the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
OceanMesh2D 1.0: MATLAB-based software for two-dimensional unstructured mesh generation in coastal ocean modeling
Keith J. Roberts
William J. Pringle
Joannes J. Westerink
OceanMesh2D is a set of MATLAB functions with preprocessing and post-processing utilities to generate two-dimensional (2-D) unstructured meshes for coastal ocean circulation models. Mesh resolution is controlled according to a variety of feature-driven geometric and topo-bathymetric functions. Mesh generation is achieved through a force balance algorithm to locate vertices and a number of topological improvement strategies aimed at improving the worst-case triangle quality. The placement of vertices along the mesh boundary is adapted automatically according to the mesh size function, eliminating the need for contour simplification algorithms. The software expresses the mesh design and generation process via an objected-oriented framework that facilitates efficient workflows that are flexible and automatic. This paper illustrates the various capabilities of the software and demonstrates its utility in realistic applications by producing high-quality, multiscale, unstructured meshes.
- Article
(11552 KB) - Full-text XML
- BibTeX
- EndNote
Many phenomena in the coastal ocean, such as tides, tsunamis, and storm surges, can be accurately modeled by the shallow water equations. Unstructured meshes are often used for numerical simulations of the coastal ocean because they can resolve the large range of horizontal length scales necessary for accurate hydrodynamic predictions and can conform well to complicated shoreline boundaries. The accuracy and the associated computational expense of the mesh are in direct conflict, which makes the mesh design process challenging. Computational work is governed by the distribution of vertices (mesh resolution) and accuracy is determined, in part, by the representation of relevant geometrical and bathymetric features that may influence the simulation. Due to this balance between accuracy and computational work, the prescription of the mesh resolution often leads to a highly subjective mesh generation process, which is often handled through software based on a graphical user interface (GUI), e.g., the Surface-water Modeling System (https://www.aquaveo.com/software/sms-surface-water-modeling-system-introduction, last access: 8 May 2019), Blue Kenue (https://nrc.canada.ca/en/research-development/products-services/software-applications/blue-kenuetm-software-tool-hydraulic-modellers, last access: 8 May 2019), and Delft's Flexible Mesh suite (https://www.deltares.nl/en/software/delft3d-flexible-mesh-suite/, last access: 8 May 2019). Although GUIs allow the user to carefully edit detailed aspects of the mesh, they do not promote automation, objectivity, or reproducibility. To address this issue, the ocean modeling community has developed approaches and tools to support the automated generation of unstructured meshes for coastal circulation problems (Hagen et al., 2002; Bilgili et al., 2006; Gorman et al., 2006, 2008; Lambrechts et al., 2008; Conroy et al., 2012; Engwirda, 2017; Candy and Pietrzak, 2018; Avdis et al., 2018; Remacle and Lambrechts, 2018). Most works have either tried to minimize topo-bathymetric interpolation error on the mesh (e.g., Gorman et al., 2006) or construct the mesh based on resolving relevant physical processes in the domain and/or preserving the geometry of the shoreline boundary (e.g., Conroy et al., 2012; Engwirda, 2017). An iterative a posteriori method that aims to keep the local truncation error constant throughout the mesh has also been employed (Hagen et al., 2002).
Table 1The parameters (defined in Sect. 3.3) that are used to generate the three example meshes for this paper, which were released with the tool kit. The final mesh quality (defined in Sect. 3.1.1) and the number of iterations in the mesh generator to achieve this are noted.

Modern interpreter-based programming environments such as MATLAB and Python are attractive for many users to develop mesh generators because they include a plethora of built-in or community-developed functions, toolboxes, and packages that are freely available. For instance, a simple and easily adaptable mesh generator based on the concept of force equilibrium and written in a few dozen MATLAB lines is DistMesh2D (Persson and Strang, 2004). The simplicity of the force equilibrium algorithm makes it attractive as a general-purpose mesh generator by allowing users and developers to adapt it for various applications (e.g., Engsig-Karup et al., 2008; Liu, 2009; Nguyen et al., 2010; Wang et al., 2014). However, due to the general nature of DistMesh2D, it tends to be computationally inefficient for the large and highly multiscale geophysical domains that are encountered in coastal ocean hydrodynamic modeling problems. Additionally, there are a number of preprocessing steps that must be performed to prepare the geospatial data for meshing and a number of post-processing steps to make sure the mesh is amenable for simulation. For instance, one must obtain a shoreline boundary that will lead to a mesh that is practical to simulate with. By integrating the tools to preprocess the geospatial data into the mesh generator directly, it reduces the time spent performing these essential tasks and largely automates the mesh development process.
In a related previous work, the Advanced Mesh generator (ADMESH; Conroy et al., 2012) implemented a DistMesh2D-based coastal ocean mesh generator in MATLAB. In this work, we build on many of the ideas described in ADMESH with the following primary improvements: (a) a focus on computational efficiency to enable the software to become practically useful even for large geophysical datasets (e.g., ∼1 km resolution global topo-bathy) in the MATLAB scripting language; (b) the inclusion of preprocessing and post-processing workflows; (c) a greater variety of mesh size functions and flexibility in their application, which offers more control over mesh resolution placement; and, critically, (d) code written in an open-source environment for the benefit of the community. The codes place emphasis on facilitating automatic mesh design workflows that lead to the creation of meshes and the necessary model inputs for a numerical simulation. These mesh generation workflows (i.e., a user-specified MATLAB control script) are typically represented by a few lines of MATLAB code and take from minutes to an hour to generate relatively large, multiscale, high-fidelity meshes (potentially global to channel scale) and their auxiliary components automatically.
The software is written in an objected-oriented framework that is divided into a set of stand-alone classes. Special effort has been made to ensure that only open-source functions are required to generate a mesh. Further, in its current state the software contains a number of post-processing functions specific to the ADvanced CIRCulation model (ADCIRC; Luettich and Westerink, 2004), but these can be adapted to other solvers in the future. The rest of this paper is structured as follows: we begin by introducing the framework and organization of the code, followed by a detailed description of each of the four stand-alone classes.
1.1 Example problems
To demonstrate the overall workflow and the design of the classes, three examples located along the East Coast and Gulf Coast of the United States of America are documented (Fig. 1). The first example produces a mesh of the Jamaica Bay estuary in New York (JBAY), demonstrating the utility of the software in incorporating high-resolution ( arcsec or approximately 3 m horizontal resolution) light detection and ranging (lidar) datasets with fine-resolution (∼15 m) triangular elements nearshore. The second example meshes the Galveston Bay in Texas (GBAY), demonstrating the utility of a new mesh size function that can be used to target resolution along deep-draft marine navigation and tidal channels. The third example demonstrates how the software can produce truly multiscale unstructured meshes in less than 1 h by building a mesh of the western Atlantic Ocean with focused refinement around Puerto Rico and the US Virgin Islands (PRVI). See Table 1 for details on the various options and/or parameters that were used to generate these example meshes.
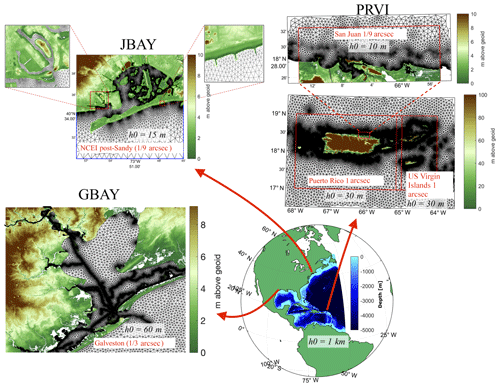
Figure 1The geographical location and triangulation of the three meshes used as examples in this work. The minimum mesh sizes (h0) are annotated in black text, and the names of the digital elevation models (DEMs) used in the construction of the mesh size functions are annotated in red text on each panel. The color map indicates topographical data (bathymetric data were removed for the production of this figure) in the DEMs, which are freely available through the NOAA bathymetric data viewer website (https://coast.noaa.gov/dataviewer, last access: 8 May 2019).
The automated generation of geophysical-use unstructured meshes often requires a number of user-defined parameters and a variety of geospatial data as inputs. As a result, the mesh is strongly related to the algorithms and data that were used to create it. These task- and object-specific properties of the mesh generation process provide the motivation behind the development of an objected-oriented programming (OOP) approach. In this software, the use of OOP leads to automation and promotes the usage of efficient workflows.
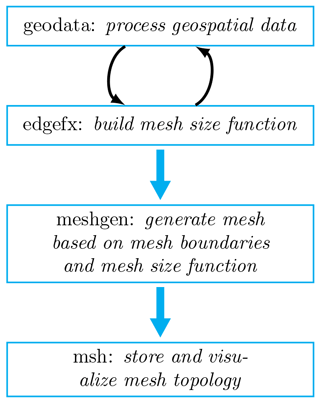
OceanMesh2D is composed of four classes (geodata, edgefx, meshgen, and msh; see Fig. 2) and a utilities directory containing various stand-alone functions. The geodata class is used as a preprocessor to mesh generation and creates an appropriate meshing boundary from user-supplied geospatial datasets and inputs. The edgefx class enables the user to build standardized mesh size functions with a variety of parameters and constraints. The meshgen class is associated with mesh generation, inheriting various options from the geodata and edgefx classes. The msh class is a data storage class for the mesh and related attributes. Additional technical information can be found in the user guide (Roberts and Pringle, 2018a).
Although each individual class is stand-alone, there is a specific workflow that is typically followed to build coastal ocean meshes with the OceanMesh2D software (Fig. 2). The structure of this workflow enables the user to create numerous instances of the geodata and edgefx classes that can be subsequently passed to the meshgen class. Numerous instances of the geodata and edgefx classes can be combined to seamlessly mesh high-resolution insets contained within wider-coverage geospatial datasets. The ability to incorporate datasets over a wide range of scales is particularly useful and pragmatic given the finite computational memory and highly variable horizontal resolution of available high-resolution topo-bathymetric data.
In the following section, each of the four classes that comprise OceanMesh2D are described.
3.1 Mesh generation: meshgen class
Mesh generation is achieved through the use of the DistMesh2D algorithm with a number of modifications to help improve the quality of the final triangulation, the speed of the mesh generation, and the memory footprint of the overall application. It is noted that the architecture of the OceanMesh2D software could additionally support other mesh generation packages besides DistMesh2D, such as JIGSAW-GEO (Engwirda, 2017). In its current state, the class is a wrapper function around the DistMesh2D algorithm that automatically uses classes that describe the meshing domain and the mesh size functions. However, it can be used as a stand-alone 2-D mesh generator with a polygonal boundary and mesh size function.
For coastal mesh generation, a key advantage of using the DistMesh2D smoothing-based algorithm over Delaunay refinement and/or frontal Delaunay mesh generation algorithms is that the boundary is implicitly defined through a signed distance function. While the boundary of the meshing domain is stored as a set of linear segments, these segments do not represent the boundary of the final mesh as all vertices can move during mesh generation in accordance with the mesh size function. The final mesh boundary that approximates the shoreline is thus dependent on the mesh size function and post-processing strategies that we employ to ensure that there are no self-intersecting boundaries or small disconnected portions of the mesh. Thus, the need for shoreline approximation preprocessing (e.g., Gorman et al., 2007) to define the mesh boundary as required by Delaunay refinement and/or frontal Delaunay mesh generation approaches (Gorman et al., 2008) is eliminated. In this section, we document the mesh improvement strategies that occur during the execution of the DistMesh2D algorithm that lead to a high-quality approximate representation of the domain and are in congruence with mesh size functions.
3.1.1 Termination criterion
In the DistMesh2D algorithm, the vertices of the mesh are allowed to move iteratively to achieve a force equilibrium state in which the edges of the triangulation are in balance with an external force. After some number of meshing iterations, the algorithm must then terminate. Persson and Strang (2004) proposed a termination criterion based on convergence to a configuration of vertices in which negligible movement of the mesh vertices would occur with additional meshing iterations. In practice, our studies have found that a configuration of vertices with negligible movement is difficult to achieve within hundreds of meshing iterations for coastal ocean mesh domains because of the complex shoreline boundary and mesh size functions. Thus, we propose an alternative termination criterion based on element quality.
The notion of what constitutes a high-quality mesh is application dependent. Mesh quality can be viewed as a combination of geometric element measures, application dependencies, and numerics (Shewchuk, 2002). A geometric measure of triangle equilateral-ness can be calculated through
where AE is the area of the triangle and (λE)i is the length of the ith edge of the triangle. qE=1 corresponds to an equilateral triangular element and qE=0 indicates a triangle that degenerates to a line. A mesh with a sufficiently high minimum bound on qE is often desired (Shewchuk, 2002; Persson and Strang, 2004; Engwirda, 2017). However, we find that a minimum bound on qE is a strict measure for large domains with millions of elements and complex shoreline features, which is difficult to achieve within the modified DistMesh2D algorithm (Fig. 3). Instead, we use the following termination criterion:
where the overline and σ denote the mean and standard deviation, respectively, and qL3σ is the “three-sigma lower control limit” element quality used as a proxy for the minimum element quality.
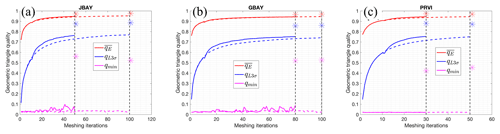
Figure 3The geometric triangle quality q, Eq. (1), as a function of iterations in the mesh generation process for the three mesh examples (Fig. 1 and Table 1). The dotted and solid lines indicate the progression of quality metrics with the mesh improvement strategies turned off and on, respectively, during mesh generation. At the end of mesh generation, a secondary round of mesh improvement strategies is applied and the resulting quality after this step is indicated by the colored asterisk. In each panel, the dotted vertical black line demarcates when the mesh generation process finished.
Upon termination through the above criterion the majority of triangles are of adequate quality. Moreover, in the approach used here, a number of mesh-cleaning steps are performed after this mesh generation termination criterion has been met (Sect. 3.1.3) in order to improve a typically small number of the worst quality (Fig. 3).
3.1.2 Mesh improvement strategies during mesh generation
Approximately every 10 meshing iterations the qL3σ element quality starts to saturate. The termination criteria can be met more quickly by relying on the following mesh improvement strategies that are conducted every 10 iterations (except item 4, which is executed every meshing iteration):
-
edges in the mesh that are greater than 2 times the length as given by the mesh size function (at the midpoint of the edge) are bisected;
-
edges that are half as short as their intended length are deleted;
-
a vertex not on the mesh boundary that is connected to less than or equal to four vertices is deleted (this is also performed when the termination criterion is satisfied); and
-
triangles with exceedingly thin angles (<5∘) and large angles (>175∘) are removed every iteration.
Improvement strategies one and two add and delete vertices when they are part of edges that are too long and short, which produces a set of new edges that more closely approximate the mesh size function. Improvement strategy three directly reduces the occurrence of low vertex-to-vertex connectivity (valency of three or four), for which a valency of six is ideal (Canann et al., 1993). Note that improvement strategy one also helps to reduce high vertex-to-vertex connectivity indirectly by avoiding steep transitions in the element size at which valencies greater than six tend to develop. The fourth improvement strategy removes triangles with small and large angles, allowing neighboring vertices to form a triangulation that has a better geometric quality.
We demonstrate the benefit of using these mesh improvement strategies through the three example meshes (Fig. 1, Table 1). The time evolution of the geometric quality demonstrates the direct benefit of these mesh improvement strategies. Figure 3 illustrates that in all three examples the mesh improvement strategies lower the number of iterations necessary to achieve the termination criterion. Further, the rate at which qL3σ increases is accelerated when mesh improvement strategies are enabled. Note that in the subsequent iteration after each improvement cycle (10 iterations), a slight degradation in the geometric quality (Fig. 3) can occur as edges and vertices are decimated. For the development of large multiscale meshes, 20–50 iterations can often save 5–20 min for the problems to reach the termination criterion. Based on the termination criterion and the improvements listed here, we generally find that complex coastal ocean meshes are generated in approximately 30–100 iterations. Thus, the maximum allowed number of iterations is commonly set to 100, which typically takes a few minutes to half an hour to compute depending primarily on the geometric complexity of the boundary and the ratio of domain size to minimum element size.
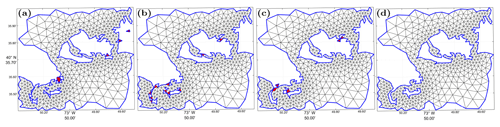
Figure 4Mesh triangulation within the JBAY example before and after different stages of the Make_Mesh_Boundaries_Traversable function enabling mesh traversability. (a) After initial mesh generation (before entry to function); (b) after deleting offending exterior elements; (c) after deleting offending interior elements; (d) after exit of function once all offending exterior and interior elements are deleted and traversability is obtained. The thick blue line indicates the mesh boundary at each stage, and red patches indicate the elements that are deleted between stages (subplots).
3.1.3 Mesh improvement strategies after mesh generation
After mesh generation has terminated, a secondary round of mesh improvement strategies is applied that is focused towards improving the geometrically worst-quality triangles that often occur near the boundary of the mesh and can make simulation impossible (e.g., Fig. 4a). Low-quality triangles can occur near the mesh boundary because the geospatial datasets used may contain features that have horizontal length scales smaller than the minimum mesh resolution. To handle this issue, a set of algorithms is applied that iteratively addresses the vertex connectivity problems. The application of the following mesh improvement strategies results in a simplified mesh boundary that conforms to the user-requested minimum element size.
Topological defects in the mesh can be removed by ensuring that it is valid, defined as having the following properties:
-
the vertices of each triangle are arranged in counterclockwise order;
-
conformity (a triangle is not allowed to have a vertex of another triangle in its interior); and
-
traversability (the number of boundary segments is equal to the number of boundary vertices, which guarantees a unique path along the mesh boundary).
Properties one and two are handled with the fixmesh.m function that was provided with the original DistMesh2D package. Property three (traversability) is often not satisfied upon termination of the mesh generator because a simplification of the shoreline was not applied. Fragmented patches of triangles may appear near the shoreline boundary, destroying traversability (Fig. 4).
A function, called Make_Mesh_Boundaries_traversable, was developed to iteratively remove patches of elements that are either disconnected from the major portion of the mesh or are not disconnected but prevent traversability. The former set of offending elements is defined as being “exterior” disjoint components of the mesh. Exterior disjoint components of the mesh are defined as follows: starting from a random seed element in the mesh, the total area of a connected set of elements (i.e., elements that share an edge) is smaller than a user-defined threshold μco. The user-defined threshold can be defined in terms of either the total mesh area fraction or an absolute area cutoff (by default we set μco=0.25, which is equivalent to a 25 % total mesh area fraction cutoff). These patches are identified and removed through the use of a breadth-first search (BFS) (Fig. 4a and b). The latter set of offending elements is defined as being “interior” elements of the mesh that interfere with the traversability of the mesh boundary path. First, an offending vertex that has more than two connecting boundary edges is identified. One of the elements connected to this vertex is chosen to be deleted based on a hierarchy: first, triangles that have two boundary edges and, second, triangles with the lowest quality, qE (Fig. 4b and c). Offending exterior and interior elements are deleted iteratively until traversability is achieved (Fig. 4c and d).
After ensuring traversability, three additional functions, depicted visually in Fig. 5, are applied to the mesh in the following order to improve mesh quality.
-
Fix_single_connec_edge_elements. Elements that share an edge with only one other element (singly connected elements) poorly approximate geospatial datasets and are thus removed from the mesh iteratively (Fig. 5a and d).
-
bound_con_int. This bounds the vertex-to-vertex connectivity (e.g., Fig. 5b and e) in the mesh to a user-defined value in order to improve mesh quality and gradation and also increase solution accuracy and computational speed (Massey, 2015).
-
direct_smoother_lur. This provides additional improvement to the mesh quality by moving non-boundary vertices based on a single-step implicit operation (Balendran, 1999) (Fig. 5c and f). The application of this function significantly enhances the statistical distribution of qE (Fig. 3).
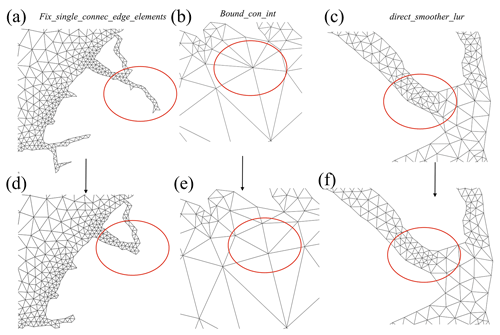
Figure 5The mesh improvement strategies that are applied in sequence from left to right after mesh generation, with the red ovals denoting areas of change in the connectivity along with the function's name that performs the operation. (a–c) Various regions in the mesh before the improvement strategy and (d–f) after improvement. Panels (a) and (d) indicate the deletion of elements that share an edge with only one other element (singly connected elements); (b) and (e) illustrate the reduction of the vertex-to-vertex connectivity to an upper bound of six using the algorithms documented in Massey (2015); and (c) and (f) illustrate the single-step implicit smoothing operation (Balendran, 1999) that is used to maximize the overall mesh quality.
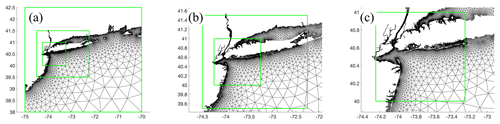
Figure 6An example of the multiscale meshing technique applied to a set of domains around the New York–Long Island area. The green boxes are specified by the user. The minimum resolution of the outermost green box in each panel is different: (a) 1 km, (b) 500 m, and (c) 35 m. Notice how the regions of overlap gradually transition into each other.
3.1.4 Multiscale meshing approach
The DistMesh2D algorithm uses memory inefficiently for the development of multiscale regional and global meshes of the coastal ocean because it requires a uniform vertex spacing to initialize. The memory inefficiency becomes especially problematic when employing high-resolution elements locally to fully incorporate the information contained in high-resolution geospatial datasets while using coarser mesh resolution elsewhere. To reduce the memory overhead when constructing regional coastal meshes using the DistMesh2D algorithm, the meshgen class has been specifically developed to allow the user to pass multiple instances of the boundary description (geodata) and mesh size (edgefx) classes to the meshgen class, an approach that we term “multiscale meshing”. Instances of these classes are defined within axis-aligned bounding boxes (rectangles) that reflect the available geospatial dataset coverage and can be partially or fully nested any number of times with largely disparate mesh sizes between nests. Examples of the multiscale meshing technique are shown in Fig. 1 (PRVI) and Fig. 6 in which the mesh sizes seamlessly transition between the different DEM extents.
Only minor modifications to the DistMesh2D algorithm were involved in enabling the multiscale meshing capability. The nested domains are evaluated in a loop inside DistMesh2D in a hierarchical order from comparatively coarser- to fine-resolution minimum mesh sizes. The hierarchical evaluation of the force function enables vertices of the mesh to move between the nested boxes so long as the outer box fully encloses the inner box. Since the finest local meshing boundary and mesh size function take precedent within each nested box, it enables many variable-resolution geospatial datasets to be included into the mesh generation process simultaneously. In order for the multiscale meshing capability to work, it requires smooth mesh size transitions between nests. A routine (smooth_outer.m) was developed to ensure that a smooth resolution transition occurs between nested boxes by using a marching method (Persson, 2006) that has been adapted for structured grids.
In contrast to the development of nested coastal circulation models (Deleersnijder et al., 2010; Nash and Hartnett, 2014; Debreu et al., 2012; Brown et al., 2016; Pringle et al., 2018) the application of the multiscale meshing capability allows for the construction of a single seamless unstructured mesh with mesh size transitions that are bounded by the user-defined allowable limit, while the resolution is not significantly altered away from the boundaries of their nests. The multiscale approach is beneficial over traditional structured grid nesting approaches employed by ocean models because it avoids the need for an explicit coupling paradigm in the numerical solver as well as issues associated with interpolation and smoothing at the interfaces between disparate-resolution grids that ultimately reduce numerical accuracy.
3.2 Geospatial data: geodata class
The geodata class is a preprocessor to the mesh generator. It is used to create an appropriate mesh boundary description from user-supplied input files. The geodata class also stores the region of the digital elevation model (DEM) that overlaps the desired meshing domain efficiently in memory. These DEM data are used in the construction and computation of a number of mesh size functions (see edgefx class) and msh methods. The following section describes the methodologies to prepare the mesh boundary description.
3.2.1 Projections
Users often want an ability to bound placement needs to be accurate in mesh resolution sizes in certain parts of a large coastal modeling domain. In order to accurately enforce these constraints on the Earth, a projection from the spherical geometry of the Earth to a planar one is necessary. In this software, the mesh is generated and output in the World Geographic Coordinate System (WGS84). For the formation of some mesh size functions that rely on bathymetric gradients and distances, we use a simple relationship between WGS84 degrees and planar meters to calculate the underlying grid spacing:
where δlon and δlat define the DEM resolution in WGS84 degrees between meridians and parallels, respectively, RE is the mean radius of the Earth (≈6378 km), and are the distances between meridians and parallels in meters, and ϕ is the latitude in radians. To enforce mesh resolution constraints, we use the Haversine formula to convert between WGS84 and meters. An assumption is made that the length in geographic degrees forms a horizontal (i.e., latitude parallel) edge starting at the point at which it is defined. The distance between the start and end point of this edge is converted to great circle distances using the Haversine method, and then we invert the Haversine formula and solve for WGS84 degrees by assuming that the distance between latitudes is zero:
where h* is the length of the edge in meters, and hd is the length of the edge in WGS84 degrees. The assumption that the edge length extrudes along a latitude parallel is reasonable in practice because the mesh size function constraints matter mostly in areas of relatively high mesh refinement, and in these locations the variation in ϕ is small.
3.2.2 Automatic mesh boundary definition
Since a coastline is often approximated by a series of piecewise linear segments, the mesh boundary is often unbounded on the ocean side and is not a polygon (i.e., the first point does not equal the last). Thus, users often have to turn their segments that represent the shoreline into a closed polygon for any meshing algorithm to work properly. To make this process automatic, we enable the user to specify the meshing region as a rectangular box, bbox. The mesh domain is then defined as the intersection of the area enclosed by the bbox and the area enclosed by the shoreline polygon. The boundary of the meshing domain is implicitly defined through the use of a signed distance function, d, whereby the distance to the nearest coastline point is zero (Persson and Strang, 2004). Note that a negative value of the signed distance function indicates a point within the mesh boundary, and a positive value of the signed distance function indicates a point outside the mesh boundary.
In addition to defining the meshing boundary, the signed distance function is also used to form mesh size functions (see Sect. 3.3) and is used during the execution of the DistMesh2D meshing algorithm. To ensure the calculation of the signed distance is computationally efficient, the calculation relies on a combination of the MATLAB class version of the approximate nearest-neighbor (ANN) method (Arya and Mount, 1993; Mount and Arya, 2006) (to obtain the absolute distance) and a points-in-polygon test function (inpoly.m; Engwirda, 2017) (to get the sign). The ANN method has high computational efficiency with a negligible memory footprint in comparison to the dsegment.m function available in DistMesh2D. Further, the inpoly.m function is several hundred times quicker (O(log N) vs. O(n2)) than MATLAB's built-in inpolygon.m function.
In our methodology, the shoreline polygon is internally partitioned into mainland and island polygons (this categorization is defined below). New vertices are added to the shoreline polygon so that it conforms to the user-requested minimum mesh resolution (h0) inside the bbox. Vertices are decimated outside bbox to save both memory and time during the mesh generation process since the calculation of the signed distance function is proportional to the number of shoreline vertices.
-
The segments of shoreline polygon that intersect with bbox are read into memory.
-
The segments of shoreline polygon are classified into three types: mainland, inner, or outer.
- a.
The mainland category contains segments that are not totally enclosed inside the bbox.
- b.
The inner (i.e., islands) category contains polygons totally enclosed inside the bbox.
- c.
The outer category is the union of the mainland, inner, and bbox.
- a.
-
New vertices are added on these segments so that no two consecutive vertices along it are further than apart. This is necessary for an accurate re-projection of the points that exit the meshing domain during the execution of the DistMesh2D algorithm (Persson and Strang, 2004).
-
All segments are smoothed using an n-point moving average. Simultaneously, small islands that have an area less than (p⋅h0)2 are removed, where n and p are user-specified integers (n=5, p=4 by default).
As an example, the following steps are applied to a shoreline extracted from a National Centers for Environmental Information (NCEI) post-Sandy DEM (JBAY in Fig. 1), leading to a classification of shoreline points that is crucial for correct automatic meshing of the complicated coastal domain it describes without human intervention (Fig. 7).
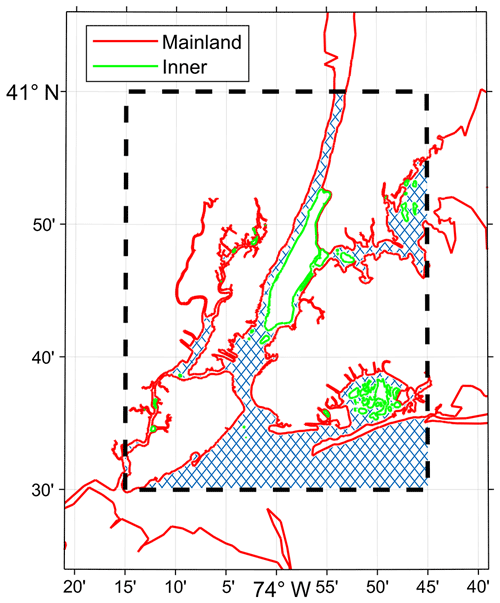
Figure 7Example of boundary treatment in and around New York, United States; the bounding box of the mesh domain, bbox, is indicated by the thick dashed black line, the meshing domain is hatched in blue, and the categorization of land boundary types is indicated according to the colored lines.
The capability to use geometric contours extracted directly from geospatial datasets in the mesh generation process without the need for shoreline simplification algorithms or external shoreline datasets improves workflow efficiency and automation. Further, by using a geometric contour, the resulting shoreline boundary in the mesh is consistent with the topo-bathymetric dataset that is subsequently interpolated onto the mesh vertices. Since many coastal mesh generators rely on the Global Self-consistent Hierarchical High-resolution Shorelines (GSHHS) dataset (Wessel and Smith, 1996), we consider the automatic geospatial data processing algorithms to represent a significant step forward towards more comprehensive coastal modeling efforts. For example, the GSHHS dataset is largely insufficient for meshes with a desired resolution finer than 100 m as it often misses critical connections between water bodies (Fig. 8).
3.3 Automatic mesh size function: edgefx class
The careful placement of mesh resolution is critical to create meshes that lead to accurate but efficient simulations. There are a number of heuristics used to design unstructured meshes for shallow water flow applications. A review of some common resolution heuristics utilized in coastal ocean modeling can be found in Greenberg et al. (2007). We have considered a variety of constraints involved in the formation of the mesh size functions by integrating and adapting past work on the topic. The various mesh size functions are detailed in this section.
Mesh resolution is distributed in the domain according to a mesh size function. The mesh size functions are constructed on a structured grid that relates every point in the meshing domain to a desired mesh size h or, more precisely, a triangular edge length (hence edgefx). Defining the mesh size function on a structured grid has advantages over an unstructured one (Conroy et al., 2012; Engwirda, 2017) in relation to computational efficiency when storing, querying, interpolating, and performing calculations. Further, bathymetric data are often defined on structured grids, and in these cases, computing the mesh size function directly on the same grid can minimize seabed interpolation error for the mesh size function calculation. Given these factors, we calculate our mesh size functions on Cartesian grids defined in geographical coordinates (i.e., WGS84). A major drawback to this approach is that the entire domain must be uniformly refined, which becomes particularly severe for relatively large meshing domains. This impacts the scalability of the subsequent mesh generation process for regional and global coastal mesh generation, but the multiscale mesh capability (Sect. 3.1.4) alleviates this problem.
Each individual mesh size function is based on shoreline data and/or the bathymetric datasets that were passed to the edgefx class constructor. Currently, the software supports a variety of mesh size functions that are used in the ocean modeling community: wavelength to grid size (Westerink et al., 1994; Luettich Jr. and Westerink, 2013), topographic length scale (Greenberg et al., 2007; Lambrechts et al., 2008), Euclidean distance from the shoreline (Persson and Strang, 2004), approximate feature size of the shoreline (Persson, 2006; Koko, 2015), thalweg and/or polyline (Heinzer et al., 2012), and Courant–Friedrichs–Lewy (CFL) limiting (Bilgili et al., 2006). Each mesh size function can either be incorporated or omitted based on the user's requirements. The mesh size function is graded using a marching algorithm (Persson, 2006) to ensure that the triangle-to-triangle change in edge length is bounded below a user-defined percent, αg.
3.3.1 Distance and feature size
A high degree of refinement is often necessary near the shoreline boundary to capture its geometric complexity. If mesh resolution is poorly distributed, critical conveyances may be missed, leading to larger-scale errors in the nearshore circulation (Greenberg et al., 2007). Thus, a mesh size function that is equal to a user-defined minimum mesh size h0 along the shoreline boundary, growing as a linear function of the signed distance d from it, may be appropriate:
where αd is the percent change in mesh size with distance from the shoreline boundary. Equation (5) is what we call the distance mesh size function and was originally presented in the DistMesh2D algorithm (Persson and Strang, 2004).
One major drawback of the distance mesh size function is that the minimum mesh size will be placed evenly along straight stretches of shoreline. If the distance mesh size function generates too many vertices, a feature mesh size function that places resolution according to the geometric width of the shoreline should be employed instead (Conroy et al., 2012; Koko, 2015). In this function, the feature size (e.g., the width of channels and/or tributaries and the radius of curvature of the shoreline) along the coast is estimated by computing distances to the medial axis of the shoreline geometry. Here we have implemented an approximate medial axis method closely following Koko (2015). This involves finding local extrema in the gradient of the d, which in practice amounts to defining a medial point as a location where and d<0 (Koko, 2015). Sometimes due to the configuration of the mesh size function grid juxtaposed on the shoreline geometry, medial points inside small channels may be lost. These medial points can be recovered by classifying mesh size function grid points as medial points if both adjacent neighbors (in the north–south or east–west directions) are outside of the domain but the mesh size function point under question is within the domain. Once the medial points are computed, the local feature size hlfs is calculated as
where αR is the user-specified number of desired elements per local feature size (commonly ), and dMA is the absolute distance to the nearest medial point. Since the medial axis is an approximation, the identification of the full set of medial points depends on the horizontal resolution of the mesh size function. This implies that the feature mesh size calculation will work best when computed on a structured grid with a resolution similar or finer than the horizontal resolution of the supplied geophysical datasets.
To demonstrate the efficacy of the feature mesh size function, we use a 1∕9 arcsec (∼3 m) topo-bathy DEM to generate an approximate 10 m minimum element size mesh of Jamaica Bay in New York, US (JBAY; Fig. 1), with αR=3. Relatively coarse resolution is placed along linear regions of the sandbar, while the dark patches indicate where higher resolution is automatically placed around points of high curvature in the coastline and through channels. For example, two close-ups are shown in which higher resolution is placed along a narrow constriction and around perpendicular coastal groins along a beach.
3.3.2 Wavelength
In shallow water theory, the wave celerity, and hence the wavelength λ, is proportional to the square root of the depth of the water column. This relationship indicates that more mesh resolution at shallower depths is required to resolve waves that are shorter than those in deep water. With this considered, a mesh size function hwl that ensures a certain number of elements are present per wavelength (usually of the M2-dominant semi-diurnal tidal species) can be deduced:
where and are the wavelength and period (≈12.42 h) of the M2 tidal wave, g is the acceleration due to Earth's gravity, b is the bathymetric depth, and αwl is the user-specified number of elements chosen to resolve the wavelength. If the M2 wavelength is sufficiently captured, the diurnal species will also be sufficiently resolved since their wavelengths are approximately twice as large as the M2. In general, the wavelength parameter αwl is set to a value somewhere between 25 and 100 (Westerink et al., 1994; Le Provost and Lyard, 1997).
3.3.3 Topographic length scale
The distance, feature size, and/or wavelength mesh size functions can lead to coarse mesh resolution in deeper waters that under-resolve and smooth over the sharp topographic gradients that characterize the continental shelf break. These slope features can be important for coastal ocean models in order to capture dissipative effects driven by the internal tides, transmissional reflection at the shelf break that controls the astronomical tides, and trapped shelf waves (Huthnance, 1995). The scaling of the slope parameter, commonly called the topographic length scale, is usually represented by the following:
where 2π∕αslp is the number of elements that resolve the topographic slope, and ∇b is the gradient of the bathymetry evaluated on a structured grid of horizontal resolution h0. The 2π factor is a convention introduced by Lyard et al. (2006) so that αslp can be set to a value similar in magnitude to αwl, e.g., around 10–30.
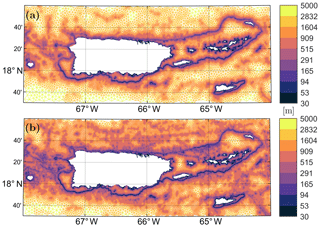
Figure 9Mesh resolution (defined as the local element circumradius in meters) in the PRVI example (see Table 1) around the Puerto Rico and US Virgin Islands inset region, with (a) and without (b) the Rossby radius slope filter applied. The “thermal” color palette from cmocean (Thyng et al., 2016) is used in this figure.
Typically the gradient of the bathymetry often contains a high degree of noise, which results in high mesh refinement with the application of hslp despite the fact that small features have marginal effects on shallow water flow, particularly in deep water (LeBlond, 1991). We would like to filter bathymetric features that are not relevant to the underlying shallow water processes, like the astronomical tides. Therefore, we propose low-pass filtering the bathymetry before calculating the gradient. In this low-pass filter, we propose a filter cutoff length based on an estimate of the local Rossby radius of deformation:
where f is the Coriolis parameter. By local we mean that we discretely bin values of LR in the meshing domain and apply a low-pass filter to binned grid points with a cutoff set to LR at the bin midpoint. For this approach to work correctly, partitioning the meshing domain is critical because the meshing domain often spans large regions of latitude with highly varying f. Here, the PRVI example (Fig. 1 and Table 1) is used to demonstrate the effect of the Rossby radius slope filter (Fig. 9). The mesh with the Rossby radius slope filter focuses mesh resolution at large and relatively shallow features such as the continental shelf break, avoiding the placement of fine resolution over deep and small-scale features that are not comparable to LR. As a result, the mesh with the filtered seabed has 27 % fewer vertices in the illustrated region.
3.3.4 Channel thalwegs and polylines
Closer to the shoreline, the width of the nearshore geometry through which water must flow eventually becomes the dominant length scale instead of LR. Thus, constraints imposed by continuity normally become more important than dynamic balances in determining spatial scales in estuaries (LeBlond, 1991). Following this logic, the representation of the cross-sectional area of the channel that connects the ocean to the estuary is important in order to simulate an accurate exchange of water.
The predominant conveyance through a watercourse is often approximated by a series of neighboring points that connect local minimums in bathymetric depth. These locations are referred to collectively as a thalweg and are represented as polylines in the geographic information system (GIS) framework. The level of mesh refinement near and around the thalweg can affect the bathymetric representation in the mesh through aliasing local minimums in bathymetric depth. Often the associated length scale of these features is too small to efficiently resolve through the other mesh size functions. Instead we propose a mesh size function to locally enhance mesh refinement around thalwegs.
Thalwegs can be located by thresholding upslope area (O'Callaghan and Mark, 1984) in a DEM with GIS software such as GRASS. One difficulty with thresholding upslope area to identify submerged channels is that it may produce spurious nonphysical channel networks, especially in areas of flat bathymetry.
Similar to the feature-constraint algorithm (Heinzer et al., 2012) this mesh size function treats the thalwegs as a set of connected vertices that forms polylines and operates on the polylines that intersect with the meshing domain. The mesh resolution is distributed as follows.
-
A circular region in the mesh size function is formed on each thalweg point with a diameter, dia, equal to
where θ is the angle of reslope.
-
In each circular region, the mesh size function is assigned resolution by
This assumes the thalweg has a cross-sectional area that resembles a V shape with a bank angle of θ (which is set to 60∘ by default) and that the stencil becomes larger as b increases (Fig. 10). The parameter αch is a user-defined value that is chosen to scale resolution according to the user's desire.
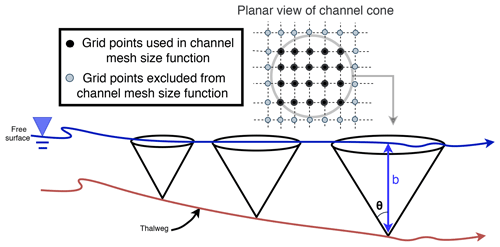
Figure 10A schematic illustrating the channel mesh size function implementation. The thalweg (deepest part of a channel) is depicted by the maroon line. Mesh size function grid points (defined at the free-surface vertical contour) that fall within the channel cones (centered along the thalweg with an assumed bank angle of θ from the vertical) used to estimate the width of the channel are set to follow Eq. (12).
As the water column deepens, the horizontal length scale greatly enlarges, which implies that the dynamical effects from small-scale features like thalwegs should weaken. This dynamic is qualitatively captured through Eq. (11) by the enlargement of the thalweg region in the mesh size function as the water depth increases. Additionally, the quotient αch in Eq. (12) alters how the resolution scales with bathymetric depth to further reflect the fact that the horizontal length scale tends to grow as the water becomes substantially deeper, thus reducing the resolution around thalwegs.
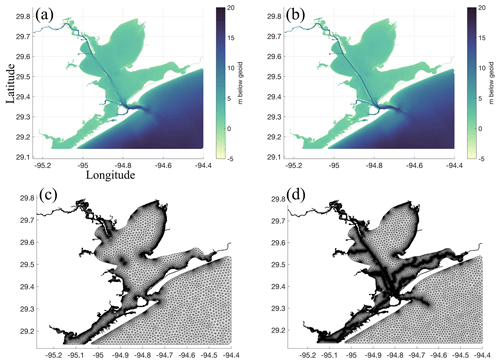
Figure 11Panels (a) and (c) show the bathymetry and mesh connectivity in the GBAY example (Fig. 1 and Table 1) created without the thalweg mesh size function enabled; (b) and (d) are with the thalweg mesh size function enabled. The “deep” color palette from cmocean (Thyng et al., 2016) is used in the palettes in panels (a) and (b).
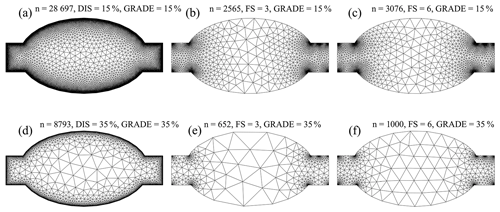
Figure 12Depiction of mesh resolution interactions between the grade (αg), distance (DIS), and feature (FS) mesh size functions. (a–c) The resolution with a grade equal to 15 % (αg=0.15) and (d–f) with a grade equal to 35 % (αg=0.35). Panels (a) and (d) depict how mesh resolution is distributed with a distance mesh size function, while panels (b, e) and (c, f) show how the mesh size varies with the feature mesh size function with αR equal to 3 and 6, respectively. In the title of each panel, the number of vertices n in the triangulation is shown.
As an example of this mesh size function, a mesh is built in and around Galveston Bay, Houston (GBAY; Fig. 1 and Table 1), a shallow estuary with a heavily trafficked shipping channel along its centerline. In this example, we have provided the thalweg points by thresholding the Galveston DEM (Fig. 1) with an upslope area of 10 000 cells using GRASS GIS. Visually, the mesh generated using the channel mesh size function clearly captures the bathymetric feature of the Houston Ship Channel to a higher degree of accuracy (Fig. 11). The channel mesh size function provides a mechanism to localize high-resolution elements around polylines that can be extracted from GIS software suites. Many mesh generation packages include methods for selective and ad hoc mesh size variations in order to resolve local seabed features. In our approach, we try to make the application of mesh size variation more objective by assuming a channel width and depth dependence to scale mesh sizes. Further, the polylines extracted here originate from a DEM and are not hand drawn to further improve objectivity and model design reproducibility.
3.3.5 Finalizing the mesh size function
The final mesh size function, h, is determined by applying the minimum function to the set of individual local mesh size functions, i.e.,
Note that it is possible to operate on any given subset of mesh size functions. Following this, h is further refined based on mesh size transition bounds (Sect. 3.3.6), Courant–Friedrichs–Lewy limiting (Sect. 3.3.7), and global user-defined maximum (hmax) and minimum (h0) mesh size bounds.
3.3.6 Mesh size gradation
It is necessary to ensure a mesh size smoothness limit αg such that for any two adjacent vertices xi, xj connected by an edge, the local increase in mesh size is bounded above such that
This bound on the mesh size gradation is enforced with the marching method that was introduced in Sect. 3.1.4. A smoothness criterion is essential to produce a mesh that can simulate physical processes with a practical time step, as sharp gradients in mesh resolution typically lead to triangles with highly skewed angles that result in low numerical accuracy (Shewchuk, 2002). In general, a smoother edge length function is congruent with a higher overall triangle quality but with more triangles in the mesh. It is important to note that the rate of mesh resolution increase is bounded above by the grade; therefore, if the distance parameter in Eq. (5) is set to a value lower than the grade (αd<αg), then grading should have no effect on the mesh size function.
Figure 12 demonstrates the relative effects of the distance and feature mesh size functions and their interaction with the grade. To illustrate this mesh size function, we built a mesh over an estuary-like geometry with the distance (αd=0.15 and αd=0.35) and feature (αR=3 and αR=6) mesh size functions, each using two different gradation bounds (αg=0.15 and αg=0.35). The distance mesh size function focuses resolution on the mesh boundary, which is often not necessary to resolve areas that are geometrically simple. Further, the use of a distance mesh size function often results in comparatively larger triangles in the center of the geometry, especially with a relatively high grade (i.e., 35 %; Fig. 12d). In shallow estuaries, this can be undesirable as the bathymetric representation of high conveyance channels in the center of the estuary will be inaccurate, aliasing the transported mass and energy. In contrast, the feature mesh size function places a uniform number of triangles across the widest axis of the feature (Fig. 12e and f). It focuses mesh resolution on regions that are narrow and/or where the shoreline has high curvature. The net result is a comparatively smaller number of vertices than the distance mesh size function (for αR<20 in this example). Depending on the selection of αR in the local feature size equation (Eq. 6), the size of the mesh resolution in the center of the estuary can be bounded even when using a relatively high mesh grade (αg>0.25). This is advantageous because a higher grade can dramatically lower the overall vertex count. Conversely, a relatively low grade (αg<0.20) can hinder the feature mesh size function from expanding efficiently and may be somewhat counterproductive to its purpose.
3.3.7 Courant–Friedrichs–Lewy (CFL) limiting
The computational expense of a computational model and the associated code is significantly affected by the time step that must be used to ensure stability and accuracy. For models that use explicit time stepping schemes, a necessary condition for numerical stability is determined by the Courant–Friedrichs–Lewy (CFL) condition. Although this is not a sufficient condition, it is a practical way to gauge the success of a new mesh. The CFL condition states that the Courant number (Cr) must be less than or equal to a critical value that is numerical scheme dependent. Additionally, the accuracy of a numerical scheme is impacted by the Cr as high values tend to give poorer accuracy even in implicit solvers. For the application of solving the shallow water equations the Cr can be estimated and bounded in the mesh (Bilgili et al., 2006). We define an estimate of Cr at the vertices of the mesh by adding the shallow water wave speed with an estimate of the anticipated flow speed:
where u is the magnitude of the flow, g is the acceleration due to gravity, H is the total water depth, Δt is the time step, and ΔX is the element size or the shortest connected edge to each vertex. Since the wave speed is a function of depth and ΔX is equivalent to the mesh size, h, the user can estimate the CFL condition a priori for a given Δt. Note that to obtain this a priori estimate of Cr in Eq. (15), we set H≈b and approximate the flow speed with the longwave linear orbital velocity, i.e., , where η is the wave amplitude, which we set to 1 m by default. Applying these approximations and rearranging gives the following CFL-limiting condition on the mesh size:
where b is set to a minimum of 1 m to allow the CFL condition to be satisfied overland in the case that inundation were to occur.
Thus, the user can specify a value of Δt to bound the mesh resolution based on some value of Cr<1. The aim of CFL limiting is to help facilitate a mesh to be simulated with a certain time step when using explicit time stepping numerical models. However, this often comes with a loss of mesh resolution that may be critical for resolving important conveyances, so the user must consider reasonable values of Δt based on the minimum edge length. To avoid this choice, we have also implemented an option that automatically selects a suitable Δt that satisfies the condition Eq. (16) for the hdis or hlfs (whichever is induced) mesh size functions. The purpose of this is to preserve the nearshore resolution while applying the CFL limiting to other mesh size functions that may give higher refinement offshore.
To demonstrate the CFL-limiting option, we return to the JBAY example (Fig. 1 and Table 1) generated using the feature mesh size function. In one instance of the mesh, no CFL limiting is used (TwoCFL); in another instance, CFL limiting with Δt=2 s (TwCFL) is invoked. In the generation of TwCLF, the mesh size function is conservatively bounded by Cr=0.5 to allow for a buffer of the effects of nonlinearities, bathymetric interpolation, and mesh smoothing. After the mesh is generated, the NCEI post-Sandy DEM is interpolated onto each vertex using a cell-averaging approach (see interp method in Sect. 3.4), and the resulting CFL is calculated by Eq. (15) with Δt=2 s. The use of the CFL limiter acts to shift the distribution of Cr to smaller values (Fig. 13). The maximum Cr decreases from 3.64 to 0.96 and the mean Cr shifts from 0.68 to 0.36. In the mesh with the CFL limiting, there are no vertices that violate the CFL condition compared to 10 492 in the mesh without it. CFL limiting thus reduces the number of vertices by locally coarsening h (TwCFL has 45.6 % fewer vertices than TwoCFL). Again, the user must be careful when selecting Δt as CFL limiting may lead to choke points in small channels nearshore, which are generally the first areas that violate the CFL (Fig. 14). Depending on the application this may or may not be tolerable.
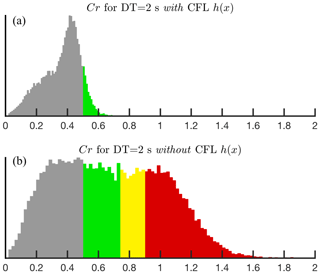
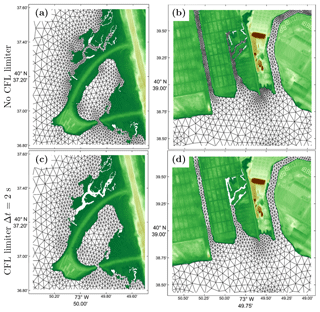
Figure 14Selected close-up regions in Jamaica Bay, New York, of the mesh connectivity built with the JBAY example script (Fig. 1 and Table 1): (a, c) West Pond, Queens; (b, d) Old Howard Beach, Queens. Panels (a) and (b) show the mesh connectivity without invoking the CFL limiter, and panels (c) and (d) show it when using the CFL-limiting option with Δt=2 s.
Although the above example demonstrates that the Cr of all vertices is reduced to under 1 when using the CFL-limiting mesh size function, the maximum Cr is still 0.96 for Δt=2 s, which may be too close to the theoretical condition to simulate without instabilities. Based on our experience we need to impose a stricter CFL condition such as Cr<0.5 to ensure numerical stability, accuracy, and to minimize numerical artifacts. To ensure that this more conservative condition is fully satisfied, we propose the CheckTimestep post-processing function (Algorithm 1). This function iteratively deletes vertices in the mesh associated with edges that violate the CFL. With each deletion, the vertices on the outer fan containing all the connected elements are smoothed using the Laplacian operator. The algorithm relies on MATLAB's implementation of the Bowyer–Watson incremental Delaunay triangulation to preserve the mesh connectivity outside of the modification patch. For example, in the JBAY example with CFL limiting, CheckTimestep converged after five iterations, resulting in a mesh with approximately 2240 fewer vertices but one that fully satisfied Cr<0.5 everywhere for Δt=2 s. In addition to ensuring the CFL condition is fully met, CheckTimestep in practice is often used to explore how the mesh would have to be modified in order to achieve a stable simulation for a particular Δt.

3.4 Mesh container: msh class
To store the triangulation and related files, the msh data storage class contains triangulation-related attributes and support for solver-specific input files. While the underlying purpose of the msh class is to store the mesh data, the OOP framework enables specific methods to be associated with it. This enables the msh class to act as an intermediary between the numerical solver and the user to assist in the creation of solver-specific files and perform common data-driven operations on the mesh.
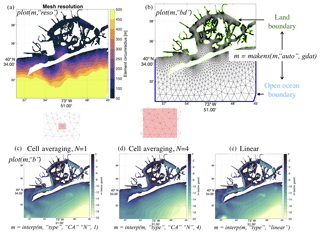
Figure 15Illustration of key msh methods: plot can be used to visualize mesh resolution (a), mesh triangulation, boundary types (b), and seabed topography (c–e); interp interpolates seabed topography onto the mesh using cell-averaging or built-in griddedInterpolant methods (c–e); and makens classifies mesh boundary vertices into land and open ocean types automatically using the native geodata class (b).
Substantial effort is often required after the triangulation is constructed to enable simulation with a coastal ocean solver such as ADCIRC, FVCOM, SELFE, or SCHISM. For example, the mesh often needs to be visualized and quality checked, boundary conditions must be specified, and seabed topography must be interpolated onto the mesh vertices (Fig. 15). Rather than have each user independently write their own methods to accomplish these tasks, we believe it to be more advantageous to place these static or dynamic methods inside the msh class that can be edited by everyone using version control software.
Table 2Wall-clock time in seconds (percent of total) for the steps involved in mesh generation. The preprocessing includes reading and processing the geospatial data (in geodata) and forming the mesh size functions (in edgefx). The vertex relocation timings include the time elapsed in the initial point rejection, vertex re-projection back into the meshing domain, vertex movement, and mesh improvement strategies during mesh generation (Sect. 3.1.2). The cleaning category includes the time spent on mesh improvement strategies after mesh generation (Sect. 3.1.3).
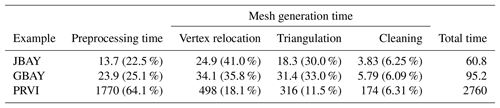
Figure 15 illustrates a few of the key methods associated with the msh class (see the user guide for a complete list) that we have implemented, such as the visualization of mesh triangulation, resolution, seabed topography, and boundary types. Further, a standardized method for interpolating seabed topography, which employs a generalized cell-averaging approach by default, has been developed. The method can also be used as a wrapper to the built-in MATLAB griddedInterpolant function with nearest, linear, and various higher-order interpolation methods. Comparison of the mesh seabed topography using cell-averaging and linear interpolation methods is shown in Fig. 15c–e. Also included is a msh method to automatically classify mesh boundary vertices into open ocean, enclosed islands, and mainland types based on the native geodata class (Fig. 15b).
The total and component-based wall-clock times for generating each of the three examples presented in this study are shown in Table 2. Overall, the small examples (JBAY and GBAY) complete in under 2 min, and the large PRVI example takes approximately 45 min. Consistently for all examples, vertex relocation consumes slightly more time than Delaunay triangulation, and the mesh cleaning (post-processing improvement strategies) accounts for approximately 6 % of the total time. The relative balance between mesh generation and preprocessing times depends on the resolution of the shoreline and the size of the meshing domain. For example, in the small domain problems (JBAY and GBAY), the preprocessing time makes up roughly a quarter of the total time. In contrast, in the PRVI example, which meshes most of the northwestern Atlantic ocean using four separate geodata and edgefx classes, the preprocessing time accounts for 64 % of the total time.
A self-contained model development tool kit to automate the generation of two-dimensional (2-D) triangular unstructured meshes for coastal ocean models was developed. The overarching goal of the software is to reduce the complexity and hours spent constructing real-world unstructured meshes to the degree that it allows one to more carefully and systemically study the impact on the coastal circulation. This software is expressed as an objected-oriented approach composed of four MATLAB classes. Each class was designed to simplify the necessary preprocessing and post-processing procedures for mesh generation, leading to a self-contained model development tool. While the scripting-based approach used to generate meshes promotes automation and approximate reproducibility, the pointers contained within the script do not adequately describe the provenance attribution of the geospatial datasets and computing environment used. In the future, employing formal research data management practices in the context of geophysical mesh generation (Avdis et al., 2018; Candy and Pietrzak, 2018) into OceanMesh2D would be beneficial to heighten reproducibility.
For coastal mesh generation, a key advantage of using the DistMesh2D smoothing-based algorithm over Delaunay refinement and/or frontal Delaunay mesh generation algorithms is that the boundary is implicitly defined using a signed distance function. The implicit definition of the mesh boundary enables the vertices, including the boundary vertices that represent the highly irregular shoreline boundary, to move during the mesh generation step in accordance with the mesh size function. In contrast, Delaunay refinement and advancing front schemes incrementally modify the triangulation starting from a partitioning of the polygonal boundary and then propagate into the interior of the meshing domain. This aspect of front-based mesh generation schemes requires that the shoreline boundary be simplified in accordance with the mesh size function before mesh generation commences, which can be a challenging step.
A set of common coastal-ocean-relevant mesh size functions were built into the mesh size function class (edgefx) that can handle a variety of user-based constraints and facilitate the approximate reproducibility of mesh vertex locations. The implementation of these mesh size functions was largely borrowed from preexisting literature with some minor enhancements. We presented a polyline mesh size function to locally enhance resolution around and near marine navigation channels and deep-draft channels (i.e., thalwegs). These features are found by thresholding upslope area calculated from a digital elevation model (DEM) using GIS software. The polyline mesh size functions may have interesting future applications for the development of overland meshes that seamlessly mate with ocean meshes. For example, the user could provide a set of lines that characterize overland ridges so that the polyline mesh size function can be used to locally enhance mesh resolution to better capture the local maximums in topographic heights. Since the representation of the inter-tidal and floodplain zone in the mesh is critical for coastal flooding applications, ensuring that overland features like hills and levees are correctly represented in the mesh is an important feature. In its current state, the toolbox is able to constrain piecewise linear segments that may represent, e.g., a series of levees; however, if there is a large degree of disparity between the point spacing on the constraints and the mesh size function, then the resulting mesh will be of poor quality.
To ensure that a mesh is computationally stable with a user-requested time step (relevant when simulating with explicit–semi-implicit numerical models), a CFL-limiting mesh size function similar to Bilgili et al. (2006) was introduced. In this approach, we estimate the Courant (Cr) number based on shallow water wave theory and ensure that the final mesh size function satisfies the CFL condition (Cr<1). Although applying CFL limiting to the mesh size function was shown to help encourage stability by lowering the Cr, the resulting unstructured mesh may not necessarily satisfy the CFL condition due to that fact that bathymetric interpolation from the DEM is not easily constrained. Thus, an iterative algorithm to be applied after the mesh was developed (CheckTimestep) to locally alter the connectivity by decimating vertices that violate the CFL condition. Depending on the user choice of time step and the various mesh size constraints, the algorithm decimates vertices in certain regions (e.g., small constricted channels) that may or may not be tolerable for the problem at hand. In such regions, anisotropic mesh elements (e.g., Piggott et al., 2009) that could be generated using mesh size functions, which include a directional component, may be more beneficial than isotropic equilateral elements. Thus, implementing anisotropic mesh size functions into the software, along with the testing of the resultant meshes in real coastal ocean problems, is an interesting direction for future work.
We emphasized the expensive nature of building large-scale high-fidelity mesh size functions, which motivates the use of a multiscale meshing approach. This approach reflects the often sparse spatial coverage and heterogeneous nature of freely available digital elevation data that are often used in the construction of the mesh size functions. Multiscale meshing allows the user to build (extremely) high-resolution local mesh size functions that are embedded in larger-scale ocean domains. The end result is a mesh that seamlessly transitions from the high-refinement region to coarser elements outside the region of interest. This is practically useful to accurately model coastal flooding in small regions (e.g., a city or a small island – here we show an example of the approach with the mesh refinement region around Puerto Rico and the US Virgin Islands) that may be susceptible to storms and tropical cyclones (TCs) passing over it. For large-scale TC-driven storm surge events, it has been shown that a large model domain is essential to capture the pre-event conditions that can alter the modeled severity of the event (Blain et al., 1994). In forecasting scenarios, the multiscale meshing approach could be used to mesh around the predicted land-falling region based on the cone of uncertainty of the path of the storm to locally higher resolution. This approach could generate meshes for the prediction of coastal flooding on the fly as new forecast data become available. Given the local nature of the mesh refinement in this approach, these meshes could be computationally more efficient with smaller minimum element sizes than preexisting ones, e.g., the US National Ocean Service's (NOS) Hurricane Storm Surge Operational Forecast System (HSSOFS) mesh (Technology Riverside Inc. and AECOM, 2015), which covers entire swaths of coastline with medium-level resolution.
The objected-oriented structure of the software enables each component to be used in isolation and/or under workflows different to that presented here. For instance, mesh size functions constructed through the edgefx class could be used with other mesh generators to distribute vertices. Furthermore, the ability of OceanMesh2D to automatically adapt user-supplied shoreline datasets to a mesh size function is a new feature to the authors' knowledge. This ability could be used as a stand-alone feature to produce polygonal boundaries that approximate the shoreline with a variety of spatial constraints for other mesh generator packages or GIS applications.
Three examples were used for demonstration in this study (Fig. 1 and Table 1). A further three separate examples are illustrated in the user guide (Roberts and Pringle, 2018a). All six examples are released with this version of the OceanMesh2D package. They can be used to become familiar with the software, for testing purposes, and as templates for scripts used to generate the user's custom mesh.
The OceanMesh2D mesh generator toolbox is hosted on the following GitHub page: https://github.com/CHLNDDEV/OceanMesh2D (last access: 8 May 2019). The version release presented in this paper is available as a Zenodo archive: https://doi.org/10.5281/zenodo.1341385 (Roberts and Pringle, 2018b). The software requires no paid MATLAB toolboxes to generate meshes; however, some auxiliary functions (e.g., those that create ADCIRC input files) not used in primary workflows may. A user guide (Roberts and Pringle, 2018a) and a suite of examples are available from the main GitHub page. All components of the OceanMesh2D toolbox are free software released under the GNU General Public License version 3.0. Full details on the license, including the compatible copyright notices of third party routines included in the package, are provided in the LICENSE file in the source distribution.
The geospatial datasets required to execute the three examples presented in this study can be accessed at the Zenodo archive: https://doi.org/10.5281/zenodo.2605388 (Roberts and Pringle, 2019). Additionally, the PRVI example requires the global shoreline dataset, GSHHS (Wessel and Smith, 1996) (full-resolution ESRI shapefile version), and the SRTM global land–ocean topography dataset (Sandwell et al., 2014) (“topo15_compressed.nc”), which are freely accessible at the links included in the respective references.
KR designed the framework of the software. KR and WP equally contributed to the coding and development of the software, design and testing of the provided examples, and the preparation of the paper and its associated figures. JW provided the research environment and intellectual discussion necessary for the software's development and eventual realization of this paper.
The authors declare that they have no conflict of interest.
We would like to thank the two anonymous reviewers who helped improve the presentation and quality of this paper. We thank Darren Engwirda at Columbia University in the city of New York for his useful functions to perform the points-in-polygon test and mesh size gradation limiting. Our gratitude goes to Chris Massey at the US Army Corps of Engineers ERDC Coastal and Hydraulics Laboratory for his function to bound the vertex connectivity. The m_map (https://www.eoas.ubc.ca/~rich/map.html, last access: 8 May 2019) and cmocean (Thyng et al., 2016) (https://matplotlib.org/cmocean/, last access: 8 May 2019) toolboxes are widely used in plotting and mapping related routines within OceanMesh2D, for which we are grateful for the authors' work. We appreciate the valuable feedback provided by Darren Engwirda and Per-Olof Persson at the University of California, Berkeley. The authors wish to thank Damrongsak Wirasaet at the University of Notre Dame for many helpful discussions and his comments on an initial draft that led to an improvement in the quality of this paper.
This research has been supported by the National Science Foundation (grant no. ACI-1339738).
This paper was edited by James R. Maddison and reviewed by two anonymous referees.
Arya, S. and Mount, D. M.: Approximate Nearest Neighbor Queries in Fixed Dimensions, in: Proc. 4th Ann. ACM-SIAM Symposium on Discrete Algorithms (SODA), 25–27 January 1993, Austin, Texas, USA, 271–280, 1993. a
Avdis, A., Candy, A. S., Hill, J., Kramer, S. C., and Piggott, M. D.: Efficient unstructured mesh generation for marine renewable energy applications, Renewable Energy, 116, 842–856, https://doi.org/10.1016/j.renene.2017.09.058, 2018. a, b
Balendran, B.: A Direct Smoothing Method for Surface Meshes, in: Proceedings of the 8th International Meshing Roundtable, 10–13 October 1999, South Lake Tahoe, California, USA, 189–193, available at: http://imr.sandia.gov/papers/abstracts/Ba142.html (last access: 8 May 2019), 1999. a, b
Bilgili, A., Smith, K. W., and Lynch, D. R.: BatTri: A two-dimensional bathymetry-based unstructured triangular grid generator for finite element circulation modeling, Comput. Geosci., 32, 632–642, https://doi.org/10.1016/j.cageo.2005.09.007, 2006. a, b, c, d
Blain, C. A., Westerink, J. J., and Luettich, R. A.: The influence of domain size on the response characteristics of a hurricane storm surge model, J. Geophys. Res., 99, 467–479, https://doi.org/10.1029/94JC01348, 1994. a
Brown, J. M., Norman, D. L., Amoudry, L. O., and Souza, A. J.: Impact of operational model nesting approaches and inherent errors for coastal simulations, Ocean Modelling, 107, 48–63, https://doi.org/10.1016/j.ocemod.2016.10.005, 2016. a
Canann, S. A., Stephenson, M. B., and Blacker, T.: Optismoothing: An optimization-driven approach to mesh smoothing, Finite Elements Anal. Design, 13, 185–190, https://doi.org/10.1016/0168-874X(93)90056-V, 1993. a
Candy, A. S. and Pietrzak, J. D.: Shingle 2.0: generalising self-consistent and automated domain discretisation for multi-scale geophysical models, Geosci. Model Dev., 11, 213–234, https://doi.org/10.5194/gmd-11-213-2018, 2018. a, b
Conroy, C. J., Kubatko, E. J., and West, D. W.: ADMESH:An advanced, automatic unstructured mesh generator for shallow water models, Ocean Dynam., 62, 1503–1517, https://doi.org/10.1007/s10236-012-0574-0, 2012. a, b, c, d, e
Debreu, L., Marchesiello, P., Penven, P., and Cambon, G.: Two-way nesting in split-explicit ocean models: Algorithms, implementation and validation, Ocean Model., 49-50, 1–21, https://doi.org/10.1016/j.ocemod.2012.03.003, 2012. a
Deleersnijder, E., Legat, V., and Lermusiaux, P. F. J.: Multi-scale modelling of coastal, shelf and global ocean dynamics, Ocean Dynam., 60, 1357–1359, https://doi.org/10.1007/s10236-010-0363-6, 2010. a
Engsig-Karup, A. P., Hesthaven, J. S., Bingham, H. B., and Warburton, T.: DG-FEM solution for nonlinear wave-structure interaction using Boussinesq-type equations, Coast. Eng., 55, 197–208, https://doi.org/10.1016/j.coastaleng.2007.09.005, 2008. a
Engwirda, D.: JIGSAW-GEO (1.0): Locally orthogonal staggered unstructured grid generation for general circulation modelling on the sphere, Geosci. Model Dev., 10, 2117–2140, https://doi.org/10.5194/gmd-10-2117-2017, 2017. a, b, c, d, e, f
Gorman, G. J., Piggott, M., Pain, C., de Oliveira, C., Umpleby, A., and Goddard, A.: Optimisation based bathymetry approximation through constrained unstructured mesh adaptivity, Ocean Model., 12, 436–452, https://doi.org/10.1016/j.ocemod.2005.09.004, 2006. a, b
Gorman, G. J., Piggott, M. D., and Pain, C. C.: Shoreline approximation for unstructured mesh generation, Comput. Geosci., 33, 666–677, https://doi.org/10.1016/j.cageo.2006.09.007, 2007. a
Gorman, G. J., Piggott, M., Wells, M., Pain, C., and Allison, P.: A systematic approach to unstructured mesh generation for ocean modelling using GMT and Terreno, Comput. Geosci., 34, 1721–1731, https://doi.org/10.1016/j.cageo.2007.06.014, 2008. a, b
Greenberg, D. A., Dupont, F., Lyard, F. H., Lynch, D. R., and Werner, F. E.: Resolution issues in numerical models of oceanic and coastal circulation, Cont. Shelf Res., 27, 1317–1343, https://doi.org/10.1016/j.csr.2007.01.023, 2007. a, b, c
Hagen, S. C., Horstmann, O., and Bennett, R. J.: An Unstructured Mesh Generation Algorithm for Shallow Water Modeling, Int. J. Comput. Fluid Dynam., 16, 83–91, https://doi.org/10.1080/10618560290017176, 2002. a, b
Heinzer, T. J., Williams, M. D., Dogrul, E. C., Kadir, T. N., Brush, C. F., and Chung, F. I.: Implementation of a feature-constraint mesh generation algorithm within a GIS, Comput. Geosci., 49, 46–52, https://doi.org/10.1016/j.cageo.2012.06.004, 2012. a, b
Huthnance, J. M.: Circulation, exchange and water masses at the ocean margin: the role of physical processes at the shelf edge, Prog. Oceanogr., 35, 353–431, https://doi.org/10.1016/0079-6611(95)80003-C, 1995. a
Koko, J.: A Matlab mesh generator for the two-dimensional finite element method, Appl. Math. Comput., 250, 650–664, https://doi.org/10.1016/j.amc.2014.11.009, 2015. a, b, c, d
Lambrechts, J., Comblen, R., Legat, V., Geuzaine, C., and Remacle, J.-F.: Multiscale mesh generation on the sphere, Ocean Dynam., 58, 461–473, https://doi.org/10.1007/s10236-008-0148-3, 2008. a, b
LeBlond, P. H.: Tides and their Interactions with Other Oceanographic Phenomena in Shallow Water (Review), in: Tidal hydrodynamics, edited by: Parker, B. B., John Wiley & Sons, Inc., New York, USA, 357–378, 1991. a, b
Le Provost, C. and Lyard, F.: Energetics of the M2 barotropic ocean tides: an estimate of bottom friction dissipation from a hydrodynamic model, Prog. Oceanogr., 40, 37–52, https://doi.org/10.1016/S0079-6611(97)00022-0, 1997. a
Liu, J.: Open and traction boundary conditions for the incompressible Navier–Stokes equations, J. Comput. Phys., 228, 7250–7267, https://doi.org/10.1016/j.jcp.2009.06.021, 2009. a
Luettich, R. A. and Westerink, J. J.: Formulation and Numerical Implementation of the 2D/3D ADCIRC Finite Element Model Version 44.XX, Tech. rep., available at: http://www.unc.edu/ims/adcirc/adcirc_theory_2004_12_08.pdf last access: 8 May 2019), 2004. a
Luettich Jr., R. A. and Westerink, J. J.: Continental Shelf Scale Convergence Studies with a Barotropic Tidal Model, in: Quantitative Skill Assessment for Coastal Ocean Models, edited by: Lynch, D. R. and Davies, A. M., https://doi.org/10.1029/CE047p0349, 2013. a
Lyard, F., Lefevre, F., Letellier, T., and Francis, O.: Modelling the global ocean tides: modern insights from FES2004, Ocean Dynam., 56, 394–415, https://doi.org/10.1007/s10236-006-0086-x, 2006. a
Massey, T. C.: Locally constrained nodal connectivity refinement procedures for unstructured triangular finite element meshes, Eng. Comput., 31, 375–386, https://doi.org/10.1007/s00366-014-0357-y, 2015. a, b
Mount, D. M. and Arya, S.: ANN: A Library for Approximate Nearest Neighbor Searching, version 1.1.1, available at: http://www.cs.umd.edu/~mount/ANN/ (last access: 8 May 2019), 2006. a
Nash, S. and Hartnett, M.: Development of a nested coastal circulation model: Boundary error reduction, Environ. Model. Softw., 53, 65–80, https://doi.org/10.1016/j.envsoft.2013.11.007, 2014. a
Nguyen, V.-T., Peraire, J., Khoo, B. C., and Persson, P.-O.: A discontinuous Galerkin front tracking method for two-phase flows with surface tension, Comput. Fluids, 39, 1–14, https://doi.org/10.1016/j.compfluid.2009.06.007, 2010. a
O'Callaghan, J. F. and Mark, D. M.: The extraction of drainage networks from digital elevation data, Comput. Vis. Graph. Image Proc., 28, 323–344, https://doi.org/10.1016/S0734-189X(84)80011-0, 1984. a
Persson, P. O.: Mesh size functions for implicit geometries and PDE-based gradient limiting, Eng. Comput., 22, 95–109, https://doi.org/10.1007/s00366-006-0014-1, 2006. a, b, c
Persson, P. O. and Strang, G.: A Simple Mesh Generator in MATLAB, SIAM Rev., 46, 2004, https://doi.org/10.1137/S0036144503429121, 2004. a, b, c, d, e, f, g
Piggott, M. D., Farrell, P. E., Wilson, C. R., Gorman, G. J., and Pain, C. C.: Anisotropic mesh adaptivity for multi-scale ocean modelling, Philos. T. Roy. Soc. A, 367, 4591–4611, https://doi.org/10.1098/rsta.2009.0155, 2009. a
Pringle, W. J., Yoneyama, N., and Mori, N.: Multiscale Coupled Three-dimensional Model Analysis of the Tsunami Flow Characteristics around the Kamaishi Bay Offshore Breakwater and Comparisons to a Shallow Water Model, Coast. Eng. J., 60, 200–224, https://doi.org/10.1080/21664250.2018.1484270, 2018. a
Remacle, J.-F. and Lambrechts, J.: Fast and robust mesh generation on the sphere – Application to coastal domains, Comput.-Aided Design, 103, 14–23, https://doi.org/10.1016/j.cad.2018.03.002, 2018. a
Roberts, K. J. and Pringle, W. J.: OceanMesh2D: User guide – Precise distance-based two-dimensional automated mesh generation toolbox intended for coastal ocean/shallow water, ResearchGate, Computational Hydraulics Laboratory, University of Notre Dame, Notre Dame, https://doi.org/10.13140/RG.2.2.21840.61446/2, 2018a. a, b, c
Roberts, K. J. and Pringle, W. J.: CHLNDDEV/OceanMesh2D: OceanMesh2D V1.0, https://doi.org/10.5281/zenodo.1341385, 2018b. a
Roberts, K. J. and Pringle, W. J.: Datasets for OceanMesh2D V1.0, https://doi.org/10.5281/zenodo.2605388, 2019. a
Sandwell, D. T., Becker, J. J., Olson, C., and Jackson, A.: SRTM15_PLUS: Data Fusion of SRTM Land Topography with Measured and Estimated Seafloor topography, available at: ftp://topex.ucsd.edu/pub/srtm15_plus/ (last access: 8 May 2019), 2014. a
Shewchuk, J. R.: What Is a Good Linear Finite Element? – Interpolation, Conditioning, Anisotropy, and Quality Measures, Tech. rep., in: Proc. of the 11th International Meshing Roundtable, 15–18 September 2002, Ithaca, New York, USA, 2002. a, b, c
Technology Riverside Inc. and AECOM: Mesh Development, Tidal Validation, and Hindcast Skill Asessment of an ADCIRC Model for the Hurricane Storm Surge Operational Forecast System on the US Gulf-Atlantic Coast, Tech. rep., National Oceanic and Atmospheric Administration/Nation Ocean Service, Coast Survey Development Laboratory, Office of Coast Survey, Fort Collins, Colorado, https://doi.org/10.7921/G0MC8X6V, 2015. a
Thyng, K. M., Greene, C. A., Hetland, R. D., Zimmerle, H. M., and DiMarco, S. F.: True colors of oceanography: Guidelines for effective and accurate colormap selection, Oceanography, 29, 9–13, https://doi.org/10.5670/oceanog.2016.66, 2016. a, b, c
Wang, Q., Danilov, S., Sidorenko, D., Timmermann, R., Wekerle, C., Wang, X., Jung, T., and Schröter, J.: The Finite Element Sea Ice-Ocean Model (FESOM) v.1.4: formulation of an ocean general circulation model, Geosci. Model Dev., 7, 663–693, https://doi.org/10.5194/gmd-7-663-2014, 2014. a
Wessel, P. and Smith, W. H. F.: A global, self-consistent, hierarchical, high-resolution shoreline database, J. Geophys. Res.-Solid, 101, 8741–8743, https://doi.org/10.1029/96JB00104, 1996. a, b
Westerink, J. J., Luettich, R. A., and Muccino, J.: Modelling tides in the western North Atlantic using unstructured graded grids, Tellus A, 46, 178–199, https://doi.org/10.1034/j.1600-0870.1994.00007.x, 1994. a, b