the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
(GO)2-SIM: a GCM-oriented ground-observation forward-simulator framework for objective evaluation of cloud and precipitation phase
Ann M. Fridlind
Andrew S. Ackerman
Pavlos Kollias
Eugene E. Clothiaux
Maxwell Kelley
General circulation model (GCM) evaluation using ground-based observations is complicated by inconsistencies in hydrometeor and phase definitions. Here we describe (GO)2-SIM, a forward simulator designed for objective hydrometeor-phase evaluation, and assess its performance over the North Slope of Alaska using a 1-year GCM simulation. For uncertainty assessment, 18 empirical relationships are used to convert model grid-average hydrometeor (liquid and ice, cloud, and precipitation) water contents to zenith polarimetric micropulse lidar and Ka-band Doppler radar measurements, producing an ensemble of 576 forward-simulation realizations. Sensor limitations are represented in forward space to objectively remove from consideration model grid cells with undetectable hydrometeor mixing ratios, some of which may correspond to numerical noise.
Phase classification in forward space is complicated by the inability of sensors to measure ice and liquid signals distinctly. However, signatures exist in lidar–radar space such that thresholds on observables can be objectively estimated and related to hydrometeor phase. The proposed phase-classification technique leads to misclassification in fewer than 8 % of hydrometeor-containing grid cells. Such misclassifications arise because, while the radar is capable of detecting mixed-phase conditions, it can mistake water- for ice-dominated layers. However, applying the same classification algorithm to forward-simulated and observed fields should generate hydrometeor-phase statistics with similar uncertainty. Alternatively, choosing to disregard how sensors define hydrometeor phase leads to frequency of occurrence discrepancies of up to 40 %. So, while hydrometeor-phase maps determined in forward space are very different from model “reality” they capture the information sensors can provide and thereby enable objective model evaluation.
- Article
(5049 KB) - Full-text XML
- BibTeX
- EndNote
The effect of supercooled water on the Earth's top-of-atmosphere energy budget is a subject of increasing interest owing to its wide variability across climate models and its potential impact on predicted equilibrium climate sensitivity (Tan et al., 2016; McCoy et al., 2016; Frey et al., 2017). Some general circulation models (GCMs) now prognose number concentrations and mass mixing ratios for both cloud and precipitation hydrometeors of both the liquid and ice phase, which enables them to shift towards more realistic microphysical process-based phase prediction (e.g., Gettelman and Morrison, 2015; Gettelman et al., 2015). While more complete and physically sound, these models still contain multiple scheme choices and tuning parameters, creating a need for increasingly thorough evaluation and adjustment (e.g., Tan and Storelvmo, 2016; English et al., 2014).
Active remote sensing observations remain an indirect approach to evaluate models because they measure hydrometeor properties different from those produced by microphysical schemes. For each hydrometeor species within a grid cell models prognose geophysical quantities such as mass and number concentration, whereas active remote sensors measure power backscattered from all hydrometeor species present within their observation volumes. Defining which hydrometeors have an impact is a fundamental question that needs to be addressed by the modeling, as well as observational, communities. In numerical models it is not uncommon to find very small hydrometeor mixing ratio amounts as demonstrated below. They may possibly be unphysical, effectively numerical noise, and the decision of which hydrometeor amounts are physically meaningful is somewhat arbitrary. Considering sensor capabilities is one path to objectively assessing hydrometeor populations within models. On such a path it is possible to evaluate those simulated hydrometeor populations that lead to signals detectable by sensors, leaving unassessed those not detected. Sensor detection capabilities are both platform and sensor specific. Space-borne lidars can adequately detect liquid clouds globally but their signals cannot penetrate thick liquid layers, limiting their use to a subset of single-layer systems or upper-level cloud decks (Hogan et al., 2004). Space-borne radar observations, while able to penetrate multilayer cloud systems, are of coarser vertical resolution and of limited value near the surface owing to ground interference and low sensitivity (e.g., Huang et al., 2012b; Battaglia and Delanoë, 2013; Huang et al., 2012a). A perspective from the surface can therefore be more appropriate for the study of low-level cloud systems (e.g., de Boer et al., 2009; Dong and Mace, 2003; Klein et al., 2009; Intrieri et al., 2002).
Fortunately, both sensor sampling and hydrometeor scattering properties can be emulated through the use of forward simulators. Forward simulators convert model output to quantities observed by sensors and enable a fairer comparison between model output and observations; discrepancies can then be more readily attributed to dynamical and microphysical differences rather than methodological bias. For example, the CFMIP (Cloud Feedback Model Intercomparison Project) Observation Simulator Package (COSP) is composed of a number of satellite-oriented forward simulators (Bodas-Salcedo et al., 2011), including a lidar-backscattering forward simulator that has been used to evaluate the representation of upper-level supercooled water layers in GCMs (e.g., Cesana and Chepfer, 2008; Kay et al., 2016). Also, Zhang et al. (2018) present a first attempt at a ground-based radar reflectivity simulator tailored for GCM evaluation.
Here we propose to exploit the complementarity of ground-based vertically pointing polarimetric lidar and Doppler radar measurements, which have been shown uniquely capable of documenting the water phase of shallow and multilayered clouds that form near the surface and frequently contain supercooled water layers. More specifically, we present a GCM-oriented ground-observation forward-simulator ((GO)2-SIM) framework designed for objective hydrometeor-phase evaluation (Fig. 1). GCM output variables (Sect. 2) are converted to observables in three steps: (1) hydrometeor-backscattered power estimation (Sect. 3), (2) consideration for sensor capabilities (Sect. 4), and (3) estimation of specialized observables (Sect. 5). These forward-simulated fields, similar to observed fields, are used as inputs to a multi-sensor water-phase classifier (Sect. 6). The performance of (GO)2-SIM is evaluated over the North Slope of Alaska using output from a 1-year simulation of the current development version of GCM ModelE. Limitations and uncertainty are discussed in Sects. 6.3 and 7, respectively.
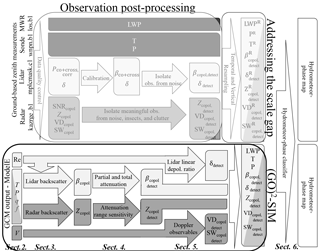
Figure 1(GO)2-SIM framework. (GO)2-SIM emulates two types of remote sensors: Ka-band Doppler radars (dark gray shading) and 532 nm polarimetric lidars (light gray shading). It then tunes and applies a common phase-classification algorithm (white boxes) to both observed (upper section) and forward-simulated (bottom section) fields. Follow-on work will describe how observation can be post-processed and resampled to reduce the scale gap before model evaluation can be performed.
To demonstrate how atmospheric model variables are converted to observables we performed a 1-year global simulation using the current development version of the ModelE GCM. Outputs from a column over the North Slope of Alaska (column centered at latitude 71.00∘ and longitude −156.25∘) are input to (GO)2-SIM. The most relevant changes from a recent version of ModelE (Schmidt et al., 2014) are the implementation of the Bretherton and Park (2009) moist turbulence scheme and the Gettelman and Morrison (2015) microphysics scheme for stratiform cloud. The implementation of a two-moment microphysics scheme with prognostic precipitation species makes this ModelE version more suitable for the forward simulations presented here than previous versions. Here ModelE is configured with a 2.0∘ by 2.5∘ latitude–longitude grid with 62 vertical layers. The vertical grid varies with height from 10 hPa layer thickness over the bottom 100 hPa of the atmosphere, coarsening to about 50 hPa thickness in the mid-troposphere, and refining again to about 10 hPa thickness near the tropopause. For the current study, the model top is at 0.1 hPa, though we limit our analysis to pressures greater than 150 hPa. Dynamics (large-scale advection) are computed on a 225 s time step and column physics on a 30 min time step. High-time-resolution outputs (every column physics time step) are used as input to (GO)2-SIM. ModelE relies on two separate schemes to prognose the occurrence of stratiform and convective clouds. The current study focuses on stratiform clouds because their properties are more thoroughly diagnosed in this model version; when performing future model evaluation, the contribution from convective clouds will also be considered.
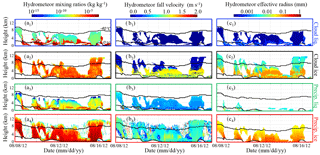
Figure 2Sample time series of ModelE outputs: (a1–4) mixing ratios, (b1–4) mass-weighted fall speed (positive values indicate downward motion) and (c1–4) effective radii for cloud droplets (1; blue boxes), cloud ice particles (2; black boxes), precipitating liquid drops (3; green boxes), and precipitating ice particles (4; red boxes). Also indicated are the locations of the 0 and −40 ∘C isotherms (horizontal black lines).
An example of 8 days of this simulation is displayed in Fig. 2. From a purely numerical modeling standpoint, the simplest approach to defining hydrometeors is to consider any nonzero hydrometeor mixing ratio as physically meaningful. Using this approach, we find that 43.5 % of the 981 120 grid cells simulated in the 1-year ModelE run contain hydrometeors, with 2.4 % of them being pure liquid, 37.8 % pure ice, and 59.8 % mixed in phase (Table 1a). However, these statistics are impacted by a number of simulated small hydrometeor mixing ratio amounts that may or may not result from numerical noise (e.g., Fig. 2a; blueish green colors). The forward-simulator framework will be used to create phase statistics of only those hydrometeors present in amounts that can create a signal detectable by sensors, hence removing the need for arbitrary filtering.
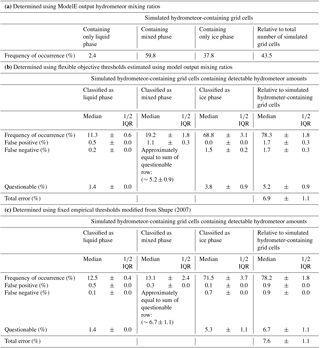
Table 1(a) Hydrometeor-phase frequency of occurrence obtained (a) from ModelE mixing ratios outside of the forward-simulator framework and (b–c) from the forward-simulation ensemble created using different backscattered power assumptions. The median and interquartile range (IQR) capture the statistical behavior of the ensemble. Results using thresholds (b) objectively determined for each forward-ensemble member and (c) modified from those in Shupe (2007). Percentage values are relative either to the total number of simulated hydrometeor-containing grid cells (426 603) or those grid cells with detectable hydrometeor amounts (333 927). Note that the total number of simulated grid cells analyzed is 981 120.
(GO)2-SIM forward-simulator inputs are, at model native resolution, mean grid box temperature and pressure as well as hydrometeor mixing ratios, area fractions (used to estimate in-cloud mixing ratios), mass-weighted fall speeds, and effective radii for four hydrometeor species: cloud liquid water, cloud ice, precipitating liquid water, and precipitating ice. In its current setup, (GO)2-SIM can accommodate any model that produces these output variables
Reaching a common objective hydrometeor definition between numerical model output and active sensors starts by addressing the fact that they are based on different hydrometeor properties (i.e., moments). Backscattering amounts observed by sensors depend on both sensor frequency and on hydrometeor properties and amounts. Hydrometeor properties that impact backscattering include size, phase, composition, geometrical shape, orientation, and bulk density. When plausible representations for these hydrometeor properties are available as part of the model formulation, fundamental radiative transfer calculations would be the most accurate way to transform model hydrometeor properties to observables. However, in most GCMs such detailed hydrometeor information is highly simplified (e.g., fixed particle size distribution shapes) or not explicitly represented (e.g., orientation and realistic geometrical shape), complicating the process of performing direct radiative transfer calculations. Chepfer et al. (2008) proposed an approach by which lidar-backscattered power can be forward simulated using model output hydrometeor effective radius. Their approach, based on Mie theory, relies on the assumption that cloud particles (both liquid and ice) are spherical and requires additional assumptions about hydrometeor size distributions and scattering efficiencies. Similarly, the COSP (Bodas-Salcedo et al., 2011) and ARM Cloud Radar Simulator for GCMs (Zhang et al., 2018) packages both use QuickBeam for the estimation of radar-backscattered power (i.e., radar reflectivity; Haynes et al., 2007). QuickBeam computes radar reflectivity using Mie theory, again under the assumption that all hydrometeor species are spherical and by making additional assumptions about the shape of hydrometeor size distributions as well as mass–size and diameter–density relationships. While some of these assumptions may be consistent with the assumptions in model cloud microphysical parameterizations, some are not adequately realistic (e.g., spherical ice) or complete for accurate backscattering estimation and it is typically very difficult to establish the sensitivity of results to all such assumptions.
To avoid having to make ad hoc assumptions about hydrometeor shapes, orientations, and compositions, which are properties that also remain poorly documented in nature, (GO)2-SIM employs empirical relationships to convert model output to observables. These empirical relationships are based on observations, direct or retrieved, with their own sets of underlying assumptions and are expected to capture at least part of the natural variability in hydrometeor properties. Additionally, empirical relationships are computationally less expensive to implement than direct radiative scattering calculations, thus enabling the estimation of an ensemble of backscattering calculations using a range of assumptions in an effort to quantify part of the backscattering uncertainty (see Sect. 7). The empirical relationships proposed require few model inputs, potentially enhancing consistency in applying (GO)2-SIM to models with differing microphysics scheme assumptions and complexity. Section 6 will show that, while the empirical relationships employed in (GO)2-SIM may not be as exact as direct radiative scattering calculations, they produce backscattering estimates of sufficient accuracy for hydrometeor-phase classification, which is the main purpose of (GO)2-SIM at this time.

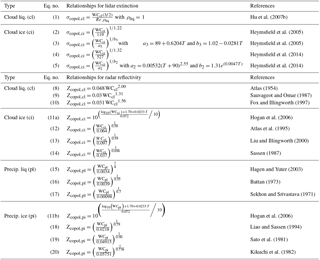
Figure 3Relationship between water content in the form of cloud liquid (blue), precipitating liquid (green), cloud ice (black) and precipitating ice (red) and (a) lidar extinction, and (b) radar copolar reflectivity. Spread emerges from using multiple differing empirical relationships (listed in Table 2) and from variability in the 1-year ModelE output (including the effects of varying temperature and effective radii).
3.1 Lidar-backscattered power simulator
At a lidar wavelength of 532 nm, backscattered power is proportional to total particle cross section per unit volume. Owing to their high number concentrations, despite their small size, cloud particles backscatter radiation of this wavelength the most.
We adopt the Hu et al. (2007b) representation of liquid cloud extinction derived from CALIPSO and CERES–MODIS observations and retrievals of liquid water content and effective radius (Table 2, Eq. 1). For cloud ice water content, a number of empirical relationships with lidar extinction have been proposed for various geophysical locations and ice cloud types using a variety of assumptions. Four of these empirical relationships are implemented in (GO)2-SIM (Table 2, Eqs. 2–5, and references therein) and used to generate an ensemble of forward simulations. Using these empirical relationships, a given water content can be mapped to a range of lidar extinction values (Fig. 3a). This spread depends both on the choice of empirical relationships and on the variability of the atmospheric conditions that affect them (i.e., atmospheric temperature and hydrometeor effective radius variability). Figure 3a also illustrates the fundamental idea that lidar extinction increases with increasing water content and that for a given water content cloud droplets generally lead to higher lidar extinction than cloud ice particles.
Lidar copolar-backscattered power (βcopol,species; ) generated by each hydrometeor species is related to lidar extinction (σcopol,species; m−1) through the lidar ratio (Sspecies; sr):
While constant values are used for the lidar ratios of liquid and ice clouds in this version of the forward simulator, we acknowledge that in reality they depend on particle size. O'Connor et al. (2004) suggest that a liquid cloud lidar ratio (Scl) of 18.6 sr is valid for cloud liquid droplets smaller than 25 µm, which encompasses the median diameter expected in the stratiform clouds simulated here. Kuehn et al. (2016) observed layer-averaged lidar ratios in ice clouds (Sci) ranging from 15.1 to 36.3 sr. Sensitivity tests indicate that adjusting the ice cloud lidar ratio to either of these extreme values in the forward simulator increases the number of detectable hydrometeors by no more than 0.6 %, changes the hydrometeor-phase frequency of occurrence statistics by less than 0.4 %, and causes less than a 0.1 % change in water-phase classification errors (not shown). Given these results, the ice cloud lidar ratio is set to the constant value of 25.7 sr, which corresponds to the mean value observed by Kuehn et al. (2016).
It is important to consider the fact that lidars do not measure cloud droplet backscattering independently of cloud ice particle backscattering. Rather, they measure total copolar-backscattered power (βcopol,total), which is the sum of the contribution from both cloud phases.
3.2 Radar-backscattered power simulator
At the cloud-radar wavelength of 8.56 mm (Ka band), backscattered power is approximately related to the sixth power of the particle diameter and inversely proportional to the forth power of the wavelength. Hereafter radar-backscattered power will be referred to as “radar reflectivity” as commonly done in the literature.
(GO)2-SIM relies on water-content-based empirical relationships to estimate cloud liquid water (cl), cloud ice (ci), precipitating liquid water (pl), and precipitating ice (pi) radar reflectivity. Different relationships are used for each species to account for the fact that hydrometeor mass and size both affect radar reflectivity. A number of empirical relationships link hydrometeor water content to copolar radar reflectivity; 13 of these empirical relationships are implemented in (GO)2-SIM (Table 2, Eqs. 8–20, and references therein) and used to generate an ensemble of forward simulations. Figure 3b illustrates the fact that for all these empirical relationships increasing water content leads to increasing radar reflectivity. As already mentioned, radar reflectivity is approximately related to the sixth power of the particle size, which explains why, for the same water content, precipitating hydrometeors are associated with greater reflectivity than cloud hydrometeors.
In reality, radars cannot isolate energy backscattered by individual hydrometeor species. Rather, they measure total copolar reflectivity (Zcopol,total; mm6 m−3), which is the sum of the contributions from all of the hydrometeor species.
In the previous section, total backscattered power resulting from all modeled hydrometeor species (without any filtering) is estimated. In order to objectively assess model hydrometeor properties, they must be converted to quantities that are comparable to observations. This necessitates the incorporation of sensor detection limitations, including attenuation and finite sensitivity. Fortunately, lidar and radar sensors are often relatively well characterized so that sensor detection capabilities can be quantified and replicated in forward simulators for an objective model-to-observation comparison.
4.1 Lidar detection capability
Following the work of Chepfer et al. (2008), the (GO)2-SIM lidar forward simulator takes into consideration the fact that lidar power is attenuated by clouds. Attenuation is related to cloud optical depth (τ), which is a function of total cloud extinction (σcopol,total; m−1) that includes the effect of cloud liquid water and cloud ice via
Lidar attenuation is exponential and two-way as it affects the lidar power on its way out and back:
Note that in some instances multiple scattering occurs before the lidar signal returns to the sensor, thus amplifying the returned signal. In theory, the multiple scattering coefficient (η) varies from 0 to 1. Sensors with large fields of view, such as satellite-based lidars, are more likely to be impacted by multiple scattering than others (Winker, 2003). In the current study, for which a ground-based lidar is simulated, a multiple scattering coefficient of unity is used. A sensitivity test in which this coefficient was varied from 0.7, such as that implemented in the CALIPSO satellite lidar simulator of Chepfer et al. (2008), to 0.3, representing an extreme case, indicated that multiple scattering had a negligible impact (less than 1 %) on the number of hydrometeors detected, the hydrometeor-phase frequency of occurrence statistics, and hydrometeor-phase classification error (not shown).
In the current simulator we assume that only cloud segments with an optical depth smaller than 3 can be penetrated, and other clouds are opaque (Cesana and Chepfer, 2013) such that total copolar-backscattered power detected () is
For the sample ModelE output shown in Fig. 2, Fig. 4a illustrates results from the lidar forward simulator for one forward-ensemble member (i.e., using a single set of lidar-backscattered power empirical relationships, specifically Eqs. 1 and 4). Figure 4a1 shows lidar total copolar-backscattered power without consideration of sensor limitations, such as attenuation, which are included in Fig. 4a2. Lidar attenuation prevents the tops of deep systems containing supercooled water layers from being observed (e.g., magenta boxes on 10 and 13 August). For the 1-year sample the forward-simulated lidar system detects only 35.5 % of simulated hydrometeor-containing grid cells. In Sect. 6 we will determine which hydrometeors (liquid water or ice) are responsible for the detected signals.
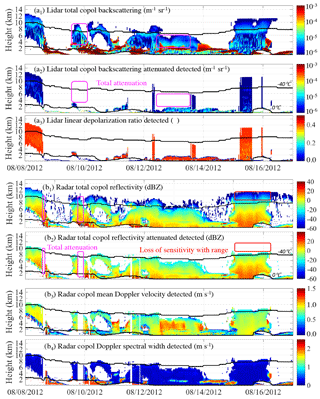
Figure 4Example outputs from the (GO)2-SIM backscattered power modules (1), sensor capability modules (2), and specialized-observables modules (3–4) for (a) lidars and (b) radars obtained using one set of empirical backscattered power relationships. This figure highlights sensor limitations ranging from attenuation (magenta boxes) to sensitivity loss with range (red boxes). Also indicated are the locations of the 0 and −40 ∘C isotherms (black lines). Note that positive velocities indicate downward motion.
4.2 Radar detection capability
Millimeter-wavelength radars are also affected by signal attenuation. Radar signal attenuation depends on both the transmitted wavelength and on the mass and phase of the hydrometeors. Liquid-phase hydrometeors attenuate radar signals at all millimeter radar wavelengths, even leading to total signal loss in heavy rain conditions. In contrast, water vapor attenuation is less important at relatively longer wavelengths (e.g., 8.56 mm; the wavelength simulated here) but can be important near wavelengths of 3.19 mm (the CloudSat operating wavelength; Bodas-Salcedo et al., 2011).
At 8.56 mm (Ka band), total copolar attenuated reflectivity (; dBZ) is given by
where attenuation is controlled by the wavelength-dependent attenuation coefficient a (dB km−1 (g m), which we take to be 0.6 at Ka band (Ellis and Vivekanandan, 2011), by the water contents of cloud liquid (WCcl; g m−3) and precipitating liquid (WCcl; g m−3), and by the thickness of the liquid layer.
In addition to attenuation, radars suffer from having a finite sensitivity that decreases with distance. Given this, the total copolar reflectivity detectable (; dBZ) is
where the radar minimum detectable signal (Zmin; dBZ) is a function of height (h; km) and can be expressed as
A value of dBZ is selected to reflect the sensitivity of the Ka-band ARM Zenith Radar (KAZR) currently installed at the Atmospheric Radiation Measurement (ARM) North Slope of Alaska observatory. This value has been determined by monitoring 2 years of observations and it reflects the minimum signal observed at a height of 1 km. The minimum detectable signal used in the simulator should reflect the sensitivity of the sensor used to produce the observational benchmark to be compared to the forward-simulator output.
For the sample ModelE output shown in Fig. 2, Fig. 4b illustrates results from the radar forward simulator for one forward-ensemble member (i.e., using a single set of radar reflectivity empirical relationships, specifically Eqs. 9, 11a, b, and 15). Figure 4b1 shows radar total copolar reflectivity without consideration of sensor limitations, while Fig. 4b2 includes the effects of attenuation and the range-dependent minimum detectable signal. Sensor limitations make it such that heavy-rain-producing systems cannot be penetrated (e.g., magenta box on 8 and 10 August) and the tops of deep systems cannot be observed (e.g., red box on 15 August). For the 1-year sample the forward-simulated radar system could detect only 69.9 % of the simulated hydrometeor-containing grid cells. In Sect. 6 we will determine the phase of the hydrometeors responsible for the detected signals.
4.3 Lidar–radar complementarity
Figure 4a2 and b2 highlight the complementarity of lidar and radar sensors. Despite sensor limitations, 532 nm lidar measurements can be used to characterize hydrometeors near the surface and infer the location of a lowermost liquid layer if one exists. In contrast, 8.56 mm radars have the ability to penetrate cloud layers and light precipitation, allowing them to determine cloud boundary locations (e.g., Kollias et al., 2016). For the 1-year sample ModelE output the combination of both sensors enables the detection of 73.0 % of the hydrometeor-containing grid cells. Real observations can be used to objectively evaluate these detectable hydrometeor populations, while nothing can be said about those that are not detectable. Note that a number of undetectable grid cells only contain trace amounts of hydrometeors, which could be the result of numerical noise. As such the approach of considering sensor detection limitations helps objectively remove numerical noise from consideration and allows model and observations to converge towards a common hydrometeor definition for a fair comparison.
In the previous section total copolar-backscattered powers are used to determine which simulated hydrometeors are present in sufficient amounts to be detectable by sensors, hence removing numerical noise from consideration. However, determining the phase of the detectable hydrometeor populations can be achieved with much greater accuracy by using additional observables.
Backscattered power alone provides a sense of hydrometeor number concentration (from lidar) and hydrometeor size (from radar), but it does not contain information about hydrometeor shape nor does it provide any hint on the number of coexisting hydrometeor species, both of which are relevant for phase determination. However, such information is available from lidar depolarization ratios and radar Doppler spectral widths.
5.1 Lidar depolarization ratio simulator
So far we have described how hydrometeors of all types and phases affect copolar radiation. It is important to note that radiation also has a cross-polar component, which is only affected by nonspherical particles. Ice particles, which tend to be nonspherical, are expected to affect this component, while we assume that cloud droplets, which tend to be spherical, do not. Taking the ratio of cross-polar to copolar backscattering thus provides information about the dominance of ice particles in a hydrometeor population. This ratio is referred to as the linear depolarization ratio (δdetect) and it can be estimated where hydrometeors are detected by the lidar.
According to an analysis of CALIPSO observations by Cesana and Chepfer (2013), cloud ice particle cross-polar backscattering (; m−1 sr−1) and cloud liquid droplet cross-polar backscattering (; m−1 sr−1) can be approximated using the following relationships:
For reasons mentioned in Sect. 4.1, multiple scattering is considered negligible in the current study such that cloud-liquid droplet cross-polar backscattering is assumed to be zero under all conditions.
5.2 Radar Doppler moment simulator
Specialty Doppler radars have the capability to provide information about the movement of hydrometeors in the radar observation volume. This information comes in the form of the radar Doppler spectrum, which describes how backscattered power is distributed as a function of hydrometeor velocity (Kollias et al., 2011). The zeroth moment of the Doppler spectral distribution (the spectral integral) is radar reflectivity, the first moment (the spectral mean) is mean Doppler velocity (VD), and the second moment (the spectral spread) is Doppler spectral width (SW). Rich information is provided by the velocity spread (i.e., SW) of the hydrometeor population, including information regarding the number of coexisting species, turbulence intensity, and spread of the hydrometeor particle size distributions. Typically, the effects of turbulence and hydrometeor size variations on the velocity spread for a single species are much smaller than the effect of mixed-phase conditions. As such, Doppler spectral width is a useful parameter for hydrometeor-phase identification.
Forward simulations of Doppler quantities have been performed for cloud models using bin microphysics (e.g., Tatarevic and Kollias, 2015) but not, to our knowledge, for GCMs using two-moment microphysics schemes.
Copolar mean Doppler velocity and copolar Doppler spectral width are subject to the same detection limitations as radar reflectivity. In fact, just like radar reflectivity, these observables are strongly influenced by large hydrometeors; that is, they are reflectivity-weighted velocity averages. Our approach begins by quantifying the contribution of each species present (Pspecies), which is determined by the species detected copolar reflectivity (; mm6 m−3) relative to the total detected copolar reflectivity (; mm6 m−3):
together with
In Eqs. (27a)–(27b) the subscript “species” represents cl, ci, pl, or pi. The attenuation coefficient (a), minimum detectable signal (Zmin), and water contents (WCs) are as in Eqs. (24) and (25b). Total mean Doppler velocity detected (VDcopol,detect; m s−1) is the reflectivity-weighted sum of the mass-weighted fall velocity of each hydrometeor species (Vspecies; m s−1):
where the mass-weighted fall velocity of each hydrometeor species (Vspecies; m s−1) is a model output. Total Doppler spectral width (SWcopol,detect; m s−1) is more complex and can be estimated following a statistical method similar to that described by Everitt and Hand (1981). It takes into consideration the properties of each individual hydrometeor species through their respective fall speed (Vspecies; m s−1) and spectral width (SWspecies; m s−1) in relation to the properties of the hydrometeor population as a whole through the total mean Doppler velocity detected (VDcopol,detect) estimated in Eq. (28):
where the spectral widths of individual species (SWspecies) are assigned climatological values. These climatological values are SWcl=0.10 m s−1 SWci=0.05 m s−1, SWpi=0.15 m s−1, and SWpl=2.00 m s−1 (Kalesse et al., 2016).
For the sample ModelE output shown in Fig. 2, Fig. 4b3 and b4 respectively show examples of forward-simulated mean Doppler velocity and Doppler spectral width estimate using one set of empirical radar reflectivity relationship.
From a purely numerical modeling perspective the simplest approach to defining the phase of a hydrometeor population contained in grid cells is to consider any nonzero hydrometeor mixing ratio species as contributing to the phase of the population. Using this approach, in the 1-year sample, we find that the detectable hydrometeor-containing grid cells are 2.4 % pure liquid, 19.4 % pure ice, and 78.2 % mixed phase (note how these water-phase statistics differ by up to 18.4 % from Sect. 2 in which all grid cells potentially including numerical noise were considered). But determining hydrometeor phase in observational space is not as straightforward. It is complicated by the fact that sensors do not record ice- and liquid-hydrometeor returns separately but rather record total backscattering from all hydrometeors. Retrieval algorithms are typically applied to the observed total backscattering to determine the phase of hydrometeor populations. However, phase-classification algorithms have limitations that require each hydrometeor species to be present not only in nonzero amounts but in amounts sufficient to produce a phase signal. Thus, hydrometeor-phase statistics obtained from a numerical model in the absence of a forward simulator are not necessarily comparable with equivalent statistics retrieved from observables, especially in instances in which one hydrometeor species dominates the grid cell and other species are present in trace amounts. A common hydrometeor-phase definition must be established to objectively evaluate the phase of simulated hydrometeor populations using observations, which requires the development of a phase-classification algorithm that can be applied to observables both forward simulated and real.
The scientific literature contains a number of phase-classification algorithms with different levels of complexity. Hogan et al. (2003) used regions of high lidar-backscattered power as an indicator for the presence of liquid droplets. Lidar-backscattered power combined with the lidar linear depolarization ratio has been used to avoid some of the misclassifications encountered when using backscattered power alone (e.g., Yoshida et al., 2010; Hu et al., 2007a, 2009, 2010; Sassen, 1991) Hogan and O'Connor (2004) proposed using lidar-backscattered power in combination with radar reflectivity. While the combination of radar- and lidar-backscattered powers is useful for the identification of mixed-phase conditions, their combined extent remains limited to single-layer clouds or to lower cloud decks because of lidar signal attenuation. Shupe (2007) proposed a technique in which radar Doppler velocity information is used as an alternative to lidar backscattering information (for ranges beyond that of lidar total attenuation) to infer the presence of supercooled water in multilayer systems. Figure 5 displays cartoons of Doppler spectra that have the same total copolar radar reflectivity but different total mean Doppler velocities (VDs) and Doppler spectral widths (SWs) resulting from different hydrometeor species and combinations, thus highlighting the added value of Doppler information. The contribution of each species to the total copolar reflectivity is indicated as a percentage in the top right of each subpanel. These scenarios show that VD tends to be relatively small for pure liquid cloud (Fig. 5a6), pure ice cloud (Fig. 5a2), and even mixed-phase non-precipitating cloud (Fig. 5a3, a5, b3) and only tends to increase when precipitation is present in cloud (Fig. 5a4, b3, b4, b5) or below cloud (Fig. 5a1, b2), making VD a seemingly robust indicator for precipitation occurrence but not for phase identification. These scenarios also show that SW tends to be relatively small in single-phase clouds without precipitation (Fig. 5a2, a6), pure precipitating ice (Fig. 5a1), and multispecies clouds with a dominant hydrometeor species (Fig. 5a3, a5). On the other hand, SW tends to be large when liquid precipitation is present (Fig. 5b1, b2, b5) and in mixed-phase clouds without a dominant species (Fig. 5b3, b4, b5). These scenarios suggest that large spectral widths are useful indicators for the presence of supercooled rain and mixed-phase conditions. Scenarios in which this interpretation of spectrum width is incorrect will be discussed in Sect. 6.3.

Figure 5Cartoon examples of radar Doppler spectra from different hydrometeor combinations: precipitating ice (red), cloud ice (black), precipitating water (green), and cloud water (blue). The contribution of each hydrometeor species to the total copolar reflectivity is indicated in the top right of each subpanel. Each radar Doppler spectrum has been normalized to have the same total copolar radar reflectivity, which highlights the fact that different hydrometeor combinations generate unique mean Doppler velocity (VD) and Doppler spectral width (SW) signatures. As discussed in Sect. 6, low spectral width signatures are assumed to be associated with ice conditions (column a), while high spectral width signatures are assumed to be associated with liquid–mixed-phase conditions (column b). Hydrometeor combinations that respect these assumptions are marked with √ marks. Exceptions to these rules (X marks) are responsible for (GO)2-SIM phase misclassifications above the level of lidar extinction. This list is not exhaustive.
Regardless of which observation they are based on, the aforementioned phase-classification schemes all rely on the assumption that hydrometeor phases when projected on observational space (e.g., lidar-backscattered power against the lidar depolarization ratio) create well-defined patterns that can be separated using thresholds.
6.1 Observational thresholds for hydrometeor-phase identification
While the thresholds used for the radar reflectivity, lidar-backscattered power, and lidar depolarization ratio are generally accepted by the remote sensing community, the same cannot be said about the radar Doppler velocity and Doppler spectral width thresholds suggested by Shupe (2007). Because simulated mixing ratios of liquid and ice hydrometeors are known in the (GO)2-SIM framework, the use and choice of all such thresholds for phase classification can be evaluated using joint frequency of occurrence histograms of hydrometeor mixing ratios for a single species and forward-simulated observable values (resulting from all hydrometeor types; Fig. 6). This exercise is repeated for each forward simulation of the ensemble in order to provide a measure of uncertainty and ensure that the choice of empirical relationship does not affect our conclusions.
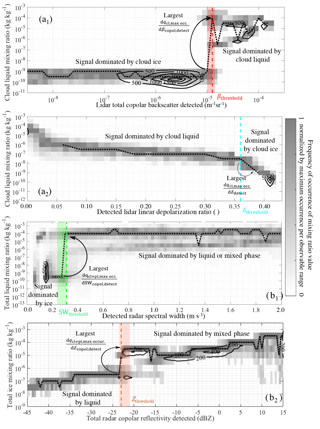
Figure 6Example of joint frequency of occurrence histograms (contours) and normalized subsets from the joint histograms (gray shading) for one (GO)2-SIM forward realization: (a1) , (a2) δdetect, (b1) SWcopol,detect, and (b2) . These are used for the determination of objective water-phase classifier thresholds (vertical colored dashed lines) that are set at the observational value with the largest change (see curved arrows) in most frequently occurring mixing ratio. These thresholds are not fixed but rather reestimated for each forward-ensemble member. The widths of the color-shaded vertical columns represent the interquartile range spreads generated from 576 different forward realizations.

Figure 7Collective illustration of hydrometeor-phase classification thresholds and phase-classification sequence. Fixed empirical thresholds modified from Shupe (2007) are displayed as gray lines. The objectively determined flexible thresholds are displayed using dashed colored lines and colored shading as in Fig. 6. Note that positive velocities indicate downward motion.
As one example, the joint frequency of occurrence histogram of lidar total copolar-backscattered power () and cloud liquid mixing ratio is plotted with the objective of isolating cloud ice particles from cloud water droplets (Fig. 6a1, black contour lines). Two distinct clusters are evident in the joint histogram in Fig. 6a1: (1) between 10−6.7 and 10−5.1 m−1 sr−1 for cloud liquid water mixing ratios between 10−10.6 and 10−8.8 kg kg−1, which we conclude result primarily from cloud ice particle contributions, and (2) between 10−4.6 and 10−3.8 m−1 sr−1 for cloud liquid water mixing ratios between 10−6.4 and 10−4.3 kg kg−1, which we conclude result primarily from cloud liquid droplet contributions. Therefore, a threshold for best distinguishing these two distinct populations should lie somewhere between 10−5.1 and 10−4.6 m−1 sr−1.
To objectively determine an appropriate threshold to separate different hydrometeor populations, we start by normalizing the joint histogram of mixing ratio values for fixed ranges of observable values of interest. This normalization is done by assigning a value of 1 to the frequency of occurrence of the most frequently occurring mixing ratio value per observable range. It is then possible to evaluate the change in this most frequently occurring mixing ratio as a function of observable value. The observable value that intersects the largest change in most frequently occurring mixing ratio is then set as the threshold value.
In the example presented in Fig. 6a1, the darkest gray shading is indicative of the most frequently occurring cloud liquid mixing ratio for each lidar-backscattered power range. The dotted black line in Fig. 6a1 connects these most frequently occurring mixing ratio values. A curved arrow points to the largest change in most frequently occurring mixing ratio as a function of . A red dashed line at 10−4.9 m−1 sr−1 indicates the lidar backscatter value that intersects this largest change in mixing ratio and represents an objective threshold value for this example forward simulation. As mentioned earlier, this threshold is expected to change with the choice of empirical relationships used in the forward simulator. For the 576 forward-simulator realizations of this version of ModelE outputs, the interquartile range of threshold values ranged from 10−5 to 10−4.85 m−1 sr−1 (red shaded vertical column).
The different panels in Fig. 6 show that similar observational patterns occur in the water mixing ratio versus lidar or radar observable histograms such that objective thresholds for hydrometeor-phase classification can be determined for all of them. The second threshold determined is for the detected lidar linear depolarization (δdetect), once again with the goal of separating returns dominated by cloud droplets versus cloud ice particles (Fig. 6a2). If we first identify the model grid cells with backscattered power above the lidar detectability threshold of 10−6 m−1 sr−1, the threshold to distinguish between ice particles and liquid droplets is 0.36 (cyan dashed line). In the 576 forward realizations from this version of ModelE this threshold is stable at 0.36. Note that this threshold is not allowed to fall below 0.05 m s−1.
The third threshold determined is the radar detected copolar spectral width (SWcopol,detect) value that separates ice-dominated from liquid- or mixed-phase-dominated returns (Fig. 6b1). We isolate the model grid cells with subzero temperatures and look for the most appropriate SWcopol,detect threshold between 0.2 and 0.5 m s−1 to isolate the ice population. For the example forward simulation we find a threshold of 0.31 m s−1 (green dashed line), and over all forward realizations this threshold ranges from 0.24 to 0.31 m s−1 (green shaded vertical column).
The last threshold determined is the radar total copolar reflectivity detected () value that separates liquid- from mixed-phase-dominated returns (Fig. 6b2). If we isolate the model grid cells with subzero temperatures, spectral widths within the liquid- to mixed-phase range, and with mean Doppler velocities smaller than 1 m s−1, the threshold to distinguish between the liquid and mixed phase is objectively set to −23 dBZ (orange dashed line). This threshold ranges from −23.5 to −21.0 dBZ over the 576 forward realizations obtained from this version of ModelE outputs (orange shaded vertical column).
The objectively determined thresholds, based on model output mixing ratios, optimize the performance of the hydrometeor-phase classification algorithm and are expected to generate the best (by minimizing false detection) hydrometeor-phase classifications. Results using these objective flexible thresholds are compared in Sect. 6.4 to results using the fixed empirical thresholds of Shupe (2007).
6.2 Hydrometeor-phase map generation
Hydrometeor-phase maps are produced for each forward realization by applying the objectively determined flexible thresholds or fixed empirical thresholds modified from Shupe (2007) as illustrated in Fig. 7.
Thresholds are applied in sequence. Where the lidar signal is detected it is used for the initial classification of liquid-dominated grid cells (Fig. 7.1, red box) and the final classification of ice-dominated grid cells (Fig. 7.1, cyan box). Grid cells initially classified as containing liquid drops by the lidar are subsequently reclassified as either liquid dominated (Fig. 7.2, orange box) or mixed phase (Fig. 7.2, outside of orange box) by the radar, which is more sensitive to the larger ice particles. Because studies suggest that supercooled water layers extend to the tops of shallow clouds, if liquid-containing grid cells were identified within 750 m of the cloud top, the radar is used to determine if there are other liquid- or mixed-phase hydrometeor populations from the range of lidar attenuation to the cloud top (Fig. 7.2; and just as in Shupe, 2007). Hydrometeor-containing grid cells either not detected by the lidar or whose initial phase classification is inconclusive (Fig. 7.1, inconclusive region) are subsequently classified using their radar moments. If radar spectral width is above the threshold grid cells are finally classified as liquid (Fig. 7.3, orange box) or mixed phase (Fig. 7.3, outside the orange box) depending on their other radar moments. If radar spectral width is below the threshold grid cells are finally classified as ice phase (Fig. 7.4). As a final step detected hydrometeors in grid cells at temperatures above 0 ∘C are reclassified to the liquid phase, while those at temperatures below −40 ∘C are reclassified to the ice phase.
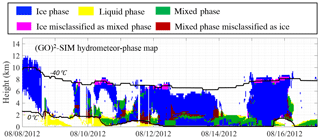
Figure 8Example output from (GO)2-SIM phase-classification algorithms (using objectively determined thresholds and one set of empirical relationships in the forward simulator). The locations of ice-phase hydrometeors (blue), liquid-phase hydrometeors (yellow), and mixed-phase hydrometeors (green) are illustrated. After evaluation against the original ModelE output mixing ratios, we found that some mixed-phase hydrometeors were misclassified as ice phase (red) and some ice-phase hydrometeors were misclassified as mixed phase (magenta). Also indicated are the locations of the 0 and −40 ∘C isotherms (black lines).
Figure 8 shows an example of (GO)2-SIM water-phase classification for one forward-ensemble member using objectively determined thresholds. During the first day of this example simulation, ModelE produced what appears to be a thick cirrus. The simulator classified this cirrus as mostly ice phase (blue). The following day of 9 August, ModelE generated enough hydrometeors to attenuate both the forward-simulated lidar and radar signals. The algorithm identified these hydrometeors as liquid phase (yellow). For the following few days (11–14 August) deep hydrometeor systems extending from the surface to about 8 km were produced. According to (GO)2-SIM they were mostly made up of ice-phase particles (blue) with two to three shallow mixed-phase layers at 2, 4, and 7 km. Finally, on 14 August hydrometeor systems appear to become shallower (2 km altitudes) and liquid topped (yellow). For the entire 1-year simulation, of the 333 927 detectable hydrometeor-containing grid cells, the phase classifier applied to our example forward-simulation ensemble member identified 12.2 % pure liquid, 68.7 % pure ice, and 19.1 % mixed-phase conditions. Hydrometeor-phase statistics estimated using this objective definition of hydrometeor phase differ by up to 60 % from those discussed at the beginning of this section that were simply based on model output nonzero mixing ratios. This indicates that a large number of grid cells containing detectable hydrometeor populations were dominated by one species and that the amounts of the other species were too small to create a phase-classification signal. This highlights the need to create a framework that both objectively identifies grid cells containing detectable hydrometeor populations and determines the phase of the hydrometeors dominating them using a phase-classification technique consistent with observations.
6.3 Phase-classification algorithm limitations
Hydrometeor-phase classification evaluation is facilitated in the context of forward simulators because inputs (i.e., model-defined hydrometeor phase) are known. Model mixing ratios are used to check for incorrect hydrometeor-phase classifications over the entire forward-realization ensemble (Table 1b).
Without any ambiguity, it is possible to identify false-positive phase classifications (Table 1b). A false-positive phase classification occurs when a grid cell containing 0 kg kg−1 of ice particles (liquid drops) is wrongly classified as ice or mixed phase (liquid or mixed phase). In this study a negligible number (0.5 %) of hydrometeor-containing model grid cells are wrongly classified as containing liquid. Similarly, a negligible number (∼0.0 %) of hydrometeor-containing model grid cells are wrongly classified as containing ice particles, whereas 1.1 % of pure liquid- or ice-containing model grid cells are wrongly classified as mixed phase. Using model mixing ratios, it is possible to determine the appropriate phase of these false-positive classifications (“False negative” row in Table 1b). An additional 1.5 % of all hydrometeor-containing model grid cells should be classified as ice phase, while a negligible number (0.2 %) of liquid water is missed.
Quantifying the number of mixed-phase false negatives (i.e., the number of grid cells that should have been, but were not, classified as mixed phase) is not as straightforward because it requires us to define mixed-phase conditions in model space. For a rough estimate of mixed-phase false negatives we check if model grid cells classified as containing a single phase contained large amounts of hydrometeors of other phase types, with a large amount being defined here as a mixing ratio greater than 10−5 kg kg−1. This mixing ratio amount was chosen because it is associated with noticeable changes in observables, as seen in Fig. 6. Using this mixed-phase definition, we find that 1.4 % of liquid-only classified grid cells contained large amounts of ice particles and 3.8 % of ice-only classified grid cells contained large amounts of liquid (“Questionable” row in Table 1b). Everything considered, only 6.9 % of model grid cells with detectable hydrometeor populations were misclassified according to their phase.
For completeness we examined the circumstances associated with the most frequent phase-classification errors. Most of these errors occurred above the altitude at which the lidar beam was completely attenuated, with only radar spectral widths used to separate liquid- or mixed-phase hydrometeors from ice-phase hydrometeors.
The first set of phase-classifier errors was a scarcity of pure ice particles (1.5 % false-negative ice phase). In the current (GO)2-SIM implementation, ice particle populations are sometimes incorrectly classified as liquid–mixed-phase populations when cloud ice and precipitating ice hydrometeors coexist. This happens because mixtures of cloud and precipitating ice particles sometimes generate large Doppler spectral widths similar to those of mixed-phase clouds (Fig. 5b6). In this example simulation ModelE produced such mixtures close to the −40 ∘C isotherm near the tops of deep cloud systems (e.g., Fig. 8, 15 August around 8 km; magenta).
In contrast, mixed-phase conditions were sometimes misclassified as pure ice (3.8 %; “Questionable” row in Table 1b). This occurred when large amounts of liquid drops coexisted with small amounts of ice particles that generated small spectral widths incorrectly associated with pure ice particles (Fig. 5a5). In this example simulation, ModelE produced such conditions just above the altitude of lidar beam extinction in cloud layers with ice falling into supercooled water layers (e.g., Fig. 8, 13 August around 3 km; red).
Other possible misclassification scenarios associated with spectral width retrievals are presented in Fig. 5 and identified with the red X marks. These other misclassification scenarios are not responsible for large misclassification errors here but could be in other simulations. As such, (GO)2-SIM errors should be quantified every time it is applied to a new region or numerical model.
6.4 Sensitivity on the choice of threshold
The performance of the objectively determined flexible phase-classification thresholds (illustrated using colored dashed lines and shading in Fig. 7) is examined against those empirically derived by Shupe (2007) with one exception (illustrated using gray lines in Fig. 7). The modification to Shupe (2007) is that radar reflectivity larger than 5 dBZ is not associated with the snow category since introducing this assumption was found to increase hydrometeor-phase misclassification (not shown). From Fig. 7 it is apparent that both sets of thresholds are very similar. We estimate that the hydrometeor-phase frequency of occurrence produced by both threshold sets is within 6.1 % of the other and that the fixed empirical thresholds modified from Shupe (2007) only produce phase misclassification in an additional 0.7 % of hydrometeor-containing grid cells (compare Table 1b to c). These results suggest that the use of lidar–radar threshold-based techniques for hydrometeor-phase classification depends little on the choice of thresholds.
Owing to the limited information content in models with regard to detailed particle property information, all forward simulators must rely on a set of assumptions to estimate hydrometeor-backscattered power. (GO)2-SIM performs an uncertainty assessment by performing an ensemble of 576 forward simulations based on 18 different empirical relationships (relationships are listed in Table 2). While the relationships used do not cover the entire range of possible backscattering assumptions, they represent an attempt at uncertainty assessment and illustrate a framework for doing so. We express the spread generated by the different empirical relationship combinations using median values and interquartile ranges (IQR; Table 1b, c). The fact that the largest interquartile range is 3.7 % suggests that the number of grid cells containing detectable hydrometeors as well as hydrometeor-phase statistics estimated using the proposed lidar–radar algorithm are rather independent of backscattered power assumptions in the forward simulator. Nevertheless, we suggest using the full range of frequency of occurrences presented in Table 1b and c for future model evaluation using observations and acknowledge that additional uncertainty is most likely present.
Ground-based active remote sensors offer a favorable perspective for the study of shallow and multilayer mixed-phase clouds because ground-based sensors are able to collect high-resolution observations close to the surface where supercooled water layers are expected to be found. In addition, ground-based sensors have the unique capability to collect Doppler velocity information that has the potential to help identify mixed-phase conditions even in multilayer cloud systems.
Because of differences in hydrometeor and phase definitions, among other things, observations remain incomplete benchmarks for general circulation model (GCM) evaluation. Here, a GCM-oriented ground-based observation forward-simulator ((GO)2-SIM) framework for hydrometeor-phase evaluation is presented. This framework bridges the gap between observations and GCMs by mimicking observations and their limitations and producing hydrometeor-phase maps with comparable hydrometeor definitions and uncertainties.
Here, results over the North Slope of Alaska extracted from a 1-year global ModelE (current development version) simulation are used as an example. (GO)2-SIM uses as input native-resolution GCM grid-average hydrometeor (cloud and precipitation, liquid, and ice) area fractions, mixing ratios, mass-weighted fall speeds, and effective radii. These variables offer a balance between those most essential for forward simulation of observed hydrometeor backscattering and those likely to be available from a range of GCMs, making (GO)2-SIM a portable tool for model evaluation. (GO)2-SIM outputs statistics from 576 forward-simulation ensemble members all based on a different combination of 18 empirical relationships that relate simulated in-cloud water content to hydrometeor-backscattered power as would be observed by vertically pointing micropulse lidar and Ka-band radar; the interquartile range of these statistics is used as an uncertainty measure.
(GO)2-SIM objectively determines which hydrometeor-containing model grid cells can be assessed based on sensor capabilities, bypassing the need to arbitrarily filter trace amounts of simulated hydrometeor mixing ratios that may be unphysical or just numerical noise. Limitations that affect sensor capabilities represented in (GO)2-SIM include attenuation and range-dependent sensitivity. In this approach 78.3 % of simulated grid cells containing nonzero hydrometeor mixing ratios were detectable and can be evaluated using real observations, with the rest falling below the detection capability of the forward-simulated lidar and radar, leaving them unevaluated. This shows that comparing all hydrometeors produced by models with those detected by sensors would lead to inconsistencies in the evaluation of quantities as simple as cloud and precipitation locations and fraction.
While information can be gained from comparing the forward-simulated and observed fields, hydrometeor-phase evaluation remains challenging owing to inconsistencies in hydrometeor-phase definitions. Models evolve ice and liquid water species separately such that their frequency of occurrence can easily be estimated. However, sensors record information from all hydrometeor species within a grid cell without distinction between signals originating from ice particles or liquid drops. The additional observables of lidar linear depolarization ratio and radar mean Doppler velocity and spectral width are forward simulated to retrieve hydrometeor phase. The results presented here strengthen the idea that hydrometeor-phase characteristics lead to distinct signatures in lidar and radar observables, including the radar Doppler moments that have not been evaluated previously. Our analysis confirms that distinct patterns in observational space are related to hydrometeor phase and an objective technique to isolate liquid, mixed-phase, and ice conditions using simulated hydrometeor mixing ratios was presented. The thresholds produced by this technique are close to those previously estimated using real observations, further highlighting the robustness of thresholds for hydrometeor-phase classification.
The algorithm led to hydrometeor-phase misclassification in no more than 6.9 % of the hydrometeor-containing grid cells. Its main limitations were confined above the altitude of lidar total attenuation where it sometimes failed to identify additional mixed-phase layers dominated by liquid water drops and containing few ice particles. Using the same hydrometeor-phase definition for forward-simulated observables and real observations should produce hydrometeor-phase statistics with comparable uncertainties. Alternatively, disregarding how hydrometeor phase is observationally retrieved would lead to discrepancies in hydrometeor-phase frequency of occurrence of up to 40 %, a difference attributable to methodological bias and not to model error. So, while not equivalent to model “reality” a forward-simulator framework offers the opportunity to compare simulated and observed hydrometeor-phase maps with similar limitations and uncertainties for a fair model evaluation.
The next steps in GCM evaluation using ground-based observations include the creation of an artifact-free observational benchmark and addressing model and observation scale differences. While the (GO)2-SIM modules presented here capture sensor limitations related to backscattered power attenuations, they do not account for sensitivity inconsistencies, clutter, and insect contamination, which affect the observations collected by the real sensors. Only a thorough evaluation of observational datasets and the application of masking algorithms to them can remediate these issues. Several approaches, from the subsampling of GCMs to the creation of reflectivity contoured frequency by altitude diagrams (CFADs), have been proposed to address the scale difference. A follow-up study will describe an approach by which vertical and temporal resampling of observations can help reduce the scale gap. Furthermore, it will be shown that, using simplified model evaluation targets based on three atmospheric regions separated by constant pressure levels, ground-based observations can be used for GCM hydrometeor-phase evaluation.
(GO)2-SIM is a step towards creating a fair hydrometeor-phase comparison between GCM output and ground-based observations. Owing to its simplicity and robustness, (GO)2-SIM is expected to help assist in model evaluation and development for models such as ModelE, specifically with respect to hydrometeor phase in shallow cloud systems.
The results here are based on ModelE tag modelE3_2017-06-14, which is not a publicly released version of ModelE but is available on the ModelE developer (password-protected) repository at https://simplex.giss.nasa.gov/cgi-bin/gitweb.cgi?p=modelE.git;a=tag;h=refs/tags/modelE3_2017-06-14 (last access: 21 June 2018). The (GO)2-SIM modules described in the current paper can be fully reproduced using the information provided. Interested parties are encouraged to contact the corresponding author for additional information on how to interface their numerical model with (GO)2-SIM.
KL developed and implemented the (GO)2-SIM forwardsimulator framework on NASA GISS's ModelE3. AMF, ASA and MK participated in developing the current version of ModelE3. AMF extracted the model simulation used in the current study. EEC and PK along with AMF and ASA actively participated in brainstorming and in revising this work and manuscript lead by KL.
The authors declare that they have no conflict of interest.
Katia Lamer and Eugene E. Clothiaux's contributions to this research were
funded by subcontract 300324 of the Pennsylvania State University with the
Brookhaven National Laboratory in support of the ARM-ASR Radar Science group.
The contributions of Ann M. Fridlind, Andrew S. Ackerman, and Maxwell Kelley
were partially supported by the Office of Science (BER), U.S. Department of
Energy, under agreement DE-SC0016237, the NASA Radiation Sciences Program,
and the NASA Modeling, Analysis and Prediction Program. Resources supporting
this work were provided by the NASA High-End Computing (HEC) Program through
the NASA Center for Climate Simulation (NCCS) at Goddard Space Flight Center.
Finally, the authors would like to thank the two anonymous reviewers and the
editor of this paper for their
comments.
Edited by: Klaus Gierens
Reviewed by: two anonymous referees
Atlas, D.: The estimation of cloud parameters by radar, J. Meteorol., 11, 309–317, 1954.
Atlas, D., Matrosov, S. Y., Heymsfield, A. J., Chou, M.-D., and Wolff, D. B.: Radar and radiation properties of ice clouds, J. Appl. Meteorol., 34, 2329–2345, 1995.
Battaglia, A. and Delanoë, J.: Synergies and complementarities of CloudSat-CALIPSO snow observations, J. Geophys. Res.-Atmos., 118, 721–731, 2013.
Battan, L. J.: Radar observation of the atmosphere, University of Chicago, Chicago, Illinois, 1973.
Bodas-Salcedo, A., Webb, M., Bony, S., Chepfer, H., Dufresne, J.-L., Klein, S., Zhang, Y., Marchand, R., Haynes, J., and Pincus, R.: COSP: Satellite simulation software for model assessment, B. Am. Meteorol. Soc., 92, 1023–1043, 2011.
Bretherton, C. S. and Park, S.: A new moist turbulence parameterization in the Community Atmosphere Model, J. Climate, 22, 3422–3448, 2009.
Cesana, G. and Chepfer, H.: Evaluation of the cloud thermodynamic phase in a climate model using CALIPSO-GOCCP, J. Geophys. Res.-Atmos., 118, 7922–7937, 2013.
Chepfer, H., Bony, S., Winker, D., Chiriaco, M., Dufresne, J. L., and Sèze, G.: Use of CALIPSO lidar observations to evaluate the cloudiness simulated by a climate model, Geophys. Res. Lett., 35, L15704, https://doi.org/10.1029/2008GL034207, 2008.
de Boer, G., Eloranta, E. W., and Shupe, M. D.: Arctic mixed-phase stratiform cloud properties from multiple years of surface-based measurements at two high-latitude locations, J. Atmos. Sci., 66, 2874–2887, 2009.
Dong, X. and Mace, G. G.: Arctic stratus cloud properties and radiative forcing derived from ground-based data collected at Barrow, Alaska, J. Climate, 16, 445–461, 2003.
Ellis, S. M. and Vivekanandan, J.: Liquid water content estimates using simultaneous S and Ka band radar measurements, Radio Sci., 46, RS2021, https://doi.org/10.1029/2010RS004361, 2011.
English, J. M., Kay, J. E., Gettelman, A., Liu, X., Wang, Y., Zhang, Y., and Chepfer, H.: Contributions of clouds, surface albedos, and mixed-phase ice nucleation schemes to Arctic radiation biases in CAM5, J. Climate, 27, 5174–5197, 2014.
Everitt, B. and Hand, D.: Mixtures of normal distributions, in: Finite Mixture Distributions, Springer, 25–57, 1981.
Fox, N. I. and Illingworth, A. J.: The retrieval of stratocumulus cloud properties by ground-based cloud radar, J. Appl. Meteorol., 36, 485–492, 1997.
Frey, W., Maroon, E., Pendergrass, A., and Kay, J.: Do Southern Ocean Cloud Feedbacks Matter for 21st Century Warming?, Geophys. Res. Lett., 44, 12447–12456, https://doi.org/10.1002/2017GL076339, 2017.
Gettelman, A. and Morrison, H.: Advanced two-moment bulk microphysics for global models. Part I: Off-line tests and comparison with other schemes, J. Climate, 28, 1268–1287, 2015.
Gettelman, A., Morrison, H., Santos, S., Bogenschutz, P., and Caldwell, P.: Advanced two-moment bulk microphysics for global models. Part II: Global model solutions and aerosol–cloud interactions, J. Climate, 28, 1288–1307, 2015.
Hagen, M. and Yuter, S. E.: Relations between radar reflectivity, liquid-water content, and rainfall rate during the MAP SOP, Q. J. Roy. Meteor. Soc., 129, 477–493, 2003.
Haynes, J., Luo, Z., Stephens, G., Marchand, R., and Bodas-Salcedo, A.: A multipurpose radar simulation package: QuickBeam, B. Am. Meteorol. Soc., 88, 1723–1727, 2007.
Heymsfield, A., Winker, D., Avery, M., Vaughan, M., Diskin, G., Deng, M., Mitev, V., and Matthey, R.: Relationships between ice water content and volume extinction coefficient from in situ observations for temperatures from 0 to −86 ∘C: Implications for spaceborne lidar retrievals, J. Appl. Meteorol. Clim., 53, 479–505, 2014.
Heymsfield, A. J., Winker, D., and van Zadelhoff, G. J.: Extinction-ice water content-effective radius algorithms for CALIPSO, Geophys. Res. Lett., 32, L10807, https://doi.org/10.1029/2005GL022742, 2005.
Hogan, R. J. and O'Connor, E.: Facilitating cloud radar and lidar algorithms: The Cloudnet Instrument Synergy/Target Categorization product, Cloudnet documentation, 2004.
Hogan, R. J., Illingworth, A., O'connor, E., and Baptista, J.: Characteristics of mixed-phase clouds. II: A climatology from ground-based lidar, Q. J. Roy. Meteor. Soc., 129, 2117–2134, 2003.
Hogan, R. J., Behera, M. D., O'Connor, E. J., and Illingworth, A. J.: Estimate of the global distribution of stratiform supercooled liquid water clouds using the LITE lidar, Geophys. Res. Lett., 31, L05106, https://doi.org/10.1029/2003GL018977, 2004.
Hogan, R. J., Mittermaier, M. P., and Illingworth, A. J.: The retrieval of ice water content from radar reflectivity factor and temperature and its use in evaluating a mesoscale model, J. Appl. Meteorol. Clim., 45, 301–317, 2006.
Hu, Y., Vaughan, M., Liu, Z., Lin, B., Yang, P., Flittner, D., Hunt, B., Kuehn, R., Huang, J., and Wu, D.: The depolarization-attenuated backscatter relation: CALIPSO lidar measurements vs. theory, Opt. Express, 15, 5327–5332, 2007a.
Hu, Y., Vaughan, M., McClain, C., Behrenfeld, M., Maring, H., Anderson, D., Sun-Mack, S., Flittner, D., Huang, J., Wielicki, B., Minnis, P., Weimer, C., Trepte, C., and Kuehn, R.: Global statistics of liquid water content and effective number concentration of water clouds over ocean derived from combined CALIPSO and MODIS measurements, Atmos. Chem. Phys., 7, 3353–3359, https://doi.org/10.5194/acp-7-3353-2007, 2007b.
Hu, Y., Winker, D., Vaughan, M., Lin, B., Omar, A., Trepte, C., Flittner, D., Yang, P., Nasiri, S. L., and Baum, B.: CALIPSO/CALIOP cloud phase discrimination algorithm, J. Atmos. Ocean. Tech., 26, 2293–2309, 2009.
Hu, Y., Rodier, S., Xu, K. m., Sun, W., Huang, J., Lin, B., Zhai, P., and Josset, D.: Occurrence, liquid water content, and fraction of supercooled water clouds from combined CALIOP/IIR/MODIS measurements, J. Geophys. Res.-Atmos., 115, D00H34, https://doi.org/10.1029/2009JD012384, 2010.
Huang, Y., Siems, S. T., Manton, M. J., Hande, L. B., and Haynes, J. M.: The structure of low-altitude clouds over the Southern Ocean as seen by CloudSat, J. Climate, 25, 2535–2546, 2012a.
Huang, Y., Siems, S. T., Manton, M. J., Protat, A., and Delanoë, J.: A study on the low-altitude clouds over the Southern Ocean using the DARDAR-MASK, J. Geophys. Res.-Atmos., 117, D18204, https://doi.org/10.1029/2012JD017800, 2012b.
Intrieri, J., Shupe, M., Uttal, T., and McCarty, B.: An annual cycle of Arctic cloud characteristics observed by radar and lidar at SHEBA, J. Geophys. Res.-Oceans, 107, 8030, https://doi.org/10.1029/2000JC000423, 2002.
Kalesse, H., Szyrmer, W., Kneifel, S., Kollias, P., and Luke, E.: Fingerprints of a riming event on cloud radar Doppler spectra: observations and modeling, Atmos. Chem. Phys., 16, 2997–3012, https://doi.org/10.5194/acp-16-2997-2016, 2016.
Kay, J. E., Bourdages, L., Miller, N. B., Morrison, A., Yettella, V., Chepfer, H., and Eaton, B.: Evaluating and improving cloud phase in the Community Atmosphere Model version 5 using spaceborne lidar observations, J. Geophys. Res.-Atmos., 121, 4162–4176, 2016.
Kikuchi, K., Tsuboya, S., Sato, N., Asuma, Y., Takeda, T., and Fujiyoshi, Y.: Observation of wintertime clouds and precipitation in the Arctic Canada (POLEX-North), J. Meteorol. Soc. Jpn., 60, 1215–1226, 1982.
Klein, S. A., McCoy, R. B., Morrison, H., Ackerman, A. S., Avramov, A., Boer, G. D., Chen, M., Cole, J. N., Del Genio, A. D., and Falk, M.: Intercomparison of model simulations of mixed-phase clouds observed during the ARM Mixed-Phase Arctic Cloud Experiment. I: Single-layer cloud, Q. J. Roy. Meteor. Soc., 135, 979–1002, 2009.
Kollias, P., Rémillard, J., Luke, E., and Szyrmer, W.: Cloud radar Doppler spectra in drizzling stratiform clouds: 1. Forward modeling and remote sensing applications, J. Geophys. Res.-Atmos., 116, D13201, https://doi.org/10.1029/2010JD015237, 2011.
Kollias, P., Clothiaux, E. E., Ackerman, T. P., Albrecht, B. A., Widener, K. B., Moran, K. P., Luke, E. P., Johnson, K. L., Bharadwaj, N., and Mead, J. B.: Development and applications of ARM millimeter-wavelength cloud radars, Meteor. Mon., 57, 17.11–17.19, 2016.
Kuehn, R., Holz, R., Eloranta, E., Vaughan, M., and Hair, J.: Developing a Climatology of Cirrus Lidar Ratios Using Univeristy of Wisconsin HSRL Observations, EPJ Web of Conferences, 16009, 2016.
Liao, L. and Sassen, K.: Investigation of relationships between Ka-band radar reflectivity and ice and liquid water contents, Atmos. Res., 34, 231–248, 1994.
Liu, C.-L. and Illingworth, A. J.: Toward more accurate retrievals of ice water content from radar measurements of clouds, J. Appl. Meteorol., 39, 1130–1146, 2000.
McCoy, D. T., Tan, I., Hartmann, D. L., Zelinka, M. D., and Storelvmo, T.: On the relationships among cloud cover, mixed-phase partitioning, and planetary albedo in GCMs, J. Adv. Model. Earth Sy., 8, 650–668, 2016.
O'Connor, E. J., Illingworth, A. J., and Hogan, R. J.: A technique for autocalibration of cloud lidar, J. Atmos. Ocean. Tech., 21, 777–786, 2004.
Sassen, K.: Ice cloud content from radar reflectivity, J. Clim. Appl. Meteorol., 26, 1050–1053, 1987.
Sassen, K.: The polarization lidar technique for cloud research: A review and current assessment, B. Am. Meteorol. Soc., 72, 1848–1866, 1991.
Sato, N., Kikuchi, K., Barnard, S. C., and Hogan, A. W.: Some characteristic properties of ice crystal precipitation in the summer season at South Pole Station, Antarctica, J. Meteorol. Soc. Jpn., 59, 772–780, 1981.
Sauvageot, H. and Omar, J.: Radar reflectivity of cumulus clouds, J. Atmos. Ocean. Tech., 4, 264–272, 1987.
Schmidt, G. A., Kelley, M., Nazarenko, L., Ruedy, R., Russell, G. L., Aleinov, I., Bauer, M., Bauer, S. E., Bhat, M. K., and Bleck, R.: Configuration and assessment of the GISS ModelE2 contributions to the CMIP5 archive, J. Adv. Model. Earth Sy., 6, 141–184, 2014.
Sekhon, R. S. and Srivastava, R.: Doppler radar observations of drop-size distributions in a thunderstorm, J. Atmos. Sci., 28, 983–994, 1971.
Shupe, M. D.: A ground-based multisensor cloud phase classifier, Geophys. Res. Lett., 34, L22809, https://doi.org/10.1029/2007GL031008, 2007.
Tan, I. and Storelvmo, T.: Sensitivity study on the influence of cloud microphysical parameters on mixed-phase cloud thermodynamic phase partitioning in CAM5, J. Atmos. Sci., 73, 709–728, 2016.
Tan, I., Storelvmo, T., and Zelinka, M. D.: Observational constraints on mixed-phase clouds imply higher climate sensitivity, Science, 352, 224–227, 2016.
Tatarevic, A. and Kollias, P.: User's Guide to Cloud Resolving Model Radar Simulator (CR-SIM), McGill University Clouds Research Group, Document available at: http://radarscience.weebly.com/radar-simulators.html (last access: 1 October 2018), 2015.
Winker, D. M.: Accounting for multiple scattering in retrievals from space lidar, Proceedings Volume 5059, 12th International Workshop on Lidar Multiple Scattering Experiments, https://doi.org/10.1117/12.512352, 2003.
Yoshida, R., Okamoto, H., Hagihara, Y., and Ishimoto, H.: Global analysis of cloud phase and ice crystal orientation from Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observation (CALIPSO) data using attenuated backscattering and depolarization ratio, J. Geophys. Res.-Atmos., 115, D00H32, https://doi.org/10.1029/2009JD012334, 2010.
Zhang, Y., Xie, S., Klein, S. A., Marchand, R., Kollias, P., Clothiaux, E. E., Lin, W., Johnson, K., Swales, D., and Bodas-Salcedo, A.: The ARM Cloud Radar Simulator for Global Climate Models: A New Tool for Bridging Field Data and Climate Models, B. Am. Meteorol. Soc., https://doi.org/10.1175/BAMS-D-16-0258.1, online first, 2018.
- Abstract
- Introduction
- GCM outputs required as inputs to the forward simulator
- Hydrometeor-backscattered power simulator
- Sensor capability simulator
- Forward simulation of specialized observables
- Water-phase classifier algorithm
- An ensemble approach for uncertainty assessment
- Summary and conclusions
- Code availability
- Author contributions
- Competing interests
- Acknowledgements
- References
- Abstract
- Introduction
- GCM outputs required as inputs to the forward simulator
- Hydrometeor-backscattered power simulator
- Sensor capability simulator
- Forward simulation of specialized observables
- Water-phase classifier algorithm
- An ensemble approach for uncertainty assessment
- Summary and conclusions
- Code availability
- Author contributions
- Competing interests
- Acknowledgements
- References