An EC-Earth coupled atmosphere–ocean single-column model (AOSCM.v1_EC-Earth3) for studying coupled marine and polar processes

Single-column models (SCMs) have been used as tools to help develop numerical weather prediction and global climate models for several decades. SCMs decouple small-scale processes from large-scale forcing, which allows the testing of physical parameterisations in a controlled environment with reduced computational cost. Typically, either the ocean, sea ice or atmosphere is fully modelled and assumptions have to be made regarding the boundary conditions from other subsystems, adding a potential source of error. Here, we present a fully coupled atmosphere–ocean SCM (AOSCM), which is based on the global climate model EC-Earth3. The initial configuration of the AOSCM consists of the Nucleus for European Modelling of the Ocean (NEMO3.6) (ocean), the Louvain-la-Neuve Sea Ice Model (LIM3) (sea ice), the Open Integrated Forecasting System (OpenIFS) cycle 40r1 (atmosphere), and OASIS3-MCT (coupler).

Results from the AOSCM are presented at three locations: the tropical Atlantic, the midlatitude Pacific and the Arctic. At all three locations, in situ observations are available for comparison. We find that the coupled AOSCM can capture the observed atmospheric and oceanic evolution based on comparisons with buoy data, soundings and ship-based observations. The model evolution is sensitive to the initial conditions and forcing data imposed on the column. Comparing coupled and uncoupled configurations of the model can help disentangle model feedbacks. We demonstrate that the AOSCM in the current set-up is a valuable tool to advance our understanding in marine and polar boundary layer processes and the interactions between the individual components of the system (atmosphere, sea ice and ocean).

1 Introduction

Single-column models (SCMs) have been used for several decades to advance our understanding of physical processes and their parameterisations in numerical models. SCMs originated from bulk models (Kraus and Turner, 1967; Niiler and Kraus, 1977). The first vertically resolved SCMs were developed in the late 1980s. For example, Betts and Miller (1986) demonstrated the added value of an atmospheric SCM framework for the development and evaluation of a convective adjustment scheme in atmospheric models, and Price et al. (1986) used an ocean SCM to study the diurnal cycle of the mixed layer in the subtropical Pacific. Research with SCMs is a valuable addition to studies with three-dimensional numerical weather prediction (NWP) models and global climate models (GCMs). By zooming into a single grid column of a host model, either in the atmosphere, the ocean, or the sea ice, one achieves a separation between resolved large-scale processes and processes parameterised in the vertical column. This means that physical processes, and the ability of their associated parameterisation schemes to produce the correct physical tendencies, can be studied in a controlled framework (Randall et al., 1996). Similar to the set-up of a three-dimensional model, initial conditions are provided, typically from a sounding, a mooring or a reanalysis profile. Although the column is decoupled from the large-scale flow, forcing mimicking the influence of the large-scale circulation on the column of interest can be applied. In practice, this is done by applying pressure gradient forcing via the geostrophic wind, horizontal advection and vertical velocity forcing to the atmospheric component of the SCM. Relaxation (nudging) is an alternative way to include forcing by the large-scale environment. Forcing types can also be applied in combination, depending on the type of model experiment being performed. In the controlled environment of an SCM, the evolution of idealised or realistic initial profiles exposed to forcing of varying complexity can be studied in an Eulerian or Lagrangian setting. The choice of experimental set-up determines how, and to what extent, different physical parameterisations within the model can be studied. Thus, an experiment needs to be designed carefully, depending on the underlying scientific question. By only evolving a single grid column, the computational cost is reduced considerably compared to experiments with a three-dimensional model. This allows for comprehensive parameter testing as more sensitivity experiments can be carried out. In summary, an SCM can be a powerful tool if its limitations are handled with care.

For these reasons, SCMs have regularly been employed to investigate the modelling of physical processes in the ocean, sea ice and atmosphere. In the ocean, single-column models, sometimes just called column models, started off as bulk mixed-layer models (Kraus and Turner, 1967; Price et al., 1986). From the start, they were used to study the impact of air–sea exchange and vertical mixing on the temporal evolution of the oceanic mixed layer. In Gaspar et al. (1990) and Large et al. (1994), these bulk models are extended to 1-D turbulence models, which can be applied in the whole column and are thus suitable for GCMs. More recent examples of oceanic SCM models being used for model development are Ling et al. (2015) and Reffray et al. (2015).

In addition to research with individual atmospheric SCMs (e.g. Betts and Miller, 1986; Randall et al., 1996), SCM intercomparison studies have focused on, e.g., convection (e.g. Bechtold et al., 2000; Betts and Miller, 1986; Ghan et al., 2000; Lenderink et al., 2004), stratocumulus (e.g. Bretherton et al., 1999; de Roode et al., 2016), mixed-phase clouds (e.g. Klein et al., 2009; Pithan et al., 2016) and the representation of the boundary layer (e.g. Baas et al., 2010; Cuxart et al., 2006; Svensson et al., 2011), as part of GABLS (GEWEX Atmospheric Boundary Layer Study; Holtslag, 2006; GEWEX: Global Energy and Water EXchanges). These studies also present a wide range of numerical approaches to initialise (e.g. idealised or based on measurements) and force the model (e.g. Eulerian or Lagrangian). Idealised model set-ups are commonly complemented by large eddy simulations (LESs) or cloud-resolving models (CRMs), capturing the atmospheric evolution in more detail. LES and CRM are used to compile forcing data or as benchmarks when evaluating the performance of parameterisations in SCMs (e.g. Beare et al., 2006; Bechtold et al., 2000; Guichard et al., 2004). The cases developed within GCSS (GEWEX Cloud System Study) and GABLS, which merged into GASS (GEWEX Global Atmospheric System Study) at the end of 2010, have been successfully used to identify and improve parameterised processes (e.g. Lenderink et al., 2004) and serve as test beds for model development. Overall, 44 % of modelling centres, which develop coupled atmosphere and ocean models, polled by Hourdin et al. (2017) reported the use of SCMs for model development and tuning. This coordinated way of working has not been, to our knowledge, as extensively utilised in the ocean or sea-ice communities.

In contrast to global climate models, SCMs have mostly been implemented uncoupled. Thus, for the majority of atmospheric studies mentioned, the surface is prescribed by boundary conditions using surface temperature or fluxes. The choice of boundary condition may influence the results. Using prescribed surface temperature has proven to lead to a very different energy content in the boundary layer (Svensson et al., 2011), while using different land models also introduces spread (Bosveld et al., 2014, and GABLS4), a subject that is currently further studied in the “Diurnal land/atmosphere coupling experiment” (DICE; http://appconv.metoffice.com/dice/dice.html, last access: 25 September 2018). There are also theoretical limitations to consider, such as problems that arise when a stably stratified boundary layer is forced with surface fluxes (Basu et al., 2008). Over sea ice, the presence of snow modulates the surface energy budget, and thus results vary depending on the description of snow in the surface model (Pithan et al., 2016). In the ocean, the depth of the mixed layer is sensitive to the coupling, especially in the tropics and during summer, when the mixed layer is shallow and quickly responding to forcing. The fast response can give rise to positive feedbacks between model biases in the atmospheric and oceanic mixed layers (Breugem et al., 2008; Toniazzo and Woolnough, 2014). It is common to develop model components using prescribed forcing; i.e. ocean and land models use near-surface observed or reanalysis mean state variables to provide atmospheric fluxes. However, this can lead to surprises when model components are interactively coupled. Atmospheric models are forced with observed sea surface temperatures (SSTs) over the ocean and often developed in a framework with an interactive land model over land, although the land model is taken as is, i.e. not developed in the interactive framework. To avoid ambiguities arising from specifications of surface boundary conditions, it is desirable to combine several SCMs into one coupled model, especially when studying boundary layer processes or processes that depend on interfacial coupling.

In the last two decades a few coupled single-column models have been developed. Clayson and Chen (2002) coupled an atmosphere and an ocean SCM to study tropical atmosphere–ocean feedbacks, and Goyette and Perroud (2012) combined a 1-D lake model with an atmospheric column model. More recently, West et al. (2016) coupled a one-dimensional sea ice and an atmospheric column model to investigate the optimal interface at which to calculate the surface energy budget.

Following this line of work, we present a coupled atmosphere–ocean sea-ice SCM (AOSCM) following the global climate host model EC-Earth (Hazeleger et al., 2010, 2012). The AOSCM provides a platform to study both physical and numerical coupling processes at the surface interface. First, we present and discuss ways to set up and force the model. This encompasses idealised and realistic initial conditions and forcing, Eulerian and Lagrangian set-ups, and short-term case-based or long-term statistical analysis. Application of the AOSCM is demonstrated at three locations, namely the midlatitudes, the tropics and the Arctic. Varying experimental designs display the versatility of the tool.

2 Model description, model set-up and data

2.1 Model components

In this study, the AOSCM is built from the atmospheric model OpenIFS (Open Integrated Forecasting System; https://confluence.ecmwf.int/display/OIFS/About+OpenIFS, last access: 25 September 2018), including the land model H-Tessel (Balsamo et al., 2009), and the ocean model NEMO (Nucleus for European Modelling of the Ocean; https://www.nemo-ocean.eu/, last access: 25 September 2018) with the sea-ice model LIM (Louvain-la-Neuve Sea Ice Model; http://www.elic.ucl.ac.be/repomodx/lim/, last access: 25 September 2018). All coupling actions between the column versions of the subcomponents NEMO and OpenIFS are performed by the coupling software OASIS3-MCT (https://portal.enes.org/oasis, last access: 25 September 2018). For model development purposes, the column model should follow the specifications of a GCM host model. In an iterative process, findings from the SCM, and specifically their impact on the large-scale circulation, can then be directly tested and evaluated in the GCM. In this way the computational cost for coupled model development is reduced. Here, the AOSCM is set up to closely match the development version of the EC-Earth model. Presently, this means that the default set-up is a column version of EC-Earth v3, except that instead of using IFS cycle 36r4, the AOSCM uses OpenIFS cycle 40r1. Future versions of EC-Earth will be based on OpenIFS. The other components, namely NEMO3.6, LIM3 and OASIS3-MCT, are used with the same version in both EC-Earth v3 and the AOSCM.

The different model components are presented with a focus on formulations and settings specific to the one-dimensional versions of the codes. Still, the description does not encompass all details on the model subcomponents. This is mainly motivated by the fact the AOSCM, as well as all its components, are continuously under development. For current settings and recent updates we refer to the AOSCM code branch and the respective model platforms.

2.1.1 OpenIFS

OpenIFS (hereafter OIFS) is developed by the European Centre for Medium-Range Weather Forceasts (ECMWF) as a version of IFS intended for research and education (Day et al., 2017). The main difference between OIFS40r1 and IFS 40r1 is the exclusion of the data assimilation component of IFS. Extensive documentation is available for IFS at https://www.ecmwf.int/en/forecasts/documentationand-support/changes-ecmwf-model/ifs-documentation (last access: 25 September 2018).

The atmospheric part of the AOSCM solves the one-dimensional version of the primitive equations:

$$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle }-\dot{\mathit{\eta }}{\displaystyle \frac{\partial u}{\partial \mathit{\eta }}}+F_u+f(v-v_{\text{g}})+P_u+{\displaystyle \frac{u_{\text{r}}-u}{{\mathit{\tau }}_a}}={\displaystyle \frac{\partial u}{\partial t}},\text{(2)}& {\displaystyle }& {\displaystyle }-\dot{\mathit{\eta }}{\displaystyle \frac{\partial v}{\partial \mathit{\eta }}}+F_v-f(u-u_{\text{g}})+P_v+{\displaystyle \frac{v_{\text{r}}-v}{{\mathit{\tau }}_a}}={\displaystyle \frac{\partial v}{\partial t}},\text{(3)}& {\displaystyle }& {\displaystyle }-\dot{\mathit{\eta }}{\displaystyle \frac{\partial T}{\partial \mathit{\eta }}}+F_T+{\displaystyle \frac{RT\mathit{\omega }}{c_{p}p}}+P_T+{\displaystyle \frac{T_{\text{r}}-T}{{\mathit{\tau }}_a}}={\displaystyle \frac{\partial T}{\partial t}},\text{(4)}& {\displaystyle }& {\displaystyle }-\dot{\mathit{\eta }}{\displaystyle \frac{\partial q}{\partial \mathit{\eta }}}+F_q+P_q+{\displaystyle \frac{q_{\text{r}}-q}{{\mathit{\tau }}_a}}={\displaystyle \frac{\partial q}{\partial t}}.\end{array}$$

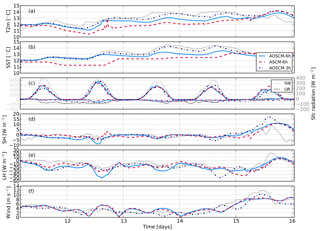
Figure 1 Simplified flow chart of the OIFS model. Routines dedicated to coupling via OASIS are coloured red.

As in the full model system, a two-time-level semi-Lagrangian scheme is used (an Eulerian scheme is also available) to integrate the momentum with horizontal wind components u and v (Eqs. 1 and 2), thermodynamics T (Eq. 3), moisture q (Eq. 4) and the continuity equation. The vertical coordinate is based on η levels, which merge orography following σ coordinates near the surface with pressure coordinates in the free atmosphere. Here, $\dot{\mathit{\eta }}$ and ω are vertical velocities in η and pressure coordinates, respectively. F_i is the horizontal advection, P_i summarises physical parameterisations and u_r, v_r, T_r and q_r denote the reference profiles used for nudging with a timescale τ_a. Furthermore, f is the Coriolis parameter, u_g and v_g are the horizontal components of the geostrophic wind, R is the moist air gas constant, c_p is the heat capacity of moist air at constant pressure, and p is the pressure. In addition to the atmospheric state variables (Eqs. 1–4), the model prognostically calculates cloud liquid, ice, rain, snow and cloud cover.

The total tendency (right-hand sides of Eqs. 1–4) to each prognostic variable is calculated as the sum of dynamical (first three terms on the left-hand side) and physical parameterisation tendencies P_i (fourth term), possibly updated by relaxation (i.e. nudging, fifth term). The order of the left-hand side of the equation is, in a simplified way, equivalent to the sequence in which the tendencies are calculated in the model (Fig. 1). In the time-stepping loop, the dynamical tendencies are determined, mainly aggregating available prescribed forcing. The pressure gradient forcing is represented by the geostrophic wind. The third term of the heat equation captures adiabatic heating through vertical motion. Calculations of tendencies from physical parameterisations are done in the same way as in the three-dimensional OIFS. Detailed discussion of the parameterisations used for these processes, namely, the radiation, turbulence, cloud and convection parameterisation schemes as well as the non-orographic gravity wave drag, orographic gravity wave drag and surface drag, can be found in the IFS documentation for cycle 40r1 (https://www.ecmwf.int/sites/default/files/IFS_CY40R1_Part4.pdf, last access: 25 September 2018). Relaxation tendencies are calculated weighing the difference between the new state, as determined by physical and dynamical tendencies, and a reference state, with the relaxation timescale τ_a. References states can, for example, be observed or modelled profiles of atmospheric variables. All forcing fields are read in at forcing time steps and linearly interpolated at intermediate model steps.

Besides visualising the sequence of main routines called during an OIFS SCM run, Fig. 1 also highlights in red communications with other AOSCM components through the coupler and the use of coupling variables. Coupling variables are also schematically shown in Fig. 4. They enter the primitive equation system (Eqs. 1–4) via the surface energy budget (Eq. 5).

$$\begin{array}{ll}\text{(5)}& {\displaystyle }& {\displaystyle }(\mathrm{1}-{\mathit{\alpha }}_i)(\mathrm{1}-f_{R_{\text{s}},i})R_{\text{s}}+R_T-\mathit{ϵ}\mathit{\sigma }{T}_{\text{sk},i}^{\mathrm{4}}+{\text{SH}}_i+{\text{LH}}_i{\displaystyle }& {\displaystyle }=Q_T={\mathrm{\Lambda }}_{\text{sk},i}(T_{\text{sk},i}-T_{\mathrm{1}})\end{array}$$

The energy budget is solved individually for each surface tile i, which in the coupled system is the ocean and/or sea ice. The downward short-wave and long-wave radiations are R_s and R_T, with the tiled albedo α_i, the tiled fraction of short-wave radiation absorbed at the surface $f_{R_{\text{s}},i}$, the surface emissivity ϵ, the Stefan–Boltzmann constant σ, the skin temperature T_sk,i and the skin layer conductivity Λ_sk,i. SH_i is the tiled sensible heat flux and LH_i the tiled latent heat flux. Upward coupling is implemented through the surface albedo and the temperature of the upper snow, sea-ice or ocean layer T₁.

2.1.2 NEMO

NEMO is based on the thermodynamics and dynamics OPA model (Océan PArallélisé) and includes the LIM3 sea-ice component. More details on NEMO can be found in Madec (2016), and Rousset et al. (2015) describes the recent version of LIM.

The ocean component NEMO3.6 is a primitive equation model based on the one-dimensional version of the Navier–Stokes equations (Eqs. 6 and 7), the hydrostatic equation, the incompressibility equation, heat and salt conservation equations (Eqs. 8 and 9), and the equation of state.

$$\begin{array}{}\text{(6)}& {\displaystyle }& {\displaystyle }-{\displaystyle \frac{\partial }{\partial z}}{\mathit{\nu }}_{\text{t}}{\displaystyle \frac{\partial u}{\partial z}}+fv+P_u+{\displaystyle \frac{u_{\text{r}}-u}{{\mathit{\tau }}_o}}={\displaystyle \frac{\partial u}{\partial t}}\text{(7)}& {\displaystyle }& {\displaystyle }-{\displaystyle \frac{\partial }{\partial z}}{\mathit{\nu }}_{\text{t}}{\displaystyle \frac{\partial v}{\partial z}}-fu+P_v+{\displaystyle \frac{v_{\text{r}}-v}{{\mathit{\tau }}_o}}={\displaystyle \frac{\partial v}{\partial t}}\text{(8)}& {\displaystyle }& {\displaystyle }-{\displaystyle \frac{\partial }{\partial z}}{K}_{\text{t}}{\displaystyle \frac{\partial T}{\partial z}}+{\displaystyle \frac{\mathrm{1}}{{\mathit{\rho }}_o{c}_p}}{\displaystyle \frac{\partial I(F_{\text{sol}},z)}{\partial z}}+P_T+{\displaystyle \frac{T_{\text{r}}-T}{{\mathit{\tau }}_o}}={\displaystyle \frac{\partial T}{\partial t}}\text{(9)}& {\displaystyle }& {\displaystyle }-{\displaystyle \frac{\partial }{\partial z}}{K}_{\text{t}}{\displaystyle \frac{\partial S}{\partial z}}+E-P+P_S+{\displaystyle \frac{S_{\text{r}}-S}{{\mathit{\tau }}_o}}={\displaystyle \frac{\partial S}{\partial t}}\end{array}$$

EC-Earth v3 uses an equation of state which is based on conservative state variables and provides better conservation constraints than other representations of the equation of state (polyTEOS10-bsq; IOC and IAPSO, 2010). That is of less importance in the 1-D version, which is therefore based on a simpler equation of state (polyEOS80-bsq; Fofonoff and Millard, 1983). The prognostic variables of the equation of state used in the 1-D version are the tracer potential temperature T, practical salinity S, and the horizontal velocity components u and v as described in Eqs. (6)–(9). Here, ν_t and K_t are the vertical turbulent viscosity and diffusivity, respectively. I(F_sol,z) denotes the penetrative part of the solar surface heat flux, and E and P are the evaporation and precipitation fluxes. P_i summarises physical parameterisations, and u_r, v_r, T_r, and S_r again describe reference profiles to which the modelled profiles can be relaxed with a timescale τ_o. The terms on the left-hand sides of the equation system capture the column forcing.

The general structure and workflow in the NEMO and LIM models are summarised in Figs. 2 and 3. The main ocean integration is organised from the time stepping routine (stp_c1d), with tracer and momentum tendencies evaluated separately. The AOSCM setting includes physical parameterisations P_i, for example describing the turbulence closure. In the standard setting, the vertical mixing scheme is based on a TKE-dependent (turbulent kinetic energy) eddy coefficient and a 1.5 turbulent closure for convection, but other turbulence schemes are implemented in the code and can easily be selected. A Langmuir circulation parameterisation is also turned on, and the effect of chlorophyll on heating due to solar penetration is taken into account. The advection of tracers is not possible in the one-dimensional framework but can, in a similar way to that applied in the atmospheric model, be approximated by relaxing profiles of both tracer and momentum fields towards reference profiles. However, this procedure is not utilised in the examples presented here.

Figure 2 Simplified flow chart of the NEMO model. Routines dedicated to coupling via OASIS are coloured red.

Figure 3 Simplified flow chart of the LIM model, part of the NEMO model if sea ice is present. Routines dedicated to coupling via OASIS are coloured red.

Communications with other components during the workflow are highlighted in red (Fig. 2). Coupling actions are performed at the beginning of the time stepping, namely receiving fields as part of the boundary condition routines, and at the end of the time stepping, when the updated SST and ice parameters are sent to the atmospheric part of the AOSCM. The surface boundary conditions for the momentum and tracer variables are given in Eqs. (10)–(13). There, τ_u,v is the surface wind stress components, ρ₀ is the in situ density and S_t is the rate of change of the sea-ice thickness budget. Only the non-penetrative part of the net surface heat flux (see Eq. 5) influences the temperature boundary condition.

$$\begin{array}{}\text{(10)}& {\displaystyle }& {\displaystyle }{\mathit{\nu }}_{\text{t}}{\displaystyle \frac{\partial u}{\partial z}}={\displaystyle \frac{{\mathit{\tau }}_u}{{\mathit{\rho }}_{\mathrm{0}}}}\text{(11)}& {\displaystyle }& {\displaystyle }{\mathit{\nu }}_{\text{t}}{\displaystyle \frac{\partial v}{\partial z}}={\displaystyle \frac{{\mathit{\tau }}_v}{{\mathit{\rho }}_{\mathrm{0}}}}\text{(12)}& {\displaystyle }& {\displaystyle }{K}_{\text{t}}{\displaystyle \frac{\partial T}{\partial z}}={\displaystyle \frac{Q_T}{{\mathit{\rho }}_{\mathrm{0}}{C}_p}}\text{(13)}& {\displaystyle }& {\displaystyle }{K}_{\text{t}}{\displaystyle \frac{\partial S}{\partial z}}={\displaystyle \frac{(E-P-S_{\text{t}})\cdot S(z=\mathrm{0})}{{\mathit{\rho }}_{\mathrm{0}}}}\end{array}$$

LIM3, the sea-ice model embedded in the oceanic component of the AOSCM, contains a thermodynamic and a dynamic component. In its 1-D version, only the thermodynamic model is currently used, including the representation of subgrid-scale distributions of ice thickness, enthalpy, salinity and age. The model includes multiple sea-ice categories of different ice thicknesses, set to five categories as a default. The distribution of sea-ice thickness categories is determined based on the mean ice thickness and is constant in time. The sea-ice concentration in each category varies due to source and sink processes of sea ice. The halo-thermodynamics parameterised in the model are solved for each ice category, which consist of one snow layer and potentially several ice layers. A brief description of the model subcomponents is given in Fig. 3.

2.1.3 OASIS3-MCT

The OASIS3-MCT coupler (Valcke, 2006) takes care of communications between the atmosphere and the ocean/sea-ice components and carries out transfers and temporal transformations of variables. Regridding is not necessary since two SCMs are coupled. Coupling between the atmospheric and oceanic models is performed by OASIS writing (oasis_put) and reading (oasis_get) actions (see Figs. 1 and 2). At every coupling step (a multiple of each model's time step), coupling variables are exchanged between the components. It is recommended to use a temporal lag between OASIS writing and reading actions to avoid long waiting times of components or possible deadlocks, even in a single-column set-up. In this framework, the variables are written a given time before the coupling time step, usually determined by the model time step, but are only read by the receiving model at the coupling time step. Thus, initialisation files of the coupling variables are needed at the start of the simulation.

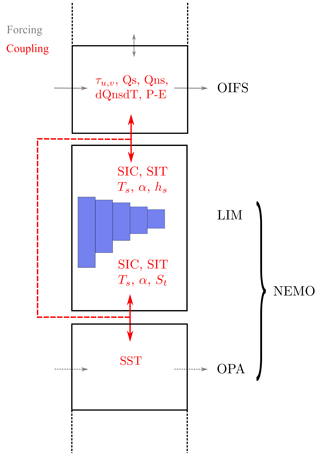
Figure 4 Schematic of coupling variables exchanged between the model components. In the polar environment all red lines represent the coupling (dashed and full), and without sea ice, coupling reduces to the dashed line. From the atmosphere, the horizontal wind stress τ_u,v, the solar flux Q_s, the non-solar fluxes Q_ns and precipitation minus evaporation P−E are passed to the ocean. In the presence of ice, the temperature sensitivity of the non-solar fluxes dQ_nsdT is coupled as well. The ocean model sends the sea surface temperature SST and, in the presence of sea ice, the aggregated sea-ice concentration SIC, sea ice thickness SIT, surface temperature T_s, surface albedo α and the snow thickness h_s. In a coupled simulation with sea ice, the ocean also receives the ice parameters SIC, SIT, T_s and α and in addition the rate of change of the sea-ice thickness S_t.

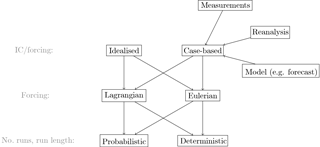
Figure 5 Guideline on how to set up an SCM experiment. Each row represents a set-up decision necessary (grey phrase on the far left) and potential approaches. IC is short for initial conditions.

Variable transfer between NEMO and OIFS is implemented in both directions (Fig. 4). From OIFS, NEMO receives surface stress, solar radiation, long-wave radiation, sensible and latent heat fluxes, the temperature sensitivity of the non-solar heat fluxes (long-wave radiation, sensible and latent heat flux), precipitation, and evaporation. In the reverse direction, only the sea surface temperature is passed in ice-free conditions. In the presence of sea ice, sea-ice albedo, thickness, fraction (areal coverage), temperature and snow thickness are also transferred from LIM to OIFS. Sea-ice parameters are available for the different sea-ice thickness categories, but the aggregated mean is transferred to the atmosphere. If sea ice is present, some ice parameters are also coupled to the ocean model. In addition to the atmospheric parameters, the ocean receives sea-ice fraction, thickness, temperature and albedo. The rate of change in ice thickness is added to the mass flux received from the atmosphere, evaporation and precipitation. OASIS3-MCT allows us to pass either instantaneous values of the coupling fields at the time of coupling or transform the field by calculating an average, maximum, minimum or sum over the period since the last coupling. As in EC-Earth v3, coupling parameters are averaged over the coupling time step.

3 How to design an (AO)SCM experiment

As mentioned in Sect. 1, the freedom in setting up the model initial conditions and forcing is both an advantage and a challenge when using the AOSCM. One needs to find a balance of forcing settings, based on the research question to be studied. Here, we briefly present some possibilities of using the (AO)SCM.

Figure 5 shows the main options to consider when designing an SCM experiment. Firstly, the question is if the model should be used in an idealised setting or following measurements, reanalysis or model data. In idealised simulations, the vertical structure of initial conditions and forcing, as well as the vertical extent of the forcing, can be simplified. If no forcing is prescribed, the model column evolves in a Lagrangian way. In an SCM it would usually be assumed that the whole column is migrating simultaneously; this is unlikely to be true in reality. The Lagrangian approach of following an air parcel needs to be adapted in an AOSCM, as disregarding relative horizontal velocities of the components is unrealistic, especially for longer simulations.

More complex experiments can be designed in a variety of ways, as for example described in Randall and Cripe (1999). They are presented here in order of increasing control on the model evolution and complexity of the set-up. It is often advisable to combine several of these forcing options.

Pressure-gradient forcing is one of the most basic large-scale forcings. It ensures that energy is supplied from the non-resolved large-scale pressure field to counteract energy loss through frictional dissipation near the surface. As the wind is forced to be close to the geostrophic wind, modulated by the timescale prescribed by the Coriolis parameter, it can be understood as a physically motivated relaxation. Unless nudging of the wind is applied, this forcing is necessary, and it is in general advisable for longer simulations. Forcing with geostrophic winds is known to introduce inertial-type oscillations into the column (e.g. Egger and Schmid, 1988). Advective tendencies of prognostic variables and vertical velocity also emulate the influence of neighbouring columns on the column of interest. As the vertical structure in the AOSCM might differ from the host model column or from measurements, one needs to ensure that the tendencies are physically reasonable and, if possible, prevent the model from drifting. Thus, it might be necessary to apply advective tendencies only over a specific height interval or to add relaxation forcing. It should be noted that the vertical velocity is often corrected from large-scale forcing (e.g. Sigg and Svensson, 2004), since it is a parameter not easily diagnosed in large-scale models. Finally, the model column can be forced by relaxation (also called nudging). This is the forcing option which is the most dependent on the actual model state at the time the forcing is applied and the only one which is not mimicking a process resolved in a three-dimensional model. Weighted with the characteristic timescale of relaxation, the AOSCM column mean profile is forced towards a reference profile, for example a sounding or mooring profile or reanalysis fields. Thus, nudging can alleviate or prevent model drift, depending on the timescale chosen. Nudging best reduces biases of state variables but has been reported to lead to problems for variables describing rates, extensively documented for precipitation (e.g. Ghan et al., 2000; Hack and Pedretti, 2000; Randall and Cripe, 1999). Nudging momentum can be very helpful when evaluating cloud microphysics (e.g. Lohmann et al., 1999) but not in a study of the boundary layer turbulence evolution. Nudging changes the equilibrium of dynamic forcing and physical parameterisations and might mask model biases. On the other hand, nudging tendencies can be evaluated and used to diagnose model drift and imbalances. Nudging is also useful as it allows the handling of inaccurate or missing information, like inertial oscillations of wind or vertical velocity forcing.

After designing initial and forcing data, the number and length of simulations needs to be decided. Measurement campaigns are usually limited in time and thus motivate shorter simulation lengths. Even if relaxation of the profile is used to prevent model drift, the impact of initial condition and forcing sensitivity might limit the model run length to which parameterisations can be evaluated.

The physical processes of interest, and the need to appropriately resolve them, determine settings of time steps, vertical grid and coupling frequency. Even though not practicable for the host model, for which settings are usually tested, it is desirable to run the SCM with highest temporal and spatial resolution. Similarly, the model can be used to develop and understand different coupling options which are less feasible in a three-dimensional model. An example of a more advanced coupling method is synchronous coupling (Lemarié et al., 2015), in which coupling fields are sent and received at the same time step.

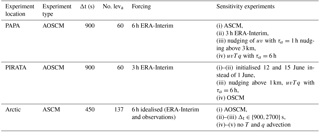
Table 1 Model settings at the three test locations with a selection of model parameters. Here, Δt is the time step and “No. lev_a” the number of atmospheric model levels. Simulations are either coupled (AOSCM), atmosphere-only (ASCM) or ocean-only (OSCM). Standard forcing includes horizontal advective tendencies, vertical velocity and geostrophic wind.

Both pressure gradient forcing and horizontal advective tendencies are calculated based on horizontal gradients. Thus, it should be noted that when using forcing based on model data, they depend on the horizontal resolution of the host model. The resolution of the forcing is the main scale information applied in the model, apart from potential timescale settings, which depend on the horizontal grid settings. In addition, the temporal resolution of the forcing steers how closely the observed temporal evolution can be captured.

4 Examples of experimental set-up and evaluation

4.1 Experimental set-up

To illustrate the versatility of the new tool, the AOSCM is applied at three different locations, namely the Pacific midlatitudes, the tropical Atlantic and the north polar region. The locations are chosen to demonstrate the model in three different climatic regions. Result from the coupled SCM (AOSCM) are compared with atmosphere-only (ASCM) or ocean-only (OSCM) simulations.

Special focus is placed on analysing the stability of the simulations; i.e. we test for model drift, compared to gridded reanalysis data (for the Pacific midlatitudes and tropical Atlantic locations). It should be noted that evaluation against reanalysis does not assume that reanalyses present the truth. However, it allows us to detect potential model drift against the forcing dataset. Simulations in the north polar region are based on reanalysis data in a semi-idealised way, which also considers a reference LES simulation. At all locations, model simulations are evaluated against point-based observations. In addition to testing for model stability, sets of experiments at the three locations analyse the sensitivity to forcing and model settings while highlighting the versatility of the AOSCM. Furthermore, current scientific questions and avenues to study them are touched upon for two of the locations (tropical Atlantic and north polar region). However, our aim is not to conclusively answer these science problems but to motivate other users to consider the AOSCM for such tasks.

An overview of the experiments at the three locations is given in Table 1.

Atmospheric initial conditions and forcing are obtained from ERA-Interim (Dee et al., 2011). Both analysis steps, which are provided every 6 h and intermediate 3-hourly forecast are used. The OIFS SCM is initialised with profiles of the non-cloud atmospheric prognostic variables. In the case of atmosphere-only simulations, the sea surface temperature is initialised and updated daily. Restart files of surface parameters required for coupled simulations are obtained from short ASCM simulations. All forcing data, horizontal advective tendencies of the prognostic variables, geostrophic wind and vertical velocities are calculated from the three-dimensional fields of ERA-Interim for each output time step.

The ocean is initialised from observed daily-mean profiles of temperature and salinity, measured to a depth of 120–500 m at the Pacific and Atlantic locations. As these depths are well below the typical mixed layers, we assume that temporally coarser data in the deeper ocean do not significantly influence the model evolution near the surface. Therefore, the observed initial profiles are extended below by monthly-mean potential temperature and salinity ORAS4 reanalysis fields (Balmaseda et al., 2013). At the Arctic location, the initial ocean profile is taken from ORAS4 data. The vertical grid is based on 75 levels, though at the Arctic location the shallow bathymetry means that only 17 levels are used. The ocean is only forced by coupling information from the atmosphere.

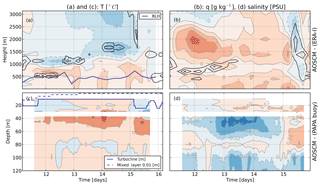
Figure 6 Coupled model biases of AOSCM-6h relative to ERA-Interim in the atmosphere (a, b) and PAPA buoy measurements in the ocean (c, d) for 11–15 July 2014. Note that the colour contours match different values for atmosphere and ocean. White areas indicate missing buoy data. Measured temperature and salinity evolution is smoothed with a 12 h running mean to remove tidal influences which are not explicitly modelled by the AOSCM. The liquid water content, i.e. the cloud, is given in panels (a) and (b) for the model and reanalysis, respectively, in black contours showing 0.1, 0.2 and 0.3 g kg⁻¹. The boundary layer height (BLH) and the turbocline depth are calculated by the AOSCM.

To ensure best performance, the equivalent resolution of the A(O)SCM is set to T511, mainly reducing the convective adjustment timescale and thereby alleviating instabilities. In contrast to EC-Earth v3, the radiation time step is equal to the dynamics time step (see Table 1). The NEMO configuration differs from the standard EC-Earth GCM settings, since it uses NEMO-C1D options (Reffray et al., 2015); i.e. the equation of state formulation and the temporal chlorophyll structure are adapted. Instead of a constant value, Sea-WiFS-based (Sea-viewing Wide Field-of-view Sensor) chlorophyll climatologies are used (NASA Goddard Space Flight Center, 2014). For the test location in the Pacific mid-latitudes, the data is the same as presented in Reffray et al. (2015). No bottom geothermal heating is parameterised, and the enhanced vertical mixing schemes of EC-Earth is turned off. The time series of observed ocean profiles are influenced by tidal oscillations. As the model does not resolve these, the oscillations in measurements are removed by applying a running mean of 12 h (the frequency of the peak in the energy spectrum, not shown) for the comparison (Fig. 6).

4.1.1 Midlatitudes: PAPA station, east Pacific

For the first experiment, we place the AOSCM at the PAPA mooring in the midlatitudinal north-east Pacific (nominally at 50^∘ N, 145^∘ W; https://www.pmel.noaa.gov/ocs/Papa, ). Observations at this location have been extensively used to develop physical parameterisation in the ocean (e.g. Gaspar et al., 1990; Reffray et al., 2015) because the buoy is situated in a region of weak horizontal advection. Reffray et al. (2015) present a reference configuration of the NEMO column model at the PAPA mooring and test various mixing parameterisations available within NEMO.

The main experiment at the PAPA location consists of a 5-day coupled atmosphere–ocean simulation, initialised on 11 July 2014 at 18:00 UTC (11:00 local time) which is forced with 6-hourly data (AOSCM-6h). An uncoupled atmosphere-only simulations with 6-hourly atmospheric forcing (ASCM-6h) and a coupled simulation with 3-hourly atmospheric forcing (AOSCM-3h) act as sensitivity runs to the main set-up. One further set of simulations highlights how model drift in the free troposphere can be minimised. Here, nudging of temperature, moisture and horizontal wind with a timescale of τ_a=6 h above a height of 3 km is applied (AOSCM-N3km6h). In addition, the model was run with the standard setting extended by relaxing the horizontal wind with a timescale of τ_a=1 h (AOSCM-Nuv0km1h). With each of the experiment settings described above, a further sixteen 29-day long simulations started at 18:00 UTC on the first of the respective months (October 2010; April, June–July, November 2011; March, August, November 2012; June–July 2013; January, April, July–September, November 2014) are run for statistical assessment.

Surface variables are evaluated using hourly averaged PAPA mooring surface measurements. The variables used here, with measurement error estimates in parentheses, are as follows: 2 m air temperature (±0.2 ^∘C), SST (±0.003 ^∘C), 10 m wind speed (±2 %), wind-speed-corrected precipitation (±4 mm h⁻¹ on 10 min filtered data with measurement threshold of 0.2 mm h⁻¹), long- and short-wave radiation (downwelling component with ±1 % error), and turbulent fluxes of heat.

4.1.2 Tropical Atlantic

The second location at which the SCM is tested, lies in the tropical Atlantic, situated at the 6^∘ S, 8^∘ E buoy of the PIRATA mooring array (Bourlès et al., 2008; Servain et al., 1998; https://www.pmel.noaa.gov/tao/drupal/disdel/, last access: 25 September 2018). We choose a boreal summer month to demonstrate the AOSCM's ability to follow the SST cooling connected to the annual cold tongue development in the tropical Atlantic (Lübbecke et al., 2010; Xie and Carton, 2004). During the period of 1–30 June 2014, mooring observations of SST, radiative fluxes, and ocean temperature and salinity are available for SCM evaluation, which are complemented by ERA-Interim for the atmosphere. We perform experiments using several settings of the AOSCM and one OSCM simulation. The atmospheric column is either forced by advective tendencies and vertical velocity only (AOSCM-Jun1/12/15), or additionally, profiles of temperature, moisture and horizontal wind are nudged above 1 km with a timescale of 6 h (AOSCM-N1km6h). For comparison, we also perform an ocean-only simulations (OSCM), which is forced by hourly precipitation, near-surface wind, temperature and moisture from ERA-Interim, and short-wave and long-wave radiation measured at the PIRATA buoy.

4.1.3 North polar region

To explore the AOSCM in an experimental setting with idealised forcing and to show the additional interaction with sea ice, we choose an Arctic summer case. For this location (76^∘ N, 160^∘ E), we have observations from the ACSE (Arctic Clouds in Summer Experiment) campaign during a warm-air advection episode in early August 2014 causing rapid ice melt (Tjernström et al., 2015). Sotiropoulou et al. (2018) use an LES to study the importance of advection for cloud evolution during this period. Here, we present results from the LES (Savre et al., 2014), in comparison with results from the ASCM, using the same experimental set-up as in Sotiropoulou et al. (2018). Furthermore, we explore the importance of coupling to the ocean/sea ice, as well as the sensitivity to atmospheric model time step and coupling frequency, in ASCM and AOSCM experiments. With the aim to separate the influence of local and remote processes, as in Sotiropoulou et al. (2018), we turn off large-scale advection of heat and moisture.

The idealised experiment, based on simplified information from observations and reanalysis (Sotiropoulou et al., 2018), assumes an initial ice concentration (100 %), surface albedo (0.65), and temperature (273.15 K, i.e. melting point of ice). The LES applies a surface friction velocity of $u_{*}=\mathrm{0.2}$ m s⁻¹ as lower boundary condition, while it is modelled in the ASCM and AOSCM using a surface roughness, updated from its default value (0.001 m) to 0.06 m to achieve approximately the same averaged u_*. The LES and the atmospheric component of AOSCM are initialised with the same vertical mean profiles, i.e. smoothed versions of soundings on 1 August, 06:00 UTC, the starting time of the simulation. The atmospheric forcing consists of a constant geostrophic wind of 5.4 m s⁻¹ and advective tendencies of temperature and humidity, all derived from 6-hourly ERA-Interim data interpolated to a vertical L137 grids but restricted vertically to the LES boundary layer height. The synoptic-scale divergence (i.e. vertical advection), is not directly taken from the ERA-Interim as it generates unrealistic results. Thus, a prescribed divergence of $\mathrm{2.3}\times {\mathrm{10}}^{-\mathrm{5}}$ s⁻¹ is applied over the first 18 simulated hours and then decreased by 50 %, in both the LES and the SCM experiments.

Figure 7 Model evolution at the PAPA buoy during 11–15 July 2014 for AOSCM-6h, ASCM-6h and AOSCM-3h. Radiative fluxes are smoothed in time with a running-mean timescale of 1 h. Measurements from the PAPA buoy in grey. All downward fluxes are positive.

4.2 Results from experiments

4.2.1 PAPA mooring – case study

During 11–15 July 2014, the PAPA mooring briefly experienced an atmospheric cold advection event, followed by a period of weak advection, which was finally ended by warm advection (not shown). A cloud, which initially caps the boundary layer, rises and dissipates after about 2 days. Only during the last day does a cloud form again, associated with the warm advection.

AOSCM-6h reproduces the general temporal evolution as given by the forcing but shows a mismatch in cloud height of up to 500 m, associated with temperature and moisture biases (Fig. 6a and b). Modelled temperatures are overestimated at and below the reanalysis cloud height and are underestimated above, with cold biases peaking at the height of the modelled cloud. In addition, the AOSCM produces too much water vapour mixing ratio relative to ERA-Interim. In the reanalysis, the cloud dissipates during 13 July, whereas at least a thin cloud persists for most of the simulation time in the three model experiments. The atmospheric boundary layer height varies around a depth of 500 m and the oceanic turbocline stays shallow, reaching at most 20 m (Fig. 6c). Atmospheric evolution and biases are similar in AOSCM-3h and ASCM-6h. During a period of weak atmospheric advection, the frequency with which forcing information is updated thus does not influence the evolution of the coupled column.

Figure 7 summarises the comparison between the modelled surface parameters and the PAPA measurements. If the model forcing is updated less frequently (A(O)SCM-6h), oscillations in the wind arise with larger amplitude than in AOSCM-3h (Fig. 7f). Oscillations occur mainly during periods of weak wind forcing and their amplitude increases with height (not shown). They are a sign of the column not being in geostrophic equilibrium and are enhanced if applying pressure gradient forcing, as this adds momentum to the column. At the location of the PAPA mooring, the frequency of inertial oscillations is about 16 h. A footprint of the artificial inertial oscillations is visible in the boundary layer height (Fig. 6a) and the turbulent surface fluxes (Fig. 7d, e). The flux oscillations arise from the oscillating near-surface shear, which generates turbulence. In the coupled simulations, temperature biases peak around 1 ^∘C (Fig. 7a, b). In ASCM-6h, a larger 2 m temperature bias can be reduced to similar values if forced with observed hourly SST instead of daily mean SST from ERA-Interim (not shown).

Comparing AOSCM-6h results to reanalysis data and PAPA measurements reveals disagreements in terms of bias signs. On the one hand, the reanalysis, and thus the forcing state, indicates that the AOSCM is too warm and moist near the surface. On the other hand, comparison to PAPA measurements points to an underestimation of atmospheric moisture (too large an upward latent heat flux) and too cold near-surface temperatures. These differences might partly be explained by deviations in the SST between reality and ERA-Interim reanalysis, which steer boundary layer dynamics via stability in different ways. It is interesting to note that when the atmospheric evolution is tightly nudged to the reanalysis, the cloud structure, as well as short- and long-wave radiation, improve compared to measurements (not shown). Near-surface temperature and latent heat flux, however, deviate even further from observations. These differences might partly be due to compensating biases but could also be due to non-representativeness of the buoy measurements for the model grid box. During the studied period, the AOSCM captures the local observations even with the likely erroneous large-scale forcing. Comparison with the large-scale forcing fields can be used to reveal potential atmospheric model drifts. However, in ERA-Interim the coupling to the ocean is not interactive and SSTs are only prescribed with daily resolution. One way to overcome this is to use measurements for the analysis since they reflect the observed coupling and are dependent on the true near-surface stability.

Table 2 Surface RMSE after 28 days evaluated with respect to PAPA mooring measurements. Statistics calculated over 16 realisations of the five main experiments at the PAPA location. Table 1 describes the experiments.

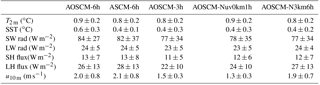
Table 3 As Table 2 but for RMSE of atmospheric profiles evaluated with respect to ERA-Interim fields.

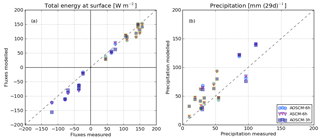
Figure 8 Accumulated fluxes, total surface energy and precipitation calculated over 29-day simulations at the PAPA mooring, compared for three main sensitivity runs AOSCM-6h, ASCM-6h and AOSCM-3h across all 16 simulations. Symbols with a light (dark) border represent results from warm (cold) months. Modelled precipitation is filtered with the measurement hourly rain threshold of 0.2 mm h⁻¹

The evolution of the atmosphere is also sensitive to the initial conditions. Initialising the model only 6 h later increases the biases during the final warm-air advection period (not shown). In this simulation the cloud cover is underestimated, thus giving increased biases in the radiative fluxes at the surface. Furthermore, in this set-up, a strong sensitivity to forcing frequency can be diagnosed, as these biases do not occur in AOSCM-3h results. Again, nudging the wind down to the surface removes the cloud biases. Initialising 18 h earlier, on the other hand only weakly influence the results.

4.2.2 PAPA mooring – statistical assessment

Root mean square error (RMSE) statistics, relative to ERA-Interim and observations, summarise results from 16 simulations for the main three set-ups AOSCM-6h, ASCM-6h and AOSCM-3h (Tables 2 and 3). Statistically significant differences are assessed by comparing the two mean values and their range of 1 standard deviation. If the values do not overlap considering only the range of variability from one variable, we call this one-sidedly statistically significant. Results are separately compiled for warm and cold periods (not shown in the tables, only in Fig. 8), with 8 of the 16 simulations falling into each category. Here, warm cases are characterised by a mean ocean mixed-layer depth of less than 10 m (June–September) and cold cases by more than 30 m (November–April). Results based on oceanic profiles are not included because the variability produced by experiment set-ups is less than the variability among the 16 different periods.

AOSCM-6h and ASCM-6h exhibit similar monthly mean biases in the considered parameters. Daily-mean SSTs used to force ASCM-6h simulations are one-sidedly statistically significantly superior to SSTs modelled by the AOSCM-6h. Reduced variability is due to a coarser temporal resolution of the forcing. The signal is largest in summer months and can be explained by SST cold biases in AOSCM runs, in some cases also present during winter. This SST bias in the AOSCM is part of a temperature bias dipole in the ocean column which intensifies with run time. Reffray et al. (2015) discuss a sensitivity of the mixing depth to a TKE length parameter, describing the deepening of the mixed layer by near-inertial waves and ocean swell or waves. In the standard TKE set-up used in EC-Earth v3, the parameter is either a function of latitude and set to 30 m at the PAPA station (stand-alone ocean model) or set to 0 m so that no additional mixing is supplied (coupled model). Setting the parameter to 0 m, thus not considering additional mixing by waves, produces very similar results to the ones presented here (Tables 2 and 3), but cold biases during the summer months are now replaced by warm biases of roughly equal strength and mixed layers that are too shallow (not shown). Reducing the value of the parameter to 10 m, as suggested by Reffray et al. (2015), and thus limiting an increase in mixing depth by internal mixing, alleviates the observed summer cold biases (not shown).

In general, the AOSCM can successfully reproduce atmosphere-only results. The added benefit of a coupled simulation is that the interactions between the marine and atmospheric boundary layer are resolved and can be studied directly. AOSCM-3h, forced with atmospheric data of higher temporal frequency, is better able to represent measurements and model reference data than AOSCM-6h, with the largest impact on momentum. Again the annual mean signal originates mainly from one subperiod, in this case the cold months, when AOSCM-3h performance exceeds that of AOSCM-6h in several aspects. Firstly, wind biases are statistically significantly reduced in the whole atmospheric column. Secondly, the mean column state bias is reduced, although not to an extent that is statistically significant. In addition to improvements in the mean state, an increase in the depth of the mixed layer is found in both atmosphere and ocean (not shown), related to reduced coupling biases, though again the change is not statistically significant.

Higher-frequency forcing is, in many cases, linked to pronounced improvements in wind representation through the reduction in oscillations in wind speed. One way of emulating this effect is to relax horizontal wind profiles in the model towards those provided by the reanalysis. Results from simulations with AOSCM-Nuv0km1h settings are summarised in the fourth columns of Tables 2 and 3. Atmospheric column and surface wind biases can be reduced by nudging the wind. SST biases are also alleviated during cold months (not shown) but atmospheric temperature and humidity biases are not sensitive to wind nudging. The ocean is affected through momentum transport during cold months. The ocean responds similarly as in AOSCM-3h simulations, though only one-sidedly statistically significant. The ocean mixed layer is deeper whereas the annual mean atmospheric boundary layer is shallower than in all other configurations. Thus, nudging of the wind components can be used to reduce model biases. However, it has to be noted that wind nudging perturbs the momentum balance. Especially when studying boundary layer turbulence parameterisation, nudging interferes with the performance of the parameterisation.

In some simulations, the free troposphere drifts away from the reanalysis state. A weak atmospheric nudging of the four main prognostic variables temperature, moisture and horizontal wind above 3 km (i.e. well above the boundary layer, AOSCM-N3km6h) reduces biases in the troposphere even below 3 km (Table 3). At the same time, the ocean state is only weakly influenced by deepening the ocean mixed layer. This way of nudging can be used even when the momentum balance at the surface is required to be unperturbed in the boundary layer.

Accumulated energy fluxes (see Eq. 5) and accumulated precipitation from the main three sensitivity runs are visualised in Fig. 8, resolving individual cases. Modelled fluxes are sampled every hour to match the measurement frequency. In summary, the model surface receives too little energy during summer and loses too much energy during winter. Considering all seasons, AOSCM-3h/6h performs best compared to ASCM-6h, but the main signal appears in different seasons. AOSCM-3h gives the best net surface energy balance during summer, and during winter AOSCM-6h exceeds the other set-ups. However, the overall variability is large and individual cases may show different results. Precipitation is larger during winter and the model produces generally more rain than observed.

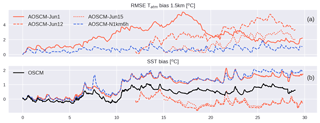
Figure 9 Atmospheric temperature root-mean square error integrated in the lower 1.5 km of the atmosphere compared to ERA-Interim and SST biases relative to PIRATA measurements for several coupled and one ocean-only simulation. More details on the presented experiments can be found in Table 1.

4.2.3 Tropical Atlantic

Our second marine test location is the tropical Atlantic. During the time of the case study, June 2014, SSTs in this area cool by 4 ^∘C. This trend is part of the cooling of the eastern tropical Atlantic due to its annual cycle (Lübbecke et al., 2010; Xie and Carton, 2004). To estimate AOSCM performance in this region, we perform a base simulation using only advective tendencies (AOSCM-Jun1 in Fig. 9). Within 10 days, two main biases develop, one atmospheric and one oceanic. Firstly, atmospheric temperatures between 0.5 and 1.5 km are overestimated, while moisture is underestimated over the same height interval (not shown). The patterns of these atmospheric biases are closely correlated and peak between 14 and 17 June. Both biases are flow-dependent, i.e. they are not connected to a model drift but reduce again after 17 June. The RMSE in the lower 1.5 km develops similarly for temperature (Fig. 9a) and moisture (not shown). Secondly, although the cooling of the ocean surface layer is partly captured, its amplitude is underestimated, leading to a warm bias of around 2 ^∘C at the end of the simulation (Fig. 9b). It is worth noting that the ocean column follows the observations well until 5 days into the simulation, when the observed ocean cooling can no longer be matched by the model. The SST bias grows, and after a short period of recovery around days 7 to 10, it increases during the course of 2 days and does not reduce significantly afterwards. Emergence of a model warm bias during the build up of SST cooling is a common model bias in the tropical Atlantic (Breugem et al., 2008; Toniazzo and Woolnough, 2014; Voldoire et al., 2018).

We demonstrate how the origins of the two biases can be traced back using several sensitivity experiments. Nudging above 3 km, as done in the PAPA case, also reduces the near-surface bias in moisture and temperature but in a weaker form (not shown). The atmospheric bias can largely be alleviated by nudging prognostic variables above 1 km with a timescale of τ_a=6 h (AOSCM-N1km6h). However, the SST evolution is not influenced by atmospheric relaxation to a height of 1 km. Inspired by the indication of a flow-dependent bias in the standard set-up, AOSCM-Jun12 and AOSCM-Jun15 are initialised further into the period. Initialising the ocean between 12 and 15 June, when the largest SST bias develops, strongly improves the SST representation in the AOSCM. The atmospheric biases develop again and are stronger when initialising on 12 June than 15 June.

Finally, the SST bias can be studied by decoupling the ocean from the atmosphere. This can either be done by nudging the atmospheric column strongly (e.g. τ_a=0.25 h) down to the surface (not shown) or by performing an ocean-only simulation (OSCM, Fig. 9b). Both simulations produce very similar evolutions of the SST bias (not shown). The similarities point to an oceanic origin of the SST bias, while differences in AOSCM-Jun1 indicate the impact of additional feedbacks on the bias development. Observations of the ocean current vector (available at 10 m depth during this period) indicate two maxima of about 50 cm s⁻¹ on 5 and 10 June (not shown), coinciding with periods of maximum SST bias in all simulations initialised on 1 June. The ocean model currently does not capture horizontal temperature advection. Temperature changes related to advection hence cannot be reproduced by the OSCM. Heat budget analyses shows these terms to be small in the region of the experiment (Deppenmeier et al., 2018; Giordani et al., 2013). However, short-timescale events are likely to be missed and can impact the budget on shorter times. Another possible oceanic origin of the bias is insufficient ocean vertical mixing of near-surface warming into the ocean. The importance of and sensitivity to vertical ocean mixing has been observed and demonstrated by Hazeleger and Haarsma (2005) and Hummels et al. (2013), among others. Too little mixing of cold water masses into the well-mixed layer as well as too little heat transport from the upper layer into the deep ocean leads to artificially warm SSTs, similar to those observed towards the end of the simulation. In the current set-up, upper-ocean vertical mixing only penetrates the first upper metres of the ocean column and then stops abruptly. Replacing the relatively strongly stratified observed profile with the more gradual profile from ORAS4 deepens the mixed layer and improves the results slightly but still only down to 20 m (not shown). This feature and its impact on the SST evolution are currently under investigation.

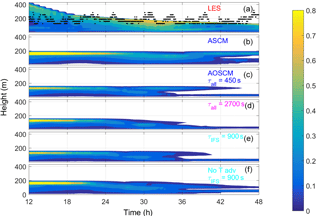
Figure 10 Time-height evolution of the simulated cloud liquid water content (g kg⁻¹) in the Arctic set-up for hours 12 to 48 with a colour scale that maximises at about 0.8 (g kg⁻¹) for (a) LES results from Sotiropoulou et al. (2018), (b) the ASCM simulation with a time step of 450 s and 137 layers, (c) AOSCM with a time step of 450 s in all components and coupling, (d) AOSCM with conditions similar to EC-Earth, i.e. 2700 s for all time steps and coupling, (e) as in (d) but with 900 s time step for the atmospheric component, and (f) as in (e) but with no temperature advection. Observational estimates of cloud top (black dots) from ACSE are also included in (a).

4.2.4 North polar region

Finally, the AOSCM is used to simulate a moist, warm-air advection event in the Arctic summer. Figure 10 shows the evolution of the liquid water content for the reference LES simulation (panel a) together with observational estimates of cloud top and different versions of the ASCM and AOSCM (panels b–f). The atmosphere-only run (panel b) is the most similar to the LES as it keeps a cloud with a top at about 200 m during the whole simulation. The formation of the cloud in the beginning of the simulations (not shown) is quite different. The LES initially forms a cloud with a top at about 800 m that slowly descends under the influence of the subsidence. In all the AOSCM simulations, a cloud also forms at that height and dissipates, and after a few hours a new cloud appears with a top at around 200 m. The evolution of the simulated cloud between hours 12 and 48 diverges from a similar state at around hour 12, with sensitivity to coupling and time step. In a simulation with short time steps in all model components and coupling at every time step (Δt=450 s, Fig. 10c), the cloud develops into a double-layered cloud at about hour 32. Using a longer time step (2700 s), as is used in EC-Earth (Fig. 10d), results in a descending and thinning cloud, which at the end of the period is only present close to the surface. Returning to a shorter time step of 900 s in the atmosphere but keeping the ocean, ice and coupling at 2700 s results in a cloud that keeps its top at 200 m for a longer time (Fig. 10e). Two simulations are run where first the temperature and then the moisture advection is turned off; the resulting cloud for the first simulation is not that different (compare Fig. 10e and f). When the moisture advection is removed, the cloud disappears before hour 12 (not shown).

The integrated liquid water content between hours 12 and 48 is presented in Fig. 11. The LES liquid water path (red) varies between 50 and 150 g m⁻² during the simulation, while the observations show a wider range. Only the ASCM (blue dashed line) reaches observed values, the coupled simulations (thick lines in blue, magenta, and cyan) produce smaller liquid water paths and little variability in sensitivity tests. In this figure, the importance of advection of moisture is clearly seen (dash–dotted cyan line, near the bottom of the figure). Without temperature advection (cyan dashed line), the cloud stays cooler and can thus hold more liquid water.

For this Arctic case, the cloud both shields the surface from the sun and increases the long-wave radiation. For the short-wave cloud effect, the surface albedo plays an important role. As discussed in Tjernström et al. (2015), the surface changes characteristics rapidly as energy is absorbed and melting occurs. Figure 12 shows the initial albedo in the simulation (averaged over hour 1) for the various simulations, calculated using the model's incoming and reflected short-wave radiation. The albedo during the first hour is a result of both the initialisation (same for all coupled simulations) and processes changing the albedo. The albedo in the AOSCM is calculated in LIM based on the sea-ice state and is quite different from the default albedo climatology provided to the ASCM. In the coupled simulations, the albedo spans about 63 to 74 %, while the ASCM's albedo is at 58 %. The LES value is 65 % and constant in time. Some of these differences can be explained by how the cloud affects the diffuse radiation and thereby the amount of reflected light at the surface. The albedo decreases over the 48 h in all simulations and decreases the most (≥15 %) in the simulation where the cloud disappears. This illustrates the complexity of the coupling and how these different processes influence the net energy received by the surface.

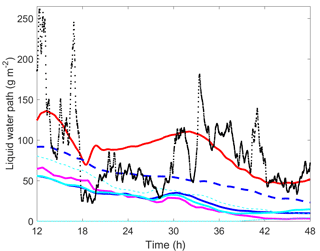
Figure 11 Liquid water path in (g m⁻²) for all Arctic simulations presented in Fig. 10. LES – red line; ASCM – blue dashed line; AOSCM with various time steps – blue (all 450 s), magenta (all 2700 s) and cyan (IFS 900 s, other 2700 s). Also included are the results from simulations without advection of temperature (dashed cyan line) and without humidity (dash–dotted cyan thin line). Observations are shown as running averages over approximately 10 min (black dots).

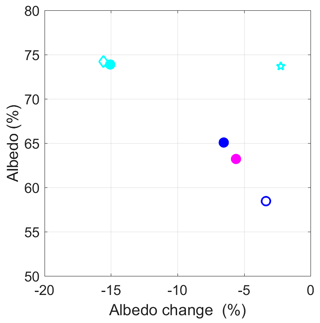
Figure 12 Mean albedo (%) change over the simulated 40 h plotted against the mean albedo for the first simulated hour for the experiments in Fig. 10; same colors as in Fig. 11; ASCM – open blue symbol; AOSCM simulations with no advection of temperature (cyan diamond) and no humidity advection (cyan star) are also included.

In Fig. 13, the net mean energy at the surface, with and without the sensible and latent heat flux contribution, is shown. The deviation from the dashed 1-to-1 line gives the magnitude of the turbulent fluxes. In all simulations, the turbulent fluxes present a net source of energy for the surface i.e. stably stratified conditions dominate. However, the observational estimate (black dot) shows a small net upward flux and the overall available energy at the surface is about 40 W m⁻² less. This analysis points to differences in the vertical structure of the atmosphere.

4.3 Evaluation of experiments

Based on results from the PAPA station and considering atmosphere-only set-ups as a benchmark, the AOSCM performs well and is in some cases even superior to the ASCM. Extending an ASCM to an AOSCM allows us to resolve coupled processes. A sensitivity to the forcing frequency is apparent, which is largely related to deteriorated winds in simulations forced with temporally coarser data. Both the horizontal advection and the vertical wind forcing are captured more realistically with increased forcing frequency. It should be noted that a linear interpolation will result in deteriorated results even for perfect forcing data. A linear functionality is likely not a good assumption for the temporal evolution of the forcing fields. Wind components can be nudged to alleviate oscillations in wind speed, while this process does not influence temperature and moisture evolution. Nudging wind down to the surface ensures that atmospheric momentum biases do not deteriorate ocean performance, but the nudging interferes with parameterisations connected to momentum, e.g. turbulence. Nudging all fields above the boundary layer with weak nudging timescale remedies biases in the free troposphere while allowing us to focus on the freely evolving surface interactions. At the PIRATA buoy, nudging above 3 km also reduces time-dependent atmospheric biases considerably. Biases are almost completely removed when reducing the lowest nudged height to 1 km. At the sea surface, a temperature bias remains even in an ocean-only setting or with a strongly nudged atmosphere. Both biases are sensitive to the initialisation time of the simulation. The sensitivity tests performed for the Arctic case, compared with both observations and an idealised LES simulation, show the complexity of how the coupling between the lower atmospheric structure, surface properties and clouds affect the energy budget at the surface. Further analysis of this case is ongoing.

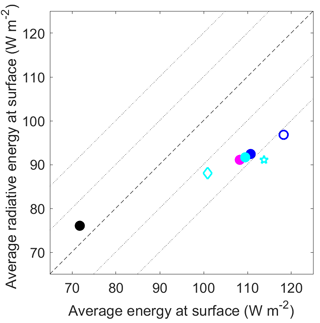
Figure 13 Average radiative energy as a function of average energy received at the surface for hours 12 to 48 for the simulations (same symbols as in Fig. 12) and observations (black dot). The thin dotted lines around the 1-to-1 line represent ±10 and 20 W m⁻².

Based on fluid dynamical theory and our results, we recommend forcing the AOSCM with advective tendencies and pressure gradient forcing in the atmosphere. The forcing frequency should be kept as high as possible, ideally based on information from the host model at every time step, e.g. for model development. If model drifts or other persistent biases are identified, nudging profiles down to the surface or above the processes of interest can enhance the stability of the simulation and keep close analogies with observations. Running several sensitivity experiments based on different forcing and coupling settings, periods for further parameter sensitivity experiment can be identified and then studied inexpensively in the AOSCM.

5 Summary and outlook

We demonstrate a coupled atmosphere–ocean single-column model (AOSCM) following the set-up of a future version of the climate model EC-Earth (v4, currently v3). The AOSCM is designed to study the physical interaction of oceanic and atmospheric boundary layer processes as well as technical aspects of the coupling. Here, we demonstrate the functionalities of the model by applying it at three locations and present analysis showing the versatility of the tool. Furthermore, we discuss possibilities of how to design process studies using the AOSCM.

As the AOSCM consists of individually compiled components, it is relatively straightforward to update and exchange routines, e.g. when newer cycles become available. At this stage, the capabilities of the EC-Earth AOSCM can be extended along several avenues. Even though the hydrometeorological variables cloud liquid, ice, rain, snow, and cloud cover are treated prognostically in OpenIFS, their profiles can currently not be forced by advective tendencies or nudging. The missing advection terms can be partially included by adding the advective tendencies of cloud liquid and ice mixing ratios to the advective tendency of water vapour mixing ratio. Similarly, advective tendency forcing could be added to both the sea-ice and ocean equation systems. Apart from the necessary model infrastructure, this requires observations or model data to compile the relevant forcing. Based on the current model without advective forcing, one option is to limit the run time of the model. In that case the relative stationarity of ocean and sea ice with respect to atmospheric movement can be assumed. Another option is to relax the ocean profile towards a reference profile, either across the whole column or only below the mixed layer. A similar feature, namely an adaptive relaxation height, is currently not available in the atmospheric part of the AOSCM. It is, however, possible to nudge only above a constant level, as we demonstrate. If this height is chosen well above the boundary layer, it is still ensured that the boundary layer is not affected by nudging, while biases in the free troposphere are limited.

Even though the model can be extended in numerous ways, it is a useful tool to explore several open science questions already in its current form. A non-extensive list of problems that can be tackled includes the following.

In the marine environment simulations similar to Atlantic Stratocumulus Transition Experiment (ASTEX) (Bretherton et al., 1999; de Roode et al., 2016), describing stratocumulus to cumulus transition, can be performed with coupled models. Independent of the location where it is placed, a coupled atmosphere–ocean SCM allows us to study the concept of stochastic air–sea fluxes decoupled from large-scale motions (Williams, 2012). An AOSCM, including sea ice, presents the opportunity to study physical processes in the polar regions. The atmosphere–ice–ocean system is strongly coupled and sensitive to even small energy imbalances at the interfaces and thus to the correct representation of sea-ice fluxes (Bourassa et al., 2013; Spengler et al., 2016). Understanding of the processes relevant for sea-ice melting and freeze-up in the changing polar regions is crucial. Work can be done along the lines of previous studies, e.g. Pithan et al. (2016), investigating Arctic air mass transformations and the local interactions with the snow surface (Lecomte et al., 2015; Sterk et al., 2013).

The AOSCM is a tool for investigating local, vertical interactions at the air–ice–ocean interface. All physical parameterisations implemented in the individual model components (see respective references) and their interactions can be tested in the current set-up. The AOSCM can furthermore yield insights into the physical processes responsible for model shortcomings in areas where the coupling at the interface plays an important role. With its low computational cost, it can furthermore help understand how choices of coupling parameters and numerical set-up influence the evolution of the whole column.