Fast sensitivity analysis methods for computationally expensive models with multi-dimensional output

Global sensitivity analysis (GSA) is a powerful approach in identifying which inputs or parameters most affect a model's output. This determines which inputs to include when performing model calibration or uncertainty analysis. GSA allows quantification of the sensitivity index (SI) of a particular input – the percentage of the total variability in the output attributed to the changes in that input – by averaging over the other inputs rather than fixing them at specific values. Traditional methods of computing the SIs using the Sobol and extended Fourier Amplitude Sensitivity Test (eFAST) methods involve running a model thousands of times, but this may not be feasible for computationally expensive Earth system models. GSA methods that use a statistical emulator in place of the expensive model are popular, as they require far fewer model runs. We performed an eight-input GSA, using the Sobol and eFAST methods, on two computationally expensive atmospheric chemical transport models using emulators that were trained with 80 runs of the models. We considered two methods to further reduce the computational cost of GSA: (1) a dimension reduction approach and (2) an emulator-free approach. When the output of a model is multi-dimensional, it is common practice to build a separate emulator for each dimension of the output space. Here, we used principal component analysis (PCA) to reduce the output dimension, built an emulator for each of the transformed outputs, and then computed SIs of the reconstructed output using the Sobol method. We considered the global distribution of the annual column mean lifetime of atmospheric methane, which requires ∼ 2000 emulators without PCA but only 5–40 emulators with PCA. We also applied an emulator-free method using a generalised additive model (GAM) to estimate the SIs using only the training runs. Compared to the emulator-only methods, the emulator–PCA and GAM methods accurately estimated the SIs of the ∼ 2000 methane lifetime outputs but were on average 24 and 37 times faster, respectively.

1 Introduction

Sensitivity analysis is a powerful tool for understanding the behaviour of a numerical model. It allows quantification of the sensitivity in the model outputs to changes in each of the model inputs. If the inputs are fixed values such as model parameters, then sensitivity analysis allows study of how the uncertainty in the model outputs can be attributed to the uncertainty in these inputs. Sensitivity analysis is important for a number of reasons: (i) to identify which parameters contribute the largest uncertainty to the model outputs, (ii) to prioritise estimation of model parameters from observational data, (iii) to understand the potential of observations as a model constraint and (iv) to diagnose differences in behaviour between different models.

1.1 Different approaches for sensitivity analysis

By far, the most common types of sensitivity analysis are those performed one at a time (OAT) and locally. OAT sensitivity analysis involves running a model a number of times, varying each input in turn, whilst fixing other inputs at their nominal values. For example, Wild (2007) showed that the tropospheric ozone budget was highly sensitive to differences in global NO_x emissions from lightning. The observation-based range of 3–8 TgN yr⁻¹ in the magnitude of these emissions could result in a 10 % difference in predicted tropospheric ozone burden. OAT sensitivity analysis is used in a variety of research fields including environmental science (Bailis et al., 2005; Campbell et al., 2008; de Gee et al., 2008; Saltelli and Annoni, 2010), medicine (Coggan et al., 2005; Stites et al., 2007; Wu et al., 2013), economics (Ahtikoski et al., 2008) and physics (Hill et al., 2012). While the ease of implementing OAT sensitivity analysis is appealing, a major drawback of this approach is that it assumes that the model response to different inputs is independent, which in most cases is unjustified (Saltelli and Annoni, 2010) and can result in biased results (Carslaw et al., 2013).

Global sensitivity analysis (GSA) overcomes this OAT issue by quantifying the sensitivity of each input variable by averaging over the other inputs rather than fixing them at nominal values. However, the number of sensitivity analysis studies using this global method has been very small. Ferretti et al. (2016) found that out of around 1.75 million research articles surveyed up to 2014, only 1 in 20 of studies mentioning “sensitivity analysis” also use or refer to “global sensitivity analysis”. A common type of GSA is the variance-based method, which operates by apportioning the variance of the model's output into different sources of variation in the inputs. More specifically, it quantifies the sensitivity of a particular input – the percentage of the total variability in the output attributed to the changes in that input – by averaging over the other inputs rather than fixing them at specific values. The Fourier Amplitude Sensitivity Test (FAST) was one of the first of these variance-based methods (Cukier et al., 1973). The classical FAST method uses spectral analysis to apportion the variance, after first exploring the input space using sinusoidal functions of different frequencies for each input factor or dimension (Saltelli et al., 2012). Modified versions of FAST include the extended FAST (eFAST) method which improves its computational efficiency (Saltelli et al., 1999) and the random-based-design (RBD) FAST method which samples from the input space more efficiently (Tarantola et al., 2006). Another widely used GSA method is the Sobol method (Homma and Saltelli, 1996; Saltelli, 2002; Sobol, 1990), which has been found to outperform FAST (Saltelli, 2002). Most applications of the Sobol and FAST methods involve a small number of input factors. However, Mara and Tarantola (2008) carried out a 100-input sensitivity analysis using the RBD version of FAST and a modified version of the Sobol method and found that both methods gave estimates of the sensitivity indices (SIs) that were close to the known analytical solutions. A downside to the Sobol method is that a large number of runs of the model typically need to be carried out. For the model used in Mara and Tarantola (2008), 10 000 runs were required for the Sobol method but only 1000 were needed for FAST.

1.2 Emulators and meta-models

If a model is computationally expensive, carrying out 1000 simulations may not be feasible. A solution is to use a surrogate function for the model called a meta-model that maps the same set of inputs to the same set of outputs but is computationally much faster. Thus, much less time is required to perform GSA using the meta-model than using the slow-running model. A meta-model can be any function that maps the inputs of a model to its outputs, e.g. linear or quadratic functions, splines, neural networks. A neural network, for example, works well if there are discontinuities in the input–output mapping, but such a method can require thousands of runs of the computationally expensive model to train it (particularly if the output is highly multi-dimensional) which will likely be too time-consuming. Here, we use a statistical emulator because it requires far fewer training runs and it has two useful properties. First, an emulator is an interpolating function which means that at inputs of the expensive model that are used to train the emulator, the resulting outputs of the emulator must exactly match those of the expensive model (Iooss and Lemaître, 2015). Secondly, for inputs that the emulator is not trained at, a probability distribution of the outputs that represents their uncertainty is given (O'Hagan, 2006). The vast majority of emulators are based on Gaussian process (GP) theory due to its attractive properties (Kennedy and O'Hagan, 2000; O'Hagan, 2006; Oakley and O'Hagan, 2004), which make GP emulators easy to implement while providing accurate representations of the computationally expensive model (e.g. Chang et al., 2015; Gómez-Dans et al., 2016; Kennedy et al., 2008; Lee et al., 2013). A GP is a multivariate normal distribution applied to a function rather than a set of variables. The original GP emulator in a Bayesian setting was developed by Currin et al. (1991) (for a basic overview, see also O'Hagan, 2006) and is mathematically equivalent to the kriging interpolation methods used in geostatistics (e.g. Cressie, 1990; Ripley, 2005). Kriging regression has been used as an emulator method since the 1990s (Koehler and Owen, 1996; Welch et al., 1992). More recently, there has been considerable interest in using this kriging emulator approach for practical purposes such as GSA or inverse modelling (Marrel et al., 2009; Roustant et al., 2012). Examples of its application can be found in atmospheric modelling (Carslaw et al., 2013; Lee et al., 2013), medicine (Degroote et al., 2012) and electrical engineering (Pistone and Vicario, 2013).

For GSA studies involving multi-dimensional output, a traditional approach is to apply a separate GP emulator for each dimension of the output space. However, if the output consists of many thousands of points on a spatial map or time series (Lee et al., 2013), then the need to use thousands of emulators can impose substantial computational constraints even using the FAST methods. A solution is to adopt a GSA method that does not rely on an emulator but is based on generalised additive modelling (Mara and Tarantola, 2008; Strong et al., 2014, 2015b) or on a partial least squares approach (Chang et al., 2015; Sobie, 2009). A separate generalised additive model (GAM) can be built for each input against the output of the expensive model, and the sensitivity of the output to changes in each input is then computed using these individual GAM models. Partial least squares (PLS) is an extension of the more traditional multivariate linear regression where the number of samples (i.e. model runs in this context) can be small, and they may even be less that the number of inputs (Sobie, 2009).

An alternative way of reducing the computational constraints is to use principal component analysis (PCA) to reduce the dimensionality of the output. This means that we require far fewer emulators to represent the outputs, reducing the GSA calculations by a large margin, although there is some loss of detail. This emulator–PCA hybrid approach has been successfully used in radiative transfer models (Gómez-Dans et al., 2016), a very simple chemical reaction model (Saltelli et al., 2012) and general circulation models (Sexton et al., 2012). While we hypothesise that both emulator-free and PCA-based methods are suited to large-scale GSA problems (e.g. those involving more than 20 input factors), a focus of our work is to determine the accuracy of these methods for a smaller-scale GSA study.

1.3 Aims of this study

Recent research comparing different GSA methods based on Gaussian process emulators has been limited in application to relatively simple models and low-dimensional output (Mara and Tarantola, 2008). Using two computationally expensive models of global atmospheric chemistry and transport – namely the Frontier Research System for Global Change/University of California at Irvine (FRSGC/UCI) and Goddard Institute for Space Studies (GISS) models – we compare the accuracy and efficiency of global sensitivity analysis using emulators and emulator-free methods, and we investigate the benefits of using PCA to reduce the number of emulators needed. We compare and contrast a number of ways of computing the first-order sensitivity indices for the expensive atmospheric models: (i) the Sobol method using an emulator, (ii) the extended FAST method using an emulator, (iii) generalised additive modelling, (iv) a partial least squares approach and (v) an emulator–PCA hybrid approach. Hereafter, we refer to (i) and (ii) as emulator-based GSA methods and (iii) and (iv) as emulator-free GSA methods.

2 Materials and methods

2.1 Atmospheric chemistry models

Global atmospheric chemistry and transport models simulate the composition of trace gases in the atmosphere (e.g. O₃, CH₄, CO, SO_x) at a given spatial resolution (latitude × longitude × altitude). The evolution in atmospheric composition over time is controlled by a range of different dynamical and chemical processes, our understanding of which remains incomplete. Trace gases are emitted from anthropogenic sources (e.g. NO from traffic and industry) and from natural sources (e.g. isoprene from vegetation, NO from lightning), they may undergo chemical transformation (e.g. formation of O₃) and transport (e.g. convection or boundary layer mixing), and they may be removed through wet or dry deposition. Global sensitivity analysis is needed to understand the sensitivity of our simulations of atmospheric composition and its evolution to assumptions about these governing processes.

In this study, we performed GSA on two such atmospheric models. We used the FRSGC/UCI chemistry transport model (CTM) (Wild et al., 2004; Wild and Prather, 2000) and the GISS general circulation model (GCM) (Schmidt et al., 2014; Shindell et al., 2006). We used results from 104 model runs carried out with both of these models from a comparative GSA study (Wild et al., 2018). This involved varying eight inputs or parameters over specified ranges using a maximin Latin hypercube design: global surface NO_x emissions (30–50 TgN yr⁻¹), global lightning NO_x emissions (2–8 TgN yr⁻¹), global isoprene emissions (200–800 TgC yr⁻¹), dry deposition rates (model value ±80 %), wet deposition rates (model value ±80 %), humidity (model value ±50 %), cloud optical depth (model value × 0.1–10) and boundary layer mixing (model value × 0.01–100). For this study, we focus on a single model output, namely the global distribution of tropospheric columns of mean methane (CH₄) lifetime at the annual timescale. The CH₄ lifetime is an important indicator of the amount of highly reactive hydroxyl radical in the troposphere (Voulgarakis et al., 2013), and we choose this output because of its contrasting behaviour in the two models. The native spatial resolution of the models is 2.8^∘ × 2.8^∘ for FRSGC and 2.5^∘ × 2.0^∘ for GISS, but we combine neighbouring grid points so that both models have a comparable resolution of 5–6^∘, giving a total of 2048 grid points for FRSGC/UCI and 2160 grid points for GISS.

2.2 Global sensitivity analysis using the Sobol and extended FAST methods

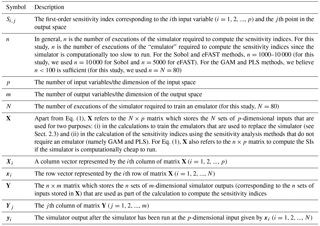
For brevity and generality, we hereafter refer to each of the atmospheric chemical transport models as a simulator. A common way of conducting global sensitivity analysis for each point in the output space of the simulator – where the output consists of, for example, a spatial map or a time series – is to compute the first-order sensitivity indices (SIs) using variance-based decomposition; this apportions the variance in simulator output (a scalar) to different sources of variation in the different model inputs. Assuming the input variables are independent of one another – which they are for this study – the first-order SI, corresponding to the ith input variable (i=1, 2, ..., p) and the jth point in the output space, is given by

$$\begin{array}{}\text{(1)}& S_{i,j}={\displaystyle \frac{\text{Var}\left[E\left({\mathit{Y}}_j\mathrm{|}{\mathit{X}}_i\right)\right]}{\text{Var}\left({\mathit{Y}}_j\right)}}\times \mathrm{100},\end{array}$$

where X_i is the ith column of the n×p matrix X (i.e. a matrix with n rows and p columns) which stores the n samples of p-dimensional inputs, and Y_j is the jth column of the n×m matrix which stores the corresponding n sets of m-dimensional outputs (Table 1). We multiply by 100 so that the SI is given as a percentage. The notation given by Var(⋅) and E(⋅) denotes the mathematical operations that compute the variance and expectation. The simplest way of computing S_i,j is by brute force, but this is also the most computationally intensive (Saltelli et al., 2008).

Table 1 Summary of algebraic terms used in this study that are common to all of most of the statistical methods described in this study. For brevity, the terms that are specific to a particular method are not listed here.

2.2.1 The Sobol method

The Sobol method, developed in the 1990s, is much faster than brute force at computing the terms in Eq. (1), in part because it requires fewer executions of the simulator (Homma and Saltelli, 1996; Saltelli, 2002; Saltelli et al., 2008; Sobol, 1990). The method operates by first generating a n×2p matrix (i.e. a matrix with n rows and 2p columns) of random numbers from a space-filling sampling design (e.g. a maximin Latin hypercube design), where n is the number of sets of inputs and p is the number of input variables. The inputs are on the normalised scale so that each element of a p-dimensional input lies between 0 and 1. Typical values for n are 1000–10 000. The matrix is split in half to form two new matrices, A and B, each of size n×p. To compute the ith SI (1 $\le i\le p)$, we define two new matrices, Ci and Di, where Ci is formed by taking the ith column from A and the remaining columns from B, and Di is formed by taking the ith column from B and the remaining columns from A. We then execute the simulator – denoted by f – at each set of inputs given by the rows of matrices A, B, Ci and Di. This gives vectors Y_A=f (A), Y_B=f (B), Y_Ci=f (Ci) and Y_Di=f (Di). Vectors Y_A and Y_Ci are then substituted into Eq. (2):

$$\begin{array}{ll}{\displaystyle }\widehat{S_{i,j}}& {\displaystyle }={\displaystyle \frac{\widehat{\text{Var}}\left[\widehat{E}\left({\mathit{Y}}_j\mathrm{|}{\mathit{X}}_i\right)\right]}{\widehat{\text{Var}}\left({\mathit{Y}}_j\right)}}\times \mathrm{100}\\ \text{(2)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{{\mathit{Y}}_{\mathrm{A}}\cdot {\mathit{Y}}_{\mathrm{Ci}}-{\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{A}}^{\left(j\right)}\right)}^{\mathbf{2}}}{{\mathit{Y}}_{\mathrm{A}}\cdot {\mathit{Y}}_{\mathrm{A}}-{\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{A}}^{\left(j\right)}\right)}^{\mathbf{2}}}}\times \mathrm{100},\end{array}$$

where ${\mathit{Y}}_{\mathrm{A}}\cdot {\mathit{Y}}_{\mathrm{Ci}}=\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{A}}^{\left(j\right)}{\mathit{Y}}_{\mathrm{Ci}}^{\left(j\right)}\right)$, and ${\mathit{Y}}_{\mathrm{A}}^{\left(j\right)}$ and ${\mathit{Y}}_{\mathrm{Ci}}^{\left(j\right)}$ are the jth elements of Y_A and Y_Ci (equivalent formula for Y_A⋅Y_A). For all p input variables, the total number of simulator runs is $\mathrm{12}\times n\times p$. Saltelli (2002) and Tarantola et al. (2006) suggested using eight variants of Eq. (2), using different combinations of Y_A, Y_B, Y_Ci and Y_Di (Appendix A). Lilburne and Tarantola (2009) proposed using the average of these eight SI estimates as they deemed this to be more accurate than a single estimate. We used this approach by Lilburne and Tarantola (2009) for this study.

2.2.2 The extended FAST method

An alternative and even faster way of estimating the terms in Eq. (1) is to use the eFAST method, first developed by Saltelli et al. (1999) and widely used since (Carslaw et al., 2013; Koehler and Owen, 1996; Queipo et al., 2005; Saltelli et al., 2008; Vanuytrecht et al., 2014; Vu-Bac et al., 2015). A multi-dimensional Fourier transformation of the simulator f allows a variance-based decomposition that samples the input space along a curve defined by

$$\begin{array}{}\text{(3)}& x_i\left(s\right)=G_i\left(\text{sin}\left({\mathit{\omega }}_{i}s\right)\right),\end{array}$$

where x=(x₁, ..., x_p) refers to a general point in the input space that has been sampled, s∈R is a variable over the range (−∞, ∞), G_i is the ith transformation function (Appendix A), and ω_i is the ith user-specified frequency corresponding to each input. Varying s allows a multi-dimensional exploration of the input space due to the x_is being simultaneously varied. Depending on the simulator, we typically require n=1000–10 000 samples from the input space. After applying the simulator f, the resulting scalar output – denoted generally by y – produces different periodic functions based on different ω_i. If the output y is sensitive to changes in the ith input factor, the periodic function of y corresponding to frequency ω_i will have a high amplitude.

More specifically, we express the model $y=f\left(s\right)=f\left(x_{\mathrm{1}}\left(s\right),x_{\mathrm{2}}\left(s\right),\mathrm{\dots },x_{\mathrm{p}}\left(s\right)\right)$ as a Fourier series:

$$\begin{array}{}\text{(4)}& y=f\left(s\right)=\sum _{j=-\mathrm{\infty }}^{\mathrm{\infty }}{A}_j\text{cos}\left(js\right)+B_j\sin \left(js\right).\end{array}$$

Using a domain of frequencies given by $j\in Z=\mathit{\{}-\mathrm{\infty },\mathrm{\dots },-\mathrm{1},\mathrm{0},\mathrm{1},\mathrm{\dots },\mathrm{\infty }\mathit{\}}$, the Fourier coefficients A_j and B_j are defined by

$$\begin{array}{}\text{(5)}& {\displaystyle }{A}_j={\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }}}\underset{-\mathit{\pi }}{\overset{\mathit{\pi }}{\int }}f\left(s\right)\cos \left(js\right).\mathrm{d}s,B_j={\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }}}\underset{-\mathit{\pi }}{\overset{\mathit{\pi }}{\int }}f\left(s\right)\sin \left(js\right).\mathrm{d}s.\end{array}$$

With ω_i stated in Eq. (3), the variance of model output attributed to changes in the ith input variable for the jth point in the output space (numerator of Eq. 1) is defined as

$$\begin{array}{}\text{(6a)}& \widehat{\text{Var}}\left[\widehat{E}\left({\mathit{Y}}_j\mathrm{|}{\mathit{X}}_i\right)\right]=\sum _{q\in Z^{\mathrm{0}}}{A}_{q{\mathit{\omega }}_i}^{\mathrm{2}}+B_{q{\mathit{\omega }}_i}^{\mathrm{2}},\end{array}$$

where Z⁰ is the set of all integers except zero. The total variance (denominator of Eq. 1) is

$$\begin{array}{}\text{(6b)}& \widehat{\text{Var}}\left({\mathit{Y}}_j\right)=\sum _{k\in Z^{\mathrm{0}}}{A}_k^{\mathrm{2}}+B_k^{\mathrm{2}}.\end{array}$$

Further details of eFAST are given in Saltelli et al. (1999). The differences between the original and the extended versions of the FAST method are given in Appendix A.

2.3 Gaussian process emulators

When the simulator is computationally expensive to run – like the atmospheric chemical transport models used here – we substitute it with an emulator which is a surrogate of the expensive simulator but much faster to run. If we are confident that the emulator is accurate, then we can compute the first-order SIs from the Sobol and eFAST methods using the outputs of the emulator rather than the simulator. Mathematically, an emulator is a statistical model that mimics the input–output relationship of a simulator. As stated in the introduction, an emulator is an interpolating function at model outputs it is trained at and gives a probability distribution and other outputs (O'Hagan, 2006).

An emulator is trained using N sets of p-dimensional inputs denoted by x₁, x₂, ..., x_N and N sets of one-dimensional outputs from the simulator given by y₁=f(x₁), y₂=f(x₂), ..., y_N=f(x_N); f represents the simulator and for our study N=80 (see Sect. 2.6). The most common form of an emulator is a GP since it has attractive mathematical properties that allow an analytical derivation of the mean and variance of the emulated output (given by $\widehat{f}\left(\mathit{x}\right)$ for a general input x). A notable exception is Goldstein and Rougier (2006), who used a non-GP emulator based on a Bayes linear approach. More formally, a GP is an extension of the multivariate Gaussian distribution to infinitely many variables (Rasmussen, 2006). The multivariate Gaussian distribution is specified by a mean vector μ and covariance matrix Σ. A GP has a mean function which is typically given by m(x)=E(f(x)) and covariance function given by c(x, x^′) = cov(f(x), f(x^′)), where x and x^′ are two different p-dimensional inputs. For the latter, we used a Matern (5/2) function (Roustant et al., 2012), which is given by

$$\begin{array}{ll}{\displaystyle }c\left(\mathit{x},{\mathit{x}}^{\prime }\right)& {\displaystyle }=s^{\mathrm{2}}+\left(\mathrm{1}+\sqrt{\mathrm{5}}\left({\displaystyle \frac{\left|\mathit{x}-{\mathit{x}}^{\prime }\right|}{\mathit{\theta }}}\right)+{\displaystyle \frac{\mathrm{5}}{\mathrm{3}}}{\left({\displaystyle \frac{\left|\mathit{x}-{\mathit{x}}^{\prime }\right|}{\mathit{\theta }}}\right)}^{\mathrm{2}}\right)\\ \text{(7)}& {\displaystyle }& {\displaystyle }\times \text{exp}\left(-\sqrt{\mathrm{5}}\left({\displaystyle \frac{\left|\mathit{x}-{\mathit{x}}^{\prime }\right|}{\mathit{\theta }}}\right)\right),\end{array}$$

where s denotes the standard deviation and θ is the vector of range parameters (sometimes called length scales). These emulator parameters are normally estimated using maximum likelihood (see Bastos and O'Hagan, 2009, for details). GP emulators for uncertainty quantification were originally developed within a Bayesian framework (Currin et al., 1991; Kennedy and O'Hagan, 2000; O'Hagan, 2006; Oakley and O'Hagan, 2004).

Developed around the same time, the kriging interpolation methods used in geostatistics are mathematically equivalent to the GP methods developed by Currin et al. (1991) (e.g. Cressie, 1990; Ripley, 2005). Kriging-based emulators have been used for 25 years (Koehler and Owen, 1996; Welch et al., 1992), with recent implementations including the DICE-Kriging R packages used for GSA and inverse modelling (Marrel et al., 2009; Roustant et al., 2012). Since the latter approach is computationally faster, we adopted the DICE-Kriging version of the GP emulator for this study. For the statistical theory behind both emulator versions and descriptions of related R packages, see Hankin (2005) and Roustant et al. (2012).

2.4 Emulator-free global sensitivity analysis

For GSA studies involving highly multi-dimensional output, the time to compute the SIs can be significantly reduced by employing an emulator-free GSA approach. In this study, we consider two such methods using (i) GAM and (ii) a PLS regression approach. For both the GAM and PLS methods, we used n=N simulator runs to compute the sensitivity indices (Table 1), and for our study these were the same N=80 runs that were used to train the emulators described in Sect. 2.3. In the descriptions of these two sensitivity analysis methods (Sect. 2.4.1 and 2.4.2), we thus use $\mathbf{X}=[{\mathit{X}}_{\mathrm{1}}{\mathit{X}}_{\mathrm{2}},\mathrm{\dots },{\mathit{X}}_{\mathrm{p}}]$ and Y to denote the matrices that store N sets of p-dimensional inputs and m-dimensional outputs.

2.4.1 The generalised additive modelling method

A GAM is a generalised linear model where the predictor variables are represented by smooth functions (Wood, 2017). The general form of a GAM is

$$\begin{array}{}\text{(8a)}& {\displaystyle }& {\displaystyle }{\mathit{Y}}_j=g\left(\mathbf{X}\right)+\mathit{\epsilon }\text{(8b)}& {\displaystyle }& {\displaystyle }g\left(\mathbf{X}\right)=s\left({\mathit{X}}_{\mathrm{1}}\right)+s\left({\mathit{X}}_{\mathrm{2}}\right)+\mathrm{\dots }+s\left({\mathit{X}}_{\mathrm{p}}\right),\end{array}$$

where X_i is the ith column of input matrix X (i=1, 2, ..., p); Y_j is the jth column of output matrix Y (j=1, 2, ..., m) since we construct a separate GAM for each point in the output space (i.e. for each latitude–longitude point in our case); s(.) is the smoothing function such as a cubic spline; and ε is a zero-mean normally distributed error term with constant variance. If we wish to include second-order terms in g(X), we would add $s\left({\mathit{X}}_{\mathrm{1}},{\mathit{X}}_{\mathrm{2}}\right)+s\left({\mathit{X}}_{\mathrm{1}},{\mathit{X}}_{\mathrm{3}}\right)+\mathrm{\dots }+s\left({\mathit{X}}_{\mathrm{p}-\mathrm{1}},{\mathit{X}}_{\mathrm{p}}\right)$ to the right-hand side of Eq. (8b). A GAM it is not an emulator as defined by O'Hagan (2006) because the fitted values of the GAM are not exactly equal to the outputs of the training data (Simon N. Wood, personal communication, 23 May 2017). It is still a meta-model and we could use it as a surrogate of the computationally expensive simulator in order to perform variance-based sensitivity analysis using, for example, the Sobol or extended FAST method. However, we have found that the number of runs of the simulator to train it in order for it to be an accurate surrogate for the simulator is too many (i.e. too computationally burdensome). Instead, it is possible to obtain accurate estimates of the first-order SIs by using a GAM to estimate the components of Eq. (1) directly (Stanfill et al., 2015; Strong et al., 2014, 2015b). To compute the ith first-order SI ($\mathrm{1}\le i\le p)$, we first recognise that taking the expectation of Eq. (8a) leads to E(Y_j)=g(X). The expression for E(Y_j|X_i) is thus the marginal distribution of E(Y_j). We could fit the full model and then compute this marginal distribution following Stanfill et al. (2015). However, an easier and quicker way is to fit a GAM to the (X_i, Y_j) “data” where X_i and Y_j are defined above. Then, E(Y_j|X_i) consists of the fitted values of this reduced model (Strong et al., 2015b). Thus, Var[E(Y_j|X_i)] (numerator of equation 1) is determined by computing the variance of the n points from this fitted GAM model. In other words,

$$\begin{array}{}\text{(9)}& \widehat{\text{Var}}\left[\widehat{E}\left({\mathit{Y}}_j\mathrm{|}{\mathit{X}}_i\right)\right]=\text{var}\left(s\left(x_{\mathrm{1},i}\right),s\left(x_{\mathrm{2},i}\right),\mathrm{\dots },s\left(x_{n,i}\right)\right),\end{array}$$

where x_k,i is the element from the kth row and ith column of matrix X. Finally, the denominator term of Eq. (1) is computed by taking the variance of the n samples of the outputs from the computationally expensive simulator that are stored in Y_j.

2.4.2 The partial least squares method

The PLS method is the only one of the four GSA methods considered here that is not variance-based (Chang et al., 2015). Multivariate linear regression (MLR) is a commonly used tool to represent a set of outputs or response variables (Y) based on a set of inputs or predictor variables (X), where X and Y are matrices (Table 1). MLR is only appropriate to use when the different inputs (columns in X) are independent and not excessive in number. In many situations, such as GSA studies, there can be a large number of input variable and/or they could be highly correlated with each other (Sobie, 2009). PLS is an extension of MLR which is able to deal with these more challenging multivariate modelling problems (Wold et al., 2001). The main reason for choosing PLS over other applicable regression approaches is that it has been shown to give similar estimates of the sensitivity indices to a variance-based GSA approach (Chang et al., 2015). Thus, for sensitivity analysis problems when the inputs are correlated, this PLS method could be considered an alternative to the variance-based GAM method which assumes that the inputs are independent. Mathematically, PLS operates by projecting X and Y into new spaces, determined by maximising the covariance between the projections of X and Y (see Sect. S1 in the Supplement for details). PLS regression is then performed where the regression coefficients represent the sensitivity indices (given as a percentage). When n>p, it is standard to estimate the PLS regression coefficients using the traditional multivariate linear regression. Thus, the p×m matrix of sensitivity indices (S) can be computed using the following formula:

$$\begin{array}{}\text{(10)}& S={\left({\mathbf{X}}^T\mathbf{X}\right)}^{-\mathrm{1}}{\mathbf{X}}^T\mathbf{Y}.\end{array}$$

2.5 Principal component analysis

As an alternative approach for speeding up the sensitivity analysis calculations, we computed the SIs from the Sobol GSA method using a hybrid approach involving PCA to reduce the dimensionality of the output space, and then used separate Gaussian process emulators for each of the transformed outputs (Gómez-Dans et al., 2016; Saltelli et al., 2012; Sexton et al., 2012). After performing the emulator runs, we then reconstruct the emulator output on the original output space, from which we compute the sensitivity indices.

PCA transforms the outputs onto a projected space with maximal variance. Mathematically, we obtain the matrix of transformed outputs Y^(PC) by

$$\begin{array}{}\text{(11)}& {\mathbf{Y}}^{\left(\mathrm{PC}\right)}={\mathbf{YA}}^{\ast },\end{array}$$

where Y is the N×m matrix of training outputs from the simulator (see Sect. 2.3), and A^∗ is a matrix whose columns are orthogonal to one another and whose ith column (${\mathit{A}}_i^{\ast })$ is chosen such that var$\left(\mathbf{Y}{\mathit{A}}_i^{\ast }\right)$ is maximised subject to the constraint ${\left({\mathit{A}}_i^{\ast }\right)}^T{\mathit{A}}_i^{\ast }=\mathrm{1}$. The vector ${\mathit{A}}_{\mathrm{1}}^{\ast }$ is called the first principal component (PC1), and we define λ₁ to be the principle eigenvalue of S= var (Y) which is the largest variance of the outputs Y with respect to PC1. The second, third, fourth columns, etc. of A^* are referred to as PC2, PC3, PC4, etc. with λ₂, λ₃, λ₄, etc. representing the second, third, fourth, etc. largest variance of Y, respectively. PC1 contains the most information in the output, followed by PC2, then PC3, etc. The number of principal components required is commonly determined by plotting the following points: (1, λ₁), (2, λ₁+λ₂), (3, ${\mathit{\lambda }}_{\mathrm{1}}+{\mathit{\lambda }}_{\mathrm{2}}+{\mathit{\lambda }}_{\mathrm{3}})$, ..., and identifying the point where the line begins to flatten out. This is equivalent to choosing a cutoff when most of the variance is explained. In this study, we included the first N_pc principal components such that 99 % of the variance is explained. The 99 % threshold was also necessary for this study to ensure that the reconstructed emulator output accurately approximated the simulator output for the validation runs (Fig. 2). While we found the 99 % threshold was necessary, other studies may find that a lower threshold (e.g. 95 %) is sufficient.

This technique of reducing the dimension of the output space from $m=\sim \mathrm{2000}$ spatially varying points to the first N_pc principal components (e.g. N_pc=5 for the FRSGC model; see Sect. 2.6) means that the number of required emulator runs to compute the sensitivity indices from the Sobol method is reduced by a factor of m∕N_pc (= ∼ 400 using above m and N_pc values). However, after having generated the N_pc sets of output vectors for the Sobol method (${\mathit{Y}}_{\mathrm{A}}^{\left(\mathrm{PC}\right)}$, ${\mathit{Y}}_{\mathrm{B}}^{\left(\mathrm{PC}\right)}$, ${\mathit{Y}}_{\mathrm{Ci}}^{\left(\mathrm{PC}\right)}$, ${\mathit{Y}}_{\mathrm{Di}}^{\left(\mathrm{PC}\right)}$; see Sect. 2.2), we need to reconstruct the m sets of output vectors which are required to compute the sensitivity indices for each of the m points in the output space. To do this, we first set the elements of the (N_pc+1)th, (N_pc+2)th, ..., m columns of the matrix A^∗ (Eq. 11) to zero and call this new matrix ${\mathbf{A}}_{\mathrm{sample}}^{\ast }$. We also form a n×m matrix ${\mathbf{Y}}_{\mathrm{sample}}^{\left(\mathrm{PC}\right)}$ whose first N_pc columns are vectors storing the emulator outputs corresponding to the first N_pc principal components, while the elements of the remaining columns are set to zero. Recall that ${\mathbf{Y}}_{\mathrm{sample}}^{\left(\mathrm{PC}\right)}$ is different from Y^(PC) where the latter has N rows (80 for this study) which correspond to the number of simulator runs required to train the emulators, whereas the number of samples n (n=10 000 for this study) refers to the number of emulator runs needed to estimate the sensitivity indices. The n×m matrix Y_sample of the reconstructed m-dimensional outputs is computed using

$$\begin{array}{}\text{(12)}& {\mathbf{Y}}_{\mathrm{sample}}={\mathbf{Y}}_{\mathrm{sample}}^{\left(\mathrm{PC}\right)}{\left({\mathbf{A}}_{\mathrm{sample}}^{\ast }\right)}^T.\end{array}$$

We use this formula to compute the Y_A, Y_B, Y_Ci and Y_Di vectors from Sect. 2.2 and the resulting sensitivity indices using Eq. (2) from the Sobol method (Sect. 2.2).

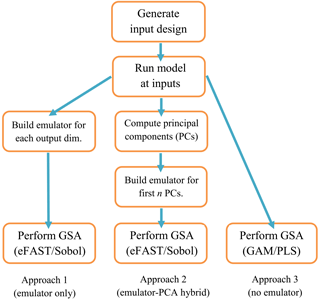
Figure 1 Flowchart for order of tasks to complete in order to perform GSA on a computationally expensive model. The ranges on the inputs, on which its design is based, are determined by expert elicitation. For approach 1, each dimension (dim.) of the output consists of a different spatial or temporal point of the same variable (CH₄ lifetime for this study). For approach 2, a PC is a linear combination of the different dimensions of the output, where n is chosen such that the first n PCs explain 99 % of the variance of the output.

2.6 Experimental setup

The sequence of tasks to complete when performing global sensitivity analysis is shown schematically in Fig. 1. The choice of inputs (e.g. parameters) to include in the sensitivity analysis will depend upon which have the greatest effects, based on expert knowledge of the model and field of study. Expert judgement is also needed to define the ranges of these inputs. A space-filling design such as maximin Latin hypercube sampling or sliced Latin hypercube sampling (Ba et al., 2015) is required in order to sample from the input space with the minimum sufficient number of model runs. We used n=10 000 for the Sobol method and n=5000 for the eFAST method, but $n=N=\mathrm{80}$ for the GAM and PLS methods. The third stage is to run the model at the set of input points specified by the space-filling sampling design.

If we are employing an emulator, the next stage is to build the emulator using the training runs. The number of training runs (N) is determined by $N=\mathrm{10}\times p$, where p is the number of input variables (Loeppky et al., 2009). We also need to perform runs of the computationally expensive simulator to validate the emulators. For this study, we ran the simulators with an additional set of inputs for validation. Comparing the emulator outputs with the simulator outputs using the validation inputs is usually sufficient, but more sophisticated diagnostics can also be carried out if needed (Bastos and O'Hagan, 2009). If employing the emulator-free approach, validation is also needed because we are using a statistical model to infer the SIs. Such a validation is not a central part of our results but is included in the Supplement (Fig. S2). For the emulator–PCA hybrid approach (Fig. 1), we found that the first 5 (for FRSGC) and 40 (for GISS) principal components were required to account for 99 % of the variance. This means that only 5–40 emulators are required to generate a global map in place of ∼ 2000 needed if each grid point is emulated separately, thus providing large computational savings.

The final stage is to compute the first-order SIs for all the inputs; these quantify the sensitivity of the output to changes in each input. The SIs are also known as the main effects. The eFAST, Sobol and GAM approaches can also be used to compute the total effects, defined as the sum of the sensitivities of the output to changes in input i on its own and interacting with other inputs. For this study, we do not consider total effects as the sum of the main effects was close to 100 % in each case.

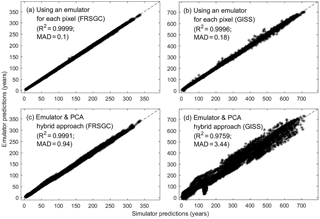
Figure 2 Annual column mean CH₄ lifetime calculated by the FRSGC and GISS chemistry models from each of 24 validation runs (x axis) versus that predicted by the emulator (y axis). In each plot, the R² and median absolute difference (MAD) are given as metrics for the accuracy of the emulator predictions. Each validation run contains ∼ 2000 different output values, corresponding to different latitude–longitude grid squares.

3 Results

3.1 Validation of the emulators

Since the emulators we employed are based on a scalar output, we built a separate emulator for each of the ∼ 2000 model grid points to represent the spatial distribution of the CH₄ lifetimes. At the 24 sets of inputs set aside for emulator validation, the predicted outputs from the emulators compared extremely well with the corresponding outputs from both chemistry models (Fig. 2a, b, R²=0.9996–0.9999, median absolute difference of 0.1–0.18 years). When PCA is used to reduce the output dimension from ∼ 2000 to 5–40 (depending on the chemistry model), the accuracy of the predicted outputs was not as good (Fig. 2c, d, R²=0.9759–0.9991, median absolute difference of 0.94–3.44 years) but was still sufficient for this study.

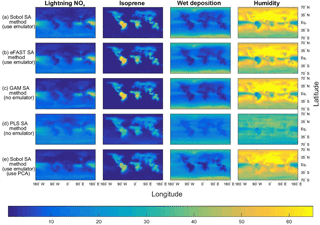
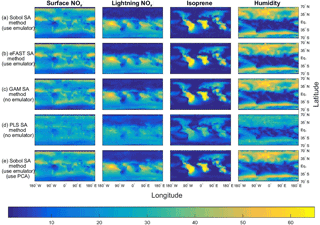
Figure 3 The sensitivity indices (percentage of the total variance in a given output) for the four dominant inputs, with the output given as the annual column mean CH₄ lifetime from the FRSGC chemistry transport model. The rows show the results from five different methods for performing sensitivity analysis (SA), whose formulae for computing the SIs are given by Eqs. (1, 2) and Sect. 2.3 (Sobol method and emulator), Eqs. (1, 6a–b), Sect. 2.3 (eFAST method and emulator), Eqs. (1, 9) (GAM method), Eq. (10) (PLS method), Eqs. (1, 2), Sect. 2.3 and 2.5 (Sobol method, emulator and PCA).

Figure 4 The sensitivity indices (percentage of the total variance in a given output) for the four dominant inputs, with the output given as the annual column mean CH₄ lifetime from the GISS chemistry model. See caption for Fig. 3 for further details about the five methods used.

3.2 Comparison of sensitivity indices

As expected, the two emulator-based global sensitivity analysis (GSA) approaches (eFAST and Sobol) produced almost identical global maps of first-order SIs (%) of CH₄ lifetime; see Figs. 3 and 4. The statistics (mean, 95th percentile and 99th percentile) of the differences in SIs between the two GSA methods over all eight inputs at 2000 output points for the FRSGC and GISS models are shown in Fig. 5 (M1 versus M2).

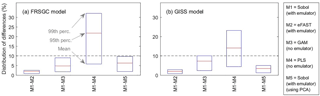
Figure 5 Statistics (mean, 95th percentile and 99th percentile) of the distribution of differences in sensitivity indices (SIs) between pairs of methods. For each comparison, the ∼ 16 000 pairs of SIs are made up of ∼ 2000 pairs of SIs for each of the eight inputs.

Our results show that the GAM emulator-free GSA method produces very similar estimates of the SIs to the emulator-based methods (Figs. 3, 4; row a vs. c for Sobol versus GAM). The 95th and 99th percentiles of differences of the emulator-based methods (e.g. Sobol) versus GAM are 5 and 9 % for FRSGC, and 7 and 10 % for GISS (Fig. 5, M1 versus M3). For both models, the PLS non-emulator-based method produced SIs that were significantly different from those using the eFAST and Sobol methods (Figs. 3, 4; row a vs. d for Sobol vs. PLS). For FRSGC, the mean and 95th percentile of the differences in SIs for the Sobol versus PLS methods are around 21 and 31 %, while for GISS the corresponding values are around 14 and 23 % (Fig. 5, M1 versus M4). Thus, our results indicate that the PLS method is not suitable for use as an emulator-free approach to estimating the SIs.

The global map of SIs using the emulator–PCA hybrid approach compared well to those from the emulator-only approach (Figs. 3, 4; row a vs. e). The 95th and 99th percentiles of differences between the two approaches were 6 and 10 %, respectively, for FRSGC (Fig. 5a, M1 versus M5) and 3 and 5 %, respectively, for GISS (Fig. 5b, M1 versus M5). These are both higher than the corresponding values for the emulator-only methods (Fig. 5, M1 versus M2; < 2 and < 3 %, respectively). These higher values for the emulator–PCA hybrid approach are also reflected in the poorer estimates of the validation outputs using this approach versus the emulator-only approach (Fig. 2). Such poorer estimates are expected because the PCA-transformed outputs only explain 99 % of the variance of the untransformed outputs used in the emulator-only approach.

4 Discussion

4.1 Comparison of sensitivity indices

Our results align with the consensus that the eFAST method or other modified versions of the FAST method (e.g. RBD-FAST) produce very similar SIs to the Sobol method. Mathematically, the two methods are equivalent (Saltelli et al., 2012) and when the analytical (true) values of the SIs can be computed, both methods are able to accurately estimate these values (Iooss and Lemaître, 2015; Mara and Tarantola, 2008). However, many studies have noted that the Sobol method requires more simulator (or emulator) runs to compute the SIs. Saltelli et al. (2012) state that $\frac{\mathrm{2}}{k}\times \mathrm{100}$ (%) more model runs are required for the Sobol method compared to eFAST, where k is the number of input factors (e.g. if k=8, then 25 % more runs are needed for Sobol). Mara and Tarantola (2008) found that the Sobol method required ∼ 10 000 runs of their model to achieve the same level of aggregated absolute error to that of FAST, which only needed 1000 runs. This is comparable to our analysis where the Sobol method required 18 000 runs of the emulator but only 1000 runs were needed for the eFAST method.

Given recent interest in applying GAMs to perform GSA (Strong et al., 2015a, b, 2014), only Stanfill et al. (2015) have compared how they perform against other variance-based approaches. The authors found that first-order SIs estimated from the original FAST method were very close to the true values using 600 executions of the model, whereas the GAM approach only required 90–150 model runs. This is roughly consistent with our results, as we estimated the SIs using 80 runs of the chemistry models for GAM and 1000 runs of the emulator for the eFAST method.

There are a limited number of studies comparing the accuracy of the SIs of the GAM method amongst different models, as in our study. Stanfill et al. (2015) found that the GAM method was accurate at estimating SIs based on a simple model (three to four parameters) as well as a more complex one (10 parameters). However, if more models of varying complexity and type (e.g. process versus empirical) were to apply the GAM approach, we expect that while GAM would work well for some models, for others the resulting SIs may be substantially different from those produced using the more traditional Sobol or eFAST methods. Saltelli et al. (1993) suggests that the performance of a GSA method can be model dependent, especially when the model is linear versus non-linear or monotonic versus non-monotonic, or if transformations are applied on the output (e.g. logarithms) or not. This is particularly true for GSA methods based on correlation or regression coefficients (Saltelli et al., 1999), which might explain why the SIs calculated from the PLS method in our analysis also disagreed with those of the eFAST/Sobol methods for the FRSGC versus GISS models. Not all GSA methods are model dependent; for example, the eFAST method is not (Saltelli et al., 1999).

4.2 Principal component analysis

For both chemistry models, using PCA to significantly reduce the number of emulators needed resulted in SIs very similar to those calculated using an emulator-only approach. For the GISS model, this was encouraging given that the spread of points and their bias in the emulator versus simulator scatter plot were noticeably larger than those of the FRSGC model (Fig. 2c, d). If we had increased the number of principle components so that 99.9 % of the variance in the output was captured rather than 99 %, following Verrelst et al. (2016), then we would expect less bias in the validation plot for GISS. However, the poor validation plots did not translate into poorly estimated SIs for the emulator–PCA approach. On the contrary, the estimated SIs for GISS are consistent with the estimated SIs using either emulator-only approach (Fig. 5).

The use of PCA in variance-based global sensitivity analysis studies is relatively new but has great potential for application in other settings. De Lozzo and Marrel (2017) used an atmospheric gas dispersion model to simulate the evolution and spatial distribution of a radioactive gas into the atmosphere following a chemical leak. The authors used principal component analysis to reduce the dimension of the spatio-temporal output map of gas concentrations to speed up the computation of the Sobol sensitivity indices for each of the ∼ 19 000 points in the output space. This emulator–PCA hybrid approach was also used to estimate the Sobol sensitivity indices corresponding to a flood forecasting model that simulates the water level of a river at 14 different points along its length (Roy et al., 2017). Using a crop model to simulate a variable related to nitrogen content of a crop over a growing season of 170 days, Lamboni et al. (2011) using PCA to reduce the dimension of the output space. However, unlike other comparable studies, the computed sensitivity indices corresponded to the principal components, i.e. to a linear combination of the 170 output values. This is permissible if the principal components can be interpreted in some physical sense. For Lamboni et al. (2011), the first PC approximately corresponded to mean nitrogen content over the whole growing season, while the second PC was the difference in nitrogen content between the first and second halves of the growing season.

4.3 Scientific context of this study

Our work extends the work of Wild et al. (2018) who used the same training inputs and the same atmospheric chemical transport models (FRSGC and GISS) but different outputs. Instead of using highly multi-dimensional output of tropospheric methane lifetime values at different spatial locations, Wild et al. (2018) used a one-dimensional output of global tropospheric methane lifetime. Using the eFAST method, the authors found that global methane lifetime was most sensitive to change in the humidity input for the FRSGC model, while for the GISS model the surface NO_x and the lightning NO_x inputs were most important for predicting methane lifetime at the global scale, followed by the isoprene, the boundary layer mixing and the humidity inputs (Wild et al., 2018). As expected, our results indicated that these same inputs explained most of the variance in the outputs for the different spatial locations. However, while the humidity SI for GISS was very low at the global scale (SI of 5 %), out study found that the SIs for humidity were very high (50–60 %) for the higher-latitude regions (Fig. 4).

4.4 Implications for large-scale sensitivity analysis studies

GSA studies for computationally expensive models involving a small number of inputs (e.g. < 10) are useful and straightforward to implement (Lee et al., 2012). However, the inferences made are limited due to the large number of parameters on which these models depend and the number of processes that they simulate. Hence, interest is growing in carrying out large-scale GSA studies involving a high number of inputs to improve understanding of an individual model (e.g. Lee et al., 2013) or to diagnose differences between models (Wild et al., 2018). For GSA studies when the number of inputs is small, our study has demonstrated that the GAM approach is a good candidate for carrying out emulator-free GSA since it calculates very similar SIs without the computational demands of emulation. A caveat is that the performance of GAM may depend on the behaviour of the model; although we have found it is a good GSA method for our models (FRSGC and GISS) and output (CH₄ lifetimes), its suitability may not be as good in all situations.

5 Conclusions

GSA is a powerful tool for understanding model behaviour, for diagnosing differences between models and for determining which parameters to choose for model calibration. In this study, we compared different methods for computing first-order sensitivity indices for computationally expensive models based on modelled spatial distributions of CH₄ lifetimes. We have demonstrated that the more established emulator-based methods (eFAST and Sobol) can be used to efficiently derive meaningful sensitivity indices for multi-dimensional output from atmospheric chemistry transport models. We have shown that an emulator-free method based on a GAM and an emulator–PCA hybrid method produce first-order sensitivity indices that are consistent with the emulator-only methods. For a reasonably smooth system with few parameters, as investigated here, the GAM and PCA methods are viable and effective options for GSA, and are robust over models that exhibit distinctly different responses. Moreover, the computational benefit of these alternative methods is apparent, with the GAM approach allowing calculation of variance-based sensitivity indices 22–56 times faster (or 37 times faster on average) compared to the eFAST or Sobol methods. Using the Sobol method, the emulator–PCA hybrid approach is 19–28 times faster (or 24 times faster on average) at computing the sensitivity indices compared to using an emulator-only approach depending on which chemistry model is used. Finally, we have provided guidance on how to implement these methods in a reproducible way.

Appendix A: Further details of the Sobol and eFAST global sensitivity analysis methods

For the Sobol method, Saltelli (2002) and Tarantola et al. (2006) suggest using eight variants of Eq. (2), using different combinations of y_A, y_B, y_Ci and y_Di :

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\widehat{S_i}}^{\text{I}}={\displaystyle \frac{{\mathit{Y}}_{\mathrm{A}}\cdot {\mathit{Y}}_{\mathrm{Ci}}-\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{A}}^{\left(j\right)}\right)\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{B}}^{\left(j\right)}\right)}{{\mathit{Y}}_{\mathrm{A}}\cdot {\mathit{Y}}_{\mathrm{A}}-\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{A}}^{\left(j\right)}\right)\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{B}}^{\left(j\right)}\right)}}\\ {\displaystyle }& {\displaystyle }{\widehat{S_i}}^{II}={\displaystyle \frac{{\mathit{Y}}_{\mathrm{B}}\cdot {\mathit{Y}}_{\mathrm{Di}}-\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{A}}^{\left(j\right)}\right)\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{B}}^{\left(j\right)}\right)}{{\mathit{Y}}_{\mathrm{B}}\cdot {\mathit{Y}}_{\mathrm{B}}-\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{A}}^{\left(j\right)}\right)\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{B}}^{\left(j\right)}\right)}}\\ {\displaystyle }& {\displaystyle }{\widehat{S_i}}^{\text{III}}={\displaystyle \frac{{\mathit{Y}}_{\mathrm{A}}\cdot {\mathit{Y}}_{\mathrm{Ci}}-\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{A}}^{\left(j\right)}\right)\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{B}}^{\left(j\right)}\right)}{{\mathit{Y}}_{\mathrm{B}}\cdot {\mathit{Y}}_{\mathrm{B}}-\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{A}}^{\left(j\right)}\right)\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{B}}^{\left(j\right)}\right)}}\\ {\displaystyle }& {\displaystyle }{\widehat{S_i}}^{\text{IV}}={\displaystyle \frac{{\mathit{Y}}_{\mathrm{A}}\cdot {\mathit{Y}}_{\mathrm{Ci}}-\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{Ci}}^{\left(j\right)}\right)\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{Di}}^{\left(j\right)}\right)}{{\mathit{Y}}_{\mathrm{Ci}}\cdot {\mathit{Y}}_{\mathrm{Ci}}-\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{Ci}}^{\left(j\right)}\right)\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{Di}}^{\left(j\right)}\right)}}\\ {\displaystyle }& {\displaystyle }{\widehat{S_i}}^{\text{V}}={\displaystyle \frac{{\mathit{Y}}_{\mathrm{A}}\cdot {\mathit{Y}}_{\mathrm{Ci}}-\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{Y}_{\mathrm{Ci}}^{\left(j\right)}\right)\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{Di}}^{\left(j\right)}\right)}{{\mathit{Y}}_{\mathrm{Di}}\cdot {\mathit{Y}}_{\mathrm{Di}}-\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{Ci}}^{\left(j\right)}\right)\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{Di}}^{\left(j\right)}\right)}}\\ {\displaystyle }& {\displaystyle }{\widehat{S_i}}^{\text{VI}}={\displaystyle \frac{{\mathit{Y}}_{\mathrm{B}}\cdot {\mathit{Y}}_{\mathrm{Di}}-\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{A}}^{\left(j\right)}\right)\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{B}}^{\left(j\right)}\right)}{{\mathit{Y}}_{\mathrm{A}}\cdot {\mathit{Y}}_{\mathrm{A}}-\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{A}}^{\left(j\right)}\right)\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{B}}^{\left(j\right)}\right)}}\\ {\displaystyle }& {\displaystyle }{\widehat{S_i}}^{\text{VII}}={\displaystyle \frac{{\mathit{Y}}_{\mathrm{B}}\cdot {\mathit{Y}}_{\mathrm{Di}}-\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{Ci}}^{\left(j\right)}\right)\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{Di}}^{\left(j\right)}\right)}{{\mathit{Y}}_{\mathrm{Ci}}\cdot {\mathit{Y}}_{\mathrm{Ci}}-\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{Ci}}^{\left(j\right)}\right)\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{Di}}^{\left(j\right)}\right)}}\\ {\displaystyle }& {\displaystyle }{\widehat{S_i}}^{\text{VIII}}={\displaystyle \frac{{\mathit{Y}}_{\mathrm{B}}\cdot {\mathit{Y}}_{\mathrm{Di}}-\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{Y}_{\mathrm{Ci}}^{\left(j\right)}\right)\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{Di}}^{\left(j\right)}\right)}{{\mathit{Y}}_{\mathrm{Di}}\cdot {\mathit{Y}}_{\mathrm{Di}}-\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{Ci}}^{\left(j\right)}\right)\left(\frac{\mathrm{1}}{N}\sum _{j=\mathrm{1}}^N{\mathit{Y}}_{\mathrm{Di}}^{\left(j\right)}\right)}}.\end{array}$$

Thus, the ith first-order Sobol SI estimate is

$$\widehat{S_i}={\displaystyle \frac{\mathrm{1}}{\mathrm{8}}}\left({\widehat{S_i}}^{\mathrm{I}}+{\widehat{S_i}}^{\mathrm{II}}+{\widehat{S_i}}^{\mathrm{III}}+{\widehat{S_i}}^{\mathrm{IV}}+{\widehat{S_i}}^{\mathrm{V}}+{\widehat{S_i}}^{\mathrm{VI}}+{\widehat{S_i}}^{\mathrm{VII}}+{\widehat{S_i}}^{\mathrm{VIII}}\right).$$

The main difference between classical FAST (Cukier et al., 1973) and extended FAST (Saltelli et al., 1999) when computing first-order SIs is the choice of transformation function G_i:

$$\begin{array}{l}{\displaystyle }\text{classical FAST}:G_i\left(z\right)={\stackrel{\mathrm{‾}}{x}}_i{e}^{{\stackrel{\mathrm{‾}}{v}}_{s}z},\\ \text{(A1a)}& {\displaystyle }({\stackrel{\mathrm{‾}}{x}}_i,{\stackrel{\mathrm{‾}}{v}}_s\text{are user-specified})\end{array}$$

$$\begin{array}{}\text{(A1b)}& \text{extended FAST}:G_i\left(z\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}+{\displaystyle \frac{\mathrm{1}}{\mathit{\pi }}}\arcsin \left(z\right).\end{array}$$

Using Eq. (A1b), Eq. (3) now becomes a straight-line equation:

$$\begin{array}{}\text{(A2)}& {\displaystyle }{x}_i\left(s\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}+{\displaystyle \frac{\mathrm{1}}{\mathit{\pi }}}{\mathit{\omega }}_{i}s.\end{array}$$