PCR-GLOBWB 2: a 5 arcmin global hydrological and water resources model

We present PCR-GLOBWB 2, a global hydrology and water resources model. Compared to previous versions of PCR-GLOBWB, this version fully integrates water use. Sector-specific water demand, groundwater and surface water withdrawal, water consumption, and return flows are dynamically calculated at every time step and interact directly with the simulated hydrology. PCR-GLOBWB 2 has been fully rewritten in Python and PCRaster Python and has a modular structure, allowing easier replacement, maintenance, and development of model components. PCR-GLOBWB 2 has been implemented at 5 arcmin resolution, but a version parameterized at 30 arcmin resolution is also available. Both versions are available as open-source codes on https://github.com/UU-Hydro/PCR-GLOBWB_model (Sutanudjaja et al., 2017a). PCR-GLOBWB 2 has its own routines for groundwater dynamics and surface water routing. These relatively simple routines can alternatively be replaced by dynamically coupling PCR-GLOBWB 2 to a global two-layer groundwater model and 1-D–2-D hydrodynamic models. Here, we describe the main components of the model, compare results of the 30 and 5 arcmin versions, and evaluate their model performance using Global Runoff Data Centre discharge data. Results show that model performance of the 5 arcmin version is notably better than that of the 30 arcmin version. Furthermore, we compare simulated time series of total water storage (TWS) of the 5 arcmin model with those observed with GRACE, showing similar negative trends in areas of prevalent groundwater depletion. Also, we find that simulated total water withdrawal matches reasonably well with reported water withdrawal from AQUASTAT, while water withdrawal by source and sector provide mixed results.

1 Introduction

The last decades saw the development of an increasing number of global hydrological models (GHMs), e.g. VIC (Liang et al., 1994; Nijssen et al., 2001), WMB (Fekete et al., 2002), WaterGAP (Döll et al., 2003), H08 (Hanasaki et al., 2008a, 2018), and Mac-PDM (Gosling and Arnell, 2011) (see Bierkens et al., 2014, Bierkens, 2015, and Kauffeldt et al., 2016, for a more extensive list, also including land surface models). GHMs have become essential tools to quantify and understand the global terrestrial water cycle, as they simulate the distributed hydrological response to weather and climate variations at higher resolution (typically 0.5^∘ × 0.5^∘) than used previously in general circulation models (GCMs), with more sophisticated run-off generation processes and river routing. As such, GHMs have been used for medium-range to seasonal flood forecasting (Bierkens and van Beek, 2009; Alfieri et al., 2013; Candogan Yossef et al., 2013) as well as for a myriad of water-related global change assessments. Examples include the projection or estimation of future flood and drought events (Sperna-Weiland et al., 2012; Dankers et al., 2013; Prudhomme et al., 2013; Wanders et al., 2015; Wanders and Wada, 2016), current and future flood hazard and risk (Pappenberger et al., 2012; Hirabayashi et al., 2013; Ward et al., 2013; Winsemius et al., 2013, 2016), global groundwater depletion (Wada et al., 2010; Gleeson et al., 2012), the contribution of terrestrial water stores to global sea level change (Konikow, 2011; Wada et al., 2012; Pohkrel et al., 2013), current and future water scarcity under climate change and increasing population growth (Hanasaki et al., 2008b; Wada et al., 2011a, b; Schewe et al., 2014; Haddeland et al., 2014; Wada and Bierkens, 2014), teleconnections between climate oscillations and water availability (Wanders and Wada, 2015), the impact of land use change on global water resources (Rost et al., 2008; Sterling et al., 2015; Bosmans et al., 2017), and trends in surface water temperature and cooling water potential (van Beek et al., 2012; van Vliet et al., 2012). More recently, the output from global hydrological models has been extended to study socioeconomic impacts, such as virtual water trade (Konar et al., 2013; Dalin et al., 2017) and future agricultural production (Elliott et al., 2013). These applications show that GHMs have become invaluable tools in support of global change research and environmental assessments.

PCR-GLOBWB (PCRaster Global Water Balance) (van Beek and Bierkens, 2009; van Beek et al., 2011) is one of the recently developed GHMs. PCR-GLOBWB is a grid-based global hydrological model developed at the Department of Physical Geography, Faculty of Geosciences, Utrecht University, the Netherlands. The model, describing the terrestrial part of the hydrological cycle, was first introduced in a technical report by van Beek and Bierkens (2009) and then formally published in a paper of van Beek et al. (2011), focusing on global water availability issues. PCR-GLOBWB was originally developed to solve the global daily surface water balance with a spatial resolution of 30 arcmin (about 50 km by 50 km at the Equator) and compare the resulting freshwater availability with monthly sectoral water demand in order to assess global-scale water scarcity (van Beek et al., 2011; Wada et al., 2011a, b). In this first version of PCR-GLOBWB (called PCR-GLOBWB 1 hereafter), similar to other global-scale hydrological models, water demand and water availability are treated independently, i.e. without direct feedback between human water use and other terrestrial water fluxes (e.g. Döll and Siebert, 2002; Wisser et al., 2010). Since it was first introduced, PCR-GLOBWB has been applied extensively in global water resource assessment studies. For instance, a recent search on Scopus (accessed on 13 April 2018) for the key-word “PCR-GLOBWB” yielded 113 publications with collectively over 2500 citations. Since the first version, several new model features have been introduced such as a comprehensive water demand and irrigation module (Wada et al., 2011b, 2014), a scheme for dynamic allocation of sectoral water demand to available surface water and groundwater resources, and the associated calculation of return flow (de Graaf et al., 2014). These features essentially introduced a two-way interaction among water demand, water withdrawal, water consumption, and availability, particularly over irrigated areas where water demand is large and return flow is significant. Nevertheless, all of these preceding studies using PCR-GLOBWB were performed at a relatively coarse resolution of 30 arcmin, limiting their subregional or local applications. Additionally, some added functionalities, such as the possibility to couple the land surface component of PCR-GLOBWB to a global MODFLOW-based groundwater model (Sutanudjaja et al., 2011, 2014; de Graaf et al., 2015, 2017) and an extension to simulate surface water temperature (van Beek et al., 2012), were incorporated in different versions based on the original PCR-GLOBWB 1, leading to divergent model code development.

The objective of this paper is to summarize and present the new version of the model, PCR-GLOBWB 2, which consolidates all components that have been developed since the original version of the model was first introduced (van Beek et al., 2011). The new version of the model, PCR-GLOBWB 2, which is able to simulate the water balance at a finer spatial resolution of 5 arcmin, supersedes the original PCR-GLOBWB 1, which has a resolution of 30 arcmin only¹. The finer resolution of PCR-GLOBWB 2 allows a much better representation of the effects of spatial heterogeneity in topography, soils, and vegetation on terrestrial hydrological dynamics (Wood et al., 2011; Bierkens et al., 2014). Likewise, it provides a better resolution for visualization that allows stakeholders and decision makers to assess model simulation output more easily and directly for the places they are specifically interested in (Sheffield et al., 2010; Beven and Cloke, 2012). To assess the possible improvements, this paper also presents the first evaluation results from the simulation of PCR-GLOBWB 2 at 5 arcmin resolution and compares them to a 30 arcmin version. As discharge data are commonly used in hydrological model performance evaluation, the simulated river discharge of PCR-GLOBWB 2 is compared to in situ discharge observations from the Global Runoff Data Centre (GRDC, 2014).

The paper is organized as follows. Section 2 provides a global description of PCR-GLOBWB 2, including its model structure and the new components and functionalities that have been added since PCR-GLOBWB 1. In Sect. 3 the global application of PCR-GLOBWB 2 is demonstrated and the results from a 58-year simulation (1958–2015) are evaluated against observations of discharge, total water storage, and reported withdrawal data. Section 4 summarizes and concludes this paper and discusses possible future developments. Section 5 provides information about availability of the model code and the underlying data.

2 PCR-GLOBWB 2 – model description

2.1 General overview

PCR-GLOBWB 2 is a state-of-the-art grid-based global hydrology and water resources model. It is a component-based model implementation in Python using open-source PCRaster Python routines (Karssenberg et al., 2010, http://pcraster.geo.uu.nl/, last access: 15 September 2017). The code is distributed through GitHub. The computational grid covers all continents except Greenland and Antarctica. Currently two versions are available: one with a spatial resolution of 5 arcmin in latitude and longitude and one with a coarser resolution of 30 arcmin. Typical time steps for hydrology and water use are 1 day while sub-daily time stepping is used for hydrodynamic river routing. For all dynamic processes involved, PCR-GLOBWB 2 uses a time-explicit scheme. For each grid cell and each time step, PCR-GLOBWB 2 simulates moisture storage in two vertically stacked upper soil layers (S₁+S₂ in Fig. 1), as well as the water exchange among the soil, the atmosphere, and the underlying groundwater reservoir (S₃ in Fig. 1). The exchange with the atmosphere is comprised of precipitation, evaporation from soils, open water, snow and soils, and plant transpiration, while the model also simulates snow accumulation and snowmelt. Sub-grid variability in land use, soils, and topography is included and influences the schemes for run-off–infiltration partitioning, interflow, groundwater recharge (from S₂ to S₃), and capillary rise (from S₃ to S₂). Run-off, generated by snowmelt, surface run-off, interflow, and baseflow, is routed across the river network to the ocean or endorheic lakes and wetlands. Routing can either be simple accumulation, simplified dynamic routing using a method of characteristics, or kinematic wave routing. In case the kinematic wave routing is used, it is also possible to use a (simplified) floodplain inundation scheme and to simulate the surface water temperature.

PCR-GLOBWB 2 includes a simple reservoir operation scheme that is applied to over roughly 6000 human-made reservoirs, which are progressively introduced according to their construction year, from the GRanD database (Lehner et al., 2011). Human water use is fully integrated within the hydrological model, meaning that at each time step (1) water demands are estimated for irrigation, livestock, industry, and households, (2) these demands are translated into actual withdrawals from groundwater, surface water (rivers, lakes, and reservoirs), and desalinization, subject to availability of these resources and maximum groundwater pumping capacity in place, and (3) consumptive water use and return flows are calculated per sector.

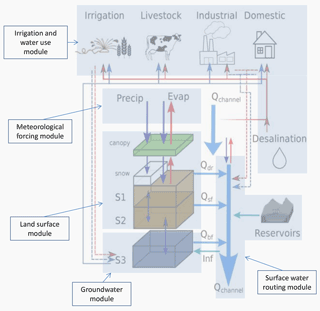
Figure 1 Schematic overview of a PCR-GLOBWB 2 cell and its modelled states and fluxes. S₁, S₂ (soil moisture storage), S₃ (groundwater storage), Q_dr (surface run-off – from rainfall and snowmelt), Q_sf (interflow or stormflow), Q_bf (baseflow or groundwater discharge), and Inf (riverbed infiltration from to groundwater). The thin red lines indicate surface water withdrawal, the thin blue lines groundwater abstraction, the thin red dashed lines return flows from surface water use, and the thin dashed blue lines return flows from groundwater use surface. For each sector, withdrawal − return flow = consumption. Water consumption adds to total evaporation. In the figure, the five modules that make up PCR-GLOBWB 2 are portrayed on the model components.

As an option PCR-GLOBWB 2 can be partially or fully coupled to a two-layer global groundwater model based on MODFLOW (de Graaf et al., 2017). Recent work (Hoch et al., 2017a, b) also includes coupling PCR-GLOBWB 2 to either Delft3D Flexible Mesh (Kernkamp et al., 2011) or LISFLOOD-FP (Bates et al., 2010), which are model codes that can be used to solve the 1-D–2-D shallow water equations (or approximations thereof) for detailed inundation studies.

2.2 Model structure and flexibility

PCR-GLOBWB 2 has a flexible modular structure (Fig. 1). The modular structure of PCR-GLOBWB 2, both in terms of model concepts and implementation (separate modules are called from a main program), makes it easy to modify or replace components according to specific objectives of the model application, to introduce new modules or components within the modelling system, and to couple it to existing codes.

There are currently five main hydrological modules in PCR-GLOBWB 2 as illustrated in Fig. 1 and briefly described in Sect. 2.3: meteorological forcing, land surface, groundwater, surface water routing, and irrigation and water use. For an extensive description of the underlying equations and methods used in each of these modules we refer to the following sources:

• the meteorological forcing module from van Beek (2008, http://vanbeek.geo.uu.nl/suppinfo/vanbeek2008.pdf);

• the land surface module, groundwater module, and surface water routing module from van Beek and Bierkens (2009, http://vanbeek.geo.uu.nl/suppinfo/vanbeekbierkens2009.pdf) and van Beek et al. (2011, https://doi.org/10.1029/2010WR009791);

• the irrigation and water use module including

  • calculation of water demand by Wada et al. (2014, https://doi.org/10.5194/esd-5-15-2014);

  • calculation of water withdrawal, consumption, and return flows by de Graaf et al. (2014, https://doi.org/10.1016/j.advwatres.2013.12.002), Wada et al. (2014, https://doi.org/10.5194/esd-5-15-2014), and Erkens and Sutanudjaja (2015, https://doi.org/10.5194/piahs-372-83-2015).

Furthermore, for details about coupling to MOFLOW we refer to

• one-way coupling from Sutanudjaja et al. (2011, https://doi.org/hess-15-2913-2011) and de Graaf et al. (2017, https://doi.org/10.1016/j.advwatres.2017.01.011);

• two-way coupling from Sutanudjaja et al. (2014, https://doi.org/10.1002/2013WR013807).

2.3 Description of the modules

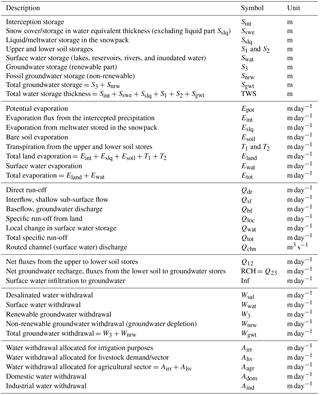
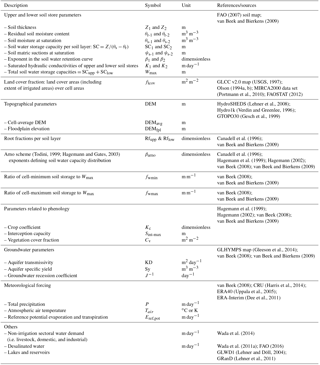
Hereafter, we briefly describe the main features of the five modules. Additionally, a (non-exhaustive) list of the model state and flux variables is provided in Table A1, whereas Table A2 lists the model inputs and parameters, including their sources.

2.3.1 Meteorological forcing module

Meteorological forcing of PCR-GLOBWB 2 uses time series of spatial fields of precipitation, temperature, and reference evaporation. Reference potential evaporation can be prescribed or calculated within the model and is used in the land surface module to calculate land-cover-specific potential evaporation based on crop factors of the various land cover types according to the FAO guidelines (Allen et al., 1998). There are two options for calculating reference potential evaporation: (1) using Hamon (1963) in case only daily mean temperature is available, or (2) using Penman–Monteith following the FAO guidelines (Allen et al., 1998) if net radiation, wind speed, and vapour pressure deficit are additionally available. See van Beek et al. (2008) for details. The resulting land-cover-specific potential evaporation is subsequently used to compute the actual evaporation for different land cover types in each cell. Apart from the calculation of evaporation, temperature is also used to partition precipitation into snow and rain and to drive snowmelt.

2.3.2 Land surface module

This core module of PCR-GLOBWB 2 covers the land–atmosphere exchange, the vertical flow among soil compartments and the eventual groundwater recharge, snow and interception storage, and the run-off generation mechanisms. These processes are simulated over a number of land cover types and aggregated proportionally based on land cover fractions within a model cell. Users can specify their own land cover classification and introduce their own land cover parameterization. The number of land cover types is configurable. The standard parameterization of PCR-GLOBWB 2 carries four land cover types consisting of tall natural vegetation, short natural vegetation, non-paddy irrigated crops, and paddy irrigated crops (i.e. wet rice). There is also a parameterization set for six land cover types (Bosmans et al., 2017), albeit still at 30 arcmin resolution only, which includes distinct types for pasture and rain-fed crops. For the standard four land cover parameterization of PCR-GLOBWB, applied in this paper, the land cover types of pasture and rain-fed crops are integrated into the short natural vegetation type.

For each land cover type, separate soil conditions can be specified. It should be noted that the soil and vegetation conditions are in any case fully spatially distributed. Thus, vegetation properties (e.g. crop factor; leaf area index, LAI) and soil properties (depth, saturated hydraulic conductivity, etc.) vary not only among land cover types but may also vary from cell to cell (e.g. per climate zone). In the standard parameterization, vegetation properties vary over the year using a monthly climatology of phenology and crop calendars (i.e. for the crop factor and LAI). The application of irrigation water for paddy and non-paddy irrigation is carried out by the irrigation and water use module. It is based on the FAO guidelines of Allen et al. (1998) and is dependent on the actual soil water storage (S₁, S₂) or paddy-inundated water storages. All fluxes, from and to the land surface module in Fig. 1, are thus calculated separately per land cover type. The resulting vertical fluxes for each land cover type are interception evaporation, bare soil evaporation, snow sublimation, and vegetation-specific transpiration. In the soil column, vertical fluxes are driven by degrees of saturation of soil layers and interact with the underlying groundwater store, S₃ (see e.g. van Beek and Bierkens, 2009; Sutanudjaja et al., 2011; Sutanudjaja, 2012, for detailed explanation). Surface run-off (Q_dr, from precipitation and snowmelt) consists of infiltration excess run-off and saturation excess run-off following a sub-grid approach that mimics variable source areas, i.e. the improved Arno scheme (Todini, 1996; Hagemann and Gates, 2003). Interflow or stormflow (Q_sf), mostly occurring in regolith soils on hillslopes, is also handled with a sub-grid approach based on a run-off parameterization by Sloan and Moore (1984). All fluxes are computed per land cover type and balanced with the available storage to arrive at the net flux that is used to update the storages for the next time step. Also, to report the overall fluxes per cell, and to pass these to other modules, the land-cover-specific fluxes are subsequently averaged (weighted by land cover type fractions).

For the standard parameterization of the land surface module the following data sets are combined (see Table A2): the cell fractions of various non-irrigation land cover types are based on the map of Global Land Cover Characteristics Database (GLCC) version 2.0 (Loveland et al., 2000) with the land cover classification following Olson (1994a, b) and the parameter sets from Hagemann et al. (1999) and Hagemann (2002). Irrigation land cover types (i.e. paddy and non-paddy), including their crop calendars and growing season lengths, are parameterized based on the data set of MIRCA2000 (Portmann et al., 2010) and the Global Crop Water Model of Siebert and Döll (2010). We refer to van Beek et al. (2011) for detailed descriptions.

2.3.3 Groundwater module

The groundwater module calculates groundwater storage dynamics subject to recharge and capillary rise (calculated by the land surface module), groundwater discharge (Q_bf, in case of a positive groundwater storage), and riverbed infiltration (Inf). Groundwater discharge (assumed to be the same as groundwater baseflow here) depends on a linear storage–outflow relationship ($Q_{\text{bf}}=S_{\mathrm{3}}/J)$ in which the proportionality constant J is calculated following the drainage theory of Kraijenhoff van de Leur (1958) based on drainage network density and aquifer properties. Riverbed infiltration occurs only in the case that Q_bf becomes 0 by groundwater withdrawal. Under persistent groundwater withdrawal (calculated with the irrigation and water use module) that is larger than the sum of recharge and riverbed infiltration, the groundwater storage S₃ is allowed to become negative. In this case, the part of the withdrawn groundwater in excess of the input (recharge and riverbed infiltration) is seen as non-renewable groundwater withdrawal leading to groundwater depletion (permanent loss of groundwater from storage). In case withdrawal becomes smaller than the input, the remaining input is used to first fill the negative storage to zero, before baseflow Q_bf commences again. As an alternative, it is also possible to limit the maximum volume of non-renewable groundwater that can be extracted.

It is possible to use a full-fledged groundwater flow model based on MODFLOW (Harbaugh et al., 2000) coupled to PCR-GLOBWB 2 in order to calculate groundwater heads and flow paths. This can be performed as a one-way coupling in which PCR-GLOBWB 2 is first run with the standard groundwater module (reservoir S₃ with only vertical fluxes) to yield time series of net groundwater recharge (recharge – capillary rise) and surface water levels. These fluxes and inputs are subsequently used to force the groundwater flow model (see e.g. Sutanudjaja et al., 2011; de Graaf et al., 2017). Another possibility is to use a two-way coupling in which the groundwater module of PCR-GLOBWB 2 is replaced by the groundwater flow model. In this case, at each time step fluxes are exchanged between the groundwater model and the land surface module, and the groundwater model and the surface water routing module (Sutanudjaja et al., 2014).

2.3.4 Surface water routing module

Following an eight-point steepest-gradient algorithm across the terrain surface (local drainage direction), all cells of the modelled domain are connected to a strictly convergent drainage network that together makes up the river basins and sub-basins of the model domain. The lowermost cell is either connected to the ocean or to an endorheic basin. Per cell, the sum of the three daily run-off fluxes (Fig. 1) is aggregated and routed along the drainage network until passing the lowermost cell and being removed from the model. Routing can be carried out in three ways of increasing complexity: (1) simple accumulation of the fluxes over the drainage network, (2) a travel-time characteristic solution (Karssenberg et al., 2007), and (3) the kinematic wave solution.

The first method is typically aggregated over longer time steps (e.g. month or year) that are larger than the travel times of water along the longest river length. The second routing method includes an estimation of cell flow velocity based on average discharge from the last 5 years and Manning's equation, which assumes the energy slope to be equal to the bed slope. This estimated velocity is used to move the volume of water in the channel of a cell the corresponding distance within one daily time step along the drainage network. This method works reasonably well for relatively steep rivers in humid climates for which the friction slope is close to the bed slope and the rivers are equally filled with water throughout the year. The third method is the kinematic wave approximation of the Saint-Venant equations with flow described by Manning's equation. Also, here, it is assumed that friction slope and bed slope are equal, which makes it valid for rivers without backwater effects. The kinematic wave is solved using a time-explicit variable sub-time stepping scheme based on the minimum Courant number. Of these methods, the kinematic wave solution simulates the propagation of the flood wave more realistically while the others provide an expedient means to approximate discharge over longer periods.

Using the kinematic wave method, it is possible to model floodplain inundation, which occurs if the discharge exceeds the bankfull capacity of a channel. The excess discharge volume is spread over the entire cell from the lowest part of the cell (based on a higher-resolution sub-grid DEM) yielding a flooded area with an approximated flood depth. In case of flooding, the simulated river flow is impacted by adjusting the wetted area and wetted perimeter and calculating a weighted Manning coefficient from the individual Manning coefficients of the floodplains and the channel.

Lakes and reservoirs are part of the drainage network. Lakes and reservoirs can extend over multiple cells, in which case the storage is subdivided by area to ensure that lake and reservoir levels are the same across their extent. The active storage of lakes and the actual storage of reservoirs are dynamically updated; for the lake outflow a standard storage–outflow relationship based on a rectangular cross section over a broad-crested weir (Bos, 1989) is used, while reservoirs follow a release strategy. This strategy is, by default, aimed at passing the average discharge, while maintaining levels between a minimum and maximum storage (Wada et al., 2014), but more elaborate strategies that take account of downstream water demand are possible (e.g. van Beek et al., 2011). Lakes and reservoir areas change based on global volume–area relationships. All surface water areas, which can be classified into several water types including river channels, inundated floodplains, lakes and reservoirs, are subject to open water evaporation calculated from reference potential evaporation multiplied with factors depending on water types and depths. Moreover, surface waters are subject to surface water withdrawal calculated with the irrigation and water use module.

If the kinematic wave approach is used, it can also be augmented with an energy routing scheme to simulate surface water temperature (van Beek et al., 2012). Finally, it should be noted that it is possible to run the routing routine from PCR-GLOBWB 2 as a stand-alone routine, which allows it to be fed with the specific discharge from other land surface models.

The routing methods that are available in PCR-GLOBWB 2 will yield significant errors for wide lowland rivers in which backwater effects are important. In this case, it is possible to replace the surface water module for part of the modelling domain with hydrodynamic models solving the shallow water equations (Hoch et al., 2017a). Hoch et al. (2017b) developed a generic coupler for this purpose that enables coupling to multiple hydrodynamic modelling codes (https://doi.org/10.5281/zenodo.597107).

Although any data set can be used to define the drainage network and locate the lakes and reservoirs, the standard parameterization of PCR-GLOBWB 2 that runs globally uses the drainage network derived from the high-resolution 30 arcsec HydroSHEDS (Lehner et al., 2008) combined with 30 arcsec GTOPO30 (Gesch et al., 1999) and 1 km Hydro1k (Verdin and Greenlee, 1996; USGS EROS Data Center, 2006), lakes taken from the Global Lakes and Wetlands Database (GLWD) (Lehner and Döll, 2004) and reservoirs obtained from GRanD (Lehner et al., 2011).

2.3.5 Irrigation and water use module

In PCR-GLOBWB 1 water demand was calculated separately from the hydrology and water availability calculated as a post-processing step by subtracting upstream demand (Wada et al., 2011a, b). In PCR-GLOBWB 2 water use (withdrawal and consumption) is fully integrated. Hereafter, the main features of the irrigation and water use module are described in the following order: water demand, water withdrawal, water consumption, and return flows.

Water demand

Irrigation water demand is calculated based on the crop composition (which changes per month and includes multi-cropping) and the irrigated area per cell. As stated above, these are obtained from MIRCA2000 (Portmann et al., 2010) and the Global Crop Water Model (Siebert and Döll, 2010). In the standard PCR-GLOBWB 2 parameterization the irrigated areas change over time. In want of detailed data, fractions of paddy and non-paddy irrigation, as well as the crop composition per month, stay fixed (as obtained from MIRCA2000), while the total irrigated area per cell changes over time and is based on the FAOSTAT (http://www.fao.org/faostat/en/\#home, last access: 15 September 2017) reported irrigated areas. Irrigation water demand is computed using the FAO guidelines (Doorenbos and Pruit, 1977; Allen et al., 1998): in case of non-paddy irrigation, water is applied whenever soil moisture falls below a pre-set value and then the soil column is replenished up to field capacity. In case of paddy irrigation, the water level is kept at a water depth of 5 cm above the surface until the late crop development stage (∼ 20 days) before the harvest. After that, no irrigation is applied anymore such that the water level is allowed to drop to zero under infiltration and evaporation (Wada et al., 2014). The net irrigation demand is augmented to account for limited irrigation efficiency and losses. In order to obtain irrigation water demand including losses, i.e. gross irrigation demand, net irrigation water demand is multiplied with (1+f_I), with f_I as a country-specific loss factor obtained from Rohwer et al. (2007).

Non-irrigation water demand covers three sectors: industry, households, and livestock. For each of these sectors, the gross demand and net demand are prescribed to the model. The calculation of net non-irrigation water demand, which varies with time, follows methods developed by Wada et al. (2014). We refer to Wada et al. (2014) for an extensive description. Trends in water demand are prescribed on an annual basis as a function of population, electricity demand, and gross domestic product (GDP) per capita. In addition, domestic water demand exhibits a seasonal variation on the basis of temperature. Domestic and industrial gross water demand is calculated from net water demand using a country-specific recycling ratio (RC) (based on development stage or GDP per capita and additionally access to domestic water demand): gross = net ∕ (1−RC). This takes into account that much of the domestic and industrial water is not consumed but returned as surface water. For livestock, the return flow is assumed to be zero, meaning all water is consumed.

Water withdrawal

The water withdrawal estimation is based on the work by de Graaf et al. (2014) and Wada et al. (2014). In PCR-GLOBWB 2 water withdrawal is set equal to gross water demand (summed over all the sectors) unless sufficient water is not available. In that case, water withdrawal is scaled down to the available water and then allocated proportionally to gross water demand per sector. Thus, no allocation preference is available in the standard parameterization of PCR-GLOBWB 2.

Water can be abstracted from three sources: surface water, groundwater (fossil and non-fossil), and desalinated water. The latter is prescribed (Wada et al., 2011a), while the fractions of the other two sources are determined as a function of their relative abundance. Groundwater and surface water availability are determined based on 2-year running means of groundwater recharge and river discharge respectively, thus keeping track of the prevalence of local resources and their temporal change (de Graaf et al., 2014). These fractions determine, on a monthly basis, from which source water is abstracted. Surface water withdrawal is ceased if river discharge falls below 10 % of the long-term average yearly discharge under naturalized flow conditions (determined by running the model without withdrawal). If, for some reason, the surface water amount is insufficient, the model falls back on groundwater to meet the resulting gap. Groundwater is first abstracted from the renewable groundwater storage, and if this is not present, non-renewable groundwater is abstracted. The amount of groundwater that can be abstracted is, however, capped by the groundwater pumping capacity, which is based on data from the IGRAC GGIS database. The described dynamic allocation scheme is not always in line with local preferences or the infrastructure. However, there is a possibility to use fractions of groundwater and surface water withdrawal reported in the literature. For urban areas, we rely on the data set of McDonald et al. (2014) that states whether a surface water distribution infrastructure is available. If this is the case, industrial and domestic water withdrawals are mainly taken from surface water before abstracting groundwater. If surface water infrastructure is limited, groundwater source is prioritized (see e.g. Erkens and Sutanudjaja, 2015). For urban areas that are not in the McDonald (2014) data set, we give preference to the dynamic allocation scheme. For irrigation, we use the ratios supplied by Siebert et al. (2010) in regions where they are said to be reliable. In regions where they are not fully reliable, we take the average ratio provided by Siebert et al. (2010) and the one provided by the dynamic allocation scheme. For regions where the data of Siebert (2010) are not reliable (i.e. extrapolated data), we give preference to the dynamic allocation scheme.

Moreover, we cannot assume that all the water demand is supplied from surface water and groundwater resources in the same cell. Ideally, data about local water redistribution networks and inter-basin transfers should be used to define surface water and groundwater service areas. Unfortunately, this information is not available at the global scale. Therefore, in our current parameterization of PCR-GLOBWB 2, we pool water availability of desalinated and surface water over zones of approximately 1 arcdeg by 1 arcdeg size that are truncated by country borders if applicable. For groundwater, 0.5 arcdeg zones are used. The downside of the current scheme is that a cell does not always have access to its nearest water resource if this lies outside its prescribed service area.

Water consumption and return flows

In case of irrigation, all the withdrawn water is applied to the soil (non-paddy) or the water level on the field (paddy). Part of that water is lost by transpiration and part by soil and open-water evaporation. Transpiration and evaporation together make up the irrigation water consumption. The remaining part of irrigated water is lost by percolation and contributes to groundwater recharge as return flow. Irrigation efficiency (not including conveyance losses) could also be calculated after the fact by the difference between withdrawal and transpiration. In the case of domestic and industrial water use, water consumption depends on the RC and equals withdrawal × (1 − RC), while withdrawal × RC constitutes return flow. All return flow is added to the surface water. For livestock, the consumption is set equal to the withdrawal and no return flow is assumed.

2.4 Model code

The original PCR-GLOBWB version 1 (van Beek et al., 2011) was written in the PCRaster scripting language. PCRaster (Wesseling et al., 1996) is a high-level programming language that started as a dynamic raster-based Geographical Information System (GIS) and is tailored to spatiotemporal modelling for environmental and earth science applications. The generic nature of PCRaster with its many pre-existing built-in hydrological functions and its syntax that reads like pseudo-code generally results in concise model codes, short development times, and limited programming errors. Karssenberg et al. (2010) developed a PCRaster Python package such that PCRaster functions, implemented in C$++$, can also be called via Python (http://www.python.org/). Using PCRaster Python makes it possible for students and beginner modellers to contribute to the model quickly, while it allows experts to be more productive and focus on the science rather than on the programming language syntax. Realizing the aforementioned advantages, PCR-GLOBWB, particularly starting from this version 2, has been rewritten in the Python scripting language.

To allow for exchanges of model components and therefore evaluate different model configurations, a component-based development approach (e.g Argent, 2004; Castronova and Goodall, 2010) was followed while developing the PCR-GLOBWB 2 model code. Each of the PCR-GLOBWB scientific modules described in Sect. 2.3 is implemented in a separate Python class that needs to implement initialization and update methods. The latter designates changes of states and fluxes per time step. Each module is initialized and executed by iteratively calling the update method via a main model script.

To run the model, a so-called initialization file or configuration file is used (with extension .ini). In this file the following aspects are defined: the spatial and temporal domain, the time step, the settings of the different modules (e.g. with surface water routing, human water use, or not), and the locations and names of the parameter files and forcing files. PCR-GLOBWB 2 uses NetCDF files for most input and all output, thus making it easier to exchange data with other scientists and use existing tools to analyse their output.

PCR-GLOBWB 2 generally runs best under Linux. In order to run PCR-GLOBWB the following additional software needs to be installed: PCRaster version 4, Python version 2.7 with Python packages NumPy and netCDF4, and GDAL version 1.8 or higher.

2.5 Differences between PCR-GLOBWB 1 and 2

PCR-GLOBWB 2 has the following new capabilities compared to PCR-GLOBWB 1 (see van Beek et al., 2011; Wada et al., 2011):

• the model was completely rewritten in PCRaster Python and now has a modular structure;

• the inputs and outputs are in the form of NetCDF files and output can be reported for daily monthly and yearly time steps;

• parameterizations are available at 30 and 5 arcmin resolutions;

• water use (demand, withdrawal, consumption, and return flow) is fully integrated;

• distinction is made between paddy and non-paddy irrigation and irrigation follows FAO guidelines;

• three different options for surface water routing are available and a surface water temperature module is fully integrated with the routing scheme;

• it is possible to run surface water routines separately with specific discharge from other sources (e.g. other land surface models);

• PCR-GLOBWB 2 can be coupled to a two-layer transient groundwater model (Sutanudjaja et al., 2014; de Graaf et al., 2017) and to the hydrodynamic models Delft3D Flexible Mesh (Kernkamp et al., 2011) or LISFLOOD-FP (Bates et al., 2010; Hoch et al., 2017b).

3 Model demonstration and evaluation

To test and evaluate the performance of PCR-GLOBWB 2, we ran the model at both 30 and 5 arcmin resolution over the period 1958–2015. We compared the results of both simulations with discharge data from the Global Runoff Data Centre (GRDC, 2014), with total basin water storage estimates from GRACE (Gravity Recovery and Climate Experiment; Wiese, 2015) and with water withdrawal data from the FAO AQUASTAT database (FAO, 2016).

3.1 Model run setup

3.1.1 Parameterization

We used the standard parameterization (parameters, forcing, and their sources in Table A2) of PCR-GLOBWB 2 at 30 and 5 arcmin spatial resolutions to simulate global hydrology at daily resolution over 1958–2015. Outputs were reported as monthly averages. The parameterization was mostly unchanged from that given in van Beek and Bierkens (2009), but newer data sets, such as the GRAND (Lehner et al., 2011) data set for reservoirs and MIRCA (Portmann et al., 2010) for crop areas, were used if available. We stress that no calibration was performed. We ran the model with human water use options turned on and used the travel-time characteristic solution routing option.

3.1.2 Forcing

The forcing data set is based on time series of monthly precipitation, temperature, and reference evaporation from the CRU TS 3.2 data set of Harris et al. (2014) downscaled to daily values with ERA40 (1958–1978, Uppala et al., 2005) and ERA-Interim (1979–2015, Dee et al., 2011). CRU is specified at 30 arcmin spatial resolution and directly usable. We used ERA40 and ERA-I results that had been resampled by ECMWF's resampling scheme from their original resolutions (∼ 1.2 and ∼ 0.7^∘) to 30 arcmin first. Here, resampling means a form of spatial downscaling whereby the values of the larger ERA40 and ERA-I grid cells are assigned to the cell centres and then spatially interpolated onto 30 arcmin grids. Precipitation was temporally downscaled by first applying a threshold of 0.1 mm day⁻¹ to the ERA daily time series to estimate the number of rain days for ERA. The amount of rainfall below this threshold was proportionally allocated to the rain days. Next, the daily rainfall totals were scaled in order to reproduce the CRU monthly precipitation total using multiplicative scaling. Equally, monthly reference potential evaporation, computed with Penman–Monteith from the CRU data set, was scaled using multiplicative scaling and downscaled to daily data proportional to Hamon (1967) evaporation calculated from daily ERA temperatures. We elected not to calculate Penman–Monteith reference evaporation directly from the ERA40 and ERA-I data, in order to avoid the large calculation times needed to process the required meteorological values. For the air temperature, an additive scaling factor was used. To better simulate snow dynamics for the 5 arcmin model, the temperature values from CRU were further spatially downscaled to 5 arcmin using a temperature lapse rate derived from the higher-resolution CRU CL 2.0 climatology (New et al., 2002). For areas in which the number of stations underlying the CRU data set was found to be small, preference was given to directly using the meteorological data from ERA. The method used to create the forcing data set is described more extensively in van Beek (2008).

3.1.3 Spin-up

The large groundwater response times for certain regions (e.g. Niger and Amazon) requires substantial spin-up for the groundwater volumes to be in equilibrium with the current climate. To reach this equilibrium, the model was spun up using the average climatological forcing over the years 1958–2000 back to back for 150 years to reach a dynamic steady state. This spin-up was executed under naturalized conditions, which means no reservoirs and no human water use.

3.1.4 Computation time and parallelization

The models were run on Cartesius, the Dutch national supercomputer (https://userinfo.surfsara.nl/systems/cartesius, last access: 15 September 2017). Without parallelization, the wall clock time for a 1-year global simulation run of the 30 arcmin model was about 1 h. This entails that a 1-year global simulation run with the 5 arcmin model might result in wall clock times of at least 36 h. Hence, to speed up computation, the 5 arcmin model domain was divided into 53 groups of river basins such that it could be run as 53 separate processes. With this simple parallelization technique, the wall clock time for a 1-year simulation run of the 5 arcmin model was reduced to about 1 h again. Note that these computation times were obtained for simulations with the travel-time characteristic routing option. Calculation times would have been significantly longer if the kinematic wave routing had been used (e.g. about 6 h for a 1-year 5 arcmin global run including parallelization).

3.2 Data used for comparison

3.2.1 River discharge

We used discharge stations from GRDC (2014) to compare simulated discharge from PCR-GLOBWB 2 with monthly reported discharge. From all the globally available stations in the database, we selected a subset of stations using the following criteria: (1) allowing a not-more-than 15 % difference in the catchment area between PCR-GLOBWB 2 and the area reported with the GRDC discharge station, (2) not more than 1 cell distance between the station location and the nearby location of a river in PCR-GLOBWB 2, and (3) at least 1 year of discharge data. This yielded 5363 stations for the 5 arcmin simulation, 3910 stations for the 30 arcmin simulation, and 3597 stations fulfilling the criteria for both resolutions. The minimum, median, and maximum catchment sizes for the GRDC stations at the 5 arcmin resolution are respectively 29, 2730, and 4.68×10⁶ km² and 31, 6560, and 4.68×10⁶ km² at the 30 arcmin resolution. As we jointly compared the performance of both simulations, we used the set of 3597 locations throughout. The average time series length of these stations is equal to 36 years.

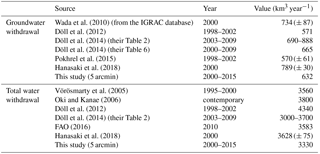
Table 1 Global water balance components and human water withdrawal (km³ year⁻¹ and mm year⁻¹) over the period 2000–2015 as obtained from the 30 and 5 arcmin simulations. The numbers are shown to high significance to show the water balance closure. This does not mean that we pretend to know global discharge with a cubic-kilometre accuracy (actual accuracy of the large fluxes is more on the order of 10³ km³).

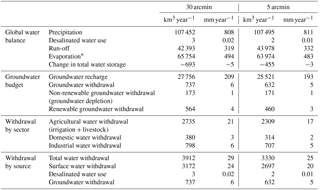
^* Includes consumptive water use for livestock, domestic, and industrial sectors.

3.2.2 Total water storage

We compared total water storage (TWS) as simulated by PCR-GLOBWB 2 with the TWS estimated from GRACE (Gravity Recovery and Climate Experiment) gravity anomalies. We used the JPL GRACE Mascon product RL05M (Wiese, 2015; Watkins et al., 2015; Wiese et al., 2016). Scanlon et al. (2016) suggest that recent developments in mascon (mass concentration) solutions for GRACE have significantly increased the spatial localization and amplitude of recovered terrestrial TWS signals. They also claim that one of the advantages of using the mascon solutions relative to traditional SH (spherical harmonic) solutions is that it makes it much easier for non-geodesists to apply GRACE data to hydrologic problems. Note that although the data of JPL RL05M are represented on a 30 arcmin lat–long grid, they represent the 3 × 3 arcdeg equal-area zones, which is the actual resolution of JPL RL05M. We compared trends on a pixel-by-pixel basis. Given the coarse resolution of GRACE products of about 300 km by 300 km, we compared correlations only for major river basins with an area of 900 000 km² and up.

3.2.3 Water withdrawal

The water withdrawal for a large number of countries is taken from FAO's AQUASTAT database (FAO, 2016). These data are on average reported every 5 years. We compared simulated water withdrawal per sector and per water source (surface water and groundwater) with reported values per country and per reporting period, whenever available.

3.3 The global water balance simulated at 30 and 5 arcmin

We calculated the main global water balance components from the 30 and 5 arcmin simulations over the period 2000–2015. The results in Table 1 show that there are some differences between the two model runs, but values are on the same order of magnitude. The small difference in precipitation is due to the fact that the area of the land cells is slightly different at the two resolutions. Differences in evaporation and run-off show that the run-off and evaporation parameterization of PCR-GLOBWB 2 is not entirely scale consistent. Differences in evaporation may also be causing the differences in irrigation water demand, which in turn may explain the differences in water withdrawal. Recently, Samaniego et al. (2017) applied their multiscale parameter regionalization (MPR; creating spatially variable parameter fields) technique to PCR-GLOBWB 2 for the Rhine basin, showing that parameterizations that yield the same hydrological fluxes at different resolutions are possible. However, a global application of this method to all PCR-GLOBWB 2 parameters is not possible yet. Nonetheless, when comparing the results of both model runs with data reported in the literature, it shows that the global water balance components are similar to recent assessments (e.g. by Rodell et al., 2015), and groundwater withdrawal and total withdrawal estimates match those of previous studies (see Table 2).

Table 2 Groundwater withdrawal and total water withdrawal compared to other studies (km³ year⁻¹).

From Table 1, it can also be seen that there is a negative change in total terrestrial water storage in both model runs. Table 1 shows that this can only be partly explained by groundwater depletion, which is localized to certain regions (see also Sect. 3.4.2). Further analysis shows that this change can also be attributed to the trends in precipitation forcing used, particularly over the tropics.

3.4 Evaluation of the 30 and 5 arcmin simulations

3.4.1 Discharge

When evaluating the simulated discharge with discharge observations from GRDC, we used the monthly values and calculated three different measures. The first one is the correlation coefficient between monthly simulated and observed GRDC time series, which is a measure of reproducing correct timing of high and low discharge. A correlation coefficient of 1 indicates perfect timing. The second measure is the Kling–Gupta efficiency coefficient or KGE (Gupta et al., 2009), which equally measures bias, differences in amplitude, and differences in timing between monthly simulated and observed GRDC time series. The KGE varies between 1 and minus infinity, where 1 means a perfect fit in terms of bias, amplitude and timing. The last metric is the anomaly correlation, i.e. the correlation among monthly time series after the seasonal signal (climatology) has been removed. This statistic measures the ability of the model to correctly simulate timing of seasonal and inter-annual anomalies from the yearly climatology. This is to test if the model is able to capture the monthly-scale and inter-annual anomalies in discharge (i.e. on the monthly scale) when the dominant seasonal trend is removed from observations and simulations. An anomaly correlation of 1 indicates perfect characterization of inter-annual anomalies and values below 0 indicate a lack thereof.

Figure 2 Maps of correlation between simulated and observed discharge time series for 3597 GRDC discharge stations; (a) results for the 5 arcmin simulation; (b) difference between results for 5 and 30 arcmin simulations.

Figure 3 Histograms of evaluation statistics showing the correlation and Kling–Gupta efficiency (KGE) values for the simulated discharge for the 30 and 5 arcmin simulations based on 3597 GRDC discharge stations, (a) correlation 30 arcmin simulation, (b) correlation 5 arcmin simulation, (c) KGE 30 arcmin simulation, and (d) KGE 5 arcmin simulation. Note that the percentage catchments with KGE < −1 are 21 and 12 % for 30 and 5 arcmin respectively.

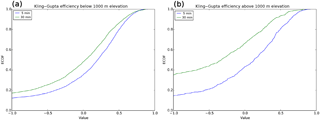
Figure 4 Cumulative frequency distributions of Kling–Gupta efficiency (KGE) values for GRDC stations that are positioned below (a) and above (b) 1000 m a.m.s.l. It can be expected that for the stations above 1000 m, the upstream area is influenced by snow dynamics.

Figure 2 shows maps of the correlation coefficients for the GRDC stations considered and Fig. 3 shows histograms of correlation and KGE values. Both figures show that the evaluation results of the 5 arcmin simulation are generally better than those of the 30 arcmin simulation. For the 30 arcmin model, the number of catchments with KGE > 0, 0.3, and 0.6 are equal to 48, 26, and 7 % of the total catchments respectively. For the 5 arcmin model, these values are respectively equal to 63, 40, and 12 % of the total catchments. Note that for both runs the standard parameterization was used. Possible explanations for the better performance of the 5 arcmin run are a better delineation of the shape of the basins, particularly the smaller ones, a better characterization of basin relief and the drainage network, more accurate sub-grid parameterization of soil and land cover due to a smaller scale gap that needs to be overcome, better estimates of the basin storage, and better snow dynamics due to the downscaling of temperature to 5 arcmin resolution. The KGE values are less favourable than the correlation coefficients. This is mostly due to biases in run-off caused by incorrect meteorological forcing. It is difficult to exactly assess which of these factors are most important in determining the improvement. Inspecting the histograms of correlation and KGE (Fig. 3) shows that the improvement is mostly apparent for the smaller sized catchments, which supports the notion that a better delineation of the catchments' shape, topography, and drainage network could be the cause. However, disentangling these individual effects would require further study. To investigate the possible effects of better snow dynamics, we classified the GRDC stations into stations below 1000 m altitude (above mean sea level) and those above 1000 m. The GRDC stations above 1000 m are expected to experience precipitation falling as snow during periods of the year. The results in Fig. 4 clearly show that the improvement is larger for the higher GRDC stations. This supports the explanation that better snow dynamics due to temperature lapsing in combination with a better resolved digital elevation model is partly responsible for the superior results at 5 arcmin. We also investigated if improvements were notably different among climate zones, by separately calculating KGEs for GRDC stations in the Köppen–Geiger zones A (tropical), B (desert), C (temperate), and D (continental). The results (not shown) show that the improvement is equally visible for climate zones A, B, and C and less so for D (continental). Without further analysis this is difficult to explain. Note, however, that the continental climate zone is somewhat under-represented in the GRDC data set due to the low measurement densities over Russia, although it is well represented in the US. Thus, it may be that the global improvements shown in Fig. 3 are somewhat positively biased.

Figure 5 Histograms of evaluation statistics showing the anomaly correlation for the simulated discharge for the 30 and 5 arcmin simulations based on 3597 GRDC discharge stations, (a) anomaly correlation half-arc-degree simulation, and (b) anomaly correlation 5 arcmin simulation.

The maps of correlations (Fig. 2) show the best results in Europe and North America where the meteorological forcing is generally more accurate as a result of more data used in the reanalysis products and higher station availability in the CRU data set. Also, monsoon-dominated basins are well simulated due to the strong seasonal nature of both forcing and related discharge. The improvement of the 5 arcmin simulation over the 30 arcmin simulation in Europe is mostly seen in the Alps and the Norwegian mountains. This reflects the fact that topography and thus snow dynamics is better represented at higher resolution as shown in Fig. 4. The least accurate results are obtained for some of the African rivers, in particular the Niger, where the groundwater recession coefficients are probably overestimated and inland delta evaporation is underestimated, for some rivers in the Rocky Mountains, which may be the result of errors in snow dynamics, and for continental eastern Europe, which is most likely explained by an overestimation of the groundwater recession constants.

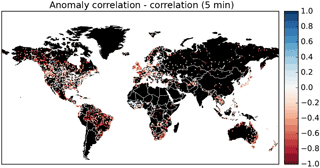
Figure 6 Map showing for the 5 arcmin run the difference between the correlation and the anomaly correlation between simulated and observed discharge time series for 3597 GRDC discharge stations; negative values mean that the correlation is higher than the anomaly correlation.

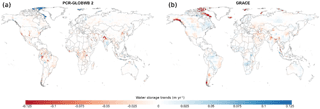
Figure 7 Comparison of PCR-GLOBWB 2 total water storage trends (m year⁻¹) with those estimated with GRACE over the period 2003–2015. (a) TWS trends simulated with PCR-GLOBWB at 5 arcmin resolution (∼ 10 km at the Equator). Negative values indicate declining TWS (e.g. groundwater-depleted regions). (b) TWS trends obtained based on the GRACE JPL RL05M Mascon product. The GRACE data were resampled to the resolution of 30 arcmin, but they actually represent the 3 × 3 arcdeg (∼ 300 km × 300 km) area, which is the native resolution of the GRACE signal.

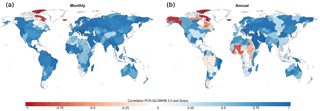
Figure 8 (a) Correlation between monthly TWS time series simulated by PCR-GLOBWB 2 and the GRACE JPL RL05M Mascon product over the period 2003–2015. (b) Comparison of annual TWS series (inter-annual variability). Comparison is only performed for the larger basins over 900 000 km², conforming to the 3 × 3 arcdeg resolution of GRACE.

Figure 9 Country water withdrawal (km³ year⁻¹) by source and evaluation of simulations with PCR-GLOBWB 2 with reported values in AQUASTAT (FAO, 2016). The scatter plots on the left (a, c, e) are for the period 1968–1992, while the right ones (b, d, f) are 1993–2015. The uppermost plots (a, b) are for total water withdrawal, the middle ones (c, d) are groundwater withdrawal, and the lowermost charts (e, f) are surface water withdrawal. The regression coefficient is based on regression to non-log-transformed data with the intercept kept at zero.

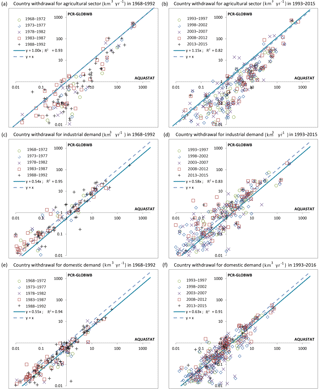
Figure 10 Country water withdrawal (km³ year⁻¹) by sector and evaluation of simulations with PCR-GLOBWB 2 with reported values in AQUASTAT (FAO, 2016). The scatter plots on the left (a, c, e) are for the period 1968–1992, while the right ones (b, d, f) are 1993–2015. The uppermost plots (a, b) are for withdrawal for agricultural purposes, the middle ones (c, d) are industrial withdrawal, and the lowermost charts (e, f) are domestic. The regression coefficient is based on regression to non-log-transformed data with the intercept kept at zero.

The histograms of the anomaly correlation are shown in Fig. 5. The anomaly correlations are generally lower than the correlations, showing that seasonality explains part of the skill in many regions where seasonal variation is dominant when compared to intra-annual or inter-annual variability. Clearly, the 5 arcmin results are much better than those of the half-degree simulation, indicating a higher skill with regard to capturing inter-annual anomalies. Figure 6 shows a map of the difference between the anomaly correlation and the correlation for the 5 arcmin case. This map shows that there are some regions where the anomaly correlation is better than the correlation (blue colours), e.g. snow-dominated regions in Canada and the Niger basin. These are catchments where the model has difficulty reproducing the correct seasonality as a result of errors in snow dynamics (Canada) or groundwater dynamics (Niger). Also, in the case of the Niger River, not representing the inner delta flooding and resulting high evaporation may be the cause of poor seasonal timing of discharge.

3.4.2 Total water storage

Figure 7 compares the trends in 5 arcmin simulated TWS with those from GRACE, estimated as the average change in metres per year over the period 2003–2015. Generally, the PCR-GLOBWB 2 simulation is able to capture major groundwater-depleted regions as suggested by GRACE, such as those in the Central Valley aquifer, the High Plains aquifer, the North China Plain aquifer, and parts of the Middle East, Pakistan, and India. For these regions, the absolute rates of TWS change (i.e. TWS declines) of PCR-GLOBWB 2 are generally larger, while the spatial pattern in the GRACE map tends to be smoother. This is mainly due to the lower resolution and spatial averaging used in the GRACE product, as well as the fact that the current PCR-GLOBWB 2 simulation does not include lateral groundwater flow among cells. In the polar regions where GRACE estimates mass loss due to melting glaciers and ice sheets, PCR-GLOBWB 2 simulates accumulation as a result of a lack of glacier parameterization. Finally, there are some clear differences over the Amazon and some parts of Africa. A possible explanation are errors in meteorological forcing data, which are not very accurate in these parts, but also problems with the over-estimation of PCR-GLOBWB's groundwater response times in these regions, which therefore fail to be sufficiently sensitive to recent changes in terrestrial precipitation.

Further analyses were conducted at basin-scale resolution, for which both TWS time series of PCR-GLOBWB 2 and GRACE JPL RL05M were averaged over a river basin area map derived from the 5 arcmin PCR-GLOBWB drainage network. We identified all river basins with sizes larger than 900 000 km², which is similar to the GRACE resolution. Smaller river basins were merged to the nearest river basins or grouped together. For the remaining map of large basins, the correlations between PCR-GLOBWB 2 and GRACE basin-average monthly and annual TWS time series were calculated. Monthly correlation provides information about PCR-GLOBWB's ability to correctly time TWS seasonal variability (with a value equal to 1 for perfect timing), while the correlation for annual time series measures inter-annual variability.

The results in Fig. 8 show that PCR-GLOBWB 2 is able to capture GRACE's TWS seasonality for most basins around the world, with the exception of some cold regions in high latitudes (e.g. the Yukon River basin, Iceland). This shortcoming is most likely due to the lack of a proper representation of glacier and ice processes in PCR-GLOBWB 2. As expected, the correlation values for inter-annual time series are generally lower than the ones for monthly time series. There are some areas with negative correlation values, such as the Amazon, Niger, and Nile river basins. Apart from the uncertainty in the GRACE signal, these deficiencies may be related to errors in model forcing and structural errors such as errors in the groundwater response time and the effects of wetlands that have not been represented sufficiently well.

3.4.3 Water withdrawal

We compared simulated water withdrawal data from PCR-GLOBWB 2 with reported withdrawal data per country from AQUASTAT (FAO, 2016). The results are shown subdivided per source (Fig. 9) and per sector (Fig. 10). Total water withdrawal and surface water withdrawal are simulated reasonably well (R² between 0.84 and 0.96 and regression slopes between 0.70 and 1.08). However, groundwater withdrawal is underestimated for the smaller water users. A likely explanation for this is occasional groundwater withdrawal by farmers during dry periods in areas that have not been mapped as irrigated crops in MIRCA, such as grasslands in Germany and the Netherlands, for example, while this groundwater withdrawal is reported in AQUASTAT.

When looking at water withdrawal per sector, results are mixed. The largest agricultural water users are well captured, but the smaller ones are clearly underestimated. This is related to the fact that in many regions of the smaller water use countries, water is used for irrigation only occasionally during dry summers, while these areas are not mapped as irrigated crops in MIRCA. Also, many of these countries use irrigation technology that is not part of MIRCA, e.g. subsurface drainage by artificially high surface water levels such as in a number of developed delta regions in the world. However, even though these smaller countries are not well represented, PCR-GLOBWB 2 is still able to capture the big water users, which have a significant impact on the water cycle and are most important for global-scale analyses.

Both industrial and domestic water withdrawals are underestimated. The underestimation of industrial water withdrawal is partly caused by the fact that we do not include water withdrawal for thermoelectric cooling of power plants. The underestimation of domestic water withdrawal comes from the fact that we assume that the priority of water allocation is proportional to demand. This means that in times of shortage, water withdrawal is reduced with an equal percentage for agriculture, industry, and domestic use. In many countries, however, there is a priority series, whereby domestic demand is first met, industrial demand next, and agricultural demand comes last. As a result, we underestimate domestic water withdrawal and it also partly causes the underestimation of industrial water withdrawal. This is corroborated by plotting gross water demand (which would be withdrawal if no shortage would occur) against AQUASTAT data. These plots (not shown here) result in a regression slope of 0.68–0.75 for industrial demand and 0.78–0.92 for domestic demand. These results thus reveal that the water allocation scheme of PCR-GLOBWB 2 should be further improved.

4 Conclusions and future work

We presented the most recent version of the open-source global hydrology and water resource model PCR-GLOBWB. This version, PCR-GLOBWB 2, has a global coverage at 5 arcmin resolution. Apart from the higher resolution, the new model has an integrated water use scheme, i.e. every day sector-specific water demand is calculated, resulting in groundwater and surface water withdrawal, water consumption, and return flows. Dams and reservoirs from the GRanD database (Lehner et al., 2011) are added progressively according to their year of construction. PCR-GLOBWB 2 has been rewritten in Python and uses PCRaster Python functions (Karssenberg et al., 2007). It has a modular structure, which makes the replacement and maintenance of model parts easier. PCR-GLOBWB 2 can be dynamically coupled to a global two-layer groundwater model (de Graaf et al., 2017; Sutanudjaja et al., 2014, 2011), and a one-way coupling to hydrodynamic models for large-scale inundation modelling (Hoch et al., 2017b) is also available.

Comparing the 5 arcmin with 30 arcmin simulations using discharge data, we clearly find an improvement in the model performance of the higher-resolution model. We find a general increase in correlation, anomaly correlation, and KGE, indicating that the higher-resolution model is better able to capture the seasonality, inter-annual anomalies, and the general discharge characteristics. Also, PCR-GLOBWB 2 is able to reproduce trends and seasonality in total water storage as observed by GRACE for most river basins. It simulates the hotspots of groundwater decline that abound in GRACE as well. Simulated total water withdrawal matches reasonably well with reported water withdrawal from AQUASTAT, while water withdrawal by source and sector provide mixed results. Future work will concentrate on further improving the water withdrawal and water allocation scheme, developing a full dynamic (two-way) coupling with hydrodynamic models, developing 5 and 1 km resolution (or higher) parameterizations of PCR-GLOBWB 2 using scale-consistent parameterizations (e.g. using MPR; Samaniego et al., 2017), incorporating a crop growth model, and solving the full surface energy balance. Other foreseeable developments are using the model in probabilistic settings and in data-assimilation frameworks.

Appendix A

Table A1 List (non-exhaustive) of state and flux variables defined in PCR-GLOBWB.

Table A2 List of model inputs and parameters.