the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Numerical experiments on vapor diffusion in polar snow and firn and its impact on isotopes using the multi-layer energy balance model Crocus in SURFEX v8.0
Alexandra Touzeau
Amaëlle Landais
Samuel Morin
Laurent Arnaud
Ghislain Picard
To evaluate the impact of vapor diffusion on isotopic composition variations in snow pits and then in ice cores, we introduced water isotopes in the detailed snowpack model Crocus. At each step and for each snow layer, (1) the initial isotopic composition of vapor is taken at equilibrium with the solid phase, (2) a kinetic fractionation is applied during transport, and (3) vapor is condensed or snow is sublimated to compensate for deviation to vapor pressure at saturation.
We study the different effects of temperature gradient, compaction, wind compaction, and precipitation on the final vertical isotopic profiles. We also run complete simulations of vapor diffusion along isotopic gradients and of vapor diffusion driven by temperature gradients at GRIP, Greenland and at Dome C, Antarctica over periods of 1 or 10 years. The vapor diffusion tends to smooth the original seasonal signal, with an attenuation of 7 to 12 % of the original signal over 10 years at GRIP. This is smaller than the observed attenuation in ice cores, indicating that the model attenuation due to diffusion is underestimated or that other processes, such as ventilation, influence attenuation. At Dome C, the attenuation is stronger (18 %), probably because of the lower accumulation and stronger δ18O gradients.
- Article
(3574 KB) - Full-text XML
-
Supplement
(3176 KB) - BibTeX
- EndNote
The isotopic ratios of oxygen or deuterium measured in ice cores have been used for a long time to reconstruct the evolution of temperature over the Quaternary (EPICA comm. members, 2004; Johnsen et al., 1995; Jones et al., 2018; Jouzel et al., 2007; Kawamura et al., 2007; Lorius et al., 1985; Petit et al., 1999; Schneider et al., 2006; Stenni et al., 2004, 2011; Uemura et al., 2012; WAIS Divide project members, 2013). They are, however, subject to alteration during post-deposition through various processes. Consequently, even if the link between the temperature and isotopic composition of the precipitations is quantitatively determined from measurements and modeling studies (Stenni et al., 2016; Goursaud et al., 2017), it cannot faithfully be applied to reconstructions of past temperature. Nevertheless, ice cores remain a primary climatic archive for the Southern Hemisphere where continental archives are rare (Mann and Jones, 2003). In Antarctica, where meteorological records only started in the 1950s (Genthon et al., 2013), they provide useful information for understanding climate variability (e.g., EPICA comm. members, 2006; Shaheen et al., 2013; Steig, 2006; Stenni et al., 2011) and recent climate change (e.g., Altnau et al., 2015; Schneider et al., 2006). When using ice cores for past climate reconstruction, parameters other than temperature at condensation influence the isotopic compositions and must be considered. Humidity and temperature in the region of evaporation (Landais et al., 2008; Masson-Delmotte et al., 2011) or the seasonality of precipitation (Delmotte et al., 2000; Sime et al., 2008; Laepple et al., 2011) should be taken into account. In addition, uneven accumulation in time and space introduces stratigraphic noise (Ekaykin et al., 2009). Records from adjacent snow pits have been shown to be markedly different under the influence of decameter-scale local effects such as wind redeposition of snow, erosion, compaction, and metamorphism (Ekaykin et al., 2014; Petit et al., 1982). These local effects reduce the signal to noise ratio. Then only stacking a series of records from snow pits can eliminate this local variability and yield information relevant to recent climate variations (Fisher and Koerner, 1994; Hoshina et al., 2014; Ekaykin et al., 2014; Altnau et al., 2015). This concern is particularly significant in the central regions of East Antarctica characterized by accumulation rates lower than 100 mm of water equivalent per year (van de Berg et al., 2006). There, strong winds can scour and erode the snow layer over depths larger than the annual accumulation (Frezzotti et al., 2005; Morse et al., 1999; Libois et al., 2014). There is thus a strong need to study post-deposition effects in these cold and dry regions.
Additionally to the mechanical reworking of the snow, the isotopic compositions are further modified in the snowpack. First, diffusion along isotopic gradients can occur within the snow grains due to solid diffusion (Ramseier et al., 1967). Second, within the porosity, the vapor isotopic composition can change due to (1) diffusion along isotopic gradients in the gaseous state, (2) thermally induced vapor transport caused by vapor pressure gradients, (3) ventilation in the gaseous state, or (4) exchanges between the gas phase and the solid phase, i.e., sublimation and condensation. In the porosity, the combination of diffusion along isotopic gradients in the vapor and of exchange between vapor and the solid phase has been suggested to be the main explanation to the smoothing of the isotopic signal in the solid phase (Ebner et al., 2016, 2017; Gkinis et al., 2014; Johnsen et al., 2000). The isotopic compositions in the solid phase are also modified by “dry metamorphism” and “ventilation” but in a less predictable way. In both cases, the vapor transport exerts an influence on the isotopic compositions in the solid phase because of permanent exchanges between solid and vapor. During “dry metamorphism” (Colbeck et al., 1983), vapor transport is driven by vapor pressure gradients, themselves caused by temperature gradients. During ventilation (Town et al., 2008), vapor moves as part of the air in the porosity because of pressure variations at the surface. Last, at the top of the snowpack, the isotopic composition of snow may also be modified through direct exchange with atmospheric vapor (Ritter et al., 2016).
To elucidate the impact of these various post-deposition processes on the snow isotopic compositions, numerical models are powerful tools. They allow one to discriminate between processes and test their impact one at a time. For instance, Johnsen et al. (2000) were able to simulate and deconvolute the influence of diffusion along isotopic gradients in the vapor at two Greenland ice-core sites, GRIP and NGRIP, using a numerical model. To do this, they define a quantity called “diffusion length”, which is the mean displacement of a water molecule during its residence time in the porosity. Using a thinning model and an equation for the diffusivity of the water isotopes in snow, they compute this diffusion length as a function of depth. It is then used to compute the attenuation ratio A∕Ao and in the end retrieve the original amplitude Ao. Additionally, the effect of forced ventilation was investigated by Neumann (2003) and Town et al. (2008) using similar multi-layer numerical models. In these models, wind-driven ventilation forces atmospheric vapor into snow. There, the vapor is condensed, especially in layers colder than the atmosphere.
We focus on the movement of water isotopes in the vapor phase in the porosity, in the absence of macroscopic air movement. In that situation, the movement of vapor molecules in the porosity is caused by vapor pressure gradients or by diffusion along isotopic gradients. Note that in the first case, the vapor transport is “thermally induced”; i.e., the vapor pressure gradients directly result from temperature gradients within the snowpack. Thus, the first prerequisite for our model is to correctly simulate macroscopic energy transfer within the snowpack and energy exchange at the surface.
The transport of vapor molecules will affect the isotopic composition in the solid phase only if exchanges between vapor and solid are also implemented. Thus, the second prerequisite is that the model includes a description of the snow microstructure and of its evolution in time. Snow microstructure is typically represented by its emerging scalar properties such as density, specific surface area, and higher-order terms often referred to as “shape parameters” (e.g., Krol and Löwe, 2016). While the concept of “grain” bears ambiguity, it is a widely used term in snow science and glaciology that we employ here as a surrogate for “elementary microstructure element” without explicit reference to a formal definition, whether crystallographic or geometrical.
Crocus is a unidimensional multi-layer model of snowpack with a typically centimetric resolution initially dedicated to the numerical simulation of snow in temperate regions (Brun et al., 1992). It describes the evolution of the snow microstructure driven by temperature and temperature gradients during dry snow metamorphism using semi-empirical variables and laws. It has been used for ice-sheet conditions in polar regions, both Greenland and Antarctica (Brun et al., 2011; Lefebre et al., 2003; Fréville et al., 2013; Libois et al., 2014, 2015). In these regions, it gives realistic predictions of density and snow type profiles (Brun et al., 1992; Vionnet et al., 2012), snow temperature profile (Brun et al., 2011), and snow specific surface area and permeability (Carmagnola et al., 2014; Domine et al., 2013). It has been recently optimized for application to conditions prevailing at Dome C, Antarctica (Libois et al., 2014). This was necessary to account for specific conditions such as high snow density values at the surface and low precipitation amounts.
The Crocus model has high vertical spatial resolution and also includes an interactive simulation of snow metamorphism in near-surface snow and firn. Therefore, it is a good basis for the study of post-deposition effects in low accumulation regions. For the purposes of this study, we thus implemented vapor transport resulting from temperature gradients and the water isotope dynamics into the Crocus model. This article presents this double implementation and a series of sensitivity tests. A perfect match with observations is not anticipated, in part because not all relevant processes are represented in the model. This study thus represents a first step towards better understanding the impact of diffusion driven by temperature gradients on the snow isotopic composition.
The isotopic composition of the snow can evolve after deposition due to several processes. Here, we first give a brief overview of such processes at the macroscopic level. Section 2.1 thus deals with the modification of the isotopic composition of a centimetric to decametric snow layer after exchanges with the other layers. Second, we consider the evolution of the isotopic composition at the microscopic level, i.e., at the level of the microstructure. The macroscopic change in the isotopic composition results from both large-scale and small-scale processes. For instance, dry metamorphism includes both vapor transport from one layer to another and vapor–ice grain exchange inside a layer.
2.1 Evolution of the composition of the snow layers at the macroscopic scale
Several studies address the evolution of the isotopic compositions in the snow column after deposition. Here we describe first the processes leading only to attenuation of the original amplitude (Sect. 2.1.1). Then we describe processes that lead to other types of signal modifications (Sect. 2.1.2). These modifications result from the transportation and accumulation of heavy or light isotopes in some layers without any link to the original isotopic signal. In some cases, the mean δ18O value of the snow deposited can also be modified.
2.1.1 Signal attenuation on a vertical profile: smoothing
In this section we consider the processes leading only to attenuation of the original amplitude of the δ18O signal by smoothing. We define the mean local pluriannual value as the average isotopic composition in the precipitation taken over 10 years. The smoothing processes, which act only on signal variability, do not modify this average value. Within the snow layers, the smoothing of isotopic compositions is caused by diffusion along isotopic gradients in the vapor phase and solid phase. The magnitude of smoothing depends on site temperature and on accumulation. Higher temperatures correspond to higher vapor concentrations and higher diffusivities in the vapor and solid phases. Oppositely, high accumulation rates ensure a greater separation between seasonal δ18O peaks (Ekaykin et al., 2009; Johnsen et al., 1977), thereby limiting the impact of diffusion. They also result in increased densification rates and therefore reduced diffusivities (Gkinis et al., 2014). Because sites with high accumulation rates also usually have higher temperatures, the resulting effect on diffusion is still unclear. These two competing effects should be thoroughly investigated, and Johnsen et al. (2000) display the damping amplitude of a periodic signal depending on wavelength and on diffusion length, strongly driven by temperature.
In Greenland, Johnsen et al. (1977) indicate that annual cycles generally disappear at depths shallower than 100 m for sites with accumulation lower than 200 kg m−2 yr−1. Diffusion along isotopic gradients exists throughout the entire snow–ice column. It occurs mainly in the vapor phase in the firn, especially in the upper layers with larger porosities. After pore closure, it takes place mostly in the solid phase at a much slower rate. Note that in the solid phase, all isotopes have the same diffusion coefficient.
2.1.2 Signal shift caused by processes leading to oriented vapor transport
We consider here the oriented movement of water molecules forced by external variables such as temperature or pressure. We use the term “oriented” here to describe an overall movement of water molecules that is different from their molecular agitation and externally forced. Three processes can contribute to oriented vapor transport and hence possible isotopic modification within the snowpack: diffusion, convection, and ventilation (Albert et al., 2002). Brun and Touvier (1987) have demonstrated that the convection of dry air within the snow occurs only in the case of very low snow density of the order of ∼ 100 kg m−3. These conditions are generally not encountered in Antarctic snow and therefore convection is not considered here. Bartelt et al. (2004) also indicate that energy transfer by advection is negligible compared to energy transfer by conduction in the first meters of the snowpack. The two other processes of ventilation and diffusion are respectively forced by variations in the surface pressure and surface temperature. In the first case, the interaction between wind and surface roughness is responsible for wind pumping, i.e., the renewal of the air of the porosity through macroscopic air movement (Albert et al., 2002; Colbeck, 1989; Neumann and Waddington, 2004). In the second case, air temperature diurnal or seasonal variations generate vertical temperature gradients within the snow (Albert and McGilvary, 1992; Colbeck, 1983). They result in vertical vapor pressure gradients responsible for vapor diffusion. These two processes are largely exclusive (Town et al., 2008) because strong ventilation homogenizes the air and vapor in the porosity and therefore prevents diffusion. Diffusion as a result of temperature gradients can coexist with ventilation only at very low air velocities (Calonne et al., 2015). It becomes the main process of vapor transport when air is stagnant in the porosity. During diffusion, lighter molecules move more quickly in the porosity, leading to a kinetic fractionation of the various isotopologues.
2.2 Evolution of the isotopic composition at the microscopic scale
2.2.1 Conceptual representation of snow microstructure as spherical grains
The term “snow grain” as used classically is an approximation. In reality, snow grains are very diverse in size, shape, and degree of metamorphism and may also be made of several snow crystals agglomerated. Moreover, they are often connected to each other, forming an ice matrix, or “snow microstructure”. However, several studies addressing snow metamorphism physical processes have relied on spherical ice elements to represent snow grains and snow microstructure (Legagneux and Domine, 2005; Flanner and Zender, 2006). Here, we consider the snow grains to be made of two concentric layers, one internal and one external, with different isotopic compositions. In terms of snow microstructure, this could correspond to the inner vs. outer regions of the snow microstructure.
The snow grain or microstructure is not necessarily homogeneous in terms of isotopic composition. On the one hand, the central part of the grain or of the microstructure is relatively insulated. This central part becomes even more insulated as the grain grows or as the structure gets coarser. On the other hand, outer layers are not necessarily formed at the same time as the central part or in the same environment (Lu and DePaolo, 2016). They are prone to subsequent sublimation–condensation of water molecules, implying that their composition varies more frequently than for the inner layers. Of course, only the bulk δ18O value of the snow grain can be measured by mass spectrometry. But considering the heterogeneity of the grain may be required to get a fine understanding of the processes. In the following, we propose splitting the ice grain compartment into two sub-compartments: grain surface and grain center. Thus, the grain surface isotopic composition evolves because of exchange with two compartments: (1) vapor in the porosity through sublimation–condensation and (2) the grain center through solid diffusion or grain center translation. The grain center composition evolves at the timescale of weeks or months, as opposed to the grain surface, where the composition changes at the timescale of the vapor diffusion, i.e., over minutes.
2.2.2 Solid diffusion within snow grains
The grain center isotopic composition may change either as a result of crystal growth and/or sublimation or as a result of solid diffusion within the grain. For solid diffusion, water molecules move in the crystal lattice through a vacancy mechanism, in a process of self-diffusion that has no particular direction and that is very slow. The diffusivity of water molecules in solid ice Dice in m2 s−1 follows the Arrhenius law. Thus, it can be expressed as a function of ice temperature T (Gkinis et al., 2014; Johnsen et al., 2000; Ramseier, 1967) using Eq. (1):
for which the symbols are listed in Table 1.
Thus at 230 K, the diffusivity is m2 s−1. Gay et al. (2002) indicate that in the first meter at Dome C, a typical snow grain has a radius of 0.1 mm. Across this typical snow grain, the characteristic time for diffusion is given by Eq. (2).
Therefore, the solid diffusion within the grain is close to zero at the timescales considered in the model. For Dome C, if we use the average temperature T of 248 K for the summer months (December to January; Table 2), the characteristic time becomes 15 months. Thus, within a summer period, the snow grain is only partially refreshed through this process. At Summit the grain size is typically larger, from 0.2 to 0.25 mm in wind-blown and wind-packed snow, and from 0.5 to 2 mm in the depth hoar layer (Albert and Shultz, 2002). The summer temperature is also higher, with an average value T of 259 K at Summit from July to September, after Shuman et al. (2001). Using a grain size of 0.25 mm, the resulting characteristic time is of the order of 30 months.
2.2.3 Snow grain recrystallization
During snow metamorphism, the number of snow grains tends to decrease with time, while the snow grain size tends to increase (Colbeck, 1983). Each grain experiences continuous recycling through sublimation–condensation, but the small grains are more likely to disappear completely. Then, there is no more nucleus for condensation at the grain initial position. Oppositely, the bigger grains do not disappear and accumulate the vapor released by the smaller ones. Concurrently to this change in grain size, the grain shape also tends to evolve. In conditions of a maintained or stable temperature gradient, facets appear at the condensing end of snow grains, while the sublimating end becomes rounded (Colbeck, 1983). In that case, the center of the grain moves toward the warm air region. This migration causes a renewal of the grain center on a proportion that can be estimated from the apparent grain displacement (Pinzer et al., 2012). Pinzer et al. (2012) use this method to obtain an estimation of vapor fluxes.
The asymmetric recrystallization of snow grains implies that the surface layer of the snow grain is eroded at one end and buried at the other end. Therefore, the composition of the grain center changes more often than if the surface layer was thickening through condensation or thinning through sublimation homogeneously over the grain surface. This means that the “inner core” of the grain gets exposed more often. Implementing this process is thus very important to have a real-time evolution of the snow grain center isotopic composition. Here, we reverse the method of Pinzer et al. (2012). Therefore, we use the fluxes of isotopes in the vapor phase computed by the model to assess the renewal of the grain center (Sect. 3.1.3.).
3.1 Description of the model SURFEX–Crocus v8.0
We first present the model structure and second describe the new module of vapor transport (diffusion forced by temperature gradients). Third, we present the integration of water isotopes in the model.
3.1.1 Model structure
The Crocus model is a one-dimensional detailed snowpack model consisting of a series of snow layers with variable and evolving thicknesses. Each layer is characterized by its density, heat content, and by parameters describing snow microstructure such as sphericity and specific surface area (Vionnet et al., 2012; Carmagnola et al., 2014). In the model, the profile of temperature evolves with time in response to (1) surface temperature and (2) energy fluxes at the surface and at the base of the snowpack. To correctly compute energy balance, the model integrates albedo calculation as deduced from surface microstructure and impurity content (Brun et al., 1992; Vionnet et al., 2012).
The successive components of the Crocus model have been described by Vionnet et al. (2012). Here we only list them to describe those modified to include water stable isotopes and water vapor transfer. Note that the Crocus model has a typical internal time step of 900 s (15 min) corresponding to the update frequency of layers properties. We only refer here to processes occurring in dry snow.
-
Snowfall. The presence or absence of precipitation at a given time is determined from the atmospheric forcing inputs. When there is precipitation, a new layer of snow may be formed. Its thickness is deduced from the precipitation amount.
-
Update of snow layering. At each step, the model may split one layer into two or merge two layers together to get closer to a target vertical profile for optimal calculations. This target profile has high resolution in the first layers to correctly simulate heat and matter exchanges. The layers that are merged together are the closest in terms of microstructure variables.
-
Metamorphism. The evolution of microstructure variables follows empirical laws. These laws describe the change in grain parameters as a function of temperature, temperature gradient, snow density, and liquid water content.
-
Snow compaction. Layer thickness decreases and layer density increases under the burden of the overlying layers and resulting from metamorphism. In the original module, snow viscosity is parameterized using the layer density and also using information on the presence of hoar or liquid water. However, this parameterization of the viscosity was designed for alpine snowpack (Vionnet et al., 2012) and may not be adapted to polar snowpacks. Moreover, since we are considering only the first 12 m of the snowpack in the present simulations, the compaction in the considered layers does not compensate for the yearly accumulation, leading to a rising snow level with time. To maintain a stable surface level in our simulations, we used a simplified compaction scheme in which the compaction rate ε is the same for all the layers. The compaction rate is obtained by dividing the accumulation rate at the site (see Sect. 3.3) by the total mass of the snow column (Eq. 3). It is then applied to all layers to obtain the density change per time step using Eq. (4).
-
Wind drift events. They modify the properties of the snow grains, which tend to become more rounded. They also increase the density of the first layers through compaction. An option allows snow to be partially sublimated during these wind drift events (Vionnet et al., 2012).
-
Snow albedo and transmission of solar radiation. In the first 3 cm of snow, snow albedo and absorption coefficient are computed from snow microstructure properties and impurity content. The average albedo value in the first 3 cm is used to determine the part of incoming solar radiation reflected at the surface. The rest of the radiation penetrates into the snowpack. Then, the absorption coefficient is used to describe the rate of decay of the radiation as it is progressively absorbed by the layers downward, following an exponential law.
-
Latent and sensible surface energy and mass fluxes. The sensible heat flux and the latent heat flux are computed using the aerodynamic resistance and the turbulent exchange coefficients.
-
Vertical snow temperature profile. It is deduced from the heat diffusion equation using the snow conductivity and the energy balance at the top and at the bottom of the snowpack.
-
Snow sublimation and condensation at the surface. The amount of snow sublimated–condensed is deduced from the latent heat flux, and the thickness of the first layer is updated. Other properties of the first layer such as density and SSA are kept constant.
3.1.2 Implementation of water transfer
The new vapor transport subroutine has been inserted after the compaction (Eq. 4) and wind drift (Eq. 5) modules and before the solar radiation module (Eq. 6). In this section, the term “interface” is used for the horizontal surface of exchange between two consecutive layers. The flux of vapor at the interface between two layers is obtained using Fick's law of diffusion (Eq. 5):
where dz(t,n) and are the thicknesses of the two layers considered in meters, Cv(t,n) and are the local vapor mass concentrations in the two layers in kg m−3, and in m2 s−1 is the effective diffusivity of water vapor in the snow at the interface. The thicknesses are known from the previous steps of the Crocus model, but the vapor mass concentrations and the interfacial diffusivities must be computed.
The effective diffusivity at the interface is obtained in two steps: first the effective diffusivities (Deff(t,n) and ) in each layer are calculated (Eq. 6); second, the interfacial diffusivity ( is computed as their harmonic mean (Eq. 7). Effective diffusivity can be expressed as a function of the snow density using the relationship proposed by Calonne et al. (2014) for layers with relatively low density. In these circumstances, the compaction occurs by “boundary sliding”, meaning that the grains slide on each other, but that their shape is not modified. It is therefore applicable to our study for which density is always below 600 kg m−3. The equation of Calonne et al. (2014) is based on the numerical analysis of 3-D tomographic images of different types of snow. It relates normalized effective diffusivity Deff∕Dv to the snow density ρsn in the layer (Eq. 6). Dv is the vapor diffusivity in air and has a value that varies depending on the air pressure and air temperature (Eq. 19 in Johnsen et al., 2000). ρice corresponds to the density of ice and has a value of 917 kg m−3.
We assume that vapor is generally at saturation in the snow layers (Neumann et al., 2008, 2009). The local mass concentration of vapor Cv in kg m−3 in each layer is given by the Clausius–Clapeyron equation (Eq. 8):
where Cv0 is the mass concentration of vapor at 273.16 K and is equal to kg m−3, Lsub is the latent heat of sublimation and has a value of 2.6×109 J m−3, Rv is the vapor constant and has a value of 462 J kg−1 K−1, ρice is the density of ice and has a value of 917 kg m−3, T0 is the temperature of the triple point of water and is equal to 273.16 K, and T is the temperature of the layer.
All layers are treated identically, except the first layer at the top and the last layer at the bottom. For the uppermost layer, the exchange of vapor occurs only at the bottom boundary. Exchanges with the atmosphere are described elsewhere in Crocus at step 9 in which surface energy balance is realized. For the lowermost layer, only exchanges taking place at the top boundary are considered, with the flux of vapor to and from the underlying medium being set to zero.
For each layer, the mass concentration of vapor in the air and the effective diffusivity are computed within the layer and in the neighboring layers. Fluxes at the top and bottom of each layer are deduced from Fick's law of diffusion (Eq. 5). They are integrated over the subroutine time step, and the new mass of the layer is computed. It is used at the beginning of the next subroutine step. We use a 1 s time step within the subroutine, which is smaller than the main routine time step of 900 s. This ensures that vapor fluxes remain small relative to the amount of vapor present in the layers. Note that the temperature profile, which controls the vapor pressure profile, is not modified within the subroutine. Physically, temperature values should change as a result of the transfer of sensible heat from one layer to another associated with vapor transport. They should also evolve due to the loss or gain of heat caused by water sublimation–condensation (Albert and McGilvary, 1992; Kaempfer et al., 2005). However, vapor transport is only a small component of heat transfer between layers (Albert and Hardy, 1995; Albert and McGilvary, 1992). In the absence of ventilation, with or without vapor diffusion, the steady-state profile for temperature varies by less than 2 % (Calonne et al., 2014). Thus, the effect can be neglected at first order.
3.1.3 Implementation of water isotopes
In the model, the isotopic composition of snow in each layer is represented by the triplicate (δ18O, d-excess, 17O-excess). Only the results of δ18O are presented and discussed here. For each parameter, two values per layer are considered independently that correspond to the “snow grain center” and the “snow grain surface”. Water vapor isotopic composition is deduced at each step from the snow grain surface isotopic composition. It is not stored independently to limit the number of prognostic variables. The isotopic compositions are used at step 1, i.e., for snowfall, and after step 5 within the new module of vapor transfer.
In the snowfall subroutine, a new layer of snow may be added, depending on the weather, at the top of the snowpack. At this step of the routine, the snow grains being deposited are presumed to be homogenous, i.e., they have the same composition in the grain surface compartment and in the grain center compartment. Their composition is deduced from the air temperature (see Sect. 3.2).
Within the vapor transport subroutine, a specific module deals with the isotopic aspects of vapor transport. It modifies the isotopic compositions in the two snow grain sub-compartments as a result of water vapor transport and the recrystallization of snow crystals. It works with four main steps:
-
an initiation step in which the vapor isotopic compositions are computed using equilibrium fractionation from the ones in the grain surface sub-compartment;
-
a transport step in which vapor moves from one layer to another, with a kinetic fractionation associated with diffusion;
-
a balance step in which the new vapor in the porosity exchanges with the grain surface compartment by sublimation–condensation (the flux is determined by the difference between the actual vapor mass concentration and the expected vapor mass concentration at saturation); and
-
a “recrystallization” step in which the grain center and grain surface isotopic compositions are homogenized, leading to an evolution of grain center isotopic composition.
The time step in this module is 1 s, the same as the time step of the subroutine.
The initial vapor isotope composition in a given layer is taken at equilibrium with the grain surface isotopic composition . Here i denotes a heavy isotope and thus stands for 18O, 17O, or D. Equilibrium fractionation is a hypothesis that is correct in layers in which vapor has reached equilibrium with ice grains both physically and chemically. This process is limited by the water vapor–snow mass transfer whose associated speed is of the order of 0.09 m s−1 (Albert and McGilvary, 1992). In our case, we are dealing with centimetric-scale layer thickness and recalculate the isotopic composition every second so that we consider the speed of the mass transfer as not limiting the equilibrium situation at the water vapor–snow interface. To compute isotopic ratios for water vapor we use the following Eqs. (9) and (10).
The equilibrium fractionation coefficients ( are obtained using the temperature-based parameterization from Ellehoj et al. (2013). Note that we make a slight approximation here by replacing molar concentrations with mass concentrations in our mass balance formulas (see Table 1 for symbol definitions).
The initial vapor mass concentration in air Cv has already been computed in the vapor transport subroutine, and the volume of the porosity can be obtained from the snow density ρsn and the thickness of the layer dz. By combining both, we obtain Eq. (11), which gives the initial mass of vapor in the layer mvap,ini.
This mass of vapor should be subtracted from the initial grain surface mass because vapor mass is not tracked outside of the subroutine (Fig. 1). The new grain surface isotope composition, after vapor individualization is given by Eq. (12).
The diffusion of isotopes follows the same scheme as the water vapor diffusion described above in Sect. 3.1.2. and Eq. (5). In Eq. (13), the gradient of vapor mass concentrations is replaced by a gradient of concentration for the studied isotopologue. The kinetic fractionation during the diffusion is realized with the Di∕D term where i stands for 18O, 17O, or 2H (Barkan and Luz, 2007).
As done for water molecule transport (Sect. 3.1.2), the flux is set to zero at the top of the first layer and at the bottom of the last layer. When the vapor concentration is the same in two adjacent layers, the total flux of vapor is null. But diffusion along isotopic gradients still occurs if the isotopic gradients are nonzero (Eq. 13). Once the top and bottom fluxes of each layer have been computed, the new masses of the various isotopes in the vapor are deduced, as are the new ratios.

Figure 1Splitting of the snow layer into two compartments, grain center and grain surface, with a constant mass ratio between them. The vapor compartment is a sub-compartment inside the grain surface compartment and is only defined at specific steps of the model.
After the exchanges between layers, the isotopic composition in the vapor has changed. However, the vapor isotopic composition is not a prognostic variable outside of the vapor transport subroutine. To record this change, it must be transferred to either the grain surface compartment or to the grain center compartment before leaving the subroutine. First, we consider exchanges of isotopes with the grain surface compartment, which is in direct contact with the vapor. Depending on the net mass balance of the layer, two situations must be considered.
-
If the mass balance is positive, condensation occurs so that the transfer of isotopes takes place from the vapor toward the grain surface. To evaluate the change in the isotope composition in the grain surface, the mass of vapor condensed Δmvap,exc must be computed. It is the difference between the mass of vapor expected at saturation and the mass of vapor present in the porosity after vapor transport. Note that temperature does not evolve in this subroutine. Nevertheless, the difference is not exactly equal to the mass of vapor that has entered the layer because of layer porosity change. The excess mass of vapor is given by Eq. (14).
Since the excess of vapor is positive, the next step is the condensation of the excess vapor. The number of excess water molecules is determined through comparison with the expected number in the water vapor phase for an equilibrium state between surface snow and water vapor. Here the condensation of excess vapor occurs without additional fractionation because (1) there is a permanent isotopic equilibrium between surface snow and interstitial vapor restored at each first step of the subroutine, and (2) kinetic fractionation associated with diffusion is taken into account during the diffusion of the different isotopic species along the isotopic gradients.
-
If the mass balance is negative, the transfer of isotopes takes place from the grain surface toward the vapor without fractionation. Ice from the grain surface sub-compartment is sublimated without fractionation to reach the expected vapor concentration at saturation. Note that the absence of fractionation at sublimation is a frequent hypothesis because water molecules move very slowly in ice lattice (Friedman et al., 1991; Neumann et al., 2005; Ramseier, 1967). Consequently, the sublimation removes all the water molecules present at the surface of grains, including the heaviest ones, before accessing inner levels. In reality, there is evidence for fractionation at sublimation. It occurs through kinetic effects associated with sublimation or simultaneous condensation or during equilibrium fractionation at the boundary, especially when invoking the existence of a thin liquid layer at the snow–air interface (Neumann et al., 2008 and references therein; Sokratov and Golubev, 2009; Stichler et al., 2001; Ritter et al., 2016). The new composition in the vapor results from a mixing between the vapor present and the new vapor recently produced. The composition in the grain surface ice compartment does not change.
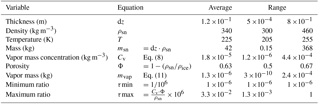
The limit between the surface compartment and the grain center compartment is defined by the mass ratio of the grain surface compartment to the total grain mass, i.e., ); see also Fig. 1. This mass ratio can be used to determine the thickness of the grain surface layer as a fraction of grain radius for spherical grains. The surface compartment must be thin to be able to react to very small changes in mass when vapor is sublimated–condensed. Our model has a numerical precision of 6 decimals and is run at a 1 s temporal resolution. Consequently, the isotopic composition of the surface compartment can change in response to surface fluxes only if its mass is smaller than 106 times the mass of the water vapor present in the porosity. This constrains the maximum value for τ: msurf<106mvap or , i.e., . Considering typical temperatures, snow densities, and layer thicknesses (Table 3), we obtain a maximum value of 3.3 . On the other hand, this compartment must be thick enough to transmit the change in isotopic compositions caused by vapor transport and condensation–sublimation to the grain center. Again, numerical precision imposes that its mass should be no less than 10−6 times the mass of the grain center compartment, and thus we get an additional constraint: . Here we use a ratio for the mass of the grain surface relative to the total mass of the layer (Fig. 1). We have run sensitivity tests with smaller and larger ratios (Sect. 4.3).
Two types of mixing between the grain surface and grain center are implemented in the model. The first one is associated with crystal growth or shrinkage because of vapor transfer. Mixing is performed at the end of the vapor transfer subroutine after sublimation–condensation has occurred. During the exchange of water between vapor and the grain surface, the excess or default of mass in the water vapor caused by vapor transport has been entirely transferred to the grain surface sub-compartment. Thus, the mass ratio between the grain surface compartment and the grain center compartment deviates from the original one. To bring the ratio τ back to the normal value of 5 , mass is transferred either from the grain surface to the grain center or from the grain center to the grain surface. This happens without fractionation; i.e., if the transfer occurs from the center to the surface, the composition of the center remains constant.
The second type of mixing implemented is the grain center translation (Pinzer et al., 2012), which favors mixing between the grain center and grain surface in the case of a sustained temperature gradient. Pinzer et al. (2012) used the apparent grain displacement to compute vapor fluxes. Here, we reverse this method and use the vapor fluxes computed from Fick's law to estimate the grain center renewal. We could transfer a small proportion of the surface compartment to the grain center every second. Instead, we choose to totally mix the snow grain every few days. The interval Δtsurf/center between two successive mixings is derived from the vapor flux within the layer using Eq. (15).
The average temperature gradient of 3 ∘C m−1 corresponds to a flux of kg m−2 s−1. The typical mass for the layer msn is 3.3 kg. Based on these values, the dilution of the grain surface compartment into the grain center should occur every 15 days. Of course, this is only an average, since layers have varying masses and since the temperature gradient can be larger or smaller. We will, however, apply this time constant for all the layers and any temperature gradient (see sensitivity tests Sect. 4.3) to ensure that the mixing between compartments occurs at the same time in all layers.
In terms of magnitude, this process is probably much more efficient for mixing the solid grain than grain growth or solid diffusion. It is thus crucial for the modification of the bulk isotopic composition of the snow layer. It creates the link between microscopic processes and macroscopic results.
Table 3Typical thickness, density, temperature, and other parameters of the snow layers in the simulations. The ratio τ is the mass ratio between the grain surface compartment and the grain center compartment. It must be chosen within the interval [10−6; 106 (CvΦ∕ρsn)] to allow for exchanges between the grain surface compartment and grain center compartment on the one hand and between the grain surface compartment and vapor compartment on the other hand (see text for details).
3.1.4 Model initialization
For model initialization, an initial snowpack is defined with a fixed number of snow layers and for each snow layer an initial value of thickness, density, temperature, and δ18O. Typically, processes of oriented vapor transport such as thermally induced diffusion and ventilation occur mainly in the first meters of snow. Therefore, the model starts with an initial snowpack of about 12 m.
The choice of the layer thicknesses depends on the annual accumulation. Because the accumulation is much higher at GRIP than at Dome C (Sect. 3.2., Table 2), the second site is used to define the layer thicknesses. About 10 cm of fresh snow is deposited every year (Genthon et al., 2016; Landais et al., 2017). This implies that to keep seasonal information, at least one point every 4 cm is required in the first meter. For the initial profile, we impose a maximal thickness of 2 cm for the layers between 0 and 70 cm of depth and 4 cm for the layers between 70 cm and 2 m of depth. As the simulation runs, merging is allowed but restricted in the first meter to a maximum thickness of 2.5 cm. Below 2 m, the thicknesses are set to 40 cm or even 80 cm. Thus, the diffusion process can only be studied in the first 2 m of the model snowpack. In the very first centimeters of the snowpack, thin millimetric layers are used to accommodate low precipitation amounts and surface energy balance. The initial density profiles are defined for each site specifically (see Sect. 3.2). The initial temperature and δ18O profiles in the snowpack depend on the simulation considered (see Sect. 3.3).
3.1.5 Model output
A data file containing the spatiotemporal evolution of prognostic variables such as temperature, density, SSA, and δ18O is produced for each simulation. Here, we present the results for each variable as two-dimensional graphs, with time on the horizontal axis and snow height on the vertical axis. The variations in the considered variable are displayed as color levels. The white color corresponds to an absence of change in the variable. As indicated above, only the first 12 m of the polar snowpack are included in the model. The bottom of this initial snowpack constitutes the vertical reference or “zero” to measure vertical heights h. The height of the top of the snowpack varies with time due to snow accumulation and snow compaction. In the text, we sometimes refer to the layer depth z instead of its height h. The depth can be computed at any time by subtracting the current height of the considered layer from the current height of the top of the snowpack.
3.2 Studied sites: meteorology and snowpack description
In this study we run the model under the conditions encountered at Dome C, Antarctica and GRIP, Greenland. We chose these two sites because they have been well studied in recent years through field campaigns and numerical experiments. In particular for Dome C, a large amount of meteorological and isotopic data is available (Casado et al., 2016a; Stenni et al., 2016; Touzeau et al., 2016). Typical values of the main climatic parameters for the two studied sites, GRIP and Dome C, are given in Table 2 along with the typical δ18O range. Dome C has lower accumulation rates of 2.7 cm ice equivalent per year (ice eq. yr−1) compared to GRIP rates of 23 cm ice eq. yr−1 (Table 2), making it more susceptible to post-deposition processes.
Table 4List of simulations described in the article with the corresponding paragraph number. The external atmospheric forcing used for Dome C is ERA-Interim reanalysis (2000–2013). However, the precipitation amounts from the ERA-Interim reanalysis are increased by 1.5 times to account for the dry bias in the reanalysis (as in Libois et al., 2014). For the second simulation at GRIP, Greenland meteorological conditions are derived from the atmospheric forcing of Dome C, but the temperature is modified () as is the longwave down (LWGRIP=0.85 LWDC+60).
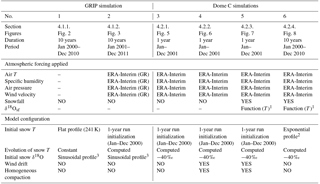
1 Using data from 1-year snowfall
sampling at Dome C (Stenni et al., 2016; Touzeau et al., 2016), we obtained
the following Eq. (16) linking δ18O in the snowfall to the local
temperature: .
2 The exponential profile of temperature used in Simulation 6 is defined
using Eq. (20):
with T(10 m)=218 K, ΔT=28 K, and z0=1.516 m. It fits well with temperature measurements of
midday in January (Casado et
al., 2016b).
3 The Greenland snowpack has an initial sinusoidal profile of δ18O defined using Eq. (19): .
Table 5List of the sensitivity tests performed at GRIP and at Dome C. The external atmospheric forcing used for Dome C is ERA-Interim reanalysis (see Table 4).
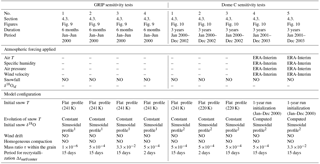
1The Greenland
snowpack has an initial sinusoidal profile of δ18O defined using
Eq. (19):
2 The Dome C snowpack has an initial sinusoidal
profile of δ18O defined using Eq. (21):
In this study, we also compare the results obtained for GRIP to results from two other Greenland sites, namely NGRIP and NEEM. GRIP is located at the ice-sheet summit, whereas the two other sites are located further north in lower elevation areas with higher accumulation rates. NGRIP is located 316 km to the NNW of the GRIP ice-drill site (Dahl-Jensen et al., 1997). GRIP and NGRIP have similar temperatures of −31.6 and −31.5 ∘C but different accumulation rates of 23 and 19.5 cm ice eq. yr−1, respectively. The NEEM ice-core site is located some 365 km to the NNW of NGRIP on the same ice ridge. It has an average temperature of −22 ∘C and an accumulation rate of 22 cm ice eq. yr−1.
The δ18O value in the precipitation at a given site reflects the entire history of the air mass, including evaporation, transport, distillation, and possible changes in trajectory and sources. However, assuming that these processes are more or less repeatable from one year to the next, it is possible to empirically relate the δ18O to the local temperature using measurements from collected samples. Here, using data from 1-year snowfall sampling at Dome C (Stenni et al., 2016; Touzeau et al., 2016), we use the following Eq. (16) to link δ18O in the snowfall to the local temperature Tair in K.
We do not provide an equivalent expression for GRIP, Greenland because the simulations run here (see Sect. 3.1.1) do not include precipitation.
The initial density profile in the snowpack is obtained from fitting density measurements from Greenland and Antarctica (Bréant et al., 2017). Over the first 12 m of snow, we obtain the following evolution (Eqs. 17 and 18) for GRIP and Dome C, respectively.
3.3 List of simulations
Table 4 presents the model configuration for the six simulations considered here. Additionally, Table 5 presents sensitivity tests performed to evaluate the uncertainties associated with grain renewal parameters.
3.3.1 Greenland simulations
The first simulation, listed as number 1 in Table 4, is dedicated to the study of diffusion along isotopic gradients. It is realized on a Greenland snowpack with an initial sinusoidal profile of δ18O (see Eq. 19) and with a uniform and constant vertical temperature profile at 241 K. In addition to comparison to δ18O profiles for GRIP and other Greenland sites, the aim of the first simulation is to compare results from Crocus model to the models of Johnsen et al. (2000) and Bolzan and Pohjola (2000) run at this site with only diffusion along isotopic profiles. To compare our results to theirs, we consider an isothermal snowpack without meteorological forcing, and we deactivate modules of surface exchanges and heat transfer. The initial seasonal sinusoidal profile at GRIP is set using Eq. (19):
where z is the depth of the layer n, ρsn is its density, ρice is the density of ice with a value of 917 kg m−3, and aGR is the average accumulation at GRIP equal to 0.23 m ice eq. yr−1 (Dahl-Jensen et al., 1993). The peak to peak amplitude value of 16 ‰ is close to the back-diffused amplitude at Summit (Sjolte et al., 2011).
The second simulation is run with evolving temperature in the snowpack. The snow temperature is computed by the model using meteorological forcing from ERA-Interim (see Table 4). In that case, the transport of isotopes in the vapor phase results from both diffusion along isotopic gradients and vapor concentration gradients. The initial snowpack is the same as in the previous simulation.
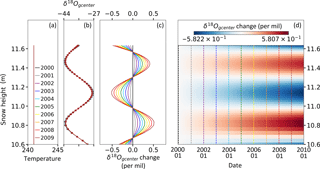
Figure 2Simulation 1: attenuation of the seasonal δ18Ogcenter variation caused by diffusion along isotopic gradients in the vapor phase over 10 years (homogeneous and constant temperature of 241 K, original signal with a mean value of −35.5 ‰ and amplitude of 16 ‰). (a) Vertical homogeneous temperature profile; (b) δ18O profile at the beginning and end of the simulation; (c) deviation of the δ18O relative to the original profile for 10 dates; (d) evolution of the deviation to the original profile of δ18O.
In the two GRIP simulations, the modules of wind compaction and weight compaction are inactive. As weight compaction is taken to compensate for yearly accumulation (Eqs. 3 and 4), applying this compaction without precipitation would lead to an unrealistic drop in snow level. The wind compaction was absent from the model of Johnsen et al. (2000) and using this module would make comparisons more difficult.
3.3.2 Dome C simulations
In Simulations 3 to 6, we take advantage of the abundant documentation of the Dome C site to disentangle the different effects on the variations in water isotopic composition. All the simulations at Dome C were performed with an evolving temperature profile. Temperatures in the snow layers were computed using a modified meteorological forcing from ERA-Interim (Dee et al., 2011; Libois et al., 2014; see details in Table 4) and the modules of energy exchange and transfer. In this series of simulations, the δ18O values thus evolve as a result of diverging and/or alternating vapor fluxes. The simulations are ordered by increasing complexity. First, in Simulation 3, the modules of homogeneous compaction and wind drift are deactivated, as is the module of snowfall. Thus, the impact of vapor transport forced by temperature gradients on the snow isotopic compositions is clearly visible. Then, in Simulation 4, the module of compaction and the module of wind drift are activated to see their impact on the isotopes. We use an accumulation rate dmsn∕dt for Dome C of 0.001 kg m−2 per 15 min (see Eq. 3). Next, in Simulation 5, snowfall is added to assess how new layers affect snow δ18O values. Lastly, in Simulation 6, the model is run over 10 years at Dome C to build up a snowpack with realistic “sinusoidal” variation in δ18O values.
4.1 Greenland
4.1.1 Results of the Crocus simulations (Simulations 1 and 2)
Figure 2 shows the result of Simulation 1, in which only diffusion along isotopic gradients is active, as in Johnsen et al. (2000). As expected the peak to peak amplitude of δ18O cycles is reduced because of diffusion. Over 10 years from 2000 to 2009, the amplitude decreases by 1.2 ‰, which corresponds to a 7.3 % variation.
Figure 3 shows the result of Simulation 2, i.e., with varying temperature in the snowpack. The attenuation is stronger than the one observed in the previous simulation. The minimum at 11.46 m increases by 1.03 ‰ over 10 years, and the maximum at 11.15 m decreases by 0.84 ‰. Thus, the total attenuation is ∼ 1.9 ‰ or 11.7 % for this height range. Below, the attenuation is smaller, with a total attenuation of only 6 % for heights between 10.54 and 10.85 m. If we compare attenuation for heights 11.46 and 11.56 m in the first and second simulation, we note that including temperature gradients leads to an increased attenuation by 50 %.

Figure 3Simulation 2: attenuation of the seasonal δ18Ogcenter variation caused by diffusion in the vapor phase over 10 years (with temperature evolution, original signal with a mean value of −35.5 ‰ and amplitude of 16 ‰). (a) Vertical temperature profile for each summer; (b) δ18Ogcenter profile for each summer; (c) evolution of the deviation to the original profile of δ18Ogcenter. Note that temperature evolves during the whole year (see Fig. S1).
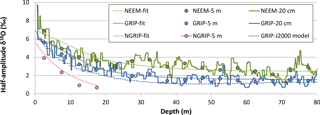
Figure 4Evolution of the δ18O semi-amplitude with depth in shallow cores at NEEM, GRIP, and NGRIP (Steen-Larsen et al., 2011; Masson-Delmotte et al., 2015; White et al., 1997; Johnsen et al., 2000). The attenuation of the semi-amplitude values with depth was fitted using an exponential equation: with A0=4.976 ‰, γ=0.08094, ‰ at GRIP and A0=4.685 ‰, γ=0.06622, ‰ at NEEM. The dotted curve corresponds to the simulated attenuation at GRIP based on the Johnsen et al. model (diffusion length σ from their Fig. 2 and wavelength λ fitted on the Eurocore core from GRIP; White et al., 1997).
Between 11.46 and 11.56 m, the δ18Ogcenter values increase over 10 years by 1 to 4 ‰. This increase is not caused only by attenuation of the original sinusoidal signal. At h=11.60 m, the values get higher than the initial maximum, which was −36 ‰ at 11.64 m. There is therefore a local accumulation of heavy isotopes in this layer as a result of vapor transport. This maximum corresponds to a local maximum in temperature and is coherent with the departure of 18O-depleted water vapor from this layer. Thus, thermally induced vapor transport not only results in signal attenuation, but can also shift the δ18O value regardless of the initial sinusoidal variations.
Lastly, in the first 2–3 cm of the snowpack, strong depletion is observed over the period, with a decrease by 2 to 3 ‰ instead of 0.5 ‰ when the temperature gradients were absent (Simulation 1). This depletion probably results from the arrival of 18O-depleted water vapor from warmer layers below. This again shows the influence of temperature gradients that were absent from the previous simulation. However, note that in this simulation we neglect precipitation and the exchange of vapor with the atmosphere. Thus, the depletion observed here may not occur in natural settings when these processes are active.
In conclusion, at GRIP the diffusion of vapor as a result of temperature gradients has a double impact on isotopic compositions. It increases the attenuation in the first 60 cm of snow because of higher vapor fluxes. And it also creates local isotopic maxima and minima in a pattern corresponding to temperature gradients in the snowpack but disconnected from the original δ18O sinusoidal signal.
4.1.2 Comparison with core data
Here, we evaluate the attenuation of the initial seasonal signal in δ18O over 10 years at two Greenland ice-core sites, NEEM and GRIP. For the first site, we use four shallow cores (NEEM2010S2, NEEM2008S3, NEEM2007S3, NEEM2008S2) published in Steen-Larsen et al. (2011) and in Masson-Delmotte et al. (2015). For the second site, we use one shallow core (1989-S1) published in White et al. (1997). For the GRIP core, only the first 80 m is considered. Therefore, the data presented correspond to deposition and densification conditions like the modern ones. For NEEM the values of the four cores are taken together. For NEEM and GRIP, the semi-amplitude is computed along the core. In the first 10 m, the maximum value every 30 cm is retained, and deeper in the firn because of compaction, the maximum value every 20 cm is retained (see also the Supplement; Fig. 4). For this study, we have chosen to estimate attenuation in years with a clearly marked seasonal cycle, a strategy that can be debated but at least documented. Consequently, from this first series of maxima, a second series of maxima is computed with a larger window of 1 m. The “attenuated amplitudes” at each level are then defined as the ratio between these 1 m maxima and the initial 1 m maxima. Maximum semi-amplitudes every 5 m are also computed and displayed in Fig. 4. The 2.5 m attenuation is slightly higher at GRIP, leading to a remaining amplitude of 86 %, than at NEEM where the remaining amplitude is 90 % (Fig. 4). The amplitude decreases with depth in parallel for the two cores, with the amplitude at NEEM always staying higher than at GRIP. For comparison with our model, we estimate attenuation after 10 years, i.e., at a depth of ∼ 5.8 m for NEEM and ∼ 5.65 m for GRIP. The remaining amplitude is 80 and 72 % at GRIP and NEEM, respectively. Our Simulation 1 produced 7 % of attenuation only in the same duration, showing that our model run on an isothermal snowpack underestimates the attenuation observed in the data.
4.1.3 Comparison with other models
At 2.5 m at NGRIP, Johnsen et al. (2000) simulate a remaining amplitude of 77 % (Fig. 4). For a depth of 5.43 m corresponding to an age of 10 years, the simulated remaining amplitude is 57 %. For Bolzan and Pohjola (2000) at GRIP after 10 years, 70 % of the initial amplitude is still preserved. The slower attenuation for Bolzan and Pohjola (2000) compared to Johnsen et al. (2000) may be due more to the different sites considered than to the different models. GRIP has higher accumulation rates that should limit diffusion. Nevertheless, the attenuation of 30 % simulated by Bolzan and Pohjola (2000) at GRIP is stronger than the attenuation of 7 % simulated in our model. Town et al. (2008, Sect. 2.1) found attenuations of a few tenths per mil after several years when implementing only diffusion, a result consistent with ours since we get a decrease by 1.2 ‰ after 10 years.
We explore below the reasons for discrepancies between models. The equation for the effective diffusivity of vapor in firn used in our study is different from the ones used by Johnsen et al. (2000) and by Bolzan and Pohjola (2000). We do not consider the tortuosity factor l or the adjustable scale factor s of Bolzan and Pohjola (2000). However, using the values given by the previous authors for l and s leads to Deff values ranging from to m2 s−1 for a density of 350 kg m−3 and a temperature of 241 K, which is coherent with our value of m2 s−1. As indicated by Bolzan and Pohjola (2000), the choice of one equation or another has little impact here.
The most probable difference lies in the way diffusion is taken into account. Johnsen et al. (2000) and Bolzan and Pohjola (2000) use a single equation of diffusion to predict the evolution of the isotopic composition of the layer. In our case, we specifically compute the fluxes in the vapor each second and at each depth level and deduce the evolution of δ18O in the grain center after sublimation–condensation and recrystallization. Denux (1996) and van der Wel et al. (2015) indicate that the model developed by Johnsen (1977) and used in Johnsen et al. (2000) overestimates the attenuation compared to observed values. For Denux (1996), the model of Johnsen (1977) should consider the presence of ice crusts and maybe also the temperature gradients in the surface snow to get closer to the real attenuation at remote Antarctic sites. Van der Wel et al. (2015) have compared the model results to a spike-layer experiment realized at Summit. Because an artificial snow layer cannot be representative of natural diffusion, they took care to evaluate diffusion based only on the natural layers present above and below the artificial layer. Van der Wel et al. (2015) propose three causes for the discrepancy between the Johnsen et al. model prediction and actual measured attenuation at GRIP. They blame either ice crusts, bad knowledge and parameterization of the tortuosity in the first meters of snow, and/or a bad description of the isotopic heterogeneity within the ice grain. In our model, the grain heterogeneity is included. Even if the parameters defining the mixing between the two compartments are not very well constrained (see Sect. 4.3), the attenuation is indeed smaller compared to the Johnsen model.
4.2 Dome C (Antarctica)
The aim of the Simulations 3 to 6, run at Dome C, is to isolate diffusion from other effects affecting water isotopic composition, i.e., wind drift and compaction.
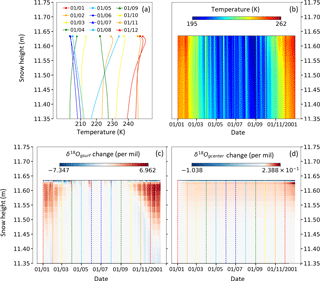
Figure 5Simulation 3: evolution of temperature and δ18O values from January to December 2001. (a) Temperature profiles for the first day of each month; (b) temperature evolution in the snowpack; (c) δ18O change in the grain surface compartment; (d) δ18O change in the grain center compartment. Here, “δ18O change” is defined as the difference between δ18O at t and at the beginning of the simulation for the selected layer.
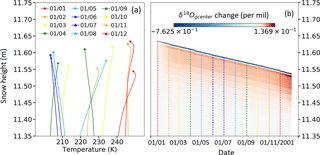
Figure 6Simulation 4: cumulative change in δ18Ogcenter values (vapor transport, compaction, and wind drift active).
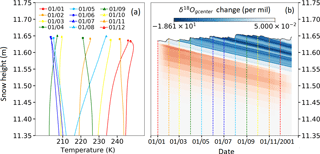
Figure 7Simulation 5: cumulative change in δ18O values at the grain center (relative to t0) over 6 months. Simulation with snowfall with varying δ18O (function of Tair), vapor transport active, wind, and weight compaction active.
4.2.1 Simulation 3: without precipitation, without wind drift, and without homogeneous compaction
Figure 5 presents the results of temperature evolution (panels a and b) and δ18O evolution (panels c and d) for Simulation 3. The main changes in δ18Ogsurf and δ18Ogcenter occur in summer (Fig. 5c and d). On the one hand, the first 20 cm of snow tend to become 18O enriched by +0.2 ‰ for the grain center compartment. On the other hand, the first centimeter becomes depleted by 1.0 ‰ for grain center. This pattern is coherent with the temperature profiles for the summer period (Fig. 5a). Vapor moves out of the warmest layers and toward colder layers where it condensates. This causes an increase in δ18O in warm layers and a decrease in colder layers. This pattern is also confirmed by snow density changes (see Fig. S2).
During winter, the temperature generally decreases toward the surface (Fig. 5a). Vapor transport is thus reversed in the first 20 cm, but this only slightly reduces the dispersion of δ18Ogcenter values. On the first of August, the temperature at the surface temporarily increases to 235 K. This warm event strongly modifies the temperature profile in the snowpack and therefore the pattern of vapor transport. It is associated with an increase in δ18O values at the surface, which is particularly visible for the δ18Ogsurf values (Fig. 5c).
Thus, vapor transport can modify δ18O values in surface snow, even in the absence of precipitation or condensation from the atmosphere. This mechanism could explain the parallel evolution of surface snow isotopic composition and temperature described by Steen-Larsen et al. (2014) and Touzeau et al. (2016) between precipitation events.
4.2.2 Simulation 4: without precipitation, with wind drift, and with homogeneous compaction
Compaction and wind drift are not presumed to directly modify the δ18O values. However, the change in densities and layer thicknesses slightly modifies the temperature profile and the diffusivities. These processes thus could have an indirect impact on δ18O values. Figure 6 shows δ18Ogcenter changes that are reduced compared to the simulation without wind drift and compaction. This is coherent with a decrease in the density changes associated with vapor transport in the case with compaction (see Fig. S5).
4.2.3 Simulation 5: with precipitation, with wind drift, with homogeneous compaction
In Simulation 5, we add precipitation to wind and weight compaction effects. Both snowfall and wind compaction are responsible for irregular changes, respectively positive and negative, in the height of the snowpack (Fig. 7). In the new deposited layers, the δ18Ogcenter values reflect the δ18O values in the precipitation. They vary as expected from −40 ‰ on 31 December to −59 ‰ in July (Figs. 7, S8). The effect of vapor transport is visible only in “old” layers that were originally homogeneous in terms of δ18O. These old layers, which were reaching the surface in January, have been buried below the new layers and are found from 11 cm of depth downward in December.
4.2.4 Simulations 6: 10-year simulation at Dome C
Simulations 6 corresponds to a simulation run over 10 years at Dome C, with variable δ18O in the precipitation. Over these 10 years, about 1 m of snow is deposited. At the end of the simulation, the vertical profile of δ18O in the new layers has an average value of −49.7 ‰ and a semi-amplitude of 4.5 ‰ (Fig. 8). Here we take into account all the maxima and minima at a vertical resolution of 9 cm of fresh snow. Based on the atmospheric temperature variations only, the isotopic composition in the precipitation should vary around an average value of −53.2 ‰, with a semi-amplitude of 8.6 ‰. The main reason for this difference is the precipitation amounts: large precipitation events in winter are associated with relatively high δ18O values. The vertical resolution chosen for the model of 2.5 cm may also contribute to the decrease in the semi-amplitude. Light snowfall events do not result in the production of a new surface layer but are integrated into the old surface layer. As expected, the peak to peak amplitude of δ18O variations is then further reduced as a result of the two vapor diffusion processes and of associated vapor–solid exchanges. The effect of vapor transport is relatively small. To help with visualization, we selected four layers and displayed the evolution of δ18O in these layers over the years (Fig. 8d). The selected layers were deposited during winter 2000 and during summer seasons 2002, 2004, and 2006.
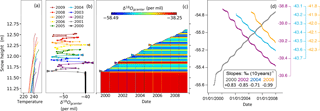
Figure 8Simulation 6: evolution of δ18Ogcenter values as a result of snowfall and vapor transport over 10 years (compaction is inactive; merging between layers is allowed but limited). (a) Temperature profiles at mid-January for each year. (b) δ18Ogcenter profile at mid-January for each year. (c) Repartition of δ18Ogcenter values as a function of time and depth. (d) Evolution of δ18Ogcenter values after burial for four selected layers (deposited in winter 2000 and summer 2002, 2004, 2006). Note that we do not present the evolution of snow composition in the first year after deposition because the thin snow layers resulting from precipitation are becoming merged.
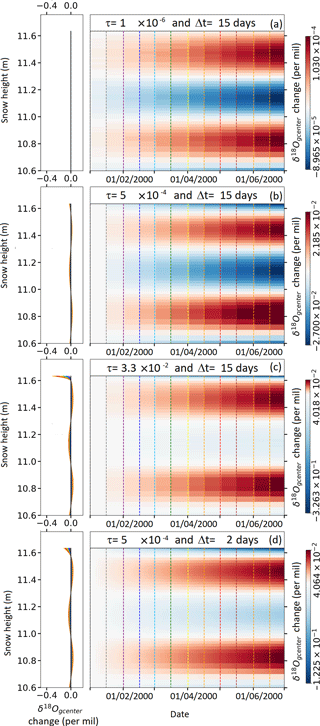
Figure 9Test of the sensitivity of the model to the ratio of mass between grain surface compartments and total grain and to the interval of mixing between the two compartments (GRIP).
For the layer deposited during winter 2000, there is an increase in δ18O values of about +0.8 ‰ over 10 years. The slope is irregular, with the strongest increases occurring during summers between November and February when vapor transport is maximal. The slope is also stronger when the layer is still close to the surface, probably because of the stronger temperature gradients in the first centimeters of snow (Fig. 8a). For the layers deposited during the summers, the evolution of δ18O values is symmetric to that observed for winter 2000. Over 10 years, i.e., between 2000 and 2009, the δ18O amplitude thus decreases by about 1.6 ‰. This corresponds to a decrease of 18 % relative to the initial amplitude in the snow layers. This is higher than the 7 % attenuation modeled in Greenland for constant temperature and the 11.7 % attenuation observed when including diffusion caused by temperature gradients (Sect. 4.1). However, the comparison between the two sites is not straightforward, because of differences in temperature and accumulation counteracting each other. On the one hand, at GRIP the diffusion is forced by low vertical gradients of δ18O of the order of 0.24 ‰ cm−1. These are much smaller than the typical δ18O gradients at Dome C, which are close to 1.10 ‰ cm−1. On the other hand, the temperature of 241 K at GRIP is higher than the 220 K measured at Dome C, thus favoring diffusion.
4.3 Sensitivity tests for duration of recrystallization
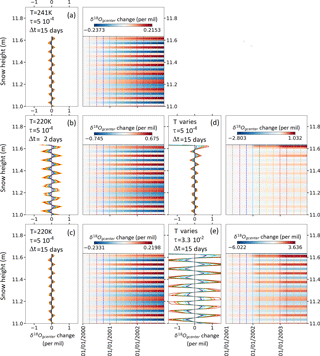
We have shown above that the attenuation of the isotopic signal seems too small, at least for the GRIP site. In parallel, the parameters τ and Δtgsurf/center of the model associated with grain renewal could only loosely be estimated, leading to uncertainty in the attenuation modeling. In this section, we perform some sensitivity tests to quantify how δ18O attenuation can be increased by exploring the uncertainty range in the renewal of the snow grain (Table 5). Indeed, the assumed values for the ratio between the grain surface and the total mass of the grain τ may have been underestimated or overestimated. The same is true for the periodicity of mixing between these two compartments Δtsurf/center.
The sensitivity tests are first designed for Greenland sites and run for 6 months, with initial amplitude of the sinusoidal δ18O signal of 16 ‰ and a fixed temperature of 241 K in all the layers (Fig. 9). First, we use a periodicity of mixing Δtsurf/center of 15 days and vary the value for the mass ratio τ: , 5 , 3.3 . In practice, for Δtsurf/center=15 days, we realize mixing on day 2 and day 16 of each month. Second, we use the usual value of for τ and change the periodicity of the mixing to 2 days.
In the first case, where and the mixing occurs every 15 days, the grain surface compartment is very small. Its original sinusoidal δ18O profile disappears in less than 1 day due to exchanges with vapor (not shown). The impact on the grain center is then very small with an increase in the first minimum by ∼ ‰ over 6 months (Fig. 9a). In this case, the attenuation due to diffusion is even reduced compared to the results displayed above.
In the second case, where and the mixing occurs every 15 days, the grain surface compartment is larger and the attenuation is slower. Thus, in the grain surface compartment, half of the original amplitude still remains at the end of the simulation (not shown). The impact on the grain center compartment is clearly visible with an increase in the first minimum by ‰ after 6 months (Fig. 9b).
In the third case, with , and mixing every 15 days, the attenuation of the sinusoidal signal in the grain surface compartment is only of 1 % because the grain surface compartment is very large. On opposite, attenuation in the grain center is quite large, i.e., the first minimum increases by ‰ after 6 months (Fig. 9c).
In the fourth case, with and mixing every 2 days, the first minimum increases by ‰ after 6 months for the grain center compartment (Fig. 9d). It is similar to the attenuation observed in the third case.
The results of these sensitivity tests suggest that the impact of vapor transfer on the grain center isotopic compositions is maximized when the grain surface compartment is large and/or refreshed often. They also clearly show that using a small grain surface compartment such as drastically reduces the impact on the grain center isotopic values. However, our best estimates for τ and Δtsurf/center were not chosen randomly (see Sect. 3.1.3). Moreover, the use of or Δtsurf/center=2 days leads to a near doubling of the δ18O attenuation (see above). This is not yet sufficient to explain the gap between our model output for isothermal simulation and the data. However, if this doubling is applicable to the case with temperature gradients, the attenuation obtained might reach the one observed in the data at GRIP.
At Dome C, sensitivity tests show that we can increase the attenuation by a factor of 3 by reducing the mixing time from 15 to 2 days (Fig. 10b–c). Similarly, if the ratio τ is put at instead of , attenuation is more than doubled over 3 years (Fig. 10d–e). Thus, at Dome C the values of τ and Δtsurf/center seem to more strongly affect the attenuation obtained compared to GRIP. This greater sensitivity at Dome C could result from the influence of temperature gradients or from steeper δ18O gradients caused by the low accumulation. The average layer thickness of 2 cm in the first meter corresponds to ∼ 4 points per year at Dome C, but 35 points per year at GRIP.
4.4 Additional missing processes
In the previous sections, we have seen that model outputs for GRIP generally lead to smaller attenuation than observed in ice cores. To improve the model compatibility with data, two kinds of approaches are possible. On the one hand, it would be useful to realize simulations adapted to on-site experiments, such as the one by van der Wel et al. (2015). This would allow for the verification of how diffusion can be improved in the model. For instance, previous studies have suggested that water vapor diffusivity within the snow porosity may be underestimated by a factor of 5 (Colbeck, 1983), but this is debated (Calonne et al., 2014). On the other hand, we also believe that other processes should probably be considered to explain the remaining attenuation. Ventilation is an additional process that has already been implemented in the snow water isotopic model of Town et al. (2008) and Neumann (2003). Because of strong porosity and sensitivity to surface wind and relief, ventilation is probably as important as diffusion in the top of the firn, even if diffusion is expected to be more effective at greater depths. For the Dome C simulation (Fig. 8), the slope d(δ18O)∕dz decreases slowly, indicating that diffusion remains almost as active at 60 cm than at 10 cm of depth. Neumann (2003) indicates that at Taylor Mouth the diffusion becomes the only process of vapor transport below 2 m of depth. For Dome C, for a temperature gradient of 3 ∘C m−1, we compute an average speed due to diffusion of m s−1. This is comparable to an air speed due to wind pumping of about m s−1 within the top meters of snow at WAIS (Buizert and Severinghaus, 2016). We conclude that, in as much as these results can be applied to Dome C, the two processes would have a comparable impact at this site in the first meters of snow. The next step for Crocus-iso development is thus to implement ventilation. Finally, we are also aware that in Antarctic central regions, the wind reworking of the snow has a strong effect in shaping the isotopic signal. A combination of stratigraphic noise and diffusion could indeed be responsible for creating isotopic cycles of non-climatic origin in the firn (Laepple et al., 2017). Wind reworking may also contribute to attenuation by mixing together several layers deposited during different seasons.
Water vapor transport and water isotopes have been implemented in the Crocus snow model, enabling the depiction of the temporal δ18O variations in the top 50 cm of the snow in response to new precipitation, the evolution of the temperature gradient in the snow, and densification. The main process implemented here to explain post-deposition isotopic variations is diffusion. We have implemented two types of diffusion in the vapor phase: (1) water vapor diffusion along isotopic gradients and (2) thermally induced vapor diffusion. The vapor diffusion between layers was realized at the centimetric scale. The consequences of the two vapor diffusion processes on isotopes in the solid phase were investigated. The solid phase was modeled as snow grains divided into two sub-compartments: (1) a grain surface sub-compartment in equilibrium with interstitial water vapor and (2) an inner grain only exchanging slowly with the surface compartment. We parameterized the speed of diffusion through the renewal time of a snow grain and the proportion of the two snow grain compartments.
Our approach based on a detailed snow model makes it possible to investigate at a fine scale the various processes explaining the variations in density and δ18O in the firn. We look specifically at the effect of the evolution of the temperature gradient, new snow accumulation, and compaction events linked to wind drift. Over the first 30 cm, the snow density variations are mainly driven by compaction events linked to wind drift. Vapor transport and long-term compaction have secondary effects. Below 30 cm, wind-drift-driven compaction is no longer visible. Because of a strong temperature gradient and low density, water vapor transport will have a significant effect down to 60 cm. δ18O is primarily driven by variations in the δ18O of precipitation as expected. The seasonal variations are then attenuated by water vapor transport and diffusion along isotopic gradients, with an increase in these effects at higher temperatures, i.e., during summer periods.
From 10-year simulations of the Crocus-iso model both at GRIP in Greenland and Dome C in Antarctica, we have estimated the post-deposition attenuation of the annual δ18O signal in the snow to about 7–18 % through diffusion. This attenuation is smaller than the one obtained from isotopic data on shallow cores in Greenland, suggesting missing processes in the Crocus model when implementing water vapor. It is also significantly smaller than the diffusion implemented by Johnsen et al. (2000), but some studies have suggested that the Johnsen isotopic diffusivity is too strong (Denux, 1996; Van der Wel et al., 2015).
We see our study as a first step toward a complete post-deposition modeling of water isotope variations. Several other developments are foreseen in this model. First, wind pumping is currently not implemented in the Crocus model. This effect, implemented in the approach of Neumann (2003) and Town et al. (2008), is expected to have a contribution as large as the effect of diffusion for the post-deposition isotopic variations. Second, in low accumulation sites like Dome C, wind scouring probably has an important effect on the evolution of the δ18O signal at depth through a reworking of the top snow layers (Libois et al., 2014). This effect has not been considered here but could be implemented in the model in the next years. It could also play a role in the preservation of anomalously strong δ18O peaks at Dome C (Denux, 1996).
Other short-term developments concern the implementation of the exchange of water vapor with the atmosphere through hoar deposition. This is particularly timely since many recent studies have explored the parallel evolution of the isotopic composition of water vapor and surface snow during summer in both Greenland and Antarctica (Steen-Larsen et al., 2014; Ritter et al., 2016; Casado et al., 2016a, b). Similarly, the implementation of the ventilation of the snowpack in the model is important, since this effect is expected to significantly contribute to signal attenuation.
Another aspect is to look at the post-deposition d-excess and 17O-excess variations in snow pits. Recent studies have shown that the relationship between 17O-excess and δ18O is not the same when looking at precipitation samples and snow pit samples in East Antarctica (Touzeau et al., 2016). This observation questions the influence of diffusion within the snowpack on second-order parameters such as 17O-excess. Indeed, 17O-excess is strongly influenced by kinetic-diffusion-driven fractionation, which may be quantified by the implementation of 17O-excess in our Crocus-iso model.
The code used in the paper is a development of the open source code for the SURFEX/ISBA–Crocus model based on version 8.0, hosted on an open git repository at CNRM (https://opensource.umr-cnrm.fr/projects/surfex_git2). Before downloading the code, you must register as a user at https://opensource.umr-cnrm.fr/. You can then obtain the code used in the present study by downloading the revision tagged “Touzeau_jan2018” of the branch touzeau_dev (last access: January 2018). The meteorological forcing required to perform the runs is available in the Supplement of the present paper.
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-11-2393-2018-supplement.
SM wrote the new module for vapor diffusion. AT inserted isotopes and isotope transport into the numerical code with the help of SM for numerical issues and physics and help from AL for concepts and hypotheses on the theory of isotopes. GP and LA provided information and references on snow microstructure and microphysics as well as direct field experience on site meteorology and accumulation conditions. AT ran the simulations and interpreted the results. AT and AL wrote the paper. All the authors corrected the paper.
The authors declare that they have no conflict of interest.
The research leading to these results received funding from the European
Research Council under the European Union Seventh Framework Programme
(FP7/2007-30 2013; ERC grant agreement no. 306045). We want to acknowledge
Anaïs Orsi and Mathieu Casado from LSCE, who contributed to this work through fertile
discussions on the model contents and its applications. We are grateful to
Mathieu Casado and Camille Bréant for providing snow pit temperature and density
profiles as well as firn density profiles for model initialization. We would
like to thank Didier Roche for his advice during model development and on
how to make the code available. We are also indebted to Jean-Yves Peterschmidt,
who provided continual help and useful tutorials on the Fortran and Python
languages. We thank Matthieu Lafaysse and Vincent Vionnet at CNRM/CEN for help with the
model and meteorological driving data. CNRM/CEN and IGE are part of LabEX
OSUG@2020. We thank three anonymous reviewers for their questions and
comments, which helped to improve the present article.
Edited by: Dan
Goldberg
Reviewed by: three anonymous referees
Albert, M. R. and Hardy, J. P.: Ventilation experiments in seasonal snow cover, IAHS Publications-Series of Proceedings and Reports-Intern Assoc Hydrological Sciences, 228, 41–50, 1995.
Albert, M. R. and McGilvary, W. R.: Thermal effects due to air flow and vapor transport in dry snow, J. Glaciol., 38, 273–281, 1992.
Albert, M. R. and Shultz, E. F.: Snow and firn properties and air–snow transport processes at Summit, Greenland, Atmos. Environ., 36, 2789–2797, 2002.
Albert, M. R., Grannas, A. M., Bottenheim, J., Shepson, P. B., and Perron, F. E.: Processes and properties of snow–air transfer in the high Arctic with application to interstitial ozone at Alert, Canada, Atmos. Environ., 36, 2779–2787, 2002.
Altnau, S., Schlosser, E., Isaksson, E., and Divine, D.: Climatic signals from 76 shallow firn cores in Dronning Maud Land, East Antarctica, The Cryosphere, 9, 925–944, https://doi.org/10.5194/tc-9-925-2015, 2015.
Barkan, E. and Luz, B.: Diffusivity fractionations of HO/HO and HO/HO in air and their implications for isotope hydrology, Rapid Commun. Mass Sp., 21, 2999–3005, 2007.
Bartelt, P., Buser, O., and Sokratov, S. A.: A nonequilibrium treatment of heat and mass transfer in alpine snowcovers, Cold Reg. Sci. Technol., 39, 219–242, 2004.
Bolzan, J. F. and Pohjola, V. A.: Reconstruction of the undiffused seasonal oxygen isotope signal in central Greenland ice cores, J. Geophys. Res.-Oceans, 105, 22095–22106, 2000.
Bréant, C., Martinerie, P., Orsi, A., Arnaud, L., and Landais, A.: Modelling firn thickness evolution during the last deglaciation: constraints on sensitivity to temperature and impurities, Clim. Past, 13, 833–853, https://doi.org/10.5194/cp-13-833-2017, 2017.
Brun, E. and Touvier, F.: Etude expérimentale de la convection thermique dans la neige, Le Journal de Physique Colloques, 48, C1-257–C1-262, 1987.
Brun, E., David, P., Sudul, M., and Brunot, G.: A numerical model to simulate snow-cover stratigraphy for operational avalanche forecasting, J. Glaciol., 38, 13–22, 1992.
Brun, E., Six, D., Picard, G., Vionnet, V., Arnaud, L., Bazile, E., Boone, A., Bouchard, A., Genthon, C., and Guidard, V.: Snow/atmosphere coupled simulation at Dome C, Antarctica, J. Glaciol., 57, 721–736, 2011.
Buizert, C. and Severinghaus, J. P.: Dispersion in deep polar firn driven by synoptic-scale surface pressure variability, The Cryosphere, 10, 2099–2111, https://doi.org/10.5194/tc-10-2099-2016, 2016.
Calonne, N., Geindreau, C., and Flin, F.: Macroscopic modeling for heat and water vapor transfer in dry snow by homogenization, J. Phys. Chem. B, 118, 13393–13403, 2014.
Calonne, N., Geindreau, C., and Flin, F.: Macroscopic modeling of heat and water vapor transfer with phase change in dry snow based on an upscaling method: Influence of air convection, J. Geophys. Res.-Earth, 120, 2476–2497, 2015.
Carmagnola, C. M., Morin, S., Lafaysse, M., Domine, F., Lesaffre, B., Lejeune, Y., Picard, G., and Arnaud, L.: Implementation and evaluation of prognostic representations of the optical diameter of snow in the SURFEX/ISBA-Crocus detailed snowpack model, The Cryosphere, 8, 417–437, https://doi.org/10.5194/tc-8-417-2014, 2014.
Casado, M., Landais, A., Masson-Delmotte, V., Genthon, C., Kerstel, E., Kassi, S., Arnaud, L., Picard, G., Prie, F., Cattani, O., Steen-Larsen, H.-C., Vignon, E., and Cermak, P.: Continuous measurements of isotopic composition of water vapour on the East Antarctic Plateau, Atmos. Chem. Phys., 16, 8521–8538, https://doi.org/10.5194/acp-16-8521-2016, 2016a.
Casado, M., Landais, A., Picard, G., Münch, T., Laepple, T., Stenni, B., Dreossi, G., Ekaykin, A., Arnaud, L., Genthon, C., Touzeau, A., Masson-Delmotte, V., and Jouzel, J.: Archival of the water stable isotope signal in East Antarctic ice cores, The Cryosphere Discuss., https://doi.org/10.5194/tc-2016-263, 2016b.
Colbeck, S. C.: Theory of metamorphism of dry snow, J. Geophys. Res., 88, 5475–5482, 1983.
Colbeck, S. C.: Air movement in snow due to wind pumping, J. Glaciol., 35, 209–213, 1989.
Dahl-Jensen, D., Johnsen, S., Hammer, C., Clausen, H., and Jouzel, J.: Past accumulation rates derived from observed annual layers in the GRIP ice core from Summit, Central Greenland, in: Ice in the climate system, Springer, 1993.
Dahl-Jensen, D., Gundestrup, N. S., Keller, K., Johnsen, S. J., Gogineni, S. P., Allen, C. T., Chuah, T. S., Miller, H., Kipstuhl, S., and Waddington, E. D.: A search in north Greenland for a new ice-core drill site, J. Glaciol., 43, 300–306, 1997.
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, I., Biblot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Greer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Holm, E. V., Isaksen, L., Kallberg, P., Kohler, M., Matricardi, M., McNally, A. P., Mong-Sanz, B. M., Morcette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thepaut, J. N., and Vitart, F.: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. Roy. Meteorol. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011.
Delmotte, M., Masson, V., Jouzel, J., and Morgan, V. I.: A seasonal deuterium excess signal at Law Dome, coastal eastern Antarctica: A Southern Ocean signature, J. Geophys. Res.-Atmos., 105, 7187–7197, 2000.
Denux, F.: Diffusion du signal isotopique dans le névé et dans la glace. Implication pour l'échantillonnage, PhD, Geosciences, Université Joseph Fourier-Grenoble 1, Grenoble, 243 pp., 1996.
Domine, F., Morin, S., Brun, E., Lafaysse, M., and Carmagnola, C. M.: Seasonal evolution of snow permeability under equi-temperature and temperature-gradient conditions, The Cryosphere, 7, 1915–1929, https://doi.org/10.5194/tc-7-1915-2013, 2013.
Ebner, P. P., Schneebeli, M., and Steinfeld, A.: Metamorphism during temperature gradient with undersaturated advective airflow in a snow sample, The Cryosphere, 10, 791–797, https://doi.org/10.5194/tc-10-791-2016, 2016.
Ebner, P. P., Steen-Larsen, H. C., Stenni, B., Schneebeli, M., and Steinfeld, A.: Experimental observation of transient δ18O interaction between snow and advective airflow under various temperature gradient conditions, The Cryosphere, 11, 1733–1743, https://doi.org/10.5194/tc-11-1733-2017, 2017.
Ekaykin, A. A., Hondoh, T., Lipenkov, V. Y., and Miyamoto, A.: Post-depositional changes in snow isotope content: preliminary results of laboratory experiments, Clim. Past Discuss., 5, 2239–2267, https://doi.org/10.5194/cpd-5-2239-2009, 2009.
Ekaykin, A. A., Kozachek, A. V., Lipenkov, V. Y., and Shibaev, Y. A.: Multiple climate shifts in the Southern hemisphere over the past three centuries based on central Antarctic snow pits and core studies, Ann. Glaciol., 55, 259–266, 2014.
Ellehoj, M. D., Steen-Larsen, H. C., Johnsen, S. J., and Madsen, M. B.: Ice-vapor equilibrium fractionation factor of hydrogen and oxygen isotopes: Experimental investigations and implications for stable water isotope studies, Rapid Commun. Mass Sp., 27, 2149–2158, 2013.
EPICA community members: Eight glacial cycles from an Antarctic ice core, Nature, 429, 623–628, 2004.
EPICA community members: One-to-one coupling of glacial climate variability in Greenland and Antarctica, Nature, 444, 195–198, 2006.
Fisher, D. A. and Koerner, R. M.: Signal and noise in four ice-core records from the Agassiz Ice Cap, Ellesmere Island, Canada: details of the last millennium for stable isotopes, melt and solid conductivity, The Holocene, 4, 113–120, 1994.
Flanner, M. G. and Zender, C. S.: Linking snowpack microphysics and albedo evolution, J. Geophys. Rese.-Atmos., 111, D12208, https://doi.org/10.1029/2005JD006834, 2006.
Fréville, H., Brun, E., Picard, G., Tatarinova, N., Arnaud, L., Lanconelli, C., Reijmer, C., and van den Broeke, M.: Using MODIS land surface temperatures and the Crocus snow model to understand the warm bias of ERA-Interim reanalyses at the surface in Antarctica, The Cryosphere, 8, 1361–1373, https://doi.org/10.5194/tc-8-1361-2014, 2014.
Frezzotti, M., Pourchet, M., Flora, O., Gandolfi, S., Gay, M., Urbini, S., Vincent, C., Becagli, S., Gragnani, R., and Proposito, M.: Spatial and temporal variability of snow accumulation in East Antarctica from traverse data, J. Glaciol., 51, 113–124, 2005.
Friedman, I., Benson, C., and Gleason, J.: Isotopic changes during snow metamorphism, in: Stable isotope geochemistry: a tribute to Samuel Epstein, edited by: Taylor Jr., H. P., O'Neil, J. R., and Kaplan, I. R., The Geochemical Society, Special Publication No.3, 211–221, 1991.
Gay, M., Fily, M., Genthon, C., Frezzotti, M., Oerter, H., and Winther, J.-G.: Snow grain-size measurements in Antarctica, J. Glaciol., 48, 527–535, 2002.
Genthon, C., Six, D., Gallée, H., Grigioni, P., and Pellegrini, A.: Two years of atmospheric boundary layer observations on a 45-m tower at Dome C on the Antarctic plateau, J. Geophys. Res.-Atmos., 118, 3218–3232, 2013.
Genthon, C., Six, D., Scarchilli, C., Ciardini, V., and Frezzotti, M.: Meteorological and snow accumulation gradients across Dome C, East Antarctic plateau, Int. J. Climatol., 36, 455–466, 2016.
Gkinis, V., Simonsen, S. B., Buchardt, S. L., White, J. W. C., and Vinther, B. M.: Water isotope diffusion rates from the NorthGRIP ice core for the last 16,000 years – Glaciological and paleoclimatic implications, Earth and Planet. Sc. Lett., 405, 132–141, 2014.
Goursaud, S., Masson-Delmotte, V., Favier, V., Preunkert, S., Fily, M., Gallée, H., Jourdain, B., Legrand, M., Magand, O., Minster, B., and Werner, M.: A 60-year ice-core record of regional climate from Adélie Land, coastal Antarctica, The Cryosphere, 11, 343–362, https://doi.org/10.5194/tc-11-343-2017, 2017.
Hoshina, Y., Fujita, K., Nakazawa, F., Iizuka, Y., Miyake, T., Hirabayashi, M., Kuramoto, T., Fujita, S., and Motoyama, H.: Effect of accumulation rate on water stable isotopes of near-surface snow in inland Antarctica, J. Geophys. Res., 119, 274–283, 2014.
Johnsen, S.: Stable isotope homogenization of polar firn and ice, Isotopes and impurities in snow and ice, International Association of Hydrological Sciences, 1, 210–219, 1977.
Johnsen, S. J., Dahl-Jensen, D., Dansgaard, W., and Gundestrup, N.: Greenland palaeotemperatures derived from GRIP bore hole temperature and ice core profiles, Tellus B, 47, 624–629, 1995.
Johnsen, S. J., Clausen, H. B., Cuffey, K. M., Hoffmann, G., Schwander, J., and Creyts, T.: Diffusion of stable isotopes in polar firn and ice: the isotope effect in firn diffusion, Physics of ice core records, 159, 121–140, 2000.
Jones, T. R., Roberts, W. H. G., Steig, E. J., Cuffey, K. M., Markle, B. R., White, J. W. C.: Southern Hemisphere climate variability forced by Northern Hemisphere ice-sheet topography, Nature, 554, 351–355, https://doi.org/10.1038/nature24669, 2018.
Jouzel, J., Masson-Delmotte, V., Cattani, O., Dreyfus, G., Falourd, S., Hoffmann, G., Minster, B., Nouet, J., Barnola, J. M., Chappellaz, J., Fischer, H., Gallet, J. C., Johnsen, S., Leuenberger, M., Loulergue, L., Luethi, D., Oerter, H., Parrenin, F., Raisbeck, G., Raynaud, D., Schilt, A., Schwander, J., Selmo, E., Souchez, R., Spahni, R., Stauffer, B., Steffensen, J. P., Stenni, B., Stocker, T. F., Tison, J. L., Werner, M., and Wolff, E. W.: Orbital and millennial Antarctic climate variability over the past 800,000 years, Science, 317, 793–796, 2007.
Kaempfer, T. U., Schneebeli, M., and Sokratov, S. A.: A microstructural approach to model heat transfer in snow, Geophys. Res. Lett., 32, L21503, https://doi.org/10.1029/2005GL023873, 2005.
Kawamura, K., Parrenin, F., Lisiecki, L., Uemura, R., Vimeux, F., Severinghaus, J. P., Hutterli, M. A., Nakazawa, T., Aoki, S., Jouzel, J., Raymo, M. E., Matsumoto, K., Nakata, H., Motoyama, H., Fujita, S., Goto-Azuma, K., Fujii, Y., and Watanabe, O.: Northern Hemisphere forcing of climatic cycles in Antarctica over the past 360,000 years, Nature, 448, 912–916, 2007.
Krol, Q. and Löwe, H.: Relating optical and microwave grain metrics of snow: the relevance of grain shape, The Cryosphere, 10, 2847–2863, https://doi.org/10.5194/tc-10-2847-2016, 2016.
Laepple, T., Werner, M., and Lohmann, G.: Synchronicity of Antarctic temperatures and local solar insolation on orbital timescales, Nature, 471, 91–94, 2011.
Landais, A., Barkan, E., and Luz, B.: Record of δ18O and 17O-excess in ice from Vostok Antarctica during the last 150,000 years, Geophys. Res. Lett., 35, L02709, https://doi.org/10.1029/2007GL032096, 2008.
Landais, A., Casado, C., Prié, F., Magand, O., Arnaud, L., Ekaykin, A., Petit, J.-R., Picard, G., Fily, M., Minster, B., Touzeau, A., Goursaud, S., Masson-Dlemotte, V., Jouzel, J., and Orsi, A.: Surface studies of water isotopes in Antarctica for quantitative interpretation of deep ice core data, C. R. Geosci., 349, 139–150, 2017.
Legagneux, L. and Domine, F.: A mean field model of the decrease of the specific surface area of dry snow during isothermal metamorphism, J. Geophys. Res., 110, F04011, https://doi.org/10.1029/2004JF000181, 2005.
Lefebre, F., Gallée, H., van Ypersele, J.-P., and Greuell, W.: Modeling of snow and ice melt at ETH Camp (West Greenland): A study of surface albedo, J. Geophys. Res.-Atmos., 108, D84231, https://doi.org/10.1029/2001JD001160, 2003.
Libois, Q., Picard, G., Arnaud, L., Morin, S., and Brun, E.: Modeling the impact of snow drift on the decameter-scale variability of snow properties on the Antarctic Plateau, J. Geophys. Res.-Atmos., 119, 11662–11681, 2014.
Libois, Q., Picard, G., Arnaud, L., Dumont, M., Lafaysse, M., Morin, S., and Lefebvre, E.: Summertime evolution of snow specific surface area close to the surface on the Antarctic Plateau, The Cryosphere, 9, 2383–2398, https://doi.org/10.5194/tc-9-2383-2015, 2015.
Lorius, C., Jouzel, J., Ritz, C., Merlivat, L., Barkov, N. I., Korotkevich, Y. S., and Kotlyakov, V. M.: A 150,000-year climatic record from Antarctic ice, Nature, 316, 591–596, 1985.
Lu, G. and DePaolo, D. J.: Lattice Boltzmann simulation of water isotope fractionation during ice crystal growth in clouds, Geochim. Cosmochim. Ac., 180, 271–283, 2016.
Mann, M. E. and Jones, P. D.: Global surface temperatures over the past two millennia, Geophys. Res. Lett., 30, 1820, https://doi.org/10.1029/2003GL017814, 2003.
Masson-Delmotte, V., Landais, A., Stievenard, M., Cattani, O., Falourd, S., Jouzel, J., Johnsen, S. J., Dahl-Jensen, D., Sveinsbjornsdottir, A., White, J. W. C., Popp, T., and Fischer, H.: Holocene climatic changes in Greenland: Different deuterium excess signals at Greenland Ice Core Project (GRIP) and NorthGRIP, J. Geophys. Res.-Atmos., 110, 1–13, 2005.
Masson-Delmotte, V., Buiron, D., Ekaykin, A., Frezzotti, M., Gallée, H., Jouzel, J., Krinner, G., Landais, A., Motoyama, H., Oerter, H., Pol, K., Pollard, D., Ritz, C., Schlosser, E., Sime, L. C., Sodemann, H., Stenni, B., Uemura, R., and Vimeux, F.: A comparison of the present and last interglacial periods in six Antarctic ice cores, Clim. Past, 7, 397–423, https://doi.org/10.5194/cp-7-397-2011, 2011.
Masson-Delmotte, V., Steen-Larsen, H. C., Ortega, P., Swingedouw, D., Popp, T., Vinther, B. M., Oerter, H., Sveinbjornsdottir, A. E., Gudlaugsdottir, H., Box, J. E., Falourd, S., Fettweis, X., Gallée, H., Garnier, E., Gkinis, V., Jouzel, J., Landais, A., Minster, B., Paradis, N., Orsi, A., Risi, C., Werner, M., and White, J. W. C.: Recent changes in north-west Greenland climate documented by NEEM shallow ice core data and simulations, and implications for past-temperature reconstructions, The Cryosphere, 9, 1481–1504, https://doi.org/10.5194/tc-9-1481-2015, 2015.
Morse, D. L., Waddington, E. D., Marshall, H.-P., Neumann, T. A., Steig, E. J., Dibb, J. E., Winebrenner, D. P., and Arthern, R. J.: Accumulation Rate Measurements at Taylor Dome, East Antarctica: Techniques and Strategies for Mass Balance Measurements in Polar Environments, Geogr. Ann. A, 81, 683–694, 1999.
Neumann, T. A.: Effects of firn ventilation on geochemistry of polar snow, PhD, Department of Earth and Space Sciences, University of Washington, Washington, 223 pp., 2003.
Neumann, T. A. and Waddington, E. D.: Effects of firn ventilation on isotopic exchange, J. Glaciol., 50, 183–194, 2004.
Neumann, T. A., Waddington, E. D., Steig, E. J., and Grootes, P. M.: Non-climate influences on stable isotopes at Taylor Mouth, Antarctica, J. Glaciol., 51, 248–258, 2005.
Neumann, T., Albert, M., Lomonaco, R., Engel, C., Courville, Z., and Perron, F.: Experimental determination of snow sublimation rate and stable-isotopic exchange, Ann. Glaciol., 49, 1–6, 2008.
Neumann, T. A., Albert, M. R., Engel, C., Courville, Z., and Perron, F.: Sublimation rate and the mass-transfer coefficient for snow sublimation, Int. J. Heat Mass. Tran., 52, 309–315, 2009.
Petit, J. R., Jouzel, J., Pourchet, M., and Merlivat, L.: A detailed study of snow accumulation and stable isotope content in Dome C (Antarctica), J. Geophys. Res., 87, 4301–4308, 1982.
Petit, J. R., Jouzel, J., Raynaud, D., Barkov, N. I., Barnola, J. M., Basile, I., Bender, M., Chappellaz, J., Davis, M., Delaygue, G., Delmotte, M., Kotlyakov, V. M., Legrand, M., Lipenkov, V. Y., Lorius, C., Pepin, L., Ritz, C., Saltzman, E., and Stievenard, M.: Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica, Nature, 399, 429–436, 1999.
Pinzer, B. R., Schneebeli, M., and Kaempfer, T. U.: Vapor flux and recrystallization during dry snow metamorphism under a steady temperature gradient as observed by time-lapse micro-tomography, The Cryosphere, 6, 1141–1155, https://doi.org/10.5194/tc-6-1141-2012, 2012.
Ramseier, R. O.: Self-diffusion of tritium in natural and syntehtic ice monocrystals, J. Appl. Phys., 38, 2553–2556, 1967.
Ritter, F., Steen-Larsen, H. C., Werner, M., Masson-Delmotte, V., Orsi, A., Behrens, M., Birnbaum, G., Freitag, J., Risi, C., and Kipfstuhl, S.: Isotopic exchange on the diurnal scale between near-surface snow and lower atmospheric water vapor at Kohnen station, East Antarctica, The Cryosphere, 10, 1647–1663, https://doi.org/10.5194/tc-10-1647-2016, 2016.
Schneider, D. P., Steig, E. J., Ommen, T. D. v., Dixon, D. A., Mayewski, P. A., Jones, J. M., and Bitz, C. M.: Antarctic temperatures over the past two centuries from ice cores, Geophys. Res. Lett., 33, L16707, https://doi.org/10.1029/2006GL027057, 2006.
Shaheen, R., Abauanza, M., Jackson, T. L., McCabe, J., Savarino, J., and Thiemens, M. H.: Tales of volcanoes and El-Niño southern oscillations with the oxygen isotope anomaly of sulfate aerosol, P. Natl. Acad. Sci. USA, 110, 17662–17667, 2013.
Shuman, C. A., Alley, R. B., Anandakrishnan, S., White, J. W. C., Grootes, P. M., and Stearns, C. R.: Temperature and accumulation at the Greenland Summit: Comparison of high-resolution isotope profiles and satellite passive microwave brightness temperature trends, J. Geophys. Res.-Atmos., 100, 9165–9177, 1995.
Shuman, C. A., Steffen, K., Box, J. E., and Stearns, C. R.: A dozen years of temperature observations at the Summit: Central Greenland automatic weather stations 1987–99, J. Appl. Meteorol., 40, 741–752, 2001.
Sime, L. C., Tindall, J. C., Wolff, E. W., Connolley, W. M., and Valdes, P. J.: Antarctic isotopic thermometer during a CO2 forced warming event, J. Geophys. Res., 113, D24119, https://doi.org/10.1029/2008JD010395 , 2008.
Sjolte, J., Hoffmann, G., Johnsen, S. J., Vinther, B. M., Masson-Delmotte, V., and Sturm, C.: Modeling the water isotopes in Greenland precipitation 1959–2001 with the meso-scale model REMO-iso, J. Geophys. Res.-Atmos., 116, D18105, https://doi.org/10.1029/2010JD015287, 2011.
Sokratov, S. A. and Golubev, V. N.: Snow isotopic content change by sublimation, J. Glaciol., 55, 823–828, 2009.
Steen-Larsen, H. C., Masson-Delmotte, V., Sjolte, J., Johnsen, S. J., Vinther, B. M., Bréon, F. M., Clausen, H., Dahl-Jensen, D., Falourd, S., and Fettweis, X.: Understanding the climatic signal in the water stable isotope records from the NEEM shallow firn/ice cores in northwest Greenland, J. Geophys. Res.-Atmos., 116, D06108, https://doi.org/10.1029/2010JD014311, 2011.
Steen-Larsen, H. C., Masson-Delmotte, V., Hirabayashi, M., Winkler, R., Satow, K., Prié, F., Bayou, N., Brun, E., Cuffey, K. M., Dahl-Jensen, D., Dumont, M., Guillevic, M., Kipfstuhl, S., Landais, A., Popp, T., Risi, C., Steffen, K., Stenni, B., and Sveinbjörnsdottír, A. E.: What controls the isotopic composition of Greenland surface snow?, Clim. Past, 10, 377–392, https://doi.org/10.5194/cp-10-377-2014, 2014.
Steig, E. J.: The south-north connection, Nature, 44, 152–153, 2006.
Stenni, B., Jouzel, J., Masson-Delmotte, V., Röthlisberger, R., Castellano, E., Cattani, O., Falourd, S., Johnsen, S. J., Longinelli, A., Sachs, J. P., Selmo, E., Souchez, R., Steffensen, J. P., and Udisti, R.: A late-glacial high-resolution site and source temperature record derived from the EPICA Dome C isotope records (East Antarctica), Earth Planet. Sc. Lett., 217, 183–195, 2004.
Stenni, B., Buiron, D., Frezzotti, M., Albani, S., Barbante, C., Bard, E., Barnola, J. M., Baroni, M., Baumgartner, M., Bonazza, M., Capron, E., Castellano, E., Chappellaz, J., Delmonte, B., Falourd, S., Genoni, L., Iacumin, P., Jouzel, J., Kipfstuhl, S., Landais, A., Lemieux-Dudon, B., Maggi, V., Masson-Delmotte, V., Mazzola, C., Minster, B., Montagnat, M., Mulvaney, R., Narcisi, B., Oerter, H., Parrenin, F., Petit, J. R., Ritz, C., Scarchilli, C., Schilt, A., Schupbach, S., Schwander, J., Selmo, E., Severi, M., Stocker, T. F., and Udisti, R.: Expression of the bipolar see-saw in Antarctic climate records during the last deglaciation, Nat. Geosci., 4, 46–49, 2011.
Stenni, B., Scarchilli, C., Masson-Delmotte, V., Schlosser, E., Ciardini, V., Dreossi, G., Grigioni, P., Bonazza, M., Cagnati, A., Karlicek, D., Risi, C., Udisti, R., and Valt, M.: Three-year monitoring of stable isotopes of precipitation at Concordia Station, East Antarctica, The Cryosphere, 10, 2415–2428, https://doi.org/10.5194/tc-10-2415-2016, 2016.
Stichler, W., Schotterer, U., Fröhlich, K., Ginot, P., Kull, C., Gäggeler, H., and Pouyaud, B.: Influence of sublimation on stable isotope records recovered from high-altitude glaciers in the tropical Andes, J. Geophys. Res., 106, 22613–22620, 2001.
Touzeau, A., Landais, A., Stenni, B., Uemura, R., Fukui, K., Fujita, S., Guilbaud, S., Ekaykin, A., Casado, M., Barkan, E., Luz, B., Magand, O., Teste, G., Le Meur, E., Baroni, M., Savarino, J., Bourgeois, I., and Risi, C.: Acquisition of isotopic composition for surface snow in East Antarctica and the links to climatic parameters, The Cryosphere, 10, 837–852, https://doi.org/10.5194/tc-10-837-2016, 2016.
Town, M. S., Warren, S. G., Walden, V. P., and Waddington, E. D.: Effect of atmospheric water vapor on modification of stable isotopes in near-surface snow on ice-sheets, J. Geophys. Res., 113, D24303, https://doi.org/10.1029/2008JD009852, 2008.
Uemura, R., Masson-Delmotte, V., Jouzel, J., Landais, A., Motoyama, H., and Stenni, B.: Ranges of moisture-source temperature estimated from Antarctic ice cores stable isotope records over glacial–interglacial cycles, Clim. Past, 8, 1109–1125, https://doi.org/10.5194/cp-8-1109-2012, 2012
Urbini, S., Frezzotti, M., Gandolfi, S., Vincent, C., Scarchilli, C., Vittuari, L., and Fily, M.: Historical behaviour of Dome C and Talos Dome (East Antarctica) as investigated by snow accumulation and ice velocity measurements, Global Planet. Change, 60, 576–588, 2008.
van de Berg, W. J., van den Broeke, M. R., Reijmer, C. H., and van Meijgaard, E.: Reassessment of the Antarctic surface mass balance using calibrated output of a regional atmospheric climate model, J. Geophys. Res.-Atmos., 111, D11104, https://doi.org/10.1029/2005JD006495, 2006.
van der Wel, L. G., Been, H. A., van de Wal, R. S. W., Smeets, C. J. P. P., and Meijer, H. A. J.: Constraints on the δ2H diffusion rate in firn from field measurements at Summit, Greenland, The Cryosphere, 9, 1089–1103, https://doi.org/10.5194/tc-9-1089-2015, 2015.
Vionnet, V., Brun, E., Morin, S., Boone, A., Faroux, S., Le Moigne, P., Martin, E., and Willemet, J.-M.: The detailed snowpack scheme Crocus and its implementation in SURFEX v7.2, Geosci. Model Dev., 5, 773–791, https://doi.org/10.5194/gmd-5-773-2012, 2012.
WAIS Divide Project Members: Onset of deglacial warming in West Antarctica driven by local orbital forcing, Nature, 500, 440–444, 2013.
White, J. W. C., Barlow, L. K., Fisher, D., Grootes, P., Jouzel, J., Johnsen, S. J., Stuiver, M., and Clausen, H.: The climate signal in the stable isotope of Summit, Greenland snow : Results of comparisons with modern climate observations, J. Geophys. Res., 102, 26425–26439, 1997.