Quantifying uncertainties in satellite NO₂ superobservations for data assimilation and model evaluation

Satellite observations of tropospheric trace gases and aerosols are evolving rapidly. Recently launched instruments provide increasingly higher spatial resolutions, with footprint diameters in the range of 2–8 km and with daily global coverage for polar orbiting satellites or hourly observations from geostationary orbits. Often the modelling system has a lower spatial resolution than the satellites used, with a model grid size in the range of 10–100 km. When the resolution mismatch is not properly bridged, the final analysis based on the satellite data may be degraded. Superobservations are averages of individual observations matching the model's resolution and are functional to reduce the data load on the assimilation system. In this paper, we discuss the construction of superobservations, their kernels, and uncertainty estimates. The methodology is applied to nitrogen dioxide tropospheric column measurements of the TROPOspheric Monitoring Instrument (TROPOMI) instrument on the Sentinel-5P satellite. In particular, the construction of realistic uncertainties for the superobservations is non-trivial and crucial to obtaining close-to-optimal data assimilation results. We present a detailed methodology to account for the representation error when satellite observations are missing due to, e.g., cloudiness. Furthermore, we account for systematic errors in the retrievals leading to error correlations between nearby individual observations contributing to one superobservation. Correlation information is typically missing from the retrieval products, where an error estimate is provided for individual observations. The various contributions to the uncertainty are analysed from the spectral fitting and the estimate of the stratospheric contribution to the column and the air mass factor for which we find a typical correlation length of 32 km. The method is applied to TROPOMI data but can be generalized to other trace gases such as HCHO, CO, and SO₂ and other instruments such as the Ozone Monitoring Instrument (OMI), the Geostationary Environment Monitoring Spectrometer (GEMS), and the Tropospheric Emissions: Monitoring of POllution (TEMPO) instrument. The superobservations and uncertainties are tested in the Multi-mOdel Multi-cOnstituent Chemical (MOMO-Chem) data assimilation ensemble Kalman filter system. These are shown to improve forecasts compared to thinning or compared to assuming fully correlated or uncorrelated uncertainties within the superobservation. The use of realistic superobservations within model comparisons and data assimilation in this way aids the quantification of air pollution distributions, emissions, and their impact on climate.

1 Introduction

The capabilities that satellite instruments have to measure trace gases in the atmosphere have increased greatly in recent years. Instruments measuring from the ultra-violet (UV) to infrared and microwaves (https://earthobservations.org/, last access: August 2023, https://ceos.org/ourwork/virtual-constellations/acc/, last access: August 2023) allow the retrieval of concentrations of a large number of gases including O₃, NO₂, SO₂, CO, CH₄, and CO₂. While a previous generation was providing measurements with footprint diameters of the order of 15–50 km, instruments like the polar-orbiting spectrometer, TROPOspheric Monitoring Instrument (TROPOMI) (Veefkind et al., 2012), and the recently launched geostationary instruments, the Geostationary Environment Monitoring Spectrometer (GEMS) (Kim et al., 2020) and Tropospheric Emissions: Monitoring of POllution (TEMPO) (Zoogman et al., 2017), provide observations with a spatial resolution at around 5 km, allowing the identification of plumes originating from individual major emitters and the estimation of their emissions (Streets et al., 2013; Georgoulias et al., 2020). At the same time, these instruments provide daily global coverage (TROPOMI) or regional hourly observations (GEMS and TEMPO), resulting in large data volumes (e.g. about half a terabyte per day for TROPOMI). Making good use of all this information is a major challenge.

In parallel, global atmospheric composition analysis systems have been developed which use data assimilation techniques to assimilate the available satellite data. In Europe, the Copernicus Atmosphere Monitoring System (CAMS) (Peuch et al., 2022) is assimilating about 24 satellite datasets in real time to constrain the concentrations of reactive gases, aerosols, and greenhouse gases (Inness et al., 2019b). Multi-decadal reanalyses have been generated by CAMS (Inness et al., 2019a) or by the Multi-mOdel Multi-cOnstituent Chemical (MOMO-Chem) data assimilation system (Miyazaki et al., 2020a).

The recent advances in satellite instruments have led to a mismatch in the resolution between models and observations. For example, the TROPOMI instrument has footprints of 5.5 by 3.5 km at nadir (about 20 km²), whereas the CAMS model grid cells are roughly 0.4 by 0.4 ° (about 2000 km²). As a result, a single model grid cell may be covered by the order of 100 observations, which will lead to large differences between individual observations and interpolated model values because trace gas concentrations vary and are strongly linked to the distribution of (point) air pollution sources. The large number of satellite observations (about 1 000 000 cloud-free NO₂ observations per day) makes the assimilation of all observations numerically very costly. Also, regional data assimilation or inverse modelling applications, e.g. van der A et al. (2024), are often implemented with a resolution of the order of 0.2° or coarser, with the order of 10–20 TROPOMI observations per grid cell. This mismatch is the main reason for introducing superobservations, namely averages of the individual observations which are representative of the scales that are resolved by the model.

Crucial for a successful analysis is high-quality information on the uncertainties in the model forecast (the error covariance matrix) and in the observations. Observation errors that are too optimistic will lead to spurious impacts in the model, degrading the quality of the analyses, while an overestimate of the observation error implies that the observations are not used to their full potential.

The model–data mismatch, or departure d, in Eq. (1) is a key quantity in data assimilation (Kalnay, 2002). Here y is the observation vector, and H is the observation operator converting the model state vector x to the observations.

$$\begin{array}{}\text{(1)}& \mathbf{d}=\mathit{y}-H\left[\mathit{x}\right]\end{array}$$

There are three sources of error contributing to non-zero d values, namely the error in the observation y; the forecast error in x; and the errors in the observation operator, which are often combined with the observation error. The error in H describes how accurately the measurement can be reconstructed from the model state represented on a finite-resolution grid. This representation error, although sometimes neglected, will often be the dominant error source. Various terms may contribute to this error, including horizontal spatial representation errors (Janjić et al., 2018; Schutgens et al., 2016; Miyazaki et al., 2012a), temporal errors (Boersma et al., 2016), vertical interpolation errors, smoothing errors (when averaging kernels are not used; see Rodgers, 2000), and forward-modelling errors (errors in the radiative transfer model included in H to describe the (satellite) observation).

In this paper, we focus on the horizontal spatial representation error (RE) because this is a major source of errors in the case of large sub-grid variability and partial coverage. Also, this error is straightforward to simulate and quantify in the framework of superobservations.

In data assimilation applications, the uncertainties in the observations are often assumed to be uncorrelated in space because of its complexity. Satellite retrieval products generally contain detailed retrieval error estimates, but these are available for individual observations, and typically, there is no information on how much errors in nearby observations may be correlated. If such correlations are neglected, the individual observations will impact the analysis too strongly.

Thinning the observational dataset through using only a subset of the observations often improves the data assimilation results and reduces correlated errors through a data density reduction, while reducing the computational cost in data assimilation (Liu and Rabier, 2002, 2003). However, thinning does not decrease the uncorrelated part of the uncertainty (Berger and Forsythe, 2003) and leads to a loss of information as well. In the case of a short-lived tracer like NO₂ with local sources, the variability within a grid cell of 40×40 km² is large and is picked up by TROPOMI. Randomly selecting one observation in a grid cell, or within a correlation length scale, implies throwing away most of the sub-grid information and leads to very noisy comparisons because the model does not resolve the fine-scale variability, especially around inhomogeneous point sources. A better approach is selecting the single observation closest to the mean or median of the observations within the grid cell (Plauchu et al., 2024), but note that this approach makes use of the information on all these observations.

An alternative to thinning is “superobbing”. In this approach, multiple observations are clustered and averaged to a single superobservation. The superobservations then replace the original observations in data assimilation applications, as illustrated in Fig. 1. This makes for a more representative and less noisy comparison, while also reducing the correlation in uncertainties between superobservations.

Superobbing can also prevent biases. The uncertainty in individual observations often scales with the column amount. This is the case for NO₂ column retrievals and is related to uncertainties in the air mass factor. If all individual observations with their individual uncertainties are assimilated in a model with a coarser resolution than the satellite, this leads to low-biased analyses because more weight is given to low observations with a small uncertainty. With the superobservation approach described in this paper, such persistent low biases are largely avoided.

Satellite trace gas retrieval products often contain a significant number of negative values. This may result from small signal-to-noise ratios (for instance, for HCHO and SO₂ column retrievals) or from a subtraction of two large numbers (the total and stratospheric columns in the case of tropospheric NO₂). These negative values are, however, essential for maintaining statistical consistency and preventing biases when averaging the observations. Data assimilation systems for atmospheric chemistry are often unable to use negative values, discarding them instead. But this practice will result in positive biases, for instance, over remote regions in the case of NO₂. The process of creating superobservations implies an averaging over individual positive and negative values, which reduces the relative percentage of negative observations. This is another advantage of using superobservations.

Various methods of superobbing exist. The clustering of observations inside the optimal interpolation analysis is introduced in Lorenc (1981), but Purser et al. (2000) points out two disadvantages with this method. First, the superobservations are not independent of the assimilation system, and second, creating superobservations requires a statistical description of the forecast system, which is not always available. Another example is the 10 s observations constructed for OCO-2 (Crowell et al., 2019). Superobbing methods generally consist of three components, namely a method to cluster the observations, to average the observations, and to average the uncertainties.

A simple way to cluster observations is using a pre-determined grid, such as a model grid (Jeuken et al., 1999; Boersma et al., 2016). This minimizes the RE between the superobservations and the model. Another approach involves clustering observations based on the proximity to a model point in both space and time. Alternatively, clustering observations based on information density can be preferable, depending on the desired properties (Duan et al., 2018; Purser, 2015). Detail is retained where necessary, and more of the structures of the original observations are preserved. This method can retain more information with fewer data points, especially for data with a heterogeneous information density, such as wind data. However, it yields an irregular grid, which may be undesirable. The irregular grid increases the RE between the superobservations and the model.

Several methods exist for averaging the clustered observations. The simplest method is to take a mean of all observations forming part of a superobservation cluster. Crowell et al. (2019) use the uncertainty in the observation as weights. Miyazaki et al. (2012a) and Boersma et al. (2016) average the observations with the overlap of the observation footprint with the superobservation grid as weights.

Various methods to compute the superobservation uncertainty have been introduced in the past. Uncertainties may be averaged in the same way as the observations have been (Inness et al., 2019b). On the other hand, Crowell et al. (2019) calculate their uncertainty as the largest of the square root of the mean variance's or the observation's standard deviation. Berger and Forsythe (2003) and Miyazaki et al. (2012a) introduce spatial error correlations between individual observations and combine the uncertainties based on these correlations. Determining the correlation between the uncertainties is difficult and can be qualitative (Miyazaki et al., 2012a).

The inflation of uncertainties is another method that is often employed to address the problem of correlated uncertainties. Chevallier (2007) demonstrated that inflating observational uncertainties gives good results. This method is often combined with thinning to account for the fact that thinned observations are still correlated (Heilliette and Garand, 2015; Bédard and Buehner, 2020). Inflation can also be used in conjunction with superobservations, as superobservation uncertainties are still spatially correlated.

In this paper, we improve and formalize the superobservation method used by Miyazaki et al. (2012a) and Boersma et al. (2016) and apply it to TROPOMI tropospheric NO₂ observations for data assimilation applications. The correlations between the retrieval uncertainties are quantified to calculate the superobservation uncertainty more accurately. Also, we derive an equation for the representation error, which has only been parameterized until now. Furthermore, we apply a correction to take systematic sampling into account. We study superobservations with NO₂ because it is one of the trace gases most affected by correlated uncertainties and representation errors, due to its short residence time and large variation in both time and space. Also, the high signal-to-noise ratio of the retrieval makes systematic errors dominant over random errors, which makes correctly handling the correlation between uncertainties more important. In particular, we discuss in detail the construction of the superobservation uncertainty, explicitly treating correlations between nearby observations and the horizontal representativity term. The applications that we have in mind for the superobservations are the assimilation of high-resolution satellite observations with global analysis systems and the model validation of global chemistry transport models or general circulation models including chemistry. These are applications that make use of the averaging kernels.

In Sect. 2, we give background information on the TROPOMI NO₂ product. Section 3 contains the method we use for superobservation construction and explains the choices for the method. We add to the existing method in Sects. 4 and 5 by quantifying the correlations between observational uncertainties and the horizontal representation error. In Sect. 6, we test different methods of constructing the superobservation uncertainty by assimilating the superobservations into the MOMO-Chem data assimilation system.

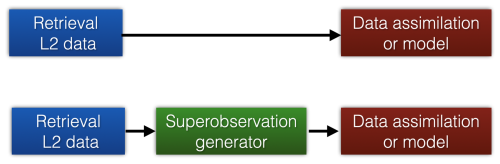
Figure 1 The superobservation approach implies that the direct assimilation of level 2 retrievals (top row) is replaced by a pre-processing step, where a superobservation generator is applied to form an intermediate set of clustered observations with the spatial resolution of the data assimilation system which is subsequently assimilated or compared with model output (bottom row).

2 Sentinel-5P TROPOMI NO₂ observations

The TROPOMI instrument (Veefkind et al., 2012) is a push-broom spectrometer and is the single payload on the Sentinel-5P satellite, which is part of the fleet of Sentinel satellites of the EU Copernicus programme. The following four aspects make TROPOMI unique: (1) the large swath width and resulting daily global coverage; (2) the large spectral range from the UV to the short-wave infrared, allowing the retrieval of a large number of trace gases like O₃, NO₂, SO₂, HCHO, CO, and CH₄, as well as aerosol properties; (3) the very high signal-to-noise ratio, which allows the retrieval of these gases with a high precision; and (4) the small pixels of down to 3.5×5.5 km² at nadir.

The TROPOMI NO₂ product data usage and details of the retrieval are provided in the product Readme file (Eskes and Eichmann, 2022), the product user manual (Eskes et al., 2022), and the algorithm theoretical baseline document (van Geffen et al., 2022a). The Sentinel-5P Validation Data Analysis Facility (https://s5p-mpc-vdaf.aeronomie.be/, last access: March 2023) is providing routine validation results with quarterly validation updates.

Two versions of the product are used in this paper. Processor version 2.2.0 became operational in the summer of 2021, including a new implementation of cloud retrieval, leading to a substantial increase in the tropospheric columns retrieved (van Geffen et al., 2022b). In combination with high-resolution a priori information (Douros et al., 2023), this improved the comparisons to ground-based remote sensing observations (Verhoelst et al., 2021). An intermediate and consistent reprocessing of the NO₂ data became available on the S5P-PAL server (https://data-portal.s5p-pal.com, last access: March 2023). These NO₂ data are no longer publicly available after completion of the official v2.4 reprocessing. In July 2022, TROPOMI v2.4.0 became operational, including a replacement of the Ozone Monitoring Instrument (OMI) and the Global Ozone Monitoring Experiment 2 (GOME-2)-derived Lambertian-equivalent reflectivity (LER) albedos in the UV-visible and near-infrared spectral ranged by the TROPOMI directionally dependent Lambertian-equivalent reflectivity (DLER) database (Tilstra, 2023). An official reprocessing of the full mission dataset (30 April 2018–present) became available in March 2023 (Copernicus Sentinel-5P, 2021). This most recent upgrade is relevant for this paper because it allows us to study the sensitivity of the tropospheric columns and air mass factors to uncertainties in the input databases. At the start of this research, the v2.4 reprocessing was not yet publicly available. Instead, we make use of a pre-release processing dataset used for the final evaluation. These data are identical to the release data but limited in scope to the first 14 d of September in 2018, 2019, 2020, 2021, and 2022. Thus, the analyses in this paper are limited to this time frame.

A crucial input for estimating the superobservation uncertainty is the error analysis of the individual tropospheric columns. For NO₂, the error budget is particularly complex since many aspects contribute significantly to the uncertainty ${\mathit{\sigma }}_{N_{\mathrm{t}}}$ of the retrieved tropospheric vertical column N_t. This follows the error propagation approach developed in Boersma et al. (2004).

$$\begin{array}{}\text{(2)}& {\mathit{\sigma }}_{N_{\mathrm{t}}}^{\mathrm{2}}={\left({\displaystyle \frac{\partial N_{\mathrm{t}}}{\partial N_{\mathrm{slant}}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{N_{\mathrm{slant}}}^{\mathrm{2}}+{\left({\displaystyle \frac{\partial N_{\mathrm{t}}}{\partial N_{\mathrm{strat}}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{N_{\mathrm{strat}}}^{\mathrm{2}}+{\left({\displaystyle \frac{\partial N_{\mathrm{t}}}{\partial M_{\mathrm{t}}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{M_{\mathrm{t}}}^{\mathrm{2}}\end{array}$$

The equation distinguishes error contributions from the slant column N_slant (uncertainties in the differential optical absorption spectroscopy (DOAS) spectral fit), the estimate of the stratospheric contribution N_strat to the total column, and the uncertainties in the tropospheric air mass factor M_t. The partial derivatives are the error propagation terms or the sensitivity of the retrieval to the various sources of uncertainty.

Note that in this equation there is no distinction between random and systematic components of the errors. All terms have quasi-systematic components, e.g. the input surface albedo is available as monthly datasets with a limited spatial resolution which introduces systematic errors, but the satellite sampling of the albedo introduces a random component. For the NO₂ slant column retrievals, the random and systematic components have been discussed in Zara et al. (2018) and van Geffen et al. (2020).

The tropospheric air mass factor M_t depends itself on the a priori NO₂ profile x_a, as well as several input parameters b,

$$\begin{array}{}\text{(3)}& M_{\mathrm{t}}=M_{\mathrm{t}}({\mathit{x}}_{\mathrm{a}},\mathbf{b})=M_{\mathrm{t}}({\mathit{x}}_{\mathrm{a}},f_{\mathrm{c}},z_{\mathrm{c}},a_{\mathrm{s}}),\end{array}$$

where f_c is the (effective) cloud fraction, z_c is the (effective) cloud height, and a_s is the surface albedo. Note that aerosols are not treated explicitly in the NO₂ retrieval but are implicitly accounted for by the effective cloud fraction and height (Boersma et al., 2004, 2011).

A basic assumption in the error estimation in Eq. (2) is that all terms are uncorrelated. There is one exception, namely a correlation term which is introduced between the cloud fraction and albedo. An error in the albedo has a direct impact on the air mass factor but also an indirect impact through the retrieved cloud fraction, partly compensating for the direct error (Boersma et al., 2004). Despite this extra correlation term, the uncertainties in the air mass factor may be overestimated. In the v2 retrievals, high biases in the albedo (or LER/DLER) are corrected by matching the observed and computed radiance levels for cloud-free pixels, which further lowers the impact of the (D)LER input on the final result (van Geffen et al., 2022b). The reduction in the uncertainty due to the albedo adjustment is not accounted for in the v2 uncertainty analysis. The air mass factor uncertainties will be further discussed below in Sect. 4.3.

The air mass factor also depends on the a priori NO₂ profile. However, as shown in Eskes and Boersma (2003), relative comparisons between a model and the NO₂ satellite observations become independent of the prior when the averaging kernel is used in the observation operator. Since the superobservations are constructed for model validation and data assimilation applications, the kernels should always be applied. Therefore we omit errors related to the a priori in the remainder of this study.

The NO₂ data product includes averaging kernel vectors A that link model profiles to the retrieved (tropospheric) columns. According to the optimal estimation theory, these kernels are part of the observation operator and are used to compute a model-equivalent y_m of the retrieval y by the following equation,

$$\begin{array}{}\text{(4)}& y_{\mathrm{m}}=x_{\mathrm{a}}+\mathbf{A}(\mathit{x}-{\mathit{x}}_{\mathrm{a}}).\end{array}$$

Here x is the tropospheric NO₂ vertical profile from the model colocated in space and time to the footprint of the satellite, and x_a is the vertical profile of layer contributions to the column. Because, for the NO₂ retrieval (which is linear to a good approximation), we have $(\mathbf{I}-\mathbf{A}){\mathit{x}}_{\mathrm{a}}=\mathrm{0}$, where I is a vector with elements 1 (Eskes and Boersma, 2003), this reduces to

$$\begin{array}{}\text{(5)}& y_{\mathrm{m}}=\mathbf{A}\mathit{x}.\end{array}$$

Note that in this paper, A refers to the NO₂ tropospheric column averaging kernel. These are computed from the total column averaging kernel by multiplying with the ratio of the total and tropospheric air mass factor (Eskes et al., 2022). Values above the troposphere as calculated by the Tracer Model 5 massive parallel (TM5-MP) are set to 0.

3 Constructing superobservations: the tiling approach

Superobservation construction consists of three components, namely clustering, averaging, and uncertainty averaging. The TROPOMI observations are clustered to the grid of the model that the superobservations will be used with, which minimizes the representation error. Additionally, this removes the need for grid interpolation during assimilation. Clustering also significantly reduces the number of TROPOMI observations.

3.1 Averaging approach

We average using the overlap of the individual observations with the grid cell as weights (Eq. 6) (Miyazaki et al., 2012a; Boersma et al., 2016).

$$\begin{array}{}\text{(6)}& y_{\mathrm{S}}={\displaystyle \frac{{\sum }_i^n{w}_i{y}_i}{{\sum }_i^n{w}_i}}\end{array}$$

In our formulation, the superobservation is the best possible estimate of the model grid box average NO₂ column, given n satellite observations. The weights w_i are obtained by covering (tiling) the grid box with the TROPOMI observations, as shown in Fig. 2. They are equal to the area overlap between the footprint of the TROPOMI observation y_i and the selected model grid box. Figure 11b shows satellite observations over Europe, with the associated superobservations shown in Fig. 11a. This method of averaging is similar to spatial binning using the data harmonization toolset for scientific Earth observation data (HARP) (http://stcorp.github.io/harp/doc/html/algorithms/regridding.html#spatial-binning, last access: August 2024). In the rest of this paper, normalized weights are used (Eq. 7).

$$\begin{array}{}\text{(7)}& {\stackrel{\mathrm{̃}}{w}}_i={\displaystyle \frac{w_i}{{\sum }_i^n{w}_i}}\end{array}$$

The tiling method has three main advantages over other averaging methods. First, it takes into account the idea that observations which only partially overlap with the superobservation area should contribute less to the superobservation average. This is especially relevant for smaller superobservations, where the difference in overlap becomes more pronounced. Second, the tiling method is not sensitive to creating biases. Last, the tiling method has a clear physical interpretation with a closed mass balance. The total amount of tropospheric NO₂ in a superobservation is the sum of the tropospheric NO₂ of the observations comprising the superobservation. The main alternative of using precision weights assumes that every observation within a superobservation is an independent measurement of the superobservation (Taylor, 1997). This is not the case here, as different pixels are independent measurements looking at different air masses.

To compare a superobservation against a model, we also need a corresponding averaging kernel, which is averaged in the same way as the observations. Multiplying Eq. (1) with w_i and summing over the satellite observations, we get the following:

$$\begin{array}{}\text{(8)}& \sum _i^n{\stackrel{\mathrm{̃}}{w}}_i{d}_i=\sum _i^n{\stackrel{\mathrm{̃}}{w}}_i{y}_i-\sum _i^n{\stackrel{\mathrm{̃}}{w}}_i{\mathbf{A}}_i{\mathbf{H}}_{\mathrm{v},\mathrm{interpol},i}\left[\mathit{x}\right]=d_S.\end{array}$$

Here x is the vector of modelled NO₂ partial columns in the vertical layers of the model for the chosen horizontal model grid box, A_i is the averaging kernel of observation y_i, and $H_{\mathrm{v},\mathrm{interpol},i}$ is the vertical interpolation between the satellite-averaged kernel pressure levels and the model pressure levels.

A horizontal interpolation operator is missing because y_S is compared with the model using a single profile of model values for the selected horizontal model grid cell. This is in contrast to an assimilation of individual observations, where typically a bi-linear interpolation operator is introduced involving neighbouring horizontal model grid cells.

$$\begin{array}{}\text{(9)}& d_{\mathrm{S}}=y_{\mathrm{S}}-{\mathbf{A}}_{\mathrm{S}}{\mathbf{H}}_{\mathrm{v},\mathrm{interpol}}\mathit{x};{\mathbf{A}}_{\mathrm{S}}=\sum _i^n{\stackrel{\mathrm{̃}}{w}}_i{\mathbf{A}}_i.\end{array}$$

Thus, the averaging kernel of the superobservation (the “superkernel” A_S) is constructed in the same way as the superobservation using the weights w_i. Note that because all individual observations are by construction compared with the same model value, we do not have to worry about correlations between A_i and x (von Clarmann and Glatthor, 2019).

Note that each TROPOMI observation comes with a unique surface pressure, which may differ substantially between neighbouring pixels over mountain terrain. To conserve the total column in the model–satellite comparison, we will follow the TROPOMI NO₂ product user manual and align the surface pressures by replacing the retrieval surface pressure with the surface pressure of the model grid cell before comparing. In this way, the kernels of all observations contributing to the superobservation will have the same pressure levels and can be averaged, as in Eq. (9). Note that the shape of the kernel is only weakly dependent on changes in the surface pressure.

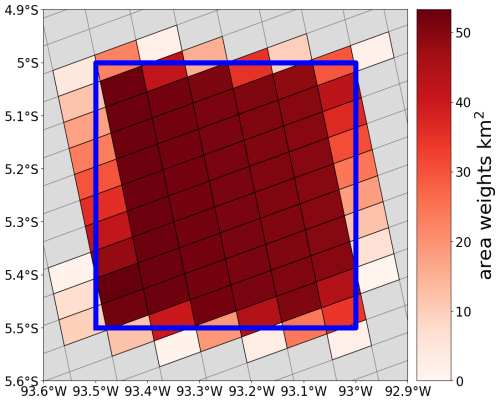
Figure 2 The tiling approach, where a model grid cell mean NO₂ tropospheric column amount is constructed as an overlapping area-weighted average of the satellite footprints covering the model grid cell. The colours indicate the weights w_i, which are the area overlap (km²) between the superobservation grid cell and satellite observation footprint. The grid cell boundary is indicated in blue.

3.2 Uncertainty averaging

A realistic superobservation uncertainty estimate is essential to guide the data assimilation and to find the right balance between the model forecast and the observations in the analysis. The total uncertainty in the superobservation σ_S is the combination of the measurement error and representation error terms, assuming that these are uncorrelated (Eq. 10).

$$\begin{array}{}\text{(10)}& {\mathit{\sigma }}_{\mathrm{S}}=\sqrt{{\mathit{\sigma }}_{\mathrm{obs}}^{\mathrm{2}}+{\mathit{\sigma }}_{\mathrm{RE}}^{\mathrm{2}}}\end{array}$$

The observational uncertainty in the superobservation depends on the uncertainty in the individual observations, as well as their correlation. To calculate the former, we apply the method from Sekiya et al. (2022), who calculate the retrieval contribution to the superobservation uncertainty using Eq. (11). This assumes a representative uniform correlation factor c, which is applied to all uncertainties within a superobservation. Here the observational uncertainty is a combination of an uncorrelated part and a correlated part. The uncorrelated part tends towards zero as the number of observations increases because the square of the standardized weights ${\stackrel{\mathrm{̃}}{w}}_i^{\mathrm{2}}$ decreases. On the other hand, the correlated part does not change much when adding more observations. As a result, the correlated part puts a lower limit on the uncertainty, which is roughly $\mathit{\sigma }\sqrt{c}$.

$$\begin{array}{}\text{(11)}& {\mathit{\sigma }}_{\mathrm{obs}}^{\mathrm{2}}=(\mathrm{1}-c)\sum _{i=\mathrm{1}}^N{\stackrel{\mathrm{̃}}{w}}_i^{\mathrm{2}}{\mathit{\sigma }}_i^{\mathrm{2}}+c(\sum _{i=\mathrm{1}}^N{\stackrel{\mathrm{̃}}{w}}_i{\mathit{\sigma }}_i{)}^{\mathrm{2}}\end{array}$$

4 Uncertainty estimate for TROPOMI NO₂

As mentioned in Sect. 3.2, the superobservation uncertainty depends on the observational uncertainties and their correlation c (Eq. 11). As shown in Eq. (2), the tropospheric column uncertainty consists of three separate sources of uncertainty, namely the stratospheric uncertainty, the slant column uncertainty, and the air mass factor uncertainty. The superobservation uncertainty in these components is calculated separately because they have different correlations, which means that their uncertainty propagates differently. Every component and its correlation are discussed individually in the sections below. Note that these components are not provided separately in the retrieval, but through using the methods from the algorithm theoretical basis document (ATBD) (van Geffen et al., 2022a), they can be reconstructed using the available information.

4.1 Stratospheric uncertainty

The tropospheric NO₂ column is obtained by subtracting an estimated stratospheric column from the total observed column. The stratospheric column is obtained by TM5-MP model simulations, while assimilating TROPOMI NO₂ column observations (Huijnen et al., 2010; Dirksen et al., 2011). With the method, the stratospheric column is constrained by the TROPOMI observations, with strong forcings in the assimilation over unpolluted areas, such as the oceans, and small adjustments over polluted regions. Subtracting the modelled stratospheric slant column from the total slant column and dividing the tropospheric air mass factor gives tropospheric NO₂ (Eq. 12).

$$\begin{array}{}\text{(12)}& N_{\mathrm{trop}}={\displaystyle \frac{N_{\mathrm{slant}}-N_{\mathrm{s},\mathrm{strat}}}{M_{\mathrm{trop}}}}\end{array}$$

The resolution of the (TM5-MP) model is 1° × 1°, and the horizontal correlation length scale used in the assimilation is about 500 km, with both being coarser than the superobservation sizes considered in this paper. Therefore, the stratospheric uncertainty is assumed to be fully correlated (c=1) between observations that are part of one superobservation.

Because fully correlated terms will influence the final superobservation error more strongly than uncorrelated or partially correlated terms, the stratospheric estimate will become relatively more important compared to other sources of uncertainty. Therefore, it is relevant to investigate this term in more detail.

There is seasonal and latitudinal variation in the stratospheric uncertainty. However, the TROPOMI NO₂ retrieval approximates the stratospheric uncertainty using a constant mean value. To improve on this, we analyse the observation-minus-forecast (OmF) departure between TROPOMI and the model column, using a geometric air mass factor for both (Eq. 13; using solar zenith angle Θ₀ and viewing zenith angle Θ). The root mean square error (RMSE) is calculated daily over 5° latitudinal bands, highlighting latitudinal and temporal uncertainties. Only areas with an average model-estimated tropospheric NO₂ column lower than 30 µmol m⁻² are included to minimize the effect of the troposphere. Figure 3 shows clear latitudinal and seasonal variations in the TROPOMI and TM5 differences. To reduce noise in the data, a block function convolution is applied to smooth the data over 15° and 2 weeks. The smoothed data are oversampled into bins of 2° by 1 d. To calculate the geometric stratospheric uncertainty σ_Strat geo for an observation, these data are linearly interpolated to their day and latitude. If an observation occurs outside of the bounds of the data, then it is set to the maximum of the data. These gaps result from the lack of observations during polar nights. Equation (14) converts the geometric stratospheric RMSE to the stratospheric uncertainty (van Geffen et al., 2022a).

$$\begin{array}{}\text{(13)}& {\displaystyle }{M}_{\mathrm{geo}}={\displaystyle \frac{\mathrm{1}}{\cos {\mathrm{\Theta }}_{\mathrm{0}}}}+{\displaystyle \frac{\mathrm{1}}{\cos \mathrm{\Theta }}}\text{(14)}& {\displaystyle };{\mathit{\sigma }}_{\mathrm{strat}}={\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{Strat}\mathrm{geo}}\times M_{\mathrm{geo}}}{M_{\mathrm{trop}}}}.\end{array}$$

Compared to the constant σ_Strat geo of 3.32 µmol m⁻² of the data product, the new uncertainty is generally lower, especially at the Equator. Areas closer to the poles can have a higher RMSE, depending on the season. This is more pronounced in the Northern Hemisphere because the higher NO₂ concentrations in the Northern Hemisphere increase the absolute errors. In winter, the polar region is not observed, and model biases will build up, affecting concentration estimates in late winter. Also, there is seasonal variation in the high latitudes which relates to the formation and breaking of the polar vortex during winter, leading to larger errors. Gradients around the Antarctic vortex are also challenging to predict, particularly during the Southern Hemisphere spring. Because the Antarctic vortex is more stable, these errors are less pronounced and occur during the Southern Hemisphere spring. High-latitude summer NO₂ levels are also difficult to predict. This relates to Arctic fire emissions from Siberia and Alaska. In TM5-MP, these are based on climatological fire intensities from the Global Fire Emissions Database (GFED) (van der Werf et al., 2017), meaning that the model is not capable of accurately predicting individual fire events and the corresponding total and stratospheric column. In contrast, in the tropics, the RMSE results are better than the mean value because of the relatively small natural variability there.

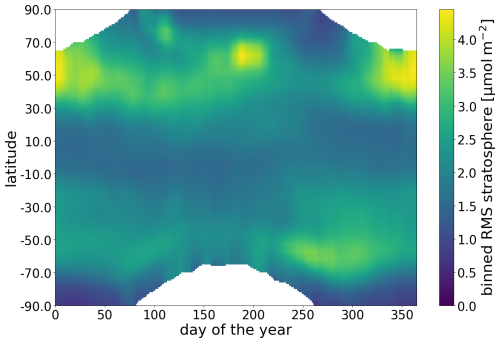
Figure 3 Zonal average of the observation (the forecast root mean square error in the TROPOMI total column) in the TM5 total column averaged over multiple years (2018–2022). Data are smoothed over 15° and 2 weeks and averaged into bins of 1° by 1 d. This result is used as the geometric stratospheric uncertainty σ_Strat geo instead of the constant in the retrieval.

4.2 Slant column

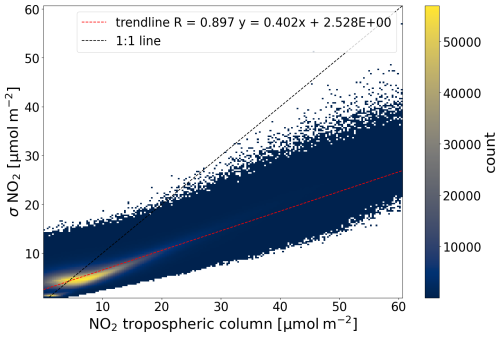
Measurement noise is contributing to the slant column uncertainty. An average random slant column uncertainty of 10.23 µmol m⁻² is found by van Geffen et al. (2020) for cloud-free scenes. Apart from a random component to the slant column uncertainty, there will also be a (regionally) systematic component. The systematic component consists of gaps in knowledge, such as missing cross sections, inaccurate ring coefficients in the DOAS fit, or the lack of an intensity offset and a correction for vibrational Raman scattering (Richter et al., 2011). These systematic effects are most pronounced over the sea in clear-sky conditions. In such circumstances, the systematic uncertainty can be larger than the random uncertainty. But because these are low-NO₂ environments, the impact on the retrieval is limited.

Any systematic error in the slant column also influences the quantification of the stratospheric error discussed in Sect. 4.1 because the slant column is assimilated for the quantification of the stratosphere. Moreover, the transport of the systematic error within the model results in a further increase in the (OmF) RMSE. Considering that the effect of the systematic error is already (partially) included in the stratospheric (OmF) RMSE discussed above, we do not separately quantify the effect of the systematic retrieval error. Instead, only the random part of the slant column uncertainty from the level 2 data is converted to a tropospheric column uncertainty through the tropospheric air mass factor (AMF) and averaged as uncorrelated using Eq. (11).

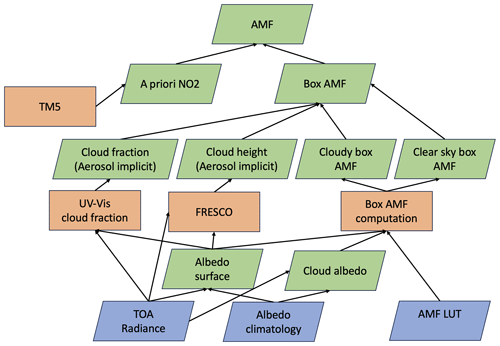
Figure 4 Diagram showing the dependencies (arrows) in the calculation of the air mass factor (AMF) as part of the TROPOMI NO₂ tropospheric column retrieval. Shown in blue are the input data (TROPOMI radiances, albedo climatology, and static data), in orange are the processing blocks (cloud properties and box AMF lookup table evaluation, TM5 chemical transport model, CTM), and in green are the (intermediate) products.

4.3 Air mass factor uncertainty

To calculate the superobservation uncertainty resulting from the air mass factor uncertainty, we use the uncertainty from the retrieval, together with a correlation c. Note that the AMF uncertainty is not part of the level 2 product but can be calculated using the available information (van Geffen et al., 2022a). Calculating the associated spatial correlation between observations is not trivial because the tropospheric air mass factor M_t is calculated through several inputs, algorithms, dependencies, and feedbacks, as shown in Fig. 4. One of these complicating factors is the use that is made of the top-of-atmosphere (TOA) radiance to correct the albedo climatology for dark scenes. Uncertainties in the algorithms and input variables induce uncertainty in the AMF. Of these uncertainties, the a priori NO₂ profile is a large contribution, typically ranging from 5 %–20 % in polluted regions. These are most affected because the low resolution of the a priori profile may result in the underestimation of hotspots (Douros et al., 2023). However, as shown in Eskes and Boersma (2003), the relative comparisons between a model and the NO₂ satellite observations become independent of the a priori profile shape when the averaging kernel is used in the observation operator. Since the superobservations are constructed for model validation and data assimilation applications, the kernels should always be applied. Therefore, we omit errors related to the a priori in the discussion below.

Other large sources of uncertainty are the effective cloud cover, the effective cloud height, and the surface albedo (or the Lambertian-equivalent reflectivity, LER). Aerosols are treated implicitly through the effective cloud fractions and cloud height, which introduces a minor uncertainty (Boersma et al., 2004, 2011). All three of these variables depend on a climatological surface albedo dataset. For the S5P-PAL NO₂ processor version 2.3.1, these are derived from OMI (440 nm) and GOME-2 (758 nm), while for v2.4.0 it is derived from TROPOMI spectra. A typical RMSE difference between these two albedo datasets at 440 nm is 0.015 or about 25 % for a typical albedo of 0.06. Furthermore, the uncertainties are spatially correlated, first of all, because of the relatively low resolution of the LER database but also because surface-modifying conditions are often spatially extensive. For example, droughts impact the surface albedo in a large area. Luckily the retrieval algorithm can partially compensate for errors in the climatological surface albedo. If the TOA radiance is lower than expected based on the albedo, then the albedo is adjusted downwards. On the other hand, if the TOA radiance is higher than expected, then it is attributed to “effective” clouds. If these clouds are placed at the correct heights (e.g. at the surface for a high-albedo anomaly), then this yields approximately the same AMF as with a perfect surface albedo (Riess et al., 2022).

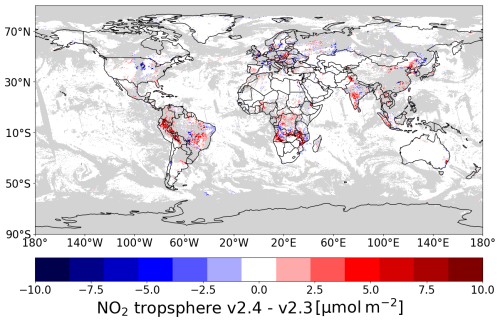
Figure 5 Difference between the tropospheric column of the v2.3.1 and v2.4 products on 14 September 2018. Data are filtered for quality assurance >0.75 (grey areas indicate cloud cover). White colours range from −8 to 8 µmol m⁻².

To estimate the spatial correlation required to estimate the superobservation uncertainty, we compare versions 2.3.1 and 2.4 of the retrieval. We use the data of the first 2 weeks of September for 2018–2022 because these were processed as the validation before the product was made publicly available. The difference between the datasets should be representative of the uncertainty resulting from the climatological surface albedo as both datasets are valid inputs. Albedo is also a key input for cloud retrieval, so this replacement also generates differences in cloud fraction and cloud pressure. One may argue that the comparison is not a good estimate of the uncertainty in v2.4 because the new TROPOMI surface albedo is likely superior. Thus, the uncertainties obtained here are overestimated. However, both maps are still climatological. This absence of temporally explicit data is probably a major source of uncertainty, making both maps uncertain.

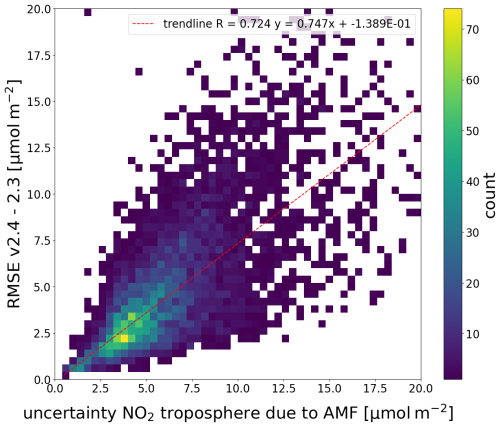
Figure 5 shows the difference in NO₂ on 14 September 2018. These differences, caused by the replacement of the albedo climatology, are spatially correlated. A correlation length is calculated as outlined in Appendix A. Here we find a correlation length of 32 km. This correlation length is then used to calculate the average correlation of a superobservation for use with Eq. (11). Using a correlation length is preferable over using an average correlation because it takes into account the fact that high-latitude superobservations have a smaller surface area than low-latitude ones and thus should have a higher average correlation if other factors are equal. Also, a correlation length is resolution-agnostic, which allows for an easy change in the superobservation resolution and a properly behaved limit towards smaller superobservations. The correlation C between two points at a distance d for a correlation length l is calculated using the exponential form, $C=\exp (-d/l)$.

We calculate the correlation for every distance within a superobservation and multiply this with the probability density function of points within a box (Philip, 2007). Integrating this yields the average correlation within a superobservation. Note that, strictly speaking, the probability density function (PDF) from Philip (2007) is for a Cartesian plane and not for a sphere, but grid cells are rectangular to a good approximation, except very close to the pole. For a 0.5° superobservation, this gives C≈0.3.

The difference between the versions is compared to the uncertainty due to the AMF, as estimated by the retrieval. The RMSE is calculated per swath in a 1° by 1° grid and then averaged. The uncertainty is averaged to the same grid. Figure 6 shows the relationship between these variables. There is a relationship between them, with an R value of 0.724. On average, the uncertainty estimated by the retrieval is higher than the RMSE, with a slope of 0.747 for the Theil–Sen estimator. Note that factors other than the surface albedo contribute to the uncertainty, such as the choice of radiative transfer model, the wavelength at which the AMF is calculated, sphericity corrections, and systematic aspects in cloud retrieval (Lorente et al., 2017). Based on this information, the difference between v2.4 and v2.3 is consistent with the retrieval uncertainty. Thus, the obtained correlation length is likely representative of AMF uncertainty.

Figure 6 Binned scatter plot between the retrieved average tropospheric uncertainty resulting from the AMF and the average RMSE of the difference between the retrieval versions. Calculated using globally available data. Trendline fit using a Theil–Sen estimator.

5 Representation error

When making superobservations, the data are clustered within a pre-defined grid. Ideally, we would always have complete coverage, and thus complete information, of the grid cell. However, this is not the case as satellite observations are often flagged due to quality concerns, for instance, linked to the presence of clouds obscuring pollution close to the surface.

In the case of incomplete information, the grid cell mean concentration can still be estimated using the available sample of observations, but the area-weighted average will be an estimate of the true average. The difference between the (population) average of the entire grid cell and the estimate using an incomplete (sample) average is the (horizontal) representation error, which we quantify in this section.

5.1 Representation error due to random removal of observations

By comparing the mean of a completely covered grid cell to a random sample mean, we can calculate the representation error (RE) for the situation, which is given by

$$\begin{array}{}\text{(15)}& \text{RE}=|\mathit{\mu }-{\overline{x}}_n|,\end{array}$$

with the true mean μ and an estimate of the mean ${\overline{x}}_n$, which depends on the number of sample observations n. To quantify the error, we perform experiments by taking a fully covered grid cell and by removing random observations to calculate the RE for n observations. Because the order in which we remove observations results in different estimates, we repeat the experiment for I number of iterations. Figure 7a shows the results of this experiment as grey lines, with every line representing one iteration.

The uncertainty σ_RE,n associated with this error is the standard deviation of the estimated mean ${\overline{x}}_n$ around the true mean μ, as follows:

$$\begin{array}{}\text{(16)}& {\mathit{\sigma }}_{\mathrm{RE},n}=\sqrt{{\displaystyle \frac{\mathrm{1}}{I}}\sum _{i=\mathrm{1}}^{i=I}(\mathit{\mu }-{\overline{x}}_n^i{)}^{\mathrm{2}}}.\end{array}$$

This standard deviation is plotted as the green line in Fig. 7a. Increasing n improves our estimate of μ, decreasing σ_RE,n. When n equals the total number of observations N in the grid cell, the estimate ${\overline{x}}_n^i$ equals μ, and the uncertainty becomes 0.

Note that σ_RE,n is the standard deviation of the sample mean to the true mean, also known as the standard error (SE). To calculate σ_RE, we can use the formula for the standard error with a correction factor because the population of observations within a superobservation (N) is finite (Bondy and Zlot, 1976; Isserlis, 1918). With this correction factor, σ_RE becomes

$$\begin{array}{}\text{(17)}& {\mathit{\sigma }}_{\mathrm{RE},n}=\text{SE}={\displaystyle \frac{\mathit{\sigma }}{\sqrt{n}}}\sqrt{{\displaystyle \frac{N-n}{N-\mathrm{1}}}}.\end{array}$$

The results from the equation are shown in Fig. 7a as the blue line. The theoretical blue line is on top of the experimental green line, which means Eq. (17) describes σ_RE very well.

Equation (17) indicates that σ_RE,n is proportional to the standard deviation σ of the observations within the grid cell. In Fig. 7, the results are divided by this grid-cell-dependent standard deviation such that different TROPOMI superobservations can be compared. To calculate the absolute value of σ_RE, estimating the standard deviation σ is crucial, as discussed in Sect. 5.3. Equation (17) also shows that the uncertainty resulting from random thinning (n=1) is equal to the standard deviation of the area that the thinned observation represents.

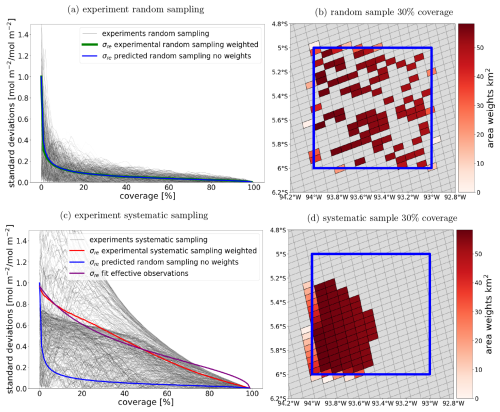
Figure 7 Results of repeatedly sampling a single grid cell to calculate σ_RE. (a) Random sampling of a single superobservation. The thin grey lines represent individual random experiments for the superobservation. The green line is the mean of the samples, and the blue line is the theoretical result from Eq. (17). (b) Example of a random sample at 30 % coverage. (c) Systematic sampling of a single superobservation. The red line is the mean of the samples, and the blue line is the theoretical result for the random case. The purple line shows the fit to the systematic mean by fitting N_eff. In this case, the fitted N_eff is 5.5 when compared to 536 observations. (d) Example of a systematic sample for 30 % coverage.

There are some difficulties in applying Eq. (17) to the superobservation RE because it applies the standard error to the mean and not a weighted average. This is also the reason why the blue and green lines in Fig. 7a do not match perfectly. For an unweighted average, they would converge with enough iterations. Generally, this only results in minor differences between the predictions and the experiments, but these errors become more pronounced if the difference in weights between observations increases. This error is most present in smaller superobservations because they have relatively more partially overlapping observations.

In Appendix B, we derive a formulation of the representation error that works with observations with different weights by introducing fractional observations. This results in Eq. (18):

$$\begin{array}{}\text{(18)}& {\mathit{\sigma }}_{\mathrm{RE},n}={\displaystyle \frac{\mathit{\sigma }}{\sqrt{N_{\mathrm{f}}{f}_{z,n}+\mathrm{1}-f_{z,n}}}}\sqrt{{\displaystyle \frac{N_{\mathrm{f}}-(N{f}_{z,n}+\mathrm{1}-f_{z,n})}{N_{\mathrm{f}}-\mathrm{1}}}}.\end{array}$$

Here f_z,n is the coverage fraction of the superobservation grid from 0–1, and N_f is the fractional population size. Note that n in Eq. (17) is replaced by N_ff_z,n.

5.2 Representation error due to systematic removal of observations

A major complicating factor is that the coverage of the superobservation is not random. A cloud field could cover the northern half of the superobservation. The valid observations then only cover the southern half of the superobservation, making it less representative of the grid cell as a whole than a random sample. We repeat the experiment from Sect. 5.1 but, instead, sample systematically. The systematic sampling of a grid cell starts by picking a random observation from the grid cell. Then the nearest observation is added to the sample, which is repeated until the grid cell is filled. This is done for multiple iterations, resulting in Fig. 7 (bottom panel), with the iterations in grey and the experimental σ_RE in red. As expected, the systematic experiment produces a higher representation error.

This increase in RE is parameterized by fitting the total population size N in the first term of Eq. (18). By lowering the population size, σ_RE increases for the same coverage, which allows us to match the curve obtained in the systematic sampling experiment. We call this fitted population size the effective population size N_eff. It is not necessary to modify the finite population correction term (second term) because this term accounts for having more complete information of the superobservation as the number of observations approaches the population size. This effect remains unchanged with systematic sampling.

$$\begin{array}{}\text{(19)}& {\mathit{\sigma }}_{\mathrm{RE},n}={\displaystyle \frac{\mathit{\sigma }}{\sqrt{N_{\mathrm{eff}}{f}_{z,n}+\mathrm{1}-f_{z,n}}}}\sqrt{{\displaystyle \frac{N-(N{f}_{z,n}+\mathrm{1}-f_{z,n})}{N-\mathrm{1}}}}\end{array}$$

Fitting the number of observations using Eq. (19) results in the purple line in Fig. 7c. The line fits well but is not perfect.

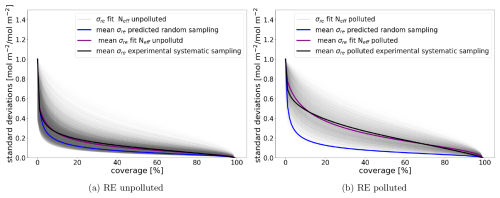
Figure 8 Result of systematically sampling multiple cells. The thin grey lines are the fit of a single cell using the number of effective observations, similar to the purple line in Fig. 7. The purple lines show the average fit for unpolluted cells (a) and polluted cells (b). The blue lines are the predicted averages over multiple superobservations using Eq. (17). The black lines are the averages over multiple superobservations when sampling systematically for unpolluted cells in panel (a) and polluted cells in panel (b).

The effective population size of a superobservation has a physical interpretation. Imagine a superobservation containing two distinct regions; there is a city with high-tropospheric NO₂ levels, and a rural area outside the city with low-tropospheric NO₂. If we were to sample the entire city (including the pollution plume from the city), the estimate of the superobservation average is not much better than with a single sample over the city. Effectively, there are only two independent observations, namely the city and the rural area. As the example illustrates, the effective population size of observations in a superobservation depends on its spatial structure. If the effective population size is the same as the regular population size, then there is no effect of systematic sampling on the superobservation. This occurs over areas such as the oceans and the Sahara, where observed tropospheric NO₂ is similar and noise-dominated. If the values within the superobservation are random, systematic sampling has no effect. On the other hand, source regions are sensitive to systematic sampling and applying it gives very different results. Major population centres, such as China, the Middle East, and Europe, all have a significantly lower effective population size than the actual population size. Regions with fire emissions, such as the savannahs in Africa, are also sensitive to systematic sampling. The effective population is a property of a location and can be quantified for that location.

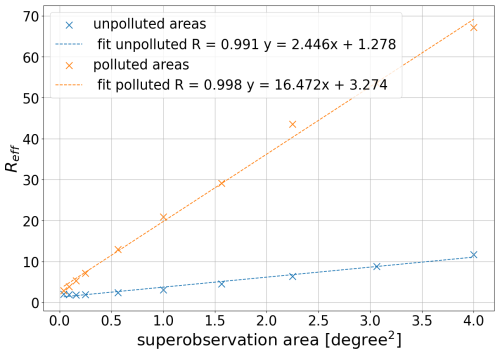
To calculate a representative effective population size for a location, ${\mathit{\sigma }}_{\mathrm{RE},n}/\mathit{\sigma }$ on that location is calculated and averaged over the dataset. The average is used to fit an effective population N_eff for that location, which we compare to the average population size for the location. The ratio R_eff between the time-averaged population size 〈N〉 and the effective population size N_eff captures how sensitive that location is to systematic sampling ($R_{\mathrm{eff}}=\langle N\rangle /N_{\mathrm{eff}}$).

While it is possible to calculate R_eff for every superobservation, this quantification would be grid-dependent, which would make the method inflexible. Instead, we calculate an average ratio R_eff for polluted superobservations and unpolluted superobservations at multiple resolutions. Superobservations over 30 µmol m⁻² are classified as polluted and are expected to be sensitive to systematic sampling. First, we calculate R_eff for every 1° superobservation for the polluted and unpolluted cases. The resulting fits are shown as the thin lines in Fig. 8. Note that there are fewer fits for the polluted case because many locations are never polluted. Then we average R_eff, which gives an R_eff of 21 and 3 for polluted and unpolluted 1° superobservations respectively. The purple line in Fig. 8 shows the average result of the fits, which matches well with the average experimental values in black for both the unpolluted and polluted case. These figures also show the average effect of systematic sampling. At 50 % coverage, the increase in RE when sampling systematically instead of randomly is 54 % for unpolluted areas and 263 % for polluted areas.

Figure 9 shows the R_eff as a function of the superobservation area, which increases as the area increases for both polluted and unpolluted superobservations. Increasing the area of a superobservation increases the distance between observations. As a result, they become more sensitive to systematic sampling. Within our software, we use the trendlines in Fig. 9 in combination with the distinction between polluted and unpolluted superobservations to quantify the R_eff of a superobservation. This allows us to calculate R_eff for different grids and to take into account latitudinal variations in grid cell size.

Figure 9 Resolution dependency of the correction for systematic sampling as a function of the area of the superobservation up to a resolution of 2°. The plot distinguishes between polluted (>30 µmol m⁻²; orange curve) and unpolluted (blue curve) grid boxes.

5.3 Sample standard deviation

Thus far, the RE has been expressed in terms of the standard deviation of the observations (tropospheric NO₂) within each grid cell. This standard deviation is estimated using the measurement variability for each superobservation individually. In practice, this procedure works well for coverages up to 30 % for 0.5° superobservations. This coverage corresponds to the point where, on average, the sample standard deviation would be more accurate than a climatological standard deviation. With this coverage, it is still possible that there are not enough available data points to calculate a reliable standard deviation, in particular for smaller superobservations. For smaller superobservations, a minimum coverage of 50 % or even 70 % may be appropriate. The optimal coverage may also vary between assimilation systems, applications, and instruments. It is a tradeoff between data quantity and quality. When fewer than five data points are available, it is impossible to calculate a reliable standard deviation. Instead, we set the standard deviation to 0.4 times the tropospheric column +2.5 µmol m⁻². This is based on the relation between the standard deviation and tropospheric column, as shown in Fig. C1 in Appendix C.

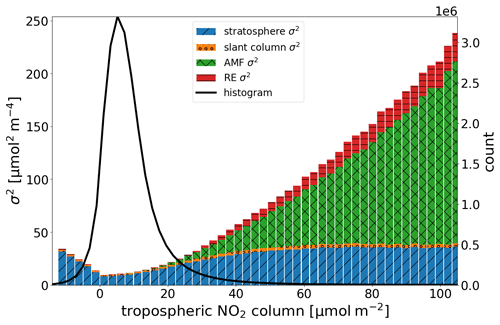
Figure 10 The division of the superobservation error variance into its components, namely stratosphere (blue), slant column (orange), air mass factor (green), and representativity (red). Computed from TROPOMI NO₂ at a 0.5° resolution. Note that the figure depicts the error variance uncertainty instead of the uncertainty because the variance is a direct sum of its contributions. The black line shows the number of observations within each column bin.

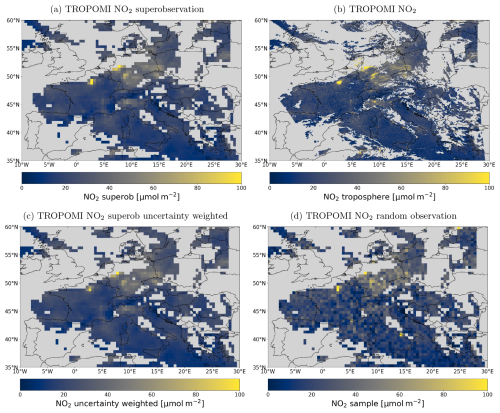
Figure 11 Panel showing various methods of pre-processing observations for data assimilation on 8 September 2018 for q_a>0.75. (a) Superobservations constructed for this research. (b) Regular TROPOMI observations. (c) Uncertainty-weighted superobservations instead of the area weights used by this research. (d) Random sample from the observations within the model grid.

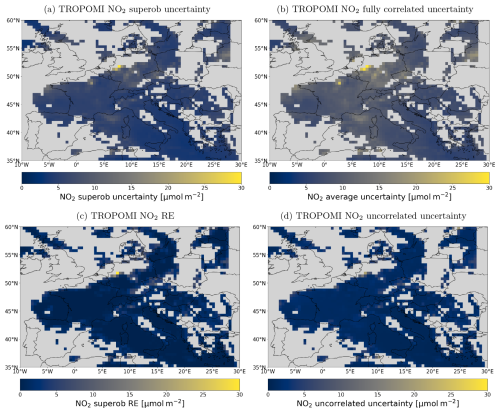
Figure 12 Panels showing various methods of pre-processing uncertainties for data assimilation and the RE on 8 September 2018 for q_a>0.75. (a) Superobservation uncertainty constructed for this research. (b) Fully correlated uncertainty (C=1). (c) Representation error. (d) Uncorrelated uncertainty (C=0).

6 Combined uncertainty in the superobservations

Figure 10 shows the contributions to the superobservation uncertainty $\left({\mathit{\sigma }}_{\mathrm{s}}^{\mathrm{2}}\right)$ as a function of the tropospheric NO₂ column. For low-tropospheric columns, the uncertainty is dominated by the stratospheric uncertainty, while for high-tropospheric columns, it is impacted most by the air mass factor with a major contribution still coming from the stratospheric uncertainty. The RE is only a minor contribution to the average uncertainty, but it varies significantly by location, depending on the coverage and standard deviation (as illustrated in Fig. 12c below) and becomes important at the edges of cloud fields. The slant column uncertainty has almost no impact on the average uncertainty, even though it is a major source of uncertainty for individual observations over clean areas. Because the slant column uncertainty is treated as dominantly uncorrelated, it is reduced significantly by the averaging process. Note that the systematic slant column uncertainty is (partly) included in the stratospheric uncertainty.

We constructed and created superobservations by combining all sources of uncertainty, as described in Sects. 3.2 and 5. Figure 11a shows the constructed tropospheric NO₂ superobservations on a grid of 0.5° × 0.5° for the overpass on 8 September 2018. Additionally, Fig. 11 shows superobservations created using weights determined from the uncertainty in the individual observations ($w_i=\mathrm{1}/{\mathit{\sigma }}_i^{\mathrm{2}}$) (Fig. 11c) and using random observations (analogous to thinning; Fig. 11d). For comparison, the satellite observations have also been included (Fig. 11b). The regular superobservations and the uncertainty superobservations are similar. Both give a realistic low-resolution representation of the original satellite data. But, as expected, the uncertainty-weighted superobservations have systematically lower values because the weights favour the smaller columns, though the difference remains subtle. The difference is most clearly observed over Paris and North Africa. On average, the uncertainty-weighted superobservations in Fig. 11 have a tropospheric column of 22.4 µmol m⁻² compared to 23.0 µmol m⁻² for the normal superobservations, which is a reduction of 2.7 %. Over polluted areas with a tropospheric NO₂ column over 30 µmol m⁻², this reduction is 5 %. With the tiling approach, we avoid such a systematic low bias. The randomly sampled observations provide a noisy picture of the data, making it much less reliable than the other methods and demonstrating the large sub-grid variability.

The spatial structure of the superobservation uncertainty is illustrated in Fig. 12a and is compared to two simplified methods of calculating the superobservation uncertainty. The associated RE is shown separately in Fig. 12c. Note how the RE is mainly present at the edges of cloud fields due to the low coverage there. Also, note how the RE is higher in high-NO₂ areas due to the higher variation in measurement in these areas. This is particularly visible over Tunis and the Ruhr area.

The assumption that the observational uncertainty is fully correlated in space results in the uncertainties shown in Fig. 12b. Uncertainties using this approach are much higher than Fig. 12a and are likely overestimated. Assuming that the uncertainty is fully uncorrelated results in a much lower uncertainty, as shown in Fig. 12d. In this case, the total uncertainty is dominated by the number of observations in the grid cell, somewhat reflecting the RE. This is a strong underestimation compared to the uncertainty shown in Fig. 12a.

6.1 Data assimilation experiments

The impact of superobservations and their uncertainties in the NO₂ analysis from NO_x emission optimization is evaluated in a state-of-the-art chemical data assimilation framework. The data assimilation system used is described in Sekiya et al. (2022) and Miyazaki et al. (2020b) and uses the CHASER 4.0 chemical transport model (Sudo et al., 2002; Sekiya et al., 2018) at 1.125° × 1.125° resolution as the forecast model and the local ensemble transform Kalman filter (LETKF) data assimilation technique (Hunt et al., 2007). The assimilation was performed with 32 ensemble members and a 2 h assimilation window. Covariance localization was applied based on species-dependent localization scales that were derived from sensitive tests in Miyazaki et al. (2012b). Covariance inflation was also applied by inflating emission factor uncertainties (i.e. ensemble spread) to a minimum predefined value. Additionally, a multiplicative covariance inflation of 7 % was applied to the concentrations. In addition to NO₂, the assimilated measurements included total columns from the thermal-infrared (TIR)/near-infrared (NIR) band of the Measurement of Pollution in the Troposphere (MOPITT) instrument (Deeter et al., 2017), OMI SO₂ planetary boundary layer vertical columns (Li et al., 2020), and Aura Microwave Limb Sounder (MLS) O₃ and HNO₃ profiles (Livesey et al., 2022).

To demonstrate the impact of different superobservation settings, the following four sensitivity runs were done for July 2019, only varying the NO₂ observations:

1. The superobservations and their uncertainties as described in this paper (Figs. 11a, 12a).

2. The superobservations with uncorrelated errors include the standard superobservations, with modified uncertainty, assuming that the observations are fully uncorrelated in space (C=0; Fig. 12d).

3. The superobservations with correlated errors include the standard superobservations with modified uncertainty, assuming that the individual observations are fully correlated in space (C=1; Fig. 12b). This is analogous to the variance-averaged uncertainty.

4. Thinning includes thinned observations for which the values of one superobservation were taken randomly as one of the available observations within a model grid cell, similar to Fig. 11d. The uncertainty is the corresponding retrieval uncertainty in this observation.

Note that the RE for thinned observations is expected to be higher than the standard superobservations. Nevertheless, the RE was set to be the same among experiments to assess the impacts of the superobservation uncertainty itself.

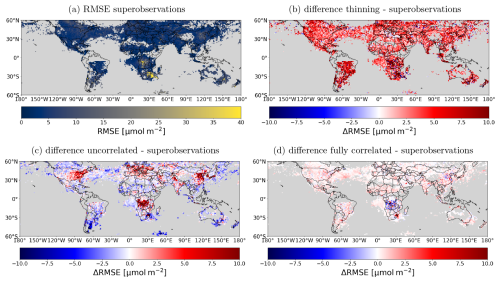
Figure 13 Panel showing the RMSE of the OmF for the superobservations and how it compares to the other experiments. The RMSE is calculated over the time dimension using only grid cells for which the tropospheric column is over 17 µmol m⁻² (Eq. 20). (a) RMSE of the superobservations. (b) Difference RMSE thinning – superobservations. (c) Difference RMSE uncorrelated – superobservations. (d) Difference RMSE fully correlated – superobservations.

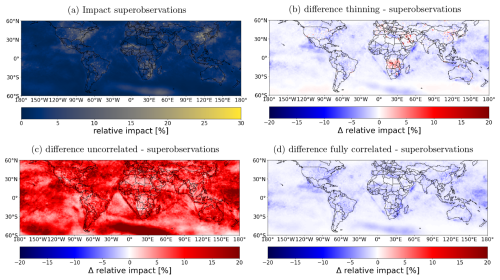
Figure 14 Panel showing the relative impact of the superobservations on the data assimilation system, and how this compares to the other experiments. (a) Relative impact of the superobservations. (b) Difference relative impact thinning – superobservations. (c) Uncorrelated – superobservations. (d) Fully correlated – superobservations.

The effectiveness of the assimilation for these four experiments was evaluated with the OmF RMSE as follows:

$$\begin{array}{}\text{(20)}& {\text{RMSE}}_{x,y}=\sqrt{{\displaystyle \frac{\mathrm{1}}{t}}\sum _{\mathrm{1}}^t(O_{t,x,y}-F_{t,x,y}{)}^{\mathrm{2}}}.\end{array}$$

Here $O_{t,x,y}$ values are the observations associated with the experiment (1, 2, and 3 in Fig. 11a and 4 in Fig. 11d), and $F_{t,x,y}$ values are the forecasted values. This is shown in Fig. 13. The relative adjustments made by data assimilation are evaluated by comparing the analysis (A_t) and forecasts (F_t) as follows:

$$\begin{array}{}\text{(21)}& \text{Impact }\left[\mathrm{\%}\right]={\displaystyle \frac{\mathrm{1}}{t}}\sum _{\mathrm{1}}^t{\displaystyle \frac{|A_t-F_t|}{F_t}}\cdot \mathrm{100}.\end{array}$$

The results are shown in Fig. 14. Additionally, the mean absolute difference (MAD) is as follows:

$$\begin{array}{}\text{(22)}& \text{MAD}={\displaystyle \frac{\mathrm{1}}{n}}\sum _{\mathrm{1}}^n\left|{\displaystyle \frac{\mathrm{1}}{t}}\sum _{\mathrm{1}}^t{O}_{t,x,y}-F_{t,x,y}\right|.\end{array}$$

RMSE and χ² metrics were evaluated for the different experiments (see Table 1). The χ² value is the ratio between the OmF errors (actual errors) and the model plus observational uncertainties (estimated uncertainty). A χ² of 1 means the residuals and uncertainties are balanced, while a higher χ² value indicates that uncertainties are underestimated, and vice versa. It is calculated as in Sekiya et al. (2022) and Zupanski and Zupanski (2006). χ² was estimated only over highly polluted areas with observation concentrations higher than 17 µmol m⁻². The impact calculation uses data between 11 and 17 h (local time), which is the time window during which TROPOMI observations are available.

Table 1 Metrics of the data assimilation experiments.

The χ² value of the standard superobservations (Obs-1) is 1.8, which means either the model or the observational uncertainties (or both) are somewhat underestimated. The χ² value can be sensitive to the choice of the covariance inflation factor through its impacts on background error covariance (i.e. model errors), as indicated by Sekiya et al. (2022). We have conducted several sensitivity calculations by perturbing the covariance inflation factor and have found that the impact on χ² is limited because the increase in background error covariance is compensated by an increase in the OmF error. The increase in spread from the covariance inflation results in a poorer forecast. The reason why χ² is higher than 1 can be due to a variety of model forecast or observation errors that are not accounted for in the covariances, such as transport errors and error correlations between superobservations.

Both the MAD and RMSE values are largest in the thinning case (Table 1). The decreased RMSE when using the superobservations indicates that averaging satellite observations leads to values which are closer to the scale that is represented by the model. The larger MAD in the thinning case reflects the fact that randomly selecting observations often results in negative tropospheric NO₂ columns, which are rejected by the assimilation system, resulting in a positive sampling bias. This effect is particularly obvious over remote areas, with some negative values due to the retrieval uncertainties. In the case of superobservations, the proportion of observations with negative tropospheric columns and their value are both significantly reduced.

The standard superobservation case had the smallest RMSE compared to both the fully correlated and the uncorrelated cases. Given the common tropospheric NO₂ fields, the difference is attributed to the differences in the superobservation uncertainty. In the uncorrelated case, corresponding to the smaller uncertainties, the data assimilation adjustments become larger than the standard superobservation case (Fig. 14c), with larger RMSEs in highly polluted areas, probably due to overcorrections (Fig. 13c). In remote areas, the RMSE improves with smaller uncertainties, suggesting that the standard superobservations overestimate its uncertainty in remote areas. The smaller MAD in the uncorrelated case reflects the reduced RMSEs in remote areas.

On the other hand, in the correlated case, the uncertainty is large, which reduced the data assimilation impact and somewhat increased the RMSE and MAD. This shows that assuming that the uncertainties are fully correlated is not so unrealistic, but it does lead to a reduction in performance almost everywhere. One exception to this is central Africa, where the lower uncertainty significantly improves the RMSE. Note that there is only a small decrease in the relative impact in this area going from the superobservations to the correlated experiment. Despite the fact that there is almost no uncertainty reduction from the superobservations, the uncertainty is still too low. It is likely that further increasing the uncertainty yields even better results than the correlated experiment. Because this effect is so strong and local, we believe it is not related to the superobservation method but instead results from fire-related errors in the observation uncertainty or model. The high absolute errors in the area have a large impact on the RMSE and MAD values, despite a small difference in the relative impact. As a result, the superobservations probably do not compare as well to the uncorrelated experiment in Table 1 as they should.

The uncertainty is similar between the thinning and fully correlated cases because the retrieval uncertainty is not as noisy as the retrieval concentrations. Correspondingly, the effect of the observations on the assimilation should be similar between the thinning and correlated cases. This is mostly true, except for some high-emission areas, such as central Africa, the Middle East, and eastern China. Here the larger OmF and RMSE values between the model and observations increases the impact of the observations on the assimilation. Also, note that thinning results in a similar χ² value to the superobservations. The larger OmF and uncertainty maintain the ratio between the two.

7 Discussion

In this paper, we presented a detailed methodology to construct superobservations and their errors and averaging kernels, improving upon the superobservations used previously by Miyazaki et al. (2012a), Boersma et al. (2016), Sekiya et al. (2022), and van der A et al. (2024). These superobservations are constructed in particular for data assimilation, inverse modelling, and model evaluation applications. The first aspect of this is an improved estimation of the superobservation uncertainties stemming from the observational uncertainties for individual TROPOMI NO₂ observations. This is achieved by quantifying the correlation between observations, allowing for a more accurate propagation of the observational uncertainties and the spatial distribution of these uncertainties. The spatial correlations for the slant column, stratosphere, and air mass factor contributions are estimated and treated separately. Uncertainties relating to the prior are not discussed because it is assumed that the kernels will be used during assimilation or model evaluation. As shown by the data assimilation experiments, realistic uncertainties are of key importance for the optimal performance of the assimilation system. The correlated experiment leads to an overestimation of the uncertainty. This is similar to the method of Inness et al. (2019b) and the HARP spatial binning method for total uncertainty variables (http://stcorp.github.io/harp/doc/html/algorithms/regridding.html#spatial-binning, last access: August 2024). On the other hand, the uncorrelated experiment underestimates the uncertainty. It is similar to the HARP spatial binning method for random uncertainty variables. Both an over- and underestimation of the uncertainty degrade the short-term forecast in the MOMO-Chem data assimilation system, as demonstrated above.

The quantification of the spatial error correlation is complicated and remains uncertain. Correlations between retrieval uncertainties in nearby satellite pixels may be caused by spatially correlated biases in the characterization of the surface reflectance or LER, aerosol, and cloud properties and may depend on the weather. For instance, rainfall or drought may locally impact the albedo, which is not described by the albedo climatology used in the retrieval. Estimating a correlation for the AMF uncertainty is particularly difficult because it results from complex interactions between algorithms and variables such as surface albedo, cloud albedo and cloud height, and unspecified systematic retrieval errors. The way that these variables are spatially correlated propagates to the correlation of the AMF uncertainty.

The stratospheric uncertainty treatment was updated. For individual observations, the stratosphere does not contribute much to the uncertainty, but for the clustered superobservations, the stratosphere is a prime source of error. We quantified a longitude- and seasonal-dependent stratospheric uncertainty, replacing the default constant uncertainty present in the TROPOMI data product. As a result, lower latitudes have significantly lower stratospheric uncertainties. Uncertainties for the higher latitudes are generally lower than the default uncertainty but can also be higher, depending on the season.

We also improved the existing method of calculating the (horizontal) RE. A simple constant parameterization was used before by Miyazaki et al. (2012a) and Boersma et al. (2016). We presented a mathematical derivation for the RE in the case of a random missing observation. This allows for an easier and more accurate computation of the RE. Additionally, we have quantified a systematic sampling correction for the case when the missing observations are clustered, as would be the case when clouds cover part of the superobservation area. This leads to higher uncertainties and a lower impact of low-coverage superobservations. The RE derivation also shows that a thinning approach (keeping just one observation per grid cell) would add a large uncertainty to the observation equal to the standard deviation of the observations within a model grid cell.

Compared to Miyazaki et al. (2012a), who postulated a fixed correlation of 0.15, our superobservations are somewhat more uncertain. However, due to the separation of the different components, the uncertainty correlation in our superobservations is spatially heterogeneous and has a different behaviour over the ocean than over polluted regions. In a further development, Sekiya et al. (2022) already separated the stratospheric error, treating it as fully correlated. However, Sekiya et al. (2022) still use the postulated correlation of 0.15 for the remaining observational uncertainties. This means that the slant column uncertainties presented here are lower than theirs, but our AMF uncertainty is higher (except for very large superobservations). Compared to Sekiya et al. (2022), our superobservations are somewhat more impactful over clean areas and somewhat less impactful over polluted areas.

When compared to thinning, the superobservations are a much less noisy representation of the satellite data and thereby improve the performance of the data assimilation. The uncertainty-weighted superobservations also provide a realistic average of the data, but they favour the small column retrievals and are therefore biased low, which is a feature we avoid using the tiling approach.

The superobservations resolve the correlations between observations within the superobservation grid cell. However, they does not describe a remaining correlation between adjacent superobservations. Inflating the superobservation uncertainty could improve the results of the assimilation, depending on the size of the superobservations.

We have focused on constructing superobservations of the same size as the grid cell of the model that they will be compared against. However, it is not obvious that this would be the most optimal configuration. According to Nyquist (Shannon, 1949), in order to capture all the variability at the size of the superobservations, we would need to oversample by introducing extra superobservations shifted in space. One may argue that for a species like NO₂ with a very inhomogeneous fine-scale distribution, interpolation in model space is not useful without knowledge of the sub-grid distribution of the emission sources. Data assimilation implementations typically introduce spatial correlation lengths covering multiple grid cells in the modelling of the background (forecast) covariance matrix B. These correlations act as low-pass filters, and the fine-scale variability for smaller length scales is not constrained in the analysis. In that case, constructing superobservations larger than a single model grid cell could be explored, as long as the horizontal correlation lengths of the assimilation system are appropriately oversampled. These coarser superobservations could be useful for satellite data with a high relative noise level (e.g. HCHO and SO₂ column observations) or reducing correlated uncertainties between observations while at the same time lowering computational costs.

8 Conclusion

In conclusion, this research has improved and formalized existing methods of creating superobservations. Superobservation uncertainties have been quantified by analysing the various aspects leading to systematic and random uncertainties in the satellite retrieval and by mathematically deriving a realistic representation error. Data assimilation experiments show that the uncertainties derived in this way lead to better forecast results than postulating either fully correlated or uncorrelated uncertainties. A thinning of the observations results in very noisy patterns of NO₂ and degraded assimilation results compared to the superobservations. Thus, we recommend the use of superobservations with quantitative uncertainties for the assimilation of atmospheric NO₂ and other trace gases.

The superobservation methodology is generic and will be applied in the future to other species, like HCHO, SO₂, CO, O₃, CH₄, and CO₂, and to other satellite instruments, like OMI, GEMS, or TEMPO. All of the concepts and mathematics described in this paper are broadly applicable. This includes the method of clustering, averaging, and uncertainty averaging. The latter does require the quantification of correlations. Calculating the RE is also species-agnostic, with only the systematic correction requiring extra quantification.

Another possible application for superobservations is the creation of level 3 data. These methods provide satellite information on regular grids. Our superobservation approach provides realistic error estimates of the grid box mean value in case the level 3 grid boxes contain multiple satellite footprints and have a lower resolution than the satellite. This is a first step towards a consistent averaging of the satellite data into monthly, seasonal, and yearly averages and specifying meaningful uncertainties for such averages. Additional considerations are needed to quantify the temporal representation and temporal correlations. Also, in our work targeting model comparisons and data assimilation, we did not consider the a priori uncertainties which may need to be quantified for level 3 data, depending on the application.

Appendix A: Correlation calculation

A1 Calculation of the grid box mean correlation from the correlation length

The mean correlation C between pairs of observations within a superobservation is calculated as an average of the correlation between all pairs of points in a superobservation. This is obtained by multiplying the probability density function (PDF) of the distance between all points in a square with the correlation as a function of the distance and integrating the result. The PDF of all points in a rectangle is taken from Philip (2007), and the correlations are calculated for a distance d and a correlation length l, assuming an exponential decay, $C=e^{-d/l}$. The correlation length l is computed using the TROPOMI v2.4–v2.3.1 differences.

For example, a 1° superobservation at 29° latitude is a 113 by 99 km rectangle resulting in a PDF, as shown in Fig. A1a. A correlation length of 32 km yields Fig. A1b. Multiplying the two functions creates Fig. A1c, and integrating this results in a correlation of 0.24 (Fig. A1d).

A2 Calculation of the correlation length

The correlation length is calculated using the inverse of the method for calculating the correlation, where a correlation is converted to a correlation length based on the PDF of distances. This requires a representative correlation of the dataset with a representative grid cell. The autocorrelation of the v2.4–v2.3.1 tropospheric column differences within a 1° superobservation is calculated using Eq. (A1) for n number of tropospheric columns x in a superobservation indexed by i and j. This is a special case of the Pearson correlation, where we assume the mean of the v2.4–v.2.3.1 retrieval difference is 0.

$$\begin{array}{}\text{(A1)}& C_{x,x}={\displaystyle \frac{{\sum }_i^n{\sum }_j^n{x}_i{x}_j}{{\sum }_i^n{x}_i^{\mathrm{2}}}}\end{array}$$

Correlations are computed within single superobservations. Figure A2a and b show the difference and the correlation on a single day. Averaging the correlation over the available data gives Fig. A2c. Because the AMF is most important for polluted observations, we filter this result for areas with an average tropospheric NO₂ concentration over 30 µmol m⁻², shown in Fig. A2d. The average correlation of the remaining data is 0.244 at an average grid box size of 113×99 km². Applying the inverse method of Sect. A1 gives a correlation length of 32 km.

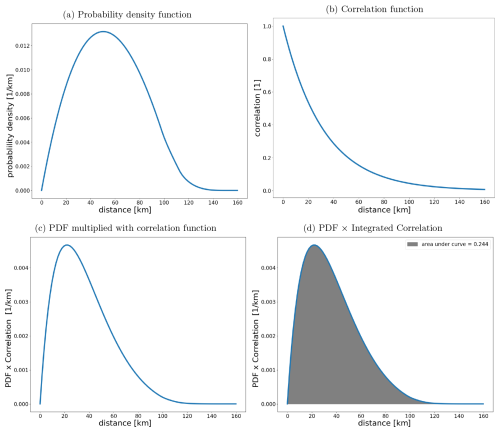
Figure A1 Panels show the computation of the superobservation correlation from a correlation length and latitude. (a) The probability density function for the distance between two points in a 1° superobservation at 29° latitude. (b) Correlation function for a correlation length of 32 km. (c) Multiplication of the PDF in panel (a) and the correlation function in panel (b). (d) Integration of the curve from panel (c). The area under the curve gives the correlation of the superobservation.

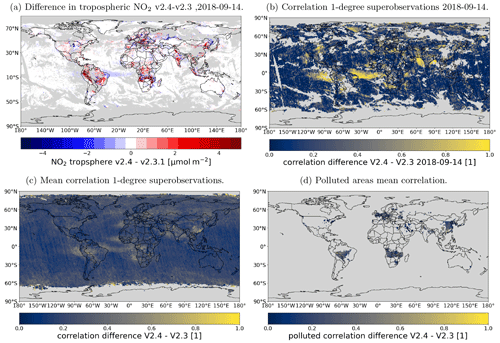
Figure A2 Panels showing the calculation of a representative correlation for the purpose of calculating a representative correlation length. (a) Difference between the v2.4 and v2.3 observations. (b) Correlations within 1° superobservations relative to dataset. (c) Average correlation in the month of September for 2018–2022. (d) Average correlation of polluted areas.

Appendix B: Fractional representation error

To use the formula of the representation error (Eq. 17) with observations with different weights, we reformulate the equation using fractional observations (n_f). Here partially overlapping observations are counted based on the fraction of overlap (o). The overlap of an observation is the ratio between the area inside the superobservation grid (a_in,i) to the total area (a_tot,i).

$$\begin{array}{}\text{(B1)}& o_i={\displaystyle \frac{a_{\mathrm{in},i}}{a_{\mathrm{tot},i}}}\end{array}$$

An observation with a 20 % overlap only counts as 0.2 observations. To take into account the size differences between satellite observations, we also normalize the overlap by the average area of the observations (including the parts outside of the superobservation).

The number of fractional observations of (n_f,n) within a superobservation is the sum of the observation area divided by the average area and multiplied by the observation overlaps, as follows:

$$\begin{array}{}\text{(B2)}& n_{\mathrm{f},n}=\sum _i^n{o}_i{\displaystyle \frac{{\stackrel{\mathrm{̃}}{a}}_i}{{\stackrel{\mathrm{̃}}{a}}_{\mathrm{avg}}}}.\end{array}$$

In this formulation, an average sized observation that completely overlaps the superobservation will count as one observation, while smaller or partially overlapping observations count for less. The total population size of fractional observations (N_f) is the sum over all observations within the superobservation, as follows:

$$\begin{array}{}\text{(B3)}& N_{\mathrm{f}}=\sum _i^N{o}_i{\displaystyle \frac{{\stackrel{\mathrm{̃}}{a}}_i}{{\stackrel{\mathrm{̃}}{a}}_{\mathrm{avg}}}}.\end{array}$$

To facilitate the comparison between superobservations with different population sizes N, the RE can be expressed in terms of a fractional coverage f ranging from 0 to 1, as follows:

$$\begin{array}{}\text{(B4)}& f_n={\displaystyle \frac{n_{\mathrm{f},n}}{N_{\mathrm{f}}}}.\end{array}$$

Replacing n with n_f,n and substituting n_f,n with $n_{\mathrm{f},n}=N{f}_n$, σ_RE becomes

$$\begin{array}{}\text{(B5)}& {\mathit{\sigma }}_{\mathrm{RE},n}={\displaystyle \frac{\mathit{\sigma }}{\sqrt{N_{\mathrm{f}}{f}_n}}}\sqrt{{\displaystyle \frac{N_{\mathrm{f}}-N{f}_n}{N_{\mathrm{f}}-\mathrm{1}}}}.\end{array}$$

However, expressing the RE in terms of fractional observations or coverage has the following two problems:

1. Because different configurations of observations have a different number of fractional observations, it is not possible to experimentally calculate σ_RE,n using Eq. (16) because the values on the x axis are different. Interpolating the values solves this, except for the case where n=1 because there are no values for 0 observations.

2. There are situations where $n_{\mathrm{f},\mathrm{1}}<\mathrm{1}$, which results in ${\mathit{\sigma }}_{\mathrm{RE},\mathrm{1}}>\mathit{\sigma }$. This should not happen because it is not possible to have fewer than one observation. In Fig. 7a, we also see that σ_RE,1 (green line) does not exceed 1 standard deviation.

Both of these problems require that for one observation n_f,1 or Nf₁ is equal to 1, irrespective of the actual n_f. More formally, there is a constraint, where

$$\begin{array}{}\text{(B6)}& N{f}_{\mathrm{1}}=\mathrm{1}.\end{array}$$

First, we redefine the fractional coverage to 0 for n=1 using the following formula:

$$\begin{array}{}\text{(B7)}& f_{z,n}=(f-f_{\mathrm{1}})\cdot {\displaystyle \frac{\mathrm{1}}{\mathrm{1}-f_{\mathrm{1}}}}.\end{array}$$

We call this new fractional coverage f_z,n. Essentially, this stretches the σ_RE,n to always range from 0 to 1 fractional coverage. Because $f_{z,\mathrm{1}}=\mathrm{0}$, the following equation satisfies the constraint:

$$\begin{array}{}\text{(B8)}& N{f}_n=N{f}_{z,n}+\mathrm{1}-f_{z,n}.\end{array}$$

Substituting Eq. (B8) into Eq. (B5) yields the final equation for the random representation error as follows:

$$\begin{array}{}\text{(B9)}& {\mathit{\sigma }}_{\mathrm{RE},n}={\displaystyle \frac{\mathit{\sigma }}{\sqrt{N_{\mathrm{f}}{f}_{z,n}+\mathrm{1}-f_{z,n}}}}\sqrt{{\displaystyle \frac{N_{\mathrm{f}}-(N_{\mathrm{f}}{f}_{z,n}+\mathrm{1}-f_{z,n})}{N_{\mathrm{f}}-\mathrm{1}}}}.\end{array}$$

Appendix C: Fallback standard deviation

For the case when there are insufficient observations to calculate a meaningful standard deviation for a grid cell, we implemented a fallback option in which the superobservation standard deviation is estimated as 0.4 times the tropospheric column +2.5 µmol m⁻², based on the trendline in Fig. C1. This relationship has a Pearson correlation of 0.9. We calculated the fallback using 0.3° superobservations, which contain on average 25 TROPOMI observations at the Equator.

Figure C1 Relationship between the superobservation tropospheric column and standard deviation for a 0.3° superobservation.