A wave-resolving two-dimensional vertical Lagrangian approach to model microplastic transport in nearshore waters based on TrackMPD 3.0

Potentially acting as a source or a sink for plastic pollution to the open ocean, nearshore waters remain a challenging context for predicting the transport and deposition of plastic debris. In this study, we present an advanced modeling approach based on the SWASH wave model and the TrackMPD (v3.0) particle transport model to investigate the transport dynamics of floating and sinking microplastics in wave-dominated environments. This approach introduces novel features such as coupling with advanced turbulence models, simulating resuspension and bedload processes, implementing advanced settling and rising velocity formulations, and enabling parallel computation. The wave laboratory experiments conducted by Forsberg et al. (2020) were simulated to validate the model's ability to reproduce the transport of diverse microplastics (varying in density, shape, and size) along a comprehensive beach profile, capturing the whole water column. Our results underscore the robustness of the proposed model, showing good agreement with experimental data. High-density microplastics moved onshore near the bed, accumulating in proximity to the wave-breaking zone, while the distribution of low-density particles varied along the coastal profile depending on the particle properties. The study also sheds light on the primary mechanisms driving microplastic transport, such as Stokes drift, wave asymmetry, and settling/rising velocities. Sensitivity analyses on calibration parameters further confirm the robustness of the model results and the influence of these factors on transport patterns. This research establishes the SWASH–TrackMPD approach as a valuable tool, opening avenues for future studies to contextualize laboratory findings within the complexities of real-world nearshore environments and further refine our comprehension of microplastic dynamics across different beaches and wave-climate conditions.

1 Introduction

Nearshore areas are highly dynamic environments influenced by complex interactions among water, sediment, biota, and human activity. These regions support high productivity and biodiversity and provide multiple ecosystem services (Liu and Stern, 2008; McLachlan and Defeo, 2017). However, they are also vulnerable to anthropogenic and natural threats, such as sea-level rise, extreme storms, and pollution (Rippy et al., 2013; d'Anna et al., 2022). Microplastic (MP, 0.1 µm to 5 mm plastic particles) pollution has emerged as a major concern, with the potential to cause significant ecological, aesthetic, and economic impacts on beaches and coastal environments. Numerous studies have reported MP pollution on beaches globally, with some revealing alarmingly high contamination levels (Turra et al., 2014; Fok and Cheung, 2015; Pérez-Alvelo et al., 2021; Tata et al., 2020; Lefebvre et al., 2021).

Despite the well-documented presence and abundance of MPs on beaches, fundamental questions regarding their transport, dispersion, trapping, and fate in nearshore waters remain unresolved (Zhang, 2017). This is primarily due to (1) the intricate nature of nearshore hydrodynamic processes and the rapid morphodynamic changes occurring within these environments (Castelle and Masselink, 2023); (2) the inherent variability in MP properties, including density, size and shape, as well as complex processes like biofouling, aggregation, and fragmentation, which influence their transport behavior (Khatmullina and Chubarenko, 2019; Jalón-Rojas et al., 2022); (3) the multiple pathways through which MPs enter the nearshore environment, including runoff from urban areas and rivers, direct discharge from ships or offshore sources, and beach litter (Lefebvre et al., 2023); and (4) the lack of high-resolution data and suitable modeling approaches to accurately capture the multidimensional aspects of MP transport in these environments.

The absence of direct field observations beyond the beach region (Chubarenko et al., 2018), within or near the surf zone water column, can be primarily attributed to the inherent difficulties associated with sampling MPs in this dynamic and often hazardous environment. Consequently, previous studies investigating microplastic transport in nearshore waters have predominantly relied on laboratory experiments in wave or wind-wave flumes (Forsberg et al., 2020; Kerpen et al., 2020; Guler et al., 2022; Larsen et al., 2023; Núñez et al., 2023). While these recent experiments have provided valuable insights into certain aspects of microplastic movement, they remain small-scale idealized representations of nearshore systems, affected by scaling issues. Furthermore, laboratory experiments on wave-driven or wind-wave-driven transport of MP are very costly approaches, which limits the number of tested configurations and their ability to capture the diversity and complexities of real-world scenarios.

To overcome these limitations, numerical modeling offers a promising tool to elucidate the transport and fate of microplastics in nearshore waters, providing a means to explore multiple scenarios that may be challenging to investigate through field or laboratory experiments (e.g., different forcings, beach morphologies, and particle characteristics). Although numerical models have been extensively developed at ocean and regional scales in recent years (e.g., Dobler et al., 2019; Jalón-Rojas et al., 2019; Lobelle et al., 2021; Baudena et al., 2022), there is a significant knowledge gap in modeling MP dynamics at the nearshore scale. In particular, there is a pressing need to develop numerical tools able to address the wave- and particle-resolved temporal and space scales of transport. Such a detailed characterization of MP dynamics remains a necessary step to avoid the use of uncontrolled bulk parameterization of transport processes. To our knowledge, prior to this study, Stocchino et al. (2019) and De Leo and Stocchino (2022) have conducted such fine numerical studies evaluating the effects of sea waves on inertial microplastic dynamics, a topic that has also been well documented through experimental research (DiBenedetto et al., 2018, 2019, 2022; De Leo et al., 2021). However, these studies were mainly dedicated to deep water transport, and several hydrodynamic processes affecting the transport in nearshore areas, such as wave asymmetry and wave breaking, and transport mechanisms like resuspension or bedload were not considered. Additionally, a more recent study by Kim and Kim (2024) modeled microplastic transport in the nearshore region, emphasizing the key role of wave breaking and rip currents. However, it exclusively focused on buoyant particles and did not consider near-bed transport processes such as deposition, resuspension, and bedload.

In this study, we aim to develop a wave-resolving 2D Lagrangian numerical model based on the SWASH (Zijlema et al., 2011) and TrackMPD (Jalón-Rojas et al., 2019) models to simulate the transport of floating and sinking microplastics (MPs) in shallow, wave-dominated environments. A major challenge for process-based modeling of the complex nearshore microplastic transport is the lack of field observations. In this context, data from laboratory studies offer a valuable opportunity to validate numerical model approaches. We use wave laboratory experiments conducted by Forsberg et al. (2020) as a validation benchmark to assess the model's capacity in simulating the transport of different types of microplastics (different shapes, densities, and sizes) along a 2D beach profile by describing the entire water column. Furthermore, we evaluate the sensitivity of model parameters to assess their influence on the simulated transport trends.

2 Methods

The process-based hydrodynamical model SWASH was utilized in this study to simulate the wave-driven hydrodynamics and generate the associated current velocity field, which is subsequently provided (offline) as input to the Lagrangian particle-tracking model TrackMPD. In this section, we provide a concise overview of both models and present the novel developments made in this study to enhance the modeling of key transport mechanisms in nearshore waters. The test case from Forsberg et al. (2020) and the sensitivity scenarios are then detailed.

2.1 The base models

2.1.1 SWASH

SWASH (Zijlema et al., 2011) is a non-hydrostatic, wave-resolving model designed to solve the non-linear shallow-water equations derived from the incompressible Navier–Stokes equations. SWASH has been particularly designed to simulate the transformation of surface waves as they propagate toward the shore, capturing the key features of surf and swash zone dynamics including non-linear shoaling, wave breaking, wave runup, and wave-driven currents. The model employs an explicit, second-order finite-difference method that ensures the conservation of both mass and momentum at the numerical level. In the present study, unidirectional cross-shore propagating waves were imposed at the left boundary of the domain, so the equations are solved in a two-dimensional vertical (2DV) plane. A structured grid is utilized for discretizing the physical domain, with a constant width in the x direction and a fixed number of layers between the bottom and the free surface in the vertical direction. The layer thickness is defined as a constant fraction of the water depth, similar to the sigma-layer coordinate system. SWASH has been validated and applied extensively in laboratory and field studies to investigate nearshore waves and wave-driven processes (Zijlema et al., 2011; Rijnsdorp et al., 2014; Suzuki et al., 2017; Zhang et al., 2018; Sous et al., 2020). Further details on the present SWASH configuration are given in Sect. 2.3.

2.1.2 TrackMPD

TrackMPD (Jalón-Rojas et al., 2019) is a Lagrangian particle-tracking model that incorporates a wide range of particle transport processes, including advection, turbulent dispersion, beaching, refloating, deposition, and resuspension. It also accounts for various microplastic behaviors such as settling/rising, biofouling, and degradation, which are contingent upon the physical properties of the particles. The model employs a fourth-order Runge–Kutta scheme to accurately advect virtual particles through a set of velocity fields. A random-walk approach is implemented to simulate the turbulent motion of particles in both the horizontal and the vertical directions as a function of the horizontal and vertical diffusivity coefficients (see Sect. 2.2.1 for more details). The settling or rising velocities of particles can be defined by users or calculated online using various empirical formulations that account for particle physical properties and other behaviors such as biofouling and degradation. TrackMPD is an open-source model and can be accessed on GitHub (https://github.com/IJalonRojas/TrackMPD, last access: September 2024). For more information about TrackMPD v1, readers can refer to Jalón-Rojas et al. (2019).

2.2 Developments

In order to enhance the Lagrangian modeling of particles in nearshore and coastal waters, significant advancements have been incorporated into TrackMPD. The focus is placed on the dynamical representation of two strong controlling factors of nearshore transport: (i) turbulent mixing, which displays striking spatial gradients forced by wave breaking and depth variations, and (ii) the main time-varying processes governing the transport of solid particles in response to the continuously evolving hydrodynamical conditions (water depth, current, shear stress), particularly deposition, erodibility, and subsequent transport. These developments ultimately led to the release of TrackMPD v2.3 and v3.0 (used in this work), which offer several key features and improvements compared to the previous version.

Firstly, TrackMPD (from v2.3) allows for the offline coupling of turbulence models, as detailed in Sect. 2.2.1, enabling a more accurate representation of turbulent dispersion effects on particle transport. Secondly, additional processes such as deposition, resuspension, and bedload have been included or improved, providing a more accurate representation of particle dynamics (Sect. 2.2.2 and 2.2.3). The resuspension process was built upon the initial simplified proposition presented by Cheng et al. (2020). Furthermore, parallel computation of particle trajectories has been implemented, leading to faster simulation times and improved computational efficiency. Additionally, while in the first version, advection was computed at an internal time step and dispersion and behavior were calculated at the output time step, the new version integrates these processes into a unified internal time step of calculation. New parameterizations for settling and rising velocities (Dellino et al., 2005; Waldschläger and Schẗtrumpf, 2019a; Jalón-Rojas et al., 2022) have also been introduced. Finally, TrackMPD now includes a verbose mode that allows users to select the degree of detail in the progress messages during simulation runs.

It is important to note that TrackMPD retains its availability for both the 2D horizontal (2DH) and the 3D approaches. However, for the specific focus of this work, we have adapted the 3D approach to a 2DV approach, focusing specifically on the dynamics within a two-dimensional vertical plane.

2.2.1 Vertical diffusivity

TrackMPD (from v2.3) offers the flexibility to set the horizontal and vertical diffusivity coefficients as either constant or varying values. In the latter case, the diffusivity coefficients are generated by an external hydrodynamic or turbulence model and read by TrackMPD in a similar way to current velocities. This approach enables the diffusivity coefficients to vary over space and time, providing a more realistic representation of the particles' transport processes.

In this study, the vertical turbulent “eddy” diffusivity ν_t was estimated from the non-dimensional analysis of surf zone turbulence presented by Feddersen (2012). This analysis has been demonstrated to provide consistent scaling for both laboratory and natural surf zone turbulence. A spectral analysis was first performed on each SWASH wave run to extract the energy flux F [N s⁻¹] over the whole domain based on the linear theory. A wave-averaged vertical eddy diffusivity [m² s⁻¹] is therefore estimated as

$$\begin{array}{}\text{(1)}& {\mathit{\nu }}_{\mathrm{t}}(x,z)=Ah{\left({\displaystyle \frac{\mathrm{1}}{\mathit{\rho }}}{\displaystyle \frac{\mathrm{d}F}{\mathrm{d}x}}\right)}^{\mathrm{1}/\mathrm{3}}\exp \left(B{\displaystyle \frac{z}{h}}\right),\end{array}$$

where x and z are the horizontal cross-shore and vertical coordinates, h is the local depth [m], ρ is the density of water [kg m⁻³], and A=0.0147 and B=1.46 following the coefficient values proposed by Feddersen (2012). The wave averaging means that the wave-breaking-induced eddy diffusivity is supposed to be driven by the turbulent field resulting from the breaking of many successive waves (Ruessink, 2010). An additional background eddy viscosity can be imposed at the beach and offshore regions. At the beach zone, the Feddersen scaling is not applicable due to the impossibility of computing energy flux in the intermittently wet and dry portion of the beach. Smoothing is applied to avoid sharp ν_t gradients in transition areas.

We propose that, for nearshore applications, as in the present study, the vertical diffusivity coefficient for particles, K_v, instead of being constant, can be assumed to be equal to the eddy diffusivity calculated using this approach, meaning that momentum and plastic particles diffuse at the same rate. This assumption is reasonable, given that the small size of microplastics causes their dynamics to be largely dominated by turbulence in these highly dynamic systems, but it requires further validation through dedicated research efforts.

2.2.2 Deposition, resuspension, and bedload conditions

Depending on user preferences, different types of particle interactions with the bed can be set. Particles reaching the bed can be deposited. Once at the bed, particles can be temporarily or permanently attached to the bed or left free for further motions. Particles can be considered definitely trapped in the bed if strong interactions with bed sediments are expected. It is also possible to dynamically evaluate their fate at each time step according to the prevailing hydrodynamic conditions. In the latter case, the particle shear stress [N m⁻²] is estimated at the position of the deposited particle at each time step as

$$\begin{array}{}\text{(2)}& {\mathit{\tau }}_{\mathrm{0}}=\mathit{\rho }{\mathit{\nu }}_{\mathrm{t}}{\displaystyle \frac{\partial U}{\partial z}}{|}_{z=\mathrm{0}},\end{array}$$

where ρ is the density of water. The shear stress can be approximated as

$$\begin{array}{}\text{(3)}& {\mathit{\tau }}_{\mathrm{0}}=\mathit{\rho }{\mathit{\nu }}_{\mathrm{t}}{\displaystyle \frac{U_{\mathrm{1}}}{\mathrm{\Delta }z}},\end{array}$$

where U₁ [m s⁻¹] and Δz [m] are the first-layer (bottom) velocity and the layer separation distance, respectively.

Similarly to the traditional approach employed for the transport of natural particles (Soulsby, 1997), the fate of the deposited particles is determined based on the magnitude of the bottom shear stress relative to critical values:

• If $\left|{\mathit{\tau }}_{\mathrm{0}}\right|<\left|{\mathit{\tau }}_{\mathrm{cr},\mathrm{1}}\right|$, the particle remains settled at the bottom.

• If $\left|{\mathit{\tau }}_{\mathrm{cr},\mathrm{1}}\right|<\left|{\mathit{\tau }}_{\mathrm{0}}\right|<\left|{\mathit{\tau }}_{\mathrm{cr},\mathrm{2}}\right|$, the particle is transported as bedload (see Sect. 2.2.3).

• If $|{\mathit{\tau }}_{\mathrm{0}}>|{\mathit{\tau }}_{\mathrm{cr},\mathrm{2}}|$, the particle is resuspended, allowing it to move again following the currents from its position on the bed.

These critical values, which can be either set up by users or calculated using empirical formulations, are written in terms of the critical Shields parameter, θ_cr, as

$$\begin{array}{}\text{(4)}& {\mathit{\tau }}_{\mathrm{cr}}={\mathit{\theta }}_{\mathrm{cr}}({\mathit{\rho }}_{\mathrm{p}}-\mathit{\rho })g{D}_{\mathrm{eq}},\end{array}$$

where g is the acceleration of gravity [m s⁻²], ρ_p the particle density [kg m⁻³], ρ the water density [kg m⁻³], and D_eq is the equivalent particle diameter [–]. The latter is calculated as

$$\begin{array}{}\text{(5)}& D_{\mathrm{eq}}=\sqrt[\mathrm{3}]{abc},\end{array}$$

where a, b, and c are the particle length [m], width [m], and height [m]. In TrackMPD v2.3, the model includes the modified Shields approach by Soulsby (1997), which provides the critical Shields parameters [–] for natural particles, for bedload,

$$\begin{array}{}\text{(6)}& {\mathit{\theta }}_{\mathrm{cr},\mathrm{1}}={\displaystyle \frac{\mathrm{0.3}}{\mathrm{1}+\mathrm{1.2}{D}_{*}}}+\mathrm{0.055}[\mathrm{1}-\exp (-\mathrm{0.02}{D}_{*}\left)\right],\end{array}$$

and resuspension,

$$\begin{array}{}\text{(7)}& {\mathit{\theta }}_{\mathrm{cr},\mathrm{2}}={\displaystyle \frac{\mathrm{0.3}}{\mathrm{1}+D_{*}}}+\mathrm{0.1}[\mathrm{1}-\exp (-\mathrm{0.05}{D}_{*}\left)\right],\end{array}$$

where D_* [–] is the reduced diameter of MP particles $D^{*}={\left(\frac{\left|\frac{{\mathit{\rho }}_{\mathrm{p}}-\mathit{\rho }}{\mathit{\rho }}\right|\cdot g}{{\mathit{\nu }}^{\mathrm{2}}}\right)}^{\mathrm{1}/\mathrm{3}}\cdot D_{\text{eq}}$. Additionally, the model incorporates the empirical formulation of Waldschläger and Schẗtrumpf (2019b), which accounts for the “hiding–exposure” effect of sediments and estimates the critical shear stress of microplastics deposited on sandy beds from the sediment shear stress as

$$\begin{array}{}\text{(8)}& {\mathit{\theta }}_{\mathrm{cr},\mathrm{p}}^{*}=\mathrm{0.5588}{\mathit{\theta }}_{\mathrm{cr}}^{*}{\left({\displaystyle \frac{D_{\mathrm{50}}}{D_{\mathrm{eq}}}}\right)}^{-\mathrm{0.503}},\end{array}$$

where ${\mathit{\theta }}_{\mathrm{cr},\mathrm{p}}^{*}$ is the critical Shields parameter of the microplastic [–], θ_cr,sed is the critical Shields parameter of the sediment bed [–] calculated using Eq. (6) or Eq. (7), D_eq [m] is the microplastic diameter, and D₅₀ [m] is the median grain size of the sediment bed. New empirical formulations can be seamlessly integrated into the model as they become available. In this study, we used Soulsby's formulations rather than Waldschläger's approach to calculate the critical shear stress of resuspension and bedload transport, as the flume experiments were performed in the absence of sediments on the bed.

2.2.3 Bedload transport

When the bedload transport condition is satisfied, it is assumed that the near-bed particle is mainly driven by the drag force, which is estimated as

$$\begin{array}{}\text{(9)}& F_{\mathrm{d}}=\mathit{\rho }{C}_{\mathrm{h}}{U}_{\mathrm{r}}^{\mathrm{2}}{D}^{\mathrm{2}},\end{array}$$

where U_r the relative fluid velocity [m s⁻¹], i.e., the difference between the fluid and the particle velocities; D is a typical dimension of the particle [m]; and C_h is an empirical particle drag coefficient [–]. Vertical forces (lift and gravity/buoyancy) are expected to weakly affect the horizontal force balance, while friction, added mass, and Basset forces are neglected but may be included in further developments of the model. Introducing the bed shear stress ${\mathit{\tau }}_{\mathrm{0}}=\mathit{\rho }{u}_{*}^{\mathrm{2}}=\mathit{\rho }{C}_{\mathrm{d}}{U}^{\mathrm{2}}$ [N m⁻²], the hydrodynamic force can be written as

$$\begin{array}{}\text{(10)}& F_{\mathrm{d}}={\displaystyle \frac{C_{\mathrm{h}}}{C_{\mathrm{d}}}}{\displaystyle \frac{U_{\mathrm{r}}^{\mathrm{2}}}{U^{\mathrm{2}}}}{\mathit{\tau }}_{\mathrm{0}}{D}^{\mathrm{2}},\end{array}$$

with C_d being the bottom drag coefficient [–]. Scaling the particle volume as $D_{\mathrm{eq}}^{\mathrm{3}}$ and using Eq. (3), the particle acceleration can be written as

$$\begin{array}{}\text{(11)}& A={\displaystyle \frac{\mathit{\nu }}{D_{\mathrm{eq}}\mathrm{\Delta }z}}{\displaystyle \frac{\mathit{\rho }}{{\mathit{\rho }}_{\mathrm{p}}}}{\displaystyle \frac{C_{\mathrm{h}}}{C_{\mathrm{d}}}}{\displaystyle \frac{U_{\mathrm{r}}^{\mathrm{2}}}{U}}.\end{array}$$

Note that ν instead of ν_t is used here based on the assumption that turbulent mixing remains weak in the bedload-active layer of the flow. Finally, discretizing in time, the bedload particle velocity U_b [m s⁻¹] at iteration n+1 can be written as

$$\begin{array}{}\text{(12)}& U_{\mathrm{b}}^{n+\mathrm{1}}=U_{\mathrm{b}}^n+A\mathrm{\Delta }t=U_{\mathrm{b}}^n+{\displaystyle \frac{\mathit{\rho }}{{\mathit{\rho }}_{\mathrm{p}}}}{\displaystyle \frac{C_{\mathrm{h}}}{C_{\mathrm{d}}}}{\displaystyle \frac{\mathit{\nu }}{D_{\mathrm{eq}}}}{\displaystyle \frac{U_{\mathrm{r}}^{\mathrm{2}}}{U}}{\displaystyle \frac{\mathrm{\Delta }t}{\mathrm{\Delta }z}}.\end{array}$$

2.3 Experimental test case

The laboratory experiments conducted by Forsberg et al. (2020) in the CASH wind-wave flume (SeaTech–MIO) were reproduced using the SWASH–TrackMPD approach, specifically under one of the two windless hydrodynamic scenarios. The model domain was designed to replicate the configuration of the flume, which has a length of 6 m. The still-water depth was set to 0.22 m, and a linearly sloping (1:20) bathymetry was implemented starting from x=1 m (Fig. 1a). The computational grid consisted of 175 points in the horizontal direction (resolution 3.45 cm) and 15σ layers in the vertical direction. A time step of 0.05 s was selected for both hydrodynamic and particle-tracking simulations. This time step is much smaller than the Stokes time for all particles (ranging from 9.4 to 35.7 s, calculated as ${\mathit{\tau }}_{\mathrm{Stokes}}=D_{\mathrm{eq}}/\left(\mathrm{12}\mathit{\nu }\mathit{\beta }\right)$ with $\mathit{\beta }=\mathrm{3}\mathit{\rho }/(\mathit{\rho }+\mathrm{2}{\mathit{\rho }}_{\mathrm{p}})$), indicating that the model's time step is sufficiently small to resolve the dynamics of the particles accurately. The SWASH model is forced at the left boundary (wave maker) by regular waves (period 1.2 s) associated with a weakly reflective boundary condition, while a Sommerfeld condition is applied at the right boundary (beach). The wave height at the boundary has been adapted to match the experimental measurement (H=9.2 cm) at the first gauge (x=1.8 m; see Fig. 1a). Numerical wave heights are generally in good agreement with experimental measurements, as illustrated in Fig. 1a. Specifically, the model tends to slightly underestimate surf zone dissipation, leading to a root mean square error (RMSE) of 2.2 cm and an average negative bias of 0.7 cm for wave heights in this region. Despite this minor discrepancy, the overall agreement in wave heights supports using SWASH simulations as a reliable hydrodynamic forcing for TrackMPD.

Figure 1 (a) Numerical domain replicating the experimental setup from Forsberg et al. (2020). The dashed black and solid blue lines represent the bottom depth and mean water level of still water, respectively. Numerical and experimental wave heights are depicted with a black line and red circles, respectively. (b) Spatial evolution of the numerical wave skewness and asymmetry, in solid and dashed lines, respectively. (c) Contours of the time-averaged horizontal velocity profile. (d) Contours of the time-averaged vertical diffusivity coefficient for particle K_v assumed to be equal to the eddy diffusivity ν_t from Eq. (1).

In line with the flume experiments, six different types of MP are implemented in TrackMPD (Table 1). The particles were selected in Forsberg et al. (2020) to represent the range of shapes (including nearly spherical pellets, fibers, and sheets) and densities typically found in coastal waters. Table 1 provides a summary of the physical properties of the plastic particles, categorized as either light or heavy based on their densities relative to the water density of 1 g cm⁻³. To accurately replicate the dynamic behavior of each particle, the model incorporated the measured rising or settling velocity values for each particle. These velocity values were obtained through precise measurements conducted in the laboratory using a vertical column with a specially designed gate at the bottom, following the protocol described in Jalón-Rojas et al. (2022).

The release of particles in the model accurately reproduced the conditions of the laboratory experiment. A total of 50 particles of each type (300 in total) were released at the beginning of the shoaling zone, at a depth between z_r=0.05 and 0.15 m and between x_r=1 and 1.5 m (see Sect. 2.4 for sensitivity tests on the release location). Each experiment ran for a sufficiently long duration, 10 min, compared to the 1.2 s wave period, allowing sufficient time for the system to reach a stationary state. To ensure the consistency and reproducibility of the model results, multiple runs of each reference scenario were performed and compared.

Table 1 Properties of MP released during the simulations.

2.4 Sensitivity analysis

To evaluate the performance and sensitivity of the SWASH–TrackMPD model approach, we conducted a series of simulations based on 6 reference scenarios and 18 sensitivity scenarios (Table 2), keeping the hydrodynamics constant. The reference scenarios involved the modeling of the six types of particles presented in Table 1, while sensitivity scenarios were focused on fibers of high and low density (similar trends have been observed for sheets and spheres).

Since the particle sizes and rising/settling velocities are known, the TrackMPD parameterization required only four free parameters: the horizontal and vertical diffusivity coefficients K_h and K_v and the drag coefficients C_h and C_d used for bedload transport calculations (Eq. 12). For each free parameter, representative values from the flume experiments were selected for the reference scenario (Table 2). A scaling factor of approximately 80 with respect to real-scale environments was considered to estimate the diffusivity parameters. For example, the typical value of 10⁻⁴ m² s⁻¹ for K_v in turbulent environments was transformed to $\mathrm{1.25}\times {\mathrm{10}}^{-\mathrm{6}}$ m² s⁻¹ at the flume scale and selected as the background value (offshore, to account for turbulence generated in the vicinity of the wave maker, and in beach regions). The depth-dependent scaling presented in Sect. 2.2.1 is used to determine K_v in the surf zone, resulting in the cross-shore and vertically varying structure displayed in Fig. 1d. The horizontal diffusivity coefficient for particles is here kept uniform throughout the domain. A common K_h value in coastal environments (0.002/0.15 m² s⁻¹ at the flume/real scale) (Bogucki et al., 2005; Diez et al., 2008) was selected for the reference scenario. Different empirical drag coefficients for the particle bedload transport C_h were selected as a function of the shape: 0.9 for sphere, 0.8 for fibers, and 0.7 for sheets. A constant and uniform smooth bottom drag coefficient C_d=0.003 was used for each simulation.

A series of sensitivity tests were then performed by varying individual parameters to assess their impact on particle dynamics (Table 2). Scenarios S1 and S2 were designed to evaluate the sensitivity of particle dynamics to the horizontal turbulent diffusivity. Scenarios S3 and S4 examined the impact of modification of the offshore background K_v, while S5 to S7 explored configurations with uniform K_v throughout the domain, with different tested values. S8 focused on the role of bottom drag. S9 and S10 explored the impact of increasing/decreasing the particle drag coefficient C_h. S11 to S14 focused on assessing the sensitivity of particle transport to the bottom dynamics condition. These scenarios included deactivation of bedload transport (S11), deactivation of resuspension (S12), decreasing the resuspension critical shear stress to the bedload value (S13), and increasing the resuspension critical shear stress by 1 order of magnitude (S14). Additionally, scenarios S15 to S18 investigated the sensitivity of particle dynamics to different release points.

Table 2 List of the tested scenarios in TrackMPD, with bold formatting used to highlight the parameter modified relative to the reference scenario.

3 Results

3.1 Reference case

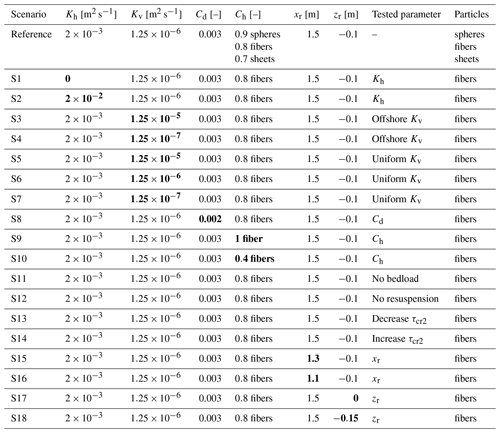
Figure 2 displays a comparison between reference simulations and laboratory observations, for each type of particle. The results are interpreted in terms of trajectories throughout the whole simulation (grey lines), along with the final positions (black dots), and cross-shore MP distributions in five distinct regions (color bars): offshore, shoaling, breaking, surf, and beach zones. Overall, the simulations demonstrate a satisfactory reproduction of the spatial distribution of the different particle types, providing a first demonstration of the reliability and accuracy of the SWASH–TrackMPD approach in capturing the dynamics of microplastics in nearshore waters. Notably, to ensure the robustness of our simulations, we conducted five simulations for each scenario, and the results consistently exhibited only minor variability in the number of particles within each region. This variability was within the same order of magnitude as that observed in the experiments, as indicated by the error bars in Fig. 2.

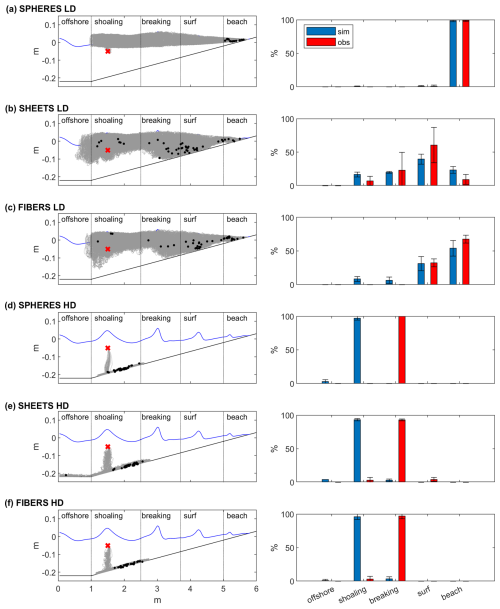
Figure 2 Trajectories (left panels) and final cross-shore distribution (right panels) of the six plastic particle types with indications of the location of the offshore, shoaling, breaking, surf, and beach zones: (a) low-density spheres, (b) low-density sheets, (c) low-density fibers, (d) high-density spheres, (e) high-density sheets, and (f) high-density fibers. The right panels compare the results of the experimental observations (Forsberg et al., 2020; red bars) and the simulations from this work (blue bars). The error bars represent the standard deviation from two experiments and five simulations. In the left panels, red crosses, grey lines, and black dots represent the release points, the trajectories, and the final position of particles for one of the five simulations, representative of the scenario.

Consistently with the experimental observations, the cross-shore distribution of the low-density MPs varied depending on their shape, highlighting the diverse range of dynamic behaviors exhibited by light particles (Fig. 2a–c). Low-density spheres, characterized by strong rising velocities, were primarily transported onshore in the surface layer through the action of Stokes drift and wave non-linearities as analyzed in Sect. 3.3. Consequently, all the particles eventually reached the beach (Fig. 2a). While also experiencing an overall onshore motion, low-density sheets depicted a broader distribution throughout the water column and in the final cross-shore position (Fig. 2b). Low-density sheets also exhibited higher variability in the final number of particles within each region in both experiments and simulations. These results can be attributed to their enhanced mobility across different layers of the water column, which are influenced by distinct transport mechanisms, as further discussed in Sect. 3.3. Like the flume observations, the model predicted the highest number of low-density sheets finishing in the surf region at the end of the experiment (Fig. 2b). However, it slightly underestimated the number of particles in this region (40 % on average in simulations compared to 60 % in observations), while it overestimated the number reaching the beach (24 % in simulations versus 9 % in observations). While difficult to interpret with the present data, this small difference may be attributed to inaccuracy in the beach zone definition and/or to complex small-scale processes related to sheet particle beaching not being accurately represented by the present transport approach. Fibers show an intermediate transport pattern between spheres and sheets. Finally, 54 % and 67 % of low-density fibers were gradually transported onshore and eventually reached the beach in the simulations and observations, respectively. A small portion of particles displayed a wider distribution in the final cross-shore position due to their mobility within the water column (Fig. 2c).

The simulated high-density particles moved onshore very close to the bed in accordance with the flume observations, yet their final position was slightly offshore. In contrast to the experimental results where particles were predominantly trapped in the breaking region, in the model, they tended to accumulate in the upper shoaling region (Fig. 2d–f). These particles settled rapidly upon release and gradually migrated onshore due to the non-linear wave behavior in the shoaling zone, until reaching a region where they remained relatively stationary, as further elaborated in Sect. 3.3. Discrepancies in the accumulation region between simulations and observations may be attributed to slight misrepresentation of the experimental undertow current or the temporal evolution of vertical mixing by the model or to inaccuracies in the definition of the compartment limits.

3.2 Sensitivity analysis

This section presents the results of the sensitivity analysis, aiming to assess the influence of model parameters that were not experimentally quantified on particle dynamics. This analysis also seeks to gain a better understanding of the relative significance of key processes, which include enhanced turbulence induced by wave breaking, bedload transport, and resuspension. Figure 3 illustrates the impact of varying the horizontal (K_h) and vertical (K_v) diffusivity parameters on the final cross-shore distribution of low- and high-density fibers. When we decreased K_h to 0 m² s⁻¹, we observed minor changes in the transport trends and final distribution of both low-density and high-density particles (Fig. 3b). When K_h was increased to 0.02 m² s⁻¹ (i.e., 10 times the reference value), it had little impact on low-density particle trends (Fig. 3i.c), but an alteration occurred for high-density particles (Fig. 3ii.c). This increase in K_h hindered approximately one-third of the high-density fibers from moving onshore, while it facilitated another third to reach the breaking zone. This outcome is likely due to an excessive increase in the stochastic transport component in the horizontal direction.

Variations in K_v also had minimal effects on the transport patterns of low-density particles, which primarily undergo suspension transport. As depicted in Fig. 3i.d–g, the cross-shore distribution of low-density fibers remained consistent across multiple scenarios: (a) the reference case, where K_v exhibited spatial variability with higher values in the breaking zone (Fig. 3i.a); (b) when K_v was reduced or increased by a factor of 10 in the offshore region (S3–S4, Fig. 3i.d and i.e); and (c) when K_v had constant values (ranging from $\mathrm{1.25}\times {\mathrm{10}}^{-\mathrm{5}}$ to $\mathrm{1.25}\times {\mathrm{10}}^{-\mathrm{7}}$ m² s⁻¹, S5–S7) throughout the entire domain (Fig. 3i.f and i.g). On the other hand, the transport behavior of high-density particles is not very sensitive to the background K_v in the offshore region (S3–S4, Fig. 3ii.d–e) but is affected when considering constant turbulent conditions through the whole domain (S5–S6). As shown in Fig. 3ii.f high-density fibers failed to move onshore when the constant K_v dropped below 10⁻⁵ m² s⁻¹ (Fig. 3ii.f and ii.g). This phenomenon is primarily attributed to the contribution of eddy diffusivity, ν_t, on the bed shear stress, leading to potential resuspension rather than a potential effect on the stochastic particles' dispersion through the water column. When ν_t reached relatively low values in the shoaling region, the decrease in shear stress (Eq. 3) precludes the activation of the resuspension condition (Sect. 2.2.2), preventing particle resuspension and subsequent onshore transport.

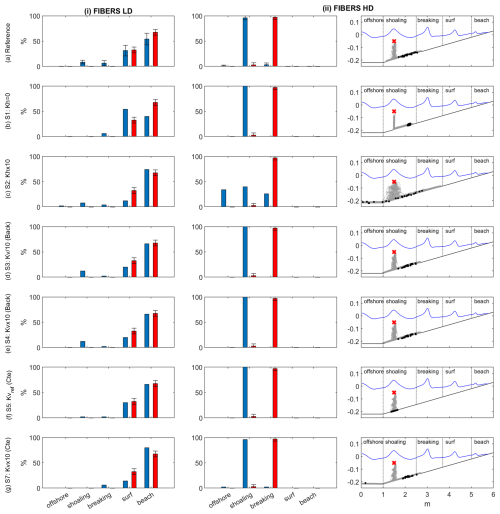
Figure 3 Final cross-shore distribution of low-density (i, left column) and high-density (ii, middle and right column) fibers with indications of the location of the offshore, shoaling, breaking, surf, and beach zones for different scenarios: (a) reference, $K_{\mathrm{h}}=\mathrm{2}\times {\mathrm{10}}^{-\mathrm{3}}$, varying K_v, $K_{\mathrm{v},\mathrm{off}}=\mathrm{1.25}\times {\mathrm{10}}^{-\mathrm{6}}$; (b) S1, K_h=0, varying K_v, $K_{\mathrm{v},\mathrm{off}}=\mathrm{1.25}\times {\mathrm{10}}^{-\mathrm{6}}$; (c) S2, $K_{\mathrm{h}}=\mathrm{2}\times {\mathrm{10}}^{-\mathrm{2}}$, varying K_v, $K_{\mathrm{v},\mathrm{off}}=\mathrm{1.25}\times {\mathrm{10}}^{-\mathrm{6}}$; (d) S3, $K_{\mathrm{h}}=\mathrm{2}\times {\mathrm{10}}^{-\mathrm{3}}$, varying K_v, $K_{\mathrm{v},\mathrm{off}}=\mathrm{1.25}\times {\mathrm{10}}^{-\mathrm{5}}$; (e) S4, $K_{\mathrm{h}}=\mathrm{2}\times {\mathrm{10}}^{-\mathrm{3}}$, varying K_v, $K_{\mathrm{v},\mathrm{off}}=\mathrm{1.25}\times {\mathrm{10}}^{-\mathrm{7}}$; (f) S5, $K_{\mathrm{h}}=\mathrm{2}\times {\mathrm{10}}^{-\mathrm{3}}$, uniform K_v, $K_{\mathrm{v}}=\mathrm{1.25}\times {\mathrm{10}}^{-\mathrm{5}}$; and (g) S7, $K_{\mathrm{h}}=\mathrm{2}\times {\mathrm{10}}^{-\mathrm{3}}$, uniform K_v, $K_{\mathrm{v},\mathrm{off}}=\mathrm{1.25}\times {\mathrm{10}}^{-\mathrm{7}}$. The red and blue bars represent the results of the experimental observations from Forsberg et al. (2020) and the simulations from this work, respectively. The error bars represent the standard deviation from two experiments.

These findings emphasize the significance of accounting for enhanced mixing resulting from wave breaking, as well as the importance of accurately estimating the order of magnitude for K_v and K_h to faithfully reproduce the transport of high-density microplastics in nearshore environments but allow for some uncertainty in their values. Therefore, the Feddersen formulation offers a physically sound estimate of the order of magnitude for ${\mathit{\nu }}_{\mathrm{t}}/K_{\mathrm{v}}$ and a more realistic depiction of their spatial evolution, without the necessity of using overestimated and/or empirical values through the whole domain.

The modification of particle and bottom drag coefficients does not appear to affect the cross-shore distribution of particles (Fig. 4a–d). The effect of bedload transport (comparison between Fig. 4a and e) also appears to be weak in the present configuration. A much stronger effect is observed for resuspension (comparison between Fig. 4a and f). When resuspension was totally deactivated, high-density particles were not able to shift onshore. One notes that the modification of the resuspension threshold, either decreasing (Fig. 4g) or increasing (Fig. 4h), does not affect the main dynamics. This absence of sensitivity, which indicates that the resuspension is overwhelmed in typical conditions, strengthens the finding of a primary role played by resuspension in the transport of heavy particles. Finally, the results remained virtually insensitive to variations in the release point's position (S15–S18, not shown). Only the release of particles closer to the offshore regions (S16) resulted in a small portion of particles remaining in the offshore region.

Figure 4 Final cross-shore distribution of high-density fibers with indications of the location of the offshore, shoaling, breaking, surf, and beach zones for different scenarios: (a) reference, C_d=0.003, C_h=0.8; (b) S8, C_d=0.002; (c) S9, C_h=1; (d) S10, C_h=0.4; (e) S11, bedload deactivated; (f) S12, resuspension deactivated; (g) S13, τ_cr2=τ_cr1; and (h) S14, τ_cr2×10.

3.3 Dominant transport mechanisms

In this section, we examine the core physical processes that govern the transport of microplastics in the simulated scenario. As analyzed in Sect. 3.1, distinct transport trends were evident for low-density and high-density microplastics. To explore these divergent behaviors, Figs. 5 and 6 depict the temporal evolution of the vertical and horizontal trajectory of a low-density sphere and a high-density fiber as they traverse the shoaling and breaking regions. These figures also include the temporal evolution of water level (η), current magnitude ($\left|U\right|$), and current direction (U_Dir) at the particles' positions. Complementary information on the cross-shore distribution of wave and wave-driven parameters, such as the mean wave height H, wave skewness Sk and asymmetry As (calculated following Grasso et al., 2011), and residual currents U_res, is provided in Fig. 1.

Low-density particles exhibited net onshore transport in the horizontal dimension (Fig. 2a) driven by the Stokes drift and wave asymmetry: superimposed onto the transport oscillating backwards and forwards due to the wave motion, the plastic particles tend to spend more time in the faster onshore-moving layer underneath the crest than in the slower offshore-moving layer below the trough. This effect, which is the well-known Stokes drift, is enhanced by the increased non-linearity and asymmetry of shoaling and surf zone waves. As shown in Fig. 5a–f, these spheres predominantly traveled in the upper water layer, closely following the water surface in the vertical coordinate, as their high buoyancy prevents significant dispersion due to turbulence. Consequently, they followed the net drift velocity aligned with the wave propagation direction, i.e., the Stokes drift (van den Bremer and Breivik, 2018) (see residual velocity in Fig. 1c). The overall transport mechanism is therefore plastic particles undergoing stronger shoreward motion at greater height reached under the crest than under the trough. This residual onshore transport is quite marginal near the offshore region (Fig. 5c) in comparison with the upper shoaling zone or the breaking region (Fig. 5d). Figure 5h highlights that currents responsible for transporting these particles exhibit significantly higher magnitudes around the crest when directed onshore (U_Dir close to 0° in Fig. 5j), compared to the offshore direction (U_Dir close to ±180°). This asymmetry between onshore and offshore transports became more pronounced within the breaking zone, characterized by prolonged shoreward motion ($-\mathrm{90}>U_{\mathrm{Dir}}<\mathrm{90}$°), as depicted in Fig. 5f. This observation finds further support in the strong negative asymmetry combined with positive skewness observed within this region, as illustrated in Fig. 1b.

Low-density sheets and fibers had higher vertical mobility (Fig. 2c and e) and were therefore influenced by different transport mechanisms. In the surface layer, the driving mechanisms for residual onshore transport are the same as those that affected low-density particles, described before. When spread throughout the water column due to buoyancy-driven settling and vertical turbulent mixing, the particles are exposed to an offshore-directed return current, i.e., the classical undertow, which compensates for the wave-induced surface mass flux (Fig. 1b–c). This undertow-driven transport is expected to be particularly effective in the breaking zone. As discussed by Forsberg et al. (2020), the sensitivity of the position of these particles along their trajectory can be compared with the uncertainty observed in deterministic chaos systems, which results in a broader spatial dispersion of particles.

Figure 6i illustrates the vertical behavior of the three types of high-density particles and the underlying transport processes, using fibers as an example. These particles were typically deposited at the bottom by gravity forces, frequently coinciding with the transition between onshore and offshore current phases and vice versa, when velocities were at their minimum. Resuspension typically occurred after deposition, causing particles to make small jumps in both onshore and offshore directions. As depicted in Fig. 6c, these jumps led to minimal residual onshore transport, while accumulation after the passage of multiple waves resulted in the transport of particles toward the upper shoaling region. Resuspension events, which can also be interpreted as saltation transport, appear here to dominate over the pure bedload motion (rolling/sliding). While producing overall consistent particle fluxes at the beach scale, no direct validation of the numerical near-bed dynamics can be performed using the present experimental data. As detailed in Sect. 3.2, resuspension can only take place if turbulence is high enough to facilitate it. Upon approaching the breaking region (Fig. 6ii), high-density particles exhibited a similar vertical behavior, but the residual onshore transport was offset by stronger return currents (Fig. 1c).

Figure 5 Temporal evolution of the depth of a low-density sphere during its transit through the shoaling (a) and breaking (b) regions, accompanied by corresponding time series of environmental hydrodynamic and trajectory variables at the particle's location: distance traveled from x=0 (c–d), water level elevation (e–f), current velocity (g–h), and velocity direction (i–j).

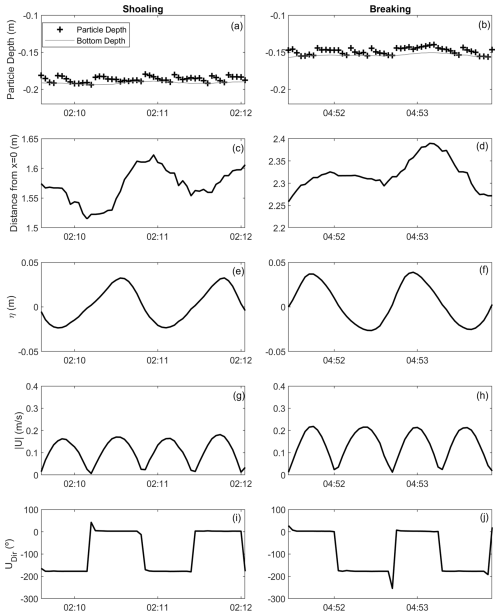
Figure 6 Temporal evolution of the depth of a high-density fiber during its transit through the shoaling (a) and breaking (b) regions, accompanied by corresponding time series of environmental hydrodynamic and trajectory variables at the particle's location: distance traveled from x=0 (c–d), water level elevation (e–f), current velocity (g–h), and velocity direction (i–j).

4 Discussion

4.1 Insights into nearshore microplastic transport

The results of this study underscore the robustness of the proposed modeling approach in advancing our understanding of microplastic transport, reinforcing several consistent findings from prior research in this field and introducing new insights, discussion points, and research perspectives. Previous studies have also recognized differences in the behavior between low-density and high-density particles and highlighted the key role of the settling/rising velocity (also expressed non-dimensionally as the Dean number) in the transport of plastic particles (Alsina et al., 2020; Kerpen et al., 2020; Guler et al., 2022; Larsen et al., 2023; Núñez et al., 2023). The experimental results from Kerpen et al. (2020), Larsen et al. (2023), and Núñez et al. (2023) also demonstrated a net onshore transport and beaching of very low-density particles. Much like in our study, Kerpen et al. (2020) and Larsen et al. (2023) illustrated that highly buoyant particles are transported at higher mean velocities and are more likely to beach due to their greater tendency to remain near the surface and escape from undertow return flow. On the other hand, Alsina et al. (2020) conducted an in-depth examination of the role of Stokes drift in the transport of plastic particles, but unlike our study, theirs focused solely on shoaling waters, omitting an examination of the effect of the non-linearity of breaking waves. Also in line with our work, Kim and Kim (2024) emphasized the significance of wave breaking for MP transport. They demonstrated that buoyant particles with more neutral buoyancy are particularly influenced by undertow currents, resulting in delayed beaching compared to highly buoyant ones.

While recent research has advanced understanding of wave non-linear processes in shallow water (e.g., Martins et al., 2020), their effects on plastic transport have received limited attention. The findings of our study suggest that the primary mechanism for high-density microplastic transport is linked to wave asymmetry, similarly to sand transport dynamics. Grasso et al. (2011) demonstrated that wave asymmetry promotes the resuspension of sand particles during the rising phase of the wave crest's velocity, followed by sedimentation, resulting in onshore transport during the waning phase until the return undertow flow counteracts this transport. This cycle is less apparent in our results, likely due to the constrained temporal evolution of vertical turbulence. Nonetheless, we also observed residual onshore transport following the passage of multiple waves. Future research may involve a more robust parameterization of this parameter to better capture its effect on particle transport. Furthermore, Guler et al. (2022) investigated the cross-shore distribution of various non-buoyant particles under different beach configurations, namely a plane bed and a barred beach. They observed varying transport patterns dependent on the particle's Dean number and the beach morphology. For instance, non-buoyant particles with a high Dean number (indicating relatively low settling velocity) tended to migrate to the beach region on the plane bed, while a hotspot of particles formed on the plateau of the barred beach. The authors attributed these differences to wave skewness and asymmetry, which increased in the surf zone of the plane bed configuration, facilitating onshore particle transport, while decreasing in the plateau region of the barred beach configuration, hindering onshore migration.

Núñez et al. (2023) also evaluated the transport behavior of high-density microplastics through laboratory experiments and observed that they were mainly trapped in the breaking zone. They also found that the cross-shore distribution of particles remained consistent under both regular and irregular wave conditions, with variations in cross-shore transport processes linked to the different timescales associated with these conditions. It should be highlighted that, in addition to the physical properties of the particles, beach morphology and wave forcing appear to play crucial roles in determining transport trends, although further investigation is needed. Wind conditions (Forsberg et al., 2020) and longitudinal currents may also impact particle transport. Consequently, the interpretation of the present results and previous research needs to be framed in the context of the specific experimental configurations employed, which are inherently limited in experimental studies. For example, the experiments from Forsberg et al. (2020) simulated in this work are characterized by stormy conditions, including relatively high and non-linear waves, as well as by the presence of intense turbulent conditions right from the onset of the shoaling region due to the wave-maker action. Less energetic conditions may thus lead to different transport patterns. The robustness and consistency demonstrated by our numerical model offer a valuable opportunity to continue building knowledge on these aspects through holistic studies that evaluate the influence of various geomorphological and wave climate conditions, in addition to exploring the underlying physical processes.

Future modeling studies using the proposed SWASH–TrackMPD approach also offer a promising avenue to bridge the gap between laboratory experiments and the complexities of real-world nearshore environments. In experimental studies, scaling effects present a significant challenge when attempting to accurately replicate the complexities of natural systems within the controlled laboratory setting. While laboratory experiments involve scaling down physical parameters such as wave heights and velocities to fit the laboratory's constraints, microplastic properties such as density, and therefore rising/settling velocities, are typically left unscaled. As discussed above, this (unscaled) parameter plays a pivotal role in predicting microplastic transport trends and hotspot formation. Our sensitivity analysis (Sect. 3.2) even demonstrated that this parameter is the primary particle property driving its transport, as the choice of erosion threshold did not significantly impact transport patterns under the simulated conditions. Future modeling studies using real-scale morphologies, environmental forcings, and accurate particle properties will be essential for validating these significant results and for reevaluating microplastic transport trends discussed in previous experimental research. These studies will also contribute to a deeper understanding of the physical processes governing transport, as discussed in this study.

4.2 Advancements, limitations, and future perspectives in modeling nearshore microplastic transport

The SWASH–TrackMPD modeling approach stands out as quite unique in its methodology and offers several distinct advantages and advanced features in (a) resolving wave transformation dynamics; (b) coupling with surf zone turbulence parameterization, or potentially with any other turbulent modeling, for accurate prediction of wave-induced turbulence effects; (c) simulating resuspension and bedload processes, drawing from traditional sediment research (Soulsby, 1997) and pioneering microplastic studies (Waldschläger and Schẗtrumpf, 2019b); and (d) implementing advanced settling and rising velocity formulations, including biofouling processes (Jalón-Rojas et al., 2022; Baudena et al., 2023). The validation provided in this work is also unique in the literature.

Several simplifications have been used to build the transport model from a computationally efficient perspective. The estimation of bed shear stress for resuspension and bedload transport was based on the molecular viscosity, i.e., assuming that turbulent mixing does not play a significant role in the near-bed region, with the critical values for motion initiation derived from formulations for natural particles. While using the Soulsby formulation for sediments is reasonably valid for spherical particles, it may be less accurate for fibers and sheets due to their anisotropic shapes and complex interactions with the flow. Even though our sensitivity test suggested that this parameter had a secondary effect on the transport of high-density microplastics in the flume, future studies will incorporate new empirical formulations for the incipient motion of microplastics with different shapes as they become available. Regarding the assumption of molecular viscosity, estimating the Stokes layer thickness as $\sqrt{\mathrm{2}\mathit{\nu }/\mathit{\sigma }}$ (σ being the angular frequency) for the present case leads to a value of about 0.6 mm, which is larger than the thickness of tested fibers and sheets. For the spheres, the top of the particles is expected to rise above the laminar layer. However, as the exact distribution of small-scale viscous/turbulent shear remains unaccessible for the present dataset, the fluid viscosity is used for each particle type to ensure robust comparisons. Further research works at finer scale are required to better frame this assumption in realistic conditions in terms of particle size and shape, bed roughness, and wave boundary layer dynamics. In addition, it is worthwhile to note that the particle near-bed dynamics, which have been shown here to be dominated by resuspension/saltation events rather than pure sliding/rolling bedload processes, cannot be directly validated due to the lack of relevant measurements. Further detailed tracking of wave-driven near-bed transport regimes should be envisioned by future laboratory works to provide suitable validation data for wave-resolving transport models.

More generally, advanced turbulence models able to inject, at the wave scale, the breaking-induced mixing in the turbulence parameterization should bring finer insight into the time-resolved particle dispersion throughout the water column. The particle transport in the mixed-phase roller and beaching/refloating mechanisms also remains nearly unexplored, while we can expect that few “surfing” events, with entrapped particles in the roller foam, may be responsible for fast onshore transport. The model also neglects inertial effects induced by particle properties on advection. While a wide range of research has highlighted the importance of inertial effects on particle advection and settling under wave oscillatory flow (DiBenedetto et al., 2018, 2019, 2022; De Leo et al., 2021; De Leo and Stocchino, 2022), this omission is supported in nearshore waters by the experimental findings of Alsina et al. (2020), which indicated that, apart from the buoyancy, such properties exert minimal influence on the net drift of low-density particles in the shoaling region. The authors also suggested that the net drift of high-density particles might be influenced by plastic density and size, but trends remain inconclusive due to particle motion variability. Indeed, in this region characterized by strong turbulent conditions and other complex processes (air–water two-phase mixing, roller), the pronounced stochastic transport characteristics may outweigh the influence of non-inertial particle effects on advection. Nevertheless, future model developments could consider incorporating the effects of particle drag on advection and settling, as proposed by Stocchino et al. (2019) and De Leo et al. (2021), to further investigate these hypotheses and refine our understanding of microplastic transport dynamics in nearshore environments.

5 Conclusions

The SWASH–TrackMPD modeling approach has proven to be a pertinent, robust, and versatile tool for investigating microplastic transport in nearshore environments. It offers unique features in terms of its ability to resolve wave transformation dynamics, consider wave-breaking-induced turbulence, and simulate resuspension and bedload processes tailored for diverse types of plastic particles. These advancements have culminated in the release of TrackMPD v3.0, marking a significant milestone in our ability to simulate microplastic dynamics in coastal environments.

The model reproduced the wave laboratory experiments conducted by Forsberg et al. (2020), accurately simulating the distribution of particles of different densities, sizes, and shapes over the beach profile and providing new insights into the key mechanisms governing their movement. Our findings underscore the critical role of rising and settling velocities in the transport of microplastics. Low-density microplastics exhibited net onshore transport driven primarily by the Stokes drift and wave asymmetry. While highly buoyant particles remained predominantly near the water surface with the net drift aligned with wave propagation direction, particles characterized by lower rising velocities were more affected by turbulent motion and had a broader final distribution over the system.

High-density microplastics exhibited a distinct transport pattern, predominantly trapped near the breaking zone. Akin to sediment transport dynamics, the breaking zone accumulation tends to result from the competing effects of near-bed transport driven by wave asymmetry and return undertow flow.

The consistency observed in the results of the sensitivity analysis also underscores the reliability of the model. It highlights the importance of accurately estimating the order of magnitude for diffusivity parameters, particularly for vertical turbulence, to ensure a faithful representation of high-density microplastic transport while allowing for some degree of uncertainty in value estimation. The adoption of the Feddersen formulation provides a physically sound estimate for these parameters and a more realistic description of their spatial distribution. Furthermore, this sensitivity analysis reaffirms the primary role played by resuspension in the transport of high-density particles while revealing that the selection of the bottom drag coefficients barely affects the outcomes.

The SWASH–TrackMPD modeling approach emerges as a valuable tool for continuing the investigation of plastic particle migration and accumulation in nearshore waters, effectively bridging the gap between laboratory experiments and real-world coastal dynamics. We recommend future modeling studies with a similar approach to the present study but incorporating real-scale morphologies and environmental forcings. Extending this modeling framework into three dimensions will enable a more comprehensive exploration of the impact of various environmental factors, including wind conditions, longitudinal currents, and rip currents. These future modeling implementations hold the potential to significantly enhance our understanding of the nearshore environment's dual role as a source and sink of plastics, improve the parameterization of beaching and refloating in global numerical models, and contribute to the development of more effective management and mitigation strategies for plastic pollution in coastal regions.