HOTSSea v1: a NEMO-based physical Hindcast of the Salish Sea (1980–2018) supporting ecosystem model development

Decadal-scale oceanographic, environmental, and ecological changes have been reported in the Salish Sea, an ecologically productive inland sea in the northeast Pacific that supports the economies and cultures of millions of people. However, there are substantial data gaps related to physical water properties that make it difficult to evaluate trends and the pathways of effects between physical ocean water properties and the productivity of marine ecosystems. With the aim of addressing these gaps, we present the Hindcast of the Salish Sea (HOTSSea) v1, a 3D physical oceanographic model developed using the Nucleus for European Modelling of the Ocean (NEMO) ocean engine, with temporal coverage from 1980–2018. We used an experimental approach to incrementally assess sensitivity to atmospheric and ocean reanalysis products used for boundary forcings and to the horizontal discretisation of the model grid (∼ 1.5 km). Biases inherited from forcings were quantified, and a simple temperature bias correction factor applied at one ocean boundary was found to substantially improve model skill. Evaluation of salinity and temperature indicates performance is best in the Strait of Georgia. Relatively large biases occur in near-surface waters, especially in subdomains with topography narrower than the model grid's horizontal resolution. However, we demonstrated that the model simulates temperature anomalies and a secular warming trend over the entire water column in general agreement with observations. HOTSSea v1 provided a first look at spatially and temporally heterogenous ocean temperature trends throughout the northern and central part of the domain where observations are sparse. Overall, despite the biases inherited from forcings and a relatively coarse horizontal discretisation, HOTSSea v1 performs well at representing temperature and salinity at the spatial–temporal scales needed to support research related to decadal-scale climate effects on marine ecosystems, fish, and fisheries. We conclude by underscoring the need to further extend the hindcast to capture a regime shift that occurred in the 1970s.

1 Introduction

The Salish Sea is an inland sea in the northeast Pacific spanning Canadian and American waters with estuarine characteristics, fjords, and high marine biodiversity (Harrison et al., 1983; Pata et al., 2022). The productive waters of the area support the economy and cultures of a rapidly growing coastal population of 8–10 million people including the port cities of Vancouver, British Columbia (BC, Canada), and Seattle, Washington (United States of America), as well as dozens of recreational, commercial, and indigenous fisheries (Georgia Strait Alliance, 2020). As global climate change unfolds and regional atmospheric and oceanographic regimes shift, within the Salish Sea there are seasonal, annual, and decadal-scale changes to physical oceanographic and atmospheric patterns that have been reported, including changes in seasonal wind patterns (Collins et al., 2009; Masson and Cummins, 2007; Preikshot, 2007; Tuller, 2004), precipitation patterns (Beamish, 1993; Morrison et al., 2002; Yin et al., 1997), ocean water temperatures (Beamish et al., 2010; Masson and Cummins, 2007), properties related to ocean acidification (Feely et al., 2009; Ianson et al., 2016; Jarníková et al., 2022), and river discharge and temperatures (Islam et al., 2019; Martins et al., 2011; Riche et al., 2014). Increasing seasonal stratification and warmer surface waters may have increased the frequency and duration of harmful algal blooms (Esenkulova et al., 2021; Moore et al., 2015). Changes to regional climate patterns appear to have increased the variability of the date of the spring phytoplankton bloom (Allen and Wolfe, 2013), which may have led to spatial–temporal mismatches between predators and prey (Allen and Wolfe, 2013; Suchy et al., 2022) and affected the composition of larval fish assemblages (Guan, 2015). Changing ocean conditions in the Salish Sea are also hypothesised to affect the abundance, composition, and spatial–temporal availability of prey for Pacific salmon via various pathways of effects (Pearsall et al., 2021). Several correlative studies link sea surface temperature and stratification with declining survival of several salmon species in the Salish Sea, particularly juvenile coho salmon (Oncorhynchus kisutch), Chinook salmon (O. tshawytscha), and steelhead (O. mykiss; Beamish, 1995; Pearsall et al., 2021; Perry, 2021; Sharma et al., 2013; Sobocinski et al., 2020, 2021; Walters and Christensen, 2019).

The patchy nature of oceanic data, particularly as we delve deeper into historical records within the Salish Sea, leads to uncertainty about the pace and spatial–temporal patterns of oceanographic change. Sparse observations also limit our ability to detect associations and evaluate mechanistic links between physical oceanographic changes and marine ecosystem dynamics. Physical oceanographic hindcasts are a pivotal tool for addressing such data gaps, offering a retrospective lens through which past oceanic conditions are reconstructed. Physical ocean models may also be coupled or linked to biogeochemical and ecosystem models using an end-to-end approach useful for evaluating mechanistic drivers and dynamic pathways of effects between water properties, marine ecosystems, fisheries, and other human uses (Libralato and Solidoro, 2009; Macias et al., 2014; Piroddi et al., 2021; Rose, 2012; Rose et al., 2010).

Although several oceanographic and biogeochemical models have been developed for the Salish Sea, attributes of these models presently limit their suitability for a long hindcast, including computational cost due to high resolution and a focus on shorter-term simulations (Jarníková et al., 2022; Khangaonkar et al., 2019; Olson et al., 2020; Soontiens et al., 2016; Soontiens and Allen, 2017), too coarse a resolution for use in the Salish Sea due to a focus on the wider BC coast (Peña et al., 2016), or a particular focus on Puget Sound (Khangaonkar et al., 2012, 2019, 2021a; MacCready et al., 2021; Moore et al., 2015). It is therefore one aim of this study to develop a physical hindcast with a particular focus on the central and northern portion of the Salish Sea (i.e. the Strait of Georgia) with adequate spatial–temporal resolution to enable a long hindcast and acceptable model skill for supporting marine ecological research and ecosystem management. Although the acceptable model error will depend on the specific research question, ecological patterns and associated processes related to plankton and fish are often orders of magnitude greater than those required to study physical and chemical processes in marine ecosystems (Fulton et al., 2019). As a local example, hindcasting the timing of the spring phytoplankton bloom in the Strait of Georgia within an error margin of several days to 1 week at subregional scales is useful for studying spatial–temporal mismatches in predators and prey (Allen and Wolfe, 2013; Gower et al., 2013; Suchy et al., 2022). Many factors hypothesised to be mechanistically linked to growth and mortality of juvenile salmon exhibit variability on timescales of 1 week or more and at spatial scales of >10 km (Pearsall et al., 2021). Another hinderance to development of a long hindcast for the area has been a lack of atmospheric and oceanic data extending back to at least 1980 to use as model forcings, and there are doubts about the adequacy of the few existing products with respect to spatial–temporal resolution. A second aim of this study is therefore to conduct experimental evaluation to identify biases inherited from external forcings (including some that only recently have been made available) to determine to what degree the available forcings limit the development of long oceanographic hindcasts in the area.

Here, we present HOTSSea v1, developed using the Nucleus for European Modelling of the Ocean (NEMO) Ocean engine (Madec et al., 2017). We describe and give a rationale for the model setup with attention to three aspects that are particularly important for developing a long hindcast for the domain: (1) the biases inherited by using various atmospheric and ocean reanalysis products as surface and boundary forcing; (2) the effect of applying temperature bias corrections to the open-ocean boundary forcing; and (3) a preliminary assessment of model performance relevant to the aforementioned research applications, including decadal-scale trends. Priority areas for improvement and further evaluation are also highlighted, and, finally, we use the model to provide a first look at decadal-scale trends in the central and northern portion of the domain where historical observations are especially sparse.

2 Model overview

The NEMO ocean engine, version 3.6, supports simulations of ocean dynamics and thermodynamic processes in three dimensions (Madec et al., 2017). The physical model framework is governed by primitive equations under hydrostatic balance using the Boussinesq approximation where density variations are neglected except in their contribution to the buoyancy force (Madec et al., 2017). HOTSSea v1 was implemented in a high-performance computing cluster (Digital Research Alliance of Canada, 2022), and the model's scope is limited to physics and hydrodynamics (e.g. tides, salinity, temperature) – biogeochemistry is not included in HOTSSea v1 due to computational cost. We used state variables of practical salinity (PSU) and potential temperature (°C), as well as the EOS-80 equation of state (Millero, 2010). Sea ice is not included in HOTSSea v1 given that it occurs only occasionally in deep inland waters of fjords such as Jervis Inlet. To address issues of omitting ice, we applied NEMO's ice-if option, where the water temperatures are limited to the local salinity-dependent freezing point.

2.1 Spatial–temporal configuration

The model domain of HOTSSea v1 includes several distinct geographic areas within the Salish Sea: the Juan de Fuca Strait, Strait of Georgia, Gulf Islands, and Puget Sound (Fig. 1). A key application of the model will be to provide forcings for biogeochemical and ecosystem models developed to investigate decadal-scale change. The model's spatial domain therefore fully encompasses the domain of an ecosystem model under parallel development that focuses on the Strait of Georgia and uses the Ecospace model framework (de Mutsert et al., 2023; Walters et al., 1999). To ensure the dynamics of the Strait of Georgia were resolved, it was deemed important to resolve the broader Salish Sea, with the connection to the open ocean via the Gulf Islands and the Juan de Fuca Strait being particularly important for resolving tides and estuarine flow (Ebbesmeyer et al., 1989; MacCready et al., 2021). The horizontal grid used in NEMO is discretised on a curvilinear orthogonal Arakawa C grid generalised to three dimensions (Arakawa and Lamb, 1977; Madec et al., 2017). The basic spatial–temporal configuration of HOTSSea v1 began with a previous configuration, SalishSeaCast, implemented at approximately 500 m horizontal resolution for the same domain (Olson et al., 2020; Soontiens et al., 2016; Soontiens and Allen, 2017). The ∼ 500 m horizontal resolution grid and bathymetry used in the SalishSeaCast model were reduced by a factor of 3 in each horizontal direction, taking the mean depth of the neighbouring cells to assign the new depths. The new grid is approximately 1.5 km in horizontal resolution and has a width of ∼ 200 km and length of ∼ 450 km (132 cells × 299 cells; Fig. 1), which matches the grid and resolution of the Ecospace ecosystem model. The grid is rotated 29° anticlockwise to true north to align with the axis of the Strait of Georgia. The bathymetry was already processed for SalishSeaCast to avoid sudden changes in depths across grid cells and maintain open channels in narrow passages. We made additional manual edits to maintain channels between islands, maintain connectivity of the main Fraser River channel to the outflow, and avoid erroneously isolating bodies of water. Some narrow water bodies such as Sechelt Inlet, Salmon Inlet, Burrard Inlet, and the Indian Arm fjord are not resolved in this setup (outlines of these areas are visible in Fig. 1). The depths of edited channel cells were approximated from depth averages taken from ∼ 80 m resolution bathymetric data (PSF, 2014). To ensure tidally driven dynamics were not lost, the main channel of the Fraser River was extended inland by manually adding non-existent river channel cells approximately 150 km in total length, following Soontiens and Allen (2017).

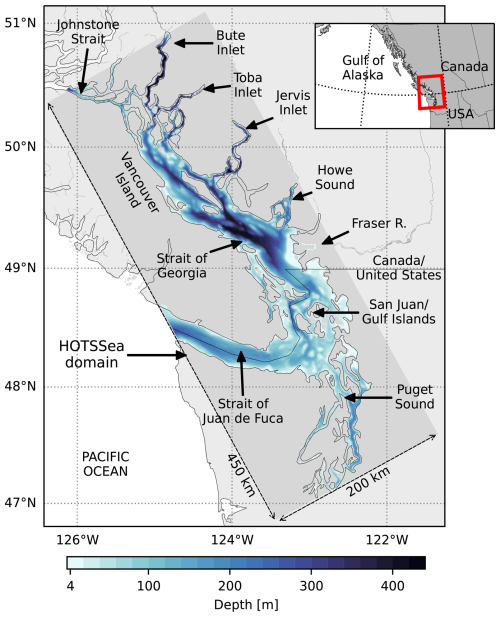
Figure 1 Map of model domain showing geographic features, extents of the HOTSSea NEMO model domain (medium grey), and bathymetry.

The vertical grid for HOTSSea v1 is divided into 40 vertical (z) levels that are gradually stretched to achieve higher resolution at the surface, ranging from 1 m vertical resolution in the upper 10 m to approximately 27 m widths at the deepest level (420 m). Partial steps were enabled to limit large changes in bathymetry between adjacent grid cells. The thickness of each layer is proportionally scaled at each time step as sea surface height (SSH) changes using a non-linear free-surface scheme referred to as the “variable volume option” (Levier et al., 2007). HOTSSea v1 uses a non-linear free-surface option to time-split the solving of the barotropic and baroclinic free surface. The barotropic and baroclinic time steps are set to 6 and 120 s, respectively, and the vertical momentum and tracer advection time stepping is set to 2 s. The model was run from 1 January 1979 to 1 January 2019, where the 1980 atmospheric forcings were duplicated and applied to 1979, such that we treat 1979 as a model spin-up year and exclude it from evaluation. A 1-year spin-up was based on a minimum estimate of deepwater residency time which elsewhere has been reported to range between 1 and 3 years (Pawlowicz et al., 2019). Initial conditions for January 1979 for temperature and salinity across the domain were generated using climatologies for December and January using SalishSeaCast outputs from 2007 to 2020. An experimental bias correction to the Ocean and Sea Ice Reanalysis v5 (ORAS5) temperature fields was applied when running the final hindcast.

2.2 Boundary conditions and forcings

2.2.1 Atmospheric

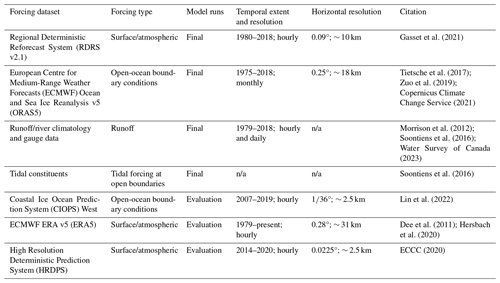
The Regional Deterministic Reforecast System (RDRS v2.1; Gasset et al., 2021) supplied the atmospheric conditions for forcing the full HOTSSea v1 hindcast. RDRS v2.1 is currently the highest-resolution atmospheric reanalysis product available extending back to 1980 (0.09°; ∼ 10 km horizontal). Two additional atmospheric forcings (Table 1) were evaluated as part of an experimental design: the European Centre for Medium-Range Weather Forecasts (ECMWF) ERA5, a global reanalysis product extending back to 1979 (hourly, at approximately 31 km horizontal resolution; Dee et al., 2011; Hersbach et al., 2020), and the High Resolution Deterministic Prediction System (HRDPS), with spatial coverage of the northern part of North America (Canada and northern United States) and with hourly coverage at ∼ 2.5 km horizontal resolution for 2014–2020 (ECCC, 2020). The RDRS v2.1 product occupies an intermediate horizontal resolution between ERA5 and HRDPS, and the three together offered an opportunity to explore the effect of horizontal resolution of atmospheric forcing on model performance in the Salish Sea.

Table 1 External forcing used in the model (n/a: not applicable).

2.2.2 Open boundaries

There are two boundaries that connect the Salish Sea to the Pacific Ocean: the mouth of the Juan de Fuca Strait in the southwest and Johnstone Strait in the north (Fig. 1). To first evaluate the effects of using different ocean boundary forcings at the mouth of the Juan de Fuca Strait, a higher-resolution model, CIOPS-W (Lin et al., 2022), was used in shorter evaluation runs (horizontal resolution 2–2.5 km; $\mathrm{1}/\mathrm{36}$°; Tables 1 and 2). ORAS5 (Tietsche et al., 2017; Zuo et al., 2019) was the only available reanalysis product with coverage for the full model hindcast and was used to supply open-ocean boundary conditions in the final model. ORAS5 has a horizontal resolution at the latitude of the Salish Sea of approximately 18 km (0.25°). At the northern boundary (Johnstone Strait), we used a monthly climatology of temperature and salinity (Dosser et al., 2020, 2021).

2.2.3 River discharge and runoff

River input into the Salish Sea periodically creates a brackish layer extending across the Strait of Georgia and drives strong estuarine circulation via the Juan de Fuca Strait (Harrison et al., 1983). The Fraser River is the largest single source of freshwater influx into the domain and supplies approximately two-thirds of the total annual freshwater input (Pawlowicz et al., 2019). Fraser River discharge is monitored as part of a long-term programme (Morrison et al., 2012). Following Soontiens and Allen (2017), we used available flow records for the Fraser River from gauges approximately 150 km inland at the city of Hope, BC (DFO, 2024), and supplemented the Fraser River flow data with climatological data for additional freshwater input downstream of the station. A climatology was used for Fraser River runoff temperatures (Morrison et al., 2002) due to a lack of long-term measurements from the lower Fraser River. The location of river outflow for the Fraser River was placed in the main channel before the river branches into a delta (at the town of Delta, BC). All other river outflows were assigned to the grid cell closest to the river mouth. Many rivers other than the Fraser River are not monitored, so climatological patterns for discharge and temperature for 150 rivers flowing into the Salish Sea were used (Morrison et al., 2012). We adapted the input file containing these river input data from the ∼ 500 m horizontal resolution model grid used by Soontiens et al. (2016) to the ∼ 1.5 km horizontal resolution used here and adjusted the outflow locations as required.

2.2.4 Tides

At the two open boundaries, tides were forced with eight tidal constituents (K1, O1, P1, Q1, M2, K2, N2, and S2). Tidal heights and currents at the Juan de Fuca Strait boundary were originally taken from WebTide (Foreman et al., 2000) and then manually tuned (Soontiens et al., 2016). At the northern open boundary sea surface height and tidal harmonics were forced for the major M2 and K1 constituents, and SSH harmonics for the O1 and S2 harmonics were configured using calculations from Thomson and Huggett (1980), with remaining constituents taken from WebTide and subsequently tuned.

3 Model evaluation

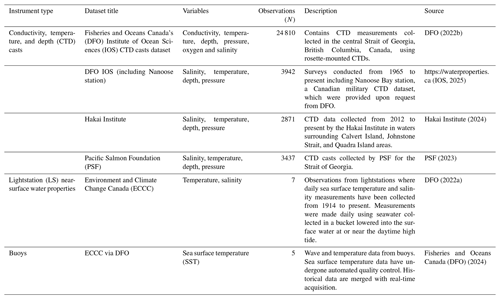
Observations were collated from various instruments and sources (Table 2) and used to do a preliminary evaluation of the model's performance with respect to sea surface temperature (SST), sea surface salinity (SSS), and temperature and salinity over depths. To understand the trade-offs between spatial–temporal resolution, tractability, and model skill, we used an experimental approach where forcings were incrementally swapped to help with isolating the most likely source of model error and bias. The NEMO-based SalishSeaCast model (v201905) outputs were used for comparison when evaluating the effect on overall model performance of changing the spatial–temporal setup, as we used this model as a foundation for the HOTSSea v1 model. As such, HOTSSea v1 shares limitations of the SalishSeaCast model, such as no wetting-and-drying capability in intertidal areas, climatologies used for river flow for all rivers except for the Fraser River, and biases in temperature and salinity. Aspects of SalishSeaCast's model skill with respect to physical properties have been previously reported (Olson et al., 2020; Soontiens et al., 2016; Soontiens and Allen, 2017). The mean temperature biases over all depths ranged from −0.21 to 0.13 °C, and for depths less than 15 m they ranged from −0.34 to 0.36 °C, respectively (Olson et al., 2020; Soontiens et al., 2016; Soontiens and Allen, 2017). The mean salinity bias over the same two depth strata ranged from −0.74 to +0.23 PSU and −1.62 to 0.23 PSU, respectively (Olson et al., 2020; Soontiens et al., 2016; Soontiens and Allen, 2017). Our results may differ because the previous study did not necessarily use the same observational data nor did it use the subdomain definitions we used. For evaluation of temperature trends in the final hindcast, we used the modelled long-term temperature trend against observations at Nanoose station, the only long-term dataset with at least biweekly depth profiles done in the model domain extending back to the beginning of the hindcast (Table 2).

Table 2 Summary of data used for model evaluation.

3.1 Experimental evaluation

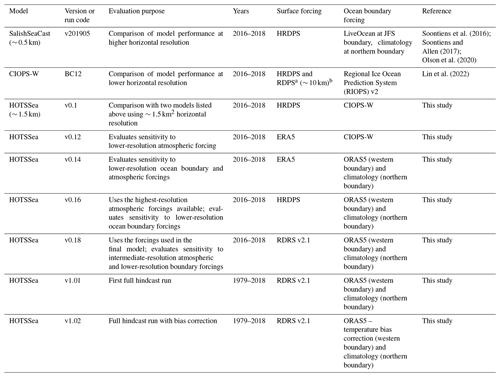
The years chosen for running preliminary experimental evaluations were 2016–2018. The available forcing data and models had coverage for those years, and generally a larger volume of evaluation data is available for the most recent years (Table 3). Experimental runs of the HOTSSea model were given run codes. The first was HOTSSea v0.1, which used the highest-resolution atmospheric and ocean boundary forcings available. This run was used to do a comparative evaluation with SalishSeaCast v201905, which has a higher horizontal resolution (∼ 500 m versus ∼ 1500 m). The LiveOcean model (Fatland et al., 2016) forcings used in SalishSeaCast at the Juan de Fuca Strait (JFS) open-ocean boundary were not available for the 2016–2018 period, so in HOTSSea v0.1 we used CIOPS-W BC12, a model also developed using the NEMO v3.6 ocean engine covering the northeast Pacific at an approximate horizontal resolution of 2.0–2.5 km (Lin et al., 2022). The HOTSSea v0.12 experiment was used to evaluate the effect of swapping from HRDPS to the ERA5 atmospheric forcings (∼ 31 km horizontal; Dee et al., 2011; Hersbach et al., 2020). At the time HOTSSea development began in 2021, ERA5 was the only climate reanalysis product available for the entirety of the hindcast period. At the time of writing, it is still the only reanalysis extending back to the 1940s, and therefore evaluation of this product for use for atmospheric forcing was a priority. The v0.14 and v0.16 experiments jointly helped evaluate the effect of using the ORAS5 (∼ 18 km horizontal; Tietsche et al., 2017; Zuo et al., 2019) dataset for ocean boundary conditions at the mouth of the Juan de Fuca Strait, which will be used in the final hindcast; the two experiments used the lowest-resolution atmospheric forcings (v0.14; ERA5) and the highest-resolution atmospheric forcings (v0.16; HRDPS) to assist with isolating the effects on model performance of ORAS5 versus the atmospheric forcings. The HOTSSea v0.18 experiment used the RDRS v2.1 atmospheric outputs for forcing, which have an intermediate horizontal resolution of ∼ 10 km (Gasset et al., 2021). To evaluate each experiment, we used data, methods, and statistics as described in the next section. Model performance was evaluated using results aggregated over the 2016–2018 period – analyses were also carried out on model results grouped by month and year, though only results aggregated for the entire period are presented here, and only the results using CTD measurements are highlighted here for brevity.

Table 3 Experimental evaluation run codes and forcings.

^a RDPS: Regional Deterministic Prediction System (used by CIOPS-W; not used herein). ^b Approximate horizontal resolutions are included in brackets where not otherwise included in Table 1.

3.2 Model–observation evaluation methods

The final hindcast was evaluated using the datasets grouped by subdomains (Table 2, Fig. 2). Subdomains were selected based on distinct geographic features, data availability, and physical characteristics.

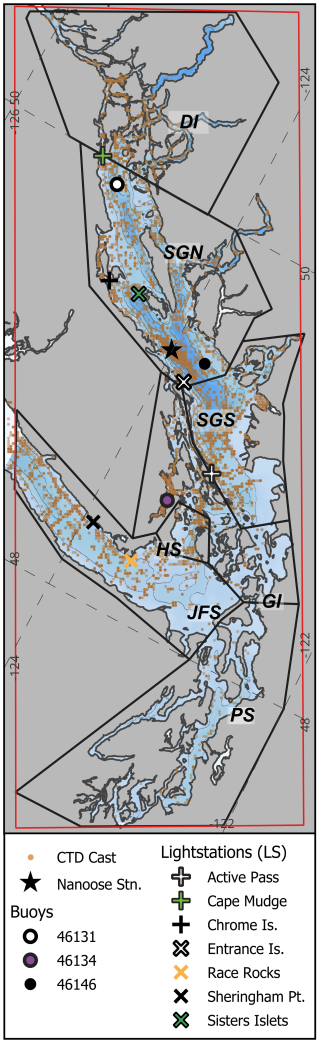
Figure 2 Map of HOTSSea v1 model domain (red rectangle) and subdomains used for analysis (black polygons; DI, Discovery Islands; SGN, Strait of Georgia North; SGS, Strait of Georgia South; HS, Haro Strait; GI, Gulf Islands; JFS, Juan de Fuca Strait; PS, Puget Sound). Locations of CTD casts are indicated by orange stippling (darker denotes higher density), and Nanoose station is indicated by the black star.

3.2.1 Vertical profiles

CTD casts were acquired from various sources (Table 2). After quality control, 27 272 CTD casts were used in the analysis of the final hindcast. These data have heterogeneous spatial coverage when aggregated by subdomain (Fig. 2; Table 4). For the model intercomparison and experimental evaluation only CTD data from 2016–2018 were used (N=8012), which also had spatially heterogenous coverage across subdomains.

Table 4 Spatial distribution of CTD data used for evaluation of the entire hindcast (1980–2018) and shorter experiments (2016–2018).

^* Brackets indicate spatial density of measurements.

The closest model grid cell and time index was found for each CTD measurement, and the measurements over depths for each CTD cast were vertically interpolated to the model depth levels. To calculate the statistics described below, CTD data were first grouped by subdomain, period, and depth strata during analysis. We highlight in the subsequent sections only the results of grouping the data first by subdomain and model depth level and second by subdomain and selected depth strata (0 to >30 m, 30 to >150 m, >150 m, and over all depths). For statistics grouped by depth strata, the depth-integrated mean from individual CTD casts within each depth grouping was first calculated. These values were treated as a single measurement (o_i) in the set of CTD casts, N, across each subdomain, with $\stackrel{\mathrm{‾}}{o}$ representing the mean of depth-integrated means. Model results were extracted for each observation and depth-integrated in the same manner.

The model error was calculated for each model–observation pair (m,o) of time series (error = m−o) with the bias being the mean error. The root mean square error (RMSE) was also calculated for each depth stratum, time frame, and subdomain. The bias and RMSE are often used to infer the accuracy of a model, whereas the centred root mean square error (CRMSE) quantifies the precision (Walther and Moore, 2005) as the variability of the model as compared with observations as

$$\begin{array}{}\text{(1)}& \mathrm{CRMSE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^N{\left(\left(m_i-\stackrel{\mathrm{‾}}{m}\right)-(o_i-\stackrel{\mathrm{‾}}{o})\right)}^{\mathrm{2}}},\end{array}$$

where o_i denotes a single observation out of a set of observations, N, with the corresponding model output denoted by m_i. The Willmott skill score (WSS) was also used, a dimensionless measure of model skill ranging from zero, denoting poor agreement between model and observations, to one, denoting perfect agreement (Willmott, 1981):

$$\begin{array}{}\text{(2)}& \mathrm{WSS}=\mathrm{1}-{\displaystyle \frac{{\sum }_{i=\mathrm{1}}^N(m_i-o_i{)}^{\mathrm{2}}}{{\sum }_{i=\mathrm{1}}^N\left(\right|m_i-\stackrel{\mathrm{‾}}{o}|+|o_i-\stackrel{\mathrm{‾}}{o}|{)}^{\mathrm{2}}}}.\end{array}$$

3.2.2 Sea surface temperature and salinity

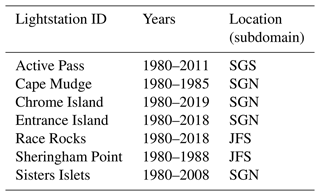
Sea surface temperature (SST) and salinity (SSS) were evaluated using measurements collected at high tide during daylight hours by lighthouse staff at seven lighthouses throughout the domain (Fig. 2; Treasury Board Secretariat, 2023). Lightstation data (LS) were available for the entirety of the hindcast period for Chrome Island, Entrance Island, and Race Rocks lighthouses, whereas others had partial coverage (Table 5). The time of day when samples were taken was not always provided in the dataset. As such, the closest tidal gauge each day was found for each lighthouse, and the high-tide time was extracted and then matched to the lighthouse sample data as required.

Table 5 Lightstation data summary used for evaluation of SST and SSS.

Sea surface temperature measurements were also available from buoys within the model domain (Fig. 2). Canadian buoy data were downloaded from online repositories (Fisheries and Oceans Canada (DFO), 2024; NOAA National Buoy Data Centre, 1971). The buoy data we prepared had heterogeneous temporal coverage of the hindcast period (Table 6). For the evaluation of the full hindcast we only used buoys with 10 or more years of data (buoy IDs: 46146, 46131, and 46134).

Table 6 Buoy data summary used for evaluation of SST.

The statistics used for evaluation of SST and SSS include the standard deviation, σ, and Pearson's R (i.e. the correlation coefficient):

$$\begin{array}{}\text{(3)}& R={\displaystyle \frac{\mathrm{1}}{{\mathit{\sigma }}_o{\mathit{\sigma }}_m}}{\displaystyle \frac{\mathrm{1}}{N}}{\sum }_{i=\mathrm{1}}^N(m_i-\stackrel{\mathrm{‾}}{m})(o_i-\stackrel{\mathrm{‾}}{o}).\end{array}$$

For plotting of results using Taylor diagrams, the σ_m and CRMSE statistics were normalised by scaling to the standard deviation of the observations to allow the display of evaluation results for multiple stations on the same plots. The normalised centred root mean square error (NCRMSE) is computed using the relationship between σ, R, and CRMSE,

$$\begin{array}{}\text{(4)}& \mathrm{CRMSE}=\sqrt{{\mathit{\sigma }}_o^{\mathrm{2}}+{\mathit{\sigma }}_m^{\mathrm{2}}-\mathrm{2}{\mathit{\sigma }}_o{\mathit{\sigma }}_{m}R};\end{array}$$

thus,

$$\begin{array}{}\text{(5)}& \mathrm{NCRMSE}=\mathrm{CRMSE}/{\mathit{\sigma }}_o,\end{array}$$

and

$$\begin{array}{}\text{(6)}& {\mathit{\sigma }}_m^{\prime }={\displaystyle \frac{{\mathit{\sigma }}_m}{{\mathit{\sigma }}_o}},\end{array}$$

where ${\mathit{\sigma }}_m^{\prime }$ denotes the normalised standard deviation. Note that in target plots, the NCRMSE has been modified by the sign of σ_m−σ_o (Kärnä et al., 2021).

3.3 Ocean boundary temperature bias correction

The ORAS5 global ocean reanalysis extends back to 1958 (Copernicus Climate Change Service, 2021), and it would be ideal to extend the model back to 1958, too; however, the magnitude of biases that would be inherited from ORAS5 was hitherto unknown. Based on the results of experiments (Table 3), we suspected biases could be substantial. To investigate, we collated observations from CTD instruments sampled between 1980 and 2018 from the mouth of the Juan de Fuca Strait (N=2162) and compared these observations to temperatures in the ORAS5 data. We chose to do this for the entire hindcast period rather than using the experiments for only 2016–2018 given the observational data available at this location for the experimental period were relatively limited. ORAS5 outputs were interpolated from monthly to daily using the cdo toolset (Schulzweida, 2022), which is the same procedure done by NEMO internal routines during model runs. Each CTD measurement was then matched to the closest ORAS5 grid point. Both the observations and the ORAS5 model data were interpolated vertically to the HOTSSea model depth levels. The ORAS5 model bias was calculated using monthly mean bias at each depth level.

Figure 3 Monthly climatology of ORAS5 temperature bias over depths at the Juan de Fuca Strait open-ocean boundary.

The analysis indicated that ORAS5 at the JFS boundary is biased warm at most depths and months except January, with the mean summer bias near the surface approaching +4 °C (Fig. 3). Surface waters in the ORAS5 model were biased fresh in the spring and summer, especially in the top 10 m where the mean bias approached −4 PSU. As a first step towards a more comprehensive bias correction, the mean monthly temperature bias for each depth level was used as a correction factor applied to the boundary conditions. We chose to prioritise temperature to isolate a single variable and because applying a bias correction factor to salinity would run a risk of introducing dynamic instability. The temperature bias correction method is acknowledged here to be a crude approach compared to various alternatives (Adachi and Tomita, 2020). The model run with the ocean boundary temperature bias correction factor applied to ORAS5 is referred to as HOTSSea v1.02. We then evaluated the change in model performance versus with no temperature bias correction (HOTSSea v1.01).

3.4 Trend analysis

The ability of the HOTSSea model to recreate observed long-term ocean temperature trends is one of the most important tests of the utility of the model. The only station in the model domain where measurements over the entire water column were collected with biweekly regularity for the entirety of the hindcast is Nanoose station, located in the central Strait of Georgia (Fig. 2). At this location, CTD casts have been sampled approximately every 2 weeks since 1979 and with less regularity back to the late 1960s. Trends in water temperature at Nanoose station were previously analysed and estimated to be 0.24 ± 0.1 °C per decade between 1970 and 2005 (Masson and Cummins, 2007; MC07). We acquired the same Nanoose station data as analysed by MC07, with updates for recent years from a digital archive at the DFO Institute of Ocean Sciences (IOS) and in the DFO IOS Water Properties Database in August 2022 (IOS, 2025). To cross-check our analysis with MC07, we also calculated the slope for the same period as that study (1970–2005), similarly using ordinary least squares linear regression, and found a similar result: a warming trend over the water column (4.5–400 m) of 0.257 °C per decade was assessed here versus 0.24 °C per decade in MC07. We attribute the difference compared to the application of a boxcar filter to the anomalies in the previous study.

To compare temperature anomalies and trends observed at Nanoose station with those predicted by the model, first obviously erroneous measurements (e.g. with coordinates on land or depths exceeding the maximum depth of ∼ 400 m at Nanoose station) were removed and units were converted to match those used in HOTSSea. The number of CTD casts ultimately used was 5692. Measurements taken in each CTD cast were interpolated to match the model depth levels of the closest HOTSSea grid cell. The mean for each depth level grouped in 2-week time intervals was calculated for the hindcast period. A climatology over depth and time was generated for the hindcast period by taking the mean across years for each depth level and 2-week block. Time series of temperature and salinity anomalies were calculated by differencing the depth-binned data and the climatology. A blind approach was then used to match each CTD cast to HOTSSea outputs where model data were only extracted for dates, times, and locations corresponding to each CTD measurement (i.e. gaps in the Nanoose time series were also present in the extracted model results). The same procedure as above was then used for the model results to generate climatologies and anomalies.

Analysis of temperature trends was conducted using the Nanoose station data and model results drawn from the same area to examine the performance of HOTSSea v1.0x at simulating long-term trends. Depths shallower than 4.5 m were omitted because the first depth at which measurements were taken was inconsistent (following MC07). The analysis of the depth-integrated anomaly trend over the entire water column (4.5–400 m) was first done, followed by analysis of the trend at each model depth. To quantify the magnitude of a linear trend, the Theil–Sen slope was used (TS; Sen, 1968; Theil, 1950). The TS approach is more robust to data gaps, outliers, and non-normal and heteroscedastic residuals than ordinary least squares linear regression (LR; Wilcox, 1998). To calculate TS, the median slope of all data pairs is found:

$$\begin{array}{}\text{(7)}& \mathrm{TS}=\mathrm{median}\left[{\displaystyle \frac{x_i-x_j}{j-i}}\right]\text{for all}i<j,\end{array}$$

where (x_i,x_j) is a pair of values in the ordered time series (j>i). The LR method used in MC07 and the TS method were compared, and we estimated the trend for the 1970–2005 period using TS to be 0.256 °C per decade, effectively the same as the LR method after accounting for measurement precision (see above). The similarity between trends estimated between the LR and TS method is consistent with findings in a previous analysis of SST in the same region (Amos et al., 2015).

Detrended residuals were analysed for periodicity, autocorrelation, non-normal distribution, and heteroskedasticity prior to choosing the test used for determining statistical significance. The data were first “deseasoned” using the climatological mean to produce anomalies, as described above. The deseasoned anomalies were detrended by removing the secular trend calculated using the TS method, and fast Fourier transform (FFT) was used to detect any remaining periodicities in the detrended and deseasoned residuals by examining the top five peaks in the power spectrum (Bluestein, 1970; Cooley and Tukey, 1965) using scipy (Virtanen et al., 2020) and numpy Python packages (Harris et al., 2020). The presence of autocorrelation was evaluated by modelling the residuals as a first-order autoregressive process (AR-1) and computing the autocorrelation function (ACF) using Bartlett's method for computing the 95 % confidence interval (Brockwell and Davis, 2016; Parzen, 1964) with the statsmodels package in Python (Seabold and Perktold, 2010). The residuals were tested for normality using the Shapiro–Wilk test, where a p value of ≤0.9 was interpreted as insufficient evidence to reject a non-normal distribution (Shapiro and Wilk, 1965) using scipy. Heteroskedasticity was evaluated using White's test (White, 1980) and the Goldfeld–Quandt test (Goldfeld and Quandt, 1965) using statsmodels.

The analysis using FFT revealed the presence of periodicity in residuals of frequencies of 5.1 and 17.7 years, confirming that the data were deseasoned at the sub-annual scale but suggesting climate modes operating at longer timescales may limit the ability of accurate secular trend estimation, a similar result to previous studies (Amos et al., 2015). The 17.7 periodicity detected is consistent with the Pacific Decadal Oscillation (PDO), the North Pacific Gyre Oscillation (NPGO), or a combination of the two. The 5-year period is approximately consistent with the El Niño–Southern Oscillation (ENSO) cycle (Andres Araujo et al., 2013; McPhaden et al., 2006).

Analysis of the data revealed that the residuals of the detrended anomalies (both model and observation) had significant autocorrelation, were not normally distributed, and had some heteroskedasticity detected at some depths. The Mann–Kendall (MK) method (Kendall, 1948; Mann, 1945), a non-parametric method, was chosen for evaluating trend significance. This method is widely used in climatological and meteorological applications (Amos et al., 2015; Gocic and Trajkovic, 2013) and has the advantage of being relatively robust to non-normal data distributions and the data gaps present in the Nanoose time series. To check for statistical significance using MK, first the S statistic is calculated,

$$\begin{array}{}\text{(8)}& S=\sum _{i=\mathrm{1}}^{n-\mathrm{1}}\sum _{j=i+\mathrm{1}}^n\mathrm{sgn}(x_j-x_i),\end{array}$$

where n is the number of data points in the time series and sgn(x_j−x_i) represents the sign function,

$$\begin{array}{}\text{(9)}& \mathrm{sgn}\left(\mathit{\theta }\right)=\left\{\begin{array}{l}+\mathrm{1},\text{if}\mathit{\theta }>\mathrm{0};\\ \mathrm{0},\text{if}\mathit{\theta }=\mathrm{0};\\ -\mathrm{1},\text{if}\mathit{\theta }<\mathrm{0}\end{array}\right\}.\end{array}$$

When the S statistic is greater than 0, it indicates that values earlier in the time series tend to be lower than those later, and the trend therefore tends positive. Next, the variance of the test statistic is required, which accounts for ties in the data:

$$\begin{array}{}\text{(10)}& \begin{array}{rl}\mathrm{VAR}\left(S\right)& ={\displaystyle \frac{\mathrm{1}}{\mathrm{18}}}\left[n\left(n-\mathrm{1}\right)\left(\mathrm{2}n+\mathrm{5}\right)\right.\\ & \left.-\sum _{p=\mathrm{1}}^m{t}_p(t_p-\mathrm{1})(\mathrm{2}{t}_p+\mathrm{5})\right],\end{array}\end{array}$$

where n is the length of the time series, m is the number of tied values, and t_p is the number of ties in the pth tied value. Using S and VAR(S), one computes the standardised normal variate Z:

$$\begin{array}{}\text{(11)}& Z_{\mathrm{MK}}=\left\{\begin{array}{l}\frac{S-\mathrm{1}}{\sqrt{\mathrm{VAR}\left(S\right)}},\text{if}S>\mathrm{0};\\ \mathrm{0},\text{if}S=\mathrm{0};\\ \frac{S+\mathrm{1}}{\sqrt{\mathrm{VAR}\left(S\right)}},\text{if}S<\mathrm{0}\end{array}\right\}.\end{array}$$

The standardised statistic, Z_MK, follows the normal distribution with E(Z)=0 and V(Z)=1. The null hypothesis – that there is no trend – may be rejected if the absolute value of Z is larger than the theoretical value of $Z_{\mathrm{1}-\mathit{\alpha }/\mathrm{2}}$ for a one-tailed test or Z_1−α for a two-tailed test (used here), where α is a chosen statistical significance level, which here was 95 %. The Z values were also used for lower confidence limits (LCLs) and upper confidence limits (UCLs). The MK test, similar to LR with a t test, requires the data be independent, and therefore serial autocorrelation must be dealt with in advance (Helsel and Hirsch, 1992). Yue et al. (2002) proposed a “pre-whitening” procedure to remove the effect of serial autocorrelation prior to estimating the trend significance using MK. When autocorrelation was present, we used the 3PW algorithm (Collaud Coen et al., 2020), which combines three pre-whitening methods to minimise risks of type I and type II errors, which we applied using the mannkendall (v1.1.1) Python code.

After comparing the model with the measurements from the Nanoose dataset, we evaluated the trend in temperature and salinity for several depth strata (<30, 30–150, >150 m, and all depths) in each grid cell in the subdomain using the same statistical methods described above, though the 3PW method was not applied due to computational cost. The analysis was limited to the Strait of Georgia and surrounding waters for several reasons: (i) preliminary results indicated that model performance was best in this part of the domain, (ii) collated observations have relatively more coverage in this area, (iii) and it is the focus of an ecosystem model under development in parallel. Mean weekly water temperatures were calculated for each grid cell, season (winter: December, January, and February; spring: March, April, and May; summer: June, July, and August; fall: September, October, and November), and depth group. When generating plots, grid cells that were shallower than a threshold set for each depth strata were masked (thresholds: 20 m for 0–>30 m; 150 m for 30–>150 m; 200 m for >150 m) and coloured grey.

4 Results

4.1 Experimental evaluation

In the first model experiment (years 2016–2018), HOTSSea v0.1 was compared with the higher-resolution SalishSeaCast model. A notable difference was that v0.1 had a mean bias taken over all depths of 0.14 °C in the Strait of Georgia South (SGS) subdomain versus −0.017 °C in SalishSeaCast (Fig. 4c). Large differences were noted in the northernmost Discovery Islands (DI) subdomain where near-surface (0–1.5 m) biases were larger in v0.1 relative to SalishSeaCast, approaching +2 °C and −4 PSU at 0.5 m (Fig. 4a, d). We attribute the warm bias in the DI subdomain to the 3-times-coarsened HOTSSea model grid relative to SalishSeaCast, limiting the model's ability to resolve the relatively narrow topography in the DI. At depths >1.5 m HOTSSea v0.1 performed well, even in the DI, with mean biases over the water column of −0.12 °C and −0.4 PSU. In the JFS subdomain, HOTSSea v0.1 performed similarly to SalishSeaCast except for the introduction of a temperature bias of 0.3–0.5 °C at depths >2 m, with the bias most pronounced at depths >20 m (Fig. 4b). A similar bias was also present in the Strait of Georgia South (SGS) subdomain (Fig. 4c). The boundary forcings were hypothesised to be the main culprit, since different boundary forcings were used here (CIOPS-W) than in SalishSeaCast (LiveOcean).

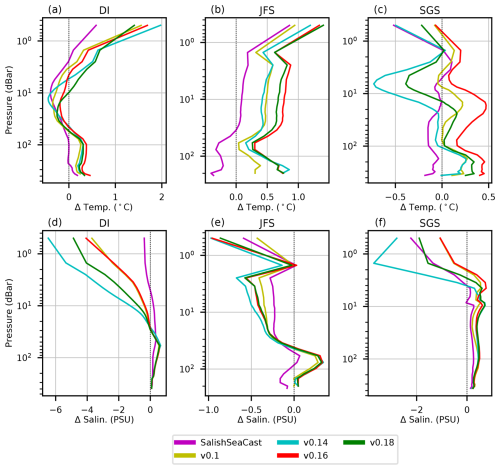
Figure 4 Model bias (model − observations) over depths using CTD data for short (2016–2018) experimental runs, highlighting temperature (a–c) and salinity (d–f) bias and CRMSE over depths (shading). HOTSSea v0.18 corresponds to the setup used in the final model run without bias correction (v1.01). HOTSSea v0.12 was omitted from the plots as results were nearly identical to v0.14. See Fig. 2 for a map of subdomains.

The v0.12 and v0.14 experiments were designed to evaluate the effect on the model's performance of using relatively coarse atmospheric forcings from ERA5 (∼ 31 km horizontal resolution) versus the relatively highly resolved HRDPS (∼ 2.5 km horizontal) forcings used in v0.1. The v0.12 and v0.14 experiments used different ocean boundary forcings, though the resulting salinity and temperature biases over depths were indistinguishable between the two (which prompted us to remove v0.12 from Fig. 4). The similarities suggest that any performance impacts of using ORAS5 (∼ 18 km horizontal resolution) versus CIOPS-W (∼ 2.5 km horizontal resolution) were masked by the relatively greater impacts of using coarse ERA5 atmospheric forcings. Among all experimental runs, v0.12 and v0.14 had the greatest near-surface biases in temperature and salinity in the northern part of the model domain (i.e. DI subdomain; Fig. 4a, d) and in the central part of the domain (i.e. SGS domain; Fig. 4c, f). We investigated possible reasons and diagnosed that winds in ERA5 are generally weak and less variable throughout the domain relative to the higher-resolution HRDPS winds.

The HOTSSea v0.16 experiment helped isolate and evaluate the effect of using ORAS5 for boundary conditions at the Juan de Fuca Strait open-ocean boundary versus the relatively highly resolved CIOPS-W. In the northernmost subdomain, the Discovery Islands (DI), v0.16 showed similar biases to v0.14 with respect to salinity and temperature over depths (Fig. 4a, d). Looking to the SGS subdomain in the central part of the model domain, a relatively large warm bias appeared in v0.16 at depths greater than 10 m (approximately +0.3 °C at 10 m depth, increasing to +0.5 °C at 100+ m depths; Fig. 4c). In the JFS subdomain closest to the open-ocean boundary, the biases in temperature at depths >5 m were greater in v0.16 than in the other subdomains and greater relative to previous experimental runs, with biases of >1 °C near the surface and +0.4 to +0.75 °C at greater depths (Fig. 4b). The v0.16 experiment's performance with respect to salinity in JFS was comparable to v0.14 (Fig. 4e). Our interpretation of these results is that in v0.16 the model inherited a warm bias in mid- and deep waters from the ORAS5 boundary conditions, evidenced by decreasing temperature bias with increasing distance from the open-ocean boundary. Contrary to expectations, using the lower-resolution ERA5 atmospheric forcings in the HOTSSea v0.14 experiment resulted in less of a warm temperature bias across all depths in the JFS subdomain at depths up to 100 m and had little discernible effect on salinity as compared with results of using the higher-resolution HRDPS outputs for atmospheric conditions in the v0.16 experiment. The better performance of v0.14 in JFS was unexpected because the model domain is relatively poorly resolved by ERA5 versus HRDPS. We suspect that wind-driven vertical mixing is biased low when using ERA5, and therefore ERA5 masks the effect of a near-surface warm bias introduced by ORAS5 by keeping the biased-warm water closer to the surface. Further investigation is warranted, and understanding the sources of biases is a priority.

In the final experimental run, HOTSSea v0.18, the RDRS v2.1 (∼ 10 km horizontal) atmospheric conditions were used, representing an intermediate between the highest-resolution HRDPS forcings available only for 2014–2020 and the lower-resolution ERA5 forcings available for the entire hindcast period. The run performed similarly or better than the previous two runs with respect to temperature and salinity in most subdomains. The JFS subdomain was an exception, where the warm temperature bias was greater than in v0.14 (Fig. 4b). As above, the increased temperature bias was unexpected since v0.14 used the relatively weak and poorly resolved ERA5 atmospheric conditions. Thus, using both higher resolution and presumably more accurate atmospheric products (RDRS and HRDPS) resulted in greater temperature bias over depths up to ∼ 80 m in the JFS subdomain. This result is consistent with the diagnosis we reached earlier that the ERA5 atmospheric forcing fields used in the v0.14 experiment masked the effects of a warm temperature bias in the JFS subdomain up to depths of ∼ 10 m due to weaker winds and a shallower mixing as compared to the more powerful HRDPS and RDRS winds in the v0.14 and v0.18 experiments, respectively.

The preliminary experiments illuminated several important factors affecting model performance related to atmospheric and ocean boundary forcings. Coarsening the model bathymetry from 500 m to 1.5 km horizontally has especially impacted model performance in areas with narrow topography when compared with SalishSeaCast but otherwise has had only a minor effect on the evaluated aspects of model performance. Puget Sound (PS) remains essentially unevaluated (though see Tables S1 and S2) due to a lack of collated data for the area, but we suspect similar issues to the DI subdomain due to narrow topography; expanding our evaluation to PS remains a priority for future work. An important takeaway was an apparent systemic temperature bias present in ORAS5, the only reanalysis for hindcasting the ocean boundary conditions to 1980 and prior available at the time of writing. The ERA5 product similarly was deemed to be inadequate for the present purposes due to underpowered winds throughout the domain (RDRS v2.1 was used instead). The experiments prompted us to verify and quantify the bias introduced at the ocean boundary and to determine if simple bias correction could hold potential to reduce or eliminate inherited biases (results below).

4.2 Bias correction of open-ocean boundary conditions

The effect of the temperature bias corrections applied in HOTSSea v1.02 substantially improved model skill versus v1.01 (Figs. 5, 6; Tables S1, S2). In the JFS subdomain, for example, temperature bias calculated over all depths was reduced from +0.66 to +0.12 °C. The HOTSSea v1.01 run without bias correction had mean temperature biases calculated over all depths of +0.21 to +0.66 °C (excluding the PS subdomain with sparse observations) versus −0.14 to +0.2 °C in HOTSSea v1.02 (Table S1). Applying the temperature bias correction improved the model's performance in the most distant subdomain from JFS, the DI subdomain – an unexpected result that emphasises the importance of accurate ocean boundary forcings.

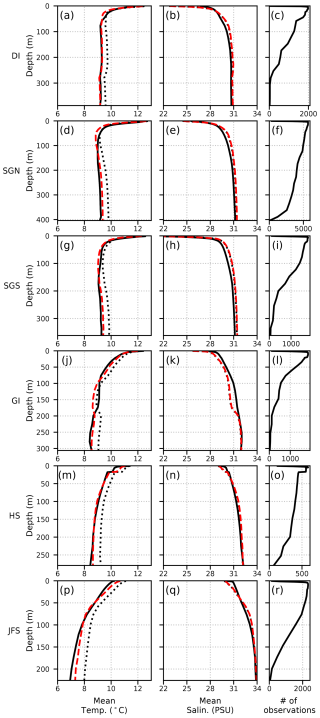
Figure 5 Results of analysis using CTD data, aggregated by subdomain, showing mean temperature and salinity over depths (solid line: observations; dashed black line: HOTSSea v1.01 without bias correction; dashed red line: HOTSSea v1.02 with bias correction).

Figure 6 Target plots of the model's temperature bias and normalised centred root mean squared error (NCRMSE) using CTD data grouped by depth strata (panels a–d) and by subdomain. Results without bias correction to western open-ocean boundary conditions (HOTSSea v1.01) are shown in grey, and results with temperature bias correction (HOTSSea v1.02) are shown in red.

4.3 Model–observation evaluation

4.3.1 Vertical profiles

Overall, the full hindcast (HOTSSea v1.02) performs best in the central and northern portion of the domain (Fig. 5). In the Strait of Georgia North (SGN) subdomain where the most CTD casts were available (N=12 288), the temperature bias over all depths over the hindcast period was −0.08 °C (0–30 m = −0.39 °C; 30–150 m = −0.14 °C; >150 m = +0.13 °C) with an overall WSS of 0.97 and a correlation coefficient (R) of 0.94 (Tables S1, S2). Performance was similar in the SGS subdomain. The normalised target and Taylor diagrams (Figs. 6, S1–S3) indicate the model captures the seasonal ocean temperature variability well, though NCRMSE was >0.5 for JFS in the west and DI subdomains in the north. Model standard deviation is generally higher than observations in shallow depths and lower in deep water. Except for JFS and DI subdomains, the mean correlation coefficient with respect to temperature taken over all depths was >0.9 (Fig. S1a; Table S1). As depths increase, correlation generally decreases. At depths greater than 150 m, the model underestimates temperature variability, and the correlation coefficient was <0.8 for DI, JFS, and SGN. The southernmost PS subdomain was omitted from analysis due to relatively few collated observations, and preparing data for this area is a priority for future work. All metrics are tabulated by subdomain and depth strata in Tables S1 and S2 for reference.

HOTSSea v1.02 model skill was relatively poor with respect to salinity compared with temperature, especially in the DI and JFS subdomains (Table S2; Figs. S2–S3). However, performance was better in the Strait of Georgia, where mean bias taken over all depths in the SGS subdomain was +0.38 PSU (WSS = 0.98 and R=0.96; Table S2). The narrow topography in the DI combined with the 1.5 km horizontal resolution likely leads to the observed error, as evidenced by experiments (Fig. 4). Another reason for salinity biases to increase in subdomains farther from the Fraser River could be that a climatology is used for estimating input from other rivers in the domain, whereas measurements are available for the Fraser River (Morrison et al., 2012). The open-ocean boundary conditions are forced using a climatology at the northern boundary in the DI subdomain, and this would affect model skill. However, the latter two explanations are considered less likely given the same boundary climatology and river forcings were used here as were used in SalishSeaCast, which performs well in the DI subdomain (Fig. 4).

4.3.2 Sea surface temperature and salinity

Time series of SST and SSS taken at lightstations in the region are some of the longest in existence and present a valuable opportunity to evaluate model performance. SST and SSS were evaluated for the full hindcast using data from sampling at lightstations and buoys with temporal coverage of at least 10 years. The Taylor plots indicate the model reproduces the variability in SST well (Fig. 7a). Most stations have NCRMSE <0.5 with a correlation coefficient greater than 0.9. HOTSSea v1.02 performs well at stations within the Strait of Georgia and relatively poorly at Sheringham Point in the Juan de Fuca Strait, where the standard deviation of the model is approximately 20 % higher than observations. The normalised target diagram (Fig. 7c) shows that the model is typically biased cold with the mean bias typically <0.75 °C. The one lightstation with >1 °C bias was Chrome Island, which is located on an island close to shore where bathymetry is poorly resolved.

Figure 7 Taylor (a, b) and target (c, d) plots evaluating HOTSSea v1.02 sea surface temperature (SST; a, c) and salinity (SSS; b, d). SST was evaluated using data from buoys (numbered) and lightstations (named), and SSS was evaluated using lightstation data only. The standard deviation (solid grey contours in Taylor diagrams) and centred root mean square error (dashed grey contours in Taylor diagrams) have been normalised to enable comparison on the same plot. Perfect agreement between model and observations on the Taylor plot would correspond to normalised standard deviation = 1, correlation = 1, and NCRMSE = 0. Perfect agreement between model and observations on the target plot would be at the centre. Arrows depict the change after applying a 1-month moving average on both the model and observation time series.

The evaluation of SSS indicates that HOTSSea v1.02 typically overestimates variability in SSS across the domain, as the normalised standard deviation of the model is greater than the observations at all stations except Chrome Island (Fig. 7b). Although the model's performance with respect to SST is better than SSS, the model's normalised standard deviation for SSS at all stations except Cape Mudge deviated by less than ±30 % of the observations. The correlation coefficient for SSS at most stations was relatively poor (0.4–0.7) compared to SST (>0.85). The target plot indicates that the model is biased fresh at the surface by approximately −1 PSU at Cape Mudge in the northern part of the domain and −2 PSU at Entrance Island in the central Strait of Georgia, whereas at other stations the fresh bias was relatively small (<−1 PSU; Fig. 7d).

Many applications of HOTSSea v1 in support of ecosystem modelling and research related to Pacific salmon are anticipated to require accuracy at weekly, monthly, or seasonal timescales rather than daily or hourly. To investigate whether the lower SSS performance was due to difficulty in capturing dynamics over hourly or daily timescales versus longer timescales, we applied a monthly moving average to both the model and observations, after which statistics were recalculated. Applying the moving average improved the evaluated statistics at all stations except Sheringham Point (Fig. 7, arrows). The improvement leads us to conclude that if research applications require bias <0.5 °C or <1.0 PSU, then averaging results to monthly timescales may ensure the accuracy is acceptable with respect to SST and SSS. As shown in Sect. 4.3.1, the model performance generally improves with depth.

4.4 Decadal temperature trend evaluation

4.4.1 Nanoose station

The model represents seasonal changes in salinity and temperature over depths well. Both the modelled and observed biweekly climatologies at Nanoose station depict a characteristic intrusion of cold water and a temperature inversion that occurs in the area in the spring and late summer or fall (Fig. 8d, e), typically associated with upwelling events and neap tides (Johannessen et al., 2014; Masson, 2002; Riche et al., 2014). Strongly stratified and warm surface layers are shown in the shallower layers in the summer in both climatologies from the observations and from the model. The model–observation biases are generally largest at depths less than 3 m for both temperature and salinity. Although at depths >10 m there is only minor bias with respect to salinity (<0.5 PSU), salinity is biased fresh in depths <3 m, especially in the summer when it approaches −3 PSU (Fig. 8c). The fresh bias observed here is not surprising; it was also apparent in the higher-resolution SalishSeaCast model (e.g. Fig. 4f; Soontiens and Allen, 2017) which formed the basis for HOTSSea; however, it remains an important area for improvement in the future and may affect model skill with respect to circulation patterns. The modelled temperatures are biased warm in the summer and cool in the winter by a maximum of approximately 1 °C at depths less than 3 m. In contrast, the modelled temperatures are consistently biased slightly high (∼ 0.5 °C) at depths over 100 m.

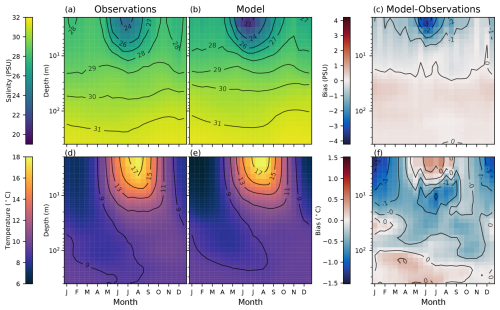
Figure 8 Biweekly climatologies and model–observation bias over depths over the hindcast period using measurements taken at Nanoose station between 1980 and 2018 (N=5692). The four panels to the left (a, b, d, e) show salinity extracted from observations (a, d) and the model (b, e). Temperatures are similarly represented from observations and the model in the bottom plots. The two plots on the right show the model bias (i.e. model − observations) over depth. Data were binned bimonthly.

After truncating the Nanoose station time series to match the model hindcast period, the monotonic temperature trend across depths 4–400 m was calculated using the MK test and the TS slope estimator. Significant autocorrelation was detected in the detrended biweekly time series, so the 3PW algorithm was used to adjust for this (see Sect. 3.4). The trend from observations at Nanoose station was evaluated to be 0.031 °C per decade but was not found to be statistically significant (LCL: −0.018; UCL: 0.08; p≤0.12). HOTSSea v1.01 without ocean boundary temperature bias correction detected no trend (0.00 °C per decade; LCL: −0.06; UCL: 0.06; p≤0.73). HOTSSea v1.02 with ocean temperature bias correction predicted an insignificant trend of 0.012 °C per decade (LCL: −0.052; UCL: 0.075; p≤0.3). Although trends over the water column for the 1980–2018 hindcast period were not significant at the 95 % confidence level, results suggested that HOTSSea v1.02 with ocean boundary temperature bias correction performs better than HOTSSea v1.01 with respect to long-term trends.

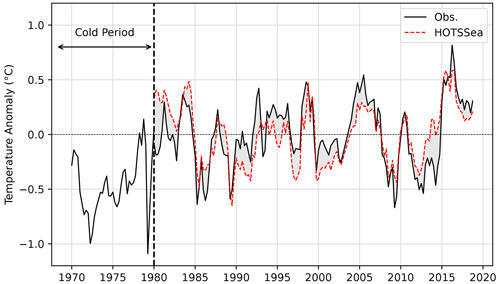
Figure 9 Temperature anomalies (seasonal) from observations (black, solid) at Nanoose station in the central Strait of Georgia versus those derived from HOTSSea v1.02 model outputs (red, dashed), depth integrated over 4.5–400 m. The grey area represents the model bias. Observations from the 1970–1980 period at Nanoose station are included to illustrate the cooler period, a multiyear swing in temperature anomalies (1977, 1978), followed by a regime shift occurring circa 1977 (Beamish et al., 1999; Hare and Mantua, 2000).

The observed inter-annual and intra-annual variability over the hindcast period is well captured by the model (Fig. 9). The largest deviations between modelled (HOTSSea v1.02) and observed temperature anomalies over the whole water column were <0.5 °C. Relatively large deviations from observations in the 1980–1983 period suggest that the 1-year spin-up may be too short, and this remains a priority area to investigate in the future. Warm anomalies as a result of a documented oceanic heat wave circa 2015–2016 (Gruber et al., 2021; Khangaonkar et al., 2021b) are generally well represented, suggesting the model is capable of reproducing extreme events. The evaluation of the trends at Nanoose station also indicate the model does not incur a detectable drift in temperature bias at this location, despite being run with no data assimilation.

The secular trend previously calculated for the 1970 to 2005 period of 0.24 °C per decade (95 % CI ± 0.1 °C; Masson and Cummins, 2007) was over 6-fold greater than calculated here for the 1980 to 2018 hindcast period. We verified that the difference was not attributable to the methods (TS vs. LR for slope estimation) by re-estimating the trend from the observations using LR for the same 1980–2018 period, finding a similar result using LR (0.038 °C per decade). The weaker secular trend calculated for the 1980–2018 period is in part due to the omission of the 1970s, a period with cold water temperature anomalies observed at Nanoose station (Figs. 9, S4). The period of the late 1970s corresponds approximately to a polarity shift in the Pacific Decadal Oscillation (PDO; Mantua et al., 1997; Mantua and Hare, 2002), a trough in the North Pacific Gyre Oscillation (NPGO; Di Lorenzo et al., 2008), which oscillates on decadal or multi-decadal timescales. The period of the late 1970s also corresponds to a trough in a multi-regime index circa 1977 that correlates with a reduction in northern Pacific fisheries catches (Beamish et al., 1999). Overall, the analysis reveals a key limitation of HOTSSea v1 – omission of the 1970s – which is thus a priority area for subsequent iterations. Our analysis also serves as an update to the MC07 analysis and confirms ocean temperatures have not subsequently reverted.

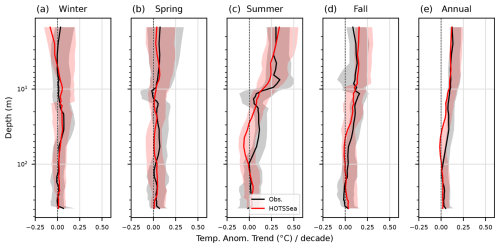
Figure 10 Seasonal and annual trends (1980–2018) over depths observed at Nanoose station compared with HOTSSea v1.02 outputs. Shading represents upper and lower 95 % confidence limits.

Analysis of trends at each depth at Nanoose station indicates that the modelled trends are in generally good agreement with observed trends (Fig. 10). Both the modelled and observed seasonal trends in the upper water column in the summer, fall, and annually were statistically significant, whereas the trends in the winter and spring were not. A deviation between the modelled and observed trends is apparent, especially in the summer, between approximately 20 and 100 m. The reason for the deviation is yet to be determined, but a similar deviation is also apparent in the analysis using CTDs in the Gulf Islands (GI) subdomain (Fig. 5). The seasonal trend patterns over depth at Nanoose station indicate that trends vary seasonally and spatially (over depths) at this location.

4.4.2 Strait of Georgia

Modelled trends from HOTSSea v1.02 were evaluated in each grid cell in the central and northern part of the model domain (Strait of Georgia and surrounding waters) over the 1980–2018 hindcast period (Fig. 11). The 0–30 m depth stratum was selected given that the evaluation of the modelled versus observed trends showed generally good agreement in approximately the top 30 m of the water column. This stratum also has special relevance for phytoplankton bloom dynamics (Allen and Wolfe, 2013). The model indicates the top 30 m is generally warming in the Strait of Georgia, with some areas experiencing statistically significant warming over the entire water column. Despite finding that the mean trend computed across all depths at Nanoose station in the winter was not statistically significant (Figs. 10a, 11f), a statistically significant warming trend in the winter was detected in the 0–30 m depth stratum in the northeastern Strait of Georgia and in Jervis Inlet (Fig. 11a). The rapid warming of Jervis Inlet is a finding consistent with trends reported for other fjords in the region (Jackson et al., 2021). The analysis of temperature trends in the spring revealed no significant warming trend (Fig. 11b), similar to the analysis of the Nanoose data (Fig. 10b). In the summer, only the waters in the central and northern Strait of Georgia generally showed a statistically significant warming trend, whereas the southern Gulf islands and surrounding waters showed no statistically significant trend (Fig. 11c). The fall season may also have experienced the most spatially consistent secular ocean temperature warming since 1980 over the 0–30 m depth range - significant trends in the fall were generally widespread apart from Howe Sound (Fig. 11d). Annualised trends were relatively low but generally statistically significant throughout the Strait of Georgia (Fig. 11e). Note that the magnitudes of all modelled trends throughout the domain are likely biased low, as the analysis of the modelled secular trend at Nanoose station was weak relative to the observed secular trend (see above).

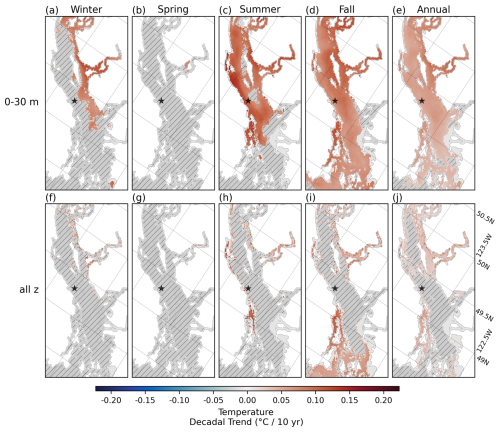
Figure 11 Mean ocean temperature trends in the Strait of Georgia computed as seasonal mean trends (columns) for two depth strata (rows), 0–30 m depth stratum and over all depths (all z), from HOTSSea v1.02 model outputs. A mask (grey) has been applied to grid cells that are shallower than the depth stratum. Grey hatching has been applied to grid cells where the trend was not statistically significant. The star symbol denotes the approximate location of Nanoose station.

5 Discussion and conclusion

To our knowledge, HOTSSea v1 represents the first 3D physical oceanographic model for the Salish Sea to be extended back to 1980, as well as the first model to use recently available forcing products to do so (e.g. RDRS v2.1, ORAS5). A highlight of the results of our evaluation of HOTSSea v1 was the skill with which the model represents observed decadal-scale ocean temperature trends at Nanoose station – without incurring any detectable drift despite being a free run with no data assimilation (Figs. 9, 10). After confirming the model's skill at recreating the trend at Nanoose station, we used the model to further our understanding of trends in areas within the central and northern part of the domain with sparse observations, offering a first glimpse at the spatial–temporal heterogeneity of ocean temperature trends in the area (Fig. 11). The 0–30 m depth range was of particular interest because changes occurring at these depths affect dynamics of spring and fall phytoplankton blooms (Masson and Peña, 2009). Most importantly, HOTSSea v1 outputs indicate that the warming trend apparent at Nanoose station is not an isolated phenomenon within the Salish Sea. Gradual ocean temperature changes such as those quantified by our analyses have the potential to affect the growth, body mass, and marine distributions of fish (Pauly, 2021; Pauly and Cheung, 2018) and support research related to the velocity of climate change (Burrows et al., 2014; Loarie et al., 2009). Anomalous events such as marine heat waves are expected to occur more frequently due to climate change, and these events can lead to key biophysical thresholds being surpassed, impacting marine organisms (Gruber et al., 2021). Given that HOTSSea v1 generally replicates observed ocean temperature anomalies and extremes, it therefore shows promise for investigating climate-related pathways of effects from physical ocean properties to marine ecosystems.

Overall, our evaluation quantifies the biases of the model at several spatial–temporal scales, with special attention to those scales and variables anticipated to be relevant for marine ecosystem model development, marine ecosystem research, and ecosystem-based fisheries management. Although variability in physical conditions at fine spatial–temporal scales (i.e. minutes to days, metres to kilometres) is an important determinant of the structure and dynamics of marine ecosystems (e.g. Jones et al., 2014), many research applications related to marine ecosystems focus on processes and mechanisms that exhibit variability on weekly or greater timescales and at spatial scales of tens of kilometres (Fulton et al., 2019). Locally, juvenile salmon enter the marine environment from natal rivers over a protracted period of weeks to months (Groot and Margolis, 1991; Healey, 1980); migrate at rates of 1.5–20 km d⁻¹ (Melnychuk et al., 2010, 2013; Trudel et al., 2009; Tucker et al., 2009; Welch et al., 2011); are widely distributed throughout the pelagic zone (Beamish et al., 2011; Riddell et al., 2018; Trudel and Tucker, 2013); and exhibit weekly, monthly, and seasonal variability in growth and mortality. We therefore expect that hindcasting physical ocean water properties at the spatial–temporal resolution used here will be of value for many studies related to Pacific salmon.

A contemporary challenge to achieving a long hindcast for the Salish Sea is related to the quality of the available products to use for boundary and atmospheric forcing. The experimental approach we used helped us isolate the effect of forcings and our model's horizontal resolution from other factors affecting model performance, revealing substantial biases inherited from both atmospheric and oceanic boundary forcings. What we learned using this approach will guide future efforts to improve and extend HOTSSea v1 and possibly other models for the domain. Using the RDRS v2.1 forcings in the final hindcast led to substantially better model performance versus using ERA5 (Sect. 4.1) – presently the only alternative to our knowledge with coverage of the full hindcast period. Wind speed biases in ERA5 have been noted in other coastal and mountainous areas (Potisomporn et al., 2023). The results of our experiments similarly indicated that locally weak winds in ERA5 resulted in reduced mixing and increased near-surface biases, leading to especially poor model performance in areas with complex and narrow topography (e.g. the Discovery Islands). Winds are an important factor determining total productivity of the Strait of Georgia (Collins et al., 2009; Johannessen et al., 2020), and thus it was fortunate that the RDRS v2.1 atmospheric reanalysis was recently made available. The experiments also revealed that the global ocean reanalysis ORAS5 outputs exhibit temperature and salinity biases at the mouth of the Juan de Fuca Strait which were inherited to some extent by our model. We suspect the main issue is that the Salish Sea is poorly resolved in ORAS5, leading to poor representation of estuarine flow and physical dynamics at the mouth of the Juan de Fuca Strait. The temperature bias correction we applied here to ORAS5 at the Juan de Fuca Strait boundary improved model performance substantially, even in areas of the domain far from the ocean boundary (Figs. 5, 6). The success of our crude bias correction serves to highlight the potential benefit of relatively advanced techniques such as statistical downscaling using machine learning or the application of data assimilation techniques to produce a reanalysis (Adachi and Tomita, 2020). Another avenue worth exploring would be to use outputs from other regional ocean hindcasts as boundary forcings, should they become available (e.g. Lin et al., 2022; Peña et al., 2016). Applying bias correction to salinity at the boundary could also be of benefit and may help with improving the model's near-surface fresh bias.

Next steps include several improvements, extensions, and applications. Our preliminary evaluation of the model prioritised the Juan de Fuca Strait and the central part of the Salish Sea (i.e. the Strait of Georgia and surrounding waters), whereas Puget Sound remains essentially unevaluated (though see Tables S1 and S2). Collated Canadian observations had relatively sparse coverage of Puget Sound (Fig. 2, Table 2), and adding more observations from American institutions therefore is a near-term priority. The reported biases in the final model are also a priority to diagnose and correct, especially near-surface fresh biases in summer months (e.g. Fig. 8c). Similar near-surface biases were reported in SalishSeaCast (Soontiens and Allen, 2017). The salinity bias is of particular concern as it may hinder the model's capability of representing circulation patterns. Evaluation of tides and the estuarine circulation is a particularly important task, as these are primary factors affecting deepwater renewal in the Salish Sea (Ebbesmeyer et al., 1989; MacCready et al., 2021). Once circulation is evaluated, one potentially promising application would be to use velocity fields from HOTSSea v1 for Lagrangian particle simulations (Hernández-Carrasco et al., 2020; Snauffer et al., 2014). Changes to regional-scale atmospheric patterns may have affected sea surface height and circulation patterns, which in turn may affect important ecosystem processes such as larval dispersal. A logical next step is to use data assimilation to combine information from dynamical simulation with observations to produce a reanalyses, with estimates for the oceanic fields that are maximally consistent with observations (Zaron, 2011). Data assimilation techniques are developing rapidly and show great promise for helping minimise model error. Finally, upgrading from NEMO v3.6 to NEMO v4.x is a priority, as new vertical mixing options and a wetting-and-drying scheme for intertidal areas hold potential for improving model skill in this domain (Madec et al., 2023).

Ultimately, we hope to extend HOTSSea further back in time, motivated by a need to capture the period prior to an oceanic regime shift that occurred circa 1977 that can be seen in the Nanoose station time series (Figs. 9, S4). The regime shift is of particular interest for fisheries-related research in the area (Beamish et al., 1999; Di Lorenzo et al., 2008; Mantua et al., 1997; Mantua and Hare, 2002; MC07). Despite various climate regime indices subsequently reverting in polarity, ocean temperatures may not have reverted. Coupling the physical model with a biogeochemical module is another potentially valuable avenue to explore, as integrating biogeochemistry into the hindcast would provide retrospective details of oxygen, nutrients, carbonate chemistry, aragonite saturation, and pH – all of which have changed since pre-industrial times in the Salish Sea (Jarníková et al., 2022). Secular ocean warming and increased seasonal variability have also had a quantifiable effect on oxygenation of deep fjord waters in the region (Jackson et al., 2021a), which may have affected the productivity or community composition of lower trophic levels (Johannessen et al., 2020). However, computational costs associated with traditional biogeochemical models are currently a challenge that would need to be overcome. The HOTSSea v1 reconstruction of temperature fields over depths should also prove useful for investigating the relative impact of pathogens and predation on fish. Warming ocean temperatures lead to greater vulnerability to pathogens and disease and thus to greater vulnerability to predation (Miller et al., 2014; Teffer et al., 2018), but concurrent increases in predator abundances make it difficult to determine whether predation is a primary or secondary mortality factor (Walters and Christensen, 2019). Available observational time series are mainly limited to surface waters, and HOTSSea v1 can help address this gap by providing ocean temperature fields at specific depths and areas occupied by fish.

In conclusion, HOTSSea v1 shows promise for improving our understanding of long-term physical changes occurring in the Salish Sea with relevance for fish, fisheries, and marine ecosystems. The model's performance with respect to salinity, temperature, decadal-scale trends, and temperature anomalies indicates HOTSSea v1 can support ecosystem research focused on dynamics that unfold over months, seasons, years, or decades. The model addresses significant gaps in historical observations and can help drive biogeochemical and ecosystem models aimed at revealing dominant drivers of ecological productivity (Hermann et al., 2023; Macias et al., 2014; Piroddi et al., 2021).