the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Reconciling surface deflections from simulations of global mantle convection
Conor P. B. O'Malley
Gareth G. Roberts
James Panton
Fred D. Richards
J. Huw Davies
Victoria M. Fernandes
Sia Ghelichkhan
The modern state of the mantle and its evolution on geological timescales are of widespread importance for the Earth sciences. For instance, it is generally agreed that mantle flow is manifest in topographic and drainage network evolution, glacio-eustasy, and the distribution of sediments. There are now a variety of theoretical approaches to predict histories of mantle convection and its impact on surface deflections. A general goal is to make use of observed deflections to identify Earth-like simulations and constrain the history of mantle convection. Several important insights into the role of radial and non-radial viscosity variations, gravitation, and the importance of shallow structure already exist. Here we seek to bring those insights into a single framework to elucidate the relative importance of popular modeling choices for predicted instantaneous vertical surface deflections. We start by comparing results from numeric and analytic approaches to solving the equations of motion that are ostensibly parameterized to be as similar as possible. Deflections predicted by such numeric and analytic models can vary by ∼ 10 %, and the difference increases to ∼ 25 % when viscosity is temperature-dependent. Including self-gravitation and the gravitational potential of the deflected surface is a relatively small source of discrepancy. However, spherical harmonic correlations between model predictions decrease dramatically with the removal of shallow structure to increasing depths and when radial viscosity structure is modified. The results emphasize the sensitivity of instantaneous surface deflections to density and viscosity anomalies in the upper mantle. They reinforce the view that a detailed understanding of lithospheric structure is crucial for relating mantle convective history to observations of vertical motions at Earth's surface.
- Article
(8703 KB) - Full-text XML
-
Supplement
(36291 KB) - BibTeX
- EndNote
Mantle convection plays a crucial role in Earth's evolution (e.g., Hager and Clayton, 1989; Parsons and Daly, 1983; Pekeris, 1935). It is well understood, for instance, that flow in the mantle is fundamental in the transfer of heat and chemicals from the deep Earth to the surface, in driving horizontal and vertical lithospheric motions (thus tectonic processes), and in magnetism via interactions with the core (e.g., Biggin et al., 2012; Davies et al., 2023; Foley and Fischer, 2017; Hoggard et al., 2016a; Holdt et al., 2022; Pekeris, 1935). In turn, many processes operating at or close to Earth's surface are impacted, including glacio-eustasy, magmatism, climate, sediment routing, natural resource distribution, drainage network evolution, and development of biodiversity (e.g., Bahadori et al., 2022; Ball et al., 2021; Braun, 2010; Chang and Liu, 2021; Hazzard et al., 2022; O'Malley et al., 2021; Salles et al., 2017; Stanley et al., 2021). Clearly, understanding the physical and chemical evolution of the mantle has broad implications. An important goal is to determine contributions to surface processes from the modern mantle and its history during, say, the last 100 million years.
Residual oceanic age–depth measurements, potential field data, seismic tomographic models, and melting histories of young mafic rocks are providing increasingly coherent observational insights into the modern and recent state of the mantle (e.g., Ball et al., 2022; Davies et al., 2023; Fichtner et al., 2009, 2013; Fichtner and Villaseñor, 2015; French and Romanowicz, 2015; Hoggard et al., 2016a; Holdt et al., 2022; Kaula, 1963; Lekić and Fischer, 2014; Priestley and McKenzie, 2013; Richards et al., 2023). Stratigraphic and geomorphic observations as well as magmatic histories provide clues about the history of mantle convection on geologic timescales (e.g., Al-Hajri et al., 2009; Czarnota et al., 2013; Flament et al., 2015; Fernandes et al., 2019; Fernandes and Roberts, 2021; Galloway et al., 2011; Gunnell and Burke, 2008; Gurnis et al., 2000; Hoggard et al., 2021; Lambeck et al., 1998; Morris et al., 2020; O'Malley et al., 2021; Stanley et al., 2021). Despite these advances, observations providing information about the history of mantle convection are sparse in places, especially within continental interiors and back through geologic time (see, e.g., Hoggard et al., 2021). Moreover, disentangling contributions from crustal, lithospheric, and sub-lithospheric processes to surface deflections remains challenging and controversial (see, e.g., Hoggard et al., 2021; Wang et al., 2022).
Theoretical approaches that retrodict histories of mantle convection can, in principle, be used to fill in spatiotemporal gaps in the observational record and disentangle contributions to surface observables from different geologic processes (e.g., Baumgardner, 1985; Bunge and Baumgardner, 1995; Davies et al., 2013; Flament et al., 2015; Ghelichkhan et al., 2021; Hager et al., 1985; Moucha and Forte, 2011; Steinberger and Antretter, 2006). Increasingly realistic geodynamic simulations can incorporate, for instance, plate motions; gravitation and deflection of gravitational potential fields; complex rheologies; viscosity laws that can include temperature, pressure, composition, grain size, and strain rate dependence; and assimilation of seismic tomographic information into flow solutions – resulting in a diverse array of retrodicted flow histories. Mineralogical phase changes, compressibility, different surface and core–mantle boundary slip conditions (e.g., no-slip, free-slip), chemical and thermal buoyancy, and plate motion constraints on mantle structure can also generate diverse predictions of mantle convection and resultant surface deflections (e.g., Baumgardner, 1985; Bunge et al., 2002, 2003; Corrieu et al., 1995; Crameri et al., 2012; Dannberg et al., 2017; Flament et al., 2014; Forte, 2007; Ghosh and Holt, 2012; Glišović and Forte, 2016; Hager and Clayton, 1989; Heister et al., 2017; Liu and Gurnis, 2008; Panasyuk et al., 1996; Ribe, 2007; Ricard, 2007; Tackley et al., 1993; Zhong et al., 2008; Zhou et al., 2018; Liu and King, 2019a).
Aside from the fundamental choice of governing equations and parameterizations underpinning simulations, mathematical and computational approaches to solve the equations of motion generate different predictions of surface deflections. These approaches sit within two broad families: numeric simulations (e.g., ASPECT, CitcomS, TERRA; Bangerth et al., 2023; Baumgardner, 1985; Zhong et al., 2000) and propagator-matrix-based, quasi-analytic techniques that can be solved in two or three dimensions, and, importantly for our purposes, spherically and spectrally (e.g., Colli et al., 2016; Hager and O'Connell, 1979; Parsons and Daly, 1983).
A challenge then is to establish whether observed surface deflections can be used to discriminate between theoretical predictions of mantle convection, and, in turn, identify models that generate realistic and testable retrodictions. In this study we are principally concerned with establishing similarities and sensitivities of predicted instantaneous vertical surface deflections. We focus on vertical motions for two reasons. First, inventories of measurements of uplift and subsidence – on timescales of mantle convection – now exist for most continents and could be compared to predictions from global simulations in future work (e.g., Fernandes and Roberts, 2021; Fernandes et al., 2024, and references therein). Secondly, many geodynamic simulations incorporate horizontal motions of the lithosphere, which limits their use as a comparator.
From an observational perspective, it would be useful to establish rules of thumb that quantify the sensitivity of surface deflections to choices made when predicting them. Many such rules are already well known from analytic and numeric solutions of the equations of motion (e.g., Colli et al., 2016; Hager and O'Connell, 1979; Holdt et al., 2022; Lees et al., 2020; Parsons and Daly, 1983). For instance, a suite of benchmark studies exist that compare predictions from numeric mantle convection simulations with analytic solutions (see, e.g., Bauer et al., 2019; Kramer et al., 2021; Zhong et al., 2008, and references therein). Those papers tend to focus on establishing the fidelity of numeric models. In contrast, our goals are to, first, understand how calculated deflections are impacted by the choice of methodology used to solve the equations of motion and, secondly, to establish sensitivities to popular assumptions incorporated into simulations. We want to know the extent to which an improved fit between predictions and observations reflects a more Earth-like density and viscosity structure versus modeling choices. Our thesis is that performing all tests in a self-consistent framework, as we do in this study, provides a straightforward way to collate insights into the sensitivities of predicted surface deflections and to simplify the comparison of predictions from different suites of models.
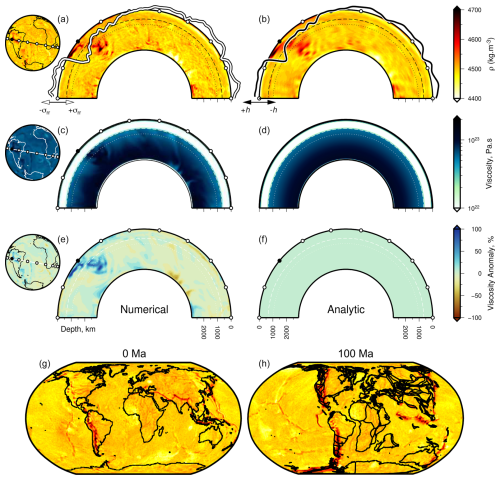
Figure 1Examples of mantle densities and viscosity used to calculate stresses and surface deflections numerically and analytically. (a) Great-circle slice (180°) through full-resolution, present-day density ρ, predicted by the numeric model TERRA with temperature-dependent viscosity (Model 11a; see Table 2 and body text); see the globe to left for the location. White circles are 20° intervals, the filled black circle indicates the orientation of the cross-section, the dashed line is the 660 km depth contour, the dotted line is the 1038 km depth contour at which depth ρ is plotted on the globe, and the white–black curve is the numeric prediction of surface normal stress σrr from Model 11a. (b) As (a) but the slice is through the spherical harmonic expansion of density structure to maximum degree l=50 (λ≈ 792 km; Model 11b); the black–white curve is surface deflection h, calculated using the (analytic) propagator matrix approach (Model 12). (c) As (a) but for a slice through the full-resolution viscosity structure of numeric model. (d) As (c) but for the mean (radial) viscosity structure, used along with the density structure shown in (b) to generate an analytic solution for surface deflection shown by the black–white curve atop (b). Panels (e) and (f) are as panels (c) and (d), but viscosity is expressed as a percentage anomaly with respect to the layer (radial) mean. (g, h) Predicted densities at 270 km depth at 0 and 100 Ma from the numeric model with viscosity independent of temperature (Model 1a). Extended results are shown in Fig. S1 in the Supplement. Plate motions and paleo-coastlines are from Merdith et al. (2021).
We start by exploring the consequences of solving the equations of motion numerically, using the TERRA software, and analytically, using the Ghelichkhan et al. (2021) propagator matrix algorithms (see Fig. 1 and the Supplement). We make use of the flexibility of numeric approaches by incorporating a variety of assumptions and parameterizations that are not amenable to analytic attack (e.g., temperature-dependent viscosity). All numeric simulations presented in this paper were driven by the plate motion history of Merdith et al. (2021, see Figs. 1g–h and S1). The models have a resolution of 60 km at their surface (see the Supplement for details of model setup and execution). We note that they do not directly assimilate information about the mantle from tomographic models. Ensuring that numeric simulations are accurate and stable means that computational burden is often considerable, and hence systematic exploration of parameter space remains challenging. In contrast, analytic approaches can yield calculated surface deflections that are (mathematically) accurate, whilst including features such as radial gravitation, with much less computational cost. Consequently, we make use of propagator matrix techniques to explore parameter space, examine benchmarks, and reproduce results. We establish the sensitivity of solutions to different parameterizations and approaches to solving the equations of motion.
There are at least two important considerations when solving the equations of motion analytically. First, solutions are only known to exist in the spherical harmonic domain for fluid bodies with radial viscosity (i.e., toroidal variations in viscosity cannot be included). Second, generating solutions in the spherical harmonic domain places practical limits on the spatial resolution of solutions. Consider that the number of spherical harmonic coefficients per degree is 2l+1, where l is degree, so for a given maximum degree L, there are (L+1)2 coefficients in total. For instance, when L=50 there are 2601 coefficients for each model. Also consider that spatial resolution increases approximately with the reciprocal of l (see Sect. 2.4). Incorporating all of the output from the numeric models (60 km at the surface) would require L≈ 880, with 776 161 coefficients, which is computationally challenging. Furthermore, observational constraints on mantle-related surface deflection are unlikely to be finer than the flexural wavelength of the overlying lithosphere, l≈ 50 (e.g., Holdt et al., 2022). With these limitations in mind, we compared surface deflections predicted using different approaches at the same resolution up to l=50 (see the Supplement and Sect. 2.5).
Most of the tests in this paper compare surface deflections calculated using the entirety of the model domains (i.e., from the core–mantle boundary – CMB – to Earth's surface). This approach simplifies like-for-like comparisons of model predictions and comparisons to increasingly complex scenarios. Since the central focus of this work is merely on quantifying contrasts in predicted instantaneous surface deflections that arise from choices made when simulating mantle convection, we wish, here, to avoid post hoc modifications (e.g., lithospheric flexure and crustal isostasy). We stress that the amplitudes of calculated deflections will then not necessarily reflect the amplitudes of true dynamic topography estimated from independent observations of, for example, oceanic age–depth residuals. In subsequent tests we examine the consequences of simply removing shallow structure, a widely used approach for estimating dynamic support from simulations (see, e.g., Flament et al., 2013; Wang et al., 2022).
With this framework in place we generate, compare, and contrast predicted surface deflections. The first suite of tests are purposefully simple, e.g., incompressible, constant gravitational acceleration (no self-gravitation or radial variation in gravitation) and have radial viscosity independent of temperature. Results are compared to estimates of sub-plate support from oceanic age–depth residuals with a view to quantifying corrections necessary to convert predicted instantaneous surface deflections into estimates of sub-plate support. We then systematically examine the impact of incorporating radial variations in gravitational acceleration, contribution to flow from deflection of the gravitational potential field, removal of shallow density structure, choice of surface and CMB slip conditions, inclusion of temperature-dependent viscosity, and amplification or reduction of viscosity and density anomalies in the upper and lower mantle (Sect. 4; Tables 2 and 3). A closed-loop modeling strategy is explored in which predicted surface deflections from these relatively complex models are compared to results from simpler reference models. Finally, a methodology for assessing effective contributions to surface topography from mantle anomalies is presented.
2.1 Equations governing predicted mantle convection
Theoretical predictions of surface displacements from mantle convection arise from the application of physical laws that take the form of conservation equations for mass, momentum, and energy (see, e.g., Hager and O'Connell, 1981; Parsons and Daly, 1983). Here, we solve those equations across a 3D spherical domain using the finite-element code TERRA (Baumgardner, 1985; Bunge and Baumgardner, 1995). Under this formulation, theoretical convection in an incompressible fluid can be expressed by the following three dimensionless equations (e.g., Baumgardner, 1985; Davies et al., 2013; McKenzie et al., 1974; Parsons and Daly, 1983). The first is the continuity condition for conservation of mass,
where u is the fluid velocity vector. Since the Prandtl number is likely to always be extremely large in this system – mantle viscosity is expected to be many orders of magnitude larger than the product of density and thermal diffusivity – inertial terms can be neglected (e.g., Parsons and Daly, 1983). The second is the equation of motion,
where
σ is the 3 × 3 stress tensor where the (radial) hydrostatic component balancing the reference density structure has been subtracted, ρ′ is the density difference due to temperature, α is the coefficient of thermal expansion; T is temperature; Tref is a radially varying reference temperature structure, which has a constant value in the mid-mantle and joins a cold thermal boundary layer near the surface and a hot one at the CMB, reaching the surface, Ts, and core–mantle boundary, TCMB, temperatures at the respective boundaries; and g is gravitational acceleration acting radially (see Table 1). This stress tensor σij is decomposed into deviatoric and lithostatic components:
where τij is the deviatoric stress tensor, p is dynamic pressure, and δij is the Kronecker delta function. The deviatoric stress tensor and the strain rate tensor, , are related by
where η is viscosity, and is the spatial partial derivative. By combining Eqs. (2), (4), and (5) we solve the equation of motion:
where g is the scalar value of g and δir is the Kronecker delta selecting the radial direction r.
We first examine predictions from models in which viscosity varies only with depth, i.e., , where η0 is reference viscosity (see Table 1), and ηr is a scaling factor dependent only on radius, plotted with model results as appropriate throughout this paper. We then include the temperature dependence of viscosity, i.e., , where
Dimensionless depth is , where = 2890 km, and dimensionless temperature is , where TCMB−Ts = 2700 K.
Finally, the heat transport equation is solved to ensure conservation of energy:
where κ is thermal diffusivity, H is internal heat generation, and Cp is specific heat capacity. See Table 1 for parameter values and units. Heat generation within the mantle depends on the distribution of radiogenic isotopes (e.g., Ricard, 2015). Concentrations of such elements can be tracked in TERRA using particles varying as a consequence of flow and melting (see, e.g., Panton et al., 2023; van Heck et al., 2016, for a full explanation). The bulk composition field, C, which varies between 0 and 1, is also tracked on particles and calculated for each of the finite elements in the model. The end-members represent completely depleted harzburgitic material (C=0) and fully enriched basaltic material (C=1). As a result, radiogenic heat production across the whole mantle volume varies, being ≈ 24 TW (5.8 × 10−12 W kg−1) at 1.2 Ga, and ∼ 18 TW (4.5 × 10−12 W kg−1) by 0 Ma. Simulations are initialized such that the average mantle composition is C=0.20 (Panton et al., 2023), and composition obeys the conservation equation:
2.2 Numerical modeling strategy
The Stokes equations described above are solved by the finite-element method on a series of stacked spherical shells composed of nodes based on a subdivision of a regular icosahedron, with an identical geometry for each shell when projected onto the CMB (see, e.g., Fig. 1 of Baumgardner, 1985). The radial spacing of consecutive shells is 45 km, which is the same as the mean horizontal spacing of the elements across the entire model domain. The stacking of identically partitioned shells leads to a finer mean horizontal resolution of ≈ 33 km at the CMB and a coarser resolution of ≈ 60 km at the surface. The surfaces of the uppermost elements in the shallowest shell lie at zero depth. To enable estimates of stress from these models to be directly compared with analytical solutions obtained from Green's functions across layer boundaries, the predicted values of deviatoric stress were calculated using the calculated velocities from the nearest shells using the interpolating linear shape functions of the underlying finite elements, while the dynamic pressure is calculated directly at the surface.
Each numerical model presented in this paper has two computational stages: “spin-up”, which is used to initialize the model, and the geologically more realistic “main” stage, from which we generate predictions of surface deflections. The spin-up stage includes 2.2 billion years of model runtime. It has the following conditions imposed to avoid sharp velocity and temperature gradients, as well as sudden reorganization of mantle flow when the main model starts. First, a free-slip condition is imposed at the surface such that horizontal velocities are free to vary. The radial (“vertical”') component of the mantle flow velocity at the surface, ur, is set to zero. While the radial velocity boundary condition is of the Dirichlet type, the horizontal free-slip boundary condition has no tangential restriction imposed on the flow velocity but rather on the tangential deviatoric stresses acting on the boundary (τrθ and τrϕ, where r, θ, and ϕ are the radial and two tangential directions, respectively), which are zero. Second, an initial, random white noise temperature field generated with power across spherical harmonic degrees 1–19 is inserted. Mean mantle temperature is initially 2000 K. Mantle convection arises naturally over the first 2 billion years of model runtime. A horizontal surface velocity condition is then applied to the surface for 200 Myr. These velocities are set to be equal to those at 1 Ga extracted from the reconstructions of Merdith et al. (2021). ur remains zero at the surface. The resultant mantle structure is used as the initial condition for the main model.
The main model routine predicts flow from 1 Ga to the present day. It includes an isothermal condition imposed at the surface, Ts = 300 K. Horizontal plate slip, applied in 1 Myr long stages, is prescribed using the plate reconstructions of Merdith et al. (2021); ur is still zero. Consequently, stirring by plate drift and slab sinking plays a role in driving mantle flow in these models. An isothermal condition is also imposed at the core–mantle boundary such that TCMB = 3000 K. A free-slip horizontal velocity boundary condition is imposed there. The radial boundary condition is ur=0. Horizontal components of slip are allowed to naturally emerge and evolve subject to lowermost mantle flow. Plume behavior is not artificially suppressed or instigated.
To ensure numerical stability and computational accuracy in these simulations, the reference viscosity, η0, is set to 4 × 1021 Pa s. This value is probably an order of magnitude greater than the viscosity of the actual upper mantle (e.g., Forte, 2007; Ghelichkhan et al., 2021; Mitrovica and Forte, 2004, and references therein). Consequently, flow velocities in the simulations are likely to be significantly slower than in actuality. An obvious cause for concern is that using actual (comparatively fast) plate velocities as surface boundary conditions atop a relatively slowly convecting “mantle” is likely to induce unrealistic flow. To address this issue, imposed plate velocities are scaled such that the root mean squared (rms) values of the actual applied velocities (≈ 5 cm yr−1 unscaled) match the rms values of surface velocities (≈ 2.5 cm yr−1) calculated during the spin-up phase (before plate velocities are imposed on the model) when the model mantle is convecting naturally and not being driven by surface velocities. The applied surface plate velocities are therefore scaled by a factor of 0.5 (i.e., ) in the simulations examined in this study. To ensure that volumetric fluxes through ridges and subduction zones are realistic, simulation runtimes are increased by a factor of 2; i.e., the 1 Myr long plate stages are run for twice their elapsed time (2 Myr), but at half the speed. All times stated throughout the rest of this paper refer to times re-scaled for real-world comparison, i.e., the actual age of the respective plate stage.
For the reference case (Model 1), these conditions lead to the density distributions shown in Fig. S1. Surface layer density anomalies occur only as a result of predicted compositional variation, since the surface temperature, Ts, is constant globally. This model represents the first of two reference numerical models examined in this contribution. It has the radial viscosity structure shown in Fig. 2c. Later, we investigate a second numerical model incorporating temperature-dependent viscosity (Eq. 7). We describe numeric and analytic approaches that use output from these models to calculate instantaneous surface deflections. Both approaches make use of spherical harmonics.
2.3 Deflections calculated using radial stresses from numeric simulations
Following Parsons and Daly (1983), surface deformation is estimated from numeric simulations of mantle convection by making use of the requirement that normal stress is continuous across the upper boundary of the solid Earth (see also McKenzie, 1977; Ricard, 2015). In other words, radial stresses generated by the solid Earth are required to be balanced by stresses generated by the overlying (oceanic or atmospheric) fluid. There are three contributions to normal stress at this boundary from the mantle: hydrostatic stress that would exist even in the absence of convection, dynamic stress arising from convection, and viscous stress which opposes fluid motion (see Sect. 2.1). To satisfy the continuity condition, these stresses must be balanced by those generated by the water (or air) column atop this boundary. If the pressure from the overlying column is hydrostatic, the resultant condition is
where σrr incorporates deviatoric viscous stresses generated by mantle convection and dynamic pressure (), obtained by solving Eq. (2). In practice, since values for this term are obtained by subtracting radial lithostatic stress from the total stress, values of σrr integrate to zero globally. gs is gravitational acceleration at Earth's surface, ρm is the mean density for the surficial layer, and ρw is the density of the overlying fluid (see Table 1). Note that we do not impose additional oceanic plate cooling, e.g., due to hydrothermal circulation at ridges. Cooling and subsequent subsidence, as well as passive return flow at ridges, arise naturally from the solution of the governing equations laid out in Sect. 2.1.
Surface deflection arising in response to predicted convective flow, h, is approximated by rearranging Eq. (10),
Deflections are estimated from radial stresses at times of interest (e.g., the present day) by rerunning one time step of the TERRA model. During that time step, a free-slip boundary condition, for which analytic approximations for surface deflection exist, is imposed instead of the plate-slip condition prescribed during the main model run routine (see Sect. 2.5; Ricard, 2015). The numeric models themselves apply a quasi-rigid condition at the surface, whereby flow is driven by estimates of real plate velocities (from Merdith et al., 2021), so the surface layers behave as a series of rigid, laterally mobile plates rather than a single rigid shell. We assess the accuracy of modifying boundary conditions in this way by converting calculated deflections into the spherical harmonic domain and comparing them to predictions generated using the analytic propagator matrix approach. The consistent boundary flux (CBF) method provides an alternative means to accurately calculate normal stresses (Zhong et al., 1993). Previous benchmarking with TERRA has shown mean errors of a few percent or less for surface deflection predictions at low harmonic degrees, l≤16 (Davies et al., 2013).
2.4 Calculated surface deflections in the spherical harmonic domain
Transforming stress, or surface deflections, calculated using numeric approaches into the frequency domain provides a straightforward means of comparing results to analytic solutions and of quantifying spectral power, i.e., the magnitude of the contribution to the total signal from different wavelengths. Since the models that we investigate are global in scope, we do so using spherical harmonics.
Any real, square-integrable function over the surface of the Earth can be described as a function of longitude θ and latitude ϕ by a linear combination of spherical harmonics of degree l and order m,
The spherical harmonic functions Ylm make up the natural orthogonal set of basis functions on the sphere, and flm represents the spherical harmonic coefficients. The spherical harmonic coefficients, flm, are calculated following the regularized least-squares methodology described in Hoggard et al. (2016a). The power at each degree, l, in the resultant interpolating function is given by
As an example, Fig. 2d shows a spherical harmonic expansion of the surface stress field predicted by Model 1 at 0 Ma (see Fig. 2a). We call this result Model 1b, and the original, full-resolution numerical result is referred to as Model 1a. The fidelity of the spherical harmonic expansion is demonstrated by the similarity of the maps and histograms shown in Fig. 2a–b and d–e.
Using the total power per degree convention, Hoggard et al. (2016a) derived a rule of thumb for estimating the power spectrum of dynamic topography (see their Supporting Information), , using the Kaula (1963) approximation for the long-wavelength gravity field of Earth as a function of l:
where G is the gravitational constant, M = 5.97 × 1024 kg is the mass of the Earth, and R≈ 6370 km is Earth's radius. The value of admittance, Z, between gravity and topography varies as a function of viscosity, as well as the depth and wavelength of internal density anomalies because of the depth and degree dependence of their respective sensitivity kernels (see, e.g., Colli et al., 2016, and references therein). However, in the upper mantle, which contributes most to surface deflections, the topography and gravity kernels are approximately proportional to one another across all but the lowest spherical harmonic degrees, even when this layer is assumed to be of relatively low viscosity (see, e.g., Colli et al., 2016, their Fig. 2). This behavior can explain why Hoggard et al. (2016a) found that assuming an average value of Z = 12 mGal km−1 provides a reasonable approximation of observed residual topographic trends; thus, we make use of that value in the remainder of the paper. Finally, it is useful to note that Jeans (1923) related spherical harmonic degree to wavelength λ, which at Earth's surface can be approximated via .
2.5 Surface deflections calculated analytically
The second methodology used to calculate surface deflection in response to mantle convection is the analytic propagator matrix technique (e.g., Craig and McKenzie, 1987; Gantmacher, 1959; Ghelichkhan et al., 2021; Parsons and Daly, 1983; Richards and Hager, 1984). The approach we take stems from the work of Hager and O'Connell (1981), who used Green's functions to solve the equations of motion in the spherical harmonic domain. Those solutions are used to generate sensitivity kernels that straightforwardly relate, for example, density or temperature anomalies in the mantle to surface deflections. The kernels are generated in the frequency domain and constructed such that surface deflection sensitivity to mantle (e.g., density) anomalies is calculated as a function of depth (or radius) and wavenumber. A global spherical harmonic implementation introduced by Hager et al. (1985) has been extended to include compressibility, the effect of warping of the gravitational potential by subsurface density distributions, and radial gravity variations calculated using radial mean density values (Corrieu et al., 1995; Forte and Peltier, 1991; Hager and O'Connell, 1981; Richards and Hager, 1984; Thoraval et al., 1994).
In this study, following Ghelichkhan et al. (2021), surface deflection for each spherical harmonic coefficient, hlm, is calculated in the spectral domain such that
Products of the sensitivity kernel, Al, and density anomalies, δρlm, of spherical harmonic degree l and order m are integrated with respect to the radius r between the core–mantle boundary and Earth's surface radii, RCMB and R, respectively. The sensitivity kernel is given by
where un(r) represents a set of poloidal variables, which are posed for the solution of the set of simultaneous equations by matrix manipulation such that
where , and y1 to y6 represent the spherical harmonic coefficients of radial velocity vr, lateral velocity vθ,ϕ, radial stress σrr, lateral stress σrθ,ϕ, gravitational potential V, and gravitational potential gradient , respectively (Hager and Clayton, 1989; Panasyuk et al., 1996). is the layer mean (l=0) density. The kernel Al includes both u1 and u3, two terms in the matrix solution to the governing equations that affect surface topography. They directly exert stress on the surface boundary (u1) and change the gravitational potential at the surface (u3). The functional forms of calculated sensitivity kernels depend on chosen radial viscosity profiles and boundary conditions (e.g., free-slip or no-slip; Parsons and Daly, 1983).
To quantify impacts of modeling assumptions and approaches used to solve the equations of motion we compare calculated surface deflections using the following metrics.
3.1 Euclidean comparisons of amplitudes
First, we calculate root mean squared difference, χ, between predicted surface deflections in the spatial domain,
where and are predicted surface deflections from the two models being compared. N is the number of points in the 1° × 1° gridded maps being compared (e.g., Fig. 3b; N = 65 341). The prefactor wϕ is proportional to cos ϕ, where ϕ is latitude and is included to correct biases in cell size with latitude; mean wϕ=1. This metric is closely associated with the mean vertical distance (L2-norm distance) between predicted and reference surfaces, i.e., . These metrics are sensitive to differences in amplitudes and locations of surface deflections.
3.2 Spectral correlation coefficients
Secondly, to aid comparisons of surface deflections as a function of scale they are converted into the frequency domain using spherical harmonics. The degree correlation spectrum, rl, is calculated using pyshtools v4.10 (Wieczorek and Meschede, 2018) such that
where f1 and f2 are the spherical harmonic coefficients of the two estimates of surface deflection being compared. They vary as a function of order m and degree l; . Sfafb is the cross-spectrum of the two functions fa and fb. We note that , and we calculate the mean value, , where L is total number of degrees. Thirdly, the correlation of the entirety of both functions can be estimated following Forte et al. (2015) such that
where ∗ indicates complex conjugation (see also Becker and Boschi, 2002; O'Connell, 1971). This metric is not sensitive to the amplitudes of surface deflections.
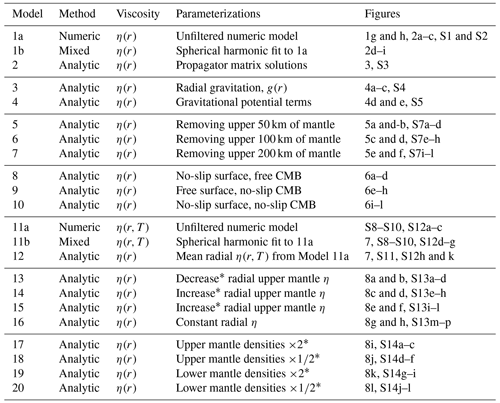
Table 2Summary of mantle convection simulations. The column labeled “Method” indicates surface deflections calculated using either “numeric” (i.e., from surface normal stresses calculated using TERRA) or “analytic” (i.e., propagator matrix) approaches; “mixed” indicates spherical harmonic fitting of surface stresses calculated using numeric code, enabling comparison with solutions to propagator matrix code. η(r) indicates models with radial viscosity (e.g., independent of temperature; Models 1–10). η(r,T) indicates models with temperature-dependent (therefore laterally varying) viscosity (Models 11–20); note that analytic Models 12–20 incorporate radial viscosity calculated using mean radial viscosity from Model 11a. An asterisk (∗) indicates with respect to Model 12. See Table 2, Sect. 4, and figures referred to in column 5 for details.
3.3 Comparing calculated power spectra
Finally, differences in power spectra between predicted and independent surface deflections are calculated such that
where L is the number of spherical harmonic degrees being considered. is the total power per degree of predicted surface deflections, where . and are total power per degree estimated independently from Kaula's law or residual oceanic age–depth measurements, respectively (Eq. 14; Hoggard et al., 2016b; Holdt et al., 2022). Once power spectra are calculated it is straightforward to compare their spectral slopes, which can be used to assess whether broad patterns of surface deflections are similar even if their amplitudes are not.
The models examined in this paper are summarized in Table 2. In terms of assumptions tested there are two families of models: those with viscosity independent of temperature (Models 1–10) and those with temperature-dependent viscosity (Models 11–20). We note that Models 12–20 incorporate mean radial viscosity from numeric Model 11a in which viscosity depends on temperature.
The two approaches used to solve the equations of motion are denoted as “numeric” and “analytic” in Table 2, which refers to solutions from the TERRA and propagator matrix code, respectively. Numeric results are generated by the direct conversion of TERRA-predicted surface stress to surface deflection as described in Sect. 2.3. To calculate analytic surface deflections, density and viscosity outputs from TERRA were first converted to respective spherical harmonic or radially averaged representations, which were then used as input for the propagator matrix code (Sect. 2.5). Results denoted as “mixed” in Table 2 are the numeric surface deflections calculated using the output from TERRA fit using spherical harmonics (thus aiding comparison to the analytic solutions; Sect. 2.4). We compare predicted deflections that arise from flow across entire model domains, i.e., from the CMB to the surface. Parameterizations of these models and resultant surface deflections are discussed in the following sections, with summary statistics given in Table 3.
Table 3Inter-model comparison of predicted surface deflections. Models being compared are summarized in Table 2. Metrics: root mean squared difference (χ, km), mean Euclidean (L2-norm) difference in predicted deflection (, km), and mean spherical harmonic correlation between models (). The standard deviation of rl distribution across degrees (sr) is also stated: note that rl≤1. All spherical harmonic representations of output from numeric code and generated by the propagator matrix code are expanded up to maximum degree, l=50. See the body of the text, figures referred to in column 6, and Table 2 for details.
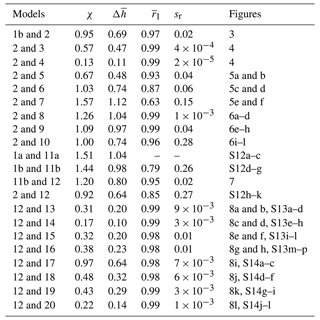
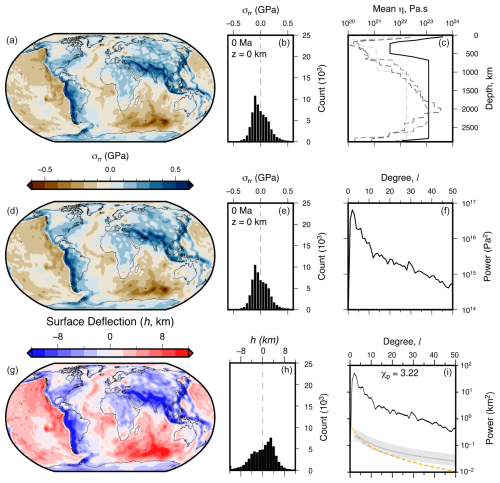
Figure 2Surface stresses and deflections from numeric simulation of mantle convection with spherical harmonic expansion up to degree 50. (a) Predicted present-day surface radial stress, σrr (Model 1a). (b) Histogram of values shown in (a). (c) The black line is the radial viscosity, η, structure used to drive Model 1a and thus produce the grid shown in panel (a). Gray dashed lines show alternative viscosity profiles of (from darkest to lightest) Mitrovica and Forte (2004) and Steinberger and Calderwood (2006), as well as μ1 and μ2 from Ghelichkhan et al. (2021). (d) Model 1b: spherical harmonic fit to Model 1a (panel a) up to maximum degree l = 50 (minimum wavelength λ≈ 792 km). (e) Histogram of values shown in panel (d). (f) Power spectrum – total power per degree – of the stress field shown in panel (d). (g) Spherical harmonic fit to surface deflections (Model 1b; up to degree l = 50). (h) Histogram of values shown in panel (g). (i) The black curve is the power spectrum of calculated water-loaded surface deflections (panel g), and the gray line and band show the expected dynamic topography from Kaula's rule using admittance Z = 12 ± 3 mGal km−1 (Kaula, 1963). The dashed orange line is the expected power spectrum for water-loaded residual topography (from Holdt et al., 2022) via the analytic solution of the special case in Eq. (15). χp is the root mean squared difference between calculated (black) and independent (orange and gray) surface deflection power (see Eq. 20). All histograms are weighted by latitude to correct to equal area. Figure S2 in the Supplement shows extended results including air-loaded deflections.
4.1 Models with viscosity independent of temperature
4.1.1 Reference models
Models 1 and 2 are the simplest explored in this paper. They were designed to be as similar as possible, with a view to quantifying differences and similarities arising solely from the choice of numeric or analytic methodology used to solve equations of motion and to calculate surface deflections. Model 1 was parameterized with the radial viscosity structure shown in Fig. 2c. Radial viscosities used in other geodynamic studies are shown alongside for comparison (Ghelichkhan et al., 2021; Mitrovica and Forte, 2004; Steinberger and Calderwood, 2006). Surface densities at 0 Ma are shown in Figs. 1 and S1. The mean uppermost density, ρm, at 0 Ma used to convert radial stresses into surface deflections (Eq. 11) is 4578 kg m−3. Note that this model is incompressible, and hence the reference density, ρ0 (Table 1), for the entire domain must approximate the average density of the whole mantle, which results in densities close to the surface tending to be larger than in actuality. Water loading is assumed (ρw = 1030 kg m−3). Figure 2d shows the spherical harmonic expansion of the surface stress field predicted by Model 1 at 0 Ma (see Fig. 2a). We call this result Model 1b. The original full-resolution numerical result is referred to as Model 1a.
Model 2 is the analytic model parameterized to be as similar as possible to Model 1. Its sensitivity kernel, generated assuming water loading, free-slip surface and CMB boundary conditions, and the radial viscosity profile shown in Fig. 2c, is shown in Fig. 3a. Values of the other parameters used to generate these kernels are stated in Table 1. Similar to many previous studies, the kernel indicates that surface deflections will be especially sensitive (across all degrees incorporated, l≤50) to density anomalies in the upper mantle (Parsons and Daly, 1983; Hager and Clayton, 1989; Ghelichkhan et al., 2021; Colli et al., 2016). Models 1 and 2 are used as points of reference for other more complex models explored in the remainder of this paper.
4.1.2 Gravitation
We start by incorporating more complex parameterizations of gravitation. Analytic Model 3 was parameterized in the same way as Model 2 with the addition of radial gravitation (following Hager and Clayton, 1989; Panasyuk et al., 1996, see Eq. 16). The solid curve in Fig. 4b shows the radial gravity function used to calculate surface deflections. It was generated using the density distribution produced by (the numerical) Model 1a (see Fig. S1) by calculating
where is layer mean density and Fcore is a factor chosen to account for core mass such that g = 9.8 m s−2 at the surface. This formulation is derived from Gauss's law assuming spherically symmetric density, combined with Newton's law of universal gravitation (Turcotte and Schubert, 2002).
Analytic Model 4 incorporates stress perturbations induced by deflections of the gravitational potential field. This model assumes g = 10 m s−2 everywhere, even within the deflected surface layer, as was the case for Models 1–2. Following Hager and Clayton (1989) and Panasyuk et al. (1996), when solving for surface deflection using propagator matrices, the effect on flow of the perturbation of gravitational potential is included via the u3 term in Eq. (17) (see also Ribe, 2007; Ricard, 2015). Sensitivity kernels for Models 3 and 4 are shown in Fig. S6 in the Supplement. TERRA simulations do not include this component in flow calculations (see Sect. 2.1).
4.1.3 Discarding shallow structure
The uppermost few hundred kilometers of geodynamic simulations are often not included in predictions of dynamic topography (see, e.g., Flament et al., 2013; Flament, 2019; Davies et al., 2019, and references therein). To quantify the impact of discarding shallow structure on our calculations, we examine differences in calculated surface deflections in the spatial and spherical harmonic domains. We present three tests, resulting in Models 5, 6, and 7, where structure shallower than 50, 100, and 200 km is removed from Model 2.
4.1.4 Changing boundary conditions
Up to now, we have only considered instantaneous analytic and numeric solutions for surface deflection where both the surface and CMB have free-slip conditions imposed (i.e., vertical component of flow velocity ur=0; horizontal components are allowed to freely vary). No gradient or Neumann constraint (e.g., on ) is imposed. This condition is generally deemed appropriate for the surface of the convecting mantle and CMB, since at both boundaries, cohesion within convecting mantle is thought to be much stronger than adhesion to the boundary. Analytic solutions for sensitivity kernels for propagator matrices also exist for no-slip Dirichlet boundary conditions, where horizontal components of u=0, which may be more appropriate when the Earth's lithosphere is implicitly included in mantle convection models, as is the case here (Parsons and Daly, 1983; Thoraval and Richards, 1997). Therefore, we test the effect of changing the surface boundary condition to no-slip on predicted surface deflections (Model 8). Although there is little reason to believe the adhesion of the CMB would be strong, for completeness, we test scenarios in which no- and free-slip conditions are assumed for the CMB and the surface, respectively (Model 9), and both have no-slip conditions (Model 10).
4.2 Models with temperature-dependent viscosity
We investigate the impact of including the temperature dependence of viscosity, η(r,T), on predicted global mantle flow in numeric models and on subsequent estimates of surface deflection. We do so by first generating numeric Model 11, which is identical to Model 1 in terms of all boundary conditions, initialization, and physical parameters, except for the fact that viscosity depends on temperature in the manner described by Eq. (7). In this model, ρm at 0 Ma is 4579 kg m−3, which is very similar to Model 1 (i.e., when viscosity is independent of temperature; Sect. 4.1.1).
The radial distribution of viscosity, but not its absolute value, plays a crucial role in determining the sensitivity of instantaneous solutions for surface deflections to density (and thermal) anomalies in the mantle (e.g., Parsons and Daly, 1983; Hager, 1984). Consequently, to assess the sensitivity of surface deflections to arbitrary changes to radial viscosity, η(r), we performed a suite of analytic tests. Since the analytic approaches require viscosity to only vary as a function of radius, we first test the impact of inserting layer mean viscosity from the present-day 3D temperature-dependent viscosity structure predicted by numeric Model 11 (Fig. S8 in the Supplement). This parameterization is used to generate (analytic) Model 12. The sensitivity kernel for Model 12 is shown in Fig. S11a in the Supplement.
We stress that the analytic solutions for instantaneous surface deflection for Models 3–10 (with adjusted parameters and boundary conditions) were simply compared with Model 2; no new numeric models were generated using TERRA. In contrast, the additional tests examined here correspond to a new TERRA model (Model 11) in which the temperature dependence of viscosity affects mantle flow across the entire runtime.
The sensitivity of surface deflections to arbitrary modification of upper and lower mantle viscosity and densities was then examined. Mean upper and lower mantle (radial) temperature-dependent viscosity was decreased or increased by an order of magnitude from that used to generate Model 12 (see the solid black curve in Fig. 8). The resultant impact on calculated surface deflections (Models 13–16) was quantified by comparison with results generated using reference Model 12 (Fig. S11). Figures 8i–l and S14 in the Supplement show the amplitudes of density anomalies in the upper and lower mantle that were systematically increased or decreased to generate Models 17–20. Similar to the tests shown in Figs. 8a–h and S13 in the Supplement, densities are amplified relative to Model 12. Radial viscosity is constant for each of these tests (black curve in Fig. 8a; i.e., the same as that used to generate Model 12).
5.1 Models with viscosity independent of temperature
5.1.1 Reference models: comparing numeric and analytic solutions
We first compare solutions generated from numeric Model 1a, with its spherical harmonic representation (Model 1b), and analytic Model 2, which were designed to be as similar as possible. Figure 1g and h show calculated densities that arise in Model 1a at 0 and 100 Ma (see Fig. S1 for extended results). The history of plate motions used to drive these models is also indicated in these figures. The resultant normal stresses, σrr, calculated at the surface of Model 1, and associated statistics are shown in Fig. 2a and b. By convention, positive stresses imply compression and hence downward surface deflection, which could manifest as lithospheric drawdown, i.e., subsidence. Prominent regions of positive stress anomalies in this model include locations atop imposed collision zones, where subduction naturally results, e.g., along the Pacific margin of South America. Negative stresses imply dilation and hence positive lithospheric support (i.e., surface uplift). Figure 2a shows dilatational stresses beneath southern Africa, for example, and along mid-oceanic ridges in the Indian Ocean and Atlantic Ocean.
Surface stresses calculated by fitting radial stresses from Model 1a with a global spherical harmonic interpolation up to maximum degree l=50, i.e., minimum wavelength of ≈ 800 km, are shown in Fig. 2d and e. The resultant power spectrum in terms of total power at each degree is shown in Fig. 2f. Aside from the lack of structure at degree 0, amplitudes decrease steadily with increasing degree (i.e., decreasing wavelength) and can be approximated by red noise. The spherical harmonic representation of deflections calculated by converting stress using Eq. (11), assuming water loading, is shown in Figs. 2g and S2. A comparison of calculated power spectra, expected surface deflection from Kaula's rule (Eq. 14), and spectra generated from observed residual ocean age–depth measurements is also included in Figs. 2 and S2 (Kaula, 1963; Hoggard et al., 2016a; Holdt et al., 2022). For completeness, surface deflections calculated assuming air loading are shown in Fig. S2f–j.
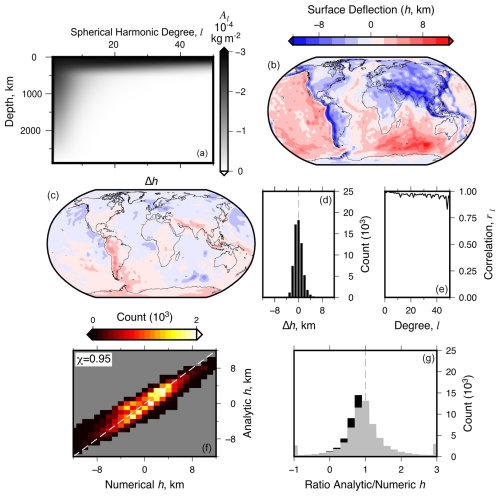
Figure 3Comparisons of numeric (Model 1b) and analytic (Model 2) estimations of surface deflections from models with identical parameterization. (a) Surface deflection sensitivity kernel Al as a function of spherical harmonic degree, l, and depth (Model 2). (b) Propagator matrix (analytic) solution for water-loaded surface deflection calculated using the sensitivity kernel shown in panel (a). Figure S3 in the Supplement shows extended results including power spectra and air-loaded deflections. (c) Difference, Δh, of surface deflections in Models 1b and 2. (d) Histogram of difference values shown in (c). (e) Spectral correlation coefficient, rl, between Models 1b and 2; Eq. (20). (f) Comparison of predicted surface deflections; χ is the root mean squared difference between predictions (Eq. 18), and the dashed gray line shows the 1:1 ratio. (g) The black bar is a histogram of ratios between analytic and numeric solutions for surface deflection as in (f). The dashed gray line is 1 (i.e., identical values). Gray bars are as the black bars, but for propagator matrix solution amplitudes scaled up by the optimal factor to fit the numeric solution (10 %). All histograms are weighted by latitude to correct to equal area.
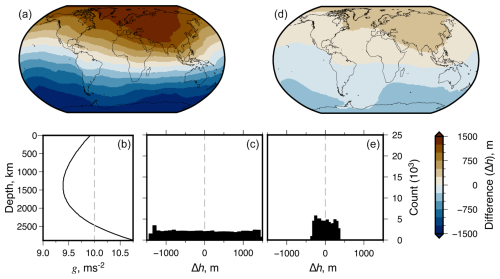
Figure 4Impact of self-gravitation (a–c) and gravitational potential of deflected surfaces (d–e) on surface deflections calculated analytically. In these tests surface deflections from models with different gravity parameterizations are compared to predictions from Model 2. (a) Difference between water-loaded surface deflections, Δh, calculated using the propagator matrix technique incorporating self-gravitation (Model 3; black curve in panel b) and g = 10 m s−2 (dashed line in panel b; Model 2). (c) Histogram of values in panel (a). (d, e) Differences in surface deflection from models with (Model 4) and without (Model 2) stress perturbations induced by the gravitational potential of the deflected surface. All histograms are weighted by latitude to correct to equal area, and they show the full extent of the results. Figures S4 and S5 in the Supplement show extended results including maps of calculated surface deflections.
Surface deflections predicted by Model 2 and its associated sensitivity kernel are shown in Fig. 3a and b. An expanded set of results including sensitivity kernels for water and air loading, as well as histograms of deflection and associated power spectra, are included in Fig. S3.
Deflections predicted from these numeric and analytic models are visually similar (see Figs. 2g and 3b). Absolute differences in amplitudes are greatest close to subduction zones (e.g., in South America and Asia; Fig. 3c). The differences are broadly normally distributed and centered on 0 (Fig. 3d). The spherical harmonic correlation between these models is high (close to 1 for all degrees; see Forte, 2007, Fig. 3e). The ratios between surface deflection values in these predictions indicate that analytic solutions tend to be damped compared to numeric solutions. This result is emphasized by the histogram shown in Fig. 3g. Multiplying amplitudes of deflections from the propagator matrix solutions by a factor of 1.1 brings them in line with the numeric solutions. These results indicate that the propagator matrix approach dampens solutions by ≈ 10 %. We note that power spectral slopes between Model 1b and 2 are similar (see Figs. 2i and S3d). These and all other results are discussed in Sect. 6.
5.1.2 Incorporating self-gravitation and gravitational potential of the deflected surface
Differences in deflections predicted by Model 2, which assumes constant g = 10 m s−2 across all radii, and Model 3, which incorporates self-consistent radial gravity profiles, are shown in Fig. 4a and c. Deviations in predicted instantaneous deflections are ∼ 10 % of maximum amplitudes predicted by Model 2 (see Table 3). Note that, for the viscosity structure used in these models, changing g in this way impacts sensitivity kernels most at low degrees l≲10 in the mid-mantle (see Figs. 2c, 3a, and S6).
We suggest that the broadly hemispherical differences in calculated deflections arise from three contributing factors. First, deviations in g between the two models are greatest in the mid-mantle, which, secondly, results in subtly different sensitivity kernels (see Fig. S6). In general, surface deflection sensitivity to mid-mantle structure is highest at low degrees (l = 1–3) and is almost negligible at higher degrees compared to contributions from near the surface. Thus it seems likely that differences between these kernels would manifest in low-degree (e.g., hemispherical) differences in surface deflections. Third, in the final time step, which is used to calculate deflections, a greater proportion of negative and positive deflections occurs in the Northern and Southern Hemisphere, respectively.
We note that incorporating radially varying gravitation into numeric simulations, which is not trivial, might materially impact calculated mantle flow fields and hence predictions of surface deflections (see, e.g., Zhong et al., 2008; Liu and King, 2019a).
As expected, induced differences in surface displacement predictions are much lower in magnitude when the gravitational potential of the deflected surface is included compared to when radial gravitation is incorporated (see Fig. 4a and d). We note that they are of the same order of magnitude as the geoid height anomalies predicted by these models. The mean Euclidean distance between the two predicted surfaces in Models 2 and 4 is only ∼ 110 m (compared to maximum amplitudes > 8 km), and the spherical harmonic correlation is very high across all degrees (see Table 3). Similar to the results for Model 3, the differences are concentrated at low spherical harmonic degree l. We stress that this test investigates the effect of the u3 term on the instantaneous solution for surface deflection (Eq. 5). It cannot be ruled out from this test that inclusion of the effect of gravitational potential field perturbation would result in greater differences across the entire model runtime of a numeric model, although it is unlikely (Zhong et al., 2008).

Figure 5Effect of removing shallow structure on surface deflections calculated analytically. Surface deflections in models with shallow structure removed are compared to those predicted by Model 2. (a) The black line shows the power spectra of predicted water-loaded surface deflection from the propagator matrix solution for Model 2 (Fig. 3b), but with the effect of the upper 50 km of the density anomaly structure ignored in the calculation (Model 5). The gray line and band show the expected dynamic topography from Kaula's rule using admittance Z = 12 ± 3 mGal km−1 (Kaula, 1963). The dashed orange line is the expected power spectrum for water-loaded residual topography from Holdt et al. (2022) via the analytic solution of the special case in Eq. (15). χp is the root mean squared difference between calculated (black) and independent (orange and gray) surface deflection power (see Eq. 20). (b) Spectral correlation coefficient, rl, of surface deflections in Models 5 and 2 (see Eq. 19). Inset: χ is the root mean squared difference in surface deflections of Models 5 and 2 (see Eq. 18). Panels (c) and (d) as well as (e) and (f) are as panels (a) and (b) but for depth cut-offs of 100 (Model 6) and 200 km (Model 7), respectively. Figure S7 in the Supplement shows extended results including maps of calculated surface deflections and differences with Model 2.
5.1.3 Excising shallow structure
As expected from examination of surface deflection sensitivity kernels (e.g., Fig. 3a), removal of shallow structure (Models 4–6) results in significantly reduced amplitudes of surface deflections (Fig. 5). Doing so results in amplitudes of power spectra that more closely align with independent estimates (Fig. 5a, c, and e). The reduction in differences is largely due to the fact that reference Model 2 has surface deflections that are much larger than independent estimates of dynamic topographic power across all degrees. We note that power spectral slopes for predicted surface deflection from Model 2 are close to those generated from Kaula's rule and observed oceanic residual depths (Figs. 2i, S2, and S3). Removing shallow structure steepens spectral slopes (i.e., reduces power at high degrees) beyond those expected from theoretical considerations (Kaula's rule) or observed from oceanic residual depths, akin to results from other work that excised shallow structure (e.g., Flament et al., 2013; Moucha et al., 2008; Steinberger, 2007). This result is emphasized by calculated spectral coherence, r, between deflections with and without shallow structure removed (see Fig. 5b, d, and f). While degree 1 and 2 structure remains coherent, coherence across degrees ≳ 20 decreases from ∼ 0.9 to as low as 0.5, which is the largest discrepancy between any models examined in this study (Fig. S7).
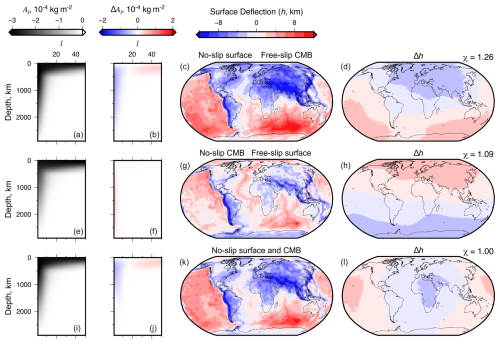
Figure 6Impact of free- and no-slip surface and core–mantle boundary conditions on surface deflections. This figure shows comparisons of surface deflections from models with different assumed boundary conditions and Model 2. (a) Water-loaded surface deflection sensitivity kernel Al for Model 8, which has a no-slip surface boundary condition but is otherwise parameterized the same as Model 2. l is the spherical harmonic degree. (b) Sensitivity kernel of Model 8 minus the sensitivity kernel of Model 2. Note that a positive difference implies reduced sensitivity compared to Model 2, and vice versa, since Al is negative. (c) Predicted water-loaded surface deflection for Model 8. (d) Difference between surface deflection predictions, Δh, for Model 8 and Model 2. Panels (e)–(h) are as (a)–(d) but for Model 9: free-slip surface boundary and no-slip CMB. Panels (i)–(l) are as (a)–(d) but for Model 10: no-slip surface and CMB boundaries.
5.1.4 Adjusting boundary conditions
Figure 6a, e, and i show predicted sensitivity kernels as a function of depth and degree for no-slip/free-slip, free-slip/no-slip, and no-slip/no-slip boundaries, respectively, where the first condition is the surface slip condition and the second the CMB slip condition. Differences in the sensitivity kernel for Model 2 (free-slip/free-slip; Fig. 3a) are shown in Fig. 6b, f, and j. Those panels, and Fig. 6c, g, and k, demonstrate that when the surface boundary condition is “no-slip”, there is decreased sensitivity to short-wavelength shallow structure and increased sensitivity to long-wavelength (low degree) structure across all depths. Figure 6d, h, and l reveal that induced misfit in the spatial domain is impacted to a greater degree than in tests of gravitation (Models 3 and 4), but not necessarily more severely than for removal of, say, the upper 200 km of density structure from surface deflection calculations. Spectral correlation with Model 2 is most severely impacted when both surface and CMB boundaries are no-slip, which is probably physically unrealistic (Model 7; see Table 3; Sect. 4.1.4).
5.2 Adjusting viscosity and density anomaly amplitudes
5.2.1 Temperature-dependent viscosity
Slices through the three-dimensional viscosity and density structure of Model 11, which incorporates temperature-dependent viscosity, are shown in Fig. 1a, c, and e. Density anomalies in the models parameterized with temperature-dependent viscosity are more localized (“sharper”) than in the models with viscosity independent of temperature (e.g., Model 1; see Figs. 7 and S8–S10 in the Supplement). This result is unsurprising since temperature-dependent viscosity provides stronger mechanical contrasts between cooler subducting regions and surrounding asthenosphere (see Figs. 1g–h and S9 in the Supplement; Zhong et al., 2000). Nonetheless, power spectra of calculated surface deflections are very similar (see Figs. S10j and 2i). This result emphasizes the relatively small impact incorporating temperature-dependent viscosity has on surface deflections compared to, say, excising shallow structure.
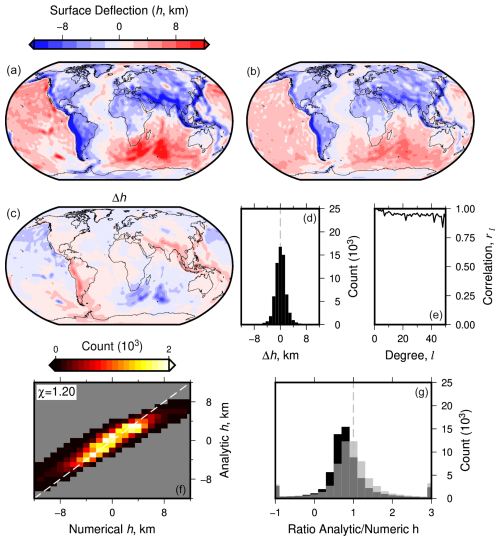
Figure 7Comparison of surface deflections calculated numerically (Model 11b) and analytically (Model 12) using results from a simulation with temperature-dependent viscosity. (a) Model 11b: spherical harmonic expansion of predicted present-day water-loaded surface deflection converted from stress output from the numeric model TERRA (Model 11a) to maximum degree l = 50. (b) Model 12: as (a) but for predictions made using the propagator matrix method. (c) Difference, Δh, between Models 11b and 12 (panels a and b). (d) Histogram of difference values shown in (c), weighted by latitude to correct to equal area. (e) Spectral correlation coefficient, rl, between predictions shown in panels (a) and (b); Eq. (19). (f) Numeric (Model 11b) versus analytic (Model 12) predictions of surface deflection; χ is the root mean squared difference between predictions (Eq. 18), and the dashed gray line is the 1:1 ratio. (g) Histogram of ratios between analytic and numeric solutions for surface deflection as in (f), weighted by latitude. The dashed gray line is 1 (i.e., identical values). Gray bars are as the black bars, but for propagator matrix solution amplitudes scaled up by the optimal factor to fit the numeric solution (24 %).
Calculated power spectra from analytic Model 12, which was generated using layer mean (radial) viscosity from Model 11a, reinforces this view (see Figs. S3a–d and S11a–d). Similar to the results obtained for models without temperature-dependent viscosity (Fig. 3), deflections calculated analytically are damped relative to numeric solutions (see Fig. 7f). The best-fit amplification factor to align propagator matrix and numeric solutions is 1.24 (24 %). The effect is greater than that seen when comparing Models 1b and 2 because of increased short-wavelength structure in Model 11 (see also Zhong et al., 2000). Nonetheless, spherical harmonic correlations, rl, are > 0.75 for all degrees examined (l≤50) and > 0.85 for most degrees. Cell-to-cell differences in surface deflections are broadly normally distributed and centered on zero (Fig. 7d).
A summary of comparisons between models with and without temperature-dependent viscosity is shown in Fig. S12 in the Supplement. Discrepancies in cell-to-cell deflections are broadly normally distributed and centered on zero, clustering along the 1:1 relationship with maximum χ=1.51 for unfiltered (numeric) models (Fig. S12b and c; see Table 3). Unsurprisingly, spherical harmonic fits and analytic results have tighter normal distributions and lower χ values. Correlation coefficients are > 0.75 for nearly all degrees in all comparisons.
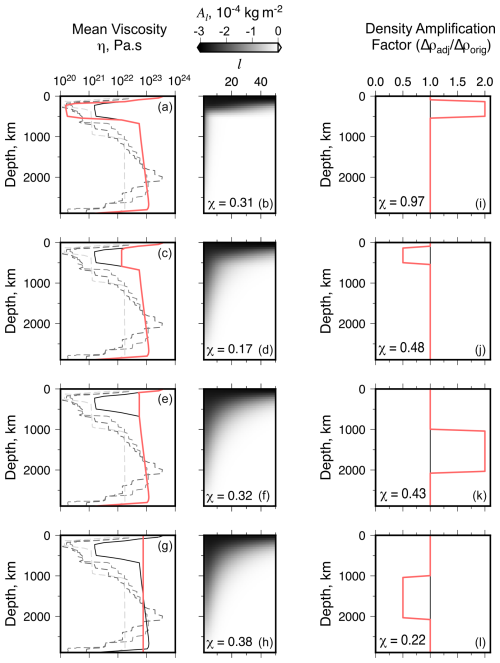
Figure 8Sensitivity of calculated analytic surface deflection to adjusted radial viscosity (a–h) and density anomalies (i–l). This figure shows comparisons of surface deflections calculated in models with modified viscosity and density to the results from Model 12 (see Table 1). (a) The black curve is the unadjusted prediction of present-day radial mean viscosity from Model 11, the red line is the adjusted radial profile with viscosity decreased by a factor of 10 between depths of ∼ 300–500 km (Model 13), and dashed gray lines show the viscosity profiles used in other studies (see Fig. 2). (b) Sensitivity kernel for the viscosity profile indicated by the red curve in panel (a); l is the spherical harmonic degree. The value of the root mean squared difference, χ, between calculated surface deflections for unadjusted and adjusted viscosity is stated (see Eq. 7). (c–h) Results from testing alternative radial viscosity (Models 14–16). Figure S13 shows extended results including maps of surface deflections and their differences. (i–l) Density anomalies (red line) adjusted by directly scaling spherical harmonic coefficients (l>0) up or down by a factor of 2 (Models 17 and 19: panels e and g) or 0.5 (Models 18 and 20: panels f and h). Viscosity structure applied in each case is the same as that used to generate Fig. 7b. Sensitivity kernels for surface deflections are not shown since they are invariant with respect to density anomalies, Δρ, depending only on viscosity structure. Figure S14 shows extended results including maps of surface deflections and their differences.
5.2.2 Sensitivity to upper and lower mantle viscosity and density anomalies
In order to explore the consequences of modified viscosity and density for calculated deflections we also systematically increased and decreased contrasts in the upper and lower mantle (Models 13–20) with respect to Model 12. Figure 8 summarizes the results, which include decreasing upper mantle viscosity by an order of magnitude, and shows the impact of using increasingly simple radial viscosity in analytic calculations. Calculated sensitivity kernels for the adjusted viscosity profiles demonstrate that decreasing upper mantle viscosity reduces the sensitivity of surface deflections to long-wavelength density structure, especially in the lower mantle (Figs. S13 and 8d, f, and h). Models 13–16 have broad similarities to reference Model 12 even when η(r) is drastically varied: average χ misfit = 0.17–0.38 km and rl > 0.97 across all degrees. These results emphasize that the viscosity adjustments we examined exert a relatively minor control on the amplitudes of instantaneous surface deflection (Table 3; see, e.g., Ghosh et al., 2010; Moucha et al., 2007; Lu et al., 2020). Of course changes in viscosity might impact the history of mantle convection and thus surface deflections.
In contrast, increasing (Model 17) or decreasing (Model 18) upper mantle densities is much more impactful on amplitudes of calculated surface deflections (see Figs. 8i–l and S14). For instance, increasing or decreasing upper mantle densities by a factor of 2 (relative to Model 12) results in χ values of 0.97 and 0.48, respectively. Modifying lower mantle densities has a much smaller impact on amplitudes of deflection (Models 18 and 19). Spherical harmonic correlation between models is approximately as good as for the radial viscosity tests (Models 13–16), which is to be expected since we do not vary locations of density anomalies here, only their amplitudes, and rl is insensitive to the amplitudes of the two results being compared. It is significant that mean vertical differences between Models 17–20 and 12 (i.e., χ and ) are higher than those calculated for Models 13–16 (in which viscosity is varied; see Table 3).
These results emphasize the relative sensitivity of instantaneous surface deflections to upper mantle density anomalies compared to, say, radial viscosity or lower mantle densities. Even quite large uncertainties in lower mantle density anomalies have relatively little impact on instantaneous surface deflections. These results reinforce the view that accounting for shallow (e.g., lithospheric and asthenospheric) densities is crucial when estimating surface deflection and dynamic topography from mantle convection simulations (e.g., Colli et al., 2016; Flament et al., 2013; Holdt et al., 2022; Wang et al., 2022).
6.1 Similarities of analytic and numeric solutions
In this paper we compare numeric and analytic predictions of instantaneous surface deflections generated by mantle convection simulations. First, we simply compared predictions from numeric and analytic approaches parameterized to be as similar as possible. In this test, the models were purposefully simple: viscosity is radial, models are incompressible, and models do not include self-gravitation or radial variation in g. Numeric solutions were transformed into the frequency (spherical harmonic) domain so that they could be compared with analytic solutions and so that power spectra could be directly compared at appropriate scales. The results show that, for parameterizations that are as similar as possible, amplitudes of analytic solutions are ≈ 10 % lower than numeric solutions (Fig. 3). If the numeric model incorporates temperature-dependent viscosity, this discrepancy increases to 25 % (Fig. 7). We interpret these results in two ways. First, once armed with viscosity and density fields, numeric and analytic approaches broadly yield similar estimates of surface deflections. Second, the relatively damped analytic solutions are a consequence of smoothing steps in the propagator matrix approach.
The smoothness of analytic solutions, and subsequent damping of topographic amplitudes, is perhaps surprising, given the fact that they are being compared with numeric models expanded into the spherical harmonic domain to the same maximum degree, l=50. However, the surface stresses used to generate Model 1a have full horizontal resolution (≈ 45 km) across depths, and only the surface layer is smoothed by spherical harmonic fitting to generate Model 1b. Therefore, Model 1b inherently contains some contribution from degrees ≥ 50 in the sense that finer-resolution density structure at depth could affect longer-wavelength flow nearer to the surface. In contrast, to generate the analytic solution (Model 2), the density structure of each layer of the model is smoothed, by expansion to maximum l=50, before integration of their contributions to surface deflection. The analytic solution would provide a better match to stress estimates from numeric models if such estimates were calculated using density structure smoothed to the same maximum l across all depths, which is currently challenging (see Sect. 1).
Nonetheless, the similarity of results indicates that the relatively low-cost propagator matrix approach can be used to explore the consequences of including additional model complexity. A systematic sweep of parameters, including radial gravitation (Fig. 4a–c) and gravitational potential field effects (Fig. 4d and e), indicates that their effects on surface deflection are relatively modest. A useful rule of thumb is that self-gravitation perturbs instantaneous surface deflections by O(1–10) % when compared to models with constant gravitational acceleration, and even less difference is observed at high degree (e.g., Ricard, 2015, their Sect. 7.02.2.5.2). Incorporating the effect of deflections of the gravitational potential field on flow has a modest impact on amplitudes of surface deflections at degrees 1–2, but overall it contributes even less than radial variation in g to surface deflections across the scales of interest. We note that incorporating full 3D self-gravitation in numeric simulations is challenging (see, e.g., Zhong et al., 2008; Liu and King, 2019b). Nonetheless, establishing its impact on the flow field over time, and the resultant impact on surface deflections, would be useful.
6.2 Importance of viscosity and shallow density anomalies for isolating dynamic support
Figure 8 demonstrates that even quite large (order of magnitude) variations in viscosity do not have much impact on instantaneous surface deflections when compared to, say, modified upper mantle density anomalies, which appears to agree with the results of Davies et al. (2019) (see also Flament, 2019; Steinberger et al., 2019). Assuming no-slip boundary conditions at Earth's surface may be appropriate for driving near-surface (lithospheric) flow throughout the main model runtime, but it less clear whether no- or free-slip boundary conditions are most appropriate for calculating instantaneous dynamic topography (see, e.g., Forte and Peltier, 1994; Thoraval and Richards, 1997). Nonetheless, all calculated sensitivity kernels in this study indicate that shallow density anomalies make significant contributions to surface topography regardless of viscosity profile or boundary conditions chosen (e.g., Fig. 3a; see also Colli et al., 2016; Parsons and Daly, 1983).
It is well known that disentangling contributions to Earth's surface topography from mantle convection, lithospheric isostasy, and flexure is important but not trivial (see, e.g., Davies et al., 2019; Cao and Liu, 2021; Fernandes and Roberts, 2021; Hoggard et al., 2021; Steinberger, 2016; Stephenson et al., 2021; Zhou and Liu, 2019; Wang et al., 2022). Previous studies simulating mantle convection have addressed this issue by discarding density anomalies in radial shells shallower than specified depths before calculating surface stresses (e.g., Spasojevic and Gurnis, 2012; Flament et al., 2013; Molnar et al., 2015). Similarly, analytic approaches have isolated contributions from the convecting mantle by only incorporating information from deep shells (e.g., Colli et al., 2018). This method has the advantage of effectively removing the effect of lithospheric cooling through time from surface deflection estimates. It also avoids the need to incorporate, say, realistic crustal or depleted lithospheric layers within the viscous flow parameterization. However, uncertain oceanic and continental lithospheric thicknesses mean that choosing appropriate cut-off depths is not simple.
Out of all the tests performed in this study, removing shallow structure resulted in the largest impact on predicted surface deflections. It modifies amplitudes of deflections, locations of uplift and subsidence, and degrees over which they are resolved, and it hence modifies power spectral scalings (Table 3, Fig. 5). Making quantitative predictions of dynamic topography from such an approach is fraught for at least two reasons. First, if the chosen depth is shallower than the lithosphere–asthenosphere boundary in places, plate and sub-plate contributions to topography will be entangled. Second, discarding deeper layers to ensure that all plate contribution is definitely avoided means that some contributions from asthenospheric flow will be missed. Thus, such a step is unlikely to be desirable if mantle flow models are to be used to understand, say, lithospheric vertical motions, or vice versa (see, e.g., Fig. 3a; Davies et al., 2019; Hoggard et al., 2016a). Given the calculated sensitivity kernels, excising layers in the upper few hundred kilometers is likely to result in predictions of surface deflections that are especially inaccurate at short wavelengths, i.e., high spherical harmonic degree. An alternative approach, which may be fruitful for future work, is the removal of structure based on appropriately calibrated plate models or globally averaged age-dependent density trends (e.g., Richards et al., 2020, 2023).
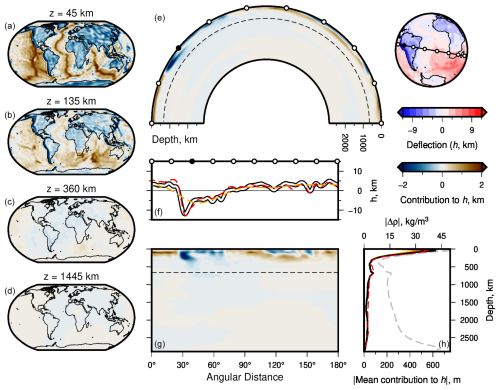
Figure 9Effective density and contributions from density anomalies to surface deflection. (a–d) Maps of the net contribution to present-day water-loaded surface deflection calculated using the propagator matrix approach (Model 12; see body text for details). Depth slices, z, at 45, 135, 360, and 1445 km depth incorporating all spherical harmonic degrees l and orders m, up to l = 50. (e) Great-circle slice (180°) showing contributions to surface deflection; the globe to the right shows the transect location and calculated surface deflection (Model 12). White circles indicate 20° intervals – note the filled black circle for orientation; the dashed line is the 660 km depth contour. (f) The white–black curve is the total surface deflection along the transect shown atop the globe in panel (e); the abscissa is aligned with panel (g), and the dashed orange line is the same but for maximum l = 10 (see Fig. S18 in the Supplement). The dashed red curve is the surface deflection from Model 2. (g) Cartesian version of panel (e); ordinate aligned with panel (h). (h) The dashed gray curve is the mean absolute value of density anomalies in Model 12 – see top axis for values. The black curve is the global mean amplitude (modulus) of the contribution from density structure in Model 12 to total surface deflection h across all l and m values; the orange line is the same but for maximum l = 10, and the dashed red line shows the results for Model 2 (see Sect. 6.3). See Figs. S15–S19 in the Supplement for extended results, demonstrating the sensitivity of surface deflections to the maximum spherical harmonic degree.
6.3 Assessing “effective” contributions to instantaneous deflections
The results emphasize the importance of considering the sensitivities of instantaneous vertical surface deflections to the location and scale of flow in the mantle. Taking inspiration from Hager and O'Connell (1981) and Parsons and Daly (1983), we calculate the net contributions from density anomaly structure to deflections as a function of radius, latitude, and longitude across all spherical harmonic degrees considered (i.e., l=1 to 50). Contributions to deflections from densities at particular radii r across all spherical harmonic degrees and orders for each latitude and longitude, (θ,ϕ), are calculated such that
where Δr is the radial width of the spherical shell included in the calculation (≈ 45 km for all shells from the surface to the CMB; see the Supplement) and Ylm represents spherical harmonic coefficients. Mean density anomalies, δρlm, within each shell at each latitude and longitude, as well as sensitivities Al at the top of each shell, are used to calculate he (see Sect. 2.5). Contributions at specific locations to surface deflections as a function of latitude and longitude, as well as spherical shell depth, are shown in Fig. 9 for Model 12 for . Results for lower maximum degrees are shown in the Supplement. Figure 9a–d show slices through effective density in the upper (at 45, 135, 360 km) and lower mantle (1445 km). A 180° cross-section showing effective densities from the core–mantle boundary to the surface beneath the Pacific to the Indian Ocean encompassing South America and southern Africa (the same transect as shown in Fig. 1) is shown in Fig. 9e. This figure again emphasizes the contribution of density anomalies in the upper mantle to surface deflections and the risks associated with discarding shallow structure when predicting dynamic topography.
6.4 Summary and future work
Encouragingly, although instantaneous surface deflections predicted by numeric and analytic solutions to the mantle convection equations of motion are sensitive to specific parameterizations, broadly coherent patterns emerge in similarly parameterized models. Calculated deflections are shown to be relatively insensitive to the methodologies used to solve the equations of motion. For instance, choosing to solve the equations of motion analytically or numerically changes calculated deflections by < 25 %, even when temperature-dependent viscosity is included throughout the duration of a simulation. Incorporated gravitational potential of deflected surfaces, self-gravitation, and viscosity anomalies each generate subtly different instantaneous surface deflections at the present day.
In contrast, removal of shallow structure produces much larger discrepancies between predicted deflections. For instance, surface deflections calculated using the entire modeling domain (core–mantle boundary to surface) have spectral slopes consistent with those of oceanic age–depth residuals; however, amplitudes are overpredicted by 1–2 orders of magnitude. In contrast, by not including the shallowest 200 km, calculated power spectra more closely match observed amplitudes, especially at spherical harmonic degrees > 10 (Fig. 5). However, the spectral slopes of predicted deflections are redder than for the oceanic residuals, which implies that a different approach to removing the contribution of lithospheric structure is required.
An obvious next step for accurately predicting modern dynamic support from mantle convection simulations is to incorporate accurate information about lithospheric structure from, for instance, tomographic models (e.g., Priestley and McKenzie, 2013; Richards et al., 2020). Another useful next step is to establish the sensitivity of surface deflections to time-dependent parameters that impact predicted flow histories, including plate motions. The results in this paper indicate that comparing predicted and observed surface deflections, combined with knowledge of lithospheric structure, could be used to identify optimal models.
Finally, the body of geologic and geomorphologic observations that could be used to test predicted histories of surface deflections from mantle convection simulations has grown substantially in the last decade (e.g., uplift and subsidence histories; Sect. 1; see, e.g., Hoggard et al., 2021, and references therein). A suite of other geologic and geophysical observables are also predicted by, or can be derived from, such simulations (e.g., mantle temperatures, heat flux, geoid, seismic velocities, true polar wander). Using them alongside histories of surface deflections to identify optimal simulations is an obvious avenue for future work (e.g., Ball et al., 2021; Lau et al., 2017; Panton et al., 2023; Richards et al., 2023). Using such data and the methodologies explored in this paper may be a fruitful way of identifying optimal simulations from the considerable inventory that already exists.
This study is concerned with quantifying sensitivities and uncertainties of Earth's surface deflections that arise in simulations of mantle convection. Calculated sensitivities of instantaneous deflection of Earth's surface to mantle density structure emphasize the importance of accurate mapping of the upper mantle. Surface deflections are somewhat sensitive to the distribution of viscosity throughout the mantle, especially to the locations and scales of density anomalies in the upper mantle. The largest discrepancies between predicted deflections seen in this study are generated when upper mantle structure is excised or altered. Doing so changes both the amplitude and distribution of calculated deflections, modifying their power spectral slopes. These results emphasize the importance of incorporating accurate models of lithospheric structure in the calculation of sub-plate support of topography and also the need to accurately determine plate contributions to topography. In contrast, the choices of methodology to estimate surface deflections – analytic or numeric – or boundary conditions are relatively small sources of uncertainty. Similarly, assumed gravitational profiles and temperature dependence of viscosity are relatively minor contributors to uncertainty given reasonable, Earth-like parameterizations. Nonetheless, these parameterizations may impact surface deflections through their role in determining how upper mantle flow evolves through geologic time. A fruitful next step could be to use the approaches developed in this paper, in combination with careful isolation of plate cooling signatures from surface deflection predictions, to test mantle convection simulations using the existing and growing body of geologic, geomorphologic, and geophysical observations.
The propagator matrix code is archived on Zenodo with the following DOI: https://doi.org/10.5281/zenodo.12696774 (Ghelichkhan, 2024); it has a CC BY 4.0 license. Radial stresses, spherical harmonic coefficients for density fields, full density fields, and viscosity profiles generated using the TERRA mantle convection simulation code are archived on Zenodo with the following DOI: https://doi.org/10.5281/zenodo.12704925 (Roberts et al., 2024). The TERRA version and system architecture used are as follows: branch – volatiles/branch, commit number 4c3ce53, system architecture – HPE Cray EX, 128 cores, 64 × dual AMP EPYC 7742 64-core. TERRA is a Fortran code built with G-Fortran. The origin of TERRA predates now widely accepted software licensing procedures; it cannot be made open-source. Nonetheless, the TERRA development team welcomes collaboration and advises interested parties to contact J. Huw Davies (daviesjh2@cardiff.ac.uk) or H.-Peter Bunge (bunge@lmu.de).
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-17-9023-2024-supplement.
Conceptualization: GGR. Formal analysis: CPBO'M, VMF, JP. Funding acquisition: GGR, JHD. Investigation: CPBO'M, GGR, JP, FDR, JHD, VMF, SG. Methodology: CPBO'M, GGR, JHD, SG, JP, SG. Supervision: GGR, JHD. Validation: CPBO'M, GGR. Visualization: CPBO'M, GGR. Writing (original draft preparation): GGR, CPBO'M. Writing (review and editing): GGR, CPBO'M, JHD, FDR, JP, VMF, SG.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
We thank Andrew Biggin, Hamish Brown, Christopher Davies, Ana Ferreira, Megan Holdt, Peter Japsen, Paula Koelemeijer, Fergus McNab, Robert Myhill, and Jamie Ward for helpful discussions. We also thank Nicolas Flament and Bernhard Steinberger for helping us to clarify our thesis. Figures were produced using GMT6 (Wessel et al., 2019).
Conor P. B. O'Malley, James Panton, and Victoria M. Fernandes were supported by the Natural Environment Research Council (grant nos. NE/T012501/1 and NE/T012633/1).
This paper was edited by Boris Kaus and reviewed by Nicolas Flament and Bernhard Steinberger.
Al-Hajri, Y., White, N., and Fishwick, S.: Scales of transient convective support beneath Africa, Geology, 37, 883–886, https://doi.org/10.1130/G25703A.1, 2009. a
Bahadori, A., Holt, W. E., Feng, R., Austermann, J., Loughney, K. M., Salles, T., Moresi, L., Beucher, R., Lu, N., Flesch, L. M., Calvelage, C. M., Rasbury, E. T., Davis, D. M., Potochnik, A. R., Ward, W. B., Hatton, K., Haq, S. S. B., Smiley, T. M., Wooton, K. M., and Badgley, C.: Coupled influence of tectonics, climate, and surface processes on landscape evolution in southwestern North America, Nat. Commun., 13, 1–18, 2022. a
Ball, P. W., White, N. J., Maclennan, J., and Stephenson, S. N.: Global Influence of Mantle Temperature and Plate Thickness on Intraplate Volcanism, Nat. Commun., 12, 1–13, https://doi.org/10.1038/s41467-021-22323-9, 2021. a, b
Ball, P. W., Duvernay, T., and Davies, D. R.: A coupled geochemical–geodynamic approach for predicting mantle melting in space and time, Geochem. Geophy. Geosy., 23, 1–31, https://doi.org/10.1029/2022gc010421, 2022. a
Bangerth, W., Dannberg, J., Fraters, M., Gassmoeller, R., Glerum, A., Heister, T., Myhill, R., and Naliboff, J.: ASPECT v2.5.0, Zenodo [code], https://doi.org/10.5281/zenodo.8200213, 2023. a
Bauer, S., Huber, M., Ghelichkhan, S., Mohr, M., Rüde, U., and Wohlmuth, B.: Large-scale simulation of mantle convection based on a new matrix-free approach, J. Comput. Sci.-Neth, 31, 60–76, https://doi.org/10.1016/j.jocs.2018.12.006, 2019. a
Baumgardner, J. R.: Three-dimensional treatment of convective flow in the Earth's mantle, J. Stat. Phys., 39, 501–511, https://doi.org/10.1007/BF01008348, 1985. a, b, c, d, e, f
Becker, T. W. and Boschi, L.: A comparison of tomographic and geodynamic mantle models, Geochem. Geophy. Geosy., 3, 1–48, https://doi.org/10.1029/2001GC000168, 2002. a
Biggin, A. J., Steinberger, B., Aubert, J., Suttie, N., Holme, R., Torsvik, T. H., Van Der Meer, D. G., and Van Hinsbergen, D. J.: Possible links between long-term geomagnetic variations and whole-mantle convection processes, Nat. Geosci., 5, 526–533, https://doi.org/10.1038/ngeo1521, 2012. a
Braun, J.: The many surface expressions of mantle dynamics, Nat. Geosci., 3, 825–833, https://doi.org/10.1038/ngeo1020, 2010. a
Bunge, H.-P. and Baumgardner, J. R.: Mantle convection modeling on parallel virtual machines, Comput. Phys., 9, 207–215, https://doi.org/10.1063/1.168525, 1995. a, b
Bunge, H.-P., Richards, M. A., and Baumgardner, J. R.: Mantle-circulation models with sequential data assimilation: Inferring present-day mantle structure from plate-motion histories, Philos. T. R. Soc. A, 360, 2545–2567, https://doi.org/10.1098/rsta.2002.1080, 2002. a
Bunge, H.-P., Hagelberg, C. R., and Travis, B. J.: Mantle circulation models with variational data assimilation: inferring past mantle flow and structure from plate motion histories and seismic tomography, Geophys. J. Int., 152, 280–301, https://doi.org/10.1046/j.1365-246X.2003.01948.x, 2003. a
Cao, Z. and Liu, L.: Origin of Three-Dimensional Crustal Stress Over the Conterminous United States, J. Geophys. Res.-Sol. Ea., 126, e2021JB022137, https://doi.org/10.1029/2021JB022137, 2021. a
Chang, C. and Liu, L.: Investigating the formation of the Cretaceous Western Interior Seaway using landscape evolution simulations, GSA Bulletin, 133, 347–361, https://doi.org/10.1130/B35653.1, 2021. a
Colli, L., Ghelichkhan, S., and Bunge, H.-P.: On the ratio of dynamic topography and gravity anomalies in a dynamic Earth, Geophys. Res. Lett., 43, 2510–2516, https://doi.org/10.1002/2016GL067929, 2016. a, b, c, d, e, f, g
Colli, L., Ghelichkhan, S., Bunge, H.-P., and Oeser, J.: Retrodictions of Mid Paleogene mantle flow and dynamic topography in the Atlantic region from compressible high resolution adjoint mantle convection models: Sensitivity to deep mantle viscosity and tomographic input model, Gondwana Res., 53, 252–272, https://doi.org/10.1016/j.gr.2017.04.027, 2018. a
Corrieu, V., Thoraval, C., and Ricard, Y.: Mantle dynamics and geoid Green functions, Geophys. J. Int., 120, 516–523, https://doi.org/10.1111/j.1365-246X.1995.tb01835.x, 1995. a, b
Craig, C. H. and McKenzie, D.: Surface deformation, gravity and the geoid from a three-dimensional convection model at low Rayleigh numbers, Earth Planet. Sc. Lett., 83, 123–136, https://doi.org/10.1016/0012-821X(87)90056-2, 1987. a
Crameri, F., Schmeling, H., Golabek, G. J., Duretz, T., Orendt, R., Buiter, S. J., May, D. A., Kaus, B. J., Gerya, T. V., and Tackley, P. J.: A comparison of numerical surface topography calculations in geodynamic modelling: An evaluation of the `sticky air' method, Geophys. J. Int., 189, 38–54, https://doi.org/10.1111/j.1365-246X.2012.05388.x, 2012. a
Czarnota, K., Hoggard, M. J., White, N., and Winterbourne, J.: Spatial and temporal patterns of Cenozoic dynamic topography around Australia, Geochem. Geophy. Geosy., 14, 634–658, https://doi.org/10.1029/2012GC004392, 2013. a
Dannberg, J., Eilon, Z., Faul, U., Gassmöller, R., Moulik, P., and Myhill, R.: The importance of grain size to mantle dynamics and seismological observations, Geochem. Geophy. Geosy., 18, 3034–3061, https://doi.org/10.1002/2017GC006944, 2017. a
Davies, D. R., Davies, J. H., Bollada, P. C., Hassan, O., Morgan, K., and Nithiarasu, P.: A hierarchical mesh refinement technique for global 3-D spherical mantle convection modelling, Geosci. Model Dev., 6, 1095–1107, https://doi.org/10.5194/gmd-6-1095-2013, 2013. a, b, c
Davies, D. R., Valentine, A. P., Kramer, S. C., Rawlinson, N., Hoggard, M. J., Eakin, C. M., and Wilson, C. R.: Earth's multi-scale topographic response to global mantle flow, Nat. Geosci., 12, 845–850, https://doi.org/10.1038/s41561-019-0441-4, 2019. a, b, c, d
Davies, D. R., Ghelichkhan, S., Hoggard, M. J., Valentine, A. P., and Richards, F. D.: Observations and Models of Dynamic Topography: Current Status and Future Directions, chap. 11, in: Dynamics of Plate Tectonics and Mantle Convection, edited by: Duarte, J., Elsevier, Amsterdam (Netherlands), Oxford (UK), Cambridge (MA, USA), https://doi.org/10.1016/B978-0-323-85733-8.00017-2, pp. 223–269, 2023. a, b
Fernandes, V. M. and Roberts, G. G.: Cretaceous to Recent net continental uplift from paleobiological data: Insights into sub-plate support, GSA Bulletin, 133, 1–20, https://doi.org/10.1130/b35739.1, 2021. a, b, c
Fernandes, V. M., Roberts, G. G., White, N., and Whittaker, A. C.: Continental-Scale Landscape Evolution: A History of North American Topography, J. Geophys. Res.-Earth, 124, 1–34, https://doi.org/10.1029/2018jf004979, 2019. a
Fernandes, V. M., Roberts, G. G., and Richards, F.: Testing Mantle Convection Simulations With Paleobiology and Other Stratigraphic Observations: Examples From Western North America, Geochem. Geophy. Geosy., 25, e2023GC011381, https://doi.org/10.1029/2023GC011381, 2024. a
Fichtner, A. and Villaseñor, A.: Crust and upper mantle of the western Mediterranean – Constraints from full-waveform inversion, Earth Planet. Sc. Lett., 428, 52–62, https://doi.org/10.1016/j.epsl.2015.07.038, 2015. a
Fichtner, A., Kennett, B. L. N., Igel, H., and Bunge, H.-P.: Full seismic waveform tomography for upper-mantle structure in the Australasian region using adjoint methods, Geophys. J. Int., 179, 1703–1725, https://doi.org/10.1111/j.1365-246X.2009.04368.x, 2009. a
Fichtner, A., Trampert, J., Cupillard, P., Saygin, E., Taymaz, T., Capdeville, Y., and Villaseñor, A.: Multiscale full waveform inversion, Geophys. J. Int., 194, 534–556, https://doi.org/10.1093/gji/ggt118, 2013. a
Flament, N.: Present-day dynamic topography and lower-mantle structure from palaeogeographically constrained mantle flow models, Geophys. J. Int., 216, 2158–2182, https://doi.org/10.1093/gji/ggy526, 2019. a, b
Flament, N., Gurnis, M., and Muller, R. D.: A review of observations and models of dynamic topography, Lithosphere, 5, 189–210, https://doi.org/10.1130/L245.1, 2013. a, b, c, d, e
Flament, N., Gurnis, M., Williams, S., Seton, M., Skogseid, J., Heine, C., and Dietmar Müller, R.: Topographic asymmetry of the South Atlantic from global models of mantle flow and lithospheric stretching, Earth Planet. Sc. Lett., 387, 107–119, https://doi.org/10.1016/j.epsl.2013.11.017, 2014. a
Flament, N., Gurnis, M., Müller, R. D., Bower, D. J., and Husson, L.: Influence of subduction history on South American topography, Earth Planet. Sc. Lett., 430, 9–18, https://doi.org/10.1016/j.epsl.2015.08.006, 2015. a, b
Foley, S. F. and Fischer, T. P.: An essential role for continental rifts and lithosphere in the deep carbon cycle, Nat. Geosci., 10, 897–902, https://doi.org/10.1038/s41561-017-0002-7, 2017. a
Forte, A. M.: Constraints on Seismic Models from Other Disciplines – Implications for Mantle Dynamics and Composition, chap. 1.23, in: Seismology and the Structure of the Earth, edited by: Romanowicz, B. and Dziewonski, A., Elsevier B. V., Amsterdam, https://doi.org/10.1016/B978-044452748-6.00027-4, pp. 805–858, 2007. a, b, c
Forte, A. M. and Peltier, R.: Viscous Flow Models of Global Geophysical Observables 1. Forward Problems, J. Geophys. Res., 96, 20131–20159, https://doi.org/10.1029/91JB01709, 1991. a
Forte, A. M. and Peltier, W. R.: The Kinematics and Dynamics of Poloidal-Toroidal Coupling in Mantle Flow: The Importance of Surface Plates and Lateral Viscosity Variations, Adv. Geophys., 36, 1–119, https://doi.org/10.1016/S0065-2687(08)60537-3, 1994. a
Forte, A. M., Simmons, N. A., and Grand, S. P.: Constraints on Seismic Models from Other Disciplines – Constraints on 3-D Seismic Models from Global Geodynamic Observables: Implications for the Global Mantle Convective Flow, in: Treatise on Geophysics, Second Edition, vol. 1, Elsevier, https://doi.org/10.1016/B978-0-444-53802-4.00028-2, pp. 853–907, 2015. a
French, S. W. and Romanowicz, B.: Broad plumes rooted at the base of the Earth's mantle beneath major hotspots, Nature, 525, 95–99, https://doi.org/10.1038/nature14876, 2015. a
Galloway, W. E., Whiteaker, T. L., and Ganey-Curry, P.: History of Cenozoic North American drainage basin evolution, sediment yield, and accumulation in the Gulf of Mexico basin, Geosphere, 7, 938–973, https://doi.org/10.1130/GES00647.1, 2011. a
Gantmacher, F. R.: The Theory of Matrices, Chelsea Publishing Company, New York, ISBN 9780821813935, 1959. a
Ghelichkhan, S.: Propagator Matrix Code for Calculating Dynamic Topography (v0.0.1), Zenodo [code], https://doi.org/10.5281/zenodo.12696774, 2024. a
Ghelichkhan, S., Bunge, H.-P., and Oeser, J.: Global mantle flow retrodictions for the early Cenozoic using an adjoint method: Evolving dynamic topographies, deep mantle structures, flow trajectories and sublithospheric stresses, Geophys. J. Int., 226, 1432–1460, https://doi.org/10.1093/gji/ggab108, 2021. a, b, c, d, e, f, g, h
Ghosh, A. and Holt, W. E.: Plate Motions and Stresses from Global Dynamic Models, Science, 335, 838–843, https://doi.org/10.1126/science.1214209, 2012. a
Ghosh, A., Becker, T. W., and Zhong, S. J.: Effects of lateral viscosity variations on the geoid, Geophys. Res. Lett., 37, 2–7, https://doi.org/10.1029/2009GL040426, 2010. a
Glišović, P. and Forte, A. M.: A new back-and-forth iterative method for time-reversed convection modeling: Implications for the Cenozoic evolution of 3-D structure and dynamics of the mantle, J. Geophys. Res.-Sol. Ea., 121, 4067–4084, https://doi.org/10.1002/2016JB012841, 2016. a
Gunnell, Y. and Burke, K.: The African Erosion Surface: A Continental-Scale Synthesis of Geomorphology, Tectonics, and Environmental Change over the Past 180 Million Years, Memoir of the Geological Society of America, 201, 1–66, https://doi.org/10.1130/2008.1201, 2008. a
Gurnis, M., Mitrovica, J. X., Ritsema, J., and Van Heijst, H.-J.: Constraining mantle density structure using geological evidence of surface uplift rates: The case of the African Superplume, Geochem. Geophy. Geosy., 1, 1–35, https://doi.org/10.1029/1999GC000035, 2000. a
Hager, B. H.: Subducted Slabs and the Geoid: Constraints on Mantle Rheology and Flow, J. Geophys. Res., 89, 6003–6015, 1984. a
Hager, B. H. and Clayton, R. W.: Constraints on the Structure of Mantle Convection Using Seismic Observations, Flow Models, and the Geoid, chap. 9, in: Mantle Convection: Plate Tectonics and Global Dynamics, edited by Peltier, W. R., Gordon and Breach Science Publishers, New York, pp. 657–763, ISBN 9780677221205, 1989. a, b, c, d, e, f
Hager, B. H. and O'Connell, R. J.: Kinematic Models of Large-Scale Flow in the Earth's Mantle, J. Geophys. Res., 84, 1031–1048, 1979. a, b
Hager, B. H. and O'Connell, R. J.: A Simple Global Model of Plate Dynamics and Mantle Convection, J. Geophys. Res., 86, 4843–4867, https://doi.org/10.1029/JB086iB06p04843, 1981. a, b, c, d
Hager, B. H., Clayton, R. W., Richards, M. A., Comer, R. P., and Dziewonski, A. M.: Lower mantle heterogeneity, dynamic topography and the geoid, Nature, 313, 541–545, https://doi.org/10.1038/314752a0, 1985. a, b
Hazzard, J. A. N., Richards, F. D., Goes, S. D. B., and Roberts, G. G.: Probabilistic Assessment of Antarctic Thermomechanical Structure: Impacts on Ice Sheet Stability, EarthArXiv, https://doi.org/10.31223/X5C35R, 2022. a
Heister, T., Dannberg, J., Gassmöller, R., and Bangerth, W.: High accuracy mantle convection simulation through modern numerical methods – II: realistic models and problems, Geophys. J. Int., 210, 833–851, https://doi.org/10.1093/gji/ggx195, 2017. a
Hoggard, M. J., White, N., and Al-Attar, D.: Global dynamic topography observations reveal limited influence of large-scale mantle flow, Nat. Geosci., 9, 1–8, https://doi.org/10.1038/ngeo2709, 2016a. a, b, c, d, e, f, g
Hoggard, M. J., White, N., and Al-Attar, D.: Supplementary Information for “Global dynamic topography observations reveal limited influence of large-scale mantle flow”, Nat. Geosci., 9, 1–34, https://doi.org/10.1038/ngeo2709, 2016b. a
Hoggard, M. J., Austermann, J., Randel, C., and Stephenson, S.: Observational Estimates of Dynamic Topography Through Space and Time, chap. 15, in: Mantle Convection and Surface Expressions, edited by: Marquardt, H., Ballmer, M., Cottaar, S., and Konter, J., AGU, https://doi.org/10.1002/9781119528609.ch15, pp. 371–411, 2021. a, b, c, d, e
Holdt, M. C., White, N. J., Stephenson, S. N., and Conway-Jones, B. W.: Densely Sampled Global Dynamic Topographic Observations and Their Significance, J. Geophys. Res.-Sol. Ea., 127, 1–32, 2022. a, b, c, d, e, f, g
Jeans, J. H.: The Propagation of Earthquake Waves, P. Roy. Soc. Lond. A, 102, 554–574, 1923. a
Kaula, W. M.: Determination of the Earth's Gravitational Field, Rev. Geophys., 1, 507–551, 1963. a, b, c
Kramer, S. C., Davies, D. R., and Wilson, C. R.: Analytical solutions for mantle flow in cylindrical and spherical shells, Geosci. Model Dev., 14, 1899–1919, https://doi.org/10.5194/gmd-14-1899-2021, 2021. a
Lambeck, K., Smither, C., and Johnston, P.: Sea-level change, glacial rebound and mantle viscosity for northern Europe, Geophys. J. Int., 134, 102–144, https://doi.org/10.1046/j.1365-246X.1998.00541.x, 1998. a
Lau, H. C. P., Mitrovica, J. X., Davis, J. L., Tromp, J., Yang, H.-Y., and Al-Attar, D.: Tidal tomography constrains Earth's deep-mantle buoyancy, Nature, 551, 321–326, https://doi.org/10.1038/nature24452, 2017. a
Lees, M. E., Rudge, J. F., and McKenzie, D.: Gravity, topography, and melt generation rates from simple 3D models of mantle convection, Geochem. Geophy. Geosy., 21, 1–29, https://doi.org/10.1029/2019gc008809, 2020. a
Lekić, V. and Fischer, K. M.: Contrasting lithospheric signatures across the western United States revealed by Sp receiver functions, Earth Planet. Sc. Lett., 402, 90–98, https://doi.org/10.1016/j.epsl.2013.11.026, 2014. a
Liu, L. and Gurnis, M.: Simultaneous inversion of mantle properties and initial conditions using an adjoint of mantle convection, J. Geophys. Res.-Sol. Ea., 113, 1–17, https://doi.org/10.1029/2008jb005594, 2008. a
Liu, S. and King, S. D.: A benchmark study of incompressible Stokes flow in a 3-D spherical shell using ASPECT, Geophys. J. Int., 217, 650–667, https://doi.org/10.1093/gji/ggz036, 2019a. a, b
Liu, S. and King, S. D.: A benchmark study of incompressible Stokes flow in a 3-D spherical shell using ASPECT, Geophys. J. Int., 217, 650–667, https://doi.org/10.1093/gji/ggz036, 2019b. a
Lu, C., Forte, A. M., Simmons, N. A., Grand, S. P., Kajan, M. N., Lai, H., and Garnero, E. J.: The Sensitivity of Joint Inversions of Seismic and Geodynamic Data to Mantle Viscosity, Geochem. Geophy. Geosy., 21, 1–29, https://doi.org/10.1029/2019gc008648, 2020. a
McKenzie, D.: Surface deformation, gravity anomalies and convection, Geophys. J. Roy. Astr. S., 48, 211–238, https://doi.org/10.1111/j.1365-246X.1977.tb01297.x, 1977. a
McKenzie, D. P., Roberts, J. M., and Weiss, N. O.: Convection in the earth's mantle: Towards a numerical simulation, J. Fluid Mech., 62, 465–538, 1974. a
Merdith, A. S., Williams, S. E., Collins, A. S., Tetley, M. G., Mulder, J. A., Blades, M. L., Young, A., Armistead, S. E., Cannon, J., Zahirovic, S., and Müller, R. D.: Extending full-plate tectonic models into deep time: Linking the Neoproterozoic and the Phanerozoic, Earth-Sci. Rev., 214, 1–44, https://doi.org/10.1016/j.earscirev.2020.103477, 2021. a, b, c, d, e
Mitrovica, J. X. and Forte, A. M.: A new inference of mantle viscosity based upon joint inversion of convection and glacial isostatic adjustment data, Earth Planet. Sc. Lett., 225, 177–189, https://doi.org/10.1016/j.epsl.2004.06.005, 2004. a, b, c
Molnar, P., England, P. C., and Jones, C. H.: Mantle dynamics, isostasy, and the support of high terrain, J. Geophys. Res.-Sol. Ea., 120, 1932–1957, https://doi.org/10.1002/2014JB011724, 2015. a
Morris, M., Fernandes, V. M., and Roberts, G. G.: Extricating dynamic topography from subsidence patterns: Examples from Eastern North America's passive margin, Earth Planet. Sc. Lett., 530, 1–13, https://doi.org/10.1016/j.epsl.2019.115840, 2020. a
Moucha, R. and Forte, A. M.: Changes in African topography driven by mantle convection: supplementary information, Nat. Geosci., 4, 707–712, https://doi.org/10.1038/ngeo1235, 2011. a
Moucha, R., Forte, A. M., Mitrovica, J. X., and Daradich, A.: Lateral variations in mantle rheology: Implications for convection related surface observables and inferred viscosity models, Geophys. J. Int., 169, 113–135, https://doi.org/10.1111/j.1365-246X.2006.03225.x, 2007. a
Moucha, R., Forte, A. M., Mitrovica, J. X., Rowley, D. B., Quéré, S., Simmons, N. A., and Grand, S. P.: Dynamic topography and long-term sea-level variations: There is no such thing as a stable continental platform, Earth Planet. Sc. Lett., 271, 101–108, https://doi.org/10.1016/j.epsl.2008.03.056, 2008. a
O'Connell, R. J.: Pleistocene Glaciation and the Viscosity of the Lower Mantle, Geophys. J. Roy. Astr. S., 23, 299–327, https://doi.org/10.1111/j.1365-246X.1971.tb01823.x, 1971. a
O'Malley, C. P. B., White, N. J., Stephenson, S. N., and Roberts, G. G.: Large-Scale Tectonic Forcing of the African Landscape, J. Geophys. Res.-Earth, 126, 1–37, https://doi.org/10.1029/2021jf006345, 2021. a, b
Panasyuk, S. V., Hager, B. H., and Forte, A. M.: Understanding the effects of mantle compressibility on geoid kernels, Geophys. J. Int., 124, 121–133, https://doi.org/10.1111/j.1365-246X.1996.tb06357.x, 1996. a, b, c, d
Panton, J., Davies, J. H., and Myhill, R.: The Stability of Dense Oceanic Crust Near the Core-Mantle Boundary, J. Geophys. Res.-Sol. Ea., 128, 1–21, https://doi.org/10.1029/2022JB025610, 2023. a, b, c
Parsons, B. and Daly, S.: The relationship between surface topography, gravity anomalies and temperature structure of convection, J. Geophys. Res., 88, 1129–1144, https://doi.org/10.1029/JB088iB02p01129, 1983. a, b, c, d, e, f, g, h, i, j, k, l, m, n
Pekeris, C. L.: Thermal Convection in the Interior of the Earth, Geophysical Supplements to the Monthly Notices of the Royal Astronomical Society, 3, 343–367, 1935. a, b
Priestley, K. and McKenzie, D.: The relationship between shear wave velocity, temperature, attenuation and viscosity in the shallow part of the mantle, Earth Planet. Sc. Lett., 381, 78–91, https://doi.org/10.1016/j.epsl.2013.08.022, 2013. a, b
Ribe, N. M.: Analytical Approaches to Mantle Dynamics, Treatise on Geophysics, 7, 167–226, https://doi.org/10.1016/B978-044452748-6.00117-6, 2007. a, b
Ricard, Y.: Physics of Mantle Convection, Treatise on Geophysics, 7, 31–88, 2007. a
Ricard, Y.: Physics of Mantle Convection, in: Treatise on Geophysics, edited by Schubert, G., chap. 7.02, pp. 23–71, Elsevier, https://doi.org/10.1016/B978-044452748-6.00115-2, 2015. a, b, c, d, e
Richards, F. D., Hoggard, M. J., White, N., and Ghelichkhan, S.: Quantifying the relationship between short-wavelength dynamic topography and thermomechanical structure of the upper mantle using calibrated parameterization of anelasticity, J. Geophys. Res.-Sol. Ea., 125, 1–36, https://doi.org/10.1029/2019JB019062, 2020. a, b
Richards, F. D., Hoggard, M. J., Ghelichkhan, S., Koelemeijer, P., and Lau, H. C. P.: Geodynamic, geodetic, and seismic constraints favour deflated and dense-cored LLVPs, Earth Planet. Sc. Lett., 602, 1–13, https://doi.org/10.1016/j.epsl.2022.117964, 2023. a, b, c
Richards, M. A. and Hager, B. H.: Geoid Anomalies in a Dynamic Earth, J. Geophys. Res., 89, 5987–6002, https://doi.org/10.1029/JB089iB07p05987, 1984. a, b
Roberts, G., O'Malley, C., Panton, J., Richards, F., Davies, H., Milanez Fernandes, V., and Ghelichkhan, S.: 'Reconciling Surface Deflections From Simulations of Global Mantle Convection': Numerical model dataset, Zenodo [data set], https://doi.org/10.5281/zenodo.12704925, 2024. a
Salles, T., Flament, N., and Müller, D.: Influence of mantle flow on the drainage of eastern Australia since the Jurassic Period, Geochem. Geophy. Geosy., 18, 280–305, https://doi.org/10.1002/2016GC006617, 2017. a
Spasojevic, S. and Gurnis, M.: Sea level and vertical motion of continents from dynamic earth models since the Late Cretaceous, AAPG Bull., 96, 2037–2064, https://doi.org/10.1306/03261211121, 2012. a
Stanley, J. R., Braun, J., Baby, G., Guillocheau, F., Robin, C., Flowers, R. M., Brown, R., Wildman, M., and Beucher, R.: Constraining Plateau Uplift in Southern Africa by Combining Thermochronology, Sediment Flux, Topography, and Landscape Evolution Modeling, J. Geophys. Res.-Sol. Ea., 126, 1–34, https://doi.org/10.1029/2020JB021243, 2021. a, b
Steinberger, B.: Effects of latent heat release at phase boundaries on flow in the Earth's mantle, phase boundary topography and dynamic topography at the Earth's surface, Phys. Earth Planet. In., 164, 2–20, https://doi.org/10.1016/j.pepi.2007.04.021, 2007. a
Steinberger, B.: Topography caused by mantle density variations: Observation-based estimates and models derived from tomography and lithosphere thickness, Geophys. J. Int., 205, 604–621, https://doi.org/10.1093/gji/ggw040, 2016. a
Steinberger, B. and Antretter, M.: Conduit diameter and buoyant rising speed of mantle plumes: Implications for the motion of hot spots and shape of plume conduits, Geochem. Geophy. Geosy., 7, 1–25, https://doi.org/10.1029/2006GC001409, 2006. a
Steinberger, B. and Calderwood, A. R.: Models of large-scale viscous flow in the Earth's mantle with constraints from mineral physics and surface observations, Geophys. J. Int., 167, 1461–1481, https://doi.org/10.1111/j.1365-246X.2006.03131.x, 2006. a, b
Steinberger, B., Nelson, P. L., Grand, S. P., and Wang, W.: Yellowstone plume conduit tilt caused by large-scale mantle flow, Geochem. Geophy. Geosy., 20, 5896–5912, https://doi.org/10.1029/2019gc008490, 2019. a
Stephenson, S. N., White, N. J., Carter, A., Seward, D., Ball, P. W., and Klöcking, M.: Cenozoic Dynamic Topography of Madagascar, Geochem. Geophy. Geosy., 22, 1–38, https://doi.org/10.1029/2020gc009624, 2021. a
Tackley, P. J., Stevenson, D. J., Glatzmaier, G. A., and Schubert, G.: Effects of an endothermic phase transition at 670 km depth on spherical mantle convection, Nature, 361, 699–704, https://doi.org/10.1038/361699a0, 1993. a
Thoraval, C. and Richards, M. A.: The geoid constraint in global geodynamics: Viscosity structure, mantle heterogeneity models and boundary conditions, Geophys. J. Int., 131, 1–8, https://doi.org/10.1111/j.1365-246X.1997.tb00591.x, 1997. a, b
Thoraval, C., Machete, P., and Cazenave, A.: Influence of mantle compressibility and ocean warping on dynamical models of the geoid, Geophys. J. Int., 117, 566–573, https://doi.org/10.1111/j.1365-246X.1994.tb03954.x, 1994. a
Turcotte, D. L. and Schubert, G.: Geodynamics, 2nd edn., Cambridge University Press, Cambridge, ISBN 9780521186230, 2002. a
van Heck, H. J., Davies, J. H., Elliott, T., and Porcelli, D.: Global-scale modelling of melting and isotopic evolution of Earth's mantle: melting modules for TERRA, Geosci. Model Dev., 9, 1399–1411, https://doi.org/10.5194/gmd-9-1399-2016, 2016. a
Wang, Y., Liu, L., and Zhou, Q.: Topography and Gravity Reveal Denser Cratonic Lithospheric Mantle Than Previously Thought, Geophys. Res. Lett., 49, e2021GL096844, https://doi.org/10.1029/2021GL096844, 2022. a, b, c, d
Wessel, P., Luis, J., Uieda, L., Scharroo, R., Wobbe, F., Smith, W. H. F., and Tian, D.: The Generic Mapping Tools Version 6, Geochem. Geophy. Geosy., 20, 1–9, https://doi.org/10.1029/2019gc008515, 2019. a
Wieczorek, M. A. and Meschede, M.: SHTools: Tools for Working with Spherical Harmonics, Geochem. Geophy. Geosy., 19, 1–19, https://doi.org/10.1029/2018GC007529, 2018. a
Zhong, S., Gurnis, M., and Hulbert, G.: Accurate determination of surface normal stress in viscous flow from a consistent boundary flux method, Phys. Earth Planet. In., 78, 1–8, https://doi.org/10.1016/0031-9201(93)90078-N, 1993. a
Zhong, S., Zuber, M. T., Moresi, L., and Gurnis, M.: Role of temperature-dependent viscosity and surface plates in spherical shell models of mantle convection, J. Geophys. Res., 105, 11063–11082, 2000. a, b, c
Zhong, S., McNamara, A., Tan, E., Moresi, L., and Gurnis, M.: A benchmark study on mantle convection in a 3-D spherical shell using CitcomS, Geochem. Geophy. Geosy., 9, 1–32, https://doi.org/10.1029/2008GC002048, 2008. a, b, c, d, e
Zhou, Q. and Liu, L.: Topographic evolution of the western United States since the early Miocene, Earth Planet. Sc. Lett., 514, 1–12, https://doi.org/10.1016/j.epsl.2019.02.029, 2019. a
Zhou, Q., Liu, L., and Hu, J.: Western US volcanism due to intruding oceanic mantle driven by ancient Farallon slabs, Nat. Geosci., 11, 70–76, https://doi.org/10.1038/s41561-017-0035-y, 2018. a
- Abstract
- Introduction
- Numeric and analytic calculations of surface deflection
- Spatial and spectral comparison of model predictions
- Model parameterizations
- Results
- Discussion
- Conclusions
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Numeric and analytic calculations of surface deflection
- Spatial and spectral comparison of model predictions
- Model parameterizations
- Results
- Discussion
- Conclusions
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement