the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Biological nitrogen fixation of natural and agricultural vegetation simulated with LPJmL 5.7.9
Johanna Braun
Jens Heinke
Sebastian Ostberg
Susanne Rolinski
Sibyll Schaphoff
Fabian Stenzel
Werner von Bloh
Friedhelm Taube
Christoph Müller
Biological nitrogen fixation (BNF) by symbiotic and free-living bacteria is an important source of plant-available nitrogen (N) in terrestrial ecosystems supporting carbon (C) sequestration and food production worldwide. Dynamic global vegetation models (DGVMs) are frequently used to assess the N and C cycles under dynamic land use and climate. BNF plays an important role in the components of both these cycles, making a robust representation of the processes and variables that BNF depends on important to reduce uncertainty within the C and N cycles and improve the ability of DGVMs to project future ecosystem productivity, vegetation patterns or the land C sink. Still, BNF is often modelled as a function of net primary productivity or evapotranspiration, and the actual drivers are neglected. We implemented plant-functional-type-specific limitations for BNF dependent on soil temperature and soil water content, as well as a cost of BNF, in the Lund–Potsdam–Jena managed Land (LPJmL) DGVM and compared the new (“C-costly”) against the previous (“Original”) approach and data from the scientific literature. For our comparison, we simulated a potential natural vegetation scenario and one including anthropogenic land use for the period from 1901 to 2016 for which we evaluate BNF and legume crop yields. Our results show stronger agreement with BNF observations for the C-costly than the Original approach for natural vegetation and agricultural areas. The C-costly approach reduced the overestimation of BNF, especially in hot spots of legume crop production. Despite the reduced BNF in the C-costly approach, yields of legume crops were similar to the Original approach. While the net C and N balances were similar between the two approaches, the reduced BNF in the C-costly approach results in a slight underestimation of N losses from leaching, emissions and harvest compared to the values in the literature, supporting further investigation of the underlying reasons, such as processes represented in DGVMs and scenario assumptions. While we see the potential for further model development, for example, to separate symbiotic and free-living BNF, the C-costly approach is a major improvement over the simple Original approach because of the separate representation of important drivers and limiting factors of BNF, and the C-costly approach also improves the ability of LPJmL to project future C and N cycle dynamics.
- Article
(9972 KB) - Full-text XML
-
Supplement
(2465 KB) - BibTeX
- EndNote
Biological nitrogen fixation (BNF) is an important source of plant-available nitrogen (N) in terrestrial ecosystems (Galloway et al., 1995). It can be separated into symbiotic (Granhall, 1981) and free-living (Reed et al., 2011) BNF, which account for the total BNF with different shares in different ecosystems (Davies-Barnard and Friedlingstein, 2020b). In natural terrestrial ecosystems, N deposition, N fixation through lightning, and BNF are the only processes that introduce additional reactive N into the system (Yu and Zhuang, 2020). In agricultural systems, increased N inputs are – together with extensive manure recycling – a major source of nitrous oxide (N2O) and ammonium () emissions (Reay et al., 2012; Tian et al., 2020) and nitrate () pollution (Moss, 2007). These inputs result from increased BNF and the deposition of additional anthropogenic N inputs, which originate mainly from synthetic fertiliser application (Lu and Tian, 2017). Promoting N-fixing crops such as forage and grain legumes for usage as green manure has been discussed (Becker et al., 1995; Fageria, 2007; Northup and Rao, 2016) to reduce N losses from nitrification, volatilisation, denitrification and leaching on agricultural land. Generally, symbiotic BNF, as well as free-living BNF, can be important for plant growth in N-limited ecosystems, and this supports carbon (C) sequestration and food production across the globe.
Briefly, BNF describes the transformation of atmospheric N2 to ammonia () by a variety of soil microorganisms providing a source of mineral N for plants at the expense of C (Yu and Zhuang, 2020). The underlying mechanisms of BNF, as well as its role within the C and N cycles and for ecosystem productivity, have been described in detail in multiple studies (e.g. Yu and Zhuang, 2020; Davies-Barnard and Friedlingstein, 2020b; Cleveland et al., 1999). Here, we focus on the representation of BNF in the Lund–Potsdam–Jena managed Land (LPJmL) dynamic global vegetation model (DGVM) (Schaphoff et al., 2018b; von Bloh et al., 2018; Lutz et al., 2019; Herzfeld et al., 2021; Porwollik et al., 2022; Heinke et al., 2023). We do not distinguish between symbiotic and free-living BNF throughout this study but only consider the total BNF as the sum of both forms.
DGVMs such as LPJmL can be used to assess the role of BNF for the productivity of natural and agricultural ecosystems and its effects on the N and C cycles under dynamic land use and climate. A solid representation of the processes behind BNF is important to reduce uncertainty and improve the model results of DGVMs, which are frequently used in impact assessments and to inform policy-makers. A variety of approaches of different complexity to model BNF have been developed. A key difference between approaches is the selection of variables that control BNF and the accounting of the C cost of BNF. For example, Cleveland et al. (1999) use actual evapotranspiration as a single explanatory variable, while Yu and Zhuang (2020) consider soil temperature, soil water content, soil mineral N and soil C content. Both of these approaches do not consider the cost of BNF neglecting the reduced C assimilation (Cleveland et al., 1999; Yu and Zhuang, 2020), while others explicitly consider a cost per amount of N fixed and a maximum amount of C that can be invested in BNF (e.g. Ma et al., 2022). Even more complex approaches consider the different pathways of N uptake that are associated with a cost (active N uptake, retranslocation and BNF) and optimise for the minimum cost (e.g. Fisher et al., 2010). Depending on the considered variables, the simulated BNF and how it is affected by climate change may strongly differ, which in turn can have strong effects on the simulated C and N fluxes and pools.
A comparison to data published by Davies-Barnard and Friedlingstein (2020a) suggests that the approach that was implemented in LPJmL (von Bloh et al., 2018) based on Cleveland et al. (1999) – in the following defined as the “Original” approach – overestimates global BNF. In addition, we identified several shortcomings of the Original approach in LPJmL. In the Original approach, BNF is a function of actual evapotranspiration, which leads to an overestimation of BNF in moist but not necessarily N-limited ecosystems and an underestimation in dry but N-limited ecosystems. In this simplified implementation, BNF is not constrained by the availability of reactive forms of N, and additional N is fixed even if the reactive soil N is sufficient to fulfil the N demand, which potentially leads to an overestimation of the ammonia pool and N losses. For cultivated grain legumes, the approach assumes no limitation of BNF at all but simply supplies all N requested by the plant that cannot be fulfilled through N uptake from mineral N pools in the soil. This leads to an overestimation of cropland BNF. In order to overcome these deficiencies, here we describe a revision of the Original approach in LPJmL with a more complex approach, referred to as “C-costly” approach in the following. The C-costly approach is inspired by Ma et al. (2022) and Yu and Zhuang (2020) and introduces plant-functional-type (PFT)-specific limitations for BNF dependent on soil temperature and soil water content, as well as a C cost of BNF. In the following, we present the C-costly BNF approach and evaluate its performance against global and site-specific data. We discuss the differences between the Original and the C-costly BNF approach for the N cycle and plant productivity.
2.1 Model description
LPJmL is a dynamic global vegetation model (DGVM) with the full terrestrial hydrology and explicit representation of agricultural management systems for cropland and pastures. We have implemented the BNF module in the most recent development branch, which is based on a consolidated version of the carbon-only model (LPJmL4, Schaphoff et al., 2018b, a), the N cycle (LPJmL5, von Bloh et al., 2018), tillage (Lutz et al., 2019), manure (Herzfeld et al., 2021), cover crop (Porwollik et al., 2022) and grazing management (Heinke et al., 2023) modules. There have been further model improvements that have not been described in publications elsewhere, including improved online coupling options with other models such as IMAGE (Müller et al., 2016) or copan:CORE (Donges et al., 2020). For a better representation of crops that are not explicitly represented (referred to as “others”), these are no longer assumed to be identical to managed grassland (Bondeau et al., 2007) but can be simulated as separate stands with distinct management inputs (e.g. fertiliser amounts).
The original spin-up protocol for LPJmL4, described in Schaphoff et al. (2013), was modified to account for the interaction between soils and plants through N supply in LPJmL5. The principal technique to accelerate the spin-up by calculating the equilibrium soil C stocks from litter decomposition (i.e. the flux of C into the soil C pools) and soil C turnover rates (or residence time) remains the same as in Schaphoff et al. (2013). However, the original code was refactored to improve the accuracy of estimates of equilibrium stocks and to apply the technique to soil C and N pools simultaneously.
In LPJmL5, an adjustment of N pools can lead to a change in plant productivity through a change in N supply from mineralisation. To account for this feedback, the C and N stock adjustments need to be repeated multiple times until the soil and the vegetation reach equilibria. The revised spin-up procedure starts with an initial period of 300 years, during which vegetation is allowed to establish. This is followed by a 2400-year period, during which soil C and N pools are updated every 15 years based on the litter decomposition and soil pool turnover rates of the preceding 10 years. This long period with repeated adjustment (160 times) of C and N pools is required to reach an equilibrium in regions with very low turnover rates (e.g. in the boreal zone). To reduce the effect of inter-annual variability on estimates of equilibrium stocks, a final adjustment is applied after 300 simulation years, using the litter decomposition and soil pool turnover rates over that period. Finally, the model is allowed to adjust to the new C and N stocks for another 500 simulation years.
To assess the effectiveness of the spin-up procedure, we conducted a 1000-year model run under the same conditions as during the spin-up period (i.e. stable pre-industrial atmospheric CO2 concentration, atmospheric N deposition and climate) for which we present results in Appendix C.
Further changes to the code since the last published version (see Porwollik et al., 2022) include various bug fixes concerning fertiliser and manure application, data output, environmental flow requirements (Jägermeyr et al., 2017), soil temperature (Schaphoff et al., 2013) and bioenergy plantations (Beringer et al., 2011). The latest code changes are now also documented in a CHANGELOG.md file as part of the code repository (Wirth et al., 2024).
2.2 BNF-relevant nitrogen cycle components in LPJmL
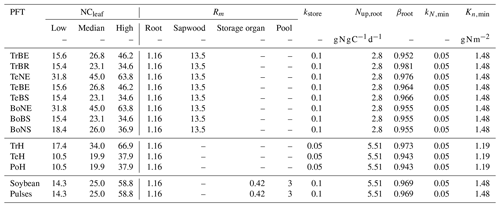
While we refer to von Bloh et al. (2018) for a detailed description and evaluation of the N cycle in LPJmL, we briefly describe the main processes that determine N deficit – which is the prerequisite for N fixation in the C-costly approach – and the Original approach here and provide the full equations in Appendix A. An N deficit is defined as the difference between the plant N demand (Eq. A4) and the active and passive N-uptake (Eq. A5) and labile-N reserves (Eq. A11).
The N demand accounts for N required to produce RuBisCo, depending on the maximum carboxylation capacity and the leaf area index (LAI) of the respective PFT (Eq. A1, first summand) and the structural N demand, depending on the current N content of the different plant compartments (Eq. A1, second summand, and Eq. A4). N reserves are included using a PFT-specific parameter (Eq. A4).
The N uptake is calculated as a combination of passive and active N uptake from the soil and is a function of the potential N uptake of the root system (Eq. A5), which is reduced to account for soil mineral N availability (Eq. A8), soil temperature (Eq. A9) and plant N starvation (Eq. A10). Labile N reserves represent the N currently available from past N uptake, BNF or retranslocation (Eq. A11).
In the Original approach, BNF was calculated from the 20-year average of annual evapotranspiration (etp) for tree and herbaceous PFTs, following the function from Cleveland et al. (1999):
The resulting BNF is added to the pool of the first soil layer. For crop PFTs, BNF equals Ndeficit and is directly added to Nlabile.
2.3 The C-costly approach
A key feature is the connection of BNF to an associated cost represented as a reduction in the net primary production (NPP). The C-costly approach calculates actual BNF (Nfix) from the potential BNF (Nfix,pot) using several reduction factors. First, the N fixation rate for the environmental conditions Nfix,env is calculated from Nfix,pot for the first two soil layers, , accounting for reductions by dimensionless soil temperature and soil water content (SWC) limitation functions (fT, fW) and the root distribution rootdist in the interval [0,1] (Ma et al., 2022):
The soil temperature limitation is increasing linearly outside the optimal temperature interval, [Topt,low,Topt,high] (Eq. 4; Fig. 1a), and it prohibits BNF if outside the tolerable temperature interval, [Tmin,Tmax], while the soil water limitation is linearly dependent on the relative soil water content, SWC (Eq. 5; Fig. 1b).
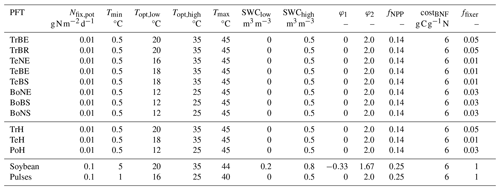
The root distribution is calculated as in Eq. (A7). Since only the fraction of roots in the first two soil layers is used for BNF, shallow root profiles lead to a higher BNF compared to deep root profiles. Nfix,pot, Tmin, Topt,low, Topt,high, Tmax, SWClow, SWChigh, φ1 and φ2 are PFT-specific parameters (Table 1), and their values are adopted from Yu and Zhuang (2020) for the natural vegetation PFTs and from Ma et al. (2022) for soybean and pulses.
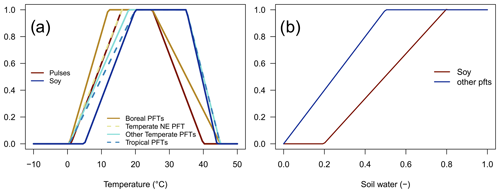
Figure 1Dimensionless temperature limitation function fT(T) (a) and soil water limitation function fW(SWC) (b).
Table 1BNF-related PFT-specific parameter values for the tropical broadleaved evergreen tree (TrBE), tropical broadleaved raingreen tree (TrBR), temperate needleleaved evergreen tree (TeNE), temperate broadleaved evergreen tree (TeBE), temperate broadleaved summergreen tree (TeBS), boreal needleleaved evergreen tree (BoNE), boreal broadleaved summergreen tree (BoBS), boreal needleleaved summergreen tree (BoNS), tropical herbaceous (TrH), temperate herbaceous (TeH), polar herbaceous (PoH), soybean and pulses.
If Nfix,env exceeds the amount of N missing to fulfil the N demand of the current day (the N deficit Ndeficit), the N fixation is reduced as follows:
Finally, if the cost of the N fixation exceeds the NPP available for BNF, then the N fixation is further reduced to match the maximum amount that can be fixed with the current day's NPP share available for BNF.
where fNPP is the maximum share (dimensionless) of NPP available for BNF, which is set to 0.14 (Kull, 2002) for the natural PFTs and to 0.25 for soybean and pulses. The average N fixer fraction (ffixer) is set to 0.05 for the tropical, to 0.01 for the temperate and to 0.03 for the boreal zone (Yu and Zhuang, 2020). PFTs only fix additional N if the N uptake from other sources is insufficient and the net primary productivity (NPP) is larger than zero. The costs of BNF are set at a moderate constant value of 6 g C g N−1 (Boote et al., 2009; Ryle et al., 1979; Patterson and Larue, 1983; Kaschuk et al., 2009).
2.4 Modelling protocol
To compare the two BNF approaches, we simulated two scenarios. The first is a potential natural vegetation (PNV) scenario, which does not include anthropogenic land use or agricultural production systems. The second is a scenario that includes agricultural land use (LU). The same input data sets were used for all scenarios. We used the climate data from the GSWP3-W5E5 data set (Kim, 2017; Cucchi et al., 2020; Lange et al., 2022), historical atmospheric N deposition (Yang and Tian, 2020), historical atmospheric CO2 concentrations (Büchner and Reyer, 2022), historical land-use patterns (Ostberg et al., 2023) and grazing management data (Stenzel et al., 2024). For both BNF approaches, we conducted spin-up simulations of 3500 years using a random permutation of the climate data from 1901 to 1930. These spin-up simulations ensure that the C and N balances are in equilibrium. Afterwards, land use is introduced, and a second spin-up period of 390 years is run to capture the effects of historical land-use change on the C and N cycle. Following the two spin-up simulations, the model is run from 1901 until 2016 using the transient input data.
2.5 Model evaluation
We compared simulated total global BNF for both approaches against several estimates which were derived empirically or reported in other modelling studies. Data on these estimates are available from Davies-Barnard and Friedlingstein (2020a). The global BNF is calculated as the sum of BNF per area times grid cell area over all grid cells:
For the evaluation we calculate the median, minimum and maximum between 2001 and 2010 and qualitatively compare these values against past estimates. We calculated the overlap between our results and the reported data if minimum and maximum values were available.
where xmin and xmax are the simulated minimum and maximum, and ymin and ymax are the minimum and maximum values from the literature.
In addition, we compared our results to data obtained at several sites for the natural vegetation (Davies-Barnard and Friedlingstein, 2020a) and legume crops (Ma et al., 2022). To evaluate legume crop BNF and yields, we conducted additional local simulations matching the coordinates of the experiments following the protocol described in Sect. 2.4 but ensured that the respective crops (soybean or pulses) were grown under the reported water management (rainfed or irrigated). We calculated the root mean square error (RMSE) as follows:
where N is the number of observations, and xn and yn are the simulated and observed values.
3.1 Comparison of the BNF approaches
Comparing the simulated BNF of both approaches to data from the literature and experiments showed a substantial improvement of the global BNF (Sect. 3.1.1), as well as the latitudinal and spatial patterns (Sect. 3.1.2).
3.1.1 Comparison to data and other models
The two approaches show large differences in the simulated BNF. While the median global BNF between 2001 and 2010 was 191 Tg N yr−1 for the Original approach, for the C-costly approach it was substantially lower, with a value of 109 Tg N yr−1 (Fig. 2a). Comparing the global BNF of both approaches to estimates from the scientific literature shows the agreement of the C-costly values with several other data sources, while the Original approach overestimates most of the literature values. In particular, the recent estimate by Davies-Barnard and Friedlingstein (2020a) was closely matched by the C-costly approach, and 60 % of the simulated data were within the range of the Davies-Barnard and Friedlingstein (2020a) data (Fig. 2a). Despite the fact that the Original approach was not derived from the empirical relationship of Cleveland et al. (1999) for the legume crops, the data from Cleveland et al. (1999) are well matched by the Original approach, and only the spread of the Cleveland et al. (1999) data is underestimated. In comparison to the data of Xu-Ri and Prentice (2017), who reported much higher values compared to the other studies, BNF is underestimated by both approaches implemented in LPJmL. However, large differences are to be expected, considering that their approach does not calculate the actual BNF but rather the BNF needed to sustain global NPP (Xu-Ri and Prentice, 2017).
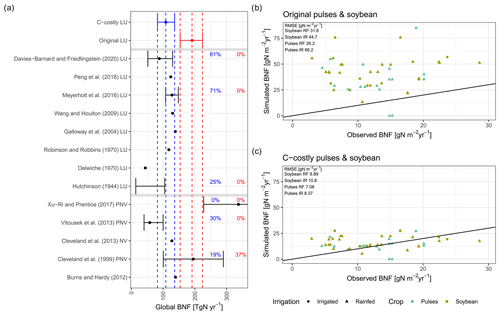
Figure 2Evaluation against global (a) and site-specific data (b, c). Global evaluation plot inspired by Davies-Barnard and Friedlingstein (2020a) showing global BNF (in Tg N yr−1) from different studies (black) compared to the Original (red) and C-costly (blue) BNF approach implemented in LPJmL. Studies are labelled by author names and whether they consider potential natural vegetation (PNV), actual natural vegetation (NV) or actual land use (LU). We assigned the Davies-Barnard and Friedlingstein (2020a) data to the LU category because they consider cropland area as grasslands and not as potential forest areas. Percentage values give the overlap between the ranges of the simulation results and the literature estimates derived using Eq. (9). Simulated values are the median between 2001 and 2010, and the ranges show the minimum and maximum. Site-specific evaluation (b, c) comparing data from observations for soybean (green) and pulses (blue) for rainfed (RF) (circle) and irrigated (IR) (triangle) experiment and simulation results is shown using the Original (b) and C-costly (c) BNF approaches. Labels show the RMSE of the two approaches.
Comparing the spatial patterns of the two approaches to those of Davies-Barnard and Friedlingstein (2020a) shows that the Original approach generally overestimated BNF in large areas of the tropics and temperate zones (Fig. C4c). The C-costly approach still overestimates BNF in the tropics and the production areas of soybean and/or pulses in India and the United States of America (USA), but the values are substantially smaller than in the Original approach (Fig. C4f). In both approaches, observed BNF is slightly underestimated in the central to western part of the USA, Canada, China, Kazakhstan, Russia and Mongolia.
On croplands, BNF was 21 Tg N yr−1 with the C-costly approach, which is within the range of 17 to 31 Tg N yr−1 reported by a recent review (Zhang et al., 2021) and other studies (Bodirsky et al., 2012; Chang et al., 2021). This contrasts with the overestimation of cropland BNF in the Original approach, which was 68 Tg N yr−1. For the two legume crop functional types representing soybean and pulses, we compared the simulation results to BNF and yield data from experiments (Figs. 2b and c and C1a and b). For all except two experiments, the Original approach strongly overestimated BNF independent of the crop and the irrigation management. Using the C-costly approach, the cropland BNF was strongly reduced by a factor of approximately 2, leading to substantially lower RMSEs. While simulation results were closer to observations, some deviations remain. Pulses generally showed lower BNF for both approaches compared to soybean, while irrigated simulations generally showed a higher BNF and overestimated BNF compared to observations for all experiments in the Original approach and for the vast majority in the C-costly approach. Crop yields barely differed between the two approaches and were comparable to observations (Fig. C1a and b).
3.1.2 Global variation in BNF
Generally, BNF decreases from low to high latitudes with similar gradients but from different levels for the two approaches (Fig. 3). In latitudes with a high share of crop legumes (e.g. 30 to 40° S), the reduction in the BNF in the C-costly approach is especially large. Both the Original and the C-costly approaches underestimate BNF at high latitudes (the Original more strongly so) compared to Davies-Barnard and Friedlingstein (2020a). The C-costly approach shows a good performance in the mid-latitudes, but both approaches overestimate BNF compared to observations in the tropics (Fig. 3). In the Original approach, especially the high BNF of cropland contributes to the overestimation. For the low latitudes, both approaches exceed the values from Davies-Barnard and Friedlingstein (2020b). However, the higher BNF in the tropics is comparable to the median of the TRENDY-N ensemble (see Sect. 4 and Kou-Giesbrecht et al., 2023).
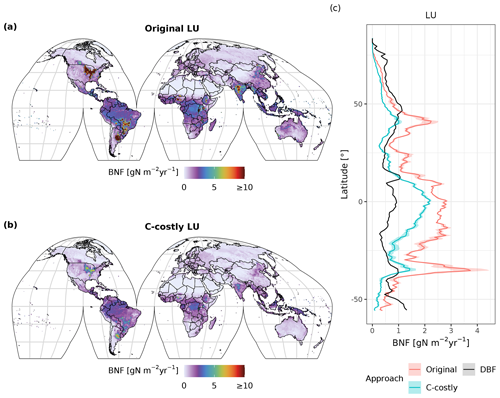
Figure 3Simulated average annual BNF (in ) for the years 2001 to 2010 using the Original (a) and C-costly (b) approaches. The average (line) and 5th to 95th percentiles (shading) of simulated and observed BNF per latitude (in ), using the Original (red) and C-costly (blue) approaches and data from Davies-Barnard and Friedlingstein (2020a) (DBF), are shown (c).
With the Original approach, mineral N was added to the first soil layer and subsequently incorporated by the PFTs via the passive and active N-uptake pathway. This did not allow a separate identification of N to be taken up via BNF from the total N uptake, except for the legume crops which fixed their entire N deficit. Using the C-costly BNF, the model separates N uptake by BNF from passive and active N uptake against N concentration gradients (Marschner et al., 1991; Fisher et al., 2010), facilitating the analysis of the share of BNF in total N uptake subsequently referred to as %Ndfa, which is commonly used to refer to this variable in the empirical literature (e.g. Herridge et al., 2008). In the PNV simulation, values for %Ndfa were between 0 % and 20 % for most of the grid cells (Figs. C7 and C8b). The distribution is bimodal, showing a peak below 5 % and one at approximately 10 %. For the dynamic land-use simulation, the values for %Ndfa are similar, but the second peak is barely distinguishable because of a higher share of %Ndfa values between 5 % and 10 % (Figs. C7 and C8a). For the crop legumes, %Ndfa is substantially higher, with the peak at around 80 % (Fig. C7d). The highest values are simulated at low latitudes, especially in India, sub-Saharan Africa and South America, while the lowest values are simulated in Canada, Russia and southern China (Fig. C8d). In the Original approach, %Ndfa of legume crops was almost exclusively 100 % (Fig. C7e).
In both approaches, BNF per area is higher for agricultural land than for natural vegetation (Fig. C3d and f). BNF is especially high in hot spots of legume crop production such as Argentina, Brazil, India and the USA (Fig. 3a and b). While the spatial pattern is similar between the two approaches, in the Original approach, the cropland BNF leads to prominent peaks in the latitudinal distribution (Fig. 3c). These peaks correspond to hot spots of legume crop production, where the C-costly approach is up to 15 lower (Fig. C4).
For natural vegetation, the differences are smaller. Here, the BNF in the Original approach is up to 4 higher compared to the C-costly approach (Fig. C4). Here, the spatial patterns differ and show a stronger reduction in the BNF in dry regions (e.g. central Australia, the Eurasian steppe regions, southeast China and parts of Africa).
The various natural PFTs contribute differently to the lower overall BNF in the C-costly approach (Figs. C5 and C6). To some extent, this reflects changes in the PFT distribution (Figs. S1 and S2 in the Supplement). For the tropical PFTs, BNF is lower for the broadleaved raingreen tree (Δ5.25 Tg N yr−1; Fig. C5b) and the herbaceous PFT (Δ14.1 Tg N yr−1; Fig. C5i) and higher for the broadleaved evergreen tree (Δ7.3 Tg N yr−1; Fig. C5a). While the temperate needleleaved evergreen tree PFT contributed to BNF in low latitudes outside its expected habitat (e.g. in India and Brazil) in the Original approach, this issue was resolved with the C-costly approach (Fig. C5c). The temperate PFTs all fix less N in the C-costly approach than in the Original approach. The reductions are smaller for the broadleaved evergreen (Δ3.6 Tg N yr−1; Fig. C5d) and summergreen (Δ3.8 Tg N yr−1; Fig. C5e) tree and the herbaceous PFT (Δ4.7 Tg N yr−1; Fig. C5j) compared to the needleleaved evergreen tree (Δ9.1 Tg N yr−1; Fig. C5c). The BNF of boreal PFTs is similar (Δ around 0.5 Tg N yr−1; Fig. C5f, g, and k) for all PFTs, except the needleleaved summergreen tree (Δ1.2 Tg N yr−1; Fig. C5h), which fixes less N in the C-costly approach. In the Original approach, the temperate herbaceous PFT contributed twice as much as in the C-costly approach to the biological N fixation of the polar vegetation (Fig. C5j). For pulses, the BNF was 14.6 Tg N yr−1, and for soybean,the BNF was 6.4 Tg N yr−1 lower with the C-costly approach.
3.2 Effects on the nitrogen and carbon cycle and productivity
In LPJmL the C and N cycles are coupled via, for example, the N limitation of gross primary productivity (GPP), which controls the amount of assimilated C, the role of plant organ carbon-to-nitrogen (C:N) ratios for maintenance respiration and the availability of the resulting NPP for BNF. Additionally, the N content of the different plant organs (leaves, roots, sapwood, heartwood and storage organs) is derived dependent on the respective C content ensuring that their C:N ratios remain within a prescribed range. As a result, the N balance components presented in the following section are strongly shaped by their C cycle counterparts as the overall C and N balances represented by LPJmL are intimately linked.
We describe the N balance as the sum over in- and outfluxes of the vegetation and the soil. Therefore, the overall balance contains a change in vegetation and soil N stocks, including organic and mineral forms of N.
3.2.1 Potential natural vegetation
Simulating only natural vegetation resulted in a positive terrestrial N balance with an average sink of 52 Tg N yr−1 for the Original approach and 54 Tg N yr−1 for the C-costly approach between 2001 and 2010 (Fig. 4a and b and Table 2). In 1901, N in- and outputs were almost balanced, and the sink remained small until the 1950s when N inputs from deposition increased, resulting in an increased sink. While the overall N balance was similar for both BNF approaches, the size of several components was different. The total BNF simulated with the Original approach was approximately double that of the C-costly BNF, leading to higher soil mineral N and organic C and N stocks. However, mineral N stocks were not utilised by the vegetation but instead lost to the atmosphere and waterbodies, leading to higher N emissions and leaching using the Original approach. Here, 112 Tg N yr−1 were emitted and 56 Tg N yr−1 were leached on average between 2001 and 2010, while for the C-costly approach, only 79 Tg N yr−1 were emitted and 39 Tg N yr−1 were leached (Table 2). All types of emissions are lower with the C-costly approach. NH3 emissions from volatilisation decrease by 14 Tg N yr−1, N2 emissions by 12 Tg N yr−1, N2O emissions by 3 Tg N yr−1 and fire emissions by 5 Tg N yr−1. Synchronised with the increase in deposition over time, emissions and leaching also increase in both approaches, with stronger increases in the C-costly approach. Overall, N inputs increased by 35 Tg N in total from 1950 to 2000 in the Original approach and by 42 Tg N in the C-costly approach, while N losses from emissions and leaching increased by 1 and 4 Tg N, respectively (Table 2).
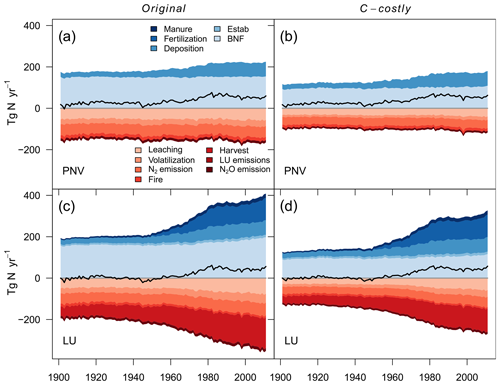
Figure 4Global terrestrial N balance. Scenarios include the Original approach, the C-costly approach for natural vegetation and actual land use. Net balance is denoted by the black line. N inputs include N from manure, synthetic fertiliser deposition, PFT establishment (Estab) and BNF. N losses include leaching, volatilisation, N2 emissions, fire N, harvested N, land-use change emissions (deforestation and product turnover) and N2O emissions from nitrification and denitrification.
Table 2N balance values for 2001 to 2010 shown in the figures. LUC (land-use change) includes deforestation emissions, product turnover and negative N fluxes.
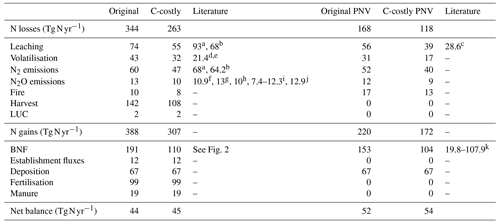
a Bouwman et al. (2013). b Zaehle et al. (2010). c Braakhekke et al. (2017). d Volatilisation from natural soils (2.4 Tg N yr−1) from Bouwman et al. (2002). e Volatilisation from manure and synthetic fertiliser on croplands and grasslands (19 Tg N yr−1) from Bouwman et al. (1997). f Galloway et al. (2004). g Sutton et al. (2013). h Tian et al. (2019). i Tian et al. (2020). j Scheer et al. (2020). k Yu and Zhuang (2020).
In addition to the changes in several N cycle components, we excepted changes in C cycle components. Overall, the C balance was similar for both approaches (Fig. C9a and b). For the PNV simulations, the only C input into the system was the NPP. The NPP was 2.2 Pg C yr−1 lower with the C-costly approach compared to the Original approach. However, C losses from heterotrophic respiration and fire were also lower by 1.9 and 0.3 Pg C yr−1, respectively.
3.2.2 Dynamic land use
The simulations with dynamic land use include agricultural production and related additional N in- and outputs. Additional inputs are N from the application of manure and synthetic fertilisers, and additional outputs are N removed through crop harvesting, grazing and emissions from land-use change. The differences in the total BNF, soil mineral N and organic C and N stocks are similar to the PNV simulations. Between 2001 and 2010, LPJmL simulated an average N sink of 44 Tg N yr−1 for the Original and 45 Tg N yr−1 for the C-costly approach (Fig. 4c and d and Table 2). Already in 1901, the N balances of the PNV and dynamic land-use simulations diverge. Since there are no synthetic fertiliser inputs in 1901, only the relatively small additional inputs from establishment and manure were counteracted by N removal through crop harvesting and land use change emissions, shifting the total N balance towards a smaller source. This persists even after inputs from manure and fertiliser were increased from the 1950s onwards, which not only resulted in higher crop yields, and therefore N removed through harvesting, but also increased N losses from emissions and leaching. As was shown for the PNV simulations, the overall N balance is similar for both approaches but with different in- and output terms driven by the higher BNF in the Original approach. N emissions and leaching for the Original approach (128 and 74 Tg N yr−1, respectively) were higher than for the C-costly approach (99 and 55 Tg N yr−1, respectively) (Table 2). Similar to the PNV scenario, all types of emissions are lower with the C-costly approach. NH3 emissions from volatilisation decrease by 11 Tg N yr−1, N2 emissions by 13 Tg N yr−1, N2O emissions by 3 Tg N yr−1 and fire emissions by 2 Tg N yr−1. N removal from harvesting was 142 Tg N yr−1 on average between 2001 and 2010 for the Original approach and 108 Tg N yr−1 for the C-costly approach. This indicates a stronger N limitation of agricultural areas in the C-costly approach. The majority of this reduction can be attributed to managed grassland and not croplands (Figs. S3 and S4).
Similar to the PNV simulations, the overall C balance barely differed between the two approaches (Fig. C9c and d). While the C input from manure and establishment was similar for both approaches, NPP was 1.8 Pg C yr−1 lower in the C-costly approach. C lost from land-use change was similar. Fire emissions and C removed through harvesting only differed by 0.1 Pg C yr−1, while heterotrophic respiration was 1.4 Pg C yr−1 lower in the C-costly approach than in the Original approach.
While the Original approach only indirectly accounts for temperature and water limitation, as these also limit evapotranspiration and NPP, the C-costly approach explicitly considers the limitation of BNF from soil temperature, water content and NPP separately. These have long been established as limiting factors for BNF. Depending on the prevailing conditions, BNF may be limited more strongly by temperature or soil moisture or a combination of both. The role of temperature was explored early on by Meyer and Anderson (1959) and was followed by numerous studies for different plant species or legume crop varieties and temperature ranges (e.g. Montañez et al., 1995). Such studies allowed the quantification of optimal temperature ranges and limits facilitating the development of functions such as fT(Tsoil), which are based on empirically derived temperature curves (e.g. Halliday and Pate, 1976). A similarly large literature body exists on the role of soil moisture (e.g. Serraj et al., 1999; Rousk et al., 2018). Valentine et al. (2018), describing the different pathways with respect to how drought stress inhibits BNF, with an important aspect being the change in nodule water potential that indicates a strong connection to soil water content. While flooding of soils can also inhibit BNF through O2 limitation, nitrogenase was shown to be more active in waterlogged environments (Jiang et al., 2021). Therefore, we are confident that our linear function for fW(SWC), assuming that only soil moisture levels that are too low limit BNF (McGechan, 1999), reflects empirical observations well. As BNF is associated with a respiratory loss of C, the net amount of C assimilated via photosynthesis (NPP) available for BNF, as well as the fixation efficiency (respiratory loss of C per gained N), forms an additional important controlling factor. A recent meta-analysis by Yao et al. (2024) highlights the importance of plant taxa for BNF in addition to abiotic factors. This is in line with early experimental work that quantified the respiratory loss of C per N fixed (Reed et al., 2011; Patterson and Larue, 1983; Voisin et al., 2003) and the total amount of NPP spent on fixation (Kaschuk et al., 2009) for different N-fixing plants and already showed that functional traits have to be considered when assessing BNF. Therefore, including NPP and a cost of fixation, as we did with the C-costly approach, is an important conceptual improvement.
The C-costly approach is not only conceptually superior to the simplistic Original approach in LPJmL, it also performs better in comparison to external data. Still, some mismatches with reference data remain, such as an overestimation of BNF in the tropics (Fig. 3c). However, the ensemble mean of a recent study evaluating the N cycle of 11 DGVMs shows a similar overestimation in the tropics and a large bias, indicating little agreement between models (Kou-Giesbrecht et al., 2023). They attributed this to the fact that BNF is typically modelled as a function of vegetation activity expressed either through NPP or evapotranspiration. Our results show that the overestimation of tropical BNF is reduced if temperature and water availability are considered separate limitations, which supports their interpretation. Furthermore, the NPP that can be used for BNF depends on the overall productivity, which certainly is higher in the tropics. It is likely that additional variables not considered in our approach constrain BNF there, such as phosphorus limitation (Vitousek, 1984; Lee et al., 2019). However, it has also been suggested that as a result of higher N losses, tropical BNF should be higher than observations imply (Hedin et al., 2009). This could be a result of uncertainties inherent to BNF measurements (Soper et al., 2021) or the limited amount of data available from tropical ecosystems.
Furthermore, simulated BNF was at the higher end of the range reported by Davies-Barnard and Friedlingstein (2020b) for the C-costly approach. One explanation is that Davies-Barnard and Friedlingstein (2020b) aggregate cropland and grassland areas, assuming that their BNF rates are identical. However, a recent study provides evidence that the BNF of crop legumes might actually be substantially higher than that of forage legumes (Herridge et al., 2022; Peoples et al., 2021), and therefore, the BNF of croplands and grassland cannot be assumed to be similar. Consistent with this, we also had to select much higher potential N fixation rates for the crop PFTs compared to the other PFTs to achieve sufficient cropland BNF (Table 1).
We expected that limiting BNF of legume crops would result in stronger N stress and reduced yields. However, yields for the legume crops were similar between the two approaches. One explanation is the direct link that the maintenance respiration of a plant organ has to its N content. Reducing the N that is taken up via BNF results in a lower organ N content and maintenance respiration and thus similar NPP. Indeed, C:N ratios are higher for the C-costly approach compared to the Original approach, indicating a lower plant N content (Fig. C2).
The average %Ndfa of legume crops was between approximately 30 % and 100 % for the C-costly approach and 100 % for the Original approach. Comparing the distribution (Fig. C7d) to %Ndfa observations shows that the values of the C-costly approach are possible but at the upper end of observations, while those of the Original approach are not supported by observations. For soybean, experimental values range from 0 % to 98 %, with an average of 52 % (Salvagiotti et al., 2008). Herridge et al. (2008) report average values between 40 % and 75 % on average and up to 97 % for experiments but only 36 % and 68 % for farmers' fields, depending on the cultivated legume crop. %Ndfa is strongly related to soil mineral N content and thus fertilisation levels. The high %Ndfa may be an indication that either fertiliser levels or active and passive N uptake and retranslocation of N at leaf senescence are underestimated by LPJmL, and respective processes should be re-evaluated. We found a higher %Ndfa for both the natural vegetation and the cropland in warm and dry areas (Fig. C8) where mineralisation of organic N is limited (Dessureault-Rompré et al., 2010).
We expected that the differences in the BNF between the two approaches would be reflected by differences in the C stocks and fluxes due to the close link of the C and N cycles in LPJmL. Both the C inflow into terrestrial C stocks from NPP and outflows from harvest, heterotrophic respiration and fire were lower in the C-costly approach, leading to a similar net C balance for the two approaches (Figs. C9 and S5). Accounting for the cost of BNF in the form of respiratory losses of NPP leads to lower NPP, which limited biomass accumulation and in turn harvest, as well as biomass available for burning and heterotrophic respiration via reduced litter accumulation. Because of the close link of the C and N cycles, the net N balance is also similar for the two approaches. The lower BNF in the C-costly approach results in lower N outfluxes, i.e. leaching, emissions and harvests. The Original approach added mineral N to the soils of the natural vegetation and managed grassland even if the vegetation was not N limited. Legume crops that received all the N that they demanded, as in the Original approach, returned high N content residues to the soil, increasing N inputs and mineral N stocks. As a result, the mineral N content of soils was higher in the Original approach, explaining the differences in yields and leaching. Similarly, soil mineral N content influences N emissions except fire emissions, which are controlled by the N content of the burned vegetation and litter. Since this also decreased, fire emissions were lower with the C-costly approach. In contrast to the lower BNF, which is in line with observations, N losses from leaching and emissions (from volatilisation, denitrification, nitrification, fire and land-use change) are underestimated by LPJmL simulations compared to observational data (see Table 2) in both approaches. The overestimation of emissions from volatilisation of soil is strongly reduced with the C-costly approach because the soil pool is lower in the C-costly approach compared to the Original approach, where BNF is directly added to the soil (see Sect. 2.2). While N2O emissions compare well to literature estimates, N2 emissions are more strongly underestimated with the C-costly approach. Similar to the soil pool, the soil is reduced because less is available for nitrification, resulting in reduced N2 emissions. Overall, the reduction shifts emissions from an over- to an underestimation of the literature values. While one source of differences is the missing representation of NOx emissions in LPJmL, this is not sufficient to fully explain the difference. However, the models of the TRENDY-N ensemble also underestimated N losses from emissions of NH3, N2O, NOx, and N2, as well as leaching (Kou-Giesbrecht et al., 2023), suggesting that processes within DGVMs and scenario assumptions need to be revised. For LPJmL, we identified several potential causes. First, the manure input accounts only for manure applied to cropland, and the total amount is in line with other sources reporting cropland manure (Zhang et al., 2021), but does not account for manure added to grasslands other than the internal recycling by grazing animals (Heinke et al., 2023). Second, N losses and emissions strongly vary between different agricultural production systems whose representation would require not only the implementation of more detailed management options but also data sets on the spatial patterns of the application of different management specifics of these systems. Third, we conducted our simulations assuming cover cropping outside the growing season on all croplands, which overestimates the extent of cover cropping and reduces N losses. However, data on cover cropping systems are not available (e.g. Porwollik et al., 2022).
While the C-costly approach improved simulation results for BNF, as well as other components of the N balance, and model results are in line with other DGVMs that represent the N cycle, we see potential for further improvement. The C-costly approach depends on multiple parameters, some of which are not well constrained. Values for the potential N fixation rate vary between species and across sites (Ma et al., 2022), and selecting one value to be representative of one PFT or even all PFTs of an entire climate zone is a strong simplification. Furthermore, experiments have shown a large variation in the respiratory cost of BNF (Reed et al., 2011; Patterson and Larue, 1983; Voisin et al., 2003), as well as the amount of NPP that different plant species invest (Kaschuk et al., 2009), which is not well reflected by the current parameterisation.
In addition, we assume a constant fraction of N fixers present in a community. However, the number of N fixers changes over time, dependent on N stress (Herben et al., 2017; Taylor et al., 2019). N fixation, the share of fixers and/or nodule abundance is low in undisturbed N-rich environments, and nodules need to be produced to increase N fixation if N availability decreases (Fisher et al., 2010; Crews, 1999). Similarly, N fixation does not cease instantaneously when N becomes more abundant but is only reduced after the share of fixers and/or nodule abundance has decreased (Thornley et al., 1995; Herben et al., 2017). In contrast, fixers are always present in LPJmL and can instantly fix N if necessary. Therefore, LPJmL likely simulates an adaptation response that is too quick for the changing N availability and overestimates the short-term capability of the community to buffer changes in N availability.
While our approach simulates the total amount of BNF well, it does not distinguish the symbiotic from free-living or heterotrophic N fixation. However, these are two different sources of N, and their share of total BNF shows large spatial heterogeneity (Davies-Barnard and Friedlingstein, 2020b). In contrast to symbiotic BNF, free-living BNF does not require NPP expenditures, and separating the two may further improve simulation results for NPP and its dependent variables.
In the following, we qualitatively compare our approach to common approaches used in crop models and DGVMs. A synthesis of nine crop models by Liu et al. (2011) showed that soil water status and N supply were the most widely considered control variables. Soil temperature was only considered by four models and plant C supply only by two models, despite their importance for limiting BNF. The C-costly approach also uses empirical factors to account for soil temperature and soil water status, whereas the role of N supply, plant C supply and plant growth stage are simulated mechanistically in LPJmL, which is a clear distinction from the models assessed by Liu et al. (2011).
Our approach is at the higher end of the complexity when compared to 11 TRENDY-N DGVMs that include the N cycle. As shown in Kou-Giesbrecht et al. (2023), five DGVMs follow an approach similar to the Original approach, calculating BNF based on evapotranspiration or NPP; three models calculate BNF as a function of N limitation; two models assume a constant BNF; and in one model BNF is derived in post-processing to close the N cycle. The remaining three models use more complex approaches which can be compared to the C-costly approach. The Community Land Model (CLM) version 5.0 (Lawrence et al., 2019) uses an approach based on Fisher et al. (2010), explicitly minimising the cost of active N uptake, retranslocation and BNF and distinguishes asymbiotic from symbiotic N fixation. In the Canadian Terrestrial Ecosystem Model (CTEM), BNF is a function of temperature, vegetation cover, soil nitrate and plant structural C pools (Arain et al., 2006; Dickinson et al., 2002). The Dynamic Land Ecosystem Model (DLEM) considers soil temperature, soil moisture status, soil C and soil N (Tian et al., 2015). While the approach used in CLM5.0 is more complex compared to the C-costly approach and addresses some of the conceptual shortcomings of the C-costly approach discussed earlier, the approach used in CTEM is of similar complexity and simulates values at the upper end of the recent literature estimates (Kou-Giesbrecht et al., 2023). However, global BNF values and latitudinal distribution simulated by CLM5.0, as shown by Kou-Giesbrecht et al. (2023) in Figs. 3 and A6, are comparable to those simulated with C-costly approach. To fully assess the advantages of such a complex approach over the C-costly approach or that of CTEM or DLEM, a comparison of the spatial patterns or of simulations at higher spatial resolution could be a worthwhile future endeavour.
Compared to the simplistic Original BNF implementation in LPJmL, the more complex C-costly approach, as described here, presents a substantial improvement of the representation of BNF in LPJmL. While the Original approach led to an overestimation of BNF and was insensitive to soil temperature and soil water conditions, the C-costly approach overcomes these issues and can help to better project future BNF and its effects on N limitation of the terrestrial biosphere, as well as losses of reactive N to the environment, including the greenhouse gas nitrous oxide (N2O). Further research is needed, especially with respect to balancing different in- and outfluxes and internal recycling rates. The current improvement of BNF simulations with LPJmL and the associated underestimation of loss terms exemplifies the scope of this problem. Our study highlights the importance of a detailed implementation of the processes controlling BNF for N cycling in DGVMs. While the C-costly approach already improved simulation results, we think that additional benefits would be gained by explicitly separating BNF by symbiotic and free-living bacteria and from accounting for the costs of other N-uptake sources, except passive N uptake.
The total N demand (Ndemand in g N m−2) at any time t is the sum of the leaf N demand for RuBisCo and structural components (Ndemand,leaf in g N m−2) and the N demand for structural components of the other plant compartments.
where Vmax (g C m−2) is the PFT-specific maximum carboxylation capacity computed based on absorbed photosynthetically active radiation (APAR) and canopy conductance (Schaphoff et al., 2018b; Sitch et al., 2003). T is the average temperature (°C) of the current day, and daylength is the duration of daylight (h). fLAI(LAI) is a dimensionless modifier to account for the current leaf area index (von Bloh et al., 2018), and Cleaf (g C m−2) is the current leaf C content.
LAI is the current leaf area index, and is the difference between the accumulated biomass increment and litterfall.
where M is one for grasses, two for trees and three for crops, equalling the number of the respective PFT plant compartments and excluding leaves, . fm is the fraction of biomass allocated to the compartment m, Rm is the C:N ratio of compartment m relative to the leaf C:N ratio, and kstore is a PFT-specific parameter to maintain the PFT labile N storage. Passive and active N uptake (Nuptake) from each soil layer l (nsoillayer=6) is calculated as a function of the potential N uptake of the root system.
where Nup,root is the PFT-specific maximum N-uptake rate per unit of fine root mass in each layer, Croot,t is the current root C, rootdistl is the fraction of roots in layer l. fN, fT and fNC are dimensionless modifiers for the availability of mineral N, soil temperature and plant N:C ratio (von Bloh et al., 2018). Croot,t is calculated as Cleaf,t in Eq. (A3). The root distribution can be calculated from the proportion of roots from the surface to soil depth z, following Jackson et al. (1996):
where zbottom is the lower boundary of the last soil layer and βroot is a PFT-specific parameter (Table A1). The root proportion of one soil layer can be calculated as
fN follows Michaelis–Menten kinetics,
where , kN,min and KN,min are the PFT-specific parameters describing the Michaelis–Menten kinetics. Θmax is the soil-type-specific fractional pore space, and dsoil,l (dimensionless) is the soil layer depth (m).
fT is the temperature function given by Thornley (1991)
where has to be fulfilled. von Bloh et al. (2018) defined Tm=15 °C, Tr=15 °C and °C, which leads to the maximum of one at temperatures of 15 °C and higher and non-zero values above −25 °C.
fNC was taken from Zaehle and Friend (2010),
where , NCleaf,min and NCleaf,max are PFT-specific parameters extracted from the TRY database (Kattge et al., 2020) (Table A1).
The labile-N values Nlabile,t are the current reserves which have accumulated via N uptake and retranslocation.
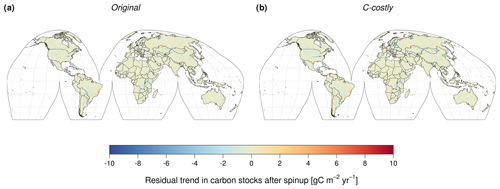
With constant forcing (i.e. stable pre-industrial atmospheric CO2 concentration, atmospheric N deposition and climate), the global C stocks showed a residual trend of −0.0106 Pg C yr−1 for the Original approach and −0.0121 Pg C yr−1 for the C-costly approach. This is 8–10 times lower than the steady-state criterion of the 0.1 Pg C yr−1 residual trend after spin-up, which is used by the Global Carbon Project to validate DGVMs for inclusion in their global C budget analysis (Friedlingstein et al., 2022). At the grid cell level, the vast majority of cells (94 % for the Original approach and 95 % for the C-costly approach) exhibited residual trends in total C stocks of less than ±1 g C m2 yr−1. The corresponding maps are shown in Fig. B1.
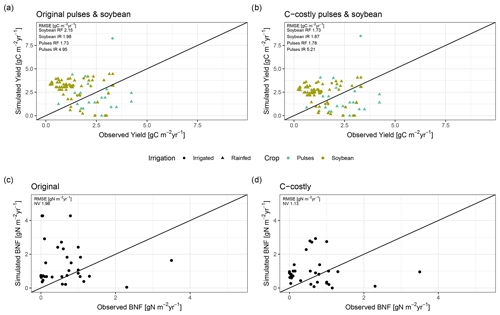
Figure C1Simulated and observed crop yields (a, b) for soybean (green) and pulses (blue) and BNF in natural vegetation (c, d).
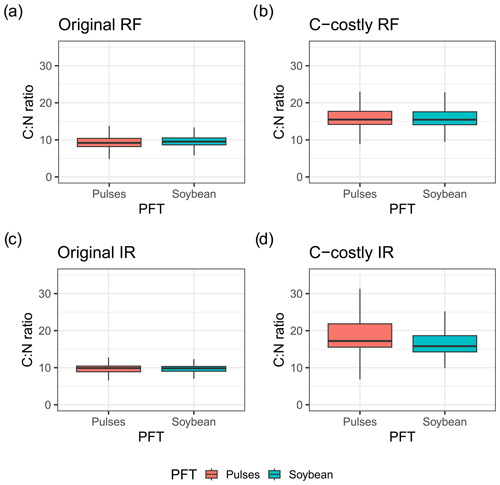
Figure C2Vegetation C:N ratio for the years 2001 to 2010 for rainfed (RF) and irrigated (IR) soybean (red) and pulses (blue) for the Original approach and C-costly approach.
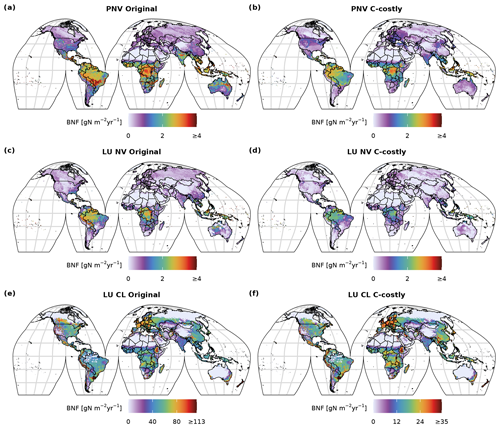
Figure C3The 2001 to 2010 average BNF (in ) of the potential natural vegetation (PNV) simulations (a, b), of the natural vegetation (NV) (c, d) and of the managed land (AG) (e, f) area fractions of the dynamic land-use (LU) simulations.
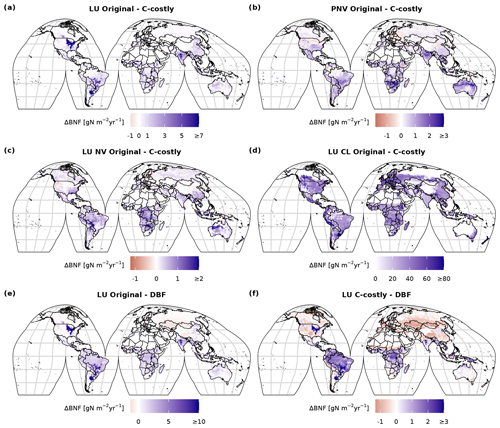
Figure C4Difference between 2001 to 2010 average BNF (in ) between the two approaches (a–d) for the dynamic land-use (LU) simulations (a), for the potential natural vegetation (PNV) simulations (b), for the area fractions of natural vegetation (NV) (c) and for the managed land (AG) (e) of the dynamic land-use simulations and the difference compared to the data from Davies-Barnard and Friedlingstein (2020a) (DBF) (e, f).
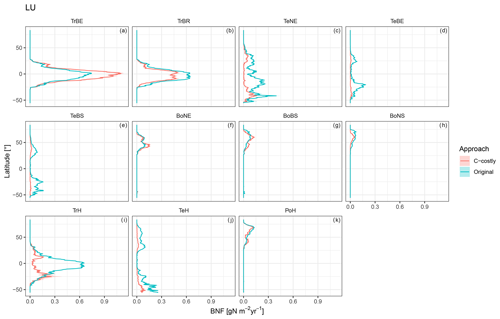
Figure C5Latitudinal distribution of BNF for each PFT for the dynamic land-use simulations for the Original approach (red) and C-costly approach (blue).
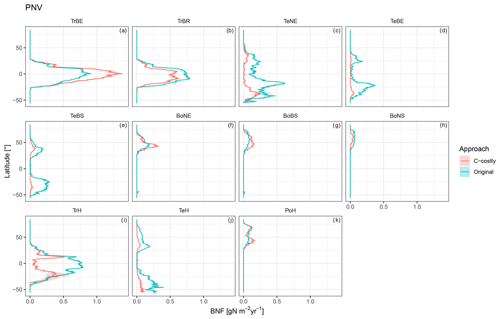
Figure C6Latitudinal distribution of BNF for each PFT for the potential natural vegetation simulations for the Original approach (red) and C-costly approach (blue).
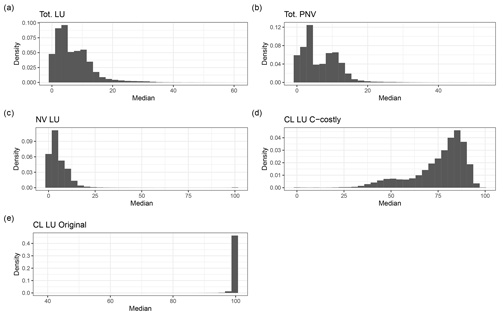
Figure C7Density distribution of the fraction of BNF of the total N uptake for the dynamic land-use simulations (a), for the potential natural vegetation (b) and for the area fractions of natural vegetation (NV) (c) and cropland (CL), using the C-costly approach (d) and the Original (e) approach for the dynamic land-use simulations.
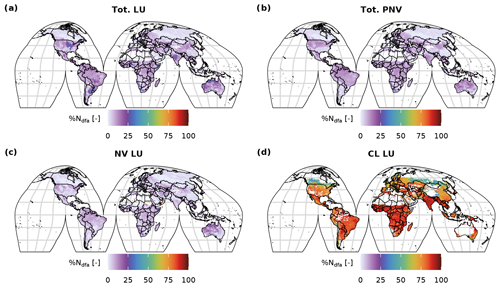
Figure C8Global distribution of the fraction of %Ndfa for the dynamic land-use (a), for the potential natural vegetation simulations (b) and the natural vegetation (c) and cropland (d) fraction of the dynamic land-use simulation.
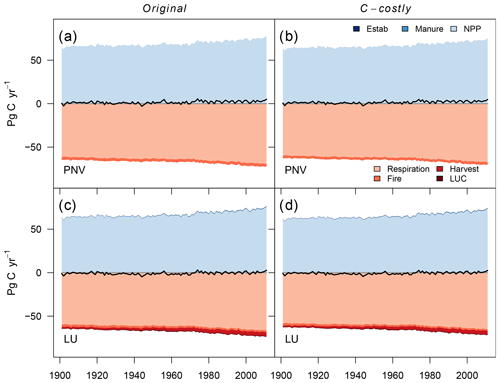
Figure C9Global terrestrial C balance. Scenarios include the Original approach and the C-costly approach for natural vegetation and actual land use. The net balance is denoted by the black line. C inputs include C from manure, PFT establishment (Estab) and NPP. C losses include heterotrophic respiration, fire emissions, harvested C and land-use change emissions (from deforestation and product turnover).
The source code of LPJmL in the exact form described here is available at https://doi.org/10.5281/zenodo.14012503 (Wirth et al., 2024) and at https://github.com/PIK-LPJmL/LPJmL (last access: 30 October 2024).
The historical climate data from the GSWP3-W5E5 data set are available from https://doi.org/10.48364/ISIMIP.982724 (Lange et al., 2022). The historical data of atmospheric N deposition and atmospheric CO2 concentrations can be obtained from https://doi.org/10.48364/ISIMIP.600567 (Yang and Tian, 2020) and https://doi.org/10.48364/ISIMIP.664235.2 (Büchner and Reyer, 2022), respectively. All input data, model code, model outputs and scripts that have been used to produce the results presented in this paper are archived at the Potsdam Institute for Climate Impact Research and are available upon request.
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-17-7889-2024-supplement.
SBW, CM, FS, SR, SiS and WvB designed the study. SBW designed and conducted the model implementation with inputs from CM, JB, SR, SiS and WvB. SBW, CM, FS, SR, SiS, WvB, SO, JH and JB contributed to the general model development and evaluation. SBW conducted the model simulations and wrote the original draft, with inputs from CM, FS, SR, SiS and WvB. SBW, CM, FS, SR, SiS, WvB, SO, JH and JB reviewed and edited the original draft. All authors discussed the simulation results and reviewed and edited the paper.
At least one of the (co-)authors is a member of the editorial board of Geoscientific Model Development. The peer-review process was guided by an independent editor, and the authors also have no other competing interests to declare.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
Fabian Stenzel acknowledges funding by the Global Challenges Foundation via Future Earth. We thank the two anonymous reviewers for their valuable feedback.
This research has been supported by the Bundesministerium für Bildung und Forschung (grant nos. 01LP1903D and 01LS2105A), the European Union's Horizon 2020 (grant nos. 101003536 and 869192), the Evangelisches Studienwerk Villigst (grant no. 851291) and Conservation International (grant no. CI-114129).
The publication of this article was funded by the Open Access Fund of the Leibniz Association.
This paper was edited by Hans Verbeeck and reviewed by two anonymous referees.
Arain, M. A., Yuan, F., and Andrew Black, T.: Soil–Plant Nitrogen Cycling Modulated Carbon Exchanges in a Western Temperate Conifer Forest in Canada, Agr. Forest Meteorol., 140, 171–192, https://doi.org/10.1016/j.agrformet.2006.03.021, 2006. a
Becker, M., Ladha, J. K., and Ali, M.: Green Manure Technology: Potential, Usage, and Limitations. A Case Study for Lowland Rice, in: Management of Biological Nitrogen Fixation for the Development of More Productive and Sustainable Agricultural Systems: Extended Versions of Papers Presented at the Symposium on Biological Nitrogen Fixation for Sustainable Agriculture at the 15th Congress of Soil Science, Acapulco, Mexico, 1994, edited by: Ladha, J. K. and Peoples, M. B., Developments in Plant and Soil Sciences, Springer Netherlands, Dordrecht, 181–194, https://doi.org/10.1007/978-94-011-0053-3_8, 1995. a
Beringer, T., Lucht, W., and Schaphoff, S.: Bioenergy Production Potential of Global Biomass Plantations under Environmental and Agricultural Constraints, GCB Bioenergy, 3, 299–312, https://doi.org/10.1111/j.1757-1707.2010.01088.x, 2011. a
Bodirsky, B. L., Popp, A., Weindl, I., Dietrich, J. P., Rolinski, S., Scheiffele, L., Schmitz, C., and Lotze-Campen, H.: N2O emissions from the global agricultural nitrogen cycle – current state and future scenarios, Biogeosciences, 9, 4169–4197, https://doi.org/10.5194/bg-9-4169-2012, 2012. a
Bondeau, A., Smith, P. C., Zaehle, S., Schaphoff, S., Lucht, W., Cramer, W., Gerten, D., Lotze-Campen, H., Müller, C., Reichstein, M., and Smith, B.: Modelling the Role of Agriculture for the 20th Century Global Terrestrial Carbon Balance, Glob. Change Biol., 13, 679–706, https://doi.org/10.1111/j.1365-2486.2006.01305.x, 2007. a
Boote, K. J., Hoogenboom, G., Jones, J. W., and Ingram, K. T.: Modeling Nitrogen Fixation and Its Relationship to Nitrogen Uptake in the CROPGRO Model, in: Quantifying and Understanding Plant Nitrogen Uptake for Systems Modeling, edited by: Ma, L., Ahuja, L. R., and Bruulsema, T., CRC Press, https://doi.org/10.1201/9781420052978, 2009. a
Bouwman, A. F., Lee, D. S., Asman, W. A. H., Dentener, F. J., Van Der Hoek, K. W., and Olivier, J. G. J.: A Global High-Resolution Emission Inventory for Ammonia, Global Biogeochem. Cy., 11, 561–587, https://doi.org/10.1029/97GB02266, 1997. a
Bouwman, A. F., Boumans, L. J. M., and Batjes, N. H.: Estimation of Global NH3 Volatilization Loss from Synthetic Fertilizers and Animal Manure Applied to Arable Lands and Grasslands, Global Biogeochem. Cy., 16, 8-1–8-14, https://doi.org/10.1029/2000GB001389, 2002. a
Bouwman, A. F., Beusen, A. H. W., Griffioen, J., Van Groenigen, J. W., Hefting, M. M., Oenema, O., Van Puijenbroek, P. J. T. M., Seitzinger, S., Slomp, C. P., and Stehfest, E.: Global Trends and Uncertainties in Terrestrial Denitrification and N2O Emissions, Philos. T. Roy. Soc. B, 368, 20130112, https://doi.org/10.1098/rstb.2013.0112, 2013. a
Braakhekke, M. C., Rebel, K. T., Dekker, S. C., Smith, B., Beusen, A. H. W., and Wassen, M. J.: Nitrogen leaching from natural ecosystems under global change: a modelling study, Earth Syst. Dynam., 8, 1121–1139, https://doi.org/10.5194/esd-8-1121-2017, 2017. a
Büchner, M. and Reyer, C. P. O.: ISIMIP3a atmospheric composition input data (v1.2), ISIMIP Repository [data set], https://doi.org/10.48364/ISIMIP.664235.2, 2022. a, b
Chang, J., Havlík, P., Leclère, D., de Vries, W., Valin, H., Deppermann, A., Hasegawa, T., and Obersteiner, M.: Reconciling Regional Nitrogen Boundaries with Global Food Security, Nat. Food, 2, 700–711, https://doi.org/10.1038/s43016-021-00366-x, 2021. a
Cleveland, C. C., Townsend, A. R., Schimel, D. S., Fisher, H., Howarth, R. W., Hedin, L. O., Perakis, S. S., Latty, E. F., Von Fischer, J. C., Elseroad, A., and Wasson, M. F.: Global Patterns of Terrestrial Biological Nitrogen (N2) Fixation in Natural Ecosystems, Global Biogeochem. Cy., 13, 623–645, https://doi.org/10.1029/1999GB900014, 1999. a, b, c, d, e, f, g, h
Crews, T. E.: The Presence of Nitrogen Fixing Legumes in Terrestrial Communities: Evolutionary vs. Ecological Considerations, Biogeochemistry, 46, 233–246, https://doi.org/10.1007/BF01007581, 1999. a
Cucchi, M., Weedon, G. P., Amici, A., Bellouin, N., Lange, S., Müller Schmied, H., Hersbach, H., and Buontempo, C.: WFDE5: bias-adjusted ERA5 reanalysis data for impact studies, Earth Syst. Sci. Data, 12, 2097–2120, https://doi.org/10.5194/essd-12-2097-2020, 2020. a
Davies-Barnard, T. and Friedlingstein, P.: Data: The Global Distribution of Biological Nitrogen Fixation in Terrestrial Natural Ecosystems, https://doi.org/10.24378/exe.2063, 2020a. a, b, c, d, e, f, g, h, i, j, k
Davies-Barnard, T. and Friedlingstein, P.: The Global Distribution of Biological Nitrogen Fixation in Terrestrial Natural Ecosystems, Global Biogeochem. Cy., 34, e2019GB006387, https://doi.org/10.1029/2019GB006387, 2020b. a, b, c, d, e, f
Dessureault-Rompré, J., Zebarth, B. J., Georgallas, A., Burton, D. L., Grant, C. A., and Drury, C. F.: Temperature Dependence of Soil Nitrogen Mineralization Rate: Comparison of Mathematical Models, Reference Temperatures and Origin of the Soils, Geoderma, 157, 97–108, https://doi.org/10.1016/j.geoderma.2010.04.001, 2010. a
Dickinson, R. E., Berry, J. A., Bonan, G. B., Collatz, G. J., Field, C. B., Fung, I. Y., Goulden, M., Hoffmann, W. A., Jackson, R. B., Myneni, R., Sellers, P. J., and Shaikh, M.: Nitrogen Controls on Climate Model Evapotranspiration, J. Climate, 15, 278–295, https://doi.org/10.1175/1520-0442(2002)015<0278:NCOCME>2.0.CO;2, 2002. a
Donges, J. F., Heitzig, J., Barfuss, W., Wiedermann, M., Kassel, J. A., Kittel, T., Kolb, J. J., Kolster, T., Müller-Hansen, F., Otto, I. M., Zimmerer, K. B., and Lucht, W.: Earth system modeling with endogenous and dynamic human societies: the copan:CORE open World–Earth modeling framework, Earth Syst. Dynam., 11, 395–413, https://doi.org/10.5194/esd-11-395-2020, 2020. a
Fageria, N. K.: Green Manuring in Crop Production, J. Plant Nutr., 30, 691–719, https://doi.org/10.1080/01904160701289529, 2007. a
Fisher, J. B., Sitch, S., Malhi, Y., Fisher, R. A., Huntingford, C., and Tan, S.-Y.: Carbon Cost of Plant Nitrogen Acquisition: A Mechanistic, Globally Applicable Model of Plant Nitrogen Uptake, Retranslocation, and Fixation, Global Biogeochem. Cy., 24, GB1014, https://doi.org/10.1029/2009GB003621, 2010. a, b, c, d
Friedlingstein, P., O'Sullivan, M., Jones, M. W., Andrew, R. M., Gregor, L., Hauck, J., Le Quéré, C., Luijkx, I. T., Olsen, A., Peters, G. P., Peters, W., Pongratz, J., Schwingshackl, C., Sitch, S., Canadell, J. G., Ciais, P., Jackson, R. B., Alin, S. R., Alkama, R., Arneth, A., Arora, V. K., Bates, N. R., Becker, M., Bellouin, N., Bittig, H. C., Bopp, L., Chevallier, F., Chini, L. P., Cronin, M., Evans, W., Falk, S., Feely, R. A., Gasser, T., Gehlen, M., Gkritzalis, T., Gloege, L., Grassi, G., Gruber, N., Gürses, Ö., Harris, I., Hefner, M., Houghton, R. A., Hurtt, G. C., Iida, Y., Ilyina, T., Jain, A. K., Jersild, A., Kadono, K., Kato, E., Kennedy, D., Klein Goldewijk, K., Knauer, J., Korsbakken, J. I., Landschützer, P., Lefèvre, N., Lindsay, K., Liu, J., Liu, Z., Marland, G., Mayot, N., McGrath, M. J., Metzl, N., Monacci, N. M., Munro, D. R., Nakaoka, S.-I., Niwa, Y., O'Brien, K., Ono, T., Palmer, P. I., Pan, N., Pierrot, D., Pocock, K., Poulter, B., Resplandy, L., Robertson, E., Rödenbeck, C., Rodriguez, C., Rosan, T. M., Schwinger, J., Séférian, R., Shutler, J. D., Skjelvan, I., Steinhoff, T., Sun, Q., Sutton, A. J., Sweeney, C., Takao, S., Tanhua, T., Tans, P. P., Tian, X., Tian, H., Tilbrook, B., Tsujino, H., Tubiello, F., van der Werf, G. R., Walker, A. P., Wanninkhof, R., Whitehead, C., Willstrand Wranne, A., Wright, R., Yuan, W., Yue, C., Yue, X., Zaehle, S., Zeng, J., and Zheng, B.: Global Carbon Budget 2022, Earth Syst. Sci. Data, 14, 4811–4900, https://doi.org/10.5194/essd-14-4811-2022, 2022. a
Galloway, J. N., Schlesinger, W. H., Levy II, H., Michaels, A., and Schnoor, J. L.: Nitrogen Fixation: Anthropogenic Enhancement-Environmental Response, Global Biogeochem. Cy., 9, 235–252, https://doi.org/10.1029/95GB00158, 1995. a
Galloway, J. N., Dentener, F. J., Capone, D. G., Boyer, E. W., Howarth, R. W., Seitzinger, S. P., Asner, G. P., Cleveland, C. C., Green, P. A., Holland, E. A., Karl, D. M., Michaels, A. F., Porter, J. H., Townsend, A. R., and Vöosmarty, C. J.: Nitrogen Cycles: Past, Present, and Future, Biogeochemistry, 70, 153–226, https://doi.org/10.1007/s10533-004-0370-0, 2004. a
Granhall, U.: Biological Nitrogen Fixation in Relation to Environmental Factors and Functioning of Natural Ecosystems [Tundra Mires, Temperate Forests], Ecol. Bull., 33, 131–144, 1981. a
Halliday, J. and Pate, J. S.: The Acetylene Reduction Assay as a Means of Studying Nitrogen Fixation in White Clover under Sward and Laboratory Conditions, Grass Forage Sci., 31, 29–35, https://doi.org/10.1111/j.1365-2494.1976.tb01112.x, 1976. a
Hedin, L. O., Brookshire, E. J., Menge, D. N., and Barron, A. R.: The Nitrogen Paradox in Tropical Forest Ecosystems, Annu. Rev. Ecol. Evol. S., 40, 613–635, https://doi.org/10.1146/annurev.ecolsys.37.091305.110246, 2009. a
Heinke, J., Rolinski, S., and Müller, C.: Modelling the role of livestock grazing in C and N cycling in grasslands with LPJmL5.0-grazing, Geosci. Model Dev., 16, 2455–2475, https://doi.org/10.5194/gmd-16-2455-2023, 2023. a, b, c
Herben, T., Mayerová, H., Skálová, H., Hadincová, V., Pecháčková, S., and Krahulec, F.: Long-Term Time Series of Legume Cycles in a Semi-Natural Montane Grassland: Evidence for Nitrogen-Driven Grass Dynamics?, Funct. Ecol., 31, 1430–1440, https://doi.org/10.1111/1365-2435.12844, 2017. a, b
Herridge, D. F., Peoples, M. B., and Boddey, R. M.: Global Inputs of Biological Nitrogen Fixation in Agricultural Systems, Plant Soil, 311, 1–18, https://doi.org/10.1007/s11104-008-9668-3, 2008. a, b
Herridge, D. F., Giller, K. E., Jensen, E. S., and Peoples, M. B.: Quantifying Country-to-Global Scale Nitrogen Fixation for Grain Legumes II. Coefficients, Templates and Estimates for Soybean, Groundnut and Pulses, Plant Soil, 474, 1–15, https://doi.org/10.1007/s11104-021-05166-7, 2022. a
Herzfeld, T., Heinke, J., Rolinski, S., and Müller, C.: Soil organic carbon dynamics from agricultural management practices under climate change, Earth Syst. Dynam., 12, 1037–1055, https://doi.org/10.5194/esd-12-1037-2021, 2021. a, b
Jackson, R. B., Canadell, J., Ehleringer, J. R., Mooney, H. A., Sala, O. E., and Schulze, E. D.: A Global Analysis of Root Distributions for Terrestrial Biomes, Oecologia, 108, 389–411, https://doi.org/10.1007/BF00333714, 1996. a
Jägermeyr, J., Pastor, A., Biemans, H., and Gerten, D.: Reconciling Irrigated Food Production with Environmental Flows for Sustainable Development Goals Implementation, Nat. Commun., 8, 15900, https://doi.org/10.1038/ncomms15900, 2017. a
Jiang, S., Jardinaud, M.-F., Gao, J., Pecrix, Y., Wen, J., Mysore, K., Xu, P., Sanchez-Canizares, C., Ruan, Y., Li, Q., Zhu, M., Li, F., Wang, E., Poole, P. S., Gamas, P., and Murray, J. D.: NIN-like Protein Transcription Factors Regulate Leghemoglobin Genes in Legume Nodules, Science, 374, 625–628, https://doi.org/10.1126/science.abg5945, 2021. a
Kaschuk, G., Kuyper, T. W., Leffelaar, P. A., Hungria, M., and Giller, K. E.: Are the Rates of Photosynthesis Stimulated by the Carbon Sink Strength of Rhizobial and Arbuscular Mycorrhizal Symbioses?, Soil Biol. Biochem., 41, 1233–1244, https://doi.org/10.1016/j.soilbio.2009.03.005, 2009. a, b, c
Kattge, J., Bönisch, G., Díaz, S., Lavorel, S., Prentice, I. C., Leadley, P., Tautenhahn, S., Werner, G. D. A., Aakala, T., Abedi, M., Acosta, A. T. R., Adamidis, G. C., Adamson, K., Aiba, M., Albert, C. H., Alcántara, J. M., Alcázar C, C., Aleixo, I., Ali, H., Amiaud, B., Ammer, C., Amoroso, M. M., Anand, M., Anderson, C., Anten, N., Antos, J., Apgaua, D. M. G., Ashman, T.-L., Asmara, D. H., Asner, G. P., Aspinwall, M., Atkin, O., Aubin, I., Baastrup-Spohr, L., Bahalkeh, K., Bahn, M., Baker, T., Baker, W. J., Bakker, J. P., Baldocchi, D., Baltzer, J., Banerjee, A., Baranger, A., Barlow, J., Barneche, D. R., Baruch, Z., Bastianelli, D., Battles, J., Bauerle, W., Bauters, M., Bazzato, E., Beckmann, M., Beeckman, H., Beierkuhnlein, C., Bekker, R., Belfry, G., Belluau, M., Beloiu, M., Benavides, R., Benomar, L., Berdugo-Lattke, M. L., Berenguer, E., Bergamin, R., Bergmann, J., Bergmann Carlucci, M., Berner, L., Bernhardt-Römermann, M., Bigler, C., Bjorkman, A. D., Blackman, C., Blanco, C., Blonder, B., Blumenthal, D., Bocanegra-González, K. T., Boeckx, P., Bohlman, S., Böhning-Gaese, K., Boisvert-Marsh, L., Bond, W., Bond-Lamberty, B., Boom, A., Boonman, C. C. F., Bordin, K., Boughton, E. H., Boukili, V., Bowman, D. M. J. S., Bravo, S., Brendel, M. R., Broadley, M. R., Brown, K. A., Bruelheide, H., Brumnich, F., Bruun, H. H., Bruy, D., Buchanan, S. W., Bucher, S. F., Buchmann, N., Buitenwerf, R., Bunker, D. E., Bürger, J., Burrascano, S., Burslem, D. F. R. P., Butterfield, B. J., Byun, C., Marques, M., Scalon, M. C., Caccianiga, M., Cadotte, M., Cailleret, M., Camac, J., Camarero, J. J., Campany, C., Campetella, G., Campos, J. A., Cano-Arboleda, L., Canullo, R., Carbognani, M., Carvalho, F., Casanoves, F., Castagneyrol, B., Catford, J. A., Cavender-Bares, J., Cerabolini, B. E. L., Cervellini, M., Chacón-Madrigal, E., Chapin, K., Chapin, F. S., Chelli, S., Chen, S.-C., Chen, A., Cherubini, P., Chianucci, F., Choat, B., Chung, K.-S., Chytrý, M., Ciccarelli, D., Coll, L., Collins, C. G., Conti, L., Coomes, D., Cornelissen, J. H. C., Cornwell, W. K., Corona, P., Coyea, M., Craine, J., Craven, D., Cromsigt, J. P. G. M., Csecserits, A., Cufar, K., Cuntz, M., da Silva, A. C., Dahlin, K. M., Dainese, M., Dalke, I., Dalle Fratte, M., Dang-Le, A. T., Danihelka, J., Dannoura, M., Dawson, S., de Beer, A. J., De Frutos, A., De Long, J. R., Dechant, B., Delagrange, S., Delpierre, N., Derroire, G., Dias, A. S., Diaz-Toribio, M. H., Dimitrakopoulos, P. G., Dobrowolski, M., Doktor, D., Dřevojan, P., Dong, N., Dransfield, J., Dressler, S., Duarte, L., Ducouret, E., Dullinger, S., Durka, W., Duursma, R., Dymova, O., E-Vojtkó, A., Eckstein, R. L., Ejtehadi, H., Elser, J., Emilio, T., Engemann, K., Erfanian, M. B., Erfmeier, A., Esquivel-Muelbert, A., Esser, G., Estiarte, M., Domingues, T. F., Fagan, W. F., Fagúndez, J., Falster, D. S., Fan, Y., Fang, J., Farris, E., Fazlioglu, F., Feng, Y., Fernandez-Mendez, F., Ferrara, C., Ferreira, J., Fidelis, A., Finegan, B., Firn, J., Flowers, T. J., Flynn, D. F. B., Fontana, V., Forey, E., Forgiarini, C., François, L., Frangipani, M., Frank, D., Frenette-Dussault, C., Freschet, G. T., Fry, E. L., Fyllas, N. M., Mazzochini, G. G., Gachet, S., Gallagher, R., Ganade, G., Ganga, F., García-Palacios, P., Gargaglione, V., Garnier, E., Garrido, J. L., de Gasper, A. L., Gea-Izquierdo, G., Gibson, D., Gillison, A. N., Giroldo, A., Glasenhardt, M.-C., Gleason, S., Gliesch, M., Goldberg, E., Göldel, B., Gonzalez-Akre, E., Gonzalez-Andujar, J. L., González-Melo, A., González-Robles, A., Graae, B. J., Granda, E., Graves, S., Green, W. A., Gregor, T., Gross, N., Guerin, G. R., Günther, A., Gutiérrez, A. G., Haddock, L., Haines, A., Hall, J., Hambuckers, A., Han, W., Harrison, S. P., Hattingh, W., Hawes, J. E., He, T., He, P., Heberling, J. M., Helm, A., Hempel, S., Hentschel, J., Hérault, B., Hereş, A.-M., Herz, K., Heuertz, M., Hickler, T., Hietz, P., Higuchi, P., Hipp, A. L., Hirons, A., Hock, M., Hogan, J. A., Holl, K., Honnay, O., Hornstein, D., Hou, E., Hough-Snee, N., Hovstad, K. A., Ichie, T., Igić, B., Illa, E., Isaac, M., Ishihara, M., Ivanov, L., Ivanova, L., Iversen, C. M., Izquierdo, J., Jackson, R. B., Jackson, B., Jactel, H., Jagodzinski, A. M., Jandt, U., Jansen, S., Jenkins, T., Jentsch, A., Jespersen, J. R. P., Jiang, G.-F., Johansen, J. L., Johnson, D., Jokela, E. J., Joly, C. A., Jordan, G. J., Joseph, G. S., Junaedi, D., Junker, R. R., Justes, E., Kabzems, R., Kane, J., Kaplan, Z., Kattenborn, T., Kavelenova, L., Kearsley, E., Kempel, A., Kenzo, T., Kerkhoff, A., Khalil, M. I., Kinlock, N. L., Kissling, W. D., Kitajima, K., Kitzberger, T., Kjøller, R., Klein, T., Kleyer, M., Klimešová, J., Klipel, J., Kloeppel, B., Klotz, S., Knops, J. M. H., Kohyama, T., Koike, F., Kollmann, J., Komac, B., Komatsu, K., König, C., Kraft, N. J. B., Kramer, K., Kreft, H., Kühn, I., Kumarathunge, D., Kuppler, J., Kurokawa, H., Kurosawa, Y., Kuyah, S., Laclau, J.-P., Lafleur, B., Lallai, E., Lamb, E., Lamprecht, A., Larkin, D. J., Laughlin, D., Le Bagousse-Pinguet, Y., le Maire, G., le Roux, P. C., le Roux, E., Lee, T., Lens, F., Lewis, S. L., Lhotsky, B., Li, Y., Li, X., Lichstein, J. W., Liebergesell, M., Lim, J. Y., Lin, Y.-S., Linares, J. C., Liu, C., Liu, D., Liu, U., Livingstone, S., Llusià, J., Lohbeck, M., López-García, Á., Lopez-Gonzalez, G., Lososová, Z., Louault, F., Lukács, B. A., Lukeš, P., Luo, Y., Lussu, M., Ma, S., Maciel Rabelo Pereira, C., Mack, M., Maire, V., Mäkelä, A., Mäkinen, H., Malhado, A. C. M., Mallik, A., Manning, P., Manzoni, S., Marchetti, Z., Marchino, L., Marcilio-Silva, V., Marcon, E., Marignani, M., Markesteijn, L., Martin, A., Martínez-Garza, C., Martínez-Vilalta, J., Mašková, T., Mason, K., Mason, N., Massad, T. J., Masse, J., Mayrose, I., McCarthy, J., McCormack, M. L., McCulloh, K., McFadden, I. R., McGill, B. J., McPartland, M. Y., Medeiros, J. S., Medlyn, B., Meerts, P., Mehrabi, Z., Meir, P., Melo, F. P. L., Mencuccini, M., Meredieu, C., Messier, J., Mészáros, I., Metsaranta, J., Michaletz, S. T., Michelaki, C., Migalina, S., Milla, R., Miller, J. E. D., Minden, V., Ming, R., Mokany, K., Moles, A. T., Molnár V, A., Molofsky, J., Molz, M., Montgomery, R. A., Monty, A., Moravcová, L., Moreno-Martínez, A., Moretti, M., Mori, A. S., Mori, S., Morris, D., Morrison, J., Mucina, L., Mueller, S., Muir, C. D., Müller, S. C., Munoz, F., Myers-Smith, I. H., Myster, R. W., Nagano, M., Naidu, S., Narayanan, A., Natesan, B., Negoita, L., Nelson, A. S., Neuschulz, E. L., Ni, J., Niedrist, G., Nieto, J., Niinemets, Ü., Nolan, R., Nottebrock, H., Nouvellon, Y., Novakovskiy, A., Network, T. N., Nystuen, K. O., O'Grady, A., O'Hara, K., O'Reilly-Nugent, A., Oakley, S., Oberhuber, W., Ohtsuka, T., Oliveira, R., Öllerer, K., Olson, M. E., Onipchenko, V., Onoda, Y., Onstein, R. E., Ordonez, J. C., Osada, N., Ostonen, I., Ottaviani, G., Otto, S., Overbeck, G. E., Ozinga, W. A., Pahl, A. T., Paine, C. E. T., Pakeman, R. J., Papageorgiou, A. C., Parfionova, E., Pärtel, M., Patacca, M., Paula, S., Paule, J., Pauli, H., Pausas, J. G., Peco, B., Penuelas, J., Perea, A., Peri, P. L., Petisco-Souza, A. C., Petraglia, A., Petritan, A. M., Phillips, O. L., Pierce, S., Pillar, V. D., Pisek, J., Pomogaybin, A., Poorter, H., Portsmuth, A., Poschlod, P., Potvin, C., Pounds, D., Powell, A. S., Power, S. A., Prinzing, A., Puglielli, G., Pyšek, P., Raevel, V., Rammig, A., Ransijn, J., Ray, C. A., Reich, P. B., Reichstein, M., Reid, D. E. B., Réjou-Méchain, M., de Dios, V. R., Ribeiro, S., Richardson, S., Riibak, K., Rillig, M. C., Riviera, F., Robert, E. M. R., Roberts, S., Robroek, B., Roddy, A., Rodrigues, A. V., Rogers, A., Rollinson, E., Rolo, V., Römermann, C., Ronzhina, D., Roscher, C., Rosell, J. A., Rosenfield, M. F., Rossi, C., Roy, D. B., Royer-Tardif, S., Rüger, N., Ruiz-Peinado, R., Rumpf, S. B., Rusch, G. M., Ryo, M., Sack, L., Saldaña, A., Salgado-Negret, B., Salguero-Gomez, R., Santa-Regina, I., Santacruz-García, A. C., Santos, J., Sardans, J., Schamp, B., Scherer-Lorenzen, M., Schleuning, M., Schmid, B., Schmidt, M., Schmitt, S., Schneider, J. V., Schowanek, S. D., Schrader, J., Schrodt, F., Schuldt, B., Schurr, F., Selaya Garvizu, G., Semchenko, M., Seymour, C., Sfair, J. C., Sharpe, J. M., Sheppard, C. S., Sheremetiev, S., Shiodera, S., Shipley, B., Shovon, T. A., Siebenkäs, A., Sierra, C., Silva, V., Silva, M., Sitzia, T., Sjöman, H., Slot, M., Smith, N. G., Sodhi, D., Soltis, P., Soltis, D., Somers, B., Sonnier, G., Sørensen, M. V., Sosinski Jr., E. E., Soudzilovskaia, N. A., Souza, A. F., Spasojevic, M., Sperandii, M. G., Stan, A. B., Stegen, J., Steinbauer, K., Stephan, J. G., Sterck, F., Stojanovic, D. B., Strydom, T., Suarez, M. L., Svenning, J.-C., Svitková, I., Svitok, M., Svoboda, M., Swaine, E., Swenson, N., Tabarelli, M., Takagi, K., Tappeiner, U., Tarifa, R., Tauugourdeau, S., Tavsanoglu, C., te Beest, M., Tedersoo, L., Thiffault, N., Thom, D., Thomas, E., Thompson, K., Thornton, P. E., Thuiller, W., Tichý, L., Tissue, D., Tjoelker, M. G., Tng, D. Y. P., Tobias, J., Török, P., Tarin, T., Torres-Ruiz, J. M., Tóthmérész, B., Treurnicht, M., Trivellone, V., Trolliet, F., Trotsiuk, V., Tsakalos, J. L., Tsiripidis, I., Tysklind, N., Umehara, T., Usoltsev, V., Vadeboncoeur, M., Vaezi, J., Valladares, F., Vamosi, J., van Bodegom, P. M., van Breugel, M., Van Cleemput, E., van de Weg, M., van der Merwe, S., van der Plas, F., van der Sande, M. T., van Kleunen, M., Van Meerbeek, K., Vanderwel, M., Vanselow, K. A., Vårhammar, A., Varone, L., Vasquez Valderrama, M. Y., Vassilev, K., Vellend, M., Veneklaas, E. J., Verbeeck, H., Verheyen, K., Vibrans, A., Vieira, I., Villacís, J., Violle, C., Vivek, P., Wagner, K., Waldram, M., Waldron, A., Walker, A. P., Waller, M., Walther, G., Wang, H., Wang, F., Wang, W., Watkins, H., Watkins, J., Weber, U., Weedon, J. T., Wei, L., Weigelt, P., Weiher, E., Wells, A. W., Wellstein, C., Wenk, E., Westoby, M., Westwood, A., White, P. J., Whitten, M., Williams, M., Winkler, D. E., Winter, K., Womack, C., Wright, I. J., Wright, S. J., Wright, J., Pinho, B. X., Ximenes, F., Yamada, T., Yamaji, K., Yanai, R., Yankov, N., Yguel, B., Zanini, K. J., Zanne, A. E., Zelený, D., Zhao, Y.-P., Zheng, J., Zheng, J., Ziemińska, K., Zirbel, C. R., Zizka, G., Zo-Bi, I. C., Zotz, G., and Wirth, C.: TRY Plant Trait Database – Enhanced Coverage and Open Access, Glob. Change Biol., 26, 119–188, https://doi.org/10.1111/gcb.14904, 2020. a
Kim, H.: Global Soil Wetness Project Phase 3 Atmospheric Boundary Conditions (Experiment 1), Data Integration and Analysis System (DIAS) [data set], https://doi.org/10.20783/DIAS.501, 2017. a
Kou-Giesbrecht, S., Arora, V. K., Seiler, C., Arneth, A., Falk, S., Jain, A. K., Joos, F., Kennedy, D., Knauer, J., Sitch, S., O'Sullivan, M., Pan, N., Sun, Q., Tian, H., Vuichard, N., and Zaehle, S.: Evaluating nitrogen cycling in terrestrial biosphere models: a disconnect between the carbon and nitrogen cycles, Earth Syst. Dynam., 14, 767–795, https://doi.org/10.5194/esd-14-767-2023, 2023. a, b, c, d, e, f
Kull, O.: Acclimation of Photosynthesis in Canopies: Models and Limitations, Oecologia, 133, 267–279, https://doi.org/10.1007/s00442-002-1042-1, 2002. a
Lange, S., Mengel, M., Treu, S., and Büchner, M.: ISIMIP3a atmospheric climate input data (v1.0), ISIMIP Repository [data set], https://doi.org/10.48364/ISIMIP.982724, 2022. a, b
Lawrence, D. M., Fisher, R. A., Koven, C. D., Oleson, K. W., Swenson, S. C., Bonan, G., Collier, N., Ghimire, B., van Kampenhout, L., Kennedy, D., Kluzek, E., Lawrence, P. J., Li, F., Li, H., Lombardozzi, D., Riley, W. J., Sacks, W. J., Shi, M., Vertenstein, M., Wieder, W. R., Xu, C., Ali, A. A., Badger, A. M., Bisht, G., van den Broeke, M., Brunke, M. A., Burns, S. P., Buzan, J., Clark, M., Craig, A., Dahlin, K., Drewniak, B., Fisher, J. B., Flanner, M., Fox, A. M., Gentine, P., Hoffman, F., Keppel-Aleks, G., Knox, R., Kumar, S., Lenaerts, J., Leung, L. R., Lipscomb, W. H., Lu, Y., Pandey, A., Pelletier, J. D., Perket, J., Randerson, J. T., Ricciuto, D. M., Sanderson, B. M., Slater, A., Subin, Z. M., Tang, J., Thomas, R. Q., Val Martin, M., and Zeng, X.: The Community Land Model Version 5: Description of New Features, Benchmarking, and Impact of Forcing Uncertainty, J. Adv. Model. Earth Sy., 11, 4245–4287, https://doi.org/10.1029/2018MS001583, 2019. a
Lee, M., Shevliakova, E., Stock, C. A., Malyshev, S., and Milly, P. C. D.: Prominence of the Tropics in the Recent Rise of Global Nitrogen Pollution, Nat. Commun., 10, 1437, https://doi.org/10.1038/s41467-019-09468-4, 2019. a
Liu, Y., Wu, L., Baddeley, J. A., and Watson, C. A.: Models of Biological Nitrogen Fixation of Legumes. A Review, Agron. Sust. Dev., 31, 155–172, https://doi.org/10.1051/agro/2010008, 2011. a, b
Lu, C. and Tian, H.: Global nitrogen and phosphorus fertilizer use for agriculture production in the past half century: shifted hot spots and nutrient imbalance, Earth Syst. Sci. Data, 9, 181–192, https://doi.org/10.5194/essd-9-181-2017, 2017. a
Lutz, F., Herzfeld, T., Heinke, J., Rolinski, S., Schaphoff, S., von Bloh, W., Stoorvogel, J. J., and Müller, C.: Simulating the effect of tillage practices with the global ecosystem model LPJmL (version 5.0-tillage), Geosci. Model Dev., 12, 2419–2440, https://doi.org/10.5194/gmd-12-2419-2019, 2019. a, b
Ma, J., Olin, S., Anthoni, P., Rabin, S. S., Bayer, A. D., Nyawira, S. S., and Arneth, A.: Modeling symbiotic biological nitrogen fixation in grain legumes globally with LPJ-GUESS (v4.0, r10285), Geosci. Model Dev., 15, 815–839, https://doi.org/10.5194/gmd-15-815-2022, 2022. a, b, c, d, e, f
Marschner, H., Häussling, M., and George, E.: Ammonium and Nitrate Uptake Rates and Rhizosphere pH in Non-Mycorrhizal Roots of Norway Spruce [Picea Abies (L.) Karst.], Trees, 5, 14–21, https://doi.org/10.1007/BF00225330, 1991. a
McGechan, W.: Simulation of Nitrogen Uptake, Fixation and Leaching in a Grass/White Clover Mixture, Grass Forage Sci., 54, 30–41, https://doi.org/10.1046/j.1365-2494.1999.00145.x, 1999. a
Meyer, D. R. and Anderson, A. J.: Temperature and Symbiotic Nitrogen Fixation, Nature, 183, 61–61, https://doi.org/10.1038/183061a0, 1959. a
Montañez, A., Danso, S. K. A., and Hardarson, G.: The Effect of Temperature on Nodulation and Nitrogen Fixation by Five Bradyrhizobium Japonicum Strains, Appl. Soil Ecol., 2, 165–174, https://doi.org/10.1016/0929-1393(95)00052-M, 1995. a
Moss, B.: Water Pollution by Agriculture, Philos. T. Roy. Soc. B, 363, 659–666, https://doi.org/10.1098/rstb.2007.2176, 2007. a
Müller, C., Stehfest, E., van Minnen, J. G., Strengers, B., von Bloh, W., Beusen, A. H. W., Schaphoff, S., Kram, T., and Lucht, W.: Drivers and Patterns of Land Biosphere Carbon Balance Reversal, Environ. Res. Lett., 11, 044002, https://doi.org/10.1088/1748-9326/11/4/044002, 2016. a
Northup, B. K. and Rao, S. C.: Effects of Legume Green Manures on Forage Produced in Continuous Wheat Systems, Agron. J., 108, 101–108, https://doi.org/10.2134/agronj15.0031, 2016. a
Ostberg, S., Müller, C., Heinke, J., and Schaphoff, S.: LandInG 1.0: a toolbox to derive input datasets for terrestrial ecosystem modelling at variable resolutions from heterogeneous sources, Geosci. Model Dev., 16, 3375–3406, https://doi.org/10.5194/gmd-16-3375-2023, 2023. a
Patterson, T. G. and Larue, T. A.: Root Respiration Associated with Nitrogenase Activity (C2H2) of Soybean, and a Comparison of Estimates 1, Plant Physiol., 72, 701–705, https://doi.org/10.1104/pp.72.3.701, 1983. a, b, c
Peoples, M. B., Giller, K. E., Jensen, E. S., and Herridge, D. F.: Quantifying Country-to-Global Scale Nitrogen Fixation for Grain Legumes: I. Reliance on Nitrogen Fixation of Soybean, Groundnut and Pulses, Plant Soil, 469, 1–14, https://doi.org/10.1007/s11104-021-05167-6, 2021. a
Porwollik, V., Rolinski, S., Heinke, J., von Bloh, W., Schaphoff, S., and Müller, C.: The role of cover crops for cropland soil carbon, nitrogen leaching, and agricultural yields – a global simulation study with LPJmL (V. 5.0-tillage-cc), Biogeosciences, 19, 957–977, https://doi.org/10.5194/bg-19-957-2022, 2022. a, b, c, d
Reay, D. S., Davidson, E. A., Smith, K. A., Smith, P., Melillo, J. M., Dentener, F., and Crutzen, P. J.: Global Agriculture and Nitrous Oxide Emissions, Nat. Clim. Change, 2, 410–416, https://doi.org/10.1038/nclimate1458, 2012. a
Reed, S. C., Cleveland, C. C., and Townsend, A. R.: Functional Ecology of Free-Living Nitrogen Fixation: A Contemporary Perspective, Annu. Rev. Ecol. Evol. S., 42, 489–512, https://doi.org/10.1146/annurev-ecolsys-102710-145034, 2011. a, b, c
Rousk, K., Sorensen, P. L., and Michelsen, A.: What Drives Biological Nitrogen Fixation in High Arctic Tundra: Moisture or Temperature?, Ecosphere, 9, e02117, https://doi.org/10.1002/ecs2.2117, 2018. a
Ryle, G. J. A., Powell, C. E., and Gordon, A. J.: The Respiratory Costs of Nitrogen Fixation in Soyabean, Cowpea, and White Clover: I. Nitrogen Fixation and the Respiration of the Nodulated Root, J. Exp. Bot., 30, 135–144, https://doi.org/10.1093/jxb/30.1.135, 1979. a
Salvagiotti, F., Cassman, K. G., Specht, J. E., Walters, D. T., Weiss, A., and Dobermann, A.: Nitrogen Uptake, Fixation and Response to Fertilizer N in Soybeans: A Review, Field Crop. Res., 108, 1–13, https://doi.org/10.1016/j.fcr.2008.03.001, 2008. a
Schaphoff, S., Heyder, U., Ostberg, S., Gerten, D., Heinke, J., and Lucht, W.: Contribution of Permafrost Soils to the Global Carbon Budget, Environ. Res. Lett., 8, 014026, https://doi.org/10.1088/1748-9326/8/1/014026, 2013. a, b, c
Schaphoff, S., Forkel, M., Müller, C., Knauer, J., von Bloh, W., Gerten, D., Jägermeyr, J., Lucht, W., Rammig, A., Thonicke, K., and Waha, K.: LPJmL4 – a dynamic global vegetation model with managed land – Part 2: Model evaluation, Geosci. Model Dev., 11, 1377–1403, https://doi.org/10.5194/gmd-11-1377-2018, 2018a. a
Schaphoff, S., von Bloh, W., Rammig, A., Thonicke, K., Biemans, H., Forkel, M., Gerten, D., Heinke, J., Jägermeyr, J., Knauer, J., Langerwisch, F., Lucht, W., Müller, C., Rolinski, S., and Waha, K.: LPJmL4 – a dynamic global vegetation model with managed land – Part 1: Model description, Geosci. Model Dev., 11, 1343–1375, https://doi.org/10.5194/gmd-11-1343-2018, 2018b. a, b, c
Scheer, C., Fuchs, K., Pelster, D. E., and Butterbach-Bahl, K.: Estimating Global Terrestrial Denitrification from Measured Product Ratios, Curr. Opin. Env. Sust., 47, 72–80, https://doi.org/10.1016/j.cosust.2020.07.005, 2020. a
Serraj, R., Sinclair, T. R., and Purcell, L. C.: Symbiotic N2 Fixation Response to Drought, J. Exp. Bot., 50, 143–155, https://doi.org/10.1093/jxb/50.331.143, 1999. a
Sitch, S., Smith, B., Prentice, I. C., Arneth, A., Bondeau, A., Cramer, W., Kaplan, J. O., Levis, S., Lucht, W., Sykes, M. T., Thonicke, K., and Venevsky, S.: Evaluation of Ecosystem Dynamics, Plant Geography and Terrestrial Carbon Cycling in the LPJ Dynamic Global Vegetation Model, Glob. Change Biol., 9, 161–185, https://doi.org/10.1046/j.1365-2486.2003.00569.x, 2003. a
Soper, F. M., Taylor, B. N., Winbourne, J. B., Wong, M. Y., Dynarski, K. A., Reis, C. R. G., Peoples, M. B., Cleveland, C. C., Reed, S. C., Menge, D. N. L., and Perakis, S. S.: A Roadmap for Sampling and Scaling Biological Nitrogen Fixation in Terrestrial Ecosystems, Methods Ecol. Evol., 12, 1122–1137, https://doi.org/10.1111/2041-210X.13586, 2021. a
Stenzel, F., Braun, J., Breier, J., Erb, K., Gerten, D., Heinke, J., Matej, S., Ostberg, S., Schaphoff, S., and Lucht, W.: biospheremetrics v1.0.2: an R package to calculate two complementary terrestrial biosphere integrity indicators – human colonization of the biosphere (BioCol) and risk of ecosystem destabilization (EcoRisk), Geosci. Model Dev., 17, 3235–3258, https://doi.org/10.5194/gmd-17-3235-2024, 2024. a
Sutton, M. A., Bleeker, A., Howard, C. M., Bekunda, M., Grizzetti, B., de Vries, W., van Grinsven, H. J. M., Abrol, Y. P., Adhya, T. K., Billen, G., Davidson, E. A., Datta, A., Diaz, R., Erisman, J. W., Liu, X. J., Oenema, O., Palm, C., Raghuram, N., Reis, S., Scholz, R. W., Sims, T., Westhoek, H., and Zhang, F. S.: Our Nutrient World: The Challenge to Produce More Food and Energy with Less Pollution, NERC/Centre for Ecology & Hydrology, Edinburgh, ISBN 978-1-906698-40-9, 2013. a
Taylor, B. N., Chazdon, R. L., and Menge, D. N. L.: Successional Dynamics of Nitrogen Fixation and Forest Growth in Regenerating Costa Rican Rainforests, Ecology, 100, e02637, https://doi.org/10.1002/ecy.2637, 2019. a
Thornley, J. H. M.: A Transport-resistance Model of Forest Growth and Partitioning, Ann. Bot.-London, 68, 211–226, 1991. a
Thornley, J. H. M., Bergelson, J., and Parsons, A. J.: Complex Dynamics in a Carbon-Nitrogen Model of a Grass-Legume Pasture, Ann. Bot.-London, 75, 79–84, https://doi.org/10.1016/S0305-7364(05)80012-5, 1995. a
Tian, H., Chen, G., Lu, C., Xu, X., Hayes, D. J., Ren, W., Pan, S., Huntzinger, D. N., and Wofsy, S. C.: North American Terrestrial CO2 Uptake Largely Offset by CH4 and N2O Emissions: Toward a Full Accounting of the Greenhouse Gas Budget, Climatic Change, 129, 413–426, https://doi.org/10.1007/s10584-014-1072-9, 2015. a
Tian, H., Yang, J., Xu, R., Lu, C., Canadell, J. G., Davidson, E. A., Jackson, R. B., Arneth, A., Chang, J., Ciais, P., Gerber, S., Ito, A., Joos, F., Lienert, S., Messina, P., Olin, S., Pan, S., Peng, C., Saikawa, E., Thompson, R. L., Vuichard, N., Winiwarter, W., Zaehle, S., and Zhang, B.: Global Soil Nitrous Oxide Emissions since the Preindustrial Era Estimated by an Ensemble of Terrestrial Biosphere Models: Magnitude, Attribution, and Uncertainty, Glob. Change Biol., 25, 640–659, https://doi.org/10.1111/gcb.14514, 2019. a
Tian, H., Xu, R., Canadell, J. G., Thompson, R. L., Winiwarter, W., Suntharalingam, P., Davidson, E. A., Ciais, P., Jackson, R. B., Janssens-Maenhout, G., Prather, M. J., Regnier, P., Pan, N., Pan, S., Peters, G. P., Shi, H., Tubiello, F. N., Zaehle, S., Zhou, F., Arneth, A., Battaglia, G., Berthet, S., Bopp, L., Bouwman, A. F., Buitenhuis, E. T., Chang, J., Chipperfield, M. P., Dangal, S. R. S., Dlugokencky, E., Elkins, J. W., Eyre, B. D., Fu, B., Hall, B., Ito, A., Joos, F., Krummel, P. B., Landolfi, A., Laruelle, G. G., Lauerwald, R., Li, W., Lienert, S., Maavara, T., MacLeod, M., Millet, D. B., Olin, S., Patra, P. K., Prinn, R. G., Raymond, P. A., Ruiz, D. J., van der Werf, G. R., Vuichard, N., Wang, J., Weiss, R. F., Wells, K. C., Wilson, C., Yang, J., and Yao, Y.: A Comprehensive Quantification of Global Nitrous Oxide Sources and Sinks, Nature, 586, 248–256, https://doi.org/10.1038/s41586-020-2780-0, 2020. a, b
Valentine, A. J., Benedito, V. A., and Kang, Y.: Legume Nitrogen Fixation and Soil Abiotic Stress: From Physiology to Genomics and Beyond, in: Annual Plant Reviews Online, Chap. 9, edited by: Foyer, C. H. and Zhang, H., John Wiley & Sons, Ltd, 207–248, https://doi.org/10.1002/9781119312994.apr0456, 2018. a
Vitousek, P. M.: Litterfall, Nutrient Cycling, and Nutrient Limitation in Tropical Forests, Ecology, 65, 285–298, https://doi.org/10.2307/1939481, 1984. a
Voisin, A. S., Salon, C., Jeudy, C., and Warembourg, F. R.: Symbiotic N2 Fixation Activity in Relation to C Economy of Pisum Sativum L. as a Function of Plant Phenology, J. Exp. Bot., 54, 2733–2744, https://doi.org/10.1093/jxb/erg290, 2003. a, b
von Bloh, W., Schaphoff, S., Müller, C., Rolinski, S., Waha, K., and Zaehle, S.: Implementing the nitrogen cycle into the dynamic global vegetation, hydrology, and crop growth model LPJmL (version 5.0), Geosci. Model Dev., 11, 2789–2812, https://doi.org/10.5194/gmd-11-2789-2018, 2018. a, b, c, d, e, f, g
Wirth, S. B., Rolinski, S., Schaphoff, S., von Bloh, W., and Müller, C.: Model Code for LPJmL5.7.9-Ccostly-Bnf, Zenodo [code], https://doi.org/10.5281/zenodo.14012503, 2024. a, b
Xu-Ri and Prentice, I. C.: Modelling the demand for new nitrogen fixation by terrestrial ecosystems, Biogeosciences, 14, 2003–2017, https://doi.org/10.5194/bg-14-2003-2017, 2017. a, b
Yang, J. and Tian, H.: ISIMIP3b N-deposition input data (v1.0), ISIMIP Repository [data set], https://doi.org/10.48364/ISIMIP.600567, 2020. a, b
Yao, Y., Han, B., Dong, X., Zhong, Y., Niu, S., Chen, X., and Li, Z.: Disentangling the Variability of Symbiotic Nitrogen Fixation Rate and the Controlling Factors, Glob. Change Biol., 30, e17206, https://doi.org/10.1111/gcb.17206, 2024. a
Yu, T. and Zhuang, Q.: Modeling biological nitrogen fixation in global natural terrestrial ecosystems, Biogeosciences, 17, 3643–3657, https://doi.org/10.5194/bg-17-3643-2020, 2020. a, b, c, d, e, f, g, h, i
Zaehle, S. and Friend, A. D.: Carbon and Nitrogen Cycle Dynamics in the O-CN Land Surface Model: 1. Model Description, Site-Scale Evaluation, and Sensitivity to Parameter Estimates, Global Biogeochem. Cy., 24, GB1005, https://doi.org/10.1029/2009GB003521, 2010. a
Zaehle, S., Friend, A. D., Friedlingstein, P., Dentener, F., Peylin, P., and Schulz, M.: Carbon and Nitrogen Cycle Dynamics in the O-CN Land Surface Model: 2. Role of the Nitrogen Cycle in the Historical Terrestrial Carbon Balance, Global Biogeochem. Cy., 24, GB1006, https://doi.org/10.1029/2009GB003522, 2010. a
Zhang, X., Zou, T., Lassaletta, L., Mueller, N. D., Tubiello, F. N., Lisk, M. D., Lu, C., Conant, R. T., Dorich, C. D., Gerber, J., Tian, H., Bruulsema, T., Maaz, T. M., Nishina, K., Bodirsky, B. L., Popp, A., Bouwman, L., Beusen, A., Chang, J., Havlík, P., Leclère, D., Canadell, J. G., Jackson, R. B., Heffer, P., Wanner, N., Zhang, W., and Davidson, E. A.: Quantification of Global and National Nitrogen Budgets for Crop Production, Nat. Food, 2, 529–540, https://doi.org/10.1038/s43016-021-00318-5, 2021. a, b
- Abstract
- Introduction
- Methods
- Results
- Discussion
- Conclusions
- Appendix A: Nitrogen demand and uptake
- Appendix B: Spin-up simulation carbon stocks
- Appendix C: Additional figures and tables
- Code availability
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Methods
- Results
- Discussion
- Conclusions
- Appendix A: Nitrogen demand and uptake
- Appendix B: Spin-up simulation carbon stocks
- Appendix C: Additional figures and tables
- Code availability
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement