The Measurement Error Proxy System Model: MEPSM v0.2

Proxy system models (PSMs) are an essential component of paleoclimate data assimilation and for testing climate field reconstruction methods. Generally, current statistical PSMs consider the noise in the output (proxy) variable only and ignore the noise in the input (environmental) variables. This problem is exacerbated when there are several input variables. Here we develop a new PSM, the Measurement Error Proxy System Model (MEPSM), which includes noise in all variables, including noise auto- and cross-correlation. The MEPSM is calibrated using a quasi-Bayesian solution, which leverages Gaussian conjugacy to produce a fast solution. Another advantage of MEPSM is that the prior can be used to stabilize the solution between an informative prior (e.g., with a non-zero mean) and the maximum likelihood solution. MEPSM is illustrated by calibrating a proxy model for δ¹⁸O_coral with multiple inputs (marine temperature and salinity), including noise in all variables. MEPSM is applicable to many different climate proxies and will improve our understanding of the effects of predictor noise on PSMs, data assimilation, and climate reconstruction.

1 Introduction

Proxy system models (PSMs) describe how biological, geological, or chemical archives are imprinted with environmental signals (Evans et al., 2013; Dee, 2015). They are an essential component of paleoclimate data assimilation (Steiger et al., 2018; Tardif et al., 2019; Sanchez et al., 2021; King et al., 2023) and of pseudoproxy experiments, e.g., testing the fidelity of climate reconstruction methods (Loope et al., 2020a, b). For PSMs, input variables include one or more environmental variables (e.g., temperature, water salinity, rainfall), and output variables include variables which can be read from natural archives, e.g., the abundance of trace elements or isotopes in carbonate archives. The processes between input and output may be linear or nonlinear fitted relationships (statistical PSMs) or more detailed physiochemical models (physiochemical PSMs). Statistical PSMs can be frequentist (i.e., the PSM is calibrated using ordinary least squares, OLS) or Bayesian (PSMs that make use of Bayes' rule). Current paleoclimate data assimilation projects often use frequentist PSMs (e.g., Steiger et al., 2018; Tardif et al., 2019) (see also example 1 in King et al., 2023), but some paleodata assimilation projects have begun to incorporate Bayesian PSMs (King et al., 2023). Current Bayesian PSMs (e.g., Tierney and Tingley, 2014, 2018; Tierney et al., 2019; Malevich et al., 2019) typically have the following form:

$$\begin{array}{}\text{(1)}& \mathit{\zeta }\sim \mathcal{N}(b_{\mathrm{0}}+f(\mathit{x},\mathit{\theta }),{\mathit{\sigma }}_{\mathit{\zeta }}^{\mathrm{2}}),\end{array}$$

where ζ is sampled from the normal distribution 𝒩(μ,σ²), where b₀ is the regression intercept, x and ζ are the input and output variables respectively (note x is a row vector of predictor matrix X), and θ is a set of parameters. These Bayesian models are based on Bayesian OLS rather than Bayesian TLS (total least squares). In comparison, an errors-in-variables (EIV) model (containing error in both x and y) may have the following form:

$$\begin{array}{}\text{(2)}& y\sim \mathcal{N}(b_{\mathrm{0}}+f(\mathit{x},{\mathit{B}}^{*}),\mathrm{d}f(\mathit{x},{\mathit{B}}^{*}{)}^{\prime }{\mathbf{\Sigma }}_{aa}\mathrm{d}f(\mathit{x},{\mathit{B}}^{*})+{\mathit{\epsilon }}_y^{\mathrm{2}}),\end{array}$$

where b₀ is the regression intercept, $\mathrm{d}f(\mathit{x},{\mathit{B}}^{*})$ is the derivative of $f(\mathit{x},{\mathit{B}}^{*})$ for each observation vector [y x], and the prime symbol (^′) is the transpose operator. Appendix A contains further information about Eq. (2). The covariance matrix Σ_aa is the covariance of the noise a associated with $\mathit{x}={\mathit{x}}^{*}+\mathit{a}$, where x^* denotes the true but unobservable part of x (so x^* is unobservable because it cannot be measured without noise). See Table 1 for notation information (including B^* explained under B). The term measurement error is used here generally to describe any uncertainty associated with the value of the predictors and the response variable, which could include both measurement uncertainty (e.g., from a thermometer) and methodological uncertainty (from the method used to “combine” several measurements, which may be spatially and temporally apart). The model in Eq. (2) is not identifiable, meaning the parameters cannot be uniquely determined without additional information, such as information about Σ_aa. A full Bayesian solution to the problem may also require reformulating the model in terms of a subspace of [Y  X]; see, e.g., Florens et al. (1974). The focus of this paper is on a quasi-Bayesian solution to Eq. (2), which leverages Gaussian conjugacy instead of a Markov chain Monte Carlo (MCMC) solution.

In this paper, EIV and WLS (weighted least squares) refer to general approaches. York (1966, 1968) introduced a root-finding solution for one-predictor WLS regression. Ludwig and Titterington (1994) presented a maximum likelihood (ML) solution for a straight line in 3-dimensional space, with heterogenous noise in all variables. Schneider (2001) briefly discussed the multivariate method of total least squares, which assumes homogenous and identically distributed noise for both predictor and response fields. Hannart et al. (2014) introduced a ML algorithm for weighted TLS (WTLS) that accounts for heterogeneity and temporal autocorrelation in the predictor noise and the response noise but lacks noise cross-correlation. Also ML solutions, by their very nature, do not incorporate prior information about the regression coefficients. This study expands the model of Hannart et al. (2014), to include both prior information and generalized noise (auto- and cross-correlation within and between the noise series), in the Measurement Error Proxy System Model (MEPSM). The general EIV model is discussed in Sect. 2.1, MEPSM is formulated in Sect. 2.2, and steps for practical implementation are given in Sect. 2.3. MEPSM is applied to a real example in Sect. 3. Further, Sect. 3.3 investigates the differences that PSM calibration using MEPSM can make to paleodata assimilation.

Table 1 Notation used.

^a The operator vec(A) means to column stack the matrix A (Henderson and Searle, 1979). ^b Superscript ⁽ⁱ⁾ refers to an index, rather than subscripting (e.g., ${}_{z_i{z}_i}$). ^c For the duplication matrix, see Magnus and Neudecker (1986).

Fuller (1990)Amiri-Simkooei and Jazaeri (2012)Hannart et al. (2014)Fang et al. (2017)

Table 2 Solutions for the EIV model. Σ_A and Σ_B are given in my notation.

^a The matrix direct sum operator ⊕ is notation to build a block diagonal matrix, e.g., $\mathrm{Diag}\left(\right[{\mathrm{\Sigma }}_{a_{\mathrm{1}}{a}_{\mathrm{1}}},\mathrm{\dots },{\mathrm{\Sigma }}_{a_n{a}_n}\left]\right)$. ^b Note though that technically ${\oplus }_i{\mathrm{\Sigma }}_{a_i{a}_i}={\mathrm{\Sigma }}_{A^{\prime }}$, not Σ_A, so ⊕ is used abstractly in this case. ^c Full: Σ_A is not constrained to a particular type.

2 Methods

2.1 The EIV model

The general EIV model can be expressed as

$$\begin{array}{}\text{(3a)}& {\displaystyle }& {\displaystyle }{\mathit{z}}_t={\mathit{z}}_t^{*}+{\mathit{q}}_t\text{(3b)}& {\displaystyle }& {\displaystyle }{\mathit{z}}_t^{*}=\left[y_t^{*}{\mathit{x}}_t^{*}\right]\text{(3c)}& {\displaystyle }& {\displaystyle }{\mathit{q}}_t=\left[v_t{\mathit{a}}_t\right]\text{(3d)}& {\displaystyle }& {\displaystyle }{y}_t^{*}=b_{\mathrm{0}}+{\mathit{x}}_t^{*}{\mathit{B}}^{*}+{\mathit{ϵ}}_t.\end{array}$$

Note that, for X^* and B^*, the superscript star also has a second use: it denotes that these entities do not include an intercept term, e.g., $\mathit{B}={\left[b_{\mathrm{0}}{{\mathit{B}}^{*}}^{\prime }\right]}^{\prime }$. From Eq. (3), the relevant covariance matrices are

$$\begin{array}{}\text{(4)}& {\mathrm{\Sigma }}_{z^{*}{z}^{*}}=\left[\begin{array}{cc}{\mathit{\sigma }}_{Y^{*}{Y}^{*}}^{\mathrm{2}}& {\mathrm{\Sigma }}_{Y^{*}{X}^{*}}\\ {\mathrm{\Sigma }}_{X^{*}{Y}^{*}}& {\mathrm{\Sigma }}_{X^{*}{X}^{*}}\end{array}\right],{\mathrm{\Sigma }}_Q=\left[\begin{array}{cc}{\mathrm{\Omega }}_V& \mathbf{0}\\ \mathbf{0}& {\mathrm{\Sigma }}_A\end{array}\right],\end{array}$$

and

$$\begin{array}{}\text{(5)}& {\mathrm{\Sigma }}_A=\left[\begin{array}{cccc}{\mathrm{\Omega }}_{A_{\mathrm{1}}}& {\mathrm{\Omega }}_{A_{\mathrm{1}}{A}_{\mathrm{2}}}& \mathrm{\dots }& {\mathrm{\Omega }}_{A_{\mathrm{1}}{A}_p}\\ {\mathrm{\Omega }}_{A_{\mathrm{2}}{A}_{\mathrm{1}}}& {\mathrm{\Omega }}_{A_{\mathrm{2}}}& \mathrm{\dots }& {\mathrm{\Omega }}_{A_{\mathrm{2}}{A}_p}\\ \mathrm{⋮}& \mathrm{⋮}& \mathrm{\ddots }& \mathrm{⋮}\\ {\mathrm{\Omega }}_{A_p{A}_{\mathrm{1}}}& {\mathrm{\Omega }}_{A_p{A}_{\mathrm{2}}}& \mathrm{\dots }& {\mathrm{\Omega }}_{A_p}\end{array}\right].\end{array}$$

See Appendix B for further information on covariance notation. These matrices describe a statistical stationary model. For example, the covariance matrix Σ_A fully specifies the lag autocovariance and lag cross-covariances of the noise variables in A, but (Σ_A)_t=Σ_A. Note this does not mean within Σ_A that ${\mathrm{\Sigma }}_{a_i{a}_i}={\mathrm{\Sigma }}_{a_j{a}_j}$ or ${\mathrm{\Omega }}_{A_i}={\mathrm{\Omega }}_{A_j}$ (those are specific cases of Σ_A). Also note that in this paper Ω_V=Σ_V. More will be said about Σ_Q in Sect. 3.1.

Table 2 summarizes the main differences between previous solutions of the EIV model. First, these methods all assume that the equation noise ϵ_t (Eq. 3d) is either zero or not separate from v_t. Earlier work by Fuller (1987) shows a way of including the equation noise separate from the response noise, but the predictor noise is limited to the p×p matrices ${\mathrm{\Sigma }}_{a_t{a}_t}$. The solutions in Table 2 relate to generalized least squares (GLS), weighted total least squares (WTLS), maximum likelihood (ML), and maximum a posteriori (MAP) methods. A general estimator is of the following form:

$$\begin{array}{}\text{(6a)}& {\displaystyle }{\mathrm{\Sigma }}_{ZZ}& {\displaystyle }=(\mathbf{Z}-{\mathit{\mu }}_Z{)}^{\prime }{\mathbb{J}}_n^{\prime }{\left[\begin{array}{cc}{\mathrm{\Sigma }}_Y& {\mathrm{\Sigma }}_{YX}\\ {\mathrm{\Sigma }}_{XY}& {\mathrm{\Sigma }}_X\end{array}\right]}^{-\mathrm{1}}{\mathbb{J}}_n(\mathbf{Z}-{\mathit{\mu }}_Z)\text{(6b)}& {\displaystyle }{\mathrm{\Sigma }}_{Z^{*}{Z}^{*}}& {\displaystyle }={\mathrm{\Sigma }}_{ZZ}-{\mathrm{\Sigma }}_{QQ}=\left[\begin{array}{cc}{\mathit{\sigma }}_{Y^{*}{Y}^{*}}^{\mathrm{2}}& {\mathrm{\Sigma }}_{Y^{*}{X}^{*}}\\ {\mathrm{\Sigma }}_{X^{*}{Y}^{*}}& {\mathrm{\Sigma }}_{X^{*}{X}^{*}}\end{array}\right]\text{(6c)}& {\displaystyle }{\mathit{B}}^{*}& {\displaystyle }={\mathrm{\Sigma }}_{X^{*}{X}^{*}}^{-\mathrm{1}}{\mathrm{\Sigma }}_{X^{*}{Y}^{*}}\text{(6d)}& {\displaystyle }{b}_{\mathrm{0}}& {\displaystyle }={\mathit{\mu }}_Z\cdot {\left[\begin{array}{cc}\mathrm{1}& -{{\mathit{B}}^{*}}^{\prime }\end{array}\right]}^{\prime },\end{array}$$

where μ_Z is the GLS mean, ${\mathrm{\Sigma }}_Y={\mathrm{\Sigma }}_{Y^{*}}+{\mathrm{\Omega }}_V$, and ${\mathrm{\Sigma }}_X={\mathrm{\Sigma }}_{X^{*}}+{\mathrm{\Sigma }}_A$. The covariance matrix ${\mathrm{\Sigma }}_{X^{*}{X}^{*}}$ is a weighted matrix, e.g., ${\mathbf{X}}^{*}{}^{\prime }{\mathrm{\Sigma }}^{-\mathrm{1}}{\mathbf{X}}^{*}$, but different ways of solving for B allow for different weightings. The assumption is then made that ${\mathrm{\Sigma }}_{B^{*}}={\mathrm{\Sigma }}_{X^{*}{X}^{*}}^{-\mathrm{1}}$ (e.g., Amiri-Simkooei and Jazaeri, 2012; Fang et al., 2017), despite the fact that different possible weightings exist. The ML method can be used to obtain a theoretically better estimation of Σ_B, but it is computationally expensive if Σ_A is not constrained. For example, in Hannart et al. (2014) Σ_A is a block diagonal matrix: ${\mathrm{\Sigma }}_A={\oplus }_{i=\mathrm{1}}^p{\mathrm{\Omega }}_{A_i}$, where ⊕ is the direct sum operator for matrices (see Table 2 footnotes). The aim of the present study is to provide a solution for the EIV model that includes a fast theory-derived approximation of Σ_B, a prior for Σ_B, and a full Σ_A, including a way to estimate Σ_A with limited initial information.

2.2 MEPSM

As in previous studies, I also ignore the equation error, so the model in Eq. (3) can be re-expressed:

$$\begin{array}{}\text{(7)}& \left[\begin{array}{c}{Z}_{\mathrm{11}}\\ Z_{\mathrm{21}}\\ \mathrm{⋮}\\ Z_{n\mathrm{1}}\end{array}\right]=\left[\begin{array}{cc}\mathrm{1}& {\mathit{x}}_{\mathrm{1}}\\ \mathrm{1}& {\mathit{x}}_{\mathrm{2}}\\ \mathrm{⋮}& \mathrm{⋮}\\ \mathrm{1}& {\mathit{x}}_n\end{array}\right]\left[\begin{array}{c}{b}_{\mathrm{0}}\\ {\mathit{B}}^{*}\end{array}\right]+\left[\begin{array}{cc}{\mathbb{I}}_n& -({{\mathit{B}}^{*}}^{\prime }\otimes {\mathbb{I}}_n)\end{array}\right]\left[\begin{array}{c}\mathit{V}\\ \mathrm{vec}\left(\mathbf{A}\right)\end{array}\right],\end{array}$$

where $\mathit{V}\sim \mathcal{N}({\mathbf{0}}_n,{\mathrm{\Omega }}_V)$, and $\mathrm{vec}\left(\mathbf{A}\right)\sim \mathcal{N}({\mathbf{0}}_{n\cdot p},{\mathrm{\Sigma }}_A)$ (see Table 1 footnotes for the operator vec). The response variable is the first column of Z, denoted as Z₁ or more generally as Y. Note also the two possible definitions of response noise for the model: $\mathit{V}=\mathit{Y}-b_{\mathrm{0}}-{\mathbf{X}}^{*}{\mathit{B}}^{*}$ and $\mathit{e}=\mathit{Y}-\mathbf{X}\mathit{B}$ (where X includes an intercept term, to match with B). The difference is that

$$\begin{array}{}\text{(8)}& \mathit{V}=\mathit{Y}-\mathbf{X}\mathit{B}+\mathbf{A}{\mathit{B}}^{*}=\mathit{e}+\mathbf{A}{\mathit{B}}^{*}.\end{array}$$

From $\mathit{e}=\mathit{V}-\mathbf{A}{\mathit{B}}^{*}$, the covariance matrix of model prediction can be expressed as

$$\begin{array}{}\text{(9)}& \mathbf{W}={\mathrm{\Omega }}_V+({{\mathit{B}}^{*}}^{\prime }\otimes {\mathbb{I}}_n){\mathrm{\Sigma }}_A({\mathit{B}}^{*}\otimes {\mathbb{I}}_n).\end{array}$$

Bayes' rule states that the posterior density function p(θ|𝒟) is proportional to the product of the likelihood function L(θ) and the prior density function p(θ):

$$\begin{array}{}\text{(10)}& p\left(\mathit{\theta }\right|\mathcal{D})\propto L(\mathit{\theta })\times p(\mathit{\theta }).\end{array}$$

Note that it does not matter if the likelihood function is a scaled distribution, e.g., a normal density function multiplied by a scalar (so it integrates to a number other than unity).

Assuming that the right-side distributions are Gaussian (or scaled Gaussian), then

$$\begin{array}{}\text{(11)}& \mathcal{N}(\mathit{B},{\mathrm{\Sigma }}_B)\propto \mathcal{N}({\mathit{B}}_{\text{ml}},{\mathrm{\Sigma }}_B^{\text{ml}})\times \mathcal{N}({\mathit{B}}_{\mathrm{0}},{\mathrm{\Sigma }}_{\mathrm{0}}),\end{array}$$

where ml refers to the maximum likelihood solution. The posterior 𝒩(B, Σ_B) integrates to unity, as expected. First I show an example by using the GLS likelihood. Let the GLS likelihood be

$$\begin{array}{}\text{(12)}& \mathcal{N}({\mathit{B}}_{\text{ml}},{\mathrm{\Sigma }}_B^{\text{ml}})=\mathcal{N}\left(({\mathbf{X}}^{\prime }{\mathrm{\Sigma }}^{-\mathrm{1}}\mathbf{X}{)}^{-\mathrm{1}}{\mathbf{X}}^{\prime }{\mathrm{\Sigma }}^{-\mathrm{1}}\mathit{Y},({\mathbf{X}}^{\prime }{\mathrm{\Sigma }}^{-\mathrm{1}}\mathbf{X}{)}^{-\mathrm{1}}\right).\end{array}$$

Now apply the Gaussian multiplication identity:

$$\begin{array}{}\text{(13)}& \begin{array}{rl}\mathcal{N}& \left(\mathbf{C}\right({\mathrm{\Sigma }}_B^{\text{ml}-\mathrm{1}}{\mathit{B}}_{\text{ml}}+{\mathrm{\Sigma }}_{\mathrm{0}}^{-\mathrm{1}}{\mathit{B}}_{\mathrm{0}}),\mathbf{C})\propto \mathcal{N}({\mathit{B}}_{\text{ml}},{\mathrm{\Sigma }}_B^{\text{ml}})\\ & \times \mathcal{N}({\mathit{B}}_{\mathrm{0}},{\mathrm{\Sigma }}_{\mathrm{0}}),\end{array}\end{array}$$

where $\mathbf{C}={\left({\mathrm{\Sigma }}_B^{\text{ml}-\mathrm{1}}+{\mathrm{\Sigma }}_{\mathrm{0}}^{-\mathrm{1}}\right)}^{-\mathrm{1}}$. Thus the mean and variance of p(θ|𝒟) are

$$\begin{array}{}\text{(14a)}& {\displaystyle }\mathit{B}& {\displaystyle }=({\mathbf{X}}^{\prime }{\mathrm{\Sigma }}^{-\mathrm{1}}\mathbf{X}+{\mathrm{\Sigma }}_{\mathrm{0}}^{-\mathrm{1}}{)}^{-\mathrm{1}}({\mathbf{X}}^{\prime }{\mathrm{\Sigma }}^{-\mathrm{1}}\mathit{Y}+{\mathrm{\Sigma }}_{\mathrm{0}}^{-\mathrm{1}}{\mathit{B}}_{\mathrm{0}})\text{(14b)}& {\displaystyle }{\mathrm{\Sigma }}_B& {\displaystyle }=({\mathbf{X}}^{\prime }{\mathrm{\Sigma }}^{-\mathrm{1}}\mathbf{X}+{\mathrm{\Sigma }}_{\mathrm{0}}^{-\mathrm{1}}{)}^{-\mathrm{1}}.\end{array}$$

The above solution is a simple example using the GLS likelihood. To obtain the solution for the EIV problem, the GLS likelihood is replaced with the WTLS likelihood $\mathcal{N}({\mathit{B}}_{\text{wtls}},{\mathrm{\Sigma }}_B^{\text{wtls}})$, where B_wtls and ${\mathrm{\Sigma }}_B^{\text{wtls}}$ are derived in Appendix C and D. Using the WTLS likelihood, simplifying the product ${\mathrm{\Sigma }}_B^{\text{ml}-\mathrm{1}}{\mathit{B}}_{\text{ml}}$ (from Eq. 13) is no longer feasible, so instead we write the mean and variance of p(θ|𝒟) simply as

$$\begin{array}{}\text{(15)}& {\displaystyle }\mathit{B}& {\displaystyle }={\left({{\mathrm{\Sigma }}_B^{\text{wtls}}}^{-\mathrm{1}}+{\mathrm{\Sigma }}_{\mathrm{0}}^{-\mathrm{1}}\right)}^{-\mathrm{1}}\left({{\mathrm{\Sigma }}_B^{\text{wtls}}}^{-\mathrm{1}}{\mathit{B}}_{\text{wtls}}+{\mathrm{\Sigma }}_{\mathrm{0}}^{-\mathrm{1}}{\mathit{B}}_{\mathrm{0}}\right)\text{(16)}& {\displaystyle }{\mathrm{\Sigma }}_B& {\displaystyle }={\left({{\mathrm{\Sigma }}_B^{\text{wtls}}}^{-\mathrm{1}}+{\mathrm{\Sigma }}_{\mathrm{0}}^{-\mathrm{1}}\right)}^{-\mathrm{1}}.\end{array}$$

2.3 Implementation

An application to calibrate a real PSM is provided in Sect. 3. Here general aspects of the solution and implementation are discussed.

The predictor noise and response noise, A and V, can be estimated as

$$\begin{array}{}\text{(17)}& {\displaystyle }\mathbf{A}& {\displaystyle }=-({\mathit{B}}^{{*}^{\prime }}\otimes {\mathbb{I}}_n){\mathrm{\Sigma }}_A({\mathbb{I}}_p\otimes {\mathbf{W}}^{-\mathrm{1}}\mathit{e})\text{(18)}& {\displaystyle }\mathit{V}& {\displaystyle }={\mathrm{\Omega }}_V{\mathbf{W}}^{-\mathrm{1}}\mathit{e}.\end{array}$$

Matrix A is needed for the calculation of both B_wtls and ${\mathrm{\Sigma }}_B^{\text{wtls}}$, while V is needed to re-estimate Ω_V if relevant (see next paragraph).

The n×n covariance matrices ${\mathrm{\Omega }}_{A_i}$ (or ${\mathrm{\Omega }}_{A_i{A}_j}$) and Ω_V ideally need information about the cross-correlation within A and autocorrelation of A and V. If the ACF (autocorrelation function) and CCF (cross-correlation function) are not available, these can potentially be estimated using an iterative procedure. The procedure begins with vectors ${\mathit{\sigma }}_A^{\mathrm{2}}$ and ${\mathit{\sigma }}_V^{\mathrm{2}}$, which are the heteroscedastic error variances (the diagonals of Σ_A and Ω_V).

1. Initialize ${\mathrm{\Sigma }}_A=\mathrm{Diag}({\mathit{\sigma }}_A\odot {\mathit{\sigma }}_A)$ and ${\mathrm{\Omega }}_V=\mathrm{Diag}({\mathit{\sigma }}_V\odot {\mathit{\sigma }}_V)$, where ⊙ denotes the Hadamard product.

2. Estimate the first posterior, 𝒩(B, Σ_B), and the predictor and response noise, A and V (Eqs. 15–18).

3. Calculate the ACF (for A and V) and the CCF (for A).

4. Estimate Σ_A and Ω_V as in Appendix E, and recalculate the posterior distribution.

3 Application

3.1 A proxy system model, uncertainties, and the prior

A bivariate (i.e., two-predictor) PSM for coral δ¹⁸O is

$$\begin{array}{}\text{(19)}& {\mathit{\delta }}^{\mathrm{18}}{\text{O}}_{\text{coral}}=b_{\mathrm{0}}+b_{\mathrm{1}}\text{SST}+b_{\mathrm{2}}\text{SSS},\end{array}$$

where SST is sea surface temperature and SSS is sea surface salinity. Note that in the coral literature, the coefficients b₁ and b₂ are commonly referred to as a₁ and a₂, but here I use the former symbols for generality. This bivariate PSM has been used in data assimilation (Sanchez et al., 2021) and Monte Carlo experiments (Thompson et al., 2022). The bivariate PSM can be extended by rewriting it in the form of Eq. (7). The MEPSM requires estimates of the time-varying uncertainty of all variables and a prior distribution for B (see below). Here the time-varying uncertainties for the predictors are obtained from recent SST and SSS products that provide the complete uncertainty field ${\mathit{\epsilon }}^{\mathrm{2}}(\mathrm{long},\mathrm{lat},t)$, i.e., the uncertainty variance for each grid cell, at each time point.

For ERSSTv5, for each grid cell and time point, the SST total uncertainty ${\mathit{\epsilon }}_T^{\mathrm{2}}(\mathrm{long},\mathrm{lat},t)$ is the sum of the parametric uncertainty and reconstruction uncertainty. These uncertainties are derived from a large reconstruction ensemble (Huang et al., 2020). The parametric uncertainty is based on the difference between the ensemble average and each ensemble member, given various internal parameters which affect SST uncertainty (including the uncertainty of the ship, buoy, or float measurement). The reconstruction uncertainty is based on the difference between each ensemble member and a pseudo-observation dataset on which the reconstruction method is trained, e.g., OISST (optimally interpolated SST). Note that the calculation of reconstruction uncertainty includes grid cells that have observational or no observational data, while the calculation of parametric uncertainty includes only grid cells that have observational data.

For HadEN4, the SSS total uncertainty ${\mathit{\epsilon }}_S^{\mathrm{2}}(\mathrm{long},\mathrm{lat},t)$ is a combination of background uncertainty and observational uncertainty (Good et al., 2013). The observational uncertainty is obtained from previous studies, while the background uncertainty is the uncertainty associated with a persistent-based forecast.

For δ¹⁸O_coral, the main known uncertainty is the analytical uncertainty, which is ∼0.05 ‰ for δ¹⁸O_coral (Osborne et al., 2013). Time variation could be included by expressing the analytical uncertainty as a relative standard deviation of the mean δ¹⁸O (the effect of this will be tested elsewhere). Other uncertainties, which are unknown at many sites, include the intra- and inter-colony noise (Sayani et al., 2019). Note also that detrending adds time-varying uncertainty, because the trend uncertainty is larger at the ends of the time series (this is applicable to all detrended variables).

For MEPSM, the matrix Σ_A can be initially constructed using Diag(σ_A⊙σ_A), where ${\mathit{\sigma }}_A^{\prime }=\left[{\mathit{\epsilon }}_T(\text{site},\cdot ),{\mathit{\epsilon }}_S(\text{site},\cdot )\right]$, “site” refers to the grid cell of a particular site, and the $(\text{site},\cdot )$ notation means over all time points. In the SST and SSS products, no information is given on the noise serial correlation, and no information exists on the noise cross-correlation between SST and SSS products. Seasonal peaks in the autocorrelation function (ACF) of SST noise could arise from, for example, seasonal changes in shipping tracks, which would affect the parametric uncertainty. Cross-correlation between SST and SSS noise might arise from sampling these variables at the same points within a particular grid cell (i.e., from the same ship) or due to seasonal variation in shipping tracks. Future work should investigate the ACF and CCF (cross-correlation function) for the SST and SSS ensembles (this is beyond the scope of the current paper). Finally, since the uncertainties in the predictors and response are fundamentally different, then Σ_Q is assumed to be a block diagonal matrix, with Ω_V and Σ_A on the block diagonal and zero-filled blocks on the block anti-diagonal (Eq. 4).

For Bayesian methods, informative prior distributions are thought to be more useful than noninformative priors (Lemoine, 2019). For example, when using a fully noninformative prior distribution, the posterior distribution will be close to the maximum likelihood distribution, which would make using the fully noninformative prior somewhat obsolete.

The prior distribution for B is obtained from previous values that were used in Monte Carlo PSM experiments (Thompson et al., 2022; Watanbe and Pfeiffer, 2022). Those previous studies did not seek to calculate Bayesian posterior distributions, but the values in those studies represent current beliefs about the coefficients and their uncertainty and can be used as a prior. The prior distribution obtained from those studies is

$$\begin{array}{}\text{(20)}& \begin{array}{rl}p\left(\mathit{B}\right)& =\mathcal{N}\left({\mathit{B}}_{\mathrm{0}},{\mathrm{\Sigma }}_{\mathrm{0}}\right)\\ & =\mathcal{N}\left(\begin{array}{c}\left[\begin{array}{c}{b}_{\mathrm{0}}\\ -\mathrm{0.22}\\ \mathrm{0.27}s\end{array}\right],\left[\begin{array}{ccc}{\mathit{\sigma }}_{b_{\mathrm{0}}}^{\mathrm{2}}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& {\mathrm{0.02}}^{\mathrm{2}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& {\mathrm{0.15}}^{\mathrm{2}}\end{array}\right]\end{array}\right),\end{array}\end{array}$$

where s=0.97 is a scaling factor between δ¹⁸O_seawater (in VSMOW) and δ¹⁸O_coral (in VPDB). The values of $b_{\mathrm{1}}=-\mathrm{0.22}$ and ${\mathit{\sigma }}_{b_{\mathrm{1}}}^{\mathrm{2}}={\mathrm{0.02}}^{\mathrm{2}}$ are from Thompson et al. (2022) and Watanbe and Pfeiffer (2022) respectively. The value of $s^{-\mathrm{1}}{b}_{\mathrm{2}}=\mathrm{0.27}$ ‰ psu⁻¹ originates from LeGrande and Schmidt (2006) and is an average ‰ per salinity value for the tropical Pacific Ocean. Regional variations in this value will probably be revealed by new datasets (DeLong et al., 2022), but for the purpose of this example of MEPSM, the value of 0.27 ‰ psu⁻¹ is used. Thompson et al. (2022) considered two values for ${\mathit{\sigma }}_{b_{\mathrm{2}}}^{\mathrm{2}}$ (i.e., ${\mathit{\sigma }}_{b_{\mathrm{2}}}^{\mathrm{2}}=\mathit{\{}{\mathrm{0.1}}^{\mathrm{2}},{\mathrm{0.2}}^{\mathrm{2}}\mathit{\}}$), so for this example an ”average” value is used (0.15²). The value of the intercept b₀ and its uncertainty ${\mathit{\sigma }}_{b_{\mathrm{0}}}^{\mathrm{2}}$ are unknown in the sense that they are site-dependent values. A prior for these unknown values can be estimated by using the other prior coefficients and SST and SSS data for a particular site. For a particular site, the prior value of b₀ can be calculated as

$$\begin{array}{}\text{(21)}& b_{\mathrm{0}}={\mathit{\mu }}_y-{\mathit{\mu }}_X\left[\begin{array}{c}-\mathrm{0.22}\\ \mathrm{0.27}s\end{array}\right],\end{array}$$

where ${\mathit{\mu }}_X=\left[{\mathit{\mu }}_{X_{\mathrm{1}}}{\mathit{\mu }}_{X_{\mathrm{2}}}\right]$ and μ_y are the mean values of the predictors and response. From ordinary least squares theory, the diagonal elements of the covariance of B are typically given as

$$\begin{array}{}\text{(22)}& {\mathit{\sigma }}_{b_j}^{\mathrm{2}}={\mathit{\sigma }}_e^{\mathrm{2}}/{\text{RSS}}_j,\end{array}$$

where ${\mathit{\sigma }}_e^{\mathrm{2}}$ is the error variance, and RSS_j is the residual sum of squares after regressing X_j on X_−j, where X_−j is the matrix X omitting column j. So for ${\mathit{\sigma }}_{b_{\mathrm{0}}}^{\mathrm{2}}$,

$$\begin{array}{}\text{(23)}& {\text{RSS}}_{\mathrm{0}}=n-n^{\mathrm{2}}{\mathit{\mu }}_X^{\prime }({\mathbf{X}}_{-\mathrm{0}}^{\prime }{\mathbf{X}}_{-\mathrm{0}}{)}^{-\mathrm{1}}{\mathit{\mu }}_X,\end{array}$$

where X₋₀ is the observed part of X not including an intercept term (different than X^*, which is the unobserved part of X). Preliminary analysis showed that the prior value for ${\mathit{\sigma }}_{b_{\mathrm{0}}}^{\mathrm{2}}$ had a large influence on the posterior distribution of B, so ${\mathit{\sigma }}_{b_{\mathrm{0}}}^{\mathrm{2}}$ only was scaled to be uninformative, i.e., ${\mathrm{10}}^{\mathrm{3}}{\mathit{\sigma }}_{b_{\mathrm{0}}}^{\mathrm{2}}$.

3.2 Coral example

Rock Islands (7.27° N, 134.38° E) is a site on the western barrier reef of Palau, western Pacific Ocean. A number of coral cores were sampled from Rock Islands (RI) and the surrounding area, but the focus here is on one core labeled RI6, which is a monthly resolved record spanning 1899–2008. The core was sampled from a narrow-entrance lagoon, in shallow water (∼2 m depth). Osborne et al. (2013) compared the coral δ¹⁸O record with temperature data from the NCEP/NCAR Reanalysis (Kalnay et al., 1996) and salinity data from LEGOS (Delcroix et al., 2011). Using the raw (not detrended or deseasonalized) RI record from 1970–2008 and ordinary least squares, Osborne et al. (2013) regressed the coral δ¹⁸O against surface temperature and salinity, producing the following equation:

$$\begin{array}{}\text{(24)}& {\mathit{\delta }}^{\mathrm{18}}{\text{O}}_{\text{coral}}=-\mathrm{0.06}\text{SST}+\mathrm{0.43}\text{SSS}-\mathrm{18.70};\end{array}$$

see Table A4 in Osborne et al. (2013). Osborne et al. (2013) attributed the small SST coefficient to the small seasonal SST range at Palau (∼1.5 °C), presumably because the small SST range makes the data scatter with δ¹⁸O more spherical than ellipsoid. They did not directly compare their raw SSS coefficient with any other data. Hence the RI δ¹⁸O record was chosen for this example, in order to further investigate the SST and SSS effects on coral δ¹⁸O at this site. In the following analysis the main differences with the analysis of Osborne et al. (2013) are that here the SST and SSS data are extracted from ERSSTv5 and HadEN4, because these products provide the uncertainty fields (Sect. 3.1). Secondly, the time period examined is from 1950–2008. Thirdly, for this study, all variables were detrended (using linear detrending and without removing the intercept), in order to ensure stationarity in the mean. For all variables, the trends at this site were weak. For example, for δ¹⁸O_coral the trend from 1950–2008 was $-\mathrm{0.00135}\pm \mathrm{0.004}$ ‰ per year. A Jupyter Notebook with these preprocessing steps is available in the Supplement. Using this updated (and detrended) data, the OLS regression was recalculated as

$$\begin{array}{}\text{(25)}& {\mathit{\delta }}^{\mathrm{18}}{\text{O}}_{\text{coral}}=-\mathrm{0.13}\text{SST}+\mathrm{0.42}\text{SSS}-\mathrm{16.25}.\end{array}$$

Next MEPSM was applied to the same data, following the steps in Sect. 2.3. Except, for the application presented here, only Σ_A was updated in step 4. Ω_V was set as ${\mathrm{\Omega }}_V=\mathrm{Diag}({\mathit{\sigma }}_V\odot {\mathit{\sigma }}_V)$ throughout, because here σ_V is thought to be mostly analytical noise, which should be approximately white (the uncertainty due to detrending is time-varying as well as white). For Σ_A, for the auto- and cross-correlation functions of the predictor noise, up to 100 lags (months) were retained to construct the submatrices ${\mathbf{R}}_{A_i}$ and ${\mathbf{R}}_{A_i{A}_j}$ (see Appendix E). Experiments with 50 and 150 lags showed little difference in the final posterior. In any application of MEPSM, the user should consider the source of the predictor and response noise in constructing Σ_A and Ω_V (as in Sect. 3.1).

Figure 1 shows the prior and the first and final posterior distributions for the SST and SSS coefficients. The first posterior distribution (dashed line) is obtained after step 2 (Sect. 2.3), while the final posterior is obtained after updating Σ_A for auto- and cross-correlation. The (final) mean SST and SSS coefficients are given in Fig. 2: $b_{\mathrm{1}}=-\mathrm{0.25}$ ‰ °C⁻¹ and b₂=0.49 ‰ psu⁻¹. Figure 2 shows the marginal plots of the 3-dimensional scatter plot (SST, SSS, δ¹⁸O), together with the prior and posterior regression lines. For Rock Island, the SST and SSS coefficients are both steeper for the final posterior, compared to the OLS equation (Eq. 25).

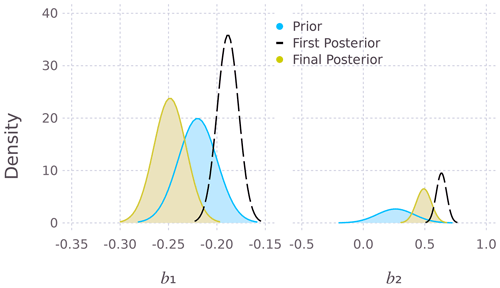
Figure 1 The prior and posterior distributions for the SST (b₁) and SSS (b₂) coefficients. The final posterior is wider than the first posterior, because the final posterior accounts for auto- and cross-correlation in Σ_A. In Figs. 1–3 the first posterior is the dashed line.

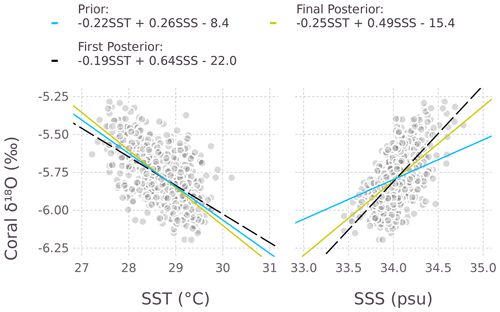
Figure 2 The regression lines of the prior and posterior distributions. In 3 dimensions, these regression lines are the sides of a plane. Each shaded point corresponds to a monthly value from 1950–2008.

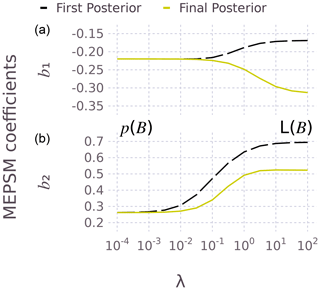
Figure 3 The effect of the regularization parameter λ on the SST (b₁, top) and SSS (b₂, bottom) coefficients. The left and right side of the plots correspond to the prior distribution p(B) and likelihood distribution L(B) respectively.

Another advantage of Bayesian analysis is that attaching a ridge parameter λ to the prior variances means that the method can be used to regularize the solution, in a way that is different than traditional methods of regularization, such as principal component analysis, where components are retained by hard thresholding. Here, the ridge parameter λ is attached to the prior and allowed to vary over the range 10⁻⁴ to 10²:

$$\begin{array}{}\text{(26)}& p\left(\mathit{B}\right)=\mathcal{N}\left(\begin{array}{c}\left[\begin{array}{c}{b}_{\mathrm{0}}\\ -\mathrm{0.22}\\ \mathrm{0.27}s\end{array}\right],\left[\begin{array}{ccc}{\mathrm{10}}^{\mathrm{3}}{\mathit{\sigma }}_{b_{\mathrm{0}}}^{\mathrm{2}}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathit{\lambda }{\mathrm{0.02}}^{\mathrm{2}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathit{\lambda }{\mathrm{0.15}}^{\mathrm{2}}\end{array}\right]\end{array}\right).\end{array}$$

Figure 3 shows the effect of λ for both the first and final posterior. As λ increases, B moves from the prior distribution to the likelihood distribution. The difference between the solid and dashed lines (for each coefficient) is because of the effect of adjusting Σ_A for auto- and cross-correlation, which becomes less relevant for small λ ($\mathit{\lambda }<{\mathrm{10}}^{-\mathrm{2}}$). More will be said about serial dependence in A below. This type of prior regularization will likely be useful for sites where the (p+1)-dimensional scatter of data (predictors plus response) is more spherical than ellipsoid. For example, a more spherical scatter of data could occur at sites where the SST range is small. In practice, the value of λ could be estimated using cross-validation methods.

Table 3 Regression parameters and their standard deviation, from four different solutions.

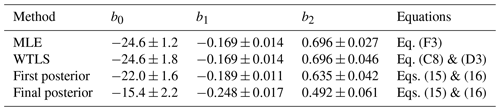
Table 3 compares the regression coefficients (and variance) from four different solutions: a ML solution (Appendix F), the WTLS method (Appendix C and D), and the MEPSM solution for the first and final posterior. The maximum likelihood estimate (MLE) and WTLS solution are basic implementations, i.e., no prior and no adjustment for autocorrelation or cross-correlation. The MLE and WTLS solutions are similar, with the variance being generally more conservative for WTLS, owing either to assumptions in the two methods or differences in method implementation, e.g., optimization for MLE versus analytical solution (with Gaussian assumptions) for WTLS. For the first posterior of MEPSM, both the mean and the variance move away from the WTLS solution and towards a tight prior: in Fig. 3 the MEPSM first posterior (on the dashed line) is the same as the λ=10⁰ solution, and the basic WTLS solution is the same as λ≥10². For the final posterior (Table 3), the SST and SSS coefficients change steepness: b₁ becomes steeper, while b₂ becomes a little less steep compared to the WTLS solution and the first posterior (also seen in Fig. 3 as the difference between the solid and dashed lines). For both coefficients (Table 3), the variance increases for the final posterior (relative to the first posterior), because the final posterior adjusts for the auto- and cross-correlation in Σ_A.

Figure 4 shows the autocorrelation of the noise in each variable (A₁ is the SST noise, and A₂ is the SSS noise), for the first and final posterior distribution. For the first posterior solution, the noise covariance in Σ_A and Ω_V is assumed to be heteroscedastic but white. This assumption is clearly not true, because all variables appear to have seasonally varying noise as shown by their autocorrelation functions (Fig. 4, left column). However, when this seasonally varying noise is included in Σ_A (but not in Ω_V), the response noise V essentially becomes white, as all the seasonal dependence moves into the predictor noise (Fig. 4, right column). Whether or not the response noise V should have seasonal variation (see Sect. 3.1) requires expert knowledge. This example is simply to illustrate the effect of including serially correlated noise in a multipredictor model. The implications of seasonally varying noise for coral PSMs will be addressed in another paper, with the application of MEPSM to a large coral database (Walter et al., 2023).

Figure 4 The autocorrelation function of the response noise (V), the SST noise A₁, and the SSS noise A₂, for the first posterior (left column) and the final posterior (right column). The predictor and response noise were calculated using Eqs. (17)–(18).

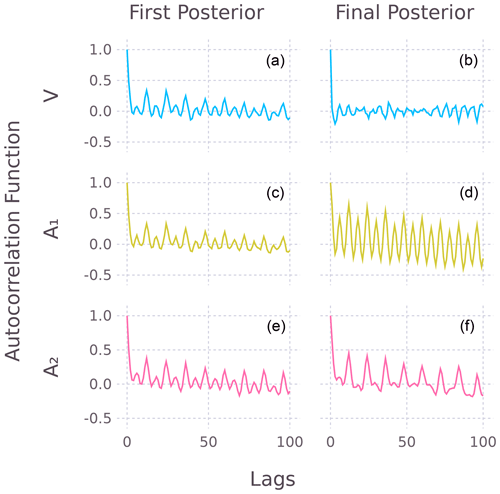
Table 4 Notation for Sect. 3.3 (unless otherwise stated in text).

^∗ In the experiments, p=5 and m=10 because there are two state variables and five grid points.

3.3 Data assimilation experiments

Two data assimilation (DA) experiments were performed using the Palau coral example. The purpose of these experiments is to investigate the effect of different H on data assimilation (Appendix G introduces DA and describes potential biases caused by misspecified H). For the experiments, the model prior covariance Σ_εε was obtained from iCESM1 (Brady et al., 2019), using a preindustrial run, and data from the last 400 years (1450–1850 CE, which is “closer” to the coral example period 1950–2007). Model SST and SSS data were extracted from a line of five grid cells, centered on the RI6 location. Although there is only one observational coral record, for these experiments, the same observational record is repeated for the five grid cells (Y^o in DA). All data were deseasonalized but kept at monthly resolution. A line of grid cells was used, so the covariance Σ_εε includes some spatial correlation. The reasons for using covariance matrices in these experiments will become apparent. The covariances Σ_εε and Σ_rr were the same for both experiments and were constructed as follows:

• ${\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}=\mathrm{Var}(\mathbf{X}-{\stackrel{\mathrm{̃}}{\mathbf{U}}}_k{\mathbf{D}}_k{\mathbf{V}}_k^{\prime })$, where $\mathbf{X}={\mathbf{UDV}}^{\prime }$ is the singular value decomposition of X, k=1:3 (means the three leading eigencomponents), and $\stackrel{\mathrm{̃}}{\mathbf{U}}$ denotes components filtered with a bandpass filter (2–20 years). Here interannual variability (as in U_k) is considered to be the state of interest. Filtering U better separates signal and noise.

• ${\mathrm{\Sigma }}_{rr}=\mathbf{FH}{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}{\mathbf{H}}^{\prime }\mathbf{F}$, where $\mathbf{F}=\mathrm{Diag}\left(\left[\frac{{\mathit{\sigma }}_V}{{\mathit{\sigma }}_{h_{\mathrm{1}}}},\mathrm{\dots },\frac{{\mathit{\sigma }}_V}{{\mathit{\sigma }}_{h_p}}\right]\right)$ and $\mathrm{Diag}\left(\mathbf{H}{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}{\mathbf{H}}^{\prime }\right)=[{\mathit{\sigma }}_{h_{\mathrm{1}}}^{\mathrm{2}},\mathrm{\dots },{\mathit{\sigma }}_{h_p}^{\mathrm{2}}]$. This means that Σ_rr is a covariance matrix with the same correlation structure as HΣ_εεH^′ but with variance scaling provided by ${\mathit{\sigma }}_V^{\mathrm{2}}=\mathrm{Var}\left(\mathit{V}\right)$, where V is from Eq. (18) (for DA, Var(V) is just the total variance of V). Also here $\mathbf{H}={\mathit{B}}_{\text{post2}}^{{*}^{\prime }}\otimes {\mathbb{I}}_p$, where B_post2 denotes the values of B for the final posterior in Table 3. In the experiments below, keeping Σ_rr constant simplifies the comparisons.

To understand the experiment results, it is useful to cast data assimilation into observation space:

$$\begin{array}{}\text{(27)}& \begin{array}{rl}{\mathit{y}}^a& =\mathbf{H}{\mathit{x}}^a=\mathbf{HK}{\mathit{y}}^{\mathrm{o}}+({\mathbb{I}}_p-\mathbf{HK})\mathbf{H}{\mathit{x}}^b\\ & ={\displaystyle \frac{\left(\mathbf{H}{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}{\mathbf{H}}^{\prime }\right){\mathit{y}}^{\mathrm{o}}+{\mathrm{\Sigma }}_{rr}{\mathit{y}}^b}{(\mathbf{H}{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}{\mathbf{H}}^{\prime }+{\mathrm{\Sigma }}_{rr})}},\end{array}\end{array}$$

where $\mathbf{K}={\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}{\mathbf{H}}^{\prime }(\mathbf{H}{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}{\mathbf{H}}^{\prime }+{\mathrm{\Sigma }}_{rr}{)}^{-\mathrm{1}}$, and x^b, y^o, and y^b are treated like column vectors (to simplify the syntax). As expected, the analysis y^a is a weighting between the prior $\mathcal{N}({\mathit{y}}^b,\mathbf{H}{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}{\mathbf{H}}^{\prime })$ and some likelihood 𝒩(y^o, Σ_rr).

In both experiments that follow, the value of H in Eq. (27) changes (but not the value of Σ_rr, as defined above). Three different $\mathbf{H}={{\mathit{B}}^{*}}^{\prime }\otimes {\mathbb{I}}_p$ are tested, which are constructed from three values of B^*: ${\mathit{B}}_{\text{ols}}^{*}=[-\mathrm{0.13},\mathrm{0.42}]$, ${\mathit{B}}_{\text{post1}}^{*}=[-\mathrm{0.189},\mathrm{0.635}]$, and ${\mathit{B}}_{\text{post2}}^{*}=[-\mathrm{0.248},\mathrm{0.492}]$ (see Eq. 25 and Table 3). The difference between the two experiments is the value of y^b=Hx^b.

The data assimilation was implemented using a reduced-rank Kalman filter (Elbern et al., 2014) (rank reduction of Σ_εε is only used in Experiment 2). A notebook and code module for the experiments is available (Fischer, 2024). Note in the following subsections that V only refers to eigenvectors (see Table 4) and not the noise from MEPSM.

3.3.1 Experiment 1

In Experiment 1, x^b (and thus y^b) is set to zero. This mimics an offline DA situation where the model prior might be centered (i.e., zero mean) and constant. In addition, a scaling parameter λ is added to the prior, i.e., $\mathcal{N}({\mathit{y}}^b,\mathbf{H}(\mathit{\lambda }{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}\left){\mathbf{H}}^{\prime }\right)$. If the prior covariance is large, then the prior is noninformative, and y^a≈y^o. Here a tighter prior is of interest, so λ is set to λ=0.1. Henceforth Σ_εε refers to a scaled prior covariance matrix, but the λ term is dropped.

.

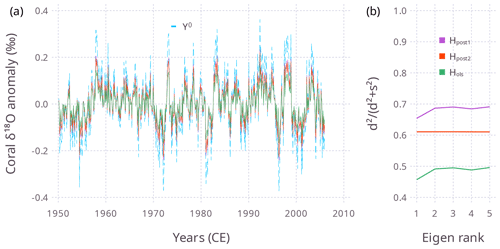
Figure 5 For Experiment 1 ($\mathit{\lambda }=\mathrm{0.1},{\mathit{y}}^b={\mathbf{0}}_p$), (a) the time series Y^a (solid lines, color key as in b) and (b) the eigenvalue shrinkage of the projection matrix (see text), for three different values of H. These experiments used five model grid points, but here Y^a is plotted for the central grid point. In (a) the dashed line is Y^o.

The DA posterior time series Y^a is shown for the three different values of H in Fig. 5a, and the eigenvalue shrinkage (explained below) is shown in Fig. 5b. For λ=0.1, the Y^a resulting from H_ols shows the most shrinkage towards the zero-mean prior (Fig. 5a).

To understand the results from theory, two pieces of information are needed (see Table 4 for notation):

• Λ(ΣC)=Λ(Σ^0.5CΣ^0.5), where Σ and C are real symmetric square matrices.

• HΣ_εεH^′ and Σ_rr have similar eigenvectors (because here Diag(F) is near constant) but different eigenvalues.

Setting y^b to zero removes the Σ_rry^b term in Eq. (27), leaving ${\mathit{y}}^a=\frac{\left(\mathbf{H}{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}{\mathbf{H}}^{\prime }\right)}{(\mathbf{H}{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}{\mathbf{H}}^{\prime }+{\mathrm{\Sigma }}_{rr})}{\mathit{y}}^{\mathrm{o}}$. The eigenvalues of the p×p projection matrix $\frac{\left(\mathbf{H}{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}{\mathbf{H}}^{\prime }\right)}{(\mathbf{H}{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}{\mathbf{H}}^{\prime }+{\mathrm{\Sigma }}_{rr})}$ are of interest here. It follows (from the points above) that the projection matrix has the same eigenvalues as

$$\begin{array}{}\text{(28)}& \begin{array}{rl}& \left(\mathbf{H}{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}{\mathbf{H}}^{\prime }{)}^{\mathrm{0.5}}\right(\mathbf{H}{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}{\mathbf{H}}^{\prime }+{\mathrm{\Sigma }}_{rr}{)}^{-\mathrm{1}}(\mathbf{H}{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}{\mathbf{H}}^{\prime }{)}^{\mathrm{0.5}}\\ & ={\mathbf{VDV}}^{\prime }({\mathbf{VD}}^{\mathrm{2}}{\mathbf{V}}^{\prime }+{\mathbf{VS}}^{\mathrm{2}}{\mathbf{V}}^{\prime }{)}^{-\mathrm{1}}{\mathbf{VDV}}^{\prime }\\ & =\mathbf{VD}({\mathbf{D}}^{\mathrm{2}}+{\mathbf{S}}^{\mathrm{2}}{)}^{-\mathrm{1}}{\mathbf{DV}}^{\prime },\end{array}\end{array}$$

where D² and S² are the eigenvalue matrices of HΣ_εεH^′ and Σ_rr respectively. So in this example, the shrinkage factors of the projection matrix can be expressed as $d_j^{\mathrm{2}}/(d_j^{\mathrm{2}}+s_j^{\mathrm{2}})$. Figure 5b shows that using H_ols shrinks the eigenvalues more than for H from MEPSM. In this introductory experiment, the results have been examined in observation space; the next experiment will consider both x^a and y^a.

3.3.2 Experiment 2

In Experiment 2, model SST and SSS data were obtained for 1950–2005 from the iCESM historical run (which ended in 2005), for x^b. The model data were deseasonalized and filtered using a low-pass (>2-year) filter (so here x^b is a smooth prior, not a zero vector). This setup mimics data assimilation with a transient prior, e.g., offline data assimilation with time windows (windows are a type of prior smoothing). Note, for this experiment, that the model trajectory does not need to strongly match the observed historic trajectory. Further, Σ_εε is not a full rank matrix (the first three eigenvalues span 98% of the total variance), so for Experiment 2 only the first three leading components of Σ_εε are used (which helps to regularize X^a). Figure 6 shows, for λ=0.1, the three time series Y^o, Y^b, and Y^a for each different H (named ${\mathbf{H}}_{\text{ols}},{\mathbf{H}}_{\text{post1}},{\mathbf{H}}_{\text{post2}}$, where the latter two refer to the first and final posterior for MEPSM). Figure 6 shows the advantage of H from MEPSM is that, for example, y^b=H_post1x^b has a greater range and thus allows y^a to better capture the peaks and troughs in y^o than can y^b=H_olsx_b. To further compare the results for the different H, (X^a, Y^a) was calculated for $\mathit{\lambda }=[{\mathrm{10}}^{-\mathrm{2}},\mathrm{\dots },{\mathrm{10}}^{\mathrm{2}}]$ and compared with $({\mathbf{X}}^{*},{\mathit{Y}}^{*})$ using the mean absolute error metric:

$$\begin{array}{}\text{(29)}& \mathrm{mae}({\mathit{Y}}^a,{\mathit{Y}}^{*})=n^{-\mathrm{1}}\sum _{i=\mathrm{1}}^n|y_i^a-y_i^{*}|.\end{array}$$

This was done similarly for $\mathrm{mae}({\mathbf{X}}^a,{\mathbf{X}}^{*})$. Note that $({\mathbf{X}}^{*},{\mathit{Y}}^{*})$, the estimated state from MEPSM, has no direct part in the DA.

Figure 7 shows that for this site, for H_post2 (and H_post1) the analysis ${\mathbf{X}}_{\text{sst}}^a$ and Y^a typically have a smaller mae compared to H_ols. Also, mae decreases as λ increases. For $\mathrm{mae}({\mathit{Y}}^a,{\mathit{Y}}^{*})$, the decrease flattens when y^a≈y^o (for λ>1, Fig. 7b), but note that Y^o is not Y^*. So in this example, it seems that a solution (X^a) better than the likelihood (y^o=Hx^a) cannot be achieved, which means that H from MEPSM wins (lower mae for ${\mathbf{X}}_{\text{sst}}^a$), because H_ols biases ${\mathbf{X}}_{\text{sst}}^a$ (Fig. 7a). For H_ols, there is less bias for ${\mathbf{X}}_{\text{sss}}^a$, perhaps owing to the relative difference between OLS and MEPSM with respect to b₂ (the SSS coefficient). Performing similar data assimilation experiments on global climate proxy datasets will better inform such issues and regional variation.

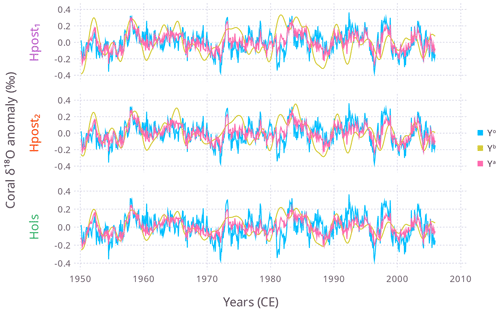
Figure 6 For Experiment 2 ($\mathit{\lambda }=\mathrm{0.1},{\mathit{y}}^b=\mathbf{H}{\mathit{x}}^b$), the time series of Y^o, Y^b, and Y^a (color key right) for three different H (on left axis). As in Fig. 5 Y^a and Y^b refer to the central grid point. In the panels, Y^o is the same, but Y^b and Y^a depend on H. Note how y^a is always between y^b and y^o.

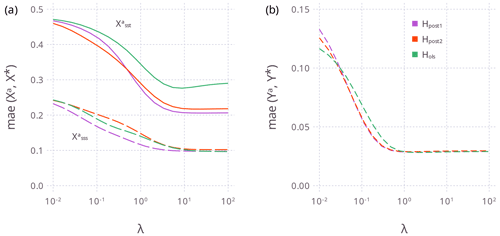
Figure 7 For Experiment 2 (y^b=Hx^b), the mean absolute error for different λ for (a) X^a and (b) Y^a (using the central grid point series) and for the three different H (color key as in b). Panel (a) shows the mae for ${\mathbf{X}}_{\text{sst}}^a$ (solid lines) and ${\mathbf{X}}_{\text{sss}}^a$ (long dashed lines), while panel (b) is the mae for Y^a (see Eq. 29). Small values of λ mean y^a≈y^b, while large λ values mean y^a≈y^o.

4 Conclusions

MEPSM is a new type of proxy system model which incorporates both prior information and generalized noise in all variables, such as cross-correlated noise within the predictor variables. DA theory and two experiments suggest that, in data assimilation, the MEPSM should have an advantage over conventional OLS-calibrated PSMs (the latter are widely employed in current paleo-DA projects). In the work presented here for MEPSM, the response noise is assumed to be independent of the predictor noise (the zero matrices in Σ_Q), but cross-correlation between the predictor and response noise is possible (if needed), by complete quadratic multiplication of Σ_Q, rather than treating Ω_V and Σ_A separately, in Eq. (9). However, for many PSMs the predictor and response noise are fundamentally different and therefore should be independent. The next step is to apply MEPSM to calibrate multiple-input proxy system models for different climate proxies (e.g., isotopes in corals, tree rings, and speleothems) and to incorporate MEPSM into current data assimilation projects.

Appendix A: Basis of Eq. (2)

Let

$$\begin{array}{}\text{(A1)}& y=f(x_{\mathrm{1}}-a_{\mathrm{1}},\mathrm{\dots },x_p-a_p).\end{array}$$

A first-order Taylor expansion gives

$$\begin{array}{}\text{(A2)}& y\approx f(x_{\mathrm{1}},\mathrm{\dots },x_p)-\sum _{k=\mathrm{1}}^p\left[{\displaystyle \frac{\partial f(x_{\mathrm{1}},\mathrm{\dots },x_p)}{\partial x_k}}{a}_k\right]\end{array}$$

such that the variance of f(x) is $\mathrm{Var}\left(f\right(\mathit{x}\left)\right)\approx \mathrm{d}f\left(\mathit{x}{)}^{\prime }{\mathbf{\Sigma }}_{aa}\mathrm{d}f\right(\mathit{x})$. The first-order Taylor expansion will be exact when f(x) is a linear function.

Appendix B: Notation for covariance

Covariance can be given in plain or scaled format, e.g.,

$$\begin{array}{}\text{(B1)}& \mathrm{\Sigma }={\mathit{\sigma }}^{\mathrm{2}}\mathbf{S}.\end{array}$$

So, just as an example, a naive covariance matrix for B could be written as follows:

$$\begin{array}{}\text{(B2)}& {\mathrm{\Sigma }}_B=({\mathbf{X}}^{*\prime }{\mathrm{\Sigma }}^{-\mathrm{1}}{\mathbf{X}}^{*}{)}^{-\mathrm{1}}={\mathit{\sigma }}^{\mathrm{2}}({\mathbf{X}}^{*\prime }{\mathbf{S}}^{-\mathrm{1}}{\mathbf{X}}^{*}{)}^{-\mathrm{1}}.\end{array}$$

In this paper I use the plain format because it simplifies many expressions.

Appendix C: The WTLS likelihood and its mean B_wtls

The target function for WTLS essentially consists of the quadratic component of the log-likelihood function:

$$\begin{array}{}\text{(C1)}& \begin{array}{rl}{\mathit{\varphi }}_{\text{wtls}}\left(\left[\mathit{B},{\mathbf{X}}^{*}\right]\right)& ={\left(\begin{array}{c}\mathrm{vec}\left(\mathbf{Z}\right)-\left[\begin{array}{c}{\mathit{Y}}^{*}\\ \mathrm{vec}\left({\mathbf{X}}^{*}\right)\end{array}\right]\end{array}\right)}^{\prime }\\ & \cdot {\mathrm{\Sigma }}_Q^{-\mathrm{1}}\left(\begin{array}{c}\mathrm{vec}\left(\mathbf{Z}\right)-\left[\begin{array}{c}{\mathit{Y}}^{*}\\ \mathrm{vec}\left({\mathbf{X}}^{*}\right)\end{array}\right]\end{array}\right),\end{array}\end{array}$$

where ${\mathit{Y}}^{*}=\left[\begin{array}{cc}{\mathbf{1}}_n& {\mathbf{X}}^{*}\end{array}\right]\mathit{B}$. For $\partial \mathit{\varphi }/\partial \mathit{B}$, Eq. (C1) reduces to

$$\begin{array}{}\text{(C2a)}& {\displaystyle \frac{\partial {\mathit{\varphi }}_{\text{wtls}}}{\partial \mathit{B}}}& {\displaystyle }={\displaystyle \frac{\partial \left[\right(\mathit{Y}-b_{\mathrm{0}}-{\mathbf{X}}^{*}{\mathit{B}}^{*}{)}^{\prime }{\mathrm{\Omega }}_V^{-\mathrm{1}}(\mathit{Y}-b_{\mathrm{0}}-{\mathbf{X}}^{*}{\mathit{B}}^{*})]}{\partial \mathit{B}}}\text{(C2b)}& {\displaystyle }& {\displaystyle }=\mathrm{2}{\stackrel{\mathrm{̃}}{\mathbf{X}}}^{\prime }{\mathrm{\Omega }}_V^{-\mathrm{1}}\mathit{V},\end{array}$$

where $\stackrel{\mathrm{̃}}{\mathbf{X}}=\left[\begin{array}{cc}{\mathbf{1}}_n& {\mathbf{X}}^{*}\end{array}\right]$. Next substitute V with Eq. (18):

$$\begin{array}{}\text{(C3)}& {\displaystyle \frac{\partial {\mathit{\varphi }}_{\text{wtls}}}{\partial \mathit{B}}}=\mathrm{2}{\stackrel{\mathrm{̃}}{\mathbf{X}}}^{\prime }{\mathbf{W}}^{-\mathrm{1}}\mathit{e}.\end{array}$$

The residual vector e can be written as

$$\begin{array}{}\text{(C4)}& \mathit{e}=(\mathit{Y}-b_{\mathrm{0}}-\mathbf{A}{\mathit{B}}^{*})-{\mathbf{X}}^{*}{\mathit{B}}^{*}\end{array}$$

or

$$\begin{array}{}\text{(C5)}& \mathit{e}=\mathit{Y}-\mathbf{X}\mathit{B}.\end{array}$$

Then setting Eq. (C3) to zero, substituting for e, and rearranging gives

$$\begin{array}{}\text{(C6)}& \begin{array}{rl}{\mathit{B}}_{\text{wtls}}& ={\left[(\mathbf{X}-\mathbf{A}{)}^{\prime }{\mathbf{W}}^{-\mathrm{1}}(\mathbf{X}-\mathbf{A})\right]}^{-\mathrm{1}}\\ & \cdot \left[(\mathbf{X}-\mathbf{A}{)}^{\prime }{\mathbf{W}}^{-\mathrm{1}}(\mathit{Y}-\mathbf{A}\mathit{B})\right]\end{array}\end{array}$$

or

$$\begin{array}{}\text{(C7)}& {\mathit{B}}_{\text{wtls}}={\left[(\mathbf{X}-\mathbf{A}{)}^{\prime }{\mathbf{W}}^{-\mathrm{1}}\mathbf{X}\right]}^{-\mathrm{1}}\left[(\mathbf{X}-\mathbf{A}){\mathbf{W}}^{-\mathrm{1}}\mathit{Y}\right],\end{array}$$

where A now may include a column of zeros (corresponding to noiseless predictors in X).

Equation (C7) expands to

$$\begin{array}{}\text{(C8)}& {\mathit{B}}_{\text{wtls}}={\left[{\mathbf{X}}^{\prime }{\mathbf{W}}^{-\mathrm{1}}\mathbf{X}-{\mathbf{A}}^{\prime }{\mathbf{W}}^{-\mathrm{1}}\mathbf{X}\right]}^{-\mathrm{1}}\left[{\mathbf{X}}^{\prime }{\mathbf{W}}^{-\mathrm{1}}\mathit{Y}-{\mathbf{A}}^{\prime }{\mathbf{W}}^{-\mathrm{1}}\mathit{Y}\right],\end{array}$$

where (${\mathbf{A}}^{\prime }{\mathbf{W}}^{-\mathrm{1}}\mathbf{X}$) is the weighted covariance between A and the predictors, and (${\mathbf{A}}^{\prime }{\mathbf{W}}^{-\mathrm{1}}\mathit{Y}$) is the weighted covariance between A and the response vector. This shows that WTLS can be expressed as an adjusted least squares problem. Hence, it can also be expressed as an augmented linear regression:

$$\begin{array}{}\text{(C9)}& \mathit{Y}-\mathbf{A}\mathit{B}=(\mathbf{X}-\mathbf{A})\mathit{B}+(\mathit{V}-\mathbf{A}\mathit{B}),\end{array}$$

which is equivalent to Eq. (7).

Appendix D: Covariance of B_wtls

One approximation for Σ_B is as follows. Let

$$\begin{array}{}\text{(D1)}& \mathit{B}=\mathbf{K}\mathit{Y}=\mathbf{K}(\mathbf{X}\mathit{B}+\mathit{e}).\end{array}$$

If KX=𝕀, then

$$\begin{array}{}\text{(D2)}& {\mathrm{\Sigma }}_B=\mathbf{K}\mathrm{\Sigma }{\mathbf{K}}^{\prime },\end{array}$$

where $\mathrm{\Sigma }=\mathrm{Diag}(\mathit{e}\otimes \mathit{e})$. For B_wtls, from Eqs. (D1) and (C7) it follows that $\mathbf{K}={\left[(\mathbf{X}-\mathbf{A}{)}^{\prime }{\mathbf{W}}^{-\mathrm{1}}\mathbf{X}\right]}^{-\mathrm{1}}(\mathbf{X}-\mathbf{A}{)}^{\prime }{\mathbf{W}}^{-\mathrm{1}}$.
Therefore,

$$\begin{array}{}\text{(D3)}& {\mathrm{\Sigma }}_B^{\text{wtls}}={\left[(\mathbf{X}-\mathbf{A}{)}^{\prime }{\mathbf{W}}^{-\mathrm{1}}\mathbf{X}\right]}^{-\mathrm{1}}\mathbf{M}{\left[(\mathbf{X}-\mathbf{A}{)}^{\prime }{\mathbf{W}}^{-\mathrm{1}}\mathbf{X}\right]}^{-{\mathrm{1}}^{\prime }},\end{array}$$

where $\mathbf{M}=(\mathbf{X}-\mathbf{A}{)}^{\prime }{\mathbf{W}}^{-\mathrm{1}}\mathrm{\Sigma }{\mathbf{W}}^{-\mathrm{1}}(\mathbf{X}-\mathbf{A})$.

Appendix E: Construction of Σ_A and Ω_V

For two predictors, Σ_A is

$$\begin{array}{}\text{(E1)}& {\mathrm{\Sigma }}_A=\left[\begin{array}{cc}{\mathrm{\Omega }}_{A_{\mathrm{1}}}& {\mathrm{\Omega }}_{A_{\mathrm{1}}{A}_{\mathrm{2}}}\\ {\mathrm{\Omega }}_{A_{\mathrm{2}}{A}_{\mathrm{1}}}& {\mathrm{\Omega }}_{A_{\mathrm{2}}}\end{array}\right].\end{array}$$

Σ_A can be constructed as

$$\begin{array}{}\text{(E2)}& {\mathrm{\Sigma }}_A=\mathrm{Diag}\left({\mathit{\sigma }}_A{)}^{\prime }\left[\begin{array}{cc}{\mathbf{R}}_{A_{\mathrm{1}}}& {\mathbf{R}}_{A_{\mathrm{1}}{A}_{\mathrm{2}}}\\ {\mathbf{R}}_{A_{\mathrm{2}}{A}_{\mathrm{1}}}& {\mathbf{R}}_{A_{\mathrm{2}}}\end{array}\right]\mathrm{Diag}\right({\mathit{\sigma }}_A),\end{array}$$

where Diag(⋅) is a diagonal matrix, and σ_A is a (n⋅p)-length vector containing the heteroscedastic “variance” of the predictor noise for each predictor (stacked vertically). The central block matrix, made up of submatrices R, will be labeled $\stackrel{\mathrm{̃}}{\mathbf{R}}$. The submatrices of $\stackrel{\mathrm{̃}}{\mathbf{R}}$ are n×n correlation matrices, containing the autocorrelation or cross-correlation information for the predictor noise A:

$$\begin{array}{}\text{(E3)}& \mathbf{R}=\left[\begin{array}{cccccc}{\mathit{\rho }}_{\mathrm{0}}& {\mathit{\rho }}_{\mathrm{1}}& {\mathit{\rho }}_{\mathrm{2}}& {\mathit{\rho }}_{\mathrm{3}}& \mathrm{\dots }& {\mathit{\rho }}_{n-\mathrm{1}}\\ {\mathit{\rho }}_{\mathrm{1}}& {\mathit{\rho }}_{\mathrm{0}}& {\mathit{\rho }}_{\mathrm{1}}& {\mathit{\rho }}_{\mathrm{2}}& \mathrm{\dots }& {\mathit{\rho }}_{n-\mathrm{2}}\\ {\mathit{\rho }}_{\mathrm{2}}& {\mathit{\rho }}_{\mathrm{1}}& {\mathit{\rho }}_{\mathrm{0}}& {\mathit{\rho }}_{\mathrm{1}}& \mathrm{\dots }& {\mathit{\rho }}_{n-\mathrm{3}}\\ {\mathit{\rho }}_{\mathrm{3}}& {\mathit{\rho }}_{\mathrm{2}}& {\mathit{\rho }}_{\mathrm{1}}& {\mathit{\rho }}_{\mathrm{0}}& \mathrm{\dots }& {\mathit{\rho }}_{n-\mathrm{3}}\\ \mathrm{⋮}& \mathrm{⋮}& \mathrm{⋮}& \mathrm{⋮}& \mathrm{\ddots }& \mathrm{⋮}\\ {\mathit{\rho }}_{n-\mathrm{1}}& {\mathit{\rho }}_{n-\mathrm{2}}& {\mathit{\rho }}_{n-\mathrm{3}}& {\mathit{\rho }}_{n-\mathrm{4}}& \mathrm{\dots }& {\mathit{\rho }}_{\mathrm{0}}\end{array}\right],\end{array}$$

where $({\mathit{\rho }}_{\mathrm{0}},{\mathit{\rho }}_{\mathrm{1}},\mathrm{\dots },{\mathit{\rho }}_{n-\mathrm{1}})$ is the auto- or cross-correlation function.

If R is an autocorrelation matrix, then ρ₀=1. Also, because the auto- or cross-correlation may become ∼0 at long lags, then ρ_>k may be set to 0, for a chosen lag k. To ensure that $\stackrel{\mathrm{̃}}{\mathbf{R}}$ is positive definite, the algorithm of Rebonato and Jaeckel (1999) is computationally fast.

Ω_V can be similarly constructed:

$$\begin{array}{}\text{(E4)}& {\mathrm{\Omega }}_V=\mathrm{Diag}\left({\mathit{\sigma }}_V{)}^{\prime }{\mathbf{R}}_V\mathrm{Diag}\right({\mathit{\sigma }}_V).\end{array}$$

Appendix F: Maximum likelihood solution of Hannart et al. (2014)

Hannart et al. (2014) defined the log-likelihood of the EIV model as (here written using the notation in this paper, rather than the notation of Hannart et al., 2014)

$$\begin{array}{}\text{(F1)}& \begin{array}{rl}\mathrm{\ell }\left(\left[{\mathit{B}}^{*},{\mathbf{X}}^{*}\right]\right)& =(\mathit{Y}-b_{\mathrm{0}}-{\mathbf{X}}^{*}{\mathit{B}}^{*}{)}^{\prime }{\mathrm{\Omega }}_V^{-\mathrm{1}}(\mathit{Y}-b_{\mathrm{0}}-{\mathbf{X}}^{*}{\mathit{B}}^{*})\\ & +\sum _i({\mathbf{X}}_i-{\mathbf{X}}_i^{*}{)}^{\prime }{\mathrm{\Omega }}_{A_i}^{-\mathrm{1}}({\mathbf{X}}_i-{\mathbf{X}}_i^{*}),\end{array}\end{array}$$

which is a reduced form of Eq. (C1), because the off-diagonal matrices ${\mathrm{\Omega }}_{A_i{A}_j}$ in Σ_A are not included. Hannart et al. (2014) wrote an iterative (fixed-point) solution in terms of X^* and B^*.

$$\begin{array}{}\text{(F2a)}& {\displaystyle }{\mathbf{X}}_i^{*}& {\displaystyle }=({\mathrm{\Omega }}_{A_i}^{-\mathrm{1}}+b_i^{\mathrm{2}}{\mathrm{\Omega }}_V^{-\mathrm{1}}{)}^{-\mathrm{1}}(b_i{\mathrm{\Omega }}_V^{-\mathrm{1}}{\overline{\mathit{y}}}_i+{\mathrm{\Omega }}_{A_i}^{-\mathrm{1}}{\mathbf{X}}_i)\text{(F2b)}& {\displaystyle }{\mathit{B}}^{*}& {\displaystyle }=\left({\mathbf{X}}^{{*}^{\prime }}{\mathrm{\Omega }}_V^{-\mathrm{1}}{\mathbf{X}}^{*}{)}^{-\mathrm{1}}{\mathbf{X}}^{{*}^{\prime }}{\mathrm{\Omega }}_V^{-\mathrm{1}}\right(\mathit{Y}-b_{\mathrm{0}}),\end{array}$$

where here ${\mathit{B}}^{*}=[b_{\mathrm{1}}{b}_{\mathrm{2}}{]}^{\prime }$, and ${\overline{\mathit{y}}}_i=\mathit{Y}-b_{\mathrm{0}}-{\mathbf{X}}_{-i}^{*}{\mathit{B}}_{-i}^{*}$. (I have included the intercept b₀ explicitly.) Confidence intervals for each b_i were calculated from the likelihood profiles (see Sect. 3 in Hannart et al., 2014).

The ML solution I provide here differs from Hannart et al. (2014), but I adopt a similar form (what follows is only for the ML estimate in the first row of Table 3). I express the log-likelihood in Eq. (F1) as a function of V and A:

$$\begin{array}{}\text{(F3)}& \mathrm{\ell }\left(\mathit{B}\right)={\mathit{V}}^{\prime }{\mathrm{\Omega }}_V^{-\mathrm{1}}\mathit{V}+\sum _i{\mathbf{A}}_i{\mathrm{\Omega }}_{A_i}^{-\mathrm{1}}{\mathbf{A}}_i,\end{array}$$

where A and V are calculated using Eqs. (17)–(18). The difference with Hannart et al. (2014) is that the likelihood here is rewritten with respect to $\mathit{e}=\mathit{Y}-\mathbf{X}\mathit{B}$ (through Eqs. 17–18), whereas the procedure of Hannart et al. (2014) is expressed with respect to $\mathit{Y}-{\mathbf{X}}^{*}{\mathit{B}}^{*}$, i.e., the main difference being X or X^*. The point here is merely to provide a basic ML solution in Table 3, in order to compare with the other solutions. Equation (F3) should work with many standard ML packages, because there is no iterative dependence on X^*.

The first row in Table 3 was calculated using Eq. (F3), and the Julia package ProfileLikelihoods.jl (VandenHeuvel, 2022).

Appendix G: MEPSM and paleodata assimilation

This appendix explores the potential advantages of MEPSM for paleodata assimilation (PDA). This is a stand-alone appendix, and notation may differ from the main text. The following notation is used for the data assimilation components:

• x^b is the climate model data, at m grid points.

• y is the proxy data, at p grid points.

• θ is the unobserved state vector, with m grid points.

• H is the operator which converts model space to proxy space.

  Matrix H is p×m. (Note that if a proxy system model has multiple inputs, then H can be formed by concatenation, e.g., H=[H_sst  H_sss] in which case m above becomes 2m.).

Data assimilation can be expressed in GLS format:

$$\begin{array}{}\text{(G1a)}& {\displaystyle }\mathit{y}& {\displaystyle }=\mathbf{H}\mathit{\theta }+\mathit{r}\text{(G1b)}& {\displaystyle }{\mathit{x}}^b& {\displaystyle }=\mathit{\theta }+\mathit{\epsilon },\end{array}$$

where $\mathit{r}\sim \mathcal{N}(\mathbf{0},{\mathrm{\Sigma }}_{rr})$ and $\mathit{\epsilon }\sim \mathcal{N}(\mathbf{0},{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }})$. In the typical offline PDA, Σ_εε is an m×m background covariance matrix. In MEPSM, the predictor noise matrix is Σ_A. Out of interest, a time-constant noise matrix could be specified as ${\mathrm{\Sigma }}_A={\mathbf{\Sigma }}_{aa}\otimes {\mathbb{I}}_n$. Note the difference between Σ_εε and Σ_aa: Σ_εε is estimated from climate model ensembles, whereas Σ_aa is from ensemble climate data reconstructions (e.g., an ensemble SST product). Also, PDA is about estimating θ, whereas MEPSM is about calibrating H (in MEPSM B contains the non-zero elements of H). Note that H is typically calibrated using observed modern climate data and proxies, over a coeval period (e.g., the 20th century). I will say more about H below.

Next concatenate the two equations above into one:

$$\begin{array}{}\text{(G2)}& \mathit{z}=\left[\begin{array}{c}\mathit{y}\\ {\mathit{x}}^b\end{array}\right]=\stackrel{\mathrm{̃}}{\mathbf{H}}\mathit{\theta }+\mathit{q},\end{array}$$

where $\stackrel{\mathrm{̃}}{\mathbf{H}}=\left[\begin{array}{c}\mathbf{H}\\ {\mathbb{I}}_m\end{array}\right]$, and let ${\mathrm{\Sigma }}_{qq}=\left[\begin{array}{cc}{\mathrm{\Sigma }}_{rr}& \mathrm{0}\\ \mathrm{0}& {\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}\end{array}\right]$. The GLS solution for θ is

$$\begin{array}{}\text{(G3)}& \begin{array}{rl}{\mathit{\theta }}^a& ={\left({\stackrel{\mathrm{̃}}{\mathbf{H}}}^{\prime }{\mathrm{\Sigma }}_{qq}^{-\mathrm{1}}\stackrel{\mathrm{̃}}{\mathbf{H}}\right)}^{-\mathrm{1}}{\stackrel{\mathrm{̃}}{\mathbf{H}}}^{\prime }{\mathrm{\Sigma }}_{qq}^{-\mathrm{1}}\mathit{z}\\ & ={\left({\mathbf{H}}^{\prime }{\mathrm{\Sigma }}_{rr}^{-\mathrm{1}}\mathbf{H}+{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}^{-\mathrm{1}}\right)}^{-\mathrm{1}}\left({\mathbf{H}}^{\prime }{\mathrm{\Sigma }}_{rr}^{-\mathrm{1}}\mathit{y}+{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}^{-\mathrm{1}}{\mathit{x}}^b\right).\end{array}\end{array}$$

For the analysis error covariance Σ^a, it is

$$\begin{array}{}\text{(G4)}& {\mathrm{\Sigma }}^a={\left({\mathbf{H}}^{\prime }{\mathrm{\Sigma }}_{rr}^{-\mathrm{1}}\mathbf{H}+{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}^{-\mathrm{1}}\right)}^{-\mathrm{1}}.\end{array}$$

Equation (G4) can also be expanded as

$$\begin{array}{}\text{(G5)}& \begin{array}{rl}{\mathrm{\Sigma }}^a& ={\mathrm{\Sigma }}^a({\mathrm{\Sigma }}^a{)}^{-\mathrm{1}}{\mathrm{\Sigma }}^a={\mathrm{\Sigma }}^a\left({\mathbf{H}}^{\prime }{\mathrm{\Sigma }}_{rr}^{-\mathrm{1}}\mathbf{H}+{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}^{-\mathrm{1}}\right){\mathrm{\Sigma }}^a\\ & =\mathbf{K}{\mathrm{\Sigma }}_{rr}{\mathbf{K}}^{\prime }+{\mathrm{\Sigma }}^a{\mathrm{\Sigma }}_{\mathit{\epsilon }\mathit{\epsilon }}^{-\mathrm{1}}{\mathrm{\Sigma }}^a,\end{array}\end{array}$$

where $\mathbf{K}={\mathrm{\Sigma }}^a{\mathbf{H}}^{\prime }{\mathrm{\Sigma }}_{rr}^{-\mathrm{1}}$. The question here is what happens if H is calibrated using a biased method (e.g., OLS). Equation (G4) suggests that Σ^a will also be biased. Ensemble filtering methods are used for their computational advantage: replacing a large m×m Σ_εε with a smaller ensemble of model x^b vectors. But the model x^b vectors are filtered in a way that ensures the resulting ensemble of δθ^a (i.e., deviation from ${\overline{\mathit{\theta }}}^a$) agrees with Eq. (G5). So ensemble filtering methods do not help if H is biased. Equation (G1) shows that the operator H is applied to the unobserved state θ, not to the “observed” x^b, so using OLS for calibrating H seems flawed. OLS calibrates a PSM on observed (but not true) data, whereas MEPSM calibrates a PSM on the unobserved state x^*.