Simple process-led algorithms for simulating habitats (SPLASH v.2.0): robust calculations of water and energy fluxes

The current representation of key processes in land surface models (LSMs) for estimating water and energy balances still relies heavily on empirical equations that require calibration oriented to site-specific characteristics. When multiple parameters are used, different combinations of parameter values can produce equally acceptable results, leading to a risk of obtaining “the right answers for the wrong reasons”, compromising the reproducibility of the simulations and limiting the ecological interpretability of the results. To address this problem and reduce the need for free parameters, here we present novel formulations based on first principles to calculate key components of water and energy balances, extending the already parsimonious SPLASH model v.1.0 (Davis et al., 2017, GMD). We found analytical solutions for many processes, enabling us to increase spatial resolution and include the terrain effects directly in the calculations without unreasonably inflating computational demands. This calibration-free model estimates quantities such as net radiation, evapotranspiration, condensation, soil water content, surface runoff, subsurface lateral flow, and snow-water equivalent. These quantities are derived from readily available meteorological data such as near-surface air temperature, precipitation, and solar radiation, as well as soil physical properties. Whenever empirical formulations were required, e.g., pedotransfer functions and albedo–snow cover relationships, we selected and optimized the best-performing equations through a combination of remote sensing and globally distributed terrestrial observational datasets. Simulations at global scales at different resolutions were run to evaluate spatial patterns, while simulations with point-based observations were run to evaluate seasonal patterns using data from hundreds of stations and comparisons with the VIC-3L model, demonstrating improved performance based on statistical tests and observational comparisons. In summary, our model offers a more robust, reproducible, and ecologically interpretable solution compared to more complex LSMs.

1 Introduction

Robust representations of water and energy fluxes provide essential foundations for the analysis of interactions and feedbacks within the soil, atmosphere, and vegetation continuum in complex land surface models (LSMs) (Wang et al., 2014; Prentice et al., 2015). These fluxes are greatly shaped by complex topography, which determines the amount of solar energy received at the surface, and by gradients of atmospheric pressure, temperature, and moisture, soil development, and gravitational potential energy, which together control vegetation dynamics and the emergent spatial patterns of ecosystem composition and structure (Tromp-van Meerveld and McDonnell, 2006; Körner, 2021; Sarmiento, 1986). Current models represent the complexity of topographic effects in various simplified ways, for example through discretization of the spatial continuum into hydrological response units (Grayson and Blöschl, 2000; Rodell et al., 2004) or predefined biomes (Liang et al., 1996) or stochastic representation of terrain and land cover at subgrid scales (Lawrence et al., 2019; Liang and Xie, 2001). Or, alternatively, models designed for large-scale applications may simply disregard terrain effects (Davis et al., 2017). This approach has arisen because models typically divide the soil–vegetation–atmosphere column into layers, or small storages, resulting in a large computational demand. So, to run models at higher resolution would increase the required computing power exponentially (Clark et al., 2017).

Although the higher precision of numerical schemes increases the accuracy of the models, the representation of some core hydrological processes still relies on empirical equations that require site-specific calibration (Clark et al., 2017). One outcome of this process is that different combinations of parameter values can produce equally acceptable results, implying a risk of obtaining “the right answers for the wrong reasons” (Grayson and Blöschl, 2000; Prentice et al., 2015), compromising the reproducibility of simulations and limiting the ecological interpretability of the results obtained.

The use of optimization algorithms for multiple parameters in ever more complex models may not necessarily improve matters and, indeed, may hide the inadequacy of concepts such as “field capacity” and “permanent wilting point” when representing one of the most important ecological quantities, the soil water availability to plants. Although these constructs make sense conceptually, they can be misleading. For example, field capacity is described as the remaining water in the soil after drainage has ceased (Kramer and Boyer, 1995; Veihmeyer and Hendrickson, 1931). Still, its value is found in laboratory tests using small soil cores, and it is arbitrarily assumed to be equivalent to the water left after applying 33 kPa of suction (or 10 kPa in sandy soils). The permanent wilting point by definition depends on the plant as well as soil properties. Nonetheless, it is assumed by convention to be equivalent to the water left after applying 1.5 MPa of suction (Kirkham, 2005). Such values are upscaled globally using pedotransfer functions (PTFs), assuming they represent conditions found in nature, but their validity is virtually impossible to test using current LSMs.

The SPLASH model (Davis et al., 2017) is a highly parsimonious, multi-purpose set of algorithms mainly designed for ecohydrological and bioclimatic analysis (see, e.g., Harrison et al., 2010; Gallego-Sala and Prentice, 2012; Ukkola et al., 2015). Even though the original SPLASH assumes a flat cell, neglecting terrain influence on the fluxes, it includes explicit effects of elevation on biophysical quantities with minimum meteorological inputs. At its core, it conceptualizes the daily cycles of water and energy fluxes, and it solves their respective budgets using analytical integrals at a daily time step (Cramer and Prentice, 1988; Davis et al., 2017). We propose new formulations to extend the original SPLASH using theory and concepts based on first principles, thus minimizing the need for free parameters while allowing the representation of processes in complex terrain.

To improve the calculations of the energy fluxes we adapted SPLASH v1.0 mathematical framework to use shortwave radiation as input instead of cloudiness as a proxy for it. Furthermore, we included terrain (slope and aspect) effects on the analytical integrals of the daily energy fluxes and updated the empirical functions used to estimate net longwave radiation.

Since one of the main applications of SPLASH is to infer the water limitation on photosynthesis (Wang et al., 2014; Stocker et al., 2018), we no longer consider the available plant water capacity to be a constant value and added the calculation of subsurface flows. Here, we enhanced SPLASH with an analytical solution for the Green–Ampt equation to calculate daily infiltration, including corrections for slope effects, and analytical solutions for lateral flow, water viscosity effects on hydraulic conductivity, and Dunne and/or Hortonian runoff generation. To upgrade the “bucket model” used in the estimation of soil water content in SPLASH we have included soil hydrophysical properties estimated by PTFs and proposed a theoretical field capacity found by equilibrating gravity with capillarity force. This new version of SPLASH also includes an analytical solution to estimate soil moisture at any depth and a simple snowpack module, which accounts for snowfall occurrence, snow mass balance, and effects on albedo. Processes that still require empirical formulations in the model (i.e., snowfall occurrence, snow albedo feedback, and the effect of soil physical properties on the water retention curve) were optimized using “big data” from remote sensing and in situ measurements.

Some simplifications were adopted in order to allow analytical solutions based on the prevalence of shallow soils and impervious bedrock in mountain regions around the world.

1. The drop of the saturated hydraulic conductivity with depth is neglected.

2. Soil moisture redistribution through the soil profile (down to 2 m) takes no longer than 1 d.

3. Water fluxes in the soil column are in a steady state.

4. The shape of the moisture profile follows Hilberts et al. (2005) and Fan et al. (2007).

5. The snow temperature is 0 °C, so implicitly the energy required to raise the snow temperature is neglected.

The proposed analytical solutions greatly reduce the computational demand compared to numerical schemes, enabling the model to perform calculations using global high-resolution datasets at daily or monthly time steps and to provide emergent spatial patterns of key model outputs such as net radiation, snowpack size, lateral flow, surface runoff, condensation, evapotranspiration, and soil water content.

The inputs of the model are precipitation, solar radiation, and air temperature. To derive terrain information (slope, aspect, and upslope contributing area) the algorithm requires a digital elevation model (DEM) when the grid functionality is used, but, if used with site-specific data (i.e., station data), these variables should be computed beforehand. To estimate some soil hydrophysical properties, the algorithm also requires soil texture, organic matter content, and thickness.

2 Methods: model description

2.1 Energy fluxes

2.1.1 Surface solar radiation

The original formulation for extraterrestrial solar radiation flux I₀ (W m⁻²) from SPLASH (Davis et al., 2017) is defined as

$$\begin{array}{}\text{(1)}& I_{\mathrm{0}}=I_{\mathrm{SC}}{d}_r\cos {\mathit{\theta }}_z,\end{array}$$

where I_SC is the solar constant (W m⁻²), d_r (unitless) is the distance factor, and cos θ_z is inclination factor. The effects of the slope inclination and orientation on the surface solar radiation were included by using a more complex formulation of cos  θ_z, parameterized after Allen et al. (2006) as follows.

$$\begin{array}{ll}{\displaystyle }\cos \left({\mathit{\theta }}_z\right)& {\displaystyle }=\sin \left(\mathit{\delta }\right)\sin \left(\mathit{\varphi }\right)\cos \left(s\right)\\ {\displaystyle }& {\displaystyle }-\sin \left(\mathit{\delta }\right)\cos \left(\mathit{\varphi }\right)\sin \left(s\right)\cos \left(\mathit{\gamma }\right)\\ {\displaystyle }& {\displaystyle }+\cos \left(\mathit{\delta }\right)\cos \left(\mathit{\varphi }\right)\cos \left(s\right)\cos \left(h\right)\\ {\displaystyle }& {\displaystyle }+\cos \left(\mathit{\delta }\right)\sin \left(\mathit{\varphi }\right)\sin \left(s\right)\cos \left(\mathit{\gamma }\right)\cos \left(h\right)\\ \text{(2)}& {\displaystyle }& {\displaystyle }+\cos \left(\mathit{\delta }\right)\sin \left(\mathit{\gamma }\right)\sin \left(s\right)\sin \left(h\right)\end{array}$$

Here, δ (rad) is the declination angle between Earth's Equator and the sun at solar noon and describes the seasonal changes at different latitude ϕ (rad); the hour angle h (rad) describes the sun's position above the horizon, s (rad) is the slope inclination, and γ (rad) is the slope orientation, or aspect, being γ=0 for slopes oriented due south with its values increasing clockwise.

The hour angle when the solar radiation flux reaches the horizon or sunset hour h_s was found by replacing Eq. (2) in Eq. (1), setting I_o=0, and solving for h.

$$\begin{array}{}\text{(3)}& h_{\mathrm{s}}=\arccos \left(-{\displaystyle \frac{\begin{array}{c}\sin \left(\mathit{\delta }\right)\sin \left(\mathit{\varphi }\right)\cos \left(s\right)-\sin \left(\mathit{\delta }\right)\cos \left(\mathit{\varphi }\right)\sin \left(s\right)\cos \left(\mathit{\gamma }\right)\\ +\cos \left(\mathit{\delta }\right)\sin \left(\mathit{\gamma }\right)\sin \left(s\right)\sin \left(h_{\mathrm{s}}\right)\end{array}}{\cos \left(\mathit{\delta }\right)\cos \left(\mathit{\varphi }\right)\cos \left(s\right)+\cos \left(\mathit{\delta }\right)\sin \left(\mathit{\varphi }\right)\sin \left(s\right)\cos \left(\mathit{\gamma }\right)}}\right)\end{array}$$

Furthermore, to simplify the notation, Eq. (3) can be rewritten as

$$\begin{array}{}\text{(4)}& h_{\mathrm{s}}=\arccos \left(-{\displaystyle \frac{r_u}{r_v}}\right),\end{array}$$

where $r_u=\sin \left(\mathit{\delta }\right)\sin \left(\mathit{\varphi }\right)\cos \left(s\right)-\sin \left(\mathit{\delta }\right)\cos \left(\mathit{\varphi }\right)\sin \left(s\right)\cos \left(\mathit{\gamma }\right)+\cos \left(\mathit{\delta }\right)\sin \left(\mathit{\gamma }\right)\sin \left(s\right)\sin \left(h_{\mathrm{s}}\right)$ and $r_v=\cos \left(\mathit{\delta }\right)\cos \left(\mathit{\varphi }\right)\cos \left(s\right)+\cos \left(\mathit{\delta }\right)\sin \left(\mathit{\varphi }\right)\sin \left(s\right)\cos \left(\mathit{\gamma }\right)$. To account for the occurrences of polar days (i.e., no sunset) or polar nights (i.e., no sunrise), h_s is set to π when $r_u/r_v\ge \mathrm{1}$ and to zero when $r_u/r_v\le -\mathrm{1}$, respectively. Here, to approximate the value of sin (h_s), the analytical solution proposed by Allen et al. (2006) is used as follows:

$$\begin{array}{}\text{(5)}& \sin \left(h_{\mathrm{s}}\right)={\displaystyle \frac{ac+b\sqrt{b^{\mathrm{2}}+c^{\mathrm{2}}-a^{\mathrm{2}}}}{b^{\mathrm{2}}+c\mathrm{2}}},\end{array}$$

where

$$\begin{array}{}\text{(6a)}& {\displaystyle }a=\sin \left(\mathit{\delta }\right)\cos \left(\mathit{\varphi }\right)\sin \left(s\right)\cos \left(\mathit{\gamma }\right)-\sin \left(\mathit{\delta }\right)\sin \left(\mathit{\varphi }\right)\cos \left(s\right),\text{(6b)}& {\displaystyle }b=\cos \left(\mathit{\delta }\right)\cos \left(\mathit{\varphi }\right)\cos \left(s\right)+\cos \left(\mathit{\delta }\right)\sin \left(\mathit{\varphi }\right)\sin \left(s\right)\cos \left(\mathit{\gamma }\right),\text{(6c)}& {\displaystyle }c=\cos \left(\mathit{\delta }\right)\sin \left(\mathit{\gamma }\right)\sin \left(s\right).\end{array}$$

Note that if we evaluate Eq. (3) for flat surfaces (s=0), it becomes $h_{\mathrm{s}}=\arccos \left(-\frac{\sin \left(\mathit{\delta }\right)\sin \left(\mathit{\varphi }\right)}{\cos \left(\mathit{\delta }\right)\cos \left(\mathit{\varphi }\right)}\right)$, which is the original SPLASH equation described by Davis et al. (2017).

The daily accumulated incoming radiation (MJ m⁻² d⁻¹) is calculated as twice the integral of Eq. (1), with cos (θ_z(h)) ranging from solar noon (h=0) to sunset (h=h_s), times the atmosphere's transmittance τ (unitless).

$$\begin{array}{}\text{(7)}& \begin{array}{rl}H& =\mathrm{2}\underset{\mathrm{0}}{\overset{h_{\mathrm{s}}}{\int }}\mathit{\tau }{I}_{\mathrm{0}}=\mathrm{2}\underset{\mathrm{0}}{\overset{h_{\mathrm{s}}}{\int }}\mathit{\tau }{I}_{\mathrm{SC}}{d}_r\cos {\mathit{\theta }}_z\mathrm{d}h\\ & ={\displaystyle \frac{\mathrm{86}\mathrm{400}}{\mathit{\pi }}}\mathit{\tau }{I}_{\mathrm{SC}}{d}_r(r_u{h}_s+r_v\sin (h_{\mathrm{s}}\left)\right)\end{array}\end{array}$$

To exploit datasets of daily average incoming shortwave radiation (SW) (W m⁻²) and phase out the empirical parameters in the previous model version, which uses the classic Ångström–Prescott formula and cloudiness data, we set H=SW (W m⁻²) ×86 400 (s d⁻¹) in Eq. (7). Then multiplying both sides of Eq. (7) by (1−β_SW), we solve for τ I_SC d_r (1−β_SW) to match the original formulation of the variable r_w (W m⁻²) as follows:

$$\begin{array}{}\text{(8)}& r_w=\mathit{\tau }{I}_{\mathrm{SC}}{d}_r(\mathrm{1}-{\mathit{\beta }}_{\mathrm{SW}})={\displaystyle \frac{\mathrm{SW}\mathit{\pi }(\mathrm{1}-{\mathit{\beta }}_{\mathrm{SW}})}{r_u{h}_s+r_v\sin \left(h_{\mathrm{s}}\right)}},\end{array}$$

where β_SW is the albedo and the other variables are previously defined.

2.1.2 Net surface radiation

The net radiation flux at the surface, I_N (W m⁻²), is defined as the difference between the net shortwave radiation flux, I_SW (W m⁻²), and the net longwave radiation flux, I_LW (W m⁻²),

$$\begin{array}{}\text{(9)}& I_{\mathrm{N}}=I_{\mathrm{SW}}-I_{\mathrm{LW}},\end{array}$$

where I_SW is computed simply as the fraction of the incoming shortwave radiation flux not reflected by the albedo, β_SW (unitless):

$$\begin{array}{}\text{(10)}& I_{\mathrm{SW}}=\mathrm{SW}(\mathrm{1}-{\mathit{\beta }}_{\mathrm{SW}}).\end{array}$$

I_LW is computed in a similar fashion as the original SPLASH by merging empirical formulations for clear and cloudy skies, both fitted using eddy covariance data from the whole FLUXNET database, thus replacing the old empirical formulations from Monteith and Unsworth (1990) and Linacre (1968) used in the first version.

$$\begin{array}{}\text{(11)}& I_{\mathrm{LW}}=(k_{\mathrm{4}}+(\mathrm{1.0}-k_{\mathrm{3}}\left)S_{\mathrm{f}}\right)(k_{\mathrm{1}}+k_{\mathrm{2}}{T}_{\mathrm{air}}),\end{array}$$

Here, k₁₋₄ represents empirical coefficients, T_air (°C) is the daily mean near-surface air temperature, and S_f (unitless) is the sunshine fraction, derived from a general form of the Ångström–Prescott equation, with parameters fitted from global databases according to Suehrcke et al. (2013).

$$\begin{array}{}\text{(12)}& s_{\mathrm{f}}={\left({\displaystyle \frac{\mathit{\tau }-{\mathit{\tau }}_o{k}_{\mathrm{5}}}{{\mathit{\tau }}_o(\mathrm{1}-k_{\mathrm{5}})}}\right)}^{\left(\mathrm{1}/k_{\mathrm{6}}\right)},\end{array}$$

Here, k₅ and k₆ represent empirical coefficients, τ is the atmosphere's transmittance, calculated as the ratio between TOA solar radiation and surface SW data, and τ_o is the clear-sky atmospheric transmittance, computed following Allen (1996). Values for the coefficients are provided in the Table 1.

Kopp and Lean (2011)Federer (1968)Wang and Zeng (2010); Barry (1996)Linacre (1968)Suehrcke et al. (2013)Suehrcke et al. (2013)Monteith and Unsworth (1990)Monteith and Unsworth (1990)

Table 1 Constants and standard values.

The daily accumulated net radiation, H_N (MJ m⁻² d⁻¹), is calculated as net positive $H_{\mathrm{N}}^{+}$ (daytime approximately) and net negative $H_{\mathrm{N}}^{-}$ (nighttime approximately), and the threshold between $H_{\mathrm{N}}^{+}$ and $H_{\mathrm{N}}^{-}$ is the hour angle when I_SW equals I_LW (h_n) (Fig. 1). It is found by setting I_N=0 in Eq. (9) as follows:

$$\begin{array}{}\text{(13)}& h_{\mathrm{n}}=\arccos \left({\displaystyle \frac{I_{\mathrm{LW}}-r_w{r}_u}{r_w{r}_v}}\right).\end{array}$$

For cases where the net radiation is always positive ($(I_{\mathrm{LW}}-r_w{r}_u)/\left(r_w{r}_v\right)\ge -\mathrm{1}$) h_n is limited to π, while for the opposite cases, where the net radiation is always negative ($(I_{\mathrm{LW}}-r_w{r}_u)/\left(r_w{r}_v\right)\ge \mathrm{1}$), h_n is limited to zero.

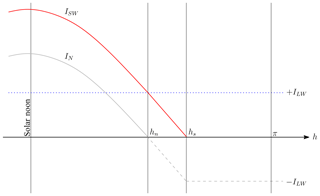
Figure 1 Conceptualization of the net radiation flux between solar noon (i.e., h=0) and solar midnight (i.e., h=π) after Davis et al. (2017).

Therefore, as described by Davis et al. (2017), $H_{\mathrm{N}}^{+}$ is defined as twice the integral of I_N from solar noon to the flux cross-over hour angle h_n (Eq. 14), while $H_{\mathrm{N}}^{-}$ is calculated as twice the integral of I_N between h_n and solar midnight (h=π) (Eq. 15).

$$\begin{array}{}\text{(14)}& {\displaystyle }{H}_{\mathrm{N}}^{+}=\mathrm{2}\underset{h=\mathrm{0}}{\overset{h_{\mathrm{n}}}{\int }}{I}_{\mathrm{N}}={\displaystyle \frac{\mathrm{86}\mathrm{400}}{\mathit{\pi }}}\left((r_w{r}_u-I_{\mathrm{LW}})h_{\mathrm{n}}+r_w{r}_v\sin \left(h_{\mathrm{n}}\right)\right)\text{(15)}& {\displaystyle }\begin{array}{rl}{H}_{\mathrm{N}}^{-}& =\mathrm{2}\left(\underset{h_{\mathrm{n}}}{\overset{h_{\mathrm{s}}}{\int }}{I}_{\mathrm{N}}-\underset{h_{\mathrm{s}}}{\overset{\mathit{\pi }}{\int }}{I}_{\mathrm{LW}}\right)\\ & ={\displaystyle \frac{\mathrm{86}\mathrm{400}}{\mathit{\pi }}}\left[r_w{r}_v\left(\sin \right(h_{\mathrm{s}})-\sin (h_{\mathrm{n}}\left)\right)+r_w{r}_u(h_{\mathrm{s}}-h_{\mathrm{n}})\right.\\ & \left.-I_{\mathrm{LW}}(\mathit{\pi }-h_{\mathrm{n}})\right]\end{array}\end{array}$$

2.2 Water fluxes and storages

2.2.1 Snowfall

The freezing temperature of the water, 0.0 °C, is the usual threshold to categorize rainfall as snowfall in several models (Pomeroy and Brun, 2001); however, other atmospheric variables like cloudiness, atmospheric pressure, and relative humidity define the snowfall formation (Jennings et al., 2018), therefore changing this temperature threshold in a narrow range across locations (Kienzle, 2008). Here, to get the rainfall–snowfall proportion it is usual to find, among different methods in the literature, linear approximations based on air temperature (Harder and Pomeroy, 2014; Marks et al., 1999; Orth and Seneviratne, 2015) or simply 100 % of the precipitation falling below 0.0 °C assigned as snowfall (Bergström, 1995; Dirmeyer et al., 2006), which might lead to miscalculations in some regions like the Alps, where up to 80 % of its annual precipitation might be in the form of snowfall (Barry, 2008).

Therefore, in the current version of the model a sigmoid curve is used to describe the rain–snow proportion (f_rain) following Kienzle (2008), who fit empirical equations using 64 years of measurements of rainfall–snowfall proportions from 113 Canadian stations as follows:

$$\begin{array}{}\text{(16)}& \begin{array}{rl}{f}_{\mathrm{rain}}& =\mathrm{5}{\left({\displaystyle \frac{T_{\mathrm{air}}-T_{\mathrm{tm}}}{\mathrm{1.4}{T}_{\mathrm{rm}}}}\right)}^{\mathrm{3}}+\mathrm{6.76}{\left({\displaystyle \frac{T_{\mathrm{air}}-T_{\mathrm{tm}}}{\mathrm{1.4}{T}_{\mathrm{rm}}}}\right)}^{\mathrm{2}}\\ & +\mathrm{3.19}\left({\displaystyle \frac{T_{\mathrm{air}}-T_{\mathrm{tm}}}{\mathrm{1.4}{T}_{\mathrm{rm}}}}\right)+\mathrm{0.5},\end{array}\end{array}$$

where T_tm (°C) is the monthly temperature threshold for the 50 % of rain–snow occurrence, and T_rm (°C) is the monthly range of temperatures for snowfall occurrence, both calculated according to Eqs. (17) and (18).

$$\begin{array}{}\text{(17)}& {\displaystyle }{T}_{\mathrm{tm}}=T_t+T_t\sin \left({\displaystyle \frac{m_{\mathrm{i}}+\mathrm{2}}{\mathrm{1.91}}}\right)\text{(18)}& {\displaystyle }{T}_{\mathrm{rm}}=T_r\left(\mathrm{0.55}+\sin (m_{\mathrm{i}}+\mathrm{4})\right)\times \mathrm{0.6}\end{array}$$

Here, m_i is a monthly index (from 1 to 12), and T_r (°C) is the annual range of temperatures for snowfall occurrence, found to be 13 °C as a first approximation by Kienzle (2008). T_t (°C) is the annual threshold for snowfall formation, defined for each year as the annual maximum air temperature when the probability of snowfall occurrence p(snow) equals or exceeds 0.5.

p(snow) was estimated using a binary logistic regression, following the method and datasets provided by Jennings et al. (2018), but reducing the number of explanatory variables to air temperature T_air (°C), elevation z (m a.s.l.), and latitude ϕ (°) as follows (Appendix A4.4):

$$\begin{array}{}\text{(19)}& p\left(\mathrm{snow}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{1}+e^{\left(k_{\mathrm{7}}+k_{\mathrm{8}}{T}_{\mathrm{air}}+k_{\mathrm{9}}z+k_{\mathrm{10}}\mathit{\varphi }\right)}}},\end{array}$$

where $k_{\mathrm{7}},k_{\mathrm{8}},k_{\mathrm{9}}$, and k₁₀ are coefficients (Table 1). Then, the snowfall is calculated by

$$\begin{array}{}\text{(20)}& \mathrm{Sf}=P_n(\mathrm{1}-f_{\mathrm{rain}}).\end{array}$$

2.2.2 Snowmelt

Snowmelt (Sm) (mm d⁻¹) was calculated using a simple relationship between available energy and the size of the snowpack SWE (mm) (snow-water equivalent) as follows:

$$\begin{array}{}\text{(21)}& \mathrm{Sm}=min\left(\mathrm{SWE},{\displaystyle \frac{H_{\mathrm{N}}^{+}}{{\mathit{\rho }}_{\mathrm{w}}{L}_{\mathrm{f}}}}\times \mathrm{1000}\right),\end{array}$$

where SWE is the size of the snowpack expressed as snow-water equivalent (mm), $H_{\mathrm{N}}^{+}$ (MJ m⁻² d⁻¹) is the daytime accumulated net radiation, ρ_w (kg m⁻³) is the water density at 0 °C, L_f (J kg⁻¹) is the latent heat of fusion, and 1000 is the factor to convert m³ to liters. Following Barry (2008), we assumed direct sublimation to be negligible; however, if there is residual energy after the melting occurs, we directed that energy to evaporate Sm, with the flux hereafter denoted simply as “sublimation” (E^swe), which reduces the amount of Sm reaching the soil or producing runoff:

$$\begin{array}{}\text{(22)}& E^{\mathrm{swe}}=min\left(S_m,{\displaystyle \frac{H_{\mathrm{A}}^{+}}{E_{\mathrm{con}}}}\times \mathrm{1000}\right),\end{array}$$

where $H_{\mathrm{A}}^{+}$ (MJ m⁻² d⁻¹) is the daytime available energy (daytime accumulated net radiation – energy used in melting), E_con (m³ J⁻¹) is the energy-to-water equivalent conversion factor (Davis et al., 2017), and 1000 is the factor to convert m³ to liters. Thus, the water from snowmelt reaching the soil is

$$\begin{array}{}\text{(23)}& {\mathrm{Sm}}_e=\mathrm{Sm}-E^{\mathrm{swe}}.\end{array}$$

2.2.3 Snowpack

The size of the snowpack, expressed as snow-water equivalent SWE (mm), is computed as a simple balance using the previous-day SWE, inputs, and outputs as follows:

$$\begin{array}{}\text{(24)}& {\mathrm{SWE}}_n={\mathrm{SWE}}_{n-\mathrm{1}}+\mathrm{Sf}-\mathrm{Sm}.\end{array}$$

The effect of the snow on the albedo was formulated as a simple weighted average using the snow cover fraction, following Wang and Zeng (2010), Roesch and Roeckner (2006), and Niu and Yang (2007),

$$\begin{array}{}\text{(25)}& {\mathit{\beta }}_{\mathrm{sw}}={\mathit{\beta }}_o\times (\mathrm{1.0}-f_{\mathrm{snw}})+(f_{\mathrm{snw}}\times {\mathit{\beta }}_{\mathrm{snw}}),\end{array}$$

where β_o the is background albedo (Federer, 1968), and β_snw is the snow albedo, calculated according to the age of the snow, following the widely used formulation from the US Army Corps of Engineers (1956).

$$\begin{array}{}\text{(26)}& {\mathit{\beta }}_{\mathrm{snw}}=({\mathit{\beta }}_o^{\mathrm{snw}}-k_{\mathrm{11}})+k_{\mathrm{11}}{e}^{-k_{\mathrm{12}}{n}_{\mathrm{d}}}\end{array}$$

Here ${\mathit{\beta }}_o^{\mathrm{snw}}$ is the albedo of the new-fallen snow, n_d is the number of days since a snowfall event greater than 3 mm (Chen et al., 2014), and k₁₁ and k₁₂ are empirical constants. The snow cover fraction (f_snw) from Eq. (25) was estimated using a simple hyperbolic function following Dickinson et al. (1986) and Barry (1996).

$$\begin{array}{}\text{(27)}& f_{\mathrm{snw}}={\displaystyle \frac{{\mathrm{SWE}}_n}{{\mathrm{SWE}}_c+{\mathrm{SWE}}_n}}\end{array}$$

Here, SWE_c is the snow-water equivalent where f_snw starts to saturate.

The optimized parameters of Eqs. (26) and (27) using remote sensing and ground observations are listed in Table 1.

2.2.4 Infiltration

The infiltration flux rate i (mm h⁻¹) was conceptualized as a two-stage process, which can happen independently or one after another according to the magnitudes of the incoming flux r (mm h⁻¹) (rain and snowmelt) and the infiltration capacity of the soil (Fig. 2).

Figure 2 Conceptualization of the infiltration process with a constant rainfall r (modified from Tindall et al., 1999). Here, K_sat is the saturated hydraulic conductivity, and t_p and t_d stand for ponding and duration times, respectively.

The first stage, usual when the soil is dry, describes an infiltration rate lower than the infiltration capacity; thus, it is limited by the rainfall and snowmelt rate and lasts until the water flux starts to pond at t_p (Vereecken et al., 2019; Assouline, 2013). A second stage describes the system once the water starts to pond on the surface. Here the infiltration rate is limited by the infiltration capacity, which in turn decreases inversely to the water content of the soil, reaching its minimum value (equivalent to K_sat) at saturation following the Green–Ampt formulation, as described by Assouline (2013) and Tindall et al. (1999):

$$\begin{array}{}\text{(28)}& i_{t+\mathrm{1}}={\displaystyle \frac{\mathrm{d}I}{\mathrm{d}t}}=K_{\mathrm{sat}}\left({\displaystyle \frac{{\mathit{\psi }}_{\mathrm{f}}({\mathit{\theta }}_{\mathrm{sat}}-{\mathit{\theta }}_t)}{I\left(t\right)}}+\mathrm{1}\right),\end{array}$$

where K_sat (mm h⁻¹) is the saturated hydraulic conductivity, θ_t,sat (m³ m⁻³) represents the volumetric soil water content at the time t and at saturation (sat), respectively, I(t) is the cumulative infiltration at the time t, and ψ_f (mm) is the capillary head at the wetting front, which according to Tindall et al. (1999) is calculated as

$$\begin{array}{}\text{(29)}& {\mathit{\psi }}_{\mathrm{f}}={\displaystyle \frac{\mathrm{2}+\mathrm{3}\mathit{\lambda }}{\mathrm{1}+\mathrm{3}\mathit{\lambda }}}{\displaystyle \frac{{\mathit{\psi }}_b}{\mathrm{2}}},\end{array}$$

with λ being the pore size distribution index (unitless) and ψ_b (mm) the air-entry pressure, both shaping parameters of the soil water retention curve proposed by Brooks and Corey (1964) (referred to as the BC model hereafter).

Therefore, the ponding time t_p can be found by setting Eq. (28) equals to r, which yields

$$\begin{array}{}\text{(30)}& t_{\mathrm{p}}={\displaystyle \frac{K_{\mathrm{sat}}{\mathit{\psi }}_{\mathrm{f}}({\mathit{\theta }}_{\mathrm{sat}}-{\mathit{\theta }}_t)}{r(r-K_{\mathrm{sat}})}}.\end{array}$$

Moreover, to account for the slope (s) effects on t_p, the factor $\frac{\mathrm{1}}{{\cos }^{\mathrm{2}}\left(s\right)}$ is used to reduce t_p, following the analysis of Morbidelli et al. (2018); thus, the cumulative infiltration is defined as follows.

$$\begin{array}{}\text{(31a)}& {\displaystyle }\begin{array}{rl}I& =r{t}_{\mathrm{p}}+\underset{t_{\mathrm{p}}}{\overset{t_{\mathrm{d}}}{\int }}i\mathrm{d}t=r{\displaystyle \frac{t_{\mathrm{p}}}{{\cos }^{\mathrm{2}}\left(s\right)}}+K_{\mathrm{sat}}\left(t_{\mathrm{d}}-{\displaystyle \frac{t_{\mathrm{p}}}{{\cos }^{\mathrm{2}}\left(s\right)}}\right)\\ & -{\mathit{\psi }}_{\mathrm{f}}\mathrm{\Delta }\mathit{\theta }\ln \left(\mathrm{1}-{\displaystyle \frac{r\frac{t_{\mathrm{p}}}{{\cos }^{\mathrm{2}}\left(s\right)}}{{\mathit{\psi }}_{\mathrm{f}}\mathrm{\Delta }\mathit{\theta }}}\right);r>K_{\mathrm{sat}}\end{array}\text{(31b)}& {\displaystyle }I=r{t}_{\mathrm{d}};r\le K_{\mathrm{sat}}\end{array}$$

Here, t_d is the duration of the precipitation event, and Δθ is the difference between θ_sat and the previous θ at the near soil surface, which is calculated using an analytical solution of the Brooks and Corey (1964) model with the previous-day moisture and the depth of the profile (See Sect. 2.7).

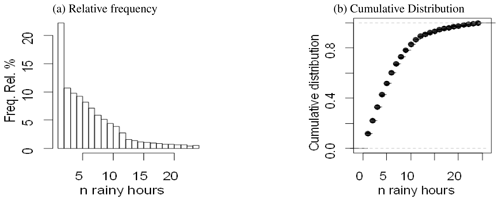
The set of equations presented above still requires rainfall intensity and the event's duration to perform the calculations; however, the “minimum inter-event time”, which is used to define a precipitation event, is not consistent in the literature and varies according to the author, location, and application, ranging from 15 min to 24 h (Dunkerley, 2008; Molina-Sanchis et al., 2016), making it difficult to define criteria for global applications. Therefore, as a simplification, an average daily rainfall duration was proposed instead, similar conceptually to the design storm, which is used in calculations for infrastructure design (Smith and Parlange, 1978). In this way, to find the average daily rainfall duration, the daily number of hours with precipitation and the daily precipitation amount were extracted from the Global Satellite Mapping of Precipitation (GsMap v6.0) dataset during the 2000–2014 period (Mega et al., 2014; Yamamoto and Shige, 2015) using the Google Earth Engine (GEE) platform, and the most frequent value was chosen (6 h).

The parameters λ and ψ_b, which shape the BC model, and K_sat were estimated using pedotransfer functions detailed in Saxton and Rawls (2006), which use soil texture and soil organic matter (SOM) as inputs.

To account for the effects of temperature and atmospheric pressure on the water viscosity and hence on K_sat (Fig. 3), we used the formula described by Hillel (1998):

$$\begin{array}{}\text{(32)}& K_{\mathrm{sat}}=k_{\mathrm{i}}{\displaystyle \frac{\mathit{\rho }g}{\mathit{\eta }}},\end{array}$$

where k_i (m²) is the soil's intrinsic permeability, ρ (kg m⁻³) is the water density, g (m s⁻²) is gravitational acceleration, and η (Pa s) is the dynamic viscosity. Thus, we simply used K_sat from the pedotransfer functions, assuming $\frac{\mathit{\rho }}{\mathit{\eta }}$ at standard conditions to find k_i, which was later replaced in Eq. (32) using actual environmental conditions.

Figure 3 Effects of elevation (atmospheric pressure and temperature) on the saturated hydraulic conductivity using a hypothetical soil with 10 % SOM, 30 % silt, and varying sand and clay.

2.2.5 Surface runoff

The runoff formulation considers the different generation mechanisms: the saturation excess overland runoff RO_D (mm d⁻¹) (Dunne runoff), which is produced after the soil becomes saturated and is frequent in humid climates or riparian areas (Vereecken et al., 2019), and the infiltration excess overland runoff RO_H (mm d⁻¹) (Hortonian runoff), which is produced when the precipitation rate exceeds the infiltration capacity and is more frequent in semi-arid climates (Grayson and Blöschl, 2000; Vereecken et al., 2019):

$$\begin{array}{}\text{(33a)}& {\displaystyle }{\mathrm{RO}}_{\mathrm{D}}=& {\displaystyle }max(\mathrm{0},W_n-W_{\mathrm{sat}}),\text{(33b)}& {\displaystyle }{\mathrm{RO}}_{\mathrm{H}}=& {\displaystyle }r-I,\end{array}$$

where r (mm d⁻¹) is water input (rainfall + snowmelt), I (mm d⁻¹) is the infiltration, and W_n,sat (mm) represents the actual and soil water content at saturation, respectively.

Therefore, the daily total RO is simply defined as

$$\begin{array}{}\text{(34)}& \mathrm{RO}={\mathrm{RO}}_{\mathrm{D}}+{\mathrm{RO}}_{\mathrm{H}}.\end{array}$$

2.2.6 Lateral flow

The lateral flow in one cell was defined at steady state as

$$\begin{array}{}\text{(35)}& q_{\mathrm{in}}=q_{\mathrm{out}},\end{array}$$

where q_in (mm d⁻¹) is the water draining into the cell from the upslope contributing area and q_out (mm d⁻¹) is the water draining out from the cell.

The lateral outgoing flow q_out (mm d⁻¹) was conceptualized using some of the TOPMODEL ideas (Beven and Kirby, 1979) on the profile transmissivity (soil hydraulic conductivity K integrated over the soil column) and the hydraulic gradient defined by local topography tan (s) as follows:

$$\begin{array}{}\text{(36)}& q_{\mathrm{out}}={\displaystyle \frac{w}{A_i}}\underset{\mathrm{0}}{\overset{z_s}{\int }}K\left(\mathit{\theta },z\right)\mathrm{d}z\tan \left(s\right),\end{array}$$

where w is the width of the profile's cross-section and A_i is the area of the cell, used here to convert the volumetric flow through the cross-section to equivalent water column units over the cell.

In order to solve the transmittance, the soil moisture distribution through the profile was conceptualized following Hilberts et al. (2005) and Fan et al. (2007) (Fig. 4) with hydrostatic equilibrium at the water table (Remson and Randolph, 1962). Here, the soil moisture redistribution after infiltration was assumed to last less than 1 d within the first 2 m of soil depth, implying a permanent shape of the moisture profile.

Similarly to Fan et al. (2007), due to the lack of information on how K_sat decreases with depth, the model assumes K_sat to be constant through the first 2 m of depth, extending the original 1.5 m proposed by Fan et al. (2007).

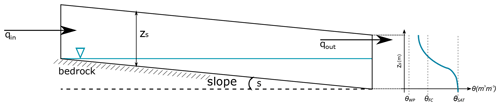
Figure 4 Conceptualization of the soil moisture profile in a shallow soil column, after Hilberts et al. (2005) and Fan et al. (2007). We assumed a cell with low spatial resolution and next to a stream.

Therefore, we defined the transmissivity of the profile as the sum of the transmissivities in the unsaturated and saturated parts of the profile as follows:

$$\begin{array}{}\text{(37)}& \begin{array}{rl}T& =\underset{\mathrm{0}}{\overset{z}{\int }}K\left(\mathit{\theta },z\right)\mathrm{d}z=T_{\mathrm{uns}}+T_{\mathrm{sat}}=\underset{\mathrm{0}}{\overset{z_{\mathrm{wtd}}}{\int }}K\left(\mathit{\theta },z\right)\mathrm{d}z\\ & +\underset{z_{\mathrm{wtd}}}{\overset{z}{\int }}K\left(\mathit{\theta },z\right)\mathrm{d}z.\end{array}\end{array}$$

Thus, to approximate the distribution of θ(z) through the unsaturated part of the soil column, the BC model was used with the total soil water potential (matric+gravitational) after Hino et al. (1988) and Beldring et al. (1999):

$$\begin{array}{}\text{(38)}& \mathit{\theta }\left(z\right)={\mathit{\theta }}_{\mathrm{r}}+\left({\mathit{\theta }}_{\mathrm{sat}}-{\mathit{\theta }}_{\mathrm{r}}\right){\left({\displaystyle \frac{{\mathit{\psi }}_{\mathrm{m}}+{\mathit{\psi }}_{\mathrm{g}}\left(z\right)}{{\mathit{\psi }}_b}}\right)}^{-\mathit{\lambda }},\end{array}$$

where θ_r (m³ m⁻³) is the residual soil water content, ψ_m (mm) is the soil matric potential, and ψ_g(z) (mm) is the gravitational potential.

The hydraulic conductivity, K(θ) (mm h⁻¹), was defined according to Brooks and Corey (1964) as follows:

$$\begin{array}{}\text{(39)}& K\left(\mathit{\theta }\right)=K_{\mathrm{sat}}{\left({\displaystyle \frac{\mathit{\theta }}{{\mathit{\theta }}_{\mathrm{sat}}}}\right)}^{\left(\mathrm{3}+\frac{\mathrm{2}}{\mathit{\lambda }}\right)}.\end{array}$$

Therefore, replacing Eq. (38) in Eq. (39) and solving the integral analytically for the unsaturated part, the transmissivity is defined as

$$\begin{array}{}\text{(40)}& \begin{array}{rl}{T}_{\mathrm{uns}}& =\underset{\mathrm{0}}{\overset{z_{\mathrm{wtd}}}{\int }}K\left(\mathit{\theta },z\right)\mathrm{d}z={\displaystyle \frac{K_{\mathrm{sat}}{\mathit{\psi }}_b}{\mathrm{3}\mathit{\lambda }+\mathrm{1}}}\left[{\left({\displaystyle \frac{{\mathit{\psi }}_b}{{\mathit{\psi }}_{\mathrm{m}}}}\right)}^{\mathrm{3}\mathit{\lambda }+\mathrm{1}}\right.\\ & \left.-{\left({\displaystyle \frac{{\mathit{\psi }}_b}{{\mathit{\psi }}_{\mathrm{m}}+z_{\mathrm{wtd}}}}\right)}^{\mathrm{3}\mathit{\lambda }+\mathrm{1}}\right],\end{array}\end{array}$$

where z_wtd (m) is the depth to the water table, found when ${\mathit{\psi }}_{\mathrm{m}}+{\mathit{\psi }}_{\mathrm{g}}={\mathit{\psi }}_b$.

The transmissivity in the saturated part of the profile T_sat is calculated as

$$\begin{array}{}\text{(41)}& T_{\mathrm{sat}}=\underset{z_{\mathrm{wtd}}}{\overset{z}{\int }}K\left(\mathit{\theta },z\right)\mathrm{d}z=K_{\mathrm{sat}}(z-z_{\mathrm{wtd}}).\end{array}$$

The lateral incoming flux q_in was formulated using a simple linear reservoir model (Buytaert et al., 2004; Yang et al., 2018; Vogel and Kroll, 1996), with a decaying volumetric flux as a function of time:

$$\begin{array}{}\text{(42)}& Q_{\mathrm{f}}=Q_o{K_b}^t,\end{array}$$

where Q_f is the final flux after the time t and Q_o (m³ d⁻¹) is the initial volumetric flow soon after the precipitation event. If we set the cease of drainage at field capacity we get

$$\begin{array}{}\text{(43)}& \underset{t\to \mathrm{\infty }}{lim}{Q}_o{K_b}^t=Q_{\mathrm{fc}},\end{array}$$

where Q_fc (m³ d⁻¹) is the volumetric flow after the time t (d), and K_b is the recession constant (unitless), which was found using the drainable porosity; see Appendix A. Therefore, the total volume result of a daily (1 d) recharge (R>0) over the upslope area (Fig. 5), theoretically, can be approximated by

$$\begin{array}{}\text{(44)}& A_{\mathrm{u}}R\left(\mathrm{1}d\right)=\underset{t_{\mathrm{0}}}{\overset{t}{\int }}{Q}_o{K_b}^t\mathrm{d}t,\end{array}$$

where A_u is the upslope area (m²), R is the recharge (mm d⁻¹), which is defined as infiltration minus evapotranspiration $R=I-E^{\mathrm{a}}$ and t₀ is the time at Q_o.

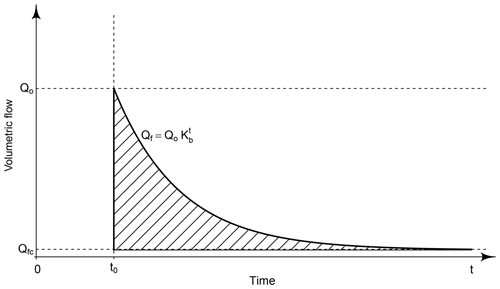
Figure 5 Conceptualization of the recharge from the upslope after one precipitation at t₀ using a simple linear reservoir model. The shaded area represents Eq. (44).

Therefore, if we find t from both Eqs. (43) and (44), we can set

$$\begin{array}{}\text{(45)}& {\displaystyle \frac{\mathrm{1}}{\ln \left(K_b\right)}}\ln \left({\displaystyle \frac{Q_{\mathrm{fc}}}{Q_o}}\right)={\displaystyle \frac{\mathrm{1}}{\ln \left(K_b\right)}}\ln \left({\displaystyle \frac{A_{\mathrm{u}}R\ln \left(K_b\right)}{Q_o}}+\mathrm{1}\right),\end{array}$$

which, solving for Q_o yields

$$\begin{array}{}\text{(46)}& Q_o=Q_{\mathrm{fc}}-A_{\mathrm{u}}R\ln \left(K_b\right),\end{array}$$

where Q_fc can be found by setting θ to field capacity in Eqs. (38) and (40). Thus,

$$\begin{array}{}\text{(47)}& q_{\mathrm{in}}=\left\{\begin{array}{ll}\frac{Q_{\mathrm{fc}}-A_{\mathrm{u}}R\ln \left(K_b\right)}{\mathrm{Ai}};& \text{if}R>\mathrm{0}\wedge \mathit{\theta }>{\mathit{\theta }}_{\mathrm{fc}}\\ \frac{{Q_{\mathrm{in}}}_{n-\mathrm{1}}{K_b}^{\mathrm{\Delta }t}}{A_i};& \text{if}R\le \mathrm{0}\wedge \mathit{\theta }>{\mathit{\theta }}_{\mathrm{fc}}\\ \mathrm{0};& \text{if}\mathit{\theta }\le {\mathit{\theta }}_{\mathrm{fc}}.\end{array}\right.\end{array}$$

2.2.7 Evapotranspiration

The actual evapotranspiration, $E_n^{\mathrm{a}}$ (mm d⁻¹), is computed following the original formulation of Davis et al. (2017) with modifications to account for the reduction in available energy, which is diverted to snow melting and sublimation, if any. It starts by defining the actual instantaneous evapotranspiration E^a (mm h⁻¹) as the minimum between supply S_W (mm h⁻¹) and demand D_p (mm h⁻¹) rates (Federer, 1982).

$$\begin{array}{}\text{(48)}& E^{\mathrm{a}}=min(S_{\mathrm{W}},D_p)\end{array}$$

Then, the daily integration of this flux is computed using an analogous form to the daily energy flux calculation (Fig. 6) as follows:

$$\begin{array}{}\text{(49)}& E_n^{\mathrm{a}}=\mathrm{2}\underset{h=\mathrm{0}}{\overset{h_{\mathrm{n}}}{\int }}{E}^{\mathrm{a}}=\mathrm{2}\left(\underset{h=\mathrm{0}}{\overset{h_{\mathrm{i}}}{\int }}{S}_{\mathrm{W}}+\underset{h_{\mathrm{i}}}{\overset{h_{\mathrm{n}}}{\int }}{D}_p\right),\end{array}$$

where h (rad) is the hour angle and h_i is the cross-over angle when the supply is equal to the demand.

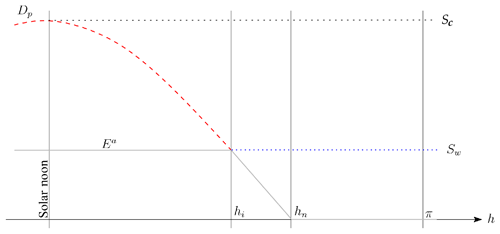
Figure 6 Conceptualization of the actual instantaneous evapotranspiration flux between solar noon (i.e., h=0) and solar midnight (i.e., h=π), modified from Davis et al. (2017). The evaporative demand D_p (red dashed line) is maximum at solar noon, equivalent to the maximum supply rate, Sc. The actual supply rate S_W is constant throughout the day and depends on soil moisture limitations.

The evaporative demand D_p is defined following the Priestley and Taylor (1972) formulation for potential evapotranspiration:

$$\begin{array}{}\text{(50)}& D_p=\mathrm{3.6}\times {\mathrm{10}}^{\mathrm{6}}{E}_{\mathrm{con}}{I}_{\mathrm{N}},\end{array}$$

where I_N (W m⁻²) is the instantaneous net radiation, and E_con (m³ J⁻¹) is the energy-to-water conversion factor, defined following the Priestley–Taylor theory (hereafter PT), with adjustments proposed by Yang and Roderick (2019), which reproduce the feedback between the surface temperature and E^a (hence their effect on I_N), thus replacing the need for a Priestley–Taylor α_PT coefficient.

$$\begin{array}{}\text{(51)}& E_{\mathrm{con}}={\displaystyle \frac{s}{L_{\mathrm{v}}{\mathit{\rho }}_{\mathrm{w}}(s+\mathrm{0.24}\mathit{\gamma })}}\end{array}$$

Here, L_v (J kg⁻¹) is the latent heat of vaporization, ρ_w (kg m⁻³) is the water density, s (Pa K⁻¹) is the slope of the temperature–pressure curve, γ (Pa K⁻¹) is the psychrometric constant, and 0.24 is the constant defined by Yang and Roderick (2019). Equations for temperature and pressure dependencies to calculate ρ_w and γ were used, while only temperature-dependent equations were used for s and L_v (Davis et al., 2017).

The stress factor controlling the evaporative supply rate S_W was conceptualized as a piecewise linear function, where we assumed the stress follows the depletion of the water content in the plant-available water region (Fig. 7).

Figure 7 Conceptualization of the stress factor controlling the evaporative supply rate S_W.

Therefore, S_W is defined as

$$\begin{array}{}\text{(52)}& S_{\mathrm{W}}=\left\{\begin{array}{ll}{S}_c\frac{W_{n-\mathrm{1}}-W_{\mathrm{pwp}}}{W_{\mathrm{fc}}-W_{\mathrm{pwp}}};& \text{if}{W}_{\mathrm{pwp}}\le W_n<W_{\mathrm{fc}}\\ S_c& \text{if}{W}_n\ge W_{\mathrm{fc}},\end{array}\right.\end{array}$$

where S_c (mm h⁻¹) is the maximum evaporative supply rate, and W_n−1 is the previous-day soil water content.

Here, Davis et al. (2017) adopt S_c as a constant, following Federer (1982); however, Federer (1982) points out that this value should change according to morphological traits of the vegetation (i.e., root density and depth).

Therefore, since $E^{\mathrm{a}}=\min (S_{\mathrm{W}},D_p)$, and under well-watered conditions S_W=S_c, S_c with a value higher than the maximum D_p (at solar noon) will not affect the resultant E^a.

Thus, to estimate S_c so it applies for non-vegetated areas as well, the supply rate is approximated as the maximum rate of evaporation as follows:

$$\begin{array}{}\text{(53)}& \mathrm{Sc}=D_{\mathrm{pMAX}}=r_x\left(\left(r_w\right(r_u+r_v\left)\right)-I_{\mathrm{LW}}\right),\end{array}$$

where, to simplify the notation, r_x (mm m² W⁻¹ h⁻¹) is equal to 3.6×10⁶ E_con.

The upper limit of Eq. (52) is the water content at field capacity W_fc (mm), which was defined as the amount of water held after the drainage ceased (Kramer and Boyer, 1995). This was calculated by setting the total water potential to equilibrium, following Remson and Randolph (1962):

$$\begin{array}{}\text{(54)}& {\mathit{\psi }}_{\mathrm{m}}+{\mathit{\psi }}_{\mathrm{g}}=\mathrm{0},\end{array}$$

where the matric potential ψ_m was calculated following Saxton and Rawls (2006):

$$\begin{array}{}\text{(55)}& {\mathit{\psi }}_{\mathrm{m}}=A(\mathit{\theta }{)}^{-B},\end{array}$$

with

$$\begin{array}{}\text{(56a)}& {\displaystyle }A& {\displaystyle }=e^{\ln \left(\mathrm{33}\right)+B\ln \left({\mathit{\theta }}_{\mathrm{33}}\right)},\text{(56b)}& {\displaystyle }\mathit{\theta }& {\displaystyle }=W_n/\left(\mathrm{1000}z\right),\text{(56c)}& {\displaystyle }B& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathit{\lambda }}}={\displaystyle \frac{\ln \left(\mathrm{1500}\right)-\ln \left(\mathrm{33}\right)}{\ln ({\mathit{\theta }}_{\mathrm{33}}-\ln ({\mathit{\theta }}_{\mathrm{1500}})}},\end{array}$$

where θ₃₃ is the volumetric water content at 33 kPa (usually assumed to be field capacity), θ₁₅₀₀ is the volumetric water content at 1500 kPa, and z (m) is the depth of the soil profile. Then, using the minimum between 2 m and the depth to the bedrock as a reference plane, the gravitational potential is defined as

$$\begin{array}{}\text{(57)}& {\mathit{\psi }}_{\mathrm{g}}={\mathit{\rho }}_{\mathrm{w}}g{W}_n.\end{array}$$

Therefore, W_fc can be found by replacing Eqs. (55) to (57) in Eq. (54) and solving for W_n (see Appendix A for intermediate steps).

$$\begin{array}{}\text{(58)}& W_{\mathrm{fc}}=\mathrm{1000}z{\left({\displaystyle \frac{\mathrm{1000}A}{{\mathit{\rho }}_{\mathrm{w}}gz}}\right)}^{\frac{\mathrm{1}}{\mathrm{1}+B}}\end{array}$$

The lower limit of Eq. (52) is defined as the water content at permanent wilting point W_pwp (mm), which was computed as

$$\begin{array}{}\text{(59)}& W_{\mathrm{pwp}}={\mathit{\theta }}_{\mathrm{1500}}\times \mathrm{1000}z.\end{array}$$

In order to adopt the best option to compute soil hydrophysical properties (θ₃₃, θ₁₅₀₀,θ_sat and K_sat) and hence the thresholds proposed, a set of the most widely used PTFs in LSMs were evaluated (Van Looy et al., 2017) and tested with a global dataset of soil physical properties which was compiled from different sources. The models, ranging in complexity, from the most simple mathematical formulations are described in Table 2.

Cosby et al. (1984)Balland et al. (2008)Saxton and RawlsTóth et al. (2015)(Zhang and Schaap, 2017)

Table 2 Evaluated pedotransfer functions and their use in land surface models.

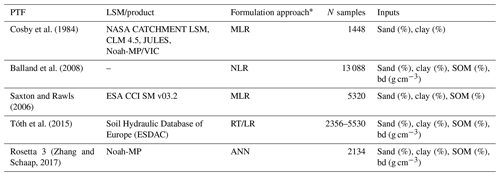
^* MLR, multiple linear regression; ANN, artificial neural network; RT, regression tree; LR, linear regression; NLR, nonlinear regression.

Thus, finally Eq. (49) is solved analytically as

$$\begin{array}{}\text{(60)}& \begin{array}{rl}{E}_n^{\mathrm{a}}& ={\displaystyle \frac{\mathrm{24}}{\mathit{\pi }}}\left(S_{\mathrm{W}}{h}_{\mathrm{i}}+r_x{r}_v{r}_w(\sin h_{\mathrm{n}}-\sin h_{\mathrm{i}})\right.\\ & \left.+(r_x{r}_u{r}_w-r_x{I}_{\mathrm{LW}})(h_{\mathrm{n}}-h_{\mathrm{i}})\right),\end{array}\end{array}$$

where the intersection hour angle h_i is found by setting Eq. (50) equal to Eq. (52) and solving for h:

$$\begin{array}{}\text{(61)}& h_{\mathrm{i}}=\arccos \left({\displaystyle \frac{S_{\mathrm{W}}}{r_x{r}_v{r}_w}}+{\displaystyle \frac{I_{\mathrm{LW}}}{r_v{r}_w}}-{\displaystyle \frac{r_u}{r_v}}\right).\end{array}$$

2.2.8 Condensation

The daily dew formed by condensation C_n (mm d⁻¹) is assumed to represent 10 % of the water equivalent (Eq. 52) of the negative net radiation $H_{\mathrm{n}}^{-}$ (Eq. 15) (Jones, 2013). The remnant energy is assumed to be lost as convective heat. Thus,

$$\begin{array}{}\text{(62)}& C_n=\mathrm{100}{E}_{\mathrm{con}}{H}_{\mathrm{n}}^{-}.\end{array}$$

2.2.9 Soil water content

Once inputs and outputs are calculated, the total soil water content W_n (mm) can now be calculated using a simple balance expression, with the previous-day soil water content W_n−1 as follows:

$$\begin{array}{}\text{(63)}& W_n=W_{n-\mathrm{1}}+I+q_{\mathrm{in}}-q_{\mathrm{out}}-{\mathrm{RO}}_{\mathrm{H}}-E_n^{\mathrm{a}}.\end{array}$$

Furthermore, to calculate the water content (SWC) (mm) accumulated to any depth (z^′) for further comparison with the observations, if we assume the same moisture profile from Eq. (26), it can be defined as

$$\begin{array}{}\text{(64)}& \mathrm{SWC}=\underset{\mathrm{0}}{\overset{z^{\prime }}{\int }}\mathit{\theta }\left(z\right)\mathrm{d}z={\left.{\mathit{\theta }}_{\mathrm{r}}z+{\displaystyle \frac{({\mathit{\psi }}_{\mathrm{m}}+{\mathit{\psi }}_z)({\mathit{\theta }}_{\mathrm{r}}-{\mathit{\theta }}_{\mathrm{sat}}){\left(\frac{{\mathit{\psi }}_b}{{\mathit{\psi }}_{\mathrm{m}}+{\mathit{\psi }}_z}\right)}^{\mathit{\lambda }}}{\mathit{\lambda }-\mathrm{1}}}\right|}_{\mathrm{0}}^{z^{\prime }}.\end{array}$$

2.3 Initial conditions

The SPLASH algorithm assumed steady-state conditions as the initial state for the simulations, which is reached by looping n times the first year of data until the water balance is preserved.

$$\begin{array}{}\text{(65)}& \sum \left(f_{\mathrm{rain}}{P}_n+C_n+{\mathrm{Sm}}_n+q_n^{\mathrm{in}}\right)=\sum \left(E_n^{\mathrm{a}}+q_n^{\mathrm{out}}+\mathrm{RO}\right)\end{array}$$

3 Methods: simulation protocol and performance evaluation

3.1 Point-scale simulations

Point-scale simulations with the SPLASH model were run at individual sites (Figs. 8 and 10) with their entire daily time series of meteorological measurements. Due to different variables measured by the different networks of monitoring, the performance evaluation with the pooled data was done separately per network. The statistics used for the evaluation were the coefficient of determination (R²), the root mean squared error (RMSE), bias, and the slope of the regression for observations vs. simulations. To evaluate the seasonal patterns of fluxes and storages, all the results were aggregated as daily means and grouped by climate zone using the Köppen–Geiger climate classification system (Beck et al., 2018). Only direct measurements were used for the performance evaluations, while some indirect observations were estimated using the variation with previous-day observations to visualize seasonal patterns of some fluxes (e.g., Sf and Sm_e). To complement the analysis and interpretation of the results, simulations with the three-layer variable infiltration capacity model (VIC-3L) (Liang et al., 1996; Liang and Xie, 2001) were performed using the same inputs and in the same way as SPLASH, without local calibration.

Figure 8 FLUXNET stations used for the I_LW parameter calibration.

Figure 9 SNOTEL stations used for albedo and snow cover analysis.

Figure 10 SNOTEL soil moisture and SWE validation sites.

Vegetation properties, soil parameters, and initial soil moisture, all required by VIC-3L, were extracted at the site locations from Schaperow and Li (2020). Extra forcing data required by the VIC-3L, like wind speed and vapor pressure, not measured at the SNOwpack TELemetry (SNOTEL) sites, were extracted from the daily high-resolution GRIDMET (Abatzoglou, 2013) and DAYMET (Thornton et al., 2020) datasets, respectively. Since some quantities computed by SPLASH are not standard outputs of the VIC-3L model (e.g., $H_{\mathrm{N}}^{+}$ and C_n), some calculations were applied to obtain comparable outputs (Appendix A3.1). To compare seasonal patterns of soil moisture a relative moisture content was calculated with the observations and results from SPLASH in the same way as the VIC output:

$$\begin{array}{}\text{(66)}& \mathrm{\Theta }={\displaystyle \frac{W_n-W_{\mathrm{pwp}}}{W_{\mathrm{sat}}-W_{\mathrm{pwp}}}},\end{array}$$

where W_sat is the water content (mm) at saturation. W_n and W_pwp are as defined in Sect. 2.2.7.

3.2 Spatially distributed simulations

Spatially distributed simulations were performed to visualize major spatial patterns of the fluxes and storages, test the computational performance of the model at different resolutions, and evaluate how the global parameters and assumptions of the model hold.

Global simulations were run at a resolution of 5 km, regional simulations (e.g., North America) at a resolution of 1 km, and micro-catchments at a resolution of 90 m. Since the model lacks a routing algorithm, to test the runoff–lateral flow simulations against streamflow observations, yearly aggregated quantities were used.

VIC spatially distributed simulations of runoff across the US were obtained from Kao et al. (2022). These simulations, conducted independently, employed VIC calibrated with historical hydrological data and were exclusively used for evaluating streamflow against SPLASH simulations run with identical inputs (i.e., DAYMET, Thornton et al., 2018).

4 Methods: fitting and optimization of empirical functions

Parameters from the selected equations (pedotransfer functions) were optimized using the Nash–Sutcliffe (NSE) coefficient, which relates the variance of the residuals to the variance of the data as the objective function (Nash and Sutcliffe, 1970; Gupta and Kling, 2011). Here, an NSE closer to 1.0 expresses ideal estimates. The probabilistic model for snowfall occurrence was fitted using a binomial family generalized linear model (GLM), while the albedo-related functions were fitted using nonlinear least squares. To assess the accuracy of the snowfall probability estimation, the receiver operating characteristic (ROC) curve was used, which plots the true positive rate (specificity) against the false positive rate (sensitivity) using a probability of 0.5 as a threshold. Here the area under the curve (AUC) closer to 1.0 expresses a better overall prediction (Fawcett, 2006).

5 Methods: input data

5.1 Eddy covariance towers

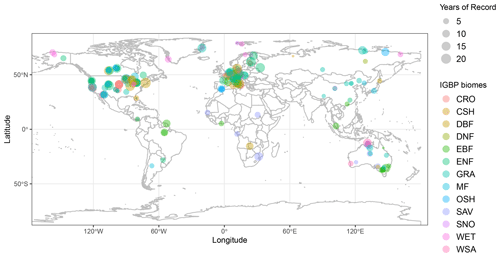
Data from the whole FLUXNET database (Pastorello et al., 2020), comprising 212 stations distributed around the world (Fig. 8), were used to update the empirical functions to compute net longwave radiation, superseding the equations formulated by Monteith and Unsworth (1990) and Linacre (1968) used in the first version of SPLASH.

All the data were aggregated to daily means, while the originally reported latent heat flux was transformed to its equivalent in water flux density (mm d⁻¹) by using the heat of vaporization corrected for field conditions.

To test the validity of the theorized daily cycles and cross-over angles, positive values of net radiation were subsetted and aggregated daily, which in theory should be equivalent to Eq. (14). A simple threshold for measured albedo of 0.3 was used to identify snow presence; then, latent heat measurements when snow was present were excluded from the estimations of daily evapotranspiration and condensation, trying to prevent the latent heat used in melting, refreeze, and sublimation from introducing error into the evaluations.

5.2 Meteorological and hydrometric stations

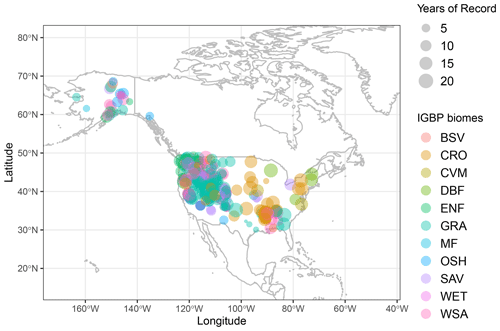
To estimate the parameters used in the snow cover and albedo functions, 315 stations reporting snow-water equivalent or snow depth from the SNOwpack TELemetry (SNOTEL) network (Serreze et al., 1999), managed by the US Natural Resources Conservation (NCAR) service, were used together with remote sensing data (Fig. 9); most of these stations also report solar radiation, precipitation, air temperature, and volumetric soil moisture at different depths.

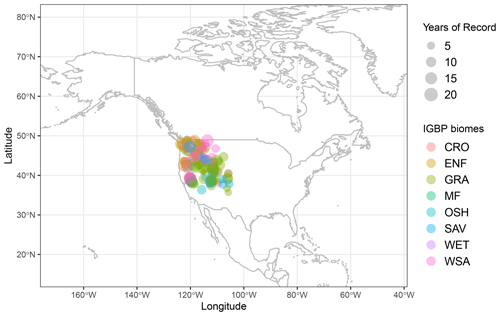
To evaluate the model, we subset sites in mountain regions with joint measurements of snow, soil physical properties (i.e., texture, bulk density, and SOM), and soil moisture deeper than 30 cm, resulting in 127 sites (Table A5). Data from the DAYMET database (Thornton et al., 2018) were used whenever the solar radiation was not reported (Fig. 10).

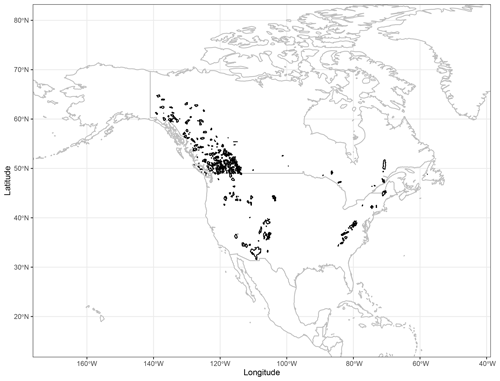
To fit the binary logistic regression used to estimate the probability of snowfall occurrence p(snow), the dataset described by Jennings et al. (2018) was used, which comprises 11 924 stations distributed over the Northern Hemisphere, adding a total of 17 810 805 binary observations of snowfall (Fig. 11).

Figure 11 Stations providing snowfall observations from the Jennings et al. (2018) dataset.

To test the model capabilities predicting streamflow, with its improvements accounting for slope, small watersheds with areas between 5 and 2000 km² located in mountain regions of Canada and the USA were selected from the global GSIM database (Do et al., 2018) due to the quality of the available forcing data over these regions. The GSIM database provides curated streamflow data from multiple sources and geographic watershed boundaries (Fig. 12). Only watersheds with natural cover higher than 90 % and streamflow data covering at least 10 years since 1980 were subset (Table A6), resulting in 15 963 station years. Here, the separation of surface runoff and baseflow was done following the method described by Ladson et al. (2013).

Figure 12 GSIM watersheds for streamflow validation.

To evaluate the spatial patterns produced by the model with long-term data, hydrometeorological and soil moisture measurements from the Rietholzbach Research Catchment were used. These datasets are publicly available and described by Seneviratne et al. (2012) and Hirschi et al. (2017). To test the model in regions where the rainfall and runoff response is mainly dominated by subsurface flow (Crespo et al., 2011; Correa et al., 2020), hydrometeorological data from the tropical Andes, compiled by Ochoa-Tocachi et al. (2018), were used.

5.3 Soil physical properties and terrain

To calibrate the pedotransfer functions which compute field capacity (θ₃₃) and wilting point (θ₁₅₀₀) a dataset containing data on water retention, texture, organic matter content (SOM), and bulk density was compiled from the US Natural Resources Conservation service through the “soilDB” R package (Skovlin and Roecker, 2018) and the “Wosis” databases (Batjes et al., 2020). Both databases have global coverage and resulted in a total of 68 567 usable samples (at least one of the response variables (θ_fc or θ_wp) and all the predictors) out of 324 380 (Fig. 13).

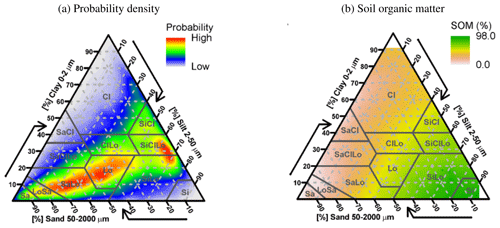
Figure 13 θ_fc and θ_wp measurements used to calibrate the pedotransfer functions. (a) Probability density of the soil samples according to their textural classes. (b) Average soil organic matter content of the samples per textural class.

To optimize the functions to estimate soil moisture at saturation (θ_sat) and saturated hydraulic conductivity (K_sat) data were gathered from the HYBRAS (Ottoni et al., 2018), SWIG (Rahmati et al., 2018), UNSODA (Leij et al., 1996), and University of Florida (IFAS, 2007) datasets for a total of 9346 usable samples out of 15 160 (Fig. 14).

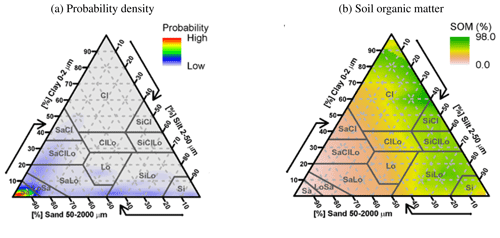
Figure 14 K_sat and θ_sat measurements used to calibrate the pedotransfer functions. (a) Probability density of the samples according to their textural classes. (b) Average soil organic matter content of the samples per textural class.

To test the model for the EC sites, abovementioned soil physical properties were retrieved from the SoilGrids.org (https://soilgrids.org/, last access: 26 January 2021) dataset (Hengl et al., 2017), while the “soilDB” R package (Skovlin and Roecker, 2018) was used to retrieve soil data at SNOTEL sites.

Slope, slope orientation (aspect), and upslope area were computed using the TauDEM software (Tarboton, 2016) from the global SRTM digital elevation model resampled to 250 m (Jarvis et al., 2008).

5.4 Remote sensing

To fit the functions that calculate the snow cover fraction and the snow cover effect on the albedo, data from the MODIS MOD10A1 500m daily product (Hall et al., 2016) were compared against 15 years (2001–2015) of daily data from the 315 SNOTEL stations described previously in this section (Fig. 9).

Information on the biome classification, used to interpret the data, was gathered from the simple typology defined by the International Geosphere–Biosphere Programme (IGBP), available as a MODIS product (MOD12Q1) (Friedl et al., 2019).

To assess the spatial patterns of evapotranspiration in selected small watersheds, the SEBAL algorithm (Bastiaanssen et al., 1998a, b), implemented in Google Earth Engine (GEE) by Laipelt et al. (2021), was used with Landsat 5 atmospherically corrected surface reflectances from 1994–2007 and Landsat 8 from 2014.

To propose a reasonable assumption for the duration of a precipitation event, the global hourly precipitation GsMAP dataset was used. This dataset has 0.1° resolution and was built using retrievals from NASA's satellite constellation, including infrared, microwave, and radar sensors (20 sensors), merged and corrected with NOAA’s ground stations (Mega et al., 2014; Yamamoto and Shige, 2015). Since the gauge count is also available within the dataset, only pixels with three or more gauges were used to extract and analyze the hourly data using GEE.

5.5 Spatially distributed forcing

For the global simulations at 5 km of resolution, monthly precipitation data from Beck et al. (2019) were resampled and subset to 2010–2016, and air temperature was obtained from the Terraclim dataset (Abatzoglou et al., 2018), together with the solar radiation produced by Ryu et al. (2018), which uses MODIS atmospheric and albedo retrievals as some of the inputs.

For regional simulations (e.g., North America), 1 km resolution temperature and precipitation from CHELSA (Karger et al., 2017) were used, while the solar radiation from Ryu et al. (2018) was downscaled using the theoretical effects of terrain described in Sect. 2.1.1. Elevation datasets at 1 and 5 km resolution used in the respective runs were obtained from Amatulli et al. (2018). While the soil data were resampled from the global 250 m SoilGrids dataset (Hengl et al., 2017) (sand, clay, organic matter, coarse fraction, and bulk density), the soil depth and thickness were averaged between SoilGrids and the Pelletier et al. (2016) datasets.

6 Results

6.1 Fitting and optimization results

6.1.1 Net longwave radiation functions

Quadratic equations were the best fit for both incoming and outgoing longwave radiation during clear-sky conditions, noticeably improving the predictions for temperatures below 0 °C, particularly useful for regions at high elevations (Fig. 15a and b). The net longwave equation, resulting from algebraically subtracting LW_IN−LW_OUT, showed a very small quadratic coefficient, which was neglected to adopt a simpler linear equation (Fig. 15c).

Figure 15 Clear-sky longwave radiation as a function of air temperature. (a) Clear-sky incoming longwave radiation. (b) Clear-sky outgoing longwave radiation. (c) Clear-sky net longwave radiation.

6.1.2 Snowfall probability

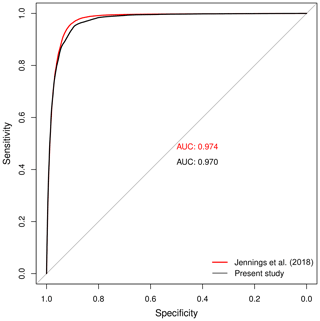
The performance of the snowfall occurrence calculation resulted in an AUC of 0.97 (Fig. 16), which considering a maximum value of 1.0 suggests that this method is highly accurate.

Figure 16 Evaluation of the predicted snowfall probability using an ROC curve.

6.1.3 Snow cover fraction and snow albedo correction

The simple hyperbolic function used to describe the response of the snow cover fraction to the size of the snowpack suggests that the inflection starts when the SWE reaches 140 mm, and most of the variation in snow cover (up to 80 %) happens in the first 1000 mm of SWE. Moreover, the standard deviations of SWE aggregated by biomes show that in the sampled period values higher than 1000 mm are uncommon (Fig. 17a).

The snow aging function suggests that a reduction of about 50 % of the albedo can happen in the first 10 d without new snow falling and the lowest albedo can reach 0.4 (Fig. 17b).

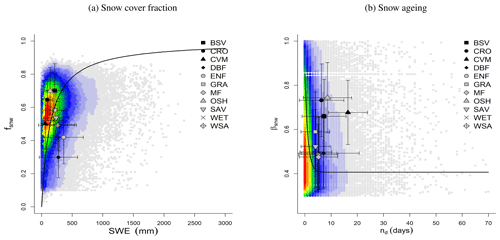
Figure 17 Ground-based observations of snow against satellite retrievals. The color scale represents the plotted point density, where blue indicates lower densities and red indicates higher densities. (a) Daily snow cover fraction from MODIS (f_snw) vs. daily SNOTEL SWE. The black line shows the optimized Eq. (27). (b) MODIS albedo (β_snw) when the snow cover exceeds 70 % vs. days without fresh snowfall (n_d) from the daily SNOTEL SWE. The black line shows the optimized Eq. (26).

6.1.4 Pedotransfer functions

From the models tested (Table 2), the nonlinear equations from Balland et al. (2008), which were fit to the largest dataset, outperformed the other models. Further optimization of these equations (Eqs. A25a, A25b, A25c) using the full dataset employed for this evaluation yielded a slight improvement of around 10 % for field capacity (θ₃₃) and saturation (θ_sat) (Fig. 20). The new parameters are detailed in Table A1.

$$\begin{array}{}\text{(67a)}& {\displaystyle }{\mathit{\theta }}_{\mathrm{1500}}={\mathit{\theta }}_{\mathrm{33}}\left(c_{\mathrm{wp}}+(d_{\mathrm{wp}}-c_{\mathrm{wp}}){\mathrm{CLAY}}^{\mathrm{0.5}}\right)\text{(67b)}& {\displaystyle }{\mathit{\theta }}_{\mathrm{33}}={\mathit{\theta }}_{\mathrm{sat}}\left(c_{\mathrm{fc}}+(d_{\mathrm{fc}}-c_{\mathrm{fc}}){\mathrm{CLAY}}^{\mathrm{0.5}}\right)e^{\frac{a_{\mathrm{fc}}\mathrm{SAND}-b_{\mathrm{fc}}\mathrm{SOM}}{{\mathit{\theta }}_{\mathrm{sat}}}}\text{(67c)}& {\displaystyle }{\mathit{\theta }}_{\mathrm{sat}}=\mathrm{1}-{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{b}}}{{\mathit{\rho }}_{\mathrm{p}}}}\text{(67d)}& {\displaystyle }{K}_{\mathrm{sat}}={\mathrm{10}}^{a_{\mathrm{ks}}+b_{\mathrm{ks}}{\log }_{\mathrm{10}}({\mathit{\rho }}_{\mathrm{p}}-{\mathit{\rho }}_{\mathrm{b}})+c_{\mathrm{ks}}\mathrm{SAND}}\end{array}$$

Here, θ₁₅₀₀ is wilting point (water held at 1500 kPa), θ₃₃ is field capacity (water held at 33 kPa), θ_sat is saturation, K_sat is the saturated hydraulic conductivity, and, SAND, CLAY, and SOM refer to sand, clay, and organic matter contents (%). a, b, and c are constants with the subscripts referring to wilting point, field capacity, or hydraulic saturated conductivity, respectively, ρ_b is the bulk density, and ρ_p is the particle density, calculated as follows (Balland et al., 2008):

$$\begin{array}{}\text{(68)}& {\mathit{\rho }}_{\mathrm{p}}={\displaystyle \frac{\mathrm{1}}{\frac{\mathrm{SOM}}{\mathrm{1.3}}+\frac{\mathrm{1}-\mathrm{SOM}}{\mathrm{2.65}}}}.\end{array}$$

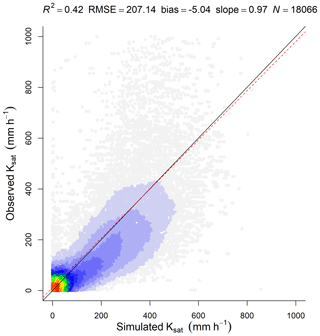
K_sat estimated by the Saxton and Rawls (2006) PTF was the best-performing model; however, it leads to unrealistic values when the drainable porosity (θ_sat−θ₃₃) is relatively high. Thus a simple saturating curve was adopted here, which yields similar estimations to Saxton and Rawls (2006) at the lower end of the drainable porosity but flattens at a fitted K_sat maximum of 623 mm h⁻¹.

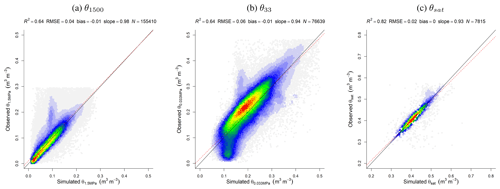
Figure 18 Correlation of observed and simulated values of soil hydrophysical properties. The color scale represents the plotted point density, where blue indicates lower densities and red indicates higher densities. (a) Permanent wilting point (θ₁₅₀₀). (b) Field capacity (θ₃₃). (c) Soil porosity or saturation point (θ_sat).

Figure 19 Correlation of observed and simulated values of saturated hydraulic conductivity K_sat. The color scale represents the plotted point density, where blue indicates lower densities and red indicates higher densities.

6.2 Fluxes

6.2.1 Net longwave radiation

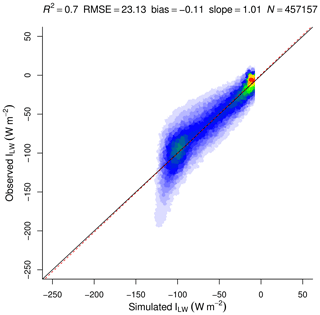
The evaluation of I_LW shows the values clustering around −100 and 0 W m²; nonetheless, the simple linear model was able to explain 70 % of the variance with a very low bias (−0.11) (Fig. 20).

Figure 20 Correlation of observed and simulated values of I_LW, with data from all the sites pooled. The color scale represents the plotted point density, where blue indicates lower densities and red indicates higher densities.

6.2.2 Daytime net radiation

The daytime net radiation, or positive net radiation, was compared against 87 EC sites distributed over mountain regions covering several biomes. The comparison, using all the data pooled at daily resolution shows, that the model is able to explain more than 70 % of the observations' variance with a very small bias (Fig. 21). The evaluation also shows that the highest overestimation happens in ecosystems with sparse vegetation (BSV biome).

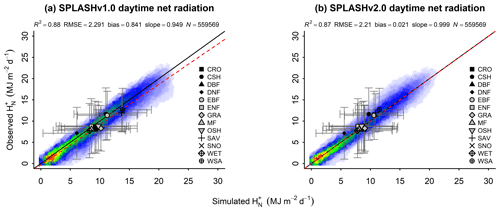
Figure 21 Correlation of observed and simulated values of $H_{\mathrm{N}}^{+}$ with data from all the sites pooled. The color scale represents the plotted point density, where blue indicates lower densities and red indicates higher densities. (a) Simulations with SPLASH v1.0. (b) Simulations with SPLASH v2.0.

The seasonal patterns of $H_{\mathrm{N}}^{+}$ averaged by climate zone show a classic bell-shaped curve, peaking during the summer months, with greater deviations from the mean appearing in climate zones with no dry season (Cfb, Dfc). SPLASH simulations reproduce the observations more closely than the VIC results in most of the climate zones, noticeably outperforming VIC in climate zones with dry summers (Csa, Csb). SPLASH overestimation happens primarily in cold deserts during summer months (BWk), while underestimation is noticeable in temperate zones with no dry season (Cfa) and in the hot steppe (BSh), both during summer months (Fig. 22).

Figure 22 Mean seasonal cycle of $H_{\mathrm{N}}^{+}$ per climate zone. The gray areas show 1 SD from the observed mean. Climate zones are described in Table A3.

6.2.3 Evapotranspiration

The performance evaluation of $E_n^{\mathrm{a}}$ using the data from all the EC stations shows the model reproducing 50 % of the variance of daily observations with a small bias and the slope of the regression of observations simulations equal to 0.072. The standard deviation of the data aggregated by biome, in the observation axis, shows that at a daily time step $E_n^{\mathrm{a}}$ is highly variable, and there is no clear difference between woody and herbaceous ecosystems. The evaluation shows a greater underestimation for evergreen broadleaf forests (EBF), while the greater overestimation happens in deciduous broadleaf forests (DBF). Furthermore, the lowest $E_n^{\mathrm{a}}$ is shown by ecosystems with sparse vegetation (OSH) and the highest by EBF (Fig. 23).

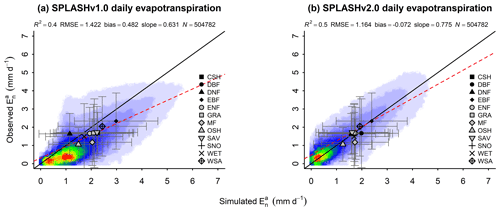
Figure 23 Correlation of observed and simulated values of $E_n^{\mathrm{a}}$ with data from all the sites pooled. The color scale represents the plotted point density, where blue indicates lower densities and red indicates higher densities. (a) Simulations with SPLASH v1.0. (b) Simulations with SPLASH v2.0.

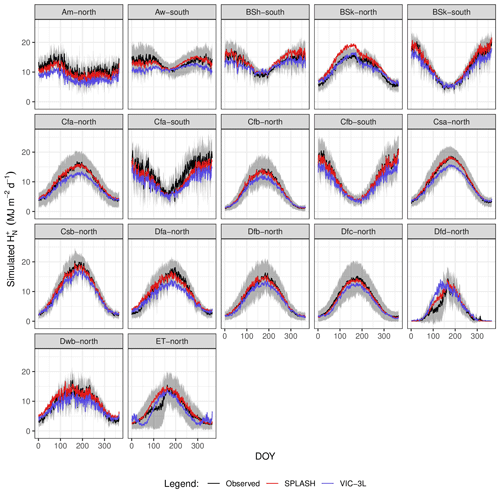
The seasonal patterns of $E_n^{\mathrm{a}}$ broadly follow the pattern of $H_{\mathrm{N}}^{+}$ in zones with no water limitations (Cf* and Cf* types), and the polar tundra exhibits similar patterns but with a higher difference between summer and winter months. Arid zones (BS* and BW* types) show a very different pattern compared to $H_{\mathrm{N}}^{+}$. SPLASH simulations correctly reproduced most of the seasonal patterns and for certain climate zones (BSk, Csb, Dsc) outperformed VIC simulations. Although SPLASH captures the overall seasonal patterns, it overestimates $E_n^{\mathrm{a}}$ at Dsc sites, while, similarly to the VIC results, it underestimates $E_n^{\mathrm{a}}$ in the polar tundra (ET) and at the Cfb sites in the Southern Hemisphere (Fig. 24).

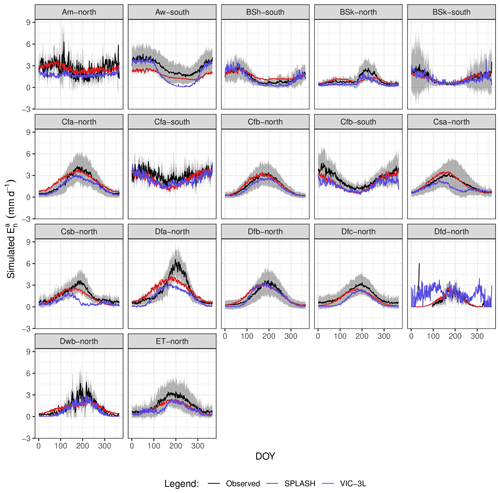
Figure 24 Mean seasonal cycle of $E_n^{\mathrm{a}}$ per climate zone. The gray areas show 1 SD from the observed mean. Climate zones are described in Table A3.

At a global scale, SPLASH produces major spatial patterns that roughly follow the distribution of the Köppen–Geiger climate zones. In northern latitudes it overestimates $E_n^{\mathrm{a}}$ during summer months; nonetheless, it outperforms VIC-3L, which produces high values during winter (Fig. 25).

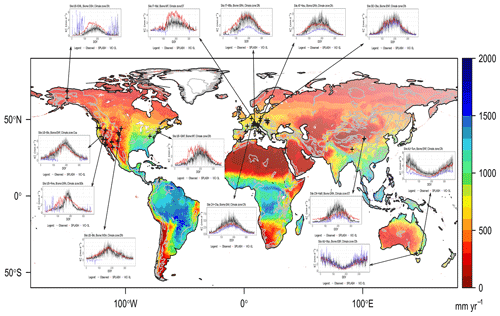
Figure 25 Spatial patterns of mean annual E^a for the period 2010–2016 at 5 km resolution along with site simulation examples from the mountains. Inset plots show seasonal cycles where observations are in black, SPLASH v2.0 simulations are in red, and VIC-3L simulations are in blue. The gray areas show 1 SD from the observed mean.

The simulations, with the long-term data from Rietholzbach, exhibit good overall agreement with the lysimeter-based observations (Fig. 26c). However, a minor but systematic overestimation happens during the spring months. Here, the spatial patterns produced by SPLASH show higher magnitudes on south-facing slopes and at the valley bottom close to the outlet, coinciding with the area where a small forest is present (Seneviratne et al., 2012) (Fig. 26c). These patterns contrast with the spatially distributed LE, calculated from Landsat 5 retrievals, which shows a more uniform LE, except for a few forest patches, where LE spikes (Fig. 26d). Both datasets barely agree over the small forest at the valley bottom.

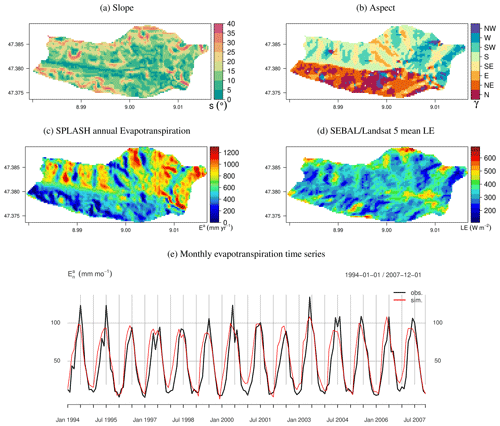
Figure 26 Spatial and temporal patterns of evapotranspiration in a small wet temperate watershed in Rietholzbach, Switzerland. (a) Slope in degrees. (b) Slope orientation; N stands for north, S for south, and so on. (c) Mean annual simulated evapotranspiration 1994–2007. (d) Mean instantaneous LE from L5's clear-sky pixels during 1994–2007. (e) Time series of monthly evapotranspiration, as well as simulated and lysimeter-based observations.

In the tropical watershed, the spatial patterns of $E_n^{\mathrm{a}}$ produced by SPLASH (Fig. 27c) show better agreement with the RS LE than in the temperate watershed, as shown by some emergent cold spots in the northern part of the watershed (Fig. 27e). Moreover, in both datasets, slopes facing the Equator show higher magnitudes compared to flat areas; however, in the SPLASH results, this difference is stronger than in the RS LE estimation.

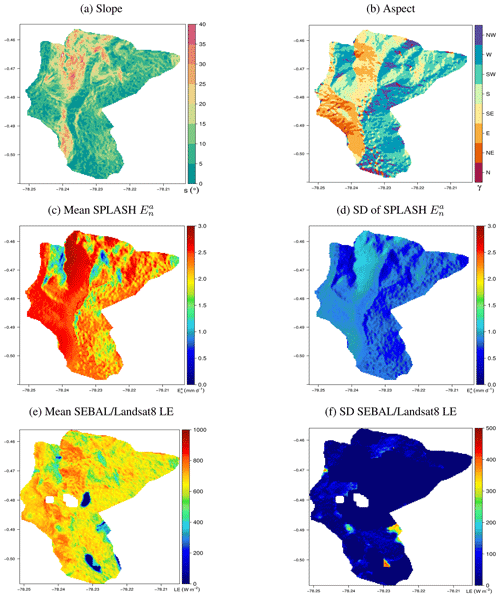
Figure 27 Spatial patterns of daily evapotranspiration in a wet tropical watershed in Jatunhuayco, Ecuador. (a) Slope in degrees. (b) Slope orientation; N stands for north, S for south, and so on. (c) Mean daily evapotranspiration during 2014. (d) Standard deviation of the daily evapotranspiration during 2014. (e) Mean instantaneous LE from L8's clear-sky pixels during 2014. (f) Standard deviation of the instantaneous LE from L8's clear-sky pixels during 2014.

6.2.4 Condensation

The model showed the poorest performance simulating C_n, capturing only around 18 % of the variance, with a bias of 0.913. The slope of the regression of observations vs. simulations points to overestimations at high simulated values; however, it shows a massive improvement from version 1.0 (Fig. 28). Most of the observations seem to cluster in the 0–10 mm yr⁻¹ range, with the greatest underestimation occurring in broadleaf evergreen forests, while C_n is overestimated in barren and sparsely vegetated ecosystems.

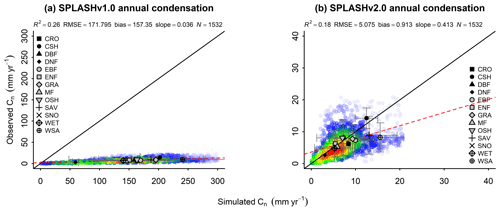
Figure 28 Correlation of observed and simulated values of C_n with data from all the sites pooled. The color scale represents the plotted point density, where blue indicates lower densities and red indicates higher densities. (a) Simulations with SPLASH v1.0. (b) Simulations with SPLASH v2.0.

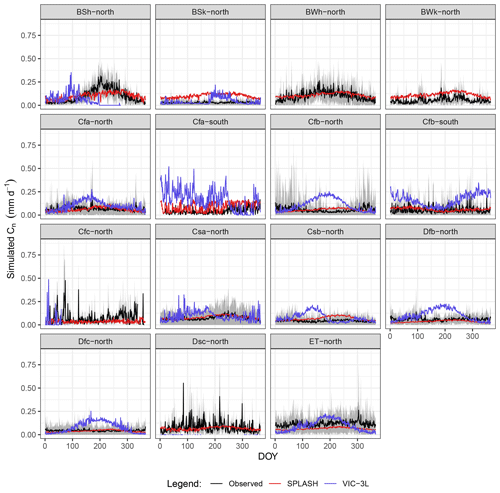
Just arid climate zones (B* types) showed seasonal patterns of C_n and potentially important magnitudes, and both dimensions are captured by SPLASH. However, the SPLASH model is still underestimating C_n in the hot steppe (BSh) and overestimating C_n in the cold steppe and desert (e.g., BSk and BWk). In some climate zones with no apparent seasonal pattern and with random peaks through the year (e.g., Cfc and Dsc) the SPLASH model shows a smother prediction, underestimating all the peaks. Compared to the VIC simulations, the SPLASH model seems to reproduce the general patterns more reasonably (Fig. 29).

Figure 29 Mean seasonal cycle of C_n per climate zone. The gray areas show 1 SD from the observed mean. Climate zones are described in Table A3.

6.2.5 Snowfall

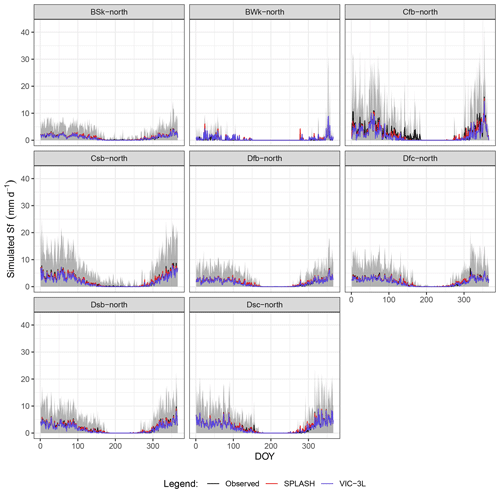
The seasonal patterns of Sf show differences in the magnitudes between climate zones with and without a dry season only in temperate types (Cfb, Csb), while wet continental (Df*) types did not show noticeable differences with their dry counterparts (Ds*). Arid climates (B*), on the other hand, showed the lowest magnitudes. The patterns simulated by SPLASH match the observations for all the climate zones almost perfectly, in agreement with the VIC simulations as well. Some underestimation is noticeable at the end of the winter in the wet temperate zone (Cfb) (Fig. 30).

Figure 30 Mean seasonal cycle of Sf per climate zone. The gray areas show 1 SD from the observed mean. Climate zones are described in Table A3.

6.2.6 Snowmelt

Seasonal patterns of Sm appear more clearly in the continental climate zones (D* types) with an expected peak at the beginning of spring; the other climate zones apparently do not show a general pattern. The SPLASH model was able to simulate the start of the melting process in all the climate zones; however, it captures the seasonal pattern only in wet continental climates (Df*), while overestimating Sm in their dry counterparts (Ds*). Overall the seasonal patterns from SPLASH seem to agree with the simulations better than the results of the VIC model, which shows a temporal lag at the start and peak of the melting period (Fig. 31).

Figure 31 Mean seasonal cycle of Sm per climate zone. The gray areas show 1 SD from the observed mean. Climate zones are described in Table A3.

6.2.7 Surface runoff and lateral flow

The SPLASH simulations of total streamflow (TSF) (RO+q_out) in the watersheds were able to explain 71 % of the variation, while the estimations of surface runoff accounted for 69 % of the variation. The bias in both analyses shows a systematic underestimation of this flux, especially at the lower end (Fig. 32).

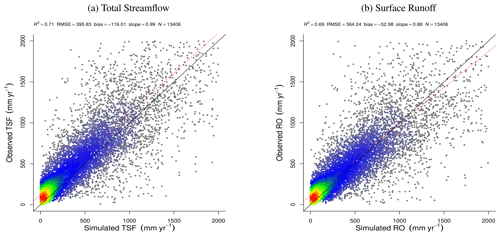
Figure 32 Correlation of observed and simulated values of discharge with data from all the watersheds pooled. The color scale represents the plotted point density, where blue indicates lower densities and red indicates higher densities. (a) Total streamflow. (b) Surface runoff.

SPLASH simulations of TSF and RO in the same watersheds as VIC showed that although VIC achieved slightly better performance, SPLASH can achieve very similar R² values. The slope of simulated vs. observed data suggests that SPLASH, without any local calibration, can reach 80 % of the accuracy of VIC calibrated with historical data (Fig. 33).

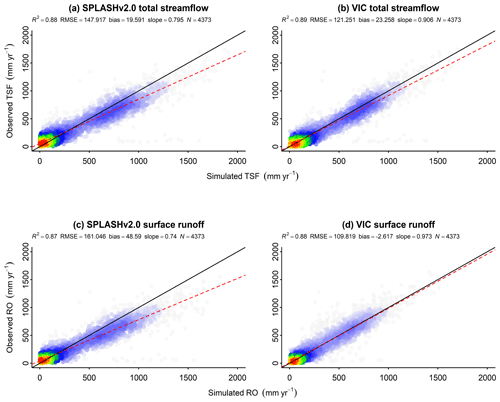
Figure 33 Correlation of observed and simulated values of discharge with data from all the watersheds pooled. The color scale represents the plotted point density, where blue indicates lower densities and red indicates higher densities. (a) Total streamflow. (b) Surface runoff.

Tracking down the source of the systematic underestimation by analyzing the time series of observed and simulated TSF from Rietholzbach in detail, the underestimation appeared greater during winter months when the precipitation is below the average. On the other hand, when the precipitation is peaking, overestimation occurs in some years, seemingly without showing any systematic pattern (Fig. 34f).

The simulated time series of baseflow index BFI $\left(\frac{q_{\mathrm{out}}}{q_{\mathrm{out}}+\mathrm{RO}}\right)$ roughly follows the temporal dynamics of the observations. Overestimations appear in the winter months due to the underestimations of surface RO during these months (Fig. 34e). Furthermore, the spatial patterns resulting from the simulation show that the runoff is higher in areas surrounding the stream, which emerges from the flux accumulation at the valley bottom (Fig. 34b).

Moreover, the lateral flow is mostly produced in the north-facing slopes and in some areas next to the main stream, upslope from the main outlet. The BFI is close to 1 in most of the watershed, except in areas close to the stream, suggesting that most of the simulated hydrological response is subsurface flow (Fig. 34a).

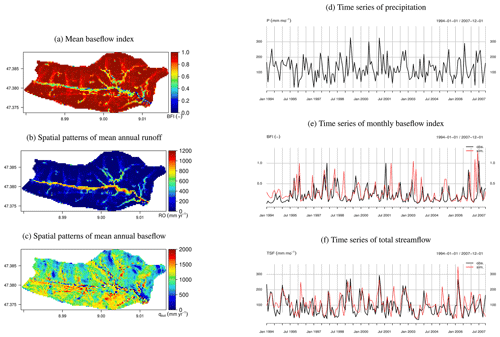
Figure 34 Spatial and temporal patterns of runoff in a small wet temperate watershed in Rietholzbach, Switzerland. (a) Spatial patterns of mean soil water content in the first 2 m during 1994–2007. (b) Spatial patterns of mean annual runoff during 1994–2007. (c) Spatial patterns of mean annual baseflow during 1994–2007. (d) Time series of precipitation 1994–2007. (e) Time series of SWC in the first 1 m of depth during 1994–2007. (f) Time series of total streamflow during 1994–2007.

The monthly means of BFI from the long-term data from Rietholzbach suggest that the underestimation of surface RO is indeed systematic and the major discrepancies appear in November and December (Fig. 35).

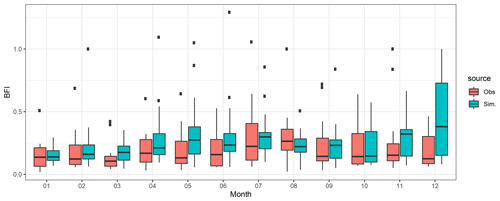
Figure 35 Mean monthly BFI for 1994–2007 in a small wet temperate watershed in Rietholzbach, Switzerland, for the period 1994–2007.

At a daily time step, the results of the simulation in the tropical watershed show that the performance of SPLASH simulating fast storm response is poor, and the model fails in capturing the expected runoff peaks during relatively big storms at a daily timescale (Fig. 36e). Nonetheless, the spatial patterns generated by SPLASH in this small watershed reproduce mostly saturation excess runoff in areas close to the streams (Fig. 36a), while the simulated lateral flow appears stable spatially and over time (Fig. 36c and d).

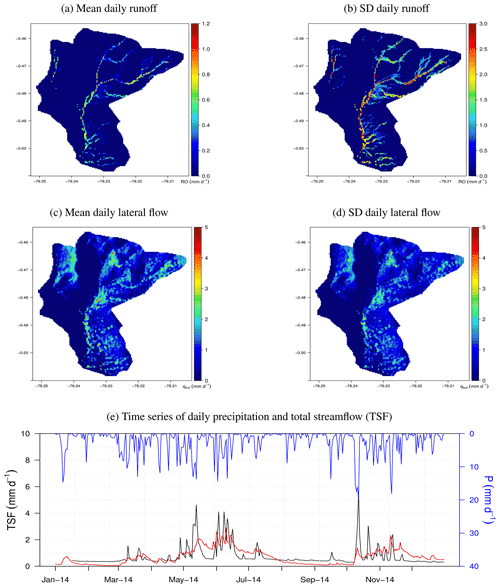
Figure 36 Spatial and temporal patterns of daily fluxes in a tropical small watershed in Jatunhuayco, Ecuador. (a) Mean daily runoff during 2014. (b) Standard deviation of the daily runoff in 2014. (c) Mean daily lateral flow during 2014. (d) Standard deviation of the daily lateral flow during 2014. (e) Time series of daily precipitation and total streamflow during 2014.

6.3 Storages

6.3.1 Snow-water equivalent

The simple formulations proposed to simulate SWE were able to explain 88 % of the observed variation across 127 SNOTEL sites located in mountain regions. The mean value of the observations aggregated by biome shows that SWE in evergreen needleleaf forest (ENF) is the largest among the biomes, while the lowest value was from open–deciduous canopies (OSH, DBF). The bias suggests that SPLASH is underestimating SWE at low values; however, the huge variation of the observations in all biomes suggests that the differences are not significant (Fig. 37).

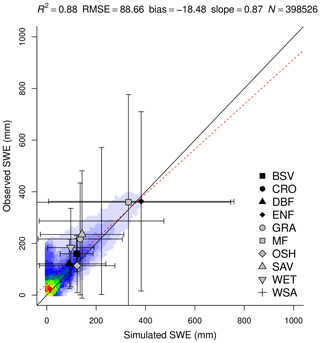
Figure 37 Correlation of observed and simulated values of daily SWE, with values of all sites pooled. The color scale represents the plotted point density, where blue indicates lower densities and red indicates higher densities.

The seasonal patterns of SWE depict the well-known bell-shaped curve during winter with great deviations from the seasonal mean. Here, the sites in the temperate climate zones without a dry season showed the greatest deviation (Cfb). The SPLASH model was able to reproduce the seasonal patterns in all the climate zones. It underestimates, to different degrees, the averages within the range of the observations, which contrasts with the overestimation of the VIC simulations. Nonetheless, SPLASH captures the length of the snow-covered period almost perfectly, failing only in the Cfb zone, where it overestimates SWE during the melting period; here VIC outperforms SPLASH (Fig. 38).

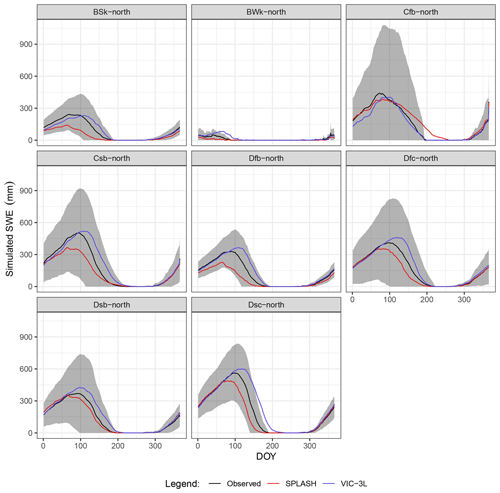
Figure 38 Mean seasonal cycle of SWE per climate zone. The gray areas show 1 SD from the observed mean. Climate zones are described in Table A3.

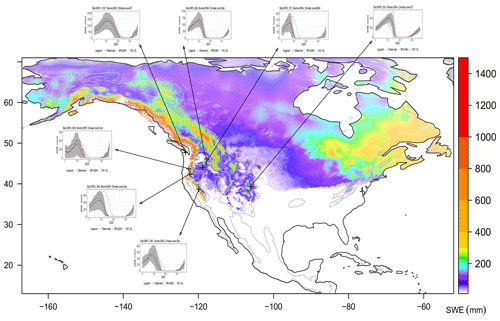
The spatially distributed high-resolution simulation over North America showed strong patterns defined by the topography, with higher SWE over the mountain regions and variations according to the slope exposure. A well-defined lower boundary for the snow-covered area emerged in the eastern US around 40° of latitude, coinciding with the transition from climates Cfa to Dfa, while on mountain summits the simulated SWE fades at around 35° (Fig. 39).

Figure 39 Spatial patterns of mean monthly maximum SWE for the period 2010–2016 over North America at 1 km resolution, along with site simulation examples from the mountains. The gray areas show 1 SD from the observed mean.

6.3.2 Soil water content

The performance evaluation of daily SWC was done with data from stations measuring soil moisture deeper than 30 cm located in the mountain regions, resulting in 16 EC (Fig. 40a) and 127 SNOTEL (Fig. 40b) stations. Comparison among biomes was not possible due to the different depths of measurement at each station. This shows, for example, because of mostly superficial measurements, wetlands at the lower end of the observation axis (Fig. 40b). Nevertheless, the SPLASH model was able to explain 86 % of the variation in the EC dataset, which is around 7 times smaller than the SNOTEL dataset where SPLASH explained 54 % of the variation. The evaluation also shows that SWC was overestimated by the SPLASH model in grassland ecosystems (GRA) and in open shrublands (OSH) (Fig. 40).

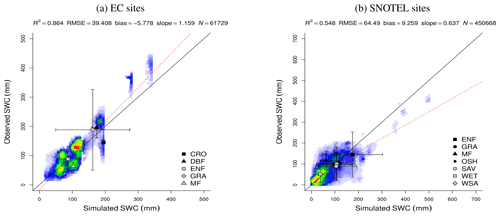
Figure 40 Correlation of observed and simulated values of daily SWC, with values of all sites pooled. The color scale represents the plotted point density, where blue indicates lower densities and red indicates higher densities.

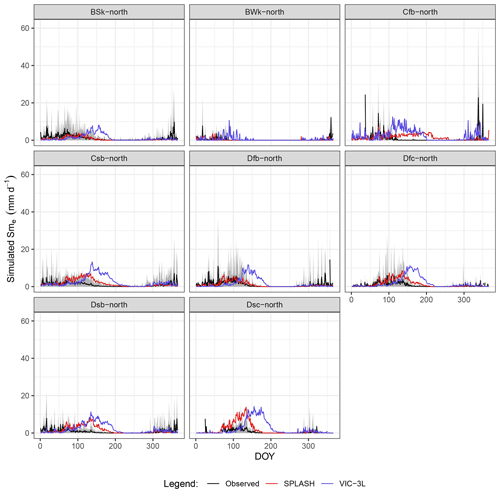
The seasonal patterns of Θ, extracted from the data and simulations at SNOTEL sites, show a sinusoidal shape in all the climate zones. The highest point appears during the first half of the spring and the lowest point by the end of the summer. Most of the climate zones show huge deviations from the mean, especially the zones without a dry season (e.g., Cfb, Dfc), except for the cold desert (BWk) where this variation is smaller.

The SPLASH model shows reasonable agreement of the seasonal pattern for climate zones with warm and dry summers (i.e., Csb, Dsb) and for the cold steppe (BSk). In these climate zones, SPLASH reproduces the seasonality in a better way than VIC.

In some continental climates (Dfb, Dfc, Dsc), SPLASH produces a similar pattern to the observed mean but downshifted inside the expected deviation. In these climate zones, the VIC model approaches the observed mean only during spring–summer months. In the warm-summer temperate climate with no dry season (Cfb), SPLASH is not able to reproduce the seasonal pattern, and the amplitude of the sinusoidal shape is too small to match the observations. Here, VIC agrees with the observations briefly during winter. In the cold desert (BWk) SPLASH does not produce a seasonal pattern, and the average through the year remains close to the minimum. Here VIC overestimates Θ during spring and produces negative values during the spring and summer months (Fig. 41).

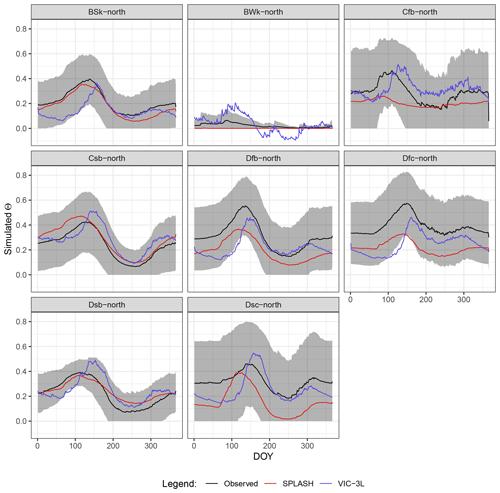
Figure 41 Mean seasonal cycle of Θ per climate zone. The gray areas show 1 SD from the observed mean. Climate zones are described in Table A3.

The spatially distributed simulation of relative soil moisture saturation shows that the patterns of the annual average roughly follow the global climate zone distribution. At this resolution, the model was incapable of reproducing the streams and most of the mountain regions emerged as areas half- to low-saturated (Fig. 42).

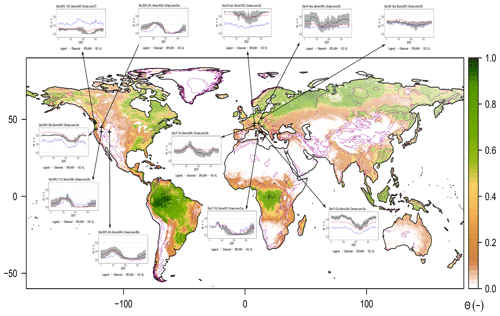
Figure 42 Spatial patterns of mean annual Θ for the period 2010–2016 at 5 km resolution along with site simulation examples from the mountains. The gray areas show 1 SD from the observed mean.

The spatial patterns of the total soil water content in the temperate watershed show an emergent accumulation at the valley bottom, shaping the stream. Here, the SD is very small, suggesting that the valley bottom remains wet most of the year (Fig. 43d).

The different patterns over north- and south-facing slopes show the former with more water content over the latter but more variations over time. The emergent variations in the north-facing slope are shaped by the inclination of the slope, while on the south-facing slope, this pattern seems to follow the aspect (Fig. 43c).

The time series of soil water content over the first meter of depth was poorly reproduced by SPLASH, and in some years the simulation matches the observations (e.g., 2006); however, in most of the years the droughts are underestimated and the peaks are overestimated (Fig. 43e).

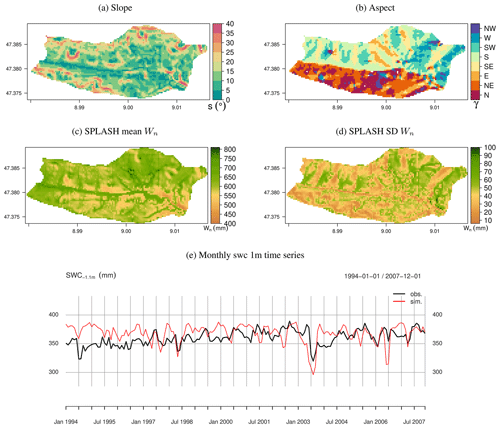
Figure 43 Spatial and temporal patterns of soil water content in a small wet temperate watershed in Rietholzbach, Switzerland. (a) Slope in degrees. (b) Slope orientation; N stands for north, S for south, and so on. (c) Mean annual simulated soil water content in the whole column during 1994–2007. (d) The standard deviation of the daily soil water content in the whole column during 1994–2007. (e) Time series of monthly soil water content, simulated and observed over the first 1 m of depth.

In the tropical watershed, the spatial patterns of the daily average W_n show the emergent stream at the valley bottom; according to the simulations the daily water content here is more variable than in the rest of the watershed (Fig. 44d), contrary to the temperate watershed where this pattern was opposite. Here the east–west aspects define the spatial patterns, and the eastern flanks show less water content than their western counterparts (Fig. 44c).

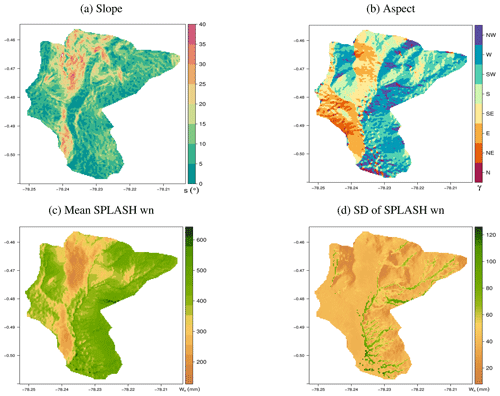
Figure 44 Spatial patterns of daily soil water content in a wet tropical watershed in Jatunhuayco, Ecuador. (a) Slope in degrees. (b) Slope orientation; N stands for north, S for south, and so on. (c) Mean daily soil water content during 2014. (d) Standard deviation of the daily soil water content during 2014.

7 Discussion

The updated SPLASH model showed reasonable agreement with the observations in all the fluxes analyzed here without any local calibration or prescribed land cover information. The data requirements to run the model (precipitation, solar radiation, air temperature, elevation, and soil texture) are modest; the open-source code, compiled in a ready-to-use package, facilitates replication.

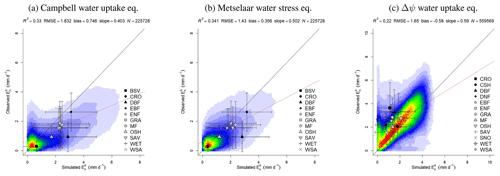
Figure 45 Simulation experiments against EC observations using different soil water stress and water uptake functions. The color scale represents the plotted point density, where blue indicates lower densities and red indicates higher densities. (a) Using the Campbell and Norman (1998) water uptake function at mountain sites. (b) Using the Metselaar and de Jong van Lier (2007) water stress function and a constant Sc=1.05 (mm h⁻¹) (Federer, 1982) at mountain sites. (c) Using the gradient of water potential soil-leaf Δψ to drive the water uptake in the entire FLUXNET database.

The analytical approach used to solve the energy and water fluxes allowed the model to run with high-resolution data on global scales without using statistical–dynamical flux parameterizations or hydrological unit responses. Emergent patterns produced by the model follow the natural accumulation of soil moisture downslope. Most of the fluxes and storages analyzed here agree with – and sometimes outperform – the more complex VIC-3L model, which was chosen for comparison due to its wide use in ecohydrological applications and its well-known good performance.

SPLASH assumes background albedo, a parameter particularly crucial due to its synergy with water fluxes, to be constant for all biomes. This contrasts with the VIC model, which uses monthly albedo per vegetation class (Gao et al., 2009). Nonetheless, SPLASH showed overall good agreement of $H_{\mathrm{n}}^{+}$ with the observations, suggesting that the snow effect on the albedo is much stronger than the effects of the phenology in snow-covered regions (Xiao et al., 2017). This global albedo assumption, however, is more likely to be the cause of the discrepancy of $H_{\mathrm{n}}^{+}$ in ecosystems with sparse vegetation cover (e.g., BSV and OSH), where the extent of exposed soil and its moisture status modify the albedo (Campbell and Norman, 1998; Barry, 2008).

Although the ground heat flux is ignored by the model, an improvement in the calculation of $H_{\mathrm{n}}^{+}$ is noticed relative to the previous version (Davis et al., 2017), where the overestimation in the arid desert (BWh) is fixed with the new parameterization of the longwave radiation and the overestimation in the polar tundra (ET) is corrected by the new included feedback of snow albedo.

Simulated actual evapotranspiration ($E_n^{\mathrm{a}}$) is underestimated to various degrees in all biomes. As model performance for $H_{\mathrm{n}}^{+}$ is high, this suggests that the $E_n^{\mathrm{a}}$ discrepancies are related to the empirical parameterization of the water supply and uptake (S_W). Theoretically, this should be driven by the soil-to-leaf-water potential gradient (Δψ) (Prentice et al., 2014), thus reflecting different plant strategies to deal with drought. However, when this idea was tested during the development stage, the performance of the simulations decreased (Fig. 45c), probably due to the calculation method used for the leaf water potential and its assumptions (both taken from the literature): the canopy well coupled to the atmosphere at pre-dawn (thus T_s=T_a) and the relative water content of the leaf close to saturation (Appendix A4).

Although in this version of SPLASH, we propose a physically based calculation for the upper threshold of S_W, its response to the water deficit is conceptualized as a linear function, which has been reported as the most simple and reasonable empirical description (e.g., Federer, 1982). Nonetheless, several authors report more complex formulations depicting convex (Campbell and Norman, 1998), concave (Metselaar and de Jong van Lier, 2007), or trapezoidal (Feddes and Raats, 2004) shapes. Some of these formulations were tested during the development stage of the model, with no significant improvement over the simple linear formulation (Fig. 45).

From this experimentation, the assumption made on the maximum supply rate S_c as the maximum rate of evaporation yielded the best approximations. This assumption makes more sense in bare-ground areas; however, in vegetated areas, this value should reflect the plant controls on transpiration, which ideally needs to be addressed with ideas based on eco-evolutionary optimality theory (Harrison et al., 2021).

Since SPLASH seems to reproduce the evapotranspiration better over non-water-limited areas, in such areas, slopes facing the Equator (south-facing slopes in the Northern Hemisphere) should, in theory, show higher values than their opposite-facing counterparts, which receive less radiation (Körner, 2021; Chapin et al., 2011).

This spatial pattern is indeed produced by SPLASH in the Rietholzbach experimental catchment. However, here the latent heat calculated from the Landsat 5 retrievals does not show any strong differences between north- and south-facing slopes. It is still unclear if the spatial patterns from Landsat are correct; the SEBAL algorithm used the calculate LE is limited to clear-sky pixels only, and thus a large amount of data was excluded from the calculation. Furthermore, this algorithm computes an instantaneous $\frac{\mathrm{LE}}{\mathrm{Rn}-G}$ (at the satellite overpass), and then it assumes this proportion is constant through the day, so the daily E^a can be calculated from the daily accumulated Rn measured on the ground (Bastiaanssen et al., 1998a). Therefore, a more accurate estimation from SEBAL would involve terrain-corrected independent calculations of Rn at Landsat spatial resolution, which were unavailable at the time of this comparison. Land use in Rietholzbach also plays a key role in shaping the spatial patterns of LE.

SPLASH in theory reflects the environment the plants experience. The spin-up routine produces an initial state of equilibrium, and thus in areas with natural vegetation the spatial patterns produced by SPLASH should reflect this vegetation cover to some degree. This is shown in the agreement (to some extent) of the spatial patterns of $E_n^{\mathrm{a}}$ produced by SPLASH compared with the Landsat 8 LE in the tropical watershed, which always had natural vegetation. This microclimatic gradient created by the slope and aspect is particularly important to explain outlier populations existing beyond their major distribution zone, which can colonize their surroundings during rapid climatic changes (Chapin et al., 2011).

Although the results presented here are encouraging, more rigorous comparisons are needed to evaluate how well the fluxes produced by SPLASH reflect patterns of naturally occurring vegetation.

The less-than-optimal performance of SPLASH simulating condensation is mainly due to the lack of other environmental variables needed to calculate the dew point and surface temperature, such as air humidity, wind speed, and aerodynamic resistance. Nonetheless, the simple assumption made to estimate this flux (10 % of $H_{\mathrm{N}}^{-}$) reproduces the seasonal Cn better than VIC. The major discrepancies of VIC's Cn happen during the spring–summer months, suggesting that some of the heat lost as Cn (latent) is actually lost from the surface by convection, cooling the leaves. The yearly magnitudes of dew formed by Cn suggest that its impact on the water balance is minimal in most climate zones, except for hot arid climate zones (BSh), where Cn has ecological importance, in agreement with the observations reported by Guo et al. (2016) and Yu et al. (2020).

The size of the snowpack (SWE) simulated by SPLASH agrees more than 80 % with the observations; however, its seasonal patterns show a systematic underestimation in most of the climate zones. Since the seasonal patterns of the snowfall (Sf) produced by SPLASH match the observations in all the climate zones, the snowmelt (Sm) is reasonably well predicted in the steppe (BSk) and the wet continental climates (Df*). In these climate zones, the discrepancies seem to be due to the redistribution of snow by the wind, which is greatly dependent on the structure of the vegetation (Barry, 2008; Pomeroy and Brun, 2001) and is not considered by the model. In dry continental and temperate climates (Ds*, Csb), on the other hand, SPLASH systematically underestimates SWE. Here the cause is more likely to be neglecting the “cold content” of the snow, which in turn causes an overestimation of Sm. This effect is stronger at high elevations where the temperature is lower; here VIC delivers better estimations than SPLASH (Fig. 45). Moreover, despite the discrepancies in the simulated magnitudes at these sites, the duration of the snow-covered period is reasonably predicted, considering that the multi-annual variation can be up to 1 month (Körner, 2021).

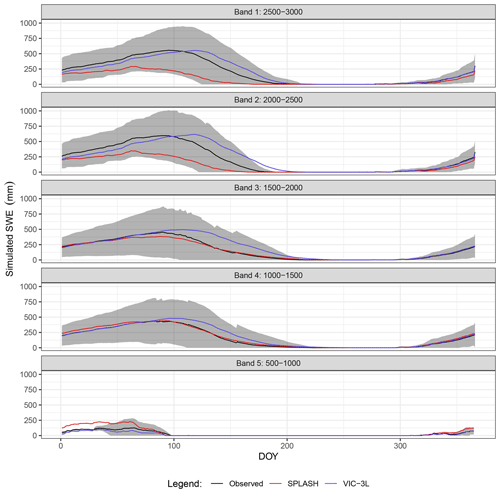
Figure 46 Mean seasonal cycle of SWE over dry temperate climates (Csb) per elevation band. Results aggregated every 500 m a.s.l. The lines show the means, while the gray shaded area shows the SD.

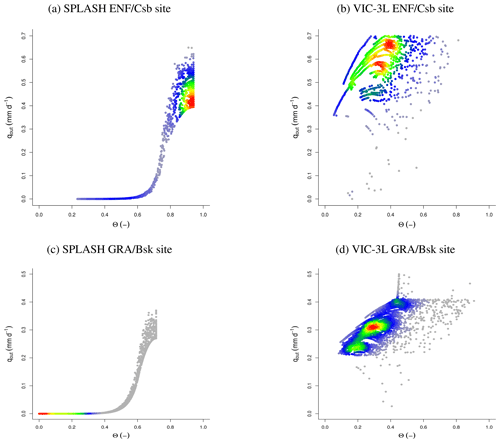
Figure 47 Emergent response of the lateral flow to soil moisture from an ENF in a temperate climate, with a dry and warm summer (Csb) (site SNTL:529), simulated from (a) SPLASH and (b) VIC-3L. The same relationship from a GRA in an arid cold steppe (Bsk) (site SNTL:871), simulated from (c) SPLASH and (d) VIC-3L.

Although in theory, different sets of parameters in the snow albedo functions, depending on the complexity of the canopy, should yield more accurate predictions (e.g., Romanov, 2003), the performance of SPLASH simulating SWE shows that one set of parameters is able to deliver reasonable approximations for all types of biomes. Such an approximation was possible using roughly 10⁶ of RS and ground data points spawned over 15 years at 315 stations during the optimization process. The use of one set of parameters is nothing new and has been done for a long time; however, in previous studies, the number of observations and available tools limited the spatial representativity of these calibrations (Clark et al., 2017). Nonetheless, the parameters found in SPLASH for the snow albedo decay function are consistent with the values proposed in the Noah model by Livneh et al. (2010), although in SPLASH there are no different sets of parameters for accumulation and melt seasons.

The spatial patterns of the surface runoff generated by SPLASH in the small watersheds show that most of this flux is generated in the saturated zone in the valley bottom, in agreement with what is expected in montane regions (Grayson and Blöschl, 2000; Weizu and Freer, 1995).

Moreover, the spatial patterns of BFI produced by SPLASH in Rietholzbach agree with previous studies which show that most of the streamflow is produced by subsurface flow, especially interflow (Von Freyberg et al., 2014; Gurtz et al., 2003). However, the poor performance of SPLASH simulating the daily surface runoff in the Andean catchment suggests that the assumption made for the event duration does not hold for this area, or the saturated zone close to the stream, which controls this flux in Andean catchments (Correa et al., 2020), is underestimated.

Although the simulations of soil moisture are overall reasonable and the results mostly matched the temporal dynamics of the observations, two recurrent errors were observed among the simulations (or a combination of these errors): the resultant soil moisture appears up- or downshifted randomly (first error), or the amplitude of the variations is different from what is observed (second error).

The first type of error seems to be related to the estimation of the bucket size, which in turn is defined by the pedotransfer functions and soil data. Although the pedotransfer functions were optimized with a global dataset, which covers a wide spectrum of textural classes with a wide range of SOM combinations, the empirical nature of these equations is a well-documented source of error (Pachepsky et al., 2015; Van Looy et al., 2017; Paschalis et al., 2022). This error might explain why the evapotranspiration and total streamflow agree with the observations in Rietholzbach, but the performance of the soil moisture simulation was very poor.

The second type of error was less recurrent with the SNOTEL dataset, which includes actual measurements of soil properties, suggesting that the data obtained from SoilGrids for the EC sites might be a source of this error. The coarser volumetric fraction (stoniness) in particular can reduce the size of the bucket dramatically here. However, a rigorous evaluation and sensitivity analysis are needed to define this source of error in a broader modeling context.

The spatial patterns of soil moisture at a global scale show how the assumption of the model of a maximum depth breaks the hydrological connectivity in large watersheds. Here, the model forces the water to flow down instead of laterally if the bedrock is not in the first 2 m of depth. On the other hand, in small watersheds, the hydrological connectivity emerges from the conceptualization of the model accumulating the moisture at the valley bottom and shaping the streams.

Furthermore, the lateral flow simulated by SPLASH is strongly related to the soil water content, consistent with what has been reported in Rietholzbach (Teuling et al., 2010) and in Andean watersheds (Crespo et al., 2011).

The exponential decay of the saturated conductivity with depth, widely used in TOPMODEL-type models, was deliberately excluded from the model. The saturated hydraulic conductivity is highly dependent on the organic matter content and was calculated using a weighted average (by depth) of SOM as an input. Since SOM generally decreases exponentially with depth (Kramer and Gleixner, 2008; Hobley and Wilson, 2016; Bai et al., 2016) this estimated K_sat should be reproducing the decay to some degree. However, the available data used for the optimization of the pedotransfer functions calculating K_sat were biased towards sandy and loamy-sand soils, affecting the performance in the rest of the textural classes.

The lateral flow equation proposed here is based on the profile transmissivity, originally proposed by TOPMODEL and the assumption of steady-state flow. However, it has been reported that the steady-state flow assumption holds better in wet catchments with high hydraulic gradients. In dry catchments or during dry periods, areas of the catchment may lose their hydrological connectivity (Woods et al., 1997; Tague and Band, 2001).

Analyzing the response of the lateral flow to soil moisture generated by SPLASH, the minimum q_out reflects stable gravity-driven drainage (which in shallow soils defines the baseflow), while the maximum q_out appears as pulses resulting from individual precipitation events, mimicking the behavior of the interflow (Fig. 47a). This response is consistent in both wet and arid sites, albeit with varying magnitudes (Fig. 47c).

In VIC3-L, however, q_out reaches values of the order of hundreds (truncated in the figure), while soil moisture is not even saturated (Fig. 47b). In the comparable region of the analysis, the upper envelope of the scattered points shows a linear threshold and a sharp transition to a plateau. The flux here seems to display relatively high values when the soil moisture is close to the wilting point, which is theoretically impossible.

Despite the limitations discussed, the updated SPLASH model provides fast and parsimonious means to generate robust estimates of water and energy budgets across regions, regardless of their topographic complexity and spatial scale. The calibration-free approach enhances the model’s portability and the ecological interpretability of the results. Moreover, since the structure of the model contains fewer moving parts than any other LSMs, it facilitates formulating ecologically driven working hypotheses on why results do not match the observations in the case of big discrepancies. With targeted refinements, SPLASH could become an even more robust tool for ecohydrological modeling and for exploring hydrological impacts of global change.

Appendix A: Derivations and extended mathematical analysis

A1 Recession constant

Analyzing the flux from one cell, according to the linear reservoir model (Eq. 42) and the BC model (Eq. 39), the maximum (initial) lateral flux will happen when the soil is saturated. In the same way, it will be close to zero at field capacity. Thus, if we set the volume of the drainable porosity equal to the total volume drained by Eq. (42), then

$$\begin{array}{}\text{(A1)}& (W_{\mathrm{sat}}-W_{\mathrm{fc}})\mathrm{Ai}=\underset{\mathrm{0}}{\overset{t}{\int }}{Q}_{\mathrm{sat}}{K_b}^t\mathrm{d}t.\end{array}$$

Solving both Eqs. (42) and (A1) for t, we can set

$$\begin{array}{}\text{(A2)}& {\displaystyle \frac{\mathrm{1}}{\ln \left(K_b\right)}}\ln \left({\displaystyle \frac{Q_{\mathrm{fc}}}{Q_{\mathrm{sat}}}}\right)={\displaystyle \frac{\mathrm{1}}{\ln \left(K_b\right)}}\ln \left({\displaystyle \frac{\mathrm{Ai}(W_{\mathrm{sat}}-W_{\mathrm{fc}})\ln \left(K_b\right)}{Q_{\mathrm{sat}}}}+\mathrm{1}\right).\end{array}$$

Therefore, solving Eq. (A2) for K_b, we get

$$\begin{array}{}\text{(A3)}& K_b=e^{\frac{Q_{\mathrm{fc}}-Q_{\mathrm{sat}}}{\mathrm{Ai}(W_{\mathrm{sat}}-W_{\mathrm{fc}})}}.\end{array}$$

A2 Actual field capacity

Replacing Eqs. (55), (56b), and (57) in Eq. (54) yields

$$\begin{array}{}\text{(A4)}& A(\mathit{\theta }{)}^{-B}-{\mathit{\rho }}_{\mathrm{w}}g\mathit{\theta }(\mathrm{1000}z)=\mathrm{0}.\end{array}$$

Then, converting units to SI and simplifying, we can substitute

$$\begin{array}{}\text{(A5)}& c={\displaystyle \frac{\mathrm{1000}}{{\mathit{\rho }}_{\mathrm{w}}g}},\end{array}$$

where 1000 is a factor to correct the units. This can be rearranged to

$$\begin{array}{}\text{(A6)}& c{\displaystyle \frac{A}{z}}={\displaystyle \frac{\mathit{\theta }}{{\mathit{\theta }}^{-B}}}.\end{array}$$

Thus, solving Eq. (A3) for θ,

$$\begin{array}{}\text{(A7)}& \mathit{\theta }={\left({\displaystyle \frac{cA}{z}}\right)}^{\frac{\mathrm{1}}{\mathrm{1}+B}}.\end{array}$$

A3 Comparable quantities from the VIC-3L model

A3.1 $H_{\mathrm{N}}^{+}$ from $\stackrel{\mathrm{‾}}{I_{\mathrm{N}}}$

VIC-3L provides daily $\stackrel{\mathrm{‾}}{I_{\mathrm{N}}}$ (W m⁻²) as output, so the comparable quantity representing the total input of energy can be found as

$$\begin{array}{}\text{(A8)}& H_{\mathrm{N}}^{+}=\mathrm{86}\mathrm{400}\stackrel{\mathrm{‾}}{I_{\mathrm{N}}}+H_{\mathrm{N}}^{-}.\end{array}$$

Among the outputs from the VIC-3L model are I_SWmax and I_LW, so if at solar noon (h=0) $I_{\mathrm{SW}}=I_{\mathrm{SW}}max$ and at h=h_n, I_SW=I_LW, then

$$\begin{array}{}\text{(A9)}& \begin{array}{rl}& I_{\mathrm{SW}}max\cos h_{\mathrm{n}}=I_{\mathrm{LW}},\\ & \Rightarrow h_{\mathrm{n}}=\arccos {\displaystyle \frac{I_{\mathrm{LW}}}{I_{\mathrm{SW}}max}},\end{array}\end{array}$$

where I_SW=I_LW, and I_SW=0 at h=h_s also implies the line

$$\begin{array}{}\text{(A10)}& \mathrm{0}=I_{\mathrm{SW}}max-\left({\displaystyle \frac{I_{\mathrm{SW}}max-I_{\mathrm{LW}}}{h_{\mathrm{s}}}}\right)h_{\mathrm{n}}.\end{array}$$

Solving for h_s yields

$$\begin{array}{}\text{(A11)}& h_{\mathrm{s}}=h_{\mathrm{n}}\left(\mathrm{1}+{\displaystyle \frac{I_{\mathrm{LW}}}{I_{\mathrm{SW}}max}}\right).\end{array}$$

Then, the area representing $H_{\mathrm{N}}^{-}$ is

$$\begin{array}{}\text{(A12)}& H_{\mathrm{N}}^{-}={\displaystyle \frac{\mathrm{86}\mathrm{400}}{\mathit{\pi }}}(\mathit{\pi }-h_{\mathrm{s}})I_{\mathrm{LW}}+{\displaystyle \frac{(h_{\mathrm{s}}-h_{\mathrm{n}})I_{\mathrm{LW}}}{\mathrm{2}}}.\end{array}$$

A3.2 C_n from latent heat components

VIC-3L provides daily average of the net latent heat as output, along with its components used to melt or refreeze soil and snow, so C_n was computed simply as the remnant negative latent heat after the components were subtracted from the net latent heat.

$$\begin{array}{}\text{(A13)}& \begin{array}{rl}{C}_n& =({\mathrm{OUT}}_{\mathrm{LATENT}}+{\mathrm{OUT}}_{\mathrm{FUSION}}+{\mathrm{OUT}}_{\mathrm{MELT}\mathrm{ENERGY}}\\ & +{\mathrm{OUT}}_{\mathrm{RFRZ}\mathrm{ENERGY}})\times (\mathrm{86.4}/\mathrm{2260})-{\mathrm{OUT}}_{\mathrm{EVAP}}\end{array}\end{array}$$

Here, the factor $(\mathrm{86.4}/\mathrm{2260})$ transforms from W m⁻² to mm d⁻¹ assuming constant water density and vaporization heat of 2260 kJ kg⁻¹.

A4 Water uptake and water stress functions

A4.1 Water uptake from Δψ

Transpiration can be defined following Campbell and Norman (1998) as

$$\begin{array}{}\text{(A14)}& E=S_{\mathrm{W}}=\left({\displaystyle \frac{{\mathit{\psi }}_{\mathrm{s}}-{\mathit{\psi }}_{\mathrm{L}}}{R_{\mathrm{p}}}}\right),\end{array}$$

where ψ_s is the soil water potential, ψ_L the leaf water potential, and R_p the total plant hydraulic resistance from the root to the leaf.

Then, without soil moisture limitations (ψ_s=0), the transpiration becomes

$$\begin{array}{}\text{(A15)}& E_{\max }=D_p=\left({\displaystyle \frac{-{\mathit{\psi }}_{\mathrm{L}}}{R_{\mathrm{p}}}}\right).\end{array}$$

Then, solving Eq. (A15) for R_p and replacing in Eq. (A14) results in

$$\begin{array}{}\text{(A16)}& S_{\mathrm{W}}=D_p\left(\mathrm{1}-{\displaystyle \frac{-{\mathit{\psi }}_{\mathrm{s}}}{{\mathit{\psi }}_{\mathrm{L}}}}\right),\end{array}$$

where ψ_L is found using the first law of thermodynamics: $\mathrm{dU}=\mathrm{dQ}-\mathrm{PdV}$, where dU is the change in internal energy, dQ is the instantaneous heat input, and PdV is the work done at constant pressure.

So, if $\mathit{\psi }=\frac{U}{\mathrm{Vw}}$ and $\mathrm{PdV}=\frac{-\mathrm{nRT}}{P}\mathrm{dP}$ from the ideal gas law, assuming dQ=0 at pre-dawn, then

$$\begin{array}{}\text{(A17)}& {\mathit{\psi }}_{\mathrm{L}}={\displaystyle \frac{\mathrm{1}}{\mathrm{Vw}}}\underset{P\mathrm{1}}{\overset{P\mathrm{2}}{\int }}{\displaystyle \frac{\mathrm{nRT}}{P}}\mathrm{dP}={\displaystyle \frac{\mathrm{RT}}{\mathrm{Vw}}}\ln {\displaystyle \frac{e_{\mathrm{L}}^{\mathrm{a}}}{e_{\mathrm{L}}^s}},\end{array}$$

where Vw is the molar volume, and $e_{\mathrm{L}}^{\mathrm{a}}$ and $e_{\mathrm{L}}^s$ are the actual and saturation vapor pressure at the leaf surface; its proportion was assumed as 0.98 (Nobel, 1983).

A4.2 Water uptake from Campbell and Norman (1998)

$$\begin{array}{}\text{(A18)}& S_{\mathrm{W}}=D_p\left(\mathrm{1}-{\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}{\displaystyle \frac{{\mathit{\psi }}_{\mathrm{s}}}{{\mathit{\psi }}_{\mathrm{L}}}}\right)\end{array}$$

A4.3 Water stress function from Metselaar and de Jong van Lier (2007)

$$\begin{array}{}\text{(A19)}& S_{\mathrm{W}}=Sc{\displaystyle \frac{{\mathrm{\Theta }}^{a+\mathrm{1}}-{\mathrm{\Theta }}_W^{a+\mathrm{1}}}{{\mathrm{\Theta }}_l^{a+\mathrm{1}}-{\mathrm{\Theta }}_W^{a+\mathrm{1}}}},\end{array}$$

with the following.

$$\begin{array}{}\text{(A20)}& {\displaystyle }\mathrm{\Theta }={\displaystyle \frac{\mathit{\theta }-{\mathit{\theta }}_{\mathrm{r}}}{{\mathit{\theta }}_{\mathrm{s}}-{\mathit{\theta }}_{\mathrm{wp}}}}\text{(A21)}& {\displaystyle }{\mathrm{\Theta }}_l={\displaystyle \frac{{\mathit{\theta }}_l-{\mathit{\theta }}_{\mathrm{r}}}{{\mathit{\theta }}_{\mathrm{s}}-{\mathit{\theta }}_{\mathrm{wp}}}}\text{(A22)}& {\displaystyle }{\mathrm{\Theta }}_W={\displaystyle \frac{{\mathit{\theta }}_{\mathrm{wp}}-{\mathit{\theta }}_{\mathrm{r}}}{{\mathit{\theta }}_{\mathrm{s}}-{\mathit{\theta }}_{\mathrm{wp}}}}\text{(A23)}& {\displaystyle }{\mathit{\theta }}_l={\mathit{\theta }}_{\mathrm{wp}}+A\times ({\mathit{\theta }}_{\mathrm{s}}-{\mathit{\theta }}_{\mathrm{wp}})\text{(A24)}& {\displaystyle }\mathit{\alpha }=\mathrm{3}+\mathrm{2}\mathit{\lambda }\end{array}$$

Here, λ is a parameter for the BC water retention model, A is an empirical parameter defining the curvature of the function, θ_wp θ_s, θ, and θ_r are the volumetric water content at wilting point, saturation, and residual levels, respectively, and Sc=1.05 (mm h⁻¹) after Federer (1982).

A4.4 Rainfall event duration

The rainfall duration followed a Pareto distribution (Fig. A1a). Events lasting between 0 and 1 h had the highest frequency, while around 80 % of the events lasted less than 6 h (Fig. A1b). Here 6 h was the chosen parameter.

Figure A1 Distribution of daily rainy-hour counts from GsMap global hourly data for 2000–2014. (a) Relative frequencies. (b) Cumulative probability.

A5 Pedotransfer functions

From the models tested (Table 2), the equations from Balland et al. (2008), which use the largest dataset and nonlinear formulations, outperformed the other models with the explained variance exceeding 60 % for permanent wilting point (θ₁₅₀₀), field capacity (θ₃₃), and saturation (θ_sat) (Fig. A2).

The PTFs for computing K_sat showed poor performances for all the models, and most of the measurements seem to cluster around 0 to 50 mm h⁻¹, which is only captured by the Cosby et al. (1984) model. Overall, the explained variance of all the models did not reach 10 % (Fig. A3). Here, K_sat values exceeding 526 mm h⁻¹ were considered to be outliers (percentile 90 %) and excluded from the analysis; similar maximum values were presented by Van Looy et al. (2017).

K_sat estimated by the Saxton and Rawls (2006) PTF was the best-performing model; however, it leads to unrealistic values when the drainable porosity (θ_sat−θ₃₃) is relatively high. So, a simple exponential saturating curve was adopted here, which yields similar estimations to Saxton and Rawls (2006) at the lower end of the drainable porosity but it flattens at a fitted K_sat maximum of 623 mm h⁻¹.

Furthermore, to improve these estimations, the equations from Balland et al. (2008) (Eqs. A25a, A25b, A25c, A25d) were optimized using the full dataset employed for this evaluation, resulting in the parameters detailed in Table A1.

$$\begin{array}{}\text{(A25a)}& {\displaystyle }{\mathit{\theta }}_{\mathrm{1500}}={\mathit{\theta }}_{\mathrm{33}}\left(c_{\mathrm{wp}}+(d_{\mathrm{wp}}-c_{\mathrm{wp}}){\mathrm{CLAY}}^{\mathrm{0.5}}\right)\text{(A25b)}& {\displaystyle }{\mathit{\theta }}_{\mathrm{33}}={\mathit{\theta }}_{\mathrm{sat}}\left(c_{\mathrm{fc}}+(d_{\mathrm{fc}}-c_{\mathrm{fc}}){\mathrm{CLAY}}^{\mathrm{0.5}}\right)e^{\frac{a_{\mathrm{fc}}\mathrm{SAND}-b_{\mathrm{fc}}\mathrm{SOM}}{{\mathit{\theta }}_{\mathrm{sat}}}}\text{(A25c)}& {\displaystyle }{\mathit{\theta }}_{\mathrm{sat}}=\mathrm{1}-{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{b}}}{{\mathit{\rho }}_{\mathrm{p}}}}\text{(A25d)}& {\displaystyle }{K}_{\mathrm{sat}}={\mathrm{10}}^{a_{\mathrm{ks}}+b_{\mathrm{ks}}{\log }_{\mathrm{10}}({\mathit{\rho }}_{\mathrm{p}}-{\mathit{\rho }}_{\mathrm{b}})+c_{\mathrm{ks}}\mathrm{SAND}}\end{array}$$

Here, θ₁₅₀₀ is the wilting point (water held at 1500 kPa), θ₃₃ is the field capacity (water held at 33 kPa), θ_sat is saturation, K_sat is the saturated hydraulic conductivity, and SAND, CLAY ,and SOM refer to sand, clay, and organic matter contents (%). a, b, and c are constants with the subscripts referring to wilting point, field capacity, or hydraulic saturated conductivity, respectively; ρ_b is the bulk density, and ρ_p is the particle density, calculated as follows (Balland et al., 2008):

$$\begin{array}{}\text{(A26)}& {\mathit{\rho }}_{\mathrm{p}}={\displaystyle \frac{\mathrm{1}}{\frac{\mathrm{SOM}}{\mathrm{1.3}}+\frac{\mathrm{1}-\mathrm{SOM}}{\mathrm{2.65}}}}.\end{array}$$

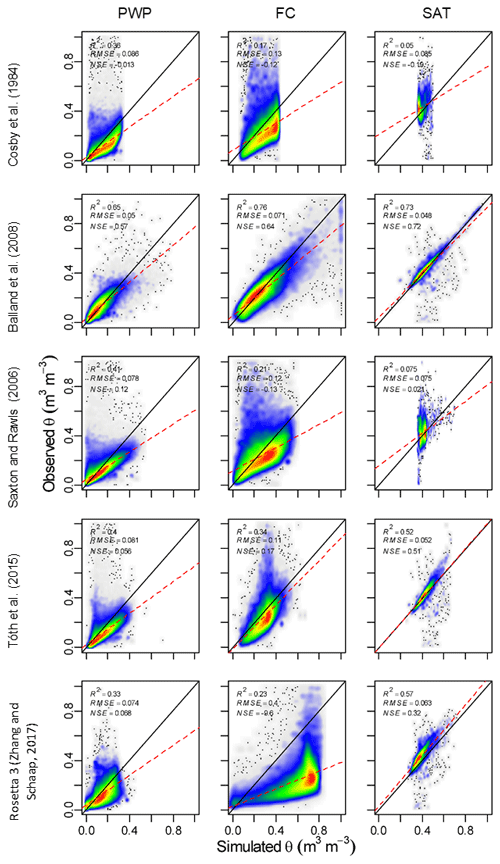
Figure A2 Evaluation of different pedotransfer functions to estimate θ₁₅₀₀, θ₃₃, and θ_sat for n=68 567. The color scale represents the plotted point density, where blue indicates lower densities and red indicates higher densities.

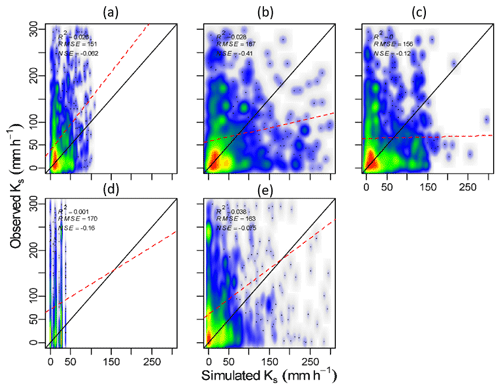
Figure A3 Evaluation of different pedotransfer functions to estimate K_sat. The color scale represents the plotted point density, where blue indicates lower densities and red indicates higher densities. (a) Cosby et al. (1984). (b) Balland et al. (2008). (c) Saxton and Rawls (2006). (d) Tóth et al. (2015). (e) Rosetta 3 (Zhang and Schaap, 2017).

Table A1 Updated parameters for the Balland et al. (2008) PTFs.

Table A2 IGBP biomes and their description.

Table A3 Köppen–Geiger climate zones after Beck et al. (2018). T_cold is the air temperature of the coldest month (°C); T_hot is the air temperature of the warmest month (°C); T_mon10 is the number of months with air temperature >10 °C (unitless); P_dry is the precipitation in the driest month (mm per month); P_sdry is the precipitation in the driest month in summer (mm per month); P_wdry is precipitation in the driest month in winter (mm per month); P_swet is precipitation in the wettest month in summer (mm per month); P_wwet is precipitation in the wettest month in winter (mm per month). $P_{\mathrm{threshold}}=\mathrm{2}\times \mathrm{MAT}$ if >70 % of precipitation falls in winter, and $P_{\mathrm{threshold}}=\mathrm{2}\times \mathrm{MAT}+\mathrm{28}$ if >70 % of precipitation falls in summer; otherwise, $P_{\mathrm{threshold}}=\mathrm{2}\times \mathrm{MAT}+\mathrm{14}$.

Wohlfahrt et al. (2008)Bristow et al. (2016)Leuning et al. (2005)Kilinc et al. (2013)Merbold et al. (2014)Zielis et al. (2014)Imer et al. (2013)Etzold et al. (2011)Ammann et al. (2009)Dietiker et al. (2010)Shi et al. (2006)Kato et al. (2006)Acosta et al. (2013) ()Lindauer et al. (2014)Westergaard-Nielsen et al. (2013)Reverter et al. (2010)Serrano-Ortiz et al. (2011)López-Blanco et al. (2017)Valentini et al. (1996)Marcolla et al. (2003)Marcolla et al. (2011)Montagnani et al. (2009)Galvagno et al. (2013)Novick et al. (2016)Goldstein et al. (2000)Meyers (2016)Chu et al. (2018a)Goulden (2018a)Goulden (2018b)Goulden (2018c)Belshe et al. (2012)Amiro et al. (2010)Amiro et al. (2010)Zeller and Nikolov (2000)Frank et al. (2014)Chu et al. (2018b)Kelsey and Green (2020)Euskirchen et al. (2012a)Euskirchen et al. (2017)Euskirchen et al. (2012b)Irvine et al. (2007)Campbell et al. (2004)Barr et al. (2013a)Anthoni et al. (1999)Anthoni et al. (2002)Ruehr et al. (2012)Chu et al. (2018c)Monson et al. (2002)Fellows et al. (2020)Fellows et al. (2020)Fellows et al. (2020)Goulden (2018d)Goulden (2018e)Goulden (2018f)Goulden (2018g)Barr et al. (2013b)Baldocchi et al. (2015)Baldocchi et al. (2015)Wolf et al. (2016)Scott et al. (2015)Barron-Gafford et al. (2013)Anderson-Teixeira et al. (2011)Anderson-Teixeira et al. (2011)Remy et al. (2019)

Table A4 Eddy covariance stations used in the performance evaluation. Lat. is latitude (°), Long. is longitude (°), and Net. is the network; here FLX, EUR, and AME stand for FLUXNET, EuropeFlux, and AmeriFlux, respectively. Climate refers to the Köppen–Geiger climate zone and “biome” as defined by the IGBP (Table A2) (Friedl et al., 2019). Elev. is the elevation in m a.s.l., Slop. and Asp. are the slope (°) and aspect (°), respectively, and Au. is the upslope draining area (km²).

Table A5 SNOTEL stations used in the performance evaluation. Lat. is latitude (°), Long. is longitude (°), and Climate refers to the Köppen–Geiger climate zone with “biome” as defined by the IGBP (Table A2) (Friedl et al., 2019). Elev. is the elevation in m a.s.l., Slop. and Asp. are the slope (°) and aspect (°), respectively, Au. is the upslope draining area (km²), and depth is the maximum depth of the soil profile (m) where the soil moisture was measured.

Table A6 GSIM hydrometric stations used in the streamflow performance evaluation. Lat. is latitude (°), Long. is longitude (°), Climate refers to the three largest Köppen–Geiger climate zones in the watershed, and “biome” refers to the three largest biomes in the watershed, as defined by the IGBP (Table A2) (Friedl et al., 2019). Elev. is the elevation range in m a.s.l. Area is the watershed area (km²), and “river” lists the river name and country.