the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Low sensitivity of three terrestrial biosphere models to soil texture over the South American tropics
Félicien Meunier
Wim Verbruggen
Hans Verbeeck
Marc Peaucelle
Drought stress is an increasing threat for vegetation in tropical regions, within the context of human-induced increase of drought frequency and severity observed over South American forests. Drought stress is induced when a plant's water demand is not met with its water supply through root water uptake. The latter depends on root and soil properties, including soil texture (i.e. the soil clay and sand fractions) that determines the soil water availability and its hydraulic properties. Hence, soil clay content is responsible for a significant fraction of the spatial variability in forest structure and productivity. Soil-textural properties largely vary at the spatial resolution used by Terrestrial Biosphere Models (TBMs) and it is currently unclear how this variability affects the outputs of these models used to predict the response of vegetation ecosystems to future climate change scenarios. In this study, we assessed the sensitivity of the carbon cycle of three state-of-the-art TBMs, i.e. ORganizing Carbon and Hydrology in Dynamic EcosystEms (ORCHIDEEv2.2), Ecosystem Demography model version 2 (ED2), and Lund–Potsdam–Jena General Ecosystem Simulator (LPJ-GUESS) to soil-textural properties at the regional level over the South American tropics using model default pedotransfer functions. For all three TBMs, the model outputs, including gross primary productivity (GPP), aboveground biomass (AGB), soil carbon content and drought stress, were shown to be mostly insensitive to soil-texture changes representative of the spatial variability in soil properties, except for a small region characterised by very low water availability in ORCHIDEEv2.2 and ED2. We argue that generic pedotransfer and simple drought stress functions, as currently implemented in TBMs, should be reconsidered to better capture the role of soil texture and its coupling to plant processes. Similarly, we suggest that better estimates of the soil-texture uncertainty resulting from soil-texture data aggregate should be considered in the future. Those steps forward are critical to properly account for future increasing drought stress conditions in tropical regions.
- Article
(1809 KB) - Full-text XML
-
Supplement
(4735 KB) - BibTeX
- EndNote
Over the last 3 decades, the Amazon tropical forest has been facing an increase in environmental pressures, including the severity and length of drought events (Spinoni et al., 2014). This trend is projected to be exacerbated by the end of the century (Duffy et al., 2015), also resulting from the rapid deforestation rates and the regional precipitation recycling (Staal et al., 2020). Observations and manipulative field experiments have revealed a clear sensitivity of the Amazon forest to severe drought, potentially leading to large-scale increase in tree mortality and decrease in forest productivity through reduced photosynthesis (Nepstad et al., 2007; Phillips et al., 2009; Gatti et al., 2014; Doughty et al., 2015; Corlett, 2016; Feldpausch et al., 2016). Increasing tree mortality in the Amazon is thought to be induced by soil moisture deficit (low water supply) combined with low air humidity and high air temperature (high water demand), which when combined, leads to either hydraulic failure or stomatal closure that may cause carbon starvation in trees (Rowland et al., 2015). Increased vulnerability of the Amazon forest to drought stress will have large impacts on the regional and global carbon, nutrient and water cycles as well as the coupled climate system, and has been proposed as one of the factors involved in the observed decline of the Amazon carbon sink strength (Brienen et al., 2015; Maeda et al., 2015; O'Connell et al., 2018; Hubau et al., 2020).
Soil water availability is intimately related to root distribution (De Deurwaerder et al., 2021), root and soil depth (Jackson et al., 1996), as well as soil properties including texture. By modulating the retention and accessibility of water (and nutrients) to the trees (Silver et al., 2000; Laurance et al., 1999), soil texture, and especially the clay fraction, shapes forest structure, function and its spatio-temporal dynamics. At the regional level, clay and nutrient gradients were shown to explain a substantial part of the variability in forest biomass, soil carbon pools, and forest productivity across the Amazon basin (Laurance et al., 1999; Aragão et al., 2009; Jiménez et al., 2014). The intensity of the dry season and the availability of nutrients (e.g. phosphorus) affect species distribution (Condit et al., 2013; Jirka et al., 2007), while soil moisture gradients have also been shown to affect plant traits and leaf area index (LAI) (Fyllas et al., 2009; Flack-Prain et al., 2021). Furthermore, by affecting canopy conductance and hence carbon assimilation, soil moisture directly impacts the dynamics of water and carbon fluxes at the tree level (Harris et al., 2004).
In order to study the resilience of the Amazon forest to future drought and deforestation, Terrestrial Biosphere Models (TBMs) are key tools that integrate ecophysiological processes at different spatio-temporal scales and the response of ecosystems to environmental changes. In most TBMs, water availability directly affects carbon assimilation through so-called drought stress functions that modulate leaf stomatal conductance. Joetzjer et al. (2014) showed that the amplitude and timing of plant response to moisture deficit was highly sensitive to these unconstrained functions, which prevented the accurate representation of the impact of drought over the Amazon rainforest. Consequently, current TBMs are unable to simulate the spatial variability of forest productivity and biomass over the Amazon (Johnson et al., 2016). Drought stress response parameterisation and sensitivity were also shown to affect the coupling strength between the land surface and the atmospheric boundary layer and thus the performance of coupled climate models (Combe et al., 2016). To better capture the drought stress effect on vegetation, unprecedented efforts are being made in the community to improve the representation of plant hydraulics in TBMs (e.g. Christoffersen et al., 2016; Xu et al., 2016; Mencuccini et al., 2019). However, less effort has been spent on enhancing the representation of the belowground compartments, despite its key role in drought stress (Carminati and Javaux, 2020). Roots, soils, their interactions, and their effect in TBMs have not received as much attention as they should. In this study, we primarily focus on the impact of soil texture on TBMs but also call for more research into other belowground components.
In TBMs, soil moisture is determined by soil hydrology submodels which typically rely on soil-textural information and pedotransfer functions. The TBMs use a rather limited number of pedotransfer functions while soil-texture inputs often resume to a few products with different spatial resolutions (horizontally and vertically). The main products used for regional and global simulations are the FAO/UNESCO soil map of the world (Batjes, 1997), the Harmonized World Soil Database (Nachtergaele et al., 2008), and the more recent SoilGrids250m products (Hengl et al., 2017; Poggio et al., 2021). Those gridded soil maps are not independent of one another, and often aggregated at lower spatial resolution to match other model forcings (e.g. meteorological drivers) which results in average soil properties that neglect inter- and intra-grid cell heterogeneity. Yet, most TBMs do not consider the uncertainty in the influence of soil texture in vegetation activity and drought when applied at large scales.
To date, the existing evaluations of the response of TBMs to soil properties mainly focused on hydrology and water fluxes. These analyses tend to show a lack of sensitivity of TBMs to soil texture and composition. For instance, Li et al. (2012) showed that the performance of CABLE remained insensitive to parameters of soil water dynamics across three contrasting sites, even after improving critical processes related to root functioning. In line with these results, Tafasca et al. (2020) investigated the impact of soil texture on soil water fluxes and storage at different scales with ORganizing Carbon and Hydrology in Dynamic EcosystEms (ORCHIDEE), as part of the Land Surface, Snow and Soil moisture Model Intercomparison Project (LS3MIP; van den Hurk et al., 2016). They showed that, while the model exhibits realistic behaviours at the local scale, it is weakly sensitive to the choice of soil-texture maps at the global scale. The effect of soil representation on vegetation and carbon has been sporadically assessed in the literature. By applying the Ecosystem Demography model, version 2 (ED2) over the Amazon rainforest, Longo et al. (2018) showed different sensitivities of the aboveground biomass (AGB) to soil texture, depending on the rainfall regimes at two contrasting sites. While this study suggests that soil hydraulic properties mediate the Amazon ecosystem response to rainfall regimes, the authors highlighted that the current parameterisation of the model does not account for the diversity in soil types and is limited for representing certain configurations such as clay-rich soils.
Since soil is a major carbon pool and a key driver of water and nutrient availability for plants, we expect a large model sensitivity to soil properties, which should propagate into the simulated vegetation and the ecosystem biogeochemical cycles. This assumption especially applies in a tropical region like South America that frequently suffers from drought and is characterised by heavily weathered and poor soils. To test this assumption, we explored the sensitivity of the vegetation carbon dynamics to soil texture in three state-of-the-art TBMs, representative of the main classes of commonly used TBMs: Lund–Potsdam–Jena General Ecosystem Simulator (LPJ-GUESS), ED2, and ORCHIDEE v2.2. Model sensitivity to soil texture was assessed based on the inter- and intra-grid cell variability in clay content as quantified from the SoilGrid250m database. For each simulation, we present the sensitivity of soil carbon pools, gross primary productivity (GPP), and AGB resulting from the different soil configurations, for both the conditions after the model spin-up and the historical simulation spanning the 1860–2016 period. Results of the different simulations for the three models are compared to one another and with existing observation products to assess model robustness. We finally discuss the main findings in light of implemented mechanisms and propose future development to improve the representation of the soils and drought stress in TBMs.
2.1 Study region
This study focuses on the South American tropical region, ranging from 90 to 30∘ W in longitude and from 15∘ N to 20∘ S in latitude. The spatial resolution of the simulations was set to 1∘. To drive the model, we used the 6-hourly CRU-NCEP v7 meteorological forcing dataset (Viovy, 2018). Climate variables include air temperature and humidity, incoming short-wave and long-wave radiation, precipitation rate, surface pressure, and winds. No land-use changes were applied to any simulation but a land-cover mask representative of the current plant functional type (PFT) distribution as derived from the ESA-CCI land-cover map (Poulter et al., 2015) is applied by default to ORCHIDEE simulations. This land-cover map corresponds to the year 2015, which is consistent with remote-sensing products used for model evaluation described below (see Sect. 2.5).
2.2 Vegetation models
In this study, we explored the sensitivity to soil texture of important model outputs (e.g. GPP, soil carbon) of three state-of-the-art TBMs with different levels of complexity. These TBMs, namely LPJ-GUESS, ED2, and ORCHIDEE v2.2, are briefly described in the next three subsections while a more detailed list of parameters, pedotransfer functions, and description of the impact of drought stress on plant productivity for each model can be found in Sect. S1 in the Supplement.
2.2.1 LPJ-GUESS
The Lund–Potsdam–Jena General Ecosystem Simulator (LPJ-GUESS) model is a process-based dynamic vegetation model which can simulate the global vegetation distribution with its associated carbon, nitrogen, and water cycles (Smith et al., 2001, 2014; Oberpriller et al., 2022). The model has three possible modes of representing vegetation. The population mode is inherited from the LPJ model (Sitch et al., 2003), while the individual and cohort modes correspond to the vegetation representation of the GUESS model (Smith et al., 2001). For this study, the model was run in cohort mode (default vegetation representation). Cohorts represent the properties of the average individuals belonging to an age class of a given PFT. However, for herbaceous PFTs, the LPJ-GUESS model simulates only one average individual per patch. The coarsest spatial level in this model is the grid cell, for which soil texture, meteorological drivers, and nitrogen deposition should be provided. Different stands will each occupy a fraction of a given grid cell, representing different land cover and management types (natural vegetation, cropland, managed forests, etc.). Each stand contains one (population mode) or multiple (cohort and individual modes) replicate patches. The latter allows the model to account for heterogeneity in age distribution of the vegetation, due to stochastic differences in population dynamics. Within each patch, the different cohorts will grow and compete for light, water, and soil nitrogen.
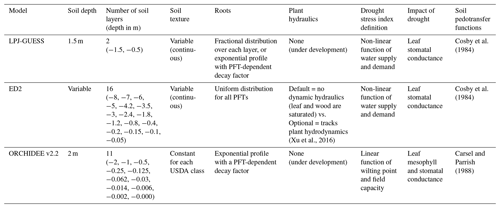
Soil hydrology is represented by a multi-layer bucket model, where water can percolate between the different soil layers and drains at the bottom (Gerten et al., 2004). Soil depth is hard-coded to 1.5 m and subdivided into 15 layers of 10 cm thickness each. Soil moisture in the top two layers (20 cm) is available for surface evaporation. Yet, only 2 large layers are defined for percolation: excess water from the top layers (down to 50 cm) percolates into the bottom layers (remaining 100 cm), where it is distributed between the 10 layers depending on their water capacity. Soil hydraulic properties are derived from pedotransfer functions that require sand and clay contents for each grid cell (Cosby et al., 1984; Prentice et al., 1992; Haxeltine and Prentice, 1996). These are assumed to remain constant over the complete soil column. Soil water content is given as a fraction (0–1) of the available water capacity, which is in turn defined as the difference between the volumetric water content at field capacity and wilting point. Plant drought stress is expressed by the ratio between water supply and atmospheric water demand. If water supply is smaller than water demand, the PFT will be drought-stressed and canopy conductance will be reduced. Water supply is calculated as the product of a PFT-specific daily maximum transpiration rate (emax), daily maximum root water uptake, and a factor which represents the leaf-phenological status as a fraction of the potential leaf cover. Daily maximum root water uptake is given as a function of the fractional root distribution and plant-available water content, summed over all soil layers. In the standard LPJ-GUESS parameterisation, this function is simply the product of both factors, further scaled by the total foliar projective cover in order to account for spatial overlap between cohorts.
2.2.2 ED2
The Ecosystem Demography model, version 2 (ED2) is a cohort-based vegetation model that simulates the energy, water, and carbon cycles of terrestrial ecosystems while accounting for their horizontal and vertical heterogeneities (Medvigy et al., 2009). The model was designed to be compatible with multiple configurations: it can be run as a stand-alone TBM over a single location, over a regional grid, or coupled with an atmospheric model distributed regionally (Knox et al., 2015). The coarsest hierarchical level of ED2 is the polygon within which time-varying meteorological forcing above the canopy is assumed uniform. Each polygon is subdivided into one or multiple sites with the aim of representing landscape-scale variations in abiotic properties like soil texture. Within the simulated sites, the horizontal heterogeneities in the ecosystem are simulated through a set of patches that represent the aggregation of all areas with a similar disturbance history. Finally, in each patch, the plant community population is tracked as a collection of plant cohorts, defined by their functional type and size. The ED2 has a typical time step of 10 min for the energy and water fluxes but can simulate succession and demography over larger (i.e. century) timescales.
In ED2, plant water availability is determined through a physically based soil-hydrology submodel, which encompasses heat, enthalpy, and water fluxes between different soil layers and the potentially existing temporary surface water. Water flux between soil layers is based on Darcy's law (Darcy, 1856; Bonan, 2008), surface runoff of water is simulated using a simple extinction function while subsurface drainage depends on the bottom boundary condition (e.g. free drainage, zero-flow, saturated water table). In ED2, soil depth, the number of soil layers, and layer thickness can be prescribed by the user but in the tropics, the soil is typically discretised into 16 layers along a 8 m depth soil profile with increasing layer thickness from top to bottom (Longo et al., 2019a). Most of the soil-hydraulic properties in ED2 are derived from the LEAF-3 model (Walko et al., 2000) and follow the parameterisation by Cosby et al. (1984) which is based on the soil volumetric fraction of sand and clay. Soil water retention and hydraulic conductivity curves are respectively based on Clapp and Hornberger (1978) and Brooks and Corey (1964), corrected for partially or completely frozen soil water. Drought stress negatively impacts plant productivity through a non-linear, soil-dependent wilting function, based on the ratio of water demand (plant transpiration) and supply (root water uptake). The latter is proportional to the soil water field capacity minus the soil water at the wilting point, integrated from the deepest soil layer accessible by plant roots to the soil surface. Rooting depth is related to plant height through an allometric relationship and root biomass is distributed over the soil layers according to their relative thickness.
2.2.3 ORCHIDEE v2.2
The process-based gridded vegetation model ORCHIDEE (ORganizing Carbon and Hydrology in Dynamic EcosystEms) is designed to simulate the fluxes of matter and energy, as well as the vegetation dynamics at the regional level (Krinner et al., 2005). ORCHIDEE v2.2 is the land component of the IPSL (Institut Pierre Simon Laplace) climate model developed for the Coupled Model Intercomparison Project Phase 6 (CMIP6; Eyring et al., 2016; Peylin et al., 2022). For a given vegetation, soil type, and climatic conditions, the model simulates physiological processes of an average ecosystem on a half-hourly time step, based on a combination of a dozen PFTs representing the major biomes on Earth.
Drought stress effect on vegetation is simulated through a physically based soil hydrology scheme and saturation-based Richards equation (Richards, 1931). The soil is discretised into 11 layers along a 2 m depth profile with increasing layer thickness from the top to the bottom (de Rosnay et al., 2002). Infiltration is processed before soil moisture redistribution while unsaturated values of hydraulic conductivity and diffusivity follow the models of Mualem (1976) and van Genuchten (1980). Soil parameters are set constant for each dominant USDA soil-texture class (Carsel and Parrish, 1988) provided as input. In ORCHIDEE, the soil texture is uniform over the soil column and only the saturated hydraulic conductivity decreases exponentially with depth to account for soil compaction and bioturbation (d'Orgeval et al., 2008). To compute infiltration and surface runoff, the model also accounts for horizontal variations in soil hydraulic conductivity (Vereecken et al., 2019). Soil evaporation and transpiration depend on soil moisture and properties, and transpiration is limited by stomatal resistance which increases when soil moisture drops from field capacity to wilting point. For each PFT, the root density decreases exponentially with depth up to 2 m, thus influencing the drought stress factor on transpiration. The drought stress factor will impact stomatal and mesophyll conductance at the leaf level and hence carbon assimilation. Finally, assimilated carbon is dynamically allocated to several vegetation pools, including the leaves. This will directly influence the seasonality in leaf area index (LAI), which has a feedback on the partitioning between soil evaporation and transpiration, and thus the resulting soil moisture.
2.3 Soil scenarios and simulation protocol
We performed three regional simulations with each model, using different soil-texture maps. These three soil maps represent the soil texture corresponding to the average (Mean clay), minimum (Min. clay), and maximum (Max. clay) topsoil clay content of each grid cell from SoilGrids250m (Poggio et al., 2021), see Fig. 1. Soil texture and hence hydraulic properties were assumed to be vertically uniform for each model and simulation. For each model, both the soil depth and the number of soil layers were set up according to the most default model configurations for the tropics (Table 1).
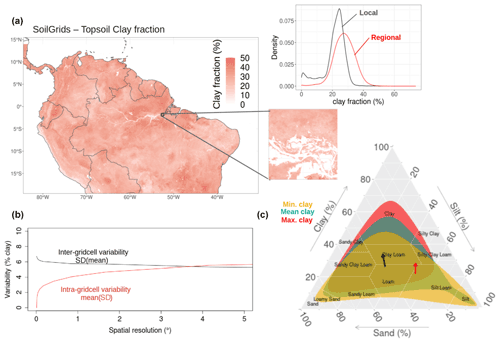
Figure 1Topsoil (0–5 cm) clay fraction spatial distribution as defined by the latest version of SoilGrids with a magnified example of a grid cell (a). The Min., Mean, and Max. clay scenarios are those soil types that are characterised respectively by the minimum, average, and maximum clay fraction content in each grid cell, excluding those without soil-textural information (for instance the rivers as illustrated in the magnified map). In panel (a), the density plot reveals the clay fraction distribution at the regional and local (magnified grid cell) levels. Subplot (b) shows both the intra-grid cell (i.e. mean of the standard deviation (SD) of the clay content) and the inter-grid cell (the standard deviation (SD) of the mean clay content) variability as a function of the spatial resolution. Subplot (c) is the resulting soil-texture distribution for each scenario. The arrows in subplot (c) show the average change of soil texture moving from the Min. clay to Mean clay scenario (black) and observed (red) changes in soil texture after deforestation (Eleftheriadis et al., 2018).
Table 1Summary of the representation of soil, roots, and soil drought stress for each model in their default version.
For each scenario, long-term spin-up with pre-industrial atmospheric CO2 concentration from 1860 (287.14 ppm) were performed to each grid cell starting from near-bare ground conditions. This was achieved by recycling the initial 10 years of CRU-NCEP until soil and vegetation carbon pools reached an equilibrium. The spin-up runs were continued with historical simulations from 1860 to 2016 for each model using the full CRU-NCEP forcing dataset and varying atmospheric CO2 concentration according to Friedlingstein et al. (2020).
We did not change any model parameters (with the exception of the soil textural information) compared to the model default parameterisation for the tropics. More detail on each model's parameter sets can be found in the aforementioned references describing the three models. In ED2, we simulated four competing PFTs (grass, early-, mid-, and late-successional tropical trees) similarly to Longo et al. (2019a) for Amazon regional runs. To facilitate inter-model comparisons, we chose to run multiple ED2 simulations for each polygon rather than simulating multiple sites per polygon. For the LPJ-GUESS model, we activated all PFTs as for global simulations (Sitch et al., 2003; Ahlström et al., 2012), but due to bioclimatic limits only tropical broadleaf evergreen and raingreen trees as well as C4 grasses emerged from the simulation with nonzero biomass.
2.4 Evaluation datasets
We used three different datasets to assess the model robustness and performance under the three soil scenarios. Firstly, we compared the spatial distribution of aboveground biomass (AGB) as simulated by the models with the integrated biomass map of Avitabile et al. (2016) over the study region. This biomass map is one of the reference products used by the International Model Benchmarking system (ILAMB; Collier et al., 2018) to evaluate TBMs, e.g. in the global carbon budget exercise (Friedlingstein et al., 2020). Secondly, we contrasted the model outputs of the average ecosystem gross primary production (GPP) with a moderate-resolution dataset of vegetation GPP derived from MODIS satellite data (MOD17A2), see Running et al. (2015). Finally, we differentiated the soil organic carbon stocks produced by each vegetation model/scenario with those derived from local observations upscaled to the globe in SoilGrids. We used those datasets for qualitative comparison only and not with the objective to improve model accuracy and/or precision.
2.5 Analyses
To assess the relative importance of the intra-grid cell variability, we aggregated the topsoil clay fraction in SoilGrids from its finest (250 m) to a much coarser (5∘) resolution with the R package “raster”. For each resolution, we compared the intra-grid cell variability with the inter-grid cell variability. We defined the intra-grid cell variability as the average of the clay fraction standard deviation (SD) within each grid cell, and the inter-grid cell variability as grid-level SD of the average clay fraction of each grid cell.
All the results from the vegetation model simulations presented below are either (i) averages of the last 10 years of either the spin-up or the historical period (2006–2016) or (ii) the averages of the very last year of the historical period (2016). We particularly focused on the inter-model and inter-scenario comparison of GPP at the ecosystem and the PFT levels, as well as the resulting ecosystem-level AGB and soil carbon. For each simulation of each model, we also computed the normalised soil drought stress index (SDI) from the model outputs whose definition is model-specific (see Sect. S1) but always normalised between 0 (full stress) and 1 (no stress). We related SDI to the ecosystem GPP through quantile regression analyses using the R package “quantreg”. We used a quantile regression given the nature of the vegetation productivity response to SDI: for SDI close to 1, the GPP variability is high (other resources can limit GPP) while for SDI to 0, the GPP is necessarily low. To evaluate the model performance, we averaged the model outputs (GPP, AGB, soil carbon) for each grid cell and vegetation model/scenario over the period of observation of the remote-sensing products (see previous section). We compared the resulting maps through a correlation analysis to compare their spatial distribution, and compared their density distribution through standard metrics (mean, root mean squared error).
The soil textures across the 3 scenarios were also classified according to the 12 major soil-texture categories defined by the United States Department of Agriculture (Soil Survey Manual, 2002), using the “soiltexture” R package (Moeys, 2018), which allowed us to quantify soil class frequencies for each soil scenario and to define transition matrix when switching from 1 soil-textural map to another. All analyses and plots were performed in R version 3.6.3.
3.1 Intra- and inter-grid cell variability in topsoil clay content
With the native spatial resolution of the SoilGrids product (250 m), we observed a wide distribution in clay content over the South American tropics ranging from nearly 0 % to 74 %, with a median around 28 % and a standard deviation of 7 % (Fig. 1a). Such extreme clay content values can also be found within grid cells when using the spatial resolution typically applied in TBMs: in the magnified 1∘ grid cell (∼111 km at the Equator) of Fig. 1a, clay fraction varied between 0 % and 58 % with a median and a standard deviation of 23 % and 7 %, respectively. When SoilGrids was aggregated from its finest to coarser spatial resolutions, we observed a rapidly increasing intra-grid cell variability in soil texture: over the whole region, the average intra-grid cell variability (i.e. the mean standard deviation) in clay content strongly raised by 4 % from 250 m to 1∘, and kept increasing up to 6 % at 5∘. At 1∘ resolution and coarser, the variability within and between grid cells reached similar orders of magnitude (Fig. 1b).
A clear shift from sandy/silty soils toward more clayey soils can be observed when moving from the Min. Clay to the Max. Clay scenario (Figs. 1c and S1A in the Supplement). The mean clay fraction reached 17 %, 28 %, and 34 % for the Min. clay, Mean clay, and the Max. clay scenario, respectively (Fig. 1c). The resulting changes in sand fraction density distributions were less marked, except for the Min. clay scenario (Fig. S1B).
3.2 Models performance in default configuration
In their most default configuration, all three models showed poor performances in capturing the spatial variability in AGB (Figs. 2 and S2 in the Supplement), GPP (Fig. 3), and soil carbon content (Figs. S3 and S4 in the Supplement) as estimated from independent products, regardless of the soil scenarios.
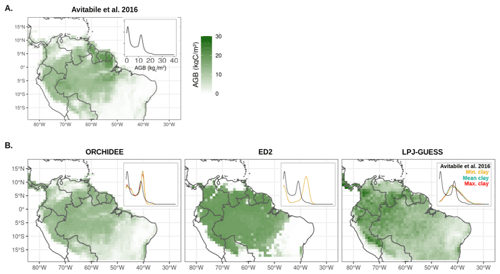
Figure 2Aboveground biomass (AGB) spatial distribution, as generated by Avitabile et al. (2016) (a) or as predicted at the end of the historical period (average over the 2006–2016 period) by the three terrestrial biosphere models used in this study for the Mean clay scenario (b). The upper-right corners in each plot represent the AGB density distributions over the simulated region for all three scenarios (coloured lines) and the observations (black). Note that the land cover was prescribed in the ORCHIDEE model, while it was an emergent property of the ED2 and LPJ-GUESS models.
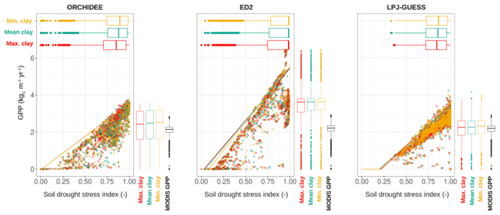
Figure 3Ecosystem GPP as a function of the soil drought stress index (SDI) as predicted at the end of the historical period (2016) by each terrestrial biosphere model used in this study. The SDI values range between 0 and 1, with no stress represented by SDI=1, full stress conditions represented by SDI=0. The boxplots represent the distributions of the stress index for each scenario and the coloured lines are the 95 % quantile regression per scenario (with the same colour legend). Each dot is a grid cell (1∘ resolution).
The reference AGB map from Avitabile et al. (2016) shows a bimodal distribution in biomass over the South American tropics as a reflection of the distribution in forest (12.5 ± 2.7 kgC m−2) versus non-forest biomes (2.4 ± 2.3 kgC m−2, see Fig. 2). Both the ORCHIDEE v2.2 and ED2 models not only reproduced this bimodal distribution (non-forest peak at 3.1 ± 2.3 and 0.7 ± 1.5 kgC m−2; forest peak at 12.3 ± 1.8 and 17.5 ± 2.4 kgC m−2, respectively), but also overestimated the overall AGB on average (8.0 and 11.4 kgC m−2 for both models, respectively while data average is 6.7 kgC m−2). On the contrary, LPJ-GUESS simulated a unimodal biomass distribution with an overestimated average biomass of 12.0 ± 5.5 kgC m−2. The spatial correlation of AGB between the map of Avitabile et al. (2016) and the models varied between 0.35 (LPJ-GUESS) and 0.82 (ORCHIDEE), with an intermediate performance for ED2 (0.67).
When compared to remote-sensing estimates over the 2006–2016 period, ORCHIDEE v2.2 and ED2 overestimated the GPP with simulated average values of 2.4 ± 1.0 and 3.3 ± 1.5 , respectively, compared to reference values of 2.2 ± 0.3 . Only LPJ-GUESS simulated similar average values of 2.2 ± 0.6 .
Finally, all three models overestimated soil carbon content compared to the information from the SoilGrid database with LPJ-GUESS, ED2, and ORCHIDEE v2.2, respectively, simulating mean values of 14.8 ± 6.3, 10.6 ± 8.2, and 7.6 ± 2.9 kgC m−2 for a reference value of 4.3 ± 1.7 kgC m−2. Also the simulated spatial distributions of the soil carbon content were drastically different from the reference one (Figs. S3 and S4), regardless of the soil scenario. The spatial correlations of soil carbon between SoilGrids250m and the models were systematically low: 0.10 for ORCHIDEE, 0.25 for ED2, and 0.26 for LPJ-GUESS.
The relative better performance of the ORCHIDEE model in capturing the spatial variability in vegetation and average soil carbon stocks can be partly explained by the use of a land-cover map to constrain vegetation type distribution compared to ED2 and LPJ-GUESS for which the PFT distribution is an emergent property of the models.
3.3 Model sensitivity to clay content variability
Large differences in all investigated model outputs existed between models for the same soil scenario. However, the performance of each model was almost independent of the soil scenario for all investigated products (AGB, GPP, soil carbon). All three models exhibited a strong correlation between the soil drought stress index (SDI) and the overall ecosystem productivity, as illustrated by the quantile regression analysis (Fig. 3). Across the three scenarios, we observed that increasing clay content slightly increased drought stress (i.e. decreased SDI) by 2.6 %, 0.7 %, and 1.5 % (change of the drought stress index from the Min. clay to the Max. clay scenario) for ORCHIDEE, ED2, and LPJ-GUESS, respectively (horizontal boxplots in Fig. 3). This increase in simulated drought stress was accompanied by a decrease in productivity for all three models, respectively by 2.7 %, 1.9 % and 3.2 % (vertical boxplots in Fig. 3).
Nonetheless, we observed substantial changes in PFT-level GPP simulated for the three scenarios for some grid cells (Fig. 4), especially for the ORCHIDEE model, which indicates some shifts in the simulated PFT composition. This situation occurred in about 3 % of the grid cells for ED2, 6 % of the grid cells for LPJ-GUESS, and 7 % for ORCHIDEE when switching from the Mean clay scenario to the Min. clay or the Max. clay scenario (Fig. S5 in the Supplement). Yet, these PFT-level shifts in GPP compensate for each other when aggregated at the ecosystem level, resulting in similar total GPP and spatial distributions that remain almost unaffected by shifts in soil composition (Fig. 3). Not only did the simulated SDI and GPP not change substantially, but we also observed very limited shifts in soil carbon content (Figs. S3 and S4) and AGB (Figs. 2 and S2) in response to changes in soil clay content (Fig. 2). Between the Min. clay and Max. clay scenarios, we observed a 3.0 %, 0.7 %, and 4.2 % increase in the average simulated AGB, and a −11.9 %, 10.1 %, and 7.6 % change in soil carbon content, as simulated by ORCHIDEE, ED2, and LPJ-GUESS. All the aforementioned observations also apply to state conditions resulting from the spin-up phase (as exemplified for the AGB spatial distribution at the end of the spin-up for all three models and all three scenarios, see Fig. S6 in the Supplement).
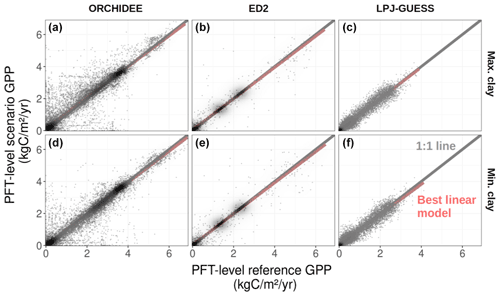
Figure 4Scenario (Max. clay: a–c and Min. clay: d–f) versus reference (Mean clay scenario) GPP for each TBM used in this study. Each dot is the PFT-level GPP over a specific grid cell (1∘ resolution) at the end of the historical period (2016).
We observed some substantial impacts of the scenario on the ecosystem GPP (up to a 100 % change of ecosystem GPP) for some of the soil-textural class transitions (which represent the frequency of soil class changes when moving from one soil-textural map to another), but those transitions were rather rare events and hence limited to a small area of the simulated region (Fig. 5). The most frequent transitions were within the same soil class (the diagonal of the soil transition matrix of Fig. 5a): those represented 32 % of all transitions between the Mean clay and the Min. clay scenarios, and 43 % of all transitions between the Mean clay and the Max. clay scenarios and were almost unaffected by the soil clay content (relative change of ecosystem GPP between −0.6 % and 2.1 % for all models and scenarios). For both ED2 and ORCHIDEEv2.2, the most important changes occurred over (very) low water-availability regions (Mean Annual Precipitation or MAP<1000 mm for ED2, MAP<2000 mm for ORCHIDEE) while the sensitivity to soil texture was independent of the water availability in LPJ-GUESS (Fig. 6). Yet, only a small fraction of the water-limited area was concerned by changes of simulated state variables: 20 % of the grid cells with MAP<1000 showed a relative change of the ecosystem GPP larger than 10 % in both ED2 and ORCHIDEEv2.2. Moreover, positive and negative shifts balanced one another and hence had a very limited impact on the regional ecosystem productivity (Figs. 3 and 6). This was partly due to a lack of sensitivity of the pedotransfer functions to the explored range of variations of soil texture (Fig. S7 in the Supplement), leading to narrower soil hydraulic parameter distributions compared to previously generated at this spatial scale (Montzka et al., 2017).
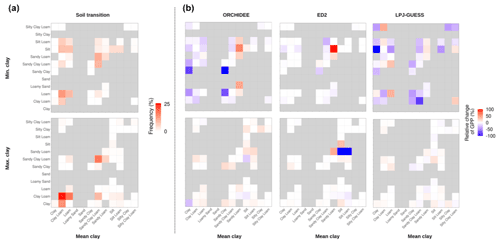
Figure 5Soil transition matrix representing the frequencies of moving from one soil class to another when changing the soil-textural map (a) and the relative change of ecosystem gross primary production (GPP) for each category of transition and terrestrial biosphere model (b) as predicted by each TBM at the end of the historical period. In (a), the colour intensity represents the frequency of each transition. The grey cells are transitions that did not occur in the simulated scenarios.
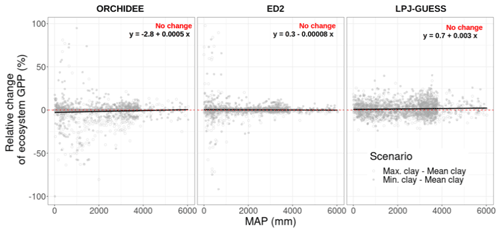
Figure 6Relative change of the annual ecosystem GPP at the end of the historical simulation with the mean annual precipitation (MAP) for both scenarios (shapes) and all three TBMs considered in this study, across the entire simulated region (each point is a grid cell). The MAP is the annual average over the last 10 years (2006–2016) of the CRU-NCEP dataset forcing. R2 of all linear models were lower than 0.01.
Finally, we note that the LPJ-GUESS model crashed for some specific soil textures. Those soil textures occur naturally in the field and were relatively frequent in our simulations, especially in the Min. clay scenario (5.4 % of the grid cells). The problem occurred for silty soils with low fractions of both sand (<12 %) and clay (25 %). The default pedotransfer functions applied to those specific soil textures led to volumetric water content at field capacity larger than the water content at saturation (see Fig. S8 in the Supplement), which caused the model to crash during model initialisation for those particular grid cells.
The South American tropics frequently suffer from (mega)droughts such as the 2015–2016 El Niño event, which severely impacted ecosystems on the continent. These droughts result from the increasing environmental pressures, including climate change and deforestation (Staal et al., 2020). In a recent study, Yang et al. (2022) linked patterns of forest biomass changes with drought severity and duration as well as soil clay content, which indicates that both water demand and supply (or both climate and soil/roots) influence forest functioning. In contrast to that study, we found here that the aboveground biomass simulated by three state-of-the-art TBMs was mostly insensitive to soil texture, except for some limited areas with low water availability in ED2 and ORCHIDEEv2.2.
In TBMs, plants and soils are coupled by a drought stress function which depends on soil moisture. We suggest that the overall lack of sensitivity that we observed originates from the combination of two main limitations in the current implementation of the hydrology submodel in TBMs: (1) the shifts in soil texture resulting from the spatial variability in soil clay content does not translate into realistic shifts in soil hydraulic properties (Fig. S7) and (2) the implemented drought stress functions do not properly capture the effect of changes in soil hydraulic properties on vegetation. Both limitations should be rapidly tackled in order to improve TBM performance (Fisher and Koven, 2020) and are briefly discussed below.
Current TBMs use a limited number of generic, widespread pedotransfer functions, which can be class-based or continuous. However, most of these functions were developed and calibrated decades ago (1984 and 1988, see Table 1) with fewer and less geographically spread calibration data than what are available today. On top of the limited size of the training data (especially for the tropical regions), the main drawback of these pedotransfer functions resides in their inability to capture the variability and non-linearity of many parameters for given soil-textural classes. For example, in their review, Van Looy et al. (2017) highlighted large differences in saturated hydraulic conductivity within each soil class derived from different data sources and location. As a result, by using generic and global functions, soil parameters in TBMs are substantially different from region-specific observations (Kishné et al., 2017; Van Looy et al., 2017). Such generic, global functions could therefore lead to inaccurate characterisation of the soil properties, as illustrated by the LPJ-GUESS crashes with realistic soil compositions (Fig. S8). Since no generic functions are able to properly capture soil properties at the global scale (Patil and Singh, 2016), intermediate solutions should be implemented in TBMs for a better representation and scaling of soil properties. For example, region-specific pedotransfer functions, regional calibration, ensemble simulations using multiple pedotransfer models, or the combination of regional pedotransfer functions could be used to estimate the uncertainties that soil properties are responsible for (Hodnett and Tomasella, 2002; Barros and de Jong van Lier, 2014; Medeiros et al., 2014).
Soils have a direct, strong role in the response of plants to drought (Carminati and Javaux, 2020). All three vegetation models used in our study apply simple drought stress functions that depend on the available water and the water demand (Table 1 and Sect. S1). We observed that shifting soil properties from low to high clay content barely affected the simulated soil drought stress despite substantial changes in soil texture and classification (Figs. 1, 3 and S1). Even if the sensitivity to soil texture might slightly increase with drought stress (Fig. 6) and hence under future climate change scenarios, it confirms that generic drought stress functions are not suitable to capture the impact of changes in plant water availability on plant processes, as suggested from previous studies (Uribe et al., 2021; Joetzjer et al., 2014; Combe et al., 2016) and argues for a better representation of root–soil coupling in TBMs. To reproduce the annual pattern of net ecosystem exchange of carbon over the Amazon with the Simple Biosphere Model (SiB3), Baker et al. (2008) demonstrated the importance of combining multiple mechanisms, not only related to soil water distribution but also on root dynamic schemes. Indeed, the Amazon forest was shown to have high GPP during the dry season (Green et al., 2020; Negrón Juárez et al., 2007; Saleska et al., 2003), and the role of water uptake with deep roots is currently not properly simulated in TBMs, e.g. because of the shallow soils (and hence root systems) that are simulated (Table 1), (Verbeeck et al., 2011; Nepstad et al., 1994). Recent developments in the TBM community have focused on improved plant hydraulics but to a lesser extent to the root–soil interactions (Xu et al., 2016). Recent studies have demonstrated the need for a better representation of root water uptake in drying soils to simulate plant response to drought stress and its impact on biomass. For instance, the new dynamic root scheme (Joetzjer et al., 2022) coupled to explicit plant hydraulic processes in ORCHIDEE managed to reproduce observed water and carbon dynamics at the Caxiuanã throughfall exclusion field experiment in eastern Amazonia (Yao et al., 2021). Although they better capture biomass and flux dynamics at the site level, the new implementations of plant hydraulics is empirical and complex, and leads to an increased number of model parameters and hence to a larger required size of field observational data to calibrate it. Such data are not readily available for a large number of sites or a larger area and/or might be difficult to measure, especially in complex ecosystems like tropical forests. The process of model complexification might also result in over-fitted simulations at the site level, mainly focusing on climate factors (e.g. drought) while overlooking the unconstrained soil and root properties. Better estimate of water demands based on eco-evolutive optimality theories (Prentice et al., 2014), root biomass (Franklin et al., 2012), and soil–root interactions (Lu et al., 2020; Vanderborght et al., 2021) could help bridge the gap between complex and over-parameterised models on the one hand and simple unrealistic model-specific functions on the other.
Soil texture and clay content have a direct, strong impact on the distribution and mineralisation of carbon and nutrients in soils (e.g. Hassink, 1992; Telles et al., 2003; Plante et al., 2006; Zinn et al., 2007). In our simulations, the three TBMs could not reproduce SoilGrid soil carbon distribution and showed very low sensitivity to changes in clay content (Figs. S3 and S4) despite long-term spin-up during which we expected large differences between equilibrium states induced by different soil composition. This further highlights the poor representation of soil processes in TBMs and their coupling to vegetation dynamics. As for the relationship between soil hydraulic properties and texture, we argue that current development focusing on soil processes in TBMs (e.g. nutrient mineralisation, soil organic carbon) should systematically assess model sensitivity to soil properties and texture parameters.
By selecting the dominant soil-texture class, a significant fraction of the soil spatial heterogeneity is omitted in TBMs running at coarse spatial resolution. This effect has already been documented in Tafasca et al. (2020), who suggested that spatial aggregation statistically enhances medium textures, leading to excessive evapotranspiration and insufficient total runoff. Accounting for subgrid variability in soil texture and moisture through systematic sensitivity analysis, or directly representing this effect in TBMs with models (Qu et al., 2015) could alleviate these uncertainties and improve model performance. Intra-grid cell variability in soil texture might have large impacts on simulating vegetation dynamics, especially in demographic models for which plant competition and access to resources drive ecosystem composition and dynamics (i.e. growth/mortality) (Rowland et al., 2015; Johnson et al., 2016). In addition to the aggregation bias, we also expect substantial biases in simulated ecosystem properties resulting from intrinsic uncertainties from soil products. In SoilGrids, maps of soil properties are generated using machine-learning methods that account for direct soil observations and environmental variables describing vegetation, climate, topography, geology, and hydrology. However, the number of soil observations available over the Amazon tropics is very low (10 or fewer soil-textural observations for grid cell of 70 000 km2 for many grid cells in the studied area), potentially leading to high uncertainties in regional soil properties at fine resolution (see Fig. S6 from Poggio et al., 2021).
Realistically reproducing the South American tropics in silico suppose that TBMs accurately represent the most essential processes driving ecosystem functioning. In the context of increasing drought intensity and severity, a better representation of the impacts of soils on plant productivity and status is urgently needed. More generally, the belowground compartment should receive more attention from the vegetation modelling community. It has been long known that root and soil depth critically influence drought tolerance (Nepstad et al., 1994; Fan et al., 2017), yet this knowledge has not been integrated in most TBMs (Verbeeck et al., 2011). In this study, we focused on soil texture only, but further research should include other soil properties (e.g. soil structure see Fatichi et al., 2020) and root traits. Other critical processes are impacting this region and require as much attention. The Amazon basin has gone through intense deforestation activities for more than 3 decades. Among the consequences of such environmental pressure, deforestation increases drought (Staal et al., 2020) and modifies soil properties (Veldkamp et al., 2020). Interestingly, the impact of deforestation on soil texture is of the same order as the one investigated in this study (Fig. 1c). These processes and their interactions should be accounted for in the next generation of TBMs.
The TBMs are keystones of global carbon and water budget assessments. Past developments strongly focused on representing plant processes and their response to climate. Despite their importance and recent efforts from the TBM community, belowground processes have remained overlooked. Here, we showed that the carbon-related processes are mostly insensitive to soil texture over the South American tropics for all three investigated TBMs (LPJ-GUESS, ORCHIDEE, and ED2). These results suggest a poor representation of the soil–vegetation coupling in TBMs, mainly because of inadequate pedotransfer functions and soil drought stress definitions. To date, the use of generic pedotransfer and drought stress functions is common in the TBMs which are used for carbon and water budget assessments, as well as future projections, which leads to large errors in the model predictions. Appropriately representing soil spatial heterogeneity (through better estimates of the impact of soil-texture uncertainties) and soil–plant coupling, such as the non-linearity of soil–root resistance, is a major challenge that needs to be urgently addressed in TBMs. This will lead to a better representation of the effect of drought stress on vegetation and to a reduction of the carbon budget uncertainties, which is particularly needed in complex and heterogeneous ecosystems such as tropical forests.
SoilGrids250m data are available at: https://soilgrids.org/ (SoilGrids web portal, 2022). CRUNCEPv7 data are available at: https://rda.ucar.edu/datasets/ds314.3/ (Viovy, 2018). The code used to generate the results, soil scenario, and to reproduce the figures of this manuscript is available on Github (https://github.com/femeunier/SoilSensitivity (last access: 11 October 2022) with an archived version on Zenodo (https://doi.org/10.5281/zenodo.6226622, Meunier, 2022) corresponding to tag v1. The code source of the ORCHIDEE v2.2 model is available at: https://forge.ipsl.jussieu.fr/orchidee/browser/branches/ORCHIDEE_2_2?order=name (ORCHIDEE in tags/ORCHIDEE_2_0 – ORCHIDEE, 2022), please contact the ORCHIDEE team at https://orchidee.ipsl.fr/contact/ (last access: 11 October 2022) before any intended usage of the model. The ED2.2 model is available at https://doi.org/10.5281/zenodo.3365659 (Longo et al., 2019b). LPJ-GUESS is a worldwide developed and refined terrestrial biosphere model. The model code is managed and maintained by the Department of Physical Geography and Ecosystem Science, Lund University, Sweden. The source code can be made available with a collaboration agreement under the acceptance of certain conditions. For this reason, a DOI for the model code is not available. Additional details and information can be found at the LPJ-GUESS website (http://web.nateko.lu.se/lpj-guess, last access: 10 October 2022).
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-15-7573-2022-supplement.
All co-authors designed the study. FM ran the ED2 simulations, MP ran the ORCHIDEE v2.2 simulations, and WV ran the LPJ-GUESS simulations. FM analysed the model outputs, and wrote the first version of the manuscript. All co-authors critically revised it.
At least one of the (co-)authors is a member of the editorial board of Geoscientific Model Development. The peer-review process was guided by an independent editor, and the authors also have no other competing interests to declare.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research was funded by the Fonds Wetenschappelijk Onderzoek (FWO grant no. G018319N). The computational resources and services used in this work were provided by the VSC (Flemish Supercomputer Center), funded by the Research Foundation – Flanders (FWO) and the Flemish Government – department EWI. ORCHIDEE simulations were performed using HPC resources from GENCI-TGCC (grant no. A0110106328). During the preparation of this article, Félicien Meunier was funded by the FWO as a junior postdoctoral researcher and is thankful to this organisation for its financial support (FWO grant no. 1214720N). Wim Verbruggen was funded by the ArboreSens (Dryland woody vegetation sensitivity to soil texture and precipitation variability) dissemination and support project (BELSPO STEREO III; grant no. SR/02/209). Marc Peaucelle was supported by the H2020 Marie Skłodowska-Curie Actions (LEAF-2-TBM grant no. 891369). Hans Verbeeck was supported by the European Research Council Starting Grant 637643 TREECLIMBERS.
This paper was edited by Carlos Sierra and reviewed by two anonymous referees.
Ahlström, A., Schurgers, G., Arneth, A., and Smith, B.: Robustness and uncertainty in terrestrial ecosystem carbon response to CMIP5 climate change projections, Environ. Res. Lett., 7, 044008, https://doi.org/10.1088/1748-9326/7/4/044008, 2012.
Aragão, L. E. O. C., Malhi, Y., Metcalfe, D. B., Silva-Espejo, J. E., Jiménez, E., Navarrete, D., Almeida, S., Costa, A. C. L., Salinas, N., Phillips, O. L., Anderson, L. O., Alvarez, E., Baker, T. R., Goncalvez, P. H., Huamán-Ovalle, J., Mamani-Solórzano, M., Meir, P., Monteagudo, A., Patiño, S., Peñuela, M. C., Prieto, A., Quesada, C. A., Rozas-Dávila, A., Rudas, A., Silva Jr., J. A., and Vásquez, R.: Above- and below-ground net primary productivity across ten Amazonian forests on contrasting soils, Biogeosciences, 6, 2759–2778, https://doi.org/10.5194/bg-6-2759-2009, 2009.
Avitabile, V., Herold, M., Heuvelink, G. B. M., Lewis, S. L., Phillips, O. L., Asner, G. P., Armston, J., Ashton, P. S., Banin, L., Bayol, N., Berry, N. J., Boeckx, P., de Jong, B. H. J., DeVries, B., Girardin, C. A. J., Kearsley, E., Lindsell, J. A., Lopez-Gonzalez, G., Lucas, R., Malhi, Y., Morel, A., Mitchard, E. T. A., Nagy, L., Qie, L., Quinones, M. J., Ryan, C. M., Ferry, S. J. W., Sunderland, T., Laurin, G. V., Gatti, R. C., Valentini, R., Verbeeck, H., Wijaya, A., and Willcock, S.: An integrated pan-tropical biomass map using multiple reference datasets, Glob. Change Biol., 22, 1406–1420, https://doi.org/10.1111/gcb.13139, 2016.
Baker, I. T., Prihodko, L., Denning, A. S., Goulden, M., Miller, S., and da Rocha, H. R.: Seasonal drought stress in the Amazon: Reconciling models and observations, J. Geophys. Res., 113, G00B01, https://doi.org/10.1029/2007JG000644, 2008.
Barros, A. H. C. and de Jong van Lier, Q.: Pedotransfer Functions for Brazilian Soils, in: Application of Soil Physics in Environmental Analyses: Measuring, Modelling and Data Integration, edited by: Teixeira, W. G., Ceddia, M. B., Ottoni, M. V., and Donnagema, G. K., Springer International Publishing, Cham, 131–162, https://doi.org/10.1007/978-3-319-06013-2_6, 2014.
Batjes, N. H.: A world dataset of derived soil properties by FAO–UNESCO soil unit for global modelling, Soil Use Manage., 13, 9–16, https://doi.org/10.1111/j.1475-2743.1997.tb00550.x, 1997.
Bonan, G. B.: Forests and Climate Change: Forcings, Feedbacks, and the Climate Benefits of Forests, Science, 320, 1444–1449, 2008.
Brienen, R. J. W., Phillips, O. L., Feldpausch, T. R., Gloor, E., Baker, T. R., Lloyd, J., Lopez-Gonzalez, G., Monteagudo-Mendoza, A., Malhi, Y., Lewis, S. L., Vásquez Martinez, R., Alexiades, M., Álvarez Dávila, E., Alvarez-Loayza, P., Andrade, A., Aragão, L. E. O. C., Araujo-Murakami, A., Arets, E. J. M. M., Arroyo, L., Aymard C, G. A., Bánki, O. S., Baraloto, C., Barroso, J., Bonal, D., Boot, R. G. A., Camargo, J. L. C., Castilho, C. V., Chama, V., Chao, K. J., Chave, J., Comiskey, J. A., Cornejo Valverde, F., da Costa, L., de Oliveira, E. A., Di Fiore, A., Erwin, T. L., Fauset, S., Forsthofer, M., Galbraith, D. R., Grahame, E. S., Groot, N., Hérault, B., Higuchi, N., Honorio Coronado, E. N., Keeling, H., Killeen, T. J., Laurance, W. F., Laurance, S., Licona, J., Magnussen, W. E., Marimon, B. S., Marimon-Junior, B. H., Mendoza, C., Neill, D. A., Nogueira, E. M., Núñez, P., Pallqui Camacho, N. C., Parada, A., Pardo-Molina, G., Peacock, J., Peña-Claros, M., Pickavance, G. C., Pitman, N. C. A., Poorter, L., Prieto, A., Quesada, C. A., Ramírez, F., Ramírez-Angulo, H., Restrepo, Z., Roopsind, A., Rudas, A., Salomão, R. P., Schwarz, M., Silva, N., Silva-Espejo, J. E., Silveira, M., Stropp, J., Talbot, J., ter Steege, H., Teran-Aguilar, J., Terborgh, J., Thomas-Caesar, R., Toledo, M., Torello-Raventos, M., Umetsu, R. K., van der Heijden, G. M. F., van der Hout, P., Guimarães Vieira, I. C., Vieira, S. A., Vilanova, E., Vos, V. A., and Zagt, R. J.: Long-term decline of the Amazon carbon sink, Nature, 519, 344–348, https://doi.org/10.1038/nature14283, 2015.
Brooks, R. H. and Corey, A. T.: Hydraulic Properties of Porous Media, Hydrology Paper, Vol. 3, Colorado State University, Fort Collins, 1964.
Carminati, A. and Javaux, M.: Soil Rather Than Xylem Vulnerability Controls Stomatal Response to Drought, Trends Plant Sci., 25, 868–880, https://doi.org/10.1016/j.tplants.2020.04.003, 2020.
Carsel, R. F. and Parrish, R. S.: Developing joint probability distributions of soil water retention characteristics, Water Resour. Res., 24, 755–769, https://doi.org/10.1029/WR024i005p00755, 1988.
Christoffersen, B. O., Gloor, M., Fauset, S., Fyllas, N. M., Galbraith, D. R., Baker, T. R., Kruijt, B., Rowland, L., Fisher, R. A., Binks, O. J., Sevanto, S., Xu, C., Jansen, S., Choat, B., Mencuccini, M., McDowell, N. G., and Meir, P.: Linking hydraulic traits to tropical forest function in a size-structured and trait-driven model (TFS v.1-Hydro), Geosci. Model Dev., 9, 4227–4255, https://doi.org/10.5194/gmd-9-4227-2016, 2016.
Clapp, R. and Hornberger, G.: Empirical equations for some soil hydraulic properties, Water Resour. Res., 14, 601–604, https://doi.org/10.1029/WR014I004P00601, 1978.
Collier, N., Hoffman, F. M., Lawrence, D. M., Keppel-Aleks, G., Koven, C. D., Riley, W. J., Mu, M., and Randerson, J. T.: The International Land Model Benchmarking (ILAMB) System: Design, Theory, and Implementation, J. Adv. Model. Earth Sy., 10, 2731–2754, https://doi.org/10.1029/2018MS001354, 2018.
Combe, M., de Arellano, J. V.-G., Ouwersloot, H. G., and Peters, W.: Plant water-stress parameterization determines the strength of land–atmosphere coupling, Agr. Forest Meteorol., 217, 61–73, https://doi.org/10.1016/j.agrformet.2015.11.006, 2016.
Condit, R., Engelbrecht, B. M. J., Pino, D., Pérez, R., and Turner, B. L.: Species distributions in response to individual soil nutrients and seasonal drought across a community of tropical trees, P. Natl. Acad. Sci. USA, 110, 5064–5068, https://doi.org/10.1073/pnas.1218042110, 2013.
Corlett, R. T.: The Impacts of Droughts in Tropical Forests, Trends Plant Sci., 21, 584–593, https://doi.org/10.1016/j.tplants.2016.02.003, 2016.
Cosby, B. J., Hornberger, G. M., Clapp, R. B., and Ginn, T. R.: A Statistical Exploration of the Relationships of Soil Moisture Characteristics to the Physical Properties of Soils, Water Resour. Res., 20, 682–690, https://doi.org/10.1029/WR020i006p00682, 1984.
Darcy, H.: Les Fontaines Publiques de la Ville de Dijon: Exposition et Application des Principes a Suivre et des Formulesa Employer dans les Questions de Distribution d’Eau, edited by: Dalmont, V., Paris, 647 pp., ISBN 10 2012576001, ISBN 13 9782012576001, 1856.
De Deurwaerder, H. P. T., Visser, M. D., Meunier, F., Detto, M., Hervé-Fernández, P., Boeckx, P., and Verbeeck, H.: Robust Estimation of Absorbing Root Surface Distributions From Xylem Water Isotope Compositions With an Inverse Plant Hydraulic Model, Front. For. Glob. Change, 4, 76, https://doi.org/10.3389/ffgc.2021.689335, 2021.
de Rosnay, P., Polcher, J., Bruen, M., and Laval, K.: Impact of a physically based soil water flow and soil-plant interaction representation for modeling large-scale land surface processes, J. Geophys. Res.-Atmos., 107, 4118, https://doi.org/10.1029/2001JD000634, 2002.
d'Orgeval, T., Polcher, J., and de Rosnay, P.: Sensitivity of the West African hydrological cycle in ORCHIDEE to infiltration processes, Hydrol. Earth Syst. Sci., 12, 1387–1401, https://doi.org/10.5194/hess-12-1387-2008, 2008.
Doughty, C. E., Metcalfe, D. B., Girardin, C. A. J., Amézquita, F. F., Cabrera, D. G., Huasco, W. H., Silva-Espejo, J. E., Araujo-Murakami, A., da Costa, M. C., Rocha, W., Feldpausch, T. R., Mendoza, A. L. M., da Costa, A. C. L., Meir, P., Phillips, O. L., and Malhi, Y.: Drought impact on forest carbon dynamics and fluxes in Amazonia, Nature, 519, 78–82, https://doi.org/10.1038/nature14213, 2015.
Duffy, P. B., Brando, P., Asner, G. P., and Field, C. B.: Projections of future meteorological drought and wet periods in the Amazon, P. Natl. Acad. Sci. USA, 112, 13172–13177, https://doi.org/10.1073/pnas.1421010112, 2015.
Eleftheriadis, A., Lafuente, F., and Turrión, M.-B.: Effect of land use, time since deforestation and management on organic C and N in soil textural fractions, Soil Till. Res., 183, 1–7, https://doi.org/10.1016/j.still.2018.05.012, 2018.
Eyring, V., Bony, S., Meehl, G. A., Senior, C. A., Stevens, B., Stouffer, R. J., and Taylor, K. E.: Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization, Geosci. Model Dev., 9, 1937–1958, https://doi.org/10.5194/gmd-9-1937-2016, 2016.
Fan, Y., Miguez-Macho, G., Jobbágy, E. G., Jackson, R. B., and Otero-Casal, C.: Hydrologic regulation of plant rooting depth, P. Natl. Acad. Sci. USA, 114, 10572–10577, https://doi.org/10.1073/pnas.1712381114, 2017.
Fatichi, S., Or, D., Walko, R., Vereecken, H., Young, M. H., Ghezzehei, T. A., Hengl, T., Kollet, S., Agam, N., and Avissar, R.: Soil structure is an important omission in Earth System Models, Nat. Commun., 11, 522, https://doi.org/10.1038/s41467-020-14411-z, 2020.
Feldpausch, T. R., Phillips, O. L., Brienen, R. J. W., Gloor, E., Lloyd, J., Lopez-Gonzalez, G., Monteagudo-Mendoza, A., Malhi, Y., Alarcón, A., Álvarez Dávila, E., Alvarez-Loayza, P., Andrade, A., Aragao, L. E. O. C., Arroyo, L., Aymar C. G. A., Baker, T. R., Baraloto, C., Barroso, J., Bonal, D., Castro, W., Chama, V., Chave, J., Domingues, T. F., Fauset, S., Groot, N., Honorio Coronado, E., Laurance, S., Laurance, W. F., Lewis, S. L., Licona, J. C., Marimon, B. S., Marimon-Junior, B. H., Mendoza Bautista, C., Neill, D. A., Oliveira, E. A., Oliveira dos Santos, C., Pallqui Camacho, N. C., Pardo-Molina, G., Prieto, A., Quesada, C. A., Ramírez, F., Ramírez-Angulo, H., Réjou-Méchain, M., Rudas, A., Saiz, G., Salomão, R. P., Silva-Espejo, J. E., Silveira, M., ter Steege, H., Stropp, J., Terborgh, J., Thomas-Caesar, R., van der Heijden, G. M. F., Vásquez Martinez, R., Vilanova, E., and Vos, V. A.: Amazon forest response to repeated droughts, Global Biogeochem. Cy., 30, 964–982, https://doi.org/10.1002/2015GB005133, 2016.
Fisher, R. A. and Koven, C. D.: Perspectives on the Future of Land Surface Models and the Challenges of Representing Complex Terrestrial Systems, J. Adv. Model. Earth Sy., 12, e2018MS001453, https://doi.org/10.1029/2018MS001453, 2020.
Flack-Prain, S., Meir, P., Malhi, Y., Smallman, T. L., and Williams, M.: Does economic optimisation explain LAI and leaf trait distributions across an Amazon soil moisture gradient?, Glob. Change Biol., 27, 587–605, https://doi.org/10.1111/gcb.15368, 2021.
Franklin, O., Johansson, J., Dewar, R. C., Dieckmann, U., McMurtrie, R. E., Brännström, Å., and Dybzinski, R.: Modeling carbon allocation in trees: a search for principles, Tree Physiol., 32, 648–666, https://doi.org/10.1093/treephys/tpr138, 2012.
Friedlingstein, P., O'Sullivan, M., Jones, M. W., Andrew, R. M., Hauck, J., Olsen, A., Peters, G. P., Peters, W., Pongratz, J., Sitch, S., Le Quéré, C., Canadell, J. G., Ciais, P., Jackson, R. B., Alin, S., Aragão, L. E. O. C., Arneth, A., Arora, V., Bates, N. R., Becker, M., Benoit-Cattin, A., Bittig, H. C., Bopp, L., Bultan, S., Chandra, N., Chevallier, F., Chini, L. P., Evans, W., Florentie, L., Forster, P. M., Gasser, T., Gehlen, M., Gilfillan, D., Gkritzalis, T., Gregor, L., Gruber, N., Harris, I., Hartung, K., Haverd, V., Houghton, R. A., Ilyina, T., Jain, A. K., Joetzjer, E., Kadono, K., Kato, E., Kitidis, V., Korsbakken, J. I., Landschützer, P., Lefèvre, N., Lenton, A., Lienert, S., Liu, Z., Lombardozzi, D., Marland, G., Metzl, N., Munro, D. R., Nabel, J. E. M. S., Nakaoka, S.-I., Niwa, Y., O'Brien, K., Ono, T., Palmer, P. I., Pierrot, D., Poulter, B., Resplandy, L., Robertson, E., Rödenbeck, C., Schwinger, J., Séférian, R., Skjelvan, I., Smith, A. J. P., Sutton, A. J., Tanhua, T., Tans, P. P., Tian, H., Tilbrook, B., van der Werf, G., Vuichard, N., Walker, A. P., Wanninkhof, R., Watson, A. J., Willis, D., Wiltshire, A. J., Yuan, W., Yue, X., and Zaehle, S.: Global Carbon Budget 2020, Earth Syst. Sci. Data, 12, 3269–3340, https://doi.org/10.5194/essd-12-3269-2020, 2020.
Fyllas, N. M., Patiño, S., Baker, T. R., Bielefeld Nardoto, G., Martinelli, L. A., Quesada, C. A., Paiva, R., Schwarz, M., Horna, V., Mercado, L. M., Santos, A., Arroyo, L., Jiménez, E. M., Luizão, F. J., Neill, D. A., Silva, N., Prieto, A., Rudas, A., Silviera, M., Vieira, I. C. G., Lopez-Gonzalez, G., Malhi, Y., Phillips, O. L., and Lloyd, J.: Basin-wide variations in foliar properties of Amazonian forest: phylogeny, soils and climate, Biogeosciences, 6, 2677–2708, https://doi.org/10.5194/bg-6-2677-2009, 2009.
Gatti, L. V., Gloor, M., Miller, J. B., Doughty, C. E., Malhi, Y., Domingues, L. G., Basso, L. S., Martinewski, A., Correia, C. S. C., Borges, V. F., Freitas, S., Braz, R., Anderson, L. O., Rocha, H., Grace, J., Phillips, O. L., and Lloyd, J.: Drought sensitivity of Amazonian carbon balance revealed by atmospheric measurements, Nature, 506, 76–80, https://doi.org/10.1038/nature12957, 2014.
Gerten, D., Schaphoff, S., Haberlandt, U., Lucht, W., and Sitch, S.: Terrestrial vegetation and water balance – hydrological evaluation of a dynamic global vegetation model, J. Hydrol., 286, 249–270, https://doi.org/10.1016/j.jhydrol.2003.09.029, 2004.
Green, J. K., Berry, J., Ciais, P., Zhang, Y., and Gentine, P.: Amazon rainforest photosynthesis increases in response to atmospheric dryness, Sci. Adv., 6, eabb7232, https://doi.org/10.1126/sciadv.abb7232, 2020.
Harris, P. P., Huntingford, C., Cox, P. M., Gash, J. H. C., and Malhi, Y.: Effect of soil moisture on canopy conductance of Amazonian rainforest, Agr. Forest Meteorol., 3–4, 215–227, https://doi.org/10.1016/j.agrformet.2003.09.006, 2004.
Hassink, J.: Effects of soil texture and structure on carbon and nitrogen mineralization in grassland soils, Biol. Fert. Soils, 14, 126–134, https://doi.org/10.1007/BF00336262, 1992.
Haxeltine, A. and Prentice, I. C.: A General Model for the Light-Use Efficiency of Primary Production, Funct. Ecol., 10, 551–561, https://doi.org/10.2307/2390165, 1996.
Hengl, T., de Jesus, J. M., Heuvelink, G. B. M., Gonzalez, M. R., Kilibarda, M., Blagotić, A., Shangguan, W., Wright, M. N., Geng, X., Bauer-Marschallinger, B., Guevara, M. A., Vargas, R., MacMillan, R. A., Batjes, N. H., Leenaars, J. G. B., Ribeiro, E., Wheeler, I., Mantel, S., and Kempen, B.: SoilGrids250m: Global gridded soil information based on machine learning, PLOS ONE, 12, e0169748, https://doi.org/10.1371/journal.pone.0169748, 2017.
Hodnett, M. and Tomasella, J.: Marked differences between van Genuchten soil water-retention parameters for temperate and tropical soils: A new water-retention pedo-transfer functions developed for tropical soils, Geoderma, 108, 155–180, https://doi.org/10.1016/S0016-7061(02)00105-2, 2002.
Hubau, W., Lewis, S. L., Phillips, O. L., Affum-Baffoe, K., Beeckman, H., Cuní-Sanchez, A., Daniels, A. K., Ewango, C. E. N., Fauset, S., Mukinzi, J. M., Sheil, D., Sonké, B., Sullivan, M. J. P., Sunderland, T. C. H., Taedoumg, H., Thomas, S. C., White, L. J. T., Abernethy, K. A., Adu-Bredu, S., Amani, C. A., Baker, T. R., Banin, L. F., Baya, F., Begne, S. K., Bennett, A. C., Benedet, F., Bitariho, R., Bocko, Y. E., Boeckx, P., Boundja, P., Brienen, R. J. W., Brncic, T., Chezeaux, E., Chuyong, G. B., Clark, C. J., Collins, M., Comiskey, J. A., Coomes, D. A., Dargie, G. C., de Haulleville, T., Kamdem, M. N. D., Doucet, J.-L., Esquivel-Muelbert, A., Feldpausch, T. R., Fofanah, A., Foli, E. G., Gilpin, M., Gloor, E., Gonmadje, C., Gourlet-Fleury, S., Hall, J. S., Hamilton, A. C., Harris, D. J., Hart, T. B., Hockemba, M. B. N., Hladik, A., Ifo, S. A., Jeffery, K. J., Jucker, T., Yakusu, E. K., Kearsley, E., Kenfack, D., Koch, A., Leal, M. E., Levesley, A., Lindsell, J. A., Lisingo, J., Lopez-Gonzalez, G., Lovett, J. C., Makana, J.-R., Malhi, Y., Marshall, A. R., Martin, J., Martin, E. H., Mbayu, F. M., Medjibe, V. P., Mihindou, V., Mitchard, E. T. A., Moore, S., Munishi, P. K. T., Bengone, N. N., Ojo, L., Ondo, F. E., Peh, K. S.-H., Pickavance, G. C., Poulsen, A. D., Poulsen, J. R., Qie, L., Reitsma, J., Rovero, F., Swaine, M. D., Talbot, J., Taplin, J., Taylor, D. M., Thomas, D. W., Toirambe, B., Mukendi, J. T., Tuagben, D., Umunay, P. M., van der Heijden, G., Verbeeck, H., Vleminckx, J., Willcock, S., Wöll, H., Woods, J. T., and Zemagho, L.: Asynchronous carbon sink saturation in African and Amazonian tropical forests, Nature, 579, 80–87, https://doi.org/10.1038/s41586-020-2035-0, 2020.
Jackson, R. B., Canadell, J., Ehleringer, J. R., Mooney, H. A., Sala, O. E., and Schulze, E. D.: A global analysis of root distributions for terrestrial biomes, Oecologia, 108, 389–411, https://doi.org/10.1007/BF00333714, 1996.
Jiménez, E. M., Peñuela-Mora, M. C., Sierra, C. A., Lloyd, J., Phillips, O. L., Moreno, F. H., Navarrete, D., Prieto, A., Rudas, A., Álvarez, E., Quesada, C. A., Grande-Ortíz, M. A., García-Abril, A., and Patiño, S.: Edaphic controls on ecosystem-level carbon allocation in two contrasting Amazon forests, J. Geophys. Res.-Biogeo., 119, 1820–1830, https://doi.org/10.1002/2014JG002653, 2014.
Jirka, S., McDonald, A. J., Johnson, M. S., Feldpausch, T. R., Couto, E. G., and Riha, S. J.: Relationships between soil hydrology and forest structure and composition in the southern Brazilian Amazon, J. Veg. Sci., 18, 183–194, https://doi.org/10.1111/j.1654-1103.2007.tb02529.x, 2007.
Joetzjer, E., Delire, C., Douville, H., Ciais, P., Decharme, B., Fisher, R., Christoffersen, B., Calvet, J. C., da Costa, A. C. L., Ferreira, L. V., and Meir, P.: Predicting the response of the Amazon rainforest to persistent drought conditions under current and future climates: a major challenge for global land surface models, Geosci. Model Dev., 7, 2933–2950, https://doi.org/10.5194/gmd-7-2933-2014, 2014.
Joetzjer, E., Maignan, F., Chave, J., Goll, D., Poulter, B., Barichivich, J., Maréchaux, I., Luyssaert, S., Guimberteau, M., Naudts, K., Bonal, D., and Ciais, P.: Effect of tree demography and flexible root water uptake for modeling the carbon and water cycles of Amazonia, Ecol. Model., 469, 109969, https://doi.org/10.1016/j.ecolmodel.2022.109969, 2022.
Johnson, M. O., Galbraith, D., Gloor, M., De Deurwaerder, H., Guimberteau, M., Rammig, A., Thonicke, K., Verbeeck, H., von Randow, C., Monteagudo, A., Phillips, O. L., Brienen, R. J. W., Feldpausch, T. R., Lopez Gonzalez, G., Fauset, S., Quesada, C. A., Christoffersen, B., Ciais, P., Sampaio, G., Kruijt, B., Meir, P., Moorcroft, P., Zhang, K., Alvarez-Davila, E., Alves de Oliveira, A., Amaral, I., Andrade, A., Aragao, L. E. O. C., Araujo-Murakami, A., Arets, E. J. M. M., Arroyo, L., Aymard, G. A., Baraloto, C., Barroso, J., Bonal, D., Boot, R., Camargo, J., Chave, J., Cogollo, A., Cornejo Valverde, F., Lola da Costa, A. C., Di Fiore, A., Ferreira, L., Higuchi, N., Honorio, E. N., Killeen, T. J., Laurance, S. G., Laurance, W. F., Licona, J., Lovejoy, T., Malhi, Y., Marimon, B., Marimon Junior, B. H., Matos, D. C. L., Mendoza, C., Neill, D. A., Pardo, G., Peña-Claros, M., Pitman, N. C. A., Poorter, L., Prieto, A., Ramirez-Angulo, H., Roopsind, A., Rudas, A., Salomao, R. P., Silveira, M., Stropp, J., ter Steege, H., Terborgh, J., Thomas, R., Toledo, M., Torres-Lezama, A., van der Heijden, G. M. F., Vasquez, R., Guimarães Vieira, I. C., Vilanova, E., Vos, V. A., and Baker, T. R.: Variation in stem mortality rates determines patterns of above-ground biomass in Amazonian forests: implications for dynamic global vegetation models, Glob. Change Biol., 22, 3996–4013, https://doi.org/10.1111/gcb.13315, 2016.
Kishné, A., Yimam, Y., Morgan, C., and Dornblaser, B.: Evaluation and improvement of the default soil hydraulic parameters for the Noah Land Surface Model, Geoderma, 285, 247–259, https://doi.org/10.1016/j.geoderma.2016.09.022, 2017.
Knox, R. G., Longo, M., Swann, A. L. S., Zhang, K., Levine, N. M., Moorcroft, P. R., and Bras, R. L.: Hydrometeorological effects of historical land-conversion in an ecosystem-atmosphere model of Northern South America, Hydrol. Earth Syst. Sci., 19, 241–273, https://doi.org/10.5194/hess-19-241-2015, 2015.
Krinner, G., Viovy, N., de Noblet-Ducoudré, N., Ogée, J., Polcher, J., Friedlingstein, P., Ciais, P., Sitch, S., and Prentice, I. C.: A dynamic global vegetation model for studies of the coupled atmosphere-biosphere system, Global Biogeochem. Cy., 19, GB1015, https://doi.org/10.1029/2003GB002199, 2005.
Laurance, W. F., Fearnside, P. M., Laurance, S. G., Delamonica, P., Lovejoy, T. E., Rankin-de Merona, J. M., Chambers, J. Q., and Gascon, C.: Relationship between soils and Amazon forest biomass: a landscape-scale study, Forest Ecol. Manag., 118, 127–138, https://doi.org/10.1016/S0378-1127(98)00494-0, 1999.
Li, L., Wang, Y.-P., Yu, Q., Pak, B., Eamus, D., Yan, J., van Gorsel, E., and Baker, I. T.: Improving the responses of the Australian community land surface model (CABLE) to seasonal drought: Improving CABLE in response to drought, J. Geophys. Res.-Biogeo., 117, G04002, https://doi.org/10.1029/2012JG002038, 2012.
Longo, M., Knox, R. G., Levine, N. M., Alves, L. F., Bonal, D., Camargo, P. B., Fitzjarrald, D. R., Hayek, M. N., Restrepo-Coupe, N., Saleska, S. R., da Silva, R., Stark, S. C., Tapajós, R. P., Wiedemann, K. T., Zhang, K., Wofsy, S. C., and Moorcroft, P. R.: Ecosystem heterogeneity and diversity mitigate Amazon forest resilience to frequent extreme droughts, New Phytol., 219, 914–931, https://doi.org/10.1111/nph.15185, 2018.
Longo, M., Knox, R. G., Medvigy, D. M., Levine, N. M., Dietze, M. C., Kim, Y., Swann, A. L. S., Zhang, K., Rollinson, C. R., Bras, R. L., Wofsy, S. C., and Moorcroft, P. R.: The biophysics, ecology, and biogeochemistry of functionally diverse, vertically and horizontally heterogeneous ecosystems: the Ecosystem Demography model, version 2.2 – Part 1: Model description, Geosci. Model Dev., 12, 4309–4346, https://doi.org/10.5194/gmd-12-4309-2019, 2019a.
Longo, M., Knox, R., Medvigy, D. M., Levine, N. M., Dietze, M., Swann, A. L. S., Zhang, K., Rollinson, C., di Porcia e Brugnera, M., Scott, D., Serbin, S. P., Kooper, R., Pourmokhtarian, A., Shiklomanov, A., Viskari, T., and Moorcroft, P.: Ecosystem Demography Model, version 2.2 (ED-2.2) (rev-86), Zenodo [code], https://doi.org/10.5281/zenodo.3365659, 2019b.
Lu, J., Zhang, Q., Werner, A. D., Li, Y., Jiang, S., and Tan, Z.: Root-induced changes of soil hydraulic properties – A review, J. Hydrol., 589, 125203, https://doi.org/10.1016/j.jhydrol.2020.125203, 2020.
Maeda, E. E., Kim, H., Aragão, L. E. O. C., Famiglietti, J. S., and Oki, T.: Disruption of hydroecological equilibrium in southwest Amazon mediated by drought, Geophys. Res. Lett., 42, 7546–7553, https://doi.org/10.1002/2015GL065252, 2015.
Medeiros, J. C., Cooper, M., Dalla Rosa, J., Grimaldi, M., and Coquet, Y.: Assessment of pedotransfer functions for estimating soil water retention curves for the amazon region, Rev. Bras. Cienc. Solo, 38, 730–743, https://doi.org/10.1590/S0100-06832014000300005, 2014.
Medvigy, D., Wofsy, S. C., Munger, J. W., Hollinger, D. Y., and Moorcroft, P. R.: Mechanistic scaling of ecosystem function and dynamics in space and time: Ecosystem Demography model version 2, J. Geophys. Res.-Biogeo., 114, G01002, https://doi.org/10.1029/2008JG000812, 2009.
Mencuccini, M., Manzoni, S., and Christoffersen, B.: Modelling water fluxes in plants: from tissues to biosphere, New Phytol., 222, 1207–1222, https://doi.org/10.1111/nph.15681, 2019.
Meunier, F.: Data for the publication “Low sensitivity of three terrestrial biosphere models to soil texture over the South-American tropics” (v1.0.0), Zenodo [data set], https://doi.org/10.5281/zenodo.6226622, 2022.
Moeys, J.: The soil texture wizard: R functions for plotting, classifying, transforming and exploring soil texture data, 104, https://cran.r-project.org/web/packages/soiltexture/vignettes/soiltexture_vignette.pdf (last access: 11 October 2022), 2018.
Montzka, C., Herbst, M., Weihermüller, L., Verhoef, A., and Vereecken, H.: A global data set of soil hydraulic properties and sub-grid variability of soil water retention and hydraulic conductivity curves, Earth Syst. Sci. Data, 9, 529–543, https://doi.org/10.5194/essd-9-529-2017, 2017.
Mualem, Y.: A new model for predicting the hydraulic conductivity of unsaturated porous media, Water Resour. Res., 12, 513–522, https://doi.org/10.1029/WR012i003p00513, 1976.
Nachtergaele, F. O., van Velthuizen, H., Verelst, L., Batjes, N. H., Dijkshoorn, J. A., van Engelen, V. W. P., Fischer, G., Jones, A., Montanarella, L., Petri, M., Prieler, S., Teixeira, E., Wilberg, D., and Shi, X.: Harmonized World Soil Database (version 1.0), https://research.wur.nl/en/publications/harmonized-world-soil-database-version-10 (last access: 11 October 2022), 2008.
Negrón Juárez, R. I., Hodnett, M. G., Fu, R., Gouden, M. L., and von Randow, C.: Control of dry season evapotranspiration over the Amazonian forest as inferred from observation at a Southern Amazon forest site, J. Climate, 20, 2827–2839, https://doi.org/10.1175/JCLI4184.1, 2007.
Nepstad, D. C., de Carvalho, C. R., Davidson, E. A., Jipp, P. H., Lefebvre, P. A., Negreiros, G. H., da Silva, E. D., Stone, T. A., Trumbore, S. E., and Vieira, S.: The role of deep roots in the hydrological and carbon cycles of Amazonian forests and pastures, Nature, 372, 666–669, https://doi.org/10.1038/372666a0, 1994.
Nepstad, D. C., Tohver, I. M., Ray, D., Moutinho, P., and Cardinot, G.: Mortality of Large Trees and Lianas Following Experimental Drought in an Amazon Forest, Ecology, 88, 2259–2269, https://doi.org/10.1890/06-1046.1, 2007.
Oberpriller, J., Herschlein, C., Anthoni, P., Arneth, A., Krause, A., Rammig, A., Lindeskog, M., Olin, S., and Hartig, F.: Climate and parameter sensitivity and induced uncertainties in carbon stock projections for European forests (using LPJ-GUESS 4.0), Geosci. Model Dev., 15, 6495–6519, https://doi.org/10.5194/gmd-15-6495-2022, 2022.
O'Connell, C. S., Ruan, L., and Silver, W. L.: Drought drives rapid shifts in tropical rainforest soil biogeochemistry and greenhouse gas emissions, Nat. Commun., 9, 1348, https://doi.org/10.1038/s41467-018-03352-3, 2018.
ORCHIDEE in tags/ORCHIDEE_2_0 – ORCHIDEE: http://forge.ipsl.jussieu.fr/orchidee/browser/tags/ORCHIDEE_2_0/ORCHIDEE/, last access: 23 February 2022.
Patil, N. G. and Singh, S. K.: Pedotransfer Functions for Estimating Soil Hydraulic Properties: A Review, Pedosphere, 26, 417–430, https://doi.org/10.1016/S1002-0160(15)60054-6, 2016.
Peylin, P., Ghattas, J., Cadule, P., Cheruy, F., Ducharne, A., Guenet, B., Lathière, J., Luyssaert, S., Maignan, F., Maugis, P., Ottle, C., Polcher, J., Viovy, N., Vuichard, N., Bastrikov, V., Guimberteau, M., Lanso, A.-S., MacBean, N., Mcgrath, M., Tafasca, S., and Wang, F.: The global land surface model ORCHIDEE – Tag2.0, in preparation, 2022.
Phillips, O. L., Aragão, L. E. O. C., Lewis, S. L., Fisher, J. B., Lloyd, J., López-González, G., Malhi, Y., Monteagudo, A., Peacock, J., Quesada, C. A., van der Heijden, G., Almeida, S., Amaral, I., Arroyo, L., Aymard, G., Baker, T. R., Bánki, O., Blanc, L., Bonal, D., Brando, P., Chave, J., de Oliveira, Á. C. A., Cardozo, N. D., Czimczik, C. I., Feldpausch, T. R., Freitas, M. A., Gloor, E., Higuchi, N., Jiménez, E., Lloyd, G., Meir, P., Mendoza, C., Morel, A., Neill, D. A., Nepstad, D., Patiño, S., Peñuela, M. C., Prieto, A., Ramírez, F., Schwarz, M., Silva, J., Silveira, M., Thomas, A. S., ter Steege, H., Stropp, J., Vásquez, R., Zelazowski, P., Dávila, E. A., Andelman, S., Andrade, A., Chao, K.-J., Erwin, T., Di Fiore, A., Honorio, C. E., Keeling, H., Killeen, T. J., Laurance, W. F., Cruz, A. P., Pitman, N. C. A., Vargas, P. N., Ramírez-Angulo, H., Rudas, A., Salamão, R., Silva, N., Terborgh, J., and Torres-Lezama, A.: Drought Sensitivity of the Amazon Rainforest, Science, 323, 1344–1347, https://doi.org/10.1126/science.1164033, 2009.
Plante, A. F., Conant, R. T., Stewart, C. E., Paustian, K., and Six, J.: Impact of Soil Texture on the Distribution of Soil Organic Matter in Physical and Chemical Fractions, Soil Sci. Soc. Am. J., 70, 287–296, https://doi.org/10.2136/sssaj2004.0363, 2006.
Poggio, L., de Sousa, L. M., Batjes, N. H., Heuvelink, G. B. M., Kempen, B., Ribeiro, E., and Rossiter, D.: SoilGrids 2.0: producing soil information for the globe with quantified spatial uncertainty, SOIL, 7, 217–240, https://doi.org/10.5194/soil-7-217-2021, 2021.
Poulter, B., MacBean, N., Hartley, A., Khlystova, I., Arino, O., Betts, R., Bontemps, S., Boettcher, M., Brockmann, C., Defourny, P., Hagemann, S., Herold, M., Kirches, G., Lamarche, C., Lederer, D., Ottlé, C., Peters, M., and Peylin, P.: Plant functional type classification for earth system models: results from the European Space Agency's Land Cover Climate Change Initiative, Geosci. Model Dev., 8, 2315–2328, https://doi.org/10.5194/gmd-8-2315-2015, 2015.
Prentice, I. C., Cramer, W., Harrison, S. P., Leemans, R., Monserud, R. A., and Solomon, A. M.: A global biome model based on plant physiology and dominance, soil properties and climate, J. Biogeogr., 19, 117–134, 1992.
Prentice, I. C., Dong, N., Gleason, S. M., Maire, V., and Wright, I. J.: Balancing the costs of carbon gain and water transport: testing a new theoretical framework for plant functional ecology, Ecol. Lett., 17, 82–91, https://doi.org/10.1111/ele.12211, 2014.
Qu, W., Bogena, H. R., Huisman, J. A., Vanderborght, J., Schuh, M., Priesack, E., and Vereecken, H.: Predicting subgrid variability of soil water content from basic soil information, Geophys. Res. Lett., 42, 789–796, https://doi.org/10.1002/2014GL062496, 2015.
Richards, L. A.: Capillary conduction of liquids through porous mediums, Physics, 1, 318–333, https://doi.org/10.1063/1.1745010, 1931.
Rowland, L., da Costa, A. C. L., Galbraith, D. R., Oliveira, R. S., Binks, O. J., Oliveira, A. A. R., Pullen, A. M., Doughty, C. E., Metcalfe, D. B., Vasconcelos, S. S., Ferreira, L. V., Malhi, Y., Grace, J., Mencuccini, M., and Meir, P.: Death from drought in tropical forests is triggered by hydraulics not carbon starvation, Nature, 528, 119–122, https://doi.org/10.1038/nature15539, 2015.
Running, S., Mu, Q., and Zhao, M.: MOD17A2H MODIS/Terra Gross Primary Productivity 8-Day L4 Global 500m SIN Grid V006, NASA EOSDIS Land Processes DAAC [data set], https://doi.org/10.5067/MODIS/MOD17A2H.006, 2015.
Saleska, S. R., Miller, S. D., Matross, D. M., Goulden, M. L., Wofsy, S. C., da Rocha, H. R., de Camargo, P. B., Crill, P., Daube, B. C., de Freitas, H. C., Hutyra, L., Keller, M., Kirchhoff, V., Menton, M., Munger, J. W., Pyle, E. H., Rice, A. H., and Silva, H.: Carbon in Amazon forests: unexpected seasonal fluxes and disturbance-induced losses, Science, 302, 1554–1557, https://doi.org/10.1126/science.1091165, 2003.
Silver, W. L., Neff, J., McGroddy, M., Veldkamp, E., Keller, M., and Cosme, R.: Effects of Soil Texture on Belowground Carbon and Nutrient Storage in a Lowland Amazonian Forest Ecosystem, Ecosystems, 3, 193–209, https://doi.org/10.1007/s100210000019, 2000.
Sitch, S., Smith, B., Prentice, I. C., Arneth, A., Bondeau, A., Cramer, W., Kaplan, J. O., Levis, S., Lucht, W., Sykes, M. T., Thonicke, K., and Venevsky, S.: Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model, Glob. Change Biol., 9, 161–185, https://doi.org/10.1046/j.1365-2486.2003.00569.x, 2003.
Smith, B., Prentice, I. C., and Sykes, M. T.: Representation of vegetation dynamics in the modelling of terrestrial ecosystems: comparing two contrasting approaches within European climate space, Global Ecol. Biogeogr., 10, 621–637, https://doi.org/10.1046/j.1466-822X.2001.t01-1-00256.x, 2001.
Smith, B., Wårlind, D., Arneth, A., Hickler, T., Leadley, P., Siltberg, J., and Zaehle, S.: Implications of incorporating N cycling and N limitations on primary production in an individual-based dynamic vegetation model, Biogeosciences, 11, 2027–2054, https://doi.org/10.5194/bg-11-2027-2014, 2014.
Soil and Survey Manual: https://www.nrcs.usda.gov/wps/portal/nrcs/detailfull/soils/ref/?cid=nrcs142p2_054262 (last access: 22 February 2022), 2002.
SoilGrids web portal: https://soilgrids.org, last access: 11 October 2022.
Spinoni, J., Naumann, G., Carrao, H., Barbosa, P., and Vogt, J.: World drought frequency, duration, and severity for 1951–2010, Int. J. Climatol., 34, 2792–2804, https://doi.org/10.1002/joc.3875, 2014.
Staal, A., Flores, B. M., Aguiar, A. P. D., Bosmans, J. H. C., Fetzer, I., and Tuinenburg, O. A.: Feedback between drought and deforestation in the Amazon, Environ. Res. Lett., 10, 044024, https://doi.org/10.1088/1748-9326/ab738e, 2020.
Tafasca, S., Ducharne, A., and Valentin, C.: Weak sensitivity of the terrestrial water budget to global soil texture maps in the ORCHIDEE land surface model, Hydrol. Earth Syst. Sci., 24, 3753–3774, https://doi.org/10.5194/hess-24-3753-2020, 2020.
Telles, E. C. C., de Camargo, P. B., Martinelli, L. A., Trumbore, S. E., da Costa, E. S., Santos, J., Higuchi, N., and Oliveira Jr., R. C.: Influence of soil texture on carbon dynamics and storage potential in tropical forest soils of Amazonia, Global Biogeochem. Cy., 17, 1040, https://doi.org/10.1029/2002GB001953, 2003.
Uribe, M. R., Sierra, C. A., and Dukes, J. S.: Seasonality of Tropical Photosynthesis: A Pantropical Map of Correlations With Precipitation and Radiation and Comparison to Model Outputs, J. Geophys. Res.-Biogeo., 126, e2020JG006123, https://doi.org/10.1029/2020JG006123, 2021.
van den Hurk, B., Kim, H., Krinner, G., Seneviratne, S. I., Derksen, C., Oki, T., Douville, H., Colin, J., Ducharne, A., Cheruy, F., Viovy, N., Puma, M. J., Wada, Y., Li, W., Jia, B., Alessandri, A., Lawrence, D. M., Weedon, G. P., Ellis, R., Hagemann, S., Mao, J., Flanner, M. G., Zampieri, M., Materia, S., Law, R. M., and Sheffield, J.: LS3MIP (v1.0) contribution to CMIP6: the Land Surface, Snow and Soil moisture Model Intercomparison Project – aims, setup and expected outcome, Geosci. Model Dev., 9, 2809–2832, https://doi.org/10.5194/gmd-9-2809-2016, 2016.
van Genuchten, M. Th.: A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils, Soil Sci. Soc. Am. J., 44, 892, https://doi.org/10.2136/sssaj1980.03615995004400050002x, 1980.
Van Looy, K., Bouma, J., Herbst, M., Koestel, J., Minasny, B., Mishra, U., Montzka, C., Nemes, A., Pachepsky, Y. A., Padarian, J., Schaap, M. G., Tóth, B., Verhoef, A., Vanderborght, J., van der Ploeg, M. J., Weihermüller, L., Zacharias, S., Zhang, Y., and Vereecken, H.: Pedotransfer Functions in Earth System Science: Challenges and Perspectives, Rev. Geophys., 55, 1199–1256, https://doi.org/10.1002/2017RG000581, 2017.
Vanderborght, J., Couvreur, V., Meunier, F., Schnepf, A., Vereecken, H., Bouda, M., and Javaux, M.: From hydraulic root architecture models to macroscopic representations of root hydraulics in soil water flow and land surface models, Hydrol. Earth Syst. Sci., 25, 4835–4860, https://doi.org/10.5194/hess-25-4835-2021, 2021.
Veldkamp, E., Schmidt, M., Powers, J. S., and Corre, M. D.: Deforestation and reforestation impacts on soils in the tropics, Nat. Rev. Earth Environ., 1, 590–605, https://doi.org/10.1038/s43017-020-0091-5, 2020.
Verbeeck, H., Peylin, P., Bacour, C., Bonal, D., Steppe, K., and Ciais, P.: Seasonal patterns of CO2 fluxes in Amazon forests: Fusion of eddy covariance data and the ORCHIDEE model, J. Geophys. Res., 116, G02018, https://doi.org/10.1029/2010jg001544, 2011.
Vereecken, H., Pachepsky, Y., Bogena, H., and Montzka, C.: Upscaling Issues in Ecohydrological Observations, in: Observation and Measurement of Ecohydrological Processes, edited by: Li, X. and Vereecken, H., Springer, Berlin, Heidelberg, 435–454, https://doi.org/10.1007/978-3-662-48297-1_14, 2019.
Viovy, N.: CRUNCEP Version 7 – Atmospheric Forcing Data for the Community Land Model, Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory [data set], https://doi.org/10.5065/PZ8F-F017, 2018.
Walko, R. L., Band, L. E., Baron, J., Kittel, T. G. F., Lammers, R., Lee, T. J., Ojima, D., Pielke, R. A., Taylor, C., Tague, C., Tremback, C. J., and Vidale, P. L.: Coupled Atmosphere–Biophysics–Hydrology Models for Environmental Modeling, J. Appl. Meteorol., 39, 931–944, https://doi.org/10.1175/1520-0450(2000)039<0931:CABHMF>2.0.CO;2, 2000.
Xu, X., Medvigy, D., Powers, J. S., Becknell, J. M., and Guan, K.: Diversity in plant hydraulic traits explains seasonal and inter-annual variations of vegetation dynamics in seasonally dry tropical forests, New Phytol., 212, 80–95, https://doi.org/10.1111/nph.14009, 2016.
Yang, H., Ciais, P., Wigneron, J.-P., Chave, J., Cartus, O., Chen, X., Fan, L., Green, J. K., Huang, Y., Joetzjer, E., Kay, H., Makowski, D., Maignan, F., Santoro, M., Tao, S., Liu, L., and Yao, Y.: Climatic and biotic factors influencing regional declines and recovery of tropical forest biomass from the 2015/16 El Niño, P. Natl. Acad. Sci. USA, 119, e2101388119, https://doi.org/10.1073/pnas.2101388119, 2022.
Yao, Y., Joetzjer, E., Ciais, P., Viovy, N., Cresto Aleina, F., Chave, J., Sack, L., Bartlett, M., Meir, P., Fisher, R., and Luyssaert, S.: Forest fluxes and mortality response to drought: model description (ORCHIDEE-CAN-NHA, r7236) and evaluation at the Caxiuanã drought experiment, Geosci. Model Dev. Discuss. [preprint], https://doi.org/10.5194/gmd-2021-362, in review, 2021.
Zinn, Y. L., Lal, R., Bigham, J. M., and Resck, D. V. S.: Edaphic Controls on Soil Organic Carbon Retention in the Brazilian Cerrado: Texture and Mineralogy, Soil Sci. Soc. Am. J., 71, 1204–1214, https://doi.org/10.2136/sssaj2006.0014, 2007.





