Characterizing uncertainties of Earth system modeling with heterogeneous many-core architecture computing

The physical and heat limits of semiconductor technology require the adaptation of heterogeneous architectures in supercomputers, such as graphics processing units (GPUs) with many-core accelerators and many-core processors with management and computing cores, to maintain a continuous increase in computing performance. The transition from homogeneous multi-core architectures to heterogeneous many-core architectures can produce non-bit-for-bit reproducibility that leads to numerical perturbations and uncertainties in simulation results, which could blend with errors due to coding bugs. The development of a methodology to identify computational perturbations and secure model correctness is a critically important step in model development on computer systems with new architectures. Thus, we have developed a methodology to characterize the uncertainties in the heterogeneous many-core computing environment. This methodology contains a simple multi-column atmospheric model consisting of typical discontinuous physical parameterizations defined by the selection programming structure, an efficient ensemble-based test approach, and an application to the GPU-based high-performance computing (HPC) and Sunway systems. Statistical distributions from ensembles of the heterogeneous systems show quantitative analyses of computational perturbations and acceptable error tolerances. The methodology aims to enable one to fully distinguish between perturbations caused by platforms and discrepancies caused by software bugs, and it provides encouraging references for verifying the reliability of supercomputing platforms and discussing the sensibility of Earth system modeling to the adaptation of new heterogeneous many-core architectures.

1 Introduction

The improvement of the resolution of numerical simulations requires an increase in computing power. Due to physical and heat limits, regular increases in the processing frequency of supercomputing processors came to a stop roughly a decade ago. Since then, increases in the number of processors, the design of inexact hardware (Düben et al., 2014), and heterogeneous many-core architectures have been used to continue increasing computing performance. For heterogeneous many-core architectures, the major computing power is provided by many-core accelerators, such as NVIDIA graphics processing units (GPUs) (Vazhkudai et al., 2018) as well as Intel Xeon Phi Many Integrated Cores (MICs) and many-core processor Sunway computing processing elements (CPEs) (Fu et al., 2016). Dubbed inexact (Palem and Lingamneni, 2013) or heterogeneous, many-core architecture computing can produce nonidentical floating-point arithmetic outputs. The differences between arithmetic units and compilation flows can sometimes cause numerical perturbations and generate uncertainties (Zhang et al., 2020).

Earth system models (ESMs) are based on mathematical equations, including dynamical and parameterization processes, established by dynamical, physical, chemical, and biological processes to resolve more details of interacting atmosphere, ocean, sea-ice, and land surface components through numerical methods consisting of millions of lines of legacy codes (Flato, 2011), such as the Community Earth System Model (CESM). Perturbations can cause sudden changes in discontinuous physical parameterizations (Yano, 2016) defined by selection structures in programming, such as cloud bottom and cloud top (Zhang and McFarlane, 1995) as well as the top of the planetary boundary layer (Sun and Ogura, 1980) in atmosphere modules and the mixed-layer depth in ocean modules (Kara et al., 2000).

The traditional method to secure the correctness of ESMs for computing environment changes is a cumbersome process. For example, data from a climate simulation of several hundred years (typically 400) on the new machine are analyzed and compared to data from the same simulation on a “trusted” machine by senior climate scientists (Baker et al., 2015). A CESM ensemble-based consistency test (CESM-ECT) is then currently used to evaluate climate consistency for the ongoing state of computing environment changes (Baker et al., 2015; Milroy et al., 2016). However, all of the abovementioned methods focus on homogeneous multi-core architecture computing. For heterogeneous many-core architecture computing, the difference in computing environments between master and slave cores can cause perturbations whenever a slave core or an accelerator is involved. Hence, there is a lack of methodology for identifying and characterizing the computational perturbations in heterogeneous many-core computing environments.

Therefore, the goal of this article is to design a methodology to characterize the uncertainties of Earth system modeling in heterogeneous many-core computing environments and discuss its influence on numerical simulations. The methodology contains a simple multi-column atmospheric model consisting of typical discontinuous physical parameterizations defined by the selection programming structure to study uncertainties through sudden changes, an efficient ensemble-based test approach to characterize uncertainties through quantitative analyses, and a software application to verify the reliability of heterogeneous many-core systems.

The rest of the paper is organized as follows: Sect. 2 provides background information on uncertainties in floating-point computation; Sect. 3 details the methodology to characterize uncertainties; Sect. 4 shows the results of experiments with the methodology; and, finally, the summary and discussion are given in Sect. 5.

2 Uncertainties in floating-point computation

2.1 The origins of uncertainties

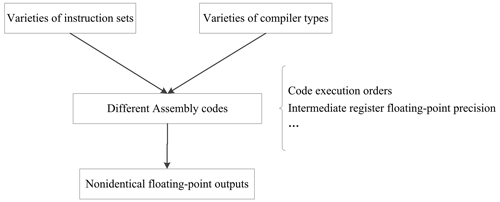
During ESM code porting with a homogeneous computing approach, changes in computing environments can cause simulation results that are no longer bit-for-bit (BFB) identical to previous output data (Baker et al., 2015), either due to hardware architecture transitions (such as the transitions from IBM processors to Intel processors around the year 2010) or compiler configurations (such as the changes from Intel compilers to GNU compilers) (Rosinski and Williamson, 1997; Arteaga et al., 2014). Figure 1 shows a schematic illustration of the sources of nonidentical floating-point outputs. In the process of translating a high-level programming language into machine language codes, different compilers and/or instruction sets can cause assembly code differences, such as different code execution order and/or different intermediate register floating-point precision, eventually causing nonidentical floating-point output.

Figure 1 Schematic illustration of sources of nonidentical floating-point outputs.

2.2 Uncertainties in heterogeneous many-core architecture computing

The heterogeneous computing approach introduces even more sources of uncertainty. Firstly, the heterogeneous way of computing introduces an additional level of domain or task decomposition compared with homogeneous computing. The different algorithmic design already means that there are different layouts of data elements and different sequences of computing. For example, Fu et al. (2017b​​​​​​​) carried out adjustments of both the computational sequence and the loop structures so as to achieve a suitable level of parallelism for CPE clusters. Secondly, in some cases, one would face a hardware difference between the master cores and slave cores in a heterogeneous scenario. The master cores and slave cores require a slightly different hardware design to implement the floating-point arithmetic, thereby leading to hardware-generated differences in corner cases related to denormalized numbers. Therefore, compared with homogeneous computing using master cores only, heterogeneous computing can cause nonidentical floating-point outputs whenever a slave core or accelerator is involved. Hence, the model is perturbed constantly during integration on a heterogeneous supercomputing platform (Zhang et al., 2020).

For GPU-based high-performance computing systems, GPU devices are introduced as accelerators for general-purpose scientific and engineering applications (Xiao et al., 2013), such as the GPU-based Princeton Ocean Model (POM) (Xu et al., 2015) and the GPU-based COSMO regional weather model by MeteoSwiss (Fuhrer et al., 2018). The fixed instruction set, streaming assembly (SASS), and compiler (NVCC) are used in GPU-based systems to achieve cost-effective data processing (Stephenson et al., 2015). For GPU-based high-performance computing (HPC) systems, the difference in the central processing unit (CPU) and GPU math libraries can cause different floating-point results for a given input. Functions compiled for the GPU will use the NVIDIA Compute Unified Device Architecture (CUDA) math library implementation, whereas functions compiled for the CPU will use the host compiler math library implementation (e.g., glibc on Linux; Whitehead and Fit-Florea, 2011). For the Sunway TaihuLight, which is the Chinese homegrown supercomputing platform, the master and slave cores are integrated into the same processor (SW26010), as shown in Fig. 2. Each SW26010 processor can be divided into four identical core groups (CGs), which are connected through the “network on chip”. Each CG includes one management processing element (MPE) and one CPE cluster with 8 × 8 CPEs. For the Sunway system, in order to achieve the maximum aggregated computing power and minimize the complexity of the micro-architecture, the MPEs and CPEs have different functions; therefore, programs are generally computed in a hybrid mode in order to use the instruction sets separately (Fu et al., 2016). The MPEs and CPEs use a slightly different hardware design to implement the floating-point arithmetic, thereby leading to hardware-generated differences in corner cases related to denormalized numbers. The Sunway TaihuLight has realized high-resolution scientific computing with high-efficiency, such as version 5 of the Community Atmosphere Model (CAM5) (Fu et al., 2017a, b) and CESM1.3 (Zhang et al., 2020). After the domain-based task decomposition in the traditional message passing interface (MPI) parallelism (first-level parallelism) among the core groups, the Sunway machine requires a CPE-based task decomposition and communication between the MPE and CPEs within each core group (second-level parallelism) (Zhang et al., 2020). Upgraded from a SW26010 processor, the new-generation Sunway supercomputer has been constructed using a SW26010P processor. Using the new-generation Sunway supercomputer, higher-resolution ESMs have been developed. Thus, identification and understanding of the characteristics of floating-point computation uncertainties in heterogeneous architectures are urgently demanded.

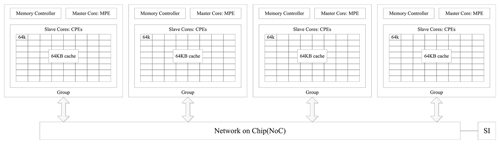
Figure 2 A schematic illustration of the general architecture of the Sunway SW26010 processor. Each processor consists of four core groups, and each core group includes a memory controller, a master core (MPE), and 64 slave cores (CPEs), each of which has a 64 KB scratch pad fast memory, called LDM (local data memory). The four core groups are linked together by the network on chip, and the whole CPU is linked with other CPUs by the system interface (SI) network (courtesy of Fu et al., 2016).

In this study, we focus on unavoidable perturbations caused by the hardware design difference between master cores and slave cores. We start from the Goff–Gratch equation (Goff and Gratch, 1946) and examine the floating-point results. The Goff–Gratch equation is a formula that calculates the saturated vapor pressure (SVP); it is highly nonlinear and widely used in cloud parameterizations such as the Zhang and McFarlane cumulus convection parameterization (ZM) scheme (Zhang and McFarlane, 1995) and the Morrison and Gettelman two-moment stratiform microphysics scheme (Morrison and Gettelman, 2008). The Goff–Gratch equation is given by the following:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}\log p& =-\mathrm{7.90298}(T_{\mathrm{bt}}/T-\mathrm{1})+\mathrm{5.02808}\log (T_{\mathrm{bt}}/T)\\ & -\mathrm{1.3816}\times {\mathrm{10}}^{-\mathrm{7}}({\mathrm{10}}^{\mathrm{11.344}(\mathrm{1}-T/T_{\mathrm{bt}})}-\mathrm{1})\\ & +\mathrm{8.1328}\times {\mathrm{10}}^{-\mathrm{3}}({\mathrm{10}}^{-\mathrm{3.49149}(T_{\mathrm{bt}}/T-\mathrm{1})}-\mathrm{1})+\log p_{\mathrm{bt}},\end{array}\end{array}$$

where log refers to the logarithm in base 10, p is the SVP, T is the absolute atmospheric temperature in degrees kelvin, T_bt is the steam-point temperature (here, T_bt is 373.15 K), and p_bt is p at the steam-point pressure (here, p_bt is 1013.25 hPa). Single values are used to calculate the Goff–Gratch equation in order to avoid introducing different layouts of data elements and different sequences of computing. The computing environments include homogeneous computing using only the Intel x86 CPU, homogeneous computing using only the MPE, heterogeneous computing using both CPUs and GPUs (CPU–GPU), and heterogeneous computing using both MPEs and CPEs (MPE–CPE). The Fortran codes of the Goff–Gratch equation are the same in all homogeneous computing environments (CPU-only and MPE-only), as shown in Fig. 3a. In all heterogeneous computing environments (CPU–GPU and MPE–CPE), the Goff–Gratch equation is implemented for the GPU with CUDA Fortran (Fig. 3b) and for the CPE in a hybrid mode, where the MPE major task (in Fortran) manages CPE subtasks (in C language) (Fig. 3c). For the experiments, the same Fortran codes are used to implement the Goff–Gratch equation, and the same parameter and input data are used to run the program. Either the CPU–GPU or MPE–CPE implementation forms a heterogeneous many-core architecture computing environment. The different realizations are defined by whether the Goff–Gratch equation is calculated in the slave core (GPU or CPE) or master core (CPU or MPE). Next, we give an example of compiler changes to measure the scale of the perturbations involved with slave cores. The Goff–Gratch equation in Fortran (Fig. 3a) is replaced by C language using only the Intel x86 CPU. The input data point T is 234.917910298505. The floating-point results are shown in Table 1. The different results of CPU-only (Fortran language) and CPU-only (C language) are caused by compiler changes. The different results of CPU-only (or MPE-only) and CPU–GPU (or MPE–CPE) are caused by the difference in hardware designs between the master and slave cores. Note that the same digits from CPU–GPU and MPE–CPE occurring by chance, given the simplicity of the Goff–Gratch equation, do not mean that the GPU and CPE have the same hardware designs to implement the floating-point arithmetic. For heterogeneous computing, differences in hardware designs (to implement floating-point arithmetic) between the master and slave cores can generate a perturbation due to slave cores. The key question is, however, whether or not such perturbations caused by slave cores affect the scientific results. Next, we will design a methodology to characterize the uncertainties in heterogeneous many-core architecture computing and discuss its influences on the numerical solution.

Figure 3 The codes of the Goff–Gratch equation in homogeneous and heterogeneous computing environments.

Table 1 The SVP results using the Goff–Gratch equation with the difference in compiler configurations and computing environments.

3 Methodology to characterize uncertainties

3.1 The general idea behind developing the methodology

As noted, heterogeneous many-core architecture computing can cause nonidentical floating-point outputs that lead to frequent ESM simulation perturbations when using GPUs or CPEs and, thus, generate unique uncertainties. However, identifying computational perturbations and securing model correctness with heterogeneous many-core architecture computing has two major challenges. First, the heavy legacy of codes limits the efficiency of refactoring and optimizing a complex ESM on heterogeneous systems, which makes it extremely difficult to examine the codes line by line. Hence, an urgent demand exists for a straightforward metric to measure uncertainties instead of counting nonidentical floating-point outputs in each expression evaluation. Second, the complexity of the model makes it difficult for us to identify and mitigate the possible adverse impact of computational perturbations on the sciences enabled by the models. To overcome these challenges, our methodology includes (1) the design of a simple model that consists of typical discontinuous physical parameterizations defined by selection programming structure to study the uncertainties due to the perturbations induced from slave cores or accelerators. The model should be simple enough so that porting, running, and the comparison of results between different supercomputing platforms can be easily performed. As the model is simulating chaotic dynamics, resulting in the differences between simulations growing exponentially, we also (2) develop an ensemble approach to quantitatively characterize uncertainties and (3) implement an application to verify the reliability of heterogeneous many-core systems.

3.2 A simple model to study hardware design differences

Intending to study the uncertainties produced by hardware design differences, we design a multi-column atmospheric model. First, to meet simplicity needs, the advection term describing the local variation due to its horizontal transport is used as a representation of the interaction between large-scale and local convection (Li et al., 2016). The governing equations of the simple model are as follows:

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\partial T}{\partial t}}=-u\left(z\right){\displaystyle \frac{\partial T}{\partial x}},\end{array}$$

and

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{\partial q}{\partial t}}=-u\left(z\right){\displaystyle \frac{\partial q}{\partial x}}.\end{array}$$

Here, T and q are the respective temperature and specific humidity, and u is the horizontal wind velocity as a function of height z. u is fixed as time mean outputs from the CAM5 climate simulation on the homogeneous multi-core platform at the Qingdao Pilot National Laboratory for Marine Science and Technology (QNLM) for the period from 1850 to 1860. The distance Δx is set to be about 277.5 km.

Second, the deep convective adjustment terms, F_T and F_q, are used to control the water vapor content in the atmosphere (Emanuel and Živković-Rothman, 1999), which include selection programming structure outputs, such as cloud bottom and cloud top. Thus, the governing equations become

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{\partial T}{\partial t}}=-u\left(z\right){\displaystyle \frac{\partial T}{\partial x}}+F_T,\end{array}$$

and

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\partial q}{\partial t}}=-u\left(z\right){\displaystyle \frac{\partial q}{\partial x}}+F_q.\end{array}$$

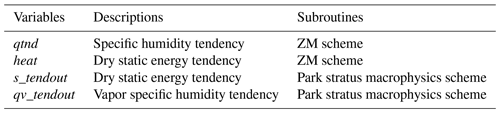
F_T and F_q are calculated in tendency equations using the ZM scheme (Zhang and McFarlane, 1995) along with the dilute convective available potential energy (CAPE) modification (Neale et al., 2008). With a set of thermodynamic properties of source air estimated from the grid-mean values at the level of maximum moist static energy (MSE)​​​​​​​ and surface fluxes, a deep convective updraft plume rises from zb with a specified lateral entrainment rate if the dilute CAPE is larger than 70 J kg⁻¹ (Park et al., 2014). CAPE is defined as follows:

$$\begin{array}{}\text{(6)}& \mathrm{CAPE}=\underset{\mathrm{Zb}}{\overset{\mathrm{NBL}}{\int }}g{\displaystyle \frac{T_{\mathrm{vp}}-T_{\mathrm{ve}}}{T_{\mathrm{ve}}}}\mathrm{d}z,\end{array}$$

where NBL is the neutral buoyancy level of the parcel lifted from the most unstable level in the boundary layer; T_vp and T_ve are the virtual temperatures of the parcel and environment, respectively; and g is the acceleration due to gravity. z_b is defined as the cloud bottom. The cloud top, z_t, is satisfied as follows:

$$\begin{array}{}\text{(7)}& \left[h_{\mathrm{u}}\right(z_{\mathrm{t}})\le h^{*}(z_{\mathrm{t}}\left)\right]\mathit{\&}\left[h_{\mathrm{u}}\right(z_{\mathrm{t}}+\mathrm{1})>h^{*}(z_{\mathrm{t}}+\mathrm{1}\left)\right]=\mathrm{True},\end{array}$$

where h_u is the moist static energy (MSE) of the lifted air parcel, and h^* is the saturation MSE of the environment (Wang and Zhang, 2018). MSE is defined as follows:

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{\partial m_{\mathrm{u}}{h}_{\mathrm{u}}}{\partial z}}=E_{\mathrm{u}}\stackrel{\mathrm{‾}}{h}-D_{\mathrm{u}}\widehat{h},\end{array}$$

where m_u is the updraft cloud mass flux; E_u and D_u are the mass entrainment and detrainment rate, respectively; and $\stackrel{\mathrm{‾}}{h}$ and $\widehat{h}$ are the MSE of the grid mean and the MSE detrained from updrafts, respectively.

Third, the vertical macrophysics adjustment terms, Y_T and Y_q, are used to supplement large-scale stratiform precipitation. Thus, the governing equations become

$$\begin{array}{}\text{(9)}& {\displaystyle \frac{\partial T}{\partial t}}=-u\left(z\right){\displaystyle \frac{\partial T}{\partial x}}+F_T+Y_T,\end{array}$$

and

$$\begin{array}{}\text{(10)}& {\displaystyle \frac{\partial q}{\partial t}}=-u\left(z\right){\displaystyle \frac{\partial q}{\partial x}}+F_q+Y_q.\end{array}$$

Y_T and Y_q are calculated in tendency equations using the Park stratus macrophysics scheme (Park et al., 2014). The Park scheme is defined as stratiform condensation/evaporation and cloud fraction parameterization (Donahue and Caldwell, 2018). The Park scheme diagnoses the liquid stratus fractions (αl)​​​​​​​ based on the assumption that the subgrid distribution of the total liquid relative humidity (RH), v_l, follows a triangular probability density function (PDF), where $v_l\equiv q_{\mathrm{t}}/\stackrel{\mathrm{‾}}{q_{\mathrm{s}}}$, q_t is the total liquid specific humidity, and $\stackrel{\mathrm{‾}}{q_{\mathrm{s}}}$ is the grid-mean saturation specific humidity over water. The Park scheme also computes the grid-mean net condensation rate of water vapor into liquid stratus condensate.

The simple model is designed to simulate tropical areas where convection is most active. The model contains 144 columns in a latitudinal circle, with a 1.9^∘ × 2.5^∘ resolution, a cyclic boundary condition, and 30σ​​​​​​​ vertical levels. The surface pressure is fixed at 1000 hPa, and the top model layer is about 2.26 hPa. The time integration step size is 30 min. The difference scheme for advection is the Lax–Wendroff method. The initial conditions for T and q are obtained from CAM5 outputs on QNLM after starting a spin-up of 10⁵ time steps.

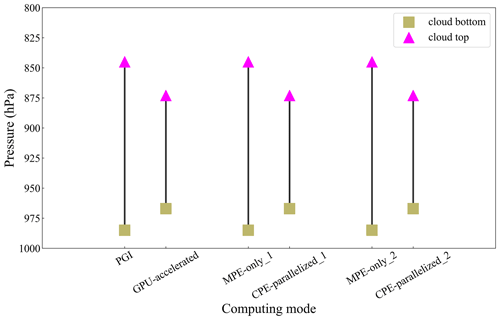
Mixed-precision or mixed-language approaches can cause simulation results that are no longer BFB identical to previous output data (Düben et al., 2017; Tintó Prims et al., 2019). To illustrate the influence of computational perturbations on simulation results, we first give an example with homogeneous computing to study the uncertainties in the simple model. First, we design a mixed-language compiling mode of the simple model in which the Goff–Gratch equation is replaced by C language only using the CPU. The Fortran and C version of the simple model have 64 bit variables and the same Intel compilers. Next, we change the variable precision in the Goff–Gratch equation to 32 bit in order to simulate larger perturbations. Table 2 shows an example of the deviated digits of the mean surface air temperature (SAT) at 209 time steps in the simple model using mixed-precision and mixed-language approaches. The SAT is the output in the 64 bit simple model. Figure 4 shows sudden changes in the cloud bottom and cloud top when the variable precision in the Goff–Gratch equation is set to 32 bit at 209 time steps. Thus, software changes can cause results with non-BFB reproducibility, and the computational perturbations caused by the change in variable precision are large enough to cause obvious uncertainties.

Table 2 The results of the mean SAT for the simple model for a 2.84^∘ N latitudinal circle at 209 time steps with the different compiler configurations.

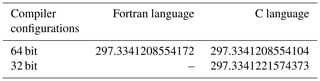
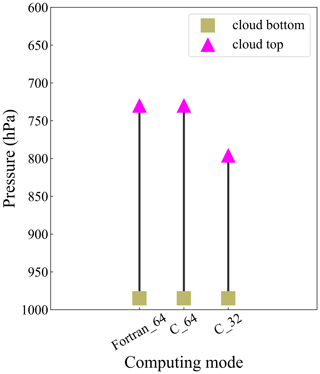
Figure 4 The cloud bottom and cloud top in the simple model of the Goff–Gratch equation in the Fortran and C languages at 209 time steps.

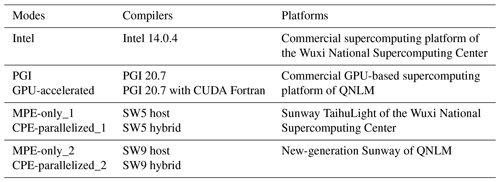
For heterogeneous many-core architecture computing, hardware design differences can cause nonidentical floating-point outputs, as described in Sect. 2.2. We use the simple model to study the uncertainties via the sudden changes in the cloud bottom and cloud top. We design seven simple model modes that are applied to homogeneous and heterogeneous computing, as listed in Table 3. The Intel mode refers to homogeneous computing on a trusted machine. The simple model is implemented for the GPU with CUDA Fortran and the CPE with hybrid schemes. The PGI (Portland Group, Inc) and MPE-only modes refer to compiling and running with the same type of CPUs and MPEs, which is similar to homogeneous programs but different from the Intel mode in terms of compilers and processor architectures, whereas the GPU-accelerated and CPE-parallelized modes are heterogeneous programs. We use the result of a 2.84^∘ N latitudinal circle as an example to illustrate the outputs of the simple model. For homogeneous computing, nonidentical floating-point outputs caused by hardware design differences do not cause changes in the cloud bottom and cloud top. However, heterogeneous many-core architecture computing can cause sudden changes compared with homogeneous computing at 255 time steps, as shown in Fig. 5.

Table 3 The list of computing modes for the simple model.

Figure 5 The cloud bottom and cloud top with homogeneous computing and heterogeneous many-core computing on the GPU-based HPC system, Sunway TaihuLight, and the new-generation Sunway system at 255 time steps.

3.3 An ensemble approach to characterizing uncertainties

In this study, a quantitative analysis approach based on ensembles is used to objectively characterize the uncertainties generated by hardware design differences. Characterizing the natural variability is difficult with a single run of the original simulation. A large ensemble refers to a collection of multiple realizations of the same model simulation that are generated to represent possible system states. Ensembles created by small perturbations to the initial conditions are commonly used in climate modeling to reduce the influence of the initial condition uncertainty (Sansom et al., 2013) and diagnose the influence of computing environment changes (Düben et al., 2017; Tintó Prims et al., 2019; Baker et al., 2015). We generate a 100-member ensemble of 260 time steps in the simple model. The ensemble is formed by perturbing the initial temperature with random noise multiplied by 0.1 from a Gaussian distribution with a zero mean and unit variance.

Statistical distributions collected from ensemble simulations help characterize the internal variability of the climate model system (Baker et al., 2015). Note that measurements for characterizing uncertainties are estimates, and we ignore the printing-phase errors of floating-point numbers (Andrysco et al., 2016). First, we compute the mean horizontal standard deviation of the state variables to get a set of time series scores for each ensemble member. The horizontal standard deviation is calculated by variable for a latitudinal circle. We design seven simple model modes applied to homogeneous and heterogeneous computing, as listed in Table 3. Following Table 3, the Intel mode is used as a baseline and denotes homogeneous computing on a trusted machine. The uncertainties are evaluated using the root-mean-square error (RMSE) and the mean absolute percentage error (MAPE) of the ensemble mean scores between the different modes, as listed in Table 3. Next, for the GPU-accelerated and CPE-parallelized modes, we add different perturbations with different orders of magnitude to the function variables listed in Table 4, when transferred from GPUs to the CPU or from CPEs to the MPE, in order to simulate the accumulated perturbations caused by hardware design differences by determining the critical state of the consistent climate.

Table 4 The list of variables and added perturbations.

3.4 An application to verify the reliability of heterogeneous many-core systems

We further discuss the implementation of the methodology to verify the reliability of heterogeneous many-core systems. Firstly, the simple model in homogeneous and heterogeneous modes should be designed. In homogeneous modes, the simple model is the serial program operated by the Fortran language. Refactoring and porting the simple model in heterogeneous modes is the most demanding step. In this study, the simple model includes dynamical process, consisting of advection, and physical parameterizations, consisting of deep convection and macrophysics. In order to avoid data dependency, we only parallelize the parameterizations over different columns using GPUs or CPEs. The computation of each column is completely independent in the parameterizations, as this can avoid introducing different layouts of data elements and different sequence of computing. The simple model codes on homogeneous and heterogeneous computing must be mathematically equivalent and stable.

Next, the time series of the cloud bottom and cloud top need to be compared to study uncertainties. Based on sudden changes in the outputs, a 100-member ensemble of 260 time steps in the simple model is then generated with different many-core architecture computing. Statistical distributions collected from ensemble simulations help characterize uncertainties, including quantitative analyses of computational perturbations and acceptable error tolerances.

It is noted that, for a bounded model state variable (e.g., q), the probability often exhibits non-Gaussian distributions because of the lower bound. In this study, when q falls below zero, it will be pulled back to zero (Li et al., 2016). In addition, we control some basic computing conditions, such as numerical stable codes like numeric constants written with the “d” notation (Bailey, 2008), no optimization, unified double-precision variables, and a 64 bit platform. Input files and ensemble simulation output files are in text format.

4 Experimental studies

4.1 The performance on the GPU-based HPC system

4.1.1 Brief description of the GPU-based HPC system at QNLM

The GPU computing system that we used for our experiment consists of a NVIDIA Tesla V100. Each Tesla V100 GPU contains 80 multithreaded streaming multiprocessors (SMs) and 16 GB of global DDR4 (double-data-rate 4) memory. Each SM contains 64 FP32 cores, 32 FP64 cores, and 8 tensor cores. ESMs are generally implemented for CUDA programs, which are written to use massive numbers of threads, each with a unique index, and executed in parallel (Kelly, 2010).

4.1.2 Results

Most physical parameterizations are structurally suitable for parallel architectures and demonstrate a high speedup when migrating from CPU to GPU, such as the chemical kinetics modules (Linford et al., 2009) and the microphysics scheme (Mielikainen et al., 2013) in the WRF (Weather Research and Forecasting) model, the shortwave radiation parameterization of CAM5 (the fifth version of the Community Atmospheric Model; Kelly, 2010), and the microphysics module of GRAPES (the Global/Regional Assimilation and Prediction System; Xiao et al., 2013). Therefore, we implement the simple model on the GPU-based HPC system at QNLM.

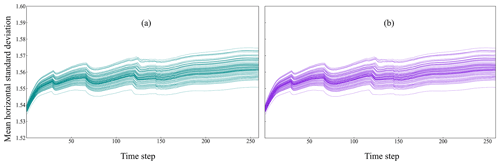
Following sudden changes in the cloud bottom and cloud top shown in Fig. 5, we discuss the influence of heterogeneous many-core architecture computing on the scientific correctness of numerical simulations carried out on GPU-based HPC systems. Figure 6 shows the mean horizontal standard deviation of the simple model of ensemble simulations in the PGI and GPU-accelerated modes. The results show that heterogeneous many-core architecture computing does not change the scientific correctness of simulation results on the GPU-based HPC system at QNLM.

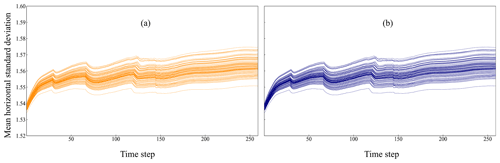
Figure 6 The time series of the mean horizontal standard deviation of atmospheric temperature for a 2.84^∘ N latitudinal circle in the (a) PGI and (b) GPU-accelerated modes.

We carry out quantitative analyses to characterize the uncertainties on the GPU-based HPC systems. We compute the RMSE and MAPE among the Intel, PGI, and GPU-accelerated modes, as shown in Table 5. The RMSE and MAPE of temperature between the GPU-accelerated and PGI modes characterize the uncertainties in heterogeneous many-core architecture computing with GPUs. The RMSE and MAPE between the PGI and Intel modes characterize the uncertainties due to compiler changes in homogeneous computing environments. The results of heterogeneous many-core architecture computing are larger than those of homogeneous computing, which makes it easier to generate sudden changes in simulation results.

Table 5 The RMSE and MAPE of atmospheric temperature between different modes.

Next, we add ​​​​​​​O(10⁻⁹), ​​​​​​​O(10⁻¹⁰), and O(10⁻¹¹) perturbations when GPUs transport data to the CPU, as described in Sect. 3.3. The PDFs of the simple model are shown in Fig. 7 to ensure acceptable error tolerances when using GPUs. We find that the differences between the PGI and GPU-accelerated modes are accompanied by an increase in the order of magnitude of perturbations.

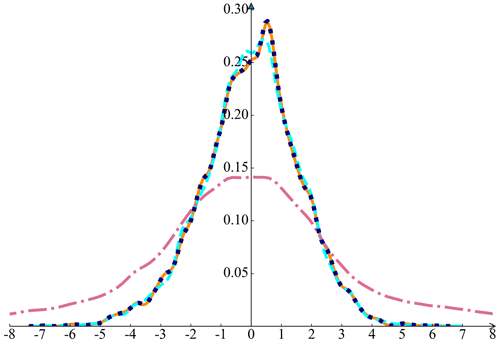
Figure 7 The PDFs of atmospheric temperature for the PGI and the GPU-accelerated modes with an increasing order of magnitude of perturbations. The PDF of PGI is represented by the orange line. The PDFs of the GPU-accelerated mode with the O(10⁻¹¹), O(10⁻¹⁰), and O(10⁻⁹) perturbations are represented by the black dotted line, the cyan line, and the pink line, respectively. Note that the orange line and black dotted line overlap.

4.2 The performance on the Sunway TaihuLight system

4.2.1 Brief description of the Sunway TaihuLight system

Sunway TaihuLight is the first Chinese system to reach number one on the “TOP500” list. The system is built using Chinese homegrown heterogeneous many-core processors (SW26010), and its peak performance is 125 PFlops. Each SW26010 includes four MPEs (256 CPEs) with a 64 bit instruction set and basic compiler components, including C/C$++$ and Fortran compilers (Fu et al., 2016). Unlike the GPU-accelerated HPC systems, where data transfer has to go between different processors and accelerators, the on-chip heterogeneity of the SW26010 processor enables a uniform memory space to facilitate data transfer and leads to a uniform programming model between the MPE and CPEs. ESMs are generally computed in a hybrid mode to use the instruction sets separately, and the MPE major task (in Fortran) manages CPE subtasks (in C language).

4.2.2 Results

Considering great breakthroughs in optimizing high-resolution CESM simulations on the heterogeneous many-core system (Zhang et al., 2020), we choose the Sunway TaihuLight as one of the heterogeneous running platforms. First, we focus on whether results with non-BFB reproducibility, as shown in Fig. 5, generated by hardware design differences will cause scientific errors on the Sunway TaihuLight system. Figure 8 shows the mean horizontal standard deviation of the temperature of the simple model of ensemble simulations in the MPE-only_1 and CPE-parallelized_1 modes. The distribution is indistinguishable overall, which demonstrates that heterogeneous many-core architecture computing will not affect the scientific correctness of the simple model despite uncertainties in the Sunway TaihuLight system.

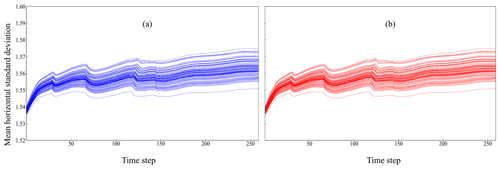
Figure 8 The time series of the mean horizontal standard deviation of atmospheric temperature for a 2.84^∘ N latitudinal circle in the (a) MPE-only_1 and (b) CPE-parallelized_1 modes.

Although Fig. 5 displays uncertainties in the CPE-parallelized modes, it is necessary to undertake quantitative analyses to characterize uncertainties. Thus, we compute the RMSE and MAPE among the Intel, MPE-only_1, and CPE-parallelized_1 modes, as shown in Table 5. Next, we add O(10⁻⁹), O(10⁻¹⁰), and O(10⁻¹¹) perturbations when CPEs transport data to the MPE on the Sunway TaihuLight system, as described in Sect. 3.3. The PDFs of the simple model are shown in Fig. 9. We find that, with an increasing order of magnitude of perturbations, the difference between the MPE-only_1 and CPE-parallelized_1 modes with additional perturbation becomes larger. It is noted that nonidentical floating-point outputs caused by hardware design differences should be within a certain range with the utilization of CPEs on the Sunway TaihuLight system.

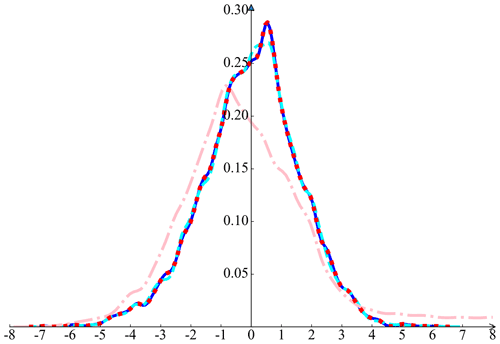
Figure 9 The PDFs of the atmospheric temperature for the MPE-only_1 and the CPE-parallelized_1 modes with an increasing order of magnitude of perturbations. The PDF of the MPE-only_1 mode is represented by the blue line. The PDFs of the CPE-parallelized_1 mode with the O(10⁻¹¹), O(10⁻¹⁰), and O(10⁻⁹) perturbations are represented by the red dotted line, the cyan line, and the pink line, respectively. Note that the blue line and the red dotted line overlap.

Figure 10 The time series of the mean horizontal standard deviation of the atmospheric temperature for a 2.84^∘ N latitudinal circle in the (a) MPE-only_2 and (b) CPE-parallelized_2 modes.

4.3 The performance on the new-generation Sunway system

The new-generation Sunway system is built using an upgraded heterogeneous many-core processor (SW26010P), which is similar to the SW26010 in terms of architecture. ESMs are also generally computed in a hybrid mode.

As a new heterogeneous system, the new-generation Sunway requires reliability verification in preparation for ESMs code porting. Following the sudden changes shown in Fig. 5, we discuss its influence on the scientific correctness of numerical simulation on the new-generation Sunway system. Figure 10 shows the mean horizontal standard deviation of the temperature of the simple model of ensemble simulations in the MPE-only_2 and CPE-parallelized_2 modes. The results show that heterogeneous many-core architecture computing does not change the scientific correctness of simulations on the new-generation Sunway system.

Quantitative analyses of uncertainties are also required on the new-generation Sunway system. We compute the RMSE and MAPE between the MPE-only_2 and Intel and between the CPE-parallelized_2 and MPE-only_2 modes, as shown in Table 5. Finally, we add O(10⁻⁹),O(10⁻¹⁰), and O(10⁻¹¹) perturbations when CPEs transport data to the MPE on the new Sunway system. The PDFs of the simple model are shown in Fig. 11 to ensure the acceptable error tolerances when using CPEs.

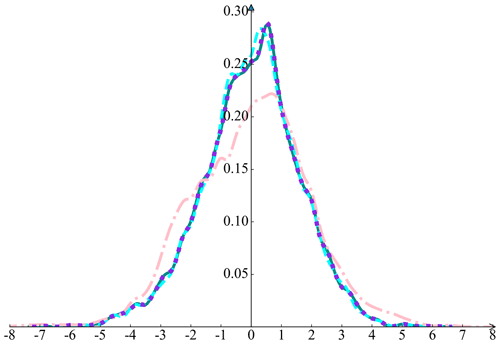
Figure 11 The PDFs of the atmospheric temperature for the MPE-only_2 and the CPE-parallelized_2 modes with an increasing order of magnitude of perturbations. The PDF of the MPE-only_2 mode is represented by the dark green line. The PDFs of the CPE-parallelized_2 mode with the O(10⁻¹¹), O(10⁻¹⁰), and O(10⁻⁹) perturbations are represented by the violet dotted line, the cyan line, and the pink line, respectively. Note that the dark cyan line and the violet dotted line overlap.

5 Summary and discussions

Numerical simulation advancements, which demand tremendous computing power, drive the progressive upgrade of modern supercomputers. In terms of architecture, due to physical and heat limits, most of the large systems during the last decade have used a heterogeneous structure to continuously improve the performance. Currently, heterogeneous many-core architectures include graphics processing unit (GPU) accelerators and the Sunway hybrid structure consisting of master and slave cores. However, differences in hardware designs exist between master (CPU and MPE) and slave cores (GPU and CPE) in heterogeneous many-core architecture computing environments. Therefore, compared with homogeneous computing, heterogeneous numerical integration can cause perturbations in Earth system simulations and, thus, generate uncertainties whenever a slave core or accelerator is involved. Hence, the characterization of uncertainties and an understanding of whether or not they affect the scientific results of modeling in heterogeneous many-core architectures are urgently demanded.

In this study, we explore a methodology to characterize the uncertainties of Earth system modeling with heterogeneous many-core architecture computing, and we seek to understand the scientific consequences of perturbations caused by a slave core or accelerator. The developed method includes a simple multi-column atmospheric model, consisting of typical physical processes sensitive to perturbations, and an efficient ensemble-based approach to characterize uncertainties. The simple model is used to study the perturbation-related uncertainties via the sudden changes in cloud bottom and cloud top by applying to homogeneous and heterogeneous systems that include GPU-based and Sunway HPC systems. First, in the homogeneous computing environment, we add perturbations to simulate the heterogeneous behavior related to slave core involvement in the computation, and we examine the influence of perturbation amplitudes on the determination of the cloud bottom and cloud top in both homogeneous and heterogeneous systems. Then, we compute the probability density function (PDF) of generated clouds in both homogeneous and heterogeneous computing environments with an increasing order of magnitude of perturbations. It is found that heterogeneous many-core architecture computing generates a consistent PDF structure with respect to that generated in homogeneous systems, although heterogeneous computing can slightly change the instant-layer index of the cloud bottom and cloud top with small perturbations within tiny precision differences. A series of comparisons of PDFs between homogeneous and heterogeneous systems show consistently acceptable error tolerances when using slave cores in heterogeneous many-core architecture computing environments.

Our current efforts demonstrate that perturbations involved with slave cores do not affect the scientific result of the simple model. However, refactoring and optimizing the legacy ESMs for new architectures requires verification in the form of quality assurance. Traditional tools, such as the Community Earth System Model ensemble-based consistency test (CESM-ECT), focus on evaluating climate consistency within homogeneous multi-core architecture systems (Baker et al., 2015; Milroy et al., 2016). For heterogeneous many-core architecture computing, such tools cannot distinguish code errors from unavoidable computational perturbations due to slave cores or accelerators. Based on the CESM-ECT, we are going to develop a new tool to verify the correctness of ESMs on heterogeneous many-core systems in a follow-up study. Such a tool shall first include the ensemble that captures the natural variability in the modeled climate system in the master-core-only mode and will then include perturbations using master–slave core parallelization. Second, the tool shall have a new function to measure the consistent behavior of the ensemble as the perturbation magnitude increases. Eventually, the tool will use a quantitative criterion to measure the correctness of ESMs on heterogeneous HPC systems. In addition, ESMs have many interacting and complex dynamical and parameterization processes that can magnify or reduce perturbations in the process of computation with different orders of magnitude. Thus, our current efforts focus on designing the most sensitive and typical discontinuous atmospheric physical processes to study the coarse-grained uncertainties. In follow-up studies, we intend, in a fine-grained manner, to combine more physical processes of ESMs into the simple model in an attempt to find hot spots prone to computational perturbations.

Climate science advances and societal needs require Earth system modeling with an ever increasing level of resolution in order to better resolve regional changes/variations as well as extreme events. Given that model resolution is intractable with the computing resources available, increasing the model resolution for Earth modeling demands greener supercomputing platforms with more affordable energy consumption. In the future, heterogeneous hardware shall progressively advance toward achieving better performance and lower energy consumption. Quality assurance of heterogeneous many-core computing environments is critical for building confidence in ESM porting, optimization, and development. Our methodology provides a protocol for verifying the reliability of new heterogeneous many-core systems.