the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
CREST-VEC: a framework towards more accurate and realistic flood simulation across scales
Shang Gao
Mengye Chen
Jonathan Gourley
Naoki Mizukami
Yang Hong
Large-scale (i.e., continental and global) hydrologic simulation is an appealing yet challenging topic for the hydrologic community. First and foremost, model efficiency and scalability (flexibility in resolution and discretization) have to be prioritized. Then, sufficient model accuracy and precision are required to provide useful information for water resource applications. Towards this goal, we craft two objectives for improving US current operational hydrological models: (1) vectorized routing and (2) improved hydrological processes. This study presents a hydrologic modeling framework, CREST-VEC, that combines a gridded water balance model and a newly developed vector-based routing scheme. First, in contrast to a conventional fully gridded model, this framework can significantly reduce the computational cost of river routing by at least 10 times, based on experiments at regional (0.07 vs. 0.002 s per step) and continental scales (0.35 vs. 7.2 s per step). This provides adequate time efficiency for generating operational ensemble streamflow forecasts and even probabilistic estimates across scales. Second, the performance using the new vector-based routing is improved, with the median-aggregated NSE (Nash–Sutcliffe efficiency) score increasing from −0.06 to 0.18 over the CONUS (contiguous US). Third, with the lake module incorporated, the NSE score is further improved by 56.2 % and the systematic bias is reduced by 17 %. Lastly, over 20 % of the false alarms on 2-year floods in the US can be mitigated with the lake module enabled, at the expense of only missing 2.3 % more events. This study demonstrated the advantages of the proposed hydrological modeling framework, which could provide a solid basis for continental- and global-scale water modeling at fine resolution. Furthermore, the use of ensemble forecasts can be incorporated into this framework; and thus, optimized streamflow prediction with quantified uncertainty information can be achieved in an operational fashion for stakeholders and decision-makers.
- Article
(8243 KB) - Full-text XML
- BibTeX
- EndNote
Flooding all over the world has affected millions of people, especially those who reside in floodplains (Tellman et al., 2021). In the US, flooding, as the primary cause of billion-dollar weather disasters, has cost USD 3.9 billion monetary losses and 15 deaths per year over the past four decades according to the NOAA National Centers for Environmental Information U.S.: Billion-Dollar Weather and Climate Disasters (2021). In light of frequent flooding in the US, several public agencies have been operating real-time flood forecasting systems, such as the NOAA NSSL (National Severe Storms Laboratory) FLASH project (https://flash.ou.edu, last access: 10 May 2022) and NOAA Office of Water Prediction (OWP). However, flood warnings are still either missed or unverified due to uncertainties ranging from precipitation forcing, hydrologic model structure, model parameterization, and/or hydrologic routing. As revealed by Martinaitis et al. (2017), 12.8 % of flash floods in the US go completely unwarned every year, let alone falsely warned. Apart from pursuing accurate weather forecasts, improving hydrologic simulation is the key to issuing flood warnings properly.
Flow routing in hydrology is the lateral transport of water on the land surface, subsurface, and in waterways (namely, hydrologic compartments). It is an inseparable component in hydrologic simulation to redistribute and exchange water between compartments and is also relatively time-consuming. In a lumped hydrologic model (watershed as an integrated unit), routing can be simplified to time convolution, such as the unit hydrograph (UH) or referred to as “impulse response function” (IRF) (Chow, 1988). However, variable velocities over the land surface and in waterways are difficult to be physically considered. Parameterization is a pragmatic approach, but too many parameters could lead to equifinality (Beven, 2006). In addition, only outlet streamflow can be simulated in a lumped model. A semi-distributed model was thus created to resolve flow pathways using digital elevation models (Quinn et al., 1991). Owing to ever-increasing computing power, gridded hydrologic models with spatially distributed routing have become feasible over large domains (Shaad, 2018). Terrain (or hillslope) routing and river channel routing at grid scales can be explicitly represented in model settings with distributed solvers such as linear reservoirs (Liston et al., 1994; Wang et al., 2011; Shen et al., 2017), kinematic wave models (Vergara et al., 2016), and diffusive wave models (Lighthill and Whitham, 1955; Ponce et al., 1978; de Almeida and Bates, 2013). More recently, vector-based routing has attracted more attention instead of raster-based routing for large-scale (i.e., continental and global extent) simulation. In theory, vector-based routing and raster-based routing differ in defining unit catchments and river networks. For instance, a raster-based routing model discretizes both catchments and river networks on Cartesian coordinates, while a vector-based routing model builds upon the irregular shape of unit catchments (i.e., polygon) and river networks (i.e., polyline).
The pioneering experiment of vector-based routing dates back to the early 2000s, in which river network models were incorporated in emerging GIS (geographic information system) software (Wang et al., 2000). With the burgeoning availability of global-scale hydrography datasets (e.g., HydroSHEDS and NHDPlus), vector-based routing models have been gaining considerable interest in recent years (David et al., 2011; Lehner and Grill, 2013; Mizukami et al., 2016; Paiva et al., 2011; Yamazaki et al., 2011). Among those developments, three frameworks have become popular and stand out in the hydrologic model community. First, David et al. (2011) introduced the RAPID routing framework that is based on the Muskingum method. The RAPID has been coupled with the National Water Model operated by the NOAA OWP (Office of Water Prediction) (Lin et al., 2018) and the GLoFAS (Global Flood Awareness System) developed by the ECWMF (European Center for Median-Range Weather Forecasts). Second, Yamazaki et al. (2011) developed the CaMa-Flood framework which generates flood inundation at a large scale by solving the 1D diffusive equation and spilling water over floodplains. Third, the recent development of the mizuRoute framework by Mizukami et al. (2016) offers terrain routing and multiple channel routing schemes (e.g., IRF and kinematic wave), making it more physically based compared to RAPID, which ignores terrain routing. The mizuRoute has been used together with the hydrologic framework SUMMA (Structure for Unifying Multiple Model Alternatives) (Knoben et al., 2021) and is planned to be implemented in the CESM (Community Earth System Model). These vector-based routing models overcome several challenges for large-scale hydrologic simulations faced by raster-based routing models. First, higher model resolution in raster-based models comes at the expense of higher computational cost, which prohibits global hydrological simulations at tens or hundreds of meters. However, the vector-based routing model is much more scalable and computationally efficient, irrespective of increasing resolution. Second, river networks can be more realistically represented in a vector form. In conventional hydrologic models, the river network in a raster form has to be delineated based on a DEM as a preprocessing step. River networks generated in such a way do not always align well with natural river centerlines. For studies investigating hydrologic connectivity in particular, river grid cells in a raster form can easily become discontinuous without considering river topology. Alternatively, river networks in popular hydrography data are digitalized based on satellite optical imagery and manual inspection (Lin et al., 2021). Another weakness of raster-based routing stems from the traditional D8 flow strategy, which means water in the central grid can only be permitted to flow through one of its neighboring grid cells (Tarboton, 1997). On the contrary, vector-based routing offers a more flexible approach from vector representation of river networks.
To date, modern vector-based routing models such as RAPID and mizuRoute have neglected the subsurface routing, which is either assumed to be minimum (Mizukami et al., 2021) or treated the same way as surface routing (Lin et al., 2019; Y. Yang et al., 2021). However, subsurface routing is an important hydrologic process and dominates over regions that have intermittent flow behaviors (Freeze, 1972). For flood simulation, ignoring subsurface routing could underestimate the peak flow and miscalculate the flood timing, both of which directly affect decision-making processes. An equally important research thrust is the representation of lakes and reservoirs in vector formats, since they markedly alter flow response not only at a local scale, but also downstream of rivers. One of the functions of lakes and reservoirs in the US is for flood control, and thus simulation without incorporating such a process is likely to result in falsely issued flood warnings.
In light of the advantages of vector-based routing, this study introduces a coupled modeling framework, CREST-VEC (Coupled Routing and Excess STorage with VECtor routing), which strives to facilitate real-time flood forecasting across scales. This framework seamlessly integrates the current operational flash flood forecast model structure – CREST model and the vector-based routing framework – mizuRoute. We utilize a case study to demonstrate the advantages of this coupled framework and to investigate some updates we made to improve the existing routing scheme. Four questions are posed in this regional case study: (1) What are the performance gains for CREST-VEC compared to the CREST model? (2) Does the included subsurface routing improve model performance? (3) Can a simple natural lake simulation improve model performance in a downstream urban area? (4) How does the CREST-VEC model adopt to flood warnings? In the second part, we apply this framework to the continental US for a comprehensive evaluation. We ask one additional question: For how many floods are there false alarms without considering reservoir operations? It is anticipated that findings from this work could motivate the future development of large-scale hydrologic models and raise awareness on whether and how much flood forecasts by model simulations should be trusted without the proper representation of lakes.
2.1 Hydrography data
In this study, we use the vectorized river network and HRU (hydrologic response unit) dataset derived from the high-accuracy MERIT Hydro (Multi-Error-Removed-Improved-Terrain hydrography) dataset (Yamazaki et al., 2017, 2019). The flow lines were created from the 90 m DEM data (MERIT DEM), covering the full global land surface (60∘ S–90∘ N). A minimum channelization threshold of 25 km2 (upstream area) was applied to restrict river channel grid cells in the MERIT Hydro dataset. The HRUs were processed along with flow lines by the TauDEM software and trimmed with the HydroBASINS level-II boundaries. Detailed processing of the hydrography data is listed in Lin et al. (2019). This set of hydrography data has been validated against 30-year Landsat imagery (Lin et al., 2021) and empowered the global reconstruction of historical streamflow (Lin et al., 2019; Y. Yang et al., 2021). Over the CONUS, we have obtained 341 921 river reaches and the same number of unit catchments for the routing component.
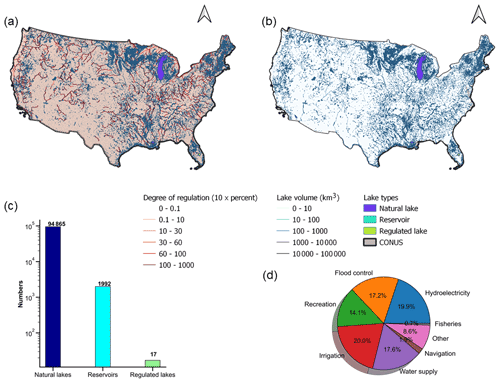
Lakes and reservoirs in the US play a significant role in regulating streamflow (Tavakoly et al., 2021). Major river basins (e.g., Mississippi and Columbia River Basins) are highly regulated, as shown in Fig. 1a and b with results obtained from Lehner et al. (2011). The HydroLAKES dataset provides a global catalog of lake polygons and pour points that can be easily integrated into hydrologic models (Messager et al., 2016). Over 1 million natural lakes and constructed reservoirs were identified globally, with a minimum surface area larger than 10 ha. Over the US, there are 96 874 lakes recorded in the HydroLAKES data, of which 94 865 are natural lakes without human intervention, and 1992 (17) lakes are reservoirs (regulated lakes), as shown in Fig. 1c. Of the regulated lakes or reservoirs, 20.0 % are primarily used for irrigation, 19.9 % for hydroelectricity, 17.6 % for water supply, 17.2 % for flood control, 14.1 % for recreation, 1.9 % for navigation, 0.7 for fisheries, and 8.6 % for other functions (Fig. 1d). The total lake volume, estimated from the lake bathymetry, is a required field in our modeling framework to approximate outflow.
2.2 Forcing data
Forcing data are required as model inputs to drive the hydrologic model. Hourly precipitation rates are obtained from the MRMS (Multi-Radar Multi-Sensor) data, operated at the NOAA NSSL (Zhang et al., 2016). The MRMS is a state-of-the-art radar-gauge merged product, providing instantaneous rates at a 1 km spatial resolution over the CONUS and parts of southern Canada and northern Mexico. We used the 1 h accumulated and gauge-corrected precipitation product in this study for streamflow simulation. The performance and hydrologic utility of MRMS data have been corroborated in previous studies (Li et al., 2020, 2021). The daily temperature from the PRISM (Parameter-elevation Relationships on Independent Slopes Model) is used to simulate snow accumulation and melt (PRISM Climate Group, 2014). The PRISM team routinely collects meteorological data from meteorological stations over the US and interpolates them into 4 km gridded data based on the elevation dependence (Daly et al., 2008). The potential evapotranspiration (PET) data are obtained from the USGS FEWS data port (https://earlywarning.usgs.gov/fews, last access: 1 August 2022) at daily and 1∘ spatial resolution (Allen et al., 1998). Forcing data at different spatial resolutions is re-gridded to a 1 km model resolution. All of these data are collected from the simulation period in complete calendar days from 2015 to 2020.
2.3 CREST model
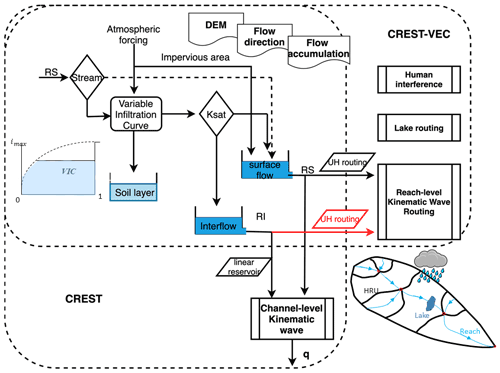
As jointly developed by the University of Oklahoma (OU) and NASA, the CREST model has been released for a decade (Wang et al., 2011). It is a distributed hydrologic model whose primary purposes are (1) flood simulation and forecasting, (2) evaluating the hydrologic utility of satellite precipitation datasets, and (3) water resources management (Xue et al., 2013; Tang et al., 2016; Gourley et al., 2017; Gao et al., 2021; Li et al., 2021; Chen et al., 2022). Owing to its relatively simple structure and computationally efficient simulation, the CREST model has been promoted by the NOAA NSSL for real-time flash flood forecasting over the continental US and its territories (Gourley et al., 2017; Flamig et al., 2020). As shown in Fig. 2, the effective rain (deficit of rainfall rates and evaporation rates) reaches the land surface and is partitioned into fast runoff from urban impervious area ratio and infiltration into the soils. A VIC (variable infiltration curve) model is incorporated to determine the infiltration rate (Liang et al., 1994). Surface runoff is generated when infiltration rates become higher than the maximum infiltration capacity. In the meantime, slow-flowing interflow is produced while soil water content is depleted. In the CREST model, flow routing is handled in two ways. Terrain routing and in-channel river routing are done by the kinematic wave model which simplifies the Saint-Venant equation by ignoring the acceleration and forcing terms (Vergara et al., 2016). The interflow is routed by a conceptual linear reservoir with parameterized velocity (Shen et al., 2017). We refer to the CREST model hereafter as a standalone package that couples the water balance model with gridded terrain and channel routing. The original code is written in C++.
To account for snowmelt, we coupled the original CREST model with the Snow-17 model, which is part of the National Weather Service River Forecast System in the US (Franz et al., 2008). The Snow-17 model is a conceptual snowmelt scheme that simulates snow accumulation and ablation based on temperature and precipitation as inputs (Anderson, 2006). Although the physics behind it is not as comprehensive as the energy balance model, Snow-17 is advantageous for having less required input data and performing “at least as good as” energy-based models (Ohmura, 2001).
2.4 mizuRoute
The mizuRoute river routing model, developed at the NCAR (National Center for Atmospheric Research), is a vector-based routing framework that incorporates both terrain and channel routing for large-domain river routing applications (Mizukami et al., 2016, 2021). For the terrain routing, the IRF or UH is used with parameters associated with gamma distribution to adjust the shape and scale. For the channel routing, user-defined options are IRF, kinematic wave with Lagrangian solution, and kinematic wave with Euler solution. A recent version of mizuRoute (Version 2.0.1) includes two lake routing schemes (Gharari et al., 2022; Vanderkelen et al., 2022) – one based on Döll et al. (2003) with a simple level-pool equation for natural lakes and the other more complicated one based on Hanasaki et al. (2006), which includes reservoir operation rules. These two schemes have been applied to the other global hydrologic models (e.g., WaterGAP, VIC, and CWatM) to account for regulated streamflow. The original code is written in Fortran.
The current version of mizuRoute does not explicitly account for subsurface runoff routing over terrain, which is critical in the Great Plains and regions where streams are intermittent across a year (Salas et al., 2018). In this study, we enable an option to turn on or off subsurface routing as defined in the model configuration file. Similar to surface runoff routing, the subsurface flow is routed using the IRF scheme but with a much slower velocity and reduced magnitude. We use a two-parameter gamma distribution function to materialize the IRF method as shown in Eq. (1):
where t is the time variable, a is a shape parameter, and θ is a time-scale parameter. Both a and θ determine the flood peaking time and flashiness. After calculating instantaneous rates based on the gamma function, we use convolution to compute flow rates Q at time t. R(t−s) is the (sub)surface runoff at time (t−s), and s is an increment of time from 0 to tmax (also denoted as the time window). The default values of a and θ for hillslope surface routing are set to 2.5 and 8000. For subsurface flow routing, the a and θ are 10 and 86 400, respectively.
2.5 CREST-VEC
The framework CREST-VEC and the difference compared to its precedent CREST model are shown in Fig. 2. The main difference comes from the routing process, where the original CREST model routes surface flow and interflow via a kinematic wave routing model and a conceptual linear reservoir model in a gridded manner. However, the CREST-VEC model requires area-averaged time series of surface and subsurface flow at each river reach to be separately routed downstream. The gridded outputs from the CREST model (i.e., surface runoff and subsurface runoff) are extracted and averaged over each unit catchments or HRU using the newly developed Python package EASYMORE (EArth SYstem Modeling REmapper), publicly available from https://github.com/ShervanGharari/EASYMORE (last access: 14 May 2022). The framework is loosely coupled with two models written in different programming languages. A bash file subsequently calls three executables after model compilation (CREST-EASYMORE-mizuRoute). The input files for this model chain include forcing data (gridded precipitation, potential evaporation, and temperature), topography data (gridded digital elevation model, flow direction, flow accumulation, river network topology, and hydrologic response unit), and configuration files. The topography data can be accessed from the HydroSHEDS website, which consists of grid-based and vector-based topography data.
We use the IRF scheme in this study for both terrain routing and channel routing and activate the lake model with the Döll et al. (2003) lake model. The lake parameters such as the outflow coefficient a and exponent b of Eq. (3) are based on suggested values in Döll et al. (2003) and Gharari et al. (2022). For lakes that have monitored storage provided by the USGS (US Geological Survey), we directly insert storage time series into the model. As reservoir operation is not considered in this study, we exclude observed streamflow that is regulated by reservoirs and regulated lakes, as shown in Fig. 1c. Thus, only results from natural lakes, which account for 98 % of US lakes or reservoirs, are considered valid for statistical comparison. To initialize model states, especially for initial lake volumes, we warm up the CREST-VEC model from 1948 to 2014 using the GLDAS forcing (Global Land Data Assimilation System) at a daily time step:
where a and b are the outflow coefficient (1 d−1) and exponent, respectively, Sf is the actual lake storage (m3), and Sf, max is the maximum lake storage (m3).
3.1 Case study: Houston region
As mentioned in the objectives of this study, we first conduct a case study analysis to assess the relative contributions of subsurface flow routing and lake routing to streamflow simulation based on the CREST-VEC framework. The original CREST model is used as a benchmark. We chose the Houston region (Fig. 3a) because there are two large natural lakes – Lake Barker and Lake Addicks – that impact hydrologic simulations (Fig. 1a). For the CREST model with gridded routing, we calibrate the model using the DREAM (Differentiable Evolution Adaptive Metropolis) optimizer (Vrugt et al., 2009) from 1 June 2016 to 1 June 2017 at an hourly time step and performed the evaluation from 1 June 2017 to 1 January 2020. The NSCE is used as the objective function for calibration, and the model is warmed up for 1 year from 1 June 2015 to 1 June 2016. We run the CREST model at three spatial resolutions: 1 km, 250 m, and 90 m. To be comparable with CREST-VEC simulations, whose hydrography data are built upon a 90 m resolution DEM, we only use the CREST model results at 90 m for statistical comparisons and use the results at 1 km and 250 m to assess computational efficiency. The evaluation metrics shown in Fig. 3c are based on the evaluation period. The river flows from 22 stream gauges are curated from the USGS.
3.1.1 Model speedup
Figure 3b shows the computational cost (elapsed time at seconds per step) for a series of model configurations for the routing process. All the tests were run on a single core Intel i7-6700K CPU (4.00 GHz). The grid-based CREST model costs 0.01, 0.08, and 0.12 s per step at 1 km, 250 m, and 90 m resolutions, respectively. However, the CREST-VEC model can reduce this to approximately 0.002 s per step, regardless of grid resolutions from the forcing data. There is little difference among the three scenarios (i.e., CREST-VEC, CREST-VEC + subq: CREST-VEC plus subsurface routing, and CREST-VEC + subq + lake: CREST-VEC with subsurface routing and lake routing). Relatively speaking, CREST-VEC can speed up the current operational CREST model at 1 km by 10×, let alone at finer resolutions.
3.1.2 Performance improvement
Regarding model skills, the CREST model and CREST-VEC achieve similar median NSE (Fig. 3c) based on observations from 22 stream gauges, even though the CREST model takes advantage of automatic calibration. CREST-VEC and CREST-VEC + subq overestimate flows downstream of two natural lakes, resulting in poor scores. But after incorporating lake routing schemes, the CREST-VEC + subq + lake model achieves not only better median scores but also less spread (quantified by the interquartile range). Notably, both CREST-VEC + subq and CREST-VEC + subq + lake have positive NSE values and smaller uncertainty ranges, primarily owing to the included subsurface routing. The time series in Fig. 4 highlights the model performance at three stream gauges affected by upstream lakes. The CREST-VEC overestimates streamflow by a considerable amount (i.e., 3 times higher than observation in Hurricane Harvey), resulting in low NSE scores: 0.11, 0.16, and 0.18, respectively. With lake routing considered in the CREST-VEC + subq + lake, the simulated streamflow aligns well with observations, achieving NSE scores of 0.61, 0.65, and 0.64, respectively. Although the CREST model captures streamflow magnitude after calibration with the NSE scores, 0.37, 0.52, and 0.54, the peak timing is at least 1 d delayed for Hurricane Harvey. In summary, the advantages for the general CREST-VEC framework against the gridded CREST model are threefold: (1) improve computational efficiency by at least 10 times, (2) improve overall model skill, and (3) reduce uncertainty ranges.

Figure 3(a) Map of the study area (Houston region) showing river networks and water bodies. (b) Computation time per step for CREST at three resolutions and CREST-VEC model at four configurations on the x axis. (c) Nash–Sutcliffe efficiency values for CREST and CREST-VEC model.

Figure 4Performance of models downstream of two lakes. The Nash–Sutcliffe efficiency coefficients are obtained from the CREST-VEC model with lake routing and subsurface routing. Three plots of time series of stream gauges (from upstream to downstream: 08073500, 08073600, 08074000) are pointed to beside the map, and the Hurricane Harvey event is highlighted in the red box and insets. Base map copyright © Google Map.
3.2 CONUS simulation
Moving towards continental-scale hydrologic simulation, the CREST-VEC model excels at reducing computational costs, leaving room for quantifying uncertainties from forcing, model structure, and parameters in real time. The ensuing question is whether and how much the new lake routing improves a continental simulation. To answer this question, we simulate CREST-VEC with and without lake routing over the CONUS from 1 June 2016 to 1 January 2020 at an hourly time step. Notably, subsurface routing is activated for both models with and without lake routing, and thus we expect the difference in results to be primarily due to lake simulation. Streamflow data from 5350 stream gauges in the same period are collected and used for model verification. For this case, the CREST-VEC model parameters are based on the pre-configured CONUS-wide parameters, the same as those used by Flamig et al. (2020).
3.2.1 Model speedup
Table 1 lists the model performance with respect to total computational costs and evaluation scores of streamflow simulation. CREST-VEC certainly improves streamflow simulation not only via a higher resolution (from 1 km to 90 m) but with faster computational speed (149.2–29.9 h in total; 7.2–0.37 s per step for the routing step only). Considering all preprocessing steps altogether, the CREST-VEC model is still at least 4 times faster than the original framework. To be noted, a considerable amount of time is spent on mapping gridded runoff data to a vector form (>50 % of the time). Future attention should be drawn to how to optimize efficiency while preserving certain degrees of accuracy for this process.
3.2.2 Performance improvement
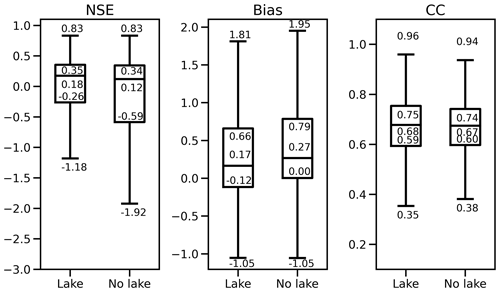
The median NSE score increased from −0.06 (gridded) to 0.12 (no lake) and 0.18 (lake). The fraction of gauges with positive NSE scores improved from 41.8 % (gridded CREST) to 50.6 % (CREST-VEC without lake) and to 56.2 % (CREST-VEC with lake). However, the CREST-VEC results are more biased than the gridded CREST results, partly due to the systematic overestimation of streamflow by the IRF routing scheme in the CREST-VEC. The difference would be primarily attributed to the different routing processes, as CREST permits leakage in the interflow reservoir, thereby leading to lower positive bias. The results with lake simulation have reduced bias from 27 % to 17 %, since part of the water is being held in the lake. The CC (correlation coefficient), however, does not vary much between scenarios with and without lake simulation, as shown in Fig. 5. One of the reasons is that the CREST-VEC model does not simulate regulated lakes or reservoirs which have strong control of streamflow time shifts. Notably, the IQRs (interquartile ranges) of NSE and bias for the lake simulation are lower than without lakes, meaning that this method particularly boosts scores at gauge locations that had poor performance previously.
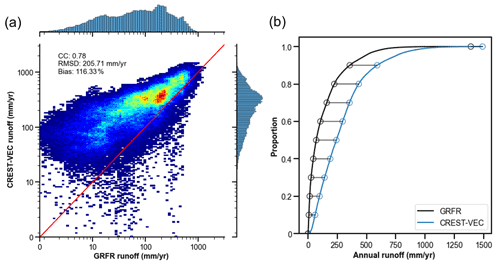
Figure 6 depicts the spatial map of model skill (with lake) and its difference between scenarios with and without lake simulation. CREST-VEC with the lake module in regions like the West Coast and Upper Mississippi River Basin have relatively good performance (NSE >0.4), yet over the Great Plains and East Coast, the model bias is high (bias >1), yielding low NSE scores. Similar issues are found in the literature with other models (Clark et al., 2008; Newman et al., 2015; Mizukami et al., 2017; Salas et al., 2018; Lin et al., 2019; Knoben et al., 2020; Y. Yang et al., 2021; Tijerina et al., 2021). Taking the Great Plains as an example (highlighted box in Fig. 6c), the model physics of CREST-VEC does not correctly represent the real hydrologic processes by two means. First, the surface runoff (before routing) simulated by CREST-VEC is biased. We compare the annual surface runoff by CREST-VEC with the public community dataset GRFR (Global Reach-level Flood Reanalysis) in Fig. 7. The runoff in GRFR is simulated by the VIC model and undergoes stringent bias correction against observations via the discrete quantile mapping technique (Y. Yang et al., 2021; Lin et al., 2019). There is a 116.3 % higher surface runoff by the CREST-VEC than the GRFR, partly explaining the high bias and low NSE scores in this region. We suspect the singular bulk soil layer represented in the CREST model yields such systematic differences. Second, the missing representation of playas, small and rain-fed lakes that are prominent in the Great Plains, leads to falsely produced runoff (Solvik et al., 2021). However, even when accounting for multiple hydrologic model structures, performance in this region is still ranked as one of the poorest (Clark et al., 2008; Knoben et al., 2020). For example, Knoben et al. (2020) analyzed 36 hydrologic models over the US, in which the maximum KGE (Kling–Gupta efficiency) scores out of those models are lower than 0.5 over the Great Plains.
Table 1Statistical comparison of model performance over the continental US. Bold numbers indicate the best metrics among the three model configurations. The computational speed is calculated as an average speed over a whole simulation period.
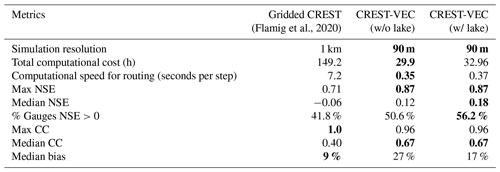

Figure 6Spatial map of model performance with the lake (left column) and the difference between with lake simulation and without lake simulation (right column). (a) NSE scores; (b) NSE differences (results with lake minus results without lake); (c) bias; (d) bias difference; (c) CC (correlation coefficient); (f) CC difference. The blue box in (c) highlights the region where high positive bias is present.
3.3 How likely are floods falsely detected?
In this section, we shift gears to explore how likely US floods are falsely detected if no lake simulations are included. We selected 283 gauges that are downstream of natural lakes (Fig. 8), with most of them located in the middle and eastern US. The hourly time series of streamflow of those gauges are compared against advised flood thresholds (2-year flooding) provided by the USGS. They fit a log-Pearson III type distribution to the annual maxima streamflow from long-term records and extract values with the given flood frequency. Following a similar approach as in Y. Yang et al. (2021), consecutive yet independent events have to be 2 d apart from one another. From there, we calculated the POD (probability of detection, FAR (false alarm ratio, and CSI (critical success index) based on the contingency table.
As expected, median FAR is reduced from 0.63 (without lake simulation) to 0.50 (with lake), resulting in a slightly higher CSI of 0.36 than that of 0.31 for no lake simulation (Fig. 8a). Additionally, previous research reported that simulation results with the lake module mitigate the seasonal variability of the river discharge (Tokuda et al., 2021). The decrease in FAR values implies five instances: (1) decrease in false alarms while hits remain the same; (2) increase in hits while false alarms remain the same; (3) decrease in false alarms while increase in hits; (4) decrease in both false alarms and hits; and (5) increase in both false alarms and hits. We find, however, that POD values decrease from 0.87 without lakes to 0.85 with lakes, from which we can infer that both hits and false alarms are decreasing, but false alarms decrease at a higher rate. That is a fact of reducing simulated flood peak, which results in fewer hits in flood forecasts but less false-alarm floods. As most studies focus on flood detection, they inevitably arrive at more falsely detected floods. Too many false alarms could make people disregard the warnings despite a real threat, causing the “cry wolf” effect.
The maps in Fig. 8b display the distributions of flood detectability with lake simulation and its improvements compared to results without lake simulation. High POD and FAR values coexist in the Great Plains, where the model simulates considerably higher streamflow values than observations. Moderate FAR values are found near the Florida Panhandle and parts of Georgia. Lower FAR values are found in the Midwest and West Coast. Compared to results without the lake, FAR values are reduced reasonably over the East Coast, Midwest, Gulf Coast, and West Coast, although POD values remain relatively unchanged or even decreased.
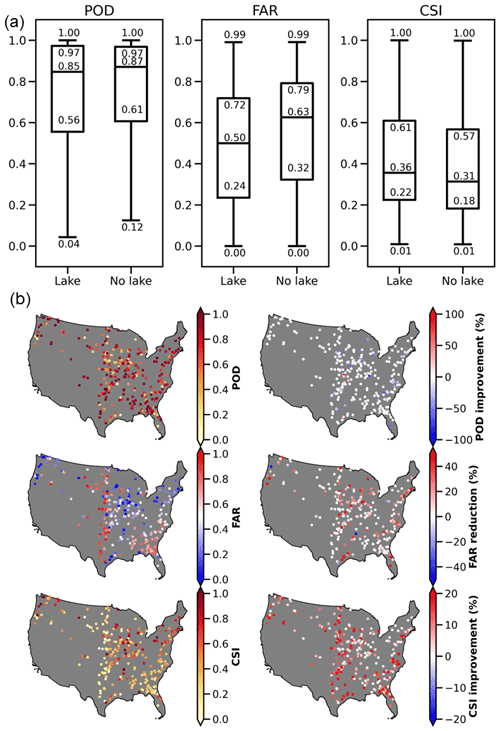
Figure 8Flood detection performance comparing lake simulation and no lake simulation. (a) Similar to Fig. 5, but for flood detectability; (b) similar to Fig. 6, but for flood detectability.
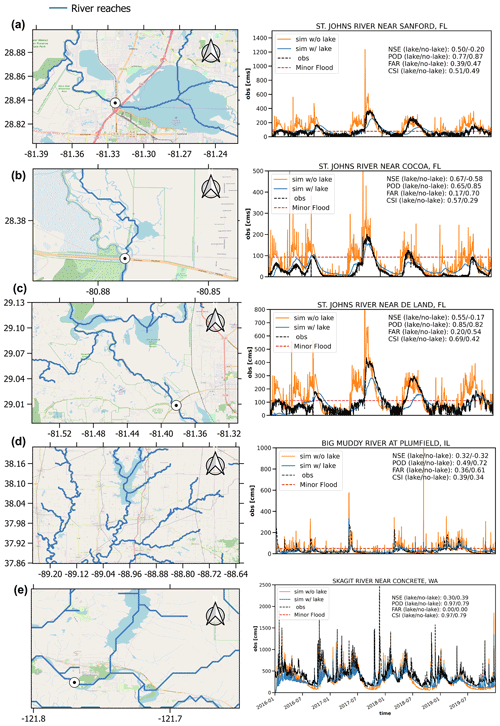
Figure 9Five case examples of streamflow time series at gauges downstream of lakes: (a) St. Johns River near Sanford, FL; (b) St. Johns River near Cocoa, FL; (c) St. Johns River near De Land, FL; (d) Big Muddy River at Plumfield, IL; (e) Mississippi River at Clinton, IA. Base map copyright © Google Map.
Five local cases are shown in Fig. 9, which depicts the river topology and time series of hourly streamflow. One can infer that these lakes are not heavily regulated from recorded streamflow time series, therefore showing the effectiveness of our model. In Fig. 9a, the simulated streamflow without lakes is heavily overestimated, peaking at 1200 m3 s−1 in the year 2017, whereas the actual flow rate is around 400 m3 s−1. The scenario with lake simulation, however, produces a magnitude much closer to the observation. Due to decreased systematic bias, the lake scenario boosts the NSE score from −0.2 to 0.5. There is also an 8 % less chance of issuing false alarms than in the model without lake simulation. Figure 9b shows a case where FAR is reduced from 0.70 to 0.17, a reduction rate of 75.7 %. The flood detectability, i.e., CSI, is greatly improved from 0.29 to 0.57. Figure 9c exemplifies a case with all improved metrics (i.e., NSE, POD, FAR, and CSI). All these three cases in Fig. 9a–c are located along the St. Johns River, in which we expect a systematic improvement along this river after incorporating the lake simulation. Figure 9d displays more common cases where a reduction in FAR comes at the expense of reducing POD (i.e., flood detection), almost at the same pace. Figure 9e shows that although the model with lakes produces better baseflow, it underestimates flood peaks, resulting in lower NSE values (0.3) than in the case without lakes (0.4). It implies that parameters governing the lake outflow need to be improved.
4.1 Vector vs. raster-based routing
In this study, we compare the advantages of vector-based routing with respect to conventional raster-based routing in two aspects: (1) model efficiency and (2) model accuracy. Overall, the vector-based routing shows great promise, as it speeds up the routing process by at least 10 times, compared to grid-based routing, for both the regional simulation (0.07 vs. 0.002 s per step) and the CONUS simulation (0.35 vs. 7.2 s per step). In terms of results against observations, the CONUS-wide performance is improved regarding NSE values. However, the variable river reach lengths (from hundreds of meters to tens of kilometers) in large-scale simulation pose challenges for estimating routing parameters such as the time and shape parameters in a unit hydrograph. Second, most land surface models are still grid-based, making a type mismatch (grid-based land surface model vs. vector-based routing model) (Lehner and Grill, 2013). To integrate the two, we need a processing step by mapping surface and subsurface runoff onto representative HRUs. Different aggregation strategies are present and subject to the primary purpose of interest. At present, there is an ongoing effort to seamlessly integrate these two processes together (Gharari et al., 2020). However, it is yet to be efficient and draws further attention to improving this mapping scheme. Third, the many-to-one river network is established but not for one-to-many, meaning that river bifurcation is challenging to represent and tackle (Yamazaki et al., 2014).
Raster-based routing comes at the resolution of the input DEM data, albeit at a slower computational speed. Having matured over the years, most raster-based routing models are seamlessly integrated with water balance models so that the model can be set up with minimum effort by a modeler.
As one objective of this study, we wanted to examine the potential improvement from the with-lake configuration in streamflow simulation over a wide range of hydrometrical and geographical settings in the CONUS, rather than provide some optimal model setup and parameterization at the CONUS scale, which we believe is far beyond our scope and several steps forward from the current CREST-VEC or any existing CONUS models. As far as what qualifies as “an adequate base simulation”, there may be some room for debate but there should be some bottom-line principles: first, one should be clearly aware of the sources of uncertainties, including forcing, model structure, parameterization, streamflow observation as the reference, etc. Optimization, although effective in improving the model performance, compensates for uncertainties from the other sources simply via adjusting model parameters. This has been acceptable for operational purposes but is not appropriate for this study where a modification of the model structure is introduced. Instead, we use an a priori parameter set that was developed based on remote sensing datasets and also evaluated at the CONUS scale (Vergara et al., 2016). The physical base of these a priori parameters set a solid foundation for examining the new with-lake configuration, and thus should not be compromised via parameter tuning.
The CREST-VEC model by no means represents all physical hydrological processes. Instead, it is a conceptual flood forecast model that aims to deliver timely flood information to stakeholders, decision-makers, and broader users. We admit that some processes such as vadose zone modeling, snow melting, hillslope routing, in-channel river routing, and reservoir operations are simplified, and some processes such as vegetation and groundwater modeling are missing from the current version. For the lake module, we expect to include more sophisticated multilayer decision processes instead of a level-pool process. Lake evaporation is another important factor to be considered for improved water balance. Since it is a compromise between model complexity and efficiency, we hope to continuously push the envelope on this front to optimize the real-time flood forecast system.
4.2 Room for improving large-scale hydrologic simulation
Large-scale hydrologic simulation is still a long-standing challenge for the hydrologic community, especially with debates on developing a “one-model-fits-all” structure or a “malleable” structure (Burek et al., 2020; Clark et al., 2015b; Fenicia et al., 2011; Savenije, 2009). The CREST model, in our study, systematically overestimates surface runoff over the Great Plains and Southeast, a result of some misrepresented or missing processes, yet excels in flash flood simulation. Diverse hydrologic model structures, on the other hand, hope to overcome individual limitations and offer joint benefits (Horton et al., 2021). We, therefore, promote the “malleable” model structure from the efficiency point of view – a flexible structure disables redundant hydrologic processes. Then, the central question becomes: How do we adapt the model to variable catchment processes? In such a context, intercomparisons and discussions of different hydrologic models in varying catchment processes become particularly valuable (Clark et al., 2015b; Knoben et al., 2020; Tijerina et al., 2021). Notably, simply relying on the NSE or KGE score to assess the model performance can be misleading (Clark et al., 2021).
Hydrologic calibration is powerful in boosting model accuracy, yet large-scale models oftentimes suffer from the complexity that impedes credible model calibration. River routing schemes and their parameters can affect streamflow simulations, especially at fine time scales such as sub-daily scales (Mizukami et al., 2021). Our current study used an IRF scheme in which the impulse response function is derived from a diffusive wave equation (see Lohman et al., 1996; Mizukami et al., 2016) and includes two parameters: diffusivity and celerity. These parameters need to be exposed to calibration in addition to the hydrologic model parameters. Furthermore, to fully understand the routing model's impact on streamflow simulations, it is necessary to consider other routing schemes including a diffusive wave model as well as a kinematic wave model, which may be suited for flood forecasting.
Lastly, the computational costs for large-scale simulation can be optimized from accelerated hardware (multi-core CPUs and GPUs) once codes are parallelized and scalable. Advances in ROM (reduced-order modeling), a surrogate model which develops a parsimonious solution to replace the computationally intensive part, hold promise to reduce costs (Clark et al., 2015a). For instance, to integrate reservoir simulation into the CREST-VEC system, we can build an offline ML model which is promising in mimicking human decisions (T. Yang et al., 2021) and plug it into the system.
4.3 Towards improved flood forecasting with lake routing
Flood forecasts are difficult because of their rarity, and their hits and misses are typically low while false alarms are high (Bartholmes et al., 2009; Cloke and Pappenberger, 2009). Results in this study demonstrate a dilemma in which the model with a lake module reduces false alarms but at the cost of more missed flood events compared to the one without a lake module. Although the combined metric CSI has a certain degree of improvement, this leaves a question: Should we reduce a large number of false alarms at the expense of missing a small number of real events? Before discussing this point, we acknowledge that the current lake routing process is simple and imperfect, and improvement in this process possibly leads to an optimal situation where both false alarms and misses can be improved. However, in most situations, tradeoffs exist in hydrologic predictions. A good strategy in our case would be running both simulations with and without the lake module concurrently and making the “without lake” results the worst-case scenario. Since the CREST-VEC model has the advantage of efficiency, running two scenarios is totally feasible. A decision-maker can be trained to assess the situation – results from two scenarios disagree – from the perspective of flood severity and consequences.
This study compares a conventional raster-based routing scheme with the emerging vector-based routing approach in hydrologic models for regional cases and continental simulations. From the continental run, we demonstrate the improvement in streamflow simulation after incorporating the lake storage and release module. Last but not least, flood-related false alarms can be greatly reduced by including the lake module. The following points summarize the primary findings of the study:
-
Vector-based routing can accelerate continental-scale river routing by up to 10 times, compared to a grid-based routing, for both a regional case (0.07 s per step) and a continental case (0.002 s per step). This leaves adequate room for generating ensemble predictions with variable forcing, parameters, and/or model structures. Furthermore, it improves streamflow simulation from −0.06 to 0.18, according to the aggregated median NSE values.
-
A newly developed lake model increases the NSE score by 56.2 % and reduces systematic bias by 17 % for the continental simulation.
-
Flood false-alarm ratios can be mitigated by 20.6 % after enabling the lake module at the expense of missing 2.3 % more floods on a continental scale.
We recommend the use of ensemble simulations stemming from different model structures to overcome and adapt to varying catchment processes. Optimized streamflow prediction with quantified uncertainty information can be achieved in an operational manner for stakeholders and decision-makers. Future studies can fully investigate the limitation and uncertainty of different forcing, parameters, and/or model structures to catchment signatures such as climatology, dominant hydrologic processes, lithology, etc. Vector-based routing, in such a context, can enable a fair comparison by excluding the effect of different routing schemes while focusing on discrepancies in water balance models alone. For future work, we hope to have the best possible model-simulated streamflow product in the US, fused with multimodel structures and observations. Another direction is to improve current lake and reservoir outflow simulation with a hybrid model: process-based and ML-based.
The CREST-VEC model code is publicly available in Zenodo: https://doi.org/10.5281/zenodo.6305817 (Li, 2022). The MRMS radar-based precipitation data are archived at the Iowa State University https://mesonet.agron.iastate.edu/archive/ (last access: 3 July 2021). The daily temperature data PRISM are accessed from the Oregon State University: https://prism.oregonstate.edu (last access: 16 September 2020). The hydrography MERIT-Hydro river network data (ESRI shapefile)are available at https://www.reachhydro.org/home/params/merit-basins (last access: 10 August 2021). The HydroLAKES Version 1.0 global lake data are downloaded at https://www.hydrosheds.org/page/hydrolakes (last access: 11 August 2021).
ZL, YH, and JG conceived this study; ZL and NM implemented the model code and simulated the model in this study; ZL, SG, and MC designed the experiments and analyzed the data; ZL wrote the original draft; all co-authors contributed to reviewing and revising the manuscript.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Zhi Li is sponsored by the University of Oklahoma Hydrology and Water Security (HWS) program (https://www.ouhydrologyonline.com/, last access: 31 July 2022) and Graduate College Hoving Fellowship.
This paper was edited by Charles Onyutha and reviewed by Daisuke Tokuda and four anonymous referees.
Allen, R. G., Pereira, L., Raes, D., and Smith, M.: Crop Evapotranspiration, Food and Agriculture Organization of the United Nations, Rome, Italy, FAO publication 56, 290 pp., ISBN 92-5-104219-5, 1998.
Anderson, E. A.: Snow accumulation and ablation model – SNOW-17, US National Weather Service, Silver Spring, MD, 61, 2006.
Bartholmes, J. C., Thielen, J., Ramos, M. H., and Gentilini, S.: The european flood alert system EFAS – Part 2: Statistical skill assessment of probabilistic and deterministic operational forecasts, Hydrol. Earth Syst. Sci., 13, 141–153, https://doi.org/10.5194/hess-13-141-2009, 2009.
Beven, K.: A manifesto for the equifinality thesis, J. Hydrol., 320, 18–36, https://doi.org/10.1016/j.jhydrol.2005.07.007, 2006.
Burek, P., Satoh, Y., Kahil, T., Tang, T., Greve, P., Smilovic, M., Guillaumot, L., Zhao, F., and Wada, Y.: Development of the Community Water Model (CWatM v1.04) – a high-resolution hydrological model for global and regional assessment of integrated water resources management, Geosci. Model Dev., 13, 3267–3298, https://doi.org/10.5194/gmd-13-3267-2020, 2020.
Chen, M., Li, Z., and Gao, S.: Multisensor Remote Sensing and the Multidimensional Modeling of Extreme Flood Events, in: Remote Sensing of Water-Related Hazards, edited by: Zhang, K., Hong, Y., and AghaKouchak, A., https://doi.org/10.1002/9781119159131.ch5, 2022.
Chow, V. T., Maidment, D. R., and Mays, L. W.: Applied Hydrology: McGraw-Hill Series in Water Resources and Environmental Engineering, McGraw-Hill, Inc., New York, 1988.
Clark, M. P., Slater, A. G., Rupp, D. E., Woods, R. A., Vrugt, J. A., Gupta, H. V., Wagener, T., and Hay, L. E.: Framework for Understanding Structural Errors (FUSE): A modular framework to diagnose differences between hydrological models, Water Resour. Res., 44, W00B02, https://doi.org/10.1029/2007WR006735, 2008.
Clark, M. P., Fan, Y., Lawrence, D. M., Adam, J. C., Bolster, D., Gochis, D. J., Hooper, R. P., Kumar, M., Leung, L. R., Mackay, D. S., Maxwell, R. M., Shen, C., Swenson, S. C., and Zeng, X.: Improving the representation of hydrologic processes in Earth System Models, Water Resour. Res., 51, 5929–5956, https://doi.org/10.1002/2015WR017096, 2015a.
Clark, M. P., Nijssen, B., Lundquist, J. D., Kavetski D., Rupp, D. E., Woods, R. A., Freeer, J. E., Gutmann, E. D., Wood, A. W., Gochis, D. J., Rasmussen, R. M., Tarboton, D. G., Mahat, V., Flerchinger G. N., and Marks, D. G.: A unified approach for process-based hydrologic modeling: 1. Modeling concept, Water Resour. Res., 51, 2498–2514, https://doi.org/10.1002/2015WR017198, 2015b.
Clark, M. P., Vogel, R. M., Lamontagne, J. R., Mizukami, N., Knoben, W. J. M., Tang, G., Shervan, G., Freer J. E., Whitfield, P. H., Shook, K. R., and Papalexiou, S. M.: The abuse of popular performance metrics in hydrologic modeling, Water Resour. Res., 57, e2020WR029001, https://doi.org/10.1029/2020WR029001, 2021.
Cloke, E. and Pappenberger, F.: Ensemble flood forecasting: A review, J. Hydrol., 375, 613–626, https://doi.org/10.1016/j.jhydrol.2009.06.005, 2009.
Daly, C., Halbleib, M., Smith, J. I., Gibson, W. P., Doggett, M. K., Taylor, G. H., Curtis, J., and Pasteris, P. A.: Physiographically-sensitive mapping of temperature and precipitation across the conterminous United States, Int. J. Climatol., 28, 2031–2064, 2008.
David, C. H., Maidment, D. R., Niu, G., Yang, Z., Habets, F., and Eijkhout, V.: River Network Routing on the NHDPlus Dataset, J. Hydrometeorol., 12, 913–934, 2011.
de Almeida, G. A. M. and Bates, P.: Applicability of the local inertial approximation of the shallow water equations to flood modeling, Water Resour. Res., 49, 4833–4844, https://doi.org/10.1002/wrcr.20366, 2013.
Döll, P., Kaspar, F., and Lehner, B.: A global hydrological model for deriving water availability indicators: model tuning and validation, J. Hydrol., 270, 105–134, https://doi.org/10.1016/S0022-1694(02)00283-4, 2003.
Fenicia, F., Kavetski, D., and Savenije, H. H. G.: Elements of a flexible approach for conceptual hydrological modeling: 1. Motivation and theoretical development, Water Resour. Res., 47, W11510, https://doi.org/10.1029/2010WR010174, 2011.
Flamig, Z. L., Vergara, H., and Gourley, J. J.: The Ensemble Framework For Flash Flood Forecasting (EF5) v1.2: description and case study, Geosci. Model Dev., 13, 4943–4958, https://doi.org/10.5194/gmd-13-4943-2020, 2020.
Franz, K. J., Hogue, T. S., and Sorooshian, S.: Operational snow modeling: Addressing the challenges of an energy balance model for National Weather Service forecasts, J. Hydrol., 360, 48–66, 2008.
Freeze, R. A.: Role of subsurface flow in generating surface runoff: 2. Upstream source areas, Water Resour. Res., 8, 1272–1283, https://doi.org/10.1029/WR008i005p01272, 1972.
Gao, S., Chen, M., Li, Z., Cook, S., Allen, D., Neeson, T., Yang, T., Yami, T., and Hong, Y.: Mapping dynamic non-perennial stream networks using high-resolution distributed hydrologic simulation: A case study in the upper blue river basin, J. Hydrol., 600, 126522, https://doi.org/10.1016/j.jhydrol.2021.126522, 2021.
Gharari, S., Clark, M. P., Mizukami, N., Knoben, W. J. M., Wong, J. S., and Pietroniro, A.: Flexible vector-based spatial configurations in land models, Hydrol. Earth Syst. Sci., 24, 5953–5971, https://doi.org/10.5194/hess-24-5953-2020, 2020.
Gharari, S., Vanderkelen, I., Tefs, A., Mizukami, N., Stadnyk, T. A., Lawrence, D., and Clark, M. P.: A Flexible Multi-Scale Framework to Simulate Lakes and Reservoirs in Earth System Models, Earth and Space Science Open Archive, https://doi.org/10.1002/essoar.10510902.1, 2022.
Gourley, J. J., Flamig, Z. L., Vergara, H., Kirstetter, P., Clark, R. A., III, Argyle, E., Arthur, A., Martinaitis, S., Terti, G., Erlingis, J. M., Hong, Y., and Howard, K. W.: The FLASH Project: Improving the Tools for Flash Flood Monitoring and Prediction across the United States, B. Am. Meteorol. Soc., 98, 361–372, https://doi.org/10.1175/BAMS-D-15-00247.1, 2017.
Hanasaki, N, Kanae, S., and Oki, T.: A reservoir operation scheme for global river routing models, J. Hydrol., 327, 22–41, 2006.
Horton, P., Schaefli, B., and Kauzlaric, M.: Why do we have so many different hydrological models? A review based on the case of Switzerland, Wiley Interdiscip. Rev., Water, e1574, https://doi.org/10.1002/wat2.1574, 2021.
Knoben, W. J. M., Freer, J. E., Peel, M. C., Fowler, K. J. A., and Woods, R. A.: A brief analysis of conceptual model structure uncertainty using 36 models and 559 catchments, Water Resour. Res., 56, e2019WR025975, https://doi.org/10.1029/2019WR025975, 2020.
Knoben, W. J. M., Clark, M., Bates, J., Bennet, A., Gharari, S., Marsh, C., Nijssen, B., Pietroniro, A., Spiteri, R., Tarboton, D. J., and Wood, A. J.: Community Workflows to Advance Reproducibility in Hydrologic Modeling: Separating model-agnostic and model-specific configuration steps in applications of large-domain hydrologic models, Earth and Space Science Open Archive, https://doi.org/10.1002/essoar.10509195.1, 2021.
Lehner, B. and Grill, G.: Global river hydrography and network routing: baseline data and new approaches to study the world's large river systems, Hydrol. Process., 27, 2171–2186, https://doi.org/10.1002/hyp.9740, 2013.
Lehner, B., Liermann, C. R., Revenga, C., Vörösmarty, C., Fekete, B., Crouzet, P., Döll, P., Endejan, M., Frenken, K., Magome, J., Nilsson, C., Robertson, J. C., Rödel, R., Sindorf, N., and Wisser, D.: High-resolution mapping of the world's reservoirs and dams for sustainable river-flow management, Front. Ecol. Environ., 9, 494–502, https://doi.org/10.1890/100125, 2011.
Li, Z.: CREST-VEC: A framework towards more accurate and realistic flood simulation across scales (v1.0), Zenodo [code], https://doi.org/10.5281/zenodo.6305817, 2022.
Li, Z., Chen, M., Gao, S., Hong, Z., Tang, G., Wen, Y., Gourley, J. J., and Hong, Y.: Cross-examination of similarity, difference and deficiency of gauge, radar and satellite precipitation measuring uncertainties for extreme events using conventional metrics and multiplicative triple collocation, Remote Sens., 12, 1258, https://doi.org/10.3390/rs12081258, 2020.
Li, Z., Chen, M., Gao, S., Luo, X., Gourley, J. J., Kirstetter, P., Yang, T., Kolar, R., McGovern, A., Wen, Y., Rao, B., Yami, T., and Hong, Y.: CREST-iMAP v1. 0: A fully coupled hydrologic-hydraulic modeling framework dedicated to flood inundation mapping and prediction, Environ. Model. Softw., 141, 105051, https://doi.org/10.1016/j.envsoft.2021.105051, 2021.
Liang, X., Lettenmaier, D. P., Wood, E. F., and Burges, S. J.: A simple hydrologically based model of land surface water and energy fluxes for general circulation models, J. Geophys. Res., 99, 14415–14428, https://doi.org/10.1029/94JD00483, 1994.
Lighthill, M. J. and Whitham, G. B.: On kinematic waves I. Flood movement in long rivers, Proc. R. Soc. Lond., 229, A229281–316, https://doi.org/10.1098/rspa.1955.0088, 1955.
Lin, P., Rajib, M. A., Yang, Z., Somos-Valenzuela, M., Merwade, V., Maidment, D. R., Wang, Y., and Chen, L.: Spatiotemporal Evaluation of Simulated Evapotranspiration and Streamflo over Texas Using the WRF-Hydro-RAPID Modeling Framework, J. Am. Water Resour. Assoc., 54, 40–54, https://doi.org/10.1111/1752-1688.12585, 2018.
Lin, P., Pan, M., Beck, H. E., Yang, Y., Yamazaki, D., Frasson, R., David, C. G., Durand, M., Pavelsky, T. M., Allen, G. H., Gleason, C. J., and Wood, E. F.: Global reconstruction of naturalized river flows at 2.94 million reaches, Water Resour. Res., 55, 6499–6516, https://doi.org/10.1029/2019WR025287, 2019.
Lin, P., Pan, M., Wood, E.F. Yamazaki, D., and Allen, G. H.: A new vector-based global river network dataset accounting for variable drainage density, Sci Data, 8, 28, https://doi.org/10.1038/s41597-021-00819-9, 2021.
Liston, G. E., Sud, Y. C., and Wood, E. F.: Evaluating GCM land surface hydrology parameterizations by computing river discharges using a runoff routing model, J. Appl. Met., 33, 394–405, 1994.
Lohman, D., Nolte-holube, R., and Raschke, E.: A large-scale horizontal routing model to be coupled to land surface parametrization schemes, Tellus A, 48, 708–721, https://doi.org/10.1034/j.1600-0870.1996.t01-3-00009.x, 1996.
Martinaitis, S. M., Gourley, J. J., Flamig, Z. L., Argyle, E. M., Clark, R. A., III, Arthur, A., Smith, B. R., Erlingis, J. M., Perfater, S., and Albright, B.: The HMT Multi-Radar Multi-Sensor Hydro Experiment, B. Am. Meterorol. Soc., 98, 347–359, 2017.
Messager, M. L., Lehner, B., Grill, G., Nedeva, I., and Schmitt, O.: Estimating the volume and age of water stored in global lakes using a geo-statistical approach, Nat. Comm., 13603, https://doi.org/10.1038/ncomms13603, 2016.
Mizukami, N., Clark, M. P., Sampson, K., Nijssen, B., Mao, Y., McMillan, H., Viger, R. J., Markstrom, S. L., Hay, L. E., Woods, R., Arnold, J. R., and Brekke, L. D.: mizuRoute version 1: a river network routing tool for a continental domain water resources applications, Geosci. Model Dev., 9, 2223–2238, https://doi.org/10.5194/gmd-9-2223-2016, 2016.
Mizukami, N., Clark, M. P., Newman, A. J., Wood, A. W., Gutmann, E. D., Nijssen, B., Rakovec, O., and Samaniego, L.: Towards seamless large-domain parameter estimation for hydrologic models, Water Resour. Res., 53, 8020–8040, https://doi.org/10.1002/2017WR020401, 2017.
Mizukami, N., Clark, M. P., Gharari, S., Kluzek, E., Pan, M., Lin, P., Beck, H. E., and Yamazaki, D.: A vector-based river routing model for Earth System Models: Parallelization and global applications, J. Adv. Model. Earth Sy., 13, e2020MS002434, https://doi.org/10.1029/2020MS002434, 2021.
Newman, A. J., Clark, M. P., Sampson, K., Wood, A., Hay, L. E., Bock, A., Viger, R. J., Blodgett, D., Brekke, L., Arnold, J. R., Hopson, T., and Duan, Q.: Development of a large-sample watershed-scale hydrometeorological data set for the contiguous USA: data set characteristics and assessment of regional variability in hydrologic model performance, Hydrol. Earth Syst. Sci., 19, 209–223, https://doi.org/10.5194/hess-19-209-2015, 2015.
NOAA National Centers for Environmental Information (NCEI): U.S. Billion-Dollar Weather and Climate Disasters, https://doi.org/10.25921/stkw-7w73, 2022.
Ohmura, A.: Physical basis for the temperature-based melt-index method, J. Appl. Meteorol., 40, 753–761, 2001.
Paiva, R. C. D., Collischonn, W., and Tucci, C. E. M.: Large scale hydrologic and hydrodynamic modeling using limited data and a GIS based approach, J. Hydrol., 406, 170–181, https://doi.org/10.1016/j.jhydrol.2011.06.007, 2011.
Ponce, V. M., Li, R.-M., and Simons, D. B.: Applicability of kinematic and diffusion models, J. Hydraul. Div., 104, 353–360, 1978.
PRISM Climate Group, Oregon State University, https://prism.oregonstate.edu (last access: 16 September 2020), 2014.
Quinn, P., Beven, K., Chevallier, P., and Planchon, O.: The prediction of hillslope flow paths for distributed hydrological modelling using digital terrain models, Hydrol. Process., 5, 59–79, https://doi.org/10.1002/hyp.3360050106, 1991.
Salas, F. R., Somos-Valenzuela, Marcelo A., Dugger, A., Maidment, D. R., Gochis, D. J., David, C. H., Yu, W., Ding, D., Clark, E. P., and Noman, N.: Towards Real-Time Continental Scale Streamflow Simulation in Continuous and Discrete Space, J. Am. Water Resour. Assoc. 54, 7–27, https://doi.org/10.1111/1752-1688.12586, 2018.
Savenije, H. H. G.: HESS Opinions “The art of hydrology”, Hydrol. Earth Syst. Sci., 13, 157–161, https://doi.org/10.5194/hess-13-157-2009, 2009.
Shaad, K.: Evolution of river-routing schemes in macro-scale models and their potentials for watershed management, Hydrol. Sci. J., 63, 1062–1077, https://doi.org/10.1080/02626667.2018.1473871, 2018.
Shen, X., Hong, Y., Zhang, K., and Hao, Z.: Refining a distributed linear reservoir routing method to improve performance of the CREST model, J. Hydrol. Eng., 22, 04016061, https://doi.org/10.1061/(ASCE)HE.1943-5584.0001442, 2017.
Solvik, K., Bartuszevige, A. M., Bogaerts, M., and Joseph, M. B.: Predicting playa inundation using a long short-term memory neural network, Water Resour. Res., 57, e2020WR029009, https://doi.org/10.1029/2020WR029009, 2021.
Tang, G., Zeng, Z., Long, D., Guo, X., Yong, B., Zhang, W., and Hong, Y.: Statistical and Hydrological Comparisons between TRMM and GPM Level-3 Products over a Midlatitude Basin: Is Day-1 IMERG a Good Successor for TMPA 3B42V7?, J. Hydrometeorol., 17, 121–137, 2016.
Tarboton, D. G.: A new method for the determination of flow directions and upslope areas in grid digital elevation models, Water Resour. Res., 33, 309–319, https://doi.org/10.1029/96WR03137, 1997.
Tavakoly, A. A., Gutenson, J. L., Lewis, J. W., Follum, M. L., Rajib, A., LaHatte, W. C., and Hamilton, C. O.: Direct integration of numerous dams and reservoirs outflow in continental scale hydrologic modeling, Water Resour. Res., 57, e2020WR029544, https://doi.org/10.1029/2020WR029544, 2021.
Tellman, B., Sullivan, J. A., Kuhn, C. Kettner, A. J., Doyle, C. S., Brakenridge, G. R., Erickson, T. A., and Slayback, D. A.: Satellite imaging reveals increased proportion of population exposed to floods, Nature, 596, 80–86, https://doi.org/10.1038/s41586-021-03695-w, 2021.
Tijerina, D., Condon, L., FitzGerald, K., Dugger, A., O'Neill, M. M., Sampson, K., Gochis, D., and Maxwell, R.: Continental hydrologic intercomparison project, phase 1: A large-scale hydrologic model comparison over the continental United States, Water Resour. Res., 57, e2020WR028931, https://doi.org/10.1029/2020WR028931, 2021.
Tokuda, D., Kim, H., Yamazaki, D., and Oki, T.: Development of a coupled simulation framework representing the lake and river continuum of mass and energy (TCHOIR v1.0), Geosci. Model Dev., 14, 5669–5693, https://doi.org/10.5194/gmd-14-5669-2021, 2021.
Vanderkelen, I., Gharari, S., Mizukami, N., Clark, M. P., Lawrence, D. M., Swenson, S., Pokhrel, Y., Hanasaki, N., van Griensven, A., and Thiery, W.: Evaluating a reservoir parametrization in the vector-based global routing model mizuRoute (v2.0.1) for Earth system model coupling, Geosci. Model Dev., 15, 4163–4192, https://doi.org/10.5194/gmd-15-4163-2022, 2022.
Vergara, H., Kirstetter, P., Gourley, J. J., Flamig, Z. L., Hong, Y., Arthur, A., and Kolar, R.: Estimating a-priori kinematic wave model parameters based on regionalization for flash flood forecasting in the Conterminous United States, J. Hydrol., 541, 421–433, https://doi.org/10.1016/j.jhydrol.2016.06.011, 2016.
Vrugt, J. A., ter Braak, C., Diks, C., Robinson, B. A., Hyman, J. M., and Higdon, D.: Accelerating Markov Chain Monte Carlo Simulation by Differential Evolution with Self-Adaptive Randomized Subspace Sampling, Int. J. Nonlinear Sci. Numer. Simul., 10, 273–290, https://doi.org/10.1515/ijnsns.2009.10.3.273, 2009.
Wang, J., Hong, Y., Li, L., Gourley, J. J., Khan, S. I., Yilmaz, K. K., Adler, R. F., Policelli, F. S., Habib, S., Irwn, D., Limaye, A. S., Korme, T., and Okello, L.: The coupled routing and excess storage (CREST) distributed hydrological model, Hydrol. Sci. J., 56, 84–98, 2011.
Wang, X., White-Hull, C., Dyer, S., and Yang, Y.: GIS-ROUT: A River Model for Watershed Planning, Environ. Plann. B, 27, 231–246, https://doi.org/10.1068/b2624, 2000.
Xue, X., Hong, Y., Limaye, A. S., Gourley, J. J., Huffman, G. J., Khan, S. I., Doriji, C., and Chen, S.: Statistical and hydrological evaluation of TRMM-based Multi-satellite Precipitation Analysis over the Wangchu Basin of Bhutan: Are the latest satellite precipitation products 3B42V7 ready for use in ungauged basins?, J. Hydrol., 499, 91–99, https://doi.org/10.1016/j.jhydrol.2013.06.042, 2013.
Yamazaki, D., Kanae, S., Kim, H., and Oki, T.: A physically based description of floodplain inundation dynamics in a global river routing model, Water Resour. Res., 47, 1–21, https://doi.org/10.1029/2010WR009726, 2011.
Yamazaki, D., Sato, T., Kanae, S., Hirabayashi, Y., and Bates, P. D.: Regional flood dynamics in a bifurcating mega delta simulated in a global river model, Geophys. Res. Lett., 41, 3127–3135, https://doi.org/10.1002/2014GL059744, 2014.
Yamazaki, D., Ikeshima, D., Tawatari, R., Yamaguchi, T., O'Loughlin, F., Neal, J. C., Sampson, C. C., Kanae, S., and Bates, P. D.: A high-accuracy map of global terrain elevations, Geophys. Res. Lett., 44, 5844–5853, https://doi.org/10.1002/2017GL072874, 2017.
Yamazaki, D., Ikeshima, D., Sosa, J., Bates, P. D., Allen, G. H., and Pavelsky, T. M.: MERIT Hydro: A High-Resolution Global Hydrography Map Based on Latest Topography Dataset, Water Resour. Res., 55, 5053–5073, https://doi.org/10.1029/2019WR024873, 2019.
Yang, T., Zhang, L., Kim, T., Hong, Y., Zhang, D., and Peng, Q.: A large-scale comparison of Artificial Intelligence and Data Mining (AI&DM) techniques in simulating reservoir releases over the Upper Colorado Region, J. Hydrol., 602, 126723, https://doi.org/10.1016/j.jhydrol.2021.126723, 2021.
Yang, Y., Pan, M., Lin, P., Beck, H. E., Zeng, Z., Yamazaki, D., David, C. H., Lu, H., Yang, K., Hong, Y., and Wood, E. F.: Global Reach-Level 3-Hourly River Flood Reanalysis (1980–2019), B. Am. Meteorol. Soc., 102, E2086–E2105, 2021.
Zhang, J., Howard, K., Langston, C., Kaney, B., Qi, Y., Tang, L., Grams, H., Wang, Y., Cocks, S., Martinaitis, S., Arthur, A., Cooper, K., Brogden, J., and Kitzmiller, D.: Multi-Radar Multi-Sensor (MRMS) Quantitative Precipitation Estimation: Initial Operating Capabilities, B. Am. Meteorol. Soc., 97, 621–638, https://doi.org/10.1175/BAMS-D-14-00174.1, 2016.