the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A scalability study of the Ice-sheet and Sea-level System Model (ISSM, version 4.18)
Yannic Fischler
Martin Rückamp
Christian Bischof
Vadym Aizinger
Mathieu Morlighem
Angelika Humbert
Accurately modelling the contribution of Greenland and Antarctica to sea level rise requires solving partial differential equations at a high spatial resolution. In this paper, we discuss the scaling of the Ice-sheet and Sea-level System Model (ISSM) applied to the Greenland Ice Sheet with horizontal grid resolutions varying between 10 and 0.25 km. The model setup used as benchmark problem comprises a variety of modules with different levels of complexity and computational demands. The core builds the so-called stress balance module, which uses the higher-order approximation (or Blatter–Pattyn) of the Stokes equations, including free surface and ice-front evolution as well as thermodynamics in form of an enthalpy balance, and a mesh of linear prismatic finite elements, to compute the ice flow.
We develop a detailed user-oriented, yet low-overhead, performance instrumentation tailored to the requirements of Earth system models and run scaling tests up to 6144 Message Passing Interface (MPI) processes. The results show that the computation of the Greenland model scales overall well up to 3072 MPI processes but is eventually slowed down by matrix assembly, the output handling and lower-dimensional problems that employ lower numbers of unknowns per MPI process. We also discuss improvements of the scaling and identify further improvements needed for climate research. The instrumented version of ISSM thus not only identifies potential performance bottlenecks that were not present at lower core counts but also provides the capability to continually monitor the performance of ISSM code basis. This is of long-term significance as the overall performance of ISSM model depends on the subtle interplay between algorithms, their implementation, underlying libraries, compilers, runtime systems and hardware characteristics, all of which are in a constant state of flux.
We believe that future large-scale high-performance computing (HPC) systems will continue to employ the MPI-based programming paradigm on the road to exascale. Our scaling study pertains to a particular modelling setup available within ISSM and does not address accelerator techniques such as the use of vector units or GPUs. However, with 6144 MPI processes, we identified issues that need to be addressed in order to improve the ability of the ISSM code base to take advantage of upcoming systems that will require scaling to even higher numbers of MPI processes.
- Article
(9229 KB) - Full-text XML
- BibTeX
- EndNote
Projections of future sea level rise are a major societal demand. The future mass loss of ice sheets and glaciers is one of the primary sources of sea level rise (Church et al., 2013). Today, projections are still subject to large uncertainties, which stem in particular from the climate forcing and ice-sheet model characteristics (such as the initial state or ability to represent processes adequately Goelzer et al., 2020; Edwards et al., 2021; Crawford et al., 2021). While the momentum balance can be solved using a higher-order approximation (HO, also called Blatter–Pattyn, Blatter, 1995; Pattyn, 2003) representing the physical system reasonably well, the benefits of HO pay out only if the resolution is sufficiently high (Rückamp et al., 2020a), especially in the vicinity of the grounding line where the ice sheet goes afloat (Cornford et al., 2020). The grid resolution requirement comes with additional computational costs, a limiting factor that needs to be overcome. In addition, standalone ice sheet projections are challenged by large spread in climate forcing fields (e.g. Goelzer et al., 2020). As a consequence, atmosphere and ocean models will be run in the future at higher spatial resolutions, so when ice sheet codes are coupled with other components of Earth system models (ESMs), they need to reach a level of computational performance – especially in terms of parallel scalability – comparable to that of ocean and atmosphere models.
Since complex bed topographies, rugged coastlines of ice sheets and small scale features form an irregular geometry (e.g. narrow confined fjords in Greenland or small pinning points in Antarctic ice shelves), unstructured meshes are best suited. This motivated the development of codes based on finite element and finite volume discretizations with triangular or Voronoi meshes (Larour et al., 2012; Gagliardini et al., 2013; Hoffman et al., 2018; Berends et al., 2021) – such as the Ice-sheet and Sea-level System Model (ISSM, Larour et al., 2012). The flexible multi-physics ISSM model provides full Stokes, HO, shallow shelf and shallow ice approximations for the momentum balance, making it particularly versatile and flexible.
To study the performance of ISSM, we select a real-life system as a test case: the Greenland Ice Sheet (GrIS) simulated at different horizontal resolutions – covering the range from what is today's standard for long-term simulations (Plach et al., 2019), such as paleo-spinups, up to the present-day highest resolutions in projections such as the ones used in the international benchmark experiment ISMIP6 (Goelzer et al., 2020; Rückamp et al., 2020a). This way, we contribute a “user-oriented” performance analysis tailored to the requirements of ESMs. Such an in-depth performance analysis has not yet been performed for ISSM and comes timely with the first exascale-ready ESMs (Golaz et al., 2019) ushering a new era of climate modelling. While Message Passing Interface (MPI) scalability is not sufficient for reaching exascale performance, it seems to be necessary as corroborated, for example, by the MPI-based programming style of the 24 applications chosen for the exascale computing project (see http://www.exascaleproject.org/about, last access: 8 April 2022).
Several metrics have been proposed to quantify “scalability”, that is, the performance response of a code when additional hardware resources are made available (see, e.g. Perlin et al., 2016). “Strong scaling” shows the performance of a fixed-size problem when additional cores are employed to solve it. The baseline measurement is, in theory (as in Amdahl's law), the runtime with one core, but this is infeasible for many realistic model setups due to memory and runtime limitations. “Weak scaling” (or Gustavson's law), on the other hand, reflects the fact that usually the problem size increases with the size of the compute system. In our study, we mainly investigate how ISSM performs on a particular, fixed-size model setup using from 96 to 6144 cores, i.e. over almost 2 orders of magnitude in core count, but we also show performance for various resolutions of the same domain. These results give us insight into both strong and weak scaling issues and allow us, in particular, to determine the model throughput in simulated years per (wall-clock) day (SYPD), which is an important measure for an ESM's performance.
Numerical models such as the ISSM are generally based on a discretization of the underlying system of partial differential equations (PDEs) leading to a fully discrete system of nonlinear or linear algebraic equations to be solved. In the context of finite elements, the computational domain is partitioned using a computational mesh consisting of elements (e.g. triangles or quadrilaterals in 2-D, tetrahedra or prisms in 3-D), and the discrete unknowns are specified per node, per element or per face of the mesh, depending on the specific finite element scheme and the used approximation order. The discrete unknowns are called degrees of freedom (DOF), and their total number then specifies the size of the discrete linear or nonlinear system to be solved. With increasing mesh resolution as well as higher order of shape functions, the number of DOF is increasing for a particular PDE boundary value problem (e.g. Wriggers, 2008). In parallel computing, the problem is distributed over a number of cores leaving each core with a particular number of DOF/core. Studies on performance in other disciplines have shown (Bnà et al., 2020) that a certain minimum number of DOF/core is required to ensure good performance. For the software package PETSc (Balay et al., 2021a), on which ISSM is built, the recommendation is a minimum of 10 000 DOF/core.
The employed model setup in our study comprises a variety of modules with different levels of complexity. Sophisticated performance analyses that identify the impact of such a multi-physics problem for overall code performance do exist for ocean models (Reuter et al., 2015; Huang et al., 2016; Prims et al., 2018; Koldunov et al., 2019) and, in somewhat less detail, for the atmosphere (Neumann et al., 2019); however, they are not yet standard for ice sheet codes. Most studies analyse the performance of the stationary Stokes problem. For MALI1 (MPAS-Albany Land Ice, HO, finite elements, Hoffman et al., 2018), this was presented by (Tezaur et al., 2015a, b) and revealed a good overall scalability. Similarly, Gagliardini et al. (2013) achieved a good weak and strong scaling efficiency for Elmer/Ice (full Stokes finite elements). A study mostly focused on the scalability and computational performance issues was conducted in Isaac et al. (2015) in a greatly simplified setting (e.g. a prescribed temperature field), whereas Brædstrup et al. (2014) ported a time-dependent shallow ice model to GPUs and discussed the key challenges of achieving good computational performance on this type of hardware architecture. In a transient setup, Dickens (2015) analysed the scalability and performance of PISM's (Parallel Ice Sheet Model, hybrid SIA and SSA, finite differences, Bueler and Brown, 2009) compute and output phases (i.e. I/O). They found the I/O component to be a considerable bottleneck, while the compute phase scaled well. As we will see, however, for sophisticated multi-physics and multi-resolution codes such as ISSM, a finer-grained analysis is necessary to shed light on the drivers of scalability issues (see also Chang et al., 2018).
A first scaling analysis of ISSM has been conducted in Larour et al. (2012), presenting the efficiency of the stress balance module up to 180 compute cores for a case of the GrIS using the direct solver MUMPS. In our study, we extend the performance analysis of ISSM to cover the entire code base using a high-resolution model setup as well as several lower-resolution ones executed on 96 to 6144 cores. Here we rely on an iterative solver – based on recommendations in Habbal et al. (2017), we selected GMRES preconditioned with block Jacobi method.
In addition, to pinpoint the effect of different models on the overall performance, we develop an instrumentation scheme that provides detailed performance information closely related to an Earth system scientist's view of the code. The challenge here is to develop a setup that does not introduce much overhead, as otherwise the results of instrumented runs would not be representative for the original code base. As a result, then, such an analysis can become part of the standard production environment providing insight into the code's performance as algorithms or the code's environment (e.g. the underlying hardware, middleware or libraries) change. To that end, a setup is developed that limits the instrumentation overhead through careful filtering but leaves the code base untouched.
The paper is structured as follows: we start by introducing the underlying physical model (the details of the mathematical models are given in Appendix A) and the employed test setup applied to GrIS (Sect. 2). We then present the software design of ISSM, its parallelization scheme and how it supports efficient simulations (Sect. 3). The main part of this study is the measurement of the runtime. We present our low-overhead sustainable performance measurement instrumentation in Sect. 4, and the results are presented in Sect. 5. Section 6 contains a discussion of the results, including the options for further code optimization, followed by a discussion from the prospective of coupled ice sheets integrated into ESMs, i.e. exchanging variables with atmosphere and ocean models rather than just obtaining data from them. A short Conclusions section wraps up this presentation.
2.1 Description of the model
For this study, we focus on a selected subset of the capabilities of ISSM; e.g. we employ only the HO approximation of the stress balance. This approximation is currently used in ice sheet projections and, in terms of the ice sheet code run as a part of a fully coupled ESM, it is the most comprehensive level of physics that we expect to be practical in ESMs. We also do not incorporate other sophisticated modules, such as subglacial hydrology, or advanced approaches for computation of surface mass balance (SMB). The mathematical model is given in detail in the Appendix A1. For a more exhaustive model description, the reader is referred to Rückamp et al. (2019).
The mathematical models for the different modules (Sect. A1, Eqs. A2–A23) are discretized using the finite element method on an unstructured mesh that is fixed in time. The computation within a time step is conducted in a sequence of different modules (see Fig. 1 for a schematics of the main execution substeps), which means that the different balance equations for momentum, mass and energy are not solved in a coupled fashion. Furthermore, the stress balance module solves a nonlinear PDE system using a fixed-point Picard iteration where each step involves the solution of a linear equation system. The balance equations for enthalpy and momentum are solved consecutively, no iteration between the two modules is done within a time step. The total number of DOF, the quantity that determines the size of the matrix for the linear equation systems, differs substantially between different modules. The fields for velocity, enthalpy, ice thickness and ice level set are computed at each vertex of the mesh using piecewise-linear (P1) finite elements. The enthalpy equation is stabilized with ASUPG (anisotropic streamline upwind Petrov–Galerkin method, Rückamp et al., 2020b).
2.2 Description of the benchmark problem
The results presented in this study are based on a setup of the GrIS that has previously been used for future projections (Rückamp et al., 2019) and is utilized here with slight modifications. The bed topography is BedMachine v3 (Morlighem et al., 2017). The ice thermodynamics are computed with an enthalpy scheme (Sect. A1.4) initialized with the enthalpy field from a paleo-climate spinup similar to Rückamp et al. (2019). Surface topography and 3-D velocity are also taken from this spinup. Grounding line evolution (Eq. A22) uses the sub-element parameterization of the friction coefficient (Seroussi et al., 2014). Climate forcing fields are read in at each time step in the SMB module.
The main difference with Rückamp et al. (2019) is that the moving front module is enabled during the scalability tests to capture its performance. The calving front motion is solved by a level-set method (Eq. A23), which tracks the ice front according to a kinematic calving front condition (Bondzio et al., 2016, 2017). Here, we assume a moving front configuration where the advance of the calving from (i.e. by glacier velocity) is compensated by the sum of calving and frontal melting. These settings basically specify a system close to an equilibrium.
Each horizontal mesh is generated with a higher resolution denoted by REShigh in fast-flowing regions (initial ice surface velocity ), while maintaining a relatively low, RESlow, resolution in the interior. This statically adaptive mesh generation strategy allows for a variable resolution and gives more computational resources to regions of dynamic complexity. Simulation measurements are performed on five meshes (Fig. A1, Table 1) using 15 vertical sigma layers refined towards the base where vertical shearing becomes more important. The meshes differ by employing five different horizontal grid resolutions with REShigh as specified in Table 1. The highest resolution is approximately 250 m, which is close to the resolution of the bed topography dataset used in our study.
Table 1Overview of problem setups used in our study. Note that (a) the vertices and elements of the 3-D mesh describe the full mesh (i.e. ice-covered and non-ice-covered elements), (b) the minimum DOF is the DOF from the 2-D mass transport module and (c) the maximum DOF is the DOF from the 3-D stress balance horizontal module.

In order to measure the performance, we conduct 30 time steps in each run, but we only measure time steps from 11 to 30. Since we allow in each time step the individual modules to reach their convergence criteria, we intentionally exclude the timings from a cold start based on a poor initial guess.
The convergence criteria (see the Appendix) for the linear iteration of the stress balance is the Euclidean norm , and the relative tolerance (no ϵ3 set). The thermal solver is using . Stress balance and thermal modules are set to use at most 100 nonlinear iterations, but this limit is never reached in all cases observed.
2.3 Experimental environment
All experiments are conducted on dedicated compute nodes of the Lichtenberg high-performance computing (HPC) system with two 48-core Intel Xeon Platinum 9242 per compute node and 384 GB of main memory each, connected with an InfiniBand HDR100 network providing point-to-point connections between nodes. For all runs, we employ 48 MPI processes on each node pinned to NUMA nodes. The fact that we only use half of the available hardware cores is due to the fact that at G250 resolution, each MPI process requires 7.4 GB of memory, when the mesh is distributed on only 48 processes. Even the shrinking memory consumption with an increasing number of processes (e.g. 5.9 GB per process on 96 processes) does not overcome this limitation, while we only use a few nodes. The demand of memory per process shrinks with a rising number of processes, but it is a limitation of our setup. Each experiment runs three repetitions, and results fall within a standard deviation of 10 %. The basis for our instrumentation is the latest ISSM public release 4.18, which is compiled with GCC 10.2 (optimization level “-O2”), Open MPI 4.0.5 (Graham et al., 2006) and PETSc 3.14 (Balay et al., 2021b). For profiling and tracing we use Score-P 7.0 (Knüpfer et al., 2012) and for data analysis Cube GUI 4.6 (Geimer et al., 2007) and Vampir 9.18 (Nagel et al., 1996).
We compiled both ISSM and PETSc with “-O2” as well as with “-O3 -march=cascadelake -mtune=cascadelake”. On a 480-core configuration, the entire calculation (without loading the model) took 1955 s compiled with “-O2” and 1930 s when compiled with higher-level optimization. With 1536 cores, we observed execution times of 763 and 748 s, respectively. So the compiler optimization level has an impact of less than 2 % in both cases. As the impact of the more aggressive compiler optimizations is low, we stick to “-O2”, as it avoids some potential numerical issues that can arise with more aggressive compiler options. Optimization level “-O2” is also employed for Open MPI and PETSc in the module tree provided for the Lichtenberg HPC system by the computing centre of TU Darmstadt.
Nevertheless, in general, vector units which are generated during compilation with native compiler flags are important for overall performance of codes. The fact that ISSM does not benefit from vector instructions is a sign that the performance of ISSM is memory bandwidth limited. Therefore node-level performance optimizations are a future need that pure MPI scaling cannot overcome.
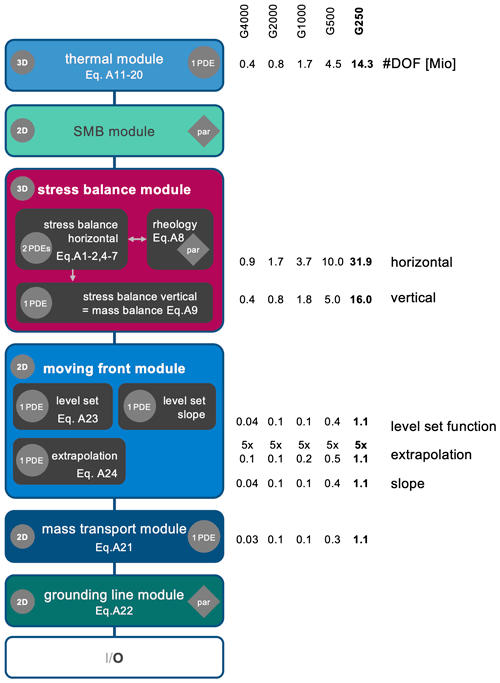
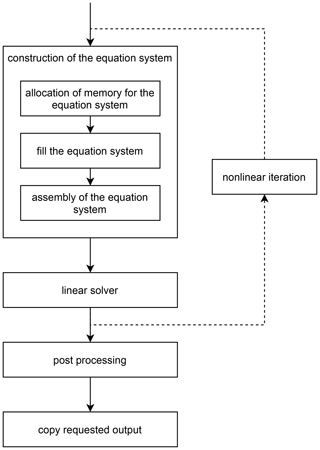
Figure 1The sequence of modules in a transient time step in ISSM. Small grey circles indicate the dimension of the equations of the module (3-D, 2-D). Larger grey circles with PDEs are denoting if and how many partial differential equations are solved. Diamonds with “par” indicate that only an algebraic equation is evaluated. On the right side, we list the DOF for particular mesh resolutions and modules.
ISSM is implemented in multiple modules, which run in a predefined sequence illustrated in Fig. 1 for the transient solution in our GrIS setup. While these modules all utilize the same 2-D mesh, the same vertical layer structure and the same data distribution, they strongly differ in the number of DOF ranging from a large linear equation system for the velocity field in three dimensions to the comparatively low-cost computations needed for two dimensional fields in the mass transport module (the equations solved are given in Appendix A). The solution procedure in each module belongs to one of three different types. The SMB module and the grounding line module calculate an algebraic solution, the mass transport module and the moving front module solve linear PDEs, and the thermal module and the stress balance module solve nonlinear PDEs. The file output for the results of the simulation is carried out in the last step of the sequence.
Although these modules solve different mathematical problems, the modular software designs enables a similar structure for the implementation of the linear and nonlinear equations. This generalized form of the solution sequence of ISSM is shown in Fig. 2.
The first step of each sequence step that involves the solution of a PDE is identical and consists of constructing the equation system. Within this step, memory is allocated, the entries of the system matrix are filled in on each mesh element, and the global matrix is assembled. The main difference between the modules lies in how the equation matrix is filled. Here, the code iterates over all elements of the mesh and computes an element matrix, whose entries depend on the PDE being discretized. The element entries are then assembled into a global matrix. Next, the equation system is solved. If a module contains a nonlinear iteration – this is the case for the horizontal stress balance and the thermal module – in each step of the nonlinear solver material properties or basal constraints are updated, and the global linear equation system is solved in the same fashion as for linear PDEs. The nonlinear iteration is repeated until the convergence criterion is reached. Subsequently, the results are post-processed, and the geometry of the mesh is updated as needed. Finally, the requested file output is selected.
While running multiple modules in parallel is not possible due to data dependencies, ISSM parallelizes the solution sequence of individual modules. For this it uses an even distribution of the elements, which is constant over time and independent of the modules, and each module handles the parallelization in the same way. During the construction of the equation system, memory is allocated locally, the element matrices are computed, and the equation system is filled, without any MPI communication. Thereafter, entries which are assigned to other MPI processes are communicated in the assembly of the equation system, leading to many MPI calls. The parallel linear solver then solves the equation system and the solution is distributed to all MPI processes in the post-processing. In the case of a nonlinear system, a convergence criterion has to be computed, and the nonlinear iteration has to be updated, potentially involving additional MPI calls. In the final selection of the requested output, data are stored in vectors or reduced to scalars. Both operations again lead to MPI communication.
Large code bases such as ISSM are developed and used over decades. The environment in which they are executed, on the other hand, i.e. the hardware, the operating systems, underlying libraries and compilers, is in a constant state of flux. As a consequence, code development needs not only to address the representation of physics but also to account for these changing operating environments, in particular, the increase in the number of compute cores. Modernizing a code or porting it from one operating environment to the other is likely to affect overall performance. In particular, modules that do not play a significant role with respect to compute time with a low core count may end up taking a significantly larger chunk of compute time on a larger parallel system and thereby significantly affect the overall performance and scalability. In addition, a code like ISSM is never in a final state. The development of new modules, the implementation of new algorithms in existing modules, code optimizations to exploit GPU accelerators or vector units, or an update of used libraries can have a substantial (positive or negative) performance impact. As a consequence, a continuous performance monitoring of ISSM is an essential feature allowing to assess the performance on the shifting computational ground the code lives on. For this reason, the code version of ISSM that we started out with had a basic timing setup to monitor the performance of the eight modules accounted for in Fig. 3, as well as of the setup stage and the linear solver.
As will be shown in the next section, we need to dig deeper to develop a sufficient understanding of the performance behaviour of ISSM. To gather this information, we developed a sustainable performance measurement environment which provides performance information that correlates with the algorithmic view of domain scientists. Sustainability here includes three main factors: (1) the instrumented code needs to be easy to build and use, (2) the instrumentation results need to refer to identifiable modules in the code, and (3) measurements must not lead to a significant computational overhead, as this would distort results.
Profiling information for a code can be created in two different ways: sampling and/or instrumentation. With sampling-based tools, the execution is interrupted at regular intervals and that state recorded (e.g. with HPC toolkit, cf. Tallent et al., 2009), whereas with the instrumentation approach, calls to monitoring functions are inserted into the source code (or an intermediate representation) manually or automatically. Instrumentation has the advantage that it measures exactly the same regions in each run, thereby improving comparability of results. The main potential disadvantage of instrumentation over sampling is the overhead resulting from too many logging calls, which can be avoided by efficient filtering.
In our work, we use the Score-P instrumentation tool (Knüpfer et al., 2012), whose output in the cubex format is also used by a variety of other analysis and visualization tools. These cubex files can be used in subsequent tools like Cube GUI (Geimer et al., 2007), Vampir (Nagel et al., 1996), Scalasca (Geimer et al., 2010) or Extra-P (Calotoiu et al., 2013) to gain performance information and provide visualizations or hints for improvement potential.
In this work, we go beyond the instrumentation of the top-level modules and develop an instrumentation that enables an in-depth analysis of ISSM behaviour which is closely tied to the algorithmic view of domain scientists through making judicious use of the features provided by Score-P. Score-P generates profiles and traces based on compiler instrumentation supporting filtering and manually defined user regions. Additionally, Score-P hooks into the PMPI interface (the MPI profiling interface) of the MPI library and is therefore able to track each MPI call with little overhead. This is important as calls to MPI functions are likely causes of synchronization overhead that we might encounter. In addition, Score-P is able to generate similarly instrumented interfaces for user-defined libraries, which we employ to wrap calls to the PETSc library. Our timing profile thus includes every PETSc call. This is beneficial since the PETSc calls provide much more context information than MPI calls by themselves. So the profile contains the information whether an MPI call belongs to an assembly, the solver or some other PETSc algorithm, respectively.
In order to develop a low-overhead instrumentation, we start out with a full instrumentation (which is generated automatically without effort on our part) and then analyse which modules account for a significant chunk of the runtime. Repeating this several times and taking the modular structure of ISSM (see Sect. 3) as a guideline then provides us a structure for efficient instrumentation. The functionality of Score-P whitelist instrumentation is limited to the instrumentation of entire functions or methods. To gain more detailed information on the creation of the equation system, which is implemented in one function, we instrument six code regions within this function manually by bracketing them with Score-P instrumentation calls. In the end, we provide Score-P with a whitelist of 52 functions to instrument and instrument six code regions manually. In the following, we refer, for simplicity, to 58 instrumented regions (IR). In fact, the maintenance of an instrumented version of ISSM would be easier if the six regions were functions, as, in that case, no Score-P instrumentation code would need to be inserted in ISSM.
These 58 functions cover the so-called “hot paths” of the main parts of the code, i.e. the modules and call paths where most of the computing time is spent. We mention that this process of finding the hot paths of a code has since been (partially) automated with the Performance Instrumentation Refinement Automation framework (PIRA) tool (Arzt et al., 2021). When we started this work, PIRA was not yet able to deal with a code base such as ISSM.
Since we paid attention to include all functions and methods which are on the call path to a function we instrument, in order to get the context of each measured region, our function whitelist includes the entry point of each physics module (which have also been measured by ISSM internal timings), the calls of the individual solution sequences and the top-level calls of the logical steps of the algorithms, e.g. allocation of memory, computation of element matrices, assemble of matrices and vectors and the linear solver.
Table 2 illustrates the impact of instrumentation for a model run for 30 steps with the G250 resolution on 3072 MPI processes. In addition to the 58 ISSM functions whose instrumentation was triggered through filtering or bracketing of regions, we see that 56 different functions of PETSc and 33 different MPI function are called and measured. The number of calls to instrumented functions of ISSM is quite low (57 million), the number of PETSc functions called (84 billion) is roughly 1500 times higher but is far exceeded by the 15 trillion MPI calls.
Even with this high number of calls to MPI functions, the instrumentation overhead remains low: The profiling of the 15 trillion MPI calls results in a runtime overhead of about 2.5 %. When, in addition, the 84 billion PETSc functions are instrumented, we do not detect any noteworthy additional overhead, the same holds for the addition of the 57 million calls related to ISSM. On the other hand, a fully automatic instrumentation of ISSM results in an overhead of over 13 000 % according to our measurements on a coarser grid. Fully instrumented binaries are not executable in reasonable time, and any performance evaluations made on their basis may have little relevance with respect to the original code.
Table 2Details of our filter, the final profile and the overhead of the measurement environment 30 time steps of G250 with 3072 MPI processes.

The bottom line is that our instrumentation scheme keeps overhead low, even for large-scale runs, thus ensuring that the measured code is representative of the original source. As a result, it is quite feasible to periodically run an instrumented version of the code as part of the regular work of domain scientists, as a safeguard against surprises arising, for example, from a changed MPI library.
Through the performance analysis of ISSM we recognized, for example, that the matrix of the equation system in the stress balance horizontal module is being reallocated in each iteration of the nonlinear iteration scheme. Since the structure of the matrix does not change during these iterations, we modified the code to pre-allocate the matrices. Reusing them saved substantial time in the allocation and assembly of the equation system of the stress balance horizontal module. For example, running with 3072 cores, the time for matrix allocation was reduced by 91 %, the time for matrix assembly was reduced by 85 %, and the overall runtime of stress balance horizontal module decreased by 31 %. The performance numbers shown in the following section are based on this optimized version.
Pre-allocation is not an option for the thermal module due to dynamic changes in boundary condition type at the base (see Eqs. A16–A19) that may necessitate changes in the matrix structure. Since the nonlinear iteration scheme of the thermal module only needs one to three nonlinear iterations in our setup, the reallocation does not matter as much as in the stress balance horizontal module anyway.
In this section, we present the results of the measurements for the entire transient time step (Fig. 3) as well as for individual modules (Figs. 4–7). Output handling was measured and manually excluded in the post processing of the profiles and thus is not reflected in the runtimes shown. We also excluded the time for the initial loading of the model. We focus on the results for the highest resolution (G250) first and compare the throughput of different resolutions afterwards. The number of MPI processes (and the number of DOF) is plotted on the x axis, and the y axis shows the runtime in seconds. Due to the log scale of both axes, linear scaling is represented by straight lines. All plots employ the same scale for the y axis for easier comparison.
5.1 Transient step
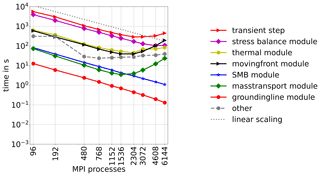
Figure 3 displays the total runtime for 20 time steps and a breakdown to the individual modules for the transient step. From 2304 MPI processes on, the transient step deviates from linear scaling and, most importantly, the computational costs start to rise from 3072 MPI processes onward.
However, the stress balance module scales linearly up to 3072 MPI processes and reasonably above that. Although the stress balance module does not scale linearly, its runtime is still monotonously declining over the number of employed MPI processes. In contrast, the earlier increase (i.e. at a lower number of MPI processes) in the runtime of the thermal, mass transport and moving front modules is more prominent. Since they scale worse than the transient solution, they become more relevant with increasing numbers of processors. The worst scalability is found for the moving front module, which contributes even more than the stress balance module from 4608 MPI processes on. The main reason for these discrepancies in the scaling behaviour is the fact that the individual modules solve equations with differing numbers of total DOF and different computing costs per element. In the following, we discuss the scaling behaviour and the algorithmic parts which cause it. Modules that do not solve any PDEs (SMB and grounding line modules) scale linearly and are not further investigated.
5.2 Stress balance module
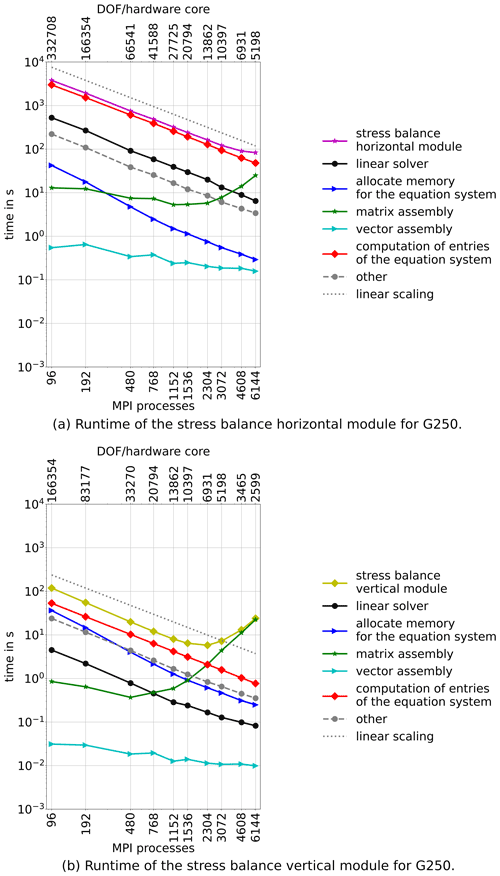
Since the stress balance module is the most time consuming module of ISSM, it is the most important module with respect to performance optimization and thus discussed first. Exploiting the natural anisotropy of the problem, the horizontal and vertical components are solved in an uncoupled fashion, and the structure of the solution procedure varies between these two main components. Therefore, we present them here separately. The runtime of both modules is displayed in Fig. 4.
We observe that the stress balance horizontal module is by far more expensive to solve than the vertical, which is expected due to more DOF in the former. The scaling behaviour of both modules differs significantly with the stress balance vertical module scaling worse. For the horizontal stress balance module, runtime is still monotonously declining at 6144 MPI processes but starts to deviate from the linear scaling. The stress balance vertical module exhibits a minimum runtime at 2304 MPI processes and slows down by about a factor of 4 with 6144 MPI processes. In the horizontal case, linear scaling breaks down when the DOF per MPI process fall below 10 000, while the vertical case never reaches 10 000 DOF per MPI process.
The execution time of the stress balance horizontal module and the stress balance vertical module on low core counts is dominated by the costs for the computation of the entries of the matrix, which scales linearly with the number of cores for setups considered in this work. Most notably, the costs for the matrix assembly are in both cases rising from 1152 cores on despite the large difference in the size of the problem. The linear solver does not represent a problem either in the stress balance horizontal module or in stress balance vertical module: it does not need a significant amount of time and its scaling is sufficient. While the stress balance vertical module is solved in a linear equation system, the nonlinear equation system of the stress balance horizontal module has to be solved iteratively and needs approximately 12 iterations per time step for this particular application.
5.3 Thermal module
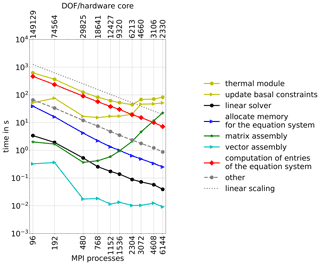
The runtime for the thermal module is presented in Fig. 5. The linear scaling of the module breaks down with about 12 000 DOF per MPI process and, after reaching a minimum at 2304 MPI processes, the execution time rises again. The execution time is dominated by three components: the computation of matrix system entries, the matrix assembly and the update of basal constraints. The assembly of the matrix system scales only up to 768 MPI process, which corresponds to about 18 600 DOF per MPI process.
The thermal module contains a nonlinear iteration scheme in which the basal boundary conditions are updated. This update is expensive, and the execution time does not change much as the number of cores increases. Furthermore, Fig. 5 shows that the costs of the linear solver can be neglected. The computation of the convergence criteria and the post-processing of the results (summarized as “other”) do not need significant runtime and scale linearly within the range of our experiments.
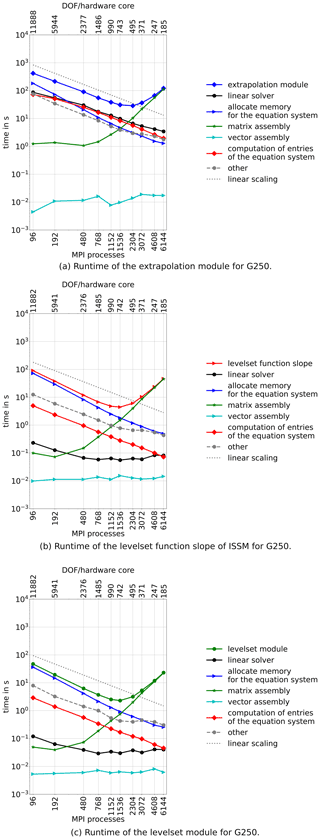
5.4 Moving front module
The moving front module consists of three individual modules: (1) a level-set module that is executed first, followed by (2) a module evaluating the slope of the level-set function and lastly (3) the extrapolation module. As shown in Fig. 3, the moving front module becomes as costly as the very expensive stress balance module, while slowing down even more than the thermal module above 3072 MPI processes.
The runtime of each step is displayed in Fig. 6. All three constituent models scale up to 768–1152 MPI processes and are mainly limited by the assembly of the equation system. Whereas in the extrapolation module the matrix assembly does not even scale for ∼ 12 000 DOF per MPI processes, in the level-set and level-set slope modules, the costs for the matrix assembly rise once DOF per MPI processes is below 10 000.
The amount of time required for allocation of memory for the level-set and level-set slope modules is similar to that of stress balance and thermal modules. In contrast, the allocation of memory is more time consuming for the extrapolation module. This is likely due to repeatedly solving a diffusion equation that accumulates larger costs.
The linear solver does only take a significant amount of time in the extrapolation module and scales linearly. The execution time of the linear solver of the level-set and level-set slope modules is negligible. Other routines are summarized in the dashed grey line, but because of an almost linear scaling, they do not play an important role.
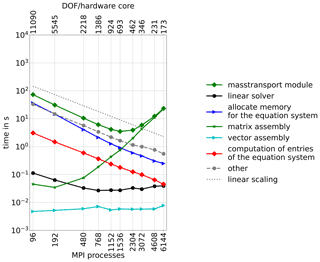
5.5 Mass transport module
This module is characterized by a particularly low number of DOF which is 30 times smaller than in the horizontal stress balance and 13 times less than in the thermal module. The overall module scales up to 1536 MPI processes (Fig. 7) despite the number of DOF per MPI process being already as low as 693. Figure 7 reveals that matrix assembly is the main scaling problem of the mass transport module once the number of DOF per MPI process drops below about 5500. The linear solver has negligible overall costs; however, its linear scaling ends at the same number of cores (and with the same DOF/core) as the assembly of the matrix system is becoming more costly than the allocation of memory. Other routines – such as averaging over depth and the update of constraints, to name the most expensive ones – scale linearly and are not further investigated at this point.
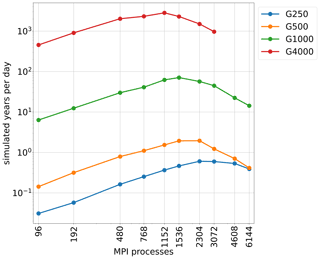
5.6 Throughput of the transient solution
Of high interest in terms of planning simulations is the quantity SYPD, as it reflects the total time needed to conduct a certain simulation. As the typical applications of ice sheet models vary strongly in simulated time periods and resolution, we conducted here simulations with coarse resolutions (G4000), a resolution that is still higher than that used in the current paleo-simulations, as well as with the highest resolution we could afford (G250). We estimated SYPD from our simulations of 20 time steps and scaled them up to 1 year by also taking into account differing time step sizes for each resolution. As displayed in Fig. 8, SYPD is approaching a maximum at 1152–2304 MPI processes with a decline at higher numbers of cores. The coarser the resolution, the larger the SYPD. Increasing spatial resolution requires a smaller time step strongly impacting the throughput at high resolutions.
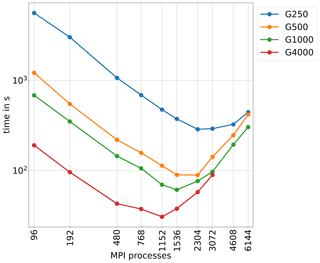
5.7 Scalability comparison for different resolutions
As our ability to assess the scalability of the code might be limited by the size of the problem we solve, we are conducting in this last part a comparison for simulations of Greenland in different resolutions. Figure 9 displays the total runtime for five different resolutions. The corresponding DOF per MPI process for the different modules is presented in Fig. 1, and an overview of the minimum and maximum number of DOF for each resolution is given in Table 1. There is a factor of about 34 between the maximum and the minimum DOF between G250 and G4000. The overall behaviour is similar for all resolutions: the code scales linearly until a threshold and execution time is rising from that minimum on. The minimum in execution time is reached at 2304 MPI processes for the high resolutions (G250 and G500). For lower resolution (and lower DOF), the minimum shifts towards lower number of MPI processes. For G4000, the minimum is reached at half of the number of MPI processes than for G250 and G500.
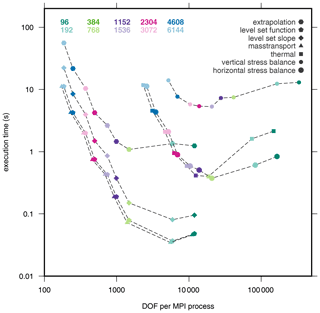
Figure 10Execution time for matrix assembly for various modules. Symbols are representing the modules, while the colour is denoting the number of MPI processes.
The performance analysis for the components of individual modules reveals that the major scaling issue is the assembly of the equation system matrix as shown in Figs. 4–7. Figure 10 displays the costs of matrix assembly in all modules vs. the DOF per MPI process. It reveals that the execution time for matrix assembly is reaching a plateau (vertical stress balance and extrapolation modules) or potentially approaching a plateau from a certain DOF per MPI process onwards. The minimum is similar for the 3-D cores at about 10 000 DOF per MPI process, whereas the minimum of 2-D modules is below that value. The range of costs for matrix assembly is varying for 2-D modules by a factor of 104–614, while it is for 3-D modules only a factor of 5–60 with the minimum of five being found for the vertical stress balance module. The matrix assembly costs for the two modules with nonlinear iterations (horizontal stress balance and thermal modules) scale for larger numbers of MPI processes very similarly to each other.
Matrix assembly consists almost entirely of MPI communication, and the cost of communication increases from a certain point on as the number of MPI processes grows. The allocation of memory and the computation of entries of the equation system, on the other hand, are both core-local computations and hence scale linearly with the number of cores. In particular, this part of the computation will scale further, because elements are distributed evenly on MPI processes, no matter how many or few elements are computed on each core. In all these modules, the runtime contribution of vector assembly is insignificant and the linear solver is either insignificant or scales well.
Our measurements reveal that the scalability is breaking down in all modules by poor performance of the matrix assembly. The tipping point mainly depends on the costs of the allocation of memory and the time for computing the element entries of an individual PDE, the amount of elements per MPI process and the data locality of the assembly, which impacts the amount of inter-core communication required for the assembly. So, for a fixed core count, increasing DOF increases performance but, with an increasing number of MPI processes, the communication overhead of the assembly starts dominating at some point. Similar behaviour was also found in other studies (e.g. Perlin et al., 2016). This is also clearly reflected in Fig. 11, which shows the increasing runtime of matrix assembly as the number of cores increases.
While not in the focus of the current study, we also noticed that the output routine does not scale well either. The main reason for this is an indexing scheme tailored towards post-processing in the MATLAB/Python user interface which does not exhibit good data locality and leads to a large number of MPI calls. Here, we suggest the more data-local indexing scheme already used in the creation of the equation system. The compatibility to the user interface could then be achieved in a reordering post-processing of the results, which can be done trivially in parallel by distributing different output vectors and different time steps among available cores.
The performance analysis of an ice sheet code needs to keep the challenging numerical underpinnings of the problem in mind: the code solves in a sequential fashion a number of different modules, each of which solves an equation system of a very different type and with a different number of DOF. Therefore, this type of code is inherently prone to the situation that a particular domain decomposition may be optimal for the module with the largest number of DOF and scale well with increasing core counts, while the performance of the module with a smaller number of DOF may not experience any improvement – or even worsen – with increasing core counts.
Also other components of ESMs are facing the issue that modules with fewer DOF are limiting scalability. For the finite volume sea ice–ocean model FESOM2(Finite-volumE Sea ice–Ocean Model, version 2.0), similar scalability issues were found for 2-D computations (Koldunov et al., 2019) such as the sea ice module and the linear solver. For FESOM2, the problem boils down to a large number of short but too frequent communications that were suggested to be addressed by widening the halo layer.
Our analysis reveals that the migration of lateral margins is becoming costly with increasing number of cores. This module includes the extrapolation of some solution fields performed via solving a diffusion equation over the ice-free regions constrained by the values calculated in the ice-covered region. This approach generates the smallest stiffness matrices in the overall sequence because ISSM treats Dirichlet boundary conditions with a lifting method so that only the unconstrained degrees of freedom are included in the stiffness matrix. Since all vertices located on ice are constrained, the unconstrained degrees of freedom are only those that correspond to the vertices that are outside of ice, and one ends up with a very small number of DOF per MPI process. One approach to address this problem would be to use an alternative approach for treating Dirichlet boundary conditions such as including entries for all nodes in the stiffness matrix, setting rows of constrained nodes to 0 except along the diagonal and changing the right-hand side to the value of the constraint.
In addition, wherever a low number of DOF per MPI process is limiting scalability with increasing core counts, the number of DOF could be increased by switching to P2 (quadratic) elements. In this context, one must find a reasonable balance between increasing the size of the problem for the sake of making the node computation more expensive while keeping communication constant, and increasing total computational costs disproportionally with respect to the additional knowledge gain. At this point, it should also be mentioned that the bedrock topography is only insufficiently known, and resolutions finer than 150 m are to date limited by the lack of input data for such simulations.
In order to increase the throughput, new modelling strategies are worth investigating. The nonlinear iterations are contributing to the overall costs of a time step significantly. Depending on the particular application, the number of nonlinear iterations may be reduced. Thus far, nothing is known about the effect of such a reduction, and care must be taken not to miss abrupt changes in the system. A simulation study comparing the resulting evolution of the temperature field with and without iterative update of the basal constraints can assess this effect. It is here also worth considering employing error indicators to steer the number of nonlinear iterations. Similar to error indicators used for adaptive mesh refinement (dos Santos et al., 2019), physics-based approaches may be particularly attractive.
Future simulation strategies may comprise more on-the-fly analyses than is currently standard in ice sheet codes. So far, only few scalars are computed, while an in-depth analysis is conducted in the post-processing. Some analyses may be conducted on the level of processors, while others need to be run globally. In particular, sensitivity studies for tuning model parameters would benefit from such an on-the-fly analysis with simulations producing unrealistic results quickly terminated.
From the perspective of ice sheet codes running coupled in ESMs, we recommend to consider higher resolutions even if long timescales are anticipated, as this leads to better scaling than coarse resolution. If the anticipated SYPDs cannot be met, the ice sheet code is to be run at its peak performance rather than the maximum number of cores available. To this end, investigations of optimal sharing of resources between codes of ESMs should be conducted. Similar to ESMs (Bauer et al., 2021), ISSM still falls short in reasonable SYPD for the tasks ahead. Taking the ocean model FESOM2 as the target – this is the most suitable candidate for coupling to ISSM due to its unstructured meshes and excellent parallel scalability – our results in Fig. 8 for the highest resolution mesh indicate that we would need about a factor 20 improvement in model throughput for the future versions of ISSM in order to match approximately 10–15 SYPDs demonstrated by FESOM2 in an operational configuration on a high-resolution mesh (Koldunov et al., 2019).
By means of the performance analysis we also identified some avenues for future improvement of the code. The reuse of the equation system matrix is also applicable to the multiple executions of the extrapolation step, and a change of indexing in the requested outputs module can be used to improve the memory locality. Furthermore, our instrumentation is suitable for efficient tracing and load imbalance detection. The major load imbalances occur in the computation of matrix entries and lead to load-imbalanced matrix assembly. The matrix assembly is clearly a key computation that warrants further investigation. We also want to emphasize here, that we investigated the performance of an HO application only and that other issues may arise for other momentum balance choices.
Although our performance instrumentation leads to a very modest overhead, this can be further diminished. About 99 % of the MPI calls belong to three functions, MPI_Iprobe, MPI_Test and MPI_Testall, and about 90 % of the PETSc calls recorded by Score-P refer to setvalue() routines used in filling buffers for matrix assembly. If the MPI calls are not of interest, they can be disabled in groups via the Score-P interface, or individual functions can be excluded by implementing and preloading a functionless PMPI interface. Currently, the library wrapping interface of Score-P does not allow for the easy exclusion of certain functions in a library (i.e. a whitelist/blacklist functionality for library functions). However, the overhead of our instrumentation would clearly be reduced further if instrumentation of these low-level PETSc calls could be avoided.
To analyse the practical throughput of a typical application of ISSM, we conducted transient HO simulations for the Greenland Ice Sheet in five different horizontal resolutions. We present runtime measurements for individual code modules based on an instrumentation of the ice sheet code with Score-P. We conclude that ISSM scales up to 3072 MPI processes in the highest resolution that we tested (G250). While it was expected that the stress balance module would dominate the runtime, we found that simulating the motion of the lateral margins becomes the main cost factor from 4608 MPI processes on. We find major scaling challenges in HO due to the assembly of the system matrix, in particular, when the number of DOF per MPI process is falling below 10 000. The maximum throughput for all horizontal resolutions in HO was reached at 1152–2304 MPI processes and is particularly small for the highest resolution due to severe time step restrictions.
This study also showed that meaningful in-depth performance analysis of ISSM can be performed at little cost and with minimal code changes, which could be eliminated completely in the future by a very limited refactoring of the code. An instrumented, user-oriented, low-overhead profiling version of ISSM can then be built from the unmodified main source of ISSM. Thus, scientists using ISSM can monitor performance of their code as their computational environment evolves without having to worry about carrying instrumentation code into their new code branch. Future advances in instrumentation with respect to the filtering of library routines could further decrease instrumentation overhead to the level where it is negligible, thereby allowing continuous performance monitoring, which would provide valuable information for the creation of execution models of ISSM and its modules.
A1 Mathematical model
Let Ωi(t)⊆ℝ3 be a three-dimensional domain with . All equations are given in Cartesian coordinates, of which x and y are in the horizontal plane and z is parallel to the direction of gravity and positive upwards. Let the following function be given:
with being the velocity for the time . We assume the ice to have constant density and hence being incompressible. Let the viscosity being given as , with for . The pressure is given as , with for . The temperature is given as , with for , similarly the enthalpy is , with for . Let the ice thickness being given as , with for . The normal vector be the normal vector field on pointing out of the ice body by convention. The boundary at the ice–atmosphere transition is denoted by Γs, the ice–bed interface Γb and the calving front as Γcf.
A1.1 Momentum balance
The momentum balance used in this study is the Blatter–Pattyn higher-order approximation (Blatter, 1995; Pattyn, 2003). This approximation is reducing the Stokes equation to two PDEs for the horizontal velocities vx,vy by neglecting the bridging stresses and assuming the vertical component of the momentum balance to be hydrostatic.
where hs is the surface topography of the ice sheet, ρi the ice density and g the gravitational acceleration. From the vertical component of the momentum balance, we find the pressure in HO to be
with the normal deviatoric stresses in x and y directions, respectively. They are evaluated from the constitutive relation with Dij the strain-rate tensor components.
The boundary condition of the momentum balance is at all boundaries a stress boundary condition but of a different kind. The ice surface Γs is treated as traction-free. At the ice base, Γb the kinematic boundary condition of the momentum balance is given as the no penetration condition with n reducing in HO to a normal vector in the z direction only. The stress boundary condition in tangential direction is given by the friction law that is implemented in terms of basal stress; thus, τb=f(vb) as
with the tangential vectors t1,t2 and the basal drag . The basal velocity is then determined by a friction law. Basal drag and velocity are two-dimensional vectors acting in the basal tangential plane. We use a Weertman-type friction law with submelt sliding:
reformulated as a Neumann boundary condition (Rückamp et al., 2019) with Cb the drag coefficient, the basal temperature relative to pressure melting point, and γ, , parameters given in Table A1.
Finally, at the (vertical) calving front Γcf, the boundary condition is
with zsl the elevation of the sea level.
A1.2 Rheology
The viscous rheology of ice is treated with a regularized Glen flow law (Eq. A8), a temperature-dependent rate factor for cold ice and a water-content-dependent rate factor for temperate ice.
with the creep exponent n=3, the flow rate factor A depending on temperature and water content W, the enhancement factor Ei, and de the second invariant of the strain-rate tensor Dij.
A1.3 Mass balance
The ice is treated as an incompressible material and hence the mass balance reduces to div v=0, which is used in HO to derive the vertical velocity:
with the vertical velocity at the ice base hb(x,y). This quantity is given by the kinematic boundary condition at the ice base that is assumed to be quasi-static:
with BMB the basal melt rate.
A1.4 Enthalpy balance
We solve the enthalpy balance equation to resolve cold-, temperate- or polythermal-ice states (Eq. A11, Aschwanden et al., 2013; Kleiner et al., 2015). The evolution equation for enthalpy E reads as
with q the heat flux and Ψ the source term. The advection dominated problem is stabilized with the anisotropic streamline upwind Petrov–Galerkin (ASUPG) method (Rückamp et al., 2020b). The heat flux is given by
with , ki the thermal conductivity and ci the specific heat capacity of ice. The discontinuous conductivity, Keff, is treated with a geometric mean (Rückamp et al., 2020b). The source term reads
with representing strain heating and (⋅)pmp denoting quantities at the pressure melting point. For solid ice, Epmp is defined as
where is the pressure melting point temperature, β is the Clausius–Clapeyron constant, and T0 is the melting point at standard pressure.
The temperature field is then diagnostically computed from the enthalpy transfer rules:
with Tref a reference temperature and L the latent heat of fusion.
At the ice surface Γs, the boundary condition is given by the surface skin temperature with zero water content. Four different cases need to be considered for the boundary condition at the ice base Γb:
Cold base (dry). If the glacier is cold at the base and without a basal water layer (i.e. E<Epmp and Hw=0), then
Temperate base. If the glacier is temperate at the base without an overlying temperate ice layer with melting conditions at the base (i.e. E≥Epmp, Hw>0 and ), then
Temperate ice at base. If the glacier is temperate at the base with an overlying temperate ice layer (i.e. E≥Epmp, Hw>0 and ), we let
Cold base (wet). If the glacier is cold but has a liquid water layer at the base which is refreezing (i.e. E<Epmp and Hw>0), then
Here is the temperature relative to the melting point, Hw is the basal water layer thickness. In addition to the temperate base condition, E≥Epmp, it is necessary to check if there is a temperate layer of ice above, . The type of basal boundary condition – Neumann or Dirichlet – is therefore time dependent and therefore also requires a nonlinear iteration.
The jump condition on Γb gives the basal mass balance BMB
with the frictional heating Fb due to basal sliding, the upward heat flux in the ice qi, and the heat flux qgeo entering the ice at the base.
A1.5 Mass transport
Ice thickness evolution equation reads as
with H the ice thickness, SMB the surface accumulation rate (surface mass balance). For grounded ice, the surface topography is computed from . For floating ice, and with ρsw being the seawater density.
A1.6 Grounding line evolution
For HO the grounding line position is obtained from hydrostatic equilibrium: let the thickness of flotation be given by Hf, then
with ρoc the density of the ocean and grounded and floating parts are defined as
A1.7 Evolution of the horizontal margins
The terminus evolution (for both, marine terminating glaciers, as well as ice shelves) is given by the kinematic calving front condition using a level-set method. The level-set function, φ, is defined as
where Ωc is the subdomain where there is no ice. The level set therefore defines implicitly the terminus where . The level set is updated at each time step using the level-set equation:
where vf is the ice-front speed, taken as , where c is the calving rate, and .
For filling the required physical variables at elements that are activated due to expansion of the ice sheet area, an extrapolation is required. This is done by solving a 2-D diffusion equation for each variable (⋅):
and assuming a diffusion coefficient of 1. Equation (A24) is solved for 3-D fields individually for each vertical layer () and for H.
A1.8 Surface mass balance
While in general the derivation of SMB may require an energy balance model to compute, from precipitation, air temperature and radiation, the surface skin temperature and SMB, we restrict use in this study a simple approach and compute surface melting is parameterized by a positive degree day (PDD) method (Reeh, 1991; Calov and Greve, 2005).
A1.9 Convergence criteria
ISSM employs three different convergence criteria (Larour et al., 2012). A residual convergence criterion ϵres<ϵ1 is based on an Euclidean norm between the current and the previous iteration steps ensures the convergence of the linear system. The relative norm ϵrel<ϵ2 uses the infinity norm to ensure convergence in relative terms. In addition, an absolute norm ϵabs<ϵ3 controls the convergence in absolute terms.
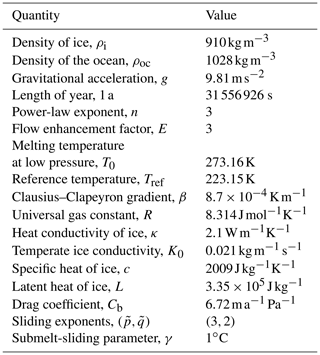
A1.10 Parameters
A2 Mesh and horizontal velocity field
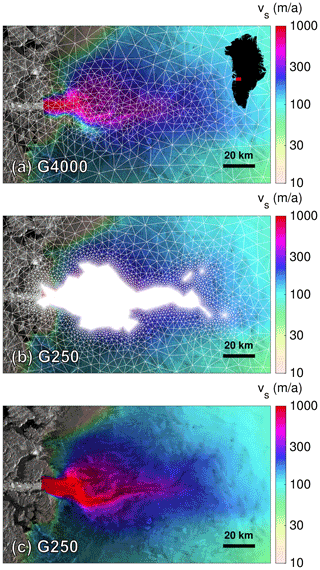
Figure A1Horizontal mesh and simulated surface velocities, vs, of the Jakobshavn Isbræ: (a) G4000, (b) G250 and (c) the same as panel (b) but without mesh. The location is shown by the red inset in panel (a). The background image is a RADARSAT mosaic (Joughin, 2015; Joughin et al., 2016).
ISSM version 4.18 (Larour et al., 2012) is open source and freely available at https://issm.jpl.nasa.gov/ (last access: 23 March 2022). A copy of the source code including minor changes and scripts to build ISSM on the HHLR is available on https://doi.org/10.48328/tudatalib-613 (Fischler, 2021a). The Greenland setup is available on https://doi.org/10.48328/tudatalib-614 (Fischler and Rückamp, 2021) and the generated profiles are stored at https://doi.org/10.48328/tudatalib-612 (Fischler, 2021b).
CB, YF, MR, AH and VA designed the study. YF conducted the performance measurements and instrumented the code. MR contributed the ISSM Greenland setup. All authors discussed the results and text. YF and CB wrote Sects. 3 and 4. AH and YF wrote Sects. 5 and 6. AH wrote major parts of Sect. 1 and the Appendix. MM contributed ISSM design philosophy and insights into implementations. VA contributed the comparison to other ESM codes and strategies in terms of numerics.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Simulations for this study were conducted on the Lichtenberg high-performance computer of Technical University of Darmstadt. The authors would like to thank the Hessian Competence Center for High Performance Computing – funded by the Hessian State Ministry of Higher Education, Research and the Arts – for helpful advice. Angelika Humbert thanks Simone Bnà for discussions. Angelika Humbert and Martin Rückamp acknowledge support from the German Federal Ministry for Education and Research (BMBF) within the GROCE-2 project (grant no. 03F0855A), to which this work contributed optimal HPC setting options for coupled ice–ocean simulations. We thank Thomas Zwinger and the anonymous reviewer for very useful comments on the manuscript.
The work of Christian Bischof was partially funded by the German Science Foundation (DFG) (project no. 265191195) within SFB 1194. The work of Yannic Fischler was partially funded by the Hessian LOEWE initiative within the Software-Factory 4.0 project.
This paper was edited by Steven Phipps and reviewed by Thomas Zwinger and one anonymous referee.
Arzt, P., Fischler, Y., Lehr, J.-P., and Bischof, C.: Automatic Low-Overhead Load-Imbalance Detection in MPI Applications, in: EuroPar 2021, Springer International Publishing, Cham, 19–34, ISBN 978-3-030-85665-6, 2021. a
Aschwanden, A., Aðalgeirsdóttir, G., and Khroulev, C.: Hindcasting to measure ice sheet model sensitivity to initial states, The Cryosphere, 7, 1083–1093, https://doi.org/10.5194/tc-7-1083-2013, 2013. a
Balay, S., Abhyankar, S., Adams, M. F., Brown, J., Brune, P., Buschelman, K., Dalcin, L., Dener, A., Eijkhout, V., Gropp, W. D., Karpeyev, D., Kaushik, D., Knepley, M. G., May, D. A., McInnes, L. C., Mills, R. T., Munson, T., Rupp, K., Sanan, P., Smith, B. F., Zampini, S., Zhang, H., and Zhang, H.: PETSc Users Manual, Tech. Rep. ANL-95/11 - Revision 3.15, Argonne National Laboratory, https://www.mcs.anl.gov/petsc (last access: 8 April 2022), 2021a. a
Balay, S., Abhyankar, S., Adams, M. F., Brown, J., Brune, P., Buschelman, K., Dalcin, L., Dener, A., Eijkhout, V., Gropp, W. D., Karpeyev, D., Kaushik, D., Knepley, M. G., May, D. A., McInnes, L. C., Mills, R. T., Munson, T., Rupp, K., Sanan, P., Smith, B. F., Zampini, S., Zhang, H., and Zhang, H.: PETSc Web page, https://www.mcs.anl.gov/petsc (last access: 8 April 2022), 2021b. a
Bauer, P., Düben, P. D., Hoefler, T., Quintino, T., Schulthess, T. C., and Wedi, N. P.: The digital revolution of Earth-system science, Nature Computat. Sci., 1, 104–113, 2021. a
Berends, C. J., Goelzer, H., and van de Wal, R. S. W.: The Utrecht Finite Volume Ice-Sheet Model: UFEMISM (version 1.0), Geosci. Model Dev., 14, 2443–2470, https://doi.org/10.5194/gmd-14-2443-2021, 2021. a
Blatter, H.: Velocity and stress fields in grounded glaciers: a simple algorithm for including deviatoric stress gradients, J. Glaciol., 41, 333–344, https://doi.org/10.3189/S002214300001621X, 1995. a, b
Bnà, S., Spisso, I., Olesen, M., and Rossi, G.: PETSc4FOAM: A Library to plug-in PETSc into the OpenFOAM Framework, Tech. Rep. ANL-95/11 – Revision 3.15, PRACE, https://prace-ri.eu (last access: 8 April 2022), 2020. a
Bondzio, J. H., Seroussi, H., Morlighem, M., Kleiner, T., Rückamp, M., Humbert, A., and Larour, E. Y.: Modelling calving front dynamics using a level-set method: application to Jakobshavn Isbræ, West Greenland, The Cryosphere, 10, 497–510, https://doi.org/10.5194/tc-10-497-2016, 2016. a
Bondzio, J. H., Morlighem, M., Seroussi, H., Kleiner, T., Rückamp, M., Mouginot, J., Moon, T., Larour, E. Y., and Humbert, A.: The mechanisms behind Jakobshavn Isbræ's acceleration and mass loss: A 3-D thermomechanical model study, Geophys. Res. Lett., 44, 6252–6260, https://doi.org/10.1002/2017GL073309, 2017. a
Brædstrup, C. F., Damsgaard, A., and Egholm, D. L.: Ice-sheet modelling accelerated by graphics cards, Comput. Geosci., 72, 210–220, https://doi.org/10.1016/j.cageo.2014.07.019, 2014. a
Bueler, E. and Brown, J.: Shallow shelf approximation as a “sliding law” in a thermodynamically coupled ice sheet model, J. Geophys. Res., 114, https://doi.org/10.1029/2008JF001179, 2009. a
Calotoiu, A., Hoefler, T., Poke, M., and Wolf, F.: Using automated performance modeling to find scalability bugs in complex codes, Extra-P, https://doi.org/10.1145/2503210.2503277, 2013. a
Calov, R. and Greve, R.: A semi-analytical solution for the positive degree-day model with stochastic temperature variations, J. Glaciol., 51, 173–175, https://doi.org/10.3189/172756505781829601, 2005. a
Chang, J., Nakshatrala, K., Knepley, M., and Johnsson, L.: A performance spectrum for parallel computational frameworks that solve PDEs, Concurrency and Computation: Practice and Experience, 30, e4401, https://doi.org/10.1002/cpe.4401, 2018. a
Church, J., Clark, P., Cazenave, A., Gregory, J., Jevrejeva, S., Levermann, A., Merrifield, M., Milne, G., Nerem, R., Nunn, P., Payne, A., Pfeffer, W., Stammer, D., and Alakkat, U.: Sea level change, in: Climate Change 2013: The Physical Science Basis. Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., et al., Cambridge University Press, Cambridge, 1137–1216, https://doi.org/10.1017/CBO9781107415324.026, 2013. a
Cornford, S. L., Seroussi, H., Asay-Davis, X. S., Gudmundsson, G. H., Arthern, R., Borstad, C., Christmann, J., Dias dos Santos, T., Feldmann, J., Goldberg, D., Hoffman, M. J., Humbert, A., Kleiner, T., Leguy, G., Lipscomb, W. H., Merino, N., Durand, G., Morlighem, M., Pollard, D., Rückamp, M., Williams, C. R., and Yu, H.: Results of the third Marine Ice Sheet Model Intercomparison Project (MISMIP+), The Cryosphere, 14, 2283–2301, https://doi.org/10.5194/tc-14-2283-2020, 2020. a
Crawford, A., Benn, D., Todd, J., Astrom, J., Bassis, J., and Zwinger, T.: Marine ice-cliff instability modeling shows mixed-mode ice-cliff failure and yields calving rate parameterization, Nat. Commun., 12, 2701, https://doi.org/10.1038/s41467-021-23070-7, 2021. a
Dickens, P.: A Performance and Scalability Analysis of the MPI Based Tools Utilized in a Large Ice Sheet Model Executing in a Multicore Environment, in: Algorithms and Architectures for Parallel Processing, edited by: Wang, G., Zomaya, A., Martinez, G., and Li, K., Springer International Publishing, Cham, 131–147, https://doi.org/10.1007/978-3-319-27140-8_10, 2015. a
dos Santos, T. D., Morlighem, M., Seroussi, H., Devloo, P. R. B., and Simões, J. C.: Implementation and performance of adaptive mesh refinement in the Ice Sheet System Model (ISSM v4.14), Geosci. Model Dev., 12, 215–232, https://doi.org/10.5194/gmd-12-215-2019, 2019. a
Edwards, T. L., Nowicki, S. M., Marzeion, B., Hock, R., Goelzer, H., Seroussi, H., Jourdain, N., Slater, D. A., Turner, F. E., Smith, C. J., McKenna, C. M., Simon, E. G., Abe-Ouchi, A., Gregory, J. M., Larour, E. Y., Lipscomb, W. H., Payne, A. J., Shepherd, A. P., Agosta, C., Alexander, P. M., Albrecht, T., Anderson, B. M., Asay-Davis, X. S., Aschwanden, A., Barthel, A. M., Bliss, A. K., Calov, R., Chambers, C., Champollion, N., Choi, Y., Cullather, R. I., Cuzzone, J. K., Dumas, C., Felikson, D., Fettweis, X., Fujita, K., Galton-Fenzi, B. K., Gladstone, R. M., Golledge, N. R., Greve, R., Hattermann, T., Hoffman, M. J., Humbert, A., Huss, M., Huybrechts, P., Immerzeel, W. W. W., Kleiner, T., Kraaijenbrink, P. D., Le clec'h, S., Lee, V., Leguy, G. R., Little, C. M., Lowry, D. P., Malles, J. H., Martin, D. F., Maussion, F., Morlighem, M., O'Neill, J. F., Nias, I. J., Pattyn, F., Pelle, T., Price, S. F., Quiquet, A., Radić, V., Reese, R., Rounce, D. R., Rückamp, M., Sakai, A., Shafer, C., Schlegel, N. J., Shannon, S. R., Smith, R. S., Straneo, F., Sun, S., Tarasov, L., Trusel, L. D., Van Breedam, J., Van De Wal, R. S., Van Den Broeke, M. R., Winkelmann, R., Zekollari, H., Zhao, C., Zhang, T., and Zwinger, T.: Projected land ice contributions to twenty-first-century sea level rise, Nature, 593, 74–82, https://doi.org/10.1038/s41586-021-03302-y, 2021. a
Fischler, Y.: GMD 2021 ISSM v4.18 Source Code and Build Scripts, TU data lib [code], https://doi.org/10.48328/tudatalib-613, 2021a. a
Fischler, Y.: GMD 2021 ISSM on HHLR Scaling Profiles, TU data lib [data set], https://doi.org/10.48328/tudatalib-612, 2021b. a
Fischler, Y. and Rückamp, M.: GMD 2021 ISSM Greenland Setup, TU data lib [data set], https://doi.org/10.48328/tudatalib-614, 2021. a
Gagliardini, O., Zwinger, T., Gillet-Chaulet, F., Durand, G., Favier, L., de Fleurian, B., Greve, R., Malinen, M., Martín, C., Råback, P., Ruokolainen, J., Sacchettini, M., Schäfer, M., Seddik, H., and Thies, J.: Capabilities and performance of Elmer/Ice, a new-generation ice sheet model, Geosci. Model Dev., 6, 1299–1318, https://doi.org/10.5194/gmd-6-1299-2013, 2013. a, b
Geimer, M., Kuhlmann, B., Pulatova, F., Wolf, F., and Wylie, B.: Scalable Collation and Presentation of Call-Path Profile Data with CUBE, 645–652, 2007. a, b
Geimer, M., Wolf, F., Wylie, B., Ábrahám, E., Becker, D., and Mohr, B.: The SCALASCA performance toolset architecture, Concurr. Comp. Pract. E., 22, 702–719, https://doi.org/10.1002/cpe.1556, 2010. a
Goelzer, H., Nowicki, S., Payne, A., Larour, E., Seroussi, H., Lipscomb, W. H., Gregory, J., Abe-Ouchi, A., Shepherd, A., Simon, E., Agosta, C., Alexander, P., Aschwanden, A., Barthel, A., Calov, R., Chambers, C., Choi, Y., Cuzzone, J., Dumas, C., Edwards, T., Felikson, D., Fettweis, X., Golledge, N. R., Greve, R., Humbert, A., Huybrechts, P., Le clec'h, S., Lee, V., Leguy, G., Little, C., Lowry, D. P., Morlighem, M., Nias, I., Quiquet, A., Rückamp, M., Schlegel, N.-J., Slater, D. A., Smith, R. S., Straneo, F., Tarasov, L., van de Wal, R., and van den Broeke, M.: The future sea-level contribution of the Greenland ice sheet: a multi-model ensemble study of ISMIP6, The Cryosphere, 14, 3071–3096, https://doi.org/10.5194/tc-14-3071-2020, 2020. a, b, c
Golaz, J.-C., Caldwell, P. M., Van Roekel, L. P., Petersen, M. R., Tang, Q., Wolfe, J. D., Abeshu, G., Anantharaj, V., Asay-Davis, X. S., Bader, D. C., Baldwin, S. A., Bisht, G., Bogenschutz, P. A., Branstetter, M., Brunke, M. A., Brus, S. R., Burrows, S. M., Cameron-Smith, P. J., Donahue, A. S., Deakin, M., Easter, R. C., Evans, K. J., Feng, Y., Flanner, M., Foucar, J. G., Fyke, J. G., Griffin, B. M., Hannay, C., Harrop, B. E., Hoffman, M. J., Hunke, E. C., Jacob, R. L., Jacobsen, D. W., Jeffery, N., Jones, P. W., Keen, N. D., Klein, S. A., Larson, V. E., Leung, L. R., Li, H.-Y., Lin, W., Lipscomb, W. H., Ma, P.-L., Mahajan, S., Maltrud, M. E., Mametjanov, A., McClean, J. L., McCoy, R. B., Neale, R. B., Price, S. F., Qian, Y., Rasch, P. J., Reeves Eyre, J. E. J., Riley, W. J., Ringler, T. D., Roberts, A. F., Roesler, E. L., Salinger, A. G., Shaheen, Z., Shi, X., Singh, B., Tang, J., Taylor, M. A., Thornton, P. E., Turner, A. K., Veneziani, M., Wan, H., Wang, H., Wang, S., Williams, D. N., Wolfram, P. J., Worley, P. H., Xie, S., Yang, Y., Yoon, J.-H., Zelinka, M. D., Zender, C. S., Zeng, X., Zhang, C., Zhang, K., Zhang, Y., Zheng, X., Zhou, T., and Zhu, Q.: The DOE E3SM Coupled Model Version 1: Overview and Evaluation at Standard Resolution, J. Adv. Model. Earth Sy., 11, 2089–2129, https://doi.org/10.1029/2018MS001603, 2019. a
Graham, R. L., Woodall, T. S., and Squyres, J. M.: Open MPI: A Flexible High Performance MPI, in: Parallel Processing and Applied Mathematics, edited by: Wyrzykowski, R., Dongarra, J., Meyer, N., and Waśniewski, J., Springer Berlin Heidelberg, Berlin, Heidelberg, 228–239, https://doi.org/10.1007/11752578_29, 2006. a
Habbal, F., Larour, E., Morlighem, M., Seroussi, H., Borstad, C. P., and Rignot, E.: Optimal numerical solvers for transient simulations of ice flow using the Ice Sheet System Model (ISSM versions 4.2.5 and 4.11), Geosci. Model Dev., 10, 155–168, https://doi.org/10.5194/gmd-10-155-2017, 2017. a
Hoffman, M. J., Perego, M., Price, S. F., Lipscomb, W. H., Zhang, T., Jacobsen, D., Tezaur, I., Salinger, A. G., Tuminaro, R., and Bertagna, L.: MPAS-Albany Land Ice (MALI): a variable-resolution ice sheet model for Earth system modeling using Voronoi grids, Geosci. Model Dev., 11, 3747–3780, https://doi.org/10.5194/gmd-11-3747-2018, 2018. a, b
Huang, X., Tang, Q., Tseng, Y., Hu, Y., Baker, A. H., Bryan, F. O., Dennis, J., Fu, H., and Yang, G.: P-CSI v1.0, an accelerated barotropic solver for the high-resolution ocean model component in the Community Earth System Model v2.0, Geosci. Model Dev., 9, 4209–4225, https://doi.org/10.5194/gmd-9-4209-2016, 2016. a
Isaac, T., Stadler, G., and Ghattas, O.: Solution of Nonlinear Stokes Equations Discretized By High-Order Finite Elements on Nonconforming and Anisotropic Meshes, with Application to Ice Sheet Dynamics, SIAM J. Sci. Comput., 37, B804–B833, https://doi.org/10.1137/140974407, 2015. a
Joughin, I.: MEaSUREs Greenland Ice Sheet Mosaics from SAR Data, Version 1. Boulder, Colorado USA, NASA National Snow and Ice Data Center Distributed Active Archive Center, https://doi.org/10.5067/6187DQUL3FR5, 2015. a
Joughin, I., Smith, B. E., Howat, I. M., Moon, T., and Scambos, T. A.: A SAR record of early 21st century change in Greenland, J. Glaciol., 62, 62–71, https://doi.org/10.1017/jog.2016.10, 2016. a
Kleiner, T., Rückamp, M., Bondzio, J. H., and Humbert, A.: Enthalpy benchmark experiments for numerical ice sheet models, The Cryosphere, 9, 217–228, https://doi.org/10.5194/tc-9-217-2015, 2015. a
Knüpfer, A., Rössel, C., Mey, D. a., Biersdorff, S., Diethelm, K., Eschweiler, D., Geimer, M., Gerndt, M., Lorenz, D., Malony, A., Nagel, W. E., Oleynik, Y., Philippen, P., Saviankou, P., Schmidl, D., Shende, S., Tschüter, R., Wagner, M., Wesarg, B., and Wolf, F.: Score-P: A Joint Performance Measurement Run-Time Infrastructure for Periscope,Scalasca, TAU, and Vampir, in: Tools for High Performance Computing 2011, edited by: Brunst, H., Müller, M. S., Nagel, W. E., and Resch, M. M., Springer Berlin Heidelberg, Berlin, Heidelberg, 79–91, https://doi.org/10.1007/978-3-642-31476-6_7, 2012. a, b
Koldunov, N. V., Aizinger, V., Rakowsky, N., Scholz, P., Sidorenko, D., Danilov, S., and Jung, T.: Scalability and some optimization of the Finite-volumE Sea ice–Ocean Model, Version 2.0 (FESOM2), Geosci. Model Dev., 12, 3991–4012, https://doi.org/10.5194/gmd-12-3991-2019, 2019. a, b, c
Larour, E., Seroussi, H., Morlighem, M., and Rignot, E.: Continental scale, high order, high spatial resolution, ice sheet modeling using the Ice Sheet System Model (ISSM), J. Geophys. Res.-Earth Surf., 117, F01022, https://doi.org/10.1029/2011JF002140, 2012. a, b, c, d, e
Morlighem, M., Williams, C. N., Rignot, E., An, L., Arndt, J. E., Bamber, J. L., Catania, G., Chauché, N., Dowdeswell, J. A., Dorschel, B., Fenty, I., Hogan, K., Howat, I., Hubbard, A., Jakobsson, M., Jordan, T. M., Kjeldsen, K. K., Millan, R., Mayer, L., Mouginot, J., Noël, B. P. Y., O'Cofaigh, C., Palmer, S., Rysgaard, S., Seroussi, H., Siegert, M. J., Slabon, P., Straneo, F., van den Broeke, M. R., Weinrebe, W., Wood, M., and Zinglersen, K. B.: BedMachine v3: Complete bed topography and ocean bathymetry mapping of Greenland from multibeam echo sounding combined with mass conservation, Geophys. Res. Lett., 44, 11051–11061, https://doi.org/10.1002/2017GL074954, 2017. a
Nagel, W., Arnold, A., Weber, M., Hoppe, H.-C., and Solchenbach, K.: VAMPIR: Visualization and analysis of mpi resources, Supercomputer, 12, 69–80, 1996. a, b
Neumann, P., Düben, P., Adamidis, P., Bauer, P., Brück, M., Kornblueh, L., Klocke, D., Stevens, B., Wedi, N., and Biercamp, J.: Assessing the scales in numerical weather and climate predictions: Will exascale be the rescue?, Philos. T. Roy. Soc. A, 377, 2142, https://doi.org/10.1098/rsta.2018.0148, 2019. a
Pattyn, F.: A new three-dimensional higher-order thermomechanical ice-sheet model: basic sensitivity, ice-stream development and ice flow across subglacial lakes, J. Geophys. Res., 108, 2382, https://doi.org/10.1029/2002JB002329, 2003. a, b
Perlin, N., Zysman, J. P., and Kirtman, B. P.: Practical scalability assessment for parallel scientific numerical applications, CoRR, abs/1611.01598, https://doi.org/10.48550/arXiv.1611.01598, 2016. a, b
Plach, A., Nisancioglu, K. H., Langebroek, P. M., Born, A., and Le clec'h, S.: Eemian Greenland ice sheet simulated with a higher-order model shows strong sensitivity to surface mass balance forcing, The Cryosphere, 13, 2133–2148, https://doi.org/10.5194/tc-13-2133-2019, 2019. a
Prims, O. T., Castrillo, M., Acosta, M. C., Mula-Valls, O., Lorente, A. S., Serradell, K., Cortés, A., and Doblas-Reyes, F. J.: Finding, analysing and solving MPI communication bottlenecks in Earth System models, J. Comput. Sci., 36, 100864, https://doi.org/10.1016/j.jocs.2018.04.015, 2018. a
Reeh, N.: Parameterization of melt rate and surface temperature on the Greenland ice sheet, Polarforschung, 59, 113–28, 1991. a
Reuter, B., Aizinger, V., and Köstler, H.: A multi-platform scaling study for an OpenMP parallelization of a discontinuous Galerkin ocean model, Comput. Fluids, 117, 325–335, 2015. a
Rückamp, M., Greve, R., and Humbert, A.: Comparative simulations of the evolution of the Greenland ice sheet under simplified Paris Agreement scenarios with the models SICOPOLIS and ISSM, Polar Sci., 21, 14–25, https://doi.org/10.1016/j.polar.2018.12.003, 2019. a, b, c, d, e
Rückamp, M., Goelzer, H., and Humbert, A.: Sensitivity of Greenland ice sheet projections to spatial resolution in higher-order simulations: the Alfred Wegener Institute (AWI) contribution to ISMIP6 Greenland using the Ice-sheet and Sea-level System Model (ISSM), The Cryosphere, 14, 3309–3327, https://doi.org/10.5194/tc-14-3309-2020, 2020a. a, b
Rückamp, M., Humbert, A., Kleiner, T., Morlighem, M., and Seroussi, H.: Extended enthalpy formulations in the Ice-sheet and Sea-level System Model (ISSM) version 4.17: discontinuous conductivity and anisotropic streamline upwind Petrov–Galerkin (SUPG) method, Geosci. Model Dev., 13, 4491–4501, https://doi.org/10.5194/gmd-13-4491-2020, 2020b. a, b, c
Seroussi, H., Morlighem, M., Larour, E., Rignot, E., and Khazendar, A.: Hydrostatic grounding line parameterization in ice sheet models, The Cryosphere, 8, 2075–2087, https://doi.org/10.5194/tc-8-2075-2014, 2014. a
Tallent, N. R., Mellor-Crummey, J. M., and Fagan, M. W.: Binary Analysis for Measurement and Attribution of Program Performance, SIGPLAN Not., 44, 441–452, https://doi.org/10.1145/1543135.1542526, 2009. a
Tezaur, I. K., Perego, M., Salinger, A. G., Tuminaro, R. S., and Price, S. F.: Albany/FELIX: a parallel, scalable and robust, finite element, first-order Stokes approximation ice sheet solver built for advanced analysis, Geosci. Model Dev., 8, 1197–1220, https://doi.org/10.5194/gmd-8-1197-2015, 2015a. a
Tezaur, I. K., Tuminaro, R. S., Perego, M., Salinger, A. G., and Price, S. F.: On the Scalability of the Albany/FELIX first-order Stokes Approximation ice Sheet Solver for Large-Scale Simulations of the Greenland and Antarctic ice Sheets, Procedia Comp. Sci., 51, 2026–2035, https://doi.org/10.1016/j.procs.2015.05.467, 2015b. a
Wriggers, P.: Nonlinear Finite Element Methods, Springer, Berlin, Heidelberg, 4, https://doi.org/10.1007/978-3-642-56865-7, 2008. a
formerly Albany/FELIX
- Abstract
- Introduction
- Description of the model and the experiment environment
- Software design of ISSM
- Sustainable performance measurement
- Scalability of ISSM
- Discussion
- Conclusions
- Appendix A
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Description of the model and the experiment environment
- Software design of ISSM
- Sustainable performance measurement
- Scalability of ISSM
- Discussion
- Conclusions
- Appendix A
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References