Variability and extremes: statistical validation of the Alfred Wegener Institute Earth System Model (AWI-ESM)

Coupled general circulation models are of paramount importance to quantitatively assessing the magnitude of future climate change. Usual methods for validating climate models include the evaluation of mean values and covariances, but less attention is directed to the evaluation of extremal behaviour. This is a problem because many severe consequences of climate change are due to climate extremes. We present a method for model validation in terms of extreme values based on classical extreme value theory. We further discuss a clustering algorithm to detect spatial dependencies and tendencies for concurrent extremes. To illustrate these methods, we analyse precipitation extremes of the Alfred Wegener Institute Earth System Model (AWI-ESM) global climate model and from other models that take part in the Coupled Model Intercomparison Project CMIP6 and compare them to the reanalysis data set CRU TS4.04. The clustering algorithm presented here can be used to determine regions of the climate system that are then subjected to a further in-depth analysis, and there may also be applications in palaeoclimatology.

1 Introduction

Coupled general circulation models are frequently utilised to quantitatively assess the magnitude of future climate change. Validating these models by simulating different climate states is essential for understanding the sensitivity of the climate system to both natural and anthropogenic forcing. Usual methods for validating climate models include the evaluation of mean values and covariances and the comparison of empirical cumulative distribution functions. These analyses can also be conducted over seasonal and annual averages (climatologies) or along latitudinal and longitudinal transects (Tapiador et al., 2012). The comparison of climate indices is also common in model validation (Sillmann et al., 2013; Zhang et al., 2011). While climate models are able to reproduce many climate phenomena across the globe, their reliability regarding extremes requires additional evaluation. Changes in the intensity and frequency of extremes have drawn much attention during recent decades (IPCC, 2012; Rahmstorf and Coumou, 2011; Horton et al., 2016), mainly due to their large impacts on the natural environment, economy and human health (Ciais et al., 2005; Kovats and Kristie, 2006). For instance, the summer heatwave over Central Europe in 2003 resulted in extensive forest fires, crop yield reductions and fatalities (de Bono et al., 2004; Vandentorren et al., 2004). During the 20th and early 21st century, the frequency of high-temperature extremes increased in Europe (Dong et al., 2017), even after the apparent levelling off of global mean temperatures after 2000 (Trenberth and Fasullo, 2013), and a similar development has been observed for precipitation extremes (Fischer and Knutti, 2016). Due to the inherent nature of extreme events, their evolution differs from that of the mean and the variance (Schär et al., 2004; IPCC, 2012) and also depends on the strength of the events themselves (Myhre et al., 2019).

In particular, the concurrent occurrence of climate extremes at different locations may have especially large impacts on agriculture (Toreti et al., 2019), human societies and economies (Jongman et al., 2014), and the climate system itself (Zscheischler et al., 2014). Large-scale climate extremes can furthermore cause serious problems for insurance and reinsurance companies (Mills, 2005). For these reasons, an increasing amount of research is being conducted on multivariate analysis of extremes with a focus on their concurrent appearance (Shaby and Reich, 2012; Dombry et al., 2018; Kornhuber et al., 2020; Ionita et al., 2021a), and new tools have been created for the analysis of extremes in climate models (Weigel et al., 2021).

A particular challenge for the analysis of extreme events is the fact that extreme events are typically rare and that it is therefore difficult to build informative statistics based solely on the extreme events themselves. Two common approaches are used to overcome this issue: peaks over threshold and block maxima. In the peaks-over-threshold approach, a fixed threshold is selected. The distribution of the data exceeding this threshold can then be approximated by a generalised Pareto distribution if some additional assumptions are fulfilled (see McNeil et al., 2015, chap. 7.2, for more details). The peaks-over-threshold approach is frequently applied in climatology and hydrology (Acero et al., 2011; Fowler and Kilsby, 2003; Kiriliouk et al., 2019). The block-maxima approach, on the other hand, follows the idea of splitting the time axis into blocks of a sufficiently large size and investigating the block-wise maxima of the data. Under suitable conditions, the distribution of these block-wise maxima can be approximated by a generalised extreme value (GEV) distribution for large sample sizes.

In this work, we will evaluate the performance of the fully coupled Alfred Wegener Institute Earth System Model (AWI-ESM1.1LR) (Shi et al., 2020; Lohmann et al., 2020; Ackermann et al., 2020) in terms of its accuracy regarding variability and extremes of precipitation, putting special focus on spatially concurrent precipitation extremes. Our main questions are whether the model is able to accurately reproduce extreme events in different regions and whether spatial dependencies and concurrent extremal events are modelled adequately. We compare model data from a historical run of the AWI-ESM to the global precipitation reanalysis data set CRU TS4.04 (Harris et al., 2020b). We start with investigating variability and extremes locally using empirical statistical parameters and by fitting a GEV distribution to annual precipitation maxima. Afterwards, following an approach by Bernard et al. (2013), we use a clustering algorithm to group spatio-temporal climate data into different spatial regions based on their similarity in terms of extremal behaviour and the concurrency of their extremes. This clustering is based on the theory of max-stable copulae, which has been used in prior work to investigate spatial dependence of extreme precipitation events, for example in Bargaoui and Bárdossy (2015); Zhang et al. (2013); Qian et al. (2018). In those papers, an analysis of bivariate distributions is performed. In our work, we first construct for each pair of locations a measure for their similarity in terms of extremes. This measure is then used as a basis for the clustering algorithm to group the data into spatial regions of comparable extremal behaviour. The resulting clusters for model and observational data are compared and used to analyse the ability of the climate model to reproduce spatial dependencies of precipitation extremes.

In this article, our main focus is on the AWI-ESM, and we present our methods using data from this model. We also present a measure for the model accuracy in regard to extremal precipitation and apply it to a set of different CMIP6 models. In the main text, results will be discussed for the AWI-ESM and for the model identified as having the best model accuracy. In the Supplement to this paper, the results for the other CMIP6 models investigated are presented.

Model validation in terms of precipitation extremes is already an active research topic. Tabari et al. (2016) investigate the performance of global and regional climate models using the peaks-over-threshold approach. An evaluation of regional and global climate models using extreme precipitation indices is conducted by Bador et al. (2020), revealing a tendency for stronger extremes in regional models. A similar result was obtained by Mahajan et al. (2015) by comparing climate model and observational precipitation data over the United States using GEV distributions. Timmermans et al. (2019) conduct pairwise comparisons of the precipitation extremes of numerous gridded observation-based data sets and find considerable differences between the data sets, especially in mountainous regions. Precipitation extremes over India are investigated by Mishra et al. (2014) using GEV distributions and comparisons of indices with a focus on changes over time.

It is also not a new approach to apply clustering algorithms to climate data. For example, it has been used to define climate zones in the United States (Fovell and Fovell, 1993) and globally (Zscheischler et al., 2012) and to find regions with similar trends in their climatic change over Europe (Carvalho et al., 2016). Those analyses focus on mean values and on their temporal differences, respectively, while we apply clustering specifically to uncover connections regarding climate extremes.

The article is structured as follows. After introducing the data sets in Sect. 2, we present the methods used in Sect. 3. The results from their application to the data are presented in Sect. 4. A section on conclusions and discussions finalises the article.

2 Data

The observational data are reanalysed monthly precipitation data in mm over land (excluding Antarctica) from the CRU TS4.04 data set (Harris et al., 2020b; University of East Anglia Climatic Research Unit, 2020) with data ranging from 1901 to 2019. We restrict the timeframe to the years 1930 to 2014 in order to have a sufficiently large area with non-missing data and to be consistent with the climate model data. The grid size is $\mathrm{0.5}\times {\mathrm{0.5}}^{\circ }$, and the data have been obtained by interpolating observations from more than 4000 weather stations using angular distance weighting. At some locations and time points, no data from nearby weather stations were available to use for interpolation. In these cases, the creators of the CRU TS4.04 data set used a value from a climatology instead. These climatology values are not very informative in terms of extremes and using too many of them would distort the analyses; therefore, all grid points with more than 5 % climatology values and all grid points with at least 12 consecutive months of climatology values are excluded from our analysis. This results in the exclusions of large regions in northern and central Africa, Indonesia, central Asia, and at the poles. In the figures showing geographical data in this paper, these regions are coloured in grey. The climate model used is the coupled model AWI-ESM1.1LR. It is based on the AWI Earth System Model (AWI-ESM1), which consists of the AWI Climate Model (Sidorenko et al., 2015; Rackow et al., 2018), but with interactive vegetation. The model is comprised of the atmosphere model ECHAM6 (Stevens et al., 2013), which is run with the T63L47 setup (i.e. a horizontal resolution of $\mathrm{1.85}\times {\mathrm{1.85}}^{\circ }$ and 47 vertical layers) and the ocean–sea ice model FESOM1.4 (Wang et al., 2014), which employs an unstructured grid, allowing for varying resolutions from 20 km around Greenland and in the North Atlantic to around 150 km in the open ocean (CORE2 mesh). The land surface processes are computed by the land surface model JSBACH2.11 (Reick et al., 2013). The model considers the surface runoff toward the coasts, deploying a hydrological discharge model that also includes freshwater fluxes by snowmelt (Hagemann and Dümenil, 1997). AWI-ESM1 has been extensively used and described in the context of palaeoclimate changes and changes in the recent and future climate (Shi et al., 2020; Lohmann et al., 2020; Ackermann et al., 2020; Niu et al., 2021). The historical run is documented in Danek et al. (2020) and has been directly used in Ackermann et al. (2020) and Keeble et al. (2021). Furthermore, the model takes part in CMIP6/PMIP4 activities (Brierley et al., 2020; Brown et al., 2020; Otto-Bliesner et al., 2021; Kageyama et al., 2021a, b).

The Coupled Model Intercomparison Project (CMIP), coordinated by the Working Group on Coupled Modelling (WGCM) of the World Climate Research Programme (WCRP) has the goal of supporting and facilitating the analysis of climate model data by providing a set of common standards regarding the formatting and availability of model output. Additionally, in order to enhance model comparability, all models participating in CMIP are required to run a set of standardised experimental setups (Diagnostic, Evaluation and Characterization of Klima experiments; DECK experiments) and a simulation of the historical climate from 1850 to 2014 (the historical simulations we also use in our analysis). CMIP is divided into different phases, reflecting the advancements of climate modelling; the current phase (CMIP6) started in 2016. More information on CMIP can be found in Eyring et al. (2016). The model outputs are made available by the Earth System Grid Federation (ESGF;  Cinquini et al., 2014).

In our analysis, we restrict the timeframe of the model data to the years 1930 to 2014, as in the observational data. We investigate monthly precipitation (the sum of convective precipitation and large-scale precipitation) in millimetres per month. We use bilinear interpolation to scale the reanalysis data to the grid of the atmospheric component of the climate model and take into account only those interpolated grid points that correspond to locations with given observed data, excluding the oceans and the regions with incomplete data mentioned above.

3 Methods

3.1 Univariate analysis

In this subsection, the time series of each spatial location (henceforth referred to as grid point) is investigated separately, and all operations and analyses described are therefore conducted for each grid point. Since the focus of this work is not on evaluating the effects of longtime trends, we apply a seasonal–trend decomposition using Loess (Cleveland et al., 1990) on the data and subtract the trend from the data but add the mean value of the trend, resulting in data for which we assume temporal stationarity. Following this, as a first comparison between the data sets, we investigate differences in the empirical mean and empirical standard deviation of the annually maximised precipitation data.

The theoretical foundation for the application of the GEV distribution is as follows. For a random variable X with an unknown probability distribution, we investigate the distribution of the maximum of independent and identically distributed (i.i.d.) copies $X_{\mathrm{1}},\mathrm{\dots },X_n$ of it: $Y^{\left(n\right)}:={max}_{i=\mathrm{1},\mathrm{\dots },n}\left(X_i\right)$. We assume that for suitable normalising sequences a_n>0 and b_n, Y⁽ⁿ⁾ converges in distribution if n tends to infinity:

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{Y^{\left(n\right)}-b_n}{a_n}}\stackrel{\mathcal{D}}{⟶}H.\end{array}$$

In this case, as shown by Fréchet (1927), Fisher and Tippett (1928), and Gnedenko (1943), the distribution of Y⁽ⁿ⁾ can be approximated by a GEV distribution for a large (fixed) value of n. This distribution depends on three parameters, called location (μ), scale (σ>0) and shape (γ), and its cumulative distribution function is given by

$$\begin{array}{}\text{(2)}& F_{\mathit{\mu },\mathit{\sigma },\mathit{\gamma }}\left(x\right)=\left\{\begin{array}{ll}\exp \left(-\exp \left(-\frac{x-\mathit{\mu }}{\mathit{\sigma }}\right)\right)& \mathit{\gamma }=\mathrm{0}\\ \exp \left(-max{\left(\mathrm{0},\mathrm{1}+\mathit{\gamma }\frac{x-\mathit{\mu }}{\mathit{\sigma }}\right)}^{-\frac{\mathrm{1}}{\mathit{\gamma }}}\right)& \mathit{\gamma }\ne \mathrm{0}.\end{array}\right.\end{array}$$

The GEV distribution has widely been used as a model for block-wise maximised data (for example, Coles et al., 2003; Onwuegbuche et al., 2019; Villarini et al., 2011). Following this approach, we group our monthly precipitation data from observations and climate model into 1-year block maxima and fit a GEV distribution to the block-wise maxima at each grid point. When selecting a block size, a bias–variance tradeoff has to be taken into account. For a low block size, the resulting parameter estimates tend to be biased because the convergence to the GEV distribution holds only asymptotically. A high block size, on the other hand, will lead to a limited amount of block-wise maxima that can be analysed and therefore to a higher variance in the estimates (see McNeil et al., 2015, chap. 7). In our case, we have a relatively small block size of 12 (months per year) and 90 block-wise maxima (years of investigation).

To estimate the distribution parameters, we use the method of probability-weighted moments developed by Hosking (1985) as implemented in the R package “EnvStats” of Millard and Kowarik (2013). As shown by Hosking et al. (1985), this method yields estimators with a relatively low variance and bias compared to the maximum likelihood approach, especially for small- and medium-sized samples. We test the goodness of fit using a one-sample Kolmogorov–Smirnov (KS) test at a 5 % significance level. The null hypothesis of the test is that the annually maximised data follow the GEV distribution having the probability-weighted moments estimates as distribution parameters.

We also use the parametric bootstrap method with 2500 resamples to compute 95 % confidence intervals for each GEV parameter and for the 95 % quantiles of the distributions. Confidence intervals for the GEV parameters based on asymptotic normality also exist for the probability-weighted moments estimators, but they have a high bias and variance if the shape parameter is far away from zero, as shown by Hosking et al. (1985). In our data, such a value is estimated for the shape parameter for several time series, and comparisons between the confidence intervals based on bootstrap and those based on asymptotic normality also confirmed large differences in these cases. For the sake of methodological consistency (and because we also use the bootstrap for the confidence intervals of the 95 % quantiles), we calculated the GEV parameter confidence intervals using bootstrap for all time series. Since this method is quite time-consuming, it could also be appropriate to choose the method of confidence interval calculation based on the estimated shape parameter value.

To compare the performance of different CMIP6 models, we introduce average weighted quantile difference (AWQD) as a measure for the accuracy of the extremal precipitation. For this measure, the absolute differences between model and observational 95 % GEV quantiles, weighted with the cosine of the latitude, are averaged. The weighting accounts for the fact that the grid cells do not have an equal size for all grid points, and the average is taken because of the different model resolutions. Let 𝒢 denote the set of grid points. For g∈𝒢, let ${\widehat{q}}_{\mathrm{0.95},\text{mod}}\left(g\right)$ and ${\widehat{q}}_{\mathrm{0.95},\text{obs}}\left(g\right)$ denote the estimated quantiles. Using these notations, we define

$$\begin{array}{}\text{(3)}& \begin{array}{rl}\text{AWQD}:=& {\displaystyle \frac{\mathrm{1}}{\left|\mathcal{G}\right|}}\sum _{g\in \mathcal{G}}\cos \left(\mathrm{lat}\left(g\right)\right)\cdot \\ & \left|{\widehat{q}}_{\mathrm{0.95},\text{mod}}\left(g\right)-{\widehat{q}}_{\mathrm{0.95},\text{obs}}\left(g\right)\right|.\end{array}\end{array}$$

3.2 Comparison of spatial distributions

To compare the spatial distributions of climate extremes, we introduce a hierarchical clustering algorithm (using average linking) to determine regions with similar extremal behaviour. This approach is similar to the idea proposed in Bernard et al. (2013). The hierarchical clustering is based on concepts from extreme value statistics that will be discussed in the following.

Assume that two real-valued random variables (X,Y) have a copula function C: [0,1] × [0,1] → [0,1], meaning that their joint distribution function can be written in terms of the copula and the marginal distribution functions as $F_{X,Y}(x,y)=C\left(F_X\right(x),F_Y(y\left)\right)$ for all $x,y\in \mathbb{R}$. Thus, if (X,Y) is the weak limit of block-wise maxima of a sequence of i.i.d. two-dimensional variables when the block size goes to infinity (a similar condition as in Sect. 3.1 but extended to two-dimensional random variables), it follows that X and Y are (jointly) GEV distributed. It also follows that the copula must fulfil $C(u^t,v^t)=C^t(u,v)$ for all $u,v\in [\mathrm{0},\mathrm{1}]$ and t>0 (see McNeil et al., 2015, Theorem 7.44 and 7.45). Such a copula is called max-stable, and it can be written as follows:

$$\begin{array}{}\text{(4)}& C(u,v)=\exp \left(\left(\ln u+\ln v\right)A_{X,Y}\left({\displaystyle \frac{\ln u}{\ln u+\ln v}}\right)\right),\end{array}$$

which uses a function A_X,Y: [0,1] → [$\frac{\mathrm{1}}{\mathrm{2}},\mathrm{1}$] called the Pickands dependence function (Pickands, 1981). The function A_X,Y is convex and satisfies $max(w,\mathrm{1}-w)\le A_{X,Y}\left(w\right)\le \mathrm{1}$ for all $w\in [\mathrm{0},\mathrm{1}]$. The extremal coefficient is now defined as 2 times its value at the point 0.5:

$$\begin{array}{}\text{(5)}& {\mathit{\theta }}_{X,Y}:=\mathrm{2}\cdot A_{X,Y}\left(\mathrm{0.5}\right).\end{array}$$

The extremal coefficient takes its minimal possible value of 1 if X and Y are comonotonic (meaning specifically that it holds ${\mathit{\theta }}_{X,X}=\mathrm{1}$ for all X). The maximal possible value of 2 is obtained if X and Y are stochastically independent. To estimate the extremal coefficient, we use the madogram estimator as described in Ribatet et al. (2015) and Cooley et al. (2006) and rewrite θ_X,Y as

$$\begin{array}{}\text{(6)}& {\mathit{\theta }}_{X,Y}={\displaystyle \frac{\mathrm{1}+\mathrm{2}{\mathit{\nu }}_{X,Y}}{\mathrm{1}-\mathrm{2}{\mathit{\nu }}_{X,Y}}},\end{array}$$

with the madogram ${\mathit{\nu }}_{X,Y}=\frac{\mathrm{1}}{\mathrm{2}}\mathbb{E}\left[\right|F_X\left(X\right)-F_Y\left(Y\right)\left|\right]$. The madogram can be estimated by replacing F_X and F_Y with their empirical counterparts. For a data sample $(x_{\mathrm{1}},y_{\mathrm{1}}),\mathrm{\dots },(x_n,y_n)$, we then obtain

$$\begin{array}{}\text{(7)}& {\widehat{\mathit{\nu }}}_{X,Y}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}n(n+\mathrm{1})}}\sum _{i=\mathrm{1}}^n\left|\sum _{j=\mathrm{1}}^n\right({\mathbf{1}}_{x_j\le x_i}-{\mathbf{1}}_{y_j\le y_i}\left)\right|,\end{array}$$

and consequently define an estimator

$$\begin{array}{}\text{(8)}& {\widehat{\mathit{\theta }}}_{X,Y}={\displaystyle \frac{\mathrm{1}+\mathrm{2}{\widehat{\mathit{\nu }}}_{X,Y}}{\mathrm{1}-\mathrm{2}{\widehat{\mathit{\nu }}}_{X,Y}}}.\end{array}$$

Hierarchical clustering algorithms require a dissimilarity function $D:\mathcal{G}\times \mathcal{G}\to \mathbb{R}$ that must fulfil $D(g_{\mathrm{1}},g_{\mathrm{2}})=D(g_{\mathrm{2}},g_{\mathrm{1}})\ge \mathrm{0}$ and $D(g_{\mathrm{1}},g_{\mathrm{1}})=\mathrm{0}$ for all grid points $g_{\mathrm{1}},g_{\mathrm{2}}\in \mathcal{G}$ (for an introduction to hierarchical clustering algorithms, see Murtagh and Contreras, 2012). Based on the properties of the extremal coefficient discussed above, we define such a dissimilarity function as follows:

$$\begin{array}{}\text{(9)}& D_{\mathrm{0}}(g_{\mathrm{1}},g_{\mathrm{2}}):={\widehat{\mathit{\theta }}}_{X,Y}-\mathrm{1},\end{array}$$

with X and Y representing the GEV distributions at the grid points g₁ and g₂, respectively.

Note that the extremal coefficient is invariant under rank transformations and that it does not depend on the values of the GEV parameters of the marginal distributions. In fact, in Ribatet et al. (2015); Cooley et al. (2006), it was only used in the special case of margins following a $\mathrm{GEV}(\mathrm{1},\mathrm{1},\mathrm{1})$ distribution. It may be desirable to also include the dissimilarity of the marginal distributions in the clustering. As a further generalised dissimilarity measure we propose

$$\begin{array}{}\text{(10)}& \begin{array}{rl}{D}_{\mathit{\lambda }}\left(g_{\mathrm{1}},g_{\mathrm{2}}\right):=& \left(\mathrm{1}-\mathit{\lambda }\right)D_{\mathrm{0}}\left(g_{\mathrm{1}},g_{\mathrm{2}}\right)+\mathit{\lambda }\left({\displaystyle \frac{\mathrm{1}}{\mathrm{3}}}{d}_{\mathit{\mu }}\left(g_{\mathrm{1}},g_{\mathrm{2}}\right)\right.+\\ & \left.{\displaystyle \frac{\mathrm{1}}{\mathrm{3}}}{d}_{\mathit{\sigma }}\left(g_{\mathrm{1}},g_{\mathrm{2}}\right)+{\displaystyle \frac{\mathrm{1}}{\mathrm{3}}}{d}_{\mathit{\gamma }}\left(g_{\mathrm{1}},g_{\mathrm{2}}\right)\right),\end{array}\end{array}$$

where $\mathit{\lambda }\in [\mathrm{0},\mathrm{1}]$ is a weighting parameter and $d_{\mathit{\mu }}(g_{\mathrm{1}},g_{\mathrm{2}}):=\frac{|{\widehat{\mathit{\mu }}}_{g_{\mathrm{1}}}-{\widehat{\mathit{\mu }}}_{g_{\mathrm{2}}}|}{{max}_{h_{\mathrm{1}},h_{\mathrm{2}}\in \mathcal{G}}|{\widehat{\mathit{\mu }}}_{h_{\mathrm{1}}}-{\widehat{\mathit{\mu }}}_{h_{\mathrm{2}}}|}\in [\mathrm{0},\mathrm{1}]$ is the normalised distance between the location parameter estimates at the grid points g₁ and g₂ (analogous for d_σ and d_γ). Instead of an equal weighting, it would also be possible to use different weights for d_μ, d_σ and d_γ, but the selection of a set of weights that is clearly better suited to describing GEV distribution dissimilarity is difficult. It could be a good idea to put more weight on the shape parameter since this parameter describes the heavy-tailedness of the distribution and therefore the strength of its extremes relative to the non-extreme values. On the other hand, we will see in the next section that the uncertainty in the shape parameter estimation is considerably higher than the uncertainty in the estimation of the other two parameters, at least for our data, which would speak against weighting shape parameter differences too strongly.

To choose a suitable number of clusters, we consider an approach by Salvador and Chan (2004) called the L method. In each step of the hierarchical clustering, the two clusters with minimal dissimilarity are combined; therefore, we can plot the number of clusters versus the dissimilarity between them, resulting in a graph called the evaluation graph. The dissimilarity between clusters necessarily grows as the total number of clusters is reduced. The idea of Salvador and Chan (2004) is to find a point from which on the growth rate of the dissimilarity measure increases considerably. It can then be expected that the clusters up to this point combine rather similar data points, whereas combining the data points to larger clusters would yield artificial results. To determine such a point of change, first a suitable range of the number of clusters is selected. For our example, we consider different ranges, starting with 10 clusters and having no more than 550 clusters. For each possible point of change c in this range, the horizontal axis of the graph is divided into the two parts to the left and the right of that point, and a linear regression line is fitted to each of the two partial graphs. The root-mean-squared errors (RMSEs) of the two regression lines are weighted with the number of points involved in the regression analysis and summed up. The point of change with the minimal combined RMSE is chosen as the suitable cluster number. As an alternative method, we set the number of clusters to the highest possible number such that a fixed threshold dissimilarity between clusters is not exceeded (threshold method). This number can easily be read off of the evaluation graph.

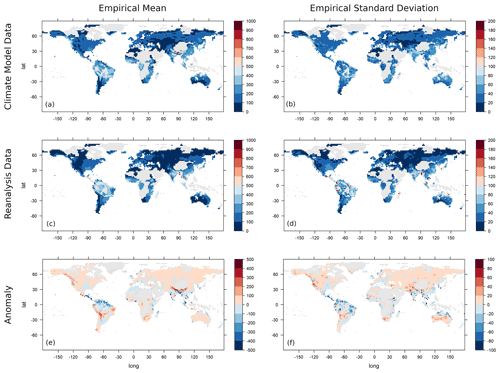
Figure 1 The empirical mean (a, c, e) and empirical standard deviation (b, d, f) of the annual maxima of monthly precipitation of the AWI-ESM model data set (a, b) and the CRU TS4.04 reanalysis data set (c, d) and their difference (model data minus reanalysis data) (e, f). Values exceeding the scale limits are truncated. Values are given in millimetres per month.

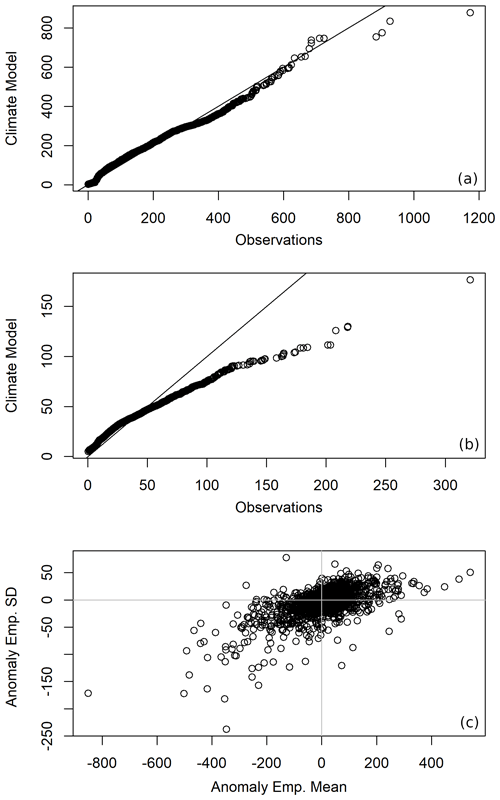
Figure 2 Quantile–quantile (Q–Q) plots comparing the empirical mean values (a) and the empirical standard deviations (b) of the annually maximised monthly precipitation of the CRU TS4.04 reanalysis data set and the AWI-ESM model data set. The deviance of the empirical mean and standard deviation are plotted against each other in (c). Values are given in millimetres per month.

4 Results

We start with calculating the empirical mean and standard deviation of the annually maximised data for each grid point, as can be seen in Fig. 1. In most regions, similar mean values can be observed. A notable overestimation of the annual maxima of monthly precipitation by the climate model takes place in the Himalayas and along the western coasts of the Americas. Underestimation occurs most prominently in the Amazon region and parts of Central America, as well as in Bangladesh and East Asia. Looking at the standard deviation, a similar pattern to that of the empirical mean can be observed, but it has a stronger tendency for underestimation, which also occurs in India and the northern part of Australia. In Fig. 2a and b, quantile–quantile plots (Q–Q plots) of the empirical mean and standard deviation are displayed. The quantiles of the empirical mean are generally similar, but the highest quantiles show a strong discrepancy. Regarding the standard deviation, this tendency is much more pronounced, corresponding to the larger areas of underestimation of empirical standard deviation we identified in Fig. 1. The difference in empirical mean and the difference in empirical standard deviation are plotted against each other in Fig. 2c). It is visible that in many cases overestimation (underestimation) of the empirical mean also corresponds to overestimation (underestimation) of the empirical standard deviation. A similar case of heteroscedasticity has also been noted in Lohmann (2018) when investigating Holocene climate.

As pointed out by Katz and Brown (1992), the frequency of extreme events is strongly influenced by changes (or, in this case, misestimation) in the mean and in the variance of a distribution. Therefore, an overestimation or underestimation of extremes can be expected in certain regions based on the results in Figs. 1 and 2.

When fitting the GEV distributions to the data and applying KS tests to check the goodness of fit, the hypothesis that the data follow a GEV distribution with the estimated parameters is not rejected for almost all grid points in both the observational and climate model data, except for in parts of the Sahara and some isolated points.

Figure 3 The p values of Kolmogorov–Smirnov tests for the hypothesis that the data follow a GEV distribution with parameters estimated using probability-weighted moments. Test results for the AWI-ESM climate model (a) and for the CRU TS4.04 reanalysis data (b).

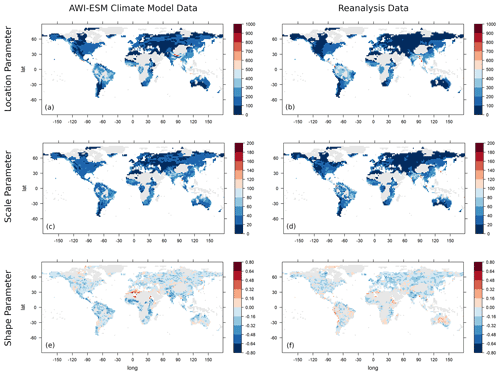
Figure 4 The estimated GEV parameters location (a, b), scale (c, d) and shape (e, f) for the AWI-ESM climate model data (a, c, e) and reanalysis data (b, d, f). Values exceeding the scale limits are truncated. Values are given in millimetres per month.

The three GEV parameters estimated are location, scale and shape, with location and scale very roughly corresponding to mean and variance, and the shape parameter yielding information about the degree of heavy-tailedness. The estimated parameter values are shown in Fig. 4. In Fig. 5, the differences between model and observational parameters are shown. Shaded areas are areas in which the model parameter falls into the 95 % confidence interval of the corresponding observation parameter and vice versa. We can observe a similarity between the anomaly of the location parameters and the anomaly of the empirical means discussed above, and we can likewise obtain the similarity between the anomalies of scale parameters and empirical standard deviations. For the location parameter, we observe large differences quite often, and the parameters estimated for one data set seldom fall into the confidence interval derived from the other data set. The estimated scale parameters are covered more often by the confidence intervals derived from the other data set, although there are also large regions with a high difference in the two estimates. The estimated shape parameters are covered by the confidence intervals at many locations, but it needs to be noted that the estimator of the shape parameter is known to be sensitive to small variations in the data. Therefore, the confidence intervals calculated using the parametric bootstrap tend to be large and not particularly informative. In Fig. 6, the anomalies of the 95 % upper quantiles of the estimated GEV distributions are depicted, again with shaded areas indicating quantiles lying within the confidence levels determined using a parametric bootstrap. Climate extremes are most strongly overestimated by the model in the mountainous regions of the Himalayas, the Andes and the Rocky Mountains. An underestimation of climate extremes takes place most notably in the Amazon region and parts of eastern Asia. This corresponds well to the regions of overestimation and underestimation of the empirical means and standard deviations and the implications of such misestimations discussed above.

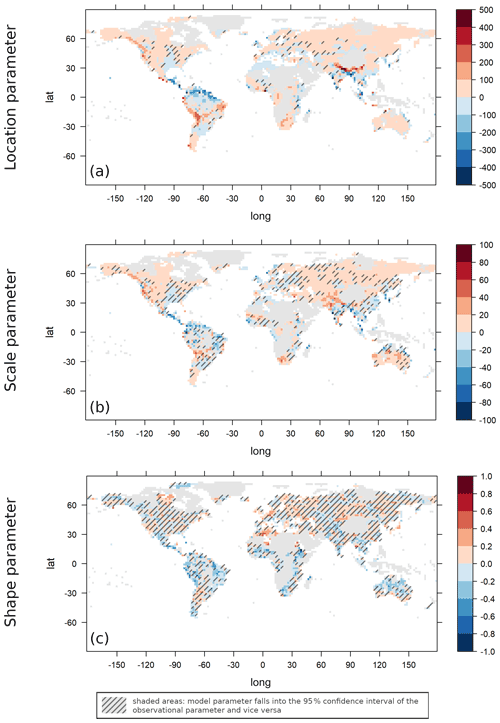
Figure 5 Difference between AWI-ESM model and observational GEV parameter estimates: location parameter (a), scale parameter (b) and shape parameter (c). Values exceeding the scale limits are truncated. Values are given in millimetres per month.

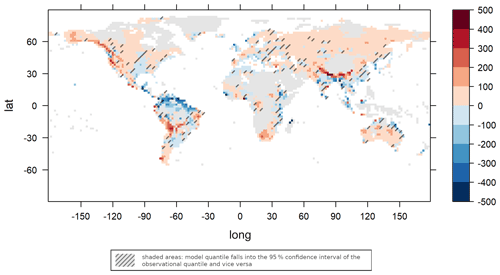
Figure 6 Difference between the 0.95 quantiles of the estimated GEV distribution for AWI-ESM model and observational data. Values exceeding the scale limits are truncated. Values are given in millimetres per month.

We apply the hierarchical clustering algorithms using the two dissimilarity measures D₀ and D_0.25 as introduced in the previous section. The numbers of clusters determined using the L method with selected cluster ranges (from 10 to a maximal number of clusters m) and using the threshold method with selected threshold dissimilarities h are documented in Table 1.

Table 1 The number of clusters for the AWI-ESM climate model and observational data determined with the L Method (m data) and the threshold method (h data) for different ranges and thresholds and for the dissimilarity measures D₀ (a) and D_0.25 (b).

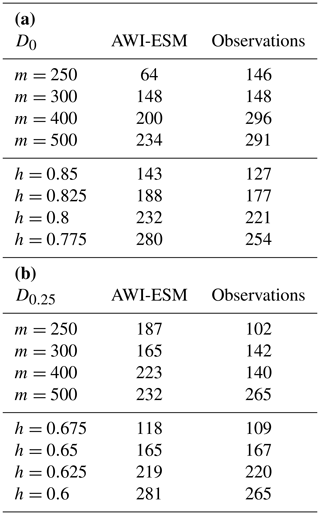
The results of the L method seem to depend rather strongly on the data set investigated and the value of m (compare the results for m=250 and m=300 for measure D₀), making this method less suitable for the comparison of two data sets. The threshold method generally predicts a similar but (in most cases) slightly lower cluster number for observational data than for climate model data. In Fig. 7, the clusters for both data sets are depicted using the threshold method for dissimilarity measure D₀ with threshold h=0.825 and for dissimilarity measure D_0.25 with threshold h=0.65.

To exemplify the differences and similarities in the clusterings, we have a closer look at Europe in the D₀ clusterings. In the model data, there is one cluster covering western Spain and Portugal, one cluster covering eastern Spain, and one cluster consisting of southern France and Italy. Great Britain and Denmark are in the same cluster, and the northern parts of France together with Belgium and the Netherlands are in another. One cluster covers Germany and Switzerland, and in eastern Europe we see several clusters covering larger areas in a longitudinal direction, e.g. one cluster over Poland, one over Ukraine, and one over Turkey and Greece. The clusters in the observational data set show a slightly different picture. Here, the whole Iberian Peninsula is in one cluster, and one large cluster extends over northern France, Belgium, the Netherlands, Germany and the western parts of Poland. On the other hand, Great Britain and Denmark are now in two separate clusters. Regarding other parts of the world, it is worth noting that in all four clusterings a large cluster covering the Sahara (or at least all parts of it for which there are observations available) can be identified. There are no clusters extending over two regions that are very far apart from each other, and in general clusters tend to cover more area in the longitudinal direction than in the latitudinal one.

Figure 7 Clustering of AWI-ESM model data (a, b) and observational data (c, d) with the dissimilarity measure D₀ and threshold h=0.825 (a, c) and with the dissimilarity measure D_0.25 and threshold h=0.65 (b, d).

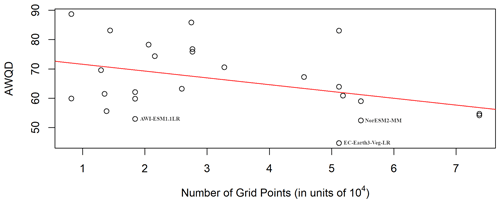
Figure 8 The average weighted quantile difference (AWQD) of the 27 CMIP6 models considered plotted against the model resolution (number of model grid points in units of 10⁴). The linear regression line (intercept 73.310, slope −2.368) is shown in red.

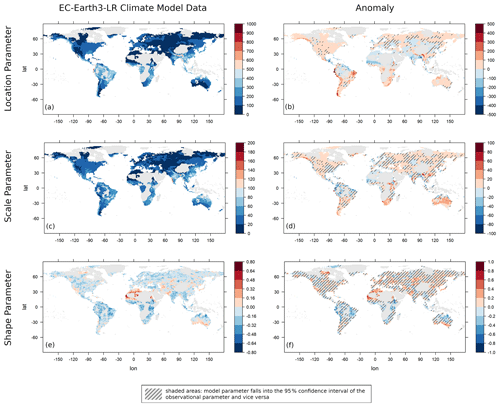
Figure 9 GEV parameters estimated using the EC-Earth3-Veg-LR climate model (a, c, e) and their anomaly compared to the reanalysis GEV parameters (b, d, f). The GEV parameters are location (a, b), scale (c, d) and shape (e, f). Values exceeding the scale limits are truncated. Values are given in millimetres per month.

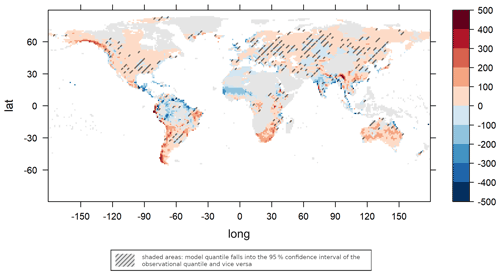
Figure 10 Difference in the 0.95 quantiles for the estimated GEV distribution from EC-Earth3-Veg-LR model and the observational data. Values exceeding the scale limits are truncated. Values are given in millimetres per month.

Table 2 The number of clusters for the EC-Earth3-Veg-LR climate model and the observational data determined with the L method (m data) and the threshold method (h data) for different ranges and thresholds and for the dissimilarity measures D₀ (a) and D_0.25 (b).

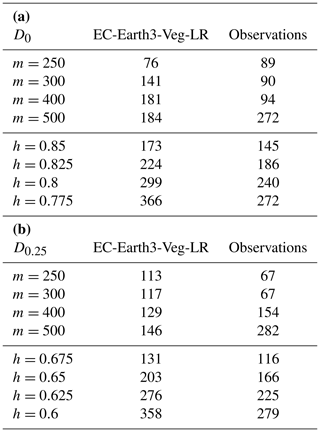
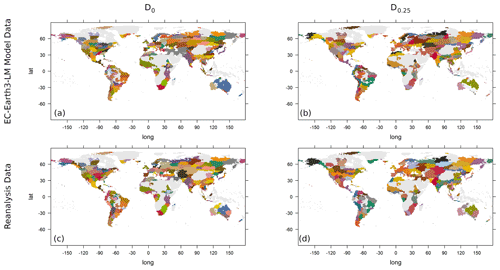
Figure 11 Clustering of the EC-Earth3-Veg-LR model data (a, b) and the observational data (c, d) with the dissimilarity measure D₀ and threshold h=0.825 (a, c) and with dissimilarity measure D_0.25 and threshold h=0.65 (b, d).

For the AWI-ESM, we calculated an AWQD of 52.98, making it the third best of all 27 CMIP6 models analysed. A full table of the models and their AWQDs is provided in the Supplement to this paper. In Fig. 8, the AWQDs are plotted against the model resolution (the total number of model grid points in units of 10⁴). A linear regression (shown as a red line; intercept: 73.310; slope: −2.368) indicates that models with a higher resolution have a tendency to describe extremal precipitation better. A test of the significance of the slope parameter (null hypothesis of the slope parameter being equal to zero) was significant at the 5 % level with a p value of 0.0357. The best model in terms of the AWQD is the high-resolution model EC-Earth3-Veg-LR (EC-Earth Consortium, 2020) with a value of 44.71. We will now discuss results for this model in more detail, while results for the other models can be found in the Supplement. For the EC-Earth3-Veg-LR, the estimated GEV parameters and anomalies are shown in Fig. 9. The differences in the 95 % quantiles are depicted in Fig. 10. The numbers of clusters determined using the L method and the threshold method are found in Table 2, and images of clusterings are shown in Fig. 11. Q–Q plots and plots of KS tests are similar to the corresponding plots for the AWI-ESM and can be found in the Supplement to this paper. The EC-Earth3-Veg-LR model predicts climate extremes better than AWI-ESM in the Himalayas and in the Amazon region (cf. Fig. 6 and 10), while it overestimates precipitation extremes more strongly than the AWI-ESM at the western coast of South America. The number of clusters is in general higher than for the AWI-ESM, in part probably due to the higher model resolution (320×160 compared to 192×96). Note that this increased resolution is also the reason for the different values for the cluster numbers of the reanalysis data in Tables 1 and 2 because in each case reanalysis data were interpolated to the climate model resolution. When again comparing the clusters over Europe using the D₀ dissimilarity measure, it can be observed that in the western part of Europe model and observational clusters are similar in general, with only slight differences over the Iberian Peninsula and with an area covering southern France and northern Italy that is in one cluster in the model data and in two different clusters in the observational data. In eastern Europe and Scandinavia, the differences between the clusterings are larger, and thus it is more difficult to see correspondences. The general remarks that have been made about the clusterings while discussing the AWI-ESM data also apply here.

5 Conclusions

We presented approaches and methods to validate climate model outputs by comparing their extremal behaviour to the extremal behaviour of observational data. To illustrate these methods, we compared precipitation extremes between the AWI-ESM and the CRU TS4.04 data set of reanalysed observations. After an analysis of empirical statistical parameters, we fitted the data to GEV distributions and analysed the differences in estimated parameters. Following this, we continued with an analysis of spatial concurrence of extremes based on a hierarchical clustering approach and a dissimilarity measure derived from bivariate copula theory. While the empirical statistics are similar for many parts of the world, we can also identify larger regions of overestimation and underestimation of empirical means and standard deviations by the climate model. These misestimations often go hand in hand with a similar misestimation of the standard deviation (heteroscedasticity), but for the standard deviation a stronger tendency for underestimation can be observed. Misestimations of mean and standard deviations translate into a misestimation of extreme values, and this can be confirmed by the comparison of the fitted GEV distribution parameters and the 0.95 quantiles derived from them. The shape parameter, indicative of the heavy-tailedness of the distribution, is in general similar between model and observational data, but because of the difficulties in reliably estimating this parameter from data (that are in turn a result of the rareness of extreme events in the data), these results have to be taken with caution.

The cluster analysis based on spatial dependencies and the occurrence of concurrent extremes shows that there is generally a good agreement between identified clusters. The number of clusters is also similar in general, with a slight tendency for a higher cluster number in the model data. Since it is mostly large-scale weather events and teleconnections contributing to concurrent climate extremes, this may indicate that the basic physical behaviour underlying them is in general well captured by the AWI-ESM. Further analyses can be conducted to investigate the reasons for different clusterings over selected regions in detail.

In addition to the AWI-ESM, several other CMIP6 models are also analysed. A comparison of the model accuracy, measured using an averaged quantile difference, shows a tendency for higher-dimensional models to capture extremal behaviour better.

In this work, a clustering algorithm based on bivariate extremal coefficients is used to perform a spatial analysis of extreme values. Extremal coefficients are also used to model multivariate spatial distributions of extremal precipitation using max-stable processes. This method was first developed by Smith (1990) and Schlather (2002) and was then extended by Opitz (2013) and Ribatet et al. (2015), and it has been used successfully to model precipitation over Switzerland (Ribatet, 2017). The models based on max-stable processes assume spatial stationarity (i.e. the spatial dependence between two points depends only on their distance). This assumption is justifiable for small regions like Switzerland, but it makes the models in their present form unsuitable for global data. Castro-Camilo and Huser (2020) created a model for the spatial distributions of extreme tail dependencies based on factor copulae, allowing them to use the relaxed assumption of local spatial stationarity and therefore to apply their model to the whole contiguous United States. From the area of parametric copulae, vine copulae have also been employed to model precipitation data by Vernieuwe et al. (2015) and by Nazeri Tahroudi et al. (2021). A further possibility is the application of non-parametric multivariate copulae. Marcon et al. (2014) used an estimator based on Bernstein polynomials to model the common distribution of up to seven variables in their analysis of French precipitation data. Copulae based on Bernstein polynomials are also used in multivariate extreme value analysis with a focus on multiple testing (Neumann et al., 2019). In global climate models, the number of dimensions is much higher than seven, and thus the method by Marcon et al. (2014) is not directly transferable.

The clustering approach presented here focuses on the comparison of extremal events at different locations, thereby supplementing the analyses of climate extremes that are often focused on extremes at a specific location (Zhang et al., 2011). An application to daily data that has been annually or seasonally maximised is also possible but is beyond the scope of this paper. In order to investigate extreme precipitation within the area covered by one cluster in more detail, the spatially stationary max-stable models or the copulae-based models mentioned above could be employed. Most of the clusters cover only a small region, therefore spatial stationarity might be a reasonable assumption, although it is not a direct consequence of the data being in the same cluster. In addition to model validation, the definition of regions with concurrent extremes may turn out to be useful for assessments of risks in an economical context and for insurance. It needs to be noted, however, that extremes in climate models and in gridded reanalysis data sets tend to be damped because of the spatial averaging performed during the creation of the data (Bador et al., 2020). Another possible field of application is palaeoclimatology. The spatial distribution of precipitation extremes is known to have changed markedly in the past (Lohmann et al., 2020; Ionita et al., 2021b), and clustering based on climate models could be used to generalise the sparse existing palaeoclimatic data to larger regions.