the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Irrigation quality and management determine salinization in Israeli olive orchards
Vladimir Mirlas
Asher Aizenkod
Naftali Goldshleger
Olive (Olea europaea L.) orchard brackish water irrigation with incorrect irrigation management reduces soil fertility and degrades soil health through soil salinization. This study was conducted in the Beit She'an Valley, one of the main agricultural regions in Israel, in an olive orchard in which a combination of soil salinization and poor drainage conditions impedes plant development and causes severe economic damage. By combining various research methods, including soil salinity monitoring, field experiments, remote sensing (frequency domain electromagnetic – FDEM), and unsaturated soil profile saline water movement modeling, the salinization processes were quantified. Irrigation water conductance of 3.13 dS m−1 points to salinization within the tree upper root zone, whereas the modeling results suggest that salinization danger is greater with brackish treated wastewater rather than with lower-salinity brackish irrigation groundwater and that irrigation with potable water can help reduce salt accumulation and recover damaged plots.
- Article
(3306 KB) - Full-text XML
-
Supplement
(377 KB) - BibTeX
- EndNote
Soil salinity surveys and studies across the world and Israel indicate that irrigation with poor water quality and improper irrigation management causes soil salinization and degradation, and damages soil fertility (Wada et al., 2016; Pandit et al., 2020). Soil salinity monitoring in the Jezre'el Valley began in 1987, following a soil salinity survey that showed intensive salinization and often alkalinization of the upper soil horizons (Benyamini et al., 2005, 1998, 2000). Earlier studies had shown that these processes were enhanced by a semi-confined shallow aquifer (Kruseman and De Ridder, 1976), causing upward water flow during winter and spring seasons and reducing downward rain and irrigation percolation during the summer and fall seasons (Gafni and Salinger, 1992).
Most of the soil salinization problems in the Beit She'an Valley are associated with the use of poor-quality irrigation water (conductivity above 3 dS m−1). The soil salinity is constantly increasing owing to irrigation with high-salinity-treated wastewater and blocking of the natural drainage to the underlying groundwater (Mirlas et al., 2006a; Mirlas, 2012). At a lemon tree plantation in the Jordan Valley, it was found that an increase in irrigation water salinity to 3.7 times freshwater salinity increased soil salinity by 3.8 to 4.1 times in a few years (Abu Awwad, 2001). An additional effect of treated effluent irrigation in the Jordan Valley was decreasing pH in parallel to soil salinity increase (Mohammad and Mazahreh, 2003). In the Beit She'an Valley, high saline–sodic concentration in irrigation damaged the soil's hydraulic conductivity, increasing runoff and causing silt–clay chalk soil erosion (Mandal et al., 2008a; Bhardwaj et al., 2008).
While global-scale land surface–soil–biosphere–atmosphere models enable a regional water balance (Boone et al., 2017; Guimberteau et al., 2018; Katz et al., 2018), understanding water and solute movement processes in unsaturated soil layers requires a mathematical description and numerical model development (Leij et al., 1991; Simunek and van Genuchten, 1995; van Genuchten and Wagenet, 1989; Celia et al., 1990; Kool et al., 1985). Principal component analysis (PCA) suggests that soil hydraulic conductivity is one of the factors affecting soil quality (Mandal et al., 2008b). Water and solute movement models in an unsaturated soil layer are based on Richards' equation for one-dimensional movement of water under saturation variability (Celia et al., 1990; Bear, 1972), and root water uptake is calculated by the van Genuchten equation (van Genuchten, 1987). In such models, the soil hydraulic conductivity coefficient in the saturated media varies as a function of the soil's hydraulic conductivity.
Soil moisture may be evaluated through atmospheric conditions (Garrigues et al., 2015) or calculated as a function of suction (pressure head) and hydraulic conductivity in an unsaturated condition. Salt leaching and accumulation are significant in arid and semi-arid areas (Wada et al., 2016). Salt motion models are commonly based on the Fickian convection–dispersion equation for solute transport (Toride et al., 1993) and complex models that should also consider absorption processes, anion and cation exchange, and more. Several modeling platforms such as HYDRUS (Simunek et al., 1998) and WASTRC-1 (Mirlas et al., 2006b) are widely used. WASTRC-1, a one-dimensional water and solute movement model under saturated conditions, was found to fit the soil characteristics of Hula Valley irrigated fields in Israel. In both the HYDRUS and WASTRC-1 models, various soil hydraulic conditions such as drainage, irrigation, and layer saturation depth can be considered. Soil density, saturated hydraulic conductivity, field moisture, suction, and root zone development among other factors are prerequisites for model calibration, parameter validation, and, consequently, proper water and solute movement simulation (Garrigues et al., 2015).
Salinization during irrigation is a dynamic process as the number of salts in the soil and their composition change during irrigation in both the surface area and in the soil profile. Soil salinity mapping by the traditional sampling method is expensive and time-consuming, with mapping accuracy directly depending on the distance between the sampling points (Pandit et al., 2018). Remote sensing technologies that are based on active electromagnetic (EM) radiation are being widely adopted for soil salinity mapping. Ground-based EM methods measure electrical conductivity (EC) in subsurface and substratum horizons and can thus recognize salinity anomalies in the field before salinization approaches the surface (Farifteh et al., 2007). EM induction sensors measure the soil profile salinity by recording the soil's apparent electrical conductivity (ECa).
Frequency domain electromagnetic (FDEM) techniques are a powerful tool for mapping soils and detecting changes in soil types related to salinity. FDEM sensors work within a range of 30 cm to 5 m of depth and perform best while scanning the area from about 1 m above the ground (Ben Dor et al., 2009a). By applying FDEM with other active and passive remote sensing methods, EC values in given soil layers were attained for the soil in the Jezre'el Valley (Ben Dor et al., 2009b).
The soils of the Beit She'an Valley were selected for research as it is one of the most important agricultural areas in Israel. They consist of brown clay soils (grumusols) and calcritic soils, with the latter's profile characterized by thin layers and formation layers of marl with high water absorption capacity. The soil stratification influences the potential to drain and wash excess salts that accumulate during the irrigation season, which preserve ventilated root conditions. Sodium-rich soil has up to 30 % cation exchangeable capacity, which exacerbates the ventilation conditions necessary for plants. The combination of soil stratification and poor drainage conditions impedes plant development, and, in some cases, soil structure destruction and salt accumulation in the root zone cause plant degeneration due to water absorption difficulties (Machado and Serralheiro, 2017). Consequently, crop irrigation by brackish water in the Beit She'an area might cause economic damage.
The irrigation water sources in the area are of variable quality: springs and Jordan River water are considered of acceptable quality (fresh), while groundwater and effluent water might be of poor quality (brackish). In this latter case, irrigation without clear irrigation criteria might steadily damage soil fertility. Defining an irrigation regime for local soil and water quality conditions is therefore of great importance for preventing crop and economic damage in the Beit She'an Valley. The required knowledge should indicate how water and salt move in soil and correlate with salinity processes and irrigation management capability (Pandit et al., 2018). Combining remote sensing (FDEM) methods with water and salt movement models in the unsaturated soil layer may enable the effective identification of soil salinization processes. In turn, this may result in improved planning and control for irrigation systems.
As integrative knowledge of harvesting demonstration needed for irrigation management, this study's objective was to assess soil salinization processes because of low-quality irrigation at the Kibbutz Meirav olive plantation in the Beit She'an Valley.
2.1 Research site background and geographical framework
The Beit She'an area is a unique agricultural area due to a combination of warm and dry climate (potential annual evaporation of 2400 mm at the meteorological service, Eden Farm Station), saline water irrigation, and heavy soils. The study site is a mature (2002) olive plantation located 1100 m north of the Kibbutz Meirav (Fig. 1).
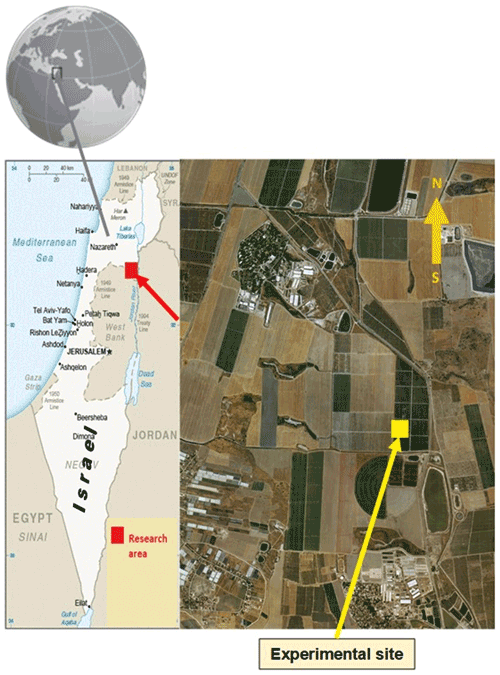
Figure 1Study site location (regional map: after CIA factbook, 2021; photo: Survey of Israel, 2021).
The planting intervals between the trees and rows are 7 and 4 m. The rainfall amount at the study site was 154, 253, and 281 mm in 2007/2008, 2008/2009, and 2009/2010 hydrological years, respectively. The soil at the study site is layered, with a practically impervious shallow layer of travertine found in different locations of the plantation as well as layers of marl at greater depth. Soil salinity stains were observed together with trees suffering from lack of ventilation, salting, and excess irrigated water. Following the soil sample particle size analysis results, the soil mechanical components at the research site consist of clay (40 %–50 %), silt (25 %–30 %), and sand (20 %–30 %) (Fig. 2).
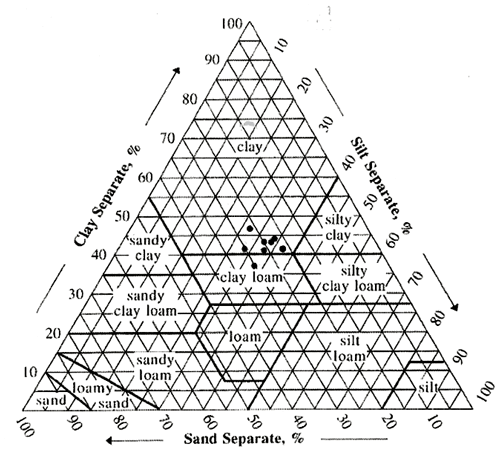
Figure 2The mechanical composition (soil texture triangle) of soil at the research site. The depth range of the travertine layer is from 110 cm at the southern edge to 55–60 cm at the northern edge of the site (Fig. 3).
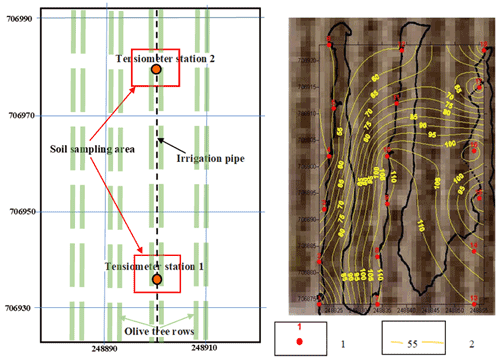
Figure 3Depth of the travertine layer from the soil surface in centimeters (background aerial photo is an insert from Fig. 1; orthophoto). 1 – lithological borehole; 2 – isoline of travertine layer depth from the soil surface.
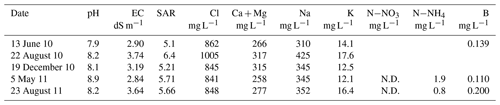
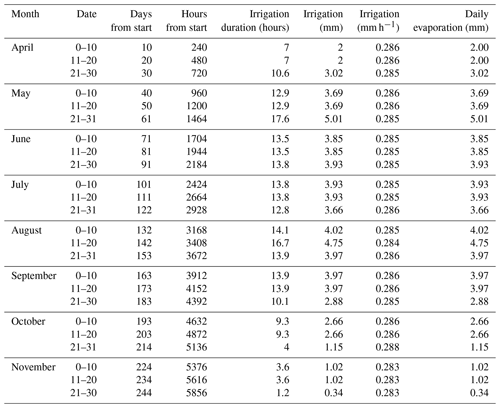
The Kibbutz Meirav olive plantation irrigation water quality test results for different seasons during the study period are presented in Table 1. The main irrigation water sources in the area are Jordan River water and local groundwater whose salinity and SAR (sodium adsorption ratio) are very high, mainly due to high sodium chloride concentrations (Flexer et al., 2006). The chloride concentration is in a range of 800–1700 mg L−1 and electrical conductivity is above 3.5 dS m−1. Local authorities intend to dilute the local water with effluent water and reduce the chloride concentration in the water to 800 mg L−1. The acceptable amount of irrigation from May to November is 0.285 mm h−1.
The olive plantation drip irrigation regime in one extension along the row that was used for the study calibration was 1 L s−1 every 40 cm daily, with a cumulative water amount from April to November (harvest) between 631 and 1272 m3 per 1000 m2. Nitrogen fertilizer given by dosing pumps was 15–20 kg for the season regardless of the amount of water.
2.2 Research methodology
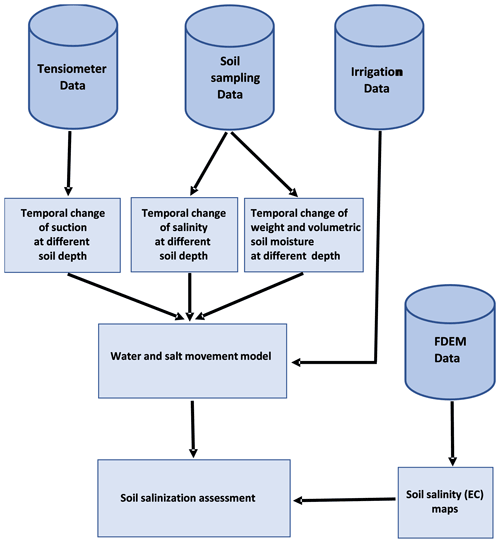
This study integrates field experiments with water and salt movement models in the unsaturated soil strata. Field experiments including a remote sensing method (FDEM) were utilized to supply the required data for water and salt movement modeling and soil salinity mapping during soil salinization monitoring under different irrigation conditions (Corwin and Lesch, 2005). The suction and soil moisture monitoring during the irrigation period was conducted near two tensiometer stations characterizing suction and soil moisture conditions. The first station characterized irrigation by about 80 % of the acceptable amount of irrigation (lack of water) and the second station characterized irrigation by about 120 % of the acceptable amount of irrigation (excess water). The field experiment was conducted in spring before the beginning of summer irrigation, which made it possible to evaluate the soil salinization dynamics when water enters practically dry soil after winter precipitation salt washing. The experiment included soil sampling to measure soil moisture and soil salinity coupled to FDEM mapping. The integration of the various data processing types and modeling finally yielded a soil salinization spatial–temporal illustration of the different irrigation regimes (Fig. 4).
2.3 Research procedures
2.3.1 Soil suction monitoring
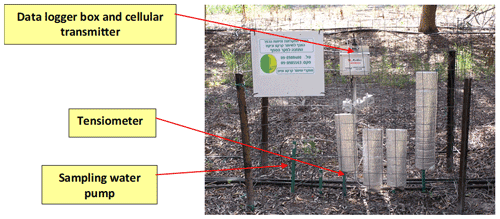
Continuous soil suction monitoring included two transmitting tensiometer stations (Mottes Tensiometers, Ltd.). The two stations were installed 50 m from each other. At each station, four tensiometers were installed, measuring the soil suction at depths of 20, 40, 60, and 70 cm from the soil surface and under the olive tree rows. The tensiometer system sampled soil suction values (in mBar) every 30 min that were transmitted to the company's website (https://www.tensiograph.com/?action=lang=en, last access: 12 June 2021) every 4 h, enabling online data availability through a client interface. During the study, selected soil solution samples were pumped from the tensiometers and analyzed at the lab (Fig. 5).
2.3.2 Soil salinity and moisture monitoring
Soil moisture and salinity monitoring were made by simultaneous soil sampling every 2 weeks from September until December 2011. Soil samples were taken at depths of 0–20, 40–60, 20–40, and 70 cm or down to the depth of the travertine layer. Drilling was done along the olive rows between the trees. Each sample characterized a particular tensiometer depth as well as the distance from the irrigation pipe and closest dripper. The laboratory salt composition delineation included electrical conductivity (EC), saturation percentage (SP), sodium adsorption ratio (SAR), Na, Ca+Mg, Cl, and SO4 ion concentrations, general chalk, mechanical composition, and soil moisture. Soil moisture weight is calculated by subtracting the weight of the dry soil from the weight of the moist soil and then dividing by the weight of the dry soil, which is expressed by a unitless fraction number.
2.3.3 Field experiment
From 22 to 28 March 2011, a field experiment was conducted with the purpose of obtaining soil salinity parameters before the irrigation season. These parameters were needed to build and adapt the moisture and salt motion model for the upper soil unsaturated layer. The experiment included moisture and salinity measurements through manual soil sampling and FDEM soil salinity mapping. Near each tensiometer station, three control lines were marked perpendicular to the dripper line, whereas the line center was positioned near the dripper. Near the first tensiometer station, the distance between the control lines (1A, 1B, 1C) was 50 cm, and near the second tensiometer station (2A, 2B, 2C) it was 40 cm (according to distance changes between the drippers so that each control line was extended from the middle between the three rows). Soil sampled for laboratory salt composition and moisture tests was taken for each control line, at a central point adjacent to the dripper, and 30, 80, 180, and 330 cm distances from the central sampling point on both sides. Together with soil sampling, values of soil suction from the tensiometers were also measured. The first soil sampling was done at 08:30 UTC+2 before irrigation on control lines 1A and 2A. At 09:00 UTC+2, drip irrigation began with an intensity of 1.6 L h−1 and stopped at 10:15 UTC+2. At 12:15 UTC+2 immediately after the irrigation finished (2 h after irrigation commences), sampling was done on lines 1B and 2B at the central point and 30 cm distance from it on both sides. On 23 and 24 March, a total of 30 mm of rain fell, which was recorded by the rainfall automatic monitoring system.
2.3.4 FDEM measurements and mapping of soil electrical conductivity
Measurements were done along the control lines and in the area between the tree row in the experiment site. Three measuring lines with 7 m length were spaced 0.5 m apart near the first tensiometer station. The measurement lines were made perpendicular to the irrigation dripper pipeline. Mapping was done after 3 h of irrigation. The device was hung by a strap at the height of 1 m above the ground, with the operator walking along the sampling lines without stopping within the line. Five frequency channels (62525, 22075, 7825, 2275, and 975 Hz) were used for characterizing soil layer depth intervals at 0–30, 0–45, 0–60, 0–75, and 0–100 cm, respectively. Interpolation and spatial soil salinity mapping (in EC, dS m−1) were performed using SURFER software (Surfer Ver. 7.02, 2000).
2.3.5 Water and salt movement mode development and application for soil salinization assessment and prediction
The water and salt movement model in the upper unsaturated soil layer and up to the travertine layer was made in the HYDRUS 1D software. The one-dimensional model characterizes the cross section to a depth of 60 cm above the travertine layer.
The water and salt movement, a basic mathematical model of one-dimensional equations for an unsaturated soil state, was
where W is volumetric moisture, H is suction, K(W) is hydraulic conductivity of unsaturated soil state, E is plant root moisture absorption function, Ks is hydraulic conductivity of soil in a saturated state, C is soil solution salt concentration, D∗ is the soil salt diffusion coefficient, S is the soil salt absorbing (or releasing) function because of moisture changes, and t is time.
The hydraulic model used was the van Genuchten–Mualem (no hysteresis) single porosity model (van Genuchten, 1980). As a soil salinization model, Crank–Nicolson was used as a time weighting scheme (Crank and Nicolson, 1947) and the Galerkin finite scheme (Fletcher, 1983) was used for a space weighting scheme equilibrium model. For water movement relation with the root zone, the Feddes water uptake reduction model (Feddes et al., 2001) was used, with maximum concentration to passive root solute uptake of 0.5 (cRoot). The one-dimensional model calculated the volumetric moisture and total salinity in a soil profile down to the model's lower boundary. In the HYDRUS 1D software, the unsaturated layer parameters are automatically determined by the soil type. The lower boundary of the water movement model was calculated as a constant flow along with the travertine layer.
The irrigation input to the soil profile through the model's upper boundary was calculated as the water supply according to an incremental irrigation regime. Evapotranspiration and transpiration values as well as root zone activity were determined from the field data and changed during the irrigation season. The models were calibrated according to the field experiment data. The calibrated model was used to assess and predict soil salinization due to irrigation with different water quality: 3.13 dS m −1 (available today), 1.5 dS m −1 (potable water), and 5.5 dS m −1 (brackish water). The time step of the model was a month, and the salinity and moisture distributions during this month were used as the initial conditions for the following month.
3.1 Soil moisture and salinization dynamics in the autumn following the intensive summer irrigation
Near the first tensiometer station at a depth of about 60 cm of the travertine layer and irrigation by about 80 % of the acceptable amount of irrigation (lack of water), the soil salinity was about 11–12 dS m −1 in the soil profile in September (Fig. 6). After the last irrigation cycle at the beginning of October, the soil salinity decreased to 4–8 dS m −1 throughout the soil profile, especially in the top layer. Soil weight moisture increased from 0.22–0.25 to 0.33 at the top of the soil profile. Then, before the rainfall in mid-December, soil salinization gradually increased, and the most intense salinization growth to 14 dS m −1 was found in the upper layer (0–20 cm) of soil. The weight moisture values gradually decreased to 0.2–0.25, whilst the highest values were noted in the upper layer of the soil profile.
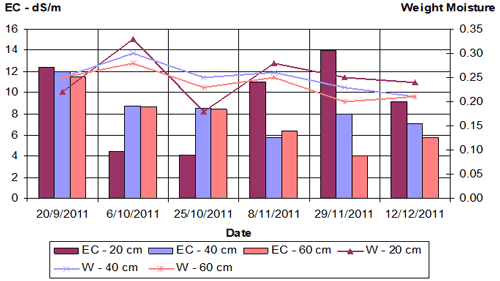
Figure 6Changes in soil salinity (EC) and soil weight moisture (W) during the autumn near the first tensiometer station.
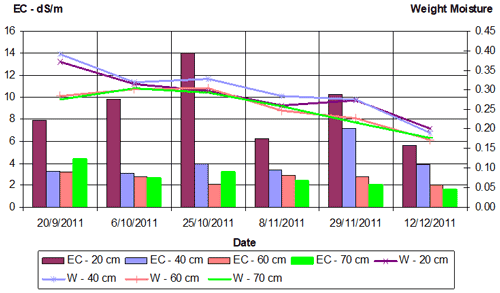
Figure 7Changes in soil salinity (EC) and soil weight moisture (W) during the autumn near the second tensiometer station.
Near the second tensiometer station with a travertine layer depth of about 70 cm and irrigation by about 120 % of the acceptable amount of irrigation (excess water), soil salinity was lower: between 2.0 and 4.0 dS m −1. In the upper layer (0–20 cm), soil salinity exceeded 6 dS m −1, and after the last irrigation cycle at the beginning of October, it increased to 14 dS m −1 with a gradual decrease to previous values during November–December. The moisture weight values were almost the same throughout the soil profile and gradually decreased from 0.35 to 0.2 during the monitoring period.
The SAR values under irrigation conditions of about 80 % of the acceptable amount of irrigation ranged from 4 to 12. The SAR values increased with soil profile depth. Under irrigation conditions of about 120 % of the acceptable amount of irrigation (excess water), SAR values were found to be lower, ranging from 3 to 6, with an increase toward the upper soil layer.
Near the first tensiometer station with a depth of about 60 cm of the travertine layer and irrigation by about 80 % of the acceptable amount of irrigation (lack of water) at the end of September, the chloride concentration was high throughout the soil profile and ranged from 3200 to 3500 mg L−1. At the end of the irrigation period, the chloride concentration again increased to a range of 3500–4000 mg L−1 in the upper layer (20 cm). After the last irrigation cycle at the beginning of October, the chloride concentration decreased to 1000 mg L−1 in the upper layer (20 cm). After the end of irrigation, the chloride concentration again increased to a range of between 3500 and 4000 mg L−1 in this layer. The sulfate concentration hardly changed and ranged from 300 to 550 mg L−1 throughout the soil profile.
Near the second tensiometer station with a travertine layer at a depth of about 70 cm and irrigation of about 120 % of the acceptable amount of irrigation (excess water), chloride concentrations were found to be lower, ranging from 400 to 3000 mg L−1 during the study period. The chloride concentration increased during irrigation and decreased at the end of irrigation in the deeper soil layers. No clear relationship was found between the chloride concentration and the soil moisture. The sulfate concentration ranged from 100 to 600 mg L−1 throughout the soil profile.
The amount of general chalk in the soil was very high and hardly changed during the study period. The amount of general chalk ranged from 70 % to 85 % and did not depend on soil moisture and irrigation regime.
3.2 Assessment of drip irrigation effect on soil salinization
The soil suction that was measured in situ using the first tensiometer station is shown in Fig. 8. In station 1, the soil suction before irrigation varied from 140 to 300 mbar depending on the depth of the measured soil layer, while after irrigation it dropped to 40–130 mbar. Due to the highest moisture, the maximal soil suction decrease was observed in the upper soil layer (0–20 cm), while in the upper soil layer (0–20 cm) sinusoidal oscillations were observed due to daily (day–night) changes in temperature and humidity. At other depths, once settled, the suction had a small tendency to increase during the study period.
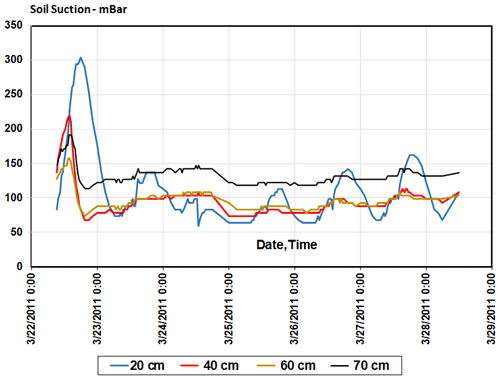
Figure 8Soil suction on the different depths of the soil profile measured at the first tensiometer station.
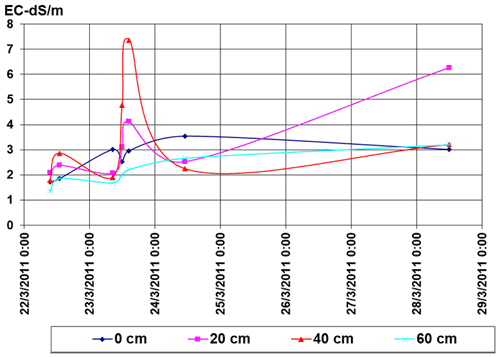
Laboratory soil salinity measurements characterized the dissolved salt concentration in the soil saturated solution near the drippers. Soil salinity near the first tensiometer station ranged from 1.5 dS m−1 before irrigation to 7.5 dS m−1 after 22 h from when irrigation commenced. Salinity differences by depth are irregular, but the rain event on 23 March 2011 was noticed at 40 cm and the increase of 20 cm during the following days may indicate capillary movement (Fig. 9).
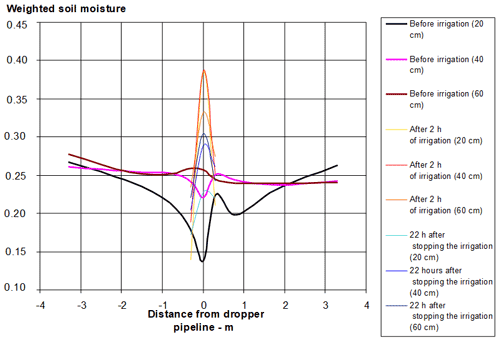
The highest soil salinity from 4.1 to 7.4 dS m −1 was detected at depths of 20–40 cm. The presence of a salinization peak in the soil layer at a depth of up to 40 cm was associated with the leaching of salts to a depth with irrigation water. The subsequent increase in salinization of the upper soil layer was caused by the evaporative concentration of salts at the soil surface. SAR values varied from 9±1 to 3±1 depending on the depth of the soil layer, and its distribution was like the salinity distribution. Active chalk values ranged from 15 %–20 % to 30 %–33 %, with higher concentration at a depth of 20–60 cm, which did not change during the experiment. Weighted soil moisture ranged from 0.14 to 0.36, which increased with depth.
During the study, the period-averaged weighted soil moisture varied from 0.25 to 0.30, with a dependency on distances from the dripper with an affected radius of up to 30 cm. Soil moisture increased with irrigation right away in the upper soil layer under the dripper from 0.14 to 0.37 after 2 and 22 h; after irrigation stopped it decreased to 23 % (Fig. 10).
3.3 Soil salinity mapping using FDEM device
EC values obtained from FDEM measurements characterize the dissolved salt amount and soil moisture. The maps show the salt flushing area progressing to a depth of 50–60 cm (Fig. 11). The salt flushing area width was about 0.5 m, demonstrating EC lower than 2 dS m−1 and reaching EC values of 2.5 dS m−1 between rows. At a depth of 60–80 cm, the soil salinity had a maximum of 2.5–3.0 dS m−1. The travertine layer from a depth of 80 cm is probably dry, which does not enable ion movement; this appears as very low salinity values. This suggests that for matching EC values with laboratory results, the FDEM strata should be in full saturation conditions (ECsat). Otherwise, the correlation between soil moisture and salinity is necessary. This relationship depends on the lithological and chemical composition of the local soil profile. Figure 12 shows the correlation between the ratio of laboratory EC measurements (ECsat) to FDEM EC measurements and weighted soil moisture according to soil characteristics of the study site.
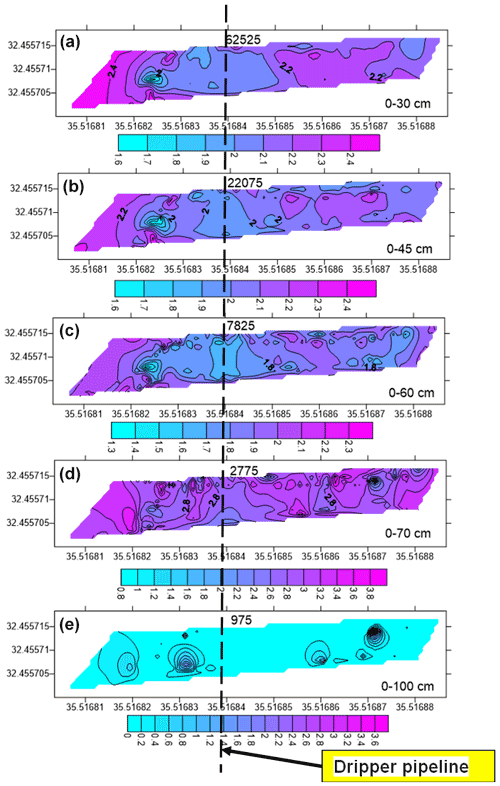
Figure 11FDEM EC values for the different depths of the soil profile from the soil surface: (a) up to 30 cm; (b) up to 45 cm; (c) up to 60 cm; (d) up to 70 cm; (e) up to 100 cm.
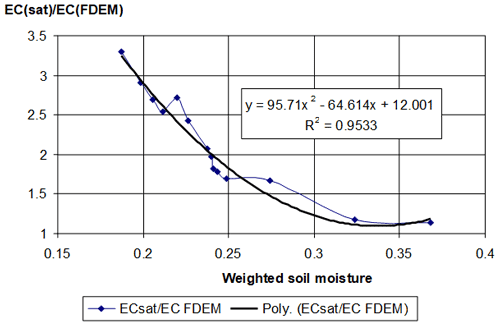
Figure 12Correlation between the ratio of EC (sat) to EC FDEM and the weighted soil moisture at the Kibbutz Meirav mature olive plantation test site.
Thus, under a weighted soil moisture content of 0.2, the EC values obtained using the FDEM device (EC FDEM) will be approximately 3 times lower than those measured in the soil saturation extract laboratory measurements (EC (sat)). Provided the weighted soil moisture is greater than 0.32, EC measurements using FDEM would be close to the laboratory soil test results.
3.4 Water and salt movement modeling for soil salinization prediction of different irrigation water quality
Fitting the model to the study site conditions was based on comparing the model calculation results with measurements taken during the field experiment. The comparison was made for soil volumetric moisture and soil salinity values in EC. The best fit between model calculation and soil mechanical composition field measurements was obtained for the silty clay type soil (Fig. 2). The volumetric moisture model calibration was like the calculated results (Fig. 13). The hydraulic conductivity of the soil saturated conditions according to the model was 0.02 cm h−1.
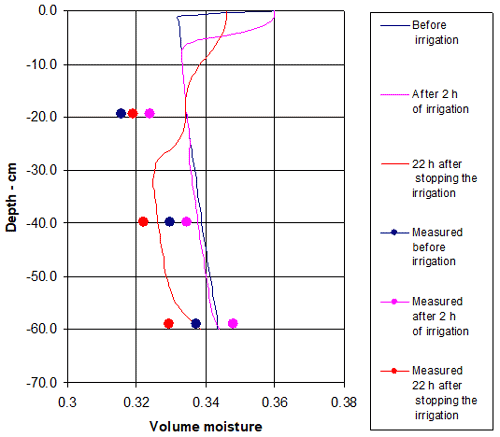
Figure 13Comparison of volumetric moisture values measured in a study section with computerized values in the model. Model calibration results.
Differences between soil volumetric moisture measured in the field and calculated in the model were maximal −0.0187 (5.9 % of the measured), minimal −0.0029 (0.88 %), and on average −0.0077 (2.39 %). The soil salinity values calculated in the model were similar to the salinity distribution obtained from the soil samples at the study site. However, differences between soil salinity measured in the field and the one calculated in the model ranged from 34 % to 11 % and were on average −28.8 % (1.08 (dS m−1)). This is because the soil salt movement model did not include the salts' release and absorption processes in the soil. Soil suction, according to the calibrated model calculations, decreased in the upper soil layer (up to 20 cm of depth) immediately after the irrigation began.
In deeper layers, it started after 2 h, while 12 h after irrigation ended soil suction began to rise owing to soil drying. Changes in volume soil moisture were consistent with changes in soil suction. Moisture increased immediately after irrigation in the upper soil layer from 0.33 to 0.36 almost to a saturated state. After 2 h (end of irrigation) the moisture began decreasing. The results in the model show that in the deep layers (below 30 cm from the soil surface) the moisture continued to decrease, probably due to a rather small amount of water and irrigation span. As a result of irrigation by relatively saline water (3.13 dS m−1), soil salinity (salt concentration) increased in the upper soil layer (up to 30 cm of depth) but decreased at the bottom of the soil profile (Fig. 14). In both model and field measurements, the border between these opposite salinity dynamics approximately corresponded to the root system depth, as intensive development of trees appears at depths below 35 cm.
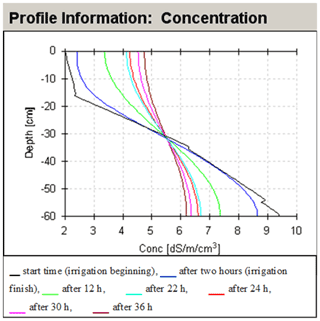
Figure 14Changes in soil salinity in the soil profile calculated in the model. Calibration results of the model.
Figure 15 shows the process of salts accumulating (or washing away) at the model's outer boundaries. Near the soil surface at the TOP boundary, the salt concentration initially decreased due to soil washing by irrigation, and after irrigation finished it gradually increased over 36 h owing to evaporation from 2.5 to 4.7 dS m−1. At the root zone bottom (ROOT boundary), the salt concentration was constant, with a small tendency to decrease. The salt concentration at the lower model boundary (BOT) gradually decreased from 9.2 to 6.2 dS m−1, which is probably related to the horizontal movement of water together with dissolved salts from the dripper to the travertine layer.
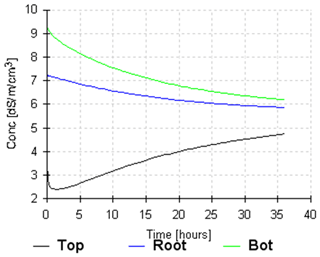
Figure 15Changes in salt concentration calculated in the model at the upper model boundary (TOP), at the root zone bottom (about 35 cm from the ground surface) (ROOT), and the lower model boundary (BOT).
The soil-salinity-calibrated model simulates soil salinity patterns, with different water quality irrigation between April and December. The data input to the model for calculating the irrigation duration per day and daily evapotranspiration included the olive plantation irrigation and daily evaporation as well as evapotranspiration from the Eden Farm meteorological station (Table 2).
Initial salt concentration values in the model soil profile (the 1 April) were taken from the field experiment soil sampling results. Soil profile and salt accumulation predictions during the irrigation season show that under current water quality conditions (3.13 dS m−1) soil salinity may rise to 15–16 dS m−1 (Fig. 16a). The most intense soil salinity change from 2.0 to 4.0 dS m−1 per month was in June, immediately after irrigation increased. The model calculation results are consistent with soil salinity monitoring during 2011 (Fig. 6). Irrigation by potable water (Fig. 16b) reduced soil salinity to 7–9 dS m−1.
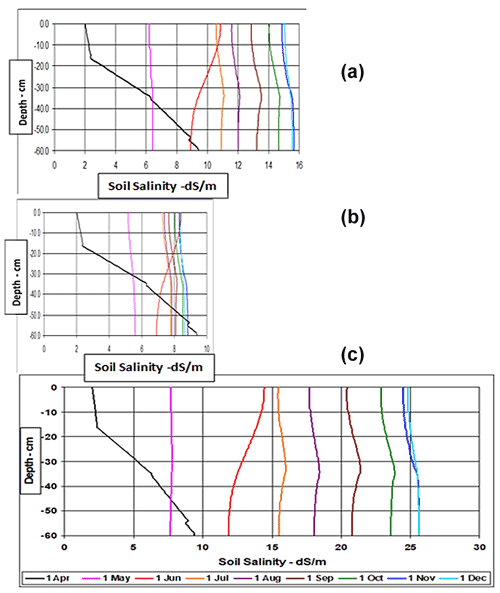
Figure 16Salt accumulation predictions in the soil during the irrigation season under different water salinity: (a) 3.13 dS m−1 (available today); (b) 1.5 dS m−1 (potable water); (c) 5.5 dS m−1 (brackish water).
Irrigation by brackish water during the summer months (Fig. 16c) caused substantial increases in soil salinity, reaching a very high EC value of about 24–26 dS m−1. Irrigating with such water during the summer months might increase EC in 2–3 dS m−1 per month on average owing to salt accumulation in the soil profile. Brackish water irrigation (EC>5 dS m−1) might cause the entire soil profile to turn saline to a point that could harm the trees.
The combined use of various research methods, including soil salinity monitoring, field experiments, remote sensing (FDEM), and water and salt movement modeling in the unsaturated soil profile, allowed salinization process assessment of calcritic soils in an irrigated olive plantation in the Beit She'an Valley. Under the existing drip irrigation regime, water with a dissolved salt content of 3.13 dS m−1, and the presence of an impermeable travertine layer close to the soil surface, the salinization process is characterized by salt accumulation tendency in the trees' upper root zone after the summer irrigation season. During irrigation, the soluble salts are rapidly leached in the soil layer upper 20–30 cm down to the dripper depth and sides. However, within 24 h after the irrigation cycle completion, as the soil dries through evapotranspiration the soil salinity level near the surface begins to increase again.
The FDEM device made it possible to study the dissolved salts' spatial distribution and concentration, with reference to the soil's existing weight moisture distribution at the time of measurement. The FDEM EC maps show the salt flushing area development at a depth of 50–60 cm and a width of ∼50 cm. The soil salinity and moisture field sampling combination and the FDEM measurements demonstrated correlation in EC for a given soil type. This relationship indicates that the soil FDEM salinity mapping accuracy and cost-effective upscaling potential will probably turn it into a standard method in future agriculture.
The one-dimensional model created for water and dissolved salt transport showed the danger of using brackish water for irrigation. Since soil salinization exceeds an acceptable level for trees, the use of potable water for irrigation, if possible, will help to reduce soil salinization. To enable a tailor-made irrigation scheme, a database including changes in physical and chemical parameters affecting soil salting processes should be established, which will enable contemporary mapping and salinity forecasting as well as the effect of hydrochemical factors on various soil and irrigation conditions for the database-specific region.
Data and code are available in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-15-129-2022-supplement.
VM designed and carried out the field experiments and performed the HYDRUS simulations. NG designed and carried out the field experiments and performed measurements and mapping of the soil electrical conductivity using an FDEM device. AA did the irrigation data processing, and YA analyzed the results and prepared the paper with contributions from all co-authors.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is based on the results of scientific research carried out as
project 855-0066-12 “Identification and assessment of soil salinization
risk as a result of agricultural activity in the Beit She'an Valley” by a
team of researchers and technical personnel of the Soil Erosion Research
Station of the Ministry of Agriculture and Rural Development (MOAG), Israel:
Vladimir Mirlas (main researcher), Naftaly Goldshleger (researcher), Asher Aizenkod (researcher, field survey center, MOAG), Roei Ben-Binyamin (technician), Yochai Barnay-Betsalel and Moshe Gottesman (technicians), and Ivan Sapogineth (technician, the Eastern R&D Center, Ariel University).
The authors particularly thank the technical team of
the SERS and the Eastern R&D Center, Ariel University: Roei Ben-Binyamin,
Yochai Barnay-Betsalel, Moshe Gottesman, Efraim Fizik, and Ivan Sapogineth for their
assistance in the field investigations.
The authors wish to thank David Wilson, Ruishan Chen, Douglas Karlen, and
also the two anonymous reviewers for their helpful contribution to the
paper.
The paper is dedicated to our friend Naftali Goldshleger, who passed away in 2019.
This research has been supported by the Ministry of Agriculture and Rural Development (MOAG), Israel (grant no. 855-0066-12), and the Jewish National Fund (KKL–JNF) (grant no. 855-0066-12).
This paper was edited by Bethanna Jackson and reviewed by two anonymous referees.
Abu Awward, A., M.: Influence of different water quantities and qualities on lemon trees and soil salt distribution at the Jordan Valley, J. Agricultural Water Management, 52, 53–71, 2001.
Bear, J.: Dynamics of Fluid in Porous Media, Elsevier, New York, NY, 39–63, 1972.
Ben Dor, Y., Metternicht, G., Goldshleger, N., Mor, E., Mirlas, V., and Basson, U.: Review of remote sensing-based methods to assess soil salinity, in: Remote sensing of soil salinization, Impact on land management, edited by: Metternicht, G. and Zinck, J. A., CRC Press, Taylor and Francis Group, LLC, New York, USA, 39–63, https://doi.org/10.1201/9781420065039, 2009a.
Ben Dor, Y., Goldshleger, N., Mor, E., Mirlas, V., and Basson, U.: Combined active and passive remote sensing methods for assessing soil salinity: a case study from Jezre'el Valley, Northern Israel, in: Remote sensing of soil salinization, Impact on land management, edited by: Metternicht, G. and Zinck, J. A., CRC Press, Taylor and Francis Group, LLC, New York, USA, 236–253, https://doi.org/10.1201/9781420065039, 2009b.
Benyamini, Y., Marish, S., Mirlas, V., and Gotesman, M.: Soil Salinization and Rehabilitation, in: Proc., The Ann. Meeting, 22–24 March 1998, Israel Geog. Soc., Tel-Aviv, Israel, 128–129, 1998.
Benyamini, Y., Marish, S., Mirlas, V., and Gotesman, M.: Impact of Subsurface Drainage on Groundwater Regime in Irrigated Fields in Israel, in: Proc. Inter. Conf. “Water and Environment: Resolving Conflicts in the Development of Dry Lands”, Beer-Sheba, The Center for Water Science and Technology (CWST), Ben-Gurion University of the Negev, Israel, 4–7 June, 56–57, 2000.
Benyamini, Y., Mirlas, V., Marish, S., Gotesman M., Fizik, E., and Agassi, M.: A survey of soil salinity and groundwater level control systems in irrigated fields in the Jezre'el Valley, Israel, J. Agricultural Water Management, 76, 181–194, 2005.
Bhardwaj, A. K., Mandal, U. K., Bar-Tal, A., Gilboa, A., and Levy, G. J.: Replacing saline-sodic irrigation water with treated wastewater: effects on saturated hydraulic conductivity, slaking and swelling, J. Irrigation Science, 26, 139–146, 2008.
Boone, A., Samuelsson, P., Gollvik, S., Napoly, A., Jarlan, L., Brun, E., and Decharme, B.: The interactions between soil–biosphere–atmosphere land surface model with a multi-energy balance (ISBA-MEB) option in SURFEXv8 – Part 1: Model description, Geosci. Model Dev., 10, 843–872, https://doi.org/10.5194/gmd-10-843-2017, 2017.
Celia, M. A., Bououtas, E. T., and Zarba, R. L.: A general mass-conservative numerical solution for the unsaturated flow equation, Water Resour. Res., 26, 1483–1496, 1990.
CIA: The world factbook, Israel, picture inventory, available at: https://www.cia.gov/the-world-factbook/countries/israel/, last access: 12 June 2021.
Corwin, D. L. and Lesch, S. M.: Apparent soil electrical conductivity measurements in agriculture, Computer Electronics in Agriculture, 46, 11–43, 2005.
Crank, J. and Nicolson, P.: A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type, P. Camb. Philos. Soc., 43 pp., 50–67, 1947.
Farifteh, J., van der Meer, F., Atzberger, C., and Carranza, E. J. M.: Quantitative analysis of salt-affected soil reflectance spectra: A comparison of two adaptive methods (PLSR and ANN), Remote Sens. Environ., 110, 59–78, 2007.
Feddes, R., Hoff, H., Bruen, M., Dawson, T., de Rosnay, P., Dirmeyer, P., Jackson, R. B., Kabat, P., Kleidon, A., Lilly, A., and Pitman, A. J.: Modeling root water uptake in hydrological and climate models, B. Am. Meteorol. Soc., 82, 2797–2809, https://doi.org/10.1175/1520-0477(2001)082<2797:MRWUIH>2.3.CO;2, 2001.
Fletcher, C.: Computational Galerkin Methods, Springer-Verlag New York Inc, 303 pp., https://doi.org/10.1007/978-3-642-85949-6, 1983.
Flexer, A., Anker, Y., Davidson, L., Rosenthal, E., Yellin-Dror, A., and Guttman, J.: Groundwater salinization in the Jordan Valley – Quo Vadis, in: Water in the Middle East, edited by: Hambright, K. D., Ragep, F. J., and Ginat, J., University of Oklahoma Press: Norman, 100–110, 2006.
Gafni, A. and Salinger, Y.: Hydraulic and salinity regime of two affected sites in the Jezre'el Valley, Israel, J. Hydrol. Proc., 6, 55–65, 1992.
Garrigues, S., Olioso, A., Carrer, D., Decharme, B., Calvet, J.-C., Martin, E., Moulin, S., and Marloie, O.: Impact of climate, vegetation, soil and crop management variables on multi-year ISBA-A-gs simulations of evapotranspiration over a Mediterranean crop site, Geosci. Model Dev., 8, 3033–3053, https://doi.org/10.5194/gmd-8-3033-2015, 2015.
Guimberteau, M., Zhu, D., Maignan, F., Huang, Y., Yue, C., Dantec-Nédélec, S., Ottlé, C., Jornet-Puig, A., Bastos, A., Laurent, P., Goll, D., Bowring, S., Chang, J., Guenet, B., Tifafi, M., Peng, S., Krinner, G., Ducharne, A., Wang, F., Wang, T., Wang, X., Wang, Y., Yin, Z., Lauerwald, R., Joetzjer, E., Qiu, C., Kim, H., and Ciais, P.: ORCHIDEE-MICT (v8.4.1), a land surface model for the high latitudes: model description and validation, Geosci. Model Dev., 11, 121–163, https://doi.org/10.5194/gmd-11-121-2018, 2018.
Katz, H., Farber, R., Chaniel, G., Ankar, Y., Cohen, H., and Cahan, R.: Rhamnolipid-enhanced Pseudomonas putida biofilm formation on hydrophilic surfaces with toluene as the bacterium's sole carbon source, Int. Biodeterior. Biodegr., 127, 87–94, https://doi.org/10.1016/j.ibiod.2017.11.019, 2018.
Kool, J. B., Parker, J. C., and van Genuchten, M. T.: Determining soil hydraulic properties from one-step outflow experiments by parameter estimation: I, Theory and numerical studies, Soil Sci. Soc. Am. J., 49, 1348–1354, 1985.
Kruseman, G. P. and De Ridder, N. A.: Analysis and Evaluation of Pumping Test Data, International Institute for Land Reclamation and Improvement/ILRI, Wageningen, International Institute for Land Reclamation, The Netherlands, 18–20 pp., 1976.
Leij, F. G., Skaggs, T. H., van Genuchten, M. T.: Analytical solutions for solute transport in three-dimensional semi-infinite porous media, Water Resour. Res., 27, 2719–2733, 1991.
Machado, R. M. A. and Serralheiro, R.: Soil Salinity: Effect on Vegetable Crop Growth, Management Practices to Prevent and Mitigate Soil Salinization, Horticulturae, 3, 30, https://doi.org/10.3390/horticulturae3020030, 2017.
Mandal, U. K., Bhardwaj, A. K., Warrington, D. N., Goldstein, D., Bar-Tal, A., and Levy, G. J.: Changes in soil hydraulic conductivity, runoff, and soil loss due to irrigation with different types of saline-sodic water, Geoderma, 144, 509–516, 2008a.
Mandal, U. K., Warrington, D. N., Bhardwaj, A. K., Bar-Tal, A., Kautsky, L., Minz, D., and Levy, G. J.: Evaluating impact if irrigation water quality on a calcareous clay soil using principal component analysis, Geoderma, 144, 189–197, 2008b.
Mirlas, V.: Assessing soil salinity hazard in cultivated areas using MODFLOW model and GIS tools: A case study from the Jezre'el Valley, Israel, J. Agriculture Water Management, 109, 144–154, 2012.
Mirlas, V., Benyamini, Y., Gottesman, M., Fizik, E., and Agassi, M.: Long-term changes in groundwater regime of a semi-confined aquifer in Jezre'el Valley, Israel, J. Soil Water Conserv., 1, 98–112, 2006a.
Mirlas, V., Benyamini, Y., Miron, M., Peres, M., and Yasur, E.: Development of groundwater flow and salt transport models for the non-saturation zone of the soil in the Hula Valley, Annual meeting of the Israel Geography Society, 1–3 January 2006, Jerusalem, Israel, 63–64, 2006b, (in Hebrew).
Mohammad, M., J. and Mazahreh, N.: Changes in soil fertility parameters to irrigation of forage crops with secondary treated wastewater, J. Communication in Soil Science and Plant Analysis, 34, 1281–1294, 2003.
Pandit, R., Parrotta, J. A., Chaudhary, A. K., Karlen, D. L., Mascia Vieira, D. L., Anker, Y., Chen, R., Morris, J., Harris, J., and Ntshotsho, P.: Responses to halt land degradation and to restore degraded land, in: IPBES Assessment Report on Land Degradation and Restoration, edited by: Montanarella, L., Scholes, R. J., and Brainich, A., 435–528, UNEP, UNDP, FAO, Geneva, United Nations, 2018.
Pandit, R., Parrotta, J. A., Chaudhary, A. K., Karlen, D. L., Luis, D., Vieira, M., Anker, Y., Chen, R., Morris, J., Ntshotsho, P., Pandit, R., Parrotta, J. A., Chaudhary, A. K., Douglas, L., Luis, D., Vieira, M., Anker, Y., Chen, R., Morris, J., and Harris, J.: A framework to evaluate land degradation and restoration responses for improved planning, Ecosyst. and People, 15, 1–18, 2020.
Simunek, J. and van Genuchten, M. T.: Numerical model for simulating multiple solute transport in variably-saturated soil, in: Proc. “Water Pollution III: Modeling, Measurement, and Prediction”, edited by: Wrobel, L. C. and Latinopoulos, P., Computation Mechanics Publ, Ashurst Lodge, Ashjur, Southamption, UK, 21–30, 1995.
Simunek, J., Sejna, M., and van Genuchten, M. T.: The HYDRUS-1D software package for simulating the one-dimensional movement for water, heat, and multiple solutes in variably-saturated media, version 2.0, IGWMC-TPS 70. U.S., Salinity laboratory, Agricaltural Research Service, U.S. Department of Agriculture, Riverside, California, 1998.
Surfer Ver.7.02, Surface Mapping System, Golden Software, Inc., available at: https://www.goldensoftware.com/products/surfer (last access: 12 June 2021), 2000.
Survey of Israel, National orthophoto layer 0.5 m resolution, available at: https://www.govmap.gov.il/?c=204000,595000&z=0&b=2, last access: 6 December 2021.
Toride, N., Leij, F. J., and van Genuchten, M. T.: A comprehensive set of analytical solution for no equilibrium solute transport with first-order decay and zero-order production, Water Resour. Res., 29, 2167–2182, 1993.
van Genuchten, M. T.: A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils, J. Soil Science Society of America, available at: https://doi.org/10.2136/sssaj1980.03615995004400050002x, 1980.
van Genuchten, M. T.: A numerical model for water and solute movement in and below the root zone, Research Report No 121, U.S. Salinity laboratory, USDA, ARS, Riverside, California, 1987.
van Genuchten, M. T. and Wagenet, R. J.: Two-site/two region models for pesticide transport and degradation: Theoretical development and analytical solutions, Soil Sci. Soc. Am. J., 53, 1303–1310, 1989.
Wada, Y., Flörke, M., Hanasaki, N., Eisner, S., Fischer, G., Tramberend, S., Satoh, Y., van Vliet, M. T. H., Yillia, P., Ringler, C., Burek, P., and Wiberg, D.: Modeling global water use for the 21st century: the Water Futures and Solutions (WFaS) initiative and its approaches, Geosci. Model Dev., 9, 175–222, https://doi.org/10.5194/gmd-9-175-2016, 2016.