the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The Grell–Freitas (GF) convection parameterization: recent developments, extensions, and applications
Saulo R. Freitas
Georg A. Grell
Haiqin Li
Recent developments and options in the GF (Grell and Freitas, 2014; Freitas et al., 2018) convection parameterization are presented. The parameterization has been expanded to a trimodal spectral size to simulate three convection modes: shallow, congestus, and deep. In contrast to usual entrainment and detrainment assumptions, we assume that beta functions (BFs), commonly applied to represent probability density functions (PDFs), can be used to characterize the vertical mass flux profiles for the three modes and use the BFs to derive entrainment and detrainment rates. We also added a new closure for nonequilibrium convection that improved the simulation of the diurnal cycle of convection, with a better representation of the transition from shallow to deep convection regimes over land. The transport of chemical constituents (including wet deposition) can be treated inside the GF scheme. The tracer transport is handled in flux form and is mass-conserving. Finally, the cloud microphysics have been extended to include the ice phase to simulate the conversion from liquid water to ice in updrafts with resulting additional heat release and the melting from snow to rain.
- Article
(16812 KB) - Full-text XML
- BibTeX
- EndNote
Convection parameterizations (CPs) are components of atmospheric models that aim to represent the statistical effects of a subgrid-scale ensemble of convective clouds. They are necessary in models in which the spatial resolution is not sufficient to resolve the convective circulations. These parameterizations often differ fundamentally in closure assumptions and parameters used to solve the interaction problem, leading to a large spread and uncertainty in possible solutions.
A seminal work by Arakawa and Schubert (1974) provided the framework upon which numerous CPs were constructed. Following this, new ideas were implemented, such as including stochasticism (Grell and Devenyi, 2002; Lin and Neelin, 2003) and the super parameterization approach (Grabowski and Smolarkiewicz, 1999; Randall et al., 2003), to name a few. An additional complication is the use of convective parameterizations on so-called “gray scales”, which is gaining attention rapidly (Kuell et al., 2007; Gerard et al., 2009; Arakawa et al., 2011; Grell and Freitas, 2014; Kwon and Hong, 2017).
The original Grell and Freitas (2014, hereafter GF2014) scheme was based on a convective parameterization developed by Grell (1993) and expanded by Grell and Devenyi (2002, hereafter GD2002) to include stochasticism by expanding the original scheme to allow for a series of different assumptions that are commonly used in convective parameterizations and that have proven to lead to large sensitivity in model simulations. In GF, scale awareness (following Arakawa et al., 2011) was added for application to gray scales, at which convection is partially resolved. Aerosol awareness was implemented by including a cloud condensation nuclei (CCN) dependence for the conversion from cloud water to rainwater, in addition to using an empirical approach that relates precipitation efficiency to CCN.
The GF has been used operationally in the Rapid Refresh prediction system (RAP; Benjamin et al., 2016) at the Environmental Modeling Center (EMC) at the National Center for Environmental Prediction (NCEP) of the National Weather Service (NWS) in the US, at the Global Modeling and Assimilation Office of NASA Goddard Space Flight Center, and in the Brazilian Center for Weather Forecast and Climate Studies (CPTEC/INPE). Scale awareness was evaluated in a nonhydrostatic global model with smoothly varying grid spacing from 50 to 3 km (Fowler et al., 2016) and also in a cascade of global-scale simulations with uniform grid size spanning from 100 km to a few kilometers using the NASA Goddard Earth Observing System (GEOS) global circulation model (GCM) (Freitas et al., 2018, 2020).
The use of GF in other modeling systems and for other applications required further modifications to represent physical processes such as momentum transport, cumulus congestus clouds, modifications of cloud water detrainment, and better representation of the diurnal cycle of convection. These new features are described in this paper.
In Sect. 2, we will describe the new implementations and options; Sect. 3 will show some results from both single-column models and full 3D simulations, and Sect. 4 will conclude and summarize results.
2.1 The trimodal formulation
The original unimodal steady-state updraft deep plume has been replaced by a trimodal formulation, which allows up to three characteristic convective modes (Johnson et al., 1999): shallow, congestus, and deep. This approach lies between the two extremes of having a single bulk cloud (e.g., Tiedtke, 1989; Grell, 1993, and many others) and a full spectral cloud size approach (e.g., Arakawa and Schubert, 1974; Grell et al., 1991; Grell, 1993; Moorthi and Suarez, 1992; Baba, 2019). To be clear, we are not claiming to represent three plumes, but BFs characterizing plumes. For example, the BF for deep convection is a statistical average of deep plumes in the grid box and may include impacts from several plumes.
Each mode of our trimodal formulation is characterized by a BF that determines average lateral mixing. For each mode we assume a characteristic initial gross lateral entrainment rate to represent an approximate size of one of the three modes of convection in the grid box. Section 2.2 provides details on this formulation, including how the entrainment and detrainment rates (lateral mixing) are derived from the BFs. The deep and congestus modes are accompanied by convective-scale saturated downdrafts sustained by rainfall evaporation. Associated with each mode, a set of closures to determine the mass flux at the cloud base was introduced to adequately account for the diverse regimes of convection in a given grid cell. The three modes transport momentum, tracers, water, and moist static energy. For mass and energy, the spatial discretization of the tendency equation is conservative on machine precision. The three modes are allowed to cohabit a given model grid column. The parameterization is performed over the entire spectrum executing first the shallow, next the congestus, and finally the deep mode. In this manner, the convective tendencies resulting from the development of each mode may be applied as a forcing for the next one. In this paper, however, the results shown do not include feedback from the shallower modes. The impacts of a successive application will be looked at in a future study.
2.1.1 Shallow convection
The source parcels for the shallow convecting plumes are defined by mixing the environmental moist static energy (MSE) and water vapor mixing ratio over a user-specified depth layer (currently, the lowest atmospheric layer with 30 hPa depth). Then, an excess MSE and moisture perturbation associated with the surface fluxes are added when calculating the forcing and checking for trigger functions, as described in GF2014. The cloud base is defined by the first model level where the source air parcel lifted from the surface without any lateral entrainment is positively buoyant. Above the cloud base, shallow convection growth and cloud properties will strongly depend on the description of the vertical mass flux distribution and resulting entrainment and detrainment rates. Since the BFs are part of all three types of convection, the method will be described in detail in Sect. 2.2. The shallow convection cloud tops are determined following two criteria. One is defined by the first vertical layer at which the buoyancy becomes negative. The second is defined by the first thermal inversion layer above the planetary boundary layer (PBL) height. The inversion layer is found following two conditions:
- i.
the first derivative (, where is the grid-scale air temperature) must have a local maximum, and
- ii.
the absolute value of the second derivative must be zero (inflexion point).
The effective cloud top is defined by the layer that has the lower vertical height. The closures for the determination of the mass flux at cloud base, suitable for the shallow moist convection regime, are the following.
Raymond (1995) establishes the equilibrium for the boundary layer budget of the moist static energy. In this case, the flux out at the cloud base of shallow convection counterbalances the flux in from surface processes. This closure is called boundary layer quasi-equilibrium (BLQE). The BLQE closure provides a reasonable diurnal cycle of shallow convection over land, as the resulting mass flux at cloud base is tightly connected with the surface fluxes. The equation for the mass flux at cloud base (mb) from this closure reads
where hc and are the in-cloud and environmental moist static energy, respectively, g is gravity, p is pressure, and the integral is determined from the surface to the cloud base. is approximated by the grid-scale moist static energy, and its tendency is given by adding the tendencies from the grid-scale advection, diffusion in the planetary boundary layer, and radiation.
Grant (2001) introduced a closure based on the boundary layer convective-scale vertical velocity (w∗) and the air density at the cloud base (ρ). In this closure, mb is simply given by
Rennó and Ingersoll (1996) and Souza (1999) applied the concept of convection as a natural heat engine to provide a closure for the updraft mass flux at cloud base:
where η is the thermodynamic efficiency, Fin is the buoyancy surface flux, and TCAPE is the total convective available potential energy, which is approximated by the standard convective available potential energy (CAPE) calculated from the vertical level of the air parcel source to the cloud top (Souza, 1999).
2.1.2 Congestus and deep convection
Congestus and deep convection share several properties and will be described together in this section. Both allow associated convective-scale saturated downdrafts (see Grell, 1993, for further details). As for shallow convection, they are distinguished by different characteristic initial gross entrainment rates (see Sect. 2.2) that represent the deep and congestus modes. The cloud bases are found following the same procedure described for the shallow convection. For deep convection, the cloud top is defined by the vertical layer where the buoyancy becomes negative. For congestus convection, the thermal inversion layer closest to the 500 hPa pressure level defines the cloud top for the congestus mode.
The closure formulations to determine the cloud-base mass fluxes for deep convection are described in GD2002. For congestus, the closures BLQE (Eq. 1) and based on w* (Eq. 2) described in Sect. 2.1.1 are available, as is the instability (measured as the cloud work function) removal using a prescribed timescale of 1800 s (see Sect. 2.3 for further details).
2.2 Representation of normalized vertical mass flux profiles
The new version applies analytical beta functions to represent the average statistical mass flux of the plumes. We assume that the average normalized mass flux profiles for updrafts (Zu) and downdrafts (Zd) in the grid box may be represented by a beta function (BF), which is given by
where c is defined below (Eq. 6) as a normalization constant to ensure that the total integral is 1, rk is the location of the mass flux maximum given by the ratio between the pressure depth from which the normalized maximum mass flux of the cloud is in relation to the cloud base related to the total depth of the cloud,
α and β determine the skewness of the function, and Γ is the gamma function. In GF they depend to a large extent on where the maximum of the BF is located. For shallow and congestus convection, the maximum is located towards the cloud base. For shallow convection, it is assumed to be at or just above the level of free convection. For congestus, we assume this level to be higher at half of the congestus cloud depth. For deep convection, this level is given by the level where the stability changes sign; the stability is given by the difference from in-cloud moist static energy and environmental saturation moist static energy. This is equivalent to assuming that the strong increase in static stability at those levels will – statistically – lead to an increase in detrainment and a possible decrease in updraft radius (not necessarily updraft vertical velocity). For deep convection, we assume
Then, α is imply given by
where rkm is the value of rk at the level of maximum mass flux. α and β determine the skewness of the BF. For shallow convection we use β=2.2 and for congestus convection β=1.3. The downdrafts are assumed to reach maximum mass flux – in a statistical sense – at or below cloud base; therefore,
with β=4pstart here as the downdraft originating level.
Once the normalized mass flux profiles are defined, the entrainment and detrainment rates are adjusted accordingly. First, an initial entrainment rate is given that is meant to characterize the type of convection in the grid box. This is assumed to be the initial rate at the cloud base. In the version of the parameterization that is used in the Rapid Refresh hourly update cycle at the National Weather Service of the US (hereafter RAP) and is available to the community using GitHub, we use
for deep, congestus, and shallow convection, respectively, with
where γ,δ represents the entrainment and detrainment rates (m−1). With initial γ, δ, and the PDFs for Zu defined, the effective lateral mixing (given through entrainment and detrainment rates γ∗ and δ∗), in a statistically averaged sense, must be related to the vertical mass flux profiles. They are simply given by
where z is the vertical height and zmax is the vertical height at which the maximum value of Zu is located. A comparison to observed mass flux profiles using a single-column model approach is given in Fig. 4 and described later in this section in more detail.
The use of BFs enables interesting options for introducing completely mass-conserving stochastic parameter perturbations (SPPs) with a possibly significant increase in spread. It may of course also be used for training and tuning purposes. The operational version of the RAP uses the GF scheme with BFs without tuning and so far without any stochastic applications. However, we are also planning on using some of the approaches described next for SPP stochastics in the near future. In the next section we will describe possible ways to apply stochastics and/or use this approach for tuning.
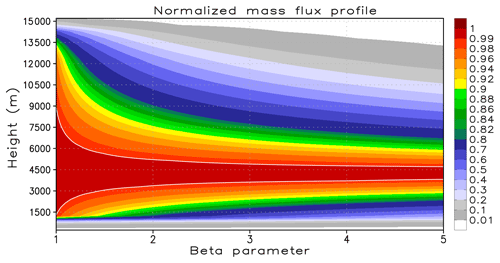
Figure 1The universe of solutions for the normalized updraft mass flux profile (Zu) for a case in which the cloud base resides at 1.2 km of height, the height of maximum Zu is 4.3 km, and the cloud top is at 15.1 km of height. The horizontal axis denotes the range of variation of the beta parameter. The white contour lines delimit the solution domain where .
2.3 Options for stochastic approaches
Following from Sect. 2.2 and Eq. (4), we use the requirement
where rmax relates to the vertical level at which the mass flux profile reaches its maximum value. In this way, the function is unequivocally defined once β and rmax are specified. The two parameters β and rmax may be stochastically perturbed. The rmax is used to move the level of maximum mass flux up or down, and the β is used to define the shape of the profile. The allowed range of the beta parameter is [1, 5]. For example, Fig. 1 introduces the universe of solutions for Zu of the deep convection updraft for a case in which the heights of cloud base, maximum mass flux, and the cloud top are 1.2, 4.3, and 15.1 km, respectively. Choosing β closer to 1 results in a very gentle shape of the mass flux in the troposphere, but with a very sharp increase (decrease) at cloud base (cloud top) with large entrainment (detrainment) mass rates. Increasing β, the profile becomes curved and, above the level of maximum Zu, the detrainment rates dominate over the entrainment. An appropriate choice of the β parameter implies, for example, a more even detrainment of condensate water through the upper troposphere or a sharper, narrower detrainment at the very deep cloud-top layer.
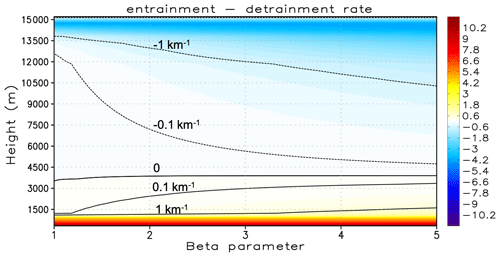
Figure 2The universe of solutions for the effective net mass exchange rate (entrainment – detrainment, km−1) for the case shown in Fig. 1. The black contour lines demark the transition from mostly entraining to mostly detraining plumes.
To give an example, using Eqs. (10) and (11), zmax is defined as 4.3 km in Fig. 1. Figure 2 introduces the difference between the effective entrainment and detrainment rates () for the case shown in Fig. 1. Assuming β closer to 1 implies a very large effective entrainment and detrainment at cloud base and top with very small net mass exchange in between. Increasing β makes the entrainment and detrainment layers wider and smoother.
The above-described options for stochastically perturbing vertical mass flux distributions may also be used in fine tuning of model performance, in particular for operational forecasting applications. Those parameters allow slight changes in the vertical distribution of heating and drying and may be used to improve biases in temperature and moisture profiles. As is the case with parameters and assumptions in convective parameterizations in general, the values proposed in Sect. 2.2 may, of course, not be universal, and optimal values may need adjustments for each host model.
2.4 Diurnal cycle closure
Convection parameterizations based on the use of CAPE for closure and/or trigger function prove difficult in accurately representing the diurnal march of convection and precipitation associated with the diurnal surface heating in an environment of weak large-scale forcing. In nature, shallow and congestus convective plumes start a few hours after sunrise, moistening and cooling the lower and mid-troposphere. These physical processes prepare the environment for the deep penetrative and larger rainfall-producing convection, which usually occurs in the mid-afternoon to early evening. Models, in general, simulate a more abrupt transition, with the rainfall peaking in phase with the surface fluxes, earlier than observations indicate (Betts and Jakob, 2002).
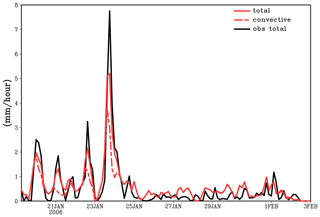
Figure 3Total (red solid), convective (red dashed), and observed total precipitation rates (mm per hour) with the GF scheme using the TWP-ICE soundings.
In addition to a more accurate timing of the precipitation forecast, a realistic representation of the diurnal cycle in a global model should also improve the forecast of the near-surface maximum temperature. Additionally, it improves the subgrid-scale convective transport of tracers, which should be especially relevant for carbon dioxide over vegetated areas. Moreover, as models configured at cloud-resolving scales can intrinsically capture the diurnal cycle of convection, global models with good skill in the diurnal cycle representation should yield a smoother transition from non-resolved to resolved scales. Lastly, it seems plausible that benefits for the data assimilation are also expected with a better diurnal cycle representation.
In the effort to improve the diurnal cycle in the GF scheme, we adopted a closure for nonequilibrium convection developed by Bechtold et al. (2014, hereafter B2014), which, as we further demonstrate, notably improves the simulation of the diurnal cycle of convection and precipitation over land. B2014 proposed the following equation for the convective tendency for deep convection, which represents the stabilization response in the closure equation for the mass flux at cloud base:
where Π is called the density-weight buoyancy integral, and τ and τBL are appropriate timescales. The tendency of the second term on the right side of Eq. (13) is the total boundary layer production given by
where the virtual temperature tendency includes tendencies from grid-scale advection, diffusive transport, and radiation. T∗ is a scale temperature parameter, and the integral is performed from the surface (ps) to the cloud base (pb). The justification for subtracting a fraction of the boundary layer production is that Π already contains all the boundary layer heating but it is not totally available for deep convection.

Figure 4(a) On the left is the two-season mean mass flux associated with all cumulus clouds (solid curves), congestus (dotted), deep (dashed), and overshooting convection (dotted–dashed) using wind-profiler (black) and CPOL-based (red) measurements taken at the profiler site (From Kumar et al., 2016, © American Meteorological Society; used with permission). (b) On the right are the TWP-ICE mean mass flux (kg m2 s−1) profiles from all cumulus clouds (in black), shallow (in blue), congestus (in green), and deep convection (in red) with GF SCM simulation.
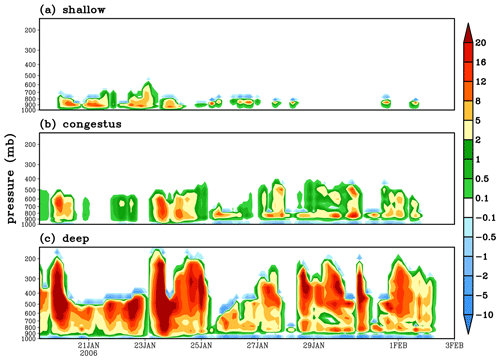
Figure 5Convective heating tendencies (K d−1) of (a) shallow, (b) congestus, and (c) deep convection with the GF scheme using the TWP-ICE soundings.
In GF, we follow B2014 to introduce an additional closure using the concept of the cloud work function (CWF) available for the deep convection overturning. The CWF is calculated as
where A is the total updraft CWF, zb and zt are the height of the cloud base and cloud top, respectively, g is the gravity, cp is the specific heat of dry air, Zu is the normalized mass flux, is the grid-scale air temperature, and hu and are the updraft and grid-scale saturated moist static energy, respectively. The parameter γ is given by Grell (1993, Eq. A15). Following B2014, the boundary layer production is given by
where τBL is the boundary layer timescale given by B2014 (Eq. 15 therein) and the integral is performed from the surface (zsurf) to the cloud base. From Eqs. (15) and (16), the available CWF (Aavail) is given by
and the rate of instability removal is given by , where τ is a prescribed timescale that is currently 1 and 0.5 h for deep and congestus modes, respectively.
While the impact for the GEOS modeling system was a substantial improvement, this may depend on other physical parameterizations and how tendencies are applied in a GCM. For this reason, in GF this closure is optional. It can be combined with any of the other closures previously available in the scheme for deep convection.
2.5 Inclusion of the ice-phase process
The thermodynamical equation employed in the GF scheme uses the moist static energy (h) as a conserved quantity for non-entraining air parcels with adiabatic displacements:
where h has the usual definition,
and cp is the isobaric heat capacity of dry air, T is the temperature, g is the gravity, z is the height, Lv the latent heat of vaporization, and qv the water vapor mixing ratio. However, h is not conserved if glaciation transformation occurs, and this process was not explicitly included in GF until now. Incorporating the transformation of liquid water to ice particles, Eq. (18) now reads
where Lf is the latent heat of freezing, and qi is the ice mixing ratio. With the extended Eq. (20), the general equation for the in-cloud moist static energy including the entraining process solved in this version of GF is
where (dh)entr represents the modification of the in-cloud moist static energy associated with the internal mixing with the entrained environmental air. Overall, the associated additional heating has a small impact on the total convective heating tendency.
The partition between liquid- and ice-phase contents is represented by a smoothed Heaviside function that increases from 0 to 1 in the finite temperature range [235.16, 273.16] K, which is given by fract_liq = .
The melting of precipitation falling across the freezing level is represented by adding an extra term to the grid-scale moist static energy tendency:
where M is the mass mixing ratio of the frozen precipitation that will melt in a given model vertical layer of the pressure depth Δp.
In this section, applications associated with the features described in the previous section are discussed.
3.1 The trimodal characteristics revealed by single-column simulations
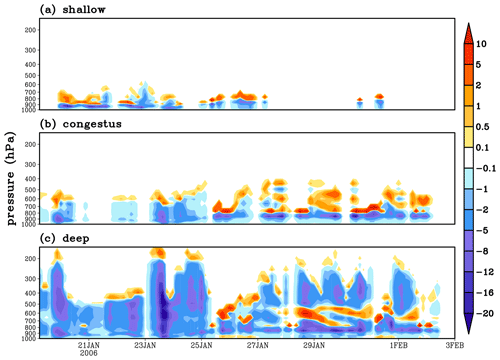
The GF convection scheme was implemented into the Common Community Physics Package (CCPP) Single Column Model (SCM; Firl et al. 2018), and SCM simulations were executed using data (Xie et al., 2010) from the Tropical Warm Pool International Cloud Experiment (TWP-ICE; May et al., 2008) to demonstrate the trimodal characteristics and the value of using BFs. TWP-ICE is a comprehensive field campaign that took place in January and February 2006 over Darwin, Australia.
Strong precipitation events are observed during the active monsoon period with a major mesoscale convective system (MCS) on 23 January 2006, followed by a suppressed monsoon with relatively weak rainfall (Fig. 3). The periods 19–25 January and 26 January–2 February 2006 are defined as active monsoon and suppressed monsoon periods for the subsequent quantitative analysis. As shown in Fig. 3, GF captures all the peak precipitation events during the active monsoon period. The heavy precipitation in the active monsoon period appears underestimated, while the light precipitation events in the suppressed monsoon period may be overestimated. However, exact agreement cannot be expected. Precipitation data for this data set were derived from radar data; derivation of large-scale forcing data is also not trivial. Some of this is also obvious in the calculation and discussion of the Q1 and Q2 profiles (later in this section). The convective precipitation contributes about 78 % of the total precipitation during the active monsoon period and contributes as much as 94 % of total precipitation during the suppressed monsoon period.
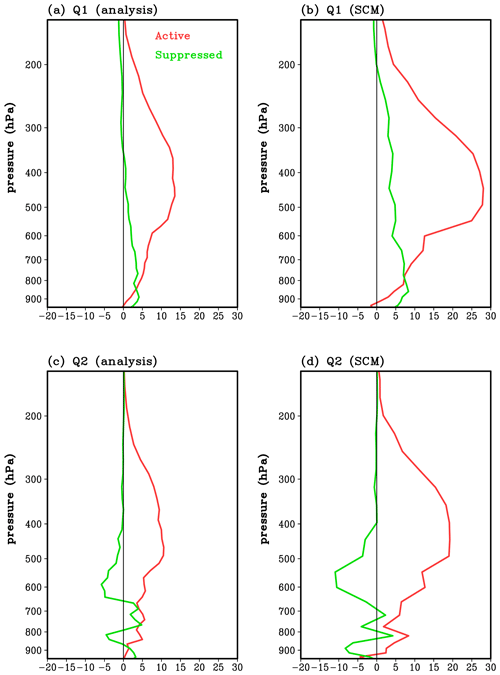
Figure 7The diabatic heating source (Q1, K d−1) profiles from (a) sounding analysis, (b) SCM simulation, and diabatic drying sink (Q2, K d−1) from (c) sounding analysis and (d) SCM simulation. The active monsoon period is in red, and the suppressed period is in green.
To test the approximation of the normalized mass flux with our generalized normalized mass flux approach, we compare the simulated mass flux profiles with observations, as analyzed by Kumar et al. (2016). Of particular importance for us is whether the predicted mass flux for deep convection is able to characterize deep convective clouds in the area, since this will determine maximum entrainment and detrainment in the GF parameterization. For completeness we also compare congestus and shallow clouds. The mean mass flux during the whole TWP-ICE simulation period from all cumulus clouds (deep, congestus, and shallow) is shown in Fig. 4b. The congestus mass flux (green), which is weaker than the mass flux for deep convection, has its maximum at around 7 km of height. The maximum mass flux from deep convection (red) and all convective types (black) is around 6 km and a bit under 6 km, respectively. Kumar et al. (2016) estimated the convective mass flux for two wet seasons (October 2005–April 2006 and October 2006–April 2007) from radar observations over Darwin, Australia. Although the TWP-ICE simulation period (19 January–2 February 2006) is much shorter, the shape of the mass flux profiles in Fig. 4b is quite similar to their observations, shown in Fig. 4a, which is from Fig. 13 of Kumar et al. (2016, © American Meteorological Society; used with permission).
Figure 5 shows the convective heating rate of shallow (Fig. 5a), congestus (Fig. 5b), and deep convection (Fig. 5c). In the case of the shallow convection (Fig. 5a) the environment is warmed in the lower levels and cooled at cloud tops. Temperature tendencies are derived using
Here, ϱ is the change in moist static energy (h) or water vapor (q) per unit mass, and mb(CU) is the cloud-base mass flux for deep, congestus, or shallow convection.
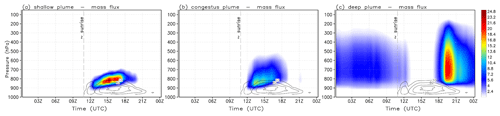
Figure 8The diurnal cycle of the three convective modes as represented by the GF convection parameterization in a single-column model experiment with the GEOS-5 modeling system. The black contours represent the vertical diffusivity coefficient for heat (m2 s−1). The color contours show the updraft mass flux expressed in 10−3 kg m−2 s−1.
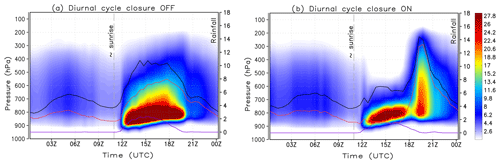
Figure 9Color shading is the time average of the diurnal cycle of the total vertical mass flux of the three convective modes: shallow, congestus, and deep (10−3 kg m2 s−1). The rainfall is depicted by graphic lines: black, red, and purple represent the total precipitation and the convective part from deep and congestus plumes, respectively. The scale for rainfall appears on the right vertical axis (mm d−1). Panel (a) represents the results without the diurnal cycle closure, and panel (b) is with.
More low-level heating due to shallow convection occurs during the active monsoon stage. The congestus (Fig. 5b) and deep (Fig. 5c) convection cools the boundary layer mainly through downdrafts and evaporation of rainfall, and it also cools the troposphere through the evaporation of detrained cloud condensates at cloud tops. On 23 January 2006, the strong heating from the lower troposphere to 500 and 200 hPa for congestus and deep convection, respectively, corresponds to the heavy precipitation in Fig. 3. Figure 6 shows the convective drying tendencies of shallow (Fig. 6a), congestus (Fig. 6b), and deep convection (Fig. 6c). The entraining of low-level environmental moist air into the convection plumes and raining out results in drying of the lower atmosphere, while the detrained cloud water–ice at the cloud top leads to some cooling. The strongest drying for deep convection on 23 January 2006 (Fig. 6c) from the lower troposphere to 200 hPa also corresponds to the heavy precipitation in Fig. 4.
The heating and drying features of the single-column model (SCM) simulation with the GF convection scheme are further validated by the diabatic heating source (Q1) and drying sink (Q2), which were defined by Yanai et al. (1973), from sounding analysis. The averaged profiles of Q1 and Q2 derived from constrained variational objective analysis observation (Xie et al., 2010) are shown in Fig. 7a and c, while the SCM-simulated Q1 and Q2 are given in Fig. 7b and d. The shape of Q1 and Q2 in active or suppressed periods from the simulation agrees with the observations very well, but with a stronger magnitude. The maximum Q1 and Q2 between 350 and 550 hPa in the active monsoon period corresponds to the heavy precipitation in Fig. 3. The Q1 and Q2 from observations and simulations were mainly distributed at low levels in the suppressed period, consistent with the study from Xie et al. (2010).

Figure 10Time average of the diurnal cycle of the grid-scale vertical moistening (a, c) and heating (b, d) tendencies associated with the three convective modes (shaded colors) and precipitation (contour: red dashed, green solid, and purple dashed represent the total precipitation and the convective precipitation from deep and congestus plumes, respectively). The upper (bottom) panels show results without (with) the diurnal cycle closure.
3.2 Evaluation of the diurnal cycle closure
Santos e Silva et al. (2009, 2012) discussed the diurnal cycle of precipitation over the Amazon Basin in detail using the TRMM rainfall product (Huffman et al., 2007), observational data from an S-band polarimetric radar (S-POL), and rain gauges obtained in a field experiment during the wet season of 1999. Their analysis indicated that peak in rainfall is usually late in the afternoon (between 17:00 and 21:00 UTC), despite existent variations associated with wind regimes. In addition, over the Amazon, a secondary period of convection activity is observed during the night as reported by Yang et al. (2008) and Santos e Silva et al. (2012). In general, this is associated with squall line propagation in the Amazon Basin (Cohen et al., 1995; Alcântara et al., 2011). This bimodal pattern of convective activity can be identified with observational analysis of vertical profiles of moistening and heating (Schumacher et al., 2007).
Here we evaluate the GF scheme with the B2014 closure by applying it in the NASA GEOS GCM configured as a single-column model (SCM). The GEOS SCM with GF was run from 24 January to 25 February 1999 using the initial conditions and advective forcing from the TRMM_LBA field campaign data. The simulation started on 00:00 Z 24 January 1999 with 1-month time integration. Model results were averaged in time to express the mean diurnal cycle. An initial glance at the three convection modes in the GF scheme is given by Fig. 8, where the time-averaged mass fluxes (10−3 kg m−2 s−1) of each mode are introduced. The contour lines in black represent the vertical diffusivity coefficient for heat (m2 s−1), describing the diurnal development of the planetary boundary layer (PBL) over the Amazon forest. The PBL development seems to be well represented with a fast evolution in the first hours after sunrise and stabilizing around noon with a realistic vertical depth between 1 and 1.5 km. Both shallow (Fig. 8a) and congestus (Fig. 8b) modes start a few hours after sunrise with cloud base around the PBL top and cloud tops below ∼ 700 and 550 hPa, respectively. Those two modes precede the deep convection (Fig. 8c) development during the late afternoon (local time is UTC−4 h) with cloud tops reaching 200 hPa.
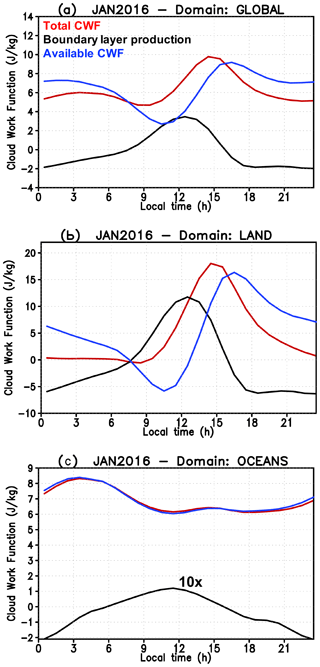
Figure 12The monthly mean (January 2016) diurnal variation of the total cloud work function (red color), boundary layer production (black), and available cloud work function (blue). The curves also represent the areal average over (a) the entire globe, (b) the land regions, and (c) the oceans. In panel (c) the boundary layer production is multiplied by 10 for clarity.
Figure 9 shows the mean diurnal cycle of the net vertical mass flux (the sum of shallow, congestus, and deep modes) as well as the total and convective precipitation. The chosen closures for the mass flux at cloud base were the BLQE for shallow and the adaptation of B2014 for congestus and deep modes, as described at the end of Sect. 2.3. For congestus, we only retained the first term of Eq. (17); for deep, the simulations were performed without and with the second term of Eq. (17). This allowed us to evaluate its role in defining the phase of the diurnal march of the precipitation.
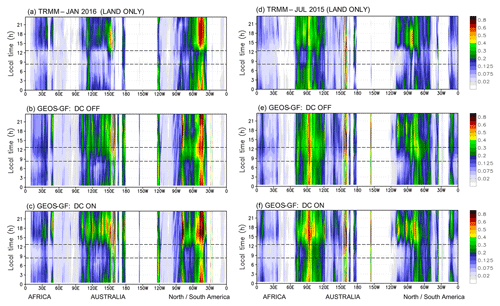
Figure 13Global Hovmöller diagram (average over latitudes 40∘ S to 40∘ N) of the diurnal cycle of precipitation (mm h−1) from remote-sensing-derived observations (TRMM, a, d) and the NASA GEOS GCM applying the GF scheme without the diurnal cycle closure (b, e, DC OFF) and with (c, f, DC ON). The results account for precipitation only over land regions and are monthly means for January 2016 (a, b, c) and July 2015 (d, e, f), respectively.
Figure 9a shows the model results without applying the diurnal cycle closure (i.e., retaining only the first term of Eq. 17) for deep convection. In this case, the three convective modes coexist, triggered just a few hours after sunrise (∼ 11:00 UTC), with the deep convection occurring too early and producing maximum precipitation at about 15:00 UTC (∼ 11:00 local time). Conversely, we observed a clear separation between the convective modes when applying the full equation of the diurnal cycle closure (Fig. 9b), reducing the amount of potential instability available for the deep convection. In this case, there is a delay of the precipitation from the deep penetrative convection with the maximum rate taking place between 18:00 and 21:00 UTC, more consistent with observations of the diurnal cycle over the Amazon region.
Figure 10 introduces the grid-scale vertical moistening and heating tendencies associated with the three convective modes for the simulations without and with the diurnal cycle closure. The net effect (moistening minus drying) of the three convective modes, not including the diurnal cycle closure for the deep mode, appears in the Fig. 10a. As the three modes coexist most of the time and as the drying associated with the deep precipitating plumes dominates, water vapor is drained from the troposphere, with a shallow lower-level layer of moistening associated with the precipitation evaporation driven by downdrafts. However, by including the full formulation of the diurnal cycle closure (Fig. 10b), a much smoother transition is simulated with a late morning and early afternoon low to mid-tropospheric moistening by shallow and congestus convection, followed by a late afternoon and early evening tropospheric drying by the rainfall from the deep cumulus. Associated with the delay of precipitation, the peak downdraft occurrence is correspondingly displaced. On the right, Fig. 10c and d introduce the results for the heating tendencies. A similar discussion applies to these tendencies, with the peak of the atmospheric heating delayed by a few hours, when the diurnal cycle closure is applied (Fig. 10d). Note that the warming from the congestus plumes somewhat offsets the low-troposphere cooling associated with the shallow plumes.
3.3 Global-scale three-dimensional modeling
A global-scale evaluation of the diurnal cycle closure is shown in this section applying GF within the NASA GEOS GCM (Molod et al., 2015). The GEOS GCM was configured with c360 spatial resolution (∼ 25 km) and was run in free forecast mode for all of January 2016. Each forecast day covered a 120 h time integration, with output available every hour. Atmospheric initial conditions were provided by the Modern-Era Retrospective Analysis for Research and Applications Version 2 (MERRA-2; Gelaro et al., 2017). The simulations applied the FV3 nonhydrostatic dynamical core on a cubed-sphere grid (Putman and Lin, 2007). Resolved grid-scale cloud microphysics apply a single-moment formulation for rain, liquid, and ice condensates (Bacmeister et al., 2006). The longwave radiative processes are represented following Chou and Suarez (1994), and the shortwave radiative processes are from Chou and Suarez (1999). The turbulence parameterization is a nonlocal scheme primarily based on Lock et al. (2000), acting together with the local first-order scheme of Louis and Geleyn (1982). The sea surface temperature is prescribed following Reynolds et al. (2002).
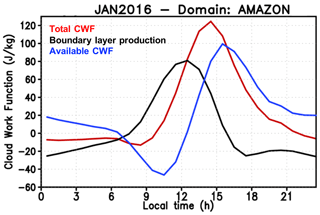
We first demonstrate the impact of the boundary layer production on the cloud work function (CWF) available for the deep convection overturning. Figure 11 shows the monthly mean of the diurnal variation of the three quantities given by Eqs. (10), (11), and (12). The figure represents the monthly mean (January 2016) diurnal variation of the total cloud work function, boundary layer production, and available cloud work function, all area-averaged over the Amazon Basin.
The total CWF tightly follows the surface fluxes as the air parcels that form the convective updrafts originate close to the surface in the PBL. The boundary layer production presents similar behavior, peaking at noon and developing negative values during the nights. The combination of the two terms following Eq. (17) defines the available CWF for convection overturning. A negative range of the available CWF, associated with the negative buoyancy contribution below the level of free convection, in the early mornings to approximately noon prevents the model from developing convective precipitation in that period and shifts the maximum CWF to late afternoon, which is much closer to the observed diurnal cycle of precipitation over the Amazon region.
A global perspective of these three quantities is shown in Fig. 12. As before, the curves represent the monthly mean (January 2016) diurnal variation of the total cloud work function, boundary layer production, and available cloud work function. Here the averaged area corresponds to the global domain (Fig. 12a), only the land regions (Fig. 12b), and only the oceans (Fig. 12c). Over oceans, the boundary layer production is small in comparison with the total CWF; over land (Fig. 12b), it is comparable in magnitude with the total CWF, pushing the available CWF to peak closer to the late afternoons and early evenings. On global average (Fig. 12a), the boundary layer production still plays a substantial role, with a clear effect on the timing of the maximum available CWF.
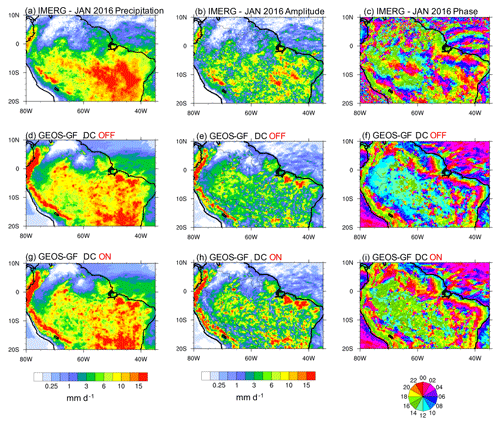
Figure 14The January 2016 monthly mean precipitation, amplitude, and phase of the diurnal harmonic over the Amazon Basin. The top panels (a–c) show the quantities of the GPM IMERG retrieval. In the middle (d–f) and lower rows (g–i), panels show model simulations with the diurnal cycle closure turned off and on, respectively.
A perspective of the precipitation simulation with the GEOS-5 GCM with the GF scheme and the impact of the diurnal cycle closure is provided by Fig. 13. Here, the January 2016 (left column) and July 2015 (right column) averages of the diurnal cycle of precipitation are depicted. Figure 13a and d show the rainfall estimation by the TRMM Multi-satellite Precipitation Analysis (TMPA version 3B42; Huffman et al., 2007). Also, the precipitation simulated by the GEOS GF, including the diurnal cycle closure (at middle, Fig. 13c and e) or not (lower panels, Fig. 13d and f), is depicted. The precipitation fields were averaged over the latitudes between 40∘ S and 40∘ N taking into account only the land regions. The vertical axis represents the local time.
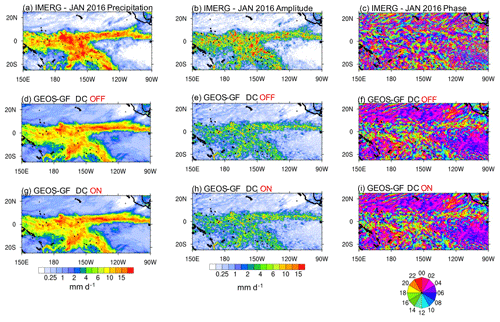
Figure 15The January 2016 monthly mean precipitation, amplitude, and phase of the diurnal harmonic over the tropical Pacific Ocean. The top panels (a–c) show the quantities of the GPM IMERG retrieval. In the middle (d–f) and lower rows (g–i), panels show model simulations with the diurnal cycle closure turned off and on, respectively.
The TRMM estimation evidences two peaks of precipitation rate: a nocturnal peak around 03:00 LST over oceans (not shown) and another one in late afternoon (15:00 to 18:00 LST) over land. A significant gap of rainfall in the mornings is also seen in both months. We found somewhat of an overestimation of the precipitation in comparison with the estimates produced by the TRMM retrieval technique (Fig. 13a and d). However, the simulations that apply the diurnal cycle closure (Fig. 13c and f) are superior regarding the phase in comparison with the simulations that apply the total CWF (Fig. 13b and e) for the closure. As shown in Fig. 13c and f, the diurnal cycle closure adapted from B2014 used in these simulations shows a much better representation of the morning to early afternoon gap of the precipitation, which peaks much closer to the time of TRMM retrieval. In particular, model improvements are noticeable over the Amazon region (denoted by “South America”). Similar improvements are also evident over Africa and Australia.
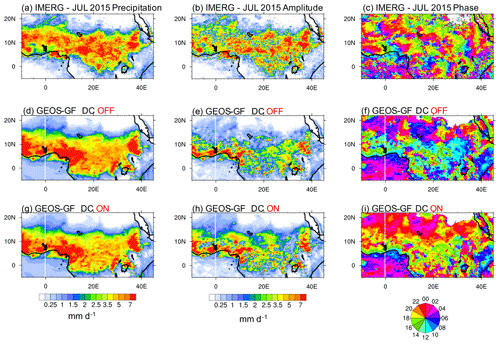
Figure 16The July 2015 monthly mean precipitation, amplitude, and phase of the diurnal harmonic over a portion of equatorial Africa. The top panels (a–c) show the quantities of the GPM IMERG retrieval. In the middle (d–f) and lower rows (g–i), panels show model simulations with the diurnal cycle closure turned off and on, respectively.
For a more detailed analysis of the diurnal cycle of the precipitation we use higher-spatial- and temporal-resolution retrievals from the Global Precipitation Measurement (GPM) with the Integrated Multi-satellitE Retrievals for GPM (IMERG, version 6; Huffman et al., 2019). The IMERG has 0.1∘ spatial and h temporal resolutions. Also, we adopt the technique of calculating the diurnal harmonics using a Fourier transform and focus on the phase and amplitude of the first harmonic. The GPM IMERG retrievals were first interpolated to the GEOS-5 grid spatial resolution (∼ 25 km) and temporal accumulation (1 h). Figure 14 shows the mean precipitation and the mean amplitude and phase of the first harmonic over the Amazon Basin. The diurnal phase was shifted to the local solar time (LST), and 12:00 LST is associated with the time of maximum insolation in a cloud-free sky condition. The IMERG mean precipitation (Fig. 14a) shows the typical summer pattern over the Amazon Basin, with the maximum accumulated precipitation occurring south of the Equator following the annual southward shift of the Intertropical Convergence Zone (ITCZ). The domain average precipitation estimated by IMERG was 5.62 mm d−1. The correspondent field as simulated by GEOS-5 is shown in Fig. 14d and g without (DC OFF) and with (DC ON) the adaptation of the B2014 diurnal cycle closure, respectively. Both simulations show a very similar pattern, and they are also reasonably comparable with the IMERG in the inner part of the continent. However, the simulations suffer from spurious precipitation along the Andes mountains triggered by numerical noise associated with the steep terrain and the use of a sigma-type vertical coordinate. The simulated domain average precipitation was 6.69 (6.59) mm d−1 for the case DC OFF (ON), which is roughly 18 % larger than IMERG. It seems plausible that the precipitation excess is mostly associated with the spurious generation along the steep terrain. The central column of Fig. 14 shows the January 2016 mean amplitude of IMERG (panel b) and model simulations (panels e and h). The domain average amplitude corresponds to 61, 51, and 62 % of the precipitation of IMERG, model DC OFF, and DC ON, respectively. The right column of Fig. 14 shows the diurnal phase of the three data sets. Following Kousky (1980) the maximum precipitation, which forms just inland along the coast in the late afternoon, is associated with the development of the sea breeze front. With the sea breeze penetrating further inland, another maximum occurs during the nighttime due to the convergence formed with the onshore flow. Both features are present in the simulations (Fig. 14f and i), but the case DC ON better simulates the timing, being closer to the IMERG. As for the Amazon Basin interior, the IMERG shows a nighttime maximum associated with the squall lines that form along the northern coast of Brazil and propagate long distances across the basin (Alcântara et al., 2011). Both simulations were unable to capture the propagation of these convective lines. However, it is clear that the case DC OFF (Fig. 14f) simulates a maximum amplitude too early, between 10:00 and 14:00 LT, whereas the case with the diurnal cycle ON (Fig. 14i) is closer to the timing of the IMERG (Fig. 14c), with the peaks occurring between 14:00 and 18:00 LT.
Correspondent analysis over the tropical Pacific Ocean for January 2016 is included in Fig. 15; the domain average precipitation estimated by IMERG was 4.53 mm d−1, whereas GEOS-5 with DC OFF and DC ON simulated ∼ 4.21 mm d−1 in both configurations. For the amplitudes, the amounts were 2.16, 1.47, and 1.45 mm d−1, respectively. The left column of Fig. 15 shows that the spatial distribution of the precipitation simulated by GEOS-5 (panels d and g) remarkably resembles the IMERG retrieval (panel a), although the domain average precipitation amounts are underestimated by about ∼ 10 %. The former discussion also applies to the amplitudes, as shown in the central column of Fig. 15. For the phase, most of the precipitation peaks occur through the nighttime (panel c), and the simulations with GEOS-5 have a similar pattern. The fact that both simulations are nearly the same in terms of the precipitation amount and its diurnal cycle over the ocean is explained by Fig. 12c.
The diurnal cycle of precipitation of the north equatorial portion of Africa for July 2015 is discussed based on the results shown in Fig. 16. The domain average precipitation (amplitude) is 2.51 (2.12), 2.79 (1.45), and 2.8 (1.8) mm d−1 for panels a (b), d (e), and g (h), respectively. Note that the simulated mean precipitation amounts are about 11 % larger than the IMERG estimation. For the diurnal phase (Fig. 16c), the IMERG retrieval shows a mix of late afternoon (16:00–20:00 LT) and nighttime (00:00–04:00 LT) maximum amplitudes. As before, the simulations show contrasting results for the timing of precipitation. Without the diurnal cycle closure, the precipitation peaks occur too early (mostly 10:00–14:00 LT, Fig. 16f), whereas with that closure, those peaks take place mainly after 14:00–16:00 LT (Fig. 16i).
Figure 17 displays the results for July 2015 over the contiguous United States and part of the neighboring countries. The domain average precipitation (amplitude) is 2.60 (2.37), 2.52 (1.59), and 2.42 (1.8) mm d−1 for panels a (b), d (e), and g (h), respectively. Model simulations underestimate the mean precipitation by about 5 %–10 %. As in the other regions, the model's monthly mean spatial distribution of the precipitation looks realistic, although it underestimates the amount in the southeast and overestimates the rainfall over the eastern part of Gulf of California. According to IMERG, the peaks of precipitation occur in the late afternoon over the southeast and central-western part of the region and in the nighttime over the central-eastern part of the domain (Fig. 17c). Over the central part of the US, both simulations did not capture the nighttime precipitation well. However, the simulation DC ON (Fig. 17i) seems to be closer to IMERG over the central-western portion.
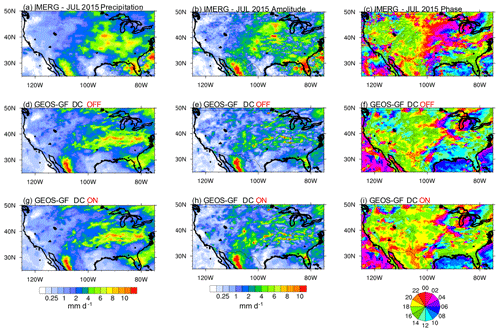
Figure 17The July 2015 monthly mean precipitation, amplitude, and phase of the diurnal harmonic over the contiguous United States and part of the neighboring countries. The top panels (a–c) show the quantities of the GPM IMERG retrieval. In the middle (d–f) and lower rows (g–i), panels show model simulations with the diurnal cycle closure turned off and on, respectively.
We describe a set of new features recently implemented in the GF convection parameterization. The main new aspects are as follows.
-
The unimodal approach has been replaced by a trimodal formulation representing the three modes: shallow, congestus, and deep convection. Each mode has a distinct initial gross entrainment and a set of closure formulations for the mass flux at the cloud base.
-
The normalized mass flux profiles are now prescribed following a continuous and smooth beta function. From the cloud base, cloud top, and a free parameter that shapes the BF, the normalized mass flux profile and the entrainment and detrainment rates are determined. Together with the mass flux at the cloud base defined by the selected closure, these parameters also determine, e.g., the vertical drying and heating tendencies associated with the subgrid-scale convection. Using a BF to describe the statistical average of a characteristic convection type means that the BF may in fact represent several plumes in the grid box. Additionally, this approach may be used to implement stochasticism with temporal and spatial correlations as well as memory dependence that lead to significant changes in the vertical distribution of heating and drying without disturbing mass conservation. Future work will address this possibility. Finally, the use of the BFs may help fine-tune the model skill by removing water vapor and temperature biases.
-
An optional closure for nonequilibrium convection updated from Bechtold et al. (2014) is available. This closure has significantly improved the GF scheme's ability in the NASA GEOS GCM to represent the diurnal cycle of convection over land, also with potential beneficial impacts on data assimilation and tracer transport.
The new features of the GF scheme, as described in this paper, further extend the capabilities of this convection parameterization to be applied to a wide range of spatial scales and environmental problems.
The GF convection scheme within the Global Model Test Bed (GMTB) Single Column Model is available from the GMD-paper branch at https://github.com/GF-GMD/ccpp-physics (last access: 26 August 2021), https://doi.org/10.5281/zenodo.5278281 (Li et al., 2021). Public access to the NASA GEOS GCM source code is available at https://github.com/GEOS-ESM/GEOSgcm (last access: 25 August 2021) on tag Jason-3.0. The authors are available for recommendations on applying the several options present in the GF scheme, as well as for instructions for its implementation in other modeling systems.
The data can be obtained from the ARM website at https://www.arm.gov/research/campaigns/twp2006twp-ice (last access: 27 August 2021) and https://doi.org/10.5281/zenodo.5292370 (Li, 2021).
SRF and GAG developed the model code and performed the simulations. HL conducted the simulations and produced the results shown in Sect. 3.1. All authors prepared the paper.
The authors declare that they have no conflict of interest.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The first author acknowledges the support of NASA/GFSC – USRA/GESTAR grant no. NNG11HP16A. This work was also supported by the NASA Modeling, Analysis, and Prediction (MAP) program. Computing was provided by the NASA Center for Climate Simulation (NCCS).
This research has been supported by NASA/GFSC – USRA/GESTAR (grant no. NNG11HP16A).
This paper was edited by Richard Neale and reviewed by two anonymous referees.
Alcântara, C. R., Silva Dias, M. A. F., Souza, E. P., and Cohen, J. C. P.: Verification of the Role of the Low Level Jets in Amazon Squall Lines, Atmos. Res., 100, 36–44, https://doi.org/10.1016/j.atmosres.2010.12.023, 2011.
Arakawa, A. and Schubert, W. H.: Interaction of a cumulus cloud ensemble with the large-scale environment, Part I, J. Atmos. Sci., 31, 674–701, https://doi.org/10.1175/1520-0469(1974)031<0674:IOACCE>2.0.CO;2, 1974.
Arakawa, A., Jung, J.-H., and Wu, C.-M.: Toward unification of the multiscale modeling of the atmosphere, Atmos. Chem. Phys., 11, 3731–3742, https://doi.org/10.5194/acp-11-3731-2011, 2011.
Baba, Y.: Spectral cumulus parameterization based on cloud-resolving model, Clim. Dynam., 52, 309–334, https://doi.org/10.1007/s00382-018-4137-z, 2019.
Bacmeister, J. T., Suarez, M. J., and Robertson, F. R.: Rain reevaporation, boundary layer-convection interactions, and Pacific rainfall patterns in a AGCM, J. Atmos. Sci., 63, 3383–3403, 2006.
Bechtold, P., Semane, N., Lopez, P., Chaboureau, J., Beljaars, A., and Bormann, N.: Representing Equilibrium and Nonequilibrium Convection in Large-Scale Models, J. Atmos. Sci., 71, 734–753, https://doi.org/10.1175/JAS-D-13-0163.1, 2014.
Benjamin, S. G., Weygandt, S. S., Brown, J. M., Hu, M., Alexander, C. R., Smirnova, T. G., Olson, J. B., James, E. P., Dowell, D. C., Grell, G. A., Lin, H., Peckham, S. E., Smith, T. L., Moninger, W. R., Kenyon, J. S., and Manikin, G. S.: A North American hourly assimilation and model forecast cycle: The Rapid Refresh, Mon. Weather Rev., 144, 1669–1694, https://doi.org/10.1175/MWR-D-15-0242.1, 2016.
Betts, A. K. and Jakob, C.: Study of diurnal cycle of convective precipitation over Amazonia using a single column model, J. Geophys. Res., 107, 4732, https://doi.org/10.1029/2002JD002264, 2002.
Chou, M.-D. and Suarez, M. J.: An efficient thermal infrared radiation parameterization for use in general circulation models, NASA Tech. Memorandum 104606 – Vol. 3, NASA, Goddard Space Flight Center, Greenbelt, MD, 1994.
Chou, M.-D. and Suarez, M. J.: A Solar Radiation Parameterization for Atmospheric Studies, NASA Tech. Memorandum 104606 – Vol. 15, NASA, Goddard Space Flight Center, Greenbelt, MD, 1999.
Cohen, J. C. P., Silva Dias, M. A. F., and Nobre, C. A.: Environmental conditions associated with Amazonian squall lines: a case study, Mon. Weather Rev., 123, 3163–3174, 1995.
Firl, G., Carson, L., Bernardet, L., and Heinzeller, D.: Global Model Test Bed Single Column Model v2.1 User and Technical Guide, 26 pp., available at: https://dtcenter.org/sites/default/files/community-code/scm-ccpp-guide-v2-1.pdf, last access: 26 August 2021.
Fowler, L. D., Skamarock, W. C., Grell, G. A., Freitas, S. R., and Duda, M. G.: Analyzing the Grell-Freitas convection scheme from hydrostatic to non hydrostatic scales within a global model, Mon. Weather Rev., 144, 2285–2306, https://doi.org/10.1175/mwr-d-15-0311.1, 2016.
Freitas, S. R., Grell, G. A., Molod, A., Thompson, M. A., Putman, W. M., Santos e Silva, C. M., and Souza, E. P.: Assessing the Grell-Freitas convection parameterization in the NASA GEOS modeling system, J. Adv. Model. Earth Sy., 10, 1266–1289, https://doi.org/10.1029/2017MS001251, 2018.
Freitas, S. R., Putman, W. M., Arnold, N. P., Adams, D. K., and Grell, G. A.: Cascading toward a kilometer-scale GCM: Impacts of a scale-aware convection parameterization in the Goddard Earth Observing System GCM, Geophys. Res. Lett., 47, e2020GL087682, https://doi.org/10.1029/2020GL087682, 2020.
Gelaro, R., McCarty, W., Suarez, M. J., Todling, R., Molod, A., Takacs, L., Randles, C. A., Darmenov, A., Bosilovich, M. G., Reichle, R., Wargan, K., Coy, L., Cullather, R., Draper, C., Akella, S., Buchard, V., Conaty, A., da Silva, A. M., Gu, W., Kim, G., Koster, R., Lucchesi, R., Merkova, D., Nielsen, J. E., Partyka, G., Pawson, S., Putman, W., Rienecker, M., Schubert, S. D., Sienkiewicz, M., and Zhao, B.: The Modern–Era Retrospective Analysis for Research and Applications, Version 2 (MERRA–2), J. Climate, 30, 5419–5454, https://doi.org/10.1175/JCLI-D-16-0758.1, 2017.
Gerard, L., Piriou, J., Brožková, R., Geleyn, J., and Banciu, D.: Cloud and Precipitation Parameterization in a Meso-Gamma-Scale Operational Weather Prediction Model, Mon. Weather Rev., 137, 3960–3977, 2009.
Grabowski, W. and Smolarkiewicz, P.: CRCP: a Cloud Resolving Convection Parameterization for modeling the tropical convecting atmosphere, Physica D, 133, 1–4, https://doi.org/10.1016/S0167-2789(99)00104-9, 1999.
Grant, A. L. M.: Cloud-base fluxes in the cumulus-capped boundary layer. Q. J. Roy. Meteor. Soc., 127, 407–421, https://doi.org/10.1002/qj.49712757209, 2001.
Grell, G.: Prognostic evaluation of assumptions used by cumulus parameterizations, Mon. Weather Rev., 121, 764–787, 1993.
Grell, G. A. and Devenyi, D.: A generalized approach to parameterizing convection combining ensemble and data assimilation techniques, Geophys. Res. Lett., 29, 38-1–38-4, https://doi.org/10.1029/2002GL015311, 2002.
Grell, G. A. and Freitas, S. R.: A scale and aerosol aware stochastic convective parameterization for weather and air quality modeling, Atmos. Chem. Phys., 14, 5233–5250, https://doi.org/10.5194/acp-14-5233-2014, 2014.
Grell, G. A., Kuo, Y.-H., and Pasch, R.: Semi-prognostic tests of cumulus parameterization schemes in the middle latitudes, Mon. Weather Rev., 119, 5–31, 1991.
Huffman, G. J., Adler, R. F., Bolvin, D. T., Gu, G. J., Nelkin, E. J., Bowman, K. P., Hong, Y., Stocker, E. F., and Wolff, D. B.: The TRMM multi-satellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales, J. of Hydrometeorol., 8, 38–55, 2007.
Huffman, G. J., Bolvin, D. T., Braithwaite, D., Hsu, K., Joyce, R., Kidd, C., Nelkin, E. J., Sorooshian, S., Tan, J., and Xie, P.: Algorithm Theoretical Basis Document (ATBD) Version 5.2 for the NASA Global Precipitation Measurement (GPM) Integrated Multi-satellitE Retrievals for GPM (I-MERG), GPM Project, Greenbelt, MD, 38 pp., available at: https://gpm.nasa.gov/sites/default/files/document_files/IMERG_ATBD_V06.pdf (last access: 25 August 2021), 2019.
Johnson, R. H., Rickenbach, T. M., Rutledge, S. A., Ciesielski, P. E., and Schubert, W. H.: Trimodal Characteristics of Tropical Convection, J. Climate, 12, 2397–2418, https://doi.org/10.1175/1520-0442(1999)012<2397:TCOTC>2.0.CO;2, 1999.
Kousky, V. E.: Diurnal Rainfall Variation in Northeast Brazil, Mon. Weather Rev., 108, 488–498, 1980.
Kuell, V., Gassmann, A., and Bott, A.: Towards a new hybrid cumulus parametrization scheme for use in non-hydrostatic weather prediction models. Q. J. Roy. Meteor. Soc., 133, 479–490, https://doi.org/10.1002/qj.28, 2007.
Kumar, V. V., Protat, A., Jakob, C., Williams, C. R., Rauniyar, S., Stephens, G. L., and May, P. T.: The Estimation of Convective Mass Flux from Radar Reflectivities, J. Appl. Meteorol. Clim., 55, 1239–1257, 2016.
Kwon, Y. C. and Hong, S.-Y.: A Mass-Flux cumulus parameterization scheme across gray-zone resolutions, Mon. Weather Rev., 145, 583–598, https://doi.org/10.1175/MWR-D-16-0034.1, 2017.
Li, H.: GF-GMD/SCM & forcing data, Zenodo [data set], https://doi.org/10.5281/zenodo.5292370, 2021.
Li, H., Grell, G. A., and Freitas, R. S.,: GF- GMD/ccpp-physics: GMD-paper branch (GMD-paper), Zenodo [code], https://doi.org/10.5281/zenodo.5278281, 2021.
Lin, J. W.-B. and Neelin, J. D.: Toward stochastic deep convective parameterization in general circulation models, Geophys. Res. Lett., 30, 1162, https://doi.org/10.1029/2002GL016203, 2003.
Lock, A. P., Brown, A. R., Bush, M. R., Martin, G. M., and Smith, R. N. B.: A new boundary layer mixing scheme. Part I: Scheme description and single-column model tests, Mon. Weather Rev., 138, 3187–3199, 2000.
Louis, J. and Geleyn, J.: A short history of the PBL parameterization at ECMWF, Proc. ECMWF Workshop on Planetary Boundary Layer Parameterization, Reading, United Kingdom, ECMWF, 1982.
May, T. P., Mather, J. H., Vaughan, G., Jakob, C., McFarquhar, G. M., Bower, K. N., and Mage, G. G.: The Tropical Warm Pool International Cloud Experiment, B. Am. Meteorol. Soc., 89, 629–645, 2008.
Molod, A., Takacs, L., Suarez, M., and Bacmeister, J.: Development of the GEOS-5 atmospheric general circulation model: evolution from MERRA to MERRA2, Geosci. Model Dev., 8, 1339–1356, https://doi.org/10.5194/gmd-8-1339-2015, 2015.
Moorthi, S. and Suarez, M. J.: Relaxed Arakawa Schubert: A parameterization of moist convection for general circulation models, Mon. Weather Rev., 120, 978–1002, 1992.
Putman, W. and Lin, S.-J.: Finite Volume Transport on Various Cubed Sphere Grids, J. Comput. Phys., 227, 55–78, https://doi.org/10.1016/j.jcp.2007.07.022, 2007.
Randall, D., Khairoutdinov, M., Arakawa, A., and Grabowski, W.: Breaking the Cloud Parameterization Deadlock, B. Am. Meteorol. Soc., 84, 1547–1564, 2003.
Raymond, D. J.: Regulation of moist convection over the west pacific warm pool, J. Atmos. Sci., 52, 3945–3959, 1995.
Rennó, N. and Ingersoll, A. P.: Natural convection as a heat engine: A theory for CAPE, J. Atmos. Sci., 53, 572–585, 1996.
Reynolds, R. W., Rayner, N. A., Smith, T. M., Stokes, D. C., and Wang, W.: An improved in situ and satellite SST analysis for climate, J. Climate, 15, 1609–1625, 2002.
Santos e Silva, C. M., Gielow, R., and Freitas, S. R.: Diurnal and semidiurnal rainfall cycles during the rain season in SW Amazonia, observed via rain gauges and estimated using S-band radar, Atmos. Sci. Lett., 10, 87–93, https://doi.org/10.1002/asl.214, 2009.
Santos e Silva, C. M., Freitas, S. R., and Gielow, R.: Numerical simulation of the diurnal cycle of rainfall in SW Amazon basin during the 1999 rainy season: the role of convective trigger function, Theor. Appl. Climatol., 109, 473–483, 2012.
Schumacher, C., Zhang, M. H., and Ciesielski, P. E.: Heating Structures of the TRMM Field Campaigns, J. Atmos. Sci., 64, 2593–2610, https://doi.org/10.1175/JAS3938.1, 2007.
Souza, E. P.: Estudo Teórico e Numérico da Relação entre Convecção e Superfícies Heterogêneas na Região Amazônica, PhD thesis, São Paulo University, São Paulo, SP, Brazil, 1999 (in Portuguese).
Tiedtke, M.: A Comprehensive Mass Flux Scheme for Cumulus Parameterization in Large-Scale Models, Mon. Weather Rev., 117, 1779–1800, 1989.
Xie, S., Hume, T., Jakob, C., Klein, S. A., McCoy, R. B., and Zhang, M.: Observed large-scale structures and diabatic heating and drying profiles during TWP-ICE, J. Climate, 23, 57–59, 2010.
Yanai, M., Esbensen, S., and Chu, J.: Determination of bulk properties of tropical cloud clusters from large-scale heat and moisture budgets, J. Atmos. Sci., 30, 611–627, 1973.
Yang, S., Kuo, K. S., and Smith, E. A: Persistent Nature of Secondary Diurnal Modes of Precipitation over Oceanic and Continental Regimes, J. Climate, 21, 4115–413, https://doi.org/10.1175/2008JCLI2140.1, 2008.