Inclusion of a suite of weathering tracers in the cGENIE Earth system model – muffin release v.0.9.23

The metals strontium (Sr), lithium (Li), osmium (Os) and calcium (Ca), together with their isotopes, are important tracers of weathering and volcanism – primary processes which shape the long-term cycling of carbon and other biogeochemically important elements at the Earth's surface. Traditionally, because of their long residence times in the ocean, isotopic shifts in these four elements observed in the geologic record are almost exclusively interpreted with the aid of isotope-mixing, tracer-specific box models. However, such models may lack a mechanistic description of the links between the cycling of the four metals to other geochemically relevant elements, particularly carbon, or climate. Here we develop and evaluate an implementation of Sr, Li, Os and Ca isotope cycling in the Earth system model cGENIE. The model offers the possibility to study the dynamics of these metal systems alongside other more standard biogeochemical cycles, as well as their relationship with changing climate. We provide examples of how to apply this new model capability to investigate Sr, Li, Os and Ca isotope dynamics and responses to environmental change, for which we take the example of massive carbon release to the atmosphere.

1 Introduction

The evolution of life and climate on Earth is intrinsically linked to the dynamics of carbon, oxygen and nutrients at the Earth's surface. While complex interactions on a range of spatial and temporal scales determine the distribution of these elements between surficial (non-lithological) reservoirs like oceans, atmosphere, biomass and soils, the total amount and isotopic distribution of these elements is ultimately governed by the balance between crustal weathering, marine sediment deposition and mantle inputs associated with oceanic crust formation. The geological record shows that the abundance of these elements at Earth's surface has varied on timescales of thousands to millions of years. For example, the changing composition of mantle fluxes into the ocean and nutrient supply during weathering of large mountain ranges were potentially drivers of the accumulation of surficial oxygen during the Archean and Proterozoic (e.g., Kump and Barley, 2007; Campbell and Allen, 2008). Increased basalt weathering in the Cenozoic could have led to a continuous decline in CO₂ concentrations, contributing to the reconstructed long-term cooling trend (e.g., Kent and Muttoni, 2013; Mills et al., 2014) while the emplacement of large igneous provinces (LIPs) repeatedly led to climatic and biotic crises by increasing the supply of mantle-derived carbon and nutrients to the oceans, e.g., during oceanic anoxic events (e.g., Erba et al., 2010; Jenkyns, 2010; Bottini et al., 2012; Monteiro et al., 2012; Percival et al., 2015). At the other (late Quaternary) end of the geological timescale, the supply of particulate iron from airborne ground rock to the oceans of the Quaternary has been invoked as a mechanism to drive glacial–interglacial carbon cycle dynamics (e.g., Martin, 1990; Martínez-Garcia et al., 2011; Loveley et al., 2017; Hooper et al., 2019), linking erosion of the land surface, trace metal cycles in the ocean, and atmospheric pCO₂ (Ridgwell and Watson, 2002).

Understanding mass fluxes between the lithosphere and Earth's dynamic surface are thus key to understanding climate change over geological timescales. However, past changes cannot be reconstructed directly. Instead, variations in the oceanic content and isotopic composition of trace metals like strontium (Sr), osmium (Os), lithium (Li) and calcium (Ca) preserved in marine sediments are used to study lithological processes. The dynamics of these metals are controlled by processes that also shape the long-term carbon and nutrient cycles, namely continental and oceanic weathering and direct mantle emissions, and variations in their isotopic compositions can be linked more directly to changes in these processes since radioactive decay and mass-dependent fractionation form isotopically distinct lithological metal reservoirs. Furthermore, the long residence time of these metals in the ocean, which is generally assumed to be greater than the mixing time of the ocean, generally removes the complexity of spatially heterogeneous marine records since their marine distribution is comparably homogeneous (e.g., Faure and Mensing, 2005), and marine sedimentary records are typically understood as capturing global signals.

Despite laboratory methods to measure and reconstruct the evolving trace metal composition of seawater have become increasingly precise, our ability to interpret these records is limited by our incomplete mechanistic understanding of the cycling of these metals and their isotopes. Mass balances and box models have been most commonly used to interpret geological records of trace metal variations (e.g., Tejada et al., 2009; Misra and Froelich, 2012; Kristall et al., 2017; Them et al., 2017). However, they cannot mechanistically resolve spatially heterogeneous metal burial, and hence they often rely on assumed global fluxes and residence times based on today's ocean, which might not always be applicable throughout the geological record. Additionally, they tend not to include effects of Earth system feedbacks (e.g., climate-driven weathering flux changes, sediment dissolution), the simulation of which requires information about spatially heterogeneous climate and ocean variables, bathymetry, and continental configuration. In contrast, more mechanistic and spatially resolved Earth system models of intermediate complexity (EMIC) aim to capture spatial heterogeneity in marine sources and sinks while making numerical compromises elsewhere (such as in omitting atmospheric dynamics). Of relevance here, the EMIC “cGENIE” has been used successfully to study marine biogeochemical cycles (including C and Ca) under various boundary conditions and external forcings (e.g., Ridgwell and Zeebe, 2005; Ridgwell et al., 2007; John et al., 2014; Death et al., 2014; Turner and Ridgwell, 2016; Hülse e al., 2019). Adding a mechanistic description of the cycling of Sr, Os, Li and Ca (plus isotopes) in cGENIE thus allows us to test their behavior under environmental perturbations alongside nutrient, redox and carbon dynamics (plus climate change) and to compute their spatial distributions and marine residence times under different assumptions about source and sink mechanisms.

Here, we present an implementation of the marine cycling of Sr, Os, Li and Ca in cGENIE. We evaluate the model's performance by comparing simulations of pre-industrial trace metal distributions in the oceans to seawater measurements and study their equilibration times under imposed geochemical perturbations compared to established seawater residence times.

2 Observational constraints

We first provide a brief review of Sr, Os, Li and Ca cycling in the ocean (Sect. 2.1–2.4), as well as their observed concentrations and isotopic compositions in seawater (Sect. 2.5) and their applications as proxies for Earth system processes (Sect. 2.6).

2.1 Strontium

Of the four metal cycles simulated in this study, Sr has the second-highest marine concentration (3 to 4 times more abundant than Li and more than a billion times more abundant than Os, Angino et al., 1966). The main source for marine Sr is continental weathering, replenishing the ocean reservoir through rivers and potentially groundwater discharge (Basu et al., 2001; Beck et al., 2013). Smaller sources include hydrothermal input of mantle-derived Sr and refluxes from diagenetic alteration of carbonates at the seafloor. The chemical and physical similarity of Sr to Ca leads to its substitution in aragonite and, to a lesser degree, calcite (Fietzke and Eisenhauer, 2006; Rüggeberg et al., 2008; Böhm et al., 2012; Stevenson et al., 2014). Angino et al. (1966) argue that biological uptake is the dominant driver of spatial gradients in Sr concentrations in today's oceans, and Krabbenhöft et al. (2010) predict that marine carbonate burial could be the most important sink of seawater Sr. The concentration of Sr incorporated into biogenic carbonates depends on the mineralogy and the growth rate with higher $\mathrm{Sr}/\mathrm{Ca}$ ratios in aragonite precipitated at fast growth rates (Rickaby et al., 2002; Stevenson et al., 2014). In contrast, direct effects of temperature on elemental fractionation during the formation of calcite, the major carbonate buried in marine sediments, are small (Tang et al., 2008). Assuming rivers to be the only supply of continental Sr to the oceans and that the marine Sr reservoir size is in equilibrium, Hodell et al. (1989) estimate the marine residence time of Sr to be 1.9–3.45 Myr. Considering the potentially appreciable Sr influx from groundwater, the actual residence time might be at or below the lower end of this estimate, and it may be even more different if the marine Sr reservoir is not currently in equilibrium with Sr inputs, as suggested by, e.g., Vance et al. (2009).

Strontium has four stable isotopes (0.56 % ⁸⁴Sr, 9.87 % ⁸⁶Sr, 7.04 % ⁸⁷Sr, 82.53 % ⁸⁸Sr) (Veizer, 1989), ⁸⁷Sr being the product of β decay of ⁸⁷Rb (half-life 4.88×10¹⁰ years, Faure and Mensing, 2005). Radiogenic Sr isotope ratios are reported as ${}^{\mathrm{87}}\mathrm{Sr}{/}^{\mathrm{86}}\mathrm{Sr}$ ratios, whereas stable Sr isotope ratios are reported as ${\mathit{\delta }}^{\mathrm{88}/\mathrm{86}}\mathrm{Sr}$, which is the per mill (‰) deviation in the ${}^{\mathrm{88}}\mathrm{Sr}{/}^{\mathrm{86}}\mathrm{Sr}$ relative to the NBS987 standard (${\mathit{\delta }}^{\mathrm{88}/\mathrm{86}}\mathrm{Sr}=(\frac{({}^{\mathrm{88}}\mathrm{Sr}{/}^{\mathrm{86}}\mathrm{Sr}{)}_{\mathrm{sample}}}{({}^{\mathrm{88}}\mathrm{Sr}{/}^{\mathrm{86}}\mathrm{Sr}{)}_{\mathrm{std}}}-\mathrm{1})\cdot \mathrm{1000}$, Fietzke and Eisenhauer, 2006). Elemental fractionation during magmatic processes creates different $\mathrm{Rb}/\mathrm{Sr}$ ratios that over time generate reservoirs with distinct Sr isotopic signatures, with the continental crust being considerably more radiogenic than the mantle (Faure and Mensing, 2005). Dust and rainwater isotopic signatures, both radiogenic and stable, are generally lower than modern-day seawater values (Pearce et al., 2015). Volcanic material brings un-radiogenic particulate Sr into sediments and can over time significantly affect the radiogenic composition of dissolved Sr in the sediment column while having little effect on the isotopic composition of dissolved Sr in seawater (Elderfield and Gieskes, 1982; Pearce et al., 2015). Changes in isotope abundances caused by kinetic and equilibrium mass-dependent fractionation during carbonate formation are much smaller, and one can thus assume that the ${}^{\mathrm{87}}\mathrm{Sr}{/}^{\mathrm{86}}\mathrm{Sr}$ of seawater and deposited carbonates is only controlled by inputs to the ocean (Krabbenhöft, 2011). By contrast, variations in ${\mathit{\delta }}^{\mathrm{88}/\mathrm{86}}$Sr are only controlled by fractionation during chemical processes, biogenic carbonate formation being the most important one in the ocean (e.g., Krabbenhöft et al., 2010). There is no evidence for a general dependence of ${\mathit{\delta }}^{\mathrm{88}/\mathrm{86}}$Sr fractionation during biogenic carbonate formation on environmental conditions, although temperature and growth rate effects were observed in some calcifying species (Fietzke and Eisenhauer, 2006; Böhm et al., 2012; Stevenson et al., 2014; Vollstaedt et al., 2014).

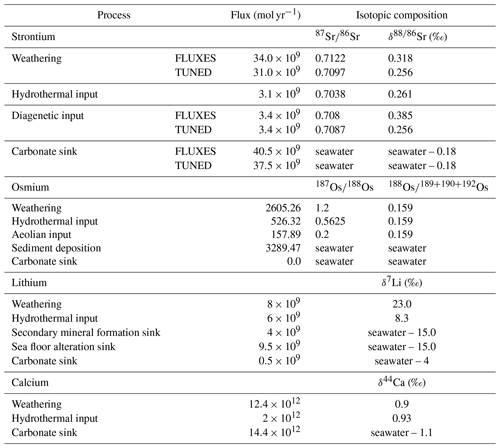
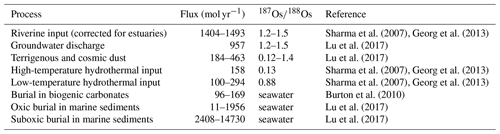
A list of the different sources and sinks of Sr, together with flux estimates and isotopic values, is given in Table 1. The Sr cycle is also summarized in Fig. 2.

Pearce et al. (2015)Kristall et al. (2017)Kristall et al. (2017)Allègre et al. (2010)Peucker-Ehrenbrink et al. (2010)Pearce et al. (2015)Kristall et al. (2017)Allègre et al. (2010)Peucker-Ehrenbrink et al. (2010)Kristall et al. (2017)Basu et al. (2001)Beck et al. (2013)Pearce et al. (2015)Krabbenhöft et al. (2010)Stevenson et al. (2014)Kristall et al. (2017)Krabbenhöft et al. (2010)Menzies and Seyfried (1979)Kristall et al. (2017)

Table 1 Estimates of pre-industrial Sr fluxes between surface reservoirs and their isotopic composition.

2.2 Osmium

Osmium, a siderophile (affinity for iron) and chalcophile (affinity for sulfur) element, is compatible during mantle melting and as such is accumulated in Earth's core (Goldschmidt, 1922). As a result, it is one of the rarest elements in the Earth's crust and the oceans. Because of its low concentrations, the ability to measure Os in seawater was only developed in the past few decades, limiting the number of observations of marine Os concentrations and isotopic compositions.

The cycling of Os at the Earth's surface is similar to that of radiogenic Sr in many aspects. Oxidative weathering of sediments exposed at the land surface is currently the most important natural source of Os to the oceans (Peucker-Ehrenbrink and Ravizza, 2000; Lu et al., 2017). The estimated annual input of such Os to the oceans via aeolian and riverine transport and groundwater discharge is about 5 times larger than all other natural inputs combined (Lu et al., 2017). Hydrothermal inputs constitute the next largest source of oceanic Os, with high- and low-temperature systems being of roughly equal importance (Georg et al., 2013). The high-temperature hydrothermal source can be split into a basaltic and a peridotitic source (Burton et al., 2010). Unlike for Sr, cosmic and terrestrial dust are significant sources of marine Os (Sharma et al., 2007). Os is removed from the ocean by deposition at the seafloor, predominantly under suboxic conditions and in association with organic matter, and in ferro-manganese nodules (Lu et al., 2017). Os incorporation into biogenic carbonates constitutes an additional but minor sink (Burton et al., 2010). The marine residence time of Os is inherently uncertain given the uncertainty in Os fluxes. Estimates range from 3–50 kyr (Sharma et al., 1997; Levasseur et al., 1998; Oxburgh, 2001).

Os has seven naturally occurring isotopes (0.02 % ¹⁸⁴Os, 1.59 % ¹⁸⁶Os, 1.51 % ¹⁸⁷Os, 13.29 % ¹⁸⁸Os, 16.22 % ¹⁸⁹Os, 26.38 % ¹⁹⁰Os, 40.98 % ¹⁹²Os). ¹⁸⁶Os has such a long half-life that it can also be treated as stable over geologic time, whereas ¹⁸⁷Os is radiogenic due to the β decay of ¹⁸⁷Re (Faure and Mensing, 2005). The isotopic composition of Os in marine sediments provides insight into changing fluxes between different Os reservoirs, particularly weathering-related Os fluxes from the continents and mantle-derived fluxes from volcanic activity. During partial melt in the upper mantle, Os is more compatible than rhenium (Re), leading to an increased $\mathrm{Re}/\mathrm{Os}$ ratio in continental crust relative to the mantle (Dąbek and Halas, 2007) and therefore elevated ${}^{\mathrm{187}}\mathrm{Os}{/}^{\mathrm{188}}\mathrm{Os}$ ratios in the continental crust compared to the mantle. No isotopic fractionation has been observed during Os uptake into macroalgae (Racionero-Gómez et al., 2017), nor is it assumed to occur during other transfers between surface reservoirs.

A list of the different sources and sinks of Os together with flux estimates and isotopic values is given in Table 2. The Os cycle is also summarized in Fig. 2.

Sharma et al. (2007)Georg et al. (2013)Lu et al. (2017)Lu et al. (2017)Sharma et al. (2007)Georg et al. (2013)Sharma et al. (2007)Georg et al. (2013)Burton et al. (2010)Lu et al. (2017)Lu et al. (2017)

Table 2 Estimates of pre-industrial Os fluxes between surface reservoirs and their isotopic composition. In the calculation of Os burial with Ca carbonate, the estimates of Ca burial in Table 4 were used.

2.3 Lithium

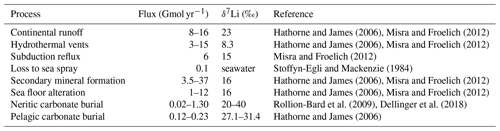
Lithium is the 25th most abundant element in the Earth's crust, and it is more concentrated in continental crust than in oceanic crust (Baskaran, 2011). Weathering, in particular of silicate rocks, releases dissolved Li to rivers and soils where it is partially removed and bound during clay formation (Kısakűrek et al., 2005; Dellinger et al., 2015; Pogge von Strandmann et al., 2017). The remaining dissolved Li is transported to the oceans via rivers and groundwater. Aeolian transport only contributes a minor flux of Li to the oceans (Baskaran, 2011). Li is also added to the oceans by hydrothermal vents and submarine weathering, but the size of this flux is more uncertain (Chan et al., 1992; Hathorne and James, 2006). Removal from the ocean happens predominantly via Li adsorption onto clay minerals, with a minor proportion buried as Li-containing biogenic calcite (Hathorne and James, 2006). These removal fluxes are dependent on the abundance of inorganic carbon and pH (or carbonate saturation) (Hall and Chan, 2004; Marriott et al., 2004) and are not spatially uniform (Hathorne and James, 2006). The residence time of Li in the ocean is estimated to be 0.3–3 Myr (Stoffyn-Egli and Mackenzie, 1984) with more recent estimates closer to 1 Myr (Vigier and Goddéris, 2015).

Li has two stable isotopes (7.52 % ⁶Li and 92.48 % ⁷Li, Penniston-Dorland et al., 2017). The isotopic composition of Li is expressed as δ⁷Li, which is the ‰ deviation of the ${}^{\mathrm{7}}\mathrm{Li}{/}^{\mathrm{6}}\mathrm{Li}$ ratio from the L-SVEC standard (${\mathit{\delta }}^{\mathrm{7}}\mathrm{Li}=(\frac{({}^{\mathrm{7}}\text{Li}{/}^{\mathrm{6}}\text{Li}{)}_{\mathrm{sample}}}{({}^{\mathrm{7}}\text{Li}{/}^{\mathrm{6}}\text{Li}{)}_{\mathrm{std}}}-\mathrm{1})\cdot \mathrm{1000}$). While earlier studies suggested considerable spatial variability in seawater δ⁷Li (Carignan et al., 2004), more recent studies suggest that seawater is remarkably homogeneous in its δ⁷Li (Hall et al., 2005; Rosner et al., 2007; Penniston-Dorland et al., 2017) consistent with its long residence time. Isotope fractionation has been observed during clay formation, adsorption onto minerals and incorporation of Li into calcite shells (Pistiner and Henderson, 2003; Rudnick et al., 2004; Dellinger et al., 2015; Hindshaw et al., 2019) in magmatic systems (Parkinson et al., 2007; Penniston-Dorland et al., 2017), as well as potentially in aqueous solutions (Richter et al., 2006). Isotopic differences in weathered lithologies and post-weathering formation of secondary minerals in rivers and soils result in large spatial and temporal variability of the δ⁷Li of continental runoff (Huh et al., 1998; Pistiner and Henderson, 2003; Dellinger et al., 2015; Pogge von Strandmann and Henderson, 2015). Temporal variations in the amount of secondary mineral formation on land have the potential to drive shifts in seawater δ⁷Li over geological time (Misra and Froelich, 2012; Pogge von Strandmann and Henderson, 2015). Fractionation during biogenic carbonate formation results in carbonate δ⁷Li values that are a few per mill lower than seawater, but this offset seems to be carbonate producer dependent (Hathorne and James, 2006).

A list of the different sources and sinks of Li, together with flux estimates and isotopic values, is given in Table 3. The Li cycle is also summarized in Fig. 2.

Hathorne and James (2006)Misra and Froelich (2012)Hathorne and James (2006)Misra and Froelich (2012)Misra and Froelich (2012)Stoffyn-Egli and Mackenzie (1984)Hathorne and James (2006)Misra and Froelich (2012)Hathorne and James (2006)Misra and Froelich (2012)Rollion-Bard et al. (2009)Dellinger et al. (2018)Hathorne and James (2006)

Table 3 Estimates of pre-industrial Li fluxes between surface reservoirs and their isotopic composition. In the calculation of Li burial with calcium carbonate, the estimates of calcium burial in Table 4 were used, assuming a 50:50 split in calcium carbonate burial fluxes between neritic and pelagic environments (Milliman, 1993).

2.4 Calcium

Calcium cycling is closely linked to the C cycle, both shaping and shaped by the size of C reservoirs and C fluxes at the Earth's surface. Similar to Sr, Os and Li, the dominant Ca source for today's oceans is weathering-derived dissolved and particulate Ca in continental runoff. Input through hydrothermal vents near ocean ridges is on the order of 20 % of the riverine flux (e.g., Milliman, 1993; DePaolo, 2004). Unlike Sr, Os and Li, Ca plays an important role in many biological systems, predominantly as an electrolyte and building block for biogenic minerals (e.g., shells, exoskeletons, bones and teeth). In the ocean, Ca ions are incorporated into biogenic minerals (e.g., foraminiferal tests and calcareous nannoplankton), or form hydrogenetic or authigenic minerals (Fantle et al., 2020) if waters are highly saturated ($\mathrm{\Omega }=a_{{\mathrm{Ca}}^{\mathrm{2}+}}\cdot a_{{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}}/K_{\mathrm{sp}}$). The resulting minerals will tend to be dissolved in undersaturated conditions or buried, compacted and lithified under saturated conditions. Carbonate formation creates the biggest long-term Ca and C sinks in today's oceans, and marine carbonate accumulation and dissolution constitute a significant buffer mechanism to stabilize marine and atmospheric pCO₂ during periods of enhanced exogenic C input (see Ridgwell and Zeebe, 2005). The residence time of Ca in seawater is estimated to be 0.5–1.3 million years (Milliman, 1993; Sime et al., 2007; Griffith et al., 2008).

Ca has 6 stable isotopes (96.941 % ⁴⁰Ca, 0.647 % ⁴²Ca, 0.135 % ⁴³Ca, 2.086 % ⁴⁴Ca, 0.004 % ⁴⁶Ca, 0.187 % ⁴⁸Ca). ⁴⁸Ca has such a long half-life that it can be treated as a stable isotope, whereas a small component of the ⁴⁰Ca in a rock mineral is radiogenic (via decay of ⁴⁰K; $t_{\mathrm{1}}/\mathrm{2}=\mathrm{1.248}$ Ga) and accumulates in continental crust over geological timescales (Fantle and Tipper, 2014). The isotopic composition of Ca is reported as either ${\mathit{\delta }}^{\mathrm{44}/\mathrm{40}}\mathrm{Ca}$ or ${\mathit{\delta }}^{\mathrm{44}/\mathrm{42}}$Ca, which are the ‰ deviations in ${\mathit{\delta }}^{\mathrm{44}/\mathrm{40}}\mathrm{Ca}$ and ${\mathit{\delta }}^{\mathrm{44}/\mathrm{42}}$Ca, respectively, from NIST SRM-915a, SRM-915b, or modern seawater (see Fantle and Tipper, 2014, for discussion): (${\mathit{\delta }}^{\mathrm{44}/\mathrm{40}}\mathrm{Ca}=(\frac{({}^{\mathrm{44}}\mathrm{Ca}{/}^{\mathrm{40}}\mathrm{Ca}{)}_{\mathrm{sample}}}{({}^{\mathrm{44}}\mathrm{Ca}{/}^{\mathrm{40}}\mathrm{Ca}{)}_{\mathrm{std}}}-\mathrm{1})\cdot \mathrm{1000}$ and ${\mathit{\delta }}^{\mathrm{44}/\mathrm{42}}\mathrm{Ca}=(\frac{({}^{\mathrm{44}}\mathrm{Ca}{/}^{\mathrm{42}}\mathrm{Ca}{)}_{\mathrm{sample}}}{({}^{\mathrm{44}}\mathrm{Ca}{/}^{\mathrm{42}}\mathrm{Ca}{)}_{\mathrm{std}}}-\mathrm{1})\cdot \mathrm{1000}$). We use the ${\mathit{\delta }}^{\mathrm{44}/\mathrm{40}}\mathrm{Ca}$ notation in this study, from now on shortened to δ⁴⁴Ca, with NIST SRM-915a as standard. Dissolution of carbonates and silicates, as well as the precipitation of secondary silicate minerals, control the Ca isotopic composition in soil pore fluids, lakes and rivers (Farkaš et al., 2007; Tipper et al., 2008; Hindshaw et al., 2013; Fantle and Tipper, 2014; Kasemann et al., 2014; Perez-Fernandez et al., 2017). Both biotic and abiotic precipitation of carbonates fractionate Ca isotopically, generating minerals with low δ⁴⁴Ca values relative to aqueous Ca²⁺. The isotopic fractionation factor is most strongly a function of precipitation rate (and thus and solution chemistry, e.g. DePaolo, 2011) and is close to one (Δ∼0) in the marine sedimentary column (see reviews in Blättler et al., 2012; Fantle and Tipper, 2014). In the ocean, species-dependent fractionation has been observed for several groups of calcifiers, with a small dependence on temperature (e.g., Nägler et al., 2000).

A list of the different sources and sinks of Ca, together with flux estimates and isotopic values, is given in Table 4. The Ca cycle is also summarized in Fig. 2.

Berner and Berner (2012)Zhu and Macdougall (1998)Holmden et al. (2012)Tipper et al. (2016)Berner and Berner (2012)Fantle and Tipper (2014)Berner and Berner (2012)Holmden et al. (2012)Fantle and Tipper (2014)Berner and Berner (2012)Holmden et al. (2012)Fantle and Tipper (2014)Fantle et al. (2012)Fantle and Tipper (2014)Holmden et al. (2012)Fantle and Tipper (2014)

Table 4 Estimates of pre-industrial Ca fluxes between surface reservoirs and their isotopic composition. ${\mathit{\delta }}^{\mathrm{44}/\mathrm{40}}\mathrm{Ca}$ is given relative to NIST SRM915a (offset by $+\mathrm{1.8825}\pm \mathrm{0.07}$ from seawater, Holmden et al., 2012).

2.5 Metal distributions in seawater

Dissolved Sr, Os, Li and Ca are largely homogeneous in seawater, which is illustrated in Fig. 1 by sorting all seawater measurements – independent of location and depth – by their measured value. Measurements of a perfectly homogeneous – salinity-normalized – seawater property would appear as a horizontal line in this plot (for Sr, Li, Ca), since the same value would be measured everywhere in the ocean. Most trace metal measurements have a difference of less than 1 standard deviation from the respective mean, suggesting very small spatial heterogeneities. In particular, most measured isotopic compositions are analytically indistinguishable from the standard deviation of the overall data population. Larger differences between lowest and highest measured metal concentrations indicate heterogeneity (potentially horizontal and/or vertical gradients) in metal abundances or are an artifact of the small number of sub-surface measurements. One possible example is Sr, which is reportedly less abundant in surface waters and waters in the North Atlantic than in deeper waters and sites outside the North Atlantic (see Fig. F1). Higher Li concentrations in the surface ocean compared with deeper waters are only reported in one study, Angino and Billings (1966), while no vertical gradients are apparent in Fabricand et al. (1967) and Hall (2002). These differences suggest that the spread in Li concentrations in Fig. 1 could be the result of analytical uncertainty rather than real gradients in dissolved Li. In contrast, Os concentrations, which are not salinity-normalized in our compilation, have a relative spread of Os concentrations (factor 2 between the lowest and highest measurements) that is larger than that of salinity (maximum factor of 1.1 Talley, 2002) with a considerable variation in Os concentration between sites and measurement techniques (Gannoun and Burton, 2014). Ca (salinity-normalized) values show no spatial heterogeneity.

Figure 1 Sr (a, e, i), Li (b, f), Os (c, g) and Ca (d, h) composition of modern seawater. Shown are composites of all published measured concentrations (a–d) and isotope ratios (e-i) with reported errors. From these, we calculated mean concentrations and isotope ratios weighted by the reported error (the more uncertain a value, the less it contributes to the mean), which are indicated by horizontal lines. Shading indicates a single weighted standard deviation around the means. Data are taken from Angino et al. (1966), Fabricand et al. (1967), Bernat et al. (1972), Brass and Turekian (1974), De Villiers (1999), Pearce et al. (2015), Mokadem et al. (2015), and the compilation of Wakaki et al. (2017) for Sr; Angino and Billings (1966), Fabricand et al. (1967), Chan (1987), Chan and Edmond (1988), You and Chan (1996), Moriguti and Nakamura (1998), Tomascak et al. (1999), James and Palmer (2000), Košler et al. (2001), Nishio and Nakai (2002), Hall (2002), Bryant et al. (2003), Pistiner and Henderson (2003), Millot et al. (2004), Choi et al. (2010), Pogge von Strandmann et al. (2010), Phan et al. (2016), Lin et al. (2016), Henchiri et al. (2016), Weynell et al. (2017), Fries et al. (2019), Gou et al. (2019), Hindshaw et al. (2019), Murphy et al. (2019), and Pogge von Strandmann et al. (2019b) for Li; Levasseur et al. (1998), Woodhouse et al. (1999) and Gannoun and Burton (2014) for Os; and Fabricand et al. (1967), De Villiers (1999), and Fantle and Tipper (2014) for Ca. The decade of publication is indicated by color as measurement techniques for some metals and isotopes have improved over time. Concentrations of Sr, Li and Ca are normalized to a salinity of 34.90. Os concentrations could not be salinity-normalized because of missing salinity measurements at one out of three measurement sites (Woodhouse et al., 1999).

2.6 Application of Sr, Os, Li and Ca isotopes as proxies of weathering and mantle emissions

The isotopic differences between Sr, Os, Li and Ca in the ocean and exogenic reservoirs make these metals important proxies for mass exchange occurring between the surficial Earth system and the mantle, continental crust (all four) and extra-terrestrial material (Os). Because they record different geochemical pathways, behave differently in water and have different predominant host lithologies, their combined interpretative power is much greater than any one single proxy used in isolation and which is the basis of our model development philosophy here.

Radiogenic Sr and Os isotopes have previously mostly been used separately as proxies for the balance between the weathering of old and juvenile basalt or direct mantle emissions (e.g., Hodell et al., 1990; Goddéris and François, 1995; Tejada et al., 2009; Finlay et al., 2010; Bottini et al., 2012; Dickson et al., 2015). However, in combination, they also provide information about sedimentary rock weathering since continental Sr is primarily derived from carbonates while Os resides predominantly in shales and evaporites (e.g., Peucker-Ehrenbrink et al., 1995). Li is orders of magnitude more abundant in silicates than in carbonates and thus is regarded as the most direct proxy for silicate weathering (Kısakűrek et al., 2005; Millot et al., 2010; Pogge von Strandmann et al., 2020). The isotopic composition of dissolved Li is also not affected by plant growth (Lemarchand et al., 2010; Clergue et al., 2015) or phytoplankton growth (Pogge von Strandmann et al., 2016). Instead, the light Li isotope (⁶Li) is preferentially taken up by secondary minerals (clays, oxides, zeolites) formed during weathering, enriching residual waters in ⁷Li. Hence, surface water δ⁷Li is controlled by the ratio of primary rock dissolution to secondary mineral formation, known as the weathering congruency (Misra and Froelich, 2012; Pogge von Strandmann and Henderson, 2015), which in turn can act as a tracer of weathering intensity (that is, the ratio of the weathering rate to the denudation rate, Dellinger et al., 2015; Pogge von Strandmann et al., 2017; Murphy et al., 2019; Gou et al., 2019). This also relates to the efficiency of CO₂ drawdown, as weathering-derived cations cannot assist carbon sequestration in the ocean if they are retained on the continents in secondary minerals (Pogge von Strandmann and Henderson, 2015; Pogge von Strandmann et al., 2017). Ca isotopes have also been used to examine weathering processes in the geological record (Kasemann et al., 2005; Farkaš et al., 2007; Kasemann et al., 2008; Blättler et al., 2011; Holmden et al., 2012; Fantle and Tipper, 2014; Kasemann et al., 2014), and additionally are crucial proxies for the quantification of carbonate precipitation rates (Pogge von Strandmann et al., 2019b), including authigenesis (Fantle and Ridgwell, 2020). Furthermore, Ca isotopes have been considered a potential temperature proxy (e.g., Nägler et al., 2000), but this application might be complicated by the strong control of aqueous chemistry on Ca fractionation (DePaolo, 2011). Alongside Ca, stable Sr isotopes provide information about the dominant form of carbonate burial (Paytan et al., 2021) and growth rate in marine calcifiers, mostly influenced by temperature and pCO₂ (Stevenson et al., 2014; Müller et al., 2018). Likewise, changes in the $\mathrm{Sr}/\mathrm{Ca}$ ratio in calcifiers reflect shifts in ecosystem structure, carbonate mineralogy and calcification rate (Stoll and Schrag, 2001).

While each system individually gives valuable insight into Earth system dynamics, in concert these trace metal systems can provide information on feedbacks and event durations, as well as improve the accuracy of our reconstructions (e.g., Kasemann et al., 2008).

3 Model implementation

For this paper, we developed a series of parameterizations of marine cycling of Sr, Os and Li and Ca isotopes in the Earth system model cGENIE, focusing on the elemental and isotopic fluxes most essential to tracking external metal additions or weathering rate changes. Our implementation is hence deliberately not exhaustive in this initial paper, and representation of elemental cycles, particularly with respect to processes occurring in terrestrial freshwater environments and at the seafloor, could be further improved upon (Sect. 5 discusses ideas for added complexity). The present section provides an overview of the existing implementation.

cGENIE is best described as a modeling framework (Lenton et al., 2007) and comprises, in our study, modules for ocean physics (GOLDSTEIN, Edwards and Marsh, 2005), marine biogeochemistry (BIOGEM, Ridgwell et al., 2007), continental weathering and runoff (ROKGEM, Colbourn et al., 2013), sea-floor sediment formation (SEDGEM, Ridgwell and Hargreaves, 2007), atmospheric chemistry (ATCHEM) and atmospheric energy balance (EMBM, Ridgwell et al., 2007). As such, our implementation of cGENIE includes a 3D ocean combined with a 2D atmosphere and can capture the cycling of carbon and a range of other elements relevant for biogeochemical studies of the ocean water column and at the sea–sediment and sea–air interfaces, as well as climate-sensitive continental runoff and explicit sedimentary carbonate burial.

Figure 2 Processes included in the cGENIE trace metal implementation and the number of the subsection describing their implementation. Hashed arrows indicate processes during which isotopic fractionation occurs in the model.

Figure 2 shows a conceptual model of the Sr, Os, Li and Ca cycles in cGENIE with arrows of different colors showing mass fluxes of different metals. The implementation of these processes involves code additions to the modules ROKGEM, BIOGEM and SEDGEM that are described in the following sections. Each code addition requires the model user to set parameters controlling the respective metal fluxes. These parameters, as well as a parameter set that reproduces the present-day marine distributions of Sr, Os, Li and Ca in steady-state metal cycles, are provided in Appendix E, together with example experiments as part of the model code release.

3.1 Marine Sr, Os, Li and Ca sources

Continental weathering is the main source for marine Sr, Os, Li and Ca today and changes in the weathered lithology or weathering intensity are invoked as major drivers of the evolution of trace metal concentrations and their isotopic compositions in seawater over time (e.g., Misra and Froelich, 2012; Kristall et al., 2017). ROKGEM, the weathering module of cGENIE, provides a framework for calculating climate- and CO₂-dependent additions of Ca, Mg and alkalinity from carbonate weathering (following Berner, 1994) and silicate weathering (following Brady, 1991) to the ocean (see Colbourn et al., 2013, for a full description of the weathering module). By applying linear and exponential relationships of temperature and carbonate and silicate weathering rates, respectively, ROKGEM modifies user-given baseline weathering fluxes according to climatic variations. Additional (optional) modifiers can be selected to represent the effect of changes in precipitation, vegetation and atmospheric CO₂ concentration.

The modification of weathering fluxes is either calculated locally, based on a geographic distribution of carbonates and silicates taken from user input (“2-D case”, described in more detail in the Supplement) or globally, based on a globally averaged change in climate (“0-D case”). In both implementations, the ROKGEM module calculates a drainage map based on a prescribed continental topography and determines the coastal locations where weathering input (either of regionally variant composition in the 2D case or homogeneous in the 0D case) is added to the ocean. The flux of metals added to the ocean in these locations is determined by the size of the model catchment and can optionally be scaled by the proportion of global runoff entering the ocean (when rg_opt_weather_runoff=.true.).

Depending on the primary source rock, we tied the rate M of Sr, Os or Li ion delivery to the ocean to Ca and magnesium (Mg) input rates from weathering of carbonates (${\mathrm{Ca}}_{{\mathrm{CaCO}}_{\mathrm{3}}}$) and/or silicates (${\mathrm{Ca}}_{{\mathrm{CaSiO}}_{\mathrm{3}}}$), related by a constant ratio k:

$$\begin{array}{}\text{(1)}& {\displaystyle }{M}_{{\mathrm{CaCO}}_{\mathrm{3}}}=k_{{\mathrm{CaCO}}_{\mathrm{3}}}\cdot {\mathrm{Ca}}_{{\mathrm{CaCO}}_{\mathrm{3}}},\text{(2)}& {\displaystyle }{M}_{{\mathrm{CaSiO}}_{\mathrm{3}}}=k_{{\mathrm{CaSiO}}_{\mathrm{3}}}\cdot {\mathrm{Ca}}_{{\mathrm{CaSiO}}_{\mathrm{3}}}.\end{array}$$

ROKGEM allows for different CaSiO₃ weathering schemes, including one which separates total CaSiO₃ weathering into contributions from granite and basalt weathering. For this case, we imposed individual parameters for Sr weathering for each lithology. Because the amount and isotopic composition of weathering-derived Os is mostly dependent on organic matter content (Jaffe et al., 2002; Georg et al., 2013; Dubin and Peucker-Ehrenbrink, 2015), whereas the 0D weathering scheme in ROKGEM only differentiates between Os delivery from CaSiO₃ and CaCO₃ weathering. To enable a more realistic simulation of continental Os weathering fluxes, we extended the 2D weathering schemes in ROKGEM to trace Os and its isotopes. While slightly computationally more expensive, Os weathering fluxes can be tied to specific lithologies in these schemes, including organic-rich shales.

The effect of secondary mineral formation on land on Li concentrations and isotope abundances in continental runoff is simulated based on the empirical relationships between the weathering Li flux (${\text{Li}}_{{\mathrm{CaSiO}}_{\mathrm{3}}}$) and the ratio of weathering to denudation rate (WD, also referred to as weathering congruency) reported in Pogge von Strandmann et al. (2020):

$$\begin{array}{}\text{(3)}& {\text{Li}}_{{\mathrm{CaSiO}}_{\mathrm{3}}}=k_{{\mathrm{CaSiO}}_{\mathrm{3}}}\cdot {\mathrm{Ca}}_{{\mathrm{CaSiO}}_{\mathrm{3}}}\cdot e^{\mathrm{0.4883}\cdot \log \left(\text{WD}\right)}.\end{array}$$

cGENIE derives an estimate of WD from the climate weathering modifier, which adjusts the chemical weathering flux from silicates on the basis of a deviation of climate (e.g., surface land temperature) from some reference value (and a value of WD of 1.0).

To represent the vast range of chemical conditions and reaction rates at the sediment–water interface in the ocean efficiently, three biogeochemically distinct depositional environments are represented in the SEDGEM module: (1) shallow seafloor with reef-building biota (“reef”), (2) shallow seafloor, assumed depleted in oxygen with reef-building biota absent and characterized by organic rich sediments (“muds”), and (3) plankton-derived carbonate (and opal) deposition in the open ocean (“deep sea”). CaCO₃ deposition and dissolution, as well as elemental fluxes across the sediment–water interface, are parameterized differently in each of these environments, with masks used to distinguish the different environments.

Mantle-derived metal input via hydrothermal vents is also parameterized in the SEDGEM module and the fluxes to ocean bottom waters occur only in grid cells that represent deep sea. We parameterized this flux such that a global total input flux is prescribed, but it is then either distributed equally across deep-sea grid cells or according to an easily adjustable, spatially explicit map (e.g., following the line of mid-ocean ridges). There is no differentiation between seafloor areas with predominant high- or low-temperature hydrothermal venting in our implementation, and hence we make no isotopic distinction spatially between fluxes from the seafloor. Recrystallization of SrCO₃ is an additional source of Sr to the water column (see above). Its parameterization is similar to that for hydrothermal inputs, except that elemental fluxes from recrystallization only occur in bottom waters of grid cells labeled as “reef”. The size and rate of this Sr flux can also either be set as a total global or an area-weighted value.

To account for inputs at the air–sea interface (only assumed to be relevant for Os, as described in the previous section), we added the option to prescribe a spatially explicit field of annual input into the surface ocean (or technically anywhere into the water column).

3.2 Marine Sr, Os, Li and Ca sinks

Ca export from the surface ocean is linked to the export of particulate organic carbon (POC) by a constant CaCO₃:POC ratio (rain ratio) (see Ridgwell et al., 2007, for a description of POC export simulation in cGENIE). We parameterize the incorporation of Os, Li and Sr into carbonates by scaling their export in carbonates to the Ca export. This can be done by setting either a constant Sr, Li and Os to Ca ion ratio ($r_{M/\mathrm{Ca}}$) or a constant scaling factor α that links the local Sr/Li/Os-to-Ca ratio in seawater to the Sr/Li/Os-to-Ca ratio in the precipitate (following, e.g., Tang et al., 2008):

$$\begin{array}{}\text{(4)}& {\displaystyle }{\text{export}}_{\mathrm{metal}}=k\cdot {\text{export}}_{\mathrm{Ca}},\text{(5)}& {\displaystyle }k=r_{M/\mathrm{Ca}}+\mathit{\alpha }\cdot [\text{Metal}{]}_{\mathrm{water}}/[\mathrm{Ca}{]}_{\mathrm{water}}.\end{array}$$

The Sr/Li/Os-to-Ca ratio of the precipitate is then used to calculate the metal consumption during carbonate formation, as well as metal release during carbonate dissolution. To reflect the different Sr/Li/Os-to-Ca ratios in pelagic compared to reef carbonates, a separate factor can be set for reef production. Reef CaCO₃ immediately contributes to surface sediments, whereas pelagically formed CaCO₃ sinks through the water column, and might be dissolved before reaching the deep-sea sediment–water interface as a result of local chemical equilibria.

We further included the sequestration of Sr and Li in seafloor sediments due to seafloor weathering by scaling the metal flux into the uppermost sediment layer (fMetal) to the metal concentration of the overlying ocean grid cell ([Metal]):

$$\begin{array}{}\text{(6)}& \mathit{\text{f}}\text{Metal}=k\cdot \left[\text{Metal}\right].\end{array}$$

This burial occurs in all grid cells that are labeled as deep sea. In the absence of better constraints on depositional mechanisms, we include a mathematically similar sink for Os. For a desired global burial rate B (mol s⁻¹), the value of k can be estimated by considering the total area of deep-sea A_deep (m²) and equilibrium metal concentration [Metal] (mol kg⁻¹):

$$\begin{array}{}\text{(7)}& k={\displaystyle \frac{B/A_{\mathrm{deep}}}{\left[\text{Metal}\right]}}.\end{array}$$

Our model calculates Li burial during clay formation locally at the sea–sediment interface. The burial flux fLi_clay is scaled to the concentrations of Li in the deepest grid box of the water column and the detrital flux into the sediments:

$$\begin{array}{}\text{(8)}& \mathit{\text{f}}{\text{Li}}_{\mathrm{clay}}=k\cdot \left[\text{det}\right]\cdot \left[\mathrm{Li}\right].\end{array}$$

To test implications of Os burial with particulate organic carbon, we included an option for [O₂]-sensitive scavenging from the water column. In the surface ocean, organic carbon is exported as a function of the concentration of inorganic carbon, light, nutrient availability (PO${}_{\mathrm{4}}^{\mathrm{3}-}$ in our set up), sea ice cover and temperature (Ridgwell et al., 2007). This export production of organic carbon is split into dissolved and particulate organic carbon (DOC and POC) at an adjustable ratio. DOC is advected and diffused in the ocean, while POC is instantly exported to deeper water layers. Remineralization of organic matter can either be set to follow empirical decay functions or to depend on local temperature and redox conditions. Depending on which chemical species are accounted for in a particular experiment, the redox state is calculated based on oxygen, sulfate, methane, nitrate and iron oxide concentrations. O₂ is exchanged between the atmosphere and the ocean at the air–sea interface, depending on the solubility of O₂ in water. In the ocean, O₂ is released during primary production in the surface ocean and consumed during remineralization of DOC and POC under oxic conditions. Sulfur, iron, methane and nitrogen cycling are less relevant for the redox state in the modern open ocean but influenced POC fluxes in the past and are described in detail in van de Velde et al. (2021), Reinhard et al. (2020) and Naafs et al. (2019). Following the example of existing scavenging parameterization schemes in cGENIE, we implemented this by scaling the flux of scavenged Os (f_scav) to the local concentrations of Os and POC:

$$\begin{array}{}\text{(9)}& f_{\mathrm{scav}}=k\cdot \left[\mathrm{Os}\right]\cdot \left[\mathrm{POC}\right].\end{array}$$

Since there is evidence that Os needs to be reduced in order to be buried, we include a switch to use the scavenging code only where ambient [O₂] falls below some specified threshold.

3.3 Isotopes

cGENIE tracks isotopes in total molar abundances rather than delta notation or ratios so that they can be advected and diffused like any other tracer. Li has two stable isotopes, and thus its implementation follows that of other elements with two stable isotopes (e.g., C, Ridgwell, 2001; Ridgwell et al., 2007). The addition of Sr, Os and Ca isotopes needed different approaches because they have more than two principal stable isotopes. We chose to reduce the number of traced isotopes to three for Sr and Os and to two for Ca because these subsets contain the most abundant isotopes of the respective element (Sr) and/or are most relevant for their application as seawater proxies (Sr, Os and Ca). Calcium is thus currently treated like an element with two stable isotopes in cGENIE. To track three isotopes rather than two, we track two isotopes explicitly and one implicitly by subtracting from the bulk abundance of the trace metal. In the case of Sr, abundances of ⁸⁷Sr and ⁸⁸Sr are tracked explicitly. The abundance of ⁸⁶Sr is then taken as the difference between the abundances of the two explicitly tracked isotopes and the bulk Sr abundance, since ⁸⁴Sr can be neglected. Os has more than two stable isotopes, but only two of them, ¹⁸⁷Os and ¹⁸⁸Os, are currently used as a proxy system, and thus these two isotopes are tracked explicitly and the bulk Os abundance contains all remaining stable isotopes.

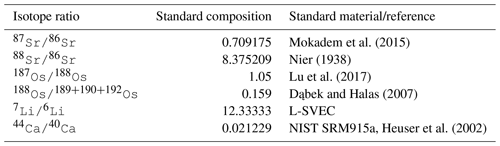
Every metal flux in the model is accompanied by fluxes of the traced isotopes. The scale of these isotope fluxes depends on the size of the metal flux and the relative abundance of the respective isotope, derived from the model configuration in which the model user prescribes the isotopic composition of marine metal inputs and outputs. For simplicity, the user can prescribe these isotopic compositions in delta notation for stable isotopes and ratios for radiogenic isotopes. The model then converts these values into molar isotope abundances, using the isotope standards listed in Table 5 (international standards where available and observations of modern-day seawater otherwise). If required, these internal standards can be changed by the user, although this currently requires an edit to the code.

Mokadem et al. (2015)Nier (1938)Lu et al. (2017)Dąbek and Halas (2007)Heuser et al. (2002)

Table 5 Isotopic standards in cGENIE.

Given the current lack of evidence for Os isotopic fractionation outside of the lithosphere (e.g. Nanne et al., 2017), we do not include a fractionation factor for marine Os sinks (or rather, it is assume to be 1.0). For Sr and Li, we account for isotopic fractionation during carbonate and secondary mineral formation. In its default setting, cGENIE uses constant fractionation factors for Sr, Li and Ca fluxes, but we have included optional schemes to simulate environmental controls on stable Li and Ca isotope fractionation. For Li, we included an optional correction of riverine δ⁷Li for weathering congruency (following Pogge von Strandmann et al., 2020) and the temperature sensitivity of Li isotope fractionation during terrestrial and marine clay formation (Millot et al., 2010):

$$\begin{array}{}\text{(10)}& {\displaystyle }{\mathit{\delta }}^{\mathrm{7}}{\mathrm{Li}}_{\mathrm{runoff}}={\mathit{\delta }}^{\mathrm{7}}{\mathrm{Li}}_{{\mathrm{CaSiO}}_{\mathrm{3}}}-\mathrm{5.4079}\cdot \log \left(\text{WD}\right),\text{(11)}& {\displaystyle }{\mathit{\delta }}^{\mathrm{7}}{\mathrm{Li}}_{\mathrm{runoff}}={\mathit{\delta }}^{\mathrm{7}}{\mathrm{Li}}_{\mathrm{runoff}}+k\cdot (T-T_{\mathrm{0}}),\text{(12)}& {\displaystyle }{\mathrm{\Delta }}^{\mathrm{7}}{\mathrm{Li}}_{\mathrm{burial}}={\mathrm{\Delta }}^{\mathrm{7}}{\mathrm{Li}}_{\mathrm{burial}}+k\cdot (T-T_{\mathrm{0}}),\end{array}$$

with ${\mathit{\delta }}^{\mathrm{7}}{\mathrm{Li}}_{{\mathrm{CaSiO}}_{\mathrm{3}}}$ being the assumed δ⁷Li of weathered silicates at the reference temperature, k the isotopic effect of a 1 ^∘C temperature change and T₀ being the reference temperature. A consistency check prevents the resulting δ⁷Li_runoff from falling below the composition of continental crust. If these functions are not used, the absence of simulated Li fractionation in freshwater should be taken into account by setting the parameters for terrestrial Li input based on the composition of river water rather than weathered Li at the reference temperature.

cGENIE also offers two different choices for Ca isotope fractionation during carbonate formation (in addition to the default of a fixed fractionation), carbonate ion concentration-dependent fractionation following Gussone et al. (2005) and saturation state (Ω)-dependent fractionation following Tang et al. (2008):

$$\begin{array}{}\text{(13)}& \begin{array}{rl}& {\mathrm{\Delta }}^{\mathrm{44}/\mathrm{40}}{\mathrm{Ca}}_{\mathrm{CaCO}\mathrm{3}}=-\mathrm{1.31}+\mathrm{3.69}\cdot \left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]\times {\mathrm{10}}^{\mathrm{3}},\\ & {\mathrm{\Delta }}^{\mathrm{44}/\mathrm{40}}{\mathrm{Ca}}_{\mathrm{CaCO}\mathrm{3}}=-\mathrm{0.066649}\cdot \mathrm{\Omega }-\mathrm{0.320614}.\end{array}\end{array}$$

These fractionation schemes are explored in Appendix C, as well as in Fantle et al. (2020).

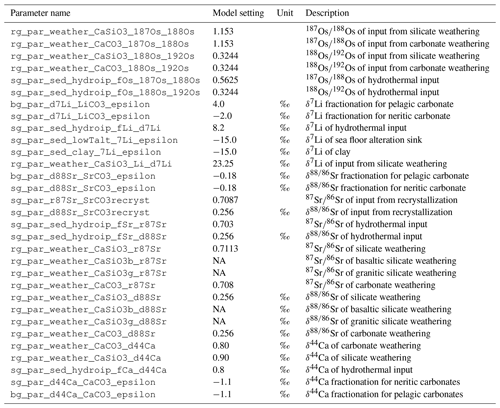
The model parameters required to set isotopic fractionation of Os, Li and Sr are listed in Table E8.

4 Model configuration and validation

The three-dimensional grid of cGENIE allows for comparison of the spatial pattern produced by the simulated set of processes to observations, which can further bolster or challenge our assumptions about global trace metal cycling on diverse timescales. Here we set up the model to represent the pre-industrial state of trace metal cycling, and compare the model output to measured modern seawater profiles.

4.1 Pre-industrial configuration

We initialized cGENIE with a modern-day geography on a 36×36 grid with eight depth layers in the ocean (following Ridgwell and Hargreaves, 2007) and with a pre-industrial CO₂ concentration of 278 ppm. Marine biological productivity is simulated using a single-nutrient scheme as outlined in Ridgwell et al. (2007), but here it is done with a constant CaCO₃:POC rain ratio set to 0.043, in line with typical paleo-configurations of the model (Panchuk et al., 2008). Burial and dissolution of CaCO₃ in deep-sea sediments follows Ridgwell and Hargreaves (2007). This configuration results in a pelagic CaCO₃ burial rate of 0.125 PgC yr⁻¹, close to the observationally calibrated CaCO₃ sink of Ridgwell and Hargreaves (2007). In addition to the pelagic environment, covering 350.6 million square kilometers, we simulated reef deposition on shelves, which covers 5.5 million square kilometers in our particular (low-resolution) modern model grid (see Appendix D). The sediment model bathymetry was derived from ETOPO5, Data Announcement 88-MGG-02, 1988). Reefal deposition was simulated in grid cells representing marine sediments shallower than 1000 m and not further polewards than 41.8^∘ N/S, on the basis that reefal carbonate deposition is predominantly a tropical and subtropical process. We prescribe a reefal CaCO₃ sink of 0.05 PgC yr⁻¹ associated with these environments (approximately 40 % of the deep-sea value). Temperature-dependent terrestrial silicate and carbonate weathering (Lord et al., 2016) formulations were selected, with the baseline temperature and rates of carbonate and silicate weathering set to 8.48 ^∘C, 8.4 and 6.0 Tmol yr⁻¹, respectively. Silicate weathering was split into the CO₂-consuming weathering components: CaSiO₃ ($\mathrm{2}/\mathrm{3}$) and MgSiO₃ ($\mathrm{1}/\mathrm{3}$). In the absence of a numerical representation of hydrothermal cation exchange (Coogan and Gillis, 2018), we balanced the Ca and Mg cycles by including a constant exchange between sedimentary Ca and dissolved Mg of 2.0 Tmol yr⁻¹ at the seafloor. To close the long-term carbon cycle, we prescribed a fixed rate of organic C burial of 0.031 PgC yr⁻¹ with ${\mathit{\delta }}^{\mathrm{13}}\mathrm{C}=-\mathrm{30}$ ‰, as well as a total exogenic carbon influx of 0.103 PgC yr⁻¹ with ${\mathit{\delta }}^{\mathrm{13}}\mathrm{C}=-\mathrm{6}$ ‰. This net input can be regarded as the result of 0.103 PgC yr⁻¹ subaerial outgassing with ${\mathit{\delta }}^{\mathrm{13}}\mathrm{C}=-\mathrm{4.6}$ ‰ (Mason et al., 2017), hydrothermal emissions of 0.018 PgC yr⁻¹ with ${\mathit{\delta }}^{\mathrm{13}}\mathrm{C}=-\mathrm{6}$ ‰ at mid-ocean ridges and consumption of 0.018 PgC yr⁻¹ with δ¹³C=2 ‰ during seafloor weathering (Cocker et al., 1982).

Table 6 summarizes the trace metal fluxes we prescribed to simulate the pre-industrial trace metal cycling, consistent with the observational constraints provided in Tables 1–4. We used the 0D weathering scheme for computational efficiency, but since a differentiation between carbonate and silicate derived Os does not capture the lithology dependence of the Os weathering flux appropriately, we prescribed the net abundance and isotopic composition of Os in continental runoff rather than lithology-specific compositions. We also did not simulate Os scavenging in these pre-industrial spin-ups because the dependence of marine Os burial on organic matter abundance and redox state are uncertain and today's ocean is predominantly oxic. However, in Appendix A1 and A2 we included the results of two pre-industrial Os cycle spin-ups – one with the 2D weathering scheme and the second with Os scavenging under occurring anoxic conditions and accounting for 50 % of marine Os burial. Note that the prescribed hydrothermal metal fluxes are net fluxes of high- and low-temperature hydrothermal activity. The specific model parameters that need to be prescribed to achieve these fluxes are given in the Supplement and in the GitHub repository containing all relevant configuration files, which can be accessed as outlined under “code availability”.

In running the model to steady state, we assume that metal fluxes are currently in equilibrium. This is a common assumption when modeling weathering tracer isotopes and their perturbations in the geological record (e.g., Misra and Froelich, 2012; Bauer et al., 2017). However, given the long residence time estimates in today's ocean, it is likely that at least the Sr, Li and Ca cycles are not fully in steady state today (i.e., Derry, 2009). For example, Paytan et al. (2021) inferred that the marine Sr has constantly fluctuated over the last 35 Myr. Constant Os isotopic compositions of seawater over the last millennia suggest that Os has reached steady state since the last deglaciation. However, residence time estimates of >20 kyr based on modern day Os fluxes put this into question (Oxburgh, 2001). The newly implemented tracers in cGENIE can be used to study different equilibria and transient adaptations of the marine metal reservoirs to new boundary conditions. For example, we were not able to simulate the observed marine Sr reservoir using the observed Sr input fluxes, which indicates an imbalance between observed Sr fluxes and the marine Sr reservoir. Hence, we simulated two different steady states for Sr under pre-industrial boundary conditions: one with a best estimate of pre-industrial Sr fluxes (hereafter referred to as FLUXES) and one tuned to best fit the spatial mean of observations (TUNED).

Table 6 Metal fluxes for pre-industrial spin-up.

The model spin-up was carried out in three stages to improve computational efficiency. The first stage (20 kyr) was carried out with a “closed” marine carbonate system, where the marine C and alkalinity reservoirs are artificially restored by balancing losses through CaCO₃ burial with external inputs to the ocean. During this stage, the climate and ocean dynamics adjust to the physical boundary conditions and ocean–atmosphere C exchanges come into balance. In the second phase (500 kyr), the marine carbonate system was “open” so that prescribed inputs from terrestrial weathering and the mantle and marine burial dynamically adjusted to balance one another. During the third stage (15 Myr), when ocean dynamics, C, nutrient and Ca cycles were already equilibrated, the prescribed Sr, Os and Li sources were added, and the model was run until metal concentrations and their isotopic composition in the ocean were at steady state. The model calculations were accelerated during the last two stages of the spin-up using the time-stepping method introduced by Lord et al. (2016).

4.2 Comparison between simulated and observed trace metal contents of seawater

One advantage of simulating trace metal cycles within a 3D Earth system model is that we can test simulated metal concentrations and isotopes against observed spatial patterns. In the following sections, the simulated pre-industrial distribution of each metal is compared against observational data shown in Sect. 2.5.

4.2.1 Strontium

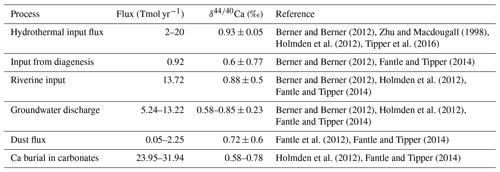
Figure 3 compares Sr concentrations and isotopic compositions in our simulation with observations. The simulated marine Sr reservoir is more homogeneous than observed in terms of concentrations and isotopic composition. The FLUXES simulation, in which we prescribe observationally constrained marine Sr inputs, results in more radiogenic and isotopically heavy marine Sr than observed. To yield a steady-state marine ${}^{\mathrm{87}}\mathrm{Sr}{/}^{\mathrm{86}}\mathrm{Sr}$ close to observations, we need to assume that the continental Sr supply is on average less radiogenic than observed (in agreement with, e.g., Pearce et al., 2015). Similarly, the observed fractionation factor for stable Sr isotopes during biogenic CaCO₃ formation is too large to equilibrate the model at the observed low ${\mathit{\delta }}^{\mathrm{88}/\mathrm{86}}$Sr if we do not assume that all Sr sources only provide mantle-like light Sr (${\mathit{\delta }}^{\mathrm{88}/\mathrm{86}}\mathrm{Sr}=\mathrm{0.256}$ ‰, TUNED simulation). Corroborating the conclusion of, e.g., Vance et al. (2009), this suggests that the isotopic composition of marine dissolved Sr is currently not at equilibrium.

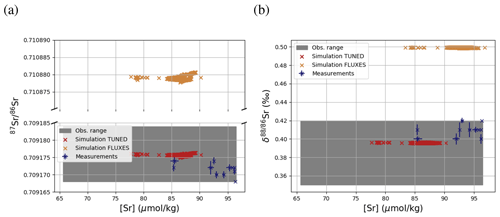
Figure 3 Comparison between measured and simulated concentrations (a) and isotopic composition (b) of dissolved Sr in seawater. The displayed data points are paired measurements of Sr concentrations and isotope ratios (Wakaki et al., 2017), while the gray box also indicates the full range of concentrations and isotopic compositions (separate measurements of Sr concentration or isotope ratios) (Angino et al., 1966; Fabricand et al., 1967; Bernat et al., 1972; Brass and Turekian, 1974; De Villiers, 1999; Mokadem et al., 2015). Observations and model results are salinity-normalized.

The simulations capture the homogeneous vertical profiles of Sr concentrations observed at most sites (see Figs. F1 and F5). One exception are modeled Sr concentrations in the North Atlantic, which are high compared with older measurements. Given that these low observed North Atlantic values come from one of the first studies measuring Sr concentrations in seawater (Angino et al., 1966) and that other studies of North Atlantic seawater yielded higher Sr concentrations (e.g., De Villiers, 1999), this difference could be partially the result of analytical errors, although influences from seasonal or inter-annual variability not captured by the model cannot be ruled out.

4.2.2 Osmium

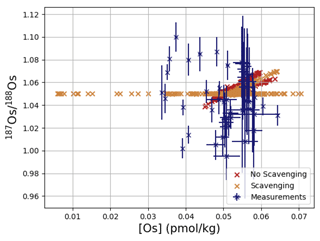
Os concentrations and isotopes are generally more spatially homogeneous in the simulation compared with observations. For 80 % of the paired measurements of Os concentrations and isotopic compositions, one or more cGENIE simulated grid cells fall within measurement uncertainty. The remaining 20 % of the Os observational data (those measurements with the lowest Os concentrations and isotopic ratios) were not reproduced in any grid cells in our simulation. This discrepancy between model simulation and observations is not the result of the simplified homogeneous terrestrial Os input in the model. In a repetition of the model experiment but employing spatially variable Os input (see Fig. A1), we found no appreciable change to the simulated ranges of Os concentrations and isotope ratios in the oceans, i.e., no appreciable increase in spatial heterogeneity. Since the low Os concentrations not captured by the model are observations from surface and intermediate waters from the East Pacific (Fig. F6, Woodhouse et al., 1999; Gannoun and Burton, 2014), some processes affecting Os removal in that region might instead be missing in our model. For example, Woodhouse et al. (1999) suggested that Os could bind onto organic matter in the water column under low-oxygen conditions.

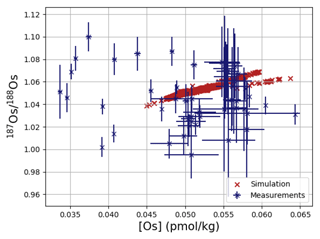
Figure 4 Comparison between measured and simulated concentrations and isotopic composition of dissolved Os in seawater. Shown are all available measured Os concentrations and isotope ratios for the modern ocean alongside the values of all ocean grid cells in the simulation. Data are taken from Levasseur et al. (1998), Woodhouse et al. (1999), and Gannoun and Burton (2014).

We tested the effect of increased Os removal with particulate organic matter from anoxic water masses in cGENIE by associating half of the marine Os burial with the optional Os scavenging sink (Eq. 9, see the results of our sensitivity study in Sect. A2). The true magnitude of Os burial associated with organic matter is uncertain, but we assumed here that it is responsible for all suboxic Os removal, which is estimated to account for at least 50 % of total marine burial flux that we assumed (Lu et al., 2017). Adding such dependence of Os burial on environmental conditions increased the range of simulated Os concentrations beyond that observed; i.e., Os scavenging is more than capable of producing the observed spatial heterogeneity in Os concentrations. However, there is no known Os isotopic fractionation associated with scavenging or burial; in the absence such fractionation, scavenging does not increase the range of simulated marine Os isotope ratios. Observations from sites outside the East Pacific show no vertical Os concentration gradients, which is well reproduced by our simulation set-up. The Os isotopic composition shows a uniform vertical distribution in the simulations, which is consistent with observations at all sites (see Fig. F6). While our initial simulation is thus consistent with the majority of Os measurements, we showed that cGENIE provides the necessary framework to investigate regionally variable environmental controls on the marine Os reservoir.

4.2.3 Lithium

Similar to Sr and Os, the model simulations fall within the range of observed concentrations and isotopic compositions of dissolved Li, although they are more homogeneous than observed (see Fig. 5). cGENIE can be used to explore whether environmental influences on local Li inputs and burial can explain this disparity, though underestimated measurement uncertainties and inter-laboratory inconsistencies, particularly in older studies, could also contribute to the spread in observed values. For example, the high concentrations, which are underrepresented in our simulation (see Figs. F7 and F3), come from one study in the Caribbean Sea (Angino and Billings, 1966), a marginal ocean that is not representative of the open ocean and which might not be sufficiently resolved in the coarse grid of cGENIE. However, Angino and Billings (1966) was one of the first studies measuring Li concentrations in seawater, and their measurements may be associated with much larger uncertainties than reported. Were these measurements excluded, the spatial mean of observed Li concentrations would be lower, and the model could be retuned by prescribing slightly lower Li fluxes in and out of the ocean, which would be permissible given the current range of flux estimates (see Table 3).

Figure 5 Comparison between measured and simulated concentrations and isotopic composition of dissolved Li in seawater. The displayed data points are measurements of Sr concentrations and isotope ratios on the same samples (Hall, 2002), while the gray box also indicates the range of concentrations and isotopic compositions that were measured separately (Angino and Billings, 1966; Fabricand et al., 1967; Chan, 1987; Chan and Edmond, 1988; You and Chan, 1996; Moriguti and Nakamura, 1998; Tomascak et al., 1999; James and Palmer, 2000; Košler et al., 2001; Nishio and Nakai, 2002; Bryant et al., 2003; Pistiner and Henderson, 2003; Millot et al., 2004; Choi et al., 2010; Pogge von Strandmann et al., 2010; Lin et al., 2016; Henchiri et al., 2016; Phan et al., 2016; Weynell et al., 2017; Fries et al., 2019; Gou et al., 2019; Hindshaw et al., 2019; Murphy et al., 2019; Pogge von Strandmann et al., 2019b). Observations and model results are salinity-normalized.

Only one measured vertical profile of Li isotopes is available in the literature (Hall, 2002), and it shows no vertical δ⁷Li variation, which is reproduced by our simulation. The simulated ⁷Li is offset from the profile reported by Hall (2002) since we tuned the model to the average of reported seawater ⁷Li measurements but the profile in Hall (2002) contains some of the most ⁷Li-enriched published seawater values.

4.2.4 Calcium

Simulated concentrations of dissolved Ca and its homogeneous isotopic composition closely resemble the observations, the spread in observed Ca isotope ratios likely being due to measurement uncertainty given the large reported error bars (see Fig. 1). Repeating our model spin-up with different parameterizations of Ca isotope fractionation during biogenic carbonate formation did not appreciably increase the simulated range of marine Ca isotope ratios (see our sensitivity study in Sect. C). Similar to the average Ca concentration in seawater, the uniform vertical distribution is well captured by the model simulation (see Fig. F8). Likewise, no vertical $\mathrm{Sr}/\mathrm{Ca}$ gradients are observed or simulated. Observed $\mathrm{Sr}/\mathrm{Ca}$ ratios are in between simulation results with tuned and untuned marine Sr reservoirs. This is an artifact of the tuning to mean observed Sr concentrations, which is lower than the mean Sr concentrations of the sites shown in Fig. F8 because it includes the anomalously depleted samples from the North Atlantic. This mismatch is another indication that the Sr measurements reported in Angino et al. (1966) might be associated with a larger uncertainty than reported.

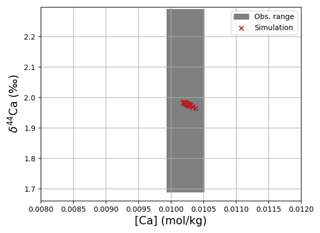
Figure 6 Comparison between measured and simulated concentrations and isotopic composition of dissolved Ca in seawater. The gray box indicates the range of concentrations and isotopic compositions that were measured on separate samples (Fabricand et al., 1967; De Villiers, 1999; Fantle and Tipper, 2014). Observations and model results are salinity-normalized.

4.3 Transient perturbation experiments

Adding the new metal cycles to cGENIE now enables us to study their transient behavior under external forcings in a fully coupled system, including effects from ocean circulation and primary productivity changes, climate-sensitive weathering, and marine carbonate accumulation and dissolution. Here we present one such example, where we instantaneously release either 1000 or 5000 Pg C into the atmosphere to produce temporary weathering responses which gradually re-equilibrate the model (similar to Lord et al., 2016). These scenarios allow us to showcase the sensitivity of the simulated metal systems and to discuss the Earth system processes that shape their transient evolution. Our experiments are set up to understand model behavior rather than to compare against any particular geological records or represent any particular event, although the choices of carbon release relate to estimates associated with differing “hyperthermal” events of the Paleogene (e.g., Panchuk et al., 2008; Kirtland Turner and Ridgwell, 2013). It is also important to note that some of these scenarios generate isotopic perturbations smaller than the analytical uncertainty of real-world measurements.

Table 7 Marine trace metal concentrations and residence times in our pre-industrial spin-up compared to those reported in literature (see scientific background).

In our spin-up, the prescribed metal fluxes result in residence times within the range of published estimates (Table 7). Li has the longest residence time in our simulations, and thus the largest inertia to external perturbations. Sr and Ca follow, with Os being the most responsive system.

Figure 7 Transient changes in modeled Sr, Os, Li, Ca, composition of seawater, and atmospheric CO₂ and temperature following instant releases of 1000 and 5000 Pg C. Shown are changes (a) in concentrations, and (b) in the isotopic composition of seawater.

Figure 7 shows the modeled transient response of Sr, Os, Li, Ca concentrations and isotopic compositions to an exogenic CO₂ pulse, together with mean global ocean dissolved inorganic carbon (DIC) δ¹³C, atmospheric CO₂ and temperature. After the instantaneous carbon release, atmospheric CO₂ concentration increases and the δ¹³C of seawater decreases on the timescale of years. The increase in atmospheric CO₂ and invasion of CO₂ into the ocean also suppresses biogenic carbonate formation in the surface ocean and leads to the dissolution of pelagic carbonates. Over the next ∼10 000 years, “carbonate compensation” removes the majority of the initial excess carbon from the atmosphere (Lord et al., 2016). Increased atmospheric CO₂ also enhances the greenhouse effect and thus leads to a rise in global mean air temperature, altering the hydrological cycle and speeding up reaction kinetics, in turn resulting in increased rates of continental crust weathering. After a few tens of thousands of years, increased continental weathering supplies enough alkalinity to the ocean to reverse the dissolution of carbonates on the seafloor and increase carbonate burial. Through enhanced silicate weathering and carbonate burial, the remaining excess carbon is sequestered over the timescale of ∼100 000 years after the initial emissions pulse. Over the same timescale, temperature, which due to Earth system feedbacks initially recovers more slowly than atmospheric CO₂ concentrations, returns to pre-emissions values and ends the phase of enhanced weathering.

Metal input from continental weathering (and marine carbonate dissolution for Sr and Ca) leads to a transient growth of marine metal reservoirs and isotopic excursions. Increased continental weathering increases the influx of radiogenic Sr and Os, driving the respective marine reservoirs to more radiogenic isotopic compositions. The continental crust is also depleted in heavy stable isotopes compared to seawater, such that the increased weathering influx reduces the ${\mathit{\delta }}^{\mathrm{88}/\mathrm{86}}$Sr, δ⁷Li and δ⁴⁴Ca values of seawater. The isotopic composition of carbonates and silicates in continental crust is spatially uniform in our set-up, and cGENIE does not simulate any isotopic effects associated with changes in erosion rate. By default, isotopic shifts due to changes in secondary mineral formation and dissolution in freshwater systems are also not simulated. However, such a shift has been deduced from observed δ⁷Li isotope excursions (e.g., for δ⁷Li, Lechler et al., 2015). Enabling the climate-sensitive parameterization of δ⁷Li in continental runoff demonstrates that this can increase the excursion amplitude to be more consistent with perturbations in the geologic record (see our sensitivity study in Sect. B).

At steady state, alkalinity and Ca²⁺ inputs to the ocean are equal. Since the alkalinity supply is entirely derived from climate-sensitive continental weathering but one-third of the Ca²⁺ influx is derived from a constant hydrothermal source, the climate-driven increase in weathering results in a temporarily larger supply of alkalinity than of Ca²⁺, which does not occur in C-cycle simulations without an igneous Ca²⁺ source at the seafloor (e.g., Lord et al., 2016; Vervoort et al., 2019). The imbalance between alkalinity and Ca²⁺ input is small (10 % of the Ca²⁺ input at its peak), but cumulatively enough excess alkalinity is supplied to cause a slight reduction of the steady-state marine Ca and Sr reservoirs (by ∼0.5 % following the emission of 5000 Pg C). Our assumption of a climate-insensitive Ca²⁺ source at the seafloor is a simplification since there is evidence that this flux varies with bottom-water properties, in particular temperature (e.g., Krissansen-Totton and Catling, 2017). However, the temperature sensitivity of the seafloor Ca²⁺ influx is likely lower than that of continental weathering (Brady and Gíslason, 1997), and temperature change is dampened in the deep ocean. Thus, even if the temperature sensitivity of hydrothermal Ca²⁺ input was considered, a temporary imbalance of alkalinity and Ca²⁺ supplies during a transient warming event is likely when alkalinity and Ca²⁺ enter the ocean via different pathways. Our set-up thus produces an upper limit for such a transient imbalance between alkalinity and Ca²⁺ supply, assuming constant seafloor fluxes.

In the presented simulations, only the excursion amplitudes of radiogenic ${}^{\mathrm{87}}\mathrm{Sr}{/}^{\mathrm{86}}\mathrm{Sr}$ and δ⁷Li assuming climate-driven runoff modifications are larger than measurement uncertainty in present-day seawater (see Figs. 3–6). Stronger or prolonged climate change, a larger isotopic offset between seawater and continental runoff, or a more sensitive weathering regime would be required to produce detectable weathering changes in the other isotope systems. Regardless, our idealized perturbation of the modern system illustrates the differing responses of all five isotope systems to a C emission pulse. Specifically, we find that the timings of excursion peaks and minima differ strongly between the isotope systems, which might provide a “fingerprint” of rapid C injection. For instance, the radiogenic ${}^{\mathrm{187}}\mathrm{Os}{/}^{\mathrm{188}}\mathrm{Os}$ and negative ${\mathit{\delta }}^{\mathrm{88}/\mathrm{86}}$Sr and δ⁴⁴Ca excursions peak a few tens of thousands of years after the C injection, while the radiogenic ${}^{\mathrm{87}}\mathrm{Sr}{/}^{\mathrm{86}}\mathrm{Sr}$ and negative δ⁷Li excursions take hundreds of thousands of years to reach their full amplitude. These time lags result from different residence times and fractionation processes.

With the shortest residence time, estimated both from present-day inventories and in our simulation (see Table 7), Os is the first metal to re-equilibrate after the perturbation. The excursions in Os concentration and isotopes are only driven by enhanced weathering rates, and thus both recover within 300 kyr once atmospheric temperature, and with it continental weathering rates, decrease sufficiently. The radiogenic ${}^{\mathrm{87}}\mathrm{Sr}{/}^{\mathrm{86}}\mathrm{Sr}$ excursion, however, continues to grow until weathering rates have fully returned to pre-event levels because concentration-dependent Sr sinks adapt more slowly to enhanced continental Sr input as a result of the longer residence time. The re-equilibration of the marine Sr reservoir is substantially slower than that of the Os reservoir for the same reason. However, the removal of marine Sr is also dependent on carbonate chemistry, since marine carbonate preservation constitutes the largest marine Sr sink. Biogenic carbonate preservation initially decreases because of the pH and carbonate saturation drop following the C injection, but it increases during the C cycle recovery as a result of enhanced weathering-related alkalinity input. Increased marine carbonate burial causes the marine Ca reservoir to re-equilibrate on a similar timescale to Os, although Ca has a substantially longer residence time in our spin-up. The effect is not strong enough to stop the growth of the marine Sr reservoir, but it reduces its growth rate. Isotopic fractionation of Ca and Sr during biogenic carbonate formation enhances the speed of the δ⁴⁴Ca recovery and stops the ${\mathit{\delta }}^{\mathrm{88}/\mathrm{86}}$Sr excursion from growing, despite continued excess input of isotopically light continental Sr. Li has the longest residence time of the four metals in our simulations, and Li burial is only dependent on the marine Li concentration and not carbonate chemistry. Hence, the marine Li reservoir continues to grow until all excess weathering stops. Once more dissolved Li is buried than added to the ocean, i.e., the marine Li reservoir shrinks, the δ⁷Li trend reverses because excess sources of isotopically light Li cease and isotopically light Li is preferentially buried during clay formation, enriching seawater in the heavier ⁷Li. In the longer term, stable isotope fractionation during the removal of excess Sr, Li and Ca from the ocean results in transient positive ${\mathit{\delta }}^{\mathrm{88}/\mathrm{86}}$Sr, δ⁷Li and δ⁴⁴Ca excursions which, in the case of Sr and Li, last for several million years. In our simulations, the staggered timings of the ${}^{\mathrm{187}}\mathrm{Os}{/}^{\mathrm{188}}\mathrm{Os}$ and ${}^{\mathrm{87}}\mathrm{Sr}{/}^{\mathrm{86}}\mathrm{Sr}$ excursion peaks, as well as the δ⁴⁴Ca and δ⁷Li excursion minima, are thus predominantly the result of different elemental residence times, while enhanced carbonate burial is the main reason for the time lag between δ⁷Li and ${\mathit{\delta }}^{\mathrm{88}/\mathrm{86}}$Sr and the coincidence of the excursion minima of ${\mathit{\delta }}^{\mathrm{88}/\mathrm{86}}$Sr and δ⁴⁴Ca.

5 Potential for further model development

Incorporation of Sr, Os, Li and Ca cycle dynamics in cGENIE constitutes a useful tool to study perturbations of marine metal reservoirs during environmental changes and, importantly, in concert with other biogeochemical tracers. Several extensions of this model can be envisaged to include the representation of metal-specific processes that we did not address in this initial cGENIE implementation. Firstly, the SEDGEM module could be expanded by adding temperature dependency to the fluxes of Sr, Os, Li, Ca, C and Mg related to seafloor alteration. Although secular variation in Cenozoic climate altered these fluxes by an order of magnitude less than those connected to terrestrial weathering (Krissansen-Totton and Catling, 2017), this extra model feature could still improve the simulated metal isotope response to long-term environmental change and constrain metal fluxes in warmer Earth system states. Secondly, the weathering module ROKGEM could be extended to simulate C and S release from organic shale weathering alongside Os fluxes to better capture the climatic and biogeochemical effects of changing shale weathering. Thirdly, celestite-bound Sr could be added as an additional particulate Sr tracer to improve the representation of Sr cycling in oceans with higher celestite stability than at present. Similarly, growth rate-dependent isotope fractionation factors could be implemented in the ecosystem module ECOGEM (Ward et al., 2018). However, the benefit of more complex biological metal cycles will have to be weighed against increased computational costs and the need to constrain additional rate constants and fractionation factors.

6 Conclusions

Sr, Os, Li and Ca isotope records can help identify mantle activity and lithological responses to climate change in the geological record if processes governing their distribution in the ocean and their response to geological perturbations are well understood. Our implementation of the marine cycling of Sr, Os, Li and Ca in the Earth system model cGENIE allows us to investigate these processes and their consistency with observations. Simulating pre-industrial Sr, Os, Li and Ca distributions in the ocean, the model achieves slightly more homogeneous fields than observed but is consistent with the widely used assumption of homogeneous metal isotope distributions in a fully equilibrated state (e.g., Elderfield, 1986; Chan and Edmond, 1988). It reproduces the mostly homogeneous mean observed depth profiles of concentrations and isotopic compositions well but partially deviates from local observations. This could be an artifact of measurement uncertainties, non-equilibrated cycles in today's ocean, or local processes that are not resolved or parameterized in cGENIE. We showed how this new cGENIE tracer development provides an opportunity to investigate the consistency between reported metal compositions in the ocean and marine sources and sinks. Further investigations of the differences between cGENIE simulations and observations thus have the potential to improve our understanding of present-day marine trace metal cycling. Furthermore, the new implementation can be used to study the response of these metal cycles to transient environmental change. As an example, we showed how these systems respond to a sudden CO₂ release through perturbation to their input and output fluxes on different timescales. cGENIE thus becomes a valuable tool to quantitatively interrogate the environmental signals of these isotope systems as preserved in sedimentary records and their relationship to more traditional isotope systems such as carbon.

Appendix A: Sensitivity studies of the Os cycle

We tested two additional Os cycle set-ups besides the pre-industrial spin-up described in the main paper: one with a 2D continental weathering scheme in which Os delivery is tied to organic-rich shale and basalt weathering, and one assuming that half of marine Os deposition happens through association with POC in anoxic conditions. The following two subsections show the two set-ups and the simulation results.

A1 Continental Os inputs calculated with a 2D weathering scheme

We added Os and stable isotope (¹⁸⁷Os and ¹⁸⁸Os) tracers to the 2D weathering schemes available in ROKGEM (Colbourn et al., 2013). Derived from Suchet and Probst (1995), Bluth and Kump (1994), Gibbs and Kump (1994), and Gibbs et al. (1999), these weathering schemes calculate alkalinity and DIC fluxes entering coastal grid cells based on lithology-specific dependencies on runoff. Depending on the scheme, the model user can specify the locations of five or six pre-defined lithologies (carbonates, sandstone, shales, basalt, granites), the relative contribution of weathering fluxes from these lithologies to the overall input of carbonate- and silicate-derived weathering fluxes to the ocean, and parameters that define the sensitivity of these fluxes to runoff changes. Similarly, flux and isotopic composition of Os derived from each of these lithologies can now be prescribed by changing the input files of ROKGEM (see the cGENIE.muffin manual, p. 372–373, for a step-by-step guide). To test the effect of spatially explicit Os weathering fluxes on the isotopic composition of dissolved Os in the ocean, we tied the continental Os weathering flux to shale and basalt weathering, which are assumed to be dominant continental Os sources (Li et al., 2009). We ascribed typical isotopic compositions (${}^{\mathrm{187}}\mathrm{Os}{/}^{\mathrm{188}}\mathrm{Os}=\mathrm{2.2}$ for shales, Dubin and Peucker-Ehrenbrink, 2015, and ${}^{\mathrm{187}}\mathrm{Os}{/}^{\mathrm{188}}\mathrm{Os}=\mathrm{1.0}$ for basalt, Peucker-Ehrenbrink and Jahn, 2001) to Os derived from these lithologies and Os yields that resulted in the same global Os weathering input as in the pre-industrial spin-up presented in the main text (2605 mol Os yr⁻¹ with ${}^{\mathrm{187}}\mathrm{Os}{/}^{\mathrm{188}}\mathrm{Os}=\mathrm{1.2}$).

Table A1 Model parameters setting Os scavenging under sub-oxic conditions.

Figure A1 shows the simulated spatial pattern of Os weathering flux alongside measurements. The comparison between Os concentrations in rivers and in cGENIE runoff is complicated by the high reactivity of Os in river deltas (Turekian et al., 2007), which might result in lower Os addition to the open than to the coastal ocean. However, there is general agreement between the measured and simulated isotopic composition of local Os weathering fluxes. This spatially heterogeneous Os weathering flux does not change the ranges of simulated marine Os concentrations and isotope ratios substantially (Fig. A2), suggesting that assumptions about the homogeneity of marine Os inputs are not the cause of differences between the simulated and observed marine Os reservoir.

Figure A1 Spatially explicit Os weathering flux using the ROKGEM 2D weathering scheme “GEM_CO2” and observed Os river fluxes (colored dots) based on measured Os concentrations (a) and their isotopic composition (b) in rivers (Levasseur et al., 1999) and annual river runoff (Milliman and Farnsworth, 2013).

A2 Marine Os sequestration by association with POC

Another possible explanation for the wider range of observed compared with simulated Os concentrations and isotopic ratios in seawater is spatially-variable Os burial rates. The inclusion of Os cycling in cGENIE enables for the first time the simulation of the effects of heterogeneous marine biogeochemistry on Os burial. As part of the Os cycle implementation, we included options for simulating enhanced Os burial in suboxic settings and Os scavenging by POC in cGENIE, since it is assumed that low oxygen concentrations and/or burial of organic matter intensify Os sequestration (Lu et al., 2017), although rates and exact mechanisms are still uncertain. Here, we present an alteration of the previously presented spin-up of the pre-industrial Os cycle by including enhanced Os deposition via association with POC in sub-oxic conditions and scaled this sink to account for 50 % of marine Os burial (see parameter choices in Table A1).

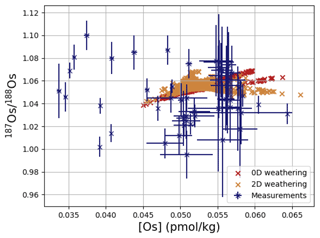
Figure A2 Cross plot of measured and simulated Os concentrations and isotopic compositions in seawater, comparing the modern ocean measurements against every ocean grid cell for spin-ups using both the 0D and 2D weathering schemes.

Spatially variable Os burial rates increase the range of simulated Os concentrations in seawater beyond that observed (Fig. A3). While we found that the previous range of simulated Os concentrations covered only half of the observed range, we cannot assess if the lowest simulated Os concentrations with sub-oxic Os scavenging are realistic for the pre-industrial ocean, since only a few Os measurements from oxygen-poor water masses with high POC fluxes are available. However, the range of measured isotopic compositions of Os in seawater is also not reproduced by including spatially variable Os burial. Further modeling and Os measurements in diverse marine settings are urgently needed to address these discrepancies.

Figure A3 Cross plot of measured and simulated Os concentrations and isotopic compositions in seawater with and without Os scavenging under sub-oxic conditions.

A3 Marine ${}^{\mathrm{187}}\mathrm{Os}{/}^{\mathrm{188}}\mathrm{Os}$ signal of large C injections with O₂-sensitive Os scavenging

We tested the implications of dynamic Os scavenging on the isotopic response of the marine Os reservoir to climate change by repeating the previously shown C injection simulations with the Os scavenging scheme.

Figure A4 Time series of marine ${}^{\mathrm{187}}\mathrm{Os}{/}^{\mathrm{188}}\mathrm{Os}$ changes in response to an immediate release of two different masses of C into the atmosphere–ocean system with and without Os scavenging from the water column

Figure A4 shows that the inclusion of Os scavenging from O₂-poor water masses only results in small changes to the simulated evolution of ${}^{\mathrm{187}}\mathrm{Os}{/}^{\mathrm{188}}\mathrm{Os}$ in the C injection experiments. Enhanced remineralization of particulate organic matter in the warmer ocean overcompensates for the effects of reduced marine oxygenation and leads to less Os scavenging and hence a transient growth of the marine Os reservoir. Because the marine Os reservoir grows larger in the simulation with Os scavenging than in the simulation without Os scavenging, the amplitude of the isotopic excursion is smaller.

Appendix B: Climate-sensitive continental Li fluxes

The abundance and isotopic composition of riverine Li depends primarily on the weathering regime and temperature during clay formation and not on the host lithology (Pogge von Strandmann et al., 2020). Simulations of continental Li fluxes based on rock weathering rates alone therefore do not capture the full variability of the Li cycle under climate change if the latter shifts the weathering regime. ROKGEM does not provide a detailed land surface model, but we included the first-order approximations of the sensitivity of continental Li fluxes on the weathering regime and temperature described in Sect. 3. Here, we show the different simulated response of the marine Li reservoir to a transient warming event with and without these approximations. For this purpose, we repeated the C injection experiments with the optional dependence of continental Li fluxes on the ratio of chemical to physical weathering rates and temperature.

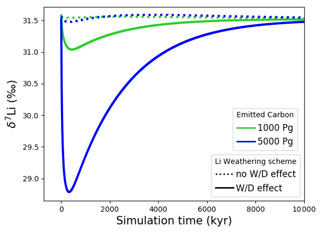
Figure B1 Time series of marine δ⁷Li changes in response to an immediate release of two different amounts of C into the atmosphere–ocean system with and without effects of the ratio of weathering to denudation rate ($W/D$) and temperature on the composition of riverine Li.

Figure B1 shows that appreciable isotopic changes in the marine Li reservoir are only simulated if the continental Li flux changes with changing $W/D$ and temperature. In the simulation with the larger C release, a sudden temperature increase, +7 ^∘C at the peak and +3 ^∘C sustained for almost 100 kyr, resulted in a marine negative δ⁷Li excursion of −3 ‰. Although our simulation is set up to represent pre-industrial metal cycles, this amplitude is at the lower end of δ⁷Li excursions recorded during the Paleocene–Eocene Thermal Maximum, a past C injection event with a similar global mean temperature change (Gehler et al., 2016; Pogge von Strandmann et al., 2019a). cGENIE provides the necessary functionalities to further investigate this and other past δ⁷Li excursions by enabling the user to prescribe and test early Eocene constraints on the Li cycle, including baseline weathering regimes and rates, the scale of marine clay and evaporite formation and hydrothermal inputs, and the Li concentration in seawater.

Appendix C: Ca isotope fractionation during biogenic carbonate formation

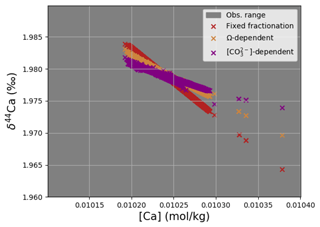
Figure C1 Cross plot of measured and simulated Ca concentrations and isotopic compositions in seawater using different Ca isotope fractionation schemes.

cGENIE contains three different parameterizations for Ca isotope fractionation during carbonate formation. By default, a fixed user-prescribed fractionation factor is applied across the whole ocean. Alternatively, the fractionation factor can be made dependent on the local concentration of carbonate ions (following Gussone et al., 2005 and Komar and Zeebe, 2016) or the local saturation state (following Tang et al., 2008). A detailed discussion of these approaches can be found in Fantle and Ridgwell (2020). Here, we show the effect of these schemes on the simulated distribution of ${\mathit{\delta }}^{\mathrm{44}/\mathrm{40}}\mathrm{Ca}$ in pre-industrial seawater and surface sediments.

Figure C2 The ${\mathit{\delta }}^{\mathrm{44}/\mathrm{40}}\mathrm{Ca}$ of CaCO₃ in the top layer of marine sediments in simulations with different Ca isotope fractionation schemes: (a) fixed fractionation, (b, c) fractionation dependent on local conditions.

We tuned the mean seawater ${\mathit{\delta }}^{\mathrm{44}/\mathrm{40}}\mathrm{Ca}$ to the same value in all simulations by varying the isotopic composition of continental Ca input, hence the mean composition of seawater aligns in all three simulations but the spatial variability differs. The simulated range of ${\mathit{\delta }}^{\mathrm{44}/\mathrm{40}}\mathrm{Ca}$ is largest with a fixed fractionation factor because local conditions reduce the fractionation factor across most of the ocean in the simulations with dynamic fractionation factors. The smallest ${\mathit{\delta }}^{\mathrm{44}/\mathrm{40}}\mathrm{Ca}$ range is simulated when the fractionation factor is dependent on the local concentration of carbonate ions. However, these differences are negligible compared to measurement uncertainty.

In contrast to seawater, the top layer of marine sediments shows substantial differences in ${\mathit{\delta }}^{\mathrm{44}/\mathrm{40}}\mathrm{Ca}$ in the three simulations (Fig. C2), with generally higher ${\mathit{\delta }}^{\mathrm{44}/\mathrm{40}}\mathrm{Ca}$ and large spatial variability when the fractionation factor is set by environmental conditions. Sedimentary carbonate ${\mathit{\delta }}^{\mathrm{44}/\mathrm{40}}\mathrm{Ca}$ is highest at the poles and decreases towards the Equator when the fractionation factor varies with saturation state, while the opposite gradients are simulated using the carbonate-ion-dependent fractionation scheme from Gussone et al. (2005). This illustrates that the surface ocean fractionation factor is shifted in opposing directions by changing carbonate ion abundance in these fractionation schemes Fantle and Ridgwell (2020).

Appendix D: Map of locations with prescribed reefal carbonate deposition

Figure D1 Locations with prescribed benthic carbonate deposition representing carbonate reefs. Reef grid cells are highlighted in brown.

Appendix E: Model parameters for pre-industrial spin-up

Table E1 Model parameters setting continental weathering-related trace metal fluxes.

NA: not available.

Table E2 Model parameters setting hydrothermal metal input.

Table E3 Model parameters setting the Os, Li and Sr contents of calcite shells.

NA: not available.

Table E4 Model parameters setting Os scavenging.

NA: not available.

Table E5 Model parameters for weathering-related trace metal fluxes.

Table E6 Model parameters for Sr recrystallization.

NA: not available.

Table E7 Model parameters for metal deposition in sediments.

Table E8 Model parameters for the representation of isotopes and isotopic fractionation.

NA: not available.

Appendix F: Observed and simulated metal distributions in the water column

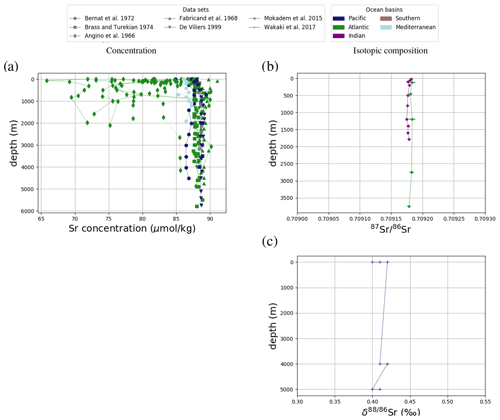
Figure F1 Measured Sr ocean profiles. Composites of all available profiles of measured concentrations (a) and isotopic compositions (b) are shown. Data are taken from Angino et al. (1966), Fabricand et al. (1967), Bernat et al. (1972), Brass and Turekian (1974), De Villiers (1999), Mokadem et al. (2015), and Wakaki et al. (2017). Sr concentrations are normalized to a salinity of 34.90.

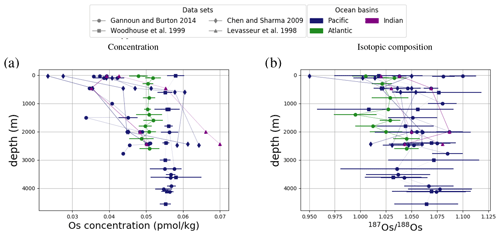
Figure F2 Measured Os ocean profiles. Composites of all available profiles of measured concentrations (a) and isotopic compositions (b) are shown. Data are taken from Levasseur et al. (1998), Woodhouse et al. (1999), and Gannoun and Burton (2014).

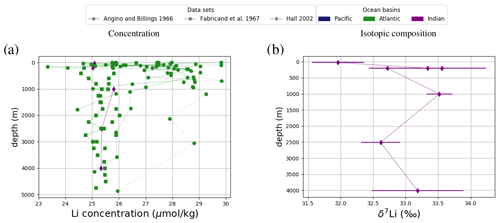
Figure F3 Measured Li ocean profiles. Composites of all available profiles of measured concentrations (a) and isotopic compositions (b) are shown. Data are taken from Angino and Billings (1966), Fabricand et al. (1967), Chan (1987), and Hall (2002). Li concentrations are normalized to a salinity of 34.90.

Figure F4 Composites of all available ocean Ca concentration (a) and Sr/Ca profiles (b). Data are taken from Fabricand et al. (1967) and De Villiers (1999). Ca concentrations are normalized to a salinity of 34.90.

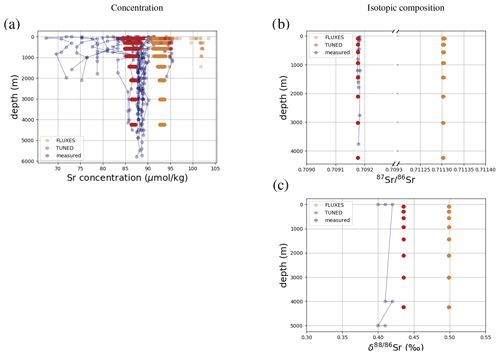
Figure F5 Comparison between measured and simulated Sr profiles in seawater. Composites of all available measured Sr concentration (a) and isotope ratio (b, c) profiles and all profiles in the simulation are shown. Data are taken from Angino et al. (1966), Fabricand et al. (1967), Bernat et al. (1972), Brass and Turekian (1974), De Villiers (1999), and Mokadem et al. (2015). Sr concentrations are normalized to a salinity of 34.90.

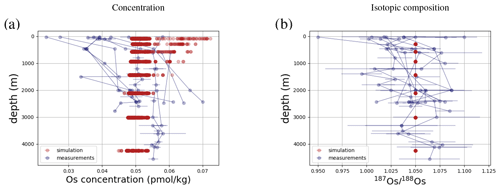
Figure F6 Comparison between measured and simulated Os vertical profiles in seawater. Composites of all available measured Os concentration (a) and isotope ratio (b) profiles and all profiles in the simulation are shown. Data are taken from Levasseur et al. (1998), Woodhouse et al. (1999), and Gannoun and Burton (2014).

Figure F7 Comparison between measured and simulated Li profiles in seawater. Composites of all available measured Li concentration (a) and isotope ratio (b) profiles and all profiles in the simulation are shown. Data are taken from Angino and Billings (1966), Fabricand et al. (1967), Chan (1987), Chan and Edmond (1988), You and Chan (1996), Moriguti and Nakamura (1998), Tomascak et al. (1999), James and Palmer (2000), Košler et al. (2001), Nishio and Nakai (2002), Hall (2002), Bryant et al. (2003), Pistiner and Henderson (2003), Millot et al. (2004), Choi et al. (2010), and Lin et al. (2016). Li concentrations are normalized to a salinity of 34.90.

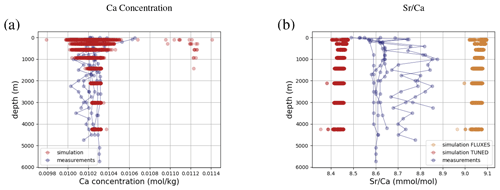
Figure F8 Comparison between measured and simulated Ca (a) and $\mathrm{Sr}/\mathrm{Ca}$ (b) profiles in seawater. Composites of all available measured concentration profiles and all profiles in the simulation are shown. Data are taken from Fabricand et al. (1967), De Villiers (1999), and Fantle and Tipper (2014). Ca concentrations are normalized to a salinity of 34.90.

Appendix G: Site-specific model–data comparison

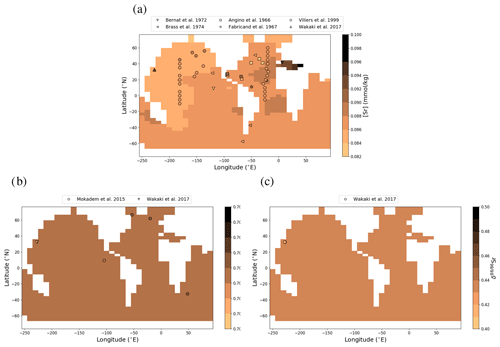
Figure G1 Comparison between measured and simulated Sr concentrations (a) and isotopic composition (b, c) in surface waters. Measurements are shown as symbols on the map, with the color indicating the respective value. Data are taken from Angino et al. (1966), Fabricand et al. (1967), Bernat et al. (1972), Brass and Turekian (1974), De Villiers (1999), Mokadem et al. (2015), and Wakaki et al. (2017).

Appendix H: Seawater measurements used for the model evaluation

Summary tables of all Sr, Os, Li, and Ca concentration measurements; their locations; and references are provided as separate spreadsheets in the Supplement. Ca isotope ratios in seawater were taken from the compilation in Fantle and Tipper (2014).