Optimization of the sulfate aerosol hygroscopicity parameter in WRF-Chem

A new sulfate aerosol hygroscopicity parameter (${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$) parameterization is suggested that is capable of considering the two major sulfate aerosols, H₂SO₄ and (NH₄)₂SO₄, using the molar ratio of ammonium to sulfate (R). An alternative ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterization method is also suggested that utilizes typical geographical distribution patterns of sulfate and ammonium, which can be used when ammonium data are not available for model calculation. Using the Weather Research and Forecasting model coupled with Chemistry (WRF-Chem), the impacts of different ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterizations on cloud microphysical properties and cloud radiative effects in East Asia are examined. Comparisons with the observational data obtained from an aircraft field campaign suggest that the new ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterizations simulate more reliable aerosol and cloud condensation nuclei concentrations, especially over the sea in East Asia, than the original ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterization in WRF-Chem that assumes sulfate aerosols as (NH₄)₂SO₄ only. With the new ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterizations, the simulated cloud microphysical properties and precipitation became significantly different, resulting in a greater cloud albedo effect of about −1.5 W m⁻² in East Asia than that with the original ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterization. The new ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterizations are simple and readily applicable to numerical studies investigating the impact of sulfate aerosols in aerosol–cloud interactions without additional computational expense.

1 Introduction

Aerosols impact global climate by directly scattering and absorbing radiation. Aerosols also play an important role as potential cloud condensation nuclei (CCN). Increases in the CCN number concentration could increase the cloud optical depth, suppress local precipitation, and prolong cloud lifetime (Twomey, 1974; Albrecht, 1989). Therefore, the aerosol-induced changes in cloud microphysical properties can alter the Earth's radiation budget and hydrological cycle. Such aerosol–cloud interactions possibly cause the greatest uncertainty in the estimation of climate forcing due to their complexity (Myhre et al., 2013). Understanding the role of aerosols as CCN (CCN activation) is therefore important for predicting future climate. CCN activation depends on the chemical and physical properties of aerosols (Köhler, 1936; Abdul-Razzak et al., 1998; Dusek et al., 2006; Fountoukis and Nenes, 2005; Khvorostyanov and Curry, 2009; Ghan et al., 2011). Soluble aerosol species have high potential to become CCN, and differences in aerosol solubility could exert a considerable impact on CCN activation (Nenes et al., 2002; Kristjánsson 2002).

Sulfate aerosols are one of the major components of natural and anthropogenic aerosols, contributing to a large portion of the net radiative forcing due to aerosol–cloud interactions (Boucher et al, 2013). They are highly soluble and, therefore, easily activated to become cloud droplets. Recently, Zelinka et al. (2014) estimated that the contribution of sulfate aerosols to the net effective radiative forcing from aerosol–cloud interaction (ERFaci) is about 64 %. Sulfate aerosols are mainly present as sulfuric acid (H₂SO₄) and ammonium sulfate ((NH₄)₂SO₄) in the atmosphere (Charlson and Wigley, 1994), but they have a very different hygroscopicity parameter (κ) that represents the water affinity of aerosols and determines the efficiency of CCN activation (Petters and Kreidenweis, 2007). Despite the importance of sulfate aerosols in the estimation of ERFaci, many atmospheric models simply assume that sulfate aerosols have a single sulfate aerosol hygroscopicity parameter (${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$) value (Ackermann et al., 1998; Stier et al. 2006; Pringle et al., 2010; Mann et al., 2010; Chang et al., 2017; Tegen et al., 2019).

Especially in East Asia, the distribution of the ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ value could vary significantly because sulfur dioxide and ammonia are emitted from inland China on a massive scale (Kurokawa et al., 2013; Qu et al., 2016; Kang et al., 2016; Liu et al., 2017), and the distribution of H₂SO₄ and (NH₄)₂SO₄ are closely related to the emissions and chemical reactions of sulfur dioxide and ammonia. Sulfur dioxide is oxidized to H₂SO₄ and then neutralized to form (NH₄)₂SO₄ by ammonia. Generally, sulfur dioxide is released from industry and from the sea surface, and ammonia is discharged from livestock and farmland. For this reason, the ratio of ammonium to sulfate is observed to decrease as the distance from land increases (Fujita et al., 2000; Paulot et al., 2015; Kang et al., 2016; Liu et al., 2017). Thus, applying a single hygroscopicity parameter for all sulfate aerosols in atmospheric models can lead to uncertainty in quantifying CCN activation, particularly in East Asia.

This study proposes a new ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterization that aims at simultaneously considering the two major sulfate aerosols, i.e., (NH₄)₂SO₄ and H₂SO₄, in WRF-Chem (the Weather Research and Forecasting model coupled with chemistry). First, we describe the calculation of κ for different size modes of aerosols and suggest a new parameterization of ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$. The performance of the new ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterization in estimating the effects of aerosol–cloud interactions is examined for the domain of East Asia. The model results are compared with the aircraft measurement data obtained during the Korea–United States Air Quality Campaign (KORUS-AQ; Al-Saadi et al., 2016). Finally, we address the effects of the new ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterizations in simulating (or calculating) cloud microphysical properties and cloud radiative effects in East Asia.

2 Model description

2.1 The WRF-Chem model

WRF-Chem version 3.8.1 is designed to predict mesoscale weather and atmospheric chemistry (Grell et al., 2005; Fast et al., 2006; Skamarock et al., 2008; Peckham et al., 2011). The aerosol size and mass distributions are calculated with the Modal Aerosol Dynamics Model for Europe (MADE; Ackermann et al., 1998) that includes three lognormal distributions for Aitken-, accumulation-, and coarse-mode particles. MADE considers the new particle formation process of homogeneous nucleation in the H₂SO₄ and H₂O system (Wexler et al., 1994; Kulmala et al., 1998). The model also treats inorganic chemistry systems as the default option and organic chemistry systems as coupling options. Inorganic chemistry systems include the chemical reactions of three inorganic ionic species: ${\mathrm{SO}}_{\mathrm{4}}^{-\mathrm{2}}$, ${\mathrm{NO}}_{\mathrm{3}}^{-}$, and ${\mathrm{NH}}_{\mathrm{3}}^{+}$ (Ackermann et al., 1998). The Secondary Organic Aerosol Model (SORGAM), an optional model to calculate secondary organic aerosol (SOA) chemistry processes (Schell et al., 2001), is coupled to MADE (MADE/SORGAM). MADE/SORGAM treats atmospheric aerosols as an internal mixture of sulfate, nitrate, ammonium, organic carbon (OC), elemental carbon (EC), sea salt, and dust aerosols. Additionally, gas-phase chemical processes are calculated in Regional Acid Deposition Mechanism version 2 (RADM2; Chang et al., 1989). RADM2 simulates the concentrations of air pollutants, including inorganic (14 stable, 4 reactive, and 3 abundant stable) and organic (26 stable and 16 peroxy radicals) chemical species.

For the microphysics calculation, we use the CCN activation parameterizations (Abdul-Razzak and Ghan, 2000, hereafter ARG) and Morrison double-moment microphysics scheme (Morrison et al., 2009). The CCN activation is determined by meteorological factors (e.g., updraft) and physicochemical properties of aerosols based on the assumption of internally well-mixed aerosols. Detailed model designs for the modeling studies of aerosol–cloud interactions in WRF-Chem can be found in Gustafson et al. (2007), Chapman et al. (2009), Grell et al. (2011), and Bar et al. (2015).

For the physics parameterization, we use the following configurations: the Rapid and accurate Radiative Transfer Model for GCMs (RRTMG) for the shortwave and longwave radiative transport processes (Iacono et al., 2008); the Yonsei University scheme (YSU scheme) for the atmospheric boundary layer processes (Hong et al., 2006); and the Unified NOAH (NCEP Oregon State University, Air Force, and the Hydrologic Research Laboratory) land surface model for land surface processes (Tewari et al., 2004).

2.2 Calculation of the hygroscopicity parameter

The CCN activation parameterization is based on the Köhler theory, which is described using the water activity and the surface tension of the solution droplets. The water activity is estimated from detailed information on aerosols such as the van't Hoff factor, osmotic coefficient, molecular weight, mass, and density of aerosols. If aerosol chemical information is fully provided, CCN activation could almost be accurately calculated using the Köhler theory (Raymond and Pandis, 2003); however, it is very computationally expensive (Lewis, 2008). Petters and Kreidenweis (2007) proposed a single quantitative measure of aerosol hygroscopicity, known as the hygroscopicity parameter (κ). This method does not require detailed information on aerosol chemistry and, therefore, reduces the computational cost when calculating the water activity. For this reason, κ values are applied in many observational, experimental, and numerical studies (Zhao et al., 2015; Chang et al., 2017, Shiraiwa et al., 2017; Gasteiger et al., 2018). κ can be determined separately for the three lognormal modes (Aitken, accumulation, and coarse modes). That is, κ_i is the volume-weighted average of κ_j for mode i:

$$\begin{array}{}\text{(1)}& {\mathit{\kappa }}_i\equiv {\sum }_{j=\mathrm{1}}^J{\mathit{\epsilon }}_{ij}{\mathit{\kappa }}_j,\end{array}$$

where ε_ij is the volume ratio of chemical j in mode i ($=V_{ij}/V_{\text{tot},i},V_{\text{tot},i}={\sum }_{j=\mathrm{1}}^J{V}_{ij}$, and V_ij is the volume of chemical j in mode i), and κ_j is the individual hygroscopicity parameter for chemical j. In Eq. (1), the temperature is assumed to be 298.15 K. The upper end of the κ value for hygroscopic species of atmospheric relevance is around 1.40 (Petter and Kreidenweis, 2007).

2.3 Limitation of previous ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterizations

CCN activation is affected by κ values (e.g., Nenes et al., 2002; Kristjánsson 2002). H₂SO₄ has a κ value that is more than 2 times higher than (NH₄)₂SO₄: 1.19 for ${\mathit{\kappa }}_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$ and 0.53 for ${\mathit{\kappa }}_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$ (Clegg and Wexler, 1998; Petters and Kredenweis 2007; Good et al., 2010). Such large disparities in the ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ between different sulfate species could cause large variability in the estimation of ERFaci. However, many aerosol modules simplify the physical and chemical characteristics of aerosols, often neglecting some chemical species (Kukkonen et al., 2012; Im et al., 2015; Bessagnet et al., 2016). Sulfate aerosols are usually prescribed as a single species of either H₂SO₄ or (NH₄)₂SO₄. Some models consider H₂SO₄ as the representative sulfate aerosol when the neutralization reaction between H₂SO₄ and ammonia is not considered or when only the binary sulfuric acid–water nucleation is considered (e.g., Wexler et al., 1994; Kulmala et al., 1998; Stier et al., 2006; Kazil and Lovejoy, 2007; Korhonen et al., 2008; Mann et al., 2010). Some other models consider (NH₄)₂SO₄ as the representative sulfate aerosol when studying aerosol–CCN closure (e.g., VanReken et al., 2003), or when including the ternary sulfuric acid–ammonia–water nucleation process or the neutralization reaction between sulfate and ammonia (Kulmala et al., 2002; Napari et al., 2002; Grell et al., 2005; Elleman and Covert, 2009; Watanabe et al., 2010). To reduce the uncertainty of ERFaci, more speciated ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameters need to be utilized in the calculation of cloud droplet activation process – at least for the two main sulfate aerosols, H₂SO₄ and (NH₄)₂SO₄. Here, we suggest a new method of representing ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ that considers both H₂SO₄ and (NH₄)₂SO₄ using the molar ratio of ${\mathrm{NH}}_{\mathrm{4}}^{+}$ to ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$. We also suggest an alternative method that utilizes the spatial distribution of ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$, based on the distinct distribution patterns of ${\mathrm{NH}}_{\mathrm{4}}^{+}$ and ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$over land and sea.

2.4 New parameterization of ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$

H₂SO₄ is completely neutralized as (NH₄)₂SO₄ when ammonia is abundant (Seinfeld and Pandis, 2006). During the neutralization process of H₂SO₄, 1 mol of ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ takes up 2 mol of ${\mathrm{NH}}_{\mathrm{4}}^{+}$ and forms 1 mol of (NH₄)₂SO₄. Here, the assumption is that ammonia neutralizes ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ ions prior to nitrate ions (Seinfeld and Pandis, 2006), and sulfate aerosols appear only in the form of H₂SO₄ and (NH₄)₂SO₄. In the calculation of ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$, the proportion of H₂SO₄ and (NH₄)₂SO₄ is determined using the ammonium to sulfate molar ratio $R=n_{{\mathrm{NH}}_{\mathrm{4}}^{+}}/n_{{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}}$, where $n_{{\mathrm{NH}}_{\mathrm{4}}^{+}}$ is the molar concentration of ${\mathrm{NH}}_{\mathrm{4}}^{+}$ ions, and $n_{{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}}$ is the molar concentration of ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ ions. Generally, sulfate aerosols are completely neutralized as (NH₄)₂SO₄ under high R conditions (R>2) and are partially neutralized under low R conditions (R<2) (Waggoner et al., 1967; Fisher et al., 2011). Using R and the Zdanovskii–Stokes–Robinson relationship (i.e., $V_{\mathrm{d}}=V_{\mathrm{w}}+V_{\text{tot}},V_{\text{tot}}={\sum }_{j=\mathrm{1}}^J{V}_j$, where V_d is the droplet volume, V_w is the volume of water, and V_j is the volume of the chemical j), a representative ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ is defined as follows:

$$\begin{array}{}\text{(2)}& {\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}={\mathit{\epsilon }}_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}{\mathit{\kappa }}_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}+{\mathit{\epsilon }}_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}{\mathit{\kappa }}_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}},\end{array}$$

where ${\mathit{\epsilon }}_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$ is the volume fraction of H₂SO₄ in the total volume of sulfate aerosols (defined as $V_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}/V_{{\mathrm{SO}}_{\mathrm{4}}}$, where $V_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$ is the volume concentration of H₂SO₄, and $V_{{\mathrm{SO}}_{\mathrm{4}}}$ is the total volume concentration of sulfate aerosols), and ${\mathit{\epsilon }}_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$ is calculated in the same manner for (NH₄)₂SO₄ (defined as $V_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}/V_{{\mathrm{SO}}_{\mathrm{4}}}$, where $V_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$ is the volume concentration of (NH₄)₂SO₄). In this study, we use 1.19 and 0.53 to represent ${\mathit{\kappa }}_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$ and ${\mathit{\kappa }}_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$, respectively (Clegg and Wexler, 1998; Petters and Kredenweis 2007; Good et al., 2010). The volume fractions of H₂SO₄ and (NH₄)₂SO₄ are calculated as follows:

$$\begin{array}{llll}{\displaystyle }& {\displaystyle }\text{(i)}& {\displaystyle }& {\displaystyle }\text{if}R=\mathrm{0},\text{then}{\mathit{\epsilon }}_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}=\mathrm{1}\text{and}{\mathit{\epsilon }}_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}=\mathrm{0},\\ {\displaystyle }& {\displaystyle }\text{(ii)}& {\displaystyle }& {\displaystyle }\text{if}\mathrm{0}<R<\mathrm{2},\text{then}\\ \text{(3)}& {\displaystyle }& {\displaystyle }& {\displaystyle }& {\displaystyle }{\mathit{\epsilon }}_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}={\displaystyle \frac{\left[\left(\mathrm{1}-\frac{R}{\mathrm{2}}\right)\times n_{{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}}\right]\times \frac{m_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}}{{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}}}{V_{\mathrm{SO}\mathrm{4}}}}{\displaystyle }& {\displaystyle }& {\displaystyle }& {\displaystyle }\text{and}\\ {\displaystyle }& {\displaystyle }& {\displaystyle }& {\displaystyle }{\mathit{\epsilon }}_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}={\displaystyle \frac{\left(\frac{R}{\mathrm{2}}\times n_{{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}}\right)\times \frac{m_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}}{{\mathit{\rho }}_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}}}{V_{\mathrm{SO}\mathrm{4}}}},\\ {\displaystyle }& {\displaystyle }\text{(iii)}& {\displaystyle }& {\displaystyle }\text{if}R>\mathrm{2},\text{then}{\mathit{\epsilon }}_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}=\mathrm{0}\text{and}{\mathit{\epsilon }}_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}=\mathrm{1}.\end{array}$$

Here, m and ρ indicate the molar mass and density of the specific chemical species, respectively. To be more realistic, ammonium bisulfate may also need to be considered: when the number of ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ is smaller than ${\mathrm{NH}}_{\mathrm{4}}^{+}$, the sulfates appear as a mixture of ammonium bisulfates and sulfuric acids, and when the number of ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ is greater than ${\mathrm{NH}}_{\mathrm{4}}^{+}$ but not twice as large as ${\mathrm{NH}}_{\mathrm{4}}^{+}$, the sulfates appear as a mixture of ammonium bisulfates and ammonium sulfates (Nenes et al., 1998; Moore et al., 2011, 2012). For simplicity, however, such partitioning is not considered in this study. As a result, sulfate aerosols are treated as (NH₄)₂SO₄ when R is greater than two (R>2) and as H₂SO₄ when R is zero (R=0). This method is applicable to the models that consider both ${\mathrm{NH}}_{\mathrm{4}}^{+}$ and ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ ions. If ${\mathrm{NH}}_{\mathrm{4}}^{+}$ data are not available in a model, we suggest an alternative method to represent ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ based on the typical geographical distribution pattern of sulfate aerosols available from observations, as discussed below.

Observational studies show the distinctly different distribution patterns of the two dominant sulfate aerosol species, i.e., (NH₄)₂SO₄ over land and H₂SO₄ over sea (Fujita et al., 2000; Paulot et al., 2015; Kang et al., 2016; Liu et al., 2017). Such distribution patterns are related to the sources of sulfate and ammonium. In general, sulfate aerosols are emitted from land and sea, whereas ammonium is mostly produced from land. Sulfur dioxide is produced from fossil fuel combustion, volcanic eruptions, and dimethyl sulfide (DMS) via air–sea exchanges, and then forms sulfate aerosols (Aneja 1990; Jardin et al., 2015). Wind transportation of pollutants could also cause high concentrations of sulfate aerosols over the sea (Liu et al., 2008). In contrast, ammonium is emitted from livestock, fertilizer, and vehicles (Sutton et al., 2013; Paulot et al., 2014; Bishop et al., 2015; Liu et al., 2015; Stritzke et al., 2015); therefore, it is concentrated mostly on land. Ammonium is usually not abundant enough to fully neutralize H₂SO₄ in the marine boundary layer (Paulot et al., 2015; Ceburnis et al., 2016). Thus, when ammonium information is not available, the ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ can be alternatively estimated by considering the land and sea fractions as follows:

$$\begin{array}{}\text{(4)}& {\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}=f\times {\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}},\text{land}}+\left(\mathrm{1}-f\right)\times {\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}},\text{sea}},\end{array}$$

where f represents the fraction of land at each grid point; unity means entire land, zero means entire sea, and the value in between represents the fraction of land at the grid points in coastal areas. ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}},\text{land}}$ and ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}},\text{sea}}$ represent ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ over land and sea, respectively (i.e., ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}},\text{land}}={\mathit{\kappa }}_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}=\mathrm{0.53}$ and ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}},\text{sea}}={\mathit{\kappa }}_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}=\mathrm{1.19}$).

3 Experimental setup

Model simulations are carried out for 36 d from 00:00 UTC on 10 May to 00:00 UTC on 15 June 2016 and the first 5 d are used as spin-up. Observational data for sulfate aerosols and CCN during this period were obtained from the KORUS-AQ campaign, and they indicated that sulfate aerosols were widely distributed throughout East Asia due to the stagnation of high-pressure systems and the transportation of pollutants from China. The domain covers East Asia (i.e., 2700 km×2700 km; 20–50^∘ N, 105–135^∘ E) with 18 km grid spacing and 50 vertical levels from sea level pressure to 100 hPa. The initial and boundary conditions are provided by the National Center for Environment Prediction–Climate Forecast System Reanalysis (NCEP–CFSR; Saha et al., 2014). The 4DDA (Four-Dimensional Data Assimilation) analysis nudging is used. Anthropogenic emission inventories are obtained from the Emissions Database for Global Atmospheric Research–Hemispheric Transport of Air Pollution (EDGAR–HTAP; Janssens-Maenhout et al., 2015). Natural source emission inventories adopt the Model of Emissions of Gases and Aerosols from Nature (MEGAN; Guenther et al., 2006).

We conduct four simulations with different ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterizations: (1) AS uses a single ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ of 0.53 (i.e., ${\mathit{\kappa }}_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$), assuming that all sulfate aerosols are completely neutralized by ammonium, which is a default setting in WRF-Chem; (2) SA uses a single ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ of 1.19 (i.e., ${\mathit{\kappa }}_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$), assuming that all sulfate aerosols are H₂SO₄; (3) RA applies the new ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterization that calculates the volume-weighted mean ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ using the molar ratio of ammonium to sulfate (R, i.e., Eq. 2); and (4) LO adopts different ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ values for land and sea, assuming that sulfate aerosols are completely neutralized as (NH₄)₂SO₄ over land and are H₂SO₄ only over sea (i.e., Eq. 4).

4 Results and discussion

4.1 Distribution of sulfate and ammonium

The simulated sulfate and ammonium distributions are compared with the observational data that were measured onboard the NASA DC-8 aircraft during the KORUS–AQ campaign (https://www-air.larc.nasa.gov/missions/korus-aq/, last access: 18 July 2019) in and around the Korean Peninsula in May and June of 2016. The measurements were taken within the boundary layer. The mass concentration of sulfate and ammonium were obtained using the method described in Dibb et al. (2003).

In Fig. 1, the mass concentration of sulfate and ammonium simulated by AS are compared with the KORUS-AQ aircraft observations (OBS) following the flight track. The simulated sulfate shows a positive bias but has a high temporal correlation with OBS (r=0.78). The simulated ammonium is less biased than sulfate but indicates a moderate temporal correlation with OBS (r=0.58). Overall, it seems reasonable to state that the WRF-Chem model can calculate the distribution of sulfate aerosols well enough.

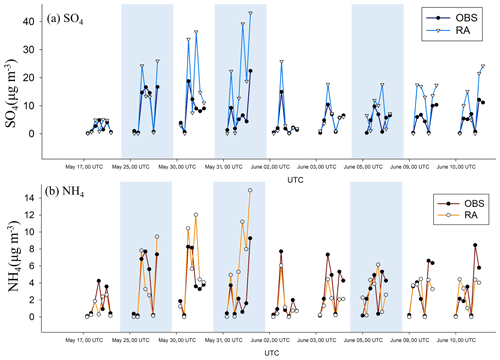
Figure 1 Time variation of the mass concentrations of (a) sulfate and (b) ammonium measured by the NASA DC-8 aircraft (OBS, black line) and simulated by RA (colored line). The blue shaded regions denote the time over the sea.

Figure 2 shows the 30 d averaged mass concentration of sulfate and ammonium and the molar ratio (R) of ammonium to sulfate over the model domain. During the KORUS-AQ campaign period, high-pressure systems often covered East China and the Yellow Sea, and this led to stagnating sulfate and ammonium concentrations. However, sulfate and ammonium are distributed differently due to different sources. Pollutants emitted from the Asian continent are often transported by westerly and southerly winds. Sulfate is highly concentrated in China and the northern part of the Yellow Sea, and DMS emission from the sea also contributes to the formation of sulfate aerosols over the sea. Ammonium is widely distributed throughout China due to the use of fertilizers over farmlands (Paulot et al., 2014; Van Damme et al., 2014; Warner et al., 2017). The concentration of ammonium is generally low over the sea, but it is high over the northern part of the Yellow Sea due to wind transport.

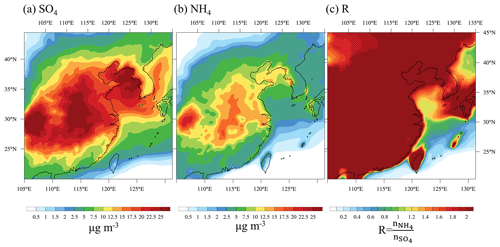
Figure 2 The 30 d averaged (00:00 UTC on 16 May to 00:00 UTC on 15 June 2016) spatial distribution of the mass concentrations of (a) sulfate and (b) ammonium, and (c) the molar ratio of ammonium to sulfate (R) at the surface, from AS.

The distribution of R is associated with the distribution of sulfate and ammonium (Fig. 2). In general, R is high (R>2) over land on account of the high anthropogenic emissions of continental ammonium, and R is low (R<2) over remote seas because the ammonium concentration is small. However, high R is also shown over the Yellow Sea in Fig. 2. This is because the ammonium concentration increases when the westerlies carry continental pollutants over the Yellow Sea during the simulation period. Based on the distribution of R, sulfate aerosols are expected to be almost completely neutralized over land (e.g., (NH₄)₂SO₄) and partially neutralized over sea ((NH₄)₂SO₄+H₂SO₄).

4.2 Distribution of κ

Figure 3 shows the average κ of the accumulation-mode aerosols in AS and the difference between RA and AS and between LO and AS.

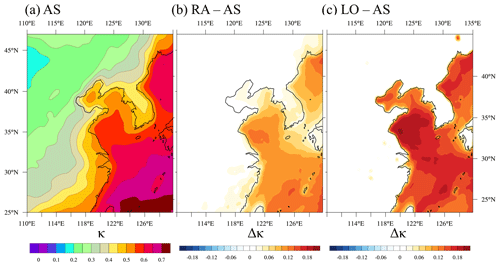
Figure 3 (a) Spatial distribution of the hygroscopicity parameter (κ) in the accumulation mode simulated by AS, and the difference in κ (b) between RA and AS and (c) between LO and AS, at the surface.

The accumulation mode is selected because sulfate aerosols are dominant in this mode. AS simulates κ values that are roughly consistent with the observed mean κ values in the literature (i.e., κ over land is about 0.3 and κ over sea is about 0.7; Andreas and Rosenfeld, 2008), but it varies significantly between land and sea. The κ over land is expected to be lower than the κ over sea because continental aerosols usually include more hydrophobic aerosol species such as black carbon and organic carbon from industry, whereas maritime aerosols consist mainly of hygroscopic substances, i.e., sea salt and non-sea salt sulfates originating from DMS. The variation in κ is also influenced by chemical reactions and meteorological factors, i.e., wind transportation of aerosols and scavenging of aerosols due to precipitation, as well as gravitational settling.

Compared with AS, RA and LO show a pronounced difference in κ over sea (Fig. 3b, c). That is, RA and LO produce significantly higher κ over the sea than AS does because the ammonium concentration is not sufficient to neutralize sulfate completely over the sea (i.e., R<2). RA predicts slightly higher continental κ following the coastal regions than AS because R occasionally becomes low due to the intrusion of maritime air masses that have very low concentrations of ammonium. Maritime κ of RA is lower than that of LO because the transportation of continental pollutants increases the portion of ammonium over the Yellow sea.

4.3 CCN activation

According to the Köhler theory, changes in κ directly influence CCN activation. In this study, the CCN activation rate (f_CCN) is defined as the ratio of the CCN number concentration at 0.6 % supersaturation to the total aerosol number concentration. Simulated f_CCN is compared with the aircraft measurements during the KORUS-AQ campaign (OBS). During this campaign, aerosol and CCN number concentrations were measured by a condensation particle counter (CPC; TSI, 3010) and a CCN counter (CCNC; DMT, CCN-100), respectively (Park et al., 2020). The CPC measures the number concentration of aerosols larger than 10 nm in diameter, and the CCNC measures the CCN number concentration at 0.6 % supersaturation.

The model simulations capture the temporal variation of f_CCN well (r≈0.7 for the linear correlation with OBS; Fig. 4).

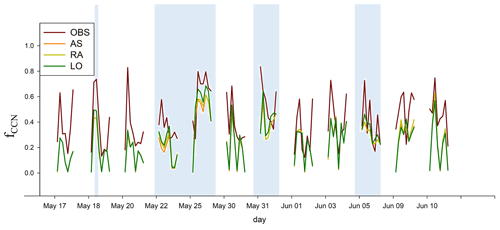
Figure 4 Time variation in the CCN activation fractions at 0.6 % supersaturation (f_CCN) measured by the NASA DC-8 aircraft (OBS) and simulated by AS, RA, and LO. The blue shaded regions denote the time over the sea.

However, f_CCN values are underestimated mainly due to the underestimation of CCN concentrations. The average aerosol (CN) number concentrations for the flight track in all simulations (AS, SA, RA, and LO) and the actual observed values during the flight are 5934 and 5794 cm⁻³, respectively. Thus, unlike Georgiou et al. (2018), who showed that WRF-Chem coupled with MADE/SORGAM tended to overestimate aerosol number concentrations, our simulations only slightly overestimated aerosol number concentrations. The average CCN number concentration at 0.6 % supersaturation for the AS, RA, and LO simulations are 982, 1027, and 1057 cm⁻³, respectively, but the observation was 2154 cm⁻³. Such underestimated CCN concentrations seem to be due to the systematic error in WRF-Chem. As discussed in Tuccella et al. (2015), the uncertainty of the updraft velocity parameterization and bulk hygroscopicity of aerosols lead to an underestimation of the CCN concentration and CCN efficiency (CCN/CN) by a factor of 1.5 and 3.8, respectively. Nevertheless, over land, AS, RA, and LO simulate similar values of f_CCN because continental sulfate aerosols are generally expected to be a fully neutralized form of sulfate (i.e., (NH₄)₂SO₄). This was not the case over sea. During KORUS-AQ, the aircraft passed over the Yellow Sea on 22 and 25 May 2016 (blue shading in Fig. 4). On this occasion, LO simulates the highest f_CCN over the sea among all simulations because LO uses the prescribed ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ value of ${\mathit{\kappa }}_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$ over sea. RA simulates slightly lower f_CCN over the sea because transportation of continental pollutants over the sea can be taken into account, as observed during the KORUS-AQ campaign. The transported air pollutants increase the ammonium concentration over the sea, neutralize H₂SO₄, reduce the hygroscopicity of sulfate aerosols, and consequently decrease f_CCN. Simulated f_CCN in RA has a high spatiotemporal correlation with the observation over the Yellow Sea (i.e., 0.83), whereas AS shows a rather lower correlation (i.e., 0.65). Such difference stems from the fact that R values vary significantly over the Yellow sea due to the transportation of anthropogenic chemicals by westerlies, and such variability is taken into account in RA. This improvement highlights the importance of appropriate chemical representation in atmospheric models. Compared with the RA and LO simulations, AS predicts the lowest f_CCN because the lowest ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ ($={\mathit{\kappa }}_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}})$ is prescribed over sea as well as over land.

We conducted a reliability test that has been often used to evaluate the performance of air quality models. Kumar et al. (1993) proposed the following three criteria for judging model reliability: (1) the normalized mean squared error (NMSE) below 0.5; (2) the fractional bias (defined as $\mathrm{2}\times \frac{\stackrel{\mathrm{‾}}{\text{OBS}}-\stackrel{\mathrm{‾}}{\text{sim}}}{\stackrel{\mathrm{‾}}{\text{OBS}}+\stackrel{\mathrm{‾}}{\text{sim}}}$, where OBS indicates the observed values, sim indicates the simulated values, and the bar above the symbols indicates the average) between −0.5 and 0.5; and (3) the ratio of the model values to the observed values (defined as sim∕OBS) between 0.5 and 2.0. These values for AS, RA, and LO are compared in Table 3. It indicates that RA and LO satisfy all three criteria, but AS does not satisfy two of the three criteria as it predicts a rather high normalized NMSE and fractional bias. Between RA and LO, LO seems somewhat closer to the observations than RA, but the difference is small for these calculations.

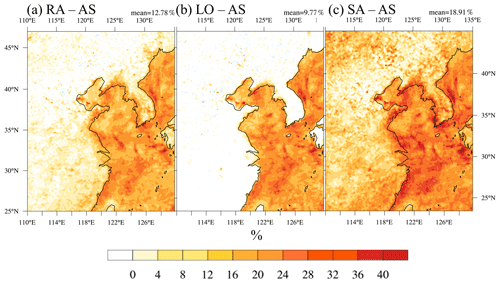
The variation in ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ almost directly influences the change in the column-integrated f_CCN (Fig. 5).

Figure 5 Percentage difference in the column-integrated CCN activation fraction at 0.6 % supersaturation (f_CCN) in AS and sensitivity simulations: (a) RA – AS, (b) LO – AS, and (c) SA – AS.

RA predicts higher f_CCN than AS over the coastal land regions because the occasionally very low ammonium concentration lowers R and affects the CCN activation. Meanwhile, SA prescribes ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ value 2 times as high as AS does and produces about 20 % higher f_CCN values.

4.4 Cloud microphysical properties

Different ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterizations affect simulated cloud microphysical properties. Figure 6 shows the relative differences in the simulated column-integrated cloud droplet number concentration (CDNC) in RA, LO, and SA from AS. All three produce higher ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ values than AS and, therefore, simulate higher CDNCs. However, the differences in CDNC do not exactly correspond to the differences in f_CCN (Fig. 5) because cloud droplet activation is also affected by in-cloud supersaturation and other meteorological factors. SA simulates higher CDNC than AS over both land and sea, but RA and LO simulate higher CDNC mostly only over sea. RA and LO produce similar CDNC distributions over the Yellow Sea (compare Fig. 6a and b) although RA produces smaller f_CCN than LO (compare Fig. 5a and b). As in Moore et al. (2011), the reason for this may be that the sensitivity on f_CCN decreases so much because supersaturation is so high that most aerosols can act as CCN regardless of their critical supersaturation. That is, the supersaturation over the Yellow Sea is high enough to activate most aerosols to cloud droplets. Over land, RA simulates higher CDNC (up to 12 %) than AS in southeast China and the Korean Peninsula, but LO simulates CDNC similar to AS. The results of RA seem to be related to the dilution of ammonium concentrations along the coastal land regions due to the intrusion of maritime air. However, such variation in ammonium cannot be taken into account in LO.

Figure 6 Same as Fig. 5 except for the cloud droplet number concentration (CDNC).

Overall, high CDNCs in RA, LO, and SA (Table 1) result in less precipitation but larger liquid water path (LWP), compared with AS (Table 2). Precipitation reduction is more pronounced over sea because of larger relative differences in CDNC. These results agree well with some previous studies – i.e., high CDNCs suppress local precipitation, prolong cloud lifetime, and consequently increase net LWP, which is known as the cloud lifetime effect (Albrecht, 1989). Obviously, SA, which assumes sulfate aerosols are all H₂SO₄ particles, produces the highest CDNC and also the largest differences in all other properties in Table 2. Less rainwater in SA than in any other simulations may also imply that precipitation scavenging of aerosols was less efficient and, therefore, that more aerosols (CCN) were retained to produce more cloud drops and a longer cloud lifetime. On average, SA has 103 cm⁻³ more aerosols over sea and 116 cm⁻³ more aerosols over land than LO. These surplus aerosols certainly have the potential to simulate a higher number of CCN in SA than in LO.

Table 1 Domain-averaged differences ($=\frac{\text{sensitivity simulation-AS}}{\text{AS}}\times \mathrm{100}\mathit{\%})$ of the CCN activation fraction at 0.6 % supersaturation (f_CCN) and the cloud droplet number concentration (CDNC) in percent. The data are averaged from 00:00 UTC on 15 May to 00:00 UTC on 15 June.

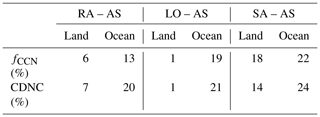
Table 2 Domain-averaged water budgets of AS and their differences from other simulations. The data are averaged from 00:00 UTC on 15 May to 00:00 UTC on 15 June. Rainwater in this study refers to the liquid phase of water that has a potential to become rainfall in the model. LWP stands for liquid water path, and IWP stands for ice water path.

Table 3 Values of the three criteria suggested in Kumar et al. (1993).

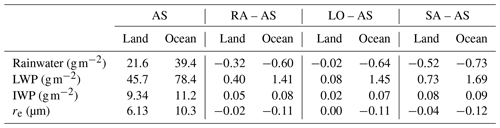
For the same LWP condition, high CDNC induces small effective radii (r_e). RA, LO, and SA simulate smaller r_e than AS, and the maximum difference in r_e amounts to 1.46, 1.38, and 1.48 µm, respectively. However, the domain-averaged differences in r_e are not as substantial as the differences in other cloud microphysical properties (Table 2). This may be related to somewhat larger LWPs in RA, LO, and SA than in AS as well as the sufficient water supply during droplet growth. All simulations in this study have high water vapor path (WVP) conditions ($\text{WVP}>\mathrm{30}\mathrm{kg}{\mathrm{m}}^{-\mathrm{2}}$) throughout the whole domain. According to Qiu et al. (2017), cloud droplets have low competition for water vapor and a high chance of collision–coalescence under high WVP conditions (i.e., WVP>1.5 cm or 15 kg m⁻²). If LWP is similar, the r_e difference could be larger among the simulations than those that are shown herein.

Figure 7 The simulated 30 d averaged (00:00 UTC on 16 May to 00:00 UTC on 15 June 2016) cloud radiative effect (CRE) for (a) AS and the differences (ΔCRE) between (b) RA and AS, (c) LO and AS, and (d) SA and AS.

4.5 Cloud radiative effects

Cloud microphysical properties determine cloud optical properties and, therefore, control the cloud radiative effects. For a fixed LWP, high CDNC is usually associated with low r_e but high cloud optical thickness. Then optically thick clouds reflect more sunlight and strengthen the cloud radiative cooling effect at the top of the atmosphere (TOA), which is known as the cloud albedo effect (Twomey, 1974). We calculate the cloud radiative effect at the TOA (CRE) by subtracting the clear-sky downward radiation from the net all-sky downward radiation (including clouds) (Hartmann, 2016).

RA, LO, and SA simulate optically thicker clouds that reflect more sunlight and exert stronger cooling effects at the TOA than AS (Fig. 7). For the domain average, the differences in CRE for RA, LO, and SA from AS amount to about −1.7, −1.5, and $-\mathrm{2.1}\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}$, respectively. These differences are most pronounced over sea (Fig. 7b, c, d). Such pronounced difference over sea may be affected by the large cloud fraction around the East China Sea due to the East Asian summer monsoon (Pan et al., 2015). That is, a large cloud fraction exerts a large CRE cooling, so the impact of the new parameterization of ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ on CRE could be substantial under large cloud fraction conditions. Note that CRE is similar over land and over the sea in the latitude band from 25 to 28^∘ N in AS (Fig. 7a), but the CRE differences between RA, LO and SA, and AS are much higher over the sea than over land (Fig. 7b, c, d). Such an enhanced cooling effect over the sea can be explained by increases in CDNC (Fig. 6) and, somewhat, by increases in LWP (Table 2). According to some previous studies, the contribution of CDNC and LWP to CRE could be larger than 56 % (Sengupta et al., 2003; Goren and Rosenfeld, 2014).

5 Summary and conclusions

This study introduces a new hygroscopicity parameterization method for sulfate aerosols in the WRF-Chem model and demonstrates the impacts of different ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterization on simulating cloud microphysical properties in East Asia. The new ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterization considers the composition effect of H₂SO₄ and (NH₄)₂SO₄, using the molar ratio of ammonium to sulfate, R. We also suggest an alternative ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterization – ${\mathit{\kappa }}_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$ for land and ${\mathit{\kappa }}_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$ for sea – which utilizes information on the typical observed geographical distribution of sulfate aerosols, in cases where ammonium data are not available. The performance of the new ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterizations was evaluated by comparing it with observational data obtained from a field campaign in East Asia, and it was demonstrated that the new parameterizations could produce more reliable aerosol and CCN concentrations than the previous method, which used a single ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ value (i.e., ${\mathit{\kappa }}_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$). It should be noted that the κ values of 0.53 and 1.19 for (NH₄)₂SO₄ and H₂SO₄ that we used in this study were derived from humidified tandem differential mobility analyzer (HTDMA) measurements, instead of being derived from CCN, which were 0.61 and 0.90, respectively (Petters and Kreidenweis, 2007). If CCN-derived κ values were used, CDNC would generally have decreased because κ became lower and the contrast between (NH₄)₂SO₄ and H₂SO₄ would have been decreased to a certain degree. In the context of cloud droplet activation, CCN-derived κ values might be more appropriate to use because they would be measured under cloudy (i.e., supersaturated) conditions. However, in this study, we try to manifest the effect of different κ values of the two major sulfate species, and this was the main reason for choosing HTDMA-derived κ values that show a greater difference between (NH₄)₂SO₄ and H₂SO₄, instead of CCN-derived values that show a smaller difference.

The effect of the new ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterizations is indicated as substantially different cloud microphysical properties, especially over the sea (about 20 % increases in CDNC). The increases in CDNC suppress local precipitation, prolong cloud lifetime, and consequently reflect more sunlight, i.e., a larger cooling effect (about 1.5 W m⁻²), than the simulation with the original ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterization in WRF-Chem that assumes ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}={\mathit{\kappa }}_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$ for all sulfate aerosols. These results indicate that the estimated cloud radiative forcing due to aerosol–cloud interactions can vary significantly with different ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterizations.

The importance of oceanic sulfate aerosols on radiative forcing is highlighted in recent studies which suggested that DMS (precursor of oceanic sulfate aerosols) emissions significantly contribute to the total radiative forcing due to aerosol–cloud interactions (Carslaw et al., 2013; Yang et al., 2017). The new ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterizations could be more appropriate for studying the effects of oceanic sulfate aerosols on climate, compared with other approaches that use a single ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ (i.e., ${\mathit{\kappa }}_{({\mathrm{NH}}_{\mathrm{4}}{)}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$) or an empirical relationship between (NH₄)₂SO₄ and CCN to calculate CCN activation (Boucher and Anderson, 1995; Kiehl et al., 2000). All in all, the new ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterization is capable of considering the variation in ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ and simulates more reliable results, compared with the previous method using a single ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ value in the calculation of cloud microphysical properties. Many atmospheric models neglect the differences in hygroscopicity between H₂SO₄ and (NH₄)₂SO₄ for simplicity. However, this could result in large uncertainties in estimating CRE, especially in East Asia, as demonstrated in our results.

Therefore, we propose this new parameterization of ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ that considers both of the dominant sulfate aerosols, H₂SO₄ and (NH₄)₂SO₄, when investigating the effects of sulfate aerosols on climate – especially for East Asia, which shows distinctly different emission patterns over land and sea. The new parameterizations are applicable to calculate CCN activation without additional treatments of the chemical reactions and computational expenses. The new parameterization introduced in this study is expected to work effectively in the domain where land and sea are almost evenly distributed or in the regions with a varying distribution of ammonium to sulfate molar ratio. However, we only tested the performance of the new ${\mathit{\kappa }}_{{\mathrm{SO}}_{\mathrm{4}}}$ parameterization in East Asia due to the limited amount of observational data available to validate the performance of CCN activation. Therefore, further studies are needed for different regions where observational data are available to confirm the reliability of our new parameterization.

In this study, we did not discuss other important aerosol species. For instance, the proportion of mass concentrations of nitrate ions are almost as large as sulfate ions (Zhang et al., 2012; Moore et al., 2012), and nitrate also has spatiotemporally varying hygroscopicity due to the complex chemical reactions with other chemicals, i.e., ammonium, sodium, and calcium. In this work, we only made changes in the representation of sulfate aerosol species and did not alter any other chemical processes, and we find that the amount of nitrate and sea salt aerosols in the AS, RA, and LO simulations were similar. Perhaps this implies that the different treatment of sulfate aerosols did not significantly affect nitrate and sea salt aerosols. However, it is difficult to estimate how the presence of nitrate and sea salt aerosols impacted the results in our simulations. Future studies may need to address such important issue in more detail.