JlBox v1.1: a Julia-based multi-phase atmospheric chemistry box model

As our knowledge and understanding of atmospheric aerosol particle evolution and impact grows, designing community mechanistic models requires an ability to capture increasing chemical, physical and therefore numerical complexity. As the landscape of computing software and hardware evolves, it is important to profile the usefulness of emerging platforms in tackling this complexity. Julia is a relatively new programming language that promises computational performance close to that of Fortran, for example, without sacrificing the flexibility offered by languages such as Python. With this in mind, in this paper we present and demonstrate the initial development of a high-performance community mixed-phase atmospheric 0D box model, JlBox, written in Julia.

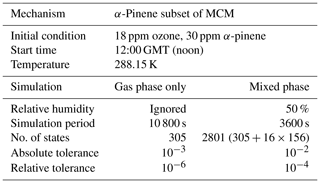
In JlBox v1.1 we provide the option to simulate the chemical kinetics of a gas phase whilst also providing a fully coupled gas-particle model with dynamic partitioning to a fully moving sectional size distribution, in the first instance. JlBox is built around chemical mechanism files, using existing informatics software to parse chemical structures and relationships from these files and then provide parameters required for mixed-phase simulations. In this study we use mechanisms from a subset and the complete Master Chemical Mechanism (MCM). Exploiting the ability to perform automatic differentiation of Jacobian matrices within Julia, we profile the use of sparse linear solvers and pre-conditioners, whilst also using a range of stiff solvers included within the expanding ODE solver suite the Julia environment provides, including the development of an adjoint model. Case studies range from a single volatile organic compound (VOC) with 305 equations to a “full” complexity MCM mixed-phase simulation with 47 544 variables. Comparison with an existing mixed-phase model shows significant improvements in performance for multi-phase and mixed VOC simulations and potential for developments in a number of areas.

1 Introduction

Mechanistic models of atmospheric aerosol particles are designed, primarily, as a facility for quantifying the impact of processes and chemical complexity on their physical and chemical evolution. Depending on how aligned these models are with the state of the science, they have been used for validating or generating reduced-complexity schemes for use in regional to global models (Zaveri et al., 2008; Riemer et al., 2009; Amundson et al., 2006; Korhonen et al., 2004; Roldin et al., 2014; Hallquist et al., 2009; Kokkola et al., 2018). This is based on the evaluation that “full” complexity schemes are too computationally expensive for use in large-scale models. With this in mind, the community has developed a spectrum of box models that focus on a particular process or experimental facility (e.g. Riemer and Ault, 2019), or use a combination of hybrid numerical methods to capture process descriptions for use in regional to global models (e.g. Zaveri et al., 2008; Kokkola et al., 2018). Recent studies are also exploring coupling the latter with numerical techniques for reducing systematic errors through assimilation of ambient measurements (e.g. Sherwen et al., 2019).

With ongoing investments in atmospheric aerosol monitoring technologies, the research community continues to hypothesise and identify new processes and molecular species deemed important to improve our understanding of their impacts. This continually expanding knowledge base of processes and compounds, however, likewise requires us to expand our aerosol modelling frameworks to capture this increased complexity. It also raises an important question about the appropriate design of community-driven process models that can adapt to such increases in complexity, and also about how we ensure our platforms exploit emerging computational platforms, if appropriate.

In this paper we present a new community atmospheric 0D box model, JlBox, written in Julia. Whilst the first version of JlBox, v1.1, has the same structure and automatic model generation approach as PyBox (Topping et al., 2018), we present significant improvements in a number of areas. Julia is a relatively new programming language, created with the understanding that “Scientific computing has traditionally required the highest performance, yet domain experts have largely moved to slower dynamic languages for daily work” (Julia Documentation: https://julia-doc.readthedocs.io/en/latest/manual/introduction/, last access: 8 February 2021). Julia promises computational performance close to that of Fortran, for example, without sacrificing the flexibility offered by languages such as Python (Perkel, 2019). In JlBox v1.1 we evaluate the performance of a one-language-driven simulation that still utilises automated property predictions provided by UManSysProp and other informatics suites (Topping et al., 2018). The choice of programming language when building new and sustainable model infrastructures is clearly influenced by multiple factors. These include issues around training, support and computational performance to name a few. Python has seen a persistent increase in use across the sciences, in part driven by the large ecosystem and community-driven tools that surrounds it. This was the main factor behind the creation of PyBox. Likewise, in this paper we demonstrate that the growing ecosystem around Julia offers a number of significant computational and numerical benefits to tackle known challenges in creating aerosol models using a one-language approach. Specifically, we make use of the ability to perform automatic differentiation of Julia code using tools now available in that ecosystem. In JlBox we demonstrate the usefulness of this capability when coupling particle-phase models to a gas-phase model where deriving an analytical jacobian might be deemed too difficult.

In the following sections we describe the components included within the first version of JlBox, JlBox v1.1. In Sect. 2 we briefly describe the theory on which JlBox is based, including the equations that define implementation of the adjoint sensitivity studies. In Sect. 3 we discuss the code structure, including parsing algorithms for chemical mechanisms, and the use of sparse linear solvers and pre-conditioners, whilst also using a range of stiff solvers included within the expanding ODE solver suite DifferentialEquations.jl. In Sect. 4 we then demonstrate the computational performance of JlBox relative to an existing community of gas-phase and mixed-phase box models, looking at a range of mechanisms from the Master Chemical Mechanism (MCM; Jenkin et al., 1997, 2002). In Sect. 5 we discuss the relative merits of JlBox in comparison with other models whilst presenting a narrative on required future developments. We present JlBox as a platform for a range of future developments, including the addition of internal/external aerosol processes currently not captured. It is our hope that the demonstration of Julia-specific functionality in this study will facilitate this process.

2 Model description

The gas-phase reaction of chemicals in atmosphere follows the gas kinetics equation:

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left[C_i\right]=-\sum _j{r}_j{S}_{ij},r_j=k_j\prod _{\forall i,S_{ij}>\mathrm{0}}[C_i{]}^{S_{ij}},\end{array}$$

where [C_i] is the concentration of compound i, r_j is the reaction rate of reaction j, k_j is the corresponding reaction rate coefficient, and S_ij is the value of the stoichiometry matrix for compound i and j. The above ordinary differential equation (ODE), Eq. (1), fully determines the concentrations of gas-phase chemicals at any time given reaction coefficients k_j, a stoichiometry matrix {S_ij} and initial values. All chemical kinetic demonstrations in this study are provided by the MCM (Jenkin et al., 1997, 2002), but the parsing scheme allows for any mechanism provided in the standard Kinetics PreProcessor (KPP) format (Damian et al., 2002). When adding aerosol particles to the system, more interactions have to be considered in order to predict the state of the system, including concentrations of components in the gas and particulate phase. In JlBox v1.1 we only consider the gas–aerosol partitioning to a fully moving sectional size distribution, recognising the need to use hybrid sectional methods when including coagulation (e.g. Kokkola et al., 2018). We discuss these future developments in Sect. 5. We use bulk-absorptive partitioning in v1.1 where gas-to-particle partitioning is dictated by gas-phase abundance and equilibrium vapour pressures above ideal droplet solutions. This process is described by the growth–diffusion equation provided by Jacobson (2005) (pages 543, 549, 557, 560).

$$\begin{array}{ll}\text{(2)}& {\displaystyle \frac{\mathrm{d}\left[C_{i,k}\right]}{\mathrm{d}t}}=& {\displaystyle }\mathrm{4}\mathit{\pi }{R}_k{n}_k{D}_{i,k}^{\text{eff}}\left(\left[C_i\right]-\left[C_{i,k}^{\mathrm{s}}\right]\right),\text{(3)}& {\displaystyle }\left[C_{i,k}^{\mathrm{s}}\right]=& {\displaystyle }\exp \left({\displaystyle \frac{\mathrm{2}{m}_{\text{w},i}}{\mathit{\sigma }{R}_k{\mathit{\rho }}_i{R}_{*}T}}\right){\displaystyle }& {\displaystyle }\cdot {\displaystyle \frac{\left[C_{i,k}\right]}{\left[C_{\text{core},k}\right]\times \text{core\_diss}+{\sum }_i\left[C_{i,k}\right]}}{\displaystyle \frac{p_i^{\mathrm{s}}{R}_{*}T}{N_{\mathrm{A}}}},\\ \text{(4)}& {\displaystyle }{D}_{i,k}^{\text{eff}}=& {\displaystyle }{\displaystyle \frac{D_i^{*}}{\mathrm{1}+K_{n,i}\left(\frac{\mathrm{1.33}{K}_{n,i}+\mathrm{0.71}}{K_{n,i}+\mathrm{1}}+\frac{\mathrm{4}}{\mathrm{3}}\frac{\mathrm{1}-{\mathit{\alpha }}_i}{{\mathit{\alpha }}_i}\right)}},\end{array}$$

where [C_i,k] is the concentration of compound i component in size bin k, $\left[C_{i,k}^{\mathrm{s}}\right]$ is the effective saturation vapour concentration over a curvature surface of size bin k (considering Kelvin effect), $D_{i,k}^{\text{eff}}$ is the effective molecular diffusion coefficient, R_k is the size of particles in size bin k, n_k the respective number concentration of particles, [C_core,k] is the molar concentration of an assumed involatile core in v1.1 that may dissociate into core_diss components. For example, for an ammonium sulfate core, core_diss is set to 3.0, m_w,i is the molecular weight of condensate i, ρ_i is liquid-phase density, $p_i^{\mathrm{s}}$ is pure component saturation vapour pressure, $D_i^{*}$ is the molecular diffusion coefficient, K_n,i is Knudsen's number, α_i is accommodation coefficient, σ is the surface tension of the droplet, R_* is the universal gas constant, N_A is Avogadro's number, and T is temperature.

As we have to keep track of the concentration of every compound in every size bin, this significantly increases the complexity of the ODE relative to the gas-phase model:

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}=f(y;\mathit{p}),y=(C_{\mathrm{1}},C_{\mathrm{2}},\mathrm{\dots },C_n;C_{\mathrm{1},\mathrm{1}},C_{\mathrm{2},\mathrm{1}},\mathrm{\dots },C_{n,m}),\end{array}$$

where y represents the states of the ODE, n is the number of chemicals, m is the number of size bins, p is a vector of parameters of the ODE, and f(y) is the RHS function implicitly defined by Eqs. (1) and (2). We extend the original ODE state y with concentrations of each chemical on each size bin. A simple schematic is provided in Fig. 1. Imagine there are n=800 components in the gas phase. In the configuration displayed in Fig. 1, the first 800 cells hold the concentration of each component in the gas phase. If our simulation has one size bin, the proceeding cells hold the concentration of each component in the condensed phase. If our simulation has two size bins, the proceeding 800 cells hold the concentration of each component in the second size bin and so on. The gas-phase simulation of a mechanism with n=800 chemicals has to solve an ODE with 800 states, while the mixed-phase simulation with m=16 size bins will have 13 600 ($=\mathrm{800}+\mathrm{800}\times \mathrm{16}$) states. Meanwhile, the size of the Jacobian matrix (required by implicit ODE solvers) will increase in a quadratic way from 800×800 to 13 600×13 600.

Figure 1 Array layout for ODE states y in Eq. (5).

Sensitivity analysis is useful when we need to investigate how the model behaves when we perturb the model parameters and initial values. One approach is to see how all the outputs change due to one perturbed value by simply subtracting the original outputs from the perturbed outputs, or, in a local sense, solving an ODE whose RHS is the partial derivative of the respective parameter. However, this approach would be very expensive when we want the sensitivity of a scalar output with respect to all the parameters. This is often the case when doing data assimilation. The adjoint method can efficiently solve the problem. Imagine there is some scalar function g(y), and we would like to compute its sensitivity against some parameters p. Introducing the adjoint vector λ(t) with the shape of g(y)'s gradient, the adjoint method could compute this in two steps (Damian et al., 2002):

1. Solve the ODE Eq. (6) in a backward order.

2. Numerically integrate formula Eq. (7).

$$\begin{array}{}\text{(6)}& {\displaystyle }& {\displaystyle \frac{\mathrm{d}\mathit{\lambda }}{\mathrm{d}t}}=-{\displaystyle \frac{\partial f(y;p)}{\partial y}}\mathit{\lambda },\mathit{\lambda }\left(t_{\mathrm{F}}\right)={\displaystyle \frac{\partial g}{\partial y}}\left(t_{\mathrm{F}}\right)\text{(7)}& {\displaystyle }& {\displaystyle \frac{\partial g}{\partial p}}=\underset{t_{\mathrm{0}}}{\overset{t_{\mathrm{F}}}{\int }}{\displaystyle \frac{\partial f(y;p)}{\partial p}}\mathit{\lambda }\left(t\right)\mathrm{d}t\end{array}$$

JlBox implements the adjoint sensitivity algorithm with the help of an auto-generated Jacobian matrix $\partial f(y;p)/\partial y$. Users only need to supply the gradient function of the scalar function with respect to ODE states $\partial g/\partial y$ as well as the Jacobian function $\partial f(y;p)/\partial p$ of the RHS function with respect to parameters so as to get the sensitivity of the scalar function with respect to parameters $\partial g/\partial p$ at time t_F. Both are provided automatically through the automatic differentiation provided by Julia.

3 Implementation

JlBox is written in pure Julia and is presently only dependent on the UManSysProp Python package for parsing chemical structures into objects for use with fundamental property calculations during a pre-processing stage. The pre-processing stage also includes extracting the rate function, stoichiometry matrix and other parameters from a file that defines the chemical mechanism using the common KPP format, followed by a solution to the self-generated ODEs using implicit ODE solvers. Specifically, the model consists of six parts:

1. Run a chemical mechanism parser.

2. Perform rate expression formulation and optimisation.

3. Perform RHS function formulation.

4. Create a Jacobian of RHS function.

5. Preparation and calculation for partitioning process.

6. Adjoint sensitivity analysis where required.

Figure 2 highlights the workflow of an implementation of JlBox, used as either a forward or adjoint model. As detailed in the section on Code availability, JlBox was designed with both performance and ease of use in mind, where users can download, install and test it as a package from the Julia package manager in the command-line interface. To use the model, one has to construct a configuration object containing all the parameters and initial conditions that the model requires and then supply it to JlBox's run_simulation_* function. The results are provided as a solution object from DifferentialEquation.jl providing a state vector at any time through interpolation (≥2 order), along with the respective name vector. Examples can be found in the example/ subfolder in the project repository which we refer to in Sect. B.

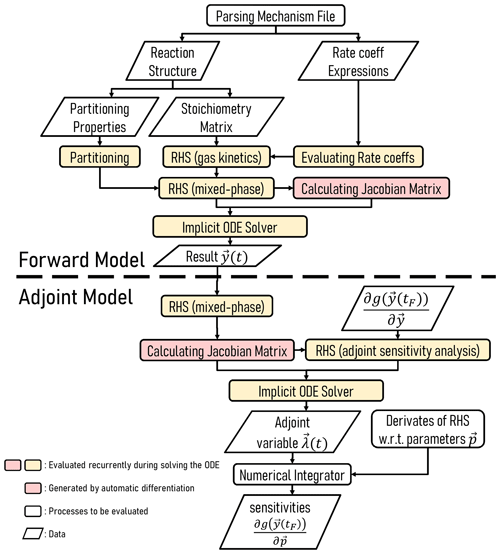
Figure 2 Schematic illustrating the structure of JlBox v1.1, whether in forward or adjoint configuration.

3.1 Mechanism parsing and property predictions

Like PyBox, JlBox builds the required equations to be solved by reading a chemical mechanism file. In the examples provided here, we use mechanisms extracted from the Master Chemical Mechanism (MCM) to build the intended model for simulation. A preview of a mechanism file is given in Listing 1.

Listing 1 Example of the MCM file.

There are two sections in each line of the mechanism file separated by the : symbol: the first represents a single gas-phase chemical reaction where reactants before the = symbol will react with each other with a fixed ratio and produce the products after the = symbol. For example, a A + b B = c C + d D represents a units of A and b units of B will react and produce c units of C and d units of D.

Upon reading each set of equations, JlBox will assign unique numbers for reactants and products if encountered for the first time; then it will fill in the stoichiometry matrix S_ij with stoichiometry coefficients where i is the number of the equation (depicted at the beginning of each line) and j is the number of the reactants and products. The stoichiometry matrix is firstly built as a list of triplets $(i,j,S_{ij})$ for fast insertion of elements, and then it is transformed into the compressed sparse column (CSC) format, which is more memory efficient for calculating the RHS of gas-kinetics.

The latter part of a line of the chemical mechanism file, after the symbol :, represents the expression of reaction rate coefficient k_j(y;p). The expression consists of prescribed combinations of basic arithmetic operators + - * / **, basic math functions, photolysis coefficients J(1), …, J(61), ambient parameters and intermediate variables which have explicit expressions determined by the chemical mechanism. The drawback of this approach is that pre-processing is separated from simulation, and automatic code generation could, in theory, introduce errors that are hard to debug. However, such a drawback is avoided in JlBox with the help of Julia's meta-programming, which assembles the function for calculating reaction rate coefficients “on the fly”. Since the abstract representation of the function is in the tree format, JlBox also does constant folding optimisation to the function where expressions are replaced by their evaluated values if all of the values inside the expressions are found to be constants. For example, the expression 1.2*EXP(1000/TEMP) will be replaced by 34.340931863060504 given a constant temperature at 298.15 K. To further reduce computation, when a reaction rate coefficient is constant, the related expression is deleted from the function which is called at every time step to update the coefficients, and the respective initial value of the coefficient is set to be the constant.

The gas–aerosol partitioning process requires additional pre-processing of several parameters of each compound required by the growth equation. These are listed in Eqs. (2) to (4). Python packages UManSysProp (Topping et al., 2018) and OpenBabel (O'Boyle et al., 2011) are called during the pre-processing stage to calculate thermodynamic properties required by those parameters.

3.2 Gas kinetics and gas–aerosol partitioning process

When solving the ODE, the RHS function of the gas-phase kinetics firstly updates the non-constant rate coefficients k_j(y;p) and then constructs the reaction rate r_j from concentrations of compounds [C_i], their stoichiometry matrix (S_ij), and rate coefficients k_j.

$$\begin{array}{}\text{(8)}& r_j=k_j\prod _{\forall i,S_{ij}>\mathrm{0}}[C_i{]}^{S_{ij}}\end{array}$$

Following this, the model calculates the rate of change (loss/gain) of reactants and products in each equation and sums the loss/gain of the same species across different equations using the following:

$$\begin{array}{}\text{(9)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left[C_i\right]=-\sum _j{r}_j{S}_{ij}.\end{array}$$

There are two ways to implement this. The first projects the structure to program instructions executed by the RHS function. The second stores it as data and the RHS function loops through the data to calculate the result.

The first method is intended to statically figure out the symbolic expressions of the loss and gain for each species as combinations of rate coefficients and gas concentrations, and to generate the RHS function line by line from the relevant expressions. This method is straightforward and fast, especially for small cases. However, it consumes lots of memory and time for compiling when the mechanism file is large (i.e. >1000 equations).

The other approach is to use spare matrix manipulation because of the sparse structure of the stoichiometry matrix in atmospheric chemical mechanisms. Considering equation numbers as columns, compounds numbers as rows and signed stoichiometry (positive for products and negative for reactants) as values, most columns of the stoichiometry matrix have limited (usually ≤4) nonzero values because most equations have a limited number of reactants and products. Therefore, the accumulated rate of change of each compound can be expressed as a sparse matrix–vector product of the stoichiometry matrix and the rates of equations vector while the rates of equations vector can be calculated by loops with cached indices. This method has comparable speed to the previous one and consumes much less memory when compiling and running.

The gas–aerosol partitioning component of JlBox simulates the condensational growth of aerosols in discrete size bins where each particle has the same size. Please note that as we use a fully moving distribution in v1.1, when we further refer to a size bin we retain a discrete representation with no defined limits per bin.

$$\begin{array}{ll}\text{(10)}& {\displaystyle \frac{\mathrm{4}}{\mathrm{3}}}\mathit{\pi }{n}_k{\mathit{\rho }}_k{R}_k^{\mathrm{3}}& {\displaystyle }=m_k{\displaystyle }{m}_k& {\displaystyle }=m_{\text{core},k}+\sum _i{m}_{i,k}\\ {\displaystyle }{m}_{i,k}& {\displaystyle }={\displaystyle \frac{m_{\text{w}.i}\left[C_{i,k}\right]}{N_{\mathrm{A}}}}\\ {\displaystyle }{\mathit{\rho }}_k& {\displaystyle }={\left(\sum _i{\displaystyle \frac{m_{i,k}}{m_k{\mathit{\rho }}_i}}+{\displaystyle \frac{m_{\text{core},k}}{m_k{\mathit{\rho }}_{\text{core}}}}\right)}^{-\mathrm{1}}\end{array}$$

JlBox computes the rate of loss/gain for gas-phase and condensed-phase substances through all size bins. Firstly, for each size bin k, the corresponding concentrations of each compound in the condensed phase $\mathit{\left\{}\right[C_{i,k}\left]\right|\forall i\mathit{\}}$ are summed. Then the model calculates all the values required by the RHS of Eq. (2). As we adopted the moving bin scheme in v1.1, it keeps track of the bin sizes R_k as they grow during the process following formulas Eq. (10) where for each size bin k, m_k denotes mass of all the particles, m_i,k denotes condensed mass of compound i, m_core,k denotes the mass of inorganic core of the particles, and ρ_core denotes the density of inorganic core. Finally, the rate of change of a given species $\mathrm{d}\left[C_{i,k}\right]/\mathrm{d}t$ is summed across all bins to give the corresponding loss/gain of gas-phase concentrations according to conservation law.

$$\begin{array}{}\text{(11)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left[C_i\right]=-\sum _j{r}_j{\mathbf{S}}_{ij}-\sum _k{\displaystyle \frac{d}{\mathrm{d}t}}\left[C_{i,k}\right]\end{array}$$

The combination of the gas-phase Eq. (9) and condensed-phase Eq. (11) rate of change expressions provides the overall RHS function Eq. (5) of a multi-phase.

Please note we explicitly simulate the partitioning of water between the gaseous and condensed phase following every other condensate. We appreciate this may significantly reduce the run-time of the box model. However, in this instance we wish to retain the explicit nature of the partitioning process before applying any simplifications, as we briefly discuss in Sect. 5.2

3.3 Numerical methods and automatic differentiation

JlBox uses the DifferentialEquations.jl library to solve the ODE, assembling the RHS function in a canonical way: function dydt!(dydt::Array{<:Real,1}, y::Array{<:Real,1}, p::Dict , t::Real). There is a variety of solvers (>100) available in the DifferentialEquations.jl package, from which we generally choose semi-implicit/implicit solvers including Rosenbrock, singly diagonally implicit Runge–Kutta and backward differentiation formula (BDF) types of solvers as our problem is numerically stiff. Most of the available solvers are adaptive meaning that they would choose every time step in an adaptive sense to achieve some absolute and relative errors given by the user. Higher error tolerance allows larger time steps, resulting in faster simulation time and vice versa. The error tolerance could also influence the convergence of fully implicit ODE solvers due to the non-linear nature of the ODE, so it may fail to converge if the tolerance is too high. Note that native Julia ODE solvers in the OrdinaryDiffEq.jl sub-package make use of the parallel (dense) linear solver while the CVODE_BDF solver in Sundials.jl sub-package does not. This could mean that the native TRBDF2 solver could be faster than CVODE_BDF on multiprocessor machines, although they adopt similar algorithms. This would need to be profiled across a range of examples.

Since all the states in the ODE (Eqs. 1, 2) represent the atmospheric abundance of compounds in each phase, it is important to preserve the non-negativeness of those states. This can be ensured by rejecting any states with negative figures and shrinking the time step. Users can specify whether to enable it in the configure object, and it is only available in native Julia solvers in the OrdinarDiffEq.jl subpackage.

The Jacobian matrix of the RHS $\partial f(y;p)/\partial y$ is needed in implicit ODE solvers as well as in adjoint sensitivity analysis. The accuracy of the Jacobian matrix, however, has variable requirements in each case. For implicit ODE solvers, when doing forward simulations, the accuracy of the matrix only affects the rate of convergence instead of the accuracy of the result. Some methods like BDF and Rosenbrock–Wanner, by design, could tolerate inaccurate Jacobian matrices (Wanner and Hairer, 1996, p114). Meanwhile, for adjoint sensitivity analysis, accurate Jacobian matrices are needed as they explicitly appear in the RHS function of Eq. (6).

JlBox implements an analytical Jacobian function for both gas kinetics and the partitioning process as well as those generated using finite differentiation and automatic differentiation. Theoretically, an analytical Jacobian is the most accurate and efficient approach but can be laborious to implement due to the nature of the equations involved and therefore error-prone due to manual imputation. The finite-difference approximation can have low numerical accuracy and high-performance costs due to multiple evaluations of the RHS function, although it is the simplest to implement and is applicable to most functions. Automatic differentiation shares the advantages of both methods mentioned previously; it has the convenience of automatically generating a Jacobian matrix from the Julia-based model, much like the finite-difference method, whilst retaining the accuracy of the analytical solution. Based on the fact that all programs are combinations of primitive instructions, an auto-differentiation library could generate the derivative of a program according to the chain rule and predefined derivatives of primitive instructions. The only limitation is that the RHS function must be fully written in the Julia language, and this dictates any additional work that might be required. JlBox uses the ForwardDiff.jl library to perform auto-differentiation. The library introduces the dual-number trick with the help of Julia's multiple dispatch mechanism.

To improve performance and reduce memory consumption, JlBox has special treatments for computing the Jacobian of mixed-phase RHS. Firstly, the gas kinetic part $\partial f_i/\partial y_j{|}_{\mathrm{1}\le i,j\le n}$ is produced analytically because it is sparse and has simple analytical form, while auto-differentiation tools will waste lots of memory and time as they treat it as a dense matrix. Secondly, according to Eq. (11), one part of the Jacobian could be expressed as the sum of another part:

$$\begin{array}{ll}\text{(12)}& {\displaystyle }& {\displaystyle \frac{\partial f_i}{\partial y_j}}\left|{}_{\mathrm{1}\le i\le n,n+\mathrm{1}\le j\le n+nm}\right|{\displaystyle }& {\displaystyle }={\displaystyle \frac{\partial }{\partial y_j}}\left(-\sum _{ni+\mathrm{1}\le k\le (n+\mathrm{1})i}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{y}_k\right)\\ {\displaystyle }& {\displaystyle }=-\sum _{ni+\mathrm{1}\le k\le (n+\mathrm{1})i}{\displaystyle \frac{\partial f_k}{\partial y_j}},\end{array}$$

which could also reduce computation. We only have to compute the Jacobian of Eq. (2) using methods mentioned previously. For comparison of performance and accuracy, JlBox implements two auto-differentiated Jacobians for aerosol processes called “coarse_seeding” and “fine_seeding” with and without the optimisations mentioned above. According to benchmark results presented in Appendix Table B1, it was found those optimisations could significantly reduce memory usage without effecting the performance.

3.4 Sparse linear solvers and pre-conditioners

As the size of the Jacobian matrices grow quickly (O(n²)) following the growth of number of states n, it becomes increasingly slow when simulating a multi-phase model on the full MCM which has 47 544 states when using 16 size bins. The majority of time is spent in solving the dense linear equation Mx=b where $\mathbf{M}=\mathbf{I}-\mathit{\gamma }\mathbf{J}$, J is the Jacobian matrix, γ is a scalar set by ODE solver, and x and b are some vectors.

Following the Kinetic PreProcessor (KPP) and AtChem model approach (Sommariva et al., 2020; Damian et al., 2002), as the Jacobian is quite sparse JlBox introduces the option to use sparse linear solvers provided by DifferentialEquations.jl. Specifically JlBox is optimised for the iterative sparse linear solver GMRES in CVODE_BDF by providing pre-conditioners which could drastically reduce the number of iterations of iterative sparse linear solvers like GMRES. Theoretically, a pre-conditioner P is a rough approximation of the matrix M so that P⁻¹M has less condition number than M. It is “rough” in the sense that the pre-condition process of solving ${\mathbf{P}}^{-\mathrm{1}}\mathit{x}=\mathit{b}$ is easier. In practice, the pre-conditioner P is stored in lower–upper (LU) factored form so that solving ${\mathbf{P}}^{-\mathrm{1}}\mathit{x}=\mathit{b}$ is a simple back substitution that sometimes needs to be updated to retain proximity with the changing Jacobian.

In JlBox, the functions for solving ${\mathbf{P}}^{-\mathrm{1}}\mathit{x}=\mathit{b}$ and updating P are specified by “prec” and “psetup” arguments inside the CVODE_BDF solver. JlBox provides default prec and psetup as a tri-diagonal pre-conditioner following the approach used in AtChem (Sommariva et al., 2020). In psetup, a full Jacobian is calculated in sparse format followed by taking its tridiagonal values forming the approximated tridiagonal M. A LU factorisation is then calculated using the Thomas algorithm and stored in a cache so that prec can solve the linear equation quickly.

3.5 Adjoint sensitivity analysis

In this section we demonstrate the ability to build and deploy an adjoint model. Using it to quantify sensitivity typically relies on experimental data and processes that will be incorporated in future versions. Nonetheless, the example given in Sect. 4.2 demonstrates the ability to evaluate the sensitivity of predicted secondary organic aerosol to all gas-phase kinetic coefficients. An adjoint sensitivity analysis computes the derivatives of a scalar function g(y) of the ODE states with respect to some parameters p of the RHS function f(y;p). The actual computation reformulates solving the ODE Eq. (6) in a backward order and numerically integrating formula Eq. (7). It is worth noting that the equation is in the linear form, so using an implicit method that linearises the RHS function like the Rosenbrock method may give a good result. The Rosenbrock method explicitly includes the Jacobian function as an estimation of the RHS function. In this case, such an estimation is an exact representation which enables longer time steps. The BDF may also benefit from this for the same reason, with the number of Newton steps reduced to one or two. As the Jacobian matrix is frequently called, a fast and accurate Jacobian function is needed. With this in mind, the special treatment of automatic differentiation mentioned in Sect. 3.3 delivered a 10× improvement in performance compared with the one that simply wraps the RHS with the AD function. For the second step, we adopt the adaptive Gauss–Kronrod quadrature to calculate the formula accurately.

Solving the ODE Eq. (6) in a backward manner poses a significant problem as we need to evaluate (an accurate) Jacobian matrix in a backward order (from t_F to t₀) which requires accessing the states y(t) at given time points in backward order. The only way to achieve that is to store a series of states y_i at some checkpoints t_i. The stored states alone are sufficient for using ODE solvers with a fixed time step, but an adaptive ODE solver is needed for better error control which requires accessing y(t) at an arbitrary time t. Thus we need to interpolate those states into dense outputs. Since the time derivative of y is easily accessible in the form of $\mathrm{d}y/\mathrm{d}t=f\left(y\right)$, we can use Hermite interpolation or higher order interpolation to enhance the accuracy of the interpolation. JlBox utilises the solution object of DifferentialEquations.jl (which internally implements Hermite interpolation) to provide y(t) at any given point $t_{\mathrm{0}}\le t\le t_{\mathrm{F}}$.

4 Model output

The goal of JlBox is to provide a high-performance mechanistic atmospheric aerosol box model that also retains the flexibility and usability of Python implementations, for example. Not only should it have comparable performance, if not run faster, than other models for a given scenario, it should have the capacity for integrating benchmark chemical mechanisms with coupled aerosol process descriptions. In this section we validate the output of JlBox against PyBox since the model process representations are identical, whilst also investigating the relative performance as the “size” of the problem scales.

4.1 Verification against existing box models

To test the numerical correctness of JlBox, we ran our model together with existing box model including PyBox and KPP with identical scenarios. JlBox is designed as a more efficient version of PyBox, so it is expected to have identical results in both gas- and mixed-phase scenarios. Meanwhile, gas-phase models constructed from the widely used KPP software could provide some guarantee that the results from JlBox is useful. However, aerosol processes are not available in KPP; as a result we could only compare outputs of gas kinetics. We prepared two test scenarios with gas-phase simulation only and multi-phase simulation. The settings of the simulations are listed in Table 1. Additionally, in the multi-phase simulation, we set the initial aerosol to be an ideal representation of an ammonium sulfate solution satisfying a lognormal size distribution with an average geometric mean diameter of 0.2 micrometres and a standard deviation of 2.2, discretised into 16 bins. The bins are linearly separated in log-space where a fixed volume ratio between bins defines the centre of the bin and bin width. The upper and lower size range and required number of bins define the centre (radius) of each bin accordingly. The saturation vapour pressure threshold of whether to include the gas-to-particle partitioning of a specific chemical is chosen to be 10⁻⁶ atm based on an extremely low absorptive partitioning coefficient for a wide range of pre-existing mass loadings. For all simulations presented in this paper we use the vapour pressure technique of Joback and Reid (1987). Whilst known to systematically under predict saturation vapour pressures for species of atmospheric interest (Bilde et al., 2015), we use it for illustrative purposes here, and any of the methods included within UManSysProp can be called within JlBox. For gas-phase-only simulations, we use α-pinene as an indicative VOC degradation scheme. The simulations to compare JlBox with PyBox and KPP are performed on a PC with a CPU of 8-core AMD Ryzen 1700X at 3.6 GHz and 16 GB RAM.

Table 1 Initial conditions and solver configurations.

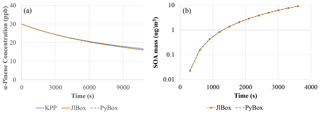
Figure 3 clearly shows that JlBox and PyBox produced identical results, as designed. Although very close, there is around 1 % deviation between the KPP-generated model and the other two models. A possible explanation includes differences between ODE solvers as JlBox and PyBox used CVODE while KPP used LSODEs. For mixed-phase simulations, JlBox and PyBox again generate identical values for secondary organic aerosol mass, as expected.

Figure 3 Comparison of gas-only (a) and multi-phase (b) simulation.

4.2 Evaluation of adjoint sensitivity analysis

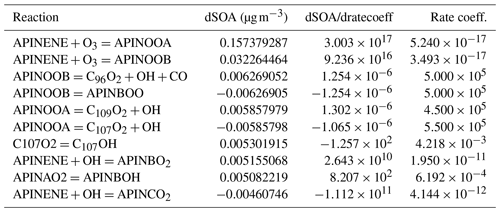
A demonstration of an adjoint sensitivity analysis is conducted to calculate the partial derivative of secondary organic aerosol (SOA) mass at the end of the simulation with respect to the rate coefficients of each equation in the mechanism. The configurations of the simulation are the same as the mixed-phase α-pinene scenario (Table 1) presented in the previous section.

The results presented in Table 2 highlighted the top 10 (in terms of absolute magnitude) estimated deviations of SOA mass dSOA under a 1 % change of rate coefficients because the derivate itself ($\text{dSOA}/\text{dratecoeff}$) is not comparable due to different units involved. The reactions between α-pinene and ozone have the most substantial effect. The order of the equations simply highlights the flow of α-pinene to its subsequent products. This could be attributed to the fact that the system has not reached the equilibrium state (also illustrated in the growth of SOA mass in Fig. 3). Another interesting point is that competing reactions have similar sensitivities but opposite signs to the reactions of APINOOB, APINOOA, and APINENE+OH. The competing reactions between α-pinene and ozone is an outlier with a ratio of 5 between the two. A plausible explanation is that for those reactions with opposite sensitivities, the products of one leads to little or no SOA while the other contributes more, so when the former reaction is accelerated due to its perturbed rate coefficient, it reduces the ability of the latter reaction to produce SOA. As a result, the two reactions have opposite sensitivities. For the reactions of APINENE and O3, it is possible that the APINOOA and APINOOB pathways both produce SOA, and the first produces more than the second one. When the rate coefficient of the second reaction is increased, the decrease in SOA due to less APINOOA does not offset the increase in SOA due to more APINOOB, which leads to a smaller but still positive sensitivity of SOA. As we state earlier, a deeper analysis with alternative options for saturation vapour pressures and process inclusion may reveal important dependencies.

Table 2 Sensitivities of SOA mass with respect to gas-phase rate coefficients. The units of the last two columns depend on the number of reactants.

4.3 Performance on large-scale problems

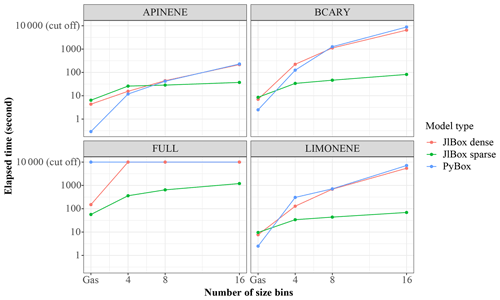
In this section we demonstrate the performance of JlBox on “large-scale” problems where both KPP and PyBox fail to solve due to constraints imposed by the model workflow and language dependencies as shown in Appendix B. We define “large-scale” problems as those beyond single VOCs or gas-phase-only simulations. Equipped with a sparse linear solver and auto-generated tridiagonal preconditioner, JlBox is ideal for simulating larger mechanisms than we present above. With this in mind, the largest possible mechanism accessible from the MCM suite is selected, which contains 16 701 chemical equations and 5832 species. Moreover, we performed 72 h mixed-phase simulations with 16 moving bins. This means that JlBox has to solve a system of stiff ODEs of 47 544 variables that requires solving matrices of 47 544×47 544 at each time step. The initial conditions are taken from an existing representative chamber study on mixed VOC systems (Couvidat et al., 2018, Tables 1 and 2) (see Appendix A) with 16 experiments in two sets. We use average values of temperature where ranges are provided. In addition, instead of using the relative humidity selected in those studies, we performed perturbed simulations with a low-relative-humidity (RH) scenario (10 %) and high-RH scenario (80 %) respectively to investigate possible dependence on stiffness according to variable partitioning from the gas to the condensed phase. All the simulations were executed on the ETH Zurich Euler cluster, requesting 4 cores and 7 GB memory each to exploit parallelism between different initial conditions. This was chosen as a PC would have to run them in sequential order making it too time consuming.

The elapsed time taken by JlBox is plotted in Fig. 4. The average time is around 7 h which is approximately $\mathrm{1}/\mathrm{10}$ of simulation time. In addition, the maximum memory consumption is 8216 MB and average consumption is 4273 MB. This represents a significant reduction when compared to the memory required to store a Jacobian matrix in a dense double-precision format. Note that the Euler cluster provides three types of CPU nodes equipped with Intel XeonE3 1585Lv5, XeonGold 6150 and AMD EPYC 7742 and the simulation jobs are distributed to all three kinds of node. Although XeonE3 has better single-core performance compared to the other two, the time variations between different scenarios far exceeds the variations due to the difference in processors.

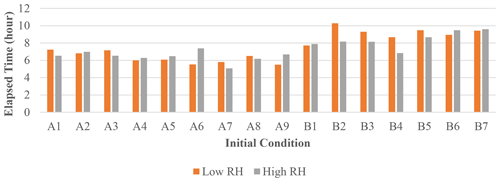
Figure 4 Elapsed time of 72 h mixed-phase simulations. The initial conditions used for each case are listed in Appendix A.

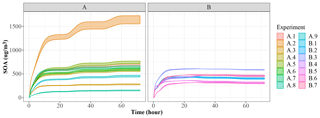
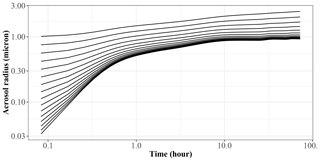
Figure 5 shows the generation of SOA mass in the 72 h period. JlBox captures a diurnal change of photolysis rate as is depicted in experiment A. We remind the reader that we have no depositional loss, or variable emissions, and that we are using the boiling point method of Joback and Reid (1987) for estimating saturation vapour pressures. We also present a time series plot (Fig. 6) for experiment A1 with the high-RH scenario. Small size bins went through condensational growths within this first few hours as expected from the gas–aerosol partitioning process.

Figure 5 Time series plot of SOA mass from the same case studies used in profiling total simulation time. In this study, as noted in the text, we use a predictive technique that under-predicts the saturation vapour pressure to create the maximum number of viable condensing products.

Figure 6 Time series plot of size bins for experiment A1 with the high-RH scenario.

5 Discussion

5.1 Comparison with other models

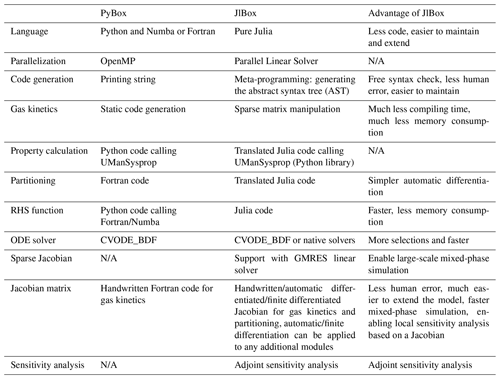
JlBox is developed based on the PyBox model (Topping et al., 2018): they have similar structures, rely on the same methods for calculating pure component properties and provide almost identical results. Despite these similarities, we feel JlBox has made significant improvements over PyBox in terms of readability, functionality, scalability and efficiency from both a programming and algorithmic sense (Table 3). The Julia programming language makes the most significant contribution to those improvements in that it promises a high-performance environment, close to Fortran, without sacrificing the flexibility of Python. For example, the directly translated partitioning code in JlBox can run at a comparable speed to the individual Fortran routines in PyBox, and the multiple dispatching mechanism makes it trivial for implementing the automatic differentiation. As a result, JlBox elegantly solves the “two-language problem” without compromising anything by writing everything in Julia. It spares users from editing “code in code” like PyBox and makes it easier to maintain the code base and to extend the model. The homogeneous code base of JlBox also enables a convenient migration to other devices like GPUs considering there is already a GPU backend for Julia.

Table 3 Comparison between JlBox and PyBox.

As for algorithmic advances, the automatic differentiation method for generating Jacobian matrices is not only the most effective addition but also a fundamental one. It is an accurate and convenient way to calculate the Jacobian matrix which only requires an RHS function fully written in Julia. With Jacobian matrices available, the number of RHS evaluations is dramatically reduced since the implicit ODE solver no longer needs to estimate the Jacobian matrix using finite differences. Also, without automatic differentiation, it will not be so easy to build the adjoint model of a fully coupled process model which explicitly requires the Jacobian matrix for the entire model, let alone to extend the model with more processes. Besides, the adaptation of sparse matrices for gas kinetics reduced the compilation cost to a small constant value enabling the JlBox to simulate large-scale mechanisms such as the entire MCM, which for PyBox typically remains limited by memory.

Compared to other models like KPP (Damian et al., 2002) and AtChem (Sommariva et al., 2020), JlBox is unique due to its ability to perform coupled mixed-phase simulation efficiently, especially on large mechanisms such as the full MCM where the vanilla KPP variant often fails to compile. JlBox is written in pure standard Julia without any string manipulation to codes, in contrast to KPP and AtChem, which enables full IDE support making it more developer friendly.

5.2 Future development

There are a number of processes and algorithmic implementations not included in this version of JlBox that would be useful for further use in a scientific capacity. These include coagulation, hybrid sectional methods and auto-oxidation products schemes to name a few (Ehn et al., 2014; Hallquist et al., 2009; Riemer et al., 2009). As we state earlier, the purpose of this development stage was to create and profile the first Julia implementation of an aerosol box model for the scientific community that would demonstrably exploit the exciting potential this emerging language has to offer. In version 1.0 we provide a fully coupled model. We could, and will, provide options for implementing simplified approaches to aerosol process, such as operator splitting, and assume instantaneous equilibration for water in a range of sub-saturated humid conditions. Indeed, these methods have proven to provide robust mechanisms for mitigating computational efficiency barriers if implemented correctly. However, our ethos with JlBox is to build and develop a platform for a benchmark community box model that exploits the aforementioned benefits that Julia provides. This includes the ability to exploit existing and emerging hardware and software platforms as we try to tackle the growing chemical and process complexity associated with aerosol evolution. We hope that, with version 1.0, the community can help develop and expand this new framework.

Quantifying the importance, or not, of process and chemical complexity requires a multifaceted approach. With the proliferation of data-science-driven approaches across most scientific domains, Reichstein et al. (2019) note that the next generation of earth system models are likely to merge machine learning (ML) and traditional process-driven models to attempt to solve the aforementioned challenges in complexity whilst exploiting the rich and growing datasets of global observations. Julia is being used in the development of ML frameworks, with libraries such as Flux-ML enabling researchers to embed process-driven models within the back propagation pipeline (Innes, 2018). This opens up the possibility to develop observation-driven parameterisations in hybrid mechanistic-ML frameworks, which helps with the issue around provenance in ML parameterisation developments.

JlBox will continually grow and we encourage uptake and further developments.

Appendix A: Initial condition of Sect. 4.3

Table A1 Initial condition for anthropogenic VOC experiments from Couvidat et al. (2018). Concentrations in ppb, temperature (T) in Kelvin and relative humidity in %.

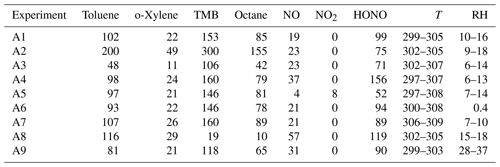
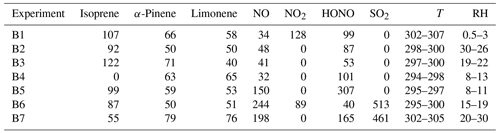
Table A2 Initial condition for biogenic VOC experiments from Couvidat et al. (2018). Concentrations in ppb, temperature (T) in Kelvin and relative humidity in %.

Appendix B: Performance benchmarking

In Table B1, we measured the elapsed time and total allocated memory of simulations using varying ODE solvers and techniques of computing the Jacobian matrix mentioned in Sect. 3.3. We chose two ODE solvers: CVODE_BDF and TRBDF2. CVODE_BDF is part of the Sundials suite developed by Lawrence Livermore National Laboratory. It is a widely used high-performance ODE solver suitable for large-scale stiff ODE problems. TRBDF2 is a Julia-native library implemented in OrdinaryDiffEq.jl. It uses the classical TRBDF2 scheme (Hosea and Shampine, 1996) while benefiting from a high-performance linear solver provided by the Julia community.

Table B1 Elapsed time and total allocated memory of the multi-phase APINENE simulation in Sect. 4.1 with different ODE solvers and Jacobian matrix evaluation techniques.

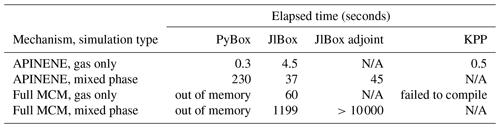
In Table B2 the elapsed time of PyBox, JlBox and KPP are measured, with initial conditions and parameters in Sects. 4.1 and 4.2. We fine tuned JlBox on its ODE solver options to achieve the best performance. For the APINENE mechanism, CVODE with dense Jacobian was found to be the fastest on the gas-phase-only simulations, CVODE with sparse Jacobian was fastest for the multi-phase simulation, while the Julia-native TRBDF2 solver runs better on the adjoint sensitivity analysis. For the full MCM, due to memory restrictions, the only practical option is to use the CVODE ODE solver with the FGMRES sparse linear solver.

Table B2 Performance comparison of PyBox, JlBox and KPP based on elapsed time of forward and adjoint simulation in Sects. 4.1 and 4.2 and simulation of full MCM with the same initial condition.

As shown in Fig. 6, we conducted simulations with varying size bins and mechanism complexity to further illustrate the scaling property of JlBox compared with PyBox. We built simulations around two additional mechanisms that represent beta-caryophyllene and limonene (referred to using identifiers BCARY and LIMONENE respectively), which are subsets of the full MCM. The configurations of simulations are set to be identical to those provided in Table 1. The results in Table B2 and Fig. 6 show that the sparse multi-phase JlBox (referred to as “JlBox sparse”) performs much better than PyBox, especially for large simulations, because the performance reliance on using a sparse Jacobian scales roughly linearly with the number of size bins.The same is not true when using a dense Jacobian within JlBox (referred to as “JlBox dense”). For gas-phase-only simulations, interestingly the simulation overhead of JlBox is larger than PyBox for simulations of a single VOC but outperforms PyBox when simulating the entire MCM. Indeed, in this scenario, PyBox ran out of memory in our simulations.

Figure B1 Performance comparison between JlBox and PyBox with different numbers of size bins and mechanisms.