the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A new parameterization of ice heterogeneous nucleation coupled to aerosol chemistry in WRF-Chem model version 3.5.1: evaluation through ISDAC measurements
Setigui Aboubacar Keita
Eric Girard
Jean-Christophe Raut
Maud Leriche
Jean-Pierre Blanchet
Jacques Pelon
Tatsuo Onishi
Ana Cirisan
In the Arctic, during polar night and early spring, ice clouds are separated into two leading types of ice clouds (TICs): (1) TIC1 clouds characterized by a large concentration of very small crystals and TIC2 clouds characterized by a low concentration of large ice crystals. Using a suitable parameterization of heterogeneous ice nucleation is essential for properly representing ice clouds in meteorological and climate models and subsequently understanding their interactions with aerosols and radiation. Here, we describe a new parameterization for ice crystal formation by heterogeneous nucleation in water-subsaturated conditions coupled to aerosol chemistry in the Weather Research and Forecasting model coupled with chemistry (WRF-Chem). The parameterization is implemented in the Milbrandt and Yau (2005a, b) two-moment cloud microphysics scheme, and we assess how the WRF-Chem model responds to the run-time interaction between chemistry and the new parameterization. Well-documented reference cases provided us with in situ data from the spring 2008 Indirect and Semi-Direct Aerosol Campaign (ISDAC) over Alaska. Our analysis reveals that the new parameterization clearly improves the representation of the ice water content (IWC) in polluted or unpolluted air masses and shows the poor performance of the reference parameterization in representing ice clouds with low IWC. The new parameterization is able to represent TIC1 and TIC2 microphysical characteristics at the top of the clouds, where heterogenous ice nucleation is most likely occurring, even with the known bias of simulated aerosols by WRF-Chem over the Arctic.
- Article
(3077 KB) - Full-text XML
- BibTeX
- EndNote
The Arctic is warming faster than the global mean, and projections for the future suggest that this tendency will continue (IPCC, 2013). The contribution of aerosols to the changing climate of the Arctic is poorly known. Aerosols perturb the radiative balance directly by absorbing radiation and indirectly due to aerosol effects on cloud properties. This leads to increases in shortwave scattering efficiency and infrared radiation (IR) emissivity alterations of Arctic clouds (Zhao and Garrett, 2015; Shindell and Faluvegi, 2009). The radiative properties and lifetime of clouds are particularly sensitive to aerosol concentration, composition and size. While the uncertainties associated with the indirect effects of aerosols on liquid clouds are still large, the effect of ice nucleation is even less well understood. Ice particle formation in tropospheric clouds significantly changes cloud microphysical properties, radiation balance and precipitation efficiency. At the core of the problem, ice nucleation causes multiple changes to cloud behavior, which at present are difficult to quantify. In its latest report, the IPCC (Intergovernmental Panel on Climate Change) was unable to estimate the radiative forcing of aerosols on clouds through ice nucleation (Boucher et al., 2013).
The detailed process of ice nucleation in cold clouds is complex and remains a major challenge for parameterization in atmospheric models. This is especially the case for polar ice clouds, for which the paucity of observations is a serious limitation (Curry et al., 1996; Kanji et al., 2017; McFarquhar et al., 2017). For instance, instead of assuming that cloud particles are distributed homogeneously, to investigate model response and climate sensitivity, some models have based their parameterization on in situ observations (Kay et al., 2016; Cirisan et al., 2020). However, the strong coupling between clouds and state variables, particularly temperature and moisture or relative humidity, requires a dynamic coupling of the cloud microphysics interactively with the atmospheric state variables. Among these coupling processes, the efficiency of ice-nucleating particles (INPs) to activate cloud formation is critical given the rarity of INPs in the pristine atmosphere. Two approaches are used to treat the INP efficiency: a singular and deterministic method, or a stochastic method (Pruppacher and Klett, 1997). While the singular approach assumes nucleation to occur at specific relative humidity and temperature (e.g., Wheeler and Bertram, 2012; Murray et al., 2012), the stochastic method allows for time-dependent state variables following the classical nucleation theory (CNT) (Pruppacher and Klett, 1997; Cirisan et al., 2020). It is also our approach in this study, whereby we assume that freezing occurs at any location on the INP surface with equal probability. This is one attempt to best represent in situ observations, yet it is still not fully physically comprehensive and one exploration step. The ultimate general method is still a matter of intense research (Vali, 2014; Wright and Petters, 2013).
Most atmospheric models use simple time-independent parameterizations of ice nucleation, predicting ice crystal number concentration either as a function of temperature (Fletcher, 1962; Cooper, 1986) or ice supersaturation (e.g., Meyers et al., 1992). These parameterizations do not include a limitation of ice crystal number concentration by the number of available ice nuclei particles and can lead to very poor estimation of ice crystal number concentration, in particular if they are applied outside the range of measurements used to constrain them (Prenni et al., 2007). This is particularly true for ice clouds in Arctic conditions (Keita and Girard, 2016). In the CNT model, a crucial fitting parameter is the contact angle (θ), quantifying the wettability of a solid particle surface by ice via the Young–Dupré equation. It is generally described as a single contact angle for an entire aerosol population, which does not work well for predicting the fractions of INPs on dust aerosol or on particles that have heterogeneous surfaces (Hoose and Möhler, 2012).
In recent years, with increasing data on ice nucleation from field and laboratory studies, new time-independent parameterizations have been developed, often based on empirical fits to atmospheric INP measurements as a function of temperature and aerosol particle size distributions (e.g., Connolly et al., 2013; Welti et al., 2012; Phillips et al., 2013; DeMott et al., 2010, 2015; Cirisan et al., 2020). Despite significant advances, they are of limited use in large-scale models operating over a wide range of temperatures. More complex CNT parameterizations than those using contact angle (θ probability density function or PDF) come at high computational costs (Welti et al., 2012; Murray et al., 2012; Niedermeier et al., 2014). In the particular context of climate simulations in Arctic atmospheric and chemical conditions, there is a need for efficient parameterizations of heterogeneous ice nucleation using simplified approaches to limit computational time.
In Keita et al. (2019), the parameterization of Girard et al. (2013) for water-subsaturated conditions based upon the CNT approach was implemented in the online Weather Research and Forecasting model coupled with chemistry (WRF-Chem) (Grell et al., 2005). This parameterization is suitable to represent the formation of ice clouds in the Arctic. It assumes that INPs are mainly mineral dust particles, which is consistent with recent results from the NETCARE (Network on Climate and Aerosols: Addressing Key Uncertainties in Remote Canadian Environments) project (Abbatt et al., 2019). This parameterization considered physicochemical properties of INPs, which are important in Arctic conditions, especially during winter and early spring (Eastwood et al., 2009; Keita and Girard, 2016) when sulfuric acid is often a dominant component of the aerosol, known as Arctic haze. Two types of ice clouds (TICs) were characterized Grenier et al. (2009). A TIC1 is an ice cloud seen by lidar but unseen by radar and is composed of a relatively large number of nonprecipitating small ice crystals; its ice crystal number concentration is higher than 10 L−1. This cloud can have an upper part composed of low concentrated precipitating ice crystals. The second type, TIC2, is an ice cloud seen by radar and lidar characterized by a low concentration of larger precipitating ice crystals with an ice crystal number concentration lower than 10 L−1. After spatial and temporal evaluation of the model, Keita et al. (2019) showed the ability of the parameterization to discriminate TIC1 and TIC2 clouds observed during the Indirect and Semi-Direct Aerosol Campaign (ISDAC) (McFarquhar et al., 2011). However, the study of Keita et al. (2019) was constrained by a prescribed concentration of aerosols with a fixed acid concentration.
In this paper, we investigate ice heterogeneous nucleation for the first time in a fully coupled aerosol and chemistry parameterization. We evaluate the response of the WRF-Chem model to the realistic time-dependent interaction between aerosols predicted by the chemistry module and the contact angle approach proposed by Girard et al. (2013). The new parameterization significantly improves the treatment of ice nucleation by discriminating TIC1 and TIC2 cloud formation as a function of the aerosol chemical composition. Each cloud is closely analyzed against observational data from three detailed flights conducted during ISDAC (2008). This study is part of the NETCARE project addressing key uncertainties in remote Canadian environments with the objective of assessing the impact of aerosols on Arctic ice clouds.
The paper is organized as follows. Section 2 briefly describes the Milbrandt and Yau (2005a, b) scheme for cloud microphysics and the presentation of ice heterogeneous nucleation parameterization coupled with aerosol chemistry. Section 3 presents the test cases from ISDAC and Sect. 4 the evaluation of the new parameterization against ISDAC. Section 5 is dedicated to the conclusion.
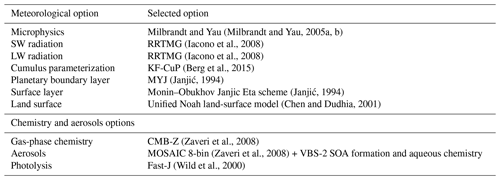
The new scheme for ice crystal formation by heterogeneous nucleation in the deposition mode is implemented in WRF-Chem version 3.5.1. WRF-Chem is a regional, fully coupled “online” model (Grell et al., 2005), for which all prognostic meteorological, chemical and aerosol variables are fully integrated within WRF-ARW, a mesoscale meteorological model; it uses the same grid, time step, advection scheme and physics schemes as WRF-ARW. Several schemes are available in WRF-Chem for cloud microphysics. We choose the Milbrandt and Yau (2005a, b), MY05, for its ability to simulate Arctic clouds in previous works (Keita et al., 2019; Keita and Girard, 2016).
2.1 Overview of the two-moment version of the cloud microphysical scheme MY05
MY05 (Milbrandt and Yau, 2005a, b) is a bulk cloud microphysics parameterization with one-, two- and three-moment versions. We use the two-moment version available in WRF-Chem. It includes the following prognostic variables: the mass mixing ratio qx and the number concentration Nx, with respectively representing cloud liquid water (c), cloud ice water (i), rain (r), snow (s), hail (h) and graupel (g). The time evolutions of the hydrometeor mass mixing ratio and number concentration are respectively governed by the following prognostic equations:
and
where ρ is the density of air, U the 3D velocity vector, VQx the mass-weighted fall speed, NT,x the total number concentration per unit volume, VNx the number-weighted fall speed and K the turbulent diffusion matrix. The right-hand side terms of both equations respectively represent advection and divergence, turbulent mixing, sedimentation, and microphysical tendencies (marked by the “s” subscript).
The mass of a single hydrometeor for the x category is parameterized as a power law of the form
where , with ρx the bulk density (Table 1) for spherical particles x (cloud liquid water, rain, snow, graupel and hail). Cloud ice crystals are assumed to be bullet rosettes (Schoenberg Ferrier, 1994) with ci=440 kg m−3. The size spectrum of each category is described by a common generalized gamma distribution function (Schoenberg Ferrier, 1994) of the form
where Nx(D) is the number concentration of hydrometeor x per unit volume per unit diameter D, αx is the shape parameter controlling the size dispersion, λx is the slope and νx is a second size dispersion parameter. The size distribution of cloud droplets is represented in MY05 by αx=1 and λx=3. For all other hydrometeors νx=1, leading to the form
where N0x is the intercept parameter given by
The four ice-phase hydrometeors follow the size distribution above. The cloud ice water category represents pristine ice crystals. The snow category includes crystals with radii greater than 100 µm and aggregates. The graupel category includes moderate-density graupel formed from heavily rimed ice or snow. The hail category corresponds to high-density hail and frozen raindrops. For each ice-phase hydrometeor x, the total number concentration NT,x (kg−1) and the mass mixing ratio qT,x (kg kg−1) are respectively given by
and
where mx(D) is obtained from Eq. (3).
Table 2Source and sink terms listed according to the hydrometeor category, which gains mass and number, except for self-collections or when the loss is to water vapor.

Microphysical processes represented in MY05 are summarized in Table 2, where processes are listed according to the hydrometeor category. The source and sink terms for the two-moment (mass content) scheme are from previous studies (Kong and Yau, 1997; Schoenberg Ferrier, 1994) and depend on the size distribution function. The primary sources of ice crystals in the atmosphere are heterogeneous and homogeneous ice nucleation. Homogeneous freezing is the spontaneous freezing of a water (or haze) droplet. According to Pruppacher and Klett (1997), the homogeneous freezing rate of cloud droplets is dominant at temperatures below ∘C. In the range −30 to −50 ∘C, MY05 follows DeMott et al. (1994) with
In a given time step Δt, ΔNfreeze is the number of droplets freezing homogeneously and J is the nucleation rate for pure water. For homogeneous nucleation,
with the volume V approximated by the mean droplet diameter in centimeters. Therefore, the fraction of cloud droplets freezing in one time step may be written as
where Dmc is the mean volume diameter of cloud droplets. Heterogeneous ice nucleation needs INPs, a minor fraction of the tropospheric aerosol, which exhibits micro surface structures to facilitate the formation of ice crystals. In the presence of INPs, if thermodynamic conditions are favorable, ice crystals can form by heterogeneous nucleation through four different modes. Deposition nucleation and condensation freezing can occur without the presence of supercooled droplets. For clouds below 0 ∘C primarily composed of supercooled liquid droplets, ice crystal can form by immersion and contact freezing. This conceptual definition of heterogeneous ice nucleation (Pruppacher and Klett, 1997) is used in MY05. Contact freezing follows Young (1974) wherein the number concentration of contact INPs is a function of temperature according to Meyers et al. (1992). In the contact-freezing formation mode, ice nucleation occurs on a solid particle colliding with a supercooled liquid droplet. Immersion freezing of raindrops and cloud water droplets follows the parameterization of Bigg (1953). The deposition mode involves the growth of ice directly from the vapor phase, whereas condensation freezing occurs if the ice phase is formed immediately after condensation of water vapor on a solid particle as liquid intermediate. In the original version of MY05, deposition and condensation freezing are functions of water vapor supersaturation with respect to ice, Si, following Meyers et al. (1992):
where Nm,i is the number of ice crystals predicted per unit volume due to deposition and condensation freezing. The Meyers et al. (1992) parameterization for deposition and condensation freezing depends only on supersaturation. It was derived from ground-based measurements. These approximations may lead to an overestimation of Nm,i when the number concentration of particles acting as INPs is low, such as in Arctic conditions (Eidhammer et al., 2009). Moreover, the immersion-freezing mode from Pruppacher and Klett (1997) has been extended to include freezing of immersed INPs inside an aqueous solution or wet aerosol (Vali et al., 2015), which is a significant process of Arctic ice cloud formation (Eastwood et al., 2008).
2.2 A new parameterization of ice heterogeneous nucleation coupled with chemistry for MY05 in WRF-Chem
The new parameterization focuses on heterogeneous ice nucleation for uncoated INPs and for sulfuric-acid-coated INPs in the deposition mode, i.e., in water-subsaturated conditions. In this approach, INPs are assumed to be mineral dust particles following Girard et al. (2013). For contact freezing and immersion freezing from supercooled cloud droplets, the parameterizations remain unchanged. As condensation freezing is uncertain (Vali et al., 2015), this process is no longer included in the model. The modified version of MY05 including our new parameterization described below is hereafter referred to as MYKE.
The parameterization is based on the CNT, a stochastic approach in which the nucleation rate Jd depends on the contact angle between an ice embryo and its INPs. Following CNT, in each time step Δt the number concentration of nucleated ice crystals Nf is given by
where Ad is the total surface area of dust particles and Nt is the total number concentration of available INPs. In previous studies using this approach (Keita and Girard, 2016; Keita et al., 2019; Girard et al., 2013; Khvorostyanov and Curry, 2009; Morrison et al., 2005b; Liu et al., 2007; Hoose et al., 2010; Chen et al., 2008), Ad and Nt were prescribed and constant over time, although the concentration of atmospheric INPs varied tremendously in time and space, as well as in their composition and origins. The new MYKE parameterization within WRF-chem now considers the temporal and spatial variation of Ad and Nt. Jd, the nucleation rate of embryos per unit surface of particles (Pruppacher and Klett, 1997; Martin, 2000; Hung et al., 2003; Pant et al., 2004; Parsons et al., 2004b; Archuleta et al., 2005; Pant et al., 2006), is defined as
where B=1026 is the kinetic coefficient (Pruppacher and Klett, 1997), k is the Boltzmann constant (J K−1), T is the temperature in Kelvin, and ΔG∗ is the critical Gibbs free energy for the formation of an ice embryo (J) and is defined as
where J m−2 is the surface tension between ice and water vapor, ρi=0.5 g cm−3 is the bulk ice density and Rv=461.5 is the gas constant for water vapor. The function f(cos θ) is a monotonic decreasing function of the cosine of the contact angle θ as defined by Pruppacher and Klett (1997) for a curved substrate:
where and , with rg being the critical germ size expressed as
where νw is the volume of a water molecule.
In the CNT, the contact angle θ is a very important variable because it represents the ability of an INP to form ice. The lower the contact angle, the better an INP the aerosol is. Numerous laboratory studies have found realistic values of θ based on the physicochemical composition of aerosols (e.g., Marcolli et al., 2007; Eastwood et al., 2008; Fornea et al., 2009; Welti et al., 2009; Kanji and Abbatt, 2010; Welti et al., 2009). The CNT approach using these values was subsequently applied successfully in climate and forecast models at different scales (Khvorostyanov and Curry, 2009; Morrison et al., 2005a; Liu et al., 2007; Chen et al., 2008). For example, using the parameterization of Girard et al. (2013) based on laboratory studies from Eastwood et al. (2008, 2009), Keita et al. (2019) were able to simulate Arctic clouds forming in polluted and clean air masses with a prescribed contact angle of 26 and 12∘, respectively. These studies were, however, limited because the contact angles represent extreme cases that must be prescribed arbitrarily before the simulation, and they assumed homogeneity of the degree of acidity of clouds in space and time throughout the whole domain.
For the first time, a real-time variable contact angle is used here in the CNT approach by coupling MY05 with the chemical module in WRF-Chem. This coupling is between MY05 and the MOSAIC (Model for Simulating Aerosol Interactions and Chemistry) aerosol module (Zaveri et al., 2008). MOSAIC simulates a wide variety of aerosol species: sulfates, methanesulfonate, nitrate, chloride, carbonate, ammonium, sodium, calcium, black carbon (BC), primary organic mass (OC), liquid water and other inorganic mass (OIN). OIN represents unspecified inorganic species such as silica (SiO2), other inert minerals and trace metals lumped together assimilated to mineral dust. MOSAIC uses a sectional approach to represent aerosol size distributions by dividing the size distribution for each species into several size bins (four or eight available in WRF-Chem) and assumes that the aerosols are internally mixed in each bin. MOSAIC considers the major aerosol processes of inorganic aerosol thermodynamic equilibrium, binary aerosol nucleation, coagulation and condensation but does not include secondary organic aerosol (SOA) formation in the version used in this study. MOSAIC is a good compromise between accuracy and computing performance. It is used in WRF-Chem with four chemical mechanisms.
The coupling is done by expressing θ as a function of the aerosol neutralization fraction fn in dust particles internally mixed with sulfate, nitrate and ammonium (Zhang et al., 2007; Fisher et al., 2011), which is between 0 and 1 and is defined as
This was motivated by several previous studies (Jouan et al., 2012; Grenier and Blanchet, 2010; DeMott et al., 2010; Blanchet and Girard, 1994; Keita et al., 2019; Keita and Girard, 2016) suggesting that the acidification of ice nuclei by the oxidation of sulfur dioxide forming sulfuric acid in the Arctic greatly alters the microphysical response of ice clouds. Such ice clouds tend to have bigger and fewer ice crystals than ice clouds formed in pristine environments. For instance, Kulkarni et al. (2014) showed that, except for quartz, acid-coated dust makes less effective INPs in the deposition mode but has similar effectiveness in the immersion-freezing mode, i.e., in water-supersaturated regime. Based on X-ray diffraction analyses, they argued that acid treatment caused structural deformations of the surface dust, and the lack of structured order reduced the ice nucleation properties of coated particles in the deposition mode. Moreover, they suggested that, at water-supersaturated conditions, surface chemical reactions might not change the original ice-nucleating properties permanently because coating material could be removed by dissolution. Panda et al. (2010) concluded that sulfuric-acid-treated kaolinite particles could result in the formation of aluminum sulfate that can easily be dissolved in water. Considering these recent findings and our objective to develop a simplified parameterization to limit computational time, we choose to use the CNT formula for deposition mode but with a specific factor, the neutralization fraction fn, indicating the degree of acidity of the coating of dust particles.
Moreover, θ has been derived by Eastwood et al. (2008, 2009) from heterogeneous nucleation rates on kaolinite particles obtained in laboratory measurements. As a best fit, they found limiting values of in polluted air and in clean air. Kaolinite represents a significant component of mineral dust (Glaccum and Prospero, 1980). It is also found to be an efficient ice nucleus in the deposition mode, requiring relative humidity with respect to ice (RHi) below 112 % in order to initiate ice crystal formation (Eastwood et al., 2009). This is a typical microphysical condition found in Arctic ice clouds. Recent studies from Kumar et al. (2018, 2019a, b) showed that
-
the relevance of quartz particles as atmospheric INPs is uncertain,
-
INP activity of dust particles not only depends on their composition but also on their chemical exposure history, and
-
the exposition of dust particles to acidic air masses decreases their INP activity.
Thus, using kaolinite as a proxy for dust particles in our parameterization is reasonable in the current state of knowledge on dust particle composition in the atmosphere, in particular in the Arctic atmosphere where our parameterization applies. Keita and Girard (2016), after analyzing the slope between the nucleation rate and the saturation over ice for TIC1 and TIC2 clouds (see Fig. 16 in Keita and Girard, 2016), observed for a given Si that
-
the slope is the largest for the smallest accessible contact angle, and
-
the decrease in the slope with the increasing contact angle is very nonlinear.
These results are consistent with laboratory experiments (Sullivan et al., 2010) showing a rapid increase in the contact angle with acidity on coated INPs. These results motivated us to parameterize the contact angle θ as a function of the aerosol neutralization fraction fn under a concave form. Simple concave functions follow the power law:
with p larger than 1. We have chosen a quadratic (p=2) form for simplicity:
We have also added a sensitivity simulation under a biquadratic form (p=4) to test the influence of the exponent p on the concave form of the contact angle with the neutralization fraction:
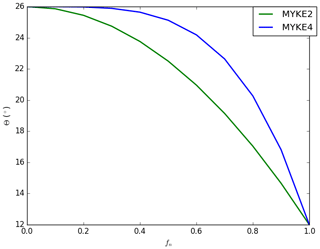
Both formulations, referred to as MYKE2 (Eq. 20) and MYKE4 (Eq. 21), are implemented in MY05 and tested hereafter. They imply that θ is close to 26∘ for with a more (Eq. 21) or less (Eq. 20) rapid decrease between 0.5 and 1 as shown in Fig. 1. The coupling between MY05 and MOSAIC is done by taking information from MOSAIC for Ad and Nt as needed to compute Eq. (13) and for fn to compute Eqs. (20) and (21). These parameters are computed assuming the same aerosol size bin definition as in MOSAIC.
ISDAC took place during April 2008 at the North Slope of Alaska. The objective was to study the role of Arctic aerosols in cloud microphysical properties and in the surface energy budget. Numerous studies have been based upon data from ISDAC (McFarquhar et al., 2011; Lawson et al., 2019). Among them, several studies investigated detailed parameters of ice clouds by analyzing the ISDAC database (Jouan et al., 2012; DeMott et al., 2010) or by running atmospheric models on case studies highlighted during the campaign (Keita and Girard, 2016; Matrosov et al., 2019; Keita et al., 2019). For instance, Keita et al. (2019) analyzed microphysical properties of TICs for ISDAC flights in nonpolluted and polluted environment using WRF simulations. Flights F13, F21 and F29 studied by Keita et al. (2019) were typical of a TIC1 cloud (F13) formed in a pristine air mass and of two TIC2 representative cloud cases (F21 and F29) formed in a polluted air mass. Here, our goal is to show the potential of the new ice nucleation parameterization to discriminate TIC1 and TIC2 cloud formation as a function of the aerosol chemical composition. Each cloud type is closely investigated using detailed observations from three flights conducted during ISDAC.
The simulations with WRF-Chem including MYKE are done over the whole period of ISDAC (McFarquhar et al., 2011), from 1 to 30 April 2008, on the domain shown in Fig. 2, which is identical to that described by Keita et al. (2019). The three test cases (F13, F21 and F29) are included in this period. The domain is based on a Lambert projection centered on Barrow, Alaska (now Utqiagvik), over 160 × 100 grid cells with a horizontal resolution of 10 km and 55 vertical levels between the surface and 50 hPa. The first 4 d of the simulation (1 to 4 April included) are used for model spin-up. Three simulations are performed: the first one uses the original MY05 scheme (the REF simulation), the second one uses the new parameterization given in Eq. (20) (the MYKE2 simulation) and the third one uses the new parameterization described by Eq. (21) (the MYKE4 simulation). WRF-Chem options and parameterizations used in these simulations are summarized in Table 3. As in Keita et al. (2019), meteorological initial and boundary conditions use NCEP (National Centers for Environmental Prediction) Global Forecast System (GFS) Final Analysis (FNL) data (), and the simulations are nudged to GFS FNL updated every 6 h above the planetary boundary layer (PBL).
Figure 2Model domain (yellow) used in this study centered over Fairbanks with a horizontal resolution of 10 km. The cities of Barrow (now Utqiagvik; 71.18∘ N,156.44∘ E) and Fairbanks (64.83∘ N,147.77∘ E) over which the F12, F13, F21 and F29 flights took place are also shown with orange dots.
For the chemical module, the CBM-Z (Carbon Bond Mechanism) photochemical mechanism (Zaveri and Peters, 1999) coupled with MOSAIC is used. CBM-Z has 67 species and 164 reactions in a lumped structure approach that classifies organic compounds according to their internal bond types. Rates for photolytic reactions are derived using the Fast-J photolysis rate scheme (Wild et al., 2000). Eight size bins are used in MOSAIC. Chemical initial and boundary conditions are taken from the global chemical-transport model MOZART-4 (Model for OZone And Related chemical Tracers, version 4) (Emmons et al., 2010). The fire emissions inventory used is the Fire INventory from NCAR (FINN-v1) (Wiedinmyer et al., 2011). FINN-v1 provides emissions on a per fire basis based on event count information from the Moderate Resolution Imaging Spectrometer (MODIS). The anthropogenic emissions come from the inventory developed within the POLARCAT Model Intercomparison Model Project (POLMIP), which includes SO2 from both eruptive and noneruptive continuous degassing volcanism (Fisher et al., 2011; Jouan et al., 2014). During winter and spring 2008, sustained eruptive activity was recorded at Kamchatka and the Aleutian Islands (Fisher et al., 2011; Jouan et al., 2014; Atkinson et al., 2013; Burton et al., 2012). Noneruptive activity was common throughout our simulation period (Fisher et al., 2011; Jouan et al., 2014; Atkinson et al., 2013). Soil-derived (dust) and sea salt aerosol emissions are computed online into WRF-Chem respectively based upon the wind erosion formulation of Shaw et al. (2008) and the GOCART (Global Ozone Chemistry Aerosol Radiation and Transport model) sea salt emission module (Chin et al., 2000). For biogenic emissions, the Model of Emissions of Gases and Aerosols from Nature (MEGAN) (Guenther, 2007) computes them online using characteristics of the surface (class of vegetation, soil humidity and temperature, for instance).
This section presents comparisons of WRF-Chem simulations (REF, MYKE2 and MYKE4) against observations, followed by a discussion of the results. Although the comparison between simulated results and observations is presented in the following along the entire vertical profile inside the clouds, the discussion focuses on the altitudes above the 500 hPa level, where heterogeneous nucleation is the most important process. According to Jouan et al. (2012), most of the differences between TIC1 and TIC2 events were confined at cloud top where ice nucleation mostly occurs and air is supersaturated with respect to ice. To compare simulations with observations along the ISDAC flight tracks, simulated results are averaged in a grid box of 10 by 10 km2 centered on the location of the flight. ISDAC in situ measurements have been averaged every 20 s, corresponding to a vertical resolution of ∼45 hPa (∼450 m), during ascents and descents through clouds. Simulated WRF outputs are linearly interpolated to the pressure levels of these observations and temporally averaged over a 3 h period, encompassing the area of ISDAC flights. Some statistics are computed using the same method. First, we present some meteorological and chemical properties, followed by an analysis of cloud microphysical properties.
4.1 Temperature and relative humidity over ice
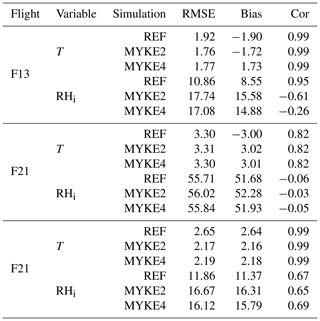
Table 4 presents biases (Bias), Pearson correlation coefficients (Cor) and root mean square errors (RMSE) for the temperature T and relative humidity over ice RHi for the three simulations (REF, MYKE2 and MYKE4) and above the 500 hPa level. According to Jouan et al. (2012), the uncertainties on the measurements are estimated at ±0.5 ∘C for T and ±11 % for RHi. Note that vertical profiles of T and RHi for flights F13, F21 and F29 are very close to results obtained by Keita et al. (2019). As expected, due to the nudging, the new heterogeneous ice nucleation parameterization does not significantly impact T and RHi. The lowest temperatures at the top of the clouds, where the process of heterogeneous ice nucleation is important, are relatively well reproduced by MYKE2 and MYKE4 simulations with similar statistics (Cor ≃0.99, RMSE ≃2, Bias ∘C), except along F21 flight (Cor ≃0.82, RMSE ≃3.3, Bias ∘C), for which the observed increase in temperature caused by the heat exchanged at cold temperatures is not adequately represented by the model. For that flight, the three simulations underestimate RHi by ±50 % at the top of the cloud. These biases are consistent with the large-scale GFS FLN fields and result in an underestimation of the altitude of the top of the cloud by the model for F21.
4.2 Aerosol properties
Figure 3 shows the comparison between observed and simulated (REF, MYKE2 and MYKE4) vertical profiles of total aerosol number concentrations (Na). The Passive Cavity Aerosol Spectrometer Probe (PCASP) externally mounted under a wing of the Convair-580 aircraft sampled ambient clear air just before entering the cloud regions for all flights except F21. The optical particle counter (PCASP) provided particle size distributions and number concentrations in the geometric diameter size range 0.12–3 µm. To allow a fair comparison between WRF-Chem-simulated and PCASP-measured Na, the model concentrations are summed over bins 3 to 6, corresponding to sizes between 0.156 and 2.5 µm. According to Shantz et al. (2014), the uncertainty in number concentration measured by the PCASP is approximately 10 %. First, the model does not reproduce the observed vertical variability. This may be due to the small sampling domain and time taken during ISDAC, which make comparisons between model simulations and the observed variability difficult, especially at the low horizontal resolution of 10 km used here. For F13, the air mass is relatively clean, with a weak vertical variability of aerosol number concentrations remaining mostly below 210 cm−3 on the whole column with mean concentrations around 73 cm−3, very close to the simulation mean of 86 cm−3. For F29, the PCASP shows that there is a much higher concentration of aerosol particles in the lower troposphere (more than twice that observed during F13, e.g., larger than 400 cm−3), particularly at altitudes above 550 hPa near cloud top where peak concentrations exceeding 1000 cm−3 have been measured. Comparing the two flights, between 550 hPa and 400 hPa, the simulated aerosol number concentration is overestimated by a factor of 3 above observations for flight F13 and underestimated by 1 order magnitude for flight F29 (Fig. 3). These discrepancies are consistent with Mölders et al. (2011), who analyzed aerosol concentrations during polar night around Fairbanks and showed an overestimation of aerosol concentrations over the nonpolluted site and an underestimation at an polluted site by using WRF-Chem. They concluded that discrepancies result from uncertainty in emissions, especially at Fairbanks. While most models agree that Arctic aerosols can be attributed to a mixture of anthropogenic sources, mesoscale models have difficulty properly simulating aerosol concentrations over the Arctic (Shindell et al., 2008; Eckhardt et al., 2015; Schwarz et al., 2013; Raut et al., 2017). Moreover, even if the simulated results show the same order of magnitude for Na above 550 hPa (Fig. 3), whereas observations show a large difference between the two flights, we expect that the differences between simulated results for cloud microphysical properties for these two flights could be mainly explained by a combination of differences in the physicochemical properties of aerosols and the altitude of the simulated cloud top.
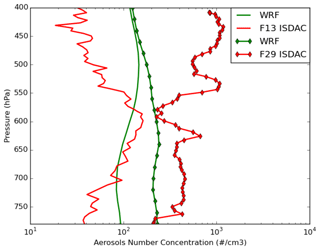
Figure 3Comparison of the observed (red) and simulated (green) WRF vertical profiles of total aerosol number concentrations. Observations were measured by the PCASP in situ sensor onboard the Convair-580 just before entering the clouds for flights F13 (solid lines) and F29 (solid lines with diamond markers) Note that PCASP measurements were not available during flight F21.
Figure 4 presents simulated (REF, MYKE2 and MYKE4) vertical profiles of sulfate (SO4), ammonium (NH4) and nitrate (NO3) molar aerosol concentrations along flights F13, F21 and F29, respectively. Unfortunately, no observation of the aerosol chemical composition was available during the campaign to evaluate those results. Vertical distributions indicate a rather constant structure of aerosol molar concentrations for F13, with a mean value around 6.2 nmol cm−3 for both SO4 and NH4 and a value of 0.5 nmol cm−3 for NO3 (Fig. 4). For F21 and F29 simulated results show peak aerosol concentrations in the mid-troposphere up to a factor of 2 compared to F13 and a larger vertical gradient, with large and moderate depletion in the boundary layer for F21 and F29 (Fig. 4b and c). F21 and F29 have NH4 mean values of 8 and 10.2 nmol cm−3, respectively, and SO4 mean values both around 7 nmol cm−3. These values and the vertical structures correspond relatively well with mean observed concentrations for NH4 and SO4 of 7 nmol cm−3 seen during the ARCTAS (Arctic Research of the Composition of the Troposphere from Aircraft and Satellites) and ARCPAC (Aerosol, Radiation, and Cloud Processes affecting Arctic Climate) campaigns in April 2008 (Fisher et al., 2011). Fisher et al. (2011) showed that volcanic sources (Aleutian Islands and Kamchatka) accounted for 12 %–24 % of the sulfate at all altitudes, with a peak contribution in the mid-troposphere. The volcanic source is discharged directly in the free troposphere and is thus less affected by deposition than surface sources. This is also supported by satellite observations from the Ozone Monitoring Instrument (OMI) over the North Slope of Alaska, which shows much larger SO2 concentrations at the end of ISDAC. Clouds sampled during both F21 and F29 appear to form mostly in air masses containing dust and smoke, possibly with a highly acidic coating.
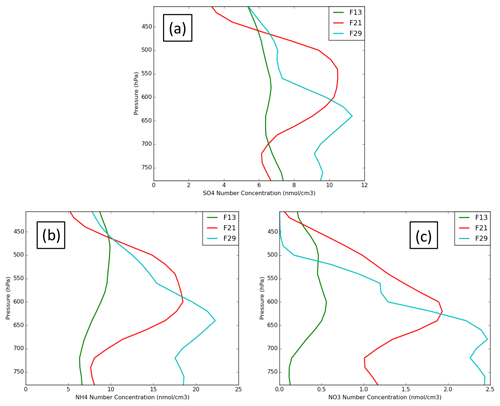
Figure 4Vertical profiles of sulfate (a), ammonium (b) and nitrate (c) molar aerosol concentration along flights F13 (green), F21 (red) and F29 (light blue).
Figure 5 presents the vertical profile of the neutralization fraction fn (full line, see Eq. 18) and the contact angle θ (dashed, see Eqs. 20 and 21) for MYKE2 (Fig. 5a) and for MYKE4 (Fig. 5b) along the top of the three flights F13, F21 and F29. Results obtained with MYKE2 and MYKE4 using the same value of the neutralization fraction are very similar. Results from the two simulations are therefore discussed together. The difference lies in the curve shape of the contact angle θ: MYKE4 simulates a more rapid decrease for than MYKE2 (Fig. 1). This prescription substantially increases θ values in MYKE4 more than in MYKE2 along the vertical profile by up to 3∘, especially at the cloud top where nucleation is the dominant process. This change has a positive impact on the nucleation rate: a smaller contact angle in the MYKE2 simulation indeed tends to decrease the critical Gibbs free energy to form ice embryos (Eq. 15), hence leading to a higher nucleation rate of ice crystals. The θ profile in F13 presents a constant shape with values around 17.5 and 20.5∘ for MYKE2 and MYKE4, respectively. Focusing on MYKE4 for F21, the large contact angle around 21∘ corresponds to acid INPs, i.e., a smaller fn than F13, and a decrease in the nucleation rate. Although F29 also shows significant acidity around 400 hPa (Fig. 4b), with higher concentrations of SO4 than F13, it tends to neutrality around 500 hPa in relation to the increase in ammonium at this altitude in comparison to higher altitudes and the negligible amount of nitrate in the upper part of the cloud (Fig. 4b and c).
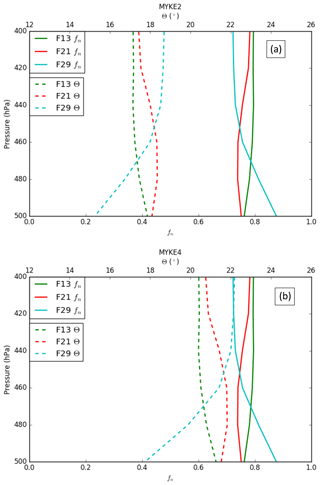
Figure 5Vertical profiles of the neutralization fraction (fn, full line) and the contact angle (θ, dashed line) for MYKE2 (a) and MYKE4 (b) along flights F13 (green), F21 (red) and F29 (light blue).
Our results reveal that the model broadly reproduces Na from the ground to the 500 hPa level, but it has difficulty representing Na in the upper part, even if observations and model results remain of the same order of magnitude. MYKE2 and MYKE4 simulations show higher θ values at cloud top for F21 and F29 in comparison to F13, thus differencing the acidic from the nonacidic cases as expected. In the following section, we will examine the effect of interactive chemistry on the cloud microphysical variables.
4.3 Cloud microphysical structure
Details of the retrieval of cloud microphysical properties and associated uncertainties from the several cloud probes onboard the Convair-580 aircraft are given in Jouan et al. (2012). Figure 6 presents the comparison of the observed and simulated (REF, MYKE2 and MYKE4) vertical profiles of IWC (uncertainties: ±75 %) along the three flights. Observed IWC vertical profiles for F13 and F29 continuously decrease between 800 and 400 hPa, with values in the range of 10−1 to 10−2 kg kg−1. For flight F21, observed IWC shows a large variability in its vertical structure. IWC values simulated by both MYKE2 and MYKE4 are very similar, with a slight improvement for MYKE2 simulating more IWC. This agrees with the θ difference between MYKE2 and MYKE4 (Fig. 5). A smaller contact angle in the MYKE2 simulation tends to decrease the critical Gibbs free energy to form ice embryos (Eq. 15), hence leading to a higher nucleation rate of ice crystals and higher IWC. Both MYKE2 and MYKE4 broadly capture observed values with a low bias: and g kg−1 for F13; and g kg−1 for F21; and g kg−1 for F29. In contrast, REF strongly underestimates IWC values with a negative bias of 0.01 g kg−1 for F13 and 0.03 g kg−1 for F29. Note that REF does not have any noticeable IWC cloud at these levels in flight F21.
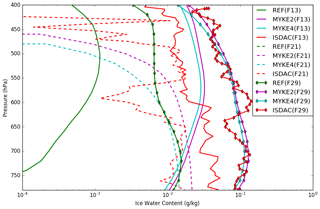
Figure 6Comparison of the observed (red) and simulated (REF in green, MYKE2 in purple and MYKE4 in cyan) vertical profiles of IWC along flights F13 (solid lines), F21 (dashed lines) and F29 (solid line with diamond markers).
Figure 7 presents a comparison between observed and simulated (REF, MYKE2 and MYKE4) vertical profiles of ice number concentration (Ni) (uncertainties: ±50 %) in the upper part of the cloud where heterogeneous ice nucleation processes are dominant above 500 hPa during flights F13, F21 and F29. The airborne ISDAC vertical profile for the TIC1 observed during F13 varies between 70 and 200 L−1 and is rather constant with altitude. The REF simulation strongly underestimates Ni by 2 orders of magnitude, corresponding rather to a TIC2. MYKE2 and MYKE4 reproduce the observed Ni within the ranges of uncertainties well, while MYKE4 is slightly closer to observations with a bias of 25 L−1. The TIC2 cloud type observed along F21 and F29 flight tracks is characterized by a small concentration of ice crystals ranging between 1 and 30 L−1. For F21, while REF is not able to simulate a persistent cloud, both MYKE2 and MYKE4 show a cloud with Ni close to observations typical of TIC2 under 450 hPa in the range of uncertainties (±50 %). As expected, due to the biases of temperature and relative humidity over ice, the model underestimates the cloud-top altitude for F21. For F29, both MYKE2 and MYKE4 show an increase in Ni compared to REF, which has the best statistics, while MYKE2 and MYKE4 simulations are overestimated by 1 order of magnitude. However, it is reasonably close to satellite observations as analyzed by Keita et al. (2019). Their analysis revealed a large discrepancy in Ni between ISDAC flights and satellite estimations for F29 in the upper part of the cloud. We can notice here that the order of magnitude of Ni for F29 estimated from satellites can call into question the classification of F29 as a TIC2, especially as Jouan et al. (2012), using a flight track above Barrow (now Utqiagvik) instead of Fairbanks, classified this cloud as a TIC1. This discrepancy between airborne measurements, simulated results and satellite observations can be due to the small sampling domain during ISDAC versus the low resolution of satellite products and of the model grid.
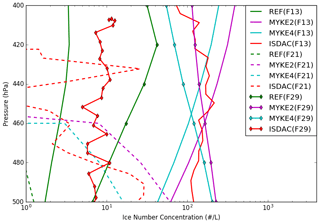
Figure 7Comparison of the observed (red) and simulated (REF in green, MYKE2 in purple and MYKE4 in cyan) vertical profiles of Ni along flights F13 (solid lines), F21 (dashed lines) and F29 (solid line with diamond markers).
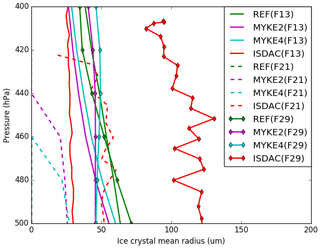
Figure 8 presents the comparison of the observed and simulated (REF, MYKE2 and MYKE4) vertical profiles of the mean ice crystal radius (Ri) with uncertainties of ±97 %) along the F13, F21 and F29 flights. Observations show that, although having the same IWC magnitude (Fig. 6), the TIC1 and TIC2 differ in their Ni (Fig. 7) and Ri values. Flight F13 (TIC1), with a large Ni concentration, has Ri values around 25 µm, while both F21 and F29 refer to TIC2 with a low Ni and Ri at least a factor of 2 larger. The INP acid coating in TIC2 inhibits the ice nuclei properties of the INPs, slowing the rate of ice nucleation in comparison to uncoated Ni. Subsequently, this decrease in the nucleation rate increases the amount of available supersaturated water vapor and allows the rapid growth of activated ice crystals. It could explain the persistence of low Ni and the large Ri. For flight F13, MYKE2 and MYKE4 simulate the TIC1 formation above 450 hPa relatively well in the observation range, while below 450 hPa they both overestimate Ri by a factor of 2. For this TIC1 cloud, MYKE2 and MYKE4 give the smallest error in comparison to REF. For flight F21, MYKE2 and MYKE4 improve the comparison of simulated Ri against observations, showing large ice crystals even if the cloud-top altitude is underestimated. For flight F29, observed values of Ri are even larger. MYKE2 and MYKE4 show a little improvement in comparison to REF but only above around 450 hPa, with larger simulated ice crystals than REF. For flights F21 and F29, MYKE2 and MYKE4 underestimate the observed Ri by a factor of 2.
4.4 Discussion
Our analysis shows the poor performance of the original REF parameterization in representing ice heterogeneous nucleation with low IWC and reveals that the MYKE parameterization can significantly improve the representation of the IWC at all vertical levels in polluted or unpolluted air masses. Along the three flights, RHi is therefore lower in the MYKE2 and MYKE4 simulations than in the REF run at cloud top. This may be due to the new parameterization promoting ice nucleation through a reduction of the available supersaturated water vapor. The new parameterization, with the variation in time and space of Ad and Nt, better represents Ni and Ri values at the top of TICs for flights F13 and F21 where the nucleation occurs. The pronounced slope of observed Ri above the 500 hPa level in TIC2 cases (Fig. 8) indicates rapid growth of the ice crystals, which consume supersaturated water vapor faster than it is made available in the model. Finally, for flight F29, the new parameterization slightly improves Ri at the top of the clouds, while under around the 450 hPa level, simulated results show better agreement for the REF simulation. The reason for that is not clear. However, Fig. 5 shows a decrease in θ with altitude between 450 and 500 hPa in connection with an increase in the ammonium molar concentration (Fig. 5b), which leads to a more efficient heterogeneous nucleation of ice at this altitude with smaller ice crystals and larger concentrations.
Finally, from the comparison of the three simulations, we can assess the ability of the new scheme to discriminate TIC1 and TIC2 clouds. For F13, while REF results in a TIC2 cloud, MYKE2 and MYKE4 simulations produce a TIC1 in agreement with observations. As shown before, the orders of magnitude of Na at the top of the cloud for F13 and F29 are similar, but the neutralization fraction fn shows more acidic aerosols for F29. For both cases, close values of IWC allow us to compare MYKE results for Ni and Ri. Looking at the top of the cloud (above the 440 hPa level), Ni is lower for F29 than for F13 and Ri is larger for F29 than for F13, responding to acid aerosol through the variation of the contact angle. Within the limit of our calculation, the new parameterization significantly improves the representation of nucleation in TIC1 for F13 versus TIC2 for F29 at the cloud tops, despite the model bias of simulated aerosols by WRF-Chem over the Arctic (Mölders et al., 2011). The comparison between simulations of F21 and F13 cases with MYKE is not so clear. Even if, at the top of the cloud, Ni is lower for F21 than for F13 as expected, Ri is smaller for F21 than for F13, which is not consistent with TICs. However, the comparison of the fn fraction at the cloud tops shows similar values for F21 and F13 near acid neutrality. This result highlights the importance of a consistent simulation of aerosol physicochemical properties to create a valuable simulation of microphysical ice cloud properties with our new parameterization of heterogeneous ice nucleation.
In general, regarding overall simulated results, MYKE4 shows better agreement with observations than MYKE2 for TIC1 and TIC2 clouds. It is well known that the effect of acid coating on INPs is to reduce their ability to form ice crystals, and this effect increases with the amount of acid (Sullivan et al., 2010; Yang et al., 2011). Moreover, our results suggest that even a low acidity on INPs leads to an important decrease in the heterogeneous ice nucleation rate because, for MYKE4, θ increases more rapidly when acid coating increases, i.e., decrease in the fn fraction (Fig. 1).
A new parameterization of ice heterogeneous nucleation for water-subsaturated conditions, based upon the CNT approach and coupled with real-time chemistry information, is proposed within the WRF-Chem model. The coupling with chemistry helps to link the contact angle θ to the aerosol neutralization fraction, which is a good proxy for the acidity of aerosols. This new parameterization is implemented in the Milbrandt and Yau (2005a, b) two-moment cloud microphysical scheme available in WRF-Chem. It is particularly designed to simulate Arctic ice clouds. In the Arctic, ice clouds are separated into two classes: (1) TIC1 clouds characterized by large concentrations of very small crystals and TIC2 clouds characterized by low concentrations of larger ice crystals. TIC2 clouds induce significant ice crystal precipitation or so-called diamond dust, a notoriously deficient variable to simulate in polar atmospheric models despite its significant contribution to annual snowfall that is generally reported as “trace” in station observations. The model including the original Milbrandt and Yau (2005a, b) scheme and the modified one are applied to three test cases observed during ISDAC: one TIC1 and two TIC2 clouds. For each case, results are analyzed in terms of meteorology, chemistry and cloud microphysical properties by comparison between the new (MYKE2 and MYKE4) and original (REF) parameterization of ice nucleation within the cloud microphysical scheme and with available observations.
Our results show the poor performance of the REF parameterization in representing Arctic ice cloud types at low IWC and underline the fact that the MYKE2 and MYKE4 parameterizations significantly improve the representation of IWC, especially in the top region of the clouds where nucleation dominates, in both polluted and unpolluted air masses. MYKE2 and MYKE4 simulations are in better agreement with observations for the three flights. In contrast, REF always strongly underestimates IWC values with a negative bias and does not see any noticeable IWC cloud at these levels during flight F21.
Aerosol number concentrations are simulated with the same order of magnitude as observations under the 550 hPa level, whereas above the 550 hPa level, the simulated value is overestimated by a factor of 3 for flight F13 and underestimated by 1 order magnitude for flight F29. Despite known difficulties in simulating aerosol concentrations in WRF-Chem over the Arctic region (Mölders et al., 2011), our parameterization achieves the proper representation of cloud types TIC1 for flight F13 versus TIC2 for flights F21 and F29 in the nucleation region at cloud top. Values and vertical structures of ammonium and sulfate molar aerosol concentrations for flights F21 and F29 correspond fairly well to mean observed concentrations, i.e., 7 and 5.5 nmol cm−3, during the ARCTAS and ARCPAC campaigns, respectively, with known contributions from volcanic sources peaking in the mid-troposphere. MYKE2 and MYKE4 simulations are similar, showing higher θ values at cloud top for flights F21 and F29 in comparison to flight F13, thus differencing the acidic from the nonacidic cases as expected, and a low sensitivity to the arbitrarily parameterized curve shape.
For the TIC1 case, REF strongly underestimates the ice crystal number concentration by at least 2 orders of magnitude and overestimates the mean radius, resulting in the false representation of an ice cloud corresponding rather to a TIC2. In contrast, the new parameterization captures the cloud type well, with representative microphysical structure (IWC, ice crystal mean radius and ice crystal number concentration) at the top of the cloud where nucleation occurs. TIC2 clouds observed along the F21 and F29 flight tracks are characterized by a small concentration of ice crystals ranging between 1 and 30 L−1. MYKE2 and MYKE4 simulate those ice crystal number concentrations within the range of observation uncertainties. For flight F21, REF is not able to simulate a persistent cloud, while both the MYKE2 and MYKE4 simulations show a cloud with an ice crystal concentration close to observations. Corresponding values are typical of TIC2 cloud under the 450 hPa level even if the model underestimates the cloud-top altitude as a result of biases in the simulated temperature and relative humidity over ice. MYKE2 and MYKE4 also improve the ice crystal mean radius, showing larger ice crystals than REF. For flight F29, both MYKE2 and MYKE4 show an increase in the ice crystal concentration compared to REF, which has the best statistics, but the MYKE2 and MYKE4 results are still overestimated by 1 order of magnitude. MYKE2 and MYKE4 slightly improve the representation of the ice crystal mean radius in comparison to REF above the 450 hPa level, with larger simulated ice crystals than REF. For both TIC2 flights, MYKE2 and MYKE4 nevertheless underestimate the observed mean radius by a factor of 2. Comparing the two versions of the parameterization for the three cases, in general, MYKE4 presents a slight improvement compared to MYKE2, in agreement with θ dependency. Because this difference is small, the dependency of the contact angle on the aerosol neutralization fraction under a concave form should be considered a sufficient condition to improve the representation of heterogeneous ice nucleation in Arctic ice clouds.
In our simulations, secondary organic aerosol (SOA) formation is not considered. However, the concentration of their precursor species, mainly biogenic and aromatic volatile organic compounds, should be low in the ISDAC region and period as suggested by the WRF-Chem simulation. However, results obtained later during the NETCARE campaign (2015) show a potential contribution of SOA to the total mass of Arctic aerosols, but their precursors are not yet identified in the Arctic, which is a new challenge in simulating their formation (Abbatt et al., 2019). Moreover, as our parameterization is dedicated to the simulation of Arctic ice cloud types, we are confident that the combination of CBM-Z and MOSAIC is appropriate even if CBM-Z is a relatively simple gas-phase mechanism and if SOA formation is not considered. Indeed, our results suggest that it is enough to consider the chemical impact on heterogeneous ice nucleation though the degree of aerosol acidity acting as INPs. Despite the huge challenge, our parameterization seems promising. Further studies will help with validations against satellite data and future campaigns. In particular, future flight campaigns should include simultaneously measurements of cloud microphysics properties, aerosol number size distribution, aerosol chemical composition and ice nuclei number concentrations. The next step will be to extend simulations to quantify the role of the ice nucleation of acid pollution in radiation, the atmospheric water balance and, ultimately, the Arctic climate.
WRF-Chem is an open-source community model. The source code of WRF-Chem model version 3.5.1 is available at http://www2.mmm.ucar.edu/wrf/users/download/get_source.html (NCAR and UCAR, 2020a). The new scheme for ice crystal formation by heterogeneous nucleation described in this paper is implemented in WRF-Chem version 3.5.1 and permanently archived at https://doi.org/10.5281/zenodo.4033654 (Keita et al., 2020). Indirect and Semi-Direct Aerosol Campaign (ISDAC) data are available from the ARM data archive (online at https://www.arm.gov/data/data-sources/cldmicroprop-51, ARM, 2020). Meteorological initial and boundary conditions use NCEP (National Centers for Environmental Prediction) Global Forecast System (GFS) Final Analysis (FNL) data available at https://rda.ucar.edu/datasets/ds083.2/ (NCAR and UCAR, 2020b). Chemical initial and boundary conditions are taken from the global chemical-transport model MOZART-4 (Model for OZone And Related chemical Tracers, version 4) (Emmons et al., 2010) at https://www.acom.ucar.edu/wrf-chem/mozart.shtml (last access: September 2020). The fire emissions inventory used is the Fire INventory from NCAR (FINN-v1) (Wiedinmyer et al., 2011) available at http://bai.acom.ucar.edu/Data/fire/ (last access: September 2020).
SAK and EG developed and implemented the parameterization with the support of JCR and ML. SAK performed the simulations with the technical support of TO. SAK analyzed results and wrote the paper with the support of JCR, ML and JPB. All authors contributed to the paper and to the analysis.
The authors declare that they have no conflict of interest.
As we know that Eric Girard had numerous discussions with our colleague Allan Bertram on the form of the dependency between the contact angle and the aerosol neutralization fraction, we would like to thank him for his invaluable help. We thank NETCARE (Network on Climate and Aerosols: Addressing Key Uncertainties in Remote Canadian Environments) and NSERC (Natural Sciences and Engineering Research Council of Canada) for funding support and ARM (Atmospheric Radiation Measurement Program) for the data collected during ISDAC. Computer modeling benefited from access to IDRIS HPC resources (GENCI allocations A003017141 and A005017141) and the IPSL mesoscale computing center (CICLAD: Calcul Intensif pour le CLimat, l'Atmosphère et la Dynamique). We acknowledge the use of the WRF-Chem preprocessor tools mozbc and fire_emiss provided by the Atmospheric Chemistry Observations and Modeling Lab (ACOM) of NCAR.
This paper was edited by Samuel Remy and reviewed by three anonymous referees.
Abbatt, J. P. D., Leaitch, W. R., Aliabadi, A. A., Bertram, A. K., Blanchet, J.-P., Boivin-Rioux, A., Bozem, H., Burkart, J., Chang, R. Y. W., Charette, J., Chaubey, J. P., Christensen, R. J., Cirisan, A., Collins, D. B., Croft, B., Dionne, J., Evans, G. J., Fletcher, C. G., Galí, M., Ghahremaninezhad, R., Girard, E., Gong, W., Gosselin, M., Gourdal, M., Hanna, S. J., Hayashida, H., Herber, A. B., Hesaraki, S., Hoor, P., Huang, L., Hussherr, R., Irish, V. E., Keita, S. A., Kodros, J. K., Köllner, F., Kolonjari, F., Kunkel, D., Ladino, L. A., Law, K., Levasseur, M., Libois, Q., Liggio, J., Lizotte, M., Macdonald, K. M., Mahmood, R., Martin, R. V., Mason, R. H., Miller, L. A., Moravek, A., Mortenson, E., Mungall, E. L., Murphy, J. G., Namazi, M., Norman, A.-L., O'Neill, N. T., Pierce, J. R., Russell, L. M., Schneider, J., Schulz, H., Sharma, S., Si, M., Staebler, R. M., Steiner, N. S., Thomas, J. L., von Salzen, K., Wentzell, J. J. B., Willis, M. D., Wentworth, G. R., Xu, J.-W., and Yakobi-Hancock, J. D.: Overview paper: New insights into aerosol and climate in the Arctic, Atmos. Chem. Phys., 19, 2527–2560, https://doi.org/10.5194/acp-19-2527-2019, 2019. a, b
Archuleta, C. M., DeMott, P. J., and Kreidenweis, S. M.: Ice nucleation by surrogates for atmospheric mineral dust and mineral dust/sulfate particles at cirrus temperatures, Atmos. Chem. Phys., 5, 2617–2634, https://doi.org/10.5194/acp-5-2617-2005, 2005. a
Atmospheric Radiation Measurement (ARM) user facility: CLDMICROPROP-51, available at: https://www.arm.gov/data/data-sources/cldmicroprop-51, last access: September 2020. a
Atkinson, D. E., Sassen, K., Hayashi, M., Cahill, C. F., Shaw, G., Harrigan, D., and Fuelberg, H.: Aerosol properties over Interior Alaska from lidar, DRUM Impactor sampler, and OPC-sonde measurements and their meteorological context during ARCTAS-A, April 2008, Atmos. Chem. Phys., 13, 1293–1310, https://doi.org/10.5194/acp-13-1293-2013, 2013. a, b
Berg, L. K., Shrivastava, M., Easter, R. C., Fast, J. D., Chapman, E. G., Liu, Y., and Ferrare, R. A.: A new WRF-Chem treatment for studying regional-scale impacts of cloud processes on aerosol and trace gases in parameterized cumuli, Geosci. Model Dev., 8, 409–429, https://doi.org/10.5194/gmd-8-409-2015, 2015. a
Bigg, E. K.: The formation of atmospheric ice crystals by the freezing of droplets, Q. J. Roy. Meteor. Soc., 79, 510–519, https://doi.org/10.1002/qj.49707934207, 1953. a
Blanchet, J.-P. and Girard, E.: Arctic “greenhouse effect”, Nature, 371, p. 383, https://doi.org/10.1038/371383a0, 1994. a
Boucher, O., Randall, D., Artaxo, P., Bretherton, C., Feingold, G., Forster, P., Kerminen, V.-M., Kondo, Y., Liao, H., Lohmann, U., Rasch, P., Satheesh, S., Sherwood, S., B., S., and Zhang, X.: Clouds and Aerosols, in: Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013. a
Burton, S. P., Ferrare, R. A., Hostetler, C. A., Hair, J. W., Rogers, R. R., Obland, M. D., Butler, C. F., Cook, A. L., Harper, D. B., and Froyd, K. D.: Aerosol classification using airborne High Spectral Resolution Lidar measurements – methodology and examples, Atmos. Meas. Tech., 5, 73–98, https://doi.org/10.5194/amt-5-73-2012, 2012. a
Chen, F. and Dudhia, J.: Coupling an Advanced Land Surface–Hydrology Model with the Penn State–NCAR MM5 Modeling System. Part I: Model Implementation and Sensitivity, Mon. Weather Rev. 129, 569–585, https://doi.org/10.1175/1520-0493(2001)129<0569:CAALSH>2.0.CO;2, 2001. a
Chen, J.-P., Hazra, A., and Levin, Z.: Parameterizing ice nucleation rates using contact angle and activation energy derived from laboratory data, Atmos. Chem. Phys., 8, 7431–7449, https://doi.org/10.5194/acp-8-7431-2008, 2008. a, b
Chin, M., Rood, R. B., Lin, S.-J., Müller, J.-F., and Thompson, A. M.: Atmospheric sulfur cycle simulated in the global model GOCART: Model description and global properties, J. Geophys. Res.-Atmos., 105, 24671–24687, https://doi.org/10.1029/2000jd900384, 2000. a
Cirisan, A., Girard, E., Blanchet, J.-P., Keita, S., Gong, W., Irish, V., and Bertam, A.: Modellings of the observed INP concentration during Arctic summer campaigns, Atmosphere, 11, 916, https://doi.org/10.3390/atmos11090916, 2020. a, b, c
Connolly, P. J., Möhler, O., Field, P. R., Saathoff, H., Burgess, R., Choularton, T. W., and Gallagher, M. W.: Corrigendum to: “Studies of heterogeneous freezing by three different desert dust samples;;, Atmos. Chem. Phys., 9, 2805–2824, 2009, Atmos. Chem. Phys., 13, 10079–10080, https://doi.org/10.5194/acp-13-10079-2013, 2013. a
Cooper, W. A.: Ice Initiation in Natural Clouds, Meteor. Mon., 43, 29–32, https://doi.org/10.1175/0065-9401-21.43.29, 1986. a
Curry, J. A., Schramm, J. L., Rossow, W. B., and Randall, D.: Overview of Arctic Cloud and Radiation Characteristics, J. Climate, 9, 1731–1764, https://doi.org/10.1175/1520-0442(1996)009<1731:OOACAR>2.0.CO;2, 1996. a
DeMott, P. J., Meyers, M. P., and Cotton, W. R.: Parameterization and Impact of Ice initiation Processes Relevant to Numerical Model Simulations of Cirrus Clouds, J. Atmos. Sci., 51, 77–90, https://doi.org/10.1175/1520-0469(1994)051<0077:PAIOII>2.0.CO;2, 1994. a
DeMott, P. J., Prenni, A. J., Liu, X., Kreidenweis, S. M., Petters, M. D., Twohy, C. H., Richardson, M. S., Eidhammer, T., and Rogers, D. C.: Predicting global atmospheric ice nuclei distributions and their impacts on climate, P. Natl. Acad. Sci. USA, 107, 11217–11222, https://doi.org/10.1073/pnas.0910818107, 2010. a, b, c
DeMott, P. J., Prenni, A. J., McMeeking, G. R., Sullivan, R. C., Petters, M. D., Tobo, Y., Niemand, M., Möhler, O., Snider, J. R., Wang, Z., and Kreidenweis, S. M.: Integrating laboratory and field data to quantify the immersion freezing ice nucleation activity of mineral dust particles, Atmos. Chem. Phys., 15, 393–409, https://doi.org/10.5194/acp-15-393-2015, 2015. a
Eastwood, M. L., Cremel, S., Gehrke, C., Girard, E., and Bertram, A. K.: Ice nucleation on mineral dust particles: Onset conditions, nucleation rates and contact angles, J. Geophys. Res., 113, D22203, https://doi.org/10.1029/2008jd010639, 2008. a, b, c, d
Eastwood, M. L., Cremel, S., Wheeler, M., Murray, B. J., Girard, E., and Bertram, A. K.: Effects of sulfuric acid and ammonium sulfate coatings on the ice nucleation properties of kaolinite particles, Geophys. Res. Lett., 36, L02811, https://doi.org/10.1029/2008gl035997, 2009. a, b, c, d
Eckhardt, S., Quennehen, B., Olivié, D. J. L., Berntsen, T. K., and Cherian, R.: Corrigendum to “Current model capabilities for simulating black carbon and sulfateconcentrations in the Arctic atmosphere: a multi-model evaluationusing a comprehensive measurement data set” published in Atmos. Chem. Phys., 15, 9413–9433, 2015, Atmos. Chem. Phys., https://doi.org/10.5194/acp-15-9413-2015-corrigendum, 2015. a
Eidhammer, T., DeMott, P. J., and Kreidenweis, S. M.: A comparison of heterogeneous ice nucleation parameterizations using a parcel model framework, J. Geophys. Res., 114, D06202, https://doi.org/10.1029/2008jd011095, 2009. a
Emmons, L. K., Walters, S., Hess, P. G., Lamarque, J.-F., Pfister, G. G., Fillmore, D., Granier, C., Guenther, A., Kinnison, D., Laepple, T., Orlando, J., Tie, X., Tyndall, G., Wiedinmyer, C., Baughcum, S. L., and Kloster, S.: Description and evaluation of the Model for Ozone and Related chemical Tracers, version 4 (MOZART-4), Geosci. Model Dev., 3, 43–67, https://doi.org/10.5194/gmd-3-43-2010, 2010. a, b
Fisher, J. A., Jacob, D. J., Wang, Q., Bahreini, R., Carouge, C. C., Cubison, M. J., Dibb, J. E., Diehl, T., Jimenez, J. L., Leibensperger, E. M., Lu, Z., Meinders, M. B. J., Pye, H. O. T., Quinn, P. K., Sharma, S., Streets, D. G., van Donkelaar, A., and Yantosca, R. M.: Sources, distribution, and acidity of sulfate–ammonium aerosol in the Arctic in winter–spring, Atmos. Environ., 45, 7301–7318, https://doi.org/10.1016/j.atmosenv.2011.08.030, 2011. a, b, c, d, e, f
Fletcher, N. H.: The physics of rainclouds, Cambridge University Press, 1962. a
Fornea, A. P., Brooks, S. D., Dooley, J. B., and Saha, A.: Heterogeneous freezing of ice on atmospheric aerosols containing ash, soot, and soil, J. Geophys. Res., 114, D13201, https://doi.org/10.1029/2009jd011958, 2009. a
Girard, E., Dueymes, G., Du, P., and Bertram, A. K.: Assessment of the effects of acid-coated ice nuclei on the Arctic cloud microstructure, atmospheric dehydration, radiation and temperature during winter, Int. J. Climatol., 33, 599–614, https://doi.org/10.1002/joc.3454, 2013. a, b, c, d, e
Glaccum, R. A. and Prospero, J. M.: Saharan aerosols over the tropical North Atlantic – Mineralogy, Mar. Geol., 37, 295–321, https://doi.org/10.1016/0025-3227(80)90107-3, 1980. a
Grell, G. A., Peckham, S. E., Schmitz, R., McKeen, S. A., Frost, G., Skamarock, W. C., and Eder, B.: Fully coupled “online” chemistry within the WRF model, Atmos. Environ., 39, 6957–6975, https://doi.org/10.1016/j.atmosenv.2005.04.027, 2005. a, b
Grenier, P. and Blanchet, J.-P.: Investigation of the sulphate-induced freezing inhibition effect from CloudSat and CALIPSO measurements, J. Geophys. Res., 115, D22205, https://doi.org/10.1029/2010jd013905, 2010. a
Grenier, P., Blanchet, J., and Muñoz‐Alpizar, R.: Study of polar thin ice clouds and aerosols seen by CloudSat and CALIPSO during midwinter 2007, J. Geophys. Res., 114, D09201, https://doi.org/10.1029/2008jd010927, 2009. a
Guenther, A.: Corrigendum to ”Estimates of global terrestrial isoprene emissions using MEGAN (Model of Emissions of Gases and Aerosols from Nature)” published in Atmos. Chem. Phys., 6, 3181–3210, 2006, Atmos. Chem. Phys., 7, 4327–4327, https://doi.org/10.5194/acp-7-4327-2007, 2007. a
Hoose, C. and Möhler, O.: Heterogeneous ice nucleation on atmospheric aerosols: a review of results from laboratory experiments, Atmos. Chem. Phys., 12, 9817–9854, https://doi.org/10.5194/acp-12-9817-2012, 2012. a
Hoose, C., Kristjánsson, J. E., Chen, J.-P., and Hazra, A.: A Classical-Theory-Based Parameterization of Heterogeneous Ice Nucleation by Mineral Dust, Soot, and Biological Particles in a Global Climate Model, J. Atmos. Sci., 67, 2483–2503, https://doi.org/10.1175/2010jas3425.1, 2010. a
Hung, H., Malinowski, A., and Scot, T. M.: Kinetics of Heterogeneous Ice Nucleation on the Surfaces of Mineral Dust Cores Inserted into Aqueous Ammonium Sulfate Particles, J. Phys. Chem. A, 107, 1296–1306, https://doi.org/10.1021/jp021593y, 2003. a
Iacono, M. J., Delamere, J. S., Mlawer, E. J., Shephard, M. W., Clough, S. A., and Collins, W. D.: Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models, J. Geophys. Res., 113, D13103, https://doi.org/10.1029/2008jd009944, 2008. a, b
IPCC: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 1535 pp., 2013. a
Janjić, Z. I.: The Step-Mountain Eta Coordinate Model: Further Developments of the Convection, Viscous Sublayer, and Turbulence Closure Schemes, Mon. Weather Rev., 122, 927–945, https://doi.org/10.1175/1520-0493(1994)122<0927:TSMECM>2.0.CO;2, 1994. a, b
Jouan, C., Girard, E., Pelon, J., Gultepe, I., Delanoë, J., and Blanchet, J.-P.: Characterization of Arctic ice cloud properties observed during ISDAC, J. Geophys. Res.-Atmos., 117, D23207, https://doi.org/10.1029/2012jd017889, 2012. a, b, c, d, e, f
Jouan, C., Pelon, J., Girard, E., Ancellet, G., Blanchet, J. P., and Delanoë, J.: On the relationship between Arctic ice clouds and polluted air masses over the North Slope of Alaska in April 2008, Atmos. Chem. Phys., 14, 1205–1224, https://doi.org/10.5194/acp-14-1205-2014, 2014. a, b, c
Kanji, Z. A. and Abbatt, J. P. D.: Ice Nucleation onto Arizona Test Dust at Cirrus Temperatures: Effect of Temperature and Aerosol Size on Onset Relative Humidity, Am. Chem. Soc., 114, 935–941, https://doi.org/10.1021/jp908661m, 2010. a
Kanji, Z. A., Ladino, L. A., Wex, H., Boose, Y., Burkert-Kohn, M., Cziczo, D. J., and Krämer, M.: Overview of Ice Nucleating Particles, Meteor. Mon., 58, 1.1–1.33, https://doi.org/10.1175/amsmonographs-d-16-0006.1, 2017. a
Kay, J. E., L'Ecuyer, T., Chepfer, H., Loeb, N., Morrison, A., and Cesana, G.: Recent Advances in Arctic Cloud and Climate Research, Current Climate Change Reports, 2, 159–169, https://doi.org/10.1007/s40641-016-0051-9, 2016. a
Keita, S., Girard, E., Raut, J.-C., Pelon, J., Blanchet, J.-P., Lemoine, O., and Onishi, T.: Simulating Arctic Ice Clouds during Spring Using an Advanced Ice Cloud Microphysics in the WRF Model, Atmosphere, 10, 433, https://doi.org/10.3390/atmos10080433, 2019. a, b, c, d, e, f, g, h, i, j, k, l, m, n
Keita, S. A. and Girard, E.: Importance of Chemical Composition of Ice Nuclei on the Formation of Arctic Ice Clouds, Pure Appl. Geophys., 173, 3141–3163, https://doi.org/10.1007/s00024-016-1294-z, 2016. a, b, c, d, e, f, g, h
Keita, S. A., Girard, E., Raut, J.-C., Leriche, M., Blanchet, J.-P., Pelon, J., Onishi, T., and Keita, A. C.: paper_gmd-2020-50 (Version 1.0), Zenodo, https://doi.org/10.5281/zenodo.4033654, 2020. a
Khvorostyanov, V. I. and Curry, J. A.: Critical humidities of homogeneous and heterogeneous ice nucleation: Inferences from extended classical nucleation theory, J. Geophys. Res., 114, D04207, https://doi.org/10.1029/2008jd011197, 2009. a, b
Kong, F. and Yau, M. K.: An explicit approach to microphysics in MC2, Atmosphere-Ocean, 35, 257–291, https://doi.org/10.1080/07055900.1997.9649594, 1997. a
Kulkarni, G., Sanders, C., Zhang, K., Liu, X., and Zhao, C.: Ice nucleation of bare and sulfuric acid-coated mineral dust particles and implication for cloud properties, J. Geophys. Res.-Atmos., 119, 9993–10 011, https://doi.org/10.1002/2014JD021567, 2014. a
Kumar, A., Marcolli, C., Luo, B., and Peter, T.: Ice nucleation activity of silicates and aluminosilicates in pure water and aqueous solutions – Part 1: The K-feldspar microcline, Atmos. Chem. Phys., 18, 7057–7079, https://doi.org/10.5194/acp-18-7057-2018, 2018. a
Kumar, A., Marcolli, C., and Peter, T.: Ice nucleation activity of silicates and aluminosilicates in pure water and aqueous solutions – Part 2: Quartz and amorphous silica, Atmos. Chem. Phys., 19, 6035–6058, https://doi.org/10.5194/acp-19-6035-2019, 2019a. a
Kumar, A., Marcolli, C., and Peter, T.: Ice nucleation activity of silicates and aluminosilicates in pure water and aqueous solutions – Part 3: Aluminosilicates, Atmos. Chem. Phys., 19, 6059–6084, https://doi.org/10.5194/acp-19-6059-2019, 2019b. a
Lawson, R. P., Woods, S., Jensen, E., Erfani, E., Gurganus, C., Gallagher, M., Connolly, P., Whiteway, J., Baran, A. J., May, P., Heymsfield, A., Schmitt, C. G., McFarquhar, G., Um, J., Protat, A., Bailey, M., Lance, S., Muehlbauer, A., Stith, J., Korolev, A., Toon, O. B., and Krämer, M.: A Review of Ice Particle Shapes in Cirrus formed In Situ and in Anvils, J. Geophys. Res.-Atmos., 124, 10049–10090, https://doi.org/10.1029/2018JD030122, 2019. a
Liu, X., Penner, J. E., Ghan, S. J., and Wang, M.: Inclusion of Ice Microphysics in the NCAR Community Atmospheric Model Version 3 (CAM3), J. Climate, 20, 4526–4547, https://doi.org/10.1175/jcli4264.1, 2007. a, b
Marcolli, C., Gedamke, S., Peter, T., and Zobrist, B.: Efficiency of immersion mode ice nucleation on surrogates of mineral dust, Atmos. Chem. Phys., 7, 5081–5091, https://doi.org/10.5194/acp-7-5081-2007, 2007. a
Martin, S. T.: Phase Transitions of Aqueous Atmospheric Particles, Chem. Rev., 100, 3403–3454, https://doi.org/10.1021/cr990034t, 2000. a
Matrosov, S. Y., Maahn, M., and de Boer, G.: Observational and Modeling Study of Ice Hydrometeor Radar Dual-Wavelength Ratios, J. Appl. Meteorol. Clim., 58, 2005–2017, https://doi.org/10.1175/JAMC-D-19-0018.1, 2019. a
McFarquhar, G. M., Ghan, S., Verlinde, J., Korolev, A., Strapp, J. W., Schmid, B., Tomlinson, J. M., Wolde, M., Brooks, S. D., Cziczo, D., Dubey, M. K., Fan, J., Flynn, C., Gultepe, I., Hubbe, J., Gilles, M. K., Laskin, A., Lawson, P., Leaitch, W. R., Liu, P., Liu, X., Lubin, D., Mazzoleni, C., Macdonald, A.-M., Moffet, R. C., Morrison, H., Ovchinnikov, M., Shupe, M. D., Turner, D. D., Xie, S., Zelenyuk, A., Bae, K., Freer, M., and Glen, A.: Indirect and Semi-direct Aerosol Campaign, B. Am. Meteorol. Soc., 92, 183–201, https://doi.org/10.1175/2010bams2935.1, 2011. a, b, c
McFarquhar, G. M., Baumgardner, D., and Heymsfield, A. J.: Background and Overview, Meteor. Mon., 58, v–ix, https://doi.org/10.1175/amsmonographs-d-16-0018.1, 2017. a
Meyers, M. P., DeMott, P. J., and Cotton, W. R.: New Primary Ice-Nucleation Parameterizations in an Explicit Cloud Model, J. Appl. Meteorol., 31, 708–721, https://doi.org/10.1175/1520-0450(1992)031<0708:NPINPI>2.0.CO;2, 1992. a, b, c, d
Milbrandt, J. A. and Yau, M. K.: A Multimoment Bulk Microphysics Parameterization. Part I: Analysis of the Role of the Spectral Shape Parameter, J. Atmos. Sci., 62, 3051–3064, https://doi.org/10.1175/JAS3534.1, 2005a. a, b, c, d, e, f, g
Milbrandt, J. A. and Yau, M. K.: A Multimoment Bulk Microphysics Parameterization. Part II: A Proposed Three-Moment Closure and Scheme Description, J. Atmos. Sci., 62, 3065–3081, https://doi.org/10.1175/JAS3535.1, 2005b. a, b, c, d, e, f, g
Mölders, N., Tran, H. N. Q., Quinn, P., Sassen, K., Shaw, G. E., and Kramm, G.: Assessment of WRF/Chem to simulate sub–Arctic boundary layer characteristics during low solar irradiation using radiosonde, SODAR, and surface data, Atmos. Pollut. Res., 2, 283–299, https://doi.org/10.5094/apr.2011.035, 2011. a, b, c
Morrison, H., Curry, J. A., and Khvorostyanov, V. I.: A New Double-Moment Microphysics Parameterization for Application in Cloud and Climate Models. Part I: Description, J. Atmos. Sci., 62, 1665–1677, https://doi.org/10.1175/JAS3446.1, 2005a. a
Morrison, H., Curry, J. A., Shupe, M. D., and Zuidema, P.: A New Double-Moment Microphysics Parameterization for Application in Cloud and Climate Models. Part II: Single-Column Modeling of Arctic Clouds, J. Atmos. Sci., 62, 1678–1693, https://doi.org/10.1175/JAS3447.1, 2005b. a
Murray, B. J., O'Sullivan, D., Atkinson, J. D., and Webb, M. E.: Ice nucleation by particles immersed in supercooled cloud droplets, Chem. Soc. Rev., 41, 6519–6554, https://doi.org/10.1039/c2cs35200a, 2012. a, b
National Center for Atmospheric Research (NCAR) and University Corporation for Atmospheric Research (UCAR): WRF Source Codes and Graphics Software, available at: https://www2.mmm.ucar.edu/wrf/users/download/get_source.html, last access: September 2020a. a
National Center for Atmospheric Research (NCAR) and University Corporation for Atmospheric Research (UCAR): NCEP FNL Operational Model Global Tropospheric Analyses, continuing from July 1999, available at: https://doi.org/10.5065/D6M043C6, last access: September 2020b. a
Niedermeier, D., Ervens, B., Clauss, T., Voigtländer, J., Wex, H., Hartmann, S., and Stratmann, F.: A computationally efficient description of heterogeneous freezing: A simplified version of the Soccer ball model, Geophys. Res. Lett., 41, 736–741, https://doi.org/10.1002/2013gl058684, 2014. a
Panda, A. K., Mishra, B., Mishra, D., and Singh, R.: Effect of sulphuric acid treatment on the physico-chemical characteristics of kaolin clay, Colloids and Surface. A, 363, 98–104, https://doi.org/10.1016/j.colsurfa.2010.04.022, 2010. a
Pant, A., Fok, A., Parsons, M. T., Mak, J., and Bertram, A. K.: Deliquescence and crystallization of ammonium sulfate-glutaric acid and sodium chloride-glutaric acid particles, Geophys. Res. Lett., 31, L12111, https://doi.org/10.1029/2004GL020025, 2004. a
Pant, A., Parsons, M. T., and Bertram, A. K.: Crystallization of Aqueous Ammonium Sulfate Particles Internally Mixed with Soot and Kaolinite: Crystallization Relative Humidities and Nucleation Rates, J. Phys. Chem. A, 110, 8701–8709, https://doi.org/10.1021/jp060985s, 2006. a
Parsons, M. T., Mak, J., Lipetz, S. R., and Bertram, A. K.: Deliquescence of malonic, succinic, glutaric, and adipic acid particles, J. Geophys. Res.-Atmos., 109, D06212, https://doi.org/10.1029/2003jd004075, 2004b. a
Phillips, V. T. J., Demott, P. J., Andronache, C., Pratt, K. A., Prather, K. A., Subramanian, R., and Twohy, C.: Improvements to an Empirical Parameterization of Heterogeneous Ice Nucleation and Its Comparison with Observations, J. Atmos. Sci., 70, 378–409, https://doi.org/10.1175/jas-d-12-080.1, 2013. a
Prenni, A. J., Petters, M. D., Kreidenweis, S. M., DeMott, P. J., and Ziemann, P. J.: Cloud droplet activation of secondary organic aerosol, J. Geophys. Res.-Atmos., 112, D10223, https://doi.org/10.1029/2006jd007963, 2007. a
Pruppacher, H. R. and Klett, J. D.: Microphysics of Clouds and Precipitation, Atmospheric and oceanographic sciences library, Kluwer Academic Publishers, 1997. a, b, c, d, e, f, g, h
Raut, J.-C., Marelle, L., Fast, J. D., Thomas, J. L., Weinzierl, B., Law, K. S., Berg, L. K., Roiger, A., Easter, R. C., Heimerl, K., Onishi, T., Delanoë, J., and Schlager, H.: Cross-polar transport and scavenging of Siberian aerosols containing black carbon during the 2012 ACCESS summer campaign, Atmos. Chem. Phys., 17, 10969–10995, https://doi.org/10.5194/acp-17-10969-2017, 2017. a
Schoenberg Ferrier, B.: A Double-Moment Multiple-Phase Four-Class Bulk Ice Scheme. Part I: Description, J. Atmos. Sci., 51, 249–280, https://doi.org/10.1175/1520-0469(1994)051<0249:ADMMPF>2.0.CO;2, 1994. a, b, c
Schwarz, J. P., Gao, R. S., Perring, A. E., Spackman, J. R., and Fahey, D. W.: Black carbon aerosol size in snow, Sci. Rep., 3, 1356, https://doi.org/10.1038/srep01356, 2013. a
Shantz, N. C., Gultepe, I., Andrews, E., Zelenyuk, A., Earle, M. E., Macdonald, A. M., Liu, P. S. K., and Leaitch, W. R.: Optical, physical, and chemical properties of springtime aerosol over Barrow Alaska in 2008, International J. Climatol., 34, 3125–3138, https://doi.org/10.1002/joc.3898, 2014. a
Shaw, W. J., Jerry Allwine, K., Fritz, B. G., Rutz, F. C., Rishel, J. P., and Chapman, E. G.: An evaluation of the wind erosion module in DUSTRAN, Atmos. Environ., 42, 1907–1921, 2008. a
Shindell, D. and Faluvegi, G.: Climate response to regional radiative forcing during the twentieth century, Nat. Geosci., 2, 294–300, https://doi.org/10.1038/ngeo473, 2009. a
Shindell, D. T., Chin, M., Dentener, F., Doherty, R. M., Faluvegi, G., Fiore, A. M., Hess, P., Koch, D. M., MacKenzie, I. A., Sanderson, M. G., Schultz, M. G., Schulz, M., Stevenson, D. S., Teich, H., Textor, C., Wild, O., Bergmann, D. J., Bey, I., Bian, H., Cuvelier, C., Duncan, B. N., Folberth, G., Horowitz, L. W., Jonson, J., Kaminski, J. W., Marmer, E., Park, R., Pringle, K. J., Schroeder, S., Szopa, S., Takemura, T., Zeng, G., Keating, T. J., and Zuber, A.: A multi-model assessment of pollution transport to the Arctic, Atmos. Chem. Phys., 8, 5353–5372, https://doi.org/10.5194/acp-8-5353-2008, 2008. a
Sullivan, R. C., Petters, M. D., DeMott, P. J., Kreidenweis, S. M., Wex, H., Niedermeier, D., Hartmann, S., Clauss, T., Stratmann, F., Reitz, P., Schneider, J., and Sierau, B.: Irreversible loss of ice nucleation active sites in mineral dust particles caused by sulphuric acid condensation, Atmos. Chem. Phys., 10, 11471–11487, https://doi.org/10.5194/acp-10-11471-2010, 2010. a, b
Vali, G.: Interpretation of freezing nucleation experiments: singular and stochastic; sites and surfaces, Atmos. Chem. Phys., 14, 5271–5294, https://doi.org/10.5194/acp-14-5271-2014, 2014. a
Vali, G., DeMott, P. J., Möhler, O., and Whale, T. F.: Technical Note: A proposal for ice nucleation terminology, Atmos. Chem. Phys., 15, 10263–10270, https://doi.org/10.5194/acp-15-10263-2015, 2015. a, b
Welti, A., Lüönd, F., Stetzer, O., and Lohmann, U.: Influence of particle size on the ice nucleating ability of mineral dusts, Atmos. Chem. Phys., 9, 6705–6715, https://doi.org/10.5194/acp-9-6705-2009, 2009. a
Welti, A., Lüönd, F., Kanji, Z. A., Stetzer, O., and Lohmann, U.: Time dependence of immersion freezing: an experimental study on size selected kaolinite particles, Atmos. Chem. Phys., 12, 9893–9907, https://doi.org/10.5194/acp-12-9893-2012, 2012. a, b
Wheeler, M. J. and Bertram, A. K.: Deposition nucleation on mineral dust particles: a case against classical nucleation theory with the assumption of a single contact angle, Atmos. Chem. Phys., 12, 1189–1201, https://doi.org/10.5194/acp-12-1189-2012, 2012. a
Wiedinmyer, C., Akagi, S. K., Yokelson, R. J., Emmons, L. K., Al-Saadi, J. A., Orlando, J. J., and Soja, A. J.: The Fire INventory from NCAR (FINN): a high resolution global model to estimate the emissions from open burning, Geosci. Model Dev., 4, 625–641, https://doi.org/10.5194/gmd-4-625-2011, 2011. a, b
Wild, O., Zhu, X., and J., P. M.: Fast-J: Accurate Simulation of In- and Below-Cloud Photolysis in Tropospheric Chemical Models, J. Atmos. Chem., 37, 245–282, https://doi.org/10.1023/A:1006415919030, 2000. a, b
Wright, T. P. and Petters, M. D.: The role of time in heterogeneous freezing nucleation, J. Geophys. Res.-Atmos., 118, 3731–3743, https://doi.org/10.1002/jgrd.50365, 2013. a
Yang, F., Tan, J., Zhao, Q., Du, Z., He, K., Ma, Y., Duan, F., Chen, G., and Zhao, Q.: Characteristics of PM2.5 speciation in representative megacities and across China, Atmos. Chem. Phys., 11, 5207–5219, https://doi.org/10.5194/acp-11-5207-2011, 2011. a
Young, K. C.: A Numerical Simulation of Wintertime, Orographic Precipitation: Part I. Description of Model Microphysics and Numerical Techniques, J. Atmos. Sci., 31, 1735–1748, https://doi.org/10.1175/1520-0469(1974)031<1735:ANSOWO>2.0.CO;2, 1974. a
Zaveri, R. A. and Peters, L. K.: A new lumped structure photochemical mechanism for large-scale applications, J. Geophys. Res.-Atmos., 104, 30387–30415, https://doi.org/10.1029/1999jd900876, 1999. a
Zaveri, R. A., Easter, R. C., Fast, J. D., and Peters, L. K.: Model for Simulating Aerosol Interactions and Chemistry (MOSAIC), J. Geophys. Res.-Atmos., 113, D13204, https://doi.org/10.1029/2007JD008782, 2008. a, b, c
Zhang, Q., Jimenez, J. L., Worsnop, D. R., and Canagaratna, M.: A Case Study of Urban Particle Acidity and Its Influence on Secondary Organic Aerosol, Environ. Sci. Technol., 41, 3213–3219, https://doi.org/10.1021/es061812j, 2007. a
Zhao, C. and Garrett, T. J.: Effects of Arctic haze on surface cloud radiative forcing, Geophys. Res. Lett., 42, 557–564, https://doi.org/10.1002/2014gl062015, 2015. a
- Abstract
- Introduction
- Description of the new scheme for ice heterogeneous nucleation in WRF-Chem
- Configuration of the model for typical TIC1 and TIC2 clouds observed during ISDAC
- Results and discussion
- Conclusions
- Code and data availability
- Author contributions
- Competing interests
- Acknowledgements
- Review statement
- References
- Abstract
- Introduction
- Description of the new scheme for ice heterogeneous nucleation in WRF-Chem
- Configuration of the model for typical TIC1 and TIC2 clouds observed during ISDAC
- Results and discussion
- Conclusions
- Code and data availability
- Author contributions
- Competing interests
- Acknowledgements
- Review statement
- References