FORests and HYdrology under Climate Change in Switzerland v1.0: a spatially distributed model combining hydrology and forest dynamics

We present FORHYCS (FORests and HYdrology under Climate Change in Switzerland), a distributed ecohydrological model to assess the impact of climate change on water resources and forest dynamics. FORHYCS is based on the coupling of the hydrological model PREVAH and the forest landscape model TreeMig. In a coupled simulation, both original models are executed simultaneously and exchange information through shared variables. The simulated canopy structure is summarized by the leaf area index (LAI), which affects local water balance calculations. On the other hand, an annual drought index is obtained from daily simulated potential and actual transpiration. This drought index affects tree growth and mortality, as well as a species-specific tree height limitation. The effective rooting depth is simulated as a function of climate, soil, and simulated above-ground vegetation structure. Other interface variables include stomatal resistance and leaf phenology.

Case study simulations with the model were performed in the Navizence catchment in the Swiss Central Alps, with a sharp elevational gradient and climatic conditions ranging from dry inner-alpine to high alpine. In a first experiment, the model was run for 500 years with different configurations. The results were compared against observations of vegetation properties from national forest inventories, remotely sensed LAI, and high-resolution canopy height maps from stereo aerial images. Two new metrics are proposed for a quantitative comparison of observed and simulated canopy structure. In a second experiment, the model was run for 130 years under climate change scenarios using both idealized temperature and precipitation change and meteorological forcing from downscaled GCM-RCM model chains.

The first experiment showed that model configuration greatly influences simulated vegetation structure. In particular, simulations where height limitation was dependent on environmental stress showed a much better fit to canopy height observations. Spatial patterns of simulated LAI were more realistic than for uncoupled simulations of the forest landscape model, although some model deficiencies are still evident. Under idealized climate change scenarios, the effect of the coupling varied regionally, with the greatest effects on simulated streamflow (up to 60 mm yr⁻¹ difference with respect to a simulation with static vegetation parameters) seen at the valley bottom and in regions currently above the treeline. This case study shows the importance of coupling hydrology and vegetation dynamics to simulate the impact of climate change on ecosystems. Nevertheless, it also highlights some challenges of ecohydrological modeling, such as the need to realistically simulate the plant response to increased CO₂ concentrations and process uncertainty regarding future land cover changes.

1 Introduction

Of the manifold effects of climate change, many are expected to impact the interactions between the water cycle and forest dynamics. As a result of higher temperatures and shifts in precipitation regimes, an increase in the frequency and intensity of drought events is predicted (Allen et al., 2010), as experienced in Europe in 2003 and 2018. This may greatly affect tree growth and mortality, even in locations currently not subject to high water stress (Choat et al., 2012; Martin-Benito and Pederson, 2015). This affects hydrologically relevant vegetation properties such as leaf area index (LAI) (Tesemma et al., 2015), root depth, or biomass (Bréda et al., 2006) and stomatal conductance, which vary with stand age or species composition (Ewers et al., 2005; Ford et al., 2011). These changes might affect streamflow and also feed back on local conditions for growth by altering water availability. For example, various studies have shown that trees growing in thinner stands are subject to lower water stress, so that artificial thinning may mitigate drought effects on tree growth and mortality (Elkin et al., 2015) and increase water yield (McLaughlin et al., 2013). Also, hydrological sensitivity of catchments to climate change seems to depend on vegetation properties, with mixed forests showing a more stable water yield than catchments dominated by broadleaf or coniferous forests (Creed et al., 2014). Furthermore, increased atmospheric CO₂ is expected to impact hydrology through its effects on stomatal activity and plant productivity (Trancoso et al., 2017), although the long-term effects are still subject to high uncertainty and debate (Medlyn et al., 2011). Another ecohydrologically relevant component of global change is land cover change, driven not only by a change in human land use, but also by natural vegetation dynamics. Increases in forested area usually reduce streamflow (Andréassian, 2004; Bosch and Hewlett, 1982), although the magnitude of such changes varies strongly with catchment characteristics such as climate, soil and forest age (Andréassian, 2004). Also, catchment response is often nonstationary, especially in the case of afforestation or reforestation, where streamflow strongly depends on stand age (Farley et al., 2005). Recent model developments have aimed at improving predictions by including transient vegetation parameters to simulate the transition between forest and non-forest (Du et al., 2016; Nijzink et al., 2016).

Mountainous regions are particularly sensitive to global change. Among the main effects are the changing significance of seasonal snow storage (Speich et al., 2015), altered species composition in temperature-limited ecosystems (Mayor et al., 2017), and an upwards shift of the treeline (Gehrig-Fasel et al., 2007). Given the high significance of mountains for large-scale water supply (Viviroli et al., 2003), it is crucial to estimate how the factors affecting water supply will change in the future. In Switzerland, mountains make up two-thirds of the territory and are of high importance for nature conservation, energy production, tourism, and farming, among other sectors (SCNAT, 2012). Modeling studies predict a change in runoff regime due to increased temperatures, changing precipitation seasonality, and glacier melt (Rössler et al., 2014), with important but locally varying consequences for hydropower generation (Gaudard et al., 2014) and farming (Milano et al., 2015). Climate impacts on forests also vary locally, with an increase in drought stress predicted at lower elevations and improved growth conditions in energy-limited high-altitude forests (Bugmann et al., 2014), leading to shifting spatial patterns of species composition, tree biomass and canopy cover (Bugmann et al., 2014; Fuhrer et al., 2006). The increased frequency of extreme droughts will probably be a more important factor than a change in long-term averages (Fuhrer et al., 2006). Additionally, abandonment of high-mountain pastures, driven by socioeconomic processes, is an important factor of land-use change (Price et al., 2016), interacting with climate change to allow the tree line to shift upwards (Gehrig-Fasel et al., 2007). These developments and predictions highlight the need for an integrated simulation of hydrology, forest dynamics, and land-use change in Switzerland.

1.1 Coupled models of hydrology and forest dynamics

Interactions between hydrology and vegetation dynamics are included in various types of dynamic models, with widely different areas of application, levels of complexity, and spatial and temporal resolutions (Fatichi et al., 2016). One such domain is that of land surface models (LSMs), which represent land surface processes in climate models (e.g., CLM; Lawrence et al., 2011). The main role of vegetation in these models is the partitioning of energy between sensible and latent heat fluxes. The latter consist of evaporation and transpiration, thus representing the coupling between the vegetation, hydrology, and atmosphere. Over time, the representation of vegetation and evaporative fluxes in LSMs grew increasingly complex, moving from a simple vegetation-independent bucket model in early applications to a detailed description of vegetation processes, in particular physiological processes such as photosynthesis, carbon assimilation, and nutrient cycling (see review by Seneviratne et al., 2010). For a representation of vegetation dynamics, climate models are sometimes coupled with dynamic global vegetation models (e.g., LPJ; Sitch et al., 2003), which can also be used for offline simulations. Although the primary objective of these models is to simulate vegetation patterns, they usually include a representation of terrestrial water balance and are able to simulate river discharge (Gerten et al., 2004).

While these models typically operate at the global scale, and for computational efficiency simplify vegetation to a single average individual per plant type and coarse grid cell, some ecosystem models have been developed to depict vegetation structure, such as the dynamic vegetation model LPJ-GUESS (Smith et al., 2001), which is based on individual plants. Like LPJ, this model contains a soil hydrology module that can be used to calculate discharge, but such predictions were greatly improved by adding a coupling to a routing scheme (Tang et al., 2013). A sensitivity analysis by Pappas et al. (2013) pointed out that, despite of its detailed mechanistic representation of transpirational demand and stomatal closure that affects carbon uptake, water stress effects are represented inaccurately in LPJ-GUESS. As the various effects of water shortage on trees are well documented (McDowell et al., 2008), this may be seen as a weakness of LPJ-GUESS, especially since important plant functions, like cavitation or leaf area reduction under drought conditions are not implemented yet (Pappas et al., 2013; Manusch et al., 2014).

Another type of model representing the interface of hydrology and vegetation is the forest water balance model. These models usually simulate the local water balance of forest stands to predict the influence of climatic change or forest management practices on growth conditions for trees. Examples include WAWAHAMO (Zierl, 2001) or BILJOU (Granier et al., 1999). These models may be coupled with dynamic forest models (Lischke and Zierl, 2002; Seely et al., 2015) or run with vegetation parameters assimilated from forest inventories (Zierl, 2001; De Cáceres et al., 2015) or remote sensing (Chakroun et al., 2014). Moreover, most forest dynamics models include a water balance module (Bugmann and Cramer, 1998; Seidl et al., 2012). However, its role is usually restricted to quantifying soil moisture stress, and it is seldom used to predict streamflow.

Various hydrological models operating at the catchment scale have been used to evaluate the effect of land-use change and the resulting change in vegetation on streamflow. Such models include distributed models with a high spatial resolution, allowing for a detailed mapping of static vegetation parameters, e.g., DHSVM (Wigmosta et al., 1994). Other models include a simple vegetation growth module, such as SWAT (Watson et al., 2008) or SWIM (Wattenbach et al., 2005). More complex models include a detailed representation of average plant biomass growth, carbon and nutrient cycling, and hydrological processes, such as RHESSys (Tague and Band, 2004) or Tethys-Chloris (Fatichi et al., 2012).

Furthermore, the impact of vegetation dynamics on streamflow has also been studied with models that were not originally developed to this effect. For example, Sutmöller et al. (2011) used the physically based distributed hydrological model WaSiM-ETH (Schulla, 2015) to perform hydrological simulations with vegetation parameters derived from an individual-based forest model driven by different forest management scenarios, which influence forest structure and species composition. Also, Schattan et al. (2013) applied the semi-conceptual hydrological model PREVAH (Gurtz et al., 1999) with vegetation parameters obtained from the forest landscape model TreeMig (Lischke et al., 2006). In the original versions of both these hydrological models, vegetation parameters were parameterized as a function of season and land cover class only. This one-way coupling impacted mean annual streamflow by about 10 mm yr⁻¹ in two large catchments in Switzerland, whereas the effect on the local water balance reached 40 mm yr⁻¹ in individual cells. Similarly, a modeling experiment by Köplin et al. (2013) showed that including transient land cover changes, such as forest cover increase or decrease or glacier retreat, could substantially affect water balance predictions. Such experiments highlight the importance of considering the dynamics and spatial variability in vegetation properties in hydrological simulations.

So far, most of the models combining hydrology and vegetation processes have a strong biogeochemical focus, whereas successional dynamics and interspecific competition are rarely considered. Couplings between models that explicitly simulate forest dynamics and hydrological models have so far mostly been the object of experimental studies. The results from these experiments show that coupling these processes may substantially alter model results and behavior (Sutmöller et al., 2011; Schattan et al., 2013). This gives an opportunity to increase the confidence in simulated impacts of climate change on forested ecosystems. For reliable country-level predictions of long-term climate impacts on water resources and forest structure and composition in a mountainous country such as Switzerland, a model should

• explicitly simulate the feedbacks between forest properties and hydrology;

• return estimates of streamflow and (evapo)transpiration as well as tree species distribution and biomass;

• operate at a spatial resolution fine enough to account for the great variability in climate, topography, and land cover;

• be able to simulate the hydrology of non-vegetated areas such as glaciers, bare rock, or built-up;

• take into account the possibility of forest expansion and retreat; and

• not be too complex, so that it can be run for large areas and long periods at a reasonable computational cost.

None of the models discussed above fulfill all of these criteria. This motivated the development of a spatially distributed model combining hydrology and forest dynamics, presented below.

1.2 Aims of this work

In this paper, we present a newly developed distributed ecohydrological model, FORHYCS (FORests and HYdrology under Climate change in Switzerland). This model combines two existing models, the hydrological model PREVAH (Gurtz et al., 1999) and the forest landscape model TreeMig (Lischke et al., 2006). FORHYCS is spatially distributed and operates on a grid of regular cells. The model outputs are hydrological quantities, such as catchment-integrated streamflow and maps of runoff, transpiration, evaporation or snow cover and maps of forest properties, such as biomass, leaf area index (LAI), species distribution and tree density. In FORHYCS, the two source models are run simultaneously and exchange information through shared variables. FORHYCS may be run in uncoupled mode (i.e., parallel simulations of hydrology and forest dynamics, without any transfer of information between the two source models), with a one-way coupling (transfer of information from the forest landscape model to the hydrological model or vice versa) or in fully coupled mode.

Like its parent models, FORHYCS may be described as semi-conceptual. Hydrological processes (evaporation, transpiration, soil moisture dynamics, and runoff generation) and forest dynamics (growth, mortality, establishment, and migration of tree species) are based on physical and ecological theory as well as empirical approaches. Thus, the degree of complexity of FORHYCS is lower than other coupled ecohydrological models, such as RHESSys (Tague and Band, 2004). Also, unlike these models, the focus of the ecological part is on forest dynamics, similar to the addition to SWIM proposed by (Wattenbach et al., 2005). However, FORHYCS differs from the latter approach in that growth and mortality are simulated at the level of species and size classes, instead of a single biomass pool per cell. Both TreeMig and PREVAH were designed for applications at an intermediate spatial resolution, with a cell size between 100 m and 1 km.

The goal of this paper is to explore the interplay of hydrology and forest dynamics in a coupled model. The questions to be answered are (1) “How does the coupling impact the behavior and the performance of both TreeMig and PREVAH, compared to uncoupled simulations?”; (2) “Which aspects of the forest–hydrology coupling are of greatest importance for simulation results?”; and (3) “What are the implications of model coupling for simulations under climate change?”

The model is tested in five subcatchments of the Navizence catchment (27 to 87 km²), located in the Swiss Central Alps. To answer the first question, a full forest succession is modeled for the period 1500–2015, starting from bare soil. The forest model is run in uncoupled mode to serve as a reference simulation. For the coupled runs, various configurations are tested, with different aspects of the coupling between hydrology and forest dynamics switched on and off. The outputs are then compared to forest inventory data, as well as gridded datasets of leaf area index (LAI) and canopy height. To assess the effect of the coupling on hydrological predictions, simulated streamflow from coupled and uncoupled model runs is compared against a time series of daily measurements. Furthermore, to assess the behavior of the coupled and uncoupled model under climate change, the model is run for a century under artificial climate change scenarios. In these future model runs, the significance of two further aspects of the forest–hydrology coupling are examined, including the effect of elevated CO₂ on stomatal resistance and the potential forest expansion into high-elevation meadows as a result of climate and land-use change.

2 Methods and data

2.1 FORHYCS model description

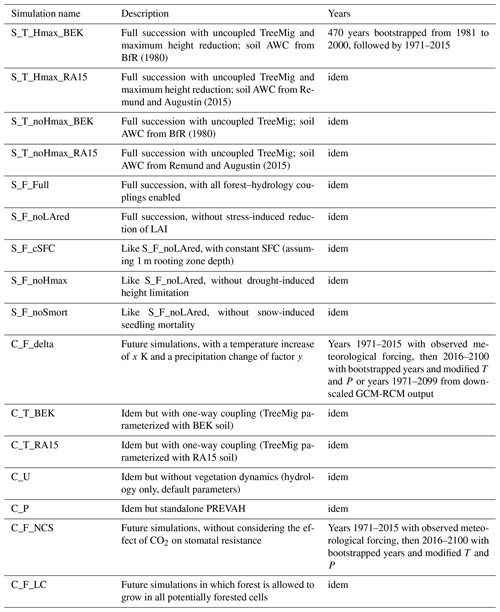
The two original models operate at a different temporal resolution; while TreeMig simulates forest dynamics with an annual time step, PREVAH calculates daily values, with an internal time step of 1 h. Both original models are run simultaneously over the same domain and exchange information through shared variables. Figure 1a shows the flow of a simulation; hydrology is simulated on a daily basis with vegetation properties given by the forest model for the previous year. This is based on the assumption that effects of the current-year water balance on the forest structure and composition are negligible. An annual drought index (DI), influencing tree growth and mortality (Sect. 2.1.3), is calculated in each cell from the transpiration simulated in the hydrological model over the whole simulation year (Sect. 2.1.4). Based on the number of trees per species and height class in each cell, annual maximal values of leaf area index (LAI) and fractional canopy cover (FCC) are calculated. These values are converted to daily values using a temperature-dependent phenology module (Sect. 2.1.2). The rooting zone water storage capacity (SFC) is updated annually as a function of long-term climate (Sect. 2.1.5). Furthermore, the model includes the effects of snow-induced mortality for some species using an additional mortality function based on snow cover duration (Sect. 2.1.6).

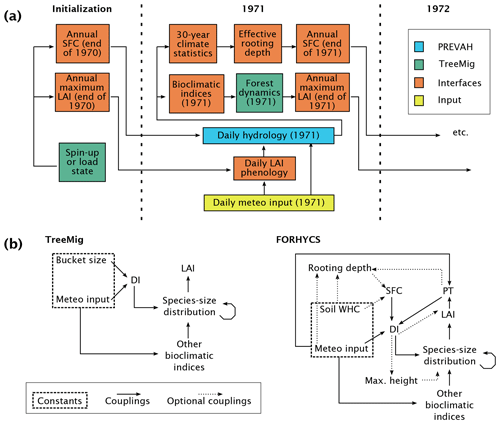
Figure 1 (a) Flow of a FORHYCS simulation starting in the example year 1971. The initial state can be loaded from a file or a spin-up can be performed. The hydrological calculations are performed daily. At the end of the simulation year, bioclimatic indices are calculated and passed to TreeMig, which simulates forest dynamics with an annual time step. Long-term climate statistics are updated at the end of the year based on the daily calculations, and the effective rooting depth module is run with the updated climate indices. The forest model returns an annual maximal LAI value. To be used in hydrological calculations, this value is converted to daily values based on simulated leaf phenology. Another important interface variable is the rooting zone storage capacity SFC. (b) Schematic overview of the couplings between climate, above-ground forest structure, and the rooting zone in TreeMig (left) and FORHYCS (right). TreeMig's forest structure (species–size distribution) depends on its previous state and is influenced by the annual bioclimatic indices. Unlike the other indices, which depend on meteorological input only, the drought index (DI) further depends on a constant soil moisture storage capacity (“bucket size”). In FORHYCS, the drought index further depends on canopy structure, through its influence on potential transpiration (PT). Additional optional couplings in FORHYCS are the dynamic simulation of a climate-dependent storage capacity of the rooting zone (through varying effective rooting depth), a limitation of maximum tree height under dry conditions, and a drought-dependent reduction of leaf area.

2.1.1 Source models

The semi-conceptual hydrological model PREVAH (Gurtz et al., 1999) in its fully distributed form (Schattan et al., 2013; Speich et al., 2015) solves the water balance of each grid cell by calculating evapotranspiration, soil water balance, and runoff generation at a sub-daily time step. The core of PREVAH is based on the structure of the widely used model HBV (Bergström, 1992), combined with a conceptual runoff routing scheme (Gurtz et al., 1999). Successive model developments enabled or improved the treatment of interception (Menzel, 1996), snowpack dynamics (Zappa et al., 2003), glacier runoff (Klok et al., 2001), and groundwater runoff (Gurtz et al., 2003). PREVAH was used, among other applications, to estimate the impact of climate change on discharge (Zappa and Kan, 2007). Climate impact studies were also conducted using the distributed outputs of PREVAH (Speich et al., 2015).

The spatially explicit forest landscape model TreeMig (Lischke et al., 2006) simulates forest establishment, growth, and mortality, as well as seed dispersal. Originally based on a gap model (Lischke et al., 1998), TreeMig calculates the number of trees per species and height in each cell and operates at an annual time step. Inter- and intraspecific competition is represented through light distribution within the canopy, which depends on the distribution of trees of different heights within a stand and thus on leaf area (Lischke et al., 1998). TreeMig was used to predict climate impact on tree species distribution in Switzerland (Bugmann et al., 2014), as well as to simulate forest response to land abandonment (Rickebusch et al., 2007) and the feedbacks between forests and avalanches (Zurbriggen et al., 2014). Abiotic drivers of forest dynamics are represented by three bioclimatic indices: mean temperature of the coldest month, degree-day sum, and drought (see Sect. 2.1.3 for the latter).

2.1.2 Canopy structure and leaf phenology

Leaf area index (LAI) is calculated in TreeMig to account for mutual shading and competition for light (Lischke et al., 1998). In FORHYCS, LAI is passed to the hydrological model, replacing the land-cover-specific parameterization in PREVAH. The allometric equations of Bugmann (1994) relate leaf area to diameter at breast height (D; in centimeters). As D is allometrically linked to tree height, leaf area is calculated for each group of trees of the same species and height class, then summed to obtain the value for the whole stand as follows:

$$\begin{array}{}\text{(1)}& A_{\mathrm{l}}=\sum _{\mathrm{sp}=\mathrm{1}}^{\mathrm{nspc}}\sum _{\mathrm{hc}=\mathrm{1}}^{\mathrm{nhcl}}{\mathrm{SLA}}_{\mathrm{sp}}\times a_{\mathrm{1},\mathrm{sp}}\times D_{\mathrm{sp},\mathrm{hc}}^{\mathrm{a}\mathrm{2},\mathrm{sp}}\times p_{\mathrm{d},\mathrm{sp}},\end{array}$$

where A_l is the total all-sided stand leaf area (in square meters), nspc is the number of species (30 in FORHYCS), nhcl is the number of height classes (16), SLA_sp is the specific leaf area (in square meters per kilogram), a_1,sp (in kilograms per centimeter) and a_2,sp (unitless) are species-specific allometric parameters (Bugmann, 1994), and p_d,sp is a dimensionless reduction term accounting for seasonal variations in leaf area, ranging from 0 to 1 (see below and in the Supplement). The reference area in TreeMig is the size of a forest plot, set to 833 m² (1∕12 ha), which is the reference area in many gap models (e.g., Bugmann, 1994), so that

$$\begin{array}{}\text{(2)}& \mathrm{LAI}=A_{\mathrm{l}}{k}_{\mathrm{c}}/\mathrm{833},\end{array}$$

where k_c is a factor to convert from true to projected leaf area, set to 0.5 for broadleaves and 0.4 for conifers following Hammel and Kennel (2001). Fractional canopy cover f_c is also calculated from the number of trees per species and height class, using the equation of Zurbriggen et al. (2014) as follows:

$$\begin{array}{}\text{(3)}& \begin{array}{rl}& f_{\mathrm{c}}=\\ & \left[\mathrm{1}-\exp \left(-\mathrm{1}\times \sum _{\mathrm{sp}=\mathrm{1}}^{\mathrm{nspc}}\sum _{\mathrm{hc}=\mathrm{1}}^{\mathrm{nhcl}}(n_{\mathrm{sp},\mathrm{hc}}/\mathrm{833})\times {\mathrm{CA}}_{\mathrm{sp},\mathrm{hc}}\right)\right],\end{array}\end{array}$$

where CA_sp,hc is the total crown area for trees of each species and height class.

$$\begin{array}{}\text{(4)}& {\mathrm{CA}}_{\mathrm{sp},\mathrm{hc}}=\left(k_{\mathrm{a}\mathrm{1},\mathrm{sp}}\times h_{\mathrm{hc}}^{\mathrm{2}}+k_{\mathrm{a}\mathrm{2},\mathrm{sp}}\times h_{\mathrm{hc}}\right)\times n_{\mathrm{sp},\mathrm{hc}},\end{array}$$

where k_a1,sp and k_a2,sp are species-specific allometric parameters, and h_hc is the (upper) height of the height class (hc). Minimum values for LAI and f_c are set to 0.2 and 0.1, respectively, to account for a minimal cover by grass and shrubs, as well as bare stems. Annual maximum LAI may be reduced as a function of the drought stress of the previous years, as described below in Sect. 2.1.3. It is worth noting that leaf area and crown area are calculated independently from each other, both using empirical relationships with tree size.

To obtain daily values for LAI and f_c, a leaf phenology module has been implemented. The variable p_d,sp reflects the phenological status of species “sp” in a given cell and varies between 0 (no leaves) and 1 (full foliage). This module also defines the start and end of the growing season in each cell, which is required to calculate the climatic indices for the rooting depth module (Sect. 2.1.5). In each cell, the growing season lasts as long as p_d,sp is greater than 0.5 for the dominant species. Daily values of p_d,sp are simulated in spring with the model of Murray et al. (1989), which depends on the number of chill days in winter and accumulated growing degree days in summer. When p_d,sp reaches a value of 1, the foliage is assumed to be fully developed. The onset of leaf senescence in autumn is simulated using the model of Delpierre et al. (2009), which depends on temperature and photoperiod. For broadleaves, the end of the growing season is set to 14 d after the onset of senescence, and p_d,sp is linearly reduced from 1 to 0 during this period. Although the leaf area is not varied throughout the year for evergreen conifers, p_d,sp is still simulated to define the start and end of the growing season. For these species (as well as for the deciduous conifer Larix decidua), the development of p_d,sp following the onset of senescence is calculated using the formulation of Scherstjanoi et al. (2014). The parameters for the empirical models of Murray et al. (1989) and Delpierre et al. (2009) were calibrated against phenological observations across Switzerland (Defila and Clot, 2001). The species-specific parameters and a description of the calibration procedure are given in the Supplement.

2.1.3 Drought and its effects on forest growth, mortality, and structure

The drought index used in TreeMig is based on the ratio of annual to potential evapotranspiration, as calculated with a module modified from Thornthwaite and Mather (1957). This scheme requires a monthly precipitation sum and temperature average for each cell, as well as the plant-available water storage capacity. Evaporative demand is calculated using an empirical, temperature-dependent approach, and monthly soil water balance is simulated based on water supply and demand, after accounting for interception (see Bugmann and Cramer, 1998, for a full description of this scheme). This approach has a number of drawbacks. First, it does not consider the effect of variations in vegetation properties on evaporative supply and demand, thus neglecting feedbacks between vegetation density, transpiration, and drought (see e.g., Kergoat, 1998). Also, the Thornthwaite–Mather routine does not account for snow-related processes, which can lead to large errors in the estimation of evapotranspiration, diminishing the representativeness of the index for growth conditions (Anderegg et al., 2013). Furthermore, empirical evapotranspiration formulations such as the Thornthwaite–Mather routine rely to a large extent on calibrated values. These may not be transferrable to climatic conditions that differ from the calibration period (Bartholomeus et al., 2015), limiting the ability of the model to make predictions under a changing climate. For these reasons, this abiotic drought index was replaced by a relative transpiration index (Speich et al., 2018a). This index is similar to the evapotranspiration deficit index presented above but is based on transpiration rather than evapotranspiration as follows:

$$\begin{array}{}\text{(5)}& \mathrm{DI}=\mathrm{1}-{\displaystyle \frac{{\sum }_{\mathrm{d}=\mathrm{de}}^{\mathrm{ds}}{E}_{T,\mathrm{act},\mathrm{d}}}{{\sum }_{\mathrm{d}=\mathrm{de}}^{\mathrm{ds}}{E}_{T,\mathrm{pot},\mathrm{d}}}},\end{array}$$

where de and ds are the first and last day of the period for which the drought stress is calculated, and $E_{T,\mathrm{pot},\mathrm{d}}$ and $E_{T,\mathrm{act},\mathrm{d}}$ are modeled daily canopy transpiration sums (in millimeters per day). Here, DI is calculated for the entire year, so that de =1 and ds =365. Furthermore, to account for delayed effects of drought on tree physiology (Hammel and Kennel, 2001), the average of the last 3 years is used here. Transpiration is reduced from the potential rate through the effect of low soil moisture or high atmospheric vapor pressure deficit (VPD) on stomatal resistance (Eq. 14 in Speich et al., 2018a). The rationale behind this index is based on the fact that stomatal closure is one of the first responses of a plant to water deficit. Therefore, the time during which stomatal resistance is increased due to drought is the time during which adverse physiological effects of water shortage (e.g., cavitation, reduced carbon uptake) are likely to occur, and DI serves as a proxy for all these processes. The effect of VPD was included to account for the effects of high evaporative demand on plant-internal hydraulics (Zierl, 2001). The drought stress function f_DS determines the relative drought-induced limitation of annual growth (Bugmann, 1994).

$$\begin{array}{}\text{(6)}& f_{\mathrm{DS}}=\sqrt{max\left(\mathrm{0},\mathrm{1}-{\displaystyle \frac{\mathrm{DI}}{k_{\mathrm{DT}}}}\right)},\end{array}$$

where k_DT is a species-specific drought tolerance parameter, indicating the value of DI at which growth is completely suppressed. This growth reduction function can take values between 0 (complete growth suppression) and 1 (unstressed conditions). Annual growth of the trees of the same species and height class is the product of a species-specific maximal growth, an environmental reduction function f_env, and a further reduction term accounting for shading. The environmental reduction function is the geometric mean of f_DS and two other stress functions, representing the effects of temperature and nitrogen availability (Bugmann, 1994). While the effects of temperature are taken into account in this study, nitrogen availability is kept spatially and temporally constant. These two environment-dependent stress functions are further described in Sect. S1.2 of the Supplement (for a description of the effects of light competition and shading, we refer to (Lischke et al., 2006). The same reduction function is used to simulate mortality in addition to background mortality and applies if it is more severe than mortality caused by low productivity. Lischke and Zierl (2002) parameterized k_DT for the 30 tree species represented in TreeMig by overlaying modeled DI with inventory-derived maps of species distribution. The values range between 0.27 and 0.5. However, this parameterization did not lead to satisfactory simulations of species composition in the case study of this paper. Therefore, species-specific k_DT was defined based on a combination of the rankings by Lischke and Zierl (2002) and Niinemets and Valladares (2006). Table S7 in the Supplement lists the k_DT values used in this study.

FORHYCS accounts for two additional effects of drought stress: a limitation of maximum height and a reduction of annual maximal LAI. The former is parameterized following Rasche et al. (2012); i.e., species-specific maximum tree height may be reduced as a function of the bioclimatic indices DI and DDEGS (degree-day sum; see Sect. S1.2 of the Supplement). The parameter k_redmax, which is also species-specific, indicates the fraction of maximum height that can be attained by trees if one of the environmental vitality functions is at its minimum. The more severe of the two reductions (drought or degree-days) is applied. Unlike in the formulation of Rasche et al. (2012), where the reduction is a linear function of the bioclimatic indices, the impact functions (Eq. 6 for drought and S8 for degree-day sum) are used here.

The LAI reduction function follows the formulation of Landsberg and Waring (1997), where the fraction of carbon allocated to roots increases under stress, whereas allocation to foliage and stem decreases. Since allocation is not explicitly simulated in FORHYCS, the following formulation is purely phenomenological. For all size classes of a given species, leaf area is scaled by the ratio of the foliage allocation coefficient under current η_l and unstressed conditions η_l,u. Eq. (1) is thus modified as follows:

$$\begin{array}{}\text{(7)}& \begin{array}{rl}{A}_{\mathrm{l}}& =\sum _{\mathrm{sp}=\mathrm{1}}^{\mathrm{nspc}}\sum _{\mathrm{hc}=\mathrm{1}}^{\mathrm{nhcl}}{\mathrm{SLA}}_{\mathrm{sp}}\times a_{\mathrm{1},\mathrm{sp}}\times D_{\mathrm{sp},\mathrm{hc}}^{\mathrm{a}\mathrm{2},\mathrm{sp}}\times p_{\mathrm{d},\mathrm{sp}}\\ & \times {\mathit{\eta }}_{\mathrm{l},\mathrm{sp}}/{\mathit{\eta }}_{\mathrm{l},\mathrm{u},\mathrm{sp}}.\end{array}\end{array}$$

The allocation coefficients for foliage are calculated as follows:

$$\begin{array}{}\text{(8)}& {\mathit{\eta }}_{\mathrm{l}}=\mathrm{1}-{\mathit{\eta }}_{\mathrm{r}}-{\mathit{\eta }}_{\mathrm{s}},\text{ and }{\mathit{\eta }}_{\mathrm{l},\mathrm{u}}=\mathrm{1}-{\mathit{\eta }}_{\mathrm{r},\mathrm{u}}-{\mathit{\eta }}_{\mathrm{s},\mathrm{u}},\end{array}$$

where η_r and η_r,u are the allocation coefficients to roots and η_s and η_s,u are the allocation coefficients to the stem under current and unstressed conditions, respectively. Following Landsberg and Waring (1997), η_r,u is set to 0.229, and η_r increases with increasing stress by the following relation:

$$\begin{array}{}\text{(9)}& {\mathit{\eta }}_{\mathrm{r}}={\displaystyle \frac{\mathrm{0.8}}{\mathrm{1}+\mathrm{2.5}\left(\mathrm{1}-f_{\mathrm{env}}\right)}},\end{array}$$

where f_env is the geometrical mean of the drought and low temperature stress functions (Eqs. 6 and S8). The carbon allocated to the stem is related to η_r as follows:

$$\begin{array}{}\text{(10)}& \begin{array}{rl}& {\mathit{\eta }}_{\mathrm{s}}=\left(\mathrm{1}-{\mathit{\eta }}_{\mathrm{r}}\right)/\left(p_{\mathrm{l},\mathrm{s}}+\mathrm{1}\right),\mathrm{and}\\ & {\mathit{\eta }}_{\mathrm{s},\mathrm{u}}=\left(\mathrm{1}-{\mathit{\eta }}_{\mathrm{r},\mathrm{u}}\right)/\left(p_{\mathrm{l},\mathrm{s}}+\mathrm{1}\right),\end{array}\end{array}$$

where p_l,s is the ratio of the growth rates of leaves and stems, in terms of their change in relation to diameter at breast height D. In FORHYCS, p_l,s is calculated using the allometric equations used to calculate leaf and stem biomass:

$$\begin{array}{}\text{(11)}& p_{\mathrm{l},\mathrm{s}}={\displaystyle \frac{\mathrm{d}{w}_{\mathrm{l}}/\mathrm{d}D}{\mathrm{d}{w}_{\mathrm{s}}/\mathrm{d}D}}={\displaystyle \frac{k_{\mathrm{l},\mathrm{1}}{D}^{k_{l,\mathrm{2}}}}{k_{\mathrm{s},\mathrm{1}}{D}^{k_{\mathrm{s},\mathrm{2}}}}},\end{array}$$

where k_l,1 and k_l,2 are allometric parameters for leaf biomass, and k_s,1 and k_s,2 are allometric parameters for stem biomass (Bugmann, 1994). It is important to stress that FORHYCS does not explicitly simulate carbon assimilation. Hence, Eqs. (9) and (10) are only used to determine a reduction factor for leaf area (Eq. 8) and have no direct influence on simulated tree growth, stem biomass, and rooting depth.

2.1.4 Partitioning of transpiration and soil evaporation

The implementation of the new drought index (see Sect. 2.1.3 above) required some changes to the evapotranspiration routine in the hydrological model. While the relative transpiration index is based on estimates of actual and potential transpiration, PREVAH does not explicitly differentiate between transpiration and soil evaporation. Therefore, a new local water balance routine was implemented, based on the standalone model FORHYTM (Speich et al., 2018a). This module combines the soil water balance formulation of the HBV model (Bergström, 1992), which is also implemented in PREVAH, with the transpiration and evaporation scheme of Guan and Wilson (2009) and a Jarvis-type (Jarvis, 1976) parameterization of canopy resistance. A full description is given in Speich et al. (2018a).

The parameterization of canopy resistance differs from the original formulation in two ways. First, the effect of atmospheric vapor pressure deficit (VPD) on stomatal conductance is represented with a negative exponential function instead of a linear function. Second, an additional canopy resistance modifier (f₅) was implemented to account for the effect of atmospheric CO₂ concentration (C_a [µmol mol⁻¹]). This function is based on the results of Medlyn et al. (2001).

$$\begin{array}{}\text{(12)}& f_{\mathrm{5}}={\left(\mathrm{1}-j_{\mathrm{c}}\left({\displaystyle \frac{\min (C_{\mathrm{a}},\mathrm{700})}{\mathrm{350}}}-\mathrm{1}\right)\right)}^{-\mathrm{1}},\end{array}$$

where j_c represents the fractional change in conductance in response to an increase in C_a from 350 to 700 µmol mol⁻¹ and was set to 0.1 for coniferous forests, 0.25 for broadleaf forests, and 0.18 for mixed forests (the forest type in each cell is determined based on the relative share of above-ground biomass belonging to conifers and broadleaves). These values were set based on the results reported by Medlyn et al. (2001); coniferous species had a value of j_c between 0 and 0.2, whereas broadleaves had values up to 0.4. Therefore, for conifers, a value of 0.1 was selected. For broadleaves, as there seemed to be some acclimation for trees growing in elevated CO₂, a more conservative (than 0.4) value of 0.25 was chosen. The value for mixed forests corresponds to the arithmetic mean of the two. This affects both potential and actual transpiration so that, with all other factors kept constant, increases in C_a will reduce the level of drought stress. The rationale for implementing this new water balance scheme is to account for the effect of variations in vegetation properties (e.g., LAI) on physiological drought in forests. As FORHYCS includes the possibility of changing land cover classes in a cell, some non-forested cells may become forested over the course of a simulation. As vegetation parameters (such as LAI and effective rooting depth) are prescribed as a function of land cover for non-forested cells, this shift inevitably introduces an artificial discontinuity in the simulation. To reduce this discontinuity, the new water balance scheme is also used for potentially forested land cover types. On the other hand, for land cover types that cannot become forested, the original water balance scheme of PREVAH (Gurtz et al., 1999) is applied.

2.1.5 Rooting zone storage capacity

The rooting zone water holding capacity, SFC, is calculated as the product of effective root depth Z_e and soil water holding capacity κ (Federer et al., 2003). While κ is assumed to remain constant, Z_e is assumed to vary as a function of vegetation characteristics and climate. The approach used to parameterize Z_e is the carbon cost–benefit approach of Guswa (2008, 2010). This approach rests on the assumption that plants dimension their rooting systems in a way that optimizes their carbon budget. The optimal rooting depth is the depth at which the marginal carbon costs of deeper roots (linked to root respiration and construction) starts to outweigh the marginal benefits (i.e., additional carbon uptake due to greater availability of water for transpiration). The implementation of this model in FORHYCS follows the procedure described by Speich et al. (2018b). Effective rooting depth, expressed as an average over the whole cell, is calculated for both overstory (trees) and understory (shrubs and non-woody plants). The storage volume SFC for a given cell is defined as the sum of these two area-averaged rooting depths, multiplied with soil water holding capacity κ. A full description of this implementation is given in Speich et al. (2018b). The underlying equation is:

$$\begin{array}{}\text{(13)}& {\displaystyle \frac{{\mathit{\gamma }}_{\mathrm{r}}\times D_{\mathrm{r}}}{L_{\mathrm{r}}}}=w_{\mathrm{ph}}\times f_{\mathrm{seas}}\times {\displaystyle \frac{\mathrm{d}\langle T\rangle }{\mathrm{d}{Z}_{\mathrm{e}}}},\end{array}$$

where γ_r is root respiration rate (in milligrams of carbon per gram of roots per day), D_r is the root length density (in centimeters of roots per cubic centimeter of soil), L_r is the specific root length (in centimeters of roots per gram of roots), w_ph is the photosynthetic water use efficiency (in grams of carbon per cubic centimeter of H₂O), f_seas is the growing season length (fraction of a year), and 〈T〉 is the mean daily transpiration (in millimeters per day) during the growing season. The left hand side represents the marginal cost of deeper roots, and the right hand side the marginal benefits; solving for Z_e gives the optimal rooting depth. Any equation can be used to relate d〈T〉 to dZ_e. In this implementation, the probabilistic models of Milly (1993) and Porporato et al. (2004) are used for the understory and overstory, respectively. These two models reflect the differing water uptake strategies of grasses and trees (Guswa, 2010). Both models estimate transpiration based on soil water holding capacity κ and long-term averages of climatic indices. Evaporative demand is represented by potential transpiration, and rainfall is represented as a marked Poisson process characterized by the frequency (λ; in events per day) and mean intensity (α; in millimeters per event) of events. In FORHYCS, these variables are calculated as rolling means with a window of 30 years, including only the growing seasons. Potential transpiration for the understory and overstory are taken from the calculations of the local water balance module (Sect. 2.1.4), and the rainfall characteristics are taken from modeled effective precipitation (i.e., after accounting for interception). The start and end of the growing season are determined based on the phenology module (Sect. 2.1.2). In addition, mean daily air temperature is calculated over the growing season to adjust respiration rate. The plant-specific parameters in Eq. 13 are summarized in the variable PP_o, defined as follows:

$$\begin{array}{}\text{(14)}& {\mathrm{PP}}_{\mathrm{o}}={\displaystyle \frac{{\mathit{\gamma }}_{\mathrm{r},\mathrm{20}}{D}_{\mathrm{r}}}{L_{\mathrm{r}}{w}_{\mathrm{ph}}}},\end{array}$$

where γ_r,20 is the root respiration rate at 20 ^∘C. The actual root respiration rate is dependent on annually averaged temperature via a Q₁₀ function. For further details, please refer to Speich et al. (2018b). A higher value of PP_o indicates a greater difficulty for the plant to develop additional roots. In FORHYCS, PP_o was set to $\mathrm{1.263}\times {\mathrm{10}}^{-\mathrm{4}}$ for conifers and $\mathrm{1.01}\times {\mathrm{10}}^{-\mathrm{4}}$ for broadleaved species. At the cell level, PP_o was averaged based on the relative share of above-ground biomass belonging to conifers and broadleaves. For the understory, the corresponding parameter PP_u is set to $\mathrm{1.512}\times {\mathrm{10}}^{-\mathrm{4}}$.

2.1.6 Snow-cover induced seedling mortality

For seedlings of the high-mountain species Larix decidua, Pinus cembra, and P. montana, the model also includes the effect of snow-induced fungal infections via the variable FDSA (final day of snow ablation), as described by Zurbriggen et al. (2014). An additional mortality term is calculated as follows:

$$\begin{array}{}\text{(15)}& {\mathit{\mu }}_{\mathrm{s}}=a\times {\mathrm{FDSA}}^{\mathrm{2}}+b\times \mathrm{FDSA}+c,\end{array}$$

where a, b, and c are empirical parameters fitted by Zurbriggen et al. (2014) for Larix decidua and for the two aforementioned Pinus species. If μ_s is greater than background mortality or the mortality term integrating light, temperature, and water stress, it is applied instead for the seedlings of these species. This aspect of the model was implemented to examine the feedback between forest dynamics and avalanches on a small spatial scale (Zurbriggen et al., 2014) but was never tested on landscape scale. Here, FDSA is defined as the last day of the year with more than 5 mm of snow water equivalent.

2.1.7 Uncoupled mode and one-way coupling

The methods have so far described the model FORHYCS in its fully coupled version. It is also possible to run FORHYCS in uncoupled mode (without any information transfer between the hydrological and forest models) or with a one-way coupling (information transfer from the forest model to the hydrological model only). An uncoupled FORHYCS run consists essentially of a PREVAH run and a TreeMig run, happening independently from each other. Uncoupled FORHYCS differs from other PREVAH implementations mainly through the parameterization of soil and surface properties. As mentioned in Sect. 4.2, previous applications of PREVAH in Switzerland have used soil depth and water holding capacity from the agricultural suitability map BEK (BfR, 1980). Preliminary analyses in this project have shown that this parameterization gave implausible results when used with the newly implemented water balance module (Sect. 2.1.4). Therefore, to ensure comparability between coupled and uncoupled runs, all FORHYCS runs use the soil parameterization from Remund and Augustin (2015) (see Sect. 2.2.2) in forested cells. In uncoupled runs, it is assumed that the rooting depth of forests is 1 m. As this dataset was developed based on forest soil profiles, values for cells outside currently forested areas are not reliable (Jan Remund, Meteotest, personal communication, 2015). To simulate forest expansion under climate and land-use change scenarios, it was nevertheless assumed that cell values of the RA2015 (Remund and Augustin, 2015) dataset represent the water storage capacity for 1 m of soil depth. To account for shallower rooting of non-forest vegetation types, a land-cover-dependent rooting depth parameter was introduced. The parameter values for different land cover types are given in Table S6. Non-vegetated land cover classes (e.g., built-up or bare rocks) use the same standard soil parameters as in the original PREVAH (Gurtz et al., 1999). Another difference between FORHYCS and PREVAH is the parameterization of canopy resistance. Whereas PREVAH gives a minimum canopy resistance for each land cover class (i.e., normalized by leaf area index), the new water balance module requires a minimum stomatal resistance. Following Guan and Wilson (2009), minimum stomatal resistance was set to 180 s m⁻¹ for forests, 130 s m⁻¹ for meadows and grasslands, and 210 m⁻¹ for shrubs.

One-way coupling is similar to the modeling experiment of Schattan et al. (2013); vegetation variables from TreeMig are passed to PREVAH, but there is no feedback from the hydrological to the forest model. This configuration uses the abiotic drought index calculated with FORCLIM-E (Bugmann and Cramer, 1998). In this study, TreeMig was run with two soil datasets (BEK and RA2015; see below). In all cases, the hydrological part of the model uses the RA2015 dataset. In this study, rooting zone storage capacity SFC of the hydrological model was kept constant in one-way coupled mode, assuming a rooting depth of 1 m. Enabling climate-dependent adaptation of SFC in this mode would impact simulation results for the hydrology part but not for the forest.

2.2 The Navizence case study

2.2.1 Catchment description

The Navizence catchment is located in the Swiss Central Alps and covers an area of 255 km². To enable the future migration of tree species that are currently not represented in the catchment, the modeling area extends beyond the catchment to form the rectangular area shown in Fig. 2 (1079 km²). The catchment is characterized by a sharp elevational gradient, with elevations ranging from 522 to 4505 m a.s.l. Like in its neighboring valleys, this gradient is reflected in the hydro-climatic conditions. Due to the shielding effect of mountain ranges, the Rhône valley, where the catchment outlet is located, is the driest region of Switzerland, with the mean annual precipitation (MAP; 1981–2010) at Sion totaling 603 mm (MeteoSwiss, 2014). However, the valley presents a strong altitudinal precipitation gradient, with MAP exceeding 2500 mm at 3000 m a.s.l., most of it falling as snow (Reynard et al., 2014).

Tree species composition shows a rather clear altitudinal zonation, with drought-resistant species (Pinus sylvestris and Quercus spp.) dominating at lower elevations, whereas Picea abies, Larix decidua, and Abies alba dominate the subalpine stage, and the treeline is formed by Larix decidua and Pinus cembra. The landscape is heavily influenced by human activity, with a large fraction of land occupied by settlements, cropland, vineyards, and pastures. Furthermore, nearly all forests in the area are subject to management in various forms and degrees of intensity, with a considerable impact on forest dynamics. Specifically, many forests were clear-cut between the Middle Ages and the nineteenth century, mostly for fuel (Burga, 1988). In the first half of the twentieth century, the quantitatively most important anthropogenic disturbance factors were litter collecting and wood pasture by goats (Gimmi et al., 2008). Nowadays, these practices have been largely abandoned, and timber harvesting plays a limited role in the region. As a result of past and current anthropogenic factors, the main deviations from potential natural forest composition are (1) silvicultural practices favoring certain species, such as Pinus sylvestris and Larix decidua (2) effects of litter removal and grazing, and (3) a replacement of L. decidua and Pinus cembra by mountain pastures (Büntgen et al., 2006) and dwarf shrubs (Burga, 1988) near the treeline.

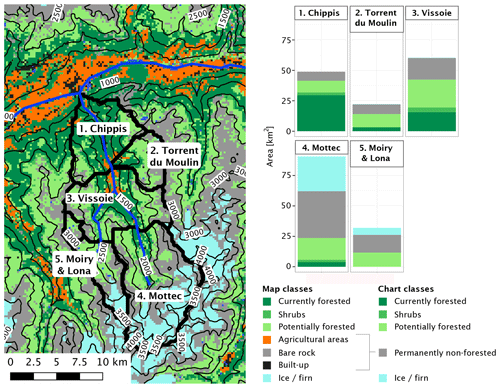
Figure 2 Map of the study area, including the Navizence catchment and the subcatchments used in this study. Streamflow measurements are available for the subcatchments 2 through 5. As the lowest part of the Navizence catchment (subcatchment 1) differs greatly from the others in terms of elevation and current land cover, modeled streamflow is also examined for this subcatchment, although no measurements are available. Forest-related model outputs are evaluated over the entire currently forested area, inside and outside the catchment. Streams are drawn for reference only.

Currently, three major hydropower plants are operational in the valley, with a total installed capacity of 164 MW and a mean net annual production of 570 GWh. The main reservoir is the artificial lake Lac de Moiry, located in a lateral valley, with a storage capacity of 77 million m³. A system of pipelines has been built to divert water from the Navizence, as well as from a neighboring catchment, into the lake.

2.2.2 Input data

Three kinds of spatial data are needed to run the model: daily meteorological data, time-invariant physiographic data, and spatially distributed model parameters for PREVAH. These parameters represent environmental factors not related to vegetation, such as snow, glacier, and runoff generation processes. Further information on the parameterization of PREVAH is given in Sect. S1.7 of the Supplement. The model is driven by daily values for precipitation (in millimeters), air temperature (in degrees Celsius), global radiation (in watts per square meter), wind speed (in meters per second), relative air humidity (percent), and sunshine duration SSD (in hours), provided by the Swiss Meteorological Office MeteoSwiss (Begert et al., 2005).

Physiographic data consists of information on soil, topography and land cover. Soil is represented in terms of water holding capacity κ (in millimeters of water depth per millimeter of soil depth) and soil depth. Two different datasets are used for soil properties. In previous applications in Switzerland, both PREVAH and TreeMig used grids of κ and soil depth from a countrywide agricultural suitability map (BfR, 1980; hereafter referred to as “BEK”). The resulting rooting zone storage capacities (SFC; in millimeters) in the forested cells of the study region range between 3.75 and 110 mm. As this dataset was not specifically developed for use in forests, and some values are implausibly low, Remund and Augustin (2015) generated a new countrywide dataset (RA2015) of rooting zone storage capacity, on the basis 1234 forest soil profiles throughout Switzerland, combined with a lithological map. This dataset gives the volume of water that can be stored in the soil for a depth of up to 1 m, with lower values in cells where soil is assumed to be shallower. SFC in the new dataset ranges from 71 to 223 mm in forested cells of the study region. Figure S1 shows the rooting zone storage capacity in forested cells of the study region for both soil parameterizations. For coupled simulations, only the RA2015 parameterization is used. To facilitate a comparison with results from previous studies, the parent models PREVAH and TreeMig are also run with the BEK parameterization.

2.2.3 Comparison data and metrics of agreement

This section describes the data against which model outputs were compared, including three datasets of vegetation properties and one dataset of streamflow measurements. These datasets are used to plausibilize model outputs and serve as a basis for the choice of model configuration. Daily streamflow was obtained from the operator of the power plants. These data include an accounting of the amount of water diverted through the different pipelines. From this, time series of natural streamflow were reconstructed, which were used as observations. Further details on the streamflow data are given in Sect. S1.9 of the Supplement.

The simulated stem numbers and above-ground biomass were compared against data from the first Swiss National Forest Inventory(NFI; Bachofen et al., 1988). As the sampling plots of the NFI are distributed on a regular grid, each plot is randomly selected from all forest plots in that region and may not be considered representative for a larger area. It is therefore not sensible to compare simulated and observed biomass at the scale of single inventory plots. Instead, the 245 NFI plots in the study area were aggregated to seven classes based on aspect and elevation, with four elevation bands for north-facing plots and three for south-facing plots. This way, each class has a sample size of at least 30 plots, which ensures that the averages are representative. For comparison with inventory data, simulated biomass was also averaged over the same strata.

Simulated LAI was compared to the remotely sensed LAI dataset provided by Copernicus at 300 m resolution (Copernicus Service Information , 2017). This dataset uses measurements of the satellite Proba-V and its temporal coverage starts in January 2014. The LAI 300 m rasters were resampled to match the resolution and extent of the model input and output, then stratified as described above. For each cell of the original LAI 300 m grids, the maximum value of the 10 d periods contained between May and July of the years 2014 through 2016 was used as an estimate of maximum LAI, independent of intra-annual fluctuations. As forest properties are also shaped by local processes not represented in the model (e.g., disturbance or forest management), a direct cell-by-cell correspondence of simulated and observed values is not expected. Furthermore, cells of the remote sensing dataset are spatially heterogeneous and may include non-forested parts. However, it was still assumed that over larger domains, a good correspondence between simulated and observed LAI would be indicative of good model performance. Therefore, the simulations and observations were also stratified by elevation and aspect. As the number of cells is relatively large, smaller elevation bands were chosen than for inventory data. The cells are divided between north- and south-facing aspects, then binned into nine elevation bands. These elevation bands have a fixed width of 200 m, except the lowest (<700 m a.s.l.) and highest (>2100 m a.s.l.). Each zone contains between 100 and 714 forested cells. Model outputs and observations are only evaluated over the areas classified as forests or shrubland in the model input.

Figure 3 (a) Schematic representation of the canopy division into discrete height classes, as used in the model–data comparison. The cumulative fractional cover of a height class is the total visible crown area of that and higher classes, divided by the total vegetated area. In this example, a road (in grey) crosses the cell, which reduces the total vegetated area. (b) For each 200 m×200 m cell, the shade of green represents the lowest height class for which 95 % of the 1 m×1 m cells are lower or equal (H95). (c) An example of a very sparsely vegetated 200 m×200 m cell. The shade of green shows the height of each 1×1 cell. Cells with a height of 0 m are assumed to be bare and are marked black. This cell is located in an area disturbed by a wildfire in 2003. (d) An example of a mountain forest, located at 2000 m a.s.l. The bare areas in this cell are mostly covered by rocks. (e, f) An illustration of the 1−ABC index of agreement between observed and simulated forest structure, applied to the cells shown in (c) and (d). The open dots and solid lines show the cumulative sum of 1×1 cells belonging to each discrete height class, starting from the right (i.e., from the highest class), normalized by the area of the 200 m×200 m cell which is not bare. The full dots and dashed lines represent the cumulative relative coverage of each height class as simulated by FORHYCS. As the wildfire is not reflected in the model, the simulation shows a fully developed forest in the cell shown in (c), leading to a poor match between simulated and observed canopy structure. On the other hand, the forest simulated in the cell shown in (d) corresponds well to the observed structure, leading to a high 1−ABC score.

The recently developed Switzerland-wide vegetation height dataset at 1 m resolution of Ginzler and Hobi (2016), derived from stereo aerial images, was compared against simulated canopy structure. To compare the level of agreement between observed and simulated canopy structure, two novel metrics were introduced. The rationale behind these metrics is illustrated in Fig. 3. Both measures are based on the discrete height classes used in TreeMig and use the cumulative fractional cover of each height class, starting from the highest class. In the illustrative example of Fig. 3a), the cumulative fractional cover of the height class 5–10 m corresponds to the visible crown area of the height classes 5–10 m and 10–15 m, divided by the potentially vegetated area (i.e., excluding the area occupied by a road, shown in grey). In each cell of the model grid, the fractional cover of each height class is calculated from the simulated species–size distribution using the procedure described in Eqs. (3) and (4). For each height class i, the cumulative fractional cover f_c,i is defined as follows:

$$\begin{array}{}\text{(16)}& \begin{array}{rl}& f_{\mathrm{c},i}=\\ & \left[\mathrm{1}-\exp \left(-\mathrm{1}\times \sum _{\mathrm{sp}=\mathrm{1}}^{\mathrm{nspc}}\sum _{\mathrm{hc}=i}^{\mathrm{nhcl}}\left(n_{\mathrm{sp},\mathrm{hc}}/\mathrm{833}\right)\times {\mathrm{CA}}_{\mathrm{sp},\mathrm{hc}}\right)\right].\end{array}\end{array}$$

The procedure used to calculate fractional cover is based on the assumption that trees are randomly distributed in space and accounts for overlap between crowns. For example, applying Eq. (16) to the upper three height classes will return the fractional cover for the trees belonging to these classes, accounting for overlap between them. This assumes that shading of lower parts of their crowns by smaller trees can be neglected.

As can be seen in the examples in Fig. 3c and d, each cell from the model grid covers 200×200 cells of the observations grid. Therefore, for each model cell, the observed fractional cover is calculated from the relative number of high-resolution cells belonging to each height class. Observed cells with a height of 0 m represent non-vegetated surfaces such as roads, water bodies or buildings and were excluded from the analysis. Indeed, as the model does not contain any land cover information on subgrid level, these elements are an irreducible source of disagreement between observations and simulations. On the other hand, observation cells with a height between 0 and 1.37 m are assumed to be covered by ground vegetation and decrease the total fractional canopy cover in a coarse cell. The first cell-level measure of agreement is the difference in observed and simulated H95, i.e., the lowest height class for which the cumulated fractional cover (starting from 0) equals or exceeds 95 % of the total fractional cover. Fig. 3b shows the H95 of the observations, at the level of model cells. The second measure of agreement is illustrated in Fig. 3e and f. The cumulative fractional cover of each class (starting from the top) is plotted for observations and simulations. The better the agreement, the closer the curves are to each other. Therefore, the second measure of agreement, termed 1−ABC (where ABC stands for “area between the curves”), is defined as the fraction of the plot area not contained between the curves. The plot in Fig. 3e applies this to the cell shown in Fig. 3c and represents a case with a poor agreement between simulations and observations. Indeed, this area was devastated by a wildfire and is thus currently very sparsely forested. As this fire is not represented in the model, the simulations indicate a fully developed forest. Even in this extreme case, the ABC does not exceed 40 % of the plot area. Therefore, a 1−ABC score of 0.6 can be considered a poor fit. On the other hand, the sample cell in Fig. 3d and f show a good agreement between observations and simulations, with 1−ABC exceeding 0.99. These two measures of agreement can be used to evaluate the performance of a model by examining their distribution over the whole simulation domain. A better performing model will have a higher proportion of cells with a ΔH95 (difference of the 95th percentile of tree height between observed and simulated forest structure) close to 0 and a 1−ABC close to one. Furthermore, the spatial distribution of ΔH95 and 1−ABC may give insight into the factors that contribute to agreement or disagreement between simulations and observations.

2.2.4 Simulation experiments

To evaluate the behavior of the coupled model FORHYCS and the importance of the different forest–hydrology couplings implemented, two series of simulation experiments have been conducted. An overview of the different simulation runs is given in Table 1. In a first series of experiments, the simulations start with no forest, and a full succession is modeled. The names for these simulations start with “S”. The second part of the name indicates whether these experiments were conducted in fully coupled mode “F” or in one-way coupled mode “T”. The next part indicates which couplings are switched on and off, as per Table 1. Finally, for the one-way coupled runs, the fourth part of the name indicates the source of the soil water holding capacity BEK or “RA15”; see the next paragraph. In a second series of experiments, starting with “C”, the model was run with several climate change scenarios (see below). In this set of experiments, the model was run in uncoupled (U), one-way coupled (T) and fully coupled mode (F). In addition, a simulation with standalone PREVAH was run, “P”. For the fully coupled simulations, two additional experiments were run (see below), testing the effect of CO₂ on stomatal resistance, “_NCS”, standing for “No CO₂ effect on stomatal resistance”, and land cover change “_LC”.

Remund and Augustin (2015)Remund and Augustin (2015)

Table 1 Overview of the conducted simulation experiments.

In the succession experiments, the simulations start with no forest, and a full succession is modeled. The simulations span a period of 515 years, where the last 45 years are the years 1971 to 2015. For the first 470 years, the meteorological forcing consists of years bootstrapped from the period 1981 to 2000. In two cases (S_T_BEK and S_T_RA15), the model is run in uncoupled mode, and only the forest output is evaluated. This is equivalent to a standard TreeMig run. The difference between the two runs is the parameterization of the rooting zone storage capacity for the (abiotic) drought stress module (FORCLIM-E; Bugmann and Cramer, 1998). In the first case, the storage capacity in each cell is given by the soil depth and water holding capacity given in the Swiss soil map for agricultural suitability (referred to as BEK; BfR, 1980), as in previous TreeMig applications in Switzerland (e.g., Bugmann et al., 2014). In the second case, the parameterization of Remund and Augustin (referred to as RA15; 2015) is used. As noted in Sect. 2.2.2, the soil water holding capacity is much larger in the RA2015 dataset for most cells. As a result, the (abiotic) drought index also shows great differences between the two model runs. Figure S1c and d show the difference in mean annual drought index (1971–2015), and maximum annual drought index between the BEK and RA2015 parameterizations. Due to the considerable effect of maximum height reduction (Sect. 2.1.3) on the coupled model, two additional TreeMig runs were performed with this effect enabled, to facilitate the comparison between coupled and uncoupled runs.

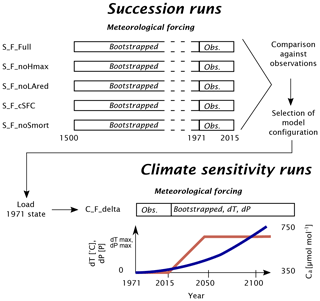
Figure 4 Workflow of the various simulation experiments conducted in this study. The succession runs (S_) use bootstrapped meteorological forcing for 470 years, followed by observed forcing for the period 1971–2015. FORHYCS is run with several configurations, as described in Table 1. The output from each run is then compared against observations, based on which one configuration is selected for the runs under idealized climate change (C_). The modifiers for temperature and precipitation (red line) are scaled linearly between 0 and their maximum in the period 2016–2050. Atmospheric CO₂ concentration C_a (blue line, approximate illustration) has no effect on the temperature and precipitation modifiers but impacts the canopy resistance.

In coupled mode, FORHYCS is run with different configurations, with the various couplings described in Sect. 2.1 switched on or off (maximum height reduction, stress-induced leaf area reduction, dynamically varying rooting depth, and snow-induced seedling mortality). Based on pilot study results, the configuration S_F_noLAred (all couplings switched on, except leaf area reduction) was selected as the best configuration, as it produced the most plausible long-term biomass dynamics (see Sect. 3.2.1) and shows a good fit to observed canopy structure (see Sect. 3.2.2), and the other configurations in Table 1 differ from S_F_noLAred by only one process switched on or off.

The configuration S_F_noLAred is also used for the second set of model runs, which start in the year 1971 and end in 2100. In the idealized climate change runs, the sensitivity to a ramp-shaped climate change is evaluated (see Fig. 4). In the period 1971–2015, observed forcing is used. From 2016 to 2100, years are randomly selected from the period 1981–2015 (excluding the abnormally dry and hot year 2003). Furthermore, from 2016 on, daily temperature is incremented by a given number of degrees dT, and daily precipitation is scaled by a given factor dP. The values of these factors are given in Table 1. To emulate a gradual progression of climate change, these factors are scaled linearly between 0 and their full value between 2016 and 2050. The runs C_F_NCS test the impact of the CO₂ effect on stomatal closing, implemented through Eq. (12). In these runs, the CO₂ response function is always set to 1; i.e., stomatal response to high CO₂ is switched off, whereas in all other runs, this effect is active. In all the runs presented so far, forest growth is restricted to the currently forested cells. In the C_F_LC runs, forest is allowed to grow in all potentially forested land cover classes. Thus, the potential ecohydrological consequences of land abandonment and rising treelines are examined. In addition to the runs with delta change, three runs were performed with meteorological forcing from downscaled regional climate simulations, generated in the CH2018 project (National Centre for Climate Services, 2018). CH2018 contains the output of climate model runs from the EURO-CORDEX initiative (Kotlarski et al., 2014) , downscaled to a 2 km×2 km grid. While there are 39 climate model chains available in the CH2018 dataset, running FORHYCS with each of them would be beyond the scope of this study. Instead, the three chains selected by Brunner et al. (2019) to represent dry, intermediate, and wet conditions were used. The characteristics of the three chains are given in Table 2. For more information on the model chains, we refer to Brunner et al. (2019). It is worth noting that precipitation in the GCM-RCM chains is higher than in the observations for this region. Mean annual precipitation differs by 300 to 600 mm yr⁻¹, depending on period and subcatchment (see Fig. S2 in the Supplement). Due to these differences, a comparison of the absolute model outputs between delta change runs and GCM-RCM chain runs is of little value. Therefore, the analysis shall focus on the difference between coupled and uncoupled runs for the different scenarios. Precipitation also differs in terms of event frequency (Fig. S3) and mean intensity (Fig. S4); the latter is consistently higher for the three GCM-RCM chains, whereas for the former, observed values lie between the two extreme values of the model chains. The model chains also differ with regard to temperature; the mean annual and seasonal (May–October) temperatures in two arbitrarily selected grid cells (one in the bottom of the Rhone valley at 667 m a.s.l. and one near the treeline at 2160 m a.s.l.) are shown in Fig. S5.

Table 2 Characteristics of the three climate model chains used in the C_F_scen runs: global climate model (GCM), regional climate model (RCM), relative concentration pathway (RCP), and spatial resolution of the climate model.

3 Results

3.1 Plausibilization of simulated streamflow

To evaluate model efficiency, the Kling–Gupta efficiency (KGE, Gupta et al., 2009) was applied to daily streamflow for the period April 2004–December 2008 in subcatchments 2 to 5 (Table 3). The scores were calculated for three different model runs: uncoupled FORHYCS (C_U), fully coupled FORHYCS (C_F), and the original PREVAH (C_P; the version used in Speich et al., 2015) for reference. There is little difference between the scores of these three runs, and no model version consistently outperforms the others. The last four columns of Table 3 show the observed and simulated mean annual streamflow for the period 2005–2007 (the years for which there are no gaps in the observations). The sums simulated by PREVAH are consistently greater than for FORHYCS, with differences between PREVAH and uncoupled FORHYCS ranging between 40 (Moiry) and 172 mm yr⁻¹ (Chippis). The values simulated with coupled FORHYCS are somewhat higher than with the uncoupled version at the lower elevation subcatchments (35 mm yr⁻¹ in subcatchment 1 and 6 mm yr⁻¹ in subcatchment 2) but almost equal in the two high-elevation catchments 4 and 5. Figure 5a shows the daily values (30 d rolling means) for subcatchment 3 (Vissoie; analogous figures for the other gauged subcatchments are given in Figs. S6–S8). The main differences between PREVAH and the FORHYCS runs occur in late summer and autumn, where streamflow simulated by PREVAH is consistently higher. The differences between the two FORHYCS versions are shown in Fig. 5b). The greatest differences occur in winter and early spring, with some peaks in spring 2005 and 2006 and consistently higher streamflow in the winters 2006–2007 and 2007–2008.

Table 3 Kling–Gupta Efficiency (KGE) scores obtained by three different model configurations – standalone PREVAH (C_P), uncoupled FORHYCS (C_U), and fully coupled FORHYCS (C_F) – against daily observed streamflow data for the period 2004–2008 (first three columns) and mean annual streamflow sums Q_a [mm yr⁻¹] for the period 2005–2007 (observed and simulated).

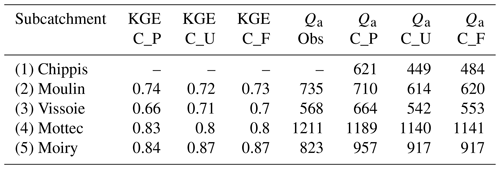
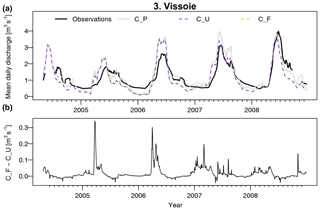
Figure 5 (a) Observed vs. simulated daily streamflow for subcatchment 3 (Vissoie) for the period 2004–2008. For clarity, the plot shows rolling averages with a 30 d window. The plot shows results for two FORHYCS runs, uncoupled (C_U), and fully coupled (C_F). For reference, the results obtained with standard PREVAH (C_P) are also shown. (b) Difference in simulated daily streamflow between the coupled and uncoupled versions of FORHYCS. Unlike in (a), values are not shown as rolling averages. Streamflow simulated with coupled FORHYCS is usually higher than for the uncoupled version, and the greatest differences occur in winter and spring.

3.2 Forest spin-up with different model configurations

3.2.1 Biomass and species composition

Figure 6 shows the above-ground biomass simulated with FORHYCS using the configuration S_F_noLAred (fully coupled succession simulation with all vegetation–water couplings switched on except leaf area reduction; analogous figures for the other configurations are provided in the Supplement; Figs. S9 to S16). In addition, the bar shows the average above-ground biomass of trees in plots of the first Swiss national forest inventory (1982–1986; Bachofen et al., 1988). The simulations start in 1500 with no trees. Biomass increases quickly at the beginning, so that in most zones, values close to 100 t ha⁻¹ are reached within the first 40 years. The initial species composition consists of various broadleaf species, among which the maple species Acer campestre and A. pseudoplatanus. After this initial state, Pinus sylvestris (mainly at lower elevations) and Larix decidua (mainly at higher elevations) start developing. Finally, Quercus species (lower elevations, mainly Q. pubescens and Q. petraea), Abies alba (north-facing slopes), and Picea abies develop, with the latter becoming dominant at higher elevations. At the end of the simulation, the forest seems to have reached a state in which the relative importance of species changes little over time. At lower elevations, the state at the end of the simulation is close to that reached after the first 100 or 200 years. By contrast, at high elevations, the replacement of L. decidua by P. abies occurs over a much longer time.

At low elevations, simulated biomass is higher than the inventory value, especially on north-facing slopes. By contrast, simulated biomass is lower than the observed value at intermediate elevations. Unlike in simulations, for slopes reaching below 1346 m, there is almost no Quercus and Acer biomass in the inventory data, and the share of other broadleaves is also much smaller. Also at intermediate elevations, FORHYCS simulates a higher biomass for Acer and other broadleaves. However, L. decidua makes up one-third of observed biomass in that elevation band, while it is practically nonexistent in the simulations. Also at higher elevations, the simulated biomass of L. decidua is much lower than in the inventory data.

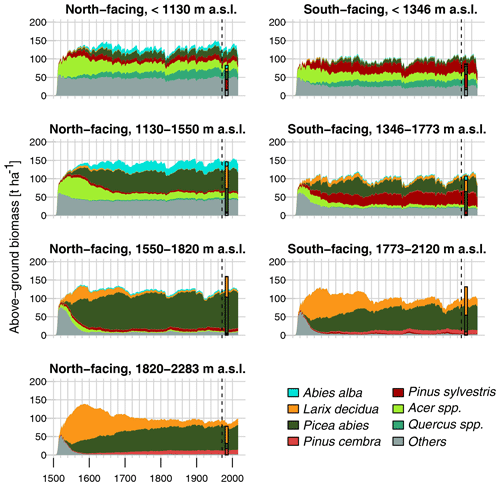
Figure 6 Above-ground tree biomass simulated with FORHYCS using the configuration S_noLAred (Table 1). The graphs show annual values, averaged over seven clusters of cells. The bar shows the above-ground biomass in the same area, from the first Swiss national forest inventory (1982–1986; Bachofen et al., 1988). The limits of the elevation bands were set so that each cluster contains at least 30 forest inventory plots. The dashed line marks the year 1971, from when meteorological data are available. Simulation years before 1971 use meteorological data bootstrapped from the years 1981–2000.

The results of S_T_noHmax_BEK (one-way coupled succession simulation with low soil moisture storage capacity; Fig. S9) differ greatly from those in Fig. 6. Pinus sylvestris is dominant at intermediate elevations, whereas high elevations are dominated by L. decidua. P. abies is hardly represented, and simulated biomass for broadleaves is very low. Fluctuations of simulated biomass are also much higher, with increases or decreases of up to 70 t ha⁻¹ within 20 years. For S_T_noHmax_RA15 (one-way coupled succession simulation with high soil moisture storage capacity; Fig. S10), biomass equals or exceeds 200 t ha⁻¹ in all strata except at the highest elevations. The mesophilous species Abies alba and P. abies dominate at all elevations. For TreeMig runs with maximum height reduction (S_T_Hmax_BEK and S_T_Hmax_BEK; Figs. S11 and S12), species composition is similar to the results of standard TreeMig but with much lower biomass.

The configuration S_F_Full differs from S_F_noLAred in that LAI is reduced as a function of drought or low temperatures. Biomass simulated with this configuration (Fig. S13) is markedly higher than with S_F_noLAred, especially at lower and intermediate elevations, while species composition is similar. Biomass also fluctuates more for S_F_Full at lower and intermediate elevations. For S_F_noHmax (no reduction of maximum tree height due to water availability or temperature; Fig. S14) and S_F_cSFC (constant rooting depth of 1 m; Fig. S15), biomass is also higher than for S_F_noLAred. In the former case, species composition is similar to S_F_noLAred, whereas for S_F_cSFC, the share of relatively drought intolerant species is larger at lower elevations (e.g., higher share of P. abies and lower share of Pinus sylvestris). Biomass simulated with S_F_noSmort (no snow-induced sapling mortality; Fig. S16) shows no apparent difference from S_F_noLAred.

3.2.2 Canopy structure

The distribution of the two metrics of agreement between observed and simulated canopy structure is shown in Fig. 7. The distribution of ΔH95 shows large differences between the model configurations. While S_T_noHmax_RA15 has its maximum count of ΔH95 at 25.2 m and overestimates H95 in almost all cells, S_T_noHmax_BEK shows a much flatter distribution, with a large number of under- and overestimations. By contrast, the TreeMig runs with maximum height limitation have their maximum count at 0 m, suggesting a better fit. Most of the FORHYCS runs show a similar pattern, with a peak close to 0 m, and most values contained between −16.8 and 21 m. S_F_noHmax, however, has its maximum at 16.8 m and overestimates H95 in almost all cells. The distribution of the 1−ABC scores, shown in the lower plot, also sets apart the two configurations with the largest overestimation of H95, S_T_noHmax_RA15, and S_F_noHmax. These runs have their highest density at a lower value than the other configurations. The other FORHYCS runs all have their highest density around 0.95. While S_F_Full shows a distribution of ΔH95 that is very similar to S_F_noLAred and S_F_noSmort, its density distribution for 1−ABC differs from that of the other two configurations. S_F_Full has a lower density around 0.95 but a higher density between 0.7 and 0.85, indicating a lower degree of agreement between observations and simulation for this configuration.

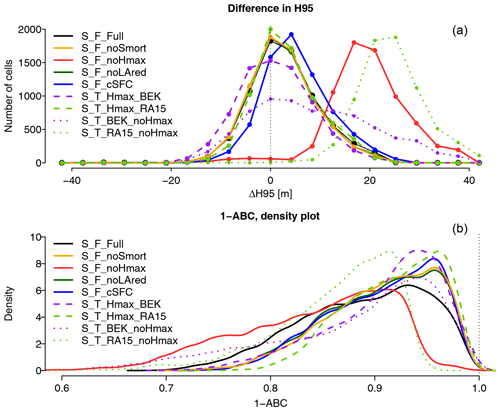
Figure 7 Distribution of the two goodness-of-fit metrics for canopy structure described in Sect. 2.2.3 over all forested cells of the simulation domain (n=7138). Graph (a) shows the distribution of ΔH95 (difference between H95 for simulated and observed data) for the different model configurations listed in Table 1. More values closer to 0 indicate a better agreement between observed and simulated canopy structure. As H95 uses the height classes of TreeMig, the results are given as discrete values with an interval of 4.2 m. Graph (b) shows the density distribution of the 1−ABC scores (bandwidth =0.0075). The better the agreement between observed and simulated canopy structure, the more values are close to 1.

3.2.3 Leaf area index

Figure 8 shows a comparison of the Copernicus 300 m LAI and values simulated with the different TreeMig and FORHYCS configurations listed in Table 1. For the observations, the average forest LAI for the different elevation and aspect classes range approximately between 2 and 4. The lowest values occur on south-facing slopes below 700 m a.s.l. (i.e., close to the bottom of the Rhône valley). LAI of the south-facing slopes increases steadily with elevation up to 1700–1900 m a.s.l., where it reaches a value of 4. For cells over 2100 m a.s.l., LAI is again somewhat smaller. LAI is generally higher on north-facing slopes. There is little difference among the elevation bands between 700 and 2100 m a.s.l. Average LAI is always around 4 in that elevational range. Smaller values occur only in the lowest and highest elevation bands. The TreeMig runs differ greatly in the range and pattern of simulated LAI. For S_T_Hmax_BEK, parameterized with available water capacity (AWC) from the soil suitability map (BfR, 1980), the values range between 2 and 6. The highest values occur in the lowest elevation band and, for north-facing slopes, at 1700–1900 m a.s.l. Except for the lowest elevation band, LAI on north-facing slopes is markedly higher than on south-facing slopes, with differences of up to 2.5. By contrast, for S_T_Hmax_RA15, which uses the AWC from Remund and Augustin (2015), the absolute values are much higher and the variability much lower. For all elevation bands, values range between 6.5 and 7.5. The results for TreeMig runs with height limitation are almost equal to the standard version.

There is less difference in patterns and absolute values among the FORHYCS runs. The absolute values range from 4 to 7. Spread is lowest for the two highest elevation bands, where all configurations give a value of approximately 6, for both north- and south-facing slopes. At lower elevations, there is a clear difference between the two aspect classes, with consistently higher values for the north-facing slopes. The difference between configurations increases with decreasing elevation and is somewhat higher on south-facing slopes. The configuration S_F_cSFC consistently returns the largest values. On north-facing slopes, the values are lowest for S_F_noLAred. This is also the case at higher elevations on south-facing slopes, whereas at lower elevations, S_noHmax returns the lowest values. In most cases, the results of S_F_Full and S_F_noLAred are similar. Up to 1300–1500 m a.s.l. on north-facing slopes, S_F_Full gives somewhat higher values, whereas on south-facing slopes, the value for S_F_noLAred is higher. In all cases, the symbols for S_F_noSmort are indistinguishable from S_F_noLAred.

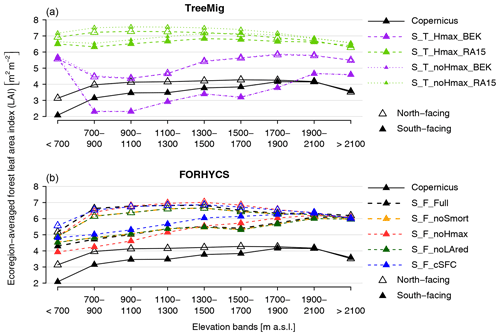
Figure 8 Observed and simulated leaf area index (LAI), averaged over elevation bands and aspect classes. The observed values show the average of cell-level maximum LAI of the period 2014–2016. The simulated values correspond to the averages of the largest annual maximum LAI values in the last three years of the succession runs (2013–2015). Graph (a) shows LAI simulated with TreeMig, using two different parameterizations for soil moisture storage capacity. The purple symbols show results of TreeMig runs parameterized with the soil suitability map (BfR, 1980), whereas the green symbols correspond to TreeMig runs parameterized with the dataset of Remund and Augustin (2015). Graph (b) shows the results of the various FORHYCS succession runs, with the configurations listed in Table 1.

3.3 Climate change runs

3.3.1 Differences between uncoupled, one-way coupled, and fully coupled model runs

Figure 9 shows how area-averaged LAI and rooting zone storage capacity SFC change for all future simulations (the results are shown here as rolling means with a 30-year window; a version without smoothing is given in Fig. S17). LAI and SFC are averaged over two of the strata used in Fig. 6, the lowest stratum of south-facing cells (Fig. 9a and c) and the highest stratum of north-facing cells (Fig. 9b and d). Figure 9a shows the results of the coupled run for the low-elevation south-facing cells. At the end of the succession run, LAI is approximately 6, and over the next century the values range between 3.5 and 6.5 for all runs except the dry GCM-RCM chain. Long-term average LAI is lower for warmer and drier runs. In particular, under the dry GCM-RCM chain, LAI starts to decrease sharply around 2050, with values less than 2 at the end of the simulation (Fig. S17). The plot of annual values (Fig. S17) shows that under warmer scenarios, the variability in LAI is much higher, with LAI decreasing much more in certain years than in less warm scenarios. In other years, annual LAI values strongly converge between scenarios. For SFC, values decrease for drying scenarios and increase for wetting scenarios, with consistently higher values for the GCM-RCM chains than for the delta change runs. The high-elevation north-facing cells (Figs. 9b, S17b) also show a decrease in long-term average LAI and an increase in variability under drying and warming scenarios. Also here, the dry GCM-RCM chain stands out, with a sharp decrease in LAI from the middle of the century. SFC initially increases in all scenarios. Around 2050 (when the temperature and precipitation modifiers reach their maximum), SFC starts decreasing, with a faster decrease in drying delta change runs.

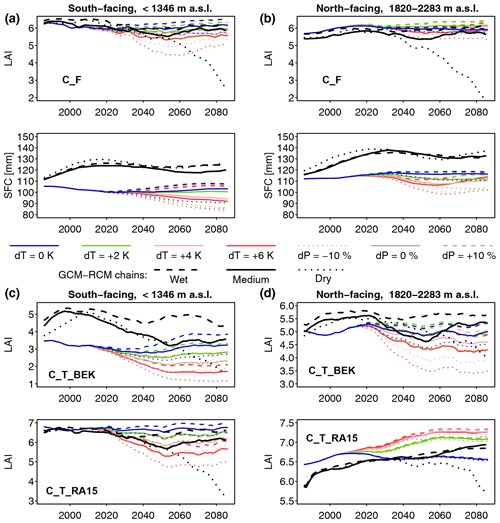
Figure 9 (a) Annual maximum LAI (top) and rooting zone storage SFC (bottom) under idealized climate change scenarios, simulated using coupled FORHYCS (C_F). LAI and SFC are averaged over the cells belonging to the lowest elevation class with south-facing slopes (same stratification as for Fig. 6. The results are shown as 30-year rolling means. In the delta change runs, both LAI and SFC generally increase under wetting delta runs and decrease under drying delta runs, although trends are not always monotonic. While the wet and medium scenarios are in the same range as the delta runs, the dry scenario leads to a marked decrease from about 2050. (b) Same as panel (a) but for the highest elevation class with north-facing slopes. Also here, LAI increases under wet scenarios and decreases under dry scenarios. SFC trajectories show large differences between scenarios. (c) LAI simulated with TreeMig, with the two different soil parameterizations (C_T_BEK and C_T_RA15). Note the different scales on the y axis. LAI simulated with C_T_BEK is markedly lower than for C_F, whereas the C_T_RA15 values are somewhat higher. (d) Same as panel (c) but for the highest elevation class with north-facing slopes.

Due to the similarity of LAI simulated by TreeMig with and without height reduction (cf. Fig. 8), only the results for the version without height reduction are shown. LAI differs greatly between the two TreeMig simulations, especially for the low-elevation south-facing cells (Figs. 9c, S17c). With C_T_BEK (one-way coupling with low soil moisture storage capacity), LAI is approximately at 3.5 at the end of the succession run and decreases to less than 1.5 in the warmest and driest scenario (T6_P-10). Unlike with fully coupled FORHYCS, the dry GCM-RCM chain leads to values within the range of the delta runs at the end of the simulations. By contrast, under C_T_RA15 (one-way coupling with high soil moisture storage capacity), LAI decreases from 6.5 to 5 in the T6_P-10 scenario. Interannual variability increases with C_T_RA15 but not with C_T_BEK (Fig. S17c). Here, as for the fully coupled runs, the dry GCM-RCM chain leads to substantially lower values than the other runs. In the high-elevation north-facing cells, the LAI trajectories diverge between the two TreeMig parameterizations. Under C_T_BEK, as for the lower elevation cells, LAI decreases under the T6_P-10 scenario while interannual variability increases. On the other hand, with C_T_RA15, LAI increases under all warming delta change runs. LAI also decreases noticeably under the dry GCM-RCM chain but remains around 5.5 at the end of the simulation.

Figure 10a shows simulated annual streamflow (30-year rolling means) for subcatchment 1 (Chippis), as simulated with uncoupled FORHYCS (equivalent graphs for the other subcatchments are provided in Figs. S18 to S21 in the Supplement). From initially 550 mm yr⁻¹, streamflow decreases by about 50 % under the most extreme warming and drying delta scenario (temperature increase of 6 K and precipitation decrease by 10 %). The three GCM-RCM chains show little difference to each other, no clear trends and consistently lead to higher mean annual runoff than all delta change runs. Figure 10b, c, and d show the difference in annual streamflow to the uncoupled run (Fig. 10a), for the one-way coupled runs (C_T_BEK and C_T_RA15) and the fully coupled FORHYCS runs (C_F), respectively. In all cases, streamflow is higher in the coupled runs. For C_T_BEK, the difference is approximately 30 mm yr⁻¹ at the end of the succession and increases under idealized climate change. The increase is greater for warmer scenarios, with a difference of 60 mm yr⁻¹ for the warmest delta change scenarios (T6_Py) at the end of the simulation. For the GCM-RCM chains, the difference is usually smaller than for most delta change runs. The difference in annual streamflow is much less for C_T_RA15 and ranges between 5 and 20 mm yr⁻¹. Here, the difference in streamflow decreases with idealized climate change, with a more pronounced decrease for the warmer delta change scenarios. For the fully coupled runs, the initial difference is around 30 mm yr⁻¹, which is similar to the initial difference for C_T_BEK. During idealized climate change, the difference does not increase as much as for C_T_BEK: the largest difference on the order of 40 mm yr⁻¹. The only exception is the dry GCM-RCM chain, where streamflow difference starts increasing sharply around 2050 to reach 60 mm yr⁻¹ at the end of the simulation. Unlike for TM_BEK, the delta change scenarios with the greatest difference by the end of the simulation are the three warming and drying scenarios.

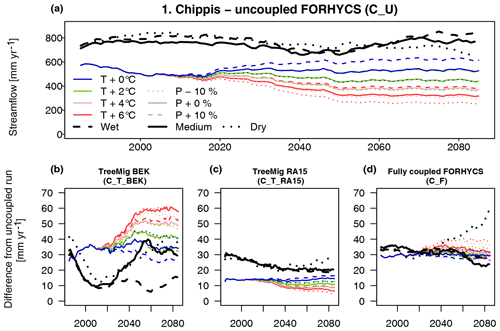
Figure 10 (a) Simulated annual streamflow (30-year rolling means) in the Chippis subcatchment (lowest elevation; most forested). In the warmest dry delta change scenario (T6_P-10), annual streamflow is reduced approximately by half, from 550 to less than 300 mm yr⁻¹. (b, c) Difference in annual streamflow in the runs with one-way coupling, relative to the uncoupled run. (d) Difference in annual streamflow in the fully coupled FORHYCS run, relative to the uncoupled run. In all coupled runs, streamflow is greater than in the uncoupled version, due to lower LAI (see Figs. 8 and 9; the standard PREVAH value for forest LAI is 8) and, for the fully coupled version, smaller rooting zone storage capacity SFC.

3.3.2 Effect of CO₂ concentration

The increase in stomatal resistance due to increased CO₂ concentration (Eq. 12) has a minimal effect on streamflow and area-averaged forest properties (see Fig. S22 in the Supplement). In C_F_NCS (the runs in which Eq. 12 is set to one), streamflow is consistently lower than in the C_F runs. The greatest difference occurs towards the end of the simulation period in the Chippis subcatchment, with differences up to 10 mm yr⁻¹. The differences are largest in the simulations with a precipitation increase. Regarding vegetation properties, the differences in LAI and SFC, averaged over the strata used in Fig. 6, never exceed 0.05 m² m⁻² and 1 mm, respectively.

3.3.3 Effect of land-use change

Figure 11 shows the difference in annual streamflow (30-year annual means) between a fully coupled run without land-use change (C_F) and a run in which forest is allowed to grow in all cells with a “potentially forested” land cover type (see Fig. 2). The three subcatchments shown here differ by elevation and distribution of land cover classes. Chippis is the lowest subcatchment and has few cells belonging to the potentially foreste' land cover classes. By contrast, the high-elevation subcatchments Mottec and Moiry are barely forested (Mottec) or have no forest cells at all (Moiry). In the warmest scenarios, LAI and rooting zone storage capacity reached values of 5.5 and 120 mm, respectively, by the end of the simulation even in the highest elevation band of meadows (cells above 2700 m a.s.l.). In all cases, allowing land cover change leads to a decrease in streamflow. The magnitude of this change depends greatly upon the warming scenario. When no warming is assumed, the difference in streamflow relative to the simulation without land cover change is approximately 10 mm yr⁻¹. In all three subcatchments, the difference is greatest under warmer and wetter scenarios. The difference increases rapidly until 2050 (when the temperature and precipitation modifiers reach their maximum), whereas the increase is slower or partially reversed between 2050 and 2100.

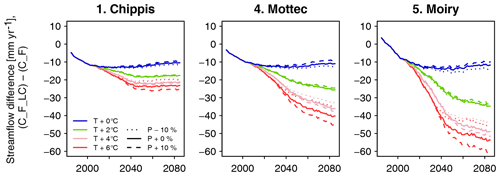
Figure 11 Difference in simulated annual streamflow (30-year rolling means) between the standard fully coupled runs (C_F) and the coupled runs with land abandonment (C_F_LC) for three contrasting subcatchments. In the land abandonment scenario, forest is allowed to grow in all cells classified as meadows and alpine vegetation. The Chippis subcatchment has relatively few meadows, whereas they occupy about a third of the high-elevation catchment Moiry (see Fig. 2). Forest expansion leads to streamflow reduction due to the higher leaf area and potentially deeper roots. As most meadows are located at high elevations, the effect of forest expansion on streamflow greatly depends on the warming scenario.

4 Discussion

4.1 Effect of coupling on hydrological simulations

The plausibilization of simulated streamflow (Sect. 3.1) showed that PREVAH in its original version, as well as coupled and uncoupled FORHYCS yielded similar goodness-of-fit scores in the four gauged subcatchments of this study. The differences between standard PREVAH and the two FORHYCS versions are much larger than between coupled and uncoupled FORHYCS. As noted in Sect. 2.1.7, the main difference between standard PREVAH and uncoupled FORHYCS is the parameterization of rooting zone storage capacity SFC. As this difference is considerable (see Fig. S1), the differences in daily streamflow seen in Fig. 5 are to a large extent due to the differing SFC parameterizations. Due to the small differences between the results of coupled and uncoupled FORHYCS, it is not possible to conclude whether varying vegetation properties has led to an improvement of model performance. In the fully coupled version, simulated LAI is quite close to the default values in PREVAH (cf. Fig. 8; standard summer LAI for forests in PREVAH is 8). As seen in Fig. 8, LAI is smaller when simulated with C_T_BEK in most elevation bands. A comparison of the simulated streamflow shown in Sect. 3.1 with output from a one-way coupled simulation with C_T_BEK (not shown) shows differences of only 3 mm yr⁻¹ between one-way and two-way couplings, except in the ungauged catchment 1 (Chippis), where the difference is 24 mm yr⁻¹. This suggests that the effect of the coupling on hydrological model outputs varies spatially, which is in line with the findings of Schattan et al. (2013).

The relatively modest effect of the coupling on simulated streamflow, especially in the high-elevation subcatchments, is consistent with the findings of Schattan et al. (2013), whose study domain also included the Navizence catchment. They found a differential effect of transient vegetation parameters on simulated streamflow, with the greatest effects at low elevations (where LAI is much lower than the generic parameter value of the hydrological model) and above the current treeline (where the forest may expand in the future). The issue of scale is also of relevance; as forested cells make up a relatively small fraction of each subcatchment (Fig. 2), even an important change in the water balance of some forested cells will have little influence on catchment-integrated streamflow. The most extreme example of change in vegetation parameters in this study in the runs using meteorological forcing from the GCM-RCM model chain representing dry conditions. In this run, forest LAI greatly decreases throughout the study region (Fig. 9), leading to a difference in simulated streamflow of up to 60 mm yr⁻¹ between the coupled and uncoupled runs (Fig. 10). This shows the value of including vegetation dynamics for hydrological modeling under severe change.

While leaf area and rooting depth are among the most sensitive vegetation parameters for surface water partitioning (Milly, 1993; Nijzink et al., 2016; Speich et al., 2018a), FORHYCS does not represent all possible impacts of forest dynamics on hydrological processes. For example, forest properties have been related to hydrological model parameters relating to snow (Seibert, 1999) or soil properties (Johst et al., 2008). Badoux et al. (2006) found that forest site type was a good indicator of the dominant runoff processes. While this does not imply a causal relationship between forest characteristics and runoff generation in all cases, some of the differences between runoff processes could be explained by forest properties, such as hydrophobicity of conifer needle litter, which promotes fast runoff processes. On the other hand, forest soils are often associated with low runoff coefficients. Johst et al. (2008) parameterized the soil moisture recharge BETA as a function of land cover type. This parameter, which controls the partitioning of precipitation between plant-available soil moisture and runoff generation, is also used in the local water balance modules of PREVAH and FORHYCS (see Speich et al., 2018a). Speich et al. (2018a) found that BETA was a relatively sensitive parameter for the physiological drought index of FORHYCS. Currently, snow and runoff generation parameters are static in PREVAH and FORHYCS. As they have been obtained through regionalization, it may be challenging to relate their values to specific forest properties. However, representing the effects of forest dynamics on these processes might further reduce the dependence on calibrated and regionalized parameter values.

4.2 Effect of coupling on forest simulations

To assess the effect of various forest-hydrology couplings on the performance of the forest models, several outputs and state variables were compared against observations. For various reasons, a perfect match between simulated and observed vegetation properties cannot be expected. First, the model simulates the potential natural vegetation dynamics, without considering forest management or disturbances such as fire or avalanches, which again have impacts on stand age. Second, the succession is modeled using bootstrapped meteorological forcing data, which do not contain any trends and may differ greatly from the actual climate in past centuries. Third, the spatial scales of model outputs and observations are not the same. For all these reasons, the comparison against observations serves as a plausibilization rather than a rigorous validation of the model. Nevertheless, it is assumed that when aggregated to a larger scale, a qualitative comparison with observations can still give some indication of the skill of the model. The fully coupled FORHYCS gave reasonable results for biomass, species composition and stand structure (simulated LAI is discussed in the next paragraph). It is important to remember that the coupled and uncoupled forest simulations used two different drought indices, one that depends on transfer variables from PREVAH equations and one that is calculated before the simulations, respectively (see Sect. 2.1.3). The species-specific drought tolerance parameters used with one index cannot be used with the other. Therefore, it is difficult to assess to what extent the differences in model outputs are due to the coupling or to the different parameterization. In any case, representing the effect of water availability (and low temperatures) on maximum height greatly improved the simulation of canopy structure, also in uncoupled models, as seen by the better fit to observed canopy structure for the runs which include this effect (Fig. 7). By contrast, reducing leaf area as a function of stress leads to poorer results regarding canopy structure, as well as unrealistic biomass fluctuations. Two main effects happen in the model as a result of LAI reduction, which are as follows: (1) the drought index (Eq. 5) is lower than it would be without LAI reduction; (2) the light distribution is modified; i.e., lower height classes get more light than they would get without LAI reduction. These two effects both promote tree growth, which explains why the model simulates higher biomass. This higher growth also eventually leads to greater mortality, after the number and size of trees have grown fast for some years. This explains the more dynamic pattern when LAI reduction is activated (Fig. S13).

Simulated leaf area index (LAI) varies greatly between the TreeMig and FORHYCS runs (Fig. 8). The pattern of LAI simulated with C_T_BEK (one-way coupling with low soil moisture storage capacity) across elevation bands follows the distribution of soil moisture storage capacity, which is displayed in Fig. S1. Indeed, the flat areas at the bottom of the Rhône valley are the only areas where storage capacity exceeds 100 mm. Therefore, LAI is high for the lowest elevation band. By contrast, storage capacity on the slopes is much lower, so LAI initially sharply decreases with elevation. With C_T_RA15, water is hardly limiting, so LAI is high at all elevations. LAI simulated with FORHYCS shows a similar pattern to the remotely sensed data, with an initial increase with elevation and consistently higher values on north-facing than on south-facing slopes, except at the highest elevations. The absolute values, however, are consistently higher than the observations, sometimes offset by a factor of 2. Various factors hinder a direct, quantitative comparison of measured and simulated LAI. First, the 300 m×300 m cells of the remotely sensed dataset may contain non-forested surfaces, such as pastures, clearings, roads, or water bodies, even if the cell is classified as forest. The model does not consider this type of spatial heterogeneity. This is especially relevant in regions with a high spatial variability in land cover, as is the case in this study region. Second, remotely sensed LAI is subject to some uncertainty, due for example to the clumping of needles in coniferous forests (Garrigues et al., 2008). Despite a good overall performance, the authors of the validation report for the Copernicus LAI 300, product Camacho et al. (2016, p. 83), note that forests were underrepresented in the validation dataset. Therefore, it is difficult to say to what extent FORHYCS overestimated LAI in this study. Schleppi et al. (2011) measured LAI at 91 forested sites across Switzerland and used a regression against stand parameters to predict LAI in forests throughout the country. Their measured values range between 1 and 7. They noted a decrease of LAI with elevation, as well as a limitation of LAI due to water availability for sites with annual precipitation below 1000 mm. The values simulated by FORHYCS thus appear plausible at intermediate elevations, where the effects of both water availability and low temperatures are moderate. By contrast, terrestrial LAI measurements at the bottom of the Rhône valley (Dobbertin et al., 2010) are between 2 and 2.5. Despite the presence of patches with more mesic forest types, especially in the proximity of water bodies (Matthias J. R. Speich, personal observation, 2017), such values can be taken as representative for the xeric forests in the Rhône valley. The values simulated by TreeMig and FORHYCS are much higher than this for this elevation band. At high elevations, the decrease in LAI is not as pronounced in the simulations as in the observations (Fig. 8). These results suggest that the spatial variability in LAI is somewhat underestimated by the model, especially where an environmental factor is particularly limiting.

4.3 Effect of coupling on model behavior under climate change

The models used in this study are very similar to those used in the simulation experiment of Lischke and Zierl (2002). In that experiment, they coupled the gap model DisCForM, from which TreeMig was later derived, with a point-scale water balance model which is conceptually similar to the new local water balance module of FORHYCS. They found that the coupling of forest dynamics and water balance had a stabilizing effect on the simulated system under climate change. In their experiment, coupled simulations converged towards low LAI and lower levels of physiological drought. This effect is not visible to the same extent in the simulations conducted here. The effect of warming on forests is less pronounced in the fully coupled runs, as evidenced by the evolution of streamflow differences in Fig. 10. However, it cannot be excluded that this is due to the different drought tolerance parameters or to the lesser sensitivity of the FORHYCS drought index to changes in temperature. In contrast to the study of Lischke and Zierl (2002), FORHYCS includes some additional mechanisms through which the system can react to changes in climate, such as the adaptation of rooting depth and maximum tree height. Some processes may even have a destabilizing influence on the system, such as the high fluctuations in biomass introduced by the stress-induced leaf area reduction.

An exception to the generally resilient behavior of forests under climate change are the GCM-RCM runs representative for dry conditions. In these runs, the forest greatly deteriorates throughout the study region, even under the C_F configuration (Fig. 9). Interestingly, under this meteorological forcing, precipitation is higher than in the delta change scenarios, in which this severe reduction of forest LAI does not occur (see Sect. 2.2.4 and Fig. S2). Therefore, the high stress causing this LAI reduction must have been caused mainly by changes in potential evaporation or temporal precipitation distribution. While this study has shown a range of possible model behaviors under various climate change scenarios, future research should examine more formally the effect of different bioclimatic factors on the behavior of forest models under climate change. For example, understanding the physiological significance of bioclimatic drought indices is important to interpret how a forest model responds to different scenarios (Speich, 2019). Also, rooting depth has been shown to be an important interface variable for the coupling of hydrology and vegetation dynamics. In the runs presented in this study, ecoregion-integrated rooting zone storage capacity fluctuated by up to 30 mm over the course of a simulation covering 130 years. The rooting depth formulation used in FORHYCS responds to bioclimatic and edaphic conditions in complex and nonlinear ways (Guswa, 2008, 2010; Speich et al., 2018b). As the inclusion of this variable is rather new in dynamic models, its magnitude and dynamics should be plausibilized against empirical evidence, using e.g., inverse modeling (Nijzink et al., 2016)

4.4 Effect of additional processes

4.4.1 CO₂ concentration

Results of this modeling experiment have shown that an increase in atmospheric CO₂ concentration has almost no effect on hydrological processes and vegetation dynamics as modeled by FORHYCS. In this implementation, the physiological effect of elevated CO₂ concentration is represented by an additional modifier function to the stomatal resistance parameterization. All else being equal, an increase in C_a leads to an increase in stomatal resistance and thus to a decrease in potential and actual transpiration. This slows down canopy water use and thus leads to lower levels of simulated physiological drought. This formulation does not account for other physiological impacts of elevated C_a, such as enhanced photosynthetic rates or possible acclimation effects. The physiological effect of increased C_a is a source of uncertainty in forest models, due to widely differing process formulations among models (Medlyn et al., 2001). For example, our results contrast with the simulations of (Scherstjanoi et al., 2014), who applied a modified version of LPJ-GUESS and found a crucial influence of C_a on simulated future forest biomass in Switzerland. These differences between models are partly due to the knowledge gaps regarding the underlying processes. According to Medlyn et al. (2011), models that do not consider the physiological effects of C_a at all are likely to underestimate future forest productivity, whereas some other models are likely to yield overestimates due to an improper representation of other limiting factors. From an ecohydrological point of view, the large-scale effects of increased C_a have been the object of a number of recent studies. For example, Trancoso et al., 2017) found that decreases in streamflow in Australian catchments were caused by vegetation greening, which was in turn driven by elevated C_a. These studies suggest that the stomatal effects of increased C_a (transpiration reduction) are more than offset by enhanced vegetation growth. This is not the case in this study, where the only visible effect was an increase in streamflow, whereas vegetation properties were not affected at all.

4.4.2 Land cover change

In this simulation experiment, allowing the forest to grow in areas currently covered by meadows caused a reduction of streamflow of up to 60 mm yr⁻¹ at subcatchment level (Fig. 11). This is a substantially greater effect than in the simulation experiment of Schattan et al. (2013), who found a change in annual runoff on the order of 10 mm yr⁻¹ in regions currently above the treeline as they become forested under simulated climate change. Under the scenario used in their study, temperature was projected to increase by 3–4 K by the end of the century. A major difference with this study is that they only varied LAI, whereas in this study, the development of both LAI and rooting depth were simulated. Both of these variables probably had a major impact on simulated streamflow. These spectacular results must be considered in the light of several potential sources of uncertainty in the model formulation. First, FORHYCS does not account for competition by other vegetation types, which may slow down the expansion of forests. Also, other factors that make the current treelines an extreme environment are not considered by FORHYCS, such as the steep slopes and shallow soils. For example, it was shown that during the warmest period of the Holocene, only stunted trees were able to establish at high elevations, although the climate would have allowed a forest to grow (Theurillat and Guisan, 2001). Another aspect to consider is that at the beginning of the simulation, meadows and alpine vegetation types were parameterized with a prescribed rooting depth of 22 cm. This value was set arbitrarily, and if it was actually higher for these vegetation types, the hydrological impact of forest expansion would be exaggerated in the simulations.

5 Conclusions and Outlook

This study presented a proof of concept for a dynamic, spatially distributed model combining hydrological processes and forest dynamics. The main interface variables are a leaf area index, the rooting depth, and a physiological drought index. This model was applied in a case study in a valley with a sharp topographical and hydro-climatic gradient.

The motivation behind developing this model was to apply it to climate change impact studies in which the spatio-temporal forest dynamics and water balance of Switzerland are simulated together. The closer integration of these ecosystem processes would increase the confidence in these model projections, compared to uncoupled models that do not account for changes in the environment besides climate. The research considered questions of (1) how model coupling impacts the results of simulated water balance and forest dynamics, (2) which aspects of the coupling were particularly relevant, and (3) how model coupling affects simulation results under climate change. From the hydrological point of view, the coupling had only a modest effect on catchment-integrated streamflow, although this effect was not uniform in space; the greatest effects occurred at low elevations and in regions currently above the treeline. Regarding forest simulations, model results were compared against multiple data sources to examine model behavior and pinpoint potential weaknesses. In a comparison with a new high-resolution canopy height dataset, two new indices of agreement between observed and simulated forest structure were developed. This comparison confirmed the importance of specifying an environmental limitation on maximum tree height, as this greatly improved the realism of simulated canopy structure and biomass. Also, a dynamic parameterization of rooting depth led to better model performance. In combination with remotely sensed LAI data, this model–data comparison showed that the coupled model was better able to reproduce observed spatial patterns, although it also highlighted potential deficiencies in the way drought impacts are represented. Under (idealized) climate change, the forests in the coupled model show greater resilience, which translates into a reduced sensitivity of mean annual streamflow to changes in temperature and precipitation. In some cases, the behavior of the model seems exaggerated but demonstrates the importance of explicitly modeling relevant processes. This was the case with regard to the possible expansion of forests above the current treeline. On the other hand, the effects of increased CO₂ concentration on plant physiology are less than what observations suggest, highlighting the challenges of incorporating physiological principles into phenomenological models. As these areas are the object of active research, it is expected that new analyses will provide an opportunity to test model behavior under these novel conditions and possibly to improve process formulations.