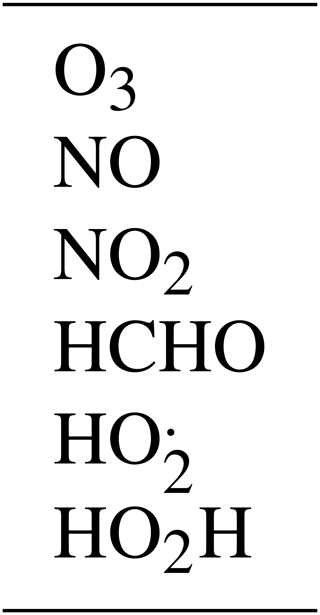the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A mass- and energy-conserving framework for using machine learning to speed computations: a photochemistry example
Anthony S. Wexler
Large air quality models and large climate models simulate the physical and chemical properties of the ocean, land surface, and/or atmosphere to predict atmospheric composition, energy balance and the future of our planet. All of these models employ some form of operator splitting, also called the method of fractional steps, in their structure, which enables each physical or chemical process to be simulated in a separate operator or module within the overall model. In this structure, each of the modules calculates property changes for a fixed period of time; that is, property values are passed into the module, which calculates how they change for a period of time and then returns the new property values, all in round-robin between the various modules of the model. Some of these modules require the vast majority of the computer resources consumed by the entire model, so increasing their computational efficiency can either improve the model's computational performance, enable more realistic physical or chemical representations in the module, or a combination of these two. Recent efforts have attempted to replace these modules with ones that use machine learning tools to memorize the input–output relationships of the most time-consuming modules. One shortcoming of some of the original modules and their machine-learned replacements is lack of adherence to conservation principles that are essential to model performance. In this work, we derive a mathematical framework for machine-learned replacements that conserves properties – say mass, atoms, or energy – to machine precision. This framework can be used to develop machine-learned operator replacements in environmental models.
- Article
(115 KB) - Full-text XML
- Companion paper
- BibTeX
- EndNote
Complex systems require large models that simulate the wide range of physical and chemical properties that govern their performance. In the air quality realm, models include CMAQ (Foley et al., 2010), CAMx (Yarwood et al., 2007), WRF-Chem (Grell et al., 2005), and GEOS-Chem (Eastham et al., 2014). In the climate change arena, models include HadCM3 (Jones et al., 2005), GFDL CM2 (Delworth et al., 2012), ARPEGE-Climat (Somot et al., 2008), CESM (Kay et al., 2015), and E3SM (Golaz et al., 2019). These models employ operator splitting, also called the method of fractional steps (Janenko, 1971), in their structure so that each module can be tasked with representing one or a small number of physical and/or chemical processes. This modular structure enhances model maintenance and sustainability while enabling diverse physical and chemical processes to interact. Each module is tasked with simulating its processes over a fixed period of time, each module called in turn until they have all returned their results. Usually, the computational performance of these models is governed by one or two modules that consume the vast majority of the computer resources. In air quality models, this is usually the photochemistry and/or aerosol dynamics modules. In climate models, this is usually the radiative energy transport module.
Machine learning has been used to improve the computational efficiency of modules in atmospheric models for decades (Potukuchi and Wexler, 1997). As machine learning algorithms have improved, these efforts have matured (Hsieh, 2009; Kelp et al., 2018; Rasp et al., 2018; Keller and Evans, 2019; Pal et al., 2019). But the effort to replace physical and chemical operators with machine-learned modules is challenging because small systematic errors can build. For instance, a 0.1 % error over a 1 h time step could lead to a 72 % error after a month of simulation. This problem is compounded if the replacement module does not conserve quantities that are essential to model accuracy, such as atoms in a photochemical module, molecules and mass in an aerosol dynamics module, or energy in a radiative transfer module.
Recent efforts at developing and using machine-learned replacement modules has focused on memorizing how the quantities change. Some have also explored enforcing physical constraints when memorizing these quantities via postprediction balancing approaches (Krasnopolsky et al., 2010), introducing a penalty into the cost function (Beucler et al., 2019) or incorporating hard constraints on a subset of the output in neural network architecture (Beucler et al., 2019). All of these approaches focus on memorizing how quantities change and incorporate some correction strategy after all or a portion of the quantities have been predicted. If instead we focus on how the fluxes between quantities change, we can guarantee adherence to conservation principles to machine precision without a postprediction correction. In photochemical modules, the fluxes are how atoms move between chemical species as reactions progress. In aerosol dynamics, the fluxes are the condensation and evaporation or coagulation processes that move material between the gas and particle phases or between particle sizes. In radiative transfer, the fluxes are the energy movements between spatial domains.
In this work, we derive a mathematical framework that enables the use of machine learning tools to memorize these fluxes. We focus this work on atmospheric photochemistry and provide an example for a simple photochemical reaction mechanism because the number of species and the complexity of the problem exercises many aspects of the framework.
In general, the atmospheric chemistry operator solves
where C is a vector containing the current concentration of the chemical species, T is temperature, and RH is the relative humidity. A full list of symbols can be found in Appendix A. The right-hand side can be written as
where A is a matrix describing the stoichiometry, and R is a vector of reactions. The form of the right-hand side assures mass balance because it is composed of reactions that destroy one species while creating one or more other ones, all in balance, described by A. The R terms take forms such as kCiCj, where k is the rate constant for a reaction between species; JCi, where J is the photolysis reaction rate; or k(Ci(x1)−Ci(x2)), where k is a diffusion or mass transport rate constant between two spatial locations or between the gas and particle phases.
In the method of fractional steps, all modules integrate their equations forward for a fixed time step, Δt, that we call the operator-splitting time step. Combining these two equations and integrating gives
or in matrix form
where Sj equals . Sj is the flux integral. For atmospheric photochemistry, it is the flux of atoms between molecules. For aerosol dynamics, it is the flux of molecules condensing on or evaporating from particles or the flux of small particles coagulating on large particles. For radiative transfer, Sj is the energy between spatial coordinates. We are able to pull the A out of the integral if it is a constant, which is usually the case or can be approximated as such.
Using machine learning tools to learn the relationship
has advantages over memorizing a concentration–concentration relationship because of the following:
- a.
The formulation in Eq. (3) conserves mass.
- b.
The R terms are simpler to memorize because they do not contain the complexity in A.
- c.
There are fewer concentrations directly influencing S than C, so the machine learning algorithm should be simpler.
The difficulty resides in developing the training and testing sets needed to train and test the machine learning algorithm corresponding to Eq. (4). In principle, we can run a model many times, generate a data set, and then learn that data using machine learning techniques. That is, we can run many models that integrate Eq. (1) to find the relationship between concentrations at two time steps to develop our machine learning training set. But such models do not provide the value of S, and since the chemical system is stiff, the integrators make many complex calls to calculate the right-hand side of Eq. (1) and integrate it. Another way of saying this is that the ΔC is easily available from the models, but the S is not.
If we have many sets of ΔC values, in principle we can invert Eq. (3b) to obtain the corresponding S values. The difficulty with this approach is that there are more elements of S than ΔC, so a conventional inverse cannot be applied. Instead, we employ the generalized inverse of A to obtain S via the relationship
where AG is the generalized inverse of A. In the case that there are as many fluxes as quantities (A is a square matrix), and the quantities are coupled but linearly dependent (A is full rank), then AG is the true inverse of A and readily calculable. If the system is overdetermined, where A is a rectangular matrix with more quantities than fluxes but has full column rank, then a left inverse can calculate AG. An overdetermined system is typical in an aerosol module calculating condensation and evaporation, where fluxes depend on two quantities. However, if A is underdetermined, meaning there are more fluxes than known quantities, or A is otherwise rank-deficient from linear dependency, there is an infinite number of generalized inverses AG. This means that given values for ΔC, Eq. (5) will not give reliable values for S.
Given sufficient constraints, AG will be unique and provide the desired values of S that are needed to develop a machine learning training set. Ben-Israel and Greville (2003) show that the inverse can be unique if the solutions, S, are restricted to lie in a subspace that defines the “legal” solutions, and these restrictions are sufficiently constraining. The constrained generalized inverse of A produces solutions, S, that lie in the legal subspace defined by good examples of solutions. S is given by
where is the generalized inverse of A restricted to the subspace of all possible solutions by the projection PS, which in turn is defined by a set of basis vectors that define the subspace. Before we discuss obtaining the basis vectors, we first need to discuss how to obtain the projection, PS.
Assume for the moment that we have the basis vectors Sk. We concatenate them (column-wise) to form the matrix U:
The projection onto the subspace defined by these basis vectors Sk and the matrix U is then (Mukhopadhyay, 2014)
where U+ is the transpose of U.
Atmospheric-chemistry problems are stiff, so the U+U may be ill-conditioned. One source of this ill-conditioning, which can also hamper machine learning tools, is that the concentrations are often orders of magnitude apart. The modules use actual concentrations to make the mechanism easier to understand and debug. Normalizing the concentrations helps with both learning and stiffness and ill-conditioning. Ill-conditioned problems can hamper matrix inversion. Since the S vectors describe the subspace where the solutions must reside, their magnitude does not matter, just their direction. So we normalize the S vectors by dividing by the average of the nonzero values. Mathematically, we form a diagonal square matrix, NS, with the averages on the diagonal and calculate the normalized S with
Since NS is diagonal, the inverse is simply the reciprocal of each diagonal element. The ΔC values are recovered from the Snorm values via
Atmospheric-chemistry problems are also high-dimensional. Typical air quality models may have 100 to 200 chemical species, and since the vertical-column-mixing timescale is similar to the slower timescales of the chemistry, some models solve the vertical transport and chemistry simultaneously. Since typical air quality models have 10 to 20 vertical cells, the dimension of the problem is 1000 to 4000. Even though the inverse only has to be calculated once, this inversion may be intractable. Providing that the condition number of U+U is not too large, Gram–Schmidt orthonormalization can be performed on the Si vectors before carrying out Eqs. (7) and (8), in which case they will describe the same subspace, but now the matrix U+U will be the identity matrix, which is its own inverse.
Now let us return to the question of how to find the basis vectors that define the “legal” subspace of S. These can be developed by solving Eq. (1) using Euler's method, in which case Eq. (3) becomes
that is
The value of Δt does not matter since it just changes the length of Sk, not its direction and therefore not its value in describing the subspace. The original module that calculates Rk can be run many times under many conditions to generate a set of Sk vectors that span the subspace. Then locality-preserving projections (LPPs), principal component analysis (PCA), or another similar algorithm can be used to find a minimum set of vectors that define the subspace.
The following overview aims to put into context the procedure outlined in this paper. The focus of this paper is on deriving and conducting the mass balancing framework and inverse problem detailed in steps 1–9. Steps 10–13 are provided for context: these include machine learning, operator replacement, and benchmarking. In principle, any machine learning algorithm can be used with the framework described here in steps 1–9.
-
Determine which species are active in the photochemical mechanism, that is, not the steady-state or buildup species.
-
From the mechanism, extract the A matrix for these species.
-
Using a representative set of atmospheric concentrations, T, RH, and actinic flux, use Eq. (10) and the photochemical module to generate data that match values of ΔC and S for many values of C, T, RH, and actinic flux for the models operator-splitting time step.
-
Normalize the S vectors by dividing each by the average of its nonzero elements. Use these averages to form the NS matrix, which relates S to Snorm via Eq. (9).
-
Use the Snorm vectors and Eq. (7) to form the U matrix and then the U+U matrix. What is the condition number of the U+U matrix? If the system is large and not ill-conditioned, use Gram–Schmidt orthonormalization on the S vectors before calculating U and U+U, in which case U+U should be an identity matrix or a subset of one.
-
Use Eq. (8) to calculate PS.
-
Use Eq. (6) to calculate the constrained generalized inverse .
-
Use Eq. (5) to calculate values of S from the values of ΔC.
-
Compare the values of S obtained from steps 3 and 7 to make sure they are very similar, using the dot product to calculate the angle between them. If they are, we have a good .
-
Use neural networks or another machine learning algorithm to memorize the S(C) relationship obtained using (a) Eq. (5) and (b) many runs of the mechanism for a wide range of C, T, RH, and actinic flux values.
-
Replace the mechanism with the neural network to calculate S(C) and Eq. (3b) to march forward.
-
Clock the speed improvement.
-
Calculate standard measures of performance such as mass balance, bias, and error compared to runs using the complete mechanism.
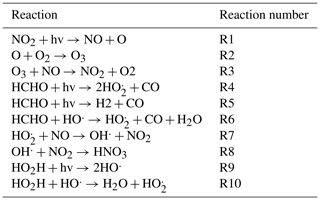
We tested the methods described above on the following very simplified set of photochemical reactions used by Michael Kleeman at the University of California, Davis, when teaching the modeling of atmospheric photochemistry. Although this mechanism is abbreviated, it contains the essential components of all atmospheric photochemical mechanisms related to ozone formation: NOx chemistry, volatile organic compound (VOC) chemistry, and the formation of peroxy radicals from VOC chemistry that then react with NO to form NO2 and OH, both of which may react to terminate.
The 10 reactions are given in Table 1. The oxygen atom and hydroxyl radical are assumed to be in a steady state, so there are six active species, which are listed in Table 2.
The resulting A matrix represents the stoichiometry of the reactions, where the rows correspond to each species and the columns to each reaction:
As in prior efforts (Kelp et al., 2018; Keller and Evans, 2019), we employed a box model in Julia to generate 60 independent days of output for both ΔC and S, recording data every 6 min. We are interested in the set of S vectors that form a basis describing the subspace that contains the desired S vectors. First, the transformation in Eq. (9) is performed to normalize the sample S vectors. In this example, we use LPP (He and Niyogi, 2004), which is similar to PCA but more robust for this application. Here the LPP yields a basis set of seven vectors, which form the columns of the U matrix:
High condition numbers mean that the matrix inversion is problematic at best. The condition number of U+U is approximately 12. This is several orders of magnitude smaller than the same problem but without the NS transformation of Eq. (9), where the condition number was 1888. This suggests that the NS transformation has potential to reduce ill-conditioning arising from stiffness in S. The condition number of 12 after the NS transformation ensures that the inversion needed to make the projection PS in Eq. (8) is numerically tractable.
The resulting symmetric block diagonal projection PS is equal to
And Eq. (6) gives us
Since U and have seven and six independent columns, respectively, but 10 rows, and the row rank is equal to the column rank, there must be linearly dependent rows. One manifestation of this is that the first two rows of U and are identical or nearly so. The S values computed from may not be identical to the original S corresponding to the ΔC values. However, all S values calculated from Eq. (5) using the above are “legal”, in other words, within the subspace defined by the basis set U. Furthermore, the inverse by definition satisfies so that even if a calculated S is not identical to the S from the original box model output, it can be used in Eq. (3b) to return a ΔC identical to that of the box model output.
Large models of the environment require the solution of large systems of equations over long periods of time. These models consume vast quantities of computational resources, so approximations are necessarily employed so that the models are computationally tractable. Machine learning tools can be used to dramatically improve the speed of these models, enabling a more faithful representation of the physics and chemistry while also improving runtime performance. But this field is in its infancy. To help facilitate the use of machine learning tools in these environmental models, we have developed a framework that (a) enables machine learning algorithms to learn flux terms, assuring that conservation principles dictated by the physics and chemistry are adhered to, and (b) allows parameters easily calculated by geophysical models to be used to back-calculate these flux terms that can then be used to train the machine learning algorithm of choice. Applications of this framework in environmental models include any process where conservation principles apply, such as conservation of atoms in chemical reactions; conservation of molecules during phase change; and conservation of energy in, say, radiative transfer calculations.
| Ci(t) | concentration at time t |
| Ci(t+Δt) | concentration at time t+Δt |
| the number of molecular species | |
| Δt | operator-splitting time step |
| Rj(t) | contribution to ΔCi from each reaction |
| the number of reactions, m>n | |
| A | a sparse stoichiometry matrix relating ΔCi to Sj; most element values are 0, 1, or −1 |
| AG | generalized inverse of A |
| constrained generalized inverse of A | |
The most current version of the MATLAB script used to generate and the projection is available at https://doi.org/10.5281/zenodo.3712457 (Sturm, 2020a) and the input data at https://doi.org/10.5281/zenodo.3733502 (Sturm, 2020b). The exact version of the script used to produce the results used in this paper is named GenerateAG.m and is archived on Zenodo (https://doi.org/10.5281/zenodo.3733594; Sturm and Wexler, 2020). The input files required for this script as well as the Julia mechanism are available on Zenodo as S.txt and delC.txt (https://doi.org/10.5281/zenodo.3733503; Sturm, 2020c). Both the restricted inverse script and the input data are available under a Creative Commons Attribution 4.0 International license.
ASW initiated the project and is responsible for the conceptualization of the mass balancing framework. ASW and POS contributed to the formal analysis, including the generalized inverse and preconditioning approach. POS developed the model code using Julia and MATLAB.
The authors declare that they have no conflict of interest.
Michael Kleeman at University of California, Davis, contributed the photochemical mechanism, which was modified to create the data needed to calculate the restricted inverse.
The LPP MATLAB program was written by Deng Cai at the Zhejiang University College of Computer Science and Technology, China.
Both the Fortran and LPP programs were essential in calculating the restricted inverse described in this paper.
This paper was edited by David Topping and reviewed by two anonymous referees.
Ben-Israel, A. and Greville, T. N.: Generalized inverses: theory and applications, Springer Science & Business Media, 2003.
Beucler, T., Rasp, S., Pritchard, M., and Gentine, P.: Achieving Conservation of Energy in Neural Network Emulators for Climate Modeling, arXiv, available at: https://arxiv.org/abs/1906.06622 (last access: 17 June 2020), 2019.
Delworth, T. L., Rosati, A., Anderson, W., Adcroft, A. J., Balaji, V., Benson, R., Dixon, K., Griffies, S. M., Lee, H.-C., and Pacanowski, R. C.: Simulated climate and climate change in the GFDL CM2. 5 high-resolution coupled climate model, J. Climate 25, 2755–2781, https://doi.org/10.1175/JCLI-D-11-00316.1, 2012.
Eastham, S. D., Weisenstein, D. K., and Barrett, S. R.: Development and evaluation of the unified tropospheric–stratospheric chemistry extension (UCX) for the global chemistry-transport model GEOS-Chem, Atmos. Environ. 89, 52–63, https://doi.org/10.1016/j.atmosenv.2014.02.001, 2014.
Foley, K. M., Roselle, S. J., Appel, K. W., Bhave, P. V., Pleim, J. E., Otte, T. L., Mathur, R., Sarwar, G., Young, J. O., Gilliam, R. C., Nolte, C. G., Kelly, J. T., Gilliland, A. B., and Bash, J. O.: Incremental testing of the Community Multiscale Air Quality (CMAQ) modeling system version 4.7, Geosci. Model Dev., 3, 205–226, https://doi.org/10.5194/gmd-3-205-2010, 2010.
Golaz, J. C., Caldwell, P. M., Van Roekel, L. P., Petersen, M. R., Tang, Q., Wolfe, J. D., Abeshu, G., Anantharaj, V., Asay-Davis, X. S., and Bader, D. C.: The DOE E3SM coupled model version 1: Overview and evaluation at standard resolution, J. Adv. Model Earth. Sy., 11, 2089–2129, https://doi.org/10.1029/2018MS001603, 2019.
Grell, G. A., Peckham, S. E., Schmitz, R., McKeen, S. A., Frost, G., Skamarock, W. C., and Eder, B.: Fully coupled “online” chemistry within the WRF model, Atmos. Environ., 39, 6957–6975, https://doi.org/10.1016/j.atmosenv.2005.04.027, 2005.
He, X. and Niyogi, P.: Locality preserving projections, Advances in neural information processing systems 16, MIT Press, 153–160, 2004.
Hsieh, W. W.: Machine learning methods in the environmental sciences: Neural networks and kernels, Cambridge university press, 2009.
Janenko, N. N.: The method of fractional steps, Springer, 1971.
Jones, C., Gregory, J., Thorpe, R., Cox, P., Murphy, J., Sexton, D., and Valdes, P.: Systematic optimisation and climate simulation of FAMOUS, a fast version of HadCM3, Clim. Dynam., 25, 189–204, 2005.
Kay, J. E., Deser, C., A. Phillips, A., Mai, A., Hannay, C., Strand, G., Arblaster, J. M., Bates, S., Danabasoglu, G., and Edwards, J.: The Community Earth System Model (CESM) large ensemble project: A community resource for studying climate change in the presence of internal climate variability, B. Am. Meteorol. Soc., 96, 1333–1349, https://doi.org/10.1175/BAMS-D-13-00255.1, 2015.
Keller, C. A. and Evans, M. J.: Application of random forest regression to the calculation of gas-phase chemistry within the GEOS-Chem chemistry model v10, Geosci. Model Dev., 12, 1209–1225, https://doi.org/10.5194/gmd-12-1209-2019, 2019.
Kelp, M. M., Tessum, C. W., and Marshall, J. D.: Orders-of-magnitude speedup in atmospheric chemistry modeling through neural network-based emulation, arXiv preprint arXiv:1808.03874, 2018.
Krasnopolsky, V. M., Rabinovitz, M. S., Hou, Y. T., Lord, S. J., and Belochitski, A. A.: Accurate and Fast Neural Network Emulations of Model Radiation for the NCEP Coupled Climate Forecast System: Climate Simulations and Seasonal Predictions, Mon. Weather Rev., 138, 1822–1842, https://doi.org/10.1175/2009MWR3149.1, 2010.
Mukhopadhyay, N.: Quick Constructions of Non-Trivial Real Symmetric Idempotent Matrices, Sri Lankan Journal of Applied Statistics 15, 57–70, https://doi.org/10.4038/sljastats.v15i1.6794, 2014.
Pal, A., Mahajan, S., and Norman, M. R.: Using Deep Neural Networks as Cost-Effective Surrogate Models for Super-Parameterized E3SM Radiative Transfer, Geophys. Res. Lett., 46, 6069–6079, https://doi.org/10.1029/2018GL081646, 2019.
Potukuchi, S. and Wexler, A. S.: Predicting vapor pressures using neural networks, Atmos. Environ., 31, 741–753, https://doi.org/10.1016/S1352-2310(96)00203-8, 1997.
Rasp, S., Pritchard, M. S., and Gentine, P.: Deep learning to represent subgrid processes in climate models, P. Natl. Acad. Sci. USA, 115, 9684–9689, https://doi.org/10.1073/pnas.1810286115, 2018.
Somot, S., Sevault, F., Déqué, M., and Crépon, M.: 21st century climate change scenario for the Mediterranean using a coupled atmosphere–ocean regional climate model, Global Planet. Change, 63, 112–126, https://doi.org/10.1016/j.gloplacha.2007.10.003 2008.
Sturm, P. O.: A MATLAB Script to Generate a Restricted Inverse, Zenodo, https://doi.org/10.5281/zenodo.3712457, 2020a.
Sturm, P. O.: Photochemical Box Model in Julia, Zenodo, https://doi.org/10.5281/zenodo.3733502, 2020b.
Sturm, P. O.: Photochemical Box Model in Julia, v0.1.0, Zenodo, https://doi.org/10.5281/zenodo.3733503, 2020c.
Sturm, P. O. and Wexler, A. S.: A MATLAB Script to Generate a Restricted Inverse, v0.2.0, Zenodo, https://doi.org/10.5281/zenodo.3733594, 2020.
Yarwood, G., Morris, R. E., and Wilson, G. M.: Particulate matter source apportionment technology (PSAT) in the CAMx photochemical grid model, Air Pollution Modeling and Its Application XVII, Springer, 478–492, https://doi.org/10.1007/978-0-387-68854-1_52, 2007.