A multirate mass transfer model to represent the interaction of multicomponent biogeochemical processes between surface water and hyporheic zones (SWAT-MRMT-R 1.0)

Surface water quality along river corridors can be modulated by hyporheic zones (HZs) that are ubiquitous and biogeochemically active. Watershed management practices often ignore the potentially important role of HZs as a natural reactor. To investigate the effect of hydrological exchange and biogeochemical processes on the fate of nutrients in surface water and HZs, a novel model, SWAT-MRMT-R, was developed coupling the Soil and Water Assessment Tool (SWAT) watershed model and the reaction module from a flow and reactive transport code (PFLOTRAN). SWAT-MRMT-R simulates concurrent nonlinear multicomponent biogeochemical reactions in both the channel water and its surrounding HZs, connecting the channel water and HZs through hyporheic exchanges using multirate mass transfer (MRMT) representation. Within the model, HZs are conceptualized as transient storage zones with distinguished exchange rates and residence times. The biogeochemical processes within HZs are different from those in the channel water. Hyporheic exchanges are modeled as multiple first-order mass transfers between the channel water and HZs. As a numerical example, SWAT-MRMT-R is applied to the Hanford Reach of the Columbia River, a large river in the United States, focusing on nitrate dynamics in the channel water. Major nitrate contaminants entering the Hanford Reach include those from the legacy waste, irrigation return flows (irrigation water that is not consumed by crops and runs off as point sources to the stream), and groundwater seepage resulting from irrigated agriculture. A two-step reaction sequence for denitrification and an aerobic respiration reaction is assumed to represent the biogeochemical transformations taking place within the HZs. The spatially variable hyporheic exchange rates and residence times in this example are estimated with the basin-scale Networks with EXchange and Subsurface Storage (NEXSS) model. Our simulation results show that (1), given a residence time distribution, how the exchange fluxes to HZs are approximated when using MRMT can significantly change the amount of nitrate consumption in HZs through denitrification and (2) source locations of nitrate have a different impact on surface water quality due to the spatially variable hyporheic exchanges.

1 Introduction

Broadly defined, the hyporheic zone (HZ) is the area of the stream bed and stream bank in which stream water mixes with shallow groundwater (Runkel et al., 2003) or through which subsurface pathways begin and end at the stream (Cardenas, 2015). The HZ has been recognized as a critical component of a stream's ecosystem (Boano et al., 2014; Boulton et al., 1998; Ward, 2016; Wondzell, 2011; Liao and Cirpka, 2011). It is a location of interacting physical, chemical, and biological systems (Ward, 2016). Biogeochemical gradients in HZs can significantly impact the cycling of carbon and nitrogen (Claret and Boulton, 2009; Briggs et al., 2013). Most studies of the HZ focused on low-order streams (e.g., Briggs et al., 2009; Harvey et al., 2013; Hoagland et al., 2017; Mulholland et al., 1997; Triska et al., 1989; Valett et al., 1996; Ward et al., 2016) because they are more logistically tractable. On the other hand, the role of the HZ for large- or higher-order streams is not well understood due to inadequate or difficult to obtain direct measurements (Tank et al., 2008; Ye et al., 2017; Zarnetske et al., 2012) and the challenge of scaling up the process understanding from plot-scale measurements to reach scale. For large rivers, numerical experiments may provide some insights on the role of HZs.

Hyporheic exchange and biogeochemical processes within HZs are largely absent in reach-scale models (Helton et al., 2010). We need a modeling framework that integrates the physical and biogeochemical processes in the surface water and HZs in order to bridge the gap in reach-scale models and answer questions of when and where HZs become important. An integrated hydrologic model that couples land surface processes with spatially explicit three-dimensional groundwater flow processes, such as SWAT-MODFLOW (Bailey et al., 2016), can explicitly simulate hyporheic processes. However, it is often computationally demanding to capture the hyporheic zones that are highly variable in space and time, and it requires more model parameters that are difficult to characterize (Painter, 2018). In reality, hydrologic exchange between surface water and groundwater was commonly modeled by the transient storage model to investigate the physical processes governing riverine solute transport (Bencala and Walters, 1983; Briggs et al., 2009; Boano et al., 2014; Runkel et al., 2003; Haggerty and Gorelick, 1995; Zaramella et al., 2003) because it is simple, accessible, and adaptable (Knapp and Kelleher, 2020). The transient storage model is a lumped model representing first-order exchange between the main channel and well-mixed storage zones or dead zones, usually parameterized with a conservative tracer test. The transport of solute between the storage zone and channel is simply determined by the solute concentration difference between the channel and storage zone and an exchange coefficient (Bencala and Walters, 1983). It has been modified to include various zones with one exchange coefficient within each zone (Briggs et al., 2010; Neilson et al., 2010) and to simulate reactive solute within the storage zones by coupling with a chemical equilibrium model (Runkel et al., 1996); however, the transient storage model is not capable of representing the long solute tail observed in the stream (Cardenas, 2015; Painter, 2018). Coupled with a transient storage zone solute transport model, Ye et al. (2012) used a dynamic hydrologic network model to simulate dissolved nutrient retention processes during transient flow events at the channel network scale. They assumed a constant exchange rate and simple uptake of nutrient in the storage zone, but the interplay between mass exchange and biogeochemical processes, as well as hydrological and geological control on mass exchange rates, was ignored.

In this study, to model the exchange between the channel and HZs, we extended the transient storage model by using the multirate mass transfer (MRMT) formulation and incorporating a spectrum of transition times that is commonly used to simulate the late‐time solute and contaminant tails observed in porous media (e.g., Haggerty and Gorelick, 1995; Wang et al., 2005; Liu et al., 2008; Fernandez-Garcia and Sanchez-Vila, 2015). The MRMT formulation is a discrete equivalent to convolution-based representations of model mass exchange, which can be solved in the Lagrangian domain (Silva et al., 2009). Painter (2018) recently generalized the convolution-based model to include multicomponent reactive transport with general nonlinear reactions and tested the model using a single reach and assuming a steady-state hyporheic flow field. It has not yet been integrated in watershed modeling. Here we generalized the MRMT model to include mass transfer between the stream channel and multiple storage zones according to a spectrum of rates within each storage zone. We developed an integrated model, referred to as SWAT-MRMT-R, based on two open-source codes to simulate in-stream biogeochemical processes, mass transfer between the stream and HZ, and biogeochemical processes in HZs. These two codes are the Soil and Water Assessment Tool (SWAT) watershed model (Neitsch et al., 2011) and the subsurface flow and reactive transport code, PFLOTRAN (Lichtner et al., 2017). We applied the integrated model to the Hanford Reach of the Columbia River, a large river in southern Washington State of the United States. At the simulated reach, major impacts on stream nutrients come from the contaminated groundwater, irrigation return flows, and groundwater seepage resulting from irrigated agriculture (Evans et al., 2000).

This paper starts with an overview of the components in the SWAT-MRMT-R modeling framework, followed by a description of each component (Sect. 2). The model is then applied to the Hanford Reach using the spatially variable hyporheic exchange rates and residence times estimated with the basin-scale Networks with EXchange and Subsurface Storage (NEXSS) model (Gomez-Velez and Harvey, 2014) (Sect. 3). We focus on the nitrate dynamics in the results (Sect. 4), varying modeled processes and parameters. Finally, model limitation and future work are discussed.

2 SWAT-MRMT-R model description

2.1 Modeling framework

Our modeling framework is built within the in-stream nutrient submodel in SWAT, considering distinguished biogeochemical processing in both the water column and hyporheic zones. The SWAT model was developed by the United States Department of Agriculture to predict the impact of land management on water, nutrients, and sediments of large ungauged basins (Neitsch et al., 2011), and it is widely used worldwide. A schematic description of the modeling framework is shown in Fig. 1. At the top of Fig. 1a, the processes pointed to by the blue arrow are reactions related to the water column. The processes in the orange circle at the bottom of the figure are example reactions related to the hyporheic zones (shown as black rectangular prisms with orange streamlines) in the vertical and lateral directions. The orange streamlines represent the river water entering the vertical and lateral hyporheic zones and returning back to the river within the same reach over a distribution of travel times; i.e., each streamline carries a residence time (τ_s) and exchange flux (q_s). In this study, the residence time and exchange flux are estimated by NEXSS (Gomez-Velez and Harvey, 2014), which will be briefly described in Sect. 3.3. We use an MRMT model to represent solute mass transfer dynamics between the channel and storage zones, capturing the effect of hyporheic exchange in the fate and transport of solutes along the river corridor. In this model, all of the reactions and exchange processes shown in Fig. 1a are simply conceptualized as a series of hyporheic batch reactors connected to a stream batch reactor through mass exchange as shown in Fig. 1b. The hyporheic zones do not communicate with each other but only with the stream water. The mass exchange between the hyporheic reactor and the stream reactor is provided by NEXSS through user input. In other words, we only use the NEXSS output, and it is not part of the model development. The batch reactors in Fig. 1b are simulated simultaneously with the implicit time stepping through the Newton–Raphson method in batch mode (i.e., no transport) of PFLOTRAN (Lichtner et al., 2017). In this study, we only modified the in-stream nutrient transformation module in SWAT and did not modify the hydrologic flow and solute transport by taking advantage of the operator splitting approach in which the solute transport and the reaction steps are solved separately in SWAT. The model in this study is not limited by the number of storage zones. The user can provide the number of zones through the input file without having to modify the code. In the following, we describe each of these components and their coupling in detail.

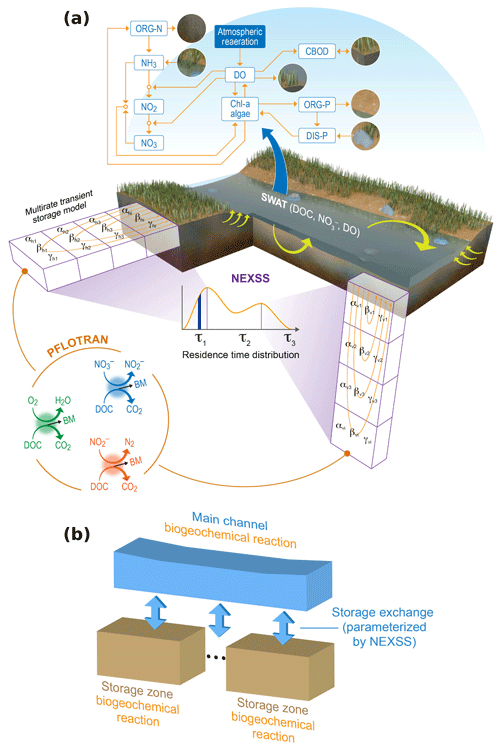
Figure 1 Schematics of coupling SWAT, MRMT, and microbial reactions in HZs. The top of figure (a) shows reactions in the stream water column. In the circle are representative reactions in the HZs. Rectangular prisms are sub-storage zones. The orange curves in the rectangular prisms are streamlines. Residence time distributions for lateral and vertical HZs are estimated by NEXSS. α_i is the exchange rate corresponding to residence time τ_i in the sub-storage zone i. β_i and γ_i represent reaction rates for different reactions in the sub-storage zone i. (b) The simplified conceptual model of (a). All chemical transformation processes shown are solved using PFLOTRAN.

2.2 Mass exchange processes between the channel and storage zones

MRMT is commonly used to simulate the late‐time solute and contaminant tails in porous media (e.g., Haggerty and Gorelick, 1995; Wang et al., 2005; Liu et al., 2008; Fernandez-Garcia and Sanchez-Vila, 2015). We use it here to simulate mass transfer between the stream channel and multiple storage zones according to a spectrum of rates within each storage zone. The mass exchange rate of a solute component due to hyporheic exchange is

$$\begin{array}{}\text{(1)}& m_{s,j}=(C_j-C_{s,j})q_{s}L,\end{array}$$

where j is the solute component of interest (O₂, ${\mathrm{NO}}_{\mathrm{3}}^{-}$, dissolved organic carbon (DOC), ${\mathrm{NO}}_{\mathrm{2}}^{-}$, etc.), $s=\mathrm{1},\mathrm{\dots },N$ is the storage zone, m_s,j is the mass exchange rate of the jth component (MT⁻¹), C_j is the concentration in the main channel (ML⁻³), C_s,j is the concentration of the jth component in the sth storage zone (ML⁻³), q_s is water exchange flux per reach length (L³ L⁻¹ T⁻¹), and L is the length of the reach.

2.3 Mass balance equations of the coupled system

Considering the biogeochemical processes in the water column, storage zones, and hyporheic exchange, the final mass balance equations for dissolved components in the channel and storage zones are

$$\begin{array}{}\text{(2)}& {\displaystyle }\begin{array}{rl}AL{\displaystyle \frac{\partial C_j}{\partial t}}+\sum _{s=\mathrm{1}}^N{m}_{s,j}=& AL(D{\displaystyle \frac{{\partial }^{\mathrm{2}}{C}_j}{\partial x^{\mathrm{2}}}}-u{\displaystyle \frac{\partial C_j}{\partial x}}\\ & +\sum _{m=\mathrm{1}}^M{a}_{m,j}{r}_m)\end{array}\end{array}$$

and

$$\begin{array}{}\text{(3)}& {\displaystyle }{A}_{s}L{\displaystyle \frac{\partial C_{s,j}}{\partial t}}=m_{s,j}+A_{s}L\sum _{ms=\mathrm{1}}^{Ms}{a}_{ms,j}{r}_{ms}.\end{array}$$

The area of the storage zones is calculated as a function of each storage zone's water exchange flux (q_s) and storage residence time (τ_s):

$$\begin{array}{}\text{(4)}& A_s=q_s{\mathit{\tau }}_s,\end{array}$$

where A is the cross-sectional area of the channel (L²), A_s is the cross-sectional area of the storage zone s (L²), t is time (T), τ_s is the storage residence time (T), r_m is the reaction rate of the mth ($m=\mathrm{1},\mathrm{\dots },M$) reaction in the channel water (ML⁻³ T⁻¹), a_m,j is the stoichiometry of the jth component in the mth reaction i (–), r_ms is the reaction rate of the msth ($ms=\mathrm{1},\mathrm{\dots },M_s$) reaction in the storage zone (ML⁻³ T⁻¹), a_ms,j is the stoichiometry of the jth component in the msth reaction i (–), D is longitudinal dispersion (L² T⁻¹), and u is flow velocity in the channel (LT⁻¹). The other variables are defined in Eq. (1).

Equations (1) to (4) are a parsimonious version of the general form of the MRMT model (e.g., Haggerty and Gorelick, 1995; Anderson and Phanikumar, 2011) in which a discrete number of storage zones, each with different geometry, linear rate, and biogeochemical reactions, are considered.

2.4 Water column biogeochemical processes

The in-stream submodel within SWAT is based on the QUAL2E (Brown and Barnwell, 1987) model. QUAL2E simulates major interactions of the nutrient cycle, atmospheric aeration, algae production, benthic oxygen demand, and carbonaceous oxygen uptake (Fig. 1). Details of the processes and transformation rates can be found in Brown and Barnwell (1987) and Neitsch et al. (2011). Major processes shown in Fig. 1 in the channel water column are summarized below:

1. Algae growth and respiration. Algae grow via photosynthesis and die via respiration. As algae grow and die, they form an organic part of the in-stream nutrient cycle. Nutrient limitation factor is considered for algal growth.

2. Nitrogen cycle. The transformation from organic nitrogen to ammonia, to nitrite, and finally to nitrate is stepwise.

3. Phosphorus cycle. Organic phosphorus is mineralized to soluble phosphorus available for uptake by algae.

4. Transformation of dissolved oxygen (DO). Concentrations of DO can be changed due to atmospheric reaeration, photosynthesis, plant respiration, benthic demand, biochemical oxygen demand, and nitrification.

Algae, organic nitrogen, and phosphorus can also be removed from the stream by settling. All of the reactions described above contribute to r_m in Eq. (2).

2.5 Storage zone biogeochemical processes

Although any type of biogeochemical process of interest can be simulated by the model, we focus on the following reactions for aerobic respiration and denitrification in each storage zone:

$$\begin{array}{}\text{(R1)}& {\displaystyle }\begin{array}{rl}& {\mathrm{CH}}_{\mathrm{2}}\mathrm{O}+f_{\mathrm{1}}{\mathrm{O}}_{\mathrm{2}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{5}}}\left(\mathrm{1}-f_{\mathrm{1}}\right){{\mathrm{NH}}_{\mathrm{4}}}^{+}\to f_{\mathrm{1}}{\mathrm{CO}}_{\mathrm{2}}\\ & +{\displaystyle \frac{\mathrm{1}}{\mathrm{5}}}\left(\mathrm{1}-f_{\mathrm{1}}\right){\mathrm{C}}_{\mathrm{5}}{\mathrm{H}}_{\mathrm{7}}{\mathrm{O}}_{\mathrm{2}}\mathrm{N}+{\displaystyle \frac{\mathrm{1}}{\mathrm{5}}}\left(\mathrm{3}+\mathrm{2}{f}_{\mathrm{1}}\right){\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\displaystyle \frac{\mathrm{1}}{\mathrm{5}}}\left(\mathrm{1}-f_{\mathrm{1}}\right){\mathrm{H}}^{+},\end{array}\text{(R2)}& {\displaystyle }\begin{array}{rl}& {\mathrm{CH}}_{\mathrm{2}}\mathrm{O}+\mathrm{2}{f}_{\mathrm{2}}{\mathrm{NO}}_{\mathrm{3}}^{-}+{\displaystyle \frac{\mathrm{1}}{\mathrm{5}}}\left(\mathrm{1}-f_{\mathrm{2}}\right){\mathrm{NH}}_{\mathrm{4}}^{+}\to \mathrm{2}{f}_{\mathrm{2}}{\mathrm{NO}}_{\mathrm{2}}^{-}+f_{\mathrm{2}}{\mathrm{CO}}_{\mathrm{2}}\\ & +{\displaystyle \frac{\mathrm{1}}{\mathrm{5}}}\left(\mathrm{1}-f_{\mathrm{2}}\right){\mathrm{C}}_{\mathrm{5}}{\mathrm{H}}_{\mathrm{7}}{\mathrm{O}}_{\mathrm{2}}\mathrm{N}+{\displaystyle \frac{\mathrm{1}}{\mathrm{5}}}\left(\mathrm{3}+\mathrm{2}{f}_{\mathrm{2}}\right){\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\displaystyle \frac{\mathrm{1}}{\mathrm{5}}}\left(\mathrm{1}-f_{\mathrm{2}}\right){\mathrm{H}}^{+},\end{array}\text{(R3)}& {\displaystyle }\begin{array}{rl}& {\mathrm{CH}}_{\mathrm{2}}\mathrm{O}+{\displaystyle \frac{\mathrm{4}}{\mathrm{3}}}{f}_{\mathrm{3}}{\mathrm{NO}}_{\mathrm{2}}^{-}+{\displaystyle \frac{\mathrm{1}}{\mathrm{5}}}\left(\mathrm{1}-f_{\mathrm{3}}\right){\mathrm{NH}}_{\mathrm{4}}^{+}\to {\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}{f}_{\mathrm{3}}{\mathrm{N}}_{\mathrm{2}}+f_{\mathrm{3}}{\mathrm{CO}}_{\mathrm{2}}\\ & +{\displaystyle \frac{\mathrm{1}}{\mathrm{5}}}\left(\mathrm{1}-f_{\mathrm{3}}\right){\mathrm{C}}_{\mathrm{5}}{\mathrm{H}}_{\mathrm{7}}{\mathrm{O}}_{\mathrm{2}}\mathrm{N}+{\displaystyle \frac{\mathrm{1}}{\mathrm{15}}}\left(\mathrm{9}+\mathrm{16}{f}_{\mathrm{3}}\right){\mathrm{H}}_{\mathrm{2}}\mathrm{O}\\ & +{\displaystyle \frac{\mathrm{1}}{\mathrm{15}}}\left(\mathrm{3}+\mathrm{17}{f}_{\mathrm{3}}{\mathrm{H}}^{+}\right),\end{array}\end{array}$$

where Reactions (R1), (R2), and (R3) are associated with the electron acceptors O₂, ${\mathrm{NO}}_{\mathrm{3}}^{-}$, and ${\mathrm{NO}}_{\mathrm{2}}^{-}$, respectively, and f₁, f₂, and f₃ are the fractions of the electron equivalents in CH₂O used for energy production in each reaction. We used the approach proposed by Song et al. (2017) and Song et al. (2018) to model the reaction rates for R1, R2, and R3, denoted as r₁, r₂, and r₃, which contribute to r_ms in Eq. (3):

$$\begin{array}{}\text{(5)}& r_i=e_i{r}_i^{\mathrm{kin}},i=\mathrm{1},\mathrm{2},\mathrm{3}.\end{array}$$

These reaction rates incorporate unregulated and regulated effects. In particular, the unregulated effect is represented by a Monod-type kinetics coefficient ($r_i^{\mathrm{kin}}$) of the form

$$\begin{array}{}\text{(6)}& r_i^{\mathrm{kin}}=k_i{\displaystyle \frac{a_i}{K_{a_i}+a_i}}{\displaystyle \frac{d_i}{K_{d_i}+d_i}}\left(\mathrm{BM}\right),\end{array}$$

where k_i, K_a,i, and $K_{d_i}$ denote the reaction rate (mol mol ⁻¹ d⁻¹), half-saturation constants associated with the electron acceptors (mol L⁻¹), and half-saturation constants for donors (mol L⁻¹), respectively, a_i is the concentration of electron acceptor (mol L⁻¹), d_i is the concentration of electron donor (mol L⁻¹), and BM is the concentration of biomass (mol L⁻¹).

On the other hand, the regulated effect is dictated by the enzyme activity (e_i) and determined by the cybernetic control law (Young and Ramkrishna, 2007) as follows (Song et al., 2018):

$$\begin{array}{}\text{(7)}& e_i={\displaystyle \frac{r_i^{\mathrm{kin}}}{{\sum }_i^{\mathrm{3}}{r}_i^{\mathrm{kin}}}}.\end{array}$$

This approach associates a community's traits with functional enzymes without directly considering the dynamics of individual microbial species or their guilds that synthesize their enzymes (i.e., the entire microbial community is treated as a single organism) and allowed the estimation of reaction stoichiometries and rates of denitrification, as well as the biomass degradation rate (Song et al., 2017). Rather than using empirical inhibition kinetics, the formulation in Eq. (7) enables the oxygen regulation of denitrification in response to environmental variation (Song et al., 2018).

2.6 Numerical solution of the nonlinear reaction system

In SWAT, dissolved nutrients are transported with the water, and those sorbed to sediments are allowed to be deposited with the sediments on the bed of the channel (Neitsch et al., 2011). PFLOTRAN is an open-source, massively parallel reactive multiphase flow and multicomponent transport code. It has well-established documentation (https://www.pflotran.org/documentation/, last access: 5 August 2020). Nutrient transport and reactions in SWAT are solved sequentially. We modified the explicit time-stepping algorithm in the original code for in-stream chemistry so the resulting nonlinear system of equations from the transformations taking place within the stream water and storage zones is simulated simultaneously with the implicit time stepping through the Newton–Raphson method in the batch mode (i.e., no transport) of the PFLOTRAN (Lichtner et al., 2017) model.

During each time step, the initial condition in the water column was calculated using the following equation (Neitsch et al., 2011):

$$\begin{array}{}\text{(8)}& C_{j,i}={\displaystyle \frac{m_{j,\mathrm{wb}}+m_{j,\mathrm{flowin}}}{V_{\mathrm{stored}}+V_{\mathrm{flowin}}}},\end{array}$$

where C_j,i is the initial concentration of dissolved component j in the water (ML⁻³) within reach i, m_j,wb is the amount of component j in the water body at the beginning of the time step (M), m_j,flowin is the amount of component j added to the water body with inflow at the end of the time step (M), V_stored is the volume of water stored in the channel at the beginning of the time step (L³), and V_flowin is the volume of water entering the channel at the end of the time step (L³) calculated using the Muskingum routing method (Overton, 1966).

3 Numerical experiment

3.1 Site description

We tested our model in a ninth-order reach of the upper Columbia–Priest Rapids watershed located in southern Washington State (46.23–46.86^∘ N, 118.14–120.25^∘ W). The selected reach is adjacent to the Hanford site downstream of the Priest Rapids Dam, representing a regulated river section with significant agricultural nutrient inputs. The Priest Rapids watershed has a semiarid climate with a Mediterranean precipitation pattern. Winters are cold with a mean temperature of ca. −2.2 ^∘C. Water is pumped from the river for irrigation, and runoff is returned to the river through canal drains. This watershed is dominated by agricultural activities on irrigated land. The Columbia River is the primary source of surface water for irrigation. Major crops in the watershed include alfalfa, potatoes, spring barley, winter wheat, corn, and orchards. Sources of pollutants entering the Columbia River are irrigation return flows and groundwater seepage associated with irrigated agriculture. Dilution in the river results in contaminant concentrations that are below drinking water standards.

3.2 SWAT model configuration

We set up the SWAT model by combining a series of geospatial data. We derived topography information from the United States Geological Survey (USGS) National Elevation Dataset (https://lta.cr.usgs.gov/NED, last access: 5 August 2020) with a spatial resolution of 30 m. Land covers including shrubland, forestland, grassland, developed land, barren land, and cultivated land were derived from the United States Department of Agriculture Cropland Data Layer (https://nassgeodata.gmu.edu/CropScape/, last access: 5 August 2020) with a spatial resolution of 30 m. Figure 2a shows the shapes of the reaches within the watershed. A reach is a section of stream between two defined points. Figure 2b compares the coarser reaches (green lines) generated for SWAT with those (black lines) defined in the National Hydrography Database (NHD Plus v2; http://nhd.usgs.gov, last access: 5 August 2020) at a selected location. NHD Plus v2 is used by NEXSS for residence time and exchange flux estimations. Highlighted in cyan is the main channel of the Columbia River. Climate data for the period of 2001–2015 from the North America Land Data Assimilation System (https://ldas.gsfc.nasa.gov/nldas/NLDAS2forcing.php, last access: 5 August 2020) were used to obtain precipitation, temperature, relative humidity, solar radiation, and wind speed. Discharges of water and nitrate at the USGS 12472900 station near the Priest Rapids Dam were used as inputs. In addition, we obtained nitrogen and phosphorus fertilizer application rates (USDA-ERS, 2018), tillage intensity (CTIC, 2008), and planting and harvesting information (USDA, 2010) for crop management (Qiu and Malek, 2019).

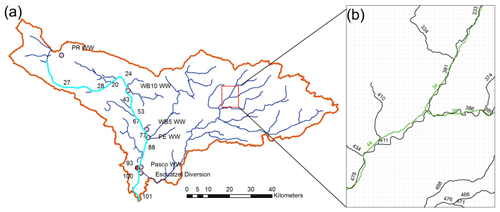
Figure 2 Reaches created by SWAT. The main channel of the Columbia River is highlighted in cyan (a). Numbers identify the individual reaches, the red circle is the area where field samples for dissolved organic carbon were collected, pink circles are the main wasteways carrying irrigation return flow water from farms and irrigation system operations, and the red rectangle shows the selected location for the mapping between SWAT and NHD Plus v2 that is used for NEXSS simulation. Panel (b) shows the mapping between NEXSS (black lines) and SWAT (green lines) for the rectangle area. The numbers in (b) are reach identifications.

3.3 Mass exchange parameters

Quantifying hyporheic exchange in streams is difficult. Exchange rate coefficients are often determined by tracer injection in the stream (e.g., Harvey et al., 2013; Gooseff et al., 2011; Laenen and Bencala, 2001). Assuming steady uniform flow, the river corridor hydrologic exchange model NEXSS in Gomez-Velez and Harvey (2014) can estimate hydrologic exchange flux rates and distribution of residence times that can be used to parameterize the exchange rate coefficients. NEXSS is a single tool that consolidates multiple previously published geomorphic and hyporheic flow models for the analysis of exchange at the basin scale (Gomez-Velez et al., 2015). The river network is discretized into individual reaches of length L, where values of channel width, bankfull width, depth, bankfull depth, discharge, average channel velocity, median grain size, channel slope, sinuosity, and regional hydraulic head gradient in the x and y direction are prescribed. The model is applied in two steps: geomorphic characterization and hyporheic exchange modeling. For each channel reach, the hyporheic exchange modeling predicts average hyporheic exchange flux per unit area of streambed and residence time distributions, as well as median residence time for vertical exchange beneath submerged bedforms (ripples, dunes, and alternate bars) and lateral exchange outside the wetted channel through emergent alternate bars and meanders. To estimate the net amount of vertical exchange flux, vertical exchange is conceptualized as a three-dimensional process assuming a homogeneous and isotropic porous medium. The boundary conditions of the system are the following. The top boundary at the sediment–water interface has a prescribed head distribution, lateral boundaries (y=0) or w_bf (bankfull channel width) are impervious ($q_y(x,y=\mathrm{0},z)=q_y(x,y=w_{\mathrm{bf}},z)=\mathrm{0})$, and the bottom boundary has a prescribed flux, which is defined as q_u≈0.57 K J_y (Boano et al., 2009), where K is hydraulic conductivity and J_y is the mean head gradient across the alluvial valley. Basal flux through the dunes and ripples induced by the regional groundwater flow are defined as q_b = KJ_x (Elliott and Brooks, 1997), where J_x is the mean head gradient along the valley in the downstream direction. The lateral exchange is conceptualized as a steady and two-dimensional process, and the flow is solved by the vertically integrated groundwater flow equation with the Dupuit–Forchheimer assumption. Following Gomez et al. (2012), the river is conceptualized as sinusoidal with wavelength λ (L, length) and amplitude α (L). A prescribed hydraulic head ${\mathit{\psi }}_s\left(x\right)={\mathit{\psi }}_{\mathrm{0}}+(J_x/\mathit{\sigma })s\left(x\right)$ is assigned along the river stretch, where ψ₀ (L) is the free surface elevation at the downstream end of the river above the horizontal bottom, s(x) (L) is the arc length along the boundary, $\mathit{\sigma }=s\left(\mathit{\lambda }\right)/\mathit{\lambda }$ is sinuosity, and J_x is the mean head gradient along the valley in the downstream direction. The boundary at a distance λ from the channel axis has a prescribed head $\mathit{\psi }(x,y=\mathit{\lambda })=J_{x}x+J_y\mathit{\lambda }$, where J_y is the mean head gradient across the alluvial valley. The upgradient and downgradient boundaries of the domain along the reach are assumed to be periodic with a prescribed head drop $\mathit{\psi }(x=\mathrm{0},y)=\mathit{\psi }(x=\mathrm{2}\mathit{\lambda },y)-\mathrm{2}\mathit{\lambda }{J}_x$. A particle tracking scheme is used to estimate the flux-weighted residence time distribution and median residence time for the exchange zones. Detailed description of NEXSS and its assumptions can be found in Gomez-Velez and Harvey (2014) and its supporting information. Consistent with Gomez-Velez et al. (2015), we considered two storage zones corresponding to lateral and vertical exchange. NEXSS estimates these parameters for long-term average flow conditions and mean monthly flow conditions, and therefore it can only capture the seasonal dynamics of flow.

Note that additional preprocessing is needed to match the scales of NEXSS and the model proposed in this study. NEXSS simulations are performed within the National Hydrography Database, which is characterized by reach lengths that range from 23 m to 43 km within the watershed of interest. Depending on the threshold of land cover, soil, and slope in defining the hydrologic response units in SWAT, SWAT reaches may or may not overlap with NEXSS reaches. In the current configuration, NEXSS reach is different from the discretization used in the stream network delineated for the SWAT simulation (Fig. 2b). To address this issue of mapping the NEXSS exchange metrics onto the SWAT stream network, we implemented a procedure that matches channels and transfers parameters over a rectangular grid that covers the entire watershed. As the reaches from the two networks do not exactly overlap (see Fig. 2b), we used a grid size of 200 m to search for matching reaches. Reaches that intersected with this grid and the length of each reach within each grid cell are calculated. For example, NEXSS reaches 386 and 380 in Fig. 2b contribute to SWAT reach 36. NEXSS reaches that do not overlap with those of SWAT are not considered, e.g., reach 374. To calculate the exchange flow for SWAT reach 36, exchange fluxes from NEXSS 386 and 380 are multiplied by the area of the channel bed and added together. The residence time for SWAT reach 36 is then calculated using residence time weighted by exchange flow of each contributing NEXSS reach. NEXSS reaches that do not overlap with those of SWAT are not considered. Input files to the code include (1) the reach identification number, vertical and lateral exchange fluxes, vertical and lateral residence times, reach width, and reach length within a grid from NEXSS and (2) the reach identification number and reach length within a grid from SWAT. Binary trees are created for both of the stream networks for NEXSS and SWAT to facilitate the search. When more than two reach segments of the two networks landed in the same grid cells, the matching reaches are found.

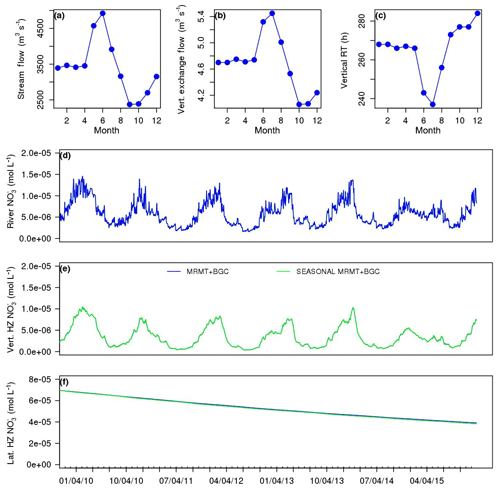
Mapping the NEXSS output to the simulated watershed, we found that the reaches along the Columbia River are characterized by vertical residence times ranging from 8 h to 10 d and lateral residence times ranging from 17 d to 10 years (Fig.  3). The vertical and lateral residence times for the reaches highlighted in Fig. 2a are shown in Table S1 in the Supplement. Compared to other reaches in the watershed, the Columbia River is characterized by a relatively larger exchange flow and shorter residence times in vertical storage zones (Fig. 3). Hydraulic conductivity, head gradient, stream geomorphology, and flow paths together determine the hyporheic residence times (Kasahara and Wondzell, 2003; Cardenas et al., 2008). The vertical exchange residence times are short probably due to their hydraulic and geomorphic conditions that favor ripple and dune formation (Gomez-Velez et al., 2015). For example, hyporheic flow around steps and riffles with coarse-textured alluvium can result in short residence time distributions for hyporheic exchange flows (Kasahara and Wondzell, 2003). Vertical exchange flow is dominant along the Columbia River.

Figure 3 NEXSS simulated vertical (a, c) and lateral (b, d) residence times (h) and exchange flux (m s⁻¹) in the watershed and scatter plot of exchange flow (m³ s⁻¹) versus residence time (h) (e). Solid circles in (e) are for reaches along the Columbia River.

3.4 Parameters for biogeochemical reactions

Parameters for reactions in the stream water are default from SWAT. The selection of reaction parameters for HZs is informed by the denitrification experiments and modeling synthesis reported in Li et al. (2017) and Song et al. (2017), respectively. Stegen et al. (2016) showed that significant O₂ is maintained in the HZ at the location shown by the red circle in Fig. 2a, which implies that aerobic respiration can take place in the HZ. Therefore, aerobic respiration and denitrification reactions are considered in this study. The parameters for biogeochemical reactions are the same as in Song et al. (2018), which were based on parameters derived from the aforementioned experiment, as well as parameters for aerobic respiration, assuming it is energetically more favorable than ${\mathrm{NO}}_{\mathrm{3}}^{\mathrm{-}}$ reduction. The uptake rates (k_i in Eq. 6) of oxygen, nitrate, and nitrite are 68.94, 28.26, and 23.28 mmol mmol⁻¹ d⁻¹, respectively. The biomass degradation rate is 0.242 mmol mmol⁻¹ d⁻¹. The other parameters are not repeated here.

3.5 Case scenarios

Starting from the BASE case, for which mass transfer and reactions in the HZ were not simulated, we added mass transfers using two storage zones to represent vertical and lateral exchanges, and within each zone only one exchange rate calculated from the NEXSS mean residence time was used. The latter case is referred to as MRMT. The mass transfer parameters for this case were estimated by NEXSS using the long-term average flow conditions. Then reactions in the HZs were added to isolate the impact of physical and biological processes on nitrate levels in the river in order to answer the questions of the role of HZs and biogeochemical processes in HZs to nitrate concentration attenuation in the surface water, and this case is referred to as MRMT+BGC. Additional cases with exchange and BGC include the following.

1. The residence time and exchange flux are replaced with those predicted by NEXSS using seasonal flow conditions. For this case, the NEXSS model was run 12 times using mean monthly streamflow conditions. The exchange fluxes and residence times now change monthly instead of being constants throughout the whole simulation.

2. The single storage zone in the vertical and lateral is replaced with sub-storage zones within a storage zone, which assumes a distribution of residence times to evaluate whether the commonly used single transient storage model is sufficient for model nitrate attenuation in the river.

3. Nitrate in the hyporheic zones is pulse increased to see how surface water quality will be affected when pulsed nitrate from the legacy waste intrudes into the HZs, which could be caused by a flow event.

4. Irrigation return flows are added along the river as point sources to study if the river can quickly dilute the contaminant concentration from those sources because of the high discharge rate.

For case MRMT+BGC, the initial conditions for DOC, nitrate, and DO in the HZs were set to 0.0637, 0.079, and 0.287 mmol L⁻¹, respectively, which are the average concentrations of those observed in the field. Initial BM concentration is 0.01 mmol L⁻¹. As there is not a working model for DOC in the version of SWAT (SWAT rev664) used for this study, we fitted an exponential relationship of DOC and stream discharge (shown in the Supplement Fig. S1) in the Columbia River using the limited measurement of DOC in the stream and stream discharge at the time of the measurements. This relationship is used to calculate DOC in the stream.

To represent multiple exchange rates according to a residence time distribution, the discrete form of the probability density function of residence time is written as

$$\begin{array}{}\text{(9)}& p\left({\mathit{\tau }}_s\right)=\sum _j{P}_j\mathit{\delta }({\mathit{\tau }}_s-{\mathit{\tau }}_{s,j}),\end{array}$$

where τ_s,j is the residence time of the jth sub-storage zone and P_j is the probability of occurrence of the residence time in the jth sub-storage zone such that

$$\begin{array}{}\text{(10)}& \sum _j{P}_j=\mathrm{1}.\end{array}$$

τ_s,j can be determined from the following equation using the interpolation method:

$$\begin{array}{}\text{(11)}& f_j=\underset{{\mathit{\tau }}_s-\mathrm{\Delta }{\mathit{\tau }}_s}{\overset{{\mathit{\tau }}_s+\mathrm{\Delta }{\mathit{\tau }}_s}{\int }}p\left({\mathit{\tau }}_s\right)d{\mathit{\tau }}_s,\end{array}$$

in which f_j is defined as the fraction or the area under the curve of the distribution function that is between τ_s−Δτ_s and τ_s+Δτ_s of the sub-storage zone within the vertical or horizontal storage zones that has an average residence time τ_s. Here we assume an equal fraction for each sub-storage zone; i.e., a vertical or horizontal storage is evenly divided into N_s sub-storage zones. To extract N_s residence times for the sub-storage zones in a given HZ with mean residence time τ_m, we use the exponential distribution $P=\mathrm{1}-e^{-{\mathit{\tau }}_s/{\mathit{\tau }}_m}$. We have one distribution for the vertical HZ and one for the lateral HZ with means equal to the vertical and lateral residence time calculated from NEXSS. N_s discrete residence time values with their corresponding probability were then extracted from this distribution for both HZs. For example, if N_s=10, the fraction of each sub-storage zone is 0.1. The average residence time of each sub-storage corresponds to a value with probability less than or equal to 0.05, 0.15, 0.25, 0.35, 0.45, 0.55, 0.65, 0.75, 0.85, and 0.95. The minimum and maximum residence times are discrete values that are less than or equal to the given probability of 0.05 and 0.95, respectively. The maximum residence is interpolated from the equation $\mathrm{1}-e^{-{\mathit{\tau }}_s/{\mathit{\tau }}_m}=\mathrm{0.95}$. The other discrete residence times are similarly solved.

4 Results

4.1 MRMT with single vertical and lateral storage zones

Compared to the BASE case, pure mass exchange by MRMT has little impact on the downstream nitrate level in the river due to the small exchange flow compared to the stream discharge (Fig. 4a). Vertical HZ reached dynamic steady state in the selected reach, but the concentration in the lateral HZ is still decreasing (Fig. 4b, c), indicating a continuous loss in concentrations in the HZ due to slow mass transfer.

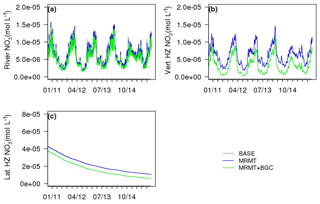
Figure 4 Comparison of nitrate in the river (a), vertical HZ (b), and lateral HZ (c) between cases BASE, MRMT, and MRMT+BGC at reach 93.

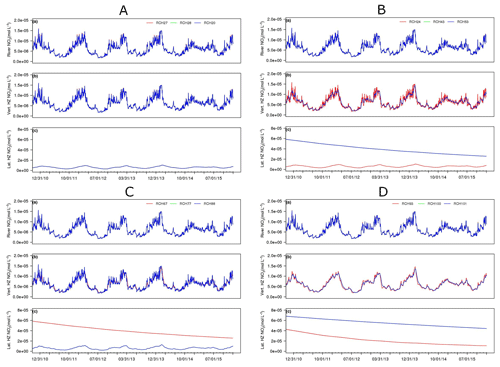
Figure 5 shows the concentration of nitrate in selected reaches (from upstream to downstream) along the Columbia River for case MRMT. The selected reach numbers are shown in Fig. 2a. In general, nitrate concentrations in the stream and HZs are nearly identical for reaches with similar residence times. Exchange with HZs of longer residence times slows the transport of nitrate in the stream (retardation) as can be inferred from the delayed peak concentration in the vertical HZs of reaches RCH53 and RCH101 in Fig. 5b and d. Stream nitrate concentrations are in dynamic steady state with the vertical HZ. They are also in dynamic steady state with the lateral HZ for reaches RCH27, RCH24, RCH28, RCH20, RCH77, and RCH88, suggesting that lateral exchange can be important too. It is not true for RCH53, RCH67, RCH93, RCH100, and RCH101 as their residence times are much longer.

Figure 5 Comparison of nitrate in the river (a), vertical HZ (b), and lateral HZ (c) between reaches at the upstream (A), in the middle of the stream (B, C), and at the downstream (D) using MRMT.

4.2 HZ microbial respiration

Including the respiration reactions in the simulation results in the consumption of stream nitrate (green line in Fig. 4a) because the reaction time is faster compared to vertical HZ residence times in some reaches along the river but on a similar order. Nitrate concentration in the vertical HZ at the selected reach (RCH93) drops due to the respiration reactions, creating a concentration difference between the channel and HZs further decreasing the concentration in the channel compared with case MRMT. Lateral HZ is diffusion limited (slow exchange), and hence there is not much dynamics in nitrate concentration (Fig. 4c).

4.3 Seasonal exchange flux and residence time

For this case, dynamic exchange parameters were generated using NEXSS driven by long-term averaged monthly stream discharges. During the simulation, exchange parameters were updated each month. Figure 6a, b, and c show the change in vertical exchange flux and residence time for RCH101 (outlet) as stream discharge changes: a 50 % change in stream discharge results in about a 12 % change in exchange flux and residence time. Using the seasonal exchange fluxes does not have a significant effect on the stream water nitrate concentration (Fig. 6d, e, f).

Figure 6 Effect of streamflow dynamics (a) on hyporheic exchange (b, c) and the nitrate concentration in the stream (d), vertical HZ (e), and lateral HZ (f) using exchange rates derived from annual discharge (blue line) and seasonal discharge (green line) at the outlet.

4.4 Multiple sub-storage zones

Zhang and Baeumer (2007) showed that the long tail behavior in stream tracer can be approximated by a small number of mass transfer coefficients. We started with 10 mass transfer coefficients or sub-storage zones for both the lateral and vertical HZs. Using exponential residence time distribution and 10 sub-storage zones in both the lateral and vertical HZs, we had 10 discrete residence times with the mean residence time in the lateral and vertical HZs from NEXSS following the procedure described in Sect. 3.5. Given the total lateral and vertical HZ volumes calculated using the exchange flux and mean residence time from NEXSS, we assumed that (1) the exchange flux from the NEXSS estimation is equally distributed in each sub-storage zone and (2) larger fluxes are associated with longer residence times. The second assumption is based on the theory in Elliott and Brooks (1997) that exchange flow paths with higher fluxes penetrate deeper in the streambed with homogeneous and isotropic material and are associated with longer residence times. Compared to the single-rate simulation, the simulation with multiple exchange rates and uniform hyporheic exchange fluxes removes only 3 % more nitrate in the HZ of the Columbia River reaches due to denitrification (Fig. 7a) and 40 % less nitrate removal in the HZs of the Columbia River reaches (Fig. 7b) when high exchange flux is associated with long residence time. These results show that the assumption of the exchange flux associated with each sub-storage zone can have a significant effect on the estimation of HZ nitrate removal, and there is a need for more research on the reliable estimation of these exchange fluxes.

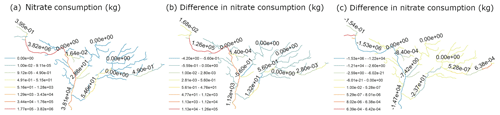
Figure 7 Total nitrate consumption through HZ denitrification at the end of simulation using a single storage zone in both vertical and lateral HZs (a). Change in nitrate consumption with 10 sub-storage zones in both vertical and lateral HZs compared to the simulation with a single storage zone using uniform exchange flux (b) and nonuniform exchange flux (c).

4.5 Pulsed nitrate increase in HZs

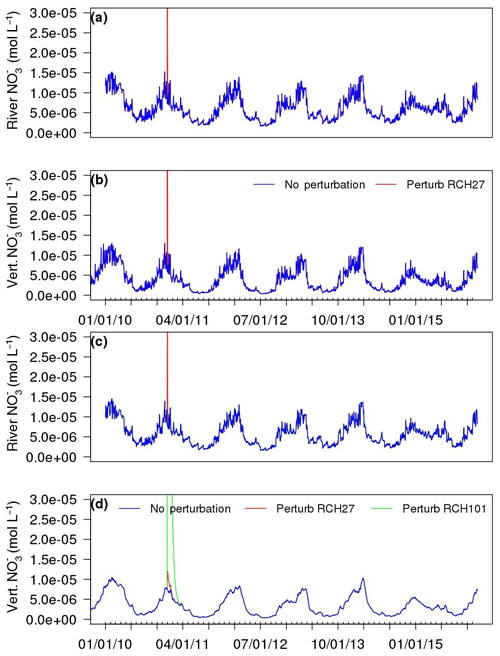
Contaminant can enter the stream during the upwelling of nitrate‐contaminated groundwater from the legacy waste site. We changed the nitrate concentration to 0.3 mmol L⁻¹ in the vertical HZ of RCH27 and RCH101 separately at the beginning of 2011. Because the residence time in the HZ of RCH27 is 30 times faster than RCH101 (Table S1 in the Supplement), the stream and HZ nitrate concentration reached steady state instantaneously (Fig. 8a, b), and the high concentration pulse propagated downstream (Fig. 8c, d) because of the longer residence time downstream. The local perturbation at the outlet (RCH101) results in a small change in stream water concentration because of the longer residence time (Fig. 8c, d). At the outlet, it takes 112 d for the reach concentration to return to a pre-perturbed condition. It has been observed in the field that higher stream nitrate concentrations than those shown in the BASE case can occur. The field observation may be explained by the contaminant intrusion as tested here. The nonequilibrium behavior shown in this test indicates that the dynamic mass contribution from the groundwater should be considered in this model as it affects concentrations in the HZs.

Figure 8 Nitrate concentration in the stream and vertical HZ at RCH27 (a, b) and at the outlet (c, d) with and without HZ perturbation using MRMT+BGC.

4.6 Irrigation return flows

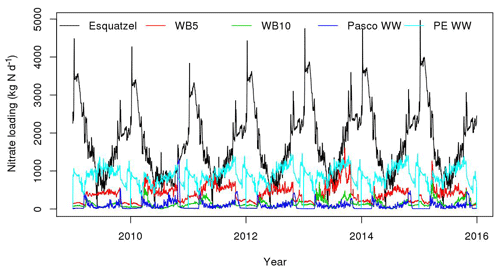
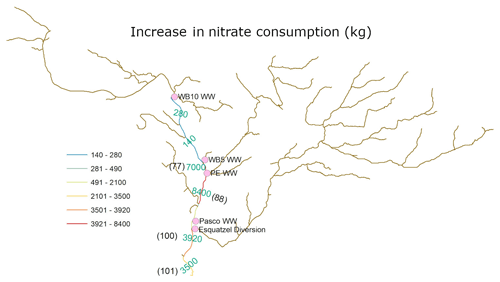
There are five major wasteways carrying return flow water into the Columbia River (Fig. 2a). The Bureau of Reclamation, Pacific Northwest Region, has recorded nitrate loading from these wasteways. We generated an hourly nitrate loading (Fig. 9) at five source points and reran the MRMT+BGC case. Wasteways WB5 and PE flow into RCH77 and RCH88, respectively. Wasteways WB10, Pasco, and Esquatzel Diversion flow into RCH43, RCH93, and RCH100, respectively. Because the lateral residence times of the aforementioned reaches are much longer than the vertical times, the following discussion will only focus on vertical exchanges. The residence times of RCH77, RCH88, and RCH100 are 8.49, 7.88, and 258 hr, respectively. The short residence times at RCH77 and RCH88 result in fast delivery of nutrient and carbon into the HZs and a higher reaction rate for denitrification at these locations compared to RCH100. The vertical HZ volumes of RCH77 and RCH88 are 14 % and 13 % of that of RCH100. Total upstream nitrate loadings at RCH77 and RCH88 are 28 % and 106 % of that from Esquatzel Diversion into RCH100 alone. At the end of the simulation, the total denitrification at RCH77 and RCH88 is 7000 and 8400 kg due to nitrate loading from the irrigation flow only. They are 178 % and 214 % of that at RCH100 where total denitrification is 3920 kg (Fig. 10). In other words, HZ denitrification can remove more nitrate at RCH77 and RCH88 even though the loadings and HZ volumes are smaller compared to those at RCH100. Compared to RCH77 and RCH88, nitrate loadings into reaches with longer residence times, such as RCH100 and RCH101, have more negative effects on river water quality.

Figure 9 Nitrate loadings at five wasteways along the Columbia River.

Figure 10 Increase in HZ nitrate consumption (kg) through denitrification due to irrigation return flow compared to case MRMT+BGC. Text in green shows the amount of nitrate consumption, pink solid circles are the locations of irrigation wasteways, and numbers in parentheses are reaches of interest.

5 Discussion

Our study focuses on the effect of bedform-induced (vertical) and sinuosity-driven (lateral) hyporheic exchange derived under steady-state conditions on stream water quality in large rivers using the SWAT-MRMT-R model we developed. Our studied system is dominated by inlet conditions if there are no additional sources in the HZs.

5.1 Coupled effect of physical and biogeochemical processes

Coupling reactive transport in channel and HZs and MRMT in a large river using the mean residence times and exchange fluxes calculated from NEXSS, our simulations show that HZs can attenuate the peak nitrate concentrations in the stream with mass transfer and biogeochemical reactions with a 11.6 % concentration reduction on average compared to the base case without MRMT. However, for biogeochemically inactive zones, hyporheic exchange (physical process) alone is not effective in attenuating nitrate in the surface water due to the relatively small exchange flow in the vertical HZs. Depending on the channel morphologic features and the river channel aquifer's physical properties in an individual river corridor, lateral HZ can play an equally important role in storage and biogeochemical transformation in certain reaches as the vertical HZ (Fig. 5), which echoes the findings in Gomez-Velez et al. (2015).

5.2 Effect of dynamic hyporheic exchange

The Hanford Reach of the gravel-bed Columbia River exhibits frequent hydrologic mixing and steep physicochemical gradients caused by the combined effects of large, long-term river stage fluctuations driven by snowmelt runoff and short-term fluctuations driven by upstream flow regulation at the Priest Rapids Dam (Graham et al., 2017; Stegen et al., 2016; Song et al., 2018). Gravel-bed river corridors, which are common worldwide (Nilsson et al., 2005; Sawyer and Cardenas, 2009; Hauer et al., 2016), exhibit coarse-textured sediments with high hydraulic conductivity. Hydrologic exchange due to dam operation and high hydraulic conductivity can drive river water into and out of the river banks, creating high-frequency lateral exchanges in these types of river corridors. The study in Zhou et al. (2017) indicated the exchange fluxes in the shallow water near the river banks of the Columbia River were stronger than those in the center of the channel due to a large pressure gradient between the groundwater and river stage. This is not captured by the steady-state NEXSS model, which could result in an inaccurate estimation of the attenuation capability of the HZs and recovery time for the stream water quality.

5.3 Effect of multirate mass transfer using multiple rates

Short residence times could provide a faster supply of DOC into the HZs. Including the short residence time can frequently change the chemical signature of the stream water in the HZ and could be used to explain, for example, the response of microbial community composition in Stegen et al. (2016). The importance of the biogeochemical processes in HZs on surface water quality could be affected by the fraction of this short residence time if the Damköhler number for oxygen ($D{a}_{{\mathrm{O}}_{\mathrm{2}}}$) is greater than 1 (Zarnetske et al., 2012). Our simulation with multiple rates shows that channel hyporheic zone nitrate removal due to denitrification could increase or decrease compared to a single rate (Fig. 7) depending on how the exchange flux for each sub-storage zone is approximated. MRMT simulation with the uniform exchange flux approximation makes almost no difference in HZ nitrate consumption compared to the single rate simulation, while there is much less (40 %) nitrate consumption when large fluxes are assumed to be associated with longer residence times. It has yet to be verified by field studies.

5.4 Implications for source water quality treatment

Spatial perturbation in the HZs and including point sources of irrigation return flow show that high-concentration pulses of nitrate may stay in the stream before being attenuated (Fig. 8c, d). This has implications for the effort to treat water quality in groundwater and irrigation return flows before entering the reaches with longer residence times, particularly for streams impacted by agricultural activities.

5.5 Limitations and future development

There are limitations in the current model such as (1) the lack of nitrification processes, (2) source uncertainties, e.g., lack of groundwater contribution to the HZs in the model, (3) uncertainty in the exchange rates and residence times calculated by NEXSS, (4) uncertainty in the rates for biogeochemical reactions in the HZs, and (5) lack of field observations for model comparison and application. For example, the shape of residence time distributions can be drastically changed due to heterogeneity in stream sediment hydraulic conductivity as shown in the study of Pryshlak et al. (2015). We only considered denitrification processes in our study case, which is reasonable in this study as the Damköhler number for oxygen ($D{a}_{{\mathrm{O}}_{\mathrm{2}}}$) is >1 based on residence times calculated from NEXSS and assumed oxygen uptake rate. If $D{a}_{{\mathrm{O}}_{\mathrm{2}}}$ becomes less than 1, nitrification processes which dominate short residence times (Zarnetske et al., 2012) should be included in the model to better quantify the role of HZs as a net sink of nitrate. These processes can be easily implemented in PFLOTRAN. Also, we only evaluated the denitrification process using a single set of reaction rate parameters in the river corridors. However, nutrient uptake in streams can be highly spatially variable (McClain et al., 2003). Our perturbation and return flow simulations show that source term can have a big impact on stream water quality. The effect of HZs on stream water quality can be compromised by the upwelling of nitrate‐contaminated groundwater through the addition of nitrate to the stream or altering features of the hyporheic zone (Azizian et al., 2017). These factors need to be evaluated and combined with field characterizations and model developments in future studies.

Field experiments in large rivers are challenging due to the large spatial extent, spatial heterogeneity, and high stream discharge. A decision has to be made as to how and where to sample across the watershed. One of the advantages of the model developed in this study is that it can be used to cost effectively define the reaches that are biogeochemical hot spots using physically derived parameters before conducting field experiments. The model can then be combined with experiment data collected at those locations for a better mechanistic understanding of river corridor functioning and model improvement.

As we mentioned earlier, this model is an extension of the transient storage model. The sub-storage zones are assumed to be well mixed, and they only communicate with the stream water, not with each other. This assumption is unlike the integrated model SWAT-MODFLOW which can rigorously resolve the redox sensitivity at each location in the modeling domain. Future model development will consider approximating each storage zone as an advection dispersion system like the model in Painter (2018) so that redox zonation in the storage zones can be represented. Models of different conceptualizations will be evaluated on the effect of the watershed biogeochemical processing function and whether model complexity is warranted for reach-scale process understanding.

6 Conclusion

Based on the widely used open-source models SWAT and PFLOTRAN, we developed an integrated model, SWAT-MRMT-R, to account for hyporheic exchange and biogeochemical processes within HZs that are often absent in reach-scale modeling. In this model, the MRMT module can incorporate a spectrum of transition times to represent solute mass transfer dynamics between the channel and storage zones. The model is flexible such that different shapes of residence time distributions (e.g., exponential, power-law, or lognormal distribution) and biogeochemical reactions in stream water and HZs can be easily implemented. Exchange parameters in our study were estimated from NEXSS. Although our demonstration of the model uses mass transfer parameters derived from steady-state discharge conditions, it is applicable to dynamic conditions as well once the corresponding mass transfer parameters are available. An integrated model as developed in this study can serve as a base framework to answer questions related to the significance of HZs in surface water quality in higher-order river networks where the characterization of HZs can be challenging. Our simulation results show that it is critical to better approximate the hydrologic exchange flux that enters into each sub-storage zone given a residence time distribution because it can have a significant impact on how much nitrate can be removed through denitrification in HZs. Efforts are needed to treat water quality in groundwater and irrigation return flows before entering the reaches with longer residence times. It is worth noting that this model has a multitude of parameters at reach scale. For real-world, large-scale studies, model validation at multiple points within the study area is necessary.