BPOP-v1 model: exploring the impact of changes in the biological pump on the shelf sea and ocean nutrient and redox state

The biological pump of the ocean has changed over Earth's history, from one dominated by prokaryotes to one involving a mixture of prokaryotes and eukaryotes with trophic structure. Changes in the biological pump are in turn hypothesized to have caused important changes in the nutrient and redox properties of the ocean. To explore these hypotheses, we present here a new box model including oxygen (O), phosphorus (P) and a dynamical biological pump. Our Biological Pump, Oxygen and Phosphorus (BPOP) model accounts for two – small and large – organic matter species generated by production and coagulation, respectively. Export and burial of these particles are regulated by a remineralization length (z_rem) scheme. We independently vary z_rem of small and large particles in order to study how changes in sinking speeds and remineralization rates affect the major biogeochemical fluxes and O and P ocean concentrations. Modeled O and P budgets and fluxes lie reasonably close to present estimates for z_rem in the range of currently measured values. Our results highlight that relatively small changes in z_rem of the large particles can have important impacts on the O and P ocean availability and support the idea that an early ocean dominated by small particles was nutrient rich due to the inefficient removal of P to sediments. The results also suggest that extremely low oxygen concentrations in the shelf can coexist with an oxygenated deep open ocean for realistic values of z_rem, especially for large values of the small-particle z_rem. This could challenge conventional interpretations that the Proterozoic deep ocean was anoxic, which are derived from shelf and slope sediment redox data. This simple and computationally inexpensive model is a promising tool to investigate the impact of changes in the organic matter sinking and remineralization rates as well as changes in physical processes coupled with the biological pump in a variety of case studies.

1 Introduction

The “biological pump” describes the production of organic matter at the surface of the ocean (an oxygen source), its downward export/sinking flux, remineralization at depth (an oxygen sink) and burial. This set of processes acts against the homogenization of tracer concentrations by the ocean circulation, maintaining large-scale tracer gradients (Sarmiento and Gruber, 2006). In today's world, the biological pump plays a key role in transferring carbon from the atmosphere/surface ocean to the deep ocean and in so doing lowers atmospheric CO₂ and creates oxygen demand in deeper waters (Lam et al., 2011; Kwon et al., 2009). Those deeper waters with the greatest oxygen demand relative to oxygen supply can be driven hypoxic (O₂<60 mmol m⁻³), suboxic (O₂<5 mmol m⁻³) or even anoxic – as is being seen in parts of the ocean today (Keeling et al., 2010). By combining surface oxygen production and organic carbon burial, the biological pump plays a role in determining the long-term source of oxygen to the atmosphere. The biological pump also provides a means of efficiently transferring organic matter and the nutrients it contains to marine sediments if sinking through the water column happens fast enough compared to remineralization for the material to hit the bottom (Sarmiento and Gruber, 2006). Hence the biological pump plays a key part in balancing the input of phosphorus to the ocean with a corresponding output flux of phosphorus buried in marine sediments. Through Earth's history, the characteristics, efficiency and impact of the biological pump are thought to have changed dramatically due to the evolution of increasingly large and complex marine organisms (Ridgwell, 2011; Logan et al., 1995; Boyle et al., 2018). Life in the ocean began as just prokaryotes, presumably attacked by viruses, with slow sinking of the resulting tiny particles. Now the marine ecosystem is a mix of prokaryotic cyanobacteria and heterotrophs and size-structured eukaryotic algae, mixotrophs, and heterotrophs all the way up to large jellyfish, fish, and whales. Some of the resulting particles sink very fast (McDonnell and Buesseler, 2010).

How changes in the biological pump have affected ocean nutrient and redox state at different times in Earth history is a subject of active research and hypothesis generation. Previous work has highlighted the Neoproterozoic Era, spanning from 1000 to 541 million years ago, as being of particular interest because it saw a shift of dominance from prokaryotes to eukaryotes and a series of dramatic shifts in the climate, biogeochemical cycling and ocean redox state (Katz et al., 2007; Brocks et al., 2017). A common paradigm has been to assume that a progressive rise of oxygen in the atmosphere (of uncertain cause) drove the oxygenation of the deep ocean at this time through air–sea gas exchange and mixing, but equally, increases in the efficiency of the biological pump could have lowered ocean phosphorus concentration and thus oxygenated the ocean (Lenton et al., 2014). Recent data show a series of transient ocean oxygenation events ∼660–520 Ma, which get more frequent over time, suggesting a complex interplay of processes on multiple timescales, including changes in the biological pump and ocean phosphorus inventory (Lenton and Daines, 2018).

During the Phanerozoic Eon there have been further changes to the biological pump. In particular, a rise of eukaryotic algae from the early Jurassic onwards is hypothesized to have increased the efficiency of the biological pump and thus oxygenated shallow waters (Lu et al., 2018) but presumably deoxygenated deeper waters, at least in the short term. In the oceanic anoxic events (OAEs) that occurred during the Mesozoic Era there were major increases in prokaryotic nitrogen fixation yet evidence for a eukaryote-dominated biological pump (Higgins et al., 2012), raising interesting questions as to whether this reinforced anoxia at depth.

Previous modeling work has examined the impact of changes in the organic matter remineralization length/depth (z_rem) in the 3-D GENIE intermediate complexity model (Meyer et al., 2016; Lu et al., 2018). Both studies clearly demonstrated the important control of the z_rem on ocean oxygen concentrations – as it gets larger the oxygen minimum zone shifts to greater depths. Furthermore, Lu et al. (2018) showed that an increase in z_rem can explain an observed deepening of the oxycline from the Paleozoic to Meso-Cenozoic in the ocean redox proxy I/Ca. However, coarse 3-D models such as GENIE do not really resolve shelf seas and their dynamics, which are distinct from those of the open ocean. Furthermore, GENIE only accounts for one organic carbon species, overlooking processes of transformation of organic material, such as coagulation and fragmentation, which contribute to modulating the efficiency of the organic matter vertical export and burial (Wilson et al., 2008; Karakaş et al., 2009; Boyd and Trull, 2007).

In this study, we take a more idealized approach, exploring how changes in the properties of the biological pump may have affected the shelf sea and open ocean nutrient and redox state using a new Biological Pump, Oxygen and Phosphorus (BPOP) box model. This model combines a box representation of the marine O and P cycles with an intermediate complexity representation of the biological pump transformations, including two classes of particulate organic matter (POM). BPOP allows us to modify the properties of two POM pools, whose abundance is regulated by the processes of production and coagulation. We focus on changes in the characteristic depths at which the two POM pools are remineralized, i.e. the particle remineralization length scale (z_rem), and study the resulting equilibrium budgets and fluxes. The model has a deliberately simplified treatment of redox carriers and is designed to focus on ocean P and ocean redox steady states, not on longer-term controls on atmospheric oxygen. In the following sections we describe the model, provide an evaluation of its performance in the context of modern observations and flux estimates, and finally present and discuss our model results.

Table 1 List of the state variables in the model and of their units.

Table 2 Parameters set that describes geometry of the box model.

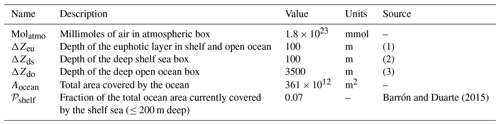
Notes: (1) we assume a constant average euphotic layer depth of 100 m in both shelf and open sea; (2) the shelf sea is assumed to be 200 m deep in total, in line with the definition of shelf sea by Barrón and Duarte (2015); and (3) we assume an average open ocean depth of 3600 m (including euphotic layer).

2 Model description

Here we describe the Biological Pump, Oxygen and Phosphorus (BPOP) model. The model was implemented using MATLAB, and the equations are solved by the built-in ode15s solver. BPOP can easily run on a single core, integrating 50 million years of time in less than a minute on an ordinary machine and is therefore computationally efficient. We refer to the user manual (see the Supplement) for further information on how to run the model.

2.1 Variables and circulation

The box model resolves explicitly for each relevant box the local concentrations of three types of tracers: molecular oxygen O₂ (O), inorganic dissolved phosphorus (P) and sediment organic phosphorus (SedP_org). The total budgets of P and O, respectively P^TOT and O^TOT, are also independently integrated from the net sources and sinks of the two tracers over the entire model domain, for the purpose of checking mass conservation. The entire set of state and diagnostic variables in the model and their units are listed in Table 1. In the following subsections we describe the geometry of the box model and discuss the physical and geochemical fluxes that drive the dynamics of the tracers. Box properties are listed in Table 2, while the set of parameters adopted for the modeled physical and geochemical fluxes can be found in Table 3.

Table 3 Parameter set pertaining to the initial conditions of the model, circulation mass fluxes and boundary fluxes.

Notes: (1) Chavez and Messié (2009) estimate 5.5 Sv (sverdrups) in the four major upwelling systems alone; (2) compare to 38 Sv (Sarmiento and Gruber, 2006), 17 Sv of mixing flux in the Southern Ocean alone (Meyer et al., 2015), estimated open ocean downwelling 38.5 Sv and upwelling 34.5 Sv (Ganachaud and Wunsch, 2000); (3) cross-shelf mass exchange due to lateral recirculation, tides and mixing aimed at including exchange processes other than upwelling (Fennel et al., 2005; Cole et al., 2015; Wollast, 1998); (4) minimal assumption for vertical mixing in nearshore regions due to seasonal and eddy mixing; see also Sect. 3.2 Sensitivity to parameter choices; (5) up to 70 % of river outflow reaches the open ocean; see Sharples et al. (2017); and (6) calculated from the equilibrium solution given P_in.

2.1.1 Box properties and physical fluxes of inorganic tracers

The box model includes four ocean boxes, one atmospheric box and two sediment boxes (Fig. 1a). The ocean and sediment boxes are equally split between shelf sea and open ocean, both including one surface ocean box and one deep ocean box.

O and P are exchanged between the four ocean boxes through advection and mixing, including an upwelling recirculation between shelf sea and open ocean (Wollast, 1998). For a generic tracer concentration C and in the ith box, the physical exchange flux (in millimoles per cubic meter per year) is represented by

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }\text{AdvMix}(C{)}^i={\sum }_j{\text{MassFlux}}_{ij}/V^i\cdot (C_j-C_i),\end{array}$$

where MassFlux_ij represents the volumetric flow between the ith box and any adjacent box j, while Vⁱ is the volume of the ith box.

Figure 1 Box model scheme with a representation of the physical and boundary fluxes affecting inorganic tracers in the water column and atmosphere, where blue arrows indicate advective and mixing fluxes and yellow arrows indicate air–sea gas exchange fluxes. The model includes seven boxes: surface shelf (ss), deep shelf (ds), surface open ocean (so), deep open ocean (do), atmosphere (at), shelf sediments (s) and open ocean sediments (o).

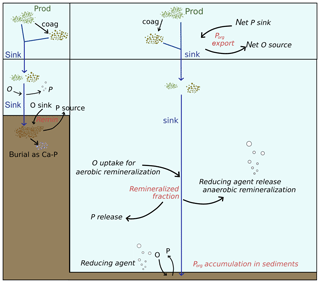
Figure 2 Representation of the physical and biogeochemical fluxes affecting the P_org cycling in the model. Even though some processes (such as burial as Ca–P) are here represented in detail only in one box, the set of biogeochemical processes regulating the P_org dynamics in shelf sea and open ocean (both water column and sediments) is the same, as described in Sect. 2.2.

For each surface box i, air–sea gas exchange allows O fluxes between the ocean and the atmosphere (at). The flux (in millimoles of O₂ per cubic meter per year) is positive when directed into the ocean and depends on the gas transfer velocity K_W, atmospheric pressure p_at (here assumed constant) and Henry's constant K_Henry, as in

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle }{\text{AirSea}}^i=K_W\cdot (O^{\text{at}}\cdot p_{\text{at}}/K_{\text{Henry}}-O^i)\cdot A^i/V^i,\end{array}$$

where K_W (in meter per year) is a function of the prescribed mean temperature T_mean and wind speed W_speed (Sarmiento and Gruber, 2006).

2.1.2 Initialization and boundary fluxes

The model is initialized with an even concentration of P (P_ini) in all the ocean boxes, zero oxygen (O_ini) and zero SedP_org ((P_org)_ini). A constant input of P from rivers (P_in) into the surface ocean replenishes the P ocean reservoir despite the burial flux (net sink of P_org) into the sediments. P_in is in part delivered directly to the surface open ocean (Sharples et al., 2017). At equilibrium, the organic phosphorus (P_org) burial flux balances P_in. Oxidative weathering determined by atmospheric oxygen O^at constitutes a net sink flux for O. The weathering flux (per year) depends on a constant baseline flux W₀, and it scales like the square root of the oxygen mixing ratio normalized to present values $O_{{\text{mix}}_{\mathrm{0}}}$ (Lenton et al., 2018), following

$$\begin{array}{}\text{(3)}& {\displaystyle }\text{OxyWeath}=W_{\mathrm{0}}\cdot \sqrt{O^{\text{at}}/O_{{\text{mix}}_{\mathrm{0}}}}.\end{array}$$

2.2 Biological pump details

The modeled tracer cycles are coupled with a set of biological transformations, i.e. the biological pump, governing the cycle of production, and remineralization and burial of P_org in the water column and in the sediments. P_org in the water column is resolved implicitly; at each time step all the produced P_org that does not reach the sediments is instantaneously remineralized. In this sense, in our model no P_org can accumulate in the ocean water column, and we only calculate fluxes of water column P_org without treating P_org as a state variable. This scheme is similar to the one used to represent detrital POM in some modern ocean biogeochemical models (Moore et al., 2004). P and O biological fluxes are coupled with a fixed Redfield ratio OP_Red. The next few paragraphs describe the cycle of production, coagulation, export, remineralization and burial that constitute the biological pump representation. The full set of parameters used to resolve the P_org cycle is provided in Table 4.

Table 4 Parameters set pertaining to the P_org cycle of the model and coupled biogeochemical fluxes.

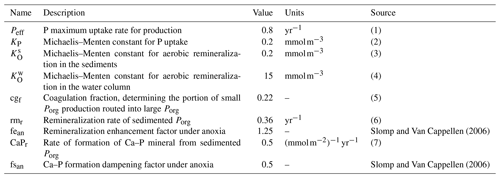
Notes: (1) maximum P uptake rate, meant to account for environmental limitations of phytoplankton growth rate (such as light and temperature); the magnitude of the rate takes into account that we are not explicitly resolving phytoplankton concentrations (order of 10⁻² mmol P); see also production in Gruber et al. (2006) and Yool and Tyrrell (2003); (2) measured values vary in the range from 0.01 mmol m⁻³ up to a few millimoles per cubic meter, varying for different phytoplankton types; see Lomas et al. (2014), Tantanasarit et al. (2013), Krumhardt et al. (2013), Lin et al. (2016) and Klausmeier et al. (2004); (3) measured half-saturation constant for oxygen uptake varies in the range of 0.1–3 mmol m⁻³ (Ploug, 2001); (4) biogeochemical models commonly switch to anaerobic respiration below 4 mmol m⁻³ (Paulmier et al., 2009); measurements suggest a value close to 19 mmol m⁻³ (DeVries and Weber, 2017); (5) Cavan et al. (2017) showed that small particles are about 85 % of the total sinking particles abundance in the coastal region at export depth; the parameter was further tuned to bring the model closer to modern ocean conditions; (6) on the same order of magnitude as Gruber et al. (2006); (7) unmeasured – given the analogous adopted functional form, we assume Ca–P formation to happen on a timescale close to that of P_org coagulation in the water column in models with explicit particle pools (Gruber et al., 2006).

2.2.1 Particle classes, production and coagulation

The model includes two P_org classes that get produced, exported and remineralized in the ocean water column, which are small P_org (SP_org) and large P_org (LP_org). The use of two P_org classes is in line with modern ocean in situ observations, which reveal a bimodal distribution of the particle sizes and sinking speeds (Riley et al., 2012; Alonso-González et al., 2010). Moreover, it allows a better reproduction of the commonly observed Martin power-law decay of the particle export flux with the use of a remineralization length scheme of export and burial fluxes (Boyd and Trull, 2007).

Organic matter production happens only in the surface ocean boxes through the uptake of P. This is regulated by a maximum rate P_eff and a Michaelis–Menten kinetics with constant K_P. Production (in millimoles of P per cubic meter per year) in each ith box only generates SP_org, according to

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle }{\text{Prod}}^i=P_{\text{eff}}\cdot (P^i/(P^i+K_{\mathrm{P}}\left)\right)\cdot P^i.\end{array}$$

LP_org is generated via the coagulation of SP_org at the surface after production. As we do not explicitly solve for the concentrations of SP_org and LP_org, we assume that the coagulation (in millimoles of P per cubic meter per year) of SP_org into LP_org in each box i is proportional to the rate of production of small particles as follows:

$$\begin{array}{}\text{(5)}& {\displaystyle }{\text{Coag}}^i={\text{cg}}_f\cdot {\text{Prod}}^i.\end{array}$$

This is a necessary simplifying assumption compared to the usual coagulation models, which define the flux as the square of the particle concentration (Boyd and Trull, 2007; Gruber et al., 2006), given the fact that our model does not resolve this variable. Coagulation impacts the relative contribution of small and large particles to the export and burial fluxes by subtracting from the local SP_org pool and adding to the LP_org pool.

2.2.2 Physical fluxes of organic material

The implicit representation of the organic matter in the water column implies that no organic matter is accumulated in the ocean. In our baseline version of the model, corresponding to the results presented in this paper, SP_org and LP_org are redistributed throughout the water column exclusively by implicitly modeled gravitational sinking before being buried, accumulated in the sediments or remineralized. Even though the vertical export by downwelling and mixing (Stukel and Ducklow, 2017) and the lateral organic matter redistribution (Lovecchio et al., 2017; Inthorn et al., 2006) may be important when working with suspended SP_org ($z_{\text{rem}}^{\mathrm{S}}=\mathrm{0}$), these fluxes are not currently accounted for in the model.

2.2.3 Remineralization length scheme

The export and sedimentation fluxes of P_org through the water column are represented by a remineralization length scheme. In this representation, the vertical fluxes of organic matter f(z) vary exponentially with depth. The shape of the exponential depends on the value of the remineralization length (z_rem) of each organic matter species as follows:

$$\begin{array}{}\text{(6)}& {\displaystyle }{\displaystyle }{f}^k\left(z\right)=f_{\mathrm{0}}^k\cdot e^{-\frac{z-z_{\mathrm{0}}}{{z_{\text{rem}}}^k}},\end{array}$$

where $f_{\mathrm{0}}^k$ is the flux (in millimoles of P per square meter per year) at the reference depth z₀, and the index k indicates the organic matter pool of reference, either small (S) or large (L). This representation of the export flux is convenient, as it does not depend on the specific choice of z₀ (Boyd and Trull, 2007).

The remineralization length z_rem indicates the distance through which the particle flux becomes 1∕e times (about 36 %) the flux at the reference depth (Buesseler and Boyd, 2009; Marsay et al., 2015). This quantity is expressed in meters and can be calculated as the ratio between the particle sinking speed and the remineralization rate of the particle (Cavan et al., 2017). Consequently, z_rem implicitly contains information on several particle-inherent properties (among which are density, size, shape and organic matter liability) as well as information about the surrounding environment, e.g. the type of heterotrophs that feed upon the organic material (McDonnell and Buesseler, 2010; Baker et al., 2017). For simplicity, we assume that the remineralization length of small and large particles does not vary between shelf sea and open ocean boxes. We examine the potential impact of this limitation in the Discussion section of the paper.

2.2.4 Sediments and burial

SP_org and LP_org accumulate in the sediments as SedP_org, which is calculated as a density per unit of area. The flux (in millimoles of P per square meter per year) into the sediment box i depends on the organic matter fluxes into the overlaying deep ocean box j and on the remineralization length of the two pools as in

$$\begin{array}{ll}{\displaystyle }{\text{SedFlx}}^i=& {\displaystyle }({{\text{Flx\_SP}}_{\mathrm{org}}}^j\cdot \text{exp}\left(-\mathrm{\Delta }{Z}_j/{z_{\text{rem}}}^{\mathrm{S}}\right)\\ \text{(7)}& {\displaystyle }& {\displaystyle }+{{\text{Flx\_LP}}_{\mathrm{org}}}^j\cdot \text{exp}\left(-\mathrm{\Delta }{Z}_j/{z_{\text{rem}}}^{\mathrm{L}}\right)).\end{array}$$

The accumulated SedP_org is partially slowly remineralized and partially irreversibly buried in a mineral form. Phosphorus burial as mineral Ca–P is modeled as a function of the square of SedP_org that accumulates in the sediments and is regulated by a constant rate coefficient CaP_r. Ca–P formation happens at a lower rate under low-oxygen conditions (CaP${}_{\mathrm{r}}^{\ast }={\mathrm{CaP}}_{\mathrm{r}}\cdot f{s}_{\text{an}}$ with fs_an<1), in agreement with observations and previous models (Slomp and Van Cappellen, 2006). The transition from aerobic and anaerobic conditions is controlled by a Michaelis–Menten type of function of the oxygen concentration in the deep ocean box j overlaying the sediment box i. The oxic and anoxic terms sum to the total formation term (in millimoles per square meter per year) as in

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\text{CaPform}}^i={\left({{\text{SedP}}_{\mathrm{org}}}^i\right)}^{\mathrm{2}}\cdot \\ {\displaystyle }& {\displaystyle }[{\text{CaP}}_r\cdot O^j/\left(O^j+{K_{\mathrm{O}}}^s\right)\\ \text{(8)}& {\displaystyle }& {\displaystyle }+\left({\text{CaP}}_r\cdot f{s}_{\text{an}}\right)\cdot \left(\mathrm{1}-O^j/\left(O^j+{K_{\mathrm{O}}}^s\right)\right)].\end{array}$$

This flux is essential to balance the continuous P river input, therefore preventing the ocean from overflowing with nutrients.

2.2.5 Remineralization in the water column and sediments

At each time step, remineralization in the water column completely depletes the P_org that has not reached the sediments. In the two surface boxes, remineralization of P_org that is not exported below the euphotic layer uses up part of the oxygen that was released by production. For this reason, net oxygen production in each surface box is proportional to the export of P_org below the euphotic layer. The overall loss of P due to export (in millimoles of P per cubic meter per year) from a surface box i to a deep box j via gravitational sinking, is calculated as

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{\text{VExp}}^i=& ({{\text{Flx\_SP}}_{\mathrm{org}}}^i\cdot \text{exp}(-(\mathrm{\Delta }{Z}_{\text{eu}}/\mathrm{2})/{z_{\text{rem}}}^{\mathrm{S}})\\ & +\text{Flx\_}{{\text{LP}}_{\mathrm{org}}}^i\cdot \text{exp}(-(\mathrm{\Delta }{Z}_{\text{eu}}/\mathrm{2})/{z_{\text{rem}}}^{\mathrm{L}}))/\mathrm{\Delta }{Z}_i\end{array},\end{array}$$

where the fluxes per unit of area of SP_org and LP_org in the surface boxes depend on production and coagulation as described in Sect. 2.2.1.

At depth, the remineralization of P_org that does not reach the sediments happens through both aerobic and anaerobic processes, completely depleting the remaining P_org. The amount of inorganic P released in each deep box j by water-column remineralization (in millimoles of P per cubic meter per year) is therefore calculated as

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\text{Wc}{\text{Rem}}^j=({{\text{Flx\_SP}}_{\mathrm{org}}}^j\cdot \left(\mathrm{1}-\text{exp}\left(-\mathrm{\Delta }{Z}_j/{z_{\text{rem}}}^{\mathrm{S}}\right)\right)\\ \text{(10)}& {\displaystyle }& {\displaystyle }+{{\text{Flx\_LP}}_{\mathrm{org}}}^i\cdot \left(\mathrm{1}-\text{exp}\left(-\mathrm{\Delta }{Z}_j/{z_{\text{rem}}}^{\mathrm{L}}\right)\right))/\mathrm{\Delta }{Z}_j.\end{array}$$

In each deep ocean box i, aerobic remineralization uses some of the available oxygen and is therefore limited by Michaelis–Menten kinetics with a half-saturation constant ${K^{\mathrm{w}}}_{\mathrm{O}}$ (DeVries and Weber, 2017). Anaerobic remineralization takes up the entire remaining P_org that is not remineralized aerobically and releases a product, which bubbles up to the atmosphere, reacting with atmospheric oxygen. In our model, the reducing agent produced by anaerobic remineralization is methane gas, and it is only produced when the sediments and the deep shelf water column have gone anoxic. As we do not track other oxidizing agents such as SO₄, there is nothing for the methane to be oxidized by until it reaches the surface ocean, and as the surface ocean is equilibrated with the atmosphere, the fact that we assume oxidation in the atmosphere is a reasonable approximation. In each sediment box i, remineralization of SedP_org happens in a similar way to remineralization in the water column, with an aerobic and an anaerobic component. However, remineralization in the sediments is not instantaneous but rather happens at a fixed rate which depends on the oxygenation state of the overlaying water column. Aerobic remineralization takes up oxygen from the overlaying deep water box j and happens at a rate rm_r, while being limited by a Michaelis–Menten coefficient. Anaerobic remineralization releases its product to the atmosphere and happens at a faster rate ${{\text{rm}}_{\mathrm{r}}}^{\ast }={\text{rm}}_{\mathrm{r}}\cdot {\mathrm{fe}}_{\text{an}}$ with fe_an>1, in agreement with recent observations and previous models (Slomp and Van Cappellen, 2006). The release of P_org from a sediment box i into the overlaying ocean box due to sediment remineralization (in millimoles of P per cubic meter per year) is therefore the sum of the two terms as in

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\text{SedRem}}^i=({\text{rm}}_{\mathrm{r}}\cdot {{\text{SedP}}_{\mathrm{org}}}^i\cdot \left(O^j/\left(O^j+{K_{\mathrm{O}}}^s\right)\right)\\ {\displaystyle }& {\displaystyle }+({\text{rm}}_{\mathrm{r}}\cdot {\mathrm{fe}}_{\text{an}})\\ \text{(11)}& {\displaystyle }& {\displaystyle }\cdot {{\text{SedP}}_{\mathrm{org}}}^i\cdot \left(\mathrm{1}-O^j/\left(O^j+{K_{\mathrm{O}}}^s\right)\right))/\mathrm{\Delta }{Z}_{\mathrm{d}}.\end{array}$$

2.3 Equations summary

The dynamics of the 11 state variables in the model are regulated by just as many equations. We summarize here the major terms for P, O and SedP_org in the surface ocean (s), deep ocean (d), atmosphere (at) and sediments, without distinguishing between coastal and open ocean boxes and assuming that all terms have been scaled with dimensions of the reference boxes or number of moles (atmosphere). A full set of equations including the explicit formulation of all the flux terms for each box can be found in the Appendix.

$$\begin{array}{ll}\text{(12)}& {\displaystyle }& {\displaystyle \frac{\text{d}{P}^{\mathrm{s}}}{\mathrm{d}t}}=P_{\text{in}}+\text{AdvMix}(P{)}^{\mathrm{s}}-\text{VExp}\text{(13)}& {\displaystyle }& {\displaystyle \frac{\mathrm{d}{P}^{\mathrm{d}}}{\mathrm{d}t}}=\text{AdvMix}(P{)}^{\mathrm{d}}+\text{WcRem}+\text{SedRem}\text{(14)}& {\displaystyle }& {\displaystyle \frac{\mathrm{d}{O}^{\mathrm{s}}}{\mathrm{d}t}}=\text{AdvMix}(O{)}^{\mathrm{s}}+\text{VExp}\cdot {\text{OP}}_{\text{Red}}+\text{AirSea}{\displaystyle }& {\displaystyle \frac{\mathrm{d}{O}^{\mathrm{d}}}{\mathrm{d}t}}=\text{AdvMix}(O{)}^{\mathrm{d}}-{\text{WcRem}}_{\text{Aer}}\cdot {\text{OP}}_{\text{Red}}\\ \text{(15)}& {\displaystyle }& {\displaystyle }-{\text{SedRem}}_{\text{Aer}}\cdot {\text{OP}}_{\text{Red}}\text{(16)}& {\displaystyle }& {\displaystyle \frac{\mathrm{d}{\text{SedP}}_{\mathrm{org}}}{\mathrm{d}t}}=\text{SedFlx}-\text{CaPform}-\text{SedRem}\cdot \mathrm{\Delta }{Z}_{\mathrm{d}}{\displaystyle }& {\displaystyle \frac{\mathrm{d}{O}^{\text{at}}}{\mathrm{d}t}}=-\sum \text{AirSea}-{\text{WcRem}}_{\text{Ana}}\cdot {\text{OP}}_{\text{Red}}\\ \text{(17)}& {\displaystyle }& {\displaystyle }-{\text{SedRem}}_{\text{Ana}}\cdot {\text{OP}}_{\text{Red}}-\text{OxyWeath},\end{array}$$

where P_in is the river input of P to the surface of the ocean and AdvMix indicates the advective and mixing physical fluxes of the variable of interest (which differ for each box according to the circulation scheme); Exp is the export flux of P_org in P units; WcRem indicates the water column complete remineralization of the organic material in P units, which is split into an anaerobic (Ana) and aerobic (Aer) component; SedRem indicates the sediment remineralization of SedP_org in P units (also aerobic and anaerobic); AirSea represents the air–sea flux exchange of O; OxyWeath is the O weathering flux sink; SedFlx is the SedP_org accumulation flux as regulated by the remineralization length scheme at the bottom of the water column; and finally CaPform represents the sediment burial flux of P in mineral form. For each box, flux terms are rescaled with the appropriate box geometry.

2.4 Strategy: sensitivity studies for varying z_rem

In order to characterize the model, we analyze the equilibrium budgets and fluxes of the state variables for varying z_rem values separately for SP_org and LP_org, respectively ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$. We adopt a range of z_rem values that fall close to modern observations (Cavan et al., 2017; Buesseler and Boyd, 2009; Marsay et al., 2015) and takes into consideration our future aim to apply the model to simulate the impact of the time evolution of the early biological pump (at the Neoproterozoic–Paleozoic transition). For this reason, we do not push the range as far as what would be needed to consider the impact of fast sinking rates typical of silicified or calcified small phytoplankton (McDonnell and Buesseler, 2010; Lam et al., 2011). In our sensitivity simulations, ${z_{\text{rem}}}^{\mathrm{S}}$ is in the range of 0–40 m, while ${z_{\text{rem}}}^{\mathrm{L}}$ varies in the range of 50–450 m.

3 Evaluation

3.1 Timescales

Starting from the initial values listed in Table 3, the modeled state variables evolve towards equilibrium for any pair of values of ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$ in the explored interval. Simple mass conservation checks show no hidden source or sink of tracers in the boxes of the model. Figure 3 illustrates an example of evolution of the variables for ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$ in the middle of the interval of explored values for both particle types. In all the ocean boxes, P shows an initial oscillation that evolves on timescales of tens of thousands of years (Fig. 3a, b), as expected by the typical timescale of evolution of the tracer (Lenton and Watson, 2000). This is followed by a slower drift, which depends on the dynamics of the deep water oxygen content, as the release and burial of P in the sediments depend on the level of oxygenation of the deep ocean and especially of the deep shelf sea. P reaches complete equilibrium as soon as the deep ocean boxes become stably oxygenated. The timescales of the evolution of O are slower and lie on the order of tens of millions of years (Lenton and Watson, 2000). Oxygen in the deep shelf overcomes hypoxia after the first few millions of years and then slowly evolves towards equilibrium on the same timescale of O in the other ocean boxes. The dynamics of SedP_org are also strongly driven by level of oxygenation of the deep shelf sea. The dynamical response of the model to changes in the biological pump is rapid subsequent to the model equilibrating considering the given initial conditions. For example, step changes in the z_rem values of the particles result in a transition time to a new equilibrium that is on the order of a few tens of thousands of years, which is the typical timescale of the P cycle.

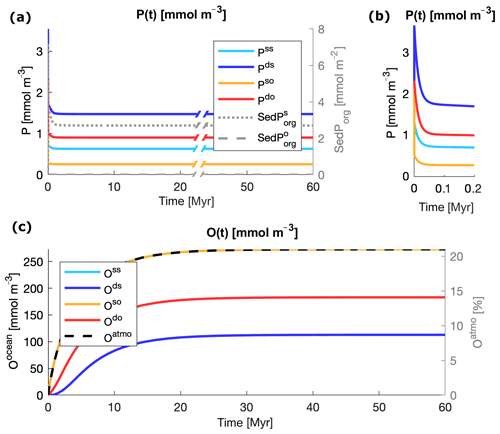
Figure 3 Evolution of the state variables from the initial conditions listed in Table 2 and remineralization lengths roughly in the middle of the interval of explored values, ${z_{\text{rem}}}^{\mathrm{S}}=\mathrm{20}$ m and ${z_{\text{rem}}}^{\mathrm{L}}=\mathrm{250}$ m. (a) Evolution of inorganic phosphorus P in the water column (left axis) and of organic phosphorus in the sediments SedP_org (right axis). (b) A zoomed-in view of the dynamics of P in the first 200 000 years. (c) Evolution of oxygen in the water column (left axis) and atmosphere (right axis). In (c) the two lines O^ss and O^so are overlapping; the two variables evolve closely due to the coupling of the surface ocean with the atmosphere via air–sea gas exchange.

3.2 Modern ocean budgets and fluxes

Modern estimates of the ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$ vary depending on the region of sampling and on the local community structure, with most of the measurements focusing on large or heavy particles and most studies focusing on the open ocean (Iversen and Ploug, 2010; Cavan et al., 2017; Lam et al., 2011). Furthermore, only a very limited number of measurements account for both microbial and zooplankton remineralization, the latter disregarded by lab measurements of z_rem (Cavan et al., 2017). Considering the fundamental role of the shelf sea in our model (always accounting for >98 % of the total burial), we evaluate modeled tracer budgets and fluxes for values of ${z_{\text{rem}}}^{\mathrm{L}}$ that lie around 76 m, as measured in situ by Cavan et al. (2017) for a modern shelf sea. We pose no restrictions on ${z_{\text{rem}}}^{\mathrm{S}}$ due to the lack of precise measurements. A summary of our evaluation is provided in Table 5.

Table 5 Summary of the model evaluation provided in Sect. 3. Modern observations and estimates are compared to model results obtained for ${z_{\text{rem}}}^{\mathrm{L}}$ in the range of measured values for a modern shelf sea (Cavan et al., 2017).

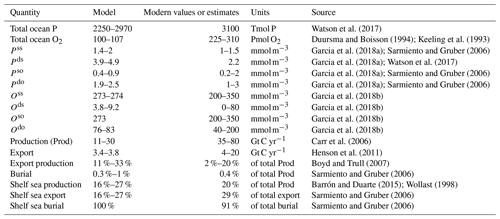
In the above-mentioned range of z_rem, our model predicts equilibrium budgets of between 2250 and 2970 Tmol P for phosphorus and an oxygen budget of between 100 and 107 Pmol O₂ in the entire ocean, compared to the estimated total P reservoir of 3100 Tmol P (Watson et al., 2017) and estimated ocean O₂ reservoir of between 225 and 310 Pmol O₂ (Keeling et al., 1993; Duursma and Boisson, 1994). Due to the relative size of the ocean boxes, it is important to underline that total budgets are strongly driven by the deep open ocean budget and that the low-oxygen reservoir of our model may be connected to an underestimation of the deep open ocean oxygenation.

Deep shelf P and O concentrations lie in the ranges of 3.9–4.9 mmol m⁻³ and 3.8–9.2 mmol m⁻³, respectively (Figs. 5 and 6). Deep shelf nutrient concentrations are higher than expected by about a factor of 2 compared to modern values, possibly due to the fact that our model does not store any P_org in the water column or due to an underestimation of the vertical supply of nutrients to the surface shelf (e.g. via mixing). Limiting deep P concentrations via lower remineralization or higher burial rates, however, also results in sensibly lower production rates. In the deep open ocean, P and O concentrations fall in the ranges of 1.9–2.5 mmol m⁻³ and 76–83 mmol m⁻³, respectively. For any combination of ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$, O levels in surface ocean boxes lie between 273 and 274 mmol m⁻³, a good approximation of average modern surface values (Garcia et al., 2018b). In general, the deep shelf always shows the highest P values and lowest O concentrations compared to the other ocean regions, while, as expected, the surface shelf sea is richer in P compared to the surface open ocean.

Figure 4 Total ocean budgets of (a) P and (b) O at equilibrium for varying ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$.

In order to compare the modeled fluxes to modern estimates, we converted our results into carbon (C) units assuming a C:P Redfield ratio of 106. However, recent studies found a substantially higher mean C:P ratio for the modern ocean (Martiny et al., 2014); therefore our derived C fluxes may be a conservative estimate. Modeled biological fluxes in C units, such as production and export, fall just below the low end of present estimates (Fig. 7). Our model predicts a total primary production of between 11 and 30 Gt C yr⁻¹, and an export below the euphotic layer ranges between 3.4 and 3.8 Gt C yr⁻¹. These must be compared to an expected value of production of between 35 and 80 Gt C yr⁻¹ (Carr et al., 2006) and an estimated export flux of at least 4 Tmol C yr⁻¹ (Henson et al., 2011). Despite the absolute fluxes being at the low end of the present estimates, modeled export production (the export to production ratio) and the burial to production ratio compare well to range of present estimates. The modeled export corresponds to between 11 % and 33 % of total production, strongly depending on ${z_{\text{rem}}}^{\mathrm{S}}$, compared to an expected range of 2 %–20 % (Boyd and Trull, 2007). Buried P_org corresponds to between 0.3 % and 1 % of total production, compared to an expected 0.4 % (Sarmiento and Gruber, 2006).

In terms of the shelf contribution to the total fluxes, model results also fall close to present estimates. Modeled production in the surface shelf sea represents between 16 % and 27 % of total production (expected 20 %) (Barrón and Duarte, 2015; Wollast, 1998). The fraction of modeled export and burial that happens in the shelf region represent, respectively, [16 %, 27 %] and nearly 100 % of the total ocean fluxes, compared to estimated modern values of 29 % and 91 % (Sarmiento and Gruber, 2006). Our overestimation of the shelf contribution to the burial fluxes may be due to the underestimation of the z_rem of open-ocean particles compared to observations (Cavan et al., 2017; Lam et al., 2011), i.e. our choice of using the same value of ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$ for both the coastal and the open ocean box. This simplifying assumption limits the capacity of P_org to reach the deep sediment layer in the open ocean. We explore potential limitations of this choice in the Discussion section.

4 Results

4.1 Budgets and fluxes sensitivity to changes in z_rem

Around the lowest values of ${z_{\text{rem}}}^{\mathrm{L}}$ adopted in the present study, i.e. in the range of 50–100 m, our model shows a strong sensitivity of the total and local ocean P and O budgets to small changes in ${z_{\text{rem}}}^{\mathrm{L}}$ (Fig. 4). This is true for any ${z_{\text{rem}}}^{\mathrm{S}}$, with minor differences between low and high ${z_{\text{rem}}}^{\mathrm{S}}$ values. For smaller ${z_{\text{rem}}}^{\mathrm{L}}$, the model shows a sharp increase in P concentrations in all the ocean boxes and a substantial decrease in O levels at depth (Figs. 5 and 6), which are coupled with high levels of production and remineralization and low rates of sedimentation (Fig. 7). Essentially, slow sinking and/or rapid remineralization results in inefficient removal of P to shelf sea sediments, requiring the ocean concentration of P to rise considerably for P output to balance (fixed) P input to the ocean.

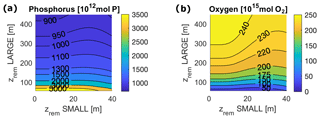
Figure 5 Local P concentration in each ocean box for varying ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$ for the following: (a) surface shelf sea, ss; (b) surface open ocean, so; (c) deep shelf sea, ds; and (d) deep open ocean, do. Surface ocean boxes, as well as deep ocean boxes, are plotted on the same scale.

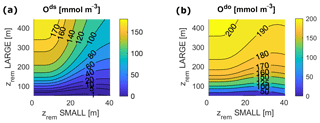
Figure 6 O concentrations at equilibrium for varying ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$ for the following: (a) deep shelf sea, ds; (b) deep open ocean, do. Surface ocean boxes (not shown) have nearly constant values of O for any set of z_rem due to the air–sea gas exchange, which strongly couples them to the atmosphere.

Our model results show that for any pair of values of ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$ in the entire explored range, the biological pump is able to oxygenate the surface ocean (surface O levels lie close to 273 mmol m⁻³) and, for most values, also to maintain the deep ocean above the level of hypoxia (Fig. 6). The model shows a substantial difference between the deep shelf and the deep open ocean; while the latter is substantially oxygenated (O>50 mmol m⁻³) for nearly any values of ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$, the deep shelf is hypoxic or even suboxic for a broad range of small values of ${z_{\text{rem}}}^{\mathrm{L}}$, especially close to modern shelf ${z_{\text{rem}}}^{\mathrm{L}}$ observations. Considering the wide spatial extension of our boxes, we expect these low oxygen levels to indicate the development of local anoxia in the deep shelf.

In a limited interval of small ${z_{\text{rem}}}^{\mathrm{S}}$ values (roughly ${z_{\text{rem}}}^{\mathrm{S}}<\mathrm{6}$ m), model results depend only on the LP_org properties due to the rather irrelevant contribution of SP_org to export and remineralization. For larger z_rem values (${z_{\text{rem}}}^{\mathrm{S}}>\mathrm{6}$ m and ${z_{\text{rem}}}^{\mathrm{L}}>\mathrm{100}$ m), model results show a strong interdependence of equilibrium budgets and absolute fluxes on both ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$. Interestingly, in this range of values, export production depends very strongly on the small particle properties, ranging between 10 % for low ${z_{\text{rem}}}^{\mathrm{S}}$ and 30 % for high ${z_{\text{rem}}}^{\mathrm{S}}$, an overall trend that also affects the ratio of deep remineralization to surface production (Fig. 7).

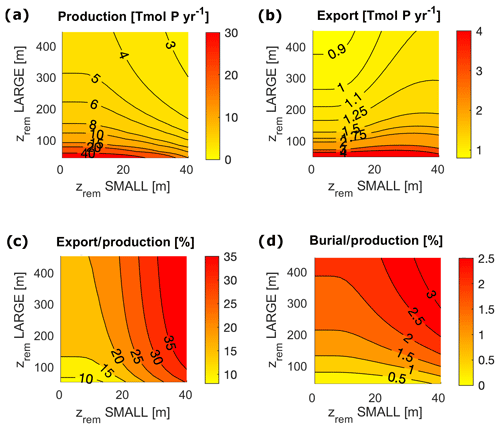
Figure 7 Biological pump fluxes in P units for the entire ocean for varying ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$ in the following cases: (a) P_org surface production; (b) P_org export through the euphotic layer depth; (c) export / production, i.e. export to production ratio; and (d) burial to production ratio.

It is also important to notice that, for any couple of ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$, modeled tracer concentrations and fluxes fall in a range of values that never exceeds by orders of magnitude the modern observed values. Considering all of the ocean boxes, P concentrations vary in the range of roughly 0.2 and 9 mmol m⁻³, while O levels lie between 0.5 and 205 mmol m⁻³. Production in carbon units lies in the interval [7.6, 70.7 Gt C yr⁻¹].

4.2 Budgets and fluxes contribution by particle class

The relative role of small and large particles in modeled biological and physical fluxes depends on a combination of their inherent properties (z_rem) and coagulation. In our simple model, coagulation of SP_org into LP_org after production in surface boxes affects a constant fraction (cg_f=0.22) of the produced particles. This fraction was determined by model tuning to modern ocean conditions and lies close to modern ocean observations of the large-particle fraction (15% of the total particles) at export depth (Cavan et al., 2017).

For ${z_{\text{rem}}}^{\mathrm{L}}>\mathrm{100}$ m, LP_org efficiently removes P from the water column, limiting production. The contribution of SP_org to the total export below the euphotic layer, however, is strongly dominated by the value of ${z_{\text{rem}}}^{\mathrm{S}}$, with a null contribution to export for all values of ${z_{\text{rem}}}^{\mathrm{S}}<\mathrm{10}$ m and increasing values above it. This trend is reflected in the deep water small-particle fraction (Fig. 8c, d). Small particles contribute up to 73 % to export in both ocean boxes and up to 60 % to the sediment accumulation in the shelf sea, with the highest contribution to sediment accumulation being reached for large ${z_{\text{rem}}}^{\mathrm{S}}$ and low ${z_{\text{rem}}}^{\mathrm{L}}$. Our model highlights therefore the different role of large and small particles in the determination of the equilibrium budgets and fluxes. Coagulation into large (fast sinking and less liable) particles is essential to maintain high enough sedimentation and burial rates, therefore allowing O accumulation in the system. At the same time, small (slow sinking and more liable) particles tune the total magnitude of export and remineralization below the euphotic layer, affecting the distribution of oxygen and nutrients throughout the water column.

5 Discussion

5.1 Model limitations and robustness

5.1.1 General limitations

BPOP consists of a simple box model with four ocean boxes, two sediment boxes and one atmospheric box. As with every box model, BPOP only allows a very rough and fundamental representation of the topography and circulation of the ocean as well as of the exchange fluxes between ocean, atmosphere and sediments. Even though this may be a limitation in the context of the study of the well-known modern (and future) ocean, such a computationally inexpensive model can be a useful tool to for a first exploration of a large variety of projected conditions. In the context of understanding past ocean changes, often characterized by a limited availability of observational data, the use of such a simple model constitutes instead an effective and honest approach to understanding global shifts in budgets and fluxes. Furthermore, BPOP explicitly distinguishes between the well-sampled shelf sea and the less known open ocean of deep time; therefore allowing the relation of shelf data with large-scale open ocean conditions.

The model deliberately simplifies the redox carriers and processes represented, neglecting denitrification and iron and sulfate reduction. Including additional oxidants and/or methane consumption in deeper water column would be expected to intensify anoxia results at depth. However, our current results suggest that the model is underestimating the ocean total oxygen budget overall, mostly driven by the deep open ocean reservoir. This suggests that neglecting these additional processes in our simple box model does not lead to an overestimation of oxygen accumulation at depth. Including additional state variables and processes could also lead to more complex dynamical behaviors (Wallmann, 2010).

We include anaerobic remineralization of P_org as being faster than aerobic degradation, but in reality this is not the case for carbon – which is remineralized at a similar or slower rate under anoxic vs. oxic conditions (Burdige, 2007; Hedges et al., 1999; Dale et al., 2015). Hence, in reality, under anoxic conditions, there is preferential regeneration of phosphorus and organic C:P burial ratios rise considerably, altering the long-term steady state of atmospheric oxygen (Van Cappellen and Ingall, 1996). We do not consider these aspects here because to do so would require adding state variables for organic carbon (as distinct from organic phosphorus) and because our focus here is on changes in ocean phosphorus and ocean redox under an unchanged oxygen steady state. In future work we intend to elaborate the model in order to explore long-term effects on atmospheric oxygen.

5.1.2 Limitations connected to the biological pump representation

In our model we adopt a very simplified representation of the biological pump, including two particle classes, “small” and “large”, generated by production and coagulation, assuming that, on average, ${z_{\text{rem}}}^{\mathrm{S}}<{z_{\text{rem}}}^{\mathrm{L}}$. This scheme resembles the one commonly used in ocean biogeochemical models (Gruber et al., 2006; Jackson and Burd, 2015). Our model does not include a dissolved organic matter (DOM) pool for reasons mostly connected to the implicit representation of the biological pump and the complete remineralization of the non-sedimented organic material at each integration step. For the same reason, we do not resolve particle P_org concentrations, and therefore we model the coagulation flux as a constant fraction of production. A more physical representation of coagulation would require this flux to scale with the square of the particle concentrations (Boyd and Trull, 2007). Such a further development could potentially lead to increase large particle export for high surface P concentrations leading to high production and particle concentrations (and vice versa). We reserve this improvement as our first step for further model developments, which will include an explicit P_org representation.

Modeled particles get remineralized through the water column according to their characteristic z_rem. Even though for simplicity we do not use a continuous spectrum of z_rem, the use of two particle classes is in line with observations showing two distinct peaks in the observed distribution of the sinking speeds of the particles (Riley et al., 2012; Alonso-González et al., 2010). Furthermore, this simplification still allows us to closely approximate the empirical particle flux curve as a function of depth, also known as Martin's curve (Boyd and Trull, 2007).

We assume that ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$ do not vary between the shelf sea and the open ocean. However, modern ocean observations show cross-shore changes in the phytoplankton community structure and sinking speeds (Barton et al., 2013). Our simplifying assumption may therefore cause the overestimation of the relative contribution of the shelf sea to the total burial flux of P_org. Despite this, we believe that this choice is still convenient in the context of the current model, as it allows us to reduce the number of parameters in such a simple box model representation of the biological pump of the ocean.

Observations suggest that hard-shelled phytoplankton types, especially calcified cells, contribute substantially to the vertical export and burial of the organic material thanks to extremely large z_rem despite their small size (Lam et al., 2011; Iversen and Ploug, 2010). In the present study we focus on an interval of ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$ values that are most likely to resemble the biological pump conditions of the Neoproterozoic–early Paleozoic ocean, before the evolution of such phytoplankton types. However, the model allows the exploration of different ranges of ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$ values and the tuning of the rate of coagulation in order to explore the influence of these phytoplankton classes.

Even though bacterial remineralization is thought to be the dominant pathway for organic matter recycling on a global scale, especially at low latitudes (Rivkin and Legendre, 2001), modern ocean coastal environments are also characterized by high grazing rates. The evolution of zooplankton and increasingly large grazers may have had a different impact on the effective ${z_{\text{rem}}}^{\mathrm{S}}$ and low ${z_{\text{rem}}}^{\mathrm{L}}$, given additional P_org transformations such as particle fragmentation due to sloppy feeding (Cavan et al., 2017; Iversen and Poulsen, 2007). These processes can limit the large-particle burial rates, while resulting in the deep production of small particles, suspended particulate organic matter (s-POM) and DOM. Our model does not currently account for particle fragmentation, however the process could be easily considered in future model developments. In this context, new processes such as the sedimentation and burial of large grazers should also be considered.

5.1.3 Sensitivity to parameter choices

We discuss here the model sensitivity to changes in a set of significant parameters adopted to describe its geometry, circulation and biological processes. Overall, none of the sensitivity experiments showed significant changes in the model results and conclusions; trends in budgets and fluxes obtained varying ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$ and our main results regarding the relative deep shelf and open ocean oxygenation remain unchanged.

Among the geometrical box model parameters, a key value is represented by the percentage of shelf sea area (𝒫_shelf). An increase (e.g. doubling) in 𝒫_shelf results in an overall decrease in the total budget of P and increase in O due to the larger ratio of burial to production, which is facilitated by a larger extension of the surface of shallow water. Interestingly, deep shelf anoxia is enhanced for larger 𝒫_shelf; i.e. anoxia is observed for a wider range of ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$ values, while the deep ocean tends to be more oxygenated. Despite a doubling of 𝒫_shelf, however, model results largely remain in the same range of those found for modern 𝒫_shelf.

We explored the effect of varying the physical circulation parameters. Changes in upwelling (Upw), have an important impact on the budgets of the modeled ocean. An increase in Upw induces a lowering of P levels, especially in the deep shelf, due to their recirculation towards the surface and consequent uptake by production. This is coupled with an overall larger equilibrium O budget due to higher storage in the deep open ocean and consequent recirculation into the deep shelf. Deep shelf suboxia is still possible but for a more limited range of ${z_{\text{rem}}}^{\mathrm{L}}$ values. Changes in vertical mixing in the open ocean (Mix_vo) affect the overall P and O budgets mostly for high ${z_{\text{rem}}}^{\mathrm{L}}$. For lower Mix_vo, the O budget decreases due to lower O storage at depth, while P increases. Changes in vertical mixing on the shelf (Mix_vs), instead, have a minor impact on the total budgets and fluxes of the model, while locally modulating shelf oxygen and nutrient concentrations. Lateral mixing fluxes (Mix_ls, Mix_ld) were included in our model for means of generalization and in order to account for the influence of non-upwelling margins, with a lower value than in previous studies (Fennel et al., 2005). Changes in Mix_ls and Mix_ld result in significant changes in the deep ocean storage of tracers and open ocean production, with little impact on the budget of the other ocean boxes. However, in this case also, our main conclusions remain unaffected.

We explored the impact of changing the portion of nutrients delivered directly to the open ocean, P_open. Even large changes in this parameter do not significantly affect the results of the model, indicating that the relative levels of P and O at equilibrium are determined by the internal physical and biogeochemical dynamics of the model, rather than by boundary conditions.

Lastly, we explored the model sensitivity to the choice of key biogeochemical parameters representing rates of transformation. Both increasing coagulation (cg_f) and the use of higher rates of formation of mineral Ca–P (CaP_r) result in a general increase in O levels and decrease in nutrient availability due to larger sedimentation and burial rates. However, we find again no substantial change in the model behavior nor in the relative contribution to budgets and fluxes of each modeled ocean box.

Furthermore, we have tested the impact of having sediment remineralization rates that vary with the z_rem of the particles, under the assumption that the liability of small and large particles may be different. In our experiment, we increased the remineralization rm_r rate linearly with z_rem by 40 % of our baseline value (${{\text{rm}}_{\mathrm{r}}}^{\mathrm{0}}$), with ${{\text{rm}}_{\mathrm{r}}}^{\mathrm{0}}$ being found at the center of the interval of explored values of $z_{\text{rem}}=[\mathrm{0},$ 450 m]. Under these conditions, we obtained a higher decoupling between the influence of ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$ on budgets and fluxes, both being more strongly driven by the small particle properties for large values of ${z_{\text{rem}}}^{\mathrm{L}}$.

5.2 Model applications

5.2.1 Past changes in the biological pump

The evolution of larger and heavier cells during the Neoproterozoic and across the Neoproterozoic–Paleozoic transition is hypothesized to have caused significant changes in the nutrient and redox state of the ocean (Lenton and Daines, 2018). Our new model can be used to assess the impact of this evolution in both the shelf and the open ocean. Our first model results highlight that for small ${z_{\text{rem}}}^{\mathrm{L}}$, i.e. for an early biological pump with reduced capacity of export and burial, nutrient levels and production rates are particularly high. At the same time, an increase in ${z_{\text{rem}}}^{\mathrm{S}}$ alone, fueling higher remineralization rates at depth, can induce anoxia in the deep shelf while still maintaining the deep open ocean substantially oxygenated. The possibility of a coexistence of an anoxic deep shelf with an oxygenated deep open ocean has important implications for the interpretation of deep time redox proxy data, which come almost exclusively from shelf and slope environments yet have been widely used to infer deep ocean anoxia for most of the Proterozoic Eon (Lenton and Daines, 2017). We plan to use our model to further explore these changes from a time-frame perspective, introducing time-varying boundary conditions (such as changes in P_in) and parameter properties.

Phytoplankton evolution as well as the development of heavier and larger marine organisms continued throughout the Phanerozoic (Katz et al., 2007). BPOP can also be used to explore the role of the biological pump in the onset of OAEs in the course of the Mesozoic Era, likely induced by enhanced productivity due to an upwelling intensification (Higgins et al., 2012). During the Mesozoic Era, the evolution of dinoflagellates and calcareous and silica-encased phytoplankton also likely impacted the export and burial rates in a significant way (Katz et al., 2004). By extending the range of explored values of ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$ or possibly including the effect of grazing and/or an additional heavy POM class for shelled organisms, BPOP can also be used to study the consequences of such an evolution.

5.2.2 Future changes in the biological pump

Predicted future changes connected to global warming include, among others, changes in ocean temperature, pH and stratification (Gruber et al., 2004), with additional repercussions on plankton community structure, production, remineralization and export rates (Laufkötter et al., 2017; Acevedo-Trejos et al., 2014; Kwon et al., 2009). Our results show that around values of ${z_{\text{rem}}}^{\mathrm{L}}$ measured for the modern shelf environment (Cavan et al., 2017), modeled equilibrium budgets and fluxes are very sensitive to small changes in z_rem. This indicates a potentially high sensitivity of the modern ocean to small changes in the biological pump, which may be particularly important in the deep shelf, where the boundary with suboxia is especially close (Keeling et al., 2010). Our model can be used to get a first assessment of the large-scale combined effect of predicted changes in the biological pump with expected shifts in the physical ocean properties.

5.2.3 Exploring past and future changes in geometry, physics and biogeochemistry

In the present study we have focused on the impact of changes in ${z_{\text{rem}}}^{\mathrm{S}}$ and ${z_{\text{rem}}}^{\mathrm{L}}$ on the equilibrium budget and fluxes in the ocean. However, BPOP can be used to explore the effect of global changes in other physical or biogeochemical processes coupled with the biological pump dynamics. Aside from testing the robustness of our results, the sensitivity tests presented in Sect. 5.1.3 serve also as a first exploration of the possibility to apply the model to these further studies. We discuss here a few examples of past changes that could be explored with the present model.

Through Earth's history, variations in the distribution of continents and in the mean sea level height likely impacted the percentage of shelf sea area (𝒫_shelf) throughout the global ocean (Katz et al., 2007). Changes in climate and therefore in the mean temperature are expected to have affected both the air–sea gas exchange of oxygen – Schmidt number N_Sch(T_mean) – and vertical mixing – Mix_vo (Petit et al., 1999). Reduced vertical mixing in warm periods is also expected to be relevant in the future because of global warming (Gruber et al., 2004). Changes in temperature are also known to impact biological activity directly, e.g. by increasing remineralization rates (rm_r) (Laufkötter et al., 2017), and indirectly, e.g. affecting production and mortality rates through changes in the mixed layer depth (Polovina et al., 1995). Climatic shifts can also cause changes in the intensity of alongshore winds and therefore in the upwelling circulation (Sydeman et al., 2014). Lastly, the model can be used to test the impact of changes in the biogeochemical cycles, including shifts in the Redfield ratio as well as global changes in the P input (P_in) to the ocean (Reinhard et al., 2017; Filippelli, 2008).

6 Conclusions and outlook

This paper provides a description, evaluation and discussion of the new BPOP model. BPOP is aimed at exploring the effects of changes in the biological pump on the shelf and open ocean nutrient and redox state as well as on P and O fluxes. This model can be adopted for a large variety of studies aimed at exploring the impact of changes in the biological pump, i.e. the particle remineralization length scale z_rem, in past and future ocean settings. Furthermore, it allows us to couple changes in POM properties with changes in the geometry, circulation and boundary conditions of the ocean.

Despite its simple representation of the ocean circulation and the biological pump, the model can reasonably simulate values of the current P and O tracer budgets and biological pump fluxes. The model predicts potentially large variations in these P and O budgets and fluxes for past and future changes in the POM remineralization length. Our preliminary results also indicate that the early ocean may have been nutrient rich, with high levels of production and remineralization and that a suboxic deep shelf setting may have been compatible with an oxygenated deep open ocean.

We plan to apply this model to study the time evolution of the P and O budgets in both the shelf and the open ocean environment across the Neoproterozoic–Phanerozoic transition. Further developments of the model will be aimed at accounting for successive evolutionary innovations, including particle fragmentation due to grazing.

Appendix A: Equations

A1 Air–sea gas exchange of oxygen

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{N}_{\text{Sch}}=\mathrm{1638}-\mathrm{81.83}\cdot T_{\text{mean}}+\mathrm{1.483}\cdot {T_{\text{mean}}}^{\mathrm{2}}\\ \text{(A1)}& {\displaystyle }& {\displaystyle }-\mathrm{0.008004}\cdot {T_{\text{mean}}}^{\mathrm{3}}{\displaystyle }& {\displaystyle }{K}_W=\mathrm{0.31}\cdot {W_{\text{speed}}}^{\mathrm{2}}\cdot \sqrt{\mathrm{660}/N_{\text{Sch}}}\cdot {\mathrm{10}}^{-\mathrm{2}}\\ \text{(A2)}& {\displaystyle }& {\displaystyle }\cdot (\mathrm{24}\cdot \mathrm{365.25})\end{array}$$

A2 Surface shelf sea (ss)

$$\begin{array}{ll}\text{(A3)}& {\displaystyle }& {\displaystyle }{V}^{\text{ss}}=\mathrm{\Delta }{Z}_{\text{eu}}\cdot A_{\text{ocean}}\cdot {\mathcal{P}}_{\text{shelf}}\text{(A4)}& {\displaystyle }& {\displaystyle }{\text{Prod}}^{\text{ss}}=P_{\text{eff}}\cdot (P^{\text{ss}}/(P^{\text{ss}}+K_{\mathrm{P}}\left)\right)\cdot P^{\text{ss}}\text{(A5)}& {\displaystyle }& {\displaystyle }{{\text{Flx\_SP}}_{\mathrm{org}}}^{\text{ss}}=({\text{Prod}}^{\text{ss}}-{\text{cg}}_{\mathrm{f}}\cdot {\text{Prod}}^{\text{ss}})\cdot \mathrm{\Delta }{Z}_{\text{eu}}\text{(A6)}& {\displaystyle }& {\displaystyle }{{\text{Flx\_LP}}_{\mathrm{org}}}^{\text{ss}}={\text{cg}}_{\mathrm{f}}\cdot {\text{Prod}}^{\text{ss}}\cdot \mathrm{\Delta }{Z}_{\text{eu}}{\displaystyle }& {\displaystyle }{{\text{VExp\_SP}}_{\mathrm{org}}}^{\text{ss}}={{\text{Flx\_SP}}_{\mathrm{org}}}^{\text{ss}}\\ \text{(A7)}& {\displaystyle }& {\displaystyle }\cdot \text{exp}\left(-(\mathrm{\Delta }{Z}_{\text{eu}}/\mathrm{2})/{z_{\text{rem}}}^{\mathrm{S}}\right){\displaystyle }& {\displaystyle }{{\text{VExp\_LP}}_{\mathrm{org}}}^{\text{ss}}={{\text{Flx\_LP}}_{\mathrm{org}}}^{\text{ss}}\\ \text{(A8)}& {\displaystyle }& {\displaystyle }\cdot \text{exp}\left(-(\mathrm{\Delta }{Z}_{\text{eu}}/\mathrm{2})/{z_{\text{rem}}}^{\mathrm{L}}\right){\displaystyle }& {\displaystyle }{\text{VExp\_TOTbyV}}^{\text{ss}}=\left({{\text{Flx\_SP}}_{\mathrm{org}}}^{\text{ss}}+{{\text{Flx\_SP}}_{\mathrm{org}}}^{\text{ss}}\right)\\ \text{(A9)}& {\displaystyle }& {\displaystyle }/\mathrm{\Delta }{Z}_{\text{eu}}{\displaystyle }& {\displaystyle \frac{\text{d}{P}^{\text{ss}}}{\mathrm{d}t}}=P_{\text{in}}\cdot \left(\mathrm{1}-P_{\text{open}}\right)/V^{\text{ss}}+(\text{Upw}\cdot (P^{\text{ds}}-P^{\text{ss}})\\ {\displaystyle }& {\displaystyle }+{\text{Mix}}_{\text{ls}}\cdot (P^{\text{so}}-P^{\text{ss}})+{\text{Mix}}_{\text{vs}}\cdot (P^{\text{ds}}-P^{\text{ss}}))\\ \text{(A10)}& {\displaystyle }& {\displaystyle }\cdot \text{spy}/V^{\text{ss}}-{\text{VExp\_TOTbyV}}^{\text{ss}}{\displaystyle }& {\displaystyle }{\text{AirSea}}^{\text{ss}}=K_W\cdot (O^{\text{at}}\cdot p_{\text{at}}/K_{\text{Henri}}-O^{\text{ss}})\\ \text{(A11)}& {\displaystyle }& {\displaystyle }\cdot (A_{\text{ocean}}\cdot P_{\text{shelf}})/V^{\text{ss}}\text{(A12)}& {\displaystyle }& {\displaystyle }{\text{OProd}}^{\text{ss}}={\text{OP}}_{\text{Red}}\cdot {\text{VExp\_TOTbyV}}^{\text{ss}}{\displaystyle }& {\displaystyle \frac{\text{d}{O}^{\text{ss}}}{\mathrm{d}t}}=(\text{Upw}\cdot \left(O^{\text{ds}}-O^{\text{ss}}\right)\\ {\displaystyle }& {\displaystyle }+{\text{Mix}}_{\text{ls}}\cdot \left(O^{\text{so}}-O^{\text{ss}}\right)+{\text{Mix}}_{\text{vs}}\cdot \left(O^{\text{ds}}-O^{\text{ss}}\right))\\ \text{(A13)}& {\displaystyle }& {\displaystyle }\cdot \text{spy}/V^{\text{ss}}+{\text{AirSea}}^{\text{ss}}+{\text{OProd}}^{\text{ss}}\end{array}$$

A3 Deep shelf sea (ds)

$$\begin{array}{ll}\text{(A14)}& {\displaystyle }& {\displaystyle }{V}^{\text{ds}}=\mathrm{\Delta }{Z}_{\text{ds}}\cdot A_{\text{ocean}}\cdot {\mathcal{P}}_{\text{shelf}}\text{(A15)}& {\displaystyle }& {\displaystyle }{{\text{VIn\_SP}}_{\mathrm{org}}}^{\text{ds}}={{\text{VExp\_SP}}_{\mathrm{org}}}^{\text{ss}}\text{(A16)}& {\displaystyle }& {\displaystyle }{{\text{VIn\_LP}}_{\mathrm{org}}}^{\text{ds}}={{\text{VExp\_LP}}_{\mathrm{org}}}^{\text{ss}}{\displaystyle }& {\displaystyle }{{\text{Rem\_SP}}_{\mathrm{org}}}^{\text{ds}}={{\text{VIn\_SP}}_{\mathrm{org}}}^{\text{ds}}\\ \text{(A17)}& {\displaystyle }& {\displaystyle }\cdot \left(\mathrm{1}-\text{exp}\left(-\mathrm{\Delta }{Z}_{\text{ds}}/{z_{\text{rem}}}^{\mathrm{S}}\right)\right)/\mathrm{\Delta }{Z}_{\text{ds}}{\displaystyle }& {\displaystyle }{{\text{Rem\_LP}}_{\mathrm{org}}}^{\text{ds}}={{\text{VIn\_LP}}_{\mathrm{org}}}^{\text{ds}}\\ \text{(A18)}& {\displaystyle }& {\displaystyle }\cdot \left(\mathrm{1}-\text{exp}\left(-\mathrm{\Delta }{Z}_{\text{ds}}/{z_{\text{rem}}}^{\mathrm{L}}\right)\right)/\mathrm{\Delta }{Z}_{\text{ds}}{\displaystyle }& {\displaystyle }{{\text{AerRem\_SedP}}_{\mathrm{org}}}^{\text{ds}}={\text{rm}}_{\mathrm{r}}\cdot {{\text{SedP}}_{\mathrm{org}}}^{\mathrm{s}}/\mathrm{\Delta }{Z}_{\text{ds}}\\ \text{(A19)}& {\displaystyle }& {\displaystyle }\cdot \left(O^{\text{ds}}/\left(O^{\text{ds}}+{K_{\mathrm{O}}}^{\mathrm{s}}\right)\right){\displaystyle }& {\displaystyle }{{\text{AnaRem\_SedP}}_{\mathrm{org}}}^{\text{ds}}=({\text{rm}}_{\mathrm{r}}\cdot {\text{fe}}_{\text{an}})\cdot {{\text{SedP}}_{\mathrm{org}}}^{\mathrm{s}}/\mathrm{\Delta }{Z}_{\text{ds}}\\ \text{(A20)}& {\displaystyle }& {\displaystyle }\cdot \left(\mathrm{1}-O^{\text{ds}}/\left(O^{\text{ds}}+{K_{\mathrm{O}}}^{\mathrm{s}}\right)\right){\displaystyle }& {\displaystyle \frac{\text{d}{P}^{\text{ds}}}{\text{dt}}}=(\text{Upw}\cdot \left(P^{\text{do}}-P^{\text{ds}}\right)+{\text{Mix}}_{\text{ld}}\cdot \left(P^{\text{do}}-P^{\text{ds}}\right)\\ {\displaystyle }& {\displaystyle }+{\text{Mix}}_{\text{vs}}\cdot \left(P^{\text{ss}}-P^{\text{ds}}\right))\cdot \text{spy}/V^{\text{ds}}\\ {\displaystyle }& {\displaystyle }+({{\text{Rem\_SP}}_{\mathrm{org}}}^{\text{ds}}+{{\text{Rem\_LP}}_{\mathrm{org}}}^{\text{ds}}+{{\text{AerRem\_SedP}}_{\mathrm{org}}}^{\text{ds}}\\ \text{(A21)}& {\displaystyle }& {\displaystyle }+{{\text{AnaRem\_SedP}}_{\mathrm{org}}}^{\text{ds}}){\displaystyle }& {\displaystyle }{\text{AerRemWcO}}^{\text{ds}}={\text{OP}}_{\text{Red}}\cdot \left({{\text{Rem\_SP}}_{\mathrm{org}}}^{\text{ds}}+{{\text{Rem\_LP}}_{\mathrm{org}}}^{\text{ds}}\right)\\ \text{(A22)}& {\displaystyle }& {\displaystyle }\cdot \left(O^{\text{ds}}/\left(O^{\text{ds}}+{K_{\mathrm{O}}}^{\mathrm{w}}\right)\right)\text{(A23)}& {\displaystyle }& {\displaystyle }{\text{AerRemSedO}}^{\text{ds}}={\text{OP}}_{\text{Red}}\cdot {{\text{AerRem\_SedP}}_{\mathrm{org}}}^{\text{ds}}{\displaystyle }& {\displaystyle \frac{\text{d}{O}^{\text{ds}}}{\mathrm{d}t}}=(\text{Upw}\cdot \left(O^{\text{do}}-O^{\text{ds}}\right)+{\text{Mix}}_{\text{ld}}\cdot \left(O^{\text{do}}-O^{\text{ds}}\right)\\ {\displaystyle }& {\displaystyle }+{\text{Mix}}_{\text{vs}}\cdot (O^{\text{ss}}-O^{\text{ds}}))\cdot \text{spy}/V^{\text{ds}}-{\text{AerRemWcO}}^{\text{ds}}\\ \text{(A24)}& {\displaystyle }& {\displaystyle }-{\text{AerRemSedO}}^{\text{ds}}\end{array}$$

A4 Surface open ocean (so)

$$\begin{array}{ll}\text{(A25)}& {\displaystyle }& {\displaystyle }{V}^{\text{so}}=\mathrm{\Delta }{Z}_{\text{eu}}\cdot A_{\text{ocean}}\cdot (\mathrm{1}-P_{\text{shelf}})\text{(A26)}& {\displaystyle }& {\displaystyle }{\text{Prod}}^{\text{so}}=P_{\text{eff}}\cdot (P^{\text{so}}/(P^{\text{so}}+K_{\mathrm{P}}\left)\right)\cdot P^{\text{so}}\text{(A27)}& {\displaystyle }& {\displaystyle }{{\text{Flx\_SP}}_{\mathrm{org}}}^{\text{so}}=({\text{Prod}}^{\text{so}}-{\text{cg}}_{\mathrm{f}}\cdot {\text{Prod}}^{\text{so}})\cdot \mathrm{\Delta }{Z}_{\text{eu}}\text{(A28)}& {\displaystyle }& {\displaystyle }{{\text{Flx\_LP}}_{\mathrm{org}}}^{\text{so}}={\text{cg}}_{\mathrm{f}}\cdot {\text{Prod}}^{\text{so}}\cdot \mathrm{\Delta }{Z}_{\text{eu}}{\displaystyle }& {\displaystyle }{{\text{VExp\_SP}}_{\mathrm{org}}}^{\text{so}}={{\text{Flx\_SP}}_{\mathrm{org}}}^{\text{so}}\\ \text{(A29)}& {\displaystyle }& {\displaystyle }\cdot \text{exp}\left(-(\mathrm{\Delta }{Z}_{\text{eu}}/\mathrm{2})/{z_{\text{rem}}}^{\mathrm{S}}\right){\displaystyle }& {\displaystyle }{{\text{VExp\_LP}}_{\mathrm{org}}}^{\text{so}}={{\text{Flx\_LP}}_{\mathrm{org}}}^{\text{so}}\\ \text{(A30)}& {\displaystyle }& {\displaystyle }\cdot \text{exp}\left(-(\mathrm{\Delta }{Z}_{\text{eu}}/\mathrm{2})/{z_{\text{rem}}}^{\mathrm{L}}\right){\displaystyle }& {\displaystyle }{\text{VExp\_TOTbyV}}^{\text{so}}=\left({{\text{Flx\_SP}}_{\mathrm{org}}}^{\text{so}}+{{\text{Flx\_SP}}_{\mathrm{org}}}^{\text{so}}\right)\\ \text{(A31)}& {\displaystyle }& {\displaystyle }/\mathrm{\Delta }{Z}_{\text{eu}}{\displaystyle }& {\displaystyle \frac{\text{d}{P}^{\text{so}}}{\mathrm{d}t}}=P_{\text{in}}\cdot P_{\text{open}}/V^{\text{ss}}+(\text{Upw}\cdot (P^{\text{ss}}-P^{\text{so}})+{\text{Mix}}_{\text{ls}}\\ {\displaystyle }& {\displaystyle }\cdot (P^{\text{ss}}-P^{\text{so}})+{\text{Mix}}_{\text{vo}}\cdot (P^{\text{do}}-P^{\text{so}}))\cdot \text{spy}/V^{\text{so}}\\ \text{(A32)}& {\displaystyle }& {\displaystyle }-{\text{VExp\_TOTbyV}}^{\text{so}}{\displaystyle }& {\displaystyle }{\text{AirSea}}^{\text{so}}=K_W\cdot \left(O^{\text{at}}\cdot p_{\text{at}}/K_{\text{Henri}}-O^{\text{so}}\right)\\ \text{(A33)}& {\displaystyle }& {\displaystyle }\cdot (A_{\text{ocean}}\cdot (\mathrm{1}-{\mathcal{P}}_{\text{shelf}}\left)\right)/V^{\text{so}}\text{(A34)}& {\displaystyle }& {\displaystyle }{\text{OProd}}^{\text{so}}={\text{OP}}_{\text{Red}}\cdot {\text{VExp\_TOTbyV}}^{\text{so}}{\displaystyle }& {\displaystyle \frac{\text{d}{O}^{\text{so}}}{\mathrm{d}t}}=(\text{Upw}\cdot \left(O^{\text{ss}}-O^{\text{so}}\right)+{\text{Mix}}_{\text{ls}}\cdot \left(O^{\text{ss}}-O^{\text{so}}\right)\\ {\displaystyle }& {\displaystyle }+{\text{Mix}}_{\text{vo}}\cdot (O^{\text{do}}-O^{\text{so}}))\cdot \text{spy}/V^{\text{so}}\\ \text{(A35)}& {\displaystyle }& {\displaystyle }+{\text{AirSea}}^{\text{so}}+{\text{OProd}}^{\text{so}}\end{array}$$

A5 Deep open ocean (do)

$$\begin{array}{ll}\text{(A36)}& {\displaystyle }& {\displaystyle }{V}^{\text{do}}=\mathrm{\Delta }{Z}_{\text{do}}\cdot A_{\text{ocean}}\cdot (\mathrm{1}-P_{\text{shelf}})\text{(A37)}& {\displaystyle }& {\displaystyle }{{\text{VIn\_SP}}_{\mathrm{org}}}^{\text{do}}={{\text{VExp\_SP}}_{\mathrm{org}}}^{\text{so}}\text{(A38)}& {\displaystyle }& {\displaystyle }{{\text{VIn\_LP}}_{\mathrm{org}}}^{\text{do}}={{\text{VExp\_LP}}_{\mathrm{org}}}^{\text{so}}{\displaystyle }& {\displaystyle }{{\text{Rem\_SP}}_{\mathrm{org}}}^{\text{do}}={{\text{VIn\_SP}}_{\mathrm{org}}}^{\text{do}}\\ \text{(A39)}& {\displaystyle }& {\displaystyle }\cdot \left(\mathrm{1}-\text{exp}\left(-\mathrm{\Delta }{Z}_{\text{do}}/{z_{\text{rem}}}^{\mathrm{S}}\right)\right)/\mathrm{\Delta }{Z}_{\text{do}}{\displaystyle }& {\displaystyle }{{\text{Rem\_LP}}_{\mathrm{org}}}^{\text{do}}={{\text{VIn\_ LP}}_{\mathrm{org}}}^{\text{do}}\\ \text{(A40)}& {\displaystyle }& {\displaystyle }\cdot \left(\mathrm{1}-\text{exp}\left(-\mathrm{\Delta }{Z}_{\text{do}}/{z_{\text{rem}}}^{\mathrm{L}}\right)\right)/\mathrm{\Delta }{Z}_{\text{do}}{\displaystyle }& {\displaystyle }{{\text{AerRem\_SedP}}_{\mathrm{org}}}^{\text{do}}={\text{rm}}_{\mathrm{r}}\cdot {{\text{SedP}}_{\mathrm{org}}}^{\mathrm{o}}/\mathrm{\Delta }{Z}_{\text{do}}\\ \text{(A41)}& {\displaystyle }& {\displaystyle }\cdot \left(O^{\text{do}}/\left(O^{\text{do}}+{K_{\mathrm{O}}}^{\mathrm{s}}\right)\right){\displaystyle }& {\displaystyle }{{\text{AnaRem\_SedP}}_{\mathrm{org}}}^{\text{do}}=({\text{rm}}_{\mathrm{r}}\cdot {\text{fe}}_{\text{an}})\cdot {{\text{SedP}}_{\mathrm{org}}}^{\mathrm{o}}/\mathrm{\Delta }{Z}_{\text{do}}\\ \text{(A42)}& {\displaystyle }& {\displaystyle }\cdot \left(\mathrm{1}-O^{\text{do}}/\left(O^{\text{do}}+{K_{\mathrm{O}}}^{\mathrm{s}}\right)\right){\displaystyle }& {\displaystyle \frac{\text{d}{P}^{\text{do}}}{\mathrm{d}t}}=(\text{Upw}\cdot \left(P^{\text{so}}-P^{\text{do}}\right)+{\text{Mix}}_{\text{ld}}\cdot \left(P^{\text{ds}}-P^{\text{do}}\right)\\ {\displaystyle }& {\displaystyle }+{\text{Mix}}_{\text{vo}}\cdot \left(P^{\text{so}}-P^{\text{do}}\right))\cdot \text{spy}/V^{\text{do}}\\ {\displaystyle }& {\displaystyle }+({{\text{Rem\_SP}}_{\mathrm{org}}}^{\text{do}}+{{\text{Rem\_LP}}_{\mathrm{org}}}^{\text{do}}+{{\text{AerRem\_SedP}}_{\mathrm{org}}}^{\text{do}}\\ \text{(A43)}& {\displaystyle }& {\displaystyle }+{{\text{AnaRem\_SedP}}_{\mathrm{org}}}^{\text{do}}){\displaystyle }& {\displaystyle }{\text{AerRemWcO}}^{\text{do}}={\text{OP}}_{\text{Red}}\cdot \left({{\text{Rem\_SP}}_{\mathrm{org}}}^{\text{do}}+{{\text{Rem\_LP}}_{\mathrm{org}}}^{\text{do}}\right)\\ \text{(A44)}& {\displaystyle }& {\displaystyle }\cdot \left(O^{\text{do}}/\left(O^{\text{do}}+{K_{\mathrm{O}}}^{\mathrm{w}}\right)\right)\text{(A45)}& {\displaystyle }& {\displaystyle }{\text{AerRemSedO}}^{\text{do}}={\text{OP}}_{\text{Red}}\cdot {{\text{AerRem\_SedP}}_{\mathrm{org}}}^{\text{do}}{\displaystyle }& {\displaystyle \frac{\text{d}{O}^{\text{do}}}{\mathrm{d}t}}=(\text{Upw}\cdot \left(O^{\text{so}}-O^{\text{do}}\right)+{\text{Mix}}_{\text{ld}}\cdot \left(O^{\text{ds}}-O^{\text{do}}\right)\\ {\displaystyle }& {\displaystyle }+{\text{Mix}}_{\text{vo}}\cdot \left(O^{\text{so}}-O^{\text{do}}\right))\cdot \text{spy}/V^{\text{do}}-{\text{AerRemWcO}}^{\text{do}}\\ \text{(A46)}& {\displaystyle }& {\displaystyle }-{\text{AerRemSedO}}^{\text{do}}\end{array}$$

A6 Shelf sea sediments (s)

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\text{SedFlx}}^{\mathrm{s}}={{\text{VIn\_SP}}_{\mathrm{org}}}^{\text{ds}}\cdot \text{exp}\left(-\mathrm{\Delta }{Z}_{\text{ds}}/{z_{\text{rem}}}^{\mathrm{S}}\right)\\ \text{(A47)}& {\displaystyle }& {\displaystyle }+{{\text{VIn\_LP}}_{\mathrm{org}}}^{\text{ds}}\cdot \text{exp}\left(-\mathrm{\Delta }{Z}_{\text{ds}}/{z_{\text{rem}}}^{\mathrm{L}}\right){\displaystyle }& {\displaystyle }{\text{CaPform}}^{\mathrm{s}}={\text{CaP}}_{\mathrm{r}}\cdot {\left({{\text{SedP}}_{\mathrm{org}}}^{\mathrm{s}}\right)}^{\mathrm{2}}\\ {\displaystyle }& {\displaystyle }\cdot \left(O^{\text{ds}}/\left(O^{\text{ds}}+{K_{\mathrm{O}}}^{\mathrm{w}}\right)+{\text{fs}}_{\text{an}}\right.\\ \text{(A48)}& {\displaystyle }& {\displaystyle }\left.\cdot \left(\mathrm{1}-O^{\text{ds}}/\left(O^{\text{ds}}+{K_{\mathrm{O}}}^{\mathrm{w}}\right)\right)\right){\displaystyle }& {\displaystyle }{{\text{Rem\_SedP}}_{\mathrm{org}}}^{\text{ds}}={{\text{AerRem\_SedP}}_{\mathrm{org}}}^{\text{ds}}\\ \text{(A49)}& {\displaystyle }& {\displaystyle }+{{\text{AnaRem\_SedP}}_{\mathrm{org}}}^{\text{ds}}{\displaystyle }& {\displaystyle \frac{{{\text{dSedP}}_{\mathrm{org}}}^s}{\mathrm{d}t}}={\text{SedFlx}}^{\mathrm{s}}-{\text{CaPform}}^{\mathrm{s}}\\ \text{(A50)}& {\displaystyle }& {\displaystyle }-{{\text{Rem\_SedP}}_{\mathrm{org}}}^{\text{ds}}\cdot \mathrm{\Delta }{Z}_{\text{ds}}\end{array}$$

A7 Open ocean sediments (o)

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\text{SedFlx}}^{\mathrm{o}}={{\text{VIn\_SP}}_{\mathrm{org}}}^{\text{do}}\cdot \text{exp}\left(-\mathrm{\Delta }{Z}_{\text{do}}/{z_{\text{rem}}}^{\mathrm{S}}\right)\\ \text{(A51)}& {\displaystyle }& {\displaystyle }+{{\text{VIn\_LP}}_{\mathrm{org}}}^{\text{do}}\cdot \text{exp}\left(-\mathrm{\Delta }{Z}_{\text{do}}/{z_{\text{rem}}}^{\mathrm{L}}\right){\displaystyle }& {\displaystyle }{\text{CaPform}}^{\mathrm{o}}={\text{CaP}}_{\mathrm{r}}\cdot {\left({{\text{SedP}}_{\mathrm{org}}}^{\mathrm{o}}\right)}^{\mathrm{2}}\cdot (O^{\text{do}}/\left(O^{\text{do}}+{K_{\mathrm{O}}}^{\mathrm{w}}\right)\\ \text{(A52)}& {\displaystyle }& {\displaystyle }+{\text{fs}}_{\text{an}}\cdot \left(\mathrm{1}-O^{\text{do}}/\left(O^{\text{do}}+{K_{\mathrm{O}}}^{\mathrm{w}}\right)\right)){\displaystyle }& {\displaystyle }{{\text{Rem\_SedP}}_{\mathrm{org}}}^{\text{do}}={{\text{AerRem\_SedP}}_{\mathrm{org}}}^{\text{do}}\\ \text{(A53)}& {\displaystyle }& {\displaystyle }+{{\text{AnaRem\_SedP}}_{\mathrm{org}}}^{\text{do}}{\displaystyle }& {\displaystyle \frac{{{\text{dSedP}}_{\mathrm{org}}}^{\mathrm{o}}}{\mathrm{d}t}}={\text{SedFlx}}^{\mathrm{o}}-{\text{CaPform}}^{\mathrm{o}}\\ \text{(A54)}& {\displaystyle }& {\displaystyle }-{{\text{Rem\_SedP}}_{\mathrm{org}}}^{\text{do}}\cdot \mathrm{\Delta }{Z}_{\text{do}}\end{array}$$

A8 Atmosphere (at)

$$\begin{array}{ll}\text{(A55)}& {\displaystyle }& {\displaystyle }{\text{AirSea}}^{\text{at}}=\left({\text{AirSea}}^{\text{ss}}+{\text{AirSea}}^{\text{so}}\right)/({\text{Mol}}_{\text{atmo}}\cdot {\mathrm{10}}^{\mathrm{3}}){\displaystyle }& {\displaystyle }{\text{AnaRemWc}}^{\text{ds}}={\text{OP}}_{\text{Red}}\cdot \left({{\text{Rem\_SP}}_{\mathrm{org}}}^{\text{ds}}+{{\text{Rem\_LP}}_{\mathrm{org}}}^{\text{ds}}\right)\\ \text{(A56)}& {\displaystyle }& {\displaystyle }\cdot \left(\mathrm{1}-O^{\text{ds}}/(O^{\text{ds}}+{K_{\mathrm{O}}}^{\mathrm{w}})\right){\displaystyle }& {\displaystyle }{\text{AnaRemWc}}^{\text{do}}={\text{OP}}_{\text{Red}}\cdot \left({{\text{Rem\_SP}}_{\mathrm{org}}}^{\text{do}}+{{\text{Rem\_LP}}_{\mathrm{org}}}^{\text{do}}\right)\\ \text{(A57)}& {\displaystyle }& {\displaystyle }\cdot \left(\mathrm{1}-O^{\text{do}}/\left(O^{\text{do}}+{K_{\mathrm{O}}}^{\mathrm{w}}\right)\right){\displaystyle }& {\displaystyle }{\text{AnaRemWc}}^{\text{at}}=({\text{AnaRemWc}}^{\text{ds}}\cdot V^{\text{ds}}\\ \text{(A58)}& {\displaystyle }& {\displaystyle }+{\text{AnaRemWc}}^{\text{do}}\cdot V^{\text{do}})/({\text{Mol}}_{\text{atmo}}\cdot {\mathrm{10}}^{\mathrm{3}}){\displaystyle }& {\displaystyle }{\text{AnaRemSed}}^{\text{at}}=({{\text{AnaRem\_SedP}}_{\mathrm{org}}}^{\text{ds}}\cdot V^{\text{ds}}\\ \text{(A59)}& {\displaystyle }& {\displaystyle }+{{\text{AnaRem\_SedP}}_{\mathrm{org}}}^{\text{do}}\cdot V^{\text{do}})/{\text{Mol}}_{\text{atmo}}\text{(A60)}& {\displaystyle }& {\displaystyle }\text{OxyWeath}=W_{\mathrm{0}}\cdot \sqrt{O^{\text{at}}/{\mathrm{O}}_{{\mathrm{mix}}_{\mathrm{0}}}}/{\text{Mol}}_{\text{atmo}}\text{(A61)}& {\displaystyle }& {\displaystyle \frac{\text{d}{O}^{\text{at}}}{\mathrm{d}t}}=-{\text{AirSea}}^{\text{at}}-{\text{AnaRemWc}}^{\text{at}}-\text{OxyWeath}\end{array}$$

A9 Diagnostics: total budgets of P and O

$$\begin{array}{ll}\text{(A62)}& {\displaystyle }& {\displaystyle }{P}_{\text{sources}}=P_{\text{in}}\cdot {\mathrm{10}}^{-\mathrm{15}}{\displaystyle }& {\displaystyle }{P}_{\text{sinks}}=({\text{CaPform}}^{\mathrm{s}}\cdot A_{\text{ocean}}\cdot P_{\text{shelf}}\\ \text{(A63)}& {\displaystyle }& {\displaystyle }+{\text{CaPform}}^{\mathrm{o}}\cdot A_{\text{ocean}}\cdot \left(\mathrm{1}-P_{\text{shelf}}\right))\cdot {\mathrm{10}}^{-\mathrm{15}}\text{(A64)}& {\displaystyle }& {\displaystyle \frac{\text{d}{P}^{\text{TOT}}}{\mathrm{d}t}}=P_{\text{sources}}-P_{\text{sinks}}\text{(A65)}& {\displaystyle }& {\displaystyle }{O}_{\text{sources}}=\left({\text{OProd}}^{\text{ss}}\cdot V^{\text{ss}}+{\text{OProd}}^{\text{so}}\cdot V^{\text{so}}\right)\cdot {\mathrm{10}}^{-\mathrm{18}}{\displaystyle }& {\displaystyle }{O}_{\text{sinks}}=(\left({\text{SedRemO}}^{\text{ds}}+{\text{AerRem}}^{\text{ds}}\right)\cdot V^{\text{ds}}\\ {\displaystyle }& {\displaystyle }+\left({\text{SedRemO}}^{\text{do}}+{\text{AerRem}}^{\text{do}}\right)\cdot V^{\text{do}}\\ \text{(A66)}& {\displaystyle }& {\displaystyle }+\text{OxyWeath}\cdot {\text{Mol}}_{\text{atmo}})\cdot {\mathrm{10}}^{-\mathrm{18}}\text{(A67)}& {\displaystyle }& {\displaystyle \frac{\text{d}{O}^{\text{TOT}}}{\mathrm{d}t}}=O_{\text{sources}}-O_{\text{sinks}}\end{array}$$