the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The Air-temperature Response to Green/blue-infrastructure Evaluation Tool (TARGET v1.0): an efficient and user-friendly model of city cooling
Ashley M. Broadbent
Andrew M. Coutts
Kerry A. Nice
Matthias Demuzere
E. Scott Krayenhoff
Nigel J. Tapper
Hendrik Wouters
The adverse impacts of urban heat and global climate change are leading policymakers to consider green and blue infrastructure (GBI) for heat mitigation benefits. Though many models exist to evaluate the cooling impacts of GBI, their complexity and computational demand leaves most of them largely inaccessible to those without specialist expertise and computing facilities. Here a new model called The Air-temperature Response to Green/blue-infrastructure Evaluation Tool (TARGET) is presented. TARGET is designed to be efficient and easy to use, with fewer user-defined parameters and less model input data required than other urban climate models. TARGET can be used to model average street-level air temperature at canyon-to-block scales (e.g. 100 m resolution), meaning it can be used to assess temperature impacts of suburb-to-city-scale GBI proposals. The model aims to balance realistic representation of physical processes and computation efficiency. An evaluation against two different datasets shows that TARGET can reproduce the magnitude and patterns of both air temperature and surface temperature within suburban environments. To demonstrate the utility of the model for planners and policymakers, the results from two precinct-scale heat mitigation scenarios are presented. TARGET is available to the public, and ongoing development, including a graphical user interface, is planned for future work.
- Article
(6366 KB) - Full-text XML
- BibTeX
- EndNote
Policymakers and decision makers are increasingly aware of the cooling potential of green and blue infrastructure (GBI). Recent examples of this include the Australian Federal Government's 20 Millon Trees Program (Commonwealth of Australia, 2017) and Singapore Green Plan (Singapore Ministry of Environment and Water Resources, 2006). Governments and urban planners wish to evaluate the cooling effects of design and planning options. Urban climate models are becoming more complex, allowing more complete representation of urban physics. However, the complexity of urban climate models renders them inaccessible to consultants (Elasson, 2000), who typically work for designers and planners. Commonly used urban climate models, such as the Weather Research and Forecasting (WRF) model (Skamarock et al., 2008) and ENVI-met (Bruse, 1999), require trained research scientists and significant computational resources to run. As a result, consultants usually provide generic and unsubstantiated estimates of cooling magnitudes. Consequently, there is a need for simple, computationally efficient, and scientifically defensible urban climate models that can be used by consultants to provide reliable estimates of cooling to governmental planners and policymakers.
There are a number of existing micro-to-local-scale urban models capable of modelling GBI. The most complex models are primarily based on computational fluid dynamics (CFD) techniques. These include ENVI-met, hand-coded CFD models (such as OpenFOAM; OpenFOAM, 2011; or STAR-CD; CD-adapco, 2011) and other CFD-based approaches (Bailey et al., 2014, 2016; Kunz et al., 2000; Schlünzen et al., 2011; Yamada and Koike, 2011; Bruse, 1999). ENVI-met is the most commonly used urban microclimate model. However, numerous ENVI-met studies have reported concerns with model accuracy, particularly for representation of vegetation (Ali-Toudert and Mayer, 2006; Krüger et al., 2011; Acero and Herranz-Pascual, 2015; Spangenberg et al., 2008). In addition, the complexity of configuration and computational intensity of all CFD-based models (i.e. 24 h of simulation requiring 24 h of computation time) puts their usage out of the reach of non-specialized users.
A second group of commonly used models, such as SOLWEIG (Lindberg et al., 2008) and RayMan (Matzarakis et al., 2007, 2010), focus on radiation fluxes in urban areas. These models have been used to assess GBI cooling, especially tree shading. However, the limitations of these models may not allow a complete assessment of GBI cooling because the effects of evapotranspiration are neglected. The Temperatures of Urban Facets in 3-D (TUF-3D) model (Krayenhoff and Voogt, 2007) and a vegetated derivative (VTUF-3D) (Nice et al., 2018) provide a precise representation of urban canyon physical processes. However, TUF-3D and VTUF-3D require a high level of computer power, modelling experience, and parameter set-up.
The canyon air temperature (CAT) model (Erell and Williamson, 2006) shows potential as a computationally efficient model that calculates air temperatures using urban building and vegetation geometry and moisture availability. However, the lack of surface temperature prediction makes it difficult to derive human thermal comfort indexes. The Town Energy Balance (TEB) model (Masson, 2000) has emerged as a popular urban area parameterization scheme. The TEB-Veg (Lemonsu et al., 2012; Redon et al., 2017) variation includes urban vegetation and provides functionality to assess cooling impacts of GBI. However, the TEB-Veg model configuration and application requires a level of modelling skill normally outside the capability of environmental consultants.
While not an air temperature model, the Local-Scale Urban Meteorological Parameterization Scheme (LUMPS) (Grimmond and Oke, 2002) has been widely used to assess the impacts of GBI on surface energy balance (SEB). The Surface Urban Energy and Water Balance Scheme (SUEWS) (Järvi et al., 2011), a superset of LUMPS with added urban water balance functionality, provides a means to assess vegetation (and associated soil) transpiration impacts at local scales. SUEWS shows good performance in SEB evaluations for Vancouver and Los Angeles (Järvi et al., 2011), Helsinki (Järvi et al., 2014), and Singapore (Demuzere et al., 2017). Due to the success and simplicity of LUMPS, we use it as a key component of the model presented here.
The lack of an efficient yet accessible tool for assessing GBI is identified as a research gap. Here we introduce and evaluate a new model called The Air-temperature Response to Green/blue-infrastructure Evaluation Tool (TARGET). TARGET is a simple modelling tool that calculates surface temperature and street-level (below roof height) air temperature in urban areas. TARGET is designed to make quick and accurate assessments of urban temperatures and GBI cooling impacts with minimal input data requirements. TARGET calculates the average air temperature at street level in urban areas but does not represent micro-scale variations of radiation exchange or wind flow at the human scale. The model is designed to be used at the urban canyon to block scales (100–500 m). We recommend a minimum spatial resolution of 100 m for air temperature simulations and 30 m for surface temperature. It can be used to assess the canyon-averaged impacts of street-scale interventions or larger-scale suburban greening projects. TARGET is a climate-service-oriented tool that provides a first-order approximation of the impacts of GBI on surface temperature and street-level air temperature to provide scientific guidance to practitioners during the planning process. The computational efficiency of the model is such that a user (with 1–2 h of training) can calculate in minutes the 100 m horizontal resolution cooling effects, on a normal desktop computer, across an entire suburb/local government area or neighbourhood.
The main aims of this paper are the following: (1) to provide a technical description of TARGET, (2) to provide detailed evaluation of model performance, and (3) to provide proof of concept and illustrate how the model can be operationalized by consultants and practitioners.
2.1 Model overview
As outlined in Fig. 1, TARGET treats each model grid point as an idealized urban canyon with roofs, walls, and ground-level facets. Roof width (Wroof), building height (H), tree width (Wtree), and street width (W) are used to define the geometry of the canyon. The thermal and radiative characteristics of roofs and walls are considered to be uniform. At street level, the surfaces can be defined as concrete, asphalt, grass, irrigated grass, and water. Trees are represented at roof height, and the surfaces beneath trees are considered to be representative of the ground-level surfaces. To represent the first-order shading impacts of trees, we effectively represent the tree canopy as part of the urban canyon. As shown in Fig. 1, the width of the canyon (and therefore the amount of radiation that enters and leaves the canyon) is modulated by the planar area of trees. The simple method implies that none of the radiation effectively “intercepted” by trees enters the canyon. The area underneath trees (not shown in planar land cover maps) is added to the model to represent the additional thermal mass. This simple approach allows for a first-order representation of two major process associated with trees: solar shading and longwave trapping.
Additionally, water bodies are treated separate to all other surfaces using an independent module. More details about the model process are shown in Fig. 2. For each grid point, the average surface characteristics are used to calculate an aggregated surface temperature (Tsurf). Tsurf is converted to an average canopy layer air temperature (Tac) using an estimated canopy wind speed (Ucan) and above-canopy air temperature (Tb). A uniform Tb for all grid points is diagnosed for each time step using reference meteorological variables.
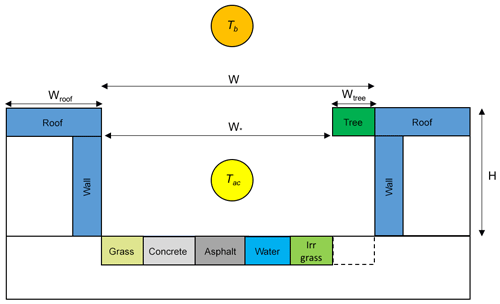
Figure 1Schematic of TARGET urban canyon set-up. Tac is the canopy layer air temperature, and Tb is the above-canopy air temperature, which is a uniform value across the whole domain. Wroof is the roof width, Wtree is the tree width, W is canyon width, and . The surface beneath trees is assumed to be representative of canyon ground-level surfaces.
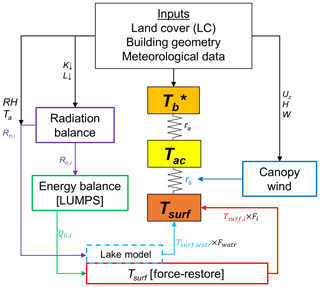
Figure 2Overview of approach used in TARGET. Tac is street-level (urban canopy layer) air temperature (∘C), Tb is the air temperature above the urban canopy layer (∘C), Tsurf,i is the surface temperature for surface type i, K↓ is incoming shortwave radiation (W m−2), L↓ is incoming longwave radiation (W m−2), Ta is reference air temperature (∘C), Rn is net radiation (W m−2), RH is relative humidity (%), Fi is the fraction of land cover type i (%), QH,i is the sensible heat flux for surface i from LUMPS (W m−2), QG,i is the storage heat flux for surface type i from LUMPS (W m−2), Uz is the reference wind speed (m s−1), H is the average building height (m), W is the average street width (m), rs is the resistance from the surface to the canopy (s m−1), and ra is the resistance from urban canopy to the atmosphere (s m−1). is a homogeneous value for the whole domain, which is diagnosed through the processes laid out in Sect. 2.7.
2.2 Input data requirements
2.2.1 Land cover
TARGET uses simple data inputs that are intended to be easily accessible. The model requires the user to define the plan area of buildings (Aroof), concrete (Aconc), asphalt (Aasph), grass (Agras), irrigated grass (Aigrs), tree (Atree), and water (Awatr). These land cover categories are self-explanatory and describe most of the surfaces present in urban areas. Local governments often have geographical information system (GIS) datasets of land cover and/or land use that can be used for land cover input data. Further, we intend to develop a graphical user interface (GUI) that allows users to easily input land cover datasets and define the model domain. This feature will allow users to convert and upload GIS data (e.g. shape and raster files) directly into the model. The Wroof, Wtree, W, W*, and wall area (Awall) are calculated from plan area land cover inputs. However, average building height (m) must be user-defined or set to a domain average value. If detailed land cover data are not available, input data can be defined from existing land-use lookup tables or from databases such as the World Urban Database and Portal Tool (WUDAPT) (Mills et al., 2015; Ching et al., 2018). See Wouters et al. (2016) for an example of how the WUDAPT data could be integrated.
2.2.2 Meteorological data
TARGET requires reference meteorological data to drive the model and calculate street-level air temperature. The following meteorological variables are required: incoming shortwave (solar) radiation (K↓), incoming longwave (terrestrial) radiation (L↓), relative humidity (RH), reference wind speed (typically at 10 m) (Uz), and air temperature (Ta). The user must define the height above ground of reference Uz and Ta. Meteorological data should be representative of a nearby airport or an open site with minimal buildings. At a minimum, reference meteorological data should conform to World Meteorological Organization guidelines (Oke, 2007).
2.3 Radiation calculation
The net radiation of the ith surface type (Rn,i) is calculated using the following:
where αi is surface albedo, ϵi is surface emissivity, and σ is the Stefan–Boltzmann constant ( W m−2 K−4). The αi and ϵi values are predefined for each surface (see Table 1). The right-hand side of the equation accounts for net longwave radiation. The modelled from two time steps (t) previously is used to calculate L↑. This is necessary to avoid circular logic in model calculations; modelled is calculated using the storage heat flux (QG,i), which takes Rn from the previous time step. The time lag does not significantly affect calculations when a 30 min time step is used. The average sky view factor (SVFi) is included to broadly represent the interception of incoming and outgoing short- and longwave radiation by buildings and trees on the radiation balance. Addition of SVF restricts the net radiation exchange of each facet to its total view factor occupied by sky. It assumes that walls and ground surfaces have similar longwave emission relative to the sky and that the solar radiation receipt can be approximated by SVF, on average. This simplification means that the model makes no distinction between lit and unlit buildings walls and roads. SVFi for ground-level, wall, and roof facets is defined as (Sparrow and Cess, 1978)
The Rn,i is then used to calculate a QG,i for each surface type.
Table 1Parameter set-up for all TARGET simulations in this article.

1 Oke (1987). 2 Stewart et al. (2014). 3 Järvi et al. (2014).
4 Narita et al. (1984). 5 Asaeda and Ca (1993). 6 Grimmond et al. (1993). 7 Doll et al. (1985).
α is the surface albedo, ϵ is the surface emissivity,
C is the volumetric heat capacity (J m−3 K−1) (×106), κ is the thermal diffusivity (m2 s−1) (), Tm is the average soil (ground) temperature
(∘C), αpm is the LUMPS empirical parameter (alpha
parameter), relating to surface moisture, β is the LUMPS empirical
parameter (beta parameter), and Tm bracketed values
are used in Mawson Lakes suburb
simulations, derived from 1-month spin-up.
a Soil layer beneath water layer. b The traditional
force–restore method is not well suited to urban surfaces (e.g. roof and
walls) — we use an artificially low thermal diffusivity to represent a thin
layer. This is discussed further in Sect. 2.5. c Roof
and wall layers are represented by the same model parameters. n/a: not
applicable.
2.4 Storage heat flux (QG) calculation
The storage heat flux (QG,i) for the ith land cover class is calculated using an adapted version of the objective hysteresis model (OHM) (Grimmond and Oke, 2002):
where and the three a coefficients are defined using cited values for each surface (see Table 1). The a coefficients capture the hysteresis pattern commonly observed between the Rn and QG,i in urban areas. See Grimmond and Oke (1999) for a full description of the OHM and the role of the a parameters in QG,i calculations. The QG,i is then used to calculate the Tsurf for each land cover type using the “force–restore” method.
2.5 Surface temperature calculation (force–restore)
The force–restore method is an efficient method for calculating surface temperature (Bhumralkar, 1975; Deardorff, 1978) and is an alternative to multilayer conduction approaches used in other climate models. The force–restore method is used to ensure that the model remains computationally efficient. The ground layer is conceptually divided into two layers with uniform vertical temperature: a thin surface layer and a deep soil layer. The forcing term, which is driven by QG,i, heats the surface layer. The restore term, driven by deep soil temperature, dampens the forcing term. The change in surface temperature Tsurf for surface i, with respect to time (t), is calculated as (Jacobs et al., 2000)
where Ci is the volumetric heat capacity (J m−3 K−1), τ is the period (86 400 s), D is the damping depth of the diurnal temperature wave , , and κ represents thermal diffusivity. The average soil (ground) temperature (∘C) (Tm) is calculated using
where , the damping depth for the annual temperature cycle (m).
The force–restore method, which assumes two layers each of uniform temperature, cannot be applied to more complex surfaces such as water, trees, walls, or roofs. For roofs we set C at a realistic value and use κ as a tuning parameter to represent layers of thermally active mass characteristic of most building roofs, which are often thinner than ground-level surfaces. This approach produces accurate Tsurf,roof results (see Sect. 3.2), but ongoing work is needed to represent roofs in a physically realistic and efficient manner. For simplicity, the wall surfaces are assumed to have the same thermal properties as roofs. For trees, we assume that Tsurf,tree is equal to Ta (see Fig. B3 for justification), and a simple water body model is used to calculate Tsurf,watr.
2.6 Simple water body model
The water model is used for modelling small inland water bodies, such as lakes and wetlands. Our analysis suggests that the OHM–force–restore method cannot be used to reliably reproduce water surface temperatures. We tested the OHM modifications and parameters used by Ward et al. (2016) and found substantial over-predictions of surface water temperature (over 10 ∘C) during the day. As such, we developed a simple water body model to stand in for the OHM–force–restore method. The water model in TARGET is based on a single water layer, overlaying a soil layer. Essentially, the force–restore surface temperature model is implemented and is overlain by a homogeneous mixed water layer (i.e. neglecting thermal stratification) representing a water body of depth dwatr (m). The model is designed to apply to water bodies of 0.1–1.0 m depths. The water model is based on the pan evaporation model of Molina Martínez et al. (2006), which closely follows that of the lake model of Jacobs et al. (1998). The water body model also determines the surface energy balance of the water surface. The energy balance model for the water layer is given by Molina Martínez et al. (2006):
where Sab is absorbed shortwave radiation (W m−2), Ln is the net longwave radiation (W m−2), QG,watr is the convective heat flux at the bottom of the water layer and into the soil below (W m−2), and ΔQS,watr is the change in heat storage of the water layer (W m−2). Solar radiation penetrates the water surface and is absorbed as described by Beer's law (Molina Martínez et al., 2006):
where Kn is the net shortwave radiation (W m−2), βk is the amount of shortwave radiation immediately absorbed by the water layer (set to 0.45) (Molina Martínez et al., 2006), and η is the extinction coefficient. Here, η is calculated according to Subin et al. (2012), for the water layer with depth dwatr (m):
A correction factor for the solar path length zenith angle is often applied to Eq. (9) (Molina Martínez et al., 2006), but this is omitted from TARGET to reduce complexity.
The QG,watr into the soil at the base of the water layer is given by Molina Martínez et al. (2006):
where Cwatr is the volumetric heat capacity of water (4.18×106 J m−3 K−1), κwatr is the eddy diffusivity of water (m2 s−1), and the change in depth is Δdwatr=dwatr (the depth of the water layer). κwatr is a complex function accounting for thermal stratification of water and surface friction velocity. To reduce complexity, and assuming a mixed homogeneous water layer, a constant κwatr is selected based on shallow lakes reported in Salas De León et al. (2016). The change in temperature ΔT (∘C) is the difference between the water temperature Tsurf,watr (∘C) and the soil temperature beneath the water layer Tsoil (∘C). Tsoil is calculated using the force–restore model, where QG,watr is equivalent to QG,i in Eq. (6):
To represent the radiation that is not absorbed by the water but is absorbed by the underlying soil layer, Kn−Sab is added to QG,watr.
The latent heat flux (QE,watr) (W m−2) is given by Arya (2001):
where ρv is the density of moist air (kg m−3), Lv is the latent heat of vaporization (i.e. 2.43 MJ kg−1), hv is the bulk transfer coefficient for moisture (Hicks, 1972; Jones et al., 2005), Uz is the reference wind speed, qs is the saturated specific humidity at Tsurf,watr, and qa is the specific humidity of the air for the given Ta.
The sensible heat flux above the water surface is given by Molina Martínez et al. (2006):
where ρa is the density of dry air (=1.2 kg m−3), Cp the specific heat of air (1013 J kg−1 K−1), and hc the bulk transfer coefficient for heat (hc=hv).
Returning to Eq. (9), net long wave radiation , leaving ΔQS,watr from the energy balance equation, which is defined as (Molina Martínez et al., 2006)
where Δt is change in time (s), and Cwatr is the volumetric heat capacity of water (J m−2 K−1). Solving for ΔTsurf,watr and adding the change in temperature to the previous time step () gives the new water layer temperature.
2.7 Calculation of urban canopy layer air temperature (Tac)
To calculate Tac we first calculate a domain Tb for each time step. Assuming air temperature at 3 times the building height (3H) is consistent between the neighbourhood of interest and the reference weather station location, we extrapolate reference air temperature at measurement height to 3H assuming a constant flux layer and using a bulk Richardson-number-based approximation (Mascart et al., 1995). Through this simple calculation we define a domain constant Tb with the basic representation of atmospheric stability in TARGET.
The canyon air temperature is then calculated using a modified version of the canopy air temperature equation from the Community Land Model Urban (CLMU) (Oleson et al., 2010):
where Fi and Tsurf,i are the 2-D fractional coverage and surface temperature of surface i in the canyon, cs is the conductance from the surface to the urban canopy layer (m s−1), and ca is the conductance from the urban canopy to the above-canopy surface layer (m s−1). In Eq. (16) we assume roofs are connected to the canyon via two resistances in series, thus representing the additional impediment to the transfer of heat from a rooftop into the canyon. We hypothesize that the heat transfer from roofs to the canyon air can be approximated by two resistances in series (the canyon-to-atmosphere resistance, ca, and surface-to-canyon resistance, cs). The logic here is that resistance to heat transfer from the roof surface to the canyon should be greater than ca or cs independently. Through sensitivity testing we are able to demonstrate that this assumption improves predicted canyon air temperature. The ca is calculated following Masson (2000) and using the stability coefficients from Mascart et al. (1995). The cs term is from Masson (2000):
where and Ucan is the wind speed in the canyon (m s−1) (Kusaka et al., 2001):
where Utop is the wind speed at the top of the canyon (m s−1). Utop is estimated at 3H based on the observed wind speed at a nearby observational site (ideally an airport) using a logarithmic relationship. Airports are relatively devoid of roughness elements, and wind speed is typically measured at 10 m above the surface. As such, the assumption of a logarithmic profile through the roughness sublayer (Masson, 2000) is imposed.
3.1 Overview
As part of the model evaluation, we conduct a range of simulations that test model performance for both Tsurf and Tac. These validation experiments are focused on clear sky summertime conditions. Clear sky is chosen because the local cooling effects of GBI are most notable during these conditions. First, we test the model's ability to simulate Tsurf for each land cover type that can be prescribed in TARGET (i.e. dry grass, asphalt etc.), using ground-based observations of Tsurf (Sect. 3.2). These simulations by land cover type provide a detailed assessment of model parameters and the underlying energy balance dynamics and resulting Tsurf for each land cover class. Second, we conduct suburb-scale simulations of Mawson Lakes, Adelaide, for which we have high-resolution remotely sensed Tsurf observations and in situ Tac data (Sect. 3.3). The suburb-scale simulations reflect the way the model is intended to be used by practitioners.
3.2 Land cover simulations
To test model performance at simulating Tsurf of different land cover classes and perform sensitivity analysis on a number of model parameters, we use ground-based observations of Tsurf from the Melbourne metropolitan area. Coutts et al. (2016) deployed infrared temperature sensors (SI-121, Apogee), during February 2012 (5 min averages), across a range of land cover types including asphalt, concrete, grass, irrigated grass, steel roof, and water. Infrared sensors were mounted above the aforementioned surface types installed at heights of approximately 1.5–2 m. The conditions during this period represented near-typical summertime conditions in Melbourne, including a number of days (15, 24, and 25 February) when air temperature exceeded 30 ∘C (see Fig. B1). These hotter days were characterized by northerly winds, which bring hot and dry air from Australia's interior and often result in heatwave conditions in Melbourne. Additionally, there was at least one cloudy day when incoming shortwave radiation (K↓) dropped significantly and a negligible amount of rainfall occurred (17 February). To compare the Coutts et al. (2016) observations with TARGET we run the model for each surface type (i.e. 100 % grass or roof etc.) with radiation forcing data from the Melbourne Airport weather station during the time period in question. The Tb calculation is not needed since we only calculated Tsurf for this part of the model evaluation. The 30 min output from TARGET is compared with Tsurf observations, and statistics are calculated.
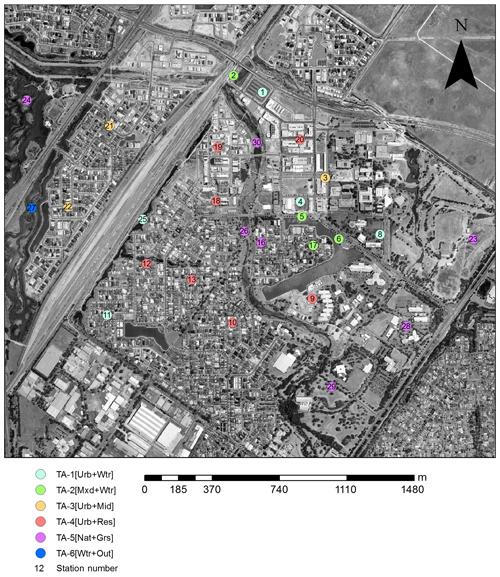
Figure 3Mawson Lakes suburb with weather station locations. The numbers indicate individual weather stations, while the colour coding specifies groups of sites with statistically similar thermal characteristics. The names of each cluster indicate the average land surface characteristics: urban sites with nearby water (TA-1[Urb+Wtr]), mixed land use with nearby water (TA-2[Mxd+Wtr]), urban mid-rise-type sites (TA-3[Urb+Mid]), urban residential sites (TA-4[Urb+Res]), natural grass-dominated sites (TA-5[Nat+Grs]), and a single outlier site (TA-6[outlier]) (Broadbent et al., 2018b).
3.3 Suburb-scale simulations (Mawson Lakes)
In addition to the land cover category testing, we also conduct suburb-scale simulations of Tsurf and Tac for Mawson Lakes, Adelaide (Fig. 3). The suburb-scale simulations use observational data from the Mawson Lakes field campaign, conducted during 13–18 February 2011, which represented average summertime conditions in Adelaide (Broadbent et al., 2018b). For these simulations, the model is run on 30 m (Tsurf) and 100 m (Tac) grids over the Mawson Lakes suburb for the period 13–18 February (Fig. B2). Remotely sensed land cover data from the campaign are used to define land cover, and building morphology is defined using lidar data (see Broadbent et al., 2018b). The Mawson Lakes simulations use the same parameter set-up as above (summarized in Table 1) and are forced with meteorological data from the Kent Town Bureau of Meteorology (ID 023090) weather station. Modelled Tsurf is validated using observed remotely sensed Tsurf (night – 15 February and day – 16 February), which is resampled to 30 m resolution (Broadbent et al., 2018b). To validate Tac, we use data from 27 automatic weather stations (AWSs) that were also deployed during the Mawson Lakes field campaign (see Fig. 3 for AWS locations).
4.1 Land cover simulations
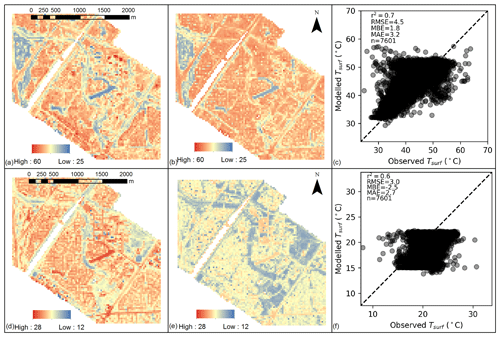
The surface temperature for each land cover class is simulated for a 14-day period during February 2012. The results show that modelled surface temperature for all three impervious surfaces (concrete, asphalt, and roof) is reasonably well predicted, with a mean bias error (MBE) of 0.88, −0.22, and −1.16 ∘C, respectively (Fig. 4a–f). The root mean square error (RMSE) values for impervious surfaces are around 3.5–4 ∘C. These RMSE values represent about 15 % of diurnal Tsurf variation, which implies good model skill given the simplicity of the approach.
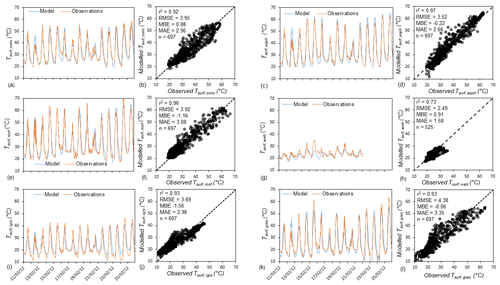
Figure 4Observed vs. modelled (a, b) Tsurf,conc, (c, d) Tsurf,asph, (e, f) Tsurf,roof, (g, h) Tsurf,watr, (i, j) Tsurf,irgs, and (k, l) Tsurf,gras. All time series plots are for the period 11–25 February. Note that the water site only had observational data for the period 11–21 February due to instrument failure; r2 is the correlation coefficient, RMSE is the root mean square error, MBE is the mean bias error, and MAE is the mean absolute error.
The night of the 16 February is not well captured at the concrete and asphalt sites. The Tsurf,conc and Tsurf,asph are under-predicted (up to 5 ∘C cooler than observations) on the night of 16 February, which may have been caused by warm air advection. The TARGET approach cannot account for the effects of warm air advection on surface temperature, as there is no feedback between Tac and Tsurf. Despite this limitation, the broad timing and magnitude of heating and cooling are well captured for all three impervious land cover types.
Model performance for Tsurf,watr had a low MBE of 0.91 ∘C, but the r2 value of 0.76 suggests the model captured diurnal Tsurf,watr variation less accurately than other surfaces (Fig. 4g–h). In particular, daily maximum Tsurf,watr values are under-predicted on hotter days (e.g. 14 February). TARGET uses a different module for water bodies (see Sect. 2.6). This simple module treats water as a single layer overlying soil. Despite the under-prediction on 14 February, the simple water body model can reproduce Tsurf,watr to an acceptable standard.
Modelled Tsurf,irgs had a MBE (−1.56 ∘C) comparable to that of impervious surfaces (Fig. 4i–j). However, the RMSE for irrigated grass (3.69 ∘C) represents approximately 20 % of diurnal Tsurf,igrs variation, suggesting model error is slightly higher than for the impervious surfaces. Generally Tsurf,igrs is slightly over-predicted at night and under-predicted at the daily maxima. This skewing of the scatter plot suggests that thermal inertia is too high in the model. Overall, the model is skillful enough to capture the timing and amplitude of Tsurf,igrs.
Dry grass had a small MBE (0.06 ∘C) but the largest RMSE of the surfaces tested (4.38 ∘C). However, this RMSE only equated to approximately 10 %–15 % of diurnal Tsurf,gras variability (Fig. 4k–l) as dry grass had the largest amplitude of surface temperature variability. Dry grass exhibited the same skewing in the scatter plot as irrigated grass, with a general over-prediction of night-time temperatures and under-prediction of daytime maxima.
4.2 Suburb-scale simulations (Mawson Lakes)
4.2.1 Surface temperature
In addition to the land cover simulations, we conduct suburb-scale modelling of the Mawson Lakes site. These simulations reveal how the TARGET model can be operationalized by practitioners who want to assess the cooling benefits of blue infrastructure or greening initiatives. Suburb-scale simulations are conducted using the same parameters as above (Table 1). We run the model at 30 m spatial resolution for Tsurf simulations and 100 m for simulations of Tac. Figure 5 shows the predicted Tsurf for the Mawson Lakes domain plotted against observed Tsurf. The Mawson Lakes simulations revealed the initial conditions of the Tm parameter (which represents the average temperature in the ground layer) are important for good model performance. A spin-up period (1 month) had to be used to obtain initial Tm values for each surface type. This can be quickly and easily achieved by running the force–restore module for a single point for each surface type. A future version of the model will automatically spin up initial Tm values. The model output also shows that some of the input land cover is poorly categorized, resulting in the population of grid points in which modelled Tsurf is over-predicted. Additionally, errors in the observed Tsurf caused by heterogeneity of roof emissivity also contribute to apparent inaccuracies of modelled Tsurf. In general, the daytime Tsurf is slightly over-predicted, and the complexity of spatial variability is not fully captured. However, this is a positive result given that only eight land cover classes are represented in the model. Overall, the daytime Tsurf is well predicted, with the range and magnitude of Tsurf captured by the model.
The results suggest that night-time Tsurf is under-predicted by model. The range of modelled nocturnal Tsurf variability (8 ∘C) is much smaller than observed variability (18 ∘C). This under-prediction of variability could reflect the fact that some processes that dictate the rate of nocturnal cooling are not fully accounted for in this approach. Nevertheless, the general spatial patterns of Tsurf are captured well. Further, given that the range of Tsurf is smaller at night, this under-prediction is of minimal consequence for modelled Tac. The nocturnal Tsurf of impervious surfaces is also under-predicted in the land cover simulations (i.e. Sect. 4.1) under warm advection conditions. Although warm advection conditions were not observed during the Mawson Lakes campaign, it is worthwhile further investigating this phenomenon in future work to negate its effect and improve nocturnal Tsurf accuracy.
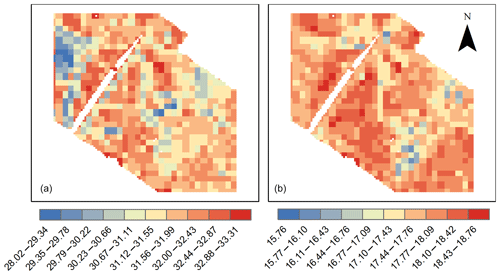
4.2.2 Air temperature
Spatial plots of modelled 03:00 and 15:00 Tac are shown in Fig. 6. The modelled air temperatures are biased towards warmer air temperature in urban areas and cooler air temperature in rural areas. These biases are partly driven by the lack of advection in the model. Without atmospheric mixing, the local impacts of pervious and impervious surfaces are exaggerated, causing an additional cooling and warming effect in rural and urban areas, respectively However, the general patterns of Tac are reasonable and as expected. We also extract modelled Tac from the grid points where the 27 AWSs are located (grid points were centred at the AWS) for a 2-day period (15–16 February 2011) (Fig. 7). The Tac is generally well predicted (Fig. 7), with a RMSE of 2.0 ∘C. These results have about the same accuracy as simulations, from the same site, conducted using a more sophisticated and computationally expensive urban climate model called SURFEX (Broadbent et al., 2018a). Although a simple model, TARGET appears to be as accurate as more complex models. Additionally, TARGET does not require the user to provide above-canyon forcing data (e.g. Tb), which are needed for other models and are not easily obtained. TARGET tends to over-predict average Tac at all urban sites (Fig. 8). Residential sites (TA-4[Urb+Res] cluster [red]) are too warm during the day. This over-prediction is likely due to the uniform wall and roof thermal parameters used, which are not representative of residential areas. Further, the lack of horizontal mixing may have exacerbated warmer temperatures in these areas. By contrast, the TA-5[Nat+Grs] cluster is too cool at night. The model predicts the formation of a stable layer with cool air trapped near the surface. Overall, the diurnal range and average Tac are well captured by the model.
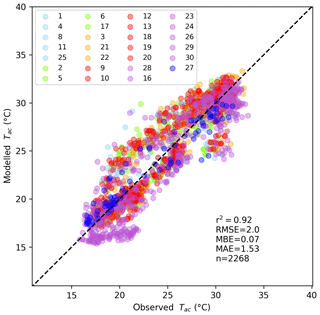
Figure 7Modelled Tac vs. observed Tac for Mawson Lakes weather stations (15–16 February 2011, 30 min data). The numbers and colours correspond to individual stations and clusters shown in Fig. 3.
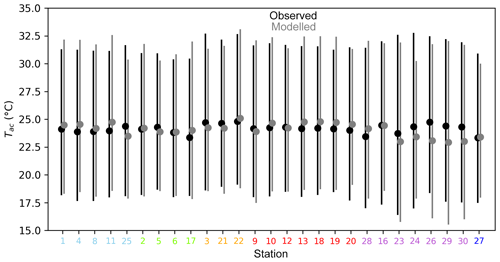
Figure 8Box plot of modelled Tac (grey) vs. observed Tac (black) for Mawson Lakes, with average, min, and max Tac shown. Box plots are generated from 30 min data from the period 15–16 February 2011. The numbers and colours (x axis) correspond to individual stations and clusters in Fig. 3.
Finally, there is some hysteresis in Fig. 6, indicating that modelled Tac is slightly out of sync with observed Tac. This could be due to the approach used to diagnose Tb, which assumes a constant Ri in the surface layer and therefore heats up too quickly during the morning. Improvement in the Tb term is an area for future model development. However, we believe it is important that TARGET calculates Tb, as this makes the model much more accessible to non-expert users. Given the simplicity and computational efficiency of the model approaches used, TARGET shows good skill for predicting urban Tac. Overall, the air temperature evaluation shows we can have confidence in the accuracy of the model and its potential to be used by practitioners.
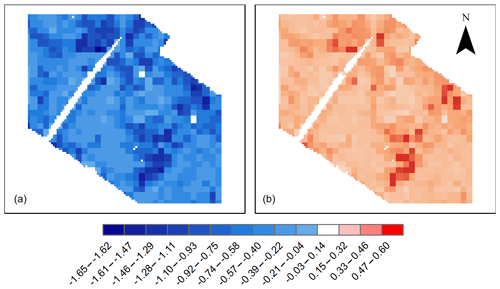
To demonstrate how TARGET can be used by practitioners to predict GBI cooling impacts, two simple heat mitigation scenarios are presented: (1) a doubling of existing tree cover (“2×TREE”) (Fig. 9) and (2) all dry grass converted to irrigated grass (“IRRIGATION”) (Fig. 10). The 2×TREE scenario assumes a maximum tree coverage of 75 %. The results presented here represent the local maximum cooling potential of GBI. In reality, the cooling local magnitude will be decreased by advection, which TARGET does not represent.
The 2×TREE scenario shows maximum cooling of 3.0 ∘C during the day and a smaller effect (<0.25 ∘C) at night (Fig. 9). The IRRIGATION scenarios suggests that increasing irrigation can have a small warming effect (<0.75 ∘C) at night and cooling of up to 1.75 ∘C at 15:00 (Fig. 10). The amount of land cover change differs in each scenario. As such, we calculate the cooling sensitivity (γ) as
where ΔLC is the average land cover change (fraction) (Table 2); this metric demonstrates the average ΔTac per 10 % surface change. Model results suggest that trees are about 2.5 times more effective at providing cooling at 15:00 (Table 2). The results for both heat mitigation simulations are within the expected magnitudes based on previous heat mitigation modelling studies (Grossman-Clarke et al., 2010; Middel et al., 2015; Daniel et al., 2016; Broadbent et al., 2018a). These simulations demonstrate that TARGET not only reproduces observations accurately but can be used with confidence to efficiently assess the efficacy of heat mitigation measures.
As discussed above, TARGET aims to be a simple and accessible urban climate model that provides scientifically defensible and accurate urban temperature predictions. To achieve simplicity, the model necessarily makes some assumptions and omissions that users should be aware of. TARGET is primarily intended to model urban temperatures during clear sky conditions. The model does not simulate rainfall and therefore should not be used for periods containing significant precipitation. Further, the model can be used to simulate street-level air temperature and surface temperature for days to weeks (i.e. a heatwave) but has not been tested or validated for longer-scale simulations (i.e. months to years).
For computational efficiency, the model assumes no horizontal advection inside or above the urban canopy layer. In general, advection reduces the local impacts (i.e. cooling directly adjacent the cooling intervention) of GBI due to atmospheric mixing, and therefore we expect TARGET to provide estimates of near-maximum cooling benefits. In reality, cooling effects will be diminished by advection, especially during the day and during high wind conditions.
As mentioned, the force–restore method is used for roof and wall surfaces with an artificially reduced κ value. Although this approach generally performed well, it is our intention to develop and integrate a more realistic formula for modelling roof and wall QG,i. A conduction model, although more computationally expensive, would allow more flexibility as different types of roof (which do vary significantly) could be represented. Furthermore, wall surfaces are treated the same as roofs in TARGET, which is unrealistic. The improved representation of walls and roofs is a key area for future model development.
In addition, the QG,i (hence the heat transfer to the urban canopy atmosphere, as the residual) is parameterized according to Rn and the building parameters. This means that the dependency on the other atmospheric conditions, such as air temperature, wind speed, and humidity, is neglected in TARGET. However, given that the OHM (used to calculate QG,i) was developed based on observational data collected during summertime clear sky conditions, we are confident that TARGET will provide reasonable results during summer. Ongoing testing is needed to ascertain the limitations of the use of the OHM in TARGET.
The QG,i calculation for water sources used a different method to other surfaces (see Sect. 2.6). Further, a resistance formulation is used to calculate the QH,i over water bodies (see Eq. 14), whereas QH,i for the non-water surfaces is calculated as a residual (and not temperature- and wind-speed-dependent). These different model formulations for water may lead to artificial non-physical discrepancies. However, testing does not reveal any unexpected behaviour. As TARGET is a climate-service-oriented tool, we think that good model performance is more important than the consistency of physics schemes used.
This paper has presented TARGET, a simple and user-friendly urban climate model that is designed to be accessible to urban planners and policymakers. The model contains a number of key limitations that are outlined above. However, despite these caveats, rigorous testing suggests TARGET shows excellent potential for modelling the cooling effects of GBI projects. We believe this novel model is well balanced between complexity and accuracy. The computational efficiency of the model and the reduced amount of input data required ensure that non-skilled users can use the model to ascertain reliable urban cooling estimates. Ongoing work will be done to improve TARGET, including the creation of a GUI, the addition of human thermal comfort indices, and the improvements to model physics outlined above.
TARGET is distributed under the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 Generic (CC BY-NC-SA 4.0). TARGET code cannot be used for commercial purposes. Java code is available at https://doi.org/10.5281/zenodo.1310138 (Broadbent et al., 2018c).
| a1 | Objective hysteresis model (OHM) parameter |
| a2 | Objective hysteresis model (OHM) parameter |
| a3 | Objective hysteresis model (OHM) parameter |
| Aasph | land cover asphalt plan area (m2) |
| Aconc | land cover concrete plan area (m2) |
| Agras | land cover grass plan area (m2) |
| Aigrs | land cover irrigated grass plan area (m2) |
| Atree | land cover tree plan area (m2) |
| Aroof | land cover building plan area (m2) |
| Awall | land cover wall plan area (m2) |
| Awatr | land cover water plan area (m2) |
| Cwatr | volumetric heat capacity of water (J m−2 K−1) |
| ca | conductance from the urban canopy to the above-canopy surface layer (m s−1) |
| cs | conductance from the surface to the urban canopy layer (m s−1) |
| Cwatr | volumetric heat capacity of water (4.18×106 J m−3 K−1) |
| Cp | specific heat of air (1013 J kg−1 K−1) |
| dwatr | depth of water body (m) |
| Dy | damping depth for the annual temperature cycle (m) |
| η | extinction coefficient |
| Fi | fraction of land cover type i (%) |
| H | average building height (m) |
| hc | bulk transfer coefficient for heat (hc=hv) |
| hv | bulk transfer coefficient for moisture () |
| Kn | net shortwave radiation (W m−2) |
| K↓ | incoming shortwave radiation (W m−2) |
| Ln | net longwave radiation (W m−2) |
| L↓ | incoming longwave radiation (W m−2) |
| L↑ | outgoing longwave radiation (W m−2) |
| Lv | latent heat of vaporization (=2.43 MJ kg−1) |
| QE,watr | latent heat flux for water surface (W m−2) |
| QG,i | storage heat flux for surface type i from LUMPS (W m−2) |
| QG,watr | convective heat flux at the bottom of the water layer (and into the soil below) (W m−2) |
| QH,i | sensible heat flux for surface i from LUMPS (W m−2) |
| QH,watr | sensible heat flux for water surface (W m−2) |
| ra | resistance from the urban canopy to the atmosphere (s m−1) |
| RH | relative humidity (%) |
| Ri | Richardson number |
| Rn | net radiation (W m−2) |
| Sab | absorbed shortwave radiation (W m−2) |
| SVF | sky view factor |
| rs | resistance from the surface to the canopy (s m−1) |
| Ta | reference air temperature (∘C) |
| TARGET | CRC for Water Sensitive Cities microclimate Toolkit model |
| Tac | street-level (urban canopy layer) air temperature (∘C) |
| Tb | air temperature above the urban canopy layer (∘C) |
| Tm | average soil (ground) temperature (∘C) |
| Thigh | upper-level temperature for Richardson number calculation (∘C) |
| Tlow | lower-level temperature for Richardson number calculation (∘C) |
| Tsoil | soil temperature (∘C) |
| Tsurf | surface temperature from the force–restore model (∘C) |
| Ucan | wind speed in canyon (m s−1) |
| Utop | wind speed at the top of the canyon (m s−1) |
| Uz | reference wind speed (m s−1) |
| W | average street width (m) |
| W* | average street width minus tree width (m) |
| Wtree | tree width (m) |
| Wroof | roof width (m) |
| α | surface albedo |
| αpm | LUMPS empirical parameter (alpha parameter), relating to surface moisture |
| β | LUMPS empirical parameter (beta parameter) |
| βk | amount of shortwave radiation immediately absorbed by the water layer (set to 0.45) |
| ΔQS,watr | change in heat storage of the water layer (W m−2) |
| ϵ | surface emissivity |
| κ | thermal diffusivity (m2 s−1) |
| κwatr | eddy diffusivity of water (m2 s−1) |
| λC | plan area ground-level surfaces (m2) |
| ρa | density of dry air (i.e. 1.2 kg m−3) |
| ρv | density of moist air (kg m−3) |
| σ | Stefan–Boltzmann constant ( W m−2 K−4) |
B1 Meteorological conditions during validation periods
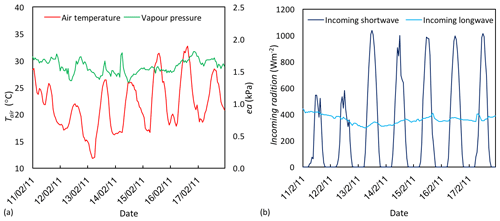
As outlined in Sect. 3, we conduct model validation experiments during two different periods. A summary of the meteorological conditions for land cover (Melbourne; Fig. B1) and suburb-scale (Mawson Lakes; Fig. B2) simulations are provided in the figures below.
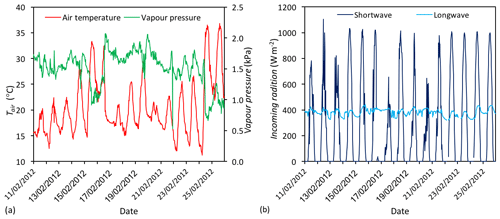
Figure B1Meteorological conditions during the land cover validation period. Data source: Melbourne Airport Bureau of Meteorology (ID 086282) weather station.
B2 Tree surface temperature
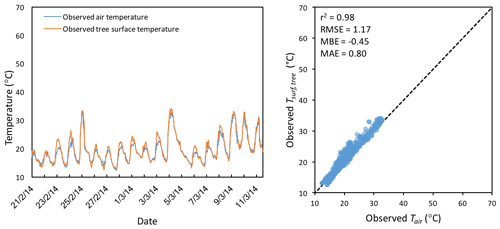
To assess Ttree we obtain observational data from a tree experiment completed in Melbourne, which included Tsurf observations of the tree canopy (collected during February 2014). We also obtain Bureau of Meteorology meteorological forcing data for the 2014 case study period. This period (not shown) was very similar to the February 2012 period (Fig. B1) used above. The tree data confirm that Ta is an excellent predictor of Ttree.
AMB, AMC, KAN, MD, HW, ESK, and NJT assisted with model development and design. AMB conducted model evaluation and analysis. All authors contributed to the writing of the manuscript.
The authors declare that they have no conflict of interest.
At Monash University, Ashley M. Broadbent and Kerry A. Nice were funded by
the Cooperative Research Centre for Water Sensitive Cities, an initiative of
the Australian Government. While at Arizona State University,
Ashley M. Broadbent was supported by NSF Sustainability Research Network
(SRN) Cooperative Agreement 1444758, NSF grant EAR-1204774, and NSF
SES-1520803. Matthias Demuzere and Hendrik Wouters were funded by the
Cooperative Research Centre for Water Sensitive Cities. The contribution of
Matthias Demuzere was funded by the Flemish regional government through a
contract as a FWO (Fund for Scientific Research) post-doctoral research
fellow. E. Scott Krayenhoff was supported by NSF Sustainability Research
Network (SRN) Cooperative Agreement 1444758 and NSF
SES-1520803.
Edited by: Astrid Kerkweg
Reviewed by: three anonymous referees
Acero, J. A. and Herranz-Pascual, K.: A comparison of thermal comfort conditions in four urban spaces by means of measurements and modelling techniques, Build. Environ., 93, 245–257, https://doi.org/10.1016/j.buildenv.2015.06.028, 2015. a
Ali-Toudert, F. and Mayer, H.: Numerical study on the effects of aspect ratio and orientation of an urban street canyon on outdoor thermal comfort in hot and dry climate, Build. Environ., 41, 94–108, https://doi.org/10.1016/j.buildenv.2005.01.013, 2006. a
Arya, P. S.: Introduction to Micrometeorology, Academic Press, San Diego, USA, 2001. a
Asaeda, T. and Ca, V. T.: The subsurface transport of heat and moisture and its effect on the environment: A numerical model, Bound.-Lay. Meteorol., 65, 159–179, https://doi.org/10.1007/BF00708822, 1993. a
Bailey, B. N., Overby, M., Willemsen, P., Pardyjak, E. R., Mahaffee, W. F., and Stoll, R.: A scalable plant-resolving radiative transfer model based on optimized GPU ray tracing, Agr. Forest Meteorol., 198-199, 192–208, https://doi.org/10.1016/j.agrformet.2014.08.012, 2014. a
Bailey, B. N., Stoll, R., Pardyjak, E. R., and Miller, N. E.: A new three-dimensional energy balance model for complex plant canopy geometries: Model development and improved validation strategies, Agr. Forest Meteorol., 218–219, 146–160, https://doi.org/10.1016/j.agrformet.2015.11.021, 2016. a
Bhumralkar, C. M.: Numerical experiments on the computation of ground surface temperature in an atmospheric general circulation model, J. Appl. Meteorol., 14, 1246–1258, 1975. a
Broadbent, A. M., Coutts, A. M., Tapper, N. J., and Demuzere, M.: The cooling effect of irrigation on urban microclimate during heatwave conditions, Urban Climate, 23, 309–329, 2018a. a, b
Broadbent, A. M., Coutts, A. M., Tapper, N. J., Demuzere, M., and Beringer, J.: The microscale cooling effects of water sensitive urban design and irrigation in a suburban environment, Theor. Appl. Climatol., 134, 1–23, 2018b. a, b, c, d
Broadbent, A. M., Coutts, A. M., Nice, K. A., Demuzere, M., Krayenhoff, E. S., Tapper, N. J., and Woulters, H.: TARGETv1.0 Java code, Zenodo, https://doi.org/10.5281/zenodo.1310138, 2018c. a
Bruse, M.: The influences of local environmental design on microclimate- development of a prognostic numerical Model ENVI-met for the simulation of Wind, temperature and humidity distribution in urban structures, PhD thesis, University of Bochum, Bochum, Germany, 1999 (in German). a, b
CD-adapco: http://www.cd-adapco.com/ (last access: 12 February 2019), 2011. a
Ching, J., Mills, G., Bechtel, B., See, L., Feddema, J., Wang, X., Ren, C., Brousse, O., Martilli, A., Neophytou, M., Mouzourides, P., Stewart, I., Hanna, A., Ng, E., Foley, M., Alexander, P., Aliaga, D., Niyogi, D., Shreevastava, A., Bhalachandran, P., Masson, V., Hidalgo, J., Fung, J., Andrade, M., Baklanov, A., Dai, W., Milcinski, G., Demuzere, M., Brunsell, N., Pesaresi, M., Miao, S., Mu, Q., Chen, F., and Theeuwes, N.: WUDAPT: An Urban Weather, Climate, and Environmental Modeling Infrastructure for the Anthropocene, B. Am. Meteorol. Soc., 99, 1907–1924, https://doi.org/10.1175/BAMS-D-16-0236.1, 2018. a
Commonwealth of Australia: National Landcare Programme. 20 Million Trees Program, http://www.nrm.gov.au/national/20-million-trees (last access: 12 February 2018), 2017. a
Coutts, A. M., Harris, R. J., Phan, T., Livesley, S. J., Williams, N. S., and Tapper, N. J.: Thermal infrared remote sensing of urban heat: Hotspots, vegetation, and an assessment of techniques for use in urban planning, Remote Sens. Environ., 186, 637–651, 2016. a, b
Daniel, M., Lemonsu, A., and Viguié, V.: Role of watering practices in large-scale urban planning strategies to face the heat-wave risk in future climate, Urban Climate, 23, 287–308, 2018. a
Deardorff, J. W.: Efficient Prediction of Ground Surface Temperature and Moisture, With Inclusion of a Layer of Vegetation, J. Geophys. Res., 83, 1889–1903, https://doi.org/10.1029/JC083iC04p01889, 1978. a
Demuzere, M., Harshan, S., Järvi, L., Roth, M., Grimmond, C., Masson, V., Oleson, K., Velasco, E., and Wouters, H.: Impact of urban canopy models and external parameters on the modelled urban energy balance in a tropical city, Q. J. Roy. Meteor. Soc., 143, 1581–1596, 2017. a
Doll, D., Ching, J. K. S., and Kaneshiro, J.: Parameterization of subsurface heating for soil and concrete using net radiation data, Bound.-Lay. Meteorol., 32, 351–372, https://doi.org/10.1007/BF00122000, 1985. a
Elasson, I.: The use of climate knowledge in urban planning, Landscape Urban Plan., 48, 31–44, 2000. a
Erell, E. and Williamson, T.: Simulating air temperature in an urban street canyon in all weather conditions using measured data at a reference meteorological station, Int. J. Climatol., 26, 1671–1694, https://doi.org/10.1002/joc.1328, 2006. a
Grimmond, C. S. B. and Oke, T.: Heat storage in urban areas: Local-scale observations and evaluation of a simple model, J. Appl. Meteorol., 38, 922–940, https://doi.org/10.1175/1520-0450(1999)038<0922:HSIUAL>2.0.CO;2, 1999. a
Grimmond, C. S. B., Oke, T. R., and Cleugh, H.: The role of “rural” in comparisons of observed suburban-rural flux differences, in: Exchange Processes at the Land Surface for a Range of Space and Time Scales. Proc. Yokohama Symposium, Yokohama, Japan, 13–16 July 1993, vol. IAHS Publi, 165–174, 1993. a
Grimmond, C. S. B. and Oke, T.: Turbulent Heat Fluxes in Urban Areas: Observations and a Local-Scale Urban Meteorological Parameterization Scheme (LUMPS), J. Appl. Meteorol., 41, 792–810, 2002. a, b
Grossman-Clarke, S., Zehnder, J. A., Loridan, T., and Grimmond, C. S. B.: Contribution of land use changes to near-surface air temperatures during recent summer extreme heat events in the Phoenix metropolitan area, J. Appl. Meteorol. Clim., 49, 1649–1664, 2010. a
Hicks, B. B.: Some evaluations of drag and bulk transfer coefficients over water bodies of different sizes, Bound.-Lay. Meteorol., 3, 201–213, https://doi.org/10.1007/BF02033919, 1972. a
Jacobs, A. F. G., Heusinkveld, B. G., and Lucassen, D. C.: Temperature variation in a class A evaporation pan, J. Hydrol., 206, 75–83, https://doi.org/10.1016/S0022-1694(98)00087-0, 1998. a
Jacobs, A. F. G., Heusinkveld, B. G., and Berkowicz, S. M.: Force-restore technique for ground surface temperature and moisture content in a dry desert system, Water Resour. Res., 36, 1261–1268, 2000. a
Järvi, L., Grimmond, C., and Christen, A.: The Surface Urban Energy and Water Balance Scheme (SUEWS): Evaluation in Los Angeles and Vancouver, J. Hydrol., 411, 219–237, https://doi.org/10.1016/j.jhydrol.2011.10.001, 2011. a, b
Järvi, L., Grimmond, C. S. B., Taka, M., Nordbo, A., Setälä, H., and Strachan, I. B.: Development of the Surface Urban Energy and Water Balance Scheme (SUEWS) for cold climate cities, Geosci. Model Dev., 7, 1691–1711, https://doi.org/10.5194/gmd-7-1691-2014, 2014. a, b
Jones, I., George, G., and Reynolds, C.: Quantifying effects of phytoplankton on the heat budgets of two large limnetic enclosures, Freshwater Biol., 50, 1239–1247, https://doi.org/10.1111/j.1365-2427.2005.01397.x, 2005. a
Krayenhoff, E. S. and Voogt, J. A.: A microscale three-dimensional urban energy balance model for studying surface temperatures, Bound.-Lay. Meteorol., 123, 433–461, https://doi.org/10.1007/s10546-006-9153-6, 2007. a
Krüger, E., Minella, F., and Rasia, F.: Impact of urban geometry on outdoor thermal comfort and air quality from field measurements in Curitiba, Brazil, Build. Environ., 46, 621–634, https://doi.org/10.1016/j.buildenv.2010.09.006, 2011. a
Kunz, R., Khatib, I., and Moussiopoulos, N.: Coupling of mesoscale and microscale models – an approach to simulate scale interaction, Environ. Modell. Softw., 15, 597–602, 2000. a
Kusaka, H., Kondo, H., Kikegawa, Y., and Kimura, F.: A simple single-layer urban canopy model for atmospheric models: Comparison with multi-layer and slab models, Bound.-Lay. Meteorol., 101, 329–358, 2001. a
Lemonsu, A., Masson, V., Shashua-Bar, L., Erell, E., and Pearlmutter, D.: Inclusion of vegetation in the Town Energy Balance model for modelling urban green areas, Geosci. Model Dev., 5, 1377–1393, https://doi.org/10.5194/gmd-5-1377-2012, 2012. a
Lindberg, F., Holmer, B., and Thorsson, S.: SOLWEIG 1.0 – modelling spatial variations of 3D radiant fluxes and mean radiant temperature in complex urban settings, Int. J. Biometeorol., 52, 697–713, https://doi.org/10.1007/s00484-008-0162-7, 2008. a
Mascart, P., Noilhan, J., and Giordani, H.: A modified parameterization of flux-profile relationships in the surface layer using different roughness length values for heat and momentum, Bound.-Lay. Meteorol., 72, 331–344, https://doi.org/10.1007/BF00708998, 1995. a, b
Masson, V.: A physically-based scheme for the urban energy budget in atmospheric models, Bound.-Lay. Meteorol., 94, 357–397, 2000. a, b, c, d
Matzarakis, A., Rutz, F., and Mayer, H.: Modelling radiation fluxes in simple and complex environments–application of the RayMan model, Int. J. Biometeorol., 51, 323–34, https://doi.org/10.1007/s00484-006-0061-8, 2007. a
Matzarakis, A., Rutz, F., and Mayer, H.: Modelling radiation fluxes in simple and complex environments: basics of the RayMan model, Int. J. Biometeorol., 54, 131–139, https://doi.org/10.1007/s00484-009-0261-0, 2010. a
Middel, A., Chhetri, N., and Quay, R.: Urban forestry and cool roofs: Assessment of heat mitigation strategies in Phoenix residential neighborhoods, Urban For. Urban Gree., 14, 178–186, 2015. a
Mills, G., Ching, J., See, L., Bechtel, B., and Foley, M.: An Introduction to the WUDAPT project, in: Proceedings of the 9th International Conference on Urban Climate, Toulouse, France, 20–24 July 2015. a
Molina Martínez, J. M., Martínez Alvarez, V., González-Real, M. M., and Baille, A.: A simulation model for predicting hourly pan evaporation from meteorological data, J. Hydrol., 318, 250–261, https://doi.org/10.1016/j.jhydrol.2005.06.016, 2006. a, b, c, d, e, f, g, h
Narita, K., Sekine, T., and Tokuoka., T.: Thermal properties of urban surface materials: study on heat balance at asphalt pavement, Geogr. Rev. Japan, 57, 639–651, 1984. a
Nice, K. A., Coutts, A. M., and Tapper, N. J.: Development of the VTUF-3D v1. 0 urban micro-climate model to support assessment of urban vegetation influences on human thermal comfort, Urban Climate, 24, 1052–1076, 2018. a
Oke, T.: Boundary Layer Climates, 2nd edn., Routledge, London, UK and New York, USA, 1987. a
Oke, T. R. (2007). Siting and exposure of meteorological instruments at urban sites, in: Air pollution modeling and its application XVII, edited by: Borrego, C. and Norman, A. L., Springer, Boston, MA, 615–631, https://doi.org/10.1007/978-0-387-68854-1_66, 2007. a
Oleson, K., Bonan, G., Feddema, J., Jackson, T., Vertenstein, M., and Kluzek, E.: Technical description of an urban parameterization for the Community Land Model (CLMU), available at: http://opensky.ucar.edu/islandora/object/technotes:492 (last access: 12 February 2019), 2010. a
OpenFOAM: http://www.openfoam.com/ (last access: 12 February 2019), 2011. a
Redon, E. C., Lemonsu, A., Masson, V., Morille, B., and Musy, M.: Implementation of street trees within the solar radiative exchange parameterization of TEB in SURFEX v8.0, Geosci. Model Dev., 10, 385–411, https://doi.org/10.5194/gmd-10-385-2017, 2017. a
Salas De León, D. A., Alcocer, J., Ardiles Gloria, V., and Quiroz-Martínez, B.: Estimation of the eddy diffusivity coefficient in a warm monomictic tropical lake, J. Limnol., 75, 161–168, https://doi.org/10.4081/jlimnol.2016.1431, 2016. a
Schlünzen, K. H., Grawe, D., Bohnenstengel, S. I., Schlüter, I., and Koppmann, R.: Joint modelling of obstacle induced and mesoscale changes – Current limits and challenges, J. Wind Eng. Ind. Aerod., 99, 217–225, https://doi.org/10.1016/j.jweia.2011.01.009, 2011. a
Singapore Ministry of Environment and Water Resources: The Singapore Green Plan 2012: Beyond Clean and Green Towards Environmental Sustainabiliity, available at: http://unpan1.un.org/intradoc/groups/public/documents/apcity/unpan026598.pdf (last access: 12 February 2019), 2006. a
Skamarock, W., Klemp, J., Dudhi, J., Gill, D., Barker, D., Duda, M., Huang, X.-Y., Wang, W., and Powers, J.: A Description of the Advanced Research WRF Version 3, Tech. rep., https://doi.org/10.5065/D6DZ069T, 2008. a
Spangenberg, J., Shinzato, P., Johansson, E., and Duarte, D.: Simulation of the influence of vegetation on microclimate and thermal comfort in the city of São Paulo, Revista da Sociedade Brasileira de Arborização Urbana, 3, 1–19, 2008. a
Sparrow, E. and Cess, R.: Radiation heat transfer, augmented edn., Harper Collins, London, UK, 1978. a
Stewart, I. D., Oke, T. R., and Krayenhoff, E. S.: Evaluation of the “local climate zone” scheme using temperature observations and model simulations, Int. J. Climatol., 34, 1062–1080, 2014. a
Subin, Z. M., Riley, W. J., and Mironov, D.: An improved lake model for climate simulations: Model structure, evaluation, and sensitivity analyses in CESM1, J. Adv. Mode. Earth Syst., 4, 1–27, https://doi.org/10.1029/2011MS000072, 2012. a
Ward, H. C., Kotthaus, S., Järvi, L., and Grimmond, C. S. B.: Surface urban energy and water balance scheme (SUEWS): development and evaluation at two UK sites, Urban Climate, 18, 1–32, 2016. a
Wouters, H., Demuzere, M., Blahak, U., Fortuniak, K., Maiheu, B., Camps, J., Tielemans, D., and van Lipzig, N. P. M.: The efficient urban canopy dependency parametrization (SURY) v1.0 for atmospheric modelling: description and application with the COSMO-CLM model for a Belgian summer, Geosci. Model Dev., 9, 3027–3054, https://doi.org/10.5194/gmd-9-3027-2016, 2016. a
Yamada, T. and Koike, K.: Downscaling mesoscale meteorological models for computational wind engineering applications, J. Wind Eng. Ind. Aerod., 99, 199–216, https://doi.org/10.1016/j.jweia.2011.01.024, 2011. a
- Abstract
- Introduction
- Model description
- Methods and data
- Model evaluation results and discussion
- Heat mitigation scenarios
- Limitations of the model
- Conclusions and future work
- Code and data availability
- Appendix A: List of symbols
- Appendix B
- Author contributions
- Competing interests
- Acknowledgements
- References
- Abstract
- Introduction
- Model description
- Methods and data
- Model evaluation results and discussion
- Heat mitigation scenarios
- Limitations of the model
- Conclusions and future work
- Code and data availability
- Appendix A: List of symbols
- Appendix B
- Author contributions
- Competing interests
- Acknowledgements
- References