Explicit aerosol–cloud interactions in the Dutch Atmospheric Large-Eddy Simulation model DALES4.1-M7

Large-eddy simulation (LES) models are an excellent tool to improve our understanding of aerosol–cloud interactions (ACI). We introduce a prognostic aerosol scheme with multiple aerosol species in the Dutch Atmospheric Large-Eddy Simulation model (DALES), especially focused on simulating the impact of cloud microphysical processes on the aerosol population. The numerical treatment of aerosol activation is a crucial element for simulating both cloud and aerosol characteristics. Two methods are implemented and discussed: an explicit activation scheme based on κ-Köhler theory and a more classic approach using updraught strength. Sample model simulations are based on the Rain in Shallow Cumulus over the Ocean (RICO) campaign, characterized by rapidly precipitating warm-phase shallow cumulus clouds.

We find that in this pristine ocean environment virtually all aerosol mass in cloud droplets is the result of the activation process, while in-cloud scavenging is relatively inefficient. Despite the rapid formation of precipitation, most of the in-cloud aerosol mass is returned to the atmosphere by cloud evaporation. The strength of aerosol processing through subsequent cloud cycles is found to be particularly sensitive to the activation scheme and resulting cloud characteristics. However, the precipitation processes are considerably less sensitive. Scavenging by precipitation is the dominant source for in-rain aerosol mass. About half of the in-rain aerosol reaches the surface, while the rest is released by evaporation of falling precipitation. The effect of cloud microphysics on the average aerosol size depends on the balance between the evaporation of clouds and rain and ultimate removal by precipitation. Analysis of typical aerosol size associated with the different microphysical processes shows that aerosols resuspended by cloud evaporation have a radius that is only 5 % to 10 % larger than the originally activated aerosols. In contrast, aerosols released by evaporating precipitation are an order of magnitude larger.

1 Introduction

Aerosol–cloud interactions (ACI) remain a major source of uncertainty for future climate predictions (e.g. Boucher et al., 2013; Fan et al., 2016). The effect of changes in the aerosol population on the cloud radiative properties (Twomey, 1977) and the formation of precipitation (Albrecht, 1989) in warm-phase shallow cumulus clouds have long been recognized. However, cloud responses in different cloud regimes have proven to be complex and the net effect on climate is not well established (Rosenfeld et al., 2014). Aerosol-induced changes can be buffered by compensating cloud mechanisms, e.g. the lifetime effect might be weaker than implied by simple arguments and commonly assumed in climate models (Stevens and Feingold, 2009). In convective clouds increased aerosol concentrations might invigorate updraughts and increase precipitation formation (e.g. Koren et al., 2008; Fan et al., 2018).

Although the microphysics of the cloud processes is relatively well known, the representation in global climate models (GCMs) requires simplifications accompanied by high uncertainties (e.g. Seinfeld et al., 2016). Climate models neither resolve cloud structures nor the micro-scale processes determining the cloud properties, and they have to rely on parameterizations. Consequently, quantification of the influence of changes in aerosol distribution on climate remains difficult. On the other side of the modelling spectrum, process-based small-scale simulations (e.g. Roelofs, 1992) describe the microphysical processes in high detail, but they cannot model the effect of aerosol–cloud interactions on the macro-scale thermodynamics and structure of a cloud. To bridge this gap, cloud-resolving models play a role, in particular large-eddy simulation (LES) models. For these models, present-day computational power is sufficient to resolve cloud structures in mesoscale domain sizes ($>\mathrm{10}\mathrm{km}\times \mathrm{10}$ km) to simulate and connect spatial and temporal scales of aerosol–cloud interactions (e.g. Bretherton, 2015; Schneider et al., 2017). Typical spatial and temporal resolutions of ∼10 m and ∼1 s are generally considered high resolution. However, this is still too coarse to simulate the processes on particle level that take place on the Kolmogorov length scales in the order of 1 mm. These processes (e.g. condensation, collision-coalescence) remain parameterized in LES. Nevertheless, the resolution and explicit calculation of turbulence allows for a certain level of internal variability resulting from inter- and intra-cloud variations. While some clouds develop to considerable height and produce strong precipitation, others dissipate before forming rain and their influence on the aerosol population might be very different. Moreover, processing of the aerosol population by one cloud influences the microphysical processes in subsequent clouds. For example, when one cloud depletes the aerosol population by wash out, this might lead to larger cloud droplets in the subsequent cloud formed on the depleted aerosol population. This might lead to faster rain formation and an even further depletion of the aerosol population. This underlines the non-linear character of the interaction between aerosols and clouds and the need to simultaneously simulate the clouds and the aerosol population.

LES has become a widely used tool in research on structure and behaviour of clouds. An important research topic is the influence of changes in aerosol concentration on the cloud characteristics. However, the emphasis remains on the cloud processes and the numerical description of the distribution of cloud water over the cloud or rain droplets. Numerous numerical methods have been developed to describe the hydrometeor size distribution. Traditionally, there was a distinction between bulk and bin schemes. In the former, droplet size distributions are described by one or more moments (total number, mass, etc.) of the hydrometeor size distribution, while other moments are diagnosed from implicitly assumed size distribution shape. In bin schemes, the shape of the size distribution is more free to evolve as the particle size distribution is divided into bins of different sizes. Recent advances complement this choice by Lagrangian particle-based methods, e.g. Andrejczuk et al. (2008) or Shima et al. (2009). Lebo and Seinfeld (2011) developed an extensive 2-D bin method that resolves the hydrometeor characteristics as well as the solute mass dissolved in the hydrometeors. For a detailed overview and comparison of these methods, see Khain et al. (2015) and Grabowski et al. (2019).

In LES modelling, less attention is devoted to the other side of ACI, i.e. the feedback of cloud microphysical processes on the aerosol distribution. This is reflected in the often relatively simple representation of the aerosol population. Nowadays, methods based on a fixed cloud droplet number or (infinite) ambient aerosol concentration are almost completely replaced by methods that include the aerosol size distribution in a prognostic way. Aerosol composition, however, is often assumed to be uniform.

In larger-scale models, more attention is focused on a description of the chemical composition of the aerosol population. However, due to coarse resolution and computational limitations, methods still employ traditional modal (bulk) and bin schemes. In a modal aerosol scheme, several fixed-shape size distributions (i.e. modes) are chosen in such a way that the sum of these distributions approximates a certain (observed) aerosol population. An example of a modal scheme is M7 (Vignati et al., 2004), which will be used in this study. In bin schemes (e.g. SALSA; Kokkola et al., 2008), the aerosol size distribution is discretized into a number of bins according to particle size. The two methods are a good example of the trade-off between accuracy and computational cost. The modal approach requires a relatively low number of prognostic variables, is computationally efficient, and is used in GCMs (e.g. EC-Earth; van Noije et al., 2014; and ECHAM-HAMMOZ; Schultz et al., 2018). However, the shape of the aerosol size distribution in each mode is assumed to always resemble a log-normal shape. The shape of the total aerosol distribution in bin schemes is more free to evolve, but this comes at a much higher computational cost.

Recent examples of studies with a focus on multiple aerosol species and/or (aqueous-phase) chemistry are the inclusion of the SALSA aerosol module in UCLALES (Tonttila et al., 2017) and PALM (Kurppa et al., 2019). This bin scheme allows for multiple aerosol species, but the added value of taking into account the aerosol composition on simulating clouds in an LES model has not yet been explored. The implementation in UCLALES still uses a uniform composition in the aerosol distribution, while the study with the PALM model is focused on urban climates under dry conditions. Another promising example is the aqueous-phase chemistry extension of the libcloudph++ library (Arabas et al., 2015), described in Jaruga and Pawlowska (2018). The added attributes of chemical composition to the super-droplets in this method open up a range of possibilities to interactively calculate multiple aerosol species and their behaviour in clouds and precipitation.

In this work, we focus on closing the loop of aerosol–cloud interactions and quantify the contribution of different cloud processes to changes in the aerosol distribution. We take a step forward with the DALES model and combine microphysical cloud processes with M7 (Vignati et al., 2004): a multi-species modal representation of the aerosol distribution. From the perspective of pollution and atmospheric budgets, we opted to implement an aerosol framework with multiple species. This also allows for explicit calculation of aerosol characteristics like hygroscopicity. Consequently, aerosol activation can be based on the characteristics of the aerosol population instead of using a parameterization solely based on, for example, updraught velocity. Including multiple aerosol species also allows for a better future coupling to gas-phase chemistry and semi-volatile species and accommodates emission-based simulations, so less assumptions on the atmospheric composition are needed. In contrast to the SALSA and libcloudph++ aerosol frameworks, the computational cost of M7 is considerably lower and allows for longer simulations.

This work is motivated by our earlier work (de Bruine et al., 2018) in which the removal of aerosol by clouds on the global scale using the EC-Earth-TM5 model was investigated. This work showed that different (reasonable) choices in the parameterization of wet removal have a considerable impact on simulated global aerosol burdens. By revisiting the aerosol–cloud interactions in LES simulations we aim to answer the following questions:

• What are the effects of the aerosol–cloud interactions on the aerosol (size) distribution?

• How do the characteristics of the aerosol change due to cloud processes and which cloud processes are responsible?

• Does the relative importance of the different microphysical processes change for different aerosol species (e.g. small vs. coarse or hygroscopic vs. hygrophobic aerosol)?

The paper is structured as follows. A short description of the standard version of the DALES model and the cloud microphysics numerical scheme is given in Sect. 2, together with a more elaborate explanation of the new modal aerosol scheme and additional cloud-microphysical calculations in Sect. 2.2. The case set-up and simulation ensemble are outlined in Sect. 3.1. The results are separated into two parts: the differences in cloud microphysical properties between simulations are discussed in Sect. 3.2.1 and the effects on the aerosol characteristics in Sect. 3.2.2. The overall results are discussed in Sect. 4 and general conclusions are drawn in Sect. 5.

2 Model description

The model used in this study is the Dutch Atmospheric Large-Eddy Simulation (DALES) (Heus et al., 2010; Ouwersloot et al., 2017), version 4.1. DALES was initially designed to study the physics of the atmospheric boundary layer. Previous research has expanded the application of DALES and combines the physics with chemistry and biology. Applications using the DALES model include (gas-phase) chemistry (e.g. Vilà-Guerau de Arellano et al., 2011), direct aerosol effects (Barbaro et al., 2013, 2014), semi-volatile species (Aan de Brugh et al., 2013), and interaction with the biosphere (Vilà-Guerau de Arellano et al., 2014).

In this study we conduct simulations at a horizontal resolution of $\mathrm{\Delta }x=\mathrm{\Delta }y=\mathrm{100}$ m with a domain size of 12.8 km×12.8 km using a periodic boundary condition. The vertical resolution is Δz=40 m with a domain height of 5040 m. The time step is limited by the Courant–Friedrichs–Lewy (CFL) criterion and diffusion number (Wesseling, 1996), but never longer than 2 s. Time integration is done using a 3rd-order Runge–Kutta scheme based on the work of Wicker and Skamarock (2002). Advection is calculated using a 5th-order scheme for momentum and heat, while a monotonous scheme (Hundsdorfer et al., 1995) is used for moisture and aerosol fields to ensure positive values.

2.1 Dynamics and moist processes

In DALES version 4.1, the cloud-microphysical scheme is a bulk scheme for precipitating liquid-phase clouds, distinguishing between cloud water and precipitation. Cloud liquid water is diagnosed using a classic saturation adjustment (Sommeria and Deardorff, 1977). The cloud droplet number concentration is a fixed parameter, regardless of simulated amount of cloud water. However, the cloud droplet number concentration can be adjusted to simulate different pollution levels.

For the calculation of precipitation, two schemes have been implemented in DALES. The first scheme is based on Seifert and Beheng (2001), with updated numerical representation of the rain drop size distribution and sedimentation (Seifert and Beheng, 2006; Stevens and Seifert, 2008) and rain evaporation (Seifert, 2008); in the remainder of this work, this scheme is referred to as the SB scheme. The second cloud scheme is based on Khairoutdinov and Kogan (2000), but it is valid only for (drizzle formation in) stratocumulus clouds. In this work, we will simulate shallow cumulus and thus use the SB scheme. For more information and details on the implementation of this scheme in DALES, see Sect. 2.8 of Heus et al. (2010).

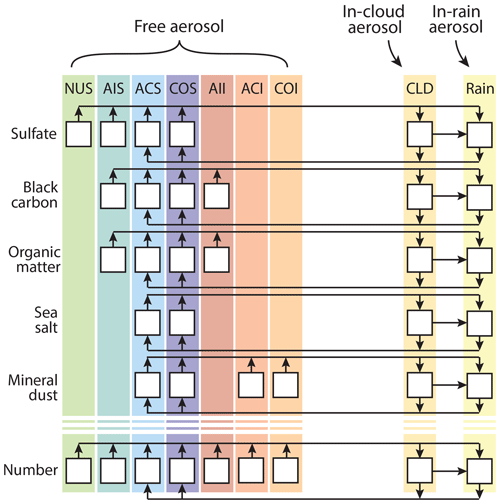
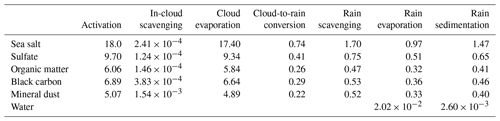
Figure 1 Overview of the aerosol framework, where the free aerosol section is the original M7 representation of the aerosol population. The extension of this framework in the current work is represented by the prognostic variables for in-cloud and in-rain aerosol mass. Cloud and rain particle number coincide with the corresponding parameters in the SB bulk microphysics scheme. Arrows represent possible pathways for the aerosols to transfer between states.

2.2 Aerosol framework

The aerosol population is described by the modal aerosol scheme M7 (Vignati et al., 2004). The modal representation is compatible to the existing SB cloud microphysics scheme since this uses a 2-moment bulk approach as well. By using M7, cloud activation can be based on fundamental principles linked to the explicit simulation of the properties of the aerosol species (see Sect. 2.2.2). Moreover, calculations of the cloud microphysical processes can also be directly linked to their influence on the aerosol distribution. This framework allows for the simulation of an external mixture of multiple aerosol species. In future development, this will be coupled to atmospheric chemistry, including aqueous-phase chemistry.

2.2.1 Numerical representation

In the M7 scheme (see Fig. 1) the aerosol population is described by a combination of five aerosol species: sulfate, black carbon, particulate organic matter (POM), sea salt, and mineral dust. The aerosol species are distributed over seven log-normal modes, hence the name M7, with prescribed mode widths σ. Four of these modes represent soluble aerosols of different sizes, i.e. nucleation, Aitken, accumulation, and coarse sizes and are abbreviated as NUS, AIS, ACS, and COS, respectively. The remaining three modes represent insoluble aerosol in the sizes of Aitken, accumulation, and coarse aerosol, abbreviated as AII, ACI, and COI, respectively. As visualized in Fig. 1, each mode is described by one prognostic variable for number concentration, plus a maximum of five variables for the mass of the different aerosol species that are contained in that mode. For example, the Aitken soluble mode contains the masses of three species (sulfate, black carbon, and organic matter) and thus has $\mathrm{1}+\mathrm{3}=\mathrm{4}$ prognostic variables. The M7 framework includes a numerical treatment for temporal evolution, or “ageing”, by, for example, coagulation as well as sedimentation of the aerosol. However, these are not applied in this work as the associated timescales for these processes are long compared to those of the interaction between aerosol, clouds, and precipitation.

To connect the description of aerosol to the SB microphysics scheme, the M7 framework is extended with two additional modes containing the in-hydrometeor (i.e. cloud droplet and raindrop) aerosol. Similar to the free aerosol modes, both the in-cloud and in-rain aerosols are described by one variable for number concentration and five variables for the in-hydrometeor aerosol mass concentration for each aerosol species. This modal approach leads to the implicit assumption that the in-hydrometeor aerosol mass is homogeneously distributed over the cloud or rain drop distributions, i.e. aerosol concentrations do not change with hydrometeor size. As a result, size (and mass) information of the original free aerosol mode is lost once aerosols are incorporated into cloud and raindrops. In more technical terms, the external mixture of seven modes for the free aerosol is transformed to one internal mixture of aerosols in the hydrometeor mode. Although this approach might not be completely realistic, the aerosol distribution in clouds and rain have been found to be homogeneous in later stages of the cloud life cycle due to frequent collision-coalescence (e.g. Roelofs, 1992).

Note that the cloud and rain droplet modes do not necessarily need to have a log-normal shape like the aerosol modes. Instead, the SB microphysics scheme assumes a generalized Γ distribution, better resembling the droplet size distributions found in clouds and rain. The cloud droplet number N_c and raindrop number N_r are used in the calculations of the cloud microphysics, together with cloud liquid water q_c and rain water q_r.

The combination of the aerosol framework and the individual microphysical processes opens up the opportunity to explicitly simulate the transfer of aerosol between the free, in-cloud and in-rain aerosol state by the individual processes. The current numerical implementation focuses on the mode-specific activation and size resolved aerosol scavenging described in this section. Note that there are numerous other processes involved in the interaction between aerosols and clouds. Our framework is not yet linked to the calculation of (gas-phase) chemistry. Also, our model does not include aqueous-phase oxidation of dissolved species which might influence the aerosol size distribution (e.g. Feingold and Kreidenweis, 2002; Ovchinnikov and Easter, 2010). Neither does our model calculate the formation of secondary aerosol nor the influence clouds can have on that process (e.g. Wehner et al., 2015).

2.2.2 Activation

In the new aerosol representation, activation of aerosols can be based on the κ-Köhler method as defined in Petters and Kreidenweis (2007). This method describes the relationship between the dry radius of a particle and its ability to act as a cloud condensation nucleus (CCN), where hygroscopicity is expressed in a single hygroscopicity parameter κ. At a given supersaturation S, and depending on hygroscopicity, aerosols with a radius larger than the critical radius r_c will be activated to form cloud droplets. Based on Eq. (10) in Petters and Kreidenweis (2007), r_c is calculated for the aerosol mode k as

$$\begin{array}{}\text{(1)}& r_{\mathrm{c},k}={\left({\displaystyle \frac{\mathrm{4}{A}^{\mathrm{3}}}{\mathrm{27}{\mathit{\kappa }}_k{\ln }^{\mathrm{2}}S}}\right)}^{\mathrm{1}/\mathrm{3}},\text{with}A={\displaystyle \frac{\mathrm{4}{\mathit{\sigma }}_{\mathrm{s}/\mathrm{a}}{M}_{\mathrm{w}}}{RT{\mathit{\rho }}_{\mathrm{w}}}}\end{array}$$

and with mode mean hygroscopic parameter κ_k, supersaturation (saturation ratio) S, surface tension of a water–air interface σ_s∕a, molar mass of water M_w, density of water ρ_w, gas constant R, and ambient temperature T. Note that r_c,k (m) can change between aerosol modes as κ_k depends on the relative mass of the aerosol species within a mode, calculated following Eq. (5).

Using the log-normal properties of the M7 aerosol modes, the activated fraction of aerosol for mode k is given by

$$\begin{array}{}\text{(2)}& f_k=\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathrm{erfc}\left(-{\displaystyle \frac{\ln (r_{c,k}/{\stackrel{\mathrm{̃}}{r}}_k)}{\sqrt{\mathrm{2}}\ln \left({\mathit{\sigma }}_k\right)}}\right),\end{array}$$

with erfc indicating the complementary error function, ${\stackrel{\mathrm{̃}}{r}}_k$ is the mode median radius and σ_k is the mode geometric standard deviation. This equation can be applied to both aerosol number and aerosol mass by replacing ${\stackrel{\mathrm{̃}}{r}}_k$ by the number median radius r_n,k or mass median radius r_m,k respectively. These are calculated as

$$\begin{array}{}\text{(3)}& {\displaystyle }{r}_{n,k}{\displaystyle }={\left({\displaystyle \frac{\mathrm{6}{M}_k}{\mathit{\pi }{N}_k{\mathit{\rho }}_k}}\right)}^{\mathrm{1}/\mathrm{3}}\exp \left(-{\displaystyle \frac{\mathrm{3}{\ln }^{\mathrm{2}}{\mathit{\sigma }}_k}{\mathrm{2}}}\right),\end{array}$$

$$\begin{array}{}\text{(4)}& {\displaystyle }{r}_{m,k}{\displaystyle }=r_{n,k}\exp \left(\mathrm{3}{\ln }^{\mathrm{2}}\right({\mathit{\sigma }}_k\left)\right),\end{array}$$

with N_k (kg⁻¹) the aerosol number mixing ratio, M_k (kg kg⁻¹) the sum of the aerosol mass mixing ratio of all species, and ρ_k (kg m⁻³) the mean aerosol density in mode k.

Mean properties for each mode k are calculated as the volume-mean averages of the different aerosol species i within that mode, following

$$\begin{array}{}\text{(5)}& {\displaystyle }{\mathit{\phi }}_k{\displaystyle }={\displaystyle \frac{\sum _i{V}_{i,k}{\mathit{\phi }}_i}{\sum _i{V}_{i,k}}},V_{i,k}={\displaystyle \frac{m_{i,k}}{{\mathit{\rho }}_i}}.\end{array}$$

Here, V_i,k and m_i,k are the volume and mass, respectively, of species i in mode k; φ_i is substituted by the species-specific hygroscopic parameter κ or density ρ (kg m⁻³) to calculate the mode mean values used in Eqs. (1) and (3). Values for density ρ and the hygroscopic parameter κ for the five M7 aerosol species are given in Table 1.

Table 1 Values of density ρ and the hygroscopic parameter κ for the five aerosol species considered in M7.

^* van Noije et al. (2014), ${}^{**}$ Pringle et al. (2010).

As stated above, DALES uses an “all-or-nothing” saturation adjustment scheme in which cloud liquid water q_c is a diagnostic variable. Therefore, we use a fixed value of supersaturation (S=0.4 %) in Eq. (1), which is representative for the simulated case (Derksen et al., 2009). However, by fixing S, the model omits the competition for moisture between particles (aerosols and cloud droplets) or the role of supersaturation in this process. Moreover, by directly linking supersaturation levels to particle activation, we implicitly assume that the equilibration time of the droplets is instantaneous or considerably shorter than the model time step. This might lead to an overestimation of activated droplets as some particles would activate at a certain supersaturation but did not have enough time to grow to the respective critical radius. This process would be better captured by a numerical framework that directly calculates condensational growth. However, including this in a multi-species aerosol scheme would be computationally too demanding. To assess the impact of using a fixed supersaturation on the cloud characteristics in our simulations, we will perform sensitivity simulations with different values of S. Although fixing the value of S is an approximation, it does allow for an interactive calculation of cloud droplet number concentration based on simulated aerosol.

A modal representation of the aerosol size distribution poses a fundamental problem for the numerical calculation of aerosol activation. Cloud activation strongly modifies the shape of the aerosol size distribution by removing the larger particles exclusively. However, in the subsequent time step, the model again assumes a full log-normal distribution. This effectively redistributes aerosol mass and number to all sizes of the log-normal size distribution, including aerosols exceeding the critical radius, which allows for additional activation. Frequent repeated activation and redistribution of aerosol might lead to a possible “runaway activation”, which depletes the complete aerosol population and yields unrealistically high cloud droplet number. To avoid this runaway activation in the κ-Köhler-based scheme, activation in a cloudy grid cell is allowed only once. Additional activation is suppressed until the grid cell becomes cloud free again.

To be able to disentangle effects of the numerical description of activation from other processes, an alternative method for activation is implemented. This method is based on the work by Pousse-Nottelmann et al. (2015), hereinafter PN15. This activation method is also geared towards a modal representation of the aerosol distribution, but it calculates N_c using updraught velocity w and the number concentration of soluble mode particles larger than 35 nm, N_>35, as given by Eq. (2) in PN15:

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{\partial N_{\mathrm{c}}}{\partial t}}{|}_{\text{acti}}=max\left\{{\displaystyle \frac{\mathrm{1}}{\mathrm{\Delta }t}}\left[\mathrm{0.1}{\left({\displaystyle \frac{w{N}_{>\mathrm{35}}^t}{w+\mathit{\alpha }{N}_{>\mathrm{35}}^t}}\right)}^{\mathrm{1.27}}-N_{\mathrm{c}}^{t-\mathrm{1}}\right],\mathrm{0}\right\},\end{array}$$

with w as the updraught vertical velocity, Δt the length of the time step, $N_{\mathrm{c}}^{t-\mathrm{1}}$ the number of cloud droplets present, $N_{>\mathrm{35}}^t$ the number concentration of soluble or mixed aerosol particles larger than 35 nm, and α=0.023 cm⁴ s⁻¹ as an empirically derived constant. N_>35 is calculated as the sum of the soluble accumulation and coarse mode number concentrations, plus the fraction of soluble Aitken mode particles above 35 nm, evaluated using Eq. (2). As described in PN15, activation is assumed to progress from the biggest to the smallest particles in each mode.

By including updraught velocity w and the existing cloud droplet number $N_{\mathrm{c}}^{t-\mathrm{1}}$, this formulation does include competition for moisture between condensation on existing droplets and activation of new particles. However, the strongest limitation of this formulation is found in the prefactor of 0.1. This prefactor was determined in Zubler et al.  (2011) by comparison of their model outcome against satellite data with respect to the cloud droplet effective radius. The combination of this prefactor and the subtraction of $N_{\mathrm{c}}^{t-\mathrm{1}}$ poses such a strong limitation on aerosol activation that runaway activation does not occur in the PN scheme.

2.2.3 Scavenging

With the addition of prognostic variables for the aerosol population, scavenging has to be addressed in the aerosol budget. Our implementation of aerosol scavenging is based on the framework by Croft et al. (2009, 2010) and distinguishes between scavenging by cloud droplets (i.e. in-cloud scavenging) and by falling precipitation (i.e. below-cloud scavenging). Because scavenging by falling raindrops also takes place within a cloud, this process is referred to as rain scavenging in the remainder of this work to avoid confusion. The separation of scavenging by cloud droplets and precipitation matches the description in the cloud microphysics scheme that makes a similar distinction between cloud and rain droplets. The calculation of the scavenging efficiency is implemented into the model using a look-up table approach. For each aerosol mode, the size-dependent scavenging efficiencies for in-cloud scavenging are determined using aerosol median radii ranging from 10⁻² to 10³ µm and median cloud drop radii between 5 and 50 µm. Rain scavenging is defined for aerosol median radii from 10⁻³ to 10³ µm and rainfall intensities between 10⁻² and 10² mm h⁻¹.

2.2.4 In-hydrometeor processes

All microphysical processes that were previously implemented in DALES (i.e. autoconversion, accretion, sedimentation, self-collection, and break-up) now have to take into account the in-hydrometeor aerosol mass and the transfer of aerosol mass between free, in-cloud, and in-rain states. For these processes it is assumed that the aerosol mass is dissolved in the hydrometeor water and homogeneously distributed over the cloud and rain drop distributions, i.e. the aerosol concentration does not change with hydrometeor size. With this assumption, the fraction of transformed in-hydrometeor aerosol mass is equal to the transformed fraction of water. For example, if 2 % of the cloud water is transformed to rain by autoconversion, then 2 % of the in-cloud aerosol mass is transferred to the in-rain mode as well.

With the introduction of a prognostic variable for N_c in DALES, the process of cloud droplet self-collection has to be added to the microphysical framework. For this, we use the parameterization of SB described in Seifert and Beheng (2006) Eq. (9):

$$\begin{array}{}\text{(7)}& {\displaystyle \frac{\partial N_{\mathrm{c}}}{\partial t}}{|}_{\text{sc}}=-k_{cc}{\displaystyle \frac{({\mathit{\nu }}_c+\mathrm{2})}{({\mathit{\nu }}_c+\mathrm{1})}}{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{0}}}{\mathit{\rho }}}{q}_{\mathrm{c}}^{\mathrm{2}}-{\displaystyle \frac{\partial N_{\mathrm{c}}}{\partial t}}{|}_{\text{au}},\end{array}$$

where $k_{cc}=\mathrm{4.44}\times {\mathrm{10}}^{\mathrm{9}}$ m³ kg⁻² s⁻¹ is a constant describing the cloud–cloud collision efficiency; ν_c (−) the width parameter in the generalized Γ distribution for cloud droplets; ρ (kg m⁻³) the air density, where ρ₀=1.225 kg m⁻³ is the reference air density; and q_c is cloud liquid water (kg kg⁻¹). The last term on the right-hand side represents subtraction of the colliding particles involved in the autoconversion process.

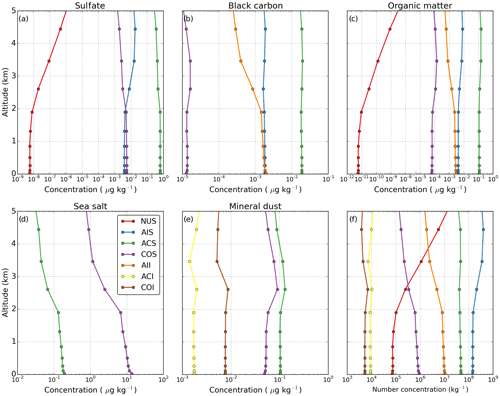
Figure 2 Initial vertical profiles of aerosol mass concentration (µg kg⁻¹) of (a) sulfate, (b) black carbon, (c) particulate organic matter, (d) sea salt, (e) mineral dust, and (f) number concentration (kg⁻¹) extracted from the TM5 model (Bergman et al., 2019). Aerosol modes are specified by different colours, which are consistent between panels. Circles correspond to the TM5 model levels. Note the break in the horizontal axis in panel (c).

2.2.5 Evaporation and aerosol resuspension

An explicit calculation of raindrop evaporation is given by the SB microphysical framework and was previously implemented in the DALES model. With the saturation adjustment approach in DALES, aerosol resuspension resulting from cloud evaporation cannot be calculated in a similar way. Instead, it is based on the diagnostic variable for cloud liquid water q_c. Evaporation of cloud water is calculated as the difference between q_c in the current time step and the previous time step if q_c decreases. Note that this approach neglects the changes in q_c due to advection. However, to disaggregate the different sources and sinks of q_c, cloud water needs to be calculated prognostically. The corresponding transfer of aerosol particle number is calculated as

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{\partial N_{\mathrm{c}}}{\partial t}}{|}_{\text{evpc}}=\left\{\begin{array}{ll}\frac{q_{\mathrm{c},t-\mathrm{1}}-q_{\mathrm{c},t}}{q_{\mathrm{c},t-\mathrm{1}}}\frac{N_{\mathrm{c}}}{\mathrm{\Delta }t}& \text{if}{q}_{\mathrm{c},t-\mathrm{1}}>q_{\mathrm{c},t},\\ \mathrm{0}& \text{otherwise}.\end{array}\right.\end{array}$$

By applying this relation, we implicitly assume a Marshall–Palmer size distribution for the cloud droplets so that the evaporated fraction of cloud water equals the fraction of cloud drop number that is resuspended (de Bruine et al., 2018, Appendix A).

For the in-hydrometeor processes a one-to-one relation is used for the fraction of transferred water and the fraction associated aerosol mass. However, for the evaporation of clouds and/or rain, we have to take into account that the evaporation of water does not immediately lead to the resuspension of aerosol (e.g. Gong et al., 2006). Only upon complete evaporation of a hydrometeor is aerosol mass released. Hence, the resuspended aerosol mass fraction is not equal to the evaporated fraction of water. We use a similar approach as de Bruine et al. (2018) to account for this effect (Eq. 4 therein). Additionally, as the number of aerosol particles incorporated into the hydrometeors is not explicitly tracked, we apply the commonly used assumption that one evaporated hydrometeor releases one aerosol particle (Mitra et al., 1992). The resuspended aerosols are assumed to follow a log-normal size distribution with a width of σ=1.5 (Pousse-Nottelmann et al., 2015) and are divided between the ACS and COS modes based on the aerosol radius that divides these two modes in M7, i.e. 0.5 µm (Vignati et al., 2004). The aerosols with radius <0.5 µm are transferred to the ACS mode and the aerosols with radius >0.5 µm are transferred to the COS mode.

3 Sample simulations

3.1 Model set-up

3.1.1 RICO case

To test and validate the explicit aerosol–cloud interaction framework, the simulations are based on the Rain in Cumulus over the Ocean (RICO) field campaign (Rauber et al., 2007). This campaign, which took place during November 2004 to January 2005, is characterized by shallow, precipitating maritime cumulus clouds. RICO is widely used in research on cloud processes in (trade wind) cumulus clouds, and it served as the test case in an intercomparison project of 12 LES models (van Zanten et al., 2011). It is especially well suited for the testing of our new framework because of the rapid development of precipitation, and thus including the “full suite” of aerosol–cloud interactions. Initial profiles for moisture, temperature, and wind as well as large-scale tendencies and surface fluxes are the same as the those prescribed in van Zanten et al. (2011).

3.1.2 Aerosol initialization

Although the RICO campaign did include aerosol observations, these were fairly restricted. The aerosol size distribution was measured on aircraft flight RF12, and the measurements were fitted to a bimodal log-normal distribution of aerosols with uniform composition, assuming characteristics of ammonium bisulfate (see van Zanten et al., 2011, Sect. 2.2.3 therein), despite the marine nature of the environment. The campaign did not collect in situ data of aerosol composition that can be used to initialize and validate the M7 aerosol variables for our simulations. Instead we use vertical aerosol profiles of the region where RICO took place from a simulation with the chemistry transport model TM5 (van Noije et al., 2014; Bergman et al., 2019). The simulations were originally carried out for a remote-sensing experiment within the AeroCom project (http://aerocom.met.no, last access: 5 December 2019) by the Royal Netherlands Meteorological Institute (KNMI) in 2017.

Since TM5 uses the same modal aerosol framework M7, a one-to-one translation of the aerosol scalar fields can be made. The only difference between the latest version of TM5 (Bergman et al., 2019) and DALES in the aerosol representation is the inclusion of secondary organic aerosol in the TM5 model. This is expressed in the presence of POM in the soluble nucleation (NUS) mode, which does not exist in DALES. The corresponding mass is negligible, but it is incorporated into the POM Aitken soluble (AIS) mode mass nevertheless.

Petters and Kreidenweis (2007)Pousse-Nottelmann et al. (2015)

Table 2 Overview and description of the different simulations performed in this study.

The TM5 output is provided on native model pressure fields. These pressure fields are transformed to altitude coordinates using corresponding temperature fields. Since our simulations concern a case over the ocean, no corrections for topography are needed. The resulting transformation yields nine levels in the lowest 5000 m, which is the vertical extent of the DALES model simulations. Of these pressure levels, four are located near the surface (i.e. below 1000 m). Linear interpolation is used between these levels and the values between top and bottom of DALES grid boxes are averaged and assigned to the DALES vertical grid. Resulting profiles are shown in Fig. 2.

The aerosol population mainly consists of sea salt particles, as expected for this ocean region, with trade winds blowing from the open ocean. The sea salt mass concentration in the lowest 2000 m is 10.0 µg m⁻³. The other species account for 0.69 µg m⁻³ (sulfate), 0.19 µg m⁻³ (mineral dust), 0.14 µg m⁻³ (organic matter), and 0.027 µg m⁻³ (black carbon). Additionally, the sea salt mass concentration shows a decrease with height, explained by the fact that it is locally generated. The concentrations of the other species are more or less constant with height or even show a slight increase with height. For the pristine environment in the RICO campaign, these species are advected into the region and display characteristics of an aged aerosol population. For example, the mineral dust particles are considerably smaller than the sea salt particles and mainly reside in the soluble modes.

The total number concentration in the lowest 2000 m is 202 cm⁻³, mainly consisting of Aitken mode particles (150 cm⁻³). Of all aerosol particles, 83 cm⁻³ activates at a supersaturation of 0.4 %. This value is diagnosed by applying the κ-Köhler theory with the characteristic values of the different species shown in Table 1.

Figure 3 (a) Instantaneous horizontal cross sections of the cloud and aerosol spatial distribution at t=5.5 h. Occurrence of clouds and precipitation is indicated by the hatching. The underlying colour scale indicates sea salt aerosol mass concentration. Average wind speed and direction in the cloud layer (500–2000 m) is denoted in the top-right corner. The black line indicates the vertical cross section shown in the right panel. (b) Vertical cross section of sea salt aerosol concentration, with cloud (outline) and precipitation (hatching) indicated separately. Arrow in the top right corner indicates the zonal component of the wind.

3.1.3 Overview

To establish a baseline for the model results, the first simulation (BASE) uses the base version of DALES. This version uses a prescribed, fixed cloud drop number concentration (i.e. 70 cm⁻³) and follows the settings described for the model intercomparison by van Zanten et al. (2011). The second simulation uses a lower cloud drop number concentration (30 cm⁻³), which corresponds to the actual observed mean values (see Sect. 3.2.1). This simulation is referred to as BASE30.

In the KAPPA simulation, aerosols are activated using the κ-Köhler-based aerosol activation scheme. Based on this simulation, two sensitivity simulations are performed using supersaturations of 0.2 % and 1.0 % (SAT0.2 and SAT1.0, respectively). To test the results of the κ-Köhler activation, the alternative activation scheme by Pousse-Nottelmann et al. (2015) is used in the PN simulation. An overview of the different simulations is given in Table 2. Because we do not simulate the emission of new aerosol during the simulations, the originally 24 h long simulations in van Zanten et al. (2011) are shortened to 6 h. In longer simulations, the washout by precipitation would deplete the aerosol population to unrealistically low levels. The first 3 h of the simulation are considered spin-up and discarded in the analysis of the results. Although the simulation has not yet fully equilibrated after 3 h, metrics like liquid water path and cloud fraction only show a slow change after that as can be seen in Fig. 3 in van Zanten et al. (2011).

3.2 Results

A qualitative overview of the simulated cloud scene for the RICO campaign is shown in Fig. 3. These cross sections display the internal variability within the LES model domain that results from the high spatial resolution. Both large and small cloud structures are found in the simulated domain, and developing clouds coexist with readily precipitating clouds. Simulations show characteristics typical for shallow cumulus clouds, which is in accordance with observations. Clouds are sparsely spread over the domain, covering about 10 % of the total sky. The cloud base is located at about 500 m and cloud tops reach up to 2000–2500 m.

The interaction between the clouds and aerosol is clearly visible in the strong reduction of aerosol mass in the presence of liquid water. In addition, changes to the aerosol distribution as a result of cloud processing and/or washout are reflected in the inhomogeneities of the aerosol field in the regions where clouds no longer exist. More details of the influence of clouds and precipitation on the aerosol concentration are shown in Fig. 3b. Here, we can observe a decreased aerosol concentration in the precipitation field (around 4 km). In contrast, an increased aerosol concentration is found below the clouds (around 8 km) as a result of evaporating precipitation between cloud base and the surface.

Further results of the simulations will be discussed in two steps. Section 3.2.1 will focus on the cloud characteristics and compare the results of the different simulations. Section 3.2.2 addresses the effect of the cloud microphysics on the aerosol distribution. The strength of the aerosol fluxes associated with the cloud microphysical processes are quantified, as well as the location in the vertical column where these processes take place. In addition, the differences between the aerosol species are discussed. Particular attention is given to the typical aerosol size associated with the various processes in clouds and precipitation.

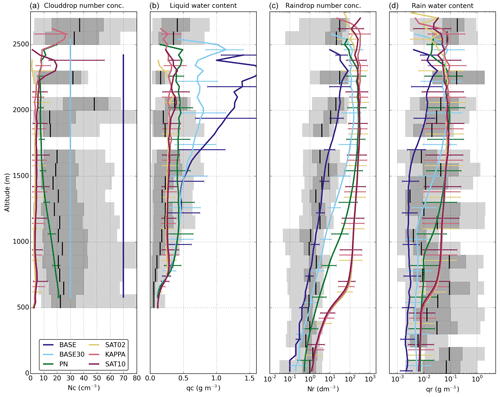
Figure 4 Validation of modelled cloud and rain characteristics against observations of (a) cloud droplet number concentration N_c, (b) cloud liquid water q_c, (c) rain drop number concentration N_r, and (d) rain water content q_r. Observations are grouped by altitude using increments of 100 m. Median value is shown by vertical black bars, light grey shading indicates the 5th to 95th percentiles, and dark grey indicates the 25th to 75th percentiles. Median simulated values are represented by coloured lines with the error bars indicating the 25th to 75th percentiles.

3.2.1 Cloud microphysics

To evaluate the modelled cloud characteristics produced in the different simulations, we follow the analysis by van Zanten et al. (2011). Domain-averaged cloud characteristics are shown in Fig. 4, which is constructed to resemble Fig. 8 in van Zanten et al. (2011). Similar to their work we use an aggregate of 1 Hz Fast-FSSP (forward scattering spectrometer probe) measurements on flights RF06-RF12 with the C-130 aircraft (Rauber et al., 2007). Cloud characteristics are filtered using the condition q_c>0.01 g kg⁻¹, while rain characteristics use the condition q_r>0.001 g kg⁻¹.

The above-mentioned aircraft observations show values for N_c up to 90 cm⁻³, but mean values are around 30 cm⁻³ while median values are about 20 cm⁻³, slightly decreasing with altitude. This is considerably lower than the default fixed value of N_c of 70 cm⁻³ used in the BASE simulation, which was the prescribed value for the simulations in van Zanten et al. (2011). The BASE30 simulation uses N_c=30 cm⁻³, based on the observed mean N_c of the aircraft observations. In the other simulations, N_c is not prescribed but interactively calculated from the aerosol distribution. The new framework with explicit κ-Köhler activation used in the KAPPA simulation yields values for N_c of about 4–10 cm⁻³. Increasing the values for critical supersaturation to 1 % in the SAT1.0 simulation shows an insignificant increase in median N_c of about 1 cm⁻³. Decreasing S to 0.2 % in the SAT0.2 simulation shows a similar decrease in the modelled amount of N_c. When using the alternative activation scheme in the PN simulation, N_c values of 30 cm⁻³ are found at cloud base, but N_c decreases to about 10 cm⁻³ at an altitude of about 1500 m and remains constant above this level.

The relatively low N_c in the KAPPA, SAT0.2, and SAT1.0 simulations is the direct result of prohibiting “repeated activation” as discussed above in Sect. 2.2.2. With the absence of additional in-cloud activation, droplets only activate at cloud base and are distributed over the whole cloud, leading to low N_c. Although in-cloud activation is allowed in the PN simulation, the governing equation also severely limits how much of the available aerosol is activated. Both simulations show a decrease in N_c with altitude as most activation takes place near cloud base.

Simulated cloud liquid water content q_c increases with the calculated or assumed N_c. The BASE simulation has the highest (fixed) value of N_c and simulates q_c with a continuous increase up to 1.5 g m⁻³ at 2500 m altitude. The BASE30 simulation shows a similar profile up to an altitude of 1500 m. From there to cloud top, q_c is considerably lower, with values around 0.7 g m⁻³. The PN simulation follows the BASE and BASE30 simulations up to 1200 m, but levels off at values around 0.4 g m⁻³. The KAPPA simulation diverges from the other simulations as it levels off at 0.25 g m⁻³. In comparison, observations of the RICO campaign show a somewhat slower continuous increase with height (as expected for shallow cumulus clouds) to about 0.25 g m⁻³ around 1250 m and above.

Above-mentioned differences in q_c are accompanied by substantial differences in domain averages in liquid water path (LWP). Consistent with q_c the BASE and BASE30 simulations calculate the highest LWP: 11.4 and 11.1 g m⁻², respectively. The lowest LWP is simulated by KAPPA: 4.43 g m⁻², while PN has an average LWP of 8.81 g m⁻². The relative differences in LWP are larger than q_c because the simulations also differ in average cloud fraction. When considering actual volume occupied by clouds (i.e. q_c>0.01 g kg⁻¹) in the cloud layer between 500 and 2000 m, BASE and BASE30 are again highest and virtually equal (2.04 % and 2.07 %, respectively). KAPPA deviates most from this and calculates 1.58 %. In the PN simulation this is 1.97 %.

While the observations of the cloud characteristics are fairly well constrained, values for precipitation show considerably more spread. Hence, a logarithmic scale is used for both N_r and q_r. Observed rain water content q_r fluctuates greatly with median values between 0.001 and 2 g m⁻³.

Simulated values show more stable values and smoother profiles. Simulations with the highest q_c show the lowest values for q_r. The BASE simulation calculates values for q_r of about 0.0025 g m⁻³ up to an altitude of 1500 m, above which the values increase with height to 0.03 g m⁻³ at 2300 m. The BASE30 simulation shows a substantially higher amount of rainwater in the lowest 1100 m with a median of about 0.006 g m⁻³. From there q_r increases to 0.01 g m⁻³ at 2000 m altitude. In the KAPPA simulation q_r is similar to the BASE30 simulation near the surface. However, in KAPPA q_r shows a sharp increase between 500 and 600 m followed by gradual increases to 0.01 g m⁻³ at 2000 m. The PN simulation shows a similar profile, with the sharp increase located around 1000 m to the same value of 0.01 g m⁻³.

Observations indicate values of N_r around 1 dm⁻³ up to 1000 m, increasing to 10 dm⁻³ at 2000 m and even higher above. The BASE simulation shows the lowest values for N_r, in accordance with q_r. From 10 to 100 dm⁻³ at the surface, N_r continuously increases to 10–100 dm⁻³ at the cloud tops. The BASE30 simulation calculates higher N_r values at all altitudes, especially in the upper half of the cloud layer. In the KAPPA simulation, values for N_r are substantially higher. Surface values are around 1 dm⁻³, but they increase with a much steeper slope to 100 dm⁻³ in the lower parts of the cloud layer around 1000 m. From there, N_r shows a steady increase to 350 dm⁻³ at the top of the cloud layer. Note the stark contrast of high values for N_r combined with low values of N_c. The vertical profile in PN is in between the BASE/BASE30 and the KAPPA simulations. It resembles the profile found in BASE30, albeit with higher values.

The differences in q_c and precipitation are all related to the simulated (or prescribed) cloud droplet concentration N_c. The initial conditions (i.e. total water content and temperature) under which the clouds form are the same in all simulations. By decreasing N_c, the liquid water is distributed over less droplets leading to larger cloud droplets. This leads to a faster rain formation as the droplets grow more quickly. From a macro-dynamic perspective, a lower N_c decreases the water holding capacity of a cloud. This is reflected in the profiles of q_c. Near cloud base all simulations show the same q_c, but in the KAPPA and PN simulations the water holding capacity is reached and all excess water is transformed into precipitation. This level is maintained in the rest of the cloud layer. In the BASE and BASE30 simulations, this limit is not reached and q_c keeps increasing throughout the cloud layer. Another interesting result is that a decrease in N_c leads to an increase in N_r (reversed order of the simulations in Fig. 4a and c). The cloud droplets in the KAPPA simulation (and to a somewhat lesser extent in the PN simulation) are so large that collision-coalescence of cloud droplets quickly results in rain size droplets (i.e. autoconversion). In the BASE and BASE30 simulations, the cloud droplets are smaller and more collisions are needed to form raindrops. Indeed, we find that the strength of autoconversion is higher in the KAPPA and PN simulations than in the BASE and BASE30 simulations, and autoconversion takes place at lower altitudes (not shown). In the BASE and BASE30 simulations, most rainwater is gained through the collection of cloud droplets by falling raindrops (accretion).

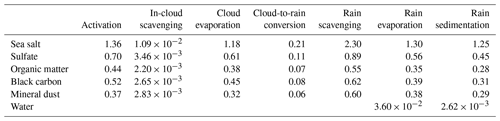
Table 3 Domain-averaged total column microphysical process strengths (kg kg⁻¹ d⁻¹) in the KAPPA simulation for the different aerosol species, divided by the species total column aerosol mass (kg kg⁻¹) and rescaled to have the unit per day (d⁻¹). Reported values can be thus interpreted as timescales, e.g. activation processes 1.36 times the total column sea salt aerosol mass per day.

Table 4 Same as Table 3 but for the PN simulation.

A full validation and direct comparison of the simulation results with observations would require inputs derived from co-located observations of both aerosol size distributions and composition as well as an elaborate investigation of the influence of model set-up, i.e. convergence of results regarding model resolution and domain size (e.g. Matheou et al., 2011). Nevertheless, it is noteworthy that the KAPPA simulation with the lowest N_c best resembles the observed q_c, while setting N_c to the observed values in the BASE30 simulation results in an overestimation of q_c. In our framework, N_c can no longer be adjusted to improve the simulated values of the other cloud microphysical properties, but it follows from the aerosol population and calculated thermodynamics. In this way, the results of our framework can act as a starting point for further improvement of the numerical implementation of the microphysical processes. Possible pathways for improvement are discussed in Sect. 4.

3.2.2 Aerosol microphysics

In this section we focus on changes to aerosol population as a result of cloud microphysical processes. Here, we discuss the results of the KAPPA and PN simulations. As shown above, the different numerical descriptions of activation (Sect. 2.2.2) cause substantial differences in the cloud and rain characteristics. This, in turn, yields differences in the feedback to the aerosol population. A comparison between the two simulations provides insight into the network of the different microphysical processes and the overall impact on the aerosol distribution.

Section 3.2.3 describes the influence of the different microphysical processes to the bulk properties of the aerosol (i.e. domain average of the aerosol mass) and the resulting vertical profiles of aerosol mass and number at the end of the simulation. Section 3.2.4 subsequently focusses on the aerosol size in more detail. This is done by comparing the typical aerosol size associated with the different microphysical processes (i.e. typical aerosol size after resuspension from raindrops compared to the initially activated aerosols).

3.2.3 Contribution of individual processes to the aerosol budget

The effective influence of the different microphysical processes on the five aerosol species is shown in Tables 3 and 4 for the KAPPA and PN simulations, respectively. The values are scaled to the species-specific total mass and thus can be interpreted as a processing timescale.

The in-cloud aerosol mass has two source processes: activation and in-cloud scavenging by cloud droplets, displayed in the first two columns of Tables 3 and 4. For both simulations, we find that virtually all in-cloud aerosol mass (>99 %) is gained through activation while in-cloud scavenging of interstitial aerosol is negligible. The relatively low values for N_c lead to rather ineffective in-cloud scavenging. Most of the in-cloud aerosol mass is resuspended to the atmosphere after evaporation of cloud droplets carrying the aerosol. In the KAPPA simulation ∼87 % of the in-cloud aerosol is resuspended, while in the PN simulation this cloud evaporation fraction is ∼96 %. The activation scheme in the PN simulation activates more aerosol and thus calculates higher N_c. This delays precipitation formation, which is reflected in higher q_c in clouds and higher LWP and cloud fraction as discussed in Sect. 3.2.1. Consequently, less aerosol is removed from the atmosphere by precipitation and resuspended when the cloud evaporates instead.

Corresponding aerosol fluxes for activation and cloud evaporation are 13 times larger in PN compared to KAPPA, i.e. in the PN simulation clouds process a total of 18.0 times the available sea salt aerosol mass per day instead of 1.36 when using the KAPPA activation. Due to the large cloud evaporation fraction, the large activation flux does not directly lead to a similar increase in cloud-to-rain conversion of aerosol. Instead, we find that conversion is “only” ∼3.5 times stronger in the PN simulation compared to the KAPPA simulation (e.g. conversion of the available sea salt mass: 0.74 d⁻¹ in PN vs. 0.21 d⁻¹ in KAPPA).

The strength of interaction between aerosol and clouds differs greatly between aerosol species. For example, the processing rate of sea salt by cloud activation (1.36 d⁻¹ in KAPPA) is 2.6 times larger than for mineral dust (0.52 d⁻¹ in KAPPA). As expected, the most hygroscopic species are most susceptible to the activation process. However, note that the combination of the different species within a log-normal mode of the aerosol framework determines the activation for that mode (see Sect. 2.2.2). As a result, organic matter is processed more slowly than black carbon despite the higher hygroscopicity of this species. Because the simulated case is over the ocean and relatively remote, species like black carbon have aged significantly and mainly reside in the accumulation mode. Therefore, it is activated alongside the highly hygroscopic sea salt aerosol in the accumulation mode. The differences in the rates for resuspension after cloud evaporation and cloud-to-rain conversion closely follow those of the activation process. This is caused by the fact we assume an internal aerosol mixture of the in-cloud aerosol mass. Cloud processes thus act similar on the aerosol species as soon as they are incorporated into cloud droplets.

Besides cloud-to-rain conversion, falling precipitation gains additional aerosol mass by rain scavenging. In fact, this process is the dominant source for in-rain aerosol mass. Comparing the process strengths in the KAPPA simulation of cloud-to-rain conversion (e.g. 0.21 d⁻¹ for sea salt) and rain scavenging (2.30 d⁻¹ for sea salt), we find that 89 %–91 % of the in-rain aerosol mass is gained by falling precipitation. This is a direct result of the high q_r in this simulation. The lower q_r in the PN simulation (see Fig. 4) corresponds to a lower scavenging by precipitation. With a relative contribution of 64 %–70 %, falling precipitation remains the most dominant source process for in-rain aerosol mass. Interestingly, cloud-to-rain conversion and scavenging together process a relatively similar amount of aerosol mass in both simulations.

Once the aerosol is incorporated into rain, it can be removed from the atmosphere by sedimentation (rainout) or it can be resuspended upon evaporation of the rain drops, shown in the last two columns of Tables 3 and 4. The strength of these two processes is about the same. In the KAPPA simulation, 51 %–56 % of the aerosol mass is resuspended by evaporating rain, while in the PN simulation this is 40 %–45 %. This difference is again linked to the slower rain water formation in the PN simulation (i.e. smaller N_r; see Fig. 4). Less cloud drops are transformed to rain, which are on average larger and thus less prone to evaporate. Because the aerosol mass is only released upon complete evaporation of rain, this leads to a lower evaporating fraction. The precipitation rate (i.e. water that reaches the surface) is the same in both simulations (see Tables 3, 4, and Fig. 4). This leads to a removal of aerosol in the PN simulation that is 17 % (sea salt) to 48 % (black carbon) higher than in the KAPPA simulation.

The above-mentioned balance between the two sink processes for in-rain aerosol (i.e. resuspension vs. sedimentation) is substantially different than for the rainwater itself. In the KAPPA simulation, 93 % of the falling precipitation evaporates, which leads to the resuspension of only 51 %–56 % of the in-rain aerosol mass. A similar ratio is found in the PN simulation: 86 % evaporated rainwater vs. 40 %–45 % resuspended aerosol. As explained in Sect. 2.2.5, the fraction of released aerosol mass is always lower than the fraction of evaporated rain water. However, the disparity exceeds the correction by Gong et al. (2006) because below the cloud falling precipitation keeps gaining additional in-rain aerosol through scavenging, whereas the amount of water only decreases.

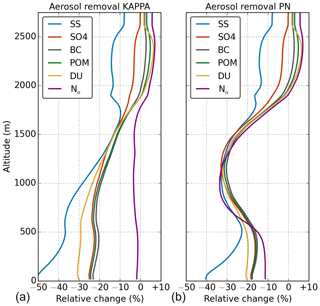
Figure 5 Vertical profile of domain-averaged aerosol mass and number concentration after 6 h for the KAPPA (a) and PN (b) simulations relative to the initial profile.

The combination of the microphysical processes discussed above leads to the ultimate removal of aerosol shown in Fig. 5. Total column aerosol mass at the end of the simulation has decreased 24 % in the KAPPA simulation and 21 % in the PN simulation. The two simulations show different vertical profiles of the remaining aerosol, which is the result of the different balance between microphysical described processes above. In the KAPPA simulation, rain scavenging was found to account for about 90 % of the in-rain aerosol. Consequently, the removal is strongest near the surface and decreases with height. The small local maximum around 400 m reflects evaporation of precipitation below the cloud base, while the zone of activation at the cloud base is visible in the local minimum around 600 m. When using the PN activation scheme, aerosol removal and the governing processes change considerably. The importance of cloud-to-rain conversion for the in-rain aerosol mass increases in the PN simulation compared to KAPPA. Consequently, aerosol removal in the cloud layer is enhanced by −30 %. In contrast, net removal below the cloud layer decreased as a result of resuspended aerosol mass originating from the cloud layer.

The decrease in aerosol number is substantially different between the KAPPA and PN simulations. While the reduction in aerosol number in KAPPA is limited (<3 %), the PN simulation calculates removal of aerosol number up to −34 %. The dominant removal by rain scavenging in the KAPPA simulation is most effective for large particles and thus results in the removal of the largest particles. Moreover, when droplets evaporate, the smallest droplets evaporate first and thus resuspend the smallest aerosols first since the aerosol mass in rain is distributed homogeneously over all available rainwater. This further increases the tendency for large particles to be removed from the atmosphere. The resulting removal of aerosol number in the KAPPA simulation is therefore much smaller than the removal in aerosol mass. In the PN simulation, aerosols are cycled through the clouds more frequently. Due to collision-coalescence of cloud droplets, resuspended aerosols will be larger than the initially activated particles. This results in removal of aerosol number in the cloud layer but has no effect on aerosol mass.

The behaviour of the different aerosol species is similar in the PN and KAPPA simulations and mainly determined by the typical aerosol particle size because the effectivity of scavenging as well as activation increases with aerosol size. The largest decrease is found for sea salt, followed by mineral dust. Profiles of sulfate, organic matter, and black carbon are similar and display the weakest removal. The vertical profile for sea salt stands out due to the vertical distribution of this species, which decreases strongly with height (see Fig. 2). The concentrations of the other species are relatively constant with altitude. Due to this, resuspension of sea salt aerosol brought down from the cloud layer is not sufficient to replenish the sea salt aerosol scavenged by falling precipitation close to the surface.

3.2.4 Changes in the aerosol size distribution

Analysis of the remaining aerosol total mass and number in the previous section (Sect. 3.2.3) already indicates that changes in the cloud characteristics might cause substantial differences in the cloud processes influence on the aerosol size distribution. To better quantify this cloud processing, the following section will compare the median radius for particles associated with the different microphysical processes.

Table 5 Typical dry aerosol median radius (nm) associated with the microphysical processes for the KAPPA and PN simulations.

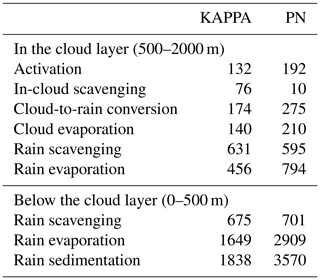
An overview of the typical aerosol median radius associated with the cloud and rain microphysical processes is shown in Table 5. At the beginning of a cloud cycle, we find an average median radius of activated aerosols of 132 nm in the cloud layer (between 500 and 2000 m) in the KAPPA simulation. In the PN simulation this radius is 192 nm. This increase of 45 % is caused by the substantially stronger cycling of aerosol through the clouds in the PN simulation. Inside the clouds, droplets are merged into larger droplets by collision-coalescence. When these cloud droplets evaporate, larger and less numerous aerosol particles are resuspended to the atmosphere. Because a larger fraction (compare Tables 3 and 4) of the cloud droplets are actually resuspended to the atmosphere in the PN simulation, this “cloud processing” has a stronger effect on the aerosol population.

Additionally, the higher evaporation fraction in the PN simulation also has a direct influence on the size of the resuspended aerosols. As explained in Sect. 2.2.5 aerosols are only resuspended when a droplet completely evaporates. Because the smallest droplets evaporate first, the smallest incorporated aerosols are also resuspended first, since the aerosol concentration is homogeneously distributed over the hydrometeor size distribution. When the evaporation fraction increases, larger droplets can evaporate completely increasing the average resuspended aerosol size. In the KAPPA simulation, resuspended aerosol particles resulting from cloud evaporation are 6 % larger (140 nm) than the initially scavenged aerosols. In the PN simulation, the resuspended aerosols are 9 % larger (210 nm).

Interstitial aerosols scavenged by cloud droplets are substantially smaller than the activated aerosols as the largest particles have been activated. In the KAPPA simulation the typical radius of scavenged interstitial aerosol is 76 nm, compared to 10 nm in the PN simulation. The activation scheme in the PN simulation activates a larger amount of particles, leaving even less interstitial aerosol for in-cloud scavenging. In both simulations, in-cloud scavenging is relatively weak and has no substantial influence on the typical aerosol size associated with the other processes.

The cloud-to-rain converted droplets contain aerosols with a median radius of 174 nm, which is 32 % larger than the activated aerosol in the KAPPA simulation. In the PN simulation, the relative size of aerosols involved in cloud-to-rain conversion is 275 nm (+43 %). This increase in aerosol size is again linked to the higher cloud evaporation fraction. Higher cloud evaporation allows larger droplets to evaporate completely, but the largest ones still remain and are converted to raindrops. In fact, by now evaporating more droplets, conversion is further shifted towards the large-end tail of the cloud droplet size distribution. Consequently, the typical aerosol radius for cloud-to-rain conversion increases together with the typical radius for resuspension.

Due to the strength of rain scavenging in the simulations, in-rain aerosol mass grows considerably. As a result, raindrops evaporating in the cloud layer produce aerosols with a median radius of 456 nm in the KAPPA simulation. In the PN simulation, the average aerosol radius associated rain evaporation is 794 nm. This difference is caused by the fact that the rain water and in-rain aerosol mass is distributed over fewer and therefore larger rain droplets in the PN simulation. This leads to a direct increase in the typical aerosol size associated with the evaporation of precipitation.

The average median radius of the aerosol particles scavenged by falling precipitation is 631 nm in the cloud layer in the KAPPA simulation. Note that this exceeds the typical median radius for evaporated aerosols. The preference for scavenging to remove the largest particles still plays a role for aerosols of this size, i.e. rain scavenging is an order of magnitude more effective for mass than number (Croft et al., 2009, their Fig. 1).

Below the cloud layer (<500 m), falling precipitation has had more time to collect aerosol mass. Additionally, outside the cloud the evaporation fraction is substantially higher. This leads to a considerable increase in the size of the resuspended aerosols. In the KAPPA simulation, the typical median aerosol radius is 1.65 µm, 12.5 times larger than the initially activated aerosols. The average size of the resuspended aerosols in the PN simulation is 2.91 µm. This is an even stronger increase of 15.2 times the size of the originally activated aerosols. Note that these large resuspended aerosols are prone to sedimentation, a process that has been left out of the current simulations.

To summarize, the results of the KAPPA and PN simulations illustrate that the influence of cloud processing on the aerosol size distribution depends on how much of the in-cloud and in-rain aerosol is ultimately removed. Due to collision-coalescence of cloud droplets, aerosol mass is redistributed over fewer droplets. Complete evaporation of these droplets would release aerosol particles larger than those originally activated and scavenged. However, when the clouds produce precipitation, the largest cloud droplets containing most aerosol mass are the droplets most likely to be converted to precipitation and to be removed from the atmosphere. Subsequent evaporation of the remaining droplets then also leads to a decrease in the average aerosol size. It thus depends on the balance between evaporation fraction and precipitation, whether the average size of the resuspended aerosols is larger or smaller than the initially activated aerosols. With a high evaporation fraction, fewer droplets are transformed to rain and these contain larger aerosols on average. Additionally, when precipitation is formed, scavenging of aerosols by falling precipitation adds a substantial amount of aerosol mass to the rainwater. The aerosols released by evaporation of these raindrops increase the average aerosol size considerably.

4 Discussion

The aerosol framework now implemented in the DALES model is specifically designed to gain insight into the aerosol–cloud interactions and the effect on the aerosol population in particular. By incorporating aerosols into the modelling framework and coupling it to the cloud microphysics, there is no longer a need for assumptions on how cloud characteristics change due to changes in the aerosol population. Instead, measured (or modelled in large-scale models) aerosol concentrations can be used to calculate corresponding cloud characteristics. An important feature of the aerosol framework is the ability to simulate multiple aerosol species, so aerosol activation can be based on the aerosol characteristics in a fundamental way, i.e. through κ-Köhler theory. Moreover, the effect of ACI on the aerosol population can be determined for individual aerosol species.

However, this increased complexity requires additional validation of the simulated aerosol population. To better constrain model results, there is particular interest in co-located cloud and aerosol measurements in, next to, and below clouds. Examples of recent campaigns collecting these types of measurements are GoAmazon2014/5 (Martin et al., 2017) and DACCIWA (Flamant et al., 2018). Observations of both aerosol size distribution and chemical composition are invaluable to the level of detail we pursue here. Measurements of aerosols near cloud base in combination with N_c provide insight into the process of activation. Cloud processing of aerosols can be investigated by determining the aerosol characteristics near cloud edges or at the location of dissipating clouds. Additionally, measuring aerosols in the wake of a precipitation zone allows for the validation of the effect of rain scavenging and evaporation of precipitation on the aerosol population. As discussed in Sect. 3.1.3, the original simulation length by van Zanten et al. (2011) was shortened from 24 to 6 h to avoid a too strong depletion of the aerosol population by washout. This would let the simulations diverge too much from the original case, decrease the already low simulated N_c, and strengthen the rain formation at the expense of cloud evaporation without precipitation.

Including aerosol emission and chemical formation to sustain aerosol levels would facilitate longer simulations. However, without observation-based constraints on these processes, this would introduce additional uncertainty and partly negate the goal of this work to have a model that includes both sides of ACI: the effect of aerosols on cloud and vice versa. Simulated N_c would be a direct result of the chosen emission strength, basically going back to the BASE simulations in which N_c is prescribed.

The exploratory analysis performed in this work only considered domain-averaged values of the clouds and aerosol. However, the richness of LES modelling allows for a deeper understanding of the aerosol–cloud interactions. Translating model data into quantitative results that do justice to the resolved complexity in LES simulations requires more comprehensive techniques. For example, convective cell tracking described in Heikenfeld et al. (2019) enables this kind of research by tracking individual clouds and averaging their statistics.

The introduction of aerosols puts increased demands on the numerical implementation of the cloud microphysical processes as well. Section 3.2.1 showed a trade-off between correct simulation of N_c and q_c. Because the aerosol population now determines the cloud characteristics, a previously prescribed value like N_c can no longer be adjusted to improve model results. Especially cases like the RICO campaign (with a pristine environment and low values for N_c) might reveal issues that were previously hidden. At the same time, combined with detailed observations, our framework is an excellent starting point to improve the microphysics parameterization in LES models. Parameters of the microphysics framework that might strongly influence the model outcome are (1) the radius that separates cloud from raindrops and (2) the parameters that describe the size distribution of the hydrometeors. Moreover, processes like autoconversion and accretion, as well as cloud droplet self-collection, do not depend on N_c in the current numerical implementation of the cloud microphysics in DALES. A well-validated case of both aerosol and cloud characteristics could provide a good starting point to evaluate the accuracy of modelled microphysical processes and its sensitivity to these critical parameters.

The difference in N_c between the KAPPA and PN simulations translated into substantial differences in the resulting aerosol population. In fact, this difference in N_c is part of a more general issue on how to numerically address the microphysical process of aerosol activation. The number of activated aerosol particles is largely determined by the maximum value of supersaturation near cloud base (e.g. Derksen et al., 2009). Supersaturation is the result of the balance between the source of available moisture resulting from the dynamics and the sink of moisture by condensation on aerosols and cloud droplets. Currently, DALES uses a diagnostic description of cloud liquid water and a fixed value for supersaturation. Although this gives a strict limitation on which aerosols can grow to cloud droplets, the modal aerosol framework does not allow this sharp cut-off in the size distribution. In subsequent time steps, aerosol mass and number are redistributed within the log-normal modes. Consequently, a part of the large-end tail of the size distribution is considered to be large enough to activate each time step. This results in a “runaway” activation yielding unrealistic N_c>200 cm⁻³ (not shown). This problem was also recognized in Pousse-Nottelmann et al. (2015), but the PN activation scheme limits activation by subtracting the number of existing cloud droplets N_c from the calculated amount of newly activated aerosols. Furthermore, a hard limit is set by only allowing particles larger than 35 nm to activate. A complete solution to this problem would be to use a sectional or bin approach to describe the aerosol population, which does allow changes to the shape of the size distribution and thus a sharp cut-off that results from activation. However, this flexibility comes with high computational cost, especially with a focus on the chemical composition of the aerosol population and the inclusion of multiple aerosol species (e.g. Kurppa et al., 2019, Table 2). A future improvement to DALES would be to replace the diagnostic calculation of cloud water by a prognostic variable. Supersaturation and activation can then be calculated interactively and be determined by the balance between available moisture resulting from the dynamics and available surface of aerosol and existing cloud droplets to condense on.

In Sect. 3.2.2, the comparison between the KAPPA and PN simulations illustrated important aspects of the interaction between aerosol and clouds. Here, we found an interesting competition between growth of aerosols through cloud processing and removal of the largest particles by precipitation. Future research could investigate the mechanisms that determine the balance between processing and removal. Settings like the pristine ocean of the RICO campaign alone might not be suitable for this as the low values of N_c inherently lead to rapid formation of precipitation and strong scavenging by falling precipitation. Simulations with higher aerosol burden and different meteorological settings should be used to investigate a large range of different cloud regimes.

5 Conclusions

The implementation of an explicit aerosol framework is a step forward in the simulation of aerosol–cloud interactions in the DALES model (Heus et al., 2010; Ouwersloot et al., 2017) as we can now quantify the feedback of the cloud microphysics on the aerosol population. Moreover, the aerosol module M7 (Vignati et al., 2004) represents an external mixture of multiple aerosol species. This allows an explicit and more fundamental approach to calculating aerosol activation by using κ-Köhler theory (Petters and Kreidenweis, 2007). Evaluation for the Rain in Shallow Cumulus over the Ocean (RICO) campaign (Rauber et al., 2007) showed that DALES reproduces the precipitating shallow cumulus clouds typical for this case. After evaluation with the RICO observations, our framework has been used to explore the feedback of aerosol–cloud interactions on the aerosol population. The main findings of this study are the following:

1. In the clean background atmosphere, virtually all in-cloud aerosol mass is gained through activation regardless of the activation scheme. In-cloud scavenging is inefficient at the low simulated cloud droplet concentrations. Despite the relatively rapid formation of precipitation, only 5 %–15 % of the aerosol mass is converted to rain.

2. Most of the in-rain aerosol mass is gained through scavenging by falling precipitation. It is the most dominant removal process of aerosol (mass) from the atmosphere. For the aerosol mass incorporated into rain, resuspension after evaporation of falling precipitation is of similar magnitude as the aerosol mass removed from the atmosphere by precipitation reaching the surface. This is in stark contrast to the evaporation to sedimentation ratio of rain water, of which only ∼10 % reaches the surface in our simulations.

3. The strength of aerosol–cloud interaction differs considerably between aerosol species. Timescales associated with the ultimate removal of aerosol by sedimentation range from almost 4 d for organic matter to less than a day for sea salt. For water, the timescale is even slower due to the strong evaporation of precipitation caused by the meteorological conditions in RICO.

4. The change in aerosol radius between activated aerosol and aerosol resuspended from evaporated cloud droplets is found to be relatively small (5 %–10 %). In contrast, the median radius of aerosols released by evaporating precipitation is an order of magnitude larger than the initially scavenged aerosol.

Future research will focus on evaluation of the M7–DALES framework under more polluted regimes in which cloud processing of the aerosol population may differ substantially. Additionally, further development includes the implementation of M7 aerosol microphysical processes (e.g. coagulation) and inclusion of aqueous-phase oxidation of dissolved (gaseous) species. The diagnostic approach to cloud water will be replaced by a prognostic calculation to incorporate the interaction between aerosols and clouds through changes in supersaturation.