the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
PALEO-PGEM v1.0: a statistical emulator of Pliocene–Pleistocene climate
Philip B. Holden
Neil R. Edwards
Thiago F. Rangel
Elisa B. Pereira
Giang T. Tran
Richard D. Wilkinson
We describe the development of the “Paleoclimate PLASIM-GENIE (Planet Simulator–Grid-Enabled Integrated Earth system model) emulator” PALEO-PGEM and its application to derive a downscaled high-resolution spatio-temporal description of the climate of the last 5×106 years. The 5×106-year time frame is interesting for a range of paleo-environmental questions, not least because it encompasses the evolution of humans. However, the choice of time frame was primarily pragmatic; tectonic changes can be neglected to first order, so that it is reasonable to consider climate forcing restricted to the Earth's orbital configuration, ice-sheet state, and the concentration of atmosphere CO2. The approach uses the Gaussian process emulation of the singular value decomposition of ensembles of the intermediate-complexity atmosphere–ocean GCM (general circulation model) PLASIM-GENIE. Spatial fields of bioclimatic variables of surface air temperature (warmest and coolest seasons) and precipitation (wettest and driest seasons) are emulated at 1000-year intervals, driven by time series of scalar boundary-condition forcing (CO2, orbit, and ice volume) and assuming the climate is in quasi-equilibrium. Paleoclimate anomalies at climate model resolution are interpolated onto the observed modern climatology to produce a high-resolution spatio-temporal paleoclimate reconstruction of the Pliocene–Pleistocene.
- Article
(18875 KB) - Full-text XML
-
Supplement
(48322 KB) - BibTeX
- EndNote
A high-resolution climate reconstruction of the Pliocene–Pleistocene will provide an unprecedented opportunity to advance the understanding of many long-standing hypotheses about the origin and maintenance of biodiversity. Climate is among the strongest drivers of biodiversity and has played an important role throughout the history of life on Earth (Svenning et al., 2015). Indeed, changes in climate over time have influenced core biological patterns and processes such as diversification, adaptation, species distribution, and ecosystem functioning (Svenning et al., 2015; Nogués-Bravo et al., 2018). However, studies on the relationship between climate and biodiversity are still limited by the lack of high-resolution, deep-time spatio-temporal paleoclimatic estimates, as the few studies available are at very sparse time slices (Lima-Ribeiro et al., 2015). Thus, a high-resolution spatio-temporal paleoclimate data series of the past 5×106 years will be useful to address many pressing questions on biodiversity dynamics. For instance, did the onset of glacial cycles promote more extinctions than recent climate cycles? Do species hold “evolutionary memory” of the warmer temperature of the Miocene? How did biodiversity respond to the increase in strength and frequency of glacial cycles during the Pliocene? Such knowledge is essential to understand biodiversity patterns and to forecast how organisms will respond to the current anthropogenic climatic change (Nogués-Bravo et al., 2018).
Spatio-temporal paleoclimatic estimates are essential to drive process-based models that are capable of exploring causal mechanisms (Nogués-Bravo et al., 2018). For instance, a recent ecological coupling study using climate emulation addressed the role of natural climate variability in shaping the evolution of species diversity in South America during the late Quaternary (Rangel et al., 2018). That study used a paleoclimate emulator (Holden et al., 2015) of the climate model PLASIM (Planet Simulator)-ENTS (Holden et al., 2014). The key limitations of the climate emulator were the lack of ocean dynamics in PLASIM-ENTS and the simplified emulation approach, which only considered orbital forcing; large-scale approximations were made to account for the effects of time-varying ice sheets and CO2. Here we address these weaknesses by using ensembles of a fully coupled atmosphere–ocean GCM with varied orbit, ice-sheet, and CO2 boundary conditions. However, simulation alone would not be possible for an application of this ambition. We use the computationally fast low-resolution AOGCM (atmosphere–ocean general circulation model) PLASIM-GENIE (Holden et al., 2016), a coupling of the spectral atmosphere model Planet Simulator (PLASIM; Fraedrich, 2012) to the Grid-Enabled Integrated Earth system model (GENIE; Lenton et al., 2006), but even with this relatively simple model a 5×106-year transient simulation would demand ∼300 CPU years of computing, which could not readily be parallelized. We overcome this intractability by using statistical emulation.
Emulators are computationally fast statistical representations of process-driven simulators, most useful when the application of the simulator would be computationally intractable (Sacks et al., 1989; Santner et al., 2003; O'Hagan, 2006). Climate applications of emulation have included the exploration of multi-dimensional parameter input space in order to, for instance, generate probabilistic outputs (Sansó et al., 2008; Rougier et al., 2009; Harris et al., 2013) or calibrate simulator inputs (Sham Bhat et al., 2012; Olson et al., 2012; Holden et al., 2013). Climate emulators have also been developed as fast surrogates of the simulator for use in coupling applications (Castruccio et al., 2014; Holden et al., 2014). In addition to Rangel et al. (2018), coupling applications have included climate change impacts on energy demands (Labriet et al., 2015; Warren et al., 2019) and adaptation to sea-level rise (Joshi et al., 2016).
Our methodology uses principal component analysis to project spatial fields of model output onto a lower-dimensional space of the dominant simulated patterns of change and then derives regression relationships between the simulator inputs and the coefficients of the dominant patterns. The method is analogous to the widely used pattern-scaling technique (Tebaldi and Arblaster, 2014), which assumes that an invariant pattern of simulated change can be scaled by global warming. Our approach extends this by including several (here 10) principal components for each climate variable, thereby allowing us to capture non-linear patterns of change. The regression approach we use involves Gaussian process (GP) emulation (Rasmussen, 2004).
GP emulators are non-parametric regression models that have become widely used tools in a variety of scientific domains. We train the emulators using ensembles of paleoclimate simulations, driven by variable orbital, CO2, and ice-sheet forcing inputs, in order to predict spatial fields of bioclimatic variables as functions of these inputs. This builds on previous studies that have emulated two-dimensional climate fields from CO2 forcing (Holden and Edwards, 2010; Holden et al., 2014), orbital forcing (Bounceur et al., 2015; Holden et al., 2015), combined CO2 and ice-sheet forcing (Tran et al., 2016), and combined orbital and CO2 forcing (Lord et al., 2017). Lord et al. (2017) additionally considered two ice-sheet states (modern and a reduced Pliocene configuration), but, to our knowledge, these three Pliocene–Pleistocene forcings have not previously been varied together except in the emulation of scalar indices (Araya-Melo et al., 2015). Ice-sheet forcing complicates the emulation problem because ice sheets are three-dimensional input fields. Although climate emulators with dimensionally reduced input and output fields have been developed (Holden et al., 2015; Tran et al., 2018), we simplify the problem by assuming there is an approximate equivalence between the ice-sheet state and global sea level. This reduces the emulation to the more usual problem of relating scalar inputs to high-dimensional outputs.
The motivation for our approach is to generate spatio-temporal climate fields for use in dynamic coupling applications that need temporal variability and therefore cannot use snapshot AOGCM simulations. To this end, we need forcing time series that extend back 5×106 years and have sufficient temporal resolution to capture orbitally forced climate variability. For PALEO-PGEM v1.0 we use the sea-level reconstructions of Stap et al. (2017) for the whole period and their CO2 reconstruction prior to 800 000 BP (when ice core records are not available).
PALEO-PGEM was built from quasi-equilibrium simulations of the intermediate-complexity AOGCM PLASIM-GENIE. The component modules, coupling, and pre-industrial climatology are described in detail in Holden et al. (2016). PLASIM-GENIE is not flux corrected. The moisture flux correction required in the Holden et al. (2016) tuning was removed during a subsequent calibration (Holden et al., 2018). PLASIM-GENIE has been applied to studies on Eocene climate (Keery et al., 2018) and climate–carbon-cycle uncertainties under strong mitigation (Holden et al., 2018).
We applied PLASIM-GENIE at a spectral T21 atmospheric resolution (5.625∘) with 10 vertical layers, and a matching ocean grid with 16 logarithmically spaced depth levels. We enabled the ocean BIOGEM (Ridgwell et al., 2007) and terrestrial ENTS (Williamson et al., 2006) carbon-cycle modules, as described in Holden et al. (2018). We do not consider ocean biogeochemistry outputs here.
The 2000-year spun-up simulations required for emulation were performed with atmosphere–ocean gearing enabled (Holden et al., 2018). In geared mode, PLASIM-GENIE alternates between conventional coupling (for 1 year) and a fixed-atmosphere mode (for 9 years), reducing spin-up time by an order of magnitude, to roughly 4 d CPU.
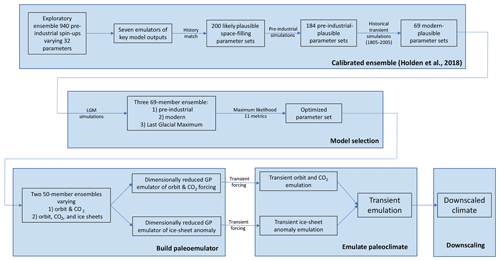
We first provide a summary of the entire approach in five steps, as illustrated schematically in Fig. 1. Each step is described in more detail in Sect. 4.
-
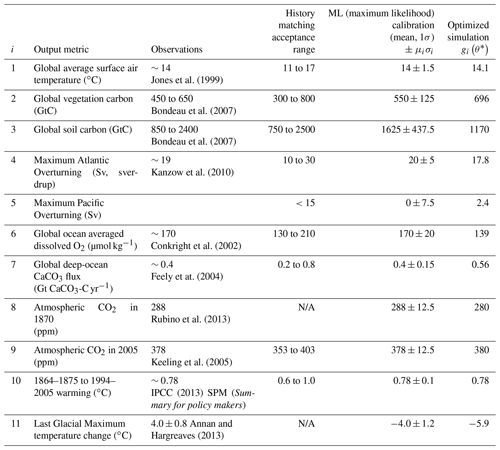
Ensemble calibration: we previously developed a 69-member ensemble of plausible parameter sets using “history matching” (see, e.g., Williamson et al., 2013). Applying any of these parameter sets to PLASIM-GENIE gives a reasonable climate–carbon-cycle simulation of the present day, as evaluated by 10 large-scale metrics; all 69 parameter sets produce simulated outputs that lie within the 10 history match acceptance ranges listed in Table 1. This step has been published elsewhere (Holden et al., 2018).
-
Model selection: we do not address parametric uncertainty in PALEO-PGEM and so required a single favoured PLASIM-GENIE parameter set. One of the 69 history-matched parameter sets was identified by picking the parameter set whose simulator output had the largest likelihood (defined in Sect. 4.1) and this “optimized” parameter set was used in all subsequent simulations. We require PALEO-PGEM to describe glacial states and so, as part of the calibration, we performed an additional ensemble with the 69 parameter sets forced by Last Glacial Maximum (LGM) boundary conditions. The calibration considered simulated LGM cooling in addition to the 10 present-day metrics (Table 1).
-
Paleoemulator construction: PALEO-PGEM was constructed via a two-stage process, in both stages applying Gaussian process emulation to a singular value decomposition of the outputs of a PLASIM-GENIE simulation ensemble (cf. Wilkinson, 2010; Bounceur et al., 2015; Holden et al., 2015; Lord et al., 2017). The first stage emulated the simulated climate response to variable orbital and CO2 forcing, while the second stage emulated the incremental climate anomaly due to the presence of glacial ice sheets. The motivation for this two-stage approach was to impose physical meaning on the decomposition by isolating the ice-sheet-forced components from the orbitally and CO2-forced components. Note that we do not assume a linear superposition of the forcing components, and interactions between ice sheets, CO2, and orbit are represented in the second stage (see Sect. 4.2). All simulations used the optimized parameter set and only varied the climate forcing.
-
Paleoclimate emulation: forcing time series of orbital parameters, atmospheric CO2 concentration and sea level (as a proxy for ice-sheet volume) were applied to the two-stage emulator at 1000-year intervals to generate emulated climates at the native climate model resolution.
-
Downscaling. The emulated climates were converted to anomalies with respect to the emulated pre-industrial state and interpolated onto a high-resolution grid. These interpolated anomalies were applied to the observed climatology to derive a high-resolution paleoclimate reconstruction at 1000-year intervals from 5 Ma.
4.1 The optimized parameter set θ∗
Given computational constraints we chose to neglect parametric uncertainty in PALEO-PGEM and selected a single “optimized parameter set” for all simulations. Earlier work (Holden et al., 2018) had developed a calibrated ensemble of 69 plausible PLASIM-GENIE parameter sets through a history matching approach. In summary, these authors built and applied emulators of seven scalar metrics (items 1–7 in Table 1) to search for plausible input space. They considered hundreds of millions of potentially valid model parameterizations, each selected randomly by drawing from priors for 32 varied input parameters (Table 2). Each of these 32-element parameter vectors were applied to the seven emulators in turn, and 200 of them were selected to maximize a criterion that combined the distance of candidate points to the other points already in the design (to ensure the design points fully span the input space) and the probability (according to the emulator) of reasonably simulating the observational targets: global average surface air temperature, global vegetation carbon, global soil carbon, Atlantic overturning circulation strength, Pacific Ocean overturning circulation strength, global average dissolved ocean oxygen concentration, and global average calcium carbonate flux to the ocean floor. The 200 parameter sets were applied to simulation ensembles of the pre-industrial state and transient historical CO2 emissions forcing (1805 to 2005). Finally, 69 of these parameter sets were selected as acceptable on the basis of the seven pre-industrial metrics and three additional metrics that relate only to the transient simulations (items 8–10 in Table 1): emissions-forced CO2 concentration in 1870 and 2005 and transient warming (from 1865 to 2005).
Table 2Prior distributions for PLASIM-GENIE varied parameters (uniform between ranges in log or linear space as stated).Prior distributions are discussed and derived from Holden et al. (2010, 2013a, b, 2014, 2016). The final column tabulates the optimized parameter set.
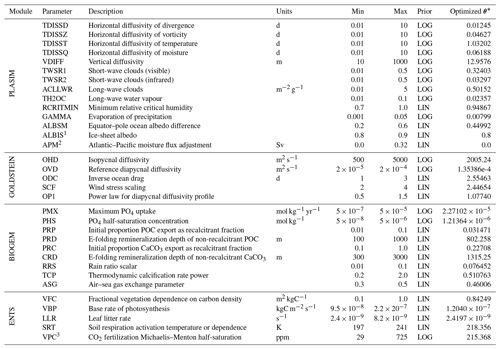
(1) ALBIS ice-sheet
albedo was fixed at 0.8 in the final ensemble. (2) APM was fixed at zero in
the final ensemble (no flux correction). (3) VPC was not constrained by the
emulator filtering as this parameter has no effect in the pre-industrial spin-up state. The final calibration step, selecting 69 simulations that satisfy present-day plausibility after the
historical transient was primarily an exercise to calibrate the VPC parameter.
In addition to these 10 plausibility tests of Holden et al. (2018), we also required the optimized model to exhibit a reasonable response to glacial ice sheets. We therefore performed an additional 69-member PLASIM-GENIE ensemble, applying Last Glacial Maximum forcing of 180 ppm CO2 concentration, “ICE-5G” LGM ice sheets (Peltier, 2004), and the LGM orbital configuration of Berger (1978), with an eccentricity of 0.0019, obliquity of 22.949∘, and longitude of the perihelion at vernal equinox of 114.4∘.
For each of j=1,..., 69 parameter combinations, we calculate a score Pj which indicates how successful simulation j was, in terms of matching the observations for each of the 11 metrics. These are tabulated in the “Calibration” column of Table 1, where μi denotes the observational estimate for metric i and σi an estimate of uncertainty, cognizant of both observational and model error.
where gi(θj) is the output of the simulator corresponding to the ith metric when it is run at parameter setting θj. The optimized parameter set θ∗ was selected to be the ensemble member with the highest score, equivalent to minimizing a weighted sum of squared errors. This optimized parameter set was used in all simulations that follow. The optimized output metrics are provided in Table 1 and the input parameter values in Table 2. The most notable bias is the cold LGM when compared to observational target, though the optimized model lies within the 3.1 to 5.9 ∘C ranges simulated by the CMIP5/PMIP3 (Coupled Model Intercomparison Project 5/Palaeoclimate Modelling Intercomparison Project 3) and PMIP2 ensembles (Masson Delmotte et al., 2013).
The climate sensitivity of the optimized parameter set is 3.2 ∘C. The Maximum Atlantic Overturning is 17.8 Sv, at a depth of 1.1 km with the 10 Sv contour, an indicator of the location of NADW (North Atlantic Deep Water) formation, at a latitude of 56∘ N. Under LGM forcing, Atlantic overturning weakens to a peak of 11.1 Sv at a depth of 1.0 km and the 10 Sv contour shifts southward to 45∘ N. Under doubled CO2 forcing, Atlantic overturning weakens substantially to a peak of 7.6 Sv at a depth of 0.4 km.
4.2 Ensemble design
Our approach to emulating climate output fields relies on dimension reduction using the singular value decomposition. This is a statistical technique which rotates the data onto a new orthogonal coordinate system, so that the first coordinate is in the direction of maximum variance in the data, the second coordinate is then in the direction of maximum variance conditional on being orthogonal to the first coordinate, etc. The new coordinates are often called principal components (or empirical orthogonal functions), and whilst they are orthogonal, they are not expected to cleanly isolate distinct physical processes. In order to impose a physical separation of the components, and therefore to enforce a clean response to a distinct forcing, we chose to build the emulator as a two-stage process. We first decomposed and emulated the smoothly varying climate response to changing orbit and CO2 concentration with fixed present-day ice sheets (the “E1” emulator). The land–sea mask is held fixed at the present day in all simulations. We then separately emulated the incremental climate response to a change in ice-sheet state under the same orbital and CO2 forcing (the “E2” emulator) so that the final emulation is the sum of these two components.
To build the E1 and E2 emulators, two separate 50-member boundary-condition ensembles were performed (BC1 and BC2) with the optimized parameter set. The statistical design of both ensembles was the same 5×50 maximin Latin hypercube (MLH,) varying the three orbital parameters, the CO2 concentration, and the ice-sheet state. The only difference between the two ensembles was that the fifth hypercube variable, reserved for ice sheets, was ignored for the BC1 ensemble and the present-day ice-sheet configuration imposed for all BC1 simulations. The BC1 ensemble is designed to simulate the model response to orbit and CO2 forcing only, while the BC2 ensemble simulates the different response driven by the presence of glacial ice sheets under the same set of choices of orbital and CO2 forcing.
The sampling strategy for the orbital variables (eccentricity e, the longitude of the perihelion at the vernal equinox ω, and obliquity ε) followed Araya-Melo et al. (2015), uniformly sampling esin ω and ecos ω in the range −0.05 to 0.05 and ε in the range 22 to 25∘. This transformation was chosen because the insolation at any point in space and time of year is generally well approximated as a linear combination of these terms. Carbon dioxide was varied uniformly in log space, in the range log(160 ppm) to log(1000 ppm). For ice sheets, relevant only to the BC2 ensemble, four states were allowed in the training ensemble, being the Peltier Ice-5G ice sheets (Peltier, 2004) at 10, 13, 15, and 20 ka. These times were chosen as they correspond to well-spaced ice-volume intervals as evidenced by benthic δ18O (Lisiecki and Raymo, 2005). These times correspond to sea-level falls of 29, 45, 64, and 107 m relative to modern values in the Stap et al. (2017) reconstruction that we use to force the time-series emulation (Sect. 6).
In contrast to Araya-Melo et al. (2015), we did not restrict input space to exclude combinations of high CO2 and high glaciation levels, preferring instead to use all BC1 ensemble members (i.e. including those with high CO2) in the BC2 ice-sheet anomaly ensemble. This maintained the maximin and orthogonal properties of the MLH design and moreover avoided any risk of extrapolation outside of training input space during the Pliocene. Present-day (∼400 ppm) CO2 levels can be associated with significant (∼50 m) sea-level falls according to the Stap et al. (2017) reconstructions (see Fig. 2). However, the trade-off for this simplicity is that realistic input space during glacial periods was less well sampled than it would be for a more targeted ensemble of the same size (cf. Araya-Melo et al., 2015).
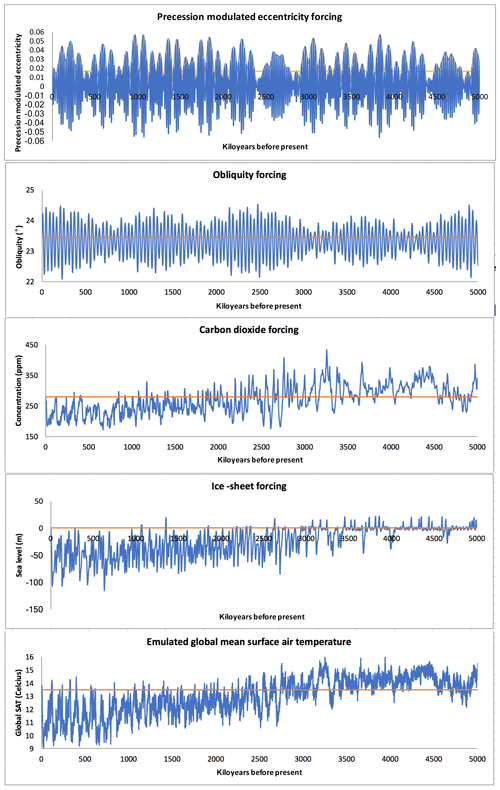
Figure 2Emulator time-series forcing and reconstructed global surface air temperature. Orbital forcing is Berger and Loutre (1991, 1999). Ice-sheet forcing is the sea-level reconstruction of Stap et al. (2017). Carbon dioxide forcing after 800 000 BP is ice core data (Luethi et al., 2008), using the Stap et al. (2017) reconstruction in the earlier period.
Emulators were built for four bioclimatic variables: the mean temperature of the warmest and coolest quarters and the mean daily precipitation of the wettest and driest quarters. Each variable was calculated on a grid-point basis as the maximum and minimum of the DJF (December–January–February), MAM (March–April–May), JJA (June–July–August), and SON (September–October–November) seasons. These emulated variables were chosen as being of bioclimatic relevance (cf. Rangel et al., 2018) and suitable for a wide range of ecological and impact coupling applications, defining the extremes of climate experienced over each grid cell during a (decadally averaged) annual cycle. Emulators of DJF and JJA temperature and precipitation were also built for validation purposes (Sect. 6.1).
We derived emulators from inputs of esin ω, ecos ω, ε, log(CO2), and sea-level S, each normalized on the range −1 to 1. Sea level provides a proxy for ice-sheet volume and hence ice-sheet state (under the assumption of an invariant correspondence between ice sheets and sea level). This neglects the asymmetry of ice sheets under glaciation and deglaciation. The E1 emulator was built from the outputs of the BC1 ensemble (after centring the data, by subtracting the ensemble mean field M from each simulation before singular value decomposition). The E2 emulator was built from the anomaly outputs BC2–BC1. For E2, we appended the training data with a synthetic 50-member ensemble with the hypercube inputs repeated except that sea level was randomly assigned to be between −25 and +100 m. In these synthetic data, no simulations were performed, but instead all the climate anomalies were set to zero, equivalent to performing a second ice-sheet-forced ensemble with a present-day ice sheet (and therefore with no anomaly by construction). This was needed so that the ice-sheet anomaly emulator can be used when glacial ice sheets are absent (i.e. sea level greater that −25 m), i.e. when the ice-sheet-emulated anomaly (E2) is trained to be zero and the emulation is determined only by the orbit and CO2 emulator (E1). Note that this approach neglected the loss of Antarctic and/or Greenland ice, compared to modern values, that is implicit when paleo sea level exceeded the present day.
All emulators were built following the “one-step emulator” algorithm described by Holden et al. (2015), summarized briefly here. For each ensemble member, we formed the 2048-element vector which describes the 64×32 output field to be emulated. The vectors for the N ensemble members were combined into a (2048×N) matrix Y describing the entire ensemble output of that variable. The matrices Y used to train the E1 emulators comprised decadally averaged outputs of the BC1 ensemble, and these matrixes were centred by subtracting the ensemble mean field. The matrices for the E2 emulators were constructed from the decadally averaged anomalies BC2–BC1. This separation of the forcing elements is a key difference with earlier work; every BC1 member has an identical BC2 member with the same inputs except for the incremental ice-sheet forcing, which cleanly isolates the emulation of ice-sheet forcing from the orbital and CO2 forcing.
Singular value decomposition was performed to reduce the dimensionality of the simulation fields:
where L is the (2048×N) matrix of left singular vectors (“components”), D is the N×N diagonal matrix of the square roots of the eigenvalues, and R is the N×N matrix of right singular vectors (“component scores”). This decomposition produced a series of orthogonal components, ordered by the percentage of variance explained. We truncated the decompositions, considering only the first 10 components. Each of the 10 retained sets of scores thus comprised a vector of N coefficients, representing the projection of each simulation onto the respective component. As each simulated field is a function of the input parameters, so are the coefficients that comprise the scores, so that each component score can be emulated as a scalar function of the input parameters to the simulator.
We used Gaussian process (GP) emulation (Rasmussen, 2004) in preference to stepwise linear regression. The principal motivation for using this more sophisticated approach was that GPs are highly flexible non-parametric regression models which have greater modelling power than linear models. Linear models live in a finite dimensional space defined by polynomial functions of the covariates. Gaussian processes live in a much richer space of functions. An additional motivation was that GP emulation provides both a central estimate and an estimate of uncertainty and therefore provides us with a means to generate uncertain climate emulations in the absence of parametric uncertainty. It is important to note that emulator uncertainty is entirely distinct from (and therefore incremental to) parametric uncertainty.
Gaussian process models are generalized models but nevertheless require some user choices, the most important being the choice of covariance function. We used an anisotropic covariance function (different length scales for each input dimension) and estimated the unknown length scale parameters using the type II maximum likelihood estimators (Rasmussen and Williams, 2006). In order to evaluate the optimal covariance function, we considered the cross-validation metric P; see Sect. 4.3.1 of Holden et al. (2014):
where is the coefficient of determination of the emulator of principal component c, evaluated under leave-one-out cross-validation of all simulations, and Vc is the percentage of the total variance explained by that component, summed across the leading 10 components. The metric is designed to quantify the percentage of the spatial variance explained by the emulator, capturing the explained variance due to principal component truncation (only 10 components are considered) and to the emulation itself (i.e. the explained variance of the simulated component scores).
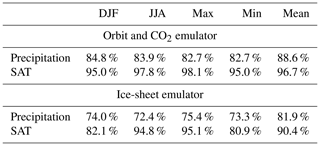
Table 3 summarizes the cross-validation of the eight emulators (i.e. four bioclimatic variables, two forcing categories). The second column tabulates the percentage of variance explained by the leading 10 principal components, , and represents the maximum variance that could be explained by the emulators if they were perfect. The remaining columns tabulate the metric P when building the emulator with a series of different covariance functions, the alternatives being available in the DiceKriging R package (Roustant et al., 2012). The reduction in variance explained (relative to column 2) reflects additional errors due to emulation.
Table 3Optimization of the Gaussian process covariance function. The variance explained by the first 10 components of the decomposition is quantified by “PC variance explained”, which would be the expected variance explained if the emulators were perfect. The percentage of variance explained by the emulators is quantified by the metric P (Eq. 3, including 10 components) for each of the eight emulators, considering various tested covariance functions. A power exponential is favoured for the final emulator, having similar average performance to exponential covariance function but outperforming it for the more difficult precipitation variables.
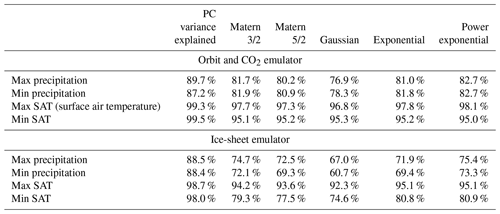
The temperature decompositions explain 94 %–99 % of the ensemble variance, compared to 87 %–90 % for the precipitation decompositions. Under emulation, the variance explained is 81 %–98 % for the temperature fields and 73 %–83 % for precipitation fields. The emulator performance is weaker for precipitation because the low-order components needed to explain much of the ensemble variability are more difficult to emulate.
The power exponential was found to give comparable or better performance compared to the other covariance functions in all eight emulators and was therefore chosen as the default covariance function and used in all analysis that follows.
Table 4 summarizes the variance explained under cross-validation of the seasonal and annual average emulators used in the following Sect. 7. DJF (JJA) temperature emulator performance is similar to min (max) temperature emulator performance, suggesting that Northern Hemisphere temperature is more difficult to emulate than Southern Hemisphere temperature, as would be expected for the ice-sheet emulator in particular. The performance of the various seasonal precipitation emulators is similar (82.7 % to 84.8 % for the orbit and CO2 emulator, 72.4 % to 75.4 % for the ice-sheet emulator), but annual precipitation is easier to emulate than seasonal precipitation (88.6 % for the orbit and CO2 emulator, 81.9 % for the ice-sheet emulator).
The emulators generate a paleoclimate as
where M is the simulation mean field that was subtracted to centre the ensemble before decomposition (Sect. 5). To generate a paleoclimate time series, we therefore require time series of the boundary condition inputs , and S.
For the orbital parameter inputs, we applied the 5×106-year calculation of Berger and Loutre (1991, 1999). We used CO2 from Antarctic ice cores for the last 800 000 years (Luethi et al., 2008). Prior to 800 000 BP, and for the entire sea-level record, we used the CO2 and sea-level reconstructions of Stap et al. (2017). These authors used a zonally averaged energy balance model coupled to a six-level ocean model, a thermodynamic sea-ice model and to one-dimensional mass-balance modules for each of the five major Cenozoic ice sheets (East and West Antarctica, Greenland, Laurentide, and Eurasian). The Stap model is forced with benthic δ18O records and uses an inversion routine to de-convolve the temperature and ice-volume components of the isotope signal and generate a self-consistent time series of CO2 and sea level (ice volume).
Figure 2 plots the forcing time series and an illustrative application of the emulator, for which we emulated the time-varying annual mean surface air temperature field and plotted its area-weighted global average through time.
In order to validate the emulators, we performed a series of experiments with Mid-Holocene (MH), Last Glacial Maximum (LGM), Last Interglacial (LIG) and mid-Pliocene warm period (MPWP) CO2, ice sheets, and orbital forcing. These time slices have been well-studied in Paleo-Modelling Inter-comparison Projects and are well suited to exploring variability driven by all three forcings. The MH and LIG responses are dominantly forced by orbit, while the MPWP is dominantly forced by CO2 and the LGM by both CO2 and ice-sheet state.
7.1 Mid-Holocene emulated ensemble
To assist comparison with readily available PMIP2 data (Braconnot et al., 2007), we here emulate seasonal (DJF and JJA) fields rather than seasonal (MAX and MIN) fields, plotted in Fig. 3. Uncertainty is associated with the emulation of the component scores. Gaussian process emulation quantifies this uncertainty by providing a mean prediction and an estimate of the uncertainty associated with that prediction. We generated a 200-member emulation ensemble with MH forcing. The 200 ensemble members differ because we do not assume the mean prediction for the emulated component scores but instead draw randomly from the posterior distributions. In Fig. 3 this ensemble is summarized with mean and standard deviation fields. (We note that for applications in which climate uncertainty is not addressed, it is appropriate to use the mean predictions of principal component scores to generate the best estimate.)
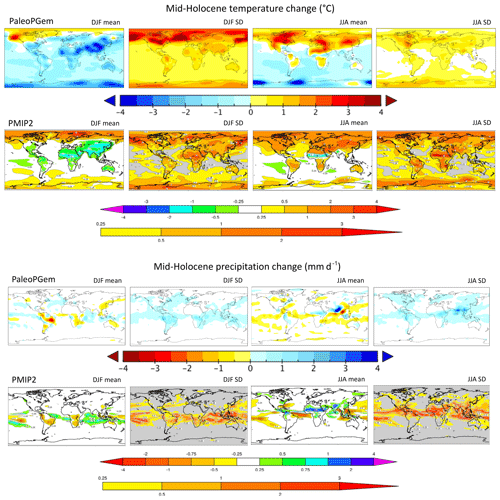
Figure 3PALEO-PGEM emulated ensemble comparison with PMIP2 ocean–atmosphere–vegetation ensemble (Braconnot et al., 2007) for the Mid-Holocene.
Figure 3 (top panels) compares emulated MH surface temperature (anomalies relative to pre-industrial) with the PMIP2 OAV (coupled atmosphere–ocean–vegetation) ensemble. In northern winter DJF, high-latitude warming is apparent in the emulated ensemble mean, although it is of uncertain sign (variability > mean). Cooling is apparent over all other land regions. In northern summer JJA, robust warming is apparent at mid- to high latitudes, while changes in variable signs are apparent in the tropics, with cooling apparent over the Sahel, India, and SE Asia. Each of these features is also found in the PMIP ensemble. The most significant difference is Antarctic cooling of ∼3 ∘C in PALEO-PGEM, which contrasts with a warming signal in the ensemble mean of PMIP2 (although we note the DJF Antarctic cooling of 0.5 ∘C was simulated in HadCM3M2). A significant cold Antarctic bias is also apparent during the Last Interglacial (Sect. 7.4). High southern latitudes are poorly modelled by PLASIM-GENIE. The pre-industrial state exhibits a warm Antarctic bias, with greatly understated sea ice, a slow Antarctic Circumpolar Current, and weak, northerly shifted zonal winds (Holden et al., 2016), which are likely associated with the well-known difficulties of resolving Southern Ocean wind stress at low meridional resolution (Tibaldi et al., 1990; Schmittner et al., 2010).
Figure 3 (lower panels) compares emulated MH precipitation with the PMIP2 OAV ensemble. In DJF, significant drying is emulated over central and northwestern South America, southern Africa, eastern Asia, and northern Australia, while wetter conditions are emulated over northeastern South America. In JJA the largest changes are seen as a strengthening of the Asian monsoon precipitation, and significantly wetter conditions are also seen over the Sahel and western South America. These changes all reflect a general agreement with PMIP2.
7.2 Last Glacial Maximum emulated ensemble
We follow the emulated ensemble procedure for the Last Glacial Maximum. Figure 4 (upper panels) compares the emulated Last Glacial Maximum temperatures with the PMIP2 OA (ocean–atmosphere) ensemble. We neglect the OAV LGM ensemble because it has only two simulations. LGM cooling is dominated by cooling of up to ∼40 ∘C over the Northern Hemisphere glacial ice sheets. The most significant differences are apparent in the emulated uncertainty, which is understated by a factor of roughly 2 relative to PMIP. This is expected because the emulator is built from a single parameterization of PLASIM-GENIE and therefore does not capture uncertain climate sensitivity. We note that by applying the principles of invariant temperature pattern scaling (Tebaldi and Arblaster, 2014), the temperature uncertainties due to neglected climate sensitivity could be approximated by inflating the variance of the principal component scores.
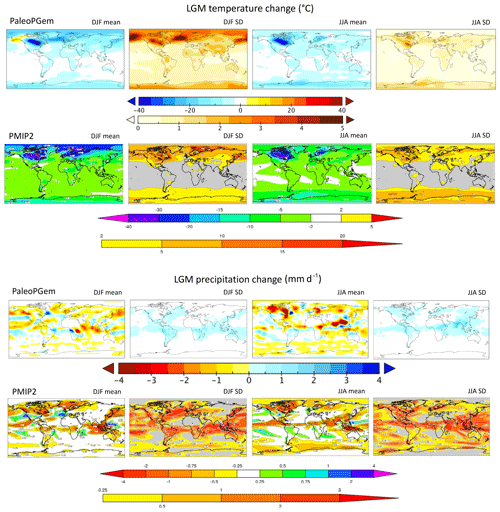
Figure 4PALEO-PGEM emulated ensemble comparison with the PMIP2 ocean–atmosphere ensemble (Braconnot et al., 2007) for the Last Glacial Maximum. Note the different scales for SD temperature. Reduced variance in PALEO-PGEM is due to the understated uncertainty of climate sensitivity, which arises from the neglect of parametric uncertainty.
Figure 4 (lower panels) compares emulated Last Glacial Maximum precipitation with the PMIP2 OA ensemble. In DJF, the drying apparent in central Africa, northern America, and the Amazon are captured by the emulator, while JJA drying at northern latitudes and in the Asian and African monsoon regions and increased precipitation in South America are common to the emulator and the PMIP2 ensemble.
7.3 Glacial–interglacial variability
The emulated global temperature change over the last 800 000 years is plotted in Fig. 5, reflecting the familiar glacial cycles and compared to the observationally based global temperature reconstructions of Koehler et al. (2010). Ten separate emulators were built (following the steps described in Sect. 5 applied to annual average temperature), and the mean prediction time series for all 10 emulators are plotted.
The Last Glacial Maximum cooling across these 10 emulators is 4.1±0.2 ∘C, which compares to uncertainty estimates of ±0.3 ∘C when emulated values are drawn randomly from a single emulator. The emulated estimates are lower than the simulated LGM cooling of 5.9 ∘C (Table 1) and may reflect bias in the ice-sheet emulator under the extreme of LGM forcing; the ice-sheet emulator was only able to explain 81 % of the variance of cold season temperatures (Table 3). However, the seasonal patterns of emulated change are reasonable (Fig. 4) and the annual average cooling is well-centred on the 3.1 to 5.9 ∘C range simulated by the CMIP5/PMIP3 and PMIP2 ensembles (Masson-Delmotte et al., 2013).
Maximum warming of 0.3±0.1 ∘C is emulated in the Last Interglacial (Marine Isotope Stage 5), peaking at 125 ka. This is consistent with CMIP estimates of 0.0±0.5 ∘C, but lower than data-based estimates of ∼1 to 2 ∘C (Masson-Delmotte et al., 2013). Maximum warming in Marine Isotope Stage 11 is 0.1±0.2 ∘C, peaking at 401 ka.
7.4 Last Interglacial transients
Zonally averaged emulated temperature changes are compared with the Last Interglacial transient model inter-comparison of Bakker et al. (2013) in Fig. 6 and Table 5. The latitudinal temporal trends are well captured by the emulator, considering the inter-model spread of Bakker et al. (2013). Notably, temperatures in June–July–August generally peak earlier (∼125 ka) than temperatures in December–January–February (∼120 ka). A maximum warming of ∼2 to 3 ∘C is emulated in northern summer mid- to high latitudes, peaking at 126 ka and consistent with inter-model estimates in the range 0.3 to 5.3 ∘C, peaking between 125 and 128 ka. Eight of the emulated peak warming estimates are consistent within the 1σ multi-model uncertainty ranges, and the remaining two are consistent within 2σ multi-model uncertainty (Table 5). The clearest difference is seen in Antarctic winter, where cooling of up to 3 ∘C is emulated, significantly greater than in any of the models.
7.5 The mid-Pliocene warm period
The emulated climate of the mid-Pliocene warm period is plotted in Fig. 7. The only emulator forcing is CO2 increased to 405 ppm, as assumed in the model inter-comparison of Haywood et al. (2013). Ice sheets are fixed at the present day, in contrast to Haywood et al. (2013), where the boundary conditions included a reduced West Antarctic Ice Sheet.
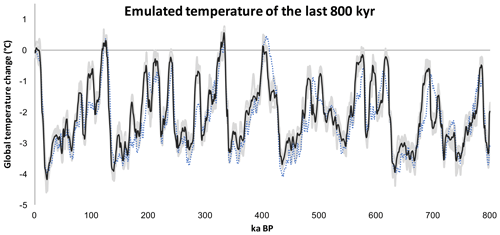
Figure 5Emulated global temperature over the last 800 000 years. An emulator was built 10 times, and the mean prediction time series of each emulator are plotted as grey lines, with the mean of these plotted as the single black line. The blue dotted line is the observationally based reconstruction of Koehler et al. (2010).
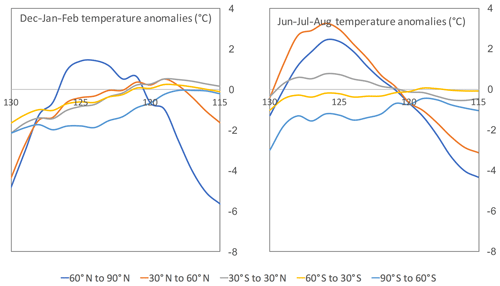
Figure 6Emulated Last Interglacial temperature anomalies with respect to pre-industrial temperatures. An emulator was built 10 times, and the mean prediction time series of each emulator are plotted. Data are provided for December–January–February and June–July–August averaged over five latitude bands; cf. Figs. 2 and 3 of Bakker et al. (2013).
Table 5Last Interglacial peak warming (∘C) and year of peak warming (BP) compared to the model inter-comparison ±1σ ranges of Bakker et al. (2013). Emulated data are provided for December–January–February and June–July–August, compared to January and July data in the model inter-comparison, and comparisons are provided for five latitude bands.

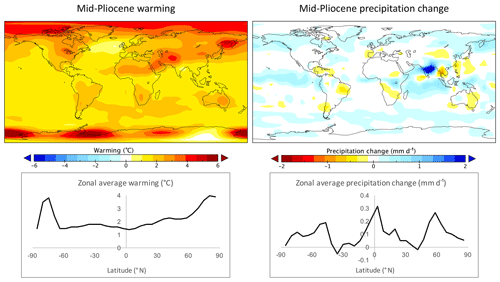
Figure 7Emulated mid-Pliocene temperature and precipitation anomalies with respect to pre-industrial values. The ice-sheet and orbital inputs are set to pre-industrial values, and the emulated change is driven by an assumed CO2 concentration of 405 ppm.
Ensemble-averaged emulated warming is 1.6±0.2 ∘C and global precipitation change 0.10±0.01 mm d−1. These compare to multi-model estimates of 1.8 to 3.6 ∘C and precipitation changes of 0.09 to 0.18 mm d−1 in Experiment 2 (the coupled atmosphere–ocean configuration) of Haywood et al. (2013). Emulated high-latitude warming of ∼4 ∘C is low-biased, but within the wide multi-model uncertainty range of ∼3 to 14 ∘C. Similarly, the emulated peak precipitation change of ∼0.3 mm d−1 near the Equator is low-biased, but within the multi-model range of ∼0 to 1.3 mm d−1.
A spatial resolution higher than the native resolution of the underlying climate model may be required for paleo-applications given the scale dependency of many patterns and processes (e.g. Rahbek, 2005), such as scale-dependent climate heterogeneity (Rangel et al., 2018). We address this need by interpolating the low-resolution climate model anomalies onto fine-resolution climatological data. This approach is widely used in climate impact assessment (e.g. Osborn et al., 2016) and has also been applied in paleo-applications in anthropology (Melchionna et al., 2018) and ecology (Rangel et al., 2018).
Downscaling can be performed in any given grid. Here we illustrate downscaling on a global hexagonal grid build on a geodesic dome because it minimizes geographic distortions in shape, area, and distance that are common to map projections. The hexagonal grid is composed of 17 151 quasi equal-area cells of 6918±859 km2 whose area variation is not spatially structured.
The four present-day (pre-industrial) emulated bioclimatic variables E were linearly interpolated onto the geodesic grid. All emulations used the mean prediction, and the E1 and E2 emulators were both truncated at 10 principal components. Contemporary observations of the bioclimatic variables C were derived from WorldClim (Hijmans et al., 2005), which provides temperature and precipitation estimates at 1 km2 resolution, interpolated from temporally averaged measurements (1950 to 2000) from ∼15 000 to 50 000 weather stations globally (depending upon the variable). The raw emulated climate data E and the difference with observed climatology E0−C are illustrated in Fig. 8.
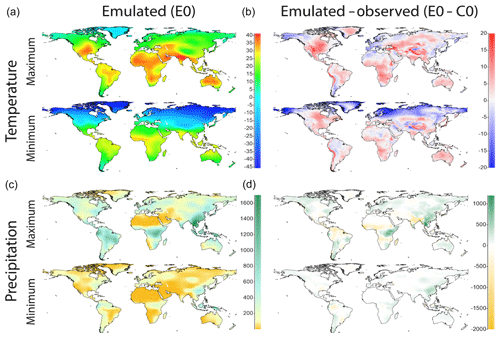
Figure 8Downscaling the emulated climate. Panels (a) and (c) are the pre-industrial emulations of the seasonal bioclimatic variables at native (T21) model resolution, interpolated into the high-resolution grid. Panels (b) and (d) illustrate the differences with respect to high-resolution climatology (Hijmans et al., 2005).
The emulated climatology is reasonable, accepting the low resolution of the underlying climate model. Cold biases are generally confined to northern winter high latitudes. Warm biases are more modest except for the Tibetan Plateau and Andes where the lapse rate cooling in these narrow mountain chains is poorly resolved by the climate model (but corrected for by the downscaling approach described below). Excess precipitation bias is mostly apparent in the (wet-season) monsoon regions. Deserts are generally well resolved in the emulator, a notable exception being the hyper-arid Atacama, which is an orography-driven feature that cannot be captured at low resolution. Conversely, orography-driven precipitation is understated in the Tibetan Plateau. Precipitation is also understated in the Sahel.
We apply anomaly adjustments to derive downscaled emulated climate fields through time Ct. This approach preserves the high-resolution spatial heterogeneity of climatology. In the case of temperature this is straightforward. Emulated anomalies Et−E are interpolated onto the hexagonal grid and applied additively; i.e. . For precipitation, the situation is more complex. In arid regions that are not well captured by the emulator, a multiplicative anomaly approach is preferable , preserving hyper-arid (topographically forced) desert and preventing unphysical negative precipitation when . Conversely, in wet regions that are understated by the emulator, a multiplicative anomaly approach can create unphysically high precipitation, but an additive approach ensures a physically reasonable solution. A pragmatic solution to this is to apply an additive precipitation anomaly when E0<C0 and a multiplicative precipitation anomaly when E0>C0. This approach is well-behaved, noting that the additive and multiplicative anomalies are equivalent when E0=C0. Consider, when E0<C0,
and the additive anomaly partially compensates for the low bias in emulated climatological precipitation. Conversely, when E0>C0,
and the multiplicative anomaly partially compensates for the high bias in emulated climatological precipitation.
The present-day climatology and downscaled emulated LGM climate are illustrated in Fig. 9. An animation of the entire 5 000 000-year reconstruction is provided as a Supplement.
PALEO-PGEM is to our knowledge the first attempt to provide a detailed spatio-temporal description of the climate of the entire Pliocene–Pleistocene period. It is essential to understand the main limitations of our modelling framework, discussed below, some of which may induce large errors or uncertainties in specific applications or even rule out certain applications completely. For all practical purposes and for the foreseeable future, substantial uncertainties exist in any paleoclimate reconstruction as a result of incomplete knowledge, computing limitations, and irreducible climatic noise. Ideally, these uncertainties should be quantified in relation to any reconstruction and their implications propagated through the analysis. Our approach provides an estimate of inherent uncertainty derived from the emulation step of the reconstruction and thus underestimates the full uncertainty, but nevertheless in some aspects remains comparable to the uncertainty in state-of-the-art reconstructions of particular periods as measured by the variance across ensembles of PMIP simulations.
Compared to state-of-the-art models, PLASIM-GENIE is a relatively low-resolution, intermediate-complexity climate model. This implies that processes operating at spatial and temporal scales below the native resolution of the climate model cannot be properly represented, although certain aspects of spatial variation are reintroduced in a highly idealized way by the downscaling process. The temporal effects of dynamical processes operating at sub-millennial timescales are further filtered out by the approximation inherent in the emulator construction that the climate is in quasi-equilibrium with the forcing, which is then only resolved at 1000-year time intervals.
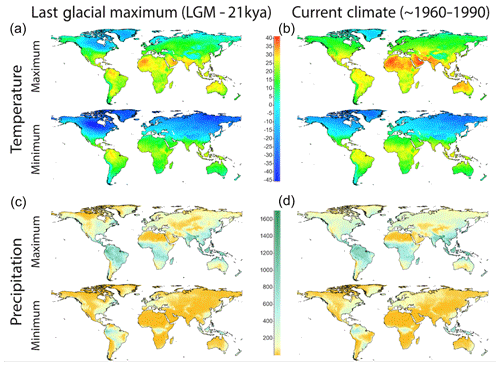
Figure 9Downscaled emulated climate. Panels (a) and (c) are the downscaled emulated bioclimatic variables at the Last Glacial Maximum. Panels (b) and (d) are the present-day climatology (Hijmans et al., 2005). Note that downscaled climates are derived by applying emulated anomalies to this present-day climatology. An animation of the complete 5 Ma reconstruction is provided as Supplement.
In applications where (downscaled) time-slice simulations are adequate and are available from higher-complexity models and/or multi-model ensembles (Sect. 7), these would normally be preferable to PALEO-PGEM as errors and biases will generally be smaller, particularly in high latitudes, regions of steep topography, close to coastlines, or in known regions of locally extreme climate. We note that HadCM3 climate simulations (Singarayer et al., 2017), downscaled to 1∘ resolution are available back to 120 ka (Saupe et al., 2019), which would provide preferable (or supplementary) climate data for applications restricted to this time domain.
The emulator uncertainty captures much of the uncertainty seen in multi-model inter-comparisons (Figs. 3 and 4), but PALEO-PGEM cannot fully represent model uncertainty because it is derived from a single configuration of a single model. Most clearly in this respect, the 90 % uncertainty range of climate sensitivity (3.8±0.6 ∘C) is understated relative to multi-model estimates of 3.2±1.3 ∘C (Flato et al., 2013). Some significant biases in spatial patterns are also apparent, most clearly temperature biases in high southern latitudes.
Emulator forcing is limited to orbit, CO2, and ice sheets. Ice meltwater forcing is not considered, so that millennial variability, especially important in North Atlantic, is neglected. The land–sea mask and orography are held fixed, so that ocean circulation changes driven by changing gateways (e.g. the closing Panama isthmus, with implications for the thermohaline circulation) are neglected and feedbacks driven by changing orography are neglected, especially important in regions of rapid tectonic uplift.
The representation of ice sheets applies Peltier ICE-5G deglaciation ice sheets (Peltier, 2004), assuming a fixed relationship between global sea-level reconstructions (derived from benthic oxygen isotopes) and the spatial form and extent of ice sheets. This approximation neglects the substantial asymmetry between build-up and decay phases of ice sheets and assumes that ice sheets were located similarly in all previous Pliocene–Pleistocene glaciations, which may not have been the case. Particular caution is therefore essential when applying the climate reconstruction at locations near the margins of ice sheets.
We apply a downscaling approach because spatial climate gradients can be critically important for ecosystem dynamics, especially in mountainous regions which are poorly resolved at native climate model resolution (Rangel et al., 2018). The downscaling approximation assumes that the lapse rate within a downscaled grid cell does not change with time, but it does capture the first-order effect of topographic complexity by assuming a constant present-day lapse rate. Similarly, the downscaling cannot capture feedbacks between atmospheric circulation and high-resolution topography, which could alter the patterns of rain shadowing. However, for many applications, it is preferable to neglect this second-order feedback rather than to neglect the first-order effect of a rain shadow that could not be resolved at native climate model resolution (e.g. the Atacama), which downscaling imposes through the baseline climatology. Other simplifications include the implicit assumptions of fixed mountain glaciers and ecotone distributions. In short, the high-resolution reconstructions should not be interpreted as a faithful reconstruction of high-resolution climate but should serve to introduce a more realistic degree of spatial variability.
We have used dimensionally reduced emulators of the intermediate-complexity AOGCM PLASIM-GENIE, downscaled onto high-resolution observed climatology, to generate a high-resolution transient climate reconstruction of the last 5×106 years. The reconstruction substantially improves on a previous emulated reconstruction (Rangel et al., 2018) in the following ways.
-
The underlying climate model is a fully coupled AOGCM. Rangel et al. (2018) used PLASIM-ENTS (Holden et al., 2014), which has a slab ocean and therefore neglected ocean circulation feedbacks.
-
The new simulation ensembles considered climate forcing by orbit, CO2, and ice sheets. Rangel et al. (2018) considered only orbit forcing, with large-scale adjustments to crudely approximate the effects of CO2 and ice sheets.
-
We use Gaussian process emulation. Rangel et al. (2018) used linear regression emulation, which cannot capture complex (non-linear) relationships between inputs and outputs.
These improvements allow us to provide a global emulation; the previous emulation was inappropriate for the Northern Hemisphere due to the crude approximation of the response to ice-sheet forcing. Additionally, we were able to extend the emulation back to 5×106 years; the previous emulation was limited by the length of an existing 800 000-year transient GENIE simulations (Holden et al., 2010) for CO2 and ice-sheet forcing. Finally, GP emulation provides uncertainty estimates that we show in Figs. 3 and 4 and can be used to provide a reasonable proxy for model error, neglected in our single-parameterization boundary condition ensembles.
The limitations of the reconstruction (see Sect. 9 for details) arise from the underlying climate model (low-resolution, intermediate-complexity), the approximated boundary conditions (in particular the use of only five ice-sheet states), uncertainties in the forcing time series (especially for sea level and CO2), the assumption of quasi-equilibrium (so that, e.g., millennial variability is neglected) and the limitations of downscaling. We note that the emulations and associated uncertainty compare favourably to existing ensembles of simulations with higher-complexity models (Figs. 3 and 4). We note further that reconstructing climates with different forcing time series is straightforward. Future improvements are anticipated by including a representation of changing topography. For instance, the Andes have uplifted by 25 % to 40 % of their 3700 m present-day elevation over the last 5×106 years (Gregory-Wodzicki, 2000) and Himalayan uplift has been associated with intensification of the Asian monsoon about 3.6 to 2.6 Myr ago (Zhisheng et al., 2001). Ensembles that address changing orography, land sea masks, and ocean gateways will improve the simulated climate and allow the extension of the emulation further back in time, to periods in which it would be unreasonable to ignore tectonically driven change.
The Supplement contains all of the files needed to build the emulators. PALEO-PGEMv1.0_5M_1Ka.mp4 is an animation of the four bioclimatic variables over 5Ma. PALEO-PGEMv1.0.R is the R code to build and run the emulators. A series of files are inputs to the R code. These are ensemble.dat (the ensemble input design for the BC1/BC2 ensembles), 5000_1000_forcing.dat (time series forcing for 5 Ma at 1 kyr intervals), MH_forcing.dat (Mid-Holocene ensemble forcing), LGM_forcing.dat (Last Glacial Maximum forcing), and area.dat (grid cell areas for area weighting). Two subdirectories contain the simulation data: data (outputs of the BC1 PLASIM-GENIE ensemble) and icedata (outputs of the BC2 PLASIM-GENIE ensemble). Supporting data are included in two spreadsheets: ensemble (supporting calculations for the ensemble design) and 5000ka_forcing (supporting calculations for the time series forcing). PALEO-PGEMv1.0.R was saved with settings to emulate DJF temperature and produce a 5 Ma time series using the GP mean prediction (no emulator uncertainty), 10 principal components, and a power exponential covariance function. Each of these settings can be changed as documented in the code. The code outputs the area-weighted average to screen and three data sets to file: emul.dat (the full spatio-temporal output), mean.dat, and SD.dat (the mean and standard deviation of the emulated fields, most relevant when code is set to generate an ensemble, e.g. with MH or LGM forcing).
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-12-5137-2019-supplement.
PBH, NRE, and TFR developed the concept. PBH performed the PLASIM-GENIE simulations, using boundary conditions developed by GTT. PBH and RDW developed the GP emulators. TFR and EBP developed the downscaling, with advice from PBH and NRE. PBH wrote the paper with contributions from all authors.
The authors declare that they have no conflict of interest.
Philip B. Holden and Neil R. Edwards were funded by NERC (grant no. NE/P015093/1). Elisa B. Pereira is supported by a doctorate fellowship from Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brasil (CAPES) – Finance Code 001.
This paper was edited by Didier Roche and reviewed by Michel Crucifix and one anonymous referee.
Annan, J. D. and Hargreaves, J. C.: A new global reconstruction of temperature changes at the Last Glacial maximum, Clim. Past, 9, 367–376, https://doi.org/10.5194/cp-9-367-2013, 2013.
Araya-Melo, P. A., Crucifix, M., and Bounceur, N.: Global sensitivity analysis of the Indian monsoon during the Pleistocene, Clim. Past, 11, 45–61, https://doi.org/10.5194/cp-11-45-2015, 2015.
Bakker, P., Stone, E. J., Charbit, S., Gröger, M., Krebs-Kanzow, U., Ritz, S. P., Varma, V., Khon, V., Lunt, D. J., Mikolajewicz, U., Prange, M., Renssen, H., Schneider, B., and Schulz, M.: Last interglacial temperature evolution – a model inter-comparison, Clim. Past, 9, 605–619, https://doi.org/10.5194/cp-9-605-2013, 2013.
Berger, A.: Long term variations of caloric insolation resulting from the Earth’s orbital elements, Quaternary Res., 9, 139–167, 1978.
Berger, A. and Loutre, M.-F.: Insolation values for the climate of the last 10 million years, Quaternary Sci. Rev., 10, 297–317, https://doi.org/10.1016/0277-3791(91)90033-Q, 1991.
Berger, A. and Loutre, M.-F.: Parameters of the Earths orbit for the last 5 Million years in 1 kyr resolution, PANGAEA, https://doi.org/10.1594/PANGAEA.56040, 1999.
Bondeau, A., Smith, P. C., Zaehle, S., Schaphoff, S., Lucht, W., Cramer, W., Gerten, D., Lotze-Campen, H., Müller, C., Reichstein, M., and Smith, B.: Modelling the role of agriculture for the 20th century global terrestrial carbon balance, Global Change Biol., 13, 679–706, 2007.
Bounceur, N., Crucifix, M., and Wilkinson, R. D.: Global sensitivity analysis of the climate-vegetation system to astronomical forcing: an emulator-based approach, Earth Syst. Dynam., 6, 205–224, https://doi.org/10.5194/esd-6-205-2015, 2015.
Braconnot, P., Otto-Bliesner, B., Harrison, S., Joussaume, S., Peterchmitt, J.-Y., Abe-Ouchi, A., Crucifix, M., Driesschaert, E., Fichefet, Th., Hewitt, C. D., Kageyama, M., Kitoh, A., Laîné, A., Loutre, M.-F., Marti, O., Merkel, U., Ramstein, G., Valdes, P., Weber, S. L., Yu, Y., and Zhao, Y.: Results of PMIP2 coupled simulations of the Mid-Holocene and Last Glacial Maximum – Part 1: experiments and large-scale features, Clim. Past, 3, 261–277, https://doi.org/10.5194/cp-3-261-2007, 2007.
Castruccio, S., McInerney, D. J., Stein, M. L., Liu Crouch, F., Jacob, R. L., and Moyer, E. J.: Statistical emulation of climate model projections based on precomputed GCM runs, J. Climate, 27, 1829–1844, 2014.
Feely, R. A., Sabine, C. L., Lee, K., Berelson, W., Kleypas, J., Fabry, V. J., and Millero, F. J.: Impact of anthropogenic CO2 on the CaCO3 system in the oceans, Science, 305, 362–366, 2004.
Flato, G., Marotzke, J., Abiodun, B., Braconnot, P., Chou, S. C., Collins, W., Cox, P., Driouech, F., Emori, S., Eyring, V., Forest, C., Gleckler, P., Guilyardi, E., Jakob, C., Kattsov, V., Reason, C., and Rummukainen, M.: Evaluation of Climate Models. In: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assess- ment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013.
Fraedrich, K.: A suite of user-friendly global climate models: hysteresis experiments, Eur. Phys. J. Plus, 127, 1–9, https://doi.org/10.1140/epjp/i2012-12053-7, 2012.
Gregory-Wodzicki, K. M.: Uplift history of the Central and Northern Andes: a review, GSA Bull., 7, 1091–1105, 2000.
Harris, G. R., Sexton, D. M., Booth, B. B., Collins, M., and Murphy, J. M.: Probabilistic projections of transient climate change, Clim. Dynam., 40, 2937–2972, 2013.
Haywood, A. M., Hill, D. J., Dolan, A. M., Otto-Bliesner, B. L., Bragg, F., Chan, W.-L., Chandler, M. A., Contoux, C., Dowsett, H. J., Jost, A., Kamae, Y., Lohmann, G., Lunt, D. J., Abe-Ouchi, A., Pickering, S. J., Ramstein, G., Rosenbloom, N. A., Salzmann, U., Sohl, L., Stepanek, C., Ueda, H., Yan, Q., and Zhang, Z.: Large-scale features of Pliocene climate: results from the Pliocene Model Intercomparison Project, Clim. Past, 9, 191–209, https://doi.org/10.5194/cp-9-191-2013, 2013.
Hijmans, R. J., Cameron, S. E., Parra, J. L., Jones, P. G., and Jarvis, A.: Very high resolution interpolated climate surfaces for global land areas, Int. J. Climatol., 25, 1965–1978, 2005.
Holden, P. B. and Edwards, N. R.: Dimensionally reduced emulation of an AOGCM for application to integrated assessment modelling, Geophys. Res. Lett., 37, L21707, https://doi.org/10.1029/2010GL045137, 2010.
Holden, P. B., Edwards, N. R., Wolff, E. W., Lang, N. J., Singarayer, J. S., Valdes, P. J., and Stocker, T. F.: Interhemispheric coupling, the West Antarctic Ice Sheet and warm Antarctic interglacials, Clim. Past, 6, 431–443, https://doi.org/10.5194/cp-6-431-2010, 2010.
Holden, P. B., Edwards, N. R., Gerten, D., and Schaphoff, S.: A model-based constraint on CO2 fertilisation, Biogeosciences, 10, 339–355, https://doi.org/10.5194/bg-10-339-2013, 2013.
Holden, P. B., Edwards, N. R., Garthwaite, P. H., Fraedrich, K., Lunkeit, F., Kirk, E., Labriet, M., Kanudia, A., and Babonneau, F.: PLASIM-ENTSem v1.0: a spatio-temporal emulator of future climate change for impacts assessment, Geosci. Model Dev., 7, 433–451, https://doi.org/10.5194/gmd-7-433-2014, 2014.
Holden, P. B., Edwards, N. R., Garthwaite, P. H., and Wilkinson, R. D.: Emulation and interpretation of high-dimensional climate outputs, J. App. Stats., 42, 2038–2055, 2015.
Holden, P. B., Edwards, N. R., Fraedrich, K., Kirk, E., Lunkeit, F., and Zhu, X.: PLASIM-GENIE v1.0: a new intermediate complexity AOGCM, Geosci. Model Dev., 9, 3347–3361, https://doi.org/10.5194/gmd-9-3347-2016, 2016.
Holden, P. B., Edwards, N. R., Ridgwell, A., Wilkinson, R. D., Fraedrich, K., Lunkeit, F., Pollitt, H. E., Mercure, J.-F., Salas, P., Lam, A., Knobloch, F., Chewpreecha U., and Viñuales, J. E.: Climate-carbon cycle uncertainties and the Paris Agreement, Nat. Clim. Change, 8, 609–613, https://doi.org/10.1038/s41558-018-0197-7, 2018.
IPCC: Summary for Policymakers, in: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013.
Joshi, S. R., Vielle, M., Babonneau, F., Edwards, N. R., and Holden, P. B.: Physical and Economic Consequences of Sea-Level Rise: A Coupled GIS and CGE Analysis Under Uncertainties, Environ. Resour. Eco., 65, 813–839, 2016.
Jones, P. D., New, M., Parker, D. E., Martin, S., and Rigor, I. G.: Surface air temperature and its changes over the past 150 years, Rev. Geophys., 37, 173–199, 1999.
Kanzow, T., Cunningham, S. A., Johns, W. E., Hirschi, J. J.-M., Marotzke, J., Baringer, M. O., Meinen, C. S., Chidichimo, M. P., Atkinson, C., Beal, L. M., Bryden, H. L., and Collins, J.: Seasonal Variability of the Atlantic Meridional Overturning Circulation at 26.58∘ N, J. Climate, 23, 5678–5698, 2010.
Keeling, C. D., Piper, S. C., Bacastow, R. B., Wahlen, M., Whorf, T. P., Heimann, M., and Meijer, H. A.: Atmospheric CO2 and 13CO2 exchange with the terrestrial biosphere and oceans from 1978 to 2000: observations and carbon cycle implications in: A History of Atmospheric CO2 and its effects on Plants, Animals, and Ecosystems, edited by: Ehleringer, J. R., Cerling, T. E., and Dearing, M. D., Springer Verlag, New York, 2005.
Keery, J. S., Holden, P. B., and Edwards, N. R.: Sensitivity of the Eocene climate to CO2 and orbital variability, Clim. Past, 14, 215–238, https://doi.org/10.5194/cp-14-215-2018, 2018.
Koehler, P., Bintanja, R., Fischer, H., Joos, F., Knutti, R., Lohmann, G., and Masson-Delmotte, V.: What caused Earth's temperature variations during the last 800,000 years? Data-based evidence on radiative forcing and constraints on climate sensitivity, Quaternary Sci. Rev., 29, 129–145, https://doi.org/10.1016/j.quascirev.2009.09.026, 2010.
Conkright, M. E., Locarnini, R. A., Garcia, H. E., O’Brien, T. D., Boyer, T. P., Stephens, C., and Antonov, J. I.: World Ocean Atlas 2001: Objective Analysis, Data, Statistics and Figures, CD-ROM Documentation, National Oceanographic Data Center, Silver Spring, MD, 2002.
Labriet, M., Joshi, S. R., Babonneau, F., Edwards, N. R., Holden, P. B., Kanudia, A., Loulou, R., and Vielle, M.: Worldwide impacts of climate change on energy for heating and cooling, Mitig. Adapt. Strateg. Glob. Change, 20, 1111–1136, doi10.1007/s11027-013-9522-7, 2015.
Lenton, T. M., Williamson, M. S., Edwards, N. R., Marsh, R., Price, A. R., Ridgwell, A. J., Shepherd, J. G., Cox, S. J., and The GENIE team: Millennial timescale carbon cycle and climate change in an efficient Earth system model, Clim. Dynam., 26, 687–711, 2006.
Lima-Ribeiro, M. S., Varela, S., González-Hernández, J., Oliveira, G. de, Diniz-Filho, J. A. F., and Terribile, L. C.: Ecoclimate: a database of climate data from multiple models for past, present, and future for macroecologists and biogeographers, Biodiversity Info., 10, 1–21, 2015.
Lisiecki, L. E. and Raymo, M. E.: A Pliocene-Pleistocene stack of 57 globally distributed benthic δ18O records, Paleoceanography, 20, PA1003, https://doi.org/10.1029/2004PA001071, 2005.
Lord, N. S., Crucifix, M., Lunt, D. J., Thorne, M. C., Bounceur, N., Dowsett, H., O'Brien, C. L., and Ridgwell, A.: Emulation of long-term changes in global climate: application to the late Pliocene and future, Clim. Past, 13, 1539–1571, https://doi.org/10.5194/cp-13-1539-2017, 2017.
Luethi, D., Le Floch, M., Bereiter, B., Bluner, T., Barnola, J.-M., Siegenthaler, U., Raynaud, D., Jouzel, J., Fischer, H., Kawamura, K., and Stocker, T. F.: High-resolution carbon dioxide concentration record 650,000–800,000 years before present, Nature, 453, 379–382, 2008.
Masson-Delmotte, V., Schulz, M., Abe-Ouchi, A., Beer, J., Ganopolski, A., González Rouco, J. F., Jansen, E., Lambeck, K., Luterbacher, J., Naish, T., Osborn, T., Otto-Bliesner, B., Quinn, T., Ramesh, R., Rojas, M., Shao X., and Timmermann, A.: Information from Paleoclimate Archives, in: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Chang, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
Melchionna, M., Di Febbraro, M., Carotenuto, F., Rook, L, Mondanaro, A., Castiglione, S., Serio, C., Vero, V. A., Tesone, G., Piccolo, M., Diniz-Filho, J. A. F., and Raia, P.: Fragmentation of Neanderthals' pre-extinction distribution by climate change, Palaeogeogr. Paleoclim. Palaeoecol., 496, 146–154, https://doi.org/10.1016/j.palaeo.2018.01.031, 2018.
Nogués-Bravo, D., Rodríguez-Sánchez, F., Orsini, L., de Boer, E., Jansson, R., Morlon, H., Fordham, D. A., and Jackson, S. T.: Cracking the Code of Biodiversity Responses to Past Climate Change, Trend. Ecol. Evolut., 33, 765–776, https://doi.org/10.1016/j.tree.2018.07.005, 1–12, 2018.
O'Hagan, A.: Bayesian analysis of computer code outputs: a tutorial, Reliabil. Eng. Sys. Safe., 91, 1290–1300, 2006.
Olson, R., Sriver, R., Goes, M., Urban, N. M., Matthews, H. D., Haran, M., and Keller, K.: A climate sensitivity estimate using Bayesian fusion of instrumental observations and an Earth System model, J. Geophys. Res.-Atmos., 117, D04103, https://doi.org/10.1029/2011JD016620, 2012.
Osborn, T. J., Wallace, C. J., Harris, I. C., and Melvin, T. M.: Pattern scaling using ClimGen: monthly-resolution future climate scenarios including changes in the variability of precipitation, Clim. Change, 134, 353–369, 2016.
Peltier, W.: Global isostasy and the surface of the ice-age Earth: The ICE-5G (VM2) model and GRACE, Annu. Rev. Earth Pl. Sc., 32, 111–149, https://doi.org/10.1146/annurev.earth.32.082503.144359, 2004.
Rahbek, C.: The role of spatial scale and the perception of large-scale species-richness patterns, Ecol. Lett., 8, 224–239, 2005.
Rangel, T. F., Edwards, N. R., Holden, P. B., Diniz-Fiho, J. A. F., Gosling, W. D., Coelho, M. T. P., Cassemiro, F. A. S., Rahbek, C., and Colwell, R. K.: Biogeographical cradles, museums, and graves in South America: Modelling the ecology and evolution of diversity, Science, 361, eaar5452, https://doi.org/10.1126/science.aar5452, 2018.
Rasmussen, C. E.: Gaussian processes in machine learning, in: Advanced Lectures on Machine Learning, edited by: Bousquet, O., von Luxburg, U., and Rätsch, G., Springer, Berlin, Heidelberg, New York, 2004.
Rasmussen C. E. and Williams, C. K. I.: Gaussian Processes for Machine Learning, the MIT Press, available at: http://www.GaussianProcess.org/gpml (last access: 2 December 2019), 2006.
Ridgwell, A., Hargreaves, J. C., Edwards, N. R., Annan, J. D., Lenton, T. M., Marsh, R., Yool, A., and Watson, A.: Marine geochemical data assimilation in an efficient Earth System Model of global biogeochemical cycling, Biogeosciences, 4, 87–104, https://doi.org/10.5194/bg-4-87-2007, 2007.
Rougier, J., Sexton, D. M., Murphy, J. M., and Stainforth, D.: Analyzing the climate sensitivity of the HadSM3 climate model using ensembles from different but related experiments, J. Climate, 22, 3540–3557, 2009.
Roustant, O., Ginsbourger, D., and Deville, Y.: DiceKriging, DiceOptim: Two R Packages for the Analysis of Computer Experiments by Kriging-Based Metamodeling and Optimization, J. Stat. Softw., 51, 1–55, 2012.
Rubino, M., Etheridge, D. M., Trudinger, C. E., Allison, C. E., Battle, M. O., Langenfelds, R. L., Steele, L. P., Curran, M., Bender, M., White, J. W. C., Jenk, T. M., Blunier, T., and Francey, R. J.: A revised 1000 year atmospheric δ13C-CO2 record from Law Dome and South Pole, Antarctica, J. Geophys. Res.-Atmos., 118, 8482–8499, https://doi.org/10.1002/jgrd.50668, 2013.
Sacks, J., Welch, W. J., Mitchell, T. J., and Wynn, H. P.: Design and analysis of computer experiments, Stat. Sci., 4, 409–423, 1989.
Sansó, B., Forest, C. E., and Zantedeschi, D.: Inferring climate system properties using a computer model, Bay. Anal., 3, 1–37, 2008.
Santner, T. J., Williams, B. J., and Notz, W. I.: The design and analysis of computer experiments, Springer Verlag, 2003.
Saupe, E. E., Myers, C. E., Townsend Peterson, A., Soberón, J., Singarayer, J., Valdes, P., and Qiao, H.: Non-random latitudinal gradients in range size and niche breadth predicted by spatial patterns of climate, Global Ecol. Biogeogr., 28, 928–942, https://doi.org/10.1111/geb.12904, 2019.
Schmittner, A., Silva, T. A. M., Fraedrich, K., Kirk, E., and Lunkeit, F.: Effects of mountains and ice sheets on global ocean circulation, J. Climate, 24, 2814–2829, https://doi.org/10.1175/2010JCLI3982.1, 2010.
Sham Bhat, K., Haran, M., Olson, R., and Keller, K.: Inferring likelihoods and climate system characteristics from climate models and multiple tracers, Environmetrics, 23, 345–362, 2012.
Singarayer, J. S., Valdes, P. J., and Roberts, W. H. G.: Ocean dominated expansion and contraction of the late Quaternary tropical rainbelt, Sci. Rep., 7, 9382, https://doi.org/10.1038/s41598-017-09816-8, 2017.
Stap, L. B., van de Wal, R. S. W., de Boer, B., Bintanja, R., and Lourens, L. J.: The influence of ice sheets on temperature during the past 38 million years inferred from a one-dimensional ice sheet-climate model, Clim. Past, 13, 1243–1257, https://doi.org/10.5194/cp-13-1243-2017, 2017.
Svenning, J. C., Eiserhardt, W. L., Normand, S., Ordonez, A., and Sandel, B.: The Influence of Paleoclimate on Present-Day Patterns in Biodiversity and Ecosystems, Annu. Rev. Ecol. Evolut. System., 46, 551–572, 2015.
Tebaldi, C. and Arblaster, J. M.: Pattern scaling: Its strengths and limitations, and an update on the latest model simulations, Clim. Change 122, 459–471, 2014.
Tibaldi, S., Palmer, T. N., Brankovic, C., and Cubasch, U.: Extended-range predictions with ECMWF models: Influence of horizontal resolution on systematic error and forecast skill, Quarternary J. Roy. Meteor. Soc., 116, 835–866, 1990.
Tran, G. T., Oliver, K. I. C., Sobester, A., Toal, D. J. J., Holden, P. B., Marsh, R., Challenor, P., and Edwards, N. R.: Building a traceable climate model hierarchy with multi-level emulators, Adv. Stat. Clim. Meteorol. Oceanogr., 2, 17–37, https://doi.org/10.5194/ascmo-2-17-2016, 2016.
Tran, G. T., Oliver, K. I. C., Holden, P. B., Edwards, N. R., and Challenor, P.: Multi-level emulation of complex climate model responses to boundary forcing data, Clim. Dynam., 52, 1505–1531, https://doi.org/10.1007/s00382-018-4205-4, 2018.
Warren, R. F., Edwards, N. R., Babonneau, F., Bacon, P. M., Dietrich, J. P., Ford, R. W., Garthwaite, P., Gerten, D., Goswami, S., Haurie, A., Hiscock, K., Holden, P. B., Hyde, M. R., Joshi, S. R., Kanudia, A., Labriet, M., Leimbach, M., Oyebamiji, O. K., Osborn, T., Pizzileo, B., Popp, A., Price, J. Riley, G., Schaphoff, S., Slavin, P., Vielle, M., and Wallace, C.: Producing Policy-relevant Science by Enhancing Robustness and Model Integration for the Assessment of Global Environmental Change, Environm. Modell. Softw., 111, 248–258, https://doi.org/10.1016/j.envsoft.2018.05.010, 2016.
Wilkinson, R. D.: Bayesian calibration of expensive multivariate computer experiments, in: Large scale inverse problems and the quantification of uncertainty, edited by: Biegler, L. T., Biros, G., Ghattas, O., Heinkenschloss, M., Keyes, D., Mallick, B. K., Tenorio, L., Van Bloemen Waanders, B., and Wilcox, K., Wiley Series in Computational Statistics, 2010.
Williamson, M. S., Lenton, T. M., Shepherd, J. G., and Edwards, N. R.: An efficient numerical terrestrial scheme (ENTS) for Earth system modelling, Ecol. Model., 198, 362–374, https://doi.org/10.1016/j.ecolmodel.2006.05.027, 2006.
Williamson, D., Goldstein, M., Allison, L., Blaker, A. Challenor, P., Jackson, L., and Yamazaki, K.: History matching for exploring and reducing climate model parameter space using observations and a large perturbed physics ensemble, Clim. Dynam., 41, 1703–1729, https://doi.org/10.1007/s00382-013-1896-4, 2013.
Zhisheng, A., Kutzbach, J. E., Prell, W. L., and Porter, S. C.: Evolution of Asian monsoons and phased uplift of the Himalaya–Tibetan plateau since Late Miocene times, Nature, 411, 62–66, 2001.
- Abstract
- Introduction
- The model PLASIM-GENIE
- Experimental overview
- The simulation ensembles
- Emulator construction
- Emulator cross-validation and model selection
- Validation of reconstructed climate fields
- Downscaling
- Limitations of the approach
- Conclusions and summary
- Code availability
- Author contributions
- Competing interests
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- The model PLASIM-GENIE
- Experimental overview
- The simulation ensembles
- Emulator construction
- Emulator cross-validation and model selection
- Validation of reconstructed climate fields
- Downscaling
- Limitations of the approach
- Conclusions and summary
- Code availability
- Author contributions
- Competing interests
- Financial support
- Review statement
- References
- Supplement