the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The ESCAPE project: Energy-efficient Scalable Algorithms for Weather Prediction at Exascale
Andreas Müller
Willem Deconinck
Christian Kühnlein
Gianmarco Mengaldo
Michael Lange
Nils Wedi
Peter Bauer
Piotr K. Smolarkiewicz
Michail Diamantakis
Sarah-Jane Lock
Mats Hamrud
Sami Saarinen
George Mozdzynski
Daniel Thiemert
Michael Glinton
Pierre Bénard
Fabrice Voitus
Charles Colavolpe
Philippe Marguinaud
Yongjun Zheng
Joris Van Bever
Daan Degrauwe
Geert Smet
Piet Termonia
Kristian P. Nielsen
Bent H. Sass
Jacob W. Poulsen
Per Berg
Carlos Osuna
Oliver Fuhrer
Valentin Clement
Michael Baldauf
Mike Gillard
Joanna Szmelter
Enda O'Brien
Alastair McKinstry
Oisín Robinson
Parijat Shukla
Michael Lysaght
Michał Kulczewski
Milosz Ciznicki
Wojciech Piątek
Sebastian Ciesielski
Marek Błażewicz
Krzysztof Kurowski
Marcin Procyk
Pawel Spychala
Bartosz Bosak
Zbigniew P. Piotrowski
Andrzej Wyszogrodzki
Erwan Raffin
Cyril Mazauric
David Guibert
Louis Douriez
Xavier Vigouroux
Alan Gray
Peter Messmer
Alexander J. Macfaden
Nick New
In the simulation of complex multi-scale flows arising in weather and climate modelling, one of the biggest challenges is to satisfy strict service requirements in terms of time to solution and to satisfy budgetary constraints in terms of energy to solution, without compromising the accuracy and stability of the application. These simulations require algorithms that minimise the energy footprint along with the time required to produce a solution, maintain the physically required level of accuracy, are numerically stable, and are resilient in case of hardware failure.
The European Centre for Medium-Range Weather Forecasts (ECMWF) led the ESCAPE (Energy-efficient Scalable Algorithms for Weather Prediction at Exascale) project, funded by Horizon 2020 (H2020) under the FET-HPC (Future and Emerging Technologies in High Performance Computing) initiative. The goal of ESCAPE was to develop a sustainable strategy to evolve weather and climate prediction models to next-generation computing technologies. The project partners incorporate the expertise of leading European regional forecasting consortia, university research, experienced high-performance computing centres, and hardware vendors.
This paper presents an overview of the ESCAPE strategy: (i) identify domain-specific key algorithmic motifs in weather prediction and climate models (which we term Weather & Climate Dwarfs), (ii) categorise them in terms of computational and communication patterns while (iii) adapting them to different hardware architectures with alternative programming models, (iv) analyse the challenges in optimising, and (v) find alternative algorithms for the same scheme. The participating weather prediction models are the following: IFS (Integrated Forecasting System); ALARO, a combination of AROME (Application de la Recherche à l'Opérationnel à Meso-Echelle) and ALADIN (Aire Limitée Adaptation Dynamique Développement International); and COSMO–EULAG, a combination of COSMO (Consortium for Small-scale Modeling) and EULAG (Eulerian and semi-Lagrangian fluid solver). For many of the weather and climate dwarfs ESCAPE provides prototype implementations on different hardware architectures (mainly Intel Skylake CPUs, NVIDIA GPUs, Intel Xeon Phi, Optalysys optical processor) with different programming models. The spectral transform dwarf represents a detailed example of the co-design cycle of an ESCAPE dwarf.
The dwarf concept has proven to be extremely useful for the rapid prototyping of alternative algorithms and their interaction with hardware; e.g. the use of a domain-specific language (DSL). Manual adaptations have led to substantial accelerations of key algorithms in numerical weather prediction (NWP) but are not a general recipe for the performance portability of complex NWP models. Existing DSLs are found to require further evolution but are promising tools for achieving the latter. Measurements of energy and time to solution suggest that a future focus needs to be on exploiting the simultaneous use of all available resources in hybrid CPU–GPU arrangements.
- Article
(3682 KB) - Full-text XML
- BibTeX
- EndNote
Numerical weather and climate prediction capabilities represent substantial socio-economic value in multiple sectors of human society, namely for the mitigation of the impact of extremes in food production, renewable energy, and water management, infrastructure planning, and for finance and insurance whereby weather-sensitive goods and services are traded. Despite significant progress achieved over past decades (Bauer et al., 2015) there are substantial shortcomings in our ability to predict, for example, weather extremes with sufficient lead time and the impact of climate change at a regional or national level. Extreme weather events caused over 500 000 casualties and over USD 2 trillion in economic damages in the past 20 years (Wallemacq and House, 2018). Another example is the prediction of climate change mitigation and adaptation targets. Failure to meet these targets is ranked among the leading threats to global society (World Economic Forum, 2019).
One of the key sources of model error is limited spatial (and temporal) resolution (Palmer, 2014), which implies that key physical processes that drive global circulation, like deep convection in the tropics and mesoscale eddies in the ocean, are only crudely represented in models by contemporary parametrisations. In addition, deficiencies in the representation of process interactions between the atmosphere and ocean–sea ice, as well as the atmosphere and land, including a time-varying biosphere, are highly relevant strategic targets to improve the representation of the internal variability of the Earth system in models (Katzav and Parker, 2015). However, better spatial resolution and enhanced model complexity translate immediately into significant computational challenges (Schulthess et al., 2019), wherein spatial resolution is the most demanding because a doubling of resolution roughly translates into 8 times more computations (doubling the horizontal resolution in both directions and a corresponding decrease in the time step). The critical resolution threshold at which global weather and climate models may eventually be able to overcome the bulk of the limiting deficiencies is unclear; however, O(1 km) emerges as a defendable intermediate target (Shukla et al., 2010; Neumann et al., 2019).
The ESCAPE project was motivated by the need to run Earth system models at much higher resolution and complexity than presently available, but within the same time-critical path of daily production for weather forecasts and with the same production throughput needed for decadal–centennial climate projections as used today. This translates to computing one simulated year per wall-clock day. Energy efficiency is a key requirement as power envelopes for HPC systems cannot be scaled up at the same rate as the computing demand. Obviously, this presents a substantial challenge to all aspects of computing, namely the choice and implementation of numerical methods and algorithms and the programming models to map memory access and communication patterns onto specific hardware (Wehner et al., 2011).
The ECMWF specific strategic target is to provide skilful predictions of high-impact weather up to 2 weeks ahead by 2025 based on a global 5 km scale Earth system model ensemble, complemented by the corresponding high-resolution data assimilation system for creating the initial conditions. This system needs sufficient model complexity in the atmosphere (physics and chemistry), oceans, sea ice, and land to represent all processes acting on such scales and a sufficiently large ensemble size so that complex probability distributions of extreme forecast features can be sampled well enough. In terms of computational demand this is comparable to the 1 km resolution target for a single forecast.
The supercomputers used for numerical weather prediction (NWP) have changed dramatically over the past decades, and ECMWF's Integrated Forecasting System (IFS; Wedi et al., 2015, and references therein) has exhibited rather different levels of sustained performance: from 40 % to 50 % on the parallel vector–processor Cray XMP, YMP, and C90 architectures between 1984 and 1996; 30 % on the Fujitsu similar-type VPP700 and 5000 systems between 1996 and 2002; down to 5 %–10 % on the scalar multi-core IBM P5-7 and Cray XC30, as well as 40 architectures operated between 2002 and today. Despite sustained performance declining, overall flop performance increased exponentially owing to Moore's law, Dennard scaling, and processor pricing (e.g. Flamm, 2018) so that significant upgrades of model resolution, complexity, and ensemble size remained affordable in terms of capital cost and power supply. However, as this technological evolution is slowing down, new concepts for designing algorithms and for mapping the associated computational patterns onto the available architectures – from the processor to system level – are needed (Lawrence et al., 2018). Many of the algorithms used in NWP were designed well before the multi-core era, but even though they contain highly tuned shared- and distributed-memory parallelisation, they only achieve such limited sustained performance because of (i) a poor ratio of data communication to computations (viz. arithmetic density) in some of the compute kernels (hereinafter “kernels” for brevity), (ii) sequential tasking due to strong physical and data dependencies, and (iii) algorithmic intricacies required to accurately and efficiently solve a multi-scale and multiphase fluid dynamics problems on a rotating sphere.
If the envisioned increase in model fidelity is constrained by only marginally growing power envelopes and decelerating general-purpose processor speed, then performance issues need to be addressed at the root, and a more radical redesign of the basic algorithms and their implementations used for weather prediction needs to be considered. This is why ESCAPE investigates both HPC adaptation and alternative numerical formulations of physically and computationally clearly identifiable model components – herein introduced as Weather & Climate Dwarfs – followed by a detailed analysis of their respective computational bottlenecks and subsequent hardware- and algorithm-dependent optimisations.
The weather and climate dwarf idea is introduced in Sect. 2. In Sect. 3 the usefulness of the dwarf concept is illustrated with the example of the spectral transform dwarf. The paper ends with conclusions and outlook in Sect. 4.
2.1 Motivation
In 2004, Phillip Colella introduced the seven dwarfs of algorithms for high-end simulation in the physical sciences (Colella, 2004 quoted after Kaltofen, 2011). These were later extended to the 13 Berkeley dwarfs (Asanović et al., 2006, 2009), which are meant to represent characteristic patterns of computation and communication. These dwarfs were created to cover the characteristic computational properties of a broad range of scientific applications. These dwarfs are the basis for the OpenDwarfs benchmark suite (Feng et al., 2012; Krommydas et al., 2015; Johnston and Milthorpe, 2018) and were also applied to benchmark cloud computing in Phillips et al. (2011). In a similar fashion, Kaltofen (2011) introduced the seven dwarfs of symbolic computation.
Following this idea, we categorise key algorithmic motifs specific to weather prediction and climate models and identify their specific computational and communication patterns, which in return are crucial for the entire model performance. The dwarfs thus represent domain-specific mini-applications (Messer et al., 2016) which include direct input from the domain scientist together with documentation, timers for profiling purposes, and error estimates for verification purposes. In this way the dwarfs facilitate the communication of NWP domain-specific knowledge on algorithmic motifs with specialists in other domains. Different implementations of the dwarfs can be used as a first step towards optimising and adapting weather prediction and climate models to new hardware architectures and to benchmark current and future supercomputers with simpler but relevant applications. Identifying these key algorithms thus allows for better collaboration between operational weather prediction centres, hardware vendors, and academia. The concept of dwarfs is different from the existing separation of weather and climate models into different model components, such as atmosphere, land surface, and ocean, for which separate dynamical core and physical parametrisation packages already exist. Instead, dwarfs define a stand-alone and more manageable subcomponent in a hierarchy of model complexity for specific targets such as adaptation to GPUs, exploring alternative programming models, and developing performance portable domain-specific languages. But dwarfs can also be used by domain scientists for developing alternative algorithms, even across model components.
The fundamental starting point of the ESCAPE project is to identify the dwarfs in the participating weather and climate models (Fig. 1) and to adapt them to different hardware architectures. The knowledge gained in this adaptation is used to research alternative numerical algorithms, which are better suited for those new architectures, and experiment with alternative programming models towards improving the overall energy efficiency of weather prediction applications.
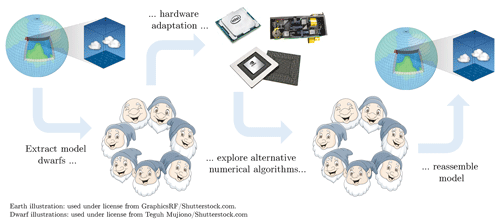
Figure 1Illustration of the main idea behind the ESCAPE project. The entire model is broken down into smaller building blocks called dwarfs. These are adapted to different hardware architectures. Based on the feedback from hardware vendors and high-performance computing centres, alternative numerical algorithms are explored. These improvements are eventually built into the operational model.
2.2 List of ESCAPE dwarfs
Table 1 gives an overview of the dwarfs defined in the ESCAPE project. These dwarfs have been chosen because they represent key algorithms that are representative of any weather and climate model or because their computational and communication patterns represent one of the most runtime-consuming parts of weather forecasting systems (Fig. 2). Prototype implementations addressing specific hardware (by default CPU) were developed for selected dwarfs. Each prototype implementation comes with documentation (Mengaldo, 2016; Müller et al., 2017) as well as timers and error measures. The timers enable a quick assessment of the speed-up due to the optimisations, whereas the error measures verify to what extent the optimisations affect the results. Table 1 also lists the models in which each dwarf was identified and from which its prototype implementations originated. The models include the IFS with the spectral transform method (IFS-ST), the Finite-Volume Module of the IFS (IFS-FVM), ALARO–AROME, and COSMO–EULAG. In order to explore alternative discretisations in ESCAPE, a new global shallow-water model called GRASS (Global Reduced A-grid Spherical-coordinate System) was developed. Table 1 further shows which dwarfs have prototypes that are based on the data structure framework Atlas (Deconinck et al., 2017) used to ease adaptation to future architectures and to avoid code duplication across prototypes. Atlas handles both the mesh generation and parallel communication aspects. In the ESCAPE project, Atlas has been improved and extended by adding support for limited area grids as well as for accelerators via GridTools (Deconinck, 2017a, b). Table 1 also shows the programming model adopted for each of the dwarf prototypes. In particular, a message-passing interface (MPI) was used for distributed-memory parallelism, OpenMP and OpenACC for shared-memory parallelism, and two domain-specific language (DSL) solutions – CLAW and GridTools – for hardware-specific optimisations. Apart from DSL, all dwarfs were coded in modern Fortran.
Table 1Overview of dwarfs identified in the ESCAPE project, short description of the computational characteristics of each dwarf, and the models in which we identified the dwarf. Stand-alone applications including documentation, profiling, and verification capabilities called prototypes have been released for many of the dwarfs. The column “Atlas” shows which of the dwarfs have prototypes that are based on the data structure framework Atlas (Deconinck et al., 2017). Dwarfs for which prototypes with MPI and OpenMP or OpenACC are available can be used with both programming models together as a hybrid parallelisation. LAITRI is used in the full model in each MPI process individually and therefore does not include MPI parallelisation inside the dwarf. Further explanations can be found in the references given in the last column.
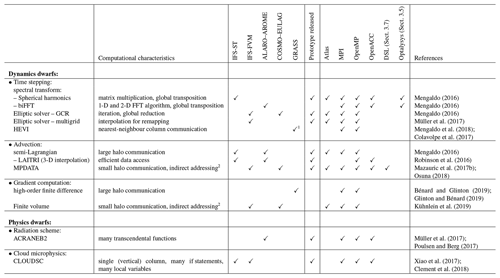
1 The GRASS model currently only solves the shallow-water equations. Research on horizontally explicit and vertically implicit (HEVI) time integration methods was performed to explore future options 2 when using unstructured meshes.
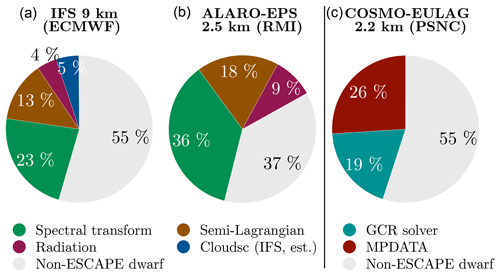
Figure 2Portion of the forecast runtime spent in ESCAPE dwarfs for the three different models: IFS (a), ALARO ensemble prediction system (EPS) (b), and COSMO–EULAG (c). The measurements for the IFS were taken during an operational run on 352 nodes (1408 MPI processes, 18 OpenMP threads per process). The limited area models ALARO-EPS and COSMO–EULAG each used 576 MPI processes for the simulations shown here. The IFS and ALARO-EPS are both based on the spectral transform method, with the latter employing 2-D FFTs. For this reason panels (a) and (b) share one legend. COSMO–EULAG uses different methods and panel (c) has its own legend. The vertical line separates the two different legends. The data used to create this and the following figures have been published in Müller et al. (2019).
In addition to identifying computational and communication patterns in existing models, there was a search for new algorithms that show significant potential to reduce runtime and energy consumption. This led to the development of a multigrid preconditioner that reduces iterations of the Krylov-subspace solver employed in the semi-implicit time integration of IFS-FVM (Müller et al., 2017) and a HEVI time integration scheme with significantly improved stability (Colavolpe et al., 2017). The latter avoids global communications, which also motivated the development of high-order finite-difference methods for reduced longitude–latitude grids on the sphere (Bénard and Glinton, 2019; Glinton and Bénard, 2019). Furthermore, on the hardware side, ESCAPE explored fast Fourier transforms (FFTs) and spherical harmonics on optical (co-)processors (Macfaden et al., 2017) to potentially scale these transforms towards higher resolutions at a fixed energy cost. An overview of the work with the optical processor can be found in Sect. 3.5.
As an example of the cycle involved in identifying, isolating, testing, adapting, optimising, and considering alternative solution procedures for a specific algorithmic motif in the ESCAPE project, the work on the spectral transform dwarf is illustrated in more detail.
Below is a short description of the domain-specific spectral transform with a discussion of computational challenges, primarily focused on the data structures and data access patterns used in IFS. Subsequently, we present the work done on adapting and optimising the dwarf for GPUs, CPUs, and optical processors and finish with a comparison of the results obtained for the different architectures and a discussion on the sustainability of the chosen techniques.
3.1 Background
Each time step of IFS is split between computations in physical space (i.e. a grid point representation) and computations with respect to spectral space (i.e. spectral coefficients at different wavenumbers). Semi-Lagrangian advection, physical parametrisations, and products of terms are computed most efficiently in grid point space, while horizontal gradients, semi-implicit calculations, and horizontal diffusion are computed more efficiently in spectral space. The transform between these two spaces is performed on the sphere with spherical harmonics, that is, computing these results along longitudes in a fast Fourier transform (FFT) and a Legendre transform (LT) along latitudes. Limited area models replace the Legendre transform with another FFT, which leads to the name biFFT.
In spectral transform methods, such as the one used in IFS (Wedi et al., 2013), the specific form of the semi-implicit system facilitating large time steps (and thus time-to-solution efficiency) is derived from subtracting a system of equations linearised around a horizontally homogeneous reference state. The solution of this specific form is greatly accelerated by the separation of the horizontal and the vertical part, which matches the large anisotropy of horizontal to vertical grid dimensions prevalent in atmospheric and oceanic models. In spectral transform methods one uses the special property of the horizontal Laplacian operator in spectral space on the sphere:
where ψ symbolises a prognostic variable, a is the Earth radius, and (n,m) are the total and zonal wavenumbers of the spectral discretisation (Wedi et al., 2013). This conveniently transforms the 3-D Helmholtz problem into an array (for each zonal wavenumber) of 2-D matrix operator inversions with the dimension of the vertical levels square – or vertical levels times the maximum truncation NT, defined shortly, in the case of treating the Coriolis term implicitly – resulting in a very efficient direct solver. The computational aspects and especially the data layout are illustrated with the inverse spectral transform from spectral to grid point space.
The inverse spectral transform begins with the spectral data , which is a function of field index f (for the variable surface pressure at a single level and for wind vorticity, wind divergence, and temperature at each height level), real and imaginary part i, and wavenumbers (zonal wavenumber and total wavenumber , where NT is the spectral truncation). This deviates from the usual notation in which total wavenumber goes from m to NT because it simplifies the separation between even and odd n using column-major order like in Fortran; i.e. the field index f is the fastest-moving index and the zonal wavenumber m is the slowest-moving index. Typical dimensions can be seen in the operational high-resolution (9 km) forecast run at ECMWF: the number of fields is in this case 412 for the direct transform and 688 for the inverse transform, and the number of zonal wavenumbers is given by the truncation NT=1279. The number of latitudes is , and the number of longitudes increases linearly from 20 next to the poles to next to the Equator.
We take advantage of the symmetry of the Legendre polynomials for even n and antisymmetry for odd n. The coefficients of the Legendre polynomials are pre-computed and stored in for even n and for odd n, where ϕ stands for the latitudes of our Gaussian mesh. Only latitudes on the Northern Hemisphere are computed. Latitudes on the Southern Hemisphere are reconstructed from the northern latitudes. In the same way the spectral data are split for each m into an even part and odd part . Fields (indexed f) are all independent in the parallel transform. The inverse Legendre transform is performed by computing the following matrix multiplications using basic linear algebra subprograms (BLAS):
The resulting array for the symmetric and antisymmetric parts are now combined into the Fourier coefficients on the Northern and Southern Hemisphere:
These Fourier coefficients are finally used to compute the fields in grid point space at each latitude ϕ and longitude λ via FFT:
3.2 Computational challenges
The computations in grid point space require all fields to be on the same computational node. The summation over the total wavenumber n in the Legendre transform (Eq. 2) makes it most efficient to have all total wavenumbers (for a given field) on the same node, and the Fourier transform (Eq. 3) over (i,m) makes it most efficient to have all of the zonal wavenumbers m with the real and imaginary part on the same node. This is only possible if the data are transposed before and after the spectral transform as well as between Legendre and Fourier transform. These transpositions produce substantial communication, which increases the contribution of the spectral transform to the overall runtime for future resolutions (Fig. 3).
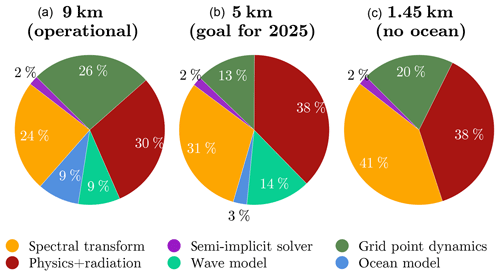
Figure 3Cost profiles of the significant components of the IFS NWP model in percent of CPU time at the operational 9 km horizontal resolution with 137 vertical levels (a), the anticipated future horizontal resolution of 5 km with 137 vertical levels (b), and an experimental resolution of 1.45 km with 62 vertical levels (c). The grid point dynamics represents the advection and grid point computations related to the dynamical core, the semi-implicit solver represents the computations and communications internal to spectral space, spectral transform relates to the communications and computations in the transpositions from grid point to spectral and reverse as well as the FFT and DGEMM computations (see also spectral transform schematic below), physics + radiation relates to the cost of physical parametrisations including radiation, and finally the additional components of the wave and ocean models are accounted for but nonetheless excluded in the 1.45 km simulation. All of these profiles have been obtained through measurements on ECMWF's Cray XC40 supercomputer.
Simplified simulations of the MPI communications performed in ESCAPE indicate that the strong scalability of the communication time for the spectral transform transpositions is better than for the halo communication required by (large) semi-Lagrangian advection halos and the global norm computation commonly used in semi-implicit methods (Zheng and Marguinaud, 2018).
These results indicate that halo communication will become almost as costly as the transpositions in the spectral transform method if a very large number of MPI processes is involved. An alternative which avoids transpositions and halo communication is given by the spectral element method shown in Müller et al. (2018) with explicit time integration in the horizontal direction. This leads to a very small amount of data communicated in each time step because this method only communicates the values that are located along the interface between different processor domains. This method, however, requires much smaller time steps, which leads overall to an even larger communication volume (Fig. 4). Figure 4 is based on the model comparison presented in Michalakes et al. (2015) and does not include all of the optimisations for the spectral element method presented in Müller et al. (2018). The spectral transform results are based on the operational version of IFS and do not contain the optimisations presented in this paper. Both models have significant potential for optimisation, and it is not obvious which method will have the lowest communication volume when fully optimised, but key for both is an approach that allows for reasonably large time steps. Regardless, the only way to avoid waiting time during communication is to enable the concurrent execution of various model components such that useful computation can be done during data communication (Mozdzynski et al., 2015; Dziekan et al., 2019).
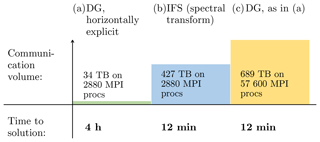
Figure 4Overall communication volume comparing the spectral element (SEM) from Müller et al. (2018) and the global spectral transform methods. The SEM requires a substantially lower amount of communication at the same number of cores, but due to the smaller time step it requires a much higher frequency of repeated communications for the given 2 d simulation. Extrapolating the number of MPI processes to achieve the same time to solution would result in a larger amount of communication for the SEM. Here we assume SEM Δt=4 s and IFS Δt=240 s; communication volume is calculated for a 48 h forecast SEM as 290.4 kB per MPI task and Δt, and IFS is calculated as 216 mB MPI task and Δt. As a result, the SEM time to solution is estimated as 20× IFS based on the performance results in Michalakes et al. (2015).
3.3 GPU optimisation
For the GPU version, the prototype is restructured to (a) allow the grid-based parallelism to be fully exposed to (viz. exploited by) the GPU in a flexible manner, (b) ensure that memory coalescing is achieved, and (c) optimise data management.
To achieve performance, the two-dimensional grid over the sphere is augmented with a third dimension that represents multiple fields. The computations are inherently parallel across this grid, so all this parallelism can be exposed to the GPU for maximal performance. In contrast, the original implementation had a sequential loop over one of the dimensions (at a high level in the call tree of the application). By restructuring the code for each operation, loops over the three dimensions become tightly nested. These loops are mapped to the GPU via OpenACC directives to collapse to a single loop.
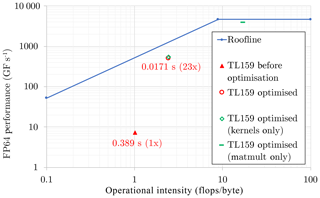
Figure 5Roofline plot for the spectral transform dwarf at 125 km resolution (NT=159) on the NVIDIA Tesla P100 GPU. The full time step of the original prototype is represented by the solid red triangle. The corresponding time step for the optimised prototype is represented by the red circle. Also included are partial results for kernels only (open green diamond atop the red circle) and matrix multiplication only (green dash). Each point is positioned in the plot according to its operational intensity: points under the sloping region of the roofline are limited by available memory bandwidth, and points under the horizontal region are limited by peak computational performance.
Similarly, for library calls it is important to maximise the exposure of parallelism through batching computations using provided interfaces. On the GPU we perform all of the matrix multiplications in the Legendre transform (Eq. 2) with a single batched call of the DGEMM routine from the cuBLAS library. The different matrices in Eq. (2) have different sizes because the total wavenumber goes from 0 to NT. To use the fully batched matrix multiplication each matrix is padded with zeroes up to the largest size, since the library currently does not support differing sizes within a batch. This step results in a 10-fold increase in the overall number of floating point operations but still improves the overall performance (Fig. 5). The FFT in Eq. (3) is performed with the cuFFT library, batching over the vertical (field) dimension. Multiple calls are still needed for each latitude since FFTs cannot be padded in a similar way to matrix multiplications. Therefore, the implementation remains suboptimal. There would be scope for further improvements if an FFT batching interface supporting differing sizes were to become available.
Sometimes matrix transposes are necessary, but where possible these were pushed into the DGEMM routine library calls, which have much higher-performing implementations of transposed data accesses. Transpose patterns remain within the kernels involved in transposing grid point data from column structure to latitudinal (and inverse) operations, which naturally involve transposes and are thus harder to fix through restructuring. However, using the “tile” OpenACC clause, which instructs the compiler to stage the operation through multiple relatively small tiles, the transpose operations can be performed within fast on-chip memory spaces such that the access to global memory is more regular.
Data allocation on the GPU is expensive, as is data movement between the CPU and GPU. Hence, the code is structured such that the fields stay resident on the GPU for the whole time step loop: all allocations and frees have been moved outside the time step loop with the reuse of temporary arrays, and thus all data transfer has been minimised. Arranging the model data consecutively in memory ensures that multiple threads on the GPU can cooperate to load chunks of data from memory in a “coalesced” manner. This allows for a high percentage of available memory throughput.
The restructured algorithm achieves an overall speed-up factor of 23× compared to the initial version, which also used cuBLAS and cuFFT but followed the CPU version more closely. Matrix multiplication performance is higher than the overall performance (in flops) and the operational intensity is increased into the compute-bound regime. Note that matrix multiplication is associated with O(N3) computational complexity for O(N2) memory accesses. The extra padding operations lead to larger N and therefore also to increased operational intensity. More details about the single-GPU optimisations can be found in Mazauric et al. (2017b).
For multiple GPU arrangements there is a large benefit from high-bandwidth interconnects (i.e. NVLink, NVSwitch) due to the relative importance of communication for the transpositions; see Sect. 3.2. For full-bandwidth connectivity when using more than four GPUs, the NVSwitch interconnect on the DGX-2 server transfers up to 300 GB s−1 between any pair of GPUs in the system, or equivalently 2.4 TB s−1 of total throughput.
When running a single application across multiple GPUs, it is necessary to transfer data between the distinct memory spaces. Traditionally, such transfers needed to be realised via host memory and required the participation of the host CPU. Not only did this introduce additional latency, but also limited the overall bandwidth to the bandwidth offered by the peripheral component interconnect express (PCIe) bus connecting CPU and GPUs. However, more recent MPI implementations are CUDA-aware. This means that pointers to GPU memory can be passed directly into the MPI calls, avoiding unnecessary transfers (both in the application and in the underlying MPI implementation). This is particularly useful when using a server that features high-bandwidth connections between GPUs, in which case the CUDA-aware MPI will use these links automatically. Moving our dwarf to a CUDA-aware MPI gave us a speed-up of 12× (Fig. 6).
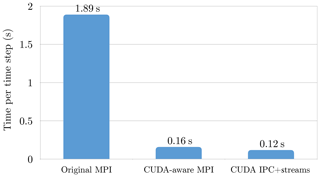
Figure 6Computational performance of the spectral transform dwarf at 18 km resolution (NT=639) on four NVIDIA V100 GPUs of the DGX1 with the original MPI implementation (left), CUDA-aware MPI communication (middle), and NVLink-optimised communication (right). This resolution is currently used operationally for the members of the ensemble forecast at ECMWF.
However, even with this optimisation the all-to-all operations remained inefficient because communication between different GPUs was not exchanged concurrently. Perfect overlap was achieved by implementing an optimised version of the all-to-all communication phase directly in CUDA using the interprocess communication (IPC) application programming interface (API). Using memory handles rather than pointers, CUDA IPC allows users to share memory spaces between multiple processes, thus allowing one GPU to directly access memory on another GPU. This allowed for another speed-up of about 30 % (Fig. 6).
Figure 7 compares a DGX-2 with NVSwitch and the DGX-1 for a spectral transform at 18 km resolution (NT=639). The NVIDIA multi-process service allows for the oversubscription of GPUs; e.g. the 8-GPU result on DGX-2 uses 16-MPI tasks. Oversubscription, a technique common to other architectures, can be beneficial to spread out load imbalances resulting from the grid decomposition and hide latencies.
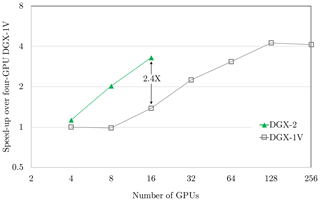
Figure 7Computational performance of the spectral transform dwarf at 18 km resolution (NT=639) on up to 16 GPUs on one DGX-2 and up to 32 DGX-1 servers connected with Infiniband. The DGX-1V uses MPI for ≥ eight GPUs (due to lack of all-to-all links); all others use CUDA IPC. DGX-2 results use preproduction hardware. The points were connected with lines for the purpose of improving readability.
The scaling on DGX-1V is limited because with an increasing number of GPUs some messages go through the lower-bandwidth PCIe and Intel QuickPath Interconnect (QPI) links and/or Infiniband when scaling across multiple servers. On DGX-2 all 16 GPUs have full connectivity; i.e. the maximum peak bandwidth of 300 GB s−1 between each pair of GPUs is available. The performance scales well up to the full 16 GPUs on DGX-2, and is 2.4× faster than the result obtained with the 16-GPU (two-server) DGX-1V. The speed-up going from 4 to 16 GPUs on DGX-2 is 3.2×, whereas the ideal speed-up would be 4×. Preliminary investigations reveal that this deviation from ideal scaling is not primarily due to communication overhead but due to load imbalance between the MPI tasks for a given spherical grid decomposition. This indicates that better scaling might be observed with a more balanced decomposition. More details about the multi-node optimisation of the spectral transform dwarf can be found in Douriez et al. (2018).
The first results on the supercomputer Summit of the Oak Ridge National Laboratory are shown in Fig. 8. At this large scale we observe a speed-up between 12.5× (on 480 nodes) and 23.7× (on 1920 nodes) when comparing the optimised GPU version with the initial CPU version of the spectral transform dwarf on the same number of nodes. These simulations were run at 2.5km resolution (NT=3999) and use 240 fields. In operational application the number of fields should be larger (see Sect. 3.1). It has been verified that the GPU-optimised dwarf from ESCAPE is capable of running on a huge number of GPUs on Summit with a significant speed-up.
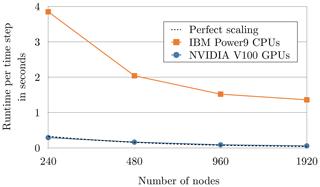
Figure 8Strong scaling comparison between the GPU-optimised version and initial CPU version of the spectral transform dwarf on Summit at the Oak Ridge National Laboratory. All of these simulations use 2.5 km resolution (NT=3999) with 240 fields. The GPU version uses six V100 GPUs per node, which leads to a maximum number of 11 520 GPUs. The perfect scaling was chosen such that it goes through the GPU result at 480 nodes to illustrate the scaling efficiency of the GPU version. The points were connected with lines for the purpose of improving the readability of the plot.
3.4 CPU optimisation
The spectral transform dwarf is based on the operational implementation used in IFS that has been continuously optimised over multiple decades. According to profiling results, it clearly appeared that the main computationally intensive kernels are the FFT and matrix multiplication executed by a dedicated highly tuned library (such as the Intel Mathematics Kernel Library, called MKL). In support of this work different data scope analysis tools were explored; see Mazauric et al. (2017a). The first optimisation strategy concentrated the effort on non-intrusive optimisations, which have the advantage of being portable and maintainable. Among these optimisations, the use of extensions to the ×86 instruction set architecture (ISA) such as SSE, AVX, AVX2, and AVX-512 is notable because it indicates how much of the source code can be vectorised by the compiler. When the compiler failed at vectorising some loops or loop nests, a deeper investigation of how to use compiler directives followed. As the different instruction sets are not supported by all processors, the study proposed an intra-node scalability comparison among several available systems (at the time of benchmarking).
System tuning using Turbo frequency (TUR), Transparent Huge Page (THP), and memory allocator (MAP) can be done without modifying the source code. This exposes both performance gains and interesting information on dwarf behaviour. Indeed, on the ATOS BullSequana ×400 supercomputer with Intel® Xeon Broadwell E5-2690v4 processors, enabling TUR offers a gain equal to 11 %; enabling THP gives 22 %, MAP gives 27 %, and finally the best performance (35 % performance gain) is achieved by the combination of MAP and TUR. This shows that memory management is a key point. More details about the single-node CPU optimisation can be found in Mazauric et al. (2017b).
Multi-node optimisation for CPUs focused on improving the MPI communication. The largest potential for optimisations was found to be in the preparation phase of point-to-point communications. During the preparation phase the sender side gathers the local data into a contiguous buffer (pack operation) and hands it off to the MPI library. On the receiver side, data are then scattered from a contiguous user buffer to their correct location (unpack operation). Pack and unpack are nearly inevitable with scattered data because remote direct memory access (RDMA) with no gather–scatter operations is known to often be less effective, notably due to the memory-pinning latency (Wu et al., 2004). It also means that the sender and receiver must exchange their memory layout as they may differ. The performance improvement came from reordering the loops for both pack and unpack following the memory layout of the scattered buffer. This optimisation decreases the number of tests (i.e. copy or not copy) and avoids scanning memory multiple times, leading to a global performance gain on the whole dwarf of about 20 % (Fig. 9a). The computational performance on up to 30 ATOS BullSequana ×400 nodes equipped with Intel® Xeon Skylake 6148 processors is shown in Fig. 9b. The work has been performed on ATOS internal HPC resources. This optimisation can be directly applied to the operational model IFS due to its non-intrusiveness. More details about the multi-node optimisation on CPUs can be found in Douriez et al. (2018).
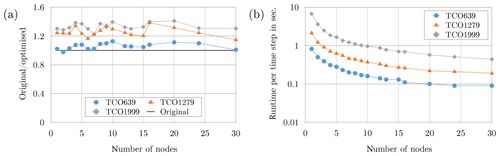
Figure 9Performance measurements on up to 30 Intel® Xeon Skylake 6148 nodes. Panel (a) shows the speed-up at 18 km resolution (NT=639) with regards to different optimisations of the communication preparation phase. Panel (b) shows the computational performance for three different resolutions of 18 km (NT=639), 9 km (NT=1279), and 5 km (NT=1999) representative of current and future operational requirements. Note the use of log scale. The points were connected with lines for the purpose of improving readability. All of these results have been obtained through measurements on the ATOS BullSequana ×400 supercomputer of ATOS internal HPC resources.
The speed-up of the GPU optimisations came from using highly optimised GPU libraries for batched DGEMM and FFT and avoiding the transposition of temporary arrays. On the CPU, one can equally apply these improvements in the handling of temporary arrays, which led to the development of a new serial spectral transform inside Atlas used operationally at ECMWF for post-processing purposes. Post-processing is run in serial mode due to the large number of concurrent post-processing jobs. Compared to the previous serial transform employed in ECMWF product generation, there is a speed-up of 2 to 3 times, in particular for limited area domains (Fig. 10).
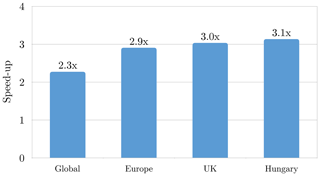
Figure 10Speed-up of the spectral transform by porting optimisations introduced in the GPU version back to the CPUs. The baseline for this comparison is the current operational post-processing library used at ECMWF. This version of the spectral transform allows for the computation on limited area domains. The speed-up is given here for the global transform and three examples of limited domains (Europe, UK, and Hungary).
3.5 Optical processors
The fundamental idea behind optical processors is to encode information into a laser beam by adjusting the magnitude and phase in each point of the beam. Optalysys has been investigating an optical implementation of the spectral transform dwarf – biFFT – for limited area models as well as spherical harmonics for global models. This information becomes the Fourier transform of the initial information in the focal plane of a lens. The information can be encoded into the optical beam by using spatial light modulators (SLMs) as illustrated in Fig. 11. The result of the Fourier transform can be recorded by placing a camera in the focal plane of a lens. A photo of an early prototype is shown in Fig. 12.
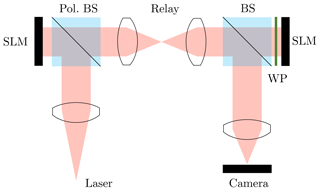
Figure 11Illustration of the fundamental idea behind the optical processor. The laser beam is emitted on the bottom left. Two spatial light modulators (SLMs) are used together to input the complex function. The system uses a beam splitter (BS) and an optical relay to image one reflective SLM onto another, followed by a lens assembly which approximates an ideal thin lens and renders the optical Fourier transform on a camera sensor. The half-waveplate (WP) before the second SLM is used to rotate linearly polarised light onto the axis of SLM action (the direction in which the refractive index switches), thus causing it to act as a phase modulator.

Figure 12Photo of the first prototype of the optical processor. The final product is built into an enclosure of similar size like a GPU.
SLMs are optical devices with an array of pixels which can modulate an optical field as it propagates through (or is reflected by) the device. These pixels can modulate the phase (essentially applying a variable optical delay) or polarisation state of the light. Often they modulate a combination of the two. When combined with polarisers, this polarisation modulation can be converted into an amplitude modulation. Hence, the modulation capability of a given SLM as a function of “grey level” can be expressed by a complex vector, which describes an operating curve on the complex plane. Each pixel of the SLM is generally a one-parameter device; arbitrary complex modulation is not offered by the SLM, only some subset. This is one of the key issues with regards to exploiting the optical Fourier transform.
Sensor arrays – essentially common camera sensors – are used to digitise the optical field. They are in general sensitive to the intensity of the light, which is the magnitude of the amplitude squared. This poses a difficulty to sensitively measuring the amplitude. Moreover, sensor arrays are not sensitive to optical phase. The latter can be overcome with a method that allows the optical phase to be derived from intensity-only measurements. This is achieved by perturbing transformed functions with a specified disturbance, measuring the resulting change in the output, and deducing the phase from the properties of the Fourier transforms.
Each pixel of the SLM is addressable with an 8-bit value (256 levels). The SLM is not capable of independently modulating the magnitude and phase of the optical field. In the Optalysys processing system, the SLMs are configured to modulate both the amplitude and phase in a coupled manner such that optimal correlation performance is achieved. The optical Fourier transform and all of the functions are inherently two-dimensional. The propagating light beam can be thought of as a 2-D function propagating and transforming along a third direction. The system is most naturally applied to 2-D datasets, and many problems can be mapped to an appropriate representation.
A critical aspect to realising the potential of optical processing systems is the interface to a traditional computing platform. Bridging this gap has been a significant undertaking for Optalysys and has resulted in the development of a custom PCIe drive board. This board interfaces to a host machine over PCIe and has direct memory access (DMA) to the system memory (RAM). It provides an interface to four SLMs and two cameras. The cameras are 4 K (4096×3072). Initially, they operate at 100 Hz, but a future firmware upgrade will unlock 300 Hz operation and 600 Hz half-frame operation, dramatically increasing the potential data throughput.
There are currently two options for the SLMs. One option is using high-speed binary (bright–dark) SLMs which operate at 2.4 kHz. This offers correlation at binary precision. The second option is greyscale SLMs which operate at 120 Hz. This is currently the only option to reach more than binary precision. The performance of the entire processor is determined by the part with the lowest frequency. The main bottleneck with multiple-bit precision is the operating frequency of the greyscale SLM. There is currently no easy solution to increase the frequency of greyscale SLMs.
Optical processing is more appropriately applied to cases in which high-throughput relatively complex operations are the priority, with less of an emphasis on numerical precision. More details about the Optalysys optical processor have been published in Macfaden et al. (2017) and Mazauric et al. (2017b). The results from the optical processing tests will be discussed in the next section.
3.6 Comparison between processors in terms of runtime and energy consumption
A lot of the speed-up achieved by running the spectral transform on accelerators is lost if the CPUs are idle during the computation on the accelerators. The cost of data transfer between the CPU and accelerator needs to be considered but has not been included in the speed-up numbers in this section. To take full advantage of high-bandwidth connected accelerators the entire simulation has to be run on the same node, which requires substantially reducing the memory footprint of the model.
For the CPUs and GPUs used in this paper the overall cost is dominated by the cost of the hardware and therefore by the number of sockets and devices required to reach the desired runtime. In addition to the number of devices we also compare the energy consumption. The large number of zero operations caused in the optimised GPU version by the padding of the matrices in the Legendre transform makes it impossible to do a fair comparison between a CPU and GPU by comparing metrics based on floating point operations, including comparing roofline plots.
In the full operational model the 18 km resolution ensemble member (NT=639) using 30 nodes on the Cray XC40 takes about 1.4 s per time step and the spectral transform component is about 15 % (0.21 s) of the overall runtime. Measurements with the dwarf on the Cray XC40 at 18 km resolution (NT=639) resulted in 4.35 s per time step on a single node (four MPI tasks, 18 threads per task) and 1.77 s on two nodes. The energy consumption was measured at around 0.3 Wh on the Cray XC40, which compares to 0.026 Wh measured on four V100 GPUs on a DGX1 that take 0.12 s per time step. The energy measurement on the XC40 is based on proprietary power management counters. The measurement on the V100 GPUs uses the NVIDIA-smi monitoring tool. Tests in ESCAPE on the latest generation of Intel Skylake CPUs have shown 0.12 s per time step using 13 Intel® Xeon Skylake 6148 nodes (connected via a fat-tree EDR network) as shown in Fig. 9. This parallel CPU version has not seen the more radical changes which have been used in redesigning the algorithm for the parallel GPU and serial CPU version.
A comparison between CPUs and an optical processor with a greyscale SLM is shown in Fig. 13. The energy consumption of the optical processor is much lower than for the CPU. The runtime of the optical processor is larger due to the relatively slow performance of the greyscale SLM, which is currently necessary to reach the precision required for NWP applications. The latter does not allow users to exploit the superior energy to solution of optical processors in time-critical NWP applications; more details about the comparison between CPUs and optical processors can be found in Van Bever et al. (2018). In general, for hybrid arrangements of CPUs and accelerators, we conclude that optimising the energy to solution requires algorithmic changes that facilitate the simultaneous use of all the available processors.
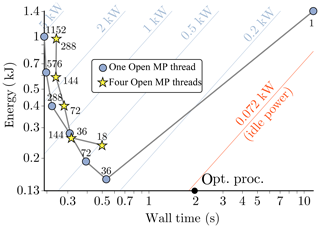
Figure 13Log–log plot of the energy consumption vs. wall-clock time for the biFFT dwarf corresponding to the combination of one direct and one inverse transformation for 525 fields. Each data point is the result of averaging the outcome of two separate runs. Grey lines connect runs with the same number of OpenMP threads (one and four). Added are lines of constant power (light blue lines), including the power delivered by a node in the idle state (orange line). Indices next to each data point denote the number of MPI tasks. The black dot represents the estimate of the Optalysys optical processor when using a greyscale SLM. The performance of the optical processor at binary precision is much higher (not shown).
3.7 Sustainability of code optimisation techniques
The optimisation results presented in Sect. 3.6 are just an example for one of the dwarfs. Similar improvements have been achieved for the advection scheme MPDATA (Douriez et al., 2018) and the radiation scheme ACRANEB2 (Poulsen and Berg, 2017). These optimisations are hardware-specific and will be difficult to maintain on upcoming new architectures. As a strategy towards performance portability and sustainability we have worked in the ESCAPE project on domain-specific languages through the GridTools framework. The main goal of the GridTools library is to provide a solution for weather and climate models to run one code on many different architectures (portability) and achieve good performance (performance portability). However, the main operational product of GridTools has so far focused on solutions for lat–lon grid models like COSMO. The work developed in the ESCAPE project aimed to extend the DSL support for irregular grids, the efficient generation of back ends for multiple architectures, and evaluating DSL useability.
The DSL developments have been used to implement a portable version of the MPDATA dwarf. The DSL version hides such details as the nested loops and the OpenACC directives used to specify properties of the GPU kernel and data layouts of the Fortran arrays. Furthermore, the DSL allows users to compose several of these operators together, which is used by the library to apply advanced performance optimisations like loop fusion or software-managed caches. Comparing the Fortran OpenACC kernel with the DSL version gives us a speed-up of 2.1× for the DSL version. This speed-up could also be achieved by hand-tuned optimisation. The DSL prevents the repeated manual effort of tuning the code for multiple architectures. At the same time, the DSL allows optimisations to be performed which would otherwise make the code unreadable. More details about this work, including code examples on how to use the new back end to GridTools, can be found in Osuna (2018).
In addition to GridTools, ESCAPE explored domain-specific languages via the CLAW DSL (Clement et al., 2018) for the cloud microphysics dwarf. In particular, the use of the single column abstraction (SCA), whereby physical parametrisations are defined solely in terms of a single horizontal column, enables domain scientists to define governing equations purely in terms of vertical dependencies without needing to account for parallelisation issues. The CLAW DSL then inserts loops over the data-parallel horizontal dimension specific to the hardware architecture and programming model (OpenMP, OpenACC) via source-to-source translation, allowing multiple architectures to be targeted from a single source code. A GPU implementation of the CLOUDSC dwarf generated by automated source translation tools has been used to generate similar performance results to the ones presented by Xiao et al. (2017) on K80 GPUs using the OpenACC back end of the CLAW DSL.
The ESCAPE project has introduced the concept of Weather & Climate Dwarfs as fundamental domain-specific building blocks into the weather and climate community. Dwarf categorisation of computational and communication patterns has been extremely useful in further breaking down the complexity of weather prediction and climate models, as well as advancing their adaptation to future hardware. Prototype implementations of the dwarfs have been used to work on code optimisation and benchmarking new architectures. Dwarfs include measures for verifying scientific correctness of the implementations, documentation, and input from domain scientists. Our dwarfs are small enough to be fairly easy to learn, and at the same time they represent a significant part of the performance of the whole weather prediction model.
The paper gives an overview of the dwarfs identified in the ESCAPE project, while illustrating in fair detail the optimisation cycle within ESCAPE applied to the spectral transform dwarf that historically encapsulates perhaps the most fundamental algorithmic motif in operational global weather models (Williamson, 2007).
To avoid code duplication we used the data structure and mesh handling framework provided by Atlas. Atlas has been extended in ESCAPE to support limited area grids and DSL with GridTools. The participating weather models and most prototype implementations are based on Fortran, and all our optimisations can be incorporated into Fortran code including the use of CUDA functions on GPUs by calling C functions from Fortran. Selected code optimisations are now routinely used in ECMWF services. Besides optimisations of the existing code, improved algorithms have been developed that are specifically targeted at improving performance on large-scale systems, which include a multigrid preconditioner for the elliptic solver to reduce iteration counts in iterative solvers, a HEVI time integration scheme with significantly improved stability and alternative finite-difference methods on the sphere in the context of reducing global communications across large processor counts, and include alternative solution procedures for spectral transforms at a fixed energy cost, with FFTs and spherical harmonics realised on optical processors.
Code optimisations performed in the ESCAPE project targeted Intel CPUs, Intel Xeon Phi processors, NVIDIA GPUs, and Optalysys optical processors. In NWP applications, the bottleneck in terms of performance is usually the memory bandwidth between the processor and main memory. Having fast interconnects can provide a significant speed-up. Having all of the processing units used by the simulation connected with such a fast interconnect is still a challenge. Using accelerators only for a small part of the code reduces their benefit if the associated CPUs are idle while the accelerators perform their computations. Hence, a large part of the code has to be moved to the accelerator (see Fuhrer et al., 2018; Schalkwijk et al., 2015) or computations on the CPU are overlapped with computations on the accelerator (see Dziekan et al., 2019).
Most of the work done in the ESCAPE project in terms of code optimisation focused on hardware-specific optimisations. This makes the optimisations difficult to maintain on upcoming new hardware architectures. As an approach towards performance portability, ESCAPE explored a DSL prototype for advection with MPDATA by using the GridTools framework and a prototype of the cloud microphysics dwarf by using the CLAW DSL. DSLs are a promising tool to enable good performance on multiple architectures while maintaining a single code base. However, designing a domain-specific language that is user-friendly and at the same time close to hand-tuned performance on each architecture is challenging. When assessing the efficacy of diverse numerical methods – e.g. finite-volume vs. spectral spatial discretisation or Eulerian vs. Lagrangian time stepping – it is important to account for all computational costs. Spectral transforms with semi-implicit, semi-Lagrangian time integration have always been considered poorly suited for large supercomputers due to the high volume of communication. Our work indicates that thanks to much larger time steps the overall communication cost is not necessarily worse than for other more local methods. Again, overlapping different parts of the model such that useful computation can be done while data are communicated is a way forward and needs to be high priority in future research.
When moving towards very high-resolution global simulations of O(1 km) or less and considering exascale computations on a variety of emerging HPC architectures, there is continued interest and a need to pursue fundamentally different algorithmic approaches that simply do not communicate beyond a certain halo size while retaining all other favourable properties, such as removing time-step size restrictions as in the semi-Lagrangian advection with semi-implicit time stepping. Such approaches, as well as the identification of dwarfs in sea ice and ocean model components of the Earth system, are crucial for the performance of coupled applications and are further investigated in ESCAPE-2. These algorithms will utilise DSLs for performance portability.
The data structure framework Atlas is available at https://github.com/ecmwf/atlas (last access: 27 September 2019) under an Apache License 2.0. The GridTools framework used as a domain-specific language approach for MPDATA is available at https://github.com/GridTools/gridtools (last access: 27 September 2019) under a BSD-3-Clause licence. The CLAW DSL used for the cloud microphysics dwarf is available at https://github.com/claw-project/claw-compiler (last access: 27 September 2019) under a BSD-2-Clause licence. Model codes developed at ECMWF are the intellectual property of ECMWF and its member states, and therefore the IFS code and the IFS-FVM code are not publicly available. Access to a reduced version of the IFS code may be obtained from ECMWF under an OpenIFS licence (see http://www.ecmwf.int/en/research/projects/openifs for further information; last access: 27 September 2019). The ALARO and ALADIN codes, along with all their related intellectual property rights, are owned by the members of the ALADIN consortium and are shared with the members of the HIRLAM consortium in the framework of a cooperation agreement. This agreement allows each member of either consortium to licence the shared ALADIN–HIRLAM codes to academic institutions of their home country for noncommercial research. Access to the codes of the ALADIN system can be obtained by contacting one of the member institutes or by submitting a request in the contact link below the page of the ALADIN website (http://www.umr-cnrm.fr/aladin/, last access: 27 September 2019), and the access will be subject to signing a standardised ALADIN–HIRLAM licence agreement. The COSMO–EULAG model, along with all of its related intellectual property rights, is owned by the members of the COSMO consortium under the cooperation agreement. This agreement allows each member of the COSMO consortium to licence the COSMO–EULAG code (http://www.cosmo-model.org/content/consortium/licencing.htm, last access: 27 September 2019) without fee to academic institutions of their home country for noncommercial research. The code of the GRASS model is the intellectual property of Météo-France and is not publicly available. The code of the ESCAPE dwarfs is the intellectual property of ECMWF. A licence for educational and noncommercial research can be obtained from ECMWF (see http://www.hpc-escape.eu for contact details; last access: 27 September 2019). For the GPU optimisation of the spectral transform dwarf we used the PGI compiler version 17.10, CUDA 9.0.176, and OpenMPI 2.1.3. For the GPU optimisation of the MPDATA dwarf we used the PGI compiler version 17.10, CUDA 9.2.88, and OpenMPI 2.1.3. CUDA includes the compiler nvcc used to compile the library function wrappers, the libraries themselves, and the profiling tool nvprof, which we used for profiling on the GPUs. For the CPU optimisation we used Intel compilers and libraries version 2018.1.163. This includes the compilers icc and ifort and the libraries MKL and MPI. The work on the optical processor Optalysys used the MATLAB software version 2017b.
The data used to create the figures can be downloaded from https://doi.org/10.5281/zenodo.3462374 (Müller et al., 2019).
AnM performed energy measurements for the spectral transform dwarf, implemented the optimised spectral transform for post-processing, performed the simulations on Summit, worked on the implementation of the MPDATA dwarf, supported maintenance for all dwarf prototypes, and assembled the paper. WD is the main developer of the data structure framework Atlas and contributed the work on improving and extending Atlas. He was also involved in creating, supporting, and maintaining all of the dwarf prototypes. CK and PKS are the main developers of IFS-FVM and contributed to the corresponding elliptic solver and MPDATA dwarfs. GiM was involved in the creation of the dwarfs and provided improvements to early drafts of the paper. MLa and VC provided DSL work for the cloud microphysics dwarf. NW and PetB supervised the entire ESCAPE project as coordinators. They were also involved in writing and improving the paper. NW performed the measurements for the cost profiles in Fig. 3. MD implemented the semi-Lagrangian dwarf prototype. SJL supported the work on HEVI time integration methods. MH, SS, and GeM were involved in creating initial versions of the dwarf prototypes. SS also contributed the code for energy measurements on the Cray XC40 supercomputer. DT provided project management for the ESCAPE project. MicG and PiB implemented the GRASS model. FV and CC worked on HEVI time-stepping methods. PhM and YZ performed simulations of communication costs. JVB, DD, GS, and PT provided energy and runtime measurements for ALARO, analysed the components of the RMI ensemble prediction system, and implemented limited area support in Atlas. KPN, BHS, JWP, and PerB provided work on the radiation dwarf. CO and OF provided work on GridTools and were involved in adding GPU support to Atlas. MiB contributed work on HEVI DG. MikG and JS worked on improving the preconditioning for the elliptic solver. EO'B, AlM, OR, ParS, and MLy provided the LAITRI dwarf and created initial CPU optimisations and OpenACC ports for all of the dwarf prototypes. MK, MC, WP, SC, MaB, KK, MP, PawS, and BB worked on performance modelling using the roofline model, which allowed for a better understanding of the experimental measurements. ZP and AW compared different time integration methods, supported optimisation of IFS-FVM, and provided energy measurements of COSMO–EULAG. ER, CM, DG, LD, and XV provided the CPU optimisations for the spectral transform and MPDATA dwarf prototypes. AG and PeM contributed the GPU optimisations for the spectral transform and MPDATA dwarf prototypes. AJM and NN contributed the work on using optical processors for the spectral transform.
The authors declare that they have no conflict of interest.
The authors thank three anonymous referees for their thorough reviews and many detailed suggestions that helped to improve the presentation. This research used resources of the Oak Ridge Leadership Computing Facility, which is a DOE Office of Science User Facility supported under contract DE-AC05-00OR22725.
This research has been supported by the European Commission, H2020 Future and Emerging Technologies (ESCAPE (grant no. 671627)). This work has also been supported by HPC resources provided by the Poznan Supercomputing and Networking Center and corresponding research activities under MAESTRO grant number DEC-2013/08/A/ST6/00296 in the National Science Centre (NCN). An award of computer time was provided by the INCITE programme.
This paper was edited by Chiel van Heerwaarden and reviewed by three anonymous referees.
Asanović, K., Bodik, R., Catanzaro, B. C., Gebis, J. J., Husbands, P., Keutzer, K., Patterson, D. A., Plishker, W. L., Shalf, J., Williams, S. W., and Yelick, K. A.: The landscape of parallel computing research: a view from Berkeley, Tech. Rep. UCB/EECS-2006-183, EECS Department, University of California, Berkeley, available at: http://www2.eecs.berkeley.edu/Pubs/TechRpts/2006/EECS-2006-183.pdf (last access: 27 September 2019), 2006. a
Asanović, K., Wawrzynek, J., Wessel, D., Yelick, K., Bodik, R., Demmel, J., Keaveny, T., Keutzer, K., Kubiatowicz, J., Morgan, N., Patterson, D., and Sen, K.: A view of the parallel computing landscape, Comm. ACM, 52, 56–67, https://doi.org/10.1145/1562764.1562783, 2009. a
Bauer, P., Thorpe, A., and Brunet, G.: The quiet revolution of numerical weather prediction, Nature, 525, 47–55, https://doi.org/10.1038/nature14956, 2015. a
Bénard, P. and Glinton, M.: Circumventing the pole problem of reduced lat-lon grids with local schemes. Part I: analysis and model formulation, Q. J. Roy, Meteor. Soc., 145, 1377–1391, https://doi.org/10.1002/qj.3509, 2019. a
Clement, V., Ferrachat, S., Fuhrer, O., Lapillonne, X., Osuna, C. E., Pincus, R., Rood, J., and Sawyer, W.: The CLAW DSL, in: Proceedings of the Platform for Advanced Scientific Computing Conference – PASC'18, ACM Press, https://doi.org/10.1145/3218176.3218226, 2018. a
Colavolpe, C., Voitus, F., and Bénard, P.: RK-IMEX HEVI schemes for fully compressible atmospheric models with advection: analyses and numerical testing, Q. J. Roy. Meteor. Soc., 143, 1336–1350, https://doi.org/10.1002/qj.3008, 2017. a
Colella, P.: Defining software requirements for scientific computing, DARPA HPCS Presentation, 2004. a
Deconinck, W.: Development of Atlas, a flexible data structure framework, Tech. rep., ECMWF, available at: http://arxiv.org/abs/1908.06091 (last access: 27 September 2019), 2017a. a
Deconinck, W.: Public release of Atlas under an open source license, which is accelerator enabled and has improved interoperability features, Tech. rep., ECMWF, available at: http://arxiv.org/abs/1908.07038 (last access: 27 September 2019), 2017b. a
Deconinck, W., Bauer, P., Diamantakis, M., Hamrud, M., Kühnlein, C., Maciel, P., Mengaldo, G., Quintino, T., Raoult, B., Smolarkiewicz, P. K., and Wedi, N. P.: Atlas – a library for numerical weather prediction and climate modelling, Comput. Phys. Commun., 220, 188–204, https://doi.org/10.1016/j.cpc.2017.07.006, 2017. a, b
Douriez, L., Gray, A., Guibert, D., Messmer, P., and Raffin, E.: Performance report and optimized implementations of weather & climate dwarfs on multi-node systems, Tech. rep., ECMWF, available at: http://arxiv.org/abs/1908.06097 (last access: 27 September 2019), 2018. a, b, c
Dziekan, P., Waruszewski, M., and Pawlowska, H.: University of Warsaw Lagrangian Cloud Model (UWLCM) 1.0: a modern large-eddy simulation tool for warm cloud modeling with Lagrangian microphysics, Geosci. Model Dev., 12, 2587–2606, https://doi.org/10.5194/gmd-12-2587-2019, 2019. a, b
Feng, W., Lin, H., Scogland, T., and Zhang, J.: OpenCL and the 13 dwarfs: a work in progress, in: Proceedings of the third joint WOSP/SIPEW International Conference on Performance Engineering – ICPE'12, ACM Press, https://doi.org/10.1145/2188286.2188341, 2012. a
Flamm, K.: Measuring Moore's law: evidence from price, cost, and quality indexes, National Biuro of Economic Research, Working Paper No. 24553, April 2018, https://doi.org/10.3386/w24553, 2018. a
Fuhrer, O., Chadha, T., Hoefler, T., Kwasniewski, G., Lapillonne, X., Leutwyler, D., Lüthi, D., Osuna, C., Schär, C., Schulthess, T. C., and Vogt, H.: Near-global climate simulation at 1 km resolution: establishing a performance baseline on 4888 GPUs with COSMO 5.0, Geosci. Model Dev., 11, 1665–1681, https://doi.org/10.5194/gmd-11-1665-2018, 2018. a
Glinton, M. R. and Bénard, P.: Circumventing the pole problem of reduced lat-lon grids with local schemes. Part II: validation experiments, Q. J. Roy. Meteor. Soc., 145, 1392–1405, https://doi.org/10.1002/qj.3495, 2019. a
Johnston, B. and Milthorpe, J.: Dwarfs on accelerators: enhancing OpenCL benchmarking for heterogeneous computing architectures, in: Proceedings of the 47th International Conference on Parallel Processing Companion – ICPP'18, ACM Press, https://doi.org/10.1145/3229710.3229729, 2018. a
Kaltofen, E. L.: The “seven dwarfs” of symbolic computation, in: Numerical and Symbolic Scientific Computing, edited by: Langer, U. and Paule, P., Springer, 95–104, https://doi.org/10.1007/978-3-7091-0794-2_5, 2011. a, b
Katzav, J. and Parker, W. S.: The future of climate modeling, Climatic Change, 132, 475–487, https://doi.org/10.1007/s10584-015-1435-x, 2015. a
Krommydas, K., Feng, W., Antonopoulos, C. D., and Bellas, N.: OpenDwarfs: characterization of dwarf-based benchmarks on fixed and reconfigurable architectures, J. Signal Process. Sys., 85, 373–392, https://doi.org/10.1007/s11265-015-1051-z, 2015. a
Kühnlein, C., Deconinck, W., Klein, R., Malardel, S., Piotrowski, Z. P., Smolarkiewicz, P. K., Szmelter, J., and Wedi, N. P.: FVM 1.0: a nonhydrostatic finite-volume dynamical core for the IFS, Geosci. Model Dev., 12, 651–676, https://doi.org/10.5194/gmd-12-651-2019, 2019.
Lawrence, B. N., Rezny, M., Budich, R., Bauer, P., Behrens, J., Carter, M., Deconinck, W., Ford, R., Maynard, C., Mullerworth, S., Osuna, C., Porter, A., Serradell, K., Valcke, S., Wedi, N., and Wilson, S.: Crossing the chasm: how to develop weather and climate models for next generation computers?, Geosci. Model Dev., 11, 1799–1821, https://doi.org/10.5194/gmd-11-1799-2018, 2018. a
Macfaden, A. J., Gordon, G. S. D., and Wilkinson, T. D.: An optical Fourier transform coprocessor with direct phase determination, Sci. Rep.-UK, 7, 13667, https://doi.org/10.1038/s41598-017-13733-1, 2017. a, b
Mazauric, C., Raffin, E., and Guibert, D.: Recommendations and specifications for data scope analysis tools, Tech. rep., ECMWF, available at: http://arxiv.org/abs/1908.06095 (last access: 27 September 2019), 2017a. a
Mazauric, C., Raffin, E., Vigouroux, X., Guibert, D., Macfaden, A., Poulsen, J., Berg, P., Gray, A., and Messmer, P.: Performance report and optimized implementation of weather & climate dwarfs on GPU, MIC and Optalysys optical processor, Tech. rep., ECMWF, available at: http://arxiv.org/abs/1908.06096 (last access: 27 September 2019), 2017b. a, b, c
Mengaldo, G.: Batch 1: definition of several weather & climate dwarfs, Tech. rep., ECMWF, available at: http://arxiv.org/abs/1908.06089 (last access: 27 September 2019), 2016. a
Mengaldo, G., Wyszogrodzki, A., Diamantakis, M., Lock, S.-J., Giraldo, F., and Wedi, N. P.: Current and emerging time-integration strategies in global numerical weather and climate prediction, Arch. Comput. Method. E., 26, 663–684, 1–22, https://doi.org/10.1007/s11831-018-9261-8, 2019.
Messer, O. E. B., D'Azevedo, E., Hill, J., Joubert, W., Berrill, M., and Zimmer, C.: MiniApps derived from production HPC applications using multiple programing models, Int. J. High Perform. C., 32, 582–593, https://doi.org/10.1177/1094342016668241, 2016. a
Michalakes, J., Govett, M., Benson, R., Black, T., Juang, H., Reinecke, A., and Skamarock, B.: AVEC Report: NGGPS Level-1 Benchmarks and software evaluation, Tech. rep., NOAA, Boulder, US, available at: https://repository.library.noaa.gov/view/noaa/18654 (last access: 27 September 2019), 2015. a, b
Mozdzynski, G., Hamrud, M., and Wedi, N. P.: A partitioned global address space implementation of the European Centre for Medium Range Weather Forecasts Integrated Forecasting System, Int. J. High Perform. Comput. Appl., 29, 261–273, https://doi.org/10.1177/1094342015576773, 2015. a
Müller, A., Kopera, M. A., Marras, S., Wilcox, L. C., Isaac, T., and Giraldo, F. X.: Strong scaling for numerical weather prediction at petascale with the atmospheric model NUMA, Int. J. High Perform. C., 2, 411–426, https://doi.org/10.1177/1094342018763966, 2018. a, b, c
Müller, A., Gillard, M., Nielsen, K. P., and Piotrowski, Z.: Batch 2: definition of novel weather & climate dwarfs, Tech. rep., ECMWF, available at: http://arxiv.org/abs/1908.07040 (last access: 27 September 2019), 2017. a, b
Müller, A., Deconinck, W., Kühnlein, C., Mengaldo, G., Lange, M., Wedi, N., Bauer, P., Smolarkiewicz, P. K., Diamantakis, M., Lock, S.-J., Hamrud, M., Saarinen, S., Mozdzynski, G., Thiemert, D., Glinton, M., Bénard, P., Voitus, F., Colavolpe, C., Marguinaud, P., Zheng, Y., Van Bever, J., Degrauwe, D., Smet, G., Termonia, P., Nielsen, K. P., Sass, B. H., Poulsen, J. W., Berg, P., Osuna, C., Fuhrer, O., Clement, V., Baldauf, M., Gillard, M., Szmelter, J., O'Brien, E., McKinstry, A., Robinson, O., Shukla, P., Lysaght, M., Kulczewski, M., Ciznicki, M., Pia̧tek, W., Ciesielski, S., Błażewicz, M., Kurowski, K., Procyk, M., Spychala, P., Bosak, B., Piotrowski, Z., Wyszogrodzki, A., Raffin, E., Mazauric, C., Guibert, D., Douriez, L., Vigouroux, X., Gray, A., Messmer, P., Macfaden, A. J., and New, N.: The ESCAPE project: Energy-efficient Scalable Algorithms for Weather Prediction at Exascale [Data set], Zenodo, https://doi.org/10.5281/zenodo.3462374, 2019. a, b
Neumann, P., Düben, P., Adamidis, P., Bauer, P., Brück, M., Kornblueh, L., Klocke, D., Stevens, B., Wedi, N., and Biercamp, J.: Assessing the scales in numerical weather and climate predictions: will exascale be the rescue?, Philos. T. R. Soc. A, 377, 20180148, https://doi.org/10.1098/rsta.2018.0148, 2019. a
Osuna, C.: Report on the performance portability demonstrated for the relevant weather & climate dwarfs, Tech. rep., ECMWF, available at: http://arxiv.org/abs/1908.06094 (last access: 27 September 2019), 2018. a
Palmer, T.: Climate forecasting: Build high-resolution global climate models, Nature, 515, 338–339, https://doi.org/10.1038/515338a, 2014. a
Phillips, S. C., Engen, V., and Papay, J.: Snow white clouds and the seven dwarfs, in: 2011 IEEE Third International Conference on Cloud Computing Technology and Science, IEEE, https://doi.org/10.1109/cloudcom.2011.114, 2011. a
Poulsen, J. W. and Berg, P.: Tuning the implementation of the radiation scheme ACRANEB2, Tech. rep., DMI report 17–22, available at: http://www.dmi.dk/fileadmin/user_upload/Rapporter/TR/2017/SR17-22.pdf (last access: 27 September 2019), 2017. a
Robinson, O., McKinstry, A., and Lysaght, M.: Optimization of IFS subroutine LAITRI on Intel Knights Landing, Tech. rep., PRACE White Papers, https://doi.org/10.5281/zenodo.832025, 2016.
Schalkwijk, J., Jonker, H. J. J., Siebesma, A. P., and Meijgaard, E. V.: Weather forecasting using GPU-based Large-Eddy Simulations, B. Am. Meteorol. Soc., 96, 715–723, https://doi.org/10.1175/bams-d-14-00114.1, 2015. a
Schulthess, T. C., Bauer, P., Wedi, N., Fuhrer, O., Hoefler, T., and Schär, C.: Reflecting on the goal and baseline for exascale computing: a roadmap based on weather and climate simulations, Comput. Sci. Eng., 21, 30–41, https://doi.org/10.1109/mcse.2018.2888788, 2019. a
Shukla, J., Palmer, T. N., Hagedorn, R., Hoskins, B., Kinter, J., Marotzke, J., Miller, M., and Slingo, J.: Toward a new generation of world climate research and computing facilities, B. Am. Meteorol. Soc., 91, 1407–1412, https://doi.org/10.1175/2010bams2900.1, 2010. a
Van Bever, J., McFaden, A., Piotrowski, Z., and Degrauwe, D.: Report on energy-efficiency evaluation of several NWP model configurations, Tech. rep., ECMWF, available at: http://arxiv.org/abs/1908.06115 (last access: 27 September 2019), 2018. a
Wallemacq, P. and House, R.: Economic losses, poverty and disasters 1998-2017, Tech. rep., available at: https://www.unisdr.org/we/inform/publications/61119 (last access: 27 September 2019), 2018. a
Wedi, N. P., Hamrud, M., and Mozdzynski, G.: A fast spherical harmonics transform for global NWP and climate models, Mon. Weather Rev., 141, 3450–3461, https://doi.org/10.1175/mwr-d-13-00016.1, 2013. a, b
Wedi, N. P., Bauer, P., Deconinck, W., Diamantakis, M., Hamrud, M., Kühnlein, C., Malardel, S., Mogensen, K., Mozdzynski, G., and Smolarkiewicz, P.: The modelling infrastructure of the Integrated Forecasting System: recent advances and future challenges, Tech. Rep. 760, Eur. Cent. For Medium-Range Weather Forecasts, Reading, UK, https://doi.org/10.21957/thtpwp67e, 2015. a
Wehner, M. F., Oliker, L., Shalf, J., Donofrio, D., Drummond, L. A., Heikes, R., Kamil, S., Kono, C., Miller, N., Miura, H., Mohiyuddin, M., Randall, D., and Yang, W.-S.: Hardware/software co-design of global cloud system resolving models, J. Adv. Model. Earth Sy., 3, M10003, https://doi.org/10.1029/2011ms000073, 2011. a
Williamson, D. L.: The evolution of dynamical cores for global atmospheric models, J. Meteorol. Soc. Jpn., 85, 241–269, https://doi.org/10.2151/jmsj.85b.241, 2007. a
World Economic Forum: The 2019 global risks report, available at: https://www.weforum.org/reports/the-global-risks-report-2019, last access: 27 September 2019. a
Wu, J., Wyckoff, P., and Panda, D.: High performance implementation of MPI derived datatype communication over InfiniBand, in: 18th International Parallel and Distributed Processing Symposium, 2004, Proceedings, IEEE, https://doi.org/10.1109/ipdps.2004.1302917, 2004. a
Xiao, H., Diamantakis, M., and Saarinen, S.: An OpenACC GPU adaptation of the IFS cloud microphysics scheme, ECMWF Tech. Memo. No. 805, https://doi.org/10.21957/g9mjjlgeq, 2017. a
Zheng, Y. and Marguinaud, P.: Simulation of the performance and scalability of message passing interface (MPI) communications of atmospheric models running on exascale supercomputers, Geosci. Model Dev., 11, 3409–3426, https://doi.org/10.5194/gmd-11-3409-2018, 2018. a





