the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Evaluation of lossless and lossy algorithms for the compression of scientific datasets in netCDF-4 or HDF5 files
Xavier Delaunay
Aurélie Courtois
Flavien Gouillon
The increasing volume of scientific datasets requires the use of compression to reduce data storage and transmission costs, especially for the oceanographic or meteorological datasets generated by Earth observation mission ground segments. These data are mostly produced in netCDF files. Indeed, the netCDF-4/HDF5 file formats are widely used throughout the global scientific community because of the useful features they offer. HDF5 in particular offers a dynamically loaded filter plugin so that users can write compression/decompression filters, for example, and process the data before reading or writing them to disk. This study evaluates lossy and lossless compression/decompression methods through netCDF-4 and HDF5 tools on analytical and real scientific floating-point datasets. We also introduce the Digit Rounding algorithm, a new relative error-bounded data reduction method inspired by the Bit Grooming algorithm. The Digit Rounding algorithm offers a high compression ratio while keeping a given number of significant digits in the dataset. It achieves a higher compression ratio than the Bit Grooming algorithm with slightly lower compression speed.
- Article
(1365 KB) - Full-text XML
-
Supplement
(858 KB) - BibTeX
- EndNote
Ground segments processing scientific mission data are facing challenges due to the ever-increasing resolution of on-board instruments and the volume of data to be processed, stored and transmitted. This is the case for oceanographic and meteorological missions, for instance. Earth observation mission ground segments produce very large files mostly in netCDF format, which is standard in the oceanography field and widely used by the meteorological community. This file format is widely used throughout the global scientific community because of its useful features. The fourth version of the netCDF library, denoted netCDF-4/HDF5 (as it is based on the HDF5 layer), offers “Deflate” and “Shuffle” algorithms as native compression features. However, the compression ratio achieved does not fully meet ground processing requirements, which are to significantly reduce the storage and dissemination cost as well as the I/O times between two modules in the processing chain.
In response to the ever-increasing volume of data, scientists are keen to compress data. However, they have certain requirements: both compression and decompression have to be fast. Lossy compression is acceptable only if the compression ratios are higher than those of lossless algorithms and if the precision, or data loss, can be controlled. There is a trade-off between the data volume and the accuracy of the compressed data. Nevertheless, scientists can accept small losses if they remain below the data's noise level. Noise is difficult to compress and of little interest to scientists, so they do not consider data degradation that remains under the noise level as a loss (Baker et al., 2016). In order to increase the compression ratio within the processing chain, “clipping” methods may be used to degrade the data before compression. These methods increase the compression ratio by removing the least significant digits in the data. Indeed, at some level, these least significant digits may not be scientifically meaningful in datasets corrupted by noise.
This paper studies compression and clipping methods that can be applied to scientific datasets in order to maximize the compression ratio while preserving scientific data content and numerical accuracy. It focuses on methods that can be applied to scientific datasets, i.e. vectors or matrices of floating-point numbers. First, lossless compression algorithms can be applied to any kind of data. The standard is the “Deflate” algorithm (Deutsch, 1996) native in netCDF-4/HDF5 libraries. It is widely used in compression tools such as zip, gzip, and zlib libraries, and has become a benchmark for lossless data compression. Recently, alternative lossless compression algorithms have emerged. These include Google Snappy, LZ4 (Collet, 2013) or Zstandard (Collet and Turner, 2016). To achieve faster compression than the Deflate algorithm, none of these algorithms use Huffman coding. Second, preprocessing methods such as Shuffle, available in HDF5, or Bitshuffle (Masui et al., 2015) are used to optimize lossless compression by rearranging the data bytes or bits into a “more compressible” order. Third, some lossy/lossless compression algorithms, such as FPZIP (Lindstrom and Isenburg, 2006), ZFP (Lindstrom, 2014) or Sz (Tao et al., 2017), are specifically designed for scientific data – and in particular floating-point data – and can control data loss. Fourth, data reduction methods such as Linear Packing (Caron, 2014a), Layer Packing (Silver and Zender, 2017), Bit Shaving (Caron, 2014b), and Bit Grooming (Zender, 2016a) lose some data content without necessarily reducing its volume. Preprocessing methods and lossless compression can then be applied to obtain a higher compression ratio.
This paper focuses on compression methods implemented for netCDF-4 or HDF5 files. These scientific file formats are widespread among the oceanographic and meteorological communities. HDF5 offers a dynamically loaded filter plugin that allows users to write compression/decompression filters (among others), and to process data before reading or writing them to disk. Consequently, many compression/decompression filters – such as Bitshuffle, Zstandard, LZ4, and Sz – have been implemented by members of the HDF5 user community and are freely available. The netCDF Operator toolkit (NCO) (Zender, 2016b) also offers some compression features, such as Bit Shaving, Decimal Rounding and Bit Grooming.
The rest of this paper is divided into five sections. Section 2 presents the lossless and lossy compression schemes for scientific floating-point datasets. Section 3 introduces the Digit Rounding algorithm, which is an improvement of the Bit Grooming algorithm that optimizes the number of mantissa bits preserved. Section 4 defines the performance metrics used in this paper. Section 5 describes the performance assessment of a selection of lossless and lossy compression methods on synthetic datasets. It presents the datasets and compression results before making some recommendations. Section 6 provides some compression results obtained with real CFOSAT and SWOT datasets. Finally, Sect. 7 provides our conclusions.
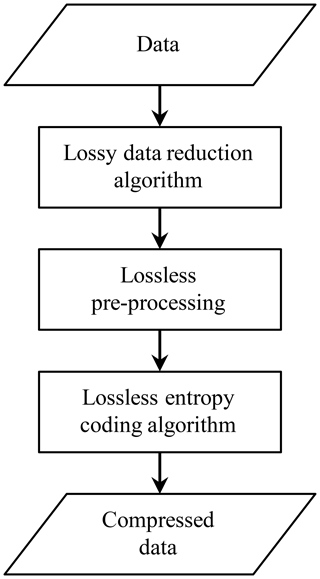
Compression schemes for scientific floating-point datasets usually entail several steps: data reduction, preprocessing, and lossless coding. These three steps can be chained as illustrated in Fig. 1. The lossless coding step is reversible. It does not degrade the data while reducing its volume. It can be implemented by lossless compression algorithms such as Deflate, Snappy, LZ4 or Zstandard. The preprocessing step is also reversible. It rearranges the data bytes or bits to enhance lossless coding efficiency. It can be implemented by algorithms such as Shuffle or Bitshuffle. The data reduction step is not reversible because it entails data losses. The goal is to remove irrelevant data such as noise or other scientifically meaningless data. Data reduction can reduce data volume, depending on the algorithm used. For instance, the Linear Packing and Sz algorithms reduce data volume, but Bit Shaving and Bit Grooming algorithms do not.
This paper evaluates lossless compression algorithms Deflate, LZ4, and Zstandard; Deflate because it is the benchmark algorithm, LZ4 because it is a widely-used, very-high-speed compressor, and Zstandard because it provides better results than Deflate both in terms of compression ratios and of compression/decompression speeds. The Deflate algorithm uses LZ77 dictionary coding (Ziv and Lempel, 1977) and Huffman entropy coding (Huffman, 1952). LZ77 and Huffman coding exploit different types of redundancies to enable Deflate to achieve high compression ratios. However, the computational cost of the Huffman coder is high and makes Deflate compression rather slow. LZ4 is a dictionary coding algorithm designed to provide high compression/decompression speeds rather than a high compression ratio. It does this without an entropy coder. Zstandard is a fast lossless compressor offering high compression ratios. It makes use of dictionary coding (repcode modeling) and a finite-state entropy coder (tANS) (Duda, 2013). It offers a compression ratio similar to that of Deflate coupled with high compression/decompression speeds.
This paper also evaluates Shuffle and Bitshuffle. The Shuffle groups all the data samples' first bytes together, all the second bytes together, etc. In smooth datasets, or datasets with highly correlated consecutive sample values, this rearrangement creates long runs of similar bytes, improving the dataset's compression. Bitshuffle extends the concept of Shuffle to the bit level by grouping together all the data samples' first bits, second bits, etc.
Last, we evaluate the lossy compression algorithms Sz, Decimal Rounding and Bit Grooming. We chose to evaluate the Sz algorithm because it provides better rate-distortion results than FPZIP and ZFP, see Tao et al. (2017). The Sz algorithm predicts data samples using an n-layers prediction model and performs an error-control quantization of the data before variable length encoding. Unpredictable data samples are encoded after a binary representation analysis: the insignificant bits are truncated after computation of the smallest number of mantissa bits required to achieve the specified error bound. The Decimal Rounding algorithm achieves a uniform scalar quantization of the data. The quantization step is a power of 2 pre-computed so as to preserve a specific number of decimal digits. The Bit Grooming algorithm creates a bitmask to remove the least significant bits of the mantissa of IEEE 754 floating-point data. Given a specified total number of significant digits, nsd, the Bit Grooming algorithm tabulates the number of mantissa bits that has to be preserved to guarantee the specified precision of nsd digits: to guarantee 1–6 digits of precision, Bit Grooming must retain 5, 8, 11, 15, 18, and 21 mantissa bits respectively. The advantage is that the number of mantissa bits that must be preserved is computed very quickly. The disadvantage is that this computation is not optimal. In many cases, more mantissa bits are preserved than strictly necessary. Table 1 provides an example using the value of π with a specified precision of nsd =4 digits. This table reproduces some of the results from Table 1 in Zender (2016a). The Bit Grooming algorithm preserves 15 mantissa bits. Table 1 shows that only 12 bits were actually necessary. Optimizing the number of mantissa bits preserved has a favorable impact on the compression ratios since it allows more bits to be zeroed, thus creating longer sequences of zero bits. In the next section, we propose the Digit Rounding algorithm to overcome this limitation of the Bit Grooming algorithm.
The Digit Rounding algorithm is similar to the Decimal Rounding algorithm in the sense that it computes a quantization factor q, which is a power of 2, in order to set bits to zero in the binary representation of the quantized floating-point value. It is also similar to Sz's error-controlled quantization (Tao et al., 2017) in the sense that the quantization error is bounded. The difference with the Decimal Rounding algorithm and with Sz's error-controlled quantization is that the Digit Rounding algorithm adapts the quantization factor to each sample value to achieve a specified relative precision of nsd digits.
The Digit Rounding algorithm uses uniform scalar quantization with reconstruction at the bin center:
where is the quantized value of sample value si. The quantization error is bounded by:
The number of digits di before the decimal separator in value si is:
We want to preserve nsd significant digits of sample value s. This is approximately equivalent to having a rounding error of less than half the last tenth digit preserved. The quantization error shall thus be lower than or equal to:
This condition guarantees that the Digit Rounding algorithm always preserves a relative error lower than or equal to half the value of the least significant digit. Combining Eqs. (2) and (4), we look for the highest quantization factor qi such that:
Moreover, in order to lower the computational cost and increase compression efficiency, we seek a quantization factor that is a power of two. This allows bit-masking instead of division, and creates sequences of zero bits:
We thus look for the greatest integer pi such that
Finally, we take value pi such that:
The log computation in Eq. (3) is the more computationally intensive, but optimization is possible because only the integer part of the result is useful. The optimization consists of computing the number of digits before decimal separator d from binary exponent ei and mantissa mi of value si, which in binary representation is written:
The mantissa mi is a number between 0.5 and 1. Hence, using Eq. (3) we obtain:
The log 10(mi) value is tabulated. Only 5 tabulated values are used in our implementation, enough to provide a good precision. The tabulated values v for log 10(mi) are such that v≤log 10(mi). They are provided in the Supplement. Number di of significant digits before the decimal separator in sample value si is thus approximated with the following equation:
This computation slightly underestimates the values for di but provides
a more conservative quantization, guaranteeing the specified number of
significant digits. The optimization slightly decreases the achievable
compression ratios in exchange for a much higher compression speed. The
Digit Rounding algorithm is summarized below.

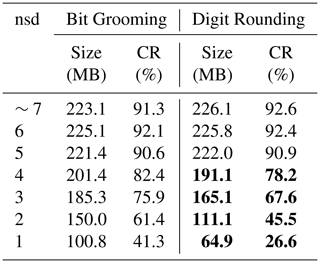
We have developed an HDF5 dynamically loaded filter plugin so as to apply the Digit Rounding algorithm to netCDF-4 or HDF5 datasets. It should be noted that data values rounded by the Digit Rounding algorithm can be read directly: there is no reverse operation to Digit Rounding, and users do not need any software to read the rounded data. Table 2 provides the results of the Digit Rounding algorithm on the value of π with specified precisions nsd varying from 1 to 8 digits. It can be compared to the Bit Grooming results provided in Table 2 in Zender (2016a). For a specified precision of nsd =4 digits, the Digit Rounding algorithm preserves 11 bits in the mantissa and sets the 12th bit to 1. Compared to the Bit Grooming algorithm, 3 more bits have been set to 0. Table 3 provides the maximum absolute errors, the mean absolute errors and the mean errors (defined in Sect. 4) obtained with varying nsd values on an artificial dataset composed of 1 000 000 values evenly spaced over the interval [1.0,2.0). This is the same artificial dataset used in Table 3 in Zender (2016a). It shows that Digit Rounding always preserves an absolute error lower than or equal to half the value of the least significant digit, i.e. . We compare the compression ratio obtained with the Digit Rounding algorithm to that obtained with the Bit Grooming algorithm for the same meteorological data from MERRA re-analysis studied in Zender (2016a). Table 4 reports the Bit Grooming results extracted from Table 6 in Zender (2016a) and provides the results of the Digit Rounding algorithm. The same lossless compression is employed: Shuffle and Deflate with level 1 compression. From nsd =7 to nsd =5, Digit Rounding and Bit Grooming provide similar compression ratios with a slight advantage for the Bit Grooming algorithm. However, from nsd =4 to nsd =1, the compression ratios obtained with Digit Rounding are clearly better.
Table 2Representation of the value of π in IEEE-754 single-precision binary representation (first row) and results preserving a varying number of significant digits (nsd) with the Digit Rounding algorithm. This table can be compared to Table 2 in Zender (2016a) providing the Bit Grooming results for π.
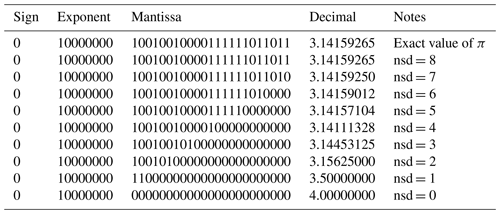
Table 3Maximum absolute errors, mean absolute errors and mean errors of the Digit Rounding algorithm preserving a varying number of significant digits (nsd) on an artificial dataset composed of 1 000 000 values evenly spaced over the interval [1.0,2.0). The error metrics are defined in Sect. 4.
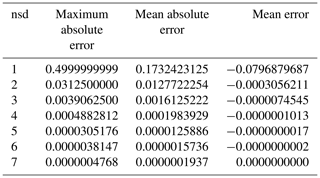
Table 4Comparison of the Bit Grooming and Digit Rounding algorithms for the compression of a MERRA dataset. Shuffle and Deflate (level 1) are applied. The compression ratio (CR) is defined by the ratio of the compressed file size over the reference data size (244.3 MB) obtained with Deflate (level 5) compression. Bit Grooming results are extracted from Zender (2016a). Bold values indicate where Digit Rounding performs better than Bit Grooming.
The following section first defines the various performance metrics used hereinafter, then studies the performance of various lossless and lossy compression algorithms – including Digit Rounding – when applied to both synthetic and real scientific datasets.
One of the features required for lossy scientific data compression is control over the amount of loss, or the accuracy, of the compressed data. Depending on the data, this accuracy can be expressed by an absolute or a relative error bound. The maximum absolute error is defined by where si are the sample values of the original dataset and are the sample values of the compressed dataset. An absolute error bound specifies the maximum absolute error, eabs, allowed between any sample of the original and compressed data: . The maximum relative error is defined by . A relative error bound specifies the maximum relative error, erel, allowed between any sample of the original and compressed data: . The absolute error bound can be useful for data with a single dynamic range of interest. The relative error bound can be useful for data where both very low and very high values are pertinent.
A near-nearly exhaustive list of metrics for assessing the performance of lossy compression of scientific datasets is provided in Tao et al. (2019). For the sake of conciseness, only a few of them are presented in this paper. The following metrics were chosen for this study:
-
compression ratio CR(F) to evaluate the reduction in size as a result of the compression. It is defined by the ratio of the original file size over the compressed file size:
-
compression speed CS(F) and decompression speed DS(F) to evaluate the speed of the compression and decompression. They are defined by the ratio of the original file size over the compression or decompression time:
The compression and decompression speeds are expressed in MB s−1. Those reported in this paper were obtained on a Dell T1600 with an Intel Xeon E31225 4-core CPU at 3.1 GHz, and a 4 GB memory under the RedHat 6.5 (64-bit) OS with compression and decompression run on a single core. Parallel compression has not been considered in this work.
The following metrics were chosen to assess the data degradation of the lossy compression algorithms:
-
maximum absolute error defined previously. It is used to evaluate the maximum error between the original and compressed data;
-
mean error to evaluate if any bias is introduced into the compressed data. It is defined as the mean of the pointwise difference between the original and compressed data:
-
mean absolute error to evaluate the mean data degradation. It is defined as the mean of the pointwise absolute difference between the original and compressed data:
-
SNR to evaluate the signal to compression error ratio. It is defined by the ratio of the signal level over the root mean square compression error and is expressed in decibels (dB):
These metrics are used in the following sections to evaluate various lossless and lossy compression algorithms, including Digit Rounding.
5.1 Analytical datasets
Synthetic datasets s1 and s3D with known statistics were generated in order to test the compression algorithms under variable conditions. Dataset s1 is a noisy sinusoid of 1 dimension with a maximum absolute value of 118. The data volume of this dataset is 4 MB. Dataset s3D is a noisy sinusoid pulse of 3 dimensions with a maximum absolute value of 145. The data volume of this dataset is 512 MB. The Supplement describes these datasets in greater detail.
5.2 Performance assessment of lossless compression methods
The lossless compression algorithms evaluated are Deflate and Zstandard with or without the Shuffle or Bitshuffle preprocessing step. LZ4 is always evaluated with the Bitshuffle preprocessing step because it was imposed in the LZ4 implementation we used. We ran a lossless compression algorithm using the h5repack tool from the HDF5 library, version 1.8.19, Deflate implemented in zlib 1.2.11, Zstandard version 1.3.1 with the corresponding HDF5 filter available on the HDF web portal (http://portal.hdfgroup.org/display/support/Filters, last access: 26 August 2019), and the implementation of LZ4 and Bitshuffle in python package Bitshuffle-0.3.4. The compression was performed by calling the h5repack tool. The Supplement provides the command lines and options used.
Figures 2 and 3 provide the results obtained for the compression and decompression of dataset s1 and dataset s3D respectively. The vertical bars represent the results for different compression levels: from 1 to 9 for Deflate level dfl_lvl, from 1 to 22 for Zstandard level zstd_lvl, and only one level for LZ4. First, it can be observed that preprocessing steps Shuffle or Bitshuffle have a similarly favorable impact both on the compression ratio and on the compression/decompression speeds. Second, the compression level parameters dfl_lvl and zstd_lvl have little influence on the compression ratio. However, the compression/decompression speeds decrease as compression levels increase, particularly with Zstandard compression levels. Third, the compression ratios obtained with Deflate and Zstandard are similar, but the compression speeds of Zstandard at low compression levels are far higher, and the decompression speeds of Zstandard are always higher. Fourth, Bitshuffle+LZ4 provides a slightly lower compression ratio than Shuffle+Deflate or Shuffle+Zstandard, with a compression speeds similar to Shuffle+Deflate or Shuffle+Zstandard at low compression level parameters dfl_lvl or zstd_lvl. Finally, the compression/decompression speeds obtained with Zstandard and LZ4 for the compression of dataset s3D are much lower than that achieved for the compression of dataset s1. Further investigations are required to understand why the compression/decompression speeds are lower, but it might be related to HDF5 chunking.
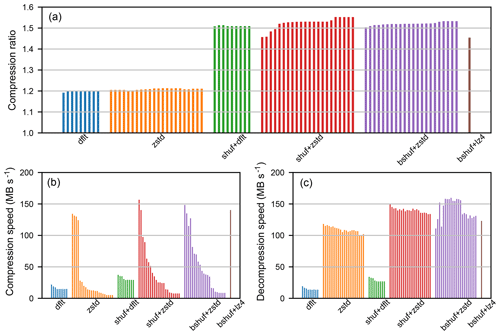
Figure 2Results obtained for the lossless compression of the s1 dataset with Deflate (dflt), Zstandard (zstd), Shuffle and Deflate (shuf+dflt), Shuffle and Zstandard (shuf+zstd), Bitshuffle and Zstandard (bshuf+zstd), Bitshuffle and LZ4 (bshuf+lz4). Compression ratios (a), compression speeds (b), and decompression speeds (c). Vertical bars represent the results for different compression levels: from 1 to 9 for Deflate, from 1 to 22 for Zstandard, only one level for LZ4.
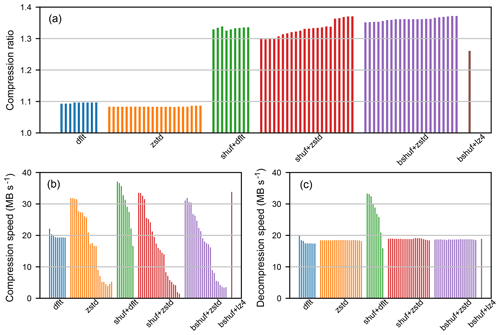
Figure 3Results obtained for the lossless compression of the s3D dataset with Deflate (dflt), Zstandard (zstd), Shuffle and Deflate (shuf+dflt), Shuffle and Zstandard (shuf+zstd), Bitshuffle and Zstandard (bshuf+zstd), Bitshuffle and LZ4 (bshuf+lz4). Compression ratios (a), compression speeds (b), and decompression speeds (c).
To summarize, these results show that preprocessing by Shuffle or Bitshuffle is very helpful in increasing compression efficiency. They also show that Zstandard can provide higher compression and decompression speeds than Deflate at low compression levels. However, on the s3D dataset, we observed that Zstandard compression and decompression speeds are lower than those obtained with Deflate. Therefore, Deflate and Zstandard are both options to consider for the lossless compression of scientific datasets as long as they follow the Shuffle or Bitshuffle preprocessing step.
5.3 Performance assessment of lossy compression methods
The lossy compression algorithms evaluated are error-bounded compression algorithms. They can constrain either the maximum absolute error or the maximum relative error, or both. The compression algorithms evaluated are Sz, Decimal Rounding, Bit Grooming and the Digit Rounding algorithm introduced in this paper. The Sz compression algorithm works in both error-bounded modes. Decimal Rounding allows a specific number of decimal digits to be preserved. In this sense, it bounds the maximum absolute error. Bit Grooming allows a specific number of significant digits to be preserved. In this sense, it bounds the maximum relative error. Like the Bit Grooming algorithm, Digit Rounding preserves a specific number of significant digits and bounds the maximum relative error.
We ran Sz version 2.1.1 using the h5repack tool and Sz HDF5 filter plugin, applying the Deflate lossless compression algorithm integrated in the Sz software. We ran the Decimal Rounding and Bit Grooming algorithms using NCO version 4.7.9, applying Shuffle and Deflate compression in the call to the NCO tool. Last, we ran the Digit Rounding algorithm using the h5repack tool and custom implantation of the algorithm in an HDF5 plugin filter. The Supplement provides the command lines and options used.
5.3.1 Performance comparison in absolute error-bounded compression mode
This section compares the performance of the absolute error-bounded compression algorithms: Sz and Decimal Rounding. The results reported were obtained by applying Sz configured with the options SZ_BEST_SPEED and Gzip_BEST_SPEED. Shuffle and Deflate with dflt_lvl =1 were applied after Decimal Rounding.
Table 5 compares the results obtained in absolute error-bounded compression mode for eabs=0.5. This corresponds to dsd =0 significant decimal digits preserved, or in other words, a rounding to the nearest integer. Both Sz and Decimal Rounding algorithms respect the specified maximum absolute error value. Moreover, none introduces a statistical bias: the mean absolute errors of both algorithms – not shown in Table 5 – are very close to zero. The errors introduced by these two algorithms are similar. However, it can be seen that Decimal Rounding provides a higher compression ratio than Sz for dataset s1. On the other hand, Sz provides a higher compression ratio for dataset s3D. Sz may perform better on dataset s3D because it is smoother than dataset s1. Indeed, Sz integrates a prediction step. This prediction might often fail because dataset s1 is very noisy. This may explain the lower compression ratio for s1 dataset. Decimal Rounding, however, does not make any predictions, which may explain why it achieves a better compression than Sz for dataset s1. The lower compression/decompression speeds obtained with Sz on the dataset s3D are not well understood and might be related to HDF5 chunking as previously mentioned.
Table 5Compression results of the absolute error-bounded compression algorithms Sz and Decimal Rounding on datasets s1 and s3D.

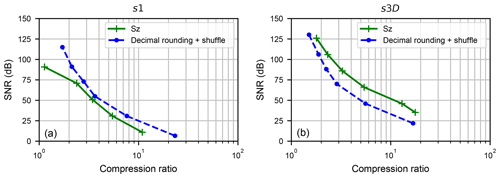
Figure 4Comparison of the compression results (SNR vs. compression ratio) of the Sz and Decimal Rounding algorithms in absolute error-bounded compression mode, on the s1 dataset (a) and s3D dataset (b).
Figure 4 compares Sz and Bit Grooming algorithms in terms of SNR versus compression ratio. This figure was obtained with the following parameters:
-
For the Sz algorithm, the absErrBound parameter was successively set to , , , , , 5;
-
For the Decimal Rounding algorithm, the dsd parameter was successively set to 4, 3, 2, 1, 0, −1.
For dataset s1, Decimal Rounding has a higher SNR than Sz for a given compression ratio. On the contrary, for dataset s3D, Sz has a higher SNR than Decimal Rounding for a given compression ratio. Both Sz and Bit Grooming algorithms seem valuable for error-bounded compression.
5.3.2 Performance comparison in relative error-bounded compression mode
This section compares the performance of the relative error-bounded compression algorithms: Sz, Bit Grooming, and Digit Rounding. The results reported were obtained by applying Sz configured with the options SZ_DEFAULT_COMPRESSION and Gzip_BEST_SPEED. Shuffle and Deflate with dflt_lvl=1 were applied after the Bit Grooming and Decimal Rounding algorithms.
We first focus on the results obtained with dataset s1. The number of significant digits – nsd parameter – in the Bit Grooming and Digit Rounding algorithms was set to 3. As the maximum absolute value in the s1 dataset is 118, the maximum absolute error should be lower than 0.5. In order to be able to compare Sz configured with a relative error bound with those algorithms, we configured the relative error bound to obtain a maximum absolute error of 0.5: the pw_relBoundRatio parameter in Sz was set to 0.00424. The results are provided in Table 6. It can be observed that all three algorithms respect the maximum absolute error of 0.5, which corresponds for dataset s1 to a relative error of 0.00424. On this dataset, Sz provides higher compression ratio and compression speed than the other two algorithms. Bit Grooming is too conservative. It preserves more mantissa bits than strictly necessary to achieve the required precision. This behavior is illustrated in Table 1 with the value of π. In contrast, Digit Rounding adapts the quantization step to each value of the input dataset. Doing so, it can achieve the required precision while preserving less mantissa bits than Bit Grooming does. This results both in a higher compression ratio but also in higher errors than Bit Grooming. Results obtained for Bit Grooming with nsd =2 are also provided for completeness. With this parameter, Bit Grooming provides slightly higher compression ratio and compression speed than Digit Rounding does.
Table 6Compression results of the relative error-bounded compression algorithms Sz, Bit Grooming, and Digit Rounding on dataset s1.

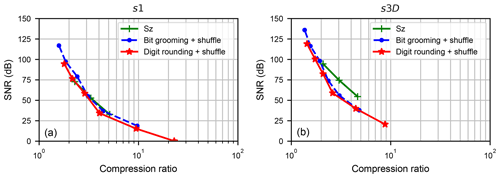
Figure 5Comparison of the compression results (SNR vs. compression ratio) of the Sz, Bit Grooming and Digit Rounding algorithms in relative error-bounded compression mode, on the s1 dataset (a) and s3D dataset (b).
Figure 5a compares Sz, Bit Grooming, and Digit Rounding algorithms in terms of SNR versus compression ratio. This figure has been obtained with the following parameters:
-
For the Sz algorithm, the pw_relBoundRatio parameter was successively set to , , ;
-
For the Bit Grooming algorithm, the nsd parameter was successively set to 6, 5, 4, 3, 2, 1;
-
For the Digit Rounding algorithm, the nsd parameter was successively set to 6, 5, 4, 3, 2, 1.
All three algorithms provide similar SNR versus compression ratio results, with a slight advantage for the Bit Grooming algorithm. Figure 6a compares the compression ratio obtained as a function of parameter nsd, which is the user-specified number of significant digits. Even though nsd is not a parameter of the Sz algorithm, we related the pw_relBoundRatio to the nsd parameters for dataset s1 (i.e. pw_relBoundRatio ) and plotted the compression ratio obtained with the Sz algorithm on the same figure. It can be seen that, whatever the nsd specified by the user, the compression ratios obtained with Digit Rounding are higher than the compression ratio obtained with the Bit Grooming algorithm. It can also be seen that the compression ratios obtained with the Sz algorithm are even higher.
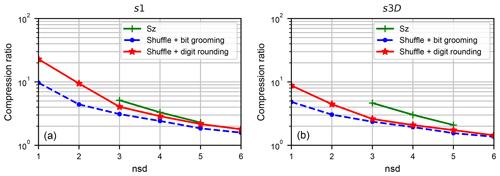
Figure 6Compression ratio as a function of the user-specified number of significant digits (nsd) for the Sz, Bit Grooming and Digit Rounding algorithms, on the s1 dataset (a) and s3D dataset (b).
We now focus on the results obtained with dataset s3D. The number of significant digits – nsd parameter – in the Bit Grooming and Digit Rounding algorithms was set to 3. As the maximum absolute value in the s3D dataset is 145, the pw_relBoundRatio parameter in Sz was set to 0.00345. Results are provided in Table 7. It can be observed that all three algorithms comply with the relative error bound specified. However, as previously mentioned, the Bit Grooming algorithm is too conservative. This is why results obtained with nsd =2 are also provided. On this dataset, Sz provides higher compression ratio than the other two algorithms but lower compression speed than Bit Grooming. At nsd =3, Digit Rounding provides slightly higher compression ratio than Bit Grooming but with lower compression speed.
Table 7Compression results of Sz, Bit Grooming, and Digit Rounding in relative error-bounded compression mode on dataset s3D.

Figure 5b compares Sz, Bit Grooming, and Digit Rounding algorithms in terms of SNR versus compression ratio. This figure has been obtained with the following parameters:
-
For the Sz algorithm, the pw_relBoundRatio parameter was successively set to , , ;
-
For the Bit Grooming algorithm, the nsd parameter was successively set to 6, 5, 4, 3, 2, 1;
-
For the Digit Rounding algorithm, the nsd parameter was successively set to 6, 5, 4, 3, 2, 1.
The Bit Grooming and Digit Rounding algorithms provide similar compression ratios, but even higher compression ratios are obtained with Sz. Figure 6b compares the compression ratio obtained as a function of the nsd parameter, which is the user-specified number of significant digits. As for dataset s1, we related pw_relBoundRatio to the nsd parameters for dataset s3D (i.e. pw_relBoundRatio ) and plotted the compression ratio obtained with the Sz algorithm on the same figure. Whatever the nsd specified by the user, the compression ratios obtained with the Digit Rounding algorithm are higher than the compression ratio obtained with the Bit Grooming algorithm. The compression ratios obtained with Sz are even higher.
Those results show that the Digit Rounding algorithm can be competitive with the Bit Grooming and Sz algorithms in relative error-bounded compression mode. It is thus applied to real scientific datasets in the next section.
6.1 Application to a CFOSAT dataset
Chinese-French Oceanography Satellite (CFOSAT) is a cooperative program between the French and Chinese space agencies (CNES and CNSA respectively). CFOSAT is designed to characterize the ocean surfaces to better model and predict ocean states, and improve knowledge of ocean/atmosphere exchanges. CFOSAT products will help marine and weather forecasting and will also be used to monitor the climate. The CFOSAT satellite will carry two scientific payloads – SCAT, a wind scatterometer; and SWIM, a wave scatterometer – for the joint characterization of ocean surface winds and waves. The SWIM (Surface Wave Investigation and Monitoring) instrument delivered by CNES is dedicated to measuring the directional wave spectrum (density spectrum of wave slopes as a function of direction and wavenumber of the waves). The CFOSAT L1A product contains calibrated and geocoded waveforms. By the end of the mission in 2023/2024, CFOSAT will have generated about 350 TB of data. Moreover, during routine phase, the users should have access to the data less 3 h after their acquisition. The I/O and compression performance are thus critical.
Currently, the baseline for compression of the CFOSAT L1A product involves a clipping method as a data reduction step, with Shuffle preprocessing and Deflate lossless coding with a compression level dfl_lvl of 3. Compression with a clipping method is like compression in an absolute error-bounded mode. It defines the least significant digit (lsd) and “clips” the data to keep only lsd decimal digits. The lsd is defined specifically for each dataset variable. The full list is provided in the Supplement with all the command lines and parameters used for running the compression methods described in this section.
We studied the following compression methods:
-
CFOSAT clipping followed by Shuffle and Deflate (dflt_lvl =3): the baseline for the compression of CFOSAT datasets;
-
CFOSAT clipping followed by Shuffle and Zstandard (zstd_lvl =2) for higher compression speeds;
-
Sz followed by Deflate in the absolute error bounded mode;
-
Decimal Rounding followed by Shuffle and Deflate (dflt_lvl =1);
-
Bit Grooming (nsd =8) followed by Shuffle and Deflate (dflt_lvl =1);
-
Digit Rounding (nsd =8) followed by Shuffle and Deflate (dflt_lvl =1).
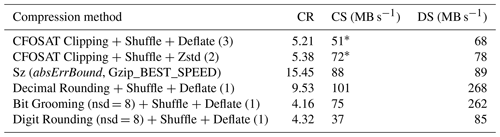
We first focused on the ground_range_5 variable of the CFOSAT L1A product. This variable is an array of 18 451×3215 values in double precision. The data volume is 452.58 MB (uncompressed). The CFOSAT clipping method defines an lsd of 3 for this variable. In absolute error-bounded mode, Decimal Rounding is configured to keep the same number of decimal digits as CFOSAT clipping: dsd =3; Sz is configured with absErrBound . In relative error-bounded mode, Bit Grooming and Digit Rounding are configured with nsd =8. The compression results are provided in Table 8. Compared to the CFOSAT baseline compression, Zstandard compression is more than twice faster while offering a similar compression ratio. On this dataset, the use of Sz instead of the CFOSAT Clipping method increases the compression ratio by a factor of 11. Sz prediction step seems to be very efficient on this dataset. Decimal Rounding increases the compression ratio by a factor of 2.5 “only”, but provides the fastest decompression. In the relative error-bounded mode, Digit Rounding provides a higher compression ratio than Bit Grooming but lower compression/decompression speeds.
Table 8Compression results for the ground_range_5 variable in the CFOSAT L1A product.
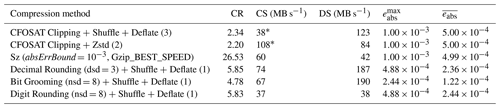
* The time taken for the CFOSAT Clipping method is not taken into account in the compression speed computation.
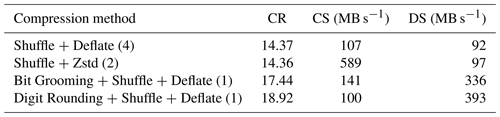
The results for the compression of the full CFOSAT L1A product of 7.34 GB (uncompressed) are provided in Table 9. The maximum absolute error and the mean absolute error are not provided because this dataset contains several variables compressed with different parameters. Compared to the CFOSAT baseline compression, Zstandard increases the compression speed by about 40 % while offering a similar compression ratio. It was not possible to apply Sz compression on the full dataset since Sz configuration file has to be modified to adapt the absErrBound to the lsd defined for each dataset variable. The way around this entails processing each variable one after the other. Sz provides a compression ratio almost 3 times higher than the baseline with faster compression and decompression. Decimal Rounding is configured on a per-variable basis to keep the precision required by the scientists on each variable. It increases the compression ratio by a factor of 1.8 with twice faster compression and decompression compared to the baseline. The compression ratios achieved with Bit Grooming or Digit Rounding in the relative error-bounded mode are lower. This is not the mode targeted for the compression of CFOSAT datasets. The usability of Sz being reduced by the fact that the error bound cannot be easily configured to achieve the precision required variable per variable, our recommendation is to use the Decimal Rounding algorithm. It achieves faster and more effective compression than CFOSAT Clipping method and bounds the absolute errors.
6.2 Application to SWOT datasets
The Surface Water and Ocean Topography Mission (SWOT) is a partnership between NASA and CNES, and continues the long history of altimetry missions with an innovative instrument known as KaRin, which is a Ka band synthetic aperture radar. The launch is foreseen for 2021. SWOT addresses both oceanographic and hydrological communities, accurately measuring the water level of oceans, rivers, and lakes.
SWOT has two processing modes, so two different types of products are generated: high-resolution products dedicated to hydrology, and low-resolution products mostly dedicated to oceanography. The Pixel Cloud product (called L2_HR_PIXC) contains data from the KaRin instrument's high-resolution (HR) mode. It contains information on the pixels that are detected as being over water. This product is generated when the HR mask is turned on. The Pixel Cloud product is organized into sub-orbit tiles for each swath and each pass, and this is an intermediate product between the L1 Single Look Complex products and the L2 lake/river ones. The product granularity is a tile 64 km long in the along-track direction, and it covers either the left or right swath (∼60 km wide). The SWOT mission will generate about 20 PB of data during the mission lifetime. Compression algorithms and performance are thus very critical. The mission center is currently defining files format and structure, and thus in this section we evaluated different compression options.
The compression of two different datasets was evaluated:
-
A simplified simulated SWOT L2_HR_PIXC pixel cloud product of 460 MB (uncompressed);
-
A realistic and representative SWOT L2 pixel cloud dataset of 199 MB (uncompressed).
The current baseline for the compression of the simplified simulated SWOT L2 pixel cloud product involves Shuffle preprocessing and Deflate lossless coding with a compression level dfl_lvl of 4. However, the compression method for the official SWOT L2 pixel cloud product has not yet been defined. A required precision is defined by the scientists as a number of significant digits (nsd) for each dataset variable. The full list is provided in the Supplement. We studied the following lossless or relative error bounded compression methods:
-
Shuffle and Deflate (dflt_lvl =4): the current baseline for the compression of SWOT datasets;
-
Shuffle and Zstandard (zstd_lvl =2) lossless alternative;
-
Sz with Deflate in the relative error bounded mode;
-
Bit Grooming followed by Shuffle and Deflate
(dflt_lvl =1); -
Digit Rounding followed by Shuffle and Deflate
(dflt_lvl =1).
We first focused on the height variable of the SWOT L2_HR_PIXC pixel cloud product. This variable is a list of 1 421 888 values in double precision. The data volume is 10.85 MB (uncompressed). A precision of 6 significant digits is required for this variable (nsd =6). Sz is configured in the relative error bounded mode with pw_relBoundRatio . Bit Grooming and Digit Rounding are configured with nsd =6. The results are provided in Table 10. Compared to the SWOT baseline compression, Zstandard compression is more than 10 times faster while offering a similar compression ratio. On this dataset, Digit Rounding provides the highest compression ratio with compression/decompression speeds similar to the one obtained with Bit Grooming. The lowest errors are obtained with Bit Grooming but with a compression ratio slightly lower than Digit Rounding. The compression ratio obtained with Sz is even lower.
Table 10Compression results for the height variable in the simplified simulated SWOT L2_HR_PIXC pixel cloud product.

Table 11Compression results for the pixel_area variable in the representative SWOT L2 pixel cloud product.

Next we focused on the pixel_area variable of the representative SWOT L2 pixel cloud product. This variable is a list of 1 300 111 values in double precision. The data volume is 9.92 MB (uncompressed). A precision of 11 significant digits is required for this variable (nsd =11). Sz is configured in the relative error bounded mode with pw_relBoundRatio only because it cannot achieve higher precision. Bit Grooming and Digit Rounding are configured with nsd =11. The results are provided in Table 11. Compared to the SWOT baseline compression, Zstandard compression is more than 7 times faster while offering a similar compression ratio. Sz provides the highest compression ratio but does not allow achieving the required precision of 11 digits. Moreover, in this configuration Sz compression is very slow. As for the height variable, Digit Rounding provides the highest compression ratio with compression/decompression speeds similar to the one obtained with Bit Grooming. The lowest errors are obtained with Bit Grooming but with a compression ratio lower than Digit Rounding.
Table 12 provides the results of the compression of the full simulated SWOT L2_HR_PIXC pixel cloud product. The maximum absolute error and the mean absolute error are not provided because this dataset contains several variables compressed with different parameters. Compared to the SWOT baseline compression, Zstandard increases the compression speed by over 5 times, while offering a similar compression ratio. Sz compression was not applied because it does not allow achieving the high precision required on some variables. Bit Grooming and Digit Rounding were configured on a per-variable basis to keep the precision required by the scientists on each variable. Compared to the baseline, Bit Grooming and Digit Rounding increase the compression respectively by 20 % and 30 % with similar compression speeds and faster decompression.
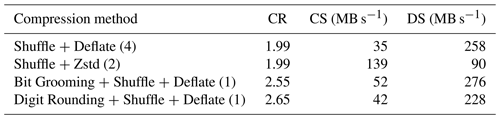
The results for the compression of the representative SWOT L2 pixel cloud product are provided in Table 13. Compared to the baseline, Zstandard compression is nearly 4 times faster while offering a similar compression ratio. Bit Grooming increases the compression ratio by 29 % with higher compression speed. And Digit Rounding increases the compression ratio by 34 % with slightly lower compression speed than Bit Grooming. Bit Grooming and Digit Rounding provide the fastest decompression. Our recommendation for the compression of SWOT datasets is thus to use the Digit Rounding algorithm to achieve high compression, at the price of a lower compression speed than the lossless solutions, considering that for SWOT the driver is product size, and taking into account the ratio between compression time and processing time.
This study evaluated lossless and lossy compression algorithms both on synthetic datasets and on realistic simulated datasets of future science satellites. The compression methods were applied using netCDF-4 and HDF5 tools. It has been shown that the impact of the compression level options of Zstandard or Deflate on the compression ratio achieved is not significant compared to the impact of the Shuffle or Bitshuffle preprocessing. However, high compression levels can significantly reduce the compression speed. Deflate and Zstandard with low compression levels are both reasonable options to consider for the compression of scientific datasets, but must always follow a Shuffle or Bitshuffle preprocessing step. It has been shown that Zstandard can speed-up the compression of CFOSAT and SWOT datasets compared to the baseline solution based on Deflate.
The lossy compression of scientific datasets can be achieved in two different error-bounded modes: absolute and relative error-bounded. Four algorithms have been studied: Sz, Decimal Rounding, Bit Grooming and Digit Rounding. One useful feature of the last three is that the accuracy of the compressed data can easily be interpreted: rather than defining an absolute or a relative error bound, they define the number of significant decimal digits or the number of significant digits. In absolute error-bounded mode, Sz provides higher compression ratios than Decimal Rounding on most datasets. However for the compression of netCDF/HDF5 datasets composed of several variables, its usability is reduced by the fact that only one absolute error bound can be set for all the variables. It cannot be easily configured to achieve the precision required variable per variable. This is why we rather recommend the Decimal Rounding algorithm to achieve fast and effective compression of the CFOSAT dataset. In relative error-bounded mode, the Digit Rounding algorithm introduced in this work provides higher compression ratios than the Bit Grooming algorithm from which it derives, but with lower compression speed. Sz can provide even higher compression ratios but fails to achieve the high precision required for some variables. This is why we rather recommend the Digit Rounding algorithm to achieve relative error bounded compression of SWOT datasets with a compression ratio 30 % higher than the baseline solution for SWOT compression.
The Digit Rounding software source code is available from CNES GitHub at https://github.com/CNES/Digit_Rounding (last access: 26 August 2019). The datasets are available upon request to Xavier Delaunay (xavier.delaunay@thalesgroup.com) or to Flavien Gouillon (flavien.gouillon@cnes.fr). The Supplement details the datasets and provides the command lines used for running the compression tools.
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-12-4099-2019-supplement.
XD designed and implemented the Digit Rounding software and wrote most of the manuscript. AC performed most of the compression experiments and generated the analytical datasets. FG provided the scientific datasets used in the experiments, supervised the study, and contributed both to its design and to the writing of the manuscript.
The authors declare that they have no conflict of interest.
This work was funded by CNES and carried out at Thales Services. We would like to thank Hélène Vadon, Damien Desroches, Claire Pottier and Delphine Libby-Claybrough for their contributions to the SWOT section and for their help in proofreading. We also thank Charles S. Zender and the anonymous reviewers their comments, which helped improving the quality of this paper.
This research has been supported by the Centre National d'Etudes Spatiales (CNES) (grant no. 170850/00).
This paper was edited by Steve Easterbrook and reviewed by Charles Zender, Dingwen Tao, and one anonymous referee.
Baker, A. H., Hammerling, D. M., Mickelson, S. A., Xu, H., Stolpe, M. B., Naveau, P., Sanderson, B., Ebert-Uphoff, I., Samarasinghe, S., De Simone, F., Carbone, F., Gencarelli, C. N., Dennis, J. M., Kay, J. E., and Lindstrom, P.: Evaluating lossy data compression on climate simulation data within a large ensemble, Geosci. Model Dev., 9, 4381–4403, https://doi.org/10.5194/gmd-9-4381-2016, 2016.
Caron, J.: Compression by Scaling and Offset, available at: http://www.unidata.ucar.edu/blogs/developer/en/entry/compression_by_scaling_and_offfset (last access: 27 September 2018), 2014a.
Caron, J.: Compression by bit shaving, available at: http://www.unidata.ucar.edu/blogs/developer/entry/compression_by_bit_shaving (last access: 27 September 2018), 2014b.
Collet, Y.: LZ4 lossless compression algorithm, available at: http://lz4.org (last access: 27 September 2018), 2013.
Collet, Y. and Turner, C.: Smaller and faster data compression with Zstandard, available at: https://code.fb.com/core-data/smaller-and-faster-data-compression-with-zstandard/ (last access: 27 September 2018), 2016.
Deutsch, L. P.: DEFLATE compressed data format specification version 1.3, Tech. Rep. IETF RFC1951, Internet Engineering Task Force, Menlo Park, CA, USA, https://doi.org/10.17487/RFC1951, 1996.
Duda, J.: Asymmetric numeral systems: entropy coding combining speed of Huffman coding with compression rate of arithmetic coding, arXiv:1311.2540v2 [cs.IT], 2013.
Huffman, D. A.: A method for the construction of minimum redundancy codes, Proceedings of the IRE, 40, 1098–1101, https://doi.org/10.1109/JRPROC.1952.273898, 1952.
Lindstrom, P.: Fixed-Rate Compressed Floating-Point Arrays, IEEE T. Vis. Comput. Gr., 20, 2674–2683, https://doi.org/10.1109/TVCG.2014.2346458, 2014.
Lindstrom, P. and Isenburg, M.: Fast and Efficient Compression of Floating-Point Data, IEEE T. Vis. Comput. Gr., 12, 1245–1250, https://doi.org/10.1109/TVCG.2006.143, 2006.
Masui, K., Amiri, M., Connor, L., Deng, M., Fandino, M., Höfer, C., Halpern, M., Hanna, D., Hincks, A. D., Hinshaw, G., Parra, J. M., Newburgh, L. B., Shaw, J. R., and Vanderlinde, K.: A compression scheme for radio data in high performance computing, Astron. Comput., 12, 181–190, https://doi.org/10.1016/j.ascom.2015.07.002, 2015.
Silver, J. D. and Zender, C. S.: The compression-error trade-off for large gridded data sets, Geosci. Model Dev., 10, 413–423, https://doi.org/10.5194/gmd-10-413-2017, 2017.
Tao, D., Di, S., Chen, Z., and Cappello, F.: Significantly Improving Lossy Compression for Scientific Data Sets Based on Multidimensional Prediction and Error-Controlled Quantization, 2017 IEEE International Parallel and Distributed Processing Symposium (IPDPS), Orlando, FL, USA, 29 May–2 June 2017, 1129–1139, https://doi.org/10.1109/IPDPS.2017.115, 2017.
Tao, D., Di, S., Guo, H., Chen, Z., and Cappello F.: Z-checker: A Framework for Assessing Lossy Compression of Scientific Data, Int. J. High Perform. C., 33, 285–303, https://doi.org/10.1177/1094342017737147, 2019.
Zender, C. S.: Bit Grooming: statistically accurate precision-preserving quantization with compression, evaluated in the netCDF Operators (NCO, v4.4.8+), Geosci. Model Dev., 9, 3199–3211, https://doi.org/10.5194/gmd-9-3199-2016, 2016a.
Zender, C. S.: netCDF Operators (NCO), version 4.6.1, Zenodo, https://doi.org/10.5281/zenodo.61341, 2016b.
Ziv, J. and Lempel, A.: A universal algorithm for sequential data compression, IEEE T. Inform. Theory, 23, 337–343, https://doi.org/10.1109/TIT.1977.1055714, 1977.
- Abstract
- Introduction
- Compression algorithms
- The Digit Rounding algorithm
- Performance metrics
- Performance assessment with synthetic data
- Application to scientific datasets
- Conclusions
- Code and data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Compression algorithms
- The Digit Rounding algorithm
- Performance metrics
- Performance assessment with synthetic data
- Application to scientific datasets
- Conclusions
- Code and data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement