An optimization for reducing the size of an existing urban-like monitoring network for retrieving an unknown point source emission

This study presents an optimization methodology for reducing the size of an existing monitoring network of the sensors measuring polluting substances in an urban-like environment in order to estimate an unknown emission source. The methodology is presented by coupling the simulated annealing (SA) algorithm with the renormalization inversion technique and the computational fluid dynamics (CFD) modeling approach. This study presents an application of the renormalization data-assimilation theory for optimally reducing the size of an existing monitoring network in an urban-like environment. The performance of the obtained reduced optimal sensor networks is analyzed by reconstructing the unknown continuous point emission using the concentration measurements from the sensors in that optimized network. This approach is successfully applied and validated with 20 trials of the Mock Urban Setting Test (MUST) tracer field experiment in an urban-like environment. The main results consist of reducing the size of a fixed network of 40 sensors deployed in the MUST experiment. The optimal networks in the MUST urban region are determined, which makes it possible to reduce the size of the original network (40 sensors) to $\sim \mathrm{1}/\mathrm{3}$ (13 sensors) and 1∕4 (10 sensors). Using measurements from the reduced optimal networks of 10 and 13 sensors, the averaged location errors are obtained as 19.20 and 17.42 m, respectively, which are comparable to the 14.62 m obtained from the original 40-sensor network. In 80 % of the trials with networks of 10 and 13 sensors, the emission rates are estimated within a factor of 2 of the actual release rates. These are also comparable to the performance of the original network, whereby in 75 % of the trials the releases were estimated within a factor of 2 of the actual emission rates.

1 Introduction

In the case of an accidental or deliberate release of a hazardous contaminant in densely populated urban or industrial regions, it is important to accurately retrieve the location and the intensity of that unknown emission source for risk assessment, emergency response, and mitigation strategies by the concerned authorities. This retrieval of an unknown source in various source reconstruction methodologies is completely dependent on the contaminant's concentrations detected by some pre-deployed sensors in the affected area or a nearby region. However, the pre-deployment of a limited number of sensors in that region required an optimal strategy for the establishment of an optimized monitoring network to achieve maximum a priori information regarding the state of emission. It is also required to correctly capture the data while extracting and utilizing information from a limited and noisy set of concentration measurements. Establishing optimal monitoring networks for the characterization of unknown emission sources in complex urban or industrial regions is a challenging problem.

The problem of monitoring network optimization is complex and may consist of a first deployment of the sensors, updating an existing network, reducing the size of an existing network, or increasing the size of an existing network. These problems are independent and each one has its own requirements. The degree of complexity also depends on (i) the network type (mobile network deployed only in an emergency, permanent mobile network, permanent static network), (ii) the scale (local, regional, etc.), and (iii) the topography of the area of interest (flat terrain without obstacles, complex terrain, cities, urban, industrial regions, etc.). It is important to note that the optimization also depends on the objective of a network design, such as the reconstruction of an emitting source, analysis of the air quality, and/or the triggering of an alert. This study is focused on reducing the size of an existing network at a local scale in an urban-like terrain for source reconstruction.

This study presents an optimization methodology for reducing the size of an existing monitoring network in a geometrically complex urban environment. The measurements from a reduced optimal network can be used for the source term estimation (STE) of an unknown source in an urban region with almost the same level of source detection ability as the original network of a larger number of samplers. The establishment of an optimal network required sensor concentration measurements, along with the availability of meteorological data, an atmospheric dispersion model, the choice of an STE procedure, and an optimization algorithm. These types of networks can have great applications in the oil and gas industries for the estimation of emissions of greenhouse gases (GHGs) like methane. In order to utilize an inversion method to estimate methane emissions, accurate measurements of methane in a network of high-precision sensors downwind of a possible source are a prerequisite. However, these sensors may not be deployed in large numbers due to their high cost. Alternatively, low-cost sensors (which may not be as high precision) can rapidly be deployed specifically for collecting the initial measurements. Using these less accurate measurements and the proposed optimization methodology, a reduced optimal network can quickly be designed to provide the “best” positions for the deployment of high-precision sensors to obtain accurate methane measurements. These high-precision measurements can be utilized in an inversion method to estimate accurate methane emissions. A similar and very useful application of the method proposed here can be applied for the estimation of methane emissions from landfills.

Ko et al. (1995) showed that the optimization of sensor networks is an NP-hard (i.e., nondeterministic polynomial time hardness) problem, which means that it is difficult for an exhaustive search algorithm to solve all instances of the problem because it requires considerable time. Various optimization algorithms have been proposed to find the best solution, but these methods are not applicable to all cases, especially for large problems. To solve such problems, metaheuristic algorithms are efficient. Some studies have discussed the optimization of sensor distribution and number for gas emission monitoring; e.g., Ma et al. (2013), Ngae et al. (2019). Ma et al. (2013) used a direct approach with a Gaussian dispersion model to optimize sensor networks in homogeneous terrains. However, the present study utilizes an inverse approach by solving the adjoint transport–diffusion equation with a building-resolving computational fluid dynamics (CFD) model for an urban environment. This methodological approach for an optimal monitoring network (i.e., coupling of the optimization algorithm, inverse tracers transport modeling, and CFD) includes the geometric and flow complexity inherent in an urban region for the optimization process. Recently, for a different application point of view, Ngae et al. (2019) also described an optimization methodology for determining an optimal sensor network in an urban-like environment using the available meteorological conditions only. The CFD computations also required a considerable amount of time to compute the flow and dispersion in an urban environment. However, in order to apply the proposed methodology in an emergency situation for an area of interest in a complex urban or industrial environment, an archive database of CFD calculations can be established for a wide range of meteorological and turbulence conditions and can be utilized in the optimization process.

In this study, a simulated annealing (SA) stochastic optimization algorithm (Jiang et al., 2007; Abida et al., 2008; Abida and Bocquet, 2009; Saunier et al., 2009; Kouichi et al., 2016; Kouichi, 2017; Ngae et al., 2019) is utilized. The SA algorithm was designed in the context of statistical physics. It incorporates a probabilistic approach to explore the search space and converges iteratively to the solution. This algorithm is often used and recommended to solve the problems of sensor network optimization (Abida, 2010). The network optimization process consists of finding the best set of sensors that leads to the minimum of a defined cost function. A cost function can be defined as a regularized norm square of the distance between the measurements and forecasts, which is also used for the STE (Sharan et al., 2012). In this study, two canonical problems are considered independently. (i) The first is the optimization of the measuring network. Optimization consists of selecting the best positions of the sensors among a set of potential locations. This choice is operated in a search space constituted by all the possible networks (of a specific size) and based on a cost function that quantitatively describes the quality of the networks. (ii) The second is the identification of the unknown source. The STE is studied in the framework of a parametric approach. Here the challenge is to determine the parameters of the source (intensity and position) using measurements from the sensors of an optimally designed network.

The reduced optimal networks are validated using an STE technique to estimate the unknown parameters of a continuous point source. The STE problem for atmospheric dispersion events has been an important topic of much consideration as reviewed in Rao (2007) and Hutchinson et al. (2017). Often, the source term is estimated using a network of static sensors deployed in a region. In an inverse process for the STE, the adjoint source–receptor relationship, concentrations, and meteorological measurements are required. The adjoint source–receptor relationship is defined by an inverse computation of the atmospheric transport–dispersion model (Pudykiewicz, 1998). This relationship is often affected by nonlinearities in the flow field by building effects in complex scenarios arising in urban environments, where the backward and forward dispersion concentrations will not match. Various inversion methods can be classified in two major categories: probabilistic and deterministic. The probabilistic category treats source parameters as random variables associated with the probability distribution. This includes the Bayesian estimation theory (Bocquet, 2005; Monache et al., 2008; Yee et al., 2014), Monte Carlo algorithms using Markov chains (MCMC) (Gamerman and Lopes, 2006; Keats, 2009), and various stochastic sampling algorithms (Zhang et al., 2014, 2015). Deterministic methods use cost functions to assess the difference between observed and modeled concentrations and are based on an iterative process to minimize this difference (Seibert, 2001; Penenko et al., 2002; Sharan et al., 2012). Among the other approaches, advanced search algorithms like the genetic algorithm (Haupt et al., 2006), the neural network algorithm (Wang et al., 2015), and other regularization methods (Ma et al., 2017; Zhang et al., 2017) have been used for the STE. In this study, we utilized the renormalization inversion method (Issartel, 2005) for the STE using measurements from the optimal networks, which is deterministic in nature and does not require any prior information on the source parameters. The renormalization inversion approach was successfully applied and validated for the retrieval of an unknown continuous point source in flat terrain (Sharan et al., 2009) and also in an urban-like environment (Kumar et al., 2015b). Initially, the renormalization inversion method was proposed to estimate emissions from the distributed sources (Issartel, 2005). Sharan et al. (2009) and other studies have shown that this technique is also effective for estimating continuous point sources. For these applications, the hypothesis of a linear relationship between the receptor and the source was assumed. For homogeneous terrains, the adjoint functions can analytically be computed based on the Gaussian solution of the diffusion–transport equation to estimate a continuous point release. However, the flow field in urban or industrial environments is quite complex, and the asymmetry of the flow and the dispersed plume in urban regions is generated mainly by the presence of buildings and other structures. In general, Gaussian models are unable to capture the effects of complex urban geometries on adjoint sensitivities between sources and receptors, and if dense gases are involved, the Gaussian distribution hypothesis fails. Recently, Kumar et al. (2015b, 2016) have extended the applications of the renormalization inversion technique to retrieve an unknown emission source in urban environments, whereby a CFD approach was used to generate the adjoint receptor–source relationship. In this process, a coupled CFD–renormalization source reconstruction approach was described for the identification of an unknown continuous point source located at the ground surface or at a horizontal plane corresponding to a known or predefined altitude above the ground surface or an elevated release in an urban area.

This study deals with a case of optimally reducing the size of an existing monitoring network. For this purpose, a predefined network of sensors deployed in an area of interest is considered to determine an optimized network with a smaller number of sensors but with comparable information. This work explores two requirements of the optimal networks that modify the spatial configuration of an existing network by moving the sensors and also reducing the number of sensors of an existing large network. In real situations, this methodology can be applied for the optimization of mobile networks deployed in an emergency situation. The methodological approach to optimally reduce the size of an existing monitoring network in an urban environment is presented by coupling the SA stochastic algorithm with the renormalization inversion technique and the CFD modeling approach. The concentration measurements obtained from the optimally reduced sensor networks in 20 trials of the Mock Urban Setting Test (MUST) field tracer experiment are utilized to validate the methodology by estimating an unknown continuous point source in an urban-like environment.

2 Source term estimation method: the renormalization

In the context of an inversion approach, source parameters are often determined using concentration measurements at the sensor locations and a source–receptor relationship. The release is considered continuous from a point source located at the ground or at a horizontal plane corresponding to an altitude of a known source height. Since the optimization methodology presented in the next section utilizes some concepts from the renormalization inversion methodology (Sharan et al., 2009), the renormalization theory to estimate a continuous point release is briefly presented in the following subsections.

2.1 Source–receptor relationship

A source–receptor relationship is an important concept in the source reconstruction process and it can be linear or nonlinear. This study deals with the linear relationship because except for nonlinear chemical reactions, most of the other processes occurring during the atmospheric transport of trace substances are linear: advection, diffusion, convective mixing, dry and wet deposition, and radioactive decay (Seibert and Frank, 2004). A source–receptor relationship between the measurements and the source function is defined based on a solution of the adjoint transport–diffusion equation that exploits the adjoint functions (retroplumes) corresponding to each receptor (Pudykiewicz, 1998; Issartel et al., 2007). These retroplumes provide sensitivity information between the source position and the sensor locations. Let us consider a discretized domain of N grid cells in a two-dimensional space $\mathbf{x}=(x,y)$, a vector of M concentration measurements $\mathit{\mu }=({\mathit{\mu }}_{\mathrm{1}},{\mathit{\mu }}_{\mathrm{2}},\mathrm{\dots },{\mathit{\mu }}_M{)}^T\in {\mathbb{R}}^M$, and an unknown source vector s(x)∈ℝ^N to estimate. The measurements μ are related to the source vector s by the use of sensitivity coefficients (also referred to as adjoint functions) (Hourdin and Talagrand, 2006). The sensitivity coefficients describe the backward propagation of information from the receptors toward the unknown source. These vectors are related by the following linear relationship:

$$\begin{array}{}\text{(1)}& \mathit{\mu }=\mathbf{As}+\mathit{ϵ},\end{array}$$

where ϵ∈ℝ^M is the total measurement error and $\mathbf{A}\in {\mathbb{R}}^{M\times N}$ is the sensitivity matrix with $\mathbf{A}\left(\mathbf{x}\right)=\left[\mathbf{a}\right({\mathbf{x}}_{\mathrm{1}}),\mathbf{a}({\mathbf{x}}_{\mathrm{2}}),\mathrm{\dots },\mathbf{a}({\mathbf{x}}_N\left)\right]$. Here, each column vector a(x_i)∈ℝ^M of the matrix A represents the potential sensitivity of a grid cell with respect to all M concentration measurements.

For a given set of concentration measurements μ, the source estimate function s(x) in Eq. (1) can easily be estimated by formulating a constrained optimization problem. This optimization problem minimizes a cost function J(s)=s^Ts, subjected to a constraint $\mathit{ϵ}=\mathit{\mu }-\mathbf{As}=\mathrm{0}$. Using the method of Lagrangian multipliers, s(x) can be estimated as a least-norm solution:

$$\begin{array}{}\text{(2)}& \mathbf{s}={\mathbf{A}}^T{\mathbf{H}}^{-\mathrm{1}}\mathit{\mu },\end{array}$$

where H⁻¹ is the inverse of the Gram matrix H=AA^T. This estimate (Eq. 2) is not satisfactory because it generates artifacts at the grid cells corresponding to the measurement points. Adjoint functions become singular at these points and have very large values. These large values do not represent a physical reality but rather artificial information. This was highlighted by Issartel et al. (2007), who reduced this artificial information by a process of renormalization.

2.2 Renormalization process

This process involves a weight function $\mathbf{W}\left(\mathbf{x}\right)\in {\mathbb{R}}^{N\times N}$ in space, which is purely a diagonal matrix with the diagonal elements w_jj>0 such that $\sum _{i=\mathrm{1}}^N{w}_{jj}=M$. The introduction of W transforms the source–receptor relationship in Eq. (1) to

$$\begin{array}{}\text{(3)}& \mathit{\mu }={\mathbf{A}}_{\mathrm{w}}\mathbf{Ws}+\mathit{ϵ},\end{array}$$

where the modified sensitivity matrix A_w is defined as ${\mathbf{A}}_{\mathrm{w}}={\mathbf{AW}}^{-\mathrm{1}}=\left[{\mathbf{a}}_{\mathrm{w}}\right({\mathbf{x}}_{\mathrm{1}}),{\mathbf{a}}_{\mathrm{w}}({\mathbf{x}}_{\mathrm{2}}),\mathrm{\dots },{\mathbf{a}}_{\mathrm{w}}({\mathbf{x}}_N\left)\right]$ in which the column vector ${\mathbf{a}}_{\mathrm{w}}\left({\mathbf{x}}_i\right)=\mathbf{a}\left({\mathbf{x}}_i\right)/w\left({\mathbf{x}}_i\right)$ of A_w is the weighted sensitivity vector at x_i. Considering a similar approach as outlined in the previous subsection, a new constrained optimization problem can be formulated for Eq. (3) to estimate s(x). This optimization problem minimizes a cost function J(s)=s^TWs, subjected to a constraint $\mathit{ϵ}=\mathit{\mu }-{\mathbf{A}}_{\mathrm{w}}\mathbf{Ws}=\mathrm{0}$, and deduces the following expression s_w of s (Appendix A in Kumar et al., 2016):

$$\begin{array}{}\text{(4)}& {\mathbf{s}}_{\mathrm{w}}={\mathbf{A}}_{\mathrm{w}}^T{\mathbf{H}}_{\mathrm{w}}^{-\mathrm{1}}\mathit{\mu },\end{array}$$

where ${\mathbf{H}}_{\mathrm{w}}^{-\mathrm{1}}$ is the inverse of ${\mathbf{H}}_{\mathrm{w}}={\mathbf{A}}_{\mathrm{w}}{\mathbf{WA}}_{\mathrm{w}}^T$.

The weight function in the above-discussed renormalization process is computed by using an iterative algorithm proposed by Issartel et al. (2007) (Appendix A). A brief derivation for the estimation of an unknown point source (i.e., location and intensity) from the renormalization inversion is described in Appendix B.

3 The combinatorial optimization of a monitoring network

A predefined large network of n sensors deployed in an area of interest is considered to determine an optimized network with a smaller number of sensors but with comparable information. For a given number of p sensors such that p<n, one determines an array of p sensors among n, which delivers a maximum of information. It is a combinatorial optimization problem that consists of choosing p sensors among n, thus constituting an optimal network. The optimal network will consist of p sensors for which a defined cost function is minimum. The number of possible choices ⁿC_p (number of combinations of p among n) is very high when an initial network is sufficiently instrumented (n large) and p is small with respect to n. As the number of combinations to be tested is very large, the minimum of a cost function will be evaluated by a stochastic algorithm, viz. simulated annealing (SA).

3.1 Cost function

A cost function is defined (based on renormalization theory) as a function that minimizes the quadratic distance between the observed and simulated measurements according to the H_w norm (Issartel et al., 2012), where H_w is the Gram matrix defined in Sect. 2.2. A cost function (say J_s(x)) to minimize is defined (Appendix C) as follows:

$$\begin{array}{}\text{(5)}& J_{\mathrm{s}}\left(\mathbf{x}\right)=\mathrm{1}-{\displaystyle \frac{{\mathbf{s}}_{\mathrm{w}}^{\mathrm{2}}}{{\mathit{\mu }}^T{\mathbf{H}}_{\mathrm{w}}^{-\mathrm{1}}\mathit{\mu }}},\end{array}$$

where s_w is given by Eq. (4). A global minimum of the cost function J_s(x) is evaluated by the SA algorithm.

3.2 Simulated annealing (SA) algorithm for the sensor's network optimization

The problem of optimization of a network is solved using a simulated annealing algorithm. The SA optimization algorithm is utilized here for the determination of the optimal networks by comparing its performance with the genetic algorithm (GA) (Kouichi, 2017). These algorithms of different search techniques (SA probabilistic and GA evolutionary) are evaluated based on the same cost function. The results showed that the optimal networks retained by the GA and the SA are quantitatively and qualitatively comparable (Kouichi, 2017). SA is advantageous because it is relatively easy to implement and takes smaller computational time in comparison to GA. Both the SA and GA optimization algorithms in the framework of this approach (based on renormalization theory) have little influence on the estimation of the parameters of a source (Kouichi, 2017).

SA is a random optimization technique based on an analogy with thermodynamics. The technique was introduced to computational physics over 60 years ago in the classic paper by Metropolis et al. (1953). The algorithm of simulated annealing is initiated by starting from an admissible network. At the subsequent steps, the system moves to another feasible network, according to a prescribed probability, or it remains in the current state. However, it is crucial to explain how this probability is calculated. The mobility of the random walk depends on a global parameter T, which is interpreted as “temperature”. The initial values of T are large, allowing for the free exploration of large extents of the state space (this corresponds to the “melted state” in terms of the kinetic theory of matter). In the subsequent steps, the temperature is lowered, allowing the algorithm to reach a local minimum.

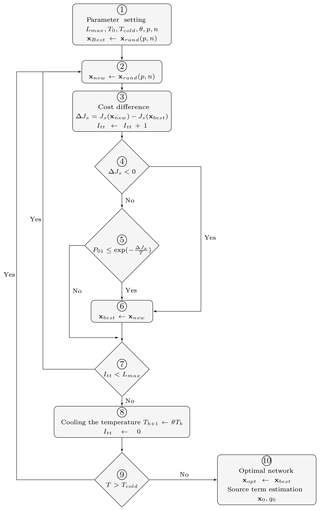
For SA, each network is considered as a state of a virtual physical system, and the objective function is interpreted as the internal energy of this system in a given state. According to statistical thermodynamics, the probability of a physical system to be in the same state follows the Boltzmann distribution and depends on its internal energy and the temperature level. By analogy, the physical quantities (temperature, energy, etc.) become pseudo-quantities. And during the minimization process, the probabilistic treatment consists of accepting a new network selected in the neighborhood of the current network following the same Boltzmann distribution and depending on both the cost difference between the new and current networks and on the pseudo-temperature (simply called temperature). To find the solution, SA incorporates the temperature into a minimization procedure. So at high temperature (i.e., starting temperature), the space of solution is widely explored, while at lower temperature the exploration is restricted. The algorithm is stopped when the cold temperature is reached. It is necessary to choose the law of decreasing temperature, called the cooling schedule. Different approaches to parameterize SA are explored in Siarry (2016). Kirkpatrick et al. (1983) proposed an average probability to determine the initial (starting) temperature. Nourani and Andresen (1998) compared the widely used cooling schedules (exponential, logarithmic, and linear). The SA algorithm starts the minimization of an objective function at annealing temperature from a single stochastic point, and then it searches for the minimal solutions by attempting all the points in the search domain with respect to their temperature value. The algorithm is depicted in a flow diagram in Fig. 2, and a step-by-step implementation of the SA procedure for an optimized monitoring network in an urban environment is described as follows.

Step 1. Parameter setting and initialization

Network parameters (n and p). The variable n is the number of possible locations of the sensors and p is the optimal network number of sensors.

Starting temperature (T₀). T₀ is also called the highest temperature. It was determined from the Metropolis law: $T_{\mathrm{0}}=-\frac{\stackrel{\mathrm{‾}}{\left(\mathrm{\Delta }{J}_{\mathrm{s}}\right)}}{\log \left(P_{\mathrm{0}}\right)}$, where $\stackrel{\mathrm{‾}}{\left(\mathrm{\Delta }{J}_{\mathrm{s}}\right)}$ is an average of the difference of cost functions calculated for a large number of cases. P₀ is an acceptance probability and following the recommendations of Kirkpatrick et al. (1983), it was set to 0.8. Start iterations (I_tt=0).

Length of the bearing (L_max). The length of the bearing is the number of iterations to be performed at each temperature level. An equilibrium is reached for this number of iterations and any significant improvement of the cost function can be expected. No general rule is proposed to determine a suitable length. This number is often constant and proportional to the size of the problem.

The temperature decay factor (θ). The temperature remains constant for L_max iterations corresponding to each bearing. We used the exponential schedule due to its efficiency as denoted by Nourani and Andresen (1998). Then, as the temperature decreases the law between two bearings varies as $T_{b+\mathrm{1}}=\mathit{\theta }{T}_b$, with $\mathrm{0}<\mathit{\theta }<\mathrm{1}$, where b represents a bearing. So, a decay pattern was retained by the bearings.

The cold temperature (T_cold). T_cold is often called the stopping temperature. There is no clear rule to set this parameter. It is possible to stop calculations when no improvement in the cost function is observed during a large number of combinations. One can estimate this number and take into account the maximum length L_max of each bearing; thus, the cold temperature can be expressed as a fraction of the starting temperature T₀.

Assigning the first best set of sensors, ${\mathbf{x}}_{\mathrm{Best}}\leftarrow {\mathbf{x}}_{\mathrm{rand}}(p,n)$. The variable x_rand(p,n) corresponds to a vector of p sensor locations randomly chosen among the n possible locations. A new solution is randomly explored. This vector is assigned to the first best set of sensors.

Step 2. Assigning a new set of sensors

This step involves ${\mathbf{x}}_{\mathrm{new}}\leftarrow {\mathbf{x}}_{\mathrm{rand}}(p,n)$, where x_rand(p,n) corresponds to a vector of p sensors locations randomly chosen among the n possible locations. This vector is assigned to a new set (x_new) of sensors.

Step 3. Cost difference

Given a sensor location x_new, the cost function J_s(x_new) is computed as follows:

• set the μ vector by using the measurements at the x_new locations;

• set rows of matrix A using the sensitivity at the x_new locations;

• determine w(x), H_w, and a_w iteratively using the algorithm in Eq. (A2);

• compute the source term s_w(x) using Eq. (4) and

• compute the cost function J_s(x_new) using Eq. (5).

J_s(x_best) is computed like J_s(x_new) using the same precedent steps. A cost difference is then calculated using $\mathrm{\Delta }{J}_{\mathrm{s}}=J_{\mathrm{s}}\left({\mathbf{x}}_{\mathrm{new}}\right)-J_{\mathrm{s}}\left({\mathbf{x}}_{\mathrm{best}}\right)$. Increment the iterations $(I_{\mathrm{tt}}\leftarrow I_{\mathrm{tt}}+\mathrm{1})$.

Step 4. Test of sign of ΔJ_s

If ΔJ_s<0, the error associated with x_new is less than that with x_best, and thus x_new will become the next “best network” (step 6). If this condition is not satisfied, the algorithm can jump out of a local minimum (step 5).

Step 5. Conditional jump

When ΔJ_s>0, the algorithm has the ability to jump out of any local minima if the condition $P_{\mathrm{01}}\le \exp (-\frac{\mathrm{\Delta }{J}_{\mathrm{s}}}{T})$ is satisfied, where P₀₁ is the acceptance probability (a random number between 0 and 1), and T is the current annealing temperature. It means that x_new will be the next best network even if the associated error is greater than that of x_best. If $P_{\mathrm{01}}>\exp (-\frac{\mathrm{\Delta }{J}_{\mathrm{s}}}{T})$, go to step 7.

Step 6. Update x_best

In this step, x_best is updated by x_new.

Step 7. Maximum iteration check

If the maximum number of iterations of a bearing (L_max) is reached, a state of equilibrium is then achieved for this temperature and one can cool the actual temperature (step 8). If not, continue iterations (step 2).

Step 8. Temperature cooling

Temperature is cooled using the cooling schedule and the iteration variable is reset to zero.

Step 9. Cold temperature test

The cold temperature (T_cold) is also known as the stopping temperature. If this temperature is reached, the algorithm is stopped. When T_cold is not reached, other temperature bearings are performed using the cooling schedule.

Step 10. Optimal network

At this step, the last best network x_best is the optimal network. Source parameters are then estimated using the concentration measurements and retroplumes only for sensors from the obtained optimal network as follows: (i) x₀ is estimated at the position of the maximum of the source estimate function s_w(x), and (ii) the intensity q₀ is given by $q_{\mathrm{0}}={\mathbf{s}}_{\mathrm{w}}\left({\mathbf{x}}_{\mathrm{0}}\right)/w\left({\mathbf{x}}_{\mathrm{0}}\right)$.

In stochastic optimization algorithms, especially in SA, it was observed that there is no guarantee for the convergence of the algorithm with such a strong cooling (Cohn and Fielding, 1999; Abida et al., 2008). However, chances are that a near-optimal network configuration can be reached. Due to this, one or more near-optimal networks can be obtained from this methodology that satisfy the conditions of a nearly overall optimum condition.

4 The Mock Urban Setting Test (MUST) tracer field experiment

The MUST field experiment was conducted by the Defense Threat Reduction Agency (DTRA) in 2001. It aimed to help develop and validate numerical models for flow and dispersion in an idealized urban environment. The experimental design and observations are described in detail in Biltoft (2001) and Yee and Biltoft (2004). In this experiment, an urban canopy was represented by a grid of 120 containers. These containers were arranged along 12 rows and 10 columns on the army ground in the Utah desert, USA. Each container has dimensions of 2.54 m high, 12.2 m long, and 2.42 m wide. The spacing between the horizontal lines is 12.9 m, while the columns are separated by a distance of 7.9 m. The total area thus formed is approximately 200×200 m². The experiment consists of 63 releases of a flammable gas (propylene C₃H₆) that is not dangerous or harmful in quantities and could be released through the dissemination system into the open atmosphere (Biltoft, 2001). Different wind conditions (direction, speed, atmospheric stability) as well as different positions for gas emissions (inside or outside the MUST urban canopy at different heights) were considered. These gas emissions were carried out under stable, very stable, and neutral stability conditions. In this study, 20 trials in various atmospheric stability conditions are selected and the meteorological variables are taken from an analysis of meteorological and micro-meteorological observations in Yee and Biltoft (2004) (Table 1). It is noted that the errors related to meteorological data can affect the accuracy of the source term estimation (Zhang et al., 2014, 2015), although this error is not considered in this study. In each trial, the gas was continuously released for ≈15 min, during which concentration measurements were made. These concentration measurements were carried out by 48 photoionization detectors (PIDs); 40 sensors were positioned on four horizontal lines at 1.6 m of height (Fig. 1), and 8 sensors were deployed in the vertical direction at a tower located approximately in the center of the MUST array.

Table 1 The meteorological values (wind speed (S₀₄), wind direction (α₀₄) at 4 m level of mast S), turbulence (the Obukhov length (L), friction velocity (u_*), turbulent kinetic energy (k) at 4 m level of tower T), and source parameters (source height (z_s), release duration (t_s), release rate (q_s)) in 20 selected trials of the MUST field experiment (Biltoft, 2001; Yee and Biltoft, 2004). Here, trial nos. 1–20 are assigned for continuation and simplicity, but these do not correspond to the same assigned trial number for a given trial name in the MUST experiment.

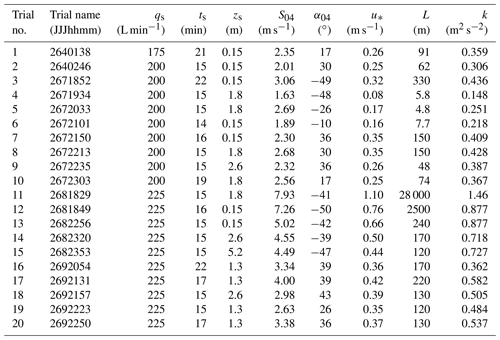
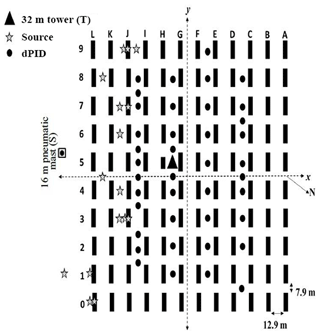
Figure 1 A schematic diagram of the MUST geometry showing 120 containers and source (stars) and receptor (black filled circles) locations. In a given trial only one source was operational.

Figure 2 Flow diagram of the simulated annealing procedures to determine an optimized monitoring network.

5 CFD modeling for retroplumes in an urban environment

The flow field in atmospheric dispersion models in geometrically complex urban or industrial environments cannot be considered homogeneous throughout the computational domain. This is because the buildings and other structures in that region influence and divert the flow into unexpected directions. Consequently, the dispersion of a pollutant and computations of the adjoint functions (retroplumes) are affected by the flow field induced by these structures in an urban region. Recently, Kumar et al. (2015a) utilized a CFD model to compute the flow field and forward dispersion in 20 trials of the MUST field experiment. In order to reconstruct an unknown continuous point source, the computed flow field is then used to compute the retroplumes for all selected trials (Kumar et al., 2015b). The CFD computations of the flow field presented in Kumar et al. (2015a) and retroplumes computed in Kumar et al. (2015b) are utilized in the proposed optimization methodology described in this study to obtain optimal monitoring networks. In these studies, the CFD model fluidyn-PANACHE was utilized to calculate the flow field, considering a subdomain of calculation (whose dimensions are 250×225 m² with a height of 100 m) that consists of the MUST urban array created by the containers, sources, receptors, and other instruments in this experiment. This subdomain is embedded in a larger computational domain (dimensions of 800×800 m² with a height of 200 m) to ensure a smooth transition of the flow between the edges of the domain and the obstacle zone. This extension of the outer domain far from the main experimental site is essential to reduce effects of the inflow boundary conditions imposed at the inlet of the outer domain. A more detailed description of the CFD model and its simulations for the MUST field experiment, e.g., boundary conditions and the turbulence model, is presented in Kumar et al. (2015a) and briefly discussed in the Supplement. An unstructured mesh was generated in both domains with more refinement in the urbanized area in the inner subdomain and at the positions of the receptors, thus generating 2 849 276 meshes.

The simulation results with fluidyn-PANACHE in each MUST trial were obtained with inflow boundary conditions from vertical profiles of the wind (U), the turbulent kinetic energy (k), and its dissipation rate (ϵ). These inflow profiles include the following: (i) a wind profile as in Gryning et al. (2007), which includes profiles in stable and neutral conditions and a profile based on the stability function by Beljaars and Holtslag (1991) in very stable conditions; (ii) a temperature profile, which includes logarithmic profiles based on Monin–Obukhov similarity theory; and (iii) turbulence profiles, in which k and ϵ profiles are based on an approximate analytical solution of one-dimensional k−ϵ prognostic equations (Yang et al., 2009). The atmospheric stability effects in the CFD model fluidyn-PANACHE are included through the inflow boundary condition (via advection). The fluidyn-PANACHE model includes a planetary boundary layer (PBL) model that serves as an interface between the meteorological observations and the boundary conditions required by the CFD solver. The observed turbulence parameters, e.g., (i) sensible heat flux (Q_h), the Obukhov length (L), (iii) surface friction velocity (u_*), and the temperature scale (θ_*), were used to derive the vertical profiles of mean velocity and potential temperature. As an example, the wind velocity vectors around some containers for trial 11 are shown in Fig. S1.1 in the Supplement. This figure shows the deviations in the wind speed and its direction due to the obstacles in an urban-like environment. It should be noted that the MUST experiment took place under neutral to stable and strongly stable conditions. However, the only atmospheric stability effects included in the CFD model are through the specification of inflow boundary conditions. Atmospheric stability has a profound impact on dispersion and would thus influence the adjoint functions. However, as presented and discussed in our previous study (Kumar et al., 2015a), even with specification of the stability-dependent inflow boundary conditions only, the predicted forward concentrations from the CFD model are in good agreement with the measured concentrations for all 20 trials in different atmospheric stability conditions. However, at microscales, small irregularities can also break the repeated flow patterns found in a regular array of containers with an identical shape (Qu et al., 2011). In addition, uncertainties associated with the thickness and the properties of the material of the container wall also affect flow pattern and the resulting concentrations and adjoint functions (Qu et al., 2011). Accordingly, the atmospheric stratification and stability effects should also be included through surface cooling or heating in the CFD model as well as stability effects from inflow boundary conditions. Since the released gas propylene is heavier than air and behaves as a dense gas, a buoyancy model was used to model the body force term in the Navier–Stokes equations. The buoyancy model is suitable for the dispersion of heavy gases for which a density difference in the vertical direction drives the body force.

In order to compute the retroplumes in each MUST trial, first the CFD simulations were performed to compute the converged flow field in the computational domain. Second, the flow field is reversed and used in the standard advection–diffusion equation to compute the adjoint functions a_i(x). In this computation of the retroplumes corresponding to each receptor in a selected trial, the advection–diffusion equation is solved by considering a receptor as a virtual point source with a unit release rate at the height of that receptor. Also, the meteorological conditions remained invariant during the whole experimental period in a trial. Details about the retroplumes and the correlated theory of duality verification (i.e., comparison of the concentrations predicted with the forward (direct) model and the adjoint model) for all 20 trials of the MUST field experiment are given in Kumar et al. (2015b), and we have utilized the same retroplumes in this study for the optimization process. Since we are concerned with establishing an optimized monitoring network in a domain that contains the MUST urban array, the retroplumes are computed in the inner subdomain only. Consequently, all the computations for an optimized monitoring network were carried out in the inner subdomain only. The sensors in the optimized monitoring network are intended to deploy at a fixed vertical height above the ground surface. Accordingly, the retroplumes corresponding to only 40 receptors at 1.6 m of height were utilized in computations for the optimized monitoring networks in the MUST urban environment.

6 Results and discussion

The calculations were performed by coupling the SA algorithm to a deterministic renormalization inversion algorithm and the CFD adjoint fields to optimally reduce the size of an existing monitoring network in an urban-like environment of the MUST field experiment. The network optimization process consists of finding the best set of sensors that leads to the lowest cost function. In this study, the validation is realized following two separate steps. The first step consists of forming two optimal monitoring networks by using the presented optimization methodology, which makes it possible to reduce the size of an original network of 40 sensors to approximately one-third (13 sensors) and one-fourth (10 sensors). The second step consists of comparing the a posteriori performance of the obtained reduced-size optimal networks with the MUST original network of 40 sensors at 1.6 m above the ground surface. In first step, a comparison (based on a cost function) with networks of the same size (e.g., 10 sensors) was implicitly performed during the optimization process. As the SA is an iterative algorithm, during the optimization process networks of the same size are compared at each iteration and the best one is retained. The networks have also been generated randomly like in Efthimiou et al. (2017); however, the search space of the problem is very large. In our case, the number of compared networks is equivalent to the number of iterations (as an example for an optimal network of 10 sensors, $\sim \mathrm{3}\times {\mathrm{10}}^{\mathrm{4}}$ configurations are compared). Here, the comparison is based on a cost function and inspired by the renormalized data-assimilation method. The cost function quantifies the quadratic distance between the observed and the simulated measurements. The “optimal network” produces the best description of the observations (i.e., corresponds to the minimal quadratic distance) and permits the a posteriori estimation of the location and emission rate of an unknown continuous point source in an urban-like environment.

The size of the MUST predefined (original) network is 40 sensors, and the sizes of the optimized networks are fixed after performing a first optimization with the number of sensors from 4 to 16 (Kouichi, 2017). This first evaluation showed that for some trials, a small number of sensors could not allow for the correct reconstruction of the source, and divergences in the calculations have been noted. Accordingly, the source estimation obtained for different trials and network sizes shows that, very often, networks of fewer than eight sensors may not characterize the source correctly. On the other hand, beyond 13 sensors, the source estimation is not significantly improved, and the associated errors were roughly constant (Kouichi, 2017). Therefore, in order to ensure an acceptable estimate of the source for all the trials, the sizes of the optimized network are fixed as 10 and 13 sensors (1∕4 and $\sim \mathrm{1}/\mathrm{3}$, respectively, of the original network of 40 sensors).

The optimization calculations were performed using MATLAB on a computer with the configuration Intel^® Core^™ i7-4790 CPU @ 3.60 GHz and 16 GB of RAM. The averaged computational time for the optimization of one 10-sensor network was ≈2.5, and it was ≈8.5 h for the 13-sensor network. In computations, a value of parameter T₀=10 was fixed according to the scale of the cost function and using the methodology described in step 1, and $T_{\mathrm{cold}}={\mathrm{10}}^{-\mathrm{13}}$ was used for both optimal sensor networks; θ is a decay factor of the temperature for an exponential cooling schedule that describes a procedure of the temperature decrease. The best cooling schedule is the exponential decay as demonstrated by Nourani and Andresen (1998) and Cohn and Fielding (1999); θ was fixed as 0.9 following the recommendation in the literature (Siarry, 2014). This value allows for sufficiently slow cooling in order to give more chances for the algorithm to explore a large search space and to avoid the local minima. L_max is taken as 100 and 200 for the 10- and 13-sensor networks, respectively, following the recommendation in Siarry (2014) and according to the number of possible combinations that increases with the number of sensors (8.5×10⁸ for 10 sensors and 1.2×10¹⁰ for 13 sensors).

Figure 3 The optimal networks of 10 (a–c) and 13 sensors (d–f), respectively, for trials 5 (very stable), 11 (neutral), and 19 (stable). Blank and filled black circles respectively represent all (40) potential positions and the optimal positions of sensors.

Figure 3 shows the optimal networks of 10 and 13 sensors, respectively, for three representative trials in the MUST urban array: trials 5 (very stable), 11 (neutral), and 19 (stable). These three trials correspond to one trial each in neutral, stable, and very stable atmospheric conditions during the release. The optimal monitoring networks of 10 and 13 sensors for all 20 selected MUST trials are shown in Figs. S2.1 and S2.2.

In order to analyze the performance of the optimal monitoring configurations of smaller sizes, source reconstructions were performed to estimate the unknown location and the intensity of a continuous point release. These source reconstruction results were obtained using the information from the optimal monitoring networks formed by 10 and 13 sensors in each MUST trial. In this performance evaluation process, the retroplumes and the concentration measurements were utilized from the sensors corresponding to these optimal networks. The retroplumes were computed using CFD simulations, considering the dispersion in a complex terrain. The source reconstruction results from both the optimal monitoring networks were also compared with results computed from the initial MUST network formed by 40 sensors (Kumar et al., 2015b). As in practice, the number of measurements is limited, but this comparison allowed for the conclusion that in urban areas, the optimal reduction of a network size is possible without significantly degrading its efficiency for source estimation.

Table 2 Source estimation results from the different monitoring networks for each selected trial of the MUST field experiment. $E_l^p$ and $E_q^p$ respectively denote the location error (m) and ratio of the estimated to true source intensity with the corresponding monitoring network. Here, the superscript p on $E_l^p$ and $E_q^p$ represents the number of sensors in an optimal network. “Skeleton” refers to the number of sensors common to the optimal networks of 10 and 13 sensors for a given MUST trial.

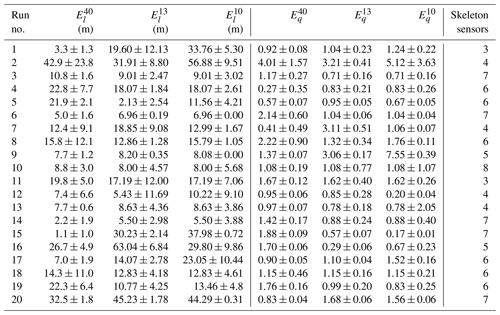
Source estimation results from the different monitoring networks are shown in Table 2 for all 20 selected trials of the MUST experiment. These results are presented in terms of the location error $\left(E_l^p\right)$, which is an Euclidean distance between the estimated and the true source location, and $E_q^p$ is a ratio of the estimated to the true source intensity. The corresponding monitoring network is represented by a superscript p (representing the number of sensors in an optimal network) on $E_l^p$ and $E_q^p$. In order to quantify the uncertainty, 10 % Gaussian noise was added at each measurement. Accordingly, 50 simulations for the source reconstruction were performed with these noise measurements using the optimal networks for each trial. The average and the standard deviation of $E_l^p$ and $E_q^p$ are calculated, and the results are also presented in Table 2.

For a given trial, the skeleton parameter represents the common sensors between two optimal networks of different sizes (with 10 and 13 sensors). These results show that the SA algorithm coupled with renormalization inversion theory and the CFD modeling approach succeeded in reducing the size of an existing larger network to estimate unknown emissions with similar accuracy in an urban environment.

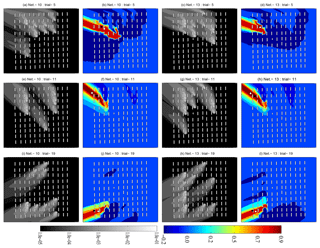
Figure 4 Isopleths of the renormalized weight function (w(x)) (gray in first and third columns) and the normalized source estimate function $\left({\mathbf{s}}_{\mathrm{w}}^n\right(\mathbf{x})={\mathbf{s}}_{\mathrm{w}}(\mathbf{x})/max({\mathbf{s}}_{\mathrm{w}}\left(\mathbf{x}\right)\left)\right)$ (colored in second and fourth columns) for both optimal networks of 10 and 13 sensors, respectively, for trials 5 (very stable), 11 (neutral), and 19 (stable). The black and white filled circles respectively represent the true and estimated source locations.

Figure 4 shows isopleths of the renormalized weight function (also called the visibility function) and the normalized source estimate function ${\mathbf{s}}_{\mathrm{w}}^n\left(\mathbf{x}\right)={\mathbf{s}}_{\mathrm{w}}\left(\mathbf{x}\right)/max\left({\mathbf{s}}_{\mathrm{w}}\right(\mathbf{x}\left)\right)$ corresponding to both optimal monitoring networks for three representative trials (e.g., 5, 11, and 19) of the MUST experiment. These isopleths for all 20 selected MUST trials are shown in Fig. S3. As already discussed in the literature, the visibility function includes the natural information associated with a monitoring network for source retrieval in a domain and physically interprets the extent of regions seen by the network (Issartel, 2005; Sharan et al., 2009). This function is independent of the effective values of the concentration measurements and depends only on the geometry of the monitoring network. Hence, this leads to a priori information about the unknown source apparent to the monitoring network. A statistical parameter, a factor of g (FAg), for the source reconstruction results from each monitoring network is presented in Table 3, where FAg represents the percentage of trials in which the source intensity is estimated within a factor of g of the actual emission rates. The statistics calculated with the original 40-sensor network show that the average location error for all 20 trials is 14.62 m, and in 75 % of the trials, the intensity of the source is estimated within a factor of 2 of the actual emission rates. In 90 % of the trials, intensity was estimated within a factor of 3, and it was estimated within a factor of 4 in 95 % of the trials (Table 3). If trial 2 is considered, large location errors (greater than 30 m) and intensity values ranging between a factor of 3 and 5 were observed (Table 2) independently of the number of sensors in the networks. If we consider trials 15, 16, and 20, it was noted from the numerical results that larger location errors do not necessarily correspond to high intensity errors (Table 2).

Table 3 Statistics for the source reconstruction results from each monitoring network. Here, $E_l^p$ is the averaged location error for all 20 trials corresponding to each network. FAg represents the percentage of trials in which the source intensity is estimated within a factor of g.

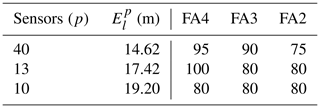
From the distribution of the optimized sensors in the networks in Fig. 3 for trials 5, 11, and 19 as well as in Figs. S2.1 and S2.2 for all selected trials, it was noted that a larger number of sensors are close to the source position in the optimal networks in most of the trials. The source reconstruction results from the optimal monitoring networks formed by 10 sensors have an averaged location error $\left(E_l^{\mathrm{10}}\right)$ of 19.20 m for all 20 trials in the MUST experiment (Tables 2 and 3). In most of the trials, the location and the intensity of a continuous point emission are estimated accurately and close to the true source parameters. The location error is minimum in trial 14 ($E_l^{\mathrm{10}}=\mathrm{5.50}$ m) and maximum in trial 2 ($E_l^{\mathrm{10}}=\mathrm{56.88}$ m) (Table 2). For this configuration of the optimal sensor network, the source intensity in 80 % of the trials is estimated within a factor of 2 of the true release rates (Tables 2 and 3).

For all 20 trials, the averaged location error $E_l^{\mathrm{13}}$ is 17.42 m for the optimal networks formed by 13 sensors, which is smaller than the averaged $E_l^{\mathrm{10}}=\mathrm{19.20}$ m obtained with 10 sensors (Tables 2 and 3). The location error is observed as a minimum in trial 5 ($E_l^{\mathrm{13}}=\mathrm{2.13}$ m) and as a maximum in trial 16 ($E_l^{\mathrm{13}}=\mathrm{63.04}$ m) (Table 2). For this optimal network, in 80 % of the trials, the source intensity is estimated within a factor of 2 of the actual emission rates. It was noted from the evaluation results that the increase in the number of sensors in a network has little influence on the accuracy of the estimated intensity (Tables 2 and 3).

In some trials, it was also noted that the distance of an estimated source to a real source decreases with a decrease in sensor number and also increases with the number of sensors in some other cases. It may be because the information added by a new sensor was not necessarily beneficial. It is noticeable that in a particular meteorological condition (i.e., wind direction, wind speed, and atmospheric stability), some of the sensors in a network may have little contribution to the STE. So, increasing the number of sensors may not always provide the best estimation because with the addition of more sensors, we also add more model and measurement errors in the estimation process. These errors can affect the source estimation results in some trials. In some cases, it may also depend on the sensitiveness of the added sensor's position in an extended optimal network to the source estimation. It is also noted that for a monitoring network, not only the number of sensors but also the sensor distribution (or sensor position) affects the information captured from the network.

In fact, both optimal networks for each trial show a diversity of structures independently of the number of sensors considered. For this, the skeleton was used to analyze the heterogeneity of the structures of different optimal networks. A skeleton with seven sensors is considered a strong common base for the networks. This is the case for trials 3, 6, 14, 15, and 20 (Table 2). It is noted that the overall results obtained are comparable (few differences between the results obtained by the networks). For these networks, a strong common base leads to a near-global optimum. If we consider networks with a weak common base, the skeleton was formed by up to three sensors, particularly in trials 1 and 11. The performances do not systematically converge independently of the size of the networks. Thus, for trial 1, better results were obtained with a network formed by 13 sensors compared to that by 10 sensors. This result reflects the fact that the algorithm with the network formed by 13 sensors probably converges toward a near-global optimum. For trial 11, it was also noted that the performances obtained by the two networks are identical. This shows that the networks with different sensor configurations may lead to a nearly overall optimum. This result is in coherence with Kovalets et al. (2011) and Efthimiou et al. (2017). Considering a network of 10 sensors, they show for the same experimental data that the best source reconstruction is possible with only 5 % or 10 % of the randomly selected total network combinations.

Considering the networks of intermediate structures with skeletons varying from four to six sensors, for trials 2, 4, 5, 7, 8, 9, 12, 13, 16, 17, 18, and 19, no obvious trend is noticed. These results tend to show that for a given trial, one or more optimal networks can satisfy the conditions of a nearly overall optimum (to be minimized). The obtained optimal networks may have a more or less common structure (having a greater or lesser number of skeletons).

Moreover, uncertainties calculated for different network sizes do not show an obvious trend. Indeed, a general relationship between the number of samplers and the uncertainties is not obvious. One may notice that changing the size of the network (increasing or decreasing the number of sensors) can lead to the growth or diminution of the uncertainties in the source parameter estimations. As an example, for trial 7 uncertainties grow, while for trial 17 uncertainties diminish (Table 2).

It should be noted that this study deals with the case of reducing the number of sensors in order to obtain an optimal network from an existing large network. This optimization was carried out under the constraints of an existing network of the original 40 sensors in the MUST field experiment. If one compares the performances of the obtained optimal monitoring networks of smaller sizes with the initial (original) network of 40 sensors in the MUST environment, both optimal networks provide satisfactory estimations of unknown source parameters. The 40-sensor network gives an averaged location error of 14.62 m for all trials, and the release rate was estimated within a factor of 2 in 75 % of the trials. However, reducing the number of sensors to $\sim \mathrm{1}/\mathrm{3}$ of the original 40 sensors, the 13-sensor optimal networks also give comparable source estimation performances with an averaged location error of 17.42 m. Even with the 13-sensor optimal networks, source intensities in 80 % of the trials were accurately estimated within a factor of 2. Similarly for the 10-sensor optimal networks, the averaged location error (19.20 m) is slightly larger than that obtained from the 13- and 40-sensor networks. However, reducing the number of sensors to 1∕4 gives extra advantages in the case of limited sensor availability for a network in emergency scenarios, such as accidental or deliberate releases, in complex urban environments.

It should also be noted that the optimization evaluation in this study is performed using the MUST set of measurements, and this makes it more likely that the resulting sensor configuration performs well in reconstructing the source (in other words, the same measurements should not be used for the optimization and for the reconstructions). However, this does not limit the application of the proposed methodology for some important practical applications like accurate emission estimations. In fact, this can be considered a limitation of the data used for this application because for a complete process of optimization and then evaluation one requires a sufficiently long set of measurements so that all the data can be divided into two parts, (i) one part for designing an optimal sensor network and (ii) another part for the evaluation of the designed optimal network. However, the durations of the releases in the MUST field experiment were not sufficiently long to divide all the data from a test release separately into two parts for designing the optimal sensor network and then its evaluation. In further evaluations of the resulting optimal sensor configuration, a different set of concentration measurements can be constructed by adding some noise to the measurements. For a continuous release in steady atmospheric conditions, the average value of the steady concentration in a test release is not expected to deviate drastically from the mean values in each segment of the complete data. So this new set of concentration measurements with added noise can partially fulfill the purpose of evaluating a designed optimal network. As shown in Table 2, the errors in the estimated source parameters are small even with the new sets of concentration measurements constructed by adding 10 % Gaussian noise. This exercise shows that even if we have utilized a partially different set of the measurements for the evaluation of the optimal networks, the optimal networks have almost the same level of source detection ability in an urban-like environment. However, realistic data are required for further evaluation of the optimization methodology.

Although the MUST field experiment has been widely utilized for the validation of atmospheric dispersion models and inversion methodologies for unknown source reconstruction in an urban-like environment, its experimental domain was only approximately 200 m × 200 m (with buildings represented by a grid of containers) and can be considered small for a real urban environment. Thus, it may not quite represent a real urban region in terms of scale, meteorological variability, and nonuniform terrain or roughness–canopy structure. However, the methodology presented here is general in nature to apply to a real urban environment. The methodology involves the utilization of a CFD model, which can generally include the effects of urban geometry, meteorological variability, and nonuniform terrain or roughness–canopy structure in a real urban environment. It is also noted that the optimal network design would depend on diurnal and spatial variability in meteorological conditions, which may increase or decrease the optimum number of sensors and may also change the “best positions” to be instrumented by sensors.

7 Conclusions

This study describes an approach for optimally reducing the size of an existing monitoring network of sensors in a geometrically complex urban environment. It is a matter of reducing the size of networks while retaining the capabilities of estimating an unknown source in an urban region. Given an urban-like environment of the MUST field experiment, the renormalization inversion method was chosen for the source term estimation. It was coupled with the CFD model fluidyn-PANACHE for the generation of the adjoint fields. Combinatorial optimization by simulated annealing consisted of choosing a set of sensors that leads to an optimal monitoring network and allows for an accurate unknown source estimation. This study demonstrates how the renormalization inversion technique can be applied to optimally reducing the size of an existing large network of concentration samplers for quantifying a continuous point source in an urban-like environment with almost the same level of source detection ability as the original network with a larger number of samplers.

The numerical calculations were performed by coupling the simulated annealing stochastic algorithm to the renormalization inversion technique and the CFD modeling approach to optimally reduce the size of an existing monitoring network in urban-like environment of the MUST field experiment. The optimal networks were constructed to reduce the size of the original networks (40 sensors) to approximately one-third (13 sensors) and one-fourth (10 sensors). The 10- and 13-sensor optimal networks have estimated average location errors of 19.20 and 17.43 m, respectively, and have comparable source estimation performances with an averaged location error of 14.62 m from the original 40-sensor network. In 80 % of trials with optimal networks of 10 and 13 sensors, the emission rates are estimated within a factor of 2 of the actual release rates. These are also comparable to the performance of the original 40-sensor network, whereby in 75 % of the trials the releases were estimated within a factor of 2 of the actual release.

It was shown that in most of the MUST trials, the number of sensors in optimal networks slightly influences the location error of an estimated source, and this error tends to increase as the number of sensors decreases. In 20 MUST trials, an analysis of the networks formed by 10 and 13 sensors revealed the heterogeneity of their structures in an urban domain. It was observed that for some trials, optimal networks had a strong common structure. This tends to prove that a certain number of sensors have a primordial role in reconstructing an unknown source. It would reflect the fact that disjoint sets of sensors can lead to the best estimate of an unknown source in an urban region. This opens enormous prospects for assessing the relative importance of each sensor in a source reconstruction process in an urban environment. Defining a global optimal network for all meteorological conditions is a complex problem, but it is of greater importance that one may realize. This challenge consists of defining an optimal static network able to reconstruct the sources in all varied meteorological conditions. This information can be of great importance to determine an optimal monitoring network by reducing the number of sensors for the characterization of unknown emissions in complex urban or industrial environments.

Appendix A: Weight function

Issartel et al. (2007) demonstrated that a weight function, which reduces the artifacts of the adjoint functions at the measurement points, must verify the following renormalization criterion:

$$\begin{array}{}\text{(A1)}& {\mathbf{a}}_{\mathrm{w}}^T\left(\mathbf{x}\right){\mathbf{H}}_{\mathrm{w}}^{-\mathrm{1}}{\mathbf{a}}_{\mathrm{w}}\left(\mathbf{x}\right)\equiv \mathrm{1}.\end{array}$$

From an iterative algorithm by Issartel et al. (2007), w(x) is determined as

$$w_{\mathrm{0}}\left(\mathbf{x}\right)=\mathrm{1},$$

and

$$\begin{array}{}\text{(A2)}& w_{k+\mathrm{1}}\left(\mathbf{x}\right)=w_k\left(\mathbf{x}\right)\sqrt{{\mathbf{a}}_{wk}^T\left(\mathbf{x}\right){\mathbf{H}}_{wk}^{-\mathrm{1}}{\mathbf{a}}_{wk}\left(\mathbf{x}\right)}.\end{array}$$

Appendix B: Identification of point source

Following Sharan et al. (2009), consider a point source of continuous release at a position ${\mathbf{x}}_{\mathbf{o}}=(x_o,y_o)$ and with the intensity q_o. The point source is thus expressed as a function of the preceding parameters: $\mathbf{s}\left(\mathbf{x}\right)=q_o\mathit{\delta }(\mathbf{x}-{\mathbf{x}}_{\mathbf{o}})$. The relationship between the source and the measurements (Eq. 3) becomes $\mathit{\mu }=q_o{\mathbf{a}}_{\mathrm{w}}\left({\mathbf{x}}_{\mathbf{o}}\right)w\left({\mathbf{x}}_{\mathbf{o}}\right)+\mathit{ϵ}$. By replacing the measurement term in Eq. (4), one obtains

$$\begin{array}{}\text{(B1)}& {\mathbf{s}}_{\mathrm{w}}=q_{o}w\left({\mathbf{x}}_{\mathbf{o}}\right){\mathbf{A}}_{\mathrm{w}}^T{\mathbf{H}}_{\mathrm{w}}^{-\mathrm{1}}{\mathbf{a}}_{\mathrm{w}}\left({\mathbf{x}}_{\mathbf{o}}\right);\end{array}$$

s_w reaches its maximum at position x_o as the renormalization criterion (Eq. A1) is satisfied only at this position. Thus, s_w(x) at x_o becomes

$$\begin{array}{}\text{(B2)}& {\mathbf{s}}_{\mathrm{w}}\left({\mathbf{x}}_{\mathbf{o}}\right)=q_{o}w\left({\mathbf{x}}_{\mathbf{o}}\right),\end{array}$$

which estimates the source intensity $q_o={\mathbf{s}}_{\mathrm{w}}\left({\mathbf{x}}_{\mathbf{o}}\right)/w\left({\mathbf{x}}_{\mathbf{o}}\right)$.

Appendix C: Derivation of the cost function

A cost function is defined (based on the renormalization theory) as a function that minimizes the quadratic distance between the observed and the simulated measurements according to the H_w norm (Issartel et al., 2012). H_w is the Gram matrix defined in Sect. 2.2. The quadratic distance between the real and the simulated concentration measurements according to the H_w norm is given by

$$\begin{array}{}\text{(C1)}& J={∥\mathit{\mu }-\widehat{\mathit{\mu }}∥}_{{\mathbf{H}}_{\mathrm{w}}^{-\mathrm{1}}}^{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left[(\mathit{\mu }-\widehat{\mathit{\mu }}{)}^T{\mathbf{H}}_{\mathrm{w}}^{-\mathrm{1}}(\mathit{\mu }-\widehat{\mathit{\mu }})\right].\end{array}$$

When considering a point source, $\widehat{\mathit{\mu }}$ is written by $\widehat{\mathit{\mu }}=q_o{\mathbf{a}}_{\mathrm{w}}\left(\mathbf{x}\right)w\left(\mathbf{x}\right)$, where q_o and x are respectively the intensity and the position of a point source. By replacing $\widehat{\mathit{\mu }}$ in Eq. (C1), one obtains (Sharan et al., 2012; Issartel et al., 2012)

$$\begin{array}{}\text{(C2)}& \begin{array}{rl}J& =J(q_o,\mathbf{x})\\ & ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left[(\mathit{\mu }-q_o{\mathbf{a}}_{\mathrm{w}}(\mathbf{x}\left)w\right(\mathbf{x}\left){)}^T{\mathbf{H}}_{\mathrm{w}}^{-\mathrm{1}}\right(\mathit{\mu }-q_o{\mathbf{a}}_{\mathrm{w}}\left(\mathbf{x}\right)w\left(\mathbf{x}\right))\right].\end{array}\end{array}$$

For a fixed x in Eq. (C2), J reaches a strict local minimum if the following two conditions are satisfied.

$$\begin{array}{}\text{(C3)}& {\displaystyle \frac{\partial J(q_o,\mathbf{x})}{\partial q_o}}=\mathrm{0}\text{(C4)}& {\displaystyle \frac{{\partial }^{\mathrm{2}}J(q_o,\mathbf{x})}{\partial q_o^{\mathrm{2}}}}>\mathrm{0}\end{array}$$

For each fixed x, the first condition (Eq. C3) gives an estimate ($\stackrel{\mathrm{̃}}{q_{\mathrm{0}}}$) of q₀ as $\stackrel{\mathrm{̃}}{q_{\mathrm{0}}}=\frac{{\mathbf{a}}_{\mathrm{w}}^T\left(\mathbf{x}\right){\mathbf{H}}_{\mathrm{w}}^{-\mathrm{1}}\mathit{\mu }}{w\left(\mathbf{x}\right)}$. The second condition (Eq. C4) is always satisfied as $\frac{{\partial }^{\mathrm{2}}J(q_o,\mathbf{x})}{\partial q_o^{\mathrm{2}}}=w^{\mathrm{2}}\left(\mathbf{x}\right)>\mathrm{0}$, ∀x (Sharan et al., 2012). Corresponding to the estimate $\stackrel{\mathrm{̃}}{q_{\mathrm{0}}}$ from the first condition (Eq. C3), the cost function J from Eq. (C2) leads to the following expression (Issartel et al., 2012):

$$\begin{array}{}\text{(C5)}& J(\stackrel{\mathrm{̃}}{q_{\mathrm{0}}},\mathbf{x})={\displaystyle \frac{{\mathit{\mu }}^T{\mathbf{H}}_{\mathrm{w}}^{-\mathrm{1}}\mathit{\mu }}{\mathrm{2}}}\left[\mathrm{1}-{\displaystyle \frac{{\mathbf{s}}_{\mathrm{w}}^{\mathrm{2}}}{{\mathit{\mu }}^T{\mathbf{H}}_{\mathrm{w}}^{-\mathrm{1}}\mathit{\mu }}}\right],\end{array}$$

where s_w is the same as given in Eq. (4) and ${\mathit{\mu }}^T{\mathbf{H}}_{\mathrm{w}}^{-\mathrm{1}}\mathit{\mu }$ is a positive constant. Considering Eq. (C5), it is obvious that the minimization of J also corresponds to the maximization of the term $\frac{{\mathbf{s}}_{\mathrm{w}}^{\mathrm{2}}}{{\mathit{\mu }}^T{\mathbf{H}}_{\mathrm{w}}^{-\mathrm{1}}\mathit{\mu }}$ or minimization of the term $\left[\mathrm{1}-\frac{{\mathbf{s}}_{\mathrm{w}}^{\mathrm{2}}}{{\mathit{\mu }}^T{\mathbf{H}}_{\mathrm{w}}^{-\mathrm{1}}\mathit{\mu }}\right]$. Accordingly, the minimum value of the cost function J in Eq. (C5) leads to the following expression of the cost function (say J_s(x)) to minimize:

$$\begin{array}{}\text{(C6)}& J_{\mathrm{s}}\left(\mathbf{x}\right)=\mathrm{1}-{\displaystyle \frac{{\mathbf{s}}_{\mathrm{w}}^{\mathrm{2}}}{{\mathit{\mu }}^T{\mathbf{H}}_{\mathrm{w}}^{-\mathrm{1}}\mathit{\mu }}}.\end{array}$$

A global minimum of the cost function J_s(x) is evaluated by the SA algorithm.