A parallel workflow implementation for PEST version 13.6 in high-performance computing for WRF-Hydro version 5.0: a case study over the midwestern United States

The Weather Research and Forecasting Hydrological (WRF-Hydro) system is a state-of-the-art numerical model that models the entire hydrological cycle based on physical principles. As with other hydrological models, WRF-Hydro parameterizes many physical processes. Hence, WRF-Hydro needs to be calibrated to optimize its output with respect to observations for the application region. When applied to a relatively large domain, both WRF-Hydro simulations and calibrations require intensive computing resources and are best performed on multimode, multicore high-performance computing (HPC) systems. Typically, each physics-based model requires a calibration process that works specifically with that model and is not transferrable to a different process or model. The parameter estimation tool (PEST) is a flexible and generic calibration tool that can be used in principle to calibrate any of these models. In its existing configuration, however, PEST is not designed to work on the current generation of massively parallel HPC clusters. To address this issue, we ported the parallel PEST to HPCs and adapted it to work with WRF-Hydro. The porting involved writing scripts to modify the workflow for different workload managers and job schedulers, as well as to connect the parallel PEST to WRF-Hydro. To test the operational feasibility and the computational benefits of this first-of-its-kind HPC-enabled parallel PEST, we developed a case study using a flood in the midwestern United States in 2013. Results on a problem involving the calibration of 22 parameters show that on the same computing resources used for parallel WRF-Hydro, the HPC-enabled parallel PEST can speed up the calibration process by a factor of up to 15 compared with commonly used PEST in sequential mode. The speedup factor is expected to be greater with a larger calibration problem (e.g., more parameters to be calibrated or a larger size of study area).

1 Introduction

Physically based hydrological models contain detailed physical mechanisms to model the hydrological cycle, but many complex physical processes in these models are parameterized. For example, the state-of-the-art Weather Research and Forecasting Hydrological (WRF-Hydro) modeling system (Gochis et al., 2018) has dozens of parameters that can be dependent on land and river type and are typically specified in lookup tables. Therefore, these hydrological models need to be calibrated before they can be applied to research over different regions. In this context, calibration refers to adjusting the values of the model parameters so that the model can closely match the behavior of the real system it represents. In some cases, the appropriate value for a model parameter can be determined through direct measurements conducted on the real system. In many situations, however, the model parameters are conceptual representations of abstract watershed characteristics and must be determined through calibration. In fact, model calibration is the most time-consuming step, not only for hydrological models, but also for Earth system model development, because both parametric estimation and parametric uncertainty analysis require hundreds – if not thousands – of model simulations to understand how perturbations in model parameters affect simulations of dominant physical processes and to find the optimum value of a single parameter.

WRF-Hydro is a numerical model that can simulate the entire hydrological cycle using advanced high-resolution data such as satellite and radar products. Compared with the traditional land-surface model (LSM) used by WRF, WRF-Hydro provides a framework for the multiscale representation of surface flow, subsurface flow, channel routing, and baseflow, as well as a simple lake–reservoir routing scheme. As a physics-based model, WRF-Hydro includes many complicated physical processes that are nonlinear and must be parameterized. The default parameters given by WRF-Hydro may be valid for one region but not for another region. Hence, the calibration of related model parameters is often required in order to use the model in a new domain. In particular, for a large spatial domain such as the entire contiguous United States, in order to develop the optimal parameter sets in a reasonable amount of time, the calibration must be conducted on high-performance computing (HPC) systems in parallel instead of in sequential mode. To date, no such calibration tool can efficiently calibrate WRF-Hydro on HPC resources. Typically, each physics-based model needs a calibration code that is custom designed to work with that particular numerical model and its set of physics parameterizations, software architecture, and solvers. These custom-designed calibration codes are highly challenging and do not offer flexibility. Therefore, a more flexible and generic calibration tool is needed that can calibrate any code that uses Message-Passing Interface–Open Multi-Processing (MPI–OpenMP) for parallelization on HPC systems.

One widely used generic and independent calibration tool is the parameter estimation tool (PEST). PEST (Doherty, 2016) conducts calibration automatically based on mathematical methods and is thus applicable for optimizing nonlinear parameters. Compared with manual calibration, automatic calibration is more efficient and effective because it avoids interference from human factors (Madsen, 2000; Getirana, 2010). The uniqueness of PEST is that it operates independently of models: there is no need to develop additional programs for a particular model except preparing the files required by PEST (as described in Sect. 3.2). PEST has four modes of operation (Doherty, 2016). One of the modes is regularization mode, which supports the use of Tikhonov regularization and is found to be better for serving environmental models because, if implemented properly, it supports model predictions of minimum error variance, is numerically stable, and embraces rather than eschews the heterogeneity of natural systems. Singular value decomposition (SVD) can be used as a regularization device to guarantee the numerical stability of the calibration problem. The parallel PEST is able to distribute many runs across many computing nodes using master–worker parallel programming. To our best knowledge, however, no approach is available that allows users to submit jobs using PEST parallelization to a typical supercomputing facility that uses job scheduling and workload management such as Simple Linux Utility for Resource Management (SLURM), Portable Batch System (PBS), and Cobalt. A previous study (Senatore et al., 2015) used PEST to calibrate WRF-Hydro over the Crati River Basin in southern Italy. Because the study area was relatively small, the authors were able to conduct the calibration using PEST in sequential mode (Alfonso Senatore, personal communication, 2018).

The objective of this study is to (1) port the parallel PEST to HPC clusters operated by the U.S. Department of Energy (DOE) and adapt it to work with WRF-Hydro, (2) evaluate the performance of the HPC-enabled parallel PEST linked to WRF-Hydro by calibrating a flood event, and (3) explore the scale-up capability and computational benefits of the HPC-enabled parallel PEST by assigning different computing resources to the entire calibration process.

2 Model description

2.1 Study area

The case presented here is one of the worst floods experienced by greater Chicago area in the past 3 decades; the storm occurred on 18 April 2013. According to the National Weather Service (NWS), the heaviest 24 h accumulated rainfall during this storm reached 201.4, 171.1, and 136.4 mm across Illinois, Iowa, and Missouri, respectively. The Mississippi River crested at 10.8 m (1.7 m above flood stage), and the Illinois River crested in Peoria, Illinois, at 8.95 m; this river cresting broke the previous record of 8.78 m, set in 1943, and was 4.55 m above the historical normal river stage (NWS, 2013). Campos and Wang (2015) conducted three-domain nested WRF simulations to understand the dynamical and microphysical mechanisms of the event. Our study builds on the smallest domain of that study, which covers Illinois and the majority of Iowa and Missouri at a spatial resolution of 3 km (Fig. 1). The domain size is ∼495 000 km² (747 km from west to east; 657 km from south to north).

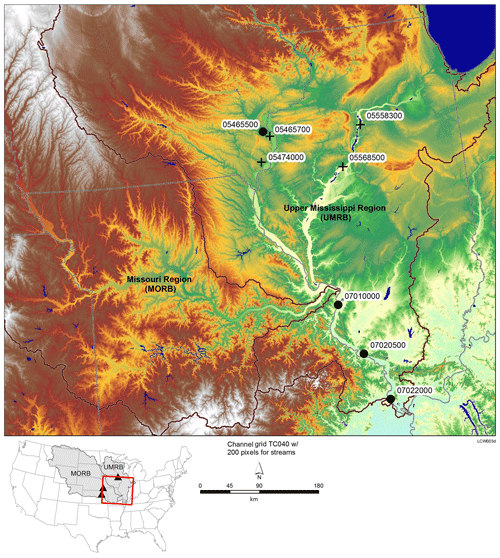
Figure 1 Eight USGS sites over the study area. The boundaries of the Upper Mississippi River Basin (UMRB) and Missouri River Basin (MORB) are highlighted. The four black circles indicate the sites that are used for calibrations; the four black crosses are sites that are used for transferability assessment. USGS site numbers corresponding to the site indices used in this study are as follows. Station 1: 05465500; Station 2: 07010000; Station 3: 07020500; Station 4: 07022000; Station 5: 05465700; Station 6: 05474000; Station 7: 05558300; Station 8: 05568500. The three inflow stations indicated by the black triangles on the lower left map are 06807000, 06887500, and 05389500.

2.2 WRF-Hydro configuration

This study employs WRF-Hydro version 5 with a basic configuration. This configuration does not use nudging techniques or spatially distributed soil-related parameters as used in the National Water Model configuration. WRF-Hydro has been tested in several different cases that focused on different hydrometeorological forecasting and simulation problems (e.g., Yucel et al., 2015; Senatore et al., 2015; Arnault et al., 2016), and it shows reasonable accuracy in simulated streamflow after being carefully calibrated. For details of the WRF-Hydro modeling system, see Gochis et al. (2018). Currently, two LSMs are available in WRF-Hydro for representing land-surface column physics: Noah (Chen and Dudhia, 2001) and Noah Multi-parameterization (Noah-MP; Niu et al., 2011). We utilize the Noah-MP LSM because compared with the Noah LSM it shows obvious improvements in reproducing surface fluxes, skin temperature over dry periods, snow water equivalent, snow depth, and runoff (Niu et al., 2011). Noah-MP is configured at a grid spacing of 3 km, and the aggregation factor is 15; that is, starting from a 3 km LSM resolution in the domain shown in Fig. 1, hydrological routing is performed at a grid resolution of 200 m, with 3285 south–north × 3735 west–east grid cells. We use a time step of 10 s for the routing grid in order to maintain model stability and prevent the numerical dispersion of overland flood waves. WRF-Hydro is configured to be in offline or uncoupled mode – there is no online interaction between the WRF-Hydro hydrological model and the WRF atmospheric model. Overland flow, saturated subsurface flow, gridded channel routing, and a conceptual baseflow are active in this study. The gridded channel network uses an explicit, one-dimensional, variable time-stepping diffusive wave. The time step of 10 s also meets the Courant condition criteria for diffusive wave routing on a 200 m resolution grid. A direct output-equals-input “pass-through” relationship is adopted to estimate the baseflow. Although the baseflow module is not physically explicit, it is important because the water flow in the channel routing is contributed by both the overland flow and baseflow. If the overland flow is active as it is in this study, it passes water directly to the channel model. In this case the soil drainage is the only water resource flowing into the baseflow buckets. However, if the overland flow is deactivated but channel routing is still active, then WRF-Hydro collects excess surface infiltration water from the land model and passes this water into the baseflow bucket. This bucket then contributes the water from both overland and soil drainage to the channel flow. Therefore, the baseflow must be active if the overland flow is switched off. This study does not consider lakes and reservoirs.

We use the geographic information system (GIS) tool developed by the WRF-Hydro team (Sampson and Gochis, 2018) to delineate the stream channel network, open-water (i.e., lake, reservoir, and ocean) grid cells, and groundwater–baseflow basins. Meteorological input for WRF-Hydro includes hourly precipitation; near-surface air temperature, humidity, and wind speed; incoming shortwave and longwave radiation; and surface pressure. In this study, the hourly precipitation is from the National Centers for Environmental Prediction (NCEP) Stage IV analysis at a spatial resolution of 4 km. The Stage IV data are based on combined radar and gauge data (Lin and Mitchell, 2005; Prat and Nelson, 2015) and have been shown to be temporally well correlated with high-quality measurements from individual gauges (see, e.g., Sapiano and Arkin, 2009; Prat and Nelson, 2015). The other hourly meteorological inputs are from the second phase of the multi-institution North American Land Data Assimilation System project, phase 2 (NLDAS-2) (Xia et al., 2012a, b), at a spatial resolution of 12 km. NLDAS-2 is an offline data assimilation system featuring uncoupled LSMs driven by observation-based atmospheric forcing.

During the 15 d period of this studied case, light to moderate rain occurred on 8 through 11 April 2013, followed by a relatively dry period from 12 to 15 April. Then a heavy rain event began on 16 April and peaked on 18 April. The heaviest rain band moved east of the study area on 19 April. The rainy event ended over the study area on 20 April (see Fig. S1 in the Supplement). We start the WRF-Hydro simulation on 1 October 2012 and run the model for 6 months to reach equilibrium. This 6-month period is considered spin-up time and is excluded from model calibration and evaluation. We calibrate the river discharge calculated by the WRF-Hydro model from 00:00 UTC 9 April to 00:00 UTC 12 April 2013, considering it long enough to achieve our objective. We then evaluate the model performance against U.S. Geological Survey (USGS) observed river discharge from 00:00 UTC 12 April to 00:00 UTC 25 April 2013.

3 Calibration

3.1 Platforms

We customized the parallel PEST to work on three different workload managers and job schedulers: SLURM at the National Energy Research Scientific Computing Center (NERSC), PBS at the Argonne National Laboratory Computing Resource Center (LCRC), and Cobalt at the Argonne Leadership Computing Facility. The tests presented here are conducted on Edison and Cori at NERSC and Bebop at Argonne LCRC, which all use the SLURM workload manager and job scheduler.

The interface we have built between the parallel PEST and the management software is, in general, used for (1) setting the number of workers and the nodes for each worker to conduct a model run (WRF-Hydro here); (2) setting up the working directory for the workers; (3) finding the nodes that are available; (4) identifying the nodes that work for each worker; (5) passing the global files (the same for all the working directory) to all the workers (these files include the lookup table files that are not to be calibrated, the namelist files for both the LSM and hydrological sector, and restart files generated by the previous simulations or spin-up period); and (6) submitting the job for the entire calibration process, including the parallel PEST and parallel WRF-Hydro. The job can be submitted as a fresh run or as a restart in terms of the calibration process. The main difference for this interface on different management software is that different management software has its own way to identify available nodes and to submit jobs. These differences require minor changes in the scripts we developed, which involves finding and identifying available nodes for workers, and submitting jobs for the specific management software. See detailed comments in the published code and scripts.

3.2 PEST files and settings

PEST requires three file types in both sequential and parallel modes. They are template files to define the parameters to be calibrated, an instruction file to define the format of model-generated output files, and a control file to supply PEST with the size of the problem and the settings for the calibration method. The parallel PEST uses a master–worker paradigm that starts model runs simultaneously by different workers (or in different folders). The master of the parallel PEST communicates with each of its workers many times during a calibration. To run PEST in parallel mode, one also needs a management file to inform PEST where the working folder is for each worker and what the names and paths are for each model input file that PEST must write (i.e., lookup tables that come from template files) and each model output file that PEST must read (such as frsxt_pts_out.txt). The management file also sets the maximum running time for each worker. For workers that take longer than the maximum running time, PEST will stop the model run by that particular worker and assign that model run to another worker if there is one with nothing else to do.

To the best of our knowledge, however, the parallel PEST is not designed to run on HPCs directly. We developed scripts and an interface to enable parallel PEST to run on HPCs using SLURM, PBS, or Cobalt workload managers and job schedulers. The development involved writing scripts to modify the workflow for different workload managers and job schedulers, as well as to connect the parallel PEST to WRF-Hydro. These developments enable parallel PEST to have many workers to run at the same time; each worker runs a parallel code (here WRF-Hydro) that uses more than one node, which could significantly reduce the wall-clock time for model calibrations. Although this master–worker parallelism may not be as efficient as a fully MPI approach, it is sufficient for model calibration and requires the least effort for the current parallel PEST to run on HPC systems.

Table 1 Calibrated 22 parameters and the optimum parameters found after five iterations based on the four USGS stations indicated by the solid circles in Fig. 1.^∗

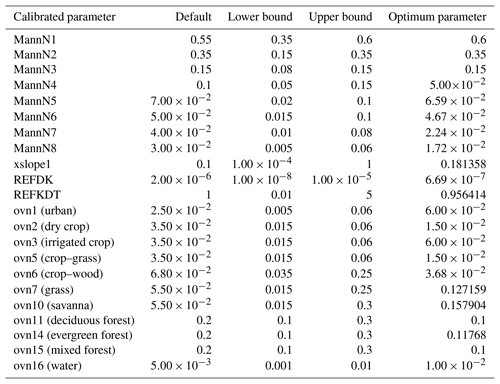
^∗ MannN numbers are the Manning's roughness coefficients in CHANPARM.TBL; xslope1 is the first number of the nine SLOPE_DATA (deep drainage) in GENPARM.TBL; REFDK and REFKDT are saturated soil lateral conductivity and the infiltration scaling parameter, respectively, in GENPARM.TBL; ovn numbers are the Manning's roughness coefficients for different land-use types.

This study presents calibration results from PEST using SVD-based regularization mode to ensure numerical stability (Tonkin and Doherty, 2005). We focus on calibrating 22 parameters (see Table 1 and a detailed description in Sect. 3.3) using 96 observation points and 22 items of prior information for the calibrated parameters. In each item of prior information, a value equal to its default value provided by WRF-Hydro v5.0 (or the log of its default value) is assigned for each adjustable parameter, assuming that default values are the preferred values. All prior information equations are assigned a weight of 1.0. We assigned five different regularization groups to the prior information: Manning's roughness coefficients specified by Strahler stream order in CHANPARM.TBL to one group; the parameters in HYDRO.TBL (Manning's roughness coefficients for overland flow as a function of vegetation types) to another group; and three global parameters for Noah-MP – deep drainage (SLOPE), the infiltration scaling parameter (REFKDT), and saturated soil lateral conductivity (REFDK) – in GENPARM.TBL to the remaining three groups. The 96 observation points are given different weights based on the inversed mean of their observed discharge during the studied period (see the detailed description in Sect. 3.3 and 4.1). For a detailed description of these settings see the PEST user manual (Doherty, 2016).

3.3 Calibrated experiments

The primary objective of this study is to build a bridge for linking parallel PEST and WRF-Hydro on the basis of HPC clusters and to explore the computational benefits of this bridge. We do not attempt to extensively assess each individual tool or address questions in each individual domain, such as optimizing the objective functions in PEST or calibrating WRF-Hydro for a long time period considering all the relevant parameters to achieve an optimal parameter set. The calibration period thus is limited to only 3 d, which we believe is long enough to achieve our objective and to understand WRF-Hydro's sensitivity to the calibrated parameters. We calibrated WRF-Hydro using four USGS sites (referred to as Station 1, Station 2, Station 3, and Station 4 hereafter), as shown in Fig. 1. (More USGS sites could be included if one manually reallocated the stations that were not properly assigned to the desired location on the channel network by the GIS tool.) As shown by the lower left index map in Fig. 1, the study area (the red box) only covers the lower part of the Upper Mississippi River Basin (UMRB) and a portion of the Missouri River Basin (MORB). In order to prepare observation datasets of streamflow contributed only from the drainage area within the model domain, we identified inflows entering the model domain at three different sites, namely sites 05411500, 06807000, and 06887500, as indicated by the black solid triangles in the index map of Fig. 1. The outflows of combined UMRB and MORB can be found at the three outlets, namely sites 07010000, 07020500, and 07022000 (Stations 2, 3, and 4, respectively, as shown by black solid circles in Fig. 1). These outlets are located sequentially at the main Mississippi River after the confluence of the Mississippi River and Missouri River. Thus, the observed streamflow contributed by drainage area within the model domain can be calculated by subtracting the sum of the discharge at the three sites (black triangles; recognized as inflow) from the discharge at each of the three outlet sites (black circles; recognized as outflow). The final derived observations of streamflow (or adjusted streamflow observation data) from the drainage area within this model domain are prepared for model calibration and validation. To prove this concept, we validated the consistency of the sum of observed drainage areas at inflow sites plus modeled drainage area with the overall drainage area at the outlet. The drainage area (UMRB and MORB) at outlet site 07010000 is 1.8×10¹² m². The sum of drainage areas at three inflow sites is about 1.4×10¹² m² (2.0×10¹¹, 1.1×10¹², and 1.4×10¹¹ m² for site 05411500, 06807000, and 06887500, respectively) and the modeled drainage area is 0.36×10¹² m²; the total area is 1.76×10¹² m². This indicates that the flows from the sum of three inflow sites and the modeled result represent 98 % of the drainage area at outflow site 07010000. Therefore, the adjusted streamflow observation data are qualified for model calibration. We then transfer the calibrated parameters to other sub-basins in the study area to assess the transferability of the calibrated parameters. Although many parameters, including spatially distributed parameters and constant parameters in the lookup tables, affect the model performance, we calibrate only the parameters in lookup tables and do not consider the spatial variability of other parameters or their scaling factors. On the other hand, we acknowledge that some studies calibrated a single scaling factor (without considering its spatial variability, however) of overland roughness coefficients (OVROUGHRTFAC) rather than the actual value of each land type in the lookup table (e.g., Kerandi et al., 2018). Although this approach reduces the number of calibrated parameters, it has less flexibility because changing one factor will change all the parameters that use the same proportion.

For the calibration exercises we conduct here, the retention depth factor (RETDEPRTFAC) is fixed at 0.001. This value is reasonable because the modeled discharge of our particular configuration (Sect. 2.2) using default parameters is lower than observed discharge. Reducing this factor from 1 to 0.001 keeps less water in water ponds and more water on the surface so it can contribute to river discharge. First, we calibrate 48 parameters based on a 3 d simulation from 9 to 11 April 2013 (Table S1 in the Supplement). This calibration uses the estimation mode in PEST and considers an equal weight for all four USGS stations. We calibrate Manning's roughness coefficients for both channels and land-use types, SLOPE, the REFKDT, and REFDK. Manning's roughness coefficients control the hydrograph shape and the timing of the peaks; the SLOPE, REFKDT, and REFDK control the total water volume. Second, based on the knowledge we learn from the 48-parameter calibration (see details in Sec. 4.1), for the same 3 d period, we reduce the number of calibrated parameters from 48 to 22 according to the sensitiveness of the WRF-Hydro model to the adjustable parameters. For example, during the calibration we find that Manning's roughness coefficients for several land types barely change because these land types (e.g., tundra, snow–ice) are not present in the study area. We also learn that even though the calibrated WRF-Hydro parameters can generate discharge results that closely resemble observations, the physical meaning of several parameters is not appropriate because of the wide range of those parameters that we set in the PEST control file. For example, the Manning's roughness coefficient for stream order 1 (0.199) is calibrated smaller than that for stream order 2 (0.218); the overland roughness coefficients for evergreen needleleaf forest (0.043) and mixed forest (0.023) are calibrated smaller than for cropland–woodland (0.046). Neither of these is true in the real world. We therefore adjust the range of many parameters according to the literature (Soong et al., 2012) to maintain their physical meanings (Table 1). On the other hand, we find that by using the same absolute weight for all four stations, the calibration helps three stations (Station 2, 3, and 4) with large water volumes to generate more reasonable results than do the default parameters; however, the calibrated results for Station 1, which has a relatively small volume of water, are not always better than the discharge that is modeled by using default parameters. Thus, we assign a higher weight (9.0) for Station 1 than for the other three stations (1.0) according to the inversed mean of observed discharge over these four stations in April 2013. The ratio of the weights between Station 1 and the other three stations stays similar even if the means are calculated based on different time periods.

3.4 Statistics

This study employs three statistical criteria: the Nash–Sutcliffe efficiency (NSE; Nash and Sutcliffe, 1970; Moriasi et al., 2007), root mean square error (RMSE), and Pearson correlation coefficient (PCC). RMSE and PCC evaluate model performance in terms of bias and temporal variation. NSE quantitatively describes the accuracy of modeled discharge compared with the mean of the observed data. Equation (1) calculates the NSE with defined variables:

$$\begin{array}{}\text{(1)}& \mathrm{NSE}=\mathrm{1}-{\displaystyle \frac{\sum _{t=\mathrm{0}}^n{\left(Y_t^{\mathrm{obs}}-Y_t^{\mathrm{sim}}\right)}^{\mathrm{2}}}{\sum _{t=\mathrm{0}}^n{\left(Y_t^{\mathrm{obs}}-Y_{\mathrm{mean}}^{\mathrm{obs}}\right)}^{\mathrm{2}}}},\end{array}$$

where $Y_t^{\mathrm{obs}}$ is the tth observed value from USGS sites for river discharge, $Y_t^{\mathrm{sim}}$is the tth simulated value from the WRF-Hydro output, $Y_{\mathrm{mean}}^{\mathrm{obs}}$ is the temporal average of USGS observed discharge, and n is the total number of observation time points. An efficiency of 1 (NSE = 1) corresponds to a perfect match between modeled discharge and observed data. An efficiency of 0 (NSE = 0) indicates that the model predictions are as accurate as the mean of the observed data. An efficiency below zero (NSE < 0) occurs when the model is worse than the observed mean. Essentially, the closer the NSE is to 1, the more accurate the model is.

4 Results

4.1 WRF-Hydro calibration and validation

Based on the knowledge we gained from the 48-parameter 3 d calibration, we adjust the range of critical parameters in the PEST control file to maintain their physical meanings. For example, we set the Manning's roughness coefficient larger for stream order 1 than for stream order 2. We also adjust the parameter range of the overland roughness coefficient for multiple land covers, such as cropland and forests. We exclude the parameters that are not sensitive to WRF-Hydro streamflow for this study in order to constrain the problem size due to the limits of computational resources. However, if one has an area of interest that is much larger with more land types than the study area here, then there would be more parameters to calibrate. Meanwhile, hundreds of constant parameters in the Noah-MP model could affect the WRF-Hydro results (Cuntz et al., 2016) and can be calibrated as well. Both these situations would increase the burden of WRF-Hydro calibration. We perform the same 3 d calibration from 9 to 11 April 2013. Figure 2 shows the results of the 3 d modeled discharge using default and calibrated parameters after five iterations, as well as observed discharge. The four stations are calibrated by considering different weights. While the model performance for Station 1 using the default and calibrated parameters is similar, the calibration improves the model performance over the drainage areas represented by Stations 2, 3, and 4 significantly. The modeled discharge using the default parameter underestimates the streamflow by 24 %–33 %. PEST detects this underestimation, immediately adjusts the parameters, and increases the modeled discharge during the first iteration. After the third iteration, the difference in calibrated results between different iterations is relatively small. We allow PEST to conduct five iterations and use the parameters obtained from the fifth iteration as our optimum parameters. As shown in Table 2, when the optimum parameters are used, the modeled discharges are much closer to the observations than the modeled results using default parameters. The NSEs for the four stations increased from −4.8 (Station 2), −18.8 (Station 3), and −57.0 (Station 4) to 0.75, −0.03, and −0.42, respectively, being closer to 1. It is noteworthy that although NSE values between 0.5 and 0.65 have been suggested to indicate a model of sufficient quality, we see much lower NSE values for Stations 3 and 4 with calibration results close to the observations. This may be because the objective function used in PEST is the sum of squared weighted residuals (SSWR), which is calculated differently from NSE. Thus even if SSWR reaches a small value, the NSE might still be far from 0.5. Incorporating other measures into the objective function of PEST may improve the robustness of PEST calibrations. The RMSEs decreased from 902.2, 1001.3, and 1399.3 m³ s⁻¹ to 188.6, 228.7, and 219.1 m³ s⁻¹, respectively.

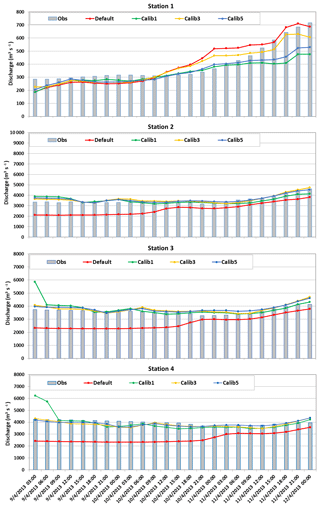
Figure 2 Observed and modeled discharge (m³ s⁻¹) using default and calibrated parameters during a 3 d calibration period (9–11 April 2013) over the four stations indicated by the black circles in Fig. 1. The observed discharge for Stations 2, 3, and 4 has been adjusted to exclude the inflows from the catchments that are not covered by the current study area.

Table 2 Statistics of model performance using optimum and default (in parentheses) parameters for Stations 1–4 during the calibration and validation period.^∗

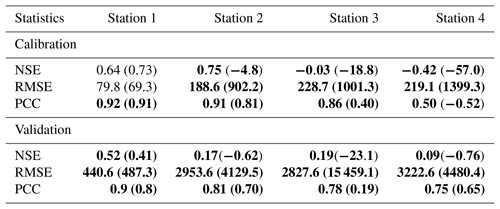
^∗ The calibration is for 3 d (9–11 April) and includes 22 parameters. The validation period is 12–24 April. Bold typeface indicates the calibrated model results are closer to observations compared with the default model results. NSE and PCC are unitless (RMSE: m³ s⁻¹).

During the validation period, compared with the modeled discharge using default parameters, as shown in Table 2, the NSEs for all four stations are increased to be closer to 1; RMSEs are significantly decreased, and the correlation coefficients between the observed and modeled discharge are increased from 0.8, 0.7, 0.19, and 0.65 to 0.9, 0.81, 0.78, and 0.75. Compared with the results of calibration using the estimation mode (no regularization) in PEST (not illustrated), the SVD-based regularization generates a slightly better hydrograph shape with 1 d later discharge peaks that are closer to the observations. However, as shown in Fig. 3, a problem remains with the hydrograph shapes of the modeled discharge, especially with the modeled peak discharge. For Station 1, WRF-Hydro almost captures the timing of the peak discharge, but it still underestimates the discharge by ∼25 %. One of the reasons perhaps is that this study uses a direct pass-through baseflow module, which does not account for slow discharge and long-term storage of the baseflow. Therefore, the largest contribution to river discharge is from precipitation, and groundwater does not contribute much discharge to the channels in a long-term view, as is also true for the other three large river stations. As a result, the contribution from the baseflow to the river discharge in model simulations does not stay as long as in real situations. In the observations, the river discharge decreases from the peak at a speed of ∼500 m³ s⁻¹ d⁻¹, while the modeled river discharge decreases from the peak at a speed of ∼1667 m³ s⁻¹ d⁻¹. Using an exponential storage–discharge function for the baseflow may improve this situation. Other reasons include the fact that the parameter range we set in the PEST control file is perhaps not wide enough, as we can see from Table 1 that several optimal parameters hit the bound of parameter ranges. Allowing wider parameter ranges may improve the calibration results.

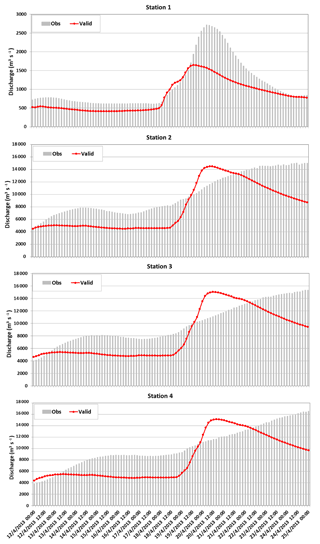
Figure 3 Observed and modeled discharge (m³ s⁻¹) during a validation period (12–24 April 2013) using optimum parameters identified from a 3 d calibration over the four stations indicated by black circles in Fig. 1. As in Fig. 2, the observed discharge for Stations 2, 3, and 4 has been adjusted.

Alternatively, instead of calibrating the stations that have large drainage areas and water coming from outside the current model domain, we have also tested calibrating small flows at local stations that have relatively small drainage areas covered by the current study area. This requires generating a new high-resolution GIS data file to distribute the stations of interest. We first run the WRF-Hydro model for 6 months using default parameters to spin up the model, and then we calibrate the model based on observations of these local stations. Results including figures and tables are shown in the Supplement. The calibration results are improved compared to the results that use default parameters, although further improvements are still needed. This again may be because the parameter range is not wide enough to consider the possible values of parameters that work for these specific areas represented at local stations, as we see many optimal parameters hit the bound of the parameter range. More tests to figure out a better set of parameters are needed for future investigation, which is beyond the scope of this study.

4.2 Computational benefits of parallel PEST on HPCs

The ability to scale up the calibration of WRF-Hydro by using the parallel PEST on HPC systems is determined by two factors: the scale-up capability of parallel PEST and the scale-up capability of WRF-Hydro. In calibrating WRF-Hydro, PEST first makes as many model runs as there are adjustable parameters to calculate the Jacobian matrix (Doherty, 2016). The Jacobian matrix has a column for each calibrated parameter and a row for each observation and each item of prior information set in the PEST control file. These model runs are independent between workers and can be easily parallelized. Each worker runs the model with temporarily incremented parameters that are defined in the template and control files. Then, PEST needs to make additional model runs to test parameter updates. Different from calculating the Jacobian matrix, these additional runs are performed by using different Marquardt lambdas, and the search for a Marquardt lambda that achieves the best set of parameters is a serial iterative process. The lambda to use for the next run depends on the outcome of the model run conducted using the previously chosen lambda. Although serial testing of Marquardt lambdas may quickly find the optimal Marquardt lambda in the first or second series of model runs, it is an inefficient use of computing resources because other processors are idle while only one process is searching for the lambdas. This is especially true when the model domain is large and requires extensive computing resources. This study employs partial parallelization for the lambda-testing procedure (Doherty, 2016), so multiple workers can be used to calculate parameter upgrades based on a series of lambda values that are related to each other by a factor of RLAMFAC set in the PEST control file. We set the value of PARLAM to −9999 in the management file so only one cycle of parallel WRF-Hydro runs is devoted to testing Marquardt lambdas. For additional details on these parameters and their settings see the PEST user manual (Doherty, 2016).

Table 3 Experiments designed to test the scale-up capability and computational benefits of the HPC-enabled parallel PEST linked to WRF-Hydro.^∗

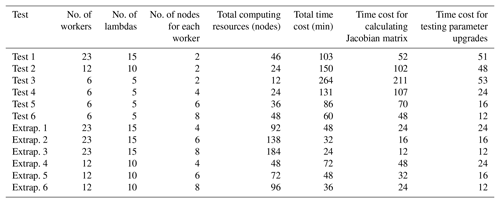
^∗ The tests were conducted on Edison at NERSC. Edison is a Cray XC30 with a peak performance of 2.57 petaflops per second. It has 5586 nodes, 24 cores per node, and ∼61 GB of physical memory per node.

In this study we test the computational performance of the HPC-enabled parallel PEST using different numbers of workers (6, 12, and 23) for the 22-parameter calibration. As shown in Table 3, we conducted six experiments: Test 1 uses 23 workers, Test 2 uses 12 workers, and Test 3 uses 6 workers. All three tests use two nodes for each worker to run WRF-Hydro in parallel. The maximum number of lambda-testing runs undertaken per iteration is set to 15, 10, and 5 for Tests 1, 2, and 3, respectively, to ensure that only one cycle of WRF-Hydro runs is devoted (using 15, 10, and 5 workers from Tests 1, 2, and 3, respectively) to testing Marquardt lambdas. Note that the maximum number of lambda-testing runs should be set equal to or less than the number of workers available. Otherwise, another cycle of WRF-Hydro runs needs to be conducted. In fact, generating more Marquardt lambdas does not always guarantee that the best Marquardt lambdas are generated. In contrast, it may make the model convergence slower (here, PEST) or even lead to model failure.

In order to test the trade-offs between the computing nodes used for running parallel WRF-Hydro and the workers used for running parallel PEST, Tests 4, 5, and 6 use the same number of workers (six) as Test 3 but use different numbers of nodes for each worker to run WRF-Hydro in parallel. Explicitly, Test 4 uses four nodes per worker, Test 5 uses six nodes per worker, and Test 6 uses eight nodes per worker. The maximum number of lambda-testing runs undertaken per iteration is set to five for Tests 4, 5, and 6. Note that the time costs in Table 3 are limited to only one iteration. Conducting more iterations will increase the cost of wall-clock time and computing resources but will not change the conclusion for the scale-up capability and computational benefits for the HPC-enabled parallel PEST linked to WRF-Hydro.

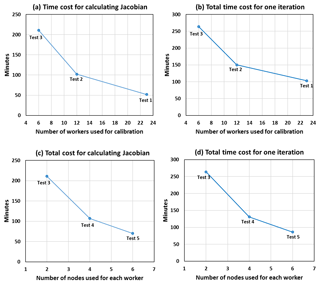
Figure 4 Time cost for calculating the Jacobian matrix and total time cost for one iteration for five experiments (see Table 3) using different numbers of workers to conduct PEST (a, b) and different numbers of nodes for each worker (c, d) to conduct WRF-Hydro.

PEST needs to run the WRF-Hydro model at least as many times as the number of calibrated parameters (22 here). In fact, PEST runs the model 23 times in the first iteration with initial parameter values and for the first Jacobian matrix. From the second iteration, it runs the model 22 times to calculate the Jacobian matrix. Therefore, if there are fewer than 23 workers, the time cost for the first round of Jacobian matrix calculation will increase accordingly. For example, as shown in Fig. 4a, when we assign 12 (and 6) workers to parallel PEST, the time cost for calculating the Jacobian matrix is increased by a factor of 2 (and 4) compared with the time cost when using 23 workers. The time cost for the parameter upgrade stays similar for the three experiments because they all conducted only one cycle of WRF-Hydro simulations to test the Marquardt lambdas. As a result, the total time cost for Test 2 is ∼1.5 times more than that for Test 1, and the total time cost for Test 3 is ∼1.5 times more than that for Test 2 (Fig. 4b). By extrapolating the speedup curve shown in Fig. 4a and b, we expect the total time cost to be ∼1516 min when using only one worker (or sequential mode), which is about 15 times slower compared with running PEST in parallel mode using 23 workers. For this particular study with 22 adjustable parameters, we expect that the time cost will most likely stay the same, even if one increases the number of workers to more than 23, because PEST runs WRF-Hydro only 23 or 22 times for each iteration. Assigning more workers for this particular study would most likely render some workers idle, which is not an efficient use of computing resources. PEST may run WRF-Hydro more than 22 times (e.g., 44 times) if higher-order finite differences are employed; in this case, assigning more workers (e.g., 45 workers) may further speed up the calibration process. On the other hand, for the same case study as we presented here and using the same number of nodes for running parallel WRF-Hydro, we can estimate the computing speedup by assuming an increase in the number of calibrated parameters to 50. This would be the case, for example, to evaluate model sensitiveness to the physics in Noah-MP or the spatial variabilities of certain parameters. We then expect to use 51 workers to calculate the Jacobian matrix in only one cycle. This would then be 28–30 times faster than running PEST using one worker (or in sequential mode). Similarly, if 100 parameters were used for the calibration for the same case study, a factor of up to 60 speedup in the calibration process would be achieved by running the HPC-enabled parallel PEST.

In addition, by increasing the number of nodes for each worker to conduct WRF-Hydro (Tests 3, 4, 5, and 6), the time cost for the entire calibration process is significantly reduced (Fig. 4c and d). Specifically, WRF-Hydro scales up well when using four, six, and eight nodes, and thus both the time spent on calculating the Jacobian matrix and the time spent on testing the parameter upgrades are decreased by 49 %, 67 %, and 77 %, respectively, when using four, six, and eight nodes compared with using two nodes. Therefore, the total time spent is also decreased when using more nodes for each worker (see Table 3). Moreover, if one has a larger study area, such as the entire contiguous United States, we expect WRF-Hydro to have an even better scale-up capability (e.g., on dozens of nodes) than in this study.

While the numbers in Table 3 and Fig. 4 are helpful to demonstrate the scale-up capability of each component (PEST and WRF-Hydro), they do not answer questions such as the following: if one has a certain number of nodes, how many workers and how many nodes per worker should be used to achieve the highest efficiency of the WRF-Hydro calibration using HPC-enabled PEST? On the other hand, one may have unlimited computational resources but would like to complete the calibration in a short time period. We present a scalability analysis below to answer these questions. First, we generate more scenarios using different numbers of workers and nodes per worker by extrapolating the existing time and computing costs based on the experiments that have been conducted. These scenarios use 23 or 12 workers and four, six, or eight nodes per worker, respectively. Since we have conducted simulations using the same number of nodes per worker, the cost for these scenarios can be easily and accurately predicted.

As shown in Fig. 5, compared with Test 3 (which requires the fewest computing resources – 12 nodes in total), having more workers (with the same number of nodes for each worker, e.g., Tests 1 and 2) takes more time than the ideal curve. The ideal curve assumes a linear speedup based on the time cost of Test 3. However, using the same number of workers and increasing the number of nodes for each worker (e.g., Tests 4, 5, and 6) can achieve the ideal speedup. Even when using 12 workers, increasing the number of nodes for each worker can still achieve a speedup close to the ideal curve (Extrap. 4, 5, and 6). Using 23 workers and increasing the number of nodes for each worker will not achieve the ideal speedup (Extrap. 1, 2, and 3). Therefore, if one only has a certain number of nodes available, we recommend using a relatively small number of workers but a large number of nodes for each worker. For example, if one has 48 nodes, then there are three options that can be considered: using 23 workers and two nodes per worker; using 12 workers and four nodes per worker; and using 6 workers and eight nodes per worker. Other partitions (16×3; or 8×6) between numbers of workers and nodes per worker are not as efficient as above. These three options will cost 103, 72, and 60 min, respectively, to finish one iteration. Thus, using six workers and eight nodes per worker is the most efficient way to spend the limited computing resources. On the other hand, if one would like to conduct the calibration in a short time period without any limits for the computing resources, then using 23 workers and eight nodes (perhaps even more nodes depending on the scale-up capability of WRF-Hydro) will finish one iteration in ∼24 min.

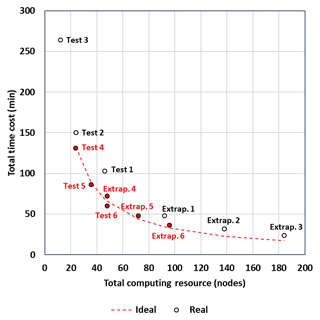
Figure 5 Total time cost and total computing resources needed for each test and extrapolated scenario, which use different numbers of workers and different numbers of nodes per worker. The dash line is an ideal curve, which assumes a linear decrease in terms of time cost when more computing resources are used, built on Test 3. All the circles are real costs for time and computing resources for each test and extrapolated scenario. The red text and filled circles indicate that those specific tests meet the ideal speedup curve.

4.3 Evaluation of spatial transferability of the calibrated parameters

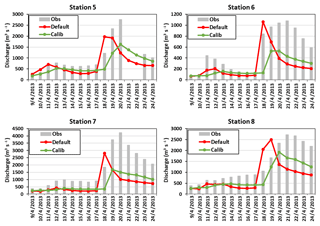
To assess the transferability of the calibrated parameters, we apply the optimum parameters obtained from the calibration for the four stations (black circles) in Fig. 1 to another set of four stations (crosses in Fig. 1) in the study area. All four sites are located on relatively small rivers, so the lag time between precipitation peak and discharge peak is much shorter than that for Stations 2, 3, and 4. The assessment compares the observed discharge with the closest grid cells from the discharge output of WRF-Hydro. Figure 6 shows the observed and modeled discharge using the default and optimum parameters. Overall, WRF-Hydro's default parameters underestimate the discharge and misrepresent the timing of discharge peaks compared with observations over the four assessed stations (Stations 5, 6, 7, and 8). By using the calibrated parameters from other sites over the area, the model results increase the discharge and shift the hydrograph shape so they are much closer to the observations than model results using default parameters. The absolute error of simulated discharge decreases by 13.1 %, 38.3 %, and 71.6 %, respectively, over Stations 6 through 8 (Station 5 shows a 6 % increase in absolute error) compared with the default simulated discharge. We also find that using SVD-based regularization for the PEST calibration captures the timing of the discharge peak better than using the estimation mode, which is 1 d earlier than the observations in reaching the discharge peak.

Figure 6 Observed and modeled daily averaged discharge (m³ s⁻¹) over the four stations indicated by the black crosses in Fig. 1 for 9–24 April using the default and optimum parameters (shown in Table 1) identified by the 3 d calibration.

5 Summary and discussion

WRF-Hydro is a new, and perhaps the first practical, computer code that can run on HPC systems and model the entire hydrological cycle using physics-based submodels and high-resolution input datasets (e.g., radar). The hydrological community has desired this capability for decades, although it requires intensive computing resources. Thus, the calibration of this model would ideally be conducted on HPCs in parallel as well, especially when the model covers a large domain rather than the basin scale. This study ports an independent model calibration tool, parallel PEST, to HPC clusters and links it to WRF-Hydro to help WRF-Hydro users calibrate the model within a much shorter wall-clock time period. The bridge we build here (between parallel PEST and WRF-Hydro on the basis of HPC systems) can be applied to any other hydrological models and ESMs that use parameterizations to represent model physics. We present the operational feasibility of the HPC-enabled parallel PEST by evaluating the performance of calibrated WRF-Hydro against observations in hydrograph features, such as the volume and timing of flood events. We examine the scale-up capability and computational benefits of the tool by assigning different computing resources for PEST and for WRF-Hydro. While this study presents the optimum parameters identified from the calibration of the particular flood event, the parameters can be significantly different if one uses different physics, such as an exponential storage–discharge function for a groundwater model or reach-based channel routing. Our preliminary testing shows that using exponential storage-discharge function with the default parameters provided by WRF-Hydro, the modeled discharge was larger than that of observations for this particular study. Thus, the calibration will need to adjust the parameters to reduce the discharge. Our study finds that for calibrating 22 parameters, using the same computing resources for running WRF-Hydro, the HPC-enabled PEST calibration tool can speed up WRF-Hydro calibration by a factor of 15 compared with running PEST in sequential mode. The speedup factor can be larger when there are more parameters to be calibrated.

The following are several key points that we would like to highlight and to inform future studies.

1. In this study, we consider using the prior or regularization information only for the parameters that we calibrate. As is the case with solving inverse problems, prior information is added to improve the smoothness of the solutions. In order to build a more comprehensive calibration, an important aspect that can be considered is to enrich the prior with available historical data (e.g., April and May from the past few years). Hence, the regularization objective function in PEST will constitute not only the discrepancies between parameters and their “current estimates” but also the discrepancies between WRF-Hydro simulations and preferred values (which is the observed time series of historical discharge). Additionally, one can use the pilot-points technique described by Doherty (2005) in conjunction with parameter estimation to add more flexibility to the calibration process. This will be potentially beneficial in improving the predictions.

2. To focus on our main goal, we calibrate only the parameters in lookup tables. We acknowledge that using a single value to represent the physics for a large domain could be problematic, especially when we expect the HPC-enabled parallel PEST to execute with WRF-Hydro for large domains. This situation often needs parameter regionalization. For example, WRF-Hydro version 5.0 has many spatially distributed parameters available, such as OVROUGHRTFAC – the overland flow roughness scaling factor, RETDEPRTFAC – the factor of maximum retention depth, and soil-related parameters (when compiled with SPATIAL_SOIL = 1). Calibrating these spatial parameters based on the grid scale (e.g., catchments) rather than a single value will give the model more flexibility and may thus better fit the observations (Hundecha and Bardossy, 2004; Wagener and Wheater, 2006). In practice, for example, one can include regional OVROUGHRTFACs (e.g., their lower–upper bounds and default values) in the PEST control file based on catchments. However, the selection of the locations and sizes of catchments may introduce significant uncertainties to the calibration results, which require systematic and comprehensive investigation and understanding of the study area.

3. This study is limited to calibrating the observed streamflow only based on the format of one of the WRF-Hydro model outputs for individual stations (frxst_pts_out.txt). It is feasible, however, to calibrate other variables as long as the observation data are available. For example, one can either find the closest point from the gridded output (of WRF-Hydro) to the observation location and then compare that model grid to observations, or one can change the WRF-Hydro input–output code to output other variables in the frxst_pts_out.txt file, so they can still use the same interface we developed here to calibrate other variables in addition to the discharge.

4. The optimal parameter set obtained from this study is from the fifth iteration of parallel PEST by testing five Marquardt lambdas. Testing different numbers of lambdas or calibrating different numbers of parameters may generate a different set of optimal parameters. These parameter sets can all make physical sense and be equally good for reproducing observed discharges. This phenomenon is called equifinality (Beven and Freer, 2001; Savenije, 2001), which is an important source of model uncertainty. To reduce the model uncertainty by reducing the equifinality, hydrologists carry out additional modeling objectives for model evaluation to find more useful parameter sets (Mo and Beven, 2004; Gallart et al., 2007). Alternatively, inspired by no. 3 discussed above, one can calibrate the WRF-Hydro model based on more than one variable, such as discharge and soil moisture (or heat flux or water table depth), to reduce the number of optimal parameter sets and thus reduce the model uncertainty of predictions for these variables.

5. While this study ported the parallel PEST to an HPC system and linked it to WRF-Hydro, we note that BEOPEST is available in the PEST family. BEOPEST has the same functionality as parallel PEST but uses a different approach for communication between master and workers. Working with HPC-enabled BEOPEST may save total time cost since BEOPEST uses the Transmission Control Protocol and the Internet Protocol instead of message files (reading input and writing output between master and workers) for communication. We expect it to be relatively straightforward to use BEOPEST to calibrate WRF-Hydro on HPCs since the interface remains the same, except one needs to copy the template and instruction files in addition to the global files (see Sect. 3.1) into each working folder.