Development and evaluation of pollen source methodologies for the Victorian Grass Pollen Emissions Module VGPEM1.0

We present the first representation of grass pollen in a 3-D dispersion model in Australia, tested using observations from eight counting sites in Victoria. The region's population has high rates of allergic rhinitis and asthma, and this has been linked to the high incidence of grass pollen allergy. Despite this, grass pollen dispersion in the Australian atmosphere has not been studied previously, and its source strength is untested. We describe 10 pollen emission source methodologies examining the strengths of different immediate and seasonal timing functions, and the spatial distribution of the sources. The timing function assumes a smooth seasonal term, modulated by an hourly meteorological function. A simple Gaussian representation of the pollen season worked well (average r=0.54), but lacked the spatial and temporal variation that the satellite-derived enhanced vegetation index (EVI) can provide. However, poor results were obtained using the EVI gradient (average r=0.35), which provides the timing when grass turns from maximum greenness to a drying and flowering period; this is due to noise in the spatial and temporal variability from this combined spatial and seasonal term. Better results were obtained using statistical methods that combine elements of the EVI dataset, a smooth seasonal term and instantaneous variation based on historical grass pollen observations (average r=0.69). The seasonal magnitude is inferred from the maximum winter-time EVI, whereas the timing of the season peak is based on the day of the year when the EVI falls to 0.05 below its winter maximum. Measurements are vital to monitor changes in the pollen season, and the new pollen measurement sites in the Victorian network should be maintained.

1 Introduction

Pollen is a biological particle, produced by plants to transfer haploid genetic material during reproduction. With allergenic properties pollen can be a human irritant, and is strongly linked to seasonal allergic rhinitis and asthma. Melbourne, in the state of Victoria, on the south-east coast of Australia, has the highest prevalence of allergic rhinitis in the world (Bousquet et al., 2008), and is a city of approximately 4.9 million inhabitants (ABS, 2018). Prior to 2017, pollen forecasts in Melbourne were generated manually by aeroallergen scientists, relying on persisting the previous day's pollen count and an interpretation of forecasted weather (Schäppi et al., 1998). However, despite the availability of a simple pollen forecast, they were not connected to the likelihood of thunderstorms, which proved fatal on the afternoon of 21 November 2016 (Lindstrom et al., 2017). During rush hour, a north–south line of thunderstorms developed west of Melbourne, and swept eastwards across the city. In the following hours, 9900 people visited hospitals with breathing difficulties, overwhelming the emergency services. It is possible that strong winds collected large quantities of grass pollen from north-western pasture regions, which were concentrated along the edge of the gust front. Victoria had experienced the world's largest epidemic thunderstorm asthma event. In the aftermath, the state government funded better planning of healthcare resources to improve preparedness and response arrangements for similar events in the future (Davies et al., 2017; Lindstrom et al., 2017). This plan included the development of a pilot thunderstorm asthma early-warning service using statistical pollen forecasts (Silver et al., 2019), operated by the Bureau of Meteorology (BOM), and the concurrent development of a pollen forecasting system, built around pollen emission and transport modelling. The pollen emissions component is called the Victorian Grass Pollen Emissions Module version 1.0 (VGPEM1.0).

Pollen is generally not included in air quality models because its atmospheric lifetime is usually too short to be of interest. Recently human exposure to pollen has become a focus, particularly in the Northern Hemisphere (e.g. Sofiev et al., 2015; Zhang et al., 2014) and urban areas (Skjøth et al., 2013), such that detailed vegetation taxa maps are being produced for pollen forecasting (McInnes et al., 2017).

Techniques to model atmospheric concentrations of pollen have included statistical techniques and dispersion models. Statistical techniques using standard multiple regression analyses have predicted whether airborne pollen concentrations will be higher or lower than a long-term mean with >87 % accuracy (Smith and Emberlin, 2006), but require decade-long datasets (Emberlin et al., 2007), and are improved by the availability of multiple sampling sites. Statistical models require a representation of the flowering season, but perform poorly if the timing of the flowering season changes (Beggs et al., 2015), whereas in urban areas, they are subject to local-scale turbulence and heat island effects (Emberlin and Norrishill, 1991). Meteorological dispersion models can capture these effects, but are more computationally demanding to run. Physical dispersion of pollen includes (1) emission from the pollen source regions, (2) atmospheric transport and (3) deposition, using measurements to validate the predictions.

Kawashima and Takahashi (1999) were amongst the first to develop a numerical description of pollen within a dispersion model, using a flowering map to simulate the cedar pollen season in the Tohoku district of Japan. In the US, the Biogenic Emission Inventory System was adapted to emit birch and ragweed pollen and predicted the timing of the birch pollen peak to within 2 d (Efstathiou et al., 2011). An understanding of pollen release biology and accurate meteorological data are crucial for pollen forecasting (Pasken and Pietrowiez, 2005). Wozniak and Steiner (2017) modelled pollen from 13 different taxa based on plant functional type mapping for the US, which could be used on climatic timescales. Indeed, the climate-induced spread of ragweed is predicted to double the number of Europeans suffering allergic responses by 2060 (Lake et al., 2017). In Germany, Helbig et al. (2004) simulated hazel and alder pollen emissions and transport, but did not verify their predictions as no pollen measurements were available. Schueler and Schlunzen (2006) simulated oak pollen emission in northern Germany via the incorporation of landscape structural mapping, finding that oak pollen plumes were transported up to 100 km away. The EMPOL 1.0 model for birch pollen across all of Europe was comprehensively evaluated by Zink et al. (2013). The Finnish Meteorological Institute has developed the System for Integrated modeLling of Atmospheric coMposition (SILAM; Sofiev, 2017, and references therein), to calculate the concentrations of six pollen species at a 10 km resolution on an hourly basis for all of Europe. This group have found that the most important input parameter is temperature (Siljamo et al., 2013).

Studies of pollen have focused on those taxa with a high allergenic burden, which differs depending on region. In Europe, birch tree pollen is the major allergen and has been the focus of intense research activity (Siljamo et al., 2013; Sofiev et al., 2013; Siljamo et al., 2007; Sofiev et al., 2006). However, birch is not common in Australia. Ragweed pollen, which is a common allergic trigger in the Northern Hemisphere, grows in the north-east and east of Australia but not elsewhere (Bass et al., 2000). Native Australian grasses such as wallaby and kangaroo grass are generally not wind-pollinated and produce little pollen, whereas introduced agricultural pasture grasses such as ryegrass (Lolium perenne) and canary grass are high pollen emitters (Smart et al., 1979). Ryegrass is grown extensively in Victoria and produces large volumes of pollen in spring. In southern Australia most of the allergenic burden has been attributed to ryegrass via skin prick tests (Girgis et al., 2000; Bellomo et al., 1992). Further, the rupturing of ryegrass pollen grains releases much smaller starch particles that are capable of causing asthma (Taylor and Jonsson, 2004; Suphioglu et al., 1992). Therefore, VGPEM1.0 focuses on pasture grass and has the following goals. First, to improve public health emergency planning and response arrangements around thunderstorm asthma, by providing a tool for appropriate information providers (i.e. Melbourne Pollen Count and Victorian Department of Health and Human Services). Second, that the VGPEM will feed into other forecasting models such as BOM's thunderstorm asthma forecast.

This paper documents the first representation of grass pollen in a 3-D dispersion model in Australia. As the greatest uncertainty is in the pollen emission characteristics, we develop and evaluate 10 methodologies, using observations from eight counting sites in Victoria. First we describe these grass pollen observations, and determine their correlations with observed meteorological variables. Second, the grass pollen emission methodologies are described and tested at a spatial resolution of 3 km. The best performing method is recommended for VGPEM1.0.

2 Observations and characteristics of grass pollen

Despite Australians having high rates of asthma and allergy compared to other Western nations (Lai et al., 2009), few Australian pollen observation sites for routine monitoring or research existed in 2016 (Beggs et al., 2015). In Australia, all pollen sampling is performed using Burkard volumetric pollen traps (de Morton et al., 2011). Samples are histologically stained and counted manually under a microscope by trained personnel who reference the samples to pollen taxonomic standards. One limitation of this method is that pollen cannot be classified into particular species, or even genus, based on visual examination alone.

The University of Melbourne (UoM) operated a pollen count site in Victoria sporadically from the late 1970s to 1990, but since 1991 it has counted annually over the 3-month period from October to December, coinciding with the grass pollen season (Ong et al., 1995). In Victoria, routine pollen counting since 2017 distinguishes between 15 pollen taxa, with Haberle et al. (2014) finding that 70 % of the total pollen measured at the UoM site is Cupressaceae from a nearby cemetery. However we concentrate on the Poaceae (grass) pollen, as it is the dominant outdoor human allergen in Australia. DNA sequencing at the UoM indicates that ryegrass could have contributed 60 %–90 % of the grass pollen counted over the 2016 pollen season (personal communication, E. Newbigin). The amount of grass pollen during the season in any particular year in Melbourne is strongly related to the amount of spring rainfall, which promotes grass growth and flowering (de Morton et al., 2011). The cumulative grass pollen count over the season in Melbourne ranges between 1500 and 5000 grains m⁻³, with daily maximums reaching 400 grains m⁻³ (Medek et al., 2016). In Melbourne, the highest pollen counts are usually associated with northerly continental air masses (de Morton et al., 2011), with an evening peak coinciding with the onset of the stable nocturnal boundary layer and descending air (Ong et al., 1995).

Two other pollen counting sites close to Melbourne at Burwood and Geelong, which are run by Deakin University, have been in operation since 2012. Five new sites were introduced in 2017 around Victoria and are situated within university or hospital grounds (Fig. 1a, b and Table 1). Pollen sampling occurred daily during the 2017 grass pollen season at 09:00 AEDT , representing the mean daily pollen concentration from 09:00 AEDT the previous day to 08:59 AEDT on the day of collection. Pollen observations from these eight sites are used to assess the accuracy of pollen predictions in this study.

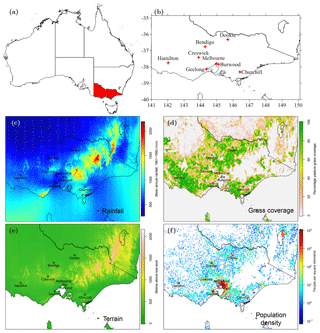
Figure 1 Maps of (a) Victoria within Australia, (b) pollen observing sites within the domain, (c) mean annual rainfall, (d) pasture grass coverage, (e) terrain and (f) population density. Data sources: (c) BOM, (d) ABARES, (e) Geoscience Australia and (f) the Bureau of Statistics.

In Australia, grass pollen counts are graded “low” if the count is 19 m⁻³ or less, “moderate” if it is between 20 and 49 m⁻³, “high” if it is between 50 and 99 m⁻³ and “extreme” if it is above 100 m⁻³. Whilst epidemiological studies commonly use annual pollen totals, we use a daily pollen risk classification system because we aim to predict daily pollen concentrations. The Australian grass count categories are similar to those used in the UK and Europe for the low and medium count categories, but the Australian extreme category is reached at pollen counts up to 3 times lower than in Europe and the US (Zink et al., 2013; Osborne et al., 2017; US National Allergy Bureau, 2019). Between 20 and 60 d in each Melbourne season are observed in the moderate or above category, and up to 37 d are observed in the high or above category (Medek et al., 2016). However, it is clear that climate change is impacting the timing and strength of the grass pollen season (Ziska and Beggs, 2012), as are changes to agricultural practices and the expanding boundary of the city. These changes highlight the importance of long-term observations and the need to sustain the new pollen observation sites in Victoria.

3 Treatment of pollen in VGPEM1.0

Pollen is set up in VGPEM1.0 as an inert particle tracer. The pollen source methodologies are tested using the CSIRO Chemical Transport Model (C-CTM), a framework of modules designed to calculate the concentrations of gases and aerosol which are subjected to emission, dispersion and deposition within the atmosphere (Cope et al., 2009). The C-CTM has been used to model the impacts of anthropogenic emissions on urban air sheds (Chambers et al., 2019; Paton-Walsh et al., 2018), to model volatile organic compounds from vegetation (Emmerson et al., 2019, 2018, 2016) and also to investigate the health impacts of reducing the sulfur content in shipping fuels (Broome et al., 2016). The C-CTM is driven by meteorology from the Australian Community Climate and Earth System Simulator model (ACCESS, Puri et al., 2013), run at a 3 km resolution using boundary conditions from ERA-Interim for a domain covering Victoria (Fig. 1a). ACCESS provides the meteorological parameters necessary for pollen emission and transport, namely wind speed and direction, temperature, relative humidity (RH) and rainfall.

Particles are output as micrograms per cubic metre (µg m⁻³) in the C-CTM, and require unit conversion to calculate grains per cubic metre (consistent with the pollen observations), using the mass of one pollen grain. Grass pollen diameters are found in the range from 30 to 40 µm (Brown and Irving, 1973). Early calculations by Smart et al. (1979) estimated the mass of one ryegrass pollen grain in Melbourne to be $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{9}}$ g, which converts to a very low density of 44.5 kg m⁻³ using a 35 µm diameter. The grass pollen density is a large source of uncertainty. Whilst Smart's study is local to our work, studies of pollen from other grass taxa yield much higher densities, for example 980 kg m⁻³ for Secale (rye) (Durham, 1946) and Dactylis glomerata (Stanley and Linskens, 1974).

The pollen density also impacts on the dry deposition velocity, which controls the length of time the pollen grain is airborne. The C-CTM dry deposition parameter follows Stoke's law. Sugita et al. (1999) measured Gramineae (grass) pollen with a fall speed of 3.5 cm s⁻¹. Skjøth et al. (2007) suggest the deposition of grass pollen is 4 times larger than the 1 cm s⁻¹ estimated for birch pollen, and consistent with the 4.3 cm s⁻¹ measured by Durham (1946) on Secale (rye). We will assume that each pollen particle is 35 µm in diameter, spherical and has a density of 1000 kg m⁻³, which is consistent with values used by Melbourne-based researchers (de Morton et al., 2011; Knox, 1993), and similar to the grass pollen density used in Zhang et al. (2014). A 35 µm particle with a density of 1000 kg m⁻³ yields a deposition velocity of 4.6 cm s⁻¹, which is similar to Skjøth et al. (2013). Using these values, the estimated mass of each pollen grain is $\mathrm{22.4}\times {\mathrm{10}}^{-\mathrm{9}}$ g.

This work relates exclusively to forecasting the presence of intact grass pollen grains in the air, within Victoria, Australia, and does not consider thunderstorm cells or the interactions of grass pollen grains within them. The process of re-entrainment of pollen grains once they are deposited to the ground is not considered, nor is the rupturing process that releases the allergenic contents of the grains – present on small starch particles. Whilst the impacts of pollen rupturing on numbers of cloud condensation nuclei has been investigated by Wozniak et al. (2018), ruptured pollen grains are not routinely monitored in Victoria. Future development of VGPEM may incorporate some of these processes.

Table 1 Locations of the Burkard pollen sampling network in Victoria arranged west to east, and their nearest automatic weather station (AWS). Code refers to site names within figures of this paper. UoM refers to the University of Melbourne.

3.1 Pollen emissions framework

Pollen emission and transport has never been modelled in Australia; therefore, we trial three different emission frameworks and vary their inputs. In some instances we test parameters proven not to work elsewhere and for other pollen taxa, to investigate whether Australian ryegrass pollen characteristics are different. The first framework is a spatio-temporal decomposition of factors, the second is a pollen production–loss model and the third is a derivative of the statistical model for daily grass pollen concentrations used in the BOM's pilot forecasting system (Silver et al., 2019). The pollen emission rate E at grid-point (x,y) and time t is expressed as follows:

$$\begin{array}{}\text{(1)}& E(x,y,t)=I(x,y,t)\times G(x,y,t)\times S(x,y),\end{array}$$

where I is the immediate timing (hour-by-hour variation due to changes in prevailing meteorology), G describes the gross seasonal timing (also termed the “phenology factor”) and S provides the spatial source distribution for a given season. The functions I, G and S are each dependent on other factors, which may include modelled meteorology, land use data or satellite data; these details are discussed in subsequent sections.

Table 2 gives the combinations of options for calculating E that are tested in this study. Each emission methodology is run for three months between October and December 2017 to cover the period of the pollen measurements. The modelled pollen is also averaged on a 24-hourly basis (to 09:00 AEDT each day) to be consistent with the 2017 pollen observations.

Table 2 Options tested for pollen emission in this study. EVI denotes the enhanced vegetation index.

3.1.1 Immediate timing (I)

We consider two representations of the immediate timing function (I). The first, and simplest, assumes that emissions are related to transport and are therefore proportional to the surface wind speeds, used in scenarios E1, E2 and E3. The second method, used in scenarios E4, E5, E6, E7 and E8 accounts for several meteorological factors, treating them as having independent effects.

$$\begin{array}{}\text{(2)}& I(x,y,t)=f_{\mathrm{h}}\cdot f_{\mathrm{RH}}\cdot f_{\mathrm{PR}}\cdot f_{\mathrm{WS}}\cdot f_{\mathrm{TM}},\end{array}$$

where the terms f_h, f_RH, f_PR, f_WS and f_TM represent the response to hour of the day, RH, precipitation, wind speed and temperature, respectively. This approach is similar to Sofiev et al. (2013, Eq. 12), representing pollen emissions from birch trees. The assumption is that grass pollen emissions are greatest when conditions are hotter, windier, drier, with less rain and around midday. The midday assumption stems from an observational study conducted near Melbourne which showed that the peak timing of ryegrass pollen release (measured as the number of exposed anthers) occurs in the early afternoon (Smart and Knox, 1979, Fig. 6). As ryegrass flowers in spring when mornings are cool and damp, the anthers need to dry before pollen is released. This timing is represented as a Gaussian distribution with a mean at the local solar noon (12:00 AEDT) and a standard deviation σ_h, of either 2 or 4 h (Smart and Knox, 1979). The larger σ_h parameter allows for a wider peak in pollen around noon in the later scenarios E6, E7 and E8.

For RH we adapt the approach of Sofiev et al. (2013), who used a piece-wise linear relationship scaled from one (RH of 50 % or less) to zero (RH of 80 % or above). For wind speed, Sofiev et al. (2013) assumed a smaller emission rate (f_stagnant=0.33) in stagnant conditions and scaled smoothly to a saturation value (1.0) for higher wind speeds. We adapt this approach to the case of RH, but use a logistic function ($f_{\mathrm{l}}(y;\mathit{\alpha },c)=\frac{\mathrm{1}}{\mathrm{1}+e^{-\mathit{\alpha }(y-c)}}$, for location parameter c and rate parameter α), where the rate and location parameters are set to yield $f_{\mathrm{l}}(\mathrm{50};{\mathit{\alpha }}_{\mathrm{RH}},c_{\mathrm{RH}})=\mathrm{0.95}$ and $f_l(\mathrm{80};{\mathit{\alpha }}_{\mathrm{RH}},c_{\mathrm{RH}})=\mathrm{0.05}$, with α_RH being negative, meaning that the assumed emissions rate decreases with increasing humidity. The final f_RH is then

$$\begin{array}{}\text{(3)}& f_{\mathrm{RH}}=f_{\mathrm{stagnant}}+(\mathrm{1}-f_{\mathrm{stagnant}})\cdot f_{\mathrm{l}}(\mathrm{RH};{\mathit{\alpha }}_{\mathrm{RH}},c_{\mathrm{RH}}).\end{array}$$

The equation for the temperature term (f_TM) is identical to the RH term (Eq. 3), but taking temperature (^∘C) as the argument and with different rate and location parameters. These are defined such that $f_{\mathrm{l}}(\mathrm{6};{\mathit{\alpha }}_{\mathrm{TM}},c_{\mathrm{TM}})=\mathrm{0.05}$ and $f_{\mathrm{l}}(\mathrm{24};{\mathit{\alpha }}_{\mathrm{TM}},c_{\mathrm{TM}})=\mathrm{0.95}$. The implied rate parameter (α_TM) is positive, meaning that grass pollen emissions are assumed to increase with increasing temperature.

A similar approach is taken for precipitation (f_PR), with the logistic rate and location parameters constrained to satisfy $f_{\mathrm{l}}(\mathrm{0};{\mathit{\alpha }}_{\mathrm{PR}},c_{\mathrm{PR}})=\mathrm{0.95}$ and $f_{\mathrm{l}}(\mathrm{0.5};{\mathit{\alpha }}_{\mathrm{PR}},c_{\mathrm{PR}})=\mathrm{0.05}$, where the precipitation is given in units of millimetres per hour (mm h⁻¹) and α_PR is negative. We cannot impose a constraint of the function being 1.0 for zero precipitation, as the logistic function approaches 1.0 asymptotically. Instead, we scale the result based on the function's value for zero humidity (defined above as 0.95), resulting in

$$\begin{array}{ll}{\displaystyle }{f}_{\mathrm{PR}}=& {\displaystyle }{f}_{\mathrm{stagnant}}+(\mathrm{1}-f_{\mathrm{stagnant}})\cdot f_{\mathrm{l}}(\mathrm{PR};{\mathit{\alpha }}_{\mathrm{PR}},c_{\mathrm{PR}})/\\ \text{(4)}& {\displaystyle }& {\displaystyle }{f}_{\mathrm{l}}(\mathrm{0};{\mathit{\alpha }}_{\mathrm{PR}},c_{\mathrm{PR}}).\end{array}$$

As noted above, the effect from wind speed (f_WS) is assumed to scale smoothly from a lower rate of 0.33 for f_stagnant in still conditions. We follow the parameterisation of Sofiev et al. (2013, Eq. 11):

$$\begin{array}{}\text{(5)}& f_{\mathrm{WS}}=f_{\mathrm{stagnant}}+(\mathrm{1}-f_{\mathrm{stagnant}})\cdot (\mathrm{1}-\exp (-\mathrm{WS}/U_{\mathrm{satur}}\left)\right),\end{array}$$

where wind speeds (m s⁻¹) are scaled by a saturation wind speed (U_satur=5 m s⁻¹), above which the wind speed does not promote the release of pollen.

3.1.2 The gross timing (G)

We consider two representations of the gross timing, a Gaussian distribution to represent the growth and decline of the springtime pollen season, and the enhanced vegetation index (EVI). The Gaussian distribution (Eq. 6) is normalised to integrate to the theoretical maximum spatial production of ryegrass pollen over the season, estimated by Smart et al. (1979) as 464 kg ha⁻¹ of ryegrass pollen in grasslands to the north of Melbourne.

$$\begin{array}{}\text{(6)}& {\displaystyle }G(x,y,t)={\displaystyle \frac{F}{\sqrt{\mathrm{2}\mathit{\pi }{\mathit{\sigma }}^{\mathrm{2}}}}}\exp \left[-{\displaystyle \frac{(d-n{)}^{\mathrm{2}}}{\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}}}}\right],\end{array}$$

where d is the day number (from 1 October to 31 December = 92 d) within the season, n is the mean day number of that season (46.5), σ is the standard deviation (26.7) and F is a normalisation factor of $\mathrm{9.53}\times {\mathrm{10}}^{-\mathrm{8}}$, so that seasonal emissions integrate to 464 kg ha⁻¹. This Gaussian representation is used in scenarios E1, E5, E6 and E7.

We apply a second Gaussian representation in scenario E8 which uses the shapes of the 2017 observed pollen time-series to shift the distribution by either moving the mean earlier or later in the grass season, and/or adjusting the standard deviation to be tighter or wider. The curves are fitted by optimising the root mean squared error (RMSE) between the pollen counts and the original Gaussian distribution (shown in the Supplement). The peak of the grass pollen season is earlier in Bendigo and Dookie than day 46.5, thus all grassland north of 37^∘ S replaces n with 34.7 and σ reduces to 15.5 (F remains the same as above). The peaks in observed pollen at Creswick and Churchill are later in the season and count more pollen than other sites; thus, at locations south of 37^∘ S and east of 143.5^∘ E, n is replaced by 50.5, σ is narrowed to 19.3 and F increased to $\mathrm{1.2}\times {\mathrm{10}}^{-\mathrm{7}}$. At sites west of 143.5^∘ E (i.e. Hamilton), the peak of the pollen observations are greater and distributed more tightly, thus n reverts to 48.1, σ is narrowed to 7.7 and F is increased further to $\mathrm{1.56}\times {\mathrm{10}}^{-\mathrm{7}}$.

3.1.3 Enhanced vegetation index (EVI)

Devadas et al. (2018) developed a non-linear statistical model for pollen concentrations using satellite greenness indices across areas surrounding a receptor point. The EVI is a measure of landscape greenness, which is less affected by saturation in higher biomass regions than the widely used normalised difference vegetation index (Huete et al., 2002). The EVI value typically increases rapidly with time during spring due to foliage growth in deciduous trees or grass growth. In the Victorian temperate climate, fresh grass rapidly dries (or “cures”) in late spring and early summer, causing a fall in the EVI. Given the absence of deciduous forests in Australia, most of the temporal variation in the EVI is due to grass growth and curing. Here we investigate a relationship between the timing of the pollen season and the gradient in the EVI over a region in the south-west of Victoria, spanning 37.3–38.3^∘ S and 142.0–143.3^∘ E (appearing as dashed lines in Fig. 3). This region is upwind of Melbourne, in terms of the prevailing climatological wind, and has high agricultural activity.

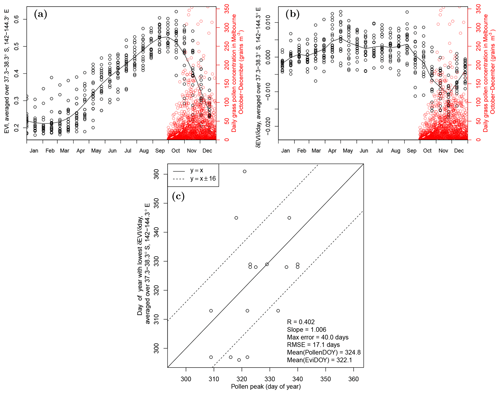
Figure 2 (a) A 16-year climatology in EVI (black) from south-west Victoria (averaged over the region from 37.3 to 38.3^∘ S and 142.0 to 143.3^∘ E, shown in each panel of Fig. 3) and the grass pollen record in Melbourne (red); the full sequence of data is shown as circles, with a locally weighted polynomial regression overlaid (Cleveland, 1979). The EVI data are 16 d composites. (b) As in panel (a) except presenting the derivative of the 16 d EVI with respect to time. (c) The day of the year of the minimum of the $\frac{\partial \mathrm{EVI}}{\partial \mathrm{t}}$ for each year plotted against the day of the year of the maximum pollen; when assessing the timing of the grass pollen peak, the grass pollen time-series was smoothed using a cubic smoothing spline. The dashed lines in (c) represent 16 d either side of a given day, which is the width of the MODIS EVI compositing window.

Using the Moderate Resolution Imaging Spectroradiometer (MODIS) MOD13C1 data (from the Terra satellite at 0.05^∘ resolution), Fig. 2a shows that the gradient in averaged EVI drops off rapidly, around the same time as the pollen season peaks. Fig. 2b shows that the first derivative of EVI is with the grass pollen time-series at UoM. If we examine inter-annual variation, assessing the day of the year when the EVI falls most rapidly (represented as the middle of the 16 d EVI compositing window) and the day of the year when the grass pollen peaks (having first applied a smoothing spline to the pollen time-series), a relationship between these two quantities is observed: the Pearson correlation is 0.4, the slope of the linear regression is 1.006 and the means of the two Julian dates differs by only 2.7 d (Fig. 2c). This agreement is especially notable given the uncertainty induced by the wide EVI compositing window.

Figure 3 Relationship between the timing of the peak in grass pollen in Melbourne and the timing of the sharpest drop in EVI at each MODIS pixel: the correlation (a) and the root mean squared error in the timing (b). Also shown are the average timing (c) and rate (d) of the fastest fall in EVI at each point in the domain. The dashed rectangle in south-west Victoria (spanning 37.3–38.3^∘ S and 142.0–143.3^∘ E) displays the region over which the EVI time-series were averaged for Fig. 2. “argmin” refers to the minimum argument.

Taking this one step further, we apply a similar analysis to each individual 0.05${}^{\circ }\times {\mathrm{0.05}}^{\circ }$ MODIS pixel (Fig. 3). Given the high deposition velocity of grass pollen grains (4.6 cm s⁻¹, as discussed above), the contribution of pollen emitted from the productive grassland areas in western Victoria to observations recorded in Melbourne is likely to be minimal. However, this analysis may help inform our understanding about the relationship between the remotely-sensed vegetation index and broad-scale features of the pollen season. The timing of the fall in the EVI in south-west Victoria not only correlates well with the timing of the grass pollen season experienced in Melbourne (Fig. 3a), but the differences in timing are also relatively small (Fig. 3b). The north-west of the state is generally much drier than the south-east (Fig. 1c), and the north-west area dries out earlier in the year (Fig. 3c). Areas identified as crops or pasture (Fig. 1d) demonstrate a more rapid fall in EVI (Fig. 3d).

This exploratory analysis suggests that in this bioclimate the broad parameters of the pollen season can be diagnosed from the EVI fields. On a broad temporal scale, a fall in the EVI over pollen source regions is associated with increasing pollen emissions. In light of this, we consider an EVI-based representation of the gross timing (G):

$$\begin{array}{}\text{(7)}& G(x,y,t)=max\left(\mathrm{0},-{\displaystyle \frac{\partial \mathrm{EVI}(x,y,t)}{\partial t}}\right).\end{array}$$

The $max(\cdot )$ function ensures that the emissions are strictly positive. We note that Eq. (7) incorporates both temporal and spatial information, and can thus be used to represent the spatial distribution, in which case we can set S=1.0 for all grid-points (x,y) (scenario E3). Alternatively, we can use the same spatial forcing (based on an assumed land use classification) to provide an extra spatial constraint. ∂EVI is used in scenarios E2 and E4.

3.1.4 The spatial function (S)

Mapped grass and pasture for Victoria were extracted from the Australian Land Use and Management (ALUM) classification (ABARES, 2017) and were re-gridded from a 50 m resolution to the 3 km grid used by the C-CTM. ALUM includes 193 categories of which only three are assumed to overlap with grazing pastures (“Grazing modified pastures”, “Native/exotic pasture mosaic” and “Grazing irrigated modified pastures”); the fractional coverage of these three classes together is shown in Fig. 1d. We include larger-scale maps of the pasture grass coverage surrounding the pollen count sites in the Supplement. While many cultivated cropping cereals grown in the region are also grasses (e.g. wheat and barley), they are mostly self-pollinating and thus produce very little pollen compared with wind-pollinated grass species such as ryegrass. The area to the east of Melbourne is mountainous and therefore not arable (Fig. 1e), whereas the region to the north-west is arid (Fig. 1c). The most productive areas of pasture grass in Victoria are found in the west of the region near Hamilton and south-west of Churchill. The ALUM grass map is used in scenarios E1, E2, E4, E5, E6, E7 and E8.

3.1.5 Pollen production–loss model

In reality, there is a finite amount of grass pollen available for release at a given time, and once exhausted by in-plant dry and wet deposition, or pollen release, the pollen reservoir is only replenished at a finite rate. Scenario E7 is a production–loss model for this pollen reservoir.

$$\begin{array}{ll}\text{(8)}& {\displaystyle }& {\displaystyle }E(x,y,t)=A(x,y,t)\cdot I(x,y,t){\displaystyle }& {\displaystyle }A(x,y,t)=A(x,y,t-\mathit{\delta }t)+P(x,y,t-\mathit{\delta }t)\\ \text{(9)}& {\displaystyle }& {\displaystyle }-L(x,y,t-\mathit{\delta }t)\text{(10)}& {\displaystyle }& {\displaystyle }P(x,y,t)=S(x,y,t)\cdot G(x,y,t)\cdot \left({\displaystyle \frac{\mathit{\delta }t}{T}}\right)\text{(11)}& {\displaystyle }& {\displaystyle }L(x,y,t)=A(x,y,t)\cdot \exp (-\mathit{\lambda }\cdot \mathit{\delta }t),\end{array}$$

where emissions, E, are set to be the product of the available pollen reservoir, A, and the instantaneous emission factor, I, at grid-point (x,y) and time t. δt is the model time-step. The pollen produced, P, is given by the product of the spatial and gross-timing terms, proportional to the fraction of the grass pollen season covered between t and t+δt. L is the amount lost between t and t+δt, T is the total length of the grass pollen season and λ is the loss rate due to direct deposition before the pollen leaves the plant. This loss can occur direct to the ground or due to animals brushing past, and differs from the in-atmosphere wet and dry deposition rates. Zink et al. (2013) suggest that this loss process is similar to a half-life, which we extend to provide a variable loss rate accelerated in wet conditions. The loss decay parameter (λ), is defined as a piece-wise polynomial function based on the rain rate such that pollen has a half-life on the plant of 2 d in dry conditions and 12 h in wet conditions, with the latter corresponding to a rain rate of 2 mm h⁻¹.

3.1.6 Statistical models

In parallel to the emission–dispersion modelling presented here, statistical forecasting methods have been trialled for use in Victoria. These models are non-linear regression equations that use weather model data, derived parameters from the MODIS EVI and land use maps as predictors. These data can be decomposed into a slow-moving seasonal component (similar to the gross-timing term described above) and a second component that accounts for day-to-day variation. The models were trained on daily pollen count data, and thus cannot resolve higher-resolution temporal variation. The gross-timing function smooths out much of the day-to-day variation, and is modulated by the immediate-timing term when estimating temporal variability in the emissions module. The two statistical models are described in detail in Silver et al. (2019), and summarised here. “V1” used data from Melbourne spanning from 2000 to 2016 (scenario E9), whereas “V2” also used the 2017 data from the eight Victorian sites (scenario E10). The V1 model was developed ahead of the 2017 pollen season before counts were available at the new pollen sites, as the BOM required input for their pilot thunderstorm asthma service. The seasonal component was represented as a Cauchy distribution (which decays more slowly than a Gaussian distribution), with a fixed scale parameter (k=19 d). The magnitude of the pollen season (corresponding to the maximum of the seasonal term) was estimated by univariate linear regression on the winter-time maximum EVI. The timing of the seasonal maximum was estimated by the day of the year when the EVI falls to 0.05 below its winter-time maximum. The magnitude and timing were smoothed spatially using an inverse cubed distance weighting.

Both V1 and V2 were constructed as generalised additive models (Wood, 2006), a form of multivariate regression that allows for a non-linear influence of the predictor variable on the response variable. The response variable used was the log (x+1)-transformed pollen count. The log of the Cauchy term and a number of derived weather parameters were considered for inclusion in the model. Each model was built up via forward step-wise variable selection; starting with a “null model” (predicting nothing but the mean), terms were considered for inclusion. Each predictor was trialled as having a linear or alternatively non-linear effect on the response variable, and the out-of-sample prediction skill was tested. The combination of predictor and form (i.e., linear or non-linear) that yielded the biggest gain in predictive skill was retained. This procedure was repeated until the incremental impact of additional terms on predictive skill was negligible. The model skill was tested by leaving out entire pollen seasons, fitting the model without these data, then assessing the model using the out-of-sample subset. Model skill was quantified using the Pearson correlation between predicted and observed pollen.

The statistical models were adapted for 3-D dispersion modelling to use hourly meteorological inputs (or daily, in the case of precipitation). The adapted forms of the two models are as follows:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\log (\mathrm{1}+{\mathrm{P}}_{\mathrm{1}}(x,y,t\left)\right)=-\mathrm{0.290}+\mathrm{0.970}\cdot {\mathrm{R}}_{\mathrm{1}}(x,y,d)\\ {\displaystyle }& {\displaystyle }-\mathrm{0.183}\cdot \log \left(\mathrm{PR}\right(x,y,d)+\mathrm{1})-\mathrm{0.117}\cdot \log \left(\mathrm{PR}\right(x,y,d\left)\right)\\ \text{(12)}& {\displaystyle }& {\displaystyle }+f_{\mathrm{TM}\mathrm{1}}(x,y,t)+f_{\mathrm{RH}\mathrm{1}}(x,y,t){\displaystyle }& {\displaystyle }\log (\mathrm{1}+{\mathrm{P}}_{\mathrm{2}}(x,y,t\left)\right)=\mathrm{1.225}+\mathrm{0.770}\cdot {\mathrm{R}}_{\mathrm{2}}(x,y,d)\\ {\displaystyle }& {\displaystyle }-\mathrm{0.033}\cdot \mathrm{WS}(x,y,t)+f_{\mathrm{RH}\mathrm{2}}(x,y,h)\\ \text{(13)}& {\displaystyle }& {\displaystyle }+f_{\mathrm{TM}\mathrm{2}}(x,y,t)+f_{\mathrm{PR}}(x,y,d),\end{array}$$

where P is the predicted pollen emission for version i at grid-point (x,y) and time t, R_i is the seasonal term based on the EVI parameters at grid-point (x,y) and for day d (outlined below), and WS is the wind speed (m s⁻¹). In both versions of the statistical model, the variable selection process assigned a non-linear response to the temperature, f_TMi (^∘C) and RH f_RHi (%). Only V2 uses a non-linear term for daily precipitation, f_PR (mm). The non-linear relationships between pollen emission and increasing temperature, RH and precipitation are shown in Fig. 4. The shaded regions correspond to plus or minus twice the standard error of the GAM term, and are greater in regions of the distribution with fewer observations. For example, there were far fewer observations at the upper tail of the temperature range considered, and the standard errors are correspondingly larger.

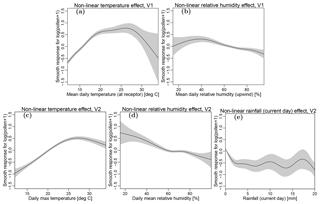
Figure 4 The shape of the non-linear terms in the statistical models related to temperature (a and c), relative humidity (b and d) and rainfall (e) for V1 (a and b) and V2 (c, d and e). The shaded regions correspond to plus or minus twice the standard error of the GAM term.

The statistical parameterisations were based on ambient pollen concentrations rather than emissions; thus, the non-linear terms take transport and dilution processes into account. The shapes of these relationships are similar to those described by Erbas et al. (2007) for grass pollen in Melbourne, and also by Zink et al. (2013) for birch pollen in Europe. The temperature response in both models increased until 25 to 30 ^∘C (Fig. 4a, c). The decline in pollen response at higher temperatures is likely due to dilution with higher planetary boundary layers. On days in November where the temperature is above 25 ^∘C, the maximum modelled boundary layer height is nearly double the height modelled on days below 25 ^∘C. Thus, the assumption of declining emissions with increased temperature is likely incorrect. There is relatively little non-linearity with humidity. The general trend is for increased concentrations (or emissions) in drier conditions, explained by the drying required before anther dehiscence. The rainfall term shows a sharp decline until about 2 mm d⁻¹, after which little additional pollen suppression occurs, although there is considerable uncertainty given the relative paucity of high-rainfall days. The suppression of grass pollen concentrations (or emissions) is likely due to the low potential for anther dehiscence in moist conditions, and the wet deposition of ambient pollen.

The seasonal term based on the EVI parameters is given as

$$\begin{array}{ll}\text{(14)}& {\displaystyle }& {\displaystyle }{\mathrm{R}}_i(x,y,d)=\log \left({\mathrm{SF}}_i\right(x,y)\cdot f_{\mathrm{C}}(d,{\mathit{\mu }}_i(x,y),k\left)\right),\text{where}\text{(15)}& {\displaystyle }& {\displaystyle }{f}_{\mathrm{C}}(d,\mathit{\mu },k)={\left(\mathit{\pi }\cdot k\cdot \left[\mathrm{1}+{\left({\displaystyle \frac{d-\mathit{\mu }}{k}}\right)}^{\mathrm{2}}\right]\right)}^{-\mathrm{1}}{\displaystyle }& {\displaystyle }{\mathrm{SF}}_{\mathrm{1}}(x,y)=max(-\mathrm{4355.913}+\mathrm{21490.343}\\ \text{(16)}& {\displaystyle }& {\displaystyle }\cdot E_{\max ,\mathrm{smoothed}}(x,y),{\mathrm{10}}^{-\mathrm{10}})\text{(17)}& {\displaystyle }& {\displaystyle }{\mathit{\mu }}_{\mathrm{1}}(x,y)=E_{\mathrm{drop},\mathrm{smoothed}}(x,y)\text{(18)}& {\displaystyle }& {\displaystyle }{\mathrm{SF}}_{\mathrm{2}}(x,y)=\mathrm{267.627}+\mathrm{8853.990}\cdot E_{\max ,\mathrm{smoothed}}(x,y)\text{(19)}& {\displaystyle }& {\displaystyle }{\mathit{\mu }}_{\mathrm{2}}(x,y)=\mathrm{202.478}+\mathrm{0.385}\cdot E_{\mathrm{drop},\mathrm{smoothed}}(x,y),\end{array}$$

where the scale factor parameter SF_i(x,y) is based on the smoothed value of the winter-time maximum EVI ($E_{\max ,\mathrm{smoothed}}(x,y)$), whereas the timing of the peak of the pollen season (μ_i(x,y)) is assumed to scale linearly with the smoothed field of the day of the year when the EVI drops 0.05 below its winter-time maximum (see Silver et al., 2019, for further details). The statistical approach accounts for inter-annual variation via the EVI time-series at each grid cell. Higher winter-time peak EVI values are associated with higher cumulative grass pollen counts over the following season.

3.2 Statistical evaluation

The skill of the pollen forecasts depends in part on how well the meteorology is predicted. The Pearson correlation indicates the strength of the correspondence without consideration of differences in magnitude, whereas the index of agreement (IOA, described in the Supplement) is a good indicator of model performance. The normalised mean bias (NMB) gives the relative difference between the model and observations.

To determine the best pollen emission methodology, we look for skill in the ability of VGPEM1.0 to forecast the possibility of the pollen being classed as high or extreme (>50 grains m⁻³), which is a level at which health impacts may be felt more strongly. The number and timing of predicted high pollen days is evaluated quantitatively for consistency and accuracy, by calculating the probability of detection (POD), the false alarm ratio (FAR) and the equitable threat score (ETS) from a simple table of model outcomes (Table 3). The POD is the fraction of correctly identified high model forecasts compared with the observations, between zero and one:

$$\begin{array}{}\text{(20)}& \mathrm{POD}={\displaystyle \frac{a}{a+c}}.\end{array}$$

Table 3 The 2×2 contingency table describing each model outcome. The model outcomes a, b, c and d then become the variables in Eqs. (20)–(23).

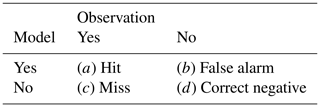
The FAR puts a value between zero and one regarding how many of the predicted high pollen days did not correspond with an observed high pollen day:

$$\begin{array}{}\text{(21)}& \mathrm{FAR}={\displaystyle \frac{b}{a+b}}.\end{array}$$

The ETS is the fraction of modelled high pollen days that were correctly predicted and is adjusted for correctly modelled days occurring with random chance. The ETS value is between $-\mathrm{1}/\mathrm{3}$ and 1, with a score of 0 indicating no skill; this is defined as

$$\begin{array}{}\text{(22)}& \mathrm{ETS}={\displaystyle \frac{a-a_{\mathrm{random}}}{a+b+c-a_{\mathrm{random}}}},\end{array}$$

where

$$\begin{array}{}\text{(23)}& a_{\mathrm{random}}={\displaystyle \frac{(a+c)\times (a+b)}{a+b}}.\end{array}$$

As Zink et al. (2013) point out, low skill scores are given to models where the pollen concentrations are close to observed concentrations yet fall into separate “risk” categories. For example, the model predicts 48 grains m⁻³ and classes the risk category as “moderate”, whereas the observations are 52 grains m⁻³ and the risk category is “high”. Therefore, we also evaluate the modelled pollen against the observations in terms of their Pearson correlation, RMSE and Gerrity score. Statistical evaluations using categorised and non-categorised pollen counts will show how the Australian grass pollen thresholds impact our results. The Gerrity score puts a value on the accuracy of VGPEM1.0 in predicting all of the observed pollen categories, relative to that of random chance (Gerrity, 1992). Gerrity scores range between −1 and 1, with 0 indicating no skill and 1 being a perfect model. Calculation of Gerrity scores is complex and is described fully in the Supplement.

The best forecasting methodology will have a high Pearson correlation, Gerrity score, POD and ETS, and a low FAR and small RMSE.

4 Results and discussion

4.1 Verification of meteorology

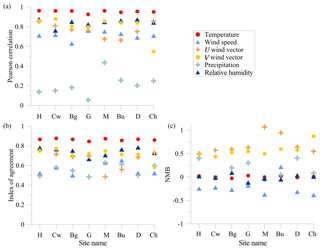
Meteorological variables are extracted from the ACCESS runs at the locations of the AWSs closest to the pollen observation sites (Table 1). At some pollen observation sites the AWSs are located more than 10 km away, or nearly 30 km away in the case of Dookie. A direct comparison is made of hourly temperature, wind speed, wind vectors, precipitation and RH between ACCESS and the AWS observations, using the Pearson correlation, IOA and NMB. (Fig. 5). Here the NMB is normalised by the mean of the absolute value of the observations (as opposed to the mean of the observations) because wind vectors contain negative values. Temperature and RH are both modelled with a high degree of accuracy at all sites, demonstrating a high Pearson correlation (average r=0.9), almost no bias, and high IOA (average IOA=0.8). Predicted wind speeds are biased slightly low (average $\mathrm{NMB}=-\mathrm{0.2}$). The V (north–south) component is approximately as well modelled as the U (east–west) component (average V r=0.80 compared to average U r=0.77). Precipitation has a low degree of bias (average NMB=0.17) but is not particularly well correlated with the observations (average r=0.21), and has a lower overall IOA (average IOA=0.55).

Figure 5 Comparison of observed and modelled meteorological variables at automatic weather station sites nearest to the pollen observation sites. (a) Pearson correlation. (b) Index of agreement. (c) Normalised mean bias.

4.2 Observed and modelled pollen correlations with meteorology

We assess which measured AWS meteorological variables are most strongly related to the observed pollen. Figure 6a shows that observed grass pollen is most strongly correlated with temperature at the majority of sites (average r=0.44), and most negatively correlated with RH (average $r=-\mathrm{0.34}$).

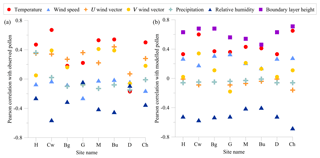
Figure 6 Pearson correlations of (a) observed pollen with observed meteorological variables from the nearest automatic weather station, and (b) modelled pollen with modelled meteorological variables.

Observed wind speed is not strongly related to observed grass pollen, except when combined with direction, specifically the U wind vector is generally a stronger predictor of pollen (average r=0.32) than the V wind vector (average r=0.22). We include a wind rose for each AWS site in the Supplement to determine the strength of the winds. The roses show a strong southerly influence, corresponding with an afternoon sea breeze at most sites apart from Churchill, located within an east–west aligned valley. Sites further west in Victoria (Hamilton and Creswick) also show a northerly influence, generally with a greater percentage of wind speeds above 4 m s⁻¹ than elsewhere. Precipitation washes pollen from the air, but shows no correlation here as rain during the 2017 season was infrequent (average r=0). Pollen observations at Dookie are the least correlated with any of the meteorological variables, perhaps because the closest AWS is 29 km away.

Figure 6b shows Pearson correlations for the modelled pollen against ACCESS meteorology, using scenario E8 as an example that uses the meteorological timing function. The strengths of the modelled correlations are broadly similar to those observed in Fig. 6a, but the model is more strongly coupled to wind speed (average r=0.25) and less correlated with the U wind vector than is observed (average $r=-\mathrm{0.07}$). However, the observed U and V correlations are not strong, and do not point to particular locations being strong pollen sources. Inverse modelling may help pinpoint productive grass pollen regions for each site. We extracted the boundary layer height from the model (unavailable in the observations), which showed that the modelled grass pollen is more strongly correlated with atmospheric dilution (average r=0.61) than it is to temperature (average r=0.44). Average modelled diurnal boundary layer evolution during November 2017 in Melbourne increases after sunrise at 05:00 AEDT to a peak of 1780 m at 13:00 AEDT. The height declines during the afternoon coincident with a southerly sea breeze, but is still above 1200 m at 17:00 AEDT. The nocturnal boundary layer is around 200 m. Over 77 % of grass pollen is found at ground level (Damialis et al., 2017) due to its size and density. The lifetime of our model pollen over 1 km is 6 h. The model RH is more negatively correlated with grass pollen levels (average $r=-\mathrm{0.52}$) than is observed. The observed relationship may be weaker, as the pollen measurements are not coincident with the AWS.

4.3 Verification of pollen source methodologies

The modelled pollen concentrations are first normalised by the observed seasonal mean across all observation sites, which is equal to 47 grains m⁻³. This normalisation allows the evaluation of trends in the daily grass pollen concentrations without considering their magnitude, as this can be corrected later. For 2017, observed individual site means range from 31 grains m⁻³ at Melbourne to 60 grains m⁻³ at Creswick. The lowest means are found in the densely populated regions of Geelong, Melbourne and Burwood (see Fig. 1f). Figure 7 shows correlations and statistical results for each pollen observation site. Numbers of observed days in the lumped high and extreme category (>50 grains m⁻³) are above 20 d for all sites.

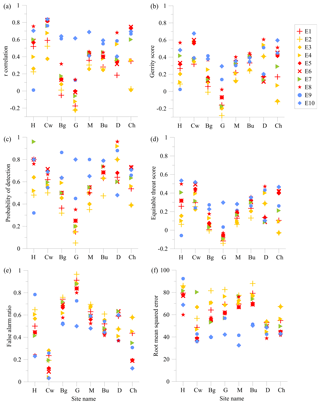
Figure 7 Results from the pollen emission methodology scenarios: (a) Pearson correlation, (b) Gerrity score, (c) POD, (d) ETS, (e) FAR and (f) RMSE. The sites are presented from west to east, and red refers to Gaussian methodologies, yellow refers to ∂EVI methodologies, green refers to the production–loss model and blue refers to statistical methodologies. A higher score is better for the Pearson correlation, Gerrity score, POD and ETS. A lower score is better for the FAR and RMSE.

E1, E2 and E3 used wind speed as the immediate timing function, which provided poor prediction skill scores (average r=0.25, 0.18 and 0.17 respectively), similar to results by Viner et al. (2010) and Zink et al. (2013). Wind promotes pollen emissions, but the plant must flower first – a process not controlled by wind speed. Wind also correlates poorly with pollen observations due to the competing effects of strength versus increased ventilation and mixing (Sofiev et al., 2013). Subsequent method E5 used the meteorological timing function that included temperature and RH and performed better (average r=0.43). Sofiev et al. (2013) also showed that observed birch pollen in Europe was negatively correlated with RH. Widening the timing of the peak pollen emission from 2 to 4 h, as included in E6, improved results further over E5 (average r=0.44).

At most sites the Gaussian description of the season performed better than the ∂EVI, shown by improvements in the FAR of E1 over E2, both of which used wind speed as the immediate timing descriptor (average FAR=0.57 and 0.61 respectively), and E5 over E4, both of which used the meteorological timing function (average FAR=0.48 and 0.52 respectively). These results indicate that using ∂EVI data as descriptors of the pollen season results in poor skill at most of the sites. The ∂EVI data are very noisy. However, E4 using the ∂EVI data and a meteorological timing function gives a good Gerrity score (0.54) and high POD (0.92) and ETS (0.40) at Dookie. When other elements of the EVI data are used in the statistical models (E9 and E10), such as the winter maximum and the day on which the EVI falls below 0.05 of the winter maximum, the pollen prediction is much improved at most sites (average POD E9=0.67 and E10=0.69). The performance of E10 indicated improvements in forecasting skill at all sites with the exceptions of Dookie and perhaps Bendigo. E10 predicted the lowest FAR of high pollen predictions at five of the eight observation sites (average FAR=0.37). The ETS adjusts the model score for achieving high pollen predictions at random. E10 achieves higher ETS scores at four of the eight sites (average ETS=0.35). Both the statistical emission parameterisations assume an underlying Cauchy distribution, which is modulated by the effects of wind, temperature, RH and rainfall. At each model grid cell, the peak and magnitude of this bell curve is calculated from statistics inferred from the EVI gradient.

The pollen production and loss model E7 had a very high POD (0.96) at Hamilton, but the method was less effective elsewhere with high FAR and RMSE scores at the other observation sites (average FAR=0.55 and RMSE=63). E7 used the Gaussian distribution for the seasonal term which could be improved upon, but the method was superseded by the good performance of the statistical models (with the exception of E9 in Hamilton and Geelong).

The Geelong pollen observations are not well modelled by most of the emission methodologies with Gerrity scores mainly in the negative region and high FAR>0.8. E10 provides the best scores by far at Geelong with a 0.62 Pearson correlation and 0.3 Gerrity score, although, overall, results are poorer for Geelong than any other site. The wind rose for Geelong shows the strong Southern Ocean influence, and there are few grass-filled pixels between the coast and the pollen count site which the model relies upon (Supplement).

The sites vary considerably in terms of surrounding land use, whereas all of the pollen in the model comes from pasture grass. This impacts the individual site performance against the pollen observations. Hamilton, Dookie and Churchill are close to pollen source areas. Creswick is surrounded by forest. The Burwood and UoM sites are in heavily built up areas with green space, which is not included in the model pasture grass maps.

Comparing the results of the non-categorised Pearson correlation and RMSE against the categorised Gerrity score yields minor differences between 0.1 and 0.2 units, and suggests that the Australian grass pollen thresholds influence the analysis by about 15 %. If the best performing scenario for each observation site and under all scoring methods is counted from Fig. 7, shifted Gaussian methodology E8 is best 12 times, statistical representation E9 is best 4 times and E10 is best 25 times. E9, built using data prior to the 2017 season, has a stronger dependence on precipitation than E10, which is not supported by the correlation of 2017 pollen with meteorology. This suggests that the V2 statistical approach to the immediate timing combined with an EVI-based approach to the gross timing and a spatial source is likely to produce the most accurate pollen forecasts.

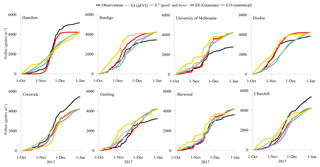
It is useful to plot the observed and modelled pollen as a cumulative time-series, as this indicates the timing of increased and decreased pollen counts (Fig. 8). Here we focus on the best performing scenarios from each of the seasonal emission methods, capturing the range in descriptions of the pollen season. The observations show an “S” shaped profile, with increased pollen gradients in November. By the end of the 2017 season, all modelled profiles reach a cumulative total of 4200 grains m⁻³ due to normalisation to the same observed mean value.

Figure 8 Cumulative time-series for pollen across the 2017 season. Sites arranged from west to east.

The ∂EVI method E4 tends to emit grass pollen too early in the season compared with observations at most sites. However at Dookie the shape of the season in E4 and E8 is more similar to the observations, and E4 captures the mid-November change when pollen counts decrease better than E10. The observed pollen at Dookie experienced a much larger grass pollen input from the middle of October to early November than E10 (but is represented well by E8). There is little additional observed pollen at Dookie after early November, which is at least 20 d earlier than at the other sites. At Melbourne, Bendigo and Burwood, both E8 and E10 predict the early part of the grass pollen season very well, but emitted too much modelled pollen towards the end of the season. The steeper gradient in E8 and E10 at Melbourne between the middle and the end of November shows that too much pollen was emitted during this period. In contrast, observed pollen at Churchill, Creswick, and Hamilton shows a rapid increase in emissions at the end of November that is not matched by either E8 or E10. However, the observations suggest that additional pollen continues to be emitted towards the end of December at Creswick and Churchill, prolonging the season. Scenario E8 captures the steep November gradient at Hamilton very well.

The observed and modelled pollen cumulative profiles in Melbourne, Geelong and Burwood are less smooth than the other regional sites, perhaps indicating more atmospheric variability near the coasts. It might also indicate the larger distances between the urban sites and the grass pollen production regions (more transport and less local production), compared with the monitoring sites within grass pollen production areas (less transport and more local production). Here we also note the apparent lack of an “S” shape in the modelled profiles at Geelong, which may account for the poor model performance at this site.

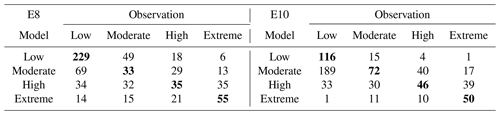
Table 4 splits the best model predictions from E8 and E10 into low, moderate, high and extreme categories for direct comparison with observed categories. Here data from all counting sites are combined to ensure a large sample size. The diagonal in each table highlights the number of days the model has correctly predicted the observed category. Values far from the diagonal indicate the model has under- or over-predicted the observed pollen. We want to avoid occasions where the observed pollen is extreme, but the model predicts low pollen. Table 4 shows that both E8 and E10 have good skill in predicting low observed pollen days. Both models also show high occurrences of predicting moderate pollen when the observed category is low. Siljamo et al. (2013) found difficulties in modelling moderate category days, which is not the case here. Both models are equally good at predicting the high and extreme observed categories. E10 has fewer occurrences of predicting extreme pollen on days when observations were low than E8. However, there are six cases in E8 and one in E10 that predict low pollen when the observations are extreme. These cases occur around the 10–11 November within the city at Geelong, Melbourne and Burwood. Examining the meteorology from this period (pollen counts are date-stamped at 09:00 AEDT, but represent the preceding 24 h) shows that the model has captured the observed temperature, wind speed, direction and zero rainfall. The observed wind direction is from the south and south-east, bringing mainly clean, marine air. However observed pollen is extreme on these days, suggesting a highly localised source. One explanation is that only pasture grass is considered in the model, whereas grass is usually present in most other land use categories. There is green space within most cities on both public and private land, and grass plants are efficient at colonising disturbed areas such as road verges. Correlations between observed pollen at each site are not particularly strong (average r²=0.28), suggesting that the pollen sources may not be related, or are highly localised. The modelled correlations between all sites are very strong because they share the same pollen source characteristics (average r²=0.80). Inverse modelling could highlight where other grass land use categories contribute to grass pollen. Future development of VGPEM could consider the sub-grid-scale grass fraction using high-resolution satellite data sources.

Table 4 The number of days the model predicts a particular observed pollen category for E8 (left) and E10 (right). Data from all Victorian sites are combined. Bold text highlights where the model captures the correct observed category.

5 Conclusions

The aim of this work was to develop and assess the utility of a grass pollen emission methodology for use in a pollen forecasting tool for Victoria, Australia. Our work is the first of its kind for Australia, and whilst initially based in the state of Victoria, future work will see the methodology applied nationally.

Grass pollen was observed during 2017 at eight sites in Victoria, showing the strongest correlations with temperature (positive) and RH (negative). Correlations of grass pollen with wind speed and precipitation were not strong.

A total of 10 grass pollen emission source methodologies were presented in this work. Most used the locations of pasture grass in Victoria in combination with meteorological parameters and a seasonal pollen emission parameter. The seasonal parameter was either based on a simple Gaussian representation of time variation, or on the enhanced vegetation index that measures greening from satellite. Each source methodology was run using a host transport model driven by ACCESS numerical weather predictions, at a spatial resolution of 3 km. The pollen was treated as an inert particle with a diameter of 35 µm and a density of 1000 kg m⁻³; however, these parameters are uncertain and impact the aerodynamic properties of the pollen.

Comparison of predicted meteorology with observations showed that ACCESS is very good at predicting temperature but less so for precipitation, compared with other meteorological parameters. Wind speeds are biased a little low, but are not the strongest correlating meteorological parameter for observed pollen. The use of wind speed as the immediate timing function in the pollen emissions framework also performed poorly. The key to predictive skill in immediate timing was to use a meteorological timing function that incorporates the parameters most correlated with observed pollen, namely temperature and RH.

Grass pollen source terms using the ∂EVI data did not perform particularly well, with the Victorian grass pollen season perhaps better described by a simple Gaussian variation. Whilst emission method E8 worked well, the method is limited by fixed timings for the start and end of the pollen season, and the distributions were only trained on the 2017 Victorian observation data. These data may not account for regional variation or inter-annual variability.

Implementing the maximum EVI value and the date on which the EVI falls to 0.05 below this maximum within a statistical methodology predicted pollen concentrations with much better skill. The smoothed statistics for E10 used 16 years of observational data from the UoM and 1 year from the seven other Victorian sites. The smoothed statistical approach is modulated by the hourly effects of wind, temperature, RH and rainfall, which introduces temporal variation. The EVI also varies spatially and temporally, meaning that this method is suitable for future years and for other regions of Australia. Additional training data will be included to model pollen in other Australian regions to account for the different seasonal flowering times of other grass species (e.g. C4 grasses) (Beggs et al., 2015). The E10 methodology will be implemented in VGPEM1.0.

Long-term observations are vital to record the grass pollen emission strength across Victoria in future years, particularly tracking changes brought about by climate change, changes to agricultural practices and the growth of cities into rural areas. The new Victorian pollen observation stations established after the thunderstorm asthma event in November 2016 should be maintained to aid with forecasting of potential threats in future. Advances in technology may provide automated pollen counting which would improve the temporal resolution and the possibility of recognising ruptured pollen grains. These technologies are required to support pollen forecasting, and to constrain future modelling of the pollen rupturing process.