Reanalysis of the PacIOOS Hawaiian Island Ocean Forecast System, an implementation of the Regional Ocean Modeling System v3.6

A 10-year reanalysis of the PacIOOS Hawaiian Island Ocean Forecast System was produced using an incremental strong-constraint 4-D variational data assimilation with the Regional Ocean Modeling System (ROMS v3.6). Observations were assimilated from a range of sources: satellite-derived sea surface temperature (SST), salinity (SSS), and height anomalies (SSHAs); depth profiles of temperature and salinity from Argo floats, autonomous Seagliders, and shipboard conductivity–temperature–depth (CTD); and surface velocity measurements from high-frequency radar (HFR). The performance of the state estimate is examined against a forecast showing an improved representation of the observations, especially the realization of HFR surface currents. EOFs of the increments made during the assimilation to the initial conditions and atmospheric forcing components are computed, revealing the variables that are influential in producing the state-estimate solution and the spatial structure the increments form.

1 Introduction

The Pacific Integrated Ocean Observing System (PacIOOS, 2018) has produced daily forecasts of the ocean state surrounding the Hawaiian Islands since 2009. To facilitate the forecasts a data assimilation procedure is used to incorporate recent observational data into the model to produce the optimal initial state from which to forecast. A number of modeling studies have been performed with older versions of this model to examine various features of the modeling framework, such as the state estimation (Matthews et al., 2012), nested models (Janeković et al., 2013), and the vorticity budget (Souza et al., 2015). In this work, we perform an extended reanalysis from 2007 to 2017 in order to produce a consistent dataset for further studies of the dynamics around Hawai`i.

The PacIOOS forecast system uses the time-dependent incremental strong-constraint four-dimensional variational data assimilation (I4D-Var) scheme (Courtier et al., 1994; Moore et al., 2004) within the Regional Ocean Modeling System (ROMS) (Matthews et al., 2012; Moore et al., 2011c; Powell et al., 2008) to best reduce the residuals between the model and observations, while maintaining a physically consistent solution. The class of methods known as 4D-Var are state-estimation techniques that create a quadratic cost function to be minimized over a defined time window utilizing observations at the time they occur in a physically consistent manner to adjust the initial state, boundary conditions, and atmospheric forcing to represent the measurements. The I4D-Var scheme is used in operational centers around the world and solves for increments to the model state, boundary conditions, and atmospheric forcing using the model physics as a constraint. The combination of I4D-Var within ROMS has been used in previous studies of various regions (Broquet et al., 2009; Matthews et al., 2012; Powell et al., 2008; Souza et al., 2015; Zhang et al., 2010). The details of the model and the observations used within this study are provided in Sect. 2.

Our model domain covers the Hawaiian Island Archipelago (Fig. 1), a dynamically active region for both the ocean and atmosphere. The North Equatorial Current (NEC), flowing from the east, splits upon encountering the island of Hawai`i, with the bulk transport traveling around the south of the island and continuing west, while the North Hawaiian Ridge Current (NHRC) follows the ridge of the other islands in the chain to the north. In the atmosphere, there are persistent trade winds from the northeast that, combined with steep mountainous terrain on the islands, cause wind wakes in lee of the peaks, particularly on the islands of Hawai`i and Maui. This introduces strong temperature gradients, increases the seasonal variability (Sasaki and Klein, 2012), and drives currents such as the Hawaiian Lee Countercurrent (HLCC) (Chavanne et al., 2002; Smith and Grubišić, 1993; Xie et al., 2001).

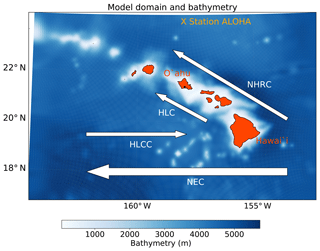
Figure 1 Model domain and bathymetry, with mean currents labeled from Lumpkin and Flament (2013).

There are two main objectives to this study: to assess the skill and performance of the state-estimation model and to analyze the increments made to the initial, boundary, and atmospheric forcing terms. For the first objective, we compare the state-estimate solution with a free-running forecast over the decadal time period and examine how the performance changes over time utilizing observations derived from satellites and it situ measurements. In addition, PacIOOS operates seven high-frequency radar stations sites across the Hawaiian Islands. The first station was constructed in 2010, with the remaining six becoming operational over the period from 2011 to 2015. These instruments produce high-resolution (both spatially and temporally) surface current velocities in the vicinity of the islands of O`ahu and Hawai`i. The use of HFR observations within a state-estimation scheme has been shown to produce a significantly improved representation of surface currents (Kerry et al., 2016; Souza et al., 2015). The impact of the radar stations will be a key focal point. The performance assessment is achieved through the statistics produced by the state estimation in Sect. 3, followed by a comparison with observations in Sect. 4. The forecast skill, a measure of the accuracy for a forecast system, is computed with reference to a persistence assumption (Sect. 5).

Section 6 focuses on the second objective of the paper, to examine the increments to the initial state and atmospheric forcing to determine how the model is adjusted. By evaluating the empirical orthogonal functions (EOFs) of these increments we determine the spatial patterns in the variability. Since physical modes are not always independent (Simmons et al., 1983), the interpretation of EOF modes must be undertaken with some caution. As such the resulting modes will not necessarily represent a physical phenomenon, but will highlight the variable spatial patterns made over time by the I4D-Var algorithm.

2 Numerical model and data assimilation system

2.1 Model configuration

The Regional Ocean Modeling System (ROMS) version 3.6 is used to simulate the physical ocean around the Hawaiian Islands. ROMS is a free-surface, hydrostatic, primitive equation model using a stretched coordinate system in the vertical to follow the underwater terrain. In order to allow varying time steps for the barotropic and baroclinic components, ROMS utilizes a split-explicit time stepping scheme (for more details on ROMS, see Shchepetkin and McWilliams, 1998, 2003, 2005).

The Hawaiian Island domain covers 164–153^∘ W longitude and 17–23^∘ N latitude, with bathymetry provided by the Hawaiian Mapping Research Group (HMRG, 2017), shown in Fig. 1. The grid has 4 km horizontal resolution with 32 vertical s levels configured to provide a higher resolution in the more variable upper regions. The configuration model, including the method for assimilating surface HFRs and the associated vertical stretching scheme, is identical to the one first presented in Souza et al. (2015).

Tidal forcing is produced using the OSU Tidal Prediction Software (OTPS) (Egbert et al., 1994), which is based on the Laplace tidal equations from the TOPEX/Poseidon Global Inverse Solution (TPXO). Tidal constituents included in this simulation are the eight main harmonics, M₂, S₂, N₂, K₂, K₁, O₁, P₁, and Q₁, as well as two long-period and one nonlinear constituent: M_f, M_m, and M₄. To avoid any long-term drifting of the tidal phases related to constituents we do not consider, the tidal harmonics are updated each year to define the phases in terms of the start of that year.

Lateral boundary conditions are taken from the HYbrid Coordinate Ocean Model (HYCOM) (Chassignet et al., 2007) and are applied daily. Within ROMs, we apply the boundary differently for each variable; Chapman (Chapman, 1985) conditions are applied to the free surface, Flather (Flather, 1976) conditions for transferring momentum from 2-D barotropic energy out of the domain, and 3-D momentum and tracer variables are clamped to match HYCOM. A sponge layer of 12 grid cells (48 km) linearly relaxes the viscosity by a factor of 4 and diffusivity by a factor of 2 close to the boundary to account for imbalances between HYCOM and ROMS.

From 2007 to 2009, atmospheric forcing fields (excluding the wind) are provided by the National Center for Environmental Prediction (NCEP) reanalysis fields (Kistler et al., 2001). For the wind forcing, a combination of two different forcings is utilized: (i) a 1∕2^∘ resolution CORA/NCEP wind product (Milliff et al., 2004) that combines QuikScat measurements with NCEP wind fields and (ii) the CORA/NCEP winds blended with the results from a 1∕12^∘ resolution PSU/NCAR mesoscale model (MM5; Yang et al., 2008a) of the Hawaiian islands (Van Nguyen et al., 2010). The MM5 model was forced at its boundaries with the global NCEP fields; hence, it is a consistent dynamical downscaling of the global fields. The MM5 model domain is smaller than the ocean grid domain, extending only to 160.5^∘ W in the lee. Therefore, for (ii), we must blend the modeled and CORA/NCEP winds to generate a consistent field for the entire region with 1∕12^∘ winds where available and 1∕2^∘ winds everywhere else.

To blend the two, we convert the MM5 winds to anomalies by subtracting a 30-day mean centered about the record of interest. We compute the mean for the same period from the CORA/NCEP winds. The difference between the two means provides a bias estimate. The bias is removed from the MM5 anomalies and the CORA/NCEP mean is added. Within a 1^∘ box around the boundary of the MM5 data, we taper the anomalies to zero with a cosine filter to avoid abrupt changes to the field. This step ensures that the mean of the CORA/NCEP field is preserved, while its structure and variability is greatly enhanced by the MM5.

From July 2009, atmospheric forcing is provided locally by a high-resolution Weather Regional Forecast (WRF) model (WRF-ARW, 2017). WRF supplies information about surface air pressure, surface air temperature, longwave and shortwave radiation, relative humidity, rainfall rate, and 10 m wind speeds. The ocean model is forced using these data every 6 h, taken from the atmospheric model with 6 km resolution across the entire domain.

Prior to the experiment, a 6-year non-assimilative model was run using the same initial state, boundary conditions, and atmospheric forcing. The variability of the model is used to produce an estimate of the background error covariances used within I4D-Var, as well as the mean sea surface height to use with sea level anomaly observations.

The cost function of the I4D-Var method penalizes for the increments made to the initial conditions, the boundary conditions, and the forcing and for the deviations of the model state from the observations. A detailed derivation of the cost function can be found in Kerry et al. (2016), Penenko (2009), Weaver et al. (2003), Stammer et al. (2002), and Talagrand and Courtier (1987). To formulate the solution, we must provide estimates of the uncertainty matrices in both the model and observations. The model uncertainty matrix, P, is estimated using the variability of the 6-year run described above, while the observation uncertainty matrix, R, is assumed to be diagonal (i.e., observations are independent). The implementation of I4D-Var in ROMS is covered extensively in Moore et al. (2011a, b, c).

2.2 Experiment setup

The reanalysis covers a period of 10 years from July 2007 to July 2017. The period of assimilation for the I4D-Var cycles is 4 days, which corresponds to the limit of the linearity assumption within the domain (Matthews et al., 2011). The atmospheric forcing is adjusted every 6 h, while the boundaries are every 12 h. An analysis of these adjustments is performed in Sect. 6.

During each I4D-Var cycle, a minimization procedure is applied. The nonlinear model is first integrated forward to estimate the background state (the first outer loop). Then the tangent-linear and adjoint models are integrated in multiple inner loops to minimize the cost function (J). After the last inner loop the nonlinear model is updated (see Fig. 1 of Moore et al., 2011c). Prior methodological experiments yielded that for our setting a sufficient reduction in J (and an acceptable computational cost) can be achieved using a single outer loop with 13 inner loops (Souza et al., 2015).

Several 4- and 8-day forecasts are performed from the end of each cycle using the assimilated state as initial conditions, and the short-range (1–4 days) and midrange (5–8 days) forecasts are evaluated for skill.

2.3 Observations

Observational data used within this study include satellite measurements of the ocean surface of temperature, height, and salinity, in situ depth profiles of temperature and salinity, and surface velocities from high-frequency radar. Observations within one Rossby radius (∼ 80 km) of the domain's boundary are neglected. It should be emphasized that no observations were withheld from the assimilation for the purpose of validation. The I4D-Var method seeks to represent the observations by exploiting the linearized model dynamics. Therefore, all available observations are used to constrain this representation.

2.3.1 Satellite-derived measurements

Sea surface temperature (SST) observations are available from two sources at different time periods: initially we used the Global Ocean Data Assimilation Experiment High Resolution Sea Surface Temperature (GHRSST) level 4 OSTIA Global Foundation Sea Surface Temperature Analysis (Naval Oceanographic Office, 2005), referred to as OSTIA for this work. The data are distributed by the Physical Oceanography Distributed Active Archive Center (PO.DAAC) using optimal interpolation to combine data from the Advanced Very High Resolution Radiometer (AVHRR), the Advanced Along Track Scanning Radiometer (AATSR), the Spinning Enhanced Visible and Infrared Imager (SEVIRI), the Advanced Microwave Scanning Radiometer-EOS (AMSRE), the Tropical Rainfall Measuring Mission Microwave Imager (TMI), and in situ data. This distribution provides a highly smoothed daily gridded global dataset at the surface at a 6 km spatial resolution, accurate between 0.2 and 0.5 ^∘C in the domain.

Beginning in April 2008, we switched to using the GHRSST level 4 K10_SST global 1 m sea surface temperature analysis dataset (Naval Oceanographic Office, 2008) produced by the Naval Oceanographic Office and referred to as NAVO for this work. Also distributed by PO.DAAC, this product combines, in a weighted average, data from AVHRR, AMSRE, and the Geostationary Operational Environmental Satellite (GOES) imager. This distribution provides a daily gridded global dataset at 1 m of depth at a 10 km spatial resolution, accurate to 0.4 ^∘C in the domain.

Sea surface height (SSH) observations are derived using sea level anomaly data from the Archiving, Validation and Interpretation of Satellite Oceanographic data (AVISO) delayed-time along-track information. The data come from multiple altimeter satellites measuring the anomaly with respect to a 20-year mean SSH, homogenized against one of the missions to ensure consistency. Each track has approximately 7 km spatial resolution and will usually make multiple passes through our domain each day. To convert from sea level anomaly to sea surface height we add the mean SSH field taken from the 6-year model run described above, to which we add the barotropic tidal prediction from TPXO. The accuracy of the swaths depends on the source satellite and ranges from 5 to 7 cm. We use the AVISO product that has been fully filtered and quality controlled until May 2016. At the time of the experiment, the delayed time data were unavailable beyond May 2016, so the near-real-time data were used.

Sea surface salinity (SSS) data are taken from Aquarius mission daily L3 gridded dataset (NASA Aquarius project, 2015) distributed by PO.DAAC. The satellite uses a combination of radiometers and scatterometers to estimate the surface salinity mapped to a coarse 1^∘ resolution. Errors for this product are around 0.2 ppt. Data for this product are available from August 2011 until June 2015.

2.3.2 In situ measurements

Depth profiles of temperature and salinity are obtained from threes sources: the Hawai`i Ocean Time-Series (HOT) shipboard conductivity–temperature–depth (CTD) casts, the global network of Argo floats, and autonomous Seagliders operated by the University of Hawai`i.

The HOT project conducts monthly cruises to the deep water station ALOHA (A Long-term Oligotrophic Habitat Assessment; located at 23^∘45^′ N, 158^∘00^′ W; see Fig. 1) in order to develop continuous datasets of physical and biochemical ocean parameters. CTD stations of temperature and salinity are concentrated in the region around the station, although some are also established along the ship route.

HOT also conducts regular Seaglider missions departing from station ALOHA. In addition, PacIOOS conducts occasional Seaglider surveys in areas close to the south coast of O`ahu. The buoyancy-driven autonomous underwater vehicles take profiles and transects at depth of temperature and salinity.

Observations from the global Argo float network are available from the Argo array network (USGODAE, 2016). The free-drifting floats profile temperature and salinity during ascension and descension every 10 days of depths down to 2000 m (Oka and Ando, 2004). Argo measurements tend to occur in the model domain at a rate of about one to two profiles per day.

Representational errors for HOT CTDs, Argo floats, and Seagliders are defined by the variance of observational data from all available sources across our domain sorted into depth bins. These profiles resemble a typical temperature–salinity profile, with a peak temperature error of 0.8 K and peak salinity error of 0.15 ppt occurring in the mixed layer at a depth around 100 m.

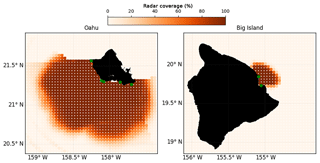
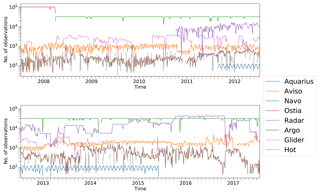
Figure 2 Composite image of percentage coverage for all radar sites (situated at green dots) when all are operational. Where two sites overlap the greater value is taken to indicate the level of coverage at each point.

Figure 3 Number of observations used within data assimilation run. Note that there tend to be orders-of-magnitude more satellite or remotely sensed observations than in situ.

2.3.3 High-frequency radar measurements

HFR measurements of surface currents are available from PacIOOS at seven sites around the Hawaiian islands: five around the southwest of O`ahu and two on the east coast of Hawai`i. Data are available from the first site in October 2010 with the other sites coming online at various times, the most recent being October 2015. The range for the HFRs on O`ahu extend approximately 150 km from the coast, while the two Hawai`i sites are focused on currents around the northeast of the island and have a shorter range. At the range limits, HFR data are less reliable due to the higher noise level of the returns. Figure 2 shows the percentage availability of data in the region. HFR measurements from any return location that is missing more than 20 % of its data over the 4-day assimilation period are ignored. Both spatially and temporally, the resolution for all sites is significantly higher than the model resolution. The HFR data are low-pass filtered at 3 h to remove the high-frequency signals that may not be resolved by the model (atmospheric forcing fields are every 6 h). We then provide the spatial field of data every 3 h. The associated error is calculated individually for each spatial point as the accuracy of the measurements is determined by the levels of interference, which increases with range. For each observation point we calculate the power spectral density and calculate the noise as per Zanife et al. (2003), with a minimum of 7 cm s⁻¹. At the extreme, errors may reach 17 cm s⁻¹.

The numbers of observations for each 4-day cycle from all sources are shown in Fig. 3. Sea surface temperature measurements from both OSTIA and NAVO are consistently the most available observation source, and by the end of the time period HFR is supplying a similar quantity. In situ measurements, which include both temperature and salinity for each of the instruments, provide a smaller amount of data by an order of magnitude.

Figure 4 Time series of percentage reduction in the I4D-Var cost function; in the left column are pre-HFR observations and in the right column are post-HFR observations, with the mean value given in parentheses. Dashed lines mark the limit of 0, below which there is no reduction in the cost function for that variable. (a) Total cost function reduction for all observations; (b) sea surface height observations, (c) temperature observations; (d) salinity observations; (e) HFR observations.

3 Assimilation statistics

In this section we examine the state estimate to quantify the performance during our time period.

3.1 Cost function reduction

I4D-Var minimizes the residuals between the model and observations over each 4-day cycle. We calculate the percentage reduction between the initial and final cost function for each cycle to assess how the assimilation performs over time. Additionally, the I4D-Var algorithm reports the individual contributions by the state variables considered by the data assimilation to the total cost function. Hence we can examine the cost function in detail for those observation types that are most critical for its reduction. However, it should be noted that for this decomposition we do not distinguish between observation sources.

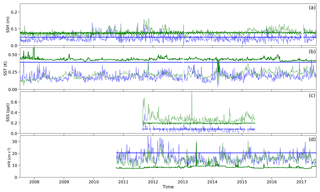
Figure 4 shows the time series of the total reduction and the percentage reduction in the cost function for each of the variables we observe: sea surface height, temperature, salinity, and HFR. A value of 0 means the final cost function is the same as the initial and no reduction has occurred. The plot is split into two distinct time periods, before and after the HFR observations, in order to assess changes in the relative contributions of each variable to the overall reduction.

The total cost function of all data (Fig. 4a) is on average halved for each cycle, with an improvement from 49 % of the original value to 55 % when HFR observations are available. Looking at the breakdown in Fig. 4b–e, we see that the final cost function associated with the other observed variables (sea surface height, temperature, and salinity) is reduced by a smaller percentage than before HFR was included. Given that the structure of the cost function is determined by the type and number of observations, this change in contribution to the cost function reduction can be expected when adding a large number of HFR measurements to the data assimilation.

Salinity measurements tend to contribute the least improvement, ranging from 34 % (pre-HFR) to 16 % (post-HFR). Salinity data are the least numerous (Fig. 3) and SSS fields taken from Aquarius are subject to high noise levels (0.2 ppt) and coarse spatial resolution. The mid-2014 drop in cost function reduction for salinity data coincides with the loss of two Seagliders. After the cessation of Seaglider missions salinity data were only available through Aquarius (until mid-2015) and sporadic Argo profiles.

The cost function associated with HFR measurements is reduced by 60 % of the initial value, meaning the model is closer to the HFR observations after the assimilation.

Figure 5 (a) Gantt chart of remotely sensed observations used in the study. (b) Optimality of I4D-Var data assimilation with the dashed line representing the theoretical minimum.

3.2 Optimality

Another measure of performance is the theoretical minimum value of the cost function (J_min). For a linear system and assuming that the error matrices P and R have been determined correctly, J_min is a chi-squared variable whose degrees of freedom are given by the number of assimilated observations (N_obs) (Bennett, 2002). The expected value of J_min is then given by

$$\begin{array}{}\text{(1)}& {\displaystyle }\langle J_{\text{min}}\rangle ={\displaystyle \frac{N_{\text{obs}}}{\mathrm{2}}}.\end{array}$$

Using above the equation, an optimality value (γ) can be defined:

$$\begin{array}{}\text{(2)}& {\displaystyle }\mathit{\gamma }={\displaystyle \frac{\mathrm{2}\cdot J_{\text{min}}}{N_{\text{obs}}}},\end{array}$$

which should reach a value of 1 with a standard deviation of $\sqrt{\mathrm{2}/N_{\text{obs}}}$.

This optimality value provides a simple representation of how consistently the error matrices (P and R) are specified, since the error covariances normalize the cost function. Figure 5 shows a time series of the calculated optimality value for the model run, in addition to a timeline of the availability of certain observations for reference. Over the full time period the mean optimality is 0.95. However, there are large significant deviations over the course of the time period. In the pre-HFR period the optimality is low, suggesting that the error bounds on observations are too wide. Since SST is the dominant source of observations before HFR, the prescribed errors associated with SST may be too large.

Post-HFR, the optimality value increases, suggesting the errors in this period are underestimated. A large optimality value arises when the cost function is large (i.e., large differences between the model and observations). There were two anomalous cycles in 2011; the first coincides with the introduction of a second radar site. From 2012 onwards the optimality value is generally good, if highly variable. The increase in optimality given the available observations points to an underestimation of HFR errors or at the least a persistent difference between the model and HFR observations.

3.3 Error consistency

The consistency of the assimilation can be assessed by comparing the error matrices P and R specified a priori with the observation and background error covariances determined a posteriori (Desroziers et al., 2005). Using the difference between the observation j (y_j) and the modeled background value (x^b) mapped to the observation location by the operator ℋ_j,

$$\begin{array}{}\text{(3)}& {\displaystyle }{d}_j^{\text{ob}}=y_j-{\mathcal{H}}_j\left(x^{\text{b}}\right),\end{array}$$

and the difference between x^b and the analysis value (x^a) mapped to the observation location,

$$\begin{array}{}\text{(4)}& {\displaystyle }{d}_j^{\text{ab}}={\mathcal{H}}_j\left(x^{\text{a}}\right)-{\mathcal{H}}_j\left(x^{\text{b}}\right),\end{array}$$

one can compute the expected a posteriori background error:

$$\begin{array}{}\text{(5)}& {\displaystyle }{\stackrel{\mathrm{̃}}{\left({\mathit{\sigma }}_i^{\text{b}}\right)}}^{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{p_i}}\sum _{j=\mathrm{1}}^{p_i}\left({\mathcal{H}}_j\right(x^{\text{a}})-{\mathcal{H}}_j(x^{\text{b}}\left)\right)(y_j-{\mathcal{H}}_j(x^{\text{b}}\left)\right),\end{array}$$

where i refers to the observation type and p_i is the number of observations of that type.

Figure 6 Time series of spatially averaged background (blue) and observation (green) errors, with thick lines showing a priori values and thin lines the posterior calculated using Eqs. (5) and (7). (a) Sea surface height; (b) sea surface temperature; (c) sea surface salinity; and (d) HFR.

Similarly, using the difference between the observation j and the modeled analysis value (x^a) mapped to the observation,

$$\begin{array}{}\text{(6)}& {\displaystyle }{d}_j^{\text{oa}}=y_j-{\mathcal{H}}_j\left(x^{\text{a}}\right),\end{array}$$

the expected a posteriori observation error can be calculated:

$$\begin{array}{}\text{(7)}& {\displaystyle }{\stackrel{\mathrm{̃}}{\left({\mathit{\sigma }}_i^{\text{b}}\right)}}^{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{p_i}}\sum _{j=\mathrm{1}}^{p_i}(y_j-{\mathcal{H}}_j(x^{\text{a}}\left)\right)(y_j-{\mathcal{H}}_j(x^{\text{b}}\left)\right).\end{array}$$

For a detailed description of the above diagnostics the reader is referred to Desroziers et al. (2005, 2009). If the variances in P and R are correctly specified a priori, they will be consistent with the a posteriori errors defined above. Figure 6 shows both the a priori and a posteriori errors for the remotely sensed data. The observation a priori values are calculated as the mean error of the observations in each cycle, while the background a priori values are defined as the variability of a free-running nonlinear model. If the a posteriori errors are typically larger than the a priori, it implies the initial errors in P and R are underestimated. Conversely, if they are smaller the initial errors are likely overestimated.

Figure 6a shows that sea surface height errors are consistent, while sea surface temperature, shown in Fig. 6b, suggests the a priori errors are overestimated. The a priori observation errors for NAVO SST observations are defined with a minimum error of 0.4 K, but the a posteriori errors are more typically around 0.25 K. The a priori background errors also appear overestimated.

Sea surface salinity observation errors (Fig. 6c) are slightly underestimated but generally consistent, as are the background errors. The HFR observation errors (Fig. 6d) also appear to be underestimated, with most a priori errors close to the minimum value of 7 cm s⁻¹. The a posteriori errors suggest that a typical value of around 12–15 cm s⁻¹ would be more appropriate. The a priori background errors are reasonably consistent with the a posteriori; if anything, they are slightly overestimated.

This error consistency analysis supports the conclusions in Sect. 3.2 that the SST observation errors are overestimated and HFR values are underestimated. It is worth noting that these diagnostics are only estimates used to characterize the errors and are not the true posterior error.

Figure 7 Time series of root mean squared anomalies (RMSAs) between remotely sensed observations and two model realizations: the state estimate (orange) and the forecast (blue). (a) Sea surface height; (b) sea surface temperature; (c) sea surface salinity; and (d) HFRs.

4 Comparison with observations

Because I4D-Var relies on the model physics to represent observations through time, it should provide better forecasts. Time-invariant methods (3D-Var, optimal interpolation) that perturb the state at single times may better reduce the time-fixed cost function, but can add nonphysical structures that generate noisy forecasts.

In this section, we examine the state-estimate solution by comparing the model to observations. For reference, the observations are also compared against the forecast starting from the same time as each state-estimate cycle. The initial and boundary as well as atmospheric and tidal forcings are initially the same for both runs; however, the initial and boundary conditions and atmospheric forcing are altered as part of the state-estimate solution.

For comparing fields we use the root mean squared anomaly (RMSA) and the anomaly correlation coefficient (ACC), defined as

$$\begin{array}{l}\text{(8)}& {\displaystyle }& {\displaystyle }\mathrm{RMSA}(\mathit{x},\mathit{y})=\sqrt{{\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^N{\left((x_i-\stackrel{\mathrm{‾}}{x})-(y_i-\stackrel{\mathrm{‾}}{y})\right)}^{\mathrm{2}}}{\displaystyle }\text{and}\\ \text{(9)}& {\displaystyle }& {\displaystyle }\mathrm{ACC}(\mathit{x},\mathit{y})={\displaystyle \frac{{\sum }_{i=\mathrm{1}}^N(x_i-\stackrel{\mathrm{‾}}{x})(y_i-\stackrel{\mathrm{‾}}{y})}{\sqrt{{\sum }_{i=\mathrm{1}}^N(x_i-\stackrel{\mathrm{‾}}{x}{)}^{\mathrm{2}}{\sum }_{i=\mathrm{1}}^N(y_i-\stackrel{\mathrm{‾}}{y}{)}^{\mathrm{2}}}}},\end{array}$$

where N is the number of observations and x represents the model values at the same location and time as the observations y. The RMSA provides a measure of the residual between the model and observations, while the ACC determines the strength of the relationship between the two. We can calculate values for a single spatial point throughout time or for all spatial points at a single time; however, we require at least 20 available observation values to get a representative statistic. The gridded satellite products are ideally suited to this analysis, while the depth profiles from in situ measurements are binned into 50 m depth layers to ensure a minimum number of values. Here it must be noted that our validation is limited to data that have been employed for the assimilation. The I4D-Var scheme uses the linearized model dynamics to produce the covariance between the model and the observations. This allows the model to optimally represent the observations in time and space rather than replicate them. As such, the desire is to use every available observation to constrain this representation. Unlike time-invariant statistical methods, we do not withhold any observations because they are sampling the dynamical subspaces of a system of unknown dimension. Since the observations covary in space and time, some particular observations may not have a significant impact on the cost function and their representation may suffer. We seek to identify these results.

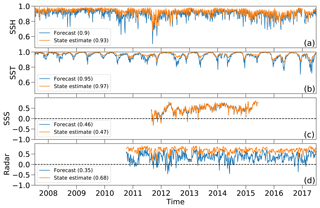
Figure 8 Time series of anomaly correlation coefficients (ACC) between remotely sensed observations and two model realizations; the state estimate (orange) and the forecast (blue). (a) Sea surface height; (b) sea surface temperature; (c) sea surface salinity; and (d) HFRs.

Figure 9 Spatial maps of RMSA for SST observation sources for the forecast (a, c) and the state estimate (b, d). (a, b) OSTIA data (2007–2008); (c, d) NAVO data (2008–2017). The typical error of representativeness is around 0.4 K.

4.1 Remotely sensed observations

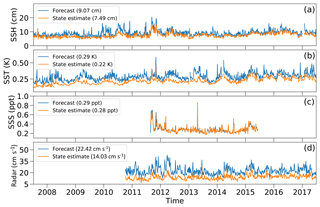
Figure 7 shows the RMSA between the observations and the models for each source of remotely observed data. The state-estimate solution reduces the RMSA compared with the forecast by 1.58 cm (17 %), 0.07 K (24 %), 0.01 ppt (3 %), and 8.39 cm s⁻¹ (37 %) for sea surface height, sea surface temperature, sea surface salinity, and HFR, respectively. In Fig. 7a the RMSA of the state-estimate solution is close to the typical observational error of 7 cm, while in Fig. 7b we see the RMSA is comfortably less than the 0.4 K representative error. Sea surface salinity is only marginally improved by the state-estimate solution, but is slightly over the prescribed observational error of 0.2 ppt. The RMSA of the currents associated with HFR observations, shown in Fig. 7d, is improved greatly by the state estimation; however, the mean value of 14 cm is around double the typical error prescribed a priori of 7 cm. As shown in the previous sections, this error was underestimated.

The ACC is also improved by the state estimate for all variables, as shown in Fig. 8. For sea surface height, temperature, and salinity the improvement is small due to a significant agreement in the forecast with gains of 0.03, 0.02, and 0.01, respectively. The improvement in HFR is much more significant, with an average correlation improvement from 0.35 to 0.68. As shown in Fig. 8d the free-running forecast model can diverge from the observations enough to become negatively correlated over a cycle, while the state-estimate solution is consistently positively correlated.

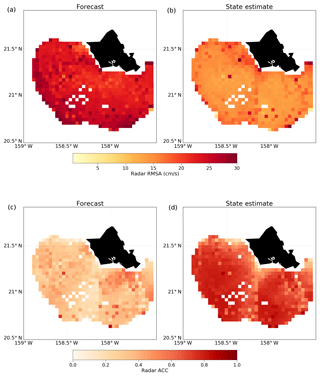
Figure 10 Spatial maps of HFR statistics for south O`ahu for the forecast (a, c) and the state estimate (b, d). (a, b) RMSA; (c, d) ACC.

Figure 9 shows the spatial RMSA between the forecast and analyses model solutions and the observations for both sources of sea surface temperature observations: OSTIA and NAVO. In both cases there is a clear reduction in the RMSA, with the largest source of error in the areas leeward of the islands, most notably the island of Hawai`i. This is due to higher heat flux variability from a reduction in cloud cover (Matthews et al., 2012; Yang et al., 2008b). Even in this peak area, the state-estimate solution is around the observational error of representativeness of 0.4 K, meaning the model is performing well with regards to SST.

Both RMSA and ACC between the experiments and HFR observations are shown in Fig. 10 for the island of O`ahu. The RMSA of the free-running forecast is reasonably uniform across the region covered by the HFR, around 20–25 cm s⁻¹, with some varying values around the extent of the radar coverage. The inclusion of HFR observations in the state-estimate solution leads to significantly reduced values of 12–15 cm s⁻¹, a reduction of almost half. The ACC is also significantly improved from a weak correlation to a consistently strong positive one.

As discussed in Souza et al. (2015), there are several reasons the model can differ from surface current observations: the discretization of the model, imperfect stratification, differing barotropic-to-baroclinic tide conversion at Kaena Ridge, or mixing parameters that do not capture the real baroclinic mixing. This may lead to a different location of the currents in the model from those observed by the HFR; however, the model does a good job of reducing these errors (Janeković and Powell, 2012). The HFRs located on the island of Hawai`i have a smaller coverage region, but the level of improvement from the forecast to the state-estimate solution is consistent with the O`ahu results shown here.

Figure 11 RMSA (solid) and ACC (dashed) profiles of subsurface temperature (a) and salinity (b) for Argo floats, Seagliders, and HOT CTDs for the forecast (blue) and the state estimate (orange). Data were binned into 50 m intervals.

4.2 Subsurface observations

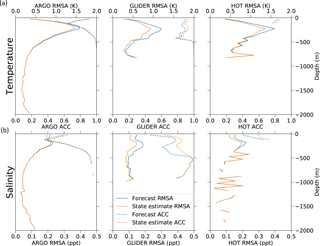
The in situ observation sources are Argo floats, Seagliders, and HOT CTDs, which also show an improvement in the state estimate over the forecast. The subsurface temperature RMSA values are reduced by an average of 0.03 K and salinity by 0.01 ppt. The average RMSA is within the representative errors for both variables at 0.8 K and 0.15 ppt, respectively. However, there are several occasions when the RMSA value for a cycle exceeds that limit when there are very few in situ observations available.

Figure 11 shows the RMSA and ACC profiles for temperature and salinity for each source of subsurface observation. For all three sources, the greatest RMSA between the models and observations is along the thermocline where minor differences in thermocline depth lead to temperature differences. The state estimate improves the RMSA in this region by 10–15 %. The thermocline location is also the source of the lowest correlation between the observations and the model, which is improved by the state estimate by ∼ 5 %. There is a high RMSA for Seagliders at the base of their profiles (close to 1000 m). In this instance the state estimate does not result in an improvement of the forecast. Many of the glider missions operated in the shallow waters off the south coast of O`ahu where processes are at much finer scale than can be resolved at 4 km resolution. As such, the observational representation errors were higher.

For subsurface salinity (Fig. 11b), the improvements made by the state-estimate solution occur almost exclusively above 500 m for Argo floats and HOT CTDs. As with temperature the largest improvement is at the top of the thermocline. There are some low ACC values lower down in the profile between both models and the observations, but both the forecast and state estimate perform equally at this depth. Seagliders produce the biggest improvement in subsurface salinity model performance, with the state-estimate solution up to 20 % better than the forecast for both RMSA and ACC. The peak improvement is at the top of the thermocline, but there are improvements throughout the profile.

Figure 12 Mean skill metric for remotely sensed observations as a function of forecast length. Solid lines: skill (see Eqs. 10 and 11); dashed lines: standard deviation of skill. (a) Sea surface height; (b) sea surface temperature; (c) sea surface salinity; (d) HFRs; and (e) subsurface temperature.

5 Forecast skill

In this section we quantify the model skill by using a skill score evaluated as the improvement against a reference field (Murphy, 1988). For the reference, we take the model value at the spatial location of each observation at the time of initialization for each 8-day cycle and assume persistence of this value throughout the 8-day cycle (persistence assumption). The skill score (SS) for the state-estimate analysis and forecast is then defined using the ratios of RMSAs with respect to the observations:

$$\begin{array}{}\text{(10)}& {\displaystyle }& {\displaystyle }{\mathrm{SS}}_{\text{a}}=\mathrm{1}-{\displaystyle \frac{\mathrm{RMSA}({\mathit{x}}^{\text{a}},\mathit{y})}{\mathrm{RMSA}({\mathit{x}}^{\mathrm{0}},\mathit{y})}},\text{(11)}& {\displaystyle }& {\displaystyle }{\mathrm{SS}}_{\text{f}}=\mathrm{1}-{\displaystyle \frac{\mathrm{RMSA}({\mathit{x}}^{\text{f}},\mathit{y})}{\mathrm{RMSA}({\mathit{x}}^{\mathrm{0}},\mathit{y})}},\end{array}$$

where the superscripts a, f, and 0 refer to the analysis, free-running forecast, and persistence, respectively, and y indicates the observations. Under this measure, a SS of 1 represents a perfect fit between the model and observations, while a value of zero indicates where the model and persistence values perform exactly the same. If the model is better than persistence, then the skill score will lie in the range $\mathrm{0}<\mathrm{SS}<\mathrm{1}$ and the degree of improvement over persistence is determined by how close to 1 the score is. Conversely, a negative SS means the model is further from the observations than persistence.

For this verification we wish to examine the effect of forecast length on the skill. Starting with the same initial conditions as each state-estimate cycle we produce an 8-day forecast, the length of two state-estimate cycles. The RMSA is calculated every 3 h for each 8-day forecast, the corresponding state-estimate cycles, and the persistence field from the start of the forecast.

Figure 13 EOF1 and PC1 of initial condition increments for temperature, east–west velocity, and north–south velocity (all averaged 0–100 m) and of forcing perturbations applied to surface heat flux. The EOFs were calculated using the routines described in Dawson (2016).

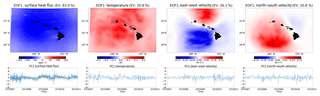
Figure 12 shows the mean SS over all cycles for remotely sensed observations. For SSH, SST, and HFR, the skill for both the state-estimation and free-running forecast is positive throughout, indicating that both models are successful over persistence in representing those variables. SSS, however, is close to zero and slightly negative, meaning the models provide no better information than persistence. SST values are consistently the highest, with a reduction in skill versus persistence for both models once per day. This is expected as initial conditions are used for persistence values and the diurnal cycle will move ocean temperatures close to this persistence value once per day. The state-estimate skill for HFR has a consistent value of 0.5 regardless of the forecast day, while the skill of the free-running forecast decreases within the first 12 h and is closer to 0.2 for the rest of the forecast period. This decrease in skill is driven by the fact that the radials are dominated by the semidiurnal baroclinic and barotropic tides.

6 Analysis of increments

During each I4D-Var 4-day window, the initial model field and time-varying boundary and surface forcings are adjusted to minimize the residuals. The initial condition increments form a single record for each cycle, while the boundary and surface forcings are perturbed every time they are applied to the model. The perturbations applied to the boundary exhibit only a minor influence on the model (not shown) due to the mean advection speed (≈20 cm s⁻¹) and sponge layer dampening near the boundaries. We focus our analysis on the increments of the initial conditions and the surface forcing.

Because we are analyzing the increments (rather than the state) to the initial conditions and forcing fields, the mean increment should be zero (unless there is a bias in the model), and we are looking to examine the variability. Over the entire reanalysis period, the mean biases between the model and observations for the different types are temperature (−0.0048 K), salinity (0.0049 ppt), SSH (−7 mm), and HFR (0.06 cm s⁻¹). A consistent pattern or principal component may suggest a repeated correction to account for missing or misrepresented physics in the model.

Over the 10-year reanalysis, there are 917 analysis cycles with 16 surface forcing adjustments (four per day) per cycle. We calculated the empirical orthogonal functions (EOFs) (Hannachi, 2004) of the increments applied to the forcing and the initial conditions to analyze the dominant spatial patterns of the adjustments.

For each cycle, the initial perturbation of the primary model prognostic variables are examined: sea surface height, temperature, salinity, east–west velocity, and north–south velocity. With the exception of sea surface height, each variable is averaged over the upper 100 m to cover the mixed layer depth in the domain (Matthews et al., 2012). The increments for salinity and sea surface height as a percentage of the initial conditions are insignificant (<1 %), while temperature increments (2–10 %) and the two velocity fields (10–20 %) are significant enough to analyze.

The assimilation was configured to optimize the surface forcing increments every 6 h (to avoid overadjustment). The time of day potentially impacts forcing variables, particularly surface heat flux, so we calculate EOFs on the increments for each of the four distinct times of day they occur (00:00, 06:00, 12:00, 18:00 UTC). Due to the size of the model grid, the number of records, and the computational resources available the EOF calculation is limited to a 4-year period, with approximately 1500 records. Several different periods were examined with no significant differences in the structure of the modes or their percentage of variance explained. The time of day does impact the percentage of variance explained by each mode, most notably for surface heat flux for which the effect of diurnal solar heating occurs. However, the overall locations and magnitudes of the peaks and troughs as well as the temporal evolution of PCs do not exhibit significant differences for each time of day, so we present one of the modes for each considered variable.

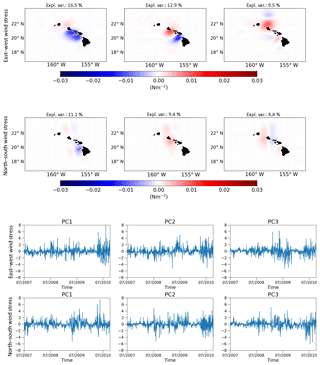
Figure 14 Spatial EOF patterns and principal components (PCs) of wind stress perturbations for the period prior to the assimilation of HFR measurements (June 2007–September 2010).

The four key surface forcing terms are surface heat flux, surface salinity flux, east–west wind stress, and north–south wind stress. Of these, increments in surface salinity flux are quite small compared to their initial value, while increments in surface heat flux (10 %–15 % of initial value) and the wind stresses (15 %–20 % of initial value) are significant.

For surface heat flux and near-surface temperature, we observe that the EOF1 modes represent 63 % and 20.8 % of the variability, respectively, with a consistent sign over the region (Fig. 13). This mode essentially accounts for the bias between our ocean model and the WRF atmospheric model used to force the surface. Unfortunately, WRF was not integrated loosely coupled to the ROMS using the ROMS SST field; rather, it was run using persistent estimates of daily SST during its integration. It must be noted, however, that the monopole structure of the EOF1 does not represent a constant offset between ROMS and WRF since the actual perturbation of surface heat flux and increment applied to near-surface temperature are given by the products of the respective EOF1 and the PC1. As can be seen in the lower panels of Fig. 13, the temporal evolution of the PC1 for both surface heat flux and near-surface temperature adjustments is dominated by high-frequency, nonphysical variance.

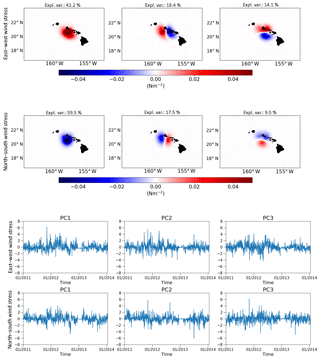
Figure 15 Spatial EOF patterns and principal components (PCs) of wind stress perturbations for the period including the assimilation of HFR measurements (January 2011–January 2014).

The EOF1 modes of the near-surface velocity increments explain 26.1 % and 20.8 % of the variance, respectively. Both modes exhibit a strong impact south of the main Hawaiian Islands. The structure of the wind stress curl in this region results in the spin-up of cyclonic and anticyclonic eddies to the north and south of the lee side of each island, respectively (Chavanne et al., 2002). As a consequence, a zone of strong current shear is created between the North Equatorial Current and the Hawaiian Lee Counter Current (Lumpkin and Flament, 2013) (see also Fig. 1). The EOF1 modes of the near-surface velocity increments are responsible for adjusting the state estimate for the significant eddy activity in the lee of Hawai`i.

The EOFs of surface wind stress increments are confined to relatively small regions of the model domain (Figs. 14 and 15). A significant change occurs after the HFR observations come online. During the period prior to the availability of the HFR data (June 2007–September 2010), the wind stress was primarily adjusted in the lee regions where the winds are forced between islands (e.g., Kaiwi, `Alenuihāhā Channels, and to a smaller degree over the Kaua`i Channel; Fig. 14). The wind stress curl in these regions plays an important role as a vorticity source to the ocean (Souza et al., 2015). Hence the adjustment of wind stress in the channels between the islands is critical for a reliable representation of ocean conditions. The magnitude and sign of the PCs of the wind stress adjustments for this period are driven by day-to-day variability (Fig. 14, lower panels). Also, the PCs of the east–west wind stress and north–south wind stress are largely uncorrelated, aggravating an interpretation of the adjustments in terms of a larger-scale atmospheric pattern or wind stress curl.

With the integration of the HFR measurements (October 2010), the dominant wind stress increments occur across the shallow region close to the south coast of O`ahu (Fig. 15). The first mode for both east–west and north–south wind stress exhibits a monopole structure adjusting the wind stress uniformly across the area covered by the HFR and its vicinity. The second modes have an east–west dipole structure that will either increase or decrease the wind stress shear around the HFR region. Similarly to the pre-HFR period, the PCs of the wind stress increments are dominated by day-to-day variability and do not represent a physical mode.

7 Conclusions

We have presented a 10-year reanalysis of the PacIOOS Hawaiian Island Ocean Forecast System and assessed the performance of the state-estimate solution and free-running forecasts. Using a time-dependent incremental strong-constraint four-dimensional variational data assimilation (I4D-Var) scheme, we show that the model represents the observational data well over the time period. The state-estimate solution reduces the RMSA compared to the forecast by 3 % (salinity) to 37 % (surface velocities). A limitation of the model–observation comparison is given by the fact that in the absence of a sufficient number of independent observations, only assimilated data could be used for the validation.

The largest reduction of the cost function of the state-estimate solution occurs when minimizing the residuals to HFR data, with SST also accounting for a significant improvement. On average, the assimilation achieves the near-optimal solution; however, the variability is heavily influenced by the HFR observations. The analysis suggests that the observational errors associated with HFR are too low and results could be improved by redefining these errors. This is supported by the increase in variability and upward trend of optimality towards the end of the time period during which HFR observations are most numerous.

The increments made by the reanalysis have revealed that sea surface height and salinity initial conditions are not significantly adjusted by the I4D-Var procedure, whereas temperature and velocity account for a significant change from the forecast field. For the atmospheric forcing, surface salinity is insignificant, but the adjustments made to surface heat flux and wind stresses alter the forcings by up to 20 %. This corresponds to cost function statistics that point to HFR and temperature as the two dominant observation sources.

The dominant EOF mode for adjustments of surface heat flux and near-surface temperature exhibits a monopole structure, indicating a slight bias correction between the ocean and atmospheric model. The leading modes of wind stress increments are concentrated in the region south of O`ahu. The wind stress heavily influences the surface currents and adjustments are mostly made as a consequence to HFR data. Additional analysis reveals that wind stress adjustments in the channels between the islands dominated the increments in the period prior to the radar-based measurements of surface currents.

The reanalysis has provided the testing for improvements to the PacIOOS operational forecast system. The data are being used to update the back catalog available to the public at http://www.pacioos.hawaii.edu (last access: 22 December 2018) and will influence the future results from daily forecasts. Analysis of the I4D-Var increments has provided a greater understanding of the variability in the region and will provide the basis for a move towards ensemble forecasting in the region.