The [simple carbon project] model v1.0

We construct a carbon cycle box model to process observed or inferred geochemical evidence from modern and paleo settings. The [simple carbon project] model v1.0 (SCP-M) combines a modern understanding of the ocean circulation regime with the Earth's carbon cycle. SCP-M estimates the concentrations of a range of elements within the carbon cycle by simulating ocean circulation, biological, chemical, atmospheric and terrestrial carbon cycle processes. The model is capable of reproducing both paleo and modern observations and aligns with CMIP5 model projections. SCP-M's fast run time, simplified layout and matrix structure render it a flexible and easy-to-use tool for paleo and modern carbon cycle simulations. The ease of data integration also enables model–data optimisations. Limitations of the model include the prescription of many fluxes and an ocean-basin-averaged topology, which may not be applicable to more detailed simulations.

In this paper we demonstrate SCP-M's application primarily with an analysis of the carbon cycle transition from the Last Glacial Maximum (LGM) to the Holocene and also with the modern carbon cycle under the influence of anthropogenic CO₂ emissions. We conduct an atmospheric and ocean multi-proxy model–data parameter optimisation for the LGM and late Holocene periods using the growing pool of published paleo atmosphere and ocean data for CO₂, δ¹³C, Δ¹⁴C and the carbonate ion proxy. The results provide strong evidence for an ocean-wide physical mechanism to deliver the LGM-to-Holocene carbon cycle transition. Alongside ancillary changes in ocean temperature, volume, salinity, sea-ice cover and atmospheric radiocarbon production rate, changes in global overturning circulation and, to a lesser extent, Atlantic meridional overturning circulation can drive the observed LGM and late Holocene signals in atmospheric CO₂, δ¹³C, Δ¹⁴C, and the oceanic distribution of δ¹³C, Δ¹⁴C and the carbonate ion proxy. Further work is needed on the analysis and processing of ocean proxy data to improve confidence in these modelling results.

1 Introduction

A box model divides regions of the ocean into boxes or grids based on some property of the composite water masses, such as temperature, density or chemical composition. The model equations describe the evolution of tracers in the model's boxes due to the various fluxes between each box (Fig. 1). Box models differ from more complex models such as general circulation models (GCMs), mainly due to their reduced spatial resolution (i.e. much larger grids or boxes) and with major processes and fluxes typically prescribed rather than calculated in the model. Box models range in complexity from simple, basin-averaged models (e.g. Stommel, 1961; Sarmiento and Toggweiler, 1984; Toggweiler, 1999) to more complex, multi-basin ocean models (Hain et al., 2010) and full Earth carbon cycle models (Zeebe, 2012). Box models, despite being simpler than GCMs, have been useful in illustrating key concepts in oceanography. For example, Sarmiento and Toggweiler (1984), Siegenthaler and Wenk (1984), and Knox and McElroy (1984) used simple four-box ocean–atmosphere models to show that the LGM CO₂ drawdown could have resulted from increased biological productivity and/or reduced ocean overturning circulation. More recently, Hain et al. (2010) used a box model to show that a range of ocean physical and biological mechanisms were required to cause lower atmospheric CO₂ levels in the LGM, and Zhao et al. (2017) used a similar model to explore ocean ventilation ages in the LGM–deglacial and Holocene periods. Despite the development of highly complex coupled atmosphere–ocean models for climate simulations, box models continue to be applied to resolve problems in the carbon cycle.

Our motivation in constructing a new box model of the full carbon cycle, the [simple carbon project] model v1.0 (SCP-M), is to contribute a simple, easy-to-use, open-access model implemented with freely available software, that is consistent with physical and biogeochemical oceanography, that caters for important features of the carbon cycle, and that has explicit avenues for data integration, optimisation and inversion. Recent advances in physical oceanography have refined our understanding of global ocean circulation and mixing fluxes. For example, Talley (2013) provided a simplified interpretation of the global ocean as a handful of large-scale processes, some of which are operating across all basins – as is the case with the global overturning circulation. De Boer and Hogg (2014) described a simple model of deep ocean mixing of water masses under the influence of sea-floor topography. These high-level concepts are easy to apply to box models. Furthermore, the growing pool of paleo proxy data across carbon isotopes and reconstructions (e.g. carbonate ion) presents an opportunity to progress model–data integrations using a number of different proxies. SCP-M caters for a range of proxies including the carbon isotopes and carbonate ion proxy, with the capacity for additional elements with minimal programming effort. The model–data experiment described in this paper provides a direct linkage between paleo data and discrete values for ocean parameters in the LGM and late Holocene periods, thus contributing to our understanding of the LGM–Holocene carbon cycle transition. Combined with the expanding dataset of paleo observations, and with advances in computing power, data-aligned models such as SCP-M have the potential to improve our understanding of past changes in climate across many other time frames. Furthermore, there are a number of features of the carbon cycle outside ocean circulation and biology which influence proxy indicators, particularly the carbon isotopes. Omitting these features could lead to erroneous modelling outcomes, particularly in the case of the terrestrial biosphere, which strongly influences atmospheric CO₂ and δ¹³C (e.g. Francois et al., 1999). We compiled SCP-M to include a broad range of carbon cycle mechanisms, including carbonate production and dissolution, marine sediments, terrestrial biosphere, anthropogenic emissions sources, and continental weathering. Finally, SCP-M is computationally cheap and quick to run. A 10 000-year simulation takes approximately 30 s to process on a regular laptop, enabling exhaustive exploration of parameter space in optimisations that incorporate large datasets. While box models are not new, we argue that these features contribute to a new tool that is well-equipped to tackle a wide range of applications in paleoceanography, paleoclimate and the modern carbon cycle.

In this paper we describe SCP-M and illustrate its application alongside LGM and late Holocene ocean and atmosphere data, with several insights for the transition between the two periods, plus modelling of the modern and future carbon cycle under the influence of anthropogenic emissions. Emphasis is placed on the model description and configuration.

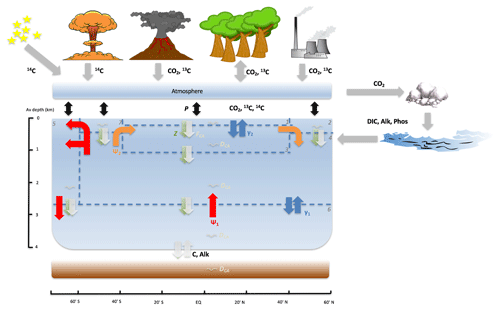
Figure 1 SCP-M: configured as a seven-box ocean model plus atmosphere with marine sediments, continents and the terrestrial biosphere. The exchange of elemental concentrations, e.g. $C_i(i=\mathrm{1},\mathrm{7})$, occurs due to fluxes between boxes. Ψ₁ (red arrows) is global overturning circulation (GOC), Ψ₂ (orange arrows) is Atlantic meridional overturning circulation (AMOC), γ₁ (blue arrows between boxes 4 and 6) is deep–abyssal mixing, γ₂ (blue arrows between boxes 1 and 3) is low-latitude thermohaline mixing, Z (green downward arrows) is the biological pump, F_CA (white downward arrows) is the carbonate pump, D_CA (white squiggles) is carbonate dissolution and P (black, bidirectional arrows) is the air–sea gas exchange. Box 1: low-latitude–tropical surface ocean; box 2: northern surface ocean; box 3: intermediate ocean; box 4: deep ocean; box 5: Southern Ocean; box 6: abyssal ocean; box 7: subpolar southern surface ocean.

2 SCP-M description

SCP-M is focussed on the ocean carbon cycle and is configured to estimate the time evolution of oceanic dissolved inorganic carbon (DIC) and its constituents: δ¹³C, Δ¹⁴C, plus alkalinity, phosphorus, oxygen, and atmospheric CO₂, δ¹³C and Δ¹⁴C. It contains a simple yet realistic representation of large-scale ocean physical processes, with an overlay of ocean chemistry and biology (Fig. 1). SCP-M simulates sources and sinks of carbon across the ocean and atmosphere, marine sediments, and terrestrial biosphere. Volcanic emissions, sedimentary weathering, rivers and anthropogenic emissions are prescribed fluxes. A range of carbon cycle features are included because the concentrations of carbon in the ocean and atmosphere (and its isotopes in particular) are sensitive to many sources and sinks, and omitting them makes it difficult to compare model results with the carbon data that indelibly feature their imprint. For example, regrowth in the terrestrial biosphere imparts a clear signature on the atmosphere and ocean δ¹³C data profile after the LGM (e.g. Francois et al., 1999; Ciais et al., 2012; Hoogakker et al., 2016). In addition, the atmospheric radiocarbon source, marine sediments, volcanic emissions, continental weathering and now anthropogenic emissions exert important influences on carbon cycle observations.

SCP-M was designed to compare model results with data and to solve for optimal parameter combinations. Within SCP-M, realistic implementation of physical processes upon a sound biogeochemical platform enables their transmission into paleo chemical tracer signals, for which proxy data exist. Many of the key ocean physical and biological processes are prescribed in the model, allowing them to be free parameters in model–data experiments. SCP-M itself is implemented with a matrix framework which enables more boxes to be added, ocean basins to be separated, elements to be added and exploration of a range of hypotheses, all with minimal programming effort.

2.1 Model topology

The box model is mostly conceptual in nature and is designed to test high-level concepts. Therefore, excessive detail and complication are to be avoided. However, key processes that are critical to the validity of any hypothesis being tested must be represented as well as possible.

The ocean is a key part of the global carbon cycle and pre-eminent in hypotheses of glacial–interglacial carbon cycles (e.g. Kohfeld and Ridgewell, 2009; Sigman et al., 2010). Talley (2013) provided an observationally based description of ocean circulation in terms of its constituent water masses, circulation and mixing fluxes, including estimates of the present-day magnitudes of those fluxes. The Talley (2013) model builds on the models of Broecker (1991), Gordon (1991), Schmitz (1996), Lumpkin and Speer (2007), Kuhlbrodt et al. (2007), Talley (2008), and Marshall and Speer (2012). Key features of the Talley (2013) model include the following.

• Atlantic thermocline water moves north, ultimately reaching the North Atlantic, driven by advection and surface buoyancy changes. High-salinity North Atlantic Deep Water (NADW) forms in the north by cooling, densification and convection and then travels south to rise up into the Southern Ocean via wind-driven upwelling and Ekman flows, forming Lower Circumpolar Deep Water (LCDW). This water comprises the upper (orange arrows) Atlantic meridional overturning circulation (AMOC) in SCP-M (Fig. 1).

• A fraction of the upwelled LCDW sinks to become Antarctic Bottom Water (AABW) under the influence of cooling and brine rejection, south of the Antarctic Circumpolar Current (ACC). AABW moves northward along the ocean floor via adiabatic advection (Talley, 2013) in all basins. It upwells into deep water in the Pacific and Indian oceans and also into NADW in the Atlantic via upwelling with diapycnal diffusion (Talley, 2013). The combined LCDW–AABW–PDW–IDW–NADW global overturning circulation (GOC) is represented by the red arrows in Fig. 1.

• Pacific Deep Water–Indian Deep Water (PDW–IDW) upwells at low latitudes and returns to the Southern Ocean above the NADW, forming the core of the Upper Circumpolar Deep Water (UCDW), which is identified by Talley (2013) as low-oxygen-content (old) water. A part of the upwelled PDW–IDW joins AABW formation, with the bulk of it moving north from the Southern Ocean at shallow and intermediate depths. These waters become fresher and warmer and join Antarctic Intermediate Water (AAIW) and Subantarctic Mode Water (SAMW) at the base of the subtropical thermocline (advection with surface buoyancy fluxes).

• Joined thermocline waters, AAIW–SAMW, and upwelled thermocline waters from the Pacific and Indian oceans form the upper-ocean transport moving towards the North Atlantic.

A key contribution of the Talley (2013) study is that GOC is the pre-eminent process in distributing water throughout the global oceans. Talley (2013) provided a 2-D “collapsed” interpretation of a 3-D ocean layout based on the observation that similar large-scale processes (i.e. GOC) operate in all three major ocean basins, and this interpretation can directly inform a box model topology. The Talley (2013) 2-D global ocean view used in SCP-M captures the features described above in a simple ocean box model format. Talley (2013) also provided observation-based estimates of the ocean transport fluxes, which are scaled according to their ocean basin domain. For example, the GOC and AABW formation process is common to all basins and thus accounts for the largest flux of 29 Sverdrups (Sv, 10⁶ m³ s⁻¹). The AMOC–NADW sinking cell is confined to the Atlantic Basin and represents a smaller flux (19 Sv) of water (Talley, 2013).

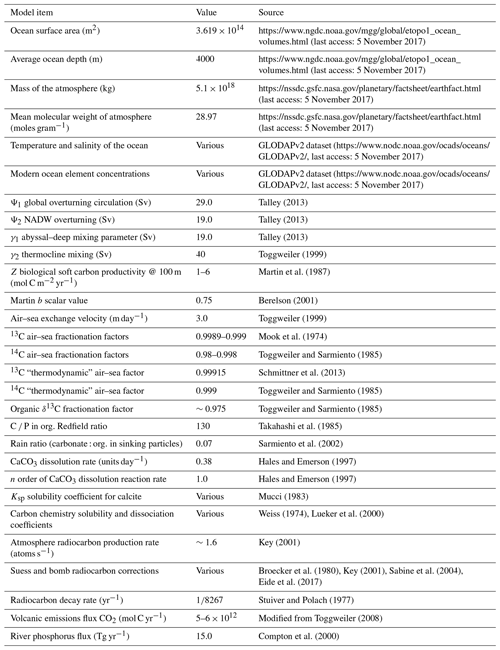
The SCP-M dimensions are designed to be consistent with measured estimates of the ocean surface area, average depth, and total ocean and atmosphere volumes. The model is divided into boxes according to latitude and depth, but not by longitude. Therefore, it does not distinguish between the Atlantic, Pacific and Indian basins and does not allow for compositional variations with longitude. Each box has a surface area and depth (and therefore volume) and corresponds to a location in the global ocean with reference to latitude and average depth. It is simple to add more boxes to divide the model into ocean basins.

SCP-M contains seven ocean boxes as shown in Fig. 1. The rationale for dividing the ocean into boxes is that there are regions of the ocean that are relatively well-mixed, or at least similar in terms of their prevailing element flux behaviour. For the depth of the surface boxes, this rationale conveniently translates to the maximum wintertime mixed layer depth (MLD) (e.g. Kara et al., 2003; de Boyer Montegut et al., 2004). We choose a depth of 100 m for box 1, the low-latitude surface box, which is a reasonable approximation to the 20–150 m seasonally varying MLD for the middle and low latitudes estimated by de Boyer Montegut et al. (2004) and consistent with the depth of a similar box in the Toggweiler (1999) model. This box represents the photic zone over much of the ocean, from 40^∘ S to 40^∘ N. Craig (1957) estimated the depth of this layer as 75 m ± 25 m, a value used by Keeling and Bolin (1968) in their simple ocean box model. We choose 250 m of depth for the NADW box (box 2) and the subpolar surface box (box 7) as per Toggweiler (1999). These boxes are deeper than the low-latitude surface box (de Boyer Montegut et al., 2004) in order to capture the regions of deepwater upwelling (subpolar Southern Ocean) and convective downwelling (North Atlantic). The MLD in these regions can vary between 70 and >500 m of depth depending on seasonal variations (de Boyer Montegut et al., 2004). An intermediate-depth box (3) resides below the low-latitude surface box and extends from 100 m to 1000 m of depth. This box captures northward-flowing AAIW and SAMW from upwelled NADW–PDW–IDW (e.g. Talley, 2013). Box 4 is the deep ocean box, extending from 1000 m to 2500 m of depth, and incorporates the upwelling abyssal waters in all basins and downwelled NADW. This water is channelled back to the surface in the subpolar surface box and the Southern Ocean box, as per the wind-driven upwelling of Morrison and Hogg (2013) and Talley (2013). The Southern Ocean box (5) extends from 80 to 60^∘ S and from the ocean surface to 2500 m of depth. This box encompasses the Southern Ocean, the ACC and deepwater formation from southward-flowing upwelled NADW–PDW–IDW (Talley, 2013). The abyssal box (6) extends the full range of the ocean, from 2500 to 4000 m of depth (our assumed average depth of the ocean). This box is the pathway for northward-flowing AABW and incorporates mixing with overlying deep water and advection–upwelling (Talley, 2013).

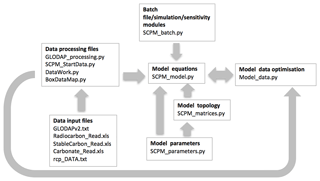
Figure 2 SCP-M Python and ancillary files with their linkages. Arrows refer to the direction of file linkages and the order of their activation during the routine of setting up and running the model. SCP-M is currently implemented in Python 3.6, although it has been run on other versions of Python. The folder or file structure separates model and data files. All files and user manuals are available from https://doi.org/10.5281/zenodo.1310161 (O'Neill et al., 2018).

2.2 The model parameters, processes and equations

2.2.1 Basic features

Figure 2 shows the suite of files used to execute SCP-M. We have chosen a modular approach to reduce the complexity of each of the model files. The SCP-M routine includes data processing for the model's boxes based on geographic coordinates, model calibration to the data, model simulations, model–data optimisation, and charting and/or tabular output. SCP-M is implemented in Python 3.6, with the code and download (including user instructions) available at https://doi.org/10.5281/zenodo.1310161 (O'Neill et al., 2018).

In short, SCP-M calculates the evolution of an element or species concentration in each model box as a function of time and flux parameters (e.g. inputs and outputs to each box) or processes, such as uptake or regeneration. The model includes ocean circulation and mixing fluxes, air–sea gas exchange, chemical and biological transformations, and sources and sinks of carbon. The model equations are a set of partial differential equations, one for each element in the model. These are solved with a straightforward, first-order, Euler-forward time-stepping method with a standard time step of 1 year. We find the model to be stable and approaching steady state for most of the simulations that we undertook. However, this stability can be challenged by scenarios with strong forcing. With the Euler method, errors can propagate in proportion to the step size. This can be resolved by revising the selection of parameter inputs or starting data values or by reducing the size of the time step in each model run.

2.2.2 The ocean circulation and mixing

There are four ocean physical parameters in SCP-M. Ψ₁ and Ψ₂ are advection terms that represent the physical transport of water from one box to another, containing the element or species concentration of its box of origin. Ψ₁ represents GOC (e.g. Sarmiento and Toggweiler, 1984; Marshall and Speer, 2012; Talley, 2013) that infiltrates all basins (Talley, 2013) and is shown by the red arrows in Fig. 1. The Ψ₁ parameter allows variable allocation between transport from the deep ocean box (box 4) into the subpolar surface box (box 7) and directly into the polar box (box 5) via α. Ψ₂ represents the AMOC. This is the region of northward-flowing intermediate waters in the Atlantic Ocean and the formation of NADW (Dickson and Brown, 1994; Talley, 2013), shown as orange arrows in Fig. 1. γ₁ and γ₂ are bidirectional mixing terms that exchange element or species concentrations between boxes without any net advection of water (blue arrows in Fig. 1). γ₁ is bidirectional mixing between the deep and abyssal boxes of the form described by Lund et al. (2011) and De Boer and Hogg (2014). γ₂ is a low-latitude, intermediate–shallow box “thermocline” mixing parameter, which governs the constant bidirectional exchange between these two boxes (Liu et al., 2016).

The influence of each of the ocean parameters is prescribed in box model space by matrix equations, with one matrix for each parameter. Each row and column position in the matrix corresponds to a box location. The atmosphere box is treated separately from the ocean boxes, and it does not enter the ocean parameter matrices. The volumetric circulation or mixing parameters, in Sv, are multiplied by the oceanic element concentration (mol m⁻³) to produce a molar flux exchanged between ocean boxes. For example, the change in concentration of carbon (as DIC) in the deep box (box 4) from ocean physical parameters is estimated by

$$\begin{array}{ll}\text{(1)}& {\displaystyle }{\left[{\displaystyle \frac{\mathrm{d}{C}_{\mathrm{4}}}{\mathrm{d}t}}\right]}_{\mathrm{phys}}& {\displaystyle }={\displaystyle }& {\displaystyle \frac{{\mathrm{\Psi }}_{\mathrm{1}}(C_{\mathrm{6}}-C_{\mathrm{4}})}{V_{\mathrm{4}}}}+{\displaystyle \frac{{\mathrm{\Psi }}_{\mathrm{2}}(C_{\mathrm{2}}-C_{\mathrm{4}})}{V_{\mathrm{4}}}}+{\displaystyle \frac{{\mathit{\gamma }}_{\mathrm{1}}(C_{\mathrm{6}}-C_{\mathrm{4}})}{V_{\mathrm{4}}}},\end{array}$$

where C_i is the concentration of DIC in each box in mol m⁻³ and V_i is the volume of each box in m³. There is no vertical flux between box 4 and box 3 (intermediate box) in Eq. (1). We assume that this vertical flux is small compared with the lateral transport and compared with the mixing fluxes between boxes 4 and  6 (and boxes 1 and 3 in Eq. 2 below). We assume that the boundary between boxes 3 and 4 is the divide between northward-flowing water sourced from AAIW and SAMW, which overlies southward return flow from AMOC and PDW–IDW. The fluxes out of box 4 are shown by the terms −Ψ₁C₄, −Ψ₂C₄ and −γ₁C₄, with the fluxes into boxes 5, 6 and 7 treated in the equations for those boxes. For the low-latitude surface box (box 1),

$$\begin{array}{}\text{(2)}& {\left[{\displaystyle \frac{\mathrm{d}{C}_{\mathrm{1}}}{\mathrm{d}t}}\right]}_{\mathrm{phys}}={\displaystyle \frac{{\mathit{\gamma }}_{\mathrm{2}}(C_{\mathrm{3}}-C_{\mathrm{1}})}{V_{\mathrm{1}}}}.\end{array}$$

We assume that box 1 represents the shallow, mixed layer of the ocean (e.g. Kara et al., 2003; de Boyer Montegut et al., 2004), which is mainly influenced by surface processes. We prescribe vertical mixing between this box and the underlying intermediate box (3) via the γ₂ parameter. This represents the thermocline mixing described by Liu et al. (2016). We assume that lateral transport of northward-flowing water underlies box 1, involving box 7 (subpolar Southern Ocean), box 3 and box 1 (northern ocean). This intermediate-depth water is colder and denser than the overlying mixed layer, given its provenance of AAIW, SAMW and deep-upwelled NADW–PDW–IDW (Talley, 2013). These ocean circulation and mixing operations (e.g. Eqs. 1 and 2) can be vectorised for all boxes using sparse matrices, as follows.

$$\begin{array}{}\text{(3)}& {\left[{\displaystyle \frac{\mathrm{d}\mathit{C}}{\mathrm{d}t}}\right]}_{\mathrm{phys}}={\displaystyle \frac{({\mathrm{\Psi }}_{\mathrm{1}}{\mathbf{T}}_{\mathbf{1}}+{\mathrm{\Psi }}_{\mathrm{2}}{\mathbf{T}}_{\mathbf{2}}+{\mathit{\gamma }}_{\mathrm{1}}{\mathbf{E}}_{\mathbf{1}}+{\mathit{\gamma }}_{\mathrm{2}}{\mathbf{E}}_{\mathbf{2}})\cdot \mathit{C}}{\mathit{V}}}\end{array}$$

where

$$\begin{array}{}\text{(4)}& \mathit{C}=C_i,\mathrm{for}i=\mathrm{1},\mathrm{7}\end{array}$$

$$\begin{array}{}\text{(5)}& \mathit{V}=V_i,\mathrm{for}i=\mathrm{1},\mathrm{7}\end{array}$$

and T₁, T₂, E₁ and E₂ are sparse matrices defined as

$$\begin{array}{}\text{(6)}& {\mathbf{T}}_{\mathbf{1}}=\left(\begin{array}{ccccccc}\mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& -\mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& (\mathrm{1}-\mathit{\alpha })& -\mathrm{1}& \mathrm{0}& \mathit{\alpha }\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& -\mathrm{1}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathit{\alpha }& \mathrm{0}& \mathrm{0}& -\mathit{\alpha }\end{array}\right)\end{array}$$

$$\begin{array}{}\text{(7)}& {\mathbf{T}}_{\mathbf{2}}=\left(\begin{array}{ccccccc}\mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& -\mathrm{1}& \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& -\mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\\ \mathrm{0}& \mathrm{1}& \mathrm{0}& -\mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}& -\mathrm{1}\end{array}\right)\end{array}$$

$$\begin{array}{}\text{(8)}& {\mathbf{E}}_{\mathbf{1}}=\left(\begin{array}{ccccccc}\mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& -\mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}& \mathrm{0}& -\mathrm{1}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\end{array}\right)\end{array}$$

$$\begin{array}{}\text{(9)}& {\mathbf{E}}_{\mathbf{2}}=\left(\begin{array}{ccccccc}-\mathrm{1}& \mathrm{0}& \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{1}& \mathrm{0}& -\mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\end{array}\right)\end{array}$$

Given that we have applied the global ocean interpretation of Talley (2013) to the SCP-M layout, we have also adopted the observationally based estimates for the large-scale ocean fluxes for the modern ocean from the same study: GOC (Ψ₁, 29 Sv), AMOC (Ψ₂, 19 Sv) and deep–abyssal mixing (γ₁, 19 Sv). For thermocline mixing between boxes 1 and 3 (γ₂), we have adopted the value for the corresponding flux from Toggweiler (1999) of 40 Sv.

2.2.3 Biological flux parameterisation

The biological pump (e.g. Broecker, 1982) is a descriptor of marine biological activity, whereby organisms consume nutrients in shallow waters, die, sink and then release those nutrients at depth. For example, carbon is taken up by shallow-water-dwelling phytoplankton through photosynthesis and then sequestered in deeper waters after sinking, breaking down and remineralising their nutrient load back into the water column. Volk and Hoffert (1985) made the distinction between the soft tissue pump (STP) for soft-tissued organisms and the carbonate pump (carbonate-shelled organisms). We also distinguish between the two pumps, as they have different effects on carbon and alkalinity balances and therefore pCO₂ and carbonate dissolution. This section deals with the STP, and a following section deals with the carbonate pump. Most STP organic matter is remineralised in the shallow to intermediate ocean depths, leading to a decrease in the export of carbon as depth increases. According to Henson et al. (2011), only ∼15 %–25 % of organic material is exported to >100 m of depth, with most recycled in the shallower waters.

Martin et al. (1987) modelled the soft-bodied organic flux of carbon observed from sediment traps in the northeast Pacific to create a simple power rule which is easily applicable to modelling. The Martin et al. (1987) equation produces a flux of organic carbon, which is a function of depth from a base organic flux at 100 m of depth (the “Martin reference depth”). The flux at 100 m of depth was estimated by Martin et al. (1987) to be between 1.2 and 7.1 mol C m⁻² yr⁻¹ from eight station observations in the northeast Pacific Ocean. Sarmiento and Gruber (2006) estimated a range of 0.0–5.0 mol C m⁻² yr⁻¹, with some localised higher values, across the global ocean. Equation (10) shows the general form of the Martin et al. (1987) equation:

$$\begin{array}{}\text{(10)}& F=F_{\mathrm{100}}{\left({\displaystyle \frac{z}{\mathrm{100}}}\right)}^b,\end{array}$$

where F is a flux of carbon in mol C m⁻² yr⁻¹, F₁₀₀ is an estimate of carbon flux at 100 m of depth, z is depth in metres and b is a depth scalar. In SCP-M, the Z parameter implements the Martin et al. (1987) equation. Z is an estimate of biological productivity at 100 m of depth (in mol C m⁻² yr⁻¹) and, coupled with the Martin et al. (1987) depth scalar, controls the amount of organic carbon that sinks from each model surface box to the boxes below. Each subsurface ocean box receives a flux of carbon from the box above it, at its ceiling depth (also the floor of the overlying box), and loses carbon as a function of the depth of the bottom of the box. Remineralisation in each box is accounted for as the difference between the influx and outflux of organic carbon. The biological flux out of the surface box 1 is shown by

$$\begin{array}{}\text{(11)}& {\left[{\displaystyle \frac{\mathrm{d}{C}_{\mathrm{1}}}{\mathrm{d}t}}\right]}_{\mathrm{bio}}={\displaystyle \frac{Z_{\mathrm{1}}{S}_{\mathrm{1}}{\left(\frac{{\mathrm{d}}_{f\mathrm{1}}}{{\mathrm{d}}_{\mathrm{0}}}\right)}^b}{V_{\mathrm{1}}}},\end{array}$$

where Z₁ is the biological flux of carbon prescribed for surface box 1 in mol C m⁻² yr⁻¹, S₁ is the surface area of surface box 1, d₀ is the reference depth of 100 m for the Z parameter value (Martin et al., 1987), and d_c and d_f are the ceiling and floor depths of a box, respectively. The dimensionless parameter b is the depth power function of the Martin et al. (1987) equation, which tapers biological production and export below depths of 100 m. The net biological flux for intermediate-depth box 3 is given by

$$\begin{array}{}\text{(12)}& {\left[{\displaystyle \frac{\mathrm{d}{C}_{\mathrm{3}}}{\mathrm{d}t}}\right]}_{\mathrm{bio}}={\displaystyle \frac{Z_{\mathrm{1}}{S}_{\mathrm{1}}\left[{\left(\frac{d_{\mathrm{c}\mathrm{3}}}{d_{\mathrm{0}}}\right)}^b-{\left(\frac{d_{\mathrm{f}\mathrm{3}}}{d_{\mathrm{0}}}\right)}^b\right]}{V_{\mathrm{3}}}}.\end{array}$$

The process is vectorised using sparse matrices in the following:

$$\begin{array}{}\text{(13)}& {\left[{\displaystyle \frac{\mathrm{d}\mathit{C}}{\mathrm{d}t}}\right]}_{\mathrm{bio}}={\displaystyle \frac{\mathit{Z}\mathit{S}\cdot \left({\mathbf{B}}_{\mathbf{out}}+{\mathbf{B}}_{\mathbf{in}}\right)}{\mathit{V}}},\end{array}$$

where Z is an array of the Z_i ($i=\mathrm{1},\mathrm{7}$) parameter, which varies across the surface boxes, and S is the array of surface box surface areas S_i ($i=\mathrm{1},\mathrm{7}$). As with the ocean parameters, the biological flux of carbon is divided by the box volume array V to return concentrations in mol m⁻³. B_out and B_in are sparse matrices as follows.

$$\begin{array}{ll}\text{(14)}& {\displaystyle }& {\displaystyle }{\mathbf{B}}_{\mathbf{out}}={\displaystyle }& {\displaystyle }\left(\begin{array}{ccccccc}-{\left(\frac{d_{\mathrm{f}\mathrm{1}}}{d_{\mathrm{0}}}\right)}^{-b}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& -{\left(\frac{d_{\mathrm{f}\mathrm{2}}}{d_{\mathrm{0}}}\right)}^{-b}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ -{\left(\frac{d_{\mathrm{f}\mathrm{3}}}{d_{\mathrm{0}}}\right)}^{-b}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ -{\left(\frac{d_{\mathrm{f}\mathrm{4}}}{d_{\mathrm{0}}}\right)}^{-b}& -{\left(\frac{d_{\mathrm{f}\mathrm{4}}}{d_{\mathrm{0}}}\right)}^{-b}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& -{\left(\frac{d_{\mathrm{f}\mathrm{4}}}{d_{\mathrm{0}}}\right)}^{-b}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& -{\left(\frac{d_{\mathrm{f}\mathrm{5}}}{d_{\mathrm{0}}}\right)}^{-b}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& -{\left(\frac{d_{\mathrm{f}\mathrm{7}}}{d_{\mathrm{0}}}\right)}^{-b}\end{array}\right)\end{array}$$

$$\begin{array}{ll}\text{(15)}& {\displaystyle }& {\displaystyle }{\mathbf{B}}_{\mathbf{in}}={\displaystyle }& {\displaystyle }\left(\begin{array}{ccccccc}\mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ {\left(\frac{d_{\mathrm{c}\mathrm{3}}}{d_{\mathrm{0}}}\right)}^{-b}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ {\left(\frac{d_{\mathrm{c}\mathrm{4}}}{d_{\mathrm{0}}}\right)}^{-b}& {\left(\frac{d_{\mathrm{c}\mathrm{4}}}{d_{\mathrm{0}}}\right)}^{-b}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& {\left(\frac{d_{\mathrm{c}\mathrm{4}}}{d_{\mathrm{0}}}\right)}^{-b}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ {\left(\frac{d_{\mathrm{c}\mathrm{6}}}{d_{\mathrm{0}}}\right)}^{-b}& {\left(\frac{d_{\mathrm{c}\mathrm{6}}}{d_{\mathrm{0}}}\right)}^{-b}& \mathrm{0}& \mathrm{0}& {\left(\frac{d_{\mathrm{c}\mathrm{6}}}{d_{\mathrm{0}}}\right)}^{-b}& \mathrm{0}& {\left(\frac{d_{\mathrm{c}\mathrm{6}}}{d_{\mathrm{0}}}\right)}^{-b}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\end{array}\right)\end{array}$$

The value of the parameter Z in each surface box is specified to vary as a fraction of the global value for Z in SCP-M (presently 5.0 mol C m⁻² yr⁻¹). There are higher fractions in the northern and southern oceans and smaller fractions in the low-latitude and polar oceans (e.g. Sarmiento and Gruber, 2006). During the model set-up we manually tuned the individual surface box values by multiplying the global value for Z by a scalar unique to each box. The values were tuned to align the model's output with GLODAPv2 data for DIC, phosphorous, alkalinity, the carbonate ion and carbon isotopes in each of the ocean boxes (Table 1). The resulting range for Z (1.1–5.33 mol C m⁻² yr⁻¹) compares with the observations-based range of Martin et al. (1987) of 1.2–7.1 mol C m⁻² yr⁻¹ and Sarmiento and Gruber (2006) of 0–5 mol C m⁻² yr⁻¹. We chose a value for the dimensionless b depth decay parameter of 0.75, which falls in the range of Gloege et al. (2017) of 0.68–1.13 and the error range of Berelson (2001) of 0.82±0.16. We found a global value of 0.75 to produce a better fit to the GLODAPv2 data when calibrating the model. The biological flux of other elements and species, such as phosphorous and alkalinity, are calculated from the biological carbon flux using so-called Redfield ratios (e.g. Redfield et al., 1963; Takahashi et al., 1985; Anderson and Sarmiento, 1994).

2.3 pCO₂ and carbonate

Modelling air–sea gas exchange, atmospheric pCO₂ and the “carbonate pump” rests on a realistic estimation of pCO₂ in the ocean. For example, only a fraction of DIC in seawater can exchange with the atmosphere, and this fraction is estimated by the oceanic pCO₂. DIC itself consists of three major constituents: carbonic acid, bicarbonate and carbonate. Their relative proportions depend on total DIC, alkalinity, pH, temperature and salinity (Zeebe and Wolf-Gladrow, 2001).

Table 1 Values for the Z biological production parameter (at 100 m of ocean depth) used in the SCP-M model calibration. A global value for Z was tuned in each surface box using scalars (column 3) to yield unique values for each surface box (column 4).

pCO₂ is estimated by subtracting alkalinity from DIC. However, this is only accurate to ±10 % (Sarmiento and Gruber, 2006), which may cause problems for scenario analysis and sensitivity testing within such a large error band. More complex calculations can require numerous iterations and can be computationally expensive (e.g. Toggweiler and Sarmiento, 1985; Zeebe and Wolf-Gladrow, 2001; Follows et al., 2006). We apply the routine of Follows et al. (2006) in SCP-M, which is a direct solution, rather than an iterative approach to solve for pCO₂ at each time step of a model run. This was demonstrated by Follows et al. (2006) to be sufficiently accurate for modelling purposes. The calculation takes inputs of DIC, alkalinity, temperature, salinity, phosphorous and silicate to estimate pCO₂.

Solving for pCO₂ enables the calculation of the concentrations of the three species of DIC, which further enables estimation of the dissolution and burial of carbonate in the water column and sediments. The latter is an important part of the oceanic carbon and alkalinity cycles and provides important feedbacks to atmospheric CO₂ on 1000-year time frames (e.g. Farrell and Prell, 1989; Anderson et al., 2007; Mekik et al., 2012; Yu et al., 2014b).

2.3.1 The carbonate pump

According to Emerson and Hedges (2003), ∼20 %–30 % of CaCO₃ formed in the ocean's surface is preserved in ocean floor sediments, with the rest dissolved in the water column. Klaas and Archer (2002) estimated that 80 % of the organic matter fluxes in the ocean below 2000 m are driven by organic matter associated with carbonate ballast. Therefore, the so-called “carbonate pump” is a relatively efficient transport of carbon and alkalinity in the ocean. According to Farrell and Prell (1989), the carbonate pump is a dynamic process, and the dissolution and burial in sediments of CaCO₃ is observed to vary across (and within) glacial–interglacial cycles.

To replicate this flux of carbon and alkalinity, a term is added to the carbon cycle equation to represent the flux of calcium carbonate (shells) out of the surface boxes into the abyssal box and sediments. This is an extension of the surface organic carbon flux Z described in Eq. (13) via the “rain ratio” parameter. The rain ratio is a common term in ocean biogeochemistry (e.g. Archer and Maier-Reimer, 1994; Ridgewell, 2003) and refers to the ratio between shell-based “hard” carbon and organic “soft” carbon fluxes in the biologically driven rain of carbon from the ocean's surface. Sarmiento et al. (2002) estimated a global average value for the rain ratio of 0.06±0.03, with local maxima and minima of 0.10 and 0.02, respectively, providing a narrow range of global values. We apply the rain ratio as a parameter multiplied by the organic flux parameter Z. We chose an initial value of 0.07, which provided appropriate values for DIC, alkalinity and dissolution in the model's boxes during the model spin-up (with reference to GLODAPv2 data). The combination delivers the physical production and export of calcium carbonate at the Martin reference depth (100 m).

Once the production and export flux at the Martin reference depth is established, the distribution of calcium carbonate in the boxes below is a function of dissolution. According to Milliman et al. (1999), the theory that calcium carbonate only dissolves at great depths in carbonate-undersaturated water is “one of the oldest and most strongly held paradigms in oceanography” (e.g. Sverdrup et al., 1941). However, in nature, the alkalinity and carbonate ion concentration profiles suggest that 30 %–60 % of carbonate produced is dissolved in shallower water that is saturated (Harrison et al., 1993; Milliman et al., 1999). Theories for this outcome include the emergence of locally undersaturated waters due to remineralisation of biological carbon (Jansen et al., 2002) and dissolution by zooplankton grazing (Milliman et al., 1999). Battaglia et al. (2016) found similar skill in model results for replicating observed dissolution profiles, whether a non-saturation-dependent or saturation-dependent dissolution constant was used. Battaglia et al. (2016) recommended the use of a basic non-saturation-dependent (i.e. constant) dissolution parameter in Earth carbon system models for computing efficiency, with limited loss of accuracy. As such, we include two parts to the dissolution equation: a non-saturation-dependent dissolution constant, to reflect the “unknown” processes that likely cause the observed dissolution of calcium carbonate in waters that are saturated, and a saturation-state-dependent component using the dissolution function of Morse and Berner (1972). We include the latter to enable dynamic feedback to take place in the carbonate system after model perturbations. The saturation-dependent dissolution is a function of the average carbonate ion composition for each box relative to its temperature- and pressure-dependent saturation concentration (Morse and Berner, 1972; Millero, 1983). We choose the median depth of each box for the calculation in the ocean boxes and the floor of the abyssal box for the sediment surface dissolution. We assume 100 % of calcium carbonate takes the form of calcite. If the surface export flux of CaCO₃ is greater than dissolution in the ocean boxes, then the remainder escapes to the sediments. This is a flux out of the ocean of alkalinity and carbon in the ratio of 2:1 assumed for carbonate shells (Sarmiento and Gruber, 2006). DIC and alkalinity can return to the abyssal box from the sediments via undersaturation-driven dissolution in the abyssal water overlying the sediments.

The net flux of carbonate between ocean boxes and out of the ocean and into the sediments is shown in vectorised Eq. (16):

$$\begin{array}{}\text{(16)}& {\left[{\displaystyle \frac{\mathrm{d}\mathit{C}}{\mathrm{d}t}}\right]}_{\mathrm{carb}}={\displaystyle \frac{\left(F_{\mathrm{CA}}\mathit{Z}\mathit{S}\right)}{\mathit{V}}}+(\mathit{\zeta }+\mathit{ϵ}){\mathrm{CaCO}}_{\mathrm{3}},\end{array}$$

where F_CA is the rain ratio, ζ is the constant background dissolution rate, ϵ is the saturation-state-dependent dissolution function of Morse and Berner (1972) and Millero (1983), and CaCO₃ is the concentration of calcium carbonate in each box. The dissolution equation of Morse and Berner (1972) operates on CaCO₃, which is calculated by multiplying Ca by ${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$, where Ca is estimated from salinity in each box as per Sarmiento and Gruber (2006).

2.3.2 Air–sea gas exchange

CO₂ is transported across the air–sea interface by gaseous exchange. According to Henry's law, the partial pressure of a gas [P] above a liquid in thermodynamic equilibrium will be directly proportional to the concentration of the gas in the liquid:

$$\begin{array}{}\text{(17)}& \left[P\right]=K_{\mathrm{HC}},\end{array}$$

where K_H is the solubility of a gas in mmol m⁻³ atm⁻¹ and C is its concentration in the liquid. Many ocean models specify the air–sea gas exchange of CO₂ as a function of the pCO₂ differential between ocean and atmosphere, a CO₂ solubility coefficient (e.g. Weiss, 1974), and a so-called “piston” or gas transfer velocity, which governs the rate of gas exchange, in m s⁻¹ (e.g. Toggweiler, 1999; Zeebe, 2012; Hain et al., 2010; Watson et al., 2015). We adopt the same approach in estimating the exchange of CO₂ between a surface box and the atmosphere:

$$\begin{array}{}\text{(18)}& {\left[{\displaystyle \frac{\mathrm{d}{C}_{\mathrm{1}}}{\mathrm{d}t}}\right]}_{\mathrm{gas}}=P_{\mathrm{1}}{S}_{\mathrm{1}}{K}_{{\mathrm{0}}_{\mathrm{1}}}\left({p\mathrm{CO}}_{{\mathrm{2}}_{\mathrm{at}}}-{p\mathrm{CO}}_{{\mathrm{2}}_{\mathrm{1}}}\right)\mathit{\rho },\end{array}$$

where P₁ is the piston velocity parameter in box 1 in m s⁻¹. P is allowed to vary in each surface box, enabling scenario analysis such as the variation of sea-ice cover in the polar box  (e.g. Stephens and Keeling, 2000; Ferrari et al., 2014). $K_{{\mathrm{0}}_{\mathrm{1}}}$ is the solubility of CO₂ in mol kg⁻¹ atm⁻¹ (Weiss, 1974), subsequently converted into mol m⁻³ by multiplying by seawater density ρ. ${p\mathrm{CO}}_{{\mathrm{2}}_{\mathrm{1}}}$ and pCO${}_{{\mathrm{2}}_{\mathrm{at}}}$ are the partial pressures of CO₂ in surface ocean box 1 and the atmosphere, respectively, in ppm. The equation is vectorised as follows:

$$\begin{array}{}\text{(19)}& {\left[{\displaystyle \frac{\mathrm{d}\mathit{C}}{\mathrm{d}t}}\right]}_{\mathrm{gas}}=\mathit{P}\mathit{S}{\mathit{K}}_{\mathrm{0}}\left({p\mathrm{CO}}_{{\mathrm{2}}_{\mathrm{at}}}-{p\mathrm{CO}}_{\mathrm{2}}\right)\mathit{\rho },\end{array}$$

where P=P_i ($i=\mathrm{1},\mathrm{7}$), with zero values for non-surface boxes, and ${\mathit{K}}_{\mathrm{0}}=K_{{\mathrm{0}}_i}$ ($i=\mathrm{1},\mathrm{7}$).

2.4 Sea surface temperature and salinity

Ocean box temperature and salinity are forced in SCP-M, not calculated by the model. Each box has a prescribed value for temperature and salinity, which can be time dependent. During initialisation, the model takes box-averaged values for temperature and salinity from the GLODAPv2 database. The values can be varied between model experiments, for example Holocene versus LGM reconstructions. We argue that this approach is plausible given the availability of temperature and salinity proxy–data inputs for a range of paleo (e.g. Adkins et al., 2002; Kohfeld and Chase, 2017), modern (e.g. Olsen et al., 2016) and future scenarios (e.g. IPCC, 2013a). For the modern and future scenarios (Sect. 3.3), we forced temperature with time series data and projections. The temperature and salinity values feed into the calculations for ocean pCO₂, which further enables the calculation of air–sea gas exchange and the species of DIC in seawater (H₂CO₃, HCO₃₋ and ${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$).

2.5 Atmosphere and terrestrial carbon cycle

SCP-M incorporates the terrestrial biosphere, continental weathering and river run-off into the ocean, plus an atmospheric radiocarbon source and volcanic and industrial emissions.

V is a constant prescribed flux of volcanic emissions of CO₂ in SCP-M. Toggweiler (2008) estimated this volcanic flux of CO₂ emissions at 4.98×10¹² mol yr⁻¹ using a carbon cycle model which balanced volcanic emissions with land-based weathering sinks. The weathering of carbonate and silicate rocks also creates DIC and alkalinity run-off into rivers, which finds its way into the ocean (Amiotte Suchet et al., 2003). Relative alkalinity and DIC concentrations affect ocean pCO₂ and carbonate ion levels, which impacts atmospheric CO₂ and the dissolution and burial of carbonates (Sarmiento and Gruber, 2006). We apply the approach of Toggweiler (2008), whereby silicate and carbonate weathering fluxes of DIC and alkalinity enter only the low-latitude surface ocean box (box 1):

$$\begin{array}{}\text{(20)}& {\left[{\displaystyle \frac{\mathrm{d}{C}_{\mathrm{1}}}{\mathrm{d}t}}\right]}_{\mathrm{weath}}=(W_{\mathrm{SC}}+(W_{\mathrm{SV}}+W_{\mathrm{CV}}\left){\mathrm{AtCO}}_{\mathrm{2}}\right),\end{array}$$

where W_SC is a constant silicate weathering term set at $\mathrm{0.75}\times {\mathrm{10}}^{-\mathrm{4}}$ mol m⁻³ yr⁻¹, W_SV is a variable rate of silicate weathering per unit of atmosphere CO₂ (ppm) set to 0.5 mol m⁻³ atm⁻¹ CO₂ yr⁻¹ and W_CV is the variable rate of carbonate weathering with respect to atmosphere CO₂ set at 2 mol m⁻³ atm⁻¹ CO₂ yr⁻¹ (Toggweiler, 2008).

Alkalinity is added to the ocean in the ratio of 2:1 to DIC (Toggweiler, 2008). In the case of silicate rocks, weathering is also a weak sink of CO₂ (e.g. Toggweiler, 2008; Hogg, 2008). The atmospheric sink of CO₂ is calculated by multiplying Eq. (20) by the volume of the low-latitude surface ocean box (box 1) and subtracting from atmospheric CO₂. Equation (20) is vectorised by multiplying by a vector of boxes with only a non-zero value for box 1.

The terrestrial biosphere may act as a sink of CO₂ during periods of biosphere growth (e.g. post-glacial regrowth), via carbon fertilisation, or a source of CO₂ (e.g. glacial reduction) via respiration. We employ a two-part model of the terrestrial biosphere with a long-term (woody forest) and short-term (grassland) terrestrial biosphere box as described by Raupach et al. (2011) and Harman et al. (2011), with net primary productivity (NPP) and respiration parameters controlling the balance between the uptake and release of carbon. NPP is positively affected by atmospheric CO₂, the so-called “carbon fertilisation” effect (e.g. Raupach et al., 2011). Respiration is assumed proportional to the carbon stock. The biosphere also preferentially partitions the lighter carbon isotope ¹²C, leading to a relative enrichment in δ¹³C in the atmosphere during net uptake of CO₂. The change in atmospheric CO₂ from the terrestrial biosphere in the model is given by

$$\begin{array}{ll}\text{(21)}& {\displaystyle }& {\displaystyle }{\left[{\displaystyle \frac{{\mathrm{dAtCO}}_{\mathrm{2}}}{\mathrm{d}t}}\right]}_{\mathrm{NPP}}={\displaystyle }& {\displaystyle }-N_{\mathrm{pre}}\mathrm{RP}\left[\mathrm{1}+\mathit{\beta }\mathrm{LN}\left({\displaystyle \frac{{\mathrm{AtCO}}_{\mathrm{2}}}{{\mathrm{AtCO}}_{\mathrm{2}\mathrm{pre}}}}\right)\right]+{\displaystyle \frac{C_{\mathrm{stock}\mathrm{1}}}{k_{\mathrm{1}}}}+D_{\mathrm{forest}},\end{array}$$

where N_pre is NPP at a reference level (“pre”) of atmospheric CO₂, and RP is the parameter to split NPP between the short-term terrestrial biosphere carbon stock (fast respiration) and the long-term stock (slow respiration) (Raupach et al., 2011). β is the parameterisation of carbon fertilisation, which causes NPP to increase (decrease) logarithmically with rising (falling) atmospheric CO₂ levels, and has a typical value of 0.4–0.8 (Harman et al., 2011). C_stock1 is the short-term carbon stock and k₁ is the time frame for respiration in the short-term carbon stock (in years). For the long-term terrestrial biosphere, we substitute (1−RP) in place of RP and C_stock2 and k₂ for the long-term carbon stock and respiration rate, respectively. D_forest is a prescribed flux of deforestation emissions, which can be switched on or off in SCP-M. A δ¹³C fractionation factor is applied to the terrestrial biosphere fluxes of carbon, effecting an increase in atmospheric δ¹³C from biosphere growth and a decrease from respiration.

2.6 The complete carbon cycle equations

Equation (22) shows the full vectorised model equation for the calculation of the evolution of carbon concentration in the ocean boxes, incorporating Eqs. (1)–(21).

$$\begin{array}{ll}\text{(22)}& {\displaystyle }& {\displaystyle \frac{\mathrm{d}\left(\mathit{C}\right)}{\mathrm{d}t}}={\displaystyle }& {\displaystyle }{\left[{\displaystyle \frac{\mathrm{d}\mathit{C}}{\mathrm{d}t}}\right]}_{\mathrm{phys}}+{\left[{\displaystyle \frac{\mathrm{d}\mathit{C}}{\mathrm{d}t}}\right]}_{\mathrm{bio}}+{\left[{\displaystyle \frac{\mathrm{d}\mathit{C}}{\mathrm{d}t}}\right]}_{\mathrm{carb}}+{\left[{\displaystyle \frac{\mathrm{d}\mathit{C}}{\mathrm{d}t}}\right]}_{\mathrm{gas}}+{\left[{\displaystyle \frac{\mathrm{d}\mathit{C}}{\mathrm{d}t}}\right]}_{\mathrm{weath}}\end{array}$$

The calculation of atmospheric CO₂ is

$$\begin{array}{ll}\text{(23)}& {\displaystyle }& {\displaystyle \frac{{\mathrm{dAtCO}}_{\mathrm{2}}}{\mathrm{d}t}}={\left[{\displaystyle \frac{{\mathrm{dAtCO}}_{\mathrm{2}}}{\mathrm{d}t}}\right]}_{\mathrm{gas}}+{\left[{\displaystyle \frac{{\mathrm{dAtCO}}_{\mathrm{2}}}{\mathrm{d}t}}\right]}_{\mathrm{NPP}}{\displaystyle }& {\displaystyle }+{\left[{\displaystyle \frac{{\mathrm{dAtCO}}_{\mathrm{2}}}{\mathrm{d}t}}\right]}_{\mathrm{volcs}}+{\left[{\displaystyle \frac{{\mathrm{dAtCO}}_{\mathrm{2}}}{\mathrm{d}t}}\right]}_{\mathrm{weath}}+{\left[{\displaystyle \frac{{\mathrm{dAtCO}}_{\mathrm{2}}}{\mathrm{d}t}}\right]}_{\mathrm{anth}},\end{array}$$

where the additional term ${\left[\frac{{\mathrm{dAtCO}}_{\mathrm{2}}}{\mathrm{d}t}\right]}_{\mathrm{anth}}$ consists of a prescribed flux of δ¹³C-depleted and ¹⁴C-dead CO₂ to the atmosphere from human industrial emissions, which is activated by a model switch in SCP-M.

2.7 Treatment of carbon isotopes

Carbon isotopes are an important component in SCP-M because they are key sources of proxy data. Carbon isotope fluxes are treated largely the same as DIC in SCP-M, with minor modification. For example, carbon isotopes are typically reported in delta notation (δ¹³C and Δ¹⁴C), which is the ‰ deviation from a standard reference value in nature. SCP-M operates with a metric mol m⁻³ for the other ocean element concentrations and flux parameters. In order to incorporate δ¹³C and Δ¹⁴C into this metric for the operation of model fluxes, the method of Craig (1969) is applied to convert starting data values of δ¹³C and Δ¹⁴C from delta notation in ‰ into mol m⁻³:

$$\begin{array}{}\text{(24)}& {}^{\mathrm{13}}{C}_i=\left({\displaystyle \frac{{\mathit{\delta }}^{\mathrm{13}}{C}_i}{\mathrm{1000}}}+\mathrm{1}\right)R{C}_i,\end{array}$$

where ¹³C_i is the ¹³C concentration in box i in mol m⁻³, δ¹³C_i is δ¹³C in ‰ in box i, R is the $\frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}$ ratio of the standard (0.0112372 as per the Pee Dee Belemnite value) and C_i is the DIC concentration C in box i in mol m⁻³.

The calculation in Eq. (24) derives the fraction $\frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}$ for the data or a model starting value, multiplies that value by the standard reference value and then by the starting model concentration for DIC (C_i) in each box. This approach rests on the assumption that the fraction $\frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}$ is the same as $\frac{{}^{\mathrm{13}}\mathrm{C}}{\text{total carbon}}$. For example, there are three isotopes of carbon, each with different atomic weights. They occur in roughly the following abundances: ¹²C ∼98.89 %, ¹³C ∼1.11 % and ¹⁴C $\sim \mathrm{1}\times \mathrm{10}{}^{-\mathrm{10}}$ %. Therefore, the assumption that $\frac{{}^{\mathrm{13}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}$ = $\frac{{}^{\mathrm{13}}\mathrm{C}}{\text{total carbon}}$ is a valid approximation. Once converted from δ¹³C (‰) to ¹³C in mol m⁻³, SCP-M's ocean parameters can operate on ¹³C concentrations in each box, according to the same model flux equations used for DIC and CO₂. The ¹³C model results are then converted back into δ¹³C notation at the end of the model run in order to compare the model output with the data, which is reported in δ¹³C format. The same method is applied to Δ¹⁴C. The reference standard value for $\frac{{}^{\mathrm{14}}\mathrm{C}}{{}^{\mathrm{12}}\mathrm{C}}$ is $\mathrm{1.2}\times {\mathrm{10}}^{-\mathrm{12}}$ (Craig, 1969). Where fractionation of carbon isotopes takes place, such as biological or air–sea gas exchange, fractionation factors are simply added to the model flux equations.

2.7.1 Biological fractionation of carbon isotopes

Biological processes influence the carbon isotopic composition of the ocean (e.g. Fontugne and Duplessy, 1978). When photosynthetic organisms are active in shallow ocean waters, they preferentially partition ¹²C (the lighter carbon isotope). This activity enriches the surface ocean in ¹³C and relatively enriches the underlying waters in ¹²C when remineralisation occurs. As such, the ocean displays depletion in δ¹³C in the deep ocean relative to the shallow ocean (e.g. Curry and Oppo, 2005). In SCP-M, a fractionation factor, f, is simply multiplied by the biological flux in Eq. (13) to calculate marine biological fractionation of ¹³C and to replicate ocean distributions of δ¹³C:

$$\begin{array}{}\text{(25)}& {\left[{\displaystyle \frac{{\mathrm{d}}^{\mathrm{13}}{C}_i}{\mathrm{d}t}}\right]}_{{}^{\mathrm{13}}\mathrm{bio}}=f\cdot S_{\mathrm{st}},\end{array}$$

where f is the biological fractionation factor for stable carbon (e.g. ∼0.977 in Toggweiler and Sarmiento, 1985), and S_st is the ratio of ¹³C to ¹²C in the reference standard. The typical δ¹³C composition of marine organisms is in the range −23 to −30‰. The same method is applied for biological fractionation of ¹⁴C, but with a different fractionation factor (Toggweiler and Sarmiento, 1985).

2.7.2 Fractionation of carbon isotopes during air–sea gas exchange

Fractionation of carbon isotopes takes place during air–sea exchange (e.g. Mook et al., 1974; Siegenthaler and Munnich, 1981; Lynch-Stieglitz et al., 1995). The lighter isotope, ¹²C, preferentially partitions into the atmosphere as a net effect of bidirectional gaseous exchange. This fractionation leads to the heavily depleted δ¹³C signature for the atmosphere relative to the ocean. The approach to capture this effect in SCP-M is per Siegenthaler and Munnich (1981):

$$\begin{array}{}\text{(26)}& {\left[{\displaystyle \frac{{\mathrm{d}}^{\mathrm{13}}{C}_i}{\mathrm{d}t}}\right]}_{{}^{\mathrm{13}}\mathrm{gas}}=\mathit{\lambda }\left[\mathit{\tau }{R}_{\mathrm{At}}{p\mathrm{CO}}_{\mathrm{2}\mathrm{At}}-\mathit{\pi }{R}_i{\mathrm{pCO}}_{\mathrm{2}i}\right],\end{array}$$

where λ, the “kinetic fractionation effect” (Zhang et al., 1995), accounts for the slower equilibration rate of the carbon isotopes ¹³C and ¹⁴C across the air–sea interface compared with ¹²C (Zhang et al., 1995). R_At is the ratio of ¹³C to ¹²C in the atmosphere, and R_i is the ratio of ¹³C to ¹²C in surface ocean box i. pCO_2At is the atmospheric pCO₂, and pCO_2i is the pCO₂ in the surface ocean boxes. τ and π are the fractionation factors of carbon isotopes from air to sea and sea to air, respectively. These are temperature-dependent reactions and are calculated in SCP-M using the method of Mook et al. (1974).

2.7.3 Source and decay of radiocarbon

Natural radiocarbon is produced in the atmosphere from the collision of cosmic-ray-produced neutrons with nitrogen. The production rate is variable over time and can be influenced by changes in solar winds and the Earth's geomagnetic field intensity (Key, 2001). A mean production rate of 1.57 atom m⁻² s⁻¹ was estimated from the long-term record preserved in tree rings, although more recent estimates approach 2 atom m⁻² s⁻¹ (Key, 2001). For use in SCP-M, this estimate needs to be converted into mol s⁻¹. We first convert atoms to moles by dividing by Avogadro's number ($\sim \mathrm{6.022}\times {\mathrm{10}}^{\mathrm{23}}$). The resultant figure is multiplied by the Earth's surface area ($\sim \mathrm{5.1}\times \mathrm{10}{}^{\mathrm{18}}$ cm⁻²) to yield a production rate of $\mathrm{1.3296}\times \mathrm{10}{}^{-\mathrm{5}}$ mol s⁻¹. This source rate, divided by the molar volume of the atmosphere, is added to the equation for atmospheric radiocarbon concentration. A decay timescale for radiocarbon of 8267 years is applied to each box in the model.

3 Modelling results

The modern carbon cycle has been extensively modelled as part of efforts to understand the impact of anthropogenic emissions on climate. There are abundant data on emissions and detailed observations of the modern carbon cycle with globally coordinated ocean surveys and land-based measuring stations. In addition, numerous modelling exercises, using consensus-type emissions projection scenarios from the Intergovernmental Panel on Climate Change (IPCC), have created a body of modelling inputs and results. This provides an ideal testing ground for SCP-M. We first calibrate the model for the pre-industrial period, then simulate historical and projected human emissions under a number of scenarios.

Marcott et al. (2014)Schmitt et al. (2012)Nydal and Lövseth (1996)Stuiver et al. (1998)Reimer et al. (2009)Turnbull et al. (2017)Peterson et al. (2014)Skinner and Shackleton (2004)Marchitto et al. (2007)Barker et al. (2010)Bryan et al. (2010)Skinner et al. (2010)Burke and Robinson (2012)Davies-Walczak et al. (2014)Skinner et al. (2015, 2017)Chen et al. (2015)Hines et al. (2015)Sikes et al. (2016)Ronge et al. (2016)Yu et al. (2014b, a)(Olsen et al., 2016)Broecker et al. (1980)Key (2001)Sabine et al. (2004)Eide et al. (2017)

Table 2 Ocean and atmosphere data sources for the SCP-M modern carbon cycle calibration, projections and LGM–Holocene experiment.

The late Holocene is chosen as the initial model calibration due to the absence of industrial-era CO₂ and bomb radiocarbon. Scripps CO₂ Program data originally sourced from http://scrippsco2.ucsd.edu (last access: 10 June 2018); data currently being transitioned to http://cdiac.ess-dive.lbl.gov (last access: 10 June 2018). The Peterson et al. (2014) database incorporates ∼500 core records across the LGM and late Holocene periods.

3.1 Pre-industrial calibration

We choose the late Holocene period (6–0.2 ka) for our calibration because it has relatively good proxy data coverage (e.g. Table 2) and a relatively steady climate in the absence of perturbations such as industrial CO₂ emissions, bomb radiocarbon or glacial terminations. The late Holocene is also close to the pre-industrial period (1700s) in order to act as a starting point for modern carbon cycle simulations. To calibrate the model for the late Holocene we begin with the modern-day GLODAPv2 dataset (https://www.nodc.noaa.gov/ocads/oceans/GLODAPv2/, last access: 10 June 2018), which we average into the model's boxes on depth and latitude coordinates using one of the SCP-M scripts (Fig. 2). The GLODAPv2 database incorporates data from ∼1 million seawater samples from 700 cruises over the years 1972–2013, including data from the original GLODAP dataset, plus the CARINA and PACIFICA datasets (Olsen et al., 2016). We assume an average data year of 1990 for the data accumulated over the period 1972–2013. We make adjustments to the ocean concentrations of DIC, δ¹³C and Δ¹⁴C for the effects of industrial emissions (the “Suess” effect) and bomb radiocarbon in the atmosphere using published estimates (Broecker et al., 1980; Key, 2001; Sabine et al., 2004; Eide et al., 2017). For example, Eide et al. (2017) establish a mathematical relationship between Suess δ¹³C and CFC-12 in the ocean, which we applied using GLODAPv2 CFC-12 data to correct the ocean δ¹³C data. We force the model with late Holocene average data for atmosphere CO₂, δ¹³C and Δ¹⁴C (data sources in Table 2). The model's starting parameters are set from literature values (Table A1, Appendix), including the point estimates for ocean circulation and mixing fluxes from Talley (2013).

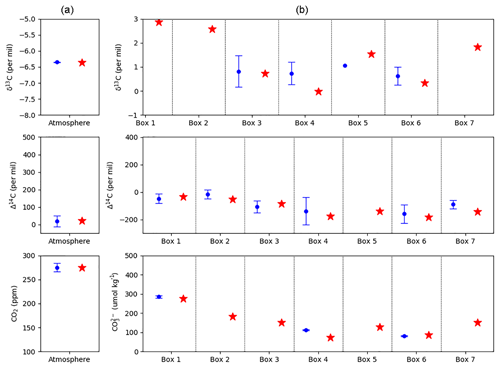
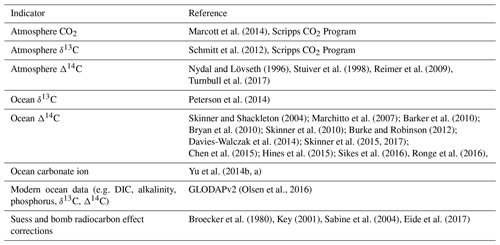
Figure 3 SCP-M late-Holocene-calibrated model results using model input parameters from the literature (Table A1). (a) Model results for atmospheric δ¹³C, Δ¹⁴C and CO₂ (red stars) plotted against late Holocene average data values (blue dots) with standard error bars. (b) The model results for oceanic δ¹³C, Δ¹⁴C and the carbonate ion proxy (red stars) plotted against late Holocene average ocean data where available (blue dots). Data sources are shown in Table 2.

Using the Suess- and bomb-adjusted GLODAPv2 ocean dataset and late Holocene atmosphere data as the starting point, combined with the literature-determined parameter values, the model is allowed to run freely for 15 kyr in spin-up. This spin-up is ample time for model equilibration and to allow slower processes such as carbonate compensation to take effect. The resulting model equilibrium ocean and atmosphere element concentrations from the spin-up are stored and then carried forward as the starting data for subsequent late Holocene simulations. Figure 3 shows the results of the model spin-up (red stars) compared with late Holocene atmosphere data and their standard error (blue dots and error bars) across the time period. We also show the model results compared with late Holocene ocean data from various sources (Table 2), which are averaged into the box model regions for comparison.

The late Holocene calibration convincingly satisfies the atmospheric data values for CO₂, δ¹³C and Δ¹⁴C. Model results are also in good agreement with the late Holocene ocean Δ¹⁴C, falling within error or very close for all boxes covered by data. The surface boxes (1, 2) are relatively enriched in Δ¹⁴C relative to deeper boxes, reflecting their proximity to the atmospheric source of ¹⁴C, although the spread of values across the ocean boxes is narrow. The surface boxes (1, 2 and 7) intuitively display more enriched δ¹³C than the intermediate (3), deep (4) and abyssal (6) boxes, mainly due to the effects of the biological pump. For most of the model's boxes, the results fall within the standard error of the late Holocene δ¹³C data. The Southern Ocean box (5) is an exception due to its extensive vertical coverage of 2500 m, incorporating the surface boundary with the atmosphere and the deep ocean, coupled with the sparse δ¹³C core data for the polar Southern Ocean (one data point, no error bars). SCP-M also exaggerates the depletion in δ¹³C in the deep box (4) relative to the data observation.

There is limited data coverage for the carbonate ion proxy (${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$), although the model replicates the available data well. ${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$ concentrations can be interpreted as alkalinity less DIC (Zeebe and Wolf-Gladrow, 2001; Yu et al., 2014b) for the purpose of analysing model results charts. ${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$ is relatively abundant in the surface boxes (e.g. boxes 1 and 2), reflecting the higher amount of alkalinity relative to carbon due to the soft tissue biological pump, which prioritises organic carbon export over alkalinity export. ${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$ is less abundant in the deep ocean (boxes 4 and 6) because there is more carbon relative to alkalinity due to the remineralisation of organic matter, a pattern that SCP-M replicates.

3.2 Sensitivity tests

We undertook parameter sensitivity tests to understand changes in atmospheric CO₂, Δ¹⁴C and δ¹³C in SCP-M. This serves two purposes: (1) to understand the directional relationship between the parameter values and these key model outputs, and evaluate whether they make sense, and (2) to inform the LGM–Holocene model–data experiment in the following section. For example, if the GOC parameter Ψ₁ displays a negative relationship with atmospheric CO₂, it would make sense to probe parameter values lower than modern to replicate the lower atmospheric CO₂ in the LGM. We varied parameter values around their modern-day settings in 10 kyr model runs and plotted the output against atmospheric CO₂, Δ¹⁴C and δ¹³C (Fig. 4).

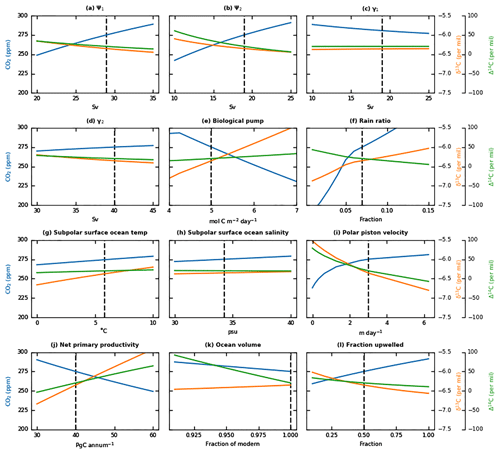
Figure 4 Univariate parameter sensitivity tests around modern-day estimated values plotted for atmospheric CO₂, Δ¹⁴C and δ¹³C versus (a) Ψ₁, (b) Ψ₂, (c) γ₁, (d) γ₂, (e) biological pump, (f) rain ratio, (g) subpolar surface box temperature, (h) subpolar surface box salinity, (i) polar box piston velocity, (j) net primary productivity, (k) ocean volume and (l) fraction of deep water upwelled into the subpolar surface box. We varied parameter input values as plotted on the x axes and show model output for atmospheric CO₂, Δ¹⁴C and δ¹³C. Atmospheric CO₂ shows the greatest sensitivity to parameters associated with ocean circulation, biology and the terrestrial biosphere. Other parameters exert less influence on atmospheric CO₂ but are important for atmospheric carbon isotope values. Modern-day estimates used in SCP-M are shown with vertical black dotted lines in each subplot (sources in the text and Appendix Table A1).

For example, Fig. 4a–d shows sensitivity variations above and below the model's modern values for ocean circulation and mixing parameters, sourced from Talley (2013) and Toggweiler (1999). Atmospheric CO₂ is very sensitive to Ψ₁ and Ψ₂ but displays limited response to γ₁ and γ₂ over the ranges analysed (Fig. 4a–d). Atmospheric Δ¹⁴C and δ¹³C are negatively related to Ψ₁ and Ψ₂. The slower ocean turnover leads to a reduced rate of upwelling and surface de-gassing of Δ¹⁴C- and δ¹³C-depleted waters, causing higher values in the atmosphere. The effect of the mixing parameters on the atmosphere variables is muted because they have a limited impact on the upwelling regime for carbon, with any upward flux of carbon offset by a downward flux (mixing).

The soft tissue export flux parameter, Z, displays an inverse relationship with CO₂ (Fig. 4e). A higher global value of Z drives the removal of carbon from the surface ocean, and the resulting CO₂ flux into the ocean from the atmosphere decreases CO₂. Lower Z leads to increased atmospheric CO₂. δ¹³C is particularly sensitive to Z, moving it well away from modern (and therefore Holocene and LGM) values from a minor perturbation. The rain ratio (Fig. 4f) increases pCO₂ in the surface ocean boxes, leading to de-gassing of CO₂ to the atmosphere, and therefore modestly decreasing atmospheric Δ¹⁴C, as the lighter ¹²C is preferentially partitioned across the air–sea interface.

Increasing surface ocean box temperature (Fig. 4g) increases atmospheric CO₂, an intuitive outcome given that warmer water absorbs less CO₂ (Weiss, 1974), and SCP-M employs a temperature- and salinity-dependent CO₂ solubility function. Air–sea fractionation of δ¹³C also decreases with higher temperatures, leading to higher atmospheric δ¹³C. According to Mook et al. (1974), air-to-sea fractionation of δ¹³C (making the atmosphere more depleted in δ¹³C) increases at a rate of approximately 0.1 ‰ ^∘C⁻¹ of cooling. SCP-M employs temperature-dependent air–sea gas δ¹³C fractionation factors (Mook et al., 1974). Δ¹⁴C is invariant to box temperature as the fractionation parameters employed in the model are not temperature dependent. CO₂ displays a weak positive relationship with surface ocean box salinity (Fig. 4h) due to the decreasing solubility of CO₂ in ocean water with increasing salinity (Weiss, 1974).

As the polar box piston velocity P slows down (Fig. 4i), atmospheric CO₂ falls. At lower values of P the polar box, a region of outgassing of CO₂ due to the upwelling of deep-sourced carbon-rich water in that part of the ocean, will exchange CO₂ with the atmosphere at a slower rate. The reduced outgassing of δ¹³C-depleted carbon to the atmosphere with a lower P leads to higher δ¹³C values in the atmosphere. Atmospheric Δ¹⁴C increases with a slowing of P as the pathways for it to invade the ocean from its atmospheric source are slower, and there is reduced outgassing of old, low Δ¹⁴C waters.

Terrestrial biosphere NPP (Fig. 4j) is a sink of CO₂ and fractionates the ratios of the isotopes of carbon, leading to higher values for δ¹³C and, to a lesser extent, Δ¹⁴C in the atmosphere. It is likely that NPP plays a feedback role and modulates CO₂, δ¹³C and Δ¹⁴C (Toggweiler, 2008). Varying the ocean surface area (Fig. 4k) has modest impacts on CO₂ and δ¹³C, but a large impact on Δ¹⁴C. Decreasing the ocean volume leads to a lower surface area for CO₂ and atmospherically produced radiocarbon to enter the ocean, causing them to increase in the atmosphere. We expect that changing the ocean surface area (from sea level), and therefore volume, leads to changes in pCO₂ on glacial–interglacial timescales. Increasing the fraction of deep water upwelled into the subpolar box (Fig. 4l) intuitively raises CO₂, but lowers δ¹³C and Δ¹⁴C, by upwelling carbon-rich and isotopically depleted water to the ocean surface boxes.

3.3 Modern carbon cycle simulation

Human fossil fuel and land use change emissions contributed ∼575 Gt carbon to the atmosphere between 1751 and 2010 (Boden et al., 2017; Houghton, 2010) and up until 2014 were growing at an accelerating rate. In response, the Earth's carbon cycle continually partitions carbon between its component reservoirs, with positive and negative feedbacks. The net effect is a build-up of carbon in most reservoirs. Given the dominance of the anthropogenic emissions source in the modern global carbon cycle, a simulation model should be able to provide a plausible replication of its effects.

Figure 5 SCP-M modelling results compared with modern atmospheric and ocean GLODAPv2 data for (a) atmospheric CO₂ and δ¹³C, (b)  atmospheric Δ¹⁴C, (c) ocean δ¹³C, (d) Δ¹⁴C, (e) DIC, and (f) the carbonate ion proxy. Projections beyond 2016 include the RCP6.0 emissions trajectory. In (a–b) we plot SCP-M model results for CO₂, δ¹³C and Δ¹⁴C (lines) for the period 1751–2100 against atmospheric data for CO₂, δ¹³C and Δ¹⁴C (red dots). The SCP-M model output closely resembles the atmospheric data record. The perturbation from industrial-era, isotopically depleted (δ¹³C) and dead (Δ¹⁴C) CO₂ is clear, as is the impact of atmospheric nuclear tests on Δ¹⁴C during 1954–1963. In the other rows we plot SCP-M model results (boxes as shown) versus GLODAPv2 data (dots and error bars, same colour as corresponding boxes). We assume an average data year of 1990 for the GLODAPv2 data accumulated over the period 1972–2013. For most of the SCP-M ocean boxes, the model results fall within or very close to error ranges of the GLODAPv2 data, despite large perturbations in the model and data from industrial-era emissions and bomb radiocarbon.

We modelled the effects of anthropogenic emissions and atmospheric nuclear bomb testing on the carbon reservoirs and fluxes in SCP-M. The experiment forces the late Holocene–pre-industrial SCP-M equilibrium described in Sect. 3.1, with estimates of industrial fossil fuel and land use change CO₂ emissions, sea surface temperature (SST) changes and atmospheric bomb ¹⁴C fluxes from historical data dating from 1751. For the future years to 2100, we force the model with the IPCC's Representative Concentration Pathway (RCP) CO₂ emissions and SST scenarios (Boden et al., 2017; Houghton, 2010; IPCC, 2013a). We compare the model results with atmospheric CO₂, δ¹³C and Δ¹⁴C historical data and published modelling results for future years from the CMIP5 project (https://cmip.llnl.gov/cmip5/, last access: 25 June 2018).

Figure 5 shows the modern carbon cycle simulation using SCP-M compared with historical atmospheric data for CO₂, δ¹³C and Δ¹⁴C and GLODAPv2 ocean data (estimated data year 1990). Importantly, SCP-M provides an appropriate simulation of the carbon cycle response to human emissions inputs by replicating the atmospheric patterns for CO₂, δ¹³C and Δ¹⁴C preserved in data observations for the period 1751–2016 (a–b). The atmospheric CO₂ and δ¹³C data are sourced from the Scripps CO₂ Program (originally sourced from http://scrippsco2.ucsd.edu, last access: 10 June 2018; data currently being transitioned to http://cdiac.ess-dive.lbl.gov, last access: 10 June 2018), and Δ¹⁴C data are sourced from Nydal and Lövseth (1996), Stuiver et al. (1998), and Turnbull et al. (2017). A key feature of the historical data is the substantial increase in human emissions from circa 1950 onwards, which is accompanied by higher atmospheric CO₂ and a steep drop in δ¹³C (Fig. 5a); this reflects δ¹³C-depleted anthropogenic emissions. The effect of emissions on atmospheric Δ¹⁴C (Fig. 5b) in the 20th century is largely overprinted by the influence of bomb radiocarbon. Emissions are seen as a slight downturn in the model and data Δ¹⁴C in the immediate lead-up to the release of bomb radiocarbon into the atmosphere and the downward trend from ∼2020 onwards. The spike in Δ¹⁴C during the period of bomb radiocarbon release lasts during the period 1954–1963 and then disperses as ¹⁴C is absorbed by the ocean. The simulation shows that SCP-M agrees with the GLODAPv2 ocean data by 1990 (Fig. 5c–f), with most boxes falling within the standard deviation of average data values, lending confidence to the model's simulation of the redistribution of carbon.

Figure 6 shows the emissions profile (a) and modelling results for atmospheric CO₂ (b) over historical time and projected forward to 2100 for the IPCC RCPs. The SCP-M output falls below the IPCC projections for atmospheric CO₂ in RCP2.6 and 4.5, but provides a close match with RCP6.0 and 8.5.

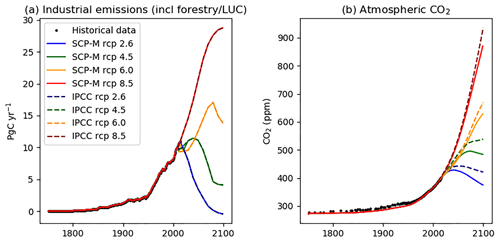
Figure 6 SCP-M RCP modelling results compared with IPCC emissions and CO₂ scenarios. Panel (a) shows the IPCC's RCP emissions pathways out to 2100, which are inputted to SCP-M for the modern carbon cycle simulation. Panel (b) shows SCP-M model output for atmospheric CO₂ (firm lines) plotted against IPCC atmospheric CO₂ projections for the RCP pathways (dashed lines). The SCP-M output undershoots the IPCC projections for RCP2.6 and 4.5, but provides a close match with RCP6.0 and 8.5.

Figure 7a shows the annual uptake of CO₂ by the ocean, modelled with SCP-M. The model begins the period close to a steady state between the atmosphere and surface ocean pCO₂, with limited transfer across the interface. Beginning circa 1950 the ocean takes up an increased load of CO₂ from the atmosphere. By 2100, SCP-M models a range of annual CO₂ uptake by the ocean of 0–6 PgC annum⁻¹ across the RCPs. This is similar to the range of values estimated by the CMIP5 models (also shown in Fig. 7a), reproduced from Jones et al. (2013). The cumulative uptake of emissions by the ocean over the period 1751–2100 (Fig. 7b) modelled by SCP-M of ∼350–750 PgC is at the upper end of the modelled range of CMIP5 models of ∼200–600 PgC over the period 1850–2100 (Jones et al., 2013). The SCP-M simulations commence in 1751 and therefore incorporate an extra 100 years of fossil fuel and land use change emissions beyond the CMIP5 model results presented in Jones et al. (2013). Wang et al. (2016) quote a range of 412–649 PgC of cumulative uptake by the ocean by 2100 from 11 CMIP5 models, a closer range to the SCP-M outcomes.

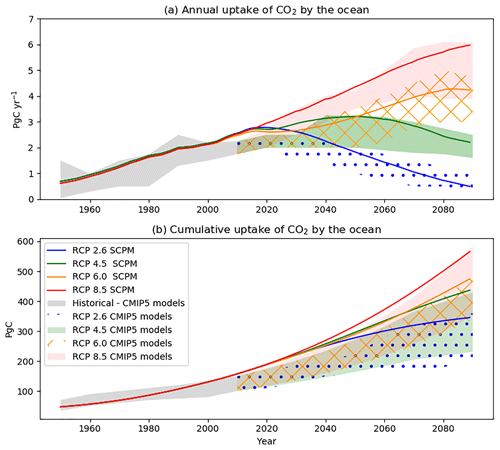
Figure 7 Panel (a) shows the annual uptake of CO₂ by the ocean in each of the RCPs over the period 1751–2100, modelled with SCP-M. By 2100, SCP-M estimates a range of 0–6 PgC yr⁻¹ across the RCPs as estimated by CMIP5 models, reproduced from Jones et al. (2013). Panel (b) shows the cumulative uptake of CO₂ by the ocean over the same period modelled with SCP-M and compared with CMIP5 models (Jones et al., 2013).

Figure 8 shows the partitioning of anthropogenic CO₂ emissions into the carbon cycle reservoirs in RCP6.0 by 2100, as simulated with SCP-M and compared with modelling results presented by the IPCC for the same scenario (IPCC, 2013b). By this time, the load of human emissions is roughly 45:55 split between the atmosphere and the combined terrestrial biosphere and ocean.

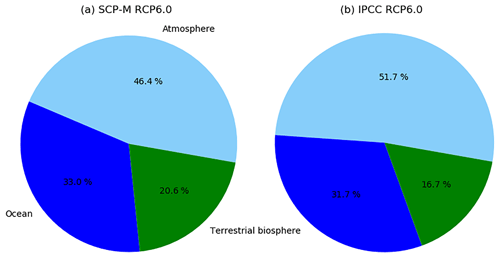
Figure 8 Relative uptake of CO₂ across the major carbon reservoirs by 2100 in RCP6.0 as modelled by SCP-M (left panel). By 2100, SCP-M projects that 46 % of industrial-era emissions will remain in the atmosphere, 33 % reside in the ocean and 21 % in the terrestrial biosphere. Shown in panel (b) are results from Earth system models reproduced from the IPCC Working Group 1 5th Assessment Report, Chapter 6 (IPCC, 2013b).

By 2100, in RCP6.0 the carbon cycle is substantially changed from the pre-industrial–late Holocene state. This is the result of the accumulation of hundreds of years of human industrial CO₂ emissions in the atmosphere and other reservoirs (Fig. 9). Anthropogenic CO₂ emissions transfer carbon to the atmosphere, ocean and terrestrial biosphere. The fluxes between the carbon reservoirs also change. In the pre-industrial state, CO₂ enters the ocean in the low latitudes and northern ocean (shown as negative fluxes in Fig. 9) and de-gasses in the Southern Ocean (positive flux) under the influence of ocean upwelling in that region. In RCP6.0, the atmospheric CO₂ concentration increases to the extent that the atmosphere–ocean pCO₂ gradient drives all surface ocean boxes to take carbon from the atmosphere (shown as large negative changes in the air–sea fluxes of carbon; red text in Fig. 9), despite warmer surface ocean temperatures towards the end of the projection (time series inputs). The terrestrial biosphere influx of carbon is dramatically increased by the carbon fertilisation effect, leading to a larger biomass stock, which in turn also causes more respiration – both inward and outward biosphere fluxes of CO₂ are therefore greatly enhanced. The weathering of silicate rocks on the continents, a weak sink of carbon, also accelerates under the effects of burgeoning atmospheric CO₂, transferring carbon from the atmosphere to the ocean via rivers. The physical fluxes of carbon within the ocean are only modestly affected, with the main exception being low-latitude thermocline mixing, which in RCP6.0 mixes a larger amount of carbon back into the surface ocean box from intermediate depths. The altered balance of DIC : alkalinity, particularly in the abyssal box, leads to a decrease in the carbonate ion concentration of abyssal waters late in the projection period, which in turn causes more dissolution of marine sediments. By 2100 this feedback brings more carbon back into the ocean, increased from 0.2 to 1.1 PgC yr⁻¹, but also alkalinity (in a ratio of 2:1 to DIC), thereby lowering whole-ocean pCO₂ – a modest negative feedback. In summary, SCP-M provides an appropriate simulation of historical atmospheric CO₂, δ¹³C and Δ¹⁴C data when forced with anthropogenic CO₂ emissions data over the same period. For the forward-looking RCP emissions projections, SCP-M falls in the range of the CMIP5 models, although the oceanic carbon uptake is exaggerated for the RCP8.5 scenario. This result suggests that a more detailed experiment, for example with non-linear representation of the piston velocity with respect to atmospheric CO₂ or prescribed feedbacks from ocean circulation and biology (e.g. Meehl et al., 2007; IPCC, 2013a, b; Moore et al., 2018), might provide a closer fit to the CMIP5 models.

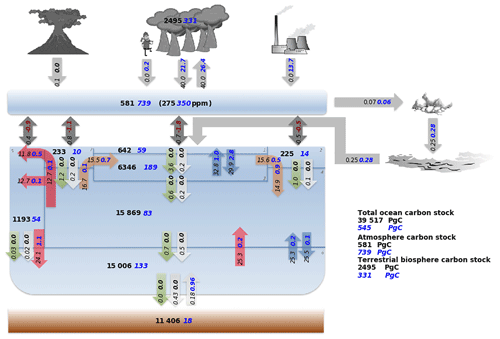
Figure 9 SCP-M-modelled pre-industrial carbon stocks and fluxes (in PgC in black text) compared with IPCC RCP6.0 emissions scenario by 2100 (shown as PgC changes with blue text for positive changes, red text for negative and black text for no change). Atmosphere, ocean and terrestrial biospheres take up the load of carbon from the industrial source. By 2100, carbon is fluxing into all ocean boxes, the terrestrial biosphere and continental sediment weathering–river fluxes. Pre-industrial outgassing of CO₂ in the Southern Ocean is reversed, and carbon is returned to the ocean via enhanced CaCO₃ dissolution. Box numbers on the diagram refer to ocean regions specified in Fig. 1. Negative fluxes on bidirectional air–sea exchange arrows are fluxes of CO₂ out of the atmosphere into the ocean.

4 LGM–Holocene model–data experiment

4.1 Background

The LGM–Holocene transition, and glacial–interglacial variations in the carbon cycle in general, remain outstanding problems in paleoceanography (e.g. Sigman and Boyle, 2000; Kohfeld and Ridgewell, 2009; Hain et al., 2010; Ferrari et al., 2014; Kohfeld and Chase, 2017). At issue is the precise cause of 80–100 ppm variations in atmospheric CO₂ across glacial and interglacial periods. These CO₂ oscillations are accompanied by striking changes in ocean and atmospheric carbon isotopes, oceanic carbonate ion distributions, and other paleo chemical indicators. Of particular interest is the transition from the LGM, ∼18–24 ka (Yokoyama et al., 2000; Clark et al., 2009; Hesse et al., 2011; Hughes et al., 2013; Hughes and Gibbard, 2015), to the Holocene (11.7 ka to present) due to the growing abundance of proxy data covering that period. The causes of abrupt atmospheric CO₂ rise at the termination of the LGM, and continuing up to the Holocene period, remain definitively unresolved. The ocean is likely the main driver of atmospheric CO₂ on the relevant timescale due to its relative size as a carbon reservoir (e.g. Broecker, 1982; Sarmiento and Toggweiler, 1984; Kohfeld and Ridgewell, 2009; Sigman et al., 2010), alongside changes in the terrestrial biosphere stock of carbon (Francois et al., 1999; Ciais et al., 2012; Peterson et al., 2014; Hoogakker et al., 2016). Active theories within the ocean realm include changes in ocean biology (Martin, 1990; Watson et al., 2000; Martinez-Garcia et al., 2014), ocean circulation and mixing (Sarmiento and Toggweiler, 1984; Toggweiler and Sarmiento, 1985; Toggweiler, 1999; Curry and Oppo, 2005; Anderson et al., 2009; Kohfeld and Ridgewell, 2009; De Boer and Hogg, 2014; Menviel et al., 2016; Muglia et al., 2018), sea-ice cover (Stephens and Keeling, 2000), whole-ocean chemistry (Broecker, 1982; Sigman et al., 2010), and composite hypotheses (Kohfeld and Ridgewell, 2009; Ferrari et al., 2014; Kohfeld and Chase, 2017). Other mechanisms proposed include ocean temperature, the terrestrial biosphere, ocean volume and shelf carbonates (Opdyke and Walker, 1992; Trent-Staid and Prell, 2002; Ridgewell et al., 2003; Ciais et al., 2012; Annan and Hargreaves, 2013). Each hypothesis listed above is supported by site-specific tracer observations (e.g. marine carbonate cores), regional data aggregation and review, literature synthesis, or modelling. Within the spectrum of hypotheses, a simple explanation of a carbon cycle mechanism or mechanisms remains elusive. Many of the early hypotheses were presented as independent or even competing in causality for the interglacial CO₂ variation (Ferrari et al., 2014).

Substantial progress has been made over the last 15 years in constraining the list of likely candidates to ocean physical and biological processes, likely in concert. The growth of paleo datasets (e.g. Oliver et al., 2010; Peterson et al., 2014; Yu et al., 2014b; Skinner et al., 2017; Zhao et al., 2017) and improvements in computing power have enabled model and model–data studies which seek to constrain the magnitude of changes in the carbon cycle across glacial–interglacial cycles (e.g. Stephens and Keeling, 2000; Toggweiler et al., 2006; Tagliabue et al., 2009; Hain et al., 2010; Bouttes et al., 2011; Hesse et al., 2011; Tschumi et al., 2011; Menviel et al., 2016; Kurahashi-Nakamura et al., 2017; Muglia et al., 2018). For example, Menviel et al. (2016) modelled slowing GOC and AMOC, with a modest increase in biological productivity in the Southern Ocean in the LGM, using δ¹³C data and an intermediate-complexity Earth system model. This differed from the finding of Muglia et al. (2018), who specifically examined the AMOC and Southern Ocean biological productivity. They found that a weaker AMOC and stronger biological productivity could account for the LGM and Holocene δ¹³C, Δ¹⁴C and ¹⁵N data. The GOC was not tested by Muglia et al. (2018). Kurahashi-Nakamura et al. (2017) contradicted both studies, diagnosing a more vigorous (but shallower) AMOC in the LGM, using a GCM with data assimilation of various proxies, notably only incorporating Atlantic data for the LGM.

(Trent-Staid and Prell, 2002; Annan and Hargreaves, 2013)(Adkins et al., 2002)(Stephens and Keeling, 2000; Ferrari et al., 2014)(Adkins et al., 2002; Grant et al., 2014)(Mariotti et al., 2013)

Table 3 Changes to ocean and atmosphere parameter settings in SCP-M to recreate the LGM background model state.

As shown in the sensitivity tests in Fig. 4, some processes do not exert a strong influence on atmospheric CO₂, but do modestly impact CO₂ and strongly impact δ¹³C and Δ¹⁴C. Where these features are posited to vary around glacial cycles, we have incorporated them as a step change from late Holocene–modern estimates in our LGM experiment.

4.2 Model–data experiments

We illustrate SCP-M's capabilities by solving for the parameter values of best fit with late Holocene and LGM ocean and atmosphere proxy data using a comprehensive model results–data optimisation. For this illustrative example, the atmosphere and ocean data are taken from published sources (Table 2), averaged for the LGM (∼18–24 ka) and late Holocene (6.0–0.2 ka) time periods and for box coordinates in SCP-M for the ocean data (depth and latitude). The mean and variance for each box are then calculated in SCP-M. First, we probe the potential for key model parameters to drive Holocene–LGM changes in atmospheric carbon variables to focus our experiment on these parameters. It is likely that the LGM-to-Holocene carbon cycle changes were dominated by the ocean (Sigman and Boyle, 2000; Kohfeld and Ridgewell, 2009), but were also accompanied by a range of physical changes in the atmosphere and terrestrial biosphere that in aggregate could be material (e.g. Sigman and Boyle, 2000; Adkins et al., 2002; Kohfeld and Ridgewell, 2009; Ferrari et al., 2014). These changes include sea surface temperature, salinity, sea-ice cover, ocean volume and atmospheric ¹⁴C production rate. Estimates of average sea surface temperature for the LGM generally fall in the range of 3–8 ^∘C cooler than the present (Trent-Staid and Prell, 2002; Annan and Hargreaves, 2013). Adkins et al. (2002) estimated that ocean salinity was 1–2 psu higher in the LGM and sea levels were ∼120 m lower (Adkins et al., 2002; Grant et al., 2014). Stephens and Keeling (2000) and Ferrari et al. (2014) highlighted the role of expanded sea-ice cover in the Southern Ocean during the LGM as a key part of the LGM CO₂ drawdown. Finally, Mariotti et al. (2013) estimated that higher atmospheric radiocarbon production accounted for $+\sim \mathrm{200}$‰ in atmospheric Δ¹⁴C in the LGM. Mariotti et al. (2013) simulated this variation in model experiments by increasing the radiocarbon production rate by a multiple of 1.15–1.30 (best guess 1.25) of the modern estimate in order to recreate LGM Δ¹⁴C values. Using these findings we define two background states for modelling purposes: a late Holocene state (Table A1 in the Appendix) and the LGM state (Table 3). Figure 10 shows the cumulative effect of these changes in SCP-M, within the late Holocene–LGM atmosphere 3-D CO₂–δ¹³C–Δ¹⁴C data space.

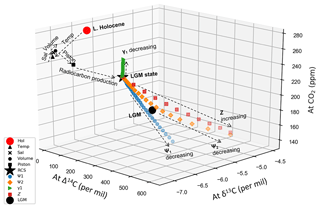
Figure 10 LGM state parameter adjustments. Using the posited LGM changes in environmental parameters in Table 3, we establish LGM foundations for exploring the impacts of varying large-scale ocean process parameters towards LGM atmospheric CO₂–δ¹³C–Δ¹⁴C data space. The red circle is our starting point for the late Holocene. From the LGM state foundation (black star), variation of global overturning circulation (Ψ₁), Atlantic meridional overturning circulation (Ψ₂) and the soft tissue biological pump (Z) drives atmospheric CO₂, δ¹³C and Δ¹⁴C into the vicinity of their LGM data values (black circle). The biological pump Z can effect the LGM CO₂ outcome, but steers δ¹³C away from the LGM value. Both Ψ₁ (3–29 Sv) and Ψ₂ (3–19 Sv) experiments run very close to the LGM data values on their own, although neither can deliver a precise hit.

These changes are the first stage of a model adjustment to analyse the potential for ocean circulation and biological changes to deliver the LGM atmospheric CO₂, δ¹³C and Δ¹⁴C values and transition the model output from the red circle (late Holocene) to the black star (the LGM background settings), and then to the black circle (LGM). The decrease in ocean surface box temperatures leads to a drop in CO₂ of ∼20 ppm and a lightening of δ¹³C by ∼0.6 ‰ owing to the increased solubility of CO₂ in colder water and the increasing fractionation of δ¹³C with decreasing temperatures, which leaves more ¹²C in the atmosphere. There is limited impact on Δ¹⁴C. Increasing salinity slightly reverses these changes to CO₂ and δ¹³C. Reducing sea surface area and volume slightly increases CO₂ and increases Δ¹⁴C as the ocean's capacity to take up these elements is reduced. Slowing down the piston velocity in the polar Southern Ocean box, as a proxy for increased sea-ice cover, slightly reduces CO₂ (reduced outgassing), increases Δ¹⁴C (slower rate of invasion to the ocean) and increases δ¹³C (reduced outgassing and sea-to-air fractionation of δ¹³C). Finally, increasing the rate of atmospheric radiocarbon production forces a shift in Δ¹⁴C (horizontal shift in Fig. 10) towards LGM levels (black star and circle in Fig. 10). In aggregate, these changes lead to a fall in CO₂ of ∼35 ppm, a fall in δ¹³C of $\sim -\mathrm{0.5}$ ‰ and an increase in Δ¹⁴C of ∼300 ‰.

From the black star in Fig. 10, the “LGM state”, we perform a focussed sensitivity test on key hypothesised drivers of LGM–Holocene carbon cycle changes (Kohfeld and Ridgewell, 2009; Sigman et al., 2010). These are slower GOC (Ψ₁), slower AMOC (Ψ₂), reduced deep–abyssal ocean mixing (γ₁) and a stronger biological pump (Z). The Z global biological production parameter, varied across 5–10 mol C m⁻² yr⁻¹ (i.e. increased), can deliver the LGM CO₂ changes, but steers δ¹³C and Δ¹⁴C away from their LGM values. γ₁ drives ancillary changes in all three variables, suggesting it is not the driver of the LGM atmospheric changes but may play a modulating role. Both Ψ₁ (3–29 Sv) and Ψ₂ (3–19 Sv) experiments run very close to the LGM data values on their own, although neither can deliver a precise hit.

Using the literature-referenced Holocene and LGM background parameter states, and informed by the sensitivity analysis in Fig. 10, we take advantage of SCP-M's fast run time to perform thousands of multi-variant simulations over the free-floating Ψ₁, Ψ₂, γ₁ and Z parameter spaces using the SCP-M batch module. We then perform an optimisation routine against the data for each period to solve for values for Ψ₁, Ψ₂, γ₁ and Z. The SCP-M batch module cycles through each set of parameter combinations, with each model simulation run for 10 000 years. Table 4 shows the experiment parameter ranges for the late Holocene and LGM model–data experiments.

Table 4 Parameter value ranges for the late Holocene and LGM model–data experiments.

The parameter input ranges for the experiments were informed by the sensitivity tests shown in Figs. 4 and 10. For example, the responses of atmospheric CO₂, δ¹³C and Δ¹⁴C to variations in Ψ₁, Ψ₂ and Z lead us to cater for lower values for Ψ₁ and Ψ₂ (weaker ocean circulation) and higher values for Z (increased biological productivity) in the LGM experiment. Where the experiments resulted in a parameter output value at the limit of the input range, the range was widened and the experiment was repeated; 16 896 and 47 616 simulations were undertaken for the late Holocene and LGM experiments, respectively.

Table 5 Late Holocene and LGM model–data parameter optimisation and associated atmospheric variable model output.

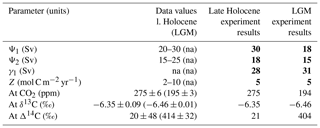
Bold font parameter results indicate those parameters that are free-floating and determined by the model and data in the experiment. The LGM experiment shows a marked decline in the strength of global overturning circulation Ψ₁ (−12 Sv) and a modest decline in Atlantic meridional overturning circulation Ψ₂ to deliver the LGM atmosphere and ocean data signal. A minor increase in deep–abyssal mixing γ₁ is also seen.

The SCP-M script harvests model output and performs a least-squares optimisation of the output against the LGM and late Holocene data for atmospheric CO₂, atmospheric, and ocean Δ¹⁴C and δ¹³C, and also the oceanic carbonate ion proxy, to source the best-fit parameter values for Ψ₁, Ψ₂, γ₁ and Z (or any parameter specified):

$$\begin{array}{}\text{(27)}& {\mathrm{Opt}}_{n=\mathrm{1}}=\mathrm{Min}\sum _{i,k=\mathrm{1}}^N{\left({\displaystyle \frac{R_{i,k}-D_{i,k}}{{\mathit{\sigma }}_{i,k}}}\right)}^{\mathrm{2}},\end{array}$$

where Opt_n=1 represents the optimal value of parameters n, R_i,k is the model output for concentration of each element i in box k, D_i,k is the average data concentration of each element i in box k and σ_i,k is the standard deviation of the data for each element i in box k. The standard deviation performs two roles. It reduces the weighting of data with high uncertainty and also normalises for the different unit scales (e.g. ppm, ‰ and µmol kg⁻¹), which allows multiple proxies in different units to be incorporated in the optimisation. Where data are unavailable for a box, that element and box combination is automatically omitted from the optimisation routine.

The late Holocene data-optimised results for Ψ₁ (30 Sv) and Ψ₂ (18 Sv) show good agreement with the Talley (2013) observations for Ψ₁ (29 Sv) and Ψ₂ (19 Sv) from the modern ocean (Table 5). The starting global value of Z, of 5 mol C m⁻² yr⁻¹, is returned in the experiment. The experiment also successfully returns values for atmospheric CO₂, δ¹³C and Δ¹⁴C within standard error for the late Holocene data series (Table 5).

The ocean and atmosphere SCP-M results for the LGM (bold stars) and late Holocene (transparent stars) experiments using the optimised parameter settings in Table 5 are plotted in Fig. 11 along with the corresponding data (blue dots with error bars). The experiment provides results within the error bounds of data for most of the box regions in both scenarios and an excellent fit to the change in the relative distribution of the proxies between ocean boxes and the atmosphere, which is preserved in the LGM and late Holocene data. A key feature of the ocean δ¹³C data is a depletion of deep ocean δ¹³C in the LGM, shown as a drop in δ¹³C values in the deep (box 4) and abyssal (box 6) boxes relative to the intermediate box (3). In the LGM δ¹³C data, there is a spread of 1 ‰ across these water masses, which narrows to 0.3 ‰ in the late Holocene data. The pattern is replicated in the LGM experiment, pointing to the important role of changes in abyssal–deep ocean water flows via Ψ₁ in delivering the ocean δ¹³C data patterns. The model shift in δ¹³C in the deep box (box 4) of 0.6 ‰ from the LGM to late Holocene is in good agreement with a global deepwater estimate of 0.49±0.23 ‰ by Gebbie et al. (2015) and an earlier estimate of 0.46 ‰ by Curry et al. (1988). The average atmospheric δ¹³C value remains largely unchanged between the two periods due to the effect of the terrestrial biosphere, which causes net uptake of CO₂ in the Holocene period (increases atmospheric δ¹³C) and net respiration of CO₂ in the LGM period (decreases atmospheric δ¹³C).

The model results also closely replicate the reduction in deep-to-shallow ocean compositional gradient in Δ¹⁴C data moving from the LGM to Holocene period (e.g. Skinner and Shackleton, 2004; Skinner et al., 2015, 2010; Burke and Robinson, 2012; Chen et al., 2015; Hines et al., 2015; Ronge et al., 2016). The LGM data show a spread of ∼300 ‰ between abyssal (box 6) and intermediate (box 3) waters, as well as deep (box 4) versus surface (boxes 1, 2 and 7) boxes. In the late Holocene data, the spread is narrowed to ∼100 ‰. This data observation was popularly characterised as the result of increased Southern Ocean upwelling of Δ¹⁴C-depleted deep water into intermediate and shallow depths in the Holocene (e.g. Skinner et al., 2010, 2015; Burke and Robinson, 2012). A slowdown in Southern Ocean upwelling in the LGM allows Δ¹⁴C-depleted water to accumulate in the deep or abyssal ocean and a widening in the Δ¹⁴C gradient between deep and shallow waters. In SCP-M, this is simulated by lower values for Ψ₁ and Ψ₂. The low-latitude surface box (box 1) enrichment in Δ¹⁴C in planktonic foraminifera in the LGM is replicated by the increased atmospheric production rate of radiocarbon applied to the LGM experiment, combined with slower ocean circulation.

SCP-M results are shown for comparison with sparse carbonate proxy data (Fig. 11 bottom panel). The model results for the carbonate ion proxy mirror the limited variation in the data between the LGM and late Holocene. The changes are most pronounced in the surface boxes (boxes 1 and 2), which are under the influence of atmospheric CO₂, and attenuate somewhat in the deeper boxes (boxes 4 and 6). Yu et al. (2014b) interpreted the relatively small changes in the carbonate ion in the deepest ocean (box 6) as the result of efficient buffering of deepwater pH by carbonate dissolution, most notably in the Pacific Ocean. The model result for the deep box (box 4) goes against the LGM–Holocene variation in the data, but given that there is only one data point for this part of the ocean and the variation itself is small, it is an uncertain outcome.

The LGM scenario shows important changes in the carbon redistributive behaviour of the ocean (Fig. 12). The stock of carbon increases in abyssal and deep boxes (blue text denotes the increase in PgC from late Holocene to LGM) and is reduced in the intermediate, low-latitude surface and northern surface boxes (red text denotes the decrease in PgC from late Holocene to LGM). The amount of carbon upwelled to the subpolar surface and deep boxes by GOC (Ψ₁) drops by ∼5–10 PgC yr⁻¹, with the most pronounced changes taking place at the abyssal–deep box boundary. The slower upwelling rate of carbon causes a reduced outgassing rate of CO₂ from the subpolar box to the atmosphere. The weaker flux of Ψ₂ also brings a reduced DIC load into the intermediate-depth ocean, the driver for lower DIC content in the intermediate and surface boxes. The optimised parameter run for the late Holocene results in a terrestrial biosphere carbon pool of 2495 PgC, which is fortuitously close to the pre-industrial estimate of Raupach et al. (2011) (2496 PgC), at the top end of acceptable values in Francois et al. (1999) and close to the “active” land carbon pool of 2370±125 estimated by Ciais et al. (2012). In the optimised LGM results, the terrestrial biosphere is reduced by 667 Pg C from the late Holocene value, which is towards the upper bound of recent estimates of this change (0–700 PgC e.g. Ciais et al., 2012; Peterson et al., 2014), but within uncertainty bounds. For example, Peterson et al. (2014) estimated a variation of 511±289 Pg C in the terrestrial biosphere carbon stock based on whole-ocean δ¹³C data, the same data used in this exercise. According to Francois et al. (1999), palynological and sedimentological data imply that the terrestrial biosphere carbon stock was 700–1350 PgC smaller in the LGM than the present. Ciais et al. (2012) pointed to the growth of a large inert carbon pool in steppes and tundra during the LGM, which may have modulated some of the active biosphere carbon signal (i.e. reduced terrestrial biosphere), a factor not explicitly covered in our modelling exercise. The terrestrial biosphere is clearly a key part of the LGM–late Holocene carbon cycle transition. The atmosphere-enriching fractionation of δ¹³C by the terrestrial biosphere during the deglacial period effectively reverses the effects of the release of δ¹³C-depleted carbon from the deep ocean to the atmosphere at the termination and leaves atmosphere δ¹³C almost unchanged from LGM values as a result (Schmitt et al., 2012). The DIC : alkalinity balances in the abyssal ocean during the LGM also drive subtle changes in the balance of carbonate outflux by sinking and influx from sediment dissolution, which build up to substantial differences in the sediment carbon stock between the LGM and Holocene simulations, mainly due to the time frames modelled in the SCP-M spin-up for each scenario (15 kyr).

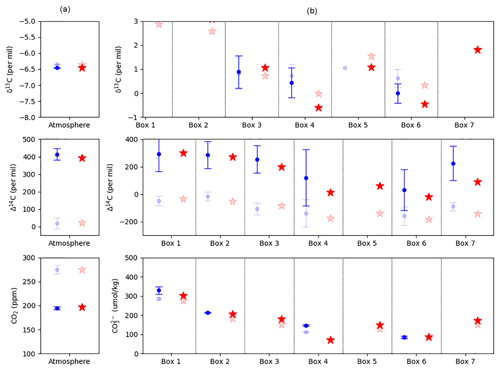
Figure 11 LGM atmosphere- and ocean-data-optimised model results. (a) The atmospheric carbon cycle results from SCP-M (red stars) plotted against LGM average data values (blue dots) with standard error bars. (b) The SCP-M ocean results plotted against LGM average ocean data where available. Corresponding Holocene data and results shown with transparent markers. The data-optimised model results show a close match for the LGM atmospheric data and most of the ocean data. The ocean δ¹³C and Δ¹⁴C data show an increased compositional gradient between shallow–intermediate depths (boxes 1–3) and deep–abyssal depths (boxes 4 and 6), an outcome replicated in the corresponding model results mainly by a slower GOC. Data sources are shown in Table 2.

5 Discussion

5.1 Model advantages and limitations

In this paper we introduce SCP-M, a box model of the global carbon cycle. We demonstrate its application to the modern and future carbon cycle with anthropogenic emissions and reconstructing potential changes across the LGM–late Holocene carbon cycle transition. In summary, SCP-M is a simple, easy-to-use model of the carbon cycle, and its fast run time enables comprehensive scenario analysis or optimisations for scenario or hypothesis testing. It takes approximately 30 s to complete a 10 000-year simulation, making the model useful for long-term paleo reconstructions of the carbon cycle. Our LGM–late Holocene experiment (Sect. 4) includes broad variations in GOC, AMOC, deep–abyssal mixing and global biological productivity. The experiments cover up to ∼47 000 parameter combinations across the LGM and late Holocene proxy data, reducing the possibility of confirmation bias or predetermined outcomes. Furthermore, the model's simplified topology (Fig. 1), although consistent with an observationally based understanding of the ocean (e.g. Talley, 2013), makes it accessible to a wide user group and potentially useful as a teaching aid to illustrate high-level concepts in the carbon cycle. The model contains data modules that directly integrate data via box mapping and averaging processes for use in calibration and for model–data experiments (Fig. 2). It also includes a model–data optimisation routine to elicit parameter values that best fit the data, as described in Sect. 4.2.

Figure 12 Late Holocene (figures in black text) and LGM (shown as PgC changes from the late Holocene) carbon stocks and fluxes modelled with SCP-M. For the LGM blue text shows positive changes (in PgC), red text shows negative and black shows no change. LGM parameter values selected from the four-parameter LGM experiment in Table 5. The LGM setting leads to a transfer of carbon from the atmosphere and terrestrial biosphere to the deep ocean. Carbon upwelled into the surface ocean falls, leading to reduced outgassing of CO₂ in the Southern Ocean boxes. Continental weathering and river fluxes of carbon are also reduced due to lower atmospheric CO₂, leading to a change in CaCO₃ burial and dissolution in marine sediments until equilibrium is restored with river input to the oceans. Box numbers on the diagram refer to ocean regions specified in Fig. 1.

A limitation of SCP-M v1.0 is that it does not distinguish between the Atlantic and Indo-Pacific Ocean basins, which is a large simplification. We argue that this is feasible for testing high-level hypotheses, for example involving large-scale ocean processes across the LGM–Holocene time periods, and the model is demonstrated to produce appropriate results in such an application. However, this framework may not be useful for testing localised or detailed problems. Given that SCP-M is a box model, there are other simplifications, including a rigid and perhaps somewhat arbitrary treatment of box boundaries (Fig. 1). For some experiments the box boundaries themselves may need to be a dynamic, model-determined output. In our LGM–Holocene example, we did not vary the abyssal box thickness across the time periods. However, this could be done very easily for the case of an experiment featuring shoaling or deepening water mass boundaries (e.g. Curry and Oppo, 2005). A key drawback of the model is that it can identify the cause of changes in proxy element concentrations in terms of parameterised processes, but cannot diagnose the root cause of these process changes. For example, with SCP-M we cannot directly answer the question of what causes GOC, AMOC or biological productivity to vary on glacial–interglacial cycles, but combined with data we can propose which of these varies (Sect. 4.2).

5.2 Modern carbon cycle simulations

Our simple forcing of SCP-M with historical and projected anthropogenic CO₂ emissions and SST (Sect. 3.3, Figs. 6–8) shows that SCP-M can reproduce historical data and the model results of more complex CMIP5 models. The SCP-M results for atmospheric CO₂ (Fig. 6), air–sea fluxes of carbon (Fig. 7) and accumulation of carbon in the various carbon reservoirs (Fig. 8) line up in the range of CMIP5 model projections. Importantly, SCP-M is shown to replicate the historical data over the period 1751–2016 for atmospheric CO₂, δ¹³C and Δ¹⁴C (Figs. 5 and 6). The historical period is a stringent test of carbon cycle models because it incorporates the influences of anthropogenic emissions, atmospheric bomb testing and an abundance of data observations of the Earth's carbon cycle response for comparison. The radioactive decay and dispersal of bomb-produced ¹⁴C provides an excellent “time clock” for the fluxes in the carbon cycle, particularly air–sea gas exchange and ocean circulation. Our experiment incorporates forcing of atmospheric ¹⁴C during 1954–1963, and SCP-M appropriately replicates the take-up of bomb ¹⁴C by the ocean from the atmosphere in the following years (Fig. 5).

However, the SCP-M modern and future simulations are simple and fail to take account of more complex potential feedbacks in the carbon cycle. These may include a wind-shift-induced slowing of AMOC and thermocline mixing or a response of ocean biological productivity to changed pCO₂, temperature and DIC in the surface ocean (e.g. Meehl et al., 2007; IPCC, 2013a, b; Moore et al., 2018). To simulate such feedbacks, the relevant parameters would need to be forced in SCP-M. A dynamical response would be expected in more complex Earth system models. The value of SCP-M is in rapidly undertaking “what-if” types of analysis to probe the effects of such changes under a variety of scenarios. For example, the high-level testing of negative emissions processes, such as alkalinity or iron seeding of the ocean, rock waste fertilisation, afforestation and/or reforestation on land, or marine fauna management, as tools for reducing atmospheric CO₂ on a global scale are feasible uses of SCP-M.

5.3 LGM–late Holocene modelling

Our model–data optimisation using SCP-M and published data (Sect. 4.2) showed that variations in the strength of large-scale ocean physical processes, particularly GOC and AMOC, can account for the LGM-to-Holocene carbon cycle changes inferred in the proxy data (Table 5). Critically, the variations are accompanied by changes in SST, sea-ice cover and the terrestrial biosphere (Table 3). The result is observed on account of ocean and atmosphere data across the proxies of CO₂, δ¹³C, Δ¹⁴C and the carbonate ion (Fig. 11). This finding is not a new one, but corroborates the model–data conclusion of Menviel et al. (2016), box modelling of Toggweiler (1999), and ¹⁴C proxy data findings of Sikes et al. (2000) and Skinner et al. (2017). The importance of GOC is at odds with Muglia et al. (2018), who found a substantially weakened AMOC and enhanced biological productivity in the Southern Ocean in the LGM, with no role examined for GOC in that study. Kurahashi-Nakamura et al. (2017) had an altogether different finding, modelling a stronger yet shallower AMOC during the LGM. Many such studies focus exclusively on the Atlantic Ocean, perhaps due to the well-understood AMOC and the more detailed proxy data coverage in that basin. For example, Curry and Oppo (2005) provided striking transects of δ¹³C in the LGM and late Holocene Atlantic Ocean, which provided evidence for large changes in the basin δ¹³C stratigraphy across the two time periods. The δ¹³C data compilations of Oliver et al. (2010) and Peterson et al. (2014) are also heavily skewed towards the Atlantic Basin.

Talley (2013) emphasised the importance of the Pacific and Indian Ocean overturning circulation limbs in the global ocean circulation regime, which implies that it is a critical part of the Earth's carbon cycle. This finding was corroborated by Skinner et al. (2017) in a recent review of Pacific Ocean radiocarbon data. The model–data results using SCP-M suggest that GOC was substantially reduced during the LGM (Table 5), accompanying enhanced storage of isotopically depleted carbon in the abyssal and deep ocean from atmospheric and terrestrial biosphere sources (Fig. 11). We posit that the release of volumes of carbon, that were greater than amounts stored in the deep–abyssal Atlantic alone, caused the atmospheric CO₂ increase at the last glacial termination. Such a movement of carbon to and from the global abyssal ocean is likely required due to the large, opposite movement in atmospheric CO₂ from the terrestrial biosphere across the same time period (Fig. 12). During the LGM, the terrestrial biosphere was reduced relative to the modern period, which was a source of CO₂ to the atmosphere, and rebounded from the LGM to the Holocene, becoming a sink of CO₂ during that period (Francois et al., 1999; Ciais et al., 2012; Peterson et al., 2014; Hoogakker et al., 2016). Incorporating the terrestrial biosphere into modelling experiments increases the magnitude of carbon uptake–release required from the ocean to satisfy the LGM and late Holocene atmospheric CO₂ and, critically, δ¹³C data (even when incorporating SST, salinity, sea-ice cover proxy and ocean volume changes). The finding underscores the importance of incorporating multiple data proxies and carbon reservoirs into glacial–interglacial carbon cycle modelling.

Our model–data experiments did not find a role of changed marine biological production in the LGM–late Holocene transition (Table 5). However, this finding was the result of testing for variations in the global value of the ocean biological productivity, impacting all surface ocean boxes in SCP-M. Other studies (e.g. Menviel et al., 2016; Muglia et al., 2018) focussed specifically on the Southern Ocean biological productivity and identified its potential role in the LGM atmospheric CO₂ drawdown. The Southern Ocean marine biology, in particular, is posited as a candidate for driving glacial–interglacial cycles of CO₂ (e.g. Martin, 1990; Martinez-Garcia et al., 2014).

6 Conclusions

The SCP-M carbon cycle box model was constructed for the purposes of scenario or hypothesis testing (quickly and easily), model–data integration and inversion, paleo reconstructions, and analysing the distribution of anthropogenic emissions in the carbon cycle. The model contains a full ocean–atmosphere–terrestrial carbon cycle with a realistic treatment of ocean processes. Despite being relatively simple in concept and construct, SCP-M can account for a range of paleo and modern carbon cycle observations. The model applications illustrated here include integration with datasets from the present day (GLODAPv2, IPCC) and ocean paleo proxy data across the LGM and late Holocene periods. Simulations of the modern carbon cycle indicate that SCP-M provides a realistic representation of the dynamic shocks from human industrial and land use change emissions and bomb ¹⁴C. A model–data experiment using LGM and late Holocene CO₂, δ¹³C, Δ¹⁴C and the carbonate ion proxy is able to resolve parameter values for ocean circulation, mixing and biology while reproducing model results that are very close to the proxy data for both time periods. The results indicate that the LGM-to-Holocene carbon cycle transition can be explained by variations in the strength of the global overturning circulation and Atlantic meridional overturning circulation when combined with a number of background changes, such as sea surface temperature, salinity, sea-ice cover, ocean volume and a varied atmospheric radiocarbon production rate. Further work on data quality and analysis is required to validate this finding, which is the subject of a separate paper. The results show promise in helping to further resolve the LGM-to-Holocene carbon cycle transition and point towards an ongoing application for data-constrained models such as SCP-M.

Appendix A: Parameters, data sources and dimensions

Talley (2013)Talley (2013)Talley (2013)Toggweiler (1999)Martin et al. (1987)Berelson (2001)Toggweiler (1999)Mook et al. (1974)Toggweiler and Sarmiento (1985)Schmittner et al. (2013)Toggweiler and Sarmiento (1985)Toggweiler and Sarmiento (1985)Takahashi et al. (1985)Sarmiento et al. (2002)Hales and Emerson (1997)Hales and Emerson (1997)Mucci (1983)Weiss (1974)Lueker et al. (2000)Key (2001)Broecker et al. (1980)Key (2001)Sabine et al. (2004)Eide et al. (2017)Stuiver and Polach (1977)Toggweiler (2008)Compton et al. (2000)

Table A1 SCP-M model dimensions, model parameter starting values and starting data used for model spin-up.