the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A new version of the CABLE land surface model (Subversion revision r4601) incorporating land use and land cover change, woody vegetation demography, and a novel optimisation-based approach to plant coordination of photosynthesis
Vanessa Haverd
Benjamin Smith
Lars Nieradzik
Peter R. Briggs
William Woodgate
Cathy M. Trudinger
Josep G. Canadell
Matthias Cuntz
The Community Atmosphere–Biosphere Land Exchange model (CABLE) is a land surface model (LSM) that can be applied stand-alone and provides the land surface–atmosphere exchange within the Australian Community Climate and Earth System Simulator (ACCESS). We describe new developments that extend the applicability of CABLE for regional and global carbon–climate simulations, accounting for vegetation responses to biophysical and anthropogenic forcings. A land use and land cover change module driven by gross land use transitions and wood harvest area was implemented, tailored to the needs of the Coupled Model Intercomparison Project 6 (CMIP6). Novel aspects include the treatment of secondary woody vegetation, which benefits from a tight coupling between the land use module and the Population Orders Physiology (POP) module for woody demography and disturbance-mediated landscape heterogeneity. Land use transitions and harvest associated with secondary forest tiles modify the annually resolved patch age distribution within secondary vegetated tiles, in turn affecting biomass accumulation and turnover rates and hence the magnitude of the secondary forest sink. Additionally, we implemented a novel approach to constrain modelled GPP consistent with the coordination hypothesis and predicted by evolutionary theory, which suggests that electron-transport- and Rubisco-limited rates adjust seasonally and across biomes to be co-limiting. We show that the default prior assumption – common to CABLE and other LSMs – of a fixed ratio of electron transport to carboxylation capacity at standard temperature (Jmax, 0∕Vcmax, 0) is at odds with this hypothesis; we implement an alternative algorithm for dynamic optimisation of this ratio such that coordination is achieved as an outcome of fitness maximisation. The results have significant implications for the magnitude of the simulated CO2 fertilisation effect on photosynthesis in comparison to alternative estimates and observational proxies.
These new developments enhance CABLE's capability for use within an Earth system model and in stand-alone applications to attribute trends and variability in the terrestrial carbon cycle to regions, processes and drivers. Model evaluation shows that the new model version satisfies several key observational constraints: (i) trend and interannual variations in the global land carbon sink, including sensitivities of interannual variations to global precipitation and temperature anomalies; (ii) centennial trends in global GPP; (iii) coordination of Rubisco-limited and electron-transport-limited photosynthesis; (iv) spatial distributions of global ET, GPP, biomass and soil carbon; and (v) age-dependent rates of biomass accumulation in boreal, temperate and tropical secondary forests.
CABLE simulations agree with recent independent assessments of the global land–atmosphere flux partition that use a combination of atmospheric inversions and bottom-up constraints. In particular, there is agreement that the strong CO2-driven sink in the tropics is largely cancelled by net deforestation and forest degradation emissions, leaving the Northern Hemisphere (NH) extratropics as the dominant contributor to the net land sink.
- Article
(10820 KB) - Full-text XML
- BibTeX
- EndNote
The Community Atmosphere–Biosphere Land Exchange model (CABLE) is a land surface model (LSM) that can be applied in stand-alone applications and also provides the land surface–atmosphere exchange within the Australian Community Climate and Earth System Simulator (ACCESS; Kowalczyk et al., 2013; Law et al., 2017; Ziehn et al., 2017). In its stand-alone configuration, CABLE was used in the IPCC 5th assessment report (IPCC, 2014) and is one of an ensemble of ecosystem and land surface models contributing to the Global Carbon Project's annual update of the global carbon budget (Le Quéré et al., 2016, 2018). The current paper describes updates to CABLE (Haverd et al., 2017) targeting two key areas that have been identified as limitations in the applicability and utility of the existing generation of LSMs: (i) land use and land cover change (LULCC, hereafter abbreviated to LUC) and (ii) adaptation of photosynthesis to changing environmental conditions.
Additional model updates based on existing parameterisations from the literature include the following: (i) drought and summergreen phenology (Sitch et al., 2003; Sykes et al., 1996); (ii) low-temperature reductions in photosynthetic rates in boreal forests (Bergh et al., 1998); (iii) photoinhibition of leaf day respiration (Clark et al., 2011); and (iv) acclimation of autotrophic respiration (Atkin et al., 2016). These are described in Appendix 2.
1.1 Land use and land cover change
The CABLE version that precedes developments described here (hereafter “Prior CABLE”) assumes fixed present-day or pre-industrial vegetation cover in the absence of land management. Capturing the impact of human LUC on the terrestrial carbon and water cycles and on land–atmosphere coupling is a key application of LSMs and associated Earth system models (ESMs) and a prerequisite for the evaluation of the models against observation-based datasets.
For the CMIP6 climate model inter-comparison process, the globally gridded Harmonised Land Use Dataset (LUH2; Hurtt et al., 2016, 2011) specifies a matrix of transitions between land use classes (e.g. primary forest, secondary forest, pasture, cropland) through time (Lawrence et al., 2016). In traditional LSMs, these transitions must be translated into annual land cover maps that specify the fraction of the land surface occupied by each plant functional type (PFT; Lawrence et al., 2012). This approach reduces the transition matrix to a set of net transitions, thereby discarding information about the gross transitions leading to land cover change. Simulations driven by gross land use transitions produce emissions that are 15–40 % higher than the net transitions alone (Hansis et al., 2015; Stocker et al., 2014; Wilkenskjeld et al., 2014).
Traditional LSMs are also unable to simulate realistic dynamics resulting from the accumulation of carbon in forests following harvest and agricultural abandonment – the so-called secondary forest sink – that is an important contributor to the extant global terrestrial carbon sink (Shevliakova et al., 2009) second only to CO2 fertilisation. This is because traditional LSMs lack the representation of woody demography that is required to simulate age effects on growth and mortality that lead to very high biomass accumulation rates in young forests compared to old-growth stands (e.g. Poorter et al., 2016; Purves and Pacala, 2008; Wolf et al., 2011).
In contrast to traditional LSMs, demography-enabled dynamic vegetation models (DVMs) can implement gross transitions directly and provide a realistic representation of secondary forest sink by explicitly simulating biomass removal and subsequent recovery following a land use event (e.g. Shevliakova et al., 2009). However, keeping track of a representative distribution of landscape elements (patches) with different times since disturbance can be computationally difficult as repeated land use events can lead to a very high number of such elements in a grid cell.
In this work, we develop a novel LUC scheme for CABLE that is driven by LUH2 gross transitions and represents age effects on biomass dynamics in all tiles with woody vegetation, including those occupied by secondary forest. This is achieved via coupling with the POP module for woody demography and disturbance-mediated heterogeneity (Haverd et al., 2013b). The key simplification in the POP approach, compared with other demography-enabled DVMs, is to compute physiological processes such as photosynthesis at the scale of a land cover tile (“grid scale”), but to partition the grid-scale biomass increment amongst sub-grid-scale patches, each subject to its own dynamics, and distinguished by the time since last disturbance. This makes tracking biomass in a large number of patch ages (as arise through both natural disturbance and human land cover change) easy and circumvents the computational difficulties of tracking land cover classes in DVMs.
1.2 Coordination of photosynthesis
Almost all global LSMs use the photosynthesis model of Farquhar et al. (1980) or a related scheme derived from this model. Different implementations result in divergent estimates of the response of photosynthesis to environmental drivers in large-scale models (e.g. Friend et al., 2014). One reason for this may be that global LSMs have mostly neglected the constraint imposed by the evolutionary ecological assumption that plants optimise productivity in their environment through relative investment in electron-transport- and Rubisco-limited steps in the photosynthesis chain, which adjust seasonally and across biomes to be co-limiting. This so-called coordination hypothesis was originally proposed by Chen et al. (1993) and has been verified experimentally by Maire et al. (2012). Its advantages as an approach to modelling photosynthetic dynamics using limited data constraints was pointed out by Wang et al. (2017), while Ali et al. (2016) have incorporated it into a global mechanistic model of photosynthetic capacity based on the optimal nitrogen allocation model of Xu et al. (2012). In this work, we will show that the assumption of a temporally invariant ratio of Rubisco and electron transport capacities (at standard temperature), adopted in Prior CABLE and typically in other LSMs, is not only inconsistent with the coordination hypothesis, but introduces large uncertainty in the simulated sensitivity of GPP to atmospheric CO2 concentration. We solve this problem by developing an algorithm for dynamic optimisation of this ratio such that coordination is achieved as an outcome of fitness maximisation.
1.3 Paper structure
The paper is structured as follows. In Sect. 2 we review the basic structure of CABLE. In Sect. 3 we describe the model developments that are the focus of this work: firstly, updates to the POP module for woody demography and disturbance; secondly, the new land use and land cover change module; thirdly, the dynamic optimisation of plant photosynthesis. In Sect. 4, we describe the modelling protocol that is used to deliver simulations for evaluating the new model version and assessing terrestrial carbon cycle implications of changing climate, CO2, land use and land cover over the historical period (1860–2016). In Sect. 5, we present the results of these simulations. Section 5.1 evaluates predictions of present-day spatial distributions of evapotranspiration, gross primary production, biomass and soil carbon. Section 5.2 evaluates predictions of biomass accumulation rates in regrowing forests. Section 5.3 illustrates the capability and behaviour of the land use implementation, showing examples of land–atmosphere carbon exchange at four locations with contrasting LUC histories. Section 5.4 shows the implications of CO2, climate and LUC on historical global and regional land–atmosphere exchange. Section 5.5 and 5.6 address the implications of simulated photosynthesis coordination for the sensitivity of photosynthesis to CO2 and for the CO2 fertilisation of global photosynthesis. Section 5.7 evaluates the new model's prediction of the annual time series of the net land carbon sink by comparison with the equivalent quantity derived from atmospheric mass balance (atmospheric growth rate + ocean sink – fossil fuel emissions). Priorities for future development are summarised in Sect. 6.
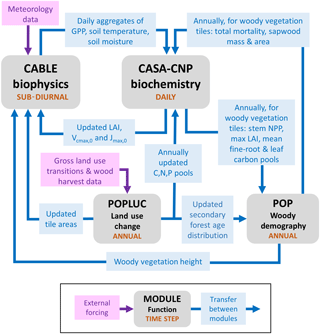
Figure 1Major sub-models of CABLE (revision 4601) showing forcing data, characteristic time steps and information flows between modules, which include fluxes, store updates, and changes to vegetation characteristics and their spatial extent (tile areas) within grid cells. Data from faster modules are aggregated before passing to slower modules. Faster modules are updated with data from slower modules at the rate of the slower time step.
Figure 1 summarises the content of CABLE and how the components interact. Further details are presented in Fig. A1 (Appendix A1) as pseudo-code for each component and Tables A1–A3 (Appendix A3), which document the parameter values and temperature response functions of photosynthesis used in this work. CABLE consists of a biophysics core (Haverd et al., 2016a; Kowalczyk et al., 2013; Wang et al., 2011), the CASA-CNP “biogeochemistry” module (Wang et al., 2010), the POP module for woody demography and disturbance-mediated landscape heterogeneity (Haverd et al., 2013c, 2014), and a completely new module for land use and land management (POPLUC).
The biophysics core (sub-diurnal time step) consists of four components: (1) the radiation module describes radiation transfer and absorption by sunlit and shaded leaves (Goudriaan and van Laar, 1994); (2) the canopy micrometeorology module describes the surface roughness length, zero-plane displacement height and aerodynamic conductance from the reference height to the air within canopy or to the soil surface (Raupach, 1994); (3) the canopy module includes the coupled energy balance, transpiration, stomatal conductance, photosynthesis and respiration of sunlit and shaded leaves (Wang and Leuning, 1998); and (4) the soil module describes heat and water fluxes within soil (six vertical layers) and snow (up to three vertical layers) and at their respective surfaces. The CASA-CNP biogeochemistry module (daily time step) inherits daily net photosynthesis from the biophysical code, calculates autotrophic respiration, allocates the resulting net primary production (NPP) to leaves, stems and fine roots, and transfers carbon, nitrogen and phosphorous between plant, litter and soil pools, accounting for losses of each to the atmosphere and by leaching. POP (annual time step) inherits annual stem NPP from CASA-CNP and simulates woody ecosystem stand dynamics, demography and disturbance-mediated heterogeneity, returning the emergent rate of biomass turnover to CASA-CNP.
The biophysics core of CABLE has been benchmarked using prescribed meteorology (e.g. Best et al., 2015; Zhang et al., 2013; Zhou et al., 2012) and its performance evaluated as part of the Australian Community Climate and Earth System Simulator climate model (Kowalczyk et al., 2013). The CASA-CNP module was developed and tested as a stand-alone module (Wang et al., 2010), and its basic performance was demonstrated as part of ACCESS (Law et al., 2017; Ziehn et al., 2017). POP (coupled to CABLE) has been evaluated against savanna data (Haverd et al., 2013b, 2016b) and boreal and temperate forest data (Haverd et al., 2014).
3.1 The Population Orders Physiology (POP) module for woody demography
In previous work, POP has been coupled to both the CABLE and HAVANA land surface schemes and demonstrated to successfully replicate the effects of rainfall and fire disturbance gradients on vegetation structure along a rainfall gradient in Australian savanna – the Northern Australian Tropical Transect (Haverd et al., 2013c, 2016b) – and leaf–stem allometric relationships derived from global forest data. For the latter, it may be argued to reflect the simultaneous development of trees in closed forest stands in terms of structural and functional (productivity) attributes (Haverd et al., 2014). The summary below is reproduced from these papers, which describe POP in detail and with full equations. To enable the extension of CABLE to simulate dynamic land use and implications for forest carbon uptake, we used the most recent version of POP's representation of growth partitioning amongst age and size classes (cohorts) of trees established in the same year; it accounts for both cohort-dependent light interception and sapwood respiration. This contrasts with the original growth partitioning, which assumed that individuals capture resources in varying proportion to their size.
POP is designed to be modular, deterministic, computationally efficient and based on defensible ecological principles. POP simulates the allometric growth of cohorts of trees that compete for light and soil resources within a patch. Parameterisations of tree growth, allometry, recruitment and mortality are broadly based on the approach of the LPJ-GUESS Dynamic Vegetation Model (Smith et al., 2001). The time step is 1 year.
Input variables to POP are annual grid-scale stem biomass increment and mean return times for two classes of disturbance: (i) “catastrophic” disturbance, which kills all individuals (cohorts) and removes all biomass in a given patch; and (ii) “partial” disturbances, such as fire, which result in the loss of a size-dependent fraction of individuals and biomass, preferentially affecting smaller (younger) cohorts. For the present study, we adopt a mean catastrophic disturbance return time of 100 years and neglect partial disturbance, such as damage caused by wildfires. Stem biomass increment is provided by the host land surface model (LSM), here CABLE.
State variables are the density of tree stems partitioned among cohorts of trees and representative patches of different age since last disturbance across a simulated landscape or grid cell. Each patch has a number of cohorts. Trees in each cohort are the same age and size because they are established simultaneously and share the same growth rate. Patches are not spatially explicit. Their areal representation in the landscape is given by the patch age distribution.
In the current implementation of POP, the annual stem biomass increment is partitioned among cohorts and patches in proportion to the current net primary production of the given cohort (Haverd et al., 2016b). For this purpose, gross primary production and autotrophic respiration for each woody tile are passed from CABLE to POP, and each is partitioned amongst patches and cohorts. Gross resource uptake is partitioned amongst cohorts and patches in proportion to light interception, which is evaluated for each cohort as the difference between downward-looking gap probabilities above and below each cohort. Gap probabilities are calculated using the geometric approach of Haverd et al. (2012). This requires estimates of cohort-specific crown cross-sectional area (related allometrically to DBH) and LAI computed using the CABLE maximum leaf area and distributed amongst patches and cohorts in proportion to sapwood area. For autotrophic respiration, leaf, fine-root and sapwood respiration components are also partitioned amongst cohorts and patches according to the size of each biomass component. Cohort-specific sapwood is prognosed by assuming sapwood conversion to heartwood at a rate 0.05 year−1. Cohort-specific leaf and root carbon pools are estimated by partitioning the aggregate values for each woody tile in proportion to leaf area index (LAI). Net resource uptake for each patch and cohort is evaluated as its gross primary production minus autotrophic respiration.
Cohort stem density is initialised as recruitment density and is episodically reset when the patch experiences disturbance. Mortality, parameterised as the sum of cohort-specific resource limitation and crowding components, reduces the stem density in the intervening period. Resource limitation mortality, a function of growth efficiency (GE; i.e. growth rate relative to biomass), is described by a logistic curve with an inflection point representing a critical GE level at which plants experience a steep increase in mortality risk due to a shortage of resources to deploy in response to stress or biotic damage (Haverd et al., 2013c). The crowding mortality component (Haverd et al., 2014) allows for self-thinning in forest canopies.
Additional mortality occurs as a result of disturbances. Patches representing stands of differing age since last disturbance are simulated for each grid cell. It is assumed that each grid cell is large enough to accommodate a landscape in which the frequency of patches of different ages follows a negative exponential distribution with an expectation related to the current disturbance interval. This assumption is valid if grid cells are large relative to the average area affected by a single disturbance event and disturbances are a Poisson process occurring randomly with the same expectation at any point across the landscape independent of previous disturbance events. To account for disturbances and the resulting landscape structure, state variables of patches of different ages are linearly interpolated between ages and weighted by probability intervals from the negative exponential distribution. The resultant weighted average of, for example, total stem biomass or annual stem biomass turnover is taken to be representative for the grid cell as a whole.
In earlier applications, CABLE–POP coupling consisted of just two exchanges: (i) stem NPP passed from the host LSM to POP and (ii) woody biomass turnover returned from POP to the host LSM. To convert between stem biomass (POP) and tree biomass (CABLE), we assume a ratio of 0.7, a representative average for forest and woodland ecosystems globally (Poorter et al., 2012). The POP biomass lost by mortality is applied as an annual decrease in the CASA-CNP tree biomass pool and replaces the default fixed biomass turnover rate. In the current work, the coupling also includes the return of sapwood area and sapwood biomass to the CASA-CNP biogeochemical module of CABLE, in which these variables respectively influence C allocation to leaves and autotrophic respiration. Combined allocation to leaves and wood is partitioned following the pipe model (Shinozaki et al., 1964) such that a target ratio of leaf area to sapwood area (a global value of 5000 is assumed) is maintained. Sapwood replaces stem-wood biomass in the CASA-CNP calculation of stem respiration. These feedbacks of POP structural variables on leaf area and autotrophic respiration result in net primary production (NPP) that reflects the area-averaged sapwood area and mass of each woody tile.
Advantages and limitations of the POP approach to simulating large-scale biomass dynamics
POP is not a replacement for a full-featured dynamic vegetation model (DVM), but does overcome key limitations of Prior CABLE and many DVMs adopted by most Earth system models (Arora et al., 2013), for which biomass turnover is often represented as a first-order decay process expressed as the product of grid cell biomass and a bulk rate parameter. This “big wood” approximation does not resolve underlying population and community processes such as recruitment, mortality and competition between individuals for limiting resources (e.g. Sitch et al., 2003) and has been demonstrated to lead to an inaccurate trajectory of biomass accumulation with stand age (Wolf et al., 2011; Haverd et al., 2014). Big wood models are additionally unable to directly exploit the wealth of information on forest stand structure and dynamics available from forest inventories. By discriminating individual and population growth and explicitly representing asymmetric competition among age and size classes of trees co-occurring within forest stands, POP overcomes the limitation of the big wood approach and has proved able to reproduce allometric relationships reflecting linkages between productivity, biomass and density in widely distributed forests (Haverd et al., 2014). This is achieved without a marked increase in model complexity or computational demand thanks to a modular design that separates the role of the parent land surface model (prognosing whole-ecosystem production) and the population dynamics model (partitioning the production among cohorts, computing mortality for each and returning the stand-level integral as whole-ecosystem biomass turnover to the parent model; Fig. 1).
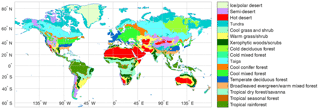
Figure 2Spatial distribution of BIOME1 biomes (Table 1) that determines the type of primary vegetation cover
Table 1CABLE primary vegetation: mapping of BIOME1 biomes to CABLE plant functional types.
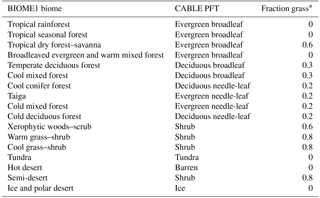
* Grass is specified as C3 where monthly minimum temperature is less than 15.5 ∘C and C4 elsewhere.
A drawback of this modular approach is that age effects on leaf area and NPP are not accounted for explicitly at the scale of the individual because these variables are computed for each woody tile and in turn distributed amongst POP patches and cohorts. Feedbacks of stand structure on leaf area and NPP thus reflect the area-averaged structural properties (sapwood area and sapwood mass) of each woody tile.
POP does not represent competitive interactions among PFTs that provide an important explanation for global biome distributions and may modulate the responses of vegetation to future climate and CO2 forcing (Smith et al., 2014). We plan to introduce PFTs and to distinguish canopy and understorey strata in a later development of the approach.
3.2 POPLUC land use and land cover change module
This development enables the simulation of the effect of LUC on land cover fractions and associated carbon flows into and out of soil, litter, vegetation and product pools.
Three land use tile types are considered: primary woody vegetation (p), secondary woody vegetation (s) and open grassy vegetation (g), the latter encompassing natural grassland, rangeland, pasture and cropland. Forcing data comprising four possible annual gross transition rates are used to drive the annual LUC-induced changes to land use area fractions. These transition rates are the following: (i) primary clearing (p → g), (ii) secondary clearing (s → g), (iii) primary harvest (p → s) and (iv) abandonment (g → s). In addition, secondary forest harvest area is used to drive changes in the secondary forest age distribution. Further, cropland and pasture area fractions are diagnosed from transitions to and from pasture and cropland and used to estimate the carbon cycle consequences of crop harvest, tillage and grazing.
3.2.1 Mapping land use tile types to CABLE plant functional types
Potential vegetation cover is prescribed using BIOME1 (Prentice et al., 1992), a semi-mechanistic climate-envelope approach, to construct global spatial distribution of biomes according to CABLE's own climate drivers, which are accumulated from 30 years (1901–1930) of meteorological inputs (Fig. 2).
Biomes (combinations of dominant plant types; Prentice et al., 1992) are mapped to a single CABLE plant functional type (PFT) or in some cases to two CABLE PFTs (one woody and one herbaceous) with fixed relative areal proportions (Table 1). We make use of five woody vegetation types (evergreen needle-leaf, evergreen broadleaf, deciduous needle-leaf, deciduous broadleaf, shrub) and six non-woody types (C3 grass, C4 grass, tundra, wetland, barren, ice). All woody vegetation tiles are represented by POP, and secondary woody vegetation tiles are assumed to be occupied by the woody PFT of the primary woody vegetation tile in the same grid cell.
3.2.2 Tracking land use area fractions and secondary forest age distribution
Each land use tile has an associated areal fraction representing its fractional area cover of the grid cell. Land transition area rates augment and deplete land use area fractions, subject to land availability. In secondary forest tiles, the areal fraction of each integral age class (0–400 years) is also tracked: a transition to secondary forest (p → s or g → s) augments the 0 age class by the same amount. A transition from secondary forest to open land (s → g) depletes the areas of the youngest age classes first, starting from 10 years. If the clearing area exceeds the area covered by age classes older than 10 years, clearing is applied uniformly across all age classes. A secondary harvest event sequentially depletes the areas of each age class, starting from the oldest, until all harvest area is satisfied, subject to land availability. Secondary forest tiles are also subject to natural disturbance, which further modifies the patch age distribution.
The POPLUC code provides the secondary forest patch age distribution to POP. POP tracks biomass in each of a set of patches with different ages based on patch-dependent growth and turnover. It then computes biomass for each integral age class represented by the secondary forest tile patch age distribution by interpolating biomass in the simulated patches.
POPLUC represents integral secondary forest ages classes from 0 to 1000 years old, although many ages may have a weight of zero. The frequency distribution is fully dynamic. In contrast, POP represents 60 patches in each woody tile spanning a distribution of ages from 0 to 1000.
3.2.3 Redistribution of carbon stocks following land use change
Changes in pool sizes of biomass, soil and litter carbon in the biogeochemical module are updated to reflect the areal changes from gross land use transitions. Analogous updates occur for nitrogen pools. The mass balance equation for the carbon density cj (g m−2) in each land use tile L with area AL (m2) that accounts for the possibility of more than one gross receiver (r) or donor (d) transition to or from the tile is
Here j=1–9 (referring to carbon in leaf, wood, fine roots, three litter pools and three soil pools) and L=1–3 (referring to primary woody, secondary woody, open land use tiles); subscript 0 refers to the value of the tile area or carbon density prior to the transitions; ΔAL refers to the total (net) change in land area of the Lth tile; and ΔAL,d refers to the absolute change in land area due to donor transitions. In Eq. (1), the first term on the LHS is the carbon stock prior to land use perturbations; the second term is the carbon lost from the tile due to donor transitions (transitions from the Lth tile) and the third term is the carbon gained by receiver transitions (transitions to the Lth tile). The term on the RHS is the carbon stock following the perturbations (i.e. the product of the new carbon density and the new tile area).
The carbon gained by receiver transitions is generally
where the total transfer of carbon is summed over all possible gross transitions (ntrans=4), and each transition contributes carbon to the receiver pool that is equal to the product of the transition area ΔAk multiplied by the carbon density of the donor pool cj,k. An exception to Eq. (2) is the transfer of carbon to the coarse woody debris pool and fine structural litter as the result of clearing or wood harvest: woody biomass residue from harvest and clearing augments the coarse woody debris pool, whereas leaf and fine-root residue augment the fine structural litter pool. In the case of secondary forest, harvest and clearing are age selective, which means that biomass loss and litter increment are affected not only by cleared or harvested secondary forest area, but also by the age distribution of the stems that are removed. Harvested and cleared biomass that is not left as residue is extracted into three product pools with turnover rates of 1, 10 and 100 years. Coefficients for allocation to these product pools, as well as the fractions of harvested and cleared biomass that remain in the landscape as litter are prescribed following Hansis et al. (2015).
Carbon losses by secondary forest harvest and clearing need to be resolved from net biomass loss in secondary forest tiles, which also includes components from natural disturbance and areal expansion. POP diagnoses a change in biomass resulting from the aggregate shift in age distribution contributed by natural disturbance, forest expansion, harvest and clearing. The proportional contributions of each of these processes to total biomass change is recorded. The carbon flux implied by this total biomass change is subsequently disaggregated according to the previously recorded proportional contributions of each process.
Carbon removal from the landscape by crop harvest and grazing are treated simply. Crops and pasture are not treated in separate land use tiles, but are simulated as grass in the open “grassy” tile of each grid cell. The areal fractions of cropland and pasture in each open tile are tracked via the gross transitions to and from these land use types. These fractions, combined with assumed respective removals of 90 % and 50 % of above-ground NPP by crop harvest and grazing (Lindeskog et al., 2013), are used to prescribe leaf-litter transfer to an agricultural product pool with a turnover time of 1 year. Following Lindeskog et al. (2013), soil carbon loss by tillage is simulated by increasing the turnover of soil carbon by 50 % in croplands. Where crops and pasture occupy more than 10 % of a grass tile, it is assumed that there is no nutrient limitation to growth.
3.3 Optimisation-based approach to plant coordination of electron-transport- and carboxylation-capacity-limited photosynthesis in C3 plants
Photosynthesis, as represented by the Farquhar et al. (1980) model, may be limited by the Rubisco-catalysed maximum rate of carboxylation (Vcmax) or the maximum rate of electron transport (Jmax). Estimates of these parameters based on leaf gas exchange measurements suggest their ratio at standard temperature (25 ∘C) to be conservative around a global mean of (e.g. Walker et al., 2014), which has led to it being widely adopted as a fixed parameter in global terrestrial biosphere models. However, as we will show in Sect. 5.5 and 5.6, the assumption of a fixed value of bJV leads to large deviations from the coordination hypothesis (Chen et al., 1993; Maire et al., 2012) that Rubisco and electron transport capacity adjust seasonally and across biomes to be co-limiting. An alternative but closely related assumption is that plants optimise bJV to minimise the nitrogen cost per unit photosynthesis. Here we describe a generic approach to dynamically optimising bJV based on this assumption.
3.3.1 Review of model for net photosynthesis
Here we review the equations of the C3 photosynthesis model (Farquhar et al., 1980) as embedded in CABLE. We note here that in CABLE these equations are coupled to the canopy environment via leaf surface energy balance and to the air above the canopy via turbulent transfer processes, which we will not review here (see Kowalczyk et al., 2006, for full description).
Net photosynthesis (An) is equated with the supply of CO2 to the intercellular air spaces:
where gsc is the stomatal conductance to CO2, cs is the concentration of CO2 at the leaf surface and ci is the intercellular CO2 concentration.
Net photosynthesis is also equated with biochemical demand for CO2, i.e. the lesser of Rubisco- and electron-transport-limited rates of carboxylation minus day respiration.
The two potentially limiting rates are given by
and
where Vcmax is the maximum catalytic activity of Rubisco in the presence of saturating levels of RuP2 and CO2; Γ∗ is the CO2 compensation point in the absence of day respiration; Kc and Ko are Michaelis–Menten constants for CO2 and O2, respectively; co is concentration of O2; and J is the electron transport rate and is related to absorbed photon irradiance Q by (Farquhar and Wong, 1984)
where α is the quantum yield of electron transport and θ a curvature parameter. Temperature response functions of Vcmax, Jmax, Γ∗, Kc and Ko are given in Table A3 (Appendix A3). The parameterisation of Rd is given by Eq. (A3) in Appendix A2.
Stomatal conductance is expressed as a linear function of An.
Following Lin et al. (2015), we set gmin to zero and adopt the following dependence of X on leaf–air vapour pressure deficit (Dleaf):
where fw, soil is related to soil moisture deficit and is parameterised according to Haverd et al. (2016a) and the PFT-dependent g1 parameter is sourced from Lin et al. (2015).
Equations (3), (4) and (8) are solved simultaneously for An, ci and gsc.
3.3.2 Dynamic optimisation of bJV: assumptions
The approach to the optimisation of bJV is based on four assumptions.
- i.
Leaf nitrogen resources may be dynamically redistributed at a 5-day timescale at no cost; i.e. bJV is optimised such that net photosynthesis (given total available leaf nitrogen) accumulated over the last 5 days (approximately the timescale for turnover of Rubisco) would have been maximised.
- ii.
Leaf nitrogen resources available for partitioning between Rubisco and electron transport capacity are proportional to effective nitrogen content (Neff) defined as the sum of prior estimates of Vcmax, 0 and Jcmax, 0 and weighted by relative cost ccost,JV:
where superscript 0 denotes prior estimate, subscript 0 denotes standard temperature, and
Neff is preserved as bJV is adjusted such that the adjusted (actual) values of Vcmax, 0 and Jmax, 0 are
and
- iii.
The prior values of Vcmax, 0 (related to leaf nitrogen and phosphorous content) and bJV are prescribed according to the synthesis of globally distributed leaf gas exchange measurements by Walker et al. (2014).
- iv.
The emerging contributions of electron-transport- and Rubisco-limited rates contribute approximately equally to total net photosynthesis (Chen et al., 1993). In practice, this requires a relative cost factor ccost, JV of 2.0 (slightly higher than a prior estimate of 1.6, which is the ratio of the linear regression slopes relating Jmax, 0 and Vcmax, 0 to leaf N; Chen et al., 1993).
3.3.3 Dynamic optimisation of bJV: method
The method for implementing these assumptions in CABLE is as follows.
- i.
Maintain a 5-day history of sub-diurnal leaf-level meteorology (absorbed PAR; leaf–air VPD difference; leaf temperature, cs) for sunlit and shaded leaves such that An,5d can be reconstructed for sunlit and shaded leaves. Other sub-diurnal variables that are required are Rd (Eq. 4), fwsoil (Eq. 9) and a scaling parameter that relates leaf-level Jmax, Vcmax and Rd to their effective “big leaf” sunlit and shaded values via integration of these parameters over canopy depth under the assumption that the leaf-level values are proportional to leaf nitrogen, which decreases exponentially from canopy top (Wang and Leuning, 1998; Eqs. C6 and C7).
- ii.
Construct a function that calculates leaf nitrogen cost per unit net photosynthesis (Neff∕An,5d). Inputs to this function are the following: (1) current estimate of bJV; (2) Neff (Eq. 10); and (3) 5-day history of sub-diurnal leaf-level meteorology.
- iii.
Implement a search algorithm to find bJV that minimises the function above for Neff∕An,5d. Here we use the golden section search algorithm (Press et al., 1993).
- iv.
Insert a call to the optimisation algorithm at the end of each day at the point in the code at which Vcmax, 0 and Jmax, 0 are being returned from the CASA-CNP biogeochemistry module to the CABLE biophysics module (Fig. A1). In this way, bJV and hence Vcmax, 0 and Jmax, 0 for sunlit and shaded leaves are updated daily based on the leaf environment of the last 5 days.
Global simulations were performed at spatial resolution, with time steps of 3 h (biophysics), 1 day (biogeochemistry) and 1 year (woody demography, disturbance, LUC). The nitrogen cycle was enabled, but not the phosphorous cycle. Recently developed parameterisations for the drought response of stomatal conductance and effects of leaf litter on soil evaporation were enabled (Haverd et al., 2016a), but not representations of the effects of groundwater and sub-grid-scale heterogeneity on the water cycle (Decker, 2015). The soil moisture response of heterotrophic respiration developed by Trudinger et al. (2016) was enabled, and the default Q10 formulation for the temperature response was replaced by that of Lloyd and Taylor (1994). For C3 PFTs, The relationship between Vcmax, 0 and leaf nutrient status was prescribed using the meta-analysis of leaf gas exchange data by Walker et al. (2014), and α and θ (Eq. 7) were prescribed to be consistent with this analysis.
4.1 Forcing data
Simulations were driven by (i) daily CRU-NCEP V7 (1901–2016; Viovy, 2016) downscaled to 3-hourly resolution using a weather generator (Haverd et al., 2013a), (ii) CO2 (1-year) resolution (Dlugokencky and Tans, 2017), (iii) gridded nitrogen deposition (10-year resolution; Lamarque et al., 2011) and (iv) gridded gross land use transitions and harvest (1500–2015) and initial land use states (1500) from the LUH2 harmonised land use dataset (Hurtt et al., 2016, 2011), re-gridded to spatial resolution and aggregated to four transitions associated with the three land use classes resolved in this study (Sect. 3.1). In this aggregation, we include all transitions to and from both the “forest” and “non-forest” components of LUH2 primary and secondary vegetation. Land use transitions and harvest are only applied in grid cells in which CABLE's primary vegetation includes a woody PFT. For simplicity, we neglect transitions from natural grassland to forest.
4.2 Simulation scenarios
Simulations (Table 2) were performed to quantify the net land–atmosphere carbon flux and attribute it to three components: (i) the land–atmosphere exchange that would occur in response to changing climate, CO2 and nitrogen deposition under a scenario of 1860 land cover (Fcc); (ii) the land–atmosphere exchange that would occur in response to land use change and management under a scenario of 1860 CO2 and nitrogen deposition and baseline (recycled 1901–1920) climate (FLUC, 0); and (iii) the additional LUC and management emissions arising from the effects of changing climate and CO2 combined with the reduction in sink capacity arising from land use conversion (FCC×L).
This allows the net flux FCC, L (combined response to CO2, climate and LUC) to be partitioned as
where
Scenario (iv) is included so that the net ecosystem production (NPP minus heterotrophic respiration) on secondary forest tiles can be partitioned between secondary forest regrowth and legacy emissions from post-harvest and post-clearing residues, which are zero in Scenario (iv). Note here that F0, L, no_residue and F0, L are slightly different (∼ 0.05 Pg C year−1 globally because of soil nitrogen feedbacks on growth and different carbon residence times in product pools vs. soil and litter). However, this difference does not affect the accuracy of reported net fluxes since Scenario (iv) is only used for flux partitioning.
Scenario (v) is included to resolve the net LUC emissions associated with grazing and cropland management as the difference F0, L–F0, L, no_Ag.
The loss of additional sink capacity (1860 reference year) FLASC can be resolved as one component of FLL × C using tile-based fluxes computed in Scenario (ii) and tile area weights computed in Scenaro (vi) as
where w1860 and wactual are the 1860 and actual grid cell tile weights and the sums are over all the tiles in each grid cell, respectively.
The initialisation phase of each scenario was designed to establish the dynamic equilibrium between model state (biomass and soil carbon pools) and the forcing data. All scenarios were initialised from zero biomass (to ensure biomass variables in POP and CASA-CNP start from the same value) and arbitrary soil carbon and nutrient stocks and brought to equilibrium with 1901–1920 climate by five repetitions of a pair of model runs. This pair comprised a full model run (1901–1920 climate, 1860 land cover, CO2, nitrogen deposition), followed by a semi-analytic spin cycle (Xia et al., 2012) adapted to include calls to the POP demography module and driven by GPP, soil moisture and temperature fields from the full model run. Due to the need to account for the legacy effects of past land use on soil carbon and secondary forest state, an additional initialisation of the vegetation and soil carbon pools as influenced by land use change and land management was performed for 1500–1710 for the scenarios with dynamic land use. To circumvent the high computational costs of the sub-diurnal solution of carbon and water fluxes, we used the same pre-computed GPP, soil moisture and temperature fields generated for the semi-analytic spin cycle. A final initialisation phase consisted of running the full model from 1711 to 1859 with dynamic land use forcing. The full model was then run for the 1860–2016 analysis period for all scenarios, with 1901–1920 meteorology recycled prior to 1901.
In addition to the above scenarios, we also explored the impact on global GPP of dynamically optimising . Simulations were performed under assumptions of dynamically optimised and fixed bJV (values of 1.6, 1.7, 1.8). For these simulations, static 1860 land cover was assumed and for computational efficiency, simulations were based on a sample of 1000 randomly distributed grid cells across the global ice-free land surface.
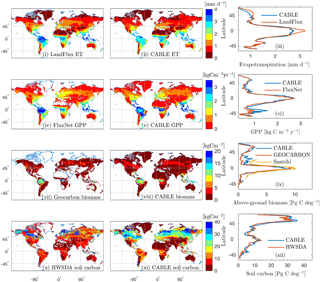
Figure 3Observation-based (i, iv, vii, x) and CABLE (ii, v, viii, xi) spatial distributions and the corresponding latitudinal distributions (iii, vi, ix, xii) of (i)–(iii) evapotranspiration, (iv)–(vi) GPP, (vii)–(ix) above-ground biomass and (x)–(xi) soil carbon (FAO/IIASA/ISRIC/ISSCAS/JRC, 2009). In the observation-based estimates, white indicates missing values. All quantities are annual means for the year 2000, except for GEOCARBON biomass (first decade of the 2000s).
5.1 Model evaluation: evapotranspiration, GPP, biomass and soil carbon
Model–data comparisons of the spatial distributions of key fluxes and stocks are presented in Fig. 3. We choose to evaluate the model against GPP, biomass and soil carbon because these are key quantities that are critical constraints on the global terrestrial carbon cycle and for which global distributions are available. We include evapotranspiration (ET) here as it is a key constraint on GPP because both ET and GPP are regulated by stomatal conductance.
The mean of evapotranspiration (ET) was obtained from the LandFlux data product (Mueller et al., 2013), which merges multiple remote sensing and flux station-based ET products into a single dataset. The CABLE and LandFlux latitudinal profile of ET differ by a mean absolute error of 0.12 mm d−1. There is an underestimate in the tropics of up to 0.4 mm d−1 (although note LandFlux 1σ uncertainty of ∼1 mm d−1 in this region), an underestimate that has been noted in previous evaluations of CABLE global ET (De Kauwe et al., 2015; Decker, 2015) and is particularly noticeable in the Amazon.
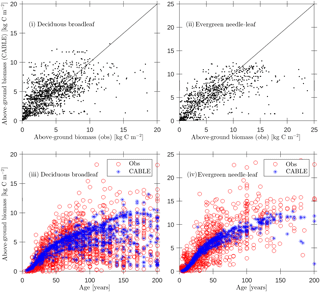
Figure 4Evaluation of CABLE (1990) above-ground biomass predictions against biomass compartments data (Teobaldelli, 2008; Teobaldelli et al., 2009) separated into deciduous broadleaf and evergreen needle-leaf classes: (i, ii) above-ground biomass predictions versus observations (solid line represents 1 : 1 line); (iii)–(iv) predictions and observations of above-ground biomass versus age.
Observation-based global gross primary production (GPP) was obtained from upscaled FLUXNET eddy covariance tower measurements (1982–2011; Jung et al., 2010). CABLE and FLUXNET estimates of the latitudinal distribution of GPP differ by a mean absolute error of 147 g C m−2 year−1. CABLE global GPP totals 134 Pg C year−1 for the year 2000, 9 % higher than the FLUXNET estimate (123 Pg C year−1). An over-prediction by CABLE is noted for Southern Hemisphere (SH) regions south of , a bias that is possibly related to SH temperate evergreen broadleaf forests being represented by the same CABLE PFT as tropical evergreen broadleaf forests (Table 1) and a fixed global value of the leaf area to sapwood area ratio.
Observation-based above-ground forest biomass at resolution for the first decade of the 2000s was obtained from the GEOCARBON product (Fig. 3vii), which is an integration of Northern Hemisphere forest biomass (Santoro et al., 2015) with a pan-tropical biomass map (Avitabile et al., 2016), itself a fusion of two existing large-scale biomass maps (Baccini et al., 2012; Saatchi et al., 2011) with local biomass data. The map covers only forest areas; forests are defined as areas with a dominance of tree cover in the GLC2000 map (Bartholomé and Belward, 2005). We also compare CABLE above-ground biomass with the product of Saatchi et al. (2011; Fig. 3ix), which is a combination of data from in situ inventory plot data, satellite lidar samples of forest structure, and optical and microwave imagery to extrapolate over the landscape, also at resolution. The CABLE and GEOCARBON latitudinal biomass estimates differ by a mean absolute error of 0.47 Pg C deg−1. Globally, CABLE's estimate for the year 2000 totals 246 Pg C of above-ground biomass (assumes an above-ground fraction of 0.7), 15 % higher than the GEOCARBON estimate of 209 Pg C. Most of the discrepancy is in China (observational uncertainties of 25–50 %), where CABLE over-predicts biomass carbon compared to GEOCARBON, but under-predicts compared to Saatchi et al. (2011).
Soil carbon density in the top 1 m of soil for the year 2000 was obtained from the Harmonized World Soil Database (HWSDA; version 1.2). (FAO/IIASA/ISRIC/ISSCAS/JRC, 2009). Latitudinal profiles of soil carbon from CABLE (total soil carbon and litter) differ from the HWSDA product by a mean absolute error of 1.8 Pg C deg−1 (Fig. 3xii), and the CABLE global total of 1426 Pg C is 7 % higher than the HWSDA estimate of 1329 Pg C. However, spatial distributions show large differences, most notably over-prediction by CABLE across much of the taiga and cold deciduous forest biomes. Another region of discrepancy is temperate south-eastern Australia, where CABLE predicts higher soil carbon (35–40 kg C m−2) than HWSDA; however, CABLE estimates are consistent with regional observation-based estimates (Viscarra Rossel et al., 2014).
5.2 Model evaluation: age dependence of biomass accumulation
5.2.1 Temperate and boreal forests
Forest inventory data for above-ground biomass and age were sourced from the Biomass Compartments Database (Teobaldelli, 2008; Teobaldelli et al., 2009). This database contains data from around 5790 plots and represents a harmonised collection of the Cannell (1982) and Usoltsev (2001) datasets covering the temperate and boreal forest region globally. In earlier work we used the database to construct biomass density plots for the purpose of calibrating the crowding mortality component of POP and to evaluate CABLE leaf-stem allometry plots relating foliage and stem biomass per tree (Haverd et al., 2014). Here we directly evaluate CABLE predictions of above-ground stem biomass for 1990 (approximate median year for the observational data; Fig. 4) for a wide range of stand ages (2–200 years). Despite significant scatter, predictions show low bias (Fig. 4i and ii) and biomass–age relationships that accord with the data (Fig. 4iii and iv): (DBL, n=1476; r2=0.35; bias error = 0.4 kg C m−2; root mean square error = 2.6 kg C m−2), (ENL, n=931; r2=0.46; bias error kg C m−2; root mean square error = 3.7 kg C m−2).
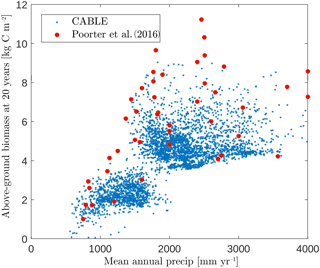
Figure 5CABLE and observation-based estimates (Poorter et al., 2016) of Neotropical secondary forest biomass after 20 years of regrowth versus mean annual precipitation. CABLE estimates are extracted from secondary forest tiles in tropical rainforest, tropical seasonal forest and tropical dry forest–savanna biomes (Fig. 2) in South America. The lower distinct cloud of CABLE-simulated values corresponds to the tropical dry forest–savanna biomes.
5.2.2 Tropical forests
CABLE regrowth rates of secondary forests in the tropical rainforest, tropical seasonal forest and tropical dry forest–savanna biomes (Fig. 2) in South America compare well with observation-based estimates by Poorter et al. (2016). This database has 1500 forest plots at 45 sites spanning the major environmental gradients across the Neotropics (Fig. 5), where mean annual rainfall is the strongest environmental predictor of biomass accumulation after 20 years (Poorter et al., 2016).
In this region, CABLE predicts that secondary forest biomass recovers to 41±6 (1σ) % of its undisturbed value after 20 years of recovery, in good agreement with observations 54±16 (1σ) % (Poorter et al., 2016). Poorter et al. (2016) emphasise high average secondary forest biomass accumulation rates in the first 20 years of regrowth compared with the uptake rate of old-growth forests. CABLE captures this distinction: mean above-ground biomass accumulation rates in the first 20 years of regrowth of 0.26±0.06 (1σ) kg C m−2 year−1 compare well with the mean of the observations of 0.31±0.13 (1σ) kg C m−2 year−1 (Poorter et al., 2016), while simulated old-growth forest rates of 0.05±0.01 (1σ) kg C m−2 year−1 (1990–2010, tropical rainforest and tropical seasonal forest biomes in South America) compare well with estimates of 0.03–0.05 kg C m−2 year−1 from the Amazon RAINFOR plot network for this period (Brienen et al., 2015).
5.3 Land use change and forest change: illustrative examples
Four examples of contrasting regional land use histories ( grid cells) are presented to illustrate carbon pool changes and the rate of land–atmosphere carbon flux from 1860 to present (Fig. 6). The landscape-scale responses reveal details that are obscured in the subsequent aggregation to regional and global scale (Sect. 5.4), but are important for demonstrating the functionality of the model at the spatial scale at which it is applied.
Each column in Fig. 6 corresponds to one site, and the four rows show the following: (1) land use transition rates for clearing (p → g + s → g), abandonment (g → s), primary forest harvest (p → s) and secondary forest harvest; (2) land use area fractions partitioned into primary woody, secondary woody and open land (open land is further partitioned into cropland, pasture and the remainder comprising rangeland and “natural grass”, meaning all other non-woody vegetation); (3) carbon stocks associated with soil and vegetation for each land use type and in product pools; and (4) land carbon flux to the atmosphere split into gross emissions (positive terms) and gross sinks (negative terms).
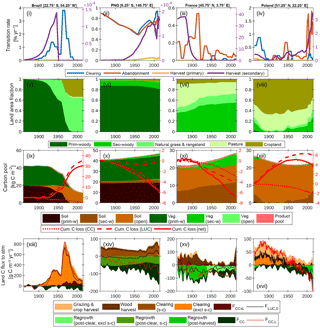
Figure 6Contrasting land use and land management for sample grid cells in Brazil, Papua New Guinea (PNG), France and Poland. (i)–(iv) Land area transition rates: clearing (p → g + s → g), abandonment (g → s), primary forest harvest (p → s) and secondary forest harvest; (v)–(viii) land cover fractions; (ix)–(xii) vegetation stocks in soil (including litter), vegetation and product pools, cumulative total carbon loss to the atmosphere from combined climate–CO2 (CC) effects, land use change and land management, and the net effect of all drivers together; (xiii)–(xvi) net land–atmosphere carbon flux (FCC, L) and its components. Positive components are the contributions from land use change and land management. “Grazing & crop harvest” refers to the net carbon flux associated with these activities, as derived by subtraction of net fluxes simulated with and without grazing and crop management. Wood harvest and clearing include legacy emissions and decay of product pools. Clearing and regrowth fluxes associated with shifting cultivation (s-c) are resolved from fluxes not associated with s-c. Regrowth on secondary forest land is resolved from legacy effects of past land use by differencing simulated net ecosystem production on secondary forest tiles, as simulated under scenarios of harvest and clearing residues being extracted to product pools versus residues left as litter. A 5-year smoothing is applied for clarity.
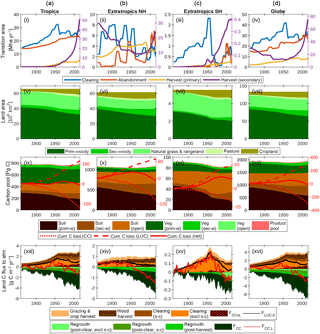
Figure 7The global terrestrial carbon balance (1860–2016) and its partitioning, as influenced by LUC, land management, CO2 and climate. Columns refer to (a) the tropics (−30 to 30∘), (b) extratropics of the Northern Hemisphere (NH; >30∘), (c) extratropics of the Southern Hemisphere (SH; <30∘) and (d) the globe, excluding permanent ice. Rows refer to the same quantities as in Fig. 6. A 5-year smoothing is applied for clarity.
5.3.1 Brazil (Fig. 6, first column)
The land use history for this grid cell is dominated by the clearing of primary forest with peak clearing events in 1940 and 1960 corresponding to respective conversion to rangeland and cropland. The 1860 carbon stocks are partitioned approximately equally between soil and vegetation. Cumulative carbon loss of 30 kg C m−2 is dominated by the vegetation carbon stock lost, with additional loss of soil carbon following conversion of forest to cropland, and is only marginally offset by net carbon gains due to differences in the effects of climate and CO2 drivers on the actual versus baseline land use. The land–atmosphere flux components indicate that the interaction flux (dominated by the loss of additional sink capacity) largely cancels FCC when all forest has been cleared. As such, the net flux (FCC, L) closely tracks FLUC, 0.
5.3.2 Papua New Guinea (Fig. 6, second column)
The land use history is dominated by shifting cultivation (s → c): secondary forest clearing and abandonment track each other closely for the whole time series. There is also additional non-s → c clearing and harvest post-1950. This leads to land area fractions that are largely constant, except for a small decrease in primary forest area post-1950 and the associated expansion of cropland and secondary forest area. Similar to the Brazil example, 1860 carbon stocks are partitioned approximately equally between soil and vegetation. The total carbon stock, particularly carbon in primary forest vegetation, increases over the time series because of cumulative carbon uptake in response to the combined effects of CO2 and climate. Land use change emissions from shifting cultivation are close to zero since emissions from s-c clearing are approximately balanced by regrowth. As such the net flux FCC, L closely tracks FCC, with small additional contributions from agricultural management and wood harvest.
5.3.3 France (Fig. 6, third column)
There is no primary forest. Land use activity is dominated by secondary forest harvest pre-1920 and the abandonment of pasture. The cessation of harvest leads to significant carbon accumulation in secondary forest vegetation post-1920. Of the total carbon accumulation since 1860 (7 kg C m−2), 4 kg C m−2 is attributable directly to LUC (first from forest regrowth post-harvest pre-1940 and then from regrowth post-abandonment post-1940) and the remainder to CO2–climate effects.
5.3.4 Poland (Fig. 6, fourth column)
This is a landscape dominated by agricultural activity. All secondary forest is cleared by 1900; however, the abandonment of cropland post-1945 leads to an expansion of secondary forest land. Carbon stocks in vegetation are very low because of secondary forest harvest. Soil carbon in open land is depleted because of cropland management (tillage and removal of biomass). The cumulative carbon loss from 1860 is 4 kg C m−2, and this is dominated by the direct effect of LUC. At the beginning of the time series, emissions to the atmosphere are dominated by contributions from cropland management and forest clearing (including legacy effects). From 1980, the land is a sink because carbon uptake by forest regrowth post-harvest and CO2–climate effects outweigh gross LUC emissions.
5.4 Land use change and forest change: global implications
Figure 7 shows the combined impacts of changing climate, CO2 and land use on the global terrestrial carbon cycle and three broad latitudinal bands in which land use activities have affected the trajectory of the net land carbon sink very differently: the tropics (−30 to 30∘), extratropics of the Northern Hemisphere (NH; >30∘), and extratropics of the Southern Hemisphere (SH; <30∘).
5.4.1 Tropics (Fig. 7, first column)
The net effect of clearing and abandonment has been a decline in forest area of 6.7×106 km2 since 1860, with clearing emissions peaking in 1954. Forest harvest (degradation) has also been a feature since 1950 and has accelerated steeply in recent decades. Cumulative sources and sinks are approximately equal, yielding negligible change in carbon stocks since 1860. Shifting cultivation (s → c) is a key feature of land use: it is useful to resolve the s → c components of the clearing and abandonment fluxes since these approximately cancel each other. The interaction flux FCC × L, which is dominated by the loss of additional sink capacity, contributes 30 Pg C to the total cumulative loss of carbon by land use change (176 Pg C since 1860).
5.4.2 Extratropics NH (Fig. 7, second column)
Forest area has declined by 3.3×106 km2 since 1860. Although the loss of primary forest areas (9.3×106 km2) is similar to tropical primary forest loss (9.6×106 km2), cumulative carbon loss from LUC is much less (92.4 Pg C) because primary vegetation carbon stocks are smaller, and those lost have been largely replaced by regrowth. Net emissions became negative (i.e. net carbon sink) in 1954, and the increasing sink trend is dominated by the effects of CO2 fertilisation and lengthening growing season, with net LUC emissions approximately constant and very close to zero in recent decades.
5.4.3 Extratropics SH (Fig. 7, third column)
This region has been subject to particularly aggressive deforestation, with 1.0×106 km2 (or one-third) of primary forest lost since 1860. Deforestation peaked and declined rapidly in 1953 and was succeeded by a period of increasing forest harvest. In contrast to the other regions, cumulative carbon loss since 1860 (7 Pg C) is a significant fraction (8 %) of the 1860 carbon stocks. The region has been a sink in recent decades due to the combined effects of CO2 fertilisation and agricultural abandonment.
5.4.4 The globe (Fig. 7, fourth column)
Global primary forest area has decreased by 20.0×106 km2, while secondary forest area has increased by 9.3×106 km2 since 1860. Cumulative LUC emissions are 287 Pg C since 1860 (243 Pg C in the absence of interactions between CO2–climate and LUC drivers) and have been counteracted by a cumulative CO2–climate-driven sink of 305 Pg C. Cumulative LUC emissions in the absence of interactions between CO2–climate and LUC drivers are 243 Pg C, and this is comparable with the BLUE bookkeeping model (261 Pg C, 1850–2005; Hansis et al., 2015) and is within the range of recent estimates (171–295 Pg C) by other models that account for gross land use transitions, as compiled by Hansis et al. (2015).
LUC emissions have been declining steadily since 1960 (albeit with a slight upturn since 2005), while the CO2–climate-driven sink is increasing rapidly and dominates the trend in the net flux. The simulated present-day (2012–2016 mean) global land–atmosphere flux of −2.2 Pg C year−1 is the balance between sources (4.1 Pg C year−1) and sinks (−6.3 Pg C year−1). Sources comprise the following: FCC × L (0.80), including loss of additional sink capacity FLASC (0.51); clearing excluding s → c (1.12); clearing s → c (0.59); wood harvest (1.20); and crop and pasture management (0.40). Sinks comprise post-clearing regrowth excluding s → c (−0.38), post-clearing regrowth (s → c; −0.55), post-harvest regrowth (−0.87) and FCC (−4.52).
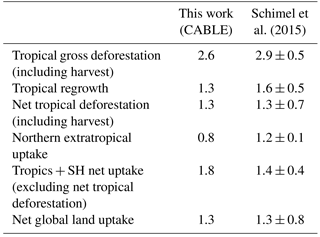
Table 3The net land carbon sink (Pg C year−1; 1990–2007) and its partitioning, as estimated by CABLE, and a synthesis using a combination of top-down and bottom-up constraints (Schimel et al., 2015).
While the FCC term dominates the sink, no sink or source term is negligible, and the FCC × L term (itself dominated by the loss of additional sink capacity) is large, pointing to the need to model the effects of land use, climate and CO2 on terrestrial carbon stocks explicitly and simultaneously, as we have done here.
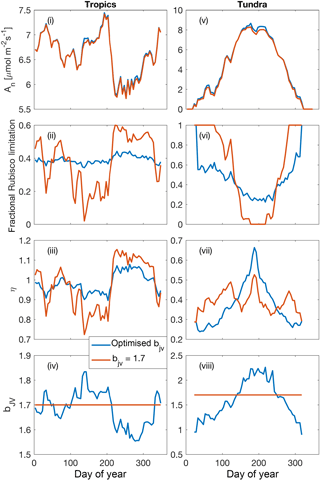
Figure 8Illustrative simulations of net photosynthesis, fractional Rubisco limitation, elasticity of net photosynthesis with respect to surface (CO2) and for shaded leaves in a tropical forest environment (2.25∘ S, 63.2∘ E) (i)–(iv) and a tundra environment (61.75∘ N, 75.75∘ W) (v)–(viii) aggregated over 5-day periods. Simulations were performed under assumptions of dynamically optimised and fixed bJV for a 365-day period (1990 meteorology, 400 ppm CO2).
Table 3 shows that CABLE's partitioning of the net land–carbon sink between the tropics and NH extratropics accords well with a recent synthesis by Schimel et al. (2015), which utilised atmospheric inversion data (selected according to assessment against aircraft vertical profile observations), biomass inventory data and an ensemble of model estimates of global land carbon uptake in response to rising CO2. Both estimates agree that the strong CO2-driven sink in the tropics is largely cancelled by net deforestation emissions, leaving the NH extratropics as the region contributing most to the net land sink, a result also supported by top-down estimates from CarbonTracker Europe (van der Laan-Luijkx et al., 2017). Note, however, a stronger tropical CO2 fertilisation effect in CABLE than estimated by Schimel et al. (2015). CABLE's high simulated CO2 fertilisation effect in tropical forests is consistent with growth rates in mature forests in Amazonia (Brienen et al., 2015; see also Sect. 5.2).
5.5 Coordination of leaf photosynthesis: illustrative examples
The effect of dynamically optimising the ratio of Jmax to Vcmax (bJV), compared with a fixed value of bJV=1.7 (Walker et al., 2014), over the course of 1 year for shaded leaves in two contrasting biomes (tropical forest and tundra) is presented in Fig. 8. While optimising bJV only slightly increases net photosynthesis, it significantly reduces variability in the fraction of Rubisco limitation compared with the assumption of fixed bJV. Periods of near-exclusive electron transport limitation (fractional Rubisco limitation close to zero) are avoided when bJV is optimised. Critical to the CO2 fertilisation effect on photosynthesis, this affects the sensitivity of net photosynthesis with respect to cs because the electron-transport-limited rate is less sensitive to cs than the Rubisco-limited rate. The proportional change in An per proportional change in cs is demonstrated using the dimensionless elasticity variable η (Fig. 8iii and vii).
Low values of elasticity occur when electron transport limitation dominates.
In the tropics, the dynamic values of bJV reflect a higher investment of nitrogen in Vcmax in the dry season (around days 200–300) when absorbed irradiance is higher, whereas in the tundra, higher investment in Jmax occurs at the height of the growing season because of the different temperature responses of Jmax and Vcmax. Overall, the effect of dynamically optimising bJV is to make electron-transport- and Rubisco-limited rates approximately co-limiting, in agreement with experimental evidence (Maire et al., 2012). The effect of increasing cs is to increase the allocation of leaf nitrogen to Jmax, resulting in reduced Vcmax . At constant Neff, the magnitude of the reduction is 10.4 % (Tropics) and 12.9 % (tundra) for an increase in cs from 366 to 567 ppm, in good agreement with CO2 acclimation effects on Vcmax inferred from Free-Air CO2 Enrichment studies (∼10 % reduction for an increase in ca from 366 to 567 ppm; Ainsworth and Rogers, 2007).
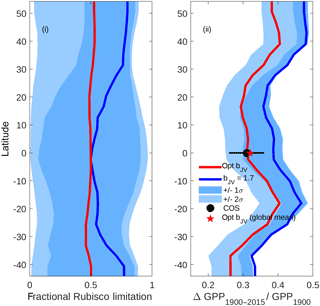
Figure 9Latitudinal profiles of (i) fractional Rubisco-limited photosynthesis (1980–2015) and (ii) the increase in gross primary production (GPP) relative to 1900 values. Simulations were performed under assumptions of dynamically optimised (red) and fixed bJV=1.7 (blue). For computational efficiency, profiles are based on a sample of 1000 randomly distributed grid cells across the global ice-free land surface. The limits of the blue shaded areas represent the results of simulations performed with fixed (dark shading) and (light shading), with lower limits corresponding to lower fractional Rubisco limitation and lower increase in GPP. In (ii), the COS value represents the trend in global GPP inferred from the carbonyl sulfide tracer (Campbell et al., 2017).
5.6 Dynamic optimisation of bJV: implications for centennial trend in global photosynthesis
The impacts of optimising bJV on fractional Rubisco limitation and centennial increase in global GPP are shown in Fig. 9. Simulations using a fixed value of bJV=1.7 (solid blue line), (limits of dark shading) and (limits of light shading) reveal that a static value of bJV translates to highly unpredictable fractional Rubisco limitation with possible values covering almost the full range from 0 to 1 at every latitude. In contrast, the fractional Rubisco limitation that is simulated when bJV is dynamically optimised has a value that is approximately 0.5 (corresponding to co-limitation) at all latitudes. Poor prediction of the fraction of Rubisco limitation under the assumption of fixed bJV translates to a wide range of GPP increase (1900–2015) relative to values in 1900, with simulated relative increases spanning a range of ∼0.2 at most latitudes. Dynamic optimisation of bJV results in predictions of centennial increase in GPP that are in good agreement with a recent estimate that uses atmospheric carbonyl sulfide (COS; Campbell et al., 2017) as a constraint.
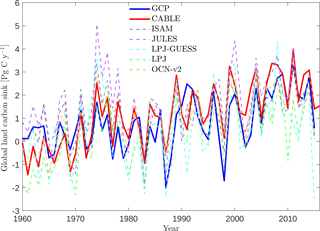
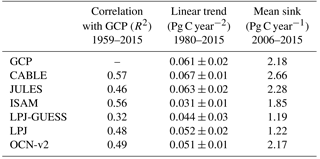
Table 4Simulated annual time series of the global land carbon sink: correlation with GCP, linear trend and mean sink.
5.7 The global net land carbon sink
Key functions of global terrestrial biosphere models such as CABLE are the attribution and projection of the global net land carbon sink. Therefore we assess CABLE predictions against observation-based estimates of this important quantity. Figure 10 depicts simulated annual times series of the global land carbon sink from CABLE and the corresponding Global Carbon Project (GCP) estimate, diagnosed as the sum of atmosphere and ocean sinks minus fossil fuel emissions (Le Quéré et al., 2016). Of the 14 land models represented in the GCP's 2016 assessment of the global carbon budget (Le Quéré et al., 2016), the five contributing simulations of the net land carbon sink (as opposed to the residual land sink, equivalent to the net land sink plus net LUC emissions, represented by all land models) are also shown in Fig. 10. For each model, the correlation of annual values with GCP estimates (1959–2015), trend (1980–2015) and magnitude (2006–2015) is quantified in Table 4. Uncertainty on the GCP estimates is 0.4 Pg C year−1 (Le Quéré et al., 2016). CABLE captures 57% of the variance in the annual sink, simulates a trend that is very similar to the GCP estimate (0.067 Pg C year−2 vs. 0.061 Pg C year−2) and simulates a mean sink for the 2006–2015 period that is 0.5 Pg C year−1 higher than GCP (2.7 Pg C year−1 vs. 2.2 Pg C year−1). One contribution to this discrepancy could be that the area of tropical forest degradation (p → s or secondary forest harvest) may be under-estimated in the LUH2 forcing dataset. In particular, CABLE simulations for the present day (2012–2016) indicate that forest degradation (secondary harvest) contributes 33 % to gross carbon losses from harvest and clearing tropical forests (Fig. 8iii) compared with 69 % (including forest disturbances such as fire) suggested by a recent remote sensing-based estimate by Baccini et al. (2017).
CABLE captures a high proportion of the variance in the GCP estimate relative to the other models in Table 4. This is in part attributable to its relatively good representation of the 1973–1974 and 1975–1976 positive anomalies corresponding to very strong La Niña events. Moisture sensitivities of both productivity and decomposition are important for capturing the response of the net flux to such events: in particular the high temporal correlation of heterotrophic respiration with NPP in water-limited environments reduces the response of the net flux compared with the response of NPP (Haverd et al., 2016c).
In contrast, CABLE under-predicts large negative anomalies corresponding to 1987–1988 and 1997–1998 El Niño events. Possible explanations are that wildfire is not represented, and the simulated drought response of tropical forests may be too weak.
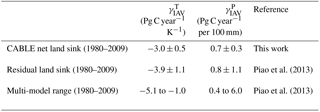
Carbon–climate sensitivity
We evaluate the global land carbon–climate sensitivity, following the analysis by Piao et al. (2013), of 10 terrestrial biosphere models. A linear model relates anomalies in the annual detrended land carbon sink (ysink) to anomalies in annual detrended temperature (xT) and precipitation (xP) with an error term ε.
Equation (18) was fitted to CABLE-simulated annual anomalies in net carbon uptake. Results are given in Table 5 and show good agreement with analysis of the residual land sink by Piao et al. (2013). Note that the residual land sink (equivalent to the net land sink plus net LUC emissions) is expected to have very similar interannual variations to the net land sink.
We have presented CABLE model developments that improve its applicability as a terrestrial biosphere model for use within an Earth system model and in stand-alone applications to attribute trends and variability in the terrestrial carbon cycle to regions, processes and drivers. Model evaluation has shown that the new model version satisfies several key observational constraints: (i) trend and interannual variations in the global land carbon sink, including sensitivities of interannual variations to global precipitation and temperature anomalies; (ii) centennial trends in global GPP; (iii) coordination of Rubisco-limited and electron-transport-limited photosynthesis; (iv) spatial distributions of global ET, GPP, biomass and soil carbon; and (v) secondary forest rates of biomass accumulation in boreal, temperate and tropical forests.
Model evaluation highlighted a few discrepancies that warrant further investigation: (i) under-prediction of ET in tropical forests in Amazonia; (ii) over-prediction of GPP in SH temperate evergreen broadleaf forests; and (iii) under-prediction of large negative anomalies in the global land carbon sink corresponding to 1987–1988 and 1997–1998 El Niño events.
Further work on the model configuration presented here should include formal benchmarking in the International Land Model Benchmarking Project framework (Hoffman et al., 2017) and model–data fusion (Trudinger et al., 2016). The latter would aim to quantify data constraints on the regional and process attribution of the global land carbon sink using multiple parameter sets that are consistent with the observations, in the same way that Trudinger et al. (2016) did for the Australian region. Data for this task would comprise observation-based constraints presented in this work extended, for example, to include remotely sensed vegetation cover.
Priorities for further process enhancement are (i) wildfire impacts on vegetation and related emissions, (ii) explicit cropland management, (iii) dynamic biogeography and PFT interactions, and (iv) dynamic allocation of carbon that optimises plant fitness.
The source code for CABLE, including revision number 4601 (Haverd et al., 2017; Kowalczyk et al., 2006), can be accessed after registration at https://trac.nci.org.au/trac/cable (last access: 26 September 2017).
A1 CABLE pseudo-code
A2 Additional model updates
Additional model updates include the following: (i) drought and summergreen phenology (Sitch et al., 2003; Sykes et al., 1996); (ii) low-temperature reductions in photosynthetic rates in boreal forests (Bergh et al., 1998); (iii) photoinhibition of leaf day respiration (Clark et al., 2011); and (iv) acclimation of autotrophic respiration (Atkin et al., 2016). These are described below.
A2.1 Drought and summergreen phenology
Prior CABLE predicts phenology based on an annual climatology of remotely sensed vegetation cover. This precludes simulating the effects of interannual variations and trends in phenology on the terrestrial carbon and water cycles and land–atmosphere exchange. We addressed this deficiency by implementing drought and summergreen phenology following the LPJ model (Sitch et al., 2003), with extensions to account for chilling requirements of bud burst (Sykes et al., 1996).
Summergreen phenology applies to deciduous forest types (deciduous needle-leaf and deciduous broadleaf; Table 1) and C3 grass when its growth is temperature limited. Leaf onset occurs when growing degree days referenced to 5 ∘C (GDD) exceed growing degree days to bud burst (GDD0). GDD0 is assumed to decline exponentially with the length of chilling period (number of days with mean temperature between 0 and 5 ∘C). This relationship represents an adaptation to weather variability: green-up is delayed long enough to minimise the risk that emerging buds will be damaged by frost. The green-up phase ends when GDD–GDD0 exceeds a threshold (set to 200 degree days). The onset of senescence occurs after a fixed period (200 days) of growth.
Raingreen phenology applies to C3 and C4 grass when they are water limited. No raingreen woody PFTs are represented in CABLE. We define “growing moisture days” (GMD) as the number of consecutive days when an indicator of plant-available soil moisture (fw, soil, Eq. 9) exceeds a threshold (set to 0.3). The green-up phase begins when GMD is greater than zero and ends when GMD exceeds a threshold (set to 21 days). Senescence begins when GMD becomes zero.
For both summergreen and raingreen phenology, green-up translates to high allocation of NPP to leaves. Leaf turnover rate is set to zero outside of the senescence period, when turnover time is set to 4 weeks.
A2.2 Low-temperature effects on boreal forest photosynthesis
Three processes that contribute to the low-temperature reduction of photosynthesis in boreal conifer forests are the following: (i) reduction caused by frozen soils; and (ii) incomplete recovery of photosynthetic capacity during spring; (iii) frost-induced autumn decline. The first effect is largely accounted for in Prior CABLE, because soil moisture limitation on stomatal conductance (Eq. 9) depends on liquid water content, meaning that soil freezing induces soil moisture limitation. Our treatment of the other two processes follows that of Bergh et al. (1998). The rate of post-winter recovery of Vcmax, 0 is held proportional to a degree-day sum referenced to 0 ∘C. Recovery is suspended for 2 days following a frost event, while a severe frost ( ∘C) also reduces Vcmax, 0. Autumn decline of Vcmax, 0 is simulated by assuming that severe frost nights reduce it progressively and irreversibly until it reaches a “dormancy” level at which it remains until the onset of spring recovery.
A2.3 Photoinhibition of leaf day respiration
In Prior CABLE, the rate of leaf respiration at standard temperature is assumed the same day and night. However, many studies have shown that at a given temperature the rate of leaf respiration in daylight is less than that in darkness (Brooks and Farquhar, 1985; Hoefnagel et al., 1998; Atkin et al., 1998, 2000). To account for this, we implement the inhibition of leaf respiration by light, as demonstrated by Brooks and Farquhar (1985), implemented by Lloyd et al. (1995) and successfully tested in the JULES land surface model for an Amazonian rainforest site by Mercado et al. (2007) and globally by Clark et al. (2011). The light-dependent non-photorespiratory leaf respiration (Rl) is thus
where I0 is the flux of incoming radiation at the top of the canopy (µmol quanta m−2 s−1) and Rd is the dark leaf respiration rate.
A2.4 Acclimation of autotrophic respiration
Prior CABLE assumes a fixed PFT-dependent value of leaf respiration at standard temperature (25 ∘C), an assumption which may lead to exaggerated latitudinal gradients in leaf respiration rates, as well as exaggerated trends in leaf respiration as global warming occurs. This is because, with sustained changes in the prevailing ambient growth temperature, leaf dark respiration (Rd, µmol m−2 s−1) acclimates to the new conditions, resulting in higher rates of Rd in cold-acclimated plants (Atkin et al., 2016, and references therein). To capture such acclimation effects, we utilise the synthesis of leaf dark respiration rates by Atkin et al. (2016) to parameterise the temperature dependence of leaf respiration at a standard temperature of 25 ∘C (Rd, 25). We then apply the same temperature acclimation response to root and stem maintenance respiration rates. Specifically, we use the linear model relating Rd, 25 to Vcmax, 25 and temperature of the warmest quarter (TWQ), here the mean temperature of the warmest 3-month period during the preceding calendar year.
In Eq. (A2), c1–c3 are taken from Atkin et al. (2016; Table S4) and c4 is an additional scaling parameter of order 1, introduced in this work with values of 0.9 (evergreen broadleaf), 1.0 (deciduous broadleaf), 1.0 (evergreen needle-leaf), 1.0 (deciduous needle-leaf), 0.8 (c3 grass) and 0.7 (other).
For consistency with Atkin et al. (2016), we adopt the “variable Q10” instantaneous temperature response of Rd (Tjoelker et al., 2001).
In the absence of data to inform a general formulation of the temperature acclimation responses of sapwood and fine-root maintenance respiration, we formulate them to be consistent with leaf temperature acclimation, but proportional to the nitrogen content of the respective compartment:
where c5 is a PFT-dependent scaling factor, and is the value of Vcmax, 0 obtained with maximum values of leaf N ∕ C and P ∕ C such that variations in leaf stoichiometry do not affect sapwood and root respiration. As in Prior CABLE, the instantaneous temperature response of Lloyd and Taylor (1994) is assumed.
A3 CABLE parameters and temperature response functions for photosynthesis used in this work
Table A1CABLE biophysics and CASA-CNP biogeochemistry parameters for evergreen needle-leaf (ENL), evergreen broadleaf (EBL), deciduous needle-leaf (DNL), deciduous broadleaf (DBL), shrub, C3 grass, C4 grass and tundra plant functional types.
a Quantum yield for electron transport (C3 plants)
or carboxylation (C4 plants).
b C4 photosynthesis follows Collatz et al. (1992).
Vcmax, 0 set to 10 µmol m−2 s−1;
.
c Higher value for tropical evergreen broadleaf.
d Applied to relationship between Vcmax, leaf N and leaf
P (Walker et al., 2014, Table 3, Model 1).
e For both summergreen and raingreen phenology, leaf turnover
rate is set to zero outside of the senescence period when turnover time is
set to 4 weeks.
f For both summergreen and raingreen phenology, green-up
translates to high (0.95) allocation of NPP to leaves, with allocation to
roots correspondingly reduced.
g Set arbitrarily high for woody PFTs to allow LAI to be controlled
by pipe model allocation constraint (to maintain prescribed leaf area to
sapwood area ratio).
VH and BS conceived, designed and performed the analysis. VH and LN coded the developments. LN, WW, CMT, MC and JGC contributed to the analysis. MC formulated the elasticity diagnostic. PRB collected and prepared the model inputs. VH drafted the paper, which all co-authors commented on and edited.
The authors declare that they have no conflict of interest.
Vanessa Haverd, Cathy M. Trudinger, Peter R. Briggs and Josep G. Canadell acknowledge support from the Earth Systems and Climate
Change Hub funded by the Australian Government's National Environmental
Science Program. The contributions of Benjamin Smith to this work were supported by the
Strategic Research Area MERGE and by a CSIRO Distinguished Visiting Science
grant. We thank Graham Farquhar for helpful discussions about the
optimisation-based approach to simulating plant coordination of
photosynthesis.
Edited by: Philippe Peylin
Reviewed by: two anonymous referees
Ainsworth, E. A. and Rogers, A.: The response of photosynthesis and stomatal conductance to rising [CO2]: mechanisms and environmental interactions, Plant, Cell Environ., 30, 258–270, 2007.
Ali, A. A., Xu, C., Rogers, A., Fisher, R. A., Wullschleger, S. D., Massoud, E. C., Vrugt, J. A., Muss, J. D., McDowell, N. G., Fisher, J. B., Reich, P. B., and Wilson, C. J.: A global scale mechanistic model of photosynthetic capacity (LUNA V1.0), Geosci. Model Dev., 9, 587–606, https://doi.org/10.5194/gmd-9-587-2016, 2016.
Arora, V. K., Boer, G. J., Friedlingstein, P., Eby, M., Jones, C. D., Christian, J. R., Bonan, G., Bopp, L., Brovkin, V., and Cadule, P.: Carbon–concentration and carbon–climate feedbacks in CMIP5 Earth system models, J. Climate, 26, 5289–5314, 2013.
Atkin, O. K., Evans, J. R., and Siebke, K.: Relationship between the inhibition of leaf respiration by light and enhancement of leaf dark respiration following light treatment, Aust. J. Plant Physiol., 25, 437–443, https://doi.org/10.1071/PP97159, 1998.
Atkin, O. K., Evans, J. R., Ball, M. C., Lambers, H., and Pons, T. L.: Leaf respiration of snow gum in the light and dark. Interactions between temperature and irradiance, Plant Physiol., 122, 915–924, https://doi.org/10.1104/pp.122.3.915, 2000.
Atkin, O., Bloomfield, K., Reich, P., Tjoelker, M., Asner, G., Bonal, D., Bonisch, G., Bradford, M., Cernusak, L., and Cosio, E.: Global variability in leaf respiration in relation to climate, plant functional types and leaf traits, New Phytol., 211, 1142–1142, 2016.
Avitabile, V., Herold, M., Heuvelink, G. B. M., Lewis, S. L., Phillips, O. L., Asner, G. P., Armston, J., Ashton, P. S., Banin, L., Bayol, N., Berry, N. J., Boeckx, P., de Jong, B. H. J., DeVries, B., Girardin, C. A. J., Kearsley, E., Lindsell, J. A., Lopez-Gonzalez, G., Lucas, R., Malhi, Y., Morel, A., Mitchard, E. T. A., Nagy, L., Qie, L., Quinones, M. J., Ryan, C. M., Ferry, S. J. W., Sunderland, T., Laurin, G. V., Gatti, R. C., Valentini, R., Verbeeck, H., Wijaya, A., and Willcock, S.: An integrated pan-tropical biomass map using multiple reference datasets, Glob. Change Biol., 22, 1406–1420, 2016.
Baccini, A., Goetz, S. J., Walker, W. S., Laporte, N. T., Sun, M., Sulla-Menashe, D., Hackler, J., Beck, P. S. A., Dubayah, R., Friedl, M. A., Samanta, S., and Houghton, R. A.: Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps, Nat. Clim. Change, 2, 182–185, 2012.
Baccini, A., Walker, W., Carvalho, L., Farina, M., Sulla-Menashe, D., and Houghton, R. A.: Tropical forests are a net carbon source based on aboveground measurements of gain and loss, Science, 358, 230–234, 2017.
Bartholomé, E. and Belward, A. S.: GLC2000: a new approach to global land cover mapping from Earth observation data, Int. J. Remote Sens., 26, 1959–1977, 2005.
Bergh, J., McMurtrie, R. E., and Linder, S.: Climatic factors controlling the productivity of Norway spruce: a model-based analysis, Forest Ecol. Manage., 110, 127–139, 1998.
Best, M. J., Abramowitz, G., Johnson, H. R., Pitman, A. J., Balsamo, G., Boone, A., Cuntz, M., Decharme, B., Dirmeyer, P. A., Dong, J., Ek, M., Guo, Z., Haverd, V., van den Hurk, B. J. J., Nearing, G. S., Pak, B., Peters-Lidard, C., Santanello, J. A., Stevens, L., and Vuichard, N.: The plumbing of land surface models: Benchmarking model performance, J. Hydrometeorol., 16, 1425–1442, 2015.
Brienen, R. J. W., Phillips, O. L., Feldpausch, T. R., Gloor, E., Baker, T. R., Lloyd, J., Lopez-Gonzalez, G., Monteagudo-Mendoza, A., Malhi, Y., Lewis, S. L., Vasquez Martinez, R., Alexiades, M., Alvarez Davila, E., Alvarez-Loayza, P., Andrade, A., Aragao, L. E. O. C., Araujo-Murakami, A., Arets, E. J. M. M., Arroyo, L., Aymard C, G. A., Banki, O. S., Baraloto, C., Barroso, J., Bonal, D., Boot, R. G. A., Camargo, J. L. C., Castilho, C. V., Chama, V., Chao, K. J., Chave, J., Comiskey, J. A., Cornejo Valverde, F., da Costa, L., de Oliveira, E. A., Di Fiore, A., Erwin, T. L., Fauset, S., Forsthofer, M., Galbraith, D. R., Grahame, E. S., Groot, N., Herault, B., Higuchi, N., Honorio Coronado, E. N., Keeling, H., Killeen, T. J., Laurance, W. F., Laurance, S., Licona, J., Magnussen, W. E., Marimon, B. S., Marimon-Junior, B. H., Mendoza, C., Neill, D. A., Nogueira, E. M., Nuñez, P., Pallqui Camacho, N. C., Parada, A., Pardo-Molina, G., Peacock, J., Pena-Claros, M., Pickavance, G. C., Pitman, N. C. A., Poorter, L., Prieto, A., Quesada, C. A., Ramirez, F., Ramirez-Angulo, H., Restrepo, Z., Roopsind, A., Rudas, A., Salomao, R. P., Schwarz, M., Silva, N., Silva-Espejo, J. E., Silveira, M., Stropp, J., Talbot, J., ter Steege, H., Teran-Aguilar, J., Terborgh, J., Thomas-Caesar, R., Toledo, M., Torello-Raventos, M., Umetsu, R. K., van der Heijden, G. M. F., van der Hout, P., Guimaraes Vieira, I. C., Vieira, S. A., Vilanova, E., Vos, V. A., and Zagt, R. J.: Long-term decline of the Amazon carbon sink, Nature, 519, 344–348, 2015.
Brooks, A. and Farquhar, G. D.: Effect of temperature on the CO2-O2 specificity of ribulose-1,5-biphosphate carboxylase/oxygenase and the rate of respiration in the light: estimates from gas exchange measurements on spinach, Planta, 165, 397–406, https://doi.org/10.1007/BF00392238, 1985.
Campbell, J. E., Berry, J. A., Seibt, U., Smith, S. J., Montzka, S. A., Launois, T., Belviso, S., Bopp, L., and Laine, M.: Large historical growth in global terrestrial gross primary production, Nature, 544, 84–87, 2017.
Cannell, M. G. R.: World Forest Biomass and Primary Production Data, Academic Press, London, UK, 391 pp., 1982.
Chen, J.-L., Reynolds, J. F., Harley, P. C., and Tenhunen, J. D.: Coordination theory of leaf nitrogen distribution in a canopy, Oecologia, 93, 63–69, 1993.
Clark, D. B., Mercado, L. M., Sitch, S., Jones, C. D., Gedney, N., Best, M. J., Pryor, M., Rooney, G. G., Essery, R. L. H., Blyth, E., Boucher, O., Harding, R. J., Huntingford, C., and Cox, P. M.: The Joint UK Land Environment Simulator (JULES), model description – Part 2: Carbon fluxes and vegetation dynamics, Geosci. Model Dev., 4, 701–722, https://doi.org/10.5194/gmd-4-701-2011, 2011.
Collatz, G., Ribas-Carbo, M., and Berry, J.: Coupled Photosynthesis-Stomatal Conductance Model for Leaves of C4 Plants, Funct. Plant Biol., 19, 519–538, 1992.
De Kauwe, M. G., Kala, J., Lin, Y.-S., Pitman, A. J., Medlyn, B. E., Duursma, R. A., Abramowitz, G., Wang, Y.-P., and Miralles, D. G.: A test of an optimal stomatal conductance scheme within the CABLE land surface model, Geosci. Model Dev., 8, 431–452, https://doi.org/10.5194/gmd-8-431-2015, 2015.
Decker, M.: Development and evaluation of a new soil moisture and runoff parameterization for the CABLE LSM including subgrid-scale processes, J. Adv. Model. Earth Sy., 7, 1788–1809, 2015.
Dlugokencky, E. and Tans, P.: Trends in atmospheric carbon dioxide, National Oceanic & Atmospheric Administration, Earth System Research Laboratory (NOAA/ESRL), available at: http://www.esrl.noaa.gov/gmd/ccgg/trends/global.html, last access: June 2017.
FAO/IIASA/ISRIC/ISSCAS/JRC: Harmonized World Soil Database (version 1.2). FAO, Rome, Italy and IIASA, Laxenburg, Austria, available at: http://www.fao.org/soils-portal/soil-survey/soil-maps-and-databases/harmonized-world-soil-database-v12/en/ (last access: 16 February 2016), 2009.
Farquhar, G. and Wong, S.: An Empirical Model of Stomatal Conductance, Funct. Plant Biol., 11, 191–210, 1984.
Farquhar, G. V., Caemmerer, S. V., and Berry, J.: A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species, Planta, 149, 78–90, 1980.
Friend, A. D., Lucht, W., Rademacher, T. T., Keribin, R., Betts, R., Cadule, P., Ciais, P., Clark, D. B., Dankers, R., Falloon, P. D., Ito, A., Kahana, R., Kleidon, A., Lomas, M. R., Nishina, K., Ostberg, S., Pavlick, R., Peylin, P., Schaphoff, S., Vuichard, N., Warszawski, L., Wiltshire, A., and Woodward, F. I.: Carbon residence time dominates uncertainty in terrestrial vegetation responses to future climate and atmospheric CO2, P. Natl. Acad. Sci. USA, 111, 3280–3285, 2014.
Goudriaan, J. and van Laar, H. H.: Modelling potential crop growth processes: textbook with exercises, Kluwer Academic Publishers, Dordrecht, 1994.
Hansis, E., Davis, S. J., and Pongratz, J.: Relevance of methodological choices for accounting of land use change carbon fluxes, Global Biogeochem. Cy., 29, 1230–1246, 2015.
Haverd, V., Lovell, J. L., Cuntz, M., Jupp, D. L. B., Newnham, G. J., and Sea, W.: The Canopy Semi-analytic Pgap And Radiative Transfer (CanSPART) model: Formulation and application, Agr. Forest Meteorol., 160, 14–35, 2012.
Haverd, V., Raupach, M. R., Briggs, P. R., Canadell, J. G., Isaac, P., Pickett-Heaps, C., Roxburgh, S. H., van Gorsel, E., Viscarra Rossel, R. A., and Wang, Z.: Multiple observation types reduce uncertainty in Australia's terrestrial carbon and water cycles, Biogeosciences, 10, 2011–2040, https://doi.org/10.5194/bg-10-2011-2013, 2013a.
Haverd, V., Smith, B., Cook, G., Briggs, P. R., Nieradzik, L., Roxburgh, S. R., Liedloff, A., Meyer, C. P., and Canadell, J. G.: A stand-alone tree demography and landscape structure module for Earth system models., Geophys. Res. Lett., 40, 1–6, 2013b.
Haverd, V., Smith, B., Cook, G. D., Briggs, P. R., Nieradzik, L., Roxburgh, S. H., Liedloff, A., Meyer, C. P., and Canadell, J. G.: A stand-alone tree demography and landscape structure module for Earth system models, Geophys. Res. Lett., 40, 5234–5239, 2013c.
Haverd, V., Smith, B., Nieradzik, L. P., and Briggs, P. R.: A stand-alone tree demography and landscape structure module for Earth system models: integration with inventory data from temperate and boreal forests, Biogeosciences, 11, 4039–4055, https://doi.org/10.5194/bg-11-4039-2014, 2014.
Haverd, V., Cuntz, M., Nieradzik, L. P., and Harman, I. N.: Improved representations of coupled soil–canopy processes in the CABLE land surface model (Subversion revision 3432), Geosci. Model Dev., 9, 3111–3122, https://doi.org/10.5194/gmd-9-3111-2016, 2016a.
Haverd, V., Smith, B., Raupach, M., Briggs, P., Nieradzik, L., Beringer, J., Hutley, L., Trudinger, C. M., and Cleverly, J.: Coupling carbon allocation with leaf and root phenology predicts tree–grass partitioning along a savanna rainfall gradient, Biogeosciences, 13, 761–779, https://doi.org/10.5194/bg-13-761-2016, 2016b.
Haverd, V., Smith, B., and Trudinger, C. M.: Process contributions of Australian ecosystems to interannual variations in the carbon cycle, Environ. Res. Lett., 11, 054013, https://doi.org/10.1088/1748-9326/11/5/054013, 2016c.
Haverd, V., Smith, B., Nieradzik, L., Briggs, P. R., Woodgate, W., Trudinger, C. M., Canadell, J. G., and Cuntz, M.: CABLE land surface model software (Subversion revision r4601, 26 September 2017), available at: https://trac.nci.org.au/trac/cable/log/branches/Users/vxh599/trunk_checks_extract_sli_optimise_JVratio_crop_harvest/core, 2017.
Hoefnagel, M. H. N., Atkin, O. K., and Wiskich, J. T.: Interdependence between chloroplasts and mitochondria in the light and the dark, Biochim. Biophys. Acta, 1366, 235–255, https://doi.org/10.1016/s0005-2728(98)00126-1, 1998.
Hoffman, F. M., Koven, C. D., Keppel-Aleks, G., Lawrence, D. M., Riley, W. J., Randerson, J. T., Ahlström, A., Abramowitz, G., Baldocchi, D. D., Best, M. J., Bond-Lamberty, B., De Kauwe, M. G., Denning, A. S., Desai, A. R., Eyring, V., Fisher, J. B., Fisher, R. A., Gleckler, P. J., Huang, M., Hugelius, G., Jain, A. K., Kiang, N. Y., Kim, H., Koster, R. D., Kumar, S. V., Li, H., Luo, Y., Mao, J., McDowell, N. G., Mishra, U., Moorcroft, P. R., Pau, G. S. H., Ricciuto, D. M., Schaefer, K., Schwalm, C. R., Serbin, S. P., Shevliakova, E., Slater, A. G., Tang, J., Williams, M., Xia, J., Xu, C., Joseph, R., and Koch, D.: 2016 International Land Model Benchmarking (ILAMB) Workshop Report, USDOE Office of Science, Washington, DC, USA, DOE/SC-0186, https://doi.org/10.2172/1330803, 2017.
Hurtt, G. C., Chini, L. P., Frolking, S., Betts, R. A., Feddema, J., Fischer, G., Fisk, J. P., Hibbard, K., Houghton, R. A., Janetos, A., Jones, C. D., Kindermann, G., Kinoshita, T., Klein Goldewijk, K., Riahi, K., Shevliakova, E., Smith, S., Stehfest, E., Thomson, A., Thornton, P., Vuuren, D. P., and Wang, Y. P.: Harmonization of land-use scenarios for the period 1500–2100: 600 years of global gridded annual land-use transitions, wood harvest, and resulting secondary lands, Clim. Change, 109, 117–161, 2011.
Hurtt, G. C., Chini, L., Frolking, S., and Sahajpal, R.: Land Use Harmonisation 2 (LUH2) v2h available at: http://luh.umd.edu/data.shtml (last access: June 2017) 2016.
IPCC: Climate Change 2014: Synthesis Report, Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Core Writing Team, Pachauri, R. K., and Meyer, L. A., IPCC, Geneva, Switzerland, 151 pp., 2014.
Jung, M., Reichstein, M., Ciais, P., Seneviratne, S. I., Sheffield, J., Goulden, M. L., Bonan, G., Cescatti, A., Chen, J., de Jeu, R., Dolman, A. J., Eugster, W., Gerten, D., Gianelle, D., Gobron, N., Heinke, J., Kimball, J., Law, B. E., Montagnani, L., Mu, Q., Mueller, B., Oleson, K., Papale, D., Richardson, A. D., Roupsard, O., Running, S., Tomelleri, E., Viovy, N., Weber, U., Williams, C., Wood, E., Zaehle, S., and Zhang, K.: Recent decline in the global land evapotranspiration trend due to limited moisture supply, Nature, 467, 951–954, 2010.
Kowalczyk, E., Wang, Y. P., Law, R. M., Davies, H. L., McGregor, J. L., and Abramowitz, G.: The CSIRO Atmosphere Biosphere Land Exchange (CABLE) model for use in climate models and as an offline model, 013, 42 pp., 2006.
Kowalczyk, E., Stevens, L., Law, R., Dix, M., Wang, Y., Harman, I., Haynes, K., Srbinovsky, J., Pak, B., and Ziehn, T.: The land surface model component of ACCESS: description and impact on the simulated surface climatology, Aust. Meteorol. Oceanogr. J., 63, 65–82, 2013.
Lamarque, J.-F., Kyle, G. P., Meinshausen, M., Riahi, K., Smith, S. J., van Vuuren, D. P., Conley, A. J., and Vitt, F.: Global and regional evolution of short-lived radiatively-active gases and aerosols in the Representative Concentration Pathways, Clim. Change, 109, 191, https://doi.org/10.1007/s10584-011-0155-0, 2011.
Law, R. M., Ziehn, T., Matear, R. J., Lenton, A., Chamberlain, M. A., Stevens, L. E., Wang, Y.-P., Srbinovsky, J., Bi, D., Yan, H., and Vohralik, P. F.: The carbon cycle in the Australian Community Climate and Earth System Simulator (ACCESS-ESM1) – Part 1: Model description and pre-industrial simulation, Geosci. Model Dev., 10, 2567–2590, https://doi.org/10.5194/gmd-10-2567-2017, 2017.
Lawrence, D. M., Hurtt, G. C., Arneth, A., Brovkin, V., Calvin, K. V., Jones, A. D., Jones, C. D., Lawrence, P. J., de Noblet-Ducoudré, N., Pongratz, J., Seneviratne, S. I., and Shevliakova, E.: The Land Use Model Intercomparison Project (LUMIP) contribution to CMIP6: rationale and experimental design, Geosci. Model Dev., 9, 2973–2998, https://doi.org/10.5194/gmd-9-2973-2016, 2016.
Lawrence, P. J., Feddema, J. J., Bonan, G. B., Meehl, G. A., O'Neill, B. C., Oleson, K. W., Levis, S., Lawrence, D. M., Kluzek, E., and Lindsay, K.: Simulating the biogeochemical and biogeophysical impacts of transient land cover change and wood harvest in the Community Climate System Model (CCSM4) from 1850 to 2100, J. Climate, 25, 3071–3095, 2012.
Le Quéré, C., Andrew, R. M., Canadell, J. G., Sitch, S., Korsbakken, J. I., Peters, G. P., Manning, A. C., Boden, T. A., Tans, P. P., Houghton, R. A., Keeling, R. F., Alin, S., Andrews, O. D., Anthoni, P., Barbero, L., Bopp, L., Chevallier, F., Chini, L. P., Ciais, P., Currie, K., Delire, C., Doney, S. C., Friedlingstein, P., Gkritzalis, T., Harris, I., Hauck, J., Haverd, V., Hoppema, M., Klein Goldewijk, K., Jain, A. K., Kato, E., Körtzinger, A., Landschützer, P., Lefèvre, N., Lenton, A., Lienert, S., Lombardozzi, D., Melton, J. R., Metzl, N., Millero, F., Monteiro, P. M. S., Munro, D. R., Nabel, J. E. M. S., Nakaoka, S.-I., O'Brien, K., Olsen, A., Omar, A. M., Ono, T., Pierrot, D., Poulter, B., Rödenbeck, C., Salisbury, J., Schuster, U., Schwinger, J., Séférian, R., Skjelvan, I., Stocker, B. D., Sutton, A. J., Takahashi, T., Tian, H., Tilbrook, B., van der Laan-Luijkx, I. T., van der Werf, G. R., Viovy, N., Walker, A. P., Wiltshire, A. J., and Zaehle, S.: Global Carbon Budget 2016, Earth Syst. Sci. Data, 8, 605–649, https://doi.org/10.5194/essd-8-605-2016, 2016.
Le Quéré, C., Andrew, R. M., Friedlingstein, P., Sitch, S., Pongratz, J., Manning, A. C., Korsbakken, J. I., Peters, G. P., Canadell, J. G., Jackson, R. B., Boden, T. A., Tans, P. P., Andrews, O. D., Arora, V. K., Bakker, D. C. E., Barbero, L., Becker, M., Betts, R. A., Bopp, L., Chevallier, F., Chini, L. P., Ciais, P., Cosca, C. E., Cross, J., Currie, K., Gasser, T., Harris, I., Hauck, J., Haverd, V., Houghton, R. A., Hunt, C. W., Hurtt, G., Ilyina, T., Jain, A. K., Kato, E., Kautz, M., Keeling, R. F., Klein Goldewijk, K., Körtzinger, A., Landschützer, P., Lefèvre, N., Lenton, A., Lienert, S., Lima, I., Lombardozzi, D., Metzl, N., Millero, F., Monteiro, P. M. S., Munro, D. R., Nabel, J. E. M. S., Nakaoka, S.-I., Nojiri, Y., Padin, X. A., Peregon, A., Pfeil, B., Pierrot, D., Poulter, B., Rehder, G., Reimer, J., Rödenbeck, C., Schwinger, J., Séférian, R., Skjelvan, I., Stocker, B. D., Tian, H., Tilbrook, B., Tubiello, F. N., van der Laan-Luijkx, I. T., van der Werf, G. R., van Heuven, S., Viovy, N., Vuichard, N., Walker, A. P., Watson, A. J., Wiltshire, A. J., Zaehle, S., and Zhu, D.: Global Carbon Budget 2017, Earth Syst. Sci. Data, 10, 405–448, https://doi.org/10.5194/essd-10-405-2018, 2018.
Leuning, R.: Modelling Stomatal Behaviour and Photosynthesis of Eucalyptus grandis, Funct. Plant Biol., 17, 159–175, 1990.
Leuning, R.: Temperature dependence of two parameters in a photosynthesis model, Plant, Cell Environ., 25, 1205–1210, 2002.
Lin, Y.-S., Medlyn, B. E., Duursma, R. A., Prentice, I. C., Wang, H., Baig, S., Eamus, D., de Dios, V. R., Mitchell, P., and Ellsworth, D. S.: Optimal stomatal behaviour around the world, Nat. Clim. Change, 5, 459–464, 2015.
Lindeskog, M., Arneth, A., Bondeau, A., Waha, K., Seaquist, J., Olin, S., and Smith, B.: Implications of accounting for land use in simulations of ecosystem carbon cycling in Africa, Earth Syst. Dynam., 4, 385–407, https://doi.org/10.5194/esd-4-385-2013, 2013.
Lloyd, J. and Taylor, J. A.: On the Temperature Dependence of Soil Respiration, Funct. Ecol., 8, 315–323, 1994.
Lloyd, J., Grace, J., Miranda, A. C., Meir, P., Wong, S. C., Miranda, H. S., Wright, I. R., Gash, J. H. C., and McIntyre J.: A simple calibrated model for Amazon rainforest productivity based on leaf biochemical properties, Plant Cell Environ., 18, 1129–1145, https://doi.org/10.1111/j.1365-3040.1995.tb00624.x, 1995.
Maire, V., Martre, P., Kattge, J., Gastal, F., Esser, G., Fontaine, S., and Soussana, J.-F.: The Coordination of Leaf Photosynthesis Links C and N Fluxes in C3 Plant Species, PLoS ONE, 7, e38345, https://doi.org/10.1371/journal.pone.0038345, 2012.
Massad, R., Tuzet, A., and Bethenod, O.: The effect of temperature on C4-type leaf photosynthesis parameters, Plant, Cell Environ., 30, 1191–1204, 2007.
Mercado, L. M., Huntingford, C., Gash, J. H. C., Cox, P. M., and Jogireddy, V.: Improving the representation of radiation interception and photosynthesis for climate model applications, Tellus B, 59, 553–565, 2007.
Mueller, B., Hirschi, M., Jimenez, C., Ciais, P., Dirmeyer, P. A., Dolman, A. J., Fisher, J. B., Jung, M., Ludwig, F., Maignan, F., Miralles, D. G., McCabe, M. F., Reichstein, M., Sheffield, J., Wang, K., Wood, E. F., Zhang, Y., and Seneviratne, S. I.: Benchmark products for land evapotranspiration: LandFlux-EVAL multi-data set synthesis, Hydrol. Earth Syst. Sci., 17, 3707–3720, https://doi.org/10.5194/hess-17-3707-2013, 2013.
Piao, S., Sitch, S., Ciais, P., Friedlingstein, P., Peylin, P., Wang, X., Ahlström, A., Anav, A., Canadell, J. G., Cong, N., Huntingford, C., Jung, M., Levis, S., Levy, P. E., Li, J., Lin, X., Lomas, M. R., Lu, M., Luo, Y., Ma, Y., Myneni, R. B., Poulter, B., Sun, Z., Wang, T., Viovy, N., Zaehle, S., and Zeng, N.: Evaluation of terrestrial carbon cycle models for their response to climate variability and to CO2 trends, Global Change Biol., 19, 2117–2132, 2013.
Poorter, H., Niklas, K. J., Reich, P. B., Oleksyn, J., Poot, P., and Mommer, L.: Biomass allocation to leaves, stems and roots: meta-analyses of interspecific variation and environmental control, New Phytol., 193, 30–50, 2012.
Poorter, L., Bongers, F., Aide, T. M., Almeyda Zambrano, A. M., Balvanera, P., Becknell, J. M., Boukili, V., Brancalion, P. H. S., Broadbent, E. N., Chazdon, R. L., Craven, D., de Almeida-Cortez, J. S., Cabral, G. A. L., de Jong, B. H. J., Denslow, J. S., Dent, D. H., DeWalt, S. J., Dupuy, J. M., Durán, S. M., Espírito-Santo, M. M., Fandino, M. C., César, R. G., Hall, J. S., Hernandez-Stefanoni, J. L., Jakovac, C. C., Junqueira, A. B., Kennard, D., Letcher, S. G., Licona, J.-C., Lohbeck, M., Marín-Spiotta, E., Martínez-Ramos, M., Massoca, P., Meave, J. A., Mesquita, R., Mora, F., Mu noz, R., Muscarella, R., Nunes, Y. R. F., Ochoa-Gaona, S., de Oliveira, A. A., Orihuela-Belmonte, E., Pe na-Claros, M., Pérez-García, E. A., Piotto, D., Powers, J. S., Rodríguez-Velázquez, J., Romero-Pérez, I. E., Ruíz, J., Saldarriaga, J. G., Sanchez-Azofeifa, A., Schwartz, N. B., Steininger, M. K., Swenson, N. G., Toledo, M., Uriarte, M., van Breugel, M., van der Wal, H., Veloso, M. D. M., Vester, H. F. M., Vicentini, A., Vieira, I. C. G., Bentos, T. V., Williamson, G. B., and Rozendaal, D. M. A.: Biomass resilience of Neotropical secondary forests, Nature, 530, 211–214, 2016.
Prentice, I. C., Cramer, W., Harrison, S. P., Leemans, R., Monserud, R. A., and Solomon, A. M.: Special Paper: A Global Biome Model Based on Plant Physiology and Dominance, Soil Properties and Climate, J. Biogeogr., 19, 117–134, 1992.
Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flannery, B. P.: Numerical Recipes in FORTRAN; The Art of Scientific Computing, Cambridge University Press, 1993.
Purves, D. and Pacala, S.: Predictive Models of Forest Dynamics, Science, 320, 1452–1453, 2008.
Raupach, M.: Simplified expressions for vegetation roughness length and zero-plane displacement as functions of canopy height and area index, Bound.-Lay. Meteorol., 71, 211–216, 1994.
Saatchi, S. S., Harris, N. L., Brown, S., Lefsky, M., Mitchard, E. T. A., Salas, W., Zutta, B. R., Buermann, W., Lewis, S. L., Hagen, S., Petrova, S., White, L., Silman, M., and Morel, A.: Benchmark map of forest carbon stocks in tropical regions across three continents, P. Natl. Acad. Sci. USA, 108, 9899–9904, 2011.
Santoro, M., Beaudoin, A., Beer, C., Cartus, O., Fransson, J. E. S., Hall, R. J., Pathe, C., Schmullius, C., Schepaschenko, D., Shvidenko, A., Thurner, M., and Wegmüller, U.: Forest growing stock volume of the northern hemisphere: Spatially explicit estimates for 2010 derived from Envisat ASAR, Remote Sens. Environ., 168, 316–334, 2015.
Schimel, D., Stephens, B. B., and Fisher, J. B.: Effect of increasing CO2 on the terrestrial carbon cycle, P. Natl. Acad. Sci. USA, 112, 436–441, 2015.
Shevliakova, E., Pacala, S. W., Malyshev, S., Hurtt, G. C., Milly, P. C. D., Caspersen, J. P., Sentman, L. T., Fisk, J. P., Wirth, C., and Crevoisier, C.: Carbon cycling under 300 years of land use change: Importance of the secondary vegetation sink, Global Biogeochem. Cy., 23, GB2022, https://doi.org/10.1029/2007GB003176, 2009.
Shinozaki, K., Yoda, K., Hozumi, K., and Kira, T.: A Quantitative Analysis of Plant Form – The Pipe Model Theory I. Basic Analyses, Jap. J. Ecol., 14, 97–105, 1964.
Sitch, S., Smith, B., Prentice, I. C., Arneth, A., Bondeau, A., Cramer, W., Kaplan, J., Levis, S., Lucht, W., and Sykes, M. T.: Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model, Glob. Change Biol., 9, 161–185, 2003.
Smith, B., Prentice, I. C., and Sykes, M. T.: Representation of vegetation dynamics in the modelling of terrestrial ecosystems: comparing two contrasting approaches within European climate space, Global Ecol. Biogeogr., 10, 621–637, 2001.
Smith, B., Wårlind, D., Arneth, A., Hickler, T., Leadley, P., Siltberg, J., and Zaehle, S.: Implications of incorporating N cycling and N limitations on primary production in an individual-based dynamic vegetation model, Biogeosciences, 11, 2027–2054, https://doi.org/10.5194/bg-11-2027-2014, 2014.
Stocker, B. D., Feissli, F., Strassmann, K. M., Spahni, R., and Joos, F.: Past and future carbon fluxes from land use change, shifting cultivation and wood harvest, Tellus B, 66, 23188, https://doi.org/10.3402/tellusb.v66.23188, 2014.
Sykes, M. T., Prentice, I. C., and Cramer, W.: A bioclimatic model for the potential distributions of north European tree species under present and future climates, J. Biogeogr., 23, 203–233, 1996.
Teobaldelli, M.: The Biomass Compartments Database, available at: http://afoludata.jrc.it/DS_Free/AF_Bio.cfm (last access: 2014), 2008.
Teobaldelli, M., Somogyi, Z., Migliavacca, M., and Usoltsev, V. A.: Generalized functions of biomass expansion factors for conifers and broadleaved by stand age, growing stock and site index, For. Ecol. Manag., 257, 3, 1004–1013,https://doi.org/10.1016/j.foreco.2008.11.002, 2009.
Tjoelker, M. G., Oleksyn, J., and Reich, P. B.: Modelling respiration of vegetation: Evidence for a general temperature-dependent Q10, Glob. Change Biol., 7, 223–230, 2001.
Trudinger, C. M., Haverd, V., Briggs, P. R., and Canadell, J. G.: Interannual variability in Australia's terrestrial carbon cycle constrained by multiple observation types, Biogeosciences, 13, 6363–6383, https://doi.org/10.5194/bg-13-6363-2016, 2016.
Usoltsev, V. A.: Forest biomass of northern Eurasia: database and geography, Russian Academy of Sciences, Ural Branch, Yekarinenburg, 2001.
van der Laan-Luijkx, I. T., van der Velde, I. R., van der Veen, E., Tsuruta, A., Stanislawska, K., Babenhauserheide, A., Zhang, H. F., Liu, Y., He, W., Chen, H., Masarie, K. A., Krol, M. C., and Peters, W.: The CarbonTracker Data Assimilation Shell (CTDAS) v1.0: implementation and global carbon balance 2001–2015, Geosci. Model Dev., 10, 2785–2800, https://doi.org/10.5194/gmd-10-2785-2017, 2017.
Viovy, N.: CRUNCEP Version 7 – Atmospheric Forcing Data for the Community Land Model, available at: ftp://nacp.ornl.gov/synthesis/2009/frescati/temp/land_use_change/original/readme.htm, last access: 24 May 2016.
Viscarra Rossel, R. A., Webster, R., Bui, E. N., and Baldock, J. A.: Baseline map of organic carbon in Australian soil to support national carbon accounting and monitoring under climate change, Glob. Change Biol., 20, 2953–2970, 2014.
Walker, A. P., Beckerman, A. P., Gu, L., Kattge, J., Cernusak, L. A., Domingues, T. F., Scales, J. C., Wohlfahrt, G., Wullschleger, S. D., and Woodward, F. I.: The relationship of leaf photosynthetic traits – Vcmax and Jmax – to leaf nitrogen, leaf phosphorus, and specific leaf area: a meta-analysis and modeling study, Ecol. Evol., 4, 3218–3235, 2014.
Wang, H., Prentice, I. C., Keenan, T. F., Davis, T. W., Wright, I. J., Cornwell, W. K., Evans, B. J., and Peng, C.: Towards a universal model for carbon dioxide uptake by plants, Nat. Plants, 3, 734–741, 2017.
Wang, Y.-P. and Leuning, R.: A two-leaf model for canopy conductance, photosynthesis and partitioning of available energy I: Model description and comparison with a multi-layered model, Agr. Forest Meteorol., 91, 89–111, 1998.
Wang, Y. P., Law, R. M., and Pak, B.: A global model of carbon, nitrogen and phosphorus cycles for the terrestrial biosphere, Biogeosciences, 7, 2261–2282, https://doi.org/10.5194/bg-7-2261-2010, 2010.
Wang, Y. P., Kowalczyk, E., Leuning, R., Abramowitz, G., Raupach, M. R., Pak, B., van Gorsel, E., and Luhar, A.: Diagnosing errors in a land surface model (CABLE) in the time and frequency domains, J. Geophys. Res., 116, G01034, https://doi.org/10.1029/2010JG001385, 2011.
Wilkenskjeld, S., Kloster, S., Pongratz, J., Raddatz, T., and Reick, C. H.: Comparing the influence of net and gross anthropogenic land-use and land-cover changes on the carbon cycle in the MPI-ESM, Biogeosciences, 11, 4817–4828, https://doi.org/10.5194/bg-11-4817-2014, 2014.
Wolf, A., Ciais, P., Bellassen, V., Delbart, N., Field, C. B., and Berry, J. A.: Forest biomass allometry in global land surface models, Global Biogeochem. Cy., 25, GB3015, https://doi.org/10.1029/2010gb003917, 2011.
Xia, J. Y., Luo, Y. Q., Wang, Y.-P., Weng, E. S., and Hararuk, O.: A semi-analytical solution to accelerate spin-up of a coupled carbon and nitrogen land model to steady state, Geosci. Model Dev., 5, 1259–1271, https://doi.org/10.5194/gmd-5-1259-2012, 2012.
Xu, C., Fisher, R., Wullschleger, S. D., Wilson, C. J., Cai, M., and McDowell, N. G.: Toward a Mechanistic Modeling of Nitrogen Limitation on Vegetation Dynamics, PLoS ONE, 7, e37914, https://doi.org/10.1371/journal.pone.0037914, 2012.
Zhang, H., Pak, B., Wang, Y. P., Zhou, X., Zhang, Y., and Zhang, L.: Evaluating surface water cycle simulated by the Australian community land surface model (CABLE) across different spatial and temporal domains, J. Hydrometeorol., 14, 1119–1138, https://doi.org/10.1175/JHM-D-12-0123.1, 2013.
Zhou, X. Y., Zhang, Y. Q., Wang, Y. P., Zhang, H. Q., Zhang, L., Vaze, J., Yang, Y. H., and Zhou, Y. C.: Benchmarking global land surface models against the observed mean annual runoff from 150 large basins, J. Hydrol., 470, 269–279, https://doi.org/10.1016/j.jhydrol.2012.09.002, 2012.
Ziehn, T., Lenton, A., Law, R. M., Matear, R. J., and Chamberlain, M. A.: The carbon cycle in the Australian Community Climate and Earth System Simulator (ACCESS-ESM1) – Part 2: Historical simulations, Geosci. Model Dev., 10, 2591–2614, https://doi.org/10.5194/gmd-10-2591-2017, 2017.