TROLL 4.0: representing water and carbon fluxes, leaf phenology, and intraspecific trait variation in a mixed-species individual-based forest dynamics model – Part 1: Model description

TROLL 4.0 is an individual-based forest dynamics model that is capable of jointly simulating forest structure, diversity, and ecosystem functioning, including the ecosystem water balance and productivity, leaf area dynamics, and the tree community functional and taxonomic composition. It represents ecosystem flux processes in a manner similar to dynamic global vegetation models, while adopting a representation of plant community structure and diversity at a resolution consistent with that used by field ecologists. Specifically, trees are modelled as three-dimensional individuals with a metric-scale spatial representation, providing a detailed description of ecological processes such as competition for resources and tree demography. Carbon assimilation and plant water loss are explicitly represented at tree level using coupled photosynthesis and stomatal conductance models, depending on the micro-environmental conditions experienced by trees. Soil water uptake by trees is also modelled. Physiological and demographic processes are parameterized using plant functional traits measured in the field. Here we provide a detailed description and discussion of the implementation of TROLL 4.0. An evaluation of the model at two tropical forest sites is provided in a companion paper (Schmitt et al., 2025). TROLL 4.0's representation of processes reflects the state of the art, and we discuss possible developments to improve its predictive capability and its capacity to address challenges in forest monitoring, forest dynamics, and carbon cycle research.

1 Introduction

Modelling vegetation dynamics remains a major challenge (Prentice et al., 2015; Song et al., 2021; Mahnken et al., 2022), and the wide variety of modelling concepts that coexist depend on models' initial objectives. Early versions of global vegetation models were developed to provide boundary conditions for energy, carbon, and water budgets in global atmospheric models (Sellers et al., 1986, 1997). With the refinement of modelling concepts and computer power, feedback loops between the atmosphere and vegetation have gradually been taken into account (Charney, 1975; Cox et al., 2000; Meir et al., 2006), leading to an improved representation of fluxes of energy, carbon, and water across the vegetation layer (Fisher et al., 2015; Moorcroft, 2003; Pitman, 2003). However, dynamic global vegetation models (DGVMs) typically adopt a simplified representation of floristic composition and vegetation structure (Fisher et al., 2014; Prentice et al., 2007). In many of these models, fluxes between vegetation and the atmosphere are still calculated in an average environment per grid cell (e.g. 1°×1°) for an average leaf of an individual drawn from a dozen plant functional types (PFTs). The diversity of plant strategies is therefore typically represented by a small number of PFTs even in highly diverse tropical forests (Fisher et al., 2014; Poulter et al., 2011).

In parallel, stand-scale process-based models have been developed to better understand the exchanges between vegetation and the atmosphere through an up-scaling of fine-scale ecophysiological processes and to account for within-stand micro-environmental heterogeneity (Wang and Jarvis, 1990; Gu et al., 1999; Williams et al., 1996; Ogée et al., 2003; Duursma and Medlyn, 2012; Fyllas et al., 2014). These process-based models are conceptually close to DGVMs, but they implement a more detailed representation of plant structure at the stand scale, and they have nurtured some important advances in DGVM development over the past decades (e.g. Chen et al., 2016). Typically used to assimilate eddy flux data, they do not include demographic processes, however.

Forest growth models have a different history as they were initially developed to predict successional dynamics and inform forest management (Watt, 1947; Botkin et al., 1972; Vanclay, 1994; Porté and Bartelink, 2002; Liang and Picard, 2013). A key innovation is gap models that represent recruitment, growth, mortality, and competition between individual trees within forest patches. Forest patches are typically the size of a canopy opening created by the fall of a dominant tree (gap or chablis; Bugmann, 2001) and modelled as horizontally homogeneous, with a spatially implicit representation of tree positions. Through the simulation of a large number of patches, gap models can represent spatial heterogeneity due to gap dynamics within stands, and larger-scale applications have been enabled by the increase in computing power and the combination with remote sensing products (Shugart et al., 2015, 2018, 2020). Overall, these models adopt a finer representation of vegetation structure than classic DGVMs, but biogeochemical processes are generally modelled more coarsely, using ideal yield curves for tree growth rates combined with limiting factors imposed by the patch environment. Since these empirical relationships can only be parameterized on the basis of a large amount of data – readily available in plantations but difficult to obtain elsewhere – gap models typically also use plant functional types to simulate diverse forest stands. The number and definition of these groups have been much discussed in the literature, with no clear consensus (Swaine and Whitmore, 1988; Vanclay, 1991; Köhler and Huth, 1998; Köhler et al., 2000; Gourlet-Fleury et al., 2005; Kazmierczak et al., 2014), and these plant functional types are difficult to transfer from one site to another (Picard and Franc, 2003; Picard et al., 2012).

Modelling vegetation from a completely different perspective and building upon flora distribution maps and biogeographic concepts (von Humboldt, 1849; Grisebach, 1872), plant species distribution models have long been developed (SDMs; Guisan et al., 2017). Generally, SDMs first estimate the envelope of environmental conditions for a species based on species occurrence data (Guisan and Thuiller, 2005; Hutchinson, 1957; Soberón, 2007), which is used to infer a probability distribution in space (Elith and Leathwick, 2009). These models require little knowledge on the processes underlying species distribution, which explains their widespread use. However, because these models are statistical in nature, their ability to project future states is unclear, and a great deal of research has been devoted to implementing process-based versions of these SDMs (Chuine and Beaubien, 2001; Ferrier and Guisan, 2006; Morin and Lechowicz, 2008; Morin and Thuiller, 2009; Kearney and Porter, 2009; Dormann et al., 2012; Journé et al., 2020).

From this brief and non-exhaustive overview it emerges that each research community in vegetation modelling emphasizes one representation of vegetation dimension – functioning, structure, or diversity – to the detriment of the others (Maréchaux et al., 2021). Data availability and computing power partly explain such trade-offs, and increasing model complexity does not necessarily translate into an increase in reliability and robustness (Mahnken et al., 2022; Prentice et al., 2015). However, a consensus has emerged in the literature that a better integration of plant species diversity, structure, and functioning should improve the predictive power of vegetation models (Purves and Pacala, 2008; Thuiller et al., 2008; McMahon et al., 2011; Evans, 2012; Dormann et al., 2012; Mokany et al., 2016; Fisher et al., 2018). For example, tree species diversity influences the productivity and resilience of forest ecosystems (Schnabel et al., 2019), and these biodiversity–ecosystem functioning relationships result from local interactions where competition for resources is a key process (Fichtner et al., 2018; Guillemot et al., 2020; Jourdan et al., 2020; Yu et al., 2024; Nemetschek et al., 2025). Similarly, the fine details of stand structure control the uptake of resources by vegetation (Braghiere et al., 2019, 2021; Brum et al., 2019; Ivanov et al., 2012; De Deurwaerder et al., 2018), and they also determine the response to environmental stresses and disturbances (Blanchard et al., 2023; Jucker et al., 2018; Seidl et al., 2014; De Frenne et al., 2019). More generally, the contribution of vegetation in biogeochemical cycles, albeit typically quantified from stand to global scales (e.g. biomass, productivity), ultimately depends on individual processes (e.g. mortality, Johnson et al., 2016) controlled by fine-scale heterogeneity and the various ecological strategies of species (Poorter et al., 2015).

Therefore, recent developments in DGVMs have sought to better represent plant community structure and diversity. Several cohort-based DGVMs have been developed to refine the representation of vegetation heterogeneity (Moorcroft et al., 2001; Fisher et al., 2015; Longo et al., 2019; Smith et al., 2001; Koven et al., 2020). Continuous representations of functional diversity have also been proposed using the distribution and covariation of traits at the individual level or trait–climate relationships (Sakschewski et al., 2015; Verheijen et al., 2015; Scheiter et al., 2013; Pavlick et al., 2013; Berzaghi et al., 2020; Van Bodegom et al., 2014). These developments represent major advances in vegetation modelling, but scale mismatches between field data and model representations limit the ability to assimilate data of various nature and resolution. While inverse modelling approaches can partially alleviate these constraints (Hartig et al., 2012; Dietze et al., 2013; LeBauer et al., 2013; Fer et al., 2018; Lagarrigues et al., 2015), they rely heavily on confidence in the model structure and can therefore raise equifinality issues (Medlyn et al., 2005) and increase rapidly in computational complexity in high-dimensional parameter sets.

Finally, most of these challenges are exacerbated for tropical forests, as they are structurally complex (Doughty et al., 2023), support a large number of tree species per hectare (up to several hundred; Wilson et al., 2012), and are more difficult to access for evaluation in the field (Schimel et al., 2015). Given that they provide a range of ecosystem services and play a major role in regional and global biogeochemical cycles (Beer et al., 2010; Bonan, 2008; Pan et al., 2011; Harper et al., 2013), tropical forests and their responses to changing environmental factors have been identified as one of the greatest sources of uncertainty in Earth system models (Koch et al., 2021; Powell et al., 2013; Restrepo-Coupe et al., 2017; Huntingford et al., 2013). Thus, many advances in vegetation modelling have been, and still are, motivated by the challenge of tropical forests.

Here we describe a major upgrade of the TROLL forest dynamics model (Chave, 1999; Maréchaux and Chave, 2017; Fischer, 2019), referred to here as TROLL 4.0. TROLL 4.0 brings together various modelling traditions, including elements of DGVMs, stand-scale process-based models, and forest gap models while adopting a species-level representation of plant diversity to jointly simulate the functioning, structure, and diversity of forest ecosystems, in particular tropical forests. TROLL is a spatially explicit forest dynamics model, with an individual- and trait-based representation (Fig. 1). Individual trees from 1 cm diameter at breast height (dbh) are explicitly represented in a three-dimensional space discretized at a resolution of 1 m, allowing a fine representation of stand structure and local interactions via explicit competition for resources. Each tree belongs to a species, with a list of mean traits per species provided as input. These traits control the physiological and demographic processes of the tree's functioning and life cycle, from recruitment and growth to seed dispersal and death. This type of trait-based parameterization is based on recent advances in plant physiology and functional ecology and has been facilitated by the expansion of large databases of functional traits (Díaz et al., 2016, 2022; Kattge et al., 2011, 2020), in particular for tropical trees (Baraloto et al., 2010a; Vleminckx et al., 2021).

In TROLL 4.0, as opposed to previous versions, a water cycle is explicitly simulated, with the state and dynamics of soil water explicitly represented and coupled with the vegetation dynamics. Carbon assimilation and water loss by transpiration are represented explicitly using a photosynthesis model coupled with a stomatal conductance model. Both take into account variation in micro-environmental conditions between and within tree crowns, as well as the newly represented tree's access to soil water. The influence of water availability on leaf-level gas exchanges, leaf phenology, tree recruitment, and death is now simulated by means of a parameterization using the leaf water potential at turgor loss point (Bartlett et al., 2012b) and mechanistic-based coordination with other hydraulic traits (Bartlett et al., 2016b). Carbon that is not consumed by the respiration of living tissues is then allocated to leaf production, carbon storage, and tree growth through allometric relationships. Compared to TROLL version 2.3.2 (Maréchaux and Chave, 2017), TROLL 4.0 includes other improvements: plant functional traits can vary among trees of the same species, tree crown shapes can be more realistic than cylinders, and leaf density can vary within the tree crowns. Altogether, the new developments made for this new TROLL version allow us to further bridge the gap between existing forest modelling approaches through a better integration of forest structure, diversity, and ecosystem functioning in the model representation.

In this contribution, we provide a detailed description of the structure and objectives of the TROLL 4.0 model, discussing how new modelling representations are an outcome of the state of knowledge and the availability of data. Finally, we discuss the limitations of the model and future developments. An evaluation of the model's ability to simulate forest structure, diversity, and functioning for two Amazonian forest sites is reported in a companion paper (Schmitt et al., 2025). The model is written in C$++$ and wrapped in the R environment through a dedicated package named rcontroll (Schmitt et al., 2023).

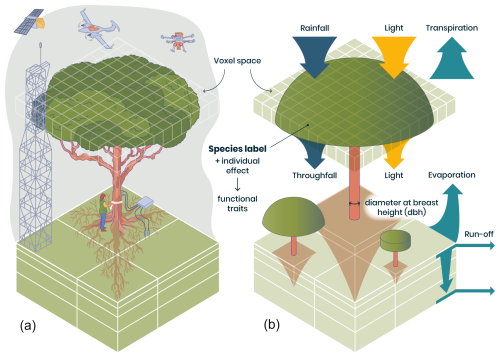
Figure 1 Representation of individual trees in a spatially explicit environment in TROLL 4.0 (b), allowing direct comparison with data of various nature (a). In TROLL 4.0, each tree is composed of a trunk, a crown whose shape evolves from a cylinder to an umbrella as the tree grows, and root biomass that decreases exponentially with soil depth. Tree dimensions are updated at each time step, depending on the net assimilated carbon that is allocated to growth and following allometric relationships depending on tree diameter at breast height (dbh). Each tree has a species label associated with plant functional traits, which, together with an individual effect randomly attributed at tree birth, determine the tree's functional traits. These traits are used to parameterize physiological and demographic processes that govern tree functioning throughout its life cycle. Light diffusion is computed explicitly at each time step and within each voxel from the canopy top to the ground. Water balance is also computed at each time step, and the resulting water availability across soil voxels influences tree functioning. With this representation of forest structure, composition, and functioning, model outputs can be directly compared with a wide range of data, including carbon and water fluxes provided by eddy flux towers, field inventories, and 3D structure estimates from remote sensing (a). In TROLL 4.0, aboveground voxels typically have a finer horizontal resolution than belowground voxels, but the latter are vertically finer and increase in thickness with depth (b). This resolution matches that of fine-scale remote sensing products or soil water content monitoring (a).

2 Model description

2.1 Environmental conditions

TROLL 4.0 simulates an idealized forest stand with a typical size of 1 to 100 ha. Parallel computing may be used to simulate several times the same stand or to simulate several forest stands with different environmental conditions. Climatic drivers are similar to those represented in many DGVMs (air temperature, vapour pressure deficit, wind speed, and light intensity above the canopy, as well as precipitation). The forest ecosystem is divided into an aboveground and belowground part. Soil is explicitly represented as a water reservoir, but soil nutrients are not modelled. The topography within a stand is assumed to be flat.

2.2 Light availability and aboveground variation in micro-climate

Above ground, the simulated forest stand is represented as a discrete grid of 1 m³ cubic voxels. Light diffuses vertically through the forest's leaf layers from the top of the canopy to the ground, with one recalculation each day. Variation in the solar zenith angle is thus neglected here, a first assumption made for the model application to tropical regions which could be reconsidered in the future. In a given voxel, light availability is the photosynthetic photon flux density in µmol photons m⁻² s⁻¹ and is computed as a function of the incident light intensity at canopy top (PPFD_top, see Table A1 for a list of symbols), the cumulated leaf density of voxels above, and the (constant) leaf density within the voxel itself. The Beer–Lambert extinction of light within the canopy allows calculating the incident PPFD (per unit ground area) above any layer at vertical extent v as

$$\begin{array}{}\text{(1)}& \mathrm{PPFD}\left(v\right)={\mathrm{PPFD}}_{\mathrm{top}}\times \exp \left[-k\times \mathrm{LAI}\left(v\right)\right],\end{array}$$

where LAI(v) is the cumulated leaf area above height v, and k is the extinction coefficient. We define $k=k_{\mathrm{geom}}\times {\text{absorptance}}_{\text{leaves}}$, where k_geom reflects the geometric arrangement of leaves in the voxel (a value of 0.5 reflecting spherical leaf distribution; Ross, 1981) and absorptance_leaves, the fraction of absorbed light within a single leaf (Long et al., 1993; Poorter et al., 1995). In the absence of sufficient relevant species-specific data, both k_geom and absorptance_leaves are assumed to be constant across species here.

The absorbed light in a layer a of thickness Δa is then

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{\mathrm{PPFD}}_{\mathrm{abs}}\left(a\right)& ={\mathrm{PPFD}}_{\mathrm{top}}\times \exp \left[-k\times \mathrm{LAI}\left(a\right)\right]\\ & -{\mathrm{PPFD}}_{\mathrm{top}}\times \exp \left[-k\times \mathrm{LAI}\left(a+\mathrm{\Delta }a\right)\right].\end{array}\end{array}$$

Assuming that leaf area per unit ground area (m² m⁻²), or dens(a), is constant within the layer, this simplifies to

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{\mathrm{PPFD}}_{\mathrm{abs}}\left(a\right)& ={\mathrm{PPFD}}_{\mathrm{top}}\times \exp \left[-k\times \mathrm{LAI}\left(a\right)\right]\\ & \times \left(\mathrm{1}-\exp \left[-k\times \mathrm{dens}\left(a\right)\right]\right).\end{array}\end{array}$$

For photosynthesis calculations, absorbed PPFD per unit ground area is converted into absorbed PPFD per unit leaf area by dividing PPFD_abs(a) by dens(a).

Air micro-environmental variation within the canopy is represented as follows. Nighttime temperature (T_night) is assumed to be constant throughout the night and within the canopy, while temperature (T) and vapour pressure deficit (VPD) vary across voxels depending on the variable $\mathit{\lambda }\left(v\right)=\frac{\mathrm{LAI}\left(v\right)}{{\mathrm{LAI}}_{\mathrm{sat}}}$ with LAI_sat a threshold LAI and LAI(v) the LAI above voxel v. At height v above ground, we calculate temperature and VPD as follows:

$$\begin{array}{}\text{(4)}& {\displaystyle }T\left(v\right)=T_{\mathrm{top}}-\mathrm{\Delta }T\times \mathit{\lambda }\left(v\right)\text{(5)}& {\displaystyle }\begin{array}{rl}\mathrm{VPD}\left(v\right)& ={\mathrm{VPD}}_{\mathrm{top}}\\ & \times \left[C_{\mathrm{VPD}\mathrm{0}}+(\mathrm{1}-C_{\mathrm{VPD}\mathrm{0}})\sqrt{(\mathrm{1}-\mathit{\lambda }\left(v\right))}\right],\end{array}\end{array}$$

where ΔT and C_VPD0 are set parameters and T_top and VPD_top are values at the top of the canopy. For any given layer a of depth Δa, temperatures and VPDs are then calculated by averaging both functions from a to a+Δa.

$$\begin{array}{}\text{(6)}& {\displaystyle }{T}_{\mathrm{mean}}\left(a\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{\Delta }a}}\underset{a}{\overset{a+\mathrm{\Delta }a}{\int }}\left(T_{\mathrm{top}}-{\displaystyle \frac{\mathrm{\Delta }T}{{\mathrm{LAI}}_{\mathrm{sat}}}}\times \mathrm{LAI}\left(v\right)\right)\mathrm{d}v\text{(7)}& {\displaystyle }\begin{array}{rl}& {\mathrm{VPD}}_{\mathrm{mean}}\left(a\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{\Delta }a}}\underset{a}{\overset{a+\mathrm{\Delta }a}{\int }}{\mathrm{VPD}}_{\mathrm{top}}\\ & \times \left[C_{\mathrm{VPD}\mathrm{0}}+{\displaystyle \frac{\left(\mathrm{1}-C_{\mathrm{VPD}\mathrm{0}}\right)}{\sqrt{{\mathrm{LAI}}_{\mathrm{sat}}}}}\sqrt{({\mathrm{LAI}}_{\mathrm{sat}}-\mathrm{LAI}\left(v\right))}\right]\mathrm{d}v\end{array}\end{array}$$

Equations (6) and (7) can then be simplified using the assumption of constant leaf density within a layer and redefining v with respect to the current layer a so that $\mathrm{LAI}\left(v\right)=\mathrm{LAI}\left(a\right)+\mathrm{dens}\left(a\right)\times v$.

This empirical representation of variation of T and VPD within the canopy is in qualitative agreement with empirical observations of micro-climate gradients within tropical forest canopies (Camargo and Kapos, 1995; Shuttleworth, 1985; Shuttleworth et al., 1989; Tymen et al., 2017), with a consistent buffering effect of forest canopies on understorey micro-environment (De Frenne et al., 2019) and a strong control by forest structure (Gril et al., 2023b, a; Tymen et al., 2017; Zellweger et al., 2019). Alternative empirical or process-based representations of micro-environmental variations (e.g. Maclean and Klinges, 2021; Ogée et al., 2003) may be tested in the future, especially for more in-depth explorations of understorey biodiversity and functioning under climate change (De Frenne et al., 2021; Haesen et al., 2023).

Wind speed attenuation inside the canopy is simulated as described in Rau et al. (2022b), who explored the effect of wind speed on forest structure in a forest exposed to cyclones using TROLL. Wind speed is usually measured above the canopy and decreases as one approaches the canopy top layer, so wind speed at the top of the canopy is (Monteith and Unsworth 2008)

$$\begin{array}{}\text{(8)}& u\left(z\right)={\displaystyle \frac{u_{\ast }}{\mathit{\kappa }}}\ln \left({\displaystyle \frac{z-d}{z_{\mathrm{0}}}}\right),\text{ if }z\ge H,\end{array}$$

where u(z) is the horizontal wind speed in m s⁻¹ at a height z (m) above ground, H is the height of the top of the canopy (m), u_∗ is the friction velocity, κ is the von Kármán constant (κ=0.40), d is the zero-plane displacement height, here assumed to be equal to 0.8H, and z₀ is the aerodynamic roughness, here assumed to be equal to 0.06H (Rau et al., 2022b). Within the canopy, wind speed decreases as (Inoue 1963)

$$\begin{array}{}\text{(9)}& u\left(z\right)=u\left(H\right)\exp \left(-\mathit{\alpha }\left(\mathrm{1}-{\displaystyle \frac{z}{H}}\right)\right),\text{ if }z<H,\end{array}$$

with α≈3 (Raupach et al., 1996). Wind speed was not computed at the voxel scale but using the coarser horizontal resolution of the belowground field (see Sect. 2.3 below, e.g. 25×25 m), and a mean top canopy height H was computed as input to Eqs. (8) and (9).

Finally, air CO₂ concentration is assumed to be constant across the canopy, in agreement with observations within a tropical forest site (Buchmann et al., 1997).

2.3 Soil water availability

In TROLL 4.0, the belowground part of the ecosystem is explicitly represented, and its discretization is specified by the user, including the number and depth of layers and horizontal dimensions of the cells. Belowground voxels are typically coarser horizontally (e.g. 25 m × 25 m, as commonly implemented in gap models; Bugmann, 2001), but finer vertically, than aboveground 1 m³ voxels. Metric-scale lateral water fluxes are difficult to parameterize and evaluate, and neglecting them here limits the computational burden. Soil layers typically increase in thickness with depth, as in most DGVMs or forest physiological models (Prentice et al., 2015) and in standard soil assessments (e.g. Hengl et al., 2017). In this representation, contrasting root depth and access to water can be represented across individual trees together with potential variation in soil properties and hydraulic state. This approach contrasts with some forest dynamics models that use a single-layer belowground representation (e.g. Gutiérrez et al., 2014; Christoffersen et al., 2016; Fyllas et al., 2014).

The water content in each belowground voxel is simulated using a bucket model, which relies on the vertical water balance for each voxel. Neglecting horizontal lateral fluxes, the water balance for a given soil column amounts to

$$\begin{array}{}\text{(10)}& \mathrm{\Delta }\mathrm{SWC}=P-I-Q-E-T-L,\end{array}$$

where SWC is the soil water content, P the incident rainfall, I the canopy interception, Q the run-off, E the evaporation from the soil, T the transpiration, i.e. the plant water uptake, and L the leakage. This water balance is established for each soil layer, with inputs from upwards and outputs downwards starting from the top layer (l=1): outputs of layer l are inputs for layer l+1, with L corresponding to the output of the deepest layer and $P-I-Q$ to the input of the top layer. The water balance for the topsoil layer thus reads

$$\begin{array}{}\text{(10a)}& \begin{array}{rl}\mathrm{\Delta }\mathrm{SWC}& =\mathrm{SWC}\left(t+\mathrm{1}\right)-\mathrm{SWC}\left(t\right)\\ & =P-I-Q-E-T-L_{\mathrm{1}\to \mathrm{2}},\end{array}\end{array}$$

with L_1→2 the water flow from the first topsoil layer to the next one, and the water balance of the other layers reads

$$\begin{array}{}\text{(10b)}& \mathrm{\Delta }\mathrm{SWC}=\mathrm{SWC}\left(t+\mathrm{1}\right)-\mathrm{SWC}\left(t\right)=L_{l-\mathrm{1}\to l}-L_{l\to l+\mathrm{1}},\end{array}$$

with $L_{l\to l+\mathrm{1}}$ the water flow from the soil layer l to soil layer l+1 that equals L if layer l is the deepest one. Note that this downward iteration neglects (i) potential hydraulic lift (upward water redistribution; see e.g. Dawson, 1993; Burgess et al., 1998; Oliveira et al., 2005) and (ii) potential interaction with the water table (Costa et al., 2023; Sousa et al., 2022). Further developments could account for these two mechanisms where they are expected to play a significant role. In particular, flooded areas could be easily represented, with a shallower soil depth and a prescribed boundary condition, i.e. a shallower water table. We now describe and discuss each term of the water balance and the corresponding modelling choices.

2.3.1 Rainfall

Rainfall (P, mm) is a model input. It is assumed that the total daily rainfall corresponds to a single event of rain per day (one storm, as in e.g. Rodriguez-Iturbe et al., 1999; Laio et al., 2001; Fischer et al., 2014; Gutiérrez et al., 2014).

2.3.2 Interception

Rainfall interception by the canopy is simulated using a model where interception depends on LAI, as proposed by Liang et al. (1994):

$$\begin{array}{}\text{(11)}& I=min\left(P,K\times \mathrm{LAI}\right),\end{array}$$

where K=0.2 mm and LAI corresponds to the leaf area index at ground level, averaged across the ground-level aboveground voxels that contribute to a single belowground voxel (typically 625 = 25² aboveground voxels contribute to one belowground voxel). Similar simple formulations of canopy interception have been used elsewhere (e.g. Liu et al., 2017), and this choice is justified by the lack of relevant data to properly parameterize more complex formulations at most field sites. More complex models of rainfall interception also exist, however (Rutter and Morton, 1977; Gash, 1979; Gash et al., 1995).

2.3.3 Run-off and infiltration

As in most bucket models coupled with a forest dynamics model, the temporal propagation of the wetting front into the soil is not explicitly simulated here because of the daily time step and the vertically lumped representation of soil moisture dynamics (e.g. Laio et al., 2001; Guimberteau et al., 2014). When the soil top layer has enough available storage to absorb the totality of the throughfall (i.e. when throughfall is smaller than the layer water content at field capacity minus the current soil water content), it is assumed that the increment in soil water content of that top layer is equal to the throughfall. Otherwise, the excess water percolates to the next layer below (L_1→2 in Eq. 10a). In the absence of an explicit wetting front, run-off occurs only when the superficial layer is already saturated, which is similar to Dunne run-off (Dunne and Black, 1970). More complex formulations of run-off exist (d'Orgeval et al., 2008; Guimberteau et al., 2014; Horton, 1933), but because of the high porosity of many tropical forest soils (Hodnett and Tomasella, 2002; Sander, 2002) and the lack of explicit topography in this version, our choice is parsimonious.

2.3.4 Soil evaporation

We assumed that water evaporates from the topsoil layer only, a reasonable assumption if the topsoil layer is not too thin. We followed Sellers et al. (1992) under which evaporation from the soil is expressed as (see Merlin et al., 2016 for a review of alternatives)

$$\begin{array}{}\text{(12)}& E={\displaystyle \frac{M_{\mathrm{w}}}{R{T}_{\mathrm{s}}}}\times {\displaystyle \frac{e_{\mathrm{s}}-e_{\mathrm{a}}}{r_{\mathrm{soil}}+r_{\mathrm{aero}}}},\end{array}$$

where E is in kg m⁻² s⁻¹, M_w is the molar mass of water vapour (M_w=18 kg mol⁻¹), R is the ideal gas constant (R=8.31 J mol⁻¹ K⁻¹), T_s is the temperature at the soil surface in Kelvin computed using Eq. (4) at ground level, e_s is the vapour pressure of the soil surface in Pa, e_a is the vapour pressure of air above the soil surface in Pa, r_soil is the soil surface resistance in s m⁻¹, and r_aero is the aerodynamic resistance to heat transfer in s m⁻¹. Soil water pressure e_s is a function of the water potential of the topsoil belowground voxel (ψ_soil, top – MPa; Jones, 2013, Eq. 5.14 therein):

$$\begin{array}{}\text{(13)}& \begin{array}{rl}{e}_{\mathrm{s}}& =e_{\mathrm{sat}}\left(T_{\mathrm{s}}\right)\times \exp \left({\displaystyle \frac{V_{\mathrm{w}}}{R{T}_{\mathrm{s}}}}\times {\mathit{\psi }}_{\mathrm{soil},\mathrm{top}}\right)\\ & =e_{\mathrm{sat}}\left(T_{\mathrm{s}}\right)\times \exp \left(\mathrm{2.17}\times {\displaystyle \frac{{\mathit{\psi }}_{\mathrm{soil},\mathrm{top}}}{T_{\mathrm{s}}}}\right),\end{array}\end{array}$$

where V_w is the partial molal volume of water ($V_{\mathrm{w}}=\mathrm{18}\times {\mathrm{10}}^{-\mathrm{6}}$ m³ mol⁻¹), and e_sat(T_s) is the saturated vapour pressure at T_s computed following the Buck equation (Jones, 2013, Appendix 4 therein). e_a is by definition equal to e_sat(T_s)−VPD_ground, where the latter is the VPD at ground level in Pa. r_soil is computed following Sellers et al. (1992, Eq. 19 therein, see also Merlin et al., 2016, Eq. 12):

$$\begin{array}{}\text{(14)}& r_{\mathrm{soil}}=\exp \left(\mathrm{8.206}-\mathrm{4.255}\times {\displaystyle \frac{{\mathit{\theta }}_{\mathrm{top}}}{{\mathit{\theta }}_{\mathrm{fc},\mathrm{top}}}}\right),\end{array}$$

where θ_top is the water content of the topsoil belowground voxel and θ_fc, top is its water content at field capacity (in m³). Aerodynamic resistance r_aero is computed as follows (Merlin et al., 2016, Eq. B10 therein):

$$\begin{array}{}\text{(15)}& r_{\mathrm{aero}}={\displaystyle \frac{\mathrm{1}}{{\mathit{\kappa }}^{\mathrm{2}}\times u\left(Z\right)}}\ln {\left({\displaystyle \frac{Z}{Z_{\mathrm{m}}}}\right)}^{\mathrm{2}},\end{array}$$

with κ again being the von Kármán constant (κ=0.40), u(Z) the wind seed (in m s⁻¹) at reference height Z, here taken at 1 m above ground, and Z_m the momentum soil roughness in metres, set to 0.001 m.

2.3.5 Transpiration

Trees transpire soil water from the belowground voxel they are rooted in (see Sect. 2.4.3). For a given tree, the total daily soil water uptake is the sum of the water transpired by leaves across its crown and across daytime half-hours (see Sect. 2.5.2). Soil layers contribute to water uptake as a function of tree-dependent weights, w_l (see Eq. 21, Sect. 2.4.3), which depend on root biomass and on the soil hydraulic state in each layer.

For each belowground voxel in layer l, the soil water potential (ψ_l) and the soil hydraulic conductivity (K_l) are computed at each time step from the soil water content in the focal voxel using the van Genuchten–Mualem soil characteristic and hydraulic conductivity curves (Mualem, 1976; van Genuchten, 1980; see Table 1 in Marthews et al., 2014). Parameters of these curves are estimated using regression models (pedotransfer functions) for tropical soils (Hodnett and Tomasella, 2002), except the saturated hydraulic conductivity, which is computed following Cosby et al. (1984; see Table 2 in Marthews et al., 2014). In practice, when only soil texture data are available, TROLL 4.0 contains a default option to apply the texture-based-only pedotransfer function provided by Tomasella and Hodnett (1998), coupled to the soil characteristic and hydraulic conductivity curves of Brooks and Corey (1964) (see Tables 1 and 2 in Marthews et al., 2014).

2.4 Representation of trees in the model

2.4.1 Species affiliation and intraspecific trait variability

In TROLL 4.0, each tree (and seed) is attributed a botanical species defined by a taxonomic binomial. It is assumed that the user has sufficiently good knowledge of the tree species growing in the study area so that a list of species-specific mean plant functional trait values can be provided as input. These are the leaf mass per area (LMA, in g m⁻²), the leaf area (LA, cm²), the leaf nitrogen content per dry mass (N, in mg g⁻¹), the leaf phosphorous content per dry mass (P, in mg g⁻¹), the wood specific gravity (wsg, in g cm⁻³), the leaf water potential at turgor loss point (π_tlp, in MPa), and three allometric parameters (dbh_thres, h_lim, a_h, all in metres; see Sect. 2.4.2). The number of species provided as input is not limited. In addition to mean plant functional trait values, it is possible to input individual trait values from which a trait variance–covariance matrix is computed (alternatively the trait variance–covariance matrix can be prescribed). With this option, for each recruited tree, the trait values are drawn from a distribution rather than attributed the species-specific mean value. For each trait i and tree j, the species-specific mean value is multiplied by a factor $e^{{\mathit{\epsilon }}_{i,j}}$, where ${\mathit{\epsilon }}_{i,j}\sim N(\mathrm{0},{\mathit{\sigma }}_i$) and σ_i is the trait-specific standard deviation on a logarithmic scale (lognormal variation). The sole exception is wood specific gravity, which we assume to be normally distributed around the mean with ${\mathit{\epsilon }}_{\mathrm{wsg},j}\sim N(\mathrm{0},{\mathit{\sigma }}_{\mathrm{wsg}}$). Trait covariance is only considered for leaf N, leaf P, and LMA, and other traits are assumed to be decoupled (Baraloto et al., 2010b). Note that with this implementation, intraspecific variation is not heritable or structured in space or time, and it is thus a surrogate for variability emerging from genetic variation or plasticity (Girard-Tercieux et al., 2023, 2024). A more realistic representation of the latter, especially light-driven trait plasticity along the vertical canopy gradient (Lamour et al., 2023b; Lloyd et al., 2010), is left for a future version.

2.4.2 Aboveground structure

Above ground, the tree geometry is represented as a three-dimensional object within the voxelized space and consists of a trunk and a crown filled with leaves. The trunk is assumed to be a cylinder characterized by its total height and its diameter (dbh, for diameter at breast height, by analogy with forest inventories). The aboveground dimensions of trees are predicted from their dbh via scaling rules. For tree j with dbh_j, we calculate its height h_j, its crown radius cr_j, and its crown depth cd_j as follows.

$$\begin{array}{}\text{(16)}& {\displaystyle }{h}_j={\displaystyle \frac{h_{\lim }\times {\mathrm{dbh}}_j}{\left(a_h+{\mathrm{dbh}}_j\right)}}\times e^{{\mathit{\epsilon }}_{h,j}}\text{(17)}& {\displaystyle }{\mathrm{cr}}_j=e^{a_{\mathrm{cr}}}\times {\mathrm{dbh}}^{b_{\mathrm{cr}}}\times e^{{\mathit{\epsilon }}_{\mathrm{cr},j}}\text{(18)}& {\displaystyle }{\mathrm{cd}}_j=\min \left({\displaystyle \frac{h_j}{\mathrm{2}}},(a_{\mathrm{cd}}+b_{\mathrm{cd}}\times h_j)\times e^{{\mathit{\epsilon }}_{\mathrm{cd},j}}\right)\end{array}$$

Here, h_lim and a_h are species-specific coefficients of the Michaelis–Menten function, and a_cr, b_cr, a_cd, and b_cd are allometric coefficients that are species-independent. ε_h, j, ε_cr, j, and ε_cd, j are tree-level variance terms to simulate intraspecific variation that are randomly drawn at tree birth with ${\mathit{\epsilon }}_{h,j}\sim N(\mathrm{0},{\mathit{\sigma }}_h$), ${\mathit{\epsilon }}_{\mathrm{cr},j}\sim N\left(\mathrm{0},{\mathit{\sigma }}_{\mathrm{cr}}\right)$, and ${\mathit{\epsilon }}_{\mathrm{cd},j}\sim N(\mathrm{0},{\mathit{\sigma }}_{\mathrm{cd}}$). Tree crown architecture is known to depend on species ecological strategies (Bohlman and O'Brien, 2006; Iida et al., 2012; Poorter et al., 2006; Laurans et al., 2024), but given that crown extents are difficult to measure reliably in the dense canopies of tropical forests, we used a single set of parameters for all the species.

In the previously published version (Maréchaux and Chave, 2017), tree crowns were represented as cylinders with homogeneous leaf densities. Since v.3.0, TROLL has also been able to model tree crowns as flexible, umbrella-like shapes with heterogeneous leaf density distributions. Small tree crowns are simulated as cylinders but consist of up to three separate 1 m layers of leaves (top, intermediate, and bottom layer). Each layer can be assigned a percentage of the total leaf area (which results from the processes of carbon allocation to leaf production and leaf shedding, see Sect. 2.6.2) to reflect gradients in leaf densities from the upmost to lower crown layers (e.g. 50 %, 30 %, 20 %; Kitajima et al., 2005), but the default is an equal distribution (33 %, 33 %, 33 %) across all layers. Once a tree surpasses 3 m in crown depth, no new layers are added. In this case, tree height directly above the tree stem (tree top height) and crown extent are derived using the same allometric equations (Eqs. 16–18), but, instead of the flat tops of small trees, it is now possible to prescribe a change in height from the centre of the crown to the crown's edges. Different geometric forms are available to describe this variation, but here we chose a simple linear decrease between the radius at the top of the crown and the radius at the bottom of the crown. The ratio between the two radii is controlled through the global parameter shape_crown, which varies between 0 (conical shape) and 1 (cylinder) and thus allows for various “conifer-like” and “broadleaf-like” shapes in between. Within the first 3 m of the resulting crown shape, leaves are allocated as before and folded around the tree trunk like an umbrella at various stages of opening (see Fig. 1b in Schmitt et al., 2023, and similar tree representations in Strigul et al., 2008). The crown shape only affects the geometry of the crown, not the amount of total leaf area allocated to it (see Sect. 2.6.2).

We also relax the assumption that tree crowns are homogeneously filled across their horizontal extent. In TROLL 4.0, crowns have small 1 m² openings (or gaps) in their crowns, parameterized as a percentage of total crown area that is not filled with leaves, f_gap. This allows for the modelling of a spatially heterogeneous light environment in the understorey (Tymen et al., 2017), with a theoretical range from f_gap=0 % (full crown cover, no openings) to f_gap=100 % (a hypothetical crown with no leaf area). When calibrating TROLL for tropical forests with airborne laser scanning (Fischer et al., 2019), we found a value of f_gap=15 % to be a good approximation for this within-crown gap fraction. If intraspecific variation in crown extent is explicitly modelled, the fraction of crown gaps is rescaled so that the absolute crown cover stays constant (i.e. the fraction of crown gaps is divided by $e^{\mathrm{2}{\mathit{\epsilon }}_{\mathrm{cr},j}}$). Within species and for trees with the same stem size (i.e. similar total sapwood area), crown extent is thus assumed to be decoupled from variation in leaf area, i.e. reflecting variation in branch angles and directions, but not branch number or biomass.

2.4.3 Belowground structure

As in other models (e.g. Xu et al., 2016), TROLL 4.0 makes the assumption that total fine root biomass is equal to leaf biomass. Future developments should endeavour to represent a more explicit belowground allocation scheme (Merganičová et al., 2019; Huaraca Huasco et al., 2021). Direct estimates of individual tree root depth and root distribution are rare in moist tropical forests (Canadell et al., 1996; Jackson et al., 1996, 1999; Nepstad et al., 1994; Cusack et al., 2024; Guerrero-Ramírez et al., 2021). Some studies have quantified the depth of tree water uptake using indirect methods, such as pre-dawn leaf water potential, or isotope labeling (Brum et al., 2019; Stahl et al., 2013a), but this does not give access to the actual rooting depth. Tree root depth was assumed here to increase with tree size and was computed as a function of tree dbh as follows (Kenzo et al., 2009, Fig. 4 therein):

$$\begin{array}{}\text{(19)}& \mathrm{RD}=\mathrm{0.35}\times {\mathrm{dbh}}^{\mathrm{0.54}},\end{array}$$

with root depth (RD, m) and diameter at breast height (dbh, cm). As in Xu et al. (2016), the exponent was based on Kenzo et al. (2009), who reported on data from excavated trees in secondary forests in Malaysia. The first parameter (0.35, root depth at dbh = 1 cm) was adjusted to avoid unrealistic water depletion of the topsoil layer. In the absence of relevant species-specific data, this allometric equation was assumed to hold for all species, even if root depth is known to be highly plastic (e.g. Rowland et al., 2023). Correlations between rooting depth and leaf phenological habit have been reported, but in drier or more seasonal sites than Amazonian rainforests (Brum et al., 2019; Hasselquist et al., 2010; Smith-Martin et al., 2020), and trait coordinations are known to be typically stronger under harsher environmental conditions (Dwyer and Laughlin, 2017; Delhaye et al., 2020).

We assumed that vertical tree root distribution follows an exponential profile, as observed empirically at the stand scale (Fisher et al., 2007; Humbel, 1978; Jackson et al., 1996). The fine root biomass in layer l, at depths ranging from z_l to $z_{l+\mathrm{1}}\left(>z_l\right)$, is computed as

$$\begin{array}{}\text{(20)}& {\mathrm{RB}}_l={\mathrm{RB}}_t\times \left(\exp \left(-\mathrm{3}{\displaystyle \frac{z_l}{\mathrm{RD}}}\right)-\exp \left(-\mathrm{3}{\displaystyle \frac{z_{l+\mathrm{1}}}{\mathrm{RD}}}\right)\right),\end{array}$$

where RB_t is the total tree fine root biomass (g), RB_l the fine root biomass in layer l (g), and RD the tree rooting depth (m). The factor 3 was determined so that about 95 % of the root biomass is contained between the soil surface and RD (note that −log(0.05) ≈ 3) (Arora and Boer, 2003). Tree roots are distributed across vertical layers but do not spread across belowground voxels horizontally. This assumption was considered a first parsimonious representation given the size of belowground voxels and the scarcity of data on root horizontal distribution worldwide, particularly in tropical biomes (see Cusack et al., 2024, where root horizontal distribution is not mentioned, but see Schenk and Jackson, 2002, for data on water-limited systems). As a result, trees only deplete the water content of the belowground voxels located below their trunk position and thus compete for water with trees sharing the same belowground voxels only (see Sect. 2.3), but this could easily be revisited in the future.

The soil water potential in the root zone, ψ_root (in MPa), captures how the plant equilibrates with the soil water state across its root profile. It is computed as the weighted mean of the belowground voxel water potentials across layers. We used the weighting scheme proposed by Williams et al. (2001; see also Bonan et al., 2014; Duursma and Medlyn, 2012), which accounts for the variation of soil water availability and conductance across layers as follows:

$$\begin{array}{}\text{(21)}& \begin{array}{rl}{\mathit{\psi }}_{\mathrm{root}}& =\sum _l{w}_{\mathrm{l}}\times {\mathit{\psi }}_l\text{ with }\\ & w_{\mathrm{l}}={\displaystyle \frac{\left({\mathit{\psi }}_l-{\mathit{\psi }}_{\mathrm{R},\min }\right)\times G_l}{\sum _{ll}\left({\mathit{\psi }}_{ll}-{\mathit{\psi }}_{\mathrm{R},\min }\right)\times G_{ll}}},\end{array}\end{array}$$

where ψ_l is the soil water potential in layer l, and ψ_R,min is the root water potential below which there is no water uptake within the layer (minimal root water potential, assumed to be −3 MPa as in Duursma and Medlyn, 2012). G_l, the soil-to-root water conductance in layer l, in mmol H₂O m⁻² s⁻¹ MPa⁻¹, is computed as follows (Gardner, 1964).

$$\begin{array}{}\text{(22)}& G_l={\displaystyle \frac{\mathrm{2}\mathit{\pi }{L}_{\mathrm{a},l}{K}_l}{\log \left(\frac{r_{\mathrm{s}}}{r_{\mathrm{r}}}\right)}}\end{array}$$

In Eq. (22), L_a,l is the total root length per unit area in the layer (in m m⁻²), with the total root length in the layer computed as RB_l×SRL where SRL is the specific root length, here assumed to be constant (10 m g⁻¹, Bonan et al., 2014; Metcalfe et al., 2008; Weemstra et al., 2016). K_l is the soil hydraulic conductivity of layer l (in mmol H₂O m⁻¹ s⁻¹ MPa⁻¹, see Sect. 2.3), r_r is the mean fine root radius, here set at 1 mm, and r_s is half the mean distance between roots, calculated with the assumption of uniform root spacing in a given layer (Newman, 1969):

$$\begin{array}{}\text{(23)}& r_{\mathrm{s}}={\displaystyle \frac{\mathrm{1}}{\sqrt{\mathit{\pi }{L}_{\mathrm{v},l}}}},\end{array}$$

where L_v,l is the total root length per unit soil volume in the layer (in m m⁻³), computed in the same way as L_a,l, but also divided by layer depth.

A range of other models have been used to infer ψ_root using the relative tree root biomass in each layer directly as weights (De Kauwe et al., 2015a; Naudts et al., 2015; Powell et al., 2013; Schaphoff et al., 2018; Sakschewski et al., 2021; Verbeeck et al., 2011). However, trees do not take up water simply as a proportion of root density but can equilibrate with the wettest soil layers (Schmidhalter, 1997; Duursma and Medlyn, 2012): the contrasting temporal variations in water availability across layers result in seasonal changes in the depth of active water withdrawal (Bruno et al., 2006; Joetzjer et al., 2022). For instance, cavitation in the driest part of the soil disconnects roots from the soil (Sperry et al., 2002; see also Fisher et al., 2006). This is likely why deeper roots, although often very rare, disproportionately contribute to sustaining forest productivity during dry seasons.

2.5 Leaf physiology

The carbon assimilated and the water transpired by a tree within a day are the sum of the leaf-level carbon and water fluxes across daytime half-hours. Leaf-level carbon assimilation is computed per crown layer of each tree, using the Farquhar–von Caemmerer–Berry model of C₃ photosynthesis (Farquhar et al., 1980, see Sect. 2.5.1), coupled to the model of stomatal conductance of Medlyn et al. (2011; see Sect. 2.5.2) as in Maréchaux and Chave (2017). In TROLL 4.0 the dependences on leaf temperature (T_l), vapour pressure deficit at the leaf surface (VPD_s), and CO₂ concentration at the leaf surface (c_s) are now determined iteratively at the leaf surface, starting from air temperature (T), air vapour pressure deficit (VPD_a), and air CO₂ concentration (c_a) averaged across the tree crown layer (see Sect. 2.2 and 2.4.2) and with transpiration computed using the Penman–Monteith equation (see Sect. 2.5.4).

2.5.1 Photosynthesis

In Farquhar et al. (1980), the leaf-level net carbon assimilation rate (A_n, µmol CO₂ m⁻² s⁻¹) is limited by either Rubisco activity (A_v, µmol CO₂ m⁻² s⁻¹) or RuBP regeneration (A_j, µmol CO₂ m⁻² s⁻¹):

$$\begin{array}{}\text{(24)}& \begin{array}{rl}{A}_{\mathrm{n}}& =min\left\{A_v,A_j\right\}-R_{\mathrm{p}}\left(T_{\mathrm{l}}\right);\\ & A_v=V_{\mathrm{cmax}}\left(T_{\mathrm{l}},{\mathit{\psi }}_{\mathrm{pd}}\right)\times {\displaystyle \frac{c_i{\mathrm{\Gamma }}^{\ast }}{c_i+K_m\left(T_{\mathrm{l}}\right)}};\\ & A_j={\displaystyle \frac{J}{\mathrm{4}}}{\displaystyle \frac{c_i-{\mathrm{\Gamma }}^{\ast }\left(T_{\mathrm{l}}\right)}{c_i+\mathrm{2}{\mathrm{\Gamma }}^{\ast }\left(T_{\mathrm{l}}\right)}},\end{array}\end{array}$$

where R_p is the photorespiration rate (µmol C m⁻² s⁻¹), V_cmax the maximum rate of carboxylation (µmol CO₂ m⁻² s⁻¹), c_i the CO₂ partial pressure at carboxylation sites, Γ^∗ the CO₂ compensation point in the absence of dark respiration, K_m the apparent kinetic constant of the Rubisco (von Caemmerer, 2000), and J the electron transport rate (µmol e⁻ m⁻² s⁻¹), which depends on PPFD through

$$\begin{array}{}\text{(25)}& \begin{array}{rl}J& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\theta }}}\left[\mathit{\alpha }\times \mathrm{PPFD}+J_{max}\left(T_{\mathrm{l}},{\mathit{\psi }}_{\mathrm{pd}}\right)\right.\\ & \left.-\sqrt{\begin{array}{c}{\left(\mathit{\alpha }\times \mathrm{PPFD}+J_{max}\left(T_{\mathrm{l}},{\mathit{\psi }}_{\mathrm{pd}}\right)\right)}^{\mathrm{2}}\\ -\mathrm{4}\mathit{\theta }\times \mathit{\alpha }\times \mathrm{PPFD}\times J_{max}\left(T_{\mathrm{l}},{\mathit{\psi }}_{\mathrm{pd}}\right)\end{array}}\right].\end{array}\end{array}$$

J_max is the maximal electron transport capacity (µmol e⁻ m⁻² s⁻¹), θ the curvature factor (unitless), and α the apparent quantum yield to electron transport (mol e⁻ mol photons⁻¹), computed following von Caemmerer (2000) as $\mathit{\alpha }=\left(\mathrm{1}-\mathrm{LSQ}\right)\times \mathrm{0.5}$, with LSQ the effective spectral quality of light, fixed at 0.15, and the factor 0.5 accounting for the fact that each photosystem absorbs half of the photons.

The V_cmax and J_max parameters depend on leaf properties, leaf temperature (T_l), and water state (through the leaf pre-dawn water potential, ψ_pd; see Eq. 37) and represent a large source of uncertainty in vegetation models (Zaehle et al., 2005; Mercado et al., 2009; Rogers et al., 2017). In tropical forest environments, Domingues et al. (2010) suggested that V_cmax and J_max are co-limited by the leaf concentration of nitrogen and phosphorus as follows (see also Walker et al., 2014):

$$\begin{array}{}\text{(26)}& {\displaystyle }\begin{array}{rl}{V}_{\text{cmax-M}}& \left(\mathrm{25}\mathrm{°}\mathrm{C}\right)=min\left\{-\mathrm{1.56}+\mathrm{0.43}\times N-\mathrm{0.37}\times \mathrm{LMA};\right.\\ & \left.-\mathrm{0.80}+\mathrm{0.45}\times P-\mathrm{0.25}\times \mathrm{LMA}\right\},\end{array}\text{(27)}& {\displaystyle }\begin{array}{rl}{J}_{\text{max-M}}& \left(\mathrm{25}\mathrm{°}\mathrm{C}\right)=min\left\{-\mathrm{1.50}+\mathrm{0.41}\times N-\mathrm{0.45}\times \mathrm{LMA};\right.\\ & \left.-\mathrm{0.74}+\mathrm{0.44}\times P-\mathrm{0.32}\times \mathrm{LMA}\right\},\end{array}\end{array}$$

with V_cmax-M and J_max-M the photosynthetic capacities at 25 °C of unstressed mature leaves on a leaf dry mass basis, in µmol CO₂ g⁻¹ s⁻¹ and µmol e⁻ g⁻¹ s⁻¹, respectively. N and P are leaf nitrogen and phosphorus concentrations in mg g⁻¹, and LMA is the leaf mass per area in g cm⁻². V_cmax-M and J_max-M can be converted into area-based V_cmax and J_max by multiplying by LMA. We used this leaf-trait-based parameterization of V_cmax(25 °C) and J_max(25 °C) in the absence of water stress (as in Fyllas et al., 2014; Mercado et al., 2011). The dependence of V_cmax and J_max on temperature was given by equations in Bernacchi et al. (2003), and the dependence on water availability was modelled by a function of ψ_pd (WSF_ns, see Sect. 2.5.3, Eq. 40).

$$\begin{array}{}\text{(28)}& {\displaystyle }\begin{array}{rl}{V}_{\mathrm{cmax}}& \left(T_{\mathrm{l}},{\mathit{\psi }}_{\mathrm{pd}}\right)=V_{\mathrm{cmax}}\left(\mathrm{25}\mathrm{°}\mathrm{C}\right)\times e^{(\mathrm{26.35}-\frac{\mathrm{65.33}}{R\times \left(T_{\mathrm{l}}+\mathrm{273.15}\right)})}\\ & \times {\mathrm{WSF}}_{\mathrm{ns}}\left({\mathit{\psi }}_{\mathrm{pd}}\right)\end{array}\text{(29)}& {\displaystyle }\begin{array}{rl}{J}_{max}& \left(T_{\mathrm{l}},{\mathit{\psi }}_{\mathrm{pd}}\right)=J_{max}\left(\mathrm{25}\mathrm{°}\mathrm{C}\right)\times e^{(\mathrm{17.57}-\frac{\mathrm{43.54}}{R\times \left(T_{\mathrm{l}}+\mathrm{273.15}\right)})}\\ & \times {\mathrm{WSF}}_{\mathrm{ns}}\left({\mathit{\psi }}_{\mathrm{pd}}\right)\end{array}\end{array}$$

R is the molar gas constant (0.008314 kJ K⁻¹ mol⁻¹), and T_l is the leaf temperature in degrees Celsius. The temperature dependence of Γ^∗ and K_m followed von Caemmerer (2000).

$$\begin{array}{}\text{(30)}& {\displaystyle }{\mathrm{\Gamma }}^{\ast }\left(T_{\mathrm{l}}\right)=\mathrm{37}\times e^{\mathrm{23.4}\times \frac{\left(T_{\mathrm{l}}-\mathrm{25}\right)}{\mathrm{298}\times R\times \left(\mathrm{273}+T_{\mathrm{l}}\right)}}\text{(31)}& {\displaystyle }\begin{array}{rl}{K}_m& \left(T_{\mathrm{l}}\right)=\mathrm{404}\times e^{\mathrm{59.36}\times \frac{\left(T_{\mathrm{l}}-\mathrm{25}\right)}{\mathrm{298}\times R\times \left(\mathrm{273}+T_{\mathrm{l}}\right)}}\\ & \times \left(\mathrm{1}+{\displaystyle \frac{\mathrm{210}}{\mathrm{248}\times e^{\mathrm{35.94}\times \frac{T_{\mathrm{l}}-\mathrm{25}}{\mathrm{298}\times R\times \left(\mathrm{273}+T_{\mathrm{l}}\right)}}}}\right)\end{array}\end{array}$$

Temperature dependencies in Eqs. (28)–(31) are consistent with Domingues et al. (2010), following recommendations from Rogers et al. (2017).

The leaf photorespiration rate R_p (Eq. 24) was assumed to be a fixed fraction (40 %) of the leaf dark respiration rate (Eqs. 32–33; Atkin et al., 2000). We used the Atkin et al. (2015) “broadleaved trees” empirical model to estimate mature leaf dark respiration rates as a function of plant functional traits:

$$\begin{array}{}\text{(32)}& \begin{array}{rl}{R}_{\mathrm{d}-\mathrm{M}}& \left(\mathrm{25}\mathrm{°}\mathrm{C}\right)=\mathrm{8.5341}-\mathrm{0.1306}\times N\\ & -\mathrm{0.5670}\times P-\mathrm{0.0137}\times \mathrm{LMA}+\mathrm{11.1}\times V_{\text{cmax-M}}\\ & +\mathrm{0.1876}\times N\times P,\end{array}\end{array}$$

with R_d−M the leaf dark respiration rate on a dry mass basis and at a reference temperature of 25 °C (in nmol CO₂ g⁻¹ s⁻¹). Multiplying R_d−M by LMA gives the area-based leaf dark respiration R_d (in µmol C m⁻² s⁻¹). The temperature dependence of mature leaf dark respiration rates was calculated as (Atkin et al., 2015, Eq. 1 therein; see also Heskel et al., 2016)

$$\begin{array}{}\text{(33)}& \begin{array}{rl}{R}_{\mathrm{d}}\left(T_l\right)& =R_{\mathrm{d}}\left(\mathrm{25}\mathrm{°}\mathrm{C}\right)\\ & \times {\left[\mathrm{3.09}-\mathrm{0.043}\times {\displaystyle \frac{(T_l+\mathrm{25})}{\mathrm{2}}}\right]}^{\frac{\left(T_{\mathrm{l}}-\mathrm{25}\right)}{\mathrm{10}}}.\end{array}\end{array}$$

Long-term acclimation to temperature is not considered in TROLL 4.0 (Kattge and Knorr, 2007; Smith and Dukes, 2013).

2.5.2 Stomatal conductance

Carbon assimilation by photosynthesis is limited by the CO₂ partial pressure at carboxylation sites, which is controlled by stomatal transport as modelled by the diffusion equation:

$$\begin{array}{}\text{(34)}& A_{\mathrm{n}}=g_{\mathrm{s}}\left(c_{\mathrm{s}}-c_i\right),\end{array}$$

with g_s the stomatal conductance to CO₂ (mol CO₂ m⁻² s⁻¹). The representation of stomatal conductance varies greatly across vegetation models (Damour et al., 2010; Bonan et al., 2014; Rogers et al., 2017; see Appendix B, Table B1) and remains an active research topic (Anderegg et al., 2018; Dewar et al., 2018; Lamour et al., 2022; Sperry et al., 2017; Wolf et al., 2016; Sabot et al., 2022). In TROLL 4.0, stomatal conductance to water vapour is simulated as (Medlyn et al., 2011)

$$\begin{array}{}\text{(35)}& g_{\mathrm{sw}}=g_{\mathrm{0}}+\mathrm{1.6}\times \left(\mathrm{1}+{\displaystyle \frac{g_{\mathrm{1}}}{\sqrt{{\mathrm{VPD}}_{\mathrm{s}}}}}\right)\times {\displaystyle \frac{A_{\mathrm{n}}}{c_{\mathrm{s}}}},\end{array}$$

where g_sw is the stomatal conductance to water vapour in mol H₂O m⁻² s⁻¹, 1.6 is the ratio of the diffusivities of H₂O to CO₂ (Massman, 1998), VPD_s is the vapour pressure deficit at the leaf surface in kPa, A_n is the assimilation rate in µmol CO₂ m⁻² s⁻¹ (Eq. 24 above), c_s is the CO₂ concentration at the leaf surface in ppm, g₀ is the minimum conductance for water vapour in mol H₂O m⁻² s⁻¹ (Duursma et al., 2019), and g₁ is a model parameter in kPa${}^{\mathrm{1}/\mathrm{2}}$. Equations (24), (34), and (35) taken together lead to two quadratic equations for c_i, one when Rubisco activity is limiting and one when RuBP regeneration is limiting, and the solution is the highest root.

The parameter g₁ varies with species ecological strategies and carbon cost of water use (Domingues et al., 2014; Franks et al., 2018; Héroult et al., 2013; Lin et al., 2015; Wolz et al., 2017). Consequently, it is expected that g₁ should differ across plant functional types (e.g. Xu et al., 2016). Here we assumed a dependence of g₁ on wood density (wsg, in g cm⁻³) as in Lin et al. (2015). We also assumed a dependence on water availability, modelled by a function of ψ_pd (WSF_s; see Sect. 2.5.3).

$$\begin{array}{}\text{(36)}& g_{\mathrm{1}}=\left(-\mathrm{3.97}\times \mathrm{wsg}+\mathrm{6.53}\right)\times {\mathrm{WSF}}_{\mathrm{s}}\left({\mathit{\psi }}_{\mathrm{pd}}\right)\end{array}$$

This parameterization of g₁ based on wood density is a matter of debate, however, and alternatives have been proposed (Wu et al., 2020; Lamour et al., 2023a).

The parameter g₀ quantifies water fluxes through the leaf cuticle (cuticular conductance) and from stomatal leaks. Although it is increasingly recognized as a key parameter explaining tree water loss in drought conditions (Cochard, 2021; Martin-StPaul et al., 2017), its values and variation with other functional traits are poorly documented (Duursma et al., 2019; Slot et al., 2021; Nemetschek et al., 2024), and here we assumed a fixed value. Note that some previous studies have defined g₀ as cuticular conductance only, ignoring stomatal leak effects and thus underestimating g₀.

Both g₀ and g₁ were assumed not to depend on temperature in the absence of clear empirical evidence for tropical forest trees (Duursma et al., 2019; Slot et al., 2021; Rogers et al., 2017), but this may be further explored in the future through measurements and experiments (Cochard, 2021).

2.5.3 Effect of water availability on leaf-level gas exchange

Under water stress, leaf-level gas exchanges and photosynthesis are impaired, but how this is represented varies greatly across models (Appendix B, Table B1; Powell et al., 2013; Trugman et al., 2018; Verhoef and Egea, 2014). A common approach is to define a single integrative water stress factor cumulating all effects along the soil–plant–atmosphere pathway, some of which are difficult to evaluate empirically (e.g. Fischer et al., 2014; Gutiérrez et al., 2014; Krinner et al., 2005; Clark et al., 2011). This factor is then used to modify the parameters of the stomatal conductance and/or photosynthesis models (Egea et al., 2011; Verhoef and Egea, 2014). Depending on models, water stress factors have been assumed to depend on soil water content or on soil water potential in the root zone (De Kauwe et al., 2015a; Drake et al., 2017; Joetzjer et al., 2014; Powell et al., 2013; Trugman et al., 2018). Alternatively, some models have implemented a water stress factor as a function of leaf water potential (ψ_leaf; Anderegg et al., 2017; Christoffersen et al., 2016; Duursma and Medlyn, 2012; Kennedy et al., 2019; Xu et al., 2016; see also the pioneer work of Tuzet et al., 2003) or used optimization approaches (Williams et al., 1996; Anderegg et al., 2018; Sabot et al., 2020; Sperry et al., 2017; Wolf et al., 2016) to account for the cost of water uptake and transportation in the plant water column. The shape of such functions remains contentious, however (Table B1), resulting in substantial differences in model predictions.

Also, there is no consensus on the relative role of stomatal and non-stomatal limitations in leaf CO₂ assimilation under drying conditions, reflecting contrasting experimental results (Drake et al., 2017; Zhou et al., 2014; Keenan et al., 2010; Appendix B, Table B2). Under stomatal limitation, stomatal closure reduces leaf gas exchanges, and the water stress factor is applied to stomatal conductance or stomatal conductance model parameters (e.g. g₁). Under non-stomatal limitations, drought (leading to increased leaf temperature and/or decreased leaf water potential) impairs the biochemical photosynthesis apparatus, which results in a reduction of photosynthetic capacities and/or mesophyll conductance (Flexas et al., 2004, 2012). In this latter case, the water stress factor is applied to V_cmax and J_max (Drake et al., 2017; Keenan et al., 2010). Some models consider only one limitation and others both (Appendix B, Table B1).

In TROLL 4.0, two water stress factors are used, one for stomatal limitation, modifying the g₁ parameter (WSF_s; Eq. 36), and one for non-stomatal limitations, modifying the V_cmax and J_max parameters of the photosynthesis model (WSF_ns; Eqs. 28 and 29). Both water stress factors are assumed to depend on the leaf pre-dawn water potential (ψ_pd; De Kauwe et al., 2015a; Verhoef and Egea, 2014), which is a function of the soil water potential in the root zone (ψ_root, Eq. 21) (Stahl et al., 2013a, but see Bucci et al., 2004; Donovan et al., 2003) as follows (Jones, 2013; Eq. 4.9 therein):

$$\begin{array}{}\text{(37)}& {\mathit{\psi }}_{\mathrm{pd}}={\mathit{\psi }}_{\mathrm{root}}-\mathit{\rho }gh\simeq {\mathit{\psi }}_{\mathrm{root}}-\mathrm{0.01}\times h,\end{array}$$

where ρ is the density of water, g the gravitational force (g=9.81 m s⁻²), and h total tree height in metres. Here, WSF_s was computed as (Zhou et al., 2013; De Kauwe et al., 2015a)

$$\begin{array}{}\text{(38)}& {\mathrm{WSF}}_{\mathrm{s}}=\exp \left(b\times {\mathit{\psi }}_{\mathrm{pd}}\right),\end{array}$$

where b is a parameter. To parameterize b, we used the relationship between the leaf water potential at turgor loss point (π_tlp in MPa) and the water potential causing 90 % of stomatal closure (ψ_gs90, in MPa): ${\mathit{\pi }}_{\mathrm{tlp}}=\mathrm{0.97}\times {\mathit{\psi }}_{\mathrm{gs}\mathrm{90}}$ (P<0.01, R²=0.4; Fig. 1 in Martin-StPaul et al., 2017) and assumed that WSF_s≈0.1 at ψ_gs90 (an approximation given the shape of Eq. 35), leading to

$$\begin{array}{}\text{(39)}& {\mathrm{WSF}}_{\mathrm{s}}=\exp \left(-\mathrm{2.23}\times {\displaystyle \frac{{\mathit{\psi }}_{\mathrm{pd}}}{{\mathit{\pi }}_{\mathrm{tlp}}}}\right).\end{array}$$

The link between the leaf water potential at stomatal closure and the leaf water potential at turgor loss point is supported by several studies (Bartlett et al., 2016b; Brodribb et al., 2003; Farrell et al., 2017; Martin-StPaul et al., 2017; Meinzer et al., 2016; Rodriguez-Dominguez et al., 2016; Trueba et al., 2019). The formulation of WSF_s in Eq. (39) was preferred over alternatives, such as a linear relationship between WSF_s and ψ_pd (Oleson et al., 2008; Powell et al., 2013; Verhoef and Egea, 2014). The latter is less supported by data and leads to threshold responses as soil water content declines and similar responses across species, in contrast with empirical evidence (Kursar et al., 2009; Zhou et al., 2013). The water stress factor for non-stomatal limitation (WSF_ns) was computed following Xu et al. (2016):

$$\begin{array}{}\text{(40)}& {\mathrm{WSF}}_{\mathrm{ns}}={\left(\mathrm{1}+{\left({\displaystyle \frac{{\mathit{\psi }}_{\mathrm{pd}}}{{\mathit{\pi }}_{\mathrm{tlp}}}}\right)}^a\right)}^{-\mathrm{1}},\end{array}$$

with a=6 estimated from data reported in Brodribb et al. (2003). In this formula, ${\mathrm{WSF}}_{\mathrm{ns}}=\mathrm{1}/\mathrm{2}$ when ψ_pd=π_tlp, in agreement with empirical findings (Brodribb et al., 2002; Manzoni, 2014).

The parameterization of WSF_s and WSF_ns based on π_tlp is supported by the fact that leaf cells need to maintain turgor to sustain functioning (Hsiao, 1973). These functions do not depend on π_tlp when ψ_pd=π_tlp, so there is a simple link between the leaf drought tolerance, as informed by π_tlp, and the response of leaf-level gas exchange to water availability. Also, these equations predict that the decline of stomatal conductance as water availability decreases precedes that of photochemistry, consistent with observations (Fig. 2; Fatichi et al., 2016; Trueba et al., 2019).

Note that, since mesophyll conductance is not explicitly represented here, the effect of water stress on photosynthetic capacities (WSF_ns) includes both direct effects on the photosynthetic machinery and indirect effects from the reduction of mesophyll conductance (Drake et al., 2017; Keenan et al., 2010). Alternative shapes of water stress factors could be explored in the future, and a more explicit representation of the water flow through the plant water column could be implemented (Paschalis et al., 2024). In the absence of a clear consensus on the effect of water stress on respiration, TROLL 4.0 does not assume that respiration depends on water availability (Flexas et al., 2006, 2005; Rowland et al., 2018, 2015; Santos et al., 2018; Stahl et al., 2013b).

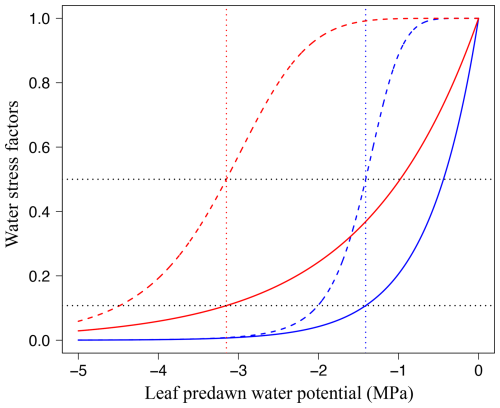
Figure 2 Responses of leaf-level gas exchange to water stress, depending on the leaf drought tolerance. Water stress factors are shown for the stomatal conductance parameter g₁ (stomatal limitation, WSF_s, Eq. 39; solid lines) and for the photosynthetic capacities J_max and V_cmax (non-stomatal limitation, WSF_ns, Eq. 40; dashed lines) as a function of leaf pre-dawn water potential (ψ_pd, MPa). WSFs are shown for a drought-vulnerable species (${\mathit{\pi }}_{\mathrm{tlp}}=-\mathrm{1.41}$ MPa, the least negative value reported in Maréchaux et al., 2015; blue lines) and for a drought-tolerant species (${\mathit{\pi }}_{\mathrm{tlp}}=-\mathrm{3.15}$ MPa, the most negative value reported in Maréchaux et al., 2015). Vertical dotted lines: π_tlp, horizontal dotted black lines: WSF_s and WSF_ns at π_tlp.

2.5.4 Leaf energy balance

In TROLL 4.0, the leaf temperature (T_l), vapour pressure deficit (VPD_s), and CO₂ concentration (c_s) at the leaf surface are computed through an iterative scheme that solves the leaf energy balance (Medlyn et al., 2007; Wang and Leuning, 1998; Duursma, 2015; Vezy et al., 2018). This is an important step because the leaf boundary layer plays a key role in gas exchanges, especially in dense tropical moist forests, given the large size of tropical tree leaves and the low wind speeds within canopies (De Kauwe et al., 2017; Jarvis and McNaughton, 1986; Meinzer et al., 1997). The iterative scheme is as follows. Initially, T_l, VPD_s, and c_s are set equal to surrounding air values (T, VPD, and c_a). Leaf photosynthesis (A_n) and stomatal conductance (g_sw) are computed using Eqs. (24), (34), and (35). Next, the boundary layer conductance and radiation conductance are computed, and finally the leaf-level transpiration rate is deduced from the Penman–Monteith equation (Eq. 41 below). After these steps, new values for T_l, VPD_s, and c_s are computed, and the above steps are repeated until leaf temperature converges, i.e. when the absolute difference between the T_l values of two consecutive iterations is lower than 0.01 °C.

The leaf-level transpiration rate E_l (in mol H₂O m⁻² s⁻¹) is calculated as

$$\begin{array}{}\text{(41)}& E_{\mathrm{l}}={\displaystyle \frac{\mathrm{1}}{\mathit{\lambda }}}\times {\displaystyle \frac{s{R}_{\mathrm{ni}}+{\mathrm{VPD}}_{\mathrm{a}}{g}_{\mathrm{H}}{C}_p{M}_{\mathrm{a}}}{s+\mathit{\gamma }\frac{g_{\mathrm{H}}}{g_{\mathrm{w}}}}},\end{array}$$

where λ is the latent heat of water vapour (in J mol⁻¹), s is the slope of the (locally linearized) relationship between saturated vapour pressure and temperature (in Pa K⁻¹, see Jones, 2013, Eq. 5.15 therein), R_ni is the isothermal net radiation (in J m⁻² s⁻¹), g_H is the total leaf conductance to heat (in mol m⁻² s⁻¹), C_p is the heat capacity of air (1010 J kg⁻¹ K⁻¹), M_a is the molecular mass of air ($\mathrm{28.96}\times {\mathrm{10}}^{-\mathrm{3}}$ kg mol⁻¹), γ the psychrometric constant (in Pa K⁻¹), and g_w the total conductance to water vapour (mol H₂O m⁻² s⁻¹). The latent heat of water vapour λ depends on air temperature as follows.

$$\begin{array}{}\text{(42)}& \mathit{\lambda }=\left(\mathrm{2.501}\times {\mathrm{10}}^{\mathrm{3}}-\mathrm{2.365}\times T\right)\times \mathrm{18}\end{array}$$

The isothermal net radiation R_ni has two components, the absorbed solar radiation (S_abs), including both PAR and NIR wavebands, and the net longwave radiation (Leuning et al., 1995; Appendix D therein):

$$\begin{array}{}\text{(43)}& R_{\mathrm{ni}}=S_{\mathrm{abs}}-B_{\mathrm{n},\mathrm{0}}\times k_{\mathrm{d}}\exp \left(-k_{\mathrm{d}}\mathrm{LAI}\right),\end{array}$$

where B_n,0 is the net longwave radiation at the top of the canopy, and k_dexp (−k_dLAI) accounts for its extinction within the canopy, with k_d set equal to 0.8. To account for the absorbed NIR radiation at a given height within the canopy in S_abs, we used the relationship reported by Kume et al. (2011; Fig. 4 therein) that links the transmitted NIR to the transmitted and incident PAR and assumed a leaf absorptance in the NIR equal to 0.1. B_n,0 is then computed as the absorbed minus the emitted longwave radiation:

$$\begin{array}{}\text{(44)}& B_{\mathrm{n},\mathrm{0}}={\mathit{\epsilon }}_{\mathrm{l}}(\mathrm{1}-{\mathit{\epsilon }}_{\mathrm{a}})\mathit{\sigma }{T}_{\mathrm{top}}^{\mathrm{4}},\end{array}$$

where T_top is the top canopy air temperature in Kelvin, σ is the Stefan–Boltzmann constant ($\mathit{\sigma }=\mathrm{5.67}\times {\mathrm{10}}^{-\mathrm{8}}$ W m⁻² K⁻⁴), ε_l is the emissivity of the canopy leaves, here assumed to be 1, and ε_a is the emissivity of the atmosphere. Several models exist for ε_a, with varying performance depending on the sky conditions (Marthews et al., 2012). We used Dilley and O'Brien (1998) here, which compromises between parsimony and performance across sky conditions (Marthews et al., 2012; Tables 2 and 5 therein).

g_H, the total leaf conductance to heat, has three components, the boundary layer conductance for free convection g_bHf, the boundary layer for forced convection g_bHu, and the radiation conductance g_r (Leuning et al., 1995; Jones, 2013):

$$\begin{array}{}\text{(45)}& g_{\mathrm{H}}=\mathrm{2}\times \left(g_{\mathrm{bHf}}+g_{\mathrm{bHu}}+g_{\mathrm{r}}\right),\end{array}$$

where the factor 2 accounts for the two sides of the leaves' g_bHf. The boundary layer conductance for free convection is given by

$$\begin{array}{}\text{(46)}& g_{\mathrm{bHf}}=\mathrm{0.5}\times D_{\mathrm{H}}\times {\left({\displaystyle \frac{\mathrm{1.6}\times {\mathrm{10}}^{\mathrm{8}}\times \left|T_{\mathrm{l}}-T\right|}{w_{\mathrm{l}}}}\right)}^{\mathrm{0.25}}\times {\displaystyle \frac{P_{\mathrm{ress}}}{RT}},\end{array}$$

where D_H is the molecular diffusivity to heat ($D_{\mathrm{H}}=\mathrm{21.5}\times {\mathrm{10}}^{-\mathrm{6}}$ m² s⁻¹), P_ress the atmospheric pressure (in Pa), R the universal gas constant (R=8.314 J mol⁻¹ K⁻¹), and T the temperature of surrounding air in Kelvin. Leaf width w_l (m) is estimated as the square root of leaf area ($w_{\mathrm{l}}=\sqrt{\mathrm{LA}})$. g_bHu, the boundary layer for forced convection (in mol m⁻² s⁻¹), is given by

$$\begin{array}{}\text{(47)}& g_{\mathrm{bHu}}=\mathrm{0.003}\times \sqrt{{\displaystyle \frac{u}{w_{\mathrm{l}}}}}\times {\displaystyle \frac{P_{\mathrm{ress}}}{RT}},\end{array}$$

where u is the wind speed in m s⁻¹ (see Eq. 9). g_r, the radiation conductance in mol m⁻² s⁻¹, varies with T_a as follows (Jones, 2013, p. 101 therein).

$$\begin{array}{}\text{(48)}& g_{\mathrm{r}}={\displaystyle \frac{\mathrm{4}\times {\mathit{\epsilon }}_{\mathrm{l}}\mathit{\sigma }{T}^{\mathrm{3}}}{C_p{M}_{\mathrm{a}}}}\end{array}$$

g_w, the total conductance to water vapour, has two components that represent hydraulic resistances in series: the stomatal conductance (g_sw, in mol H₂O m⁻² s⁻¹, Eq. 35) and the boundary layer conductance (g_bw in mol H₂O m⁻² s⁻¹) to water vapour:

$$\begin{array}{}\text{(49)}& {\displaystyle }{g}_{\mathrm{w}}={\displaystyle \frac{g_{\mathrm{bw}}\times g_{\mathrm{sw}}}{g_{\mathrm{bw}}+g_{\mathrm{sw}}}},\text{(50)}& {\displaystyle }\text{ with }{g}_{\mathrm{bw}}=\mathrm{1.075}\times \left(g_{\mathrm{bHf}}+g_{\mathrm{bHu}}\right),\end{array}$$

where 1.075 accounts for the relative diffusivities of heat and water vapour in air. Equations (9) and (50) assume that all leaves are hypostomatous (stomates on the ground-facing side of the leaves only), a reasonable assumption in tropical forests (Drake et al., 2019; Muir, 2015).

2.6 Carbon allocation

2.6.1 Net carbon uptake: whole-tree integration and respiration

At each daily time step, the individual tree net primary productivity of carbon, NPP_ind (gC), is obtained by the following balance equation (Fig. 3).

$$\begin{array}{}\text{(51)}& {\mathrm{NPP}}_{\mathrm{ind}}={\mathrm{GPP}}_{\mathrm{ind}}-R_{\mathrm{maintenance}}-R_{\mathrm{growth}}\end{array}$$

GPP_ind (gC) is computed each half-hour as the carbon assimilation rate A_n (Eq. 19), multiplied by the leaf area in each tree crown layer (LA_l, in m²), then summed over tree crown layers and cumulated across the day.

Young leaves and old leaves have been reported to have lower photosynthetic capacities and activities than mature leaves (Doughty and Goulden, 2008; Kitajima et al., 2002, 1997b; Wu et al., 2016; Albert et al., 2018; Menezes et al., 2021). For each tree, total leaf area (LA_t) is partitioned into three leaf age pools: young, mature, and old leaves so that LA_t= LA_young + LA_mature + LA_old (all in m²). These three leaf age pools are assumed to be uniformly distributed within the tree crown. In young and old leaves, the net assimilation rate is a fraction ϱ<1 of that of mature leaves so that

$$\begin{array}{}\text{(52)}& \begin{array}{rl}{\mathrm{GPP}}_{\mathrm{ind}}& =C_{\mathrm{GPP}}\times {\displaystyle \frac{\left(\mathit{\varrho }\times {\mathrm{LA}}_{\mathrm{young}}+{\mathrm{LA}}_{\mathrm{mature}}+\mathit{\varrho }\times {\mathrm{LA}}_{\mathrm{old}}\right)}{{\mathrm{LA}}_t}}\\ & \times \sum _l\sum _t{A}_{\mathrm{n}}\left(t,l\right)\times {\mathrm{LA}}_l,\end{array}\end{array}$$

where the factor C_GPP is a conversion factor, and t depicts the daytime half-hours and l the tree crown layers. Here we assume that the carbon uptake efficiency ϱ relative to mature leaves is the same in young and old leaves and ϱ=0.5, a value consistent with observations.

TROLL 4.0 partitions autotrophic respiration into maintenance respiration and growth respiration, even if both come from the same biochemical pathways (Amthor, 1984; Thornley and Cannell, 2000). Maintenance respiration (R_maintenance) has seldom been documented for stem and roots and is inferred empirically (Cavaleri et al., 2008; Meir et al., 2001; Slot et al., 2013; Weerasinghe et al., 2014). Nighttime leaf maintenance respiration is computed using Eqs. (32) and (33), using the mean nighttime temperature. As stomatal conductance and dark respiration vary less with leaf age than carbon assimilation rate (Albert et al., 2018; Kitajima et al., 2002; Villar et al., 1995), we assumed that young and old leaves have respiration and transpiration rates equal to ${\mathit{\varrho }}^{\prime }=\mathrm{0.75}$ that of mature leaves, leading to lower water use efficiency than mature leaves. Tree-level nighttime leaf respiration and daytime transpiration are computed as follows at each time step:

$$\begin{array}{}\text{(53)}& \begin{array}{rl}{X}_{\mathrm{ind}}& =C_X\times {\displaystyle \frac{\left({\mathit{\varrho }}^{\prime }\times {\mathrm{LA}}_{\mathrm{young}}+{\mathrm{LA}}_{\mathrm{mature}}+{\mathit{\varrho }}^{\prime }\times {\mathrm{LA}}_{\mathrm{old}}\right)}{{\mathrm{LA}}_{\mathrm{t}}}}\\ & \times \sum _l\left(\sum _{i}X\left(i,l\right)\right)\times {\mathrm{LA}}_l,\end{array}\end{array}$$

where X_ind is either the carbon respired by leaves during the night or the total water transpired by the tree (gC or m³, respectively), X is the leaf dark respiration (Eqs. 32 and 33) or the leaf-level transpiration rate (Eq. 41), respectively, and C_X is a factor to convert leaf-level rates in µmol C m⁻² s⁻¹ or in mol H₂O m⁻² s⁻¹ to total fluxes per individual per day (gC or m³, respectively).

Stem maintenance respiration (R_stem, in µmol C s⁻¹) was modelled assuming a constant respiration rate per volume of sapwood (39.6 µmol m⁻³ s⁻¹, Ryan et al., 1994) so that

$$\begin{array}{}\text{(54)}& R_{\mathrm{stem}}=C_{\mathrm{sresp}}\times \mathrm{39.6}\times \mathrm{SA}\times \left(h-\mathrm{cd}\right)\end{array}$$

where SA is the tree sapwood area (in m²) and C_sresp is a conversion factor. Stem respiration response to temperature was modelled using a Q₁₀ value of 2.0 (Meir and Grace, 2002; Ryan et al., 1994) and using mean daytime and nighttime temperatures. Stahl et al. (2011) reported that R_stem varies among individual trees, even when controlling for sapwood volume. However, in the absence of a clear understanding of the drivers, Eq. (4) is a parsimonious choice. In TROLL 4.0, sapwood area is computed dynamically. We used an inversion of the pipe model to derive sapwood area from the tree's leaf area (LA_t, in m²), height (h, m), and wood density following Fyllas et al. (2014; Eqs. 7 and 8 therein):

$$\begin{array}{}\text{(55)}& \mathrm{SA}=C_{\mathrm{SA}}{\displaystyle \frac{\mathrm{2}\times {\mathrm{LA}}_t}{{\mathit{\lambda }}_{\mathrm{1}}+{\mathit{\lambda }}_{\mathrm{2}}\times h+{\mathit{\delta }}_{\mathrm{1}}+{\mathit{\delta }}_{\mathrm{2}}\times \mathrm{wsg}}},\end{array}$$

with λ₁= 0.066 m² cm⁻², λ₂=0.017 m cm⁻², ${\mathit{\delta }}_{\mathrm{1}}=-\mathrm{0.018}$ m² cm⁻², and δ₂=1.6 cm³ g⁻¹, and C_SA a conversion factor. In addition to Eq. (55), there are both lower and upper limits on sapwood extent. Sapwood has a minimum thickness of 0.5 cm and any newly grown wood is always considered sapwood, irrespective of leaf area. TROLL 4.0 also imposes an upper limit on sapwood growth based on stem diameter growth so that increases in living tissue cannot exceed increases in total tissue.

Other contributions of maintenance respiration were prescribed as proportions of leaf and stem maintenance respiration. Fine root maintenance respiration was assumed to be half of leaf maintenance respiration (Malhi, 2012), and coarse root and branch maintenance respirations were assumed to account for half of stem respiration (Asao et al., 2015; Cavaleri et al., 2006; Meir and Grace, 2002).

Growth respiration (R_growth) was assumed to account for 30 % of the carbon uptake by photosynthesis (gross primary productivity) minus the maintenance respiration (Cannell and Thornley, 2000). These assumptions are commonly made in the literature but remain a major source of uncertainty in carbon flux modelling (Atkin et al., 2014; Huntingford et al., 2013).

Contrary to the last published version of TROLL, in which the allocation of NPP_ind to plant organs was fully prescribed by fixed factors ($f_{\mathrm{canopy}}=f_{\mathrm{leaves}}+f_{\mathrm{fruit}}+f_{\mathrm{twigs}}$ and f_wood; Maréchaux and Chave, 2017), the allocation scheme implemented in TROLL 4.0 can now be additionally modulated depending on the current tree state and it includes an explicit carbon storage compartment (Sect. 2.6.2 and 2.6.3; Fig. 3).

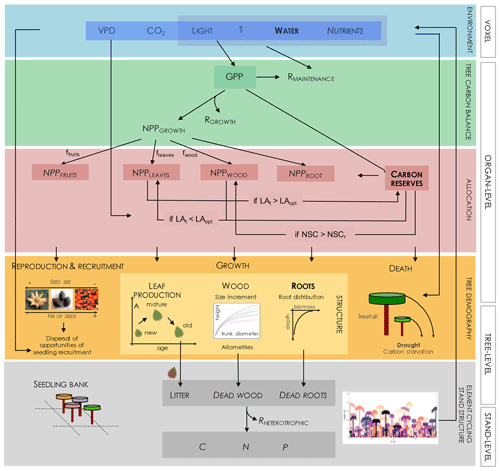
Figure 3 Diagram of structures and processes driving individual and community dynamics, as investigated under the modelling approach adopted in TROLL 4.0. Elements in bold letters refer to novel implementation in comparison to the previously published version, while italic letters refer to elements still not included in this present version. The abiotic environment is modelled at the voxel scale and drives C assimilation in the leaves (gross primary productivity, GPP) and maintenance respiration rates of the different plant organs (R_MAINTENANCE). The C amount resulting from the balance between GPP and R_MAINTENANCE can be used for tissue production (NPP_FRUITS, NPP_LEAVES, NPP_WOOD, and NPP_ROOTS) or stored (CARBON RESERVES) in the different tree organs. Both allocations induce metabolic costs (R_GROWTH and R_STORAGE; but the latter is not represented nor included). CARBON RESERVES represents non-structural carbohydrates (NSC), mainly stored as sugar or starch, and its maximal storage capacity is given by NSC_r. Allocation to these different compartments follows a hierarchical scheme initialized by default proportions (f_fruits, f_leaves, f_wood). If the tree leaf area (LA_t) exceeds the optimal leaf area (LA_opt, a function of both tree properties and its micro-environment), then the surplus of NPP_LEAVES is allocated to carbon reserves. If the tree leaf area is lower than optimal, then NPP_WOOD and, if further needed, carbon reserves are mobilized for leaf production. If carbon reserves surpass storage capacity (NSC_r), then stored carbohydrates are used for woody growth. C allocated to tissue production leads to an increase in trunk diameter and height following allometric relationships and the production of new young leaves and roots. Simultaneously with tissue turnover, this leads to the update of leaf density and root biomass distribution, influencing both the abiotic environment (e.g. light diffusion and water interception) and light and element acquisition and thus carbon assimilation and metabolism. C allocated to reproduction leads to the production of seeds, which are dispersed randomly. This generates a spatially explicit seedling bank, from which winners are locally recruited depending on both light and water availability. Tree death may be triggered by environmental or mechanical constraints or carbon starvation. In a future version, litter decomposition, wood decay, and nutrient mineralization could lead to soil nutrient availability for plant uptake and take place through the action of soil microorganisms, whose activity, and hence respiration (R_{HETEROTROPHIC}), depends particularly on temperature and soil moisture.

2.6.2 Leaf production and leaf shedding

Leaf phenology is a key driver of the variation of tropical forest productivity (Manoli et al., 2018; Restrepo-Coupe et al., 2013; Wu et al., 2017). However, its underlying drivers remain poorly understood, and its representation in vegetation models remains challenging (Chen et al., 2020; Restrepo-Coupe et al., 2017). In ORCHIDEE, Chen et al. (2020, 2021) proposed a leaf phenological scheme in which the production of young leaves is partly controlled by incident shortwave radiation, while the shedding of old leaves is controlled by vapour pressure deficit. This scheme reproduces the simultaneous increase in leaf production and litterfall observed in many Amazonian rainforest sites where productivity increases during the dry season (Chave et al., 2010; Wagner et al., 2016; Yang et al., 2021), but not the observed seasonality in productivity at some sites (e.g. GUYAFLUX eddy flux site in French Guiana; Chen et al., 2020). Additionally, this scheme overlooks the contrasted leaf phenological patterns observed across canopy individuals within and across species within communities (Nicolini et al., 2012; Loubry, 1994). In ED2, Xu et al. (2016) implemented a leaf phenological scheme driven by water availability in the root zone in a seasonally dry tropical forest. Since leaf shedding is often triggered by drought-induced loss of leaf turgor in these systems (Sobrado, 1986), leaf shedding and production are assumed to depend on the difference between leaf pre-dawn water potential and leaf water potential at turgor loss point. However, such a scheme cannot simulate the simultaneous leaf production and shedding observed in moist tropical forests.

In TROLL 4.0, we propose an alternative approach. At each time step, the optimal tree total leaf area (LA_opt) is estimated as the leaf area beyond which producing more leaves leads to a net carbon loss due to self-shading and respiration costs. LA_opt depends on tree crown size and leaf area density (Sect. 2.4.2), leaf photosynthetic capacities and respiration rate (Sect. 2.5.1), and local light environment. At each time step, the amount of carbon allocated to the production of new young leaves, NPP_leaves, and to woody growth, NPP_wood, is determined by default as ${\mathrm{NPP}}_{\mathrm{leaves}}=f_{\mathrm{leaves}}\times {\mathrm{NPP}}_{\mathrm{ind}}$, with $f_{\mathrm{leaves}}=\mathrm{0.68}\times f_{\mathrm{canopy}}$ (Chave et al., 2008, 2010; Maréchaux and Chave, 2017) and ${\mathrm{NPP}}_{\mathrm{wood}}=\mathrm{0.6}\times f_{\mathrm{wood}}\times {\mathrm{NPP}}_{\mathrm{ind}}$, where the factor 0.6 accounts for the fact that about 40 % of woody NPP is actually used for branch fall repair (Malhi et al., 2011). When leaf area LA_t exceeds LA_opt, NPP_leaves is reduced so that LA_t = LA_opt. Second, if the carbon allocated to leaf production is not sufficient to compensate for leaf loss, then the carbon attributed by default to tree woody growth is mobilized for leaf production until leaf loss is compensated for. If not sufficient, the tree carbon storage (see Sect. 2.6.3) is then also mobilized. Hence this scheme prioritizes the maintenance of the assimilating tissues over woody growth (Schippers et al., 2015). The variation of leaf area for each leaf age pool is then computed as follows:

$$\begin{array}{}\text{(56)}& \begin{array}{rl}\mathrm{\Delta }{\mathrm{LA}}_{\mathrm{young}}& ={\displaystyle \frac{\mathrm{2}\times {\mathrm{NPP}}_{\mathrm{leaves}}}{\mathrm{LMA}}}-{\displaystyle \frac{L{A}_{\mathrm{young}}}{{\mathit{\tau }}_{\mathrm{young}}}}\\ \mathrm{\Delta }{\mathrm{LA}}_{\mathrm{mature}}& ={\displaystyle \frac{{\mathrm{LA}}_{\mathrm{young}}}{{\mathit{\tau }}_{\mathrm{young}}}}-{\displaystyle \frac{{\mathrm{LA}}_{\mathrm{mature}}}{{\mathit{\tau }}_{\mathrm{mature}}}}\\ \mathrm{\Delta }{\mathrm{LA}}_{\mathrm{old}}& ={\displaystyle \frac{{\mathrm{LA}}_{\mathrm{mature}}}{{\mathit{\tau }}_{\mathrm{mature}}}}-{\displaystyle \frac{{\mathrm{LA}}_{\mathrm{old}}}{{\mathit{\tau }}_{\mathrm{old}}}},\end{array}\end{array}$$

where τ_young, τ_mature, and τ_old are the residence times in each class (in years) so that LL $={\mathit{\tau }}_{\mathrm{young}}+{\mathit{\tau }}_{\mathrm{mature}}+{\mathit{\tau }}_{\mathrm{old}}$ with LL the maximal tree leaf lifespan (in years). LL is inferred from the tree LMA using the following empirical relationships (Schmitt, 2017):

$$\begin{array}{}\text{(57)}& \begin{array}{rl}\mathrm{LL}& ={\displaystyle \frac{\mathrm{1}}{\mathrm{12}}}max(\mathrm{3},\\ & \mathrm{12.755}\times \exp \left(\mathrm{0.007}\times \mathrm{LMA}-\mathrm{0.565}\times N\right))\end{array}\end{array}$$

τ_young was fixed to min(LL$/\mathrm{3}$, $\mathrm{1}/\mathrm{12}$) yr (Doughty and Goulden, 2008; Wu et al., 2016) and τ_mature as a third of total leaf lifespan.

The loss term LA${}_{\mathrm{old}}/{\mathit{\tau }}_{\mathrm{old}}$ corresponds to the rate of leaf litterfall at each time step. In the previous TROLL version, litterfall resulted from the dynamics of leaf biomass with ${\mathit{\tau }}_{\mathrm{old}}=\mathrm{LL}-{\mathit{\tau }}_{\mathrm{young}}-{\mathit{\tau }}_{\mathrm{mature}}$. This leaf shedding scheme is passive and does not simulate the observed seasonality in leaf litterfall. Here we propose a new approach to simulate leaf shedding. We first observed that within species and sites, canopy trees can shed their leaves at different times, suggesting that causal environmental drivers should display fine-scale heterogeneity in space (unlike atmospheric shortwave radiation and vapour pressure deficit). In addition, old leaves display nutrient resorption before abscission (Albert et al., 2018; Kitajima et al., 1997a; Urbina et al., 2021); similarly, solute translocation from older to younger leaves can lower osmotic potential and leaf water potential at turgor loss point, thus increasing the drought tolerance of younger leaves to the detriment of older leaves (Pantin et al., 2012). We therefore used pre-dawn leaf water potential as a trigger of leaf shedding as in Xu et al. (2016), but with different thresholds for leaves of different ages, older leaves being more susceptible to a small decrease in tree water availability, while younger leaves can maintain turgor and grow at the same time. More specifically, we defined the following threshold.

$$\begin{array}{}\text{(58)}& {\mathit{\psi }}_{\mathrm{T},\mathrm{o}}=min\left(a_{\mathrm{T},\mathrm{o}}\times {\mathit{\pi }}_{\mathrm{tlp}},-\mathrm{0.01}\times h-b_{\mathrm{T},\mathrm{o}}\right)\end{array}$$

The first term in ψ_T,o with $a_{\mathrm{T},\mathrm{o}}<\mathrm{1}$ represents old leaves' lower ability to maintain turgor as soil dries. The second term modulates this susceptibility to drought depending on tree height (Bennett et al., 2015): it induces a susceptibility to a (small) decrease $b_{\mathrm{T},\mathrm{o}}>\mathrm{0}$ in soil water availability for large trees, while preventing them from constantly shedding their old leaves at a fast pace (see Eq. (37) and Fig. 4). τ_old is then updated using a multiplying factor $f_{\mathrm{o}}\left(\mathrm{0.001}\le f_{\mathrm{o}}\le \mathrm{1}\right)$. Initially, ${\mathit{\tau }}_{\mathrm{old}}^{\prime }=f_{\mathrm{o}}{\mathit{\tau }}_{\mathrm{old}}$ with f_o=1 , which is updated daily as follows: $f_{\mathrm{o}}^{\prime }=f_{\mathrm{o}}-{\mathit{\delta }}_{\mathrm{o}}$ when ${\mathit{\psi }}_{\mathrm{pd}}<{\mathit{\psi }}_{\mathrm{T},\mathrm{o}}$ and $f_{\mathrm{o}}^{\prime }=f_{\mathrm{o}}+{\mathit{\delta }}_{\mathrm{o}}$ when ${\mathit{\psi }}_{\mathrm{pd}}>{\mathit{\psi }}_{\mathrm{T},\mathrm{o}}$, always assuming that f_o has 0.001 as a lower bound and 1 as an upper bound.

We assumed no variation of π_tlp with tree height (Maréchaux et al., 2016). The threshold ψ_T,o jointly depends on π_tlp and tree height h to account for drought tolerance and tree height on leaf-level water stress. Practically, the tree height above which old leaves become susceptible to a small decrease in soil water availability is $H_{\mathrm{T},\mathrm{o}}=-\mathrm{100}\times \left(a_{\mathrm{T},\mathrm{o}}{\mathit{\pi }}_{\mathrm{tlp}}+b_{\mathrm{T},\mathrm{o}}\right)$ in metres: 28 m at ${\mathit{\pi }}_{\mathrm{tlp}}=-\mathrm{1.5}$ MPa and 58 m at ${\mathit{\pi }}_{\mathrm{tlp}}=-\mathrm{3}$ MPa (when $a_{\mathrm{T},\mathrm{o}}=\mathrm{0.2}$ and $b_{\mathrm{T},\mathrm{o}}=\mathrm{0.02}$; see Fig. 4). While this scheme is based on process-based observations, parameters a_T,o, b_T,o, and δ_o are currently calibrated (see Schmitt et al., 2025).

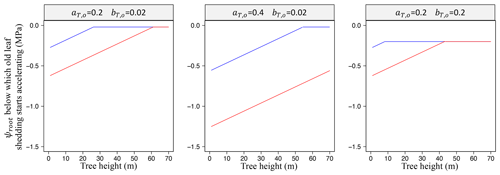
Figure 4 Effect of phenological parameters a_T,o and b_T,o (Eq. 58) on the height and drought tolerance dependencies of old leaf shedding. Variation of the soil water potential in the root zone (ψ_root; Eq. 37) below which old leaf shedding starts accelerating as a function of tree height for different values of a_T,o and b_T,o and two values of π_tlp: ${\mathit{\pi }}_{\mathrm{tlp}}=-\mathrm{1.41}$ MPa in blue, the least negative value reported in Maréchaux et al., 2015, and ${\mathit{\pi }}_{\mathrm{tlp}}=-\mathrm{3.15}$ MPa in red, the most negative value reported in Maréchaux et al. (2015), as in Fig. 2.

2.6.3 Carbon storage

In TROLL 4.0, trees can store carbon explicitly in non-structural carbohydrates. The maximum amount of carbon a tree can store and remobilize is determined as follows:

$$\begin{array}{}\text{(59)}& {\mathrm{NSC}}_{\mathrm{r}}=\mathrm{1000}\times \mathrm{0.5}\times \mathrm{0.05}\times \mathrm{1.25}\times \mathrm{AGB},\end{array}$$

where NSC_r stands for non-structural carbohydrates (gC), AGB is the tree aboveground biomass (in kg), and 1000×0.5 converts biomass in kilograms into C in grams (Elias and Potvin, 2003). It is assumed that NSC can account for 10 % of the tree biomass, half of which is mobilizable (Martínez-Vilalta et al., 2016), hence the factor 0.05. The other half of NSC supports critical metabolic functions or is no longer accessible. The factor 1.25 accounts for an additional 25 % biomass storage in coarse roots, so 1.25×AGB is total tree biomass (Ledo et al., 2018). AGB is computed following (Chave et al., 2014; Eq. 5 therein):

$$\begin{array}{}\text{(60)}& \mathrm{AGB}=\mathrm{0.0559}\times \mathrm{wsg}\times {\mathrm{dbh}}^{\mathrm{2}}\times h,\end{array}$$

where dbh is in centimetres, h in metres, and wsg in g cm⁻³. Note that Eqs. (59) and (60), together with Eq. (61) below, induce a growth–storage trade-off mediated by wood density variation across individual and species, in agreement with observations (Signori-Müller et al., 2022). The NSC storage compartment is filled by the potential carbon surplus resulting from the allocation to leaf production, i.e. $f_{\mathrm{leaves}}\times {\mathrm{NPP}}_{\mathrm{ind}}-{\mathrm{NPP}}_{\mathrm{leaves}}$, if positive. If the storage compartment has reached its maximum capacity NSC_r, then the surplus is allocated to woody growth.

2.6.4 Growth

The net primary production allocated to woody growth, NPP_wood, depends on the outcome of allocation to leaf production and carbon reserves (see Sect. 2.6.2 and 2.6.3; Fig. 3). In TROLL 4.0, hydraulic control on carbon assimilation and leaf phenology both influence carbon allocation to trunk growth (e.g. Doughty et al., 2014; Farrior et al., 2013; Friedlingstein et al., 1999), but turgor-mediated processes are not explicitly modelled (Coussement et al., 2018; Peters et al., 2023; Muller et al., 2011; Körner, 2015). NPP_wood is converted into an increment of stem volume, ΔV in m³, as follows:

$$\begin{array}{}\text{(61)}& \mathrm{\Delta }V={\mathrm{10}}^{-\mathrm{6}}\times {\displaystyle \frac{{\mathrm{NPP}}_{\mathrm{wood}}}{\mathrm{0.5}\times \mathrm{wsg}}}\times \mathrm{Senesc}\left(\mathrm{dbh}\right),\end{array}$$

where the factor 0.5 converts dry biomass units into carbon units (Elias and Potvin, 2003). The function Senesc(dbh) is designed so that the largest trees cannot allocate carbon as efficiently into growth, reflecting empirical evidence of a size-related relative growth decline in trees (Yoda et al., 1965; Ryan et al., 1997; Mencuccini et al., 2005; Woodruff and Meinzer, 2011; Stephenson et al., 2014). We assumed that trees cannot exceed a trunk diameter of ${\mathrm{dbh}}_{max}=\frac{\mathrm{3}}{\mathrm{2}}{\mathrm{dbh}}_{\mathrm{thresh}}$, where dbh_thresh depends on species-specific information provided by the user (see Sect. 2.4.1), so that

$$\begin{array}{}\text{(62)}& \begin{array}{rlr}& \mathrm{Senesc}\left(\mathrm{dbh}\right)=\mathrm{1}& \text{ when dbh}\le {\mathrm{dbh}}_{\mathrm{thresh}}\\ & \mathrm{Senesc}\left(\mathrm{dbh}\right)=max\left(\mathrm{0};\mathrm{3}-\mathrm{2}{\displaystyle \frac{\mathrm{dbh}}{{\mathrm{dbh}}_{\mathrm{thresh}}}}\right)& \text{when dbh}>{\mathrm{dbh}}_{\mathrm{thresh}}.\end{array}\end{array}$$

The trunk diameter growth increment Δdbh (m) is computed from ΔV as follows. $V=C\mathit{\pi }(\frac{\mathrm{dbh}}{\mathrm{2}}{)}^{\mathrm{2}}h$, where C is a form factor (Chave et al. 2014, Eq. 5 therein). The term h (m) is total tree height inferred from the dbh following Eq. (16), and this leads to an expression of V as a function of dbh only. This function can be inverted to estimate Δdbh as a function of ΔV, which is known from Eq. (61). Tree height and crown dimensions are then updated using Eqs. (16), (17), and (18).

2.7 Tree demography

2.7.1 Seed production, dispersal, and recruitment

The starting point for a tree life cycle, as represented in TROLL 4.0, is an event of seed dispersal into the seed bank. On each 1×1 m ground site and for each species s, a “seed” bank stores all the seeds dispersed from the mature trees as well as from an external seed rain. The seed bank is updated once a year. Here, our conceptual “seeds” represent opportunities for seedling recruitment at 1 cm dbh (henceforth denoted “reproduction opportunities”) rather than as true seeds, since not all seed dispersal events are modelled explicitly, and the seed-to-seedling transition is implicit.

In TROLL 4.0 trees are assumed to become fertile above a diameter threshold dbh_mature that depends on the tree maximum size (Visser et al., 2016) as follows.

$$\begin{array}{}\text{(63)}& {\mathrm{dbh}}_{\mathrm{mature}}=\mathrm{0.5}\times {\mathrm{dbh}}_{\mathrm{thresh}}\end{array}$$

This relationship is drawn from direct observations of the reproductive status of tree species in the tropical forest of Barro Colorado Island, Panama, with maximal tree dbh spanning a range of 0.05 to 2 m (see Fig. S9 in Visser et al., 2016; R²=0.81, n=60 species). The number of reproduction opportunities per mature tree, n_s, is assumed to be fixed and equal for all individuals, and its value is user-defined. This assumption of a fixed reproductive opportunity per tree is predicated on the fact that there is a trade-off between seed number and seed size, itself related to seed and seedling survival. Thus, the probability of germination does not depend strongly on seed size or on the number of produced seeds and can be assumed to be a zero-sum game (Coomes and Grubb, 2003; Moles et al., 2004; Moles and Westoby, 2006). Each of the n_s events is scattered away from the tree in a random direction and at a distance randomly drawn from a Rayleigh distribution, thus allowing for potential long-dispersal events. Although seed dispersal distance is known to vary depending on dispersal syndrome and plant traits (Tamme et al., 2014; Seidler and Plotkin, 2006; Muller-Landau et al., 2008), the scale parameter σ_disp of the distribution is fixed here across species and individuals.

The intensity of the external seed rain is quantified by N_tot (number of incoming seeds per hectare) and its species composition is defined by the relative abundances of species f_reg,s, both being user-defined. Hence, for each species s, n_ext,s events of dispersal due to seeds immigrating from the outside occurred, with

$$\begin{array}{}\text{(64)}& n_{\mathrm{ext},s}=N_{\mathrm{tot}}\times f_{\mathrm{reg},s}\times n_{\mathrm{ha}},\end{array}$$

with n_ha being the number of hectares of the simulated plot. These reproduction opportunities are uniformly distributed within the simulated area.

If several species are competing for recruitment in a local seed bank, one of the species is picked at random as the winner out of all the seeds present, as in a lottery model (Chesson and Warner, 1981). The recruitment event occurs only if ground-level light availability is sufficiently high. To test if this condition is met, the seedling is first attributed individual trait values depending on the species-specific averages (see Sect. 2.4.1). These trait values are then used to determine the maximum LAI (LAI_max) the seedling would support under average environmental conditions, with LAI_max defined as the threshold beyond which the seedling leaf assimilation would be less than respiration (see Sect. 2.6.2). The seedling can be recruited if the site LAI at ground level is lower than LAI_max.

Water availability is also key to seedling performance (Engelbrecht et al., 2006; Johnson et al., 2017; Kupers et al., 2019); hence, TROLL 4.0 now implements an additional dependence of water availability on seedling establishment (Craine et al., 2012; Paine et al., 2018). Seedling recruitment is possible only if the top-layer soil water potential is less negative than half the turgor loss point (${\mathit{\pi }}_{\mathrm{tlp}}/\mathrm{2}$). Such parameterization is motivated by the fact that, at turgor loss point, the seedlings would not germinate, and a certain level of turgor is needed for germination and growth (Bradford, 1990; Daws et al., 2008; Coussement et al., 2018; Hsiao, 1973; Fatichi et al., 2016).

If both conditions on light and water availability are met, the newly recruited tree is initialized with dbh = 0.01 m, a total leaf area of ${\mathrm{LA}}_{\mathrm{t}}=\mathrm{0.25}\times {\mathrm{LA}}_{\mathrm{opt}}$ distributed across the three leaf age pools in proportion to their relative span (${\mathit{\tau }}_{\mathrm{young}}/\mathrm{LL}$, ${\mathit{\tau }}_{\mathrm{mature}}/\mathrm{LL}$, ${\mathit{\tau }}_{\mathrm{old}}/\mathrm{LL}$; see Sect. 2.6.2), and a carbon storage compartment filled at half its maximum NSC_r (see Sect. 2.6.3).

The assumptions here made on tree reproduction largely reflect limited knowledge of these processes, which remain major sources of uncertainty in current models (König et al., 2022; Hanbury-Brown et al., 2022; Díaz-Yáñez et al., 2024).

2.7.2 Mortality

Mortality processes also play a key role in forest structure and carbon balance (Sevanto et al., 2014; Friend et al., 2014; Johnson et al., 2016; Esquivel-Muelbert et al., 2020; McDowell et al., 2022). TROLL 4.0 explicitly represents several important mechanisms of tree mortality. At each time step, the individual tree death rate (in events per year; Sheil et al., 1995) is

$$\begin{array}{}\text{(65)}& d=d_{\mathrm{b}}+d_{\mathrm{starv}}+d_{\mathrm{treefall}}+d_{\mathrm{drought}},\end{array}$$

where d_b is a background death rate, d_starv represents death due to carbohydrate shortage (carbon starvation), d_treefall represents death due to tree fall (including trees indirectly killed by neighbouring fallen trees), and d_drought the drought-induced tree mortality.

Background mortality d_b encapsulates death events that are not attributed to any specific mechanism in the model. The mortality rate is known to vary greatly among species, and here we assume that it is negatively correlated with tree wood density, as observed pan-tropically (King et al., 2006; Kraft et al., 2010; Poorter et al., 2008; Wright et al., 2010). This dependence illustrates a trade-off between investment in construction costs and risk of mortality (Chave et al., 2009). We assumed the following relationship:

$$\begin{array}{}\text{(66)}& d_{\mathrm{b}}=m\times \left(\mathrm{1}-{\displaystyle \frac{\mathrm{wsg}}{{\mathrm{wsg}}_{\lim }}}\right),\end{array}$$

where m (in events per year) is the reference background mortality rate for a species with low wood density and is user-specified. wsg_lim is a value large enough so that d_b always remains positive (here set at 1 g cm⁻³).

A tree can also die because of carbohydrate shortage in the case of prolonged stress (d_starv in Eq. 51). In TROLL 4.0, which includes an explicit carbohydrate storage compartment, the tree dies of carbon starvation when this compartment is empty and NPP_ind≤0 (Eq. 51).

Tree death may be caused by tree falls (term d_treefall in Eq. 65). To simulate this process, we first define a stochastic threshold Θ, depending on the tree maximal height and prescribed at tree birth. Then, the tree can fall with a probability equal to $\mathrm{1}-\frac{\mathrm{\Theta }}{h}$ (Chave, 1999) each month. As TROLL 4.0 uses a daily time step, this probability is uniformly distributed across the days of 1 month. The parameter Θ is computed for each tree, as follows:

$$\begin{array}{}\text{(67)}& \mathrm{\Theta }=h_{max}\times (\mathrm{1}-v_{\mathrm{T}}\times \left|\mathit{\zeta }\right|),\end{array}$$

where h_max is maximal tree height (i.e. the tree height computed using Eq. 16 at dbh_max), and v_T is a variance term, |ζ| is the absolute value of a random Gaussian variable with zero mean and unit standard deviation. v_T is modified at tree level so that high risks of tree fall (> 99.5th percentile of the Gaussian variable) occur at the same height for all individuals of the same species. This implicitly introduces a growth–mortality trade-off, as more slender trees (larger ratio of height to trunk diameter) should reach this height threshold quicker. The orientation of tree falls is random. Trees on the trajectory of the falling tree can be damaged, especially if they are smaller than the fallen tree (van der Meer and Bongers, 1996). To model this effect, an individual variable hurt is defined. If a tree is within the trajectory of the fallen stem or of the fallen crown, its variable hurt is updated to h and $\frac{h-\mathrm{CR}}{\mathrm{2}}$ , respectively, if it was lower, where h and CR are the tree height and crown radius of the fallen tree, respectively. The probability of dying due to another tree fall is then $\mathrm{1}-\frac{\mathrm{1}}{\mathrm{2}}\frac{h}{\mathrm{hurt}\times e^{{\mathit{\epsilon }}_{h,j}}}$, where h is the height of the focal tree and $e^{{\mathit{\epsilon }}_{h,j}}$ (see Eq. 16) accounts for the fact that slender individuals (higher tree height deviation) would be more vulnerable to tree fall. Such a tree can either fall and damage other trees itself or die standing, depending on the user choice. The hurt variable is reset to zero at each time step.

Finally, prolonged drought is also a source of mortality. Drought-induced mortality is triggered when the leaf pre-dawn water potential ψ_pd is below a lethal level (ψ_lethal), and ψ_lethal is computed from the leaf water potential at turgor loss point, using the relationship provided by the global meta-analysis of Bartlett et al. (2016b; P=0.03, R²=0.31, n=15 species from tropical dry and moist biomes), as follows.

$$\begin{array}{}\text{(68)}& {\mathit{\psi }}_{\mathrm{lethal}}=-\mathrm{0.9842}+\mathrm{3.1795}\times {\mathit{\pi }}_{\mathrm{tlp}}\end{array}$$

3 Modelling protocol

3.1 Model inputs

TROLL 4.0 requires five input files to run a simulation: (i) global parameters, (ii) species parameters, (iii) soil characteristics, and finally, meteorological drivers varying at (iv) half-hour and (v) daily steps.

The global input file contains parameters that define the simulation set-up (e.g. the number of time steps, the size of the simulated plot and of the belowground voxels) and values for biophysical parameters that remain constant throughout the simulation and are not species- or tree-specific. These include the light attenuation coefficient, allocation parameters, minimal death rate, and more (see Table A1). Parameter values can be varied across simulations to test model sensitivity, transfer across sites, or any other reason. The species input file contains mean functional traits for at least one species and with no upper bound (see Table A1). Functional trait values can be prescribed from local field measurements or retrieved from global trait databases (e.g. Kattge et al., 2020; Díaz et al., 2022).

The soil input file contains the soil variables needed for the pedotransfer functions, i.e. soil texture (proportion of silt, clay, and sand), soil organic matter content, dry bulk density, soil pH, and cation exchange capacity, for each soil layer, with the thickness of each layer. The number of soil layers is at least one and is not theoretically limited. Lacking local soil data, model users may retrieve soil parameters from online databases (e.g. Poggio et al., 2021), bearing in mind the uncertainties of such products, especially in tropical areas (Khan et al., 2024).

Meteorological drivers are provided in two files, depending on their temporal resolution in the model. Daytime temperature, vapour pressure deficit, incident irradiance, and wind speed at a reference height above the canopy are provided for every half-hour, while average nighttime temperature and cumulative rainfall are provided at a daily time step. Such data can typically be retrieved from meteorological stations embedded in eddy flux towers or from global products (Muñoz-Sabater et al., 2021), as in Schmitt et al. (2023).

3.2 Initial conditions

Two types of initial conditions are useful in most practical settings and are implemented in TROLL 4.0. First, the user can simulate forest regeneration from bare ground. In this case, forest succession is initiated by the external seed rain, the composition and intensity of which are user-defined (see above). The steady-state forest composition and structure are thus emergent properties of the community assembly mechanisms embedded in the model and the user-specified seed rain. The second option is to prescribe an initial forest state. This requires an initial forest state to be provided as an additional input file. The code is designed to adapt to the level of information provided by the inventory file, from a minimal requirement of tree dbh to the full list of individual variables for each tree. For individual variables missing in the input file, these are either computed from the model relationships or drawn at random. This second initial condition matches a real site forest state given the available data but will require careful calibration to maintain the forest state over a longer time period (e.g. Fischer et al., 2020). A more common use case is to restart new simulations from an output of a previous simulation, e.g. to perform virtual experiments controlling the initial state.

3.3 Standard outputs

TROLL 4.0 provides a range of outputs related to forest structure, forest composition and diversity, and ecosystem functioning (e.g. carbon and water fluxes; Fig. 5). It simulates forest structure and composition and provides outputs comparable to those measured in the field: tree size distribution, tree spatial distribution, biomass accumulation curve, functional trait distribution, canopy height and leaf area index maps (Maréchaux and Chave, 2017), and more generally all information that can be retrieved from a detailed field inventory or a metre-scale airborne laser scanning survey (Fischer et al., 2019). In TROLL 4.0, other outputs are also available: litterfall fluxes, carbon and water fluxes comparable to the ones provided by eddy flux towers, and soil water state (content and water potential). An evaluation of these outputs for two Amazonian forest sites is provided in a companion paper (Schmitt et al., 2025).

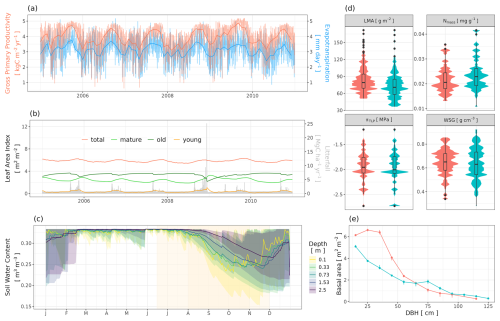
Figure 5 Examples of outputs provided by TROLL 4.0 related to ecosystem functioning, diversity, and structure. (a) Temporal variations of gross primary productivity (red) and evapotranspiration (blue) within and across years. (b) Variation in total leaf area index (red line) and leaf area index per leaf age cohort (young, mature, and old are represented by yellow, light green, and dark green lines, respectively), together with litterfall (grey bars), within and across years. (c) Mean seasonal variations of water content in soil layers of different depths, with the vertical yellow band in the background depicting the dry season. (d) Distribution of functional traits. (e) Distributions of basal area per diameter class. Panels (a), (b), and (c) show outputs for an Amazonian forest site (Paracou), and panels (d) and (e) show outputs for two Amazonian sites (Paracou, red; Tapajos, blue); see Schmitt et al. (2025) for details on simulation set-ups.

4 Discussion

TROLL 4.0 is part of a novel generation of forest growth models designed to bridge the gap between traditional forest growth models and process-based models informed by ecophysiology. It includes an integration of processes underlying ecosystem fluxes closer to a modern DGVM than most other forest growth simulators. It also includes representation of plant community structure and diversity at a resolution similar to that used by ecologists in the field. This enables a direct comparison with a range of field data, including forest inventories, trait distribution, fine- and large-scale remote sensing products, or eddy covariance data. Overall, these different features allow it to address a range of questions, from fundamental ones in community and theoretical ecology such as the mechanisms of species coexistence or the link between biodiversity and ecosystem functioning to more applied ones such as the design of forest management guidelines to sustain forest resilience under climate change. Here we discuss the assumptions of the water cycle newly included in the model, as well as transferability and limitations of the current model version.

4.1 Simulating water fluxes and forest responses to water availability

Previous versions of TROLL assume that water availability does not limit ecosystem fluxes and dynamics, a strong but reasonable assumption in a light-limited forest like in eastern Amazonia (Guan et al., 2015; Wagner et al., 2016; Maréchaux and Chave, 2017). However, such a simplification does not allow accounting for drought-induced interannual variability in forest dynamics (Bonal et al., 2008; Aguilos et al., 2018; Leitold et al., 2018) or transferring the model to sites where water availability is limiting. As droughts will be important drivers for tropical ecosystems in the future (Duffy et al., 2015), such a simplification does not allow projecting future states of forest under climate change.

In TROLL 4.0, we implemented a full water cycle. We introduced a belowground field with a hydraulic state coupled to the vegetation and a representation of the response of leaf gas exchanges to local atmospheric conditions and their control by the leaf boundary layer. This detailed representation is commonplace in DGVMs (Prentice et al., 2007), but to our knowledge, it is new for an individual-based spatially explicit forest dynamic simulator. This paves the way for explorations and projections of the independent effects of soil water availability and atmospheric demand on ecosystem functioning (Novick et al., 2016; Santos et al., 2018), community composition, and structure (Esquivel-Muelbert et al., 2019; Fauset et al., 2012; Slik, 2004; Feeley et al., 2011).

These developments have striven to follow the parsimonious principle: more complex representations do not systematically result in increased model reliability and robustness, especially if the additional parameters are poorly constrained (Mahnken et al., 2022; Prentice et al., 2015). The soil hydraulic state is simulated using a bucket model (Budyko, 1961; Manabe, 1969; Vargas Godoy et al., 2021). In the future, more complex representations of soil water dynamics could be implemented at finer temporal and spatial resolutions, such as the implementation of Richards' equation (Richards, 1931), and integration of lateral flows, but this would be at a serious computational cost. These could be compared with the current simpler representation to assess the relevance of increasing complexity in various contexts and soil data availability (Van Nes and Scheffer, 2005). However, two aspects were considered to be needed in the current version based on biological considerations. First, we implemented a multi-layer soil model, a more detailed representation compared with other models using a bucket model approach (e.g. Fischer et al., 2014; Laio et al., 2001). This was motivated by the need to account for contrasting rooting strategies and access to water among coexisting plants, which is an underexplored, but likely key, aspect of community dynamics in forests (Brum et al., 2019; De Deurwaerder et al., 2018; Ivanov et al., 2012). Second, we assumed that the depth of tree water uptake is controlled not only by the distribution of root biomass (as in Naudts et al., 2015; Sakschewski et al., 2021; Paschalis et al., 2024), but also by soil water state and its vertical variation (as in Williams et al., 1996; Duursma and Medlyn, 2012). These improvements are relevant to the temporal variation of water retrieval depth (Bruno et al., 2006) and the sustained dry-season productivity in rainforest ecosystems (Restrepo-Coupe et al., 2017).

The control of leaf gas exchange by water availability has been implemented by means of multiplicative soil water stress factors. Although the use of such factors has been debated (Powell et al., 2013; Joetzjer et al., 2014) and may underestimate the reduction of gas exchanges at midday under high evaporative demand, it has been preferred over a more explicit representation of the water flow through the plant column (e.g. Yao et al., 2022; Christoffersen et al., 2016; Cochard et al., 2021; De Cáceres et al., 2023). Although the stem hydraulic traits that would be needed for parameterizing an explicit plant water flow module have been increasingly measured over the past decades, data availability for tropical tree species remains low in regards to the actual number of species coexisting in these communities. Alternatively, correlative relationships have been used to infer these traits from more easily measured traits (Christoffersen et al., 2016; Xu et al., 2016). However, these are context-dependent (Brodribb, 2017; Rosas et al., 2019) and have at best low statistical support in rainforest communities that are loosely constrained by water availability (Dwyer and Laughlin, 2017; Delhaye et al., 2020; Maréchaux et al., 2020). Innovative methods alleviate the difficulties of robustly measuring the vulnerability of tropical trees to embolism (Cochard et al., 2016; Sergent et al., 2020; Garcia et al., 2023), and this could provide a key motivation for a more explicit module of plant water flow in TROLL (Kennedy et al., 2019; Paschalis et al., 2024). Such developments could be necessary to correctly represent the legacy of drought in forest ecosystems (Paschalis et al., 2024; Anderegg et al., 2015). However, two important aspects were taken into account in the implementation of the multiplicative water stress factors in TROLL 4.0. These factors were parameterized based on soil water potential as an independent variable, and not soil water content, the former directly controlling water availability for plants, while the effect of soil water content is strongly mediated by soil properties (Novick et al., 2022). Also, different water stress factors were used for stomatal and non-stomatal limitations in order to capture the sequence of effects of decreasing water availability on plant function (Trueba et al., 2019; Fatichi et al., 2016; Hsiao, 1973).

The effects of water availability on plant function and tree demography were implemented through trait-based parameterization, which allows a range of responses between trees and species. This was made possible through the use of leaf water potential at turgor loss point (π_tlp), a leaf-level trait that is mechanistically linked to plant responses to water availability (Bartlett et al., 2016b) and that is measurable at the community scale in diverse systems through a well-validated method (Maréchaux et al., 2016; Griffin-Nolan et al., 2019; Sun et al., 2020; Bartlett et al., 2012a). Leaf water potential at turgor loss point varies greatly across species within Amazonian forest communities (Maréchaux et al., 2015; Ziegler et al., 2019), and this diversity explains contrasting responses to water availability at the leaf and plant levels (Martin-StPaul et al., 2017; Maréchaux et al., 2018; Powell et al., 2017) and species distribution at local, regional, and global scales (Bartlett et al., 2016a; Baltzer et al., 2008; Lenz et al., 2006; Bartlett et al., 2012b). The relationships implemented here involving π_tlp have a mechanistic basis, as discussed above. However, the relationships controlling the effect of water availability on (1) leaf shedding, (2) seed germination and seedling recruitment, and (3) drought-induced mortality would deserve in-depth exploration. More generally, these three processes remain key aspects of community dynamics and ecosystem functioning in high need of sustained empirical investigation (Albert et al., 2019; Díaz-Yáñez et al., 2024; McDowell et al., 2022).

4.2 Model–data integration, transferability, and limitations

TROLL 4.0 simulates forest structure and diversity, while expanding the types of data with which its results can be compared (Schmitt et al., 2025). The individual-based species-specific representation of forest yields virtual forest inventories, including the location of each individual, their botanical identity, their dimensions, and virtual airborne laser scanning point clouds (Fischer et al., 2019; Schmitt et al., 2023). TROLL 4.0 additionally provides water, carbon, and litter flux dynamics that are directly comparable to eddy flux tower data and litter trap monitoring at fine temporal resolutions, and this specificity has numerous advantages.

The knowledge derived from field data can be directly assimilated into TROLL 4.0. As opposed to most DGVMs whose representation of vegetation does not allow this type of assimilation, this offers new perspectives for inference or calibration (Dietze et al., 2013; Fer et al., 2018; Hartig et al., 2012; LeBauer et al., 2013), which could help inform the development of DGVMs. For example, TROLL 4.0 may act as an integrator of data of different types, such as field inventories and remote sensing, to constrain allometries that would be biased or poorly grounded if relying on a unique data source (Fischer et al., 2019). Also, as many uncertainties in current DGVMs have been related to their aggregated representation of vegetation structure and biodiversity, TROLL 4.0 can be used to directly test the sensitivity of a range of processes shared with DGVMs to such representation, for example by performing simulations with different numbers and identities of species or spatial resolutions, to then inform DGVMs on the corresponding needed developments. TROLL 4.0 is also easy to use and test by field ecologists as it simulates trees, not cohorts, PFTs, or gap patches: it can reproduce classical experiments in community or ecosystem ecology (e.g. Crawford et al., 2021; Schmitt et al., 2020) while overcoming known empirical challenges such as low repeatability (Schnitzer and Carson, 2016) or limited spatial footprint (Estes et al., 2018). TROLL 4.0 can be compared with data under the control of different biophysical processes supporting a more robust evaluation and limiting equifinality issues (Franks et al., 1997; Medlyn et al., 2005). Finally, the model is parameterized based on traits directly measured in the field, improving model transferability (Rau et al., 2022a).

The individual-scale and spatially explicit representation of TROLL 4.0 comes with a computational burden. For a reference 4 ha area starting from bare ground and 600 years of simulation on a single CPU, the computational cost of TROLL 4.0 is about 1820 min compared with TROLL 2.3 (Maréchaux and Chave, 2017) of about 12 min. While the shift from a monthly to a daily time step explains the multiplication by a factor of 30 between the two versions, the addition of a belowground field and an iterative scheme to simulate leaf gas exchanges explains to a great extent the remaining factor of 5. Several developments should reduce this computational cost: tree demographic processes do not need to be simulated at the daily time step and could be represented at a monthly resolution; vegetation models already implement such nested timescales (Moorcroft, 2006). We are also confident that further computer time reduction will be brought about by code optimization. Finally, several strategies can be implemented to up-scale the outputs of individual-based models at reduced computational costs, especially by leveraging large-scale remote sensing products (Rödig et al., 2017; Sato et al., 2007; Shugart et al., 2015).

4.3 Current and future developments

TROLL 4.0 aims to reflect the state of the art in plant physiology and ecology and, as a result, reflects the corresponding knowledge gaps, which can lead to an unbalanced representation across processes. TROLL is being continuously developed, as knowledge and data availability progress, specific questions to address with the model emerge, or important limitations are identified. In a companion paper (Schmitt et al., companion paper), we use data from forest inventories, litter traps, eddy flux towers, and remote sensing products to evaluate and discuss the performance and limitations of TROLL 4.0 at two forest sites. We mention several ongoing or future developments here.

Empirical findings suggest that the contribution of undisturbed tropical forests to the global carbon sink is declining (Hubau et al., 2020; Qie et al., 2017), pointing to the need for integrated modelling to understand and predict such trends (Yao et al., 2023, 2024; Koch et al., 2021). Among the possible steps forward with TROLL 4.0 are an improved representation of stomatal conductance and its coupling with photosynthesis (Lamour et al., 2022; Dewar et al., 2018), as well as respiration response and acclimation to climatic drivers (Smith and Dukes, 2013; Collalti et al., 2020; Slot et al., 2013; Rowland et al., 2015). This notably includes the integration of light-driven plasticity in leaf traits, which has been recently highlighted as an important model development to robustly up-scale leaf-level gas exchange into ecosystem-level water and carbon balance (Fisher and Koven, 2020; Lamour et al., 2023b; Xu et al., 2021; Xu and Trugman, 2021). Improvements on the carbon budget would also be important, with more explicit carbon allocation to respiration, reproductive organs, and belowground structures, under the control of environmental drivers (Fig. 3). However, such developments would rely on limited empirical or experimental knowledge belowground (Cusack et al., 2024) and scarce information on tree reproductive strategies (Igarashi et al., 2024; Vacchiano et al., 2018; Norden et al., 2007). An improved representation and evaluation of drought-induced tree mortality would be another important step forward as it might play a key role in the observed changing dynamics and functional and floristic turnover (Esquivel-Muelbert et al., 2019; Feeley et al., 2011; Hubau et al., 2020; Qie et al., 2017). Information provided by long-term throughfall exclusion experiments would offer interesting opportunities for model development and evaluation (Powell et al., 2013; Yao et al., 2022).

Tropical forest disturbance by land use change, fire regimes, and other degradations is an important source of carbon emissions (Lapola et al., 2023) and must be represented in models. For instance, it is important to understand how edge effects affect the forest micro-climate and consequently forest dynamics, functioning, and composition (Camargo and Kapos, 1995; Nunes et al., 2022). To this end, micro-climate models could be coupled to or embedded within TROLL (Gril et al., 2023a; Maclean and Klinges, 2021). Fragmentation also impacts seed dispersal and thus seed rain and seed bank intensity and composition (Warneke et al., 2022; Cubiña and Aide, 2001). Improving TROLL's representation of seed dispersal ability and germination as a function of plant trait and dispersal mode is key to capturing the effect of forest loss and fragmentation on forest functioning and biodiversity (Seidler and Plotkin, 2006; Muller-Landau et al., 2008; Tamme et al., 2014; Chase et al., 2020; Riva and Fahrig, 2023). More generally, one overarching objective is to improve the model's representation of processes involved in forest regeneration to simulate secondary forest dynamics and resilience to disturbances (Hanbury-Brown et al., 2022; Díaz-Yáñez et al., 2024; Poorter et al., 2023; Albrich et al., 2020).

Finally, TROLL 4.0 includes major developments that should facilitate its transferability across sites. The explicit integration of the ecosystem water balance and vegetation responses to soil water availability now allows it to consider spatio-temporal extrapolation along water stress gradients. The integration of soil topography and heterogeneity would also be an important advance for improved generality. As nutrient availability is being altered by human activities (Peñuelas et al., 2013), the explicit integration of a nutrient cycle with nitrogen and phosphorous co-limitation will be a useful advance in the future (Fernández-Martínez et al., 2014; Turner et al., 2018). Similarly, the extension of tree functioning responses to a broader range of temperatures should support the transferability of TROLL to temperate and boreal forests.

5 Conclusions

TROLL 4.0 represents an advance over previous versions as it bridges forest model types, while maintaining a representation consistent with field ecology and ecosystem science. TROLL 4.0 simulates the responses of tropical forests to water availability through the explicit representation of water dynamics belowground and its coupling with leaf-level gas exchanges and demographic processes. This comes at a computational cost, and a future task is to conduct code optimization and parallelization, as well as up-scaling in combination with remote sensing products. The representation of processes in TROLL 4.0 mirrors an unbalanced state of the art, but its ability to dialogue with a range of data of various nature makes it a valuable tool to take up the fundamental and applied research challenges on tropical forests. TROLL 4.0 has benefited from observations and field experiments that feed the development of models (Medlyn et al., 2015; Paschalis et al., 2020), while modelling exercises inform and guide empirical approaches (Medlyn et al., 2016; Norby et al., 2016; Pacala and Rees, 1998). This is possible because of the fine-scale representation of forest structure and diversity and the trait-based parameterization of processes in the model.

Appendix A

Table A1 List of symbols and variables.

Appendix B

Table B1 Representation of stomatal conductance, water stress effect on leaf gas exchange, and tree transpiration in several vegetation models. g₀: cuticular or minimal stomatal conductance; i.e. g_s when A→0. A: CO₂ assimilation rate. c_s: CO₂ concentration at the leaf surface. D_s: vapour pressure deficit at the leaf surface. h_s: fractional relative humidity at the leaf surface. Γ: CO₂ compensation point. V_cmax and J_max are the maximum carboxylation rate and electron transport rate. All 0 subscripts denote the values without water stress (except for g₀ by convention). Note that stomatal conductance to H₂O is 1.6 times higher than stomatal conductance to CO₂, and here we only represent stomatal conductance to H₂O.

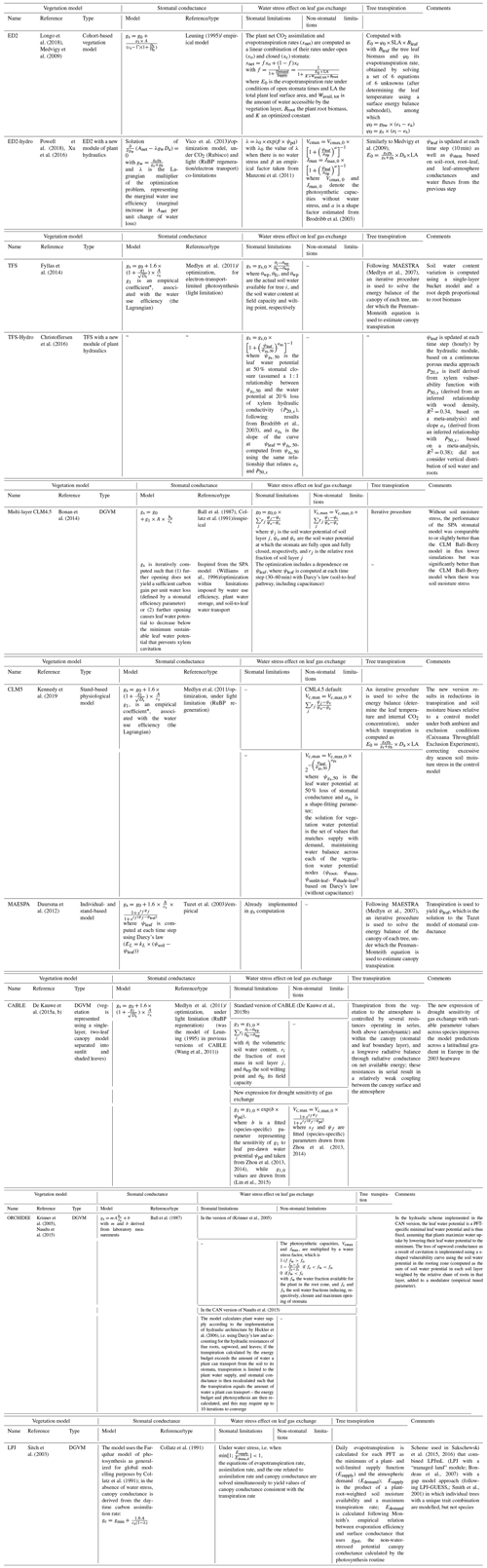
^* Although fitted empirically to leaf exchange experimental data (Lin et al., 2015), attempts have been made to relate g₁ to functional traits and/or climatological variables (wood density, Lin et al., 2015; leaf δ¹³C, Franks et al., 2018) based on the premise that water use efficiency should be associated with functional strategies. See also values reported in Domingues et al. (2014).

Table B2 Examples of observational or experimental studies that explored the relative roles of stomatal and non-stomatal limitations of photosynthesis under drought conditions.