the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Coupling the urban canopy model TEB (SURFEXv9.0) with the radiation model SPARTACUS-Urbanv0.6.1 for more realistic urban radiative exchange calculation
Robert Schoetter
Robin James Hogan
Cyril Caliot
Valéry Masson
The urban canopy model Town Energy Balance (TEB) is coupled with the radiation model SPARTACUS-Urban to improve the urban geometry simplification and the radiative transfer calculation. SPARTACUS-Urban assumes that the probability density function of wall-to-wall and ground-to-wall distances follows a decreasing exponential. This better matches the distributions in real cities than in the infinitely long street canyon employed by the classical TEB. SPARTACUS-Urban solves the radiative transfer equation using the discrete ordinate method. This allows us to take into account physical processes such as the interaction of radiation with the air in the urban canopy layer and the spectral dependence of urban material reflectivities or specular reflections. Such processes would be more difficult to account for with the radiosity method used by the classical TEB. With SPARTACUS-Urban, the mean radiant temperature, a crucial parameter for outdoor human thermal comfort, can be calculated from the radiative fluxes in the vertical and horizontal directions incident on the human body in an urban environment. TEB–SPARTACUS is validated by comparing the solar and terrestrial urban radiation budget observables with those simulated by the Monte-Carlo-based HTRDR-Urban reference model for procedurally generated urban districts that mimic the local climate zones. Improvement is found for almost all radiative observables and urban morphologies for direct solar, diffuse solar, and terrestrial infrared radiation. The TEB mean radiant temperature diagnostic for a person in the urban environment is also improved with TEB–SPARTACUS compared with the classical TEB. Based on these results, TEB–SPARTACUS could lead to more realistic results for building energy consumption, outdoor human thermal comfort, or the urban heat island effect.
- Article
(5364 KB) - Full-text XML
- BibTeX
- EndNote
Radiative exchange is a crucial physical process for the urban climate. Multiple reflections of solar radiation in the 3-D urban geometry result in a lower effective reflectivity (albedo) of a city compared to a flat surface (Krayenhoff et al., 2014). At night, downwelling terrestrial infrared radiation at the surface is higher in urban areas than in open rural areas. This is due to the emission of infrared radiation towards the ground from buildings or urban trees, which have a higher surface temperature than the radiative temperature of the sky. Radiative exchange contributes to the higher (nighttime) air temperature in urban areas compared with the surrounding rural areas (the urban heat island effect; Oke, 1982), although it is not the main cause. Shading and multiple reflections of radiation by complex geometries of buildings and vegetation alter the radiation received by buildings and humans in the urban environment compared to an open and rural environment. This is relevant to the energy consumption of buildings (Strømann-Andersen and Sattrup, 2011; Frayssinet et al., 2018) and human thermal comfort (Fröhlich and Matzarakis, 2020; Dissegna et al., 2021; Geletič et al., 2022).
Urban canopy models (UCMs) such as the Town Energy Balance (TEB; Masson, 2000) or the Building Effect Parameterisation (BEP; Martilli et al., 2002) that calculate the urban surface energy balance in mesoscale or global atmospheric models (Grimmond et al., 2010, 2011) strongly simplify both urban geometry and radiative transfer physics. The most commonly used UCM geometry is the infinitely long street canyon; the radiosity method is common for radiative exchange calculation (Schoetter et al., 2023). It assumes that radiation is reflected isotropically (Lambertian surfaces), that there is a vacuum in between the buildings, and that there is no wavelength dependence of material reflectivity (broadband materials).
Hogan (2019a) found that radiative transfer in the urban canopy layer (UCL) is governed by the probability density functions of the wall-to-wall (pww) and ground-to-wall (pgw) distances as these determine the probability that radiation passing through the UCL will be intercepted by buildings or the ground. Hogan (2019a) and Stretton et al. (2022) investigated pww and pgw for districts in real cities and found systematic differences between them and the distribution that is implicitly assumed in the use of the infinitely long street canyon geometry. This leads to incorrect mean rates of solar and thermal infrared radiation exchange between the sky, walls, and the ground. Instead, a decreasing exponential function fits pww and pgw in real cities. For urban districts where this decreasing exponential function of pww and pgw applies, the attenuation of radiation by buildings can be described by the Beer–Lambert law in the same way as that for radiation passing through the turbid atmosphere.
In light of these findings, Hogan (2019b) adapted the SPARTACUS (SPeedy Algorithm for Radiative TrAnsfer through CloUd Sides; Schäfer et al., 2016; Hogan et al., 2016) atmospheric radiation model representing the 3-D radiative interactions between clouds and the UCL (SPARTACUS-Urban). SPARTACUS-Urban is part of the land surface radiation model SPARTACUS-Surface. It is based on the 1-D discrete ordinate method and divides the UCL into the built, the urban tree, and the clear-air regions. In the vertical direction, SPARTACUS-Urban can subdivide the urban canopy into several layers, which allows for a variety of building and tree heights at each grid point. It can model physical processes such as specular reflections or the interaction of radiation with air, aerosols, or clouds in the UCL, which are difficult to account for with the radiosity method. It can also more realistically represent the interaction of radiation with trees by representing them as cylinders, thus preserving their contact surface area with air and buildings.
Hogan (2019b) validated SPARTACUS-Urban with Monte Carlo reference simulations for the specific case of forest sites without buildings. Stretton et al. (2022) evaluated the solar radiation budget simulated by SPARTACUS-Urban for urban geometries of different complexity, including real cities with simulations using the obstacle-resolving radiation model Discrete Anisotropic Radiative Transfer (DART; Gastellu-Etchegorry, 2008; Gastellu-Etchegorry et al., 2015). They find a very good performance of SPARTACUS-Urban, as long as the assumption of the decreasing exponential function for pww and pgw holds. Otherwise, larger biases appear, but the overall performance is still good. Stretton et al. (2023) successfully evaluated SPARTACUS-Urban against DART for terrestrial radiation in a central London domain for both homogeneous and heterogeneous skin surface temperature of urban facets.
Coupling SPARTACUS-Urban with UCMs promises to improve the realism of urban geometry and radiative transfer physics in these models. Furthermore, the benefits of some climate change adaptation measures (e.g. street trees or building materials with specific spectral reflectivities) can be better quantified with SPARTACUS-Urban than with the radiation schemes used by most urban canopy models. This study presents the coupling of SPARTACUS-Urban with the UCM TEB (TEB–SPARTACUS). TEB is used to simulate the energy balance of the urban surface as a function of the meteorological conditions at the top of the urban roughness sublayer (2–5 times the characteristic building height; Roth, 2000). The original TEB, hereafter referred to as TEB-Classical, represents the city as an infinitely long street canyon. It solves the energy budget separately for the roof, the walls, and the ground. TEB can solve the 1-D prognostic equations for wind speed, air temperature, humidity, and turbulence kinetic energy for the air in the UCL (surface boundary layer scheme, SBL) (Hamdi and Masson, 2008). Ground in-canyon vegetation was added by Lemonsu et al. (2012), and vertically extended in-canyon vegetation was added by Redon et al. (2017, 2020). The urban trees are represented by a turbid layer filling the entire street canyon between the height of the trunk and the height of the tree. A building energy model (Bueno et al., 2012; Pigeon et al., 2014) solves the energy budget of a representative building at the district scale, taking into account human behaviour related to the energy consumption of the buildings (Schoetter et al., 2017). TEB is used as a lower-boundary condition for cities in mesoscale atmospheric models such as Meso-NH (Lac et al., 2018), numerical weather prediction models such as AROME (Seity et al., 2011), or regional climate models such as CNRM–ALADIN (Daniel et al., 2019) and CNRM–AROME (Lemonsu et al., 2023).
This study is structured as follows. The technical aspects of the coupling between TEB and SPARTACUS-Urban are described in Sect. 2, the methodology of the TEB–SPARTACUS validation in Sect. 3, and the validation results in Sect. 4. Conclusions are drawn in Sect. 5.
In TEB, the outdoor radiative transfer is computed at each time step before the energy balance of the different urban facets is solved (Fig. 1a). The outdoor radiative transfer routines take as input the downwelling solar and terrestrial radiation at the top of the UCL, the urban and vegetation morphology parameters, the albedo, emissivity, and prognostic skin surface temperature of the urban facets. They calculate the upwelling solar and terrestrial radiation for the coupling with the atmospheric model, the solar and terrestrial radiation incident on the different urban facets, and the radiative fluxes at ground level for the calculation of the mean radiant temperature. The modular structure of TEB allows the introduction of an option to calculate outdoor radiative transfer with SPARTACUS-Urban instead of the Classical radiosity method, leaving the other routines of TEB unchanged.
2.1 TEB–SPARTACUS geometry
The original TEB (Masson, 2000) is a single-layer UCM. This means that the roof of the building is at the surface level of the atmospheric model; the walls and the road are below the surface. Schoetter et al. (2020) added the option to couple TEB with the atmospheric model on multiple levels. With the multi-layer TEB, the buildings are immersed in the atmosphere. With both the single- and multi-layer TEB, there is only one average building (Hbuild) and tree (Htree) height at each grid point. Furthermore, the radiation received and absorbed by the building walls and the trees is calculated at a single node; no vertical discretisation is performed. TEB–SPARTACUS would allow the consideration of a variety of building and tree heights at each grid point and to calculate a vertical profile of the radiation received and absorbed by the walls. However, this would require modification of the input parameters of SURFEX–TEB and also other physical routines, which are left for future development. In this article, except for the assumption of the decreasing exponential function for pww and pgw inherent to SPARTACUS-Urban, the geometric complexity of TEB is not changed.
2.2 Vertical levels of SPARTACUS-Urban when used by TEB
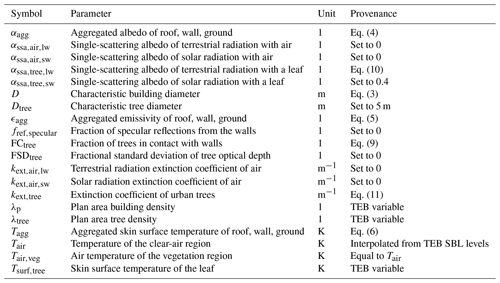
The vertical levels used by SPARTACUS-Urban for radiative transfer calculation in TEB (hereafter the TEB–SPARTACUS vertical levels) have to be defined. A maximum extension (ΔzSPTS,max) is defined for the TEB–SPARTACUS vertical levels. Its default value is 1 m. The TEB–SPARTACUS vertical levels are defined as a function of ΔzSPTS,max, Hbuild, and Htree such that one level is either completely vertically intersected by trees and/or buildings, or completely free of them (Fig. 1b, c). With this approach, no vertical interpolation of the geometric parameters of buildings and trees is required which could lead to physical inconsistencies. For a grid point with Hbuild>Htree, vertical levels with the extent ΔzSPTS,max are defined starting from the ground. The extent of the level, which would be higher than Htree, is reduced so that its height is equal to Htree (kSPTS=2 in Fig. 1b). The TEB–SPARTACUS vertical levels below Htree contain a built, tree, and clear-air region. Above Htree, further vertical levels with the extension ΔzSPTS,max are defined. The extent of the level that would be higher than Hbuild is reduced to match Hbuild (kSPTS=3 in Fig. 1b). The levels defined between Htree and Hbuild contain only buildings and clear air. A layer of clear air is placed above the buildings for numerical reasons. For a grid point with Hbuild<Htree, the TEB–SPARTACUS vertical levels are set in a similar way (Fig. 1c).
The TEB–SPARTACUS vertical levels are different from the vertical levels used for the meteorological variables in the SBL scheme. The SBL grid is defined to have a high resolution near the surface (Fig. 1b, c) because the meteorological parameters computed by the SBL scheme, such as air temperature and wind speed, have the strongest gradients close to the surface. For SPARTACUS-Urban, this does not make sense because the radiation fields are relatively homogeneous close to the surface, especially since most buildings are higher than 3 m, and there is little variation in the building density with height in the lowest metres.
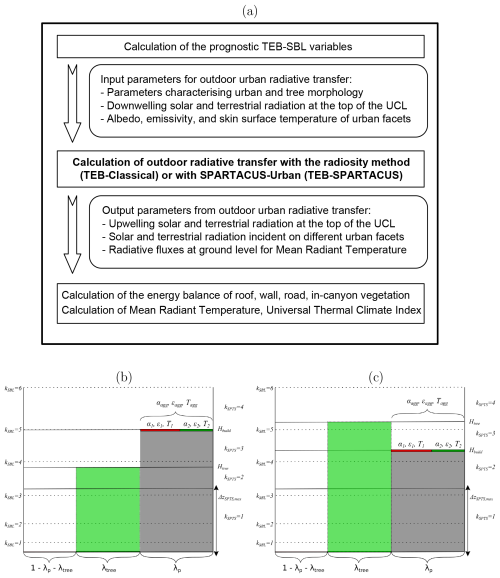
Figure 1(a) Outdoor radiative transfer calculation in the TEB model and TEB–SPARTACUS vertical levels for (b) a grid point with the buildings (grey) higher than the trees (green) (Hbuild>Htree) and (c) a grid point with the buildings lower than the trees (Hbuild<Htree). The kSBL values display the centre of the TEB surface boundary layer (SBL) mass levels, and the kSPTS values display the TEB–SPARTACUS vertical levels (continuous lines). Urban facet properties such as albedo (α), emissivity (ϵ), and skin surface temperature (T), which may show intra-facet variation in TEB (e.g. due to a part of the roofs covered by green roofs; de Munck et al., 2013) are aggregated before their use in SPARTACUS-Urban. The x axis represents the horizontal extent of buildings (λp), urban trees (λtree), and clear air () in the urban canopy layer.
2.3 SPARTACUS-Urban input and output parameters when used in TEB
The SPARTACUS-Urban input parameters, when used in TEB, are listed in Table A1, and the SPARTACUS-Urban output parameters used by TEB are listed in Table A2. Some of the input parameters are exactly the same as those in TEB. This is indicated by the “TEB variable” in Table A1. However, SPARTACUS-Urban requires some input parameters that are not present in TEB; these have to be calculated based on the TEB variables or specified, which is explained in the following. The characteristic building diameter D is calculated, assuming cylindrical buildings (Eq. 3), by combining the equations defining the plan area building density (λp; Eq. 1) and the exterior wall area density (λw; Eq. 2) as follows:
Aref is the surface area of the grid point.
As the TEB SBL levels are different from those of the TEB–SPARTACUS (Fig. 1b, c), the air temperature values from the SBL vertical levels are linearly interpolated to the centre of the TEB–SPARTACUS vertical levels.
TEB can take into account a variety of surface coverings per type of urban facet. The roofs of the buildings can be covered with native roofing material, snow, solar panels (Masson et al., 2014), or green roofs (de Munck et al., 2013). The ground may be covered by roads, bare ground, low vegetation, or snow. The building walls consist of the wall exterior material and possibly windows. In order to keep the SPARTACUS-Urban code independent of its use by TEB, it uses aggregated radiative properties for each facet. After the call of SPARTACUS-Urban, the radiation absorbed by the different surface coverings on each facet is calculated. For a facet consisting of two surface coverings (an example for the roof is shown in Fig. 1b, c) with fractional covers f1 and f2, albedos α1 and α2, emissivities ϵ1 and ϵ2, and surface temperatures T1 and T2, the aggregated values of albedo (αagg), emissivity (ϵagg), and radiative surface temperature (Tagg) used by SPARTACUS-Urban are calculated as follows:
SPARTACUS-Urban calculates the average solar (SWinc) and infrared (LWinc) radiation incident on a facet. The solar (SWabs) and infrared (LWabs) radiation absorbed by the two surface coverings is calculated as follows:
SPARTACUS-Urban represents the radiative exchanges between trees, walls, and the clear air with more detail than TEB, taking into account a more realistic shape of trees with a characteristic diameter Dtree, and a potential variability in the optical depth of trees (FSDtree). These parameters are currently specified in the code; future work could investigate whether it would be possible to link them to physiographic input variables (such as land cover) or to specify them via databases. The fraction of tree surface in contact with walls (FCtree) is calculated from the fraction of tree surface cover (λtree), assuming a random positioning of trees in the urban canyon, as follows:
The air temperature in the vegetation canopy (Tair,veg) is assumed to be equal to the air temperature in the clear-air region (Tair). SPARTACUS-Urban allows the consideration of the scattering and absorption of solar radiation in the urban canopy. This is specified by the extinction coefficients ( and ) and the single scattering albedo of the air for solar () and terrestrial radiation (). These coefficients are currently set to 0 but could be calculated as a function of air temperature, humidity, liquid water content, and aerosol concentration by coupling to an atmospheric radiation scheme.
The single-scattering albedo for solar radiation of a leaf () is assumed to be 0.4, which corresponds to a value integrated over the solar spectrum. This differs from the bulk vegetation albedo in the original TEB, as this parameter corresponds to an effective albedo after multiple reflections. The single-scattering albedo for the terrestrial radiation of a leaf () is calculated from the value of the tree emissivity (ϵtree) in TEB as follows:
The tree extinction coefficient (kext,tree) is calculated from the vertical profile of the leaf area density (LAD), assuming an isotropic orientation of the leaves as follows:
SPARTACUS-Urban allows us to take into account the fraction of specular reflections from the walls (fref,specular). It is set to 0 here but could be linked to the glazing ratio and properties of the wall and window materials.
2.4 Calculation of the mean radiant temperature
The mean radiant temperature (MRT) is a crucial input parameter for outdoor human thermal comfort indices such as the universal thermal climate index (UTCI; Blazejczyk et al., 2012). With the original TEB radiation scheme, it is calculated via the radiosity method, using the shape factors between the human body and the different urban facets (road, walls, windows, and vegetation); the detailed equations are given in the supplementary material of Kwok et al. (2019). With TEB–SPARTACUS, the MRT is calculated differently. The flux densities of the diffuse solar and infrared upwelling and downwelling radiation (, , LWup,gr, and LWdown,gr) at the ground level are known. In addition, the diffuse solar and terrestrial fluxes incident on a vertical plane at the ground level ( and LWhor,gr) can be diagnosed with TEB–SPARTACUS. The vertical and horizontal fluxes are weighted according to Thorsson et al. (2007) to obtain the average diffuse radiative flux density absorbed by the human body as follows:
where αbd (0.3) and ϵbd (0.97) are the standard (Thorsson et al., 2007) albedo and emissivity of the human body, respectively. The fluxes in the horizontal direction have a higher weight than the fluxes in the vertical direction because the human body is assumed to be in an upright position.
The average total (diffuse and direct) radiative flux density absorbed by the human body when fully exposed to solar radiation is calculated as follows:
with the mean direct solar radiative flux density incident on the human body (SWdir,bd), as given by Di Napoli et al. (2020),
is the direct solar radiation reaching the ground, and β is the solar elevation angle. Based on these fluxes, the MRT values for a human body exposed to diffuse solar radiation only (MRTshade) and a human body fully exposed to direct solar radiation (MRTsun) are calculated as follows:
The radiative fluxes are taken at ground level because the vertical profiles of the diffuse solar and terrestrial fluxes incident on a vertical plane are not outputs of the current version of SPARTACUS-Urban. It would be a bit more accurate to calculate them at 1 m above the ground, as this would better represent their average effect on the human body. The difference between the fluxes at ground level and 1 m above ground is currently neglected. By taking into account the fluxes from vertical building walls, TEB–SPARTACUS allows for a more realistic estimation of MRT in urban areas from weather models and reanalysis data than previous work considering only flat ground (Di Napoli et al., 2020).
Validation of TEB–SPARTACUS with observations of radiative and turbulent fluxes in real cities like those presented by Lipson et al. (2022) is not a promising strategy since the differences between the simulated and observed fluxes may be due to differences in the urban morphology, building material parameters, or anthropogenic heat fluxes between the real city and the simplified representation of the city in TEB. Moreover, observations themselves are uncertain. It would therefore be difficult to attribute any potential improvement in the fluxes simulated by TEB–SPARTACUS to the better representation of urban geometry or radiative transfer physics. For this reason, in this study, the radiative observables simulated by TEB are evaluated with the Monte-Carlo-based HTRDR-Urban reference model (Caliot et al., 2023). HTRDR-Urban takes the actual complex 3-D building and tree geometries into account and is used to quantify the errors due to the use of a simplified morphology in the UCM TEB. The comparison of the TEB-Classical and TEB–SPARTACUS errors allows the quantification of the potential benefits of TEB–SPARTACUS compared to TEB-Classical. All urban radiation models take into account the solar shading of trees by buildings and buildings by trees. They also account for the mutual terrestrial radiation interactions between trees and buildings. Only the way in which the urban and tree geometry and the radiative transfer physics are represented changes between the models.
3.1 HTRDR-Urban reference model of urban radiative transfer
HTRDR-Urban uses a backward Monte Carlo algorithm with the null-collision technique (Galtier et al., 2013; El Hafi et al., 2021) and accelerating grids (Villefranque et al., 2019) to solve the radiative transfer equation (RTE) for solar and terrestrial radiation. It takes into account the interaction between radiation and the atmosphere with non-grey absorption, emission, and anisotropic scattering. 3-D absorption and scattering coefficient data and scattering phase functions characterise the spectral and directional radiative properties of gases, liquid droplets, and solid particles. At the top of the atmosphere (TOA), the observed solar spectrum irradiance averaged for 2020 from Coddington et al. (2015) is prescribed. At the Earth's surface, opaque surfaces consisting of vegetation and buildings, described by triangles in a wavefront (*.obj) file are prescribed. They can be specular or Lambertian reflectors, with a potentially wavelength-dependent reflectivity. Measured spectral Lambertian reflectivities included in the Spectral Library of impervious Urban Materials (SLUM) available from the London Urban Micromet data Archive (LUMA) (Kotthaus et al., 2013, 2014) are distributed with HTRDR-Urban. The surface triangles are assigned a constant surface temperature. The MRT in HTRDR-Urban is calculated under the assumption that the human body is a cylinder with a height of 1 m and a radius of 0.14 m centred 1.1 m above the ground (Schoetter et al., 2023).
3.2 Procedurally generated urban morphologies
Exactly the same urban morphologies as those described in Sect. 4 of Schoetter et al. (2023) and Nagel et al. (2023) are investigated (Table 1). They were created with a procedural city generator, their spatial extent is 800 m × 800 m, and they mimic homogeneous urban districts covered by a type of local climate zone (LCZ; Stewart and Oke, 2012). For example, the sparsely built LCZ9 district consists only of detached houses. However, like a real LCZ9 district, they are not all exactly the same height or size. The Tornay et al. (2017) inventory of common urban morphologies in France has shown that the standard LCZ2 (compact mid-rise) and LCZ6 (open low-rise) comprises two relatively different morphologies, namely buildings forming blocks with an internal courtyard or buildings forming rows. Similar results are likely to be found in other European countries. As wind circulation and radiative transfer may be different between the block and row morphologies, the blocks of compact mid-rises (LCZ2a) and rows of compact mid-rises (LCZ2b), as well as blocks of open low-rises (LCZ6a) and rows of open low-rises (LCZ6b), are distinguished. LCZ7 is not studied because it differs from LCZ3 only in terms of construction materials.
For each district, a representative street canyon with the same λp, λw, and average building height (Hmean) as the actual district is created. The morphologies LCZ2a, LCZ2b, LCZ3, LCZ5, LCZ6a, LCZ6b, and LCZ9 will in many cases have pitched roofs. Since pitched roofs cannot be accurately represented in TEB-Classical, TEB–SPARTACUS, or SPARTACUS-Urban, the analysis for these morphologies is performed with and without pitched roofs. The evaluation of the morphologies with flat roofs allows for a rigorous quantification of potential TEB–SPARTACUS shortcomings, while the results for the morphologies with the pitched roofs give an additional indication of how TEB–SPARTACUS performs for districts where pitched roofs occur. Potential overhanging roofs, which may also occur in real cities are not considered.
A copy of the LCZ2a, LCZ4, LCZ5, and LCZ9 morphologies with trees represented by trunks, branches, and individual leaves is created. All trees have the same height (10 m), diameter (10.55 m), and leaf area index (LAI=2.24). As the trees do not intersect the buildings, more trees can be placed in the low-density morphologies than in the high-density morphologies. There are 64 trees for LCZ2a, 963 for LCZ4, 869 for LCZ5, and 1045 for LCZ9. The values of λtree are 0.01 for LCZ2a, 0.13 for LCZ4, 0.12 for LCZ5, and 0.14 for LCZ9, respectively.
A disadvantage of using procedurally generated districts is that they may not be sufficiently representative of real districts. However, for the procedurally generated districts, it is possible to perfectly control the building geometries and to know exactly which surfaces belong to the building's roofs, walls, or the ground. It is also possible to simplify the morphologies to exclude, for example, orographic effects, pitched roofs, or overhanging roofs. Schoetter et al. (2023) investigated the pww and pgw for the procedurally generated districts and found a good agreement with the decreasing exponential function assumed by SPARTACUS-Urban. Therefore, the radiative transfer in the procedurally generated districts may be close to that in real geometries for which the assumption of a decreasing exponential distribution of pww and pgw is correct.
3.3 Radiative boundary conditions
The UCL solar radiation budget consists of the downwelling and reflected solar radiation flux densities at the top of the UCL ( and ), the flux density absorbed by the roofs (), the walls (including the windows; ), the ground (), the urban trees (), and the air (). The UCL terrestrial radiation budget consists of the terrestrial radiation exchanged (absorbed minus emitted) by the sky, by the roofs, by the walls (including the windows), by the ground, by the trees, and by the air (, , , , , and ). In this study, vacuum radiative properties are assumed for the air in the UCL; hence, and .
The following boundary conditions for downwelling radiation are considered:
-
Purely direct downwelling solar radiation at the top of the UCL is achieved in HTRDR-Urban by setting the radiative properties of the atmosphere to those of a vacuum. As a result, there is no downwelling-scattered radiation at the top of the UCL. Simulations are performed for solar elevation angles (γ) of 1, 5, 10, 20, 30, 45, 60, 75, and 90°. No particular solar azimuth angle is considered; for each Monte Carlo realisation, the solar azimuth angle is randomly sampled with a uniform distribution between 0 and 360°. Schoetter et al. (2023) found that the number of Monte Carlo realisations (N) must be larger for lower values of γ than for higher ones to achieve a given accuracy of the radiative observables. For this reason, N is specified as follows:
The number of Monte Carlo realisations for γ=90° (zenith) is Nzen=106. int denotes rounding to the nearest integer. The values of Nγ are 1.0×106, 1.035×106, 1.155×106, 1.414×106, 2.0×106, 2.924×106, 5.759×106, 1.0×107, and 1.0×107 for γ values of 90, 75, 60, 45, 30, 20, 10, 5, and 1°, respectively.
-
Purely diffuse downwelling solar radiation at the top of the UCL is achieved in HTRDR-Urban by setting the atmospheric radiative properties to vacuum ones and specifying a sky model with isotropic downwelling solar radiation, resulting in a flux density of W m−2.
-
For the terrestrial radiation simulations, a 1-D atmospheric profile consisting of mid-latitude summer (MLS) conditions is used in HTRDR-Urban. For this profile, the near-surface air temperature is 294.2 K.
The downwelling direct solar, diffuse solar, and terrestrial radiation at the top of the UCL simulated by HTRDR-Urban are used as radiation forcing for HTRDR-Urban, TEB-Classical, and TEB–SPARTACUS.
3.4 Numerical tests and uncertainty quantification
The following numerical tests are performed with HTRDR-Urban, SPARTACUS-Urban, TEB-Classical, and TEB–SPARTACUS:
-
For the urban geometries without trees, simulations are made for purely direct and purely diffuse downwelling solar radiation using a uniform urban facet albedo of 0.3, which is characteristic of common building materials such as concrete or brick, although there is a wide variety of impervious urban material albedo values (Kotthaus et al., 2014). The same albedo value is chosen for all surfaces in the scene because the objective is to investigate only the effect of the changed urban geometry assumptions. An additional simulation is performed with HTRDR-Urban for the representative street canyon geometry.
-
For the urban geometries with trees, simulations with HTRDR-Urban, TEB-Classical, and TEB–SPARTACUS are made for direct and diffuse solar radiation using a uniform urban facet albedo of 0.4, which corresponds to the broadband single-scattering albedo of a leaf. For simplicity, the albedos of the other urban facets are set to the same value.
-
For all urban geometries, simulations are performed for terrestrial radiation using a uniform urban facet emissivity of 0.9, which is a value close to the observed emissivities for a variety of impervious urban surface materials (Kotthaus et al., 2014). In five sensitivity tests, the skin surface temperature (Tsurf) of all urban facets including tree leaves is set such that the difference to the near-surface air temperature of 294.2 K is −10 K (Tsurf=284.2 K), 0 K (Tsurf=294.2 K), 10 K (Tsurf=304.2 K), 20 K (Tsurf=314.2 K), and 30 K (Tsurf=324.2 K). These values span the range of plausible differences between skin surface temperature and air temperature near the surface with −10 K, corresponding to a nocturnal situation with a clear sky and a negative surface energy balance and leading to a skin surface temperature lower than the air temperature and 30 K a situation with strong solar radiation. This leads to much higher skin surface temperature than the air temperature. No distinction is made in the skin surface temperature between sunlit and shaded surfaces. This simplifies the complexity compared to a realistic situation. This simplification allows the investigation of the isolated effect of the changed urban geometry.
The SPARTACUS-Urban simulations use a vertical grid with a resolution of 1 m; the half levels of the nth grid point are located at . Hmax is the maximum building height in the district. On this vertical grid, the plan area building (λp(zn)) and the tree density (λtree(zn)) at the nth level are defined as follows:
Nbuild and Ntree are the number of buildings and trees in the district. Abuild,i, Hbuild,i and Atree,i, Htree,i are the footprint area and height of the ith building and tree. Adistrict is the area of the district.
The normalised building perimeter (npbuild(zn)) and tree perimeter (nptree(zn)) is calculated as follows:
where pbuild,i and ptree,i are the perimeters of the ith building and tree, respectively.
The characteristic scale of the building (D(zn) and tree (Dtree(zn)) scale at the nth level is then calculated, assuming cylindrical buildings and trees, as follows:
With this setup, the SPARTACUS-Urban simulations take into account the variety of building heights.
The uncertainties in the radiative observables are quantified as follows:
-
For the direct solar radiation, the simulated radiative observables are plotted as a function of γ for selected urban morphologies. The normalised mean absolute error (; Eq. 24) is defined to quantify the uncertainty in a radiative observable over different values of γ. Uncertainty is defined here as the difference between the TEB observable (OTEB,γ) and the HTRDR-Urban observable (OHTRDR,γ).
-
For the diffuse solar radiation and the terrestrial infrared radiation, the absolute error (Γ) of the radiative observable is defined as
3.5 Validation of mean radiant temperature
TEB-Classical and TEB–SPARTACUS calculate an outdoor district-average MRT value for a person in the shade (MRTshade; Eq. 16) and exposed to the sun (MRTsun; Eq. 15). HTRDR-Urban allows us to calculate the spatial distribution of MRT within the district. It is therefore possible to compare the distribution of MRT values simulated by HTRDR-Urban and the MRTsun and MRTshade values simulated by TEB. This is done here for the example of the LCZ4 district, with γ=30°; the mid-latitude summer atmospheric profile, with a near-surface air temperature of 294.2 K; and uniform surface temperatures of Tsurf=314.2 K. All surfaces have a solar albedo of 0.3 and a terrestrial infrared emissivity of 0.9. HTRDR-Urban is used to calculate a 1 m resolution MRT map. It is also used to calculate the downwelling direct solar, diffuse solar, and terrestrial radiation at the top of the UCL. These radiative fluxes are used for the meteorological forcing of TEB. The solar azimuth angle used by HTRDR-Urban is 337.5° from the north (clockwise), whereas TEB assumes a uniform street orientation with respect to the solar azimuth.
4.1 Solar radiation in urban morphologies without trees
The results for the direct-only downwelling solar radiation and the LCZ2a, LCZ4, and LCZ9 morphologies are shown in Fig. 2. The results for the other morphologies are shown in Figs. B1 to B3. For LCZ9, with its low λp and λw, most of the downwelling solar radiation () is absorbed by the ground () or reflected (), except for low values of γ when the walls absorb () most of the . This is captured by TEB-Classical and TEB–SPARTACUS. However, for TEB-Classical, is overestimated, and is underestimated for γ between 5 and 20°. This is because the infinitely long street canyon geometry used by TEB-Classical leads to shading of building walls by other buildings that is too low (Schoetter et al., 2023). TEB–SPARTACUS corrects this shortcoming of TEB-Classical almost perfectly because the cube-like LCZ9 morphology respects well the SPARTACUS-Urban assumption of a decreasing exponential function for pww and pgw (Stretton et al., 2022). Similar to the results of Caliot et al. (2023), the TEB-Classical results are almost identical to the HTRDR-Urban results for the infinitely long street canyon, which is due to the analytical solution of the radiosity method under these conditions (vacuum and Lambertian surfaces). For γ below 5°, the fraction of solar radiation absorbed by the roofs () is underestimated by both TEB-Classical and TEB–SPARTACUS because with a uniform Hbuild, the shading of the roofs by higher buildings cannot be represented. This shortcoming of TEB–SPARTACUS could be overcome by introducing a variety of building heights at each grid point in TEB, which is demonstrated by the almost perfect agreement between SPARTACUS-Urban and HTRDR-Urban.
For LCZ2a, TEB-Classical overestimates and underestimates for γ between 20 and 75° for the same reason as for LCZ9. This problem is improved by TEB–SPARTACUS, but there are still small biases of and because the selected LCZ2a with street canyons and building courtyards has pww and pgw, which deviate more from the decreasing exponential function than for LCZ9. For LCZ2a, the SPARTACUS-Urban results are also slightly different from the HTRDR-Urban results, which could be due to the deviation of pww and pgw from the decreasing exponential distribution.
For LCZ4, TEB–SPARTACUS improves and over TEB-Classical for γ above 20°. For lower γ, deficiencies of TEB–SPARTACUS remain because it does not represent the heterogeneous building height. The results for SPARTACUS-Urban show that the inclusion of a variety of building heights in TEB could significantly improve the results for the LCZ4 morphology consisting of blocks without internal courtyards.
Figure 3 shows for all urban morphologies and radiative observables. For both TEB-Classical and TEB–SPARTACUS, the highest values are found for and , while and have lower . The values are highest for the high-rise LCZ1 and LCZ4 morphologies and lowest for the low-rise LCZ3, LCZ6, LCZ8, and LCZ9 morphologies. No difference between TEB-Classical and TEB–SPARTACUS is found for because both do not consider a variety of building heights at each grid point. TEB–SPARTACUS leads to a significant improvement of the other radiative observables for most urban geometries. TEB–SPARTACUS reduces for compared to TEB-Classical by 50 % to 90 % for all morphologies, except for LCZ1 (−16 %), LCZ2a (−34 %), and LCZ2a with flat roofs (−19 %). For LCZ1, the large variety of building heights leads to a lower improvement due to TEB–SPARTACUS, whereas for LCZ2 it is the prevalence of courtyards and street canyons that leads to deviations from the decreasing exponential distribution assumption for pww and pgw. With TEB–SPARTACUS, the values for are reduced by 40 % to 70 % compared to TEB-Classical, again with the exception of LCZ1 (−13 %), LCZ2a (−11 %), and LCZ2a with flat roofs (−35 %). TEB–SPARTACUS reduces the values for by 35 % to 62 %, except for LCZ1, LCZ2a, and LCZ6a for which it increases. However, this result must be modulated since is probably only well simulated by TEB-Classical due to error compensation. The comparison of the results for pitched and corresponding flat roof morphologies shows that TEB–SPARTACUS reduces the uncertainties in the radiative observables for pitched roof morphologies to an extent comparable to that of flat roof morphologies.
Figure 4 shows the Γ values obtained for TEB-Classical and TEB–SPARTACUS for the purely diffuse downwelling solar radiation. The results are similar to those obtained for direct downwelling solar radiation. For , the Γ values are the same for TEB-Classical and TEB–SPARTACUS because both do not take into account the variety of building heights. The Γ values for are reduced by 50 % to 95 % for all morphologies, except LCZ1 and LCZ2a with flat roofs, where they are increased by 40 %. The Γ values for are reduced by 50 % to 95 % with the noted exceptions of LCZ1 (increase of 23 %), LCZ2a (decrease of only 11 %), and LCZ9 with pitched roofs (increase of 2 %). However, for LCZ9 with flat roofs, Γ is reduced by 84 % with TEB–SPARTACUS compared to TEB-Classical. The Γ for is reduced by 25 % to 97 % with TEB–SPARTACUS compared to TEB-Classical, except for LCZ1 and LCZ2a, where it increases but starts from very low values in TEB-Classical, which could be due to an error compensation.
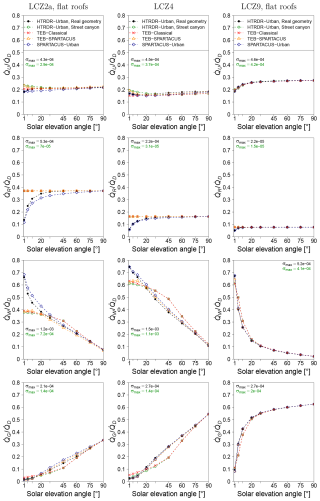
Figure 2Fraction of the downwelling direct solar radiation () that is reflected by the city (), absorbed by the roofs (), the walls (), or the ground () simulated by the reference model Monte Carlo model HTRDR-Urban, the urban radiation model SPARTACUS-Urban, and the urban canopy model TEB with the Classical (TEB-Classical) and the SPARTACUS-Urban (TEB–SPARTACUS) radiation scheme. The values of σmax indicate the maximum value of the standard deviation of the radiative observable obtained from the Monte Carlo simulations for all values of solar elevation angle.
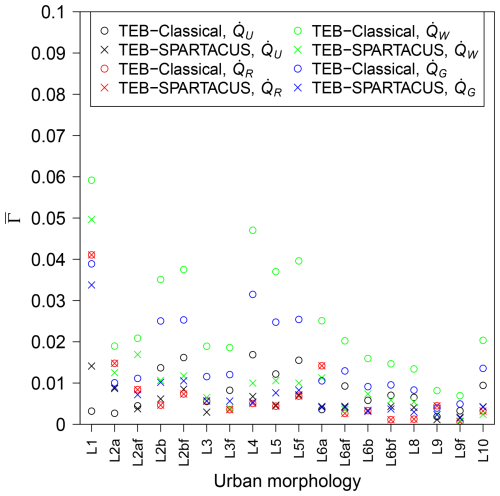
Figure 3Normalised mean absolute error (; Eq. 24) of the direct solar radiation that is reflected by the city (), absorbed by the roofs (), the walls (), or the ground () when simulated by TEB with the Classical (TEB-Classical) and the SPARTACUS-Urban (TEB–SPARTACUS) radiation scheme. L1 is LCZ1, L2af is LCZ2a with flat roofs, and so on.
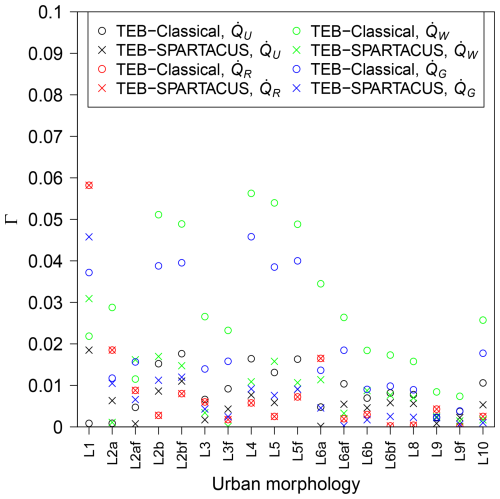
Figure 4Absolute error (Γ; Eq. 25) of the fraction of diffuse solar radiation that is reflected by the city (), absorbed by the roofs (), the walls (), or the ground () when simulated by TEB with the Classical (TEB-Classical) and the SPARTACUS-Urban (TEB–SPARTACUS) radiation scheme. L1 is LCZ1, L2af is LCZ2a with flat roofs, and so on.
4.2 Solar radiation in urban morphologies with trees
For direct downwelling solar radiation, Fig. 5 shows the results for the LCZ5 and LCZ9 districts with flat roofs and 10 m high trees. The detailed results for the LCZ2a and LCZ4 districts with flat roofs and trees are shown in Fig. C1. Figure 6 shows the values for all radiative observables and all districts with trees. The LCZ9 district is particular in the way that the trees are quite large (Htree=10 m) compared to the low-rise buildings (Hmean=6.2 m). As a consequence, the fraction of downwelling solar radiation absorbed by the trees () increases from below 0.1 for γ above 45° to above 0.5 for a γ of 1°. TEB-Classical represents the trees as a turbid layer that fills the entire street canyon between the trunk and the tree height without taking into account the individual tree borders. It therefore does not capture the increase in for low values of γ. As a result, is slightly underestimated by TEB-Classical for γ above 45° and strongly underestimated for lower γ. TEB–SPARTACUS simulates well. The other terms of the solar radiation budget are also improved with TEB–SPARTACUS compared to TEB-Classical. is significantly reduced for γ below 20° with TEB–SPARTACUS due to the enhanced shading of walls by trees compared to TEB-Classical. is reduced for γ below 60° with TEB–SPARTACUS because there is more shading from trees; it matches better with the reference HTRDR-Urban. The is lower for all γ with TEB–SPARTACUS because there are more multiple reflections of solar radiation, leading to a lower probability of reflection towards the sky. Similar to the LCZ9 district without trees, an overestimation of is found for TEB–SPARTACUS because it neglects the variety of building heights. The results for SPARTACUS-Urban show that this can be corrected to achieve near-perfect results by taking the variety of building heights into account. Similar improvements of the radiative observables with TEB–SPARTACUS compared to TEB-Classical are found for LCZ9 with pitched roofs.
For LCZ5 with flat (pitched) roofs, TEB–SPARTACUS reduces the for by 76 % (68 %), by 63 % (65 %) for , and by 16 % (20 %) for . For , there is no difference because the buildings are higher than the trees. The values for are higher for TEB–SPARTACUS than for TEB-Classical, but this could be due to the fact that for TEB-Classical the is well simulated due to error compensation. SPARTACUS-Urban almost perfectly simulates all radiative observables of the LCZ5 morphology with trees.
For LCZ4, the values are reduced by 79 % for and , by 74 % for , and by 25 % for with TEB–SPARTACUS compared to TEB-Classical and are unchanged for . SPARTACUS-Urban simulates almost perfectly all radiative observables of the LCZ4 morphology with trees.
For LCZ2a with flat (pitched) roofs, TEB–SPARTACUS reduces by 10 % (19 %) for and by 24 % (1 %) for . The values are low because not much radiation reaches the few trees in this dense mid-rise morphology; the for is almost unchanged between TEB–SPARTACUS and TEB-Classical. For , TEB–SPARTACUS leads to higher values of than TEB-Classical, which could be due to error compensation leading to good performance of TEB-Classical. SPARTACUS-Urban has similar shortcomings to LCZ2a without trees, which is due to the deviation of pww and pgw from the decreasing exponential function.
Figure 7 shows the Γ of the radiative observables for diffuse downwelling solar radiation and the urban morphologies with trees. The results are similar to those for direct solar radiation. The Γ values for are reduced by 50 % to 90 % with TEB–SPARTACUS. For , the Γ values are reduced by 73 % to 97 % with TEB–SPARTACUS, with the notable exception of LCZ2a with flat roofs (67 % increase). This could be because TEB-Classical gives good results for the wrong reason due to error compensation. The Γ values for are reduced by 48 % to 98 % for TEB–SPARTACUS, except for LCZ2a, where they increase by 24 %. For , there is no clear result. There is a decrease in the Γ values for LCZ4 and LCZ9 but an increase for LCZ2a and LCZ5.

Figure 5Fraction of the direct downwelling solar radiation () that is reflected () and that is absorbed by the roofs (), the walls (), the ground (), or urban trees () simulated by the reference Monte Carlo model HTRDR-Urban, the urban radiation model SPARTACUS-Urban, and the urban canopy model TEB with the Classical (TEB-Classical) and the SPARTACUS-Urban (TEB–SPARTACUS) radiation scheme for the LCZ5 and LCZ9 districts with trees. The values of σmax indicate the maximum value of the standard deviation of the radiative observable obtained from the Monte Carlo simulations for all values of solar elevation angle.

Figure 6Normalised mean absolute error (; Eq. 24) of the direct solar radiation that is reflected by the city (), absorbed by the walls (), the ground (), or urban trees () when simulated by TEB with the Classical (TEB-Classical) and the SPARTACUS-Urban (TEB–SPARTACUS) radiation scheme for all urban morphologies with trees. The results for the direct solar radiation absorbed by the roofs () are not shown because the differences between TEB-Classical and TEB–SPARTACUS are very small. L2a is LCZ2a, L2af is LCZ2a with flat roofs, and so on.

Figure 7Absolute error (Γ; Eq. 25) of the fraction of diffuse solar radiation that is reflected by the city (), absorbed by the walls (), the ground (), or the urban trees () when simulated by TEB with the Classical (TEB-Classical) and the SPARTACUS-Urban (TEB–SPARTACUS) radiation scheme. The results for the fraction of radiation absorbed by the roofs are not shown because they differ only slightly between TEB-Classical and TEB–SPARTACUS. L1 is LCZ1, L2af is LCZ2a with flat roofs, and so on.
4.3 Terrestrial radiation
Figure 8 shows the Γ of the terrestrial radiation radiative observables for TEB-Classical and TEB–SPARTACUS and the urban morphologies without trees. The Γ values for the terrestrial radiation exchanged by the roofs () are very small, except for LCZ1 because the variety in building heights is not taken into account. For , there is no difference in Γ between TEB–SPARTACUS and TEB-Classical.
For the terrestrial radiation exchanged by the walls (), the Γ values for TEB-Classical are larger for the mid- and high-rise morphologies and when Tsurf is greater than the near-surface air temperature of 294.2 K. For Tsurf=284.2 K, TEB–SPARTACUS reduces Γ by about 10 %, except for the low-rise LCZ9, LCZ8, and LCZ6b and the high-rise LCZ1. So there is only a small improvement for the case where the skin surface temperature is 10 K lower than the air temperature near the surface. For Tsurf=294.2 K, Γ is reduced by about 30 %, except for the low-rise LCZ9, LCZ8, and LCZ6b for which it is almost unchanged and the LCZ1 and (LCZ2 with flat roofs) for which it decreases by 85 % (80 %). The results for Tsurf=304.2 K, Tsurf=314.2 K, and Tsurf=324.2 K are similar to those for Tsurf=294.2 K. Γ is reduced by 40 % to 80 % for most morphologies, but the Γ reduction is lower or absent for LCZ9, LCZ8, and LCZ6a.
The results for the Γ values of the terrestrial radiation exchanged by the ground () are similar to those for . For Tsurf=284.2 K, TEB–SPARTACUS reduces Γ by 20 % to 30 %, except for LCZ9, LCZ8, and LCZ6b for which it is reduced by only 10 % to 15 %. For Tsurf=284.2 K, Γ is reduced by 30 % to 80 %, with the lowest reductions found for the low-rise morphologies mentioned above. For Tsurf=304.2 K, Tsurf=314.2 K, and Tsurf=324.2 K, Γ is reduced by between 55 % and 99 % for all morphologies, except for LCZ1.
For the terrestrial radiation exchanged with the sky (), the Γ values for TEB-Classical are very small for Tsurf=284.2 K and increase for higher values of Tsurf. TEB–SPARTACUS reduces the Γ values for by 50 % to 99 % for Tsurf=294.2 K, Tsurf=304.2 K, Tsurf=314.2 K, and Tsurf=324.2 K. For Tsurf=284.2 K, TEB–SPARTACUS does not reduce the Γ values for the LCZ9, LCZ8, and LCZ6b, and for the other districts, it is reduced by 50 % to 98 %.
Figure 9 shows the Γ values for the terrestrial radiation radiative observables and the urban morphologies with trees. The Γ values for the terrestrial radiation exchanged by the trees () are reduced by 45 % to 97 % with TEB–SPARTACUS compared to TEB-Classical, with the notable exception of LCZ9 with Tsurf=284.2 K. The Γ values for are lower for TEB–SPARTACUS than for TEB-Classical, except for LCZ2a with flat roofs and Tsurf>Tair. The Γ reduction is about 15 % for Tsurf=284.2 K, 40 % for Tsurf=294.2 K, 50 % to 70 % for Tsurf=304.2 K, 58 % to 86 % for Tsurf=314.2 K, and 62 % to 92 % for Tsurf=324.2 K. The Γ values for are reduced with TEB–SPARTACUS for all urban morphologies, except the LCZ9 ones. The reduction is 20 % to 30 % for Tsurf=284.2 K, 46 % to 78 % for Tsurf=294.2 K, 55 % to 99 % for Tsurf=304.2 K, 60 % to 99 % for Tsurf=314.2 K, and 64 % to 92 % for Tsurf=324.2 K. TEB–SPARTACUS reduces the Γ values of by 50 % to 96 % for Tsurf=284.2 K, by 88 % to 96 % for Tsurf=294.2 K, by 91 % to 96 % for Tsurf=304.2 K, and by 91 % to 97 % for Tsurf=314.2 K and Tsurf=324.2 K.
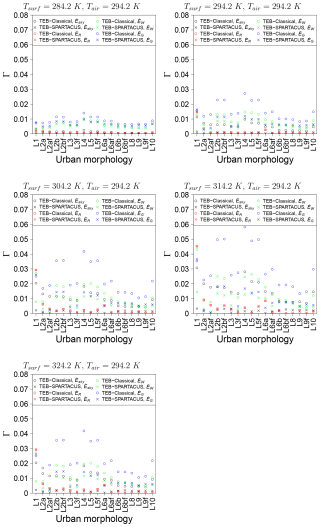
Figure 8Absolute error (Γ; Eq. 25) of the terrestrial radiation that the city exchanges with the sky () and that is exchanged by the roofs (), the walls (), and the ground () when simulated by TEB with the Classical (TEB-Classical) and the SPARTACUS-Urban (TEB–SPARTACUS) radiation scheme. is not shown because its Γ does not differ between TEB-Classical and TEB–SPARTACUS. L1 is LCZ1, L2af is LCZ2a with flat roofs, and so on.

Figure 9Absolute error (Γ; Eq. 25) of the terrestrial radiation that the city exchanges with the sky () and that is exchanged by the walls (), the ground (), and the trees () when simulated by TEB with the Classical (TEB-Classical) and the SPARTACUS-Urban (TEB–SPARTACUS) radiation scheme. L2a is LCZ2a, L2af is LCZ2a with flat roofs, and so on.
4.4 Mean radiant temperature
The spatial distribution of MRT simulated by HTRDR-Urban in the LCZ4 district (Fig. 10a) is strongly influenced by the shading from buildings. Its probability density (Fig. 10b) shows that the MRT values lie between 34 and 42 °C in the shaded areas and between 60 and 70 °C in the sunlit areas. The highest MRT values are near the walls, which are exposed to the Sun because of the reflected solar radiation. There are almost no MRT values between 42 and 60 °C, which means that the TEB approach to providing a diagnostic for MRTsun and MRTshade is useful in this case. TEB-Classical simulates a value that is too high for both MRTsun and MRTshade. The TEB–SPARTACUS values for MRTsun and MRTshade are 2.5 °C lower than the values simulated by TEB-Classical. The MRTsun value simulated by TEB–SPARTACUS agrees very well with the most frequent MRT values simulated by HTRDR-Urban in the sunlit areas. The MRTshade value simulated by TEB–SPARTACUS is still 4 °C higher than the most frequent MRT values simulated by HTRDR-Urban in the shaded areas. The general overestimation of MRTshade by TEB could be due to the consideration of the diffuse downwelling solar radiation as isotropic, whereas, in reality, part of it comes from a direction close to the Sun. In the reference model HTRDR-Urban, this is represented, leading to lower MRT values in the shaded areas because the circumsolar diffuse radiation does not reach the human body. As shown in Fig. 2, for LCZ4 and γ=30°, with TEB-Classical, not enough direct solar radiation reaches the ground and too much reaches the walls. The MRTsun value is therefore too high in TEB-Classical because too much solar radiation reflected by the walls reaches the human body, which is assumed to be in the sun. The MRTshade value is too high in TEB-Classical for the same reason. TEB–SPARTACUS corrects this problem for both MRTsun and MRTshade. The uncertainty in MRTshade arising from the use of the radiative fluxes at ground level instead of 1 m above ground level has been estimated to be 0.6 K. Since the sensitivity of thermal comfort indicators such as the UTCI to MRT is about 0.25 K (Schoetter et al., 2013), this uncertainty in MRT leads to an uncertainty of 0.15 K of such indicators. Additional output diagnostics could be added in future SPARTACUS-Urban versions to eliminate this uncertainty.
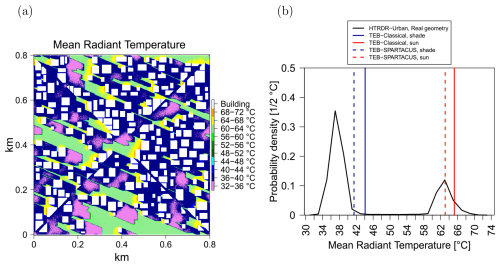
Figure 10(a) Spatial distribution at 1 m horizontal resolution of the mean radiant temperature simulated by HTRDR-Urban in the LCZ4 district with γ=30° and a solar azimuth angle of 337.5° from north (clockwise). (b) Probability density of mean radiant temperature simulated by HTRDR-Urban and the MRTsun and MRTshade values simulated by TEB-Classical and TEB–SPARTACUS.
The validation of TEB–SPARTACUS with the Monte-Carlo-based reference model HTRDR-Urban shows improvements in radiative observables related to solar and terrestrial radiation over a variety of urban morphologies.
TEB–SPARTACUS corrects a major shortcoming of the infinitely long street canyon assumption of TEB-Classical, which was documented by Schoetter et al. (2023). This shortcoming consists of the absorption of direct solar radiation that is too high (too low) by the building walls (the ground) due to the wrong distribution of wall-to-wall distances. This improvement can be of the order of 10 % of the downwelling direct solar radiation, thus potentially improving the simulated energy balance of buildings or ground vegetation and outdoor human thermal comfort.
For direct downwelling solar radiation averaged over all solar elevation angles, TEB–SPARTACUS simulates almost all radiative observables with a higher accuracy than TEB-Classical. The error is reduced by 50 % to 90 % for block-like urban morphologies such as LCZ3, LCZ4, LCZ5, LCZ8, LCZ9, and LCZ10. For these morphologies, the decreasing exponential function assumption for the distribution of wall-to-wall and ground-to-wall distances made by SPARTACUS-Urban holds. But, also for the other morphologies, the radiative observables are simulated more accurately with TEB–SPARTACUS than with TEB-Classical. For the diffuse downwelling solar radiation, the results are very similar to those for the direct downwelling solar radiation when averaging over different values of the solar elevation angle. TEB–SPARTACUS reduces the error in the radiative observables by 50 % to 95 %, with the exception of the compact high-rise LCZ1 and the dense mid-rise LCZ2. TEB–SPARTACUS improves the solar radiation absorbed by urban trees because it represents trees as cylinders, conserving the tree surface area in contact with the air and buildings. This contact area is underestimated by TEB-Classical, which treats urban trees as a homogeneous turbid layer that fills the entire street canyon in the horizontal direction and between the trunk and the tree height in the vertical direction. TEB-SPARTACUS can also represent trees higher than buildings, leading to improved results for such urban districts. As a result of the improved simulation of the interaction of radiation with urban trees, the other radiative observables are also improved. The improved representation of the radiation absorbed by urban trees could potentially improve the results of simulated evapotranspiration, photosynthesis, or CO2 uptake by trees. Uncertainties in the direct solar radiation observables for low values of the solar elevation angle are found with TEB–SPARTACUS for the high-rise districts, which is due to the neglect of the variety of building heights. These uncertainties could become more relevant in urban districts with heterogeneous building types, i.e. consisting of a mixture of LCZs. The results obtained when simulating the districts with SPARTACUS-Urban and a 1 m resolution vertical discretisation of building density and characteristic diameter show that SPARTACUS-Urban is well suited to handle such a variety of building heights. The consideration of a variety of building heights on a district scale is therefore a logical next step in the development of TEB.
Schoetter et al. (2023) found that the effective urban albedo () is an observable that is not strongly influenced by the simplifications of urban morphology such as the assumption of an infinitely long street canyon. The results of the present study are consistent with these earlier findings since only little or no improvement in the simulated effective urban albedo is found when using TEB–SPARTACUS instead of TEB-Classical.
TEB–SPARTACUS leads to a reduction in the uncertainties in simulated radiative observables for terrestrial infrared radiation. The improvement is particularly high (50 % to 99 %) when the skin surface temperature is higher than the near-surface air temperature, which is often the case in urban areas. The improvement is found for all urban morphologies, except for LCZ1, where the variety of building heights must be taken into account to obtain good results. TEB–SPARTACUS reduces the error in the simulated absorption of terrestrial infrared radiation by urban trees by 45 % to 97 % and, consequently, also the other radiative observables in urban districts with trees.
The validation of the mean radiant temperature simulated by TEB-Classical and TEB–SPARTACUS for an open high-rise district has shown that, given the bimodal distribution of MRT in the district, the strategy used in TEB of providing one MRT value for a person in the shade and one for a person in the sun is useful. Furthermore, the MRT values for shade and sun simulated by TEB–SPARTACUS are closer to the most frequent values in the shaded and sunlit areas simulated by HTRDR-Urban than those simulated by TEB-Classical. This is because the amount of solar radiation reflected by the building walls on the human body is better simulated by TEB–SPARTACUS than by TEB-Classical.
The present study has several limitations. Only urban districts with one building type and morphology were studied. In real cities, there is often a variety of building types in one district, leading, for example, to a greater variety of building heights than in the districts investigated in this study. As TEB–SPARTACUS does not represent the variety of building heights, it may predict radiative observables with less accuracy in such districts. Furthermore, no variety of urban material albedo, emissivity, or skin surface temperature were investigated. TEB–SPARTACUS may have different performances for heterogeneous districts than for the homogeneous ones that were investigated in this study. Also, only one type of urban tree with a homogeneous height and diameter was investigated. Urban districts with a variety of tree types and tree characteristics should be analysed to investigate whether the results of this study still apply to them.
In real cities, overhanging and pitched roofs are common. Simulations with HTRDR-Urban (not shown) show that such features can strongly change the direct solar radiation budget (e.g. the partitioning between the radiation absorbed by the roofs or the walls). Neither TEB-Classical nor TEB–SPARTACUS represents such features. The accuracy of the simulated radiative observables reported here may therefore be too high compared to real cities.
The mean radiant temperature simulated by TEB has only been analysed for one urban district and one solar zenith and azimuth angle. Further research is required to quantify how well the TEB diagnostics of MRT in shade and sun compare with the actual distribution of MRT in a variety of urban districts and with a variety of solar positions.
The TEB urban canopy model has been coupled with the urban radiation model SPARTACUS-Urban, which uses a decreasing exponential for the probability density function of the wall-to-wall and ground-to-wall distances. This is more realistic than the assumption of an infinitely long street canyon used by the original TEB. While the original TEB uses the radiosity method to calculate the radiative exchanges, SPARTACUS-Urban solves the RTE using the discrete ordinate method. This allows us to take into account many additional physical processes such as specular reflections, wavelength-dependent albedo of urban materials, and the interaction of radiation with the air, aerosols, or fog in the UCL. SPARTACUS-Urban also represents urban trees in a more realistic way, particularly as cylinders that represent the contact surface between trees, air, and building walls.
The TEB–SPARTACUS coupling has been made in a very simple way, preserving the geometric complexity of the original TEB; i.e. there is no variation in building height at each grid point. Furthermore, the urban material albedo and emissivities in TEB are still independent of the wavelength, and atmospheric scattering and absorption are not considered in TEB–SPARTACUS. The difference between TEB-Classical and TEB–SPARTACUS is therefore only due to the changed assumptions about the urban and tree geometry and the replacement of the radiosity method by the discrete ordinate method to calculate the radiative exchanges. With TEB–SPARTACUS, the outdoor mean radiant temperature for a cylindrical human body can be diagnosed based on the radiative fluxes in the vertical and horizontal directions using the discrete ordinate method instead of the radiosity method in TEB-Classical.
TEB–SPARTACUS has been validated against a Monte-Carlo-based reference model (HTRDR-Urban) for procedurally generated urban morphologies that mimic the local climate zones. The urban morphologies are homogeneous as there is no variety of LCZ, albedo, emissivity, or skin surface temperature at the scale of the district. A significant improvement over TEB-Classical of the key radiative observables, i.e. the direct and diffuse solar, and terrestrial radiation exchanged by the roofs, the walls, the ground, urban trees, and the sky is found when using TEB–SPARTACUS. This could improve the simulated building energy balance (e.g. the heating and air-conditioning energy consumption), outdoor human thermal comfort, urban vegetation evapotranspiration and CO2 uptake, and even the urban heat island effect.
The next step in the development of TEB–SPARTACUS is to consider a variety of building heights at each grid point as this will improve radiative observables in high-rise districts and districts with heterogeneous building heights. Also, an atmospheric radiation scheme could be used by TEB–SPARTACUS to calculate the scattering and absorption of radiation in the UCL. This can improve the simulated terrestrial radiation (Hogan, 2019b; Schoetter et al., 2023). Furthermore, TEB–SPARTACUS can be used in urban climate simulations when TEB is coupled with an atmospheric model such as Meso-NH (Lac et al., 2018) to investigate its impact on the urban heat island effect.
The following figures display the solar radiation budget for all urban morphologies with flat roofs and direct downwelling solar radiation.
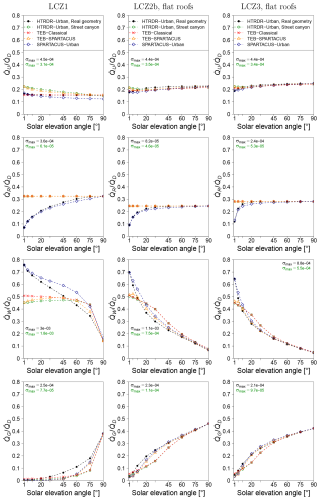
Figure B1Fraction of the downwelling direct solar radiation () that is reflected by the city (), absorbed by the roofs (), the walls (), or the ground () as simulated by the reference model Monte Carlo model HTRDR-Urban, the urban radiation scheme SPARTACUS-Urban, and the urban canopy model TEB with the Classical (TEB-Classical) and the SPARTACUS-Urban (TEB–SPARTACUS) radiation scheme. The values of σmax indicate the maximum value of the standard deviation of the radiative observable obtained from the Monte Carlo simulations for all values of solar elevation angle.

Figure B2Fraction of the downwelling direct solar radiation () that is reflected by the city (), absorbed by the roofs (), the walls (), or the ground () as simulated by the reference model Monte Carlo model HTRDR-Urban, the urban radiation model SPARTACUS-Urban, and the urban canopy model TEB with the Classical (TEB-Classical) and the SPARTACUS-Urban (TEB–SPARTACUS) radiation scheme. The values of σmax indicate the maximum value of the standard deviation of the radiative observable obtained from the Monte Carlo simulations for all values of solar elevation angle.
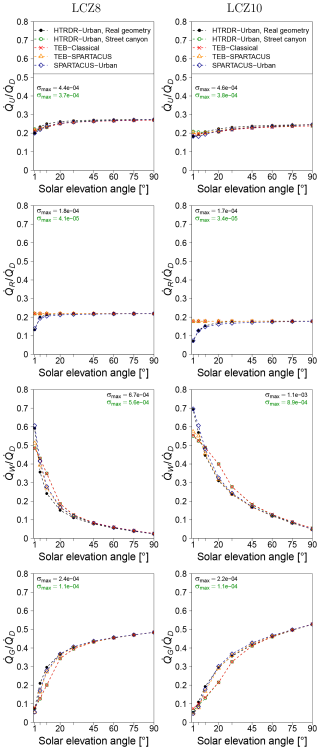
Figure B3Fraction of the downwelling direct solar radiation () that is reflected by the city (), absorbed by the roofs (), the walls (), or the ground () as simulated by the reference model Monte Carlo model HTRDR-Urban, the urban radiation model SPARTACUS-Urban, and the urban canopy model TEB with the Classical (TEB-Classical) and the SPARTACUS-Urban (TEB–SPARTACUS) radiation scheme. The values of σmax indicate the maximum value of the standard deviation of the radiative observable obtained from the Monte Carlo simulations for all values of solar elevation angle.
The following figure displays the solar radiation budget for the LCZ2a and LCZ4 morphologies with trees and direct downwelling solar radiation.
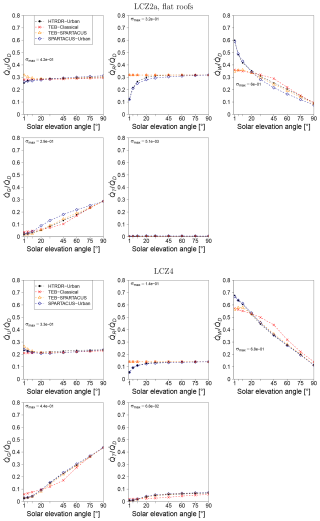
Figure C1Fraction of the downwelling direct solar radiation () that is reflected by the city (), absorbed by the roofs (), the walls (), the ground (), or the urban trees () as simulated by the reference model Monte Carlo model HTRDR-Urban, the urban radiation model SPARTACUS-Urban, and the urban canopy model TEB with the Classical (TEB-Classical) and the SPARTACUS-Urban (TEB–SPARTACUS) radiation scheme. The values of σmax indicate the maximum value of the standard deviation of the radiative observable obtained from the Monte Carlo simulations for all values of solar elevation angle.
The software archive on Zenodo (https://doi.org/10.5281/zenodo.11244064, Schoetter et al., 2024) contains the exact model version used in this article and a user manual describing the TEB–SPARTACUS namelist and how to install the model and run and plot the validation simulations to reproduce the figures in this article. TEB–SPARTACUS is also included in the free and open-source SURFEXv9.0 repository (http://www.umr-cnrm.fr/surfex/spip.php?article387, Masson et al., 2013) that is under a CeCILL-C license.
RS did the TEB and SPARTACUS-Urban coupling, the execution and analysis of the HTRDR-Urban reference simulations, and the majority of the writing. RJH prepared SPARTACUS-Urban for its coupling with TEB, provided guidance on the use of Monte Carlo reference simulations for radiative transfer, and supervised the TEB–SPARTACUS validation. CC led the HTRDR-Urban reference model development and supervised the TEB–SPARTACUS validation. VM supervised the TEB–SPARTACUS coupling. All co-authors have read the entire paper and helped to improve the original draft.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
Simone Kotthaus is acknowledged for sharing the Spectral Library of Impervious Urban Materials, and Vincent Eymet is acknowledged for his help with the creation of the optical properties files.
This research has been supported by the Agence de l'Environnement et de la Maîtrise de l'Energie (grant no. MODRADURB-1917C001) and the Agence Nationale de la Recherche (grant no. ANR-21-CE46-0013).
This paper was edited by Mohamed Salim and reviewed by two anonymous referees.
Blazejczyk, K., Epstein, Y., Jendritzky, G., Staiger, H., and Tinz, B.: Comparison of UTCI to selected thermal indices, Int. J. Biometeorol., 56, 515–535, https://doi.org/10.1007/s00484-011-0453-2, 2012. a
Bueno, B., Pigeon, G., Norford, L. K., Zibouche, K., and Marchadier, C.: Development and evaluation of a building energy model integrated in the TEB scheme, Geosci. Model Dev., 5, 433–448, https://doi.org/10.5194/gmd-5-433-2012, 2012. a
Caliot, C., Schoetter, R., Forest, V., Eymet, V., and Chung, T.-Y.: Model of Spectral and Directional Radiative Transfer in Complex Urban Canopies with Participating Atmospheres, Bound.-Lay. Meteorol., 186, 145–175, https://doi.org/10.1007/s10546-022-00750-5, 2023. a, b
Coddington, O., Lean, L. J., Doug, L., Pilewskie, P., Snow, M., and NOAA CDR Program: NOAA Climate Data Record (CDR) of Solar Spectral Irradiance (SSI), NRLSSI Version 2, NOAA National Centers for Environmental Information [data set], https://doi.org/10.7289/V51J97P6, 2015. a
Daniel, M., Lemonsu, A., Déqué, M., Somot, S., Alias, A., and Masson, V.: Benefits of explicit urban parameterization in regional climate modeling to study climate and city interactions, Clim. Dynam., 52, 2745–2764, https://doi.org/10.1007/s00382-018-4289-x, 2019. a
de Munck, C. S., Lemonsu, A., Bouzouidja, R., Masson, V., and Claverie, R.: The GREENROOF module (v7.3) for modelling green roof hydrological and energetic performances within TEB, Geosci. Model Dev., 6, 1941–1960, https://doi.org/10.5194/gmd-6-1941-2013, 2013. a, b
Di Napoli, C., Hogan, R. J., and Pappenberger, F.: Mean radiant temperature from global-scale numerical weather prediction models, Int. J. Biometeorol., 64, 1233–1245, https://doi.org/10.1007/s00484-020-01900-5, 2020. a, b
Dissegna, M. A., Yin, T., Wu, H., Lauret, N., Wei, S., Gastellu-Etchegorry, J.-P., and Grêt-Regamey, A.: Modeling Mean Radiant Temperature Distribution in Urban Landscapes Using DART, Remote Sens., 13, 1443, https://doi.org/10.3390/rs13081443, 2021. a
El Hafi, M., Blanco, S., Dauchet, J., Fournier, R., Galtier, M., Ibarrart, L., Tregan, J.-M., and Villefranque, N.: Three viewpoints on null-collision Monte Carlo algorithms, J. Quant. Spectrosc. Ra., 260, 107402, https://doi.org/10.1016/j.jqsrt.2020.107402, 2021. a
Frayssinet, L., Merlier, L., Kuznik, F., Hubert, J.-L., Milliez, M., and Roux, J.-J.: Modeling the heating and cooling energy demand of urban buildings at city scale, Renew. Sust. Energ. Rev., 81, 2318–2327, https://doi.org/10.1016/j.rser.2017.06.040, 2018. a
Fröhlich, D. and Matzarakis, A.: Calculating human thermal comfort and thermal stress in the PALM model system 6.0, Geosci. Model Dev., 13, 3055–3065, https://doi.org/10.5194/gmd-13-3055-2020, 2020. a
Galtier, M., Blanco, S., Caliot, C., Coustet, C., Dauchet, J., El Hafi, M., Eymet, V., Fournier, R., Gautrais, J., Khuong, A., Piaud, B., and Terrée, G.: Integral formulation of null-collision Monte Carlo algorithms, J. Quant. Spectrosc. Ra., 125, 57–68, https://doi.org/10.1016/j.jqsrt.2013.04.001, 2013. a
Gastellu-Etchegorry, J.-P.: 3D Modeling of satellite spectral images, radiation budget and energy budget of urban landscapes, Meteorol. Atmos. Phys., 102, 187–207, https://doi.org/10.1007/s00703-008-0344-1, 2008. a
Gastellu-Etchegorry, J.-P., Yin, T., Lauret, N., Cajgfinger, T., Gregoire, T., Grau, E., Feret, J.-B., Lopes, M., Guilleux, J., Dedieu, G., Malenovský, Z., Cook, B. D., Morton, D., Rubio, J., Durrieu, S., Cazanave, G., Martin, E., and Ristorcelli, T.: Discrete Anisotropic Radiative Transfer (DART 5) for Modeling Airborne and Satellite Spectroradiometer and LIDAR Acquisitions of Natural and Urban Landscapes, Remote Sens., 7, 1667–1701, https://doi.org/10.3390/rs70201667, 2015. a
Geletič, J., Lehnert, M., Resler, J., Krč, P., Middel, A., Krayenhoff, E., and Krüger, E.: High-fidelity simulation of the effects of street trees, green roofs and green walls on the distribution of thermal exposure in Prague-Dejvice, Build. Environ., 223, 109484, https://doi.org/10.1016/j.buildenv.2022.109484, 2022. a
Grimmond, C. S. B., Blackett, M., Best, M. J., Barlow, J., Baik, J.-J., Belcher, S. E., Bohnenstengel, S. I., Calmet, I., Chen, F., Dandou, A., Fortuniak, K., Gouvea, M. L., Hamdi, R., Hendry, M., Kawai, T., Kawamoto, Y., Kondo, H., Krayenhoff, E. S., Lee, S.-H., Loridan, T., Martilli, A., Masson, V., Miao, S., Oleson, K., Pigeon, G., Porson, A., Ryu, Y.-H., Salamanca, F., Shashua-Bar, L., Steeneveld, G.-J., Tombrou, M., Voogt, J., Young, D., and Zhang, N.: The International Urban Energy Balance Models Comparison Project: First Results from Phase 1, J. Appl. Meteorol. Clim., 49, 1268–1292, https://doi.org/10.1175/2010JAMC2354.1, 2010. a
Grimmond, C. S. B., Blackett, M., Best, M. J., Baik, J.-J., Belcher, S. E., Beringer, J., Bohnenstengel, S. I., Calmet, I., Chen, F., Coutts, A., Dandou, A., Fortuniak, K., Gouvea, M. L., Hamdi, R., Hendry, M., Kanda, M., Kawai, T., Kawamoto, Y., Kondo, H., Krayenhoff, E. S., Lee, S.-H., Loridan, T., Martilli, A., Masson, V., Miao, S., Oleson, K., Ooka, R., Pigeon, G., Porson, A., Ryu, Y.-H., Salamanca, F., Steeneveld, G., Tombrou, M., Voogt, J. A., Young, D. T., and Zhang, N.: Initial results from Phase 2 of the International Urban Energy Balance Model Comparison, Int. J. Climatol., 31, 244–272, https://doi.org/10.1002/joc.2227, 2011. a
Hamdi, R. and Masson, V.: Inclusion of a Drag Approach in the Town Energy Balance (TEB) Scheme: Offline 1D Evaluation in a Street Canyon, J. Appl. Meteorol. Clim., 47, 2627–2644, https://doi.org/10.1175/2008JAMC1865.1, 2008. a
Hogan, R. J.: An Exponential Model of Urban Geometry for Use in Radiative Transfer Applications, Bound.-Lay. Meteorol., 170, 357–372, https://doi.org/10.1007/s10546-018-0409-8, 2019a. a, b
Hogan, R. J.: Flexible Treatment of Radiative Transfer in Complex Urban Canopies for Use in Weather and Climate Models, Bound.-Lay. Meteorol., 173, 53–78, https://doi.org/10.1007/s10546-019-00457-0, 2019b. a, b, c
Hogan, R. J., Schäfer, S. A. K., Klinger, C., Chiu, J. C., and Mayer, B.: Representing 3-D cloud radiation effects in two-stream schemes: 2. Matrix formulation and broadband evaluation, J. Geophys. Res.-Atmos., 121, 8583–8599, https://doi.org/10.1002/2016JD024875, 2016. a
Kotthaus, S., Smith, T., Wooster, M., and Grimmond, S.: Spectral Library of Impervious Urban Materials, Version 1.0, Zenodo [code and data set], https://doi.org/10.5281/zenodo.4263842, 2013. a
Kotthaus, S., Smith, T. E., Wooster, M. J., and Grimmond, C.: Derivation of an urban materials spectral library through emittance and reflectance spectroscopy, ISPRS J. Photogramm. Remote Sens., 94, 194–212, https://doi.org/10.1016/j.isprsjprs.2014.05.005, 2014. a, b, c
Krayenhoff, E. S., Christen, A., Martilli, A., and Oke, T. R.: A Multi-layer Radiation Model for Urban Neighbourhoods with Trees, Bound.-Lay. Meteorol., 151, 139–178, https://doi.org/10.1007/s10546-013-9883-1, 2014. a
Kwok, Y. T., Schoetter, R., Lau, K. K.-L., Hidalgo, J., Ren, C., Pigeon, G., and Masson, V.: How well does the local climate zone scheme discern the thermal environment of Toulouse (France)? An analysis using numerical simulation data, Int. J. Climatol., 39, 5292–5315, https://doi.org/10.1002/joc.6140, 2019. a
Lac, C., Chaboureau, J.-P., Masson, V., Pinty, J.-P., Tulet, P., Escobar, J., Leriche, M., Barthe, C., Aouizerats, B., Augros, C., Aumond, P., Auguste, F., Bechtold, P., Berthet, S., Bielli, S., Bosseur, F., Caumont, O., Cohard, J.-M., Colin, J., Couvreux, F., Cuxart, J., Delautier, G., Dauhut, T., Ducrocq, V., Filippi, J.-B., Gazen, D., Geoffroy, O., Gheusi, F., Honnert, R., Lafore, J.-P., Lebeaupin Brossier, C., Libois, Q., Lunet, T., Mari, C., Maric, T., Mascart, P., Mogé, M., Molinié, G., Nuissier, O., Pantillon, F., Peyrillé, P., Pergaud, J., Perraud, E., Pianezze, J., Redelsperger, J.-L., Ricard, D., Richard, E., Riette, S., Rodier, Q., Schoetter, R., Seyfried, L., Stein, J., Suhre, K., Taufour, M., Thouron, O., Turner, S., Verrelle, A., Vié, B., Visentin, F., Vionnet, V., and Wautelet, P.: Overview of the Meso-NH model version 5.4 and its applications, Geosci. Model Dev., 11, 1929–1969, https://doi.org/10.5194/gmd-11-1929-2018, 2018. a, b
Lemonsu, A., Masson, V., Shashua-Bar, L., Erell, E., and Pearlmutter, D.: Inclusion of vegetation in the Town Energy Balance model for modelling urban green areas, Geosci. Model Dev., 5, 1377–1393, https://doi.org/10.5194/gmd-5-1377-2012, 2012. a
Lemonsu, A., Caillaud, C., Alias, A., Riette, S., Seity, Y., Le Roy, B., Michau, Y., and Lucas-Picher, P.: What added value of CNRM-AROME convection-permitting regional climate model compared to CNRM-ALADIN regional climate model for urban climate studies? Evaluation over Paris area (France), Clim. Dynam., 61, 1643–1661, https://doi.org/10.1007/s00382-022-06647-w, 2023. a
Lipson, M., Grimmond, S., Best, M., Chow, W. T. L., Christen, A., Chrysoulakis, N., Coutts, A., Crawford, B., Earl, S., Evans, J., Fortuniak, K., Heusinkveld, B. G., Hong, J.-W., Hong, J., Järvi, L., Jo, S., Kim, Y.-H., Kotthaus, S., Lee, K., Masson, V., McFadden, J. P., Michels, O., Pawlak, W., Roth, M., Sugawara, H., Tapper, N., Velasco, E., and Ward, H. C.: Harmonized gap-filled datasets from 20 urban flux tower sites, Earth Syst. Sci. Data, 14, 5157–5178, https://doi.org/10.5194/essd-14-5157-2022, 2022. a
Martilli, A., Clappier, A., and Rotach, M. W.: An Urban Surface Exchange Parameterisation for Mesoscale Models, Bound.-Lay. Meteorol., 104, 261–304, https://doi.org/10.1023/A:1016099921195, 2002. a
Masson, V.: A Physically-Based Scheme For The Urban Energy Budget In Atmospheric Models, Bound.-Lay. Meteorol., 94, 357–397, https://doi.org/10.1023/A:1002463829265, 2000. a, b
Masson, V., Le Moigne, P., Martin, E., Faroux, S., Alias, A., Alkama, R., Belamari, S., Barbu, A., Boone, A., Bouyssel, F., Brousseau, P., Brun, E., Calvet, J.-C., Carrer, D., Decharme, B., Delire, C., Donier, S., Essaouini, K., Gibelin, A.-L., Giordani, H., Habets, F., Jidane, M., Kerdraon, G., Kourzeneva, E., Lafaysse, M., Lafont, S., Lebeaupin Brossier, C., Lemonsu, A., Mahfouf, J.-F., Marguinaud, P., Mokhtari, M., Morin, S., Pigeon, G., Salgado, R., Seity, Y., Taillefer, F., Tanguy, G., Tulet, P., Vincendon, B., Vionnet, V., and Voldoire, A.: The SURFEXv7.2 land and ocean surface platform for coupled or offline simulation of earth surface variables and fluxes, Geosci. Model Dev., 6, 929–960, https://doi.org/10.5194/gmd-6-929-2013, 2013 (code available at: http://www.umr-cnrm.fr/surfex/spip.php?article387, last access: 22 January 2025). a
Masson, V., Bonhomme, M., Salagnac, J.-L., Briottet, X., and Lemonsu, A.: Solar panels reduce both global warming and urban heat island, Front. Environ. Sci., 2, 1–10, https://doi.org/10.3389/fenvs.2014.00014, 2014. a
Nagel, T., Schoetter, R., Bourgin, V., Masson, V., and Onofri, E.: Drag Coefficient and Turbulence Mixing Length of Local Climate Zone-Based Urban Morphologies Derived Using Obstacle-Resolving Modelling, Bound.-Lay. Meteorol., 186, 737–769, https://doi.org/10.1007/s10546-022-00780-z, 2023. a
Oke, T. R.: The energetic basis of the urban heat island, Q. J. Roy. Meteor. Soc., 108, 1–24, https://doi.org/10.1002/qj.49710845502, 1982. a
Pigeon, G., Zibouche, K., Bueno, B., Bras, J. L., and Masson, V.: Improving the capabilities of the Town Energy Balance model with up-to-date building energy simulation algorithms: an application to a set of representative buildings in Paris, Energ. Buildings, 76, 1–14, https://doi.org/10.1016/j.enbuild.2013.10.038, 2014. a
Redon, E., Lemonsu, A., and Masson, V.: An urban trees parameterization for modeling microclimatic variables and thermal comfort conditions at street level with the Town Energy Balance model (TEB-SURFEX v8.0), Geosci. Model Dev., 13, 385–399, https://doi.org/10.5194/gmd-13-385-2020, 2020. a
Redon, E. C., Lemonsu, A., Masson, V., Morille, B., and Musy, M.: Implementation of street trees within the solar radiative exchange parameterization of TEB in SURFEX v8.0, Geosci. Model Dev., 10, 385–411, https://doi.org/10.5194/gmd-10-385-2017, 2017. a
Roth, M.: Review of atmospheric turbulence over cities, Q. J. Roy. Meteor. Soc., 126, 941–990, https://doi.org/10.1002/qj.49712656409, 2000. a
Schäfer, S. A. K., Hogan, R. J., Klinger, C., Chiu, J. C., and Mayer, B.: Representing 3-D cloud radiation effects in two-stream schemes: 1. Longwave considerations and effective cloud edge length, J. Geophys. Res.-Atmos., 121, 8567–8582, https://doi.org/10.1002/2016JD024876, 2016. a
Schoetter, R., Grawe, D., Hoffmann, P., Kirschner, P., Grätz, A., and Schlünzen, K. H.: Impact of local adaptation measures and regional climate change on perceived temperature, Meteorol Z., 22, 117–130, https://doi.org/10.1127/0941-2948/2013/0381, 2013. a
Schoetter, R., Masson, V., Bourgeois, A., Pellegrino, M., and Lévy, J.-P.: Parametrisation of the variety of human behaviour related to building energy consumption in the Town Energy Balance (SURFEX-TEB v. 8.2), Geosci. Model Dev., 10, 2801–2831, https://doi.org/10.5194/gmd-10-2801-2017, 2017. a
Schoetter, R., Kwok, Y. T., de Munck, C., Lau, K. K. L., Wong, W. K., and Masson, V.: Multi-layer coupling between SURFEX-TEB-v9.0 and Meso-NH-v5.3 for modelling the urban climate of high-rise cities, Geosci. Model Dev., 13, 5609–5643, https://doi.org/10.5194/gmd-13-5609-2020, 2020. a
Schoetter, R., Caliot, C., Chung, T.-Y., Hogan, R. J., and Masson, V.: Quantification of Uncertainties of Radiative Transfer Calculation in Urban Canopy Models, Bound.-Lay. Meteorol., 189, 103–138, https://doi.org/10.1007/s10546-023-00827-9, 2023. a, b, c, d, e, f, g, h, i
Schoetter, R., Hogan, R. J., Caliot, C., and Masson, V.: Source code, numerical simulations, and postprocessing scripts described in the research article ”Coupling the urban canopy model TEB (SURFEXv9.0) with the radiation model SPARTACUS-Urbanv0.6.1 for more realistic urban radiative exchange calculation”, submitted to Geoscientific Model Development, Zenodo [code], https://doi.org/10.5281/zenodo.11244064, 2024. a
Seity, Y., Brousseau, P., Malardel, S., Hello, G., Bénard, P., Bouttier, F., Lac, C., and Masson, V.: The AROME-France Convective-Scale Operational Model, Mon. Weather Rev., 139, 976–991, https://doi.org/10.1175/2010MWR3425.1, 2011. a
Stewart, I. D. and Oke, T. R.: Local Climate Zones for Urban Temperature Studies, B. Am. Meteorol. Soc., 93, 1879–1900, https://doi.org/10.1175/BAMS-D-11-00019.1, 2012. a
Stretton, M. A., Morrison, W., Hogan, R., and Grimmond, S.: Evaluation of the SPARTACUS-Urban radiation model for vertically resolved shortwave radiation in urban areas, Bound.-Lay. Meteorol., 184, 301–331, https://doi.org/10.1007/s10546-022-00706-9, 2022. a, b, c
Stretton, M. A., Morrison, W., Hogan, R. J., and Grimmond, S.: Evaluation of vertically resolved longwave radiation in SPARTACUS-Urban 0.7.3 and the sensitivity to urban surface temperatures, Geosci. Model Dev., 16, 5931–5947, https://doi.org/10.5194/gmd-16-5931-2023, 2023. a
Strømann-Andersen, J. and Sattrup, P.: The urban canyon and building energy use: Urban density versus daylight and passive solar gains, Energ. Buildings, 43, 2011–2020, https://doi.org/10.1016/j.enbuild.2011.04.007, 2011. a
Thorsson, S., Lindberg, F., Eliasson, I., and Holmer, B.: Different methods for estimating the mean radiant temperature in an outdoor urban setting, Int. J. Climatol., 27, 1983–1993, https://doi.org/10.1002/joc.1537, 2007. a, b
Tornay, N., Schoetter, R., Bonhomme, M., Faraut, S., and Masson, V.: GENIUS: A methodology to define a detailed description of buildings for urban climate and building energy consumption simulations, Urban Clim., 20, 75–93, 2017. a
Villefranque, N., Fournier, R., Couvreux, F., Blanco, S., Cornet, C., Eymet, V., Forest, V., and Tregan, J.-M.: A Path-Tracing Monte Carlo Library for 3-D Radiative Transfer in Highly Resolved Cloudy Atmospheres, J. Adv. Model. Earth Sy., 11, 2449–2473, https://doi.org/10.1029/2018MS001602, 2019. a
- Abstract
- Introduction
- Technical aspects of the TEB and SPARTACUS-Urban coupling
- Methodology for TEB–SPARTACUS validation
- Results
- Discussion
- Conclusions
- Appendix A: Input and output parameters for SPARTACUS-Urban when used in TEB
- Appendix B: Results for direct-only downwelling solar radiation without trees
- Appendix C: Results for direct-only downwelling solar radiation with trees
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Technical aspects of the TEB and SPARTACUS-Urban coupling
- Methodology for TEB–SPARTACUS validation
- Results
- Discussion
- Conclusions
- Appendix A: Input and output parameters for SPARTACUS-Urban when used in TEB
- Appendix B: Results for direct-only downwelling solar radiation without trees
- Appendix C: Results for direct-only downwelling solar radiation with trees
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References