The Modular and Integrated Data Assimilation System at Environment and Climate Change Canada (MIDAS v3.9.1)

The Modular and Integrated Data Assimilation System (MIDAS) software (version 3.9.1) is described in terms of its range of functionality, modular software design, parallelization strategy, and current uses within real-time operational and experimental systems. MIDAS is developed at Environment and Climate Change Canada for both operational and research applications, including all atmospheric data assimilation (DA) elements of the Canadian operational numerical weather prediction systems. The described version of MIDAS is part of the Canadian prediction systems that became operational in June 2024. The software is designed to be sufficiently general to enable other DA applications, including atmospheric constituents (e.g. ozone), sea ice, and sea surface temperature. In addition to describing the current MIDAS applications, a sample of the results from these systems is presented to demonstrate their performance in comparison with either systems from before the switch to using MIDAS software or similar systems at other numerical weather prediction (NWP) centres. The modular software design also allows the code that implements high-level components (e.g. observation operators, error covariance matrices, state vectors) to easily be used in many different ways depending on the application, such as for both variational and ensemble DA algorithms, for estimating the observation impact on short-term forecasts, and for performing various observation pre-processing procedures. The use of a single common DA software package for multiple components of the Earth system provides both practical and scientific benefits, including the facilitation of future research on DA approaches that explicitly include the coupled connections between multiple Earth system components. To this end, work is currently underway to allow the use of MIDAS DA algorithms for initializing both deterministic and ensemble three-dimensional ocean model forecasts.

1 Introduction

Data assimilation (DA) is used in the context of numerical weather prediction (NWP) and other Earth system prediction applications to provide an estimate of the current numerical model state for initializing forecasts. This is typically accomplished using observations acquired from a diverse set of both in situ and remote sensing instruments to compute an optimal correction to a short-term model forecast within a cycling DA system. Several DA algorithms are currently employed at operational NWP centres, including at Environment and Climate Change Canada (ECCC), for initializing deterministic and ensemble forecasts at both global and regional scales. While NWP centres originally considered only the atmosphere and land surface, forecast models are increasingly coupled with other components of the Earth system, including the ocean and sea ice. Consequently, NWP centres have become involved in developing and implementing DA systems for initializing multiple components of the Earth system in addition to the atmosphere. While independent DA systems are still mostly used for initializing the separate components of coupled model forecasts, research into coupled DA approaches is starting to demonstrate some potential benefits (Penny et al., 2017). With strongly coupled DA, assimilated observations related to one Earth system component can have a direct impact on variables of the other components through the physical or statistical relationship between the forecast errors of the different components. In addition, observations that are directly related to multiple Earth system components can be assimilated in an appropriate way with a strongly coupled approach to correct variables in all involved model components. Though other approaches have been proposed (e.g. the interface solver of Frolov et al., 2016), a straightforward way to fully include coupling within the DA procedure is to use a single DA system to assimilate observations from all coupled Earth system components to simultaneously estimate the current state for the entire coupled model state. Conducting research into such a strongly coupled DA approach represents a technical challenge, since most existing DA systems have been developed in isolation from each other, often using different DA algorithms and update frequencies.

The Modular and Integrated Data Assimilation System (MIDAS) is a unified DA software package developed at ECCC for both research and operational applications. The purpose of developing a single unified software for DA is twofold. Firstly, using MIDAS instead of developing and maintaining numerous independent programs reduces the amount of redundant technical work needed for commonly required functionality. Similarly, scientific functionality specifically developed for one application can easily be tested in the context of other DA applications that employ MIDAS. The second purpose of using MIDAS for many different Earth system components is to facilitate research into the potential benefits of strongly coupled DA for initializing coupled model forecasts. Research on strongly coupled DA will be technically much easier to conduct after independent DA applications for each Earth system component are implemented and fully tested in MIDAS using the same DA algorithm and software.

There are other DA software packages developed for DA applications that share some similarities with MIDAS. This includes the Joint Effort for Data assimilation Integration (JEDI; Liu et al., 2022; Huang et al., 2023), the Data Assimilation Research Testbed (DART; Anderson et al., 2009), the Object Oriented Prediction System (OOPS; Bonavita et al., 2017), and the Parallel Data Assimilation Framework (PDAF; Nerger et al., 2020). While, like MIDAS, these are all developed to cover a variety of DA applications, specific details about their range of functionality, software design, and current operational applications differ in many ways as compared with MIDAS. Like MIDAS, OOPS is currently used for operational NWP after being recently implemented at ECMWF (ECMWF, 2023). MIDAS has been used for numerous operational applications for many years, and the number of these applications is continuing to increase, as detailed in a later section. An important technical aspect of MIDAS is that its programs are executed separately from the forecast model software, while some of the other systems previously mentioned are compiled and executed together with the forecast model and exchange information between DA and the forecast model through subroutines. While the approach used in MIDAS requires the additional procedure to read files generated by the model, it may avoid constraints on the software design and Message Passing Interface (MPI) parallelization implementation strategy that can be completely independent of the strategy used within the forecast models.

The goal of this paper is to provide an overview of the MIDAS software version 3.9.1 (ECCC, 2024a) used at ECCC to efficiently conduct scientific research and development for the DA and related tasks within many operational prediction systems, including for the NWP systems implemented during the summer of 2024. As the MIDAS software is continually being developed and modified to facilitate both research and future operational applications, it was decided to focus the description of functionality, software design, and implementation details on this particular version to avoid confusion. This description of MIDAS is intended to be helpful for an audience of developers of similar DA software at other operational NWP centres. It provides one example of how such software can be designed and provides the basic rationale supporting the design choices. Since at this time MIDAS cannot be easily installed and used outside of ECCC, the goal is not to make MIDAS available to the greater DA community. The next section describes the origins of MIDAS and the overall development strategy. Section 3 outlines the range of scientific functionality of the software, and Sect. 4 describes how this functionality is implemented in a set of Fortran programs and modules. Section 5 presents the different ways data are distributed across separate MPI tasks for efficient parallelization of the computations in MIDAS. Finally, Sect. 6 describes all current MIDAS applications in operational and experimental systems and Sect. 7 provides some discussion on ongoing and planned MIDAS developments.

2 MIDAS origins and overall development strategy

A brief description of the initial development steps of MIDAS and the reasoning behind the chosen development strategy is provided as an example for DA software developers and scientists at other NWP centres of how the constraints and requirements shared among many such centres can be addressed. Early development of MIDAS originated from a project to implement and scientifically evaluate the 4D ensemble-variational DA approach (4D-EnVar) in comparison with the then-operational 4D variational DA approach (4D-Var) for global-scale NWP (Buehner et al., 2013). The implementation of the 4D-EnVar algorithm in the existing 4D-Var software was not practical due to the extensive reliance on global variables accessible throughout the software and the convoluted design of the code that had become increasingly complex over time. Nevertheless, the decision was made to work with this existing code instead of building a completely new piece of software. To simplify the process, the code was initially reduced by only keeping the functionality needed to perform 3D variational DA (3D-Var). Since 3D-Var is closely related to the 4D-EnVar approach, software tests for 3D-Var were used to ensure this functionality was unaffected during an initial major redesign of the software. This initial redesign focused on improving the high-level structure of the code incrementally (without changing the functionality) by moving much of the existing subroutines, functions, and variables into logically organized Fortran modules and gradually removing the use of global variables. Only after this restructuring could work begin on implementing 4D-EnVar.

Once the initial work was completed for the first operational implementation of 4D-EnVar in 2014 (Buehner et al., 2015), major code restructuring continued with a focus on the data representation and low-level code for handling observations. This involved refactoring the code into the Fortran module obsSpaceData with the goal of sharing this code between the 4D-EnVar and the then operationally used ensemble Kalman filter (EnKF), which was implemented in independent Fortran software (Houtekamer et al., 2014).

Following a period of rapid large-scale refactoring of the code to encapsulate all code in a set of interrelated Fortran modules, the development strategy now focuses on the continual and incremental improvement of the code design on an “as-needed” basis without ever losing any of the existing functionality. A comprehensive set of system tests are maintained within the same repository as the Fortran code to ensure that all existing functionality is preserved when making any changes. A typical situation that motivates the need for improvements to the MIDAS code design is when the changes required to perform innovative scientific research cannot be easily introduced into MIDAS, possibly due to the high-level organization of the Fortran modules or an insufficient level of generality in existing modules. When this situation arises, a preliminary task is triggered to improve the existing code design without affecting the functionality. Once the existing code design is improved, then the new scientific functionality can be more easily introduced. With this approach, decisions about where to focus software development effort are primarily driven by the requirement to continually perform innovative scientific research and to improve the forecast quality for the atmosphere and related Earth system components without degrading the overall design or unnecessarily increasing the code complexity.

By using a continual and incremental approach to improving MIDAS in terms of scientific functionality, software design, and efficiency, the entire community of developers are always working on the same code base for both operational and research purposes. This avoids any division of the developer community into a subgroup primarily focused on improving the currently operational applications and a separate subgroup focused on longer-term developments, either technical or scientific. This is particularly important at ECCC with its relatively small community of DA scientists and developers. Changes to MIDAS are managed with GitLab using “issues” and “merge requests” to ensure coordinated and open development that incorporates mandatory code reviews and automated testing.

3 Software functionality

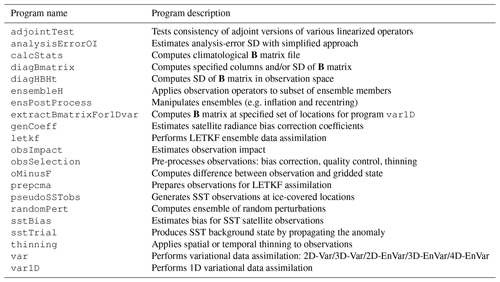
In addition to implementing both deterministic and ensemble DA algorithms, MIDAS version 3.9.1 currently also includes the ability to efficiently manipulate ensembles of states, pre-process and quality-control observations, estimate the impact of observations on short-term forecasts, estimate analysis-error standard deviation (SD) using a simple approach, calculate a highly parameterized background-error covariance matrix, and compute other diagnostic statistics from ensembles. Most of this functionality is used within numerous prediction systems operationally run in real time at ECCC as described in a later section. However, some functionality has been developed primarily for research purposes. The following subsections provide brief descriptions of the current MIDAS functionality.

3.1 Data assimilation algorithms

Two general classes of DA algorithms are implemented in MIDAS: variational DA for deterministic applications and a local ensemble transform Kalman filter (LETKF; Hunt et al., 2007) for ensemble DA applications, with many configurable variations in each general class of algorithm.

The variational DA algorithm consists of computing the state vector that minimizes a cost function measuring the “distance” from both the observations and the background state using an iterative optimization algorithm (specifically, version 2.0c of the limited-memory quasi-Newton solver of Gilbert and Lemaréchal (1989) modified to work with data distributed over MPI tasks¹). The formulation of the cost function in MIDAS is presented to introduce the mathematical notation used later and to complement the discussion on software design regarding the implementation of these mathematical operations. The cost function uses linearized observation operators and is preconditioned with respect to the background-error covariance matrix, resulting in

$$\begin{array}{ll}{\displaystyle }J\left(\mathit{v}\right)=& {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{v}}^T\mathit{v}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left(H\right({\mathit{x}}_{\mathrm{b}})+{\mathbf{HB}}^{\frac{\mathrm{1}}{\mathrm{2}}}\mathit{v}-\mathit{y}{)}^T\\ \text{(1)}& {\displaystyle }& {\displaystyle }\cdot {\mathbf{R}}^{-\mathrm{1}}\left(H\right({\mathit{x}}_{\mathrm{b}})+{\mathbf{HB}}^{\frac{\mathrm{1}}{\mathrm{2}}}\mathit{v}-\mathit{y}),\end{array}$$

where y is the vector of assimilated observations, x_b is the background state, R is the observation-error covariance matrix, B is the background-error covariance matrix, ${\mathbf{B}}^{\mathrm{1}/\mathrm{2}}$ is a possibly non-symmetric matrix related to B as $\mathbf{B}={\mathbf{B}}^{\mathrm{1}/\mathrm{2}}{\mathbf{B}}^{T/\mathrm{2}}$, H is the nonlinear observation operator that transforms a gridded state vector into a quantity comparable with the actual observation, H is the linearized version of H, and v is the so-called control vector that is determined by finding the minimum of this function. The control vector is related to the state vector as $\mathit{x}={\mathit{x}}_{\mathrm{b}}+\mathrm{\Delta }\mathit{x}$, where $\mathrm{\Delta }\mathit{x}={\mathbf{B}}^{\mathrm{1}/\mathrm{2}}\mathit{v}$ is the analysis increment. To enable the efficient determination of the value of v near the minimum, the gradient of the cost function with respect to v is also used. More details on this formulation can be found in Buehner et al. (2013).

The configuration of the variational DA algorithm can be modified by specifying the horizontal grid, vertical levels, and temporal resolution independently for both the background state and the analysis increment. For example, the analysis increment (and therefore also B and H) is often on a lower-resolution horizontal grid and at a lower temporal frequency than the background state to save computational cost, as in the so-called incremental approach (Courtier et al., 1994). Additionally, the use of a spectral transform as part of implementing the matrix–vector product with ${\mathbf{B}}^{\mathrm{1}/\mathrm{2}}$ requires that the analysis increment be on a specific type of grid that differs from the native forecast model grid of the background state. The specification of the background-error covariance matrix is very flexible, constructed as an arbitrary weighted combination of the following types of matrices:

• a climatological highly parameterized formulation based on spatially homogeneous and isotropic horizontal correlations represented in spectral space used for both global and regional NWP applications as described by Gauthier et al. (1999) and Fillion et al. (2010), respectively;

• a climatological highly parameterized formulation for the assimilation of atmospheric chemical constituents, such as ozone, also based on spatial homogeneous and isotropic horizontal correlations represented in spectral space (Gauthier et al., 1999);

• a climatological highly parameterized formulation based on the use of a diffusion operator to represent horizontal correlations with a Gaussian-like shape (e.g. Weaver et al., 2021) and able to incorporate the coastline as a boundary condition for ocean and sea ice applications as described by Caya et al. (2010; see Sect. 3); and

• an ensemble-based formulation that can use either standard spatial localization or scale-dependent localization (SDL) as described by Caron and Buehner (2018, 2022).

Note that when only using a climatological highly parameterized covariance matrix, the DA method is referred to as either 2D-Var or 3D-Var, depending on if the state vector being estimated is only 2D (e.g. for sea ice applications) or 3D (e.g. for atmospheric applications). When the ensemble-based formulation with spatial localization is used (either alone or in combination with one of the highly parameterized formulations), the approach is referred to as 3D-EnVar or 4D-EnVar, depending on if the analysis increment and ensemble covariances only include a single time or multiple times, respectively.

A special configuration of variational DA that treats each horizontal observation location independently was recently introduced mainly for research purposes. By only including the vertical and multivariate background-error covariances, this 1D variational (1D-Var) approach is useful for research related to the assimilation of satellite radiance observations. It allows greater focus on the link between the state vector of atmospheric vertical profiles and surface properties with the observed brightness temperature. Like with EnVar, the background-error covariances can use either a climatological or an ensemble-based covariance matrix or a weighted combination of both.

The implementation of the LETKF is a much more recent addition to MIDAS. To make the LETKF computationally feasible for operational applications with O(100) ensemble members, the calculation of the field of weights needed to compute the ensemble of analyses is performed on a coarse grid and then interpolated to the full-resolution grid before applying the weights to the background ensemble perturbations as introduced by Yang et al. (2009). Various flavours of the LETKF algorithm were implemented in MIDAS to facilitate the comparison by Buehner (2020; see Sect. 2 for more details) of different approaches in a realistic NWP context together with the previous stochastic EnKF algorithm: the standard LETKF (Hunt et al., 2007), a new approach for using cross-validation with the LETKF, and a stochastic formulation of the LETKF that uses perturbed observations. Subsequently, the original implementation of the LETKF with cross-validation was modified to introduce randomized subensembles to overcome problems that only appeared after extensive pre-operational testing (Caron et al., 2022). More recently, the option of using vertical grid-space covariance localization, originally proposed by Bishop et al. (2017), was introduced. This approach has been shown by Lei et al. (2018) to improve the use of satellite radiance observations.

3.2 Assimilated observations

The ability to assimilate different types of observations by any of the DA algorithms described above requires having nonlinear, tangent-linear, and adjoint versions of observation operators implemented in MIDAS. These are available for many types of meteorological atmospheric observations from both satellite-based and in situ instruments: radiosondes; aircraft; wind profilers; land stations, ships, and buoys; scatterometers; atmospheric motion vectors; radar Doppler winds; satellite-based radio occultation from global navigation satellite systems (GNSSs); ground-based GNSS stations; and microwave and infrared satellite sounders and imagers. The assimilation of all radiance observations utilizes version 13 of the software library Radiative Transfer for TOVS (RTTOV) as part of the observation operator to simulate the observed brightness temperature from the gridded state vector (Saunders et al., 2018). A recent addition to MIDAS is the ability to assimilate several types of microwave tropospheric sounding channels in cloudy non-precipitating conditions over ocean (Shahabadi and Buehner, 2021, 2024). In addition to these meteorological observations, atmospheric chemical constituent assimilation is possible for various retrieved observation types including point source values, vertical profiles, vertically integrated amounts (such as total and partial column ozone), and vertically averaged quantities, with the option of using averaging kernels when relevant. For vertical profile observations, one can select between piecewise linear interpolation or piecewise weighted averaging interpolation adapted from Rochon et al. (2007). Sea ice observation operators are also implemented for measurements from satellite-based platforms in the form of either retrievals of ice concentration from passive and active microwave sensors or direct measurements of backscatter from scatterometers (Buehner et al., 2016, and Komarov et al., 2020). In addition, observation operators for various manually generated sea ice products from the Canadian Ice Service are included. Finally, various sea surface temperature (SST) observations from both satellite-based and in situ platforms can be assimilated. The SST observations from satellite platforms are currently in the form of temperature retrievals obtained from either passive microwave or visible–infrared sensors (Skachko et al., 2024).

A unique feature of the MIDAS observation operators is their flexibility in how gridded states can be interpolated to observation locations. Some observation types are related to the gridded variables at many vertical levels but at a different horizontal location for each level. For these observations, MIDAS can use a so-called “slant-path” approach that extracts an arbitrarily slanted column of the gridded values for further computations within the operator for a specific observation type. This approach is used for measurements from ground-based weather radar, GNSS radio occultation observations, and radiances from microwave and infrared satellite sensors (Shahabadi et al., 2020).

Another feature of the interpolation to observation locations was originally implemented for sea ice observations. Some observations from satellite-based sensors are related to the spatially averaged quantity over an area much larger than a single model grid cell. For such observations, the observation operator can perform a spatial average over all analysis grid cells that fall within the observed “footprint” instead of the normal procedure of using bilinear interpolation of the gridded values to the observation location (Buehner et al., 2016). While used primarily in the context of sea ice analysis, initial testing has been performed for assimilating satellite radiance observations for high-resolution NWP to correct the large scales without constraining the small scales not resolved by these observations.

3.3 Ensemble processing

Several ways of processing ensembles of gridded state vectors are also implemented in MIDAS. These include both procedures that modify the state vectors and the computation of basic statistics of the ensemble, namely the ensemble mean and SD. The ensemble of state vectors can be modified by inflating the ensemble spread with any combination of the following approaches:

• the addition of random perturbations drawn from a multivariate Gaussian distribution with a mean of zero and covariance matrix specified in the same way as for the background-error covariances in variational DA (as described in Sect. 3.1),

• the relaxation of the ensemble perturbations towards the original background ensemble perturbations with the relaxation to prior perturbation (RTPP) approach (Zhang et al., 2004), and

• the multiplicative inflation of the ensemble perturbations referred to as the relaxation to prior spread (RTPS) approach (Whitaker and Hamill, 2012).

An ensemble of state vectors can also be modified using MIDAS by applying various methods to “recentre” the members either fully or partially around a specified alternative ensemble mean state. Typically, the same amount of recentring is applied to all ensemble members, which has the effect of shifting all members without changing the ensemble spread. However, as described by Houtekamer et al. (2019), it is also possible to apply a different amount of recentring to each member, which has the effect of increasing the ensemble spread.

Finally, the analysis ensemble can contain ensemble members with unrealistic atmospheric humidity values that far exceed the saturation point. Therefore simple procedures are implemented for limiting the humidity values to not surpass the saturation value and also to remain between a set of pressure-level-dependent minimum and maximum values.

3.4 Observation pre-processing

Several pre-processing steps implemented in MIDAS are typically required before observations can be effectively assimilated by any DA algorithm. This includes the estimation and removal of an error bias to account for the significant systematic errors that are present in several types of observations, including all types of satellite radiance observations and SST observations derived from satellite measurements. After removal of the estimated bias, numerous observation-specific quality control procedures are applied to reject observations that are either erroneous or difficult to accurately simulate with the available observation operators. Finally, many observation types also require either spatial or temporal thinning to reduce the total number of assimilated observations. This thinning is especially useful for observations that have errors with significant spatial or temporal correlations currently not accounted for in the DA algorithms.

An additional type of observation pre-processing is required for obtaining an accurate SST analysis state. To counteract the undesirable effect of spreading SST corrections from ice-free to ice-covered areas, artificial observations of SST equal to the freezing point are created in ice-covered areas. These artificial observations located in ice-covered areas are assimilated in combination with real SST observations in ice-free areas (Skachko et al., 2024).

3.5 Estimating observation impact

Two variations on the forecast sensitivity to observation impact (FSOI) approach originally introduced by Langland and Baker (2004) for estimating the impact of arbitrary subsets of observations on short-term forecast error are implemented in MIDAS. The first is suited to estimating the impact of observations within a purely ensemble-based DA system, such as the LETKF, which is similar to the approach described by Kalnay et al. (2012). The second approach is suited to estimating the impact of observations within a DA system based on the 4D-EnVar approach (Buehner et al., 2018). Both approaches use a large ensemble (256 members in the ECCC system) of short-term forecasts (typically 24 h in length) to propagate the sensitivities backwards in time from the forecast time to the analysis time. These sensitivities are then transformed, using the chain rule, into sensitivities with respect to the observations using the adjoint of the DA algorithm.

While the approaches just described for estimating the impact of observations apply to any of the observations currently assimilated, there are situations when it is useful to estimate the impact of observations from instruments that are not yet available for assimilation, such as for a new type of instrument planned for future deployment. This type of observation impact assessment is also available in MIDAS for the LETKF algorithm. Following a modified version of the approach described by Tan et al. (2007), the hypothetical observations are assimilated in combination with all existing real observations. The observation-error SD values of the hypothetical observations are essentially set to infinity for the analysis update to the ensemble mean, thereby giving no weight to these observations. On the other hand, the correct observation-error SD is used for the analysis update to the ensemble perturbations. Consequently, the hypothetical observations, for which actual observed values are not available, contribute to reducing the ensemble spread while not affecting the ensemble mean. If the ensemble DA system has good reliability or the lack of reliability can be effectively taken into account, then comparison of the ensemble spread between an experiment with and without the hypothetical observations provides an estimate of the observation impact.

3.6 Analysis-error estimation

A highly simplified procedure is implemented in MIDAS for propagating the error covariances of the state vector through a DA cycle (i.e. the repeated forecast and analysis steps performed sequentially in time) that is based on the Kalman filter equations. This is used in situations where an estimate of the uncertainty is required but only a deterministic assimilation system based on the variational DA algorithm instead of the LETKF is used. A description of this approach for estimating the analysis-error SD, originally developed in the context of the sea ice analysis system, is given by Buehner et al. (2016).

3.7 Statistics and diagnostic calculations

The existing functionality in MIDAS for efficiently reading, writing, and performing calculations with observations and either individual state vectors or ensembles of gridded state vectors makes it straightforward to implement several calculations of statistical and diagnostic quantities related to DA. This includes the computation of a highly parameterized climatological covariance matrix that is used for both specifying the background-error covariances for variational DA (Sect. 3.1) and computing random perturbations (Sect. 3.3). The calculation of this covariance matrix takes as input an ensemble of gridded model states or perturbations to states that are representative of a random sample of the appropriate probability distribution.

As described in Sect. 3.1, the background-error covariances for variational DA can be specified as any combination of several different types of matrices, some of which are quite complex. Therefore, a simple procedure is included in MIDAS to permit the visualization of the final resulting matrix by computing both individual columns of the complete covariance matrix (similar to the analysis increment obtained from assimilating a single observation) and an estimate of the matrix diagonal (i.e. the variances) for all variables and grid points. The ith column is obtained by multiplying a vector consisting of all zeros, except for the ith element, which is set to 1, by the adjoint and original versions of the covariance matrix square root. The diagonal of the matrix is estimated by a randomization approach in which a large number of realizations of a Gaussian-distributed random vector with covariance equal to the identity is multiplied by the square-root of the specified covariance matrix and the variance of the resulting ensemble of states is computed. A similar randomization approach can also be used to estimate the diagonal of a covariance matrix in observation space by simply applying the tangent-linear version of the observation operator to each gridded vector in the ensemble of states obtained with the approach just described.

4 Modular software design

This section provides a brief and high-level description of the MIDAS software design to provide an informative example that may be useful for developers of similar DA software at other operational NWP centres. The Fortran source code of MIDAS version 3.9.1 is organized within 21 programs and 111 modules. In total, the code is approximately 120 000 lines when excluding comments (ECCC, 2024a). The programs, listed in Table 1, are used to implement all of the functionality described in the previous section using a subset of the Fortran modules. The MIDAS programs and modules are all located in a single Git repository (primarily for information purposes, as no support is available for users external to ECCC; a public copy is maintained at https://github.com/ECCC-ASTD-MRD/MIDAS-src/tree/v_3.9; last access: 18 December 2024). A namelist file is used to control the configuration of programs and modules, with most programs and many modules having their own dedicated block within the namelist file to allow the setting of namelist variables to control behaviour of the program or module for a specific application.² For example, the size of the ensemble, the localization parameters, and other information used to configure the ensemble-based background-error covariance matrix for 4D-EnVar applications are located in the namelist file within the block NAMBEN which is read only by the setup routine for the Fortran module bMatrixEnsemble_mod.

Table 1 List of MIDAS programs and a short description of each.

The MIDAS Fortran code relies on a set of external libraries, including both standard math and file access libraries (LAPACK/BLAS, sqlite3, HDF5); the publicly available fast radiative transfer library RTTOV (Saunders et al., 2018); and a set of libraries developed and maintained by ECCC for accessing files in the locally used formats for both gridded model states and observations, generating random numbers, and more easily accessing observation files in the SQLite format. Currently, only the ECCC format for gridded model states (known as the RPN standard file format) is fully supported, while the observation files can be in both the ECCC format (known as BURP) and SQLite.

The source code and closely related data structures are gathered within Fortran modules. These modules are designed in a way that is similar to the “classes” in more formal object-oriented programming approaches, with the goal of maximizing the links among the data and related subroutines and functions within each module while minimizing the code links between separate modules. In particular, knowledge of the low-level details of how the data or functionality is implemented in a given module should not be required by code within the programs and other modules. This is made more explicit by using the Fortran private clause to hide the module's contents by default and then explicitly defining a minimal number of public entities at the beginning of the module source file. In this way, a user of a module can easily see how the code outside the module can access the functionality implemented in the module through the public subroutines/functions and derived-type variable definitions. Other self-imposed coding standards are implemented to facilitate readability and flexibility of the code, including the use of module prefixes for all public procedures and derived-type definitions and variables so that the origin of all non-local procedures and data is clear. For example, the module gridStateVector_mod has the prefix gsv and therefore all public subroutines and functions utilize this prefix, such as the function gsv_getField. While the original Fortran code from which MIDAS evolved made extensive use of global variables, the use of public module variables in the current version of MIDAS is restricted as much as possible. In general, the public module variables are used only for constants and a limited number of variables that have a global meaning and remain constant after being initialized. Additionally, procedure and variable names are sufficiently long and descriptive to provide useful information for developers not familiar with the code, thus improving the code readability and minimizing the need for comments within the code.

Separation of the MIDAS code within relatively independent modules facilitates the generalization of the functionality of each module, for example the removal of assumptions associated with the forecast model variables, type of vertical coordinate, and configuration of horizontal grids that can be used in MIDAS programs. This allows the same code to be used for very different applications, such as applications that work with 2D sea ice or SST fields or with 4D NWP or atmospheric chemical constituent fields. Many of the low-level modules are independent of any specific application, while others implement specific DA algorithms or other high-level functionality.

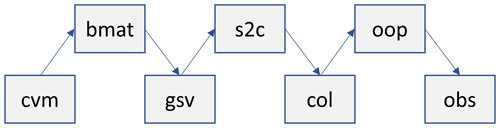
Figure 1 High-level relationship between some of the main MIDAS Fortran modules used for computing an analysis increment or background-error perturbation in observation space (see the main text for definitions of module prefixes). The upper row of modules are transformations between the data-oriented modules in the lower row. Note that each module in the upper row includes “use” statements for the two modules in the lower row to which they are directly connected.

Considering the design and relationships between modules in a general way, it is helpful to note that some modules are mainly responsible for representing data structures and performing various operations on those data structures, while others are mainly responsible for the transformation between these different data structures. As an example, Fig. 1 shows the relationship between several data-oriented modules and transformation-oriented modules that together are used in applications such as variational DA. First, the data object created with the controlVector_mod module (prefix cvm) is transformed into a gridded state vector, which is a derived-type variable defined in the gridStateVector_mod module (prefix gsv), by multiplying by the square root of the covariance matrix defined in the bMatrix_mod module (prefix bmat). This is then transformed into a single (possibly slanted) column of values at each observation location that is represented with a derived-type variable defined in the columnData_mod module (prefix col) by applying horizontal and temporal interpolation implemented in the stateToColumn_mod module (prefix s2c). This interpolation can be considered the first part of the observation operators. Finally, the column of values is transformed into values equivalent to the observations and stored in the appropriate location within the large data structure defined in the obsSpaceData_mod module (prefix obs) by applying the final part of observation operators contained in the obsOperators_mod module (prefix oop). This chain of tangent-linear transformations is represented mathematically as HB^½v.

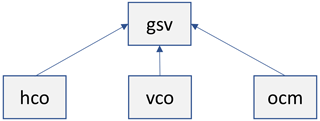
Figure 2 Relationship between the gridded state vector module (gsv) and lower-level modules that are used by this module through a composition relationship to represent the horizontal coordinate (hco), vertical coordinate (vco), and ocean mask (ocm).

Several data-oriented modules are also related to each other in a more direct way through the use of “composition”, also known as “has a” relationships. This type of relationship is used extensively in MIDAS to combine data structures and the functionality of multiple simpler modules into more complex entities. For example, many of the details included in the gridStateVector_mod data structure and functionality are actually implemented in the lower-level modules horizontalCoord_mod, verticalCoord_mod, and oceanMask_mod (with prefixes hco, vco, and ocm, respectively) as represented in Fig. 2. Therefore, it can be said that the gridded state vector “has a” horizontal coordinate, vertical coordinate, and ocean mask. As a consequence, all of the details related to the horizontal grid associated with a specific instance of the gridded state vector are represented by the data structure and functionality within the horizontalCoord_mod module. This type of relationship is extended even further in the module used to represent a complete ensemble of gridded state vectors, which is used in the context of both the EnVar and the LETKF algorithms. The ensembleStateVector_mod module relies heavily on the gridStateVector_mod module data structure and functionality to avoid code duplication.

5 Parallelization strategy

Several different strategies are used in MIDAS for distributing data over a large number of MPI tasks to reduce the volume of computations performed in parallel by each. The MPI tasks are generally organized in terms of two “dimensions” that correspond to two actual dimensions of the data themselves. Each MPI task can have multiple threads available in an additional layer of parallelization through the use of OpenMP, usually to speed up loops that perform a large number of computations. For various applications, it is often necessary to efficiently convert data currently distributed in one way into a different distribution over the MPI tasks, and therefore code for numerous data transpositions is available in MIDAS. The various MPI data distributions and associated transpositions are described in the remainder of this section.

For gridded data stored in derived-type variables defined in the gridStateVector_mod and ensembleStateVector_mod modules, the data are most commonly arranged in latitude–longitude tiles, where each MPI task only contains the data of a single non-overlapping tile. This choice of distribution facilitates several procedures related to the assimilation algorithms, including calculating the mean of ensemble, applying LETKF weights to ensemble perturbations, and computing 4D-EnVar increments from the localized ensemble. In this case, the latitude and longitude correspond to the two dimensions used to organize the MPI tasks. However, it is sometimes necessary to use other data distributions. For example, the reading of a single 4D state (such as the background state needed for variational DA) is made more efficient by distributing the data with respect to the time step such that the data for each time step can be read simultaneously in parallel by different MPI tasks and then transposed to the latitude–longitude tiles after the reading is complete. This approach is extended further when reading an ensemble of 4D states (such as for the LETKF and the ensemble-based covariance matrix of 4D-EnVar) by distributing the data with respect to both the time step and the ensemble index. In this case, each MPI task reads a single time step of a single member before transposing the entire ensemble of states to latitude–longitude tiles. The entire process of reading and transposing the hourly 256-member ensemble takes approximately 1 min of the total execution time of about 11 min (on 2352 cores) in the current global operational LETKF with 25 km horizontal grid spacing (described in Sect. 6.1). However, when writing an ensemble of states to files (such as for the LETKF), the gridded states are distributed with respect to the member index only, since all time steps for a member are stored in the same file. A different distribution is used when interpolating a 4D gridded state to observation location and time within the stateToColumn_mod module. For this, the gridded data are transposed into a distribution with respect to both the variable type and the vertical level, allowing the interpolation to be performed on each MPI task for all time steps of a single complete horizontal field (Fig. 3). With the entire horizontal field available for a given MPI task, any interpolation approach and type of grid can be used without requiring additional MPI communication, including the use of a footprint operator to horizontally average many grid-point values or the use of level-dependent horizontal positions for interpolation to create a slanted column.

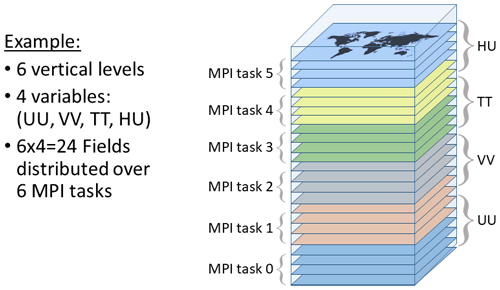
Figure 3 Schematic showing how 2D fields are distributed over MPI tasks with respect to both variables (in this example zonal and meridional wind, temperature, and humidity: UU, VV, TT, and HU, respectively) and vertical levels (six levels in this example). A different colour is used for each MPI task. This data distribution is used when interpolating to observation locations and times.

The observational data are randomly distributed over the MPI tasks for each type of observation to ensure a nearly even computational load across MPI tasks when applying the observation operators. This is accomplished using a round-robin approach to separate the observations into separate files for each MPI task. The splitting of observation files makes it very simple to read and update the files in parallel for each MPI task. The process of splitting and recombining the individual files is performed by separate programs that are parallelized for efficiency and executed within the same MPI job as the MIDAS program, just before and after the MIDAS program execution (Fig. 4). To be able to perform the interpolation from 2D fields to observation locations and times (as described above), only the latitude, longitude, and time of the observations are communicated from the random distribution to all MPI tasks (within the stateToColumn_mod module).

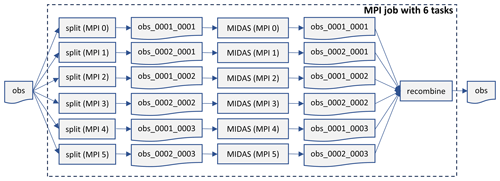
Figure 4 Schematic showing how a single observation file is first split into a separate file for each MPI task for parallel reading and updating by the MIDAS program. After the MIDAS program execution, the updated files are then recombined back into a single file. For increased efficiency, the splitting is performed independently by each MPI task to extract only the subset of observations needed for this MPI task using a round-robin strategy. In this example, we arbitrarily choose a configuration with six MPI tasks arranged in the two-dimensional decomposition as 2×3.

Another important data object that is distributed over MPI tasks is the control vector used by the minimization algorithm in variational DA to determine the analysis increment (see Sect. 3.1). The organization of the elements of this vector depends on the type of covariance matrix used to define the background error. In the case of the two types of matrices used for NWP, the control vector consists of spectral coefficients. For global applications, a triangular spherical harmonic spectral truncation is used and the spectral coefficients for the zonal and total wavenumbers are distributed over the MPI tasks using a round-robin (or cyclic) strategy. This ensures a nearly equal number of coefficients for each MPI task (Fig. 5). The spectral transforms use this data distribution as input or output and transpose the data internally (with respect to only one of the dimensions at a time) to facilitate the various steps in performing the spectral transform or its inverse. The gridded data output or input of the spectral transform subroutines is distributed with respect to latitude–longitude tiles.

Figure 5 Schematic showing an example of how the spectral coefficients (here up to a triangular truncation of T8, i.e. up to total wavenumber 8) used for the control vector in global variational data assimilation are distributed over the two-dimensional MPI decomposition (here with just 2×2 MPI tasks) following a round-robin strategy. The two values in each box represent the MPI task index over the two dimensions of the decomposition, and a different colour is used to identify each of the four MPI tasks.

The LETKF algorithm requires yet another strategy for parallelizing the most computationally demanding part of the calculation, namely the calculation of the weights that are applied to the background ensemble perturbations to obtain the analysis ensemble (e.g. see Eqs. 1–6 of Buehner, 2020). The weights are computed independently for each grid point of a relatively coarse grid (with ∼225 km grid spacing in the current operational global system). The computational cost of computing each weight strongly depends on the number of observations within the local neighbourhood of the grid point and therefore can vary greatly between different geographical regions. To ensure that the computational load is distributed relatively evenly across all MPI tasks, the weight calculations are assigned to MPI tasks using a round-robin approach. To facilitate this arbitrary distribution of the weight calculation, the limited information in observation space required to compute the weights is communicated to and duplicated on all MPI tasks. Once all of the coarse-grid weights are computed, the values for each grid point are communicated to one or more MPI tasks, where they are needed to perform bilinear interpolation to obtain the full-resolution weight fields distributed with respect to the latitude–longitude tiles. The resulting full-resolution weights can then be applied to the background ensemble perturbations (that are already distributed with respect to the latitude–longitude tiles) to obtain the analysis ensemble.

6 Operational MIDAS applications

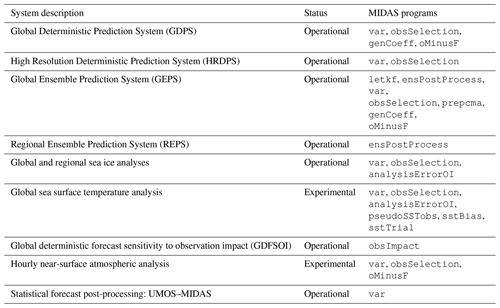
In this section, all applications of MIDAS programs in either the currently operational or the experimental systems (listed in Table 2) are briefly described. While MIDAS could be used for numerous other types of applications, it was decided to only present those applications that have been rigorously tested and evaluated prior to their operational implementation. In some cases, comparisons are described or the performance of these systems is shown with respect to a previous version before the use of MIDAS or systems at other NWP centres that implement a similar data assimilation algorithm.

Table 2 List of operational and experimental systems at ECCC that use MIDAS programs.

6.1 Numerical weather prediction

Numerous MIDAS programs are used with various configurations in all operational NWP systems. The global and high-resolution deterministic prediction systems (GDPS with 15 km grid spacing and HRDPS with 2.5 km grid spacing) both use a similar configuration of 4D-EnVar with SDL applied to the ensemble-based background-error covariance matrix. A similar configuration of 4D-EnVar is also used to produce the ensemble mean analysis for recentring the analysis ensembles in the global ensemble prediction system (GEPS with 25 km grid spacing), whereas the main ensemble analysis is performed by the LETKF algorithm with cross-validation. Both the GDPS and the GEPS also use MIDAS programs for the quality control and spatial and temporal thinning of nearly all observation types and the bias correction for satellite radiance observations. Additional spatial thinning and quality control of some observation types are also applied in GEPS to reduce the number of observations assimilated by the LETKF. The MIDAS functionality for post-processing ensembles (i.e. recentring, additive inflation, application of limits on humidity) is used in both global and regional ensemble prediction systems.

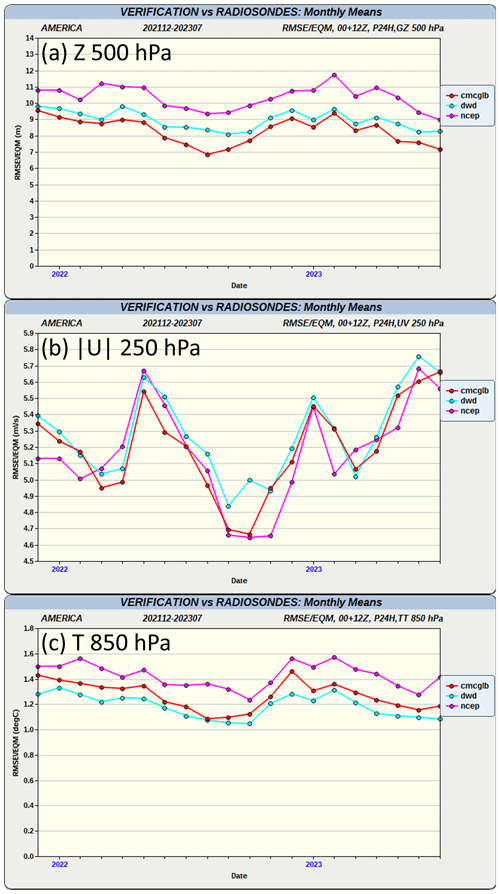
Figure 6 The RMSE of 24 h forecasts from the GDPS (in red) together with the same results from the German Weather Service (in light blue) and the US National Centers for Environmental Prediction (in pink) computed with respect to the North American network of radiosonde observations for (a) geopotential height at 500 hPa, (b) wind speed at 250 hPa, and (c) temperature at 850 hPa. (Note a similar result, but only for 500 hPa geopotential height, is available on the following public website: https://weather.gc.ca/verification/monthly_ts_e.html, last access: 18 December 2024).

A comparison of short-term forecast scores is shown to demonstrate that the quality of the analyses produced using MIDAS programs in the GDPS is comparable to analyses produced by other NWP centres that use a similar DA approach. Figure 6 shows similar values for the GDPS, the German Weather Service (DWD), and the US National Centers for Environmental Prediction (NCEP) of the monthly root-mean-square (rms) difference between 24 h forecasts and radiosonde observations of 500 hPa geopotential height, 250 hPa wind speed, and 850 hPa temperature over North America from December 2021 to July 2023.

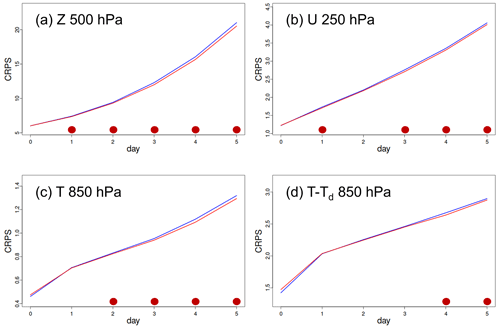
Figure 7 The continuous ranked probability score (CRPS) of 5 d ensemble forecasts from the previous EnKF system (in blue) and the new MIDAS-based LETKF system (in red) computed with respect to the global network of radiosonde observations for (a) geopotential height at 500 hPa, (b) zonal wind at 250 hPa, (c) temperature at 850 hPa, and (d) dew-point depression at 850 hPa over the period 1–25 January 2017. The filled circles along the horizontal axis indicate lead times when the difference in the score is considered statistically significant, with the colour of the circle indicating the experiment with the better score. Note that these results use an earlier configuration of the LETKF and EnKF at lower spatial resolution and without ensemble recentring.

Figure 7 shows results from GEPS experiments performed in January 2017 to compare the original MIDAS implementation of the LETKF (in red) with the previously operational ensemble DA system based on the stochastic formulation of the EnKF (in blue). The ensemble forecast quality as evaluated with the continuous ranked probability score (CRPS) with respect to the global radiosonde observations shows a small, but statistically significant, improvement (i.e. smaller CRPS values) when using the new MIDAS-based ensemble DA system. More details regarding the change in DA algorithm are provided by ECCC (2021).

6.2 Observation impact

The system for estimating the impact of all observations assimilated in the global deterministic system on 24 h forecasts, known as the global deterministic forecast sensitivity to observation impact (GDFSOI) system, has been run operationally since October 2022. It uses extended 256-member ensemble forecasts and the hybrid FSOI approach implemented in MIDAS as described by Buehner et al. (2018). Currently, the system runs every 18 h with the 24 h forecast error measured using the moist energy norm including all vertical levels between the surface and 100 hPa over the entire global domain and also over only Canada. To capture the impact of observations on stratospheric forecasts, the impact is additionally computed over the global domain for the vertical levels between 100 and 1 hPa. A separate system has recently been implemented to routinely produce a series of images that show the impact of the assimilated observations over monthly, seasonal, and annual averages. These images are published on the ECCC monitoring website, which is accessible to both internal and external users (https://hpfx.collab.science.gc.ca/~smco500/psmon/FSOI_monitoring/, last access: 18 December 2024). Figure 8 provides an example of the average observation impact on forecasts over the global and Canada domains from the surface to 100 hPa and for the global domain in the stratosphere separated by observation type and computed over a 3-month period.

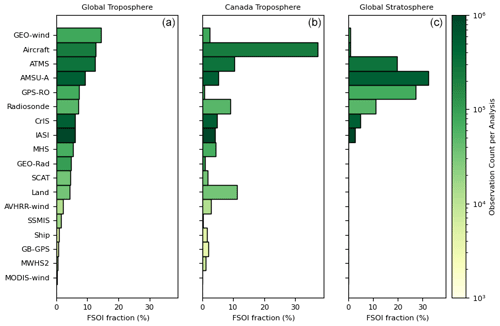
Figure 8 The average fractional observation impact on 24 h forecasts (a) over the global domain and (b) over only Canada between the surface and 100 hPa and (c) for the global domain between 100 and 1 hPa separated by observation type. The colour of each bar indicates the average number of assimilated observations per analysis. The observation types are ordered according to the magnitude of their impact on global tropospheric forecasts.

6.3 Stratospheric ozone assimilation

Currently, atmospheric constituent assimilation is conducted only for ozone as part of 4D-EnVar in the operational GDPS. Ozone assimilation was introduced to initialize ozone forecasts for the purpose of UV (ultraviolet) index forecasting and coupled radiative feedback between prognostic ozone and temperature in addition to ozone layer monitoring. Instead of ensemble background-error covariances, only univariate ozone covariances are used, resulting in ozone assimilation that is statistically independent of the NWP fields. The ozone field estimated through DA is also not used as input for the assimilation of NWP radiance observations, and instead climatological ozone is still employed. The ozone background-error correlations are obtained by fitting a third-order autoregression function to estimates initially derived from 6 h time-lag forecast differences (e.g. Bannister, 2008). The background-error variances were obtained from applying the Desroziers et al. (2005) approach with assimilation of Microwave Limb Sounder (MLS) ozone profiles followed by globally uniform scaling.

The assimilated ozone observations consist of profiles and integrated total and partial columns from a total of six satellite instruments (for more detail, see de Grandpré et al., 2024). While the assimilation and quality control of ozone observations currently utilize MIDAS programs, observation thinning and bias correction have not yet been implemented in MIDAS. Figure 9 shows example statistics of the ozone analysis and short-term forecasts relative to the MLS ozone profiles and the relative sizes of the specified forecast and observation-error SD values used for assimilation in the GDPS (all quantities are shown as percentages after normalizing by the mean MLS-observed ozone volumetric mixing ratio for each pressure level).

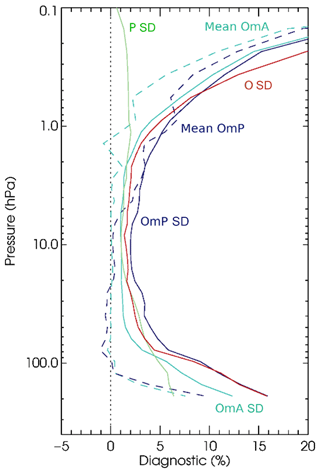
Figure 9 The global normalized mean (dashed) and SD (solid) of MLS observation minus analysis (OmA, light blue) and observation minus short-term forecast (OmP, dark blue) differences and corresponding average observation-error SD (O, red) and background-error SD (P, green) used for assimilation. Results are for the June–August 2022 period.

6.4 Sea ice

Several MIDAS programs are used for both global and regional configurations of the operational sea ice concentration analysis systems. These were recently implemented by migrating all necessary sea-ice-specific functionality from the previously used independent Fortran software into MIDAS, and tests were developed for the new functionality. The assimilation is performed with a 2D-Var approach using a diffusion operator for modelling the horizontal background-error correlations. It also uses footprint horizontal interpolation as part of the observation operator when assimilating observations that have a footprint much larger than the grid spacing of the analysis (5 and 10 km for regional and global configurations, respectively). In addition to estimating ice concentration, a measure of the associated uncertainty is produced by estimating the analysis-error SD. Observation quality control includes a procedure that rejects sea ice observations when the rms difference between the observations and the background values averaged over a swath of data exceeds a specified threshold. More details about the sea ice analysis system are given by Caya et al. (2010) and Buehner et al. (2012, 2016). The use of MPI parallelization in MIDAS greatly accelerates the computationally intensive analysis-error calculation as compared with the original software that only used OpenMP for parallelization. Overall, the use of MIDAS programs for sea ice DA did not result in any statistically significant changes to the sea ice analyses as compared with the previously operational system. However, the use of MIDAS will ease future software maintenance and facilitate research on strongly coupled DA that includes sea ice.

6.5 Sea surface temperature

As part of efforts towards developing a future atmosphere–ocean-coupled DA system (Skachko et al., 2019), a global daily SST analysis system was recently implemented using MIDAS programs. The new system will replace the current operational system that is based on legacy Fortran software and multiple separate programs and scripts employing out-of-date programming styles, making it more difficult to maintain. Like the sea ice system, the new MIDAS-based SST analysis system employs the 2D-Var DA method with background-error correlations modelled with a diffusion operator. The assimilated observations include those from moored buoys, ships, and drifters, as well as satellite measurements from infrared and microwave instruments. An estimate of analysis-error SD is also computed to provide a measure of uncertainty. The observation bias correction, quality control, and spatial thinning are all performed using MIDAS programs. The large-scale and slowly evolving bias estimates are computed separately for each satellite instrument for both day and night with respect to in situ data that are considered unbiased.

The new MIDAS-based system was initially implemented as an “experimental” system with plans to replace the current operational SST analysis system in the near future. More details about the new SST analysis system, including comparisons with the current operational system, are provided by Skachko et al. (2024).

6.6 Hourly near-surface atmospheric analysis

An hourly near-surface mesoscale analysis-only system defined on the HRDPS domain (2.5 km grid spacing) has recently been implemented at ECCC using several MIDAS programs. This system is similar to the National Centers for Environmental Prediction (NCEP) Real-Time Mesoscale Analysis (de Pondeca et al., 2011). The system relies on the 2D-Var DA approach using a background-error covariance matrix defined on a horizontal grid with 10 km grid spacing and derived using an ensemble of lagged-forecast differences (the so-called NMC method; Parrish and Derber, 1992). It combines the most recent available forecast from the HRDPS valid at the analysis time (with forecast lead times between 3 and 8 h) with all surface observations (that are available 15 min after the analysis time) to create gridded fields of temperature and humidity at 1.5 m above ground level (a.g.l.), horizontal wind components and wind gusts at 10 m a.g.l., near-surface visibility, and surface pressure.

A unique feature of this system is that the observation-error SD for each observed variable was tuned to minimize the analysis departure from observations withheld from the analysis step as proposed by Ménard and Deshaies-Jacques (2018). The MIDAS program oMinusF was used to compute observation minus analysis using 10-fold cross-validation, where a Hilbert curve was applied to select 10 % of the observations to be withheld from the assimilation. The remaining 90 % of the observations were assimilated, and the resulting analysis was compared with the withheld observations to compute an error statistic; the approach was repeated 10 times for different subsets of withheld observations. As an example, Fig. 10 shows how this method led to the adoption of a value of 2.1 m s⁻¹ for the observation-error SD for wind gust observations since this is the value that results in the best fit of the resulting analysis to the withheld observations.

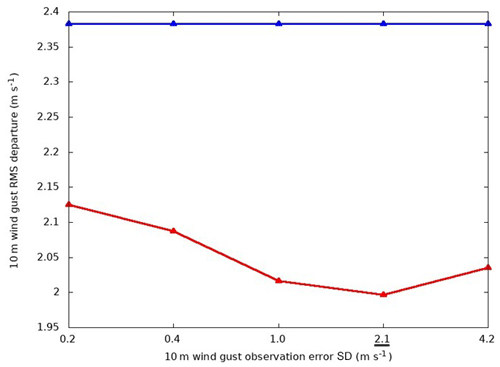
Figure 10 The red line shows the wind gust (10 m a.g.l.) rms departure of the analysis from the withheld observations for different values of the specified observation-error SD when using 10-fold cross-validation over a 2-month period during the winter of 2020. The blue line shows the SD of the observation departure from the HRDPS background state as measured using all of the wind gust observations.

6.7 Statistical forecast post-processing: UMOS–MIDAS

To reduce systematic bias and random error in raw numerical weather forecasts, the Updateable Model Output Statistics (UMOS) approach uses surface station observations together with a multiple linear regression technique to correct the forecasts at different forecast lead times for specific sites over Canada (see Wilson and Vallée, 2003). To enable the generation of post-processed fields on a grid, the post-processed forecasts at observation locations are transformed into pseudo-observations and assimilated with the 2D-Var approach implemented in MIDAS, similarly to in the previously described near-surface analysis system. So far, the approach has been applied only to temperature at 1.5 m a.g.l. The observation-error SD values assigned to the post-processed temperature forecasts were determined by finding those that minimize the departure from the resulting post-processed gridded data to observations not currently considered in the UMOS procedure. The approach is used operationally to correct the near-surface temperatures for various lead times of the GDPS and HRDPS forecasts over Canada (ECCC, 2023).

7 Summary and future plans

MIDAS is Fortran software developed at ECCC for a diverse range of both operational and research DA applications. It is currently used for most major tasks within the operational NWP systems as well as for producing sea ice, SST, and hourly near-surface atmospheric analyses and for estimating the impact of observations on short-term forecasts. Its modular software design is continually being improved, as needed, to facilitate applications to even more components of the Earth system. The use of MIDAS for many such systems will be essential to enable research on strongly coupled DA approaches that explicitly take into account the coupled connections between multiple Earth system components, especially between the atmosphere, ocean, sea ice, and land surface.

Some ongoing research and development projects involving MIDAS include testing of an LETKF configuration for high-resolution limited-area ensemble NWP, testing of grid-space vertical localization for global ensemble NWP, and application of the LETKF for initializing both deterministic and ensemble 3D ocean and sea ice model forecasts. Work also continues on the improvement of the processing and assimilation of various types of observations (including cloud-affected and surface-sensitive satellite radiances) and the addition of new observation types (such as from new satellite instruments).

The flexibility and range of applications made possible with MIDAS could constitute a powerful tool in an academic context to facilitate DA research at Canadian universities. Therefore, preliminary efforts have begun to explore the feasibility of making MIDAS accessible to collaborators external to ECCC.

Finally, given the recent rapid developments related to NWP applications of artificial intelligence and machine learning methods, it seems inevitable that work should begin on examining how such approaches can be used in combination with MIDAS. Such developments are also increasingly leading to the incorporation of graphical processing units (GPUs) in supercomputers, and therefore work will begin on enabling the MIDAS software to run efficiently on GPUs.