Simulation of snow albedo and solar irradiance profile with the Two-streAm Radiative TransfEr in Snow (TARTES) v2.0 model

The Two-streAm Radiative TransfEr in Snow (TARTES) model computes the spectral albedo and the profiles of spectral absorption, irradiance, and actinic fluxes for a multi-layer plane-parallel snowpack. Each snow layer is characterized by its specific surface area, density, and impurity content, in addition to shape parameters. In the landscape of snow optical numerical models, TARTES distinguishes itself by taking into account different shapes of the particles through two shape parameters, namely the absorption enhancement parameter B and the asymmetry factor g. This is of primary importance as recent studies working at the microstructure level have demonstrated that snow does not behave as a collection of equivalent ice spheres, a representation widely used in other models. Instead, B and g take specific values that do not correspond to any simple geometrical shape, which leads to the concept of the “optical shape of snow”. Apart from this specificity, TARTES combines well-established radiative transfer principles to compute the scattering and absorption coefficients of pure or polluted snow, as well as the δ-Eddington two-stream approximation to solve the multi-layer radiative transfer equation. The model is implemented in Python, but conducting TARTES simulations is also possible without any programming through the SnowTARTES web application, making it very accessible to non-experts and for teaching purposes. Here, after describing the theoretical and technical details of the model, we illustrate its main capabilities and present some comparisons with other common snow radiative transfer models (AART, DISORT-Mie, SNICAR-ADv3) as a validation procedure. Overall the agreement on the spectral albedo, when in compatible conditions (i.e., with spheres), is usually within 0.02 and is better in the visible and near-infrared range compared to longer wavelengths.

1 Introduction

Snow, a porous medium made of ice and air, is by far the most reflective material in the solar spectral range on Earth. Any fluctuation in the snow cover extent or changes in the surface snow properties have consequences for the global radiative budget and the climate (Qu and Hall, 2007; Räisänen et al., 2017). Snow albedo (also known as hemispherical reflectance, Schaepman-Strub et al., 2006) is the primary variable controlling the amount of solar energy absorbed in the snowpack (Flanner et al., 2011). Also of importance is the depth at which this absorption occurs. The deeper solar radiation is absorbed, the less likely the corresponding heat is to be transferred back to the surface by thermal conduction, where it can eventually be evacuated to the atmosphere through longwave emission or turbulent mixing. Hence, the warming and potential melt of the snowpack depend on the vertical profile of absorbed sunlight (Dombrovsky et al., 2019). This profile is often approximated by an exponential function decreasing with depth, with the decay length called the e-folding depth or penetration depth (Kokhanovsky, 2022). This quantity is also of great importance for photochemical processes (King and Simpson, 2001; Domine et al., 2008).

Snow optical properties are driven by the physical properties of the snow and the impurities it contains, along with the illumination conditions. The snow microstructure (i.e., the arrangement of ice and air at the micrometer scale) controls the absorption of radiation in the near-infrared range (Wiscombe and Warren, 1980) and is key to understanding some of the snow–albedo feedback loops that amplify climate change in snow-covered regions (Hall, 2004; Qu and Hall, 2007; Picard et al., 2012; Box et al., 2022). It is common to represent snow microstructure as a collection of grains with prescribed shape and size (Warren and Wiscombe, 1980; Grenfell and Warren, 1999). However, it is known that snow on the ground is generally not granular, so equivalent concepts have emerged to quantify more general microstructures. For instance, the specific surface area (SSA) (the ratio between the total air-interface surface area and the mass of ice, Domine et al., 2006) advantageously replaces the grain size as it can be rigorously defined and calculated for any porous medium made of two phases (ice and air here) even when distinct grains are not apparent. Regarding the shape, the situation is less advanced, but geometrical metrics related to the chord length distribution can provide useful information (Malinka, 2014; Krol and Löwe, 2016; Dumont et al., 2021; Robledano et al., 2023).

The thickness of the snow cover is another major driving variable in the case of shallow covers and a dark underlying ground, especially in the visible range, where light penetrates deepest (Perovich, 2007). Another important variable is the roughness of the surface, which tends to decrease the albedo (Warren et al., 1998; Leroux and Fily, 1998; Larue et al., 2020). The presence of liquid water also slightly changes the absorption coefficient in a few spectral bands (e.g., 980–1000 nm), which can be detected in spectral albedo measurements (Dumont et al., 2017; Donahue et al., 2022). More importantly it induces fast structural changes of the microstructure (Colbeck, 1982; Brun et al., 1989), usually leading to a rapid decrease in SSA and thus in albedo. Impurities, whether they are of mineral, organic, or biological origin, can also greatly affect the absorption in the visible range and drive both the albedo and the penetration (Chevrollier et al., 2022; Réveillet et al., 2022; Di Mauro et al., 2024). At last, the illumination characteristics (angular and spectral distributions) also play a role because the snow reflectance depends on the wavelength and the incidence angle. As such, neither broadband nor spectral snow albedo is strict surface snow properties, because of this dependency on the illumination characteristics. It means than even without any change in the snow properties, the surface albedo may change with changing environmental conditions (presence of clouds, sun elevation, etc.).

To account for these multiple factors, numerous snow optical models have been developed (e.g., He and Flanner, 2020). Even though most rely on the radiative transfer (RT) principles, they greatly differ in the method used to solve the RT equation (RTE, e.g., Chandrasekhar, 1960), in the representation of the medium (snow microstructure, the 1D or 3D geometry of the snowpack, surface roughness, heterogeneity of the snowpack, impurities, etc.), in the fundamental constants used (e.g., real and imaginary parts of the ice refractive index), and in the output optical quantities (e.g., albedo, absorption profile, actinic flux, transmittance). Each model has its niche of applications, from efficient but approximate code suitable to large-scale climate models to very precise solvers to investigate detailed optical behaviors (e.g., bidirectional reflectance distribution function, BRDF). To cite a few, pioneering works used phenomenological (Dunkle and Bevans, 1956; Bohren, 1987) or more rigorous (Wiscombe and Warren, 1980; Warren and Wiscombe, 1980) two-stream approximations to solve the RTE and Mie theory (Mie, 1908) or geometrical optics (Bohren and Barkstrom, 1974) to represent spherical ice particles suspended in the air. DISORT (Stamnes et al., 1988a, b) is a general robust and popular solver frequently applied to snow, usually in combination with the Mie theory, hence assuming spherical grains (Glendinning and Morris, 1999; Green et al., 2002; Gallet et al., 2011; Carmagnola et al., 2013; Dang et al., 2019). Here, we refer to this combination as “DISORT-Mie”. An advantage of DISORT is its ability to account for the radiation propagation in many directions (multi-stream). To account for other particle shapes and calculate the BRDF, an efficient code was proposed by Mishchenko et al. (1999) (available as a Python package here: https://github.com/ghislainp/mishchenko_brf, last access: 24 March 2024), but it cannot handle layering. TUV-snow is a DISORT-based coupled snow–atmosphere model specifically designed for UV radiation and photochemistry applications (Lee-Taylor and Madronich, 2002; France et al., 2011). PBSAM (Aoki et al., 2011) and SNICAR (Flanner and Zender, 2005) are fast two-stream solvers suitable for surface albedo calculation in climate simulations (Onuma et al., 2020; Usha et al., 2020). SNICAR is currently one of the most actively developed codes with a large panel of state-of-the-art parameterizations, for instance to account for snow algae (Cook et al., 2017) or to account for ice layers with the recent replacement of the two-stream solver by the adding–doubling solver (Flanner et al., 2021). Importantly, all these models are unidimensional, meaning that they describe the snowpack as a stack of homogeneous, horizontally infinite, and flat layers. This configuration is known as plane parallel. Conversely, three-dimensional RT models are necessary to account for snowpack with 3D structures, embedded objects, or light sources. Some examples are models for rough surfaces (Warren et al., 1998; Larue et al., 2020; Robledano et al., 2022), for explicit photon trajectory calculations in the snow microstructure (Kaempfer et al., 2005; Picard et al., 2009; Xiong and Shi, 2014; Letcher et al., 2022; Robledano et al., 2023), and for interactions with embedded objects or instruments (Gallet et al., 2009; Picard et al., 2016).

In this rich landscape, the Two-streAm Radiative TransfEr in Snow (TARTES) spectral model differs by two main aspects. First it relies on a simple yet state-of-the-art representation of the snow microstructure, allowing us to represent it with four parameters only: the SSA, the density, the asymmetry factor g that quantifies the forward scattering of snow, and the absorption enhancement parameter B that quantifies the lengthening of photon paths inside the ice phase due to multiple internal reflections. As a consequence, TARTES is not restricted to spherical particles, and any pair of g and B values can be used, possibly not corresponding to any particular idealized geometrical shape. It also offers the possibility of conforming with the asymptotic approximation radiative transfer (AART, Kokhanovsky and Zege, 2004) when the snowpack is semi-infinite, while still being able to simulate a multi-layered snowpack. The second main difference from other models is the use of the Python language. This facilitates rapid tests (e.g., in notebooks) and implementation of new features (e.g., impurities, Tuzet et al., 2019). While TARTES has been used over a decade (e.g., Libois et al., 2013; Shao et al., 2018; van Dalum et al., 2019; Tuzet et al., 2020; Manninen et al., 2021; Veillon et al., 2021), this paper aims at a first comprehensive and formal description of the model. Some minor but significant adjustments using the latest results on microstructure (Robledano et al., 2023) are also included, as well as a brief presentation of the ecosystem of tools relevant to snow optical computations built around TARTES.

Section 2 provides the detailed derivation of the model; Sect. 3 presents the TARTES software and the associated ecosystem; and Sect. 4 presents the results including self-consistency checks, a comparison with other models, and a presentation of its specific capabilities. Section 5 discusses how TARTES fits with the concept of the “optical shape of snow” and presents the model limitations. Section 6 concludes this study.

2 The physics behind TARTES

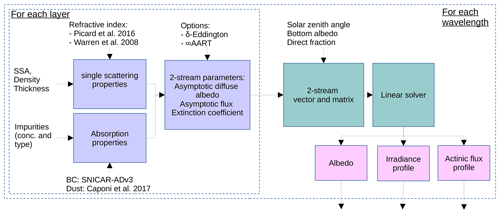
TARTES relies on the δ-Eddington approximation to solve the plane-parallel RTE and compute the spectral upwelling and downwelling fluxes within a multi-layered snowpack. To this end the single-scattering properties of each layer are computed from the SSA, density, snow grain shape, and amount of light-absorbing impurities (Fig. 1). This section provides all the theoretical details on which TARTES is built, as well as new formulations added in version 2.0.

Figure 1 Main inputs, options, and flow of computations in TARTES v2.0.

2.1 The plane-parallel radiative transfer equation

The steady-state unpolarized RTE describes the intensity (or radiance) field I propagating in an absorbing and scattering slab at depth z in a direction (θ,ϕ), where ϕ is the azimuth angle, θ is the zenith angle defined as the angle between the inward normal to the surface and the direction of light propagation, and z is defined positive from the surface downward. Such a medium is characterized by its extinction coefficient σ_e (m⁻¹), scattering coefficient σ_s (m⁻¹), and scattering phase function $p(\mathit{\theta },\mathit{\varphi },{\mathit{\theta }}^{\prime },{\mathit{\varphi }}^{\prime })$ (unitless). The absorption coefficient is obtained by energy conservation as ${\mathit{\sigma }}_{\mathrm{a}}={\mathit{\sigma }}_{\mathrm{e}}-{\mathit{\sigma }}_{\mathrm{s}}$. The phase function describes the probability for light to be scattered into the direction (θ,ϕ) when coming from the direction $({\mathit{\theta }}^{\prime },{\mathit{\varphi }}^{\prime })$. Here we consider a horizontal multi-layered snowpack. Each layer of the snowpack is assumed to be isotropic and to have homogeneous optical properties. The snowpack is illuminated at the surface by solar radiation that can be a combination of diffuse (i.e., isotropic) and direct light incident at zenith angle θ₀ and azimuth angle ϕ₀. There are no internal light sources in the snowpack, and no thermal emission is considered since TARTES focuses on the shortwave range (200–4000 nm). Along the direction s defined by (θ,ϕ), I decreases due to extinction (absorption and scattering) and increases due to scattering from all other directions $({\mathit{\theta }}^{\prime },{\mathit{\varphi }}^{\prime })$, so the RTE reads

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}I(z,\mathit{\theta },\mathit{\varphi })}{\mathrm{d}s}}& =-{\mathit{\sigma }}_{\mathrm{e}}I(z,\mathit{\theta },\mathit{\varphi })+{\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{s}}}{\mathrm{4}\mathit{\pi }}}\underset{\mathrm{0}}{\overset{\mathit{\pi }}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}p(\mathit{\theta },\mathit{\varphi },{\mathit{\theta }}^{\prime },{\mathit{\varphi }}^{\prime })\\ & \times I(z,{\mathit{\theta }}^{\prime },{\mathit{\varphi }}^{\prime })\mathrm{d}{\mathit{\varphi }}^{\prime }\sin {\mathit{\theta }}^{\prime }\mathrm{d}{\mathit{\theta }}^{\prime },\end{array}\end{array}$$

where the phase function is normalized so that $\frac{\mathrm{1}}{\mathrm{4}\mathit{\pi }}\underset{\mathrm{0}}{\overset{\mathit{\pi }}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}p(\mathit{\theta },\mathit{\varphi },{\mathit{\theta }}^{\prime },{\mathit{\varphi }}^{\prime })\mathrm{d}{\mathit{\varphi }}^{\prime }\sin {\mathit{\theta }}^{\prime }\mathrm{d}{\mathit{\theta }}^{\prime }=\mathrm{1}$. Defining μ=cos θ and ${\mathit{\mu }}^{\prime }=\cos {\mathit{\theta }}^{\prime }$, noting that dz=μds, and further defining the optical thickness such that dτ=σ_edz, Eq. (1) becomes

$$\begin{array}{}\text{(2)}& \begin{array}{rl}\mathit{\mu }{\displaystyle \frac{\mathrm{d}I(\mathit{\tau },\mathit{\mu },\mathit{\varphi })}{\mathrm{d}\mathit{\tau }}}& =-I(\mathit{\tau },\mathit{\mu },\mathit{\varphi })+{\displaystyle \frac{\mathit{\omega }}{\mathrm{4}\mathit{\pi }}}\underset{-\mathrm{1}}{\overset{\mathrm{1}}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}p(\mathit{\mu },\mathit{\varphi },{\mathit{\mu }}^{\prime },{\mathit{\varphi }}^{\prime })\\ & \times I(\mathit{\tau },{\mathit{\mu }}^{\prime },{\mathit{\varphi }}^{\prime })\mathrm{d}{\mathit{\varphi }}^{\prime }\mathrm{d}{\mathit{\mu }}^{\prime },\end{array}\end{array}$$

where the single-scattering albedo $\mathit{\omega }={\mathit{\sigma }}_{\mathrm{s}}/{\mathit{\sigma }}_{\mathrm{e}}$. Since TARTES focuses on radiative fluxes through horizontal surfaces, Eq. (2) can be azimuthally integrated, which reads

$$\begin{array}{}\text{(3)}& \mathit{\mu }{\displaystyle \frac{\mathrm{d}I(\mathit{\tau },\mathit{\mu })}{\mathrm{d}\mathit{\tau }}}=-I(\mathit{\tau },\mathit{\mu })+{\displaystyle \frac{\mathit{\omega }}{\mathrm{2}}}\underset{-\mathrm{1}}{\overset{\mathrm{1}}{\int }}p(\mathit{\mu },{\mathit{\mu }}^{\prime })I(\mathit{\tau },{\mathit{\mu }}^{\prime })\mathrm{d}{\mathit{\mu }}^{\prime },\end{array}$$

where we have defined the azimuthally averaged intensity $I(\mathit{\tau },\mathit{\mu })=\frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }}\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}I(\mathit{\tau },\mathit{\mu },\mathit{\varphi })\mathrm{d}\mathit{\varphi }$ and the azimuth-independent phase function $p(\mathit{\mu },{\mathit{\mu }}^{\prime })=\frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }}\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}p(\mathit{\mu },\mathit{\varphi },{\mathit{\mu }}^{\prime },{\mathit{\varphi }}^{\prime })\mathrm{d}\mathit{\varphi }$.

When the snowpack is at least partly illuminated by a beam source (e.g., direct solar radiation), it is useful to write $I(\mathit{\tau },\mathit{\mu })=I_{\mathrm{dir}}(\mathit{\tau },\mathit{\mu })+I_{\mathrm{diff}}(\mathit{\tau },\mathit{\mu })$, where the direct intensity I_dir corresponds to light that has not been scattered and I_diff is the diffuse intensity. At the surface the direct intensity is $F_{\mathrm{0}}\mathit{\delta }(\mathit{\mu }-{\mathit{\mu }}_{\mathrm{0}})\mathit{\delta }(\mathit{\varphi }-{\mathit{\varphi }}_{\mathrm{0}})$, where μ₀=cos θ₀, and at depth

$$\begin{array}{}\text{(4)}& I_{\mathrm{dir}}(\mathit{\tau },\mathit{\mu })={\displaystyle \frac{F_{\mathrm{0}}}{\mathrm{2}\mathit{\pi }}}\mathit{\delta }(\mathit{\mu }-{\mathit{\mu }}_{\mathrm{0}})e^{-\mathit{\tau }/{\mathit{\mu }}_{\mathrm{0}}},\end{array}$$

where F₀ is the intensity of the solar beam at the surface and δ the Dirac function.

Reporting Eq. (4) in Eq. (3), we obtain the RTE for the diffuse intensity:

$$\begin{array}{}\text{(5)}& \begin{array}{rl}\mathit{\mu }{\displaystyle \frac{\mathrm{d}{I}_{\mathrm{diff}}(\mathit{\tau },\mathit{\mu })}{\mathrm{d}\mathit{\tau }}}& =-I_{\mathrm{diff}}(\mathit{\tau },\mathit{\mu })+{\displaystyle \frac{\mathit{\omega }}{\mathrm{2}}}\underset{-\mathrm{1}}{\overset{\mathrm{1}}{\int }}p(\mathit{\mu },{\mathit{\mu }}^{\prime })I_{\mathrm{diff}}(\mathit{\tau },{\mathit{\mu }}^{\prime })\mathrm{d}{\mathit{\mu }}^{\prime }\\ & +{\displaystyle \frac{\mathit{\omega }}{\mathrm{4}\mathit{\pi }}}p(\mathit{\mu },{\mathit{\mu }}_{\mathrm{0}})F_{\mathrm{0}}{e}^{-\mathit{\tau }/{\mathit{\mu }}_{\mathrm{0}}}.\end{array}\end{array}$$

From now on I_diff will simply be referred to as I.

2.2 The δ-Eddington approximation of the phase function

Within each layer, snow is assumed to be isotropic, so the phase function depends only on the scattering angle Θ between the incident and scattered light, and we can write $p(\mathit{\mu },\mathit{\varphi },{\mathit{\mu }}^{\prime },{\mathit{\varphi }}^{\prime })=p\left(\cos \mathrm{\Theta }\right)$. This angle is such that

$$\begin{array}{}\text{(6)}& \cos \mathrm{\Theta }=\mathit{\mu }{\mathit{\mu }}^{\prime }+\sqrt{(\mathrm{1}-{\mathit{\mu }}^{\mathrm{2}})(\mathrm{1}-{{\mathit{\mu }}^{\prime }}^{\mathrm{2}})}\cos (\mathit{\varphi }-{\mathit{\varphi }}^{\prime }).\end{array}$$

p(cos Θ) can be expanded in Legendre polynomials P_l:

$$\begin{array}{}\text{(7)}& \begin{array}{rl}p\left(\cos \mathrm{\Theta }\right)& =\sum _{l=\mathrm{0}}^{\mathrm{\infty }}{\mathit{\omega }}_{\mathrm{l}}{P}_{\mathrm{l}}\left(\cos \mathrm{\Theta }\right),\\ & \mathrm{where}{\mathit{\omega }}_{\mathrm{l}}={\displaystyle \frac{\mathrm{2}l+\mathrm{1}}{\mathrm{2}}}\underset{-\mathrm{1}}{\overset{\mathrm{1}}{\int }}p\left(\cos \mathrm{\Theta }\right)P_{\mathrm{l}}\left(\cos \mathrm{\Theta }\right)\mathrm{d}\cos \mathrm{\Theta }.\end{array}\end{array}$$

By virtue of normalization ω₀=1, and the mean cosine of the scattering angle of the phase function, called the asymmetry factor g, is such that ω₁=3g. Using the addition theorem of spherical harmonics (Chandrasekhar, 1960), it can finally be shown that

$$\begin{array}{}\text{(8)}& p(\mathit{\mu },{\mathit{\mu }}^{\prime })=\sum _{l=\mathrm{0}}^{\mathrm{\infty }}{\mathit{\omega }}_{\mathrm{l}}{P}_{\mathrm{l}}\left(\mathit{\mu }\right)P_{\mathrm{l}}\left({\mathit{\mu }}^{\prime }\right).\end{array}$$

Hence, the two-term truncation of the phase function reads

$$\begin{array}{}\text{(9)}& p(\mathit{\mu },{\mathit{\mu }}^{\prime })=\mathrm{1}+\mathrm{3}g\mathit{\mu }{\mathit{\mu }}^{\prime }.\end{array}$$

To handle the strong forward scattering of snow particles, TARTES relies on the δ-Eddington approximation, which consists in writing the phase function as the sum of a strictly forward scattering component (a Dirac) and a two-term phase function (Eq. 9). Joseph et al. (1976) proposed weighting both contributions so that the asymmetry factor is conserved and the second moment of the phase function equals g² (i.e., the second moment of the Henyey–Greenstein phase function Henyey and Greenstein, 1941, with asymmetry factor g). This reads

$$\begin{array}{}\text{(10)}& p(\mathit{\mu },{\mathit{\mu }}^{\prime })=\mathrm{2}{g}^{\mathrm{2}}\mathit{\delta }(\mathit{\mu }-{\mathit{\mu }}^{\prime })+(\mathrm{1}-g^{\mathrm{2}})(\mathrm{1}+\mathrm{3}{g}^{*}\mathit{\mu }{\mathit{\mu }}^{\prime }),\end{array}$$

with $g^{*}=\frac{g}{\mathrm{1}+g}$.

Combining Eqs. (5) and (10) we obtain

$$\begin{array}{}\text{(11)}& \begin{array}{rl}\mathit{\mu }{\displaystyle \frac{\mathrm{d}I({\mathit{\tau }}^{*},\mathit{\mu })}{\mathrm{d}\mathit{\tau }}}& =-I({\mathit{\tau }}^{*},\mathit{\mu })+{\displaystyle \frac{{\mathit{\omega }}^{*}}{\mathrm{2}}}\underset{-\mathrm{1}}{\overset{\mathrm{1}}{\int }}(\mathrm{1}+\mathrm{3}{g}^{*}\mathit{\mu }{\mathit{\mu }}^{\prime })I({\mathit{\tau }}^{*},{\mathit{\mu }}^{\prime })\mathrm{d}{\mathit{\mu }}^{\prime }\\ & +{\displaystyle \frac{{\mathit{\omega }}^{*}}{\mathrm{4}\mathit{\pi }}}(\mathrm{1}+\mathrm{3}{g}^{*}\mathit{\mu }{\mathit{\mu }}_{\mathrm{0}})F_{\mathrm{0}}{e}^{-{\mathit{\tau }}^{*}/{\mathit{\mu }}_{\mathrm{0}}},\end{array}\end{array}$$

where the following variable changes have been made:

$$\begin{array}{}\text{(12)}& {\displaystyle }{\mathit{\tau }}^{*}& {\displaystyle }=\mathit{\tau }(\mathrm{1}-\mathit{\omega }{g}^{\mathrm{2}}),\text{(13)}& {\displaystyle }{\mathit{\omega }}^{*}& {\displaystyle }={\displaystyle \frac{(\mathrm{1}-g^{\mathrm{2}})\mathit{\omega }}{(\mathrm{1}-\mathit{\omega }{g}^{\mathrm{2}})}}.\end{array}$$

Hence, the δ-Eddington approximation of the phase function consists in solving Eq. (5), with τ, ω, and g replaced by τ^*, ω^*, and g^*. g^* is less than g, so the scaled phase function is less forward peaking than the original phase function, which reduces the errors in the following two-stream resolution of the RTE. Note that in this approximation the solution for direct radiation is scaled accordingly, meaning that direct radiation can propagate deeper in the snowpack, because light scattered in the forward direction is treated as unscattered light.

2.3 Equations for fluxes and Eddington approximation

In TARTES, we are interested in the vertical downward and upward fluxes in the snowpack, F⁻ and F⁺ respectively. These quantities are defined as

$$\begin{array}{}\text{(14)}& {\displaystyle }{F}^{-}\left({\mathit{\tau }}^{*}\right)& {\displaystyle }=\mathrm{2}\mathit{\pi }\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}I({\mathit{\tau }}^{*},\mathit{\mu })\mathit{\mu }\mathrm{d}\mathit{\mu },\text{(15)}& {\displaystyle }{F}^{+}\left({\mathit{\tau }}^{*}\right)& {\displaystyle }=\mathrm{2}\mathit{\pi }\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}I({\mathit{\tau }}^{*},-\mathit{\mu })\mathit{\mu }\mathrm{d}\mathit{\mu }.\end{array}$$

Integrating Eq. (11) over both positive and negative values of μ results in two differential equations:

$$\begin{array}{}\text{(16)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}{F}^{-}\left({\mathit{\tau }}^{*}\right)}{\mathrm{d}{\mathit{\tau }}^{*}}}& =-\mathrm{2}\mathit{\pi }\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}I({\mathit{\tau }}^{*},\mathit{\mu })\mathrm{d}\mathit{\mu }\\ & +\mathit{\pi }{\mathit{\omega }}^{*}\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}\underset{-\mathrm{1}}{\overset{\mathrm{1}}{\int }}(\mathrm{1}+\mathrm{3}{g}^{*}\mathit{\mu }{\mathit{\mu }}^{\prime })I({\mathit{\tau }}^{*},{\mathit{\mu }}^{\prime })\mathrm{d}{\mathit{\mu }}^{\prime }\mathrm{d}\mathit{\mu }\\ & +{\mathit{\omega }}^{*}{\mathit{\gamma }}_{\mathrm{4}}{F}_{\mathrm{0}}{e}^{-{\mathit{\tau }}^{*}/{\mathit{\mu }}_{\mathrm{0}}},\end{array}\text{(17)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}{F}^{+}\left({\mathit{\tau }}^{*}\right)}{\mathrm{d}{\mathit{\tau }}^{*}}}& =\mathrm{2}\mathit{\pi }\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}I({\mathit{\tau }}^{*},-\mathit{\mu })\mathrm{d}\mathit{\mu }\\ & -\mathit{\pi }{\mathit{\omega }}^{*}\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}\underset{-\mathrm{1}}{\overset{\mathrm{1}}{\int }}(\mathrm{1}-\mathrm{3}{g}^{*}\mathit{\mu }{\mathit{\mu }}^{\prime })I({\mathit{\tau }}^{*},{\mathit{\mu }}^{\prime })\mathrm{d}{\mathit{\mu }}^{\prime }\mathrm{d}\mathit{\mu }\\ & -{\mathit{\omega }}^{*}{\mathit{\gamma }}_{\mathrm{3}}{F}_{\mathrm{0}}{e}^{-{\mathit{\tau }}^{*}/{\mathit{\mu }}_{\mathrm{0}}},\end{array}\end{array}$$

with

$$\begin{array}{}\text{(18)}& {\mathit{\gamma }}_{\mathrm{4}}={\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}(\mathrm{2}+\mathrm{3}{g}^{*}{\mathit{\mu }}_{\mathrm{0}})\mathrm{and}{\mathit{\gamma }}_{\mathrm{3}}={\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}(\mathrm{2}-\mathrm{3}{g}^{*}{\mathit{\mu }}_{\mathrm{0}}).\end{array}$$

Next the Eddington approximation is used, which consists in expanding the intensity $I({\mathit{\tau }}^{*},\mathit{\mu })$ as

$$\begin{array}{}\text{(19)}& I({\mathit{\tau }}^{*},\mathit{\mu })=I_{\mathrm{0}}\left({\mathit{\tau }}^{*}\right)+\mathit{\mu }{I}_{\mathrm{1}}\left({\mathit{\tau }}^{*}\right),\end{array}$$

so that

$$\begin{array}{}\text{(20)}& {\displaystyle }{F}^{-}\left({\mathit{\tau }}^{*}\right)& {\displaystyle }=\mathrm{2}\mathit{\pi }\left[{\displaystyle \frac{I_{\mathrm{0}}\left({\mathit{\tau }}^{*}\right)}{\mathrm{2}}}+{\displaystyle \frac{I_{\mathrm{1}}\left({\mathit{\tau }}^{*}\right)}{\mathrm{3}}}\right],\text{(21)}& {\displaystyle }{F}^{+}\left({\mathit{\tau }}^{*}\right)& {\displaystyle }=\mathrm{2}\mathit{\pi }\left[{\displaystyle \frac{I_{\mathrm{0}}\left({\mathit{\tau }}^{*}\right)}{\mathrm{2}}}-{\displaystyle \frac{I_{\mathrm{1}}\left({\mathit{\tau }}^{*}\right)}{\mathrm{3}}}\right].\end{array}$$

This reads

$$\begin{array}{}\text{(22)}& \mathrm{2}\mathit{\pi }I({\mathit{\tau }}^{*},\pm \mathit{\mu })={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left[(\mathrm{2}\pm \mathrm{3}\mathit{\mu })F^{-}\left({\mathit{\tau }}^{*}\right)+(\mathrm{2}\pm \mathrm{3}\mathit{\mu })F^{+}\left({\mathit{\tau }}^{*}\right)\right],\end{array}$$

and therefore

$$\begin{array}{}\text{(23)}& \mathrm{2}\mathit{\pi }\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}I({\mathit{\tau }}^{*},\pm \mathit{\mu })\mathrm{d}\mathit{\mu }={\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}\left[(\mathrm{4}\pm \mathrm{3})F^{-}\left({\mathit{\tau }}^{*}\right)+(\mathrm{4}\mp \mathrm{3})F^{+}\left({\mathit{\tau }}^{*}\right)\right].\end{array}$$

Eventually,

$$\begin{array}{}\text{(24)}& \begin{array}{rl}\mathit{\pi }& {\mathit{\omega }}^{*}\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}\underset{-\mathrm{1}}{\overset{\mathrm{1}}{\int }}(\mathrm{1}\pm \mathrm{3}{g}^{*}\mathit{\mu }{\mathit{\mu }}^{\prime })I({\mathit{\tau }}^{*},{\mathit{\mu }}^{\prime })\mathrm{d}{\mathit{\mu }}^{\prime }\mathrm{d}\mathit{\mu }\\ & ={\displaystyle \frac{{\mathit{\omega }}^{*}}{\mathrm{4}}}\left[(\mathrm{4}\pm \mathrm{3}{g}^{*})F^{-}\left({\mathit{\tau }}^{*}\right)+(\mathrm{4}\mp \mathrm{3}{g}^{*})F^{+}\left({\mathit{\tau }}^{*}\right)\right].\end{array}\end{array}$$

Substituting Eqs. (23) and (24) into Eqs. (16) and (17) we obtain

$$\begin{array}{}\text{(25)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}{F}^{-}\left({\mathit{\tau }}^{*}\right)}{\mathrm{d}{\mathit{\tau }}^{*}}}& =-{\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}\left[\mathrm{7}{F}^{-}\left({\mathit{\tau }}^{*}\right)+F^{+}\left({\mathit{\tau }}^{*}\right)\right]\\ & +{\displaystyle \frac{{\mathit{\omega }}^{*}}{\mathrm{4}}}\left[(\mathrm{4}+\mathrm{3}{g}^{*})F^{-}\left({\mathit{\tau }}^{*}\right)+(\mathrm{4}-\mathrm{3}{g}^{*})F^{+}\left({\mathit{\tau }}^{*}\right)\right]\\ & +{\mathit{\omega }}^{*}{\mathit{\gamma }}_{\mathrm{4}}{F}_{\mathrm{0}}{e}^{-{\mathit{\tau }}^{*}/{\mathit{\mu }}_{\mathrm{0}}},\end{array}\text{(26)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}{F}^{+}\left({\mathit{\tau }}^{*}\right)}{\mathrm{d}{\mathit{\tau }}^{*}}}& ={\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}\left[F^{-}\left({\mathit{\tau }}^{*}\right)+\mathrm{7}{F}^{+}\left({\mathit{\tau }}^{*}\right)\right]\\ & -{\displaystyle \frac{{\mathit{\omega }}^{*}}{\mathrm{4}}}\left[(\mathrm{4}-\mathrm{3}{g}^{*})F^{-}\left({\mathit{\tau }}^{*}\right)+(\mathrm{4}+\mathrm{3}{g}^{*})F^{+}\left({\mathit{\tau }}^{*}\right)\right]\\ & -{\mathit{\omega }}^{*}{\mathit{\gamma }}_{\mathrm{3}}{F}_{\mathrm{0}}{e}^{-{\mathit{\tau }}^{*}/{\mathit{\mu }}_{\mathrm{0}}},\end{array}\end{array}$$

which can be factorized as

$$\begin{array}{}\text{(27)}& {\displaystyle \frac{\mathrm{d}{F}^{-}\left({\mathit{\tau }}^{*}\right)}{\mathrm{d}{\mathit{\tau }}^{*}}}& {\displaystyle }={\mathit{\gamma }}_{\mathrm{2}}{F}^{+}\left({\mathit{\tau }}^{*}\right)-{\mathit{\gamma }}_{\mathrm{1}}{F}^{-}\left({\mathit{\tau }}^{*}\right)+{\mathit{\omega }}^{*}{\mathit{\gamma }}_{\mathrm{4}}{F}_{\mathrm{0}}{e}^{-{\mathit{\tau }}^{\prime }/{\mathit{\mu }}_{\mathrm{0}}},\text{(28)}& {\displaystyle \frac{\mathrm{d}{F}^{+}\left({\mathit{\tau }}^{*}\right)}{\mathrm{d}{\mathit{\tau }}^{*}}}& {\displaystyle }={\mathit{\gamma }}_{\mathrm{1}}{F}^{+}\left({\mathit{\tau }}^{*}\right)-{\mathit{\gamma }}_{\mathrm{2}}{F}^{-}\left({\mathit{\tau }}^{*}\right)-{\mathit{\omega }}^{*}{\mathit{\gamma }}_{\mathrm{3}}{F}_{\mathrm{0}}{e}^{-{\mathit{\tau }}^{\prime }/{\mathit{\mu }}_{\mathrm{0}}},\end{array}$$

where

$$\begin{array}{}\text{(29)}& \begin{array}{rl}{\mathit{\gamma }}_{\mathrm{1}}& ={\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}\left[\mathrm{7}-{\mathit{\omega }}^{*}(\mathrm{4}+\mathrm{3}{g}^{*})\right]\\ & \mathrm{and}{\mathit{\gamma }}_{\mathrm{2}}=-{\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}\left[\mathrm{1}-{\mathit{\omega }}^{*}(\mathrm{4}-\mathrm{3}{g}^{*})\right].\end{array}\end{array}$$

This corresponds to two coupled first-order differential equations, with matrix A such that

$$\begin{array}{}\text{(30)}& \mathbf{A}=\left(\begin{array}{cc}-{\mathit{\gamma }}_{\mathrm{1}}& {\mathit{\gamma }}_{\mathrm{2}}\\ -{\mathit{\gamma }}_{\mathrm{2}}& {\mathit{\gamma }}_{\mathrm{1}}\end{array}\right),\end{array}$$

which has two eigenvalues k_e and −k_e, with $k_{\mathrm{e}}=\sqrt{{\mathit{\gamma }}_{\mathrm{1}}^{\mathrm{2}}-{\mathit{\gamma }}_{\mathrm{2}}^{\mathrm{2}}}$, and corresponding eigenvectors

$$\begin{array}{}\text{(31)}& {\mathit{v}}_{\mathrm{1}}=\left(\begin{array}{c}\mathrm{1}\\ \mathrm{1}/\mathrm{\Gamma }\end{array}\right)\mathrm{and}{\mathit{v}}_{\mathrm{2}}=\left(\begin{array}{c}\mathrm{1}\\ \mathrm{\Gamma }\end{array}\right),\end{array}$$

where $\mathrm{\Gamma }=\frac{{\mathit{\gamma }}_{\mathrm{1}}-k_{\mathrm{e}}}{{\mathit{\gamma }}_{\mathrm{2}}}$. A particular solution of this system is sought as

$$\begin{array}{}\text{(32)}& {\displaystyle }{F}_p^{-}\left({\mathit{\tau }}^{*}\right)& {\displaystyle }=G^{-}{e}^{-{\mathit{\tau }}^{*}/{\mathit{\mu }}_{\mathrm{0}}},\text{(33)}& {\displaystyle }{F}_p^{+}\left({\mathit{\tau }}^{*}\right)& {\displaystyle }=G^{+}{e}^{-{\mathit{\tau }}^{*}/{\mathit{\mu }}_{\mathrm{0}}}.\end{array}$$

Inserting these expressions into Eqs. (27) and (28) results in two equations with two unknowns, which give G⁻ and G⁺:

$$\begin{array}{}\text{(34)}& {\displaystyle }{G}^{-}& {\displaystyle }={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}^{\mathrm{2}}{\mathit{\omega }}^{*}{F}_{\mathrm{0}}}{(k_{\mathrm{e}}{\mathit{\mu }}_{\mathrm{0}}{)}^{\mathrm{2}}-\mathrm{1}}}\left[({\mathit{\gamma }}_{\mathrm{1}}+\mathrm{1}/{\mathit{\mu }}_{\mathrm{0}}){\mathit{\gamma }}_{\mathrm{4}}+{\mathit{\gamma }}_{\mathrm{2}}{\mathit{\gamma }}_{\mathrm{3}}\right],\text{(35)}& {\displaystyle }{G}^{+}& {\displaystyle }={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}^{\mathrm{2}}{\mathit{\omega }}^{*}{F}_{\mathrm{0}}}{(k_{\mathrm{e}}{\mathit{\mu }}_{\mathrm{0}}{)}^{\mathrm{2}}-\mathrm{1}}}\left[({\mathit{\gamma }}_{\mathrm{1}}-\mathrm{1}/{\mathit{\mu }}_{\mathrm{0}}){\mathit{\gamma }}_{\mathrm{3}}+{\mathit{\gamma }}_{\mathrm{2}}{\mathit{\gamma }}_{\mathrm{4}}\right].\end{array}$$

This overall gives the following solutions for the total (i.e., sum of direct and diffuse) downward and upward fluxes:

$$\begin{array}{}\text{(36)}& {\displaystyle }{F}_{\mathrm{tot}}^{-}\left({\mathit{\tau }}^{*}\right)& {\displaystyle }=A{e}^{-k_{\mathrm{e}}{\mathit{\tau }}^{*}}+B{e}^{k_{\mathrm{e}}{\mathit{\tau }}^{*}}+(G^{-}+{\mathit{\mu }}_{\mathrm{0}}{F}_{\mathrm{0}})e^{-{\mathit{\tau }}^{*}/{\mathit{\mu }}_{\mathrm{0}}},\text{(37)}& {\displaystyle }{F}_{\mathrm{tot}}^{+}\left({\mathit{\tau }}^{*}\right)& {\displaystyle }=\mathrm{\Gamma }A{e}^{-k_{\mathrm{e}}{\mathit{\tau }}^{*}}+{\displaystyle \frac{B}{\mathrm{\Gamma }}}{e}^{k_{\mathrm{e}}{\mathit{\tau }}^{*}}+G^{+}{e}^{-{\mathit{\tau }}^{*}/{\mathit{\mu }}_{\mathrm{0}}},\end{array}$$

where A and B are unknowns that will be determined according to the boundary conditions. Note that these above solutions are consistent with those used by Toon et al. (1989). In addition to the fluxes, the actinic flux can be derived:

$$\begin{array}{}\text{(38)}& F_{\mathrm{act}}\left({\mathit{\tau }}^{*}\right)=\mathrm{2}\mathit{\pi }\underset{-\mathrm{1}}{\overset{\mathrm{1}}{\int }}I({\mathit{\tau }}^{*},\mathit{\mu })\mathrm{d}\mathit{\mu }.\end{array}$$

Given Eq. (19), and considering the contribution of the direct radiation to the actinic flux, this overall reads

$$\begin{array}{}\text{(39)}& F_{\mathrm{act}}\left({\mathit{\tau }}^{*}\right)=\mathrm{2}\left(F^{-}\right({\mathit{\tau }}^{*})+F^{+}({\mathit{\tau }}^{*}\left)\right)+F_{\mathrm{0}}{e}^{-{\mathit{\tau }}^{*}/{\mathit{\mu }}_{\mathrm{0}}}.\end{array}$$

2.4 Alternative formulation to match the AART theory

The form of Eqs. (36) and (37) is common to all two-stream methods (e.g., Meador and Weaver, 1980). Considering a semi-infinite snowpack, it is clear that Γ corresponds to the asymptotic diffuse albedo and k_e to the asymptotic flux extinction coefficient. To allow a perfect match of the two-stream solution with the AART theory in the case of a single layer, we propose testing a new variant denoted by TARTES∞AART in the following that uses alternative expressions for Γ, k_e, G⁻, and G⁺. More specifically, following Kokhanovsky and Zege (2004) we let

$$\begin{array}{}\text{(40)}& {\displaystyle }\mathrm{\Gamma }& {\displaystyle }=\exp \left(-\mathrm{4}\sqrt{{\displaystyle \frac{\mathrm{1}-\mathit{\omega }}{\mathrm{3}(\mathrm{1}-g)}}}\right),\text{(41)}& {\displaystyle }{k}_{\mathrm{e}}& {\displaystyle }=\sqrt{\mathrm{3}(\mathrm{1}-\mathit{\omega })(\mathrm{1}-g)}.\end{array}$$

The parameters G⁻ and G⁺ are chosen so that the direct albedo of the AART theory is obtained in the case of a semi-infinite snowpack, which is given by

$$\begin{array}{}\text{(42)}& {\mathit{\alpha }}_{\mathrm{dir}}\left({\mathit{\mu }}_{\mathrm{0}}\right)=\exp \left(-{\displaystyle \frac{\mathrm{12}}{\mathrm{7}}}(\mathrm{1}+\mathrm{2}{\mathit{\mu }}_{\mathrm{0}})\sqrt{{\displaystyle \frac{\mathrm{1}-\mathit{\omega }}{\mathrm{3}(\mathrm{1}-g)}}}\right).\end{array}$$

It implies that

$$\begin{array}{}\text{(43)}& \mathrm{\Gamma }A+G^{+}={\mathit{\alpha }}_{\mathrm{dir}}{\mathit{\mu }}_{\mathrm{0}}{F}_{\mathrm{0}}.\end{array}$$

We also have $A+G^{-}=\mathrm{0}$ because the incident diffuse radiation is zero, but we need another constraint on G⁻ and G⁺. We set their sum equal to that of the δ-Eddington approximation, which is

$$\begin{array}{}\text{(44)}& G^{-}+G^{+}={\displaystyle \frac{\mathrm{3}}{\mathrm{2}}}{G}_{\mathrm{0}}\left(\mathrm{1}+g(\mathrm{1}-\mathit{\omega })\right),\end{array}$$

where

$$\begin{array}{}\text{(45)}& G_{\mathrm{0}}={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}^{\mathrm{2}}\mathit{\omega }{F}_{\mathrm{0}}}{(k_{\mathrm{e}}{\mathit{\mu }}_{\mathrm{0}}{)}^{\mathrm{2}}-\mathrm{1}}}.\end{array}$$

This finally reads

$$\begin{array}{}\text{(46)}& {\displaystyle }{G}^{-}& {\displaystyle }={\displaystyle \frac{\frac{\mathrm{3}}{\mathrm{2}}{G}_{\mathrm{0}}\left(\mathrm{1}+g(\mathrm{1}-\mathit{\omega })\right)-{\mathit{\alpha }}_{\mathrm{dir}}{\mathit{\mu }}_{\mathrm{0}}{F}_{\mathrm{0}}}{\mathrm{\Gamma }+\mathrm{1}}},\text{(47)}& {\displaystyle }{G}^{+}& {\displaystyle }={\displaystyle \frac{\mathrm{3}}{\mathrm{2}}}{G}_{\mathrm{0}}\left(\mathrm{1}+g(\mathrm{1}-\mathit{\omega })\right)-G^{-}.\end{array}$$

When these new formulas are used, τ^* in the previous Eqs. (11)–(39) must be changed to τ, without δ scaling. Note that we also tested the δ scaling with these AART formulas and found similar performance to the present TARTES∞AART formulas without scaling. These results are not reported.

2.5 Extension to a multi-layered snowpack

The equations derived so far all considered a unique homogeneous layer. For a multi-layered snowpack, the fluxes within each layer of the snowpack have the general form given by Eqs. (36) and (37), but to determine the actual fluxes, the constants A and B should be determined for each layer, which amounts to 2N unknowns ($A_i,B_i,i\in \mathit{\{}\mathrm{1},n\mathit{\}}$) for a snowpack with N layers. These unknowns are deduced from the continuity of $F_{\mathrm{tot}}^{\pm }\left({\mathit{\tau }}^{*}\right)$ at the layer interfaces (2(N−1) equations) and the top and bottom boundary conditions (2 equations). Continuity of the diffuse fluxes at ${\mathit{\tau }}_i^{*}$ between layers i and i+1 reads

$$\begin{array}{}\text{(48)}& {\displaystyle }\begin{array}{rl}{A}_i{e}^{-k_{e,i}{\mathit{\tau }}_i^{*}}& +B_i{e}^{k_{e,i}{\mathit{\tau }}_i^{*}}+G_i^{-}{e}^{-{\mathit{\tau }}_i^{*}/{\mathit{\mu }}_{\mathrm{0}}}=A_{i+\mathrm{1}}{e}^{-k_{e,i+\mathrm{1}}{\mathit{\tau }}_i^{*}}\\ & +B_{i+\mathrm{1}}{e}^{k_{e,i+\mathrm{1}}{\mathit{\tau }}_i^{*}}+G_{i+\mathrm{1}}^{-}{e}^{-{\mathit{\tau }}_i^{*}/{\mathit{\mu }}_{\mathrm{0}}},\end{array}\text{(49)}& {\displaystyle }\begin{array}{rl}{\mathrm{\Gamma }}_i{A}_i{e}^{-k_{e,i}{\mathit{\tau }}_i^{*}}& +{\displaystyle \frac{B_i}{{\mathrm{\Gamma }}_i}}{e}^{k_{e,i}{\mathit{\tau }}_i^{*}}+G_i^{+}{e}^{-{\mathit{\tau }}_i^{*}/{\mathit{\mu }}_{\mathrm{0}}}\\ & ={\mathrm{\Gamma }}_{i+\mathrm{1}}{A}_{i+\mathrm{1}}{e}^{-k_{e,i+\mathrm{1}}{\mathit{\tau }}_i^{*}}+{\displaystyle \frac{B_{i+\mathrm{1}}}{{\mathrm{\Gamma }}_{i+\mathrm{1}}}}{e}^{k_{e,i+\mathrm{1}}{\mathit{\tau }}_i^{*}}\\ & +G_{i+\mathrm{1}}^{+}{e}^{-{\mathit{\tau }}_i^{*}/{\mathit{\mu }}_{\mathrm{0}}}.\end{array}\end{array}$$

From now on we use the notation $k_i=k_{e,i}$ and define $A_i^{\prime }=A_i{e}^{-k_i{\mathit{\tau }}_{i-\mathrm{1}}^{*}}$ and $B_i^{\prime }=B_i{e}^{k_i{\mathit{\tau }}_{i-\mathrm{1}}^{*}}$. Note also that τ₀=0. The boundary conditions at the top of the snowpack, where the diffuse flux is $F_{\mathrm{0}}^{\mathrm{diff}}$, and at the bottom, where the underlying surface is assumed to be Lambertian and characterized by its albedo α_b, read

$$\begin{array}{}\text{(50)}& {\displaystyle }{A}_{\mathrm{1}}+B_{\mathrm{1}}+G_{\mathrm{1}}^{-}=F_{\mathrm{0}}^{\mathrm{diff}},\text{(51)}& {\displaystyle }\begin{array}{rl}{\mathrm{\Gamma }}_N{A}_N{e}^{-k_N{\mathit{\tau }}_N^{*}}& +{\displaystyle \frac{B_N}{{\mathrm{\Gamma }}_N}}{e}^{k_N{\mathit{\tau }}_N^{*}}+G_N^{+}{e}^{-{\mathit{\tau }}_N^{*}/{\mathit{\mu }}_{\mathrm{0}}}\\ & ={\mathit{\alpha }}_b\left(A_N{e}^{-k_N{\mathit{\tau }}_N^{*}}+B_N{e}^{k_N{\mathit{\tau }}_N^{*}}+(G_N^{-}\right.\\ & \left.+{\mathit{\mu }}_{\mathrm{0}}{F}_{\mathrm{0}})e^{-{\mathit{\tau }}_N^{*}/{\mathit{\mu }}_{\mathrm{0}}}\right).\end{array}\end{array}$$

The linear system formed by these 2N independent equations can be written as

$$\begin{array}{}\text{(52)}& \mathbf{M}\mathit{X}=\mathit{V},\end{array}$$

with

$$\begin{array}{}\text{(53)}& \mathit{X}{=}^t(A_{\mathrm{1}}^{\prime },B_{\mathrm{1}}^{\prime },\mathrm{\dots },A_i^{\prime },B_i^{\prime },\mathrm{\dots },A_N^{\prime },B_N^{\prime }).\end{array}$$

The matrix M reads

$$\begin{array}{}\text{(54)}& \left(\begin{array}{cccccccc}\mathrm{1}& \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{\dots }& \mathrm{0}& \mathrm{0}\\ e_{\mathrm{1}}^{-}& e_{\mathrm{1}}^{+}& -\mathrm{1}& -\mathrm{1}& \mathrm{0}& \mathrm{\dots }& \mathrm{0}& \mathrm{0}\\ {\mathrm{\Gamma }}_{\mathrm{1}}{e}_{\mathrm{1}}^{-}& \frac{\mathrm{1}}{{\mathrm{\Gamma }}_{\mathrm{1}}}{e}_{\mathrm{1}}^{+}& -{\mathrm{\Gamma }}_{\mathrm{2}}& -\mathrm{1}/{\mathrm{\Gamma }}_{\mathrm{2}}& \mathrm{0}& \mathrm{\dots }& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& e_{\mathrm{2}}^{-}& e_{\mathrm{2}}^{+}& \mathrm{\dots }& \mathrm{\dots }& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& {\mathrm{\Gamma }}_{\mathrm{2}}{e}_{\mathrm{2}}^{-}& \frac{\mathrm{1}}{{\mathrm{\Gamma }}_{\mathrm{2}}}{e}_{\mathrm{2}}^{+}& \mathrm{\dots }& \mathrm{\dots }& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{\dots }& \mathrm{\dots }& \mathrm{0}& \mathrm{0}\\ \mathrm{\dots }& \mathrm{\dots }& \mathrm{\dots }& \mathrm{\dots }& \mathrm{\dots }& \mathrm{\dots }& \mathrm{\dots }& \mathrm{\dots }\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{\dots }& -\mathrm{1}& -\mathrm{1}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{\dots }& -{\mathrm{\Gamma }}_N& -\mathrm{1}/{\mathrm{\Gamma }}_N\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{\dots }& ({\mathrm{\Gamma }}_N-{\mathit{\alpha }}_b)e_N^{-}& (\mathrm{1}/{\mathrm{\Gamma }}_N-{\mathit{\alpha }}_b)e_N^{+}\end{array}\right),\end{array}$$

and

$$\begin{array}{}\text{(55)}& \begin{array}{rl}\mathit{V}& ={}^t(F_{\mathrm{0}}^{\mathrm{diff}}-G_{\mathrm{1}}^{-},\mathrm{\dots },\mathrm{d}{G}_i^{-}{e}^{-{\mathit{\tau }}_i^{*}/{\mathit{\mu }}_{\mathrm{0}}},\mathrm{d}{G}_i^{+}{e}^{-{\mathit{\tau }}_i^{*}/{\mathit{\mu }}_{\mathrm{0}}},\\ & \mathrm{\dots },\left[{\mathit{\alpha }}_b(G_N^{-}+{\mathit{\mu }}_{\mathrm{0}}{F}_{\mathrm{0}})-G_N^{+}\right]e^{-{\mathit{\tau }}_N^{*}/{\mathit{\mu }}_{\mathrm{0}}}),\end{array}\end{array}$$

where we used the notation $e_i^{\pm }=e^{\pm k_i\mathrm{d}{\mathit{\tau }}_i^{*}}$, $\mathrm{d}{\mathit{\tau }}_i^{*}={\mathit{\tau }}_i^{*}-{\mathit{\tau }}_{i-\mathrm{1}}^{*}$ is the optical depth of layer i, and $\mathrm{d}{G}_i^{\pm }=G_{i+\mathrm{1}}^{\pm }-G_i^{\pm }$. The matrix M can be tridiagonalized by consecutively performing the following replacement operations on the lines M_j of M for an even $\mathrm{2}\le j<N$:

1. $M_j-{\mathrm{\Gamma }}_{i/\mathrm{2}+\mathrm{1}}{L}_{j+\mathrm{1}}\to M_j$,

2. $(\mathrm{1}-{\mathrm{\Gamma }}_{i/\mathrm{2}}{\mathrm{\Gamma }}_{i/\mathrm{2}+\mathrm{1}})M_{j+\mathrm{1}}-{\mathrm{\Gamma }}_{i/\mathrm{2}}{M}_j\to M_{j+\mathrm{1}}$.

The new matrix M reads

$$\left(\begin{array}{cccccccc}\mathrm{1}& \mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{\dots }& \mathrm{0}& \mathrm{0}\\ (\mathrm{1}-{\mathrm{\Gamma }}_{\mathrm{1}}{\mathrm{\Gamma }}_{\mathrm{2}})e_{\mathrm{1}}^{-}& (\mathrm{1}-{\mathrm{\Gamma }}_{\mathrm{2}}/{\mathrm{\Gamma }}_{\mathrm{1}})e_{\mathrm{1}}^{+}& ({\mathrm{\Gamma }}_{\mathrm{2}}^{\mathrm{2}}-\mathrm{1})& \mathrm{0}& \mathrm{0}& \mathrm{\dots }& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& (\mathrm{1}/{\mathrm{\Gamma }}_{\mathrm{1}}-{\mathrm{\Gamma }}_{\mathrm{1}})e_{\mathrm{1}}^{+}& ({\mathrm{\Gamma }}_{\mathrm{1}}-{\mathrm{\Gamma }}_{\mathrm{2}})& ({\mathit{\alpha }}_{\mathrm{1}}-\mathrm{1}/{\mathit{\alpha }}_{\mathrm{2}})& \mathrm{0}& \mathrm{\dots }& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& (\mathrm{1}-{\mathrm{\Gamma }}_{\mathrm{2}}{\mathrm{\Gamma }}_{\mathrm{3}})e_{\mathrm{2}}^{-}& (\mathrm{1}-{\mathrm{\Gamma }}_{\mathrm{3}}/{\mathrm{\Gamma }}_{\mathrm{2}})e_{\mathrm{2}}^{+}& \mathrm{\dots }& \mathrm{\dots }& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& (\mathrm{1}/{\mathrm{\Gamma }}_{\mathrm{2}}-{\mathrm{\Gamma }}_{\mathrm{2}})e_{\mathrm{2}}^{+}& \mathrm{\dots }& \mathrm{\dots }& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{\dots }& \mathrm{\dots }& \mathrm{0}& \mathrm{0}\\ \mathrm{\dots }& \mathrm{\dots }& \mathrm{\dots }& \mathrm{\dots }& \mathrm{\dots }& \mathrm{\dots }& \mathrm{\dots }& \mathrm{\dots }\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{\dots }& ({\mathrm{\Gamma }}_N^{\mathrm{2}}-\mathrm{1})& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{\dots }& ({\mathrm{\Gamma }}_{N-\mathrm{1}}-{\mathrm{\Gamma }}_N)& ({\mathrm{\Gamma }}_{N-\mathrm{1}}-\mathrm{1}/{\mathrm{\Gamma }}_N)\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{\dots }& ({\mathrm{\Gamma }}_N-{\mathit{\alpha }}_b)e_N^{-}& (\mathrm{1}/{\mathrm{\Gamma }}_N-{\mathit{\alpha }}_b)e_N^{+}\end{array}\right).$$

Accordingly, the new vector V reads

$$\begin{array}{}\text{(56)}& \begin{array}{rl}\mathit{V}& ={}^t(F_{\mathrm{0}}^{\mathrm{diff}}-G_{\mathrm{1}}^{-},\mathrm{\dots },(\mathrm{d}{G}_i^{-}-{\mathrm{\Gamma }}_{i+\mathrm{1}}\mathrm{d}{G}_i^{+})e^{-{\mathit{\tau }}_i^{*}/{\mathit{\mu }}_{\mathrm{0}}},\\ & (\mathrm{d}{G}_i^{+}-{\mathrm{\Gamma }}_i\mathrm{d}{G}_i^{-})e^{-{\mathit{\tau }}_i^{*}/{\mathit{\mu }}_{\mathrm{0}}},\mathrm{\dots },\\ & \left[{\mathit{\alpha }}_b(G_N^{-}+{\mathit{\mu }}_{\mathrm{0}}{F}_{\mathrm{0}})-G_N^{+}\right]e^{-{\mathit{\tau }}_N^{*}/{\mathit{\mu }}_{\mathrm{0}}}).\end{array}\end{array}$$

The 2N unknowns are efficiently retrieved by inversion of the tridiagonal system. Then the fluxes at each interface are calculated as follows:

$$\begin{array}{}\text{(57)}& {\displaystyle }{F}_{\mathrm{tot}}^{-}\left({\mathit{\tau }}_i^{*}\right)=A_i^{\prime }{e}^{-k_i^{*}\mathrm{d}{\mathit{\tau }}_i^{*}}+B_i^{\prime }{e}^{k_i^{*}\mathrm{d}{\mathit{\tau }}_i^{*}}+(G_i^{-}+{\mathit{\mu }}_{\mathrm{0}}{F}_{\mathrm{0}})e^{-{\mathit{\tau }}_i^{*}/{\mathit{\mu }}_{\mathrm{0}}},\text{(58)}& {\displaystyle }{F}_{\mathrm{tot}}^{+}\left({\mathit{\tau }}_i^{*}\right)={\mathrm{\Gamma }}_i{A}_i^{\prime }{e}^{k_i^{*}\mathrm{d}{\mathit{\tau }}_i^{*}}+{\displaystyle \frac{B_i^{\prime }}{\mathrm{\Gamma }}}{e}^{k_i^{*}\mathrm{d}{\mathit{\tau }}_i^{*}}+G_i^{+}{e}^{-{\mathit{\tau }}_i^{*}/{\mathit{\mu }}_{\mathrm{0}}}.\end{array}$$

Note that in practice the fluxes can be computed at any requested depth. To this end, the layer i corresponding to this depth is first identified. The ratio of the distance between the above interface and the requested depth, as well as the thickness of the layer, is used to scale $\mathrm{d}{\mathit{\tau }}_i^{*}$ in the above solutions.

2.6 Computed quantities

Beyond the fluxes (and actinic fluxes) that are the native variables returned by the above equations, it is possible to compute the energy absorbed by layer i as the sum of the absorbed upwelling E_u and downwelling E_d energy using

$$\begin{array}{}\text{(59)}& {\displaystyle }{E}_i=\underset{E_{\mathrm{u}}}{\underbrace{F_{\mathrm{tot}}^{+}\left({\mathit{\tau }}_i^{*}\right)-F_{\mathrm{tot}}^{+}\left({\mathit{\tau }}_{i-\mathrm{1}}^{*}\right)}}-\underset{E_{\mathrm{d}}}{\underbrace{\left(F_{\mathrm{tot}}^{-}\left({\mathit{\tau }}_i^{*}\right)-F_{\mathrm{tot}}^{-}\left({\mathit{\tau }}_{i-\mathrm{1}}^{*}\right)\right)}},\text{(60)}& {\displaystyle }\begin{array}{rl}{E}_{\mathrm{u}}& ={\mathrm{\Gamma }}_i{A}_i^{\prime }(e^{-k_i^{*}\mathrm{d}{\mathit{\tau }}_i^{*}}-\mathrm{1})+{\displaystyle \frac{B_i^{\prime }}{{\mathrm{\Gamma }}_i}}(e^{k_i^{*}\mathrm{d}{\mathit{\tau }}_i^{*}}-\mathrm{1})\\ & +G_i^{+}(e^{-{\mathit{\tau }}_i^{*}/{\mathit{\mu }}_{\mathrm{0}}}-e^{-{\mathit{\tau }}_{i-\mathrm{1}}^{*}/{\mathit{\mu }}_{\mathrm{0}}}),\end{array}\text{(61)}& {\displaystyle }\begin{array}{rl}{E}_{\mathrm{d}}& =A_i^{\prime }(e^{-k_i^{*}\mathrm{d}{\mathit{\tau }}_i^{*}}-\mathrm{1})+B_i^{\prime }(e^{k_i^{*}\mathrm{d}{\mathit{\tau }}_i^{*}}-\mathrm{1})\\ & +(G_i^{-}+{\mathit{\mu }}_{\mathrm{0}}{F}_{\mathrm{0}})(e^{-{\mathit{\tau }}_i^{*}/{\mathit{\mu }}_{\mathrm{0}}}-e^{-{\mathit{\tau }}_{i-\mathrm{1}}^{*}/{\mathit{\mu }}_{\mathrm{0}}}),\end{array}\end{array}$$

while the energy absorbed by the ground is given by

$$\begin{array}{}\text{(62)}& \begin{array}{rl}{E}_{\mathrm{bottom}}& =(\mathrm{1}-{\mathit{\alpha }}_b)(A_N^{\prime }{e}_N^{-}+B_N^{\prime }{e}_N^{+}\\ & +(G_N^{-}+{\mathit{\mu }}_{\mathrm{0}}{F}_{\mathrm{0}})e^{-{\mathit{\tau }}_N^{*}/{\mathit{\mu }}_{\mathrm{0}}}).\end{array}\end{array}$$

The albedo of the snowpack is also calculated as the ratio of the upward to the downward flux at the surface:

$$\begin{array}{}\text{(63)}& \mathit{\alpha }={\displaystyle \frac{\mathrm{1}}{{\mathit{\mu }}_{\mathrm{0}}{F}_{\mathrm{0}}+F_{\mathrm{0}}^{\mathrm{diff}}}}\left({\mathrm{\Gamma }}_{\mathrm{1}}{A}_{\mathrm{1}}+{\displaystyle \frac{B_{\mathrm{1}}}{{\mathrm{\Gamma }}_{\mathrm{1}}}}+G_{\mathrm{1}}^{+}\right).\end{array}$$

So far we have not specified anything about the spectral dimension of incident light. Implicitly all above derivations are valid for monochromatic radiation, so TARTES is in essence a monochromatic model. Since the single-scattering properties of the snowpack are wavelength-dependent, the matrix M and the vector V are computed at each relevant wavelength. Broadband quantities are thus obtained by summing the contribution of all wavelengths. For instance, the broadband albedo $\stackrel{\mathrm{‾}}{\mathit{\alpha }}$ is obtained through spectral integration:

$$\begin{array}{}\text{(64)}& \stackrel{\mathrm{‾}}{\mathit{\alpha }}={\displaystyle \frac{\sum _{\mathrm{1}}^N\mathit{\alpha }\left({\mathit{\lambda }}_i\right)\left(F_{\mathrm{0}}^{\mathrm{diff}}\right({\mathit{\lambda }}_i)+{\mathit{\mu }}_{\mathrm{0}}{F}_{\mathrm{0}}({\mathit{\lambda }}_i\left)\right)}{\sum _{\mathrm{1}}^N{F}_{\mathrm{0}}^{\mathrm{diff}}\left({\mathit{\lambda }}_i\right)+{\mathit{\mu }}_{\mathrm{0}}{F}_{\mathrm{0}}\left({\mathit{\lambda }}_i\right)}}.\end{array}$$

2.7 Treatment of diffuse incident radiation

As seen previously, the incident radiation in TARTES can be direct or diffuse. Wiscombe (1977) has shown that in the case of diffuse radiation the performance of the δ-Eddington approximation was limited, sometimes leading to negative values of albedo. This is why Warren and Wiscombe (1980) and Dang et al. (2019) computed the diffuse albedo as an angular average of direct albedos. In TARTES, the most accurate strategy to handle diffuse radiation is to compute the integrated sum of direct radiation coming from all directions, following an angular distribution such that p(θ₀)=cos θ₀. Hence, it requires integrating the solutions for direct incident light at various angles. As only the vector V depends on incident light characteristics, to compute the optical properties of a snowpack at various angles of incidence, M has to be calculated only once, which is computationally relatively efficient.

An alternative strategy proposed in TARTES is to consider that diffuse radiation can be approximated by direct radiation at an effective zenith angle θ_diff such that (see Eq. 42)

$$\begin{array}{}\text{(65)}& {\displaystyle \frac{\mathrm{3}}{\mathrm{7}}}(\mathrm{1}+\mathrm{2}\cos {\mathit{\theta }}_{\mathrm{diff}})=\mathrm{1},\end{array}$$

which corresponds approximately to an angle of 48.2°. This alternative is the default option in TARTES (hereinafter referred to as 48.2°). Note that in the initial version of TARTES (Libois et al., 2013) the diffuse albedo was calculated using a direct component at an angle of 53° based on equivalence tests using DISORT-Mie. This angle was changed to the approximate value of 48° on 22 June 2022 and is now obtained with the exact calculation (Eq. 65).

Note that despite the problem identified by Wiscombe (1977), the pure diffuse boundary condition of the two-stream method is implemented in TARTES (hereinafter denoted by “2S”) and should be selected for testing only as done in Sect. 4.1.1. To avoid negative albedo, we set α=0 when a negative value is obtained, which occurs when the ice absorption is very large (1400–1600 nm) (Sect. 4.1.1). The other quantities calculated by TARTES are not corrected, and we discourage using the 2S option in general.

2.8 Treatment of optically deep layers and snowpacks

When a layer is too thick, the terms $e_i^{\pm }$ become either extremely large or small, and in both cases they cannot be handled numerically. To avoid this, when a layer is too thick (practically when $k_i\mathrm{d}{\mathit{\tau }}_i^{*}>\mathrm{200}$), its optical depth is modified so that $k_i\mathrm{d}{\mathit{\tau }}_i^{*}=\mathrm{200}$. In addition, when a snowpack is very deep, energy does not penetrate through the whole snowpack; it is essentially absorbed in the topmost layers. To save computation time, the snowpack used for the calculations is reduced to the top n layers, where n is the smallest integer such that

$$\begin{array}{}\text{(66)}& \sum _{\mathrm{1}}^n{k}_i^{*}\mathrm{d}{\mathit{\tau }}_i>\mathrm{30}.\end{array}$$

At the same time, the optical thickness of the last layer is set to $\mathrm{30}/k_n$ and the underlying albedo is set to 1 to ensure the underlying surface does not absorb energy.

2.9 Single-scattering properties of snow

The previous sections detailed how the fluxes and vertical profiles of absorbed energy within a multi-layered snowpack are computed. This section details how the single-scattering properties of snow, namely σ_e, ω, and g, are determined from the snow physical properties, namely SSA, density, grain shape, and impurity contents. It is worth having in mind that the RTE applies to a continuous medium. As snow is a porous medium, it is common to define an optically equivalent continuous medium to represent it. In practice, its extinction coefficient is determined from the number concentration N (m⁻³) of snow grains and the average extinction cross section of snow grains (Kokhanovsky and Zege, 2004):

$$\begin{array}{}\text{(67)}& {\mathit{\sigma }}_{\mathrm{e}}=N\stackrel{\mathrm{‾}}{C_{\mathrm{ext}}}.\end{array}$$

This strategy, which was originally developed to compute for instance the optical properties of clouds (Stephens, 1978), implicitly assumes that scatterers are independent. Although this is unlikely to be the case in snow which is a dense medium, this formalism remains widely used since it has proved its efficiency in simulating snow optical properties in the solar spectrum where ice absorption is relatively low. Actually it remains efficient as long as the asymmetry factor is also computed assuming independent scatterers (Kokhanovsky, 2004). Using this representation, snow density is related to the average volume of snow grains $\stackrel{\mathrm{‾}}{V}$: $\mathit{\rho }=N{\mathit{\rho }}_{\mathrm{ice}}\stackrel{\mathrm{‾}}{V}$. We further assume that snow grains are large compared to the wavelength of solar radiation, so that C_ext=2Σ (where Σ is the projected area of an individual grain), and that the grains are convex so that $\mathrm{\Sigma }=S/\mathrm{4}$, where S is the total surface area of a grain. Hence, σ_e finally reads

$$\begin{array}{}\text{(68)}& {\displaystyle }{\mathit{\sigma }}_{\mathrm{e}}={\displaystyle \frac{\mathit{\rho }\mathrm{SSA}}{\mathrm{2}}},\end{array}$$

where SSA equals by definition $\frac{\stackrel{\mathrm{‾}}{S}}{{\mathit{\rho }}_{\mathrm{ice}}\stackrel{\mathrm{‾}}{V}}$. Note that this expression was originally known for convex particles only (e.g., Libois et al., 2013) but was then applied to a more general porous medium (Malinka, 2014).

The single-scattering albedo is computed after Kokhanovsky and Macke (1997), who propose an analytical expression depending on the refractive index $m=n-i\mathit{\chi }$ and grain shape 𝒮, based on Monte Carlo computations relying on the geometrical optics approximation:

$$\begin{array}{}\text{(69)}& (\mathrm{1}-\mathit{\omega })={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(\mathrm{1}-W(n\left)\right)(\mathrm{1}-e^{-\mathit{\psi }(n,\mathcal{S})c}),\end{array}$$

where

$$\begin{array}{}\text{(70)}& c={\displaystyle \frac{\mathrm{24}\mathit{\pi }\mathit{\chi }}{{\mathit{\rho }}_{\mathrm{ice}}\mathit{\lambda }\mathrm{SSA}}},\end{array}$$

and ρ_ice is the bulk density of ice. W does not depend on grain shape (for randomly oriented, convex, particles, Kokhanovsky and Macke, 1997) and is assumed to depend linearly on n based on tabulated values (Kokhanovsky, 2004, p. 61), so that in TARTES

$$\begin{array}{}\text{(71)}& W\left(n\right)=\mathrm{0.0611}+\mathrm{0.17}(n-\mathrm{1.3}).\end{array}$$

Likewise,

$$\begin{array}{}\text{(72)}& \mathit{\psi }(n,\mathcal{S})={\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}{\displaystyle \frac{B(n,\mathcal{S})}{\mathrm{1}-W\left(n\right)}},\end{array}$$

where B(n,𝒮) is the absorption enhancement parameter. Note that at low absorption Eq. (69) collapses to Eq. (6) of Libois et al. (2013). TARTES proposes three options to compute B. The first option (the only one in the previous TARTES version) is a linear dependence on n based on Kokhanovsky and Macke (1997), so that

$$\begin{array}{}\text{(73)}& B(n,\mathcal{S})=B_{\mathrm{0}}\left(\mathcal{S}\right)+\mathrm{0.4}(n-\mathrm{1.3}),\end{array}$$

where B₀(𝒮) can be prescribed by the user to account for a particular geometrical shape. For instance, for spherical particles B₀=1.25 (Libois et al., 2013).

The second option is

$$\begin{array}{}\text{(74)}& B(n,\mathcal{S})=n^{\mathrm{2}},\end{array}$$

which stems from the recent work on random media and is now the recommended and default option (Malinka, 2014; Robledano et al., 2023). The last option gives the user the possibility to prescribe a constant value or a value per wavelength.

The asymmetry factor g also depends on the detailed snow microstructure, but in the granular representation it can be computed from the scattering phase function of individual grains. At weakly absorbing wavelengths g mainly depends on snow grain shape 𝒮, but at absorbing wavelengths it also depends on the ice imaginary part of the refractive index χ and SSA. In TARTES g is calculated in consistency with B, according to the three options. In the first option g(n,𝒮) is computed after Kokhanovsky and Macke (1997):

$$\begin{array}{}\text{(75)}& g(n,\mathcal{S})=g_{\mathrm{\infty }}\left(n\right)-\left[g_{\mathrm{\infty }}\left(n\right)-g_{\mathrm{0}}(n,\mathcal{S})\right]e^{-y(n,\mathcal{S})c}.\end{array}$$

g_∞(n) is the asymmetry factor of a purely absorbing sphere, and g₀(n,𝒮) is the asymmetry factor of the non-absorbing particle of shape 𝒮. g₀ and g_∞ are both assumed to depend linearly on n, so that

$$\begin{array}{}\text{(76)}& {\displaystyle }{g}_{\mathrm{\infty }}\left(n\right)=\mathrm{0.9751}-\mathrm{0.105}(n-\mathrm{1.3}),\text{(77)}& {\displaystyle }{g}_{\mathrm{0}}(n,\mathcal{S})=g_{\mathrm{0}}\left(\mathcal{S}\right)-\mathrm{0.38}(n-\mathrm{1.3}),\end{array}$$

where g₀(𝒮) is prescribed by the user. Again the dependence on n corresponds to that of spheres (Kokhanovsky, 2004). In the second option, g=0.82 (Robledano et al., 2023), and in the third option, the user prescribes the value as a constant or as one value per wavelength.

Finally y is also assumed to depend linearly on n. In TARTES the expression corresponding to spheres is taken so that (Kokhanovsky, 2004)

$$\begin{array}{}\text{(78)}& y\left(n\right)=\mathrm{0.728}+\mathrm{0.752}(n-\mathrm{1.3}).\end{array}$$

Note that for the three options, the variables W, g_∞, and y are calculated by linear relationships (Eqs. 71, 76, and 78) corresponding to spheres. This may result in inconsistencies with respect to B and g, but given that at present these three variables have not been investigated for snow, we prefer to keep the relationship used up to now.

2.10 Impurities

At the wavelengths where ice is very weakly absorbing, the optical properties of snow are very sensitive to the presence of light-absorbing impurities. TARTES can account for such impurities, in practice black carbon (BC), dust, and humic-like substances (HULIS). For the sake of simplicity it is assumed that impurities are external to snow grains. When impurities are added in realistic, low quantities, N_i, we assume that the extinction coefficient of snow is unchanged but the absorption coefficient is altered. This supposes that impurity scattering is negligible. According to simulations at 1030 nm (Fair et al., 2022), this applies to BC in any case, as well as to dust except for fine particles (<1 µm) in high concentration (e.g., >500 ppm). When this approximation is valid, it follows that the single-scattering co-albedo is

$$\begin{array}{}\text{(79)}& (\mathrm{1}-\mathit{\omega })=(\mathrm{1}-\mathit{\omega }{)}_{\mathrm{snow}}+{\displaystyle \frac{\mathrm{1}}{{\mathit{\sigma }}_{\mathrm{e}}}}\sum _i{N}_i{C}_{\mathrm{abs}}^i,\end{array}$$

where $C_{\mathrm{abs}}^i$ is the average absorption cross section of impurities i. Rewritten as a function of the bulk mass concentration c_i (kg kg⁻¹) and using Eq. (69), it reads

$$\begin{array}{}\text{(80)}& \begin{array}{rl}(\mathrm{1}-\mathit{\omega })& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(\mathrm{1}-W(n\left)\right)(\mathrm{1}-e^{-\mathit{\psi }(n,s)c})\\ & -{\displaystyle \frac{\mathrm{2}}{\mathit{\lambda }\mathrm{SSA}}}\sum _i{\mathrm{MAE}}^i{c}_i,\end{array}\end{array}$$

where MAEⁱ is the mass absorption efficiency (in m² kg⁻¹, e.g., Caponi et al., 2017).

To calculate MAE, TARTES uses different formulations according to the particle size. For small particles compared to the wavelength (applies to BC and HULIS), the absorption cross section C_abs of an impurity of type i, of volume V_i and with complex refractive index m_i, is given by Kokhanovsky (2004):

$$\begin{array}{}\text{(81)}& C_{\mathrm{abs}}^i=-{\displaystyle \frac{\mathrm{6}\mathit{\pi }{V}_i}{\mathit{\lambda }}}\mathrm{Im}\left({\displaystyle \frac{m_i^{\mathrm{2}}-\mathrm{1}}{m_i^{\mathrm{2}}+\mathrm{2}}}\right).\end{array}$$

Dividing by ρ_iV_i, where ρ_i is the impurity bulk density, yields the mass absorption efficiency:

$$\begin{array}{}\text{(82)}& {\mathrm{MAE}}^i=-{\displaystyle \frac{\mathrm{6}\mathit{\pi }}{\mathit{\lambda }{\mathit{\rho }}_i}}\mathrm{Im}\left({\displaystyle \frac{m_i^{\mathrm{2}}-\mathrm{1}}{m_i^{\mathrm{2}}+\mathrm{2}}}\right).\end{array}$$

In TARTES, the characteristics of BC can be taken from Bond and Bergstrom (2006) (ρ_BC=1800 kg m⁻³ and $m_{\mathrm{BC}}=\mathrm{1.95}-\mathrm{0.79}i$) or by default from SNICAR-ADv3 (Flanner et al., 2021). The values for the HULIS are taken from Hoffer et al. (2006).

For large particles (applies to dust), the absorption is not simply related to the imaginary part of their refractive index and the volume but depends on the shape, size, and other impurity particularities. While Mie theory applies to spherical particles – and other more complex theories to more general shapes (Mishchenko et al., 1996) – the computation is usually intensive. Instead TARTES directly uses tabulated MAE values that can be obtained from independent calculations or from in situ measurements. More precisely, the MAE is calculated from the MAE at a specific wavelength (usually λ₀=400 nm or λ₀=550 nm) and the spectral dependence given by the Ångström absorption exponent (AAE) such as

$$\begin{array}{}\text{(83)}& \mathrm{MAE}\left(\mathit{\lambda }\right)=\mathrm{MAE}\left({\mathit{\lambda }}_{\mathrm{0}}\right){\left({\displaystyle \frac{\mathit{\lambda }}{{\mathit{\lambda }}_{\mathrm{0}}}}\right)}^{-\mathrm{AAE}}.\end{array}$$

In TARTES v2.0, values from Caponi et al. (2017) obtained from different regions in the world are implemented. For small particles (PM_2.5), available locations are Libya, Morocco, Algeria, Mali, Saudi Arabia, Kuwait, Namibia, China, and Australia, and for large particles (PM₁₀), available locations are Libya, Algeria, Bodele, Saudi Arabia, Namibia, China, Arizona, Patagonia, and Australia (Caponi et al., 2017).

3 Numerical implementation

TARTES was initially implemented in Python and then converted in part to Fortran to be integrated in the detailed snowpack model Crocus (Vionnet et al., 2012), where it can be used to compute the profile of absorption in the snowpack (Libois et al., 2015; Tuzet et al., 2017). Both versions are based on the same equations, though the Python version has more features beyond absorption calculation. Note also that the Fortran version is not systematically updated along with the Python version.

3.1 Python version

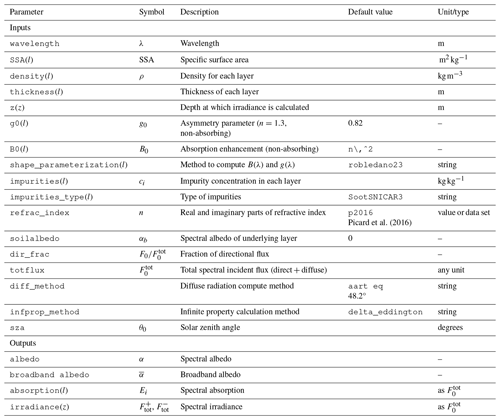
TARTES v2.0 is compatible with Python 3.7 and higher. The four main entry points for the user are the functions albedo, absorption_profile, irradiance_profile, and actinic_profile. The inputs and outputs are listed in Table 1. These functions take as inputs the wavelengths at which the computation is performed, the properties of each layer (thickness, SSA, density, B₀ and g₀, impurities), the name of the ice refractive index database (Warren and Brandt, 2008; Picard et al., 2016), the bottom albedo, and the illumination conditions (solar zenith angle, total radiation flux $F_{\mathrm{0}}+F_{\mathrm{0}}^{\mathrm{tot}}=F_{\mathrm{0}}+F_{\mathrm{0}}^{\mathrm{diff}}$, and fraction of direct radiation $F_{\mathrm{0}}/F_{\mathrm{0}}^{\mathrm{tot}}$). The outputs are the albedo, the absorption, the upwelling and downwelling irradiances, and the actinic flux for each wavelength, for each function respectively. In addition, a function allows the calculation of broadband albedo given the incident spectrum distribution.

These user functions internally call the core function tartes, which computes the intrinsic optical properties of each layer from their physical properties and impurity contents, and then call the function two_stream_rt, which solves the radiative transfer equation, eventually allowing us to compute all the quantities mentioned here above (Fig. 1).

The code has a test suite (10 tests currently) that can be automatically run using the software pytest to check the conformity of the code.

Picard et al. (2016)

Table 1 Symbols, input parameters, and outputs of the user functions in TARTES. Parameters marked with (l) are given for each layer. The (z) dimension is given by the user and is independent of the layers.

Compared to the previous version, TARTES v2.0 proposes several options to compute diffuse radiation and to compute the semi-infinite layer albedo that appears in the two-stream equation. The default values for the grain shape parameters are changed based on recent advances (Robledano et al., 2023) and likewise for the black carbon properties to match SNICAR-ADv3. The code has also been improved with the factorization of the impurity calculations (all types are now using MAE, either tabulated or calculated from the refractive index), type hinting, automatic strict formatting, modern packaging, and continuous integration for automatic publication on PyPI. The documentation has been improved, and the conformity between the equations presented in this paper and the code has been carefully checked. In addition, the SnowTARTES web application has been enhanced to calculate the irradiance profile.

3.2 Fortran version

The original TARTES code was converted in a Fortran version suitable for the integration in Crocus (Vionnet et al., 2012). Crocus predicts the evolution of a multi-layered snowpack from local meteorological forcings. For this the absorption of the solar energy in each layer needs to be computed at each time step. This is critical to compute the energy budget of the snowpack and consequently the temperature profile and gradients that control snow metamorphism (Flanner and Zender, 2005). The original optical scheme in Crocus (Brun et al., 1989) estimates the albedo, hence the total absorbed energy, in three spectral bands from empirical relationships with the grain shape and size, and then it applies an ad hoc Beer–Lambert law to distribute the absorbed energy in the layers. Using a proper radiative transfer model has many advantages: the higher spectral resolution (10 nm by default) allows us to resolve the spectral features of snow without resorting to questionable spectral averages; it computes the profile of energy in a way that is consistent with the albedo; the direct and diffuse fluxes and the solar zenith angle dependence are treated properly; and absorption by the soil, snow grain shape, and impurities are fully accounted for. However, the computation time can be significant, especially if the spectral integration is highly resolved. This is the reason why studies have developed optimized wavelength sampling strategies to reduce the number of computations needed (van Dalum et al., 2019; Veillon et al., 2021).

Although the translation of TARTES in Fortran was initially motivated by the integration in Crocus, it is a self-contained model that can be integrated into any other model. The source code is part of SURFEX (http://www.umr-cnrm.fr/surfex/, last access: 1 March 2024, Masson et al., 2013). We call this version TARTES.F hereafter.

TARTES.F was developed in 2014 exactly following the Python version. It contained the same physics and parameters. However, it has not been updated since then and now slightly differs from the most recent Python version. The main difference is the ice refractive database that is based on Warren and Brandt (2008) only (Picard et al., 2016, was not available). In 2019, impurities were added (Tuzet et al., 2017) using specific MAE values that slightly differ from the Python version (not used here).

In terms of performance, a simulation for a two-layer snowpack at 106 wavelengths repeated 10 000 times takes 3.4 s with TARTES.F on a commodity laptop, while the Python version takes 148 s, about 40 times longer.

3.3 Related software and libraries for snow optics

3.3.1 SnowTARTES web application

SnowTARTES is an interactive web application (https://snow.univ-grenoble-alpes.fr/snowtartes, last access: 24 March 2024) meant to easily compute spectral albedo and irradiance profiles using TARTES without writing code. SnowTARTES uses the Python version and thus provides exactly the same results. The snowpack is described layer by layer in a text form. In order to conduct a sensitivity analysis, any of the input parameters can be prescribed as a range (start, end, step) instead of a single value. These ranges are combined, launching multiple calculations (limited to a maximum of 10 for the sake of visibility in the plot). The calculated albedo spectra are immediately plotted (one curve for each calculation) and can be downloaded as a comma-separated-value-formatted file.

SnowTARTES offers a selection of grain shapes to chose from, each one corresponding to a pair (B₀,g₀) based on Libois et al. (2013) and Robledano et al. (2023). Similarly, it offers a selection of seven background albedo spectra (grass, ice, several soils, along with 0 and 1) extracted from the Johns Hopkins University Spectral Library (ECOSTRESS and formally ASTER library, https://speclib.jpl.nasa.gov/, last access: 24 March 2024).

3.3.2 Snowoptics Python package

The Python package Snowoptics (https://github.com/ghislainp/snowoptics, last access: 24 March 2024) provides a series of functions to compute albedo, extinction, and BRDF for a semi-infinite homogeneous snowpack using the AART theory (Kokhanovsky and Zege, 2004; Kokhanovsky, 2012). The arguments of these functions are similar (name and unit) to TARTES. The package also provides functions to compute the effect of the slope on measured albedo and to correct from the slope effect based on Picard et al. (2019), which is not available in TARTES. Here, Snowoptics is used in Sect. 4.2 to compare TARTES with AART.

3.3.3 AtmosRT Python package

Because of the impact of the illumination geometry on the spectral albedo and of the spectral distribution of incident irradiance on the broadband albedo, it is necessary to know the spectral solar irradiance. There are many available radiative transfer models for the atmosphere that can provide this information for TARTES calculations, such as SMARTS (Gueymard, 2001), MODTRAN (Berk et al., 2014), or libRadtran (Emde et al., 2016), but the offer in Python is limited. PyRTM is an unmaintained software package (https://github.com/Queens-Applied-Sustainability/PyRTM, last access: 24 March 2024) providing a Python 2 interface to access two general atmospheric radiative transfer models written in Fortran, namely SBDART (Ricchiazzi et al., 1998) and SMARTS. From this, we developed the AtmosRT package, including support for Python 3 and a few additional minor improvements for ease of use. The function atmospheric_incident_spectrum is implemented in TARTES to perform simple calculations with SBDART through AtmosRT and directly provides the total flux and the direct fraction at each wavelength as required by the TARTES functions. The function takes the solar zenith angle and cloud optical depth as input and uses the default cloud optical properties of SBDART (Ricchiazzi et al., 1998).

4 Results

Several simulations with TARTES and other models are compared in this section. By default, unless specified, we consider a semi-infinite homogeneous snowpack, i.e., made of a single layer, thick enough so that the bottom boundary does not influence the albedo and the presented profiles. The layer has an SSA of 20 m² kg⁻¹, and the density is 350 kg m⁻³, but this latter variable has no influence on thick-snow albedo in the conventional radiative transfer framework used in TARTES (Malinka, 2023). Other particular conditions of the simulations are indicated for each case.

4.1 Self-consistency checks

TARTES has a few options to select between different approximations or different modes of calculations. Here, we compare these approximations and check their consistency.

4.1.1 Diffuse illumination

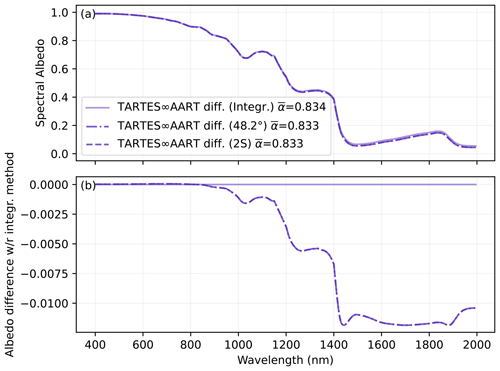
The three methods to take into account diffuse illumination in TARTES are compared in Fig. 2 for the default TARTES version and in Fig. 3 for the TARTES∞AART version, for the spectral and broadband albedo of the default semi-infinite snowpack under typical illumination for wintertime alpine snow. The reference method uses integration (denoted by “Integr.”) of n simulations in direct illumination mode with a solar zenith angle varying from 0 to 90° (with n=128 regular steps in cosine of the angle). The results show a close agreement with the direct calculations at a zenith angle of 48.2°, the equivalent angle obtained by matching the diffuse and direct expressions of AART albedo (Sect. 2.7). The latter approximation yields relatively accurate albedo, with a deviation lower than 0.003 at wavelengths <1300 nm and never exceeding 0.007 in the investigated wavelength range (up to 2000 nm). The broadband albedo difference is virtually zero (0.0006). Similar results are obtained for the TARTES∞AART variant. The maximum error is 0.011 in this case, and the broadband albedo difference is 0.001.

In contrast, the formulation using diffuse illumination for the upper boundary condition of the two-stream approximation (2S method) performs poorly in the original TARTES model, with deviations reaching nearly 0.02 at wavelengths <1300 nm and barely acceptable (>0.03) beyond 1400 nm, although the broadband albedo difference of 0.0045 probably remains small enough for most applications. The inherent difficulty in handling diffuse radiation with the δ-Eddington approximation was discussed extensively by Wiscombe (1977) and Wiscombe and Warren (1980). Conversely, the 2S method works well with the TARTES∞AART as it gives nearly equivalent results to the direct simulation at 48.2° (the dotted curves overlap in Fig. 3b). This agreement is expected as TARTES∞AART was designed to be equivalent to AART, and 48.2° is the equivalent angle for the direct and diffuse illumination in this theory.

As a conclusion, we suggest not to use the 2S method for practical applications, since it provides almost no benefit compared to the 48.2° method (at best an agreement, at worst a large error) over the spectral range of interest, and the calculation is only slightly faster than for a direct beam calculation (23 ms vs. 34 ms for the computation in Fig. 2 involving 320 wavelengths).

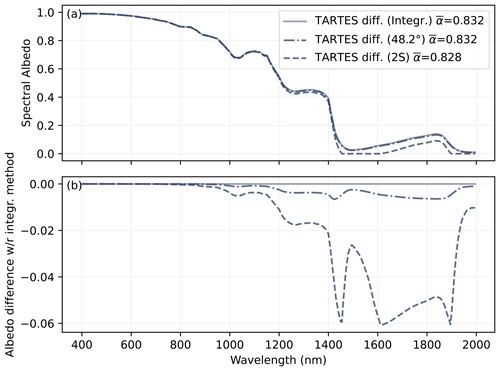
Figure 2 Comparison of albedo under diffuse illumination computed by three methods: (1) by integrating over all incident angles, (2) using a unique direct beam at the equivalent angle predicted by the AART (48.2°), and (3) using diffuse radiation for the upper boundary condition in the two-stream formulation (abbreviated 2S). The snowpack is semi-infinite with SSA = 20 m² kg⁻¹. The broadband albedo (ω) is indicated in the legend for each spectrum.

Figure 3 Same as Fig. 2 but for the TARTES∞AART variant.

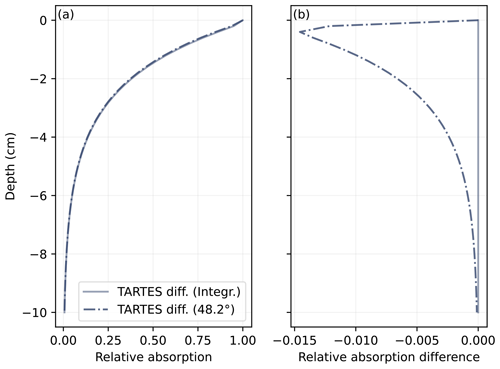
Figure 4 Comparison of the absorption profile under diffuse illumination computed by two methods: (1) by integrating over all incident angles and (2) using a unique direct beam at the equivalent angle predicted by the AART (48.2°). The snowpack is semi-infinite with SSA = 20 m² kg⁻¹.

For the profiles of irradiance, absorption, and actinic flux, only two methods are implemented: the integration and the direct 48.2° calculation. Figure 4 shows the profile of absorption close to the surface of the semi-infinite snowpack at 800 nm, a wavelength maximizing absorption since snow co-albedo (the proportion of absorbed radiation) is greater than at shorter wavelengths, and the incoming solar radiation is still relatively large compared to longer wavelengths. Only the original TARTES version is used. At this wavelength, 90 % of the absorption occurs in the topmost ≈4 cm (Fig. 4a) for the snowpack considered here. The profiles of absorption obtained with both methods look similar, with maximum differences of about 1.5 %, reaching close to the surface, as seen in Fig. 4b.

Based on these results and calculations with a shallower snowpack (not shown), the direct 48.2° calculation was chosen as the default method to simulate diffuse radiation in TARTES. The integration is in principle more accurate but requires many more computations (solving the linear system for 128 angles instead of 1) even though measuring the execution time (51 ms instead of 34 ms) does not show a difference in the same proportion because only the constant vector of the linear system depends on the angle, not the matrix. In practice, users who prefer the accuracy offered by the integration method can explicitly set this option.

4.1.2 Consistency between albedo, profile of irradiance, and profile of absorption calculations

As the albedo, irradiance, and absorption profiles in snow and the absorption below the snowpack are computed by three distinct Python functions, it is worth checking that energy is conserved across these different quantities. To this end we first compare the albedo with the absorption profile. The semi-infinite snowpack is split in numerical layers of 1 cm (top first meter), even though their properties are identical (SSA = 20 m² kg⁻¹, density = 350 m² kg⁻¹). Comparing the sum of all layer absorption A (divided by the incident irradiance, set arbitrarily to 1 W m⁻²) with the co-albedo 1−α, we found a residual numerical error $<\mathrm{2}\times {\mathrm{10}}^{-\mathrm{16}}$ for all wavelengths, which is close to the machine 64 bit floating point limit. Likewise, we checked that the calculated albedo perfectly matches the ratio of upwelling and downwelling irradiance at the surface, calculated from the vertical profiles of irradiance. These two tests are part of the automatic test suite available in the TARTES code base.

4.2 Comparison of TARTES with the asymptotic analytical radiative transfer (AART)

The comparison between TARTES and the AART to simulate the diffuse and direct albedos of a semi-infinite snowpack (a single thick homogeneous layer) is presented in Figs. 5, 6, and 7.

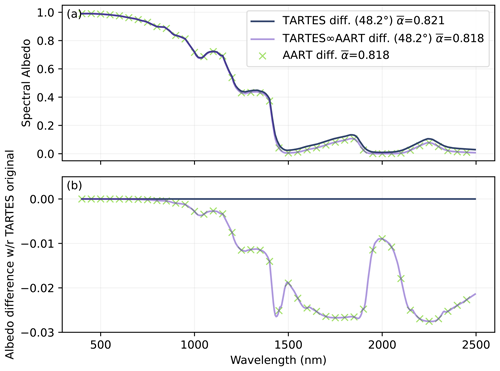
Figure 5 Comparison of the diffuse albedo spectra computed by TARTES (with 48.2°), TARTES∞AART (with 48.2°), and standalone AART under diffuse illumination. Panel (a) shows the albedo and panel (b) the difference with respect to TARTES. The snowpack is semi-infinite with SSA = 20 m² kg⁻¹.

Figure 6 Same as Fig. 5 but for direct illumination (SZA = 60°).

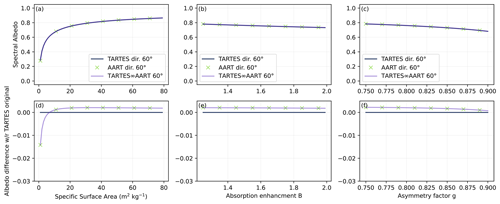
Figure 7 Comparison of direct albedo (SZA = 60°) at 1300 nm as a function of SSA, B₀, and g₀ computed by TARTES and AART. The snowpack is semi-infinite with SSA = 20 m² kg⁻¹.

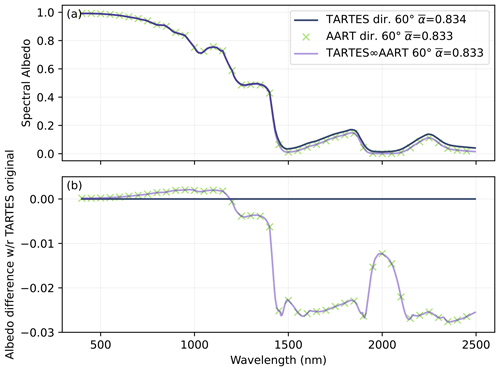
Used with the same parameters (SSA, density, B₀, and g₀), the comparison between AART and TARTES∞AART for both the diffuse and direct illuminations demonstrates that the formulation in Eqs. (40)–(41) and (46)–(47) allows our code to conform to the AART analytical expression in the case of a semi-infinite homogeneous snowpack. The maximum error is indeed $\mathrm{4}\times {\mathrm{10}}^{-\mathrm{16}}$, corresponding to numerical rounding errors. This new formulation can be useful in cases where the conformity with AART is essential.

AART is also indistinguishably similar to the original TARTES model in the visible range and up to 1400 nm on the spectrum plots in Figs. 5a and 6a. However, the residuals in Figs. 5b and 6b highlight that the differences are much larger than numerical rounding errors. Nonetheless, they remain <0.015 up to 1400 nm. At longer wavelengths the differences become noticeable and increase up to around 0.024. Interestingly, the differences between the models are mainly significant in the domain of strong ice absorption, where none of these models is expected to be valid. Indeed, AART is meant to be valid only for weak absorption (see Fig. 8 of Kokhanovsky and Zege, 2004), and TARTES uses the δ-Eddington approximation, which likewise is only relevant for weak absorption (Wiscombe, 1977). Depending on the application, the reported errors in the longer wavelengths of the solar spectrum can be either negligible (e.g., broadband albedo calculations, absorption calculation) or major (e.g., spectroscopic applications at 1550 nm as in Gallet et al., 2009).

To further explore the difference between the models, Fig. 7 shows the albedo at 1300 nm as a function of SSA, B₀, and g₀. Again we observe the perfect similitude between AART and TARTES∞AART. On the other hand, the difference with the original TARTES model is small except for very low SSA, where it reaches a maximum absolute value of 0.015. This error is small in absolute albedo but corresponds to a significant relative error considering that albedo is <0.2. The differences when B₀ and g₀ are varied are even weaker over the investigated range. Exploring other wavelengths (results not shown) indicates that the difference is much smaller in the visible range and progressively increases in the near-infrared range. These results obtained for the SSA and B₀, along with the wavelength dependence, again confirm that the models mainly diverge when the single-scattering albedo is low (it is lower for large grains than for smaller ones), which is when the absorption is strong.

To provide a more general recommendation to future users, we explored a wide range of usual conditions (λ<1400 nm, SSA in 5–100 m² kg⁻¹, and SZA in 0–70°) and found a maximum difference of 0.025 (at SSA = 5 m² kg⁻¹, SZA = 40°, and λ = 1400 nm). Furthermore, 90 % of the simulations show a very small difference <0.002, leading to the conclusion that, for a semi-infinite snowpack, TARTES is virtually equivalent to AART in most usual conditions.

4.3 Comparison of TARTES with other numerical snow radiative transfer models

TARTES is now compared to two widely used models: DISORT-Mie (with 16 streams) and SNICAR-ADv3 (online tool, http://snow.engin.umich.edu/, last access: 6 December 2024). Since the first model (and the second until a recent version) is limited to spherical particles, we consider this shape for all the simulations. In TARTES, this is achieved by letting B₀=1.25 and g₀=0.895 (Libois et al., 2013). The conditions of simulations are as similar as possible among the models. For instance, the same ice refractive index (Picard et al., 2016) is used for the three models. TARTES.F is also included in this comparison, but with a different ice refractive index (Warren and Brandt, 2008) as discussed below.

4.4 Clean semi-infinite snowpack

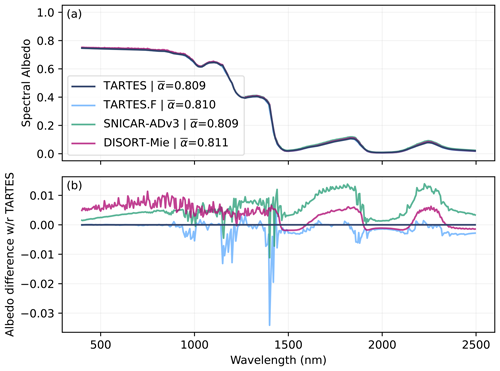
Figure 8 shows diffuse albedo simulations for the different models for a semi-infinite snowpack with SSA = 20 m² kg⁻¹. Overall the agreement is very good, with virtually unnoticeable differences in Fig. 8a, except for TARTES∞AART, which stands out for wavelengths higher than 1400 nm. The residual albedo panel (Fig. 8b) reveals small differences of around 0.01 and occasionally up to 0.03 in amplitude, which may be significant for some applications. From this comparison no outliers or particularly similar models emerge (except the new TARTES∞AART formulation). Furthermore, the presence of spikes and oscillations suggests numerical issues rather than physical differences or bugs. This is also suggested by the differences between the Python and Fortran versions of TARTES, despite a common theory and initial code. On average, TARTES appears closest to DISORT-Mie with a root mean square difference (RMSD) of 0.0035, followed by TARTES.F with a RMSD = 0.0039 and SNICAR-ADv3 with a RMSD = 0.0061. The agreement is overall much better for the shorter wavelengths <1400 nm as also noted for the comparison with AART. The differences in broadband albedo reported in Fig. 8a are very small.

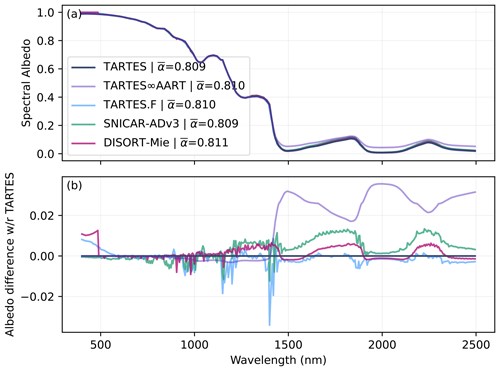
Figure 8 Comparison of diffuse albedo spectra calculated by different numerical models for a semi-infinite snowpack with SSA = 20 m² kg⁻¹.

For λ<490 nm, DISORT-Mie yields an albedo of 1.0, which is certainly a rounding error. In this highly reflective domain, the 32 bit float arithmetic used by DISORT-Mie is certainly insufficient. The difference observed in the visible range for TARTES.F is explained by the use of the refractive index database (Warren and Brandt, 2008) (hard-coded in the Fortran code) that has been recently updated with stronger absorption values (Picard et al., 2016) used for the other model simulations.

4.5 Clean two-layer snowpack

Figure 9 shows the comparison for a typical two-layer snowpack made of a thin layer of fresh snow (a 1 cm thick layer with SSA = 50 m² kg⁻¹ and density 150 kg m⁻³) on top of slightly aged snow (an infinitely thick layer with SSA = 20 m² kg⁻¹). SNICAR-ADv3 is not included because the online version used in this paper does not handle multiple layers. Overall the results are similar to the one-layer case. The maximum difference is about 0.03, the average difference is much smaller, and the errors share some similar patterns with the former comparison.

As for the single-layered snowpack, TARTES∞AART stands out in the longer wavelengths. It was mainly implemented to check the conformity of TARTES with AART from a theoretical point of view but appears to provide no practical benefit over the original TARTES model. For this reason, we do not further consider it. The original TARTES model is kept as the default in the following and in the code.

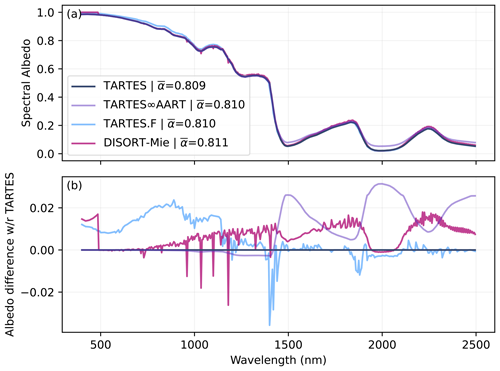
Figure 9 Comparison of diffuse albedo spectra calculated by different numerical models for a two-layer snowpack. A 1 cm layer with SSA = 50 m² kg⁻¹ and density = 150 kg m⁻³ is overlying a semi-infinite layer with SSA = 20 m² kg⁻¹.

4.5.1 Clean thin snowpack

The extreme case of a 1 cm thick snowpack with a perfectly black underlying surface (bottom albedo α_B= 0) is presented in Fig. 10. In principle, the two-stream approximation is less adequate in these conditions (corresponding to ${\mathit{\tau }}^{*}=\mathrm{7}$–17 depending on the wavelength) compared to the DISORT-Mie model. The results indeed show a degradation in the visible range, where the underlying surface has an impact (the albedo is notably lower than in Fig. 8). Nevertheless, the difference remains under 0.01 in this range, which is comparable to the more favorable case of the thick snowpack.

Figure 10 Comparison of diffuse albedo spectra calculated by different numerical models for a thin snowpack (1 cm thick) with SSA = 20 m² kg⁻¹ and density = 350 kg m⁻³ overlying a dark surface (α_b=0).

4.6 Snowpack polluted with black carbon and dust

Light-absorbing impurities can be taken into account by all models considered here. Here we compare simulations with particles much smaller than the wavelength (BC) first and then much larger than the wavelength (dust).

Figure 11 shows semi-infinite diffuse albedo spectra obtained by the three models for BC concentrations of 100, 500, and 2000 ng g⁻¹. For the sake of testing and validation, we use such extreme values compared to the typical amount found in snow (Bisiaux et al., 2012; Kang et al., 2020). Contrary to the clean snowpack, significant differences are obtained for concentrations of 500 and 2000 ng g⁻¹. The difference reaches 0.04 around 500 nm between DISORT-Mie and TARTES at the maximal concentration. Such a value, in the visible range where the solar irradiance is maximum, has a dramatic effect on the absorption. This is reflected in the differences in broadband albedo, which are limited to 0.001–0.006 between SNICAR-ADv3 and TARTES but reach 0.005–0.022 between DISORT-Mie and TARTES depending on the concentration.

Figure 11 Comparison of diffuse albedo calculated by different numerical models for different BC concentration. The snowpack is semi-infinite, SSA = 20 m² kg⁻¹, and density = 350 kg m⁻³.

Figure 12 Diffuse albedo at 550 nm as a function BC particle radius, calculated by different numerical models. The snowpack is semi-infinite, BC concentration = 500 ng g⁻¹, SSA = 20 m² kg⁻¹, and density = 350 kg m⁻³.

These differences are likely explained by the different representations of the impurities in these models. For maximal comparability, all the simulations assume the same refractive index and density of BC. They are taken from SNICAR-ADv3 (Flanner et al., 2021), which is also the default in TARTES v2.0. The three models also assume that the particles are suspended in the air (a representation known as external mixing, Flanner et al., 2012). However, the size of the particles differs for reasons inherent to each model. SNICAR-ADv3 and DISORT-Mie use Mie theory (spherical particles); however, SNICAR-ADv3 simulates a lognormal distribution of particle sizes, with a mean mass-weighted radius of 67 nm for black carbon, while our implementation of DISORT-Mie is limited to a mono-disperse collection of spheres. A radius of 67 µm is taken for Fig. 11, but this is not strictly equivalent to the SNICAR-ADv3 configuration. On the other hand, TARTES uses the Rayleigh approximation that is only valid for small particles. Comparing MAE predicted by TARTES and reported for SNICAR-ADv3 in Fig. 3a in Flanner et al. (2021), we observe (not shown) a slightly higher MAE with TARTES at 400 nm (+20 %), an agreement at 490 nm, and a slightly lower MAE at 1000 nm (−23 %), which explains the lower TARTES albedo at wavelengths <500 nm and higher at longer wavelengths observed in Fig. 11.

To illustrate the influence of the particle size, Fig. 12 shows the variations of albedo at 550 nm predicted by DISORT-Mie. TARTES compares very well with DISORT-Mie for the lowest radii (blue marker overlapping the violet curve in Fig. 12), while SNICAR-ADv3 slightly overestimates the DISORT-Mie albedo at 67 µm (green marker). This results from the fact that SNICAR simulations with BC mean radius of 67 µm include actual impurities with radii smaller and larger than 67 µm (it assumes a lognormal size distribution) for which the absorption is larger than at 67, as 67 µm appears to be very close to the minimum absorption. Nevertheless, the variations of albedo in the range 0–150 nm are relatively small (<0.02), which seems acceptable with respect to the other uncertainties on the properties of the light-absorbing particles (concentration and density).

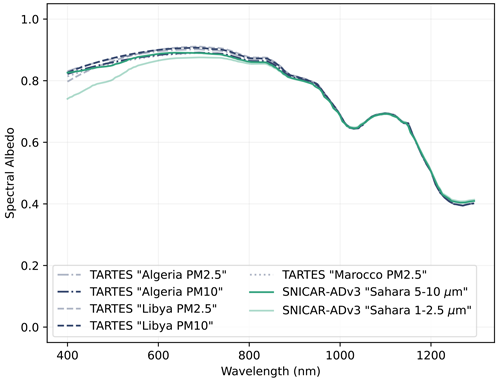
Figure 13 shows a comparison of different dust types (different origins and sizes) and models. The concentration is 100 µg g⁻¹, which is realistic in alpine snow (Dumont et al., 2020; Di Mauro et al., 2024). The agreement is again fairly good between TARTES and SNICAR-ADv3, which results from the similar MAE values for the Libya PM_2.5 and Algeria PM_2.5 dusts (400 nm = 110 and 73 m² kg⁻¹) used in TARTES, compared to the values for the Sahara used in SNICAR-ADv3 (Flanner et al., 2021, Table 2, Fig. 3).

Figure 13 Comparison of diffuse albedo spectra calculated for different dust types and sizes by two models. The snowpack is semi-infinite, dust concentration = 100 µg g⁻¹ for all types, SSA = 20 m² kg⁻¹, and density = 350 kg m⁻³.

4.7 Simulations of profiles of absorption, irradiance, and actinic flux.

Figure 14 illustrates TARTES ability to calculate profiles of absorption, irradiance, and actinic flux for a three-layer snowpack with SSA = 50, 20, and 20 m² kg⁻¹ from top to bottom; density = 300, 300, and 350 kg m⁻³; and thickness = 10 and 20 cm, with the last layer being infinitely thick. The wavelength is 600 nm. The profiles are presented relative to the incident flux; this is why the x-axis label of each graph is unitless.

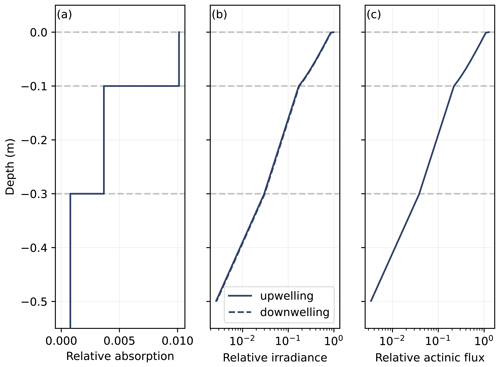
Figure 14 Profiles of (a) absorption, (b) irradiance, and (c) actinic flux for a three-layer snowpack with SSA = 50, 20, and 20 m² kg⁻¹; density = 250, 250, and 350 kg m⁻³; and thickness = 5 cm, 20 cm, and ∞. The illumination is at 60° and the wavelength is 600 nm.

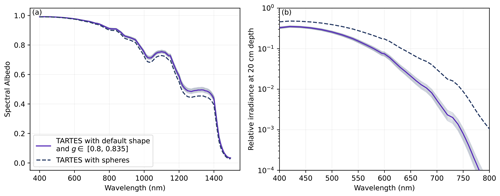
Figure 15 Spectral albedo (a) and irradiance at 20 cm depth, relative to the incident irradiance at the surface (b) for spheres and snow (i.e., B=n² and $g\in [\mathrm{0.8},\mathrm{0.835}]$ according to Robledano et al., 2023). The snowpack is semi-infinite with SSA = 20 m² kg⁻¹, and the illumination is at 60°.

Regarding the absorption profile, the convention in TARTES is to return the total radiation absorbed in every layer which is suitable for a direct input in thermodynamic calculations. The unit is the same as that of the incident flux prescribed by the user (variable totflux, usually $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{nm}}^{-\mathrm{1}}$ in real applications). Regarding the actinic flux, the convention in TARTES is to return values in the same unit as the incident flux, which is prescribed by the user in the variable totflux. The conversion from spectral irradiance $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{nm}}^{-\mathrm{1}}$ to actinic flux $\mathrm{photons}{\mathrm{s}}^{-\mathrm{1}}{\mathrm{cm}}^{-\mathrm{2}}{\mathrm{nm}}^{-\mathrm{1}}$ is left to the user. The irradiance and actinic flux profiles (Figs. 14b, c) show a series of near-linear decreasing trends in logarithm scale with varying slopes, which is equivalent to near-exponential decreases in the natural scale with the varying rate. This rate is approximately the asymptotic extinction (Libois et al., 2013), which can be deduced by approximating the AART extinction Eq. (41) as

$$\begin{array}{}\text{(84)}& k_{\mathrm{e}}=\mathit{\rho }\sqrt{{\displaystyle \frac{\mathrm{12}B\mathit{\chi }\mathrm{SSA}(\mathrm{1}-g^G)}{\mathrm{4}\mathit{\lambda }{\mathit{\rho }}_{\mathrm{ice}}}}}.\end{array}$$

This formulation is implemented in the Snowoptics package, function extinction_KZ04. Here we find k_e=9.14, 5.78, and 8.09 m⁻¹ for the layers from top to bottom, equivalent to e-folding depths ($l_{\mathrm{e}}=\mathrm{1}/k_{\mathrm{e}}$) of 11, 17, and 12 cm respectively. Calculating the vertical gradient of the irradiance logarithm from Fig. 14b (excluding 1 cm at the top and bottom of each layer) yields similar values: k_e=11.1, 5.78, and 8.09 cm respectively.

The behavior of the irradiance gradient in the top layer is affected by the proximity of the surface (where the direct radiation is progressively converted into diffuse radiation) and the junction with the next layer that has different optical properties. This tends to bend the curve, meaning that the profile of irradiance is not exactly exponential. The actinic flux shows a similar behavior.

To conclude, this example illustrates that the profiles of irradiance and actinic flux can be approximated at first order by exponential decreases whose decay can be calculated from snow properties (density, SSA, B₀, and g₀) in each layer (Eq. 84)). However, near the surface and in the presence of contrasted layers, it is recommended to use a proper multi-layered radiative transfer model such as TARTES.

5 Discussion

TARTES was designed to perform simple radiative transfer calculations in a plane-parallel multi-layered snowpack, with the unique possibility of describing the shape of the particles using two parameters also used in the AART theory, namely the absorption enhancement parameter B and the asymmetry factor g (Libois et al., 2013). This choice is important and motivated by two reasons. First these parameters are the main factors controlling the influence of the shape on the absorption and scattering properties in a weakly absorbing medium. Second, these parameters can be calculated for two-phase porous media, without assuming that snow is a collection of particles with some given geometrical shape (Malinka, 2014; Robledano et al., 2023). While the physical meaning of B and g is often presented for single particles (e.g., Libois et al., 2013), the definition of these parameters is independent of the concept of particles. For this reason we qualify these parameters as descriptive of the “optical shape of snow” without requiring the medium to be actually composed of distinct particles (spheres, fractals, or cubes). Moreover, it was found that B=n² applies very well to snow (Robledano et al., 2023) and only g varies, but in a narrow range for snow compared to across common geometrical shapes (spheres, fractals, hexagonal plates). Furthermore, the value of B=n² and the values of g clearly indicate that snow does not behave as a collection of ice spheres. These results make TARTES inherently more suitable to snow than Mie-based models. Note that most simulations presented in this paper used the values of B and g for spheres for the sole purpose of comparison with the established Mie-based models. In practice, we do not recommend running TARTES in these conditions. Instead we recommend B=n² and g=0.82 (at non-absorbed wavelengths), which is the middle of the range found by Robledano et al. (2023). These values are the defaults in TARTES v2.0. Figure 15 illustrates the difference in albedo and irradiance at depth (20 cm) when considering the default B and g values for snow or the values for spheres. The albedo is higher for snow than for spheres for a given SSA and density by 0.018 on average over the range 400–2000 nm and reaches 0.042 at 1400 nm. These values are significant for surface energy budget calculations, with a potent large impact in climate simulations (Räisänen et al., 2017). The irradiance at 20 cm depth is weaker for snow than for spheres, by about a factor 10 at 750 nm for instance. These differences can be explained by the strong forward scattering of spheres (high g) and the lower absorption enhancement parameter (low B), which tends to overestimate the penetration depth.

Despite this advantage, TARTES presents some limitations owing to its simplicity. It uses the conventional unpolarized radiative transfer, neglecting interferences, near-field and packing effects, and polarization effects. As a plane-parallel model, the surface is supposed to be perfectly flat, and surface roughness is neglected, which may impact simulations on rough terrain, especially at grazing angles. Likewise, the layers are perfectly smooth and horizontally semi-infinite. In practice, in areas where horizontal heterogeneity is strong, for instance as a result of snowdrift, this assumption might be inappropriate to simulate snow optical properties. Also, TARTES only considers snow excluding any other material that might be present in the snowpack and models its optical behavior as a homogeneous scattering medium. It means that the layers must be much thicker than the grain size (i.e., the free photon path). Regarding impurities, only their absorption is considered, and they are randomly distributed. Consistent with the choice of only using the asymmetry factor g instead of requiring the full phase function, the two-stream approximation was selected to solve the radiative transfer equation in TARTES instead of a multi-stream approach as in DISORT-based models. As a direct consequence, TARTES cannot calculate the bidirectional reflectance distribution function (BRDF), which is essential for instance for satellite remote sensing applications. TARTES was initially designed for energy balance computations and only provides hemispherically averaged quantities, namely surface albedo, absorption in each layer, and profiles of upwelling and downwelling radiation flux.

As TARTES relies on the geometrical optics approximation, the allowed range of ice particle sizes (or more generally, the length scales in the microstructure) is limited. The particles must be significantly larger than the wavelength (typically >5 µm in the solar range), which is usually valid for most snow types (Fierz et al., 2009; Walden et al., 2003). In contrast, this assumption is invalid for light-absorbing impurities such as BC that usually come as sub-wavelength-sized particles. It is still possible to account for the absorption of these small particles by neglecting their scattering. For very small particles, the Rayleigh approximation works well and allows a rigorous formulation of the absorption coefficient as a function of the particle complex refractive index and density. This approximation is acceptable for BC. For larger particles, such as dust, TARTES relies on tabulated values of mass absorption efficiency (MAE), which either can be obtained from direct measurements or can be estimated by offline Mie calculations as in SNICAR. We believe that this simple treatment of light-absorbing properties in snow is sufficient and of adequate complexity given the considerable uncertainties associated with the physical properties of light-absorbing impurities and the difficulty in measuring or simulating their concentration in snow.

Despite the differences between TARTES and the other models, the simulations of albedo presented in this paper (Sect. 4) generally show a good agreement, typically within 0.02. Notably, the errors between different models are typically lower than between the Python and FORTRAN versions of TARTES, which suggests that at this degree of agreement, most of the residual errors can result from implementation details and numerical issues rather than theoretical differences.

Possible future improvements in TARTES include the inclusion of terrain slopes, bubbly ice and slush layers, the extended impurity database, and internal mixture impurities.

6 Conclusions

TARTES and the ecosystem of tools developed around this radiative transfer model for snow allow accurate simulations of several snow optical properties, most notably the spectral albedo and irradiance profiles in the snowpack. TARTES is intended to be user-friendly and easy to improve, thanks to the Python implementation. While technically the results of this paper demonstrate that TARTES performs equally well compared to other existing models when assuming snow as a collection of ice spheres, TARTES can handle a more general representation of snow that is more representative of natural snow than historical models based on idealized shapes to represent snow grains. For this particular reason, and despite the overall simplicity of the approximations implemented in TARTES, this model is able to accurately predict the optical properties of snow with a given SSA and density and is perfectly suited for implementation in atmospheric models, including climate models.