An improved model for air–sea exchange of elemental mercury in MITgcm-ECCOv4-Hg: the role of surfactants and waves

The air–sea exchange of elemental mercury (Hg⁰) plays an important role in the global Hg cycle. Existing air–sea exchange models for Hg⁰ have not considered the impact of sea surfactants and wave breaking on the exchange velocity, leading to insufficient constraints on the flux of Hg⁰. In this study, we have improved the air–sea exchange model of Hg⁰ in the three-dimensional ocean transport model MITgcm (MIT General Circulation Model) by incorporating sea surfactants and wave-breaking processes through parameterization, utilizing the total organic carbon concentration and significant wave height data. The inclusion of these factors results in an increase of 62 %–225 % in the global transfer velocity of Hg⁰ relative to the baseline model. Air–sea exchange flux is increased in mid-latitude to high-latitude regions with high wind and wave-breaking efficiency, while it is reduced by surfactant and concentration change at low latitudes with low wind speeds and in nearshore areas with low wave heights. Compared with previous parameterizations, the updated model demonstrates a stronger dependence of Hg⁰ air–sea exchange velocity on wind speed. Our results also provide a theoretical explanation for the large variances in estimated transfer velocity between different schemes.

1 Introduction

The air–sea exchange of elemental mercury (Hg⁰) contributes up to one-third of total atmospheric mercury (Hg) emissions. This process is crucial for the global Hg cycle, as it prolongs the residence time of Hg in the biosphere (Amos et al., 2015) and reduces the reservoir of divalent mercury (Hg^II) in the surface ocean (Lavoie et al., 2013). The air–sea exchange flux of Hg⁰ is generally controlled by both kinetic (gas transfer velocity, $k_{{\mathrm{Hg}}^{\mathrm{0}}}$) and thermodynamic (partial-pressure-related concentration gradients) forcing (Wanninkhof, 1992; Wanninkhof et al., 2009; Kuss et al., 2011). However, the lack of direct measurements of Hg⁰ transfer velocity results in substantial uncertainty in estimating large-scale air–sea Hg⁰ exchange (Zhang et al., 2019). Considering that wind is the primary force driving turbulence in the upper ocean, the transfer velocity is typically parameterized with wind speed through linear (Jähne et al., 1979; Liss and Merlivat, 1986), quadratic (Wanninkhof et al., 1992; Nightingale et al., 2000), or cubic relationships (McGillis et al., 2001; Edson et al., 2011). The estimated magnitude of the global air–sea exchange of Hg ranges from 2840 to 3950 Mg a⁻¹ (Zhang et al., 2019; Liss and Merlivat, 1986; Wanninkhof et al., 1992; McGillis et al., 2001; Zhang et al., 2023). Osterwalder et al. (2021) further demonstrated that different transfer velocity parameterizations can lead to more than a 4-fold variation in air–sea exchange flux estimates along the coastal Baltic Sea (0.3 ± 0.6 to 2.6 ± 0.6 ng m⁻² h⁻¹). However, the gas transfer velocity is influenced by other environmental factors such as surfactants and waves (Wurl et al., 2017). Therefore, relying solely on wind speed may not be sufficient to quantify $k_{{\mathrm{Hg}}^{\mathrm{0}}}$.

Surfactants are ubiquitous in the sea surface microlayer (SML) and have associations with marine biological activity (Lin et al., 2002; Wurl et al., 2011). They are generally believed to affect air–sea exchange in two ways: first, surfactants act as a physicochemical barrier that suppresses Hg⁰ air–sea exchange and, second, surfactants alter sea surface hydrodynamics, thus affecting turbulent energy transfer (McKenna and McGillis, 2004; Engel et al., 2017), microscale fragmentation, and surface renewal processes. Both experimental and modeling studies reveal that surfactants have a significant inhibitory effect on the transfer velocity of various gases. Notably, a field experiment demonstrated that the injection of artificial surfactant resulted in a suppression of transfer velocity (k_w) by up to 55 % (Salter et al., 2011). Mesarchaki et al. (2015) observed that surfactants reduced the transfer velocity of N₂O by up to a factor of 3 in a large-scale wind-wave tank. Modeling research has shown that surfactants could reduce global net CO₂ exchange by 15 %–50 % (Asher et al., 1996; Tsai and Liu, 2003; Wurl et al., 2016). Studies conducted by Kock et al. (2012) in the equatorial North Atlantic demonstrated an overestimation of N₂O using conventional k_w methods, while the scheme considering the effect of surfactants (Tsai and Liu, 2003) aligned well with the observations. Nevertheless, the impact of surfactants on the Hg⁰ air–sea exchange remains unknown.

Breaking waves produce bubbles that significantly facilitate gas fluxes by increasing the air–water interface and intensifying turbulence as the bubbles rise (Asher et al., 1996; Wanninkhof et al., 2009). This is particularly pronounced for insoluble gases (Woolf and Thorpe, 1991; Kihm and Körtzinger, 2010; Vagle et al., 2010). Woolf (1997) estimated that bubbles contribute about 30 %–50 % to the global CO₂ transfer velocity, assuming a proportional relationship between bubble-mediated transfer velocity and the whitecap fraction. Historically, several models have been proposed to determine CO₂ exchange at the sea surface. Zhang et al. (2006) found that the enhancement of gas transfer velocity for O₂ and N₂ due to bubbles can be as high as 20 %. According to Reichl and Deike (2020), approximately 40 % of the net CO₂ flux between the air and the ocean is attributed to bubbles. The significance of bubble effects depends on the solubility of gases in seawater. It is anticipated that bubble effects will be more pronounced for Hg⁰, given its lower solubility. In this study, we have improved the MITgcm ocean model to gain a better understanding of the mechanisms that govern the air–sea exchange of Hg⁰ at the atmosphere–ocean interface by including the effects of surfactants and wave-breaking processes. Sensitivity experiments are also conducted to analyze the effects of individual factors on the Hg⁰ transfer velocity. Additionally, we have examined the dependence of Hg⁰ transfer velocity on wind speed.

2 Methodology

2.1 MITgcm

MITgcm (MIT General Circulation Model; http://mitgcm.org/, last access: 16 May 2024) is employed to simulate the air–sea exchange of Hg⁰. We use a configuration that has been fit to observations in a least-squares approach (ECCO v4; Forget et al., 2015) (we refer to this combined setup as “MITgcm-ECCOv4-Hg”). This three-dimensional configuration features a horizontal resolution of 1° × 1° and comprises 50 vertical layers. Near the Equator (0.5° latitude × 1° longitude) and the Arctic (approximately 40 km × 40 km), a higher horizontal resolution is adopted to better simulate ocean currents. It calculates ocean physical processes including vertical advection, diapycnal diffusion, and convective mixing based on ocean state estimates from ECCO v4. The meteorological field of atmospheric variables (temperature, wind stress, precipitation, humidity, and radiation) serves as the boundary layer of the ocean and is from the 6 h ERA-Interim reanalysis, spanning 1992 to 2017.

The model has the capacity to simulate the marine Hg cycles, which include the redox conversion between Hg⁰ and Hg^II, the methylation and demethylation of monomethylmercury (CH₃Hg) and dimethylmercury ((CH₃)₂Hg), the air–sea exchange of Hg⁰ and (CH₃)₂Hg, the partitioning between dissolved and particulate mercury, the sinking of particulate-bound Hg, and the bioaccumulation of CH₃Hg in marine food webs (Zhang et al., 2014, 2020). Biogeochemical and ecological variables, such as particulate organic carbon (POC) and dissolved organic carbon (DOC) in the ocean, are obtained from the Darwin marine ecosystem model (the Darwin Project: http://darwinproject.mit.edu/, last access: 16 May 2024; Dutkiewicz et al., 2012).

The air–sea exchange of Hg⁰ (Eq. 1) is calculated from the exchange velocity ($k_{{\mathrm{w}}_{{\mathrm{Hg}}^{\mathrm{0}}}}$) and the concentration gradient of Hg⁰ across the air–sea interface corrected and normalized by the dimensionless Henry's law constant ($C_{\mathrm{w}}-C_{\mathrm{A}}/H$) (Andersson et al., 2008), where C_w and C_A represent the concentration of Hg⁰ on the water and air sides, respectively, and H is the dimensionless Henry's law constant, which quantifies the ability of the dissolved phase to escape into the water. In the baseline parameterization, the exchange velocity of Hg⁰ on the ocean side (Eq. 2) is estimated following the quadratic relationship with wind speed proposed by Nightingale et al. (2000) for CO₂ (Eq. 3) adjusted for the Schmidt number of Hg⁰ (${\mathit{Sc}}_{{\mathrm{Hg}}^{\mathrm{0}}}$, Eq. 4) and for the proportion of ice-free sea surface areas (1−iceo). For a related parameterization in the baseline model, see Zhang et al. (2020).

Our modified expression for the air–sea exchange velocity (Eq. 7) takes into account the effects of surfactants and wave breaking, which will be described in more detail in the following two sections. We conduct a total of eight simulations (Table 2), including one baseline simulation; four simulations that comprehensively consider the effects of wave breaking and surfactants – Case 1 (SUR1 + WB1), Case 2 (SUR1 + WB2), Case 3 (SUR1 + WB3), and Case 4 (SUR1 + WB4); and three sensitive experiments that solely consider the effects of surfactants (Case A, SUR1) and wave breaking (Case B, WB1; Case C, WB3). The model is run from 1992 to 2011, allowing the response of Hg species to ocean physical and biogeochemical changes to reach a steady state. The initial conditions are extracted from previous model output in Zhang et al. (2020).

2.2 Parameterization of surfactants

Surfactants mainly originate from ocean biological activities (Lin et al., 2002), with elevated concentrations anticipated in regions characterized by increased primary productivity (PP) (Wurl et al., 2011). The concentration of surfactants at the sea surface is related to PP, which is commonly estimated from chlorophyll a (Chl a) (Tsai and Liu, 2003) for operational reasons (i.e., remote sensing). Nevertheless, recent studies have shown that Chl a cannot fully predict the occurrence of surface surfactants when used as a substitute for PP (Wurl et al., 2011; Sabbaghzadeh et al., 2017). Some strains of heterotrophic bacteria are known to produce surfactants (Satpute et al., 2010) and have been linked to a surfactant-covered ocean surface (Kurata et al., 2016). Additionally, the occurrence of surfactants is also subject to the influence of meteorological conditions, including solar radiation (Gašparović et al., 1998) and precipitation (Wurl and Obbard, 2005). Surface tension (Schmidt and Schneider, 2011), organic carbon concentration (Calleja et al., 2009; Barthelmeß et al., 2021), and sea surface temperature (Pereira et al., 2018) are also used to predict the occurrence of surface surfactants. However, most studies have not provided a clear quantitative relationship these factors and surfactants.

We model the influence of surfactant concentration ([SA]) on transfer velocity (Eq. 8) based on the empirical equation derived by Pereira et al. (2018) from a shipboard gas exchange tank experiment in the Atlantic Ocean. We adopt a relationship following Barthelmeß et al. (2021), who found a linear relationship between the concentration of total organic carbon ([TOC]) and [SA] in the Atlantic Ocean (Eq. 9). Therefore, a parameterization (hereafter referred to as SUR1) was derived using the concentration of TOC at the sea surface as an indicator of the suppression of air–sea exchange velocity by surface surfactants ($S_{\mathrm{kw}}\left[\mathit{\%}\right]=\mathrm{0.227}\left[\mathrm{TOC}\right]-\mathrm{9.817}$).

2.3 Parameterization of wave breaking

To take into account the effect of wave breaking on the air–sea exchange velocity, we separate the contributions of wave breaking (k_bub) and non-breaking (k_int) following the approach of Woolf (2005). The model agrees with measurements of CO₂ transfer at 20 °C but does not account for the dependence of k_bub on solubility. Therefore, this model is exclusively applicable to CO₂ and necessitates modifications for Hg⁰ compatibility (Jeffery et al., 2010). Here we take the influence of solubility into consideration. For the non-breaking part, we utilize the squared wind speed parameterization (Nightingale et al., 2000) previously adopted in the model (Eq. 2).

Regarding the wave-breaking component, we attempt to use four different parameterization schemes, all considering the significant wave height (H_s), friction velocity (u^*), and Ostwald solubility (α, unitless). H_s has been proved to be a more direct physical variable to estimate air–sea exchange (Li et al., 2021). Here we use climatological monthly means for 2000–2020 obtained from ERA5 reanalysis data (Hersbach et al., 2020). u^* is represented by a piecewise linear function of the wind speed (Eq. 10), as given by Edson et al. (2013). α is expressed according to Battino (1984) and Andersson et al. (2008) (Eq. 11).

The first parameterization utilizes a sea-state-dependent gas transfer velocity parameterization developed by Deike and Melville (2018), hereafter referred to as WB1 (Eq. 12). A_B is a dimensional fitting coefficient. The WB1 parameterization is based on direct numerical simulations of bubble dynamics beneath breaking waves (Deike et al., 2016), as well as on observations and modeling of wave and wave-breaking statistics (Deike et al., 2017). It has been validated by field measurements of gas transfer velocity (Bell et al., 2017; Brumer et al., 2017).

The last three parameterizations (Woolf, 1997; Asher and Wanninkhof, 1998; Asher et al., 2002) calculate the bubble-mediated transfer velocity (Eqs. 13–15, hereafter referred to as WB2–WB4) as a function of total whitecap coverage (WCC). Total whitecap coverage encompasses both the breaking crest generated by recent wave breaking (stage A whitecaps, W_A) and the sea surface foam in the process of decay (stage B whitecaps, W_B). W_A might be a better parameter for bubble-mediated transfer velocity owing to its more direct relationship with energy dissipation. Nevertheless, it exhibits weak correlation with the Reynolds number and presents challenges in measurement. Therefore, we have opted to employ the concept of total whitecap coverage for our calculations. It should also be pointed that, in the case of WB3 and WB4, we have focused exclusively on transfer via direct bubble exchange, which provides a better simulation of the transfer velocity (Blomquist et al., 2017). WCC (Eq. 16) is a function of the wind-sea Reynolds number (Eq. 17) proposed by Woolf (2005), which is estimated with friction velocity, significant wave height, and air kinematic viscosity.

Detailed parameterization and the introduction of variables are in Table 1.

Table 1 Model equation of air–sea exchange and parameterizations for wave breaking and surfactants.

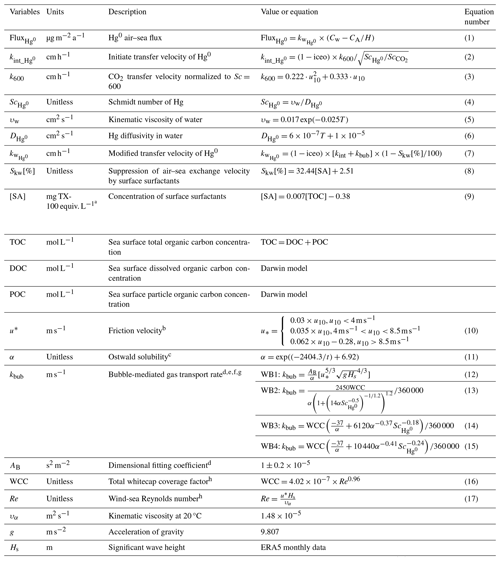
^a Surface activity was calibrated against the artificial, non-ionic surfactant Triton X-100 (TX-100, Sigma-Aldrich, Germany, molecular weight 625 g mol⁻¹). ^b Edson et al. (2013). ^c Battino (1984) and Andersson et al. (2008). ^d Deike and Melville (2018). ^e Woolf et al. (1997). ^f Asher and Wanninkhof (1998). ^g Asher et al. (2002). ^h Woolf (2005).

Table 2 Experimental setting.

^a Pereira et al. (2018). ^b Deike and Melville (2018). ^c Woolf (1997). ^d Asher and Wanninkhof (1998). ^e Asher et al. (2002).

2.4 Observation datasets

We incorporate observational data from seven cruises that involved high-resolution synchronous measurements of atmospheric and water Hg⁰ concentrations in the Atlantic, Pacific, and Southern oceans. These include data obtained by Kuss et al. (2011) during a transect from Punta Arenas, Chile, to Bremerhaven, Germany, across the Atlantic in April–May 2009. Soerensen et al. (2013) reported data from six cruises conducted between 2008 and 2010 in the Gulf of Maine, the New England Shelf, the continental slope region, and the Sargasso Sea. They also collected data along a latitudinal transect (∼ 20° N to ∼ 15° S) in the central Pacific during the METZYME cruise in October 2011 (Soerensen et al., 2014). Wang et al. (2017) obtained data during a cruise along the Antarctic coast from 13 December 2014 to 1 February 2015. Kalinchuk et al. (2021) reported data from a public cruise in the eastern Arctic Ocean from 7 September to 30 October 2018. Nerentorp Mastromonaco et al. (2017) measured continuously in the remote seas of western Antarctica, including in the Weddell Sea during winter and spring (2013) and in the Bellingshausen, Amundsen, and Ross seas during summer (2010/11). All of these studies used similar measurement methods, including Tekran trace mercury analyzers for atmospheric Hg⁰ measurements and automated continuous equilibrium systems for seawater Hg⁰ measurements. The Hg⁰ flux was calculated based on a thin-film gas exchange model (Eq. 1; Liss and Merlivat, 1986; Wanninkhof, 1992). The transfer velocity was calculated using the Nightingale et al. (2000) or Wanninkhof (1992) parameterization for instantaneous wind speeds, both of which are characterized by a quadratic relationship with wind speed. The reported data frequencies varied from 1 to 10 h. Observational data on various forms of Hg concentrations at the sea surface are summarized in Zhang et al. (2020).

3 Results and discussion

3.1 Suppression of $k_{{\mathrm{Hg}}^{\mathrm{0}}}$ by surfactants

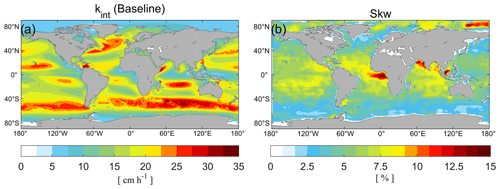
Figure 1 presents the air–sea exchange velocity calculated by the baseline model and the suppression rate of $k_{{\mathrm{w}}_{{\mathrm{Hg}}^{\mathrm{0}}}}$ caused by the surface microlayer calculated from the annual average TOC concentrations. The transfer velocity of the baseline model is zonally distributed, with higher values (33.5 cm h⁻¹) at middle to high latitudes attributed to wind-induced turbulence enhancement. In this study, we term this enhancement the transfer velocity of non-breaking waves. Our parameterization of the suppression rate is directly related to the distribution of DOC, which, in turn, is influenced by biological activity (Hansell et al., 2009). The model simulates a higher suppression rate in tropical and Arctic regions, reaching up to 16.7 % (Fig. 1b), but is 5 %–10 % in most regions. In tropical regions, organic matter resistant to degradation accumulates due to vertical stratification. In Arctic regions, terrigenous organic matter is transported to the system via high fluvial fluxes (Dittmar and Kattner, 2003). The lowest values are presented in the Southern Ocean, where deep ocean waters are more readily mixed with the surface. This finding is consistent with that of Wurl et al. (2011), who reported a more significant SML coverage between 30° N and 30° S. Our estimated suppression effect of surfactants generally aligns with Barthelmeß et al. (2021), who reported a suppression of the k_w of CO₂ by 11.5 % (±1.0 SE) inside and 9.8 % (±2.2 SE) outside the filament in the Atlantic Ocean. Similarly, Pereira et al. (2018) found that k_w suppression was reduced by 2 % to 32 % in the Atlantic in the presence of surfactants.

However, it is worth noting that other studies propose a greater impact. According to Pereira et al. (2016), the exchange of CO₂ between the ocean and atmosphere decreased by 15 % to 24 % along the northeast coast of the UK. Furthermore, Yang et al. (2021) reported that the wind speed dependence of CO₂ transfer velocity can vary by 30 % in the Southern Ocean. Frew (1997) observed a 5-fold reduction in gas transfer velocity near the coast of New England compared to the open ocean due to increased surfactant abundance and DOC content. Our lower estimate of the suppression effect might be reasonable, as the samples of these cited works were collected at different wind speeds and wind speed has a significant role in surfactant suppression. The high variation in molecular composition across diverse environments also leads to a large variation in surface activity (Barthelmeß and Engel, 2022). Therefore, the suppression relationship may change in different environments. Our surfactant parameterization used here was based on data from the Atlantic Ocean, which may not be applicable to other regions. Additionally, some research conducted in the laboratory might not fully explain processes in the natural environment (Krall and Jähne, 2014). To better explain the measured differences in Hg⁰ emissions between coastal and open-ocean areas, we need to improve our understanding of how surfactants and wind speed interact (e.g., marine aerosol emissions, surfactant abundance) to affect Hg⁰ air–sea exchange velocity and subsequent net Hg⁰ fluxes.

Figure 1 (a) The annual mean non-breaking gas transfer velocity in units of cm h⁻¹. (b) The suppression of the annual mean Hg⁰ gas transfer coefficient ($k_{{\mathrm{w}}_{{\mathrm{Hg}}^{\mathrm{0}}}}$) by surfactants in percent.

3.2 Enhancement of $k_{{\mathrm{w}}_{{\mathrm{Hg}}^{\mathrm{0}}}}$ by breaking waves

The bubble-mediated transfer velocities, calculated using four different bubble parameterizations, are shown in Fig. 2. The spatial distribution of the velocities is quite similar for all four scenarios, with relatively high values in regions with high wind speeds at middle and high latitudes, and similar to the exchange velocity of non-breaking waves (Fig. 1a). However, the magnitude varies substantially among the scenarios. The global mean bubble-mediated transfer velocities are 10.8, 9.9, 26.3, and 33.0 cm h⁻¹, respectively. Bubble-mediated transfer velocities calculated with the WB1 parameterization (Fig. 2a) and the WB2 parameterization (Fig. 2b) are comparable to those of non-breaking waves. Compared to the WB1 parameterization, the WB2 parameterization shows less variation in exchange rates across latitudes, with higher rates in low-latitude regions and lower rates in mid-latitude and high-latitude regions. The reason for this may be that WB1 has a higher wind or wave height dependence for $k_{{\mathrm{w}}_{{\mathrm{Hg}}^{\mathrm{0}}}}$ than WB2 (Fig. S1). Conversely, the WB3 (Fig. 2c) and WB4 (Fig. 2d) parameterizations significantly enhance the air–sea exchange velocity of Hg⁰ (t test on means, p<0.001). In the Southern Ocean and the North Atlantic region, bubble-mediated transfer rates can reach 105–120 cm h⁻¹, which is approximately 2–3 times higher than the transfer rates of non-breaking waves. This can be explained by the employment of total whitecap coverage rather than stage A whitecap coverage (W_A), as WCC is much higher than W_A (Monahan and Woolf, 1989). Cases 2–4 might overestimate the bubble-mediated transfer velocity. WB2 was applied for clean bubbles in quiescent water. This parameterization ignores bubbles that are mixed to a considerable depth, leading to an underestimation of the transfer velocity of poorly soluble gases (Woolf, 1997). WB3 and WB4 have been corrected using the dual-tracer method in laboratory simulations (Asher and Wanninkhof, 1998), but they were not considered adequately for all cases, which is acutely important as gas transfer is highly sensitive to the void fraction (the ratio of the air volume to the total volume) and bubble plume (Woolf et al., 2007). On the other hand, WB1 was developed by combining a mechanistic model for air entrainment and bubble statistics with empirical relationships for wave statistics. It also compares well with measured and model data for different gases (Deike and Melville, 2018). In terms of physical mechanisms, WB1 considers the process more comprehensively. Therefore, we suggest that WB1 might provide a better parameterization of wave breaking.

Our results demonstrate a higher contribution of wave breaking and bubbles to Hg⁰ air–sea exchange flux than CO₂. The bubble-mediated transfer velocity in most regions is comparable to the non-breaking transfer velocity, and it can be up to 2–3 times as high as the non-breaking transfer velocity in the high-wind-speed region. However, the bubble transfer velocity of CO₂ accounts for a comparatively small proportion of transfer velocity according to previous studies (Woolf, 1997; Reichl and Deike, 2020). Woolf (1997) estimated that bubbles contribute about 30 %–50 % of the global CO₂ transfer velocity by assuming that the transfer velocity mediated by bubbles is proportional to the coverage rate of whitecaps. Reichl and Deike (2020) estimated that 40 % of the CO₂ air–sea exchange fluxes in the Southern Ocean, North Atlantic, and Pacific are mediated by bubbles. This discrepancy could be attributed to gas solubility, as the flux of less soluble gases is more enhanced by pressure effects (bubbles are compressed by hydrostatic pressure) than more soluble gases (Bell et al., 2017; Reichl and Deike, 2020).

Figure 2 The annual mean bubble-mediated gas transfer velocity in units of cm h⁻¹. The different bubble-mediated parameterizations include (a) WB1, (b) WB2, (c) WB3, and (d) WB4.

3.3 Wind speed dependence of $k_{{\mathrm{Hg}}^{\mathrm{0}}}$

Most of the studies parameterize transfer velocity with 10 m wind speed through linear ($k_{\mathrm{w}}=\mathrm{2.8}\cdot u_{\mathrm{10}}-\mathrm{9.6}$, for 3.6<u₁₀<13 m s⁻¹; Liss and Merlivat, 1986), quadratic ($k_{\mathrm{w}}=\mathrm{0.222}\cdot u_{\mathrm{10}}^{\mathrm{2}}+\mathrm{0.333}\cdot u_{\mathrm{10}}$; Nightingale et al., 2000), or cubic relationships ($k_{\mathrm{w}}=\mathrm{0.026}\cdot u_{\mathrm{10}}^{\mathrm{3}}+\mathrm{3.3}$; McGillis et al., 2001). Gaps among wind-based equations, especially in developed wind-sea states, cause high uncertainty in different models. Recent research has shown that the transfer velocities of Hg⁰ are more sensitive to wind speed (with a higher index) using eddy covariance flux measurements ($k_{\mathrm{w}}=\mathrm{0.18}\cdot u_{\mathrm{10}}^{\mathrm{3}}$; Osterwalder et al., 2021). Additional forcing factors, such as wave breaking and sea surface activators, may result in different transport characteristics for different gases. In this section, sea surface temperature (SST), TOC concentration, and the H_s of Cases 1–4 are treated as random variables to fit the air–sea flux to the 10 m wind speed using power functions (Fig. 3):

$$\begin{array}{}\text{(18)}& {\displaystyle }\mathrm{for}\mathrm{SUR}\mathrm{1}+\mathrm{WB}\mathrm{1},k_{\mathrm{w}}=\mathrm{0.181}\cdot u_{\mathrm{10}}^{\mathrm{2.54}}\mathrm{and}{r}^{\mathrm{2}}=\mathrm{0.893};\text{(19)}& {\displaystyle }\mathrm{for}\mathrm{SUR}\mathrm{1}+\mathrm{WB}\mathrm{2},k_{\mathrm{w}}=\mathrm{0.362}\cdot u_{\mathrm{10}}^{\mathrm{2.10}}\mathrm{and}{r}^{\mathrm{2}}=\mathrm{0.963};\text{(20)}& {\displaystyle }\mathrm{for}\mathrm{SUR}\mathrm{1}+\mathrm{WB}\mathrm{3},k_{\mathrm{w}}=\mathrm{0.426}\cdot u_{\mathrm{10}}^{\mathrm{2.33}}\mathrm{and}{r}^{\mathrm{2}}=\mathrm{0.905};\text{(21)}& {\displaystyle }\mathrm{for}\mathrm{SUR}\mathrm{1}+\mathrm{WB}\mathrm{4},k_{\mathrm{w}}=\mathrm{0.487}\cdot u_{\mathrm{10}}^{\mathrm{2.34}}\mathrm{and}{r}^{\mathrm{2}}=\mathrm{0.901}.\end{array}$$

Considering sea surface films and microscale wave breaking, the relationship between Hg⁰ exchange velocity and wind speed appears to be between quadratic (Fig. 3a) and cubic (Fig. 3b and c), indicating a stronger dependence than suggested by the typically used parameterizations (Nightingale et al., 2000; McGillis et al., 2001). Compared with previous parameterizations (Fig. 3a and b), new parameterizations (Figs. 3d–g, S2) show higher transfer velocity, especially at high wind speeds, but lower velocity than that directly observed by Osterwalder et al. (2021; Fig. 3c) when wind speeds exceed 3–5 m s⁻¹. The new parameterization suggests that bubble effects play an important role in boosting Hg⁰ air–sea exchange and become more important at high wind speeds. Some previous parameterization schemes may underestimate Hg⁰ emissions when wind speeds are high enough to induce wave breaking. In comparison to gases with higher solubility such as CO₂, the air–sea exchange rate of Hg exhibits a stronger dependence on wind speed, consistent with the findings of Osterwalder et al. (2021). Indeed, microscale wave breaking enhances the transport velocity of poorly soluble gases, and bubble formation is more effective at high wind speeds.

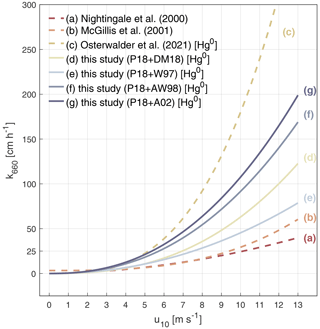
Figure 3 Wind speed dependence of transfer velocities used in gas exchange models to calculate air–sea fluxes. The k values are normalized to a Schmidt number of 660 (20 °C for CO₂ in seawater) and displayed against horizontal wind speed at 10 m (u₁₀). For comparison, other wind speed relationships of the transfer velocity calculated by Nightingale et al. (2000) and McGillis et al. (2001) and the cubic fit to measured transfer velocities of Hg⁰ during 2 d of relaxed-eddy-accumulation Hg⁰ emission measurements (Osterwalder et al., 2021) are included (dashed line, a–c). Solid curves (d–g) are the power fit to different model parameterizations (Cases 1–4). Cases 1–4 have included the effect of wave breaking and surfactants. All four schemes employ the same surfactant parameterization, SUR1, and four different bubble parameterizations (WB1, WB2, WB3, and WB4).

3.4 Hg⁰ exchange flux difference

The baseline model generally captures the spatial patterns of Hg⁰ exchange flux (Fig. 4a), with lower fluxes in Equator and polar regions and higher fluxes at mid-latitudes, which basically corresponds to the distribution of $k_{{\mathrm{w}}_{{\mathrm{Hg}}^{\mathrm{0}}}}$. Figure 4b–d illustrate the Hg⁰ exchange fluxes simulated by Cases A–C compared with the baseline. The inclusion of the sea surfactant suppression effect alone results in a reduced flux in most areas, with the largest reduction in the North Atlantic reaching −9 % (Fig. 4b). However, the impact on a global level is minor, with only a 0.9 % reduction in the global net Hg air–sea exchange flux, which equals 3808 Mg a⁻¹, compared with the baseline (3841 Mg a⁻¹). When only considering the effect of wave breaking (Fig. 4c and d), the exchange fluxes are estimated to be 4070 and 4189 Mg a⁻¹, respectively. Such values indicate an increase of 4.5 % and 11.1 % in global Hg exchange fluxes. The increased Hg⁰ evasion may increase atmospheric Hg concentrations and thus Hg deposition, as well as prolonging the Hg lifetime in biogeochemical cycles. Since only the oceanic part is considered in this model – i.e., the Hg⁰ deposition and atmospheric Hg⁰ concentration as external forcing do not change with time – the increase in air–sea exchange fluxes significantly reduces the concentration of Hg⁰ in the surface ocean (0–100 m; t test on means, p<0.001; Fig. S3) and thus alters other ocean Hg reservoirs (Fig. S4) and budgets (Fig. S5). This will result in an augmentation of the magnitude of exchange flux changes, as effective bubble-mediated transfer in the regions of the most developed wind-sea state significantly increase Hg⁰ transfer velocity (t test on means, p<0.001), while the impact of decreased concentration outweighs the slightly increased $k_{{\mathrm{w}}_{{\mathrm{Hg}}^{\mathrm{0}}}}$ where the waves are not well developed. As a result, the local variations in Case B and Case C range from −22.2 % to 40.5 % and from −28.3 % to 53.1 %. We conclude that the model changes are primarily due to the inclusion of bubble effect, whereas the inclusion of sea surface surfactants has a comparatively negligible impact on the variations in air–sea exchange fluxes.

The global net fluxes based upon the combined effect of wave breaking and surfactants (Cases 1–4) show spatial patterns similar to those of the baseline but present higher values (Figs. S6 and S7). The fluxes are 4056, 4016, 4155, and 4184 Mg a⁻¹, respectively, which are 5.6 %, 4.6 %, 8.2 %, and 8.9 % higher than the baseline (3841 Mg a⁻¹) because of the higher $k_{{\mathrm{w}}_{{\mathrm{Hg}}^{\mathrm{0}}}}$ (Fig. S8). These values are also higher than the estimates of 3360 Mg a⁻¹ by Zhang et al. (2023) and 3950 Mg a⁻¹ by Horowitz et al. (2017). The local variations range from −21.8 % to 39.5 %, −16.2 % to 28 %, −28 % to 51.3 %, and −30.7 % to 56.2 %, respectively. However, all the modeled fluxes from Case 1 to Case 4 and the baseline are within the large uncertainty range of the observations, so we cannot determine which parameterization scheme provides a more accurate estimate of air–sea exchange velocity simply by considering the current simulated results in conjunction with the available flux observations. Indeed, the fluxes are highly sensitive to concentration gradients and prevailing environmental conditions (wind speed, wave height, and surfactant concentration) with high-frequency temporal variability, modeling could therefore represent general zonal distributions (Figs. 4a and S6) rather than precise figures due to spatial- and temporal-resolution limitations. For instance, during summer in the Southern Ocean, the seawater can even be under-saturated, leading to a net deposition of Hg from the atmosphere (Nerentorp Mastromonaco et al., 2017). This is not accurately reflected in the annual mean flux modeled in our study. However, our study might explain why different research works display great uncertainty in estimating Hg⁰ exchange flux: they ignored the effect of surfactants and wave breaking. Therefore, further direct field measurements (especially micro-meteorology techniques) are necessary to assess the transfer velocity of Hg⁰, as well as the simultaneous observation of surfactants and sea waves.

Figure 4 (a) Comparison between baseline model and observations (filled circles) for net Hg⁰ air–sea exchange. Panels (b)–(d) are the difference in the annual mean net Hg⁰ evasion flux between the baseline model value and the values simulated by Cases A–C, which (b) solely consider the effect of surfactants (Case A) with the SUR1 parameterization and (c, d) consider wave breaking with the WB1 (Case B, c) and WB3 (Case C, d) parameterizations.

3.5 Model uncertainty

The parameterization of Nightingale et al. (2000) was developed from in situ experiments utilizing both volatile and non-volatile tracers, which potentially incorporate effects from wave breaking. However, the authors assumed that the transfer velocity depends only on diffusivity without taking the solubility effect into consideration. This assumption may not be valid in the presence of breaking waves. Although our scheme may result in a potential overestimation of the wave-related contributions at lower wind speeds, it has the advantage of distinguishing between different relationships with wind speed – such as linear or quadratic dependencies for non-wave processes and cubic dependencies for wave breaking – particularly at high wind speeds.

The parameterization of the surfactant suppression is quite challenging because significant spatial–temporal variations in surfactants and changes in the chemical composition of surfactants may affect the relationship between the TOC concentration and surfactant concentration (Barthelmeß et al., 2022), as well as the inhibition relationship of the sea surface film (Mustaffa et al., 2020). Since the composition of surfactant in the Atlantic Ocean may differ from other regions, extrapolating experimental findings on biological surfactants from the Atlantic Ocean to a global scale may introduce uncertainty. There is a risk of underestimating the suppressive effects of surfactants in coastal regions, as shown by Mustaffa et al. (2020), who found that the suppression of k_w was greater in coastal waters compared to oceanic waters. Barthelmeß et al. (2022) also showed that refractory DOC from coastal land sources has a more persistent impact on air–sea exchange, while the inhibitory effect of semi-unstable organic matter (dissolved glucose and isoleucine) produced by phytoplankton is stronger but has a shorter impact time. On the other hand, wave breaking and the bubble effect also show significant regional differences in the open sea and coastal waters (Callaghan et al., 2008; Woolf, 2005). The high-frequency temporal variability in the wind-wave processes and the limited resolution of wind-wave data used in this study may underestimate the variability caused by weather-scale Hg⁰ transport. Currently, there is still a lack of quantitative research on the effects of different surfactant components and bubble effects on air–sea exchange. More detailed measurements of air–sea exchange velocity and related physical quantities are needed to better understand the importance of bubble-mediated and sea-surface-film-mediated Hg exchange. In addition, since only the ocean part is considered, the atmospheric Hg⁰ concentration and deposition remain constant over time, which affects flux calculations to a substantially higher degree (Soerensen et al., 2013). To address this limitation, employing a coupled online model (Zhang et al., 2019) proves to be a valuable strategy for achieving a more accurate simulation of Hg⁰ flux.

4 Conclusion

The estimation of Hg⁰ air–sea exchange is of great uncertainty since wind speed is currently the only parameter used. Sea surfactants and breaking waves are thought to be two of the biggest drivers of uncertainty. In order to better assess the influence of surfactants and waves on Hg⁰ air–sea exchange, we integrate sea surfactants and wave-breaking processes into the air–sea exchange process of Hg⁰ within the MIT General Circulation Model (MITgcm). Seven experiments (four combined experiments and three sensitivity experiments) were conducted to explore the influence of sea surfactants and wave breaking on Hg⁰ air–sea exchange flux.

We find that surfactants can reduce the transfer velocity of Hg⁰ by 0 %–16.7 %. However, wave breaking has a much more significant impact, increasing the transfer velocity by a factor of 1–3 due to the low solubility of Hg. Therefore, we note that a lack of consideration of these processes may lead to a vast underestimation of Hg⁰ air–sea exchange flux. The new simulations that include sea surfactants and wave breaking show a much higher transfer velocity of Hg⁰ and a higher dependence of Hg on wind, which is consistent with the latest observations. Hg⁰ air–sea exchange flux is increased in mid-latitude to high-latitude regions with high wind and wave-breaking efficiency (28 %–56 %). Conversely, in low-latitude regions with lower wind speeds and in nearshore areas with reduced wave activity, the flux decreases by 16 %–31 % as the surface concentration of Hg⁰ diminishes due to higher emissions. The global mean Hg⁰ fluxes are 4016–4184 Mg a⁻¹, respectively, which are 4.6 %–8.9 % higher than the baseline (3841 Mg a⁻¹). It should be pointed out that our study does not consider changes in atmospheric Hg, and the decreases in marine Hg concentrations offset the change in transfer velocities. Therefore, we believe that the global mean Hg⁰ air–sea exchange flux will be even higher.

The results explain why different research works give such different schemes of $k_{{\mathrm{w}}_{{\mathrm{Hg}}^{\mathrm{0}}}}$. The omission of the influences of waves and surfactants during the experiment may result in a significant discrepancy when using wind speed as the only parameter in the estimation of gas exchange velocity. Theoretically, our study explains the variation among different research works and provides a universal scheme for predicting air–sea exchange transfer velocity. In addition, our parameterization schemes highlight significant uncertainty in the parameterization of surfactants and wave breaking. Traditional indirect methods, such as bulk or enclosure (flux chamber) approaches, and commonly employed flux parameterization are insufficient for effectively constraining Hg⁰ air–sea exchange flux. Thus, we highlight the necessity for direct high-resolution measurements of Hg⁰ flux, especially the synchronous observation of other parameters like wave height, surfactant concentration, and chemical composition. Because of the high sensitivity to different parameterizations at middle and high latitudes, especially in the North Atlantic (Fig. 4), we believe that synchronous observations in these regions may be helpful for modelers to develop and validate robust models for simulating the diel, seasonal, and inter-annual Hg dynamics on a local to regional scale.