A fast surrogate model for 3D Earth glacial isostatic adjustment using Tensorflow (v2.8.0) artificial neural networks

Models of glacial isostatic adjustment (GIA) play a central role in the interpretation of various geologic and geodetic data to understand and simulate past and future changes in ice sheets and sea level, as well as to infer rheological properties of the deep Earth. During the past few decades, a major advance has been the development of models that include 3D Earth structure, as opposed to 1D spherically symmetric (SS) structure. However, a major limitation in employing 3D GIA models is their high computational expense. As such, we have developed a method using artificial neural networks (ANNs) and the Tensorflow library to predict the influence of 3D Earth models with the goal of more affordably exploring the parameter space of these models, specifically the radial (1D) viscosity profile to which the lateral variations are added.

Our goal is to test whether the use of an ANN to produce a fast surrogate model can accurately predict the difference in GIA model outputs (i.e., relative sea level (RSL) and uplift rates) for the 3D case relative to the SS case. If so, the surrogate model can be used with a computationally efficient SS (Earth) GIA model to generate output that replicates that from a 3D (Earth) GIA model. Evaluation of the surrogate model performance for deglacial RSL indicates that it is able to provide useful estimates of this field throughout the parameter space when trained on only ≈15 % (≈50) of the parameter vectors considered (330 in total).

We applied the surrogate model in a model–data comparison exercise using RSL data distributed along the North American coasts from the Canadian Arctic to the US Gulf Coast. We found that the surrogate model is able to successfully reproduce the model–data misfit values such that the region of minimum misfit either generally overlaps the 3D GIA model results or is within two increments of the radial viscosity model parameter space (defined here as lithosphere thickness, upper-mantle viscosity, and lower-mantle viscosity). The surrogate model can, therefore, be used to accurately explore this aspect of the 3D Earth model parameter space. In summary, this work demonstrates the utility of machine learning in 3D Earth GIA modelling, and so future work to expand on this initial proof-of-concept analysis is warranted.

1 Introduction

Global models of glacial isostatic adjustment (GIA) have been in development since the 1970s and have several important applications (e.g., Spada, 2017; Whitehouse, 2018). Broadly speaking, through comparison of model output to a variety of both geological and geodetic datasets, they can be used to improve our understanding of ice sheet and sea level changes on decadal to 100 kyr timescales and place constraints on the rheological properties of Earth's mantle. For example, geological reconstructions of relative sea level (RSL) provide key information on past changes in regional and global ice extent during the Quaternary (e.g., Milne, 2015). Calibrated GIA models are commonly used to predict and remove the contribution of this process to observations of contemporary RSL, land motion, and gravity changes. This is done in order to better isolate signals associated with other processes, such as contemporary ice mass change (Shepherd et al., 2012) or secular changes in regional hydrology (e.g., Steffen et al., 2008; van der Wal et al., 2008; Wang et al., 2013).

To date, most GIA modelling studies have applied Earth models with a spherically symmetric geometry and so only capture variations in viscosity with depth. However, a variety of laboratory and geophysical investigations indicate strong lateral variability in Earth viscosity structure at all depths in the mantle (Karato, 2008). In the past few decades, a major improvement in the realism of GIA models has been the development of Earth models that can accommodate laterally variable viscosity structures (e.g., Latychev et al., 2005; Paulson et al., 2005; Wu, 2005; Klemann et al., 2007; Wang et al., 2008), resulting in what are referred to as “3D” Earth models. Since the development of these more realistic Earth models, a number of GIA studies have shown that the influence of lateral structure is important with respect to the applications outlined above (e.g., Paulson et al., 2007; Austermann et al., 2013; van der Wal et al., 2013, 2015; Kuchar et al., 2019). Therefore, it is important to continue to apply 3D models and improve constraints on Earth viscosity structure.

A primary limitation of 3D (Earth) GIA models (hereafter simplified to “3D GIA models”) is their greater computational expense, which, in addition to the much larger parameter set associated with two additional spatial dimensions within the Earth model, makes exploring the parameter space a major challenge. As a result, determining the optimal parameter set and quantifying parameter uncertainty has not been done with any degree of rigour. The majority of studies that have applied 3D GIA models to date have focused on considering a relatively small number of 3D Earth viscosity models (O(1–10)) to consider the influence of the additional two dimensions on predicting surface observables (e.g., Whitehouse et al., 2006; van der Wal et al., 2015; Powell et al., 2021). In defining 3D models of mantle viscosity structure, most past studies have used global and/or regional seismic velocity models to infer lateral variability in viscosity and a spherically symmetric (SS) model of viscosity variation on which to superimpose the lateral viscosity structure (e.g., Latychev et al., 2005; Wu et al., 2013). In most studies to date, only a handful, O(1), of these key model inputs have been explored. In comparison, studies focusing on the application of SS (i.e., 1D) Earth models often consider O(100) viscosity models and/or order O(1–10) ice loading histories to explore the model parameter space and map out the parametric uncertainty (e.g., Steffen and Kaufmann, 2005; Love et al., 2016; Caron et al., 2017). Recent studies using 3D Earth models have considered larger parameter sets (e.g., Bagge et al., 2021; Yousefi et al., 2021; Li et al., 2022; Pan et al., 2022). However, they remain limited sample sets of the complete Earth model parameter space. This incomplete exploration of the model parameter space is likely one of the reasons why the quality of data : model fits based on 3D Earth models has yet to improve substantially upon those obtained using 1D Earth models (e.g., Steffen et al., 2006; Spada et al., 2006; van der Wal et al., 2013; Li et al., 2018; Yousefi et al., 2021). One route to addressing this problem, in terms of identifying an optimal parameter set, is using adjoint methods (Crawford et al., 2018).

The work presented here is aimed at improving our ability to explore the parameter space of 3D GIA models via the use of a machine learning tool chain to emulate the output from a 3D GIA model. Full emulation requires the generation of a predictive probability distribution for full model output given model inputs. In this study, an artificial neural network (ANN) is used to predict a single estimate of model output for specified input, and so the term “surrogate model” is more appropriate than “emulator”. However, we often use the term “emulator” instead of “surrogate model” to improve clarity and readability. This approach has been employed successfully in other disciplines where model computational expense has been a limiting factor in exploring the parameter space (Tarasov et al., 2012; Sellevold and Vizcaino, 2021; Williams et al., 2023). A recent study (Lin et al., 2023) applied a graph-based spherical convolutional neural network algorithm to the GIA problem. Their focus was on emulating RSL for a single 1D Earth model for a wide range of ice history models, which is very different from the aims of this study. Given the high computational efficiency of the 1D GIA model, a relatively large training set of 1200 simulations was used in their analysis. In general, good results were obtained, indicating the potential utility of ANN methods in GIA applications. A primary challenge for the 3D case considered here is the much reduced computational efficiency, limiting the number of simulations that can be performed to generate a training set.

We view this study as developing a proof of concept that future studies can build upon. In this regard, we have chosen to focus this work on optimizing one of the key inputs to a 3D GIA model. Specifically, for a given model of lateral structure (lithosphere and seismic model) and ice loading, we seek to determine whether it is possible to successfully emulate model output for ≈300 different SS reference viscosity models based on a relatively small training set (O(10−100)) simulations). Our results indicate that sufficiently precise emulation can be achieved with a training set of ≈ 40–60 simulations, resulting in computational (wall) time saving of ≈85 %. Given this success, we considered an application of the emulator based on a typical GIA dataset – geological (proxy) reconstructions of RSL – to seek an optimal SS reference viscosity model for our chosen models of lateral lithosphere thickness and sub-lithosphere viscosity variations. Our inference of the optimal SS viscosity model parameters using the emulator is close to that inferred using output from the numerical 3D GIA model, thus indicating the potential of the ANNs to more efficiently search the 3D Earth model parameter space.

2 Experimental design and methods

Here we describe the individual components of the numerical models and overall experimental design of this investigation. We introduce, in Sect. 2.1, the individual models used, and then we introduce the method by which model output is processed to produce training data (Sect. 2.2). We then provide some details on the implementation and training of the ANNs (Sect. 2.3). Finally, we outline the data used in the proxy-data : model comparison (Sect. 2.4).

2.1 GIA models

We use two separate GIA models to compute RSL and radial displacement. Both solve the sea level equation (Farrell and Clark, 1976; Mitrovica and Milne, 2003; Kendall et al., 2005) and model the solid Earth response to the loading and unloading of Earth's surface through time. They each have equivalent feature sets with respect to the inclusion of compressibility (Wu and Peltier, 1982), migrating shorelines (Milne and Mitrovica, 1998; Mitrovica and Milne, 2003), and rotational feedback (Milne and Mitrovica, 1998; Mitrovica et al., 2005). However, the computational methods are different: the model that can accommodate 3D Earth structure uses a numerical finite-volume approach (Latychev et al., 2005), whereas the simpler and computationally less expensive 1D GIA model relies on the computation of viscoelastic Love numbers (Peltier, 1974) for a specified radial structure (density, elastic moduli, and viscosity). Once the Love numbers have been computed (e.g., via a normal-mode analysis, Peltier, 1976; Mitrovica and Peltier, 1992), calculation of various GIA observables, such as RSL, is computationally efficient (Mitrovica and Peltier, 1991). Hereafter this model will be referred to as the normal-mode SS model (abbreviated to “NMSS” model). A model run with a duration equivalent to a glacial cycle during the Late Pleistocene (approximately 100 kyr) typically requires less than 0.5 core hours¹ on contemporary computer hardware (surface resolution being a key factor in determining the computational time). As a result of this computational efficiency, large-scale sampling of the GIA model parameter space is feasible, with recent studies presenting results for many thousands of simulations exploring the parameter space of Earth model and ice sheet reconstructions (e.g., Steffen and Kaufmann, 2005; Love et al., 2016; Caron et al., 2017). The more complex and computationally expensive model that we use here – the Seakon model of Latychev et al. (2005) – does not have the limiting assumption of a spherically symmetric Earth structure. However, this model requires ≈1.75 core years for a typical glacial cycle experiment, which precludes its use for generating large ensembles of model output. Contemporary investigations with the Seakon model are limited to ensembles of several dozen simulations (e.g., Pan et al., 2022), and more typically fewer than a dozen simulations.

To define a 3D viscosity structure in the Seakon model, lateral viscosity variations are applied on top of a chosen spherically symmetric (radial) viscosity model. Here we employ a commonly used three-layer parameterization of this spherically symmetric viscosity structure, as in the NMSS model, composed of a high-viscosity (i.e., elastic) lithosphere above two regions with uniform viscosity. These two regions are the upper mantle (base of the lithosphere to ≈670 km depth) and lower mantle (≈670 to ≈2900 km depth). Sub-lithosphere lateral variations are applied via a set of relationships between shear-wave velocity anomalies and various depth-dependent parameters in Latychev et al. (2005) – see their Eqs. (27)–(29). Lateral lithosphere variations can be introduced using constraints that are independent of the adopted global seismic model (see the next section) and are represented as a viscoelastic layer of varying thickness with a very high ($\mathrm{1}\times {\mathrm{10}}^{\mathrm{37}}\text{Pa}\cdot \text{s}$) viscosity such that the response is essentially that of an elastic material on GIA timescales.

In order to increase the number of parameter vectors (i.e., model runs) which can be examined with the available computational resources, we use a reduced-resolution configuration of the Seakon model. The reduced-resolution configuration has a horizontal surface resolution of ≈33 km and uses ≈6 million nodes versus ≈15 km and ≈17 million nodes for the default configuration. This change results in a reduction in the CPU time to approximately one-third of the default configuration. Comparing the model output of RSL using these two grids at various times indicates that the differences are generally largest at the Last Glacial Maximum (≈20 000 years ago; Fig. S1 in the Supplement), reaching an amplitude of ≈5 m, and decrease for later times. Given the limited spatial resolution of inputs to Seakon (e.g., ice and seismic models), we consider the lower-resolution grid to be sufficiently accurate for the purpose of this analysis. As a result, with Seakon we were able to explore all 330 combinations of lithosphere thickness (LT), upper-mantle viscosity (UMV), and lower-mantle viscosity (LMV) for which we have calculated the required Love numbers for the NMSS model, representing ≈150 core years of computational resources.

Despite the broad overlap in function of the Seakon and NMSS models, they have distinct roles in this investigation. We seek to train an ANN to simulate the difference in model output between Earth models with 3D and SS structure. The Seakon numerical model is used (in 3D and SS configurations) to generate this model output. We use the Seakon code in a SS configuration rather than the NMSS code to avoid introducing any error into the calculated 3D minus 1D signal due to differences between the output of the Seakon and NMSS codes (for the same 1D configuration). Once the ANN is successfully trained, generating model output for a 3D Earth model is achieved by simply adding the ANN-derived 3D minus 1D signal to output from an efficient NMSS model with the relevant SS structure. Thus, the Seakon model is used to generate the training and validation data for the ANN. The output from the NMSS model was only used to convert the differential (3D minus 1D) signal to the full 3D signal (for both explicitly modelled (Seakon) and emulated (ANN) output).

2.2 Generation of model training inputs using the Seakon numerical model

The Seakon model is used in both SS and 3D Earth model configurations to produce the input datasets used to train the ANNs. The SS configuration (i.e., parameters varying only with depth) is used to compute the differential (3D minus 1D) signal. The primary configurations of the Seakon model used in this investigation are as follows:

1. spherically symmetric (i.e., varying only with depth and defined by three variables, LT, UMV, and LMV, as defined previously);

2. spherically symmetric perturbed using S-wave velocities from the S40RTS model (S40RTS) (Ritsema et al., 2010, plots of the relative viscosity variations in Fig. 1);

3. spherically symmetric perturbed using S-wave velocities from the S40RTS model with the addition of laterally variable lithosphere thickness from the LR18 lithosphere model (S40RTS + LR18) (Ritsema et al., 2010; Afonso et al., 2019, plot of lithosphere model LR18 in Fig. 1); and

4. spherically symmetric perturbed using S-wave velocities from the Savani model with the addition of laterally variable lithosphere thickness from the LR18 lithosphere model (Savani + LR18) (Auer et al., 2014; Afonso et al., 2019, plot of the relative viscosity variations in Fig. S2 in the Supplement).

The (full 3D) S40RTS + LR18 configuration is used to explore the application of ANNs considered here and in the proxy-data : model comparison. The Savani + LR18 configuration is used to examine the impact of an alternative laterally variable viscosity model on the ANN training and misfit results. The semi-3D S40RTS configuration is used to examine the impact of the inclusion of a laterally variable lithosphere model on the ANN results via a comparison to the S40RTS + LR18 results. The SS configuration of Seakon is used throughout the investigation to determine the differential 3D minus SS output on which the ANNs are trained and tested (as detailed below). Within each of the SS configurations we explore the parameter space of elastic LT as well as UMV and LMV. The ranges of the LT (71–120 km), UMV (0.05–5 $\times {\mathrm{10}}^{\mathrm{21}}\text{Pa}\cdot \text{s}$), and LMV(1–90 $\times {\mathrm{10}}^{\mathrm{21}}\text{Pa}\cdot \text{s}$) values used in this study are in line with previous studies which constrain these values (e.g., Lambeck et al., 2014; Roy and Peltier, 2017). The parameter space of LT, UMV, and LMV values is sampled using a Latin hypercube scheme with the goal of maximizing parameter space coverage within computational resource limitations. As a result, from the combined total of 330 realizations for each Seakon configuration (e.g., S40RTS + LR18), up to 63 parameter vectors were drawn to train the ANNs, while the remainder were only used for comparison against the emulator output. The configurations from which the training and validation data are drawn use the same ice loading history: ICE6G (Peltier et al., 2015; Roy and Peltier, 2017). In total, considering both the SS and 3D cases, the Seakon numerical model was run 1320 times for this analysis (i.e., 330 runs for each of the four configurations defined above).

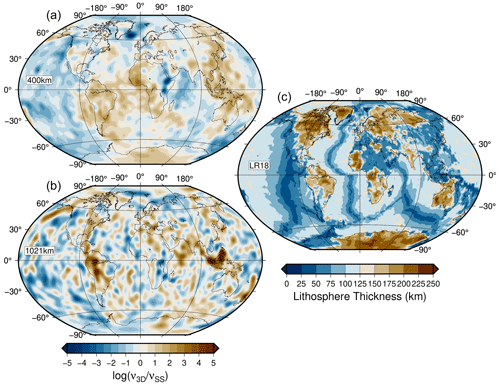
Figure 1 Panels (a) and (b) show spatial viscosity variations as $\log ({\mathit{\nu }}_{\text{3D}}/{\mathit{\nu }}_{\text{SS}})$ for two depths in the mantle, i.e., 400 and 1021 km. A value of 0 indicates that the viscosity value at that location is equivalent to the background spherically symmetric Earth model. Panel (c) shows the lithosphere thickness distribution of the LR18 model. Note that these thickness values are scaled such that the global average thickness is equivalent to the value specified in the SS configurations. The scaling depends on the target global value for the “reference” 1D viscosity profile. For most cases, the scaling is less than 1, and so the values shown are significantly reduced (by ≈ 10 %–40 %).

Preliminary results (not shown here) indicated that emulation based on the rate of change (ROC), with respect to time, of the 3D minus SS resulted in smaller prediction misfits compared to emulating RSL or radial displacement (RAD) directly. Therefore, these are the model datasets considered in the remainder of this analysis. Given that RSL is defined as 0 m at present, we can readily recover the full time series of the field by integrating the ROC of RSL backwards in time from the present.

For each 3D minus SS parameter vector, we then sample the ROC of RSL (or RAD) at 1 ° regular spacing in both latitude and longitude for each model time step (from 36 ka to present, 59 time steps in total). From each parameter vector (PV) we extract the ROC of RAD and RSL from files constructed for model performance evaluation (or training without any filtering). The ROC values of RAD and RSL are concatenated across all PVs and then evaluated using the NumPy histogram function to generate probability density functions of the ROC of RSL and RAD. This global (with respect to space, time, and Earth model parameters) distribution is then used to resample the GIA model output data points of each parameter vector for more effective and efficient training of the ANNs. The resampling or filtering is implemented such that, the most common values, i.e., those 3D minus 1D ROC values closest to 0 mm/yr , which are largely located in far-field regions, have their occurrence reduced by several orders of magnitude in the training data. This filtering reduces the input training dataset from ≈4 600 000 to ≈500 000 data points per ensemble member (i.e., the LT–UMV–LMV parameter vector for a given 3D minus 1D configuration). The net result of this processing is a reduction in the network training time and computer memory requirements and increased quality of fits in regions with larger (3D minus 1D) ROC RSL or ROC RAD anomalies (i.e., near- and intermediate-field locations). Each parameter vector results in unique input training (i.e., filtered) and comparison (i.e., unfiltered) dataset files. These files are then combined as required into a single data file for either training or comparison purposes.

2.3 Training of the ANNs

The training and implementation of the ANNs is accomplished via the Tensorflow framework (v2.8.0, Abadi et al., 2015; TensorFlow Developers, 2022). The choice of framework or library was motivated by the available support at the high-performance computing center where the network training was conducted. We anticipate that comparable results can be achieved with other frameworks. Using the model output described in Sect. 2.2, we train separate ANNs for each of the combinations of laterally variable Earth structure models (i.e., S40RTS, S40RTS + LR18, and Savani + LR18) and ice sheet history (i.e., ICE6G). As a result, each combination of laterally variable Earth structure and ice sheet history produces a separate set of ANN weights to be used with the emulator. The inputs to the ANNs can be grouped into four aspects: radial viscosity model, location, ice loading, and SS input data, more specifically (1) LT, (2) UMV, (3) LMV, (4) longitude, (5) latitude, (6) ice thickness values and timing for the current and four previous time steps, and (7) ROC of RSL or RAD prediction from the SS configuration of the Seakon model.

The prediction of the ANNs is the 3D minus 1D anomaly for the ROC of either RSL or RAD at the location and time, which corresponds to the input to the ANN. Prior to training, the input dataset is split into the online training and validation sets, with 75 % of the input data used for training and the remaining 25 % used for validation. As discussed, the training data are already filtered at this stage to emphasize regions with greater amplitude signals. Within the context of model training, the “validation set” is only used to monitor the ANN training for evidence of overfitting and contains data from all PVs included in the input dataset. ANN training and model construction (i.e., specification of the size and number of hidden layers) is done via the Keras Application Programming Interface. Training of an individual ANN usually requires no more than a dozen hours of wall time using a single NVIDIA P100 Pascal Graphics Processing Unit (GPU). The training of a given ANN is iterated until an early stopping condition, based on the mean square error (MSE) of the ANN prediction against the training dataset, is activated. This early stopping condition for RSL is set such that, if there is no improvement to the MSE of at least 0.01 mm² yr⁻² within 50 training epochs, the training stops and the set of weights which result in the lowest MSE are chosen. This approach is used to prevent, or at least minimize, overfitting of the trained ANNs (Chollet, 2021). We note there was no evidence of overfitting in the training diagnostics. The choice of using ice thickness values for the previous four time steps was motivated by preliminary testing and evaluating tradeoffs with respect to hardware limitations and quality of predictions. Generally, providing more previous time steps to the networks resulted in reduced misfits, but there were rapidly diminishing returns and technical issues (largely due to memory and storage constraints on the hardware used for training) with adding significantly more past time step data. Four previous time steps were found to be a useful balance between model expense and useful predictions.

With the Keras Application Programming Interface, we construct multilayer perceptron feed-forward ANNs. The structure of the ANN is composed of an input layer, eight fully connected hidden layers of width 512, followed by eight fully connected hidden layers of width 256, and followed by the output layer. Between the fully connected hidden layers are normalization layers which shift and scale their inputs such that the resulting distribution has a mean of 0 and a standard deviation of 1. The addition of the normalization layers helped with the convergence of the network as network depth (i.e., model layer count) increased. A variety of ANN structures were evaluated. For example, layer counts from 2 to 20 layers and widths from 8 to 1024, in steps of 2ⁿ, were varied using an initial test dataset. Some results from these initial explorations are summarized in Fig. S3 in the Supplement, which shows a ROC RSL MSE for ANNs with network widths of 64 to 1024 nodes and fully connected hidden layers (with normalization layers) between 2 and 10 nodes. Optimal results were generally found for network widths of 512 and 1024 as well as depths of 8 or 10. The configuration outlined above provides a good balance between performance and training expense. The Python scripts used for training and implementing the ANNs and for producing various GIA predictions are available in the Supplement.

2.4 Model–data comparison: source data and analysis methods

For the RSL proxy-data : model comparison, we use the RSL databases of Engelhart and Horton (2012), Love et al. (2016), and Vacchi et al. (2018), which span the eastern North American coastline from the Canadian Arctic to the US Gulf Coast. Combined, these databases contain a total of >2500 data points (including sea level index and limiting points). The locations of these data points are shown in Fig. S4 in the Supplement.

In order to quantify the data : model RSL misfits, we use the same metric as in Baril et al. (2023) for sea level index points (SLIPs) and limiting data, which are reproduced here for reference.

$$\begin{array}{}\text{(1)}& {\displaystyle }{\mathit{\delta }}_{\mathrm{SLIP}}={\displaystyle \frac{\mathrm{1}}{N}}\sqrt{\begin{array}{l}\sum _{n=\mathrm{1}}^N{\left(\frac{{\mathrm{RSL}}_{\text{data},n}-{\mathrm{RSL}}_{\text{model},n}}{{\mathrm{\Delta }}_{\mathrm{RSL},n}}\right)}^{\mathrm{2}}\\ +{\left(\frac{t_{\text{data},n}-t_{\text{model},n}}{{\mathrm{\Delta }}_{t,n}}\right)}^{\mathrm{2}}\end{array}}\text{(2)}& {\displaystyle }{\mathit{\delta }}_{\text{limit}}={\displaystyle \frac{\mathrm{1}}{N}}\sqrt{\sum _{n=\mathrm{1}}^N{\left({\displaystyle \frac{{\mathrm{RSL}}_{\text{data},n}-{\mathrm{RSL}}_{\text{model},n}}{{\mathrm{\Delta }}_{\mathrm{RSL},n}}}\right)}^{\mathrm{2}}}\end{array}$$

In Eq. (1), the RSL_model,n and t_model,n values are the model RSL and time value from the point of closest approach of the model curve to the nth SLIP. However, for limiting data, the misfit (Eq. 2) is calculated using the same time value as the data point itself. In the case of limiting data, if the RSL curve for a given model falls above/below a marine or terrestrial data point within the range of dating uncertainty, then the misfit for that data point is set to 0 (Baril et al., 2023). When examining the total δ for a given RSL database, the following values are provided: δ_SLIP, δ_ML, δ_TL, and δ_Total. Where δ_SLIP is the value from Eq. (1) for a given SLIP database, δ_ML and δ_TL are the values from Eq. (2) for marine and terrestrial limiting data, respectively, and ${\mathit{\delta }}_{\text{Total}}={\mathit{\delta }}_{\mathrm{SLIP}}+({\mathit{\delta }}_{\mathrm{ML}}+{\mathit{\delta }}_{\mathrm{TL}})/\mathrm{2}$. Contributions from limiting data are normalized by 2 since these data only provide one-sided constraints on RSL.

3 Results and discussion

3.1 Network training and performance

In this section we determine how many parameter vectors (LT/UMV/LMV) are required in the training set to obtain useful predictions from the emulator (we use “emulator” here to refer to the combination of output from the trained ANN with output from the NMSS model). In order to estimate this number, we construct several Seakon (3D minus 1D) ensembles consisting of increasing quantities of parameter vectors in the training dataset. These ensembles were determined using the S40RTS model to construct lateral viscosity variations in the mantle with lithosphere variations derived from the LR18 model. Each trained ANN incorporated the same core set of nine extreme ensemble members (i.e., members that include LT/UMV/LMV parameter values at the beginning or end of the ranges defined in Sect. 2.2). Additional supplemental parameter vectors were added to this baseline set, with 9, 18, 36, and 54 members each. The lowest number of nine supplemental parameter vectors was used to determine whether we could accurately predict the 3D minus SS difference as a function of LT/UMV/LMV, with only the core parameter vector set and a single intermediate parameter vector between each of these end-member cases (18 parameter vectors in total: 9 core plus 9 supplemental). From there we doubled the supplemental set to 18 and subsequently 36. Finally, rather than doubling the number of supplemental parameter vectors a third time, we defined an upper limit of 54 based on the rationale that requiring a larger training set would not be sufficiently resource-effective. Combining the core and supplemental sets resulted in four trained networks with N=18, 27, 45, and 63 members, respectively. To quantify the generalization of the ANNs (i.e., their accuracy with respect to parameter vectors not in the training ensemble) as a function of the training ensemble size, the mean square error (MSE) for each parameter vector in the LT/UMV/LMV space is calculated. The MSE for a given parameter vector is averaged over all locations and time steps (i.e., the full dataset described in Sect. 2.2).

Plots of the MSE for the S40RTS + LR18 configuration through the LT/UMV/LMV parameter space for the ROC RSL are shown in Fig. 2 for the different training sub-ensembles (results for N=18 are not shown). It is notable that the reduction in the MSE in going from N=27 to N=45 is more marked compared to the change from N=45 to N=63. This indicates that N=45 is close to an optimal value in terms of performance (lowering the MSE) versus the size of the training set. In general, throughout the parameter space, the MSE decreases as the number of members in the training set increases (this is particularly evident when considering the median and lowest MSE values). Furthermore, Fig. 2 shows that the thickness of the elastic lithosphere is generally a weak predictor of the 3D minus SS ROC RSL. In general, regions in the parameter space that have at least one member in the training ensemble, independent of the LT value, have lower MSE values compared to those with none. This finding is also supported by the input layer weights, where LT is consistently the lowest weight input (and thus has the lowest impact on predictions) when training ANNs. Figure 2 also shows that the prediction accuracy for a given parameter vector is generally larger when it is adjacent to another that is part of the training ensemble. As such, the distribution of training parameters is an important consideration when training the ANNs. These results indicate that the ANN has useful levels of predicative ability when considering LT/UMV/LMV values outside the training dataset.

Comparing the results in Fig. 2 to those for the other full 3D configuration, Savani + LR18 (Fig. S5 in the Supplement) indicates that these findings are valid across different velocity models. The MSE decreases as N increases, though the MSE does not appear to decrease with N as quickly as for the S40RTS + LR18 configuration. The overall lateral viscosity structure of the Savani + LR18 configuration is not significantly different from that of the S40RTS + LR18 configuration (selected layers shown in Figs. S2 and 1). As such, it is not immediately clear why there is a difference in MSE for the same values of N for different 3D Earth models. However, the general success of applying this method to two fully 3D Earth models indicates that this approach should be generally applicable regardless of the adopted velocity model. However, this preliminary conclusion should be investigated further in future work.

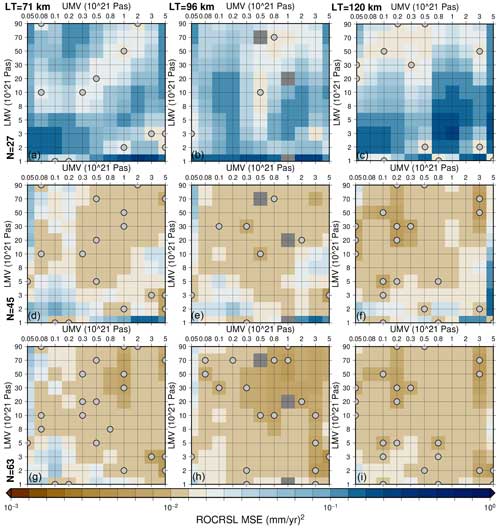
Figure 2 This plot shows the MSE (for all locations and time steps) through the parameter space (LT/UMV/LMV) for input training datasets with N=27 (a–c), 45 (d–f), and 63 (g–i) for the S40RTS + LR18 ROC RSL ANN. The parameter vectors included in the training dataset are indicated by grey circles. The columns give results for the three values of global-mean elastic lithosphere thickness: 71 km (a, d, g), 96 km (b, e, h), and 120 km (c, f, i). Note that results which are anomalous and affected by technical issues for specific ensemble members are rendered here in grey.

Despite the MSE of the full spatiotemporal datasets being a useful metric for comparison between different ANN architectures and training ensembles, it is of limited utility in describing the effectiveness of a given ANN in reproducing the geophysical output of interest. Therefore, plots showing the difference between emulated output and modelled output (for S40RTS + LR18) are provided for the RSL field at 10 ka (Figs. 3 and S6 in the Supplement, for the eastern North America and global domains, respectively) and the uplift rate at present (Figs. 4 and S7 in the Supplement, for the eastern North America and global domains, respectively). They show RSL and ROC RAD predictions for the parameter vector, which has the median MSE from the validation (i.e., not used as part of the ANN training) sub-ensemble for the N=45 case.

Comparing the scale of the emulator : model anomaly to the RSL field itself (Fig. 3), we see that the misfit is O(1 m), where the RSL field itself is generally O(10–100 m). The intermediate-field region (e.g., proximal to and south of the zero contour in Fig 3) is problematic, as the emulator : model anomaly does not decrease with the same spatial pattern as the RSL field itself (although it does broadly share the same spatial pattern), and thus there is a region where the anomaly is comparable to the RSL field itself. The spatial distribution of the emulator : model anomaly for RSL does not have a clear source, such as the viscosity and LT variations shown in Fig. 1. However, it is important to note that the sub-lithosphere (lateral) viscosity variations change with depth, and so the patterns shown are only representative within limited depth ranges. The magnitude of the pattern scales with that of RSL, and so the ice loading history is one controlling factor.

To complement Fig. 3, we also provide plots of the predicted RSL time series for the emulated and model-predicted output (together with the difference) in Fig. 5. Examining the time series data in Fig. 5, we obtain similar findings to those of Fig. 2 in that the emulator : model misfit decreases as the number of parameter vectors in the training dataset increases in most locations (e.g., there is a decrease in performance when N is increased from 45 to 63 at the Hudson Bay locality). This result is generally found across ice-covered, near-field, intermediate-field, and far-field regions. The intermediate field (e.g., northern South Carolina) is the most difficult portion of the field to emulate. The results show that ≈45 training members are generally sufficient to reproduce RSL using 3D Earth models for the ice-covered, near-field, intermediate-field, and far-field regions shown here. Examination of results using fewer training members (N=18, not shown) also indicates that fewer training members may be sufficient to produce acceptable results for regions with a greater density of training data (e.g., ice-covered regions). For the N=18 case, misfits for Hudson Bay are on the same order compared to the N=45 case. We note that, depending on the site, the difference in predicted RSL between the emulator and the Seakon results is generally small (i.e., of the same scale as proxy-data uncertainties) during the Holocene, the time interval for which the majority of RSL data exist. Although the aims and methods of this study are quite different from those in Lin et al. (2023), the RSL emulator errors obtained are broadly similar (e.g., compare our results for Hudson Bay and Barbados, respectively, to those in Fig. 2d and e in Lin et al., 2023).

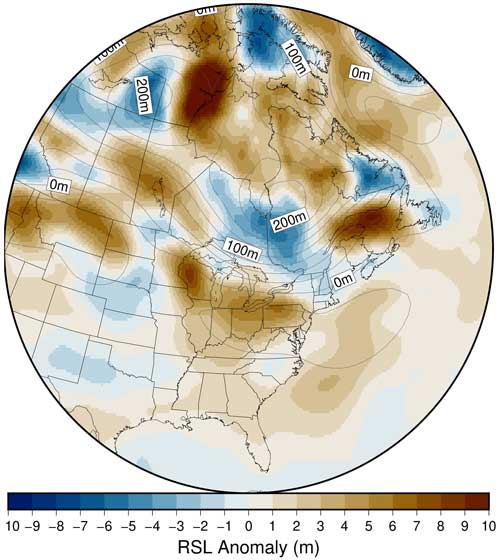
Figure 3 RSL anomaly: emulated RSL field minus the explicit (3D minus SS Seakon + NMSS) RSL field for the S40RTS + LR18 case at 10 ka. Contours denote the RSL field (from the explicit case) in 25 m increments. The Earth model parameter vector used to generate these results is that with the median MSE, calculated for all spatiotemporal data for the N=45 case. A global map of the same field is shown in Fig. S6.

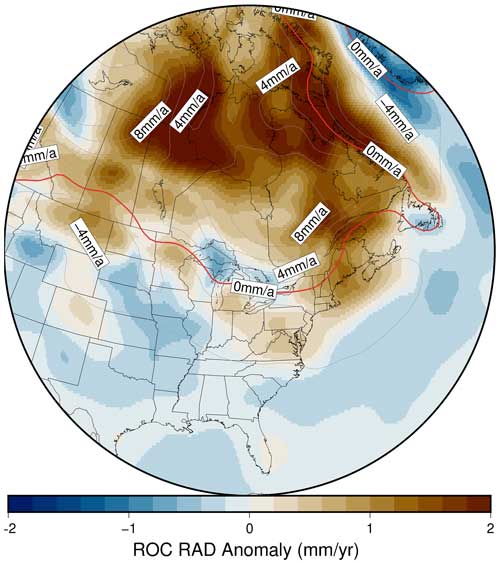
Figure 4 Emulated RAD field minus the explicit (3D minus SS Seakon + NMSS) field for the S40RTS + LR18 case at present. Contours denote the total modelled ROC RAD field (from the explicit case) in 2 mm yr⁻¹ increments; the red line denotes the 0 mm yr⁻¹ contour. The plotted parameter vector is that with the median MSE, calculated for all spatiotemporal data for the N=45 ANN. A global map of the same field is shown in Fig. S7, and an equivalent map but for 10 ka is shown in Fig. S8.

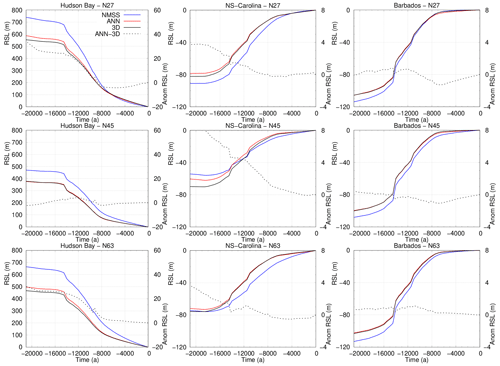
Figure 5 RSL time series for near-field (Hudson Bay), intermediate-field (northern South Carolina), and far-field (Barbados) locations for the N=27, 45, and 63 ANN training sets. RSL curves are computed using the parameter vector corresponding to the median MSE for each validation ensemble. As the parameter vector for the mean MSE generally varies with N, the resulting RSL curves also change.

When examining the emulator : model differences (or anomalies) for contemporary uplift rates, we find this method to be less accurate in comparison to RSL. The anomalies are generally of the same order of magnitude as the total modelled uplift rates for most regions (Figs. 4 and S7). However, the overall MSE results (e.g., as shown for the ROC RSL in Fig. 2) are comparable when examined over the whole spatiotemporal dataset, and so a performance comparable to that for RSL is obtained for earlier time intervals (e.g., 10 ka; Fig. S8 in the Supplement). The spatial distribution of the emulator : model anomaly for the present-day ROC of RAD more closely follows the overall distribution of the 3D Earth model's uplift field compared to the RSL results. While not investigated here, we suggest that the poorer results for this model output are a result of the input vector construction, specifically the way in which the ice sheet history is encoded. The ice sheet history comprises over half of the input vector to the ANN, and predictions of the 3D minus SS uplift difference have no change in ice sheet history within the time range used to emulate the ROC of RAD at present (previous four time steps; for ICE6G these are 0.5, 1.0, 1.5, and 2.0 ka). That is, at present, the ANN has no information to distinguish a near-field location from a far-field location when considering the input ice history data. Restricting the training data input to the ANNs or providing alternative ice history information (e.g., maximum ice thickness at that location within the last 10 kyr) may provide greater ANN accuracy. Given the relatively low accuracy of our results for contemporary uplift rates, we do not conduct data : model comparisons in Sect. 3.2.

Comparing the above results to those for the semi-3D Earth model case, i.e., S40RTS with a SS lithosphere, we find similar amplitudes of emulator : model misfit with respect to contemporary uplift rates. The emulator : model misfit for RSL is generally smaller for the same number of training parameter vectors for this simpler Earth model – of particular note is that performance within intermediate-field locations is improved (see Fig. S9 in the Supplement). Without exploring additional 3D Earth models, we cannot conclude whether this feature is a result of considering a simpler Earth model which does not incorporate the spatially variable elastic lithosphere or whether it is a limitation of our methodology (e.g., network training or architecture). Despite this, of the configurations tested here, we find that similar numbers of parameter vectors are required in the training dataset to obtain usable accuracy even for this simpler 3D Earth model.

Overall, we are able to successfully reproduce the influence of 3D Earth structures using ANNs trained using 45, or more, parameter vectors (out of a total of 330 for the LT/UMV/LMV values considered here) when considering past RSL and uplift rates. However, model–emulator misfits are generally of the same order of magnitude as the uplift and RSL rate field when considering contemporary values. As such, the emulator developed here has limited utility for comparisons to contemporary uplift and RSL rates derived from geodetic data.

Several logical extensions to the methodology applied here became apparent over the course of this investigation. The first extension would be to implement a probabilistic Bayesian artificial neural network (BANN, e.g., as described in Jospin et al., 2022). A BANN can provide estimates of the accuracy of a given prediction. Given that any error in the ROC of RSL or RAD propagates throughout the whole prediction (with respect to time), this information could be used to potentially reduce emulator : model misfits (e.g., via a cut-off where the ANN is not employed for a given prediction if the prediction confidence is too low). The second extension would be to include a parameter, or multiple parameters, in the inputs to the ANNs such that some information about the lateral Earth structure is encoded into the networks (e.g., scaling from seismic velocity anomaly to viscosity). This would allow evaluation across multiple realizations of lateral Earth structures without the need for separately trained datasets, as was done in this investigation. The final extension would be to train the ANNs on multiple ice sheet histories in order to generalize their predictions across variations of this input parameter (Lin et al., 2023). Doing so requires no changes to the ANN or training data construction, only conducting and processing of additional Seakon simulations with multiple ice sheet histories. A brief exploration (not shown here) using the ANNs trained on the ICE6G ice sheet history to emulate model output corresponding to the Australian National University (ANU) ice sheet reconstruction (Lambeck et al., 2014) resulted in large emulator : model RSL differences. This initial test underscores the need to train on multiple ice histories to produce more accurate results. Clearly, this would represent a challenge for the 3D case due to the computational inefficiency of the forward model.

3.2 Use of the emulator to identify the optimal SS viscosity model

The emulator (i.e., output from the trained ANN in combination with output from the NMSS model) is used here to examine the effects of imposing 3D viscosity variations, specifically those from the S40RTS + LR18 configuration, on reconstructions of RSL and the associated inferences of Earth structures. The ANNs were trained using 45 parameter vectors, as identified in Sect. 3.1, to provide a balance between computational expense and accuracy. As part of the validation process for the emulator and to assess the scale of impacts resulting from emulator : model differences, we calculate the model : data misfit values (Sect. 2.4) for the RSL database described in Sect. 2.4 for three different sources of model output: the NMSS model, the NMSS model combined with emulated 3D minus SS output, and the NMSS model combined with explicit 3D minus SS Seakon output. The choice to combine NMSS model output with the emulated 3D minus SS output is an end goal of the workflow, and we note that the SS Seakon output is, for the purposes of calculating the misfit, equivalent to that of the NMSS model. The results of these calculations, considering the total misfit (i.e., all RSL proxy-data types), are shown in Fig. 6. Misfit values for SLIPS, the limiting data, and all the data are shown in Fig. S10 in the Supplement for the explicit (3D minus SS + NMSS) output, with comparable misfit plots for the emulator output in Fig. S11 in the Supplement and the NMSS model output in Fig. S12 in the Supplement. These results indicate that the total misfit values are dominated by the SLIP and marine-limiting data for each of the three cases of model output.

The misfit results for the NMSS model runs are used as a baseline (or reference) for the two cases that include the influence of lateral Earth structure (modelled via Seakon or emulated via the ANNs). Comparing the results in the bottom two rows of Fig. 6 to those in the top row, we find that the emulator largely captures the impact of 3D viscosity structure on the misfit values but does not result in values that are indistinguishable from those determined from the explicit output. The emulated results are, upon visual inspection, more similar to the explicit results than the NMSS results alone. To quantify the effectiveness of the emulator across the entirety of the LT/UMV/LMV parameter space, we use the MSEs of the proxy-data : model misfit between the emulator and the explicit data as well as between the emulator and the NMSS data. For example, the emulator : NMSS MSE for the SLIP data is

$$\begin{array}{}\text{(3)}& \begin{array}{rl}& {\text{MSE}}_{\text{emulator}:\text{NMSS}}={\displaystyle \frac{\mathrm{1}}{n_{\text{LT}}{n}_{\text{UMV}}{n}_{\text{LMV}}}}\sum _{\text{LT}=\mathrm{1}}^{n_{\text{LT}}}\sum _{\text{UMV}=\mathrm{1}}^{n_{\text{UMV}}}\sum _{\text{LMV}=\mathrm{1}}^{n_{\text{LMV}}}\\ & \left({\mathit{\delta }}_{\text{SLIP}}^{\text{emulator}}\right(\text{LT},\text{UMV},\text{LMV})-{\mathit{\delta }}_{\text{SLIP}}^{\text{NMSS}}(\text{LT},\text{UMV},\text{LMV}){)}^{\mathrm{2}},\end{array}\end{array}$$

where n_LT, n_UMV, and n_LMV are, respectively, the number of LT, UMV, and LMV values in the explored parameter space, and ${\mathit{\delta }}_{\text{SLIP}}^{\text{emulator}}$ and ${\mathit{\delta }}_{\text{SLIP}}^{\text{NMSS}}$ are the SLIP misfit values as described in Sect. 2.4 for the emulator and NMSS data, respectively. The MSE provides a metric which allows for comparison of the calculated proxy-data : model misfits for the emulator, NMSS, and explicit results. In the ideal case of the misfits calculated using the emulator being identical to those from the explicit model, the emulator : explicit MSE value would be 0. MSE values for the SLIP data demonstrate that the emulator misfits are closer to those of the explicit model (${\text{MSE}}_{\text{SLIP}}=\mathrm{0.74}\times {\mathrm{10}}^{-\mathrm{3}}$) than those of the NMSS model (${\text{MSE}}_{\text{SLIP}}=\mathrm{7.11}\times {\mathrm{10}}^{-\mathrm{3}}$), which can also be concluded from Fig. 6.

Table 1 Misfits for the Canadian Arctic–Atlantic Coast (Vacchi et al., 2018), US East Coast (Engelhart and Horton, 2012), and US Gulf Coast (Hijma et al., 2015; Love et al., 2016) RSL databases broken down into the contributing misfits for sea level index points, marine- and terrestrial-limiting, and the combined total as defined in Sect. 2.4. The lowest misfit for each of the data types (i.e., SLIP, ML, TL, and total) and the corresponding combinations of SS lithospheric thickness (km), upper-mantle viscosity ($\times {\mathrm{10}}^{\mathrm{21}}\text{Pa}\cdot \text{s}$), and lower-mantle viscosity ($\times {\mathrm{10}}^{\mathrm{21}}\text{Pa}\cdot \text{s}$) are given for each region. Values are given for output generated using the NMSS, emulator (ANN-derived 3D minus SS + NMSS), and explicit (Seakon 3D minus SS + NMSS) cases. Note that the LT/UMV/LMV values for misfits of 0 in the limiting data columns for USEC are not unique and are thus left blank.

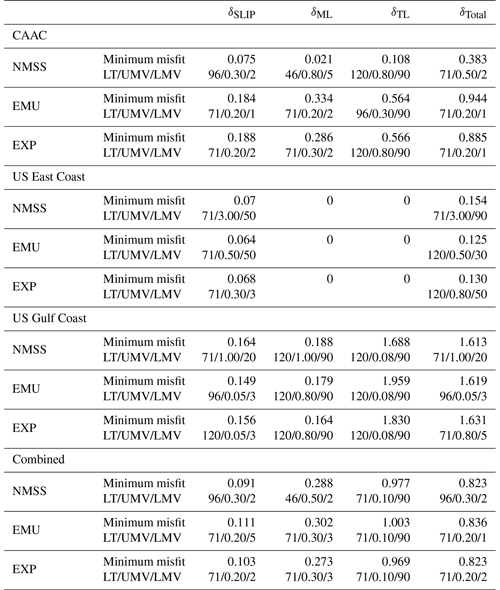
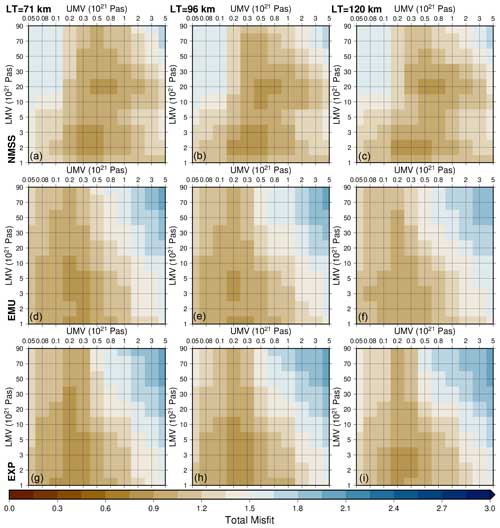
Figure 6 Proxy-data : model misfit using the RSL database (Sect. 2.4) for the NMSS model (a–c), the emulator (EMU, d–f), and the explicit 3D minus SS RSL output from Seakon added to the NMSS RSL output (EXP, g–i). The misfit varies as a function of global-mean lithosphere thickness from left to right. Results are for the S40RTS + LR18 3D model configuration.

Upon dividing the RSL dataset into the three regional subsets Canadian Arctic–Atlantic Coast (CAAC, Vacchi et al., 2018), US East Coast (USEC, Engelhart and Horton, 2012), and US Gulf Coast (USGC, Hijma et al., 2015; Love et al., 2016), we find similar results (Figs. S13, S14, and S15 in the Supplement) to those for the whole database. Overall, the proxy-data : model misfits calculated using the output of the emulator are more like the explicit results than the NMSS results alone. This result is obtained both visually and when considering the MSE values for the emulator : explicit and emulator : NMSS misfits. Since the emulator has more difficulty in reproducing the influence of lateral Earth structures in the intermediate field, for N=45, compared to near- and far-field locations (Fig. 5), it is interesting to compare the results for the USEC database (intermediate field) to the other two. For both the near-field CAAC database and the relatively distant USGC database, the MSE values of the emulator : explicit misfit results are 1 to 2 orders of magnitude smaller than the emulator : NMSS misfit. In comparison, for the intermediate-field USEC database, the MSE values of the emulator : explicit misfit results are the same order of magnitude as the emulator : NMSS misfit results.

The misfit data presented in Fig. 6 and Table 1 demonstrate that the emulator, as employed here, is successful at reproducing the region in the LT/UMV/LMV parameter space which produces the lowest proxy-data : model misfits and reproducing the relative values of proxy-data : model misfits throughout the parameter space. For the CAAC database, the use of the emulator results in a parameter vector with a minimum misfit that is either the same or within two parameter value increments (with respect to the evaluated LT/UMV/LMV values) of the explicitly derived minimum misfit parameters. This accuracy is also obtained when considering the combined dataset. For all the databases examined, the parameter vector which produces the minimum misfit obtained by emulation is closer (in parameter space) to the explicit 3D minus SS + NMSS case than the NMSS case. As such, using the emulator, we are able to identify the region of the LT/UMV/LMV parameter space that optimizes the fit for a given lateral structure model (S40RTS + LR18), e.g., the sub-region defined by UMV (0.1–0.3 $\times {\mathrm{10}}^{\mathrm{21}}\text{Pa}\cdot \text{s}$) and LMV (1–10 $\times {\mathrm{10}}^{\mathrm{21}}\text{Pa}\cdot \text{s}$) (Fig. 6). This smaller region of parameter space could then be explored using the explicit model to more accurately determine the optimal parameter vectors.

Previous work has typically used spatially confined, regional-scale analyses to mitigate the influence of lateral Earth structure when using the assumption of spherical symmetry in the GIA model (e.g., Love et al., 2016; Yousefi et al., 2018). The expectation is that, as spatial scales grow larger, those Earth models which incorporate 3D structures will outperform SS Earth models. Examining the misfit results in Fig. 6 and Table 1, we do not find that the 3D Earth model considered here consistently outperforms SS Earth models on large spatial scales. As noted in the Introduction, this has been demonstrated in many past studies (e.g., Steffen et al., 2006; Spada et al., 2006; van der Wal et al., 2013; Li et al., 2018). For some cases in our results, e.g., δ_SLIP for the US Gulf Coast, the 3D model produces a lower misfit in comparison to the SS model. However, that the 3D model results in lower proxy-data : model misfits on regional scales is expected given that we are effectively adding at least two additional parameters to the model to find the minimum proxy-data : model misfit. Despite these findings, there are features in Fig. 6 which can be used to guide future investigations. For example, the distribution and number of minima throughout the parameter space are different between the 3D and SS Earth models. The region of minimum misfit for the 3D Earth model is fairly broad but defines a single minimum in the explored parameter space rather than two distinct but relatively localized minima determined using the SS Earth models. There is a shift in the preferred UMV: for example, the UMV for the minimum misfit Earth model for the USEC δ_SLIP is $\mathrm{3}\times {\mathrm{10}}^{\mathrm{21}}\text{Pa}\cdot \text{s}$ for the SS Earth model compared to $\mathrm{0.3}\times {\mathrm{10}}^{\mathrm{21}}\text{Pa}\cdot \text{s}$) for the 3D Earth model. This shows that radial viscosity structure inferred using a SS model can be significantly biased (e.g., Lau et al., 2018; Li et al., 2022).

Overall, the SS Earth models still result in the lowest proxy-data : model misfits for the combined dataset. This suggests that our inputs to the 3D GIA model are incorrect. Given that we have investigated (in this section) only a single realization of lateral variability (to impose on a background SS Earth model) and a single ice sheet reconstruction, it is not possible to determine which one (if any) dominates in producing the higher-than-expected misfit results. Since ice sheet reconstructions (like ICE6G) are developed assuming a SS GIA model, it is not surprising that the SS Earth models outperform or give a similar quality of fit to the 3D Earth models in ice-covered areas (e.g., van der Wal et al., 2013; Li et al., 2020). This is also the reason why the optimum LT/UMV/LMV parameter set inferred here is a good approximation to the radial viscosity model assumed when constructing ICE6G (i.e., VM5a).

An important aim of future work will be to develop ice sheet models that are consistent with inferred 3D Earth structures. Previous investigations (e.g., Gomez et al., 2018; van Calcar et al., 2023) demonstrated that coupling 3D Earth models to a dynamical ice sheet model applied to Antarctica results in considerable local ice thickness changes while not significantly impacting ice sheet volume when compared to results for a SS Earth model. These more consistent 3D Earth–ice model pairings would hopefully result in improved fits to GIA-related datasets in near-field regions (compared to the SS Earth–ice model fits). In this regard, one potentially important extension of this work is to consider developing an ANN that can emulate results with different ice sheet histories. Lin et al. (2023) demonstrated that good results can be obtained with a 1D Earth model, and so there is potential to consider the case of a 3D Earth model. Again, a key challenge will be to obtain useful results in near-field regions with a relatively small training set. If successful, such an emulator could be used in coupled GIA ice sheet modelling to include the effect of lateral variations on Earth structure. This would result in computation times that are equivalent to those for coupled SS GIA–ice sheet models (i.e., ≈10 000 times more efficient than the reduced-resolution configuration used in this study).

4 Conclusions

This study provides an initial proof-of-concept assessment of using ANNs to emulate the influence of lateral Earth structure on GIA model output. We used the Tensorflow software library to produce ANNs, implement an emulator, and test the effectiveness of the emulator using model output of past (deglacial) sea level change and present-day vertical land motion from a 3D (Earth) GIA numerical model and a commonly used SS (Earth) GIA model. Our goal is to test whether the emulator can accurately predict the difference in these outputs (i.e., RSL and uplift rates) for the 3D case relative to the SS case. We pursued this application for three realizations of (global) lateral Earth structure (S40RTS, S40RTS + LR18, and Savani + LR18, Ritsema et al., 2010; Afonso et al., 2019; Auer et al., 2014) and a commonly used ice history model (ICE6G, Peltier et al., 2015; Roy and Peltier, 2017).

Our results indicate that the emulator : model differences, while not negligible, are of a scale such that useful predictions of deglacial RSL changes can be made. Evaluation of the emulator performance for deglacial RSL indicates that it is able to provide useful estimates of this field throughout the LT/UMV/LMV parameter space when trained on only ≈15 % (45) of the parameter vectors considered (330 in total). In contrast, results for present-day vertical land motion are poorer, with emulator errors on a similar order to the 3D minus SS model output. Better results when emulating vertical land motion were obtained for model time steps when ice was still present, suggesting that the performance of the emulator (for present-day rates) could be improved by modifying inputs provided to the ANNs with respect to the input ice history information (e.g., maximum ice thickness at that location within the last 10 kyr and/or a time history extending beyond the past four time steps). An important extension of this work is to consider different ice sheet models to determine whether useful results can also be achieved for variations in this important GIA model parameter.

Given the relatively accurate results obtained for RSL, we applied the emulator in a proxy-data : model comparison exercise using RSL data distributed along North American coasts, from the Canadian Arctic to the US Gulf Coast. The goals of this data : model comparison are two-fold: to determine whether the emulator can produce accurate misfit values through the entire LT/UMV/LMV parameter space considered and to evaluate whether the 3D Earth models can produce improved fits compared to the SS Earth models (for the chosen ice sheet and lateral Earth structure models). We find that the emulator is able to successfully reproduce the data : model misfit values such that, generally, the region of minimum misfit either overlaps the 3D GIA model results or is within two increments in the parameter space. The emulator can, therefore, be used to more efficiently explore this aspect of the 3D Earth model parameter space. Furthermore, the parameter values that give the best fits for the 3D and SS models are quite different, supporting previous work showing that inferences of radial viscosity structure can be significantly biased when assuming a SS structure. Thus, future work on the application of ANNs to further explore the parameter space of 3D Earth models and ice sheet histories is required.