Valid time shifting ensemble Kalman filter (VTS-EnKF) for dust storm forecasting

Dust storms pose significant risks to health and property, necessitating accurate forecasting for preventive measures. Despite advancements, dust models grapple with uncertainties arising from emission and transport processes. Data assimilation addresses these by integrating observations to rectify model error, enhancing forecast precision. The ensemble Kalman filter (EnKF) is a widely used assimilation algorithm that effectively optimize model states, particularly in terms of intensity adjustment. However, the EnKF's efficacy is challenged by position errors between modeled and observed dust features, especially under substantial position errors. This study introduces the valid time shifting ensemble Kalman filter (VTS-EnKF), which combines stochastic EnKF with a valid time shifting mechanism. By recruiting additional ensemble members from neighboring valid times, this method not only accommodates variations in dust load but also explicitly accounts for positional uncertainties. Consequently, the enlarged ensemble better represents both the intensity and positional errors, thereby optimizing the utilization of observational data. The proposed VTS-EnKF was evaluated against two severe dust storm cases from spring 2021, demonstrating that position errors notably deteriorated forecast performance in terms of root mean square error (RMSE) and normalized mean bias (NMB), impeding the EnKF's effective assimilation. Conversely, the VTS-EnKF improved both the analysis and forecast accuracy compared to the conventional EnKF. Additionally, to provide a more rigorous assessment of its performance, experiments were conducted using fewer ensemble members and different time intervals.

1 Introduction

Dust storms, identified as natural meteorological disasters, are phenomena closely associated with the prevalence of potent winds over arid regions with a loosely packed soil composition (Zhang et al., 2005; An et al., 2018). These storms enable dust particulates to ascend to remarkable heights, traversing distances of thousands of kilometers, with documented aerosol concentrations soaring to thousands of micrograms per cubic meter (µg m⁻³) (She et al., 2018). During transportation, these aerosols further participate in heterogeneous chemical reactions with SO_x and NO_x, exacerbating the severity of aerosol pollution (Song et al., 2022), thereby significantly endangering human health through respiratory and circulatory system impairments (Gross et al., 2018; Goudie, 2014). East Asia, a dominant source and recipient of dust activity (Hu et al., 2019), has witnessed intensified scholarly focus. Notably, the spring of 2021 observed the onslaught of several super dust storms – unprecedented in intensity and geographical span over the past decade (Filonchyk and Peterson, 2022) – resulting in substantial life and property losses across Mongolia and China (Gui et al., 2022; Jin et al., 2022; Tang et al., 2022). Consequently, the imperative for an accurate and timely forecasting system for dust storms is accentuated, aiming to mitigate their detrimental impacts.

In recent years, heightened public concern has fueled advancements in deciphering the physical mechanisms governing dust cycle dynamics, leading to significant strides since the 1990s. To accurately replicate dust storm behavior, numerous dust emission parameterization schemes have been devised, including MB95 (Marticorena and Bergametti, 1995), Shao96 (Shao et al., 1996; Shao, 2004), Zender03 (Zender et al., 2003), and the more recent K14 (Kok et al., 2014). Integrated within chemical transport models, these frameworks facilitate dust storm modeling exercises, exemplified by systems such as CUACE/DUST (Gong and Zhang, 2008), BSC-DREAM8b (Pérez et al., 2006; Mona et al., 2014), GEOS-Chem (Duncan Fairlie et al., 2007), and LOTOS-EUROS (Timmermans et al., 2017; Manders et al., 2017). These models are instrumental in assessing health hazards; quantifying the planet's ecosystem responses; elucidating large-scale climate drivers; and, importantly, informing the development of early warning systems capable of predicting imminent dust loads within timescales ranging from hours to days. Despite these advancements, the forecast skill of such models remains constrained by inherent uncertainties tied to input variables – such as wind velocity fields and initial/boundary conditions – as well as computational approximations necessitated by coarse spatial and temporal resolutions (Mallet and Sportisse, 2006). Of particular note, the scientific consensus highlights the emission parameterization uncertainty as the paramount source of error in dust storm simulations (Ginoux et al., 2001, 2012; Di Tomaso et al., 2017, 2022; Jin et al., 2019a, b). Consequently, the predictive prowess of numerical dust models is notably compromised under the weight of these combined limitations.

Observational studies constitute another pivotal approach in elucidating the intensity and spatial dispersion of dust storms (Akhlaq et al., 2012). Among these, satellite-based monitoring technologies have rapidly evolved into a prevalent tool for dust storm detection, offering expansive and detailed insights (Gui et al., 2022). Platforms like MODIS, Himawari, and Fengyun-4A deliver a wealth of data on aerosol characteristics, characterized by high spatial resolution and global coverage. Nonetheless, these satellite products aggregate column-integrated information and are prone to interference from cloud cover and other atmospheric constituents, thereby introducing substantial uncertainties and biases into dust load estimates. Consequently, preprocessing is imperative to ensure their reliability in depicting actual dust concentrations (Jin et al., 2019b, 2022). Concurrently, ground-based observational networks, known for their reliability and fine temporal resolution, play a crucial role in precisely measuring aerosol concentrations (She et al., 2018). China, in particular, has made substantial investments in constructing its ground monitoring infrastructure, establishing an expansive network comprising over 1600 stations nationwide. This dense grid of ground stations furnishes a granular view of dust plume dynamics across the region (Gui et al., 2022), enriching the dataset for examining east Asian dust storms and reinforcing the national observation network's capacity for comprehensive dust research.

Data assimilation stands as a potent methodology that harmoniously merges model with observations. Rooted in Bayesian principles, its objective is to ascertain the most plausible model state posterior, given the available observations, through probabilistic estimation (Law and Stuart, 2012). The realm of data assimilation encompasses two principal methodologies: variational techniques and filtering algorithms. Variational methodologies, exemplified by 4DVar, strive to determine an optimal analysis that reconciles both prior knowledge and observational constraints over a defined temporal span, achieved by optimizing a predefined cost function (Rabier and Liu, 2003). These methods are prominently employed in tasks such as inverse modeling for initial conditions and emission fields (Jin et al., 2022; Bergamaschi et al., 2010; Corazza et al., 2011), as well as in reanalysis endeavors. However, their implementation hinges on the often intricate development and maintenance of tangent linear or adjoint model forms. Furthermore, the computational burden associated with minimizing the cost function escalates dramatically with the complexity and dimensionality of the models. Conversely, filtering methodologies assimilate observations sequentially, aligning them favorably with operational forecasting frameworks. This class includes the Kalman filter (Kalman, 1960), its extension in the extended Kalman filter (Brunner et al., 2012), and the more sophisticated particle filter (Leeuwen et al., 2019). Prominent among these is the ensemble Kalman filter (EnKF), distinguished for its adeptness at managing high-dimensional systems, amenability to parallel computation (Evensen, 1994; Katzfuss et al., 2016; Houtekamer and Zhang, 2016), and reliance on ensemble members to infer background error covariance structures (Hamill, 2006; Houtekamer et al., 2014). Its virtues encompass nonlinearity accommodation, dispensing with the necessity for explicit tangent linear calculations, and computational efficacy (Bannister, 2017), rendering it a favored tool across domains, including weather prediction (Houtekamer et al., 2005) and hydrological studies (Reichle et al., 2002). Despite these strengths, the EnKF, as an extension of the Kalman filter, presumes Gaussian error distributions (Amezcua and Van Leeuwen, 2014). When dealing with non-Gaussian error statistics, EnKF can create suboptimal outcomes for the linearized dynamics or operators and sampling errors caused by finite ensemble members (Lei et al., 2010).

Uncertainty in dust storm modeling predominantly stems from the real-time estimation of dust emissions, leading to a research emphasis on emission inversion through data assimilation techniques. Studies such as those conducted by Yumimoto and Takemura (2015) leveraged long-term MODIS aerosol optical depth (AOD) retrievals for emission inversion across Asia. Similarly, Escribano et al. (2017) underscored the varying impact of distinct satellite AOD datasets on emission inversions over northern Africa and the Arabian Peninsula, revealing instances where model uncertainties outweigh observational uncertainties in determining assimilation outcomes. Building upon this foundation, recent investigations have delved deeper into the intricacies of dust emission variability in the Mongolian and Chinese Gobi deserts. This includes the assimilation of ground-level PM₁₀ concentrations (Jin et al., 2018), polar-orbiting MODIS satellite data (Jin et al., 2022), and geostationary Himawari-8 AOD measurements (Jin et al., 2019b). To refine emission inversion processes, innovations like observation bias correction (Jin et al., 2019a), adjoint-based emission source tracking (Jin et al., 2020), and grid adjustment methodologies (Jin et al., 2021) have been introduced, significantly advancing our understanding of dust emission dynamics and their environmental and climatic implications. Despite these advancements, the application of sequential forecasting methodologies utilizing filtering techniques for dust storms has received limited exploration. To address this gap, we have recently engineered an operational dust forecasting framework that integrates the ensemble Kalman filter (EnKF) with the LOTOS-EUROS model. This integration is facilitated by our custom assimilation software, PyFilter (Pang, 2024). Testing this system against the backdrop of the record-breaking dust storms of spring 2021 has demonstrated marked improvements in both the assimilated analyses and forecast results compared to standalone model forecasts. Notably, when configured with an appropriate localization radius, it consistently outperformed the EnKF, highlighting the potential for localized filters in enhancing the precision of dust storm forecasting.

Despite the encouraging outcomes of our experimental assessments, several challenges persist, chief among them being a spatial misalignment between model forecast and observations following long-distance dust transport. This disparity not only encompasses discrepancies in the estimated dust intensity but also manifests in inaccuracies regarding the timing of dust arrival and departure, as will be elaborated in Sect. 2.4. In the context of dust storm forecasting evaluation, both the intensity and the position accuracy of the dust plume are paramount. Intensity directly correlates with the amount of airborne dust, while the position is vital for understanding where the dust plume affects at a given instant. For operational forecasting and warning systems, pinpointing the correct location of impending dust impacts can carry even greater urgency than estimating dust load precisely. Quantitatively, these spatial mismatches significantly deteriorate the forecast performance when evaluated using conventional measures like the root mean square error (RMSE). The underlying causes of this spatial discrepancy and its broader ramifications on forecasting efficacy will be meticulously examined in Sect. 3.2.

The phenomenon labeled “position error” in dust aerosol simulations typically emerges following long-distance transport. This error is multifaceted, stemming from a constellation of factors including the simplification of physical processes in models, coarse spatial and temporal resolutions, indeterminate values of physical parameters (Ravela et al., 2007), and uncertainties inherent to both meteorological inputs and the precise timing of dust emissions, as we previously highlighted (Jin et al., 2021). Resembling the issues encountered in dust emission inversion, discrepancies between model forecast and observations in dust storm data assimilation efforts can also be traced back to uncertainties in dust emission estimates, where ensemble simulations incorporate varied emission scenarios. The challenge lies in the quantification of position error and its subsequent inaccurate formulation of the background error covariance matrix. Consequently, EnKF calibrates both intensity and position error, while it cannot handle position errors if the ensemble is under-dispersive with regard to position. This deficiency curtails the capacity of current assimilation methodologies to correct position error.

Position error is not an occasional issue. Instead, it is an error that accumulates as simulations progress, plaguing forecasts such as hurricanes, dust storms, convective thunderstorms, and precipitation (Dance, 2004; Nehrkorn et al., 2015; Jin et al., 2021). However, efforts explicitly targeting the mitigation of this error have been relatively scarce. One pioneering study by Brewster (2003) outlined an objective methodology to pinpoint and rectify position errors leveraging a wealth of high-resolution, densely deployed observational data. Their findings in Observing System Simulation Experiments (OSSEs) affirmed the feasibility of correcting positional errors. Jin et al. (2021) developed a grid distortion strategy grounded in image morphing techniques for post-processing, effectively realigning modeled dust plumes to conform more closely with observations. While these enhancements underscore the potential for addressing position errors, their efficacy hinges critically on the availability of a comprehensive and closely spaced observational network. Regrettably, in many practical scenarios, observational coverage is patchy and incomplete, curtailing the broad application of these corrective measures.

In this paper, the EnKF is coupled with a valid time shifting (VTS) strategy, referred to henceforth as VTS-EnKF, specifically tailored to mitigate position errors prevalent in long-distance dust storm transport. The VTS methodology, inspired by prior works such as Xu et al. (2008), Lu et al. (2011), Zhao et al. (2015), and Huang and Wang (2018), augments the EnKF by incorporating temporal flexibility to better align simulated dust plumes with observations. In practice, the VTS-EnKF enhances the background error covariance estimation for each assimilation cycle by considering not solely the immediate ensemble members but also those from neighboring time points, slightly before and after the target moment (Gasperoni et al., 2022, 2023). By doing so, this approach encapsulates a broader range of potential dust plume positions, thereby inherently compensating for transport-related inaccuracies without necessitating intricate adjustments to observations, meteorological inputs, or other underlying physical parameters. The efficacy of the VTS-EnKF was assessed against two severe dust storm events that occurred in 2021. Our findings underscore the substantial improvement offered by this hybrid method over EnKF, particularly in scenarios where significant position errors are evident in the model prior. This advancement paves the way for more precise and temporally coherent dust storm forecasting, especially amidst the complexities of long-distance transport.

This paper is organized as follows: Sect. 2 introduces the dust measurements and dust model used in the research. We also discuss that the major uncertainty of dust model forecast comes from the emission. But there is another problem: position error that remains to be solved. Then, in Sect. 3, we explain the introduction of the procedure of ensemble-based assimilation algorithm and the mechanism of position error's negative effect on EnKF. How the new assimilation method works is explained in detail afterwards. To test the performance of EnKF with VTS, sequential assimilation experiments on several dust storm events are designed. Section 4 analyses the results of experiments in terms of both the assimilation analysis and forecast performance. Section 5 concludes this paper.

2 Dust observation, model, and position error

In this paper, ground-based PM₁₀ is used as the dust observation to be assimilated after a bias-correction procedure to remove the non-dust part. The dust model adopted is LOTOS-EUROS. Considering the model processes, the greatest uncertainty in the dust simulation comes from uncertainty in the emission parameterization. Meanwhile, uncertainties from meteorology can also influence the model forecast and lead to the “position error”.

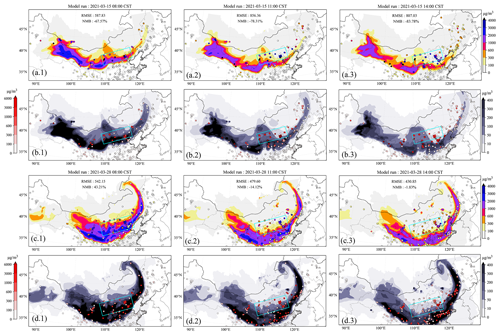
Figure 1 Evolution of the simulated dust plume from average of ensemble members (a.1–3). Their corresponding standard deviation from ensemble members (b.1–3) at 08:00, 11:00, and 14:00 on 15 March 2021, respectively. Figures below are the same except the time is at 05:00 (c.1, d.1), 08:00 (c.2, d.2), and 11:00 (c.3, d.3) on 28 March 2021, respectively. The filled circles represent ground BR-PM₁₀ observations in (a) and (c), and the model-minus-observation differences (absolute value) at various observation sites are in (b) and (d). The color bar in panel (a) and (c) represents the concentrations, and the color bar in panel (b) and (d) represents the model-minus-observation differences (left) and standard deviation (right). BR-PM₁₀: baseline-removed PM₁₀. CST: China standard time.

2.1 Ground PM₁₀ observations

Thanks to the continuous efforts and investments from the Ministry of Ecology and Environment, over 1600 ground monitoring stations have been established across China, with some locations in northern China shown in Fig. 1. These stations provide real-time hourly air quality data, and their hourly PM₁₀ concentrations serve as indispensable datasets for measuring dust load, which are used as observations to be assimilated in this paper.

Despite the advantages of low uncertainty and high time resolution, PM₁₀ observations are not assimilated directly due to the mixed state of dust and non-dust aerosols in the original PM₁₀ data. Anthropogenic activities, such as vehicle emissions, coal burning, and industrial processes (Wu et al., 2018; Liu et al., 2018), along with natural sources like volcanic eruptions, sea spray, wildfires, and wind-blown dust contribute to the total PM₁₀ concentration. Assimilating PM₁₀ data directly into a dust model may introduce biases and lead to model divergence (Jin et al., 2019a). Therefore, it is necessary to eliminate the bias before data assimilation.

In this study, the non-dust portion of PM₁₀ is approximated through a separate model. The dust observations assimilated are calculated by subtracting the non-dust fraction from the original PM₁₀ measurements. Further details regarding the baseline removal (BR) can be found in Jin et al. (2022).

2.2 Dust model

In this paper, LOTOS-EUROS v2.1 is used to simulate dust storms that occurred in east Asia. Originating from the Long-Term Ozone Simulation (LOTOS) and the European Operational Smog model (EUROS) in the 1980s, LOTOS-EUROS has undergone continuous development for various applications. It has been widely used in air quality forecasting (Curier et al., 2012; Brasseur et al., 2019; Lopez-Restrepo et al., 2020; Skoulidou et al., 2021), dust/aerosol emission inversion (Yarce Botero et al., 2021; Jin et al., 2018, 2019a, b, 2021, 2022), and source apportionment (Kranenburg et al., 2013; Timmermans et al., 2017; Pommier et al., 2020; Jin et al., 2020). In spring 2021, several super dust storm events occurred in east Asia, around 15 March and 28 March. These events, referred to as DSE1 and DSE2, are used as test cases in this study. These dust storms caused significant losses in both Mongolia and China (Jin, 2021; Chen and Walsh, 2021). Accurate forecast of such severe sandstorms is crucial for reducing health hazards and property damage.

To simulate the dust storm over east Asia, LOTOS-EUROS is configured following our recent work (Jin et al., 2022): the simulation domain is from 15 to 50° N and 70 to 140° E with a grid resolution of 0.25° × 0.25°. The model consists of 8 layers with a top at 10 km. The boundary conditions are set to zero assuming that all the dust aerosols are emitted during the simulation window. Dust emission, deposition, advection, diffusion and dry/wet deposition are considered within the model. The model output is at the interval of 1 h.

The whole model simulation period is set from 13 to 17 March for DSE1 and 27 to 30 March for DSE2, which covers the whole life cycles of emission and long-distance transport. More details can be found in Jin et al. (2022).

2.3 Uncertainties from emission and meteorology

The goal of this study is to calculate the dust concentration field that best fits both the a priori information and observations at each assimilation analysis. The optimized field will then be used as the initial condition for sequential dust forecasts, as explained in Sect. 3.1. It is essential to define and quantify the uncertainty in dust simulations. As previously mentioned, the uncertainty in emission parameterization is widely believed to be the dominant error source in dust simulation (Ginoux et al., 2001, 2012; Di Tomaso et al., 2017, 2022; Jin et al., 2019a, b). High levels of uncertainty in dust emission parameterization arise from insufficient knowledge about windblown erosion, lack of accurate input on soil characteristics, and the models' inability to resolve the fine-scale variability in wind fields governing dust emission (Escribano et al., 2017; Foroutan et al., 2017; Foroutan and Pleim, 2017; Jin et al., 2019b).

In our recent work (Jin et al., 2022), a 4DVar-based inverse modeling approach was employed to retrieve an optimal emission field for the three major dust storms in spring 2021 (Jin et al., 2022). The a priori emission, f_priori, followed the Zender03 dust emission parameterization scheme (Zender et al., 2003). To compensate for potential errors, a spatially varying multiplication factor was introduced. Mathematically, it was quantified by a background error covariance matrix, B, to describe the potential spread of the actual dust emission flux.

Another source of the uncertainties arises from the meteorological field. In our previous papers, uncertainties from meteorology and the position error were neither taken into account (Jin et al., 2022; Pang et al., 2023). In this paper, the ensemble forecast from the European Centre for Medium-Range Weather Forecasts (ECMWF) (51 ensemble members in total) is used. Each one of the model ensemble members is driven by one unique ensemble meteorology field. Its grid resolution is about 14 km. The 6-hourly short-term meteorological forecast field is interpolated to hourly values and re-gridded to match the model resolution.

In general, we assign the dust simulation uncertainty to both emission and meteorology. Ensemble emission fields $[f_{\mathrm{1}},\mathrm{\dots },f_{\mathrm{N}}]$ are generated randomly following the emission uncertainty choice f_priori and B in Jin et al. (2022). Meteorologic fields $[w_{\mathrm{1}},\mathrm{\dots },w_{\mathrm{N}}]$ are randomly selected from the total 51 ensemble meteorology. They are used to forward the LOTOS-EUROS model ℳ for the ensemble dust simulations $[{\mathit{x}}_{\mathrm{1}},\mathrm{\dots },{\mathit{x}}_{\mathrm{N}}]$ as

$$\begin{array}{}\text{(1)}& [{\mathit{x}}_{\mathrm{1}},\mathrm{\dots },{\mathit{x}}_{\mathrm{N}}]=\left[\mathcal{M}\right(f_{\mathrm{1}},w_{\mathrm{1}}),\mathrm{\dots },\mathcal{M}(f_{\mathrm{N}},w_{\mathrm{N}}\left)\right].\end{array}$$

N refers to the total ensemble number, and the choice will be explained in Sect. 3.3.

These ensemble individuals are used in the EnKF assimilation for representing the covariance dynamics of the dust plume, which resulted in more accurate dust analysis and forecast, as will be shown in Sect. 4. However, the ensemble realizations mainly represent the uncertainty in the intensity feature and hardly help resolve the positional deviation between the observation and simulation. The presence of position error would give rise to a divergent assimilation analysis, as will be illustrated in Sect. 3.1.

2.4 Position error

For all the dust events, most of the dust particles originated from the Mongolia Gobi desert and were carried by the prevailing wind towards the southeast. After several thousands of kilometers' transport, which lasted about 1–2 d, they finally arrived in the densely populated region of northern China.

Position errors are clearly visible in the simulation of two dust events (DSE1 and DSE2). Examples can be best seen in Fig. 1, which plots the evolution of LOTOS-EUROS-simulated surface dust concentration alongside BR-PM₁₀ (BR: non-dust baseline-removed) concentration observations for DSE1 (Fig. 1a) and DSE2 (Fig. 1c). The corresponding standard deviations from ensemble model simulations and the model-minus-observation differences (absolute values) are also plotted in Fig. 1b and d. In Fig. 1a.1, the model generally simulates a similar shape of the dust plume as indicated by the observations at the first instance, though the dust load intensities differ to some extent. However, during the subsequent transport, positional errors arise gradually. In Fig. 1a.2, the right part of the simulated dust plume is positioned about 100 to 200 km too far south compared to ground-based observations. Consequently, the root mean square error (RMSE) increases significantly from 587.83 µg m⁻³ at 08:00 CST to 856.36 µg m⁻³ at 11:00. This position error continues to accumulate over the following 3 h at 14:00. The development of position errors is further clearly visible against the PM₁₀ observations, especially in the light-blue box in Fig. 1a.3. The model simulation missed all the dust load there, while the observations indicate a significant amount of dust aerosols. It can also be seen in Fig. 1b.3 that the model-minus-observation differences exceed 1000 µg m⁻³ there. Similarly, for DSE2 occurring on 28 March 2021, as shown in Fig. 1c, discrepancies between observations and simulation become more explicit as time evolves, especially for the dust in the light-blue box in Fig. 1c.1 and c.2. The RMSE remains high from 542.15 µg m⁻³ at 08:00 to 479.6 µg m⁻³ at 11:00, and this error expands to a wider extent as shown in the enlarged green box in Fig. 1c.3. This position error not only limits the model forecast performance but also significantly degrades the subsequent assimilation analysis and forecast. With an ensemble-approximated background covariance unrepresentative of position error, neither the position deviation nor the intensity deviation can be fully resolved, as will be explained in Sect. 3.2.

Potential sources of position error in dust model may be attributed to inaccuracies in emission timing, uncertainties in meteorological input data (e.g., wind fields responsible for transporting dust plumes from the Gobi Desert in Mongolia and China to downwind regions), or a combination of these factors. Adjusting the emission timing profile, which characterizes the release of soil particles into the atmosphere, could partially correct the position of the dust plume. Moreover, alterations in meteorological conditions governing long-distance transport might also realign the dust plume's position. To address the position error, a comprehensive covariance matrix is necessary to account for both the potential variations in emission temporal profiles and the accumulation of uncertainties along the plume's extensive trajectory. Concurrently, a significantly larger ensemble size is required to propagate these uncertainties, featuring high degrees of freedom, into the PM₁₀ observational space. Although a sophisticated covariance matrix and a substantial ensemble size (resulting in considerable computational cost) may aid the EnKF in simultaneously resolving position and intensity errors, this approach is often prohibitively expensive. Therefore, an efficient and cost-effective alternative solution is required.

3 Assimilation methodology and experiments

EnKF is a powerful algorithm to tune the model simulation with observations, especially in intensity adjustment given the perturbed emission spreads. However, when faced with the position error, its weakness is exposed that some model-minus-observation inconsistency cannot be resolved by EnKF as illustrated in Sect. 3.1. Conversely, our EnKF with VTS can correct both the position error and the intensity. The assimilation strategy is designed and embedded in an assimilation forecast system in Sect. 3.2. Experiments are designed for the dust storms that occurred in spring 2021 and are illustrated in Sect. 3.3.

3.1 EnKF

The ensemble Kalman filter (EnKF) was first proposed by Evensen (1994). Stemming from the Kalman filter, it was designed to address high-dimensional problems by employing limited ensemble members to approximate the true background error covariance. It relies on the Gaussian distribution of errors. The EnKF has been proven to be practical and efficient in various applications, particularly in sequential forecasting with the aid of localization (Lopez-Restrepo et al., 2020; Park et al., 2022). In any sequential forecast system, the objective of assimilation analysis is to provide an optimized initial state or parameter field, which, in this study, corresponds to the 3D dust concentration. This is achieved by assimilating the available measurements. The estimated dust concentration field can then be used to forward the model for more accurate dust forecasting.

Here we use the stochastic EnKF formulated by Burgers et al. (1998). It features the perturbed observations to maintain a reliable ensemble spread. Starting from the prior dust concentration field ${\mathit{x}}_t^{f,i}$ at time t, which is calculated by model integral operator ℳ from the dust concentration field at the previous time step ${\mathit{x}}_{t-\mathrm{1}}^{\mathrm{a},i}$,

$$\begin{array}{}\text{(2)}& {\displaystyle }& {\displaystyle }{\mathit{x}}_t^{f,i}=\mathcal{M}({\mathit{x}}_{t-\mathrm{1}}^{\mathrm{a},i},f^i,w^i)\text{(3)}& {\displaystyle }& {\displaystyle }{\mathbf{X}}^f=[{\mathit{x}}_t^{f,\mathrm{1}},{\mathit{x}}_t^{f,\mathrm{2}},\mathrm{\dots },{\mathit{x}}_t^{f,\mathrm{N}}].\end{array}$$

Note that for the first analysis, the prior dust simulation is extracted from the model with the perturbed emissions as shown in Eq. (1); i represents the ensemble individual number, N is the number of ensemble, and X^f is the ensemble model simulation matrix consists of the whole ensemble individuals.

The ensemble perturbation matrix X^f′ calculates the deviation between the ensemble individuals ${\mathit{x}}_t^{f,i}$ and the ensemble mean state ${\stackrel{\mathrm{‾}}{\mathit{x}}}_t^f$.

$$\begin{array}{}\text{(4)}& {\displaystyle }& {\displaystyle }{\stackrel{\mathrm{‾}}{\mathit{x}}}_t^f={\displaystyle \frac{\mathrm{1}}{\mathrm{N}}}\sum _{i=\mathrm{1}}^{\mathrm{N}}{\mathit{x}}_t^{f,i}\text{(5)}& {\displaystyle }& {\displaystyle }{\mathbf{X}}^{f\prime }=[{\mathit{x}}_t^{f,\mathrm{1}}-{\stackrel{\mathrm{‾}}{\mathit{x}}}_t^f,{\mathit{x}}_t^{f,\mathrm{2}}-{\stackrel{\mathrm{‾}}{\mathit{x}}}_t^f,\mathrm{\dots },{\mathit{x}}_t^{f,\mathrm{N}}-{\stackrel{\mathrm{‾}}{\mathit{x}}}_t^f]\end{array}$$

Then, the background error covariance matrix P^f is approximated by X^f′ as follows:

$$\begin{array}{}\text{(6)}& {\mathbf{P}}^f={\displaystyle \frac{\mathrm{1}}{\mathrm{N}-\mathrm{1}}}{\mathbf{X}}^{f\prime }{\mathbf{X}}^{f\prime \mathrm{T}}.\end{array}$$

Afterwards, the Kalman gain K can be calculated with P^f and O.

$$\begin{array}{}\text{(7)}& \mathbf{K}={\mathbf{P}}^f{\mathcal{H}}^{\mathrm{T}}(\mathcal{H}{\mathbf{P}}^f{\mathcal{H}}^{\mathrm{T}}+\mathbf{O}{)}^{-\mathrm{1}}\end{array}$$

K weights the increments given from the observations to the prior estimation. In this paper, they are the BR-PM₁₀ observations stored in y and dust simulation stored in vector x. ℋ is the observation operator, which maps the model states into the observational space.

O is the observational error covariance matrix that weights the uncertainty of the measurements. In this case, it is the uncertainties from ground-based BR-PM₁₀ concentrations. O is defined as follows: the minimum uncertainty threshold is set to be 200 µg m⁻³. Standard deviation of observation error below the threshold is set to be 200 µg m⁻³, and that over it is set to be $\mathrm{200}+(y-\mathrm{200})\times$ 0.2 µg m⁻³. This definition can prevent the a posteriori field from getting too close to the low value observations, thus leading to model divergence. O is a diagonal matrix assuming that all the observations are independent.

In the end, the a posteriori estimation individual ${\mathit{x}}_t^{\mathrm{a},i}$ can be updated as follows:

$$\begin{array}{}\text{(8)}& {\mathit{x}}_t^{\mathrm{a},i}={\mathit{x}}_t^{f,i}+\mathbf{K}(y+{\mathit{ϵ}}^i-\mathcal{H}{\mathit{x}}_t^{f,i}).\end{array}$$

ϵⁱ represents the sampling error vector. It is a random vector subject to normal distribution. Its mean is 0, and its variance is the root of diagonal from O.

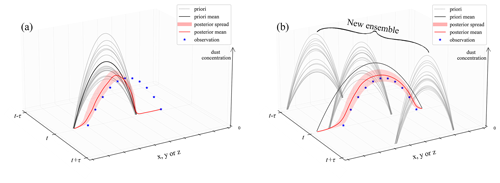
Figure 2 Strategy illustration of ensemble Kalman filter (EnKF) (a) and ensemble Kalman filter with VTS (VTS-EnKF) (b). The left-hand figure axis represents the time, and the right-hand axis represents the position of the dust field in 3D space. The vertical axis represents the intensity of the dust.

Table 1 Experiment settings.

The equations presented above describe the ensemble Kalman filter (EnKF) algorithm for dust storm assimilation, which focuses on intensity adjustment. The EnKF assimilation aims to compute an optimal a posteriori estimation given a priori information and observations. It is highly dependent on both the observations and the ensemble spread. In fact, the ensemble-based background covariance matrix, P^f, utilizes the ensemble members to approximate the true background covariance. The performance of EnKF deteriorates when position errors are present. The underlying mechanism can be best understood by examining Fig. 2a. At time point t₀, there are ensemble model simulations (dashed gray lines) distributed across the three-dimensional space. The black line and blue star represent the average of model ensemble and observations, respectively. As clearly depicted, there is a positional mismatch between the ensemble model simulations and observations. Following the assimilation analysis, the intensity of the dust plume is adjusted to better match the observations. However, in the spatial domain outside the a priori field, the dust concentration is reduced to near-zero levels. The observations in this area, containing valuable information about dust load, contribute little to correcting the dust load. This is due to the unanimous agreement on the dust load from the model ensemble, which represents low uncertainty. In such cases, the assimilation analysis favors the model results and disregards the observations. Consequently, the a posteriori estimate is biased as a result of ensemble underdispersion.

3.2 VTS-EnKF

To efficiently perform the assimilation analysis with both the intensity and position errors present, we apply a valid time shifting method in the EnKF. The strategy is illustrated in Fig. 2b. Instead of using the ensemble simulations solely at the exact assimilation analysis instant t₀, as shown in Fig. 2a, ensemble members at neighboring moments are also introduced to expand the ensemble group. These resampled ensemble members at neighboring times represent the potential positions of the actual dust plume. The enlarged ensemble exhibits a more extensive spread of the dust plume in the spatial domain compared to that displayed in Fig. 2a. The joint ensemble model simulations then capture uncertainty in both intensity and position. The a posteriori estimate (red line) is adjusted to better fit the observations, with both of these errors resolved.

Mathematically, the procedures of EnKF with VTS are very similar to those of EnKF, except that the original X^f is replaced by X^f,new, which stores the enlarged ensemble members at the assimilation analysis instant and neighboring times. It starts with

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{\mathbf{X}}^{f,\text{new}}=& [{\mathit{x}}_{t-\mathit{\tau }}^{f,\mathrm{1}},{\mathit{x}}_{t-\mathit{\tau }}^{f,\mathrm{2}},\mathrm{\dots },{\mathit{x}}_{t-\mathit{\tau }}^{f,\mathrm{N}},{\mathit{x}}_t^{f,\mathrm{1}},{\mathit{x}}_t^{f,\mathrm{2}},\mathrm{\dots },\\ & {\mathit{x}}_t^{f,\mathrm{N}},{\mathit{x}}_{t+\mathit{\tau }}^{f,\mathrm{1}},{\mathit{x}}_{t+\mathit{\tau }}^{f,\mathrm{2}},\mathrm{\dots },{\mathit{x}}_{t+\mathit{\tau }}^{f,\mathrm{N}}].\end{array}\end{array}$$

Let t be the exact assimilation time and τ be the time interval. Then, t−τ represents the time in the past, and t+τ represents the time in the future. It is noteworthy that the time axis, denoted by t−τ and t+τ, is utilized solely to illustrate the application of ensemble simulations at different time direction in the formula. However, in practical applications, ensemble members from multiple adjacent time instants can be incorporated, as demonstrated in the horizon choice utilized in this study (as presented in Table 1).

Subsequently, the ensemble-based background covariance P^f, Kalman gain K, and a posteriori state x^a will be updated with the X^f,new in Eqs. (6)–(8), respectively.

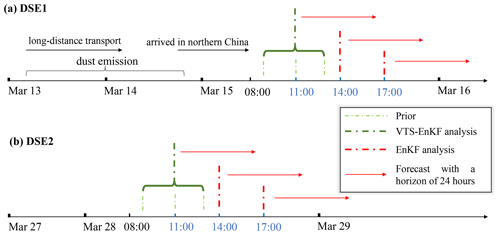
Figure 3 Sequential assimilation time set for DSE1 (a) and DSE2 (b). Take DSE1 for instance; the assimilation analysis is performed at the intervals of 3 h from 11:00 to 17:00, and the rolling forecast is done with a horizon of 24 h based on the assimilation analysis. The EnKF with VTS and EnKF is performed in turn.

The localization method is also adopted here to cut off the spurious correlation in P^f and constrain the background covariance to a certain distance. The localization matrix is constructed following Gaspari and Cohn (1999) (Eq. A.27), with a distance threshold L_thres. Details about the construction of L can be found in the Supplement. The localized P^f,local is obtained by point-to-point multiplication with the localization matrix L.

$$\begin{array}{}\text{(10)}& {\mathbf{P}}^{f,\text{local}}={\mathbf{P}}^f\circ \mathbf{L}\end{array}$$

With the localized P^f,local, the localized a posteriori estimation ${\mathit{x}}_t^{\mathrm{a},i}$ can be updated via Eqs. (7) and (8).

Both the EnKF and EnKF with VTS described above are embedded in our self-designed assimilation toolbox, PyFilter (Pang, 2024). This toolbox features a flexible interface for linking to numerical models (Pang et al., 2023), such as the dust storm forecasting model LOTOS-EUROS used in this study.

3.3 Experiment descriptions

DSE1 and DSE2 are chosen as the cases for the test. The BC-PM₁₀ observations are assimilated. The first assimilation analysis did not commence until the dust plume was detected by the ground-based observation network and a position mismatch emerged. An identification index is also designed to objectively discriminate the position error as can be found in Eq. (S6) in the Supplement. Three sequential EnKF analyses are conducted in each dust event at 3 h intervals. The timeline for DSE1 and DSE2 is depicted in Fig. 3.

Taking DSE1 as an example, the initial assimilation analysis is performed at 11:00 on 15 March, when an apparent position error was present, as illustrated in Fig. 1a.2. The last analysis is carried out at 17:00 on 15 March. As the dust loading decreases rapidly when the plume moves further southeast, no additional assimilation is performed. A rolling forecast (red line with arrow) is generated based on the optimized dust concentration field with a 24 h horizon for the purpose of examining forecast skill.

To evaluate the performance of the VTS-EnKF-implemented dust storm forecasting system, data assimilation experiments are conducted for two spring dust events in 2021. Experiment settings are shown in Table 1. Control represents the ensemble model forecast throughout the entire dust storm period. Basic and L500 denote the assimilation-based forecasts by EnKF and localized EnKF (LEnKF) with a localization distance threshold of 500 km, respectively. VTS-EnKF and VTS-L500 represent the assimilation-based forecasts by VTS-EnKF and VTS-EnKF with a localization distance threshold of 500 km. Note that various distance thresholds have been tested for localization, and a choice of 500 km is found to provide the optimal assimilation analysis and forecast in our tested cases. The metrics, root mean square error (RMSE) and normalized mean bias (NMB), are employed in this paper to evaluate system performance. Calculation of the metrics is mentioned in the Supplement.

In EnKF-based experiments, Basic and L500, the ensemble number N is set to 32, which is found to be sufficient to represent the uncertainty in the dust simulation while remaining computationally affordable. Testing with N greater than 32 shows only limited improvements. For VTS-EnKF experiments, the ensemble is expanded as they incorporate simulations from neighboring instants. To cover the potential positions of the dust plume, neighboring times with ± 1 and ± 2 h apart are empirically chosen in this paper. As demonstrated in Table 1, the ensemble number is extended to 160 when EnKF with VTS is applied, and the neighboring time stamps of 09:00, 10:00, 12:00, and 13:00 are selected. The 160 ensemble dust simulations are updated according to the EnKF principles and forwarded synchronously for the new rolling forecast; they will serve as the prior in the subsequent assimilation analysis.

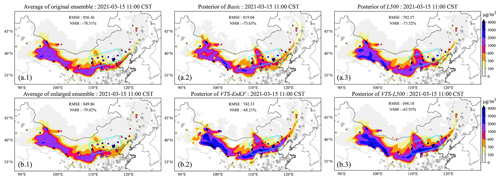
Figure 4 Spatial distribution of the simulated dust plume (SDP) on the surface from average of ensemble members at central time (a.1), the a posteriori SDP updated by EnKF (a.2), the a posteriori SDP updated by EnKF with localization (a.3), central and neighboring time ensemble model mean (b.1), the a posteriori SDP updated by VTS-EnKF (b.2), and the a posteriori SDP updated by VTS-EnKF with localization (b.3) at 11:00 CST on 15 March 2021. The filled circles are ground-based BR-PM₁₀ observations. CST: China standard time.

Experiments for the VTS-EnKF with equal ensemble members to EnKF are designed, referred to as VTS-EnKF-small and VTS-L500-small. They start with 8 central ensemble members and are extended to 32 by incorporating neighboring ± 1 and ± 2 h with 4 × 6 ensemble members. Furthermore, to test the sensitivity of neighboring time interval, VTS-EnKF experiments with different intervals are also designed. Time intervals ranging from 1 to 5 h are selected to test the impact, which are referred to as VTS-EnKF-t1, VTS-EnKF-t2, VTS-EnKF-t3, VTS-EnKF-t4, and VTS-EnKF-t5.

4 Results and discussions

The results are discussed in the aspects of assimilation analysis and model forecast. The benefits of using our EnKF with VTS algorithm for the dust storm simulation with position errors are emphasized.

4.1 Impact on assimilation analysis

There are noticeable position errors that arise with the transport of the dust storm. In Fig. 1b and d, the spatial distribution of the standard deviation (square root of the diagonal values in P^f) from 32 model ensemble members is clearly shown, along with the scatter of absolute model-minus-observation differences in two cases (DSE1, DSE2). In general, their spatial distribution corresponds well to the simulated dust field depicted in Fig. 1a and c. Concurrently, the uncertainty in the light-blue box decreases rapidly as the simulated dust plume moves southward, as illustrated in Fig. 1b.1 and b.2. This suggests that our ensemble model simulations are highly confident that there are less affected by dust aerosols. However, the observations indicate that this area remains heavily polluted. In the case of DSE2, the situation becomes more complex. The simulated dust plume in DSE2 covers most of the observation area with a high dust load, as demonstrated in Fig. 1c.1 and d.1. The uncertainty, on the other hand, reveals that the ensemble model is less confident about the dust load, especially in the light-blue box displayed in Fig. 1d.2. After 3 h, these discrepancies become more evident. The extent to which this situation affects the EnKF assimilation will be discussed in this paper. It poses a challenge to EnKF assimilation in resolving the high-value measurements in this region.

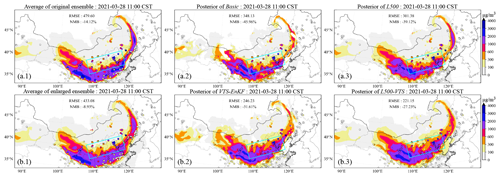
Figure 5 Spatial distribution of the simulated dust plume (SDP) on the surface from the average of ensemble members at central time (a.1), the a posteriori SDP updated by EnKF (a.2), the a posteriori SDP updated by EnKF with localization (a.3), central and neighboring time ensemble model mean (b.1), the a posteriori SDP updated by VTS-EnKF (b.2), and the a posteriori SDP updated by VTS-EnKF with localization (b.3) at 11:00 CST on 28 March 2021. The filled circles are ground-based BR-PM₁₀ observations. CST: China standard time.

Subsequent results have confirmed this theory. Figure 4 displays the spatial distribution of ground BR-PM₁₀ observations (scatter) and dust field forecasts from the average of the ensemble (Fig. 4a.1), the a posteriori field from EnKF analysis (panel a.2) and EnKF with localization (Fig. 4a.3), the average of the enlarged ensemble (Fig. 4b.1), the a posteriori field from VTS-EnKF analysis (Fig. 4b.2) and VTS-EnKF analysis with localization (Fig. 4b.3) at 11:00 on 15 March 2021 China standard time (CST). It should be noted that the average dust concentrations in Fig. 4b.1 are calculated from the 160 ensemble simulations used in VTS-EnKF, which slightly differ from the average of 32 ensemble members. In DSE1, the RMSE and NMB from the ensemble model simulation are as high as 856.36 µg m⁻³ and −78.31 %. Both EnKF and LEnKF assimilation analyses achieve very limited improvement in estimating the dust state field. As shown in Fig. 4a.2 and a.3, the RMSE and NMB remain high at 819.04 µg m⁻³ and −75.65 % in Basic and 782.57 µg m⁻³ and −73.52 % in L500. The main reason for this is the ensemble underdispersion, as described in Sect. 3.2. As observed in the light-blue box in Fig. 4a.1, the simulated dust plume is located farther southeast compared to the PM₁₀ measurements. This snapshot exhibits an apparent position error. After EnKF analysis, the simulated dust plume in the light-blue box barely changes, as depicted in Fig. 4a.2. Numerous ground stations in this area report high PM₁₀ concentrations, but the assimilated dust field fails to resolve most of them. The localization method offers limited assistance in this situation, as illustrated in Fig. 4a.3. With the unresolved positional error, the EnKF, which focuses more on intensity correction, is much less effective.

When it comes to the VTS-EnKF analysis result, an improved dust field can be noticed. Concerning the root mean square error (RMSE) and normalized mean bias (NMB), the two priors depicted in Fig. 4a.1 and b.1 exhibit highly similar performances. However, slight differences do exist. For instance, the average of the expanded 160-member ensemble used in VTS-EnKF displays a marginally broader spread. The increased ensemble size provides more room for representing background uncertainties. The enhanced capacity for this is best illustrated in Fig. 6a, which exhibits the uncertainty quantified by the enlarged ensemble simulations in VTS-EnKF formulations. This expansion of the uncertainty spread effectively addresses the issue of ensemble underdispersion, thereby boosting the EnKF's capability to handle position errors. In contrast, the relatively low uncertainty over these areas depicted in Fig. 1b.2 suggests that the EnKF method is highly confident in the absence of aerosols and does not require any modification. The observations are effectively assimilated in the VTS-EnKF analysis. As displayed in Fig. 1b.2, the dust plume within the light-blue box is adjusted to better match the observations. In particular, the dust to the east of the marked region is well represented in comparison to the a posteriori field of Basic. The RMSE and NMB are reduced to 742.33 µg m⁻³ and −68.21 %. Moreover, the a posteriori field of VTS-L500 yields an improved dust field, with the RMSE and NMB further reduced to 696.1 µg m⁻³ and −63.93 %. The implementation of the localization method eliminates spurious correlations and generates a background error covariance that more accurately describes the model uncertainties. Despite the noticeable improvements achieved in DSE1, the residual errors, as indicated by the RMSE and NMB metrics, remain relatively high. This is mainly due to some observations with extremely high value (exceeding 5000 µg m⁻³), which is far higher than the surrounding stations and hard for the EnKF to adapt. In particular, the western extent of the dust plume is covered by the insufficient stations, which results in an inadequate representation of the dust load. By incorporating neighboring ensemble, the dust plume is extended wilder. In the future research, assimilating satellite-derived dust optical depth (DOD) observations that have broader coverage may help to better constrain the enlarged ensemble.

Figure 5 presents the spatial distribution of ground-based BR-PM₁₀ observations (scatter) and dust concentration forecasts from the average of model ensemble (Fig. 5a.1), EnKF (Fig. 5a.2), and LEnKF analysis (Fig. 5a.3), as well as the average of the enlarged model ensemble (Fig. 5b.1), VTS-EnKF (Fig. 5b.2), and VTS-EnKF with localization analysis (Fig. 5b.3) at 11:00 CST on 28 March 2021. During this assimilation snapshot in DSE2, the model-simulated dust field is observed to have moved further southeast, as depicted in Fig. 5a.1. As illustrated by the light-blue box in Fig. 5a.1, the model-simulated dust plume missed most of the observations with high PM₁₀ concentrations. Consequently, although the EnKF analysis remains effective in this case, dust in the light-blue box is nearly unchanged. The RMSE and NMB are reduced to 348.13 µg m⁻³ and −45.96 % in the Basic scenario, with further reductions to 301.38 µg m⁻³ and −39.12 % when the localization method is employed in the L500 case.

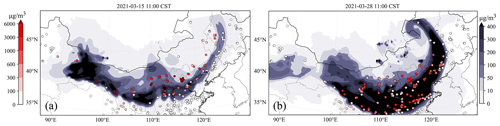
Figure 6 Spatial distribution of standard deviation from ensemble members at 11:00 in DSE1 (a) and 08:00 in DSE2 (b). The initial assimilation analysis is performed at these times. The filled circles are model-minus-observation differences (absolute value). The left-hand color bar is for model-minus-observation differences, and the right-hand color bar is for standard deviation. CST: China standard time.

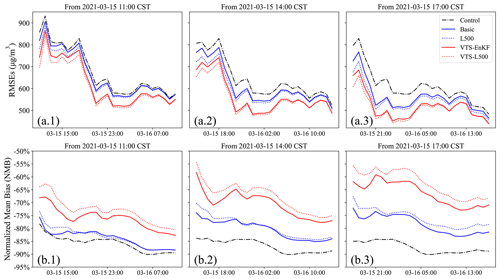
Figure 7 Time series of the 24 h root mean square error (RMSE) on the dust forecast starting from 11:00 (a.1), 14:00 (a.2), and 17:00 (a.3) and the normalized mean bias (NMB) starting from 11:00 (b.1), 14:00 (b.2), and 17:00 (b.3) on 15 March 2021. CST: China standard time.

For the enlarged ensemble, the RMSE and NMB of the a priori field for VTS-EnKF are 433.08 µg m⁻³ and −8.93 %. With VTS-EnKF assimilation, the RMSE of the a posteriori field further decreases to 246.23 µg m⁻³, and the NMB is −31.61 % in VTS-EnKF. Unlike Basic, the dust plume in light-blue box is noticeably optimized to better fit the observations. The RMSE and NMB are significantly lower than those obtained with Basic, thanks to the better-scaled background covariance displayed in Fig. 6. Moreover, by incorporating localization, the RMSE and NMB are further reduced to 221.15 µg m⁻³ and −27.23 % in VTS-L500. The dust load within the light-blue box (Fig. 5b.3) is accurately reproduced within its actual range (2000–3000 µg m⁻³).

4.2 Impact on forecast skills

In addition to the snapshots of the assimilation analysis, a comprehensive evaluation of forecast skills is also necessary to see the performance of the VTS-EnKF algorithm. A general evaluation of the forecasting skills is carried out in this section.

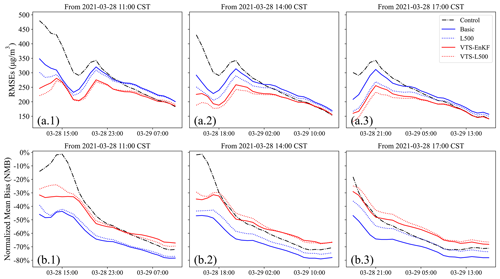
Figure 8 Time series of the 24 h root mean square error (RMSE) on the dust forecast starting from 08:00 (a.1), 11:00 (a.2), and 14:00 (a.3) and the normalized mean bias (NMB) starting from 08:00 (b.1), 11:00 (b.2), and 15:00 (b.3) on 28 March 2021. CST: China standard time.

Figure 7 presents the time series of the RMSE and NMB for the 24 h dust forecast after three assimilation analyses in DSE1 (starting from 11:00, 14:00, and 17:00). In these cases, the Control run generates a dust field with a high RMSE (ranging from over 800 µg m⁻³ to around 600 µg m⁻³) and a large NMB (consistently around −85 %). The EnKF analysis, however, does not improve this dust forecast after the initial assimilation. In fact, the RMSE and NMB of the dust forecast from the Basic scenario are nearly identical to the Control run, as evidenced by the comparison between the dashed black line and the blue line in Fig. 7a. This result can be primarily attributed to the position error discussed in Sect. 2.4. The EnKF algorithm offers minimal assistance in correcting the model simulation when position errors are present. These errors are not occasional but cumulative, as demonstrated in the subsequent two assimilation timestamps at 14:00 and 17:00, during which the assimilation analysis shows limited improvement over the situation. Moreover, it has been observed that the localization method only improves the forecast slightly in the presence of position errors. Similar for the NMB, as depicted in panel b, the improvements are also insignificant. The NMB for the Control, Basic, and L500 scenarios remains consistently around −85 % throughout the entire forecast time range.

By applying the VTS-EnKF analysis, a reduction in the RMSE compared to the model run and EnKF can be observed in Fig. 7a. There is an approximate decrease of 100 µg m⁻³ in VTS-EnKF compared to Basic, which indicates that the VTS-EnKF analysis effectively corrects the position error. At the subsequent assimilation timestamps, this situation improves, with an even greater decrease in the RMSE. The RMSE of VTS-L500 is slightly lower than that of VTS-EnKF. As for the NMB, quite promising results are achieved. In VTS-EnKF, the NMB decreases stepwise at three time points, from around −75 % at 11:00 to around −70 % at 14:00 and finally to around −65 %. The VTS-EnKF algorithm gradually takes effect over the three assimilation analyses. In VTS-L500, the localization method demonstrates its efficacy, especially after the third assimilation timestamp at 17:00. The NMB is reduced to around −60 %, which is significantly lower than that of the L500.

Figure 8 displays the time series of the RMSE and NMB on a 24 h dust forecast after three assimilation analyses in DSE2. Unlike DSE1, Basic in DSE2 does improve the dust forecast in terms of the RMSE and NMB. The RMSE drops from around 500 µg m⁻³ to less than 400 µg m⁻³ at the initial assimilation timestamp (11:00). The NMB here is higher than Control due to the complementary effect of the NMB. The overestimation is corrected, while the underestimation caused by position error is not corrected. No further reduction is observed at subsequent time points. As can be seen in Fig. 8a.2 and a.3, the RMSE of Basic remains almost constant compared to Fig. 8a.1. This indicates that the position error is not corrected, and it constitutes part of the RMSE that is difficult to eliminate. The trend of the NMB also reflects this situation. L500 is unable to correct the position error, although it does help reduce the error to some extent.

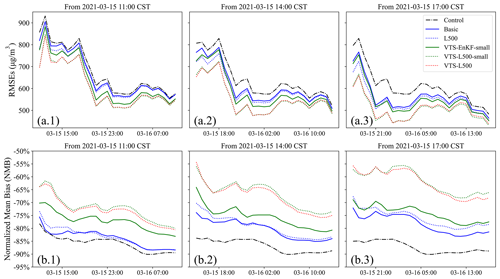
Figure 9 Time series of the 24 h root mean square error (RMSE) on the dust forecast starting from 11:00 (a.1), 14:00 (a.2), and 17:00 (a.3) and the normalized mean bias (NMB) starting from 11:00 (b.1), 14:00 (b.2), and 17:00 (b.3) on 15 March 2021. CST: China standard time.

In the scenario of the VTS-EnKF analysis, an improvement in the dust forecast of DSE2 is obtained. A general reduction of RMSE (around 50 µg m⁻³) in VTS-EnKF compared to Basic can be seen in Fig. 8a.1. Furthermore, in the subsequent forecasts, a steady decrease in RMSE is noted. The RMSE fluctuates around 250 µg m⁻³ after 14:00 and 200 µg m⁻³ after 17:00. VTS-L500 exhibits a similar pattern to VTS-EnKF for most of the forecast. Considering the NMB, as shown in Fig. 8b, the NMB of VTS-L500 demonstrates trivial superiority over VTS-EnKF. In DSE2, Basic and L500 have already achieved well-reproduced dust fields, while VTS-EnKF and VTS-L500 can further improve these fields by correcting the position error.

4.3 Assessment of fewer ensemble members

To further assess the performance of VTS-EnKF, VTS-EnKF experiments with the same ensemble members as the EnKF are designed. They are referred to as VTS-EnKF-small and VTS-L500-small, respectively. These experiments start from 8 ensemble members that are driven by randomly selected emission and meteorology field from the origin ensemble. During the initial assimilation, the extra 4 × 6 ensemble members from neighboring ± 1 and ± 2 h are randomly sampled from these 8 ensemble members. The new ensemble comprises 32 members which is equivalent to the origin ensemble number of Basic. Figure 9 displays the time series of the RMSE and NMB on a 24 h dust forecast after three assimilation analyses in DSE1. In terms of the RMSE, VTS-EnKF-small only shows slightly better performance than the EnKF. This mostly caused by the sampling error arises from limited ensemble members resampled from the central ensemble (only 8 ensemble members). However, by applying the localization, the RMSE is noticeably reduced by 100 µg m⁻³. The performance is comparable to the VTS-L500 (dashed red line) with 160 ensemble members in total. By mitigating the sampling error, the VTS-EnKF's capability of handling the position error can be revealed, which can be noticed by comparison with L500 and VTS-L500-small. This improvement can be better seen in the NMB. The NMB of VTS-L500-small is much lower than Basic and L500. Its performance is also comparable to the VTS-L500 with 160 ensemble members.

The same experiments are also carried out on DSE2. The results can be found in Fig. S2 in the Supplement. Similar to DSE1, the VTS-EnKF-small achieves a RMSE and NMB slightly better than Basic and L500, while in VTS-L500-small, noticeable improvements can been found, especially for the forecast after the second and last assimilation. Reductions of 100 µg m⁻³ in the RMSE and 20 % in the NMB are obtained.

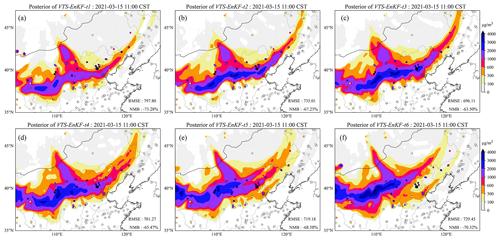
Figure 10 Spatial distribution of ground-based BR-PM₁₀ observations (scatter) and the simulated dust plume (SDP) on the surface from the a posteriori SDP updated by VTS-EnKF-t1 (a), the a posteriori SDP updated by VTS-EnKF-t2 (b), the a posteriori SDP updated by VTS-EnKF-t3 (c), the a posteriori SDP updated by VTS-EnKF-t4 (d), the a posteriori SDP updated by VTS-EnKF-t5 (e), and the a posteriori SDP updated by VTS-EnKF-t6 (f) at 11:00 CST on 15 March 2021.

4.4 Sensitivity of time interval

Previous research studies have found that an improper neighboring time interval τ can lead to undesirable results, such as less effective ensemble members (interval too small) (τ too small) or ensemble member clustering and unrepresentative ensemble covariances (τ too large) (Xu et al., 2008; Gasperoni et al., 2022, 2023). To explore the sensitivity of the choice of neighboring time interval, series of VTS-EnKF experiments with different neighboring time interval were carried out. Time intervals ranging from 1 to 6 h were tested. As shown in Fig. 10, snapshots from 6 experiments on DSE1 clearly depicts the trend. In general, all the VTS-EnKF experiments show better performance than EnKF, while in terms of specific time interval, different patterns can be noticed. For short intervals including 1 and 2 h, there is not sufficient ensemble spread to account for the position error. Thus there is still position error remaining, and the RMSE is still high. For long intervals including 5 and 6 h, the dust plume is clustered away from central dust plume. Three dust branches are noticed in VTS-EnKF-t5 and an overly backwards dust plume is noticed in VTS-EnKF-t6. In this case, 3 h interval is the best choice with the lowest RMSE (696.11 µg m⁻³) and NMB (−63.5 %).

The same experiments are also performed on DSE2, and snapshots are shown in Fig. S3 in the Supplement. Similar patterns are found for DSE2. The lowest RMSE and NMB are achieved in VTS-EnKF-t4. Too short an interval leads to inability in position error correction, and too long an interval leads to excessive dust plume. Considering both cases, a 3 h interval is the preferred choice, which holds the capability to handle position errors and not create an excessively clustered dust plume.

5 Conclusions

Chemistry transport models (CTMs) are a powerful tool for air pollutant forecasting. However, as simplified versions of the real atmospheric world, they suffer from various deficiencies, in terms of two major uncertainties in particular: emissions and meteorology. Uncertainty from meteorological fields can cause model forecast errors, especially in long-distance transport. In dust storm forecasting applications, a position error is noted that significantly degrades the overall performance of the forecast and prevents the EnKF assimilation algorithm from effectively incorporating observational data.

The background error covariance of EnKF is generally designed to represent the intensity and position uncertainty. However, when the position error is sufficiently large, the background error covariance cannot adequately represent the position error, which is highly non-Gaussian. In the case of long-distance dust storm tracking, the EnKF is incapable of thoroughly resolving the observations. Observations over low model uncertainty pixels are “ignored” by the EnKF algorithm. To address this issue, a valid time shifting method is coupled with EnKF. This VTS-EnKF methodology introduces uncertainty of the dust plume position into the background error covariance by incorporating extra ensemble simulations at neighboring time instances. This enlarged ensemble not only reflects the uncertainty of dust intensity but also reveals the potential positions of the plume, allowing for more accurate and effective assimilation and improving dust storm forecasting.

The VTS-EnKF algorithm was tested on two super dust storm events (DSE1 and DSE2) that occurred in spring 2021. Several experiments were designed to examine the performance of the VTS-EnKF algorithm in these cases, with a focus on differences between EnKF and VTS-EnKF. In terms of assimilation analysis, the VTS-EnKF analysis corrected the position error in DSE1 to a large extent. Comparison between the standard deviations from the a posteriori field of EnKF and VTS-EnKF explained it. The standard deviations from VTS-EnKF analysis indicated wider potential dust spread and were more consistent with the model-minus-observation. Observations that were “ignored” by EnKF were comprehensively resolved in VTS-EnKF, resulting in the decreased RMSE and NMB. For DSE2, the position error was not as significant as in DSE1; however, ensemble underdispersion was also observed. Nevertheless, VTS-EnKF still produced an improved dust field with a lower RMSE and NMB compared to EnKF. In both cases, the localization method helped reduce the RMSE and NMB. Regarding the forecast performance, promising results were obtained. In DSE1, the RMSE and NMB revealed that EnKF provides limited improvements compared to model run. In contrast, VTS-EnKF provided a dust field forecast with reduced errors, especially in terms of NMB. Additionally, the localization method contributed to further reducing the error. Overall, the VTS-EnKF algorithm demonstrated improved performance in assimilation analysis and forecasting for the tested dust storm events compared to the traditional EnKF approach.

Assessment of equal ensemble members between EnKF and VTS-EnKF is carried out. VTS-EnKF with smaller ensemble size shows slightly improved metrics than EnKF, while by applying localization, more reduction in the RMSE and NMB can be noticed, and its performance is comparable to the VTS-EnKF with larger ensemble size. This is due to the corrected sampling error within limited ensemble members. Comparison between them confirms VTS-EnKF's ability in handling position error. Sensitivity of neighboring time interval choice is also examined. Too short an interval leads to inability in position error correction, and too long an interval leads to an excessive dust plume. Considering both cases, the 3 h interval is the preferred choice.