Generalised drought index: a novel multi-scale daily approach for drought assessment

Drought is a complex climatic phenomenon characterised by water scarcity and is recognised as the most widespread and insidious natural hazard, posing significant challenges to ecosystems and human society. In this study, we propose a new daily based index for characterising droughts, which involves standardising precipitation and/or precipitation minus potential evapotranspiration (PET) data. The new index proposed here, the generalised drought index (GDI), is computed for the entire period available from the Iberian Gridded Dataset (1971 to 2015). Comparative assessments are conducted against the daily Standardised Precipitation Index (SPI), the Standardised Precipitation Evapotranspiration Index (SPEI), and a simple Z-Score standardisation of climatic variables. Seven different accumulation periods are considered (7, 15, 30, 90, 180, 360, and 720 d) with three drought levels: moderate, severe, and extreme. The evaluation focuses mainly on the direct comparison amongst indices in terms of their ability to conform to the standard normal distribution, added value assessment using the distribution added value (DAV), and a simple bias difference for drought characteristics. Results reveal that the GDI, together with the SPI and SPEI, follows the standard normal distribution. In contrast, the Z-Score index depends on the original distribution of the data. The daily time step of all indices allows the characterisation of flash droughts, with the GDI demonstrating added value when compared to the SPI and SPEI for the shorter and longer accumulations, with a positive DAV up to 35 %. Compared to the Z-Score, the GDI shows expected greater gains, particularly at lower accumulation periods, with the DAV reaching 100 %. Furthermore, the spatial extent of drought for the 2004–2005 event is assessed. All three indices generally provide similar representations, except for the Z-Score, which exhibits limitations in capturing extreme drought events at lower accumulation periods. Overall, the findings suggest that the new index offers improved performance and comparatively adds value to similar indices with a daily time step.

1 Introduction

Drought is known to be one of the costliest and most impactful weather-related disasters, affecting ecosystems; the economy; and sectors such as agriculture, health, and water management (Wilhite, 2000; Rhee et al., 2010; Vicente-Serrano et al., 2013; Wang et al., 2014, 2017; Lai et al., 2019). Amongst all natural disasters, droughts can spread further and have the most extended length (Jain et al., 2010), often developing in a slow manner, while, at the same time, their effects can linger in the environment long after the end of the event (Vicente-Serrano et al., 2013; Hunt et al, 2014).

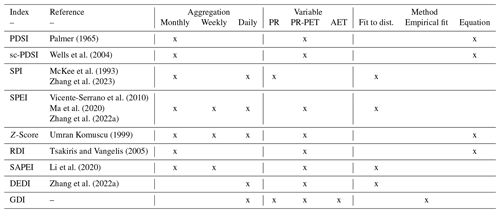
Over the years, numerous indices have been developed to assess drought conditions, particularly related to intensity and duration. One of the first proposed drought indices was the Palmer Drought Severity Index (PDSI; Palmer, 1965; Alley, 1984), which enables the measurement and evaluation of wet and dry conditions. The PDSI standardises the balance between monthly precipitation and atmospheric demand by incorporating potential evapotranspiration (PET) in its formulation. While this index was a landmark, it does have certain shortcomings. Its performance is enhanced only for the region where the index was initially defined, with its outputs being heavily influenced by the chosen calibration period. Therefore, the PDSI revealed problems related to its spatial comparison and application. To address some of these issues, Wells et al. (2004) introduced the self-calibrated PDSI, which allows spatial comparison and identifies extreme wet and dry events as rare occurrences. However, fixed timescales for computing the index remained a concern. Further developments were introduced during the following years to address these caveats. The Standardised Precipitation Index (SPI; McKee et al., 1993) is one of the indices developed which tackled the comparability and temporal scale issues (Guttman, 1998; Hayes et al., 1999). The SPI is a straightforward standardised index only requiring monthly precipitation, representing it as a standard deviation from its mean. The SPI overcomes the limitations of the self-calibrated PDSI by enabling the computation of the index at various timescales. Nevertheless, the SPI's sole use of precipitation could be a limiting factor depending on the dominating climatic conditions in certain regions. Moreover, with anthropogenic climate change, rising temperatures and the subsequent increases in evapotranspiration can also significantly increase the impact of drought events (Hu and Wilson, 2000; Vicente-Serrano et al., 2010). Therefore, including the influence of atmospheric evaporative demand in a drought index becomes imperative (Vicente-Serrano et al., 2010; Svoboda and Fuchs, 2016). To address this need, Vicente-Serrano et al. (2010) proposed the Standardised Precipitation Evapotranspiration Index (SPEI), which was further developed by Beguería et al. (2014). The SPEI combines all the features and advantages of the SPI together with the inclusion of atmospheric evaporative demand represented by the potential evapotranspiration. Both the SPI and the SPEI are indices that require data to be fitted to a theoretical probability distribution function (PDF). In the literature, numerous PDFs have been considered. For the SPI, distributions such as Pearson type III (Vicente-Serrano et al., 2006) or Gamma (McKee et al., 1993; Edwards, 1997; Wang et al., 2022; Zhang et al., 2023) have commonly been employed. On the other hand, the three-parameter log-logistic (Beguería et al., 2014; Wang et al., 2015; Ma et al., 2020) and generalised extreme value (Stagge et al., 2015; Wang et al., 2021; Zhang et al., 2023) distributions have been widely used for the SPEI. However, the best distribution to fit the data is still not clear, as the same distribution may perform differently for distinct regions (Stagge et al., 2015; Monish and Rehana, 2020; Zhang and Li, 2020). For instance, for a global dataset, Stagge et al. (2015) concluded that the Gamma (Weibull) for long (short) accumulations was the best distribution for the SPI, while the generalised extreme value was the best distribution to fit the SPEI. On the other hand, Zhang and Li (2020) concluded that the log-logistic distribution could be used as an alternative when analysing the SPI for a large river basin in China. At the same time, the log-logistic distribution, which is known to be resilient to the presence of outliers (Ahmad et al., 1988) and more appropriate for the Iberian Peninsula (Vicente-Serrano et al., 2010; Beguería et al., 2014), was deemed the best function for fitting the data for the SPEI. Usually, the SPI and the SPEI only rely on a single probability density distribution, even for large regions. To overcome this issue, there are methods to estimate the underlying distribution and associated parameters, which could, however, become computationally infeasible for large datasets (Guttman, 1999). At the same time, the method considered for estimating the parameters of a single distribution could also be computationally demanding.

Simpler drought indices which do not require fitting to a distribution also exist. One is the Z-Score, which is computed for precipitation or with the difference between precipitation and evapotranspiration by subtracting the long-term mean and dividing the result by the long-term standard deviation (Umran Komuscu, 1999; Patel et al., 2007; Akhtari et al., 2009; Jain et al., 2015). Slightly different formulations for this index also exist, such as those used by Zhang et al. (2022a, b) or the China Z-Index (Wu et al., 2001), and are also considered in the standardised reconnaissance drought index (Tsakiris and Vangelis, 2005). The advantage of the Z-Score index lies in its simple calculation being regarded as an alternative to indices which require fitting data to a distribution such as the SPI or the SPEI and that it is capable of accommodating missing values. Similarly, the Z-Score also represents a standardised departure from the mean. However, the Z-Score may not effectively represent the shorter timescales, since precipitation data are skewed (Edwards, 1997). Additionally, the index's performance may vary in regions with diverse precipitation or potential evapotranspiration patterns, where data do not assume a normal distribution. This can affect the accuracy and reliability of the index.

Although droughts are known to be a slowly evolving phenomenon in general (Wilhite and Glantz, 1985; Mishra and Singh, 2010), the concept of a flash drought has recently emerged (Wang et al., 2021, 2022; Zhang et al., 2022a; Christian et al., 2023). These types of extreme events are characterised by a sudden onset, fast aggravation, and sudden end (Christian et al., 2023). Depending on the type of climate, these short-duration events may threaten the water supply and cause significant reductions in crop yield at critical stages of plant development (Meyer et al., 1993; Dai, 2011; Vicente-Serrano et al., 2013; Hunt et al., 2014). Due to their sub-monthly timescale nature, flash droughts can only be identified with daily drought indices. Therefore, the wide spread of observational-based daily gridded datasets, such as the National Gridded Dataset for the Iberian Peninsula (IB01; Herrera et al., 2019a), the Climate Prediction Center (CPC; Xie et al., 2007; Chen et al., 2008), the E-OBS (Cornes et al., 2018), and the European Meteorological Observations (EMO-5; Thiemig et al., 2022); station-based datasets, such as the European Climate Assessment & Dataset (ECA&D, Klein-Tank et al., 2002); reanalysis data, such as ERA5 (Hersbach et al., 2020, 2023), JRA-55 (Kobayashi et al., 2015), and MERRA-2 (Gelaro et al., 2017); and regional climate model initiatives, such as the World Climate Research Programme's Coordinated Regional Climate Downscaling Experiment (CORDEX; Giorgi et al., 2009; Gutowski et al., 2016), assisted in the development of new drought indices with a daily time step (Wang et al., 2015, 2021, 2022; Jia et al., 2018; Li et al., 2020; Ma et al., 2020; Onuşluel Gül et al., 2021; Zhang et al., 2022a, b; Zhang et al., 2023). At the same time, most of these indices are still fitted to a probability distribution and/or are not standardised. Wang et al. (2015) used a daily version of the SPEI to understand if there has been any improvement in drought conditions. The authors report that the daily SPEI can provide a more comprehensive understanding of drought dynamics at a finer temporal scale. Li et al. (2020) proposed the Standardised Antecedent Precipitation Evapotranspiration Index. The index is first compared against the monthly PDSI, the SPEI, and soil moisture, revealing a similar performance against the SPEI at the monthly scale while outperforming at the weekly scale. Ma et al. (2020) computed a daily SPEI and compared it with the traditional monthly version. The authors reported that the daily index can capture more detailed drought events than the monthly counterpart. Wan et al. (2023) also considered a daily SPEI to determine the trend of drought severity and duration over 40 years (1979–2018) for China. The authors also concluded that the potential evapotranspiration was the dominant climatic factor influencing drought for most of the region. Zhang et al. (2022a) proposed the Daily Evapotranspiration Deficit Index and compared the results against the Meteorological Drought Composite Index and the SPEI for four drought events in China. The proposed index was better able to capture the start and end of the events and the peak intensity. Still, indices such as the SPI or the SPEI computed at the daily scale also prove to be demanding. The parameter estimation and the subsequent fitting to a theoretical distribution may be computationally expensive and result in a poor fit. At sub-monthly aggregation scales, the presence of outliers could hinder the parameter estimation and fit and generate values that might fall outside the range of the chosen distribution. Furthermore, periods with no precipitation may also pose difficulties in computing the SPI (Beguería et al., 2014). Table 1 displays a summary of all indices presented here.

Table 1 Examples of drought indices.

Nevertheless, daily indices are still at an early stage in comparison with the diverse monthly drought indices available. Motivated by the shortcomings illustrated before, in the present study, we propose a new daily drought index, the generalised drought index (GDI). The GDI is an index identical to the SPI or SPEI in the sense of standardising data to follow the standard normal distribution, allowing the evaluation of both short- and long-timescale droughts with a daily time step. Furthermore, the GDI allows a generalised fitting distribution which is empirically based; thus the index accepts alternative variables for drought assessment and not only precipitation. For instance, actual evapotranspiration could be regarded as an alternative to the usual precipitation minus potential evapotranspiration (P-PET). Moreover, the new index may be perceived as an alternative for removing skewness and kurtosis from climate data. Here, the GDI is computed for the Iberian Peninsula region using the IB01 dataset, covering 1971–2015. Our study contributes to the ongoing efforts to develop more effective drought monitoring tools and provides a valuable instrument for decision-makers and stakeholders to better manage the impacts of flash droughts and longer droughts consistently and solidly. Our proposed index can easily be implemented in regions with limited climatic variables and can help improve the accuracy and reliability of drought assessment, as it solely requires long time series. The introduction of the GDI can also be regarded as an important step in the evaluation of climate simulations. This is particularly relevant for high-resolution models, such as those from the EURO-CORDEX (Jacob et al., 2014, 2020; Gutowski et al., 2016) and CORDEX flagship FPS-Convection simulations (Coppola et al., 2020; Ban et al., 2021; Pichelli et al., 2021), which aim to capture extreme weather events more accurately than their coarser counterparts. With the use of daily datasets and a daily drought index, researchers can more accurately assess a model's ability to capture the fast-evolving conditions characteristic of flash droughts. Therefore, the GDI allows a better understanding of drought dynamics, facilitating the evaluation of not only long-term drought events but also short-term variability. Furthermore, with the GDI one can more easily perform studies of co-occurrence with other types of extremes, such as heatwaves or fire ignitions (Zscheischler et al., 2020; Shan et al., 2024), all on the same scale.

The following section introduces the IB01; the methodology for computing the GDI, SPI, and SPEI; and finally the simple Z-Score standardisation. Afterwards, the results are presented in Sect. 3, followed by the discussion and conclusions in Sect. 4.

2 Data and methods

2.1 Study area

The Iberian Peninsula exhibits a diverse and complex climate influenced by its geographical position, surrounded by the Atlantic Ocean to the north and west and the Mediterranean Sea to the south and east. In the northern regions of the Iberian Peninsula, such as Galicia and northern Portugal, a maritime climate prevails, characterised by mild winters and cool summers. The Atlantic Ocean influence brings relatively high precipitation throughout the year (Rios-Entenza et al., 2014). Towards the south, the climate shifts to a more Mediterranean type, with hot and dry summers. Winters remain mild and relatively wet compared to the summer months. The Mediterranean climate is associated with distinct wet and dry seasons, with most rainfall occurring during the winter (Peel et al., 2007). Droughts are a recurring and significant challenge for the Iberian Peninsula. The region has a long history of drought events, with a clear drying trend throughout the 20th century, mainly due to increased temperature (Fonseca et al., 2016; Pascoa et al., 2021). Climate change projections suggest that the frequency and intensity of droughts may amplify in the future (Sánchez et al., 2011; Seguí et al., 2016; Moemken et al., 2022; Soares et al., 2023). Rising temperatures and changing precipitation patterns may exacerbate water scarcity and put additional stress on the region's ecosystems (Soares et al., 2017; Cardoso et al., 2019; Carvalho et al., 2021; Soares and Lima, 2022).

2.2 IB01 observational dataset

The IB01 observational dataset (Herrera et al., 2019a) is a high-quality dataset that offers daily values for precipitation and for minimum and maximum temperatures with a spatial resolution of 0.1°. This dataset was constructed using an extensive network of quality-controlled observational weather stations (a maximum of 3486 for precipitation and 275 for temperatures) across the Iberian Peninsula from 1971 to 2015. Herrera et al. (2019a) reported that IB01 not only effectively captures the spatial patterns of the mean and extreme precipitation and temperatures but also exhibits a more realistic precipitation pattern than E-OBS (Cornes et al., 2018) and performs comparably to E-OBS for temperatures.

The IB01 dataset has been employed in numerous studies to characterise the present climate and was used as a benchmark for evaluating the ability of a set of EURO-CORDEX (Giorgi et al., 2009; Jacob et al., 2014, 2020; Gutowski et al., 2016) simulations to reproduce the present climate over Iberia (Herrera et al., 2020; Páscoa et al., 2021; Careto et al., 2022a, b; Lima et al., 2023a, b; Soares et al., 2022). Herrera et al. (2020) evaluated the performance of the EURO-CORDEX over the Iberian Peninsula and characterised the observational uncertainty with the use of the IB01, E-OBS-v19e, and MESAN-0.11° datasets. Páscoa et al. (2021) employed this dataset to assess the recent trends in drought events across Iberia. Careto et al. (2022a, b) evaluated the added value of using high-resolution simulations from EURO-CORDEX in characterising means and extremes of precipitation and temperature over the Iberian Peninsula. More recently, Lima et al. (2023a) used the IB01 dataset as a reference to evaluate the accuracy of a set of historical EURO-CORDEX simulations in representing the main properties of the observed climate within mainland Portugal. Based on this evaluation, a weighted multi-variable multi-model ensemble of EURO-CORDEX simulations was built and used to characterise the mean climate, extremes, and indices (Lima et al., 2023a, b), as well as water scarcity conditions over Portugal (Soares and Lima, 2022) throughout the 21st century. Based on the same weighting methodology, Soares et al. (2023) projected the future of drought events across the Iberian Peninsula. Finally, IB01 was used to critically assess the CMIP quality to project the recent past climate of Iberia (Soares et al., 2022).

2.3 Potential evapotranspiration

Potential evapotranspiration (PET) represents the maximum atmospheric water demand and is a requirement for the computation of several drought indices (Vicente-Serrano et al., 2010; Li et al., 2020; Zhang et al., 2022a, b). The FAO-56 Penman–Monteith formula (Allen et al., 1998) is one of the most widely used approaches to calculate PET. Although it was specifically designed for non-stressed grass cover, it is regarded as the most accurate estimate. However, it requires multiple variables, some of which may not be readily available, posing a drawback to its practical implementation. An alternative approach, known for its simplicity, is the Thornthwaite formulation (Thornthwaite, 1948), which only requires latitude and temperature as inputs. However, studies have shown that the Thornthwaite formulation underestimates PET in arid and semi-arid regions while overestimating it in humid tropical or equatorial regions (van der Schrier et al., 2011). Therefore, in the context of climate change and the Iberian Peninsula, with arid and semi-arid regions, this equation is not the best option for computing PET (Beguería et al., 2014).

As a compromise between formulation complexity and data availability, a modified version of the Hargreaves formulation is thus considered in this study (Droogers and Allen, 2002). The modified Hargreaves method is identical to the original Hargreaves method, in which, beyond the incorporation of maximum and minimum temperature, the precipitation is also integrated. Precipitation data are commonly accessible in most modelling and observational datasets and can serve as a proxy for cloud cover and humidity. In this study, a daily version of the modified Hargreaves formula is implemented (Farmer et al., 2011):

$$\begin{array}{}\text{(1)}& \begin{array}{rl}\mathrm{PET}& =\mathrm{0.0019}\cdot \mathrm{0.408}\cdot \mathrm{RA}\cdot (T_{\mathrm{avg}}+\mathrm{21.0584})\\ & (\mathrm{TD}-\mathrm{0.0874}\cdot P{)}^{\mathrm{0.6278}}.\end{array}\end{array}$$

More details on the calculation of the PET with the modified Hargreaves version can be found in Soares et al. (2023).

2.4 Drought indices

2.4.1 Standardised Precipitation and Standardised Precipitation Evapotranspiration indices

In this section, the Standardised Precipitation Index (SPI; McKee et al., 1993) and the Standardised Precipitation Evapotranspiration Index (SPEI; Vicente-Serrano et al., 2010) are presented. Both the SPI and the SPEI are commonly used (Edwards, 1997; Vicente-Serrano et al., 2006, 2010; Beguería et al., 2014; Wang et al., 2022; Zhang et al., 2022a, b), with the former being calculated based solely on precipitation (hereafter PR) and the latter on a simplified water balance (precipitation minus potential evapotranspiration, hereafter PR-PET). Probabilistic indices such as these allow a standardised juxtaposition and comparison across different spatial areas or between climate zones (Vicente-Serrano et al., 2010; Pohl et al., 2023).

To compute either the SPI or the SPEI, firstly, the PR and PR-PET data must be aggregated into the desired timescale through a moving window with a length equal to the timescale; i.e., a daily value is computed as the sum of the day under analysis (d) and the previous s−1 days, where s is the timescale (in days):

$$\begin{array}{}\text{(2)}& X_d=\sum _{d-(s-\mathrm{1})}^d\mathrm{data}.\end{array}$$

Subsequently, a daily yearly mean is obtained from a moving window of 31 d centred on each day d:

$$\begin{array}{}\text{(3)}& \mathrm{Se}={\displaystyle \frac{\mathrm{1}}{\mathrm{31}Y}}\sum _{i=\mathrm{1}}^Y\sum _{j=D-\mathrm{15}}^{D+\mathrm{15}}{X}_{d_{i,j}},\end{array}$$

where Y is the total number of years and D is the day of the year. For instance, 1 January corresponds to day 1, and 31 December corresponds to day 366. To ease all computations, all years are considered to have 366 d in order to include 29 February in leap years. Consequently, the value for 29 February in non-leap years is regarded as a missing value. Thus, Se is an annual mean cycle. Thirdly, this annual cycle is removed from the X_d series:

$$\begin{array}{}\text{(4)}& X_a=\sum _{i=\mathrm{1}}^Y\sum _{j=\mathrm{1}}^{\mathrm{366}}{X}_{d_{i,j}}-{\mathrm{Se}}_j.\end{array}$$

Traditionally, the removal of the seasonal cycle is not performed for the SPI and the SPEI. However, it can be regarded as a step to remove days without precipitation, which is relevant in the case of the SPI. Usually, in those situations, a factor is considered for precipitation data (Stagge et al., 2015; Wang et al., 2022; Zhang et al., 2023).

Afterwards, the X_a series are adjusted to a theoretical distribution. The log-logistic distribution (Eq. 5) was chosen to fit X_a for both the SPI (Zhang and Li, 2020) and the SPEI (Vicente-Serrano et al., 2010; Beguería et al., 2014). Therefore, the difference between the two indices lies solely in the inclusion of PET for the SPEI. To avoid issues when fitting the data to the distribution, firstly, the values of the X_a series are shifted to positive values above 0. This change does not affect the distribution or the final value.

$$\begin{array}{}\text{(5)}& f\left(x\right)={\displaystyle \frac{\mathit{\beta }}{\mathit{\alpha }}}{\left({\displaystyle \frac{x-\mathit{\gamma }}{\mathit{\alpha }}}\right)}^{\mathit{\beta }-\mathrm{1}}{\left[\mathrm{1}+{\left({\displaystyle \frac{x-\mathit{\gamma }}{\mathit{\alpha }}}\right)}^{\mathit{\beta }}\right]}^{-\mathrm{2}}\end{array}$$

The three parameters β (shape), α (scale), and γ (location) can be estimated via the maximum likelihood or with probability-weighted moments (PWMs; Hosking, 1986, 1990). Following Beguería et al. (2014), the unbiased estimator for a PWM (Hosking, 1986) was considered:

$$\begin{array}{}\text{(6)}& \begin{array}{rl}{W}_s& ={\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^N{\displaystyle \frac{\left(\frac{N-i}{s}\right)}{\left(\frac{N-\mathrm{1}}{s}\right)}}{X}_{d_i}=\\ & {\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^N{\displaystyle \frac{\mathrm{\Gamma }(N-i+\mathrm{1})/(\mathrm{\Gamma }\left(s+\mathrm{1}\right)\mathrm{\Gamma }\left(N-i-s+\mathrm{1}\right)}{\mathrm{\Gamma }\left(N\right)/\left(\mathrm{\Gamma }\left(s+\mathrm{1}\right)\mathrm{\Gamma }\left(N-s\right)\right)}}{X}_{a_i}\end{array}.\end{array}$$

Moments W_s of different orders s can be computed easily via software programming tools. Γ denotes the gamma function for natural numbers, including 0. From the first three moments (W₀, W₁, and W₂), it is possible to obtain the three parameters for the log-logistic (Singh et al., 1993):

$$\begin{array}{}\text{(7)}& {\displaystyle }\mathit{\beta }={\displaystyle \frac{\mathrm{2}{W}_{\mathrm{1}}-W_{\mathrm{0}}}{\mathrm{6}{W}_{\mathrm{1}}-W_{\mathrm{0}}-\mathrm{6}{W}_{\mathrm{2}}}},\text{(8)}& {\displaystyle }\mathit{\alpha }={\displaystyle \frac{\left(W_{\mathrm{0}}-\mathrm{2}{W}_{\mathrm{1}}\right)\mathit{\beta }}{\mathrm{\Gamma }\left(\mathrm{1}+\frac{\mathrm{1}}{\mathit{\beta }}\right)\mathrm{\Gamma }\left(\mathrm{1}-\frac{\mathrm{1}}{\mathit{\beta }}\right)}},\text{(9)}& {\displaystyle }\mathit{\gamma }=W_{\mathrm{0}}-\mathit{\alpha }\mathrm{\Gamma }\left(\mathrm{1}+{\displaystyle \frac{\mathrm{1}}{\mathit{\beta }}}\right)\mathrm{\Gamma }\left(\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{\mathit{\beta }}}\right).\end{array}$$

To convert the X_a series into the SPI or the SPEI, the cumulative distribution function (CDF) of the log-logistic is required to obtain the accumulated probability:

$$\begin{array}{}\text{(10)}& F\left(x\right)={\left[\mathrm{1}+{\left({\displaystyle \frac{\mathit{\alpha }}{X_a-\mathit{\gamma }}}\right)}^{\mathit{\beta }}\right]}^{-\mathrm{1}}.\end{array}$$

Having the accumulated probabilities, the indices can be easily obtained following the classical approximation of Abramowitz and Stegun (1968):

$$\begin{array}{}\text{(11)}& {\displaystyle }P=\mathrm{1}-F\left(x\right),\text{(12)}& {\displaystyle }P=\mathrm{1}-P,\text{if}P>\mathrm{0.5}.\end{array}$$

If P is above 0.5, then the signal of the final index is also reversed:

$$\begin{array}{}\text{(13)}& {\displaystyle }W=\sqrt{-\mathrm{2}\ln \left(P\right)},\text{(14)}& {\displaystyle }\mathrm{SPEI}=W-{\displaystyle \frac{C_{\mathrm{0}}+C_{\mathrm{1}}W+C_{\mathrm{2}}{W}^{\mathrm{2}}}{\mathrm{1}+D_{\mathrm{1}}W+D_{\mathrm{2}}{W}^{\mathrm{2}}+D_{\mathrm{3}}{W}^{\mathrm{3}}}},\end{array}$$

with C₀=2.515517, C₁=0.802853, C₂=0.010328, D₁=1.432788, D₂=0.189269, and D₃=0.001308.

2.4.2 Z-Score index

The Z-Score method is a straightforward approach used to standardise a dataset based on its mean and standard deviation (Umran Komuscu, 1999; Patel et al., 2007; Akhtari et al., 2009; Jain et al., 2015). It follows a simple rationale: (1) obtain the accumulated series and remove its seasonal cycle, as described in Sect. 2.4.1, and (2) remove the mean and divide the result by the standard deviation to get the X_a anomalies. This ensures that all data points have the same statistics for the mean and standard deviation. However, it is important to note that, while the mean and standard deviation will be consistent across all points, the underlying distribution and its parameters describing the data at each location may vary. Still, for long accumulations and as a consequence of the central limit theorem, the Z-Score and the standardised indices approach each other. The Z-Score can be computed by

$$\begin{array}{}\text{(15)}& Z\text{-Score}={\displaystyle \frac{X_a-\stackrel{\mathrm{‾}}{X_a}}{\mathit{\sigma }\left(X_a\right)}}.\end{array}$$

2.4.3 Generalised drought index

A new index, the generalised drought index (GDI), is proposed here as an alternative to the commonly used standardised drought indices, such as the SPI or the SPEI, both described in Sect. 2.3.1. The GDI is also a standardised index but introduces three upgrades which are particularly interesting when addressing drought impacts that often occur at sub-monthly scales:

• It can be calculated using any daily aggregation. For instance, 7, 15, 30, 90, 180, 360, and 720 d were chosen, ranging from weekly to biannual aggregations. Regardless of the timescale chosen, a daily index is obtained, allowing an assessment of flash droughts, which was not possible with monthly indices.

• Since fitting to a distribution is not required, any variable relevant to drought characterisation can be regarded as an input, such as PR or PR-PET, actual evapotranspiration, or PR divided by PET.

• It relies on a unique spline adjustment technique to smooth the cumulative histogram. The main advantage is the automatic fit of the empirical distribution to the data for different sites, resulting in an enhanced index.

Figure S2 (in the Supplement) shows the two sample Cramér–von Mises statistics from all land points and for each accumulation period, comparing the GDI, SPI, and SPEI cumulative distribution against the empirical cumulative distribution. This figure reveals that the spline adjustment outperforms the theoretical log-logistic fit used by both the SPI and the SPEI, as given by the lower values of the Cramér–von Mises statistics across all timescales. Moreover, the p-value is in agreement with the assumption that the H₀ hypothesis, where both samples came from the same distribution, cannot be rejected for the spline adjustment at the 5 % significance level. This result is expected, since the spline is empirically driven. However, in the case of the SPI and the SPEI, the hypothesis H₀ is rejected for most accumulations where both samples came from different distributions. Again, this result is expected, since the log-logistic distribution was assumed and used to fit the data, which for most cases does not correspond to the underlying distribution of the data.

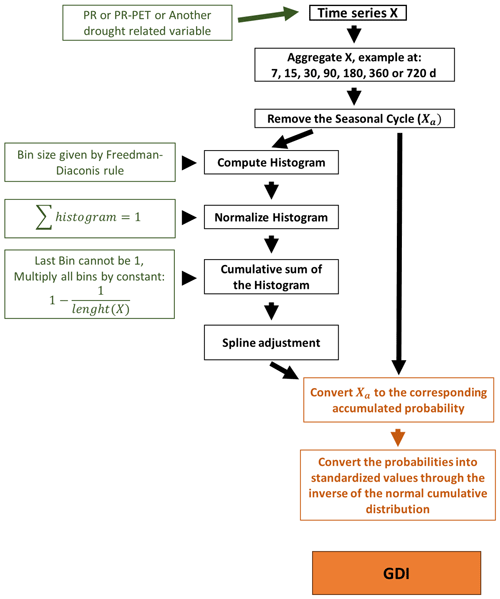
To compute the GDI, the X_a series anomalies obtained in Sect. 2.3.1 are considered. The following step is to compute a histogram of the data. The Freedman–Diaconis rule is used, which gives an optimised estimate for the bin width based on the data variability and length:

$$\begin{array}{}\text{(16)}& \mathrm{inc}=\mathrm{2}\cdot {\displaystyle \frac{\mathrm{IQR}}{\sqrt[\mathrm{3}]{N}}},\end{array}$$

where IQR is the interquartile range and N is the length of the X_a series. The histogram is defined between the minimum and maximum values and is tailored specifically for each time series. Following Soares and Cardoso (2018), the histogram series are normalised by the sum of all bins:

$$\begin{array}{}\text{(17)}& {\displaystyle }{X}_d={\displaystyle \frac{\mathrm{hist}\left(X_d\right)}{\mathrm{sum}\left(\mathrm{hist}\left(X_d\right)\right)}},\text{(18)}& {\displaystyle }{X}_d=S_N=\sum _{i=\mathrm{1}}^N{X}_{d,i}\cdot (\mathrm{1}-N^{-\mathrm{1}}).\end{array}$$

Subsequently, a cumulative sum of each bin is considered (Eq. 18). At this stage, the bins of the cumulative histogram were treated as data (x,y) points, where x represents the endpoint between the bin edges and y represents the corresponding probability. It is important to avoid 0s and 1s, since the cumulative distribution of the normal distribution tends to infinity for a probability of 0 and 1. Therefore the factor $(\mathrm{1}-N^{-\mathrm{1}})$ was considered, slightly scaling down the value for all bins. A value proportional to the length of data ($\mathrm{1}/N)$ was also appended at the minimum edge of the first bin, corresponding to the minimum value of the x_d series. Afterwards, a cubic spline technique (Fritsch and Butland, 1984) is used to smooth the cumulative histogram. With this approach the probability of any value can occur, without the need of a theoretical distribution fit.

This method allows the estimation of intermediate probabilities between the cumulative histogram points, resulting in a continuous and smooth representation of the underlying distribution, bounded by the probability of the minimum value ($\mathrm{1}/N)$ and the last bin, allowing the preservation of the daily time step for the final index. Afterwards, the original X_a series are converted into accumulated probabilities using the interpolated accumulated histogram. By using the inverse of the normal distribution, one can transform these probability values into a standardised series following the standard normal distribution with a mean of 0 and a standard deviation of 1. It is important to note that the feasibility of this approach depends on the length of the original time series, as the statistics from longer time series will tend to align more closely with the parameters of the normal distribution. This is identical to what occurs for both the SPI and the SPEI (McKee et al., 1993; Pohl et al., 2023). Figure 1 introduces a flowchart to guide the users on the steps needed to obtain the GDI.

Figure 1 Flowchart for the construction of the generalised drought index.

2.5 GDI evaluation

The performance of the GDI, SPI, SPEI, and Z-Score is assessed using the IB01 dataset for each single location to generate quantile–quantile plots, which allows us to determine the underlying distribution of all time series relative to the standard normal distribution. The percentiles considered for evaluation are constituted by a sequence from the 10th to the 90th percentile, with increments of 10. With this inter-comparative analysis, one can inspect the underlying distribution of the data and how close they are to the theoretical standard normal distribution. A wider vertical spread represents deviations of the time series from normality (linear line). Conforming results to the standard normal distribution is paramount in various statistical analyses, as it facilitates meaningful comparisons and allows the application of well-established statistical techniques. When data closely follow the standard normal distribution, they exhibit known statistical properties, simplifying the interpretation of the results (e.g., equal mean and median; 68 % of the data falls within 1 standard deviation of the mean, and 95 % of the data falls within 2 standard deviations of the mean). In the context of drought indices, compliance with normality assumptions is crucial for accurately characterising drought severity and frequency. Moreover, the standard normal distribution allows direct comparison across different spatial areas and periods, which is particularly relevant for assessing drought severity and patterns on both regional and global scales (Guttman 1998; Hayes et al., 1999; Vicente-Serrano et al., 2006, 2001; Beguería et al., 2014). As a complement, statistics including the mean, median, standard deviation, interquartile range, skewness, Yule–Kendall skewness, and kurtosis were computed for all indices, from all land points of observations.

A distribution added value (DAV; Soares and Cardoso, 2018) assessment is also performed. In this version, the DAV allows a comparison and quantification of the similarity between distributions of the different indices to the standard normal distribution. This assessment is performed for the GDI against the SPI or SPEI and for the GDI against the Z-Score for each land grid point. To compute the DAV, a histogram is first constructed. For the GDI, SPI, and SPEI, the limits considered are −5 to 5, while for the Z-Score the limits are wider, ranging from −15 to 15. The bin width was set to be constant for all datasets and is determined by the Freedman–Diaconis rule described earlier. In this context, the 75th and 25th percentiles are taken from the theoretical standard normal distribution. To build the histogram of the normal distribution, the normalised rank of each time series is first considered (this is equivalent to the empirical CDF probabilities). The probabilities range from 0 to 1, where the first value is close to $\mathrm{1}/N$ and the last value is $\mathrm{1}-\mathrm{1}/N$, where N corresponds to the data length at each location. The factor used in Eq. (17) is also considered here. These probabilities are then converted into values by considering the inverse of the standard normal distribution. Afterwards, each histogram is normalised by dividing each bin by the sum of all bins. From the histograms, a Perkins skill score (S_index; Perkins et al., 2007) is thus computed, which represents the sum of the lowest value of the two normalised histograms:

$$\begin{array}{}\text{(19)}& S_{\mathrm{index}}=\sum \min ({\mathrm{normhist}}_{\mathrm{normal}},{\mathrm{normhist}}_{\mathrm{index}}),\end{array}$$

where normhist_normal is the normalised histogram for the normal distribution and normhist_index is the normalised histogram for a specific index. A score is computed for each individual index and represents the degree of similarity between the index histogram to the standard normal distribution histogram. The Perkins skill score of each index is then used to compute the DAV:

$$\begin{array}{}\text{(20)}& \mathrm{DAV}=\mathrm{100}\cdot {\displaystyle \frac{S_{\mathrm{GDI}}-S_{\mathrm{index}}}{S_{\mathrm{index}}}},\end{array}$$

where S_index is the score obtained for the SPI, SPEI, or Z-Score. A positive percentage denotes an added value from the proposed GDI. Finally, the Pearson correlation and the root-mean-square error (RMSE) are also computed to further investigate the differences between the GDI and the other indices. All metrics mentioned aimed to assess the overall performance for daily time series.

Regarding the drought characteristics, several aspects are examined, such as the mean event severity, decadal frequency, mean event duration, and daily spatial drought extent. The drought levels considered are as follows: moderate drought with an index below −0.5, severe drought with an index below −1, and extreme drought with an index below −1.5 (McKee et al., 1993; Soares et al., 2023). The drought frequency can be defined as the average number of times any index falls below the specified threshold per decade. Mean event severity is computed by dividing the sum of all days with the index below the defined thresholds by the total number of events. The mean event duration is computed similarly and is defined as the ratio between the total number of days by the total number of drought events. These drought characteristics are computed following Spinoni et al. (2018) and Soares et al. (2023). All the statistics were computed for all indices and for the 7, 15, 30, 90, 180, 360, and 720 d timescales considering each land grid point. A comparison is then performed by studying the spatial correlation and root-mean-square error between the GDI and other indices, for moderate drought only. An assessment of the differences between the GDI against the SPI or SPEI and Z-Score is also performed, considering the drought characteristics. Additionally, the Supplement includes comparisons of the GDI against the monthly SPI and SPEI version computed with the default definitions provided by the “SPEI” package for the R programming language (Beguería et al., 2014) as a complement. Whenever it is applied, the monthly GDI is also computed by aggregating the daily index at monthly time steps, by simply averaging the daily index. An analysis of the spatial extent of drought classes (moderate, severe, and extreme) is performed for the IB01 dataset for a case study. The spatial extent is computed for each day and is defined as a percentage of land points with any index below the given thresholds. This analysis is performed for the extreme drought that affected the Iberian Peninsula in 2004 and 2005, where the evaluation period corresponds to 2 hydrological years, starting in October 2004 and ending in September 2006. Moreover, the spatial average time series of all drought indices for all time aggregations were also analysed.

3 Results

3.1 GDI general performance

The GDI, SPI, and SPEI (Fig. 2a to d) reveal percentiles close to those obtained by a normal distribution. Figure 2a displays the results for the GDI computed solely from precipitation. For the timescales below 90 d, the distributions deviate slightly from the normal, particularly near the median, while, for the longer aggregation scales, the time series deviates more from the normal distribution towards the tails. Figure 2b, for the GDI computed with PR-PET, reveals a similar pattern. However, with the inclusion of PET, the deviations from the normal distribution are reduced. For the SPI (Fig. 2c), the time series still follows the central line, although with a notorious dispersion. The pattern of the spread from all distributions remains similar for all accumulation scales, with higher deviations towards the tails of the distribution. For the SPEI (Fig. 2d), the inclusion of PET relative to the SPI (Fig. 2c) did improve the results as in Fig. 2b for the GDI, but the pattern of spread remains rather large. Both the SPI and the SPEI present a larger spread in comparison to the GDI. In the Z-Score index with PR (Fig. 2e) and PR-PET (Fig. 2d), the underlying distribution does not necessarily have to align with the normal standard distribution. However, due to the central limit theorem, for longer accumulations the time series tend towards normality, as evidenced by the alignment with the central line, despite the expected and large spread amongst all time series. Figure S3 in the Supplement shows the same but for the monthly versions of the GDI, SPI, and SPEI. Although the spread is larger for the monthly GDI in comparison to the daily version, it is still lower than the SPI and the SPEI.

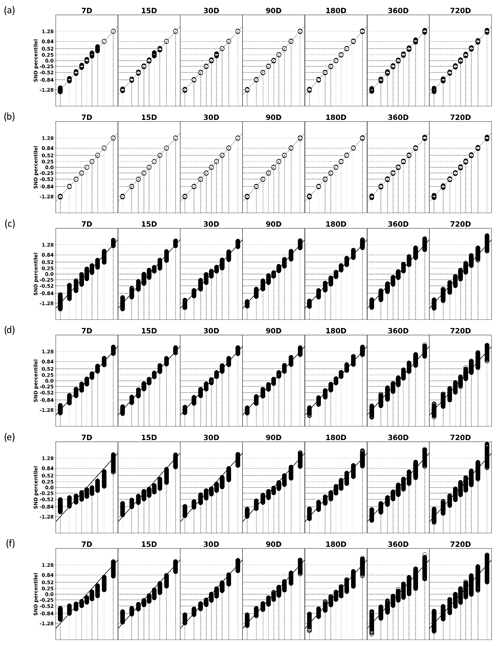
Figure 2 Quantile–quantile plot against the 10th, 20th, 30th, 40th, 50th, 60th, 70th, 80th, and 90th percentiles from the standard normal distribution for all grid points of the IB01 dataset for the (a) GDI (PR), (b) GDI (PR-PET), (c) SPI, (d) SPEI, (e) Z-Score index (PR), and (f) Z-Score index (PR-PET). All indices were computed at the daily time step. A smaller vertical spread indicates a better agreement with the standard normal distribution from all locations. The numbers of the y axis and the horizontal and vertical lines correspond to the percentiles of the standard normal distribution (SND percentile).

As a complement, Fig. S4 in the Supplement displays the statistics for all accumulation timescales and indices. The proximity of the values to zero indicates their similarity to the reference standard normal distribution. For the GDI, the mean and the median exhibit closer values, albeit with a slight deviation above 0. Nevertheless, those results, together with the low skewness and kurtosis, are good indicators of normality. For the SPI and SPEI, all metrics are near 0, although there is a more noticeable deviation among the time series in comparison with the results obtained for the GDI. Conversely, by definition, the Z-Score displays a mean of 0 and a standard deviation of 1. Still, as expected from the statistics and the quantile–quantile plot from Fig. 2, the underlying distribution clearly deviates from normality.

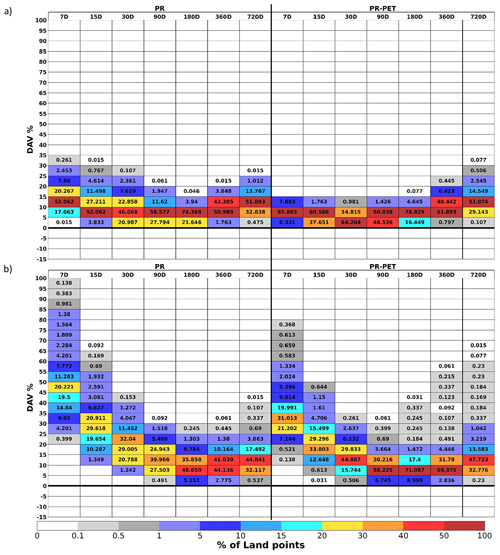
To assess the performance of the new index, the DAV metric (Eq. 20) is applied (Table 2). In this configuration, the DAV metric allows a quantification of a higher or lower degree of conformity to the standard normal distribution, relative to the other indices. The Perkins skill scores are determined for the GDI, SPI, SPEI, and Z-Score for each location individually and for chosen timescales. Table 2a shows the DAV for the GDI with PR against the SPI and shows the GDI with PR-PET against the SPEI. For each accumulation period, a histogram represents the percentage of land points within each DAV category. All locations for all accumulations clearly display positive added value. For most of the accumulation periods, more than 50 % of land points reveal gains between a DAV of 5 % to 10 %. The exceptions are for 7 d accumulation for the PR indices and 720 d for the PR-PET, where most locations exhibit higher gains. However, the intermediate aggregation timescales (30, 90, and 180 d) still reveal more than 20 % of locations falling within the neutral DAV range (−5 % to 5 %) for the PR indices. A similar trend occurs for the PR-PET indices, albeit with a more prominent result, with approximately 64 %, 48.5 %, and 16.4 % of locations for the aggregations of 30, 90, and 180 d, respectively, having DAV values up to 5 %. Following Fig. 2, this behaviour is likely attributed to the PR-PET indices offering a better representation of the normal distribution. In general, the GDI can add value, due to its improved representation of the shape of the cumulative distribution and consequently normality, as indicated in Figs. 2 and S4. Table 2b displays the DAV metric between the GDI and the Z-Score, showing that the GDI again reveals a positive added value. In this case, since the underlying distribution for the original time series does not necessarily have to follow the normal distribution, large DAV values are expected. The gains are relevant, namely for the shorter accumulations. Towards the longer accumulations, the time series for the Z-Score better aligns with the normal distribution as hinted in Fig. 2e and f, returning lower DAV values. These findings are relevant and could indicate that the fit of the data to a chosen theoretical distribution could introduce some uncertainty into the final index, while a fit to an empirical distribution can return more precise results. Table S1 displays the DAV for the daily GDI against the monthly SPI or SPEI (Table S1a) and the DAV for the monthly GDI against the monthly SPI or SPEI (Table S1b). The results obtained in Table S1a are identical to Table 2, where all locations reveal gains. However, for Table S1b, some points have a negative DAV. This behaviour hints at the fact that the added value of the index in this context is not only due to the comparison between a daily time step and a monthly time step, but also to an overall better fit to the empirical distribution.

Table 2 Distribution added value for (a) the GDI against the SPI or SPEI and (b) the GDI against the Z-Score index. Each column denotes the accumulation periods, where PR stands for accumulated precipitation (left) and PR-PET stands for accumulated precipitation minus potential evapotranspiration (right). The colours and values in each cell correspond to the percentage of land points within the respective DAV category. The Perkins skill score is built by confronting each index histogram against the normal distribution histogram. The DAV is then computed as the relative difference between each index Perkins skill score and for each location individually. The Table shows the percentage of land points falling within each DAV category.

To evaluate the degree of similarity between the GDI against the other indices, the temporal correlation and the RMSE are presented in Fig. 3. Figure 3a and b show the comparison between the GDI against the corresponding SPI and SPEI; i.e., the GDI (PR) is compared to the SPI and GDI (PR-PET) and to the SPEI. The degree of agreement for most locations is very high, with correlations close to 1. The RMSE mirrors the results obtained for the correlations, with very low values, indicating a proximity of the index values across the SPI or SPEI and the corresponding GDI. These outcomes suggest small differences amongst the indices across all timescales; i.e., the GDI can detect the same drought events as the SPI or SPEI. Fig. 3b displays the comparison between the GDI and the Z-Score, with both PR and PR-PET as input. For Fig. 3a, the correlations are still somewhat high with low RMSE, namely for the longer accumulations. A high correlation is still expected, since the same time series were used for computing both the GDI and the Z-Score. However, for the Z-Score, the prospect is different, which is expected, since the underlying distribution of the raw data is non-normal (Fig. 2), hence the larger differences found relative to the GDI. For the longer accumulations, the underlying distribution of the Z-Score data tends to be closer to the standard normal, resulting in lower RMSE values and an approximation between the GDI and the Z-Score. The dispersion of the values is also greater in comparison to Fig. 3a. For the 7 d accumulation, the correlation (RMSE) is approximately 0.9 (0.6), gradually increasing (decreasing) for longer accumulation periods. Figure S5 in the Supplement shows the correlation and RMSE of the monthly GDI against the monthly SPI or SPEI. The findings are akin to those from Fig. 3b, where the agreement between indices is higher for the longer accumulations.

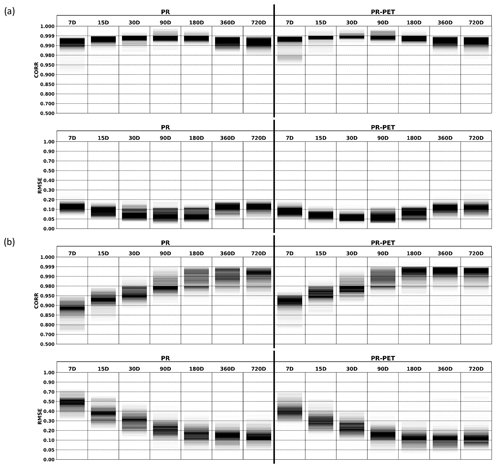
Figure 3 Pearson correlation and root-mean-square error between the GDI (a) against the SPI or SPEI and (b) against the Z-score index. Each column denotes the accumulation periods, where PR stands for accumulated precipitation (left) and PR-PET stands for accumulated precipitation minus potential evapotranspiration (right). The lines depict individual land points for the IB01 observations, with darker shading indicating a higher density of closely spaced lines.

3.2 Drought characteristics assessment

When evaluating the performance of a drought index, it is crucial to assess key characteristics such as event severity, frequency, duration, and spatial extent. Table 3 presents the spatial correlation and RMSE for drought intensity, frequency, duration, and spatial extent between the GDI against the SPI or SPEI (Table 3a) and against the Z-Score index (Table 3b). Only the results for moderate drought are considered, since, for higher drought thresholds, the lack of events may hinder this comparison. Overall, the spatial agreement of the intensity and mean duration of drought characteristics between the GDI and the SPI or SPEI (Table 3a) reduces towards the higher accumulations, as indicated by declining correlations and increasing RMSEs. Those results contrast with the findings from Fig. 3, where correlations remained high and RMSE remained low for all timescales. As for the drought frequency, although the correlation decreases for higher aggregation periods, the RMSE also decreases. Nonetheless, for all cases and regardless of the accumulation time step, higher base values from each drought characteristic, shown in Figs. S6, S8, and S10, imply potentially larger differences amongst the indices. The spatial extent in drought reveals close values between the GDI and the SPI or SPEI, with near-perfect correlation (near 1) and low RMSE values. Comparing with the Z-Score index yields similar results to Table 3a, albeit with some differences, particularly at the 7 d accumulation for drought intensity and frequency. In this case, the correlations and RMSE do not follow the previous pattern. For instance, the correlation for drought intensity is 0.917 for the PR indices and 0.909 for the PR-PET indices, contrasting with 0.938 and 0.949 obtained in the same comparison of the GDI against the SPI or SPEI. Figures S7, S9, and S11, along with Table S2, show the same results for the monthly GDI and the monthly SPI or SPEI. In this case, the comparability at shorter timescales is notably lower, particularly for PR indices, increasing towards higher accumulations.

Table 3 Spatial Pearson correlation (blue) and spatial root-mean-square error (red) between (a) the GDI against the SPI or SPEI and (b) the GDI against the Z-Score index. Each row, for both panels and from top to bottom, represents the drought intensity, the drought mean decadal frequency, and the drought mean duration. The last row in both panels displays a time Pearson correlation and root-mean-square error for the drought spatial extent. These results are presented only for moderate drought (index $<-\mathrm{0.5}$). Each column denotes the accumulation periods, where PR stands for accumulated precipitation (left) and PR-PET stands for accumulated precipitation minus potential evapotranspiration (right). The colours denote extremes of either correlation or RMSE.

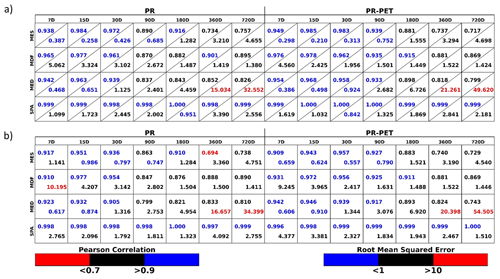
Figure 4a displays the difference between the GDI and the SPI or SPEI for the drought characteristics mean event severity, decadal frequency, mean duration, and spatial extent for the three drought classes defined: moderate (index $<-\mathrm{0.5}$), severe (index $<-\mathrm{1}$), and extreme (index $<-\mathrm{1.5}$). Regarding drought severity, the difference amongst indices increases for higher accumulations, with the GDI showing higher intensity for most locations, as indicated by the positive median value. In terms of drought decadal frequency, the differences vary more for all accumulations. At the 7 d accumulations, the GDI tends to reveal less moderate and severe events but more extreme events. Conversely, and for the PR-based indices, at 15, 30, and 90 d, the GDI slightly indicates more moderate events while showing fewer severe and extreme events. The opposite occurs for the PR-PET-based indices. It is important to note that the extreme drought class is contained within severe drought, which in turn is contained within moderate drought. This approach avoids splitting the events (Soares et al., 2023). The position of the median in this context is relevant, indicating the trend shown by most locations. For the mean event duration, not only does the dispersion of the results increase towards the longer accumulations, but the median value is also negative, suggesting systematic shorter events for the GDI within the majority of locations. For severity and duration, the differences are higher for the longer accumulations, consistent with the findings in Table 3a, where greater variability for the differences implies lower correlation and higher RMSE. In opposition to the other drought characteristics, the spatial extent reveals fewer differences across all timescales, as anticipated from the results obtained in Table 3a. In this case, extreme drought tends to reveal lower differences than moderate and severe drought. It is worth noting that the scale is not linear; thus, for higher values, the differences in the spread may not be as noticeable. Additionally, the inclusion of the PET does not noticeably change the results in this context.

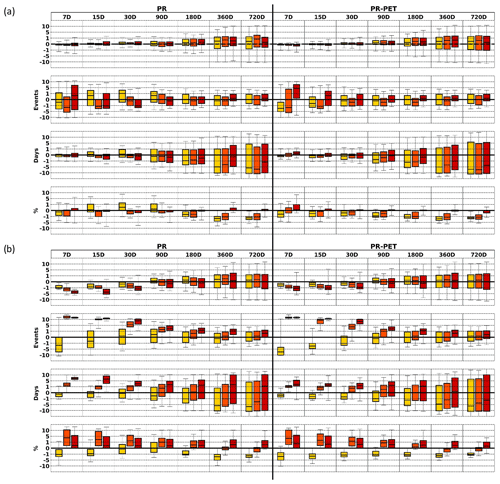
Figure 4 Boxplot of all land points featuring the difference in drought characteristics between (a) the GDI and the SPI or SPEI and between (b) the GDI and the Z-Score index. In each panel, from top to bottom: the mean event severity, the decadal frequency, the mean event duration, and the spatial extent of droughts. For the case of drought spatial extent, the differences are made for each time step. Each column denotes the accumulation periods, where PR stands for accumulated precipitation (left) and PR-PET stands for accumulated precipitation minus potential evapotranspiration (right). The different boxplots denote the results for moderate drought for index < −0.5 (yellow), severe drought for index $<-\mathrm{1}$ (orange), and extreme drought for index $<-\mathrm{1.5}$ (red). For each boxplot, the low (high) whisker denotes the 1st (99th) percentile, while the three horizontal lines within the box correspond, from bottom to top, to the 25th, 50th, and 75th percentiles.

Figure 4b illustrates the differences between the GDI and the Z-Score index. Since the Z-Score is a simple standardisation with no changes in the underlying distribution, one can anticipate larger differences, as suggested by the previous figures. Concerning mean drought severity, shorter accumulations of up to 30 d reveal that the GDI has fewer events than the Z-Score. For the higher accumulations, the differences tend to be more positive with more variability across all locations. Regarding drought decadal frequency, the same behaviour occurs for moderate drought. However, for severe and extreme drought, the GDI reveals more events than the Z-Score, decreasing towards the longer accumulations. As for the mean drought duration, a similar behaviour can be observed, albeit with smaller differences in the shorter accumulations. Furthermore, and akin to the mean event severity, differences tend to be more spread out for longer accumulations. It is noteworthy that, for severe and extreme droughts, the Z-Score may show locations without events. The same may occur for the GDI, SPI, or SPEI, although with a lower chance. This clearly occurs for extreme drought, for instance, at the 7 d accumulation Z-Score index (Figs. S6, S8, and S10). Regarding drought spatial extent, the GDI returns lower values for moderate drought and higher values for severe and extreme drought. The only exceptions are at the 360 and 720 d accumulations, where most locations reveal a slightly negative difference. Overall, the results in Fig. 4 do not indicate a significant alteration between the PR- and PR-PET-based indices, consistent with the findings in Fig. 3 for the correlation and RMSE of the time series and with Table 3. It appears that the variations between the PR and PR-PET indices are more evident within the indices themselves rather than in the comparisons performed amongst them. Figure S12 shows the same differences but for the monthly GDI against the monthly SPI or SPEI.

3.3 2004/2005 case study

A case study of an extreme drought which affected the Iberian Peninsula, starting in the autumn of 2004, is presented in Fig. 5, where the spatial extent for moderate, severe, and extreme drought are shown, computed for all timescales and indices. Figure S13 in the Supplement shows the same but for the PR-based indices. The differences between the PR- and PR-PET-based indices is minimal in terms of drought spatial extent, as expected from the previous results. The 2005 drought is widely regarded as one of the most extreme events in recent history affecting the Iberian Peninsula, characterised by a precipitation deficit during the hydrological year of 2004/2005 (García-Herrera et al., 2007; Santos et al., 2007). The patterns of the spatial extent for all drought severities for the lower accumulations (Fig. 5a, b, and c) are similar, revealing the extremely dry autumn of 2004 and spring of 2005, which were somewhat repeated in the following hydrological year. At these scales, the GDI, SPI, and SPEI exhibit similar percentages of territory in the three drought categories.

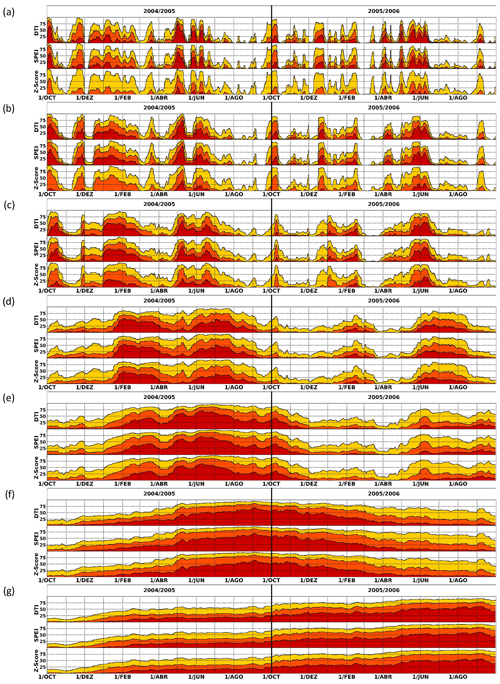
Figure 5 Time series of the daily drought spatial extent of the period from 1 October 2004 until 30 September 2006 for the IB01 with aggregations of (a) 7, (b) 15, (c) 30, (d) 90, (e) 180, (f) 360, and (g) 720 d. In each panel, the top row displays the results for the GDI, the middle row displays the results for the SPEI, and the bottom row displays the results for the Z-Score standardisation. All indices consider only the balance between precipitation and PET. Yellow denotes the results for moderate drought for index $<-\mathrm{0.5}$, light orange denotes the results for severe drought for index $<-\mathrm{1}$, and dark orange denotes the results for extreme drought for index $<-\mathrm{1.5}$.

The SPEI and GDI show that over 75 % of the land experienced extreme drought conditions from October 2004 to May 2005. Conversely, the Z-Score stands out, with lower spatial percentages of Iberia experiencing severe drought and almost no territory being classified as extreme drought. As for the longer accumulations (Fig. 5d to g), all three indices converge regarding the spatial extent of drought. At 90 and 180 d, accumulation for almost the entire year of 2005 was at least in moderate drought, returning to normal conditions in 2006. For the 360 d accumulation, the peak of drought severity occurs during the summer and autumn of 2005. It is worth noting that summer is typically one of the most critical periods for drought due to reduced precipitation and increased temperatures. For the 720 d, however, the drought conditions started in 2005 with a peak in 2006, revealing a shift relative to the previous cases due to the longer accumulation. As indicated by the results from Fig. 5a to c, the autumn of 2005 and spring of 2006 were also drier, albeit not as severe as during the previous hydrological year.

Figure 6 shows the time series of the spatial means of the PR-PET indices for the same period and event as Fig. 5 (October 2004 to September 2006). Figure S14 shows the same but for the PR based indices. The red and blue shadings denote the differences between the GDI (solid black line), the SPEI, and the Z-Score, respectively. Amongst all aggregation periods (Fig. 6a to g), the differences across indices are more visible towards the extreme values. Overall, the differences are larger for the Z-Score rather than for the SPEI. Since the Z-Score is based on a simple standardisation, it closely follows the accumulated PR-PET patterns, while the same does not occur for the other indices, hence the higher differences. Still, for the lower aggregation periods (Fig. 6a to c), the Z-Score fluctuates more relative to the SPEI and GDI. As for the GDI, the day-to-day values can reach higher extremes. Since the index is based on an empirical distribution, the maximum and minimum of the time series is dependent on the length of the data used. On the other hand, for indices such as the SPEI, the extremes are more controlled by the chosen distribution, while, for the Z-Score, the extremes are dependent on the difference in the accumulations relative to their mean. Those factors may cause a smoothing effect on the extremes for the SPEI, SPI, and Z-Score.

Figure 6 Area-averaged time series of the daily drought indices for the period from 1 October 2004 until 30 September 2006 for the IB01 dataset with aggregations of (a) 7, (b) 15, (c) 30, (d) 90, (e) 180, (f) 360, and (g) 720 d. The black line represents the GDI, while the red and blue shadings denote, respectively, the differences between the GDI and the SPEI and between the GDI and the Z-Score index. The differences are computed by taking the absolute value of each index first. Thus, if the difference is positive, it implies that the GDI is further away from the mean 0 than the other index. All indices only consider the balance between precipitation and PET.

4 Discussion and conclusions

In the present chapter, a new drought index is introduced, designated as the generalised drought index, or the GDI. This index is extremely straightforward to compute, since the fitting process to a known distribution is not required. It is empirically driven and can be regarded as an alternative to other indices such as the SPI or SPEI. The GDI is computed by generating an empirical distribution based on a smoothed cumulative histogram, where the PR or PR-PET data can be converted into probabilities and then brought back as standardised values following a normal distribution of mean 0 and a standard deviation of 1. As an example, the IB01 observational-based dataset was used to compute the GDI for Iberia. The analysis considers the IB01 period from 1971 to 2015. To compare and to assess the proposed index added value, the daily SPI, SPEI, and Z-Score were computed with a daily time step for PR- and PR-PET-based accumulations. A comparison with the monthly SPI and SPEI is also performed and shown in the Supplement.

The main distinction between the GDI and the SPI or SPEI lies in the fitting of climate data to a probability distribution function. In the case of the monthly SPI and SPEI, the fitting process is mandatory due to the scarcity of data points compared to daily data, which hinders the applicability of the GDI. Nonetheless, in this study, and since the seasonal cycle was previously removed, both the daily SPI and SPEI were fitted to the log-logistic distributions. The reason to consider the log-logistic distribution for the SPI lies in the poor fit found for the Gamma distribution. It is important to note that assuming a specific distribution for different climate types or even different accumulations can be detrimental, since the underlying distributions may differ (e.g., Stagge et al., 2015; Monish and Rehana, 2020; Zhang and Li, 2020), as also shown in Fig. S1. Those issues do not arise with the GDI. Furthermore, the SPI and SPEI may encounter difficulties in fitting data from semi-arid and arid climates with very low accumulations, such as deserts (Beguería et al., 2014). The very low accumulations, which could also occur in climate change studies with historical reference, may not be very well simulated, although alternative approaches exist, such as those of Spinoni et al. (2018) and Soares et al. (2023). On the other hand, the GDI does not have those constraints, since the distribution is built empirically by smoothing an accumulated data histogram. Apart from the distribution, the definition of the parameters in the case of the SPI and SPEI may also pose challenges, especially at the daily scale. Outliers present in the data may hinder the parameter estimation process. Additionally, as the dataset size increases, the computational expense for calculating the index also escalates, particularly when considering methods such as maximum likelihood (Beguería et al., 2014). In contrast, the GDI offers a simple and computationally efficient procedure which easily bypasses the determination of fitting parameters, making it suitable for large datasets. The performance of the GDI may be superior for larger datasets, as the underlying distribution associated with each location is better defined. Indeed, the GDI time series conforms better to the theoretical standard normal distribution, namely if PET is considered. Another potential source of uncertainty, particularly for extreme values, is associated with the Abramowitz and Stegun (1968) approximation, which performs better for values closer to the mean. For extremes, the values deviate from the true standard normal distribution, although the likelihood of the SPI or SPEI being extreme is low (Stagge et al., 2015). The GDI does not exhibit this limitation due to its empirical nature; the minimum and maximum values of the index are dependent on the size of the time series, and these values do not deviate from the standard normal as much as the other indices.

Regarding the evaluation of the proposed metric with a version of the DAV, using the normal distribution as a reference, the GDI exhibits a positive added value against the other drought indices. The gains of the proposed index against the SPI and SPEI are relevant, since both indices already conform to the standard normal distribution. Those findings could potentially indicate a reduction in the uncertainty due to the fitting procedures. Thus, this added value is not solely attributable to the different standardisation methodologies, otherwise the DAV would be closer to 0 % in this case. As for the comparison against the Z-Score, the GDI displays higher DAV percentages as expected, highlighting the relevance of the underlying distribution in thresholds based on standard deviations from the mean, such as those used in the GDI, SPI, or SPEI.

To assess the degree of similarity amongst the indices, a Pearson correlation and an RMSE were computed. The results reveal a strong agreement amongst the three indices, particularly between the GDI and the SPI or SPEI. Nevertheless, lower correlations and a higher RMSE occur for the comparison to the Z-Score. In this case, those deviations are expected, since the original underlying distribution is kept. Regarding the drought characteristics such as intensity, frequency, and duration, for moderate drought conditions, the GDI shows similar results against the SPI, SPEI, and Z-Score. Still, the proposed index reveals differences, since, for most cases and towards longer aggregation periods, the similarity amongst indices decreases.

The GDI is also evaluated in terms of drought spatial extent against the SPEI and Z-Score for the severe 2004/2005 drought event. While the GDI, SPI, and SPEI reveal very similar values for all timescales and drought severities, the Z-Score had some difficulty in representing severe and extreme drought for the lower accumulations. All indices tend to converge due to the approximation towards normality for longer accumulations. Regarding the performance of the GDI, the proposed index demonstrated a close representation of the spatial extent of drought compared to the SPEI. The same conclusions can be drawn for the PR-based indices. As for the spatial mean time series, the indices tend to grow apart towards the extreme values. Nevertheless, the differences are small, particularly for the comparison of the GDI against the SPI or SPEI. Those findings provide reassurance and present the GDI as a viable alternative to the SPI or SPEI.

The Z-Score synchronises only the statistical mean and standard deviation by setting them to 0 and 1, respectively, disregarding the underlying distribution. In contrast, the GDI, SPI, and SPEI share the same distribution and parameters: the standard normal distribution with a mean of 0 and a standard deviation of 1. PR and even PR-PET tend to be positively skewed, which may result in an underrepresentation of severe and extreme drought for shorter accumulations on threshold-based definitions. Since the GDI, SPI, and SPEI follow the standard normal distribution, this issue does not arise. If a percentile-based threshold were used, differences in decadal drought frequency, mean event duration, and spatial extent would likely be reduced. However, using a threshold based on percentiles could hinder the comparison amongst indices, as the intensity of individual events and the index value for each day would vary.

The GDI can identify the same events as the SPI or SPEI by returning similar results for most cases while revealing an enhanced performance. However, it is less computationally expensive, does not need the assumption of the characteristics of the underlying distribution of the data, and can be applied to other variables such as soil moisture or actual evapotranspiration. Compared to other studies also featuring a daily drought index (e.g., Li et al., 2020; Ma et al., 2020; Zhang et al., 2022a), the daily approach to the GDI offers a finer temporal resolution, enabling a more detailed depiction of meteorological variations and their immediate impacts on drought conditions. The higher sensitivity compared to monthly indices allows the timely identification of short-term drought events, better capturing the start and duration. This feature is particularly relevant in regions characterised by a sizeable climatic variability. Thus, the GDI is suitable for describing meteorological, hydrological, agricultural, and flash droughts using the same methodology. Therefore, the GDI could be a viable alternative for computing a standardised index for drought analysis and simulation evaluation with EURO-CORDEX simulations or the large kilometre-scale simulations from the WRCP Flagship Pilot Study on “convective phenomena over Europe and the Mediterranean”. The assessment of simulations with a daily drought index allows researchers to scrutinise models more rigorously, examining not just their ability to predict long-term trends but also their effectiveness in capturing short-term variability. With the use of a daily drought index, the assessment of a model's performance regarding frequency, severity, and duration of events is thus enhanced. Furthermore, the daily index enhances our understanding of the feedback mechanisms between meteorological droughts and their impacts on sectors such as agriculture and water management. Unlike traditional indices, which might aggregate data over longer periods and potentially smooth out critical variations, the daily index preserves the day-to-day variations in moisture availability. This is crucial for understanding drought onset, evolution, and dissipation and for predicting their impact on crop yields, water supply, and other critical resources. As climate simulations evolve, daily drought indices will undoubtedly play a key role in ensuring that the same models are able to meet the challenges posed by a rapidly changing climate.

Nevertheless, some questions are still open. Firstly, how different are the GDI results for climate change projections? The proposed index is empirically based; thus, the approaches from Spinoni et al. (2018) and Soares et al. (2023) can be considered for climate change assessment, where the entire time series is considered to build the empirical distribution. However, would it still be possible to use the historical period as a reference, conserving the absolute values for both the reference and future periods? What is the applicability and performance of the index at a global level? Other questions also arise, namely the sensitivity of the index to the potential evapotranspiration method considered and the sensitivity related to the initial variables. Furthermore, can the index be used for an ensemble-based analysis? Some of these questions will be pursued in future studies.