Carbon isotopes in the marine biogeochemistry model FESOM2.1-REcoM3

In this paper we describe the implementation of the carbon isotopes ¹³C and ¹⁴C (radiocarbon) into the marine biogeochemistry model REcoM3. The implementation is tested in long-term equilibrium simulations where REcoM3 is coupled with the ocean general circulation model FESOM2.1, applying a low-resolution configuration and idealized climate forcing. Focusing on the carbon-isotopic composition of dissolved inorganic carbon (δ¹³C_DIC and Δ¹⁴C_DIC), our model results are largely consistent with reconstructions for the pre-anthropogenic period. Our simulations also exhibit discrepancies, e.g. in upwelling regions and the interior of the North Pacific. Some of these differences are due to the limitations of our ocean circulation model setup, which results in a rather shallow meridional overturning circulation. We additionally study the accuracy of two simplified modelling approaches for dissolved inorganic ¹⁴C, which are faster (15 % and about a factor of five, respectively) than the complete consideration of the marine radiocarbon cycle. The accuracy of both simplified approaches is better than 5 %, which should be sufficient for most studies of Δ¹⁴C_DIC.

1 Introduction

Carbon isotopes are powerful tools for tracing present and past biogeochemical cycles and water masses. The stable isotope carbon-13 (¹³C) can be used to study the anthropogenic perturbation of the global carbon cycle owing to the combustion of isotopically depleted fossil fuels via the so-called ¹³C Suess effect (e.g. Keeling, 1979; Quay et al., 1992; Köhler, 2016; Graven et al., 2021). Carbon-13 may also help to decipher the exchange between atmospheric, marine, and terrestrial carbon reservoirs in the past, for example, during the last glacial cycle (Köhler et al., 2006; Ciais et al., 2012; Broecker and McGee, 2013; Jeltsch-Thömmes et al., 2019; Menking et al., 2022). Furthermore, ¹³C is a proxy for oceanic nutrients and can be employed to infer past marine biological productivity, export production, and water mass distributions assuming that calcareous tests of foraminifera are faithful recorders of dissolved inorganic ¹³C (e.g. Broecker and Peng, 1982; Lynch-Stieglitz et al., 2007; Hesse et al., 2011; Schmittner et al., 2017). The radioactive isotope carbon-14 (radiocarbon, ¹⁴C) is the most important geochemical chronometer for dating organic matter and for assessing ocean ventilation rates and pathways over the last 55 000 years (Heaton et al., 2021; Rafter et al., 2022; Skinner and Bard, 2022, Skinner et al., 2023). In addition, the penetration of bomb-produced ¹⁴C into the oceans has provided a benchmark for ocean circulation models (Matsumoto et al., 2004). Although the potential of carbon isotopes has been known for a long time, ocean general circulation models have only recently been equipped with carbon isotopes and applied in Earth system modelling studies (e.g. Tschumi et al., 2011; Holden et al., 2013; Schmittner et al., 2013; Jahn et al., 2015; Menviel et al., 2015; Buchanan et al., 2019; Jeltsch-Thömmes et al., 2019; Dentith et al., 2020; Tjiputra et al., 2020; Claret et al., 2021; Liu et al., 2021; Morée et al., 2021).

Here, we describe the implementation of both carbon isotopes ¹³C and ¹⁴C into the marine biogeochemistry model REcoM3, which is part of the AWI Earth System Model. The technical details are described in Sect. 2 and simulations in Sect. 3. Isotope results are presented in terms of δ¹³C and Δ¹⁴C, which express the relative deviations of observed ${}^{\mathrm{13}}\mathrm{C}{/}^{\mathrm{12}}\mathrm{C}$ (¹³R) and ${}^{\mathrm{14}}\mathrm{C}{/}^{\mathrm{12}}\mathrm{C}$ (¹⁴R) ratios with respect to specific standard values ¹³R_std and ¹⁴R_std, where

$$\begin{array}{}\text{(1)}& {\displaystyle }{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}={}^{\mathrm{13}}R{/}^{\mathrm{13}}{R}_{\mathrm{std}}-\mathrm{1}(\times {\mathrm{10}}^{\mathrm{3}}\mathrm{‰}),\text{(2)}& {\displaystyle }{\mathit{\delta }}^{\mathrm{14}}\mathrm{C}{=}^{\mathrm{14}}R{/}^{\mathrm{14}}{R}_{\mathrm{std}}-\mathrm{1}(\times {\mathrm{10}}^{\mathrm{3}}\mathrm{‰}),\end{array}$$

and (following Stuiver and Pollach, 1977)

$$\begin{array}{}\text{(3)}& {\mathrm{\Delta }}^{\mathrm{14}}\mathrm{C}={\mathit{\delta }}^{\mathrm{14}}\mathrm{C}-\mathrm{2}({\mathit{\delta }}^{\mathrm{13}}\mathrm{C}+\mathrm{25})(\mathrm{1}+{\mathit{\delta }}^{\mathrm{14}}\mathrm{C}/\mathrm{1000})(\times {\mathrm{10}}^{\mathrm{3}}\mathrm{‰}).\end{array}$$

Section 4 concludes with a brief summary.

2 Model description

2.1 Short overview of REcoM3

The Regulated Ecosystem Model, version 3 (REcoM3) is described in detail by Gürses et al. (2023). Here, we only give a brief summary of the common model features and describe the differences from the configuration that we use in this study. REcoM considers the marine biogeochemical cycles of carbon, nitrogen, silicon, iron, and oxygen. The ecosystem component of REcoM includes nutrients, two phytoplankton functional types (distinguishing between small phytoplankton and diatoms), one zooplankton functional type, one detritus type, and dissolved organic matter. Different from most other marine biogeochemistry models, REcoM does not rely on a fixed internal stoichiometry of phytoplankton. Instead, the composition of organic soft tissue is regulated (i.e. calculated) in response to light, temperature, and nutrient supply, which enables stoichiometric shifts between the present and past to be assessed. The model includes a sediment layer in which sinking detritus (consisting of particulate organic matter, calcite, and opal) is fully remineralized and where solutes are returned to the bottom water layer within days so that there is no accumulation of sedimentary matter. Alternatively, REcoM3 can be run with the comprehensive sediment model MEDUSA2 (Munhoven, 2021), which is described in another paper (Ye et al., 2023). Apart from the implementation of carbon isotopes, the main difference from the standard REcoM3 configuration by Gürses et al. (2023) is that REcoM3 considers two zooplankton and two detritus groups instead of one, which would require inclusion of six additional carbon-isotopic tracers at the expense of model speed. We refer to the configuration presented here as REcoM3p as an initial set-up for paleo studies. To simulate biogeochemical tracer circulation, REcoM3 needs a transport model. Here, we utilize the ocean general circulation model FESOM2.1, which is an update of FESOM2.0 (Danilov et al., 2017). The coupling of FESOM2.1 with REcoM3 is also described by Gürses et al. (2023), where all biogeochemical model equations except for carbon isotopes can be found.

2.2 Implementation of carbon isotopes

Carbon-13 and ¹⁴C are implemented as additional passive tracers, tripling the number of carbon-containing tracers in REcoM from 8 to 24. The model considers carbon isotopes for dissolved inorganic and organic carbon, small phytoplankton, diatoms, zooplankton, detritus, and calcite. As the abundances of ¹³C and ¹⁴C are small (¹³R_std≈0.0113, Assonov et al., 2020, and ${}^{\mathrm{14}}{R}_{\mathrm{std}}=\mathrm{1.170}\times {\mathrm{10}}^{-\mathrm{12}}$; Orr et al., 2017), we approximate total C with ¹²C and neglect ¹³C and ¹⁴C in the kinetic calculations of the carbonate system. For the same reason, and to ensure numerical stability in the other model calculations involving ¹³C and ¹⁴C, the model considers scaled concentrations ¹³C${}^{\prime }={}^{\mathrm{13}}\mathrm{C}{/}^{\mathrm{13}}{R}_{\mathrm{std}}$ and ¹⁴C${}^{\prime }={}^{\mathrm{14}}\mathrm{C}{/}^{\mathrm{14}}{R}_{\mathrm{std}}$, which have the same magnitude as ¹²C, following Jahn et al. (2015). As a consequence, ¹³C^′ and ¹⁴C^′ have to be rescaled when compared with observed concentrations. However, as the scaling factors cancel out when ¹³C^′ and ¹⁴C^′ are converted to δ¹³C and Δ¹⁴C, Eqs. (1)–(3) can be directly evaluated with scaled concentration ratios and ${}^{\mathrm{13}}{R}_{\mathrm{std}}{=}^{\mathrm{14}}{R}_{\mathrm{std}}=\mathrm{1}$.

We consider isotopic fractionation during air–sea gas exchange, dissolution of CO₂ in seawater, and photosynthesis by phytoplankton. In addition, the model accounts for radioactive decay and, optionally, cosmogenic production of ¹⁴C. The details are explained in the following subsections.

2.3 Carbon-13

2.3.1 Air-sea exchange

The isotopic fractionation during uptake and dissolution of ¹³CO₂ is calculated according to Zhang et al. (1995), similar to the biogeochemical protocol of the CMIP6 Ocean Model Intercomparison Project (OMIP-BGC protocol, Orr et al., 2017). That is, the air–sea exchange flux ¹³F is proportional to the difference between the saturation and in situ concentrations of aqueous ¹³CO₂:

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{}^{\mathrm{13}}F& =k_{\mathrm{w}}\left(\right[{}^{\mathrm{13}}{\mathrm{CO}}_{\mathrm{2}}^{\ast }{]}_{\mathrm{sat}}-\left[{}^{\mathrm{13}}{\mathrm{CO}}_{\mathrm{2}}^{\ast }\right])\\ & =k_{\mathrm{w}}{(}^{\mathrm{13}}{\mathit{\alpha }}_{\mathrm{k}}^{\mathrm{13}}{\mathit{\alpha }}_{\mathrm{aq}-\mathrm{g}}-\mathrm{0.0002})\\ & \cdot {(}^{\mathrm{13}}{R}_{\mathrm{atm}}\left[{\mathrm{CO}}_{\mathrm{2}}^{\ast }{]}_{\mathrm{sat}}{-}^{\mathrm{13}}{R}_{\mathrm{DIC}}{/}^{\mathrm{13}}{\mathit{\alpha }}_{\mathrm{DIC}-\mathrm{g}}\right[{\mathrm{CO}}_{\mathrm{2}}^{\ast }\left]\right),\end{array}\end{array}$$

where k_w is the CO₂ gas transfer velocity (calculated according to Wanninkhof, 2014, additionally considering sea-ice cover), and [¹³CO${}_{\mathrm{2}}^{\ast }$]_sat and [¹³CO${}_{\mathrm{2}}^{\ast }$] are the saturation and in situ concentrations of aqueous ¹³CO₂. ¹³R_atm and ¹³R_DIC are the ${}^{\mathrm{13}}\mathrm{C}{/}^{\mathrm{12}}\mathrm{C}$ concentration ratios of atmospheric CO₂ and dissolved inorganic carbon (DIC). Isotopic fractionation factors α denote kinetic fractionation during CO₂ gas transfer (¹³α_k), equilibrium fractionation during gas dissolution (¹³α_aq−g), and equilibrium fractionation between DIC and gaseous CO₂ (¹³α_DIC−g). Numerical values were taken from Zhang et al. (1995), who measured kinetic and equilibrium fractionation of ¹³C in acidified freshwater. For kinetic fractionation we employ a constant value of ¹³α_k=0.99912, which is the average between 5 °C (¹³α_k=0.99919) and 21 °C (¹³α_k=0.99905). Equilibrium fractionation between aqueous and atmospheric ¹³CO₂ is expressed as

$$\begin{array}{}\text{(5)}& {}^{\mathrm{13}}{\mathit{\alpha }}_{\mathrm{aq}-\mathrm{g}}=\mathrm{1}+\mathrm{0.001}(\mathrm{0.0049}T-\mathrm{1.31}),\end{array}$$

where T (°C) is the temperature of surface water. The numerical values of ¹³α_k and ¹³α_aq−g were determined for fresh water. To account for enhanced ¹³C fractionation in seawater associated with hydration reactions, Eq. (4) includes a correction factor of −0.0002 following Zhang et al. (1995), which is not considered in the OMIP-BGC protocol. Fractionation between DIC and gaseous CO₂ is calculated as

$$\begin{array}{}\text{(6)}& {}^{\mathrm{13}}{\mathit{\alpha }}_{\mathrm{DIC}-\mathrm{g}}=\mathrm{1}+\mathrm{0.001}\left(\right(\mathrm{0.014}f{\mathrm{CO}}_{\mathrm{3}}-\mathrm{0.107})T+\mathrm{10.53}),\end{array}$$

where fCO₃= [CO${}_{\mathrm{3}}^{\mathrm{2}-}$] $/$ DIC is the carbonate fraction of DIC.

2.3.2 Biogenic fractionation

Photosynthesis of phytoplankton leads to isotopic depletion of particulate organic carbon (POC), which is expressed following Freeman and Hayes (1992):

$$\begin{array}{}\text{(7)}& \left[{}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{POC}}\right]{=}^{\mathrm{13}}{R}_{\mathrm{POC}}\left[{}^{\mathrm{12}}{\mathrm{C}}_{\mathrm{POC}}\right]{=}^{\mathrm{13}}{R}_{\mathrm{aq}}{/}^{\mathrm{13}}{\mathit{\alpha }}_{\mathrm{p}}\left[{}^{\mathrm{12}}{\mathrm{C}}_{\mathrm{POC}}\right],\end{array}$$

where [¹³C_POC] and [¹²C_POC] are the isotopic POC concentrations in phytoplankton, ¹³R_POC is the corresponding isotopic ratio, ¹³R_aq is the ${}^{\mathrm{13}}\mathrm{C}{/}^{\mathrm{12}}\mathrm{C}$ concentration ratio of aqueous CO₂, and ¹³α_p is the isotopic fractionation factor associated with photosynthesis. Various experimental and modelling studies have determined ¹³α_p for certain phytoplankton species (Laws et al., 1995; Rau et al., 1996; Bidigare et al., 1997; Laws et al., 1997; Rau et al., 1997; Popp et al., 1998; Keller and Morel, 1999). However, it is uncertain to what extent these studies are globally representative and can be transferred into a single global modelling framework (see also the review by Brandenburg et al., 2022). Therefore, we pursue a less sophisticated but robust approach to calculating ¹³α_p, which does not rely on species-specific assumptions and has been inferred from a global dataset of 525 δ¹³C_POC field measurements spanning the period 1962–2010 CE (Young et al., 2013):

$$\begin{array}{}\text{(8)}& {}^{\mathrm{13}}{\mathit{\alpha }}_{\mathrm{p}}=\mathrm{1}+\mathrm{0.001}\left(\mathrm{17.6}\right(\mathrm{1}-\mathrm{2.02}/\left[{\mathrm{CO}}_{\mathrm{2}}^{\ast }\right]\left)\right),\end{array}$$

where [CO${}_{\mathrm{2}}^{\ast }$] is in µmol L⁻¹. As no distinction is made between different phytoplankton species in Eq. (8), the carbon-isotopic composition of small phytoplankton and diatoms in our model is the same. Similar to other models (e.g. Schmittner et al., 2013; Menviel et al., 2015; Buchanan et al., 2019; Tjiputra et al., 2020; Liu et al., 2021), we do not consider carbon-isotopic fractionation during the formation and dissolution of biogenic calcite because the effect is small and varies between species (α∼0.999–1.003 according to Ziveri et al., 2003).

2.4 Radiocarbon

Radiocarbon is subject to radioactive decay, cosmogenic production, and isotopic fractionation. The radioactive decay (applying a half-life of 5700 years, Audi et al., 2003; Bé and Chechev, 2012; Kutschera, 2013) is balanced in the model by cosmogenic ¹⁴C production fluxes or, alternatively, by prescribed atmospheric ¹⁴CO₂ concentrations corresponding to atmospheric Δ¹⁴C values.

Fractionation factors are calculated analogously to ¹³α, with ${}^{\mathrm{14}}\mathit{\alpha }={\mathrm{2}}^{\mathrm{13}}\mathit{\alpha }-\mathrm{1}$ (e.g. Craig, 1954; see also the discussion by Fahrni et al., 2017). The slow equilibration of DI¹⁴C in the deep ocean requires spinup simulations of several thousands of years, which may be computationally too expensive for high-resolution simulations. Therefore, we have implemented ¹⁴C in various ways that differ in their level of complexity and computational efficiency. The first implementation (“CC”) considers the complete ¹⁴C cycle parallel to ¹³C. The second implementation (“IC”) disregards the isotopic fractionation of ¹⁴C and radioactive decay of organic matter. In turn, DI¹⁴C and DIC have identical sources and sinks, except for atmospheric CO₂ and radioactive decay. This “inorganic” ¹⁴C approach is an approximation that is conceptually similar, but not identical, to the “abiotic” ¹⁴C modelling approach described in the OMIP biogeochemical protocol (Orr et al., 2017). In our IC approach, DIC and DI¹⁴C include biological sources and sinks. This does not apply to the OMIP-abiotic approach, which also considers alkalinity in a simplified way. In Sect. 3.3 we scrutinize the accuracy of the IC approximation. The third approach takes advantage of the fact that marine Δ¹⁴C values of DIC (Δ¹⁴C_DIC) are primarily governed by transport and radioactive decay (Fiadeiro, 1982; see also Mouchet, 2013). This implies that Δ¹⁴C_DIC can be implemented into ocean general circulation models as a single prognostic tracer without a full carbon cycle model (see Toggweiler et al., 1989, and numerous other studies later on). We evaluate this Δ¹⁴C approximation (“DA”) in an additional simulation and compare it with REcoM approaches CC and IC in Sect. 3.3 too.

A list of the various model experiments and their key features can be found in Table 1.

Table 1 List of model experiments discussed in this paper.

3 Results and discussions

3.1 Simulated ocean climatology

FESOM employs unstructured meshes with variable horizontal resolution. The default mesh of FESOM2.1-REcoM3 has about 127 000 horizontal surface nodes (Gürses et al., 2023). Here, our model resolution is radically reduced, considering 3140 surface nodes corresponding to a median horizontal resolution of 260 km (the so-called pi-mesh, see Fig. A1 in Appendix A). This configuration requires fewer computational resources and allows simulations over the time scale of marine carbon isotope equilibration to be performed (i.e. over several thousand years) within a few weeks. Vertical resolution is 47 layers using z* coordinates with non-linear free surface (for further details see Scholz et al., 2019).

In a first step we run FESOM without REcoM over 1000 years to spinup the overturning circulation and thermohaline fields. FESOM was initialized with seasonal winter temperatures and salinities by Steele et al. (2001), and driven with annually repeated atmospheric fields using Corrected Normal Year Forcing Version 2.0 (Large and Yeager, 2009; for an overview see also Griffies et al., 2012). As FESOM2.1 had originally been adjusted for higher resolution and different forcing, we retuned the model in our setup by reducing the maximum Gent–McWilliams thickness diffusivity from 2000 m² s⁻¹ originally to 1000 m² s⁻¹. After 1000 simulated years there was no significant drift of thermohaline fields and the meridional overturning circulation (MOC) had stabilized, REcoM3p was turned on, and both models were run over an additional 5000 years. At this moment, temperature and salinity drifted by about 10⁻⁶ K per year and 10⁻⁶ PSU per year in the global average, and the major biogeochemical tracer inventories drifted by less than 10⁻³ % per year (less than 10⁻³ ‰ per year regarding DI¹³C and DI¹⁴C). REcoM3p was initialized with gridded concentration fields of total alkalinity, DIC, and nitrate from version 2 of the Global Ocean Data Analysis Project (GLODAPv2, Key et al., 2015; Lauvset et al., 2016), oxygen from the World Ocean Atlas 2018 (WOA18, Garcia et al., 2019), silicate from Ocean Atlas 2013 (WOA13, Garcia et al., 2014), and dissolved iron according to Aumont et al. (2003) and Tagliabue et al. (2012). Dissolved inorganic ¹³C and ¹⁴C were initialized with DIC, assuming initial fractionation values of δ¹³C_DIC=0 ‰ and Δ¹⁴C${}_{\mathrm{DIC}}=-\mathrm{150}$ ‰ respectively. In the sediment layer all initial concentrations were close to zero. REcoM3p was forced with constant atmospheric CO₂ concentrations ([¹²CO₂]_atm=284.3 ppmv; [¹³CO₂]_atm and [¹⁴CO₂]_atm corresponding to δ¹³C${}_{\mathrm{atm}}=-\mathrm{6.61}$ ‰ and Δ¹⁴C_atm=0 ‰ respectively, following Orr et al., 2017), and with climatological mean monthly fluxes of aeolian iron deposition (Albani et al., 2014). The CO₂ concentration forcing implies that carbon-isotopic mass is only conserved in the atmosphere-ocean system when the marine isotopic inventories have reached a corresponding steady state. In our simulations this is the case after a few thousand years (see further below).

As discussed in the following, our low-resolution test setup sufficiently captures the basic thermohaline circulation structures obtained with FESOM2.0 in higher-resolution simulations (Scholz et al., 2019, 2022; compare their Figs. 14, 15, and 17 with our Figs. A2–A4 in Appendix A). Compared with observations, our simulations exhibit a warm bias for thermocline and intermediate water as well as for North Atlantic Deep Water (NADW; see Fig. A2 in Appendix A). The most notable exception is the region of the North Atlantic Gulf stream, which is not properly resolved, and where upper ocean temperatures are considerably underestimated. The temperature biases covary with salinity biases. That is, simulated salinities are also higher than observations where simulated temperatures are high, and salinities are too low where simulated temperatures tend to be low (Fig. A3). In the Atlantic, FESOM arrives at a MOC of about 16 Sv (1 Sv = 1×10⁶ m³ s⁻¹, Fig. A4), which is at the lower bound of observations, whereas the simulated overturning cell is too shallow compared with observational estimates (see Buckley and Marshall, 2016, and further references therein). For the purposes of this study, our simulations also reasonably reflect the observed large-scale pattern of DIC (Key et al., 2015; Lauvset et al., 2016). That is, low concentrations are found at upper levels of the subtropical oceans and in the freshly ventilated interior of the North Atlantic, whereas DIC concentrations progressively increase in the South Atlantic and in the deep North Pacific (Fig. A5).

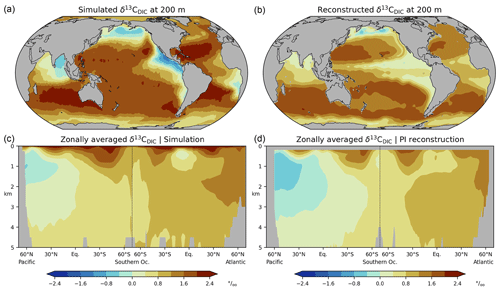
Figure 1 Preindustrial δ¹³C of DIC, (a, c) this study (simulation CC), (b, d) reconstruction (Eide et al., 2017b). (a, b) values at 200 m depth, (c, d) zonal-mean values in the Atlantic and Pacific. Map projection here and in other figures is area preserving (Equal Earth projection, Šavrič et al., 2019).

3.2 Carbon-13

We now focus on the carbon-isotopic composition of DIC near the sea surface and along zonal-mean sections through the Atlantic and Pacific. Regarding δ¹³C_DIC, we compare our model results with the gridded preindustrial (PI) δ¹³C_DIC climatology by Eide et al. (2017b). Their reconstruction does not consider the upper 200 m to exclude the ¹³C Suess effect. For the sake of completeness, we briefly note that at the sea surface our δ¹³C_DIC results are largely in line with ungridded preindustrial values determined by Kwon et al. (2022; shown in Fig. A6).

In wide areas, our simulated near-surface δ¹³C_DIC values at 200 m are within the range 1 ‰ to 2 ‰ (Fig. 1a). Higher δ¹³C_DIC values are simulated in the subtropical oceans, particularly in the Atlantic, southeast Pacific, and southern Indian Ocean. Isotopic depletion of up to $\sim -\mathrm{1}$ ‰ is found in the eastern equatorial Pacific, the subpolar North Pacific, the Bay of Bengal, and in the Angola Basin. Although our simulation captures the reconstructed spatial pattern (shown in Fig. 1b), the simulated range of δ¹³C_DIC variations is larger than in the reconstruction, that is, the model results are too high in the lower latitudes and too low in the abovementioned depletion regions (Fig. 2a).

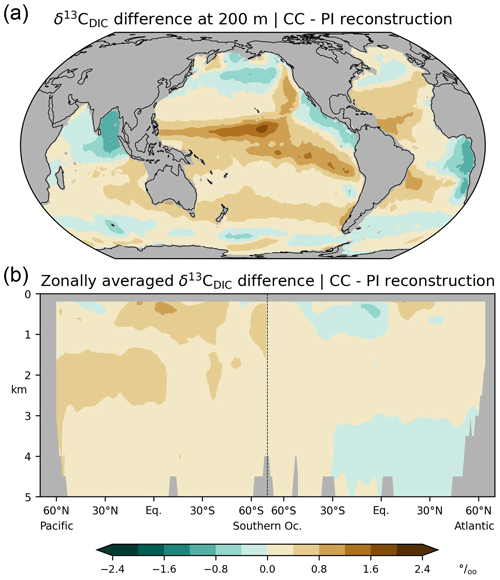
Figure 2 Differences between simulated (this study; CC) and reconstructed (Eide et al., 2017b; PI) δ¹³C of DIC for the preindustrial period; (a) at a depth of 200 m, (b) zonal-mean values in the Atlantic and Pacific.

Considering the interior of the Atlantic Ocean, our simulation yields higher δ¹³C_DIC in the North Atlantic than in the South Atlantic, and small vertical δ¹³C_DIC gradients in the high latitudes of both hemispheres (Fig. 1c). In the Pacific, our simulation displays a reversed meridional δ¹³C_DIC gradient with the strongest isotopic depletion at intermediate depths in the North Pacific. Our results are roughly in line with the reconstruction by Eide et al. (2017b, see Fig. 1d) but overestimate δ¹³C_DIC in the upper Pacific at low latitudes as well as in the North Pacific at a depth of between 1.5 and 3 km (Fig. 2b). Similar inaccuracies are seen in other models (Tagliabue an Bopp, 2008; Schmittner et al., 2013; Jahn et al., 2015; Buchanan et al., 2019; Jeltsch-Thömmes et al., 2019; Dentith et al., 2020; Tjiputra et al., 2020; Liu et al., 2021).

The differences between simulated and reconstructed δ¹³C_DIC (the δ¹³C_DIC bias for short) can be attributed to various factors. First, the reconstructed δ¹³C_DIC values may be too low in the upper ocean if the ¹³C Suess effect is not completely removed from the observations. In fact, Eide et al. (2017a) presume that they may have underestimated the ¹³C Suess effect at a depth of 200 m by about 0.1 ‰ to 0.2 ‰, which has been corroborated in recent modelling studies (Liu et al., 2021; Kwon et al., 2022). This reconstruction bias partly corresponds to the apparent simulation bias at a depth of 200 m, where our model results are 0.2 ‰ higher on global average than the reconstructed results.

To some extent, the δ¹³C_DIC bias can be further attributed by decomposing δ¹³C_DIC into biologic and thermodynamic sources:

$$\begin{array}{}\text{(9)}& {\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{DIC}}={\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{BIO}}+{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{AS}},\end{array}$$

where δ¹³C_BIO specifies the imprint of isotopic fractionation, respiration, and remineralization of organic matter in the absence of air–sea exchange. Following Broecker and Maier-Reimer (1992), δ¹³C_BIO is frequently determined from the covariation of δ¹³C_DIC with marine phosphate (PO${}_{\mathrm{4}}^{\mathrm{3}-}$). We adopt this approach, employing revised parameter values by Eide et al. (2017b) and tentatively replacing PO${}_{\mathrm{4}}^{\mathrm{3}-}$ with dissolved inorganic nitrogen (DIN) divided by 16 because PO${}_{\mathrm{4}}^{\mathrm{3}-}$ is not considered by REcoM3p:

$$\begin{array}{}\text{(10)}& {\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{BIO}}=(\mathrm{2.8}-\mathrm{1.1}{\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-})\mathrm{‰}\equiv (\mathrm{2.8}-\mathrm{0.069}\text{DIN})\mathrm{‰},\end{array}$$

where PO${}_{\mathrm{4}}^{\mathrm{3}-}$ and DIN are in µmol kg⁻¹. Equation (10) does not distinguish between preformed and remineralized nutrient concentrations and cannot be used for further separation of δ¹³C_BIO into preformed and remineralized components. The thermodynamic component δ¹³C_AS describes the effects of air–sea exchange and ocean circulation and is the residual of observed δ¹³C_DIC and reconstructed δ¹³C_BIO.

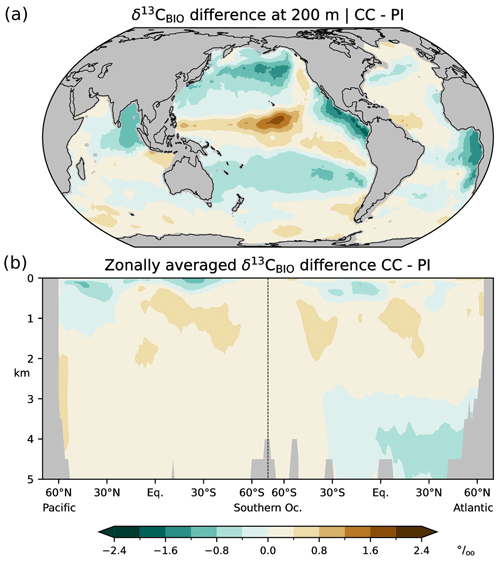
Figure 3 Differences between simulated (this study; CC) and estimated (Eide et al., 2017b; PI) δ¹³C_BIO (the biological component of δ¹³C_DIC in the absence of air–sea exchange) during the preindustrial period; (a) at a depth of 200 m, (b) zonal-mean values in the Atlantic and Pacific.

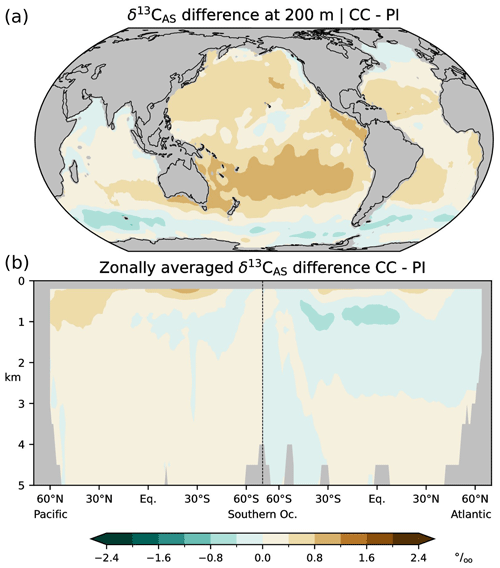
Figure 4 Differences between simulated (this study; CC) and estimated (Eide et al., 2017b; PI) δ¹³C_AS=δ¹³C_DIC−δ¹³C_BIO during the preindustrial period; (a) at a depth of 200 m, (b) zonal-mean values in the Atlantic and Pacific.

In the following we validate simulated δ¹³C_BIO and δ¹³C_AS with the corresponding values reconstructed by Eide et al. (2017b), and we compare the δ¹³C_DIC bias with the differences between the simulated and reconstructed δ¹³C_DIC components, i.e. the δ¹³C_BIO bias and δ¹³C_AS bias. Simulation CC overestimates δ¹³C_BIO in wide areas, except for subtropical and upwelling regions at 200 m and the North Atlantic below 3 km (Fig. 3). The simulation also overestimates δ¹³C_AS in the thermocline but underestimates δ¹³C_AS in the interior of the North Atlantic above about 3 km (Fig. 4). Comparing the biases of δ¹³C_DIC, δ¹³C_BIO and δ¹³C_AS, it appears that the δ¹³C_DIC bias corresponds to the δ¹³C_BIO bias in the low latitudes, upwelling regions, and the interior of the Atlantic (see Figs. 2 and 3). This points to model deficiencies in describing the sinking and regeneration of ¹³C-depleted organic carbon. On the other hand, the δ¹³C_DIC bias corresponds to the δ¹³C_AS bias in the upper thermocline of the open oceans in the Southern Hemisphere (shown in Fig. 4). Although our results may generally suffer from the coarse model resolution and simplified climate forcing, the specific reasons for this correspondence are not obvious. As a residual term δ¹³C_AS may also reflect effects of biological ¹³C cycling, which are not captured by Eq. (10). For example, δ¹³C_BIO is estimated for constant isotopic fractionation of marine organic matter of −19 ‰ whereas δ¹³C_POC varies by about 10 ‰ according to field data (Verwega et al., 2021; see also Fig. 6a).

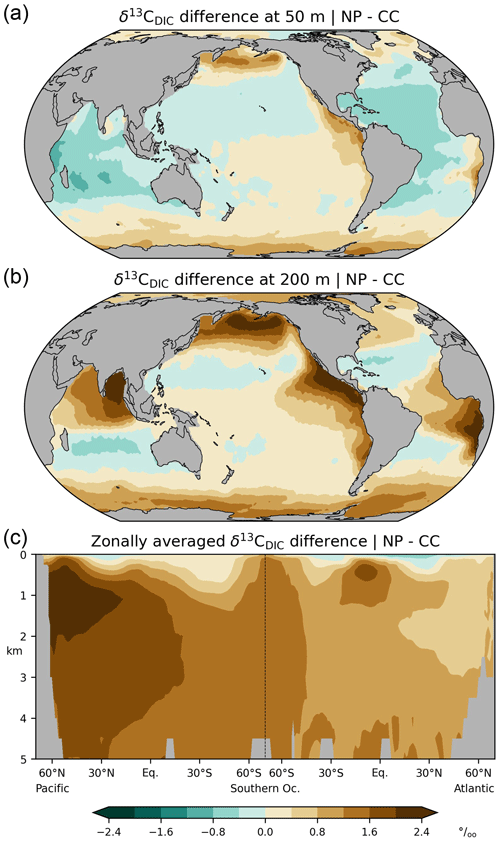
Figure 5 Changes in preindustrial δ¹³C of DIC if isotopic fractionation during photosynthesis is disabled (sensitivity experiment NP versus simulation CC), (a) at a depth of 50 m, (b) at a depth of 200 m, (c) zonal-mean values in the Atlantic and Pacific.

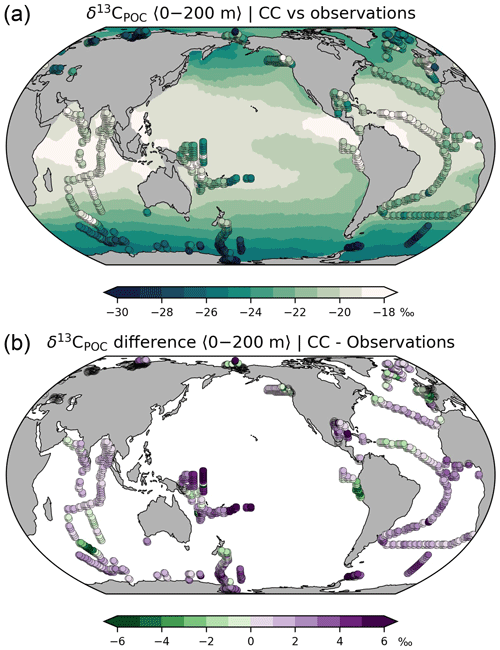
Figure 6 (a) δ¹³C of POC averaged over the upper 200 m. Shaded areas: simulation results (this study; simulation CC), dots: bulk matter observations for the period 1964–2015 (compilation by Verwega et al., 2021; see further references therein). (b) Differences between simulated and observed δ¹³C of POC.

Therefore, we explore the sensitivity of δ¹³C_DIC to photosynthetic fractionation in an additional experiment (“NP”) in which biogenic fractionation is disabled (i.e. ¹³α_p=1 in Eq. 8). Compared with the default simulation, δ¹³C_DIC|NP decreases by up to 1 ‰ in the pelagic euphotic zone whereas δ¹³C_DIC|NP increases in the disphotic zone below, which is particularly the case in highly productive regions (Fig. 5a, b). In the aphotic interior of the ocean δ¹³C_DIC|NP progressively increases from the North Atlantic towards the North Pacific by up to 2.4 ‰ (Fig. 5c). These findings are in line with similar sensitivity studies (Schmittner et al., 2013; Dentith et al., 2020) as well as with simulations comparing different parametrizations for ¹³α_p (Jahn et al., 2015; Buchanan et al., 2019; Dentith et al., 2020; Liu et al., 2021).

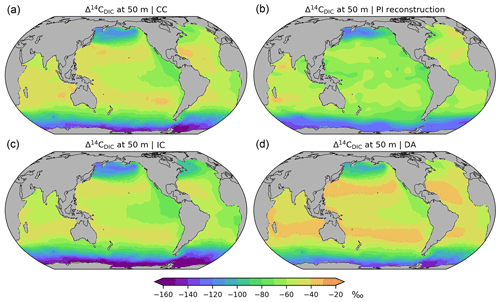
Figure 7 Preindustrial Δ¹⁴C of DIC at a depth of 50 m, (a) simulation CC considering the complete marine ¹⁴C cycle, (b) reconstruction (Key et al., 2004), (c) simulation IC applying the inorganic ¹⁴C approximation, (d) simulation DA applying the Δ¹⁴C approach. See the main text for further explanations.

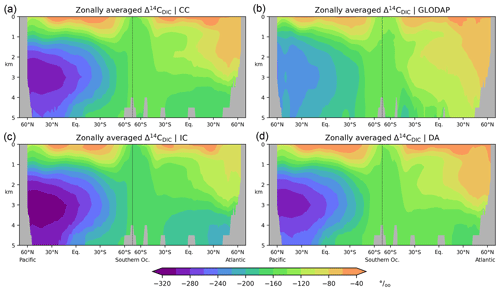
Figure 8 Preindustrial Δ¹⁴C of DIC in the Atlantic and Pacific. (a) Simulation CC, (b) reconstruction (Key et al., 2004), (c) simulation IC, (d) simulation DA. See the main text for further simulation explanations. Note the different colour scale ranges in Figs. 7 and 8.

Our default simulation with enabled photosynthetic fractionation yields δ¹³C_POC values between −18 ‰ and −25 ‰ whereas observations from the last decades range from −15 ‰ to −35 ‰ (Verwega et al., 2021; Fig. 6a). The model overestimates δ¹³C_POC at most locations (Fig. 6b; global RMS difference is 2.6 ‰). According to the sensitivity experiment NP, the overestimation of δ¹³C_POC should result in overly enriched δ¹³C_DIC in the twilight and dark zones of highly productive regions (Fig. 5b), whereas Fig. 2a indicates that the opposite is the case. However, this is only an apparent contradiction because the δ¹³C_POC observations are biased by the ¹³C Suess effect. Moreover, they exhibit a negative trend (by −3 ‰ between 1960 and 2010), which is about twice as high as the known ¹³C Suess effect on aqueous CO₂ (Verwega et al., 2021). It has been presumed that this trend also reflects a shift in the composition of phytoplankton species (Lorrain et al., 2020; Verwega et al., 2021). Neither effect is considered in our simulation. A conclusive analysis would require transient simulations, including historical values of atmospheric ¹³CO₂.

3.3 Radiocarbon

We consider Δ¹⁴C_DIC and compare our model results with gridded fields of pre-bomb Δ¹⁴C_DIC provided by the Global Ocean Data Analysis Project, version 1.1 (GLODAPv1.1, Key et al., 2004).

In the comprehensive radiocarbon cycle simulation (CC) Δ¹⁴C_DIC|CC is within the range −40 ‰ to −140 ‰ (average value: −65 ‰) near the surface (at 50 m), with the highest values in the subtropical gyres and the lowest values in the Southern Ocean (Fig. 7a). In the interior of the Atlantic, Δ¹⁴C_DIC|CC ranges between −70 ‰ and −170 ‰ and decreases from the surface to the bottom, with small vertical gradients in the high latitudes (Fig. 8a). This is superimposed by a southward decline of Δ¹⁴C_DIC values. Conversely, Δ¹⁴C_DIC decreases from south to north in the interior of the Pacific. Different from the northern North Atlantic, there is no evidence of deep-sea ventilation in the North Pacific, where our model arrives at minimum Δ¹⁴C_DIC|CC values exceeding −290 ‰ (Fig. 8a). This depletion corresponds to a ¹⁴C age τ of about 2800 years with respect to the atmosphere (calculated as $\mathit{\tau }=-\mathrm{8033}\times \ln \left[\right(\mathrm{1}+\mathrm{0.001}{\mathrm{\Delta }}^{\mathrm{14}}{\mathrm{C}}_{\mathrm{atm}})/(\mathrm{1}+\mathrm{0.001}{\mathrm{\Delta }}^{\mathrm{14}}{\mathrm{C}}_{\mathrm{DIC}}\left)\right]$).

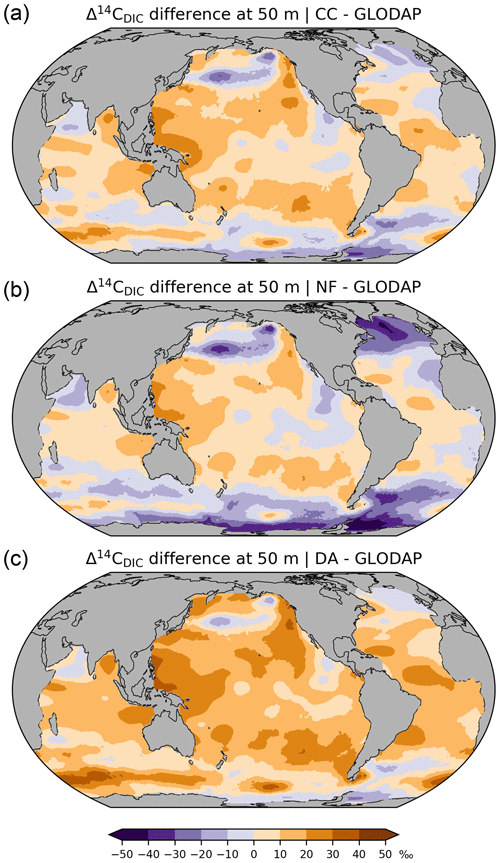
Figure 9 Differences between simulated and reconstructed preindustrial Δ¹⁴C of DIC at a depth of 50 m, (a) simulation CC minus reconstruction (GLODAP; Key et al., 2004), (b) simulation IC minus reconstruction, (c) simulation DA minus reconstruction.

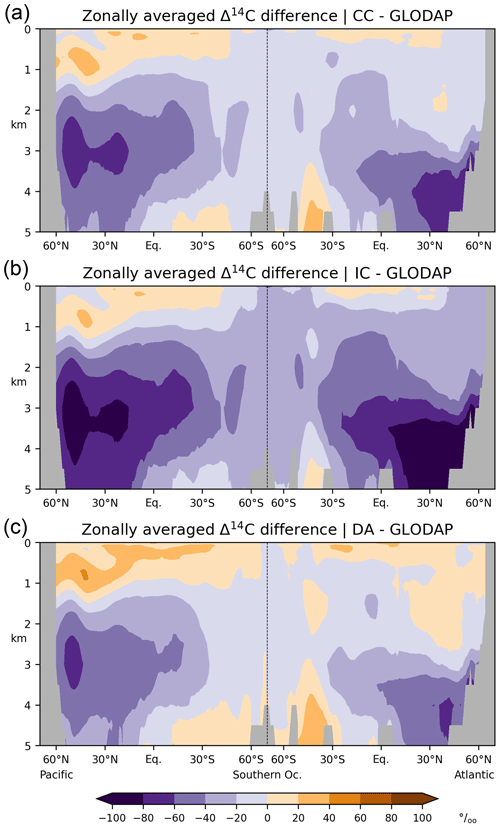
Figure 10 Differences between simulated and reconstructed preindustrial Δ¹⁴C of DIC in the Atlantic and Pacific: zonal-mean values are shown, (a) simulation CC minus reconstruction (GLODAP; Key et al., 2004), (b) simulation IC minus reconstruction, (c) simulation DA minus reconstruction. Note the different colour scale ranges in Figs. 9 and 10.

Overall, simulation CC captures the large-scale distribution of pre-nuclear Δ¹⁴C_DIC as reconstructed by GLODAPv1.1 (Figs. 7a, b, 8a, b). However, at a depth of 50 m the simulated Δ¹⁴C_DIC is too high by 10 ‰–30 ‰ in the low- and mid-latitudes, and too low by about the same amount in the high latitudes (see Fig. 9a; according to GLODAP Δ¹⁴C_DIC ranges from −50 ‰ to −170 ‰ with −71 ‰ on average). In the interior of the oceans, our model results are typically 20 ‰–60 ‰ too low (Fig. 10). The excessive depletion reaches −70 ‰ in the abyssal North Atlantic and in the North Pacific at 3 km depth (Fig. 10a). In the upper layers of the oceans, the GLODAPv1.1 data probably reflect the ¹⁴C Suess effect (Suess, 1955), which is not considered in our simulations. The excessive depletion in the deep sea indicates that the simulated MOC leads to overly shallow and weak ocean ventilation, which is particularly the case in the North Pacific. This effect is enhanced by the progressive radioactive decay of DI¹⁴C along its passage through the interior of the ocean.

Different from δ¹⁴C_DIC, Δ¹⁴C_DIC is corrected for isotopic fractionation. In practice (as well as in the comprehensive DI¹⁴C cycle modelling approach CC), the correction is made after the simultaneous determination of δ¹³C_DIC and δ¹⁴C_DIC. In the inorganic ¹⁴C (IC) modelling approach the fractionation of ¹⁴C is omitted beforehand, so that posterior corrections are not necessary. That is, δ¹⁴C_DIC|IC equals Δ¹⁴C_DIC|IC, which should equal Δ¹⁴C_DIC|CC. As the IC approach also neglects the radioactive decay of organic carbon, it considers seven tracers less than the CC approach, which is accompanied by an increase in model speed (simulated years per day) of about 15 %.

At a depth of 50 m Δ¹⁴C_DIC|IC ranges from −50 ‰ to −160 ‰ with an average value of 72 ‰ (Fig. 7c). Similar to experiment CC, the highest values of Δ¹⁴C_DIC|IC are found in subtropical surface waters. The lowest surface water values of Δ¹⁴C_DIC|IC are also found in the Southern Ocean. In the interior of the oceans, the isotopic depletion with respect to the atmosphere ranges from −90 ‰ in the North Atlantic to −310 ‰ in the North Pacific (Fig. 8c). Comparing IC with the GLODAPv1.1 reconstruction, we find that the enrichment of subtropical surface values is less pronounced in IC, whereas the depletion in the high latitudes increases (Fig. 9b). The latter is also the case in the interior of the oceans (Fig. 10b). Most notably, the outcomes of experiment IC are everywhere lower (by up to 30 ‰) than the results of simulation CC (Fig. 11a, c) which is explained as follows.

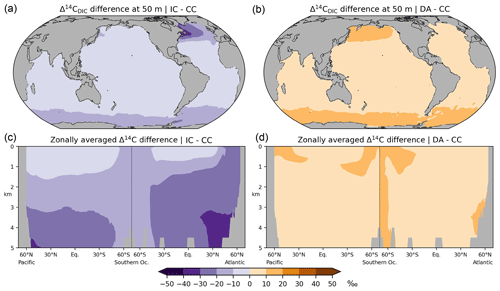
Figure 11 Absolute differences in preindustrial Δ¹⁴C_DIC between the various simulation approaches: results at a depth of 50 m  (a, b) and in the Atlantic and Pacific (c, d) are shown. (a, c) Inorganic ¹⁴C (IC) modelling approach versus complete ¹⁴C cycle (CC), (b, d) Δ¹⁴C approximation (DA) versus simulation CC.

Analogous to sensitivity experiment NP, the IC approach disregards photosynthetic fractionation, which leads to lower DI¹⁴C concentrations in the euphotic zone than in simulation CC. In addition, the IC approach disregards the DI¹⁴C enrichment of the mixed layer associated with air–sea exchange. Furthermore, as the IC approach disregards the radioactive decay of phytoplankton, the loss of DI¹⁴C due to photosynthesis is overestimated in the mixed layer. Therefore, preformed DI¹⁴C is systematically lower than in simulation CC and becomes further depleted through radioactive decay in the deep sea. This bias is similar to the lower values of “abiotic” Δ¹⁴C than “biotic” Δ¹⁴C simulated by Frischknecht et al. (2022).

Instead of computing absolute concentrations of DIC, DI¹³C, and DI¹⁴C and converting them to Δ¹⁴C_DIC a posteriori, the Δ¹⁴C approximation (DA) simulates ${}^{\mathrm{14}}{R}_{\mathrm{DIC}\mathrm{|}\mathrm{DA}}=\mathrm{1}+\mathrm{0.001}{\mathrm{\Delta }}^{\mathrm{14}}{\mathrm{C}}_{\mathrm{DIC}\mathrm{|}\mathrm{DA}}$ as a single prognostic tracer that is considered abiotic and conservative except for its radioactive decay, and that is connected to the carbon cycle only through the timescale of ¹⁴CO₂ air–sea exchange. This approach is about five times faster than the CC and IC approaches. The first results of the implementation of ¹⁴R_DIC|DA into FESOM2 were shown by Lohmann et al. (2020) for the default FESOM mesh with 127 000 horizontal surface nodes. Here, we repeated the experiment, now using the low-resolution mesh of experiments CC and IC to be able to compare the results of all approaches directly. For the same reason, we discuss model results after 5000 simulated years but point out that experiment DA has been run over 17 000 years in total. The maximum drift of Δ¹⁴C_DIC|DA between 5000 and 17 000 simulated years is about −3.5 ‰ in North Pacific Deep Water, which is much smaller than the Δ¹⁴C_DIC differences between the various modelling approaches in this study after 5000 years shown below.

At at depth of 50 m Δ¹⁴C_DIC|DA ranges from −40 ‰ to −130 ‰, with Δ¹⁴C${}_{\mathrm{DIC}\mathrm{|}\mathrm{DA}}=-\mathrm{58}$ ‰ on average (Fig. 7d). In intermediate and deep water Δ¹⁴C_DIC|DA declines from −60 ‰ in the North Atlantic to −280 ‰ in the North Pacific (Fig. 8d). At upper levels, Δ¹⁴C_DIC|DA is almost everywhere higher than Δ¹⁴C_DIC according to GLODAPv1.1 (Figs. 9c, 10c). In the deep sea, Δ¹⁴C_DIC|DA is still too low, but the depletion is less pronounced than in simulations CC and IC (Fig. 10c).

Experiment DA yields the highest Δ¹⁴C_DIC values of all three modelling approaches (Fig. 11). The DA approach assumes that DIC concentrations are constant and homogeneous (for a rigorous treatise see Mouchet, 2013). Following Toggweiler et al. (1989), our calculation of ¹⁴CO₂ air–sea exchange fluxes in simulation DA assumes a DIC concentration of 2000 mmol m⁻³ in the mixed layer, which is somewhat lower than that observed and simulated in most areas, most notably in the high latitudes (Fig. A5a, b). This leads to faster and hence higher ¹⁴C uptake in DA than in CC and IC because the ¹⁴CO₂ invasion flux is inversely proportional to the DIC concentration in the mixed layer. The absolute Δ¹⁴C_DIC differences between DA and CC are largely less than 10 ‰ (Fig. 11b, d). Moreover, the relative uncertainty of the DA approach with respect to the correct DI¹⁴C implementation (CC) is less than 5 % (Fig. 12) and actually smaller than the error of 10 % originally estimated by Fiadeiro (1982).

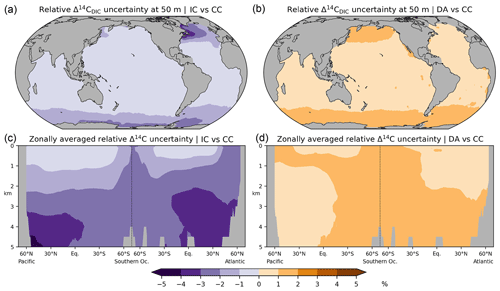
Figure 12 Relative differences in preindustrial Δ¹⁴C_DIC between the various simulation approaches: absolute values at a depth of 50 m depth (a, b) and in the Atlantic and Pacific (c, d) are shown. (a, c) No-fractionation (IC) approach versus complete ¹⁴C cycle (CC), (b, d) Δ¹⁴C approximation (DA) versus simulation CC.

4 Summary

We have added the carbon isotopes ¹³C and ¹⁴C to the marine biogeochemistry model REcoM3 and tested the implementation in long-term equilibrium simulations in which the configuration REcoM3p was coupled with the ocean general circulation model FESOM2.1. Regarding the carbon-isotopic composition of DIC (δ¹³C_DIC and Δ¹⁴C_DIC), our model results are largely consistent with marine δ¹³C_DIC and Δ¹⁴C_DIC fields reconstructed for the pre-anthropogenic period. The simulations also exhibit discrepancies, such as overly depleted δ¹³C_DIC values in upwelling regions, overly steep vertical gradients of δ¹³C_DIC and Δ¹⁴C_DIC in the interior of the North Atlantic, and excessive depletion of Δ¹⁴C_DIC in the interior of the North Pacific. To some extent, the inaccuracies of δ¹³C_DIC indicate shortcomings in modelled organic carbon cycling. The radiocarbon results (Δ¹⁴C_DIC) are insensitive to carbon cycle changes and reflect the rather shallow overturning circulation provided by our low-resolution ocean general circulation model test configuration with idealized repeat year climate forcing. As future simulations with a scientific focus will be carried out with considerably higher horizontal resolution and more realistic climate forcing, we expect some of the biases discussed in this study to decrease. These simulations should also consider transient boundary conditions of ¹³C and ¹⁴C, which provide additional benchmarks for the model. For these reasons we did not attempt to further tune REcoM3p here, e.g. by adjusting semi-empirical biogeochemical parameters such as gas transfer velocity or biogenic fractionation coefficients.

As Δ¹⁴C_DIC is dominated by radioactive decay and transport processes, we have additionally explored the accuracy of two simplified modelling approaches that are more efficient than the complete consideration (CC) of the DI¹⁴C cycle. One approach (IC) neglects isotopic fractionation but still considers biological processes. The IC approach yields lower Δ¹⁴C_DIC values than reconstructed for high-latitude surface waters and for deep and bottom waters. Another approach (DA) only considers the DI¹⁴C $/$ DIC ratio for constant and homogeneous DIC concentrations and further disregards the marine carbon cycle. It yields higher Δ¹⁴C_DIC values than reconstructed for surface water, which mitigates the isotopic depletion in the deep sea, where the DA approach therefore better agrees with the reconstruction than the other approaches. The relative uncertainty between the comprehensive and simplified approaches is less than 5 %. Therefore, the simplified Δ¹⁴C_DIC modelling approaches should be sufficiently accurate for radiocarbon dating of marine climate archives.

Appendix A

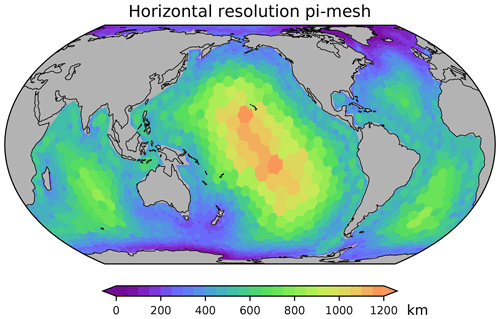
Figure A1 Horizontal resolution of FESOM2.1-REcoM used in this study. The mesh has 3140 surface nodes. See also https://fesom.de/models/meshessetups/ (last access: 20 February 2024) for an impression of the bathymetry.

Figure A2 Differences between simulated and observed (WOA09, Locarnini et al., 2010) temperatures, (a) averaged over the upper 200 m, (b) in the Atlantic and Pacific. See Scholz et al. (2019) for comparison with higher-resolution simulations.

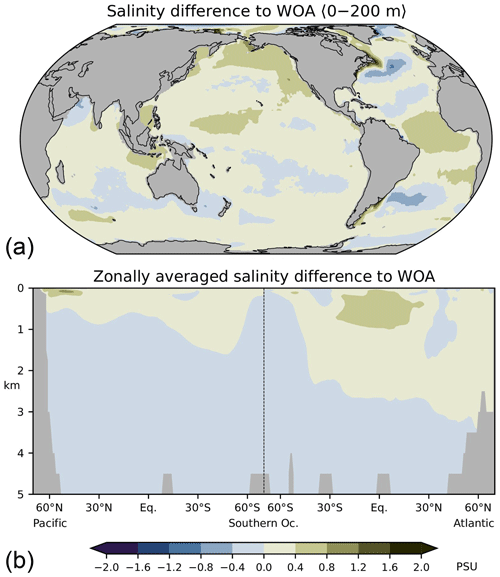
Figure A3 Differences between simulated and observed (WOA09, Antonov et al., 2010) salinities, (a) averaged over the upper 200 m, (b) in the Atlantic and Pacific. See Scholz et al. (2019) for comparison with higher-resolution simulations.

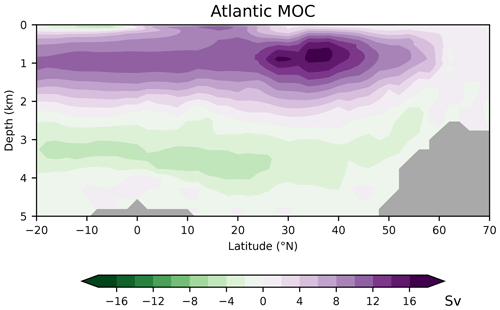
Figure A4 Simulated meridional overturning circulation (MOC) in the Atlantic. See also Scholz et al. (2019, 2022) for comparison with higher-resolution simulations.

Figure A5 Concentrations of dissolved inorganic carbon (DIC), (a, c) this study, (b, d) observations for 1972–2013 CE, normalized to the year 2002 (GLODAPv2, Key et al., 2015; Lauvset et al., 2016). (a, b) Concentrations at a depth of 50 m, (c, d) zonal-mean values in the Atlantic and Pacific. Model results are interpolated to the resolution of the observations (1° × 1° × 33 layers).

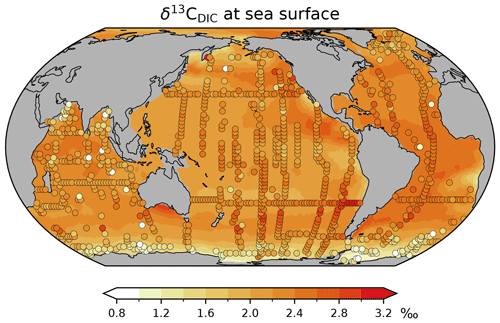
Figure A6 Preindustrial δ¹³C_DIC of surface water at a depth of about 18 m. Shaded areas: simulation CC; filled circles: reconstructed values by Kwon et al. (2022). Note that their reconstruction yields higher preindustrial δ¹³C_DIC values than Eide et al. (2017b) in thermocline and intermediate waters of the Southern Hemisphere (see the discussion by Kwon et al., 2022).