the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Improved representation of volcanic sulfur dioxide depletion in Lagrangian transport simulations: a case study with MPTRAC v2.4
Lars Hoffmann
Sabine Griessbach
Zhongyin Cai
Yi Heng
The lifetime of sulfur dioxide (SO2) in the Earth's atmosphere varies from orders of hours to weeks, mainly depending on whether cloud water is present or not. The volcanic eruption on Ambae Island, Vanuatu, in July 2018 injected a large amount of SO2 into the upper troposphere and lower stratosphere (UT/LS) region with abundant cloud cover. In-cloud removal is therefore expected to play an important role during long-range transport and dispersion of SO2. In order to better represent the rapid decay processes of SO2 observed by the Atmospheric Infrared Sounder (AIRS) and the TROPOspheric Monitoring Instrument (TROPOMI) in Lagrangian transport simulations, we simulate the SO2 decay in a more realistic manner compared to our earlier work, considering gas-phase hydroxyl (OH) chemistry, aqueous-phase hydrogen peroxide (H2O2) chemistry, wet deposition, and convection. The either newly developed or improved chemical and physical modules are implemented in the Lagrangian transport model Massive-Parallel Trajectory Calculations (MPTRAC) and tested in a case study for the July 2018 Ambae eruption. To access the dependencies of the SO2 lifetime on the complex atmospheric conditions, sensitivity tests are conducted by tuning the control parameters, e.g., by changing the release height, the predefined OH climatology data, the cloud pH value, the cloud cover, and other variables. Wet deposition and aqueous-phase H2O2 oxidation remarkably increased the decay rate of the SO2 total mass, which leads to a rapid and more realistic depletion of the Ambae plume. The improved representation of chemical and physical SO2 loss processes described here is expected to lead to more realistic Lagrangian transport simulations of volcanic eruption events with MPTRAC in future work.
- Article
(6899 KB) - Full-text XML
- BibTeX
- EndNote
Volcanic eruptions have a strong impact on human living by causing various hazards and destructive impacts on human beings' living conditions. At the ground, SO2 and acidic aerosols from eruption gases cause health hazards and increase respiratory morbidity and mortality (Hansell and Oppenheimer, 2004; Schmidt et al., 2011). The wet deposition of SO2 leads to acid precipitation, which has a destructive effect on the ecosystem and environment, including acidifying the soil, contaminating the water sources and damaging the vegetation (Delmelle et al., 2002). In the upper troposphere and lower stratosphere (UT/LS), sulfate aerosol formed by SO2 oxidation has a significant impact on the radiative forcing and energy balance of the Earth by scattering solar radiation and by absorbing and re-emitting thermal emissions (Robock, 2000; Kloss et al., 2020; Malinina et al., 2021). Satellite observations and atmospheric chemistry–transport modeling allow us to monitor the transport of volcanic ash and SO2 and to better plan for evacuation and hazard mitigation. Studies on SO2 long-range transport and dispersion can also help to better understand atmospheric dynamics – for instance, the impact of the Asian monsoon on aerosol transport (Wu et al., 2017).
Remote sensing observations from satellite instruments are widely used assets to monitor and study volcanic activity. Satellite observations provide high-resolution SO2 measurements on a global scale, which are particularly useful for initializing and evaluating the results of Lagrangian transport simulations. Among these instruments, the Atmospheric Infrared Sounder (AIRS) (Aumann et al., 2003) and the TROPOspheric Monitoring Instrument (TROPOMI) (Veefkind et al., 2012) both provide data products that are capable of detecting volcanically enhanced SO2 concentrations in the UT/LS. Hoffmann et al. (2014) proposed an SO2 index based on brightness temperature difference for AIRS observations, which is most sensitive to SO2 layers at 8 to 13 km and well suited to detect volcanic emission. The TROPOMI Level 2 SO2 product provides volcanic SO2 total column amounts for prescribed SO2 plume heights at 1, 7, and 15 km with high horizontal resolution (Theys et al., 2020). These data products provide valuable references to evaluate and improve our transport model in the present study.
For the simulation of volcanic SO2 transport, Lagrangian particle dispersion models are important tools which can resolve both small-scale features and long-range transport by calculating trajectories of ensembles of air parcels driven by deterministic (wind field and buoyancy) and stochastic (turbulence and convection) dynamics. In our past research, the Massive-Parallel Trajectory Calculations (MPTRAC) model (Hoffmann et al., 2016, 2022a) has been utilized to study volcanic eruption events, including research on source reconstruction (Heng et al., 2016; Cai et al., 2022), long-range transport (Wu et al., 2017, 2018), and large-scale parallel inverse modeling (Liu et al., 2020). Most of these studies predefined the SO2 lifetime as a constant empirical value. However, the lifetime of SO2 varies from orders of hours to weeks, depending on whether liquid or ice clouds are present or not (Eatough et al., 1994; McGonigle et al., 2004; Khokhar et al., 2005). In the gas phase, SO2 is mainly depleted by reaction with OH, whereas in the presence of clouds SO2 can be dissolved in cloud droplets and removed by precipitation or aqueous-phase oxidation. Due to the variability of the complicated atmospheric background conditions, it is hard to use a specific number to represent the local SO2 residence time.
Various studies applied Lagrangian particle dispersion models for simulations of volcanic SO2 plume transport. The study by Eckhardt et al. (2008) with the FLEXible PARTicle dispersion model (FLEXPART) considered removal of SO2 by reaction with OH radicals while aqueous-phase chemistry reactions were not considered. The study by de Leeuw et al. (2021) with the Met Office's Numerical Atmospheric-dispersion Modelling Environment (NAME) model considered the conversion of SO2 into sulfate aerosol with both gas-phase and aqueous-phase oxidation. In this work, we aim to model the removal of SO2 from volcanic plumes with representation of physical and chemical processes in the MPTRAC model, including gas- and aqueous-phase oxidation as well as wet deposition. The chemical loss is represented by first-order rate coefficients derived from predefined, climatological OH and H2O2 fields. Chemistry calculations are conducted in the Lagrangian framework rather than using a Eulerian framework, which avoids memory sharing and is well suited for parallel processing. The approach achieves a balance between computational costs and accuracy, which is similar to FLEXPART but different from the full chemistry scheme applied in NAME.
Ambae Island (15.39∘ S, 167.84∘ E), located in the South Pacific in Vanuatu, contributed the largest volcanic eruption in the year 2018. Among four main eruption phases during 2017 and 2018, the most intensive one in July 2018 injected at least 400 kt of SO2 to a peak altitude of ∼17 km (Moussallam et al., 2019). The volcanic SO2 injected into the UT/LS formed aerosol particles which have a significant impact on atmospheric radiative forcing and global climate (Kloss et al., 2020; Malinina et al., 2021). Other cases, e.g., the Raikoke eruption in 2019 (Cai et al., 2022; de Leeuw et al., 2021), Kasatochi in August 2008, Sarychev in June 2009 (Wu et al., 2017), and Nabro in June 2011 (Höpfner et al., 2015), had lifetimes of about 14, 13, 24, and 32 d, as well as SO2 mass releases of 1500, 2000, 1200, and 3650 kt, respectively. Compared to these cases, the Ambae case in July 2018 had a much shorter lifetime of ∼4 d (Malinina et al., 2021). Local reports of acid rain suggest that the eruption was accompanied by strong wet deposition, which means that the released SO2 encountered significant wet removal. As we aim to better understand and represent these processes in the MPTRAC model, we selected the Ambae eruption in July 2018 as a case study for this work.
The paper is organized as follows. Section 2 introduces the updates on the chemical and physical modules in MPTRAC and provides a brief introduction to the AIRS and TROPOMI satellite observations. In Sect. 3, simulation results for the Ambae eruption in July 2018 are presented and evaluated, including the baseline simulation and various parameter sensitivity tests on the OH chemistry module, the H2O2 chemistry module, the wet deposition module, and the convection module. Section 4 provides the summary and conclusions of the study.
2.1 The MPTRAC Lagrangian transport model
For the simulation of the dispersion and depletion of SO2 from the Ambae eruption, we applied the Massive-Parallel Trajectory Calculations (MPTRAC) model (Hoffmann et al., 2016, 2022a). Mainly, trajectories of air parcels are calculated by given horizontal winds and vertical velocities of meteorological input data, with additional stochastic perturbations being added to simulate diffusion and subgrid-scale wind fluctuations. Additionally, several improved or newly developed chemical and physical modules of MPTRAC are applied in the simulations. In particular, the SO2 mass of the air parcels is decomposed by OH oxidation and wet removal processes instead of simply using an exponential decay with a fixed lifetime as applied in our earlier studies. The new and revised modules are described in the following sections.
The transport simulations with MPTRAC are driven by the European Centre for Medium-Range Weather Forecasts’ (ECMWF’s) fifth-generation reanalysis (ERA5) (Hersbach et al., 2020) with hourly meteorological data at horizontal resolution on 137 vertical levels. This is a significant improvement in spatiotemporal resolution compared with the previous generation ERA-Interim reanalysis (Dee et al., 2011), providing only horizontal resolution on 60 vertical levels at 6 h time intervals. The higher-resolution ERA5 data are expected to lead to more accurate Lagrangian transport simulations compared to ERA-Interim (Hoffmann et al., 2019).
MPTRAC is a Lagrangian transport model developed with a hybrid MPI–OpenMP–OpenACC parallelization scheme for application on CPU/GPU heterogeneous supercomputers, aiming for good parallel performance and scaling efficiency. The computing tasks in MPTRAC are distributed over the compute nodes and compute cores by MPI and OpenMP and offloaded to GPUs by means of OpenACC for faster and more-energy-efficient computational performance (Liu et al., 2020; Hoffmann et al., 2022a). In this study, each individual simulation is conducted in parallel with 48 OpenMP threads. MPI parallel multi-processing for different model parameter settings is applied in the sensitivity tests, which significantly improves the overall runtime of the simulations. On the state-of-the-art high-performance computing system Jülich Wizard for European Leadership Science (JUWELS) at the Jülich Supercomputing Centre (Jülich Supercomputing Centre, 2019), individual Lagrangian transport simulations with 106 air parcels over a time period of 15 d require about 1.5 h of total runtime on a compute node. GPU acceleration was not considered here as there is no increase in computational speed at this problem size.
2.1.1 Hydroxyl radical oxidation in the gas phase
The hydroxyl radical (OH) is an important oxidant in the atmosphere, which causes rapid decay of many gas-phase species. In MPTRAC, the mass decay of a trace gas of an air parcel is described by an exponential formula,
Assuming that the concentration of OH is in near steady state, the pseudo-first-order reaction coefficient k is calculated as
with an effective second-order coefficient kf and a prescribed monthly zonal mean OH field. The oxidation of SO2 with OH is a termolecular reaction,
where the excited intermediate [HOSO2]* requires an inert molecule M (e.g., N2 or O2) to remove the energy and stabilize it into sulfate. In the high-pressure limit, the rate-limiting step is the production of [HOSO2]*, while in the low-pressure limit, the reaction rate depends on the abundance of M and the production of HOSO2. Thus, the effective second-order rate coefficient of the SO2–OH oxidation process is temperature- and pressure-dependent, which is described here by using a formula given by the NASA Jet Propulsion Laboratory (JPL) data evaluation (Burkholder et al., 2019) as
The high-pressure limit rate and the low-pressure limit rate were also obtained from the JPL evaluation.
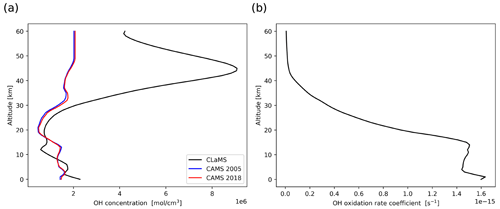
As for the prescribed zonal mean OH fields, monthly mean climatology of OH calculated from simulation of the Chemical Lagrangian Model of the Stratosphere (CLaMS) is used by default (Pommrich et al., 2014). Another OH dataset considered in this study was obtained by integrating Copernicus Atmosphere Monitoring Service (CAMS) reanalysis OH data into monthly latitude- and pressure-dependent fields, keeping consistency with the CLaMS climatology (Inness et al., 2019). The CLaMS data have 18 latitude bins and 34 pressure levels, while CAMS data have 241 latitude bins and 25 pressure levels. CLaMS has a complete chemistry scheme on the stratospheric chemistry, while the CAMS reanalysis uses a chemical mechanism most suitable for the troposphere. A comparison of the CLaMS and CAMS datasets with in situ measurements is presented in the Appendix. Whether the difference between the two OH datasets affects the MPTRAC simulations for the Ambae case study is discussed.
The formation of OH is driven by the photolysis of ozone in the troposphere and H2O in the stratosphere, which causes a strong correlation with diurnal variability (Minschwaner et al., 2011). In contrast to previous versions of MPTRAC, which did not take diurnal variability into account, the mean OH climatology concentration [OH]0 is multiplied here by a scaling factor depending on the solar zenith angle θSZA as proposed by Minschwaner et al. (2011) to model the diurnal variations,
The term sec (θSZA) is the approximate air mass factor which represents the ratio of the optical slant path to the effective vertical path. The parameter β represents the vertical optical depth. Based on Minschwaner et al. (2011), a β value of 0.6 is used for simulations covering the UT/LS region. To maintain the same mean values of the scaled data as the monthly OH field, they are divided by a normalization factor obtained by integrating the correlation factor f over longitude λ. The final OH concentration is calculated as
Figure 1 shows average vertical profiles of the different OH datasets at tropical latitudes (from 23.5∘ S to 23.5∘ N). The CLaMS OH data (Pommrich et al., 2014), calculated using methane and ozone data taken from the HALOE climatology for the year 2005 (Grooß and Russell III, 2005), are compared with the CAMS OH reanalysis data for the years 2005 and 2018, respectively. The differences in the CAMS mean profiles between 2005 and 2018 are found to be negligible. Comparing the CLaMS and CAMS OH data, these two datasets show similar concentrations in the troposphere, while in the stratosphere, CLaMS OH concentrations are much larger than CAMS OH concentrations. To further evaluate the OH fields of the climatologies, we compared them to several NASA in situ OH measurements in the troposphere at similar altitudes, solar zenith angles, and time periods and also to Microwave Limb Sounder (MLS) satellite data in the stratosphere. Both CLaMS and CAMS data showed good agreement with the in situ measurements in the troposphere. At altitudes above 20 km, CLaMS data show much better agreement with MLS observations than the CAMS reanalysis. Further details of the comparison are presented in the Appendix.
2.1.2 Hydrogen peroxide oxidation in the aqueous phase
The in-cloud oxidation pathway of SO2 is mainly dominated by the reaction with hydrogen peroxide (H2O2),
Another oxide of SO2 in liquid phase, ozone, is not considered here because its effects are expected to be negligible when pH≤5 (Rolph et al., 1992; Pattantyus et al., 2018). In contrast to OH, H2O2 has a longer atmospheric lifetime and cannot be treated as a static field as in the OH chemistry module. The reaction will rapidly deplete H2O2 in a few minutes (Pattantyus et al., 2018; Redington et al., 2009), keeping the H2O2 concentration in the aqueous phase much lower than equilibrium conditions from Henry's law (Barth et al., 1989). To approximate the concentration of H2O2 in the aqueous phase, we use an expression following Rolph et al. (1992) approximated from measurement data in Barth et al. (1989),
Here, represents Henry's law constant of H2O2 (Sander, 2015). The concentration of H2O2 in the atmosphere is defined using monthly mean zonal mean data extracted from the CAMS reanalysis. The volume mixing ratio of SO2 (in units of ppbv) is calculated in grid boxes of in the horizontal direction and 0.2 km in the vertical direction.
The concentration of the SO2 in the aqueous phase is converted into a mass concentration in the air by multiplying the cloud water volume content L; thus, the oxidation rate of SO2 by H2O2 is formulated as (Rolph et al., 1992)
Here, K′ is the dissociation constant of H2SO3 (Berglen et al., 2004), and L is the volume liquid water content of the clouds. Combining Eqs. (8) to (9), the rate coefficient used in Eq. (1) of the H2O2 aqueous-phase chemistry module is formulated as
The reaction rate coefficient is formulated as (Maass et al., 1999)
When the air parcel is located inside a grid box where the cloud water content is non-zero, the H2O2 oxidation scheme is activated to contribute to the depletion of SO2.
In reanalysis data, cloud information always has uncertainties and cannot resolve finer-scale cloud structures, which means that even in a cloudy grid box, the in-cloud oxidation may locally not take effect. Under this aspect, we implemented a control parameter allowing us to modify the cloud cover and to decrease the fraction of in-cloud oxidation. Only when a random number in the range of 0 to 1 is smaller than the given control parameter will the H2O2 chemistry be activated. At present, the cloud cover default value is given as 0.8. In future versions of MPTRAC, the meteorological cloud cover can be used instead of a predefined value.
2.1.3 Wet deposition
Irreversible in-cloud and below-cloud wet removal processes of trace gases need to be treated separately. In MPTRAC, the cloud liquid water content (CLWC) and the cloud ice water content (CIWC) of the meteorological input data are used to determine whether an air parcel is located within or below a cloud. The total column cloud water cl and the cloud depth Z are additional input variables to the wet deposition module. Similar to Pisso et al. (2019), the precipitation rate P (in units of mm h−1) is estimated from cl (in units of kg m−2) by means of a regression analysis using the ERA5 meteorological data for a region covering the Ambae eruption (10∘ S to 30∘ N, 160∘ W to 140∘ E) over the time period from 25 to 31 July 2018, as shown in Fig. 2,

Figure 2Scatter density plot of total column cloud water versus precipitation rate of ERA5 meteorological data for a region and time period covering the Ambae eruption (see text for details). Color coding indicates the normalized density of the data points. The black line represents the regression of the data as given in Eq. (12). The red line shows the expression given by Pisso et al. (2019).
For the modeling of in-cloud wet deposition, a similar exponential removal as in Eq. (1) is used with a scavenging coefficient Λ (in units of s−1). The in-cloud wet deposition process is implemented with two schemes for a choice. The first scheme is based on the rain-out rate of cloud water, which determines the removal of a soluble trace gas taken up by cloud droplets and removal by precipitation according to the solubility of the trace gas. The in-cloud scavenging coefficient is calculated by multiplying the partition ratio of the species in the aqueous phase versus the gas phase α with the cloud water removal rate (Slinn, 1974; Levine and Schwartz, 1982; Garrett et al., 2006),
where L is the volume liquid water content of the cloud (in units of m3 m−3), Z is the depth of the cloud layer determined by the pressure of cloud top and cloud bottom as taken from the meteorological input data, and α is defined by
according to the ideal gas law, where H is Henry’s law coefficient, R is the universal gas constant, and Px is the partial pressure of species x.
Combining Eqs. (13) and (14), a formula similar to the approach of the HYSPLIT model (Draxler and Hess, 1998) is obtained,
The factor η represents a temperature-dependent retention coefficient in cloud versus equilibrium concentration in liquid water. The default value of η is set following Webster and Thomson (2014), assuming the cloud between 238.15 and 273.15 K to be in the mixed phase and a retention ratio in ice clouds to be 0.15:
SO2 is a moderate soluble gas with a Henry's law constant of 1.3 M atm−1 at 298 K (Sander, 2015). However, the solubility of SO2 strongly depends on the pH value because it undergoes dissociation. In the simulations for SO2, the partition of SO2 in clouds is represented by an effective Henry's law constant related to the pH value to account for the dissolution and dissociation of SO2 in cloud water (Berglen et al., 2004),
Here K′ and K′′ are the first and second dissociation constants of SO2, using the formulation of Berglen et al. (2004), and H(SO2) is Henry's law constant (Sander, 2015). With this method, the pH value becomes a control parameter of the model affecting the wet deposition, for which we assumed a default value of 4.5, guided by earlier work (Berglen et al., 2004; Koch et al., 1999).
For comparison, we also implemented another in-cloud wet deposition scheme applying an empirical exponential expression given by
The choice of the parameters a and b follows the NAME model (Webster and Thomson, 2014).
The below-cloud wet deposition is a washout process through impact or diffusion with raindrops. With respect to SO2, the washout rate has a typical magnitude of s−1 (Maul, 1978; Martin, 1984; Elperin et al., 2015). Here, we set the parameters for SO2 to and b=0.616, which follows the settings in FLEXPART (Pisso et al., 2019).
2.1.4 Convection
Due to the limited resolution of the global meteorological input data, neither ERA-Interim nor ERA5 is capable of resolving subgrid-scale convection processes. In MPTRAC, the extreme convection parametrization (Draxler and Hess, 1998; Gerbig et al., 2003) is used to represent the effects of convective up- and downdrafts being unresolved in the meteorological input data. The lifetime and depletion of SO2 typically have a strong dependency on the atmospheric conditions at different altitudes. Testing the impact of parametrized convection on the SO2 transport simulations is part of the sensitivity tests presented in this work.
The extreme convection parametrization requires the convective available potential energy (CAPE) and the height of the equilibrium level (EL) for input. CAPE represents the vertical atmospheric instability by integrating the local buoyancy of an air parcel from the level of free convection (LFC) to the EL,
where Tv,ap is the virtual temperature of the air parcel and Tv,env is the virtual temperature of the environment. If the CAPE value is larger than a given threshold CAPE0, an air parcel will be randomly redistributed between the surface and the equilibrium level, weighted by density. The method is similarly handled in the convective transport scheme in the Stochastic Time-Inverted Lagrangian Transport (STILT) model (Gerbig et al., 2003). A more detailed description and discussion of the calculation of the CAPE and EL values in MPTRAC is given by Hoffmann et al. (2022a).
2.2 Satellite data products
2.2.1 AIRS sulfur dioxide measurements
The Atmospheric Infrared Sounder (AIRS) (Aumann et al., 2003) is an infrared spectrometer aboard the National Aeronautics and Space Administration’s (NASA's) Aqua satellite. Aqua operates in a sun-synchronous low Earth orbit at an orbit altitude of 705 km, providing nearly continuous measurements since September 2002. The AIRS instrument has across-track scanning capabilities. The swath width is 1780 km, consisting of 90 footprints per scan with a footprint size of 13.5 km ×13.5 km at nadir. The measurements take place at about 01:30 and 13:30 local time for the descending and ascending sections of the orbits, respectively.
To detect the presence of volcanic SO2 using the AIRS radiance measurements, an SO2 index defined as the brightness temperature difference between 1407.2 and 1371.5 cm−1 in the 7.3 µm SO2 waveband is used (Hoffmann et al., 2014). The SO2 index of Hoffmann et al. (2014) is most sensitive in the column density range of about 10 to 200 DU (Dobson units) at altitudes of 8 to 13 km, which covers explosive volcanic eruptions with SO2 injections into the UT/LS region. For SO2 index values larger than 4 K, the SO2 index is able to clearly detect volcanic plumes.
2.2.2 TROPOMI sulfur dioxide measurements
The TROPOspheric Monitoring Instrument (TROPOMI) (Veefkind et al., 2012) aboard the European Space Agency's Sentinel-5 Precursor satellite in a near-polar sun-synchronous orbit measures ultraviolet, visible, near-infrared, and shortwave-infrared spectra at daytime. The TROPOMI instrument provides high spatial resolution with a pixel size of 7 km ×3.5 km over a swath width of 2600 km.
The TROPOMI products include volcanic SO2 abundances for prescribed plume heights of 1, 7, and 15 km, based on a detection algorithm described by Brenot et al. (2014) which recognizes enhanced SO2 values from volcanic eruptions as well as anthropogenic sources. In this study, we use the TROPOMI Level 2 product with a priori SO2 profiles centered around 15 km (Theys et al., 2017) for the time period of 24 July to 11 August 2018 during the Ambae eruption.
The SO2 total mass of the Ambae eruption was calculated using the TROPOMI data to compare with the simulation results. TROPOMI scans the Ambae region at around 00:00 UTC. A grid with resolution of 0.1∘ covering the longitude range from 120∘ E to 110∘ W and the latitude range from 50∘ S to 30∘ N was used to calculate the average mass of SO2 in each grid box and to sum up the total mass. A filter of and the detection flag to filter out anthropogenic SO2 were used for the analysis of the TROPOMI volcanic SO2 data product as described in Theys et al. (2020). The derived SO2 total mass curve is very similar to the result of Malinina et al. (2021).
3.1 Baseline simulation
In this section, we present a baseline simulation of the dispersion and depletion of the volcanic SO2 plume of the Ambae eruption in July 2018. In our initial tests, it was found that, with only OH oxidation and wet deposition being considered, the simulations cannot fully explain the observed fast depletion of SO2. Therefore, we newly implemented the process of in-cloud oxidation with H2O2. As the plume transport in this case occurs in a high-CAPE tropical region, the convection module was also included. A CAPE threshold of 1000 J kg−1 was used to include moderate to strong subgrid-scale convection in the baseline simulation. All the parameter settings in the baseline simulation use the default values as introduced in Sect. 2. In the following sections, we will analyze the sensitivity of parameter choices for the above-mentioned chemistry and physics modules of MPTRAC with respect to the baseline simulation setup.
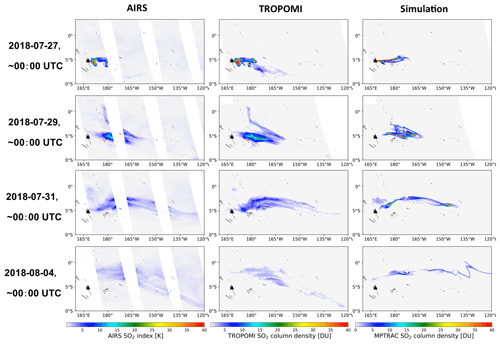
Figure 4Evolution of the Ambae SO2 plume in AIRS SO2 observations as well as column densities from TROPOMI observations and MPTRAC simulations. The time of the satellite observations shown here was restricted to ±3 h around 00:00 UTC. The black triangle shows the location of Ambae Island. MPTRAC simulation results have been sampled on the TROPOMI footprints.
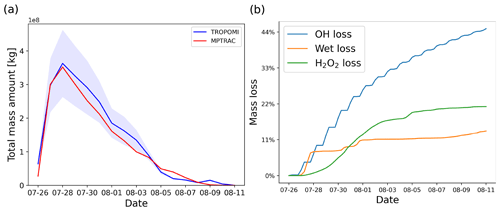
Figure 3a shows the SO2 total mass curve calculated from the TROPOMI data. The total mass of SO2 in the UT/LS region shows a strong increase on 26 July 2018, reaching a peak on 28 July, and decreases back to pre-eruption levels on 7 August 2018. According to different satellite instrument observations of the Support to Aviation Control Service (SACS, 2022), the volcanic plume is detected directly over the volcano from 26 to 27 July. The bulletin report of the Global Volcanism Program (GVP) (Krippner and Venzke, 2019) states that the main explosion occurred on 26 July and another two intense episodes, producing volcanic lightning, occurred on 27 July. Based on the different satellite measurements, observational reports as well as empirical testing, we initialized the MPTRAC baseline simulation for the Ambae case study by releasing 106 air parcels with a total mass of 450 kt starting on 26 July, 00:00 UTC, over a time period of 36 h, assuming a Gaussian vertical profile with the maximum centered at 14 km and a full width at half maximum (FWHM) of 4 km. Although there are more advanced methods available to accurately estimate the timing and vertical distribution of volcanic emissions (Hoffmann et al., 2016; Wu et al., 2017; Cai et al., 2022), we did not apply these techniques in this study because these techniques do not fully account for SO2 chemistry. This study focuses on testing the new and revised chemical and physical modules and on conducting sensitivity tests with respect to the parameter choices. As discussed below, the baseline simulation with constant emission rate and Gaussian vertical profile represents the Ambae case reasonably well so that meaningful testing and evaluation can be conducted.
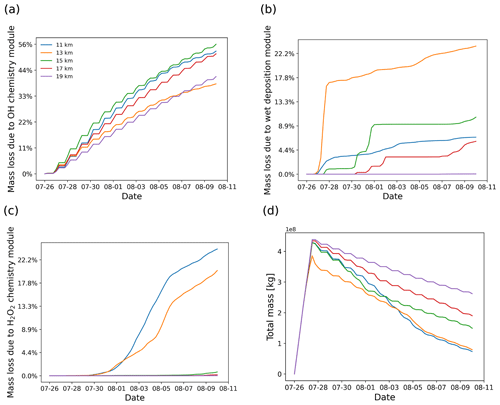
Figure 5SO2 mass loss relative to the total mass (in percent) due to OH chemistry (a), wet deposition (b), and H2O2 chemistry (c) as well as total mass curves (d) derived from simulations with different release heights centered at 11, 13, 15, 17, and 19 km.
To properly assess the total mass evolution and the SO2 plume patterns of the baseline simulation, the model output was sampled at the exact time and location as the TROPOMI satellite footprints by calculating the column density of all parcels located within a horizontal search radius of 7 km, as introduced in Cai et al. (2022). Air parcels in data gaps of the satellite observations will be excluded in the evaluation of the simulation results. The model results are multiplied by an altitude-dependent sensitivity profile derived from TROPOMI averaging kernel data. The TROPOMI averaging kernel indicates full sensitivity above 10 km of altitude, and the sensitivity only significantly decreases in the lower troposphere Cai et al. (2022). Since in this case most of the SO2 injections and the plume height were located above 10 km, the inclusion of the averaging kernel does not significantly change the model results. A lower threshold of 1 DU was applied to both the simulation data and the TROPOMI observations to eliminate the effects of noise. With this approach, the sample output of the model can be quantitatively analyzed and compared with the TROPOMI satellite observations. As shown in Fig. 3a, the MPTRAC baseline simulation yields good agreement with the total mass curve derived from the TROPOMI data. The overall SO2 lifetime from the simulation is quite similar to the observational data.
Figure 3b shows the relative mass loss relative to the total emissions over time with regard to each module. At the end of the simulation, OH chemistry, H2O2 chemistry, and wet deposition lead to a mass loss of 45 %, 14 %, and 21 % of the total mass burden, respectively. The remaining mass loss in Fig. 3a is due to air parcels leaving the study region or having SO2 mass below the filtering threshold so that they are not accounted for in the mass budget anymore. The loss rates due to in-cloud removal processes, including wet deposition and the aqueous-phase H2O2 oxidation, strongly depend on the location of the volcanic plume relative to the cloud fields. The loss due to OH oxidation is a step-shaped curve due to the diurnal variations of the OH concentration, leading to a faster loss rate at daytime and nearly zero loss at nighttime. Simulations using an OH field with diurnal variations will vary by 0.7 % compared to using an OH field without diurnal variations. Differences are relatively low in this case because the observations occur at about 13:00 local time. Overall, the diurnal variations of the OH field have little effect on the SO2 decay rates over the entire simulation period, because the observational timescale is over several days and the diurnal variations are averaging out.

Figure 6Background images represent the distributions of ERA5 cloud top height on 31 July 2018, 00:00 UTC. Dots represent air parcels released at altitudes of (a) 11 km, (b) 13 km, (c) 15 km, and (d) 17 km. A yellow dot indicates that the air parcel is below the cloud top height, triggering the wet deposition module, while a blue dot represents the opposite.
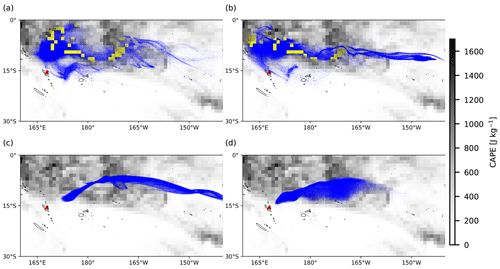
Figure 7Same as Fig. 6, but background images represent the distribution of ERA5 CAPE values on 31 July 2018, 00:00 UTC. Yellow dots indicate air parcels below the equilibrium level and local CAPE values larger than 1000 J kg−1, triggering the convection module, while blue dots represent the opposite.
Figure 4 shows comparisons of horizontal maps of the SO2 plume from the baseline simulation with AIRS and TROPOMI measurements, respectively. The bulk of the Ambae plume moved eastwards, and the moving speed is faster at lower altitudes. A small plume at heights of 10 to 12 km moved northwards after 28 July at 160 to 180∘ W, encountering strong wet deposition. The model results match the satellite observations qualitatively well with similar location and shape of the plume. At the end of the simulation the part of the plume below the cloud top is almost depleted, and the remaining part of the plume above the cloud top somewhat shows deviations from the observations due to the unpolished temporal and vertical variations of the emission estimates. Nevertheless, we consider the baseline simulation in its present form to be suitable for further evaluation and sensitivity tests.
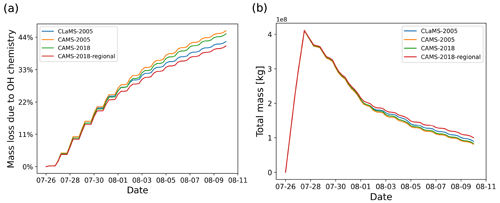
Figure 8SO2 mass loss relative to total mass (in percent) due to the OH chemistry module (a) and total mass curves (b) for simulations with different OH datasets, including CLaMS data in 2005, CAMS data in 2005 and 2018, and CAMS regional data in 2018 (see text for details).
3.2 Sensitivity test on SO2 release height
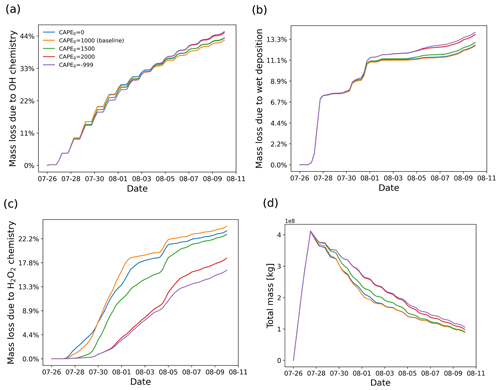
In this section, a series of simulations with air parcels released at different altitudes are presented to show the sensitivity of the plume injection height on the evolution of SO2 total mass burden. The tests use different release heights centered at 11, 13, 15, 17, and 19 km with 2 km wide uniform vertical distribution. The convection module was not activated in this test to avoid vertical mixing of air parcels down to the surface during the simulations. As shown in Fig. 5, the SO2 decay rate has an obvious dependency on release height. Releasing the volcanic SO2 at different heights leads to rather different horizontal spread and different mass loss due to wet deposition, depending on whether the SO2 plume encounters cloud regions or not.
As shown in Fig. 5b, the mass loss due to wet deposition shows particularly high sensitivity to the release height. Wet deposition occurs mainly on 27 to 28 July when releasing air parcels at altitudes below 14 km, while most of the wet deposition mass loss occurs around 1 August when releasing above 14 km. Almost no wet deposition occurs above 18 km because it is above the tropopause and the maximum cloud top height. Aqueous-phase H2O2 chemistry is most active below 14 km and has a strong sensitivity to release height, while above 14 km the H2O2 chemistry is very weak. The OH gas-phase oxidation does not show a clear correlation with release height, with contributions to mass loss ranging from 30 % to 60 % of the total mass during the simulation. However, note that the OH concentrations and temperature- and pressure-dependent rate coefficients of the OH oxidation are not linearly increasing with altitude (compare Fig. 1) over heights from 10 to 20 km. Above 15 km, the OH oxidation rate decreases with height, while below 15 km, the decay rate is controlled mainly by in-cloud removal and the OH oxidation rate quickly decreases.
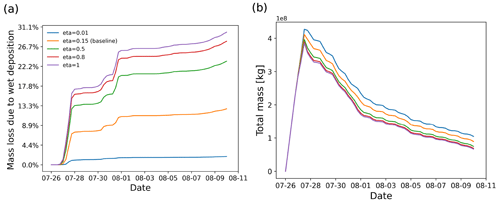
Figure 10SO2 mass loss relative to the total mass (in percent) due the wet deposition module (a) and total mass burden evolution (b), derived from different simulations with different retention ratio settings in the wet deposition module.
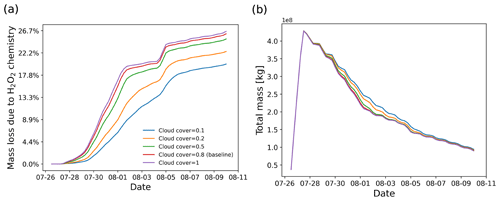
Figure 11SO2 mass loss relative to total mass (in percent) due the H2O2 chemistry module (a) and total mass burden evolution (b), derived from simulations with different cloud cover settings in the H2O2 chemistry module.
Figures 6 and 7 show the cloud top height and CAPE distributions derived from the ERA5 meteorological data as well as the particles released at different altitudes, clearly indicating which part of the plume is affected by wet removal and subgrid convection, as distinguished by yellow and blue color. The plume released at the location of Ambae Island is transported to a region with high CAPE values and abundant clouds. The wet removal and subgrid-scale convection mainly take effect at altitudes below 15 km. The maximum CAPE values range approximately from 1000 to 1600 J kg−1. In simulations with higher injection altitudes, the air parcels are transported mainly above the cloud top and are barely influenced by wet deposition and convection.
3.3 Sensitivity tests on OH chemistry
The SO2 decay rate in the OH chemistry module is calculated by Eq. (2), which considers the temperature- and pressure-dependent reaction rate kf and the OH concentration. The OH concentration is obtained from predefined monthly mean zonal mean data and the solar zenith angle correction to account for day- and nighttime conditions. The OH data used by default in MPTRAC are the monthly mean zonal mean climatology from Pommrich et al. (2014), which was calculated using the CLaMS model chemistry scheme. For another alternative, the CAMS global reanalysis provides 3 h OH data with a resolution of . To reduce memory needs and maintain consistency with the CLaMS data approach, the CAMS data are also converted into monthly mean zonal mean data. To verify the impact of inter-annual differences, we compared the results between the simulations with CAMS reanalysis data for the years 2005 (matching the CLaMS data) and 2018 (matching the Ambae eruption), respectively. For another test, simulations with regional CAMS OH data extracted from the longitude range from 160∘ E to 140∘ W are compared with global data.
As shown in Fig. 8, the inter-annual differences in the CAMS OH data are negligible (∼1 percentage point, pp). The differences between simulations with CAMS and CLaMS global OH data are ∼3 pp. The simulation with regional CAMS OH data for the location of the eruption has ∼4 pp difference compared with the global CAMS data. Overall, the inter-annual and regional differences of the OH datasets have a small influence on the amount of OH oxidation (less than 5 pp in this case), which suggests that using a monthly mean zonal mean climatology is a reasonable approach for modeling the OH loss of SO2 in the UT/LS region.
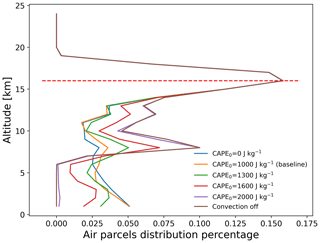
Figure 12Vertical distribution of total SO2 mass of the air parcels on 1 August 2018, 00:00 UTC, from simulations with different CAPE thresholds. The red dashed line indicates the ERA5 thermal tropopause height over the Ambae region (Hoffmann and Spang, 2022).
3.4 Sensitivity tests on wet deposition
In the Ambae case study, the wet removal in clouds plays an important role in depleting SO2 since the main plume passes through a cloud region. As introduced in Sect. 2.1.3, in-cloud wet deposition is handled as a rain-out process, which depends on the partition ratio of SO2 in the cloud droplets and the precipitation rate. The partition ratio of SO2 in liquid phase is defined with an effective Henry's law constant, depending on the assumed pH value. Here, we conducted a series of simulations to test the sensitivity to pH values in the range of 3 to 5, along with a comparison with the NAME wet deposition scheme (Webster and Thomson, 2014). As expected, higher cloud pH values lead to stronger wet deposition. The simulation with wet deposition according to the NAME scheme shows a similar deposition to the baseline simulation with the equilibrium scheme at pH 4 to 4.5. The difference between the two schemes is further reflected in the sensitivity to convection, which will be discussed in Sect. 3.6
The retention ratio represents the solute species in the ice phase versus that in the liquid hydrometeor. The retention coefficient may vary depending on temperature, pH, ventilation rate, accretion rate, and impact velocity (Stuart and Jacobson, 2006). Laboratory studies on the retention ratio of SO2 suggest a range from 1 % to 60 % (Iribarne et al., 1983; Lamb and Blumenstein, 1987; Iribarne et al., 1990). As introduced in Sect. 2.1.3, a retention coefficient dependent on temperature is applied to model the differences of wet deposition in ice and liquid cloud. Figure 10 shows the SO2 mass loss curves of simulations given different retention ratios in the range of 0.01 to 1. In this case, most of the wet deposition occurs in ice clouds, leading to a strong dependency on the retention ratio.
3.5 Sensitivity tests on H2O2 chemistry
Since the meteorological data cannot fully resolve the convection and detailed cloud structures, a parameter cloud cover was defined in the H2O2 chemistry module to represent the probability of an air parcel to be located in a cloud. When a random number in the range of 0 to 1 is larger than a given threshold for the cloud cover, the H2O2 decomposition will be skipped. Figure 11 shows the dependency of aqueous-phase H2O2 oxidation on cloud cover. Compared to full cloud cover, the amount of H2O2 oxidation in a case with only 10 % cloud cover is decreased by 8 pp. However, the SO2 total mass burden is only slightly changed.
3.6 Impact of the extreme convection parametrization
Due to better spatiotemporal resolution, the ERA5 meteorological data provide more accurate information than ERA-Interim to resolve mesoscale features (Hoffmann et al., 2019). However, convective up- and downdrafts are still underrepresented in the ERA5 data. In MPTRAC, the extreme convection parametrization is applied to represent the effects of unresolved convection in the meteorological input data. In convective columns, the convection module will randomly redistribute the air parcels between the surface and the equilibrium level if CAPE exceeds a given threshold CAPE0. As shown in Fig. 7, the SO2 plume released by the Ambae volcanic eruption was transported to a high CAPE region, which makes it a valuable case to study the potential effects of unresolved convection. In this section, the effects of parametrized convection for different thresholds CAPE0 will be discussed.
Figure 12 shows the vertical distributions of the SO2 mass of the Ambae plume for different thresholds CAPE0 from 0 to 2000 J kg−1. The case of CAPE0 being zero represents the extreme case in which convection occurs everywhere below the equilibrium level where CAPE is present. For CAPE0 larger than 1000 J kg−1, the parametrized convection is restricted to represent moderate to strong convective events only. There is almost no additional convection for CAPE0 larger than 2000 J kg−1 compared to the case without parametrized convection. When applying a larger CAPE0, more air parcels will be transported to altitudes below the equilibrium level (∼14 km).
Figure 13 shows the impact of parametrized convection on mass loss in the SO2 transport simulations for the Ambae case. The largest sensitivity is found for the H2O2 oxidation, while OH oxidation and wet deposition show little difference. This is because some air parcels are transported to heights below 14 km where the H2O2 oxidation is most active. The H2O2 chemistry is much more sensitive to height than the OH chemistry and wet deposition at altitudes where convection occurs (see Sect. 3.2). Regarding the mass evolution, the effect of the convection module enhances the depletion of SO2 below the cloud top. At the end of simulation, most of the remaining SO2 is above cloud top where the convection module takes no effect.
We present recent improvements of the chemical and physical modules in the Lagrangian transport model MPTRAC for simulating the dispersion and depletion of SO2 from volcanic eruptions. The improved modules include gas-phase OH oxidation, aqueous-phase H2O2 oxidation, wet deposition, and parametrized convection. In a case study, the modules are applied for simulations of the SO2 plume evolution of the Ambae eruption in July 2018. We present a baseline simulation in which the modeled mass evolution shows a good match with TROPOMI satellite observations.
In our simulations, the implementation of wet deposition and H2O2 oxidation significantly decreased the lifetime of SO2 in clouds. Gas-phase oxidation by OH, aqueous-phase oxidation by H2O2, and wet deposition remove about 45 %, 14 %, and 21 % of the SO2 total mass burden during a simulation time period of 15 d, respectively. Based on the baseline simulation, a series of sensitivity tests were conducted by tuning various control parameters of the modules to better understand the impacts of the chemical and physical processes on SO2 dispersion. Initially, we tested the sensitivity on the assumed injection height of the SO2 plume. The SO2 plume undergoes much faster depletion below 14 km in clouds than in the dry atmosphere because rain-out processes and aqueous-phase oxidation are bound to the presence of clouds. Variations of cloud distributions and vertical wind shear lead to rather different amount of wet deposition and aqueous-phase oxidation for different injection heights.
For the OH chemistry module, different OH monthly mean zonal mean concentration datasets have been tested. It was found that the differences in mass loss between different OH datasets (CAMS versus CLaMS, regional versus global, and year 2005 versus 2018) are limited (less than 5 pp of the total mass). Using a monthly mean zonal mean climatology of OH for simulating SO2 mass loss over time is considered a suitable approach for transport simulations covering the UT/LS region. For wet deposition, an analytic solution derived for the rain-out process according to Henry's law is considered in cloud. The assumed pH value of the effective Henry's law constant for SO2 has a strong effect on the amount of wet removal of SO2. Compared with the wet deposition scheme with a scavenging coefficient formula applied in the UK Met Office's NAME model, our simulation at an assumed pH value of 4.5 yields a similar level of wet deposition. The impact of the retention ratio of the soluble gas in ice cloud is also discussed. Due to the low temperatures in the UT/LS region, most of the regions affected by the Ambae eruption are covered with ice clouds. Therefore, the amount of wet deposition strongly depends on the assumed retention ratio. For H2O2 chemistry in the aqueous phase, the impact of cloud cover has been tested. By tuning the CAPE threshold used in the extreme convection parametrization, the vertical distribution of the SO2 plume might be strongly altered, which in turn will impact the depletion of SO2. It is found that aqueous-phase oxidation via H2O2 is mostly influenced, whereas wet deposition and OH oxidation are not so sensitive to the vertical redistribution of the air parcels due to the parametrized convection.
In this study, we improved the Lagrangian transport simulations of volcanic SO2 with MPTRAC by implementing more realistic physical and chemical process representations instead of using an exponential decay law with a fixed lifetime as in our earlier studies. However, the refinements on the modeled loss processes lead to a high sensitivity to the release vertical profile and cloud abundance. The backward trajectory method developed to estimate time- and height-resolved SO2 emissions with MPTRAC (Hoffmann et al., 2016; Wu et al., 2017) is currently incapable of taking into account the additional complexity of the revised chemistry and wet deposition parametrizations. In future work, we plan to implement more advanced inverse modeling techniques for MPTRAC to reconstruct the initial SO2 injections of volcanic eruptions, which can take the model improvements described here into account.
The representation of volcanic SO2 depletion in different atmospheric conditions above and below the cloud top in the current MPTRAC scheme considers first-order loss processes to estimate rate coefficients and lifetimes. In reality, the chemical processes affecting the lifetime of volcanic SO2 may be more complicated. Large-scale emissions of volcanic SO2 into the atmosphere will reduce the abundance of atmospheric oxides. The scattering and reduction of solar radiation by ash and other aerosol particles will reduce the photochemical regeneration of the oxides. Other factors, such as additional water release from an eruption or absorption by volcanic ash, need to be further investigated to better understand and elucidate the mechanism of their dynamics. In future work, we intend to further test and improve the current version of MPTRAC to explore its applicability to other volcanic eruption cases.
A monthly mean zonal mean OH climatology with diurnal corrections according to Eq. (6) is used as input to calculate the decomposition of SO2 due to OH oxidation. For validation of the OH data, we extracted OH values from MPTRAC as a function of the solar zenith angle and compared them with in situ measurement data provided by the NASA Earth Science Project Office (ESPO, 2022). Here, we present comparisons for April (Fig. A1) and October (Fig. A2) containing in situ measurements of campaigns SUCCESS-DC8, SONEX-DC8, POLARIS-ER2, and MAESA-ER2, covering altitudes ranging from 5 to 21 km. For the stratosphere, a comparison with OH data from MLS is shown in Fig. A3. It is found that CLaMS OH data better represent the measured OH concentrations than the CAMS reanalysis in the stratosphere. For the troposphere, the OH data from CLaMS and CAMS both match the measurements well.
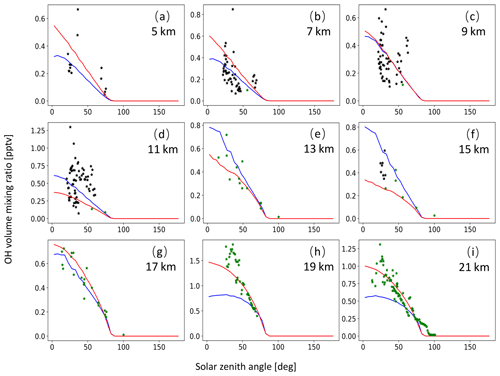
Figure A1OH volume mixing ratios used for MPTRAC based on predefined monthly mean zonal mean data for the CLaMS model (red curve) and the CAMS reanalysis (blue curve) as well as OH in situ measurements from the campaigns SUCCESS-DC8 (black points) and POLARIS-ER2 (green points). The time period being covered is the month of April. Plots in panels (a) to (i) refer to altitudes of 5, 7, 9, 11, 13, 15, 17, 19, and 21 km, respectively.
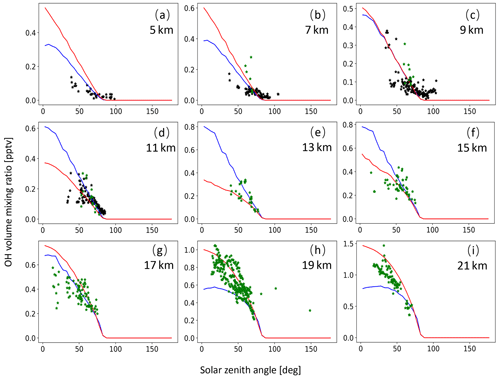
Figure A2Same as Fig. A1 but for SONEX-DC8 (black points) and MAESA-ER2 (green points) measurements in October.
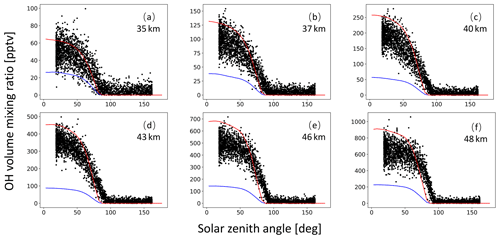
Figure A3Global average OH volume mixing ratios used in MPTRAC based on predefined monthly mean zonal mean data for the CLaMS model (red curve) and the CAMS reanalysis (blue curve) as well as MLS satellite measurements (black points). The time period being covered is May. Plots in panels (a) to (f) refer to altitudes of 35, 37, 40, 43, 46, and 48 km, respectively.
MPTRAC (Hoffmann et al., 2016, 2022a) is made available under the terms and conditions of the GNU General Public License (GPL) version 3. The release version 2.4 of MPTRAC applied in this paper has been archived on Zenodo at https://doi.org/10.5281/zenodo.7473222 (Hoffmann et al., 2022b). The git repository providing updates for MPTRAC is accessible at https://github.com/slcs-jsc/mptrac (Hoffmann et al., 2023). The running and plotting scripts for the case study in this paper are available on Zenodo at https://doi.org/10.5281/zenodo.8163071 (Liu et al., 2023). The ERA5 reanalysis (Hersbach et al., 2020) was retrieved from ECMWF's Meteorological Archival and Retrieval System (MARS). See https://www.ecmwf.int/en/forecasts/datasets/browse-reanalysis-datasets (Hersbach et al., 2020) for further details.
ML, LH, and SG jointly developed the concept of this study. ML conducted most of the model development, performed the model simulations, and analyzed the results. LH contributed to MPTRAC model development. SG contributed expertise on OH measurements. ZC, SG, LH, YH, and XW provided expertise on Lagrangian transport modeling for volcanic eruptions. ML wrote the manuscript with contributions from all co-authors.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The work described in this paper was supported by the Helmholtz Association of German Research Centres (HGF) through the Joint Lab Exascale Earth System Modelling (JL-ExaESM). We acknowledge the Jülich Supercomputing Centre for providing computing time and storage resources on the supercomputer JUWELS. We acknowledge Sandra Wallis for providing TROPOMI SO2 mass data at an earlier stage of this study.
This study has been supported by the China Scholarship Council (CSC, grant no. 202006380039), the National Natural Science Foundation of China (grant no. 41975049), the Basic Strengthening Research Program (grant no. 2021-JCJQ-JJ-1058), the Key-Area Research and Development Program of Guangdong Province (grant no. 2021B0101190003), and the Zhujiang Talent Program of Guangdong Province (grant no. 2017GC010576). The article processing charges for this open-access publication were covered by the Forschungszentrum Jülich.
This paper was edited by Simon Unterstrasser and reviewed by Nina Iren Kristiansen and one anonymous referee.
Aumann, H., Chahine, M., Gautier, C., Goldberg, M., Kalnay, E., McMillin, L., Revercomb, H., Rosenkranz, P., Smith, W., Staelin, D., Strow, L., and Susskind, J.: AIRS/AMSU/HSB on the Aqua mission: design, science objectives, data products, and processing systems, IEEE T. Geosci. Remote, 41, 253–264, https://doi.org/10.1109/TGRS.2002.808356, 2003. a, b
Barth, M. C., Hegg, D. A., Hobbs, P. V., Walega, J. G., Kok, G. L., Heikes, B. G., and Lazrus, A. L.: Measurements of atmospheric gas-phase and aqueous-phase hydrogen peroxide concentrations in winter on the east coast of the United States, Tellus, 41B, 61–69, https://doi.org/10.1111/j.1600-0889.1989.tb00125.x, 1989. a, b
Berglen, T. F., Berntsen, T. K., Isaksen, I. S. A., and Sundet, J. K.: A global model of the coupled sulfur/oxidant chemistry in the troposphere: The sulfur cycle, J. Geophys. Res.-Atmos., 109, D19310, https://doi.org/10.1029/2003JD003948, 2004. a, b, c, d
Brenot, H., Theys, N., Clarisse, L., van Geffen, J., van Gent, J., Van Roozendael, M., van der A, R., Hurtmans, D., Coheur, P.-F., Clerbaux, C., Valks, P., Hedelt, P., Prata, F., Rasson, O., Sievers, K., and Zehner, C.: Support to Aviation Control Service (SACS): an online service for near-real-time satellite monitoring of volcanic plumes, Nat. Hazards Earth Syst. Sci., 14, 1099–1123, https://doi.org/10.5194/nhess-14-1099-2014, 2014. a
Burkholder, J. B., Sander, S. P., J. Abbatt, J. R. B., Cappa, C., Crounse, J. D., Dibble, T. S., Huie, R. E., Kolb, C. E., Kurylo, M. J., Orkin, V. L., Percival, C. J., Wilmouth, D. M., and Wine, P. H.: Chemical kinetics and photochemical data for use in atmospheric studies: evaluation number 19, Tech. rep., Jet Propulsion Laboratory, Pasadena, http://jpldataeval.jpl.nasa.gov/ (last access: 31 August 2023), 2019. a
Cai, Z., Griessbach, S., and Hoffmann, L.: Improved estimation of volcanic SO2 injections from satellite retrievals and Lagrangian transport simulations: the 2019 Raikoke eruption, Atmos. Chem. Phys., 22, 6787–6809, https://doi.org/10.5194/acp-22-6787-2022, 2022. a, b, c, d, e
de Leeuw, J., Schmidt, A., Witham, C. S., Theys, N., Taylor, I. A., Grainger, R. G., Pope, R. J., Haywood, J., Osborne, M., and Kristiansen, N. I.: The 2019 Raikoke volcanic eruption – Part 1: Dispersion model simulations and satellite retrievals of volcanic sulfur dioxide, Atmos. Chem. Phys., 21, 10851–10879, https://doi.org/10.5194/acp-21-10851-2021, 2021. a, b
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011. a
Delmelle, P., Stix, J., Baxter, P., Garcia-Alvarez, J., and Barquero, J.: Atmospheric dispersion, environmental effects and potential health hazard associated with the low-altitude gas plume of Masaya volcano, Nicaragua, B. Volcanol., 64, 423–434, https://doi.org/10.1007/s00445-002-0221-6, 2002. a
Draxler, R. and Hess, G.: An overview of the HYSPLIT_4 modelling system for trajectories, dispersion and deposition, Aust. Meteorol. Mag., 47, 295–308, 1998. a, b
Eatough, D., Caka, F., and Farber, R.: The Conversion of SO2 to Sulfate in the Atmosphere, Isr. J. Chem., 34, 301–314, https://doi.org/10.1002/ijch.199400034, 1994. a
Eckhardt, S., Prata, A. J., Seibert, P., Stebel, K., and Stohl, A.: Estimation of the vertical profile of sulfur dioxide injection into the atmosphere by a volcanic eruption using satellite column measurements and inverse transport modeling, Atmos. Chem. Phys., 8, 3881–3897, https://doi.org/10.5194/acp-8-3881-2008, 2008. a
Elperin, T., Fominykh, A., and Krasovitov, B.: Precipitation scavenging of gaseous pollutants having arbitrary solubility in inhomogeneous atmosphere, Meteorol. Atmos. Phys., 127, 205–216, https://doi.org/10.1007/s00703-014-0358-9, 2015. a
ESPO: ESPO data archive, https://espoarchive.nasa.gov/archive/browse/ (last access: 31 August 2023), 2022. a
Garrett, T. J., Avey, L., Palmer, P. I., Stohl, A., Neuman, J. A., Brock, C. A., Ryerson, T. B., and Holloway, J. S.: Quantifying wet scavenging processes in aircraft observations of nitric acid and cloud condensation nuclei, J. Geophys. Res.-Atmos., 111, D23S51, https://doi.org/10.1029/2006JD007416, 2006. a
Gerbig, C., Lin, J. C., Wofsy, S. C., Daube, B. C., Andrews, A. E., Stephens, B. B., Bakwin, P. S., and Grainger, C. A.: Toward constraining regional-scale fluxes of CO2 with atmospheric observations over a continent: 2. Analysis of COBRA data using a receptor-oriented framework, J. Geophys. Res.-Atmos., 108, 4757, https://doi.org/10.1029/2003JD003770, 2003. a, b
Grooß, J.-U. and Russell III, J. M.: Technical note: A stratospheric climatology for O3, H2O, CH4, NOx, HCl and HF derived from HALOE measurements, Atmos. Chem. Phys., 5, 2797–2807, https://doi.org/10.5194/acp-5-2797-2005, 2005. a
Hansell, A. and Oppenheimer, C.: Health hazards from volcanic gases: A systematic literature review, Arch. Environ. Health, 59, 628–639, https://doi.org/10.1080/00039890409602947, 2004. a
Heng, Y., Hoffmann, L., Griessbach, S., Rößler, T., and Stein, O.: Inverse transport modeling of volcanic sulfur dioxide emissions using large-scale simulations, Geosci. Model Dev., 9, 1627–1645, https://doi.org/10.5194/gmd-9-1627-2016, 2016. a
Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horanyi, A., Munoz-Sabater, J., Nicolas, J., Peubey, C., Radu, R., Schepers, D., Simmons, A., Soci, C., Abdalla, S., Abellan, X., Balsamo, G., Bechtold, P., Biavati, G., Bidlot, J., Bonavita, M., De Chiara, G., Dahlgren, P., Dee, D., Diamantakis, M., Dragani, R., Flemming, J., Forbes, R., Fuentes, M., Geer, A., Haimberger, L., Healy, S., Hogan, R. J., Holm, E., Janiskova, M., Keeley, S., Laloyaux, P., Lopez, P., Lupu, C., Radnoti, G., de Rosnay, P., Rozum, I., Vamborg, F., Villaume, S., and Thepaut, J.-N.: The ERA5 global reanalysis, Q. J. Roy. Meteor. Soc., 146, 1999–2049, https://doi.org/10.1002/qj.3803, 2020 (data available at: https://www.ecmwf.int/en/forecasts/datasets/browse-reanalysis-datasets, last access: 20 December 2022). a, b, c
Hoffmann, L. and Spang, R.: An assessment of tropopause characteristics of the ERA5 and ERA-Interim meteorological reanalyses, Atmos. Chem. Phys., 22, 4019–4046, https://doi.org/10.5194/acp-22-4019-2022, 2022. a
Hoffmann, L., Griessbach, S., and Meyer, C. I.: Volcanic emissions from AIRS observations: detection methods, case study, and statistical analysis, in: Remote Sensing of Clouds and the Atmosphere XIX, and Optics in Atmospheric Propagation and Adaptive Systems XVII, edited by: Comerón, A., Kassianov, E. I., Schäfer, K., Picard, R. H., Stein, K., and Gonglewski, J. D., vol. 9242, p. 924214, International Society for Optics and Photonics, SPIE, https://doi.org/10.1117/12.2066326, 2014. a, b, c
Hoffmann, L., Roessler, T., Griessbach, S., Heng, Y., and Stein, O.: Lagrangian transport simulations of volcanic sulfur dioxide emissions: Impact of meteorological data products, J. Geophys. Res.-Atmos., 121, 4651–4673, https://doi.org/10.1002/2015JD023749, 2016. a, b, c, d, e
Hoffmann, L., Günther, G., Li, D., Stein, O., Wu, X., Griessbach, S., Heng, Y., Konopka, P., Müller, R., Vogel, B., and Wright, J. S.: From ERA-Interim to ERA5: the considerable impact of ECMWF's next-generation reanalysis on Lagrangian transport simulations, Atmos. Chem. Phys., 19, 3097–3124, https://doi.org/10.5194/acp-19-3097-2019, 2019. a, b
Hoffmann, L., Baumeister, P. F., Cai, Z., Clemens, J., Griessbach, S., Günther, G., Heng, Y., Liu, M., Haghighi Mood, K., Stein, O., Thomas, N., Vogel, B., Wu, X., and Zou, L.: Massive-Parallel Trajectory Calculations version 2.2 (MPTRAC-2.2): Lagrangian transport simulations on graphics processing units (GPUs), Geosci. Model Dev., 15, 2731–2762, https://doi.org/10.5194/gmd-15-2731-2022, 2022a. a, b, c, d, e
Hoffmann, L., Clemens, J., Haghighi Mood, K., and Liu, M.: Massive-Parallel Trajectory Calculations (MPTRAC) (v2.4), Zenodo, https://doi.org/10.5281/zenodo.7473222, 2022b. a
Hoffmann, L., Clemens, J., Liu, M., Haghighi Mood, K., and Lu, Y.: Massive-Parallel Trajectory Calculations (MPTRAC), https://github.com/slcs-jsc/mptrac, last access: 5 September 2023. a
Höpfner, M., Boone, C. D., Funke, B., Glatthor, N., Grabowski, U., Günther, A., Kellmann, S., Kiefer, M., Linden, A., Lossow, S., Pumphrey, H. C., Read, W. G., Roiger, A., Stiller, G., Schlager, H., von Clarmann, T., and Wissmüller, K.: Sulfur dioxide (SO2) from MIPAS in the upper troposphere and lower stratosphere 2002–2012, Atmos. Chem. Phys., 15, 7017–7037, https://doi.org/10.5194/acp-15-7017-2015, 2015. a
Inness, A., Ades, M., Agustí-Panareda, A., Barré, J., Benedictow, A., Blechschmidt, A.-M., Dominguez, J. J., Engelen, R., Eskes, H., Flemming, J., Huijnen, V., Jones, L., Kipling, Z., Massart, S., Parrington, M., Peuch, V.-H., Razinger, M., Remy, S., Schulz, M., and Suttie, M.: The CAMS reanalysis of atmospheric composition, Atmos. Chem. Phys., 19, 3515–3556, https://doi.org/10.5194/acp-19-3515-2019, 2019. a
Iribarne, J., Barrie, L., and Iribarne, A.: Effect of freezing on sulfur dioxide dissolved in supercooled droplets, Atmos. Environ., 17, 1047–1050, https://doi.org/10.1016/0004-6981(83)90287-1, 1983. a
Iribarne, J., Pyshnov, T., and Naik, B.: The effect of freezing on the composition of supercooled droplets–II. Retention of S(IV), Atmos. Environ., 24, 389–398, https://doi.org/10.1016/0960-1686(90)90119-8, 1990. a
Jülich Supercomputing Centre: JUWELS: Modular Tier-0/1 Supercomputer at the Jülich Supercomputing Centre, J. Large-scale Res. Facilities, 5, A135, https://doi.org/10.17815/jlsrf-5-171, 2019. a
Khokhar, M., Frankenberg, C., Van Roozendael, M., Beirle, S., Kuhl, S., Richter, A., Platt, U., and Wagner, T.: Satellite observations of atmospheric SO2 from volcanic eruptions during the time-period of 1996-2002, Adv. Space Res., 36, 879–887, https://doi.org/10.1016/j.asr.2005.04.114, 2005. a
Kloss, C., Sellitto, P., Legras, B., Vernier, J.-P., Jegou, F., Venkat Ratnam, M., Suneel Kumar, B., Lakshmi Madhavan, B., and Berthet, G.: Impact of the 2018 Ambae Eruption on the Global Stratospheric Aerosol Layer and Climate, J. Geophys. Res.-Atmos., 125, e2020JD032410, https://doi.org/10.1029/2020JD032410, 2020. a, b
Koch, D., Jacob, D., Tegen, I., Rind, D., and Chin, M.: Tropospheric sulfur simulation and sulfate direct radiative forcing in the Goddard Institute for Space Studies general circulation model, J. Geophys. Res.-Atmos., 104, 23799–23822, https://doi.org/10.1029/1999JD900248, 1999. a
Krippner, J. and Venzke, E.: Global Volcanism Program, 2019, Report on Ambae (Vanuatu), Bulletin of the Global Volcanism Network, 44:2, Smithsonian Institution, https://doi.org/10.5479/si.GVP.BGVN201902-257030, 2019. a
Lamb, D. and Blumenstein, R.: Measurement of the entrapment of sulfur dioxide by rime ice, Atmos. Environ., 21, 1765–1772, https://doi.org/10.1016/0004-6981(87)90116-8, 1987. a
Levine, S. and Schwartz, S.: In-cloud and below-cloud scavenging of Nitric acid vapor, Atmos. Environ., 16, 1725–1734, https://doi.org/10.1016/0004-6981(82)90266-9, 1982. a
Liu, M., Huang, Y., Hoffmann, L., Huang, C., Chen, P., and Heng, Y.: High-Resolution Source Estimation of Volcanic Sulfur Dioxide Emissions Using Large-Scale Transport Simulations, in: Computational Science – ICCS 2020, edited by: Krzhizhanovskaya, V. V., Závodszky, G., Lees, M. H., Dongarra, J. J., Sloot, P. M. A., Brissos, S., and Teixeira, J., 60–73, Springer International Publishing, https://doi.org/10.1007/978-3-030-50420-5_5, 2020. a, b
Liu, M., Hoffmann, L., and Griessbach, S.: Running script of modeling the Ambae eruption SO2 transport in July 2018 with MPTRAC v2.4, Zenodo, https://doi.org/10.5281/zenodo.8163071, 2023. a
Maass, F., Elias, H., and Wannowius, K.: Kinetics of the oxidation of hydrogen sulfite by hydrogen peroxide in aqueous solution: ionic strength effects and temperature dependence, Atmos. Environ., 33, 4413–4419, https://doi.org/10.1016/S1352-2310(99)00212-5, 1999. a
Malinina, E., Rozanov, A., Niemeier, U., Wallis, S., Arosio, C., Wrana, F., Timmreck, C., von Savigny, C., and Burrows, J. P.: Changes in stratospheric aerosol extinction coefficient after the 2018 Ambae eruption as seen by OMPS-LP and MAECHAM5-HAM, Atmos. Chem. Phys., 21, 14871–14891, https://doi.org/10.5194/acp-21-14871-2021, 2021. a, b, c, d
Martin, A.: Estimated washout coefficients for sulphur dioxide, nitric oxide, nitrogen dioxide and ozone, Atmos. Environ., 18, 1955–1961, https://doi.org/10.1016/0004-6981(84)90373-1, 1984. a
Maul, P.: Preliminary estimates of the washout coefficient for sulphur dioxide using data from an east midlands ground level monitoring network, Atmos. Environ., 12, 2515–2517, https://doi.org/10.1016/0004-6981(78)90298-6, 1978. a
McGonigle, A. J. S., Delmelle, P., Oppenheimer, C., Tsanev, V. I., Delfosse, T., Williams-Jones, G., Horton, K., and Mather, T. A.: SO2 depletion in tropospheric volcanic plumes, Geophys. Res. Lett., 31, L13201, https://doi.org/10.1029/2004GL019990, 2004. a
Minschwaner, K., Manney, G. L., Wang, S. H., and Harwood, R. S.: Hydroxyl in the stratosphere and mesosphere – Part 1: Diurnal variability, Atmos. Chem. Phys., 11, 955–962, https://doi.org/10.5194/acp-11-955-2011, 2011. a, b, c
Moussallam, Y., Rose-Koga, E. F., Koga, K. T., Medard, E., Bani, P., Devidal, J.-L., and Tari, D.: Fast ascent rate during the 2017-2018 Plinian eruption of Ambae (Aoba) volcano: a petrological investigation, Contrib. Mineral. Petrol., 174, 90, https://doi.org/10.1007/s00410-019-1625-z, 2019. a
Pattantyus, A. K., Businger, S., and Howell, S. G.: Review of sulfur dioxide to sulfate aerosol chemistry at Kilauea Volcano, Hawai'i, Atmos. Environ., 185, 262–271, https://doi.org/10.1016/j.atmosenv.2018.04.055, 2018. a, b
Pisso, I., Sollum, E., Grythe, H., Kristiansen, N. I., Cassiani, M., Eckhardt, S., Arnold, D., Morton, D., Thompson, R. L., Groot Zwaaftink, C. D., Evangeliou, N., Sodemann, H., Haimberger, L., Henne, S., Brunner, D., Burkhart, J. F., Fouilloux, A., Brioude, J., Philipp, A., Seibert, P., and Stohl, A.: The Lagrangian particle dispersion model FLEXPART version 10.4, Geosci. Model Dev., 12, 4955–4997, https://doi.org/10.5194/gmd-12-4955-2019, 2019. a, b, c
Pommrich, R., Müller, R., Grooß, J.-U., Konopka, P., Ploeger, F., Vogel, B., Tao, M., Hoppe, C. M., Günther, G., Spelten, N., Hoffmann, L., Pumphrey, H.-C., Viciani, S., D'Amato, F., Volk, C. M., Hoor, P., Schlager, H., and Riese, M.: Tropical troposphere to stratosphere transport of carbon monoxide and long-lived trace species in the Chemical Lagrangian Model of the Stratosphere (CLaMS), Geosci. Model Dev., 7, 2895–2916, https://doi.org/10.5194/gmd-7-2895-2014, 2014. a, b, c
Redington, A. L., Derwent, R. G., Witham, C. S., and Manning, A. J.: Sensitivity of modelled sulphate and nitrate aerosol to cloud, pH and ammonia emissions, Atmos. Environ., 43, 3227–3234, https://doi.org/10.1016/j.atmosenv.2009.03.041, 2009. a
Robock, A.: Volcanic eruptions and climate, Rev. Geophys., 38, 191–219, https://doi.org/10.1029/1998RG000054, 2000. a
Rolph, G., Draxler, R., and Depena, R.: Modeling Sulfur Concentrations and Depositions in the United-States During Anatex, Atmos. Environ., 26, 73–93, https://doi.org/10.1016/0960-1686(92)90262-J, 1992. a, b, c
SACS: Support to Aviation Control Service, https://sacs.aeronomie.be (last access: 31 August 2023), 2022. a
Sander, R.: Compilation of Henry's law constants (version 4.0) for water as solvent, Atmos. Chem. Phys., 15, 4399–4981, https://doi.org/10.5194/acp-15-4399-2015, 2015. a, b, c
Schmidt, A., Ostro, B., Carslaw, K. S., Wilson, M., Thordarson, T., Mann, G. W., and Simmons, A. J.: Excess mortality in Europe following a future Laki-style Icelandic eruption, P. Natl. Acad. Sci. USA, 108, 15710–15715, https://doi.org/10.1073/pnas.1108569108, 2011. a
Slinn, W. G. N.: Rate-Limiting Aspects of In-Cloud Scavenging, J. Atmos. Sci., 31, 1172–1173, https://doi.org/10.1175/1520-0469(1974)031<1172:RLAOIC>2.0.CO;2, 1974. a
Stuart, A. L. and Jacobson, M.: A numerical model of the partitioning of trace chemical solutes during drop freezing, J. Atmos. Chem., 53, 13–42, 2006. a
Theys, N., De Smedt, I., Yu, H., Danckaert, T., van Gent, J., Hörmann, C., Wagner, T., Hedelt, P., Bauer, H., Romahn, F., Pedergnana, M., Loyola, D., and Van Roozendael, M.: Sulfur dioxide retrievals from TROPOMI onboard Sentinel-5 Precursor: algorithm theoretical basis, Atmos. Meas. Tech., 10, 119–153, https://doi.org/10.5194/amt-10-119-2017, 2017. a
Theys, N., Romahn, F., and Wagner, T.: S5P Mission Performance Centre Sulphur Dioxide Readme, https://sentinel.esa.int/documents/247904/3541451/Sentinel-5P-Sulphur-Dioxide-Readme.pdf (last access: 31 August 2023), 2020. a, b
Veefkind, J., Aben, I., McMullan, K., Förster, H., de Vries, J., Otter, G., Claas, J., Eskes, H., de Haan, J., Kleipool, Q., van Weele, M., Hasekamp, O., Hoogeveen, R., Landgraf, J., Snel, R., Tol, P., Ingmann, P., Voors, R., Kruizinga, B., Vink, R., Visser, H., and Levelt, P.: TROPOMI on the ESA Sentinel-5 Precursor: A GMES mission for global observations of the atmospheric composition for climate, air quality and ozone layer applications, Remote Sens. Environ., 120, 70–83, https://doi.org/10.1016/j.rse.2011.09.027, 2012. a, b
Webster, H. and Thomson, D.: The NAME wet deposition scheme, https://library.metoffice.gov.uk/Portal/Default/en-GB/RecordView/Index/197129 (last access: 31 August 2023), 2014. a, b, c
Wu, X., Griessbach, S., and Hoffmann, L.: Long-range transport of volcanic aerosol from the 2010 Merapi tropical eruption to Antarctica, Atmos. Chem. Phys., 18, 15859–15877, https://doi.org/10.5194/acp-18-15859-2018, 2018. a
Wu, X., Griessbach, S., and Hoffmann, L.: Equatorward dispersion of a high-latitude volcanic plume and its relation to the Asian summer monsoon: a case study of the Sarychev eruption in 2009, Atmos. Chem. Phys., 17, 13439–13455, https://doi.org/10.5194/acp-17-13439-2017, 2017. a, b, c, d, e