Assessing predicted cirrus ice properties between two deterministic ice formation parameterizations

Determining the dominant ice nucleation mode in cirrus is still an open research question that impacts the ability to assess the climate impact of these clouds in numerical models. Homogeneous nucleation is generally well understood. More uncertainty surrounds heterogeneous nucleation due to a weaker understanding of the complex physio-chemical properties (e.g., ice nucleation efficiency and atmospheric abundance) of ice nucleating particles (INPs). This hampers efforts to simulate their interactions with cirrus, which is crucial in order to assess the effect these clouds have on the climate system. Kärcher and Marcolli (2021) introduced a new deterministic heterogeneous ice nucleation parameterization based on the differential activated fraction (AF), which describes the number of INPs that activate ice within a specified temperature or ice saturation ratio interval. They argued that this new approach with explicit INP budgeting, which removes INPs from the total population after they nucleate ice, could help to correct a potential overprediction of heterogeneous nucleation within cirrus when budgeting is not considered. We formulated a general circulation model (GCM)-compatible version of the differential AF parameterization for simulating only deposition nucleation within in situ cirrus and compared it to the method currently employed in the ECHAM6.3-HAM2.3 GCM that is based on cumulative AF. This default cumulative AF approach does not use explicit INP budgeting but instead implicitly budgets for INPs that nucleated ice using a differential ice crystal number concentration variable to calculate whether new ice formation should be added to the pre-existing concentration. In a series of box model simulations that were based on the cirrus sub-model from ECHAM, we found that the cumulative approach likely underpredicts heterogeneous nucleation in cirrus, as it does not account for interstitial INPs remaining from the previous GCM time step. However, as the cases that we simulated in the box model were rather extreme, we extended our analysis to compare the differential and cumulative AF approaches in two simulations in ECHAM-HAM. We find that choosing between these two approaches impacts ice nucleation competition within cirrus in our model. However, based on our 5-year simulations, the small and insignificant difference in the top-of-atmosphere radiative balance of 0.02±0.35 Wm⁻² means that the overall climate impact is negligible. We argue that while our GCM-compatible differential AF parameterization is closer to first principles, the default approach based on cumulative AF is simpler due to the lack of additional tracers required. Finally, our new approach could be extended to assess the impact of explicit versus implicit INP budgeting on the ice crystal number concentration produced by immersion freezing of mineral dust particles, as this is also an important mechanism in cirrus.

1 Introduction

Historically, clouds introduced the largest uncertainties in the projections of climate. Today, however, significant improvements in our understanding provide more confidence that cloud feedbacks will amplify climate warming in the future, for example through reductions in tropical low cloud cover (Zelinka et al., 2017, 2020; Forster et al., 2021). While more is understood about cloud feedbacks in response to a changing climate state (e.g., from the forcing associated with a quadrupling of atmospheric CO₂ as simulated by CMIP6 experiments; Eyring et al., 2016), there is less understanding of the present-day radiative forcing from the interactions between clouds and aerosol particles that can act as cloud condensation nuclei (CCN) and ice nucleating particles (INPs; Heyn et al., 2017; Storelvmo, 2017; Bellouin et al., 2020). In fact, estimates of the present-day effective radiative forcing due to aerosol–cloud interactions, which includes rapid adjustments (Sherwood et al., 2015), (e.g., a cloud glaciation effect due to elevated INP concentrations; Lohmann, 2002), are in the range of −1.36 [−2.65 to −0.07] Wm⁻² for an average period of 2005 to 2015 relative to 1850 (Bellouin et al., 2020), or −1.0 [−1.7 to −0.3] Wm⁻² for 2014 relative to 1750, based on CMIP6 experiments, as reported in the latest assessment report by the Intergovernmental Panel on Climate Change (IPCC; Forster et al., 2021).

The interactions of aerosols with liquid clouds are well established (Twomey, 1959, 1977; Albrecht, 1989; Ackerman et al., 2004; Small et al., 2009; Christensen et al., 2020), whereas the impacts of aerosols acting as INPs on mixed-phase and ice clouds (i.e., cirrus) contain a higher level of uncertainty (Storelvmo, 2017; Bellouin et al., 2020). For cirrus, the subject of this technical note, accurately simulating ice formation mechanisms is still an open research topic that impedes further understanding of cirrus climate impacts, including assessing potential climate intervention strategies (Storelvmo et al., 2013; Zhou and Penner, 2014; Penner et al., 2015; Gasparini and Lohmann, 2016; Krämer et al., 2016; Kärcher, 2017; Storelvmo, 2017; Gasparini et al., 2020; Krämer et al., 2020; Kärcher et al., 2022; Tully et al., 2022c).

Cirrus form from the nucleation of ice in the upper troposphere via homogeneous or heterogeneous nucleation. The prevalence of one mode over the other in the atmosphere remains uncertain, leaving a large gap in understanding cirrus radiative properties, as these two ice formation mechanisms can lead to vastly different cloud properties (Lohmann et al., 2008; Storelvmo, 2017; Krämer et al., 2020; Cziczo et al., 2013). Homogeneous nucleation occurs as the spontaneous freezing of aqueous solution droplets (otherwise referred to as liquid aerosols) at conditions with a temperature below roughly 238 K and a high supersaturation with respect to ice (Koop et al., 2000). Ice crystal growth following such an event is typically limited, as water vapor that has low concentrations in the upper troposphere is rapidly consumed (Ickes et al., 2015), leading to numerous and small ice crystals that act to absorb outgoing longwave (LW) radiation and re-emit it at a lower magnitude than the underlying surface. Heterogeneous nucleation occurs at a much lower ice supersaturation and at warmer temperatures than homogeneous nucleation due to the presence of an INP. Several modeling studies found that a sufficient number of INPs can inhibit homogeneous nucleation through preferential formation of ice crystals followed by rapid deposition of water vapor onto their surfaces (Lohmann et al., 2008; Storelvmo et al., 2013; Storelvmo and Herger, 2014; Storelvmo et al., 2014; Penner et al., 2015; Jensen et al., 2016). As the number of ice crystals in this case is rather limited by the availability of INPs, which are sparse in the upper troposphere (DeMott et al., 2003), they tend to be larger in size than those formed purely by homogeneous nucleation. This leads to an optically thinner cloud that is less effective at trapping LW radiation in an effect coined the “negative Twomey effect” (Kärcher and Lohmann, 2003). However, under high dynamic forcing (e.g., high vertical velocity) or without a sufficient number of INPs, heterogeneous nucleation may not be efficient enough to prevent high ice superaturations required for homogeneous nucleation.

The theory behind homogeneous nucleation is relatively well understood (Koop et al., 2000; Ickes et al., 2015), with new evidence perhaps suggesting higher freezing onsets at cold temperatures for sulfuric acid droplets (Schneider et al., 2021). However, heterogeneous nucleation in general is still a topic of substantial research (Cziczo and Froyd, 2014; Kanji et al., 2017). Specifically, the ability of certain materials to act as an INP, e.g., mineral dust (Murray et al., 2012), which is likely the most abundant INP species in the atmosphere especially downstream of source regions (Froyd et al., 2022) or black carbon particles (Mahrt et al., 2018, 2020), as well as the characterization of their abundance in the atmosphere (Li et al., 2022). Furthermore, heterogeneous nucleation can occur via several mechanisms. For example, from immersion freezing within a solution droplet or by the deposition of water vapor onto the surface of an INP (Vali et al., 2015; Kanji et al., 2017; Heymsfield et al., 2017), the former of which is thought to be the most common heterogeneous nucleation mechanism in cirrus (Kärcher and Lohmann, 2003), though newer evidence points to the abundance of deposition nucleation in the upper troposphere (Froyd et al., 2022).

Generally, the factors discussed above lead to an overall poor predictability of how INPs influence heterogeneous nucleation mechanisms in cirrus, and they contribute to uncertainties when simulating these mechanisms in numerical models. This makes it difficult to simulate the impact on ice nucleation competition in cirrus, which influences the ability to reliably estimate the radiative effects of these clouds.

Due to their coarse resolution, general circulation models (GCMs) rely on parameterizations of both homogeneous and heterogeneous nucleation based on laboratory and field-based measurements of ice formation. These parameterizations can follow either a stochastic (time dependent) approach based on ice nucleation rates or a deterministic (time independent) approach. For example, homogeneous nucleation of aqueous solution droplets is simulated in the ECHAM-HAM GCM following the stochastic approach by Koop et al. (2000) that is based on simplified assumptions of classical nucleation theory. A common method for simulating deterministic ice nucleation mechanisms is based on the activated fraction (AF or frozen fraction), i.e., the number of ice-active particles at specific temperature and/or ice saturation conditions out of a population of particles (Vali, 1971; Vali et al., 2015; Vali, 2019; Kärcher and Marcolli, 2021). This quantity is derived from cloud or continuous flow chamber experiments of the number of frozen particles (Kärcher and Marcolli, 2021). Vali (1971) and Vali (2019) defined two approaches for determining the number of INPs that become ice active. The differential AF approach describes the number of INPs that are active per temperature interval (assuming temperature decreases during a freezing experiment or as a theoretical air parcel rises within a model), whereas the cumulative AF describes the total number of active INPs between the temperature at the onset of ice activity and a given (lower) temperature. This latter quantity equates to the integral of the differential AF over the specified temperature range. However, as Kärcher and Marcolli (2021) highlight, care must be taken when determining which approach to use when calculating the number of ice crystals that can form on INPs. This is especially true for numerical models that simulate the temporal evolution of the ice saturation ratio, based on temperature, to calculate new ice crystal formation, like in ECHAM-HAM (Sect. 2.1). For example, if a model budgets INPs by removing them from the total population after they nucleate ice (i.e., explicit INP budgeting), then using the cumulative AF approach may overpredict the number of heterogeneously nucleated ice crystals (see the example in Sect. 2.1.2), as it is based on the total number of INPs that could activate between the freezing onset temperature and a given temperature (Vali, 1971, 2019).

Kärcher and Marcolli (2021) introduced a new parameterization to simulate the number of ice particles resulting from heterogeneous nucleation based on the differential AF approach (Vali, 1971, 2019) while employing INP budgeting (Sect. 2.1). They demonstrated that it is able to counteract the potential overprediction of heterogeneous nucleation in cirrus. Meanwhile, Muench and Lohmann (2020) reformulated the ice nucleation mechanisms for cirrus in the ECHAM-HAM GCM (Stevens et al., 2013; Neubauer et al., 2019; Tegen et al., 2019) to also include an AF-based approach that is, instead, based on cumulative AF. Note that this new approach in ECHAM-HAM is not the same as the cumulative AF approach described by Kärcher and Marcolli (2021). Muench and Lohmann (2020) introduced implicit INP budgeting by using a differential ice crystal number concentration (ICNC) variable (Sect. 2.1.1), which accounts for the issue stated by Kärcher and Marcolli (2021) that using the cumulative AF approach may overpredict the number of ice-active INPs (see the example in Sect. 2.1.2).

As the differential AF method introduced by Kärcher and Marcolli (2021) was applied in a process model, it does not capture the complexities of the cirrus formation environment like in a GCM. Therefore, a technical analysis is needed for the implications of using a new approach to simulate deterministic ice nucleation via AF. In this technical note, we present a comparative analysis of cirrus ICNC between a GCM-compatible differential AF parameterization based on Kärcher and Marcolli (2021) and the default AF approach used in ECHAM-HAM (Muench and Lohmann, 2020). Note that our analysis is applicable only to deposition nucleation mechanisms within in situ cirrus. Extending the analysis to other ice nucleation mechanisms, namely immersion freezing, is discussed below. In Sect. 2 we describe the box model we developed based on ECHAM-HAM to analyze these differences. In Sect. 3 we present the box model results and extend our analysis by presenting results for two simulations with the ECHAM-HAM GCM, followed by a discussion. Finally, we include concluding remarks in Sect. 4.

2 Methods

We formulated a box model to analyze deterministic, AF-based ice nucleation within cirrus clouds. The model is based on the cirrus ice nucleation scheme in the ECHAM-HAM GCM by Kärcher et al. (2006), Kuebbeler et al. (2014), and Muench and Lohmann (2020). In this note, we utilize the box model to compare a GCM-compatible differential AF approach based on Kärcher and Marcolli (2021) to understand heterogeneous nucleation to the AF approach by Muench and Lohmann (2020), hereafter abbreviated as ML20.

2.1 Ice formation mechanisms

The cirrus model in ECHAM-HAM is called from the cloud microphysics scheme and calculates the number of new ice crystals that form in in situ cirrus. It uses a sub-time-stepping approach; i.e., within a single GCM time step (i) there are several sub-time steps (j) of the cirrus scheme to simulate the temporal evolution of the ice saturation ratio (S_i) in an adiabatically ascending air parcel during the formation stage of a cloud (Kuebbeler et al., 2014; Tully et al., 2022c). In this note, we extracted only the cirrus sub-model code from ECHAM-HAM to formulate a box model of ice nucleation within cirrus (see Sect. 2.2 and 2.3). In its full form, the cirrus sub-model calculates the competition of water vapor between deposition onto pre-existing ice particles and phase transitions by homogeneous or heterogeneous nucleation mechanisms that form new ice crystals (Tully et al., 2022c).

Muench and Lohmann (2020) distinguish between two approaches (a threshold approach and a continuous approach) for heterogeneous nucleation within cirrus. For the threshold approach, as soon as the S_i reaches a critical value (i.e., a threshold), the model assumes nucleation rates are efficient enough such that all of the available aerosols that can potentially serve as INPs nucleate ice during a single step of the cirrus sub-model. For immersion freezing of internally mixed mineral dust particles, it is assumed that only 5 % of the background concentration can act as INPs (Gasparini and Lohmann, 2016; Muench and Lohmann, 2020). Heterogeneous deposition nucleation, on the other hand, is based on laboratory measurements of AF by Möhler et al. (2006), which are determined by temperature (T) and S_i and which increases continuously with decreasing T and increasing S_i. In the cirrus sub-model, this approach is applied to deposition nucleation onto externally mixed (insoluble) mineral dust particles only.

2.1.1 Default ML20 cumulative AF approach

Explicit INP budgeting is not considered for dust deposition nucleation in the default version of the cirrus sub-model in ECHAM-HAM. Instead, budgeting is implied at each cirrus sub-time step (j) through the differential ICNC (ΔICNC), following ML20, that takes the form

$$\begin{array}{}\text{(1)}& \mathrm{\Delta }{\mathrm{ICNC}}_j={\mathit{\varphi }}_j\cdot N_{\mathrm{0}}-{\mathrm{ICNC}}_{j-\mathrm{1}},\end{array}$$

where ϕ_j is the AF based on Möhler et al. (2006), N₀ is the initial INP population, and ICNC_j−1 is the ICNC from the previous cirrus sub-model time step. Negative ΔICNC values are set equal to zero. Therefore, the ICNC at each cirrus sub-model time step is only ever updated if the new ice formation exceeds the previously formed concentration. The advantage of this approach over KM21 is that it is simple (see Sect. 2.2). The activation of INPs during the lifetime of a cirrus is implicitly included by requiring that ICNC_j ≥ ICNC_j−1.

2.1.2 KM21 differential AF approach

Kärcher and Marcolli (2021), hereafter KM21, introduced a new method to describe ice nucleation by the number of activated particles. In their study, they argue that using laboratory-based cumulative AF (hereafter ϕ), when coupled to INP budgeting, overpredicts the number of ice crystals originating from heterogeneous nucleation, as ϕ is based on the total INP population (N₀). Instead, they formulated a differential AF (ψ) approach, which considers only the number of particles that can activate as a result of incremental changes in S_i during a time step j−1 to j. The method is based on the probability that the remaining INPs, following explicit INP budgeting, in the current time step j do not become ice active. Thus, ψ follows the form (Eq. 6 of KM21)

$$\begin{array}{}\text{(2)}& \begin{array}{lll}{\mathit{\psi }}_j=\frac{\mathrm{\Delta }{\mathit{\varphi }}_j}{\mathrm{1}-{\mathit{\varphi }}_{j-\mathrm{1}}},& \text{where}& \mathrm{\Delta }{\mathit{\varphi }}_j={\mathit{\varphi }}_j-{\mathit{\varphi }}_{j-\mathrm{1}},\\ & \text{and}& \mathrm{0}\le {\mathit{\psi }}_j\le \mathrm{1}.\end{array}\end{array}$$

As a short conceptual example of their argument (see also KM21; Fig. 1), let us assume two cirrus model time steps starting from ${\mathit{\varphi }}_{j=\mathrm{0}}=\mathrm{0}$. In the first cirrus model time step ${\mathit{\varphi }}_{j=\mathrm{1}}=\mathrm{0.05}$, and in the second cirrus model time step ${\mathit{\varphi }}_{j=\mathrm{2}}=\mathrm{0.1}$ under ambient temperature and S_i. Starting from an initial INP population (N₀) of 100 L⁻¹, the expected ICNC at ϕ₂=0.1 is 10 L⁻¹. Any approach needs to result in 10 L⁻¹ at this AF. However, using the cumulative AF approach as described in KM21, for ϕ₁ = 0.05 the resulting ICNC after this first step is 5 L⁻¹, which equates to $\mathrm{\Delta }N=\mathrm{5}{\mathrm{L}}^{-\mathrm{1}}$ INPs. With explicit INP budgeting, the resulting population after the first time step is N₀-ΔN=95 L⁻¹. In the second time step, ϕ₂ is 0.1. Using this value alone results in a ΔN=9.5 L⁻¹ and thus a total ICNC after this step of 14.5 L⁻¹. This is larger than 10 L⁻¹ ICNC therefore the number of activated particles is overpredicted in this case, as the INPs activated in the first time step were ignored during activation in the second time step. Using the differential AF approach as presented in Eq. (2), with ϕ₂=0.1 and ϕ₁=0.05, the resulting ψ₁=ϕ₁ equates to 0.05 and ψ₂ to roughly 0.053. When applying this to the number of available INPs after the first time step (95 L⁻¹), ΔN=5 L⁻¹, bringing the total ICNC after the second time step instead to 10 L⁻¹. Although the resulting error between the ICNC values after the second time step in this short example is not large, not accounting for previously activated INPs in a correct manner could drastically increase the amount of heterogeneous nucleation on mineral dust particles, leading to vastly different cirrus properties.

The KM21 method in its current form only considers one cirrus formation cycle, which in ECHAM-HAM occurs as a sub-loop within a single GCM time step of 7.5 min. A typical cirrus cloud exists over several GCM time steps. Between each time step, not only can the number of available INPs in a given grid box differ based on aerosol transport and vertical diffusion, but also the temperature and S_i conditions can change based on the dynamics of the model. Therefore, we made adjustments to the KM21 approach presented above for climate model compatibility (KM21_GCM). The new approach is described in more detail in Sect. 2.2.

2.2 Cirrus box model

As described previously, we formulated a box model based on the cirrus sub-model in ECHAM-HAM. It simulates the temporal evolution of S_i during the adiabatic ascent of a theoretical air parcel. As the Si is directly related to the updraft velocity (Tully et al., 2022c), to quantify the effect of vapor deposition onto newly formed or pre-existing ice crystals a fictitious downdraft is added to the updraft velocity. The resulting net updraft velocity is termed the “effective updraft velocity” and is used to calculate S_i (note that the original updraft velocity is used to compute vapor deposition onto newly formed or pre-existing ice crystals). If an environment has a high background INP concentration that leads to numerous new ice crystals forming via heterogeneous nucleation and/or if it contains a high concentration of pre-existing ice crystals (e.g., from convective detrainment), then the vapor deposition onto these ice crystals may be sufficient to prevent the development of high S_i values suitable for homogeneous nucleation.

To emulate the GCM we define starting conditions for temperature, pressure, S_i, and the updraft in order to simulate the adiabatic ascent of an air parcel during the cirrus formation stage. To simulate deterministic, AF-based ice formation onto externally mixed accumulation and coarse mode mineral dust particles (Stier et al., 2005; Zhang et al., 2012), we also defined two “freezing modes”, respectively, following Muench and Lohmann (2020). Full ice nucleation competition (Gasparini and Lohmann, 2016; Tully et al., 2022c) was also tested by adding additional modes for homogeneous nucleation of liquid sulfate aerosol, immersion freezing of internally mixed mineral dust particles, and pre-existing ice. However, the results for these latter tests are not shown in this note, as the competition between ice formation mechanisms as well as vapor deposition onto pre-existing ice crystals did not change the outcome of our box model compared to our dust deposition-only tests. The starting conditions we tested for this study are described in Sect. 2.3.

The KM21 approach was introduced in Sect. 2.1. As this method is only valid for a single cirrus formation cycle, we reformulated the parameterization in our box model for compatibility with multiple cirrus cycles in a GCM (KM21_GCM). Specifically, in order to calculate the differential AF (ψ) in the cirrus sub-model after the first GCM time step (i>1), following Eq. (2), the final AF (ϕ_j=n) from the cirrus cycle in the previous GCM time step (i−1) is required, where n is the number of cirrus sub-model time steps. As a result, we implemented a tracer in our box model that accounts for S_i oscillations to mimic tracing across GCM time steps. Following KM21, the tracer (ϕ_max) is set equal to the maximum AF value reached within a cirrus formation cycle. If in the next cycle the S_i is lower than the previous cycle, then no new ice formation can occur until the S_i increases and by extension ϕ_j exceeds ϕ_max. Note that outside of a cloud, ϕ is set equal to zero.

S_i oscillations are not the only factor to consider across GCM time steps. INP concentrations can also change. Therefore, we also trace the initial INP concentration (N_0,i) in our box model. In subsequent time steps we refer to this quantity as the previous INP concentration ($N_{\mathrm{0},i-\mathrm{1}}$). Considering both the maximum AF (${\mathit{\varphi }}_{i-\mathrm{1},j=n}$) and the previous INP concentration tracers, we reformulated the KM21 calculation of differential AF (Ψ; KM21_GCM) as the weighted average of ϕ and ψ from the INP concentration (N_0,i) of the current GCM time step (current cirrus formation cycle) as follows:

$$\begin{array}{}\text{(3)}& {\mathrm{\Psi }}_j={\displaystyle \frac{{\mathit{\varphi }}_j\cdot (N_{\mathrm{0},i}-N_{\mathrm{0},i-\mathrm{1}})-(N_{\mathrm{0},i-\mathrm{1}}\cdot {\mathit{\psi }}_j)}{N_{\mathrm{0},i}}},\end{array}$$

where ψ_j is the differential AF according to Eq. (2). The previous AF (ϕ_j−1) in this case is ${\mathit{\varphi }}_{i-\mathrm{1},j=n}$. $N_{\mathrm{0},i-\mathrm{1}}$ tracer is also set to zero outside of the cloud. Note as well that in the ECHAM-HAM GCM both $N_{\mathrm{0},i-\mathrm{1}}$ and ϕ_max are not advected or diffused.

The video supplement to this study (Tully et al., 2023a) provides more information on the theoretical understanding of our new KM21_GCM approach and compares it to our default ML20 approach. In summary, we classify different ice nucleation behaviors based on the available INP concentration, following Eq. (3). In subsequent GCM time steps, following the first, we assume that some INPs were ice active in the previous GCM time step and are thus removed by subtracting the ICNC that formed previously (ICNC${}_{i\mathrm{-}\mathrm{1},j=n}$) on INPs (N_0,i). Out of N_0,i we assume some fraction is made up of remaining (“leftover”) interstitial INPs that did not activate ice in the previous GCM time step (N_0,i−1) and the remaining fraction contains particles that are new to the system. To obtain the leftover INP concentration, we also subtract ICNC${}_{i\mathrm{-}\mathrm{1},j=n}$ from the INP concentration from the previous GCM time step.

In the first instance of ice formation in the current cirrus cycle (current GCM time step), the leftover INPs nucleate ice according to ψ_j and the newly available INPs nucleate ice according to ϕ_j as denoted in the numerator of Eq. (3). Not only does this approach consider changes in INP concentrations across GCM time steps, but it also accounts for changes in S_i. For example, if in the current GCM time step S_i is drastically lower than that in the previous time step, then no new ice formation will occur on the leftover INPs. However, ice formation can proceed on the newly available INPs if the S_i is sufficient to produce ice according to the AF calculation following Möhler et al. (2006). If the S_i increases in the current cirrus cycle compared to the previous one, then ice formation may occur on both the leftover and newly available INPs. Note that Eq. (3) also accounts for decreases in INP concentration across GCM time steps. In such a case the difference term on the left-hand side of the numerator of Eq. (3) is set to zero.

2.3 Experimental setup

There are several parameters that are available as input to our box model, including updraft, temperature, pressure, large-scale S_i, and INP concentration. For simplicity, we tested different combinations of large-scale S_i and INP concentrations over three cirrus formation cycles that emulate three GCM time steps. Each combination defines a “trend” that could be expected in a GCM over the three time steps that we used to conduct our simulations. We tested four different trends for a total of 16 tests with our cirrus box model to compare ML20 and KM21_GCM. The different combinations are summarized in Table 1. In these tests, we only considered heterogeneous nucleation on mineral dust, following the AF approaches as described in Sects. 2.1 and 2.2. We assess each case by the relative error between the KM21_GCM approach and the ML20 approach, according to Eq. (4). Finally, we conducted two simulations with the ECHAM-HAM GCM to compare ICNC fields and cloud properties between ML20 and KM21_GCM.

$$\begin{array}{}\text{(4)}& \mathrm{Error}={\displaystyle \frac{{\mathrm{ICNC}}_{\mathrm{KM}\mathrm{21}\mathrm{\_}\mathrm{GCM}}-{\mathrm{ICNC}}_{\mathrm{ML}\mathrm{20}}}{{\mathrm{ICNC}}_{\mathrm{ML}\mathrm{20}}}}\times \mathrm{100}\end{array}$$

Table 1 Summary of the different trends for large-scale S_i and aerosol concentration that are used as input to the cirrus box to compare ICNC between ML20 and KM21_GCM.

3 Results and discussion

3.1 Cirrus box model simulations

Of the 16 tests we conducted, six show agreement between ML20 and KM21_GCM in the predicted ICNC. For these cases we define agreement as a 0 % relative error between KM21_GCM and ML20 for each scenario as denoted by the white shading in Fig. 1. An additional three cases show only very small errors (<1.0 %), indicating that perhaps under most conditions the ML20 and KM21_GCM approaches do not lead to substantially different outcomes. Three additional cases show errors between 1.0 % and 10.0 %. The remaining four cases produce much larger errors (>17.0 %), which we discuss in more detail below. Note that in all cases with non-zero errors, KM21_GCM predicts higher ICNC than ML20.

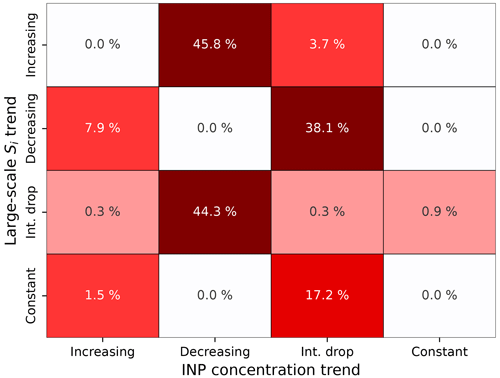
Figure 1 Heat map of maximum relative error between KM21_GCM and ML20 in the predicted ICNC from heterogeneous-only ice nucleation for the 16 tests we conducted with different combinations of large-scale S_i and INP concentration trends with the box model. Darker red shading denotes a larger non-zero error. Int. drop stands for intermediate drop.

Agreement between the ML20 and KM21_GCM approaches in the predicted ICNC is expected. On the one hand, while ML20 considers only the initial INP concentration (N₀) and does not include explicit INP budgeting, the ICNC is updated only if the amount of new ice formation as a portion of N₀ exceeds the ICNC from the previous sub-time step in the cirrus box model. As S_i increases within the updraft and the number of INPs that can nucleate ice increases based on higher S_i-dependent AF, eventually all available INPs will become ice active and ΔICNC will equate to zero, ceasing all new ice formation, as the AF cannot exceed 1.0. On the other hand, KM21_GCM follows an explicit INP-budgeting approach. Therefore, the number of newly nucleated ice crystals is proportional to a smaller number of available INPs that, in turn, is based on the number of newly formed ice crystals in each sub-time step in the cirrus box model. In the case of decreasing S_i and aerosol concentration trends, the lower S_i leads to lower AF values that prevent new ice formation after the first cycle (GCM time step). While these scenarios are valuable to understand consistency between ML20 and KM21_GCM, it is useful to examine non-zero errors between the two approaches. Therefore, the rest of this section will focus on the cases where we found disagreements between ML20 and KM21_GCM in the predicted ICNC. For brevity, only a few selected cases where we found non-zero errors are presented in this note. The remainder of the tests we conducted are presented in Appendix A for completeness.

The largest errors of 45.8 % and 44.3 % occur for the cases with a decreasing INP concentration trend, with an increasing and intermediate drop in large-scale S_i, respectively (Fig. 1). The predicted ICNC and S_i profiles for these two cases are presented in Fig. 2. A non-zero error between the predicted ICNC for KM21_GCM and ML20 occurs from the start of the second cirrus cycle in the first case (Fig. 2a) and from the start of the third cirrus cycle in the second case (Fig. 2b), where KM21_GCM predicts a higher ICNC than ML20. For the first case, this is due to the fact that KM21_GCM considers that some portion of the new INP concentration comprises leftover INPs that did not have a chance to nucleate ice by the end of the previous cirrus cycle. As the INP concentration decreases between each cycle, it is assumed that the available INPs are made up of only those that were previously available, meaning no new INPs enter the system. This emulates removal processes in the GCM (e.g., by vertical diffusion or precipitation scavenging). Therefore, our box model calculates ice formation only following the differential AF approach (ψ) in Eq. (2). As the S_i increases from roughly 1.28 from the end of the first cirrus cycle to 1.3 at the start of the second cirrus cycle, there is a large increase initially in the predicted ICNC. The rate of change of the predicted ICNC for our KM21_GCM approach decreases in subsequent sub-time steps of the cirrus model as the S_i increases only incrementally. For ML20, the implicit INP-budgeting approach prevents new ice formation from occurring at the start of the second cirrus cycle, despite a larger AF, as the number of newly formed ice crystals that could nucleate onto the fewer number of available INPs does not exceed the pre-existing ICNC. No new ice formation occurs until the S_i increases sufficiently after nearly 6 min. The error between the two approaches in this case grows in the third cirrus cycle, as no new ice formation occurs according to ML20 due to a lower availability of INPs, whereas KM21_GCM predicts higher ICNC due to the increasing S_i and the availability of leftover INPs. The box model works in much the same way for the second case presented in Fig. 2b. The exception is that for the second cirrus cycle there is no new ice formation predicted by KM21_GCM or ML20. The large-scale S_i decreases drastically at the start of this cycle and never grows sufficiently to produce an AF following Möhler et al. (2006) that exceeds the maximum AF from the first cirrus cycle (for KM21_GCM) or produces enough ice to exceed the pre-existing concentration (for ML20). At the start of the third cirrus cycle, the predicted ICNC for both KM21_GCM and ML20 follows the same behavior as the previous example (Fig. 2a).

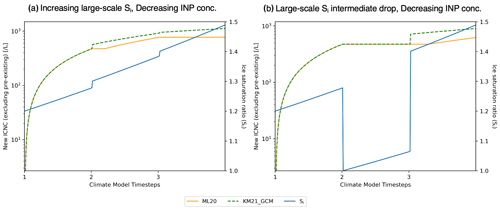
Figure 2 Temporal evolution of predicted heterogeneous-only ICNC and S_i for the cases with decreasing INP concentrations across three GCM time steps for (a) the increasing large-scale S_i and (b) the intermediate drop in large-scale S_i. Each line as noted in the legend refers to the predicted ICNC following our ML20 approach (solid orange); our GCM-compatible differential AF approach, KM21_GCM, based on KM21 (dashed green); and the S_i (solid blue) based on the large-scale S_i provided as input to our cirrus box model, which evolves according to the effective updraft velocity. Note the difference in scales between (a) and (b) for the predicted new ICNC on the left y axis of both plots.

We also find relatively large non-zero errors between KM21_GCM and ML20 for the cases with decreasing and constant large-scale S_i trends and an intermediate drop in INP concentration (Fig. 1). The profiles of the predicted ICNC and S_i for both of these cases are presented in Fig. 3. We find similar behavior for both cases, with new ice formation predicted in the first cirrus cycle and no new ice formation predicted in the second cycle due to the lower availability of INPs. A non-zero error for both cases occurs only in the third cirrus cycle after a large increase in the INP concentration (1000 to 6000 L⁻¹ for both dust modes). Following KM21_GCM, it is assumed that a significant fraction of the larger INP concentration consists of particles that are new to the system (e.g., from transport with the wind into a theoretical grid box) and a smaller fraction that did not yet have a chance to nucleate ice. Therefore the model calculates the weighted mean of the new INPs that nucleate ice cumulatively (ϕ) and the leftover INPs that follow the differential AF (ψ) following Eq. (3). However, this occurs only in the second sub-time step after the S_i increases above 1.2 within the updraft. Following the procedure in the GCM, ice formation is not calculated when the large-scale S_i≤1.2, as the Möhler et al. (2006) AF would be zero. Therefore, with our KM21_GCM approach we consider the different ice nucleation behaviors of the available INPs only in the first instance that ice formation can occur. In both cases new ice formation onto the newly available INPs is small, as the S_i is relatively low. There is no new ice formation onto any leftover INPs following the differential AF approach because the S_i decreases significantly relative to the maximum achieved in the previous cirrus cycle.

The maximum (threshold) AF is also recalculated during the first instance of ice formation in the third cirrus cycle for both cases presented in Fig. 3 to account for the larger availability of INPs. This new value is used for subsequent sub-time steps. For the case with a decreasing trend in large-scale S_i (Fig. 3a), this eventually leads to a large amount of new ice formation according to ψ (Eq. 2) as the S_i increases incrementally within the updraft. Meanwhile, ML20 does not predict any new ice formation during the third cirrus cycle in this case due to the relatively low S_i-dependent AFs that produce new ice formation that cannot exceed the pre-existing ICNC. This specific case shows the most notable difference between KM21_GCM and ML20. While both approaches account for the number of INPs contained within ice crystals, with scaling the available INP concentration for KM21_GCM and by taking away the pre-existing ICNC for ML20, we find that applying each method in the cirrus sub-model can lead to large differences in the predicted ICNC, which could have implications on cirrus climate impacts.

For the case with a constant trend in large-scale S_i (Fig. 3b), the recalculated maximum AF following KM21_GCM leads to new ice formation earlier during the third cirrus cycle than ML20.

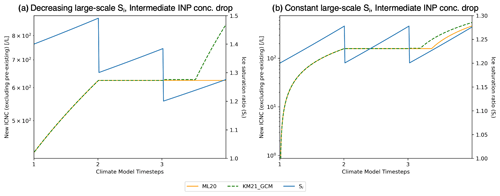
Figure 3 Temporal evolution of predicted heterogeneous-only ICNC and S_i for the cases with the intermediate drop in INP concentration for (a) the decreasing large-scale S_i and (b) the constant large-scale S_i across three GCM time steps. The lines as noted in the legend are consistent with the description under Fig. 2.

While three cases with matching large-scale S_i and INP concentration trends (increasing, decreasing, and constant) showed agreement (Fig. 1), the case where both quantities included an intermediate drop showed a small error of 0.3 %. Similarly, all cases with a constant INP concentration showed agreement, except for the case with an intermediate drop in large-scale S_i (0.9 %, Fig. 1). As the error for these cases is relatively small, and for brevity within this note, we present the predicted ICNC and S_i profiles in Appendix A. However, in summary, we find that our box model behaves similarly for both cases, albeit with different predicted ICNC values due to different INP concentrations. For both of these cases a small error occurs after a large increase of the INP concentration in the third cirrus cycle, similar to the cases presented in Fig. 3. The number of new ice crystals predicted by ML20 is less than that by KM21_GCM, consistent with the results shown previously. This is due to the fact that ML20 considers only the new INP concentration, which forms a sufficient amount of new ice crystals to exceed the pre-existing concentration.

Based on our box model results, the most significant difference between the ML20 and KM21_GCM approaches is the consideration of the previous INP concentration. ML20 mimics the default deterministic, AF-based approach by Muench and Lohmann (2020) for deposition nucleation on externally mixed mineral dust particles in the ECHAM-HAM GCM. It does not explicitly take the previous INP concentration into account and instead computes a differential ICNC based on the difference between the number of activated INPs and the pre-existing ICNC. Based on our box model results, it is likely that ML20 underpredicts the number of heterogeneously formed ice crystals under cirrus conditions compared to our KM21_GCM approach, as it neglects the different ice nucleation behaviors of available INPs (refer to the video supplement; Tully et al., 2023a). As the INP concentration changes between GCM time steps, it is reasonable to assume that some fraction of these INPs is made up of those that were previously present within the model and did not nucleate ice (leftover INPs), and the other fraction is made up of newly available INPs that have not yet been exposed to cirrus formation conditions. The KM21_GCM approach accounts for the leftover INPs and allows them to nucleate ice according to the differential AF, which, if the S_i decreases between GCM time steps, will be zero. The new approach also allows the new INPs to nucleate ice cumulatively in the first sub-time step or first instance with suitable ice formation conditions in the cirrus sub-model.

Some of the changes in large-scale S_i and INP concentrations we tested in the box model were rather extreme, in order to examine differences between KM21_GCM and ML20. However, our box model setup is limited, as we assume a constant temperature and updraft velocity. We also did not consider other processes such as ice sedimentation, transport, and mixing that would be simulated in a GCM. Furthermore, the KM21 parameterization was developed for a single air parcel within a process model that depicts ice formation within a single cirrus. It does not capture the complexities associated with changes in INP concentrations as well as S_i (among several other factors) across several hundreds of time steps in a typical GCM simulation. Therefore, we present a short analysis comparing our GCM-compatible differential AF parameterization, KM21_GCM, to our default ML20 approach for deterministic heterogeneous ice nucleation in EHCAM-HAM in Sect. 3.2.

3.2 GCM simulations

We conducted two simulations with the ECHAM6.3-HAM2.3 GCM (Stevens et al., 2013; Neubauer et al., 2019; Tegen et al., 2019) to compare the predicted ICNC between the ML20 and KM21_GCM approaches for deterministic heterogeneous ice nucleation within cirrus. Each simulation was run for 5 years between 2008 and 2012 and follows the same setup as the “Full_D19” simulation by Tully et al. (2022c), which also includes full ice nucleation competition between homogeneous nucleation on liquid sulfate aerosols, immersion freezing on internally mixed mineral dust particles, deposition nucleation on externally mixed mineral dust particles, and vapor deposition onto pre-existing ice crystals.

Figure 4 presents 5-year annual zonal mean ICNC tracers for ice originating from homogeneous (HOM) and heterogeneous (HET) nucleation in the cirrus sub-model (Kärcher et al., 2006; Kuebbeler et al., 2014; Muench and Lohmann, 2020) for ML20 and the HOM and HET differences between KM21_GCM and ML20. In this case the HET signal equates to the number tracer for heterogeneously nucleated ice on mineral dust particles (both internally and externally mixed), as this was the only active INP species for cirrus in our GCM simulations. The stippling in Fig. 4 displays insignificant data points based on an independent t test, following the false discovery rate method by Wilks (2016). This approach accounts for high spatial correlation of neighboring grid points where the null hypothesis cannot necessarily be rejected. Like in Tully et al. (2022c), these ICNC tracers are advected and diffused every GCM time step. Similarly, we calculate a 5 % significance based on the interannual variability of the 5-year simulations. For the remainder of this section, we base significance on this method.

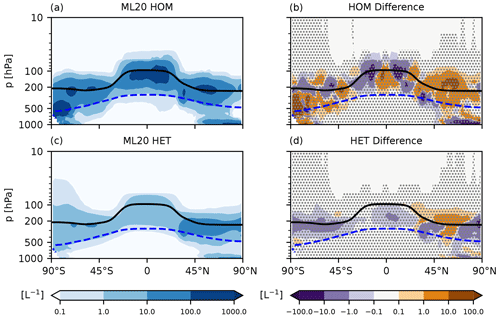
Figure 4 Five-year annual zonal mean in situ cirrus number tracers for ice originating from (a) homogeneous (HOM) and (c) heterogeneous (HET) nucleation for the ML20 simulation. The second column presents the respective ice number tracer differences between KM21_GCM and ML20 for (b) HOM and (d) HET. The black line is the WMO-defined tropopause, and the dashed blue line is the 238 K contour. The stippling in the difference plots shows insignificant data points.

In the control case, ML20, HOM clearly produces more ice in cirrus than HET, consistent with findings by Tully et al. (2022c). The HOM difference in Fig. 4b shows a mixed zonal signal by at most ±100 L⁻¹. This large change by roughly the same order of magnitude as ML20 HOM indicates that the change in HET parameterizations between ML20 and KM21_GCM affects ice nucleation competition within cirrus. One would expect that areas of positive HOM differences would correspond to areas of negative HET differences and vice versa. However, we find this is not necessarily the case in Fig. 4d. It also appears that KM21_GCM produces less HET on average than ML20 in most areas, which is inconsistent with our box model results. For those simulations KM21_GCM predicted higher ICNC values than ML20 (Sect. 3.1) due to large changes in large-scale S_i or INP concentration across the three GCM time steps we emulated. As this is not the case in our GCM simulations, it likely means that either such large changes in large-scale S_i and INP concentrations across GCM time steps do not occur frequently if at all in our model or that other factors such as temperature and updraft velocity influence our GCM results that we did not test in our box model.

In the tropics, just north of the Equator, we find that KM21_GCM produces less HET than ML20, which corresponds to an increase in HOM around the same region. Less HET in this area means that S_i growth is unimpeded with the updraft such that high values suitable for HOM occur more readily to produce more ice crystals by this mode. It is unclear whether this is reflected in the zonal profiles of cloud fraction and relative humidity (RH) differences in Fig. 5. Throughout the tropics we find only small cloud fraction and RH differences of around ±1 %; however, these signals are insignificant as denoted by the stippling.

There are significant, positive cloud fraction and RH differences between 1 % and 10 % towards the mid-latitudes and the poles in both hemispheres (Fig. 5a). In the Southern Hemisphere (SH) this corresponds to less frequent HET (Fig. 4d), which may allow more frequent high RH values suitable for HOM (Fig. 4b). As HOM occurs as a stochastic mechanism in our cirrus sub-model, the more numerous ice crystals forming in this way contribute to a higher fraction of cirrus. However, the increase in HOM is not consistent throughout the SH and is insignificant. There is a much clearer signal in the Northern Hemisphere (NH) mid-latitudes (roughly 45–60^∘ N) where both HOM and HET produce more ice in KM21_GCM than in ML20. While the positive HET ICNC difference is consistent with some of our findings from our box model results (Sect. 3.1) that showed KM21_GCM produced higher ICNC than ML20, it is insignificant for the 5 years we simulated with the GCM and is only evident in the NH. It is more likely that the GCM results confirm our box model results that show in most cases KM21_GCM and ML20 agree or have a very small error (Fig. 1).

The increase in HOM in the NH in Fig. 4b may be a result of additional latent heat release from more HET that causes air to rise and cool adiabatically and is caused by additional LW cloud-top cooling (Possner et al., 2017) from the higher cloud fractions we find in this area (Fig. 5). However, as HOM and HET, cloud fraction, and RH show positive differences, this is likely a systematic signal we find in the model.

While the zonal mean HOM and HET ICNC tracer differences for KM21_GCM (Fig. 4) are both notable (by at least ± 10 L⁻¹) relative to our control ML20 simulation, they are insignificant for the 5 years we tested. Therefore, it is difficult to describe the exact effect of choosing one deterministic ice formation parameterization (ML20 or KM21_GCM) over the other. Despite this finding, the maximum positive and significant difference for cloud fraction is 3.6 %, which equates to only a small positive top-of-atmosphere (TOA) warming effect by around 0.02±0.35 Wm⁻² that is driven predominately by a weaker shortwave (SW) cloud radiative effect (CRE). Similarly, the global mean net CRE difference between the two cases is indistinguishable from zero, 0.00±0.32 Wm⁻². These radiative differences are negligible relative to the estimated CRE from cirrus clouds of 5.7 and 4.8 Wm⁻² by Gasparini and Lohmann (2016) and Gasparini et al. (2020), respectively. Zonally the SW and LW CRE components are insignificant on a 95 % confidence level, except for a small region in the tropics (not shown).

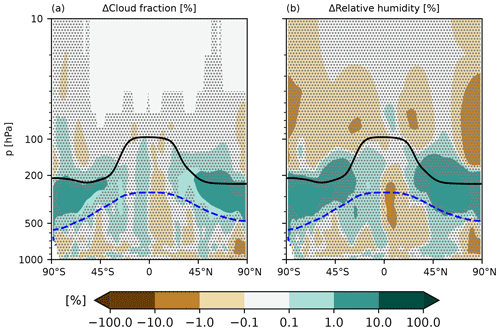
Figure 5 Five-year annual zonal mean (a) cloud fraction and (b) relative humidity differences between KM21_GCM and ML20. The black line is the WMO-defined tropopause, and the dashed blue line is the 238 K contour. The stippling in the difference plots shows insignificant data points.

Insignificant differences between ML20 and KM21_GCM in our GCM simulations relative to our box model simulations (Sect. 3) are not entirely unexpected. In the box model the changes in large-scale S_i and INP concentrations between each cirrus cycle were extreme in some cases, leading to large differences in the predicted ICNC. Such extreme changes are not unlikely in a GCM but may occur with a low frequency. In addition, we tested only heterogeneous nucleation in our box model, whereas we included full nucleation competition in our GCM simulations, following Gasparini and Lohmann (2016) and Tully et al. (2022c), that includes vapor deposition onto pre-existing ice crystal. This process was shown to have a large impact on cirrus properties in ECHAM-HAM, as it prevents S_i values from rising to high values after a sufficient number of ice crystals already formed (Kuebbeler et al., 2014; Gasparini and Lohmann, 2016).

Our GCM results do show that the choice of deterministic ice formation parameterization (ML20 versus KM21_GCM) has an impact on ice nucleation competition within cirrus. However, the small and insignificant changes in cirrus properties indicate that deposition nucleation onto externally mixed mineral dust particles does not contribute significantly to the total ice number in in situ cirrus. In fact, Tully et al. (2022c) showed that homogeneous nucleation dominates the ICNC with much higher nucleation rates than all heterogeneous nucleation mechanisms combined (immersion freezing and deposition nucleation; see their Appendix). Therefore, we argue that while the KM21_GCM approach is closer to first principles by accounting for different ice nucleation behavior of available INPs, the implicit budgeting approach by ML20 makes for a much simpler parameterization within a GCM, and it does not require additional tracers. The simulated climate with these two parameterizations is very similar in terms of TOA net radiation, despite significant differences between cirrus cloud fractions.

4 Conclusions

In this study we compared two approaches for simulating deterministic heterogeneous ice formation: a GCM-compatible version of the differential AF parameterization introduced by Kärcher and Marcolli (2021), KM21_GCM, and the default approach in the ECHAM-HAM GCM based on cumulative AF by Muench and Lohmann (2020), ML20. In a series of simulations using a box model, based on the cirrus sub-model of ECHAM-HAM (Kärcher et al., 2006; Kuebbeler et al., 2014; Muench and Lohmann, 2020), we found that ML20 underpredicts the number of ice particles originating from heterogeneous nucleation relative to KM21_GCM in cases when the large-scale S_i and INP concentration trends differed across the three cirrus cycles we simulated. This is due to the fact that ML20 does not explicitly consider changes in INP concentrations across GCM time steps nor does it consider the different ice nucleation behaviors of available INPs. KM21_GCM takes these factors into account and allows new INPs to nucleate ice according to the cumulative AF and leftover INPs to nucleate ice according to the differential AF.

We tested rather extreme changes in the large-scale S_i conditions and INP concentrations between cirrus cycles in our box model to examine the differences between the ML20 and KM21_GCM approaches. However, our setup was limited, as it did not capture all of the possible conditions and processes that are simulated in a GCM and that are relevant to assessing cirrus climate effects. Namely, we used a constant temperature and updraft velocity in our box model setup. In addition, we did not consider processes such as ice crystal sedimentation and mixing effects (e.g., entrainment). As a result, we extended our analysis of ML20 and KM21_GCM with two additional tests with the ECHAM-HAM GCM. We found that choosing one of the two deterministic ice formation approaches has an impact on ice nucleation competition within cirrus. However, the cirrus ICNC tracer differences for both homogeneous and heterogeneous nucleation were insignificant between these simulations for the 5 years that we tested (2008–2012). These results corroborate our findings from our box model simulations, which showed that out of the 16 tests we conducted six showed agreement (0 % error) and an additional three tests showed a small error between ML20 and KM21_GCM of 0.3 % (Fig. 1). This likely highlights that the GCM was often in similar regimes over the 5 years of simulation as the tests in our box model that showed zero or small errors.

It is important to note that our GCM simulations were also limited as we did not consider transport, vertical diffusion, or ice sedimentation effects on our tracers for the previous INP concentration ($N_{\mathrm{0},i-\mathrm{1}}$) and the maximum AF of the previous cirrus cycle (ϕ_max). However, these processes likely would have a small impact on $N_{\mathrm{0},i-\mathrm{1}}$ and ϕ_max and therefore would likely not lead to larger differences between KM21_GCM and ML20. An additional caveat to our GCM results is that we used the P3 ice microphysics scheme (Morrison and Milbrandt, 2015; Dietlicher et al., 2018, 2019; Tully et al., 2022c), which does not distinguish between different ice hydrometeors. Cloud ice and snow are both considered to make up the total ICNC in cirrus in our study. In our model, it is assumed that each ice crystal, including snow crystals, includes a single INP, whereas in reality there may be numerous INPs associated with snow crystal aggregates composed of several ice crystals. Therefore, by not considering collision and aggregation processes, our model may underestimate the number of previously formed ice crystals. This is unlikely to significantly impact our results as ML20 and KM21_GCM did not show significant differences.

While the KM21_GCM approach with explicit INP budgeting is closer to first principles when simulating deterministic ice formation in an iterative way following the adiabatic ascent of an air parcel, it requires additional tracers in the climate model. Not only does this require additional memory allocation and thus greater CPU demand, but it also complicates the parameterization for determining heterogeneous nucleation on externally mixed mineral dust particles in our cirrus sub-model, as we must consider changing conditions across GCM time steps, which also means that there is increased likelihood of unintended errors within the model code. Arguments are emerging that call for a simplification of cloud microphysical processes within GCMs, especially in the case that the simplified model is “equifinal” to the more complex version (i.e., the outcome is similar) (Beven, 2006; Proske et al., 2022). ML20 is a simpler parameterization for deterministic ice nucleation than KM21_GCM as it does not require tracing the maximum AF achieved in a cirrus formation cycle or the INP concentration across GCM time steps. As our results showed that differences in cloud properties as well as radiative effects were insignificant, we argue that from the perspective of understanding the impact of cirrus on the climate, the simpler ML20 approach is suitable.

Appendix A: Box model simulations of deterministic ice formation

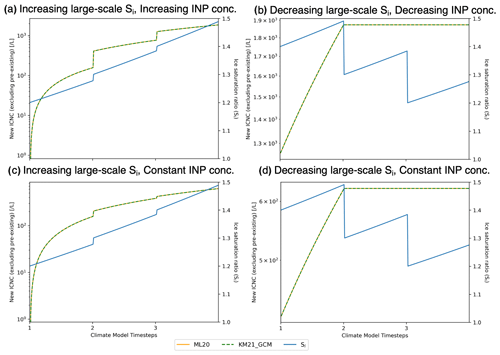
Figure A1 Temporal evolution of predicted heterogeneous-only ICNC and S_i,seed for four of the six cases that showed agreement between KM21_GCM and ML20 for (a) increasing large-scale S_i,seed and INP concentration trends, (b) decreasing large-scale S_i,seed and INP concentration trends, and for constant INP concentration with (c) increasing large-scale S_i,seed and (d) decreasing large-scale S_i,seed. The lines as noted in the legend are consistent with the description under Fig. 2.

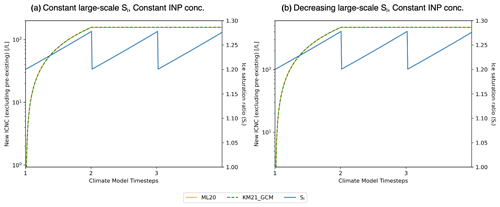
Figure A2 Temporal evolution of predicted heterogeneous-only ICNC and S_i,seed for two of the six cases that showed agreement between KM21_GCM and ML20 for the constant INP concentration trend with (a) constant large-scale S_i,seed and (b) decreasing large-scale S_i,seed. The lines as noted in the legend are consistent with the description under Fig. 2.

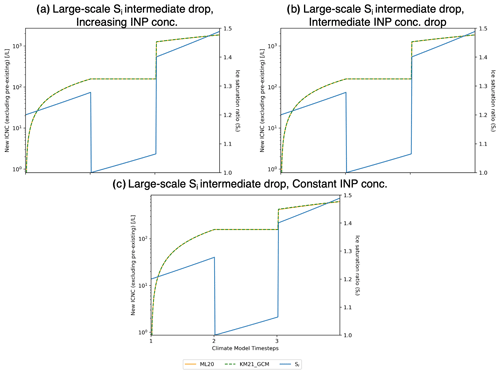
Figure A3 Temporal evolution of predicted heterogeneous-only ICNC and S_i,seed for three cases with an intermediate drop in large-scale S_i,seed that had the smallest non-zero error (<1 %) as shown in Fig. 1 for (a) increasing, (b) an intermediate drop, and (c) constant INP concentration. The lines as noted in the legend are consistent with the description under Fig. 2.

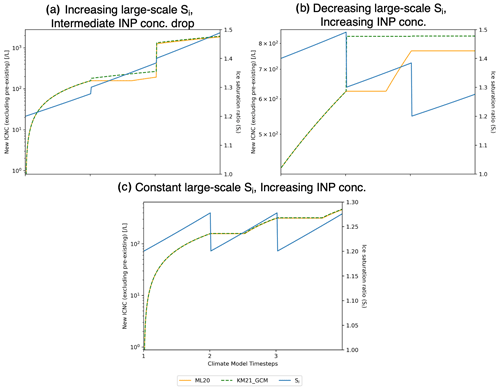
Figure A4 Temporal evolution of predicted heterogeneous-only ICNC and S_i,seed for (a) increasing large-scale S_i,seed and an intermediate drop in INP concentration, (b) decreasing large-scale S_i,seed and increasing INP concentration, and (c) constant large-scale S_i,seed and increasing INP concentration. The lines as noted in the legend are consistent with the description under Fig. 2.